Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten
|
|
|
- Dorothea Koch
- vor 8 Jahren
- Abrufe
Transkript
1 Inhalt 1 Einführung 2 Automatentheorie und Formale Sprachen Grammatiken Reguläre Sprachen und endliche Automaten Kontextfreie Sprachen und Kellerautomaten Kontextsensitive und Typ 0-Sprachen 3 Berechenbarkeitstheorie 4 Komplexitätstheorie Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 80 Kontextfreie Sprachen Zur Erinnerung Kontextfreie Grammatiken/Sprachen: alle Produktionsregeln P einer kontextfreien Grammatik G = (V, Σ, P, S) haben die Form A X, wobei A eine Variable in V ist und X eine Satzform in (V Σ) ist nach regulären Sprachen nächsthöhere Klasse in der Chomsky Hierarchie Grundlage im Compilerbau Beispiel (L = {a n b n n N}). Kontextfreie Grammatik G mit L(G) = L: S ab asb Wir zeigten bereits mit dem Pumping Lemma, dass L nicht regulär ist. Somit gibt es kontextfreie, nicht reguläre Sprachen. Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 81
2 Normalformen allgemeine Form von kontextfreien Grammatiken eignet sich kaum für algorithmische Fragestellungen Normalformen geben einfache und einheitliche Struktur vor Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 82 Chomsky Normalform Definition 56 (Chomsky Normalform (CNF)). Sei G = (V, Σ, P, S) eine kontextfreie Grammatik, in der jede Regel die Form A BC oder A a oder S ε hat, wobei A V, B, C V \ {S} und a Σ ist. Dann sagen wir, dass G in Chomsky Normalform (CNF) vorliegt. Beobachtung. Falls G in CNF vorliegt und w L(G), dann besteht jede Ableitung von w aus genau 2 w 1 Schritten. Jeder Syntaxbaum (Ableitungsbaum) ist ein Binärbaum. Satz 57. Für jede kontextfreie Grammatik G existiert eine kontextfreie Grammatik G in Chomsky Normalform, so dass L(G) = L(G ). Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 83
3 Beispiel: L = {a n b n n 1} Kontextfreie Grammatik für L Grammatik für L in CNF G : S ab asb G : S AB AF E AB AF F EB A a B b Ableitung von aabb aus G S S AF af A F aeb aabb E B aabb aabb A B aabb a a b b Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 84 Beweis: Sei eine kontextfreie Grammatik G = (V,Σ, P, S) gegeben. Wir werden sukzessive die Produktionen/Regeln, die die Chomsky Regeln verletzen, durch äquivalente Regeln ersetzen. 0 Neue Startvariable S 0 und Regel S 0 S hinzufügen. Somit erscheint die Startvariable nie auf der rechten Seite 1 ε-regeln entfernen: Für jede Variable A S 0 entferne A ε, und für jede Regel der Form B X AY (X, Y (V Σ) ) füge zusätzlich eine Regel ohne A, also B XY, ein. Beachte: Für jedes Auftreten von A auf der rechten Seite fügen wir eine Extraregel ein. Z.B. für B X AY AZ fügen wir zusätzlich B X Y AZ, B XAY Z und B XY Z ein. 2 Einzelproduktionen entfernen: Entferne Regeln der Form A B (mit A, B V {S 0 }), und für jede Regel B X (X (V Σ) ) füge die Regel A X hinzu. Es sei denn, A X war eine Einzelproduktion, die bereits entfernt wurde. 3 Ersetze letztendlich jede Regel der Form mit x i V Σ für jedes i = 1,...,k: A x 1...x k Falls k 3, dann ersetze A x 1... x k durch A x 1 A 1, A 1 x 2 A 2,..., A k 2 x k 1 x k, wobei A 1,...,A k 2 neue Variablen sind. Falls k = 2, dann ersetze jedes Terminal x i Σ (i = 1, 2) in A x 1 x 2 durch X i, und füge X i x i als neue Regel hinzu, wobei X i eine neue Variable ist. Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 85
4 Beispiel V = {S, A}, Σ = {a} S ASA A ε A aa ε 0-neue Startvariable S 0 S S ASA A ε A aa ε 1a-S ε eliminieren S 0 S ε S ASA A AA A aa ε 1b-A ε eliminieren S 0 S ε S ASA A AA AS SA A aa 2a-Einzelregel S A S 0 S ε S ASA aa AA AS SA A aa 2b-Einzelregel S 0 S S 0 ASA aa AA AS SA ε S ASA aa AA AS SA A aa 3a-S, S 0 ASA eliminieren (kurz) S 0 AX 1 aa AA AS SA ε S AX 1 aa AA AS SA A aa X 1 SA 3b- aa eliminieren (kurz) S 0 AX 1 A 1 A 1 AA AS SA ε S AX 1 A 1 A 1 AA AS SA A A 1 A 1 X 1 SA A 1 a Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 86 Greibach Normalform Definition 58 (Greibach Normalform (GNF)). Sei G = (V, Σ, P, S) eine kontextfreie Grammatik, in der jede Regel die Form A ab 1... B k (k 0) oder S ε hat, wobei A V, B 1,... B k V \ {S} und a Σ ist. Dann sagen wir, dass G in Greibach Normalform (GNF) vorliegt. Satz 59. Für jede kontextfreie Grammatik G existiert eine kontextfreie Grammatik G in Greibach Normalform, so dass L(G) = L(G ). Bemerkung. GNF kann als Erweiterung von regulären Grammatiken betrachtet werden. In regulären Grammatiken sind nur Regeln mit k = 0, 1 erlaubt. Jede kontextfreie Grammatik kann algorithmisch in eine GNF umgeformt werden. Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 87
5 Pumping Lemma für kontextfreie Sprachen Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 88 Pumping Lemma für kontextfreie Sprachen Wie kann man beweisen, dass eine Sprache nicht kontextfrei ist? Satz 60 (Pumping Lemma für kontextfreie Sprachen). Sei L eine kontextfreie Sprache über ein beliebiges Alphabet Σ. Dann existiert eine Zahl n N, so dass für alle Wörter w L mit w n eine Zerlegung w = uvxyz mit folgenden Eigenschaften existiert: 1 vy 1, 2 vxy n, 3 uv k xy k z L für alle k N. Bemerkung. Für unäre Alphabete sind beide Pumping Lemmata äquivalent, da bei Wörtern über unären Alphabeten die Reihenfolge keine Rolle spielt und somit uv k xy k z = x(vy) k uz. Wir werden noch sehen, dass jede kontextfreie Sprache über einem unären Alphabet in der Tat regulär ist. Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 89
6 Beispiel Beispiel. Die Sprache L = {a m b m c m m N} ist nicht kontextfrei. Beweis: Beweis durch Widerspruch mit Hilfe des Pumping-Lemmas. Angenommen L wäre kontextfrei. Dann gäbe es eine Pumping-Zahl n, so dass jedes Wort w = a m b m c m mit w n eine Zerlegung zulässt mit 1 vy 1, 2 vxy n, 3 uv k xy k z L für alle k N. w = uvxyz Betrachte insbesondere den Fall m = n, d.h. w = a n b n c n. Teil 2 impliziert vy kann nicht sowohl a s als auch b s und c s enthalten. Wegen Teil 1 gilt vy ε, und aus Teil 3 (angewandt mit k = 0) folgern wir uxz L. Also gibt es ein l < n mit uxz = a l b l c l, so dass vy doch a s und b s und c s enthalten muss, denn sonst w = uvxyz L. Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 90 Beweis von Satz 60 Beweis: Sei G = (V,Σ, P, S) eine Grammatik für L in CNF und V = k. Setze n = 2 k. Sei w L(G) ein Wort mit w n. Jeder Syntaxbaum von w in G ist bis auf die letzte Ebene ein Binärbaum B: D.h. innerhalb des Binärbaumes B stehen Ableitungen der Form A BC: A und in der untersten Ebene stehen Ableitungen der Form B A a mit a Σ. Weil der Binärbaum B mindestens n = 2 k Blätter hat, gibt es einen Pfad der Länge k von der Wurzel S zu einem Blatt in B. Betrachtet man also einen Pfad P maximaler Länge in B, so sind (k + 1) Knoten mit Variablen beschriftet. Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 91 C
7 Beweis von Satz 60 Teil 2 Weil G nur k Variablen hat, gibt es eine Variable, die doppelt auf P vorkommt. Genauer gibt es sogar auf dem unteren Teilstück der Länge k von P eine Variable A, die doppelt vorkommt: Betrachte nun die Teilwörter, die innerhalb des Baumes aus den beiden A s abgeleitet werden. Dies liefert eine Zerlegung w = uvxyz. Da das obere A nur k Schritte von der Blattebene entfernt ist, folgt vxy 2 k = n. Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 92 Beweis von Satz 60 Teil 3 Weil die Grammatik CNF hat, gilt ferner vy 1. Weil A doppelt vorkommt, kann der Ableitungsbaum auf folgende Art modifiziert werden, um uxz = uv 0 xy 0 z abzuleiten: Dafür führe von dem oberen A aus die Ableitung durch, die in B von dem unteren A aus durchgeführt wird. Also folgt uxz L. Ferner kann man auch an das untere A in B nochmals die Ableitung anfügen, die von dem oberen A aus durchgeführt wurde. Also folgt uv 2 xy 2 z L. Entsprechend erhält man uv k xy k z L (k 2), so dass die Behauptung folgt. Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 93
8 Weiteres Beispiel für Satz 60 Beispiel. Die Sprache L = {a h b i c j 0 h i j} {a, b, c} ist nicht kontextfrei. Beweis: Wir führen den Beweis durch Widerspruch mit Hilfe des Pumping-Lemmas. Angenommen L wäre kontextfrei. Dann gäbe es eine Pumping-Zahl n, so dass jedes Wort w = a h b i c j mit w n eine Zerlegung zulässt mit w = uvxyz 1 vy 1, 2 vxy n, 3 uv k xy k z L für alle k N. Betrachte insbesondere den Fall h = i = j = n, d.h. w = a n b n c n. Fall 1 (v oder y enthält mindestens zwei verschiedene Zeichen): Dann kann uv 2 xy 2 z nicht die Form a... ab... bc... c haben. Fall 2 (v und y enthalten jeweils höchstens Zeichen eines Typs): Da v und y jeweils nur Zeichen eines Typs enthalten, gibt es ein Zeichen, welches weder in v noch in y erscheint. Wir behandeln die drei offensichtlichen Unterfälle separat. Falls a nicht in vy enthalten ist, dann betrachte uv 0 xy 0 z = uxz, welches immer noch h = n a s, aber entweder weniger als i = n b s oder weniger als j = n c s enthält. Falls b nicht in vy enthalten ist, dann enthält vy entweder a s oder c s. Falls vy a s enthält dann ist die Anzahl der a s in uv 2 xy 2 z größer als die Anzahl der b s. Falls vy c s enthält dann ist die Anzahl der b s in uv 0 xy 0 z größer als die Anzahl der c s. Falls c nicht in vy enthalten ist, dann betrachte uv 2 xy 2 z, welches immer noch j = n c s, aber entweder mehr als h = n a s oder mehr als i = n b s enthält. In jedem Fall erhalten wir einen Widerspruch. Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 94 Gibt es nichtreguläre, kontextfreie Sprachen über Σ = {a}? Satz 61 (Unäre kontextfreie Sprachen sind regulär). Sei L eine kontextfreie Sprache über dem Alphabet Σ = {a}. Dann ist L regulär. Beweis: Sei L eine kontextfreie Sprache über Σ = {a} und sei n die Pumping-Zahl aus Satz 60. D.h. jedes Wort w L mit w n hat eine Zerlegung w = uvxyz mit 1 vy 1, 2 vxy n, 3 uv k xy k z L für alle k N. Daraus folgt, dass es zu jedem w L {a}, w n zwei Zahlen s w := uxz, l w := vy gibt, so dass w = a s w +lw und 1 l w 1, 2 l w n, 3 a s w +klw L für alle k N. Wegen Teil 2 ist die Menge M := {l w w L und w n} endlich und für q := n! gilt Sei l teilt q für alle l M. (4) R := { r q a r L und für alle i mit 1 i r/q gilt a r iq L }. Dann gilt wegen Teil 3 und (4), dass R q. Setze nun L = {w L w q} {a r+iq r R und i N}. Da {w L w q} < und R <, gibt es einen Automaten der L akzeptiert (siehe Übungsblatt). Aus der Definition von R folgt, dass für alle r R das Wort w = a r in L ist. Da r n, existiert l w n für alle Wörter der Form w = a r mit r R. Wegen (4) folgt, dass es für jedes i N ein j i gibt, so dass iq = j i l w. Demnach gilt a r+iq = a r+j i lw L für alle i N wegen Teil 3 und somit L L. Ist ferner w = a m L mit m q, so gibt es ein r R und ein i N mit m = r + iq. Also folgt, dass w L, weshalb L L. Zusammenfassend folgt, dass L regulär ist, da L regulär ist, L L, und L L. Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 95
9 CYK-Algorithmus Wortproblem für kontextfreie Sprachen Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 96 Wortproblem für kontextfreie Sprachen Wie löst man das Wortproblem für kontextfreie Sprachen? Eingabe: Kontextfreie Grammatik G = (V, Σ, P, S) in CNF und Wort w Σ Ziel: Entscheide, ob w L(G). Idee: dynamische Programmierung Für ein Wort w der Länge n sei w ij die Teilsequenz der Länge j von w, die an der i-ten Stelle beginnt. Der CYK-Algorithmus berechnet eine Tabelle (T ), deren ij-eintrag (T ij ) alle Variablen A V mit A G w ij enthält. Die Tabelle wird schrittweise für i = 1,... n und j = 1,..., n aufgebaut. Frage Was ist schlecht an einem rekursiven Ansatz für den CYK-Algorithmus? Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 97
10 Algorithmus von Cocke, Younger und Kasawi ALGORITHMUS: CYK. Eingabe: Ausgabe: kontextfreie Grammatik G = (V, Σ, P, S) in CNF und w = a 1... a n Σ JA, falls w L(G), und NEIN sonst 1 Initialisiere T i1 := {A V A a i P} für jedes i = 1,..., n. 2 Für j = 2,..., n (Schleife über Spalten) Für i = 1,..., n + 1 j Setze T ij :=. Für k = 1,..., j 1 T ij := T ij { A V (Schleife über Zeilen) A BC P mit B T ik und C T i+k,j k } Ende Schleife über k. Ende Schleife über i. Ende Schleife über j. 3 Wenn S T 1n, dann gib JA aus und sonst NEIN. (Schleife über Zeilen) (Schleife über Spalten) Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 98 Beispiel: CYK-Algorithmus Beispiel (L = {a n b n c m n, m 1}). Grammatik G für L äquivalente Grammatik G in CNF S XC X ab axb C c cc S XZ X AB AY A a Z c CZ Y XB B b C c T ij für w = aaabbbcc: A X S S 2 A X Y 3 A X Y 4 B 5 B 6 B 7 C, Z Z 8 C, Z S XZ AY Z AXBZ AAY BZ AAX BBZ AAABBBZ AAABBBCZ Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 99
11 Kellerautomaten Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 100 Kellerautomaten Anforderungen Gesucht: Automaten, die kontextfreie Sprachen akzeptieren. Benötigt: Unbegrenzten Speicher, um z.b. Sprachen wie {a n b n n N} zu erkennen. Idee: Statte NFA s mit einem Keller/Stack aus, welcher bei Übergängen manipuliert (PUSH- und POP-Operationen) werden kann. Akzeptiert: Wörter, die so abgearbeitet werden können, dass der Stack am Ende leer ist, sind in der akzeptierten Sprache ( keine Endzustände). a, A AA a, A z a ε, ε ε b, A ε ε, ε z b Akzeptiert: L = {a n b n n N} Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 101
12 PDA-Kellerautomat Definition 62 (PDA). Ein Kellerautomat (PushDown Automata) ist ein 6-Tupel Dabei ist Z eine endliche Menge von Zuständen, M = (Z, Σ, Γ, δ, z 0, ). Σ ein Alphabet, das sog. Eingabealphabet, mit Σ Z =, Γ ein Alphabet, das sog. Kelleralphabet, mit Γ Z =, δ : Z (Σ {ε}) Γ P e (Z Γ ) die Überführungsfunktion, wobei P e (Z Γ ) = {Y Z Γ Y < } die Menge der endlichen Teilmengen von Z Γ ist, z 0 Z der Startzustand und Γ das unterste Kellerzeichen ist. Wie funktioniert δ? (z a, A B 1... B k, B 1... B k ) δ(z, a, A) z z Wenn M in Zustand z ist, das Eingabesymbol a liest und A das oberste Kellerzeichen ist, dann kann M in z übergehen und A auf dem Keller durch B 1... B k ersetzen, wobei dann B 1 oberstes Kellerzeichen ist. Falls a = ε, dann spricht man vom spontanen Übergang. Falls B k = A, dann pusht man B 1... B k 1 auf den Stack/Keller. Falls k = 1 und B 1 = ε, dann popt man A vom Stack/Keller. Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 102 Konfigurationen, Relationen, PDA und Sprachen Definition 63 (Konfiguration). Eine Konfiguration eines Kellerautomaten M = (Z, Σ, Γ, δ, z 0, ) ist ein Tupel K = (z, σ, γ) Z Σ Γ, wobei (z, σ, γ) den aktuellen Zustand beschreibt. Genauer ist z der aktuelle Zustand von M, σ der noch zu lesende Teil des Eingabewortes und γ der aktuelle Kellerinhalt. Definition 64 (Relationen: M, M ). Sei M = (Z, Σ, Γ, δ, z 0, ) ein PDA. Wir definieren die Relation M (kurz ) auf der Menge der Konfigurationen von M wie folgt: Sei z, z Z, σ = aσ Σ, γ = Aγ Γ und ν Γ, dann (z, σ, γ) M (z, σ, νγ ), falls (z, ν) δ(z, a, A) (z, σ, γ) M (z, σ, νγ ), falls (z, ν) δ(z, ε, A). Mit M (kurz ) bezeichnen wir die reflexive und transitive Hülle von M. Definition 65 (akzeptierte Sprache (PDA)). Sei M = (Z, Σ, Γ, δ, z 0, ) ein PDA. Die von M akzeptierte Sprache ist N(M) := {w Σ (z 0, w, ) M (z, ε, ε) für irgendein z Z }, die Menge der Wörter, die M so abarbeiten kann, dass der Keller/Stack am Ende leer ist. Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 103
13 Kontextfreie Sprachen Satz 66 (PDA s und kontextfreie Sprachen). Sei L eine Sprache über einem beliebigen Alphabet Σ. PDA M mit N(M) = L L ist kontextfrei. Beweis ( ): Sei L eine kontextfreie Sprache, die von der kontextfreien Grammatik G = (V, Σ, P, S) erzeugt wird. Definiere M = ({z}, Σ, V Σ, δ, z, S), wobei δ genau folgende Übergänge zulässt: (z, X) δ(z, ε, A), für jede Regel A X P (z, ε) δ(z, a, a), für alle a Σ. Sei nun w Σ. Dann gilt: w L(G) es gibt eine Ableitung S w, es gibt eine Folge von Konfigurationen (z, w, S) (z, ε, ε), w N(M). Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 104 Rückrichtung von Satz 66 Sei ein PDA M = (Z, Σ, Γ, δ, z 0, ) gegeben. Wir nehmen an, dass für jeden Übergang (z, B 1... B k ) δ(z, a, A) gilt, dass k 2. Andernfalls ersetzen wir den Übergang (z, a, A) (z, B 1... B k ) durch (z, a, A) (z 1, B k 1 B k ) (z 1, ε, B k 1 ) (z 2, B k 2 B k 1 ). a, A B k 1B k z z 1 ε, B k 1 B k 2B k 1... (z k 2, ε, B 2 ) (z, B 1 B 2 ) z z ε, B 3 B 2B 3 k 2 ε, B 2 B 1B 2 Wir definieren nun G = (V, Σ, P, S), wobei V = {S} Z Γ Z, und P die folgenden Produktionen enthält: S (z 0,, z), für alle z Z, (z, A, z ) a, für alle (z, ε) δ(z, a, A), (z, A, z ) a(z 1, B, z ), für alle (z 1, B) δ(z, a, A) und z Z, (z, A, z ) a(z 1, B, z 2 )(z 2, C, z ), für alle (z 1, BC) δ(z, a, A) und z 2, z Z. Offensichtlich ist G eine kontextfreie Grammatik. Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 105
14 Rückrichtung von Satz 66 Teil 2 Behauptung 67 (Hilfslemma für Satz 66). Für alle z, z Z, A Γ und w Σ gilt: (z, A, z ) w gdw. (z, w, A) (z, ε, ε). Bevor wir die Behauptung zeigen, reduzieren wir Satz 66 auf diese. Sei also w Σ beliebig, dann gilt w N(M) (z 0, w, ) (z, ε, ε) für ein z Z, (z 0,, z ) w für ein z Z, S (z 0,, z ) w für ein z Z, w L(G). Es bleibt noch die Behauptung zu zeigen. Der Beweis spaltet sich wieder in zwei Teile (Hin- und Rückrichtung). Aber zuvor stellen wir fest, dass für alle a Σ {ε} gilt: (z, A, z ) a gdw. (z, A, z ) a P gdw. (z, ε) δ(z, a, A) (5) gdw. (z, a, A) (z, ε, ε). Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 106 Hinrichtung der Behauptung 67 Beweis ( ): Wir führen Induktion über k, die Länge einer Linksableitung von w. Der Induktionsanfang (k = 1) ergibt sich aus (5). Betrachten wir nun also eine Ableitung mit k > 1. Fall 1 ((z, A, z ) a w): Dann ist w = a. Dies ist bei k > 1 unmöglich. Fall 2 ((z, A, z ) a(z 1, B, z ) aw = w): Dann ist (z 1, B) δ(z, a, A) und nach Induktionsvoraussetzung gilt (z 1, w, B) (z, ε, ε). Daraus folgt (z, aw, A) (z 1, w, B) (z, ε, ε). Fall 3 ((z, A, z ) a(z 1, B, z 2 )(z 2, C, z ) aw = w): Dann ist (z 1, BC) δ(z, a, A) und nach Induktionsvoraussetzung gilt (z 1, u, B) (z 2, ε, ε) und (z 2, v, C) (z, ε, ε), wobei w = uv. Daraus folgt (z, auv, A) (z 1, uv, BC) (z 2, v, C) (z, ε, ε). Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 107
15 Rückrichtung der Behauptung 67 Beweis ( ): Angenommen (z, w, A) (z, ε, ε) Wir zeigen mit Induktion über die Zahl n der Schritte von M, dass dann (z, A, z ) w gilt. Der Induktionsanfang n = 1. Für a Σ {ε} gilt: (z 1, A, z ) a (z, A, z ) a P (z, ε) δ(z, a, A) (z, a, A) (z, ε, ε) Sei nun also n > 1. Wir können w zerlegen in w = au, a Σ {ε}, so dass gilt: (z, au, A) (z 1, u, γ) + (z, ε, ε) (z 1 Z, γ Γ ). Fall 1 (γ = ε): Dies kann nicht sein, weil dann (z 1, a, γ) keine Folgekonfiguration hätte (d.h. n = 1). Fall 2 (γ = B Γ): Nach Induktion gilt: (z 1, B, z ) u. Nach Definition von P gibt es ferner eine Regel (z, A, z ) a(z 1, B, z ) P. Also folgt: (z, A, z ) a(z 1, B, z ) au = w. Fall 3 (γ = BC Γ 2 ): Die Berechnung (z 1, u, BC) (z, ε, ε) wird in zwei Teile zerlegt: (z 1, u 1, BC) (z 2, u 2, C) (z 2, u 2, C) (z, ε, ε), mit u = u 1 u 2, so dass (z 1, u 1, B) (z 2, ε, ε). Daher zeigt die Induktionsvoraussetzung, dass Also ermöglicht P die Ableitung (z 1, B, z 2 ) u 1 und (z 2, C, z ) u 2. (z, A, z ) a(z 1, B, z 2 )(z 2, C, z ) au 1 (z 2, C, z ) au 1 u 2 = au = w. Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 108 Deterministisch kontextfreie Sprachen Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 109
16 Deterministischer Kellerautomat Definition 68 (DPDA - deterministischer Kellerautomat). Ein deterministischer Kellerautomat ist ein Tupel M = (Z, Σ, Γ, δ, z 0,, E), wobei (Z, Σ, Γ, δ, z 0, ) ein Kellerautomat ist, für alle z Z, a Σ und A Γ gilt: δ(z, a, A) + δ(z, ε, A) 1, E Z eine Menge von Endzuständen ist. Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 110 Determinismus vs. Nichtdeterminismus DPDA für L = {w w R w {a, b} } {a, b, } a, push A b, push B a, A ε b, B ε, ε ε z 0 z 1 ε, ε z 2 PDA für L = {ww R w {a, b} } {a, b} a, push A b, push B a, A ε b, B ε ε, ε ε, ε ε z 0 z 1 Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 111
17 Deterministisch kontextfreie Sprachen Definition 69 (akzeptierte Sprache (DPDA)). Eine Konfiguration von M ist ein Tripel (z, w,γ) Z Σ Γ, und die Relation M ist wie für PDA s definiert. M akzeptiert w Σ, falls es einen Zustand z E gibt, so dass (z 0, w, ) M (z,ε, γ) mit γ Γ. Mit N(M) bezeichnen wir die von M akzeptierte Sprache. Definition 70. Eine Sprache L heißt deterministisch kontextfrei, falls es einen deterministischen Kellerautomaten mit L = N(M) gibt. Bemerkung. Eine Sprache L ist deterministisch kontextfrei gdw. es eine sogenannte LR(k)-Grammatik (k > 0) gibt, die L erzeugt. LR(k)-Grammatiken sind kontextfreie Grammatiken für die jeder Ableitungsschritt eindeutig durch k Terminale der Eingabe bestimmt ist. Ferner gilt LR(0) LR(1)= =LR(k). Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 112 Abschlusseigenschaften det. kf. Sprachen Satz Falls L deterministisch kontextfrei ist, so ist auch L deterministisch kontextfrei. 2 Falls R regulär und L deterministisch kontextfrei ist, ist auch R L deterministisch kontextfrei. Insbesondere ist jede reguläre Sprache deterministisch kontextfrei. 3 Jede deterministisch kontextfreie Sprache ist kontextfrei. 4 Die Klasse der deterministisch kontextfreien Sprache ist weder unter Vereinigung noch unter Schnittbildung abgeschlossen. Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 113
18 Zusammenfassung Chomsky Normalform Greibach Normalform Pumping Lemma für kontextfreie Sprachen Das Wortproblem und der CYK Algorithmus Kellerautomaten (PDA s), Konfigurationen, deterministische Kellerautomaten (DPDA s) deterministisch kontextfreie Sprachen, LR(k)-Grammatik Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten 114
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen 19
 Inhalt 1 inführung 2 Automatentheorie und ormale prachen Grammatiken Reguläre prachen und endliche Automaten Kontextfreie prachen und Kellerautomaten Kontextsensitive und yp 0-prachen 3 Berechenbarkeitstheorie
Inhalt 1 inführung 2 Automatentheorie und ormale prachen Grammatiken Reguläre prachen und endliche Automaten Kontextfreie prachen und Kellerautomaten Kontextsensitive und yp 0-prachen 3 Berechenbarkeitstheorie
Theorie der Informatik
 Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 Einführung Beispiel: Aussagenlogische Formeln Aus dem Logikteil: Definition (Syntax
Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 Einführung Beispiel: Aussagenlogische Formeln Aus dem Logikteil: Definition (Syntax
Motivation. Formale Grundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen. Informales Beispiel. Informales Beispiel.
 Kontextfreie Kontextfreie Motivation Formale rundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen Bisher hatten wir Automaten, die Wörter akzeptieren Frank Heitmann heitmann@informatik.uni-hamburg.de
Kontextfreie Kontextfreie Motivation Formale rundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen Bisher hatten wir Automaten, die Wörter akzeptieren Frank Heitmann heitmann@informatik.uni-hamburg.de
Kapitel 2: Formale Sprachen Kontextfreie Sprachen. reguläre Grammatiken/Sprachen. kontextfreie Grammatiken/Sprachen
 reguläre Grammatiken/prachen Beschreibung für Bezeichner in Programmiersprachen Beschreibung für wild cards in kriptsprachen (/* reguläre Ausdrücke */)?; [a-z]; * kontextfreie Grammatiken/prachen Beschreibung
reguläre Grammatiken/prachen Beschreibung für Bezeichner in Programmiersprachen Beschreibung für wild cards in kriptsprachen (/* reguläre Ausdrücke */)?; [a-z]; * kontextfreie Grammatiken/prachen Beschreibung
Mathematische Grundlagen der Informatik 2
 Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Emanuel Duss emanuel.duss@gmail.com 12. April 2013 1 Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Dieses Dokument basiert
Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Emanuel Duss emanuel.duss@gmail.com 12. April 2013 1 Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Dieses Dokument basiert
Wortproblem für kontextfreie Grammatiken
 Wortproblem für kontextfreie Grammatiken G kontextfreie Grammatik. w Σ w L(G)? Wortproblem ist primitiv rekursiv entscheidbar. (schlechte obere Schranke!) Kellerautomat der L(G) akzeptiert Ist dieser effizient?
Wortproblem für kontextfreie Grammatiken G kontextfreie Grammatik. w Σ w L(G)? Wortproblem ist primitiv rekursiv entscheidbar. (schlechte obere Schranke!) Kellerautomat der L(G) akzeptiert Ist dieser effizient?
Informatik III. Christian Schindelhauer Wintersemester 2006/07 8. Vorlesung
 Informatik III Christian Schindelhauer Wintersemester 2006/07 8. Vorlesung 17.11.2006 schindel@informatik.uni-freiburg.de 1 Prinzip des Kellerautomats Push-Down-Automaton (PDA) Ein Kellerautomat vereinigt
Informatik III Christian Schindelhauer Wintersemester 2006/07 8. Vorlesung 17.11.2006 schindel@informatik.uni-freiburg.de 1 Prinzip des Kellerautomats Push-Down-Automaton (PDA) Ein Kellerautomat vereinigt
Vorlesung Theoretische Informatik
 Vorlesung Theoretische Informatik Automaten und Formale Sprachen Hochschule Reutlingen Fakultät für Informatik Masterstudiengang Wirtschaftsinformatik überarbeitet von F. Laux (Stand: 09.06.2010) Sommersemester
Vorlesung Theoretische Informatik Automaten und Formale Sprachen Hochschule Reutlingen Fakultät für Informatik Masterstudiengang Wirtschaftsinformatik überarbeitet von F. Laux (Stand: 09.06.2010) Sommersemester
Programmiersprachen und Übersetzer
 Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
4.9 Deterministische Kellerautomaten Wir haben bereits definiert: Ein PDA heißt deterministisch (DPDA), falls
 4.9 Deterministische Kellerautomaten Wir haben bereits definiert: Ein PDA heißt deterministisch (DPDA), falls δ(q, a, Z) + δ(q, ɛ, Z) 1 (q, a, Z) Q Σ. Die von einem DPDA, der mit leerem Keller akzeptiert,
4.9 Deterministische Kellerautomaten Wir haben bereits definiert: Ein PDA heißt deterministisch (DPDA), falls δ(q, a, Z) + δ(q, ɛ, Z) 1 (q, a, Z) Q Σ. Die von einem DPDA, der mit leerem Keller akzeptiert,
Theoretische Informatik I
 Theoretische Informatik I Einheit 2.4 Grammatiken 1. Arbeitsweise 2. Klassifizierung 3. Beziehung zu Automaten Beschreibungsformen für Sprachen Mathematische Mengennotation Prädikate beschreiben Eigenschaften
Theoretische Informatik I Einheit 2.4 Grammatiken 1. Arbeitsweise 2. Klassifizierung 3. Beziehung zu Automaten Beschreibungsformen für Sprachen Mathematische Mengennotation Prädikate beschreiben Eigenschaften
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier. Henning Fernau Universität Trier fernau@uni-trier.de
 Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
2.11 Kontextfreie Grammatiken und Parsebäume
 2.11 Kontextfreie Grammatiken und Parsebäume Beispiel: Beispiel (Teil 3): Beweis für L(G) L: Alle Strings aus L der Länge 0 und 2 sind auch in L(G). Als Induktionsannahme gehen wir davon aus, dass alle
2.11 Kontextfreie Grammatiken und Parsebäume Beispiel: Beispiel (Teil 3): Beweis für L(G) L: Alle Strings aus L der Länge 0 und 2 sind auch in L(G). Als Induktionsannahme gehen wir davon aus, dass alle
Übersicht. 3 3 Kontextfreie Sprachen
 Formale Systeme, Automaten, Prozesse Übersicht 3 3.1 Kontextfreie Sprachen und Grammatiken 3.2 Ableitungsbäume 3.3 Die pre -Operation 3.4 Entscheidungsprobleme für CFGs 3.5 Normalformen für CFGs 3.6 Chomsky-Normalform
Formale Systeme, Automaten, Prozesse Übersicht 3 3.1 Kontextfreie Sprachen und Grammatiken 3.2 Ableitungsbäume 3.3 Die pre -Operation 3.4 Entscheidungsprobleme für CFGs 3.5 Normalformen für CFGs 3.6 Chomsky-Normalform
Grammatiken. Einführung
 Einführung Beispiel: Die arithmetischen Ausdrücke über der Variablen a und den Operationen + und können wie folgt definiert werden: a, a + a und a a sind arithmetische Ausdrücke Wenn A und B arithmetische
Einführung Beispiel: Die arithmetischen Ausdrücke über der Variablen a und den Operationen + und können wie folgt definiert werden: a, a + a und a a sind arithmetische Ausdrücke Wenn A und B arithmetische
Tutorium zur theoretischen Informatik Übungsblatt 4 (2006-12-13)
 Ein verständiges Herz erwirbt Kenntnisse, und das Ohr der Weisen lauscht dem Wissen. (Die Bibel, "Buch der Sprüche", Kapitel 18 Vers 15) Inhalt 1. Empfehlenswerte Referenzen 2. Aufgabe 1 CF Grammatik für
Ein verständiges Herz erwirbt Kenntnisse, und das Ohr der Weisen lauscht dem Wissen. (Die Bibel, "Buch der Sprüche", Kapitel 18 Vers 15) Inhalt 1. Empfehlenswerte Referenzen 2. Aufgabe 1 CF Grammatik für
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Tutorium 4 26..25 INSTITUT FÜR THEORETISCHE INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu
Grundbegriffe der Informatik Tutorium 4 26..25 INSTITUT FÜR THEORETISCHE INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu
Kontextfreie Sprachen. Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester Kontextfreie Sprachen
 Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Wortproblem: der CYK-Algorithmus Pumping Lemma für kontextfreie Sprachen
Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Wortproblem: der CYK-Algorithmus Pumping Lemma für kontextfreie Sprachen
Grundlagen der Informatik II. Teil I: Formale Modelle der Informatik
 Grundlagen der Informatik II Teil I: Formale Modelle der Informatik 1 Einführung GdInfoII 1-2 Ziele/Fragestellungen der Theoretischen Informatik 1. Einführung abstrakter Modelle für informationsverarbeitende
Grundlagen der Informatik II Teil I: Formale Modelle der Informatik 1 Einführung GdInfoII 1-2 Ziele/Fragestellungen der Theoretischen Informatik 1. Einführung abstrakter Modelle für informationsverarbeitende
Formale Sprachen. Der Unterschied zwischen Grammatiken und Sprachen. Rudolf Freund, Marian Kogler
 Formale Sprachen Der Unterschied zwischen Grammatiken und Sprachen Rudolf Freund, Marian Kogler Es gibt reguläre Sprachen, die nicht von einer nichtregulären kontextfreien Grammatik erzeugt werden können.
Formale Sprachen Der Unterschied zwischen Grammatiken und Sprachen Rudolf Freund, Marian Kogler Es gibt reguläre Sprachen, die nicht von einer nichtregulären kontextfreien Grammatik erzeugt werden können.
Zusammenfassung Grundzüge der Informatik 4
 Zusammenfassung Grundzüge der Informatik 4 Sommersemester 04 Thorsten Wink 21. September 2004 Version 1.2 Dieses Dokument wurde in L A TEX 2εgeschrieben. Stand: 21. September 2004 Inhaltsverzeichnis 1
Zusammenfassung Grundzüge der Informatik 4 Sommersemester 04 Thorsten Wink 21. September 2004 Version 1.2 Dieses Dokument wurde in L A TEX 2εgeschrieben. Stand: 21. September 2004 Inhaltsverzeichnis 1
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Tutorium 27 29..24 FAKULTÄT FÜR INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Definition
Grundbegriffe der Informatik Tutorium 27 29..24 FAKULTÄT FÜR INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Definition
Formale Sprachen und Grammatiken
 Formale Sprachen und Grammatiken Jede Sprache besitzt die Aspekte Semantik (Bedeutung) und Syntax (formaler Aufbau). Die zulässige und korrekte Form der Wörter und Sätze einer Sprache wird durch die Syntax
Formale Sprachen und Grammatiken Jede Sprache besitzt die Aspekte Semantik (Bedeutung) und Syntax (formaler Aufbau). Die zulässige und korrekte Form der Wörter und Sätze einer Sprache wird durch die Syntax
Kontextfreie Sprachen
 Kontextfreie Sprachen besitzen große Bedeutung im Compilerbau Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung durch
Kontextfreie Sprachen besitzen große Bedeutung im Compilerbau Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung durch
4. Jeder Knoten hat höchstens zwei Kinder, ein linkes und ein rechtes.
 Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
Grundlagen der Theoretischen Informatik, SoSe 2008
 1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Der Zwei-Quadrate-Satz von Fermat
 Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Übung Theoretische Grundlagen Nachtrag zur Vorlesung Dirk Achenbach 21.11.2013
 Übung Theoretische Grundlagen Nachtrag zur Vorlesung Dirk Achenbach 21.11.2013 INSTITUT FÜR KRYPTOGRAPHIE UND SICHERHEIT KIT University of the State of Baden-Wuerttemberg and National Laboratory of the
Übung Theoretische Grundlagen Nachtrag zur Vorlesung Dirk Achenbach 21.11.2013 INSTITUT FÜR KRYPTOGRAPHIE UND SICHERHEIT KIT University of the State of Baden-Wuerttemberg and National Laboratory of the
Kontextfreie Sprachen
 Kontextfreie Sprachen Bedeutung: Programmiersprachen (Compilerbau) Syntaxbäume Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung
Kontextfreie Sprachen Bedeutung: Programmiersprachen (Compilerbau) Syntaxbäume Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Zusammenfassung. 1 Wir betrachten die folgende Signatur F = {+,,, 0, 1} sodass. 3 Wir betrachten die Gleichungen E. 4 Dann gilt E 1 + x 1
 Zusammenfassung Zusammenfassung der letzten LV Einführung in die Theoretische Informatik Woche 7 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 1 Wir betrachten die folgende Signatur
Zusammenfassung Zusammenfassung der letzten LV Einführung in die Theoretische Informatik Woche 7 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 1 Wir betrachten die folgende Signatur
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Erstellen von x-y-diagrammen in OpenOffice.calc
 Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Kapitel 6: Induktives Vorgehen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische
Grundbegriffe der Informatik Kapitel 6: Induktives Vorgehen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische
kontextfreie Sprachen: Normalformen
 1 kontextfreie Sprachen: Normalformen Zur Erinnerung: Kontextfreie Sprachen sind diejenigen, die von Grammatiken erzeugt werden, die auf allen linken Regelseiten nur je ein Nichtterminalsymbol haben. Aufgrund
1 kontextfreie Sprachen: Normalformen Zur Erinnerung: Kontextfreie Sprachen sind diejenigen, die von Grammatiken erzeugt werden, die auf allen linken Regelseiten nur je ein Nichtterminalsymbol haben. Aufgrund
TheGI 1: Grundlagen und algebraische Strukturen Prof. Dr.-Ing. Uwe Nestmann - 09. Februar 2010. 2. Schriftliche Leistungskontrolle (EK)
 TheGI 1: Grundlagen und algebraische Strukturen Prof. Dr.-Ing. Uwe Nestmann - 09. Februar 2010 2. Schriftliche Leistungskontrolle (EK) Punktzahl In dieser schriftlichen Leistungskontrolle sind 100 Punkte
TheGI 1: Grundlagen und algebraische Strukturen Prof. Dr.-Ing. Uwe Nestmann - 09. Februar 2010 2. Schriftliche Leistungskontrolle (EK) Punktzahl In dieser schriftlichen Leistungskontrolle sind 100 Punkte
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 3. Endliche Automaten (V) 21.05.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt Determinierte endliche Automaten (DEAs) Indeterminierte
Grundlagen der Theoretischen Informatik 3. Endliche Automaten (V) 21.05.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt Determinierte endliche Automaten (DEAs) Indeterminierte
t r Lineare Codierung von Binärbbäumen (Wörter über dem Alphabet {, }) Beispiel code( ) = code(, t l, t r ) = code(t l ) code(t r )
 Definition B : Menge der binären Bäume, rekursiv definiert durch die Regeln: ist ein binärer Baum sind t l, t r binäre Bäume, so ist auch t =, t l, t r ein binärer Baum nur das, was durch die beiden vorigen
Definition B : Menge der binären Bäume, rekursiv definiert durch die Regeln: ist ein binärer Baum sind t l, t r binäre Bäume, so ist auch t =, t l, t r ein binärer Baum nur das, was durch die beiden vorigen
Einführung. Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit (3) Vorlesungen zur Komplexitätstheorie. K-Vollständigkeit (1/5)
 Einführung 3 Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit (3) Univ.-Prof. Dr. Christoph Meinel Hasso-Plattner-Institut Universität Potsdam, Deutschland Hatten den Reduktionsbegriff
Einführung 3 Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit (3) Univ.-Prof. Dr. Christoph Meinel Hasso-Plattner-Institut Universität Potsdam, Deutschland Hatten den Reduktionsbegriff
1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage:
 Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Reguläre Sprachen Endliche Automaten
 Endliche Automaten (Folie 54, Seite 16 im Skript) Einige Vorteile endlicher deterministischer Automaten: durch Computer schnell simulierbar wenig Speicher benötigt: Tabelle für δ (read-only), aktueller
Endliche Automaten (Folie 54, Seite 16 im Skript) Einige Vorteile endlicher deterministischer Automaten: durch Computer schnell simulierbar wenig Speicher benötigt: Tabelle für δ (read-only), aktueller
Also kann nur A ist roter Südler und B ist grüner Nordler gelten.
 Aufgabe 1.1: (4 Punkte) Der Planet Og wird von zwei verschiedenen Rassen bewohnt - dem grünen und dem roten Volk. Desweiteren sind die Leute, die auf der nördlichen Halbkugel geboren wurden von denen auf
Aufgabe 1.1: (4 Punkte) Der Planet Og wird von zwei verschiedenen Rassen bewohnt - dem grünen und dem roten Volk. Desweiteren sind die Leute, die auf der nördlichen Halbkugel geboren wurden von denen auf
1. Formale Sprachen 1.2 Grammatiken formaler Sprachen
 1. Formale Sprachen 1.2 Grammatiken formaler Sprachen Die Regeln zur Bildung korrekter Wörter einer Sprache kann man in einer natürlichen Sprache formulieren. Da dies jedoch wieder Mehrdeutigkeiten mit
1. Formale Sprachen 1.2 Grammatiken formaler Sprachen Die Regeln zur Bildung korrekter Wörter einer Sprache kann man in einer natürlichen Sprache formulieren. Da dies jedoch wieder Mehrdeutigkeiten mit
Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit
 Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit Sommersemester 2011 Dozent: Prof. Dr. J. Rothe, Prof. Dr. M. Leuschel J. Rothe (HHU Düsseldorf)
Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit Sommersemester 2011 Dozent: Prof. Dr. J. Rothe, Prof. Dr. M. Leuschel J. Rothe (HHU Düsseldorf)
Informatik IC2. Balazs Simon 2005.03.26.
 Informatik IC2 Balazs Simon 2005.03.26. Inhaltsverzeichnis 1 Reguläre Sprachen 3 1.1 Reguläre Sprachen und endliche Automaten...................... 3 1.2 Determinisieren.....................................
Informatik IC2 Balazs Simon 2005.03.26. Inhaltsverzeichnis 1 Reguläre Sprachen 3 1.1 Reguläre Sprachen und endliche Automaten...................... 3 1.2 Determinisieren.....................................
Übung Theoretische Grundlagen
 Übung Theoretische Grundlagen Berechenbarkeit/Entscheidbarkeit Nico Döttling November 26, 2009 INSTITUT FÜR KRYPTOGRAPHIE UND SICHERHEIT KIT University of the State of Baden-Wuerttemberg and National Laboratory
Übung Theoretische Grundlagen Berechenbarkeit/Entscheidbarkeit Nico Döttling November 26, 2009 INSTITUT FÜR KRYPTOGRAPHIE UND SICHERHEIT KIT University of the State of Baden-Wuerttemberg and National Laboratory
Lernziele: Ausgleichstechniken für binäre Bäume verstehen und einsetzen können.
 6. Bäume Lernziele 6. Bäume Lernziele: Definition und Eigenschaften binärer Bäume kennen, Traversierungsalgorithmen für binäre Bäume implementieren können, die Bedeutung von Suchbäumen für die effiziente
6. Bäume Lernziele 6. Bäume Lernziele: Definition und Eigenschaften binärer Bäume kennen, Traversierungsalgorithmen für binäre Bäume implementieren können, die Bedeutung von Suchbäumen für die effiziente
Formale Grundlagen der Informatik 1 Kapitel 12 Zusammenfassung
 Formale Grundlagen der Informatik 1 Kapitel 12 Zusammenfassung Frank Heitmann heitmann@informatik.uni-hamburg.de 13. Mai 2014 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/17 Überblick Wir hatten
Formale Grundlagen der Informatik 1 Kapitel 12 Zusammenfassung Frank Heitmann heitmann@informatik.uni-hamburg.de 13. Mai 2014 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/17 Überblick Wir hatten
7 Rechnen mit Polynomen
 7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
Basis und Dimension. Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren.
 Basis und Dimension Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren. Definition. Sei V ein K-Vektorraum und (v i ) i I eine Familie von Vektoren
Basis und Dimension Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren. Definition. Sei V ein K-Vektorraum und (v i ) i I eine Familie von Vektoren
Grundbegriffe der Informatik Tutorium 7
 Grundbegriffe der Informatik Tutorium 7 Tutorium Nr. 16 Philipp Oppermann 16. Dezember 2014 KARLSRUHER INSTITUT FÜR TECHNOLOGIE KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum
Grundbegriffe der Informatik Tutorium 7 Tutorium Nr. 16 Philipp Oppermann 16. Dezember 2014 KARLSRUHER INSTITUT FÜR TECHNOLOGIE KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum
Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume?
 Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume? Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de WS 2013/14 Isomorphie Zwei Graphen (V 1, E 1 ) und (V
Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume? Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de WS 2013/14 Isomorphie Zwei Graphen (V 1, E 1 ) und (V
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 8: kontextfreie Grammatiken Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2009/2010 1/37 Überblick Kontextfreie Grammatiken
Grundbegriffe der Informatik Einheit 8: kontextfreie Grammatiken Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2009/2010 1/37 Überblick Kontextfreie Grammatiken
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Formale Systeme, WS 2012/2013 Lösungen zu Übungsblatt 4
 Karlsruher Institut für Technologie Institut für Theoretische Informatik Prof. Dr. Peter H. Schmitt David Farago, Christoph Scheben, Mattias Ulbrich Formale Systeme, WS 2012/2013 Lösungen zu Übungsblatt
Karlsruher Institut für Technologie Institut für Theoretische Informatik Prof. Dr. Peter H. Schmitt David Farago, Christoph Scheben, Mattias Ulbrich Formale Systeme, WS 2012/2013 Lösungen zu Übungsblatt
Einführung in die Computerlinguistik
 Einführung in die Computerlinguistik Kontextfreie Sprachen und Pushdown-Automaten Dozentin: Wiebke Petersen WS 2004/2005 Wiebke Petersen Formale Komplexität natürlicher Sprachen WS 03/04 Wiederholung c
Einführung in die Computerlinguistik Kontextfreie Sprachen und Pushdown-Automaten Dozentin: Wiebke Petersen WS 2004/2005 Wiebke Petersen Formale Komplexität natürlicher Sprachen WS 03/04 Wiederholung c
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2012
 utomaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink utomaten und Formale Sprachen 1 Der CYK-lgorithmus Beispiel
utomaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink utomaten und Formale Sprachen 1 Der CYK-lgorithmus Beispiel
a n + 2 1 auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert:
 Beispiel: Wir untersuchen die rekursiv definierte Folge a 0 + auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert: ( ) (,, 7, 5,...) Wir können also vermuten, dass die Folge monoton fallend
Beispiel: Wir untersuchen die rekursiv definierte Folge a 0 + auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert: ( ) (,, 7, 5,...) Wir können also vermuten, dass die Folge monoton fallend
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
15 Optimales Kodieren
 15 Optimales Kodieren Es soll ein optimaler Kodierer C(T ) entworfen werden, welcher eine Information (z.b. Text T ) mit möglichst geringer Bitanzahl eindeutig überträgt. Die Anforderungen an den optimalen
15 Optimales Kodieren Es soll ein optimaler Kodierer C(T ) entworfen werden, welcher eine Information (z.b. Text T ) mit möglichst geringer Bitanzahl eindeutig überträgt. Die Anforderungen an den optimalen
Theoretische Informatik SS 04 Übung 1
 Theoretische Informatik SS 04 Übung 1 Aufgabe 1 Es gibt verschiedene Möglichkeiten, eine natürliche Zahl n zu codieren. In der unären Codierung hat man nur ein Alphabet mit einem Zeichen - sagen wir die
Theoretische Informatik SS 04 Übung 1 Aufgabe 1 Es gibt verschiedene Möglichkeiten, eine natürliche Zahl n zu codieren. In der unären Codierung hat man nur ein Alphabet mit einem Zeichen - sagen wir die
Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema
 Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema 2x 4 + x 3 + x + 3 div x 2 + x 1 = 2x 2 x + 3 (2x 4 + 2x 3 2x 2 ) x 3 + 2x 2 + x + 3 ( x
Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema 2x 4 + x 3 + x + 3 div x 2 + x 1 = 2x 2 x + 3 (2x 4 + 2x 3 2x 2 ) x 3 + 2x 2 + x + 3 ( x
Grundlagen der Künstlichen Intelligenz
 Grundlagen der Künstlichen Intelligenz 27. Aussagenlogik: Logisches Schliessen und Resolution Malte Helmert Universität Basel 28. April 2014 Aussagenlogik: Überblick Kapitelüberblick Aussagenlogik: 26.
Grundlagen der Künstlichen Intelligenz 27. Aussagenlogik: Logisches Schliessen und Resolution Malte Helmert Universität Basel 28. April 2014 Aussagenlogik: Überblick Kapitelüberblick Aussagenlogik: 26.
REG versus CF. Theorem REG ist echt in CF enthalten.
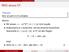 REG versus CF Theorem REG ist echt in CF enthalten. Beweis: Wir wissen: L = {a m b m m 1} ist nicht regulär. Andererseits ist L kontextfrei, wie die einfache kontextfreie Grammatik G = ({a, b}, {S}, S,
REG versus CF Theorem REG ist echt in CF enthalten. Beweis: Wir wissen: L = {a m b m m 1} ist nicht regulär. Andererseits ist L kontextfrei, wie die einfache kontextfreie Grammatik G = ({a, b}, {S}, S,
Sprachen/Grammatiken eine Wiederholung
 Sprachen/Grammatiken eine Wiederholung Was sind reguläre Sprachen? Eigenschaften regulärer Sprachen Sprachen Begriffe Symbol: unzerlegbare Grundzeichen Alphabet: endliche Menge von Symbolen Zeichenreihe:
Sprachen/Grammatiken eine Wiederholung Was sind reguläre Sprachen? Eigenschaften regulärer Sprachen Sprachen Begriffe Symbol: unzerlegbare Grundzeichen Alphabet: endliche Menge von Symbolen Zeichenreihe:
Theoretische Informatik I
 Theoretische nformatik inheit 3 Kontextfreie Sprachen 1. Kontextfreie Grammatiken 2. Pushdown Automaten 3. igenschaften kontextfreier Sprachen Theoretische nformatik inheit 3.1 Kontextfreie Grammatiken
Theoretische nformatik inheit 3 Kontextfreie Sprachen 1. Kontextfreie Grammatiken 2. Pushdown Automaten 3. igenschaften kontextfreier Sprachen Theoretische nformatik inheit 3.1 Kontextfreie Grammatiken
Kontextfreie Sprachen werden von PDAs akzeptiert
 Kontextfreie Sprachen werden von PDAs akzeptiert Sei G = (Σ, V, S, P) eine kontextfreie Grammatik. Dann gibt es einen PDA A mit L(A) = L(G). Der PDA A arbeitet mit nur einem Zustand q 0, besitzt das Kelleralphabet
Kontextfreie Sprachen werden von PDAs akzeptiert Sei G = (Σ, V, S, P) eine kontextfreie Grammatik. Dann gibt es einen PDA A mit L(A) = L(G). Der PDA A arbeitet mit nur einem Zustand q 0, besitzt das Kelleralphabet
WS 2013/14. Diskrete Strukturen
 WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
10 Kellerautomaten. Kellerautomaten
 10 Kellerautomaten Bisher hatten wir kontextfreie Sprachen nur mit Hilfe von Grammatiken charakterisiert. Wir haben gesehen, dass endliche Automaten nicht in der Lage sind, alle kontextfreien Sprachen
10 Kellerautomaten Bisher hatten wir kontextfreie Sprachen nur mit Hilfe von Grammatiken charakterisiert. Wir haben gesehen, dass endliche Automaten nicht in der Lage sind, alle kontextfreien Sprachen
Anmerkungen zur Übergangsprüfung
 DM11 Slide 1 Anmerkungen zur Übergangsprüfung Aufgabeneingrenzung Aufgaben des folgenden Typs werden wegen ihres Schwierigkeitsgrads oder wegen eines ungeeigneten fachlichen Schwerpunkts in der Übergangsprüfung
DM11 Slide 1 Anmerkungen zur Übergangsprüfung Aufgabeneingrenzung Aufgaben des folgenden Typs werden wegen ihres Schwierigkeitsgrads oder wegen eines ungeeigneten fachlichen Schwerpunkts in der Übergangsprüfung
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Algorithmen und Datenstrukturen. Große Übung vom 29.10.09 Nils Schweer
 Algorithmen und Datenstrukturen Große Übung vom 29.10.09 Nils Schweer Diese Folien Braucht man nicht abzuschreiben Stehen im Netz unter www.ibr.cs.tu-bs.de/courses/ws0910/aud/index.html Kleine Übungen
Algorithmen und Datenstrukturen Große Übung vom 29.10.09 Nils Schweer Diese Folien Braucht man nicht abzuschreiben Stehen im Netz unter www.ibr.cs.tu-bs.de/courses/ws0910/aud/index.html Kleine Übungen
Erfüllbarkeit und Allgemeingültigkeit
 Theoretische Informatik: Logik, M. Lange, FB16, Uni Kassel: 3.3 Aussagenlogik Erfüllbarkeit 44 Erfüllbarkeit und Allgemeingültigkeit Def.: eine Formel ϕ heißt erfüllbar, wennesein I gibt, so dass I = ϕ
Theoretische Informatik: Logik, M. Lange, FB16, Uni Kassel: 3.3 Aussagenlogik Erfüllbarkeit 44 Erfüllbarkeit und Allgemeingültigkeit Def.: eine Formel ϕ heißt erfüllbar, wennesein I gibt, so dass I = ϕ
Berechnungen in Access Teil I
 in Access Teil I Viele Daten müssen in eine Datenbank nicht eingetragen werden, weil sie sich aus anderen Daten berechnen lassen. Zum Beispiel lässt sich die Mehrwertsteuer oder der Bruttopreis in einer
in Access Teil I Viele Daten müssen in eine Datenbank nicht eingetragen werden, weil sie sich aus anderen Daten berechnen lassen. Zum Beispiel lässt sich die Mehrwertsteuer oder der Bruttopreis in einer
WS 2008/09. Diskrete Strukturen
 WS 2008/09 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0809
WS 2008/09 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0809
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
 50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
Grundlagen der Theoretischen Informatik
 1 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 2 Kontextfreie Grammatiken Definition: Eine Grammatik G
1 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 2 Kontextfreie Grammatiken Definition: Eine Grammatik G
Mathematische Maschinen
 Mathematische Maschinen Ziel: Entwicklung eines allgemeinen Schemas zur Beschreibung von (mathematischen) Maschinen zur Ausführung von Algorithmen (hier: (partiellen) Berechnungsverfahren). Mathematische
Mathematische Maschinen Ziel: Entwicklung eines allgemeinen Schemas zur Beschreibung von (mathematischen) Maschinen zur Ausführung von Algorithmen (hier: (partiellen) Berechnungsverfahren). Mathematische
Das Briefträgerproblem
 Das Briefträgerproblem Paul Tabatabai 30. Dezember 2011 Inhaltsverzeichnis 1 Problemstellung und Modellierung 2 1.1 Problem................................ 2 1.2 Modellierung.............................
Das Briefträgerproblem Paul Tabatabai 30. Dezember 2011 Inhaltsverzeichnis 1 Problemstellung und Modellierung 2 1.1 Problem................................ 2 1.2 Modellierung.............................
Kapitel 2: Formale Sprachen Gliederung
 Gliederung 0. Einleitung und Grundbegriffe 1. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.1. Chomsky-Grammatiken 2.2. Reguläre Sprachen 2.3. Kontextfreie Sprachen
Gliederung 0. Einleitung und Grundbegriffe 1. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.1. Chomsky-Grammatiken 2.2. Reguläre Sprachen 2.3. Kontextfreie Sprachen
Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer
 Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer Allgemein: Das RSA-Verschlüsselungsverfahren ist ein häufig benutztes Verschlüsselungsverfahren, weil es sehr sicher ist. Es gehört zu der Klasse der
Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer Allgemein: Das RSA-Verschlüsselungsverfahren ist ein häufig benutztes Verschlüsselungsverfahren, weil es sehr sicher ist. Es gehört zu der Klasse der
Deterministische Turing-Maschinen (DTM) F3 03/04 p.46/395
 Deterministische Turing-Maschinen (DTM) F3 03/04 p.46/395 Turing-Machine Wir suchen ein Modell zur formalen Definition der Berechenbarkeit von Funktionen und deren Zeit- und Platzbedarf. Verschiedene Modelle
Deterministische Turing-Maschinen (DTM) F3 03/04 p.46/395 Turing-Machine Wir suchen ein Modell zur formalen Definition der Berechenbarkeit von Funktionen und deren Zeit- und Platzbedarf. Verschiedene Modelle
2. Übungsblatt 6.0 VU Theoretische Informatik und Logik
 2. Übungsblatt 6.0 VU Theoretische Informatik und Logik 25. September 2013 Aufgabe 1 Geben Sie jeweils eine kontextfreie Grammatik an, welche die folgenden Sprachen erzeugt, sowie einen Ableitungsbaum
2. Übungsblatt 6.0 VU Theoretische Informatik und Logik 25. September 2013 Aufgabe 1 Geben Sie jeweils eine kontextfreie Grammatik an, welche die folgenden Sprachen erzeugt, sowie einen Ableitungsbaum
5.7 Kontextfreie Grammatiken und Kellerautomaten
 130 5.7 Kontextfreie Grammatiken und Kellerautomaten Im letzten Abschnitt haben wir gesehen, dass wir reguläre Sprachen auch mit Hilfe von endlichen Automaten charakterisieren können. Jetzt wollen wir
130 5.7 Kontextfreie Grammatiken und Kellerautomaten Im letzten Abschnitt haben wir gesehen, dass wir reguläre Sprachen auch mit Hilfe von endlichen Automaten charakterisieren können. Jetzt wollen wir
Analysis I für Studierende der Ingenieurwissenschaften
 Fachbereich Mathematik der Universität Hamburg WiSe 2015/16 Prof. Dr. M. Hinze Dr. P. Kiani Analysis I für Studierende der Ingenieurwissenschaften Lösungshinweise zu Blatt 2 Aufgabe 1: (12 Punkte) a) Beweisen
Fachbereich Mathematik der Universität Hamburg WiSe 2015/16 Prof. Dr. M. Hinze Dr. P. Kiani Analysis I für Studierende der Ingenieurwissenschaften Lösungshinweise zu Blatt 2 Aufgabe 1: (12 Punkte) a) Beweisen
1 topologisches Sortieren
 Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Codierungstheorie Rudolf Scharlau, SoSe 2006 9
 Codierungstheorie Rudolf Scharlau, SoSe 2006 9 2 Optimale Codes Optimalität bezieht sich auf eine gegebene Quelle, d.h. eine Wahrscheinlichkeitsverteilung auf den Symbolen s 1,..., s q des Quellalphabets
Codierungstheorie Rudolf Scharlau, SoSe 2006 9 2 Optimale Codes Optimalität bezieht sich auf eine gegebene Quelle, d.h. eine Wahrscheinlichkeitsverteilung auf den Symbolen s 1,..., s q des Quellalphabets
Binäre Bäume. 1. Allgemeines. 2. Funktionsweise. 2.1 Eintragen
 Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Musterlösungen zur Linearen Algebra II Blatt 5
 Musterlösungen zur Linearen Algebra II Blatt 5 Aufgabe. Man betrachte die Matrix A := über dem Körper R und über dem Körper F und bestimme jeweils die Jordan- Normalform. Beweis. Das charakteristische
Musterlösungen zur Linearen Algebra II Blatt 5 Aufgabe. Man betrachte die Matrix A := über dem Körper R und über dem Körper F und bestimme jeweils die Jordan- Normalform. Beweis. Das charakteristische
Theoretische Grundlagen des Software Engineering
 Theoretische Grundlagen des Software Engineering 11: Abstrakte Reduktionssysteme schulz@eprover.org Reduktionssysteme Definition: Reduktionssystem Ein Reduktionssystem ist ein Tupel (A, ) Dabei gilt: A
Theoretische Grundlagen des Software Engineering 11: Abstrakte Reduktionssysteme schulz@eprover.org Reduktionssysteme Definition: Reduktionssystem Ein Reduktionssystem ist ein Tupel (A, ) Dabei gilt: A
Stellen Sie bitte den Cursor in die Spalte B2 und rufen die Funktion Sverweis auf. Es öffnet sich folgendes Dialogfenster
 Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
3. Zusammenhang. 22 Andreas Gathmann
 22 Andreas Gathmann 3. Zusammenhang Eine der anschaulichsten Eigenschaften eines topologischen Raumes ist wahrscheinlich, ob er zusammenhängend ist oder aus mehreren Teilen besteht. Wir wollen dieses Konzept
22 Andreas Gathmann 3. Zusammenhang Eine der anschaulichsten Eigenschaften eines topologischen Raumes ist wahrscheinlich, ob er zusammenhängend ist oder aus mehreren Teilen besteht. Wir wollen dieses Konzept
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie prachen (VI) 25.06.2015 Viorica ofronie-tokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie prachen (VI) 25.06.2015 Viorica ofronie-tokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Algorithmen II Vorlesung am 15.11.2012
 Algorithmen II Vorlesung am 15.11.2012 Kreisbasen, Matroide & Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
Algorithmen II Vorlesung am 15.11.2012 Kreisbasen, Matroide & Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
Wie löst man Mathematikaufgaben?
 Wie löst man Mathematikaufgaben? Manfred Dobrowolski Universität Würzburg Wie löst man Mathematikaufgaben? 1 Das Schubfachprinzip 2 Das Invarianzprinzip 3 Das Extremalprinzip Das Schubfachprinzip Verteilt
Wie löst man Mathematikaufgaben? Manfred Dobrowolski Universität Würzburg Wie löst man Mathematikaufgaben? 1 Das Schubfachprinzip 2 Das Invarianzprinzip 3 Das Extremalprinzip Das Schubfachprinzip Verteilt
