Mathematik 1 für Maschinenbau, M. Schuchmann (SoSe 2013) Aufgabenblatt 5 (Ebenen)
|
|
|
- Christian Hilko Hofmeister
- vor 5 Jahren
- Abrufe
Transkript
1 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Aufgabenbla 5 (Ebenen) ) Geuch i eine Gleichung der Ebene E durch die Punke A(; -; ); B(; ; -) und C(; ; ) in Parameerform. ) Schreibe in Koordinaenform: E: ) Wie i die Lage der Ebenen E : - y + z = 8, E : y + z = 6, E : y + z = und E : 5 y + 5z = zueinander? ) Geuch ird die Ebenengleichung on E in Normalform: E: y + z = 5) Schreibe in Koordinaenform: E: 6) Geuch ird eine Parameerform on E: E: y + z = 8 7) Bechreiben Sie die Lage der Ebenen a) E: z= b) E: - + y = 8) E oll geprüf erden, ob der Punk P(;, -) auf der Ebene mi der Gleichung E: oder auf der Ebene mi der Gleichung F: + y + z = lieg.
2 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) 9) Beimmen Sie gegebenenfall den Schnipunk on g: r 6 und E:. ) Beimmen Sie den Schnipunk und Schniinkel on g: r 6 und E: + y + z = ) Beimmen Sie die Spurpunke on: E: + y + z = ) Berechne den Schnipunk on E: mi der -Ache. ) Wie i die Lage der Ebenen zueinander? a) E: + y + z = 8 F: + y + z = b) E: + y + z = 8 F: + y + z = 6 c) E: + y + z = 8 F: + y + z = ) Beimmen Sie die Gleichung der Schnigeraden und den Schniinkel der Ebenen E und F: E: + y + z = 8 F: + y + z =
3 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) 5) Beimmen Sie die Schnigerade der Ebenen E und F: E: - y + z = 8 F: 6) E oll der Aband der Ebene E: y + z = om Punk P(; ; ) beimm erden. Außerdem oll P an E gepiegel erden.
4 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Löungen: ) E: ) ( ) ( ) Muliplizier man die obige Normalengleichung au, o erhäl man eine Koordinaengleichung der Ebene: Somi ergib ich (- + ) =, omi ir eine Gleichung on E in Koordinaenform erhalen: E: = - Man kann die Komponenen de Vekor auch mi, y und z bezeichnen: E: - + y + z = - ) Die beiden Ebenen E : - y + z = 8 und E : y + z = 6 ind idenich, ährend E : y + z = parallel zu beiden Ebenen E und E i. Die Ebene E : 5 y + 5z = äre eder parallel zu noch idenich mi einer der Ebenen E bi E, denn der Normalenekor
5 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) n 5 5 dieer Ebene i kein Vielfache der Normalenekoren der anderen Ebenen. ) Den Normalenekor kann man einfach ableen: n Einen Punk in der Ebene E finde man auch chnell, denn dieer mu die Gleichung erfüllen. Sez man z.b. y = und z =, o ergib ich = und =. Somi äre P(; ; ) ein Punk der Ebene und ir haben eine Normalform on E: 5) E:. Möglichkei: Mi der Ebenengleichung ergib ich: () = () y = - - () z = + + Man kann zei der obigen Gleichungen (ir ählen () und ()) nach und auflöen: () + () + y = - Somi i = - - y. In () einezen ergib = y und omi = + y +. Nun ezen ir die in () ein: Dami ergib ich E: - + z =. z = + ( + y +) + (- y). Möglichkei: Der Normalenekor n i zu den beiden Richungekoren orhogonal. Dami gil
6 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) n und n. Hierau ergeben ich Gleichungen für Unbekanne: n n + n = n n + n = Dami i n bi auf die Länge fegeleg. Wir eliminieren nun eine Unbekanne, z.b. n durch Subrakion der beiden Gleichungen. Wir erhalen n =. Hier ind jez gleich Variablen enfallen. Nun können ir eine der anderen beiden Variablen auf einen Wer ezen (nich auf Null!), z.b. n =. Fall nich, ie in dieem Beipiel, gleich zei Variablen enfallen, dann ez man in der ich ergebenden Gleichung mi zei Variablen eine auf einen Wer. Sezen ir nun die Were für n und n in beipieleie die obere Gleichung ein, o ergib ich n - + =, omi n = - i. Wir haben nun einen Normalenekor gefunden (einen, da er auch eine andere Länge haben könne und omi auch Vielfache diee Vekor Normalenekoren ind): n Wir erenden den Süzekor au der Parameerform und ellen eine Normalform auf: E: Aumuliplizieren führ zur Koordinaenform: z. Möglichkei: Man geh ie bei der Möglichkei or, nur da man den Normalenekor n über da o genanne Kreuzproduk bz. Vekorproduk der beiden Richungekoren beimm. Da Vekorproduk i ein pezielle Produk zichen zei Vekoren, bei dem ich ieder ein Vekor ergib, der orhogonal zu den beiden urprünglichen Vekoren i. D.h. mi
7 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) n gil für die Skalaproduke n und n. Der Normalenekor n i zu den beiden Richungekoren orhogonal. Hier: n Nun kann man ie bei Möglichkei orgehen und die Normalengleichung und dann die Koordinaengleichung beimmen. Dabei ergib ich da (-)-fache der Koordinaengleichung au Möglichkei, da ir einen Normalenekor erhalen haben, der da (-)-fache de Normalenekor au Möglichkei darell. 6) Nun kann man ie folg orgehen. Man lö die Gleichung nach einer Variablen auf, z.b. : = 8 + y z = + y z Nun ez man die anderen beiden Variablen auf Parameer, z.b. y = r und z = : = + r y = r z = Dami haben ir berei eine Parameerform, ir müen die oberen drei Gleichungen nur in Mari-Vekor-Form chreiben:
8 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) 7) E: r a) Diee Ebene i mi der -y-ebene idenich, denn z = und und y ind beliebig. Dami äre z.b. P(; ; ) ein Punk dieer Ebene. F: z = äre eine zu E parallele Ebene. F i parallel zur -y-ebene und ha zu dieer den Aband. Z.B. i Q(; ; ) ein Punk dieer Ebene, oder R(; ; ). b) Bei Punken dieer Ebene i die z-komponene beliebig, nur zichen der - und y- Komponene mu die Beziehung + y = beehen. Diee Ebene i omi parallel zur z-ache. 8) a) Wenn dieer Punk auf der Ebene E lieg, o gib e ein und ein, o da gil, bz.: () = - + () = + + () - = + - Wir ählen zei Gleichungen au, löen diee nach und auf und manchen dann die Probe mi der nich augeählen Gleichung. Wir ählen hier () und (), denn enn ir diee addieren, erhalen ir 8 = + 5, omi = i. Einezen on = in () ergib - = +, omi = i. Die Probe mi der eren Gleichung ergib = +, omi diee erfüll i und P in E lieg. I die Ebene in Koordinaenform gegeben, o mu man nur den Punk in die Ebenengleichung einezen und prüfen, ob diee erfüll i. So bei b) P(;, -) in F: + y + z = eingeez ergib =, omi P auch in F lieg. 9) Gleichezen ergib drei Gleichungen mi drei Unbekannen: () + r = - + () -r = - + +
9 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) () -6 + r = + + Hier ergib ich genau eine Löung (man kann hier z.b. die ere Gleichung zur zeien und zur drien addieren, omi man jeeil eine Gleichung nur mi den Variablen r und erhäl, die man dann löen kann): r =, = - und =. Schnipunk i hier S(5; -, ). ) Mi der Gleichung on g ergib ich: = + r y = -r z = -6 +r In E eingeez ergib ich: ( + r) + (-r) r = + r - r r = Somi i r = und e gib einen Schnipunk. Wäre r komple enfallen und e ürde ich z.b. = ergeben, o häe g in E gelegen. Häe ich z.b. = ergeben, o äre g parallel zu E geeen. Wir können nun den Schnipunk S beimmen, enn ir r = in die Gleichung für g einezen: Schniinkel: 5 OS fl S(5; -; ) 6, n, n, n 6,, omi i in( ) 5, 79. ) Für die Berechnung de Schnipunke mi der -Ache S mu man y = und z = ezen: =
10 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Dami äre = 6 und S (6; ; ). Analog ergib ich S y (; ; ) und S z (; ; ). Diidier man die Ebenengleichung durch die reche Seie (enn diee on Null erchieden i,on ürden alle Spurpunke im Urprung liegen), o erhäl man die Achenabchniform, an der man alle Spurpunke ableen kann: + y + z = : /6 + y/ + z/ = Wäre die Ebene E: + y = gegeben, o gäbe e keinen Schnipunk mi der z-ache, da die Ebene parallel zu dieer erläuf. Wenn die Ebene in Parameerform gegeben i, dann mu für jeden Spurpunk ein Gleichungyem gelö erden, oder man müe diee in die Koordinaenform umrechnen, a u. U. eniger aufändig äre. ) Wenn ir den Schnipunk mi der -Ache direk berechnen ollen, müen ir y = und z = ezen und da Gleichungyem = - + = + - löen. Sez man danach die Löung für und in die Ebenengleichung ein, o erhäl man den Schnipunk mi der -Ache. ) a) Die beiden Ebenen ind parallel, denn die linke Seie der Ebenengleichung i idenich, omi die Normalenekoren idenich ind, aber die reche Seie unercheide ich.
11 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) b) Die beiden Ebenen ind idenich, denn die Gleichungen ind Vielfache oneinander. c) Die beiden Ebenen ind eder parallel noch idenich, denn die Normalekoren ind keine Vielfachen oneinander. Die beiden Ebenen cheiden ich in einer Schnigeraden. ) Wir eliminieren und ubrahieren die bedien Ebenengleichungen: -y - z = - Nun ezen ir z.b. z = und löen obige Gleichung nach y auf: -y - = - y = - + Nun können ir z = und y = - + eneder in die Gleichung on E oder in die on F einezen. Wir ählen E und erhalen: + (- + ) + = 8 Somi i = 6 und ir haben eine Gleichung der Schnigeraden g gefunden: Somi i = 6 y = - z = g: 6. Um den Schniinkel der beiden Ebenen beimmen zu können, mu man den Winkel zichen den Normalenekoren n E und n F beimmen. Da ich, je nachdem ie die Richungekoren ehen, auch ein Winkel a größer al 9 zichen den Normalenekoren ergeben kann, o gib man in dieem Fall 8 - a al Schniinkel an, oder man erende den Berag de Skalarproduke bei der Winkelberechung (ie beim Schniinkel zichen zei Geraden. Für den Schniinkel j gil: co( ) n n E E n n F F
12 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Hier gil: n E, n F, 6 8 ) co(.9 5) Mi F erhäl man = + + y = + + z = + und diee in die Gleichung on E eingeez ergib: + + ( + + ) + + = = 8 Löen ir nach z.b. die Gleichung nach auf, o erhalen ir = 9 -. Sezen ir die in F ein, o erhalen ir eine Gleichung der Schnigeraden: g: ) (9 6)
13 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Der Normalenekor n kann ie immer einfach an der Koordinaenform abgeleen erden. Wir beimmen deen Länge: n Al näche diidieren ir die Gleichung on E durch die Länge de Normalekor: E: / /y + /z = Wenn die reche Seie negai äre, o ird die Gleichung bei der Beimmung der HNF mi - muliplizier. Auf der rechen Seie eh nun der Aband der Ebene om Urprung (hier LE). Subrahieren ir noch auf beiden Seien, o da man auf der rechen Seie eine Null erhäl, o ergib ich durch E: / /y + /z - = die HNF al Koordinaengleichung. Von einer Normalform augehend ürde ich folgende Gleichung in ekorieller Form ergeben (für die Umandlung in Normalform urde ein Punk on E benöig, den ir erhalen, fall ir beipieleie y = z = ezen, omi ir (6; ; ) al Punk on E erhalen): 6 / E: / / Der Aband d(p, E) eine Punke P(; y; z) on E ergib ich über: 6 / d(p, E) = / / / y / z / Für den Punk P(; ; ) gil dann: d(p,e) / / / Eine eiere Möglichkei zur Beimmung de Abande eine Punke on einer Ebene i die folgende: Man konruier eine Hilfgerade g, die den Punk P al Süzekor erende und den Normalenekor der Ebene al Richungekor. Dami i die Hilfgerade enkrech zur Ebene und der Schnipunk der Geraden mi der Ebene i der Lofußpunk F. Der
14 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Aband on P und F i dann ieder der Aband der Ebene zum Punk. Diee Verfahren kann man auch anenden, enn man einen Punk an einer Ebene piegeln möche, oder enn man eine Gerade in eine Ebene projizieren möche. Hier: Die Hilfgerade i: g: n OP Wir ezen = +, y = - und z = + in E ein: ( + ) - (-) + + = = Somi i =. In die Gleichung on g eingeez, ergib ich der Orekor de Lofußpunke: OF Wir beimmen den Vekor PF und deen Länge:
15 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) PF OF OP, PF. Nun ollen ir noch zum Schlu den Punk P an der Ebene E piegeln: OP ' 5 OP PF OF' PF Alo ergib ich der gepiegele Punk P'(5; ;).
Mathematik: Mag. Schmid Wolfgang+LehrerInnenteam ARBEITSBLATT 6-13 ERMITTELN DER KREISGLEICHUNG
 ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 7 5. Semester ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE
 Mahemaik: Mag. Schmid Wolfgang Arbeibla 7. Semeer ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE Im Raum möche man naürlich nich nur Geraden ondern auch Flächen darellen. Diee Flächen bezeichne man al
Mahemaik: Mag. Schmid Wolfgang Arbeibla 7. Semeer ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE Im Raum möche man naürlich nich nur Geraden ondern auch Flächen darellen. Diee Flächen bezeichne man al
Hauptprüfung 2010 Aufgabe 4
 Haupprüfung Aufgabe Gegeben ind die Punke A(5//), B(//), C(//) und S(//5).. Zeigen Sie, da da Dreieck ABC rechwinklig und gleichchenklig i. Berechnen Sie die Koordinaen de Punke D o, da da Viereck ABCD
Haupprüfung Aufgabe Gegeben ind die Punke A(5//), B(//), C(//) und S(//5).. Zeigen Sie, da da Dreieck ABC rechwinklig und gleichchenklig i. Berechnen Sie die Koordinaen de Punke D o, da da Viereck ABCD
Geradendarstellung in Paramterform
 Vekorrechnung Theorie Manfred Gurner Seie Geradendarellung in Paramerform X X X - X - r r Die Punke auf einer Geraden laen ich folgendermaßen finden: Gegeben ei der Punk und der Richungvekor r. Dann ergib
Vekorrechnung Theorie Manfred Gurner Seie Geradendarellung in Paramerform X X X - X - r r Die Punke auf einer Geraden laen ich folgendermaßen finden: Gegeben ei der Punk und der Richungvekor r. Dann ergib
Höhere Mathematik III für die Fachrichtung Elektrotechnik und Informationstechnik Lösungsvorschläge zum 6. Übungsblatt
 Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
1. Kontrolle Physik Grundkurs Klasse 11
 1. Konrolle Phyik Grundkur Klae 11 1. Ein Luch lauer eine Haen auf und lä e da ahnungloe und chackhafe Tier bi auf 30,0 herankoen. Dann prine er i 68 k/h auf ein Opfer lo, da ofor davon renn. Nach 5,0
1. Konrolle Phyik Grundkur Klae 11 1. Ein Luch lauer eine Haen auf und lä e da ahnungloe und chackhafe Tier bi auf 30,0 herankoen. Dann prine er i 68 k/h auf ein Opfer lo, da ofor davon renn. Nach 5,0
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt Semester ARBEITSBLATT 11 LAGEBEZIEHUNG DREIER EBENEN
 Mahemaik Mag. Schmid Wolfgang Arbeisbla. Semeser ARBEITSBLATT LAGEBEZIEHUNG DREIER EBENEN Nachdem wir die Lage weier Ebenen unersuch haben, wollen wir uns nun mi der Lage von drei Ebenen beschäfigen. Anders
Mahemaik Mag. Schmid Wolfgang Arbeisbla. Semeser ARBEITSBLATT LAGEBEZIEHUNG DREIER EBENEN Nachdem wir die Lage weier Ebenen unersuch haben, wollen wir uns nun mi der Lage von drei Ebenen beschäfigen. Anders
Restkapazität. = O( V ) mal kritisch. Also gibt es insgesamt höchstens O( V E ) Augmentierungen.
 Lemma 4.5.9. Der Algorihmu von Edmond-Karp führ höchen O( V E ) Augmenierungen durch. Bewei. Eine Kane (u, v) heiße kriich auf augmenierenden Weg p gdw. c f (u, v) = c f (p). Rekapaziä Eine kriiche Kane
Lemma 4.5.9. Der Algorihmu von Edmond-Karp führ höchen O( V E ) Augmenierungen durch. Bewei. Eine Kane (u, v) heiße kriich auf augmenierenden Weg p gdw. c f (u, v) = c f (p). Rekapaziä Eine kriiche Kane
ges.: Der erste Treffpunkt ist zum Zeitpunkt 0 am Start. Danach fährt der Fahrer 1 45 min und legt dabei
 859. Zwei Auo faren mi erciedenen Gecwindigkeien 1 = 160 / bzw. 2 = 125 / dieelbe Srecke on 200 Länge. Beide Wagen aren gleiczeiig in derelben Ricung. Der arer de cnelleren Wagen mac nac 45min arzei 15min
859. Zwei Auo faren mi erciedenen Gecwindigkeien 1 = 160 / bzw. 2 = 125 / dieelbe Srecke on 200 Länge. Beide Wagen aren gleiczeiig in derelben Ricung. Der arer de cnelleren Wagen mac nac 45min arzei 15min
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 6 5. Semester ARBEITSBLATT 6 PARAMETERDARSTELLUNG EINER GERADEN
 ARBEITSBLATT PARAMETERDARSTELLUNG EINER GERADEN Eine Gerade sell man im R ensprechend zum R auf, nur daß eine z-koordinae hinzukomm: Definiion: Parameerdarsellung einer Gerade durch die Punke A und B:
ARBEITSBLATT PARAMETERDARSTELLUNG EINER GERADEN Eine Gerade sell man im R ensprechend zum R auf, nur daß eine z-koordinae hinzukomm: Definiion: Parameerdarsellung einer Gerade durch die Punke A und B:
Geometric Algebra Computing Transformationen in LA und CGA Dr. Dietmar Hildenbrand
 Geomeric Algebra Compuing Tranformaionen in LA und CGA 4.2.24 Dr. Diemar Hildenbrand Techniche Univeriä Darmad Fachbereich Mahemaik Überblick In linearer Algebra Homogene Koordinaen Tranformaionen in linearer
Geomeric Algebra Compuing Tranformaionen in LA und CGA 4.2.24 Dr. Diemar Hildenbrand Techniche Univeriä Darmad Fachbereich Mahemaik Überblick In linearer Algebra Homogene Koordinaen Tranformaionen in linearer
1. Für die Bewegung eines Fahrzeuges wurde das t-s-diagramm aufgenommen. Skizziere für diese Bewegung das t-v- Diagramm.
 Aufgaben zur gleichförigen Bewegung 1. Für die Bewegung eine Fahrzeuge wurde da --Diagra aufgenoen. Skizziere für diee Bewegung da -- Diagra. 2. Eine Radfahrerin und ein Spaziergänger i eine Hund bewegen
Aufgaben zur gleichförigen Bewegung 1. Für die Bewegung eine Fahrzeuge wurde da --Diagra aufgenoen. Skizziere für diee Bewegung da -- Diagra. 2. Eine Radfahrerin und ein Spaziergänger i eine Hund bewegen
Aufgaben zur gleichförmigen Bewegung
 Aufgaben zur gleichförigen Bewegung 860. Ein Waerrad on 5 Durcheer eh an eine 2 breien und 0,7 iefe Bach. Da Rad dreh ich in der Minue 5 al und i a Rand genau o chnell, wie der Bach fließ. Wie iel Lier
Aufgaben zur gleichförigen Bewegung 860. Ein Waerrad on 5 Durcheer eh an eine 2 breien und 0,7 iefe Bach. Da Rad dreh ich in der Minue 5 al und i a Rand genau o chnell, wie der Bach fließ. Wie iel Lier
Analytische Geometrie Übungsaufgaben 1 gesamtes Stoffgebiet
 Analyiche Geomeie Übungaufgaben geame Soffgebie Pflicheil (ohne GTR und ohne Fomelammlung): P: Zeichne die folgenden Ebenen mi Hilfe ihe Spugeaden in ein kaeiche Koodinaenyem ein: a) E: b) E: 8 c) E: P:
Analyiche Geomeie Übungaufgaben geame Soffgebie Pflicheil (ohne GTR und ohne Fomelammlung): P: Zeichne die folgenden Ebenen mi Hilfe ihe Spugeaden in ein kaeiche Koodinaenyem ein: a) E: b) E: 8 c) E: P:
Messung der Ladung. Wie kann man Ladungen messen? /Kapitel Formeln auf S.134: Elektrische Ladung
 --- Meung der Ladung Wie kann man Ladungen meen? -/Kapiel.. Formeln auf S.: Elekriche Ladung Zur Ladungmeung können wir einen au der Mielufe bekannen Zuammenhang zwichen der Ladung Q und der Sromärke I
--- Meung der Ladung Wie kann man Ladungen meen? -/Kapiel.. Formeln auf S.: Elekriche Ladung Zur Ladungmeung können wir einen au der Mielufe bekannen Zuammenhang zwichen der Ladung Q und der Sromärke I
2. Torsion geschlossener Profile
 Berache werden Balken mi einem konanen einzelligen gechloenen dünnwandigen Hohlquerchni, die durch ein konane Torionmomen M x belae werden. A B () D C M x x y Prof. Dr. Wandinger 5. Dünnwandige Profile
Berache werden Balken mi einem konanen einzelligen gechloenen dünnwandigen Hohlquerchni, die durch ein konane Torionmomen M x belae werden. A B () D C M x x y Prof. Dr. Wandinger 5. Dünnwandige Profile
Übungen zur Klausur 11M1 21/05/2008 Seite 1 von 5
 Seie von 5 Aufgabe : Eine ganzraionale Funkion. Grades habe die Nullsellen ; ;. Ihr Schaubild gehe durch P( 6). Besimme die Exremsellen. Skizziere den Graphen der Funkion. allgemeine Form einer Funkion.
Seie von 5 Aufgabe : Eine ganzraionale Funkion. Grades habe die Nullsellen ; ;. Ihr Schaubild gehe durch P( 6). Besimme die Exremsellen. Skizziere den Graphen der Funkion. allgemeine Form einer Funkion.
Staatlich geprüfte Techniker
 Auzug au dem Lernmaerial Forildunglehrgang Saalich geprüfe Techniker Auzug au dem Lernmaerial Naurwienchaf DAA-Technikum Een / www.daa-echnikum.de, Infoline: 00 83 6 50 Definiion: Die Gechwindigkei eine
Auzug au dem Lernmaerial Forildunglehrgang Saalich geprüfe Techniker Auzug au dem Lernmaerial Naurwienchaf DAA-Technikum Een / www.daa-echnikum.de, Infoline: 00 83 6 50 Definiion: Die Gechwindigkei eine
Fakultät Grundlagen. s = t. gleichförm ig
 Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
Abiturprüfung Mathematik 2009 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
Lösung Abiturprüfung 2000 Grundkurs (Baden-Württemberg)
 Lösung Abiurprüfung 2 Grundkurs (Baden-Würemberg) Analysis, Aufgabe I.1. a) ( x) = 1 [( x)3 9 ( x)]= 1 ( x3 + 9x)= 1 ( x3 9x) = ( x) Somi is (x ) punksymmerisch zum Ursprung. ( x) = 1 (x3 9x)= x(x 2 9)=
Lösung Abiurprüfung 2 Grundkurs (Baden-Würemberg) Analysis, Aufgabe I.1. a) ( x) = 1 [( x)3 9 ( x)]= 1 ( x3 + 9x)= 1 ( x3 9x) = ( x) Somi is (x ) punksymmerisch zum Ursprung. ( x) = 1 (x3 9x)= x(x 2 9)=
Arbeitsauftrag Thema: Gleichungen umformen, Geschwindigkeit, Diagramme
 Arbeiaufrag Thema: Gleichungen umformen, Gechwindigkei, Diagramme Achung: - So ähnlich (aber kürzer) könne die näche Klaenarbei auehen! - Bearbeie die Aufgaben während der Verreungunde. - Wa du nich chaff
Arbeiaufrag Thema: Gleichungen umformen, Gechwindigkei, Diagramme Achung: - So ähnlich (aber kürzer) könne die näche Klaenarbei auehen! - Bearbeie die Aufgaben während der Verreungunde. - Wa du nich chaff
Ministerium für Schule und Weiterbildung NRW M LK HT 4 Seite 1 von 9. Unterlagen für die Lehrkraft. Abiturprüfung Mathematik, Leistungskurs
 Seie von 9 Unerlagen für die Lehrkraf Abiurprüfung 9 Mahemaik, Leisungskurs. Aufgabenar Lineare Algebra/Geomerie ohne Alernaive. Aufgabensellung siehe Prüfungsaufgabe. Maerialgrundlage 4. Bezüge zu den
Seie von 9 Unerlagen für die Lehrkraf Abiurprüfung 9 Mahemaik, Leisungskurs. Aufgabenar Lineare Algebra/Geomerie ohne Alernaive. Aufgabensellung siehe Prüfungsaufgabe. Maerialgrundlage 4. Bezüge zu den
Aufgaben zur beschl. Bewegung (Abi 2007) 517. Ein Zug fährt mit 72 km/h Geschwindigkeit. Durch eine Baustelle wird er gezwungen,
 Aufgben zur bechl. Bewegung 66. (Abi 007) Ein Lieferwgen der Me,5 wird u de Sillnd durch eine konne Krf i de k Berg,0 kn bechleunig. Nchde die Gechwindigkei 7 erreich i, fähr der h Lieferwgen gleichförig
Aufgben zur bechl. Bewegung 66. (Abi 007) Ein Lieferwgen der Me,5 wird u de Sillnd durch eine konne Krf i de k Berg,0 kn bechleunig. Nchde die Gechwindigkei 7 erreich i, fähr der h Lieferwgen gleichförig
F Rück. F r Rück. Mechanische Schwingungen. Größen zur quantitativen Beschreibung :
 Mechaniche chwingungen F r Rück Gleichgewichlage r F Rück F r Rück F r Rück Gleichgewichlage Größen zur quaniaiven Bechreibung : chwingungdauer oder Periode T, Einhei: Frequenz υ /T, Einhei: / oder Hz
Mechaniche chwingungen F r Rück Gleichgewichlage r F Rück F r Rück F r Rück Gleichgewichlage Größen zur quaniaiven Bechreibung : chwingungdauer oder Periode T, Einhei: Frequenz υ /T, Einhei: / oder Hz
Technische Universität München Fakultät für Mathematik Algorithmische Diskrete Mathematik WS 2012/2013 Prof. Dr. P. Gritzmann 9.
 Noe: Name Vorname Marikelnummer Sudiengang Unerchrif der Kandidain/de Kandidaen Höraal Reihe Plaz Techniche Univeriä München Fakulä für Mahemaik Algorihmiche Dikree Mahemaik WS 0/0 Prof. Dr. P. Grizmann
Noe: Name Vorname Marikelnummer Sudiengang Unerchrif der Kandidain/de Kandidaen Höraal Reihe Plaz Techniche Univeriä München Fakulä für Mahemaik Algorihmiche Dikree Mahemaik WS 0/0 Prof. Dr. P. Grizmann
Die Bildung des Präsens funktioniert dann beispielsweise so: "lauda + mus" - wir loben.
 Präen Da Präen i die Gegenwarform. E bechreib alo Handlungen, die gerade paieren. Die Bildung i denkbar einfach und unercheide ich in den unerchiedlichen Konjugaionen (fa immer) nich. Dewegen reich e vollkommen
Präen Da Präen i die Gegenwarform. E bechreib alo Handlungen, die gerade paieren. Die Bildung i denkbar einfach und unercheide ich in den unerchiedlichen Konjugaionen (fa immer) nich. Dewegen reich e vollkommen
Abbildungsmaßstab und Winkelvergrößerung
 Abbildungmaßab und Winkelvergrößerung Abbildungmaßab Uner dem Abbildungmaßab vereh man da Verhälni /, wobei der Audruck ein negaive Vorzeichen erhäl, wenn da ild verkehr wird. Alo Abbildungmaßab V: Winkelvergrößerung
Abbildungmaßab und Winkelvergrößerung Abbildungmaßab Uner dem Abbildungmaßab vereh man da Verhälni /, wobei der Audruck ein negaive Vorzeichen erhäl, wenn da ild verkehr wird. Alo Abbildungmaßab V: Winkelvergrößerung
ZUU AUUFFGGAABBEE :: Die Wann läuft zunächst voll. Nach einiger Zeit wird etwas Wasser abgelassen und dann wird etwas zugeführt.
 Lineare Funkionen. Lösungen Lö LÖÖSSUUNNGGEENN ZZUUM.. KPPI IITTEELL ZZUU UUFFGGEE..: : a) as Pfeildiagramm zeig keine Funkion, da von h kein Pfeil ausgeh und von a zwei Pfeile. b) Is eine Funkion, denn
Lineare Funkionen. Lösungen Lö LÖÖSSUUNNGGEENN ZZUUM.. KPPI IITTEELL ZZUU UUFFGGEE..: : a) as Pfeildiagramm zeig keine Funkion, da von h kein Pfeil ausgeh und von a zwei Pfeile. b) Is eine Funkion, denn
e sx y(x)dx 2. Direkt gemäss der Definition unter Verwendung der in der Vorlesung angeführten Eigenschaften
 Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Übungsblatt 2 Physik für Ingenieure 1
 Übunbla Phyik für Inenieure 1 Ohmar Mari, (ohmar.mari@phyik.uni-ulm.de) 3. 1. 1 1 Aufaben für die Übununden Kinemaik 1 1. Ein Maepunk bewe ich nach der Gleichun () = in(ω). Konruieren ie und berechnen
Übunbla Phyik für Inenieure 1 Ohmar Mari, (ohmar.mari@phyik.uni-ulm.de) 3. 1. 1 1 Aufaben für die Übununden Kinemaik 1 1. Ein Maepunk bewe ich nach der Gleichun () = in(ω). Konruieren ie und berechnen
und zeigen Sie, dass der Punkt P auf g liegt. (c) Bestimmen Sie den Schnittwinkel der Ebenen E und E
 Übungen zum ABI 8 Geomerie (Lineare Algebra) - Lösung eie von 7 Aufgaben incl Lösungen: Aufgabe G Gegeben sind eine Ebenenscar E :( + ) x+ x + ( ) x+ + = mi, eine Ebene E: x+ x + = und der Punk P( ) (a)
Übungen zum ABI 8 Geomerie (Lineare Algebra) - Lösung eie von 7 Aufgaben incl Lösungen: Aufgabe G Gegeben sind eine Ebenenscar E :( + ) x+ x + ( ) x+ + = mi, eine Ebene E: x+ x + = und der Punk P( ) (a)
Physikalische Größe = Zahlenwert Einheit
 Phyikaliche Grundlagen - KOMPAKT 1. Phyikaliche Größen, Einheien und Gleichungen 1.1 Phyikaliche Größen Um die Ar ( Qualiä) und da Aumaß ( Quaniä) phyikalicher Eigenchafen und Vorgänge bechreiben und mi
Phyikaliche Grundlagen - KOMPAKT 1. Phyikaliche Größen, Einheien und Gleichungen 1.1 Phyikaliche Größen Um die Ar ( Qualiä) und da Aumaß ( Quaniä) phyikalicher Eigenchafen und Vorgänge bechreiben und mi
Geradlinige Bewegung Krummlinige Bewegung Kreisbewegung
 11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
Zusammenfassung: Lineare mechanische Wellen
 LGÖ K Ph -ündig Shuljahr 08/09 Zuammenfaung: Lineare mehanihe Wellen Inhalverzeihni Forhreiende ranveralwellen... Sehende ranveralwellen... 3 Refleion von ranveralwellen... ranverale Eigenhwingungen...
LGÖ K Ph -ündig Shuljahr 08/09 Zuammenfaung: Lineare mehanihe Wellen Inhalverzeihni Forhreiende ranveralwellen... Sehende ranveralwellen... 3 Refleion von ranveralwellen... ranverale Eigenhwingungen...
Physik-Übungsblatt Nr. 1: Lösungsvorschläge
 Phyik-Übungbla Nr. 1: Löungorchläge ufgabe 1: Zur Zei are Wagen mi der konanen Gechwindigkei 1 km / h, Wagen fähr mi der konanen Gechwindigkei 1 km / h in die gleiche Richung, ha aber zu eginn einen Vorprung
Phyik-Übungbla Nr. 1: Löungorchläge ufgabe 1: Zur Zei are Wagen mi der konanen Gechwindigkei 1 km / h, Wagen fähr mi der konanen Gechwindigkei 1 km / h in die gleiche Richung, ha aber zu eginn einen Vorprung
auf den Boden fallen, hört man in gleichen Zeitabständen 4 Geräusche. Welchen Abstand hat die 3. Schraube vom unteren Ende der Fallschnur?
 Aufaben zu freien Fall 0. Von der Spize eine Ture lä an einen Sein fallen. Nach 4 Sekunden ieh an ihn auf de Boden aufchlaen. a) Wie hoch i der Tur? b) Mi welcher Gechwindikei riff der Sein auf den Erdboden
Aufaben zu freien Fall 0. Von der Spize eine Ture lä an einen Sein fallen. Nach 4 Sekunden ieh an ihn auf de Boden aufchlaen. a) Wie hoch i der Tur? b) Mi welcher Gechwindikei riff der Sein auf den Erdboden
Abiturprüfung Mathematik 2014 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analytische Geometrie / Stochastik Aufgabe B 1 - Lösungen
 1 Abiturprüfung Mathematik 214 Baden-Württemberg Allgemeinbildende Gymnaien Wahlteil Analytiche Geometrie / Stochatik Aufgabe B 1 - Löungen klau_mener@eb.de.elearning-freiburg.de Wahlteil 214 Aufgabe B
1 Abiturprüfung Mathematik 214 Baden-Württemberg Allgemeinbildende Gymnaien Wahlteil Analytiche Geometrie / Stochatik Aufgabe B 1 - Löungen klau_mener@eb.de.elearning-freiburg.de Wahlteil 214 Aufgabe B
Bekommt Schüler F. noch den Bus...
 Gnuplo Inro Aufgbenellung Bekomm Schüler F. noch den Bu...... oder komm er ew zu pä in die Schule? E. Pulu 1 T. Bonow 2 1 Bichöfliche Gymnium Snk Urul Geilenkirchen 2 Sudieneminr Jülich Jülich Phyik GK11
Gnuplo Inro Aufgbenellung Bekomm Schüler F. noch den Bu...... oder komm er ew zu pä in die Schule? E. Pulu 1 T. Bonow 2 1 Bichöfliche Gymnium Snk Urul Geilenkirchen 2 Sudieneminr Jülich Jülich Phyik GK11
Die wichtigsten Inhalte der einzelnen Kapitel zur schnellen Wiederholung
 Checklien Die wichigen Inhale der einzelnen Kapiel zur chnellen Wiederholung I Kenn du eigenlich die rbeiweie der Naurwienchafler? I 1 Nenne die einzelnen Schrie, die Naurwienchafler gehen, u zu neuen
Checklien Die wichigen Inhale der einzelnen Kapiel zur chnellen Wiederholung I Kenn du eigenlich die rbeiweie der Naurwienchafler? I 1 Nenne die einzelnen Schrie, die Naurwienchafler gehen, u zu neuen
Aufgabenblatt 10: Investitionstheoretische Kostenrechnung I
 Prof. Dr. Gunher Friedl Aufgabenbla 10: Inveiionheoreiche oenrechnung I Aufgabe 10.1: Inveiionheoreiche oenrechnung, Abchreibung (Aufg. 6.2.2 im Übungbuch) Die Gechäfleiung der Brauerei Benedikiner erwäg
Prof. Dr. Gunher Friedl Aufgabenbla 10: Inveiionheoreiche oenrechnung I Aufgabe 10.1: Inveiionheoreiche oenrechnung, Abchreibung (Aufg. 6.2.2 im Übungbuch) Die Gechäfleiung der Brauerei Benedikiner erwäg
LGÖ Ks M 12 Schuljahr 2017/2018. Zusammenfassung: Abstände, Winkel und Spiegelungen
 LGÖ Ks M 12 Schuljahr 217/218 Zusammenfassung: Asände, Winkel und Spiegelungen Inhalsverzeichnis Asände 1 Winkel 5 Spiegelungen 7 Für Experen 1 Asände Asand Punk Punk: Schreiweise: Den Asand zweier Punke
LGÖ Ks M 12 Schuljahr 217/218 Zusammenfassung: Asände, Winkel und Spiegelungen Inhalsverzeichnis Asände 1 Winkel 5 Spiegelungen 7 Für Experen 1 Asände Asand Punk Punk: Schreiweise: Den Asand zweier Punke
KAPITEL 2 KÜRZESTE WEGE
 KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
Affine Geometrie 11. Jahrgang
 Affine Geomeie. Jhgng Gliedeung. Vekoen. Dellung von Vekoen. Rechnen mi Vekoen. Linee Ahängigkei. Geden- und Eenengleichungen. Gedengleichungen. Eenengleichungen in Pmeefom. Inzidenzpoleme. Punk und Gede
Affine Geomeie. Jhgng Gliedeung. Vekoen. Dellung von Vekoen. Rechnen mi Vekoen. Linee Ahängigkei. Geden- und Eenengleichungen. Gedengleichungen. Eenengleichungen in Pmeefom. Inzidenzpoleme. Punk und Gede
Karlsruher Institut für Technologie (KIT) Institut für Analysis Dr. A. Müller-Rettkowski Dipl.-Math. M. Uhl. Sommersemester 2011
 Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Bitte beginnen Sie jede neue Aufgabe auf einem neuen Blatt!
 Soereeer 010 Bla 1 (on 7) Sudiengang: BT(B) / CI(B) Seeer Prüfungfach: Phyik Fachnuer: 04, 071, 07 Hilfiel: Manukrip, Lieraur, Tachenrechner Zei:10 Minuen Ingea ind 10 Punke erreichbar. Bie beginnen Sie
Soereeer 010 Bla 1 (on 7) Sudiengang: BT(B) / CI(B) Seeer Prüfungfach: Phyik Fachnuer: 04, 071, 07 Hilfiel: Manukrip, Lieraur, Tachenrechner Zei:10 Minuen Ingea ind 10 Punke erreichbar. Bie beginnen Sie
Algorithmen II Vorlesung am
 Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
Westfälische Hochschule - Fachbereich Informatik & Kommunikation - Bereich Angewandte Naturwissenschaften. 2. Mechanik
 Wefäliche Hochchule - Fachbereich Informaik & Kommunikaion - Bereich Anewande Naurwienchafen. Mechanik Ziele der Vorleun:.) Eineilun der phikalichen Größen in kalare und ekorielle Größen.) Kinemaik Bechreibun
Wefäliche Hochchule - Fachbereich Informaik & Kommunikaion - Bereich Anewande Naurwienchafen. Mechanik Ziele der Vorleun:.) Eineilun der phikalichen Größen in kalare und ekorielle Größen.) Kinemaik Bechreibun
Stochastische Differentialgleichungen
 INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
Demo-Text für Funktionen und Kurven. Differentialgeometrie INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK. Friedrich Buckel.
 Funkionen und Kurven Differenialgeomerie Tex Nummer: 5 Sand: 9. März 6 Demo-Tex für www.mahe-cd.de INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mahe-cd.de 5 Differenialgeomerie Vorwor Das Thema Kurven is
Funkionen und Kurven Differenialgeomerie Tex Nummer: 5 Sand: 9. März 6 Demo-Tex für www.mahe-cd.de INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mahe-cd.de 5 Differenialgeomerie Vorwor Das Thema Kurven is
Aufgaben gleichmäßig beschleunigte Bewegung
 Aufaben eichäßi bechleunie Beweun 671. (Abi 1995, Grundkur) Vor der Einfahr in eine Bahnhof bre der Lokführer einen Zu i der Bechleuniun 0,850 - on 100,0 kh -1 auf 50,0 kh -1 ab und fähr i dieer Gechwindikei
Aufaben eichäßi bechleunie Beweun 671. (Abi 1995, Grundkur) Vor der Einfahr in eine Bahnhof bre der Lokführer einen Zu i der Bechleuniun 0,850 - on 100,0 kh -1 auf 50,0 kh -1 ab und fähr i dieer Gechwindikei
Wiederholung. Algorithmen und Datenstrukturen Kapitel 10. Motivation. Begriffe und Definitionen
 Algorihmen nd Daenrkren Kapiel Frank Heimann heimann@informaik.ni-hambrg.de 6. Janar 2016 Frank Heimann heimann@informaik.ni-hambrg.de 1/ Graphen Grndlagen Definiion nd Darellng Tiefen- nd Breienche Topologiche
Algorihmen nd Daenrkren Kapiel Frank Heimann heimann@informaik.ni-hambrg.de 6. Janar 2016 Frank Heimann heimann@informaik.ni-hambrg.de 1/ Graphen Grndlagen Definiion nd Darellng Tiefen- nd Breienche Topologiche
Aufgaben: 1. Gib eine Gleichung der Ebene E an, die durch A in Richtung von u und v verläuft.
 Prmeergleichung und Koordinenform einer Ebene Prmeergleichung und Koordinenform einer Ebene Die Lge einer Ebene E im Rum is durch drei Größen eindeuig fesgeleg: X. Einen Punk A, durch den die Ebene verläuf..
Prmeergleichung und Koordinenform einer Ebene Prmeergleichung und Koordinenform einer Ebene Die Lge einer Ebene E im Rum is durch drei Größen eindeuig fesgeleg: X. Einen Punk A, durch den die Ebene verläuf..
 Ergänzung Kpiel 5. Whl der Führunggröße Whl der Führunggröße für Lgeregelungen Biher wurde mei on einem prungförmigen Verluf der Führunggröße w( ugegngen. Viele regelungechniche Anwendungen weien uch ein
Ergänzung Kpiel 5. Whl der Führunggröße Whl der Führunggröße für Lgeregelungen Biher wurde mei on einem prungförmigen Verluf der Führunggröße w( ugegngen. Viele regelungechniche Anwendungen weien uch ein
(3) Weg-Zeit-Verhalten
 (3) Weg-Zei-Verhalen Vorleung Animaion und Simulaion S. Müller KOBLENZ LANDAU Wdh: Bogenlängenabelle Pfad felegen (P 0, P, P and P 3 ) 3 3 r u u P0 3 u u P 3 u u P u P Berechne Poiion für Zeipunk, i.e.
(3) Weg-Zei-Verhalen Vorleung Animaion und Simulaion S. Müller KOBLENZ LANDAU Wdh: Bogenlängenabelle Pfad felegen (P 0, P, P and P 3 ) 3 3 r u u P0 3 u u P 3 u u P u P Berechne Poiion für Zeipunk, i.e.
Von der Fourier-Reihe zum Fourier-Integral
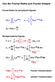 Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Das lineare H-unendlich Problem
 Das lineare H-unendlich Problem Salah-Eddine Sessou Seminarvorrag vom. Juli 6. Problemsellung Bild z P x u K Der Regler (Konroller)K ha zei Eingänge, x und den exogenen Eingang. Das H-unendlich Problem
Das lineare H-unendlich Problem Salah-Eddine Sessou Seminarvorrag vom. Juli 6. Problemsellung Bild z P x u K Der Regler (Konroller)K ha zei Eingänge, x und den exogenen Eingang. Das H-unendlich Problem
Übersicht Datenstrukturen und Algorithmen. Graphenproblem: maximale Flüsse. Graphenproblem: maximale Flüsse. Vorlesung 16: Maximaler Fluss
 Überich aenrukuren und lgorihmen Vorleung 16: Prof. r. Erika Ábrahám Theorie Hybrider Syeme Informaik 2 hp://h.rwh-aachen.de/eaching/-1/ daenrukuren-und-algorihmen/ iee Präenaion verwende in Teilen Folien
Überich aenrukuren und lgorihmen Vorleung 16: Prof. r. Erika Ábrahám Theorie Hybrider Syeme Informaik 2 hp://h.rwh-aachen.de/eaching/-1/ daenrukuren-und-algorihmen/ iee Präenaion verwende in Teilen Folien
14 Kurven in Parameterdarstellung, Tangentenvektor und Bogenlänge
 Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Figurierte Zahlen, Urnen und Kugelfarben
 Figurierte Zahlen, Urnen und Kugelfarben KLAUS-ULRICH UDER, Lüneburg HANS HUMENBERER und BERTHOLD SCHUPPAR, Dortmund Zuammenfaung: Bei einem elementaren tochatichen Problem (Ziehung von zei Kugeln au einer
Figurierte Zahlen, Urnen und Kugelfarben KLAUS-ULRICH UDER, Lüneburg HANS HUMENBERER und BERTHOLD SCHUPPAR, Dortmund Zuammenfaung: Bei einem elementaren tochatichen Problem (Ziehung von zei Kugeln au einer
1. Klausur Physik Leistungskurs Klasse
 1. Kluur Phyik Leiungkur Kle 11 1.1.1 1. uf einer gerden, horizonlen Srße fähr ein Moorrd i der konnen Gechwindigkei 9kh -1. pier zur Zei eine Mrke M. Zu elben Zeipunk re i Punk P ein Moorrd (Me einchließlich
1. Kluur Phyik Leiungkur Kle 11 1.1.1 1. uf einer gerden, horizonlen Srße fähr ein Moorrd i der konnen Gechwindigkei 9kh -1. pier zur Zei eine Mrke M. Zu elben Zeipunk re i Punk P ein Moorrd (Me einchließlich
Weg im tv-diagramm. 1. Rennwagen
 Weg im v-diagramm 1. Rennwagen Löung: (a). (a) Bechreibe die Fahr de Rennwagen. (b) Wie wei kommm der Rennwagen in den eren vier Minuen, wie wei komm er über den geamen Zeiraum? (c) Wie groß i die Durchchnigechwindigkei
Weg im v-diagramm 1. Rennwagen Löung: (a). (a) Bechreibe die Fahr de Rennwagen. (b) Wie wei kommm der Rennwagen in den eren vier Minuen, wie wei komm er über den geamen Zeiraum? (c) Wie groß i die Durchchnigechwindigkei
gegeben durch x 4 in dasselbe Koordinatensystem (Längeneinheit auf beiden Achsen: 1 cm). Zur Kontrolle: ft
 KA LK M2 13 18. 11. 05 I. ANALYSIS Leisungsfachanforderungen Für jedes > 0 is eine Funkion f gegeben durch f (x) = x + 1 e x ; x IR. Der Graph von f sei G. a) Unersuche G auf Asympoen, Nullsellen, Exrem-
KA LK M2 13 18. 11. 05 I. ANALYSIS Leisungsfachanforderungen Für jedes > 0 is eine Funkion f gegeben durch f (x) = x + 1 e x ; x IR. Der Graph von f sei G. a) Unersuche G auf Asympoen, Nullsellen, Exrem-
Übersicht. Datenstrukturen und Algorithmen. Graphenproblem: maximale Flüsse. Graphenproblem: maximale Flüsse. Vorlesung 18: Maximaler Fluss (K26)
 Überich aenrukuren und lgorihmen Vorleung 18: (K26) Joo-Pieer Kaoen Lehruhl für Informaik 2 Sofware Modeling and Verificaion Group hp://move.rwh-aachen.de/eaching/-15/dal/ 25. Juni 2015 1 Flunezwerke 2
Überich aenrukuren und lgorihmen Vorleung 18: (K26) Joo-Pieer Kaoen Lehruhl für Informaik 2 Sofware Modeling and Verificaion Group hp://move.rwh-aachen.de/eaching/-15/dal/ 25. Juni 2015 1 Flunezwerke 2
PHYSIKALISCHES PRAKTIKUM FÜR ANFÄNGER LGyGe
 10.7.08 PHYSKALSCHES PAKTKUM FÜ AFÄGE LGyGe Veruch: M 12 - Kreiel n dieem Veruch werden die Präzeionbewegung und die uaionbewegung eine Kreiel uneruch. Der Aufbau de Kreiel kann au der Abbildung de Veruch
10.7.08 PHYSKALSCHES PAKTKUM FÜ AFÄGE LGyGe Veruch: M 12 - Kreiel n dieem Veruch werden die Präzeionbewegung und die uaionbewegung eine Kreiel uneruch. Der Aufbau de Kreiel kann au der Abbildung de Veruch
Schülerkurs. Mathematik > Lineare Algebra > Lineare Gleichungen Lineare Gleichungssysteme > Teil II: Aufgaben, Lösungen.
 Michel Buhlmnn Schüleku Mhemik > Linee Algeb > Linee Gleichungen Linee Gleichungyeme > Teil II: Aufgben, Löungen Linee Gleichungen und linee Gleichungyeme duchziehen den Mhemikuneich in llen Schulfomen
Michel Buhlmnn Schüleku Mhemik > Linee Algeb > Linee Gleichungen Linee Gleichungyeme > Teil II: Aufgben, Löungen Linee Gleichungen und linee Gleichungyeme duchziehen den Mhemikuneich in llen Schulfomen
Übungsaufgaben. Physik. http://physik.lern-online.net. http://www.lern-online.net THEMA: Gleichförmige Bewegungen und Überholvorgang
 bungaufgaben Pyik p://pyik.lern-online.ne p://.lern-online.ne THEMA: leicförmige Beegungen und berolvorgang Vorgeclagene Arbeizei: Vorgeclagene Hilfmiel: Beerung: Hinei: ea 30 Minuen Tacenrecner (nic programmierbar,
bungaufgaben Pyik p://pyik.lern-online.ne p://.lern-online.ne THEMA: leicförmige Beegungen und berolvorgang Vorgeclagene Arbeizei: Vorgeclagene Hilfmiel: Beerung: Hinei: ea 30 Minuen Tacenrecner (nic programmierbar,
Abiturprüfung Mathematik 2012 (Baden-Württemberg) Berufliche Gymnasien Analysis, Aufgabe 1
 Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
= 150 kmh -1. Wie groß ist die Beschleunigung und der zurückgelegte Weg, wenn die Geschwindigkeitserhöhung in der Zeit von 10 Sekunden erfolgt?
 Aufgaben zur gleicäßig becleunigen Bewegung. Ein Auo eiger eine Gecwindigkei gleicäßig on = 0 k - auf = 50 k -. Wie groß i die Becleunigung und der zurückgelege Weg, wenn die Gecwindigkeieröung in der
Aufgaben zur gleicäßig becleunigen Bewegung. Ein Auo eiger eine Gecwindigkei gleicäßig on = 0 k - auf = 50 k -. Wie groß i die Becleunigung und der zurückgelege Weg, wenn die Gecwindigkeieröung in der
Aufgabe 1: a) (i) und (ii) und (iv) 1 Punkt b) (i) 1 Punkt c) (i) 1 Punkt d) (iv) 1 Punkt e) (B) 1 Punkt f) (iv) 1 Punkt g) (i) und (ii) 2 Punkte h
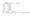 Aufgabe : a) i) un ii) un i) Punk b) i) Punk c) i) Punk ) i) Punk e) B) Punk f) i) Punk g) i) un ii) Punke i) un iii) un i) un ).5 lu.5 Punk Aufgabe : Venuri Ror Punke) a. Volumenrom Für ieen Aufgabeneil
Aufgabe : a) i) un ii) un i) Punk b) i) Punk c) i) Punk ) i) Punk e) B) Punk f) i) Punk g) i) un ii) Punke i) un iii) un i) un ).5 lu.5 Punk Aufgabe : Venuri Ror Punke) a. Volumenrom Für ieen Aufgabeneil
Lösung Abiturprüfung 1994 Leistungskurs (Baden-Württemberg)
 Lösung Abiurprüfung 1994 Leisungskurs (Baden-Würemberg) Analysis I.1. a) D f = IR / { 1 } f x= = K besiz keine Nullsellen 1x f ' x= 8 1x = 8 K besiz keine Exremsellen senkreche Asymoe : x= 1 waagereche
Lösung Abiurprüfung 1994 Leisungskurs (Baden-Würemberg) Analysis I.1. a) D f = IR / { 1 } f x= = K besiz keine Nullsellen 1x f ' x= 8 1x = 8 K besiz keine Exremsellen senkreche Asymoe : x= 1 waagereche
3 GERADL. GLEICHM. BESCHL. BEWEGUNG
 PS KINEMATIK P. Rendulić 0 GERADL. GLEICHM. BESCHL. BEWEGUNG 7 3 GERADL. GLEICHM. BESCHL. BEWEGUNG 3. Experimenelle Herleiung de WegZeiGeeze 3.. Veruchbechreibung Wirk läng der Bahn eine konane Kraf in
PS KINEMATIK P. Rendulić 0 GERADL. GLEICHM. BESCHL. BEWEGUNG 7 3 GERADL. GLEICHM. BESCHL. BEWEGUNG 3. Experimenelle Herleiung de WegZeiGeeze 3.. Veruchbechreibung Wirk läng der Bahn eine konane Kraf in
Messgrößen und gültige Ziffern 7 / 1. Bewegung mit konstanter Geschwindigkeit 7 / 2
 Die Genauigkei einer Megröße wird durch die güligen Ziffern berückichig. Al gülige Ziffern einer Maßzahl gelen alle Ziffern und alle Nullen, die rech nach der eren Ziffer ehen. Megrößen und gülige Ziffern
Die Genauigkei einer Megröße wird durch die güligen Ziffern berückichig. Al gülige Ziffern einer Maßzahl gelen alle Ziffern und alle Nullen, die rech nach der eren Ziffer ehen. Megrößen und gülige Ziffern
1. Klausur Physik Leistungskurs: Kinematik Klasse Dauer: 90 min
 1. Kluur Phyik Leiungkur: Kineik Kle 11 1.1.13 Duer: 9 in 1. Mx und Mäxchen chen ein Werennen über 1. Mx gewinn d Rennen i en 5 Vorprung. U Mäxchen bei Lune zu hlen, ren ie einen Rencheluf, bei de ber
1. Kluur Phyik Leiungkur: Kineik Kle 11 1.1.13 Duer: 9 in 1. Mx und Mäxchen chen ein Werennen über 1. Mx gewinn d Rennen i en 5 Vorprung. U Mäxchen bei Lune zu hlen, ren ie einen Rencheluf, bei de ber
Theoretische Grundlagen
 Theoreiche Grundlagen Phik Leiungkur Größen Größen Größen 5 m Grundgrößen abgeleiee Größen Zahl Einhei Länge, Mae, Zei, Sromärke, Temperaur, Soffmenge, Lichärke Gechwindigkei, Kraf, Ladung Änderunggrößen:
Theoreiche Grundlagen Phik Leiungkur Größen Größen Größen 5 m Grundgrößen abgeleiee Größen Zahl Einhei Länge, Mae, Zei, Sromärke, Temperaur, Soffmenge, Lichärke Gechwindigkei, Kraf, Ladung Änderunggrößen:
Motivation. Finanzmathematik in diskreter Zeit
 Moivaion Finanzmahemaik in diskreer Zei Eine Hinführung zu akuellen Forschungsergebnissen Alber-Ludwigs-Universiä Freiburg Prof. Dr. Thorsen Schmid Abeilung für Mahemaische Sochasik Freiburg, 22. April
Moivaion Finanzmahemaik in diskreer Zei Eine Hinführung zu akuellen Forschungsergebnissen Alber-Ludwigs-Universiä Freiburg Prof. Dr. Thorsen Schmid Abeilung für Mahemaische Sochasik Freiburg, 22. April
Elementare Lösungsmethoden für gewöhnliche Differentialgleichungen
 454 Erforderliche Kennnisse: Höhere Analysis Elemenare Lösungsmehoden für gewöhnliche Differenialgleichungen Was is eigenlich eine Differenialgleichung? Eine Differenialgleichung is eine Gleichung, in
454 Erforderliche Kennnisse: Höhere Analysis Elemenare Lösungsmehoden für gewöhnliche Differenialgleichungen Was is eigenlich eine Differenialgleichung? Eine Differenialgleichung is eine Gleichung, in
Gruppenarbeit: Anwendungen des Integrals Gruppe A: Weg und Geschwindigkeit
 Gruppenarbei: Anwendungen de Inegral Gruppe A: Weg und Gechwindigkei Die ere Ableiung der Zei-Or-Funkion x() der Bewegung eine Körper ergib bekannlich die Zei- Gechwindigkei-Funkion v(), deren ere Ableiung
Gruppenarbei: Anwendungen de Inegral Gruppe A: Weg und Gechwindigkei Die ere Ableiung der Zei-Or-Funkion x() der Bewegung eine Körper ergib bekannlich die Zei- Gechwindigkei-Funkion v(), deren ere Ableiung
Nennen Sie Vor- und Nachteile von Wasserkraftwerken Vorteile: Speicherkraftwerke, Pumpspeicherkraftwerke
 1 Waerkraf Nennen Sie Vor- und Nacheile von Waerkrafwerken Voreile: regeneraive Energie. Keine CO 2 -Emiion! kein Primärenergierägerverbrauch Spizenlafähigkei, Energiepeicherfunkion hohe Zuverläigkei hoher
1 Waerkraf Nennen Sie Vor- und Nacheile von Waerkrafwerken Voreile: regeneraive Energie. Keine CO 2 -Emiion! kein Primärenergierägerverbrauch Spizenlafähigkei, Energiepeicherfunkion hohe Zuverläigkei hoher
Lineare Algebra I - Lösungshinweise zur Klausur
 Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
existiert. In der Regel wird zusätzlich zum oben gegebenen System von Differentialgleichungen noch eine Anfangsbedingung
 0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
W. Stark; Berufliche Oberschule Freising
 9.6 Aufellen der Bewegunggleichungen der haronichen Schwingung bei unerchiedlichen Anfangbedingungen i Hilfe eine Zeiger- und Liniendiagra 9.6. Der chwingende Körper durchläuf zu Zeinullpunk eine uhelage
9.6 Aufellen der Bewegunggleichungen der haronichen Schwingung bei unerchiedlichen Anfangbedingungen i Hilfe eine Zeiger- und Liniendiagra 9.6. Der chwingende Körper durchläuf zu Zeinullpunk eine uhelage
PHYSIK. Gleichförmige Bewegungen. Datei Nr Geradlinige Bewegungen. Teil 1 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK.
 PHYSIK Geradlinige Bewegungen Teil 1 Gleichförige Bewegungen Daei Nr. 91111 Friedrich W. Buckel Geänder: 18. Januar 2013 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.ahe-cd.de 91111 Gleichförige
PHYSIK Geradlinige Bewegungen Teil 1 Gleichförige Bewegungen Daei Nr. 91111 Friedrich W. Buckel Geänder: 18. Januar 2013 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.ahe-cd.de 91111 Gleichförige
 Abiurprüfung Mahemaik 007 Baden-Würemberg (ohne CAS) Pflicheil - Aufgaben Aufgabe : ( VP) Bilden Sie die erse Ableiung der Funkion f mi f () + = ( sin ). Aufgabe : ( VP) ln Berechnen Sie das Inegral e
Abiurprüfung Mahemaik 007 Baden-Würemberg (ohne CAS) Pflicheil - Aufgaben Aufgabe : ( VP) Bilden Sie die erse Ableiung der Funkion f mi f () + = ( sin ). Aufgabe : ( VP) ln Berechnen Sie das Inegral e
Schriftliche Abiturprüfung Mathematik 2013
 Schrifliche Abiurprüfung Mahemaik 03 Aufgabe (NT 008, Nr) Pflicheil Bilden Sie die Ableiung der Funkion f mi f(x) = 3x e x+ und vereinfachen Sie so wei wie möglich ( VP) Aufgabe (HT 008, Nr ) G is eine
Schrifliche Abiurprüfung Mahemaik 03 Aufgabe (NT 008, Nr) Pflicheil Bilden Sie die Ableiung der Funkion f mi f(x) = 3x e x+ und vereinfachen Sie so wei wie möglich ( VP) Aufgabe (HT 008, Nr ) G is eine
Aufgaben Arbeit und Energie
 Aufgaben Arbei und Energie 547. Ein Tank oll i Hilfe einer Pupe i aer gefüll werden. Der Tank ha für den Schlauch zwei Anchlüe, oben und unen. ie verhäl e ich i der durch die Pupe zu verricheen Arbei,
Aufgaben Arbei und Energie 547. Ein Tank oll i Hilfe einer Pupe i aer gefüll werden. Der Tank ha für den Schlauch zwei Anchlüe, oben und unen. ie verhäl e ich i der durch die Pupe zu verricheen Arbei,
Ermittlung von Leistungsgrenzen verschiedener Lagerstrategien unter Berücksichtigung zentraler Einflussgrößen
 Ermilung von Leiunggrenzen verchiedener Lagerraegien uner Berücichigung zenraler Einflugrößen Dipl.-Wir.-Ing. (FH) Anne Piepenburg, Prof. Dr.-Ing. Rainer Brun Helmu-Schmid-Univeriä, Hamburg Lehruhl für
Ermilung von Leiunggrenzen verchiedener Lagerraegien uner Berücichigung zenraler Einflugrößen Dipl.-Wir.-Ing. (FH) Anne Piepenburg, Prof. Dr.-Ing. Rainer Brun Helmu-Schmid-Univeriä, Hamburg Lehruhl für
Differentialgleichungen
 Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Aufgaben zur Vektorrechnung
 ) Liegt der Punkt P(; -; 2) auf der Geraden 4 g: x = 5+t 2? 6 2 Aufgaben zur Vektorrechnung 2) a) Wie groß ist der Abstand der Punkte A(4; 2; -4) und B(;-2;-4) zueinander? b) Gesucht wir der Mittelpunkt
) Liegt der Punkt P(; -; 2) auf der Geraden 4 g: x = 5+t 2? 6 2 Aufgaben zur Vektorrechnung 2) a) Wie groß ist der Abstand der Punkte A(4; 2; -4) und B(;-2;-4) zueinander? b) Gesucht wir der Mittelpunkt
5. Übungsblatt zur Differentialgeometrie
 Insiu für Mahemaik Prof. Dr. Helge Glöckner Dipl. Mah. Rafael Dahmen 5. Übungsbla zur Differenialgeomerie (Aufgaben und Lösungen) SoSe 3.05.0 Gruppenübung Aufgabe G9 (Submersionen und Unermannigfaligkei)
Insiu für Mahemaik Prof. Dr. Helge Glöckner Dipl. Mah. Rafael Dahmen 5. Übungsbla zur Differenialgeomerie (Aufgaben und Lösungen) SoSe 3.05.0 Gruppenübung Aufgabe G9 (Submersionen und Unermannigfaligkei)
Freier Fall. Quelle: Lösung: (a) 1 2 mv2 = mgh h = v2. 2g = (344m s )2. 2 9,81 m s 2 = 6, m
 Freier Fall 1. Der franzöiche Fallchirpringer Michel Fournier (geb. 14.5.1944) verfolg ei ehr al 1 Jahren da Ziel in ca. 4 Höhe i eine Sraophärenballon aufzueigen und von dor abzupringen. Dabei will er
Freier Fall 1. Der franzöiche Fallchirpringer Michel Fournier (geb. 14.5.1944) verfolg ei ehr al 1 Jahren da Ziel in ca. 4 Höhe i eine Sraophärenballon aufzueigen und von dor abzupringen. Dabei will er
7.3. Partielle Ableitungen und Richtungsableitungen
 7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
Abituraufgaben Grundkurs 2009 Bayern Analysis I. dt mit D F = R.
 Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
Name: Punkte: Note: Ø:
 Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
( ) 2. Aufgabe 1: Frequenzkennlinien und BODE-Diagramm Z = Verlauf der Betragskennlinie. a) Übergang zum Frequenzgang. b) Betrag des Frequenzganges
 Aufgbe : requenzkennlinien und BODE-Digrmm Verluf der Bergkennlinie Übergng zum requenzgng T, jω jω Tjω b Berg de requenzgnge jω A ω jω jω A A ω ω Tj Tjω ω Tω Tω c db-kennlinie ω 0log A ω ω 0log Tω ω 0.log
Aufgbe : requenzkennlinien und BODE-Digrmm Verluf der Bergkennlinie Übergng zum requenzgng T, jω jω Tjω b Berg de requenzgnge jω A ω jω jω A A ω ω Tj Tjω ω Tω Tω c db-kennlinie ω 0log A ω ω 0log Tω ω 0.log
2.3 Schätzeigenschaften der OLS-Methode
 .3 Schäzeigechafe der OLS-Mehode Jede Schäzmehode wei beimme Güeeigechafe auf, die vo der Erfüllug beimmer Vorauezuge abhäge. Wa die gewöhliche Mehode der kleie Quadrae (OLS-Mehode) beriff, id beimme Schäzeigechafe
.3 Schäzeigechafe der OLS-Mehode Jede Schäzmehode wei beimme Güeeigechafe auf, die vo der Erfüllug beimmer Vorauezuge abhäge. Wa die gewöhliche Mehode der kleie Quadrae (OLS-Mehode) beriff, id beimme Schäzeigechafe
Physik A VL5 ( )
 Phik A L5 (18.10.01 Bechreiung on Bewegungen - Kinemik in drei Rumrichungen I, Rechnen mi ekoren Koordineneme Der horionle Wurf Der chräge Wurf phikliche Größen, die keine Richung hen (Me, Temperur ec.
Phik A L5 (18.10.01 Bechreiung on Bewegungen - Kinemik in drei Rumrichungen I, Rechnen mi ekoren Koordineneme Der horionle Wurf Der chräge Wurf phikliche Größen, die keine Richung hen (Me, Temperur ec.
Algorithmische Graphentheorie
 Algorihmiche Graphenheorie Sommeremeer 2014 3. Vorleung Flualgorihmen Prof. Dr. Alexander Wolff 1 Erinnerung Oh my God i an LP! Gegeben ein gericheer Graph G = (V, E) mi, V und Kanenkapaziäen c : E R >0.
Algorihmiche Graphenheorie Sommeremeer 2014 3. Vorleung Flualgorihmen Prof. Dr. Alexander Wolff 1 Erinnerung Oh my God i an LP! Gegeben ein gericheer Graph G = (V, E) mi, V und Kanenkapaziäen c : E R >0.
Übungsaufgaben zur Vektorrechnung, 6. Klasse (10. Schulstufe) 3 t 2 = 4. durch P an, welche die Gerade g schneidet.
 Übungsaufgaben zur Vekorrechnung,. Klasse (0. Schulsufe) Übungsaufgaben zur Vekorrechnung. Klasse ) Zwei Geraden im R Gegeben sind die Gerade sind enweder schneidend, parallel oder. X : g der Punk P(-
Übungsaufgaben zur Vekorrechnung,. Klasse (0. Schulsufe) Übungsaufgaben zur Vekorrechnung. Klasse ) Zwei Geraden im R Gegeben sind die Gerade sind enweder schneidend, parallel oder. X : g der Punk P(-
