Digitale Signaturen. GHR-und Chamäleon-Signaturen Björn Kaidel. FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK
|
|
|
- Katja Fried
- vor 5 Jahren
- Abrufe
Transkript
1 Digitale Signaturen GHR-und Chamäleon-Signaturen Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft
2 Socrative: Wiederholung Room: SIGNATUREN Was besagt die RSA-Annahme? Was ist Shamirs Trick? Welche Sicherheitsbegriffe erfüllt RSA-PSS? B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
3 Socrative vom letzten Mal Bei Bezug auf die aktuell besten Algorithmen ist es doch weiterhin möglich, dass z.b. geheime Algorithmen besser sind? B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
4 Socrative vom letzten Mal Bei Bezug auf die aktuell besten Algorithmen ist es doch weiterhin möglich, dass z.b. geheime Algorithmen besser sind? Ja, natürlich! Solang Annahme gilt, wissen wir aber, dass zumindest kein PPT-Angreifer existiert. Es ist aber auch denkbar, dass Annahmen gebrochen werden. (Erinnerung: Zusammenhang zu P & NP etc....) Aber irgendwie müssen wir die Parameter ja wählen :) Außerdem: Wir hatten ja aufgerundet B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
5 Socrative vom letzten Mal Bei Bezug auf die aktuell besten Algorithmen ist es doch weiterhin möglich, dass z.b. geheime Algorithmen besser sind? Ja, natürlich! Solang Annahme gilt, wissen wir aber, dass zumindest kein PPT-Angreifer existiert. Es ist aber auch denkbar, dass Annahmen gebrochen werden. (Erinnerung: Zusammenhang zu P & NP etc....) Aber irgendwie müssen wir die Parameter ja wählen :) Außerdem: Wir hatten ja aufgerundet Ist RSA-PSS Prüfungsrelevant? Ja, der Sicherheitsbeweis aber nicht (Generell: Alles aus der VL prüfungsrelevant, außer ich sage explizit etwas anderes) B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
6 Socrative vom letzten Mal Sagt man wirklich tight? B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
7 Socrative vom letzten Mal Sagt man wirklich tight? Ja! B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
8 Inhalt Genaro-Halevi-Rabin Signaturen (Kap 4.3) Chamäleon-Hashfunktionen (Kap. 3) B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
9 RSA-Signaturen: Probleme Bisher betrachtete Verfahren nur im Random-Oracle Modell sicher Offenes Problem: EUF-CMA-sichere Signatur basierend auf RSA-Annahme, dass effizient (d.h. in Praxis verwendbar) ist und kein Random-Oracle benötigt. Abhilfe : Strong-RSA-Annahme B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
10 Strong-RSA-Annahme RSA-Problem: Geg. N, e geeignet und y Z N, finde x Z N mit x e y mod N. RSA-Annahme: PPT A gilt: [ Pr A(1 k, N, e, y) = x : für eine in k vernachlässigbare Funktion negl. N = P Q, e Z ϕ(n), ] y Z N, x e negl(k) y mod N B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
11 Strong-RSA-Annahme Strong-RSA-Problem: Geg. N geeignet und y Z N, finde x Z N und e N, e > 1 mit x e y mod N. Strong-RSA-Annahme: PPT A gilt: [ Pr A(1 k, N, y) = (x, e) : für eine in k vernachlässigbare Funktion negl. ] N = P Q, e > 1, y Z N, x e negl(k) y mod N B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
12 Strong-RSA: Begriffsverwirrung Strong-RSA-Annahme stärker als RSA-Annahme Wir erlauben dem Angreifer mehr Kontrolle bzw. schwächen seine Gewinnbedingung ab Dadurch nehmen wir mehr an, da wir annehmen, dass es für den Angreifer immer noch schwierig ist, zu gewinnen B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
13 Strong-RSA: Begriffsverwirrung Strong-RSA-Annahme stärker als RSA-Annahme Wir erlauben dem Angreifer mehr Kontrolle bzw. schwächen seine Gewinnbedingung ab Dadurch nehmen wir mehr an, da wir annehmen, dass es für den Angreifer immer noch schwierig ist, zu gewinnen. Strong-RSA-Problem schwächer als RSA-Problem Gewinnbedingung vereinfacht, Problem damit (potentiell) einfacher B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
14 Strong-RSA: Begriffsverwirrung Strong-RSA-Annahme stärker als RSA-Annahme Wir erlauben dem Angreifer mehr Kontrolle bzw. schwächen seine Gewinnbedingung ab Dadurch nehmen wir mehr an, da wir annehmen, dass es für den Angreifer immer noch schwierig ist, zu gewinnen. Strong-RSA-Problem schwächer als RSA-Problem Gewinnbedingung vereinfacht, Problem damit (potentiell) einfacher Strong-RSA-Annahme RSA-Annahme, Umkehrung unklar B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
15 Genaro-Halevi-Rabin Signaturen (Kap ) Es sei h : {0, 1} P eine Hashfunktion (P = Primzahlen) B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
16 Genaro-Halevi-Rabin Signaturen (Kap ) Es sei h : {0, 1} P eine Hashfunktion (P = Primzahlen) Gen(1 k ) : erstelle N = P Q, P, Q prim und zufällig s Z N Wähle h so, dass für alle m gilt, dass ggt(h(m), ϕ(n)) = 1 pk := (N, s, h) sk := ϕ(n) = (P 1)(Q 1) B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
17 Genaro-Halevi-Rabin Signaturen (Kap ) Es sei h : {0, 1} P eine Hashfunktion (P = Primzahlen) Gen(1 k ) : erstelle N = P Q, P, Q prim und zufällig s Z N Wähle h so, dass für alle m gilt, dass ggt(h(m), ϕ(n)) = 1 pk := (N, s, h) sk := ϕ(n) = (P 1)(Q 1) Sign(sk, m) : σ := s 1/h(m) mod N B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
18 Genaro-Halevi-Rabin Signaturen (Kap ) Es sei h : {0, 1} P eine Hashfunktion (P = Primzahlen) Gen(1 k ) : erstelle N = P Q, P, Q prim und zufällig s Z N Wähle h so, dass für alle m gilt, dass ggt(h(m), ϕ(n)) = 1 pk := (N, s, h) sk := ϕ(n) = (P 1)(Q 1) Sign(sk, m) : σ := s 1/h(m) mod N Vfy(pk, m, σ) : σ h(m)? s mod N B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
19 Genaro-Halevi-Rabin Signaturen (Kap ) Es sei h : {0, 1} P eine Hashfunktion (P = Primzahlen) Gen(1 k ) : erstelle N = P Q, P, Q prim und zufällig s Z N Wähle h so, dass für alle m gilt, dass ggt(h(m), ϕ(n)) = 1 pk := (N, s, h) sk := ϕ(n) = (P 1)(Q 1) Sign(sk, m) : σ := s 1/h(m) mod N Vfy(pk, m, σ) : σ h(m)? s mod N ( : Ist möglich, wir gehen nicht weiter darauf ein.) B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
20 GHR-Signaturen: Sicherheit Theorem 70: Für jeden PPT-Angreifer A der die EUF-naCMA-Sicherheit von Σ in Zeit t A mit Erfolgswahrscheinlichkeit ɛ A bricht, existiert ein PPT-Angreifer B, der in Zeit t B t A läuft und entweder die Kollisionsresistenz von h bricht mit Erfolgswahrscheinlichkeit ɛ coll ɛ A /2, oder das Strong-RSA-Problem löst mit Erfolgswahrscheinlichkeit ɛ srsa ɛ A / B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
21 GHR-Signaturen: Beweis EUF-naCMA: Seien m 1,..., m q die Anfragen und (m, σ ) die Ausgabe von A Zwei Ereignisse: E 0 : Es existiert m i mit h(m i ) = h(m ). E 1 : Für alle i {1,..., q} gilt h(m i ) = h(m ) B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
22 GHR-Signaturen: Beweis EUF-naCMA: Seien m 1,..., m q die Anfragen und (m, σ ) die Ausgabe von A Zwei Ereignisse: E 0 : Es existiert m i mit h(m i ) = h(m ). E 1 : Für alle i {1,..., q} gilt h(m i ) = h(m ) A ruft E 0 oder E 1 hervor, also gilt ɛ A Pr[E 0 ] + Pr[E 1 ] Pr[E 0 ] ɛ A /2 oder Pr[E 1 ] ɛ A / B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
23 GHR-Signaturen: Beweis - Ereignis E 0 E 0 : Es existiert m i mit h(m i ) = h(m ). m i und m sind h-kollision. Reduziere auf Kollisionsresistenz von h. B erhält als Eingabe h, zieht (pk, sk) Gen(1 k ), simuliert A, B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
24 GHR-Signaturen: Beweis - Ereignis E 1 E 1 : Für alle i {1,..., q} gilt h(m i ) = h(m ). Reduziere auf Strong-RSA-Annahme. Annahme: Es existiert PPT A, konstruiere B B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
25 GHR-Signaturen: Beweis - Ereignis E 1 E 1 : Für alle i {1,..., q} gilt h(m i ) = h(m ). Reduziere auf Strong-RSA-Annahme. Annahme: Es existiert PPT A, konstruiere B... B erhält als Eingabe (N, y) und muss (x, e) finden mit e > 1 x e y mod N B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
26 GHR-Signaturen: srsa-reduktion Erinnerung: Gen(1 k ) : s Z N pk := (N, s, h) sk := ϕ(n) σ = s 1/h(m) mod N B verwendet (N, y) und setzt s := y Π i {1,...,q} h(m i ) mod N B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
27 GHR-Signaturen: srsa-reduktion Erinnerung: Gen(1 k ) : s Z N pk := (N, s, h) sk := ϕ(n) σ = s 1/h(m) mod N B verwendet (N, y) und setzt s := y Π i {1,...,q} h(m i ) mod N ( stellt sicher, dass s korrekt verteilt ist!) B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
28 GHR-Signaturen: srsa-reduktion Erinnerung: Gen(1 k ) : s Z N pk := (N, s, h) sk := ϕ(n) σ = s 1/h(m) mod N B verwendet (N, y) und setzt s := y Π i {1,...,q} h(m i ) mod N ( stellt sicher, dass s korrekt verteilt ist!) Signatur für Nachricht m j : σ j := y Π i {1,...,q}\{j} h(m i ) mod N B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
29 GHR-Signaturen: srsa-reduktion - Fälschung E 1 tritt ein: A gibt gültige Fälschung (m, σ ) aus mit h(m ) = h(m i ) für alle i {1,..., q}, und (σ ) h(m ) s y Π i {1,...,q} h(m i ) mod N Zusätzlich gilt: ggt(h(m ), Π i {1,...,q} h(m i )) = 1, da h auf Primzahlen abbildet und E 1 eingetreten ist B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
30 GHR-Signaturen: Shamirs Trick (σ ) h(m ) s y Π i {1,...,q} h(m i ) mod N B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
31 GHR-Signaturen: Shamirs Trick (σ ) h(m ) s y Π i {1,...,q} h(m i ) mod N Lemma 31: Seien J, S Z N und e, f aus Z, sodass ggt(e, f ) = 1 und J f S e mod N, dann gibt es einen effizienten Algorithmus, der gegeben N Z und (J, S, e, f ) Z 2 N Z2 ein x Z N berechnet, sodass x e J mod N B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
32 GHR-Signaturen: Shamirs Trick (σ ) h(m ) s y Π i {1,...,q} h(m i ) mod N Lemma 31: Seien J= y, S= σ Z N und e= h(m ), f = Π i {1,...,q} h(m i ) aus Z, sodass ggt(e, f ) = 1 und J f S e mod N, dann gibt es einen effizienten Algorithmus, der gegeben N Z und (J, S, e, f ) Z 2 N Z2 ein x Z N berechnet, sodass x e J mod N. x h(m ) y mod N Also: (x, h(m )) ist gesuchte Lösung der srsa-instanz B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
33 Ziel: EUF-CMA basierend auf RSA Kapitel 4.4 kein Teil der Vorlesung. Inhalt dort: Konstruktion einer EUF-CMA-sicheren Signatur basierend auf dem RSA-Problem. (Ohne Random Oracle!) Generelles Vorgehen: Zeige: GHR-Signaturen unter RSA-Annahme selektiv sicher. Transformation: Selektive Sicherheit EUF-naCMA Wende darauf ein paar Modifikationen an (zur Effizienzsteigerung) Führt zu EUF-naCMA-sicheren Hohenberger-Waters-Signaturen Transformation: EUF-naCMA EUF-CMA B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
34 Offene Probleme Konstruktion einer effizenten EUF-CMA-sicheren Signatur basierend auf dem RSA-Problem Hohenberger-Waters Verfahren sehr ineffizient In jedem Schritt müssen viele Primzahlen gefunden werden B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
35 Socrative B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen Room: SIGNATUREN Zusammenhang: RSA-, srsa-, Faktorisierungsannahme? Existieren Hashftk. die auf Primzahlen abbilden? Warum braucht man bei GHR eine Hashfkt. die auf Primzahlen abbildet? Auf was wird bei GHR reduziert?
36 Chamäleon-Signaturen: Motivation (Kap. 3.1) Händler Kunde Händler B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
37 Chamäleon-Signaturen: Motivation (Kap. 3.1) Angebot? Händler Kunde 100$, σ 1 Händler B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
38 Chamäleon-Signaturen: Motivation (Kap. 3.1) Angebot? Händler Kunde 100$, σ 1 100$, σ 1 99$, σ 2 Händler B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
39 Chamäleon-Signaturen: Ziel Frage: Können wir ein Signaturverfahren konstruieren, sodass K die Authentizität des Angebots von H 1 verifizieren kann, aber... K den Händler H 2 nicht davon überzeugen kann, dass das Angebot von H 1 kam? B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
40 Chamäleon-Hashfunktionen (Definition) (Kap. 3.2) Def. (Chamäleon-Hashfunktion): Eine Chamäleon-Hashfunktion CH besteht aus zwei PPT-Algorithmen (Gen CH, TrapColl CH ): B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
41 Chamäleon-Hashfunktionen (Definition) (Kap. 3.2) Def. (Chamäleon-Hashfunktion): Eine Chamäleon-Hashfunktion CH besteht aus zwei PPT-Algorithmen (Gen CH, TrapColl CH ): Gen CH (1 k ) : gibt (ch, τ) aus: ch ist eine Funktion ch : M R N M Nachrichtenraum R Zufallsraum N Zielraum M, R, N abhängig von konkreter CH! τ ist eine Trapdoor ( Falltür ) B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
42 Chamäleon-Hashfunktionen (Definition - II) TrapColl CH (τ, m, r, m ) für (m, r, m ) M R M berechnet r R, sodass ch(m, r) = ch(m, r ) B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
43 Chamäleon-Hashfunktionen (Definition - II) TrapColl CH (τ, m, r, m ) für (m, r, m ) M R M berechnet r R, sodass ch(m, r) = ch(m, r ) Wer τ kennt, kann Kollisionen berechnen Daher der Name Chamäleon -Hashfunktion Ausgabe wechselt ihr Urbild wechselt ihre Farbe B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
44 Chamäleon-Hashfunktionen (Definition - II) TrapColl CH (τ, m, r, m ) für (m, r, m ) M R M berechnet r R, sodass ch(m, r) = ch(m, r ) Wer τ kennt, kann Kollisionen berechnen Daher der Name Chamäleon -Hashfunktion Ausgabe wechselt ihr Urbild wechselt ihre Farbe Anm.: Häufig wird verlangt, dass r quasi gleichverteilt ist (spielt in der VL keine Rolle) B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
45 Kollisionsresistenz Def. 39 (Kollisionsresistenz für Chamäleon-Hashfkt.): Eine Chamäelon-Hashfunktion CH = (Gen CH, TrapColl CH ) ist kollisionsresistent, falls für alle PPT A gilt, dass B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
46 Kollisionsresistenz Def. 39 (Kollisionsresistenz für Chamäleon-Hashfkt.): Eine Chamäelon-Hashfunktion CH = (Gen CH, TrapColl CH ) ist kollisionsresistent, falls für alle PPT A gilt, dass [ (ch, τ) GenCH (1 Pr k ) A(1 k, ch) = (m, r, m, r ) : ch(m, r) = ch(m, r ] ) (m, r) = (m, r negl(k) ) für eine im Sicherheitsparameter k vernachlässigbare Funktion negl B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
47 CH-Fkt. basierend auf DLog (Kap ) Wie immer: G Gruppe, G = p prim, g Erzeuger von G B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
48 CH-Fkt. basierend auf DLog (Kap ) Wie immer: G Gruppe, G = p prim, g Erzeuger von G Gen(1 k ) : x Z p h := g x ch := (g, h) τ := x B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
49 CH-Fkt. basierend auf DLog (Kap ) Wie immer: G Gruppe, G = p prim, g Erzeuger von G Gen(1 k ) : x Z p h := g x ch := (g, h) τ := x ch beschreibt Funktion: ch : Z p Z p G ch(m, r) := g m h r B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
50 CH-Fkt. basierend auf DLog ch(m, r) = g m h r TrapColl(τ, m, r, m ) : B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
51 CH-Fkt. basierend auf DLog ch(m, r) = g m h r TrapColl(τ, m, r, m ) : Berechnet r, sodass m + x r m + x r modp B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
52 CH-Fkt. basierend auf DLog ch(m, r) = g m h r TrapColl(τ, m, r, m ) : Berechnet r, sodass r m + x r m + x r = m m x modp + r modp B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
53 CH-Fkt. basierend auf DLog ch(m, r) = g m h r TrapColl(τ, m, r, m ) : Berechnet r, sodass Damit folgt: r m + x r m + x r = m m x modp + r modp ch(m, r) = g m h r = g m+xr = g m +xr = g m h r = ch(m, r ) B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
54 CH-Fkt. basierend auf DLog - Sicherheit Theorem 40: Für jeden PPT A, der als Eingabe ch = (g, h) Gen(1 k ) erhält, in Zeit t A läuft und mit Erfolgswahrscheinlichkeit ɛ A ein Tupel (m, r, m, r ) ausgibt, sodass (m, r) = (m, r ) und ch(m, r) = ch(m, r ) gilt, existiert ein PPT B, der das DLog-Problem in G in Zeit t B t A mit Erfolgswkt. ɛ B ɛ A löst. Beweis: Ähnlich wie Beweis von DLog-Einmalsignatur (Theorem 28) B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
55 CH-Fkt. basierend auf dem RSA-Problem (Kap ) Gen(1 k ) : N = P Q, P, Q prim Primzahl e > 2 N mit ggt(e, ϕ(n)) = 1 d = e 1 mod ϕ(n) J Z N ch := (N, e, J) τ := d ch : Z N Z N Z N ch(m, r) := J m r e mod N B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
56 CH-Fkt. basierend auf dem RSA-Problem ch(m, r) := J m r e mod N TrapColl(τ, m, r, m ): B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
57 CH-Fkt. basierend auf dem RSA-Problem ch(m, r) := J m r e mod N TrapColl(τ, m, r, m ): Berechnet r wie folgt r = (J m m r e ) d mod N B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
58 CH-Fkt. basierend auf dem RSA-Problem ch(m, r) := J m r e mod N TrapColl(τ, m, r, m ): Berechnet r wie folgt r = (J m m r e ) d mod N ch(m, r) = J m r e mod N = J m (r ) e mod N = ch(m, r ) B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
59 CH-Fkt. basierend auf dem RSA-Problem: Sicherheit Theorem 42: Sei (N, e, y) eine Instanz des RSA-Problems, sodass e > 2 N eine Primzahl ist. Für jeden PPT A, der als Eingabe (N, e, J) erhält, in Zeit t A läuft und mit Erfolgswahrscheinlichkeit ɛ B ein Tupel (m, r, m, r ) mit (m, r) = (m, r ) und ch(m, r) = ch(m, r ) berechnet, existiert ein PPT B, der das RSA-Problem (mit e > 2 N und prim) in Zeit t B t A und Erfolgswkt. ɛ B ɛ A löst. Beweis: Ähnlich wie Beweis von RSA-Einmalsignatur (Theorem 30) B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
60 Socrative Room: SIGNATUREN Wieviele Hashwerte gibt es für eine feste Nachricht bei CH-Fkts.? Wieviele Urbildtupel gibt es bei einem CH-Hashwert? Was ermöglicht die Trapdoor von CH-Fkts.? B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen
Digitale Signaturen. GHR-und Chamäleon-Signaturen Björn Kaidel. FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK
 Digitale Signaturen GHR-und Chamäleon-Signaturen Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-01-12 B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen KIT
Digitale Signaturen GHR-und Chamäleon-Signaturen Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-01-12 B. Kaidel Digitale Signaturen: GHR- und Chamäleon-Signaturen KIT
Digitale Signaturen. RSA-FDH & das Random Oracle Model Jiaxin Pan (Slides from Björn Kaidel and Gunnar Hartung)
 Digitale Signaturen RSA-FDH & das Random Oracle Model Jiaxin Pan (Slides from Björn Kaidel and Gunnar Hartung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2018-10-26 B. Kaidel Digitale
Digitale Signaturen RSA-FDH & das Random Oracle Model Jiaxin Pan (Slides from Björn Kaidel and Gunnar Hartung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2018-10-26 B. Kaidel Digitale
Digitale Signaturen. RSA-FDH & das Random Oracle Model Björn Kaidel (mit Folien von Gunnar Hartung)
 Digitale Signaturen RSA-FDH & das Random Oracle Model Björn Kaidel (mit Folien von Gunnar Hartung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-12-01 B. Kaidel Digitale Signaturen:
Digitale Signaturen RSA-FDH & das Random Oracle Model Björn Kaidel (mit Folien von Gunnar Hartung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-12-01 B. Kaidel Digitale Signaturen:
Digitale Signaturen. Einmalsignaturen Gunnar Hartung, Björn Kaidel. FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK
 Digitale Signaturen Einmalsignaturen Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-11-04 B. Kaidel Digitale Signaturen: Einmalsignaturen KIT Die Forschungsuniversität
Digitale Signaturen Einmalsignaturen Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-11-04 B. Kaidel Digitale Signaturen: Einmalsignaturen KIT Die Forschungsuniversität
Digitale Signaturen. Anwendung von Einmalsignaturen Gunnar Hartung, Björn Kaidel.
 Digitale Signaturen Anwendung von Einmalsignaturen Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-11-18 G. Hartung Digitale Signaturen: Anwendung von
Digitale Signaturen Anwendung von Einmalsignaturen Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-11-18 G. Hartung Digitale Signaturen: Anwendung von
Digitale Signaturen. Sicherheitsdefinitionen Gunnar Hartung, Björn Kaidel. FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK
 Digitale Signaturen Sicherheitsdefinitionen Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-10-28 B. Kaidel Digitale Signaturen: Sicherheitsdefinitionen
Digitale Signaturen Sicherheitsdefinitionen Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-10-28 B. Kaidel Digitale Signaturen: Sicherheitsdefinitionen
Digitale Signaturen. Wiederholung Gunnar Hartung, Björn Kaidel. FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK
 Digitale Signaturen Wiederholung Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-02-10 G. Hartung Digitale Signaturen: Wiederholung KIT Die Forschungsuniversität
Digitale Signaturen Wiederholung Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-02-10 G. Hartung Digitale Signaturen: Wiederholung KIT Die Forschungsuniversität
Asymmetrische Verschlüsselungsverfahren
 Asymmetrische Verschlüsselungsverfahren Einmalsignaturen Björn Kaidel (Vertretung für Prof. Müller-Quade) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2018-02-01 B. Kaidel Asymmetrische
Asymmetrische Verschlüsselungsverfahren Einmalsignaturen Björn Kaidel (Vertretung für Prof. Müller-Quade) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2018-02-01 B. Kaidel Asymmetrische
Asymmetrische Verschlüsselungsverfahren
 Asymmetrische Verschlüsselungsverfahren Digitale Signaturen Prof. Jörn Müller-Quade mit Folien von G. Hartung und B. Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2018-01-25 J.
Asymmetrische Verschlüsselungsverfahren Digitale Signaturen Prof. Jörn Müller-Quade mit Folien von G. Hartung und B. Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2018-01-25 J.
Asymmetrische Verschlüsselungsverfahren
 Asymmetrische Verschlüsselungsverfahren Digitale Signaturen Björn Kaidel - Vertretung für Prof. Müller-Quade FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-01-19 B. Kaidel Asymmetrische
Asymmetrische Verschlüsselungsverfahren Digitale Signaturen Björn Kaidel - Vertretung für Prof. Müller-Quade FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-01-19 B. Kaidel Asymmetrische
Digitale Signaturen. seuf-cma & Pairings Björn Kaidel. FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK
 Digitale Signaturen seuf-cma & Pairings Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2018-01-19 B. Kaidel Digitale Signaturen: seuf-cma & Pairings KIT Die Forschungsuniversität
Digitale Signaturen seuf-cma & Pairings Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2018-01-19 B. Kaidel Digitale Signaturen: seuf-cma & Pairings KIT Die Forschungsuniversität
Digitale Signaturen. Sicherheitsdefinitionen Björn Kaidel. FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK
 Digitale Signaturen Sicherheitsdefinitionen Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-10-27 B. Kaidel Digitale Signaturen: Sicherheitsdefinitionen KIT Die Forschungsuniversität
Digitale Signaturen Sicherheitsdefinitionen Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-10-27 B. Kaidel Digitale Signaturen: Sicherheitsdefinitionen KIT Die Forschungsuniversität
Digitale Signaturen. seuf-cma & Pairings Gunnar Hartung, Björn Kaidel. FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK
 Digitale Signaturen seuf-cma & Pairings Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-01-20 B. Kaidel Digitale Signaturen: seuf-cma & Pairings KIT Die
Digitale Signaturen seuf-cma & Pairings Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-01-20 B. Kaidel Digitale Signaturen: seuf-cma & Pairings KIT Die
Digitale Signaturen. Anwendung von Einmalsignaturen Gunnar Hartung, Björn Kaidel.
 Digitale Signaturen Anwendung von Einmalsignaturen Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-11-15 G. Hartung Digitale Signaturen: Anwendung von
Digitale Signaturen Anwendung von Einmalsignaturen Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-11-15 G. Hartung Digitale Signaturen: Anwendung von
Digitale Signaturen. Anwendung von Einmalsignaturen Björn Kaidel (mit Folien von Gunnar Hartung)
 Digitale Signaturen Anwendung von Einmalsignaturen Björn Kaidel (mit Folien von Gunnar Hartung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-11-24 B. Kaidel Digitale Signaturen:
Digitale Signaturen Anwendung von Einmalsignaturen Björn Kaidel (mit Folien von Gunnar Hartung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-11-24 B. Kaidel Digitale Signaturen:
Digitale Signaturen. Parameterwahl & RSA-PSS Björn Kaidel (mit Folien von Gunnar Hartung)
 Digitale Signaturen Parameterwahl & RSA-PSS Björn Kaidel (mit Folien von Gunnar Hartung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-11-15 B. Kaidel Digitale Signaturen: RSA-PSS
Digitale Signaturen Parameterwahl & RSA-PSS Björn Kaidel (mit Folien von Gunnar Hartung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-11-15 B. Kaidel Digitale Signaturen: RSA-PSS
Vorlesung Digitale Signaturen im Wintersemester 2016/-17. Socrative-Fragen aus der Vorlesung vom
 Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Dozenten: Gunnar Hartung, Björn Kaidel Vorlesung Digitale Signaturen im Wintersemester 2016/-17 Socrative-Fragen aus der Vorlesung vom 25.11.2016
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Dozenten: Gunnar Hartung, Björn Kaidel Vorlesung Digitale Signaturen im Wintersemester 2016/-17 Socrative-Fragen aus der Vorlesung vom 25.11.2016
Vorlesung Digitale Signaturen im Wintersemester 2017/-18. Socrative-Fragen aus der Vorlesung vom
 Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Dozenten: Björn Kaidel Vorlesung Digitale Signaturen im Wintersemester 2017/-18 Socrative-Fragen aus der Vorlesung vom 17.11.2017 1 Quiz 1:
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Dozenten: Björn Kaidel Vorlesung Digitale Signaturen im Wintersemester 2017/-18 Socrative-Fragen aus der Vorlesung vom 17.11.2017 1 Quiz 1:
Digitale Signaturen. Einführung Björn Kaidel. FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK
 Digitale Signaturen Einführung Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-10-20 B. Kaidel Digitale Signaturen: Einführung KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft
Digitale Signaturen Einführung Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2017-10-20 B. Kaidel Digitale Signaturen: Einführung KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft
Digitale Signaturen. Einführung Gunnar Hartung, Björn Kaidel. FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK
 Digitale Signaturen Einführung Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-10-21 G. Hartung, B. Kaidel Digitale Signaturen: Einführung KIT Die Forschungsuniversität
Digitale Signaturen Einführung Gunnar Hartung, Björn Kaidel FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-10-21 G. Hartung, B. Kaidel Digitale Signaturen: Einführung KIT Die Forschungsuniversität
Übung zur Vorlesung Sicherheit Übungsblatt 3. Björn Kaidel 1 / 52
 Übung zur Vorlesung Sicherheit 21.05.2014 Übungsblatt 3 Björn Kaidel bjoern.kaidel@kit.edu 1 / 52 Kummerkasten Bitte helleren Laserpointer verwenden. Sind die Skriptlinks vertauscht? Nein! Wegen allgemeiner
Übung zur Vorlesung Sicherheit 21.05.2014 Übungsblatt 3 Björn Kaidel bjoern.kaidel@kit.edu 1 / 52 Kummerkasten Bitte helleren Laserpointer verwenden. Sind die Skriptlinks vertauscht? Nein! Wegen allgemeiner
Übung zur Vorlesung. Sicherheit Übungsblatt 5 Björn Kaidel
 Übung zur Vorlesung Sicherheit 30.06.2016 Übungsblatt 5 Björn Kaidel bjoern.kaidel@kit.edu https://b.socrative.com/login/student/ Room: SICHERHEIT Bitte gleich einloggen! 1 / 55 Evaluation (siehe Evaluations-PDF)
Übung zur Vorlesung Sicherheit 30.06.2016 Übungsblatt 5 Björn Kaidel bjoern.kaidel@kit.edu https://b.socrative.com/login/student/ Room: SICHERHEIT Bitte gleich einloggen! 1 / 55 Evaluation (siehe Evaluations-PDF)
Vorlesung Sicherheit
 Vorlesung Jörn Müller-Quade ITI, KIT basierend auf den Folien von Dennis Hofheinz, Sommersemester 2014 23.05.2016 1 / 32 Überblick 1 Symmetrische Authentifikation von Nachrichten Ziel Konstruktionen MACs
Vorlesung Jörn Müller-Quade ITI, KIT basierend auf den Folien von Dennis Hofheinz, Sommersemester 2014 23.05.2016 1 / 32 Überblick 1 Symmetrische Authentifikation von Nachrichten Ziel Konstruktionen MACs
Homomorphe Verschlüsselung
 Homomorphe Verschlüsselung Definition Homomorphe Verschlüsselung Sei Π ein Verschlüsselungsverfahren mit Enc : G G für Gruppen G, G. Π heißt homomorph, falls Enc(m 1 ) G Enc(m 2 ) eine gültige Verschlüsselung
Homomorphe Verschlüsselung Definition Homomorphe Verschlüsselung Sei Π ein Verschlüsselungsverfahren mit Enc : G G für Gruppen G, G. Π heißt homomorph, falls Enc(m 1 ) G Enc(m 2 ) eine gültige Verschlüsselung
Voll homomorpe Verschlüsselung
 Voll homomorpe Verschlüsselung Definition Voll homomorphe Verschlüsselung Sei Π ein Verschlüsselungsverfahren mit Enc : R R für Ringe R, R. Π heißt voll homomorph, falls 1 Enc(m 1 ) + Enc(m 2 ) eine gültige
Voll homomorpe Verschlüsselung Definition Voll homomorphe Verschlüsselung Sei Π ein Verschlüsselungsverfahren mit Enc : R R für Ringe R, R. Π heißt voll homomorph, falls 1 Enc(m 1 ) + Enc(m 2 ) eine gültige
RSA Full Domain Hash (RSA-FDH) Signaturen
 RSA Full Domain Hash (RSA-FDH) Signaturen Signatur RSA-FDH Sei H : {0, 1} Z N ein Random-Oracle. 1 Gen: (N, e, d) GenRSA(1 n ) mit pk = (N, e) und sk = (N, d). 2 Sign: Für eine Nachricht m {0, 1} berechne
RSA Full Domain Hash (RSA-FDH) Signaturen Signatur RSA-FDH Sei H : {0, 1} Z N ein Random-Oracle. 1 Gen: (N, e, d) GenRSA(1 n ) mit pk = (N, e) und sk = (N, d). 2 Sign: Für eine Nachricht m {0, 1} berechne
Vorlesung Sicherheit
 Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 12.05.2014 1 / 26 Überblick 1 Hashfunktionen Erinnerung Angriffe auf Hashfunktionen Zusammenfassung Hashfunktionen 2 Asymmetrische Verschlüsselung Idee Beispiel:
Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 12.05.2014 1 / 26 Überblick 1 Hashfunktionen Erinnerung Angriffe auf Hashfunktionen Zusammenfassung Hashfunktionen 2 Asymmetrische Verschlüsselung Idee Beispiel:
Ziel: Zertifiziere Pfad von Wurzel zu m mittels Signaturen. Signieren Public-Keys auf Pfad inklusive der Nachbarknoten.
 Merkle-Baum Idee: Konstruktion von Merkle-Bäumen Ersetze Signaturkette durch Baum (sogenannter Merkle-Baum). Verwenden Baum der Tiefe n für Nachrichten der Länge n. Die Wurzel erhält Label ɛ. Die Kinder
Merkle-Baum Idee: Konstruktion von Merkle-Bäumen Ersetze Signaturkette durch Baum (sogenannter Merkle-Baum). Verwenden Baum der Tiefe n für Nachrichten der Länge n. Die Wurzel erhält Label ɛ. Die Kinder
Hashfunktionen und Kollisionen
 Hashfunktionen und Kollisionen Definition Hashfunktion Eine Hashfunktion ist ein Paar (Gen, H) von pt Algorithmen mit 1 Gen: s Gen(1 n ). Gen ist probabilistisch. 2 H: H s berechnet Funktion {0, 1} {0,
Hashfunktionen und Kollisionen Definition Hashfunktion Eine Hashfunktion ist ein Paar (Gen, H) von pt Algorithmen mit 1 Gen: s Gen(1 n ). Gen ist probabilistisch. 2 H: H s berechnet Funktion {0, 1} {0,
Vorlesung Sicherheit
 Vorlesung Sicherheit Jörn Müller-Quade ITI, KIT basierend auf den Folien von Dennis Hofheinz, Sommersemester 2014 18.05.2015 1 / 30 Überblick 1 Asymmetrische Authentifikation von Nachrichten Erinnerung
Vorlesung Sicherheit Jörn Müller-Quade ITI, KIT basierend auf den Folien von Dennis Hofheinz, Sommersemester 2014 18.05.2015 1 / 30 Überblick 1 Asymmetrische Authentifikation von Nachrichten Erinnerung
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade. Nachklausur Hinweise
 Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2016 Nachklausur 12.10.2016 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2016 Nachklausur 12.10.2016 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung
Vorlesung Sicherheit
 Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 15.05.2017 1 / 25 Überblick 1 Hashfunktionen Angriffe auf Hashfunktionen Zusammenfassung Hashfunktionen 2 Asymmetrische Verschlüsselung Idee Beispiel: RSA
Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 15.05.2017 1 / 25 Überblick 1 Hashfunktionen Angriffe auf Hashfunktionen Zusammenfassung Hashfunktionen 2 Asymmetrische Verschlüsselung Idee Beispiel: RSA
RSA Full Domain Hash (RSA-FDH) Signaturen
 RSA Full Domain Hash (RSA-FDH) Signaturen Signatur RSA-FDH Sei H : {0, 1} Z N ein Random-Oracle. 1 Gen: (N, e, d) GenRSA(1 n ) mit pk = (N, e) und sk = (N, d). 2 Sign: Für eine Nachricht m {0, 1} berechne
RSA Full Domain Hash (RSA-FDH) Signaturen Signatur RSA-FDH Sei H : {0, 1} Z N ein Random-Oracle. 1 Gen: (N, e, d) GenRSA(1 n ) mit pk = (N, e) und sk = (N, d). 2 Sign: Für eine Nachricht m {0, 1} berechne
Übungsblatt 3. Stammvorlesung Sicherheit im Sommersemester Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade
 Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2015 Übungsblatt 3 Aufgabe 1. Beurteilen Sie für die folgenden Konstruktionen jeweils, ob es sich
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2015 Übungsblatt 3 Aufgabe 1. Beurteilen Sie für die folgenden Konstruktionen jeweils, ob es sich
Institut für Theoretische Informatik Prof. Dr. D. Hofheinz. Stammvorlesung Sicherheit im Sommersemester Klausur. Lösung
 Institut für Theoretische Informatik Prof. Dr. D. Hofheinz Stammvorlesung Sicherheit im Sommersemester 2017 Klausur Lösung 02.08.2017 Vorname: Nachname: Matrikelnummer: Klausur-ID: Hinweise - Schreiben
Institut für Theoretische Informatik Prof. Dr. D. Hofheinz Stammvorlesung Sicherheit im Sommersemester 2017 Klausur Lösung 02.08.2017 Vorname: Nachname: Matrikelnummer: Klausur-ID: Hinweise - Schreiben
Vorlesung Sicherheit
 Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 23.06.2014 1 / 26 Überblick 1 Zero-Knowledge-Protokolle Erinnerung Beispiel für Zero-Knowledge-Protokoll Analyse des Beispiel-Zero-Knowledge-Protokolls Proof-of-Knowledge-Eigenschaft
Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 23.06.2014 1 / 26 Überblick 1 Zero-Knowledge-Protokolle Erinnerung Beispiel für Zero-Knowledge-Protokoll Analyse des Beispiel-Zero-Knowledge-Protokolls Proof-of-Knowledge-Eigenschaft
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade. Nachklausur. Lösung Hinweise
 Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2016 Nachklausur Lösung 12.10.2016 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2016 Nachklausur Lösung 12.10.2016 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung
Institut für Kryptographie und Sicherheit Jun.-Prof. Dr. D. Hofheinz. Stammvorlesung Sicherheit im Sommersemester Nachklausur
 Institut für Kryptographie und Sicherheit Jun.-Prof. Dr. D. Hofheinz IKS Institut für Kryptographie und Sicherheit Stammvorlesung Sicherheit im Sommersemester 2013 Nachklausur 07.10.2013 Vorname: Nachname:
Institut für Kryptographie und Sicherheit Jun.-Prof. Dr. D. Hofheinz IKS Institut für Kryptographie und Sicherheit Stammvorlesung Sicherheit im Sommersemester 2013 Nachklausur 07.10.2013 Vorname: Nachname:
Beliebige Anzahl von Signaturen
 Beliebige Anzahl von Signaturen Algorithmus Signaturketten Sei Π = (Gen, Sign, Vrfy) ein Einwegsignaturverfahren. 1 Gen : (pk 1, sk 1 ) Gen(1 n ) 2 Sign : Signieren der Nachricht m i. Verwende gemerkten
Beliebige Anzahl von Signaturen Algorithmus Signaturketten Sei Π = (Gen, Sign, Vrfy) ein Einwegsignaturverfahren. 1 Gen : (pk 1, sk 1 ) Gen(1 n ) 2 Sign : Signieren der Nachricht m i. Verwende gemerkten
Asymmetrische Verschlüsselungsverfahren
 Asymmetrische Verschlüsselungsverfahren Vorlesung 4 Alexander Koch (Vertretung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-11-10 Alexander Koch Asymmetrische Verschlüsselungsverfahren
Asymmetrische Verschlüsselungsverfahren Vorlesung 4 Alexander Koch (Vertretung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 2016-11-10 Alexander Koch Asymmetrische Verschlüsselungsverfahren
Sicherheit von Merkle Signaturen
 Sicherheit von Merkle Signaturen Algorithmus Angreifer A für die Einwegsignatur EINGABE: pk, Zugriff auf eine Anfrage an Orakel Sign sk ( ) 1 Berechne (pk (i), sk (i) ) Gen(1 n ) für i = 1,...,l. Wähle
Sicherheit von Merkle Signaturen Algorithmus Angreifer A für die Einwegsignatur EINGABE: pk, Zugriff auf eine Anfrage an Orakel Sign sk ( ) 1 Berechne (pk (i), sk (i) ) Gen(1 n ) für i = 1,...,l. Wähle
Homomorphe Verschlüsselung
 Homomorphe Verschlüsselung Definition Homomorphe Verschlüsselung Sei Π ein Verschlüsselungsverfahren mit Enc : G G für Gruppen G, G. Π heißt homomorph, falls Enc(m 1 ) G Enc(m 2 ) eine gültige Verschlüsselung
Homomorphe Verschlüsselung Definition Homomorphe Verschlüsselung Sei Π ein Verschlüsselungsverfahren mit Enc : G G für Gruppen G, G. Π heißt homomorph, falls Enc(m 1 ) G Enc(m 2 ) eine gültige Verschlüsselung
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade. Klausur Hinweise
 Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2015 Klausur 21.07.2015 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung stehen
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2015 Klausur 21.07.2015 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung stehen
Vorlesung Sicherheit
 Vorlesung Sicherheit Dennis Hofheinz IKS, KIT 06.05.2013 1 / 25 Überblick 1 Hashfunktionen Erinnerung Angriffe auf Hashfunktionen Zusammenfassung Hashfunktionen 2 Asymmetrische Verschlüsselung Idee Beispiel:
Vorlesung Sicherheit Dennis Hofheinz IKS, KIT 06.05.2013 1 / 25 Überblick 1 Hashfunktionen Erinnerung Angriffe auf Hashfunktionen Zusammenfassung Hashfunktionen 2 Asymmetrische Verschlüsselung Idee Beispiel:
Asymmetrische Verschlüsselungsverfahren
 Asymmetrische Verschlüsselungsverfahren Vorlesung 4 Alexander Koch (Vertretung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 KIT 2015-11-12 Universität desalexander Landes Baden-Württemberg
Asymmetrische Verschlüsselungsverfahren Vorlesung 4 Alexander Koch (Vertretung) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 KIT 2015-11-12 Universität desalexander Landes Baden-Württemberg
Rabin Verschlüsselung 1979
 Rabin Verschlüsselung 1979 Idee: Rabin Verschlüsselung Beobachtung: Berechnen von Wurzeln in Z p ist effizient möglich. Ziehen von Quadratwurzeln in Z N ist äquivalent zum Faktorisieren. Vorteil: CPA-Sicherheit
Rabin Verschlüsselung 1979 Idee: Rabin Verschlüsselung Beobachtung: Berechnen von Wurzeln in Z p ist effizient möglich. Ziehen von Quadratwurzeln in Z N ist äquivalent zum Faktorisieren. Vorteil: CPA-Sicherheit
Institut für Theoretische Informatik Prof. Dr. Dennis Hofheinz Übungsleiter: Thomas Agrikola. Stammvorlesung Sicherheit im Sommersemester 2017
 Institut für Theoretische Informatik Prof. Dr. Dennis Hofheinz Übungsleiter: Thomas Agrikola Stammvorlesung Sicherheit im Sommersemester 2017 Übungsblatt 4 Aufgabe 1. Wir instanziieren das ElGamal-Verschlüsselungsverfahren
Institut für Theoretische Informatik Prof. Dr. Dennis Hofheinz Übungsleiter: Thomas Agrikola Stammvorlesung Sicherheit im Sommersemester 2017 Übungsblatt 4 Aufgabe 1. Wir instanziieren das ElGamal-Verschlüsselungsverfahren
Digitale Signaturen. Kapitel 8
 Digitale Signaturen Kapitel 8 Handschriftliche vs. digitale Unterschrift digitalisieren mp3 Unterschrift digitale Unterschrift von D.H. für mp3? (Scannen und als Bitmap anhängen z.b. zu leicht zu fälschen)
Digitale Signaturen Kapitel 8 Handschriftliche vs. digitale Unterschrift digitalisieren mp3 Unterschrift digitale Unterschrift von D.H. für mp3? (Scannen und als Bitmap anhängen z.b. zu leicht zu fälschen)
Sicherer MAC für Nachrichten beliebiger Länge
 Sicherer MAC für Nachrichten beliebiger Länge Korollar Sicherer MAC für Nachrichten beliebiger Länge Sei F eine Pseudozufallsfunktion. Dann ist Π MAC2 für Π = Π MAC sicher. Nachteile: Für m ({0, 1} n 4
Sicherer MAC für Nachrichten beliebiger Länge Korollar Sicherer MAC für Nachrichten beliebiger Länge Sei F eine Pseudozufallsfunktion. Dann ist Π MAC2 für Π = Π MAC sicher. Nachteile: Für m ({0, 1} n 4
Verteilte Kyroptographie
 Verteilte Kyroptographie Klassische kryptographische Verfahren Kryptographische Hash-Funktionen Public-Key-Signaturen Verteilte Mechanismen Schwellwert-Signaturen Verteilt generierte Zufallszahlen Verteilte
Verteilte Kyroptographie Klassische kryptographische Verfahren Kryptographische Hash-Funktionen Public-Key-Signaturen Verteilte Mechanismen Schwellwert-Signaturen Verteilt generierte Zufallszahlen Verteilte
Hybride Verschlüsselungsverfahren
 Hybride Verschlüsselungsverfahren Ziel: Flexibilität von asym. Verfahren und Effizienz von sym. Verfahren. Szenario: Sei Π = (Gen, Enc, Dec) ein PK-Verschlüsselungsverfahren und Π = (Gen, Enc, Dec ) ein
Hybride Verschlüsselungsverfahren Ziel: Flexibilität von asym. Verfahren und Effizienz von sym. Verfahren. Szenario: Sei Π = (Gen, Enc, Dec) ein PK-Verschlüsselungsverfahren und Π = (Gen, Enc, Dec ) ein
Asymmetrische Verschlüsselungsverfahren
 Asymmetrische Verschlüsselungsverfahren Björn Kaidel - Vertretung für Prof. J. Müller-Quade (Folien von A. Koch) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 17.11.2016 Björn Kaidel
Asymmetrische Verschlüsselungsverfahren Björn Kaidel - Vertretung für Prof. J. Müller-Quade (Folien von A. Koch) FAKULTÄT FÜR INFORMATIK, INSTITUT FÜR THEORETISCHE INFORMATIK 0 17.11.2016 Björn Kaidel
Merkle-Damgard Transformation
 Merkle-Damgard Transformation Ziel: Konstruiere H : {0, 1} {0, 1} l aus h : {0, 1} 2l {0, 1} l. Algorithmus Merkle-Damgard Konstruktion Sei (Gen, h) eine kollisionsresistente Hashfunktion mit h : {0, 1}
Merkle-Damgard Transformation Ziel: Konstruiere H : {0, 1} {0, 1} l aus h : {0, 1} 2l {0, 1} l. Algorithmus Merkle-Damgard Konstruktion Sei (Gen, h) eine kollisionsresistente Hashfunktion mit h : {0, 1}
Einführung in digitale Signaturen
 Einführung in digitale Signaturen Hannes Thalheim Universität Leipzig 8. Januar 2018 Zusammenfassung Für eine sichere Kommunikation im Web ist die Geheimhaltung von Nachrichten so wichtig wie das Wissen,
Einführung in digitale Signaturen Hannes Thalheim Universität Leipzig 8. Januar 2018 Zusammenfassung Für eine sichere Kommunikation im Web ist die Geheimhaltung von Nachrichten so wichtig wie das Wissen,
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade. Nachklausur. Lösungsvorschlag Hinweise
 Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2015 Nachklausur Lösungsvorschlag 29.09.2015 Vorname: Nachname: Matrikelnummer: Hinweise - Für
Institut für Theoretische Informatik Prof. Dr. J. Müller-Quade Stammvorlesung Sicherheit im Sommersemester 2015 Nachklausur Lösungsvorschlag 29.09.2015 Vorname: Nachname: Matrikelnummer: Hinweise - Für
3: Primzahlen. 111 S. Lucks Diskr Strukt. (WS 18/19) 3: Primzahlen
 3: Primzahlen 111 S. Lucks Diskr Strukt. (WS 18/19) 3: Primzahlen Definition 40 (Teiler, Vielfache, Primzahlen, zusammengesetzte Zahlen) Seien a, b N. a ist ein Teiler von b ( a b ), falls es ein k N gibt
3: Primzahlen 111 S. Lucks Diskr Strukt. (WS 18/19) 3: Primzahlen Definition 40 (Teiler, Vielfache, Primzahlen, zusammengesetzte Zahlen) Seien a, b N. a ist ein Teiler von b ( a b ), falls es ein k N gibt
https://b.socrative.com/login/student/
 Übung zur Vorlesung Sicherheit 23.06.2016 Übungsblatt 4 Björn Kaidel bjoern.kaidel@kit.edu https://b.socrative.com/login/student/ Room: SICHERHEIT Bitte gleich einloggen! 1 / 62 Feedback: Kummerkasten/Feedback
Übung zur Vorlesung Sicherheit 23.06.2016 Übungsblatt 4 Björn Kaidel bjoern.kaidel@kit.edu https://b.socrative.com/login/student/ Room: SICHERHEIT Bitte gleich einloggen! 1 / 62 Feedback: Kummerkasten/Feedback
https://b.socrative.com/login/student/
 Übung zur Vorlesung Sicherheit 23.06.2016 Übungsblatt 4 Björn Kaidel bjoern.kaidel@kit.edu https://b.socrative.com/login/student/ Room: SICHERHEIT Bitte gleich einloggen! 1 / 62 Feedback: Kummerkasten/Feedback
Übung zur Vorlesung Sicherheit 23.06.2016 Übungsblatt 4 Björn Kaidel bjoern.kaidel@kit.edu https://b.socrative.com/login/student/ Room: SICHERHEIT Bitte gleich einloggen! 1 / 62 Feedback: Kummerkasten/Feedback
Definition Message Authentication Code (MAC) Ein Message Authentication Code (MAC) bzgl. des Nachrichtenraumen M besteht aus den ppt Alg.
 Message Authentication Code (MAC) Szenario: Integrität und Authentizität mittels MACs. Alice und Bob besitzen gemeinsamen Schlüssel k. Alice berechnet für m einen MAC-Tag t als Funktion von m und k. Alice
Message Authentication Code (MAC) Szenario: Integrität und Authentizität mittels MACs. Alice und Bob besitzen gemeinsamen Schlüssel k. Alice berechnet für m einen MAC-Tag t als Funktion von m und k. Alice
3: Zahlentheorie / Primzahlen
 Stefan Lucks Diskrete Strukturen (WS 2009/10) 96 3: Zahlentheorie / Primzahlen 3: Zahlentheorie / Primzahlen Stefan Lucks Diskrete Strukturen (WS 2009/10) 97 Definition 37 (Teiler, Vielfache, Primzahlen,
Stefan Lucks Diskrete Strukturen (WS 2009/10) 96 3: Zahlentheorie / Primzahlen 3: Zahlentheorie / Primzahlen Stefan Lucks Diskrete Strukturen (WS 2009/10) 97 Definition 37 (Teiler, Vielfache, Primzahlen,
Blinde Signaturen, geheime Abstimmungen und digitale Münzen
 Blinde Signaturen, geheime Abstimmungen und digitale Münzen Claus Diem Im Wintersemester 2017 / 18 Crypto 1982 Geheime Abstimmungen Eine geheime Abstimmung Problem. Eine Gruppe von Personen will per Brief
Blinde Signaturen, geheime Abstimmungen und digitale Münzen Claus Diem Im Wintersemester 2017 / 18 Crypto 1982 Geheime Abstimmungen Eine geheime Abstimmung Problem. Eine Gruppe von Personen will per Brief
VI.4 Elgamal. - vorgestellt 1985 von Taher Elgamal. - nach RSA das wichtigste Public-Key Verfahren
 VI.4 Elgamal - vorgestellt 1985 von Taher Elgamal - nach RSA das wichtigste Public-Key Verfahren - besitzt viele unterschiedliche Varianten, abhängig von zugrunde liegender zyklischer Gruppe - Elgamal
VI.4 Elgamal - vorgestellt 1985 von Taher Elgamal - nach RSA das wichtigste Public-Key Verfahren - besitzt viele unterschiedliche Varianten, abhängig von zugrunde liegender zyklischer Gruppe - Elgamal
VIII. Digitale Signaturen
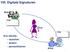 VIII. Digitale Signaturen Bob Eve Eve möchte - lauschen - ändern - personifizieren Alice 1 Aufgaben - Vertraulichkeit - Lauschen - Authentizität - Tauschen des Datenursprungs - Integrität - Änderung der
VIII. Digitale Signaturen Bob Eve Eve möchte - lauschen - ändern - personifizieren Alice 1 Aufgaben - Vertraulichkeit - Lauschen - Authentizität - Tauschen des Datenursprungs - Integrität - Änderung der
Vorlesung Sicherheit
 Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 30.04.2018 1 / 35 Überblick 1 Hashfunktionen Motivation Formalisierung Die Merkle-Damgård-Konstruktion (Weitere) Angriffe auf Hashfunktionen Zusammenfassung
Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 30.04.2018 1 / 35 Überblick 1 Hashfunktionen Motivation Formalisierung Die Merkle-Damgård-Konstruktion (Weitere) Angriffe auf Hashfunktionen Zusammenfassung
CPA-Sicherheit ist ungenügend
 CPA-Sicherheit ist ungenügend Definition CCA CCA (=Chosen Ciphertext Attack) ist ein Angriff, bei dem der Angreifer sich Chiffretext seiner Wahl entschlüsseln lassen kann. Beispiele in denen CPA nicht
CPA-Sicherheit ist ungenügend Definition CCA CCA (=Chosen Ciphertext Attack) ist ein Angriff, bei dem der Angreifer sich Chiffretext seiner Wahl entschlüsseln lassen kann. Beispiele in denen CPA nicht
Vorlesung Sicherheit
 Vorlesung Sicherheit Dennis Hofheinz IKS, KIT 29.04.2013 1 / 22 Überblick 1 Zusammenfassung und Korrektur Zusammenfassung Korrektur Definition semantische Sicherheit 2 Hashfunktionen Motivation Formalisierung
Vorlesung Sicherheit Dennis Hofheinz IKS, KIT 29.04.2013 1 / 22 Überblick 1 Zusammenfassung und Korrektur Zusammenfassung Korrektur Definition semantische Sicherheit 2 Hashfunktionen Motivation Formalisierung
Ununterscheidbarkeit von Chiffretexten
 Ununterscheidbarkeit von Chiffretexten Spiel Ununterscheidbarkeit von Chiffretexten PrivK eav A,Π (n) Sei Π ein Verschlüsselungsverfahren und A ein Angreifer. 1 (m 0, m 1 ) A. 2 k Gen(1 n ). 3 Wähle b
Ununterscheidbarkeit von Chiffretexten Spiel Ununterscheidbarkeit von Chiffretexten PrivK eav A,Π (n) Sei Π ein Verschlüsselungsverfahren und A ein Angreifer. 1 (m 0, m 1 ) A. 2 k Gen(1 n ). 3 Wähle b
Ununterscheidbarkeit von Chiffretexten
 Ununterscheidbarkeit von Chiffretexten Spiel Ununterscheidbarkeit von Chiffretexten PrivK eav A,Π (n) Sei Π ein Verschlüsselungsverfahren und A ein Angreifer. (m 0, m ) A. 2 k Gen( n ). 3 Wähle b R {0,
Ununterscheidbarkeit von Chiffretexten Spiel Ununterscheidbarkeit von Chiffretexten PrivK eav A,Π (n) Sei Π ein Verschlüsselungsverfahren und A ein Angreifer. (m 0, m ) A. 2 k Gen( n ). 3 Wähle b R {0,
Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz. Übungsblatt 5. pk = (g, y) und sk = (g, x). ? = y H(t m) t. g s
 Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz Stammvorlesung Sicherheit im Sommersemester 2014 Übungsblatt 5 Hinweis: Übungsblätter können freiwillig bei Jessica Koch, Raum 256, Geb.
Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz Stammvorlesung Sicherheit im Sommersemester 2014 Übungsblatt 5 Hinweis: Übungsblätter können freiwillig bei Jessica Koch, Raum 256, Geb.
Ununterscheidbarkeit von Chiffretexten
 Ununterscheidbarkeit von Chiffretexten Spiel Ununterscheidbarkeit von Chiffretexten PrivK eav A,Π (n) Sei Π ein Verschlüsselungsverfahren und A ein Angreifer. 1 (m 0, m 1 ) A. 2 k Gen(1 n ). 3 Wähle b
Ununterscheidbarkeit von Chiffretexten Spiel Ununterscheidbarkeit von Chiffretexten PrivK eav A,Π (n) Sei Π ein Verschlüsselungsverfahren und A ein Angreifer. 1 (m 0, m 1 ) A. 2 k Gen(1 n ). 3 Wähle b
Vorlesung Sicherheit
 Vorlesung Sicherheit Jörn Müller-Quade ITI, KIT basierend auf den Folien von Dennis Hofheinz, Sommersemester 2014 02.05.2016 1 / 22 Überblick 1 Hashfunktionen Erinnerung Formalisierung Die Merkle-Damgård-Konstruktion
Vorlesung Sicherheit Jörn Müller-Quade ITI, KIT basierend auf den Folien von Dennis Hofheinz, Sommersemester 2014 02.05.2016 1 / 22 Überblick 1 Hashfunktionen Erinnerung Formalisierung Die Merkle-Damgård-Konstruktion
Privacy-Preserving Authentication 2 Kryptografische Bausteine WS 2015/2016
 Privacy-Preserving Authentication 2 Kryptografische Bausteine WS 2015/2016 Sven Schäge, Fakultät für Mathematik, Ruhr-Universität Bochum Übersicht 1 Vorteil und Sicherheit 2 Hash Funktionen 3 Digitale
Privacy-Preserving Authentication 2 Kryptografische Bausteine WS 2015/2016 Sven Schäge, Fakultät für Mathematik, Ruhr-Universität Bochum Übersicht 1 Vorteil und Sicherheit 2 Hash Funktionen 3 Digitale
Übung zur Vorlesung Sicherheit Übungsblatt 2. Alexander Koch Björn Kaidel
 Übung zur Vorlesung Sicherheit 07.05.2014 Übungsblatt 2 Alexander Koch alexander.koch@kit.edu Björn Kaidel bjoern.kaidel@kit.edu 1 / 32 Kummerkasten In der Übung lauter und deutlicher sprechen: Wir geben
Übung zur Vorlesung Sicherheit 07.05.2014 Übungsblatt 2 Alexander Koch alexander.koch@kit.edu Björn Kaidel bjoern.kaidel@kit.edu 1 / 32 Kummerkasten In der Übung lauter und deutlicher sprechen: Wir geben
Vorlesung Sicherheit
 Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 26.06.2017 1 / 41 Überblick 1 Identifikationsprotokolle Erinnerung Sicherheitsmodell Ein sicheres Protokoll Noch ein sicheres Protokoll 2 Zero-Knowledge-Protokolle
Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 26.06.2017 1 / 41 Überblick 1 Identifikationsprotokolle Erinnerung Sicherheitsmodell Ein sicheres Protokoll Noch ein sicheres Protokoll 2 Zero-Knowledge-Protokolle
Digitale Unterschriften. Angriffe und Sicherheitsmodelle. Bemerkungen. Angriffe und Sicherheitsmodelle
 Digitale Unterschriften Auch digitale Signaturen genannt. Nachrichten aus Nachrichtenraum: M M. Signaturen aus Signaturenraum: σ S. Schlüssel sind aus Schlüsselräumen: d K 1, e K 2. SignierungsverfahrenS
Digitale Unterschriften Auch digitale Signaturen genannt. Nachrichten aus Nachrichtenraum: M M. Signaturen aus Signaturenraum: σ S. Schlüssel sind aus Schlüsselräumen: d K 1, e K 2. SignierungsverfahrenS
Existenz von Einwegfunktionen
 Existenz von Einwegfunktionen Satz Einweg-Eigenschaft von f FO Unter der Faktorisierungsannahme ist f FO eine Einwegfunktion. Beweis: f FO ist mittels FACTOR-ONEWAY effizient berechenbar. z.z.: Invertierer
Existenz von Einwegfunktionen Satz Einweg-Eigenschaft von f FO Unter der Faktorisierungsannahme ist f FO eine Einwegfunktion. Beweis: f FO ist mittels FACTOR-ONEWAY effizient berechenbar. z.z.: Invertierer
Hardcore-Prädikat. Definition Hardcore-Prädikat. Ziel: Destilliere Komplexität des Invertierens auf ein Bit.
 Hardcore-Prädikat Ziel: Destilliere Komplexität des Invertierens auf ein Bit. Definition Hardcore-Prädikat Sei Π f eine Einwegfunktion. Sei hc ein deterministischer pt Alg mit Ausgabe eines Bits hc(x)
Hardcore-Prädikat Ziel: Destilliere Komplexität des Invertierens auf ein Bit. Definition Hardcore-Prädikat Sei Π f eine Einwegfunktion. Sei hc ein deterministischer pt Alg mit Ausgabe eines Bits hc(x)
Übung zur Vorlesung Sicherheit Übungsblatt 2. Alexander Koch Björn Kaidel
 Übung zur Vorlesung Sicherheit 07.05.2014 Übungsblatt 2 Alexander Koch alexander.koch@kit.edu Björn Kaidel bjoern.kaidel@kit.edu 1 / 32 Kummerkasten In der Übung lauter und deutlicher sprechen: Wir geben
Übung zur Vorlesung Sicherheit 07.05.2014 Übungsblatt 2 Alexander Koch alexander.koch@kit.edu Björn Kaidel bjoern.kaidel@kit.edu 1 / 32 Kummerkasten In der Übung lauter und deutlicher sprechen: Wir geben
ElGamal Verschlüsselungsverfahren (1984)
 ElGamal Verschlüsselungsverfahren (1984) Definition ElGamal Verschlüsselungsverfahren Sei n ein Sicherheitsparameter. 1 Gen : (q, g) G(1 n ), wobei g eine Gruppe G der Ordnung q generiert. Wähle x R Z
ElGamal Verschlüsselungsverfahren (1984) Definition ElGamal Verschlüsselungsverfahren Sei n ein Sicherheitsparameter. 1 Gen : (q, g) G(1 n ), wobei g eine Gruppe G der Ordnung q generiert. Wähle x R Z
VI.3 RSA. - RSA benannt nach seinen Erfindern R. Rivest, A. Shamir und L. Adleman. - vorgestellt erstes Public-Key Verschlüsselungsverfahren
 VI.3 RSA - RSA benannt nach seinen Erfindern R. Rivest, A. Shamir und L. Adleman - vorgestellt 1977 - erstes Public-Key Verschlüsselungsverfahren - auch heute noch das wichtigste Public-Key Verfahren 1
VI.3 RSA - RSA benannt nach seinen Erfindern R. Rivest, A. Shamir und L. Adleman - vorgestellt 1977 - erstes Public-Key Verschlüsselungsverfahren - auch heute noch das wichtigste Public-Key Verfahren 1
Sicherheit von ElGamal
 Sicherheit von ElGamal Satz CPA-Sicherheit ElGamal ElGamal Π ist CPA-sicher unter der DDH-Annahme. Beweis: Sei A ein Angreifer auf ElGamal Π mit Erfolgsws ɛ(n) := Ws[PubK cpa A,Π (n) = 1]. Wir konstruieren
Sicherheit von ElGamal Satz CPA-Sicherheit ElGamal ElGamal Π ist CPA-sicher unter der DDH-Annahme. Beweis: Sei A ein Angreifer auf ElGamal Π mit Erfolgsws ɛ(n) := Ws[PubK cpa A,Π (n) = 1]. Wir konstruieren
Bemerkungen. Orientierung. Digitale Unterschriften. Angriffe und Sicherheitsmodelle
 Orientierung Haben bisher im Public-Key Bereich nur Verschlüsselung betrachtet. Haben dafür geeignete mathematische Strukturen und ihre Eigenschaften diskutiert. RSA, Rabin: Restklassenringe modulo n,
Orientierung Haben bisher im Public-Key Bereich nur Verschlüsselung betrachtet. Haben dafür geeignete mathematische Strukturen und ihre Eigenschaften diskutiert. RSA, Rabin: Restklassenringe modulo n,
VII. Hashfunktionen und Authentifizierungscodes
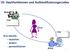 VII. Hashfunktionen und Authentifizierungscodes Bob Eve Eve möchte - lauschen - ändern - personifizieren Alice 1 Aufgaben - Vertraulichkeit Lauschen - Authentizität Tauschen des Datenursprungs - Integrität
VII. Hashfunktionen und Authentifizierungscodes Bob Eve Eve möchte - lauschen - ändern - personifizieren Alice 1 Aufgaben - Vertraulichkeit Lauschen - Authentizität Tauschen des Datenursprungs - Integrität
Aufgabe der Kryptografie
 Aufgabe der Kryptografie Eve möchte die Unterhaltung mithören und/oder ausgetauschte Informationen ändern. Alice & Bob kommunzieren über einen unsicheren Kanal. Alice & Bob nutzen Verschlüsselung und digitale
Aufgabe der Kryptografie Eve möchte die Unterhaltung mithören und/oder ausgetauschte Informationen ändern. Alice & Bob kommunzieren über einen unsicheren Kanal. Alice & Bob nutzen Verschlüsselung und digitale
Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz. Klausur Hinweise
 Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz Stammvorlesung Sicherheit im Sommersemester 2014 Klausur 22.07.2014 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung stehen
Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz Stammvorlesung Sicherheit im Sommersemester 2014 Klausur 22.07.2014 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung stehen
Ich bedanke mich bei Florian Böhl, Benny Fuhry, Gunnar Hartung, Jan Holz, Björn Kaidel, Eike Kiltz, Evgheni Kirzner, Jessica Koch, Julia Rohlfing,
 Digitale Signaturen Tibor Jager tibor.jager@rub.de Horst Görtz Institut für IT-Sicherheit Lehrstuhl für Netz- und Datensicherheit Ruhr-Universität Bochum Letzte Aktualisierung: 6. Oktober 2015 Ich bedanke
Digitale Signaturen Tibor Jager tibor.jager@rub.de Horst Görtz Institut für IT-Sicherheit Lehrstuhl für Netz- und Datensicherheit Ruhr-Universität Bochum Letzte Aktualisierung: 6. Oktober 2015 Ich bedanke
Digitale Signaturen. Andreas Spillner. Kryptografie, SS 2018
 Digitale Signaturen Andreas Spillner Kryptografie, SS 2018 Ausgangspunkt Digitale Signaturen bieten unter anderem das, was man auch mit einer eigenhändigen Unterschrift auf einem Dokument bezweckt. Beispiel:
Digitale Signaturen Andreas Spillner Kryptografie, SS 2018 Ausgangspunkt Digitale Signaturen bieten unter anderem das, was man auch mit einer eigenhändigen Unterschrift auf einem Dokument bezweckt. Beispiel:
Vorlesung Sicherheit
 Vorlesung Sicherheit Jörn Müller-Quade ITI, KIT basierend auf den Folien von Dennis Hofheinz, Sommersemester 2014 04.05.2015 1 / 20 Kummerkasten Vorlesungsfolien bitte einen Tag vorher hochladen : Sollte
Vorlesung Sicherheit Jörn Müller-Quade ITI, KIT basierend auf den Folien von Dennis Hofheinz, Sommersemester 2014 04.05.2015 1 / 20 Kummerkasten Vorlesungsfolien bitte einen Tag vorher hochladen : Sollte
Vorlesung Sicherheit
 Vorlesung Sicherheit Dennis Hofheinz IKS, KIT 13.05.2013 1 / 16 Überblick 1 Asymmetrische Verschlüsselung Erinnerung Andere Verfahren Demonstration Zusammenfassung 2 Symmetrische Authentifikation von Nachrichten
Vorlesung Sicherheit Dennis Hofheinz IKS, KIT 13.05.2013 1 / 16 Überblick 1 Asymmetrische Verschlüsselung Erinnerung Andere Verfahren Demonstration Zusammenfassung 2 Symmetrische Authentifikation von Nachrichten
Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz. Nachklausur Hinweise
 Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz Stammvorlesung Sicherheit im Sommersemester 2014 Nachklausur 29.09.2014 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung
Institut für Theoretische Informatik Jun.-Prof. Dr. D. Hofheinz Stammvorlesung Sicherheit im Sommersemester 2014 Nachklausur 29.09.2014 Vorname: Nachname: Matrikelnummer: Hinweise - Für die Bearbeitung
Digitale Signaturen. Einführung und das Schnorr Signatur Schema. 1 Digitale Signaturen Einführung & das Schnorr Signatur Schema.
 Digitale Signaturen Einführung und das Schnorr Signatur Schema 1 Übersicht 1. Prinzip der digitalen Signatur 2. Grundlagen Hash Funktionen Diskreter Logarithmus 3. ElGamal Signatur Schema 4. Schnorr Signatur
Digitale Signaturen Einführung und das Schnorr Signatur Schema 1 Übersicht 1. Prinzip der digitalen Signatur 2. Grundlagen Hash Funktionen Diskreter Logarithmus 3. ElGamal Signatur Schema 4. Schnorr Signatur
Sicherheit von hybrider Verschlüsselung
 Sicherheit von hybrider Verschlüsselung Satz Sicherheit hybrider Verschlüsselung Sei Π ein CPA-sicheres PK-Verschlüsselungsverfahren und Π ein KPA-sicheres SK-Verschlüsselungsverfahren. Dann ist das hybride
Sicherheit von hybrider Verschlüsselung Satz Sicherheit hybrider Verschlüsselung Sei Π ein CPA-sicheres PK-Verschlüsselungsverfahren und Π ein KPA-sicheres SK-Verschlüsselungsverfahren. Dann ist das hybride
Übung zur Vorlesung Sicherheit Übungsblatt 4. Björn Kaidel 1 / 70
 Übung zur Vorlesung Sicherheit 18.06.2015 Übungsblatt 4 Björn Kaidel bjoern.kaidel@kit.edu 1 / 70 RSA: Warnung! Mehrere Nachfragen nach der letzten Übung: Wir wollen zu e ein d berechnen mit e d = 1 mod
Übung zur Vorlesung Sicherheit 18.06.2015 Übungsblatt 4 Björn Kaidel bjoern.kaidel@kit.edu 1 / 70 RSA: Warnung! Mehrere Nachfragen nach der letzten Übung: Wir wollen zu e ein d berechnen mit e d = 1 mod
Vorlesung Sicherheit
 Vorlesung Sicherheit Jörn Müller-Quade ITI, KIT basierend auf den Folien von Dennis Hofheinz, Sommersemester 2014 20.04.2014 1 / 28 Überblick 1 Blockchiffren Erinnerung Angriffe auf Blockchiffren 2 Formalisierung
Vorlesung Sicherheit Jörn Müller-Quade ITI, KIT basierend auf den Folien von Dennis Hofheinz, Sommersemester 2014 20.04.2014 1 / 28 Überblick 1 Blockchiffren Erinnerung Angriffe auf Blockchiffren 2 Formalisierung
Algorithmen II Vorlesung am
 Algorithmen II Vorlesung am..03 Randomisierte Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales Forschungszentrum
Algorithmen II Vorlesung am..03 Randomisierte Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales Forschungszentrum
Vorlesung Sicherheit
 Vorlesung Sicherheit Jörn Müller-Quade ITI, KIT basierend auf den Folien von Dennis Hofheinz, Sommersemester 2014 08.06.2015 1 / 34 Überblick 1 Schlüsselaustauschprotokolle Erinnerung Weitere Schlüsselaustauschtypen
Vorlesung Sicherheit Jörn Müller-Quade ITI, KIT basierend auf den Folien von Dennis Hofheinz, Sommersemester 2014 08.06.2015 1 / 34 Überblick 1 Schlüsselaustauschprotokolle Erinnerung Weitere Schlüsselaustauschtypen
Einwegfunktionen Ziel: CPA-sichere Verschlüsselung aus Trapdoor-Einwegpermutation Später: CCA-sichere Verschlüsselung aus Trapdoor-Einwegperm.
 Einwegfunktionen Ziel: CPA-sichere Verschlüsselung aus Trapdoor-Einwegpermutation Später: CCA-sichere Verschlüsselung aus Trapdoor-Einwegperm. Spiel Invertieren Invert A,f (n) Sei f : 0, 1} 0, 1} effizient
Einwegfunktionen Ziel: CPA-sichere Verschlüsselung aus Trapdoor-Einwegpermutation Später: CCA-sichere Verschlüsselung aus Trapdoor-Einwegperm. Spiel Invertieren Invert A,f (n) Sei f : 0, 1} 0, 1} effizient
Vorlesung Sicherheit
 Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 08.05.2017 1 / 32 Überblick 1 Blockchiffren Erinnerung Varianten von DES Beispiel: AES Angriffe auf Blockchiffren 2 Formalisierung von Sicherheit (symmetrischer
Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 08.05.2017 1 / 32 Überblick 1 Blockchiffren Erinnerung Varianten von DES Beispiel: AES Angriffe auf Blockchiffren 2 Formalisierung von Sicherheit (symmetrischer
