Masterarbeit Lehrstuhl für Bioinformatik Technische Fakultät Albert-Ludwigs-Universität Freiburg
|
|
|
- Heike Becke
- vor 8 Jahren
- Abrufe
Transkript
1 B E R E C H N U N G D E R R N A - PA RT I T I O N S F U N K T I O N M I T A L G E B R A I S C H E R D Y N A M I S C H E R P R O G R A M M I E R U N G kerstin schmatzer Masterarbeit Lehrstuhl für Bioinformatik Technische Fakultät Albert-Ludwigs-Universität Freiburg 23. Februar 2012
2 Kerstin Schmatzer: Berechnung der RNA-Partitionsfunktion mit Algebraischer Dynamischer Programmierung, Masterarbeit, 23. Februar 2012 betreuer: Professor Dr. Rolf Backofen Dr. Mathias Möhl gutachter: Professor Dr. Rolf Backofen Professor Dr. Robert Giegerich
3 A B S T R A C T Prediction of secondary RNA structures is a important subarea of Bioinformatics. McCaskill developed a dynamic programming algorithm for calculating the base-pair probabilities using the partition function. It is possible to draw conclusions from this probabilities to the secondary structure of the RNA sequence. Instead of the traditional dynamic programming, we use the new technique of algebraic dynamic programming. This technique is more modular, more flexible and based on context-free grammars. In our work, we introduce a grammar to calculate the partition function of an RNA sequence. This grammar divides the RNA sequence into possible secondary RNA structure elements and calculates for each element the corresponding partition function using the energy model of Turner. For determining the base-pair probabilities, we make use of the calculated partition functions for the secondary structure elements. Z U S A M M E N FA S S U N G Die Bioinformatik bietet eine Reihe von effizienten Algorithmen für die Vorhersage von sekundären RNA-Strukturen an. Der Algorithmus von McCaskill gibt die Basenpaar-Wahrscheinlichkeiten einer RNA-Sequenz an, die Rückschlüsse auf die wahrscheinlichste sekundäre RNA-Struktur zu lässt. Für die Berechnung der Basenpaar- Wahrscheinlichkeiten wird die Partitionsfunktion, ermittelt mit Hilfe von loop-basierte Energien, verwendet. Diese lassen sich mittels dynamischer Programmierung berechnen. Mittels algebraischer dynamischer Programmierung lässt sich das Problem modularer lösen. Wir stellen eine Grammatik vor, welche die Partitionsfunktion für eine gegebene RNA-Sequenz nach der Vorgehensweise von McCaskill berechnet. Innerhalb der Grammatik werden einzelne möglichen sekundäre RNA-Strukturen betrachtet und deren Partitionsfunktionen anhand des Energiemodells von Turner ermittelt. Zur Berechnung der Basenpaar-Wahrscheinlichkeiten werden die schon bestimmten Partitionsfunktionen der Strukturelemente hinzu gezogen. iii
4 We have seen that computer programming is an art, because it applies accumulated knowledge to the world, because it requires skill and ingenuity, and especially because it produces objects of beauty. Donald E. Knuth [4] D A N K S A G U N G Zuerst möchte ich meinem Betreuer, Dr. Mathias Möhl, für seine tatkräftige Unterstützung meiner Masterarbeit danken. Vielen Dank für die hilfreichen Anregungen und die Engelsgeduld mit mir! Vielen Dank an Professor Dr. Rolf Backofen für die Möglichkeit mich mit diesem interessanten Themengebiet zu beschäftigen. Besonderen Dank schulde ich auch Georg Sauthoff und Stefan Janssen für die Bereitschaft, meine vielen Fragen zur Implementierung von Bellman s Gap zu beantworten. Vielen Dank für die Unterstützung! Ich danke meiner Familie für ihre Liebe, ihre Unterstützung und ihre vielen liebevollen Aufmunterungen. Besonders möchte ich meinen Großeltern für die finanzielle Unterstützung meiner Ausbildung danken, die mir vieles ermöglicht hat. Mein Dank gilt auch meinem besten Freund, Dr. Achim Brucker, der mich durch Höhen und Tiefen begleitet hat. Danke für deine Freundschaft! Herzlichen Dank an all meine Lektoren für die hilfreichen Anmerkungen und den Mut meine Arbeit zu lesen. iv
5 I N H A LT S V E R Z E I C H N I S i einführung 1 1 einleitung Motivation Ziel und Struktur der Arbeit 3 ii grundlagen 5 2 grundlegende algorithmen Berechnung der optimalen sekundären Struktur Berechnung der Strukturverteilung Zusammenfassung 15 3 algebraische dynamische programmierung ADP Ein neues Programmierkonzept Vergleich zur klassischen dynamischen Programmieren Das Prinzip von ADP Bellman s Gap Überblick Kurze Einführung in die Programmiersprache Im Vergleich mit manueller Implementierung Zusammenfassung 23 iii rna-partitionsfunktion 24 4 die rna-partitionsfunktion von teilsequenzen Grammatik für die Partitionsfunktion Hairpin Stack Interiorloop und Bulge Multiloop Zusammenfassung 34 5 die berechnung der rna-partitionsfunktion Von Teilsequenzen zu vollständigen Sequenzen Kodierung der Eingabe Partitionsfunktion für Outerfragmente Outerfragmente Pair Stack Interiorloop und Bulge Berechnung der vollständigen Partitionsfunktion Zusammenfassung 49 iv basenpaar-wahrscheinlichkeiten 51 6 berechnung der strukturverteilung 52 v
6 inhaltsverzeichnis vi 6.1 Berechnung der Basenpaar-Wahrscheinlichkeiten Implementierung Implementierung mit einfachen Energiefunktionen Analyse der Implementierung Zusammenfassung 58 v schluss 60 7 zusammenfassung Ausblick Zusammenfassung 61 literaturverzeichnis 63
7 A B B I L D U N G S V E R Z E I C H N I S Abbildung 1 Sekundäre Strukturelemente 7 Abbildung 2 Teilung des Multiloops 10 Abbildung 3 Die einzelnen Komponenten eines ADP-Problems 19 Abbildung 4 Übersicht von Bellman s Gap 20 Abbildung 5 Hairpin 27 Abbildung 6 Stack 28 Abbildung 7 Interiorloop 29 Abbildung 8 Linker und rechter Bulge 30 Abbildung 9 Multiloop 31 Abbildung 10 Teilung des Multiloops in der Grammatik 33 Abbildung 11 Strukturelemente der Outerfragmente 36 Abbildung 12 Kodierung der Sequenz 38 Abbildung 13 Pair in der kodierten RNA-Sequenz 41 Abbildung 14 Stack in der kodierten RNA-Sequenz 42 Abbildung 15 Interiorloop in der kodierten RNA-Sequenz 42 Abbildung 16 Bulges in der kodierten Sequenz 45 Abbildung 17 Teilung des Multiloops nach dem ersten Basenpaar 47 Abbildung 18 Teilung des Multiloops in der Grammatik 48 Abbildung 19 Überblick der Implementierung 54 Abbildung 20 Erstes Beispiel der Ausgabe 55 Abbildung 21 Zweites Beispiel der Ausgabe 56 Abbildung 22 Zeitanalyse 58 TA B E L L E N V E R Z E I C H N I S Tabelle 1 Probleme in DP und Lösung in ADP 17 vii
8 Teil I E I N F Ü H R U N G
9 E I N L E I T U N G motivation Ribonukleinsäure (RNA) ist eine Kette von Nukleotiden. In der RNA kommen die folgenden organischen Basen vor: Adenin, Guanin, Cystein und Uracil, abgekürzt mit A, G, C und U. Eine RNA kann sich in komplexe Strukturen falten. Der Grund dafür liegt in der Fähigkeit der Basen untereinander Wasserstoffbrücken und Stapelwechselwirkungen ( stacking ) auszubilden. RNA-Moleküle besitzen verschiedene Funktionen in einem sehr breiten biologischen Bereich. Im Folgenden sind einige Funktionen von RNA-Molekülen aufgezählt: RNA-Moleküle können selbst enzymatische Funktionen übernehmen. In den Ribosomen besitzen die sogenannten ribosomalen RNAs diese Eigenschaft. RNA-Moleküle können katalytisch wirksam sein. Bei der Genregulierung spielen RNA-Moleküle, die sogenannten micrornas, eine wichtige Rolle und können dabei verschiedene biologische Prozesse beeinflussen, wie Entwicklung, Differenzierung und programmierten Zelltod. Der bekannteste RNA-Typ ist die messenger RNA, die als Matrize zur Proteinsynthese dient. Small nuclear RNAs sind kleine RNA-Moleküle, die in Assoziation mit Proteinen insbesondere an der Prozessierung der messenger RNA beteiligt sind. Die unterschiedlichsten RNAs transportieren Proteine innerhalb der Zelle. Zum Beispiel holen RNAs die entsprechenden Aminosäuren, die für die Proteinsynthese benötigt werden. In der Zelle kommt die RNA meistens als Einzelstrang vor und faltet sich in sekundäre Strukturen. Die sekundäre RNA-Struktur eines RNA-Moleküls gibt Aufschluss auf dessen Funktion. Es stehen unterschiedliche Methoden der Biophysik und der Molekularbiologie zur Verfügung, um sekundäre RNA-Strukturen zu bestimmen. Die Methoden unterscheiden sich drastisch in ihrem Aufwand, Grad an Auflösung und Information. Beispiel für chemische und molekulare Methoden sind folgende zwei Verfahren: enzymatisches und chemisches Mapping und UV-Spektroskopie. Alle chemischen und molekularen Verfahren sagen nur etwas über die aktuell 2
10 1.2 ziel und struktur der arbeit 3 entstandende RNA-Struktur in der gegebene Zelle aus. Aber die RNA verändert sich je nach Temperatur ihre sekundäre RNA-Struktur. Das bedeutet es gibt nicht nur eine sekundäre RNA-Struktur, in die sich ein RNA-Molekül falten kann. Es gibt verschiedene Verfahren zur Vorhersage von sekundären RNA-Strukturen. Durch die Vorhersage von sekundären Strukturen können experimentelle Strukturanalysen verglichen, bestätigt oder widerlegt werden. Auch kann eine Aussage über die Strukturverteilung eines RNA-Moleküls bei unterschiedlichen Temperaturen gemacht werden. Dies gibt uns eine Möglichkeit die Ergebnisse experimenteller Analysemethoden zu vergleichen. Die Vorhersage von sekundären RNA-Strukturen gibt uns Aufschluss auf die biologische Funktion des analysierten Moleküls. In der Bioinformatik gibt es unterschiedliche Algorithmen zur Vorhersage der sekundären RNA-Struktur. Eine der bekanntesten Algorithmen sind der Algorithmus von Zuker [12] und der Algorithmus von McCaskill [6]. Der Algorithmus von Zuker berechnet die optimale sekundäre RNA-Struktur eines RNA-Molekühls mit minimaler freier Energie anhand eines gegebenen thermodynamischen Energiemodells. McCaskill gibt eine Algorithmus zur Vorhersage der sekundären Strukturverteilung eines RNA-Moleküls an. Beide Algorithmen lassen sich effizient mit dem Prinzip der dynamischen Programmierung lösen. 1.2 ziel und struktur der arbeit Das Ziel der Arbeit ist es, einen Algorithmus zu entwickeln, der die Basenpaar-Wahrscheinlichkeiten für eine RNA-Sequenz mit Hilfe der Vorgehensweise des Verfahrens von McCaskill [6] berechnet. Die Berechnung geschieht mit Hilfe der Partitionsfunktionen der RNA- Strukturelemente. Zur Ermittlung der Partitionsfunktionen werden die einzelnen sekundären Strukturelemente mit ihren entsprechenden Energien betrachtet. Zusätzlich soll für die Berechnung der RNA-Partitionsfunktion die neu entwickelte Programmiertechnik, die sogenannte algebraische dynamische Programmierung von R. Giegerich und C. Meyer [2], verwendet werden. Diese Methode beruht auf kontext-freie Grammatiken und Evaluationsalgebren und ermöglicht eine modularere und dadurch flexiblere Implementierung als die Methode der traditionellen dynamischen Programmierung. Die Implementierung erfolgt mit der Programmierumgebung Bellman s Gap entwickelt von G. Sauthoff [10]. Diese ist speziell für Optimierungsprobleme, die mit algebraischer dynamischer Programmierung gelöst werden, entwickelt. Zuerst stellen wir die Grundlagen und Methoden der Algorithmen, sowie der algebraischen dynamischen Programmierung vor. Danach erklären wir unsere Version des Algorithmus zur Berechnung der
11 1.2 ziel und struktur der arbeit 4 Basenpaar-Wahrscheinlichkeiten. Anschließend gehen wir kurz auf die Implementierung des Algorithmus ein.
12 Teil II G R U N D L A G E N
13 G R U N D L E G E N D E A L G O R I T H M E N 2 In diesem Kapitel werden die grundlegenden Algorithmen erklärt. Zuerst betrachten wir den Algorithmus von Zuker und Stiegler zur Berechnung sekundärer RNA-Strukturen unter Benutzung loop-basierter Energien für eine gegebene RNA-Sequenz. Als nächstes widmen wir unsere Aufmerksamkeit dem Algorithmus von McCaskill zur Berechnung der Wahrscheinlichkeiten für die jeweiligen sekundären RNA-Strukturen einer gegebenen RNA-Sequenz. 2.1 berechnung der optimalen sekundären struktur Der Algorithmus von Zuker und Stiegler [12] berechnet die optimale sekundären RNA-Strukturen für eine gegebene RNA-Sequenz unter Beachtung der freien Energien für die einzelnen Elemente der sekundären RNA-Struktur. Sei im Weiteren s = s 1...s n eine RNA-Sequenz mit Länge n, wobei s i {A, G, C, U} mit 1 i n. definition (Sekundäre RNA-Struktur) Eine sekundäre RNA-Struktur R ist eine Menge von Basenpaaren. Formal, R = {(i, j) 1 i < j n und s i, s j bildet ein Basenpaar}, wobei folgendes für alle (i, j) gilt: (i i)(i, j) R, (j j)(i, j ) R. Der Algorithmus von Zuker und Stiegler [12] betrachten keine Pseudoknoten, sprich es werden nur sekundäre RNA-Strukturen beachtet, für die gilt: ((i, j) R (i, j ) R) mit i < i < j < j Wir betrachtet nur Watson-Crick Basenpaarbindungen, sprich die Basen A und U, die Basen G und U und die Basen G und C können ein Basenpaar bilden. Jede sekundäre RNA-Struktur hat ihre eigene Energie. Diese Energie ist abhängig von den gebildeten sekundären RNA-Strukturelementen innerhalb der RNA-Struktur. definition (Sekundäre RNA-Strukturelemente) Ein sekundäres RNA-Strukturelement einer RNA-Struktur R mit schließendem Basenpaar (i, j) ist eines der folgenden: Hairpin: (i, j) R, wobei (i, j ) R für alle (i < i < j < j). 6
14 2.1 berechnung der optimalen sekundären struktur 7 Stack: (i, j) R und (i + 1, j 1) R. Interiorloop: (i, j) R und (h, l) R mit i + 1 < h < l < j 1. Die Teilsequenzen [i + 1, h 1] und [l + 1, j 1] enthalten nur ungepaarte Basen. Zusätzlich sind zwei spezielle Fälle möglich, genannt Bulge, falls (h = i + 1) < l < j 1 oder falls i + 1 < h < (l = j 1). k-multiloop: mit einem schließenden Basenpaar (i 0, j 0 ) R und k weiteren Basenpaare (i 1, j 1 ),..., (i k, j k ) R, wobei noch folgende Eigenschaften gelten: i 0 < i 1 < j 1 < < i k < j k < j 0 (l, l ) R, falls (l, l ) (i 1, j 1 ),..., (i k, j k ), wobei gilt, dass i 0 < l < l < j 0. Jedes (i l, j l ) mit l {1,..., k} ist selber eine schließendes Basenpaar einer sekundären RNA-Struktur. h l i+1 j 1 i j i j i j (a) Hairpin (b) Stack (c) Interiorloop i 2 j 2 j 1 i 3 i 1 j 3 i 0 j 0 (d) Multiloop Abbildung 1: Sekundäre Strukturelemente Abbildung 1 zeigt die sekundären RNA-Strukturen - Hairpin, Stack, Interiorloop und Multiloop.
15 2.1 berechnung der optimalen sekundären struktur 8 definition (Energie eines sekundären RNA-Strukturelements) Die Energie eines sekundären RNA-Strukturelements mit schließendem Basenpaar (i, j) ist für: einen Hairpin: eh(i, j), einem Stack: es(i, j, i + 1, j + 1) mit (i + 1, j + 1) R, einem Interiorloop: el(i, j, h, l) mit (h, l) R und einem k-multiloop: em(k, k ) = a + b k + c k mit den Gewichten a, b und c, wobei a die Energie für das schließende Basenpaar (i, j), k die Anzahl der Basenpaar innerhalb des k-multiloops und k die Anzahl der ungepaarten Basen innerhalb des k-multiloops ist. definition (Energie einer sekundären RNA-Struktur) Die freie Energie einer sekundären RNA-Struktur R ist die Summe der Energien aller sekundären Strukturelemente für jedes Basenpaar (i, j) R: E(R) = E R i,j, (i,j) R wobei E(R) die Energie der sekundären RNA-Struktur R und E R i,j die Energie der sekundären RNA-Strukturelemente mit schließendem Basenpaar (i, j) ist. Die Berechnung der freien Energie einer sekundären RNA-Struktur kann durch rekursive Formeln beschrieben werden. Dafür werden alle möglichen Fälle von sekundären RNA-Strukturen betrachtet. Die Matrizen zur Berechnung werden durch die nachfolgende Definition erklärt. definition (Zuker-Matrizen) 1. Die Matrix W i berechnet für die Sequenz s 0...s i die sekundäre RNA-Struktur mit minimaler freier Energie. W i 1 W i = min min 0 j 1<i {W j + V j,i } wobei W 0 = Die Matrix V i,j berechnet für die Sequenz s i...s j die sekundäre RNA-Struktur mit minimaler freier Energie, wobei s i und s j ein Basenpaar bilden. eh(i, j) es(i, j, i + 1, j 1) + V i+1,j 1 V i,j = min min i+1<i <j <j 1{eL(i, j, i, j ) + V i,j } min i+1<k<j {M i+1,k + M k+1,j 1 + a} wobei V i,i = 0.
16 2.1 berechnung der optimalen sekundären struktur 9 3. Die Matrix M i,j berechnet für die Sequenz s i...s j die sekundäre RNA-Struktur mit minimaler freier Energie, wobei s i und s j Teile eines Multiloops sind. M i+1,j + c M i,j 1 + c M i,j = min min 0<k i {M i,k + M k+1,j } V i,j + b wobei M i,i = 0. Eine Base s i in der RNA-Sequenz s kann nicht gebunden oder mit einer anderen Base s j gebunden sein. Dieser Basisfall wird in einer Rekursionsmatrix W i betrachtet. Falls die Base s i mit einer anderen Base s j gebunden ist, werden alle möglichen Energien der einzelnen sekundären RNA-Strukturen berechnet. Die Base s i kann mit einer anderen Base s j einen Hairpin, einen Stack, einen Loop oder einen Multiloop bilden. Die Energie für einen Hairpin, einen Stack, einen Loop können leicht berechnet werden. Im Falle eines Stack oder Loops wird die Berechnung rekursiv auf die Basenpaare s i und s j angewandt, die mit dem Basenpaar s j und s i den Stack oder Loop bilden. Im Fall eines Multiloops ist es notwendig eine zusätzliche Rekursionsmatrix für die Berechnung seiner Energie zu erstellen. Der Multiloop wird an einer Base s k geteilt, wobei i < k < j gilt und zwischen s i+1...s k und zwischen s k+1...s j 1 eine weiteres Basenpaar existiert um keinen einfachen Interiorloop zu erhalten. Die Berechnung der Energie wird dann rekursiv jeweils auf die RNA-Sequenzen s i+1...s k und s k+1...s j 1 angewandt. Abbildung 2 zeigt die Teilung eines Multiloops an einer Stelle der Base s k. Die Berechnung der Multiloop Energie geschieht in einer zusätzlichen Matrix. Die aktuell betrachteten Basen i und j können gepaart oder ungepaart sein. Eine weitere Möglichkeit ist, an einer Stelle s k den Multiloop rekursiv zu teilen, wobei i < k < j gilt. Die Berechnung der W-Matrix benötigt eine quadratische Laufzeit O(n 2 ), weil es nötig ist, einmal durch die gesamte RNA-Sequenz s mit der Länge n zu laufen und jede Base mit allen möglichen anderen Basen zu betrachten, um alle möglichen Basenpaare zu bestimmen. Die V-Matrix wird in O(n 4 ) Zeit berechnet. Die hohe Laufzeit ist auf die Betrachtung aller möglichen Interiorloops zurückzuführen. Die Berechnung der V-Matrix für alle möglichen Basenpaare (i, j) führt zu einer quadratischen Laufzeit. Im Falle eines Interiorloops wird ein weiteres Basenpaar (i, j ) gesucht, das mit dem Basenpaar (i, j) den Loop bildet. Die Suche eines weiteren Basenpaars (i, j ) benötigt auch eine quadratische Laufzeit. So vergrößert sich die Laufzeit zu O(n 4 ). Die M-Matrix benötigt O(n 3 ) Laufzeit. Hier wird für jedes mögliche Basenpaar (i, j) die Matrix einmal berechnet. Zusätzlich wird jeder
17 2.2 berechnung der strukturverteilung 10 i 2 j 2 k j 1 i 1 k+1 i 3 j 3 j 1 i 2 j 2 k k+1 i 3 i 0 j 0 i 1 j 3 (a) Multiloop Teilung an Position k (b) Geteilter Multiloop Abbildung 2: Der Multiloop wird an der Stelle k geteilt. Auf die dadurch entstandenen Teile des Multiloops wird die Berechnung der sekundären RNA-Strukturen rekursiv angewendet. mögliche Splitpunkt k eines Multiloops gesucht, der im schlimmsten Fall an jeder Base der gesamten RNA-Sequenz gesetzt werden kann. 2.2 berechnung der strukturverteilung McCaskill [6] stellt ein Methode zur Berechnung der Partitionsfunktion für RNA-Sequenzen basierend auf der Boltzmann Verteilung vor, um die Strukturverteilung einer RNA-Sequenz zu berechnen. Das Problem bei Zuker ist, dass die sekundäre RNA-Struktur mit minimaler Energie nicht immer die biologisch relevanteste ist. Für sekundäre RNA-Strukturen mit geringer Energie ist es möglich, biologisch relevanter zu sein, als alle anderen möglichen sekundären RNA-Strukturen. Daher wird ein neue Möglichkeit benötigt, um diejenige RNA-Struktur heraus zu finden, die biologisch am relevantesten ist. McCaskill berechnet für eine RNA-Sequenz die Wahrscheinlichkeit der Basenpaare mit Hilfe der Boltzmann-Verteilung. Anhand der Basenpaar-Wahrscheinlichkeiten lässt sich die wahrscheinlichste sekundäre RNA-Struktur ermitteln. definition (Boltzmann-Verteilung) Sei P(x) die Wahrscheinlichkeit für eine RNA-Struktur x. Dann ist eine Boltzmann-Verteilung gegeben durch: P(x) = exp( E(x)/(k BT)), Z wobei E(x) die Energie von x, T die Temperatur, k B die Boltzmann- Konstante ist und Z = y exp( E(y)/(k BT)), wobei y eine mögliche sekundäre RNA-Struktur ist.
18 2.2 berechnung der strukturverteilung 11 definition (Partitionsfunktion für eine RNA-Sequenz) Die Partitionsfunktion für eine RNA-Sequenz s ist: Z = R exp( E(R)/(k B T)), wobei R eine sekundäre RNA-Struktur von s, T die Temperatur und k B die Boltzmann-Konstante ist. Der Algorithmus von McCaskill berechnet die Partitionsfunktion Z für eine RNA-Sequenz s effizient. Als Energiemodell für sekundäre RNA-Strukturen wird das Modell von Zuker benutzt. Das bedeutet, dass die Energie einer sekundären RNA-Struktur der Summe aller möglichen sekundären RNA-Strukturelemente entspricht. Um eine effiziente Berechnung der Partitionsfunktion zu garantieren, ist eine Zerlegung des Problems in Teilprobleme notwendig. RNA-Sequenzen werden daher in sogenannte Strukturmengen unterteilt. definition (Strukturmengen einer RNA-Sequenz) Gegeben sei eine RNA-Sequenz s. Diese wird in vier Strukturmengen unterteilt: R all : Menge aller sekundären RNA-Strukturen von s. R i,j : Menge aller sekundären RNA-Strukturen, die nur zwischen i und j Basenpaare enthalten: R i,j = {R R (i, j ) R : i i < j j} R b i,j : Menge aller sekundären RNA-Strukturen, die (i, j) als Basenpaar haben und nur zwischen i und j Basenpaare enthalten: R b i,j = {R R (i, j) R (i, j ) R : i i < j j} R 1bd i,j : Menge aller sekundären RNA-Strukturen, die zwischen i und j mindestens ein Basenpaar haben: R 1bd i,j = {R R R : (i, j ) R : i < i < j < j} definition (Partitionsfunktion einer Strukturmenge) Sei R eine Strukturmenge. Dann ist deren Partitionsfunktion gegeben durch: Z R = R R exp( E(R)/(k B T)). Damit die Berechnung der Partitionsfunktion der Strukturmengen möglich ist, muss sicher gestellt sein, dass die Zerlegung der Strukturmengen unabhängig ist.
19 2.2 berechnung der strukturverteilung 12 definition (Unabhängige Zerlegung) Sei eine Strukturmenge R gegeben. Zwei Strukturmengen R 1 und R 2 sind eine unabhängige Zerlegung von R, falls eine bijektive Abbildung f : R R 1 R 2 existiert mit folgenden Bedingungen: f : R R 1 R 2 : R = R 1 R2 und E(R) = E(R 1 ) + E(R 2 ) mit R R, R 1 R 1 und R 2 R 2. theorem: (Unabhängige Zerlegung) Gegeben sei eine Strukturmenge R. Seien nun R 1 und R 2 zwei strukturell unabhängige Strukturmengen. Dann gilt: Z R = Z R1 Z R2 beweis: Seien R 1 und R 2 zwei strukturell unabhängige Strukturmengen. Z R = R R = e E(R)/(k BT ) R R 1 R2 e E(R)/(kBT ) R 1 und R 2 sind strukturell unabhängig. Daher folgt: Z R = e E(R)/(kBT ) + R R 1 = Z R1 Z R2 R R 2 e E(R)/(kBT ) Die rekursive Berechnung der Partitionsfunktion erfolgt anhand von Matrizen. definition (Matrizen zur Berechnung der Partitionsfunktion) Berechnung der Partitionsfunktion für R all : Q = Z Rall = R e [E(R)/(k BT )] Berechnung der Partitionsfunktion für R i,j : Q i,j = Z Ri,j = h,l Q i,h 1 Q b h,l + 1, wobei i h < l j. Berechnung der Partitionsfunktion für R b i,j : Q b i,j = Z R b = e eh(i,j)/(k BT ) i,j + e esbi(i,j,h,l)/(k BT ) Q b h,l (h,l) + (h,l) Q b h,l Qm l+1,j 1 e (a+b+c(h i 1))/(k BT),
20 2.2 berechnung der strukturverteilung 13 wobei (i < h < l < j) und esbi die jeweilige Energie für einen Stack, Interiorloop oder Bulge ist. Berechnung der Partitionsfunktion für R 1bd i,j : Q m i,j = Z R 1bd i,j = h,l (e [c(h i 1)/kT] + Q b i,h 1 ) Q b h,l e [(b+c(j l 1))/(k BT )], wobei (i < h < l < j). In dem Eintrag Q 1,n steht das Ergebnis für die gegebene RNA- Sequenz. Die Matrix Q i,j betrachtet alle sekundären RNA-Strukturen in R i,j. Hierfür werden alle RNA-Strukturen beachtet, die zusätzlich ein Basenpaar (h, l) zwischen (i, j) enthalten. Dabei wird das Produkt der Partitionsfunktion für alle RNA-Strukturen, Q i,h 1, und der von allen RNA-Strukturen mit Basenpaar (h, l), Q b i,j, summiert. Die Matrix Q b i,j summiert alle sekundären RNA-Strukturen mit schließendem Basenpaar (i, j) unter Berücksichtigung deren Energien. Für einen Multiloop wird die einfache Energiefunktion a + b k + c k angenommen. Die Konstante a ist die Energie für das schließende Basenpaar (i, j), b die Energie eines der k Basenpaare innerhalb des Multiloops und c die Energie einer der k ungepaarten Base innerhalb des Multiloops. Die Matrix Q b i,j entspricht der Partitionsfunktion Z R b für Strukturen in i,j R b i,j. Die Berechnung der Partitionsfunktion Z R 1bd behandelt den Fall, i,j dass die gegenwärtige sekundäre RNA-Struktur Teil eines Multiloops mit der oben genannten vereinfachten Energiefunktion ist. Nachdem wir die Partitionsfunktion mit Hilfe der obigen Matrizen effizient berechnen, betrachten wir im Weiteren die Berechnung der Basenpaarwahrscheinlichkeiten. Die Wahrscheinlichkeit eines Basenpaars (i, j) entspricht: p i,j = p E i,j + (h,l) p SBI i,j (h, l) + p M i,j (h, l), (h,l) wobei h < i < j < l. Es wird zwischen drei Fällen entschieden. Beim ersten Fall ist das Basenpaar das äußerste Basenpaar, bei dem die Teilsequenzen [1, i 1] und [j + 1, n] nur ungepaarte Basen enthalten. Die Wahrscheinlichkeit dafür entspricht p E i,j. Der zweite und dritte Fall berücksichtigt Basenpaare, die Teil eines Stacks, Interiorloops, Bulges oder Multiloops sind. Das schließende Basenpaar dieser Strukturen ist (h, l). Die Wahrscheinlichkeiten werden aufgeteilt - Wahrscheinlichkeit für Stack, Bulges und Interiorloops p SBI i,j (h, l) und Wahrscheinlichkeit für Multiloops p M i,j (h, l). Die drei benötigten Wahrscheinlichkeiten zur Berechnung der Basenpaarwahrscheinlichkeit p i,j greifen auf die Martizen zur Berechnung der Partitionsfunktion zu. definition (Berechnung der Basenpaarwahrscheinlichkeit) Im Folgenden ist (h, l) ein Basenpaar für das gilt i < h < l < j.
21 2.2 berechnung der strukturverteilung 14 Die Wahrscheinlichkeit p E i,j ist: p E i,j = Q 1,i 1 Q b i,j Q j+1,n Q 1,n Die Wahrscheinlichkeit p SBI i,j (h, l) entspricht: p SBI i,j (h, l) = p h,l e esbi(i,j,h,l)/(k BT ) Q b i,j Q b h,l Die Wahrscheinlichkeit p M i,j (h, l) ist: p M i,j (h, l) = p h,l 1 Q b h,l [e (i h 1)c/k BT Q m j+1,l 1 +Q m h+1,i 1 e (l j 1)c/k BT +Q m h+1,i 1 Qm j+1,l 1 ] Q b i,j e (a+b)/(k BT ) Für die Wahrscheinlichkeit p E i,j wird die Partitionsfunktion Qb i,j benötigt, die alle sekundären Strukturen mit Basenpaar (i, j) berücksichtigt. Zusätzlich werden die Partitionsfunktionen Q 1,i 1 und Q j+1,n der Teilsequenzen [1, i 1] und [j + 1, n] verwendet und multipliziert. Das Ganze wird durch die Partitionsfunktion Q 1,n aller sekundären RNA- Strukturen geteilt. Um die Wahrscheinlichkeit p SBI i,j (h, l) zu ermitteln, wird das Produkt der Partitionsfunktionen Q b i,j der sekundären Strukturen mit Basenpaar (i, j) und deren Energie e esbi(i,j,h,l) berechnet. Zusätzlich wird das Ergebnis mit der Wahrscheinlichkeit des Basenpaars p h,l multipliziert und durch die Partitionsfunktion Q b h,l aller sekundären Strukturen mit schließendem Basenpaar (h, l) geteilt. Die letzte Wahrscheinlichkeit p M i,j ist die Wahrscheinlichkeit, dass (i, j) ein Teil eines Multiloops ist. Das schließende Basenpaar für den Multiloop ist (h, l). Die Wahrscheinlichkeitsberechnung wird in drei Fälle aufgeteilt, die nach der Position des Basenpaars (i, j) bestimmt werden. Entweder ist (i, j) das Basenpaar links außen, rechts außen oder in der Mitte, sprich rechts und links gibt es mindestens noch ein weiteres Basenpaar. Die Partitionsfunktion der entsprechenden sekundären Strukturen stehen in der Matrix Q m. Nach der Addition aller Fälle benötigen wir noch die Wahrscheinlichkeit des Basenpaars (h, l). Am Schluss teilen wir die Summe durch die Partitionsfunktion 1/Q b h,l aller sekundären Strukturen mit schließendem Basenpaar (h, l). Wir haben nun eine rekursive Formel für p i,j. Durch Gebrauch des dynamischen Programmierprinzips wird dies effizient ermittelt. Die Laufzeit des Algorithmus von McCaskill beträgt O(n 4 ) bei der Länge n der gegebenen RNA-Sequenz. Es ist nötig, die ganze Sequenz einmal zudurchlaufen. Dies benötigt lineare Laufzeit. Zusätzlich sehen
22 2.3 zusammenfassung 15 wir uns jedes Basenpaar (h, l) mit i < h < l < j an. Dies entspricht auch einem linearen Aufwand. So erhalten wir eine quadratische Laufzeit. Die Berechnung der Matrizen Q benötigen zusätzliche quadratischen Aufwand. So kommen wir zu einer Laufzeit von O(n 4 ). Durch die Beschränkung der Länge von Loops kann die Laufzeit auf O(n 3 ) gebracht werden. Der Speicherplatzbedarf ist quadratisch. 2.3 zusammenfassung Sekundäre RNA-Strukturen werden zwischen Hairpins, Stacks, Interiorloops, Bulges und Multiloops unterschieden. Der Algorithmus von Zuker nimmt die Energien der einzelnen sekundären RNA-Strukturelemente und summiert diese auf. Dadurch wird die beste sekundäre RNA-Struktur ermittelt. Dies ist nicht immer die biologisch relevanteste. So benötigen wir ein anderes Kriterium. McCaskill berechnet die Wahrscheinlichkeit für jedes Basenpaar. Damit lassen sich Rückschlüsse auf sekundäre RNA-Strukturen schliessen. Beide Algorithmen werden durch dynamische Programmierung effizient implementiert.
23 A L G E B R A I S C H E N D Y N A M I S C H E N P R O G R A M M I E R U N G 3 In diesem Kapitel führen wir das Konzept der algebraischen dynamischen Programmierung (ADP) ein, das eine neue Variante der dynamischen Programmierung ist. Desweiteren stellen wir die Programmierumgebung Bellman s Gap entwickelt von G. Sauthoff vor. Diese erlaubt eine effiziente Lösung von ADP-Problemen und benutzt eine einfache und intuitive Programmiersprache. 3.1 algebraische dynamische programmierun ein neues programmierkonzept Vergleich zur klassischen dynamischen Programmieren Die Entwicklung des Prinzips der algebraischen dynamischen Programmierung (ADP) begann Verwandt ist dieses Prinzip, sowohl mit dem algebraischen Pfad Problem in der Informatik als auch mit der algebraischen Geometrie in der Mathematik. Wir halten uns an die Definitionen und Methoden, vorgestellt von Robert Giegerich und Carsten Meyer [2]. Mit ADP lassen sich kombinatorische Optimierungsprobleme in polynomieller Zeit lösen, indem das Problem rekursiv zerlegt wird und Zwischenergebnisse in Tabellen gespeichert werden. Voraussetzung ist, dass das Problem das Bellman sche Prinzip der Optimalität erfüllt [1]. Der große Unterschied zur einfachen dynamischen Programmierung (DP) liegt darin, dass ADP zur Lösung des Problems kontext freie Grammatiken, sowie Algebren und Signaturen verwendet. Das Optimalitätsproblem wird durch Anwendung der Algebra auf die entsprechende Grammatik unter Beachtung der gegebenen Signatur gelöst. Dadurch lassen sich einige Nachteile der DP lösen. Ein Überblick liefert die Tabelle 1. Ein entscheidender Vorteil von ADP ist die Möglichkeit zu einer flexibleren Implementierung als in DP. Im folgenden erklären wir das Prinzip der algebraischen dynamischen Programmierung und die dazu benötigten Elemente Das Prinzip der Algebraischen Dynamischen Programmierung definition (ADP-Problem) Ein Problem der algebraischen dynamischen Programmierung besteht aus folgenden Teilen: 16
Binäre Bäume. 1. Allgemeines. 2. Funktionsweise. 2.1 Eintragen
 Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Kapiteltests zum Leitprogramm Binäre Suchbäume
 Kapiteltests zum Leitprogramm Binäre Suchbäume Björn Steffen Timur Erdag überarbeitet von Christina Class Binäre Suchbäume Kapiteltests für das ETH-Leitprogramm Adressaten und Institutionen Das Leitprogramm
Kapiteltests zum Leitprogramm Binäre Suchbäume Björn Steffen Timur Erdag überarbeitet von Christina Class Binäre Suchbäume Kapiteltests für das ETH-Leitprogramm Adressaten und Institutionen Das Leitprogramm
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Theoretische Grundlagen der Informatik WS 09/10
 Theoretische Grundlagen der Informatik WS 09/10 - Tutorium 6 - Michael Kirsten und Kai Wallisch Sitzung 13 02.02.2010 Inhaltsverzeichnis 1 Formeln zur Berechnung Aufgabe 1 2 Hamming-Distanz Aufgabe 2 3
Theoretische Grundlagen der Informatik WS 09/10 - Tutorium 6 - Michael Kirsten und Kai Wallisch Sitzung 13 02.02.2010 Inhaltsverzeichnis 1 Formeln zur Berechnung Aufgabe 1 2 Hamming-Distanz Aufgabe 2 3
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Stellen Sie bitte den Cursor in die Spalte B2 und rufen die Funktion Sverweis auf. Es öffnet sich folgendes Dialogfenster
 Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage:
 Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Entscheidungsbäume. Definition Entscheidungsbaum. Frage: Gibt es einen Sortieralgorithmus mit o(n log n) Vergleichen?
 Entscheidungsbäume Frage: Gibt es einen Sortieralgorithmus mit o(n log n) Vergleichen? Definition Entscheidungsbaum Sei T ein Binärbaum und A = {a 1,..., a n } eine zu sortierenden Menge. T ist ein Entscheidungsbaum
Entscheidungsbäume Frage: Gibt es einen Sortieralgorithmus mit o(n log n) Vergleichen? Definition Entscheidungsbaum Sei T ein Binärbaum und A = {a 1,..., a n } eine zu sortierenden Menge. T ist ein Entscheidungsbaum
Konzepte der Informatik
 Konzepte der Informatik Vorkurs Informatik zum WS 2011/2012 26.09. - 30.09.2011 17.10. - 21.10.2011 Dr. Werner Struckmann / Christoph Peltz Stark angelehnt an Kapitel 1 aus "Abenteuer Informatik" von Jens
Konzepte der Informatik Vorkurs Informatik zum WS 2011/2012 26.09. - 30.09.2011 17.10. - 21.10.2011 Dr. Werner Struckmann / Christoph Peltz Stark angelehnt an Kapitel 1 aus "Abenteuer Informatik" von Jens
Objektorientierte Programmierung für Anfänger am Beispiel PHP
 Objektorientierte Programmierung für Anfänger am Beispiel PHP Johannes Mittendorfer http://jmittendorfer.hostingsociety.com 19. August 2012 Abstract Dieses Dokument soll die Vorteile der objektorientierten
Objektorientierte Programmierung für Anfänger am Beispiel PHP Johannes Mittendorfer http://jmittendorfer.hostingsociety.com 19. August 2012 Abstract Dieses Dokument soll die Vorteile der objektorientierten
4. Jeder Knoten hat höchstens zwei Kinder, ein linkes und ein rechtes.
 Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
t r Lineare Codierung von Binärbbäumen (Wörter über dem Alphabet {, }) Beispiel code( ) = code(, t l, t r ) = code(t l ) code(t r )
 Definition B : Menge der binären Bäume, rekursiv definiert durch die Regeln: ist ein binärer Baum sind t l, t r binäre Bäume, so ist auch t =, t l, t r ein binärer Baum nur das, was durch die beiden vorigen
Definition B : Menge der binären Bäume, rekursiv definiert durch die Regeln: ist ein binärer Baum sind t l, t r binäre Bäume, so ist auch t =, t l, t r ein binärer Baum nur das, was durch die beiden vorigen
15 Optimales Kodieren
 15 Optimales Kodieren Es soll ein optimaler Kodierer C(T ) entworfen werden, welcher eine Information (z.b. Text T ) mit möglichst geringer Bitanzahl eindeutig überträgt. Die Anforderungen an den optimalen
15 Optimales Kodieren Es soll ein optimaler Kodierer C(T ) entworfen werden, welcher eine Information (z.b. Text T ) mit möglichst geringer Bitanzahl eindeutig überträgt. Die Anforderungen an den optimalen
Welche Unterschiede gibt es zwischen einem CAPAund einem Audiometrie- Test?
 Welche Unterschiede gibt es zwischen einem CAPAund einem Audiometrie- Test? Auch wenn die Messungsmethoden ähnlich sind, ist das Ziel beider Systeme jedoch ein anderes. Gwenolé NEXER g.nexer@hearin gp
Welche Unterschiede gibt es zwischen einem CAPAund einem Audiometrie- Test? Auch wenn die Messungsmethoden ähnlich sind, ist das Ziel beider Systeme jedoch ein anderes. Gwenolé NEXER g.nexer@hearin gp
Alignment-Verfahren zum Vergleich biologischer Sequenzen
 zum Vergleich biologischer Sequenzen Hans-Joachim Böckenhauer Dennis Komm Volkshochschule Zürich. April Ein biologisches Problem Fragestellung Finde eine Methode zum Vergleich von DNA-Molekülen oder Proteinen
zum Vergleich biologischer Sequenzen Hans-Joachim Böckenhauer Dennis Komm Volkshochschule Zürich. April Ein biologisches Problem Fragestellung Finde eine Methode zum Vergleich von DNA-Molekülen oder Proteinen
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
OECD Programme for International Student Assessment PISA 2000. Lösungen der Beispielaufgaben aus dem Mathematiktest. Deutschland
 OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
ZfP-Sonderpreis der DGZfP beim Regionalwettbewerb Jugend forscht BREMERHAVEN. Der Zauberwürfel-Roboter. Paul Giese. Schule: Wilhelm-Raabe-Schule
 ZfP-Sonderpreis der DGZfP beim Regionalwettbewerb Jugend forscht BREMERHAVEN Der Zauberwürfel-Roboter Paul Giese Schule: Wilhelm-Raabe-Schule Jugend forscht 2013 Kurzfassung Regionalwettbewerb Bremerhaven
ZfP-Sonderpreis der DGZfP beim Regionalwettbewerb Jugend forscht BREMERHAVEN Der Zauberwürfel-Roboter Paul Giese Schule: Wilhelm-Raabe-Schule Jugend forscht 2013 Kurzfassung Regionalwettbewerb Bremerhaven
Wir basteln einen Jahreskalender mit MS Excel.
 Wir basteln einen Jahreskalender mit MS Excel. In meinen Seminaren werde ich hin und wieder nach einem Excel-Jahreskalender gefragt. Im Internet findet man natürlich eine ganze Reihe mehr oder weniger
Wir basteln einen Jahreskalender mit MS Excel. In meinen Seminaren werde ich hin und wieder nach einem Excel-Jahreskalender gefragt. Im Internet findet man natürlich eine ganze Reihe mehr oder weniger
Motivation. Formale Grundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen. Informales Beispiel. Informales Beispiel.
 Kontextfreie Kontextfreie Motivation Formale rundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen Bisher hatten wir Automaten, die Wörter akzeptieren Frank Heitmann heitmann@informatik.uni-hamburg.de
Kontextfreie Kontextfreie Motivation Formale rundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen Bisher hatten wir Automaten, die Wörter akzeptieren Frank Heitmann heitmann@informatik.uni-hamburg.de
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Rekursionen. Georg Anegg 25. November 2009. Methoden und Techniken an Beispielen erklärt
 Methoden und Techniken an Beispielen erklärt Georg Anegg 5. November 009 Beispiel. Die Folge {a n } sei wie folgt definiert (a, d, q R, q ): a 0 a, a n+ a n q + d (n 0) Man bestimme eine explizite Darstellung
Methoden und Techniken an Beispielen erklärt Georg Anegg 5. November 009 Beispiel. Die Folge {a n } sei wie folgt definiert (a, d, q R, q ): a 0 a, a n+ a n q + d (n 0) Man bestimme eine explizite Darstellung
1 topologisches Sortieren
 Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
2.11 Kontextfreie Grammatiken und Parsebäume
 2.11 Kontextfreie Grammatiken und Parsebäume Beispiel: Beispiel (Teil 3): Beweis für L(G) L: Alle Strings aus L der Länge 0 und 2 sind auch in L(G). Als Induktionsannahme gehen wir davon aus, dass alle
2.11 Kontextfreie Grammatiken und Parsebäume Beispiel: Beispiel (Teil 3): Beweis für L(G) L: Alle Strings aus L der Länge 0 und 2 sind auch in L(G). Als Induktionsannahme gehen wir davon aus, dass alle
Kapitel 5: Dynamisches Programmieren Gliederung
 Gliederung 1. Grundlagen 2. Zahlentheoretische Algorithmen 3. Sortierverfahren 4. Ausgewählte Datenstrukturen 5. Dynamisches Programmieren 6. Graphalgorithmen 7. String-Matching 8. Kombinatorische Algorithmen
Gliederung 1. Grundlagen 2. Zahlentheoretische Algorithmen 3. Sortierverfahren 4. Ausgewählte Datenstrukturen 5. Dynamisches Programmieren 6. Graphalgorithmen 7. String-Matching 8. Kombinatorische Algorithmen
M. Graefenhan 2000-12-07. Übungen zu C. Blatt 3. Musterlösung
 M. Graefenhan 2000-12-07 Aufgabe Lösungsweg Übungen zu C Blatt 3 Musterlösung Schreiben Sie ein Programm, das die Häufigkeit von Zeichen in einem eingelesenen String feststellt. Benutzen Sie dazu ein zweidimensionales
M. Graefenhan 2000-12-07 Aufgabe Lösungsweg Übungen zu C Blatt 3 Musterlösung Schreiben Sie ein Programm, das die Häufigkeit von Zeichen in einem eingelesenen String feststellt. Benutzen Sie dazu ein zweidimensionales
Formale Sprachen und Grammatiken
 Formale Sprachen und Grammatiken Jede Sprache besitzt die Aspekte Semantik (Bedeutung) und Syntax (formaler Aufbau). Die zulässige und korrekte Form der Wörter und Sätze einer Sprache wird durch die Syntax
Formale Sprachen und Grammatiken Jede Sprache besitzt die Aspekte Semantik (Bedeutung) und Syntax (formaler Aufbau). Die zulässige und korrekte Form der Wörter und Sätze einer Sprache wird durch die Syntax
4. AUSSAGENLOGIK: SYNTAX. Der Unterschied zwischen Objektsprache und Metasprache lässt sich folgendermaßen charakterisieren:
 4. AUSSAGENLOGIK: SYNTAX 4.1 Objektsprache und Metasprache 4.2 Gebrauch und Erwähnung 4.3 Metavariablen: Verallgemeinerndes Sprechen über Ausdrücke von AL 4.4 Die Sprache der Aussagenlogik 4.5 Terminologie
4. AUSSAGENLOGIK: SYNTAX 4.1 Objektsprache und Metasprache 4.2 Gebrauch und Erwähnung 4.3 Metavariablen: Verallgemeinerndes Sprechen über Ausdrücke von AL 4.4 Die Sprache der Aussagenlogik 4.5 Terminologie
Austausch- bzw. Übergangsprozesse und Gleichgewichtsverteilungen
 Austausch- bzw. Übergangsrozesse und Gleichgewichtsverteilungen Wir betrachten ein System mit verschiedenen Zuständen, zwischen denen ein Austausch stattfinden kann. Etwa soziale Schichten in einer Gesellschaft:
Austausch- bzw. Übergangsrozesse und Gleichgewichtsverteilungen Wir betrachten ein System mit verschiedenen Zuständen, zwischen denen ein Austausch stattfinden kann. Etwa soziale Schichten in einer Gesellschaft:
Programmiersprachen und Übersetzer
 Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Die Gleichung A x = a hat für A 0 die eindeutig bestimmte Lösung. Für A=0 und a 0 existiert keine Lösung.
 Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Grammatiken. Einführung
 Einführung Beispiel: Die arithmetischen Ausdrücke über der Variablen a und den Operationen + und können wie folgt definiert werden: a, a + a und a a sind arithmetische Ausdrücke Wenn A und B arithmetische
Einführung Beispiel: Die arithmetischen Ausdrücke über der Variablen a und den Operationen + und können wie folgt definiert werden: a, a + a und a a sind arithmetische Ausdrücke Wenn A und B arithmetische
Excel Pivot-Tabellen 2010 effektiv
 7.2 Berechnete Felder Falls in der Datenquelle die Zahlen nicht in der Form vorliegen wie Sie diese benötigen, können Sie die gewünschten Ergebnisse mit Formeln berechnen. Dazu erzeugen Sie ein berechnetes
7.2 Berechnete Felder Falls in der Datenquelle die Zahlen nicht in der Form vorliegen wie Sie diese benötigen, können Sie die gewünschten Ergebnisse mit Formeln berechnen. Dazu erzeugen Sie ein berechnetes
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
 50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
Vorkurs Informatik WiSe 15/16
 Konzepte der Informatik Dr. Werner Struckmann / Stephan Mielke, Jakob Garbe, 16.10.2015 Technische Universität Braunschweig, IPS Inhaltsverzeichnis Suchen Binärsuche Binäre Suchbäume 16.10.2015 Dr. Werner
Konzepte der Informatik Dr. Werner Struckmann / Stephan Mielke, Jakob Garbe, 16.10.2015 Technische Universität Braunschweig, IPS Inhaltsverzeichnis Suchen Binärsuche Binäre Suchbäume 16.10.2015 Dr. Werner
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Gehen wir einmal davon aus, dass die von uns angenommenen
 geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
Tutorium Informatik 1. Aufgabe 2: Formatierte Ein- und Ausgabe
 Tutorium Informatik 1 Aufgabe 2: Formatierte Ein- und Ausgabe Fachbereich: Elektrotechnik Inhaltsverzeichnis 1 Aufgabe 1 2 Benötigte Funktionen und Schlüsselwörter 2 Robert Halas / FH Regensburg - 2003
Tutorium Informatik 1 Aufgabe 2: Formatierte Ein- und Ausgabe Fachbereich: Elektrotechnik Inhaltsverzeichnis 1 Aufgabe 1 2 Benötigte Funktionen und Schlüsselwörter 2 Robert Halas / FH Regensburg - 2003
Grundlagen der Theoretischen Informatik, SoSe 2008
 1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
Abamsoft Finos im Zusammenspiel mit shop to date von DATA BECKER
 Abamsoft Finos im Zusammenspiel mit shop to date von DATA BECKER Abamsoft Finos in Verbindung mit der Webshopanbindung wurde speziell auf die Shop-Software shop to date von DATA BECKER abgestimmt. Mit
Abamsoft Finos im Zusammenspiel mit shop to date von DATA BECKER Abamsoft Finos in Verbindung mit der Webshopanbindung wurde speziell auf die Shop-Software shop to date von DATA BECKER abgestimmt. Mit
Es sollte die MS-DOS Eingabeaufforderung starten. Geben Sie nun den Befehl javac ein.
 Schritt 1: Installation des Javacompilers JDK. Der erste Start mit Eclipse Bevor Sie den Java-Compiler installieren sollten Sie sich vergewissern, ob er eventuell schon installiert ist. Gehen sie wie folgt
Schritt 1: Installation des Javacompilers JDK. Der erste Start mit Eclipse Bevor Sie den Java-Compiler installieren sollten Sie sich vergewissern, ob er eventuell schon installiert ist. Gehen sie wie folgt
EINFACHES HAUSHALT- KASSABUCH
 EINFACHES HAUSHALT- KASSABUCH Arbeiten mit Excel Wir erstellen ein einfaches Kassabuch zur Führung einer Haushalts- oder Portokasse Roland Liebing, im November 2012 Eine einfache Haushalt-Buchhaltung (Kassabuch)
EINFACHES HAUSHALT- KASSABUCH Arbeiten mit Excel Wir erstellen ein einfaches Kassabuch zur Führung einer Haushalts- oder Portokasse Roland Liebing, im November 2012 Eine einfache Haushalt-Buchhaltung (Kassabuch)
Schritt für Schritt zur Krankenstandsstatistik
 Schritt für Schritt zur Krankenstandsstatistik Eine Anleitung zur Nutzung der Excel-Tabellen zur Erhebung des Krankenstands. Entwickelt durch: Kooperationsprojekt Arbeitsschutz in der ambulanten Pflege
Schritt für Schritt zur Krankenstandsstatistik Eine Anleitung zur Nutzung der Excel-Tabellen zur Erhebung des Krankenstands. Entwickelt durch: Kooperationsprojekt Arbeitsschutz in der ambulanten Pflege
Das große ElterngeldPlus 1x1. Alles über das ElterngeldPlus. Wer kann ElterngeldPlus beantragen? ElterngeldPlus verstehen ein paar einleitende Fakten
 Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
Datenstrukturen & Algorithmen
 Datenstrukturen & Algorithmen Matthias Zwicker Universität Bern Frühling 2010 Übersicht Binäre Suchbäume Einführung und Begriffe Binäre Suchbäume 2 Binäre Suchbäume Datenstruktur für dynamische Mengen
Datenstrukturen & Algorithmen Matthias Zwicker Universität Bern Frühling 2010 Übersicht Binäre Suchbäume Einführung und Begriffe Binäre Suchbäume 2 Binäre Suchbäume Datenstruktur für dynamische Mengen
3.3 Eigenwerte und Eigenräume, Diagonalisierung
 3.3 Eigenwerte und Eigenräume, Diagonalisierung Definition und Lemma 3.3.1. Sei V ein K-Vektorraum, φ End K (V ), λ K. Wir defnieren den zu λ gehörigen Eigenraum von φ als Dies ist ein Unterraum von V.
3.3 Eigenwerte und Eigenräume, Diagonalisierung Definition und Lemma 3.3.1. Sei V ein K-Vektorraum, φ End K (V ), λ K. Wir defnieren den zu λ gehörigen Eigenraum von φ als Dies ist ein Unterraum von V.
Suche schlecht beschriftete Bilder mit Eigenen Abfragen
 Suche schlecht beschriftete Bilder mit Eigenen Abfragen Ist die Bilderdatenbank über einen längeren Zeitraum in Benutzung, so steigt die Wahrscheinlichkeit für schlecht beschriftete Bilder 1. Insbesondere
Suche schlecht beschriftete Bilder mit Eigenen Abfragen Ist die Bilderdatenbank über einen längeren Zeitraum in Benutzung, so steigt die Wahrscheinlichkeit für schlecht beschriftete Bilder 1. Insbesondere
Task: Nmap Skripte ausführen
 Task: Nmap Skripte ausführen Inhalt Einfache Netzwerkscans mit NSE Ausführen des Scans Anpassung der Parameter Einleitung Copyright 2009-2015 Greenbone Networks GmbH Herkunft und aktuellste Version dieses
Task: Nmap Skripte ausführen Inhalt Einfache Netzwerkscans mit NSE Ausführen des Scans Anpassung der Parameter Einleitung Copyright 2009-2015 Greenbone Networks GmbH Herkunft und aktuellste Version dieses
Hilfe zur Urlaubsplanung und Zeiterfassung
 Hilfe zur Urlaubsplanung und Zeiterfassung Urlaubs- und Arbeitsplanung: Mit der Urlaubs- und Arbeitsplanung kann jeder Mitarbeiter in Coffee seine Zeiten eintragen. Die Eintragung kann mit dem Status anfragen,
Hilfe zur Urlaubsplanung und Zeiterfassung Urlaubs- und Arbeitsplanung: Mit der Urlaubs- und Arbeitsplanung kann jeder Mitarbeiter in Coffee seine Zeiten eintragen. Die Eintragung kann mit dem Status anfragen,
1 Vom Problem zum Programm
 Hintergrundinformationen zur Vorlesung GRUNDLAGEN DER INFORMATIK I Studiengang Elektrotechnik WS 02/03 AG Betriebssysteme FB3 Kirsten Berkenkötter 1 Vom Problem zum Programm Aufgabenstellung analysieren
Hintergrundinformationen zur Vorlesung GRUNDLAGEN DER INFORMATIK I Studiengang Elektrotechnik WS 02/03 AG Betriebssysteme FB3 Kirsten Berkenkötter 1 Vom Problem zum Programm Aufgabenstellung analysieren
Meet the Germans. Lerntipp zur Schulung der Fertigkeit des Sprechens. Lerntipp und Redemittel zur Präsentation oder einen Vortrag halten
 Meet the Germans Lerntipp zur Schulung der Fertigkeit des Sprechens Lerntipp und Redemittel zur Präsentation oder einen Vortrag halten Handreichungen für die Kursleitung Seite 2, Meet the Germans 2. Lerntipp
Meet the Germans Lerntipp zur Schulung der Fertigkeit des Sprechens Lerntipp und Redemittel zur Präsentation oder einen Vortrag halten Handreichungen für die Kursleitung Seite 2, Meet the Germans 2. Lerntipp
7 Rechnen mit Polynomen
 7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
Programmieren I. Kapitel 7. Sortieren und Suchen
 Programmieren I Kapitel 7. Sortieren und Suchen Kapitel 7: Sortieren und Suchen Ziel: Varianten der häufigsten Anwendung kennenlernen Ordnung Suchen lineares Suchen Binärsuche oder Bisektionssuche Sortieren
Programmieren I Kapitel 7. Sortieren und Suchen Kapitel 7: Sortieren und Suchen Ziel: Varianten der häufigsten Anwendung kennenlernen Ordnung Suchen lineares Suchen Binärsuche oder Bisektionssuche Sortieren
Robot Karol für Delphi
 Robot Karol für Delphi Reinhard Nitzsche, OSZ Handel I Version 0.1 vom 24. Januar 2003 Zusammenfassung Nach der Einführung in die (variablenfreie) Programmierung mit Robot Karol von Freiberger und Krško
Robot Karol für Delphi Reinhard Nitzsche, OSZ Handel I Version 0.1 vom 24. Januar 2003 Zusammenfassung Nach der Einführung in die (variablenfreie) Programmierung mit Robot Karol von Freiberger und Krško
Lineare Differentialgleichungen erster Ordnung erkennen
 Lineare Differentialgleichungen erster Ordnung In diesem Kapitel... Erkennen, wie Differentialgleichungen erster Ordnung aussehen en für Differentialgleichungen erster Ordnung und ohne -Terme finden Die
Lineare Differentialgleichungen erster Ordnung In diesem Kapitel... Erkennen, wie Differentialgleichungen erster Ordnung aussehen en für Differentialgleichungen erster Ordnung und ohne -Terme finden Die
etutor Benutzerhandbuch XQuery Benutzerhandbuch Georg Nitsche
 etutor Benutzerhandbuch Benutzerhandbuch XQuery Georg Nitsche Version 1.0 Stand März 2006 Versionsverlauf: Version Autor Datum Änderungen 1.0 gn 06.03.2006 Fertigstellung der ersten Version Inhaltsverzeichnis:
etutor Benutzerhandbuch Benutzerhandbuch XQuery Georg Nitsche Version 1.0 Stand März 2006 Versionsverlauf: Version Autor Datum Änderungen 1.0 gn 06.03.2006 Fertigstellung der ersten Version Inhaltsverzeichnis:
Übungen zur Softwaretechnik
 Technische Universität München Fakultät für Informatik Lehrstuhl IV: Software & Systems Engineering Markus Pister, Dr. Bernhard Rumpe WS 2002/2003 Lösungsblatt 9 17. Dezember 2002 www4.in.tum.de/~rumpe/se
Technische Universität München Fakultät für Informatik Lehrstuhl IV: Software & Systems Engineering Markus Pister, Dr. Bernhard Rumpe WS 2002/2003 Lösungsblatt 9 17. Dezember 2002 www4.in.tum.de/~rumpe/se
Ohne Fehler geht es nicht Doch wie viele Fehler sind erlaubt?
 Ohne Fehler geht es nicht Doch wie viele Fehler sind erlaubt? Behandelte Fragestellungen Was besagt eine Fehlerquote? Welche Bezugsgröße ist geeignet? Welche Fehlerquote ist gerade noch zulässig? Wie stellt
Ohne Fehler geht es nicht Doch wie viele Fehler sind erlaubt? Behandelte Fragestellungen Was besagt eine Fehlerquote? Welche Bezugsgröße ist geeignet? Welche Fehlerquote ist gerade noch zulässig? Wie stellt
Anleitung über den Umgang mit Schildern
 Anleitung über den Umgang mit Schildern -Vorwort -Wo bekommt man Schilder? -Wo und wie speichert man die Schilder? -Wie füge ich die Schilder in meinen Track ein? -Welche Bauteile kann man noch für Schilder
Anleitung über den Umgang mit Schildern -Vorwort -Wo bekommt man Schilder? -Wo und wie speichert man die Schilder? -Wie füge ich die Schilder in meinen Track ein? -Welche Bauteile kann man noch für Schilder
Lineare Gleichungssysteme
 Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Lineare Funktionen. 1 Proportionale Funktionen 3 1.1 Definition... 3 1.2 Eigenschaften... 3. 2 Steigungsdreieck 3
 Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
WAS finde ich WO im Beipackzettel
 WAS finde ich WO im Beipackzettel Sie haben eine Frage zu Ihrem? Meist finden Sie die Antwort im Beipackzettel (offiziell "Gebrauchsinformation" genannt). Der Aufbau der Beipackzettel ist von den Behörden
WAS finde ich WO im Beipackzettel Sie haben eine Frage zu Ihrem? Meist finden Sie die Antwort im Beipackzettel (offiziell "Gebrauchsinformation" genannt). Der Aufbau der Beipackzettel ist von den Behörden
Handbuch ECDL 2003 Basic Modul 5: Datenbank Grundlagen von relationalen Datenbanken
 Handbuch ECDL 2003 Basic Modul 5: Datenbank Grundlagen von relationalen Datenbanken Dateiname: ecdl5_01_00_documentation_standard.doc Speicherdatum: 14.02.2005 ECDL 2003 Basic Modul 5 Datenbank - Grundlagen
Handbuch ECDL 2003 Basic Modul 5: Datenbank Grundlagen von relationalen Datenbanken Dateiname: ecdl5_01_00_documentation_standard.doc Speicherdatum: 14.02.2005 ECDL 2003 Basic Modul 5 Datenbank - Grundlagen
Approximation durch Taylorpolynome
 TU Berlin Fakultät II - Mathematik und Naturwissenschaften Sekretariat MA 4-1 Straße des 17. Juni 10623 Berlin Hochschultag Approximation durch Taylorpolynome Im Rahmen der Schülerinnen- und Schüler-Uni
TU Berlin Fakultät II - Mathematik und Naturwissenschaften Sekretariat MA 4-1 Straße des 17. Juni 10623 Berlin Hochschultag Approximation durch Taylorpolynome Im Rahmen der Schülerinnen- und Schüler-Uni
Plotten von Linien ( nach Jack Bresenham, 1962 )
 Plotten von Linien ( nach Jack Bresenham, 1962 ) Ac Eine auf dem Bildschirm darzustellende Linie sieht treppenförmig aus, weil der Computer Linien aus einzelnen (meist quadratischen) Bildpunkten, Pixels
Plotten von Linien ( nach Jack Bresenham, 1962 ) Ac Eine auf dem Bildschirm darzustellende Linie sieht treppenförmig aus, weil der Computer Linien aus einzelnen (meist quadratischen) Bildpunkten, Pixels
Bauteilattribute als Sachdaten anzeigen
 Mit den speedikon Attributfiltern können Sie die speedikon Attribute eines Bauteils als MicroStation Sachdaten an die Elemente anhängen Inhalte Was ist ein speedikon Attribut?... 3 Eigene Attribute vergeben...
Mit den speedikon Attributfiltern können Sie die speedikon Attribute eines Bauteils als MicroStation Sachdaten an die Elemente anhängen Inhalte Was ist ein speedikon Attribut?... 3 Eigene Attribute vergeben...
Guide DynDNS und Portforwarding
 Guide DynDNS und Portforwarding Allgemein Um Geräte im lokalen Netzwerk von überall aus über das Internet erreichen zu können, kommt man um die Themen Dynamik DNS (kurz DynDNS) und Portweiterleitung(auch
Guide DynDNS und Portforwarding Allgemein Um Geräte im lokalen Netzwerk von überall aus über das Internet erreichen zu können, kommt man um die Themen Dynamik DNS (kurz DynDNS) und Portweiterleitung(auch
Informatik 12 Datenbanken SQL-Einführung
 Informatik 12 Datenbanken SQL-Einführung Gierhardt Vorbemerkungen Bisher haben wir Datenbanken nur über einzelne Tabellen kennen gelernt. Stehen mehrere Tabellen in gewissen Beziehungen zur Beschreibung
Informatik 12 Datenbanken SQL-Einführung Gierhardt Vorbemerkungen Bisher haben wir Datenbanken nur über einzelne Tabellen kennen gelernt. Stehen mehrere Tabellen in gewissen Beziehungen zur Beschreibung
Dossier: Rechnungen und Lieferscheine in Word
 www.sekretaerinnen-service.de Dossier: Rechnungen und Lieferscheine in Word Es muss nicht immer Excel sein Wenn Sie eine Vorlage für eine Rechnung oder einen Lieferschein erstellen möchten, brauchen Sie
www.sekretaerinnen-service.de Dossier: Rechnungen und Lieferscheine in Word Es muss nicht immer Excel sein Wenn Sie eine Vorlage für eine Rechnung oder einen Lieferschein erstellen möchten, brauchen Sie
Inhalt. 1 Einleitung AUTOMATISCHE DATENSICHERUNG AUF EINEN CLOUDSPEICHER
 AUTOMATISCHE DATENSICHERUNG AUF EINEN CLOUDSPEICHER Inhalt 1 Einleitung... 1 2 Einrichtung der Aufgabe für die automatische Sicherung... 2 2.1 Die Aufgabenplanung... 2 2.2 Der erste Testlauf... 9 3 Problembehebung...
AUTOMATISCHE DATENSICHERUNG AUF EINEN CLOUDSPEICHER Inhalt 1 Einleitung... 1 2 Einrichtung der Aufgabe für die automatische Sicherung... 2 2.1 Die Aufgabenplanung... 2 2.2 Der erste Testlauf... 9 3 Problembehebung...
Programmierkurs Java
 Programmierkurs Java Dr. Dietrich Boles Aufgaben zu UE16-Rekursion (Stand 09.12.2011) Aufgabe 1: Implementieren Sie in Java ein Programm, das solange einzelne Zeichen vom Terminal einliest, bis ein #-Zeichen
Programmierkurs Java Dr. Dietrich Boles Aufgaben zu UE16-Rekursion (Stand 09.12.2011) Aufgabe 1: Implementieren Sie in Java ein Programm, das solange einzelne Zeichen vom Terminal einliest, bis ein #-Zeichen
Handbuch ECDL 2003 Professional Modul 2: Tabellenkalkulation Vorlagen benutzen und ändern
 Handbuch ECDL 2003 Professional Modul 2: Tabellenkalkulation Vorlagen benutzen und ändern Dateiname: ecdl_p2_02_03_documentation.doc Speicherdatum: 08.12.2004 ECDL 2003 Professional Modul 2 Tabellenkalkulation
Handbuch ECDL 2003 Professional Modul 2: Tabellenkalkulation Vorlagen benutzen und ändern Dateiname: ecdl_p2_02_03_documentation.doc Speicherdatum: 08.12.2004 ECDL 2003 Professional Modul 2 Tabellenkalkulation
Eine Logikschaltung zur Addition zweier Zahlen
 Eine Logikschaltung zur Addition zweier Zahlen Grundlegender Ansatz für die Umsetzung arithmetischer Operationen als elektronische Schaltung ist die Darstellung von Zahlen im Binärsystem. Eine Logikschaltung
Eine Logikschaltung zur Addition zweier Zahlen Grundlegender Ansatz für die Umsetzung arithmetischer Operationen als elektronische Schaltung ist die Darstellung von Zahlen im Binärsystem. Eine Logikschaltung
Einrichten einer Festplatte mit FDISK unter Windows 95/98/98SE/Me
 Einrichten einer Festplatte mit FDISK unter Windows 95/98/98SE/Me Bevor Sie die Platte zum ersten Mal benutzen können, muss sie noch partitioniert und formatiert werden! Vorher zeigt sich die Festplatte
Einrichten einer Festplatte mit FDISK unter Windows 95/98/98SE/Me Bevor Sie die Platte zum ersten Mal benutzen können, muss sie noch partitioniert und formatiert werden! Vorher zeigt sich die Festplatte
1. Einführung. 2. Weitere Konten anlegen
 1. Einführung In orgamax stehen Ihnen die gängigsten Konten des Kontenrahmens SKR03 und SKR04 zur Verfügung. Damit sind im Normalfall alle Konten abgedeckt, die Sie zur Verbuchung benötigen. Eine ausführliche
1. Einführung In orgamax stehen Ihnen die gängigsten Konten des Kontenrahmens SKR03 und SKR04 zur Verfügung. Damit sind im Normalfall alle Konten abgedeckt, die Sie zur Verbuchung benötigen. Eine ausführliche
APP-GFP/Fluoreszenzmikroskop. Aufnahmen neuronaler Zellen, mit freund. Genehmigung von Prof. Stefan Kins, TU Kaiserslautern
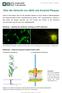 Über die Herkunft von Aβ42 und Amyloid-Plaques Heute ist sicher belegt, dass sich die amyloiden Plaques aus einer Vielzahl an Abbaufragmenten des Amyloid-Vorläufer-Proteins (amyloid-precursor-protein,
Über die Herkunft von Aβ42 und Amyloid-Plaques Heute ist sicher belegt, dass sich die amyloiden Plaques aus einer Vielzahl an Abbaufragmenten des Amyloid-Vorläufer-Proteins (amyloid-precursor-protein,
Gleichungen Lösen. Ein graphischer Blick auf Gleichungen
 Gleichungen Lösen Was bedeutet es, eine Gleichung zu lösen? Was ist überhaupt eine Gleichung? Eine Gleichung ist, grundsätzlich eine Aussage über zwei mathematische Terme, dass sie gleich sind. Ein Term
Gleichungen Lösen Was bedeutet es, eine Gleichung zu lösen? Was ist überhaupt eine Gleichung? Eine Gleichung ist, grundsätzlich eine Aussage über zwei mathematische Terme, dass sie gleich sind. Ein Term
Lange Nacht der Wissenschaft. Ein Klassiker. Die Mathematik der Kürzesten Wege
 Lange Nacht der Wissenschaft Ein Klassiker Die Mathematik der Kürzesten Wege 09.06.2007 schlechte@zib.de Konrad-Zuse-Zentrum für Informationstechnik Berlin (ZIB) http://www.zib.de/schlechte 2 Überblick
Lange Nacht der Wissenschaft Ein Klassiker Die Mathematik der Kürzesten Wege 09.06.2007 schlechte@zib.de Konrad-Zuse-Zentrum für Informationstechnik Berlin (ZIB) http://www.zib.de/schlechte 2 Überblick
Grundlagen der Künstlichen Intelligenz
 Grundlagen der Künstlichen Intelligenz 22. Constraint-Satisfaction-Probleme: Kantenkonsistenz Malte Helmert Universität Basel 14. April 2014 Constraint-Satisfaction-Probleme: Überblick Kapitelüberblick
Grundlagen der Künstlichen Intelligenz 22. Constraint-Satisfaction-Probleme: Kantenkonsistenz Malte Helmert Universität Basel 14. April 2014 Constraint-Satisfaction-Probleme: Überblick Kapitelüberblick
Datenbanken Kapitel 2
 Datenbanken Kapitel 2 1 Eine existierende Datenbank öffnen Eine Datenbank, die mit Microsoft Access erschaffen wurde, kann mit dem gleichen Programm auch wieder geladen werden: Die einfachste Methode ist,
Datenbanken Kapitel 2 1 Eine existierende Datenbank öffnen Eine Datenbank, die mit Microsoft Access erschaffen wurde, kann mit dem gleichen Programm auch wieder geladen werden: Die einfachste Methode ist,
40-Tage-Wunder- Kurs. Umarme, was Du nicht ändern kannst.
 40-Tage-Wunder- Kurs Umarme, was Du nicht ändern kannst. Das sagt Wikipedia: Als Wunder (griechisch thauma) gilt umgangssprachlich ein Ereignis, dessen Zustandekommen man sich nicht erklären kann, so dass
40-Tage-Wunder- Kurs Umarme, was Du nicht ändern kannst. Das sagt Wikipedia: Als Wunder (griechisch thauma) gilt umgangssprachlich ein Ereignis, dessen Zustandekommen man sich nicht erklären kann, so dass
Übung: Verwendung von Java-Threads
 Übung: Verwendung von Java-Threads Ziel der Übung: Diese Übung dient dazu, den Umgang mit Threads in der Programmiersprache Java kennenzulernen. Ein einfaches Java-Programm, das Threads nutzt, soll zum
Übung: Verwendung von Java-Threads Ziel der Übung: Diese Übung dient dazu, den Umgang mit Threads in der Programmiersprache Java kennenzulernen. Ein einfaches Java-Programm, das Threads nutzt, soll zum
schnell und portofrei erhältlich bei beck-shop.de DIE FACHBUCHHANDLUNG mitp/bhv
 Roboter programmieren mit NXC für Lego Mindstorms NXT 1. Auflage Roboter programmieren mit NXC für Lego Mindstorms NXT schnell und portofrei erhältlich bei beck-shop.de DIE FACHBUCHHANDLUNG mitp/bhv Verlag
Roboter programmieren mit NXC für Lego Mindstorms NXT 1. Auflage Roboter programmieren mit NXC für Lego Mindstorms NXT schnell und portofrei erhältlich bei beck-shop.de DIE FACHBUCHHANDLUNG mitp/bhv Verlag
Summenbildung in Bauteiltabellen mit If Then Abfrage
 Summenbildung in Bauteiltabellen mit If Then Abfrage Die in Bauteiltabellen ausgelesenen Werte lassen sich in jeder Spalte als Summe berechnen. So können selbstverständlich die Flächen der in der Tabelle
Summenbildung in Bauteiltabellen mit If Then Abfrage Die in Bauteiltabellen ausgelesenen Werte lassen sich in jeder Spalte als Summe berechnen. So können selbstverständlich die Flächen der in der Tabelle
Tipp III: Leiten Sie eine immer direkt anwendbare Formel her zur Berechnung der sogenannten "bedingten Wahrscheinlichkeit".
 Mathematik- Unterrichts- Einheiten- Datei e. V. Klasse 9 12 04/2015 Diabetes-Test Infos: www.mued.de Blutspenden werden auf Diabetes untersucht, das mit 8 % in der Bevölkerung verbreitet ist. Dabei werden
Mathematik- Unterrichts- Einheiten- Datei e. V. Klasse 9 12 04/2015 Diabetes-Test Infos: www.mued.de Blutspenden werden auf Diabetes untersucht, das mit 8 % in der Bevölkerung verbreitet ist. Dabei werden
8. Berechnung der kalkulatorischen Zinsen
 8. Berechnung der kalkulatorischen Zinsen 8.1. Allgemeines In der laufenden Rechnung werden im Konto 322.00 Zinsen nur die ermittelten Fremdkapitalzinsen erfasst. Sobald aber eine Betriebsabrechnung erstellt
8. Berechnung der kalkulatorischen Zinsen 8.1. Allgemeines In der laufenden Rechnung werden im Konto 322.00 Zinsen nur die ermittelten Fremdkapitalzinsen erfasst. Sobald aber eine Betriebsabrechnung erstellt
Kapitalerhöhung - Verbuchung
 Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
Novell Client. Anleitung. zur Verfügung gestellt durch: ZID Dezentrale Systeme. Februar 2015. ZID Dezentrale Systeme
 Novell Client Anleitung zur Verfügung gestellt durch: ZID Dezentrale Systeme Februar 2015 Seite 2 von 8 Mit der Einführung von Windows 7 hat sich die Novell-Anmeldung sehr stark verändert. Der Novell Client
Novell Client Anleitung zur Verfügung gestellt durch: ZID Dezentrale Systeme Februar 2015 Seite 2 von 8 Mit der Einführung von Windows 7 hat sich die Novell-Anmeldung sehr stark verändert. Der Novell Client
Das Briefträgerproblem
 Das Briefträgerproblem Paul Tabatabai 30. Dezember 2011 Inhaltsverzeichnis 1 Problemstellung und Modellierung 2 1.1 Problem................................ 2 1.2 Modellierung.............................
Das Briefträgerproblem Paul Tabatabai 30. Dezember 2011 Inhaltsverzeichnis 1 Problemstellung und Modellierung 2 1.1 Problem................................ 2 1.2 Modellierung.............................
Installation des Authorware Webplayers für den Internet Explorer unter Windows Vista
 Installation des Authorware Webplayers für den Internet Explorer unter Windows Vista Allgemeines: Bitte lesen Sie sich diese Anleitung zuerst einmal komplett durch. Am Besten, Sie drucken sich diese Anleitung
Installation des Authorware Webplayers für den Internet Explorer unter Windows Vista Allgemeines: Bitte lesen Sie sich diese Anleitung zuerst einmal komplett durch. Am Besten, Sie drucken sich diese Anleitung
WS 2008/09. Diskrete Strukturen
 WS 2008/09 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0809
WS 2008/09 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0809
Im Folgenden wird Ihnen an einem Beispiel erklärt, wie Sie Excel-Anlagen und Excel-Vorlagen erstellen können.
 Excel-Schnittstelle Im Folgenden wird Ihnen an einem Beispiel erklärt, wie Sie Excel-Anlagen und Excel-Vorlagen erstellen können. Voraussetzung: Microsoft Office Excel ab Version 2000 Zum verwendeten Beispiel:
Excel-Schnittstelle Im Folgenden wird Ihnen an einem Beispiel erklärt, wie Sie Excel-Anlagen und Excel-Vorlagen erstellen können. Voraussetzung: Microsoft Office Excel ab Version 2000 Zum verwendeten Beispiel:
Das Handbuch zu KNetAttach. Orville Bennett Übersetzung: Thomas Bögel
 Orville Bennett Übersetzung: Thomas Bögel 2 Inhaltsverzeichnis 1 Einführung 5 2 KNetAttach verwenden 6 2.1 Hinzufügen von Netzwerkordnern............................ 6 3 Rundgang durch KNetAttach 8 4 Danksagungen
Orville Bennett Übersetzung: Thomas Bögel 2 Inhaltsverzeichnis 1 Einführung 5 2 KNetAttach verwenden 6 2.1 Hinzufügen von Netzwerkordnern............................ 6 3 Rundgang durch KNetAttach 8 4 Danksagungen
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen
 Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Lernerfolge sichern - Ein wichtiger Beitrag zu mehr Motivation
 Lernerfolge sichern - Ein wichtiger Beitrag zu mehr Motivation Einführung Mit welchen Erwartungen gehen Jugendliche eigentlich in ihre Ausbildung? Wir haben zu dieser Frage einmal die Meinungen von Auszubildenden
Lernerfolge sichern - Ein wichtiger Beitrag zu mehr Motivation Einführung Mit welchen Erwartungen gehen Jugendliche eigentlich in ihre Ausbildung? Wir haben zu dieser Frage einmal die Meinungen von Auszubildenden
1. Einführung 2. 2. Erstellung einer Teillieferung 2. 3. Erstellung einer Teilrechnung 6
 Inhalt 1. Einführung 2 2. Erstellung einer Teillieferung 2 3. Erstellung einer Teilrechnung 6 4. Erstellung einer Sammellieferung/ Mehrere Aufträge zu einem Lieferschein zusammenfassen 11 5. Besonderheiten
Inhalt 1. Einführung 2 2. Erstellung einer Teillieferung 2 3. Erstellung einer Teilrechnung 6 4. Erstellung einer Sammellieferung/ Mehrere Aufträge zu einem Lieferschein zusammenfassen 11 5. Besonderheiten
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 3 1. Semester ARBEITSBLATT 3 RECHNEN MIT GANZEN ZAHLEN
 ARBEITSBLATT 3 RECHNEN MIT GANZEN ZAHLEN Wir wollen nun die Rechengesetze der natürlichen Zahlen auf die Zahlenmenge der ganzen Zahlen erweitern und zwar so, dass sie zu keinem Widerspruch mit bisher geltenden
ARBEITSBLATT 3 RECHNEN MIT GANZEN ZAHLEN Wir wollen nun die Rechengesetze der natürlichen Zahlen auf die Zahlenmenge der ganzen Zahlen erweitern und zwar so, dass sie zu keinem Widerspruch mit bisher geltenden
