3. Grundlagen der Linearen Programmierung
|
|
|
- August Ursler
- vor 8 Jahren
- Abrufe
Transkript
1 3. Grundlagen der linearen Programmierung Inhalt 3. Grundlagen der Linearen Programmierung Lineares Programm Grafische Lösung linearer Programme Normalform Geometrie linearer Programme Basislösungen Operations Research I Hochschule Bonn-Rhein-Sieg, SS
2 3. Grundlagen der linearen Programmierung Lineares Programm Lineares Programm Definition 3.1. Ein lineares Programm (LP) ist die Aufgabe, eine lineare Zielfunktion z = F(x 1,...,x n ) = c 1 x 1 + +c n x n zu maximieren oder zu minimieren unter Beachtung von linearen Nebenbedingungen der Form a i,1 x 1 + +a i,n x n b i (i = 1,...,m 1 ) a i,1 x 1 + +a i,n x n = b i (i = m 1 +1,...,m 2 ) a i,1 x 1 + +a i,n x n b i (i = m 2 +1,...,m) und meist auch von Vorzeichenbedingungen x j 0 für einige oder alle j = 1,...,n. Operations Research I Hochschule Bonn-Rhein-Sieg, SS
3 3. Grundlagen der linearen Programmierung Lineares Programm Definition 3.2. Ein Punkt oder Vektor x = (x 1,...,x n ) R n, der alle Neben- und Vorzeichenbedingungen erfüllt, heißt zulässige Lösung des LP. Eine zulässige Lösung x = (x 1,...,x n) heißt optimale Lösung des LP, wenn es keine zulässige Lösung x mit besserem Zielfunktionswert als F(x ) gibt. Mit X LP bezeichnen wir die Menge der zulässigen Lösungen des linearen Programms LP und mit X LP die Menge der optimalen Lösungen von LP. Bemerkung: Wenn aus dem Kontext heraus das lineare Programm eindeutig ist, schreiben wir auch X und X statt X LP bzw. X LP. Operations Research I Hochschule Bonn-Rhein-Sieg, SS
4 3. Grundlagen der linearen Programmierung Lineares Programm Beispiel 3.1. Ein Eisverkäufer stellt stündlich bis zu 10 kg Eis der Sorten A bzw. B her. A B Verkaufspreis 80 EUR/kg 65 EUR/kg Kosten 50 EUR/kg 40 EUR/kg Energieaufwand 5 kwh/kg 2 kwh/kg absetzbar 6 kg 9 kg Es stehen höchstens 30 kwh stündlich zur Verfügung. Entscheidungsvariablen seien die stündlich herzustellenden Mengen x 1 kg bzw. x 2 kg. Zu maximieren sei die Differenz aus Preis und Kosten. Operations Research I Hochschule Bonn-Rhein-Sieg, SS
5 3. Grundlagen der linearen Programmierung Lineares Programm Maximiere z = F(x 1,x 2 ) = 80x 1 +65x 2 50x 1 40x 2 = 30x 1 +25x 2 unter den Nebenbedingungen x 1 + x x 1 + 2x 2 30 x 1 6 x 2 9 und Vorzeichenbedingungen x 1,x 2 0. Operations Research I Hochschule Bonn-Rhein-Sieg, SS
6 3. Grundlagen der linearen Programmierung Grafische Lösung Grafische Lösung von LPs Wir betrachten zwei Entscheidungsvariablen x 1 und x 2. a 1 x 1 +a 2 x 2 = b ist die Gleichung einer Geraden im R 2. a 1 x 1 + a 2 x 2 b und auch a 1 x 1 + a 2 x 2 b beschreiben jeweils eine Halbebene mit der Geraden a 1 x 1 +a 2 x 2 = b als Rand. Auch x 1 0 und x 2 0 stellen Halbebenen dar. Der zulässige Bereich ist der Durchschnitt endlich vieler Halbebenen und somit ein sogenanntes konvexes Polyeder mit endlich vielen Eckpunkten. Operations Research I Hochschule Bonn-Rhein-Sieg, SS
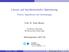
7 3. Grundlagen der linearen Programmierung Grafische Lösung x2 <= 9 x1 + x2 <= 10 Optimalpunkt 5 x1 + 2 x2 <= 30 x1 <= 6 Zielfunktion Beispiel 3.2. Die grafische Lösung zu Beispiel 3.1. Die Zielfunktion z = 30x 1 +25x 2 wirdebenfallsdurcheine Gerade dargestellt. Wachsendes z bedeutet eine Parallelverschiebung nach rechts oben. Man verschiebt so lange nach rechts oben, wie die Gerade durch X verläuft. Optimale Lösung beim Schnittpunkt der Geraden x 1 +x 2 = 10 und 5x 1 + 2x 2 = 30, also x = ( 10 3, 20 3 ). Operations Research I Hochschule Bonn-Rhein-Sieg, SS
8 3. Grundlagen der linearen Programmierung Grafische Lösung Mögliche Situationen bei grafischer Lösung (a) beschränktes X, eindeutige optimale Lösung (b) beschränktes X, nicht-eindeutige optimale Lösung (c) unbeschränktes X, eindeutige optimale Lösung (d) unbeschränktes X, nichteindeutige optimale Lösung (e) unbeschränktes X, keine optimale Lösung (f) leeres X Operations Research I Hochschule Bonn-Rhein-Sieg, SS
9 Maximumproblem Definition 3.3. Ein LP der Form n Maximiere z = F(x 1,...,x n ) = c 1 x 1 + +c n x n = c j x j j=1 n unter den Nebenbedingungen a ij x j b i (i = 1,...,m) j=1 und den Vorzeichenbedingungen x j 0 (j = 1,...,n) heißt Maximumproblem. Operations Research I Hochschule Bonn-Rhein-Sieg, SS
10 Kompakte Schreibweise Mit c,x R n,b R m und A R m n können wir ein Maximumproblem auch schreiben als: Maximiere unter den Nebenbedingungen c T x Ax b und den Vorzeichenbedingungen x 0 Operations Research I Hochschule Bonn-Rhein-Sieg, SS
11 Beispiel 3.3. Für das LP von Beispiel 3.1 lautet die kompakte Schreibweise: Maximiere unter den Nebenbedingungen (30, 25) ( x1 x 2 ( x1 x 2 ) ) und den Vorzeichenbedingungen ( x1 x 2 ) ( 0 0 ) Operations Research I Hochschule Bonn-Rhein-Sieg, SS
12 Umformung in ein Maximumproblem Satz 3.1. Zu jedem LP lässt sich ein äquivalentes LP in Form eines Maximumproblems formulieren. Beweis: Ersetze zu minimierende Zielfunktion z = F(x) durch zu maximierende Zielfunktion z = F(x) Transformiere Nebenbedingung durch Multiplikation beider Seiten mit 1 in eine Nebenbedingung. Eine Gleichung n j=1 a ijx j = b i kann durch zwei Ungleichungen n j=1 a ijx j b i und n j=1 a ijx j b i ersetzt werden. Falls für x j beliebige Werte aus R erlaubt sind, so ersetze x j durch die zwei Variablen x + j 0 und x j 0 mit x j = x + j x j. Operations Research I Hochschule Bonn-Rhein-Sieg, SS
13 Beispiel 3.4. Wir überführen das folgende LP in ein Maximumproblem: Minimiere k = 3x 1 4x 2 unter den Nebenbedingungen: 2x 1 +3x 2 7 x 1 2x 2 4 3x 1 +2x 2 = 6 x 1 0,x 2 R Operations Research I Hochschule Bonn-Rhein-Sieg, SS
14 Zunächst sorgen wir für eine Maximierung und stellen alle Nebenbedingungen als Nebenbedingungen dar: Maximiere unter den Nebenbedingungen: z = k = 3x 1 +4x 2 2x 1 +3x 2 7 x 1 +2x 2 4 3x 1 +2x 2 6 3x 1 2x 2 6 x 1 0,x 2 R Operations Research I Hochschule Bonn-Rhein-Sieg, SS
15 Nun wird durch x 2 = x + 2 x 2 mit x+ 2,x 2 0 die fehlende Vorzeichenbeschränkung eliminiert. Wir erhalten: Maximiere z = 3x 1 +4x + 2 4x 2 unter den Nebenbedingungen: 2x 1 +3x + 2 3x 2 7 x 1 +2x + 2 2x 2 4 3x 1 +2x + 2 2x 2 6 3x 1 2x x 2 6 x 1,x + 2,x 2 0 Operations Research I Hochschule Bonn-Rhein-Sieg, SS
16 Normalform Definition 3.4. Ein LP liegt in Normalform vor, wenn es die Form hat: Maximiere unter den Nebenbedingungen und Vorzeichenbedingungen z = F(x 1,...,x n ) = n j=1 c jx j n j=1 a ijx j = b i (i = 1,...,m) x j 0 (j = 1,...,n) In kompakter Darstellung: Maximiere c T x unter den Nebenbedingungen Ax = b und den Vorzeichenbedingungen x 0. Operations Research I Hochschule Bonn-Rhein-Sieg, SS
17 Umformung in Normalform Satz 3.2. Zu jedem LP lässt sich ein äquivalentes LP in Normalform formulieren. Beweis: Nach Satz 3.1 lässt sich zu jedem LP ein äquivalentes Maximumproblem formulieren. Es reicht daher zu zeigen, dass jedes Maximumproblem in Normalform überführt werden kann. Hierzu führt man für die m Ungleichungen die Schlupfvariablen x n+1,...,x n +m ein, die in der Zielfunktion mit 0 bewertet werden. Die Variablen x 1,...,x n heißen Strukturvariablen. Die Normalform ergibt sich dann durch: Operations Research I Hochschule Bonn-Rhein-Sieg, SS
18 Maximiere z = n j=1 c jx j + n+m j=n+1 0 x j unter den Bedingungen n a ij x j +x n+i = b i (i = 1,...,m) j=1 und Vorzeichenbedingungen x j 0 (j = 1,...,n+m) In Matrixschreibweise lautet die Normalform unter den Bedingungen z = F(x) = c T x Ax = b, x 0 Operations Research I Hochschule Bonn-Rhein-Sieg, SS
19 Definition 3.5. Gelten in der Matrixschreibweise für die Normalform die Eigenschaften b 0, c = c 1. c n 0. 0 und A = a 1,1 a 1,n a m,1 a m,n 0 1 so ist das LP in kanonischer Form. Operations Research I Hochschule Bonn-Rhein-Sieg, SS
20 Beispiel 3.5. Maximiere z = 30x 1 +25x 2 unter den Bedingungen x 1 + x x 1 + 2x 2 30 x 1 6 x 2 9 x 1 0 x 2 0 Für die Nebenbedingungen führen wir die Schlupfvariablen x 3,x 4,x 5,x 6 ein und erhalten Operations Research I Hochschule Bonn-Rhein-Sieg, SS
21 Maximiere unter den Bedingungen z = 30x 1 +25x 2 +0 x x 6 x 1 + x 2 + x 3 = 10 5x 1 + 2x 2 + x 4 = 30 x 1 + x 5 = 6 x 2 + x 6 = 9 und x j 0 (j = 1,...,6) Operations Research I Hochschule Bonn-Rhein-Sieg, SS
22 In Matrixschreibweise: Maximiere unter den Bedingungen z = ( ) x 1. x x 1 x 2 x 3 x 4 x 5 x 6 = und x 1. x n 0. 0 Operations Research I Hochschule Bonn-Rhein-Sieg, SS
Schranken für zulässige Lösungen
Schranken für zulässige Lösungen Satz 5.9 Gegeben seien primales und duales LP gemäß der asymmetrischen Form der Dualität. Wenn x eine zulässige Lösung des primalen Programms und u eine zulässige Lösung
OPERATIONS-RESEARCH (OR)
OPERATIONS-RESEARCH (OR) Man versteht darunter die Anwendung mathematischer Methoden und Modelle zur Vorbereitung optimaler Entscheidungen bei einem Unternehmen. Andere deutsche und englische Bezeichnungen:
Bestimmung einer ersten
Kapitel 6 Bestimmung einer ersten zulässigen Basislösung Ein Problem, was man für die Durchführung der Simplexmethode lösen muss, ist die Bestimmung einer ersten zulässigen Basislösung. Wie gut das geht,
Optimierung. Optimierung. Vorlesung 7 Lineare Programmierung II. 2013 Thomas Brox, Fabian Kuhn
Optimierung Vorlesung 7 Lineare Programmierung II 1 Lineare Programme Lineares Programm: Lineare Zielfunktion Lineare Nebenbedingungen (Gleichungen oder Ungleichungen) Spezialfall der konvexen Optimierung
4. Dynamische Optimierung
4. Dynamische Optimierung Allgemeine Form dynamischer Optimierungsprobleme 4. Dynamische Optimierung Die dynamische Optimierung (DO) betrachtet Entscheidungsprobleme als eine Folge voneinander abhängiger
Lineare Programmierung. Beispiel: Wahlkampf. Beispiel: Wahlkampf. Mathematische Schreibweise. Lineares Programm. Datenstrukturen & Algorithmen
Datenstrukturen & Algorithmen Einführung Standard- und Schlupfformen Simplex Algorithmus Matthias Zwicker Universität Bern Frühling 2009 2 Beispiel: Wahlkampf Ziel: mit möglichst wenig Werbung eine gewisse
Die Verbindung von Linearer Programmierung und Graphentheorie
Die Verbindung von Linearer Programmierung und Graphentheorie Definition 5.9. Ein kombinatorisches Optimierungsproblem entspricht einem LP, bei dem statt der Vorzeichenbedingungen x i 0 Bedingungen der
Lineare und kombinatorische Optimierung
Lineare und kombinatorische Optimierung Theorie, Algorithmen und Anwendungen Prof. Dr. Peter Becker Fachbereich Informatik Hochschule Bonn-Rhein-Sieg Wintersemester 2017/18 Peter Becker (H-BRS) Lineare
Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema
Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema 2x 4 + x 3 + x + 3 div x 2 + x 1 = 2x 2 x + 3 (2x 4 + 2x 3 2x 2 ) x 3 + 2x 2 + x + 3 ( x
Basis und Dimension. Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren.
Basis und Dimension Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren. Definition. Sei V ein K-Vektorraum und (v i ) i I eine Familie von Vektoren
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
0, v 6 = 2 2. 1, v 4 = 1. 2. span(v 1, v 5, v 6 ) = span(v 1, v 2, v 3, v 4, v 5, v 6 ) 4. span(v 1, v 2, v 4 ) = span(v 2, v 3, v 5, v 6 )
Aufgabe 65. Ganz schön span(n)end. Gegeben sei folgende Menge M von 6 Vektoren v, v,..., v 6 R 4 aus Aufgabe P 6: M = v =, v =, v =, v 4 =, v 5 =, v 6 = Welche der folgenden Aussagen sind wahr? span(v,
Simplex-Umformung für Dummies
Simplex-Umformung für Dummies Enthält die Zielfunktion einen negativen Koeffizienten? NEIN Optimale Lösung bereits gefunden JA Finde die Optimale Lösung mit dem Simplex-Verfahren! Wähle die Spalte mit
Eigenwerte und Eigenvektoren von Matrizen
Eigenwerte und Eigenvektoren von Matrizen Das Eigenwertproblem Sei A eine quadratische Matrix vom Typ m,m. Die Aufgabe, eine Zahl λ und einen dazugehörigen Vektor x zu finden, damit Ax = λx ist, nennt
Mathematischer Vorbereitungskurs für Ökonomen
Mathematischer Vorbereitungskurs für Ökonomen Dr. Thomas Zehrt Wirtschaftswissenschaftliches Zentrum Universität Basel Gleichungen Inhalt: 1. Grundlegendes 2. Lineare Gleichungen 3. Gleichungen mit Brüchen
1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage:
Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
9.2. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83
9.. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83 Die Grundfrage bei der Anwendung des Satzes über implizite Funktionen betrifft immer die folgende Situation: Wir haben eine Funktion f : V W und eine Stelle x
Fachschaft Mathematik und Informatik (FIM) LA I VORKURS. Herbstsemester 2015. gehalten von Harald Baum
Fachschaft Mathematik und Informatik (FIM) LA I VORKURS Herbstsemester 2015 gehalten von Harald Baum 2. September 2015 Inhaltsverzeichnis 1. Stichpunkte zur Linearen Algebra I 2. Körper 3. Vektorräume
Theoretische Grundlagen der Informatik
Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
Lineare Gleichungssysteme
Lineare Gleichungssysteme Sei K ein Körper, a ij K für 1 i m, 1 j n. Weiters seien b 1,..., b m K. Dann heißt a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2... a m1
x 2 2x + = 3 + Es gibt genau ein x R mit ax + b = 0, denn es gilt
- 17 - Die Frage ist hier also: Für welche x R gilt x = x + 1? Das ist eine quadratische Gleichung für x. Es gilt x = x + 1 x x 3 = 0, und man kann quadratische Ergänzung machen:... ( ) ( ) x x + = 3 +
Lineare Gleichungssysteme
Lineare Gleichungssysteme Eines der am häufigsten auftretenden Standardprobleme der angewandten Mathematik ist das Lösen linearer Gleichungssysteme, etwa zur Netzwerkberechnung in der Elektrotechnik oder
1 Aussagenlogik und Mengenlehre
1 Aussagenlogik und engenlehre 1.1 engenlehre Definition (Georg Cantor): nter einer enge verstehen wir jede Zusammenfassung von bestimmten wohl unterschiedenen Objekten (m) unserer Anschauung oder unseres
7 Rechnen mit Polynomen
7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR)
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
3. LINEARE GLEICHUNGSSYSTEME
176 3. LINEARE GLEICHUNGSSYSTEME 90 Vitamin-C-Gehalt verschiedener Säfte 18,0 mg 35,0 mg 12,5 mg 1. a) 100 ml + 50 ml + 50 ml = 41,75 mg 100 ml 100 ml 100 ml b) : Menge an Kirschsaft in ml y: Menge an
Praktische Mathematik: Lineare und Netzwerk-Optimierung (SS 2015) Praktikumsaufgaben
Technische Universität Kaiserslautern Prof Dr Sven O Krumke Dr Sabine Büttner MSc Marco Natale Praktische Mathematik: Lineare und Netzwerk-Optimierung (SS 2015) Praktikumsaufgaben Aufgabe 1 (Konvertieren
Lernziele: Ausgleichstechniken für binäre Bäume verstehen und einsetzen können.
6. Bäume Lernziele 6. Bäume Lernziele: Definition und Eigenschaften binärer Bäume kennen, Traversierungsalgorithmen für binäre Bäume implementieren können, die Bedeutung von Suchbäumen für die effiziente
Die Gleichung A x = a hat für A 0 die eindeutig bestimmte Lösung. Für A=0 und a 0 existiert keine Lösung.
Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Der Zwei-Quadrate-Satz von Fermat
Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
Primzahlen und RSA-Verschlüsselung
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
3.3 Eigenwerte und Eigenräume, Diagonalisierung
3.3 Eigenwerte und Eigenräume, Diagonalisierung Definition und Lemma 3.3.1. Sei V ein K-Vektorraum, φ End K (V ), λ K. Wir defnieren den zu λ gehörigen Eigenraum von φ als Dies ist ein Unterraum von V.
Anwendungen der Wirtschaftsmathematik und deren Einsatz im Schulunterricht
Anwendungen der Wirtschaftsmathematik und deren Einsatz im Schulunterricht Beispiele wirtschaftsmathematischer Modellierung Lehrerfortbildung, Speyer, Juni 2004-1- Beispiele wirtschaftsmathematischer Modellierung
Tangentengleichung. Wie lautet die Geradengleichung für die Tangente, y T =? Antwort:
Tangentengleichung Wie Sie wissen, gibt die erste Ableitung einer Funktion deren Steigung an. Betrachtet man eine fest vorgegebene Stelle, gibt f ( ) also die Steigung der Kurve und somit auch die Steigung
Sudoku-Informatik oder wie man als Informatiker Logikrätsel löst
Sudoku-Informatik oder wie man als Informatiker Logikrätsel löst Peter Becker Hochschule Bonn-Rhein-Sieg Fachbereich Informatik peter.becker@h-brs.de Kurzvorlesung am Studieninformationstag, 13.05.2009
Optimierung und Simulation ökonomischer Problemlagen privater Haushalte 3. Vorlesung
Optimierung und Simulation ökonomischer Problemlagen privater Haushalte 3. Vorlesung Rainer Hufnagel / Laura Wahrig 2006 Diese Woche LO - Sensitivitätsanalyse Simulation Beispiel Differenzengleichungen
Zeichen bei Zahlen entschlüsseln
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
1 Mathematische Grundlagen
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Optimalitätskriterien
Kapitel 4 Optimalitätskriterien Als Optimalitätskriterien bezeichnet man notwendige oder hinreichende Bedingungen dafür, dass ein x 0 Ω R n Lösung eines Optimierungsproblems ist. Diese Kriterien besitzen
Rekursionen. Georg Anegg 25. November 2009. Methoden und Techniken an Beispielen erklärt
Methoden und Techniken an Beispielen erklärt Georg Anegg 5. November 009 Beispiel. Die Folge {a n } sei wie folgt definiert (a, d, q R, q ): a 0 a, a n+ a n q + d (n 0) Man bestimme eine explizite Darstellung
Programmiersprachen und Übersetzer
Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
7 Die Determinante einer Matrix
7 Die Determinante einer Matrix ( ) a11 a Die Determinante einer 2 2 Matrix A = 12 ist erklärt als a 21 a 22 det A := a 11 a 22 a 12 a 21 Es ist S 2 = { id, τ}, τ = (1, 2) und sign (id) = 1, sign (τ) =
Einführung in die Algebra
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Optimierung und Simulation ökonomischer Problemlagen privater Haushalte 2. Vorlesung
Optimierung und Simulation ökonomischer Problemlagen privater Haushalte 2. Vorlesung Rainer Hufnagel / Laura Wahrig 2006 Diese Woche LO - Rechnerische Lösung - Simplex- Algorithmus LO - Auswertung des
Fall 3: Mehrere Kapazitätsengpässe
Fall 3: Mehrere Kapazitätsengpässe ei Vorliegen mehrerer Engpässe ist zunächst zu prüfen, ob ein Engpass die anderen Engpässe dominiert. Ist dies der Fall, reduziert sich das Optimierungsproblem auf den
Wir gehen aus von euklidischen Anschauungsraum bzw. von der euklidischen Zeichenebene. Parallele Geraden schneiden einander nicht.
2 Ein wenig projektive Geometrie 2.1 Fernpunkte 2.1.1 Projektive Einführung von Fernpunkten Wir gehen aus von euklidischen Anschauungsraum bzw. von der euklidischen Zeichenebene. Parallele Geraden schneiden
Optimierung für Nichtmathematiker
Optimierung für Nichtmathematiker Typische Prüfungsfragen Die folgenden Fragen dienen lediglich der Orientierung und müssen nicht den tatsächlichen Prüfungsfragen entsprechen. Auch Erkenntnisse aus den
Formelsammlung zur Kreisgleichung
zur Kreisgleichung Julia Wolters 6. Oktober 2008 Inhaltsverzeichnis 1 Allgemeine Kreisgleichung 2 1.1 Berechnung des Mittelpunktes und Radius am Beispiel..... 3 2 Kreis und Gerade 4 2.1 Sekanten, Tangenten,
Definition und Begriffe
Merkblatt: Das Dreieck Definition und Begriffe Das Dreieck ist ein Vieleck. In der Ebene ist es die einfachste Figur, die von geraden Linien begrenzt wird. Ecken: Jedes Dreieck hat drei Ecken, die meist
13. Lineare DGL höherer Ordnung. Eine DGL heißt von n-ter Ordnung, wenn Ableitungen y, y, y,... bis zur n-ten Ableitung y (n) darin vorkommen.
13. Lineare DGL höherer Ordnung. Eine DGL heißt von n-ter Ordnung, wenn Ableitungen y, y, y,... bis zur n-ten Ableitung y (n) darin vorkommen. Sie heißt linear, wenn sie die Form y (n) + a n 1 y (n 1)
WS 2009/10. Diskrete Strukturen
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Lineare Gleichungssysteme
Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
( ) als den Punkt mit der gleichen x-koordinate wie A und der
ETH-Aufnahmeprüfung Herbst 05 Mathematik I (Analysis) Aufgabe [6 Punkte] Bestimmen Sie den Schnittwinkel α zwischen den Graphen der Funktionen f(x) x 4x + x + 5 und g(x) x x + 5 im Schnittpunkt mit der
Linearen Gleichungssysteme Anwendungsaufgaben
Linearen Gleichungssysteme Anwendungsaufgaben Lb S. 166 Nr.9 Im Jugendherbergsverzeichnis ist angegeben, dass in der Jugendherberge in Eulenburg 145 Jugendliche in 35 Zimmern übernachten können. Es gibt
Darstellungsformen einer Funktion
http://www.flickr.com/photos/sigfrid/348144517/ Darstellungsformen einer Funktion 9 Analytische Darstellung: Eplizite Darstellung Funktionen werden nach Möglichkeit eplizit dargestellt, das heißt, die
Bevor lineare Gleichungen gelöst werden, ein paar wichtige Begriffe, die im Zusammenhang von linearen Gleichungen oft auftauchen.
R. Brinkmann http://brinkmann-du.de Seite 1 13.0.010 Lineare Gleichungen Werden zwei Terme durch ein Gleichheitszeichen miteinander verbunden, so entsteht eine Gleichung. Enthält die Gleichung die Variable
2 Lineare Gleichungen mit zwei Variablen
2 Lineare Gleichungen mit zwei Variablen Die Klasse 9 c möchte ihr Klassenzimmer mit Postern ausschmücken. Dafür nimmt sie 30, aus der Klassenkasse. In Klasse 7 wurden lineare Gleichungen mit einer Variablen
Lineare Optimierung Ergänzungskurs
Lineare Optimierung Ergänzungskurs Wintersemester 2015/16 Julia Lange, M.Sc. Literatur Werner, F.; Sotskov, Y.N. (2006): Mathematics of Economics and Business; Routledge; London Bemerkungen Diese Unterlagen
Optimale Steuerung. Sequentielle Quadratische Programmierung. Kevin Sieg. 14. Juli 2010. Fachbereich für Mathematik und Statistik Universität Konstanz
Optimale Steuerung Kevin Sieg Fachbereich für Mathematik und Statistik Universität Konstanz 14. Juli 2010 1 / 29 Aufgabenstellung 1 Aufgabenstellung Aufgabenstellung 2 Die zusammengesetzte Trapezregel
V 2 B, C, D Drinks. Möglicher Lösungsweg a) Gleichungssystem: 300x + 400 y = 520 300x + 500y = 597,5 2x3 Matrix: Energydrink 0,7 Mineralwasser 0,775,
Aufgabenpool für angewandte Mathematik / 1. Jahrgang V B, C, D Drinks Ein gastronomischer Betrieb kauft 300 Dosen Energydrinks (0,3 l) und 400 Liter Flaschen Mineralwasser und zahlt dafür 50, Euro. Einen
Motivation. Formale Grundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen. Informales Beispiel. Informales Beispiel.
Kontextfreie Kontextfreie Motivation Formale rundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen Bisher hatten wir Automaten, die Wörter akzeptieren Frank Heitmann heitmann@informatik.uni-hamburg.de
Mathematik. UND/ODER Verknüpfung. Ungleichungen. Betrag. Intervall. Umgebung
Mathematik UND/ODER Verknüpfung Ungleichungen Betrag Intervall Umgebung Stefan Gärtner 004 Gr Mathematik UND/ODER Seite UND Verknüpfung Kommentar Aussage Symbolform Die Aussagen Hans kann schwimmen p und
Professionelle Seminare im Bereich MS-Office
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Einführung in die Vektor- und Matrizenrechnung. Matrizen
Einführung in die Vektor- und Matrizenrechnung Matrizen Definition einer Matrix Unter einer (reellen) m x n Matrix A versteht man ein rechteckiges Schema aus reellen Zahlen, die wie folgt angeordnet sind:
Vorkurs Mathematik Übungen zu Polynomgleichungen
Vorkurs Mathematik Übungen zu en 1 Aufgaben Lineare Gleichungen Aufgabe 1.1 Ein Freund von Ihnen möchte einen neuen Mobilfunkvertrag abschließen. Es gibt zwei verschiedene Angebote: Anbieter 1: monatl.
Theoretische Grundlagen der Informatik WS 09/10
Theoretische Grundlagen der Informatik WS 09/10 - Tutorium 6 - Michael Kirsten und Kai Wallisch Sitzung 13 02.02.2010 Inhaltsverzeichnis 1 Formeln zur Berechnung Aufgabe 1 2 Hamming-Distanz Aufgabe 2 3
Definition:Eine meromorphe Modulform vom Gewicht k Z ist eine meromorphe. f : H C. (ii) C > 0, so daß f(z) im Bereich Im z > C keine Singularität hat.
Die k/2 - Formel von Renate Vistorin Zentrales Thema dieses Vortrages ist die k/2 - Formel für meromorphe Modulformen als eine Konsequenz des Residuensatzes. Als Folgerungen werden danach einige Eigenschaften
Klassenarbeit zu linearen Gleichungssystemen
Klassenarbeit zu linearen Gleichungssystemen Aufgabe : Bestimme die Lösungsmenge der Gleichungssysteme mit Hilfe des Additionsverfahrens: x + 4y = 8 5x y = x y = x y = Aufgabe : Bestimme die Lösungsmenge
DIFFERENTIALGLEICHUNGEN
DIFFERENTIALGLEICHUNGEN GRUNDBEGRIFFE Differentialgleichung Eine Gleichung, in der Ableitungen einer unbekannten Funktion y = y(x) bis zur n-ten Ordnung auftreten, heisst gewöhnliche Differentialgleichung
Grundbegriffe der Informatik
Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Umgekehrte Kurvendiskussion
Umgekehrte Kurvendiskussion Bei einer Kurvendiskussion haben wir eine Funktionsgleichung vorgegeben und versuchen ihre 'Besonderheiten' herauszufinden: Nullstellen, Extremwerte, Wendepunkte, Polstellen
Lineare Gleichungssysteme I (Matrixgleichungen)
Lineare Gleichungssysteme I (Matrigleichungen) Eine lineare Gleichung mit einer Variable hat bei Zahlen a, b, die Form a b. Falls hierbei der Kehrwert von a gebildet werden darf (a 0), kann eindeutig aufgelöst
Kapitel 15. Lösung linearer Gleichungssysteme
Kapitel 15. Lösung linearer Gleichungssysteme Lineare Gleichungssysteme Wir befassen uns nun mit der Lösung im allgemeinen nichthomogener linearer Gleichungssysteme in zweifacher Hinsicht. Wir studieren
Mathematik 1 für Wirtschaftsinformatik
Mathematik 1 für Wirtschaftsinformatik Wintersemester 2012/13 Hochschule Augsburg : Gliederung 7 Folgen und Reihen 8 Finanzmathematik 9 Reelle Funktionen 10 Differenzieren 1 11 Differenzieren 2 12 Integration
Matrizennorm. Definition 1. Sei A M r,s (R). Dann heißt A := sup die Matrixnorm. Wir wissen zunächst nicht, ob A eine reelle Zahl ist.
Matrizennorm Es seien r,s N Mit M r,s (R bezeichnen wir die Menge der reellen r s- Matrizen (also der linearen Abbildungen R s R r, und setze M s (R := M s,s (R (also die Menge der linearen Abbildungen
Algebraische Kurven. Vorlesung 26. Die Schnittmultiplizität
Prof. Dr. H. Brenner Osnabrück SS 2012 Algebraische Kurven Vorlesung 26 Die Schnittmultiplizität Es seien zwei ebene algebraische Kurven C,D A 2 K gegeben, die keine Komponente gemeinsam haben. Dann besteht
Der monatliche Tarif für ein Handy wurde als lineare Funktion der Form f(x) = k x + d modelliert (siehe Grafik).
1) Handytarif Der monatliche Tarif für ein Handy wurde als lineare Funktion der Form f(x) = k x + d modelliert (siehe Grafik). Euro Gesprächsminuten Tragen Sie in der folgenden Tabelle ein, welche Bedeutung
Übungen zum Ferienkurs Lineare Algebra WS 14/15
Übungen zum Ferienkurs Lineare Algebra WS 14/15 Linearkombinationen, Basen, Lineare Abbildungen 2.1 Lineare Unabhängigkeit Sind die folgenden Vektoren linear unabhängig? (a) 1, 2, 3 im Q Vektorraum R (b)
Logik-Programme. Eine Tatsachenklausel ist eine einelementige positive Klausel, d.h. sie hat
Logik-Programme Definition: Eine Tatsachenklausel ist eine einelementige positive Klausel, d.h. sie hat die Form {P }. Eine Prozedurklausel ist eine Klausel der Form {P, Q 1, Q 2,..., Q k } mit k 1. P
Vorlesung. Funktionen/Abbildungen 1
Vorlesung Funktionen/Abbildungen 1 1 Grundlagen Hinweis: In dieser Vorlesung werden Funktionen und Abbildungen synonym verwendet. In der Schule wird eine Funktion häufig als eindeutige Zuordnung definiert.
Absolute Stetigkeit von Maßen
Absolute Stetigkeit von Maßen Definition. Seien µ und ν Maße auf (X, Ω). Dann heißt ν absolut stetig bezüglich µ (kurz ν µ ), wenn für alle A Ω mit µ(a) = 0 auch gilt dass ν(a) = 0. Lemma. Sei ν ein endliches
Kaufmännische Berufsmatura 2007 Kanton Zürich Serie 1
Serie 1 Prüfungsdauer: 150 Minuten Hilfsmittel: Netzunabhängiger Taschenrechner Beigelegte Formelsammlung Bedingungen: Dokumentieren Sie den Lösungsweg auf dem Aufgabenblatt Unbelegte Resultate werden
Lineare Programmierung
Lineare Programmierung WS 2003/04 Rolle der Linearen Programmierung für das TSP 1954: Dantzig, Fulkerson & Johnson lösen das TSP für 49 US-Städte (ca. 6.2 10 60 mögliche Touren) 1998: 13.509 Städte in
Grammatiken. Einführung
Einführung Beispiel: Die arithmetischen Ausdrücke über der Variablen a und den Operationen + und können wie folgt definiert werden: a, a + a und a a sind arithmetische Ausdrücke Wenn A und B arithmetische
Einführung in die Lineare Optimierung
Kapitel 2 Einführung in die Lineare Optimierung lineare Modelle der relevanten Umwelt werden wegen ihrer Einfachheit häufig gegenüber nichtlinearen Ansätzen vorgezogen, lineare Optimierungsprobleme können
Lineare Funktionen. 1 Proportionale Funktionen 3 1.1 Definition... 3 1.2 Eigenschaften... 3. 2 Steigungsdreieck 3
Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen?
Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen können zwei Ebenen (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen? Wie heiÿt
Periodische Fahrpläne und Kreise in Graphen
Periodische Fahrpläne und Kreise in Graphen Vorlesung Algorithmentechnik WS 2009/10 Dorothea Wagner Karlsruher Institut für Technologie Eisenbahnoptimierungsprozess 1 Anforderungserhebung Netzwerkentwurf
Elemente der Analysis I Kapitel 2: Einführung II, Gleichungen
Elemente der Analysis I Kapitel 2: Einführung II, Gleichungen Prof. Dr. Volker Schulz Universität Trier / FB IV / Abt. Mathematik 8. November 2010 http://www.mathematik.uni-trier.de/ schulz/elan-ws1011.html
http://www.olympiade-mathematik.de 4. Mathematik Olympiade 2. Stufe (Kreisolympiade) Klasse 8 Saison 1964/1965 Aufgaben und Lösungen
4. Mathematik Olympiade Saison 1964/1965 Aufgaben und Lösungen 1 OJM 4. Mathematik-Olympiade Aufgaben Hinweis: Der Lösungsweg mit Begründungen und Nebenrechnungen soll deutlich erkennbar in logisch und
Wie löst man Mathematikaufgaben?
Wie löst man Mathematikaufgaben? Manfred Dobrowolski Universität Würzburg Wie löst man Mathematikaufgaben? 1 Das Schubfachprinzip 2 Das Invarianzprinzip 3 Das Extremalprinzip Das Schubfachprinzip Verteilt
DHBW Karlsruhe, Vorlesung Programmieren, Klassen (2)
DHBW Karlsruhe, Vorlesung Programmieren, Klassen (2) Aufgabe 3 Bankkonto Schreiben Sie eine Klasse, die ein Bankkonto realisiert. Attribute für das Bankkonto sind der Name und Vorname des Kontoinhabers,
Beispiel vor dem Beweis:
Beispiel vor dem Beweis: Beispiel vor dem Beweis: A = ¼3 6 2 3 11 2½ Beispiel vor dem Beweis: 2½ 2½ ¼3 6 A = 2 3 11 311 E 12 A = 3 6 Beispiel vor dem Beweis: 2½ 2½ ¼3 6 A = 2 3 11 311 E 12 A = 3 6 3 11
a n + 2 1 auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert:
Beispiel: Wir untersuchen die rekursiv definierte Folge a 0 + auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert: ( ) (,, 7, 5,...) Wir können also vermuten, dass die Folge monoton fallend
Pädagogische Hochschule Thurgau. Lehre Weiterbildung Forschung
Variante 1 Swisscom-Router direkt ans Netzwerk angeschlossen fixe IP-Adressen (kein DHCP) 1. Aufrufen des «Netz- und Freigabecenters». 2. Doppelklick auf «LAN-Verbindung» 3. Klick auf «Eigenschaften» 4.
Lernmaterial für die Fernuni Hagen effizient und prüfungsnah
Lernmaterial für die Fernuni Hagen effizient und prüfungsnah www.schema-f-hagen.de Sie erhalten hier einen Einblick in die Dokumente Aufgaben und Lösungen sowie Erläuterungen Beim Kauf erhalten Sie zudem
Lösen von linearen Gleichungssystemen mit zwei Unbekannten:
Lösen von linearen Gleichungssystemen mit zwei Unbekannten: 1. Additions- und Subtraktionsverfahren 3x = 7y 55 + 5x 3x = 7y 55 7y 5x + 2y = 4 3 5 werden, dass die Variablen links und die Zahl rechts vom