Kapitel 4: Beweis und Herleitung von Programmen
|
|
|
- Mareke Baum
- vor 8 Jahren
- Abrufe
Transkript
1 Funktionale Programmierung (WS2005/2006) 4/1 Kapitel 4: Beweis und Herleitung von Programmen Lernziele dieses Kapitels 1. Bedeutung der referenziellen Transparenz und des Gleichungsbeweisens 2. Strukturelle Induktion: Natürliche Zahlen, Listen, Bäume 3. Listengesetze: Dekomposition, Dualität, Fusion, Homomorphie 4. Homomorphismen zur Herleitung von Algorithmen: Mergesort, Fibonacci 5. Programmtransformationen zur Erhöhung der Effizienz: Maximale Segmentsumme
2 Funktionale Programmierung (WS2005/2006) 4/2 Referenzielle Transparenz (1) Def.: ein Ausdruck E heisst referenziell transparent, wenn jeder beliebige Teilausdruck T durch einen Ausdruck T gleichen Wertes ersetzt werden kann, ohne dass sich dabei der Wert von E ändert. Bei referenzieller Transparenz gilt die Leibniz-Regel: Beispiel: f x + f x = {nicht-striktes let} let y = f x in f x + f x = {Leibniz} let y = f x in y + f x = {Leibniz} kritische Stelle T =T E[x:=T ]=E[x:=T ] let y = f x in y + y = {Arithmetik auf Integer-Variablen} let y = f x in 2 * y = {Leibniz} let y = f x in 2 * f x = {nicht-striktes let} 2 * f x
3 Funktionale Programmierung (WS2005/2006) 4/3 Referenzielle Transparenz (2) Sprache mit Seiteneffekten: referenzielle Transparenz nicht gegeben dann z.b.: f x + f x 2 * f x, vgl. Kap. 1 funktionale Sprachen mit referenzieller Transparenz: rein funktional Haskell erlaubt Ein-/Ausgabe mit referenzieller Transparenz: Wert von I/O-Operationen ist nicht Rückgabewert der Operation, sondern die Operation selbst: Haskell let outop = putstr "ha" in do outop outop OCaml let outop = printf "ha" in outop; outop Ausgabe: haha Ausgabe: ha
4 Funktionale Programmierung (WS2005/2006) 4/4 Beweis von Programmen gegeben 1. Spezifikation, d.h. Ein-/Ausgaberelation 2. Programm gesucht: Beweis, dass Programm die Spezifikation erfüllt
5 Funktionale Programmierung (WS2005/2006) 4/5 Beweis imperativer Programme etablierte Methode: Hoare-Kalkül (Methode der Zusicherungen) Spezifikation: Vor- und Nachbedingung an Programm Aussagen über den Zustand der Belegung der Variablen Vorbedingung und Nachbedingung an jeden Programmteil Invarianten für Schleifen Substitutionsregel für Statements
6 Funktionale Programmierung (WS2005/2006) 4/6 Beweis funktionaler Programme etablierte Methode: Equational Reasoning (Gleichheitsbeweise) Spezifikation: Ein-/Ausgaberelation, was bleibt zu tun? 1. Spezifikation muss nicht ausführbar sein, z.b. Gleichungen sind keine zulässigen Funktionsdefinitionen nicht-integrierte Zusatzbedingungen 2. Spezifikation ist ausführbar, aber extrem ineffizient Programm hat gleiche Semantik, aber effizienteren Berechnungsweg Gleichheitsbeweis: schrittweise Überführung der Spezifikation in das Endprogramm durch Anwendung von Regeln (z.b. Leibniz)
7 Funktionale Programmierung (WS2005/2006) 4/7 Prinzip des Gleichheitsbeweisens Gleichungskette zwischen zwei Ausdrücken jede Gleichung gerechtfertigt durch Anwendung einer Regel Regelanwendung, um Gleichheit P = Q zu rechtfertigen: 1. gib einen Kontext E mit einer Variablen v an, sodass es Ausdrücke L und R gibt, mit denen gilt: E[v:=L ] = P und E[v:=R ] = Q 2. wähle geeignete Regel L = R (oder R = L) aus Regelbasis aus 3. gib eine Substitution(*) ϕ an, so dass L = ϕ L und R = ϕ R (*) Substitution ϕ T rein syntaktisch und simultan: für jede freie Variable x in T ersetze jedes freie Vorkommen von x in T durch einen bestimmten Ausdruck (ϕ x)
8 Funktionale Programmierung (WS2005/2006) 4/8 gegeben Beispiel einer Regelanwendung P = f (x * (y + g z)) - 1 Q = f (x * y + x * g z) - 1. Regelbasis enthält: (a * (b + c)) = a * b + a * c (Distributivgesetz) zu zeigen: P = Q 1. gib einen Kontext E mit einer Variablen v an, sodass es Ausdrücke L und R gibt, mit denen gilt: E[v:=L ] = P und E[v:=R ] = Q E = f v - 1, L = x * (y + g z), R = x * y + x * g z 2. wähle geeignete Regel L = R (oder R = L) aus Regelbasis aus wähle Distributivgesetz: L = a * (b + c), R = a * b + a * c 3. gib eine Substitution ϕ an, so dass L = ϕ L und R = ϕ R ϕ = [a:=x, b:=y, c:=g z]
9 Funktionale Programmierung (WS2005/2006) 4/9 Beweis-Skizze nur der Name der Regel wird angegeben oder eine intuitive Bezeichnung fac 0 = 1 -- fac.1 fac n n>0 = n * fac (n-1) -- fac.2 Beispiel (Beweis-Skizze): fac 2 = {fac.2} 2 * fac (2-1) = {Arithmetik} 2 * fac 1 = {fac.2} 2 * (1 * fac (1-1)) = {Arithmetik} 2 * (1 * fac 0) = {fac.1} 2 * (1 * 1) = {Arithmetik} 2 * 1 = {Arithmetik} 2
10 Funktionale Programmierung (WS2005/2006) 4/10 Korrektheit des Gleichungsbeweisens Haskell hat wichtige Eigenschaften 1. referenzielle Transparenz jede Gleichung erhält die partielle Korrektheit 2. Nicht-Striktheit der Funktionsanwendung (Laziness): Terminationsverhalten bleibt unverändert bei Verwendung einer Funktionsgleichung als Regel (z.b. fac.2) Änderung von Ersetzungsreihenfolgen 3. statisches Typsystem jeder Ausdruck hat eine definierte Semantik soetwas wie (/2).(*2) = id = ( div 2).(*2) gibt es nicht Regeln sind typabhängig: + assoziativ für Rational, aber nicht für Float
11 Funktionale Programmierung (WS2005/2006) 4/11 Unterschiedliche Ersetzungsreihenfolgen (1) bridge :: (Float,Float) -> Float -> Float -> Float bridge (x0,y0) x y = if x==x0 then y0 else y -- bridge f :: Float -> Float f x = bridge (0,1) x (sin x / x) zuerst Argumentauswertung -- f f 0 = {f} bridge (0,1) 0 (sin 0 / 0) = {Arithmetik} bridge (0,1) 0 (0 / 0) = {Arithmetik} bridge (0,1) 0 = {bridge} if 0==0 then 1 else = {==} if True then 1 else = {if-then-else} 1
12 Funktionale Programmierung (WS2005/2006) 4/12 Unterschiedliche Ersetzungsreihenfolgen (2) bridge :: (Float,Float) -> Float -> Float -> Float bridge (x0,y0) x y = if x==x0 then y0 else y -- bridge f :: Float -> Float f x = bridge (0,1) x (sin x / x) -- f zuerst Anwendung der Funktionsgleichung f 0 = {f} bridge (0,1) 0 (sin 0 / 0) = {bridge} if 0==0 then 1 else (sin 0 / 0) = {==} if True then 1 else (sin 0 / 0) = {if-then-else} 1
13 Funktionale Programmierung (WS2005/2006) 4/13 Strukturelle Induktion hier: endliche Strukturen, keine Betrachtung von Laziness Die natürlichen Zahlen als (strukturell) induktiv definierte Menge: data Nat = Zero Null Succ Nat Nachfolger deriving (Eq,Ord,Show) Wir verwenden Z und S als Abkürzung für Zero bzw. Succ. Elemente von Nat: Z (0), S Z (1), S (S Z) (2), S (S (S Z)) (3)...
14 Funktionale Programmierung (WS2005/2006) 4/14 Addition auf Nat Definition von Funktionen auf induktiv definierten Typen durch Angabe der Gleichung für jeden Datenkonstruktor add :: Nat -> Nat -> Nat add x Z = x -- add.1 add x (S y) = S (add x y) -- add.2 add :: Integer -> Integer -> Integer add x 0 = x -- add.1 add x y y>0 = 1 + add x (y-1) -- add.2 add (S Z) (S Z) S (S Z) add 1 1 2
15 Funktionale Programmierung (WS2005/2006) 4/15 Multiplikation auf Nat mul :: Nat -> Nat -> Nat mul x Z = Z -- mul.1 mul x (S y) = add x (mul x y) -- mul.2 mul :: Integer -> Integer -> Integer mul x 0 = 0 -- mul.1 mul x y y>0 = x + mul x (y-1) -- mul.2 mul (S (S Z)) (S (S (S Z))) mul S (S (S (S (S (S Z)))))
16 Funktionale Programmierung (WS2005/2006) 4/16 Schrittweise Berechnung mul (S (S Z)) (S (S (S Z))) {mul.2} add (S (S Z)) (mul (S (S Z)) (S (S Z))) {mul.2} add (S (S Z)) (add (S (S Z)) (mul (S (S Z)) (S Z))) {mul.2} add (S (S Z)) (add (S (S Z)) (add (S (S Z)) (mul (S (S Z)) Z))) {mul.1} add (S (S Z)) (add (S (S Z)) (add (S (S Z)) Z)) {add.1} add (S (S Z)) (add (S (S Z)) (S (S Z))) {add.2} add (S (S Z)) (S (add (S (S Z)) (S Z))) {add.2} S (add (S (S Z)) (add (S (S Z)) (S Z))) {add.2} S (add (S (S Z)) (S (add (S (S Z)) Z))) {add.2} S (S (add (S (S Z)) (add (S (S Z)) Z))) {add.1} S (S (add (S (S Z)) (S (S Z)))) {add.2} S (S (S (add (S (S Z)) (S Z)))) {add.2} S (S (S (S (add (S (S Z)) Z)))) {add.1} S (S (S (S (S (S Z)))))
17 Funktionale Programmierung (WS2005/2006) 4/17 Der induktive Datentyp Liste data List a = Nil leere Liste C a (List a) cons In Haskell (keine legale Quellprogrammsyntax) -- data [a] = [] -- a : [a] deriving (Eq, Ord) Elemente: Nil [] C x Nil x:[] C y (C x Nil) y:x:[] C z (C y (C x Nil)) z:y:x:[]...
18 Funktionale Programmierung (WS2005/2006) 4/18 Die Längenfunktion auf Listen len :: List a -> Nat len Nil = Z -- len.1 len (C _ xs) = S (len xs) -- len.2 len :: [a] -> Int --Integer nicht nötig, weil Speicher <= Adressraum len [] = 0 -- len.1 len (_:xs) = 1 + len xs -- len.2 len (C z (C y (C x Nil))) len (z:y:x:[]) 3 S (S (S Z))
19 Funktionale Programmierung (WS2005/2006) 4/19 Die Summenfunktion auf Listen su :: List Nat -> Nat su Nil = Z -- su.1 su (C x xs) = add x (su xs) -- su.2 su :: Num a => [a] -> a su [] = 0 -- su.1 su (x:xs) = x + su xs -- su.2 su (C (S Z) (C (S (S Z)) (C (S Z) Nil))) S (S (S (S Z))) su (1:2:1:[]) 4
20 Funktionale Programmierung (WS2005/2006) 4/20 Induktive Definition der append-funktion append (++) verkettet zwei Listen (++) :: [a] -> [a] -> [a] [] ++ ys = ys -- (++).1 (x:xs) ++ ys = x : (xs ++ ys) -- (++).2 (1:2:3:[]) ++ (4:5:6:7:8:9:[]) {(++).2} 1:((2:3:[]) ++ (4:5:6:7:8:9:[])) {(++).2} 1:2:((3:[]) ++ (4:5:6:7:8:9:[])) {(++).2} 1:2:3:([] ++ (4:5:6:7:8:9:[])) {(++).1} 1:2:3:4:5:6:7:8:9:[]
21 Funktionale Programmierung (WS2005/2006) 4/21 Induktive Definition des map-kombinators map :: (a->b) -> [a] -> [b] map f [] = [] -- map.1 map f (x:xs) = f x : map f xs -- map.2 map (^2) (1:2:3:4:[]) {map.2} (^2) 1 : map (^2) (2:3:4:[]) {(^2) } 1 : map (^2) (2:3:4:[]) {map.2} 1 : (^2) 2 : map (^2) (3:4:[]) {(^2) } 1 : 4 : map (^2) (3:4:[]) {map.2} 1 : 4 : (^2) 3 : map (^2) (4:[]) {(^2) } 1 : 4 : 9 : map (^2) (4:[]) {map.2} 1 : 4 : 9 : (^2) 4 : map (^2) [] {(^2) } 1 : 4 : 9 : 16 : map (^2) [] {map.1} 1 : 4 : 9 : 16 : []
22 Funktionale Programmierung (WS2005/2006) 4/22 Struktureller Induktionsbeweis (informell) Induktionsaxiom: (zum Beweis einer Aussage P ) für jeden Datenkonstruktor C eines induktiv definierten Typs S: 1. sei x ein beliebiges Element von S mit Wurzelsymbol C 2. Induktionsannahme: P (x i ) gelte für jede echte Teilstruktur x i von x 3. man zeige, dass P (x) gilt dann gilt die Aussage P für alle endlichen Elemente von S Basisfall, gdw. kein x i enthält Element vom Typ S Induktionsfall, gdw. mindestens ein x i enthält Element vom Typ S Problem: Wahl der Induktionsvariablen x in P (x) Spezialfälle Vollständige Induktion: Konstruktoren Zero (0) und Succ (x x+1) Listeninduktion: Konstruktoren [] (nil) und (:) (cons)
23 Funktionale Programmierung (WS2005/2006) 4/23 Strukturelles Induktionsaxiom (halbformal) sei S ein algebraischer Datentyp mit Konstruktoren { C j j N 0 j < n } #j die Anzahl der Argumente von Konstruktor C j P ein zu beweisendes Prädikat Induktionsaxiom j : 0 j < n :: x j,0,..., x j,#j 1 :: ( i : (0 i<#j x j,i S) : P (x j,i )) = P (C j x j,0...x j,#j 1 ) x : x S x endlich : P (x) Vollständige Induktion als Spezialfall P (Zero) ( x : x Nat : P (x) = P (Succ x)) x : x Nat x endlich : P (x)
24 Funktionale Programmierung (WS2005/2006) 4/24 Beweis: map f xs ++ map f ys == map f (xs++ys) {Fall.1} Induktionsvariable: xs {Fall.1}: xs==[] map f xs ++ map f ys {Fall.1}== map f [] ++ map f ys { map.1}== [] ++ map f ys {(++).1}== map f ys {(++).1}== map f ([]++ys) {Fall.1}== map f (xs++ys)
25 Funktionale Programmierung (WS2005/2006) 4/25 Beweis: map f xs ++ map f ys == map f (xs++ys) {Fall.2} Induktionsvariable: xs {Fall.2}: xs==(z:zs) map f xs ++ map f ys {Fall.2}== map f (z:zs) ++ map f ys { map.2}== (f z : map f zs) ++ map f ys {(++).2}== f z : (map f zs ++ map f ys) {Ind-A.}== f z : (map f (zs++ys)) { map.2}== map f (z:(zs++ys)) {(++).2}== map f ((z:zs)++ys) {Fall.2}== map f (xs++ys)
26 Funktionale Programmierung (WS2005/2006) 4/26 Beweis: (map f. map g) xs == map (f. g) xs {Fall.1} (q. p) x = q (p x) -- compose Induktionsvariable: xs {Fall.1}: xs==[] (map f. map g) xs {Fall.1 }== (map f. map g) [] {compose}== map f (map g []) { map.1 }== map f [] { map.1 }== [] { map.1 }== map (f. g) [] {Fall.1 }== map (f. g) xs
27 Funktionale Programmierung (WS2005/2006) 4/27 Beweis: (map f. map g) xs == map (f. g) xs {Fall.2} Induktionsvariable: xs {Fall.2}: xs==(z:zs) (map f. map g) xs {Fall.2 }== (map f. map g) (z:zs) {compose}== map f (map g (z:zs)) { map.2 }== map f (g z : map g zs) { map.2 }== f (g z) : map f (map g zs) {compose}== (f. g) z : map f (map g zs) {compose}== (f. g) z : (map f. map g) zs {Ind-A. }== (f. g) z : map (f. g) zs { map.2 }== map (f. g) (z:zs) {Fall.2 }== map (f. g) xs
28 Funktionale Programmierung (WS2005/2006) 4/28 Verwendung der vordefinierten Arithmetik Konstruktor-basierte Berechnung: langsam und inflexibel besser: eingebaute Arithmetik verwenden Bsp.: Fakultätsfunktion fac :: Integer -> Integer fac 0 = 1 fac n n>0 = n * fac (n-1) Vorsicht: Wertebereich berücksichtigen (Termination) Induktionsbeweise analog mit 0 statt Zero und (+1) statt Succ
29 Funktionale Programmierung (WS2005/2006) 4/29 Bäume als induktive Datentypen data BinTree1 a = Empty1 Fork1 { elem1::a, left1, right1 :: BinTree1 a } data BinTree2 a = Leaf2 { elem2::a } Fork2 { left2, right2 :: BinTree2 a } data BinTree3 a = Leaf3 { elem3::a } Fork3 { elem3::a, left3, right3 :: BinTree3 a } data RoseTree a = Fork4 { elem4::a, children::[rosetree a] }
30 Funktionale Programmierung (WS2005/2006) 4/30 Summenfunktion sumt auf BinTree2 sumt :: Num a => BinTree2 a -> a sumt (Leaf2 elem) = elem -- sumt.1 sumt (Fork2 left right) = sumt left + sumt right -- sumt.2 sumt (Fork2 (Fork2 (Leaf2 1) (Leaf2 2)) (Leaf2 1)) {sumt.2} sumt (Fork2 (Leaf2 1) (Leaf2 2)) + sumt (Leaf2 1) {sumt.2} sumt (Leaf2 1) + sumt (Leaf2 2) + sumt (Leaf2 1) {sumt.1} 1 + sumt (Leaf2 2) + sumt (Leaf2 1) {sumt.1} sumt (Leaf2 1) { + } 3 + sumt (Leaf2 1) {sumt.1} { + } 4
31 Funktionale Programmierung (WS2005/2006) 4/31 Beweis: leaves t == forks t + 1 data BinTree2 a = Leaf2 a Fork2 (BinTree2 a) (BinTree2 a) leaves, forks :: BinTree2 a -> Integer leaves (Leaf2 ) = 1 -- leaves.1 leaves (Fork2 l r) = leaves l + leaves r -- leaves.2 forks (Leaf2 ) = 0 -- forks.1 forks (Fork2 l r) = 1 + forks l + forks r -- forks.2
32 Funktionale Programmierung (WS2005/2006) 4/32 Beweis: leaves t == forks t + 1 {Fall.1} Induktionsvariable: t {Fall.1}: t == Leaf2 leaves t { Fall.1 }== leaves (Leaf2 ) { leaves.1 }== 1 {Arithmetik}== { forks.1 }== forks (Leaf2 ) + 1 { Fall.1 }== forks t + 1
33 Funktionale Programmierung (WS2005/2006) 4/33 Beweis: leaves t == forks t + 1 {Fall.2} Induktionsvariable: t {Fall.2}: t == Fork2 l r leaves t { Fall.2 }== leaves (Fork2 l r) {leaves.2}== leaves l + leaves r { Ind.A. }== forks l leaves r { Kommut.}== 1 + forks l + leaves r { Ind.A. }== 1 + forks l + forks r + 1 { forks.2}== forks (Fork2 l r) + 1 { Fall.2 }== forks t + 1
34 Funktionale Programmierung (WS2005/2006) 4/34 Ungleichungs-Beweis: sumt t <= leaves t * maxt t Kette von <= und == statt Kette von == leaves (Leaf2 ) = 1 -- leaves.1 leaves (Fork2 l r) = leaves l + leaves r -- leaves.2 sumt (Leaf2 x) = x -- sumt.1 sumt (Fork2 l r) = sumt l + sumt r -- sumt.2 maxt (Leaf2 x) = x -- maxt.1 maxt (Fork2 l r) = max (maxt l) (maxt r) -- maxt.2
35 Funktionale Programmierung (WS2005/2006) 4/35 Ungleichungs-Beweis: sumt t <= leaves t * maxt t {Fall.1} Induktionsvariable: t {Fall.1}: t == Leaf2 x sumt t { Fall.1 }== sumt (Leaf2 x) { sumt.1 }== x {Neutr. *}== 1 * x {leaves.1}== leaves (Leaf2 x) * x { maxt.1 }== leaves (Leaf2 x) * maxt (Leaf2 x) { Fall.1 }== leaves t * maxt (Leaf2 x) { Fall.1 }== leaves t * maxt t
36 Funktionale Programmierung (WS2005/2006) 4/36 Ungleichungs-Beweis: sumt t <= leaves t * maxt t {Fall.2} Induktionsvariable: t {Fall.2}: t == Fork2 l r sumt t { Fall.2 }== sumt (Fork2 l r) { sumt.2 }== sumt l + sumt r { Ind.A. }<= leaves l * maxt l + sumt r { Ind.A. }<= leaves l * maxt l + leaves r * maxt r { max }<= leaves l * (max (maxt l) (maxt r)) + leaves r * maxt r { max }<= leaves l * (max (maxt l) (maxt r)) + leaves r * (max (maxt l) (maxt r)) { Distr. }== (leaves l + leaves r) * max (maxt l) (maxt r) {leaves.2}== leaves (Fork2 l r) * max (maxt l) (maxt r) { maxt.2 }== leaves (Fork2 l r) * maxt (Fork2 l r) { Fall.2 }== leaves t * maxt (Fork2 l r) { Fall.2 }== leaves t * maxt t
37 Funktionale Programmierung (WS2005/2006) 4/37 Beobachtungen mehrmalige Anwendung der Induktionsannahme kann nötig oder nützlich sein bei Strukturen mit mehr als einer rekursiven Teilstruktur (z.b. Bäume) bei mehrmaligem Auftreten der Induktionsvariablen oft kann man schnell die Gleichungskette finden, wenn man 1. von oben abwärts zur Mitte bzw. 2. von unten aufwärts zur Mitte Funktionsdefinitionen einsetzt (Unfolding) und vereinfacht bei Strukturen mit einem Basisfall und einem Induktionsfall werden oft die {.1}-Regeln beim Beweis des Basisfalles und die {.2}-Regeln beim Beweis des Induktionsfalles gebraucht.
38 Funktionale Programmierung (WS2005/2006) 4/38 Listengesetze und Fold Achtung: Einschränkung auf endliche Listen ohne explizite Erwähnung Dekompositionssätze: zerlegen einer Liste Dualitätssätze: Beziehung zwischen foldl und foldr Fusionssätze: verschmelzen einer Berechnung nach einem fold mit dem fold Homomorphiesätze: wann ist eine Funktion ein Listenhomomorphismus?
39 Funktionale Programmierung (WS2005/2006) 4/39 Definitionen foldl f e [] = e -- foldl.1 foldl f e (x:xs) = foldl f (f e x) xs -- foldl.2 foldr f e [] = e -- foldr.1 foldr f e (x:xs) = f x (foldr f e xs) -- foldr.2
40 Funktionale Programmierung (WS2005/2006) 4/40 Fold-Dekompositionssätze (foldl-dec.): foldl f a (xs++ys) = foldl f (foldl f a xs) ys (foldr-dec.): foldr f a (xs++ys) = foldr f (foldr f a ys) xs falls f assoziativ mit neutralem Element e: (foldl-ass.): foldl f e (xs++ys) = f (foldl f e xs) (foldl f e ys) (foldr-ass.): foldr f e (xs++ys) = f (foldr f e xs) (foldr f e ys) Beweise: zum üben
41 Funktionale Programmierung (WS2005/2006) 4/41 Erster Dualitätssatz (1) Sei f assoziativ mit neutralem Element e. Dann gilt für jede endliche Liste xs: foldr f e xs = foldl f e xs Beweis durch Induktion über die Struktur von xs {Fall.1}: xs == [] foldr f e xs { Fall.1 }== foldr f e [] {foldr.1 }== e {foldl.1 }== foldl f e [] { Fall.1 }== foldl f e xs
42 Funktionale Programmierung (WS2005/2006) 4/42 {Fall.2}: xs == (y:ys) foldr f e xs { Fall.2 }== foldr f e (y:ys) { foldr.2 }== f y (foldr f e ys) { Ind.Ann.}== f y (foldl f e ys) {Hilfsbew.}== foldl f (f y e) ys {Neut. e } == foldl f y ys {Neut. e } == foldl f (f e y) ys { foldl.2 }== foldl f e (y:ys) { Fall.2 }== foldl f e xs Erster Dualitätssatz (2)
43 Funktionale Programmierung (WS2005/2006) 4/43 Erster Dualitätssatz, Hilfsbeweis (1) Fehlversuch! zu zeigen: f y (foldl f e ys) = foldl f (f y e) ys {Fall.1}: ys == [] f y (foldl f e ys) { Fall.1 }== f y (foldl f e []) { foldl.1 }== f y e { foldl.1 }== foldl f (f y e) [] { Fall.1 }== foldl f (f y e) ys
44 Funktionale Programmierung (WS2005/2006) 4/44 Erster Dualitätssatz, Hilfsbeweis (2) Fehlversuch! zu zeigen: f y (foldl f e ys) = foldl f (f y e) ys {Fall.2}: ys == (z:zs) f y (foldl f e ys) { Fall.2 }== f y (foldl f e (z:zs)) { foldl.2 }== f y (foldl f (f e z) zs) { Neut.e. }== f y (foldl f z zs) {? }== foldl f (f y z) zs { foldl.2 }== foldl f y (z:zs) { Neut. e }== foldl f (f y e) (z:zs) { Fall.2 }== foldl f (f y e) ys z ist i.a. nicht gleich dem neutralen Element. Induktionsannahme muss verallgemeinert werden!
45 Funktionale Programmierung (WS2005/2006) 4/45 Erster Dualitätssatz, Hilfsbeweis (1) richtig zu zeigen: f y (foldl f x ys) = foldl f (f y x) ys {Fall.1}: ys == [] f y (foldl f x ys) { Fall.1 }== f y (foldl f x []) { foldl.1 }== f y x { foldl.1 }== foldl f (f y x) [] { Fall.1 }== foldl f (f y x) ys
46 Funktionale Programmierung (WS2005/2006) 4/46 Erster Dualitätssatz, Hilfsbeweis (2) richtig zu zeigen: f y (foldl f x ys) = foldl f (f y x) ys {Fall.2}: ys == (z:zs) f y (foldl f x ys) { Fall.2 }== f y (foldl f x (z:zs)) { foldl.2 }== f y (foldl f (f x z) zs) { Ind.Ann.}== foldl f (f y (f x z)) zs { Ass. f }== foldl f (f (f y x) z) zs { foldl.2 }== foldl f (f y x) (z:zs) { Fall.2 }== foldl f (f y x) ys
47 Funktionale Programmierung (WS2005/2006) 4/47 Zweiter Dualitätssatz (1) foldr f x xs = foldl (flip f) x (reverse xs) Beweis durch Induktion über die Struktur von xs {Fall.1}: xs == [] foldr f x xs {Fall.1 }== foldr f x [] {foldr.1}== x {foldl.1}== foldl (flip f) x [] { rev.1 }== foldl (flip f) x (reverse []) {Fall.1 }== foldl (flip f) x (reverse xs)
48 Funktionale Programmierung (WS2005/2006) 4/48 {Fall.2}: xs == y:ys Zweiter Dualitätssatz (2) foldr f x xs { Fall.2 }== foldr f x (y:ys) { foldr.2 }== f y (foldr f x ys) { flip }== flip f (foldr f x ys) y { foldl.1 }== foldl (flip f) (flip f (foldr f x ys) y) [] { foldl.2 }== foldl (flip f) (foldr f x ys) [y] { Ind.Ann. }== foldl (flip f) (foldl (flip f) x (reverse ys)) [y] {foldl-dec.}== foldl (flip f) x (reverse ys ++ [y]) {reverse.2 }== foldl (flip f) x (reverse (y:ys)) { Fall.2 }== foldl (flip f) x (reverse xs)
49 Funktionale Programmierung (WS2005/2006) 4/49 Anwendung des zweiten Dualitätssatzes Herleitung einer effizienten Implementierung von reverse reverse xs Spezifikation, s.u. { id }== id (reverse xs) {foldr/id}== foldr (:) [] (reverse xs) { 2.Dual }== foldl (flip (:)) [] (reverse (reverse xs)) {rev/rev }== foldl (flip (:)) [] xs Implementierung linearer Zeit 2. Dualitätssatz verwendet Spezifikation von reverse mit quadratischer Zeit! reverse [] = [] -- reverse.1 reverse (x:xs) = reverse xs ++ [x] -- reverse.2
50 Funktionale Programmierung (WS2005/2006) 4/50 Fusionssätze (1: foldr-fusion) Sei f strikt und gelte f (g x y) = h x (f y). Dann gilt: f. foldr g a = foldr h (f a) f x x g y g a x x h f g a x x h h f a
51 Funktionale Programmierung (WS2005/2006) 4/51 Fusionssätze (2: foldl-fusion) Sei f strikt und gelte f (g x y) = h (f x) y. Dann gilt: f. foldl g a = foldl h (f a) a y g x y g f y y a g f h y y a f h h
52 Funktionale Programmierung (WS2005/2006) 4/52 Spezialfälle der Fusionssätze fold/map-fusion foldr f a. map g = foldr (f. g) a bookkeeping-law: sei f assoziativ mit neutralem Element e; dann gilt: foldr f e. concat = foldr f e. map (foldr f e) Anwendung Buchführung (f=(+),e=0): sum. concat = sum. map sum
53 Funktionale Programmierung (WS2005/2006) 4/53 Monoid Monoid: Halbgruppe mit neutralem Element, Notation (M,, e) M Menge ( ): M M M eine totale Funktion, assoziativ e ist neutrales Element bzgl. Haskell-Beispiele: (Integer,+,0), natürliche Zahlen mit Addition ([a],++,[]), (endliche) Listen mit append (a->a,.,id), Funktionen mit Komposition
54 Funktionale Programmierung (WS2005/2006) 4/54 Monoidhomomorphismus seien M 1 = (M 1, 1, e 1 ) und M 2 = (M 2, 2, e 2 ) Monoide Monoidhomomorphismus: Abbildung h : M 1 M 2 mit den Eigenschaften 1. h(e 1 ) = e 2 2. m, m M 1 : h(m 1 m ) = h(m) 2 h(m )
55 Funktionale Programmierung (WS2005/2006) 4/55 Listenhomomorphismen Beispiele für Homomorphismen von M 1 = ([a], ++, []) nach M 2 = (Integer, +, 0): length sum sum. map f es gibt viele Homomorphismen von M 1 nach M 2 Unterscheidung: durch Erzeugendensystem
56 Funktionale Programmierung (WS2005/2006) 4/56 sei M = (M,, e) ein Monoid Erzeugendensystem Erzeugendensystem: Teilmenge A M, sodass jedes m M durch wiederholte Anwendung von aus Elementen von A und e konstruiert werden kann. sei M 1 = ([a], ++, []) Satz: die einelementigen Listen bilden ein Erzeugendensystem für M 1 (Beweis: siehe Thiemann-Buch (6.1))
57 Funktionale Programmierung (WS2005/2006) 4/57 Beispiele für Listenhomomorphismen Beispiele für Homomorphismen von M 1 = ([a], ++, []) nach M 2 = (M 2,, e): Name h [x] e ( ) id [x] [] (++) map f [f x] [] (++) reverse [x] [] (flip (++)) length 1 0 (+) sum x 0 (+) product x 1 (*) sum. map f f x 0 (+) foldr g e. map f (*) f x e g (*) g ist assoziativ mit neutralem Element e
58 Funktionale Programmierung (WS2005/2006) 4/58 Erster Homomorphiesatz Original: Bird, 1988 eine Funktion h::[a]->b ist ein Homomorphismus es gibt eine assoziative Funktion g mit neutralem Element e und eine Funktion f mit der Eigenschaft f x = h [x], sodass h sich schreiben lässt als: h = foldr g e. map f
59 Funktionale Programmierung (WS2005/2006) 4/59 Definitionen Eine Listenfunktion h heisst -linksgerichtet für einen binären Operator gdw., für alle Elemente a und Listen y gilt: h ([a] ++y) = a h y -rechtsgerichtet für einen binären Operator gdw., für alle Listen x und Elemente a gilt: h (x ++[a]) = h x a Anm.: es wird nicht gefordert, dass bzw. assoziativ sind.
60 Funktionale Programmierung (WS2005/2006) 4/60 Zweiter Homomorphiesatz (Spezialisierungssatz) Original: Bird, 1987 Jeder Listenhomomorphismus lässt sich sowohl als eine linksgerichtete als auch als eine rechtsgerichtete Listenfunktion ausdrücken, d.h. sei h von ([α], +,[ ]) nach (β,,e) ein Homomorphismus dann gibt es 1. einen Operator mit a y = f a y, sodass h = foldr ( ) e 2. einen Operator mit x b = x f b, sodass h = foldl ( ) e
61 Funktionale Programmierung (WS2005/2006) 4/61 Dritter Homomorphiesatz Beweis und Beispiel nach Gibbons, 1995 Wenn h linksgerichtet und rechtsgerichtet ist, dann ist h ein Homomorphismus. Zu zeigen: wenn h links- und rechtsgerichtet ist, dann gibt es einen Operator, so dass h (x ++ y) = h x h y. assoziativ weil + assoziativ. Wir suchen eine explizite Definition für, d.h., eine Funktion g mit 1. t u = h (g t ++ g u) 2. h g h = h Idee: g liefert zu x und y äquivalente Repräsentanten im Definitionsbereich von h.
62 Funktionale Programmierung (WS2005/2006) 4/62 Hilfslemma 1 zum Beweis des dritten Homomorphiesatzes Hilfslemma 1. Für jede berechenbare Funktion h mit aufzählbarem Definitionsbereich gibt es eine berechenbare (mglw. nicht totale) Funktion g, so dass gilt: h g h = h. Beweis. Um g t zu berechnen, kann man den Definitionsbereich von h aufzählen, und das erste x zurückgeben, für das gilt: h x = t. Falls t im Wertebereich von h liegt, terminiert dieses Verfahren.
63 Funktionale Programmierung (WS2005/2006) 4/63 Hilfslemma 2 zum Beweis des dritten Homomorphiesatzes Hilfslemma 2: Die Listenfunktion h ist ein Homomorphismus gdw. für alle Listen v, w, x und y gilt: h v = h x h w = h y = h (v ++w) = h (x ++y). Beweis: h-homomorphismus :: h(v ++w) = h v h w = h x h y = h(x ++y) gelte h v = h x h w = h y = h (v ++ w) = h (x ++ y) (*) wähle g, sodass h g h = h (Hilfslemma 1) definiere durch t u = h (g t ++g u) h x h y = {Definition } h (g (h x) ++ g (h y)) = { setze v = g (h x) und w = g (h y) } h (v ++w) = { h v = h x h w = h y ( ) } h (x ++y) also: h ist Homomorphismus mit Operator (neutrales Element: h [ ]).
64 Funktionale Programmierung (WS2005/2006) 4/64 Beweis des dritten Homomorphiesatzes zu zeigen: h ist links- und rechtsgerichtet = h Homomorphismus gelte: h ist links- und rechtsgerichtet: h = foldr ( ) e = foldl ( ) e zu zeigen: h Homomorphismus zeige äquivalente Aussage nach Hilfslemma 2: h v = h x h w = h y = h(v ++ w) = h(x ++y) gelte h v = h x h w = h y zu zeigen: h (v ++ w) = h (x ++ y) [nächste Folie]
65 Funktionale Programmierung (WS2005/2006) 4/65 Beweis: h (v ++ w) = { h ist linksgerichtet } foldr ( ) e (v ++ w) = { foldr-dekomposition } foldr ( ) (foldr ( ) e w) v = { h w = h y } foldr ( ) (foldr ( ) e y) v = { foldr-dekomposition } foldr ( ) e (v ++ y) = { h ist linksgerichtet } h (v ++ y) = { h ist rechtsgerichtet } foldl ( ) e (v ++ y) = { foldl-dekomposition } foldl ( ) (foldl ( ) e v) y = { h v = h x } foldl ( ) (foldl ( ) e x) y = { foldl-dekomposition } foldl ( ) e (x ++ y) = { h ist rechtsgerichtet } h (x ++ y)
66 Funktionale Programmierung (WS2005/2006) 4/66 Anwendung: Herleitung eines Sortierverfahrens Einfügen in eine sortierte Liste: ins ins a [] = [a] ins a (b:x) a<=b = a : b : x a>b = b : ins a x ins = flip ins Sortieren basieren auf einfügen: linksgerichtet: sort = foldr ins [] rechtsgerichtet: sort = foldl ins [] Folge aus dem dritten Homomorphiesatz: sort ist ein Homomorphismus.
67 Funktionale Programmierung (WS2005/2006) 4/67 Herleitung eines Sortierverfahrens sowohl linksgerichtetes als auch rechtsgerichtetes Einfügesortieren braucht Zeit θ(n 2 ) für Liste der Länge n gesucht: Lösung, bei der die Liste in zwei etwa gleich große Teile geteilt wird, um Zeit θ(n log n) zu erreichen. Plan: Herleitung eines Sortierverfahrens, das Teilung der unsortierten Liste in zwei beliebige Teile ungleich [ ] zulässt links- und rechtsgerichtetes Einfügesortieren als Spezialfälle enthält bestimme Implementierung des Operators, so dass gilt: sort u sort v == sort (u ++ v).
68 Funktionale Programmierung (WS2005/2006) 4/68 Herleitung eines Sortierverfahrens u v { u, v sortiert } = sort u sort v { sort ist Homomorphismus } = sort (u ++ v) { sort } = foldl ins [] (u ++ v) { foldl-dekomposition } = foldl ins (foldl ins [] u) v { sort } = foldl ins (sort u) v { u sortiert } = foldl ins u v { setze mergeq = foldl ins (*) } = mergeq u v (*) Name mergeq wegen Eigenschaft von foldl ins : mergeq u [] == foldl ins u [] == u mergeq u (b:v) == foldl ins u (b:v) == foldl ins (ins u b) v == mergeq (ins u b) v
69 Funktionale Programmierung (WS2005/2006) 4/69 u v = mergeq u v Herleitung eines Sortierverfahrens mergeq u [] = u mergeq u (b:v) = mergeq (ins u b) v mergeq verwendet Eigenschaft, dass u sortiert ist mergeq verwendet nicht, dass v sortiert ist immer noch quadratische Laufzeit! Verbesserung von mergeq zu merge: Umschreiben unter Ausnutzung der Sortiertheit von v
70 Funktionale Programmierung (WS2005/2006) 4/70 Verbesserung von mergeq zu merge Abkürzung: sei a ein Element und v eine Liste: a v heisst: für alle b in v gilt a b Hilfslemma: a x a y (foldl ins (a:x) y) = (a : foldl ins x y) Beweis: durch Induktion
71 Funktionale Programmierung (WS2005/2006) 4/71 Verbesserung von mergeq zu merge zweite Liste ist leer merge u [] { merge == mergeq } = mergeq u [] { mergeq.1 } = u erste Liste ist leer merge [] v { merge == mergeq } = mergeq [] v { Abk. mergeq } = foldl ins [] v { sort } = sort v { v ist sortiert } = v
72 Funktionale Programmierung (WS2005/2006) 4/72 Verbesserung von mergeq zu merge beide Listen sind nicht leer merge (a:u) (b:v) { merge == mergeq } = mergeq (a:u) (b:v) { Abk. mergeq } = foldl ins (a:u) (b:v) { foldl.2 } = foldl ins (ins (a:u) b) v =... weiter mit Fallunterscheidung a < b und a b
73 Funktionale Programmierung (WS2005/2006) 4/73 Verbesserung von mergeq zu merge (a < b) Annahme: (a:u) und (b:v) sortiert und a < b also gilt: a u, a v und a (ins u b) merge (a:u) (b:v) { Schritte von letzter Folie } = foldl ins (ins (a:u) b) v { ins a<b } = foldl ins (a : ins u b) v { Hilfslemma } = a : foldl ins (ins u b) v { foldl.2 } = a : foldl ins u (b:v) { Abk. mergeq } = a : mergeq u (b:v) { merge == mergeq } = a : merge u (b:v)
74 Funktionale Programmierung (WS2005/2006) 4/74 Verbesserung von mergeq zu merge (a b) Annahme: (a:u) und (b:v) sortiert und a b also gilt: b (a:u) und b v merge (a:u) (b:v) { Schritte von vorletzter Folie } = foldl ins (ins (a:u) b) v { ins a b } = foldl ins (b:a:u) v { Hilfslemma } = b : foldl ins (a:u) v { Abk. mergeq } = b : mergeq (a:u) v { merge == mergeq } = b : merge (a:u) v
75 Funktionale Programmierung (WS2005/2006) 4/75 Verbesserung von mergeq zu merge, Fazit damit ergibt sich für merge... merge [] v = v merge u [] = u merge (a:u) (b:v) a<b = a : merge u (b:v) a>=b = b : merge (a:u) v... und die Einfügefunktionen sind Spezialfälle davon: ins a xs == merge [a] xs ins xs a == merge xs [a]
76 Funktionale Programmierung (WS2005/2006) 4/76 Resultierendes Sortierverfahren: mergesort mergesort :: Ord a => [a] -> [a] mergesort [] = [] -- neutrales Element mergesort [x] = [x] -- Erzeugendensystem mergesort xs = let (ys,zs) = splitat (length xs div 2) xs u = mergesort ys v = mergesort zs in merge u v -- Operator im Wertebereich -- des Homomorphismus merge :: Ord a => [a] -> [a] -> [a] merge [] v = v merge u [] = u merge (a:u) (b:v) a<b = a : merge u (b:v) a>=b = b : merge (a:u) v
77 Funktionale Programmierung (WS2005/2006) 4/77 Programmtransformationen gehen zurück auf Burstall/Darlington (1977): A transformation system for developing recursive programs Anwendung: transformiere ineffizientes in effizientes Programm Arten von Transformationsschritten unfold: ersetzen eines Funktionsnamens durch den Funktionsrumpf fold: Umkehrung von unfold def: einführen lokaler Definitionen (let/where) spec: Spezialisierung
78 Funktionale Programmierung (WS2005/2006) 4/78 Beispiel: Fibonacci-Funktion Ausgangspunkt: sehr ineffizientes Programm fib 0 = 0 -- fib.0 fib 1 = 1 -- fib.1 fib n n>1 = fib (n-2) + fib (n-1) fib (n+2) = fib n + fib (n+1) -- fib.2 Performance-steigernde Transformationen (1) einfügen einer lokalen Definition: fib (n+2) = z1 + z2 where (z1,z2) = (fib n, fib (n+1))
79 Funktionale Programmierung (WS2005/2006) 4/79 (2) Definiere eine Hilfsfunktion für die rechte Seite von fib (n+2) fib2 n = (fib n, fib (n+1)) -- fib2 (3) Anwendung von (spec) (a) fib2 0 = (fib 0, fib 1) = (0,1) (b) fib2 (n+1) { Def. fib2 } = (fib (n+1), fib (n+2)) { unfold } = (fib (n+1), fib (n+1) + fib n) { where } = (z2,z2+z1) where (z1,z2) = fib2 n Damit: fib n { fib.2 } = z1 where (z1,z2) = fib2 n { fst } = = fst (fib2 n)
80 Funktionale Programmierung (WS2005/2006) 4/80 fib2 :: Integer -> (Integer,Integer) fib2 0 = (0,1) fib2 n n>0 = (z2,z2+z1) where (z1,z2) = fib2 (n-1) fib :: Integer -> Integer fib n = fst (fib2 n) oder, Rekursion ersetzt durch foldl fib :: Integer -> Integer fib n = let f (z1,z2) = const (z2,z2+z1) in fst (foldl f (0,1) [1..n])
81 Funktionale Programmierung (WS2005/2006) 4/81 Homomorphieeigenschaften bei fib Ziel: Optimierung der foldl-berechnung repräsentieren n durch Liste von () der Länge n Homomorphismus h : ([()], +, []) (N 2 N 2,, id) fib :: Integer -> Integer fib n = fst (fibhom [ () _ <- [1..n] ] (0,1)) fibhom :: [()] -> ((Integer,Integer)->(Integer,Integer)) fibhom xs = let f (z1,z2) = (z2,z2+z1) in foldr (.) id (map (const f) xs)
82 Funktionale Programmierung (WS2005/2006) 4/82 Weitere Verbesserungen explizite Funktionskomposition ist speicherplatzaufwändig suchen nach algebraischen Möglichkeiten zur Kompaktifizierung der Komposition wir wissen: f ist eine lineare Abbildung f(z 1, z 2 ) = (z 2, z 2 + z 1 ) = ( ( ) ( z 1 z 2 ) ) T Komposition linearer Abbildungen (g f) entspricht Matrixmultiplikation nächster Schritt: Umstellung des foldr-operators auf Matrixmultiplikation
83 Funktionale Programmierung (WS2005/2006) 4/83 Einführung eines Typs von 2x2-Matrizen data M2 a = M2 {upperleft,upperright,lowerleft,lowerright::a} deriving (Eq,Show) unitmat, fibmat :: M2 Integer unitmat = M (z1,z2) -> (z1,z2) fibmat = M (z1,z2) -> (z2,z1+z2) instance Num a => Num (M2 a) where (M2 a b c d) * (M2 e f g h) = M2 (a*e+b*g) (a*f+b*h) (c*e+d*g) (c*f+d*h)
84 Funktionale Programmierung (WS2005/2006) 4/84 Fibonacci-Berechnung mittels Matrixmultiplikation fib :: Integer -> Integer fib n = lowerleft (fibhom [ () _ <- [1..n] ]) fibhom :: [()] -> M2 Integer fibhom xs = foldr (*) unitmat (map (const fibmat) xs) -- war: foldr (.) id (map (const f ) xs)
85 Funktionale Programmierung (WS2005/2006) 4/85 weitere Optimierung: effiziente Potenzierung fibopt :: Integer -> Integer fibopt n = lowerleft $ fibmat^n Laufzeitvergleiche (Zeiten mit ghci in Sekunden, ohne Ausgabe) n binär rekursiv linear rekursiv foldr (.) foldr (*) fibopt
86 Funktionale Programmierung (WS2005/2006) 4/86 Problem der maximalen Segmentsumme gesucht: Maximum der Summen aller Segmente einer Liste ganzer Zahlen Bsp.: [-3,4,-7,2,4,-5,2,3,7,-2,-1,9,3,-15,6,-2,9,-7] 22 imperative Problemlösungen (beschrieben in: Jon Bentley: Programming Pearls) Test aller Segmente: Θ(n 3 ) inkrementelles Update von Teilsummen: Θ(n 2 ) Divide-and-Conquer Lösung: Θ(n log n) Scan-Algorithmus: Θ(n) Im folgenden: formale Herleitungen funktionaler Scan-Algorithmus Θ(n) paralleler D&C-Algorithms Θ(log n)
87 Funktionale Programmierung (WS2005/2006) 4/87 Spezifikation: Problem der maximalen Segmentsumme mss :: [Integer] -> Integer mss = let segs = concat. map inits. tails in maximum. map sum. segs tails: finale Segmente, Bsp.: tails [1,2,3] [[1,2,3],[2,3],[3],[]] inits: initiale Segmente, Bsp.: map inits (tails [1,2,3]) [[[],[1],[1,2],[1,2,3]], [[],[2],[2,3]], [[],[3]], [[]]] segs: alle Segmente Bsp.: segs [1,2,3] [[],[1],[1,2],[1,2,3],[],[2],[2,3],[],[3],[]]]
88 Funktionale Programmierung (WS2005/2006) 4/88 Reduktion der Komplexität von Θ(n 3 ) auf Θ(n) {Definition mss} {concat/map} {map/.} mss = maximum. map sum. concat. map inits. tails = maximum. concat. map (map sum). map inits. tails = maximum. concat. map (map sum. inits). tails { bookkeeping } = maximum. map maximum. map (map sum. inits). tails {map/.} {map/sum} = maximum. map (maximum. map sum. inits). tails = maximum. map (maximum. scanl (+) 0). tails { Def. maximum } = maximum. map (foldr1 max. scanl (+) 0). tails { foldr Fusion } = maximum. map (foldr ( ) 0). tails where x y = max 0 (x+y) { map/foldr } = maximum. scanr ( ) 0 where x y = max 0 (x+y)
89 Funktionale Programmierung (WS2005/2006) 4/89 Akkumulierung der Zwischenergebnisse Def.: x y = max 0 (x+y) mss { vorige Folie } = maximum. scanr ( ) 0 { Def. maximum } = foldr1 max. scanr ( ) 0 { Tupling } = snd. foldr ( ) (0,0) max max max max 4 0
90 Funktionale Programmierung (WS2005/2006) 4/90 Akkumulierung der Zwischenergebnisse mss = snd. foldr ( ) (0,0) max max max max 4 0 x (acc,res) = let acc = max 0 (x+acc) in (acc, max res acc ) -- x acc Interpretation des Akkumulatorinhalts: Wert des maximalen initialen Segments
91 Funktionale Programmierung (WS2005/2006) 4/91 Anwendung von Homomorphieeigenschaften 1. segs = concat. map inits. tails: mss = let x (acc,res) = let acc = max 0 (x+acc) in (acc, max acc res) in snd. foldr ( ) (0,0) Akkumulator: Wert des maximalen initialen Segments (mis) 2. segs = concat. map tails. inits: mss = let (acc,res) x = let acc = max 0 (acc+x) in (acc, max acc res) in snd. foldl ( ) (0,0) Akkumulator: Wert des maximalen finalen Segments (mfs): mss ist eine Projektion einer linksgerichteten und rechtsgerichteten Listenfunktion. Dritter Homomorphiesatz: mss ist Projektion eines Homomorphismus h. Suche nach dem Kombinationsoperator : h (x++y) == h x h y
92 Funktionale Programmierung (WS2005/2006) 4/92 Suche nach dem Kombinationsoperator Der Homomorphismus muss enthalten: 1. maximale Segmentsumme mss 2. Summe des maximalen initialen Segments mis 3. Summe des maximalen finalen Segments mfs Problem: wie erhält man aus x und y die Werte für x y? 1. mss x y = max (max mss x mss y ) (mfs x + mis y ) 2. mis x y = max mis x (sum x + mis y ) 3. mfs x y = max mfs y (sum y + mfs x ) zusätzliches Tupling mit der Summe aller Werte nötig: 4. sum x y = sum x + sum y
93 Funktionale Programmierung (WS2005/2006) 4/93 mss als Projektion eines Homomorphismus mss :: [Integer] -> Integer mss = prj1aus4. foldr g e. map f where e = (0,0,0,0) g (mssx,misx,mfsx,sumx) (mssy,misy,mfsy,sumy) = (max (max mssx mssy) (mfsx + misy), max misx (sumx + misy), max mfsy (sumy + mfsx), sumx + sumy) f x = let xnn = max 0 x in (xnn,xnn,xnn,x) prj1aus4 (a,b,c,d) = a Übungsaufgabe: Erweiterung, so dass auch Segmentgrenzen geliefert werden
94 Funktionale Programmierung (WS2005/2006) 4/94 mss als Divide-and-Conquer mss :: [Integer] -> Integer mss [] = 0 mss xs = prj1aus4 (dc pred basic divide combine xs) where pred xs = length xs == 1 basic [x] = let xnn = max 0 x in (xnn,xnn,xnn,x) divide xs = let (ys,zs) = splitat (length xs div 2) xs in [ys,zs] combine _ [(mssx,misx,mfsx,sumx), (mssy,misy,mfsy,sumy)] = (max (max mssx mssy) (mfsx + misy), max misx (sumx + misy), max mfsy (sumy + mfsx), sumx + sumy) prj1aus4 (a,b,c,d) = a
95 Funktionale Programmierung (WS2005/2006) 4/95 Beobachtungen für mss Laufzeitreduktion von Θ(n 3 ) (Spezifikation) sequenziell: auf Θ(n) parallel: durch D&C auf Θ(log n) wichtige Gesetze/Techniken bookkeeping: vermeidet temporäre Listen fold-fusion und map-komposition: vermeidet Mehrfachdurchgänge Tupling: erhöht die Flexibilität der verknüpfenden Operatoren Zwischenergebnisse für Fold-Fusion Assoziativität für Homomorphismen
Funktionale Programmierung mit Haskell
 Funktionale Programmierung mit Haskell Dr. Michael Savorić Hohenstaufen-Gymnasium (HSG) Kaiserslautern Version 20120622 Überblick Wichtige Eigenschaften Einführungsbeispiele Listenerzeugung und Beispiel
Funktionale Programmierung mit Haskell Dr. Michael Savorić Hohenstaufen-Gymnasium (HSG) Kaiserslautern Version 20120622 Überblick Wichtige Eigenschaften Einführungsbeispiele Listenerzeugung und Beispiel
Funktionale Programmierung ALP I. Funktionen höherer Ordnung. Teil 2 SS 2013. Prof. Dr. Margarita Esponda. Prof. Dr.
 ALP I Funktionen höherer Ordnung Teil 2 SS 2013 Funktionen höherer Ordnung Nehmen wir an, wir möchten alle Zahlen innerhalb einer Liste miteinander addieren addall:: (Num a) => [a -> a addall [ = 0 addall
ALP I Funktionen höherer Ordnung Teil 2 SS 2013 Funktionen höherer Ordnung Nehmen wir an, wir möchten alle Zahlen innerhalb einer Liste miteinander addieren addall:: (Num a) => [a -> a addall [ = 0 addall
Was bisher geschah. deklarative Programmierung. funktionale Programmierung (Haskell):
 Was bisher geschah deklarative Programmierung funktional: Programm: Menge von Termgleichungen, Term Auswertung: Pattern matsching, Termumformungen logisch: Programm: Menge von Regeln (Horn-Formeln), Formel
Was bisher geschah deklarative Programmierung funktional: Programm: Menge von Termgleichungen, Term Auswertung: Pattern matsching, Termumformungen logisch: Programm: Menge von Regeln (Horn-Formeln), Formel
4. Jeder Knoten hat höchstens zwei Kinder, ein linkes und ein rechtes.
 Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
Funktionale Programmierung
 Funktionale Programmierung Jörg Kreiker Uni Kassel und SMA Solar Technology AG Wintersemester 2011/2012 2 Teil II Typen mit Werten und Ausdruck, sogar listenweise 3 Haskell Programme Programm Module ein
Funktionale Programmierung Jörg Kreiker Uni Kassel und SMA Solar Technology AG Wintersemester 2011/2012 2 Teil II Typen mit Werten und Ausdruck, sogar listenweise 3 Haskell Programme Programm Module ein
1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage:
 Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Formale Methoden in der Informatik Wiederholung klassische Logik Konkrete Datentypen (algebraische Strukturen) Abstrakte Datentypen
 Was bisher geschah Formale Methoden in der Informatik Wiederholung klassische Logik Konkrete Datentypen (algebraische Strukturen) Abstrakte Datentypen Syntax: Signatur Semantik: Axiome (FOL-Formeln, meist
Was bisher geschah Formale Methoden in der Informatik Wiederholung klassische Logik Konkrete Datentypen (algebraische Strukturen) Abstrakte Datentypen Syntax: Signatur Semantik: Axiome (FOL-Formeln, meist
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Typdeklarationen. Es gibt in Haskell bereits primitive Typen:
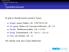 Typdeklarationen Es gibt in bereits primitive Typen: Integer: ganze Zahlen, z.b. 1289736781236 Int: ganze Zahlen mit Computerarithmetik, z.b. 123 Double: Fließkommazahlen, z.b. 3.14159 String: Zeichenketten,
Typdeklarationen Es gibt in bereits primitive Typen: Integer: ganze Zahlen, z.b. 1289736781236 Int: ganze Zahlen mit Computerarithmetik, z.b. 123 Double: Fließkommazahlen, z.b. 3.14159 String: Zeichenketten,
ALP I. Funktionale Programmierung
 ALP I Funktionale Programmierung Sortieren und Suchen (Teil 1) WS 2012/2013 Suchen 8 False unsortiert 21 4 16 7 19 11 12 7 1 5 27 3 8 False sortiert 2 4 6 7 9 11 12 18 21 24 27 36 Suchen in unsortierten
ALP I Funktionale Programmierung Sortieren und Suchen (Teil 1) WS 2012/2013 Suchen 8 False unsortiert 21 4 16 7 19 11 12 7 1 5 27 3 8 False sortiert 2 4 6 7 9 11 12 18 21 24 27 36 Suchen in unsortierten
Datenstrukturen & Algorithmen
 Datenstrukturen & Algorithmen Matthias Zwicker Universität Bern Frühling 2010 Übersicht Binäre Suchbäume Einführung und Begriffe Binäre Suchbäume 2 Binäre Suchbäume Datenstruktur für dynamische Mengen
Datenstrukturen & Algorithmen Matthias Zwicker Universität Bern Frühling 2010 Übersicht Binäre Suchbäume Einführung und Begriffe Binäre Suchbäume 2 Binäre Suchbäume Datenstruktur für dynamische Mengen
Abschnitt: Algorithmendesign und Laufzeitanalyse
 Abschnitt: Algorithmendesign und Laufzeitanalyse Definition Divide-and-Conquer Paradigma Divide-and-Conquer Algorithmen verwenden die Strategien 1 Divide: Teile das Problem rekursiv in Subproblem gleicher
Abschnitt: Algorithmendesign und Laufzeitanalyse Definition Divide-and-Conquer Paradigma Divide-and-Conquer Algorithmen verwenden die Strategien 1 Divide: Teile das Problem rekursiv in Subproblem gleicher
Programmieren I. Kapitel 7. Sortieren und Suchen
 Programmieren I Kapitel 7. Sortieren und Suchen Kapitel 7: Sortieren und Suchen Ziel: Varianten der häufigsten Anwendung kennenlernen Ordnung Suchen lineares Suchen Binärsuche oder Bisektionssuche Sortieren
Programmieren I Kapitel 7. Sortieren und Suchen Kapitel 7: Sortieren und Suchen Ziel: Varianten der häufigsten Anwendung kennenlernen Ordnung Suchen lineares Suchen Binärsuche oder Bisektionssuche Sortieren
Einfache Ausdrücke Datentypen Rekursive funktionale Sprache Franz Wotawa Institut für Softwaretechnologie wotawa@ist.tugraz.at
 Inhalt SWP Funktionale Programme (2. Teil) Einfache Ausdrücke Datentypen Rekursive funktionale Sprache Franz Wotawa Institut für Softwaretechnologie wotawa@ist.tugraz.at Interpreter für funktionale Sprache
Inhalt SWP Funktionale Programme (2. Teil) Einfache Ausdrücke Datentypen Rekursive funktionale Sprache Franz Wotawa Institut für Softwaretechnologie wotawa@ist.tugraz.at Interpreter für funktionale Sprache
SWP Prüfungsvorbereitung
 20. Juni 2011 1 Grammatiken 2 LL(1) 3 EXP 4 Datentypen 5 LP Grammatiken Angabe Erstellen Sie First- und Follow-Mengen aller Non-Terminale der folgenden Grammatik. S a S S B y B A C A A b b A x A ɛ C c
20. Juni 2011 1 Grammatiken 2 LL(1) 3 EXP 4 Datentypen 5 LP Grammatiken Angabe Erstellen Sie First- und Follow-Mengen aller Non-Terminale der folgenden Grammatik. S a S S B y B A C A A b b A x A ɛ C c
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Praktische Informatik 3: Einführung in die Funktionale Programmierung Vorlesung vom 10.11.2010: Rekursive Datentypen
 Rev. 1152 1 [23] Praktische Informatik 3: Einführung in die Funktionale Programmierung Vorlesung vom 10.11.2010: Rekursive Datentypen Christoph Lüth & Dennis Walter Universität Bremen Wintersemester 2010/11
Rev. 1152 1 [23] Praktische Informatik 3: Einführung in die Funktionale Programmierung Vorlesung vom 10.11.2010: Rekursive Datentypen Christoph Lüth & Dennis Walter Universität Bremen Wintersemester 2010/11
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Einführung in die funktionale Programmierung
 Einführung in die funktionale Programmierung Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 26. Oktober 2006 Haskell - Einführung Syntax Typen Auswertung Programmierung
Einführung in die funktionale Programmierung Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 26. Oktober 2006 Haskell - Einführung Syntax Typen Auswertung Programmierung
Lineare Gleichungssysteme I (Matrixgleichungen)
 Lineare Gleichungssysteme I (Matrigleichungen) Eine lineare Gleichung mit einer Variable hat bei Zahlen a, b, die Form a b. Falls hierbei der Kehrwert von a gebildet werden darf (a 0), kann eindeutig aufgelöst
Lineare Gleichungssysteme I (Matrigleichungen) Eine lineare Gleichung mit einer Variable hat bei Zahlen a, b, die Form a b. Falls hierbei der Kehrwert von a gebildet werden darf (a 0), kann eindeutig aufgelöst
Grundlagen der Programmierung 2. Bäume
 Grundlagen der Programmierung 2 Bäume Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 24. Mai 2006 Graphen Graph: Menge von Knoten undzugehörige (gerichtete oder ungerichtete)
Grundlagen der Programmierung 2 Bäume Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 24. Mai 2006 Graphen Graph: Menge von Knoten undzugehörige (gerichtete oder ungerichtete)
Die Gleichung A x = a hat für A 0 die eindeutig bestimmte Lösung. Für A=0 und a 0 existiert keine Lösung.
 Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Semantik von Formeln und Sequenzen
 Semantik von Formeln und Sequenzen 33 Grundidee der Verwendung von Logik im Software Entwurf Syntax: Menge von Formeln = Axiome Ax K ist beweisbar Formel ϕ beschreiben Korrektkeit Vollständigkeit beschreibt
Semantik von Formeln und Sequenzen 33 Grundidee der Verwendung von Logik im Software Entwurf Syntax: Menge von Formeln = Axiome Ax K ist beweisbar Formel ϕ beschreiben Korrektkeit Vollständigkeit beschreibt
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Was ist Logische Programmierung?
 Was ist Logische Programmierung? Die Bedeutung eines Computer-Programms kann durch Logik erklärt werden. Die Idee der logischen Programmierung besteht darin, die Logik eines Programms selber als Programm
Was ist Logische Programmierung? Die Bedeutung eines Computer-Programms kann durch Logik erklärt werden. Die Idee der logischen Programmierung besteht darin, die Logik eines Programms selber als Programm
Programmiersprachen und Übersetzer
 Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Grammatiken. Einführung
 Einführung Beispiel: Die arithmetischen Ausdrücke über der Variablen a und den Operationen + und können wie folgt definiert werden: a, a + a und a a sind arithmetische Ausdrücke Wenn A und B arithmetische
Einführung Beispiel: Die arithmetischen Ausdrücke über der Variablen a und den Operationen + und können wie folgt definiert werden: a, a + a und a a sind arithmetische Ausdrücke Wenn A und B arithmetische
7 Rechnen mit Polynomen
 7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
Übung 9 - Lösungsvorschlag
 Universität Innsbruck - Institut für Informatik Datenbanken und Informationssysteme Prof. Günther Specht, Eva Zangerle Besprechung: 15.12.2008 Einführung in die Informatik Übung 9 - Lösungsvorschlag Aufgabe
Universität Innsbruck - Institut für Informatik Datenbanken und Informationssysteme Prof. Günther Specht, Eva Zangerle Besprechung: 15.12.2008 Einführung in die Informatik Übung 9 - Lösungsvorschlag Aufgabe
Mathematischer Vorbereitungskurs für Ökonomen
 Mathematischer Vorbereitungskurs für Ökonomen Dr. Thomas Zehrt Wirtschaftswissenschaftliches Zentrum Universität Basel Gleichungen Inhalt: 1. Grundlegendes 2. Lineare Gleichungen 3. Gleichungen mit Brüchen
Mathematischer Vorbereitungskurs für Ökonomen Dr. Thomas Zehrt Wirtschaftswissenschaftliches Zentrum Universität Basel Gleichungen Inhalt: 1. Grundlegendes 2. Lineare Gleichungen 3. Gleichungen mit Brüchen
Wiederholung ADT Menge Ziel: Verwaltung (Finden, Einfügen, Entfernen) einer Menge von Elementen
 Was bisher geschah abstrakter Datentyp : Signatur Σ und Axiome Φ z.b. ADT Menge zur Verwaltung (Finden, Einfügen, Entfernen) mehrerer Elemente desselben Typs Spezifikation einer Schnittstelle Konkreter
Was bisher geschah abstrakter Datentyp : Signatur Σ und Axiome Φ z.b. ADT Menge zur Verwaltung (Finden, Einfügen, Entfernen) mehrerer Elemente desselben Typs Spezifikation einer Schnittstelle Konkreter
Das Typsystem von Scala. L. Piepmeyer: Funktionale Programmierung - Das Typsystem von Scala
 Das Typsystem von Scala 1 Eigenschaften Das Typsystem von Scala ist statisch, implizit und sicher 2 Nichts Primitives Alles ist ein Objekt, es gibt keine primitiven Datentypen scala> 42.hashCode() res0:
Das Typsystem von Scala 1 Eigenschaften Das Typsystem von Scala ist statisch, implizit und sicher 2 Nichts Primitives Alles ist ein Objekt, es gibt keine primitiven Datentypen scala> 42.hashCode() res0:
Objektorientierte Programmierung
 Objektorientierte Programmierung 1 Geschichte Dahl, Nygaard: Simula 67 (Algol 60 + Objektorientierung) Kay et al.: Smalltalk (erste rein-objektorientierte Sprache) Object Pascal, Objective C, C++ (wiederum
Objektorientierte Programmierung 1 Geschichte Dahl, Nygaard: Simula 67 (Algol 60 + Objektorientierung) Kay et al.: Smalltalk (erste rein-objektorientierte Sprache) Object Pascal, Objective C, C++ (wiederum
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lernziele: Ausgleichstechniken für binäre Bäume verstehen und einsetzen können.
 6. Bäume Lernziele 6. Bäume Lernziele: Definition und Eigenschaften binärer Bäume kennen, Traversierungsalgorithmen für binäre Bäume implementieren können, die Bedeutung von Suchbäumen für die effiziente
6. Bäume Lernziele 6. Bäume Lernziele: Definition und Eigenschaften binärer Bäume kennen, Traversierungsalgorithmen für binäre Bäume implementieren können, die Bedeutung von Suchbäumen für die effiziente
Effiziente Algorithmen und Datenstrukturen I. Kapitel 10: Lineare Algebra
 Effiziente Algorithmen und Datenstrukturen I Kapitel 10: Lineare Algebra Christian Scheideler WS 2008 19.02.2009 Kapitel 10 1 Überblick Notation Arithmetik auf großen Zahlen (Addition und Multiplikation)
Effiziente Algorithmen und Datenstrukturen I Kapitel 10: Lineare Algebra Christian Scheideler WS 2008 19.02.2009 Kapitel 10 1 Überblick Notation Arithmetik auf großen Zahlen (Addition und Multiplikation)
Erfüllbarkeit und Allgemeingültigkeit
 Theoretische Informatik: Logik, M. Lange, FB16, Uni Kassel: 3.3 Aussagenlogik Erfüllbarkeit 44 Erfüllbarkeit und Allgemeingültigkeit Def.: eine Formel ϕ heißt erfüllbar, wennesein I gibt, so dass I = ϕ
Theoretische Informatik: Logik, M. Lange, FB16, Uni Kassel: 3.3 Aussagenlogik Erfüllbarkeit 44 Erfüllbarkeit und Allgemeingültigkeit Def.: eine Formel ϕ heißt erfüllbar, wennesein I gibt, so dass I = ϕ
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen
 Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Binäre Bäume. 1. Allgemeines. 2. Funktionsweise. 2.1 Eintragen
 Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Programmieren in C. Rekursive Funktionen. Prof. Dr. Nikolaus Wulff
 Programmieren in C Rekursive Funktionen Prof. Dr. Nikolaus Wulff Rekursive Funktionen Jede C Funktion besitzt ihren eigenen lokalen Satz an Variablen. Dies bietet ganze neue Möglichkeiten Funktionen zu
Programmieren in C Rekursive Funktionen Prof. Dr. Nikolaus Wulff Rekursive Funktionen Jede C Funktion besitzt ihren eigenen lokalen Satz an Variablen. Dies bietet ganze neue Möglichkeiten Funktionen zu
Funktionale Programmierung. Funktionale Programmierung: Vorlesungsüberblick. Eigenschaften rein funktionaler Programmierung
 Funktionale Programmierung 1 Funktionale Programmierung: Vorlesungsüberblick 1. Funktionale Programmierung Prinzipien funktionaler Programmierung Funktionale Programmierung in prozeduralen Sprachen Rekursive
Funktionale Programmierung 1 Funktionale Programmierung: Vorlesungsüberblick 1. Funktionale Programmierung Prinzipien funktionaler Programmierung Funktionale Programmierung in prozeduralen Sprachen Rekursive
Scala kann auch faul sein
 Scala kann auch faul sein Kapitel 19 des Buches 1 Faulheit Faulheit ( lazy evaluation ) ist auch in C oder Java nicht unbekannt int x=0; if(x!=0 && 10/x>3){ System.out.println("In if"); } Nutzen der Faulheit?
Scala kann auch faul sein Kapitel 19 des Buches 1 Faulheit Faulheit ( lazy evaluation ) ist auch in C oder Java nicht unbekannt int x=0; if(x!=0 && 10/x>3){ System.out.println("In if"); } Nutzen der Faulheit?
Kap. 8: Speziell gewählte Kurven
 Stefan Lucks 8: Spezielle Kurven 82 Verschl. mit Elliptischen Kurven Kap. 8: Speziell gewählte Kurven Zur Erinnerung: Für beliebige El. Kurven kann man den Algorithmus von Schoof benutzen, um die Anzahl
Stefan Lucks 8: Spezielle Kurven 82 Verschl. mit Elliptischen Kurven Kap. 8: Speziell gewählte Kurven Zur Erinnerung: Für beliebige El. Kurven kann man den Algorithmus von Schoof benutzen, um die Anzahl
3. Grundlagen der Linearen Programmierung
 3. Grundlagen der linearen Programmierung Inhalt 3. Grundlagen der Linearen Programmierung Lineares Programm Grafische Lösung linearer Programme Normalform Geometrie linearer Programme Basislösungen Operations
3. Grundlagen der linearen Programmierung Inhalt 3. Grundlagen der Linearen Programmierung Lineares Programm Grafische Lösung linearer Programme Normalform Geometrie linearer Programme Basislösungen Operations
Fragen. f [ ] = [ ] f (x : y : ys) = x y : f ys f (x : xs) = f (x : x : xs) Wozu evaluiert f [1, 2, 3] (Abkürzung für f (1 : 2 : 3 : [ ]))?
![Fragen. f [ ] = [ ] f (x : y : ys) = x y : f ys f (x : xs) = f (x : x : xs) Wozu evaluiert f [1, 2, 3] (Abkürzung für f (1 : 2 : 3 : [ ]))? Fragen. f [ ] = [ ] f (x : y : ys) = x y : f ys f (x : xs) = f (x : x : xs) Wozu evaluiert f [1, 2, 3] (Abkürzung für f (1 : 2 : 3 : [ ]))?](/thumbs/24/4200701.jpg) Fragen f [ ] = [ ] f (x : y : ys) = x y : f ys f (x : xs) = f (x : x : xs) Wozu evaluiert f [1, 2, 3] (Abkürzung für f (1 : 2 : 3 : [ ]))? Wozu evaluiert [f [ ], f [ ]]? Weiteres Beispiel: f [ ] y = [
Fragen f [ ] = [ ] f (x : y : ys) = x y : f ys f (x : xs) = f (x : x : xs) Wozu evaluiert f [1, 2, 3] (Abkürzung für f (1 : 2 : 3 : [ ]))? Wozu evaluiert [f [ ], f [ ]]? Weiteres Beispiel: f [ ] y = [
TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK
 TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK WS 11/12 Einführung in die Informatik II Übungsblatt 2 Univ.-Prof. Dr. Andrey Rybalchenko, M.Sc. Ruslán Ledesma Garza 8.11.2011 Dieses Blatt behandelt
TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK WS 11/12 Einführung in die Informatik II Übungsblatt 2 Univ.-Prof. Dr. Andrey Rybalchenko, M.Sc. Ruslán Ledesma Garza 8.11.2011 Dieses Blatt behandelt
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Korrelation (II) Korrelation und Kausalität
 Korrelation (II) Korrelation und Kausalität Situation: Seien X, Y zwei metrisch skalierte Merkmale mit Ausprägungen (x 1, x 2,..., x n ) bzw. (y 1, y 2,..., y n ). D.h. für jede i = 1, 2,..., n bezeichnen
Korrelation (II) Korrelation und Kausalität Situation: Seien X, Y zwei metrisch skalierte Merkmale mit Ausprägungen (x 1, x 2,..., x n ) bzw. (y 1, y 2,..., y n ). D.h. für jede i = 1, 2,..., n bezeichnen
Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema
 Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema 2x 4 + x 3 + x + 3 div x 2 + x 1 = 2x 2 x + 3 (2x 4 + 2x 3 2x 2 ) x 3 + 2x 2 + x + 3 ( x
Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema 2x 4 + x 3 + x + 3 div x 2 + x 1 = 2x 2 x + 3 (2x 4 + 2x 3 2x 2 ) x 3 + 2x 2 + x + 3 ( x
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
 50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
Basis und Dimension. Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren.
 Basis und Dimension Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren. Definition. Sei V ein K-Vektorraum und (v i ) i I eine Familie von Vektoren
Basis und Dimension Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren. Definition. Sei V ein K-Vektorraum und (v i ) i I eine Familie von Vektoren
Java Einführung Operatoren Kapitel 2 und 3
 Java Einführung Operatoren Kapitel 2 und 3 Inhalt dieser Einheit Operatoren (unär, binär, ternär) Rangfolge der Operatoren Zuweisungsoperatoren Vergleichsoperatoren Logische Operatoren 2 Operatoren Abhängig
Java Einführung Operatoren Kapitel 2 und 3 Inhalt dieser Einheit Operatoren (unär, binär, ternär) Rangfolge der Operatoren Zuweisungsoperatoren Vergleichsoperatoren Logische Operatoren 2 Operatoren Abhängig
DATENSTRUKTUREN UND ZAHLENSYSTEME
 DATENSTRUKTUREN UND ZAHLENSYSTEME RALF HINZE Institute of Information and Computing Sciences Utrecht University Email: ralf@cs.uu.nl Homepage: http://www.cs.uu.nl/~ralf/ March, 2001 (Die Folien finden
DATENSTRUKTUREN UND ZAHLENSYSTEME RALF HINZE Institute of Information and Computing Sciences Utrecht University Email: ralf@cs.uu.nl Homepage: http://www.cs.uu.nl/~ralf/ March, 2001 (Die Folien finden
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Die reellen Lösungen der kubischen Gleichung
 Die reellen Lösungen der kubischen Gleichung Klaus-R. Löffler Inhaltsverzeichnis 1 Einfach zu behandelnde Sonderfälle 1 2 Die ganzrationale Funktion dritten Grades 2 2.1 Reduktion...........................................
Die reellen Lösungen der kubischen Gleichung Klaus-R. Löffler Inhaltsverzeichnis 1 Einfach zu behandelnde Sonderfälle 1 2 Die ganzrationale Funktion dritten Grades 2 2.1 Reduktion...........................................
Der Zwei-Quadrate-Satz von Fermat
 Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
t r Lineare Codierung von Binärbbäumen (Wörter über dem Alphabet {, }) Beispiel code( ) = code(, t l, t r ) = code(t l ) code(t r )
 Definition B : Menge der binären Bäume, rekursiv definiert durch die Regeln: ist ein binärer Baum sind t l, t r binäre Bäume, so ist auch t =, t l, t r ein binärer Baum nur das, was durch die beiden vorigen
Definition B : Menge der binären Bäume, rekursiv definiert durch die Regeln: ist ein binärer Baum sind t l, t r binäre Bäume, so ist auch t =, t l, t r ein binärer Baum nur das, was durch die beiden vorigen
11.3 Komplexe Potenzreihen und weitere komplexe Funktionen
 .3 Komplexe Potenzreihen und weitere komplexe Funktionen Definition.) komplexe Folgen: z n = x n + j. y n mit zwei reellen Folgen x n und y n.) Konvergenz: Eine komplexe Folge z n = x n + j. y n heißt
.3 Komplexe Potenzreihen und weitere komplexe Funktionen Definition.) komplexe Folgen: z n = x n + j. y n mit zwei reellen Folgen x n und y n.) Konvergenz: Eine komplexe Folge z n = x n + j. y n heißt
Whitebox-Tests: Allgemeines
 -Tests: Allgemeines Andere Bezeichnungen Logic driven, Strukturelles Der Tester entwickelt Testfälle aus einer Betrachtung der Ablauflogik des Programms unter Berücksichtigung der Spezifikation Intuitiv
-Tests: Allgemeines Andere Bezeichnungen Logic driven, Strukturelles Der Tester entwickelt Testfälle aus einer Betrachtung der Ablauflogik des Programms unter Berücksichtigung der Spezifikation Intuitiv
Entscheidungsbäume. Definition Entscheidungsbaum. Frage: Gibt es einen Sortieralgorithmus mit o(n log n) Vergleichen?
 Entscheidungsbäume Frage: Gibt es einen Sortieralgorithmus mit o(n log n) Vergleichen? Definition Entscheidungsbaum Sei T ein Binärbaum und A = {a 1,..., a n } eine zu sortierenden Menge. T ist ein Entscheidungsbaum
Entscheidungsbäume Frage: Gibt es einen Sortieralgorithmus mit o(n log n) Vergleichen? Definition Entscheidungsbaum Sei T ein Binärbaum und A = {a 1,..., a n } eine zu sortierenden Menge. T ist ein Entscheidungsbaum
Tangentengleichung. Wie lautet die Geradengleichung für die Tangente, y T =? Antwort:
 Tangentengleichung Wie Sie wissen, gibt die erste Ableitung einer Funktion deren Steigung an. Betrachtet man eine fest vorgegebene Stelle, gibt f ( ) also die Steigung der Kurve und somit auch die Steigung
Tangentengleichung Wie Sie wissen, gibt die erste Ableitung einer Funktion deren Steigung an. Betrachtet man eine fest vorgegebene Stelle, gibt f ( ) also die Steigung der Kurve und somit auch die Steigung
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Kapitel 6: Induktives Vorgehen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische
Grundbegriffe der Informatik Kapitel 6: Induktives Vorgehen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische
Algorithmen II Vorlesung am 15.11.2012
 Algorithmen II Vorlesung am 15.11.2012 Kreisbasen, Matroide & Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
Algorithmen II Vorlesung am 15.11.2012 Kreisbasen, Matroide & Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
Folge 19 - Bäume. 19.1 Binärbäume - Allgemeines. Grundlagen: Ulrich Helmich: Informatik 2 mit BlueJ - Ein Kurs für die Stufe 12
 Grundlagen: Folge 19 - Bäume 19.1 Binärbäume - Allgemeines Unter Bäumen versteht man in der Informatik Datenstrukturen, bei denen jedes Element mindestens zwei Nachfolger hat. Bereits in der Folge 17 haben
Grundlagen: Folge 19 - Bäume 19.1 Binärbäume - Allgemeines Unter Bäumen versteht man in der Informatik Datenstrukturen, bei denen jedes Element mindestens zwei Nachfolger hat. Bereits in der Folge 17 haben
Kapitel 4: Dynamische Datenstrukturen. Algorithmen und Datenstrukturen WS 2012/13. Prof. Dr. Sándor Fekete
 Kapitel 4: Dynamische Datenstrukturen Algorithmen und Datenstrukturen WS 2012/13 Prof. Dr. Sándor Fekete 4.4 Binäre Suche Aufgabenstellung: Rate eine Zahl zwischen 100 und 114! Algorithmus 4.1 INPUT: OUTPUT:
Kapitel 4: Dynamische Datenstrukturen Algorithmen und Datenstrukturen WS 2012/13 Prof. Dr. Sándor Fekete 4.4 Binäre Suche Aufgabenstellung: Rate eine Zahl zwischen 100 und 114! Algorithmus 4.1 INPUT: OUTPUT:
Diana Lange. Generative Gestaltung Operatoren
 Diana Lange Generative Gestaltung Operatoren Begriffserklärung Verknüpfungsvorschrift im Rahmen logischer Kalküle. Quelle: google Operatoren sind Zeichen, die mit einer bestimmten Bedeutung versehen sind.
Diana Lange Generative Gestaltung Operatoren Begriffserklärung Verknüpfungsvorschrift im Rahmen logischer Kalküle. Quelle: google Operatoren sind Zeichen, die mit einer bestimmten Bedeutung versehen sind.
Formale Systeme, WS 2012/2013 Lösungen zu Übungsblatt 4
 Karlsruher Institut für Technologie Institut für Theoretische Informatik Prof. Dr. Peter H. Schmitt David Farago, Christoph Scheben, Mattias Ulbrich Formale Systeme, WS 2012/2013 Lösungen zu Übungsblatt
Karlsruher Institut für Technologie Institut für Theoretische Informatik Prof. Dr. Peter H. Schmitt David Farago, Christoph Scheben, Mattias Ulbrich Formale Systeme, WS 2012/2013 Lösungen zu Übungsblatt
13. Lineare DGL höherer Ordnung. Eine DGL heißt von n-ter Ordnung, wenn Ableitungen y, y, y,... bis zur n-ten Ableitung y (n) darin vorkommen.
 13. Lineare DGL höherer Ordnung. Eine DGL heißt von n-ter Ordnung, wenn Ableitungen y, y, y,... bis zur n-ten Ableitung y (n) darin vorkommen. Sie heißt linear, wenn sie die Form y (n) + a n 1 y (n 1)
13. Lineare DGL höherer Ordnung. Eine DGL heißt von n-ter Ordnung, wenn Ableitungen y, y, y,... bis zur n-ten Ableitung y (n) darin vorkommen. Sie heißt linear, wenn sie die Form y (n) + a n 1 y (n 1)
Rekursionen (Teschl/Teschl 8.1-8.2)
 Rekursionen (Teschl/Teschl 8.1-8.2) Eine Rekursion kter Ordnung für k N ist eine Folge x 1, x 2, x 3,... deniert durch eine Rekursionsvorschrift x n = f n (x n 1,..., x n k ) für n > k, d. h. jedes Folgenglied
Rekursionen (Teschl/Teschl 8.1-8.2) Eine Rekursion kter Ordnung für k N ist eine Folge x 1, x 2, x 3,... deniert durch eine Rekursionsvorschrift x n = f n (x n 1,..., x n k ) für n > k, d. h. jedes Folgenglied
Kapitalerhöhung - Verbuchung
 Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN
 ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN CHRISTIAN HARTFELDT. Zweiter Mittelwertsatz Der Mittelwertsatz Satz VI.3.4) lässt sich verallgemeinern zu Satz.. Seien f, g : [a, b] R auf [a,
ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN CHRISTIAN HARTFELDT. Zweiter Mittelwertsatz Der Mittelwertsatz Satz VI.3.4) lässt sich verallgemeinern zu Satz.. Seien f, g : [a, b] R auf [a,
Charakteristikenmethode im Beispiel
 Charakteristikenmethode im Wir betrachten die PDE in drei Variablen xu x + yu y + (x + y )u z = 0. Das charakteristische System lautet dann ẋ = x ẏ = y ż = x + y und besitzt die allgemeine Lösung x(t)
Charakteristikenmethode im Wir betrachten die PDE in drei Variablen xu x + yu y + (x + y )u z = 0. Das charakteristische System lautet dann ẋ = x ẏ = y ż = x + y und besitzt die allgemeine Lösung x(t)
10. Public-Key Kryptographie
 Stefan Lucks 10. PK-Krypto 274 orlesung Kryptographie (SS06) 10. Public-Key Kryptographie Analyse der Sicherheit von PK Kryptosystemen: Angreifer kennt öffentlichen Schlüssel Chosen Plaintext Angriffe
Stefan Lucks 10. PK-Krypto 274 orlesung Kryptographie (SS06) 10. Public-Key Kryptographie Analyse der Sicherheit von PK Kryptosystemen: Angreifer kennt öffentlichen Schlüssel Chosen Plaintext Angriffe
1 topologisches Sortieren
 Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Was bisher geschah Funktionale Programmierung in Haskell: Algebraische Datentypen Pattern Matching Polymorphie Typklassen Rekursive Datentypen:
 Was bisher geschah Funktionale Programmierung in Haskell: Algebraische Datentypen Pattern Matching Polymorphie Typklassen Rekursive Datentypen: Peano-Zahlen, Listen, Bäume Rekursive Funktionen strukturelle
Was bisher geschah Funktionale Programmierung in Haskell: Algebraische Datentypen Pattern Matching Polymorphie Typklassen Rekursive Datentypen: Peano-Zahlen, Listen, Bäume Rekursive Funktionen strukturelle
Der Aufruf von DM_in_Euro 1.40 sollte die Ausgabe 1.40 DM = 0.51129 Euro ergeben.
 Aufgabe 1.30 : Schreibe ein Programm DM_in_Euro.java zur Umrechnung eines DM-Betrags in Euro unter Verwendung einer Konstanten für den Umrechnungsfaktor. Das Programm soll den DM-Betrag als Parameter verarbeiten.
Aufgabe 1.30 : Schreibe ein Programm DM_in_Euro.java zur Umrechnung eines DM-Betrags in Euro unter Verwendung einer Konstanten für den Umrechnungsfaktor. Das Programm soll den DM-Betrag als Parameter verarbeiten.
Zuammenfassung: Reelle Funktionen
 Zuammenfassung: Reelle Funktionen 1 Grundlegendes a) Zahlenmengen IN = {1; 2; 3; 4;...} Natürliche Zahlen IN 0 = IN {0} Natürliche Zahlen mit 0 ZZ = {... ; 2; 1; 0; 1; 2;...} Ganze Zahlen Q = { z z ZZ,
Zuammenfassung: Reelle Funktionen 1 Grundlegendes a) Zahlenmengen IN = {1; 2; 3; 4;...} Natürliche Zahlen IN 0 = IN {0} Natürliche Zahlen mit 0 ZZ = {... ; 2; 1; 0; 1; 2;...} Ganze Zahlen Q = { z z ZZ,
WS 2008/09. Diskrete Strukturen
 WS 2008/09 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0809
WS 2008/09 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0809
Elemente der Analysis I Kapitel 2: Einführung II, Gleichungen
 Elemente der Analysis I Kapitel 2: Einführung II, Gleichungen Prof. Dr. Volker Schulz Universität Trier / FB IV / Abt. Mathematik 8. November 2010 http://www.mathematik.uni-trier.de/ schulz/elan-ws1011.html
Elemente der Analysis I Kapitel 2: Einführung II, Gleichungen Prof. Dr. Volker Schulz Universität Trier / FB IV / Abt. Mathematik 8. November 2010 http://www.mathematik.uni-trier.de/ schulz/elan-ws1011.html
S=[n] Menge von Veranstaltungen J S kompatibel mit maximaler Größe J
![S=[n] Menge von Veranstaltungen J S kompatibel mit maximaler Größe J S=[n] Menge von Veranstaltungen J S kompatibel mit maximaler Größe J](/thumbs/26/8373971.jpg) Greedy-Strategie Definition Paradigma Greedy Der Greedy-Ansatz verwendet die Strategie 1 Top-down Auswahl: Bestimme in jedem Schritt eine lokal optimale Lösung, so dass man eine global optimale Lösung
Greedy-Strategie Definition Paradigma Greedy Der Greedy-Ansatz verwendet die Strategie 1 Top-down Auswahl: Bestimme in jedem Schritt eine lokal optimale Lösung, so dass man eine global optimale Lösung
Repetitionsaufgaben Wurzelgleichungen
 Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Lineare Gleichungssysteme
 Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
Grundlagen der Künstlichen Intelligenz
 Grundlagen der Künstlichen Intelligenz 27. Aussagenlogik: Logisches Schliessen und Resolution Malte Helmert Universität Basel 28. April 2014 Aussagenlogik: Überblick Kapitelüberblick Aussagenlogik: 26.
Grundlagen der Künstlichen Intelligenz 27. Aussagenlogik: Logisches Schliessen und Resolution Malte Helmert Universität Basel 28. April 2014 Aussagenlogik: Überblick Kapitelüberblick Aussagenlogik: 26.
Übungen für Woche 10
 Übungen für Woche 10 Martin Rubey 12. Januar 2011 Die folgenden Übungen sollen den Umgang mit Backtracking und kombinatorischen Spezies näherbringen. Genaue Hinweise gibt es erst auf Seite 5. Zur Erinnerung:
Übungen für Woche 10 Martin Rubey 12. Januar 2011 Die folgenden Übungen sollen den Umgang mit Backtracking und kombinatorischen Spezies näherbringen. Genaue Hinweise gibt es erst auf Seite 5. Zur Erinnerung:
Übung Theoretische Grundlagen
 Übung Theoretische Grundlagen Berechenbarkeit/Entscheidbarkeit Nico Döttling November 26, 2009 INSTITUT FÜR KRYPTOGRAPHIE UND SICHERHEIT KIT University of the State of Baden-Wuerttemberg and National Laboratory
Übung Theoretische Grundlagen Berechenbarkeit/Entscheidbarkeit Nico Döttling November 26, 2009 INSTITUT FÜR KRYPTOGRAPHIE UND SICHERHEIT KIT University of the State of Baden-Wuerttemberg and National Laboratory
1. Teilklausur. Modul "OOPM Vorlesung/Übung" 16.12.2008. Gruppe A
 Objektorientierte Programmierung und Modellierung WS 2008/2009 Institut für Informatik Prof. Dr. Ralf Lämmel Dr. Manfred Jackel 1. Teilklausur Modul "OOPM Vorlesung/Übung" 16.12.2008 Gruppe A Name Vorname
Objektorientierte Programmierung und Modellierung WS 2008/2009 Institut für Informatik Prof. Dr. Ralf Lämmel Dr. Manfred Jackel 1. Teilklausur Modul "OOPM Vorlesung/Übung" 16.12.2008 Gruppe A Name Vorname
Datenstrukturen und Algorithmen
 Datenstrukturen und Algorithmen VO 708.031 Bäume robert.legenstein@igi.tugraz.at 1 Inhalt der Vorlesung 1. Motivation, Einführung, Grundlagen 2. Algorithmische Grundprinzipien 3. Sortierverfahren 4. Halden
Datenstrukturen und Algorithmen VO 708.031 Bäume robert.legenstein@igi.tugraz.at 1 Inhalt der Vorlesung 1. Motivation, Einführung, Grundlagen 2. Algorithmische Grundprinzipien 3. Sortierverfahren 4. Halden
Algorithmen und Datenstrukturen Suchbaum
 Algorithmen und Datenstrukturen Suchbaum Matthias Teschner Graphische Datenverarbeitung Institut für Informatik Universität Freiburg SS 12 Motivation Datenstruktur zur Repräsentation dynamischer Mengen
Algorithmen und Datenstrukturen Suchbaum Matthias Teschner Graphische Datenverarbeitung Institut für Informatik Universität Freiburg SS 12 Motivation Datenstruktur zur Repräsentation dynamischer Mengen
Logik für Informatiker
 Logik für Informatiker 2. Aussagenlogik Teil 3 30.04.2012 Viorica Sofronie-Stokkermans Universität Koblenz-Landau e-mail: sofronie@uni-koblenz.de 1 Letztes Mal Aussagenlogik Syntax: welche Formeln? Semantik:
Logik für Informatiker 2. Aussagenlogik Teil 3 30.04.2012 Viorica Sofronie-Stokkermans Universität Koblenz-Landau e-mail: sofronie@uni-koblenz.de 1 Letztes Mal Aussagenlogik Syntax: welche Formeln? Semantik:
Beweisbar sichere Verschlüsselung
 Beweisbar sichere Verschlüsselung ITS-Wahlpflichtvorlesung Dr. Bodo Möller Ruhr-Universität Bochum Horst-Görtz-Institut für IT-Sicherheit Lehrstuhl für Kommunikationssicherheit bmoeller@crypto.rub.de 6
Beweisbar sichere Verschlüsselung ITS-Wahlpflichtvorlesung Dr. Bodo Möller Ruhr-Universität Bochum Horst-Görtz-Institut für IT-Sicherheit Lehrstuhl für Kommunikationssicherheit bmoeller@crypto.rub.de 6
Kapitel 6. Komplexität von Algorithmen. Xiaoyi Jiang Informatik I Grundlagen der Programmierung
 Kapitel 6 Komplexität von Algorithmen 1 6.1 Beurteilung von Algorithmen I.d.R. existieren viele Algorithmen, um dieselbe Funktion zu realisieren. Welche Algorithmen sind die besseren? Betrachtung nicht-funktionaler
Kapitel 6 Komplexität von Algorithmen 1 6.1 Beurteilung von Algorithmen I.d.R. existieren viele Algorithmen, um dieselbe Funktion zu realisieren. Welche Algorithmen sind die besseren? Betrachtung nicht-funktionaler
WS 2011/2012. Robert Giegerich Dezember 2013
 WS 2011/2012 Robert 1 AG Praktische Informatik 11. Dezember 2013 1 robert@techfak.uni-bielefeld.de Vorschau Themen heute: Funktionen höherer Ordnung (Fortsetzung) künstliche Striktheit mehr zu fold für
WS 2011/2012 Robert 1 AG Praktische Informatik 11. Dezember 2013 1 robert@techfak.uni-bielefeld.de Vorschau Themen heute: Funktionen höherer Ordnung (Fortsetzung) künstliche Striktheit mehr zu fold für
3. LINEARE GLEICHUNGSSYSTEME
 176 3. LINEARE GLEICHUNGSSYSTEME 90 Vitamin-C-Gehalt verschiedener Säfte 18,0 mg 35,0 mg 12,5 mg 1. a) 100 ml + 50 ml + 50 ml = 41,75 mg 100 ml 100 ml 100 ml b) : Menge an Kirschsaft in ml y: Menge an
176 3. LINEARE GLEICHUNGSSYSTEME 90 Vitamin-C-Gehalt verschiedener Säfte 18,0 mg 35,0 mg 12,5 mg 1. a) 100 ml + 50 ml + 50 ml = 41,75 mg 100 ml 100 ml 100 ml b) : Menge an Kirschsaft in ml y: Menge an
Theorie der Informatik
 Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 Einführung Beispiel: Aussagenlogische Formeln Aus dem Logikteil: Definition (Syntax
Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 Einführung Beispiel: Aussagenlogische Formeln Aus dem Logikteil: Definition (Syntax
2.11 Kontextfreie Grammatiken und Parsebäume
 2.11 Kontextfreie Grammatiken und Parsebäume Beispiel: Beispiel (Teil 3): Beweis für L(G) L: Alle Strings aus L der Länge 0 und 2 sind auch in L(G). Als Induktionsannahme gehen wir davon aus, dass alle
2.11 Kontextfreie Grammatiken und Parsebäume Beispiel: Beispiel (Teil 3): Beweis für L(G) L: Alle Strings aus L der Länge 0 und 2 sind auch in L(G). Als Induktionsannahme gehen wir davon aus, dass alle
Lenstras Algorithmus für Faktorisierung
 Lenstras Algorithmus für Faktorisierung Bertil Nestorius 9 März 2010 1 Motivation Die schnelle Faktorisierung von Zahlen ist heutzutage ein sehr wichtigen Thema, zb gibt es in der Kryptographie viele weit
Lenstras Algorithmus für Faktorisierung Bertil Nestorius 9 März 2010 1 Motivation Die schnelle Faktorisierung von Zahlen ist heutzutage ein sehr wichtigen Thema, zb gibt es in der Kryptographie viele weit
Also kann nur A ist roter Südler und B ist grüner Nordler gelten.
 Aufgabe 1.1: (4 Punkte) Der Planet Og wird von zwei verschiedenen Rassen bewohnt - dem grünen und dem roten Volk. Desweiteren sind die Leute, die auf der nördlichen Halbkugel geboren wurden von denen auf
Aufgabe 1.1: (4 Punkte) Der Planet Og wird von zwei verschiedenen Rassen bewohnt - dem grünen und dem roten Volk. Desweiteren sind die Leute, die auf der nördlichen Halbkugel geboren wurden von denen auf
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
(λ Ri I A+BR)v Ri = 0. Lässt sich umstellen zu
 Herleitung der oppenecker-formel (Wiederholung) Für ein System ẋ Ax + Bu (B habe Höchstrang) wird eine Zustandsregelung u x angesetzt. Der geschlossene egelkreis gehorcht der Zustands-Dgl. ẋ (A B)x. Die
Herleitung der oppenecker-formel (Wiederholung) Für ein System ẋ Ax + Bu (B habe Höchstrang) wird eine Zustandsregelung u x angesetzt. Der geschlossene egelkreis gehorcht der Zustands-Dgl. ẋ (A B)x. Die
