Chemische Analysen eklogitischer Gesteine und ihrer Mineralien vom Fundpunkt Hohl bei Wies, Koralpe, Steiermark
|
|
|
- Linda Waltz
- vor 8 Jahren
- Abrufe
Transkript
1 Mitt, naturwiss. Ver. Steiermark Band 99 S Graz 1969 Aus dem Institut für Mineralogie und Pétrographie der Universität Graz Chemische Analysen eklogitischer Gesteine und ihrer Mineralien vom Fundpunkt Hohl bei Wies, Koralpe, Steiermark Von Haymo HERITSCH und Roland WITTMANN Mit 2 Abbildungen und 10 Tabellen im Text (Eingelangt am 29. April 1969) Inhalt: Chemische Analysen und Analysenberechnungen von einem Eklogitamphibolit und einem Pyroxen-Granat-Zoisit-Schiefer ( Diallageklogit") vom Fundpunkt Hohl, südliche Koralpe, werden gegeben. Von den sie aufbauenden Mineralien: Omphazit, Na-Augit, zwei Granaten und einer Hornblende werden ebenfalls chemische Analysen gebracht, ebenso eine kurze Diskussion zur Paragenese. Der Fundpunkt: Die Gesteine des schon morphologisch sehr auffallenden Fundpunktes Hohl, südliche Koralpe, sind zuerst eingehend von KIESLINGER 1928 studiert worden. Die Schreibweise des Gehöftes ist in der älteren Literatur Holl", auf der neuen österreichischen Karte 1:50.000, Blatt 206, ist der Name jedoch Hohl" geschrieben, was hier ebenfalls verwendet wird. KIESLINGER stellt fest, daß so weit die Aufschlußverhältnisse es beurteilen lassen ein Kern von äußerst komplex zusammengesetzten Gesteinen, die er Diallageklogit" nennt, von einer Hülle von gewöhnlichem Eklogitamphibolit umgeben wird. Während Eklogitamphibolite in der Koralpe einen verbreiteten Typ darstellen, sind die Diallageklogite" nur vereinzelt zu finden. Der Fundpunkt Hohl, der in der geologischen Karte von KIESLINGER 1929 eingetragen ist, liegt in der Gemeinde Wielfressen, etwa 9 km westlich von Wernersdorf an der Straße Wies Wernersdorf St. Katharina in der Wiel. Ein auffälliger Felsturm mit der Kote 820 in unmittelbarer Nähe des Gehöftes Hohl wird von den eklogitischen Gesteinen gebildet. Die Flächenausdehnung des offensichtlich anstehenden Gesteines ist etwa 100 m X 100 m. Halden von mächtigen Blöcken umgeben den Felsturm und einzelne Blöcke sind noch in weiterer Entfernung feststellbar. Die Abbildung 1 gibt die beobachteten Verhältnisse wieder und zeigt außerdem, daß das Vorkommen von W bis NW streichenden Gneisen bis Glimmerschiefern umgeben ist, vgl. KIESLINGER Eine Probenentnahme durch die Wand, südlich von Kote 820, lieferte folgende Gesteine: Am Fuß der Felswand steht der in der Koralpe so verbreitete Typus der Eklogitamphibolite an; auch ostwärts und westlich ist der Eklogitamphibolit über längere Strecken hin am Fuß der Felswand unter der Kote 820 anstehend. In etwa 10 m darüber folgen stärker verschieferte Gesteine desselben Eklogitamphibolites. Diese Gesteine sind etwa 6 8 m mächtig. Darüber, also von etwa m über dem Fuß der Felswand bis zum Gipfel der Kote
2 S Glimmerschiefer bis Schiefergnets, anstehend Abb. 1: Fundpunkt Hohl. Lageplan und Verbreitung der eklogitischen Gesteine. folgen Gesteine, die makroskopisch eine Verschieferung kaum erkennen lassen und dem Gestein entsprechen, das von KIESLINGER 1928 als Diallag-Eklogit- Gabbro bezeichnet wurde: in typischen Gesteinen dieser Art liegen in einem sehr feinkörnigen Grundgewebe aus Zoisit, Quarz und gelegentlich etwas Disthen große rote Granate und apfelgrüne Pyroxene. Ein makroskopisch dunkler, im Dünnschliff aber sehr heller und sehr schwach pleochroitischer Amphibol kann noch hinzutreten. Die Variationsbreite in der Entwicklung und Größe der Komponenten ist beachtlich. Zielsetzung : Abgesehen von der Angabe einer offenbar älteren chemischen Analyse bei ANGEL 1924, gab es nur die chemische Analyse bei KIESLINGER 1928, wenn auch das Vorkommen selbst seither gelegentlich in der Literatur erwähnt wird und auch weitere Beobachtungen hinzugefügt werden, so z. B. von KÜMEL 1937, BECK-MANNAGETTA 1961, HERITSCH 1963 und So scheint es berechtigt, insbesondere durch chemische Analysen die Gesteine von Hohl einer eingehenden Untersuchung zu unterziehen, wobei aber nicht nur die chemische Zusammensetzung der Gesteine, sondern vor allem der sie aufbauenden Mineralphasen erfaßt werden soll. Der vorliegende Beitrag ist in diesem Sinn nur ein Teil einer noch viel ausgebreiteteren Studie, die zu gegebener Zeit veröffentlicht wird. Es wird zweifellos möglich werden, auf Grund solcher eingehender Studien die Frage der Genese, besonders im Hinblick auf neue Experimente an Eklogiten zu diskutieren, HERITSCH Material und Arbeitsmethode*. Im folgenden werden ein Eklogitamphibolit des in der Koralpe verbreiteten Typus, entsprechend etwa dem Gestein von Mauthnereck, KIES- 19
3 LINGER 1928 und vielfach in der Literatur z. B. HERITSCH 1963 aus dem Fuße der Felswand von Hohl unter Kote 820 und ein Pyroxen-Granat-Zoisit-Schiefer aus den höheren Teilen der Felswand beschrieben. Es wurde hier absichtlich eine besonders pyroxenreiche Varietät ausgewählt. Die Bearbeitung weiterer Typen, die die Variationsbreite erfassen soll, ist zur Zeit im Gang. Statt Diallag-Eklogit-Gabbro wurde als Name Pyroxen-Granat-Zoisit- Schiefer gewählt, um nicht durch den Namen schon eine genetische Aussage zu machen. KIESLINGERS 1928 Diskussion über die Namengebung ist durchaus berechtigt und die endgültig getroffene Wahl des Namens durch KIESLINGER 1928 wird als Ausweg bezeichnet. Auch in neue Nomenklaturvorschläge, FRITSCH und Mitarbeiter 1967 läßt sich das vorliegende Gestein nicht ohne weiteres einordnen. Die chemischen Analysen wurden teilweise nach klassischen Methoden, teilweise nach modernen Schnellverfahren ausgeführt. So sind die kalien flammenphotometrisch, und gravimetrisch und titrimetrisch bestimmt. Ein FRANTZ Isodynamic Separator ermöglichte die Trennung der Mineralphasen bei Korngrößen von 0,06 bis 0,1 mm, wobei sich ein forward slope von 20 und ein side slope von 15 als zweckmäßig erwies. Durch Variation der verwendeten Stromstärke zwischen 0,4 bis 1,3 Ampere gelang es alle Phasen zufriedenstellend zu trennen, besonders bei mehrmaligem Durchlauf. Optische und röntgenographische Kontrollen stellen den Reinheitsgrad fest. Eklogitamphibolit, Hohl, Fuß der Felswand, Kote 820 Gesamtge stein : Auf eine Darstellung eines mikroskopischen Befundes kann hier verzichtet werden, da das Gestein wesentlich mit dem von Mauthnereck übereinstimmt, das erstmals ausführlich von KIESLINGER 1928 und später mehrfach in der Literatur behandelt wurde, Literaturübersicht bei HERITSCH Es genügt zu vermerken, daß neben den Hauptgemengteilen Omphazit, Granat, Hornblende, Zoisit nur untergeordnet Symplektit und Quarz sowie Accessorien in den Gemengteilen auftreten. Wie die Tabellen 1 und 2 zeigen, sind die Eklogitamphibolite von Hohl und Mauthnereck einander sehr ähnlich. Der Magmentyp ist nach BURRI 1959 gabbroid bis gabbrotheralithisch und in den Tabellen von NOCKOLDS 1954, ist das Mittel von Pyroxen-Gabbro bzw. das Mittel der Gabbros überhaupt gut vergleichbar. Die Berechnung des modalen Mineralbestandes ist in einem so komplex zusammengesetzten Gestein ohne die Kenntnis der Phasen nicht durchzuführen KIESLINGER 1928:425. Dadurch, daß aber durch magnetische Separation die Hauptkomponenten abgetrennt und dann chemisch analysiert werden können, ist diese Aufgabe mit Hilfe von mehreren Gleichungen lösbar. Das Ergebnis ist in der Tabelle 3 wiedergegeben. Granat: Die Tabelle 4 enthält die chemische Analyse des Granates. Hier ist festzustellen, daß erwartungsgemäß eine sehr gute Übereinstimmung mit dem Granat von Gertrusk ANGEL und SCHAIDER 1950 besteht. Bei der Berechnung von Teilsilikaten mußte neben Rutil eine geringe Menge von Disthen, etwa 0,1 % verrechnet werden. Tatsächlich enthält der Granat, winzige, nicht näher bestimmbare Einschlüsse. Zur Kontrolle des Zusammenhanges zwischen Chemismus und Lichtbrechung, Dichte und Gitterkonstante ist es zweckmäßig diese Größen aus der 20
4 chemischen Analyse, unter der Annahme der Additivität der physikalischen Konstanten, vgl. VEGARD'sche Regel, für die Gitterkonstanten, ZEN 1950 zu berechnen. Das Ergebnis ist ebenfalls in der Tabelle 4 ausgewiesen. Die Differenzen im Brechungsquotienten in der Gitterkonstante sind verhältnismäßig gering, bei der Dichte jedoch etwas größer. Die Werte für die Gitterkonstanten, Brechungsquotienten und Dichten der reinen Endglieder wurden DEER, HOWIE at ZussMAN 1962 entnommen, vgl. auch STRUNZ In die Granatgruppen nach TRÖGER 1959 kann der vorliegende Granat zwischen Granat aus Eklogiten" und Granat aus Amphiboliten und Glaukophanschiefern" eingeordnet werden. Selbstverständlich lieferte die graphische Darstellung nach COLEMAN und Mitarbeitern 1965 dasselbe Ergebnis; danach fällt der vorliegende Granat, wie auch der von Gertrusk, zwar noch in den Bereich C der Granate aus Eklogiten in Glaukophanschiefern, jedoch an die Grenze gegen B-Granate, aus Eklogiten, in Gneis- und Migmatit-Gebieten. Merkwürdigerweise besteht keine gute Übereinstimmung mit der Analyse von Granat aus einem Eklogit von Kupplerbrunn, Saualpe, nach MOTTANA und Mitarbeitern Omphazit: Die chemische Analyse ist in Tabelle 5 wiedergegeben. Die Berechnung der chemischen Formel erfolgte mit der Basis 6 Sauerstoffe. Die Berechnung von Teilsilikaten, Ladungsausgleich usw. nach HESS 1949, bzw. OOSTEROM 1963, HUCKENHOLZ Die auch hier zu erwartende Ähnlichkeit mit dem Omphazit von Gertrusk, ANGEL & SCHAIDER 1950, ist offensichtlich. Pyroxene mit der angeführten chemischen Zusammensetzung wurden schon immer als Omphazite bezeichnet, vgl. z. B. ESSENE & FYFE 1967, in deren Diagramm auch der hier beschriebene, Pyroxen in das Omphazitfeld fällt. Bemerkenswert ist in der vorliegenden Analyse der viel niedrigere Gehalt an K2O gegenüber der Analyse des Gertrusker Omphazites, vgl. hiezu MOTTANA und Mitarbeiter 1968: 342. Das Diagramm von COLEMAN und Mitarbeitern 1965:496 ist hinsichtlich der Zuordnung von Omphaziten zu paragenetischen Typen von Eklogiten nicht sehr charakteristisch. Mit diesem Vorbehalt liegt allerdings der Omphazit von Hohl an der Grenze des Bereiches von Omphaziten aus Eklogiten der Gruppe C (Eklogite aus der Glaukophanschieferfazies) und der Gruppe B (Eklogite aus Gneis- und Migmatitgebieten). Auch hier ist die Übereinstimmung mit dem Omphazit von Kupplerbrunn, MOTTANA und Mitarbeiter 1968 nicht sehr gut. Insbesondere weichen die - und -Gehalte beträchtlich ab. Hornblende: In der Tabelle 6 ist die chemische Analyse und die Berechnung der Formel angegeben. Diese Formelberechnung erfolgte auf Grund der analytisch so schwer durchzuführenden Wasserbestimmung mit der Basis von 13 Kationen für die 6- und 4-Koordination. Diese Methode wurde bei allen Amphibolanalysen, die aus dem hiesigen Institut in den letzten Jahren herausgekommen sind, aus dem genannten Grund angewendet. Die Übereinstimmung der vorliegenden Analyse mit zahlreichen anderen Amphibolen aus Eklogiten und Eklogitamphiboliten der Koralpe bzw. auch der Saualpe ist sehr weitgehend, KORITNIG 1940, HERITSCH & KAHLER 1959, MACHATSCHKI & WALITZI 1961, etwas weniger gut, wenn auch noch zufriedenstellend, MOTTANA und Mitarbeiter Wie schon HERITSCH 1963 gezeigt hat, läßt sich die Zusammensetzung des Eklogites von Gertrusk bzw. der Eklogitamphibolite von Mauthnereck sehr 21
5 wohl aus den Mineralkomponenten im ACF-Dreieck darstellen. Viel später haben MOTTANA und Mitarbeiter 1968 dasselbe nochmals für Gertrusk und dann auch für Kupplerbrunn gezeigt. Selbstverständlich läßt sich auch der vorliegende Eklogitamphibolit von Hohl in derselben Weise darstellen, siehe Abbildung 2. Abb. 2: Fundpunkt Hohl. Darstellung des Eklogitamphibolites und seiner Komponenten (ausgefüllte Kreise), sowie des Pyroxen-Granat-Zoisit-Schiefers und seiner Komponenten (leere Kreise) im ACF-Diagramm. Pyroxen-Granat-Zoisit-Schiefer, Hohl, Felswand Kote 820 Gesteine dieser Art über ihre Namengebung ist schon oben gesprochen worden weisen eine ziemliche Variationsbreite auf. Es soll hier nicht auf die verschiedenen Varianten eingegangen werden, da das zur Z^it am hiesigen Institut laufenden Untersuchungen vorbehalten ist. Das hier behandelte Gestein ist eine pyroxenreiche Abart. Gesamtgestein : Der Farbeindruck ist auf Grund des vorliegenden Pyroxenes ein helles Grün: Geol. Soc. Am., Rock-Color-Chart: dusky yellow green 5GY5/2 bis grayish green 10GY5/2, mit roten (Granat) und weißen (Zoisit und Quarz) Flecken. Zur mikroskopischen Charakterisierung sei auf KIESLINGER 1928 und KÜMEL 1937 verwiesen. Das hier untersuchte Handstück hat große, im Dünnschliff praktisch farblose Kristalle von monoklinem Pyroxen, der auch stellenweise von einem Mörtelkranz kleiner Pyroxen-Kristalle umgeben ist. Der Granat, teilweise Körner, teilweise in charakteristischen Umwachsungsformen um Pyroxene, ist reich an kleinen Einschlüssen. In dem Raum zwischen diesen beiden Mineralien treten Anhäufungen von Zoisit und Quarz auf. Eine im 22
6 Dünnschliff nur schwach gefärbte und schwach pleochroitische Hornblende kommt nur vereinzelt vor. Tabelle 7 enthält die chemische Analyse des Pyroxen-Granat-Zoisit-Schiefers sowie die NIGGLI-Werte und die Norm. Im Vergleich zu der Tabelle 2 ist daraus zu ersehen, daß eine Zuordnung zu einem Magmentyp nur schwierig ist und daß am ehesten noch ein si-pyroxenetisches Magma paßt. Damit erscheint eine ausschließlich magmatische Entstehung bei allem Vorbehalt von Schlüssen aus einer Einzelanalyse für dieses Gestein in Frage gestellt. Die Berechnung des modalen Mineralbestandes ist auf Grund der Kenntnis der chemischen Zusammensetzung von Granat und Pyroxen bzw. aus der bekannten Zusammensetzung von Zoisit möglich. Der so bestimmte Mineralbestand ist in der Tabelle 8 angeführt. Granat: Der Granat läßt sich zwar magnetisch leicht abtrennen, jedoch ist reines Granatmaterial wegen der unvermeidlichen kleinen Einschlüsse nicht zu erhalten. Daher ist auch die Analyse der Tabelle 9 nicht auf Granat allein zu berechnen, es müssen vielmehr die Einschlüsse noch berücksichtigt werden. Die Berechnung zeigt, daß die Annahme von Zoisit, Quarz und etwas Rutil genügt, vgl. KIESLINGER Darnach kann der Granat auf Teilsilikate gerechnet werden. Das auffallende Merkmal dieses Granates ist der hohe -Gehalt, es liegt auf alle Fälle ein sehr pyropreicher Granat vor. Für einen weiteren Granat aus einem anderen Pyroxen-Granat-Zoisit-Schiefer hat HERITSCH 1966 bestimmt: a = 11,582 ± 0,004 Â und n = 1,760. Diese Werte sind ebenfalls in der Tabelle 9 angegeben, ebenso, entsprechend der Tabelle 4, die aus der chemischen Zusammensetzung berechneten Werte für Dichte, Brechungsquotienten und Gitterkonstante. Die Abweichungen belaufen sich unter Berücksichtigung des bei Tabelle 4 ausgeführten auf die zu erwartenden Beträge. Die Einordnung nach TRÖGER 1958 bzw. COLEMAN und Mitarbeiter 1965 liefert, besonders auf Grund des hohen Pyropgehaltes eine Einordnung in die Gruppe Granate aus Eklogiten" bzw. in das Feld Gruppe B-Eklogite, d. h. Granat aus Eklogit in Gneis- und Migmatit-Gebieten. Klinopyroxen: In Tabelle 10 findet sich die chemische Analyse des Klinopyroxenes und die Berechnung von Teilsilikaten und weiteren Werten nach HESS 1949, OOSTEROM 1963, HUCKENHOLZ Zur Benennung des Pyroxenes kann etwa folgendes gesagt werden: Nach DEER, HOWIE & ZUSSMAN 1963:154 ist der Ömphazit durch hohen SÌO2-, AI2O3- und Na2O-Gehalt gekennzeichnet. Na2O über 4 %, der SiO2-Gehalt bzw. 2O3-Gehalt ist nicht ziffernmäßig fixiert, jedoch folgt als Mittel aus den angeführten Analysen SÌO2 etwa 52,9 % und AI2O3 etwa 8 %. Damit ist der vorliegende Klinopyroxen nicht mehr als Omphazit zu bezeichnen. Nach ESSENE & FYFE 1967 kann aus den Teilsilikaten des Klinopyroxenes in ein Diagramm eingegangen werden, das den Namen festlegt. Hier folgt als Ergebnis Na-Augit. Der Name Diallag ist nicht eindeutig, DEER, HOWIE & ZUSSMAN1963:43 und ist als veraltet abzulehnen, STRUNZ Selbstverständlich läßt sich auch dieses Gestein als Zusammensetzung seiner Hauptkomponenten Klinopyroxen, Granate, Zoisit im ACF-Dreieck darstellen, vgl. Abbildung 2. 23
7 SiO 2 TiO 2 AI2O3 Fe2Û3 Na 2 O K2O P2O5 H2O+ Tabelle Eklogitamphibolit, Fundpunkt Hohl, südliche Koralpe 48,35 1,68 14,79 3,96 6,77 0,14 8,33 12,56 2,62 0,09 sp. 1,13 100,42 Analytiker R. WITTMANN NiGGLi-Werte al 19 fm 46 c 29 alk 6 si 105 mg 0,6 k 0,02 A C F 1 Or Ab An Wo En Fs Mt 19,4 34,3 46,3 Norm 0,5 22,2 28,5 14,3 14,0 6,7 4,8 3,2 5,8 Tabelle Vergleich des Eklogitamphibolites und des Pyroxen-Granat-Zoisit-Schiefers. Fundpunkt Hohl mit Magmentypen nach BURRI 1959 und mit dem Eklogitamphibolit vom Mauthnereck, KIESLINGER si al fm c alk k mg Gabbroid ,2 c-gabbroid ,1 0,5 0,7 Pyroxengabbroid Gabbrotheralithisch Si-pyroxenitisch , , ,5 27,5 30 4,5 12,5 7 0,2 0,2 0,7 0,45 0,7 Eklogitamphibolit Hohl ,02 0,6 Eklogitamphibolit Mauthnereck ,5 46, ,1 0,57 Pyroxen-Granat-Zoisitschiefer Hohl ,5 46,5 35,5 3,5 0,02 0,73 Tabelle 3 Modaler Mineralbestand des Eklogitamphibolites, Fundpunkt Hohl, berechnet aus der Analyse von Granat, Tabelle 4, von Omphazit, Tabelle 5, von Hornblende, Tabelle 6, bzw. aus der chemischen Zusammensetzung von Zoisit. Granat Omphazit Hornblende Zoisit Quarz 27,4 32,0 27,0 6,7 6,9 100,0 24
8 Tabelle 4 Granat aus Eklogitamphibolit, Fundpunkt Hohl Analytiker R. WITTMANN SiO 2 TiO 2 AI2O3 Fe 2 O3 H2O 38,48 0,41 21,15 1,63 20,10 0,62 6,94 10,05 99,38 Basis 24 Si Ti Fe+ 3 Fe+ 2 Mg Mn Ca Sauerstoffe 5,9501 0,050) 3,804 0,047 \ 0,1891 2,598 1,598 0,081 1,664 D AA O,U0 4,04 5,94 mandin Pyrop Spessartin Grossular Andradit 43,7 26,9 1,4 23,2 4,8 Beobachtet vorliegende Arbeit : HERITSCH 1966 : berechnet : d = 3,87 d = 3,93 g. cm~ 3 n n g. cm" 3 n = 1,774 = 1,775 = 1,779 a = 11,595 ± a = 11,595 ± a = 1L609Â 0,009A 0,005Â Tabelle 5 Omphazit aus Eklogitamphibolit, Fundpunkt Hohl Analytiker R. WITTMANN SiO2 Ti0 2 A12O3 Fe2O3 Na2O K2O H2O+ j O OC 52,83 0,39 10,04 3,62 2,15 0,05 9,18 15,54 5,53 0,02 0,66 100,01 d = 3,o5 g. cm~" J Basis 6 Si Ti F<*+ 3 Fe-+ 2 Mn Mg Ca Na K Ca Mg 2"Fe Säuerst. ^914 * ,086/ Z ' UÜ 0,342 0,011 0,099 0,065 1,01 0,002 0,495, 0,6031 o,99 0,388 0, ,5 33,5 17,0 Ac Jd Ti-A Tsch Hd Di Eh Z Y + X + W 2e 9,9 28,9 1,1 5,8 6,6 46,7 1,0 = 2,000 = 2,006 = 0,012 25
9 SiO 2 TiO 2 AI2O3 Fe2O3 Na 2 O K2O H2O+ Tabelle 6 Hornblende aus Eklogitamphibolit, Fundpunkt Hohl, Analytiker R. WITTMANN. Basis 13 Kationen 44,66 0,80 14,56 3,37 7,18 0,06 13,39 10,18 3,31 0,24 2,10 99,85 der 4- und Si Ti Fe-+ 3 Fe-+ 2 Mn Mg Ca Na K daraus OH O 6-Koord 6,3841 1,616) 0,836 0,086 0,362 0,858 0,008 2,851 1,558) 0,917? 0,045' 8,00 5,00 2,52 folgt 2,166 21,834 d = 3,16 g. cm 3 SiO 2 TÌO2 A12O3 Fe2O3 Na2O K2O P2O5 H2O+ Tabelle 7 Pyroxen-Granat-Zoisitsdiiefer, Fundpunkt Hohl, südliche Koralpe Analytiker R. WITTMANN 50,00 0,68 12,04 1,70 5,60 0,13 11,09 16,04 1,83 0,06 sp. 1,02 100,19 al fm c alk si. mg k NiGGLi-Werte A C F 14,5 46,5 35,5 3, ,73 0,02 Or Ab An Wo En Fs Mt 13,3 48,0 38,7 Norm 0,3 15,6 24,7 23,2 16,1 8,1 8,2 1,3 2,5 Tabelle 8 Modaler Mineralbestand des Pyroxen-Granat-Zoisit-Schiefers, Fundpunkt Hohl, berechnet aus der Analyse von Granat, Tabelle 9, von Pyroxen, Tabelle 10, bzw. aus der chemischen Zusammensetzung von Zoisit. Pyroxen 59,5 Granat 28,2 Zoisit 8,4 Quarz 3,9 100,0 26
10 SiO 2 TiO 2 AI2O3 Tabelle 9 Granat aus Pyroxen-Granat-Zoisitschiefer, Fundpunkt Hohl Analytiker R. WITTMANN 40,52 0,32 21,86 2,11 14,71 0,43 10,47 8,76 99,18 Verunreinigungen durch Einschlüsse: Zoisit Quarz Rutil 10,2 % 1,5 % 0,3 % beobachtet vorliegende Arbeit : d = 3,81 g. cm HERITSCH 1966 : berechnet : d = 3,86 g. cm~ 3 m an din Pyrop Spessartin Grossular Andradit 3 1 = 1,755 = 1,760 = 1,769 35,2 44,7 1,0 12,3 6,8 = 11,582 ± 0,004 A a = a = 11,573 A Tabelle 10 Pyroxen aus Pyroxen-Granat-Zoisit-Schiefer, Fundpunkt Hohl. Analytiker R. WITTMANN SÌO2 TÌO2 A12O3 Fe2O3 Na2O K2O H2O+ J Q d 0 52,97 0,78 5,64 1,19 1,92 0,06 13,52 20,10 2,57 sp. 0,92 99,67,85 g. cm J Basis 6 Si Ti Fe + 3 Fe-+ 2 Mn Mg Ca Na Ca Mg Säuerst. 0,065' 0,178 0,021 0,033 0,059 0,002 0,7361 0,7861 0,182' 48,4 41,9 9,7 2 > 00 1,03 u ' y7 Ac Jd Ti-A Tsch Hd Di En Z Y + X + W Se 3,2 14,5 2,1 2,5 6,0 66,1 5,6 = 2,000 = 1,997 = 0,006 27
11 Zusammenfassung Zusammenfassend kann gesagt werden, daß es von besonderem Interesse ist, daß räumlich so knapp nebeneinander zwei verschiedene Granate und Pyroxene vorkommen. Soweit bis jetzt überblickbar, scheint das Ausgangsmaterial hiefür von wesentlicher Bedeutung zu sein. Ausgebreitete Untersuchungen, die vom hiesigen Institut ausgeführt werden, sind zur Klärung dieser Verhältnisse noch notwendig. Literatur ANGEL F Gesteine der Steiermark. Naturwiss. Ver. Steiermark: 60, Wiss. Abh. ANGEL F. & SCHAIDER F Granat und Omphazit aus dem Eklogit des Gertrusk (Saualpe, Kärnten). Carinthia II, 58/60:33. BECK-MANNAGETTA P Zur Deutung der Eklogite im Koralpenkristallin (Zentralalpen). TSCHERMAKS Min. Petr. Mitt., dritte Folge: 7:437. BURRI C Petrochemische Berechnungsmethoden auf äquivalenter Grundlage. BIRKHÄUSER, Basel. COLEMAN R. G., LEE D. E BEATY L. B. & BRANNOCK W. W Eclogites and Eclogites usw. Bull. Geol. Soc. Am., 76:483. DEER W. A., HOWIE R. A. & ZUSSMAN J Rock-Forming Minerals 1. LONG- MANS, London. DEER W. A., HOWIE R. A. & ZUSSMAN J Rock-Forming Minerals 2. LONG- MANS, London. ESSENE E. J. & FYFE W. S Omphacite in Califomian Metamorphic Rocks. Contr. Min. Petrol., 15:1. FRITSCH W., MEIXNER H. & WIESENEDER H Zur quantitativen Klassifikation der kristallinen Schiefer, 2. Mitt. N. Jb. Min. Mtsh., 67:364. HERITSCH H Exkursion in das Kristallin der Koralpe. Mitt. naturwiss. Ver. Steiermark: 93:178. HERITSCH H Vorbericht über Untersuchungen an Eklogiten der Koralpe. Anz. math.-naturwiss. Kl., österr. Akad. Wiss.: 313. HERITSCH H Bericht über Untersuchungen an eklogitischen Gesteinen der Koralpe. Anz. math.-naturwiss. Kl., österr. Akad. Wiss.: 268. HERITSCH H. & KAHLER E Strukturuntersuchung an zwei Kluftkarinthinen. TSCHERMAKS Min. Petr. Mitt., dritte Folge, 7:218. HESS H. H Chemical Composition and Optical Properties of Common Clinopyroxenes. Am. Min., 34:621. HUCKENHOLZ H. G Der petrogenetische Werdegang der Klinopyroxene in den tertiären Vulkaniten der Hocheifel, I. Beitr. Min. Petr., 11:138. KIESLINGER A Geologie und Pétrographie der Koralpe VII, Eklogite und Amphibolite. Sitz. Berichte Akad. Wiss. Wien, math.-naturwiss. Kl., Abt. I: 137:401. KIESLINGER A Geologische Spezialkarte der Republik Österreich, Blatt Unterdrauburg. Geologische Bundesanstalt. KORITNIG S Ein Beitrag zur Kenntnis über den Karinthin". ZBl. Min. Geol. Pal., Abt. A.: 31. KÜMEL F Über basische Tiefengesteine der Zentralalpen und ihre Metamorphose. TSCHERMAKS Min. Petr. Mitt.: 49:415. MACHATSCHKI K. & WALITZI E. M Hornblenden aus Eklogiten und Amphiboliten der südlichen Koralpe. TSCHERMAKS Min. Petr. Mitt., dritte Folge, 8: Naturwissenschaftlicher Verein für Steiermark; download unter
12 MOTTANA A., CHURCH W. R. & EDGAR A. D Chemistry, Mineralogy and Petrology of an Eclogite from the Type Locality (Saualpe, Austria). Contr. Min. Petrol., 18:338. NOCKOLDS S. R Average Chemical Compositions of some Igneous Rocks. Bull. Geol. Soc. Amer., 65:1007. OOSTEROM M. G The ultramafites and layered gabbro sequences in the granulite facies rocks on Stjernöy (Finnmark, Norway). Leidse Geol. Mededel., 28:177. STRUNZ H Mineralogische Tabellen. Akad. Verlagsges., Leipzig. TRÖGER E Die Granatgruppe: Beziehungen zwischen Mineralchemismus und Gesteinsart. N. Jb. Min. Abh., 93:1. ZEN E-an Validity of VEGARD'S Law". Am. Min., 41:523. Anschrift der Verfasser: Univ.-Prof. Dr. Haymo HERITSCH und Dr. Roland WITTMANN, Universität Graz, Institut für Mineralogie und Pétrographie, A-8010 Graz. 29
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
OECD Programme for International Student Assessment PISA 2000. Lösungen der Beispielaufgaben aus dem Mathematiktest. Deutschland
 OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
Kapitalerhöhung - Verbuchung
 Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
EINFACHES HAUSHALT- KASSABUCH
 EINFACHES HAUSHALT- KASSABUCH Arbeiten mit Excel Wir erstellen ein einfaches Kassabuch zur Führung einer Haushalts- oder Portokasse Roland Liebing, im November 2012 Eine einfache Haushalt-Buchhaltung (Kassabuch)
EINFACHES HAUSHALT- KASSABUCH Arbeiten mit Excel Wir erstellen ein einfaches Kassabuch zur Führung einer Haushalts- oder Portokasse Roland Liebing, im November 2012 Eine einfache Haushalt-Buchhaltung (Kassabuch)
Die Online-Meetings bei den Anonymen Alkoholikern. zum Thema. Online - Meetings. Eine neue Form der Selbsthilfe?
 Die Online-Meetings bei den Anonymen Alkoholikern zum Thema Online - Meetings Eine neue Form der Selbsthilfe? Informationsverhalten von jungen Menschen (Quelle: FAZ.NET vom 2.7.2010). Erfahrungen können
Die Online-Meetings bei den Anonymen Alkoholikern zum Thema Online - Meetings Eine neue Form der Selbsthilfe? Informationsverhalten von jungen Menschen (Quelle: FAZ.NET vom 2.7.2010). Erfahrungen können
Stellen Sie bitte den Cursor in die Spalte B2 und rufen die Funktion Sverweis auf. Es öffnet sich folgendes Dialogfenster
 Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Zählstatistik. Peter Appel. 31. Januar 2005
 Zählstatistik Peter Appel 31. Januar 2005 1 Einleitung Bei der quantitativen Analyse im Bereich von Neben- und Spurenelementkonzentrationen ist es von Bedeutung, Kenntnis über die möglichen Fehler und
Zählstatistik Peter Appel 31. Januar 2005 1 Einleitung Bei der quantitativen Analyse im Bereich von Neben- und Spurenelementkonzentrationen ist es von Bedeutung, Kenntnis über die möglichen Fehler und
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
Alle gehören dazu. Vorwort
 Alle gehören dazu Alle sollen zusammen Sport machen können. In diesem Text steht: Wie wir dafür sorgen wollen. Wir sind: Der Deutsche Olympische Sport-Bund und die Deutsche Sport-Jugend. Zu uns gehören
Alle gehören dazu Alle sollen zusammen Sport machen können. In diesem Text steht: Wie wir dafür sorgen wollen. Wir sind: Der Deutsche Olympische Sport-Bund und die Deutsche Sport-Jugend. Zu uns gehören
Lichtbrechung an Linsen
 Sammellinsen Lichtbrechung an Linsen Fällt ein paralleles Lichtbündel auf eine Sammellinse, so werden die Lichtstrahlen so gebrochen, dass sie durch einen Brennpunkt der Linse verlaufen. Der Abstand zwischen
Sammellinsen Lichtbrechung an Linsen Fällt ein paralleles Lichtbündel auf eine Sammellinse, so werden die Lichtstrahlen so gebrochen, dass sie durch einen Brennpunkt der Linse verlaufen. Der Abstand zwischen
4. BEZIEHUNGEN ZWISCHEN TABELLEN
 4. BEZIEHUNGEN ZWISCHEN TABELLEN Zwischen Tabellen können in MS Access Beziehungen bestehen. Durch das Verwenden von Tabellen, die zueinander in Beziehung stehen, können Sie Folgendes erreichen: Die Größe
4. BEZIEHUNGEN ZWISCHEN TABELLEN Zwischen Tabellen können in MS Access Beziehungen bestehen. Durch das Verwenden von Tabellen, die zueinander in Beziehung stehen, können Sie Folgendes erreichen: Die Größe
Das große ElterngeldPlus 1x1. Alles über das ElterngeldPlus. Wer kann ElterngeldPlus beantragen? ElterngeldPlus verstehen ein paar einleitende Fakten
 Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
Das Wachstum der deutschen Volkswirtschaft
 Institut für Wachstumsstudien www.wachstumsstudien.de IWS-Papier Nr. 1 Das Wachstum der deutschen Volkswirtschaft der Bundesrepublik Deutschland 1950 2002.............Seite 2 Relatives Wachstum in der
Institut für Wachstumsstudien www.wachstumsstudien.de IWS-Papier Nr. 1 Das Wachstum der deutschen Volkswirtschaft der Bundesrepublik Deutschland 1950 2002.............Seite 2 Relatives Wachstum in der
FDAX mit Zertifikaten gehandelt
 FDAX mit Zertifikaten gehandelt Gehandelt wird ausschließlich mit Knock out Zertifikaten der Deutschen Bank. Den Grund dafür lesen Sie bitte in meinen Lehrbriefen nach. Als Broker wird Cortal Consors mit
FDAX mit Zertifikaten gehandelt Gehandelt wird ausschließlich mit Knock out Zertifikaten der Deutschen Bank. Den Grund dafür lesen Sie bitte in meinen Lehrbriefen nach. Als Broker wird Cortal Consors mit
Musterlösungen zur Linearen Algebra II Blatt 5
 Musterlösungen zur Linearen Algebra II Blatt 5 Aufgabe. Man betrachte die Matrix A := über dem Körper R und über dem Körper F und bestimme jeweils die Jordan- Normalform. Beweis. Das charakteristische
Musterlösungen zur Linearen Algebra II Blatt 5 Aufgabe. Man betrachte die Matrix A := über dem Körper R und über dem Körper F und bestimme jeweils die Jordan- Normalform. Beweis. Das charakteristische
Tipp III: Leiten Sie eine immer direkt anwendbare Formel her zur Berechnung der sogenannten "bedingten Wahrscheinlichkeit".
 Mathematik- Unterrichts- Einheiten- Datei e. V. Klasse 9 12 04/2015 Diabetes-Test Infos: www.mued.de Blutspenden werden auf Diabetes untersucht, das mit 8 % in der Bevölkerung verbreitet ist. Dabei werden
Mathematik- Unterrichts- Einheiten- Datei e. V. Klasse 9 12 04/2015 Diabetes-Test Infos: www.mued.de Blutspenden werden auf Diabetes untersucht, das mit 8 % in der Bevölkerung verbreitet ist. Dabei werden
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
 50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Sollsaldo und Habensaldo
 ollsaldo und abensaldo Man hört oft die Aussage "Ein ollsaldo steht im aben, und ein abensaldo steht im oll". Da fragt man sich aber, warum der ollsaldo dann ollsaldo heißt und nicht abensaldo, und warum
ollsaldo und abensaldo Man hört oft die Aussage "Ein ollsaldo steht im aben, und ein abensaldo steht im oll". Da fragt man sich aber, warum der ollsaldo dann ollsaldo heißt und nicht abensaldo, und warum
3. Verpackungskünstler. Berechnungen am Quader, Umgang mit Termen, räumliche Vorstellung
 Berechnungen am Quader, Umgang mit Termen, räumliche Vorstellung Päckchen, die man verschenken möchte, werden gerne mit Geschenkband verschnürt. Dazu wird das Päckchen auf seine größte Seite gelegt, wie
Berechnungen am Quader, Umgang mit Termen, räumliche Vorstellung Päckchen, die man verschenken möchte, werden gerne mit Geschenkband verschnürt. Dazu wird das Päckchen auf seine größte Seite gelegt, wie
Was meinen die Leute eigentlich mit: Grexit?
 Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
Erweiterung der Aufgabe. Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen:
 VBA Programmierung mit Excel Schleifen 1/6 Erweiterung der Aufgabe Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen: Es müssen also 11 (B L) x 35 = 385 Zellen berücksichtigt
VBA Programmierung mit Excel Schleifen 1/6 Erweiterung der Aufgabe Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen: Es müssen also 11 (B L) x 35 = 385 Zellen berücksichtigt
Leichte-Sprache-Bilder
 Leichte-Sprache-Bilder Reinhild Kassing Information - So geht es 1. Bilder gucken 2. anmelden für Probe-Bilder 3. Bilder bestellen 4. Rechnung bezahlen 5. Bilder runterladen 6. neue Bilder vorschlagen
Leichte-Sprache-Bilder Reinhild Kassing Information - So geht es 1. Bilder gucken 2. anmelden für Probe-Bilder 3. Bilder bestellen 4. Rechnung bezahlen 5. Bilder runterladen 6. neue Bilder vorschlagen
1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage:
 Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
APP-GFP/Fluoreszenzmikroskop. Aufnahmen neuronaler Zellen, mit freund. Genehmigung von Prof. Stefan Kins, TU Kaiserslautern
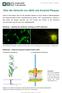 Über die Herkunft von Aβ42 und Amyloid-Plaques Heute ist sicher belegt, dass sich die amyloiden Plaques aus einer Vielzahl an Abbaufragmenten des Amyloid-Vorläufer-Proteins (amyloid-precursor-protein,
Über die Herkunft von Aβ42 und Amyloid-Plaques Heute ist sicher belegt, dass sich die amyloiden Plaques aus einer Vielzahl an Abbaufragmenten des Amyloid-Vorläufer-Proteins (amyloid-precursor-protein,
Hinweise zum Ausfüllen der Zeiterfassung
 Hinweise zum Ausfüllen der Zeiterfassung Generelle Hinweise zu Excel Ab Version VSA 4.50 wird die dezimale Schreibweise für Zeiteingaben verwendet. Die Zeiterfassung, die Sie erhalten haben wurde für Excel
Hinweise zum Ausfüllen der Zeiterfassung Generelle Hinweise zu Excel Ab Version VSA 4.50 wird die dezimale Schreibweise für Zeiteingaben verwendet. Die Zeiterfassung, die Sie erhalten haben wurde für Excel
2. Psychologische Fragen. Nicht genannt.
 Checkliste für die Beurteilung psychologischer Gutachten durch Fachfremde Gliederung eines Gutachtens 1. Nennung des Auftraggebers und Fragestellung des Auftraggebers. 2. Psychologische Fragen. Nicht genannt.
Checkliste für die Beurteilung psychologischer Gutachten durch Fachfremde Gliederung eines Gutachtens 1. Nennung des Auftraggebers und Fragestellung des Auftraggebers. 2. Psychologische Fragen. Nicht genannt.
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Gehen wir einmal davon aus, dass die von uns angenommenen
 geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
Energetische Klassen von Gebäuden
 Energetische Klassen von Gebäuden Grundsätzlich gibt es Neubauten und Bestandsgebäude. Diese Definition ist immer aktuell. Aber auch ein heutiger Neubau ist in drei (oder vielleicht erst zehn?) Jahren
Energetische Klassen von Gebäuden Grundsätzlich gibt es Neubauten und Bestandsgebäude. Diese Definition ist immer aktuell. Aber auch ein heutiger Neubau ist in drei (oder vielleicht erst zehn?) Jahren
Fachbericht zum Thema: Anforderungen an ein Datenbanksystem
 Fachbericht zum Thema: Anforderungen an ein Datenbanksystem von André Franken 1 Inhaltsverzeichnis 1 Inhaltsverzeichnis 1 2 Einführung 2 2.1 Gründe für den Einsatz von DB-Systemen 2 2.2 Definition: Datenbank
Fachbericht zum Thema: Anforderungen an ein Datenbanksystem von André Franken 1 Inhaltsverzeichnis 1 Inhaltsverzeichnis 1 2 Einführung 2 2.1 Gründe für den Einsatz von DB-Systemen 2 2.2 Definition: Datenbank
Anleitung über den Umgang mit Schildern
 Anleitung über den Umgang mit Schildern -Vorwort -Wo bekommt man Schilder? -Wo und wie speichert man die Schilder? -Wie füge ich die Schilder in meinen Track ein? -Welche Bauteile kann man noch für Schilder
Anleitung über den Umgang mit Schildern -Vorwort -Wo bekommt man Schilder? -Wo und wie speichert man die Schilder? -Wie füge ich die Schilder in meinen Track ein? -Welche Bauteile kann man noch für Schilder
Projekt 2HEA 2005/06 Formelzettel Elektrotechnik
 Projekt 2HEA 2005/06 Formelzettel Elektrotechnik Teilübung: Kondensator im Wechselspannunskreis Gruppenteilnehmer: Jakic, Topka Abgabedatum: 24.02.2006 Jakic, Topka Inhaltsverzeichnis 2HEA INHALTSVERZEICHNIS
Projekt 2HEA 2005/06 Formelzettel Elektrotechnik Teilübung: Kondensator im Wechselspannunskreis Gruppenteilnehmer: Jakic, Topka Abgabedatum: 24.02.2006 Jakic, Topka Inhaltsverzeichnis 2HEA INHALTSVERZEICHNIS
LANGFRISTIGE HAUSAUFGABE (LINEARE GLEICHUNGSSYSTEME)
 LANGFRISTIGE HAUSAUFGABE (LINEARE GLEICHUNGSSYSTEME) Aufgabe 1: Tanzkurs ( * ) Zu einem Tanzkurs erscheinen dreimal so viele Mädchen wie Jungen. Nachdem 15 Mädchen gegangen sind, sind noch doppelt so viele
LANGFRISTIGE HAUSAUFGABE (LINEARE GLEICHUNGSSYSTEME) Aufgabe 1: Tanzkurs ( * ) Zu einem Tanzkurs erscheinen dreimal so viele Mädchen wie Jungen. Nachdem 15 Mädchen gegangen sind, sind noch doppelt so viele
Was ist Sozial-Raum-Orientierung?
 Was ist Sozial-Raum-Orientierung? Dr. Wolfgang Hinte Universität Duisburg-Essen Institut für Stadt-Entwicklung und Sozial-Raum-Orientierte Arbeit Das ist eine Zusammen-Fassung des Vortrages: Sozialräume
Was ist Sozial-Raum-Orientierung? Dr. Wolfgang Hinte Universität Duisburg-Essen Institut für Stadt-Entwicklung und Sozial-Raum-Orientierte Arbeit Das ist eine Zusammen-Fassung des Vortrages: Sozialräume
Die neue Aufgabe von der Monitoring-Stelle. Das ist die Monitoring-Stelle:
 Die neue Aufgabe von der Monitoring-Stelle Das ist die Monitoring-Stelle: Am Deutschen Institut für Menschen-Rechte in Berlin gibt es ein besonderes Büro. Dieses Büro heißt Monitoring-Stelle. Mo-ni-to-ring
Die neue Aufgabe von der Monitoring-Stelle Das ist die Monitoring-Stelle: Am Deutschen Institut für Menschen-Rechte in Berlin gibt es ein besonderes Büro. Dieses Büro heißt Monitoring-Stelle. Mo-ni-to-ring
1. Weniger Steuern zahlen
 1. Weniger Steuern zahlen Wenn man arbeitet, zahlt man Geld an den Staat. Dieses Geld heißt Steuern. Viele Menschen zahlen zu viel Steuern. Sie haben daher wenig Geld für Wohnung, Gewand oder Essen. Wenn
1. Weniger Steuern zahlen Wenn man arbeitet, zahlt man Geld an den Staat. Dieses Geld heißt Steuern. Viele Menschen zahlen zu viel Steuern. Sie haben daher wenig Geld für Wohnung, Gewand oder Essen. Wenn
HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN
 HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN Zinsen haben im täglichen Geschäftsleben große Bedeutung und somit auch die eigentliche Zinsrechnung, z.b: - Wenn Sie Ihre Rechnungen zu spät
HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN Zinsen haben im täglichen Geschäftsleben große Bedeutung und somit auch die eigentliche Zinsrechnung, z.b: - Wenn Sie Ihre Rechnungen zu spät
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Es gilt das gesprochene Wort. Anrede
 Sperrfrist: 28. November 2007, 13.00 Uhr Es gilt das gesprochene Wort Statement des Staatssekretärs im Bayerischen Staatsministerium für Unterricht und Kultus, Karl Freller, anlässlich des Pressegesprächs
Sperrfrist: 28. November 2007, 13.00 Uhr Es gilt das gesprochene Wort Statement des Staatssekretärs im Bayerischen Staatsministerium für Unterricht und Kultus, Karl Freller, anlässlich des Pressegesprächs
Mobile Intranet in Unternehmen
 Mobile Intranet in Unternehmen Ergebnisse einer Umfrage unter Intranet Verantwortlichen aexea GmbH - communication. content. consulting Augustenstraße 15 70178 Stuttgart Tel: 0711 87035490 Mobile Intranet
Mobile Intranet in Unternehmen Ergebnisse einer Umfrage unter Intranet Verantwortlichen aexea GmbH - communication. content. consulting Augustenstraße 15 70178 Stuttgart Tel: 0711 87035490 Mobile Intranet
Welche Unterschiede gibt es zwischen einem CAPAund einem Audiometrie- Test?
 Welche Unterschiede gibt es zwischen einem CAPAund einem Audiometrie- Test? Auch wenn die Messungsmethoden ähnlich sind, ist das Ziel beider Systeme jedoch ein anderes. Gwenolé NEXER g.nexer@hearin gp
Welche Unterschiede gibt es zwischen einem CAPAund einem Audiometrie- Test? Auch wenn die Messungsmethoden ähnlich sind, ist das Ziel beider Systeme jedoch ein anderes. Gwenolé NEXER g.nexer@hearin gp
infach Geld FBV Ihr Weg zum finanzellen Erfolg Florian Mock
 infach Ihr Weg zum finanzellen Erfolg Geld Florian Mock FBV Die Grundlagen für finanziellen Erfolg Denn Sie müssten anschließend wieder vom Gehaltskonto Rückzahlungen in Höhe der Entnahmen vornehmen, um
infach Ihr Weg zum finanzellen Erfolg Geld Florian Mock FBV Die Grundlagen für finanziellen Erfolg Denn Sie müssten anschließend wieder vom Gehaltskonto Rückzahlungen in Höhe der Entnahmen vornehmen, um
1 C H R I S T O P H D R Ö S S E R D E R M A T H E M A T I K V E R F Ü H R E R
 C H R I S T O P H D R Ö S S E R D E R M A T H E M A T I K V E R F Ü H R E R L Ö S U N G E N Seite 7 n Wenn vier Menschen auf einem Quadratmeter stehen, dann hat jeder eine Fläche von 50 mal 50 Zentimeter
C H R I S T O P H D R Ö S S E R D E R M A T H E M A T I K V E R F Ü H R E R L Ö S U N G E N Seite 7 n Wenn vier Menschen auf einem Quadratmeter stehen, dann hat jeder eine Fläche von 50 mal 50 Zentimeter
Outlook. sysplus.ch outlook - mail-grundlagen Seite 1/8. Mail-Grundlagen. Posteingang
 sysplus.ch outlook - mail-grundlagen Seite 1/8 Outlook Mail-Grundlagen Posteingang Es gibt verschiedene Möglichkeiten, um zum Posteingang zu gelangen. Man kann links im Outlook-Fenster auf die Schaltfläche
sysplus.ch outlook - mail-grundlagen Seite 1/8 Outlook Mail-Grundlagen Posteingang Es gibt verschiedene Möglichkeiten, um zum Posteingang zu gelangen. Man kann links im Outlook-Fenster auf die Schaltfläche
Gleichungen Lösen. Ein graphischer Blick auf Gleichungen
 Gleichungen Lösen Was bedeutet es, eine Gleichung zu lösen? Was ist überhaupt eine Gleichung? Eine Gleichung ist, grundsätzlich eine Aussage über zwei mathematische Terme, dass sie gleich sind. Ein Term
Gleichungen Lösen Was bedeutet es, eine Gleichung zu lösen? Was ist überhaupt eine Gleichung? Eine Gleichung ist, grundsätzlich eine Aussage über zwei mathematische Terme, dass sie gleich sind. Ein Term
Bedienungsanleitung für den Online-Shop
 Hier sind die Produktgruppen zu finden. Zur Produktgruppe gibt es eine Besonderheit: - Seite 1 von 18 - Zuerst wählen Sie einen Drucker-Hersteller aus. Dann wählen Sie das entsprechende Drucker- Modell
Hier sind die Produktgruppen zu finden. Zur Produktgruppe gibt es eine Besonderheit: - Seite 1 von 18 - Zuerst wählen Sie einen Drucker-Hersteller aus. Dann wählen Sie das entsprechende Drucker- Modell
Lösungsmethoden gewöhnlicher Differentialgleichungen (Dgl.)
 Lösungsmethoden gewöhnlicher Dierentialgleichungen Dgl) Allgemeine und partikuläre Lösung einer gewöhnlichen Dierentialgleichung Eine Dierentialgleichung ist eine Gleichung! Zum Unterschied von den gewöhnlichen
Lösungsmethoden gewöhnlicher Dierentialgleichungen Dgl) Allgemeine und partikuläre Lösung einer gewöhnlichen Dierentialgleichung Eine Dierentialgleichung ist eine Gleichung! Zum Unterschied von den gewöhnlichen
Handbuch. NAFI Online-Spezial. Kunden- / Datenverwaltung. 1. Auflage. (Stand: 24.09.2014)
 Handbuch NAFI Online-Spezial 1. Auflage (Stand: 24.09.2014) Copyright 2016 by NAFI GmbH Unerlaubte Vervielfältigungen sind untersagt! Inhaltsangabe Einleitung... 3 Kundenauswahl... 3 Kunde hinzufügen...
Handbuch NAFI Online-Spezial 1. Auflage (Stand: 24.09.2014) Copyright 2016 by NAFI GmbH Unerlaubte Vervielfältigungen sind untersagt! Inhaltsangabe Einleitung... 3 Kundenauswahl... 3 Kunde hinzufügen...
Berechnung der Erhöhung der Durchschnittsprämien
 Wolfram Fischer Berechnung der Erhöhung der Durchschnittsprämien Oktober 2004 1 Zusammenfassung Zur Berechnung der Durchschnittsprämien wird das gesamte gemeldete Prämienvolumen Zusammenfassung durch die
Wolfram Fischer Berechnung der Erhöhung der Durchschnittsprämien Oktober 2004 1 Zusammenfassung Zur Berechnung der Durchschnittsprämien wird das gesamte gemeldete Prämienvolumen Zusammenfassung durch die
Bundesverband Flachglas Großhandel Isolierglasherstellung Veredlung e.v. U g -Werte-Tabellen nach DIN EN 673. Flachglasbranche.
 Bundesverband Flachglas Großhandel Isolierglasherstellung Veredlung e.v. U g -Werte-Tabellen nach DIN EN 673 Ug-Werte für die Flachglasbranche Einleitung Die vorliegende Broschüre enthält die Werte für
Bundesverband Flachglas Großhandel Isolierglasherstellung Veredlung e.v. U g -Werte-Tabellen nach DIN EN 673 Ug-Werte für die Flachglasbranche Einleitung Die vorliegende Broschüre enthält die Werte für
Speicher in der Cloud
 Speicher in der Cloud Kostenbremse, Sicherheitsrisiko oder Basis für die unternehmensweite Kollaboration? von Cornelius Höchel-Winter 2013 ComConsult Research GmbH, Aachen 3 SYNCHRONISATION TEUFELSZEUG
Speicher in der Cloud Kostenbremse, Sicherheitsrisiko oder Basis für die unternehmensweite Kollaboration? von Cornelius Höchel-Winter 2013 ComConsult Research GmbH, Aachen 3 SYNCHRONISATION TEUFELSZEUG
a n + 2 1 auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert:
 Beispiel: Wir untersuchen die rekursiv definierte Folge a 0 + auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert: ( ) (,, 7, 5,...) Wir können also vermuten, dass die Folge monoton fallend
Beispiel: Wir untersuchen die rekursiv definierte Folge a 0 + auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert: ( ) (,, 7, 5,...) Wir können also vermuten, dass die Folge monoton fallend
Mathematik. UND/ODER Verknüpfung. Ungleichungen. Betrag. Intervall. Umgebung
 Mathematik UND/ODER Verknüpfung Ungleichungen Betrag Intervall Umgebung Stefan Gärtner 004 Gr Mathematik UND/ODER Seite UND Verknüpfung Kommentar Aussage Symbolform Die Aussagen Hans kann schwimmen p und
Mathematik UND/ODER Verknüpfung Ungleichungen Betrag Intervall Umgebung Stefan Gärtner 004 Gr Mathematik UND/ODER Seite UND Verknüpfung Kommentar Aussage Symbolform Die Aussagen Hans kann schwimmen p und
Was ist aus der ersten Generation von Unternehmergesellschaften geworden?
 Prof. Dr. Walter Bayer / Dipl.-Kfm. Thomas Hoffmann, Jena Was ist aus der ersten Generation von Unternehmergesellschaften geworden? In diesen und den nächsten Tagen begehen die ersten Unternehmergesellschaften
Prof. Dr. Walter Bayer / Dipl.-Kfm. Thomas Hoffmann, Jena Was ist aus der ersten Generation von Unternehmergesellschaften geworden? In diesen und den nächsten Tagen begehen die ersten Unternehmergesellschaften
Dow Jones am 13.06.08 im 1-min Chat
 Dow Jones am 13.06.08 im 1-min Chat Dieser Ausschnitt ist eine Formation: Wechselstäbe am unteren Bollinger Band mit Punkt d über dem 20-er GD nach 3 tieferen Hoch s. Wenn ich einen Ausbruch aus Wechselstäben
Dow Jones am 13.06.08 im 1-min Chat Dieser Ausschnitt ist eine Formation: Wechselstäbe am unteren Bollinger Band mit Punkt d über dem 20-er GD nach 3 tieferen Hoch s. Wenn ich einen Ausbruch aus Wechselstäben
ONLINE-AKADEMIE. "Diplomierter NLP Anwender für Schule und Unterricht" Ziele
 ONLINE-AKADEMIE Ziele Wenn man von Menschen hört, die etwas Großartiges in ihrem Leben geleistet haben, erfahren wir oft, dass diese ihr Ziel über Jahre verfolgt haben oder diesen Wunsch schon bereits
ONLINE-AKADEMIE Ziele Wenn man von Menschen hört, die etwas Großartiges in ihrem Leben geleistet haben, erfahren wir oft, dass diese ihr Ziel über Jahre verfolgt haben oder diesen Wunsch schon bereits
Erklärung zum Internet-Bestellschein
 Erklärung zum Internet-Bestellschein Herzlich Willkommen bei Modellbahnbau Reinhardt. Auf den nächsten Seiten wird Ihnen mit hilfreichen Bildern erklärt, wie Sie den Internet-Bestellschein ausfüllen und
Erklärung zum Internet-Bestellschein Herzlich Willkommen bei Modellbahnbau Reinhardt. Auf den nächsten Seiten wird Ihnen mit hilfreichen Bildern erklärt, wie Sie den Internet-Bestellschein ausfüllen und
1.1 Allgemeines. innerhalb der Nachtzeit (19:00 24:00) Gesamte Normalarbeitszeit (16:00 19:00)
 Abschnitt 1 Überstunden in der Nacht 11 1.1 Allgemeines # Die Ermittlung und Abrechnung von Überstunden unter der Woche, an Sonn- und Feiertagen wurde bereits im Band I, Abschnitt 3 behandelt. Sehen wir
Abschnitt 1 Überstunden in der Nacht 11 1.1 Allgemeines # Die Ermittlung und Abrechnung von Überstunden unter der Woche, an Sonn- und Feiertagen wurde bereits im Band I, Abschnitt 3 behandelt. Sehen wir
Lineare Funktionen. 1 Proportionale Funktionen 3 1.1 Definition... 3 1.2 Eigenschaften... 3. 2 Steigungsdreieck 3
 Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
Eine Logikschaltung zur Addition zweier Zahlen
 Eine Logikschaltung zur Addition zweier Zahlen Grundlegender Ansatz für die Umsetzung arithmetischer Operationen als elektronische Schaltung ist die Darstellung von Zahlen im Binärsystem. Eine Logikschaltung
Eine Logikschaltung zur Addition zweier Zahlen Grundlegender Ansatz für die Umsetzung arithmetischer Operationen als elektronische Schaltung ist die Darstellung von Zahlen im Binärsystem. Eine Logikschaltung
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Verband der TÜV e. V. STUDIE ZUM IMAGE DER MPU
 Verband der TÜV e. V. STUDIE ZUM IMAGE DER MPU 2 DIE MEDIZINISCH-PSYCHOLOGISCHE UNTERSUCHUNG (MPU) IST HOCH ANGESEHEN Das Image der Medizinisch-Psychologischen Untersuchung (MPU) ist zwiespältig: Das ist
Verband der TÜV e. V. STUDIE ZUM IMAGE DER MPU 2 DIE MEDIZINISCH-PSYCHOLOGISCHE UNTERSUCHUNG (MPU) IST HOCH ANGESEHEN Das Image der Medizinisch-Psychologischen Untersuchung (MPU) ist zwiespältig: Das ist
Durch Wissen Millionär WerDen... Wer hat zuerst die Million erreicht? spielanleitung Zahl der spieler: alter: redaktion / autor: inhalt:
 Spielanleitung Durch Wissen Millionär werden... Diesen Traum kann man sich in diesem beliebten Quiz-Spiel erfüllen. Ob allein oder in der geselligen Runde dieses Quiz enthält 330 Fragen und 1.320 Multiple-Choice-Antworten.
Spielanleitung Durch Wissen Millionär werden... Diesen Traum kann man sich in diesem beliebten Quiz-Spiel erfüllen. Ob allein oder in der geselligen Runde dieses Quiz enthält 330 Fragen und 1.320 Multiple-Choice-Antworten.
Örtliche Angebots- und Teilhabeplanung im Landkreis Weilheim-Schongau
 Örtliche Angebots- und Teilhabeplanung im Landkreis Weilheim-Schongau Zusammenfassung der Ergebnisse in Leichter Sprache Timo Wissel Albrecht Rohrmann Timo Wissel / Albrecht Rohrmann: Örtliche Angebots-
Örtliche Angebots- und Teilhabeplanung im Landkreis Weilheim-Schongau Zusammenfassung der Ergebnisse in Leichter Sprache Timo Wissel Albrecht Rohrmann Timo Wissel / Albrecht Rohrmann: Örtliche Angebots-
einfache Rendite 0 145 85 1 160 90 2 135 100 3 165 105 4 190 95 5 210 110
 Übungsbeispiele 1/6 1) Vervollständigen Sie folgende Tabelle: Nr. Aktie A Aktie B Schlusskurs in Schlusskurs in 0 145 85 1 160 90 2 135 100 3 165 105 4 190 95 5 210 110 Arithmetisches Mittel Standardabweichung
Übungsbeispiele 1/6 1) Vervollständigen Sie folgende Tabelle: Nr. Aktie A Aktie B Schlusskurs in Schlusskurs in 0 145 85 1 160 90 2 135 100 3 165 105 4 190 95 5 210 110 Arithmetisches Mittel Standardabweichung
Letzte Krankenkassen streichen Zusatzbeiträge
 Zusatzbeiträge - Gesundheitsfonds Foto: D. Claus Einige n verlangten 2010 Zusatzbeiträge von ihren Versicherten. Die positive wirtschaftliche Entwicklung im Jahr 2011 ermöglichte den n die Rücknahme der
Zusatzbeiträge - Gesundheitsfonds Foto: D. Claus Einige n verlangten 2010 Zusatzbeiträge von ihren Versicherten. Die positive wirtschaftliche Entwicklung im Jahr 2011 ermöglichte den n die Rücknahme der
Lebensversicherung. http://www.konsument.at/cs/satellite?pagename=konsument/magazinartikel/printma... OBJEKTIV UNBESTECHLICH KEINE WERBUNG
 Seite 1 von 6 OBJEKTIV UNBESTECHLICH KEINE WERBUNG Lebensversicherung Verschenken Sie kein Geld! veröffentlicht am 11.03.2011, aktualisiert am 14.03.2011 "Verschenken Sie kein Geld" ist der aktuelle Rat
Seite 1 von 6 OBJEKTIV UNBESTECHLICH KEINE WERBUNG Lebensversicherung Verschenken Sie kein Geld! veröffentlicht am 11.03.2011, aktualisiert am 14.03.2011 "Verschenken Sie kein Geld" ist der aktuelle Rat
Erstellen von x-y-diagrammen in OpenOffice.calc
 Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
Das Leitbild vom Verein WIR
 Das Leitbild vom Verein WIR Dieses Zeichen ist ein Gütesiegel. Texte mit diesem Gütesiegel sind leicht verständlich. Leicht Lesen gibt es in drei Stufen. B1: leicht verständlich A2: noch leichter verständlich
Das Leitbild vom Verein WIR Dieses Zeichen ist ein Gütesiegel. Texte mit diesem Gütesiegel sind leicht verständlich. Leicht Lesen gibt es in drei Stufen. B1: leicht verständlich A2: noch leichter verständlich
Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer
 Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer Allgemein: Das RSA-Verschlüsselungsverfahren ist ein häufig benutztes Verschlüsselungsverfahren, weil es sehr sicher ist. Es gehört zu der Klasse der
Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer Allgemein: Das RSA-Verschlüsselungsverfahren ist ein häufig benutztes Verschlüsselungsverfahren, weil es sehr sicher ist. Es gehört zu der Klasse der
Der monatliche Tarif für ein Handy wurde als lineare Funktion der Form f(x) = k x + d modelliert (siehe Grafik).
 1) Handytarif Der monatliche Tarif für ein Handy wurde als lineare Funktion der Form f(x) = k x + d modelliert (siehe Grafik). Euro Gesprächsminuten Tragen Sie in der folgenden Tabelle ein, welche Bedeutung
1) Handytarif Der monatliche Tarif für ein Handy wurde als lineare Funktion der Form f(x) = k x + d modelliert (siehe Grafik). Euro Gesprächsminuten Tragen Sie in der folgenden Tabelle ein, welche Bedeutung
Abschlussprüfung Realschule Bayern II / III: 2009 Haupttermin B 1.0 B 1.1
 B 1.0 B 1.1 L: Wir wissen von, dass sie den Scheitel hat und durch den Punkt läuft. Was nichts bringt, ist beide Punkte in die allgemeine Parabelgleichung einzusetzen und das Gleichungssystem zu lösen,
B 1.0 B 1.1 L: Wir wissen von, dass sie den Scheitel hat und durch den Punkt läuft. Was nichts bringt, ist beide Punkte in die allgemeine Parabelgleichung einzusetzen und das Gleichungssystem zu lösen,
Projektmanagement in der Spieleentwicklung
 Projektmanagement in der Spieleentwicklung Inhalt 1. Warum brauche ich ein Projekt-Management? 2. Die Charaktere des Projektmanagement - Mastermind - Producer - Projektleiter 3. Schnittstellen definieren
Projektmanagement in der Spieleentwicklung Inhalt 1. Warum brauche ich ein Projekt-Management? 2. Die Charaktere des Projektmanagement - Mastermind - Producer - Projektleiter 3. Schnittstellen definieren
Kurzanleitung. MEYTON Aufbau einer Internetverbindung. 1 Von 11
 Kurzanleitung MEYTON Aufbau einer Internetverbindung 1 Von 11 Inhaltsverzeichnis Installation eines Internetzugangs...3 Ist mein Router bereits im MEYTON Netzwerk?...3 Start des YAST Programms...4 Auswahl
Kurzanleitung MEYTON Aufbau einer Internetverbindung 1 Von 11 Inhaltsverzeichnis Installation eines Internetzugangs...3 Ist mein Router bereits im MEYTON Netzwerk?...3 Start des YAST Programms...4 Auswahl
Die Gleichung A x = a hat für A 0 die eindeutig bestimmte Lösung. Für A=0 und a 0 existiert keine Lösung.
 Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
impact ordering Info Produktkonfigurator
 impact ordering Info Copyright Copyright 2013 veenion GmbH Alle Rechte vorbehalten. Kein Teil der Dokumentation darf in irgendeiner Form ohne schriftliche Genehmigung der veenion GmbH reproduziert, verändert
impact ordering Info Copyright Copyright 2013 veenion GmbH Alle Rechte vorbehalten. Kein Teil der Dokumentation darf in irgendeiner Form ohne schriftliche Genehmigung der veenion GmbH reproduziert, verändert
PCD Europe, Krefeld, Jan 2007. Auswertung von Haemoccult
 Auswertung von Haemoccult Ist das positiv? Nein! Ja! Im deutschen Krebsfrüherkennungsprogramm haben nur etwa 1 % der Frauen und 1,5 % der Männer ein positives Haemoccult -Ergebnis, da dieser Test eine
Auswertung von Haemoccult Ist das positiv? Nein! Ja! Im deutschen Krebsfrüherkennungsprogramm haben nur etwa 1 % der Frauen und 1,5 % der Männer ein positives Haemoccult -Ergebnis, da dieser Test eine
Spielbericht Online. Nachbearbeitung durch die Vereine ist erforderlich bei: a) Nichtantritt des angesetzten Schiedsrichters
 ist erforderlich bei: a) Nichtantritt des angesetzten Schiedsrichters b) Wenn kein Schiedsrichter angesetzt wurde und die Vereine selber das Spiel leiten müssen (vorwiegend C- bis E-JuniorenInnen) Das
ist erforderlich bei: a) Nichtantritt des angesetzten Schiedsrichters b) Wenn kein Schiedsrichter angesetzt wurde und die Vereine selber das Spiel leiten müssen (vorwiegend C- bis E-JuniorenInnen) Das
Fachdidaktik der Informatik 18.12.08 Jörg Depner, Kathrin Gaißer
 Fachdidaktik der Informatik 18.12.08 Jörg Depner, Kathrin Gaißer Klassendiagramme Ein Klassendiagramm dient in der objektorientierten Softwareentwicklung zur Darstellung von Klassen und den Beziehungen,
Fachdidaktik der Informatik 18.12.08 Jörg Depner, Kathrin Gaißer Klassendiagramme Ein Klassendiagramm dient in der objektorientierten Softwareentwicklung zur Darstellung von Klassen und den Beziehungen,
Anleitung Scharbefragung
 Projekt Evaline Anleitung Scharbefragung v.1.2 Inhalt Anleitung Scharbefragung... 1 1 Einleitung... 2 1.1 Vorlagen... 2 1.2 Journal... 2 2 Befragung Veranstaltungen / Angebote... 3 2.1 Methode... 3 2.2
Projekt Evaline Anleitung Scharbefragung v.1.2 Inhalt Anleitung Scharbefragung... 1 1 Einleitung... 2 1.1 Vorlagen... 2 1.2 Journal... 2 2 Befragung Veranstaltungen / Angebote... 3 2.1 Methode... 3 2.2
Kapitalerhöhung - Verbuchung
 Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
1 topologisches Sortieren
 Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Anwendungsbeispiele Buchhaltung
 Rechnungen erstellen mit Webling Webling ist ein Produkt der Firma: Inhaltsverzeichnis 1 Rechnungen erstellen mit Webling 1.1 Rechnung erstellen und ausdrucken 1.2 Rechnung mit Einzahlungsschein erstellen
Rechnungen erstellen mit Webling Webling ist ein Produkt der Firma: Inhaltsverzeichnis 1 Rechnungen erstellen mit Webling 1.1 Rechnung erstellen und ausdrucken 1.2 Rechnung mit Einzahlungsschein erstellen
Die reellen Lösungen der kubischen Gleichung
 Die reellen Lösungen der kubischen Gleichung Klaus-R. Löffler Inhaltsverzeichnis 1 Einfach zu behandelnde Sonderfälle 1 2 Die ganzrationale Funktion dritten Grades 2 2.1 Reduktion...........................................
Die reellen Lösungen der kubischen Gleichung Klaus-R. Löffler Inhaltsverzeichnis 1 Einfach zu behandelnde Sonderfälle 1 2 Die ganzrationale Funktion dritten Grades 2 2.1 Reduktion...........................................
Erstellen einer Collage. Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu])
![Erstellen einer Collage. Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu]) Erstellen einer Collage. Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu])](/thumbs/29/13170670.jpg) 3.7 Erstellen einer Collage Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu]) Dann Größe des Dokuments festlegen beispielsweise A4 (weitere
3.7 Erstellen einer Collage Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu]) Dann Größe des Dokuments festlegen beispielsweise A4 (weitere
Kapiteltests zum Leitprogramm Binäre Suchbäume
 Kapiteltests zum Leitprogramm Binäre Suchbäume Björn Steffen Timur Erdag überarbeitet von Christina Class Binäre Suchbäume Kapiteltests für das ETH-Leitprogramm Adressaten und Institutionen Das Leitprogramm
Kapiteltests zum Leitprogramm Binäre Suchbäume Björn Steffen Timur Erdag überarbeitet von Christina Class Binäre Suchbäume Kapiteltests für das ETH-Leitprogramm Adressaten und Institutionen Das Leitprogramm
Ergebnis und Auswertung der BSV-Online-Umfrage zur dienstlichen Beurteilung
 Ergebnis und Auswertung der BSV-Online-Umfrage zur dienstlichen Beurteilung Es waren exakt 237 Rückmeldungen, die wir erhalten, gesammelt und ausgewertet haben und damit ein Vielfaches von dem, was wir
Ergebnis und Auswertung der BSV-Online-Umfrage zur dienstlichen Beurteilung Es waren exakt 237 Rückmeldungen, die wir erhalten, gesammelt und ausgewertet haben und damit ein Vielfaches von dem, was wir
mehrmals mehrmals mehrmals alle seltener nie mindestens **) in der im Monat im Jahr 1 bis 2 alle 1 bis 2 Woche Jahre Jahre % % % % % % %
 Nicht überraschend, aber auch nicht gravierend, sind die altersspezifischen Unterschiede hinsichtlich der Häufigkeit des Apothekenbesuchs: 24 Prozent suchen mindestens mehrmals im Monat eine Apotheke auf,
Nicht überraschend, aber auch nicht gravierend, sind die altersspezifischen Unterschiede hinsichtlich der Häufigkeit des Apothekenbesuchs: 24 Prozent suchen mindestens mehrmals im Monat eine Apotheke auf,
Eva Douma: Die Vorteile und Nachteile der Ökonomisierung in der Sozialen Arbeit
 Eva Douma: Die Vorteile und Nachteile der Ökonomisierung in der Sozialen Arbeit Frau Dr. Eva Douma ist Organisations-Beraterin in Frankfurt am Main Das ist eine Zusammen-Fassung des Vortrages: Busines
Eva Douma: Die Vorteile und Nachteile der Ökonomisierung in der Sozialen Arbeit Frau Dr. Eva Douma ist Organisations-Beraterin in Frankfurt am Main Das ist eine Zusammen-Fassung des Vortrages: Busines
FAQ Spielvorbereitung Startspieler: Wer ist Startspieler?
 FAQ Spielvorbereitung Startspieler: Wer ist Startspieler? In der gedruckten Version der Spielregeln steht: der Startspieler ist der Spieler, dessen Arena unmittelbar links neben dem Kaiser steht [im Uhrzeigersinn].
FAQ Spielvorbereitung Startspieler: Wer ist Startspieler? In der gedruckten Version der Spielregeln steht: der Startspieler ist der Spieler, dessen Arena unmittelbar links neben dem Kaiser steht [im Uhrzeigersinn].
Newsletter Immobilienrecht Nr. 10 September 2012
 Newsletter Immobilienrecht Nr. 10 September 2012 Maßgeblicher Zeitpunkt für die Kenntnis des Käufers von einem Mangel der Kaufsache bei getrennt beurkundetem Grundstückskaufvertrag Einführung Grundstückskaufverträge
Newsletter Immobilienrecht Nr. 10 September 2012 Maßgeblicher Zeitpunkt für die Kenntnis des Käufers von einem Mangel der Kaufsache bei getrennt beurkundetem Grundstückskaufvertrag Einführung Grundstückskaufverträge
Programm 4: Arbeiten mit thematischen Karten
 : Arbeiten mit thematischen Karten A) Anteil der ausländischen Wohnbevölkerung an der Wohnbevölkerung insgesamt 2001 in Prozent 1. Inhaltliche und kartographische Beschreibung - Originalkarte Bei dieser
: Arbeiten mit thematischen Karten A) Anteil der ausländischen Wohnbevölkerung an der Wohnbevölkerung insgesamt 2001 in Prozent 1. Inhaltliche und kartographische Beschreibung - Originalkarte Bei dieser
Inkrementelles Backup
 Inkrementelles Backup Im Gegensatz zu einer kompletten Sicherung aller Daten werden bei einer inkrementellen Sicherung immer nur die Dateien gesichert, die seit der letzten inkrementellen Sicherung neu
Inkrementelles Backup Im Gegensatz zu einer kompletten Sicherung aller Daten werden bei einer inkrementellen Sicherung immer nur die Dateien gesichert, die seit der letzten inkrementellen Sicherung neu
How to do? Projekte - Zeiterfassung
 How to do? Projekte - Zeiterfassung Stand: Version 4.0.1, 18.03.2009 1. EINLEITUNG...3 2. PROJEKTE UND STAMMDATEN...4 2.1 Projekte... 4 2.2 Projektmitarbeiter... 5 2.3 Tätigkeiten... 6 2.4 Unterprojekte...
How to do? Projekte - Zeiterfassung Stand: Version 4.0.1, 18.03.2009 1. EINLEITUNG...3 2. PROJEKTE UND STAMMDATEN...4 2.1 Projekte... 4 2.2 Projektmitarbeiter... 5 2.3 Tätigkeiten... 6 2.4 Unterprojekte...
BERECHNUNG DER FRIST ZUR STELLUNGNAHME DES BETRIEBSRATES BEI KÜNDIGUNG
 Frist berechnen BERECHNUNG DER FRIST ZUR STELLUNGNAHME DES BETRIEBSRATES BEI KÜNDIGUNG Sie erwägen die Kündigung eines Mitarbeiters und Ihr Unternehmen hat einen Betriebsrat? Dann müssen Sie die Kündigung
Frist berechnen BERECHNUNG DER FRIST ZUR STELLUNGNAHME DES BETRIEBSRATES BEI KÜNDIGUNG Sie erwägen die Kündigung eines Mitarbeiters und Ihr Unternehmen hat einen Betriebsrat? Dann müssen Sie die Kündigung
Wie Sie mit Mastern arbeiten
 Wie Sie mit Mastern arbeiten Was ist ein Master? Einer der großen Vorteile von EDV besteht darin, dass Ihnen der Rechner Arbeit abnimmt. Diesen Vorteil sollten sie nutzen, wo immer es geht. In PowerPoint
Wie Sie mit Mastern arbeiten Was ist ein Master? Einer der großen Vorteile von EDV besteht darin, dass Ihnen der Rechner Arbeit abnimmt. Diesen Vorteil sollten sie nutzen, wo immer es geht. In PowerPoint
Repetitionsaufgaben Wurzelgleichungen
 Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
