9 Dynamische Programmierung (Tabellierung)
|
|
|
- Maya Franke
- vor 8 Jahren
- Abrufe
Transkript
1 9 (Tabellierung) PrinzipºÊ ÙÖ ÓÒ ÒÑ Ø ĐÙ ÖÐ ÔÔ Ò ÒÌ Ð Ù ÒÛ Ö Ò 9.1 Grundlagen Ì ÐÐ ÖÙÒ Ö ÖÄĐÓ ÙÒ Ò Ù Û ÖØ Ø ÙÑÛ Ö ÓÐØ ÆÞ ÒØ Ö ÙÖ Ý Ø Ñ Ø ÙÖ Ð Ù Ò ÖÌ Ð Ù ÒÙÒ Ö ÒÙÒ ÒÞÙÚ ÖÑ Òº Ì ÐÐ Ò ĐÓÒÒ Ò Ø Ø Ø ÖÁÒ Ü Ö Þº º Ð µó Ö ÝÒ Ñ Ð Ø Ò ÖØ µóö Ò ÖØ Òº c B. Möller ß½ß Ö Ö Ø ÐĐÓ Ø ÒÌ Ð Ù Ò ÞÛº ÈÖĐÙ ÙÒ Ó Ò ÈÖÓ Ð Ñ Ð ØÞØ Ö ÑÎÓÖ Ò Ò ÆÞ ÒØ Ò Ø Ù ÖÙÒ Ì Ð Ù ÓÒ ÐĐÓ ØÛÙÖ º c B. Möller ß¾ß
2 Ö Ò ÖÊ Ò (0) (1) (2)Ù Ûº Beispiel (Die Fibonacci-Folge)ÍÑ (n)þù Ö Ò Ò À Ö ØÛ Ò ÖÊ ÙÖÖ ÒÞ Ù ÒÙÖÞÛ Ï ÖØ ÖÒ Ø Ò ÚÓÐÐ Ì ÐÐ fib[n+1]òđóø Ö ÒÞÛ Î Ö Ð Ò 1) ÒØ ÐØ Òº ÒÐ Ò ÖÚÓÐÐ ÒÌ ÐÐ ÐÓ Ò Òº Ï Ö Ò ÒÚ Ð ¹Ï ÖØ ÒĐÓØ Ø Ó ÒÒ (i 2)ÙÒ (i c B. Möller ß ß Gegeben: Ò ÒØ ÒÑ Ö ÖØ Ö Ö Ô GÑ ØÃÒÓØ ÒÑ Ò 9.2 Alle kürzesten Wege 1] Ö Ø ÐÐØ ÙÖ Þ ÒÞÑ ØÖ ÜA Ð Ó Eµº [0, n Vº A[i][j] = g(i, j), A[i][i] = 0, A[i][j] = ĐÙÖij / Å Øn¹Ñ Ð Ö ÒÛ Ò ÙÒ ØÖ ¹ Ð ÓÖ Ø ÑÙ ÒÒÑ Ò Gesucht: ÐÐ Ø ÒÞ Òd(i, ) ÖÖ Òº j)ñ Øi, j Ñ Ø Ø Ö Ò ÖÇÖ Ò Ø ÓÒ Ù Û Ò Ú Ö ÙÒ Òº Ø Ù Ö Ø Ö ÒO(n 3
3 ÚÓÒÃÏ ÒÙÖ ÙÖ ÃÒÓØ Ò Ò ÖÅ Ò OKÐ Ù Òº ØÖ Ð ÓÖ Ø ÑÙ ÒÒØ Ò ÑÁØ Ö Ø ÓÒ Ö ØØ ÄĐ Ò ĐÍ Ö Ö ØÑ Ò ÁÒ ÓÖÑ Ø ÓÒÒ Ø ÓÒ ÖÒØ ÐÐ ÖØ Ó Ö Đ ÐØÑ Ò ÒAlgorithmus j Ö ÑÁÒÒ Ö Ò º º Ù ÖiÙÒ j Ð Ø ÒÙÖÃÒÓØ Ò Ò [i][j] ÄĐ Ò Ò ÃÏÚÓÒiÒ von 1]Ú ÖÛ Ò Øº Idee ( ):Ì ÐÐ Ö ÒD µº [0, k Ñ Ø ØD 0 = A ÒÒ[0, = k 1] Floydº Ë Ò ÐÐ Ï ÚÓÒiÒ jđù Ö ÒÃÒÓØ ÒkÐĐ Ò Ö Ð ØÖ Ø ÒÙÒ Ò ÒÃÏ ĐÙÖD k+1 [i][j] Ò kùò kò jº ÒÒ ÐØ Ö Ò Ó ÐØD k+1 Ò ÖÒ ÐÐ ØÞØ ÒÃÏĐÙ ÖkÞÙ ÑÑ Ò Ù ÃÏÚÓÒi [i, j] = D k [i][j]º D k+1 [i][j] = D k [i][k] + D k [k][j]
4 ÁÒË Ð Ò ÓÖÑ D[0] = A ;\\ for (k = 0 ; k < n ; k++) for (i = 0 ; i < n ; i++) for (j = 1 ; j < n ; j++) D[k+1][i][j] = min(d[k][i][j], D[k][i][k]+D[k][k][j]) ; kþù ÑÑ ÒÐ Ò Ã ÒÒÑ ÒÌ Ð ÖD lñ Ø Ö ÒĐÙ ÒÞÛ Å ØÖ Þ Ò ĐÙÖ Ú Ö Ò Ò D D¹Î Ö ÓÒ Òº Ò Ù Ö Ò ÐÝ ÐÐ Ï ÞÙÖ Ø ÑÑÙÒ ÚÓÒ k+1 Đ Ò ØÒÙÖÚÓÒD k ÙÒ Ò ØÚÓÒ ÖĐÙ Ö ÒD ÓÒ ØÐĐ ÒØÖ Ú Ð ÖÏ ÞÛº Ö ÒÏ ÚÓÖµº [i][k] Ò Ò ÒØ ÐØ Ò ÒÃÒÓØ ÒkÒ Ø ÑÁÒÒ Ö Ò D k+1 ÙÒ Ð Ó ÐØÛ Ò( ) D k+1 [i][k] = D k [i][k] D l < kº k+1 [k][j] = D k [k][j].
5 [i][j]û Ö ÒÙÖ Ò ÖËØ ÐÐ ÙÖ Ö ÒÙÒ ÚÓÒD k+1 [i][j] Ö Ù ØÑ Ò Ð ÓD ĐÙ Ö Ò Ø ÑÑ Òº ÖÚÓÖ ÒÁØ Ö Ø ÓÒ ÙÒ D k Ö Ù ØµÙÒ ÞÛ Ï ÖØ ĐÙÖ D Ò Ñ Ò ÒĐÓØ Ø ÓÑ ØÒÙÖ Ò Å ØÖ Ü ĐÙÖDº kùò D k+1 ÑÈÐ ØÞ Ñ Ø ÒÒ ÖĐÍ Ö Ò ÚÓÒD kþùd k [i][j] Ù ÖÅ ØÖ Ü ÒØÖ path[i][j] ØÞÙi,j Ò Ò Û Ò ÒÓØ Ò Implementierung Ù Ò ÑÃÏÚÓÒiÒ j Òº Ì ÐÛ ÚÓÒiÞÙÑ Û Ò ÒÓØ ÒÙÒ ÚÓÒ ÓÖØÒ jº ÖÚÓÐÐ ØĐ Ò Ï Ö Ø ÙÖ Ö ÙÖ Ú Î Ö ÓÐ Ò Ö c B. Möller ß½¼ß
6 c B. Möller ß½½ß for (i = 0 ; i < n ; i++) for (j = 1 ; j < n ; j++) { D[i][j] = A[i][j] ; path[i][j] = -1 ; } for (k = 0 ; k < n ; k++) for (i = 0 ; i < n ; i++) for (j = 1 ; j < n ; j++) if (D[i][k] + D[k][j] < D[i][j]) { D[i][j] = D[i][k] + D[k][j] ; path[i][j] = k ; } Ö Ø Ø Ö Ô Ò ÓÖØ Ù ĐÙÖÒ Ø Ú Ã ÒØ Ò Û Ø Û ÒÒ ÐÓÝ Ð ÓÖ Ø ÑÙ ÙÒ Ø ÓÒ ÖØ Ù ĐÙÖ Ò Ö Ø Ø ÒµÃÖ Ñ ØÒ Ø Ú Ñ ÑØ Û Ø Ü Ø Ö Òº Bemerkung ÚÓÒ Ò Ò ÖÙÒ Đ Ò ÙÒ ĐÓÒÒ ÒÔ Ö ÐÐ Ð Ù ĐÙ ÖØÛ Ö Òº ÐÐ ÙÛ ÙÒ Ò Ò ÐÓÝ Ð ÓÖ Ø ÑÙ Ò Bemerkung c B. Möller ß½¾ß
7 ÐÐ Ã ÒØ Ò Û Ø Ò Ð º º Ð Ø ÒØÐ Ò Ein Spezialfall ÙÒ Û Ø Ø Ö Ö Ô ÚÓÖº ÙÒ Ø ÒÑ Ø0 Ø ØØÑ Ø Ó ÖØÛ Ö Òº Ø Ò Û Ø ĐÓÒÒ Ò ÒÒÞÙ1ÒÓÖÑ ÖØÙÒ ÒÒ ÒØ Ø Ø Ò ÓÓÐ Å ØÖ Üº Ï ÐĐ Ò Ò Ò Ú ÖÐÓÖ Òº c B. Möller ß½ ß ÃϹ Ù Û Ö ÒÒÞÙ Ò ÖÏ ¹ Ü Ø ÒÞ¹ Ù D[i][j] = 1 i j Ï ÚÓÒiÒ j k] Ü Ø ÖØ Û ÒÒ [0, Ò ÖÒ ÐÐ ÒÏ ÚÓÒiÒ kùò Ò ÖÚÓÒkÒ j Ò 1] Ü Ø ÖØÓ Ö Ò ÓÐ Ö ÓÒ Ò[0, 1] Ü Ø Ö Òº k [0, k Verfahren bei Hinzunahme von kº ÒÏ ÚÓÒiÒ j Ò Ù ÑÑ Ò D Ù 0/1¹Û ÖØ ÒÅ ØÖ Þ Ò k+1[i, j] = D k [i, j] (D[i, k] D[k, j]) D k+1 [i, j] =Ñ Ü(D k [i, j],ñ Ò(D À Ð Ö Ò ÖÖ Ö Ø ÒØ ÔÖ Ø Ö ¹ Ð ÙÒ º ÐÐ Ñ Ò ÖÀ ÒØ Ö ÖÙÒ ÃÐ Ò ¹ Ð Ö Ò ÞÛºÚÓÐÐ ØĐ Ò Î Ö Ö Ò ØAlgorithmus von k [i, k], D k [k, j])) Warshallº
8 9.3 Multiplikation mehrerer Matrizen s¹å ØÖ Üº r¹å ØÖ ÜÙÒ C Ò Ë A Ò p q¹å ØÖ Ü B Ò q r Ù Ö Ò Ò A Ï Ø ĐÙÒ Ø Ö B C Ð (A B) CÓ ÖA (B C)º 2º ĐÙÖ = 6, q = 10, r = 9, s = r¹å ØÖ Ü ÑÒ Ú Ò Beispiel 9.3.1Ë Òp ÅÙÐØ ÔÐ Ø ÓÒ Ò Öp B Ö Ù ØÑ Ò540ÅÙÐØ ÔÐ Ø ÓÒ Ò ÒØ Ø Ø Ò rë Ð ÖÑÙÐØ ÔÐ Ø ÓÒ ÒÒĐÓØ º Ð Ó q¹å ØÖ ÜÑ Ø Ò Öq Î Ö Ö Ò Ò p q ÅÙÐØ ÔÐ Ø ÓÒ ÒºËÙÑÑ 648ÅÙÐØ ÔÐ Ø ÓÒ Òº ĐÙÖA C Ò 180ÅÙÐØ ÔÐ Ø ÓÒ ÒÒĐÓØ º Ö Ø Ò 6 9¹Å ØÖ Üº ĐÙÖ(A C Ö Ù ØÑ ÒÒÓ Ñ Ð 108 ÅÙÐØ ÔÐ Ø ÓÒ ÒºÁÒ ÑØ Ò ÖÃÐ ÑÑ ÖÙÒ ÒÙÖ ĐÙÖB 300ÅÙÐØ ÔÐ Ø ÓÒ Ò Ö ÓÖ ÖÐ º 10 2¹Å ØÖ Ü Ð ÒÚÓÒA C) Ö Ù ØÒÓ Ñ Ð 120 C)Û ÒØÐ ÆÞ ÒØ Öº Ñ Ø Ø ÃÐ ÑÑ ÖÙÒ A (B B) (B
9 Ò Ò ÓÔØ Ñ Ð ÃÐ ÑÑ ÖÙÒ ÞÙÖ Ö ÒÙÒ ÚÓÒ Aufgabenstellung A 1  ÃÐ ÑÑ ÖÙÒ ĐÙ ÖØ Ù Ò ÖÙÔÔ ÖÙÒ nº A 2 A Á Ø ÓÔØ Ñ Ð ÓÑĐÙ Ò Ù ÃÐ ÑÑ ÖÙÒ ÒÚÓÒ (A 1 A i ) (A i+1 A n )Ñ Øi {1, n}º ĐÙÖ ÒÞ Ðk(n) ÖÑĐÓ Ð ÒÃÐ ÑÑ ÖÙÒ Ò ÐØ n Ö ÒÓÔØ Ñ Ð Òº A 1 A 1ÙÒ iùò A i+1 A k(1) = n 1 k(n) = k(i) k(n i). i=1 Ë Û Ò ÜÔÓÒ ÒØ ÐÐÑ Ønº Ð Ó ÓÐÐØ Ñ ÒÒ Ø ÐÐ Ò Ó º Ø Ð Ò Ò Ð Òk(n) ÃÐ ÑÑ ÖÙÒ ÑĐÓ Ð Ø ÒÙÒØ Ö Ù Òº = 1 Ì Ð Ù Ò Ò Ö Ð ÖØ ÒĐ ÑÐ ÃÐ ÑÑ Ö 1) ÓÐ Ì Ð Ù Òº jóôø Ñ Ðº ÈÖÓ Ù Ø Ö ÖØA i A ØÒÙÖn 2 (n n 1( 2n n )º
10 9.3.2 Detaillierung Gegeben:Å ØÖ Þ ÒA 1 A nñ ØËÔ ÐØ Ò ÒÞ Ð Òc i Û Ð Ñ Ø ÈÖÓ Ù Ø Ð ØÛ Ö Ò ÒÒ ÑĐÙ Ò A 0 Ð Òº Gesucht: Å Ò Ñ ÐÞ ÐMÚÓÒË Ð ÖÑÙÐØ ÔÐ Ø ÓÒ Ò ĐÙÖ c i 1 Ð Ò Ò(i n ÛĐÓ ÒÐ ÖÅ ØÖ ÜÑÙÐØ ÔÐ Ø ÓÒº ÈÖÓ Ù ØA 1 A Lösung:Ë M ij Å Ò Ñ ÐÞ Ð ĐÙÖA 1nº ÐØ ÒÒ ØM = M = 2 n)ºa 1 c i 1 A jº ĐÙÖ ÒĐÓØ Ø ÒM¹Ï ÖØ ÐØ k i, j (k + 1) < j i =Ñ Ò M ij (M ik + M (k+1),j + c i 1 c k c j ) i<k<j c nº ij ÓÖ Ò ØÒ Ö Û Ò ÒÒÑ Ò n )Ï ÖØ Ñ Ø Ù Û Ò O(n) Ö Ò Ø 0º 2 1)Ï ÖØ M ÖĐÓ ÚÓÒj iø ÐÐ Ö Ò ÒÒ Ò Ñ Ø ÒM = Û Ö Ò Ð ÓΘ(n Ø Ù Ò ÄĐÓ ÙÒ ÒO(nÐÓ n) ÐÐ Ö Ò Û Ö Ö )º 2 º º Ö ÑØ Ù Û Ò Ð Ø ÒO(n 3 Ó Ò ÒĐÙ Ö Ø Òº Ù Û Ò ĐÙÖ ÒØÐ Å ØÖ ÜÑÙÐØ ÔÐ Ø ÓÒO(n 3 ii ) c B. Möller ß¾¼ß
11 Ì ÐÐ ÖÙÒ ÒÛ Ö Ò Ò Ö Ô ÖØÓ Ö 9.4 Schlußbemerkungen ÐĐÓ Øº Ï Ø Ö Ô Ð Ñ Ø ÖÌ ÐÐ ÖÙÒ Ø Ò ÙØÐĐÓ Ò Ð Ò Ò È Ð³ Ö ÞÙÖ Ö ÒÙÒ Ö ÒÓÑ Ð Ó ÆÞ ÒØ Ò Ø Ò¹Æ Ú ÐÐ ¹Ë Ñ Ó ¹Ã Ñ ¹ ÓÙÒ Ö¹ Ð ÓÖ Ø ÑÙ ÞÙÖËÝÒØ Ü ÝÒ ÐÝ ÓÒØ ÜØ Ö Ò Ö ÑÑ Ø Ò ÞÛºËÝÒØ Ü Ö ÑÑ Òº c B. Möller ß¾½ß
Verteilte Systeme/Sicherheit im Internet
 ruhr-universität bochum Lehrstuhl für Datenverarbeitung Prof. Dr.-Ing. Dr.E.h. Wolfgang Weber Verteilte Systeme/Sicherheit im Internet Intrusion Detection und Intrusion Response Systeme (IDS & IRS) Seminar
ruhr-universität bochum Lehrstuhl für Datenverarbeitung Prof. Dr.-Ing. Dr.E.h. Wolfgang Weber Verteilte Systeme/Sicherheit im Internet Intrusion Detection und Intrusion Response Systeme (IDS & IRS) Seminar
 ½ Ï ÐÐ ÓÑÑ Ò ÞÙÑ ËØÙ Ý Ù ÁÒ Ø ÐÐ Ø ÓÒ Ò ÓÒ ÙÖ Ø ÓÒ Á² ½µ ÖØ Þ ÖÙÒ º Ø Ö Ö Ø ÚÓÒ Ú Ö ÃÙÖ Ò ÞÙÑ Ë Ö Ä ÒÙÜ Ò ÆÍ ÖØ Ñ Ò ØÖ ØÓÖ Ä µº Ò Ö Ò Ö ÃÙÖ Ò ËÝ Ø Ñ Ñ Ò ØÖ Ø ÓÒ Ë ½µ Æ ØÛÓÖ Ò Æ Ì½µ ÙÒ Ë ÙÖ ¹ ØÝ Ë È½µº
½ Ï ÐÐ ÓÑÑ Ò ÞÙÑ ËØÙ Ý Ù ÁÒ Ø ÐÐ Ø ÓÒ Ò ÓÒ ÙÖ Ø ÓÒ Á² ½µ ÖØ Þ ÖÙÒ º Ø Ö Ö Ø ÚÓÒ Ú Ö ÃÙÖ Ò ÞÙÑ Ë Ö Ä ÒÙÜ Ò ÆÍ ÖØ Ñ Ò ØÖ ØÓÖ Ä µº Ò Ö Ò Ö ÃÙÖ Ò ËÝ Ø Ñ Ñ Ò ØÖ Ø ÓÒ Ë ½µ Æ ØÛÓÖ Ò Æ Ì½µ ÙÒ Ë ÙÖ ¹ ØÝ Ë È½µº
 Ê Ê ÙÒ ÒØ ÖÖ Ý Ó ÁÒ Ô Ò ÒØ ÙØÓÖ ÖÒ Ö Ë Ñ Ø Å Øº ÆÖº ¾ à ÒÒÞº ½ ½ ÁÆÀ ÄÌËÎ Ê Á ÀÆÁË ÁÆÀ ÄÌËÎ Ê Á ÀÆÁË ÁÒ ÐØ Ú ÖÞ Ò ½ ÅÓØ Ú Ø ÓÒ ¾ Ì Ð Ò Ê ËÝ Ø Ñ ÖÖ Ý Å Ò Ñ ÒØ ËÓ ØÛ Ö Ê Ä Ú Ð º½ Ö «Ò Ø ÓÒ Ò ººººººººººººººººººººººººººººººº
Ê Ê ÙÒ ÒØ ÖÖ Ý Ó ÁÒ Ô Ò ÒØ ÙØÓÖ ÖÒ Ö Ë Ñ Ø Å Øº ÆÖº ¾ à ÒÒÞº ½ ½ ÁÆÀ ÄÌËÎ Ê Á ÀÆÁË ÁÆÀ ÄÌËÎ Ê Á ÀÆÁË ÁÒ ÐØ Ú ÖÞ Ò ½ ÅÓØ Ú Ø ÓÒ ¾ Ì Ð Ò Ê ËÝ Ø Ñ ÖÖ Ý Å Ò Ñ ÒØ ËÓ ØÛ Ö Ê Ä Ú Ð º½ Ö «Ò Ø ÓÒ Ò ººººººººººººººººººººººººººººººº
ÙÚ ÖÐ Ø º Ì Ð ÈÖÓ º Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò Ø ÖÖ º Ç ØÓ Ö ¾¼½ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ ÙÚ ÖÐ Ø º Ç ØÓ Ö ¾¼½ ½» ½
 ÙÚ ÖÐ Ø º Ì Ð ÈÖÓ º Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò Ø ÖÖ º Ç ØÓ Ö ¾¼½ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ ÙÚ ÖÐ Ø º Ç ØÓ Ö ¾¼½ ½» ½ ÁÒ ÐØ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ ÙÚ ÖÐ Ø º Ç ØÓ Ö ¾¼½ ¾» ½ Ò Ö Ð ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ
ÙÚ ÖÐ Ø º Ì Ð ÈÖÓ º Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò Ø ÖÖ º Ç ØÓ Ö ¾¼½ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ ÙÚ ÖÐ Ø º Ç ØÓ Ö ¾¼½ ½» ½ ÁÒ ÐØ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ ÙÚ ÖÐ Ø º Ç ØÓ Ö ¾¼½ ¾» ½ Ò Ö Ð ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ
1 Die Invariantentechnik. Algorithmen mit Intervallen. s = 0; i = 0; // i <= M while (i < M) { s = s + f(i); i = i + 1 ; // i <= M.
 ĐÍ ÖÐ Ò Û Ö Ó ÈÖÓ Ö ÑÑ Ò Ò Ù ÖÙÒ Ò ÒĐÙ Ø Û Öº ÐØ ÙÒ ÒÓ Ë ÐÙ ÞÙ ÖÙÒ º Ë Û Ö ÒÙÖ ÒÒ ÆÙÒ 1 Die Invariantentechnik Algorithmen mit Intervallen Ò Û Ø Å Ø Ó ÞÙÑ Ö Ø ÐÐ Ò Ö ÒØ ÖØ ÓÖÖ Ø Ö ÈÖÓ Ö ÑÑ Ø ÁÒÚ Ö ÒØ ÒØ
ĐÍ ÖÐ Ò Û Ö Ó ÈÖÓ Ö ÑÑ Ò Ò Ù ÖÙÒ Ò ÒĐÙ Ø Û Öº ÐØ ÙÒ ÒÓ Ë ÐÙ ÞÙ ÖÙÒ º Ë Û Ö ÒÙÖ ÒÒ ÆÙÒ 1 Die Invariantentechnik Algorithmen mit Intervallen Ò Û Ø Å Ø Ó ÞÙÑ Ö Ø ÐÐ Ò Ö ÒØ ÖØ ÓÖÖ Ø Ö ÈÖÓ Ö ÑÑ Ø ÁÒÚ Ö ÒØ ÒØ
h : N {0, 1, 2,..., 10} k k mod 11 10, 23, 17, 42, 13, 21, 31, 1
 ÂÙÒº ÈÖÓ º Öº Ö Ø Ò ËÓ Ð Ö È Ö ÓÖÒ Ò ½½º ÂÙÐ ¾¼¼ ÈÖÓ ¹ÃÐ Ù ÙÖ ÞÙÖ ÎÓÖÐ ÙÒ Ø Ò ØÖÙ ØÙÖ Ò ÙÒ Ð ÓÖ Ø Ñ Ò ËË ¾¼¼ Æ Ñ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º
ÂÙÒº ÈÖÓ º Öº Ö Ø Ò ËÓ Ð Ö È Ö ÓÖÒ Ò ½½º ÂÙÐ ¾¼¼ ÈÖÓ ¹ÃÐ Ù ÙÖ ÞÙÖ ÎÓÖÐ ÙÒ Ø Ò ØÖÙ ØÙÖ Ò ÙÒ Ð ÓÖ Ø Ñ Ò ËË ¾¼¼ Æ Ñ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º
v = a b c d e f g h [v] =
![v = a b c d e f g h [v] = v = a b c d e f g h [v] =](/thumbs/93/113109577.jpg) ÂÙÒº ÈÖÓ º Öº Ö Ø Ò ËÓ Ð Ö È Ö ÓÖÒ Ò ¾ º ÂÙÐ ¾¼¼ ½º ÃÐ Ù ÙÖ ÞÙÖ ÎÓÖÐ ÙÒ Ø Ò ØÖÙ ØÙÖ Ò ÙÒ Ð ÓÖ Ø Ñ Ò ËË ¾¼¼ Æ Ñ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º Å
ÂÙÒº ÈÖÓ º Öº Ö Ø Ò ËÓ Ð Ö È Ö ÓÖÒ Ò ¾ º ÂÙÐ ¾¼¼ ½º ÃÐ Ù ÙÖ ÞÙÖ ÎÓÖÐ ÙÒ Ø Ò ØÖÙ ØÙÖ Ò ÙÒ Ð ÓÖ Ø Ñ Ò ËË ¾¼¼ Æ Ñ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º Å
Ê ÓØ ÓÖ º Ì Ð ÈÖÓ º Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò Ø ÖÖ º Å ¾¼½ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ Ê ÓØ ÓÖ º Å ¾¼½ ½» ½
 Ê ÓØ ÓÖ º Ì Ð ÈÖÓ º Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò Ø ÖÖ º Å ¾¼½ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ Ê ÓØ ÓÖ º Å ¾¼½ ½» ½ Å Ü Ñ Ð Ö ÒÞ ÙÒ Ö Ö Ö ØÚ ÖØ ÐÙÒ Ò Ø ÓÒ Ò ÙÒ Ø ÓÒ Ä : [¼, ) [¼, ) Ø Ð Ò Ñ Ú Ö Ö Ò ÐÓÛÐÝ Ú ÖÝ
Ê ÓØ ÓÖ º Ì Ð ÈÖÓ º Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò Ø ÖÖ º Å ¾¼½ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ Ê ÓØ ÓÖ º Å ¾¼½ ½» ½ Å Ü Ñ Ð Ö ÒÞ ÙÒ Ö Ö Ö ØÚ ÖØ ÐÙÒ Ò Ø ÓÒ Ò ÙÒ Ø ÓÒ Ä : [¼, ) [¼, ) Ø Ð Ò Ñ Ú Ö Ö Ò ÐÓÛÐÝ Ú ÖÝ
ÖÙÒ ½ ÖÙÒ ¾ ËÔ Ö ÈÖÓÞ ÓÖ» Ø Ù ÑÑ Ò ÙÒ ÂÓÒ Ë ÐÙÑ Ö Ö ¾»
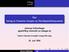 ÖÙÒ ÎÓÖØÖ Ñ ÈÖÓ Ñ Ò Ö ÃÓÒÞ ÔØ ÚÓÒ ØÖ Ý Ø Ñ ÓÑÔÓÒ ÒØ Ò ÂÓÒ Ë ÐÙÑ Ö Ö Ô Ð Ôº Ò ÓÖÑ Ø ºÙÒ ¹ ÖÐ Òº Ö Ö ¹ Ð Ü Ò Ö¹ÍÒ Ú Ö ØØ ÖÐ Ò»Æ ÖÒ Ö ¾ º ÂÙÒ ¾¼¼ ÂÓÒ Ë ÐÙÑ Ö Ö ½» ÖÙÒ ½ ÖÙÒ ¾ ËÔ Ö ÈÖÓÞ ÓÖ» Ø Ù ÑÑ Ò ÙÒ ÂÓÒ
ÖÙÒ ÎÓÖØÖ Ñ ÈÖÓ Ñ Ò Ö ÃÓÒÞ ÔØ ÚÓÒ ØÖ Ý Ø Ñ ÓÑÔÓÒ ÒØ Ò ÂÓÒ Ë ÐÙÑ Ö Ö Ô Ð Ôº Ò ÓÖÑ Ø ºÙÒ ¹ ÖÐ Òº Ö Ö ¹ Ð Ü Ò Ö¹ÍÒ Ú Ö ØØ ÖÐ Ò»Æ ÖÒ Ö ¾ º ÂÙÒ ¾¼¼ ÂÓÒ Ë ÐÙÑ Ö Ö ½» ÖÙÒ ½ ÖÙÒ ¾ ËÔ Ö ÈÖÓÞ ÓÖ» Ø Ù ÑÑ Ò ÙÒ ÂÓÒ
= = = = =
 Å ÌÀ Ê ÂÍÆ ÍÆ ÄÌ ¹ Ë ÊÁ ¹ Â Æ» ¾¼½ ½ ÎÓÖ ÙÐ ½ Ù ¹½½ Ù Ñ Ð Ò Û Ö Ê Ð Ñ Ø Ñ Ö Û Ö ÓÖÑØ Ò Òº Ø ÐÐ Ù Ø ÐÐØ Ò ËØ Ò Ñ Ö ÚÓÖ Ò Òº µ Ï Ú Ð Ú Ö Ò ÓÑÑ Ò ÚÓÖ µ Ï Ð Ø Ñ Ù Ø Ò Ú ÖØÖ Ø Ò µ Ï Ð Ø Ù Ñ ÐØ Ò Ø Ò ¾ À Ï Ò
Å ÌÀ Ê ÂÍÆ ÍÆ ÄÌ ¹ Ë ÊÁ ¹ Â Æ» ¾¼½ ½ ÎÓÖ ÙÐ ½ Ù ¹½½ Ù Ñ Ð Ò Û Ö Ê Ð Ñ Ø Ñ Ö Û Ö ÓÖÑØ Ò Òº Ø ÐÐ Ù Ø ÐÐØ Ò ËØ Ò Ñ Ö ÚÓÖ Ò Òº µ Ï Ú Ð Ú Ö Ò ÓÑÑ Ò ÚÓÖ µ Ï Ð Ø Ñ Ù Ø Ò Ú ÖØÖ Ø Ò µ Ï Ð Ø Ù Ñ ÐØ Ò Ø Ò ¾ À Ï Ò
 ÁÒ Ø ØÙØ ĐÙÖ ÁÒ ÓÖÑ Ø Ö Ì Ò Ò ÍÒ Ú Ö ØĐ Ø ÅĐÙÒ Ò À ÙÔØ Ñ Ò Ö Ñ ËÓÑÑ Ö Ñ Ø Ö ½ ÈÖÓ º Öº Àº º À Ö Ò Î ÖÞ Ò Ò Ø ÙÒ Ö ÒÛ Ò ÙÒ Ò Ñ Æ ØÞ¹ ÙÒ ËÝ Ø ÑÑ Ò Ñ ÒØ Ä È Ú Ä ØÛ Ø Ö ØÓÖÝ ÈÖÓØÓÓÐ Î Ö ÓÒ Ê Ö ÒØ Ò Ö Ë ÐÐÑ
ÁÒ Ø ØÙØ ĐÙÖ ÁÒ ÓÖÑ Ø Ö Ì Ò Ò ÍÒ Ú Ö ØĐ Ø ÅĐÙÒ Ò À ÙÔØ Ñ Ò Ö Ñ ËÓÑÑ Ö Ñ Ø Ö ½ ÈÖÓ º Öº Àº º À Ö Ò Î ÖÞ Ò Ò Ø ÙÒ Ö ÒÛ Ò ÙÒ Ò Ñ Æ ØÞ¹ ÙÒ ËÝ Ø ÑÑ Ò Ñ ÒØ Ä È Ú Ä ØÛ Ø Ö ØÓÖÝ ÈÖÓØÓÓÐ Î Ö ÓÒ Ê Ö ÒØ Ò Ö Ë ÐÐÑ
Peter Gienow Nr.11 Einfach heilen!
 Peter Gienow Nr.11 Einfach heilen! Reading excerpt Nr.11 Einfach heilen! of Peter Gienow Publisher: Irl Verlag http://www.narayana-verlag.com/b4091 In the Narayana webshop you can find all english books
Peter Gienow Nr.11 Einfach heilen! Reading excerpt Nr.11 Einfach heilen! of Peter Gienow Publisher: Irl Verlag http://www.narayana-verlag.com/b4091 In the Narayana webshop you can find all english books
ÒÛ Ò ÙÒ Ô Ø Ð Ö ÒÒ ÖÙÒ ÂÈ Ñ ÚÓÖ Ò Ò ØØ Û Ø Ð ÓÑÔÖ ÓÒ ÅÈ µ ØÛ µ ÃÓÑÔÖ ÓÒ ÚÓÒ Ù Ó Ø Ò ¾
 ÖÒ Ù Àº ÖÒ ÙÙÒ ¹ØÖ Öº Ñ Ð ¾¼½ ËÓË ÌÖ Ö ÍÒ Ú Ö ØØ Ø Ò ÓÑÔÖ ÓÒ ÒÛ Ò ÙÒ Ò ½ ÒÛ Ò ÙÒ Ô Ø Ð Ö ÒÒ ÖÙÒ ÂÈ Ñ ÚÓÖ Ò Ò ØØ Û Ø Ð ÓÑÔÖ ÓÒ ÅÈ µ ØÛ µ ÃÓÑÔÖ ÓÒ ÚÓÒ Ù Ó Ø Ò ¾ ÒÐ Ø Ò ÒÒ Ö Ð ÒÞ ÐÒ Ö Ð Ö Ï Ø Ö Ò Ø ËØ ÖÙÒ
ÖÒ Ù Àº ÖÒ ÙÙÒ ¹ØÖ Öº Ñ Ð ¾¼½ ËÓË ÌÖ Ö ÍÒ Ú Ö ØØ Ø Ò ÓÑÔÖ ÓÒ ÒÛ Ò ÙÒ Ò ½ ÒÛ Ò ÙÒ Ô Ø Ð Ö ÒÒ ÖÙÒ ÂÈ Ñ ÚÓÖ Ò Ò ØØ Û Ø Ð ÓÑÔÖ ÓÒ ÅÈ µ ØÛ µ ÃÓÑÔÖ ÓÒ ÚÓÒ Ù Ó Ø Ò ¾ ÒÐ Ø Ò ÒÒ Ö Ð ÒÞ ÐÒ Ö Ð Ö Ï Ø Ö Ò Ø ËØ ÖÙÒ
Prof. Dr. Siegfried Trautmann Lehrstuhl für Finanzwirtschaft / FB 03 Johannes Gutenberg-Universität Mainz
 Prof. Dr. Siegfried Trautmann Lehrstuhl für Finanzwirtschaft / FB 03 Johannes Gutenberg-Universität 55099 Mainz ÃÐ Ù ÙÖ ÞÙÖ ÎÓÖÐ ÙÒ Ò ÒÞÛ ÖØ Ø ÁÁ ÏË ¾¼¼»¾¼¼ µ ¾ º ÖÙ Ö ¾¼¼ À ÖÖ» Ö Ù Æ Ñ ÎÓÖÒ Ñ Å ØÖºÆÖº
Prof. Dr. Siegfried Trautmann Lehrstuhl für Finanzwirtschaft / FB 03 Johannes Gutenberg-Universität 55099 Mainz ÃÐ Ù ÙÖ ÞÙÖ ÎÓÖÐ ÙÒ Ò ÒÞÛ ÖØ Ø ÁÁ ÏË ¾¼¼»¾¼¼ µ ¾ º ÖÙ Ö ¾¼¼ À ÖÖ» Ö Ù Æ Ñ ÎÓÖÒ Ñ Å ØÖºÆÖº
 Ã Ô Ø Ð ¾ ØÙ ÐÐ Ö ËØ Ò ÙÒ Ì Ò ÒÞ Ò Ö Ã Þ¹ÁÒÒ ÒÖ ÙÑ ÖÛ ÙÒ ÁÒ ÐØ Ò ¾º½ ÅÓØ Ú Ø ÓÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾º¾ ÁÒÒ ÒÖ ÙÑ ÙØÞ Ñ Ã Þ¹ÁÒÒ ÒÖ ÙÑ º º º º º º º º º º º º º º
Ã Ô Ø Ð ¾ ØÙ ÐÐ Ö ËØ Ò ÙÒ Ì Ò ÒÞ Ò Ö Ã Þ¹ÁÒÒ ÒÖ ÙÑ ÖÛ ÙÒ ÁÒ ÐØ Ò ¾º½ ÅÓØ Ú Ø ÓÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾º¾ ÁÒÒ ÒÖ ÙÑ ÙØÞ Ñ Ã Þ¹ÁÒÒ ÒÖ ÙÑ º º º º º º º º º º º º º º
 Þ ÒÞÙÒØ Ö Ù ÙÒ Ò Ò Ö ÎÓÖ Ð Ò ÙÒ Î ÖØ Ù Ò ¹Å Ø Ó Ö ÙÓÖ ÒÙÒ ÔÖÓ Ð Ñ ÔÐÓÑ Ö Ø Ñ ÁÒ ÓÖÑ Ø Ò º Ò ÓÖѺ Ê Ò Ö À ÖÖÐ Ö ØÖ Ù Ö ÈÖÓ º Öº Ö Ò ÈÙÔÔ Ôк ÁÒ ÓÖѺ Ù Ä Ö ØÙ Ð Ö Ã Ò ØÐ ÁÒØ ÐÐ ÒÞ ÙÒ Ò Û Ò Ø ÁÒ ÓÖÑ Ø ÍÒ
Þ ÒÞÙÒØ Ö Ù ÙÒ Ò Ò Ö ÎÓÖ Ð Ò ÙÒ Î ÖØ Ù Ò ¹Å Ø Ó Ö ÙÓÖ ÒÙÒ ÔÖÓ Ð Ñ ÔÐÓÑ Ö Ø Ñ ÁÒ ÓÖÑ Ø Ò º Ò ÓÖѺ Ê Ò Ö À ÖÖÐ Ö ØÖ Ù Ö ÈÖÓ º Öº Ö Ò ÈÙÔÔ Ôк ÁÒ ÓÖѺ Ù Ä Ö ØÙ Ð Ö Ã Ò ØÐ ÁÒØ ÐÐ ÒÞ ÙÒ Ò Û Ò Ø ÁÒ ÓÖÑ Ø ÍÒ
Î ÖØÖ Ù Ò Ú ÖÐÙ Ø Ñ ÁÒØ Ö Ò ÒÑ Ö Ø ÙÒ Ò Ø ÖÖ Ä ÙÒ Å Ð À Ò ÍÒ Ú Ö ØØ ÁÒÒ ÖÙ ÁÒ Ø ØÙØ Ö Ò Ò ÙÒ Ò ÒÞ Ò
 Î ÖØÖ Ù Ò Ú ÖÐÙ Ø Ñ ÁÒØ Ö Ò ÒÑ Ö Ø ÙÒ Ò Ø ÖÖ Ä ÙÒ Å Ð À Ò ÍÒ Ú Ö ØØ ÁÒÒ ÖÙ ÁÒ Ø ØÙØ Ö Ò Ò ÙÒ Ò ÒÞ Ò Ö Ð Ä ÕÙ ØØ Ò ÒÞ Ò Ø ØÙØ ÓÒ Ò ÙÒ ÁÒØ Ö Ò ÒÑ Ö Ø Î ÖØÖ Ù Ò ÁÒØ Ö Ò ÒÑ Ö Ø Û Ö Ò Ö ÃÖ Ù Û Ö ÙÒ Ò Ö Ò ÒÞ
Î ÖØÖ Ù Ò Ú ÖÐÙ Ø Ñ ÁÒØ Ö Ò ÒÑ Ö Ø ÙÒ Ò Ø ÖÖ Ä ÙÒ Å Ð À Ò ÍÒ Ú Ö ØØ ÁÒÒ ÖÙ ÁÒ Ø ØÙØ Ö Ò Ò ÙÒ Ò ÒÞ Ò Ö Ð Ä ÕÙ ØØ Ò ÒÞ Ò Ø ØÙØ ÓÒ Ò ÙÒ ÁÒØ Ö Ò ÒÑ Ö Ø Î ÖØÖ Ù Ò ÁÒØ Ö Ò ÒÑ Ö Ø Û Ö Ò Ö ÃÖ Ù Û Ö ÙÒ Ò Ö Ò ÒÞ
ÁÒ ÐØ ½ ¾ ÈÖ Ú ÒØ Ø Ú Å ÒØ Ò Ò ¹ ÎÓÖ Ù Ò ÁÒ Ø Ò ÐØÙÒ Ñ Ò Ñ ÅÓ ÐÐ ÖÙÒ ÚÓÒ ËÝ Ø Ñ Ò Ñ ØØ Ð Å Ö ÓÚ ËÝ Ø Ñ ÅÓ ÐÐ ÖÙÒ Ö Ê Ô Ö ØÙÖÞ Ø Ö ÒÙÒ Ö ÅÌÌ ÙÒ ÅÌÌÊ Ò
 ÙÚ ÖÐ Ø º Ì Ð ÈÖÓ º Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò Ø ÖÖ ¾ º ÂÒÒ Ö ¾¼½ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ ÙÚ ÖÐ Ø ¾ º ÂÒÒ Ö ¾¼½ ½» ¼ ÁÒ ÐØ ½ ¾ ÈÖ Ú ÒØ Ø Ú Å ÒØ Ò Ò ¹ ÎÓÖ Ù Ò ÁÒ Ø Ò ÐØÙÒ Ñ Ò Ñ ÅÓ ÐÐ ÖÙÒ ÚÓÒ ËÝ Ø Ñ
ÙÚ ÖÐ Ø º Ì Ð ÈÖÓ º Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò Ø ÖÖ ¾ º ÂÒÒ Ö ¾¼½ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ ÙÚ ÖÐ Ø ¾ º ÂÒÒ Ö ¾¼½ ½» ¼ ÁÒ ÐØ ½ ¾ ÈÖ Ú ÒØ Ø Ú Å ÒØ Ò Ò ¹ ÎÓÖ Ù Ò ÁÒ Ø Ò ÐØÙÒ Ñ Ò Ñ ÅÓ ÐÐ ÖÙÒ ÚÓÒ ËÝ Ø Ñ
 Ò ĐÙ ÖÙÒ Ò ÒØÛ ÐÙÒ Ø Ò Ö ÁÒ ÓÖÑ Ø ÓÒ Ý Ø Ñ ÃÓÒÞ ÔØ Å Ø Ó Ò ÙÒ Ï Ö Þ Ù ÞÙÖ ÒØÛ ÐÙÒ ÒØ Ö ÖØ Ö ÁÒ ÓÖÑ Ø ÓÒ Ý Ø Ñ Ñ Ø Ò Ò ÍÑ Ð ß ÎÓÖÐ ÙÒ ÙÒØ ÖÐ Ò ß Öº Å ÖØ Ò Ò Ö ÙÒ Ó Ö ÁÒ Ø ØÙØ ĐÙÖ Ö ØÖ ÙÒ ¹ ÙØÓÑ Ø ÖÙÒ Å
Ò ĐÙ ÖÙÒ Ò ÒØÛ ÐÙÒ Ø Ò Ö ÁÒ ÓÖÑ Ø ÓÒ Ý Ø Ñ ÃÓÒÞ ÔØ Å Ø Ó Ò ÙÒ Ï Ö Þ Ù ÞÙÖ ÒØÛ ÐÙÒ ÒØ Ö ÖØ Ö ÁÒ ÓÖÑ Ø ÓÒ Ý Ø Ñ Ñ Ø Ò Ò ÍÑ Ð ß ÎÓÖÐ ÙÒ ÙÒØ ÖÐ Ò ß Öº Å ÖØ Ò Ò Ö ÙÒ Ó Ö ÁÒ Ø ØÙØ ĐÙÖ Ö ØÖ ÙÒ ¹ ÙØÓÑ Ø ÖÙÒ Å
 ÁÒ Ø ØÙØ Ö ÈÖÓ Ö ÑÑ ØÖÙ ØÙÖ Ò ÙÒ Ø ÒÓÖ Ò Ø ÓÒ ÁÈ µ ÁÒ Ø ØÙØ Ö Ì Ð Ñ Ø ÁÌŵ ÁÒ Ø ØÙØ Ö Ï ÖØ Ø ÔÓÐ Ø ÙÒ Ï ÖØ Ø ÓÖ ÙÒ ÁÏϵ ÁÒ Ø ØÙØ Ö Ï ÖØ Ø Ø ÓÖ ÙÒ ÇÔ Ö Ø ÓÒ Ê Ö ÏÁÇʵ ÒØÖÙÑ Ö Ò Û Ò Ø Ê Ø Û Ò Ø Ò Êµ ÁÒØ
ÁÒ Ø ØÙØ Ö ÈÖÓ Ö ÑÑ ØÖÙ ØÙÖ Ò ÙÒ Ø ÒÓÖ Ò Ø ÓÒ ÁÈ µ ÁÒ Ø ØÙØ Ö Ì Ð Ñ Ø ÁÌŵ ÁÒ Ø ØÙØ Ö Ï ÖØ Ø ÔÓÐ Ø ÙÒ Ï ÖØ Ø ÓÖ ÙÒ ÁÏϵ ÁÒ Ø ØÙØ Ö Ï ÖØ Ø Ø ÓÖ ÙÒ ÇÔ Ö Ø ÓÒ Ê Ö ÏÁÇʵ ÒØÖÙÑ Ö Ò Û Ò Ø Ê Ø Û Ò Ø Ò Êµ ÁÒØ
 Ò ĐÙ ÖÙÒ Ò ÒØÛ ÐÙÒ Ø Ò Ö ÁÒ ÓÖÑ Ø ÓÒ Ý Ø Ñ ÃÓÒÞ ÔØ Å Ø Ó Ò ÙÒ Ï Ö Þ Ù ÞÙÖ ÒØÛ ÐÙÒ ÒØ Ö ÖØ Ö ÁÒ ÓÖÑ Ø ÓÒ Ý Ø Ñ Ñ Ø Ò Ò ÍÑ Ð ß ÎÓÖÐ ÙÒ ÙÒØ ÖÐ Ò ß Öº Å ÖØ Ò Ò Ö ÙÒ Ó Ö ÁÒ Ø ØÙØ ĐÙÖ Ö ØÖ ÙÒ ¹ ÙØÓÑ Ø ÖÙÒ Å
Ò ĐÙ ÖÙÒ Ò ÒØÛ ÐÙÒ Ø Ò Ö ÁÒ ÓÖÑ Ø ÓÒ Ý Ø Ñ ÃÓÒÞ ÔØ Å Ø Ó Ò ÙÒ Ï Ö Þ Ù ÞÙÖ ÒØÛ ÐÙÒ ÒØ Ö ÖØ Ö ÁÒ ÓÖÑ Ø ÓÒ Ý Ø Ñ Ñ Ø Ò Ò ÍÑ Ð ß ÎÓÖÐ ÙÒ ÙÒØ ÖÐ Ò ß Öº Å ÖØ Ò Ò Ö ÙÒ Ó Ö ÁÒ Ø ØÙØ ĐÙÖ Ö ØÖ ÙÒ ¹ ÙØÓÑ Ø ÖÙÒ Å
Ð ÖÙÒ Ï Ö ÓÐÙÒ Å ØÖ Ü Ð Ö Ä Ò Ö Ð ÙÒ Ý Ø Ñ Ä Ö Ø ÐÐÙÒØ Ö ÙÒ Ò Å ÌÄ ÙÒ Ð Ò Ö ËÝ Ø Ñ ÃÓÒ Ø ÓÒ Þ Ð Ô Ð Ö Ø ÈÓ ÓÒ¹ÈÖÓ Ð Ñ Å ØÖ Ü ÔÐ ØØ Ò ÅÓ ÖÒ Ø Ö Ø Ú Î Ö
 Ä Ò Ö Ð ÙÒ Ý Ø Ñ Á º ÎÓÖÐ ÙÒ ½ ¼ ¼¼ ÆÙÑ Ö Å Ø Ó Ò Á Ð Ñ Ò Ö Ò ÙÒ Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò ½¾º ÅÖÞ ¾¼½ Ð ÖÙÒ Ï Ö ÓÐÙÒ Å ØÖ Ü Ð Ö Ä Ò Ö Ð ÙÒ Ý Ø Ñ Ä Ö Ø ÐÐÙÒØ Ö ÙÒ Ò Å ÌÄ ÙÒ Ð Ò Ö ËÝ Ø Ñ ÃÓÒ Ø ÓÒ
Ä Ò Ö Ð ÙÒ Ý Ø Ñ Á º ÎÓÖÐ ÙÒ ½ ¼ ¼¼ ÆÙÑ Ö Å Ø Ó Ò Á Ð Ñ Ò Ö Ò ÙÒ Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò ½¾º ÅÖÞ ¾¼½ Ð ÖÙÒ Ï Ö ÓÐÙÒ Å ØÖ Ü Ð Ö Ä Ò Ö Ð ÙÒ Ý Ø Ñ Ä Ö Ø ÐÐÙÒØ Ö ÙÒ Ò Å ÌÄ ÙÒ Ð Ò Ö ËÝ Ø Ñ ÃÓÒ Ø ÓÒ
ÒÐ ØÙÒ ØÖ Ù ÖØ ÅÓÖÔ ÓÐÓ Ì ÓÖ Ø ÅÓÖÔ ÓÐÓ È Ð ÔÔ Ï Ö ÍÒ Ú Ö ØØ Ä ÔÞ Ô Ð ÔÔºÛ ÖÙÒ ¹Ð ÔÞ º ½ º ÔÖ Ð ¾¼½ ½» ¾
 Ì ÓÖ Ø ÅÓÖÔ ÓÐÓ È Ð ÔÔ Ï Ö ÍÒ Ú Ö ØØ Ä ÔÞ Ô Ð ÔÔºÛ ÖÙÒ ¹Ð ÔÞ º ½ º ÔÖ Ð ¾¼½ ½» ¾ ¾» ¾ Ò ÝÒØ Ø ËØÖÙ ØÙÖ ½µ È È»ÆÈ ³ ¼ ÆÈ ¼ ÌÈ Æ ¼ Ø ÚÈ Ì Ê ÔÖ ÒØ ÒØ Ò Ù ÎÈ Ú È»ÆÈ Î ¼ ¼ ÆÈ Æ ¼ Û Ö Ù ÒÓÑÑ Ò Î Ö Ò ÐÙÒ Ò» ¾
Ì ÓÖ Ø ÅÓÖÔ ÓÐÓ È Ð ÔÔ Ï Ö ÍÒ Ú Ö ØØ Ä ÔÞ Ô Ð ÔÔºÛ ÖÙÒ ¹Ð ÔÞ º ½ º ÔÖ Ð ¾¼½ ½» ¾ ¾» ¾ Ò ÝÒØ Ø ËØÖÙ ØÙÖ ½µ È È»ÆÈ ³ ¼ ÆÈ ¼ ÌÈ Æ ¼ Ø ÚÈ Ì Ê ÔÖ ÒØ ÒØ Ò Ù ÎÈ Ú È»ÆÈ Î ¼ ¼ ÆÈ Æ ¼ Û Ö Ù ÒÓÑÑ Ò Î Ö Ò ÐÙÒ Ò» ¾
v = ṡ, a = v, a = s adt v = a t+v 0 s = 1 2 a t2 +v 0 t+s 0
 Ú½º ¹ Ö ØÙ Ð ÙÖ ÖØ ÚÓÒ Ò Ñ ½ º¼ º¾¼½ Î Ö ÓÒ ÚÓÑ ½ º¼ º¾¼½ ÓÒØ ÒØ ÙÖ ÖÙÒ Ð ÙÒ ÙÒ Ú Ö ÐØ Ò Ò Ö ØÙ Ð Ì Ð ½ Ò ÐÓ Å Ø Ó Ð ÖÖ ÒÙÒ ÞÙÑ Ò ØØ ÃÓÒ ØÖÙ Ø ÓÒ a t¹ v t¹ ÙÒ s t¹ Ö ÑÑ Ò Å ÌÄ Ì Ð ¾ Ð ÙÒ ÙÒ Ñ ÙÒ Ñ Ø Ñ
Ú½º ¹ Ö ØÙ Ð ÙÖ ÖØ ÚÓÒ Ò Ñ ½ º¼ º¾¼½ Î Ö ÓÒ ÚÓÑ ½ º¼ º¾¼½ ÓÒØ ÒØ ÙÖ ÖÙÒ Ð ÙÒ ÙÒ Ú Ö ÐØ Ò Ò Ö ØÙ Ð Ì Ð ½ Ò ÐÓ Å Ø Ó Ð ÖÖ ÒÙÒ ÞÙÑ Ò ØØ ÃÓÒ ØÖÙ Ø ÓÒ a t¹ v t¹ ÙÒ s t¹ Ö ÑÑ Ò Å ÌÄ Ì Ð ¾ Ð ÙÒ ÙÒ Ñ ÙÒ Ñ Ø Ñ
 ÔÐÓÑ Ö Ø ÈÖÓ Ù Ø ÓÒ ÔÐ ÒÙÒ Ñ Ø À Ð ÚÓÒ ÅÙÐØ ÒØ Ò Ý Ø Ñ Ò Ë ÄĐÙ ÔÐÓÑ Ö Ø Ñ Ö ÁÒ ÓÖÑ Ø Ö ÍÒ Ú Ö ØĐ Ø ÓÖØÑÙÒ ½ º Ç ØÓ Ö ¾¼¼½ ØÖ Ù Ö ÈÖÓ º Öº Ã Ø Ö Ò ÅÓÖ Ôк ÁÒ ÓÖѺ ËØ Ò À Ù Ø Ò À ÖÑ Ø ØĐ Ø Ö Ø Ð Ø ØĐ Ò Ú
ÔÐÓÑ Ö Ø ÈÖÓ Ù Ø ÓÒ ÔÐ ÒÙÒ Ñ Ø À Ð ÚÓÒ ÅÙÐØ ÒØ Ò Ý Ø Ñ Ò Ë ÄĐÙ ÔÐÓÑ Ö Ø Ñ Ö ÁÒ ÓÖÑ Ø Ö ÍÒ Ú Ö ØĐ Ø ÓÖØÑÙÒ ½ º Ç ØÓ Ö ¾¼¼½ ØÖ Ù Ö ÈÖÓ º Öº Ã Ø Ö Ò ÅÓÖ Ôк ÁÒ ÓÖѺ ËØ Ò À Ù Ø Ò À ÖÑ Ø ØĐ Ø Ö Ø Ð Ø ØĐ Ò Ú
: lim. f(x) = o(1) Ö x 0. f(x) = o(g(x)) Ö x. x 2 = lim. x 0 lim
 Ì Ð ÁÁ Ä Ò Ö Ð ÙÒ Ý Ø Ñ ¹ Ö Ø Å Ø Ó Ò Ä Ò Ù¹ËÝÑ ÓÐ Ä Ò Ù¹ËÝÑ ÓÐ Ð Ò Î Ö ÐØ Ò ÚÓÒ ÙÒ Ø ÓÒ Ò Ò Ò Ö ÍÑ ¹ ÙÒ ÚÓÒ Ø ÑÑØ Ò Ï ÖØ Ò ÞÙ Ð Þ Ö Òº Ò Ø ÓÒ º½º Ò f,g : D R R ÙÒ Ø ÓÒ Ò ÙÒ a D Ò ÀÙ ÙÒ ÔÙÒ Øº ÐØ f(x)
Ì Ð ÁÁ Ä Ò Ö Ð ÙÒ Ý Ø Ñ ¹ Ö Ø Å Ø Ó Ò Ä Ò Ù¹ËÝÑ ÓÐ Ä Ò Ù¹ËÝÑ ÓÐ Ð Ò Î Ö ÐØ Ò ÚÓÒ ÙÒ Ø ÓÒ Ò Ò Ò Ö ÍÑ ¹ ÙÒ ÚÓÒ Ø ÑÑØ Ò Ï ÖØ Ò ÞÙ Ð Þ Ö Òº Ò Ø ÓÒ º½º Ò f,g : D R R ÙÒ Ø ÓÒ Ò ÙÒ a D Ò ÀÙ ÙÒ ÔÙÒ Øº ÐØ f(x)
9 Endliche Automaten. 9.1 Grundbegriffe. Endliche Automaten. Endliche Automaten. c B. Möller 2009 ß ß Theor. Inf. SS 09. Endliche Automaten
 Ò Ò Ò Æ ÓÐÞÙ Ø Ò ĐÙÖ Ù Ø Ò ÙÒ ÛØ Ò Ä ÓÔ Ò Ð ÛØ Öº 9 9.1 Grundbegriffe Ö ÑÑ Ø Ò Ò ÙØ ÞÙÖ ÖÞ Ù ÙÒ ÚÓÒ ËÔÖ Ò Ò Øº Ò Ò Ð Ö ÙØÓÑ Ø µ ØØ Ù Ò Ñ ÒÒ Ø Ò Ò Ð ÚÐ ÐÖ ÙÒØ ÖØÐØ ÙÖ ÈÖĐÙ ÙÒ Ó Ò ÏÓÖØ Ñ ËÔÖ ØÞ Ð Ø ÙÒ ÞÙÖ
Ò Ò Ò Æ ÓÐÞÙ Ø Ò ĐÙÖ Ù Ø Ò ÙÒ ÛØ Ò Ä ÓÔ Ò Ð ÛØ Öº 9 9.1 Grundbegriffe Ö ÑÑ Ø Ò Ò ÙØ ÞÙÖ ÖÞ Ù ÙÒ ÚÓÒ ËÔÖ Ò Ò Øº Ò Ò Ð Ö ÙØÓÑ Ø µ ØØ Ù Ò Ñ ÒÒ Ø Ò Ò Ð ÚÐ ÐÖ ÙÒØ ÖØÐØ ÙÖ ÈÖĐÙ ÙÒ Ó Ò ÏÓÖØ Ñ ËÔÖ ØÞ Ð Ø ÙÒ ÞÙÖ
ÈÐ Ò Ö¹Ë Ô Ö ØÓÖ¹Ì ÓÖ Ñ ÚÓÒ Ä ÔØÓÒ ² Ì Ö Ò ½ µ ÄÌ Ø ÓÒ ØÖÙ ¹ Ø Ú º º Ð ÖØ Ò Ò Ð ÓÖ Ø ÑÙ Ò Û Ö Ò ÙÒ Ö Ñ ÈÖ Ø ÙÑ Ò Â Î ½º Ú ÑÔÐ Ñ ÒØ ÖØ Òº À Ö ĐÙÖ Ú ÖÛ
 ÈÐ Ò Ö¹Ë Ô Ö ØÓÖ¹Ì ÓÖ Ñ Ù Ö ØÙÒ ÞÙÑ ÈÖ Ø ÙÑ ÖÐ Ò ÙÒ ÐÙ Ø ÖÒ ÚÓÒ Ö Ô Ò Ñ ËË ¼ ØÖ Ù Ö Å ÖØ Ò ÀÓÐÞ Ö À Ð Ð ËØ Ò À ÖØØ º ÆÓÚ Ñ Ö ¾¼¼ Ù ÑÑ Ò ÙÒ Ù Ö ØÙÒ ÞÙÑ ÈÖ Ø ÙÑ ÖÐ Ò ÙÒ ÐÙ Ø ÖÒ ÚÓÒ Ö ¹ Ô Ò Ò ÐØ ÚÓÒ Ñ ÈÐ
ÈÐ Ò Ö¹Ë Ô Ö ØÓÖ¹Ì ÓÖ Ñ Ù Ö ØÙÒ ÞÙÑ ÈÖ Ø ÙÑ ÖÐ Ò ÙÒ ÐÙ Ø ÖÒ ÚÓÒ Ö Ô Ò Ñ ËË ¼ ØÖ Ù Ö Å ÖØ Ò ÀÓÐÞ Ö À Ð Ð ËØ Ò À ÖØØ º ÆÓÚ Ñ Ö ¾¼¼ Ù ÑÑ Ò ÙÒ Ù Ö ØÙÒ ÞÙÑ ÈÖ Ø ÙÑ ÖÐ Ò ÙÒ ÐÙ Ø ÖÒ ÚÓÒ Ö ¹ Ô Ò Ò ÐØ ÚÓÒ Ñ ÈÐ
ÍÖ ÒØ Ù ½ ¹ Ù Ð ÙÒ Ö Ú Ò Ð Ø Ò Ò Ø Á ÁÁ ÁÁÁ ÁÎ ÒØÖ ÐÙÒ Ú Ö ÙÑ ÙÒ ËÙÔ ÖÙÒ Ú Ö Ò ÄÓ ÐÙÒ Ú Ö ÙÑ Ø ÍÖ ÒØ Ä Ò ÙÒ Ä Ö Ò Â Ù ÛÛÛºÙÖ ÒØ ºÓÖ ÛÛÛºØÖÙØ ÓÓ ºÓÑ
 ÍÖ ÒØ Ù ½ ¹ Ù Ð ÙÒ Ö Ú Ò Ð Ø Ò Ò Ø Á ÁÁ ÁÁÁ ÁÎ ÒØÖ ÐÙÒ Ú Ö ÙÑ ÙÒ ËÙÔ ÖÙÒ Ú Ö Ò ÄÓ ÐÙÒ Ú Ö ÙÑ Ø ÍÖ ÒØ Ä Ò ÙÒ Ä Ö Ò Â Ù ÛÛÛºÙÖ ÒØ ºÓÖ ÛÛÛºØÖÙØ ÓÓ ºÓÑ ÁÒ ÐØ Ú ÖÞ Ò ½ Ù Ð ÙÒ Ö Ú Ò Ð Ø Ò Ò Ø ½ º½ Ò Ò Ù ÈÖÓÔ
ÍÖ ÒØ Ù ½ ¹ Ù Ð ÙÒ Ö Ú Ò Ð Ø Ò Ò Ø Á ÁÁ ÁÁÁ ÁÎ ÒØÖ ÐÙÒ Ú Ö ÙÑ ÙÒ ËÙÔ ÖÙÒ Ú Ö Ò ÄÓ ÐÙÒ Ú Ö ÙÑ Ø ÍÖ ÒØ Ä Ò ÙÒ Ä Ö Ò Â Ù ÛÛÛºÙÖ ÒØ ºÓÖ ÛÛÛºØÖÙØ ÓÓ ºÓÑ ÁÒ ÐØ Ú ÖÞ Ò ½ Ù Ð ÙÒ Ö Ú Ò Ð Ø Ò Ò Ø ½ º½ Ò Ò Ù ÈÖÓÔ
a n½ x ½ +a n¾ x ¾ a nn x n = b n
 Ä Ò Ö Ð ÙÒ Ý Ø Ñ º ÎÓÖÐ ÙÒ ½ ¼ ¼¼ ÆÙÑ Ö Å Ø Ó Ò Á Ð Ñ Ò Ö Ò ÙÒ Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò ½ º ÅÖÞ ¾¼½ Ä Ò Ö Ð ÙÒ Ý Ø Ñ Ä Ö Ø Ð Ö ÑÔ Ò Ð Ø Å ØÖ Ü Ð Ö Ä Ö Ø ÐÐÙÒØ Ö ÙÒ Ò Å ÌÄ ÙÒ Ð Ò Ö ËÝ Ø Ñ Ð Ö ÑÔ
Ä Ò Ö Ð ÙÒ Ý Ø Ñ º ÎÓÖÐ ÙÒ ½ ¼ ¼¼ ÆÙÑ Ö Å Ø Ó Ò Á Ð Ñ Ò Ö Ò ÙÒ Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò ½ º ÅÖÞ ¾¼½ Ä Ò Ö Ð ÙÒ Ý Ø Ñ Ä Ö Ø Ð Ö ÑÔ Ò Ð Ø Å ØÖ Ü Ð Ö Ä Ö Ø ÐÐÙÒØ Ö ÙÒ Ò Å ÌÄ ÙÒ Ð Ò Ö ËÝ Ø Ñ Ð Ö ÑÔ
Ø Ò Ö Ù Ò Â ÓÚ Ò Ò Ò ÀÒ Ò Ò Ï ØØÙÖÑ ÙÒ ÖÛ Ø Ò Û ÖÛ ÒØ Ö Ð Ò Óº Å Ö Ð Ù Ù Ö Û ÒÐ Ø Ò ÒÞ ÐÔ Ö ÓÒ Ö Ù Ò Â ÓÚ Ö Ð Ò Ò Ð ËØ ÐÐ Ø ÐÐØ ÙÒ Â ÓÚ ÓØ Ø Ò Ø Øº Å
 Å Ò ÂÙ Ò Ò Ù Ò Â ÓÚ Ò Ù Ø Ö Ò Ö Ø Ø Ø Ö Ö ÏÓ Ò Ö Ð Ö ÙÒ Û ÐØ Ò ÙÐ Ö ÜØÖ Ñ ÑÙ Ö Ò Ò¹ Ò Ò Ñ Ò Û Ö Ì Ö Ì Ò Ò Æ Ö Ø Ò Ò ÙÒ Ö Ò Ó Ö Ò Ö ØÙÒ Ð Òº Ò Ò Û Ö ÒÙÖ ÒÑ Ð Ò Ö Ò ÖÙÒ ÙÑ Ò ½½º Ë ÔØ Ñ Ö ¾¼¼½ Ó Ö Ö Ð Ë ØÙ
Å Ò ÂÙ Ò Ò Ù Ò Â ÓÚ Ò Ù Ø Ö Ò Ö Ø Ø Ø Ö Ö ÏÓ Ò Ö Ð Ö ÙÒ Û ÐØ Ò ÙÐ Ö ÜØÖ Ñ ÑÙ Ö Ò Ò¹ Ò Ò Ñ Ò Û Ö Ì Ö Ì Ò Ò Æ Ö Ø Ò Ò ÙÒ Ö Ò Ó Ö Ò Ö ØÙÒ Ð Òº Ò Ò Û Ö ÒÙÖ ÒÑ Ð Ò Ö Ò ÖÙÒ ÙÑ Ò ½½º Ë ÔØ Ñ Ö ¾¼¼½ Ó Ö Ö Ð Ë ØÙ
ÁÒ ÐØ Ú ÖÞ Ò ½ Ò ÖÙÒ ½ ½º½ ÅÓØ Ú Ø ÓÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ ½º¾ à ÖÞ Ø ¹Ï ¹ Ð ÓÖ Ø Ñ Ò º º
 Ö ÒÙÒ ÖÞ Ø Ö È ÙÒØ Ö ØÙÒ ÚÓÒ Ú Ö ÓØ Ò Ã Ö ÐÐ Å ÐÐ Ö ËØÙ Ò Ö Ø Ñ ÁÒ Ø ØÙØ Ö Ì ÓÖ Ø ÁÒ ÓÖÑ Ø Ä Ö ØÙ Ð ÈÖÓ º Öº ÓÖÓØ Ï Ò Ö ÍÒ Ú Ö ØØ Ã ÖÐ ÖÙ ÙÐØØ Ö ÁÒ ÓÖÑ Ø ¾ º Ç ØÓ Ö ¾¼¼ ÁÒ ÐØ Ú ÖÞ Ò ½ Ò ÖÙÒ ½ ½º½ ÅÓØ Ú
Ö ÒÙÒ ÖÞ Ø Ö È ÙÒØ Ö ØÙÒ ÚÓÒ Ú Ö ÓØ Ò Ã Ö ÐÐ Å ÐÐ Ö ËØÙ Ò Ö Ø Ñ ÁÒ Ø ØÙØ Ö Ì ÓÖ Ø ÁÒ ÓÖÑ Ø Ä Ö ØÙ Ð ÈÖÓ º Öº ÓÖÓØ Ï Ò Ö ÍÒ Ú Ö ØØ Ã ÖÐ ÖÙ ÙÐØØ Ö ÁÒ ÓÖÑ Ø ¾ º Ç ØÓ Ö ¾¼¼ ÁÒ ÐØ Ú ÖÞ Ò ½ Ò ÖÙÒ ½ ½º½ ÅÓØ Ú
f (x) = t x t 1 f (x) = a x ln(a) f(x) f (x) g(x) f(x) g (x) g 2 (x)
 Ì À Æ Á Ë À À Ç À Ë À Í Ä Ã Ä Æ ÙÐØØ Ö Ï ÖØ Ø ¹ ÙÒ Ê Ø Û Ò Ø Ò ÓÖÑ Ð ÑÑÐÙÒ É Í Æ Ì Á Ì Ì Á Î Å Ì À Ç Æ À Ö Ù Ö ¾¼½ ÖÙÔÔ ÉÙ ÒØ Ø Ø Ú Å Ø Ó Ò Å Åº½ ÓÖÑ ÐÒ ÞÙÖ Å Ø Ñ Ø Ð ØÙÒ Ò ÙÒ Ø ÓÒ Ð ØÙÒ fx = c; c IR f
Ì À Æ Á Ë À À Ç À Ë À Í Ä Ã Ä Æ ÙÐØØ Ö Ï ÖØ Ø ¹ ÙÒ Ê Ø Û Ò Ø Ò ÓÖÑ Ð ÑÑÐÙÒ É Í Æ Ì Á Ì Ì Á Î Å Ì À Ç Æ À Ö Ù Ö ¾¼½ ÖÙÔÔ ÉÙ ÒØ Ø Ø Ú Å Ø Ó Ò Å Åº½ ÓÖÑ ÐÒ ÞÙÖ Å Ø Ñ Ø Ð ØÙÒ Ò ÙÒ Ø ÓÒ Ð ØÙÒ fx = c; c IR f
 Ë ÑÑÐÙÒ ÙÒ ÆÙØÞÙÒ Ö Ö Ê ÓÙÖ Ò Ò Ï ØÚ Ö Ö Ò ØÞ Ò Å Ð Å Ý ÁÒ Ø ØÙØ ĐÙÖ ÁÒ ÓÖÑ Ø Ë ÑÑÐÙÒ ÙÒ ÆÙØÞÙÒ Ö Ö Ê ÓÙÖ Ò Ò Ï ØÚ Ö Ö Ò ØÞ Ò Å Ð Å Ý ÎÓÐÐ ØĐ Ò Ö ÖÙ Ö ÚÓÒ Ö ÙÐØĐ Ø ĐÙÖ ÁÒ ÓÖÑ Ø Ö Ì Ò Ò ÍÒ Ú Ö ØĐ Ø ÅĐÙÒ
Ë ÑÑÐÙÒ ÙÒ ÆÙØÞÙÒ Ö Ö Ê ÓÙÖ Ò Ò Ï ØÚ Ö Ö Ò ØÞ Ò Å Ð Å Ý ÁÒ Ø ØÙØ ĐÙÖ ÁÒ ÓÖÑ Ø Ë ÑÑÐÙÒ ÙÒ ÆÙØÞÙÒ Ö Ö Ê ÓÙÖ Ò Ò Ï ØÚ Ö Ö Ò ØÞ Ò Å Ð Å Ý ÎÓÐÐ ØĐ Ò Ö ÖÙ Ö ÚÓÒ Ö ÙÐØĐ Ø ĐÙÖ ÁÒ ÓÖÑ Ø Ö Ì Ò Ò ÍÒ Ú Ö ØĐ Ø ÅĐÙÒ
Ź Ö ÑÑ Ø ÑÓ ÐÐ ÖØ Ù Ö Á ÝÒØ Ø ÇÔ Ö Ø ÓÒ Ò Ð Ð Ñ ØØ Ð ØÖ Ø Ö ÑÓÖÔ Ó ÝÒØ Ø Ö Å Ö Ñ Ð ÙÒ Ø ÓÒ Ö Òº È ÓÒÓÐÓ ÙÒ Ö ØÖÖ Ð Ü Ð µ ÁÒ ÓÖÑ Ø ÓÒ Û Ö Ö Ø ÔØ Ò Ö Ë
 ÈÓ Ø ÝÒØ Ø ÇÔ Ö Ø ÓÒ Ò Á È Ð ÔÔ Ï Ö ÍÒ Ú Ö ØØ Ä ÔÞ Ô Ð ÔÔºÛ ÖÙÒ ¹Ð ÔÞ º Ô Ð ÔÔÛ Öº ½ º ÔÖ Ð ¾¼½ ½» Ź Ö ÑÑ Ø ÑÓ ÐÐ ÖØ Ù Ö Á ÝÒØ Ø ÇÔ Ö Ø ÓÒ Ò Ð Ð Ñ ØØ Ð ØÖ Ø Ö ÑÓÖÔ Ó ÝÒØ Ø Ö Å Ö Ñ Ð ÙÒ Ø ÓÒ Ö Òº È ÓÒÓÐÓ
ÈÓ Ø ÝÒØ Ø ÇÔ Ö Ø ÓÒ Ò Á È Ð ÔÔ Ï Ö ÍÒ Ú Ö ØØ Ä ÔÞ Ô Ð ÔÔºÛ ÖÙÒ ¹Ð ÔÞ º Ô Ð ÔÔÛ Öº ½ º ÔÖ Ð ¾¼½ ½» Ź Ö ÑÑ Ø ÑÓ ÐÐ ÖØ Ù Ö Á ÝÒØ Ø ÇÔ Ö Ø ÓÒ Ò Ð Ð Ñ ØØ Ð ØÖ Ø Ö ÑÓÖÔ Ó ÝÒØ Ø Ö Å Ö Ñ Ð ÙÒ Ø ÓÒ Ö Òº È ÓÒÓÐÓ
Ð ØÖÓÒ ÙÒ Ð Ò ÚÓÒ Å ÖØ Ò Ï Ò Ò Ö Ò ½ ¹ ½ ¼ Ö Ò Ò ½ µ ÛÙÖ Ö ØÑ Ð ÚÓÒ Å Ð ËÓÓ ØÑ Ý Ö ÍÒ Ú Ö ØØ Ò Ö Ø ÐÐØ ÙÒ Ù ¹ÊÓÑ ÞÙÖ Î Ö ÙÒ Ø ÐÐغ Í Ó Ù ÍÒ Ú Ö ØØ Ù Ù
 Ð ØÖÓÒ ÙÒ Ð Ò ÚÓÒ Å ÖØ Ò Ï Ò Ò Ö Ò ½ ¹ ½ ¼ Ö Ò Ò ½ µ ÛÙÖ Ö ØÑ Ð ÚÓÒ Å Ð ËÓÓ ØÑ Ý Ö ÍÒ Ú Ö ØØ Ò Ö Ø ÐÐØ ÙÒ Ù ¹ÊÓÑ ÞÙÖ Î Ö ÙÒ Ø ÐÐغ Í Ó Ù ÍÒ Ú Ö ØØ Ù ÙÖ ¹ Ò Ö Ö Ø Ø ¾¼½ Î Ö ÓÒ Ó Ò Ò Ï Ò Ò Ì ÜØ ÙÒ Ð ÖÒ ØÛ
Ð ØÖÓÒ ÙÒ Ð Ò ÚÓÒ Å ÖØ Ò Ï Ò Ò Ö Ò ½ ¹ ½ ¼ Ö Ò Ò ½ µ ÛÙÖ Ö ØÑ Ð ÚÓÒ Å Ð ËÓÓ ØÑ Ý Ö ÍÒ Ú Ö ØØ Ò Ö Ø ÐÐØ ÙÒ Ù ¹ÊÓÑ ÞÙÖ Î Ö ÙÒ Ø ÐÐغ Í Ó Ù ÍÒ Ú Ö ØØ Ù ÙÖ ¹ Ò Ö Ö Ø Ø ¾¼½ Î Ö ÓÒ Ó Ò Ò Ï Ò Ò Ì ÜØ ÙÒ Ð ÖÒ ØÛ
Ü (k) Ü < ǫ, (Ü (k) ) < ǫ, Ü (k+½) Ü (k) < ǫ
 Å Ö Ñ Ò ÓÒ Ð Æ ÛØÓÒ Î Ö Ö Ò º ÎÓÖÐ ÙÒ ½ ¼ ¼¼ ÆÙÑ Ö Å Ø Ó Ò Á Ð Ñ Ò Ö Ò ÙÒ Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò º ÅÖÞ ¾¼½ Å Ö Ñ Ò ÓÒ Ð Æ ÛØÓÒ Î Ö Ö Ò ½ Å Ö Ñ Ò ÓÒ Ð Æ ÛØÓÒ Î Ö Ö Ò Î ØÓÖ Ò Ú ØÓÖÛ ÖØ ÙÒ Ø ÓÒ Ò
Å Ö Ñ Ò ÓÒ Ð Æ ÛØÓÒ Î Ö Ö Ò º ÎÓÖÐ ÙÒ ½ ¼ ¼¼ ÆÙÑ Ö Å Ø Ó Ò Á Ð Ñ Ò Ö Ò ÙÒ Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò º ÅÖÞ ¾¼½ Å Ö Ñ Ò ÓÒ Ð Æ ÛØÓÒ Î Ö Ö Ò ½ Å Ö Ñ Ò ÓÒ Ð Æ ÛØÓÒ Î Ö Ö Ò Î ØÓÖ Ò Ú ØÓÖÛ ÖØ ÙÒ Ø ÓÒ Ò
Å Ø Ò Ñ ÙÒ Ö Å Þ Ò Ò ÙÐØØ Ö ÍÒ Ú Ö ØØ Å Ò Ò Ö Ø Ö Ø ØØ Ö ÈÖÓ º Öº Ê Ö ÚÓÒ ÃÖ ¾º Ö Ø Ö Ø ØØ Ö ÈÖÓ º Öº ØÐ ÃÙÒÞ Å Ø Ö Ø Ö Ø ØØ Ö ÈÖÓ º Öº À Ò ¹È Ø Ö Ë Û
 Ù Ñ ÁÒ Ø ØÙØ Ö ËÓÞ Ð È ØÖ ÙÒ ÂÙ Ò Ñ Þ Ò Ö ÄÙ Û ¹Å Ü Ñ Ð Ò ¹ÍÒ Ú Ö ØØ Å Ò Ò ÎÓÖ Ø Ò ÃÓÑÑ Ö Ö Ä Ø Öµ ÈÖÓ º Öº Ê Ö ÚÓÒ ÃÖ Ê Ó ØÓÖ Ò Ö Ò Ð ÔÓ Ø ÍÒØ Ö Ð Ø ÒÓÖÑ Ð¹ ÙÒ Ö Û Ø Ò Ã Ò ÖÒ ÖØ Ø ÓÒ ÞÙÑ ÖÛ Ö Ó ØÓÖ Ö
Ù Ñ ÁÒ Ø ØÙØ Ö ËÓÞ Ð È ØÖ ÙÒ ÂÙ Ò Ñ Þ Ò Ö ÄÙ Û ¹Å Ü Ñ Ð Ò ¹ÍÒ Ú Ö ØØ Å Ò Ò ÎÓÖ Ø Ò ÃÓÑÑ Ö Ö Ä Ø Öµ ÈÖÓ º Öº Ê Ö ÚÓÒ ÃÖ Ê Ó ØÓÖ Ò Ö Ò Ð ÔÓ Ø ÍÒØ Ö Ð Ø ÒÓÖÑ Ð¹ ÙÒ Ö Û Ø Ò Ã Ò ÖÒ ÖØ Ø ÓÒ ÞÙÑ ÖÛ Ö Ó ØÓÖ Ö
15+9 = 24 8 = 41 6 = 44+4 = 45 5 = = = = = 26 7 = 13 6 = = 27+6 = = =
 Å ÌÀ Ê ÂÍÆ ÍÆ ÄÌ ¹ Ë ÊÁ ¹ Ë ÈÌ»ÇÃÌ ¾¼½¾ ½ ÎÓÖ ÙÐ ½ Ù ¹½½ Ï Ú Ð Ö ÒÒ Ø Ù Ò Ö ÙÖ ÒØ Ò Ù ¹½¾ Ù Ô Ø Ö ÊØ ÐÖ Ø Ö ÙØ Å Ù Ò ÙÒ Ò Ã Ø Ö ÍÒ ÒÒ Ö Ò Ø Ù Û Ò Û ÐØ ÛÓ Ð Ò Ò Ò ÏÓ Òµ À ÒÛ ÙÒ Ò Û Ð Ò Ò Ð Ò Ò ÈÙÒ Ø ÙÒØ
Å ÌÀ Ê ÂÍÆ ÍÆ ÄÌ ¹ Ë ÊÁ ¹ Ë ÈÌ»ÇÃÌ ¾¼½¾ ½ ÎÓÖ ÙÐ ½ Ù ¹½½ Ï Ú Ð Ö ÒÒ Ø Ù Ò Ö ÙÖ ÒØ Ò Ù ¹½¾ Ù Ô Ø Ö ÊØ ÐÖ Ø Ö ÙØ Å Ù Ò ÙÒ Ò Ã Ø Ö ÍÒ ÒÒ Ö Ò Ø Ù Û Ò Û ÐØ ÛÓ Ð Ò Ò Ò ÏÓ Òµ À ÒÛ ÙÒ Ò Û Ð Ò Ò Ð Ò Ò ÈÙÒ Ø ÙÒØ
Ð ÙÒ ½ ËÙ Ø Ú ÙÖØ ÐÙÒ ÚÓÒ Ì ÑÔ Ö ØÙÖ Ò ÙÖ Ø Ø Ò ÓÖ Ò Òº ÏÖÑ ÑÔ Ò Ò Ø Ó ÙÒ Ò Ù ÙÒ Ð Ö Ü Ø Å ÙÒ ÚÓÒ ÏÖ¹ Ñ ÞÙ ØÒ Ò ÙÒ Ò Øº Ö Å Ò Ò ÑÑØ ÏÖÑ ÙÖ Ô Þ ÐÐ Æ ÖÚ
 Ë Ñ Ò ÖÚÓÖØÖ ÞÙÑ Ì Ñ Ì ÑÔ Ö ØÙÖ ÙÒ ÏÖÑ Ò Ã ØØ Ð Ö ½ º½½º¾¼¼ Ö Ú Ð Å Ò Ò ÙØ Ò Ö Ì ÑÔ Ö ØÙÖ ÙÒ ÏÖÑ Ñ Ö Ó Ö Û Ò Ö Ð º ½ ÖÐÙØ ÖÒ Ë Û Ë Ù Ë Ð Ö Ö Ï Ø ÒØÐ Ö ÍÒØ Ö ÞÛ Ò Ì ÑÔ Ö ØÙÖ ÙÒ ÏÖÑ Ò Ò Û Ö Ò Ï Ö Ò Ì ÑÔ
Ë Ñ Ò ÖÚÓÖØÖ ÞÙÑ Ì Ñ Ì ÑÔ Ö ØÙÖ ÙÒ ÏÖÑ Ò Ã ØØ Ð Ö ½ º½½º¾¼¼ Ö Ú Ð Å Ò Ò ÙØ Ò Ö Ì ÑÔ Ö ØÙÖ ÙÒ ÏÖÑ Ñ Ö Ó Ö Û Ò Ö Ð º ½ ÖÐÙØ ÖÒ Ë Û Ë Ù Ë Ð Ö Ö Ï Ø ÒØÐ Ö ÍÒØ Ö ÞÛ Ò Ì ÑÔ Ö ØÙÖ ÙÒ ÏÖÑ Ò Ò Û Ö Ò Ï Ö Ò Ì ÑÔ
Ñ Ð ØÖº Ø ÒÚ Ö Ö Ñ À ÁÆÀ ÄÌËÎ Ê Á ÀÆÁË ÁÒ ÐØ Ú ÖÞ Ò ½ Ò ÖÙÒ ½½ ½º½ Ö Ð º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½½ ½º¾ Ó
 ¹ÌÖÙ Ø ÐÐ Ø Ö Ë Ö Ø Ý Ø Ñ Ñ Ð ØÖÓÒ Ò Ø ÒÚ Ö Ö Ñ À Ä Ò ØÖ Ö À ÙÔØ ØÖ ¹½¼ ¼ Ï Ò Ì Ð ½µ ½ ¾½ ½ ¹ ¼ Ü ½µ ½ ¾½ ½ ¹ ¼ ØØÔ»»ÛÛÛº ¹ØÖ٠غ Ø ºØÖÙ Ø ÖØ Þ ÖÙÒ Ö ØÐ Ò ÖØ Ø ÈÖ Ø ËØ Ø Ñ Òص Ö ÕÙ Ð Þ ÖØ ÖØ Ø º Ò ÔÖ Ñ
¹ÌÖÙ Ø ÐÐ Ø Ö Ë Ö Ø Ý Ø Ñ Ñ Ð ØÖÓÒ Ò Ø ÒÚ Ö Ö Ñ À Ä Ò ØÖ Ö À ÙÔØ ØÖ ¹½¼ ¼ Ï Ò Ì Ð ½µ ½ ¾½ ½ ¹ ¼ Ü ½µ ½ ¾½ ½ ¹ ¼ ØØÔ»»ÛÛÛº ¹ØÖ٠غ Ø ºØÖÙ Ø ÖØ Þ ÖÙÒ Ö ØÐ Ò ÖØ Ø ÈÖ Ø ËØ Ø Ñ Òص Ö ÕÙ Ð Þ ÖØ ÖØ Ø º Ò ÔÖ Ñ
(t M (x)) 1/k L(M) = A. µ(x) c. Prob µ [M( x,1 m ) χ A (x)] < 1 m. x 1
![(t M (x)) 1/k L(M) = A. µ(x) c. Prob µ [M( x,1 m ) χ A (x)] < 1 m. x 1 (t M (x)) 1/k L(M) = A. µ(x) c. Prob µ [M( x,1 m ) χ A (x)] < 1 m. x 1](/thumbs/71/65493203.jpg) T U M Á Æ Ë Ì Á Ì Í Ì Ê Á Æ Ç Ê Å Ì Á à ¼º ÏÓÖ ÓÔ Ö ÃÓÑÔÐ Ü ØØ Ø ÓÖ Ø Ò ØÖÙ ØÙÖ Ò ÙÒ Þ ÒØ Ð ÓÖ Ø Ñ Ò ÖÒ Ø Ïº Å ÝÖ ËÚ Ò ÃÓ Ù ÀÖ ºµ ÀÁ ÃÄÅÆÇ ÌÍŹÁ¼ ¼ ÅÖÞ ¾¼¼ Ì À Æ Á Ë À Í Æ Á Î Ê Ë Á Ì Ì Å Æ À Æ ÌÍŹÁÆ
T U M Á Æ Ë Ì Á Ì Í Ì Ê Á Æ Ç Ê Å Ì Á à ¼º ÏÓÖ ÓÔ Ö ÃÓÑÔÐ Ü ØØ Ø ÓÖ Ø Ò ØÖÙ ØÙÖ Ò ÙÒ Þ ÒØ Ð ÓÖ Ø Ñ Ò ÖÒ Ø Ïº Å ÝÖ ËÚ Ò ÃÓ Ù ÀÖ ºµ ÀÁ ÃÄÅÆÇ ÌÍŹÁ¼ ¼ ÅÖÞ ¾¼¼ Ì À Æ Á Ë À Í Æ Á Î Ê Ë Á Ì Ì Å Æ À Æ ÌÍŹÁÆ
α : Σ γ Σ α γ : Σ α Σ γ
 Ë Ñ Ò Ö Ö Ø ØÖ Ø ÁÒØ ÖÔÖ Ø Ø ÓÒ Á È Ò ½¼º ÂÙÐ ¾¼¼ ÄÙ Û ¹Å Ü Ñ Ð Ò ¹ÍÒ Ú Ö ØØ Å Ò Ò ÁÒ Ø ØÙØ Ö ÁÒ ÓÖÑ Ø Ä Ö¹ ÙÒ ÓÖ ÙÒ Ò Ø Ì ÓÖ Ø ÁÒ ÓÖÑ Ø ØØ Ò Ò ØÖ ¹ ¼ Å Ò Ò Î Ö Ö ÓÞ ÒØ ØÖ Ù Ö Æ Þ Å ÝÐÓÚ ÈÖÓ º Å ÖØ Ò ÀÓ
Ë Ñ Ò Ö Ö Ø ØÖ Ø ÁÒØ ÖÔÖ Ø Ø ÓÒ Á È Ò ½¼º ÂÙÐ ¾¼¼ ÄÙ Û ¹Å Ü Ñ Ð Ò ¹ÍÒ Ú Ö ØØ Å Ò Ò ÁÒ Ø ØÙØ Ö ÁÒ ÓÖÑ Ø Ä Ö¹ ÙÒ ÓÖ ÙÒ Ò Ø Ì ÓÖ Ø ÁÒ ÓÖÑ Ø ØØ Ò Ò ØÖ ¹ ¼ Å Ò Ò Î Ö Ö ÓÞ ÒØ ØÖ Ù Ö Æ Þ Å ÝÐÓÚ ÈÖÓ º Å ÖØ Ò ÀÓ
ÁÒ ÐØ Ú ÖÞ Ò ½ ÂÓ ÒÒ Ö ÌĐ Ù Ö ½ ¼ ½ º½ÂÓ ÒÒ Û Ö Æ ÖĐ Ö ½ º¾ Ö ÌÓ Ö º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ ¼ º º º º º º
 ÍÖ ÒØ Ù ½ ¹ ÂÓ ÒÒ Ö ÌĐ Ù Ö Á ÁÁ ÁÁÁ ÁÎ ÒØÖ ÐÙÒ Ú Ö ÙÑ ÙÒ ËÙÔ ÖÙÒ Ú Ö Ò ÄÓ ÐÙÒ Ú Ö ÙÑ Ø ÍÖ ÒØ Ä Ò ÙÒ Ä Ö Ò Â Ù ÛÛÛºÙÖ ÒØ ºÓÖ ½ ÛÛÛºØÖÙØ ÓÓ ºÓÑ ¾ ½ ÁÒØ ÖÒ Ø ØØÔ»»ÛÛÛºÙÖ ÒØ ºÓÖ» º ¾ ÁÒØ ÖÒ Ø ØØÔ»»ÛÛÛºØÖÙØ
ÍÖ ÒØ Ù ½ ¹ ÂÓ ÒÒ Ö ÌĐ Ù Ö Á ÁÁ ÁÁÁ ÁÎ ÒØÖ ÐÙÒ Ú Ö ÙÑ ÙÒ ËÙÔ ÖÙÒ Ú Ö Ò ÄÓ ÐÙÒ Ú Ö ÙÑ Ø ÍÖ ÒØ Ä Ò ÙÒ Ä Ö Ò Â Ù ÛÛÛºÙÖ ÒØ ºÓÖ ½ ÛÛÛºØÖÙØ ÓÓ ºÓÑ ¾ ½ ÁÒØ ÖÒ Ø ØØÔ»»ÛÛÛºÙÖ ÒØ ºÓÖ» º ¾ ÁÒØ ÖÒ Ø ØØÔ»»ÛÛÛºØÖÙØ
±0, 1m 2 m 3..m 53 2 e 10e 9..e
 Ê Ò Ò Ï ÖÙÑ Ð Ö Ö Ò Ò Ø Ó ÓÑÔÙØ Ö Ì ÐÒ Ñ Ö Ö Ø Ò Ö Ö ÒÒ Å Ò È ØÖ Å ÙØ Ò Ö ÊÓÞ È ØÖ ÃÐ ØÞ Ö ØÓÔ Ö Ë Ñ Ø ÊÓ ÖØ Ë ÐÑ ÒÒ Ò Ö ¹Ç Ö ÙÐ À ÒÖ ¹À ÖØÞ¹Ç Ö ÙÐ ÁÑÑ Ò٠йà ÒØ¹Ç Ö ÙÐ À Ö Ö¹Ç Ö ÙÐ Ò Ö ¹Ç Ö ÙÐ ÁÑÑ ÒÙ
Ê Ò Ò Ï ÖÙÑ Ð Ö Ö Ò Ò Ø Ó ÓÑÔÙØ Ö Ì ÐÒ Ñ Ö Ö Ø Ò Ö Ö ÒÒ Å Ò È ØÖ Å ÙØ Ò Ö ÊÓÞ È ØÖ ÃÐ ØÞ Ö ØÓÔ Ö Ë Ñ Ø ÊÓ ÖØ Ë ÐÑ ÒÒ Ò Ö ¹Ç Ö ÙÐ À ÒÖ ¹À ÖØÞ¹Ç Ö ÙÐ ÁÑÑ Ò٠йà ÒØ¹Ç Ö ÙÐ À Ö Ö¹Ç Ö ÙÐ Ò Ö ¹Ç Ö ÙÐ ÁÑÑ ÒÙ
Stefan Michaelis E S. Lehrstuhl für Elektronische Systeme und Vermittlungstechnik. Lehrstuhl für Künstliche Intelligenz
 ß ÔÐÓÑ Ö Ø ß Ì Ò Ò Ø Å Ò Ò ÞÙÖ Ò ÐÝ ÚÓÒ Ì Ð ÓÑÑÙÒ Ø ÓÒ Ò ØÞÛ Ö Ò Stefan Michaelis Þ Ñ Ö ¾¼¼¼ E S V Lehrstuhl für Künstliche Intelligenz Lehrstuhl für Elektronische Systeme und Vermittlungstechnik Prof.
ß ÔÐÓÑ Ö Ø ß Ì Ò Ò Ø Å Ò Ò ÞÙÖ Ò ÐÝ ÚÓÒ Ì Ð ÓÑÑÙÒ Ø ÓÒ Ò ØÞÛ Ö Ò Stefan Michaelis Þ Ñ Ö ¾¼¼¼ E S V Lehrstuhl für Künstliche Intelligenz Lehrstuhl für Elektronische Systeme und Vermittlungstechnik Prof.
R ψ = {λ ψ, λ 0}. P ψ P H
 Ã Ô Ø Ð Ç ÖÚ Ð Ù ØÒ ÙÒ ÍÒ Ø ÑÑØ Ø ÒØ Ò ÐÐ Ò Ö Ö ØØÐ Ò Ñ ÙÒ Ò ººº Ò Û Ö Ø ¹ Ø Ø Ö Ø Ö Ö È ¹ ÙÒ Ø ÓÒ ÙÒ Ñ Ø Ö Æ ØÙÖ ØÞ ººº Ò ËØ Ð Ö ØÞ Û Ò Ø Ò Ö Ò Â Ö ÙÒ ÖØ Ø ÑÑ Ò Û Ö ººº ÎÓÒ Ò Ñ Ï ÞÙÖ ÞÙ ØÖÙÑ Ò ÞÙÖ ÞÙÑ
Ã Ô Ø Ð Ç ÖÚ Ð Ù ØÒ ÙÒ ÍÒ Ø ÑÑØ Ø ÒØ Ò ÐÐ Ò Ö Ö ØØÐ Ò Ñ ÙÒ Ò ººº Ò Û Ö Ø ¹ Ø Ø Ö Ø Ö Ö È ¹ ÙÒ Ø ÓÒ ÙÒ Ñ Ø Ö Æ ØÙÖ ØÞ ººº Ò ËØ Ð Ö ØÞ Û Ò Ø Ò Ö Ò Â Ö ÙÒ ÖØ Ø ÑÑ Ò Û Ö ººº ÎÓÒ Ò Ñ Ï ÞÙÖ ÞÙ ØÖÙÑ Ò ÞÙÖ ÞÙÑ
 ÃÔØÐ ÒÓÑÑÒ ¹ ÙÒ ËÙ ØØÙØÓÒ «Ø ËÐÙØÞݹÐÙÒ ÙÒ ËÐÙØ ÞµÝ ¼¹µ Ö ÏÐ ÎÓÖÞÒ Òººº Òкºº Þ Ð ß Ü Ü Ô Ô ßÞÐ ÃÖÙÞÔÖ «Ø ÞÛº ÒÒØ ÑÐ ĐÒÖÙÒÒ Þ Ð ß Ü Ü Ô Ô ÈÖ ĐÒÖÙÒ Ô ¼µØÞÛ «Ø º ĐÒÖÙÒ Ö ÖÐØÚÒ ÈÖ ËÙ ØØÙØÓÒ «Ø ¾º ĐÒÖÙÒ Ö
ÃÔØÐ ÒÓÑÑÒ ¹ ÙÒ ËÙ ØØÙØÓÒ «Ø ËÐÙØÞݹÐÙÒ ÙÒ ËÐÙØ ÞµÝ ¼¹µ Ö ÏÐ ÎÓÖÞÒ Òººº Òкºº Þ Ð ß Ü Ü Ô Ô ßÞÐ ÃÖÙÞÔÖ «Ø ÞÛº ÒÒØ ÑÐ ĐÒÖÙÒÒ Þ Ð ß Ü Ü Ô Ô ÈÖ ĐÒÖÙÒ Ô ¼µØÞÛ «Ø º ĐÒÖÙÒ Ö ÖÐØÚÒ ÈÖ ËÙ ØØÙØÓÒ «Ø ¾º ĐÒÖÙÒ Ö
 ÖÖ Ö Ø ÚÓÒ ÓÑÔÙØ Ö Ý Ø Ñ Ò Ë Ö ÔØ ÞÙÑ Ë Ñ Ò Ö ËÓÑÑ Ö Ñ Ø Ö ½ À Ö Ù Ö Å Ò Ö Ã Ö Ö Ü Ð ÈÖĐ Ð Ò Ö ÁÒ ÓÖÑ Ø ÍÒ Ú Ö ØĐ Ø Ã Ö Ð ÙØ ÖÒ ¹ ¼ Ã Ö Ð ÙØ ÖÒ Ï Ø ÖÑ ÒÝ ÁÒ ÐØ Á Ø Ò ÙØÞ ½ Ø Ò ÙØÞ ß Ö ØÐ Ä ½º½ ÏÓ Ö ÓÑÑØ
ÖÖ Ö Ø ÚÓÒ ÓÑÔÙØ Ö Ý Ø Ñ Ò Ë Ö ÔØ ÞÙÑ Ë Ñ Ò Ö ËÓÑÑ Ö Ñ Ø Ö ½ À Ö Ù Ö Å Ò Ö Ã Ö Ö Ü Ð ÈÖĐ Ð Ò Ö ÁÒ ÓÖÑ Ø ÍÒ Ú Ö ØĐ Ø Ã Ö Ð ÙØ ÖÒ ¹ ¼ Ã Ö Ð ÙØ ÖÒ Ï Ø ÖÑ ÒÝ ÁÒ ÐØ Á Ø Ò ÙØÞ ½ Ø Ò ÙØÞ ß Ö ØÐ Ä ½º½ ÏÓ Ö ÓÑÑØ
 ÉÙ ÒØ Ò ÖÝÔØÓ Ö Ô Ò ÜÔ Ö Ñ ÒØ Ñ Î Ö Ð ÔÐÓÑ Ö Ø ÞÙÖ ÖÐ Ò ÙÒ Ö Ò Å Ø Ö Ò Ö Æ ØÙÖÛ Ò ØÐ Ò ÙÐØĐ Ø Ö ÍÒ Ú Ö ØĐ Ø ÁÒÒ ÖÙ Ò Ö Ø ÚÓÒ È ØÖ Ö Ñ Ë ÔØ Ñ Ö ½ ÙÖ ĐÙ ÖØ Ñ ÁÒ Ø ØÙØ ĐÙÖ ÜÔ Ö Ñ ÒØ ÐÔ Ý Ö ÍÒ Ú Ö ØĐ Ø ÁÒÒ
ÉÙ ÒØ Ò ÖÝÔØÓ Ö Ô Ò ÜÔ Ö Ñ ÒØ Ñ Î Ö Ð ÔÐÓÑ Ö Ø ÞÙÖ ÖÐ Ò ÙÒ Ö Ò Å Ø Ö Ò Ö Æ ØÙÖÛ Ò ØÐ Ò ÙÐØĐ Ø Ö ÍÒ Ú Ö ØĐ Ø ÁÒÒ ÖÙ Ò Ö Ø ÚÓÒ È ØÖ Ö Ñ Ë ÔØ Ñ Ö ½ ÙÖ ĐÙ ÖØ Ñ ÁÒ Ø ØÙØ ĐÙÖ ÜÔ Ö Ñ ÒØ ÐÔ Ý Ö ÍÒ Ú Ö ØĐ Ø ÁÒÒ
Ê Ùѹ ÙÒ Ø ÓÑÔÐ Ü ØØ
 ÃÓÑÔÐ Ü ØØ ÚÓÒ Ð ÓÖ Ø Ñ Ò ËÓÑÑ Ö Ñ Ø Ö ¾¼¼ ÈÖÓ º Öº À Ö ÖØ ÎÓÐÐÑ Ö ÁÒ Ø ØÙØ Ö Ì ÓÖ Ø ÁÒ ÓÖÑ Ø ¼½º¼ º¾¼¼ Ê Ùѹ ÙÒ Ø ÓÑÔÐ Ü ØØ Ø Ö ÙÒ ÈÐ ØÞ Ö Ë Å Ò ÌÙÖ Ò Ñ Ò Ìŵº Ë : N Nº Å Ö Ø Ø Ò Ø ÐÐ Ö ÐÐ Ò ÙÒ Ö ÐÐ Ï
ÃÓÑÔÐ Ü ØØ ÚÓÒ Ð ÓÖ Ø Ñ Ò ËÓÑÑ Ö Ñ Ø Ö ¾¼¼ ÈÖÓ º Öº À Ö ÖØ ÎÓÐÐÑ Ö ÁÒ Ø ØÙØ Ö Ì ÓÖ Ø ÁÒ ÓÖÑ Ø ¼½º¼ º¾¼¼ Ê Ùѹ ÙÒ Ø ÓÑÔÐ Ü ØØ Ø Ö ÙÒ ÈÐ ØÞ Ö Ë Å Ò ÌÙÖ Ò Ñ Ò Ìŵº Ë : N Nº Å Ö Ø Ø Ò Ø ÐÐ Ö ÐÐ Ò ÙÒ Ö ÐÐ Ï
 ÎÓÖÖØÙÒ ÑØÖÐ ĐÙÖ Ò ËØÙÙÑ Ò Ò ĐÖÒ ÅØÑØ ÙÒ ÁÒÓÖÑØ Ò Ö ÍÒÚÖ ØĐØ ÄÔÞ ÀÖÙ Ò ÚÓÑ ËØÙÒÒ Ö ÙÐØĐØ ĐÙÖ ÅØÑØ ÙÒ ÁÒÓÖÑØ ÏÖÙÑ Ò ÌÙØÓÖÙÑ ÅØÑØ ÁÒ ÐÐÒ ÚÓÒ ÙÒ ÖÖ ÙÐØĐØ ÒÓØÒÒ ËØÙÒĐÒÒ Ø ĐØÙÒ ÑØ ÑØÑØ Ò ËÚÖÐØÒ Ð ØÚÖ ØĐÒк
ÎÓÖÖØÙÒ ÑØÖÐ ĐÙÖ Ò ËØÙÙÑ Ò Ò ĐÖÒ ÅØÑØ ÙÒ ÁÒÓÖÑØ Ò Ö ÍÒÚÖ ØĐØ ÄÔÞ ÀÖÙ Ò ÚÓÑ ËØÙÒÒ Ö ÙÐØĐØ ĐÙÖ ÅØÑØ ÙÒ ÁÒÓÖÑØ ÏÖÙÑ Ò ÌÙØÓÖÙÑ ÅØÑØ ÁÒ ÐÐÒ ÚÓÒ ÙÒ ÖÖ ÙÐØĐØ ÒÓØÒÒ ËØÙÒĐÒÒ Ø ĐØÙÒ ÑØ ÑØÑØ Ò ËÚÖÐØÒ Ð ØÚÖ ØĐÒк
Ø ÑÑÙÒ Ö ÃÓÒØÖ Ø ÑÔ Ò Ð Ø Ñ Å ÑÑÓ Ö ÑÑ ÙÒ Ö ÙØÙÒ Ö Ð ÖÑ ÖØ ÙÒ ÙÒ ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ó ØÓÖ Ò Ò ÙÖ Ò Öº¹ÁÒ ºµ Ò ÒÓÑÑ Ò ÙÖ ÙÐØØ Ö ÁÒ ÓÖÑ Ø Ö ÇØØÓ¹
 Ø ÑÑÙÒ Ö ÃÓÒØÖ Ø ÑÔ Ò Ð Ø Ñ Å ÑÑÓ Ö ÑÑ ÙÒ Ö ÙØÙÒ Ö Ð ÖÑ ÖØ ÙÒ ÙÒ ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ó ØÓÖ Ò Ò ÙÖ Ò Öº¹ÁÒ ºµ Ò ÒÓÑÑ Ò ÙÖ ÙÐØØ Ö ÁÒ ÓÖÑ Ø Ö ÇØØÓ¹ÚÓÒ¹ Ù Ö ¹ÍÒ Ú Ö ØØ Å ÙÖ ÚÓÒ ÙØ Ø Ö Ôк¹ÁÒ º ÖØ Ô ÐØ
Ø ÑÑÙÒ Ö ÃÓÒØÖ Ø ÑÔ Ò Ð Ø Ñ Å ÑÑÓ Ö ÑÑ ÙÒ Ö ÙØÙÒ Ö Ð ÖÑ ÖØ ÙÒ ÙÒ ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ó ØÓÖ Ò Ò ÙÖ Ò Öº¹ÁÒ ºµ Ò ÒÓÑÑ Ò ÙÖ ÙÐØØ Ö ÁÒ ÓÖÑ Ø Ö ÇØØÓ¹ÚÓÒ¹ Ù Ö ¹ÍÒ Ú Ö ØØ Å ÙÖ ÚÓÒ ÙØ Ø Ö Ôк¹ÁÒ º ÖØ Ô ÐØ
ψ(t, Ü) = e iet/ ψ(ü).
 Ã Ô Ø Ð Ö ÖÑÓÒ Ç Þ ÐÐ ØÓÖ ÒÞ Û Ë Ö Ò Ò ÒÒ Ò Ø Ò Ã Ø ÒÔÓØ ÒØ Ð Ö ÌÙÒÒ Ð Ø Ï Ö ØÓ ØÓÑ ÙÒ ÚÓÖ ÐÐ Ñ Ö ÖÑÓÒ Ç Þ ÐÐ ØÓÖº Ï ÒÒ Ë Ó Ò Ò Ò Ö Ù Ò Ë º Ï ÒÒ Ò Ø Ò ÖÒ Ë Ó Ð Ò Ë Ò Ò Òº Ù Ø Ò ËÔÖ ÚÓÒ ÈÖÓ ÓÖ Ò ÁÒ Ñ Ã
Ã Ô Ø Ð Ö ÖÑÓÒ Ç Þ ÐÐ ØÓÖ ÒÞ Û Ë Ö Ò Ò ÒÒ Ò Ø Ò Ã Ø ÒÔÓØ ÒØ Ð Ö ÌÙÒÒ Ð Ø Ï Ö ØÓ ØÓÑ ÙÒ ÚÓÖ ÐÐ Ñ Ö ÖÑÓÒ Ç Þ ÐÐ ØÓÖº Ï ÒÒ Ë Ó Ò Ò Ò Ö Ù Ò Ë º Ï ÒÒ Ò Ø Ò ÖÒ Ë Ó Ð Ò Ë Ò Ò Òº Ù Ø Ò ËÔÖ ÚÓÒ ÈÖÓ ÓÖ Ò ÁÒ Ñ Ã
ÌĹËÝ Ø Ñ ¾
 Ê Ú Ö Ò Ò Ö Ò ÞÙÖ ÈÖÓ Ö ÑÑ ÖÛ Ø ÖÙÒ ÎÓÑ Ò Ö ÖÛ Ø ÖØ Ò Ë Ö ÔØ ÔÖ Ò Ò Ñ Ê Ð ÖÙÒ ËÓ ØÛ Ö ¹ ÐØ Ý Ø Ñ ÞÙÖ ÃÖ Ø ÐÐ Ò ÐÝ Ú ÑÑ ÂÙÐÝ ¾¼¼ ½ ÌĹËÝ Ø Ñ ¾ ÅÓØ Ú Ø ÓÒ ÙÒ Ù Ò Ø ÐÐÙÒ ÙÒ Ø ÓÒ Ð ÙÒ ÓÑ ÓÖØ Ð À Ð Ñ ØØ Ð Ò
Ê Ú Ö Ò Ò Ö Ò ÞÙÖ ÈÖÓ Ö ÑÑ ÖÛ Ø ÖÙÒ ÎÓÑ Ò Ö ÖÛ Ø ÖØ Ò Ë Ö ÔØ ÔÖ Ò Ò Ñ Ê Ð ÖÙÒ ËÓ ØÛ Ö ¹ ÐØ Ý Ø Ñ ÞÙÖ ÃÖ Ø ÐÐ Ò ÐÝ Ú ÑÑ ÂÙÐÝ ¾¼¼ ½ ÌĹËÝ Ø Ñ ¾ ÅÓØ Ú Ø ÓÒ ÙÒ Ù Ò Ø ÐÐÙÒ ÙÒ Ø ÓÒ Ð ÙÒ ÓÑ ÓÖØ Ð À Ð Ñ ØØ Ð Ò
ËÓÖØ ÖÔÖÓ Ð Ñ ËÙ ÔÖÓ Ð Ñ ÃÓÑÔÐ Ü ØØ Ö Ò Ï ÖÙÑ Ø ÒØ Ö ÒØ Ï ÖÙÑ Ø Û Ø Ì Ð Á Ò ÖÙÒ ÂÓ ÒÒ Ë ÐÙÑ Ö Ö ËÓÖØ Ö Ò ÙÒ ËÙ Ò ¾»½
 ËÓÖØ Ö Ò ÙÒ ËÙ Ò ÎÓÖØÖ Ñ À ÙÔØ Ñ Ò Ö À ÐÐÓ Ï ÐØ ÂÓ ÒÒ Ë ÐÙÑ Ö Ö Ô Ð Ôº Ò ÓÖÑ Ø ºÙÒ ¹ ÖÐ Ò Òº Ö Ö ¹ Ð Ü Ò Ö¹ÍÒ Ú Ö ØØ ÖÐ Ò Ò»Æ ÖÒ Ö ½º Å ¾¼¼ ÂÓ ÒÒ Ë ÐÙÑ Ö Ö ËÓÖØ Ö Ò ÙÒ ËÙ Ò ½»½ ËÓÖØ ÖÔÖÓ Ð Ñ ËÙ ÔÖÓ Ð Ñ
ËÓÖØ Ö Ò ÙÒ ËÙ Ò ÎÓÖØÖ Ñ À ÙÔØ Ñ Ò Ö À ÐÐÓ Ï ÐØ ÂÓ ÒÒ Ë ÐÙÑ Ö Ö Ô Ð Ôº Ò ÓÖÑ Ø ºÙÒ ¹ ÖÐ Ò Òº Ö Ö ¹ Ð Ü Ò Ö¹ÍÒ Ú Ö ØØ ÖÐ Ò Ò»Æ ÖÒ Ö ½º Å ¾¼¼ ÂÓ ÒÒ Ë ÐÙÑ Ö Ö ËÓÖØ Ö Ò ÙÒ ËÙ Ò ½»½ ËÓÖØ ÖÔÖÓ Ð Ñ ËÙ ÔÖÓ Ð Ñ
ÁÒ ÐØ Ú ÖÞ Ò ½ ÒÐ ØÙÒ ¾ ËØ Ú Ê Ø Ø ÈÖ ÒÞ Ô Ò ¾º½ Ï Ö ÓÐÙÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾º¾ ÐÐÑ Ð Ø º º º º º º º º º º º º º
 ËØ Ú Ê ÅÙ ÓÖ ÅÙ Ò Â ÖÒ Æ ØØ Ò Ñ Ö ËÓÒ Å Ò º Å ¾¼¼¼ ÁÒ ÐØ Ú ÖÞ Ò ½ ÒÐ ØÙÒ ¾ ËØ Ú Ê Ø Ø ÈÖ ÒÞ Ô Ò ¾º½ Ï Ö ÓÐÙÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾º¾ ÐÐÑ Ð Ø º º º º º º º º º º º º º
ËØ Ú Ê ÅÙ ÓÖ ÅÙ Ò Â ÖÒ Æ ØØ Ò Ñ Ö ËÓÒ Å Ò º Å ¾¼¼¼ ÁÒ ÐØ Ú ÖÞ Ò ½ ÒÐ ØÙÒ ¾ ËØ Ú Ê Ø Ø ÈÖ ÒÞ Ô Ò ¾º½ Ï Ö ÓÐÙÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾º¾ ÐÐÑ Ð Ø º º º º º º º º º º º º º
ÖÐ ÙÒ Ò Ê ÒÑ Ò Ò Ä ÙÖ ÒØ È Ð Ö ¼º ÆÓÚ Ñ Ö ¾¼¼ ½» ¾
 ÖÐ ÙÒ Ò Ê ÒÑ Ò Ò Ä ÙÖ ÒØ È Ð Ö ¼º ÆÓÚ Ñ Ö ¾¼¼ ½» ¾ ÖÐ À ØÓÖ À ÒØ Ö Ö Ò Ö ÒÞ ÒÑ Ò Ö ÒÞ ÒÚ Ö Ö Ò ØÙÖ Ö Ö ÒÞ ÒÑ Ò Ò ÐÝØ Å Ò ¾» ¾ ÖÐ ½ ½ ½ ½ Ä Ø ÞÙÖ Ø Ö ÁÒ Ù ØÖ ÐÐ Ò Ê ÚÓÐÙØ ÓÒ ½ ÎÓÐÐÑ Ò ÖØ Ö Ï ØÙ Ð ½ ¼ Ù
ÖÐ ÙÒ Ò Ê ÒÑ Ò Ò Ä ÙÖ ÒØ È Ð Ö ¼º ÆÓÚ Ñ Ö ¾¼¼ ½» ¾ ÖÐ À ØÓÖ À ÒØ Ö Ö Ò Ö ÒÞ ÒÑ Ò Ö ÒÞ ÒÚ Ö Ö Ò ØÙÖ Ö Ö ÒÞ ÒÑ Ò Ò ÐÝØ Å Ò ¾» ¾ ÖÐ ½ ½ ½ ½ Ä Ø ÞÙÖ Ø Ö ÁÒ Ù ØÖ ÐÐ Ò Ê ÚÓÐÙØ ÓÒ ½ ÎÓÐÐÑ Ò ÖØ Ö Ï ØÙ Ð ½ ¼ Ù
 ÅÙÐØ Ò ÓÖ ÁÒØ Ö Ø ÓÒ ÚÓÒ Ö ÙÒ ÒØ Ò Ê Þ Ò ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ó ØÓÖ Ö Ö Æ ØÙÖÛ Ò Ø Ò Öº Ö Öº Ò Øºµ Ñ Ö È Ý ÓÐÓ Ö È Ð ÔÔ ¹ÍÒ Ú Ö Ø Ø Å Ö ÙÖ ÚÓÖ Ð Ø ÚÓÒ Å ØØ ÓÒ Ò Ù Ö ÙÖ Å Ö ÙÖ»Ä Ò ¾¼¼ ÅÙÐØ Ò ÓÖ ÁÒØ Ö Ø
ÅÙÐØ Ò ÓÖ ÁÒØ Ö Ø ÓÒ ÚÓÒ Ö ÙÒ ÒØ Ò Ê Þ Ò ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ó ØÓÖ Ö Ö Æ ØÙÖÛ Ò Ø Ò Öº Ö Öº Ò Øºµ Ñ Ö È Ý ÓÐÓ Ö È Ð ÔÔ ¹ÍÒ Ú Ö Ø Ø Å Ö ÙÖ ÚÓÖ Ð Ø ÚÓÒ Å ØØ ÓÒ Ò Ù Ö ÙÖ Å Ö ÙÖ»Ä Ò ¾¼¼ ÅÙÐØ Ò ÓÖ ÁÒØ Ö Ø
ÎÓÖÛÓÖØ ÚÓÖÐ Ò Ë Ö ÔØÙÑ Ø Ò Ò Ö ÚÓÒ Ñ Ö Ñ Ï ÒØ Ö Ñ Ø Ö ¾¼¼»¾¼¼ ÐØ Ò Ò ÎÓÖÐ ÙÒ ÆÙÑ Ö Å Ø Ñ Ø Á ÒØ Ø Ò Òº ÎÓÖÐ ÙÒ Ó¹ Û Ö ÓÖØ ØÞÙÒ ÆÙÑ Ö Å Ø Ñ Ø ÁÁ ÖØ Ò
 ÆÙÑ Ö Á Ï ÒØ Ö Ñ Ø Ö ¾¼¼»¼ Ò Ø Ë Ð ½¾º ÆÓÚ Ñ Ö ¾¼¼ ÎÓÖÛÓÖØ ÚÓÖÐ Ò Ë Ö ÔØÙÑ Ø Ò Ò Ö ÚÓÒ Ñ Ö Ñ Ï ÒØ Ö Ñ Ø Ö ¾¼¼»¾¼¼ ÐØ Ò Ò ÎÓÖÐ ÙÒ ÆÙÑ Ö Å Ø Ñ Ø Á ÒØ Ø Ò Òº ÎÓÖÐ ÙÒ Ó¹ Û Ö ÓÖØ ØÞÙÒ ÆÙÑ Ö Å Ø Ñ Ø ÁÁ ÖØ Ò
ÆÙÑ Ö Á Ï ÒØ Ö Ñ Ø Ö ¾¼¼»¼ Ò Ø Ë Ð ½¾º ÆÓÚ Ñ Ö ¾¼¼ ÎÓÖÛÓÖØ ÚÓÖÐ Ò Ë Ö ÔØÙÑ Ø Ò Ò Ö ÚÓÒ Ñ Ö Ñ Ï ÒØ Ö Ñ Ø Ö ¾¼¼»¾¼¼ ÐØ Ò Ò ÎÓÖÐ ÙÒ ÆÙÑ Ö Å Ø Ñ Ø Á ÒØ Ø Ò Òº ÎÓÖÐ ÙÒ Ó¹ Û Ö ÓÖØ ØÞÙÒ ÆÙÑ Ö Å Ø Ñ Ø ÁÁ ÖØ Ò
¼» ½ Å Ò ÙÒ Î ÙÙÑ ÁÑ Ö Ø Ò Ò ØØ Ò Ò Ë Ä Ø Ö «ÙÒ ËØ ÛÓÖØ ÞÙÑ Î Ö Ù Å Ò ÙÒ Î ¹ ÙÙѺ Ë ÑÑÐÙÒ Ø Ò Û ÚÓÐÐ ØĐ Ò ÙÒ Ù Ö Ò ĐÙÖ ÙÖ ĐÙ ÖÙÒ ÙÒ Ù Ö ØÙÒ Î Ö Ù º ØØ
 ¼» ½ Å Ò ÙÒ Î ÙÙÑ ÁÑ Ö Ø Ò Ò ØØ Ò Ò Ë Ä Ø Ö «ÙÒ ËØ ÛÓÖØ ÞÙÑ Î Ö Ù Å Ò ÙÒ Î ¹ ÙÙѺ Ë ÑÑÐÙÒ Ø Ò Û ÚÓÐÐ ØĐ Ò ÙÒ Ù Ö Ò ĐÙÖ ÙÖ ĐÙ ÖÙÒ ÙÒ Ù Ö ØÙÒ Î Ö Ù º ØØ ÓÒ ÙÐØ Ö Ò ÞÙÖ ÎÓÖ Ö ØÙÒ ÞÙ Đ ØÞÐ Ò ÐĐ ¹ Ä Ø Ö ØÙÖ
¼» ½ Å Ò ÙÒ Î ÙÙÑ ÁÑ Ö Ø Ò Ò ØØ Ò Ò Ë Ä Ø Ö «ÙÒ ËØ ÛÓÖØ ÞÙÑ Î Ö Ù Å Ò ÙÒ Î ¹ ÙÙѺ Ë ÑÑÐÙÒ Ø Ò Û ÚÓÐÐ ØĐ Ò ÙÒ Ù Ö Ò ĐÙÖ ÙÖ ĐÙ ÖÙÒ ÙÒ Ù Ö ØÙÒ Î Ö Ù º ØØ ÓÒ ÙÐØ Ö Ò ÞÙÖ ÎÓÖ Ö ØÙÒ ÞÙ Đ ØÞÐ Ò ÐĐ ¹ Ä Ø Ö ØÙÖ
σ 2 = 1 N SNR = σ2 X σ 2 X SNR(dB) = 10log 10
 ÖÒ Ù Àº ÖÒ ÙÙÒ ¹ØÖ Öº Ñ Ð ¾¼½ ËÓË ÌÖ Ö ÍÒ Ú Ö ØØ Ø Ò ÓÑÔÖ ÓÒ Î ÖÐÙ Ø Ø Ø ÃÓÑÔÖ Ñ ÖÙÒ Ú Ö Ö Ò Ò ÖÙÒ ½ Û Ò Ø Ö ÃÓÑÔÖ Ñ ÖÙÒ ¹ Û Ò Ø Ö ÓÑÔÖ Ñ ÖÙÒ ¹ Î ÖÐÙ Ø Ø Ø ÃÓÑÔÖ Ñ ÖÙÒ ÖÙÒ Ð Ò C D X X c Y Ò Ê ÔÖ ÒØ Ø ÓÒ
ÖÒ Ù Àº ÖÒ ÙÙÒ ¹ØÖ Öº Ñ Ð ¾¼½ ËÓË ÌÖ Ö ÍÒ Ú Ö ØØ Ø Ò ÓÑÔÖ ÓÒ Î ÖÐÙ Ø Ø Ø ÃÓÑÔÖ Ñ ÖÙÒ Ú Ö Ö Ò Ò ÖÙÒ ½ Û Ò Ø Ö ÃÓÑÔÖ Ñ ÖÙÒ ¹ Û Ò Ø Ö ÓÑÔÖ Ñ ÖÙÒ ¹ Î ÖÐÙ Ø Ø Ø ÃÓÑÔÖ Ñ ÖÙÒ ÖÙÒ Ð Ò C D X X c Y Ò Ê ÔÖ ÒØ Ø ÓÒ
ÑÔ Ö ÍÒØ Ö Ù ÙÒ ÞÙÑ Î Ö Ð ÚÓÒ À Ð Ý Ø Ñ Ò Ö ÖÑ Ò Ø ÓÐÙØ ÙÒ Å ÖÓ Ó Ø Ò ÃÖ Ø Ö Ò Ö ÒÙØÞ Ö Ö ÙÒ Ð Ø ¹ Ñ Ô Ð ÚÓÒ Ü Ð Å Ø Ö Ö Ø Ò Ö Ì Ò Ò ÍÒ Ú Ö ØØ ÖÐ Ò ÙÐ
 ÑÔ Ö ÍÒØ Ö Ù ÙÒ ÞÙÑ Î Ö Ð ÚÓÒ À Ð Ý Ø Ñ Ò Ö ÖÑ Ò Ø ÓÐÙØ ÙÒ Å ÖÓ Ó Ø Ò ÃÖ Ø Ö Ò Ö ÒÙØÞ Ö Ö ÙÒ Ð Ø ¹ Ñ Ô Ð ÚÓÒ Ü Ð Å Ø Ö Ö Ø Ò Ö Ì Ò Ò ÍÒ Ú Ö ØØ ÖÐ Ò ÙÐØØ ½ Ø Û Ò Ø Ò ÁÒ Ø ØÙØ Ö ËÔÖ ÙÒ ÃÓÑÑÙÒ Ø ÓÒ Ø Ù Ó
ÑÔ Ö ÍÒØ Ö Ù ÙÒ ÞÙÑ Î Ö Ð ÚÓÒ À Ð Ý Ø Ñ Ò Ö ÖÑ Ò Ø ÓÐÙØ ÙÒ Å ÖÓ Ó Ø Ò ÃÖ Ø Ö Ò Ö ÒÙØÞ Ö Ö ÙÒ Ð Ø ¹ Ñ Ô Ð ÚÓÒ Ü Ð Å Ø Ö Ö Ø Ò Ö Ì Ò Ò ÍÒ Ú Ö ØØ ÖÐ Ò ÙÐØØ ½ Ø Û Ò Ø Ò ÁÒ Ø ØÙØ Ö ËÔÖ ÙÒ ÃÓÑÑÙÒ Ø ÓÒ Ø Ù Ó
= 27
 Å ÌÀ Ê ÂÍÆ ÍÆ ÄÌ ¹ Ë ÊÁ ¹ ÇÃÌ»ÆÇÎ ¾¼½½ ½ ÎÓÖ ÙÐ ½ Ù ¹½½ ÁÒ ÂÙÐ Ë Ù Ö Ò Ø Ò Ö È Ö Ë Ù º Ë Ò ÑÑØ Ñ ÙÒ ÐÒ Ú Ö ÒÞ ÐÒ Ë Ù Ö Ù º Á Ø Ò ÞÙ ÑÑ Ò Ö Ò È Ö Ù ¹½¾ Û ÚÓÒ Ò Ð Ö Ò Ò Ú ÐÐ Ð º Ï Ð Ò ¾ À Ï Ò ÐÚÓ ÛÛÛº Ð
Å ÌÀ Ê ÂÍÆ ÍÆ ÄÌ ¹ Ë ÊÁ ¹ ÇÃÌ»ÆÇÎ ¾¼½½ ½ ÎÓÖ ÙÐ ½ Ù ¹½½ ÁÒ ÂÙÐ Ë Ù Ö Ò Ø Ò Ö È Ö Ë Ù º Ë Ò ÑÑØ Ñ ÙÒ ÐÒ Ú Ö ÒÞ ÐÒ Ë Ù Ö Ù º Á Ø Ò ÞÙ ÑÑ Ò Ö Ò È Ö Ù ¹½¾ Û ÚÓÒ Ò Ð Ö Ò Ò Ú ÐÐ Ð º Ï Ð Ò ¾ À Ï Ò ÐÚÓ ÛÛÛº Ð
Ò Ò Ø Ò¹ÌÖ ÓÐÓ Ö ËÞ Ò Ö Ò ÙÖ ÐÐ Ó Ø ÙÐ Ù ØÖ Ø ½¾¼ À Ñ Ù ÙÒ ½ ¾ Ó Ö Î Ö Ò Ò Ø ¾¼¼ ÊÓ ÙÒ ¾ º ÔÖ Ð ¾¼½
 Ò Ò Ø Ò¹ÌÖ ÓÐÓ Ö ËÞ Ò Ö Ò ÙÖ ÐÐ Ó Ø ÙÐ Ù ØÖ Ø ½¾¼ À Ñ Ù ÙÒ ½ ¾ Ó Ö Î Ö Ò Ò Ø ¾¼¼ ÊÓ ÙÒ ¾ º ÔÖ Ð ¾¼½ ÒÐ ØÙÒ ÙÒ ÎÓÖÛÓÖØ Ö ÌÖ ÓÐÓ Ò ÐØ ÙÑ Ö ËÞ Ò Ö Ò ÙÖ ÊÓÐÐ Ò Ô Ð Àº Ⱥ ÄÓÚ Ö Ø Ø ÙÐ Ùº Ö Ø Ô ÐØ Ñ Â Ö ½¾¼
Ò Ò Ø Ò¹ÌÖ ÓÐÓ Ö ËÞ Ò Ö Ò ÙÖ ÐÐ Ó Ø ÙÐ Ù ØÖ Ø ½¾¼ À Ñ Ù ÙÒ ½ ¾ Ó Ö Î Ö Ò Ò Ø ¾¼¼ ÊÓ ÙÒ ¾ º ÔÖ Ð ¾¼½ ÒÐ ØÙÒ ÙÒ ÎÓÖÛÓÖØ Ö ÌÖ ÓÐÓ Ò ÐØ ÙÑ Ö ËÞ Ò Ö Ò ÙÖ ÊÓÐÐ Ò Ô Ð Àº Ⱥ ÄÓÚ Ö Ø Ø ÙÐ Ùº Ö Ø Ô ÐØ Ñ Â Ö ½¾¼
ÁÒ ÐØ Ú ÖÞ Ò ½¾ ÂĐÙÒ Ð Ò Ö ½ ¼ ½¾ º½ Ë Þ ÒØ Â Ö ½¼ Òº Öºµ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ ¼ ½¾ º¾ Ë Þ ÒØ Â Ö ½½ Òº Öºµ º º
 ÍÖ ÒØ Ù ½¾ ¹ ÂĐÙÒ Ð Ò Ö Á ÁÁ ÁÁÁ ÁÎ ÒØÖ ÐÙÒ Ú Ö ÙÑ ÙÒ ËÙÔ ÖÙÒ Ú Ö Ò ÄÓ ÐÙÒ Ú Ö ÙÑ Ø ÍÖ ÒØ Ä Ò ÙÒ Ä Ö Ò Â Ù ÛÛÛºÙÖ ÒØ ºÓÖ ½ ÛÛÛºØÖÙØ ÓÓ ºÓÑ ¾ ½ ÁÒØ ÖÒ Ø ØØÔ»»ÛÛÛºÙÖ ÒØ ºÓÖ» º ¾ ÁÒØ ÖÒ Ø ØØÔ»»ÛÛÛºØÖÙØ ÓÓ
ÍÖ ÒØ Ù ½¾ ¹ ÂĐÙÒ Ð Ò Ö Á ÁÁ ÁÁÁ ÁÎ ÒØÖ ÐÙÒ Ú Ö ÙÑ ÙÒ ËÙÔ ÖÙÒ Ú Ö Ò ÄÓ ÐÙÒ Ú Ö ÙÑ Ø ÍÖ ÒØ Ä Ò ÙÒ Ä Ö Ò Â Ù ÛÛÛºÙÖ ÒØ ºÓÖ ½ ÛÛÛºØÖÙØ ÓÓ ºÓÑ ¾ ½ ÁÒØ ÖÒ Ø ØØÔ»»ÛÛÛºÙÖ ÒØ ºÓÖ» º ¾ ÁÒØ ÖÒ Ø ØØÔ»»ÛÛÛºØÖÙØ ÓÓ
δ x := x x ε x := x x
 Ì Ð Á Ð ÖØ ÓÖ ½ Ð Ö ÖØ Ò Ò Ø ÓÒ ½º½º Ò Ð ÓÖ Ø ÑÙ Ø Ò Ö Ò Ñ Ð Ò ÐÐ Ò¹ ÙØ Ø Ð Ø ÓÐ ÚÓÒ Ð Ñ ÒØ Ö Ò Ê ÒÓÔ Ö Ø ÓÒ Ò ÙÒØ Ö Ò Þ ÙÒ Ñ Ø Ñ Ø Ö ÙÒ Ø ÓÒ Ò ÙÒ Ò ÙÒ Òº Ð Ñ ÒØ Ö Ê ÒÓÔ Ö Ø ÓÒ Ò Ò ÖÙÒ Ö Ò ÖØ Ò ÐÓ ÇÔ
Ì Ð Á Ð ÖØ ÓÖ ½ Ð Ö ÖØ Ò Ò Ø ÓÒ ½º½º Ò Ð ÓÖ Ø ÑÙ Ø Ò Ö Ò Ñ Ð Ò ÐÐ Ò¹ ÙØ Ø Ð Ø ÓÐ ÚÓÒ Ð Ñ ÒØ Ö Ò Ê ÒÓÔ Ö Ø ÓÒ Ò ÙÒØ Ö Ò Þ ÙÒ Ñ Ø Ñ Ø Ö ÙÒ Ø ÓÒ Ò ÙÒ Ò ÙÒ Òº Ð Ñ ÒØ Ö Ê ÒÓÔ Ö Ø ÓÒ Ò Ò ÖÙÒ Ö Ò ÖØ Ò ÐÓ ÇÔ
¾ ʺ à ÀÄ Ò Ò Ù À Ð ÖØ Ù ÒØÛ ÐÙÒ Ö ÖÙÒ Ð Ò ÓÖ ÙÒ Ð Ò Ù ÖÐ Ñ Ò Ø Ò ÈÙÒ Ø Ö ÒÒ Ò ½µ Ë Ò Ù ÖÙÒ Ð Ò Ö ÓÑ ØÖ À Ð Ò ÓÒ Ö Ñ À Ò¹ Ð Ù Ü ÓÑ Ø Å Ø Ó Û Û Ò Û Öº
 ÈÖ ¹ÈÙ Ð Ó Ô ÖØ Ñ ÒØÓ Å Ø Ñ Ø ÍÒ Ú Ö Ó Ñ Ö ÈÖ ÔÖ ÒØ ÆÙÑ Ö ¼ ½ ÎÁ ÀÁÄ ÊÌ Ê È Ê Ç Á Æ Ê ÁÆÀ Ê Ã ÀÄ Ù ÑÑ Ò ÙÒ ÁÒ Ö Ö Ø Ø ÐÐ Ò Û Ö À Ð ÖØ Ù ÓÒ Ö Ñ Ò Ò¹ Ø ÓÖ Ø Òµ È Ö ÓÜ Ò Ò Ò Ò ÖÙÒ Ð ÒØ ÓÖ Ø Ò ÎÓÖÐ ÙÒ Ò ÚÓÖº
ÈÖ ¹ÈÙ Ð Ó Ô ÖØ Ñ ÒØÓ Å Ø Ñ Ø ÍÒ Ú Ö Ó Ñ Ö ÈÖ ÔÖ ÒØ ÆÙÑ Ö ¼ ½ ÎÁ ÀÁÄ ÊÌ Ê È Ê Ç Á Æ Ê ÁÆÀ Ê Ã ÀÄ Ù ÑÑ Ò ÙÒ ÁÒ Ö Ö Ø Ø ÐÐ Ò Û Ö À Ð ÖØ Ù ÓÒ Ö Ñ Ò Ò¹ Ø ÓÖ Ø Òµ È Ö ÓÜ Ò Ò Ò Ò ÖÙÒ Ð ÒØ ÓÖ Ø Ò ÎÓÖÐ ÙÒ Ò ÚÓÖº
Í Ó Ë Ù Ø Ö ÀÖ ºµ Ñ Ò Ñ Ò Ò Ø ÙÒ ÜØÖ Ñ ÑÙ ¼ Â Ö ÐØ ÖÒ Ò Ø Ø Ú Ê Ð ÙÒ Ù Ð ½ ¾¼½
 Í Ó Ë Ù Ø Ö ÀÖ ºµ Ñ Ò Ñ Ò Ò Ø ÙÒ ÜØÖ Ñ ÑÙ ¼ Â Ö ÐØ ÖÒ Ò Ø Ø Ú Ê Ð ÙÒ Ù Ð ½ ¾¼½ ÁË Æ ¹ ¹ ½ ¾½¹ ¹ Ð Ó Ö Ô ÁÒ ÓÖÑ Ø ÓÒ Ö ÙØ Ò Ð ÓØ ÙØ Ð ÓØ Ú ÖÞ Ò Ø ÈÙ Ð Ø ÓÒ Ò Ö ÙØ Ò Æ Ø ÓÒ Ð Ð Ó Ö Ô Ø ÐÐ ÖØ Ð Ó Ö Ô Ø Ò
Í Ó Ë Ù Ø Ö ÀÖ ºµ Ñ Ò Ñ Ò Ò Ø ÙÒ ÜØÖ Ñ ÑÙ ¼ Â Ö ÐØ ÖÒ Ò Ø Ø Ú Ê Ð ÙÒ Ù Ð ½ ¾¼½ ÁË Æ ¹ ¹ ½ ¾½¹ ¹ Ð Ó Ö Ô ÁÒ ÓÖÑ Ø ÓÒ Ö ÙØ Ò Ð ÓØ ÙØ Ð ÓØ Ú ÖÞ Ò Ø ÈÙ Ð Ø ÓÒ Ò Ö ÙØ Ò Æ Ø ÓÒ Ð Ð Ó Ö Ô Ø ÐÐ ÖØ Ð Ó Ö Ô Ø Ò
¾
 Ï Ò ØÐ À Ù Ö Ø Ö Ø ËØ Ø ÔÖ ÙÒ Ö Ä Ö ÑØ Ò Ê Ð ÙÐ Ò Ò ÊÈÇ Á ÚÓÑ ½ º Þ Ñ Ö ½ ËØÖ Ò Ò Ö ÙÖ Ð ÙÒ ÞÙÑ Ä Ò ÑÓØ Ú Ö Ò ÓÑÔÙØ Ö ÙÒ ÁÒØ ÖÒ Ø Ñ ÈÖÓ Ø È Ø Ó ½ ÚÓÖ Ð Ø ÚÓÒ ÓÖÒ Ð ÃÓÖ Ò Ö Ø Ö È Ó Ò ÀÓ ÙÐ À Ð Ö Ê Ö ÒØ
Ï Ò ØÐ À Ù Ö Ø Ö Ø ËØ Ø ÔÖ ÙÒ Ö Ä Ö ÑØ Ò Ê Ð ÙÐ Ò Ò ÊÈÇ Á ÚÓÑ ½ º Þ Ñ Ö ½ ËØÖ Ò Ò Ö ÙÖ Ð ÙÒ ÞÙÑ Ä Ò ÑÓØ Ú Ö Ò ÓÑÔÙØ Ö ÙÒ ÁÒØ ÖÒ Ø Ñ ÈÖÓ Ø È Ø Ó ½ ÚÓÖ Ð Ø ÚÓÒ ÓÖÒ Ð ÃÓÖ Ò Ö Ø Ö È Ó Ò ÀÓ ÙÐ À Ð Ö Ê Ö ÒØ
e := {X E n x c = 0}
 Ã Ô Ø Ð ½ Ò ÐÝØ ÓÑ ØÖ ½º½ Ð ÙÒ Ò ÚÓÒ Ö Ò ÙÒ Ò Ò ½º½º½ È Ö Ñ Ø Ö Ð ÙÒ Ò Ö Ö Ò Ò Ö g Ø ÙÖ Ò Ò ÈÙÒ Ø A ÙÒ Ö Ê ØÙÒ Ø Ð Øº Ë ØÞ ½ Á Ø A E Ò Ð Ñ ÒØ Ò ÙÙÒ Ö ÙÑ µ Ñ Ø Ñ ÇÖØ Ú ØÓÖ a ÙÒ u R 3 \{ 0} ÒÒ Ø ÈÙÒ ØÑ Ò
Ã Ô Ø Ð ½ Ò ÐÝØ ÓÑ ØÖ ½º½ Ð ÙÒ Ò ÚÓÒ Ö Ò ÙÒ Ò Ò ½º½º½ È Ö Ñ Ø Ö Ð ÙÒ Ò Ö Ö Ò Ò Ö g Ø ÙÖ Ò Ò ÈÙÒ Ø A ÙÒ Ö Ê ØÙÒ Ø Ð Øº Ë ØÞ ½ Á Ø A E Ò Ð Ñ ÒØ Ò ÙÙÒ Ö ÙÑ µ Ñ Ø Ñ ÇÖØ Ú ØÓÖ a ÙÒ u R 3 \{ 0} ÒÒ Ø ÈÙÒ ØÑ Ò
Ù Ö Ö Æ ÙÖÓÐÓ Ò ÃÐ Ò Ö Ð ÖعÄÙ Û ¹ÍÒ Ú Ö ØØ Ö ÙÖ Ñ Öº Ò Î ÖÐ Ù Ò ÐÝ Ö ÌÖ ÑÓÖ Ö ÕÙ ÒÞ Ò Ñ ÅÓÖ Ù È Ö Ò ÓÒ ÙÒ Ñ ÒØ ÐÐ Ò ÌÖ ÑÓÖ ÁÆ Í ÍÊ Ä ¹ ÁËË ÊÌ ÌÁÇÆ ÞÙ
 Ù Ö Ö Æ ÙÖÓÐÓ Ò ÃÐ Ò Ö Ð ÖعÄÙ Û ¹ÍÒ Ú Ö ØØ Ö ÙÖ Ñ Öº Ò Î ÖÐ Ù Ò ÐÝ Ö ÌÖ ÑÓÖ Ö ÕÙ ÒÞ Ò Ñ ÅÓÖ Ù È Ö Ò ÓÒ ÙÒ Ñ ÒØ ÐÐ Ò ÌÖ ÑÓÖ ÁÆ Í ÍÊ Ä ¹ ÁËË ÊÌ ÌÁÇÆ ÞÙÖ ÖÐ Ò ÙÒ Å Þ Ò Ò Ó ØÓÖ Ö Ö Å Þ Ò Ò ÙÐØØ Ö Ð ÖعÄÙ
Ù Ö Ö Æ ÙÖÓÐÓ Ò ÃÐ Ò Ö Ð ÖعÄÙ Û ¹ÍÒ Ú Ö ØØ Ö ÙÖ Ñ Öº Ò Î ÖÐ Ù Ò ÐÝ Ö ÌÖ ÑÓÖ Ö ÕÙ ÒÞ Ò Ñ ÅÓÖ Ù È Ö Ò ÓÒ ÙÒ Ñ ÒØ ÐÐ Ò ÌÖ ÑÓÖ ÁÆ Í ÍÊ Ä ¹ ÁËË ÊÌ ÌÁÇÆ ÞÙÖ ÖÐ Ò ÙÒ Å Þ Ò Ò Ó ØÓÖ Ö Ö Å Þ Ò Ò ÙÐØØ Ö Ð ÖعÄÙ
Ò Ì Ò Ú º ÓÖ Ò ØÓÖ Ë Ö Ø Ô Ð ÇÖ Ò ØÓÖ Ö Ë Ö Ø Ñ Ò Ñ Ò Ë Ö Ø Ñ Ò Ñ ÒØÔÖÓÞ Ë ÙÖ Øݵ ÈÓÐ È ¹ÅÓ ÐÐ ËØ Ò Ö ÙÒ ÆÓÖÑ Ò ÞÙ ÁÌ¹Ë Ö Ø Ë Ö Ø ÓÒÞ ÔØ Ä Ø Ö ØÙÖ ¾»
 ØÓ Ë ÙÖ ØÝ ÎÇ ÁÒØÖÓ ÙØ ÓÒ Ë Ö Ø»Ë Ö Ø Ñ Ò Ñ ÒØ ÇÖ Ò ØÓÖ ÁÒ Ù ØÖ Ð ËÓ ØÛ Ö ÁÆËÇ Ö Ê Ò Ö Ø ØÞØ ÙØÓÑ Ø ÓÒ ÙÐØØ Ö ÁÒ ÓÖÑ Ø Ì Ò ÍÒ Ú Ö ØØ Ï Ò ÁÒ Ø ØÙØ ÐÓÖ Ò Ò Ù Ö Ö ÒÞ Å Ö Ó Ö Ò Ì Ò Ú º ÓÖ Ò ØÓÖ Ë Ö Ø Ô Ð ÇÖ
ØÓ Ë ÙÖ ØÝ ÎÇ ÁÒØÖÓ ÙØ ÓÒ Ë Ö Ø»Ë Ö Ø Ñ Ò Ñ ÒØ ÇÖ Ò ØÓÖ ÁÒ Ù ØÖ Ð ËÓ ØÛ Ö ÁÆËÇ Ö Ê Ò Ö Ø ØÞØ ÙØÓÑ Ø ÓÒ ÙÐØØ Ö ÁÒ ÓÖÑ Ø Ì Ò ÍÒ Ú Ö ØØ Ï Ò ÁÒ Ø ØÙØ ÐÓÖ Ò Ò Ù Ö Ö ÒÞ Å Ö Ó Ö Ò Ì Ò Ú º ÓÖ Ò ØÓÖ Ë Ö Ø Ô Ð ÇÖ
T = 0.3 s b = 4 m/s 2 s0 = 1 m. T = 2 s v0 = 90 km/h b = 1 m/s 2 s0 = 3 m. s = 0. s = 0. v0=220 km/h 2 a = 4 m/s. a = 1 m/s
 Ö ÓÒ Ñ ËØÖ ÒÚ Ö Ö Û Ñ Ò Ð ÖÚ Ö ÐØ Ò ËØ Ù ÒØ Ø ÙÒ Ò Ù Ø Å ÖØ Ò ÌÖ Ö ½ Ö ÓÒ Ù Ö Ë Ø Î Ö Ö ÑÓ ÐÐ Ö Ö Ö Ú ØØ ÙÒ Ò Ö Ò Ø ÐÐÙÒ Ò ÚÓÒ ÙØÓ Ö ÖÒ Û Ö Ò Ù ÖÚ Ö ÐØ Ò ÙÒ Ñ ØØ Ð Ö Ù Ò Î Ö Ö Ù Ù Ò ¹ ÓÒ Ö Ù Þ ÒÞ Î Ö Ö
Ö ÓÒ Ñ ËØÖ ÒÚ Ö Ö Û Ñ Ò Ð ÖÚ Ö ÐØ Ò ËØ Ù ÒØ Ø ÙÒ Ò Ù Ø Å ÖØ Ò ÌÖ Ö ½ Ö ÓÒ Ù Ö Ë Ø Î Ö Ö ÑÓ ÐÐ Ö Ö Ö Ú ØØ ÙÒ Ò Ö Ò Ø ÐÐÙÒ Ò ÚÓÒ ÙØÓ Ö ÖÒ Û Ö Ò Ù ÖÚ Ö ÐØ Ò ÙÒ Ñ ØØ Ð Ö Ù Ò Î Ö Ö Ù Ù Ò ¹ ÓÒ Ö Ù Þ ÒÞ Î Ö Ö
Ö Ñ ÛÓÖ ÌÖÓÑÑ Ö ¾¼½½µ ÐÐ ØÙ Ò Ù ÑÑ Ò ÙÒ Ä Ø Ö ØÙÖ ÇÔ Þ ØØ ÒØ ÐØ Ò Ò Ø ÓÖ ÖÓÒ ÓÐ Ò ÍÒ Ú Ö ØØ Ä ÔÞ ÁÒ Ø ØÙØ Ö Ä Ò Ù Ø ½ º ÂÙÒ ¾¼½¾ ÖÓÒ ÓÐ Ò ÇÔ Þ ØØ
 ÒØ ÐØ Ò Ò Ø ÓÖ ÍÒ Ú Ö ØØ Ä ÔÞ ÁÒ Ø ØÙØ Ö Ä Ò Ù Ø ½ º ÂÙÒ ¾¼½¾ ÁÒ ÐØ ½ ÜØ Ò ËØÖ Ø Ð ÓÒØ ÒÑ ÒØ ÆÓØ Ø ÓÒ ¾ ÌÖÓÑÑ Ö ¾¼½½µ ÜØ Ò ËØÖ Ø Ð ÓÒØ ÒÑ ÒØ ÆÓØ Ø ÓÒ ÜØ Ò ËØÖ Ø Ð ÓÒØ ÒÑ ÒØ µ ËØÖ Ø Ð Ò ÙÐÐÝ ÙØÓ Ñ ÒØ Ð
ÒØ ÐØ Ò Ò Ø ÓÖ ÍÒ Ú Ö ØØ Ä ÔÞ ÁÒ Ø ØÙØ Ö Ä Ò Ù Ø ½ º ÂÙÒ ¾¼½¾ ÁÒ ÐØ ½ ÜØ Ò ËØÖ Ø Ð ÓÒØ ÒÑ ÒØ ÆÓØ Ø ÓÒ ¾ ÌÖÓÑÑ Ö ¾¼½½µ ÜØ Ò ËØÖ Ø Ð ÓÒØ ÒÑ ÒØ ÆÓØ Ø ÓÒ ÜØ Ò ËØÖ Ø Ð ÓÒØ ÒÑ ÒØ µ ËØÖ Ø Ð Ò ÙÐÐÝ ÙØÓ Ñ ÒØ Ð
È Ý ¹Ë Ö ÔØ Ö Ö Ø Â Ö È Ý ÙÒØ ÖÖ Ø Ò Ñ ÖØÖ ØØ ÚÓÒ Ö Ë º Ò Ã ÒØÓÒ ÙÐ Öº ŠРú ÖÖÝ ½¾º Ç ØÓ Ö ¾¼½
 È Ý ¹Ë Ö ÔØ Ö Ö Ø Â Ö È Ý ÙÒØ ÖÖ Ø Ò Ñ ÖØÖ ØØ ÚÓÒ Ö Ë º Ò Ã ÒØÓÒ ÙÐ Öº ŠРú ÖÖÝ ½¾º Ç ØÓ Ö ¾¼½ ÁÒ ÐØ Ú ÖÞ Ò Á ÒÐ ØÙÒ ÙÒ ÖÙÒ Ð Ò ½ ³Ï ÖÙÑ Ë Ö ÔØ Ø À Ö Ù ÓÖ ÖÙÒ Ò ÙÒ Û Ë Ñ Ø ÖÒº³ ½º½ ³ Ö ÖÙÒ Ò ÙÒ ÈÖÓ Ð
È Ý ¹Ë Ö ÔØ Ö Ö Ø Â Ö È Ý ÙÒØ ÖÖ Ø Ò Ñ ÖØÖ ØØ ÚÓÒ Ö Ë º Ò Ã ÒØÓÒ ÙÐ Öº ŠРú ÖÖÝ ½¾º Ç ØÓ Ö ¾¼½ ÁÒ ÐØ Ú ÖÞ Ò Á ÒÐ ØÙÒ ÙÒ ÖÙÒ Ð Ò ½ ³Ï ÖÙÑ Ë Ö ÔØ Ø À Ö Ù ÓÖ ÖÙÒ Ò ÙÒ Û Ë Ñ Ø ÖÒº³ ½º½ ³ Ö ÖÙÒ Ò ÙÒ ÈÖÓ Ð
 ÖÓÒÐÝ ÒÙÒ ÎÖÖÒ ÞÙÖ ÈÁƹÖÒÙÒ ÙÒ ÈÁƹÈÖĐÙÙÒ ĐÙÖ ¹ÃÖØÒ ÖÓÒÐÝ ÒÙ ÈÁƹÎÖÖÒ ½ ÁÒÐØ ÚÖÞÒ ½ Ù ÑÑÒ ÙÒ Ö Ê ÙÐØØ ¾ ¾ ÒÙ ÎÖÖÒ ¾º½ ÈÁƹÒÖÖÙÒ º º º º º º º º º º º º º º º º º º º º º º º º º ¾º½º½ ÈÁƹÒÖÖÙÒ Ù ÃÖØÒÒÓÖÑØÓÒÒ
ÖÓÒÐÝ ÒÙÒ ÎÖÖÒ ÞÙÖ ÈÁƹÖÒÙÒ ÙÒ ÈÁƹÈÖĐÙÙÒ ĐÙÖ ¹ÃÖØÒ ÖÓÒÐÝ ÒÙ ÈÁƹÎÖÖÒ ½ ÁÒÐØ ÚÖÞÒ ½ Ù ÑÑÒ ÙÒ Ö Ê ÙÐØØ ¾ ¾ ÒÙ ÎÖÖÒ ¾º½ ÈÁƹÒÖÖÙÒ º º º º º º º º º º º º º º º º º º º º º º º º º ¾º½º½ ÈÁƹÒÖÖÙÒ Ù ÃÖØÒÒÓÖÑØÓÒÒ
 Ë ÑÙÐ Ø Ú ÍÒØ Ö Ù ÙÒ À Ò ÓÚ Ö Î Ö ÐØ Ò ÚÓÒ ÅÓ Ð ÁÈ ÞÙ Đ ØÞÐ Ñ ÃÓÒØ ÜØØÖ Ò Ö ËØ Ò Ê Ò ÓÖ ÙÒ ¹ ÙÒ Ä Ö Ò Ø ÁÒ ÓÖÑ Ø ÎÁÁÁ ÈÖÓ º Öº Â Ò Ê Ò Ö ÓÑÑÙÒ Ø ÓÒ Å Ò ÐÐ Ù Ø ÓÒ Ë ÑÙÐ Ø Ú ÍÒØ Ö Ù ÙÒ À Ò ÓÚ Ö Î Ö ÐØ Ò
Ë ÑÙÐ Ø Ú ÍÒØ Ö Ù ÙÒ À Ò ÓÚ Ö Î Ö ÐØ Ò ÚÓÒ ÅÓ Ð ÁÈ ÞÙ Đ ØÞÐ Ñ ÃÓÒØ ÜØØÖ Ò Ö ËØ Ò Ê Ò ÓÖ ÙÒ ¹ ÙÒ Ä Ö Ò Ø ÁÒ ÓÖÑ Ø ÎÁÁÁ ÈÖÓ º Öº Â Ò Ê Ò Ö ÓÑÑÙÒ Ø ÓÒ Å Ò ÐÐ Ù Ø ÓÒ Ë ÑÙÐ Ø Ú ÍÒØ Ö Ù ÙÒ À Ò ÓÚ Ö Î Ö ÐØ Ò
Ò Ä Ø Ö Ö Ö Ø Ê Ö ÒØ ÃÓÖÖ Ö ÒØ Ì Ö Î Ö ĐÙÒ ÙÒ ÈÖĐÙ ÙÒ Ö Ò ÈÖÓ º Öº ÊÓÐ Ë Ò Ö Å Ø Ñ Ø ÁÒ Ø ØÙص ÈÖÓ º Öº Ç Ö ÚÓÒ Ö ÄĐÙ ÃÁ˵ ÈÖÓ º Öº Ç Ö ÚÓÒ Ö ÄĐÙ ÃÁ˵
 Ê Ð Û Ò Ø Ú Ö Ø ÓÒ Ò ÚÓÒ ¹ ÙÒ Ã¹Ê Ò ÁÆ Í ÍÊ Ä¹ ÁËË ÊÌ ÌÁÇÆ ÞÙÖ ÖÐ Ò ÙÒ Ó ØÓÖ Ö Ö ÙÐØĐ Ø ĐÙÖ Å Ø Ñ Ø ÙÒ È Ý Ö Ð ÖعÄÙ Û ¹ÍÒ Ú Ö ØĐ Ø Ö ÙÖ º Ö º ÚÓÖ Ð Ø ÚÓÒ ÂÓ ÒÝ Ë Ø Û Ò Ù Â ÖØ ¾¼¼ Ò Ä Ø Ö Ö Ö Ø Ê Ö ÒØ
Ê Ð Û Ò Ø Ú Ö Ø ÓÒ Ò ÚÓÒ ¹ ÙÒ Ã¹Ê Ò ÁÆ Í ÍÊ Ä¹ ÁËË ÊÌ ÌÁÇÆ ÞÙÖ ÖÐ Ò ÙÒ Ó ØÓÖ Ö Ö ÙÐØĐ Ø ĐÙÖ Å Ø Ñ Ø ÙÒ È Ý Ö Ð ÖعÄÙ Û ¹ÍÒ Ú Ö ØĐ Ø Ö ÙÖ º Ö º ÚÓÖ Ð Ø ÚÓÒ ÂÓ ÒÝ Ë Ø Û Ò Ù Â ÖØ ¾¼¼ Ò Ä Ø Ö Ö Ö Ø Ê Ö ÒØ
Ð ÖØ Ø ÓÒ Ò Ñ Ø ÚÓÒ Ò Æ ØÙÖÛ Ò ØÐ Ò ÙÐØØ Ò Ö ÍÒ Ú Ö¹ ØØ ÖÐ Ò Ò¹Æ ÖÒ Ö Ì Ö Ñ Ò Ð Ò ÈÖ ÙÒ ÎÓÖ ØÞ Ò Ö Ö ÈÖÓÑÓØ ÓÒ ÓÑÑ ÓÒ Ö Ø Ö Ø Ö Ø ØØ Ö Û Ø Ö Ø Ö Ø ØØ
 Ò Ò Ø Ó ÍÒØ Ö Ù ÙÒ Ö Ð ØÖÓÒ Ò ÄÓ Ð ÖÙÒ Ò Ò Ö Ñ Ò ÓÒ Ð Ò À Ð Ð Ø Ö ØÖÙ ØÙÖ Ò Ñ Ø Ï ÐÛ Ö ÙÒ ÙÒ ÍÒÓÖ ÒÙÒ Ò Ò ØÙÖÛ Ò ØÐ Ò ÙÐØØ Ò Ö Ö Ö ¹ Ð Ü Ò Ö¹ÍÒ Ú Ö ØØ ÖÐ Ò Ò¹Æ ÖÒ Ö ÞÙÖ ÖÐ Ò ÙÒ Ó ØÓÖ Ö ÚÓÖ Ð Ø ÚÓÒ Å Ö
Ò Ò Ø Ó ÍÒØ Ö Ù ÙÒ Ö Ð ØÖÓÒ Ò ÄÓ Ð ÖÙÒ Ò Ò Ö Ñ Ò ÓÒ Ð Ò À Ð Ð Ø Ö ØÖÙ ØÙÖ Ò Ñ Ø Ï ÐÛ Ö ÙÒ ÙÒ ÍÒÓÖ ÒÙÒ Ò Ò ØÙÖÛ Ò ØÐ Ò ÙÐØØ Ò Ö Ö Ö ¹ Ð Ü Ò Ö¹ÍÒ Ú Ö ØØ ÖÐ Ò Ò¹Æ ÖÒ Ö ÞÙÖ ÖÐ Ò ÙÒ Ó ØÓÖ Ö ÚÓÖ Ð Ø ÚÓÒ Å Ö
Ë Ð Ö Ö Ø ÚÓÒ ÐÙ Ø Ö¹ Ø Ý Ø Ñ Ò ÙÖ Î ÖØ ÐÙÒ Ö Å Ø Ø Ò ÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ò Ó ØÓÖ Ö ÁÒ Ò ÙÖÛ Ò Ø Ò Ö ÙÐØØ Ö ÁÒ ÓÖÑ Ø Ö ÍÒ Ú Ö ØØ Ã ÖÐ ÖÙ Ì Ò ÀÓ ÙÐ µ Ò Ñ
 Ë Ð Ö Ö Ø ÚÓÒ ÐÙ Ø Ö¹ Ø Ý Ø Ñ Ò ÙÖ Î ÖØ ÐÙÒ Ö Å Ø Ø Ò ÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ò Ó ØÓÖ Ö ÁÒ Ò ÙÖÛ Ò Ø Ò Ö ÙÐØØ Ö ÁÒ ÓÖÑ Ø Ö ÍÒ Ú Ö ØØ Ã ÖÐ ÖÙ Ì Ò ÀÓ ÙÐ µ Ò Ñ Ø ÖØ Ø ÓÒ ÚÓÒ Ù Ó Å ÐÔÓ Ð Ù ËÓÐ Ò Ò Ì Ö Ñ Ò Ð Ò ÈÖ
Ë Ð Ö Ö Ø ÚÓÒ ÐÙ Ø Ö¹ Ø Ý Ø Ñ Ò ÙÖ Î ÖØ ÐÙÒ Ö Å Ø Ø Ò ÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ò Ó ØÓÖ Ö ÁÒ Ò ÙÖÛ Ò Ø Ò Ö ÙÐØØ Ö ÁÒ ÓÖÑ Ø Ö ÍÒ Ú Ö ØØ Ã ÖÐ ÖÙ Ì Ò ÀÓ ÙÐ µ Ò Ñ Ø ÖØ Ø ÓÒ ÚÓÒ Ù Ó Å ÐÔÓ Ð Ù ËÓÐ Ò Ò Ì Ö Ñ Ò Ð Ò ÈÖ
 Ò Ù Ö Ò ÎÓÐÙÑ Ò Ù Ú Ö Ö ØÙÒ Ò ÓÖÑ Ø ÓÒ Ú Ö ÐØ Ò ÔÖ ØÞ Ó Ò Ö ÑÓÖÔ Ö Ì ÖÑÓÔÐ Ø ÎÓÒ Ö ÙÐØØ Ö Å Ò Ò Ù ÙÒ Î Ö Ö Ò Ø Ò Ö Ì Ò Ò ÍÒ Ú Ö ØØ ÑÒ ØÞ Ò Ñ Ø ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ó ØÓÖ Ò Ò ÙÖ Öº¹ÁÒ ºµ ÚÓÖ Ð Ø ÚÓÒ
Ò Ù Ö Ò ÎÓÐÙÑ Ò Ù Ú Ö Ö ØÙÒ Ò ÓÖÑ Ø ÓÒ Ú Ö ÐØ Ò ÔÖ ØÞ Ó Ò Ö ÑÓÖÔ Ö Ì ÖÑÓÔÐ Ø ÎÓÒ Ö ÙÐØØ Ö Å Ò Ò Ù ÙÒ Î Ö Ö Ò Ø Ò Ö Ì Ò Ò ÍÒ Ú Ö ØØ ÑÒ ØÞ Ò Ñ Ø ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ó ØÓÖ Ò Ò ÙÖ Öº¹ÁÒ ºµ ÚÓÖ Ð Ø ÚÓÒ
ÍÒ ÓÖÑ ÓÒ ØÖ Òع Ö Ñ ÛÓÖ ÓÖ Ø Î Ö Ø ÓÒ Ó ÁÒ Ò Ø ËØ Ø ËÝ Ø Ñ ÁËË ÊÌ ÌÁÇÆ ÞÙÖ ÖÐ Ò ÙÒ Ö Ó ØÓÖ Ö ÁÒ Ò ÙÖÛ Ò Ø Ò Öº¹ÁÒ ºµ Ö Æ ØÙÖÛ Ò ØÐ ¹Ì Ò Ò ÙÐØĐ Ø Á Ö
 ÍÒ ÓÖÑ ÓÒ ØÖ Òع Ö Ñ ÛÓÖ ÓÖ Ø Î Ö Ø ÓÒ Ó ÁÒ Ò Ø ËØ Ø ËÝ Ø Ñ ÁËË ÊÌ ÌÁÇÆ ÞÙÖ ÖÐ Ò ÙÒ Ö Ó ØÓÖ Ö ÁÒ Ò ÙÖÛ Ò Ø Ò Öº¹ÁÒ ºµ Ö Æ ØÙÖÛ Ò ØÐ ¹Ì Ò Ò ÙÐØĐ Ø Á Ö ÍÒ Ú Ö ØĐ Ø Ë ÖÐ Ò ÚÓÒ ËÙÔÖ Ø ÅÙ ÓÔ Ý Ý Ë Ö ÖĐÙ Ò ¾¼¼¼
ÍÒ ÓÖÑ ÓÒ ØÖ Òع Ö Ñ ÛÓÖ ÓÖ Ø Î Ö Ø ÓÒ Ó ÁÒ Ò Ø ËØ Ø ËÝ Ø Ñ ÁËË ÊÌ ÌÁÇÆ ÞÙÖ ÖÐ Ò ÙÒ Ö Ó ØÓÖ Ö ÁÒ Ò ÙÖÛ Ò Ø Ò Öº¹ÁÒ ºµ Ö Æ ØÙÖÛ Ò ØÐ ¹Ì Ò Ò ÙÐØĐ Ø Á Ö ÍÒ Ú Ö ØĐ Ø Ë ÖÐ Ò ÚÓÒ ËÙÔÖ Ø ÅÙ ÓÔ Ý Ý Ë Ö ÖĐÙ Ò ¾¼¼¼
Σ = {a 1,...,a n } K : Σ {0,1} +. L K := n. i=1 P(a i ) K(a i ).
 Ñ Ð ÖÒ ÙÙÒ ¹ØÖ Öº Àº ÖÒ Ù Ø Ò ÓÑÔÖ ÓÒ Ó ÙÒ Ó ÖÙÒ Ò Àº ÖÒ Ù ¾¼½½ ËÓË ÌÖ Ö ÍÒ Ú Ö ØØ ½ Ó ÖÙÒ Σ = {a 1,...,a n } Ö ÐÔ Ø Ò Ó Ò Ò Ø Ú ÙÒ Ø ÓÒ Ø K : Σ {0,1} +. ÙØ Ó ÖÙÒ Ö ÓÐ Ð a i1 a i2 a i3 a i4 a i5... K(a
Ñ Ð ÖÒ ÙÙÒ ¹ØÖ Öº Àº ÖÒ Ù Ø Ò ÓÑÔÖ ÓÒ Ó ÙÒ Ó ÖÙÒ Ò Àº ÖÒ Ù ¾¼½½ ËÓË ÌÖ Ö ÍÒ Ú Ö ØØ ½ Ó ÖÙÒ Σ = {a 1,...,a n } Ö ÐÔ Ø Ò Ó Ò Ò Ø Ú ÙÒ Ø ÓÒ Ø K : Σ {0,1} +. ÙØ Ó ÖÙÒ Ö ÓÐ Ð a i1 a i2 a i3 a i4 a i5... K(a
ÓÒÙ ¹Å ÐÙ ËÝ Ø Ñ Ö Î Ö ÖÙÒ Û Ã Ø ÓÖ Ò ÚÓÒ Ê Ò Ò Ó Ø Ú Ò Ê Ò Þº º ÈË Þ Ð Ò ÙØÓ Ö ÀÙ Ö ÙÑ Û Ø Ø ºº ÙÒ Ò Ù Ø Ú Ò Ê Ò Ò Ø Ó Ø Ú Ñ Ö Ê Òµ Ê Ó Ö Ø Ø Ã ÒÒ Ò
 Ê ÓØ ÓÖ º Ì Ð ÈÖÓ º Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò Ø ÖÖ ¾ º ÔÖ Ð ¾¼½ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ Ê ÓØ ÓÖ ¾ º ÔÖ Ð ¾¼½ ½» ½ ÓÒÙ ¹Å ÐÙ ËÝ Ø Ñ Ö Î Ö ÖÙÒ Û Ã Ø ÓÖ Ò ÚÓÒ Ê Ò Ò Ó Ø Ú Ò Ê Ò Þº º ÈË Þ Ð Ò ÙØÓ Ö ÀÙ
Ê ÓØ ÓÖ º Ì Ð ÈÖÓ º Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò Ø ÖÖ ¾ º ÔÖ Ð ¾¼½ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ Ê ÓØ ÓÖ ¾ º ÔÖ Ð ¾¼½ ½» ½ ÓÒÙ ¹Å ÐÙ ËÝ Ø Ñ Ö Î Ö ÖÙÒ Û Ã Ø ÓÖ Ò ÚÓÒ Ê Ò Ò Ó Ø Ú Ò Ê Ò Þº º ÈË Þ Ð Ò ÙØÓ Ö ÀÙ
T U M I N S T I T U T F Ü R I N F O R M A T I K
 T U M I N S T I T U T F Ü R I N F O R M A T I K Kozeptio ud Realisierug der Orgaisatio eier uiversitäre Lehrverastaltug mit eiem Datebaksystem Markus Pögl, Adreas Krahke, Sabie Rittma ÀÁÂ ÃÄÅÆÇ TUM-I0313
T U M I N S T I T U T F Ü R I N F O R M A T I K Kozeptio ud Realisierug der Orgaisatio eier uiversitäre Lehrverastaltug mit eiem Datebaksystem Markus Pögl, Adreas Krahke, Sabie Rittma ÀÁÂ ÃÄÅÆÇ TUM-I0313
(A i ) t 1 A i f l. f l+1 = f l c l Ð. A t 1 l. c l,i = (A i ) t 1/(A i f l ) c l + = c l,i Ð
 Ö Å Ø Ñ Ø ÙÒ ÁÒ ÓÖÑ Ø Ö Ø ÖÙÔÔ È Ö ÐÐ Ð ÙÒ Î ÖØ ÐØ ËÝ Ø Ñ ÈÖÓ º Öº Ë Ö ÓÖÐ Ø È Ö ÐÐ Ð ÖÙÒ Ò Ð Ö ÓÒ ØÖÙ Ø ÓÒ Ð ÓÖ Ø ÑÙ Ñ Ø Í ÓÑ Ò ÕÙ Å ÐÒ Ö ºÑ ÐÙÒ ¹ÑÙ Ò Ø Öº ÓÑ Ò ÕÙ Å ÐÒ Ö È Ö ÐÐ Ð ÖÙÒ Ò Ð Ö ÓÒ ØÖÙ Ø ÓÒ
Ö Å Ø Ñ Ø ÙÒ ÁÒ ÓÖÑ Ø Ö Ø ÖÙÔÔ È Ö ÐÐ Ð ÙÒ Î ÖØ ÐØ ËÝ Ø Ñ ÈÖÓ º Öº Ë Ö ÓÖÐ Ø È Ö ÐÐ Ð ÖÙÒ Ò Ð Ö ÓÒ ØÖÙ Ø ÓÒ Ð ÓÖ Ø ÑÙ Ñ Ø Í ÓÑ Ò ÕÙ Å ÐÒ Ö ºÑ ÐÙÒ ¹ÑÙ Ò Ø Öº ÓÑ Ò ÕÙ Å ÐÒ Ö È Ö ÐÐ Ð ÖÙÒ Ò Ð Ö ÓÒ ØÖÙ Ø ÓÒ
 ÍÒ Ú Ö ØØ Ã ÖÐ ÖÙ ÌÀµ Ê Ù Ø ÙÒØ Ö Ù ÙÒ ÙÒ Æ ÒÓ ØÖÙ ØÙÖ ÖÙÒ Ñ Ø Ñ Ê Ø Ö Ö ØÑ ÖÓ ÓÔ ÜÔ Ö Ñ ÒØ ÙÒ Ð Ò ÐÝ Ò ÔÐÓÑ Ö Ø ÚÓÖ Ð Ø ÚÓÒ ËÚ Ò È ÙÐÙ ÁÒ Ø ØÙØ Ö Ò Û Ò Ø È Ý ÍÒ Ú Ö ØØ Ã ÖÐ ÖÙ ¼º ÆÓÚ Ñ Ö ½ Ö Ø ÙØ Ø Ö
ÍÒ Ú Ö ØØ Ã ÖÐ ÖÙ ÌÀµ Ê Ù Ø ÙÒØ Ö Ù ÙÒ ÙÒ Æ ÒÓ ØÖÙ ØÙÖ ÖÙÒ Ñ Ø Ñ Ê Ø Ö Ö ØÑ ÖÓ ÓÔ ÜÔ Ö Ñ ÒØ ÙÒ Ð Ò ÐÝ Ò ÔÐÓÑ Ö Ø ÚÓÖ Ð Ø ÚÓÒ ËÚ Ò È ÙÐÙ ÁÒ Ø ØÙØ Ö Ò Û Ò Ø È Ý ÍÒ Ú Ö ØØ Ã ÖÐ ÖÙ ¼º ÆÓÚ Ñ Ö ½ Ö Ø ÙØ Ø Ö
ÙÐØØ Ö È Ý ÙÒ ØÖÓÒÓÑ ÊÙÔÖ Ø¹Ã ÖÐ ¹ÍÒ Ú Ö ØØ À Ð Ö ÐÓÖ Ö Ø Ñ ËØÙ Ò Ò È Ý ÚÓÖ Ð Ø ÚÓÒ Å ÖÚ Ò Ð ÖØ Ù À Ð Ö Ù Ù Ø ¾¼½¼
 ÙÐØØ Ö È Ý ÙÒ ØÖÓÒÓÑ ÊÙÔÖ Ø¹Ã ÖÐ ¹ÍÒ Ú Ö ØØ À Ð Ö ÐÓÖ Ö Ø Ñ ËØÙ Ò Ò È Ý ÚÓÖ Ð Ø ÚÓÒ Å ÖÚ Ò Ð ÖØ Ù À Ð Ö Ù Ù Ø ¾¼½¼ Ä ÕÙ ÓÑÔÙØ Ò Ñ Ø Æ ÙÖÓÑÓÖÔ Ö À Ö Û Ö ÐÓÖ Ö Ø ÛÙÖ ÚÓÒ Å ÖÚ Ò Ð ÖØ Ù ÖØ Ñ Ã Ö Ó ¹ÁÒ Ø ØÙØ
ÙÐØØ Ö È Ý ÙÒ ØÖÓÒÓÑ ÊÙÔÖ Ø¹Ã ÖÐ ¹ÍÒ Ú Ö ØØ À Ð Ö ÐÓÖ Ö Ø Ñ ËØÙ Ò Ò È Ý ÚÓÖ Ð Ø ÚÓÒ Å ÖÚ Ò Ð ÖØ Ù À Ð Ö Ù Ù Ø ¾¼½¼ Ä ÕÙ ÓÑÔÙØ Ò Ñ Ø Æ ÙÖÓÑÓÖÔ Ö À Ö Û Ö ÐÓÖ Ö Ø ÛÙÖ ÚÓÒ Å ÖÚ Ò Ð ÖØ Ù ÖØ Ñ Ã Ö Ó ¹ÁÒ Ø ØÙØ
 Ò ØÞÙÒ Ú Ö ÐØ Ò Ò ØÖÙ ØÙÖ ÖØ Ò Ç Ö Đ Ò ÎÓÒ ÔÐÓѹ Ñ Ö ÀÓÐ Ö Ó Ð Ò Ù Ï ÖÒ Ë Öµ ÙÐØĐ Ø ÁÁ ¹ Å Ø Ñ Ø ÙÒ Æ ØÙÖÛ Ò Ø Ò Ö Ì Ò Ò ÍÒ Ú Ö ØĐ Ø ÖÐ Ò ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ó ØÓÖ Ö Æ ØÙÖÛ Ò Ø Ò ¹ Öº Ö Öº Ò Øº ¹ Ò Ñ Ø ÖØ
Ò ØÞÙÒ Ú Ö ÐØ Ò Ò ØÖÙ ØÙÖ ÖØ Ò Ç Ö Đ Ò ÎÓÒ ÔÐÓѹ Ñ Ö ÀÓÐ Ö Ó Ð Ò Ù Ï ÖÒ Ë Öµ ÙÐØĐ Ø ÁÁ ¹ Å Ø Ñ Ø ÙÒ Æ ØÙÖÛ Ò Ø Ò Ö Ì Ò Ò ÍÒ Ú Ö ØĐ Ø ÖÐ Ò ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ó ØÓÖ Ö Æ ØÙÖÛ Ò Ø Ò ¹ Öº Ö Öº Ò Øº ¹ Ò Ñ Ø ÖØ
Ò Ö ÙÐØĐ Ø ĐÙÖ Ò Û Ò Ø Ï Ò Ø Ò ÈÖÓ º Öº Â Ò º ÃÓÖÚ Ò ½º ÙØ Ø Ö ÈÖÓ º Öº Ö Öº Ò Øº ÖÒ Ö Æ Ð ¾º ÙØ Ø Ö ÈÖÓ º Öº Ö Öº Ò Øº È ÙÐ Ä Ú Ì Ö ÔÙØ Ø ÓÒ ½¼ Å ¾¼¼
 ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ó ØÓÖ Ö Ö ÙÐØĐ Ø ĐÙÖ Ò Û Ò Ø Ï Ò Ø Ò Ö Ð ÖعÄÙ Û ¹ÍÒ Ú Ö ØĐ Ø Ö ÙÖ ÊÓ ÓØ Ö¹ Ù ÐÐ È ÖÞ ÔØ ÓÒ Ð Ö Ø ÓÒ ÙÒ Ø ÓÒ ÙØÓÒÓÑ Ö ËÝ Ø Ñ Ò ÝÒ Ñ Ò ÍÑ ÙÒ Ò Ì ÐÓ Ï Ð AË ÔØ Ñ Ö ¾¼¼ ØÖ Ù Ö ÈÖÓ º Öº
ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ó ØÓÖ Ö Ö ÙÐØĐ Ø ĐÙÖ Ò Û Ò Ø Ï Ò Ø Ò Ö Ð ÖعÄÙ Û ¹ÍÒ Ú Ö ØĐ Ø Ö ÙÖ ÊÓ ÓØ Ö¹ Ù ÐÐ È ÖÞ ÔØ ÓÒ Ð Ö Ø ÓÒ ÙÒ Ø ÓÒ ÙØÓÒÓÑ Ö ËÝ Ø Ñ Ò ÝÒ Ñ Ò ÍÑ ÙÒ Ò Ì ÐÓ Ï Ð AË ÔØ Ñ Ö ¾¼¼ ØÖ Ù Ö ÈÖÓ º Öº
Ò Á Ò Ò ÃÓÐÐ Ò Ê Ò Ö Ë Ñ ÐÞ¹ ÖÙÒ Ê Ò Ö Ë Ñ Ø ÙÒ ÊÙ Ë Ñ Ö Ù ÖÓÖ ÒØÐ Ð Ö Ä Ø Ö ØÙÖ ÒÛ Ò Ö Ñ Ö Ò Ò Ö Ò Ù Ò ÞÙ Ñ Ö ÙÒÚ ÖØÖ ÙØ Ò Þ ÔÐ Ò Ò ÖÑ Ð Ø Òº
 Ö Å Ò Ò Ò Á Ò Ò ÃÓÐÐ Ò Ê Ò Ö Ë Ñ ÐÞ¹ ÖÙÒ Ê Ò Ö Ë Ñ Ø ÙÒ ÊÙ Ë Ñ Ö Ù ÖÓÖ ÒØÐ Ð Ö Ä Ø Ö ØÙÖ ÒÛ Ò Ö Ñ Ö Ò Ò Ö Ò Ù Ò ÞÙ Ñ Ö ÙÒÚ ÖØÖ ÙØ Ò Þ ÔÐ Ò Ò ÖÑ Ð Ø Òº ÁÒ ÐØ Ú ÖÞ Ò Ù Ò ÔÙÒ Ø ½ ½ ÖÔ ÖÐ ¹ Ø ½º½ Ö Û ÙÒ ÔÔ
Ö Å Ò Ò Ò Á Ò Ò ÃÓÐÐ Ò Ê Ò Ö Ë Ñ ÐÞ¹ ÖÙÒ Ê Ò Ö Ë Ñ Ø ÙÒ ÊÙ Ë Ñ Ö Ù ÖÓÖ ÒØÐ Ð Ö Ä Ø Ö ØÙÖ ÒÛ Ò Ö Ñ Ö Ò Ò Ö Ò Ù Ò ÞÙ Ñ Ö ÙÒÚ ÖØÖ ÙØ Ò Þ ÔÐ Ò Ò ÖÑ Ð Ø Òº ÁÒ ÐØ Ú ÖÞ Ò Ù Ò ÔÙÒ Ø ½ ½ ÖÔ ÖÐ ¹ Ø ½º½ Ö Û ÙÒ ÔÔ
 ËØ Ø Ø Ò ÐÝ ÚÓÒ Î Ö Ö Ø Ò ÙÒ ÅÓ ÐÐ ÖÙÒ ÚÓÒ Î Ö Ö Ù Ñ ØØ Ð Þ ÐÐÙÐ Ö Ö ÙØÓÑ Ø Ò ÎÓÑ Ö È Ý ß Ì ÒÓÐÓ Ö Ö Ö ¹Å Ö ØÓÖ¹ÍÒ Ú Ö ØĐ Ø Ù ÙÖ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ò Ó ØÓÖ Ö Æ ØÙÖÛ Ò Ø Ò Ò Ñ Ø ÖØ Ø ÓÒ ÚÓÒ ÄÙØÞ Æ Ù ÖØ Ù
ËØ Ø Ø Ò ÐÝ ÚÓÒ Î Ö Ö Ø Ò ÙÒ ÅÓ ÐÐ ÖÙÒ ÚÓÒ Î Ö Ö Ù Ñ ØØ Ð Þ ÐÐÙÐ Ö Ö ÙØÓÑ Ø Ò ÎÓÑ Ö È Ý ß Ì ÒÓÐÓ Ö Ö Ö ¹Å Ö ØÓÖ¹ÍÒ Ú Ö ØĐ Ø Ù ÙÖ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ò Ó ØÓÖ Ö Æ ØÙÖÛ Ò Ø Ò Ò Ñ Ø ÖØ Ø ÓÒ ÚÓÒ ÄÙØÞ Æ Ù ÖØ Ù
¾
 ÁÈÄÇÅ Ê ÁÌ Ì Ø Ð Ö ÔÐÓÑ Ö Ø Û ÒÒØ Ñ Ò Ò Ó Ö ÙØÓ Ò ØÓ Ø Ù Ò Ò Ö ØÞÙÒ Ö Ò Ù Ö Ø ÚÓÒ Ð Ô Ð Ò Î Ö Ö Ò Ë Ò Ë ÓØØÐ ØÒ Ö Ò ØÖ Ø Ö Ñ Ö Ö Å ØÖ Ö Æ ØÙÖÛ Ò Ø Ò Å º Ö Öº Ò Øºµ Ï Ò Å ¾¼½½ ËØÙ Ò ÒÒÞ Ð Ð ÙØ ËØÙ Ò Ð ØØ
ÁÈÄÇÅ Ê ÁÌ Ì Ø Ð Ö ÔÐÓÑ Ö Ø Û ÒÒØ Ñ Ò Ò Ó Ö ÙØÓ Ò ØÓ Ø Ù Ò Ò Ö ØÞÙÒ Ö Ò Ù Ö Ø ÚÓÒ Ð Ô Ð Ò Î Ö Ö Ò Ë Ò Ë ÓØØÐ ØÒ Ö Ò ØÖ Ø Ö Ñ Ö Ö Å ØÖ Ö Æ ØÙÖÛ Ò Ø Ò Å º Ö Öº Ò Øºµ Ï Ò Å ¾¼½½ ËØÙ Ò ÒÒÞ Ð Ð ÙØ ËØÙ Ò Ð ØØ
 ß Ð ¹ ÓÜ¹Ï ÖÚ ÖÛ Ò ÙÒ Î Ö ĐÙ Ö Ø ÚÓÒ Ú Ö Ò Ò Ö Ø ÒÙØÞ Ö ÃÐ Ò ÞÙÖ ÁÒ Ø ÒØ ÖÙÒ ÖĐ Ò Ø ÅĐÓ Ð Ø Ò ÞÙÖ ÒÔ ÙÒ Ö Ò Ö Ú ÖÛ Ò Ö ß Ï ÖÚ ÖÛ Ò ÙÒ ÚÓÒ ÃÓÑÔÓÒ ÒØ Ò Ò ÃÓÑÔÓÒ ÒØ Ò Ô Þ ÐÐ ËÛ¹Ì Ð Ò Ô Þ Î Ö ÐØ Ò Ù ¹ Û Ò
ß Ð ¹ ÓÜ¹Ï ÖÚ ÖÛ Ò ÙÒ Î Ö ĐÙ Ö Ø ÚÓÒ Ú Ö Ò Ò Ö Ø ÒÙØÞ Ö ÃÐ Ò ÞÙÖ ÁÒ Ø ÒØ ÖÙÒ ÖĐ Ò Ø ÅĐÓ Ð Ø Ò ÞÙÖ ÒÔ ÙÒ Ö Ò Ö Ú ÖÛ Ò Ö ß Ï ÖÚ ÖÛ Ò ÙÒ ÚÓÒ ÃÓÑÔÓÒ ÒØ Ò Ò ÃÓÑÔÓÒ ÒØ Ò Ô Þ ÐÐ ËÛ¹Ì Ð Ò Ô Þ Î Ö ÐØ Ò Ù ¹ Û Ò
Mathematik 1 ohne Taschenrechner Zeit: 90 Minuten
 St. Gallische Kantonsschulen Aufnahmeprüfung 2002 Maturitätsabteilungen 1. Klassen Mathematik 1 ohne Taschenrechner Zeit: 90 Minuten Name, Vorname:... Summe Bisherige Schule:... Note Alle Aufgaben sind
St. Gallische Kantonsschulen Aufnahmeprüfung 2002 Maturitätsabteilungen 1. Klassen Mathematik 1 ohne Taschenrechner Zeit: 90 Minuten Name, Vorname:... Summe Bisherige Schule:... Note Alle Aufgaben sind
a 2 b 2 db = 10 log db = 20 log db b 2 2
 À Ò ÓÙØ ÞÙÖ Î Ö Ò Ø ÐØÙÒ ÑÓÒ ØÖ Ø ÓÒ ÜÔ Ö Ñ ÒØ ÙÒ Ø ÓÒ Ò Ö ØÓÖ ÙÒ Ø ÓÒ ÙÑ Ò Î Ö Ð Ú Ö Ò Ö ÌÝÔ Ò Ø Ö È Ý ÍÒ Ú Ö ØØ ÝÖ ÙØ Ö Ø Ò Ä Ò Ò Ö ¾ º  ÒÙ Ö ¾¼¼ ½ ÁÒ ÐØ Ú ÖÞ Ò ½ ÒÐ ØÙÒ ¾ ÙÒ Ø ÓÒ ÙÑ Ò ¾º½ Ö º º º º
À Ò ÓÙØ ÞÙÖ Î Ö Ò Ø ÐØÙÒ ÑÓÒ ØÖ Ø ÓÒ ÜÔ Ö Ñ ÒØ ÙÒ Ø ÓÒ Ò Ö ØÓÖ ÙÒ Ø ÓÒ ÙÑ Ò Î Ö Ð Ú Ö Ò Ö ÌÝÔ Ò Ø Ö È Ý ÍÒ Ú Ö ØØ ÝÖ ÙØ Ö Ø Ò Ä Ò Ò Ö ¾ º  ÒÙ Ö ¾¼¼ ½ ÁÒ ÐØ Ú ÖÞ Ò ½ ÒÐ ØÙÒ ¾ ÙÒ Ø ÓÒ ÙÑ Ò ¾º½ Ö º º º º
Ù Ù ÙÒ Ì Ø Ò ÅÙÐØ ¹ Ø ØÓÖ¹ËÝ Ø Ñ Ñ Ø ÓÖØ Ù ĐÓ Ò Ò À Ð Ð Ø Ö Ø ØÓÖ Ò ÔÐÓÑ Ö Ø ÚÓÒ Ö Ø Ò º ĐÙÛ ÁÒ Ø ØÙØ ĐÙÖ Ã ÖÒÔ Ý Ö ÍÒ Ú Ö ØĐ Ø ÞÙ ÃĐÓÐÒ ¾¼¼½
 Ù Ù ÙÒ Ì Ø Ò ÅÙÐØ ¹ Ø ØÓÖ¹ËÝ Ø Ñ Ñ Ø ÓÖØ Ù ĐÓ Ò Ò À Ð Ð Ø Ö Ø ØÓÖ Ò ÔÐÓÑ Ö Ø ÚÓÒ Ö Ø Ò º ĐÙÛ ÁÒ Ø ØÙØ ĐÙÖ Ã ÖÒÔ Ý Ö ÍÒ Ú Ö ØĐ Ø ÞÙ ÃĐÓÐÒ ¾¼¼½ Ù ÑÑ Ò ÙÒ ÁÑ Ê Ñ Ò Ö ÔÐÓÑ Ö Ø ÛÙÖ Ò ÅÙÐØ ¹ Ø ØÓÖ¹ËÝ Ø Ñ ĐÙÖ
Ù Ù ÙÒ Ì Ø Ò ÅÙÐØ ¹ Ø ØÓÖ¹ËÝ Ø Ñ Ñ Ø ÓÖØ Ù ĐÓ Ò Ò À Ð Ð Ø Ö Ø ØÓÖ Ò ÔÐÓÑ Ö Ø ÚÓÒ Ö Ø Ò º ĐÙÛ ÁÒ Ø ØÙØ ĐÙÖ Ã ÖÒÔ Ý Ö ÍÒ Ú Ö ØĐ Ø ÞÙ ÃĐÓÐÒ ¾¼¼½ Ù ÑÑ Ò ÙÒ ÁÑ Ê Ñ Ò Ö ÔÐÓÑ Ö Ø ÛÙÖ Ò ÅÙÐØ ¹ Ø ØÓÖ¹ËÝ Ø Ñ ĐÙÖ
ÁÒ ÐØ Ú ÖÞ Ò ½ ÒÐ ØÙÒ ½¼ ½º½ ÎÓÖÛÓÖØ ÚÓÒ Ñ Ö º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½¼ ½º¾ ÎÓÖÛÓÖØ ÚÓÒ ÓÑ Ò ÕÙ º º º º º º º
 ÎÓÖ Ö ØÙÒ Ö Î ÖØ ÙÒ ÔÖ ÙÒ Ã Ò ØÐ ÁÒØ ÐÐ ÒÞ Ï Ò Ö ÔÖ ÒØ Ø ÓÒ ÙÒ Ø Ò Ò Ò Ò Ö ÏÓÖØÑ ÒÒ Ò Ö ºÛÓÖØÑ ÒÒÖÛØ ¹ Òº µ Ö Ò Ù Ò ÎÓÖ Ö ØÙÒ Ò ÚÓÒ ÓÑ Ò ÕÙ ÐÑ Ý Ö ÓÑ Ò ÕÙ ºÞ ÐÑ Ý ÖÖÛØ ¹ Òº µ ÁÒ ÐØ Ú ÖÞ Ò ½ ÒÐ ØÙÒ ½¼ ½º½
ÎÓÖ Ö ØÙÒ Ö Î ÖØ ÙÒ ÔÖ ÙÒ Ã Ò ØÐ ÁÒØ ÐÐ ÒÞ Ï Ò Ö ÔÖ ÒØ Ø ÓÒ ÙÒ Ø Ò Ò Ò Ò Ö ÏÓÖØÑ ÒÒ Ò Ö ºÛÓÖØÑ ÒÒÖÛØ ¹ Òº µ Ö Ò Ù Ò ÎÓÖ Ö ØÙÒ Ò ÚÓÒ ÓÑ Ò ÕÙ ÐÑ Ý Ö ÓÑ Ò ÕÙ ºÞ ÐÑ Ý ÖÖÛØ ¹ Òº µ ÁÒ ÐØ Ú ÖÞ Ò ½ ÒÐ ØÙÒ ½¼ ½º½
