f(x) = x + 1 ±(x + 1) für 1 x < 0 ±( x + 1) für 0 x 1
|
|
|
- Linda Wagner
- vor 5 Jahren
- Abrufe
Transkript
1 Problemstellung. Die gesuchte lineare Funktion durch die Punkte (0, ) und (, 0) lautet f(x) = x + im Intervall [0, ]. Die Gleichungen für die Begrenzungslinien sind: Λ(x) = { ±(x + ) für x < 0 ±( x + ) für 0 x. Im. Quadranten hat das Quadrat eine Fläche von, die Kurve muss somit mit den Koordinatenachsen eine Fläche von 0,55 einschließen. Für die quadratische Funktion f(x) = ax + bx + c sind folgende Bedingung erforderlich: a) f(0) = = c b) f() = 0 = a + b + ; weiters folgt aus f (0) = 0 die Gleichung b = 0, daraus folgt a = und schließlich liefert die Flächenbedingung 0 x + dx =, aber nicht den geforderten Wert 0,55. Eine quadratische Funktion ist demnach ungeeignet. Für die kubische Funktion f(x) = ax + bx + cx + d ergibt sich folgendes Gleichungssystem: f(0) = f() = 0 f (0) = 0 f(x)dx = 0, 55 0 d = a + b + c + = 0 c = 0( daraus folgt b = a ) 0 ax + ( a )x + dx = 0, 55 Aus der letzten Bedingung erhält man a = 7 5 und daraus die Funktion f(x) = 7 5 x 5 x + Es bleibt zu zeigen, dass damit auch die Ausgangsbedingung c) erfüllt ist: bei x = 0 ist der Funktionswert, bei x = hat f eine Nullstelle und in diesem Intervall ist die Funktion streng monoton fallend, da f (x) = 5 x 5 x = x(7x 8) im offenen Intervall ]0, [ negativ ist. 5. a) Überprüfung der Bedingungen: i. a n (x) = x n : a) a n (0) = 0 n = b) a n () = n = = 0 c) Zu zeigen ist 0 < a n (x) < :
2 Es gilt: 0 n < x n < n (für 0 < x < ) ( ) 0 > x n > n + > x n > n = 0 ii. b n (x) = ( x) n : a) b n (0) = ( 0) n = n = b) b n () = ( ) n = 0 n = 0 c) Es ist 0 < b n (x) <, weil x in diesem Intervall zwischen 0 und liegt und damit auch jede Potenz mit n N. b) Flächen: i. A n = [ 0 ( xn )dx = x ] n + xn+ = 0 n + lim A n =. Die gesamte quadratische Fliese wird somit bemalt. n + ii. B n = [ 0 ( x)n dx = ] ( ( x)n+ = 0 ) = n + 0 n + n + lim B n = 0. Die gesamte quadratische Fliese bleibt unbemalt. n +. a) In der Grafik sind zwei Beispieltropfen P und P auf der Diagonalen dargestellt. Während der Tropfen P in den bemalten Bereich fällt und somit keinen Schaden anrichtet, sind Fliesen mit Punkten wie P im Intervall SA Ausschussware. Der x-wert von S ergibt sich als (positive) Lösung der Gleichung x = x : 5 x S = 0, 68 (Goldener Schnitt). Für die Wahrscheinlichkeit eines Ausschusses gilt (aus Symmetriegründen): p = SA ( 0, OA 68) + ( 0, 68) 0, 5 = = 8, %., Bei 5000 Fliesen erwartet man 0%, also 000 Fliesen mit Tropfen und somit etwa 8 mangelhafte Fliesen. b) Für b gelten die gleichen Überlegungen, diesmal ist S (0, 8; 0, 8) und damit p 0, 68. Es sind diesmal also etwa 68 Fliesen betroffen. Insgesamt sind also 8+68=000 Fliesen betroffen. (Anmerkung: die Kurven a und b sind im. Quadranten symmetrisch bezüglich des Punktes (0, 5; 0, 5). Auf Grund dieser Symmetrieeigenschaft könnte man obiges Ergebnis auch graphisch herleiten.)
3 Problemstellung. f k (x) = x +k. f k (0) = k. f k () = k. Daraus ergibt sich die Tangente r k im Punkt (0, 9): y = kx+9 und die Tangente s k im Punkt (; 8 + k): y = (k )x +. Der Schnittpunkt M der Tangenten: kx + 9 = kx x + x = Dieses Ergebnis ist unabhängig von k. (. Es ist M =, ) k + 9. Die Forderung y M < 0 führt auf die Ungleichung k +9 < 9 und damit k <. Der größte ganzzahlige Wert ist k =. Kurvendiskussion von f (x): f (x) = x + x + 9 ist eine Polynomfunktion. Grades, überall definiert, stetig und differenzierbar und die Wertemenge ist W = R. Sie hat genau eine Nullstelle bei ( x,, ) welche nur numerisch näherungsweise berechnet werden kann. Die Extremwerte lauten H = ; 9, 8, ( T = ) ; 8, 6 und der Wendepunkt liegt bei W = (0, 9). T = ( 0, 58; 8, 6) W = (0; 9) H = (0, 58; 9, 8) Die gesuchte Wahrscheinlichkeit ergibt sich aus dem Verhältnis der schraffierten Fläche A (siehe Abbildung) zur Fläche A des Bereichs T.
4 Der Bereich unter dem Punkt M ist hier nochmal vergrößert dargestellt: A = 0 x + 9 ( x + x + 9)dx + 0, 09 +, 5 + 0, 6 =,, x + ( x + x + 9)dx + (5, 5, ) (, + ) A = ( + 9) 9 ) = 8 Wahrscheinlichkeit: p = A, = 8, 85% A 70, 08 70, 08. Die Ursprungsgerade durch N = (x N, y N ) hat die Gleichung y N = k x N. Die Steigung der Normalen ist gleich dem negativen Kehrwert der Tangentensteigung und damit ist y N = f (x N ) x N bzw. f(x N ) f (x N ) + x N = 0. Ist nun f eine beliebige Polynomfunktion von Grad n, so ist f eine Polynomfunktion von Grad n und folglich gilt für den Grad des Produktes f(x) f (x): n + n = n. Nach dem Hauptsatz der Algebra hat eine Polynomfunktion n. Grades maximal n Nullstellen.
5 Frage Es seien r der Zylinderradius und h die Zylinderhöhe und die entsprechenden Großbuchstaben der Radius bzw. die Höhe des Kegels (vgl. Skizze). Zu zeigen: Vmax < R π H. Aus der Ähnlichkeit erhält man R r = H H h bzw. r = R H h H. Vmax = r π h = R H (H h) π h = R π H (H h Hh + h ). V (h) = R π H (H Hh + h ) = 0 mit der Lösung h = H und h = H. Die erste Lösung führt auf ein minimales Volumen. H r h R Es ist V (h) = R π ( H + 6h), somit V H gesuchte Maximum. Vmax = 9 R π H. ( ) H = R π H ( ) H + 6 H R π = H < 0 und damit das Vmax < R π H 9 R π H 9 < R π H < Frage Es sei p die Wahrscheinlichkeit eine zu erhalten. Aus der Angabe ergibt sich die folgende Wahrscheinlichkeitsverteilung für die Zufallsvariable Augenzahl : k P(X=k) 8p p p p Da die Summe aller Wahrscheinlichkeiten immer sein muss, gilt: 8p + p + p + p =. Somit ist p = 5. Damit kann jetzt die Frage beantwortet werden: ( ) 8 P (, ) + P (, ) + P (, ) + P (, ) = + 5 ( ) ( ) ( ) + + = 7 7, 78% Frage Für die Berührungspunkte der Tangente an die Funktion muss gelten, dass die. Ableitung mit der Tangentensteigung übereinstimmt, daraus folgt die Gleichung x 8x = mit den Lösungen x = und x =. Eingesetzt in die Funktion ergeben sich mögliche Berührungspunkte B = (, 95 ) und B = (, ). 7 5
6 Setzt man diese Werte in die Tangentengleichung ein, so ergeben sich mögliche Werte für k: k = 67 7 und k = 5 Zur Veranschaulichung: 8 6 B B 6 f 8 Frage Die Terme e sin(x) und 5 cos(x) sind jeweils beschränkt. Grenzwert für x + : Der Zähler geht gegen plus unendlich und der Nenner ist beschränkt, da e x gegen Null geht. Der gesuchte Grenzwert ist plus unendlich, da der Nenner immer positiv und ungleich Null ist. Grenzwert für x : Es ist lim f(x) = x + und damit sind die Voraussetzungen für die Regel von de L Hospital erfüllt: lim f(x) = lim e sin(x) cos(x) x x e x + sin(x) Das Ergebnis ist in diesem Fall Null, da der Zähler beschränkt ist und der Nenner gegen minus unendlich geht. Frage 5 Es seien r der Kreisradius, a die Rechtecksbreite und entsprechend r die Rechteckslänge. Aus U = erhält man die Nebenbedingung rπ Für die zu maximierende Fläche ergbit sich: r πr + a + r =, also a =. F (r, a) = r π + ar F (r) = r π r πr + r F (r) = rπ r = 0 r = 0, 8 π + = ( r r π r ) 6
7 Da F (r) = π < 0 ist, handelt es sich um ein Maximum. Für die Rechtecksbreite a erhält man a = 0, 8, also a = r und für die Rechteckslänge + π r = 0, π Frage 6 Gesucht ist der Mittelpunkt der Kugel M = (x M, y M, z M ) und der Kugelradius r = MT, die Kugelgleichung lautet (x x M ) + (y y M ) + (z z M ) = r. Gegeben ist die Gerade r. Diese Gerade wird mit der Geraden g durch M und T geschnitten. Da der Radius senkrecht zur gegebenen Ebene stehen muss, ergibt sich aus der Ebenengleichung direkt der Richtungsvektor der Geraden und damit eine mögliche Geradengleichung durch den Punkt T als Stützvektor für g: x = 0 + s Schneidet man nun r mit g, so ergibt sich der Schnittpunkt M aus dem Gleichungssystem + s = t, s = t und s = t, man erhält s = und t = und daraus, indem man in eine der beiden Geraden einsetzt, M = (,, ). Für den Radius: r = ( + ) + (0 + ) + ( + ) = Somit ist die Gleichung der Kugeloberfläche: (x + ) + (y + ) + (z + ) = Frage 7 a+ a (x + )dx = 0 [ x + x ] a+ a = 0 (a + ) + (a + ) (a + a) 0 = 0 Die quadratische Gleichung hat die Lösungen a = und a =. a + a 6 = 0 Frage 8 Die Wahrscheinlichkeit bei genau 0 Spielen zu gewinnen ist binomialverteilt mit p = : ( 0 0 ) ( ) 0 ( ) 0 = 0 Man gewinnt nach genau Spielen, wenn man von den ersten 0 genau 9 Mal gewinnt und auch das. Spiel gewinnt: ( 0 9 ) ( ) 9 ( ) = 5 0 Man gewinnt nach genau Spielen, wenn man von den ersten genau 9 Mal gewinnt und auch das. Spiel gewinnt: ( 9 ) ( ) 9 ( ) =
8 Die Wahrscheinlichkeit, dass einer der beiden Spieler also in maximal Spielen gewinnt liegt bei = 79, 9%. 096 Da es laut Angabe egal ist, welcher Spieler gewinnt, verdoppelt sich die Wahrscheinlichkeit: 79, 86% Frage 9 Das Dreieck liegt in der Ebene α, da die Koordinaten von jedem Punkt die Ebenengleichung erfüllen. Das Dreieck ist gleichseitig, da AB = = 8, AC = = 8 und BC = = 8 ist. Der Eckpunkt P des Tetraeders liegt genau senkrecht über bzw. unter dem Schwerpunkt S des ( gleichseitigen Dreiecks ABC. Die Koordinaten des Schwerpunktes S ergeben sich aus ( OA + OB + OC) 7 =,, ). 6 Man kann leicht nachrechnen, dass für die Höhe eines Tetraeders gilt: a (a Seitenkante). In diesem Fall: h =. Die möglichen Eckpunkte P findet man dadurch, dass man von S aus die Höhe in Richtung der normierten (Vektor mit Länge ) Normalen zur Ebene α abträgt. Der Normalvektor kann dabei direkt aus der gegebenen Ebenengleichung abgelesen werden: n =. Der normierte Vektor n 0 =. 7 ±. ( P = (,, 0) und P =, 5, 8 ) OP = OS ± h n 0 = Frage 0 Es ist y = ke kx+ und y = k e kx+. Setzt man diese Ausdrücke in die Differentialgleichung ein, so erhält man: k e kx+ ke kx+ 6e kx+ = 0 : (e kx+ ) 0 k k = 0 (k )(x + ) = 0 Die Werte für k lauten also k = und k =. 8
ist symmetrisch bezüglich der y-achse, da f( x) = f(x) ist. e x + e x = 2 2 (Substitution: a = e x )
 Problemstellung. f() e + e ist symmetrisch bezüglich der y-achse, da f( ) f() ist. Es ist f () e e. Aus f () folgt ; f(). f () e + e vor.
Problemstellung. f() e + e ist symmetrisch bezüglich der y-achse, da f( ) f() ist. Es ist f () e e. Aus f () folgt ; f(). f () e + e vor.
Analysis 2. f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt:
 Analysis 2 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f durch f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt: f (x) = 6(x
Analysis 2 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f durch f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt: f (x) = 6(x
Mathematik für Studierende der Biologie Wintersemester 2017/18. Grundlagentutorium 4 Lösungen
 Mathematik für Studierende der Biologie Wintersemester 207/8 Grundlagentutorium 4 Lösungen Sebastian Groß Termin Mittwochs 5:45 7:45 Großer Hörsaal Biozentrum (B00.09) E-Mail gross@bio.lmu.de Sprechzeiten
Mathematik für Studierende der Biologie Wintersemester 207/8 Grundlagentutorium 4 Lösungen Sebastian Groß Termin Mittwochs 5:45 7:45 Großer Hörsaal Biozentrum (B00.09) E-Mail gross@bio.lmu.de Sprechzeiten
Hauptprüfung Abiturprüfung 2015 (ohne CAS) Baden-Württemberg
 Baden-Württemberg: Abitur 01 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 01 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Baden-Württemberg: Abitur 01 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 01 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Analysis 5.
 Analysis 5 www.schulmathe.npage.de Aufgaben Gegeben ist die Funktion f durch f(x) = 2 e 2 x 2 (x D f ) a) Geben Sie den größtmöglichen Definitionsbereich der Funktion f an und führen Sie für die Funktion
Analysis 5 www.schulmathe.npage.de Aufgaben Gegeben ist die Funktion f durch f(x) = 2 e 2 x 2 (x D f ) a) Geben Sie den größtmöglichen Definitionsbereich der Funktion f an und führen Sie für die Funktion
Abiturprüfung Mathematik 2007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
1.3 Berechnen Sie die Koordinaten der Wendepunkte des Schaubildes der Funktion f mit f( x) x 6x 13
 Musteraufgaben ab 08 Pflichtteil Aufgabe Seite / BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ())
Musteraufgaben ab 08 Pflichtteil Aufgabe Seite / BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ())
Selbsteinschätzungstest Auswertung und Lösung
 Selbsteinschätzungstest Auswertung und Lösung Abgaben: 46 / 587 Maximal erreichte Punktzahl: 8 Minimal erreichte Punktzahl: Durchschnitt: 7 Frage (Diese Frage haben ca. 0% nicht beantwortet.) Welcher Vektor
Selbsteinschätzungstest Auswertung und Lösung Abgaben: 46 / 587 Maximal erreichte Punktzahl: 8 Minimal erreichte Punktzahl: Durchschnitt: 7 Frage (Diese Frage haben ca. 0% nicht beantwortet.) Welcher Vektor
Pflichtteil. Baden-Württemberg Aufgabe 1. Aufgabe 2. Musterlösung. Abitur Mathematik Baden-Württemberg Abitur Mathematik: Musterlösung
 Abitur Mathematik: Baden-Württemberg 14 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer einfachen Funktion u(x) = x und einer Verkettung v(x) = e x
Abitur Mathematik: Baden-Württemberg 14 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer einfachen Funktion u(x) = x und einer Verkettung v(x) = e x
a) Begründen Sie, dass der Graph von f symmetrisch zum Punkt S 0 2 f) Ermitteln Sie eine Gleichung der Tangente im Punkt B
 I. Wendepunkte 1. Bestimmen Sie Art und Lage der Extrempunkte sowie die Wendepunkte des Graphen der Funktion f mit der angegebenen Funktionsgleichung. a) f(x) 1 b) 12 (x + 1) (x 2) (x + 6) f(x) 1 4 x4
I. Wendepunkte 1. Bestimmen Sie Art und Lage der Extrempunkte sowie die Wendepunkte des Graphen der Funktion f mit der angegebenen Funktionsgleichung. a) f(x) 1 b) 12 (x + 1) (x 2) (x + 6) f(x) 1 4 x4
G13 KLAUSUR 1. (1) (2 VP) Bilden Sie die erste Ableitung der Funktion f mit. f(x) = e 2x+1 x
 G3 KLAUSUR PFLICHTTEIL Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () (2 VP) Bilden Sie die erste Ableitung der Funktion f mit f(x) = e 2x+. x (2) (2 VP) Gegeben ist die Funktion f mit f(x)
G3 KLAUSUR PFLICHTTEIL Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () (2 VP) Bilden Sie die erste Ableitung der Funktion f mit f(x) = e 2x+. x (2) (2 VP) Gegeben ist die Funktion f mit f(x)
Analysis 8.
 Analysis 8 www.schulmathe.npage.de Aufgaben Gegeben sind die Funktionen f a durch f a (x) = a x x + (x R x ; a R a ) a) Geben Sie die Koordinaten der Schnittpunkte der Graphen der Funktionen f a mit den
Analysis 8 www.schulmathe.npage.de Aufgaben Gegeben sind die Funktionen f a durch f a (x) = a x x + (x R x ; a R a ) a) Geben Sie die Koordinaten der Schnittpunkte der Graphen der Funktionen f a mit den
a) Im Berührungspunkt müssen die y-werte und die Steigungen übereinstimmen:
 . ANALYSIS Gegeben ist die kubische Parabel f: y = x 3 6x + 8x + a) Die Gerade g: y = k x + berührt die Parabel an der Stelle x = x 0 > 0. Bestimmen Sie den Parameter k. b) Berechnen Sie den Inhalt der
. ANALYSIS Gegeben ist die kubische Parabel f: y = x 3 6x + 8x + a) Die Gerade g: y = k x + berührt die Parabel an der Stelle x = x 0 > 0. Bestimmen Sie den Parameter k. b) Berechnen Sie den Inhalt der
Arbeiten ( )
 Lösungen für die Prüfung zu Einführung in das mathematische Arbeiten (3.2.2002). Dieses Beispiel ist eine umgekehrte Kurvendiskussion. (a) Um die Koeffizienten von f zu bestimmen, können wir ansetzen f(x)
Lösungen für die Prüfung zu Einführung in das mathematische Arbeiten (3.2.2002). Dieses Beispiel ist eine umgekehrte Kurvendiskussion. (a) Um die Koeffizienten von f zu bestimmen, können wir ansetzen f(x)
Analysis 7. f(x) = 4 x (x R)
 Analysis 7 www.schulmathe.npage.de Aufgaben Gegeben ist die Funktion f durch fx) = 4 x R) a) Führen Sie für die Funktion f eine Kurvendiskussion durch Nullstellen, Koordinaten der lokalen Extrempunkte,
Analysis 7 www.schulmathe.npage.de Aufgaben Gegeben ist die Funktion f durch fx) = 4 x R) a) Führen Sie für die Funktion f eine Kurvendiskussion durch Nullstellen, Koordinaten der lokalen Extrempunkte,
Bayern Teil 1. Aufgabe 1. Abitur Mathematik: Musterlösung. Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten:
 Abitur Mathematik: Bayern 2013 Teil 1 Aufgabe 1 a) 1. SCHRITT: DEFINITIONSMENGE BESTIMMEN Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten: 3x + 9 0 x 3 2. SCHRITT: NULLSTELLEN
Abitur Mathematik: Bayern 2013 Teil 1 Aufgabe 1 a) 1. SCHRITT: DEFINITIONSMENGE BESTIMMEN Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten: 3x + 9 0 x 3 2. SCHRITT: NULLSTELLEN
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil Wahlteil Analysis 8 Wahlteil Analysis Wahlteil Analysis 9 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 9 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Pflichtteil Wahlteil Analysis 8 Wahlteil Analysis Wahlteil Analysis 9 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 9 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Mathematik Übungsklausur 2013 Ausführliche Lösungen
 Mathematik Übungsklausur 0 Ausführliche Lösungen Analysis Aufgabe Die Nullstellen einer Funktion f mit Definitionsbereich D f sind die Lösungen der Gleichung f(x) = 0 in D f. Damit erhält man: a) f: x
Mathematik Übungsklausur 0 Ausführliche Lösungen Analysis Aufgabe Die Nullstellen einer Funktion f mit Definitionsbereich D f sind die Lösungen der Gleichung f(x) = 0 in D f. Damit erhält man: a) f: x
LMU MÜNCHEN. Mathematik für Studierende der Biologie Wintersemester 2016/17. GRUNDLAGENTUTORIUM 5 - Lösungen. Anmerkung
 LMU MÜNCHEN Mathematik für Studierende der Biologie Wintersemester 2016/17 GRUNDLAGENTUTORIUM 5 - Lösungen Anmerkung Es handelt sich hierbei um eine Musterlösung so wie es von Ihnen in einer Klausur erwartet
LMU MÜNCHEN Mathematik für Studierende der Biologie Wintersemester 2016/17 GRUNDLAGENTUTORIUM 5 - Lösungen Anmerkung Es handelt sich hierbei um eine Musterlösung so wie es von Ihnen in einer Klausur erwartet
Inhalt der Lösungen zur Prüfung 2015:
 Inhalt der Lösungen zur Prüfung : Pflichtteil... Wahlteil Analysis... 8 Wahlteil Analysis... Wahlteil Analytische Geometrie/Stochastik... Wahlteil Analytische Geometrie/Stochastik... 9 Pflichtteil Lösungen
Inhalt der Lösungen zur Prüfung : Pflichtteil... Wahlteil Analysis... 8 Wahlteil Analysis... Wahlteil Analytische Geometrie/Stochastik... Wahlteil Analytische Geometrie/Stochastik... 9 Pflichtteil Lösungen
MATHEMATIK K1. Gesamtpunktzahl /30 Notenpunkte. (1) Bestimmen Sie die erste Ableitung folgender Funktionen: a) f(x) = 2x 3 cos(x) + x
 MATHEMATIK K 06.0.206 Aufgabe 2 3 4 5 6 7 8 Punkte (max 8 2 3 5 4 3 3 2 Punkte Gesamtpunktzahl /30 Notenpunkte ( Bestimmen Sie die erste Ableitung folgender Funktionen: a f(x 2x 3 cos(x + x b g(x 2 3x
MATHEMATIK K 06.0.206 Aufgabe 2 3 4 5 6 7 8 Punkte (max 8 2 3 5 4 3 3 2 Punkte Gesamtpunktzahl /30 Notenpunkte ( Bestimmen Sie die erste Ableitung folgender Funktionen: a f(x 2x 3 cos(x + x b g(x 2 3x
Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1
![Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1 Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1](/thumbs/91/105628768.jpg) Abitur Mathematik: Bayern 2012 Teil 1 Aufgabe 1 a) DEFINITIONSMENGE f(x) = ln(x + 3) x + 3 > 0 x > 3 D f =] 3; + [ ABLEITUNG Kettenregel liefert f (x) = 1 x + 3 1 = 1 x + 3 b) DEFINITIONSMENGE 3 g(x) =
Abitur Mathematik: Bayern 2012 Teil 1 Aufgabe 1 a) DEFINITIONSMENGE f(x) = ln(x + 3) x + 3 > 0 x > 3 D f =] 3; + [ ABLEITUNG Kettenregel liefert f (x) = 1 x + 3 1 = 1 x + 3 b) DEFINITIONSMENGE 3 g(x) =
Abitur 2014 Mathematik Infinitesimalrechnung I
 Seite http://www.abiturloesung.de/ Seite 2 Abitur 204 Mathematik Infinitesimalrechnung I Die Abbildung zeigt den Graphen einer Funktion f. Teilaufgabe Teil A (5 BE) Gegeben ist die Funktion f : x x ln
Seite http://www.abiturloesung.de/ Seite 2 Abitur 204 Mathematik Infinitesimalrechnung I Die Abbildung zeigt den Graphen einer Funktion f. Teilaufgabe Teil A (5 BE) Gegeben ist die Funktion f : x x ln
Extremstellenbestimmung: A'(a) = 50 2a = 0 a = 25 und damit b = 25.
 6. Anwendungen der Differentialrechnung 6. Extremwertaufgben Eine Größe G hänge von mehreren Variablen ab. Wenn man sich dafür interesssiert, für welche Werte dieser Variablen die davon abhängige Größe
6. Anwendungen der Differentialrechnung 6. Extremwertaufgben Eine Größe G hänge von mehreren Variablen ab. Wenn man sich dafür interesssiert, für welche Werte dieser Variablen die davon abhängige Größe
Prof. Schneider Höhere Mathematik I/II Musterlösung A = x 1 = 6x 1 + x 3 x 2 = 2x 2 x 3 = x 1 + 6x 3
 Aufgabe ( Punkte) a) Bestimmen Sie die Eigenwerte und Eigenvektoren der Matrix 6 A = 6 b) Bestimmen Sie die allgemeine Lösung des Differentialgleichungssystems x = 6x + x 3 x = x x 3 = x + 6x 3 c) Bestimmen
Aufgabe ( Punkte) a) Bestimmen Sie die Eigenwerte und Eigenvektoren der Matrix 6 A = 6 b) Bestimmen Sie die allgemeine Lösung des Differentialgleichungssystems x = 6x + x 3 x = x x 3 = x + 6x 3 c) Bestimmen
K2 MATHEMATIK KLAUSUR 1. Gesamtpunktzahl /30 Notenpunkte. (1) Bilden Sie die erste Ableitung der Funktion f mit f(x) = 1 + x ln(2x + 1).
 K MATHEMATIK KLAUSUR NACHTERMIN..6 Aufgabe 3 4 6 7 8 9 Punkte (max 3 3 4 4 Punkte Gesamtpunktzahl /3 Notenpunkte ( Bilden Sie die erste Ableitung der Funktion f mit f(x = + x ln(x +. ( Bestimmen Sie das
K MATHEMATIK KLAUSUR NACHTERMIN..6 Aufgabe 3 4 6 7 8 9 Punkte (max 3 3 4 4 Punkte Gesamtpunktzahl /3 Notenpunkte ( Bilden Sie die erste Ableitung der Funktion f mit f(x = + x ln(x +. ( Bestimmen Sie das
Differenzial- und Integralrechnung II
 Differenzial- und Integralrechnung II Rainer Hauser Dezember 011 1 Einleitung 1.1 Ableitung Die Ableitung einer Funktion f: R R, x f(x) ist definiert als f (x) = df(x) dx = d f(x + h) f(x) f(x) = lim dx
Differenzial- und Integralrechnung II Rainer Hauser Dezember 011 1 Einleitung 1.1 Ableitung Die Ableitung einer Funktion f: R R, x f(x) ist definiert als f (x) = df(x) dx = d f(x + h) f(x) f(x) = lim dx
Kurvendiskussion. Gesetzmäßigkeiten. Lineare Funktionen. Funktionsgleichung
 Kurvendiskussion Gesetzmäßigkeiten Lineare Funktionen Funktionsgleichung y = mx + c m: Steigung c: y-achsenabschnitt (Funktionswert für y, bei dem der Graph die y-achse schneidet Beispiel : y = x 3 mit
Kurvendiskussion Gesetzmäßigkeiten Lineare Funktionen Funktionsgleichung y = mx + c m: Steigung c: y-achsenabschnitt (Funktionswert für y, bei dem der Graph die y-achse schneidet Beispiel : y = x 3 mit
Abitur 2017 Mathematik Infinitesimalrechnung I
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion g : x 2 4 + x 1 mit maximaler Definitionsmenge D g. Der Graph von g wird mit G g bezeichnet.
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion g : x 2 4 + x 1 mit maximaler Definitionsmenge D g. Der Graph von g wird mit G g bezeichnet.
Differenzialrechnung
 Mathe Differenzialrechnung Differenzialrechnung 1. Grenzwerte von Funktionen Idee: Gegeben eine Funktion: Gesucht: y = f(x) lim f(x) = g s = Wert gegen den die Funktion streben soll (meist 0 oder ) g =
Mathe Differenzialrechnung Differenzialrechnung 1. Grenzwerte von Funktionen Idee: Gegeben eine Funktion: Gesucht: y = f(x) lim f(x) = g s = Wert gegen den die Funktion streben soll (meist 0 oder ) g =
Übungsaufgaben zur Kurvendiskussion
 SZ Neustadt Mathematik Torsten Warncke FOS 12c 30.01.2008 Übungsaufgaben zur Kurvendiskussion 1. Gegeben ist die Funktion f(x) = x(x 3) 2. (a) Untersuchen Sie die Funktion auf Symmetrie. (b) Bestimmen
SZ Neustadt Mathematik Torsten Warncke FOS 12c 30.01.2008 Übungsaufgaben zur Kurvendiskussion 1. Gegeben ist die Funktion f(x) = x(x 3) 2. (a) Untersuchen Sie die Funktion auf Symmetrie. (b) Bestimmen
Matur-/Abituraufgaben Analysis
 Matur-/Abituraufgaben Analysis 1. Tropfen Die folgende Skizze zeigt die Kurve k mit der Gleichung y = (1 ) im Intervall 1. Die Kurve k bildet zusammen mit ihrem Spiegelbild k eine zur -Achse symmetrische
Matur-/Abituraufgaben Analysis 1. Tropfen Die folgende Skizze zeigt die Kurve k mit der Gleichung y = (1 ) im Intervall 1. Die Kurve k bildet zusammen mit ihrem Spiegelbild k eine zur -Achse symmetrische
Mathemathik-Prüfungen
 M. Arend Stand Juni 2005 Seite 1 1980: Mathemathik-Prüfungen 1980-2005 1. Eine zur y-achse symmetrische Parabel 4.Ordnung geht durch P 1 (0 4) und hat in P 2 (-1 1) einen Wendepunkt. 2. Diskutieren Sie
M. Arend Stand Juni 2005 Seite 1 1980: Mathemathik-Prüfungen 1980-2005 1. Eine zur y-achse symmetrische Parabel 4.Ordnung geht durch P 1 (0 4) und hat in P 2 (-1 1) einen Wendepunkt. 2. Diskutieren Sie
PFLICHTTEIL NT = e x (x+2) = x+2 Oder Umschreiben: f(x) = 1. = (x 2 e x ) 1, und dann Kettenregel
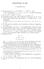 PFLICHTTEIL NT 26 F. LEMMERMEYER (1 Quotientenregel: f (x = x2 e x 2xe x x = e x (x+2 4 x = x+2 3 x 3 e. x Oder Umschreiben: f(x = 1 x 2 e = (x 2 e x 1, und dann Kettenregel x f (x = (x 2 e x 2 (2xe x
PFLICHTTEIL NT 26 F. LEMMERMEYER (1 Quotientenregel: f (x = x2 e x 2xe x x = e x (x+2 4 x = x+2 3 x 3 e. x Oder Umschreiben: f(x = 1 x 2 e = (x 2 e x 1, und dann Kettenregel x f (x = (x 2 e x 2 (2xe x
Abitur 2010 Mathematik GK Infinitesimalrechnung I
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2010 Mathematik GK Infinitesimalrechnung I Teilaufgabe 2 (4 BE) Gegeben ist für k R + die Schar von Funktionen f k : x 1 Definitionsbereich D k. Der
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2010 Mathematik GK Infinitesimalrechnung I Teilaufgabe 2 (4 BE) Gegeben ist für k R + die Schar von Funktionen f k : x 1 Definitionsbereich D k. Der
Matura2016-Lösung. Problemstellung 1
 Matura-Lösung Problemstellung. Die Funktion f( = + 9k + müsste bei = den Wert annehmen, also gilt + 9k + = k =. Wir betrachten den Bereich mit positiven Werten. Dann gilt: f ( = 8 + 8 = = ; = Bei liegt
Matura-Lösung Problemstellung. Die Funktion f( = + 9k + müsste bei = den Wert annehmen, also gilt + 9k + = k =. Wir betrachten den Bereich mit positiven Werten. Dann gilt: f ( = 8 + 8 = = ; = Bei liegt
Abiturprüfung Mathematik 2005 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A
 Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A Für jedes a > ist eine Funktion f a definiert durch fa (x) = x (x a) mit x R a Das Schaubild von f
Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A Für jedes a > ist eine Funktion f a definiert durch fa (x) = x (x a) mit x R a Das Schaubild von f
1. Fall: 2. Fall: Lösungsblatt zu: Differentialquotient. Tipp: Nullstellen. Tipp: Es reicht, wenn einer der Faktoren Null wird.
 Lösungsblatt zu: Differentialquotient Aufgabe 1: Gegeben: f(x) = 0,5x 3 1,5x² a) Bestimmen Sie die Nullstellen: Nullstellen f(x) = 0 0,5x 3 1,5x 2 = 0 ( 0,5x 2 ausklammern) 0,5x 2 (x + 3) = 0 Es reicht,
Lösungsblatt zu: Differentialquotient Aufgabe 1: Gegeben: f(x) = 0,5x 3 1,5x² a) Bestimmen Sie die Nullstellen: Nullstellen f(x) = 0 0,5x 3 1,5x 2 = 0 ( 0,5x 2 ausklammern) 0,5x 2 (x + 3) = 0 Es reicht,
) (1 BE) 1 2 ln 2. und somit
 1 Aufgaben aus dem Aufgabenpool 1 1.1 Analysis A1_1 Eine Funktion f ist durch 1 x f(x) e 1, x IR, gegeben. Ermitteln Sie die Nullstelle der Funktion f. ( ) b) Die Tangente an den Graphen von f im Punkt
1 Aufgaben aus dem Aufgabenpool 1 1.1 Analysis A1_1 Eine Funktion f ist durch 1 x f(x) e 1, x IR, gegeben. Ermitteln Sie die Nullstelle der Funktion f. ( ) b) Die Tangente an den Graphen von f im Punkt
Klausur zur Mathematik für Maschinentechniker
 SS 04. 09. 004 Klausur zur Mathematik für Maschinentechniker Apl. Prof. Dr. G. Herbort Aufgabe. Es sei f die folgende Funktion f(x) = 4x 4x 9x 6 x (i) Was ist der Definitionsbereich von f? Woistf differenzierbar,
SS 04. 09. 004 Klausur zur Mathematik für Maschinentechniker Apl. Prof. Dr. G. Herbort Aufgabe. Es sei f die folgende Funktion f(x) = 4x 4x 9x 6 x (i) Was ist der Definitionsbereich von f? Woistf differenzierbar,
Prüfungsteil B, Aufgabengruppe 1: Analysis. Bayern Aufgabe 1. BundesabiturMathematik: Musterlösung
 Abitur MathematikBayern 04 Prüfungsteil B, Aufgabengruppe BundesabiturMathematik: Prüfungsteil B, Aufgabengruppe : Bayern 04 Aufgabe a). SCHRITT: SCHNITTPUNKTE MIT DEN KOORDINATENACHSEN Die Koordinatenachsen
Abitur MathematikBayern 04 Prüfungsteil B, Aufgabengruppe BundesabiturMathematik: Prüfungsteil B, Aufgabengruppe : Bayern 04 Aufgabe a). SCHRITT: SCHNITTPUNKTE MIT DEN KOORDINATENACHSEN Die Koordinatenachsen
Klausur Mathematik I
 Klausur Mathematik I E-Techniker/Mechatroniker/Informatiker/W-Ingenieure). März 007 Hans-Georg Rück) Aufgabe 6 Punkte): a) Berechnen Sie alle komplexen Zahlen z mit der Eigenschaft z z = und z ) z ) =.
Klausur Mathematik I E-Techniker/Mechatroniker/Informatiker/W-Ingenieure). März 007 Hans-Georg Rück) Aufgabe 6 Punkte): a) Berechnen Sie alle komplexen Zahlen z mit der Eigenschaft z z = und z ) z ) =.
Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler
 Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler. (a) Bestimmen Sie die kartesische Form von Wintersemester 7/8 (..8) z = ( + i)( i) + ( + i). (b) Bestimmen Sie sämtliche komplexen Lösungen
Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler. (a) Bestimmen Sie die kartesische Form von Wintersemester 7/8 (..8) z = ( + i)( i) + ( + i). (b) Bestimmen Sie sämtliche komplexen Lösungen
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
Selbsteinschätzungstest
 D-MATH ETHZ-Semesterbeginn HS 0 Selbsteinschätzungstest Dieser Test bietet Ihnen die Möglichkeit, Ihre mathematischen Schulkenntnisse abzurufen und zu überprüfen. Die Teilnahme ist freiwillig. Bei jeder
D-MATH ETHZ-Semesterbeginn HS 0 Selbsteinschätzungstest Dieser Test bietet Ihnen die Möglichkeit, Ihre mathematischen Schulkenntnisse abzurufen und zu überprüfen. Die Teilnahme ist freiwillig. Bei jeder
Demo: Mathe-CD. Prüfungsaufgaben Mündliches Abitur. Analysis. Teilbereich 1: Ganzrationale Funktionen 1. März 2002
 Prüfungsaufgaben Mündliches Abitur Analysis Teilbereich : Ganzrationale Funktionen Hier nur Aufgaben als Demo Datei Nr. 9 März 00 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK Vorwort Die in dieser Reihe von
Prüfungsaufgaben Mündliches Abitur Analysis Teilbereich : Ganzrationale Funktionen Hier nur Aufgaben als Demo Datei Nr. 9 März 00 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK Vorwort Die in dieser Reihe von
Kurvendiskussion Ganzrationale Funktion Aufgaben und Lösungen
 Kurvendiskussion Ganzrationale Funktion Aufgaben und http://www.fersch.de Klemens Fersch 9. August 0 Inhaltsverzeichnis Ganzrationale Funktion Quadratische Funktionen f x) = ax + bx + c 8. Aufgaben...................................................
Kurvendiskussion Ganzrationale Funktion Aufgaben und http://www.fersch.de Klemens Fersch 9. August 0 Inhaltsverzeichnis Ganzrationale Funktion Quadratische Funktionen f x) = ax + bx + c 8. Aufgaben...................................................
Technische Universität München Zentrum Mathematik. Übungsblatt 4
 Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 4 Hausaufgaben Aufgabe 4. Gegeben sei die Funktion f : D R mit f(x) :=
Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 4 Hausaufgaben Aufgabe 4. Gegeben sei die Funktion f : D R mit f(x) :=
Prof. Steinwart Höhere Mathematik I/II Musterlösung A =
 Prof. Steinwart Höhere Mathematik I/II Musterlösung 9.8.6 Aufgabe Punkte a Berechnen Sie die Eigenwerte der folgenden Matrix: A 3 b Es sei 4 A. 8 5 Bestimmen Sie P, P M, und eine Diagonalmatrix D M, so,
Prof. Steinwart Höhere Mathematik I/II Musterlösung 9.8.6 Aufgabe Punkte a Berechnen Sie die Eigenwerte der folgenden Matrix: A 3 b Es sei 4 A. 8 5 Bestimmen Sie P, P M, und eine Diagonalmatrix D M, so,
( ) Dann gilt f(x) g(x) in der Nähe von x 0, das heisst. Für den Fehler r(h) dieser Näherung erhält man unter Verwendung von ( )
 64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
Gemischte Aufgaben zur Differentialund Integralrechnung
 Gemischte Aufgaben zur Differentialund Integralrechnung W. Kippels 0. Mai 04 Inhaltsverzeichnis Aufgaben. Aufgabe.................................... Aufgabe.................................... Aufgabe...................................
Gemischte Aufgaben zur Differentialund Integralrechnung W. Kippels 0. Mai 04 Inhaltsverzeichnis Aufgaben. Aufgabe.................................... Aufgabe.................................... Aufgabe...................................
Abschlussaufgabe Nichttechnik - Analysis I - Lsg.
 Analysis NT GS -.6.7 - m7_nta_l.mcd Abschlussaufgabe 7 - Nichttechnik - Analysis I - Lsg.. Gegeben sind die reellen Funktionen f k ( x) und ID fk ( ) x k x k x mit k IR k IR. Der Graph einer solchen Funktion
Analysis NT GS -.6.7 - m7_nta_l.mcd Abschlussaufgabe 7 - Nichttechnik - Analysis I - Lsg.. Gegeben sind die reellen Funktionen f k ( x) und ID fk ( ) x k x k x mit k IR k IR. Der Graph einer solchen Funktion
Koordinatengeometrie. Aufgabe 4 Untersuchen Sie die Funktion f(x) = x² 9.
 Koordinatengeometrie Aufgabe 1 Gegeben sind der Punkt P (-1; 9) sowie die Geraden g: 3x y + 6 = 0 und h: x + 4y 8 = 0. a) Die Geraden g und h schneiden einander im Punkt S. Berechnen Sie die exakten Koordinaten
Koordinatengeometrie Aufgabe 1 Gegeben sind der Punkt P (-1; 9) sowie die Geraden g: 3x y + 6 = 0 und h: x + 4y 8 = 0. a) Die Geraden g und h schneiden einander im Punkt S. Berechnen Sie die exakten Koordinaten
Aufgaben für Analysis in der Oberstufe. Robert Rothhardt
 Aufgaben für Analysis in der Oberstufe Robert Rothhardt 14. Juni 2011 2 Inhaltsverzeichnis 1 Modellierungsaufgaben 5 1.1 Musterabitur S60................................ 5 1.2 Musterabitur 3.1.4 B / S61..........................
Aufgaben für Analysis in der Oberstufe Robert Rothhardt 14. Juni 2011 2 Inhaltsverzeichnis 1 Modellierungsaufgaben 5 1.1 Musterabitur S60................................ 5 1.2 Musterabitur 3.1.4 B / S61..........................
Pflichtteil. Baden-Württemberg Aufgabe 1. Aufgabe 2. Musterlösung. Abitur Mathematik Baden-Württemberg Abitur Mathematik: Musterlösung
 Abitur Mathematik: Baden-Württemberg 2013 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer ganzrationalen Funktion u(x) = 2x 2 + 5x und einer Verkettung
Abitur Mathematik: Baden-Württemberg 2013 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer ganzrationalen Funktion u(x) = 2x 2 + 5x und einer Verkettung
K A N T O N S S C H U L E I M L E E MATHEMATIK. Grafiktaschenrechner ohne CAS, beliebige Formelsammlung
 K A N T O N S S C H U L E I M L E E W I N T E R T H U R MATURITÄTSPRÜFUNGEN 06 Klasse: 4g Profil: MN Lehrperson: Rolf Kleiner MATHEMATIK Zeit: 3 Stunden Erlaubte Hilfsmittel: Grafiktaschenrechner ohne
K A N T O N S S C H U L E I M L E E W I N T E R T H U R MATURITÄTSPRÜFUNGEN 06 Klasse: 4g Profil: MN Lehrperson: Rolf Kleiner MATHEMATIK Zeit: 3 Stunden Erlaubte Hilfsmittel: Grafiktaschenrechner ohne
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil... Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analysis 3... 5 Wahlteil Analytische Geometrie... Wahlteil Analytische Geometrie... Lösungen: 00 Pflichtteil Lösungen zur Prüfung 00: Pflichtteil
Pflichtteil... Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analysis 3... 5 Wahlteil Analytische Geometrie... Wahlteil Analytische Geometrie... Lösungen: 00 Pflichtteil Lösungen zur Prüfung 00: Pflichtteil
K A N T O N S S C H U L E I M L E E MATHEMATIK. Grafiktaschenrechner ohne CAS, beliebige Formelsammlung
 K A N T O N S S C H U L E I M L E E W I N T E R T H U R MATURITÄTSPRÜFUNGEN 017 Klasse: g Profil: MN / M Lehrperson: Rolf Kleiner MATHEMATIK Zeit: 3 Stunden Erlaubte Hilfsmittel: Grafiktaschenrechner ohne
K A N T O N S S C H U L E I M L E E W I N T E R T H U R MATURITÄTSPRÜFUNGEN 017 Klasse: g Profil: MN / M Lehrperson: Rolf Kleiner MATHEMATIK Zeit: 3 Stunden Erlaubte Hilfsmittel: Grafiktaschenrechner ohne
Übungsbeispiele Differential- und Integralrechnung
 Übungsbeispiele Differential- und Integralrechnung A) Gegeben ist die Funktion: y = 2x 3 9x 2 + 12x. a) Skizzieren Sie die Funktion im Intervall [ 0,5; 3] b) Diskutieren Sie die Funktion (Nullstellen,
Übungsbeispiele Differential- und Integralrechnung A) Gegeben ist die Funktion: y = 2x 3 9x 2 + 12x. a) Skizzieren Sie die Funktion im Intervall [ 0,5; 3] b) Diskutieren Sie die Funktion (Nullstellen,
(Tipp: Formelbuch!) x3 dx?
 Integralrechnung. bestimmte und unbestimmte Integrale (a) x ( + x ) dx =? (b) e x + e x dx =? (c) x 3 x + x x 6x + 9 dx =? (d) x cos x dx =?. Bestimmtes Integral x3 3x + 9 x dx =? 4 3. Bestimmtes Integral
Integralrechnung. bestimmte und unbestimmte Integrale (a) x ( + x ) dx =? (b) e x + e x dx =? (c) x 3 x + x x 6x + 9 dx =? (d) x cos x dx =?. Bestimmtes Integral x3 3x + 9 x dx =? 4 3. Bestimmtes Integral
Staatsexamen Herbst 2017 Differential- und Integralrechnung, Thema I
 Staatsexamen Herbst 17 Differential- und Integralrechnung, Thema I 1. a) Die Aussage ist wahr! Sei s R der Reihenwert der Reihe k=1 Da a n = s n s n 1 für n, ist also b) Die Aussage ist falsch! a k, also
Staatsexamen Herbst 17 Differential- und Integralrechnung, Thema I 1. a) Die Aussage ist wahr! Sei s R der Reihenwert der Reihe k=1 Da a n = s n s n 1 für n, ist also b) Die Aussage ist falsch! a k, also
B Anwendungen der Differenzialrechnung
 B Anwendungen der Differenzialrechnung Kurvendiskussionen Um den Verlauf eines Funktionsgraphen zu bestimmen, kann eine Wertetabelle aufgestellt werden. Dies kann jedoch sehr mühselig sein und es ist nicht
B Anwendungen der Differenzialrechnung Kurvendiskussionen Um den Verlauf eines Funktionsgraphen zu bestimmen, kann eine Wertetabelle aufgestellt werden. Dies kann jedoch sehr mühselig sein und es ist nicht
Selbsteinschätzungstest
 D-MATH ETHZ-Semesterbeginn HS 05 Selbsteinschätzungstest Dieser Test bietet Ihnen die Möglichkeit, Ihre mathematischen Schulkenntnisse abzurufen und zu überprüfen. Die Teilnahme ist freiwillig. Bei jeder
D-MATH ETHZ-Semesterbeginn HS 05 Selbsteinschätzungstest Dieser Test bietet Ihnen die Möglichkeit, Ihre mathematischen Schulkenntnisse abzurufen und zu überprüfen. Die Teilnahme ist freiwillig. Bei jeder
5.3. Aufgaben zur Kurvenuntersuchung ganzrationaler Funktionen
 .. Aufgaben zur Kurvenuntersuchung ganzrationaler Funktionen Aufgabe : Kurvendiskussion Untersuche die folgenden Funktionen auf Symmetrie, Achsenschnittpunkte, Extrem- und Wendepunkte und zeichne ein Schaubild
.. Aufgaben zur Kurvenuntersuchung ganzrationaler Funktionen Aufgabe : Kurvendiskussion Untersuche die folgenden Funktionen auf Symmetrie, Achsenschnittpunkte, Extrem- und Wendepunkte und zeichne ein Schaubild
Algebra 4.
 Algebra 4 www.schulmathe.npage.de Aufgaben In einem kartesischen ( Koordinatensystem ) sind die Punkte A( ), B( ), C(5 ), D( 4 0) und S gegeben. a) Die Punkte A, B und C liegen in einer Ebene E. Stellen
Algebra 4 www.schulmathe.npage.de Aufgaben In einem kartesischen ( Koordinatensystem ) sind die Punkte A( ), B( ), C(5 ), D( 4 0) und S gegeben. a) Die Punkte A, B und C liegen in einer Ebene E. Stellen
Mathematik verstehen 7 Lösungsblatt Aufgabe 6.67
 Aufgabenstellung: Berechne die Schnittpunkte der e k1 und k mit den Mittelpunkten M1 bzw. M und den Radien r1 bzw. r a. k1: M1 3, 4, P 5, 3 k 1, k geht durch A 0 und B 4 0 r 5 M liegt im 1. Quadranten
Aufgabenstellung: Berechne die Schnittpunkte der e k1 und k mit den Mittelpunkten M1 bzw. M und den Radien r1 bzw. r a. k1: M1 3, 4, P 5, 3 k 1, k geht durch A 0 und B 4 0 r 5 M liegt im 1. Quadranten
Aufgabe 2 Die Abbildung zeigt den Graphen einer ganzrationalen Funktion f.
 Aufgabe 1 Die Abbildung zeigt den Graphen G f einer für 1 x 3 mit x R definierten Funktion f, die bei x= 1; x=1und x=3 Nullstellen besitzt. Die Funktion F mit F( x)= 1 6 ( x2 +2 x+3 ) 3 ist eine Stammfunktion
Aufgabe 1 Die Abbildung zeigt den Graphen G f einer für 1 x 3 mit x R definierten Funktion f, die bei x= 1; x=1und x=3 Nullstellen besitzt. Die Funktion F mit F( x)= 1 6 ( x2 +2 x+3 ) 3 ist eine Stammfunktion
Abitur 2012 Mathematik Infinitesimalrechnung I
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 212 Mathematik Infinitesimalrechnung I Geben Sie zu den Funktionstermen jeweils den maximalen Definitionsbereich sowie einen Term der Ableitungsfunktion
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 212 Mathematik Infinitesimalrechnung I Geben Sie zu den Funktionstermen jeweils den maximalen Definitionsbereich sowie einen Term der Ableitungsfunktion
Lösungsblatt zu: Gebrochen rationale, Exponential- und Logarithmus Funktionen
 Lösungsblatt zu: Gebrochen rationale, Exponential- und Logarithmus Funktionen Das hast du schon gelernt: Aufgabe : a) Definitionsbereich TIPP: Definitionsbereich Nenner darf nicht Null werden x 0 x
Lösungsblatt zu: Gebrochen rationale, Exponential- und Logarithmus Funktionen Das hast du schon gelernt: Aufgabe : a) Definitionsbereich TIPP: Definitionsbereich Nenner darf nicht Null werden x 0 x
streng monoton steigend. streng monoton fallend. Ist f eine in einem Intervall stetige und im Innern des Intervalls differenzierbare Funktion mit
 3. Anwendungen ================================================================= 3.1 Monotonie Eine Funktion f heißt in ihrem Definitionsbereich D monoton steigend, wenn für alle x 1, x 2 D mit x 1 < x
3. Anwendungen ================================================================= 3.1 Monotonie Eine Funktion f heißt in ihrem Definitionsbereich D monoton steigend, wenn für alle x 1, x 2 D mit x 1 < x
Höhere Mathematik I: Klausur Prof Dr. Irene Bouw
 Höhere Mathematik I: Klausur Prof Dr. Irene Bouw Es gibt 5 Punkte pro Teilaufgabe, also insgesamt 85 Punkte. Die Klausureinsicht findet am Montag, den 5..8 ab : Uhr im H3 statt. Aufgabe. (a) Lösen Sie
Höhere Mathematik I: Klausur Prof Dr. Irene Bouw Es gibt 5 Punkte pro Teilaufgabe, also insgesamt 85 Punkte. Die Klausureinsicht findet am Montag, den 5..8 ab : Uhr im H3 statt. Aufgabe. (a) Lösen Sie
)e2 (3 x2 ) a) Untersuchen Sie den Graphen auf Symmetrie, ermitteln Sie die Nullstellen von f und bestimmen Sie das Verhalten von f für x.
 Analysis Aufgabe aus Abiturprüfung Bayern GK (abgeändert). Gegeben ist die Funktion f(x) = ( x )e ( x ). a) Untersuchen Sie den Graphen auf Symmetrie, ermitteln Sie die Nullstellen von f und bestimmen
Analysis Aufgabe aus Abiturprüfung Bayern GK (abgeändert). Gegeben ist die Funktion f(x) = ( x )e ( x ). a) Untersuchen Sie den Graphen auf Symmetrie, ermitteln Sie die Nullstellen von f und bestimmen
Klausurenkurs zum Staatsexamen (WS 2016/17): Differential und Integralrechnung 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 206/7): Differential und Integralrechnung 3 3. (Herbst 20, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 206/7): Differential und Integralrechnung 3 3. (Herbst 20, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende
 Abiturprüfung Mathematik 006 Baden-Württemberg (ohne CAS) Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit f(x) sin(4x ). Aufgabe : ( VP) Geben Sie eine Stammfunktion
Abiturprüfung Mathematik 006 Baden-Württemberg (ohne CAS) Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit f(x) sin(4x ). Aufgabe : ( VP) Geben Sie eine Stammfunktion
Studienberechtigungsprüfung Mathematik VHS Floridsdorf
 Studienberechtigungsprüfung Mathematik VHS Floridsdorf von Dr. Manfred Gurtner Würl 0/ Teil für : ) Zahlenrechnen und Taschenrechner: a) Berechnen Sie: [( 6) ( ) (+)] [( 0)+(+)] (+5) + ( ) = 5 b) Berechnen
Studienberechtigungsprüfung Mathematik VHS Floridsdorf von Dr. Manfred Gurtner Würl 0/ Teil für : ) Zahlenrechnen und Taschenrechner: a) Berechnen Sie: [( 6) ( ) (+)] [( 0)+(+)] (+5) + ( ) = 5 b) Berechnen
ETH Zürich Analysis I Zwischenprüfung Winter 2014 D-BAUG Musterlösungen Dr. Meike Akveld
 ETH Zürich Analysis I Zwischenprüfung Winter 2014 D-BAUG Musterlösungen Dr. Meike Akveld Bitte wenden! 1. Die unten stehende Figur wird beschrieben durch... (a) { (x, y) R 2 x + y 1 }. Richtig! (b) { (x,
ETH Zürich Analysis I Zwischenprüfung Winter 2014 D-BAUG Musterlösungen Dr. Meike Akveld Bitte wenden! 1. Die unten stehende Figur wird beschrieben durch... (a) { (x, y) R 2 x + y 1 }. Richtig! (b) { (x,
Das Newton-Verfahren
 1/14 Das Newton-Verfahren 11./12. Jgst. Bayern Doris Behrendt Gymnasium Marktbreit Stand: 12. März 2016 2/14 Formelsammlung Seite 72 oben, vierter Punkt: Newton-Iterationsformel: x n+1 = x n f(x n) f (x
1/14 Das Newton-Verfahren 11./12. Jgst. Bayern Doris Behrendt Gymnasium Marktbreit Stand: 12. März 2016 2/14 Formelsammlung Seite 72 oben, vierter Punkt: Newton-Iterationsformel: x n+1 = x n f(x n) f (x
Mathematik I für MB und ME
 Übungsaufgaben Aufgaben zur Wiederholung Mathematik I für MB und ME Fachbereich Grundlagenwissenschaften Prof Dr Viola Weiÿ Wintersemester 06/07 a) Stellen Sie die Gleichung a b 3+c = a +c, a, b > 0, nach
Übungsaufgaben Aufgaben zur Wiederholung Mathematik I für MB und ME Fachbereich Grundlagenwissenschaften Prof Dr Viola Weiÿ Wintersemester 06/07 a) Stellen Sie die Gleichung a b 3+c = a +c, a, b > 0, nach
Prüfungsklausur zum Modul Höhere Mathematik für Ingenieure 1
 Studiengang: Matrikelnummer: 3 4 5 6 Z Punkte Note Prüfungsklausur zum Modul Höhere Mathematik für Ingenieure 8. 7. 6, 8. -. Uhr Zugelassene Hilfsmittel: A4-Blätter eigene, handschriftliche Ausarbeitungen
Studiengang: Matrikelnummer: 3 4 5 6 Z Punkte Note Prüfungsklausur zum Modul Höhere Mathematik für Ingenieure 8. 7. 6, 8. -. Uhr Zugelassene Hilfsmittel: A4-Blätter eigene, handschriftliche Ausarbeitungen
Kugel - Kugelgleichung, Lagebeziehungen
 . Kugelgleichung. Lage Punkt / Kugel 3. Lage Gerade / Kugel 3. Standardverfahren 3. Alternative Kugel - Kugelgleichung, Lagebeziehungen. Lage Ebene / Kugel 5. Lage Kugel / Kugel (Schnittkreis, Berührungspunkt).
. Kugelgleichung. Lage Punkt / Kugel 3. Lage Gerade / Kugel 3. Standardverfahren 3. Alternative Kugel - Kugelgleichung, Lagebeziehungen. Lage Ebene / Kugel 5. Lage Kugel / Kugel (Schnittkreis, Berührungspunkt).
Dierentialrechnung mit einer Veränderlichen
 Dierentialrechnung mit einer Veränderlichen Beispiel: Sei s(t) die zum Zeitpunkt t zurückgelegte Wegstrecke. Dann ist die durchschnittliche Geschwindigkeit zwischen zwei Zeitpunkten t 1 und t 2 gegeben
Dierentialrechnung mit einer Veränderlichen Beispiel: Sei s(t) die zum Zeitpunkt t zurückgelegte Wegstrecke. Dann ist die durchschnittliche Geschwindigkeit zwischen zwei Zeitpunkten t 1 und t 2 gegeben
Eigenschaften von Funktionen. Aufgabe 1. Führen Sie eine ausführliche Funktionsuntersuchung für folgende Funktion durch:
 Aufgabe 1 Führen Sie eine ausführliche Funktionsuntersuchung für folgende Funktion durch: 1 4 2 f ( x) Ä Å x Ç 0,5x Ç 2 4 Aufgabe 2 Führen Sie eine ausführliche Funktionsuntersuchung für folgende Funktion
Aufgabe 1 Führen Sie eine ausführliche Funktionsuntersuchung für folgende Funktion durch: 1 4 2 f ( x) Ä Å x Ç 0,5x Ç 2 4 Aufgabe 2 Führen Sie eine ausführliche Funktionsuntersuchung für folgende Funktion
f(x)dx F(b) F(3) F(b).
 Aufgaben aus dem Aufgabenpool. Analysis A_ Die Abbildung zeigt den Graphen der in IR definierten Funktion f. a) Bestimmen Sie mithilfe der Abbildung einen Näherungswert für 5 f(x)dx. ( ) Die Funktion F
Aufgaben aus dem Aufgabenpool. Analysis A_ Die Abbildung zeigt den Graphen der in IR definierten Funktion f. a) Bestimmen Sie mithilfe der Abbildung einen Näherungswert für 5 f(x)dx. ( ) Die Funktion F
Lösungen: (Die Aufgaben sind fett, die Lösungen normal geschrieben.)
 KANTONSSCHULE KREUZLINGEN MATURITÄTSPRÜFUNGEN 24 TYPUS MAR MATHEMATIK / 3 Std. Klasse 4 MC / ho Lösungen: (Die Aufgaben sind fett, die Lösungen normal geschrieben.) ) Jeder Mensch hat Blut einer bestimmten
KANTONSSCHULE KREUZLINGEN MATURITÄTSPRÜFUNGEN 24 TYPUS MAR MATHEMATIK / 3 Std. Klasse 4 MC / ho Lösungen: (Die Aufgaben sind fett, die Lösungen normal geschrieben.) ) Jeder Mensch hat Blut einer bestimmten
Mathematik Abitur 2014 Lösungen
 Mathematik Abitur Lösungen Richard Reindl Analysis Aufgabengruppe Teil A. f (x) = lnx (lnx), f (x) = = lnx = = x = e, f(e) = e < x < e : lnx < = f (x) < = f fallend x > e : lnx > = f (x) > = f steigend.
Mathematik Abitur Lösungen Richard Reindl Analysis Aufgabengruppe Teil A. f (x) = lnx (lnx), f (x) = = lnx = = x = e, f(e) = e < x < e : lnx < = f (x) < = f fallend x > e : lnx > = f (x) > = f steigend.
Kurvendiskussion von Polynomfunktionen
 Kurvendiskussion von Polynomfunktionen Theorie: Für die weiteren Berechnungen benötigen wie die 1. f (x) und 2. f (x) Ableitung der zu untersuchenden Funktion f (x). Wir werden viele Gleichungen lösen
Kurvendiskussion von Polynomfunktionen Theorie: Für die weiteren Berechnungen benötigen wie die 1. f (x) und 2. f (x) Ableitung der zu untersuchenden Funktion f (x). Wir werden viele Gleichungen lösen
Durch Eliminieren der Wurzel erhalten wir die bekannte Kreisgleichung:
 Fixieren wir ein Seil der Länge r an einem Punkt M, nehmen das lose Ende in die Hand und bewegen uns so um den Punkt M herum, dass das Seil stets gespannt bleibt, erhalten wir, wie in nebenstehender Abbildung
Fixieren wir ein Seil der Länge r an einem Punkt M, nehmen das lose Ende in die Hand und bewegen uns so um den Punkt M herum, dass das Seil stets gespannt bleibt, erhalten wir, wie in nebenstehender Abbildung
Übersicht. 1. Motivation. 2. Grundlagen
 Übersicht 1. Motivation 2. Grundlagen 3. Analysis 3.1 Folgen, Reihen, Zinsen 3.2 Funktionen 3.3 Differentialrechnung 3.4 Extremwertbestimmung 3.5 Nichtlineare Gleichungen 3.6 Funktionen mehrerer Variabler
Übersicht 1. Motivation 2. Grundlagen 3. Analysis 3.1 Folgen, Reihen, Zinsen 3.2 Funktionen 3.3 Differentialrechnung 3.4 Extremwertbestimmung 3.5 Nichtlineare Gleichungen 3.6 Funktionen mehrerer Variabler
Bestimmen Sie jeweils die Lösungsmenge der Gleichung: 1. Bestimmen Sie jeweils die Lösungsmenge der Gleichung:
 Baden-Württemberg Übungsaufgaben für den Pflichtteil Gleichungslehre Stichworte: lineare Gleichungen; quadratische Gleichungen; Gleichungen höherer Ordnung; Substitution; Exponentialgleichungen; trigonometrische
Baden-Württemberg Übungsaufgaben für den Pflichtteil Gleichungslehre Stichworte: lineare Gleichungen; quadratische Gleichungen; Gleichungen höherer Ordnung; Substitution; Exponentialgleichungen; trigonometrische
1.1 Bestimmen Sie diejenigen Werte von a, für die f a mehr als eine Nullstelle hat. (3 P)
 Schriftliche Abiturprüfung 215 HMF 1 - Analysis (Pool 1) Für jeden Wert von a (a R,a ) ist eine Funktion f a durch f a (x) = a x 6 x 4 (x R) gegeben. 1.1 Bestimmen Sie diejenigen Werte von a, für die f
Schriftliche Abiturprüfung 215 HMF 1 - Analysis (Pool 1) Für jeden Wert von a (a R,a ) ist eine Funktion f a durch f a (x) = a x 6 x 4 (x R) gegeben. 1.1 Bestimmen Sie diejenigen Werte von a, für die f
Bestimme: (2x - x)dx. (x + 2) dx. (u - u + 2)du. ( 7 Ò x[ + π Ò x )dx. Berechne händisch: a) x dx
 Integrieren 1 1. Bestimme: 2 a) (2x - x)dx - 2-2 c) (u - u + 2)du -1 5 b) (x + 2) dx 0 d) ( 7 Ò x[ + π Ò x )dx 2. 1 Berechne händisch: a) x dx -1 2 b) (x - 1)dx -2 4 c) (-x + 5x -4)dx -4. Berechne von
Integrieren 1 1. Bestimme: 2 a) (2x - x)dx - 2-2 c) (u - u + 2)du -1 5 b) (x + 2) dx 0 d) ( 7 Ò x[ + π Ò x )dx 2. 1 Berechne händisch: a) x dx -1 2 b) (x - 1)dx -2 4 c) (-x + 5x -4)dx -4. Berechne von
1. Di erenzialrechnung für Funktionen einer Veränderlichen
 . Di erenzialrechnung für Funktionen einer Veränderlichen. estimmen Sie die Grenzwerte a) x + x lim x! x d) x + x lim x! x ; b) lim x! ; e) lim x! x x x + x + ; x + x x x. x x c) lim x! x + ; e an.. estimmen
. Di erenzialrechnung für Funktionen einer Veränderlichen. estimmen Sie die Grenzwerte a) x + x lim x! x d) x + x lim x! x ; b) lim x! ; e) lim x! x x x + x + ; x + x x x. x x c) lim x! x + ; e an.. estimmen
Aufgabe A2 1.1 Die Funktion ist gegeben durch 3P 21 mit Berechne die Gleichung der Tangente an das Schaubild von im Schnittpunkt mit der -Achse. 1.2 E
 Aufgabe A1 1.1 Erläutere anhand einer Skizze, ob das Integral 3P größer, kleiner oder gleich Null ist. 1.2 Für eine Funktion gilt: (1) 0 für 2 und 1 (2) 23 (3) 13 (4) 2 (5) 1 6 Welche Aussagen lassen sich
Aufgabe A1 1.1 Erläutere anhand einer Skizze, ob das Integral 3P größer, kleiner oder gleich Null ist. 1.2 Für eine Funktion gilt: (1) 0 für 2 und 1 (2) 23 (3) 13 (4) 2 (5) 1 6 Welche Aussagen lassen sich
Mathematik I Herbstsemester 2018 Kapitel 4: Anwendungen der Differentialrechnung
 Mathematik I Herbstsemester 2018 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 55 4. Anwendungen der Differentialrechnung Monotonie Krümmung Linearisierung einer Funktion Extremwerte
Mathematik I Herbstsemester 2018 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 55 4. Anwendungen der Differentialrechnung Monotonie Krümmung Linearisierung einer Funktion Extremwerte
Abschlussprüfung Fachoberschule 2016 Mathematik
 Abschlussprüfung Fachoberschule 06 Aufgabenvorschlag A Funktionsuntersuchung /6 Gegeben ist die Funktion f mit der Funktionsgleichung f ( x) = x + x; x IR. Berechnen Sie die Funktionswerte f( x ) für folgende
Abschlussprüfung Fachoberschule 06 Aufgabenvorschlag A Funktionsuntersuchung /6 Gegeben ist die Funktion f mit der Funktionsgleichung f ( x) = x + x; x IR. Berechnen Sie die Funktionswerte f( x ) für folgende
SBP Mathe Grundkurs 2 # 0 by Clifford Wolf. SBP Mathe Grundkurs 2
 SBP Mathe Grundkurs 2 # 0 by Clifford Wolf SBP Mathe Grundkurs 2 # 0 Antwort Diese Lernkarten sind sorgfältig erstellt worden, erheben aber weder Anspruch auf Richtigkeit noch auf Vollständigkeit. Das
SBP Mathe Grundkurs 2 # 0 by Clifford Wolf SBP Mathe Grundkurs 2 # 0 Antwort Diese Lernkarten sind sorgfältig erstellt worden, erheben aber weder Anspruch auf Richtigkeit noch auf Vollständigkeit. Das
Mathematik: Mag. Schmid Wolfgang+ LehrerInnenTeam ARBEITSBLATT 6-8 UMKEHRAUFGABEN ZUR KURVENDISKUSSION
 Mathematik: Mag. Schmid Wolfgang LehrerInnenTeam ARBEITSBLATT 6-8 UMKEHRAUFGABEN ZUR KURVENDISKUSSION Wir wollen uns zu diesem Aufgabenbereich noch einige komplexere Aufgabenstellungen überlegen: Beispiel:
Mathematik: Mag. Schmid Wolfgang LehrerInnenTeam ARBEITSBLATT 6-8 UMKEHRAUFGABEN ZUR KURVENDISKUSSION Wir wollen uns zu diesem Aufgabenbereich noch einige komplexere Aufgabenstellungen überlegen: Beispiel:
