Die Poincaré-Vermutung
|
|
|
- Frieda Martin
- vor 8 Jahren
- Abrufe
Transkript
1 Die Poincaré-Vermutung Dipl.-Math. Bastian Rieck Arbeitsgruppe Computergraphik und Visualisierung Interdisziplinäres Zentrum für Wissenschaftliches Rechnen 3. September 2012 B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
2 Warum dieser Vortrag? Mehr als 100 Jahre hatten Mathematiker oft verzweifelt versucht, dieses theoretische Problem zu lösen, das für Laien so gut wie unverständlich ist. (süddeutsche.de vom ; Original ohne Hervorhebung) Doch jetzt ist mathematisch beweisbar, dass die vierte Dimension wirklich existiert. (welt.de vom ) B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
3 Warum ist die Poincare -Vermutung wichtig? B. Rieck (CoVis) Die Poincare -Vermutung 3. September / 30
4 Warum ist die Poincare -Vermutung wichtig? Fru her B. Rieck (CoVis) Die Poincare -Vermutung 3. September / 30
5 Warum ist die Poincare -Vermutung wichtig? Fru her B. Rieck (CoVis) Heute Die Poincare -Vermutung 3. September / 30
6 Henri Poincaré B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
7 Henri Poincaré * 29. April 1854 in Nancy B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
8 Henri Poincaré * 29. April 1854 in Nancy 17. Juli 1912 in Paris B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
9 Henri Poincaré * 29. April 1854 in Nancy 17. Juli 1912 in Paris 1873: Mathematikstudium an der École Polytechnique B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
10 Henri Poincaré * 29. April 1854 in Nancy 17. Juli 1912 in Paris 1873: Mathematikstudium an der École Polytechnique 1879: Abschluss der Promotion B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
11 Henri Poincaré * 29. April 1854 in Nancy 17. Juli 1912 in Paris 1873: Mathematikstudium an der École Polytechnique 1879: Abschluss der Promotion Beiträge zur Mathematik (algebraische Geometrie, algebraische Topologie Zahlentheorie), Physik (Optik, Thermodynamik, spezielle Relativitätstheorie) und Philosophie. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
12 Henri Poincaré * 29. April 1854 in Nancy 17. Juli 1912 in Paris 1873: Mathematikstudium an der École Polytechnique 1879: Abschluss der Promotion Beiträge zur Mathematik (algebraische Geometrie, algebraische Topologie Zahlentheorie), Physik (Optik, Thermodynamik, spezielle Relativitätstheorie) und Philosophie. Letzter Universalist des 20. Jahrhunderts? B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
13 Henri Poincaré * 29. April 1854 in Nancy 17. Juli 1912 in Paris 1873: Mathematikstudium an der École Polytechnique 1879: Abschluss der Promotion Beiträge zur Mathematik (algebraische Geometrie, algebraische Topologie Zahlentheorie), Physik (Optik, Thermodynamik, spezielle Relativitätstheorie) und Philosophie. Letzter Universalist des 20. Jahrhunderts? 1900: Erste Formulierung der Poincaré-Vermutung B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
14 Henri Poincaré * 29. April 1854 in Nancy 17. Juli 1912 in Paris 1873: Mathematikstudium an der École Polytechnique 1879: Abschluss der Promotion Beiträge zur Mathematik (algebraische Geometrie, algebraische Topologie Zahlentheorie), Physik (Optik, Thermodynamik, spezielle Relativitätstheorie) und Philosophie. Letzter Universalist des 20. Jahrhunderts? 1900: Erste Formulierung der Poincaré-Vermutung 1904: Poincaré findet Fehler in vorherigem Beweis B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
15 Henri Poincaré * 29. April 1854 in Nancy 17. Juli 1912 in Paris 1873: Mathematikstudium an der École Polytechnique 1879: Abschluss der Promotion Beiträge zur Mathematik (algebraische Geometrie, algebraische Topologie Zahlentheorie), Physik (Optik, Thermodynamik, spezielle Relativitätstheorie) und Philosophie. Letzter Universalist des 20. Jahrhunderts? 1900: Erste Formulierung der Poincaré-Vermutung 1904: Poincaré findet Fehler in vorherigem Beweis 2001: Poincaré-Vermutung wird zu einem der 7 Millennium-Probleme des Clay Mathematics Institute. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
16 Grigori Perelman B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
17 Grigori Perelman * 13. Juni 1966 in Leningrad (St. Petersburg) B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
18 Grigori Perelman * 13. Juni 1966 in Leningrad (St. Petersburg) 1982: Perfekte Punktzahl bei internationaler Mathematik-Olympiade und Zulassung zum Studium B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
19 Grigori Perelman * 13. Juni 1966 in Leningrad (St. Petersburg) 1982: Perfekte Punktzahl bei internationaler Mathematik-Olympiade und Zulassung zum Studium 1990: Promotion in Mathematik B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
20 Grigori Perelman * 13. Juni 1966 in Leningrad (St. Petersburg) 1982: Perfekte Punktzahl bei internationaler Mathematik-Olympiade und Zulassung zum Studium 1990: Promotion in Mathematik 2002: Vorläufiger Beweis der Poincaré-Vermutung B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
21 Grigori Perelman * 13. Juni 1966 in Leningrad (St. Petersburg) 1982: Perfekte Punktzahl bei internationaler Mathematik-Olympiade und Zulassung zum Studium 1990: Promotion in Mathematik 2002: Vorläufiger Beweis der Poincaré-Vermutung 2003: Weitere erläuternde Publikationen B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
22 Grigori Perelman * 13. Juni 1966 in Leningrad (St. Petersburg) 1982: Perfekte Punktzahl bei internationaler Mathematik-Olympiade und Zulassung zum Studium 1990: Promotion in Mathematik 2002: Vorläufiger Beweis der Poincaré-Vermutung 2003: Weitere erläuternde Publikationen 2006: Bestätigung der Korrektheit des Beweises durch andere Mathematiker B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
23 Grigori Perelman * 13. Juni 1966 in Leningrad (St. Petersburg) 1982: Perfekte Punktzahl bei internationaler Mathematik-Olympiade und Zulassung zum Studium 1990: Promotion in Mathematik 2002: Vorläufiger Beweis der Poincaré-Vermutung 2003: Weitere erläuternde Publikationen 2006: Bestätigung der Korrektheit des Beweises durch andere Mathematiker 2006: Perelman lehnt Fields-Medaille ab B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
24 Grigori Perelman * 13. Juni 1966 in Leningrad (St. Petersburg) 1982: Perfekte Punktzahl bei internationaler Mathematik-Olympiade und Zulassung zum Studium 1990: Promotion in Mathematik 2002: Vorläufiger Beweis der Poincaré-Vermutung 2003: Weitere erläuternde Publikationen 2006: Bestätigung der Korrektheit des Beweises durch andere Mathematiker 2006: Perelman lehnt Fields-Medaille ab 2010: Perelman lehnt Millenniumspreis ab B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
25 Date: Wed, 20 Nov :46: (MSK) From: Grigory Perelman Reply-To: Grigory Perelman Subject: Re: geometrization To: Vitali Kapovitch That s correct. Grisha On Tue, 19 Nov 2002, Vitali Kapovitch wrote: > Hi Grisha, > Sorry to bother you but a lot of people are asking me about your preprint > "The entropy formula for the Ricci...". Do I understand it correctly > that while you can not yet do all the steps in the Hamilton program > you can do enough so that using some collapsing results you can prove > geometrization? > Vitali > B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
26 Die Poincaré-Vermutung Moderne Formulierung Jede einfach zusammenhängende geschlossene 3-Mannigfaltigkeit ist homöomorph zur 3-Sphäre. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
27 Die Poincaré-Vermutung Moderne Formulierung Jede einfach zusammenhängende geschlossene 3-Mannigfaltigkeit ist homöomorph zur 3-Sphäre. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
28 Im Folgenden Bildquelle: abstrusegoose.com B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
29 Ganz langsam... Jede einfach zusammenhängende geschlossene 3-Mannigfaltigkeit ist homöomorph zur 3-Sphäre. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
30 1-Mannigfaltigkeit Definition Eine 1-Mannigfaltigkeit ist eine Menge von Punkten, die lokal wie der 1-dimensionale euklidische Raum (R) aussieht. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
31 1-Mannigfaltigkeit Definition Eine 1-Mannigfaltigkeit ist eine Menge von Punkten, die lokal wie der 1-dimensionale euklidische Raum (R) aussieht. lokal stellen wir uns aus der Sicht eines kleinen Käfers vor B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
32 1-Mannigfaltigkeit Definition Eine 1-Mannigfaltigkeit ist eine Menge von Punkten, die lokal wie der 1-dimensionale euklidische Raum (R) aussieht. lokal stellen wir uns aus der Sicht eines kleinen Käfers vor R ist die Zahlengerade: B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
33 1-Mannigfaltigkeit Definition Eine 1-Mannigfaltigkeit ist eine Menge von Punkten, die lokal wie der 1-dimensionale euklidische Raum (R) aussieht. lokal stellen wir uns aus der Sicht eines kleinen Käfers vor R ist die Zahlengerade: B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
34 1-Mannigfaltigkeit Definition Eine 1-Mannigfaltigkeit ist eine Menge von Punkten, die lokal wie der 1-dimensionale euklidische Raum (R) aussieht. lokal stellen wir uns aus der Sicht eines kleinen Käfers vor R ist die Zahlengerade: Aus Sicht eines Käfers:. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
35 Beispiel für eine 1-Mannigfaltigkeit Die 1-Sphäre B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
36 Beispiel für eine 1-Mannigfaltigkeit Die 1-Sphäre Achtung Die 1-Sphäre bezeichnet nur die Kreislinie. Der Käfer kann also nicht in das Innere des Kreises vordringen. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
37 2-Mannigfaltigkeit Definition Eine 2-Mannigfaltigkeit ist eine Menge von Punkten, die lokal wie der 2-dimensionale euklidische Raum (R 2 ) aussieht. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
38 2-Mannigfaltigkeit Definition Eine 2-Mannigfaltigkeit ist eine Menge von Punkten, die lokal wie der 2-dimensionale euklidische Raum (R 2 ) aussieht. R 2 ist ein kartesisches Koordinatensystem mit x-achse und y-achse: B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
39 2-Mannigfaltigkeit Definition Eine 2-Mannigfaltigkeit ist eine Menge von Punkten, die lokal wie der 2-dimensionale euklidische Raum (R 2 ) aussieht. R 2 ist ein kartesisches Koordinatensystem mit x-achse und y-achse: B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
40 2-Mannigfaltigkeit Definition Eine 2-Mannigfaltigkeit ist eine Menge von Punkten, die lokal wie der 2-dimensionale euklidische Raum (R 2 ) aussieht. R 2 ist ein kartesisches Koordinatensystem mit x-achse und y-achse: Aus Sicht des Käfers: B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
41 2-Mannigfaltigkeit Definition Eine 2-Mannigfaltigkeit ist eine Menge von Punkten, die lokal wie der 2-dimensionale euklidische Raum (R 2 ) aussieht. R 2 ist ein kartesisches Koordinatensystem mit x-achse und y-achse: Aus Sicht des Käfers: B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
42 Beispiel für eine 2-Mannigfaltigkeit Die 2-Sphäre Bildquelle: Wikipedia B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
43 Beispiel für eine 2-Mannigfaltigkeit Die 2-Sphäre Achtung Die 2-Sphäre bezeichnet nur die Kugeloberfläche. Der Käfer kann also nicht in das Innere der Kugel vordringen. Bildquelle: Wikipedia B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
44 3-Mannigfaltigkeit Definition Eine 3-Mannigfaltigkeit ist eine Menge von Punkten, die lokal wie der 3-dimensionale euklidische Raum (R 3 ) aussieht. Bildquelle: Frédéric Michel B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
45 3-Mannigfaltigkeit Definition Eine 3-Mannigfaltigkeit ist eine Menge von Punkten, die lokal wie der 3-dimensionale euklidische Raum (R 3 ) aussieht. R 3 ist ein kartesisches Koordinatensystem mit x-achse, y-achse und z-achse: Bildquelle: Frédéric Michel B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
46 3-Mannigfaltigkeit Definition Eine 3-Mannigfaltigkeit ist eine Menge von Punkten, die lokal wie der 3-dimensionale euklidische Raum (R 3 ) aussieht. R 3 ist ein kartesisches Koordinatensystem mit x-achse, y-achse und z-achse: Bildquelle: Frédéric Michel B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
47 3-Mannigfaltigkeit Definition Eine 3-Mannigfaltigkeit ist eine Menge von Punkten, die lokal wie der 3-dimensionale euklidische Raum (R 3 ) aussieht. R 3 ist ein kartesisches Koordinatensystem mit x-achse, y-achse und z-achse: Aus Sicht des Käfers unserer Sicht: Bildquelle: Frédéric Michel B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
48 3-Mannigfaltigkeit Definition Eine 3-Mannigfaltigkeit ist eine Menge von Punkten, die lokal wie der 3-dimensionale euklidische Raum (R 3 ) aussieht. R 3 ist ein kartesisches Koordinatensystem mit x-achse, y-achse und z-achse: Aus Sicht des Käfers unserer Sicht: Bildquelle: Frédéric Michel B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
49 Beispiele für 3-Mannigfaltigkeiten Unser Universum ist lokal 3-dimensional. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
50 Beispiele für 3-Mannigfaltigkeiten Unser Universum ist lokal 3-dimensional. Ist unser Universum eine 3-Mannigfaltigkeit? B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
51 Beispiele für 3-Mannigfaltigkeiten Unser Universum ist lokal 3-dimensional. Ist unser Universum eine 3-Mannigfaltigkeit? Gegenwärtige Annahme in Astrophysik: Ja! B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
52 Beispiele für 3-Mannigfaltigkeiten Unser Universum ist lokal 3-dimensional. Ist unser Universum eine 3-Mannigfaltigkeit? Gegenwärtige Annahme in Astrophysik: Ja! Klassischeres Beispiel für 3-Mannigfaltigkeit: Die 3-Sphäre. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
53 Beispiele für 3-Mannigfaltigkeiten Unser Universum ist lokal 3-dimensional. Ist unser Universum eine 3-Mannigfaltigkeit? Gegenwärtige Annahme in Astrophysik: Ja! Klassischeres Beispiel für 3-Mannigfaltigkeit: Die 3-Sphäre. 3-Sphäre ist die höher-dimensionale Verallgemeinerung einer Kugel. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
54 Beispiele für 3-Mannigfaltigkeiten Unser Universum ist lokal 3-dimensional. Ist unser Universum eine 3-Mannigfaltigkeit? Gegenwärtige Annahme in Astrophysik: Ja! Klassischeres Beispiel für 3-Mannigfaltigkeit: Die 3-Sphäre. 3-Sphäre ist die höher-dimensionale Verallgemeinerung einer Kugel. Aber nicht mehr zeichenbar... B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
55 Beispiele für 3-Mannigfaltigkeiten Unser Universum ist lokal 3-dimensional. Ist unser Universum eine 3-Mannigfaltigkeit? Gegenwärtige Annahme in Astrophysik: Ja! Klassischeres Beispiel für 3-Mannigfaltigkeit: Die 3-Sphäre. 3-Sphäre ist die höher-dimensionale Verallgemeinerung einer Kugel. Aber nicht mehr zeichenbar...??? B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
56 Wie stellen sich Mathematiker die 3-Sphäre vor? Trick: Beschreibung durch Koordinaten! Die 1-Sphäre enthält alle Punkte (x, y) mit x 2 + y 2 = 1. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
57 Wie stellen sich Mathematiker die 3-Sphäre vor? Trick: Beschreibung durch Koordinaten! Die 1-Sphäre enthält alle Punkte (x, y) mit x 2 + y 2 = 1. Die 2-Sphäre enthält alle Punkte (x, y, z) mit x 2 + y 2 + z 2 = 1. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
58 Wie stellen sich Mathematiker die 3-Sphäre vor? Trick: Beschreibung durch Koordinaten! Die 1-Sphäre enthält alle Punkte (x, y) mit x 2 + y 2 = 1. Die 2-Sphäre enthält alle Punkte (x, y, z) mit x 2 + y 2 + z 2 = 1. Die 3-Sphäre enthält alle Punkte (x, y, z, w) mit x 2 + y 2 + z 2 + w 2 = 1. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
59 Zusammenfassung bisher B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
60 Zusammenfassung bisher Die 1-Sphäre ist eine 1-Mannigfaltigkeit, die im 2-dimensionalen Raum lebt. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
61 Zusammenfassung bisher Die 1-Sphäre ist eine 1-Mannigfaltigkeit, die im 2-dimensionalen Raum lebt. Die 2-Sphäre ist eine 2-Mannigfaltigkeit, die im 3-dimensionalen Raum lebt. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
62 Zusammenfassung bisher Die 1-Sphäre ist eine 1-Mannigfaltigkeit, die im 2-dimensionalen Raum lebt. Die 2-Sphäre ist eine 2-Mannigfaltigkeit, die im 3-dimensionalen Raum lebt. Die 3-Sphäre ist eine 3-Mannigfaltigkeit, die im 4-dimensionalen Raum lebt. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
63 Zurück zur Vermutung Jede einfach zusammenhängende geschlossene 3-Mannigfaltigkeit ist homöomorph zur 3-Sphäre. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
64 Was bedeutet einfach zusammenhängend? Am Beispiel der 2-Sphäre B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
65 Was bedeutet einfach zusammenhängend? Am Beispiel der 2-Sphäre B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
66 Eine Mannigfaltigkeit, die nicht einfach zusammenhängend ist Der Torus ( Fahrradschlauch ) Die grünen Schleifen lassen sich auf einen Punkt zusammenziehen. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
67 Eine Mannigfaltigkeit, die nicht einfach zusammenhängend ist Der Torus ( Fahrradschlauch ) Die grünen Schleifen lassen sich auf einen Punkt zusammenziehen. Die rote Schleife kann nicht zu einem Punkt zusammengezogen werden. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
68 Und der Nutzen? B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
69 Und der Nutzen? Stellen wir uns vor, ein kleiner Käfer lebt auf einem Torus. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
70 Und der Nutzen? Stellen wir uns vor, ein kleiner Käfer lebt auf einem Torus. Kann der Käfer herausfinden, dass er nicht auf einer Sphäre lebt? B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
71 Und der Nutzen? Stellen wir uns vor, ein kleiner Käfer lebt auf einem Torus. Kann der Käfer herausfinden, dass er nicht auf einer Sphäre lebt? Selbst wenn er das Loch in der Mitte nicht sehen kann???? B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
72 Und der Nutzen? Stellen wir uns vor, ein kleiner Käfer lebt auf einem Torus. Kann der Käfer herausfinden, dass er nicht auf einer Sphäre lebt? Selbst wenn er das Loch in der Mitte nicht sehen kann? Ja! Denn der Käfer kann überprüfen, ob seine Welt einfach zusammenhängend ist.??? B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
73 Und der Nutzen? Stellen wir uns vor, ein kleiner Käfer lebt auf einem Torus. Kann der Käfer herausfinden, dass er nicht auf einer Sphäre lebt? Selbst wenn er das Loch in der Mitte nicht sehen kann? Ja! Denn der Käfer kann überprüfen, ob seine Welt einfach zusammenhängend ist. Da der Torus nicht einfach zusammenhängend ist, weiß der Käfer, dass er nicht auf einer Sphäre lebt!!!! B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
74 Zurück zur Vermutung Jede einfach zusammenhängende geschlossene 3-Mannigfaltigkeit ist homöomorph zur 3-Sphäre. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
75 Zurück zur Vermutung Jede einfach zusammenhängende geschlossene 3-Mannigfaltigkeit ist homöomorph zur 3-Sphäre. Eine kompakte Mannigfaltigkeit dehnt sich nicht unendlich weit aus. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
76 Zurück zur Vermutung Jede einfach zusammenhängende geschlossene 3-Mannigfaltigkeit ist homöomorph zur 3-Sphäre. Eine kompakte Mannigfaltigkeit dehnt sich nicht unendlich weit aus. Eine Mannigfaltigkeit ohne Rand hat keine Kante, an der die Mannigfaltigkeit aufhört. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
77 Zurück zur Vermutung Jede einfach zusammenhängende geschlossene 3-Mannigfaltigkeit ist homöomorph zur 3-Sphäre. Eine kompakte Mannigfaltigkeit dehnt sich nicht unendlich weit aus. Eine Mannigfaltigkeit ohne Rand hat keine Kante, an der die Mannigfaltigkeit aufhört. Kurz gesagt: Geschlossen = kompakt + ohne Rand B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
78 Beispiele! Die {1, 2, 3}-Sphäre sowie der Torus sind kompakt und ohne Rand, also geschlossen. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
79 Beispiele! Die {1, 2, 3}-Sphäre sowie der Torus sind kompakt und ohne Rand, also geschlossen. Wenn wir zur {1, 2, 3}-Sphäre noch die inneren Punkte dazunehmen, so erhalten wir eine Mannigfaltigkeit mit Rand.? B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
80 Beispiele! Die {1, 2, 3}-Sphäre sowie der Torus sind kompakt und ohne Rand, also geschlossen. Wenn wir zur {1, 2, 3}-Sphäre noch die inneren Punkte dazunehmen, so erhalten wir eine Mannigfaltigkeit mit Rand. R, R 2, R 3 sind keine kompakten Mannigfaltigkeiten, da sie sich unendlich weit ausdehnen.? B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
81 Zurück zur Vermutung Jede einfach zusammenhängende geschlossene 3-Mannigfaltigkeit ist homöomorph zur 3-Sphäre. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
82 Zurück zur Vermutung Jede einfach zusammenhängende geschlossene 3-Mannigfaltigkeit ist homöomorph zur 3-Sphäre. Griechisch: homöo- = gleichartig ; morph = Gestalt B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
83 Zurück zur Vermutung Jede einfach zusammenhängende geschlossene 3-Mannigfaltigkeit ist homöomorph zur 3-Sphäre. Griechisch: homöo- = gleichartig ; morph = Gestalt Zwei Objekte sind homöomorph, wenn sie durch Dehnen, Stauchen, Verbiegen, Verzerren in einander überführt werden können. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
84 Zurück zur Vermutung Jede einfach zusammenhängende geschlossene 3-Mannigfaltigkeit ist homöomorph zur 3-Sphäre. Griechisch: homöo- = gleichartig ; morph = Gestalt Zwei Objekte sind homöomorph, wenn sie durch Dehnen, Stauchen, Verbiegen, Verzerren in einander überführt werden können. Es ist nicht erlaubt, die Objekte zu zerschneiden. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
85 Beispiel Topologen sind Menschen, die einen Donut nicht von einer Kaffeetasse unterscheiden können. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
86 Beispiel Topologen sind Menschen, die einen Donut nicht von einer Kaffeetasse unterscheiden können. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
87 Beispiel Topologen sind Menschen, die einen Donut nicht von einer Kaffeetasse unterscheiden können. Vorstellung: B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
88 Beispiel Topologen sind Menschen, die einen Donut nicht von einer Kaffeetasse unterscheiden können. Vorstellung: B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
89 Beispiel Topologen sind Menschen, die einen Donut nicht von einer Kaffeetasse unterscheiden können. Vorstellung: B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
90 Beispiel Topologen sind Menschen, die einen Donut nicht von einer Kaffeetasse unterscheiden können. Vorstellung: B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
91 Beispiel Topologen sind Menschen, die einen Donut nicht von einer Kaffeetasse unterscheiden können. Vorstellung: B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
92 Beispiel Topologen sind Menschen, die einen Donut nicht von einer Kaffeetasse unterscheiden können. Vorstellung: B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
93 Beispiel Topologen sind Menschen, die einen Donut nicht von einer Kaffeetasse unterscheiden können. Vorstellung: B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
94 Beispiel Topologen sind Menschen, die einen Donut nicht von einer Kaffeetasse unterscheiden können. Vorstellung: B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
95 Am Ziel! Jede einfach zusammenhängende geschlossene 3-Mannigfaltigkeit ist homöomorph zur 3-Sphäre. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
96 Am Ziel! Jede einfach zusammenhängende geschlossene 3-Mannigfaltigkeit ist homöomorph zur 3-Sphäre. Mit anderen Worten: Angenommen, wir haben eine Mannigfaltigkeit. Wenn diese... B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
97 Am Ziel! Jede einfach zusammenhängende geschlossene 3-Mannigfaltigkeit ist homöomorph zur 3-Sphäre. Mit anderen Worten: Angenommen, wir haben eine Mannigfaltigkeit. Wenn diese... einfach zusammenhängend B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
98 Am Ziel! Jede einfach zusammenhängende geschlossene 3-Mannigfaltigkeit ist homöomorph zur 3-Sphäre. Mit anderen Worten: Angenommen, wir haben eine Mannigfaltigkeit. Wenn diese... einfach zusammenhängend geschlossen B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
99 Am Ziel! Jede einfach zusammenhängende geschlossene 3-Mannigfaltigkeit ist homöomorph zur 3-Sphäre. Mit anderen Worten: Angenommen, wir haben eine Mannigfaltigkeit. Wenn diese... einfach zusammenhängend geschlossen 3-dimensional ist B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
100 Am Ziel! Jede einfach zusammenhängende geschlossene 3-Mannigfaltigkeit ist homöomorph zur 3-Sphäre. Mit anderen Worten: Angenommen, wir haben eine Mannigfaltigkeit. Wenn diese... einfach zusammenhängend geschlossen 3-dimensional ist... dann muss es sich um die 3-Sphäre handeln (egal, wie kompliziert sie aussieht oder beschrieben wurde)! B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
101 Wozu ist es gut? B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
102 Wozu ist es gut? Gegenwärtige Annahme in Astrophysik: Das Universum ist eine 3-Mannigfaltigkeit. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
103 Wozu ist es gut? Gegenwärtige Annahme in Astrophysik: Das Universum ist eine 3-Mannigfaltigkeit. Noch ungeklärt: Ist das Universum geschlossen? B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
104 Wozu ist es gut? Gegenwärtige Annahme in Astrophysik: Das Universum ist eine 3-Mannigfaltigkeit. Noch ungeklärt: Ist das Universum geschlossen? Falls ja, so macht die Poincaré-Vermutung eine Aussage über die Struktur unseres Universums! B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
105 Wozu ist es gut? Gegenwärtige Annahme in Astrophysik: Das Universum ist eine 3-Mannigfaltigkeit. Noch ungeklärt: Ist das Universum geschlossen? Falls ja, so macht die Poincaré-Vermutung eine Aussage über die Struktur unseres Universums! Müssen nur noch klären, ob das Universum einfach zusammenhängend ist. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
106 Wozu ist es gut? Gegenwärtige Annahme in Astrophysik: Das Universum ist eine 3-Mannigfaltigkeit. Noch ungeklärt: Ist das Universum geschlossen? Falls ja, so macht die Poincaré-Vermutung eine Aussage über die Struktur unseres Universums! Müssen nur noch klären, ob das Universum einfach zusammenhängend ist. Falls ja, so leben wir in einer 3-Sphäre! B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
107 Weitere Konsequenzen B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
108 Weitere Konsequenzen Perelman hat beiläufig große Gebiete der Mathematik revolutioniert. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
109 Weitere Konsequenzen Perelman hat beiläufig große Gebiete der Mathematik revolutioniert. Seine Arbeit setzt neue Impulse für die Forschung der nächsten Jahrzehnte! B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
110 Weitere Konsequenzen Perelman hat beiläufig große Gebiete der Mathematik revolutioniert. Seine Arbeit setzt neue Impulse für die Forschung der nächsten Jahrzehnte! Physiker haben Poincaré-Vermutung für 2 Dimensionen für String-Theorie und allgemeine Relativitätstheorie genutzt. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
111 Weitere Konsequenzen Perelman hat beiläufig große Gebiete der Mathematik revolutioniert. Seine Arbeit setzt neue Impulse für die Forschung der nächsten Jahrzehnte! Physiker haben Poincaré-Vermutung für 2 Dimensionen für String-Theorie und allgemeine Relativitätstheorie genutzt. Als Resultat haben wir Technologien wie GPS, Handys, Raumsonden... B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
112 Weitere Konsequenzen Perelman hat beiläufig große Gebiete der Mathematik revolutioniert. Seine Arbeit setzt neue Impulse für die Forschung der nächsten Jahrzehnte! Physiker haben Poincaré-Vermutung für 2 Dimensionen für String-Theorie und allgemeine Relativitätstheorie genutzt. Als Resultat haben wir Technologien wie GPS, Handys, Raumsonden... Was wird sich also noch alles aus der Poincaré-Vermutung für 3 Dimensionen ergeben? B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
113 Zum Schluss Wir müssen wissen. Wir werden wissen. David Hilbert B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
114 Lust auf mehr? Donal O Shea. Poincarés Vermutung: Die Geschichte eines mathematischen Abenteuers, ISBN George G. Szpiro. Das Poincaré-Abenteuer: Ein mathematisches Welträtsel wird gelöst, ISBN Tina S. Chang. Perelman s song, Math Horizons, Vol. 15, No. 3, S Jeff Weeks. B. Rieck (CoVis) Die Poincaré-Vermutung 3. September / 30
Die Poincaré-Vermutung
Die Poincaré-Vermutung Dipl.-Math. Bastian Rieck Arbeitsgruppe Computergraphik und Visualisierung Interdisziplinäres Zentrum für Wissenschaftliches Rechnen 19. Mai 2014 Warum dieser Vortrag? Mehr als 100
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
Informationsblatt Induktionsbeweis
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Gleichungen Lösen. Ein graphischer Blick auf Gleichungen
Gleichungen Lösen Was bedeutet es, eine Gleichung zu lösen? Was ist überhaupt eine Gleichung? Eine Gleichung ist, grundsätzlich eine Aussage über zwei mathematische Terme, dass sie gleich sind. Ein Term
Abschlussprüfung Realschule Bayern II / III: 2009 Haupttermin B 1.0 B 1.1
B 1.0 B 1.1 L: Wir wissen von, dass sie den Scheitel hat und durch den Punkt läuft. Was nichts bringt, ist beide Punkte in die allgemeine Parabelgleichung einzusetzen und das Gleichungssystem zu lösen,
Primzahlen und RSA-Verschlüsselung
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Mathematischer Vorbereitungskurs für Ökonomen
Mathematischer Vorbereitungskurs für Ökonomen Dr. Thomas Zehrt Wirtschaftswissenschaftliches Zentrum Universität Basel Gleichungen Inhalt: 1. Grundlegendes 2. Lineare Gleichungen 3. Gleichungen mit Brüchen
Grundbegriffe der Informatik
Grundbegriffe der Informatik Kapitel 6: Induktives Vorgehen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische
Persönliche Zukunftsplanung mit Menschen, denen nicht zugetraut wird, dass sie für sich selbst sprechen können Von Susanne Göbel und Josef Ströbl
Persönliche Zukunftsplanung mit Menschen, denen nicht zugetraut Von Susanne Göbel und Josef Ströbl Die Ideen der Persönlichen Zukunftsplanung stammen aus Nordamerika. Dort werden Zukunftsplanungen schon
Statuten in leichter Sprache
Statuten in leichter Sprache Zweck vom Verein Artikel 1: Zivil-Gesetz-Buch Es gibt einen Verein der selbstbestimmung.ch heisst. Der Verein ist so aufgebaut, wie es im Zivil-Gesetz-Buch steht. Im Zivil-Gesetz-Buch
Wir machen neue Politik für Baden-Württemberg
Wir machen neue Politik für Baden-Württemberg Am 27. März 2011 haben die Menschen in Baden-Württemberg gewählt. Sie wollten eine andere Politik als vorher. Die Menschen haben die GRÜNEN und die SPD in
Frohe Weihnachten und ein gutes neues Jahr!
Frohe Weihnachten und ein gutes neues Jahr! Die mit dem Stern * gekennzeichneten Übungen sind nicht verpflichtend, aber sie liefern zusätzliche Punkte. Unten wird immer mit I das reelle Intervall [0, 1]
2.1 Präsentieren wozu eigentlich?
2.1 Präsentieren wozu eigentlich? Gute Ideen verkaufen sich in den seltensten Fällen von allein. Es ist heute mehr denn je notwendig, sich und seine Leistungen, Produkte etc. gut zu präsentieren, d. h.
Zahlen und das Hüten von Geheimnissen (G. Wiese, 23. April 2009)
Zahlen und das Hüten von Geheimnissen (G. Wiese, 23. April 2009) Probleme unseres Alltags E-Mails lesen: Niemand außer mir soll meine Mails lesen! Geld abheben mit der EC-Karte: Niemand außer mir soll
Prozentrechnung. Wir können nun eine Formel für die Berechnung des Prozentwertes aufstellen:
Prozentrechnung Wir beginnen mit einem Beisiel: Nehmen wir mal an, ein Handy kostet 200 und es gibt 5% Rabatt (Preisnachlass), wie groß ist dann der Rabatt in Euro und wie viel kostet dann das Handy? Wenn
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Kreativ visualisieren
Kreativ visualisieren Haben Sie schon einmal etwas von sogenannten»sich selbst erfüllenden Prophezeiungen«gehört? Damit ist gemeint, dass ein Ereignis mit hoher Wahrscheinlichkeit eintritt, wenn wir uns
7 Rechnen mit Polynomen
7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
Kurzeinführung zum Plotten in Maple
Kurzeinführung zum Plotten in Maple Dies ist eine sehr kurze Einführung, die lediglich einen Einblick in die Visualisierung von Funktionen und Mengen gestatten soll und keinesfalls um Vollständigkeit bemüht
Kulturelle Evolution 12
3.3 Kulturelle Evolution Kulturelle Evolution Kulturelle Evolution 12 Seit die Menschen Erfindungen machen wie z.b. das Rad oder den Pflug, haben sie sich im Körperbau kaum mehr verändert. Dafür war einfach
Grundbegriffe der Informatik
Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
100 Mikrokredite und Abschluss der Pilotphase. Ruedi Winkler, Präsident Verein GO! Ziel selbstständig
100 Mikrokredite und Abschluss der Pilotphase Ruedi Winkler, Präsident Verein GO! Ziel selbstständig Vorbemerkung Wenn es um Fragen der Oekonomie geht, dann haben viele Leute den Eindruck, da könnten sie
Die Gleichung A x = a hat für A 0 die eindeutig bestimmte Lösung. Für A=0 und a 0 existiert keine Lösung.
Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Studienplan für den Diplomstudiengang Mathematik
Universität Stuttgart Fakultät Mathematik und Physik Studienplan für den Diplomstudiengang Mathematik Februar 2005 Der Diplomstudiengang Mathematik gliedert sich in den ersten und den zweiten Studienabschnitt
Qualität und Verlässlichkeit Das verstehen die Deutschen unter Geschäftsmoral!
Beitrag: 1:43 Minuten Anmoderationsvorschlag: Unseriöse Internetanbieter, falsch deklarierte Lebensmittel oder die jüngsten ADAC-Skandale. Solche Fälle mit einer doch eher fragwürdigen Geschäftsmoral gibt
Der Gabelstapler: Wie? Was? Wer? Wo?
Schreibkompetenz 16: schlusszeichen (Fragezeichen) sprechen zeichen Um eine Frage zu kennzeichnen, wird ein Fragezeichen (?) gesetzt. Fragewörter (zum Beispiel wo, wer, was, wie) zeigen an, dass ein Fragezeichen
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
Bruchrechnung Wir teilen gerecht auf
Bruchrechnung Wir teilen gerecht auf Minipizzen auf Personen. Bruchrechnung Wir teilen gerecht auf Minipizzen auf Personen. : (+) : + Wir teilen einen Teil Eine halbe Minipizza auf Personen. :? Wir teilen
Grundlagen der Theoretischen Informatik, SoSe 2008
1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
Zahlenwinkel: Forscherkarte 1. alleine. Zahlenwinkel: Forschertipp 1
Zahlenwinkel: Forscherkarte 1 alleine Tipp 1 Lege die Ziffern von 1 bis 9 so in den Zahlenwinkel, dass jeder Arm des Zahlenwinkels zusammengezählt das gleiche Ergebnis ergibt! Finde möglichst viele verschiedene
ONLINE-AKADEMIE. "Diplomierter NLP Anwender für Schule und Unterricht" Ziele
ONLINE-AKADEMIE Ziele Wenn man von Menschen hört, die etwas Großartiges in ihrem Leben geleistet haben, erfahren wir oft, dass diese ihr Ziel über Jahre verfolgt haben oder diesen Wunsch schon bereits
Konzepte der Informatik
Konzepte der Informatik Vorkurs Informatik zum WS 2011/2012 26.09. - 30.09.2011 17.10. - 21.10.2011 Dr. Werner Struckmann / Christoph Peltz Stark angelehnt an Kapitel 1 aus "Abenteuer Informatik" von Jens
Welches Übersetzungsbüro passt zu mir?
1 Welches Übersetzungsbüro passt zu mir? 2 9 Kriterien für Ihre Suche mit Checkliste! Wenn Sie auf der Suche nach einem passenden Übersetzungsbüro das Internet befragen, werden Sie ganz schnell feststellen,
1 Mathematische Grundlagen
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Zwischenablage (Bilder, Texte,...)
Zwischenablage was ist das? Informationen über. die Bedeutung der Windows-Zwischenablage Kopieren und Einfügen mit der Zwischenablage Vermeiden von Fehlern beim Arbeiten mit der Zwischenablage Bei diesen
http://www.olympiade-mathematik.de 2. Mathematik Olympiade 2. Stufe (Kreisolympiade) Klasse 7 Saison 1962/1963 Aufgaben und Lösungen
2. Mathematik Olympiade Saison 1962/1963 Aufgaben und Lösungen 1 OJM 2. Mathematik-Olympiade Aufgaben Hinweis: Der Lösungsweg mit Begründungen und Nebenrechnungen soll deutlich erkennbar in logisch und
Strom in unserem Alltag
Strom in unserem Alltag Kannst du dir ein Leben ohne Strom vorstellen? Wir verbrauchen jeden Tag eine Menge Energie: Noch vor dem Aufstehen klingelt der Radiowecker, dann schalten wir das Licht ein, wir
Virtual Roundtable: Perspektiven für SAP-Profis
Virtueller Roundtable "Perspektiven für SAP-Profis" in Kooperation mit apentia consulting der Personalberatung mit Fokus auf SAP Teilnehmer: Prof. Dr. Christian Scholz Organisation: Universität des Saarlandes
DAVID: und David vom Deutschlandlabor. Wir beantworten Fragen zu Deutschland und den Deutschen.
Manuskript Die Deutschen sind bekannt dafür, dass sie ihre Autos lieben. Doch wie sehr lieben sie ihre Autos wirklich, und hat wirklich jeder in Deutschland ein eigenes Auto? David und Nina fragen nach.
Zeichen bei Zahlen entschlüsseln
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Lineare Funktionen. 1 Proportionale Funktionen 3 1.1 Definition... 3 1.2 Eigenschaften... 3. 2 Steigungsdreieck 3
Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
Eva Douma: Die Vorteile und Nachteile der Ökonomisierung in der Sozialen Arbeit
Eva Douma: Die Vorteile und Nachteile der Ökonomisierung in der Sozialen Arbeit Frau Dr. Eva Douma ist Organisations-Beraterin in Frankfurt am Main Das ist eine Zusammen-Fassung des Vortrages: Busines
Versetzungsgefahr als ultimative Chance. ein vortrag für versetzungsgefährdete
Versetzungsgefahr als ultimative Chance ein vortrag für versetzungsgefährdete Versetzungsgefährdete haben zum Großteil einige Fallen, die ihnen das normale Lernen schwer machen und mit der Zeit ins Hintertreffen
1 topologisches Sortieren
Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Orientierungstest für angehende Industriemeister. Vorbereitungskurs Mathematik
Orientierungstest für angehende Industriemeister Vorbereitungskurs Mathematik Weiterbildung Technologie Erlaubte Hilfsmittel: Formelsammlung Taschenrechner Maximale Bearbeitungszeit: 1 Stunde Provadis
AGROPLUS Buchhaltung. Daten-Server und Sicherheitskopie. Version vom 21.10.2013b
AGROPLUS Buchhaltung Daten-Server und Sicherheitskopie Version vom 21.10.2013b 3a) Der Daten-Server Modus und der Tresor Der Daten-Server ist eine Betriebsart welche dem Nutzer eine grosse Flexibilität
Deutsches Rotes Kreuz. Kopfschmerztagebuch von:
Deutsches Rotes Kreuz Kopfschmerztagebuch Kopfschmerztagebuch von: Hallo, heute hast Du von uns dieses Kopfschmerztagebuch bekommen. Mit dem Ausfüllen des Tagebuches kannst Du mehr über Deine Kopfschmerzen
Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer
Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer Allgemein: Das RSA-Verschlüsselungsverfahren ist ein häufig benutztes Verschlüsselungsverfahren, weil es sehr sicher ist. Es gehört zu der Klasse der
Die SPD und die Grünen machen im Niedersächsischen Landtag. Alle Menschen sollen in der Politik mitmachen können.
Antrag Die SPD und die Grünen machen im Niedersächsischen Landtag einen Vorschlag: Alle Menschen sollen in der Politik mitmachen können. Menschen mit Behinderung und Menschen ohne Behinderung. Der Niedersächsische
Also: Wie es uns geht, das hat nichts mit dem zu tun, ob wir an Gott glauben.
Liebe Schwestern und Brüder, Ich möchte mit Ihnen über die Jahreslosung dieses Jahres nachdenken. Auch wenn schon fast 3 Wochen im Jahr vergangen sind, auch wenn das Jahr nicht mehr wirklich neu ist, auch
OECD Programme for International Student Assessment PISA 2000. Lösungen der Beispielaufgaben aus dem Mathematiktest. Deutschland
OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
Hinweise in Leichter Sprache zum Vertrag über das Betreute Wohnen
Hinweise in Leichter Sprache zum Vertrag über das Betreute Wohnen Sie möchten im Betreuten Wohnen leben. Dafür müssen Sie einen Vertrag abschließen. Und Sie müssen den Vertrag unterschreiben. Das steht
Arbeiten Sie gerne für die Ablage?
University of Applied Sciences Arbeiten Sie gerne für die Ablage? Ihr Studium kommt nun in die Schlussphase, denn Sie haben sich gerade zur Abschlussarbeit angemeldet. Auch wenn das Ende Ihres Studiums
Nicht kopieren. Der neue Report von: Stefan Ploberger. 1. Ausgabe 2003
Nicht kopieren Der neue Report von: Stefan Ploberger 1. Ausgabe 2003 Herausgeber: Verlag Ploberger & Partner 2003 by: Stefan Ploberger Verlag Ploberger & Partner, Postfach 11 46, D-82065 Baierbrunn Tel.
Advoware mit VPN Zugriff lokaler Server / PC auf externe Datenbank
Advoware mit VPN Zugriff lokaler Server / PC auf externe Datenbank Die Entscheidung Advoware über VPN direkt auf dem lokalen PC / Netzwerk mit Zugriff auf die Datenbank des zentralen Servers am anderen
Es gibt nur eine Bilanz die zählt: Ihre Zufriedenheit.
Es gibt nur eine Bilanz die zählt: Inhalt Im August 2013 führte die Packenius, Mademann & Partner GmbH eine Online-Kurzbefragung zum Thema Pflege durch. Die Ergebnisse sind auf ganze Zahlen gerundet. Untersuchungsdesign
Kreative Schreibtechnik Clustering
Kreative Schreibtechnik Clustering Von Heike Thormann, kreativesdenken.com Einführung 2 Clustering Einführung: Kreative Schreibtechnik Clustering Clustering (oder auch Clustern) ist eine von der amerikanischen
Skript und Aufgabensammlung Terme und Gleichungen Mathefritz Verlag Jörg Christmann Nur zum Privaten Gebrauch! Alle Rechte vorbehalten!
Mathefritz 5 Terme und Gleichungen Meine Mathe-Seite im Internet kostenlose Matheaufgaben, Skripte, Mathebücher Lernspiele, Lerntipps, Quiz und noch viel mehr http:// www.mathefritz.de Seite 1 Copyright
Inhalt. Allgemeine Einführung. Argumentationsvermögen. Räumliches Vorstellungsvermögen. Begabungen und Fähigkeiten messen
Beispielheft Inhalt Allgemeine Einführung Test Eins: Test Zwei: Test Drei: Test Vier: Test Fünf: Argumentationsvermögen Auffassungsvermögen Zahlenvermögen Sprachverständnis Räumliches Vorstellungsvermögen
DollarIndex? AUD/JPY, AUD/USD? CHF/JPY - EUR/CHF, EUR/GBP, EUR/JPY, EUR/USD -
MikeC.Kock FOREX - Wochenausblick KW 30 DollarIndex? AUD/JPY, AUD/USD? CHF/JPY - EUR/CHF, EUR/GBP, EUR/JPY, EUR/USD - NZD/JPY, NZD/USD? USD/JPY Viel wird aktuell über die wirtschaftlichen Auswirkungen
L10N-Manager 3. Netzwerktreffen der Hochschulübersetzer/i nnen Mannheim 10. Mai 2016
L10N-Manager 3. Netzwerktreffen der Hochschulübersetzer/i nnen Mannheim 10. Mai 2016 Referentin: Dr. Kelly Neudorfer Universität Hohenheim Was wir jetzt besprechen werden ist eine Frage, mit denen viele
Wissenschaftliche Grundlagen des Mathematischen Schulstoffs IV. Die erste Stunde. Die erste Stunde
Wissenschaftliche Grundlagen des Mathematischen Schulstoffs IV Was ist ist Mathematik? Der Inhalt Geometrie (seit (seit Euklid, ca. ca. 300 300 v. v. Chr.) Chr.) Die Die Lehre vom vom uns uns umgebenden
Krippenspiel für das Jahr 2058
Ev.-Luth. Landeskirche Sachsens Spielen & Gestalten Krippenspiel für das Jahr 2058 Krippenspiel für das Jahr 2058 K 125 Impressum Weihnachtsspielangebot 2009 Krippenspiel für das Jahr 2058 K 125 Die Aufführungsrechte
Lernerfolge sichern - Ein wichtiger Beitrag zu mehr Motivation
Lernerfolge sichern - Ein wichtiger Beitrag zu mehr Motivation Einführung Mit welchen Erwartungen gehen Jugendliche eigentlich in ihre Ausbildung? Wir haben zu dieser Frage einmal die Meinungen von Auszubildenden
Gutes Leben was ist das?
Lukas Bayer Jahrgangsstufe 12 Im Hirschgarten 1 67435 Neustadt Kurfürst-Ruprecht-Gymnasium Landwehrstraße22 67433 Neustadt a. d. Weinstraße Gutes Leben was ist das? Gutes Leben für alle was genau ist das
DAS LOGO. dunklem Hintergrund
DESIGN MANUAL DAS LOGO Das Logo der VBL Das Logo der VBL auf dunklem Hintergrund SO BITTE NICHT! Auf keinen Fall dürfen Änderungen an dem Logo vorgenommen werden, wie die Anwendung zusätzlicher Effekte
Screening Das Programm. zur Früherkennung von Brustkrebs
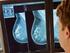Mammographie Screening Das Programm zur Früherkennung von Brustkrebs das Mammographie Screening Programm Wenn Sie zwischen 50 und 69 Jahre alt sind, haben Sie alle zwei Jahre Anspruch auf eine Mammographie-Untersuchung
4. AUSSAGENLOGIK: SYNTAX. Der Unterschied zwischen Objektsprache und Metasprache lässt sich folgendermaßen charakterisieren:
4. AUSSAGENLOGIK: SYNTAX 4.1 Objektsprache und Metasprache 4.2 Gebrauch und Erwähnung 4.3 Metavariablen: Verallgemeinerndes Sprechen über Ausdrücke von AL 4.4 Die Sprache der Aussagenlogik 4.5 Terminologie
Mit dem Tool Stundenverwaltung von Hanno Kniebel erhalten Sie die Möglichkeit zur effizienten Verwaltung von Montagezeiten Ihrer Mitarbeiter.
Stundenverwaltung Mit dem Tool Stundenverwaltung von Hanno Kniebel erhalten Sie die Möglichkeit zur effizienten Verwaltung von Montagezeiten Ihrer Mitarbeiter. Dieses Programm zeichnet sich aus durch einfachste
Lichtbrechung an Linsen
Sammellinsen Lichtbrechung an Linsen Fällt ein paralleles Lichtbündel auf eine Sammellinse, so werden die Lichtstrahlen so gebrochen, dass sie durch einen Brennpunkt der Linse verlaufen. Der Abstand zwischen
Anleitung über den Umgang mit Schildern
Anleitung über den Umgang mit Schildern -Vorwort -Wo bekommt man Schilder? -Wo und wie speichert man die Schilder? -Wie füge ich die Schilder in meinen Track ein? -Welche Bauteile kann man noch für Schilder
IT-SICHERHEIT IM UNTERNEHMEN Mehr Sicherheit für Ihre Entscheidung
IT-SICHERHEIT IM UNTERNEHMEN Mehr Sicherheit für Ihre Entscheidung IT-SICHERHEIT IM UNTERNEHMEN Mehr Sicherheit für ihre Entscheidung Entdecken Sie was IT Sicherheit im Unternehmen bedeutet IT Sicherheit
Alle Schlüssel-Karten (blaue Rückseite) werden den Schlüssel-Farben nach sortiert und in vier getrennte Stapel mit der Bildseite nach oben gelegt.
Gentlemen", bitte zur Kasse! Ravensburger Spiele Nr. 01 264 0 Autoren: Wolfgang Kramer und Jürgen P. K. Grunau Grafik: Erhard Dietl Ein Gaunerspiel für 3-6 Gentlemen" ab 10 Jahren Inhalt: 35 Tresor-Karten
Linienland, Flächenland und der Hyperraum Ein Ausflug durch die Dimensionen
Linienland, Flächenland und der Hyperraum Ein Ausflug durch die Dimensionen Stephan Rosebrock Pädagogische Hochschule Karlsruhe 23. März 2013 Stephan Rosebrock (Pädagogische Hochschule Linienland, Karlsruhe)
Arbeit zur Lebens-Geschichte mit Menschen mit Behinderung Ein Papier des Bundesverbands evangelische Behindertenhilfe e.v.
Arbeit zur Lebens-Geschichte mit Menschen mit Behinderung Ein Papier des Bundesverbands evangelische Behindertenhilfe e.v. Meine Lebens- Geschichte Warum ist Arbeit zur Lebens-Geschichte wichtig? Jeder
Bevor lineare Gleichungen gelöst werden, ein paar wichtige Begriffe, die im Zusammenhang von linearen Gleichungen oft auftauchen.
R. Brinkmann http://brinkmann-du.de Seite 1 13.0.010 Lineare Gleichungen Werden zwei Terme durch ein Gleichheitszeichen miteinander verbunden, so entsteht eine Gleichung. Enthält die Gleichung die Variable
Matrix42. Use Case - Sicherung und Rücksicherung persönlicher Einstellungen über Personal Backup. Version 1.0.0. 23. September 2015 - 1 -
Matrix42 Use Case - Sicherung und Rücksicherung persönlicher Version 1.0.0 23. September 2015-1 - Inhaltsverzeichnis 1 Einleitung 3 1.1 Beschreibung 3 1.2 Vorbereitung 3 1.3 Ziel 3 2 Use Case 4-2 - 1 Einleitung
Zahlen auf einen Blick
Zahlen auf einen Blick Nicht ohne Grund heißt es: Ein Bild sagt mehr als 1000 Worte. Die meisten Menschen nehmen Informationen schneller auf und behalten diese eher, wenn sie als Schaubild dargeboten werden.
Musterlösungen zur Linearen Algebra II Blatt 5
Musterlösungen zur Linearen Algebra II Blatt 5 Aufgabe. Man betrachte die Matrix A := über dem Körper R und über dem Körper F und bestimme jeweils die Jordan- Normalform. Beweis. Das charakteristische
Avenue Oldtimer Liebhaber- und Sammlerfahrzeuge. Ihre Leidenschaft, gut versichert
Avenue Oldtimer Liebhaber- und Sammlerfahrzeuge Ihre Leidenschaft, gut versichert Die Versicherung für aussergewöhnliche Fahrzeuge Sicherheit für das Objekt Ihrer Leidenschaft Die Versicherung von Sammlerfahrzeugen
ALEMÃO. Text 1. Lernen, lernen, lernen
ALEMÃO Text 1 Lernen, lernen, lernen Der Mai ist für viele deutsche Jugendliche keine schöne Zeit. Denn dann müssen sie in vielen Bundesländern die Abiturprüfungen schreiben. Das heiβt: lernen, lernen,
Das Blabla des LiLi-Webteams. Browser. HTML-Dateien. Links & Webadressen. ROXEN.
A Das Blabla des LiLi-Webteams Browser. HTML-Dateien. Links & Webadressen. ROXEN. Ansicht a1: Browser Das English Wort Browser wird gern direkt übersetzt mit dem deutschen Stöberer. Verstehen sollte man
Tag des Datenschutzes
Tag des Datenschutzes Datenschutz und Software: Vertrauen ist gut, Kontrolle ist besser Dr. Michael Stehmann Zur Person Rechtsanwalt Dr. Michael Stehmann Studium der Rechtswissenschaft an der Universität
Speicher in der Cloud
Speicher in der Cloud Kostenbremse, Sicherheitsrisiko oder Basis für die unternehmensweite Kollaboration? von Cornelius Höchel-Winter 2013 ComConsult Research GmbH, Aachen 3 SYNCHRONISATION TEUFELSZEUG
Das sogenannte Beamen ist auch in EEP möglich ohne das Zusatzprogramm Beamer. Zwar etwas umständlicher aber es funktioniert
Beamen in EEP Das sogenannte Beamen ist auch in EEP möglich ohne das Zusatzprogramm Beamer. Zwar etwas umständlicher aber es funktioniert Zuerst musst du dir 2 Programme besorgen und zwar: Albert, das
Wichtige Forderungen für ein Bundes-Teilhabe-Gesetz von der Bundesvereinigung Lebenshilfe. in Leichter Sprache
1 Wichtige Forderungen für ein Bundes-Teilhabe-Gesetz von der Bundesvereinigung Lebenshilfe in Leichter Sprache 2 Impressum Originaltext Bundesvereinigung Lebenshilfe e. V. Leipziger Platz 15 10117 Berlin
Südbaden-Cup. Ausstieg Champions
Südbaden-Cup Ausstieg Champions Beschreibung Der Ausstieg aus dem Turnier dient Spielern die eine weite Anreise haben sich aus dem Turnier zu verabschieden um noch am gleichen Tag heimzureisen und einen
Versetzungsregeln in Bayern
Grundschule Schüler der Jahrgangsstufen 1 und 2 rücken ohne besondere Entscheidung vor. Das Vorrücken in den Jahrgangsstufen 3 und 4 soll nur dann versagt werden, wenn der Schüler in seiner Entwicklung
Public Domain ist Aladins Wunderlampe des Internetzeitalters. Schlagen Sie Kapital aus den geistigen Werken anderer Menschen. Völlig legal.
Public Domain ist Aladins Wunderlampe des Internetzeitalters. Schlagen Sie Kapital aus den geistigen Werken anderer Menschen. Völlig legal. ebookzeile.de informiert: Der Begriff Public Domain bezeichnet
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Eine mathematische Reise ins Unendliche. Peter Koepke Universität Bonn
Eine mathematische Reise ins Unendliche Peter Koepke Universität Bonn Treffen sich die Schienen im Unendlichen? Gibt es unendlich ferne Punkte? Gibt es unendliche Zahlen? 1 Antwort: Nein! , so prostestire
Kapitalerhöhung - Verbuchung
Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
Formale Systeme, WS 2012/2013 Lösungen zu Übungsblatt 4
Karlsruher Institut für Technologie Institut für Theoretische Informatik Prof. Dr. Peter H. Schmitt David Farago, Christoph Scheben, Mattias Ulbrich Formale Systeme, WS 2012/2013 Lösungen zu Übungsblatt
Hilfedatei der Oden$-Börse Stand Juni 2014
Hilfedatei der Oden$-Börse Stand Juni 2014 Inhalt 1. Einleitung... 2 2. Die Anmeldung... 2 2.1 Die Erstregistrierung... 3 2.2 Die Mitgliedsnummer anfordern... 4 3. Die Funktionen für Nutzer... 5 3.1 Arbeiten
Lokales Netzwerk Wie kann ich lokal installierte Drucker im Netzwerk für andere Nutzer freigeben? Frage:
Wie kann ich lokal installierte Drucker im Netzwerk für andere Nutzer freigeben? Frage: Ich möchte, dass ein Drucker von verschiedenen Rechnern aus genutzt werden kann. Wie kann ich eine Druckerfreigabe
Wie ist das Wissen von Jugendlichen über Verhütungsmethoden?
Forschungsfragen zu Verhütung 1 Forschungsfragen zu Verhütung Wie ist das Wissen von Jugendlichen über Verhütungsmethoden? Wie viel Information über Verhütung ist enthalten? Wie wird das Thema erklärt?
Handbuch ECDL 2003 Modul 2: Computermanagement und Dateiverwaltung Der Task-Manager
Handbuch ECDL 2003 Modul 2: Computermanagement und Dateiverwaltung Der Task-Manager Dateiname: ecdl2_03_05_documentation Speicherdatum: 22.11.2004 ECDL 2003 Modul 2 Computermanagement und Dateiverwaltung
Wasserkraft früher und heute!
Wasserkraft früher und heute! Wasserkraft leistet heute einen wichtigen Beitrag zur Stromversorgung in Österreich und auf der ganzen Welt. Aber war das schon immer so? Quelle: Elvina Schäfer, FOTOLIA In
Betragsgleichungen und die Methode der Fallunterscheidungen
mathe online Skripten http://www.mathe-online.at/skripten/ Betragsgleichungen und die Methode der Fallunterscheidungen Franz Embacher Fakultät für Mathematik der Universität Wien E-mail: franz.embacher@univie.ac.at