1 Zinsrechnung. 1.1 Grundbegrie
|
|
|
- Annika Schwarz
- vor 8 Jahren
- Abrufe
Transkript
1 1 Zinsrechnung Als Zinsrechnung bezeichnet man alle mathematischen Formeln zur Berechnung der Zinsen, die für die Verleihung eines Geldbetrages innerhalb eines Zeitraumes anfallen. Es gibt zwei grundsätzliche Ansätze für die Verzinsung. Der Unterschied besteht in der Behandlung der bereits angefallenen aber noch nicht ausgezahlten Zinsen. Werden die Zinsen immer nur auf das Anfangskapital bezogen, spricht man von einfacher Verzinsung. Werden die Zinsen dagegen nach einer Zinsperiode genannten Zeit dem zu verzinsenden Kapital hinzugeschlagen, erhält der Gläubiger Zinsen auch auf die Zinsen, man spricht von Zinseszinsen. Beide Ansätze können aber auch verknüpft werden, was mit gemischter Verzinsung bezeichnet wird. Zinsen spielen in der Wertpapieranalyse die zentrale Rolle. Über Zinsen werden erzielte Renditen berechnet und der Wert zukünftiger Erträge ermittelt. 1.1 Grundbegrie Bei Geldgeschäften überlässt ein so genannter Gläubiger oder Kapitalgeber dem Schuldner für einen bestimmten als Laufzeit bezeichneten Zeitraum einen Anfangskapital genannten Betrag. Am Ende der Laufzeit wird vom Schuldner das Anfangskapital getilgt und zusätzlich der Zinsbetrag als Belohnung für die Überlassung des Geldes bezahlt. Die Gesamtsumme wird als Endkapital bezeichnet. Der Zinsbetrag ist ein bestimmter Prozentsatz des verliehenen Kapitals. Der auf ein Jahr bezogene Prozentsatz, wofür die Abkürzung p.a. für lateinisch pro anno gilt, wird als Zinssatz i bezeichnet, etwa i = 4%. Die reine Zahl, die vor dem Prozentzeichen steht, wird Zinsfuÿ genannt. Der Zinssatz gibt an, wie viel Prozent des Anfangskapitals nach einem Jahr als Zinsbetrag fällig sind. Bei Anlage von Euro zum Zinssatz von i = 4% werden also am Ende des ersten Jahres 40 Euro als Zinsen gut geschrieben. Der Gläubiger heiÿt so, weil er glaubt, dass der Schuldner am Ende der Laufzeit das entliehene Kapital zuzüglich einer Zinsbetrag genannten Belohnung tilgen kann. Beide Parteien können natürliche oder juristische Personen wie Banken und Unternehmen sein. Zwischen Gläubiger und Schuldner besteht ein Schuldverhältnis, das in der Regel vertraglich abgesichert ist. Eine Bank schlieÿt z.b. einen Darlehensvertrag mit dem Nehmer des Darlehens ab. Typische Geschäfte dieser Art ndet man in den folgenden Finanzbereichen. ˆ Spareinlagen bei einer Bank, der Kunde ist Gläubiger, die Bank Schuldner. ˆ Darlehen von einer Bank, der Kunde ist Schuldner, die Bank Gläubiger. 1
2 1 Zinsrechnung ˆ Anleihen von Staaten oder Unternehmen. Hier sind die Käufer die Gläubiger und die Emittenten (Staat, Unternehmen) die Schuldner. 1.2 Wofür gibt es Zins? Der Zinsbegri ist zentral für alle Bereiche der Finanzen. Zinsen haben etwas anrüchiges, da der Gläubiger sie scheinbar ohne eigene Arbeit erzielt. Zinsen werden aus vier Gründen gefordert: ˆ Inationsausgleich. Der Gläubiger möchte real nach Abzug der Geldentwertung am Ende nicht schlechter als am Anfang da stehen. ˆ Liquiditätsprämie. Der Gläubiger wird für den zeitweisen Verzicht auf die Verfügbarkeit des verliehenen Geldes belohnt. ˆ Risikoprämie. Die Unsicherheit des Gläubigers, ob der Schuldner Zinsen und Tilgung zurückzahlen kann, wird ebenfalls mit den Zinsen bezahlt. ˆ Gewinstreben. Natürlich möchte der Gläubiger durch das Verleihen von Geld auch ein Geschäft machen, das Geld arbeiten lassen, wie es so schön heiÿt. Zur Arbeit verdammt ist aber nur der Schuldner, um Kapital und Zinsen leisten zu können. Inationsausgleich ist ein ehrenwertes Anliegen, die anderen Anliegen stoÿen dagegen auf wenig Sympathie. Wegen der Risiko- und Zeitabhängigkeit der Zinsen gibt es auch keinen einheitlichen Zinssatz, sondern für jede Risikoklasse und für jede Zeit einen eigenen. Der Zinssatz ist also eine Funktion i = i(t, σ), wobei t der Parameter der Zeit und σ ein noch näher zu kennzeichnendes Maÿ für das Risiko ist. In normalen Zeiten wächst i(t, σ) monoton in t und σ. 1.3 Bestimmung des Zinssatzes Die Höhe des Zinssatzes ist natürlich marktabhängig, berücksichtigt aber auch die Bonität des Schuldners. Nach unseren grundsätzlichen Überlegungen sollte sich der Zinssatz aus vier Komponenten zusammensetzen: i = i I + i L + i R + i G, wobei jede der einzelnen Zahlen Ination, Liquidität, Risiko und Gewinn berücksichtigt. Die beiden ersten Komponenten hängen kaum vom Schuldner ab, während die Risikound die Gewinnkomponente ganz stark dessen Situation widerspiegeln. Generell gilt, 2
3 1.4 Zinsrechnung dass das Gewinnstreben mit eingegangenem Risiko wächst. Je dringender also Geld benötigt wird, umso teurer wird es. So muss im Frühjahr 2009 der Bund vertreten durch den Finanzminister rund 6 Prozent weniger Zinsen zahlen als die krisengeschüttelte Automobilindustrie. Daimler geriet dadurch in eine so verzweifelte Lage, dass einem Investor aus dem Nahen Osten rund 10 Prozent des Aktienkapitals für knapp 2 Milliarden Euro überlassen wurde. 1.4 Zinsrechnung Als Zinsrechnung bezeichnet man alle mathematischen Formeln zur Berechnung der Zinsen, die für die Verleihung eines Geldbetrages innerhalb eines Zeitraumes anfallen. Im Verlauf der Zeit wurden zwar viele unterschiedliche Formeln entwickelt, aber immer werden folgende vier Gröÿen berücksichtigt: ˆ Das Anfangskapital K 0, also die verliehene Geldsumme. ˆ Der Zinssatz i, d.h. der Prozentsatz, der den auf das Anfangskapital bezogenen Zinsbetrag für ein Jahr festlegt. ˆ Die Laufzeit t, d.h. den Zeitraum für die Überlassung des Anfangskapitals. Zeiten werden in der Finanzmathematik immer mit der Einheit Jahr angegeben. ˆ Das Endkapital K t, also die am Ende der Laufzeit fällige Geldsumme aus Anfangskapital und Zinsbetrag. Da der Zinssatz inations- und damit zeitabhängig ist, bleibt er nicht für immer konstant. Die Zinsbindung ist die Zeit, wo der Zinssatz unverändert bleibt. Zinssatz und Zinsbindung werden von Gläubiger und Schuldner je nach Marktbedingungen ausgehandelt. Wenn Sie also von einem Freund Euro bei einem Zinssatz von 2 % für vier Jahre leihen, sind K 0 = 5.000, i = 2% und t = 4. Nur das Endkapital kennen wir noch nicht. 1.5 Exponentielle Verzinsung Nach diesen grundsätzlichen Überlegungen soll jetzt eine Formel für die Verzinsung gewonnen werden. Diese soll von der Form K t = K 0 f(t) sein, wobei die Funktion f(t) den Wert zum Zeitpunkt t eines zum Zeitpunkt 0 verliehenen Euros darstellt. Der Wert jedes anderen Anfangskapitals muss dazu proportional sein. Diese Funktion muss streng monoton wachsend sein und die Bedingung f(t + s) = f(t)f(s) (1.1) 3
4 1 Zinsrechnung erfüllen, denn die Verleihung von K 0 über den Zeitraum t + s muss zum selben Endwert führen, wie die Verleihung von K 0 über den Zeitraum t und die anschlieÿende Ausleihe des Zwischenbetrags K 0 f(t) über die weitere Zeitspanne s. Bezeichnet man mit i die Zuwachsrate für ein Jahr, so gilt f(1) = 1 + i. (1.2) Die einzige Funktion, die beide Gleichungen (1.1) und (1.2) erfüllt, ist durch f(t) = (1 + i) t (1.3) gegeben. Somit gilt K t = K 0 (1 + i) t. (1.4) Denition 1.1. Jede Verzinsung, die nach diesem Gesetz erfolgt, heiÿt exponentielle Verzinsung. Die Zahl i ist der Zinssatz und t die Laufzeit. Der Zinsbetrag Z t ist die Dierenz zwischen End- und Anfangskapital. Wenn Sie also die Euro nicht von einem Freund, sondern von einer Bank zu 2 Prozent für vier Jahre bei exponentieller Verzinsung ausleihen, wird am Ende der Betrag fällig. Der Zinsbetrag ist 412,16 Euro. 1.6 Stetige Verzinsung K t = 1, = 5.412, 16 e Die Gleichung (1.4) auf Seite 4 lässt sich durch die Exponential- und Logarithmusfunktion wie folgt umschreiben: K t = K 0 e ln(1+i)t. (1.5) Setzt man so ergibt sich ĩ = ln(1 + i), K t = K 0 eĩt. (1.6) Lässt man die Tilde über dem Zinssatz weg, erhält man eine weitere Form der Verzinsung. Denition 1.2. Werden Anfangs- und Endkapital über die Zinsformel verknüpft, spricht man von stetiger Verzinsung. K t = K 0 e it (1.7) Diese Form der Verzinsung ist in den USA gebräuchlich, und wird bei Renditerechnungen verwendet. Stetige Verzinsung und exponentielle Verzinsung sind gleichwertig, was in einem Satz festgehalten werden soll. 4
5 1.7 Einfache Zinsen Satz 1.1. Die stetige Verzinsung zum Zinssatz i entspricht der exponentiellen Verzinsung zum Zinssatz e i 1. Umgekehrt entspricht der exponentiellen Verzinsung zum Zinssatz i die stetige zum Zinssatz ln(1 + i). Wegen e i 1 > i für i > 0 führt bei gleichem Zinssatz und sonst gleichen Bedingungen die stetige Verzinsung zu einem höheren Endkapital als die exponentielle. Es sei noch angemerkt, dass in der Literatur der Zinssatz bei exponentieller Verzinsung konform und der bei stetiger Verzinsung kontinuierlich genannt wird. Die stetige Verzinsung selbst wird ebenfalls zuweilen als kontinuierlich bezeichnet. Abschlieÿend ein Beispiel zu den beiden Formen der Verzinsung. Beispiel 1.1. Welchen Endwert erreicht ein Kapital von Euro zwischen dem und dem bei einem Zinssatz von i = 0, 08 mit exponentieller und stetiger Verzinsung? Wie müsste der Zinssatz der exponentiellen Verzinsung sein, damit sich derselbe Endwert wie bei der stetigen Verzinsung ergibt? Das Kapital wird genau fünf Jahre verzinst. Somit ergibt sich bei der exponentiellen Verzinsung K t = (1 + 0, 08) 5 = , 08 Euro und bei der stetigen Verzinsung K t = e 0,08 5 = , 70 Euro. Der Endwert von ,70 Euro würde bei exponentieller Verzinsung bei einem Zinssatz von ī = e i 1 = e 0,08 1 = 0, erreicht. Bei gleichem Zinssatz ergibt die stetige Verzinsung immer einer höheren Endwert als die exponentielle Verzinsung. 1.7 Einfache Zinsen Die Grundformel der exponentiellen Verzinsung (1.4) würde zur Abwicklung aller Zinsgeschäfte genügen. Die Berechnung ist mit modernen Taschenrechnern problemlos möglich, aber in früheren Zeiten nur mit Logarithmentafeln. Daher wurde die Grundformel linearisiert. Denition 1.3. Werden Anfangs- und Endkapital über die Zinsformel verknüpft, spricht man von einfacher Verzinsung. K t = K 0 (1 + it). (1.8) 5
6 1 Zinsrechnung Trägt man K t über der Zeit ab, ergibt sich eine Gerade, deshalb wird diese Form der Verzinsung auch manchmal lineare Verzinsung genannt. Für private Geldgeschäfte sind nur einfache Zinsen erlaubt, während Finanzunternehmen wie Banken auch alle anderen Verzinsungsarten gestattet sind. Betrachten wir ein Beispiel mit allen bisher bekannten Zinsformeln. Beispiel 1.2. Welchen Endwert erreicht ein Kapital von Euro zwischen dem und dem bei einem Zinssatz von i = 0, 03 mit exponentieller, stetiger und einfacher Verzinsung? Wie müsste der Zinssatz der stetigen Verzinsung sein, damit sich derselbe Endwert wie bei der exponentiellen Verzinsung ergibt? Das Kapital wird genau zwei Jahre verzinst. Somit ergibt sich bei der exponentiellen Verzinsung K t = (1 + 0, 03) 2 = , 00 Euro und bei der stetigen Verzinsung Bei der einfachen Verzinsung erhält man K t = e 0,03 2 = , 55 Euro. K t = (1 + 0, 03 2) = , 00 Euro. Der Endwert von ,00 Euro würde bei stetiger Verzinsung bei einem Zinssatz von ĩ = ln(1 + i) = 0, erreicht. Bei allen Beispielen habe ich bisher immer als Einheit der Zeit ein Jahr verwendet. Das ist so üblich und sei noch einmal festgehalten. Die Einheit der Zeit ist in der Finanzmathematik in der Regel ein Jahr. 1.8 Einuss der Laufzeit Ist die Laufzeit geringer als ein Jahr, führt die einfache Verzinsung zu höheren Zinserträgen als die exponentielle Verzinsung. Bei Laufzeiten ab einem Jahr dreht sich das zunächst langsam und dann mit wachsender Laufzeit immer deutlicher um. Das verdeutlicht die Abbildung 1.1 auf Seite 7, die das erzielte Endkapital einer Anlage von Euro zum Zinssatz von 8 Prozent bei einfacher und exponentieller Verzinsung als Funktion der Laufzeit zeigt. Für kleine Zeitabstände ist der Unterschied zwischen den beiden Formen der Verzinsung gering, daher wird auf dem Geldmarkt, wo die Verleihungszeiten nicht höher als ein Jahr sind, meistens mit linearen Zinsen gerechnet. 6
7 1.9 Auösungen nach Anfangskapital, Zeit und Zinssatz Vergleich von linearer und exponentieller Verzinsung 5000 Endkapital Zeit in Jahren Abbildung 1.1: Vergleich zwischen einfacher (linearer) und exponentieller Verzinsung. 1.9 Auösungen nach Anfangskapital, Zeit und Zinssatz Wir haben bis jetzt drei verschiedene Arten der Verzinsung kennengelernt, und zwar die exponentielle, die stetige und die lineare Verzinsung. Die drei Grundformeln lauten: Exponentielle Verzinsung: K t = K 0 (1 + i) t, (1.9) Stetige Verzinsung: K t = K 0 e it, (1.10) Einfache Verzinsung: K t = K 0 (1 + it). (1.11) In jeder Formel sind die vier Gröÿen K t, K 0, i und t beteiligt. Jede Formel lässt sich nach einer der vier Gröÿen auösen. Man kann das Ausgangskapital K 0 wie folgt aus den restlichen Gröÿen berechnen: K 0 = K t (1 + i) t, (1.12) K 0 = K t e it, (1.13) K 0 = K t 1 + it. (1.14) 7
8 1 Zinsrechnung Die Auösungen nach i folgen jetzt. i = ( Kt K 0 Als letztes gebe ich die Auösungen nach t an Zinsmethoden ) 1/t 1, (1.15) i = ln(k t) ln(k 0 ), (1.16) t i = K t K 0. (1.17) K 0 t t = ln(k t) ln(k 0 ), ln(1 + i) (1.18) t = ln(k t) ln(k 0 ), i (1.19) t = K t K 0. (1.20) K 0 i In jeder der drei Zinsformeln gehen der Zinssatz i und die Zeit t zwischen Ein- und Auszahlung ein. Die Einheit der Zeit ist ein Jahr. Die Messung der Zeit erfolgt über die Berechnung der Tage zwischen Anfangs- und Enddatum und anschlieÿender Division durch die Anzahl der Tage in einem Jahr. Das scheint banal zu sein, aber trotzdem gibt es viele verschiedene Methoden zur Berechnung von t, die ich jetzt vorstellen werde. Zunächst noch die formale Denition des Begries Zinsmethode. Denition 1.4. Jede Zinstagzählmethode, englisch day count convention, legt fest, wie viel Tage zwischen zwei Daten liegen und welche Zeit t anzurechnen ist. Meist wird nur die verkürzte Bezeichnung Zinsmethode verwendet ICMA, ISMA und ISDA Bei der Beschreibung und Festlegung der Zinsmethoden sind drei internationale Organisationen maÿgeblich beteiligt, deren Abkürzungen auch noch leicht zu verwechseln sind. ˆ ICMA: International Capital Market Association. Die International Capital Market Association (ICMA) ist eine Organisation, deren Mitglieder global und lokal tätige Banken, Zentralbanken, Börsen, Fonds- Gesellschaften und Wertpapierhändler sind. Die Regelwerke und Richtlinien von ICMA werden weltweit beachtet und angewendet. Der Sitz von ICMA ist in Zürich. ˆ ISMA: International Securities Market Association Die International Securities Market Association (ISMA) ist eine weitere groÿe internationale Organisation, die weltweit beachtete und befolgte Richtlinien und 8
9 1.10 Zinsmethoden Empfehlungen für die Wertpapiermärkte entwickelt. Die ISMA wurde 1969 als Association of International Bond Dealers (AIBD) gegründet, und hat heute fast 500 Mitglieder. ˆ ISDA: International Swaps and Derivatives Association Die International Swaps and Derivatives Association (ISDA) ist eine Handelsorganisation, die sich vorwiegend mit dem heiÿen Markt für OTC-Derivate befasst. OTC steht für over the counter und meint Finanzinstrumente, die direkt zwischen den Vertragspartnern abgeschlossen werden, und somit weder standardisiert sind noch an einer Börse gehandelt werden. Die Bedeutung dieser Organisationen für die Zinsmethoden wird im folgenden drolligen Zitat ersichtlich: The International Capital Markets Association (ICMA) has veried to IS- DA that the Day Count Convention formerly known as ACT/ACT (ISMA) is now known as ACT/ACT (ICMA) and that the two conventions are identical. Ich beschreibe die Zinsmethoden entsprechend des Internetauftritts von ICMA und übernehme deren Bezeichnungen und Abkürzungen Die kalendergenaue Zinsmethode ACT/ACT (ICMA) Diese Methode wurde also früher ACT/ACT (ISMA) genannt und geistert bis heute unter dieser Bezeichnung durch die Literatur und das Internet. Die Abkürzung ACT steht dabei für actual=taggenau. Hier werden im Anfangsjahr die Tage bis zum Jahresende genau gezählt und dabei der erste Tag mitberechnet und das Ergebnis wird durch die Anzahl der Tage des entsprechenden Jahres geteilt. Dann werden alle ganzen Jahre dazu gezählt. Abschlieÿend werden im Endjahr wieder die restlichen Tage gezählt, das Enddatum aber nicht mit einbezogen, und auch diese Zahl durch die Anzahl der Tage des Endjahrs geteilt. Diese Vorgehensweise berücksichtigt Schaltjahre ohne jede Einschränkung und ist deshalb die einzige in meinen Augen kalendergenaue Zinsmethode. Beispiel 1.3. Betrachten wir die Zeit vom bis zum Das Anfangsjahr ist ein Schaltjahr mit 366 Tagen. In diesem Jahr werden alle 311 Tage einschlieÿlich des gezählt, das ergibt den Bruch 311/366. Danach folgen fünf ganze Jahre. Im Endjahr wird der nicht gezählt, sodass nur 89 Tage zusammenkommen. Somit ist t = = 6, Beispiel 1.4. In einer anderen Variante dieses Ansatzes wird der erste Tag nicht gezählt, aber der letzte. Dann wäre bei unveränderten Daten t = = 6, Weitere Beispiele folgen später. 9
10 1 Zinsrechnung Die Zinsmethode ACT/ACT (EXCEL) Diese Zinsmethode wird in einer Excel-Funktion verwendet und in der Beschreibung act/act genannt, ich werde die Bezeichnung ACT/ACT (EXCEL) verwenden, da ihre Implementation nicht mit der beschriebenen Zinsmethode ACT/ACT (ICMA) übereinstimmt. Die Ausgestaltung von Microsoft ist sehr eigenwillig und wird im Netz heiÿ diskutiert und ist nach meinem Teststand wie folgt. Zunächst werden die Tage k zwischen Anfangs- und Endtermin kalendergenau gezählt. Die Anzahl der Tage y in einem Jahr wird wie folgt berechnet. 1. Liegen Anfangs- und dem Enddatum im gleichen Jahr, ist in einem Schaltjahr y = 366, und sonst ist y = Liegen Anfangs- und Enddatum in verschiedenen Jahren, aber innerhalb einer Dierenz von höchsten einem Jahr, ist y = 366, wenn innerhalb des Zeitraums ein Schalttag, also der fällt, sonst ist y = Liegt zwischen dem Anfangs- und dem Enddatum mehr als ein Jahr, müssen alle Jahre, einschlieÿlich der angebrochenen gezählt werden, das ergibt eine Zahl n. Dann wird die Gesamtzahl der Schaltjahre gezählt, das ergibt eine Zahl m. Dann ist y = m n. Die Zeit t zwischen Anfangs- und Enddatum ist der Bruch t = k/y. Bemerkung 1.1. Wenn Anfangs- und Enddatum innerhalb eines Jahres liegen oder sich dazwischen kein Schaltjahr bendet, liefern die Zinsmethoden ACT/ACT (EXCEL) und ACT/ACT /ICMA) das gleiche Ergebnis. Ich werde die Zinsmethoden ACT/ACT (EXCEL) nur selten in Zinsrechnungen verwenden, erwähne sie aber, weil sie in der Excel-Arbeitsblattfunktion BRTEILJAHRE implementiert und in der Beschreibung leider act/act genannt wird, obwohl sie nicht mit ACT/ACT (ICMA) übereinstimmt Zinsmethoden mit kalendergenauer Tagzählung Bei den zwei nun folgenden Zinsmethoden werden zunächst die Anzahl der Tage zwischen dem Anfangs- und dem Enddatum kalendergenau berechnet, wobei das Enddatum nicht mitgezählt wird. Diese Zahl wird anschlieÿend durch einen Nenner geteilt, der der Anzahl der Tage in einem Jahr entspricht. Die Anzahl der Tage in einem Jahr wird vereinfacht entweder auf 360 oder 365 auf 365 Tage gesetzt. Dieser seltsame Ansatz stammt aus Frankreich und England. Die Bezeichnungen sind ACT/360 bzw. ACT/365. ˆ Eurozinsmethode: ACT/360. Die Zeit t zwischen Anfangs- und Enddatum ist der Bruch t = k/360, wobei k die Anzahl der kalendergenau gezählten Tage zwischen Anfangs- und Endtermin ist. Diese Zinsmethode wird auch französisch genannt. Diese Zinsmethode wird in Deutschland u.a. bei Floating Rate Notes und am Euromarkt für fast alle Währungen angewandt. 10
11 1.10 Zinsmethoden ˆ Englische Zinsmethode: ACT/365. Die Zeit t zwischen Anfangs- und Enddatum ist der Bruch t = k/365, wobei k die Anzahl der kalendergenau gezählten Tage zwischen Anfangs- und Endtermin ist. Diese in England verbreitete Zinsmethode ist in Deutschland u.a. bei Geldmarktpapieren gebräuchlich Beispiele zu ACT/XXX Die vier Methoden mit kalendergenauer Tagzählung seien jetzt an einigen Beispielen veranschaulicht. Beispiel 1.5. Betrachten wir die Zeit vom bis zum Bei allen Methoden muss zunächst die Anzahl der Tage zwischen Anfangs- und Enddatum kalendergenau gezählt werden. Das sind hier 220 Tage. Anfangs- und Enddatum liegen in einem Jahr, deshalb haben ACT/ACT (ICMA) und ACT/ACT (EXCEL) dasselbe Ergebnis, nämlich 220/366, da der Zeitraum innerhalb eines Schaltjahrs liegt. Bei der Eurozinsmethode muss 220 durch 360 und bei der englischen Methode durch 365 geteilt werden. Die Werte für t sind deshalb wie in der Tabelle. ACT/ACT (ICMA) ACT/ACT (EXCEL) ACT/360 ACT/ / / / /365 Beispiel 1.6. Betrachten wir die Zeit vom bis zum Das sind wieder 220 Tage. Der Zeitraum liegt innerhalb desselben Jahres, aber nicht in einem Schaltjahr, somit ergibt sich bei ACT/ACT (ICMA) und ACT/ACT (EXCEL) der Wert 220/365. Da weder die Eurozins- noch die französische Methode Schaltjahre berücksichtigen, bleiben die Werte wie im vorigen Beispiel. Die Werte für t sind deshalb wie in der Tabelle. ACT/ACT (ICMA) ACT/ACT (EXCEL) ACT/360 ACT/ / /36 220/ /365 Beispiel 1.7. Betrachten wir die Zeit vom bis zum Bei der Zinsmethode ACT/ACT (ICMA) muss der Zeitraum in die Anteile der beiden Jahre aufgeteilt werden. Im Jahr 2000 sind dies 311 Tage, im Jahr 2001 weitere 55, insgesamt 366 Tage, da der zu diesem Zeitraum gehört. Bei der Methode ACT/ACT (EXCEL) wird diese Zahl durch y = 366 geteilt, denn der Zeitraum ist genau ein Jahr und enthält einen Schalttag. Die Werte für t sind deshalb wie in der Tabelle. ACT/ACT (ICMA) ACT/ACT (EXCEL) ACT/360 ACT/ / / / / /365 Beispiel 1.8. Betrachten wir die Zeit vom bis zum Bei der Zinsmethode ACT/ACT (ICMA) muss der Zeitraum in die Anteile der beiden Jahre aufgeteilt werden. Im Jahr 2000 sind dies 282 Tage, im Jahr 2001 weitere 55, insgesamt 337 Tage. Der Zeitraum ist geringer als ein Jahr, hat 337 Tage und enthält keinen Schalttag, somit ist bei der Zinsmethode ACT/ACT (EXCEL) y = 365. Die Werte für t sind deshalb wie in der Tabelle. 11
12 1 Zinsrechnung ACT/ACT (ICMA) ACT/ACT (EXCEL) ACT/360 ACT/ /366+55/ / / /365 Beispiel 1.9. Betrachten wir die Zeit vom bis zum Bei der Zinsmethode ACT/ACT (ICMA) muss der Zeitraum in die Anteile der beiden Jahre aufgeteilt werden. Im Jahr 2000 sind dies 311 Tage, im Jahr 2001 weitere 56. Der Zeitraum ist nun gröÿer als ein Jahr und hat 367 Tage. Einschlieÿlich der angebrochenen Jahre sind zwei Jahre beteiligt, also ist n = 2. Da 2000 ein Schaltjahr war, ist m = 1 und somit ist bei der Zinsmethode ACT/ACT (EXCEL) y = /2. Alle Werte von t zeigt die folgende Tabelle. ACT/ACT (ICMA) ACT/ACT (EXCEL) ACT/360 ACT/ / / /365,5 367/ /365 Beispiel Betrachten wir die Zeit vom bis zum Dieser Zeitraum enthält fünf ganze Jahre und die angebrochenen Jahre 2000 und 2006 mit 311 bzw. 89 Tagen. Somit ist bei der Zinsmethode ACT/ACT (ICMA) t = 311/ /365. Der Zeitraum enthält Tage verteilt auf n = 7 Jahre, wovon m = 2 Schaltjahre sind, nämlich 2000 und Somit ist bei der Zinsmethode ACT/ACT (EXCEL) y = ( /7) = 365, Die Werte für t sind deshalb wie in der Tabelle. ACT/ACT (ICMA) ACT/ACT (EXCEL) ACT/360 ACT/ / / /(365+2/7) 2226/ / Zinsmethoden mit vereinfachter Tagzählung (30E/360 und 30U/360) Bei diesen Methoden wird vereinfacht angenommen, dass ein Jahr 360 Tage mit 12 Monaten mit je 30 Tagen hat. Daher rührt die Bezeichnung 30/360. Dabei werde ich folgende Bezeichnungen verwenden: ˆ (D1.M1.Y 1). Das Anfangsdatum t 1 etwa der mit D1 = 11, M1 = 12 und Y 1 = ˆ (D2.M2.Y 2). Das Enddatum t 2 etwa der mit D2 = 1, M2 = 2 und Y 2 = Daraus folgt für die Anzahl der Tage zwischen beiden Daten: k = (Y 2 Y 1)360 + (M2 M1)30 + (D2 D1) Hier sind wie beschrieben die (D1.M1.Y 1) und (D2.M2.Y 2) Anfangs- und Enddatum und D1 sowie D2 Werte, die von D1 und D2 abhängen. Diese Zahl wird durch 360 geteilt und ergibt den Wert der Zeit t, d.h. t = k 360 = (Y 2 Y 1) + (M2 M1)/12 + (D2 D1)/360 Leider gibt es zwei Versionen zur Berechnung von D1 und D2. 12
13 1.10 Zinsmethoden Deutsche Zinsmethode: 30E/360 Diese Zinsmethode wird meist 30E/360 genannt. Die beiden Vorschriften zur Berechnung von D1 und D2 sind ganz einfach ˆ Falls D1 gleich 31 ist, setze D1 = 30 sonst setze D1 = D1. Es gilt also D1 = min(30, D1). ˆ Falls D2 gleich 31 ist, setze D2 = 30 sonst setze D2 = D2. Es gilt also D2 = min(30, D2). Der 31. Kalendertag spielt also keine Rolle und wird wie der 30. behandelt. Endet oder beginnt der Vertrag im Februar, werden die Tage kalendergenau gezählt, der 28. Februar, bzw. im Schaltjahr der 29. Februar sind also dann tatsächlich erst der 28. bzw. 29. Tag. Sobald der Februar aber überschritten ist, zählt auch er wie alle anderen Monate mit 30 Tagen. Diese Methode wird in Deutschland u.a. bei Sparbüchern und Termingeldern angewandt. Amerikanische Zinsmethode: 30U/360 Diese Zinsmethode wird meist 30U/360 genannt. Die beiden Vorschriften zur Berechnung von D1 und D2 sind etwas undurchsichtig: ˆ Setze D1 = 30 falls D1 der letzte Tag des Monats ist. Sonst sei D1 = D1. ˆ Setze D2 = D2. Ist aber D2 gleich 31 und D1 gleich 30, so setze D2 = 30. Die erste Bedingung führt nur im Februar zu unterschiedlichen Werten für D1, denn die Amerikaner setzen das Monatsende im Februar auf den Wert 30, die Deutschen aber nie. Deshalb liegen nach deutscher Rechnung zwischen dem und dem drei Tage, nach amerikanischer Zählung vergeht aber nur ein Tag. Für D2 ergeben sich unterschiedliche Werte, wenn der Tag des Enddatums die 31 ist, der Tag des Anfangsdatums aber nicht der 30. oder 31. Tag. Also vergehen zinsmäÿig zwischen dem und dem in Europa 89 Tage, in Amerika dagegen 90 Tage Beispiele zu 30/360 Beispiel Betrachten wir die Zeit vom bis zum Hier sind D 1 = 29 und D 2 = 31, M 1 = 2 und M 2 = 3 sowie Y 1 = 2000 und Y 2 = Nach deutschem Ansatz ergeben sich D1 = 29 und D2 = 30, während man in den USA D1 = 30 und D2 = 30 erhält. Somit sind nach der Zinsmethode 30E/360 t = ( ) + (3 2)/12 + (30 29)/360 = 391/360 und nach der Zinsmethode 30U/360 t = ( ) + (3 2)/12 + (30 30)/360 = 390/360 13
14 1 Zinsrechnung Beispiel Betrachten wir nun die Zeit vom bis zum Hier sind D 1 = 28 und D 2 = 31, M 1 = 2 und M 2 = 3 sowie Y 1 = 2000 und Y 2 = Nach deutschem Ansatz ergeben sich D1 = 28 und D2 = 30, während man in den USA D1 = 28 und D2 = 31 erhält. Somit sind nach der Zinsmethode 30E/360 t = ( ) + (3 2)/12 + (30 28)/360 = 392/360 und nach der Zinsmethode 30U/360 t = ( ) + (3 2)/12 + (31 28)/360 = 393/ Zinsmethode nach PAngV In Deutschland ist in der so genannten Preisangabeverordnung (PAngV) eine weitere Zinsmethode vorgeschrieben, die zwar umständlich zu erklären, aber besonders bei regelmäÿigen Zahlungen vorteilhaft ist. Allerdings wird diese Formel niemals zur Berechnung von Zinsen verwendet, sondern nur zur Berechnung des Eektivzinssatzes eines Kredits oder der Rendite einer Investition. Die Vorgaben sind wie folgt: Schaltjahre werden nicht berücksichtigt. Monate mit 31 Tage werden auf 30 Tage zurückgestutzt, in diesen Monaten sind dann sowohl der 30. als auch der 31. Tag das Monatsende. Im Februar sind entsprechend bereits die Tage 28 und 29 das Monatsende und erhalten die Nummer 30. Dann werden für die Zeitspanne t zwischen zwei Zeitpunkten zunächst die Monate gezählt, wobei Monate am Tag des Anfangsdatums beginnen. Für den noch verbleibenden Rest werden die Tage gezählt als Bruchteil eines Jahres hinzugefügt. Schauen wir einige Beispiele an. Beispiel a) Zeit vom bis zum bis Hier werden zunächst die 21 Monate vom bis zum veranschlagt, dazu kommt noch ein Tag im Zeitraum vom bis zum , da der letzte Tag selbst nicht mehr zählt. Somit tp = 21/12 + 1/365 = 1, b) Zeit vom bis zum bis Hier werden zunächst die 25 Monate vom bis zum veranschlagt, dazu kommen im Mai die vier Tage vom bis zum , da Monatslängen bei PAngV auf 30 Tage festgelegt sind, und noch 7 Tage im Juni 2002, also tp = 25/ /365 = 2, c) Zeit vom bis zum bis Aus dem wird trotz des Schaltjahrs der , während der auf den gestutzt wird. So kommt man auf volle 27 Monate, also tp = 27/12 = 2,
15 1.10 Zinsmethoden Die deutsche Zinsmethode PAngV ist wie gesehen für die Rechnung mit Papier und Bleistift ziemlich einfach. Für Excel oder andere Programme wird aber auch eine Formel benötigt, und die sieht schwieriger aus als die der anderen Zinsmethoden. Man geht wie folgt vor: Zunächst wird der Tag von D 1 auf D1 geändert: { D1 D1 < 31 oder D1 < 28 und M 1 = 2 D1 = (1.21) 30 D1 = 31 oder D1 28 und M 1 = 2 Genauso wird D2 berechnet. Die Zeit tp nach PAngV ist dann { Y 2 Y 1 + (M2 M1)/12 + (D2 D1)/365 tp = Y 2 Y 1 + (M2 M1 1)/12 + (D D1)/365 D2 D1 D2 < D1 (1.22) Ich rechne das schon behandelte Beispiel jetzt noch einmal stur nach dieser algorithmischen Vorschrift. Beispiel a) Zeit vom bis zum bis Hier sind D1 = D1 = 27 und D2 = D2 = 28 mit D2 D1. Somit tp = (1 4)/12 + (28 27)/365 = 1, b) Zeit vom bis zum bis Hier sind D1 = D1 = 27 und D2 = D2 = 8 mit D2 < D1. Somit tp = (6 4 1)/12 + ( )/365 = 2, c) Zeit vom bis zum bis Hier sind D1 = 30 und D2 = 30 mit D2 D1. Somit tp = (5 2)/12 + (30 30)/365 = 2, Abschlieÿende Bemerkungen Zum Schluss noch einige Anmerkungen zu den Zinsmethoden. 1. Immer wieder gern wird diskutiert, ob der Anfangs- oder Endtag verzinst wird. Sicher ist nur, dass auf keinem Fall beide Tage eingerechnet werden. Bei Sparbüchern wird in der Regel der letzte Tag und im Wertpapiergeschäft der erste Tag einer Zinsperiode mit verzinst. Bei allen Zinsmethoden mit fester Anzahl von Jahrestagen ist es egal, ob der Anfangs- oder Endtag gezählt wird. Das trit auf alle Zinsmethoden auÿer ACT/ACT (ICMA) zu. 15
16 1 Zinsrechnung 2. Weder die Bezeichnungen noch die tatsächliche Ausgestaltung der Zinsmethoden ist normiert, daher kann sich hinter 30/360 durchaus 30E/360 oder eine exotische amerikanische Sonderform verbergen. Selbstverständlich sind auch die mit Ländernamen versehenen Methoden keineswegs auf diese Länder beschränkt, noch werden in diesen Ländern ausschlieÿlich diese Methoden verwendet. Die deutsche Zinsmethode wird oft auch europäisch genannt, wie an der Bezeichnung 30E/360 zu erkennen ist. 3. Die Zinsmethode nach PAngV wird niemals zur Berechnung von Zinsen verwendet, sondern wird nur für die Bestimmung von Rendite und Eektivzinssatz eingesetzt Beispiele mit Zinsrechnung Wir kennen bis jetzt drei Arten von Verzinsung, die exponentielle, die stetige und die lineare und fünf Zinsmethoden. Bei gleichem Anfangs- und Enddatum und gleichen Zinssatz i führt ein Kapital K 0 zu 15 unterschiedlichen Endwerten K t. Ich werde das an zwei Beispielen zeigen. Beispiel Man berechne den Endwert und den Zinsbetrag bei exponentieller, stetiger und linearer Verzinsung für ein Kapital von Euro, das im Zeitraum vom bis zum bei einem Zinssatz von i = 0, 08 angelegt wurde. Man verwende alle vorgestellten Zinsmethoden, bis auf die nach PAngV. Hier sind D 1 = 12 und D 2 = 31, M 1 = 1 und M 2 = 3 sowie Y 1 = 2000 und Y 2 = Nach deutschem Ansatz ergeben sich D1 = 12 und D2 = 30, während man in den USA D1 = 12 und D2 = 31 erhält. a) ACT/ACT (ICMA). Hier müssen die Tage kalendergenau gezählt werden, also im Januar einschlieÿlich des Tage, 29 im Februar und 30 im März, also kommen 79 Tage zusammen. Diese Zahl muss durch 366 geteilt werden, da das Jahr ein Schaltjahr ist. Das ergibt dann bei exponentieller Verzinsung und bei stetiger Verzinsung sowie bei linearer Verzinsung K t = (1 + 0, 08) 79/366 = , 55 e, Z t = K t K 0 = , 55 e K t = e 0,08 79/366 = , 71 e, Z t = K t K 0 = , 71 e, K t = (1 + 0, 08 79/366) = , 76 e, Z t = K t K 0 = , 76 e. 16
17 1.11 Beispiele mit Zinsrechnung b) ACT/360. Die Tage müssen auch hier kalendergenau gezählt werden, das Jahr aber wird nur mit 360 Tagen angesetzt. Das ergibt dann bei exponentieller Verzinsung und bei stetiger Verzinsung sowie bei linearer Verzinsung K t = (1 + 0, 08) 79/360 = , 09 e, Z t = K t K 0 = , 09 e K t = e 0,08 79/360 = , 56 e, Z t = K t K 0 = , 56 e K t = (1 + 0, 08 79/360) = , 56 e, Z t = K t K 0 = , 56 e. c) ACT/365. Die Tage müssen auch hier kalendergenau gezählt werden, das Jahr aber wird nur mit 360 Tagen angesetzt. Das ergibt dann bei exponentieller Verzinsung und bei stetiger Verzinsung sowie bei linearer Verzinsung d) 30E/360. Bei dieser Zinsmethode ist K t = (1 + 0, 08) 79/365 = , 83 e, Z t = K t K 0 = , 83 e K t = e 0,08 79/365 = , 84 e, Z t = K t K 0 = , 84 e K t = (1 + 0, 08 79/365) = , 07 e, Z t = K t K 0 = , 07 e. t = 360 ( ) + 30 (3 1) + (30 12) 360 = Das ergibt dann bei exponentieller Verzinsung K t = (1 + 0, 08) 78/360 = , 69 e, Z t = K t K 0 = , 69 e 17
18 1 Zinsrechnung und bei stetiger Verzinsung sowie bei linearer Verzinsung e) 30U/360. Bei dieser Zinsmethode ist K t = e 0,08 78/360 = , 43 e, Z t = K t K 0 = , 43 e K t = (1 + 0, 08 78/360) = , 33 e, Z t = K t K 0 = , 33 e. t = 360 ( ) + 30 (3 1) + (31 12) 360 Das ergibt dann bei exponentieller Verzinsung = und bei stetiger Verzinsung sowie bei linearer Verzinsung K t = (1 + 0, 08) 79/360 = , 09 e, Z t = K t K 0 = , 09 e K t = e 0,08 79/360 = , 56 e, Z t = K t K 0 = , 56 e K t = (1 + 0, 08 79/360) = , 56 e, Z t = K t K 0 = , 56 e. Die Unterschiede sind wegen der kurzen Laufzeit noch eher gering. Unabhängig von der Zinsmethode ist der Zinsertrag bei stetiger Verzinsung höher als bei einfacher Verzinsung, diese wiederum führt zu einem höheren Zinsbeitrag als die exponentielle Verzinsung. Nun betrachten wir ein Beispiel mit langer Laufzeit. Beispiel Man berechne den Endwert bei exponentieller, stetiger und linearer Verzinsung für ein Kapital von Euro, das im Zeitraum vom bis zum bei einem Zinssatz von i = 0, 08 angelegt wurde. Man verwende alle Zinsmethoden auÿer PAngV. a) ACT/ACT (ICMA). Hier müssen die Tage kalendergenau gezählt werden, also im Jahr 2001 einschlieÿlich des insgesamt 306 Tage und im Jahr 2001 ohne den weitere 319 Tage. Dazu kommen 6 volle Jahre. Das ergibt dann bei exponentieller Verzinsung K t = (1 + 0, 08) (306/ /366) = , 20 e 18
19 1.11 Beispiele mit Zinsrechnung und bei stetiger Verzinsung sowie bei einfacher Verzinsung K t = e 0,08(306/ /366) = , 21 e K t = (1 + 0, 08(306/ /366)) = , 27 e. b) ACT/360 Hier müssen die Tage kalendergenau gezählt werden, das ergibt 2816 Tage, die dann durch 360 geteilt werden, also t = 2816/360 = 7, Das ergibt dann bei exponentieller Verzinsung und bei stetiger Verzinsung sowie bei linearer Verzinsung K t = (1 + 0, 08) 2816/360 = , 31 e K t = e 0, /360) = , 60 e K t = (1 + 0, /360) = , 78 e. c) ACT/365 Hier müssen die Tage kalendergenau gezählt werden, das ergibt 2816 Tage, die dann durch 365 geteilt werden, also t = 2816/365 = 7, Das ergibt dann bei exponentieller Verzinsung und bei stetiger Verzinsung sowie bei linearer Verzinsung K t = (1 + 0, 08) 2816/360 = , 64 e K t = e 0, /360) = , 48 e K t = (1 + 0, /360) = , 48 e. d) 30E/360 und 30U/360. Hier sind D 1 = 1 und D 2 = 15, M 1 = 3 und M 2 = 11 sowie Y 1 = 2001 und Y 2 = Nach deutschem und amerikanischen Ansatz ergeben sich D1 = 1 und D2 = 15 Bei beiden Zinsmethoden ist somit t = 360 ( ) + 30 (11 3) + (15 1) 360 Das ergibt dann bei exponentieller Verzinsung = K t = (1 + 0, 08) 2774/360 = , 41 e 19
20 1 Zinsrechnung und bei stetiger Verzinsung sowie bei linearer Verzinsung K t = e 0, /360) = , 26 e K t = (1 + 0, /360) = , 44 e. Die Laufzeit ist jetzt gröÿer als ein Jahr, daher hat die Wahl der Zinsmethode eine gröÿere Auswirkung auf den Zinsertrag. Unabhängig von der Zinsmethode ist der Zinsertrag bei einfacher Verzinsung immer deutlich geringer als bei exponentieller. Den gröÿten Zinsertrag liefert die stetige Verzinsung Zinsmethoden in Excel Die Excel-Funktion TAGE360 Wegen der groÿen Bedeutung der beiden Zinsmethoden 30E/360 und 30U/360 gibt es in Excel eine Funktion, die die Zinstage berechnet. Diese Funktion hat drei Parameter, der erste ist das Anfangsdatum, der zweite das Enddatum und der dritte ist eine logische Variable mit den Werten WAHR oder FALSCH. Soll nach der Zinsmethode 30E/360 gezählt werden, muss der dritte Parameter den Wert WAHR bekommen, während für 30U/360 FALSCH zu wählen ist. Steht etwa in der Zelle A1 als Datumswert und in der Zelle B1 als Datumswert , so liefern die Formeln =TAGE360(A1:B1;WAHR) und =TAGE360(A1:B1;FALSCH) die Werte 13 und Die Excel-Funktion BRTEILJAHRE Nun benötigt man meistens die Zeitspanne zwischen zwei Datumsangaben und nicht nur die Anzahl der Zinstage. Die Entwickler von Excel haben deshalb eine Funktion namens BRTEILJAHRE geschrieben, welche die Zeitdierenz entsprechend der vorgestellten Zinsmethoden mit Ausnahme von PAngV und ACT/ACT (ICMA) berechnet. Auch bei dieser Funktion sind die beiden ersten Parameter das Anfangsdatum und das Enddatum. Der dritte Parameter legt die Zinsmethode fest. Es sind fünf Werte möglich. ˆ Lässt man den dritten Parameter ganz weg oder 0: 30U/360 (amerikanisch), ˆ 1: ACT/ACT (EXCEL), ˆ 2: ACT/360 (Eurozins), ˆ 3: ACT/365 (Englisch), ˆ 4: 30E/360 (Deutsch). Diese Funktion liefert die nutzlose Zinsmethode ACT/ACT (EXCEL), aber nicht die international normierte Zinsmethode ACT/ACT (ICMA) und bleibt auch die in Deutschland häug gebrauchte Zinsmethode nach PAngV schuldig. 20
21 Die Zinsmethode ACT/ACT (ICMA) 1.12 Zinsmethoden in Excel Die Zinsmethode ACT/ACT (ICMA) wurde von den amerikanischen Entwicklern von Excel nicht berücksichtigt. Ich gebe deshalb in der abgebildeten Tabelle ein Schema zur Berechnung an A B C D E F G H I t 1 t 2 k 1 y 1 n k 1 y 2 Formel t / /365 1, / /365 2, / /365 2, / /365 0, / /366 7, Abbildung 1.2: Die Zinsmethode ACT/ACT (ICMA) In den Zellen A2 und B2 stehen Anfangs- und Enddatum. In den Zelle C2 bis G2 benden sich die Formeln zur Berechnung von k 1, y 1, n, k 2 und y 2. Für die Zinsmethode ACT/ACT (ICMA) müssen die Tage im Anfangsjahr ermittelt werden. Die Formel steht in der Zelle C2 und lautet =MIN(B2-A2;DATUM(JAHR(A2)+1;1;1)-A2) Liegt das Enddatum im selben Jahr wie das Anfangsdatum, vergehen im Anfangsjahr nur B2 A2 Tage, sonst aber müssen alle Tage einschlieÿlich des Jahresendes gezählt werden. Diese Zahl k 1 muss durch die Gesamtzahl y 1 der Tage des ersten Jahrs geteilt werden =DATUM(JAHR(A2);12;31)-(DATUM(JAHR(A2)-1;12;31)) In der Zelle E2 steht die Anzahl n der ganzen Jahre, also die Formel =MAX(0;JAHR(B2)-JAHR(A2)-1) Die Tage des Endjahrs stehen in der Zelle F2 und ergeben sich aus der Formel =WENN(JAHR(B2)>JAHR(A2);B2-DATUM(JAHR(B2);1;1);0) Die Tage des letzten Jahres müssen durch die Gesamtzahl der Tage dieses Jahrs geteilt werden, d.h. durch =DATUM(JAHR(B2);12;31)-(DATUM(JAHR(B2)-1;12;31)) Die Formel für die Zeitdauer nach ACT/ACT (ICMA) lautet damit =C2/D2+E2+F2/G2 und steht in Zelle I2. Die drei Formeln lassen sich zu einer einzigen Mammutformel vereinigen, die ohne Zwischenergebnisse auskommt. Dafür muss in der letzten Formel jeder Bezug auf C2, D2, E2, F2 und G2 durch die entsprechende Formel ersetzt werden, was man am besten auÿerhalb von Excel mit einem Editor durchführt. Es ergibt sich dann folgende Monsteranweisung: 21
22 1 Zinsrechnung =WENN(JAHR(B2)-JAHR(A2)=0; (B2-A2)/(DATUM(JAHR(A2);12;31)-DATUM(JAHR(A2)-1;12;31)); JAHR(B2)-JAHR(A2)-1+ (DATUM(JAHR(A2)+1;1;1)-A2) /(DATUM(JAHR(A2);12;31)-DATUM(JAHR(A2)-1;12;31)) +(B2-DATUM(JAHR(B2);1;1)) /(DATUM(JAHR(B2);12;31)-DATUM(JAHR(B2)-1;12;31))) Alle Formeln lassen sich am Ausfüllkästchen bequem nach unten ziehen. Nur für Excel-Füchse sei bemerkt, dass ich mir auch die in der Zelle H2 stehende Formel von Excel habe bilden lassen. Diese Formel ist aus der Sicht von Excel eine Zeichenfolge. Excel erlaubt, zwei Zeichenfolgen durch den Operator & zu verbinden. Die Formel für die Zelle H2 lautet somit: =C2&"/"&D2&"+"&E2&"+"&F2&"/"&G Die Zinsmethode PAngV Die deutsche Zinsmethode nach PAngV wurde von den amerikanischen Entwicklern von Excel nicht berücksichtigt. Ich gebe in der abgebildeten Tabelle ein Schema zur Berechnung an A B C D E F t 1 t 2 D1 D2 Formel t (1-4)/12+(28-27)/365 1, (5-2-1)/12 + ( )/365 2, (5-2)/12+(30-30)/365 2, (10-10)/12+(30-1)/365 0, Abbildung 1.3: Die Zinsmethode PAngV. In den Zellen A2 und B2 stehen Anfangs- und Enddatum. In den Zelle C2 und D2 benden sich die Formeln zur Berechnung von D1 bzw. D2. =WENN(ODER(TAG(A2)=31;UND(TAG(A2)>27; MONAT(A2)=2));30;TAG(A2)) (*) =WENN(ODER(TAG(B2)=31;UND(TAG(B2)>27; MONAT(B2)=2));30;TAG(B2)) (**) In der Zelle E2 steht die Formel zur Berechnung der Zeitdierenz, in der Zelle F2 der zugehörige Wert. =WENN(D2>=C2;JAHR(B2)-JAHR(A2)+(MONAT(B2)-MONAT(A2))/12+(D2-C2)/365; JAHR(B2)-JAHR(A2)+(MONAT(B2)-MONAT(A2)-1)/12+ (D C2)/365) Die drei Formeln lassen sich zu einer einzigen Mammutformel vereinigen. Dafür muss in der letzten Formel jeder Bezug auf C2 durch die mit (*) markierte Formel ersetzt werden und jeder Bezug von D2 wird durch die Formel (**) überschrieben. Dann ergibt sich folgende Monsteranweisung: 22
23 1.13 Rendite einer verzinsten Anlage WENN(WENN(ODER(TAG(B2)=31;UND(TAG(B2)>27; MONAT(B2)=2));30; TAG(B2))>= WENN(ODER(TAG(A2)=31;UND(TAG(A2)>27; MONAT(A2)=2));30; TAG(A2));JAHR(B2)-JAHR(A2)+(MONAT(B2)-MONAT(A2))/12 + (WENN(ODER(TAG(B2)=31;UND(TAG(B2)>27; MONAT(B2)=2));30;TAG(B2)) - WENN(ODER(TAG(A2)=31; UND(TAG(A2)>27; MONAT(A2)=2));30;TAG(A2))) / 365; JAHR(B2)-JAHR(A2)+(MONAT(B2)-MONAT(A2)-1)/12 + (WENN(ODER(TAG(B2)=31;UND(TAG(B2)>27; MONAT(B2)=2));30;TAG(B2)) WENN(ODER(TAG(A2)=31;UND(TAG(A2)>27; MONAT(A2)=2));30;TAG(A2)))/365) Alle Formeln lassen sich am Ausfüllkästchen bequem nach unten ziehen. Nur für Excel-Füchse sei bemerkt, dass ich mir auch die in der Zelle E2 stehende Formel von Excel habe bilden lassen. Diese Formel ist aus der Sicht von Excel eine Zeichenfolge. Excel erlaubt, zwei Zeichenfolgen durch den Operator & zu verbinden. Die Formel für die Zelle E2 lautet: = JAHR(B2) & "-" & JAHR(A2) & "+(" & WENN(D2>=C2; MONAT(B2)&"-" & MONAT(A2)& ")/12+(" & D2& "-" & C2& ")/365"; MONAT(B2)&"-" & MONAT(A2)& "-1)/12 + (" & D2& "+30-" & C2& ")/365") 1.13 Rendite einer verzinsten Anlage Die verschiedenen Arten der Verzinsung und der Zinsmethoden sind für Laien undurchsichtig, da der angegebene nominale Zinssatz nicht der tatsächlich erzielten Rendite entspricht. Die Berechnung der Rendite ist in Deutschland innerhalb der bereits erwähnten Preisangabeverordnung (PAngV) geregelt. Es sei angenommen, dass der Anleger einmalig am Anfangstermin einen Betrag von K 0 einzahlt, der bis zum Endtermin auf K t angewachsen ist. Dann ist die Rendite der Zinssatz r, der bei exponentieller Verzinsung ebenfalls von K 0 auf den Endbetrag K t geführt hätte, wobei die Zeitdierenz zwischen Anfangs- und Endtermin nach der Zinsmethode der PAngV berechnet wird. Nach Formel (1.15) auf Seite 8 gilt somit ( ) 1/tP Kt r = 1, (1.23) K 0 wobei tp die Laufzeit nach PAngV ist. Die Rendite wird auch als konformer Zinssatz bezeichnet. Die Rendite wird in Prozent mit zwei Nachkommastellen angegeben. Beispiel Eine Bank bietet Ihnen einen so genannten abgezinsten Sparbrief an. Man legt Euro am an und erhält Euro am zurück. Welche Rendite wird erreicht? Bei Renditerechnungen wird immer die Zinsmethode PAngV eingesetzt. Die Zeit tp zwischen den beiden Terminen berechnet sich nach tp = (7 1 1)/12 + ( )/365 = 1,
24 1 Zinsrechnung Damit folgt für die Rendite ( ) 1/1, r = 1 = 0, , 49 % Hinweis: Sie werden sich wundern, warum ich für die Rendite den Bezeichnung r und nicht ī verwendet habe. Das liegt daran, dass die Rendite kein tatsächlich erhobener Zinssatz, sondern ein kalkulatorischer Zinssatz ist. Ich werde für reale Zinssätze, die man als nominal oder nominell bezeichnet, immer den Buchstaben i benutzen und für kalkulatorische den Buchstaben r Die gemischte Verzinsung Die exponentielle Verzinsung war zwar in vergangenen Zeiten für nicht ganzzahlige Werte von t schwer zu berechnen, nicht aber für t = n N. Dann gilt nämlich K n = K 0 (1 + i) n = K 0 (1 + i) (1 + i) (1 + i) (1.24) } {{ } n mal Diese Form der Verzinsung wird sehr anschaulich Zinseszinsformel genannt, da sich nach einem Jahr die angesammelten Zinsen mit verzinsen, während bei linearer Verzinsung die Zinsen immer nur auf die Anfangsschuld berechnet werden. Das bereits angesammelte Kapital erhöht sich von Jahr zu Jahr um den Faktor q = (1 + i), (1.25) der deshalb Aufzinsungsfaktor genannt wird. Die Zinseszinsformel stimmt mit der exponentiellen Verzinsung für alle ganzzahligen Werte überein, dazwischen liefert sie aber keinen Wert. Daher kam man auf die Idee, lineare Verzinsung mit Zinseszinsen zu mischen. Dafür wird die Zeitspanne zwischen Anfangs- und Enddatum in drei Teile zerlegt: ˆ Zwischen dem Anfangszeitpunkt und dem Ende des ersten Jahres liege die Zeit t A. ˆ Danach folgen n volle Jahre. ˆ Im letzten Jahr vergehe dann noch die Zeit t E bis zum Endzeitpunkt t. Das Kapital verzinst sich dann wie folgt: K t = K 0 (1 + it A ) (1 + i) n (1 + it E ). (1.26) Zur Bestimmung der Zeiten t A und t E wird eine der vorgestellten Zinsmethoden verwendet. Zunächst werden im Anfangs- und Endjahr Tage k 1 und k 2 entsprechend der Zinsmethode berechnet und dann durch die Gesamttage y 1 und y 2 der jeweiligen Jahr geteilt. Damit geht die Gleichung (1.26) über in ( K t = K i k ) ( 1 (1 + i) n 1 + i k ) 2, (1.27) y 1 y 2 Denition 1.5. Wird ein Kapital wie geschildert verzinst, spricht man von gemischter Verzinsung. 24
25 Beispiele zur gemischten Verzinsung 1.14 Die gemischte Verzinsung Die beiden Grundformeln (1.26) und (1.27) seien an zwei Beispielen verdeutlicht. Beispiel Welchen Endwert erreicht ein Kapital von Euro zwischen dem und dem bei einem Zinssatz von i = 0, 05 mit gemischter und exponentieller Verzinsung, wenn die Zinsmethode ACT/ACT (ICMA) verwendet wird? Wie hoch sind die jeweiligen Renditen? ˆ Exponentielle Verzinsung. Die Zeitspanne t setzt sich aus zwei ganzen Jahren und den unterjährlichen Anteilen von 2004 und 2007 zusammen. Vom bis zum Jahresende vergehen bei genauer Zählung k 1 = = 306 Tage, da wir den 1.3. mit zählen wollen. Im Jahr 2007 kommen k 2 = = 104 Tage zusammen, denn der Auszahlungstag wird jetzt nicht mit gezählt. Für die exponentielle Verzinsung wird die Zeitspanne t = 306/ /365 = 3, benötigt. K t = , 05 t = , 21 Euro. Für die Rendite muss zunächst die Zeit tp nach PAngV bestimmt werden. Vom bis zum vergehen 37 Monate, dazu kommen weitere 14 Tage im April 2007, d.h. tp = 37/ /365 = 3, Damit folgt für die Rendite r = ( ) 3, , 21 1 = 0, , 00 % Nach PAngV muss die Rendite in Prozent mit zwei Nachkommastellen angegeben werden, somit ist r = 5, 00 Prozent. ˆ Gemischte Verzinsung. Mit den obigen Werten für k 1 und k 2 ergibt sich wegen y 1 = 366 und y 2 = 365 ( K t = , ) ( 1, , ) = , 56 Euro Die Rendite berechnet sich somit aus ( ) 3, , 56 r = 1 = 0, , 01 % Nach PAngV muss die Rendite in Prozent mit zwei Nachkommastellen angegeben werden, somit ist r = 5, 01 Prozent. Beispiel Man berechne den Endwert bei gemischter Verzinsung für ein Kapital von Euro, das im Zeitraum vom bis zum bei einem Zinssatz von i = 0, 08 angelegt wurde. Man verwende alle Zinsmethoden. 25
26 1 Zinsrechnung a) ACT/ACT (ICMA). Die Zeitspanne t setzt sich aus sechs ganzen Jahren und den unterjährigen Anteilen von 2001 und 2008 zusammen. Vom bis zum Jahresende vergehen bei genauer Zählung k 1 = = 306 Tage, da wir den 1.3. mit zählen wollen. Im Jahr 2008 kommen k 2 = = 319 Tage zusammen, denn der Auszahlungstag wird jetzt nicht mit gezählt. Somit ergibt sich K t = (1 + 0, 08(306/365)) 1, 08 6 (1 + 0, 08(319/366)) = , 19 e b) ACT/360). Bei allen Zinsmethoden ist die Anzahl n der ganzen Zinsperioden gleich. Die Tagzählungen für k 1 und k 2 unterscheiden sich nicht zwischen den drei verschiedenen Methoden ACT/XXX, nur die Werte von y 1 und y 2, diese sind bei ACT/360 immer 360. Somit ergibt sich K t = (1 + 0, 08(306/360)) 1, 08 6 (1 + 0, 08(319/360)) = , 97 e c) ACT/365). Es müssen nur die Werte für y 1 und y 2 auf 365 verändert werden. K t = (1 + 0, 08(306/365)) 1, 08 6 (1 + 0, 08(319/365)) = , 67 e d) 30E/360 und 30U/360. Die Zeitspanne t setzt sich aus sechs ganzen Jahren und den unterjährigen Anteilen von 2001 und 2008 zusammen. Vom bis zum Jahresende vergehen der Zinsmethode 30E/360 k 1 = = 300 Tage, da wir den 1.3. mit zählen wollen. Im Jahr 2008 kommen k 2 = = 314 Tage zusammen, denn der Auszahlungstag wird jetzt nicht mit gezählt. Somit ergibt sich K t = (1 + 0, 08(300/360)) 1, 08 6 (1 + 0, 08(314/360)) = , 41 e 1.15 Unterjährige Verzinsung Der wesentliche Unterschied zwischen einfacher Verzinsung und Zinseszinsen liegt in der Behandlung der bereits angesammelten Zinsen. Werden diese nach einem Jahr dem Kapital gut geschrieben und danach mitverzinst, erhöht sich der Endbetrag bei längeren Laufzeiten beträchtlich. Dieser Eekt kann noch gesteigert werden, wenn die Zinsgutschrift mehrmals im Jahr erfolgt. Man spricht dann von unterjähriger Verzinsung Zinstermin und Zinsperiode Wir benötigen zunächst zwei neue Begrie. Denition 1.6. Der Tag, an dem bei gemischter Verzinsung die Zinsgutschrift dem Kapital zugeschlagen und danach mitverzinst wird, heiÿt Zinstermin. Der Zeit zwischen zwei Zinsterminen wird als Zinsperiode bezeichnet. 26
27 1.15 Unterjährige Verzinsung Bis jetzt gab es immer nur einen Zinstermin pro Jahr, und zwar am Jahresende. An den Zinsterminen werden die angesammelten Zinsen dem Kapital zugeschlagen und danach mit verzinst. Zwischen zwei Zinsterminen gibt es nur einfache Zinsen. Auf Sparbüchern, bei Hypothekenverträgen und Sparverträgen sind die Zinstermine immer das Ende eines Jahres, bei festverzinslichen Wertpapieren ist der erste Zinstermin der Tag der Emission, z.b. der 5. Mai Bei unterjährig verzinslichen Anlagen gibt es mehr als einen Zinstermin im Jahr, die Zinsperiode ist somit kleiner als ein Jahr. Man bezeichnet mit m die Anzahl von Zinsperioden innerhalb eines Jahres, die Länge einer Zinsperiode ist daher 1/m. Die üblichen Werte für m stelle ich nun vor. ˆ m = 1. Die Länge einer Periode ist genau ein Jahr. Dies ist in Deutschland bei festverzinslichen Wertpapieren üblich, wobei die Zinstermine immer genau im Jahresabstand auf den Tag der Emission folgen, z.b. immer am 5. Mai eines Jahres liegen. ˆ m = 2. Halbjährliche Zinsperioden sind für Anleihen in Groÿ-Britannien und den USA weit verbreitet. ˆ m = 4. Vierteljährliche Zinsperioden sind bei Anleihen selten, werden aber von Bausparkassen und Hypothekenbanken gerne für Hypothekenkredite verwendet. ˆ m = 12. Monatliche Zinsperioden sind sehr selten. ˆ m =. Lässt man die Anzahl der Zinsperioden pro Jahr gegen gehen, ergibt sich als Grenzfall die bereits bekannte stetige Verzinsung. Der Name rührt daher, dass die Zinsen zu jedem Zeitpunkt sofort dem Kapital zugeschlagen und dann mitverzinst werden Formel der unterjährigen gemischten Verzinsung Auch bei der unterjährigen gemischten Verzinsung wird ein so genannter nomineller Jahreszinssatz i angegeben. Bei m Zinsperioden pro Jahr gilt dann für den tatsächlichen Periodenzinssatz i/m. Bis jetzt wurde bei der gemischten Verzinsung immer innerhalb des angebrochenen Anfangs- und des angebrochenen Endjahres mit einfacher Verzinsung gerechnet, während für alle vollen Jahre die Zinseszinsformel verwendet wurde. Diese Vorgehensweise wird beibehalten, aber der Zeitraum der einfachen Verzinsung wird auf die erste bzw. letzte Zinsperiode begrenzt und die Zinseszinsformel erfolgt für die Anzahl der vollen Zinsperioden, wobei als Zinssatz der tatsächliche Periodenzinssatz i/m verwendet wird. Damit ergibt sich die Grundformel der unterjährigen gemischten 27
28 1 Zinsrechnung Verzinsung wie folgt. ( K t = K 0 (1 + it A ) 1 + m) i n (1 + it E ). (1.28) Hier sind ˆ K 0 das Anfangskapital zum Zeitpunkt 0, ˆ i der nominelle Jahreszinssatz, ˆ m die Anzahl von Zinsperioden pro Jahr, ˆ t A die Zeit zwischen dem Anfangszeitpunkt und dem ersten Zinstermin, ˆ t E die Zeit vom letzten Zinstermin bis zum Endzeitpunkt und ˆ n die Anzahl der vollständigen Zinsperioden. Auch hier muss wieder eine Zinsmethode gewählt und entschieden werden, ob der erste oder letzte Tag in die Verzinsung eingeht. Wieder sei verabredet, den ersten Tag zu zählen. Bei den meisten Zinsmethoden spielt es aber sowieso keine Rolle. Die Zeit t A ergibt sich wieder als Bruch der Form k 1 /y 1. Dabei ist k 1 die Anzahl von Tagen bis zum nächsten Zinstermin und y 1 die Anzahl der Tage im Jahr entsprechend der Zinsmethode. Genauso wird t E berechnet. Die Gleichung (1.28) geht dann über in ( K t = K i k ) ( i ) n ( 1 + i k ) 2, (1.29) y 1 m y 2 Leider gibt es noch eine weitere Form der Zinsmethode ACT/ACT, welche ACT/ACT (ISMA) genannt wird. Hier gilt y 1 = m Länge der ersten angebrochenen Periode. Genauso wird mit y 2 verfahren. Ist etwa m = 4, so hat das erste Quartal in gewöhnlichen Jahren eine Periodenlänge von 90 Tagen, fällt der Anfangszeitpunkt in dieses Quartal, ist y 1 = 4 90 = 360. Das letzte Quartal hat dagegen eine Länge von 92 Tagen, somit wird y 1 = 4 92 = 368 falls der Anfangszeitpunkt in dieses Quartal fällt. Bei m = 12 schwankt y 1 zwischen = 336 und = 372. Denition 1.7. Wird ein Kapital wie geschildert verzinst, spricht man von unterjähriger gemischter Verzinsung. 28
29 1.15 Unterjährige Verzinsung Beispiele zur unterjährigen gemischten Verzinsung Die unterjährige gemischte Verzinsung möchte ich an zwei Beispielen verdeutlichen. Beispiel Welchen Endwert erreicht ein Kapital von Euro zwischen dem und dem bei einem Zinssatz von i = 0, 08 bei vier Zinsterminen pro Jahr? Man verwende alle vorgestellten Zinsmethoden. Die Zinsmethoden spielen nur bei den zwei Faktoren der einfachen Verzinsung eine Rolle. Die Anzahl der vollständigen Perioden ist immer gleich. Da vier Zinstermine vorhanden sind, gilt m = 4, also 1 + i/m = 1, 02. Der nächste Zinstermin nach der Einzahlung wird der sein, der letzte Zinstermin vor dem Ende ist der Im Jahr 2001 gibt es drei Zinsperioden, dazu kommen sechs volle Jahre und noch die drei Zinsperioden des Jahres 2008, das ergibt n = = 30. Dieser Teil der Lösung ist unabhängig von der Zinsmethode. ˆ ACT/ACT (ICMA). Bei beiden Methoden werden die Tage in den nicht vollständigen Perioden kalendergenau gezählt. Hier sind k 1 die genauen Tage bis zum ersten Zinstermin nach der Einzahlung, das sind k 1 = 31 Tage. Vom letzten Zinstermin vor der Auszahlung, also dem bis zum Tag der Auszahlung, also dem vergehen k 2 = = 45 Tage. Bei jeder der beiden Methoden ACT/ACT hat das erste Jahr die Länge y 1 = 365 und das letzte die Länge y 2 = 366. Damit ergibt sich als Endbetrag somit ( K t = , ) ( 1, , ) = , 64 Euro ˆ ACT/ACT(ISMA). Bei dieser Zinsmethode müssen die Tage und die Längen der Perioden kalendergenau gezählt werden. Die Zinsperiode vom bis zum hat die Länge p 1 = = 90 Tage, somit ist y 1 = 4 90 = 360 und somit t A = 31/360. Die Zinsperiode vom bis zum hat die Länge p 2 = = 92, somit ist y 2 = 4 92 = 368 und somit t E = 45/368. Der Endbetrag wird somit ( K t = , ) ( 1, , ) = , 76 Euro ˆ ACT/360. Hier werden die Tage k 1 und k 2 durch 360 geteilt: ( K t = , ) ( 1, , ) = , 25 Euro
30 1 Zinsrechnung ˆ ACT/365. Hier werden die Tage k 1 und k 2 durch 365 geteilt: ( K t = , ) ( 1, , ) = , 79 Euro. ˆ 30E/360 und 30U/360. Bei beiden Methoden vergehen vom bis zum k 1 = 30 Tage und vom bis zum k 2 = = 44 Tage. Damit ergibt sich als Endbetrag ( K t = , ) ( 1, , ) = , 49 Euro Beispiel Welchen Endwert erreicht ein Kapital von Euro zwischen dem und dem bei einem Zinssatz von i = 0, 08 bei zwei Zinsterminen pro Jahr? Man verwende alle vorgestellten Zinsmethoden. Die Zinsmethoden spielen nur bei den zwei Faktoren der einfachen Verzinsung eine Rolle. Die Anzahl der vollständigen Perioden ist immer gleich. Da es nur zwei Zinstermine gibt, gilt m = 2, also 1 + i/m = 1, 04. Der nächste Zinstermin nach der Einzahlung wird der sein, der letzte Zinstermin vor dem Ende ist der Im Jahr 2001 gibt es noch eine vollständige Zinsperiode, dazu kommen sechs volle Jahre und noch eine Zinsperiode im Jahr 2008, das ergibt n = = 14. Dieser Teil der Lösung ist unabhängig von der Zinsmethode. ˆ ACT/ACT (ICMA) und (EXCEL). Bei beiden Methoden werden die Tage in den nicht vollständigen Perioden kalendergenau gezählt. Hier sind k 1 die genauen Tage bis zum ersten Zinstermin nach der Einzahlung, das sind k 1 = = 122 Tage. Vom letzten Zinstermin vor der Auszahlung, also dem bis zum Tag der Auszahlung, also dem vergehen k 2 = = 137 Tage. Bei jeder der beiden Methoden ACT/ACT hat das erste Jahr die Länge y 1 = 365 und das letzte die Länge y 2 = 366. Damit ergibt sich als Endbetrag somit K t = ( 1 + 0, ) 1, ( 1 + 0, ) = , 27 Euro. ˆ ACT/ACT(ISMA). Bei dieser Zinsmethode müssen die Tage und die Längen der Perioden kalendergenau gezählt werden. Die Zinsperiode vom bis zum hat die Länge p 1 = = 181 Tage, somit ist y 1 = = 362 und somit t A = 122/362. Die Zinsperiode vom bis zum hat die Länge p 2 = = 184, somit ist y 2 = = 368 und somit t E = 137/368. Der Endbetrag wird somit K t = ( 1 + 0, ) 1, ( 1 + 0, ) = , 08 Euro. 30
31 1.16 Unterjährige gemischte Verzinsung mit Excel ˆ ACT/360. Hier werden die Tage k 1 und k 2 durch 360 geteilt: ( K t = , ) ( 1, , ) ˆ ACT/365. Hier werden die Tage k 1 und k 2 durch 365 geteilt: ( K t = , ) ( 1, , ) = , 34 Euro. = , 14 Euro. ˆ 30E/360 und 30U/360. Bei beiden Methoden vergehen vom bis zum k 1 = 120 Tage und vom bis zum k 2 = = 134 Tage. Damit ergibt sich als Endbetrag somit ( K t = , ) ( 1, , ) = , 04 Euro Unterjährige gemischte Verzinsung mit Excel Für die unterjährige gemischte Verzinsung habe ich das auf Seite 32 abgebildete Arbeitsblatt angelegt. Die Zellen B2 bis F2 enthalten die Eingaben. Zur besseren Lesbarkeit der Formeln habe ich diesen Zellen Namen gegeben, und zwar K0 für die Zelle B2, AnfDat und EndDat für die Zellen C2 und D2 mit Anfangs- und Enddatum sowie m für die Zelle F2, wo die Anzahl der Perioden steht. Der Zelle G2 für den Zinssatz habe ich mit rzins bezeichnet. Bei unterjähriger Verzinsung muss zunächst der nächste Zinstermin gefunden werden. Bei m Zinsperioden hat jede Zinsperiode die Länge 12/m, bei vier Zinsperioden ist etwa jede Zinsperiode drei Monate lang. Die Anfangstage der Perioden sind dann der 1.1, 1.4, 1.7 und 1.10, die Monatszahl verringert um 1 ist glatt durch die Periodenlänge 12/m teilbar und der Anfangstag ist der erste dieses Monats. Die beiden Bedingungen lauten für sich TAG(AnfDat) = 1 REST(MONAT(AnfDat)-1;12/m) = 0 und müssen durch die UND-Funktion verbunden werden und bilden dann das erste Argument der WENN-Funktion =WENN(UND(TAG(AnfDat)=1;REST(MONAT(AnfDat)-1;12/m)=0);AnfDat;XXX) An die Stelle von XXX kommt die Anweisung für den nächsten Zinstermin, wenn das Anfangsdatum nicht auf den Periodenanfang fällt. Diese Anweisung ist ziemlich lang: 31
32 1 Zinsrechnung A B C D E F Eingaben K 0 Anfang Ende i m , ,00% 4 ACT/ACT (ICMA) ACT/360 ACT/365 30E/360 30U/360 Zinstermin k y n Zinstermin k y K gemischt , , , , ,94 Renditen 8,25% 8,2565% 8,2527% 8,2528% 8,2528% tp 6, Abbildung 1.4: Berechnung des Endkapitals bei gemischter unterjähriger Verzinsung. DATUM(JAHR(AnfDat)+WENN(m-1 < MONAT(AnfDat)*m/12;1;0); WENN(m-1 <MONAT(AnfDat)*m/12;1; 1+AUFRUNDEN(MONAT(AnfDat)*m/12;0)*12/m);1) Wird dies anstelle von XXX in die obige WENN-Anweisung eingesetzt, ergibt sich dann die Formel für den Anfangstermin =WENN(UND(TAG(AnfDat)=1;REST(MONAT(AnfDat)-1;12/m)=0);AnfDat; DATUM(JAHR(AnfDat)+WENN(m-1 < MONAT(AnfDat)*m/12;1;0); WENN(m-1 <MONAT(AnfDat)*m/12;1; 1+AUFRUNDEN(MONAT(AnfDat)*m/12;0)*12/m);1)) Die Formel für den letzten Zinstermin vor dem Enddatum ist wesentlich einfacher: =DATUM(JAHR(EndDat);1+ABRUNDEN((MONAT(EndDat)-1)*m/12;0)*12/m;1) In der Zeile 12 benden sich die Formeln der Endbeträge, etwa in der Zelle B12 die Formel =K0*(1+rzins*B6/B7)*(1+rzins/m)^B8*(1+rzins*B10/B11) Die restlichen Formeln dieser Zeile ergeben sich durch Ziehen am Ausfüllkästchen nach rechts. 32
33 1.17 Das Excel-Feature Zielwertsuche 1.17 Das Excel-Feature Zielwertsuche Das Formular berechnet zu den fünf Eingabegröÿen der zweiten Zeile den Endwert. Oft wird aber auch der Endwert vorgegeben und nach dem Zinssatz gesucht, der zu diesem Endwert führt. Seien die Werte wie in der Abbildung 1.4 auf Seite 32, nur sei jetzt nach dem Zinssatz gefragt, der bei der Zinsmethode ACT/ACT (ICMA) zu einem Endbetrag von Euro führt. Klar ist, dass dieser Zinssatz kleiner als 8 Prozent sein muss. Man kann jetzt etwa versuchsweise 6 Prozent in die Zelle E2 eingeben und erhält den Endwert ,66, also einen zu kleinen Wert, der Zinssatz muss wieder erhöht werden, etwa auf 6,5 Prozent, was zu ,10 führt. Mit ein wenig Geduld wird man bald zum richtigen Wert 6,33 Prozent kommen. Diese Sucherei ist umständlich, deshalb haben die Entwickler von Excel für solche Probleme eine Lösung bereit gestellt, die so genannte Zielwertsuche. Dafür wird ein kleiner Dialog benötigt, der in den älteren Versionen von Excel über die Menüfolge Extras Zielwertsuche geönet wird. Ab der Version Excel 2007 klicken Sie auf der Registerkarte Daten in der Gruppe Datentools auf Was wäre wenn Analyse und wählen dann Zielwertsuche. Abbildung 1.5: Das Excel-Feature Zielwertsuche Es önet sich das abgebildete Dialogfeld Zielwertsuche mit seinen drei Eingabefeldern. Die Zielzelle ist die Zelle, die einen bestimmten Wert erhalten soll, das ist hier die Zelle B12. Der gewünschte Zielwert ist hier , dieser Zielwert dürfte auch in einer Zelle stehen, dann müssen Sie diese Zelle angeben. Die veränderbare Zelle ist die Zelle, die den Wert der Zielzelle bestimmt, das ist hier die Zelle E2 mit dem Zinssatz. Nach Drücken der Schaltäche OK ermittelt Excel denjenigen Wert von E2, der in der Zelle B12 zum gewünschten Wert führt, in diesem Fall 6,33 Prozent. Sie können auch das Enddatum als veränderbare Zelle verwenden und etwa die Frage stellen, an welchem Datum bei einem Zinssatz von 6,5 Prozent der Endbetrag von Euro bei der Zinsmethode ACT/ACT (ICMA) erreicht ist. Excel versucht die Lösung genau zu ermitteln und gibt neben dem Datum noch eine Tageszeit an, in unserem Fall :10:53. Die Lösung selbst muss aber ein reines Datum sein, daher muss die Tageszeit gelöscht werden. Der liefert dann mit dem Endwert von ,76 Euro die beste Näherung an den gewünschten Endwert von Euro. 33
34 1 Zinsrechnung 1.18 Gestaelte Verzinsung Bis jetzt war der Zinssatz i während der gesamten Zeit der Geldanlage fest. Es gibt aber Anlageformen mit zeitlich wechselnden Zinssätzen, meistens im jährlichen Abstand mit steigenden Zinssätzen, um den Kunden langfristig zu binden. Das gilt für Bundesschatzbriefe und vielen Sparbriefe von Banken. Aber auch auf normalen Sparbüchern wird die Verzinsung von Sparguthaben an die marktüblichen Zinssätze angepasst. Formelmäÿig ist so zu rechnen, als ob am ersten Tag, an dem der neue Zinssatz gilt, das bisher erzielte Guthaben abgehoben und dann sofort wieder eingezahlt wird. In jedem Zeitraum mit festen Zinsen wird die ausgewählte Zinsformel verwendet. Das folgende Beispiel behandelt wechselnde Zinssätze auf einem Sparbuch. Beispiel Ein Anleger zahlt am bei einem Zinssatz von 3 Prozent Euro auf ein Sparbuch ein. Die Bank senkt den Zinssatz am auf 2 Prozent. Berechnen Sie den Betrag, den der Kunde am bei der Auösung seines Sparbuchs erhält. Verwendet sei die Zinsmethode 30E/360 mit einem Zinstermin am Jahresende. Man berechne ferner die Rendite r der Anlage nach der PAngV. Zunächst wird die Entwicklung der Anlage vom bis zum bei gemischter Verzinsung mit einem Zinssatz von 3 Prozent ausgerechnet: ˆ Einschlieÿlich des gibt es 2002 k 1 = = 282 Zinstage. ˆ Dazu kommt das ganze Jahr ˆ Im Jahr 2004 fallen k 2 = = 312 Zinstage an, da der nicht mehr zählt. Somit besteht am ein Guthaben von ( K 1 = , ) ( 1, , ) Vom bis zum vergehen folgende Zeiträume ˆ k 1 = = 48 Tage vom bis ˆ Das ganze Jahr = 1.081, 61 Euro. ˆ k 2 = = 110 Tage vom bis zum , denn der letzte Tag zählt nicht mehr. Als Endkapital ergibt sich also 1.112,95 Euro. Nach PAngV vergeht zwischen dem und dem die Zeit tp = (4 3)/12 + (21 19)/365 = 4, , 34
35 1.19 Bundesschatzbriefe die Rendite beträgt somit ( ) (1/4, ) 1.112, 95 r = 1 = 0, % Anzugeben wären nach PAngV nur zwei Stellen nach dem Komma, d.h. r = 2, 65 Prozent. Beispiel Welchen Endwert erreicht ein Kapital von Euro, das zunächst zwischen dem und dem bei einem Zinssatz von i = 0, 04 und danach noch bis zum bei einem Zinssatz von i = 0, 03 bei gemischter Verzinsung angelegt wurde? Der einzige Zinstermin ist jeweils das Jahresende, die Zinsmethode sei 30E/360. Danach berechne man die Rendite. Vom bis zum vergehen nach der Zinsmethode 30E/360 insgesamt k 1 = 330 Tage. Danach folgen zwei ganze Jahre. Ab 2004 wechselt der Zinssatz auf 3 Prozent. Der Zeitraum beginnt mit drei vollen Jahren und schlieÿt mit k 2 = = 194 Tagen. Somit gilt K t = 1000(1 + 0, /360)(1, 04) 2 (1, 03) 3 (1 + 0, /360) = 1.245, 04 Nach PAngV vergeht zwischen dem und dem die Zeit von tp = 6 + 5/ /365 = 6, Somit ergibt sich aus Formel (1.23) ( ) 1/6, , 04 r = 1 = 3, 45% Bundesschatzbriefe Das bekannteste Beispiel von gestaelter Verzinsung sind die Bundesschatzbriefe. Man unterscheidet bei den Bundesschatzbriefen zwei Varianten: ˆ Typ A mit sechs Jahren Laufzeit und jährlicher Zinsausschüttung. ˆ Typ B, bei dem Zinsen und Tilgungsleistung erst am Ende der Laufzeit von sieben Jahren in einer Summe ausgezahlt werden. Bundesschatzbriefe werden in verschiedenen Ausgaben verkauft. Dabei existiert kein fester Emissionsrhythmus. Vielmehr werden immer dann neue Bundesschatzbriefe ausgegeben, wenn die Renditen der laufenden Ausgabe nicht mehr den Marktgegebenheiten entsprechen. Steigen zum Beispiel die Renditen für zehnjährige Bundesanleihen deutlich an, werden auch die Nominalzinssätze und Renditen der Bundesschatzbriefe angepasst. Das heiÿt konkret: es wird eine neue Ausgabe mit entsprechend höherer Verzinsung ausgegeben. So heiÿt es launig im Prospekt. Natürlich werden Bundesschatzbriefe immer dann ausgegeben, wenn unsere ewig klamme Bundesregierung frisches Geld braucht. 35
36 1 Zinsrechnung Der Zinssatz und damit die Rendite steigen bei beiden Bundesschatzbrief-Typen über die Laufzeit hinweg an. In der folgenden Abbildung sind die Konditionen der Anfang 2010 ausgegebenen Bundessschatzbriefe zu sehen A B C D E F ,25% 1, , ,25% ,00% 1, , ,62% ,75% 1, , ,00% ,75% 1, , ,43% ,50% 1, , ,84% ,00% 1, , ,20% ,00% 1, , ,45% Abbildung 1.6: Konditionen von zwei Bundesschatzbriefen. Typ A läuft nur sechs Jahre, wobei die Zinsen jährlich immer zum 1.3. ausgeschüttet werden. Typ B läuft dagegen sieben Jahre und sammelt die Zinsen an, am Ende der Laufzeit, d.h. am erhält der treue Kunde für je 100 Euro Nennwert 118,50 Euro ausgezahlt. Man kann aber zu jedem Zeitpunkt das Papier weiterverkaufen. In der Spalte C stehen die jährlichen Zinsen i 1, i 2,..., i 7 die von lächerlichen 0,25 % zwischen 2010 und 2011 auf 4 % zwischen 2015 und 2016 anwachsen. In der Spalte D sind die jährlichen Aufzinsungsfaktoren q 1 = 1 + i 1, q 2 = 1 + i 2,..., q 7 = 1 + i 7 zu sehen. In der Spalte E benden sich die Produkte der Aufzinsungsfaktoren p 1 = q 1, p 2 = q 1 q 2,..., p 7 = q 1 q 2 q 7. Diese Zahlen sind die Werte eines Euro, der bis zum Ende des jeweiligen Jahres angelegt wird. Die bis dahin erzielten Renditen sind in der Spalte F zu sehen. Sie ergeben sich aus der Formel Stückzinsen r k = (p k ) 1/k. Bei Bundesschatzbriefen liegen die Zinstermine immer auf dem Tag der Emission, bei dem betrachteten Beispiel also immer auf dem 1.3. eines Jahres. Als Zinsmethode wird ACT/ACT (ICMA) verwendet. Wird ein Bundesschatzbrief nicht an einem Zinstermin erworben, muss der Käufer dem Verkäufer einen Teil der zum nächsten Zinstermin ausgeschütteten Zinsen erstatten, die sogenannten Stückzinsen. Das liegt daran, dass der Bund zum Zinstermin dem dann aktuellen Eigentümer des Bundesschatzbriefes den Zinsertrag der gesamten Zinsperiode ausschüttet; Stückzinsen sind also gerade der Anteil an diesem Zinsertrag, der beim Kauftermin bereits angefallen war. Betrachten wir den Bundesschatzbrief vom Typ A und nehmen als Kauftermin den an. Der Käufer möchte einen Nennwert von Euro erwerben. Zwischen dem 1.3. und dem 1.6. liegen nach ACT/ACT (ICMA) 92 Tage, somit fallen Stückzinsen im Wert von 92 Sz = , 0025 = 0, 63 Euro
37 1.19 Bundesschatzbriefe an. Der Käufer zahlt somit 1.000,63 Euro und erwirbt den Bundesschatzbrief zum Nennwert von Euro. Die bereits vorgeleisteten Zinsen von 63 Cent werden durch die vollständige Ausschüttung des Zinsertrages von 2,50 Euro am ausgeglichen. Meist wird aber anders vorgegangen. Der Käufer gibt den Anlagebetrag vor, etwa Euro. Dieser Betrag setzt sich aus den Stückzinsen und dem Nennwert zusammen. Sei B der Anlagebetrag und N der Nennwert sowie Sz die Stückzinsen, so gilt B = N + Sz, Sz = N i k1 y1 d.h. B N = 1 + i k1/y1, wobei hier k1 die kalendergenau gezählten Tage zwischen dem letzten Zinstermin und dem Kaufdatum sind und y1 die genaue Anzahl von Tagen des entsprechenden Jahres. In unserem Beispiel erwirbt der Käufer bei einem Anlagebetrag von Euro in den Bundesschatzbrief Typ A von 2010 zum einen Nennwert von N = , /365 = 1998, 74 Euro. Auf diesen Nennwert beziehen sich die folgenden Zinserträge und die Rückerstattung des Kapitals. Dieser Bundesschatzbrief vom Typ A wird am Jahr auslaufen, der Käufer erhält dann seinen Nennwert von 1998, 74 erstattet und bekommt zusätzlich vom bis zum Zinsen auf diesen Nennwert, wobei die Zinssätze in der Spalte C der auf Seite 36 abgebildeten Excel-Tabelle stehen. Die Berechnung des Nennwerts ist bei Bundesschatzbriefen vom Typ B etwas anders, da vor dem Ende der Laufzeit die Zinsen nicht ausgeschüttet sondern gesammelt werden. Sei angenommen, dass am für Euro ein Bundesschatzbrief vom Typ B gekauft wird. Der gesuchte Nennwert N hat am den Wert ZW = N 1, , 01 = N 1, Zwischen dem und dem liegen k1 = 257 Tage, das Jahr 2012 ist ein Schaltjahr mit y1 = 366 Tagen, der Zinssatz des Jahres 2012 beträgt i = 0, 0175, der Zwischenwert ZW vergröÿert sich somit auf Damit ergibt sich N = = ZW (1 + 0, /366) = 3902, 56 Euro. 1, (1 + 0, /366) Das Beispiel ist nicht ganz wirklichkeitsnah, da der Bund so lange nach der Emission längst neue Bundesschatzbriefe ausgegeben hat und nun diese und nicht die Vorgänger verkauft. Bundesschatzbriefe dürfen aber privat veräuÿert werden und da kann die obige Rechnung einen guten Richtwert liefern. 37
38 1 Zinsrechnung Rückgabe und Verkauf von Bundesschatzbriefen Bundesschatzbriefe dürfen im ersten Jahr nach Ausgabe nicht zurückgegeben werden. Der Bund sichert sich damit den sehr niedrigen Anfangszinssatz. Nach einem Jahr darf der jeweilige Inhaber einen Betrag von Euro zurückgeben, egal wie lange er oder sie das Papier schon besitzt. Nach Ablauf von 30 Tagen dürfen weitere Euro zurückgegeben werden, usw. Hat man also Euro investiert, benötigt man 600 Tage zur vollständigen Rückgabe eines Bundesschatzbriefes. Man kann die Verfügbarkeit erhöhen, wenn man die Anlage auf mehrere Konten mit einer Höchstanlage von Euro verteilt. Bundesschatzbriefe dürfen aber privat veräuÿert werden. Der Kaufpreis ist dann natürlich anders als bei der Rückgabe an den Bund frei verhandelbar und richtet sich nach dem allgemeinen Zinsniveau. Bundesschatzbriefe können wegen ihrer hohen Sicherheit auch beliehen werden. Der Bank oder einem anderen Gläubiger dient der Bundesschatzbrief als Sicherheit, der Gläubiger wird aber in der Regel einen höheren Sollzinssatz verlangen als die Zinssätze des Bundesschatzbriefes. Auch bei der Rückgabe von Bundesschatzbriefen müssen Stückzinsen berücksichtigt werden. Sei wieder der bereits vertraute Bundesschatzbrief vom Typ A vom betrachtet und angenommen, dass der Inhaber am einen Betrag im Nennwert von Euro an den Bund zurückgibt. Sowohl 2014 als auch 2015 sind keine Schaltjahre. Zwischen dem und dem liegen 324 Tage, der Zinssatz hat die Höhe von 0,035 erreicht, der Nennwert verzinst sich einfach auf den Wert RG = (1 + 0, /365) = 4.124, 27 Euro. Dieser Betrag wird dem Verkäufer gutgeschrieben. Die Stückzinsen im Wert von 124,27 Euro muss der Verkäufer allerdings versteuern. Nun berechne ich den Rückgabewert bei sonst gleichen Daten für einen Bundesschatzbrief vom Typ B. Der ursprüngliche Nennwert von Euro hat bis zum auf den Wert W = , , 01 1, , 0275 = , = 4.234, 30 Euro. erhöht. Dieser Wert wird nun einfach bis zum Kauftermin verzinst und erreicht dann den Rückgabewert RG = 4.234, 30(1 + 0, /365) = 4.365, 86 Euro. Dieser Betrag wird dem Verkäufer gutgeschrieben. Der Rückgabewert ist höher als beim Typ A, weil anders als beim Typ A zwischenzeitlich keine Zinsgutschriften erfolgten. Die angesammelten Zinsen im Wert von 365,86 Euro muss der Verkäufer versteuern Steuerliche Behandlung Zinserträge müssen versteuert werden. Sie fallen beim Bundesschatzbrief vom Typ A jährlich an und müssen entsprechend jährlich versteuert werden. Da für Erträge aus 38
39 1.19 Bundesschatzbriefe Kapitaleinkünften ein Freibetrag von 801 Euro gilt, ist die jährliche Ausschüttung meist vorteilhaft, zumal bei den derzeitig niedrigen Zinssätzen. Beim Bundesschatzbrief vom Typ B erhält man sechs Jahre lang keine Zinsen, dafür am Ende des siebten Jahres alle angesammelten Zinsen einschlieÿlich des eingesetzten Kapitals auf einen Schlag. Im Beispiel des Bundesschatzbriefes vom Typ B mit Erstausgabe am muss bei einer Anlage im Nennwert von Euro ein Zinsertrag von , = , 91 Euro versteuert werden. Diese Art der gesammelten Ausschüttung bietet sich an, wenn man weiÿ, dass zum Zeitpunkt der Ausschüttung nur geringe andere Einkünfte zu erwarten sind, etwa bei einem Selbstständigen, der sich ein Jahr Pause von der Arbeit gönnt oder ganz zu arbeiten aufhört. 39
40 1 Zinsrechnung 1.20 Zusammenfassung Zeitmessung In der Finanzmathematik wird die zeitliche Entwicklung von Guthaben betrachtet. Am Anfang stehen daher Methoden zur Berechnung der Zeit. Es werden folgende Bezeichnungen verwendet: Bezeichner D1 M 1 Y 1 D2 M2 Y 2 t1 = (D 1, M 1, Y 1 ) t2 = (D 2, M 2, Y 2 ) N act(t1, t2) Bedeutung Anfangstag Anfangsmonat Anfangsjahr Endtag Endmonat Endjahr Anfangsdatum Enddatum Kalendergenaue Zahl von Tagen zwischen t1 und t2, wobei immer der erste Tag zählt und der letzte nicht. y1 Anzahl der Tage im Jahr Y 1 y2 Anzahl der Tage im Jahr Y 2 k1 Anzahl der Tage im Jahr Y 1 bis zum Jahresende, d.h. k1 = Nact(t1, 1.1.Y 1 + 1) k2 Anzahl der Tage im Jahr Y 2 vom Jahresanfang bis t2, d.h. k2 = Nact(1.1.Y 2, t2) n die Anzahl der ganzen Jahre zwischen t1 und t2 D1/E min(30, D1) D2/E min(30, D2) D1/U 30 falls D1 der letzte Tag des Monats ist. Sonst D1/U = D1 D2/U D2 wenn D2 < 31 oder D1/U < 30. Sonst D2/U = 30. Vereinfachte Tagzählung nach 30E/360 (deutsch) bzw. nach 30U/360 (amerikanisch) N360E = (Y 2 Y 1)360 + (M2 M1)30 + (D2/E D1/E) N360U = (Y 2 Y 1)360 + (M2 M1)30 + (D2/U D1/U) Die Zeit t wird damit wie in der folgenden Tabelle berechnet. ACT/ACT (ICMA) { ACT/360 ACT/365 30E/360 30U/360 Nact/y1 Y 2 = Y 1 k1/y1 + n + k2/y2 Y 2 > Y 1 Nact/360 Nact/365 N360E/360 N360U/360 40
41 1.20 Zusammenfassung Zeit nach PAngV Zunächst wird der Tag von D1 auf D1 geändert: { D1 D1 < 31 oder D1 < 28 und M1 = 2 D1 = 30 D1 = 31 oder D1 28 und M1 = 2 (1.30) Genauso wird D2 berechnet. Die Zeit tp nach PAngV ist dann { Y 2 Y 1 + (M2 M1)/12 + (D2 D1)/365 tp = Y 2 Y 1 + (M2 M1 1)/12 + (D D1)/ Zinsformeln D2 D1 D2 < D1 (1.31) Exponentielle Verzinsung: K t = K 0 (1 + i) t (ExpV) Stetige Verzinsung: K t = K 0 e it (SteV) Einfache Verzinsung: K t = K 0 (1 + it) (EinV) ) (1 + i m Gemischte Verzinsung: K t = K 0 (1 + i k1 1 + i k2 (GemV) y1 y2 Renditeformel: r = (K t /K 0 ) 1/tP 1 (RenF) Hier sind K 0 und K t das Anfangs- und Endkapital zu den Zeiten 0 und t. i der nominelle Jahreszinssatz Zinssatz. t die Laufzeit entsprechend der gewählten Zinsmethode. tp die Laufzeit nach PAngV. r die Rendite. m die Anzahl von Zinsperioden pro Jahr. k1 die Anzahl von Tagen vom Anfang bis zum ersten Zinstermin. y1 die Anzahl der Tage im ersten Jahr. k2 die Anzahl von Tagen vom letzten Zinstermin bis zum Ende. y2 die Anzahl der Tage im letzten Jahr. n die Anzahl der vollständigen Zinsperioden. Dabei müssen die Werte von k1, y1, k2 und y2 gemäÿ der verwendeten Zinsmethode berechnet werden. ) n ( ) 41
42 1 Zinsrechnung 1.21 Praktikumsaufgaben Aufgabe 1. Erstellen Sie die Funktion LAUFZEIT(Anfdat;Enddat;Basis) mit Visual Basic. Hier sind ˆ Anfdat: ist ein Datum, das dem Anfangsdatum entspricht. ˆ Enddat: ist ein Datum, das das Enddatum angibt. ˆ Basis: gibt an, welche Zinsmethode verwendet wird. Es sind sieben Werte möglich. Lässt man den dritten Parameter ganz weg oder 0: 30U/360 (amerikanisch), 1: ACT/ACT (EXCEL), 2: ACT/360 (Eurozins), 3: ACT/365 (Englisch), 4: 30E/360 (Deutsch), 5: ACT/ACT (ICMA), 6: PAngV. Diese Funktion stimmt also für die Parameterwerte 0 bis 4 mit der Excel-Funktion BRTEILJAHRE überein. Im Visual Basic Code werden Arbeitsblattfunktionen mit ihrem englischen Bezeichner aufgerufen, hier Excel.WorksheetFunction.YearFrac. Aufgabe 2. Erstellen Sie das abgebildete Formular, das für alle besprochene Verzinsungsarten und Zinsmethoden bei Eingabe von jeweils vier Werten den fünften berechnet. Der zu berechnende Wert soll durch ein Optionsfeld auszuwählen sein und optisch wie abgebildet von den anderen Eingabefeldern abgehoben sein. Abbildung 1.7: Ein universelles Zinsformular 42
43 1.22 Aufgaben 1.22 Aufgaben Aufgabe 1. Für die folgenden Zeiträume berechne man für alle vorgestellten Zinsmethoden die jeweils verstrichene Zeit: bis zum , bis zum , bis zum und bis zum Aufgabe 2. Man berechne den Endwert und den Zinsbetrag bei exponentieller, stetiger und einfacher Verzinsung für ein Kapital von Euro, das im Zeitraum vom bis zum bei einem Zinssatz von i = 0, 08 angelegt wurde. Man verwende alle vorgestellten Zinsmethoden, bis auf die nach PAngV und berechne jeweils auch die Rendite. Aufgabe 3. Man berechne den Endwert und den Zinsbetrag bei exponentieller, stetiger und einfacher Verzinsung für ein Kapital von Euro, das im Zeitraum vom bis zum bis bei einem Zinssatz von i = 0, 08 angelegt wurde. Man verwende alle vorgestellten Zinsmethoden, bis auf die nach PAngV und berechne jeweils auch die Rendite. Aufgabe 4. Der Zinssatz i bei stetiger Verzinsung sei so, dass aus 100 Euro innerhalb eines Monats bei der Zinsmethode 30E/ Euro werden. a) Welchen Wert hat i? b) Welchen Wert hat ein Anfangskapital von Euro nach zwei Jahren? c) Wie groÿ ist die Rendite r nach PAngV? Aufgabe 5. Eine Freundin verleiht Ihnen Euro für vier Monate und verlangt Euro zurück. Sie behauptet, ihre Rendite sei nur 3 Prozent. Wie sehen Sie das? Aufgabe 6. Eine Bank bietet einen so genannten abgezinsten Sparbrief wie folgt an: Der Kunde zahlt einmalig 900 Euro und erhält nach Ablauf von drei Jahren Euro zurück. Wie hoch ist die Rendite? Aufgabe 7. Jemand legt bei stetiger Verzinsung zu einem jährlichen Nominalzinssatz von 8 Prozent vom bis zum ein Kapital von DM an. a) Warum ist keine Zinsmethode angegeben? b) Wie hoch ist der Endbetrag? c) Wie groÿ ist die Rendite nach PAngV? d) Durch welchen Zinssatz i würde man mit exponentieller Verzinsung diesen Endbetrag erreichen? Aufgabe 8. Jemand legt bei stetiger Verzinsung zu einem jährlichen Nominalzinssatz von 8 Prozent vom bis zum ein Kapital von DM an, wobei die Zinsmethode 30E/360 verwendet wird. 43
44 1 Zinsrechnung a) Wie hoch ist der Endbetrag? b) Wie groÿ ist die Rendite nach PAngV? c) Durch welchen Zinssatz würde man auf einem Sparbuch mit gemischter Verzinsung diesen Endbetrag erreichen? Rechnen Sie mit der Zinsmethode ACT/ACT (ICMA) und einem Zinstermin am Jahresende. Aufgabe 9. An welchem Tag ist jeweils bei exponentieller, stetiger und einfacher Verzinsung ein bei einem Zinssatz von 5 Prozent am angelegtes Kapital von Euro auf Euro angewachsen? Die Zinsmethode sei 30E/360. Wie hoch ist der tatsächliche Endbetrag jeweils? Aufgabe 10. Jemand legt auf einem Sparbuch mit gemischter Verzinsung und einem Zinstermin am Jahresende zu einem jährlichen Zinssatz von 8 Prozent vom bis zum ein Kapital von DM an. a) Wie hoch ist der Endbetrag bei der Zinsmethode ACT/ACT (ICMA)? b) Wie groÿ ist die Rendite nach PAngV? c) Welcher Zinssatz ρ würde bei stetiger Verzinsung mit der Zinsmethode ACT/ACT (ICMA) zum selben Endbetrag führen? Aufgabe 11. Man berechne das Endkapital bei gemischter Verzinsung für ein Kapital von Euro, das im Zeitraum vom bis zum bei einem Zinssatz von i = 0, 08 angelegt wurde. Verwenden Sie die alle Zinsmethoden und rechnen Sie mit einer, zwei und vier Zinsperioden. Aufgabe 12. Jemand legt auf ein Bausparkonto zu einem jährlichen Zinssatz von 2 Prozent vom bis zum ein Kapital von DM an. Rechnen Sie mit vier Zinsperioden und der Zinsmethode 30E/360. a) Wie hoch ist der Endbetrag? b) Wie groÿ ist die Rendite r nach PAngV? c) Welcher Zinssatz würde bei gleicher Zinsmethode aber nur einer Zinsperiode pro Jahr zum selben Endbetrag führen? Aufgabe 13. Ein Betrag von Euro wird zwei Jahre zu einem Nominalzinssatz von 6 Prozent mit monatlicher Zinsperiode angelegt. Man berechne den Kapitalendwert und die Rendite! Aufgabe 14. Ein Bausparer zahlt am Euro auf ein Bausparkonto mit vier Zinsperioden. Nach genau vier Jahren hat er ,85 Euro auf seinem Konto. Man berechne den Nominalzinssatz und die Rendite. 44
45 1.22 Aufgaben Aufgabe 15. Herr XY zahlt am auf ein besonders günstiges Sparbuch einer niederländisch-türkischen Bank Euro ein und erhält bis zum einen Zinssatz von 4 Prozent, von da an bis zum Vertragsende am einen Zinssatz von 6 Prozent. Berechnen Sie den Betrag, den der Kunde dann erhält. Verwendet sei die Zinsmethode ACT/ACT (ICMA) mit einem Zinstermin am Jahresende. Man berechne ferner die Rendite r der Anlage nach der PAngV. Aufgabe 16. Frau XY hatte am einen Betrag von Euro auf ein Sparbuch einer Bank mit Sitz auf den Cayman-Inseln eingezahlt, und am wieder abgehoben. Der Sparzins betrug anfänglich 4 und stieg danach auf 6 Prozent. Frau XY wollte eine Rendite nach deutscher Rechnung von 5 Prozent erzielen. An welchem Tag musste dafür der Zins gewechselt werden? Die Zinsmethode war ACT/ACT (ICMA). Aufgabe 17. Frau XY erwarb am einen Bundesschatzbrief des Typs B im Wert von Euro zu den in der Abbildung 1.6 auf Seite 36 gezeigten Konditionen. Am gerät die inzwischen wieder ledige Frau XY in Geldnot und muss den Bundessschatzbrief an den Bund zurückgeben oder verkaufen. a) Welchen Rückgabewert hat das Wertpapier? b) Ein Freund bietet an, den Bundesschatzbrief zu kaufen, wobei der Kaufpreis so sein soll, dass das Papier eine Rendite von 3 Prozent erzielt, wenn es bis zum Ende der Laufzeit gehalten wird. Wie hoch wäre dieser Kaufpreis? Wie soll sich die unglückliche Frau XY entscheiden? Wie ist ihre steuerliche Situation in diesem Fall? 45
46 2 Barwert und Rendite von Zahlungsströmen Zinsen haben zwei Rollen, sie legen fest, wie sich ein heute investiertes Kapital entwickeln wird, das ist die Aufzinsungsfunktion, wofür die bereits vorgestellte Zinsrechnung entwickelt wurde. Über Kalkulationszinssätze werden aber auch die heutigen Werte von Zahlungen ermittelt, die erst in Zukunft fällig werden. Der heutige Wert einer erst später fälligen Zahlung wird als deren Barwert bezeichnet. Der Barwert ist immer geringer als der in der Zukunft fällige Betrag. Der Abschlag wird umso höher sein, je weiter in der Zukunft entfernt die Zahlung erfolgt und je höher das Ausfallsrisiko ist. Der Abschlag wird durch einen der Situation angemessenen Zinssatz berechnet, das ist die Abzinsungsfunktion der Zinsrechnung. Zinsen und Barwert hängen also eng miteinander zusammen. Während bislang lediglich eine einmalige Kapitalanlage in ihrer Wertentwicklung beobachtet wurde, sollen nun auch mehrfache Zahlungen, so genannte Zahlungsströme betrachtet sein. Renditeberechnungen und Anlageentscheidungen werden dann komplexer und erfordern neue mathematische Ansätze. Dabei hat sich die Nettobarwertmethode besonders bewährt, wobei Investitionen bezüglich ihres gegenwärtigen Wertes verglichen werden. Der Nettobarwert eines Zahlungsstroms ist die Summe seiner mit einem Kalkulationszinssatz r ermittelten Einzelbarwerte. 2.1 Konto Eine Geldanlage wird als Konto geführt. Ein Konto erfasst den Wert und die Zeit von Geschäftsvorfällen in Tabellenform, wobei Zu- und Abgänge auf zwei getrennten Spalten verbucht werden, die als Soll und Haben bezeichnet werden. Dadurch werden negative Zahlen vermieden. Zur besseren Übersicht wird nanzmathematisch nur eine Spalte verwendet, d.h. die Habenseite des Kontos besteht dann aus Zahlungen mit positiven und die Sollseite aus solchen mit negativen Vorzeichen. Ein Konto fängt mit einem Anfangsbestand an, dann folgen zu ebenfalls verbuchten Zeitpunkten Zu- uns Abüsse, die in ihrer Summe den Endbestand ergeben. In der klassischen Buchführung werden Soll- und Habenseite getrennt summiert, die Saldo genannte Dierenz und ergibt den Endbetrag. Die Bilanz eines Unternehmens hat genau wie ein normales Konto zwei Spalten, die Aktiva und Passiva genannt werden. Die Aktiva bilden die linke Spalte mit der wertmäÿigen Erfassung aller Vermögenswerte des Unternehmens. Die Passiva bilden die rechte Spalte mit der wertmäÿigen Erfassung aller Verbindlichkeiten des Unternehmens. Der Saldo ist der letzte Eintrag auf der Passivseite, es ist die Dierenz zwischen der Summe aller Vermögenswerte und der Summe aller Werte der Verbindlichkeiten. 46
47 2.2 Der Barwert 2.2 Der Barwert Die Zinsrechnung ermittelt wie sich ein heute angelegtes Kapital im Laufe der Zeit entwickeln wird. Man möchte aber auch umgekehrt wissen, welchen Wert eine erst zum Zeitpunkt t fällige Zahlung C heute hat. Man nennt diesen Wert den Barwert, englisch present value, abgekürzt PV. Aus dieser Denition des Barwerts geht nicht hervor, wie er zu berechnen ist. Sicher ist nur, dass für alle Zahlungen in der Zukunft ein Abschlag erfolgt, Euro heute sind wertvoller als Euro, die etwa eine Lebensversicherung in einem Jahr bezahlt, was wiederum wertvoller ist als eine Auszahlung desselben Betrags in zwei Jahren. Die Bewertung des in einem Jahr fälligen Betrages geschieht über die Überlegung, welcher heutige Betrag P V dann bei einem Zinssatz r auf Euro angewachsen ist, wobei bei Barwertberechnungen immer exponentielle Verzinsung und zumindest in Deutschland immer die Zinsmethode PAngV verwendet wird. Damit folgt für den Barwert eines in einem Jahr ausgezahlten Betrags von Euro P V (1 + r) = , P V = r. Damit ist das Problem aber immer noch nicht gelöst, denn es bleibt die Frage, welcher Zinssatz r in die Gleichung einzusetzen ist. Dieser Zinssatz wird sich an den gängigen Marktzinsen für Bundesanleihen orientieren und je nach Risiko der Zahlung einen Aufschlag erhalten. Im allgemeinen Fall bezieht sich der Barwert auf einen zum zukünftigen Zeitpunkt t fälligen Betrag C. Der Barwert hängt also von der Höhe des Betrags und dem Zeitpunkt seiner Fälligkeit ab, er ist deshalb eine Funktion des Paars (C, t). Der Barwert ist eine rein kalkulatorische Gröÿe und wird wie folgt berechnet: ˆ Es wird ein Zinssatz r gewählt, der dem mit der Zahlung C verbundenen Risiko entspricht. ˆ Der Barwert P V (r) ist der Wert, der bei exponentieller Verzinsung zu diesem Zinssatz von heute an bis zum Zeitpunkt t auf C anwachsen würde: P V (r) = (1 + r) t C. (2.1) Dabei wird international die Zinsmethode ACT/ACT (ICMA) und national die Zinsmethode PAngV benutzt. Der Barwert ist also der mit dem Zinssatz r diskontierte Wert von C. Der Barwert ist eine Funktion r P V (r) vom Rechnungszinssatz r. Es gilt lim r P V (0) = C, (2.2) P V (r) = 0 (2.3) Der hier verwendete Zinssatz r ist kein Zinssatz eines tatsächlichen Geldgeschäfts, sondern eine Rechengröÿe. Ich bezeichne kalkulatorische Zinssätze immer mit r. 47
48 2 Barwert und Rendite von Zahlungsströmen Beispiel 2.1. Berechnen Sie die Barwerte einer in einem halben Jahr fälligen Zahlung von Euro für die Diskontierungszinssätze von r = 0, 02 und r = 0, 08. P V (0, 02) = , 02 1/2 = , 54, P V (0, 08) = , 08 1/2 = , 45 Die beiden Barwerte unterscheiden sich also um rund Euro. 2.3 Zahlungsstrom Ein Anlagekonto wird nanzmathematisch durch einen so genannten Zahlungsstrom dargestellt. Ein Zahlungsstrom ist eine Folge von Zahlungen und den Zeitpunkten ihrer Verbuchung, also eine Folge von Paaren (C i, t i ), wobei C i der zum Zeitpunkt t i verbuchte Wert der i-ten Zahlung ist. In der tatsächlichen Kontoführung würde der Zahlungsstrom in zwei Zahlungsströme aufgeteilt, wobei der eine alle Zahlungen mit positiven und der andere alle Zahlungen mit negativen Vorzeichen umfasst. Die Zeitpunkte t i sind bei einem Konto Datumswerte wie der , in der Finanzmathematik oft aber schon Zahlen, die den Abstand zu einem Ausgangsdatum darstellen, also Zeitspannen. Bemerkung 2.1. Bei einem Zahlungsstrom wird immer still schweigend vorausgesetzt, dass die Folge der Zeiten t i aufsteigend in der Form t 0 < t 1 <... < t n angeordnet ist Beispiel eines Zahlungsstroms Betrachten wir ein Versicherungsunternehmen, das für Groÿkunden deren betriebliche Altersvorsorge renanziert. Die mathematische Abteilung geht dabei innerhalb der nächsten drei Jahre von folgenden Zahlungsverpichtungen aus. Bereits nach einem halben Jahr sind 100 Mio. Euro fällig, nach anderthalb weitere 150 Mio. Euro und nach drei Jahren noch 400 Mio. Euro. Der Zahlungsstrom ist also C = [(100, 1/2), (150, 3/2), (400, 3)]. Man kann ihn sich in Tabellenform oder auf einem Zeitstrahl veranschaulichen. Alle Angaben in Mio. Euro / /2 2 5/ t 2.4 Der Barwert eines Zahlungsstroms Man muss sich wie in dem obigen Beispiel zunächst eine Übersicht über alle Ein- und Auszahlungen sowie deren Zeitpunkten verschaen. Der Zahlungsstrom wird dann auf 48
49 2.4 Der Barwert eines Zahlungsstroms einem Zeitstrahl oder mit einer Tabelle dargestellt. Die Zeitpunkte werden dabei als Zeitspannen, d.h. als Abstände zu einem Bezugspunkt, dargestellt. Der Barwert des Zahlungsstroms ist die Summe aller Barwerte. Es wird also ein Kalkulationszinssatz r gewählt, mit dem alle Zahlungen diskontiert werden, d.h. P V (r) = n (1 + r) t i C i. (2.4) i=0 In unserem Beispiel ergibt sich in Mio. Euro P V (r) = 100 (1 + r) 0, (1 + r) 1, (1 + r) 3. Die Barwertfunktion ist streng monoton fallend, wenn alle Zahlungen positiv sind. Es gilt lim r P V (0) = n C k, (2.5) k=0 P V (r) = 0 (2.6) Den Graph dieser Funktion sehen Sie in der nächsten Abbildung: P V ( r ) ,1 0,2 0,3 0,4 0,5 0,6 Zinssatz r Abbildung 2.1: Die Barwertfunktion Das Versicherungsunternehmen muss für die künftigen Zahlungsverpichtungen in der Passivseite der Bilanz eine Rückstellung ausweisen. Dazu muss ein Wert für r gewählt werden. Je nach Gröÿe von r schwankt die Rückstellung dann zwischen 650 Mio. und 0 Mio. Euro. In der Abbildung 2.1 sind noch völlig unrealistische Zinssätze bis 60 Prozent zu sehen. Der Gesetzgeber schreibt den Versicherungsunternehmen einen Rechnungszinssatz vor, den ich r z nennen will und dessen Wert 0,03 sei. Die Rückstellung des Unternehmens beträgt deshalb in Mio. Euro P V Z := P V (r z ) = 100 (1, 03) 0, (1, 03) 1, (1, 03) 3 = 608,
50 2 Barwert und Rendite von Zahlungsströmen Wenn das Unternehmen diesen Betrag zurückstellt und ein halbes Jahr zum Rechnungszins bei exponentieller Verzinsung anlegt, verfügt es dann über 617,14 Mio. Euro, wovon 100 Mio. Euro abgehen. Der verbleibende Rest erhöht sich durch die Zinsen bis zum Zeitpunkt 1,5 auf 532,65 Mio. Euro, wovon die Zahlung über 150 Mio. Euro getragen wird. Der Rest von 382,65 Mio. Euro erhöht sich in den letzten 1,5 Jahren genau auf die nun fälligen 400 Mio. Euro. Der Rechnungszins wird sehr vorsichtig angesetzt und liegt in der Regel unterhalb des tatsächlich zu erzielenden Marktzinses, den ich mit r m bezeichne und dessen Wert 5 Prozent sei. Wenn es dem Versicherungsunternehmen mit Aktivgeschäften gelingt, diesen Marktzins zu erzielen, wird die tatsächlich benötigte Rückstellung geringer ausfallen, nämlich P V M := P V (r m ) = 100 (1, 05) 0, (1, 05) 1, (1, 05) 3 = 582, 54, d.h. das Versicherungsunternehmen hat eine stille Reserve von 25,54 Mio. Euro, die nach den drei Jahren auf 29,57 Mio. Euro angewachsen ist, wenn das Versicherungsunternehmen bei Geldanlagen den Marktzins erzielt. Man sieht das auch durch Verfolgung des Kassenbestandes des Versicherungsunternehmens. Der zurückgestellte Betrag von 608,08 Mio. Euro wächst in einem halben Jahr bei exponentieller Verzinsung zum Marktzins auf 623,10 Mio. Euro an, wovon 100 Mio. Euro abgehen. Der verbleibende Rest erhöht sich durch die Zinsen bis zum Zeitpunkt 1,5 auf 549,25 Mio. Euro, wovon die Zahlung über 150 Mio. Euro getragen wird. Der Rest wächst bis zum Ende auf 429,57 Mio. Euro, wovon nach Abzug der fälligen 400 Mio. Euro der schon errechnete Überschuss bleibt. 2.5 Äquivalenz von Zahlungsströmen Der einfache Bankkunde möchte entweder Geld anlegen oder leihen. Die Konditionen der Banken unterscheiden sich meistens nach Zeitpunkten und der Höhe der Zahlungen. Bei einer Anlage wird der Kunde zunächst eine Reihe von Einzahlungen leisten und danach das angesammelte Kapital auf einen Schlag oder als eine Folge von Zahlungen zurück erhalten. Bei einem Kredit sieht es genau umgekehrt aus, zunächst leiht die Bank einen Betrag und fordert danach Rückzahlungen. Ähnlich sieht es bei Investitionen eines Unternehmens aus. Zunächst wird über eine bestimmte Zeitspanne in eine neue Anlage investiert, was zu Geldabüssen A j zu den Zeitpunkten t j führt. Der Investition folgen dann Einnahmen E k zu den Zeitpunkten t k. Der Vergleich von zwei Zahlungsströmen ist also eine wichtige Aufgabe der Finanzmathematik. Dabei gibt es zwei Ansätze, man vergleicht entweder die Barwerte oder die Endwerte. Beim Barwertvergleich wählt man einen sinnvollen Kalkulationszinssatz r und berechnet die jeweiligen Barwerte. Beim Endwertvergleich wird eine der vorgestellten Verzinsungsarten gewählt und dann werden die sich nach den Regeln der Zinsrechnung ergebenden Endwerte verglichen. Zwei Zahlungsströme sind als gleichwertig anzusehen, wenn sie denselben Barwert oder denselben Endwert haben. Die formale Denition lautet: 50
51 2.5 Äquivalenz von Zahlungsströmen Denition 2.1. Seien A = (A j, t j ) und B = (B k, t k ) zwei Zahlungsströme. Sie heiÿen äquivalent zum Zinssatz r, wenn sie bezüglich dieses Zinssatzes denselben Barwert haben. Ist der Endwert identisch, werden sie äquivalent zum Endwert genannt. Zwei äquivalente Zahlungsströme haben also nach dieser Denition bezüglich des gewählten Zinssatzes denselben Barwert, das heiÿt aber nicht, dass sie auch zu diesem Zinssatz denselben Endwert haben. Das trit nur zu, wenn die Verzinsung exponentiell ist. Satz 2.1. Zwei zum Zinssatz r äquivalente Zahlungsströme A = (A j, t j ) und B = (B k, t k ) haben bei exponentieller Verzinsung auch denselben Endwert. Vergeht zwischen dem Anfangs- und dem Enddatum die Zeitspanne t, so gilt für den Endwert E t eines Zahlungsstroms E t = (1 + r) t P V (r) Sind alle Zahlungen positiv und die beiden Zahlungsströme nicht identisch, so gibt es genau einen Zinssatz zu dem sie äquivalent sind. In der Praxis geht man meist umgekehrt vor. Man legt eine der beiden Zahlungsströme fest, einigt sich auf einen Zinssatz r und erzwingt dann Äquivalenz. Beispiel 2.2. Ein treusorgender Vater möchte seinem Sprössling eine unbeschwerte Studienzeit ermöglichen. Er vereinbart mit seiner Bank Einzahlungen von je Euro sofort, ein halbes Jahr danach und am Ende des ersten Jahres. Die Bank zahlt vom Ende des zweiten bis zum Ende des fünften Jahrs eine Rate R. Beide Zahlungsströme sollen zum Zinssatz r = 0, 03 äquivalent sein. Welchen Wert R hat der jährliche Scheck des glücklichen Sohnes? Zunächst werden die beiden Zahlungsströme angegeben: A = [(20.000, 0), (20.000, 1/2), (20.000, 1)], B = [(R, 2), (R, 3), R, 4), R, 5)]. Der Barwert von A zum Kalkulationszinssatz r ist P V A(0, 03) = ( 1, , , 03 1) = , 06 Euro. Der Barwert des zweiten Zahlungsstroms ist P V B(0, 03) = R ( 1, , , , 03 5) = 3, R, also R = , 06/3, = , 15 Euro. Nach Satz 2.1 sind die beiden Zahlungsströme auch zum Endwert bezüglich des Zinssatzes r = 0, 03 äquivalent, wenn als Verzinsungsart die exponentielle Verzinsung gewählt wird. Der Endwert beider Zahlungsströme zum Endzeitpunkt t = 5 ist E t = (1 + r) , 06 = , 99 Euro. 51
52 2 Barwert und Rendite von Zahlungsströmen Wird aber gemischte Verzinsung gewählt, sind beide Zahlungsströme nicht äquivalent zum Endwert, denn die Endwerte unterscheiden sich beim Zinssatz r = 0, 03 geringfügig. E A = ( 1, , , , 03 4) = , 49, E B = , 15 ( 1, , , , 03 ) = , 99. Der etwas höhere Endwert des ersten Zahlungsstroms rührt daher, dass bei sonst gleichen Bedingungen die gemischte Verzinsung immer etwas günstiger als die exponentielle Verzinsung ist. 2.6 Die Nettobarwertfunktion Bei diesem Beispiel stellt sich die Frage, warum es überhaupt zum Geschäftsabschluss kam. Der Vater könnte das Geld ja zunächst selber anlegen und dann die erforderlichen Raten abzweigen. Aus seiner Sicht nimmt ihm die Bank den Aufwand der Geldanlage ab, er muss sich um nichts kümmern und hätte vielleicht als Amateur nicht einmal eine Rendite von 3 Prozent erzielt. Ganz anders wird das bei der Bank gesehen. Hier sind Pros am Werk, die sich zutrauen, das ihnen anvertraute Geld zu einem höheren Zinssatz als 3 Prozent zu vermehren. Nehmen wir an, die Anlagepros erzielen bei exponentieller Verzinsung einen Zinssatz von r = 5 Prozent. Das bedeutet für die Bank einen Gewinn, der Nettobarwert oder Kapitalwert genannt wird. Diesen werde ich jetzt genau denieren. Denition 2.2. Ein Zahlungsstrom C = (C k, t k ) heiÿt vollständig, wenn er alle Zahlungen einer Anlage oder Schuld umfasst. Die Einnahmen erhalten dabei ein positives und die Ausgaben ein negatives Vorzeichen. Der Barwert eines vollständigen Zahlungsstroms heiÿt Nettobarwert und berechnet sich durch n NP V (r) = (1 + r) t k C k. (2.7) k=0 Ich möchte noch darauf hinweisen, dass nur ich die Bezeichnung vollständig für wie in dieser Denition beschriebene Zahlungsströme verwende. Der Zahlungsstrom von Beispiel 2.2 auf Seite 51 ist vollständig, der Zahlungsstrom der Verpichtungen des Versicherungsunternehmens im Abschnitt auf Seite 48 ist es nicht, da hier nur die Ausgaben, nicht aber die zuvor erfolgten Einnahmen zu sehen sind. Ein vollständiger Zahlungsstrom besteht aus zwei Zahlungsströmen A = (A j, t j ) und E = (E k, t k ), wobei der erste Zahlungsstrom die Ausgaben und der zweite die Einnahmen beschreibt. Die Ausgaben werden im vollständigen Zahlungsstrom dann mit negativen Vorzeichen verbucht. Die Nettobarwertfunktion kann auch durch die Zahlungsströme der Ausgaben und Einnahmen ausgedrückt werden: NP V (r) = K J (1 + r) t k E k (1 + r) t j A j. (2.8) k=0 j=0 52
53 2.6 Die Nettobarwertfunktion Zur besseren Übersicht werde ich vollständige Zahlungsströme in Tabellenform ausgeben, wobei in der ersten Zeile die Zeiten stehen. Dann folgen die Zahlungsströme der Ausgaben, Einnahmen und der vollständige Zahlungsstrom. Im Beispiel des fürsorglichen Vaters benden sich die aus der Sicht der Bank vorhandenen Zahlungsströme in der folgenden Tabelle. Zeit 0 1/ Einnahmen Ausgaben vollständig Für die Nettobarwertfunktion folgt also NP V (r) = (1 + (1 + r) (1 + r) 1 ) , 15((1 + r) 2 + (1 + r) 3 + (1 + r) 4 + (1 + r) 5 ) Den Graph dieser Funktion zeigt die Abbildung N P V ( r ) ,05 0,1 0,15 0,2 Zinssatz r Abbildung 2.2: Die Nettobarwertfunktion aus Sicht der Bank. Am Graph dieser Funktion lässt sich ablesen, wie der Gewinn der Bank von dem Zinssatz abhängt, womit die Bank die Einzahlungen des Vaters selber vermehren kann. Ist der Wiederanlagezinssatz geringer als die mit dem Vater vereinbarten 3 Prozent, macht die Bank Verluste. Der sogenannte break-even-point tritt genau bei 3 Prozent ein, die Bank macht weder Verlust noch Gewinn. Gelingt es ihr, die Einlagen mit 5 Prozent zu vermehren, so winkt ein Gewinn von NP V (0, 05) = 3.238, 15 Euro. Bei 10 Prozent ist der Wert ungefähr und bei 20 Prozent fast Euro. Aus der Sicht des Vaters sieht alles spiegelbildlich aus. Hätte er selbst die drei Raten von Euro zu 5 Prozent anlegen können, hätte er 3.238,15 Euro gespart und trotzdem seinen Sohnemann mit den vier Raten von ,15 Euro beglücken können. 53
54 2 Barwert und Rendite von Zahlungsströmen 2.7 Investitionsrechnung Eine Investition ist eine mittel- bis langfristige Anlage von Finanzmitteln in Sachanlagen wie Gebäude und Inneneinrichtungen, Maschinen oder Fahrzeuge mit der Aussicht auf zukünftige Erträge. Im Rahmen der Finanzmathematik versteht man unter dem Begri Investition aber auch den Kauf von Wertpapieren. Investitionen in Sachanlagen erscheinen in der Bilanz eines Unternehmens in der Seite der Aktiva, ihre Finanzierung belastet die Passivseite. Sachgüter haben eine bestimmte Nutzungsdauer und werden in dieser Zeit steuerlich abgeschrieben, können aber natürlich bei gutem Zustand auch über diese steuerliche Nutzungsdauer hinaus im Unternehmen verwendet werden. Investitionen in Wertpapiere können nicht abgeschrieben werden, aber die Mittel zur Finanzierung gelten als Werbungskosten. Investitionsrechnungen sollen die Vor- und Nachteile von Investitionen beleuchten, Vergleiche von Investitionen ermöglichen und dienen damit der Entscheidungsndung, welche Investition getätigt werden soll. Finanzmathematisch ist jede Investition mit einem Zahlungsstrom verbunden, der alle mit ihm zusammenhängenden Ein- und Auszahlungen und deren Zeitpunkte erfasst. Dabei werden neben den Anschaungskosten auch alle Kosten für Reparaturen und Wartungsarbeiten und neben den Erträgen auch der Verkaufspreis am Ende der Nutzungsdauer berücksichtigt. Die statische Investitionsrechnung vernachlässigt den tatsächlichen Zeitpunkt der Zahlungen und rechnet diese in Durchschnittsgröÿen um, die in allen Perioden der Nutzungsdauer anfallen. Dieser mathematisch wenig anspruchsvolle Ansatz soll hier nicht weiter verfolgt werden. Dynamische Verfahren erfassen den tatsächlichen zeitlichen Anfall der Zahlungen, daher bietet sich als Basis der Investitionsentscheidung die Nettobarwertfunktion an. Die Nettobarwertfunktion wird dann als Kapitalwertfunktion bezeichnet, der Nettobarwert bei einem gegebenen Diskontierungssatz heiÿt Kapitalwert Die Kapitalwertmethode Die Kapitalwertmethode erstellt also die hier Kapitalwertfunktion genannte Nettobarwertfunktion und berechnet für einen bestimmten Kalkulationszinssatz r den Kapitalwert genannten Nettobarwert. Es wird also vorausgesetzt, dass der vollständige Zahlungsstrom der Investition vorliegt und ein sinnvoller Kalkulationszinssatz gefunden werden kann. Der Kalkulationszinssatz ist der für die betrachtete Investition vorgegebene Mindestzinssatz. Oft wird auch ein Zinssatz eingesetzt, den alternative Investitionen erwirtschaften. Weiter wird unterstellt, dass alle mit der Investition verbundenen Zahlungen und deren Zeitpunkte festliegen. Bei Finanzinvestitionen ist dies beim Kauf von festverzinslichen Wertpapieren wie etwa den Bundesschatzbriefen tatsächlich der Fall, aber schon der Kauf von Aktien ist schwierig einzuschätzen. Die Zahlungsströme von Investitionen in Sachgüter sind ähnlich schwer vorherzusehen. Die Zahlungsströme sind dann eigentlich nur Schätzungen und deshalb umso unsicherer, je weiter die Zahlungen in der Zukunft liegen. Wir setzen aber voraus, dass ein sinnvoller Kalkulationszinssatz gefunden wurde und der Zahlungsstrom festliegt. Dann wird der zum Kalkulationszinssatz gehörige und als Kapitalwert bezeichnete Nettobarwert berechnet. Ist der Kapitalwert positiv, so ist die 54
55 2.8 Der interne Zinssatz Investition günstig im Vergleich zu einer Investition, die als Verzinsung nur den Kalkulationszinssatz hat. Der Kapitalwert ist der Mehrgewinn im Vergleich mit einer Anlage zum Kalkulationszinssatz. Hat der Kapitalwert den Wert 0, so ist die Investition genauso günstig wie eine alternative Anlage zum Kalkulationszinssatz. Bei negativem Kapitalwert sind Anlagen zum Kalkulationszinssatz vorteilhafter. Beim Vergleich alternativer Investitionen ist diejenige mit dem gröÿten Kapitalwert die relativ beste. Ich betone noch einmal, dass der Kapitalwert nicht den Gewinn oder Verlust einer Investition berechnet, sondern einen zusätzlichen Gewinn oder Verlust bezogen auf eine Anlage zum Kalkulationszinssatz. Bei einem positiven Kapitalwert wird anders gesagt nicht nur der mit dem Kalkulationszinssatz verbundene Mindestgewinn, sondern noch ein Zusatzertrag in Höhe des Kapitalwerts erzielt. Beispiel 2.3. Für eine neue Fabrikhalle werden im ersten Jahr gleich am Anfang Euro und ein halbes Jahr später weitere Euro fällig. Am Ende des zweiten Jahres kann die Fabrikhalle dann für Euro verkauft werden. Alternativ können mit anderen Anlagen 7 Prozent Zinsen erwirtschaftet werden. Berechnen Sie den Kapitalwert der Investition und schätzen damit deren Vorteilhaftigkeit ein. Der vollständige Zahlungsstrom (C i, t i ) besteht aus dem Zahlungsstrom (A j, t j ) der Ausgaben und dem Zahlungsstrom (E k, t k ) der Einnahmen. Die Ausgaben werden im vollständigen Zahlungsstrom dann mit negativen Vorzeichen verbucht. Die drei Zahlungsströme benden sich in der folgenden Tabelle Zeit 0 1/2 2 Ausgaben Einnahmen 300 vollständig Die zugehörige Nettobarwertfunktion lautet NP V (r) = (1 + r) 0, (1 + r) 2, Der Kapitalwert ist der Nettobarwert dieser Investition und ergibt sich demnach durch Einsetzen von r = 0, 07, woraus sich ein Kapitalwert von 5.357,97 Euro ergibt. Die Investition lohnt sich also und ermöglicht einen zusätzlichen Ertrag von 5.357,97 Euro im Vergleich zu der alternativen Anlage. Der Graph der bei Investitionen Kapitalwertfunktion genannten Nettobarwertfunktion ist in der Abbildung 2.3 zu sehen. 2.8 Der interne Zinssatz Die Berechnung des Kapitalwerts ist die beste Methode, um die Rentabilität einer Investition zu berechnen, da der Mehrgewinn bezogen auf Alternativanlagen bestimmt wird. 55
56 2 Barwert und Rendite von Zahlungsströmen 40,00 30,00 20,00 N 10,00 P 0,00 V 0 0,02 0,04 0,06 0,08 0,1 0,12 0,14 0,16 0,18 r -10,00 )Zinssatz r -20,00 ( -30,00-40,00 Abbildung 2.3: Die Nettobarwertfunktion als Kapitalwertfunktion. Eine weitere Methode zur Einschätzung von Investitionen ist eng damit verwandt, sie heiÿt Methode des internen Zinssatz (internal rate of return = IRR). Bei dieser Methode wird einfach der Zinssatz r bestimmt, der für die Nettobarwertfunktion eine Nullstelle ist. Für einen vollständigen Zahlungsstrom (C i, t i ) ergibt sich somit der interne Zinssatz r als Lösung der Gleichung: n (1 + r) t i C i = 0. (2.9) i=0 Der Zahlungsstrom wird so eingerichtet, dass eingehende Zahlungen positiv und Ausgaben negativ sind. Werden diese Zahlungsströme wieder (A j, t j ) und (E k, t k ) genannt, folgt aus (2.9) J K (1 + r) t j A j = (1 + r) t k E k. (2.10) j=0 Die interne Zinssatz ist also genau der Zinssatz r, bei dem die Zahlungsströme der Ausgaben und Einnahmen äquivalent sind, also denselben Barwert haben. Es wird später gezeigt, dass die Gleichung (2.9) genau eine Lösung mit r > 1 hat, wenn die Zahlungen nur einmal das Vorzeichen wechseln, wenn also die ersten k Zahlungen positiv und die restlichen negativ sind oder umgekehrt. Diese Gleichung kann mit einem geeigneten Iterationsverfahren gelöst werden. Im Beispiel der Fabrikhalle ergibt sich der interne Zinssatz r als Lösung einer der beiden gleichwertigen Gleichungen k= (1 + r) 0, (1 + r) 2 = 0, (1 + r) 0,5 = (1 + r) 2. Das ergibt r = 8, 23 Prozent. Dies ist genau der Nulldurchgang des Graphen der Nettobarwertfunktion, wie Sie an Abbildung 2.3 erkennen können. 56
57 2.9 Nominale und eektive Zahlungsströme Die Anhänger der Methode des internen Zinssatzes haben eine einfache Entscheidungs- ndung: Berechne den internen Zinssatz und vergleiche ihn mit den Opportunitätskosten, in unserem Beispiel 7 Prozent. Die Investition ist genau dann lohnend, wenn der interne Zinssatz die gröÿere der beiden Zahlen ist. Die Nettobarwertmethode hat den Vorteil, dass man nicht nur weiÿ, ob die Investition lohnend ist, sondern auch die Höhe des Mehrgewinns kennt Rendite und Efektivverzinsung Der interne Zinssatz eines vollständigen Zahlungsstroms wird bei einer Investition Rendite r genannt, bei einem Kredit spricht man dagegen von der Eektivverzinsung r eff. Die Zeitspannen t i werden nach PAngV oder ACT/ACT (ICMA) berechnet. Bei einem Kredit muss in Deutschland der Vomhundertsatz des Eektivzinses auf zwei Dezimalstellen angegeben werden. Im Kapitel über Zinsrechnung war uns der Begri der Rendite schon begegnet. In der einfachen Zinsrechnung bestehen die Zahlungen aus dem zum Zeitpunkt 0 eingesetzten Kapital K 0 und dem nach einer der Zinsformeln am Endzeitpunkt berechneten Endwert K t. Wird als Zinsmethode PAngV verwendet, so ist der zugehörige Zahlungsstrom [( K 0, 0), (K t, tp )], wobei tp die Zeitdauer nach PAngV bezeichnet. Die Nettobarwertfunktion dieses Zahlungsstroms lautet NP V (r) = K 0 + K t (1 + r) tp. (2.11) Die Nullstelle r dieser Funktion ist die Rendite. Es ergibt sich in Übereinstimmung mit der Formel (1.23) auf Seite 23 r = ( Kt K 0 ) 1/tP 1, (2.12) 2.9 Nominale und eektive Zahlungsströme In der Finanzmathematik hat man es bei einer Aufgabenstellung oft mit zwei Zahlungsströmen zu tun, einem nominalen und einem eektiven. Bei Darlehen zahlen Banken nicht den Nennwert des Darlehens aus, sondern nur einen um das so genannte Disagio verringerten Betrag. Andere Bezeichnungen für das Disagio sind Damnum oder Abgeld. Das Disagio wirkt wie eine bereits vorweg gezahlte Zinsleistung und senkt damit den Nominalzinssatz, der sich auf den Nennwert des Darlehens bezieht. Das Disagio kann als Betrag oder als Prozentsatz angegeben sein. Das Disagio kann auch durch einen Auszahlungskurs bestimmt sein. Werden von einem Darlehen mit Nennwert Euro nur Euro ausgezahlt, ist der Auszahlungskurs 90 Prozent, der Disagiosatz 10 Prozent und das Disagio Dadurch unterscheiden sich der Nennwert des Darlehens und die tatsächliche Auszahlung, die Zinsberechnungen und Tilgungsraten richten sich aber immer am Nennwert der Schuld aus. Daher gibt es einen nominalen Zahlungsstrom und einen eektiven, der die tatsächlichen Zahlungen erfasst. Der interne Zinssatz wird 57
58 2 Barwert und Rendite von Zahlungsströmen immer aus dem eektiven Zahlungsstrom ermittelt, daher die Bezeichnung eektiver Zinssatz bei Darlehen. Ich stelle die wichtigsten Begrie zusammen: ˆ Der Auszahlungskurs gibt an, wie viel Prozent des Nennwerts des Darlehens tatsächlich ausgezahlt werden. ˆ Das Disagio oder Abgeld oder Damnum ist die Dierenz zwischen Nominalschuld und der tatsächlichen Auszahlung. ˆ Der Disagiosatz ist der Prozentsatz, der festlegt, welcher Teil des Nennwerts des Darlehens als Disagio einbehalten wird. ˆ Das Agio oder Aufgeld ist ein Betrag, der in der Regel bei Vertragsende zusätzlich zu leisten ist. Der nominale Zahlungsstrom wird in der Regel durch eine der vorgestellten Verzinsungsarten bestimmt, wobei alle Zinsberechnungen auf den Nennwert des Darlehens zu beziehen sind. Die Zahlen des folgenden Beispiels stammen von [4]. Beispiel 2.4. Ein Gläubiger gibt am einen Kredit von nominal DM zu 5 Prozent Nominalzins und einem Kurs von 90 Prozent aus. Die Tilgung soll am gesamtfällig erfolgen. Bis dahin muss der Schuldner einfache Zinsen bei halbjährlichen Zinsterminen am Jahresende und in der Jahresmitte zahlen. Bestimmen Sie den nominalen und den tatsächlichen Zahlungsstrom. Geben Sie dann die Nettobarwertfunktion aus Sicht des Gläubigers an. Dieser kalkuliert bei seinen sonstigen Kreditvergaben mit einem Zinssatz von 12 Prozent. Lohnt sich dieser Kredit für ihn? Wie hoch ist seine Rendite? Der Schuldner hat ein alternatives Angebot für den Kredit vorliegen, dessen eektiver Zinssatz 16 Prozent ist. Wie soll er sich entscheiden? Zunächst muss also der nominale Zahlungsstrom ermittelt werden. Die nominale Schuld ist DM und wird am ausgezahlt. Der Nominalzinssatz von 5 Prozent bezieht sich auf ein Jahr, halbjährlich sind 2,5 Prozent Zinsen zu zahlen. Am und am sind somit 25 DM bzw. 50 DM einfache Zinsen fällig und am kommt zu weiteren 50 DM einfache Zinsen die vollständige Tilgung der nominellen Schuld von DM. Der eektive Zahlungsstrom ist damit fast identisch, nur ieÿen wegen des Auszahlungskurses von 90 Prozent nur DM tatsächlich in die Taschen des Schuldners. Die tatsächlichen Leistungen von Gläubiger und Schuldner sowie die Zeitabstände sind in folgender Tabelle dargestellt, wobei in der letzten Zeile die beiden Zahlungsströme zu einem vollständigen Zahlungsstrom aus Sicht des Gläubigers stehen. In der letzten Zeile steht der nominale Zahlungsstrom. Da alle Zahlungen mit Datum angegeben sind, müssen die zeitlichen Abstände durch eine Zinsmethode ermittelt werden, in Deutschland ist dafür PAngV zu verwenden, international die Zinsmethode ACT/ACT (ICMA). 58
59 2.9 Nominale und eektive Zahlungsströme Datum PAngV 0 0, 25 0, 75 1, ACT/ACT (ICMA) Gläubiger Schuldner vollständig nominal Die Leistung des Gläubigers besteht hier aus einer einzigen Zahlung, die nominal den Wert und eektiv den Wert hat. Die Leistungen des Schuldners, also dessen Zins- und Tilgungsbeträge, sind nominal und eektiv gleich. Rechnet man die Zeitspannen nach der Zinsmethode PAngV, erhält man für die Nettobarwertfunktion aus der Sicht des Gläubigers die folgende Funktion: NP V (r) = (1 + r) 0, (1 + r) 0, (1 + r) 1,25. Der entsprechende Graph ist in der Abbildung 2.4 zu sehen. 400,00 300,00 N P V ( r ) 200,00 100,00 0,00-100,00-200,00 0 0,05 0,1 0,15 0,2 0,25 0,3 0,35 0,4-300,00-400,00 Zinssatz r Abbildung 2.4: Die Nettobarwertfunktion des Beispiels 2.4. Für r = 0, 12 ergibt sich ein Nettobarwert von 49, 45 DM. Im Vergleich zu einer Anlage zu 12 Prozent, ist dies der Mehrgewinn. Wäre umgekehrt der Schuldner nur bereit eektiv 12 Prozent Zinsen zu zahlen, müsste der Investor seinen Auszahlungsbetrag um 49, 45 DM erhöhen. Die Rendite r ist die Nullstelle der Nettobarwertfunktion, also gilt die folgende Gleichung: 0 = (1 + r) 0, (1 + r) 0, (1 + r) 1,25, 59
60 2 Barwert und Rendite von Zahlungsströmen deren Lösung bei r = 14, 51 Prozent liegt. Aus der Sicht des Schuldners ist dieser Wert die Eektivverzinsung r eff. Von diesem Wert an wird die Nettobarwertfunktion negativ. Im Vergleich zu einer Anlage zum Zinssatz von 16 Prozent ergibt sich ein Mindergewinn von 28, 31 DM. Für den Schuldner, dem nur ein Angebot von 16 Prozent vorliegt, ist das die Einsparung gegenüber diesem Angebot. Bei sonst gleichen Bedingungen würden bei einem Eektivzinssatz von 16 Prozent statt der DM sogar nur 1.771,69 DM ausgezahlt werden. International wird die Zinsmethode ACT/ACT (ICMA) verwendet. Dann lautet die Nettobarwertfunktion NP V (r) = (1 + r) (1 + r) (1 + r) Für r = 0, 12 ergibt sich ein Nettobarwert von 49, 05 Euro. Die Rendite r ist die Nullstelle der Nettobarwertfunktion, also gilt die folgende Gleichung: 0 = (1 + r) (1 + r) (1 + r) deren Lösung bei r = 14, 48 Prozent liegt. Aus der Sicht des Schuldners ist dieser Wert die Eektivverzinsung r eff. Der Grund für den horrenden Unterschied zwischen Nominalzinssatz und eektivem Zinssatz liegt in dem hohen Disagio. Aber auch die halbjährlichen Zinstermine verteuerten dieses Darlehen, wenn auch deutlich geringer. Normale Bankkunden können das Zusammenspiel von hohem Disagio und scheinbar niedrigen nominalen Zinsen nicht durchschauen, daher müssen Banken bei Krediten den Eektivzinssatz angeben, um dem Kunden Vergleiche von Angeboten zu ermöglichen Barwertberechnung mit Excel Die Berechnung von Barwerten kann mit Excel sehr einfach durchgeführt werden. Sie tragen zunächst in der ersten Spalte die Daten ein, im Beispiel von eben der , der , der und der Direkt daneben werden die Beträge des Zahlungsstroms eingesetzt. In der dritten Spalte werden dann die Zeitdierenzen zum Anfangszeitpunkt aufgelistet. Ich habe hier nach ACT/ACT (ICMA) gerechnet. In der nächsten Spalte stehen die mit (1 + r) t diskontierten Beträge, wobei der Zinssatz r hier in der Zelle B1 steht. Die korrekte Formel von Zelle D3 lautet somit =B3*(1+\$B\$1)\text{\^{}}(-C3) Diese Formel müssen Sie dann am Ausfüllkästchen nach unten ziehen. Die Summe der diskontierten Beträge ergibt den Nettobarwert zum Zinssatz r. Ich habe dafür die Excel- Funktion Summe verwendet. Zum Zinssatz von r = 0, 08 ergab dies einen Nettobarwert von 133,41 DM. Excel kann aber mehr. Im Menü Extras gibt es den Menüpunkt Zielwertsuche, der den abgebildeten kleinen Dialog önet. Sie müssen die Zielzelle angeben, das ist die 60
61 2.11 Eindeutigkeit der Rendite Abbildung 2.5: Zielwertsuche mit Excel Zelle D8 mit dem Nettobarwert und den Zielwert, also 0. Die veränderbare Zelle ist die Zelle B1 mit dem Zinssatz. Nach der Zielwertsuche steht in dieser Zelle dann die Rendite. Ab Excel 2007 erreichen Sie die Zielwertsuche durch Klicken der Registerkarte Daten, wo sich in der Gruppe Datentools die Was-wäre-wenn-Analyse mit der Zielwertsuche bendet Eindeutigkeit der Rendite Die Berechnung der Rendite entspricht mathematisch der Suche nach der Nullstelle der Nettobarwertfunktion NP V (r) = n (1 + r) t i C i mit t 0 < t 1 <... < t n. (2.13) i=0 Sollte t 0 > 0 sein, wird die Nettobarwertfunktion durch den Term (1 + r) t 0 geteilt. Die so veränderte Funktion hat dieselben Nullstellen wie die Nettobarwertfunktion, ich kann also t 0 = 0 voraussetzen. Man kann eigentlich nur dann von der Rendite sprechen, wenn die Nettobarwertfunktion nur eine Nullstelle hat, sonst muss man entscheiden, welche Nullstelle die richtige ist. Ich werde zeigen, dass ökonomisch besonders wichtige Nettobarwertfunktionen nur eine Nullstelle haben. Sehr oft besteht ein vollständiger Zahlungsstrom aus einer Folge von zunächst ausschlieÿlich negativen Zahlungen gefolgt von ausschlieÿlich positiven oder umgekehrt, abhängig davon, ob eine Investition oder ein Kredit vorliegt. In diesem Fall hat der Zahlungsstrom nur genau einen Vorzeichenwechsel bei den Zahlungen. Die Anzahl der Vorzeichenwechsel eines Zahlungsstroms beeinussen die Anzahl der möglichen Nullstellen. Es gibt eine von dem französischen Mathematiker und Philosophen Descartes 61
n... Laufzeit der Kapitalanlage = Zeit, während der Zinsen zu zahlen sind (oder gezahlt werden) in Zinsperioden (z.b. Jahre)
 3. Finanzmathematik 3.1. Zinsrechnung 3.1.1. Grundbegriffe K... Kapital (caput - das Haupt) = Betrag, der der Verzinsung unterworfen ist; Geldbetrag (Währung) z... Zinsen = Vergütung (Preis) für das Überlassen
3. Finanzmathematik 3.1. Zinsrechnung 3.1.1. Grundbegriffe K... Kapital (caput - das Haupt) = Betrag, der der Verzinsung unterworfen ist; Geldbetrag (Währung) z... Zinsen = Vergütung (Preis) für das Überlassen
Im weiteren werden die folgenden Bezeichnungen benutzt: Zinsrechnung
 4.2 Grundbegriffe der Finanzmathematik Im weiteren werden die folgenden Bezeichnungen benutzt: K 0 Anfangskapital p Zinsfuß pro Zeiteinheit (in %) d = p Zinssatz pro Zeiteinheit 100 q = 1+d Aufzinsungsfaktor
4.2 Grundbegriffe der Finanzmathematik Im weiteren werden die folgenden Bezeichnungen benutzt: K 0 Anfangskapital p Zinsfuß pro Zeiteinheit (in %) d = p Zinssatz pro Zeiteinheit 100 q = 1+d Aufzinsungsfaktor
Tutorium zur Mathematik (WS 2004/2005) - Finanzmathematik Seite 1
 Tutorium zur Mathematik WS 2004/2005) - Finanzmathematik Seite 1 Finanzmathematik 1.1 Prozentrechnung K Grundwert Basis, Bezugsgröße) p Prozentfuß i Prozentsatz i = p 100 ) Z Prozentwert Z = K i bzw. Z
Tutorium zur Mathematik WS 2004/2005) - Finanzmathematik Seite 1 Finanzmathematik 1.1 Prozentrechnung K Grundwert Basis, Bezugsgröße) p Prozentfuß i Prozentsatz i = p 100 ) Z Prozentwert Z = K i bzw. Z
ist die Vergütung für die leihweise Überlassung von Kapital ist die leihweise überlassenen Geldsumme
 Information In der Zinsrechnung sind 4 Größen wichtig: ZINSEN Z ist die Vergütung für die leihweise Überlassung von Kapital KAPITAL K ist die leihweise überlassenen Geldsumme ZINSSATZ p (Zinsfuß) gibt
Information In der Zinsrechnung sind 4 Größen wichtig: ZINSEN Z ist die Vergütung für die leihweise Überlassung von Kapital KAPITAL K ist die leihweise überlassenen Geldsumme ZINSSATZ p (Zinsfuß) gibt
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 204 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei der Rentenrechnung geht es um aus einem angesparten Kapital bzw. um um das Kapital aufzubauen, die innerhalb
SS 2014 Torsten Schreiber 204 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei der Rentenrechnung geht es um aus einem angesparten Kapital bzw. um um das Kapital aufzubauen, die innerhalb
HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN
 HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN Zinsen haben im täglichen Geschäftsleben große Bedeutung und somit auch die eigentliche Zinsrechnung, z.b: - Wenn Sie Ihre Rechnungen zu spät
HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN Zinsen haben im täglichen Geschäftsleben große Bedeutung und somit auch die eigentliche Zinsrechnung, z.b: - Wenn Sie Ihre Rechnungen zu spät
Wirtschaftsmathematik für International Management (BA)
 Wirtschaftsmathematik für International Management (BA) Wintersemester 2012/13 Hochschule Augsburg : Gliederung 1 Grundlegende 2 Grundlegende 3 Lineare Algebra 4 Lineare Programme 5 Folgen und Reihen 6
Wirtschaftsmathematik für International Management (BA) Wintersemester 2012/13 Hochschule Augsburg : Gliederung 1 Grundlegende 2 Grundlegende 3 Lineare Algebra 4 Lineare Programme 5 Folgen und Reihen 6
Rente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren Rentenperiode = Zeitabstand zwischen zwei Rentenzahlungen
 5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
Rente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren Rentenperiode = Zeitabstand zwischen zwei Rentenzahlungen
 1 3.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind
1 3.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind
Finanzmathematik. Wirtschaftswissenschaftliches Zentrum Universität Basel. Mathematik für Ökonomen 1 Dr. Thomas Zehrt
 Wirtschaftswissenschaftliches Zentrum Universität Basel Mathematik für Ökonomen 1 Dr. Thomas Zehrt Finanzmathematik Literatur Gauglhofer, M. und Müller, H.: Mathematik für Ökonomen, Band 1, 17. Auflage,
Wirtschaftswissenschaftliches Zentrum Universität Basel Mathematik für Ökonomen 1 Dr. Thomas Zehrt Finanzmathematik Literatur Gauglhofer, M. und Müller, H.: Mathematik für Ökonomen, Band 1, 17. Auflage,
.DXIPlQQLVFKHV5HFKQHQ =LQVUHFKQHQ. Für jeden Kaufmann unentbehrlich und vielseitig einsetzbar ist die Zinsrechnung. :DVVLQG=LQVHQ"
 =LQVUHFKQHQ Für jeden Kaufmann unentbehrlich und vielseitig einsetzbar ist die Zinsrechnung. :DVVLQG=LQVHQ" =LQV =LQVVDW]=LQVIX =HLW -DKU 0RQDW der Preis für die Nutzung eines Kapitals während einer bestimmten
=LQVUHFKQHQ Für jeden Kaufmann unentbehrlich und vielseitig einsetzbar ist die Zinsrechnung. :DVVLQG=LQVHQ" =LQV =LQVVDW]=LQVIX =HLW -DKU 0RQDW der Preis für die Nutzung eines Kapitals während einer bestimmten
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 221 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Wird im Bereich der Rentenrechnung die zugehörige zu Beginn eines Jahres / einer Zeitperiode eingezahlt, so spricht
SS 2014 Torsten Schreiber 221 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Wird im Bereich der Rentenrechnung die zugehörige zu Beginn eines Jahres / einer Zeitperiode eingezahlt, so spricht
Zinsen, Zinseszins, Rentenrechnung und Tilgung
 Zinsen, Zinseszins, Rentenrechnung und Tilgung 1. Zinsen, Zinseszins 2. Rentenrechnung 3. Tilgung Nevzat Ates, Birgit Jacobs Zinsrechnen mit dem Dreisatz 1 Zinsen Zinsrechnen mit den Formeln Zinseszins
Zinsen, Zinseszins, Rentenrechnung und Tilgung 1. Zinsen, Zinseszins 2. Rentenrechnung 3. Tilgung Nevzat Ates, Birgit Jacobs Zinsrechnen mit dem Dreisatz 1 Zinsen Zinsrechnen mit den Formeln Zinseszins
Prozentrechnung. Klaus : = Karin : =
 Prozentrechnung Klaus erzählt, dass bei der letzten Mathe-Arbeit 6 seiner Mitschüler die Note gut erhalten hätten. Seine Schwester Karin hat auch eine Arbeit zurück bekommen. In ihrer Klasse haben sogar
Prozentrechnung Klaus erzählt, dass bei der letzten Mathe-Arbeit 6 seiner Mitschüler die Note gut erhalten hätten. Seine Schwester Karin hat auch eine Arbeit zurück bekommen. In ihrer Klasse haben sogar
Numerische Mathematik I 4. Nichtlineare Gleichungen und Gleichungssysteme 4.1 Wo treten nichtlineare Gleichungen auf?
 Numerische Mathematik I 4. Nichtlineare Gleichungen und Gleichungssysteme 4.1 Wo treten nichtlineare Gleichungen auf? Andreas Rieder UNIVERSITÄT KARLSRUHE (TH) Institut für Wissenschaftliches Rechnen und
Numerische Mathematik I 4. Nichtlineare Gleichungen und Gleichungssysteme 4.1 Wo treten nichtlineare Gleichungen auf? Andreas Rieder UNIVERSITÄT KARLSRUHE (TH) Institut für Wissenschaftliches Rechnen und
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Grundbegriffe Gegenstand der Tilgungsrechnung ist ein von einem Gläubiger (z. B. Bank) an einen Schuldner ausgeliehener Geldbetrag S;
 1 5.3. Tilgungsrechnung Grundbegriffe Gegenstand der Tilgungsrechnung ist ein von einem Gläubiger (z. B. Bank) an einen Schuldner ausgeliehener Geldbetrag S; Bezeichnung: S... Schuld, Darlehen, Kredit
1 5.3. Tilgungsrechnung Grundbegriffe Gegenstand der Tilgungsrechnung ist ein von einem Gläubiger (z. B. Bank) an einen Schuldner ausgeliehener Geldbetrag S; Bezeichnung: S... Schuld, Darlehen, Kredit
Aufgabensammlung Grundlagen der Finanzmathematik
 Aufgabensammlung Grundlagen der Finanzmathematik Marco Papatrifon Zi.2321 Institut für Statistik und Mathematische Wirtschaftstheorie Universität Augsburg 1 Zinsrechnung Aufgabe 1 Fred überweist 6000 auf
Aufgabensammlung Grundlagen der Finanzmathematik Marco Papatrifon Zi.2321 Institut für Statistik und Mathematische Wirtschaftstheorie Universität Augsburg 1 Zinsrechnung Aufgabe 1 Fred überweist 6000 auf
Stellen Sie bitte den Cursor in die Spalte B2 und rufen die Funktion Sverweis auf. Es öffnet sich folgendes Dialogfenster
 Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Was meinen die Leute eigentlich mit: Grexit?
 Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
Wir basteln einen Jahreskalender mit MS Excel.
 Wir basteln einen Jahreskalender mit MS Excel. In meinen Seminaren werde ich hin und wieder nach einem Excel-Jahreskalender gefragt. Im Internet findet man natürlich eine ganze Reihe mehr oder weniger
Wir basteln einen Jahreskalender mit MS Excel. In meinen Seminaren werde ich hin und wieder nach einem Excel-Jahreskalender gefragt. Im Internet findet man natürlich eine ganze Reihe mehr oder weniger
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 239 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Durch die wird ein Zahlungsstrom beschrieben, der zur Rückführung eines geliehenen Geldbetrags dient. Der zu zahlende
SS 2014 Torsten Schreiber 239 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Durch die wird ein Zahlungsstrom beschrieben, der zur Rückführung eines geliehenen Geldbetrags dient. Der zu zahlende
3.3. Tilgungsrechnung
 3.3. Tilgungsrechnung Grundbegriffe Gegenstand der Tilgungsrechnung ist ein von einem Gläubiger (z. B. Bank) an einen Schuldner ausgeliehener Geldbetrag S; Bezeichnung: S... Schuld, Darlehen, Kredit Es
3.3. Tilgungsrechnung Grundbegriffe Gegenstand der Tilgungsrechnung ist ein von einem Gläubiger (z. B. Bank) an einen Schuldner ausgeliehener Geldbetrag S; Bezeichnung: S... Schuld, Darlehen, Kredit Es
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 193 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei einer Abschreibung werden eines Gutes während der Nutzungsdauer festgehalten. Diese Beträge stellen dar und dadurch
SS 2014 Torsten Schreiber 193 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei einer Abschreibung werden eines Gutes während der Nutzungsdauer festgehalten. Diese Beträge stellen dar und dadurch
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Prozentrechnung. Wir können nun eine Formel für die Berechnung des Prozentwertes aufstellen:
 Prozentrechnung Wir beginnen mit einem Beisiel: Nehmen wir mal an, ein Handy kostet 200 und es gibt 5% Rabatt (Preisnachlass), wie groß ist dann der Rabatt in Euro und wie viel kostet dann das Handy? Wenn
Prozentrechnung Wir beginnen mit einem Beisiel: Nehmen wir mal an, ein Handy kostet 200 und es gibt 5% Rabatt (Preisnachlass), wie groß ist dann der Rabatt in Euro und wie viel kostet dann das Handy? Wenn
Mathematik-Klausur vom 4.2.2004
 Mathematik-Klausur vom 4.2.2004 Aufgabe 1 Ein Klein-Sparer verfügt über 2 000, die er möglichst hoch verzinst anlegen möchte. a) Eine Anlage-Alternative besteht im Kauf von Bundesschatzbriefen vom Typ
Mathematik-Klausur vom 4.2.2004 Aufgabe 1 Ein Klein-Sparer verfügt über 2 000, die er möglichst hoch verzinst anlegen möchte. a) Eine Anlage-Alternative besteht im Kauf von Bundesschatzbriefen vom Typ
Übungsklausur. Bitte wählen Sie fünf Aufgaben aus! Aufgabe 1. Übungsklausur zu Mathematik I für BWL und VWL (WS 2008/09) PD Dr.
 Übungsklausur zu Mathematik I für BWL und VWL (WS 2008/09) PD Dr. Gert Zöller Übungsklausur Hilfsmittel: Taschenrechner, Formblatt mit Formeln. Lösungswege sind stets anzugeben. Die alleinige Angabe eines
Übungsklausur zu Mathematik I für BWL und VWL (WS 2008/09) PD Dr. Gert Zöller Übungsklausur Hilfsmittel: Taschenrechner, Formblatt mit Formeln. Lösungswege sind stets anzugeben. Die alleinige Angabe eines
Zinsrechnung 2 leicht 1
 Zinsrechnung 2 leicht 1 Berechne! a) b) c) Kapital 3 400 a) 16 000 b) 24 500 c) Zinsen 2,5% 85 400 612,50 Kapital 3 400 16 000 24 500 KESt (25% der Zinsen) 21,25 100 153,13 Zinsen effektive (2,5 Zinsen
Zinsrechnung 2 leicht 1 Berechne! a) b) c) Kapital 3 400 a) 16 000 b) 24 500 c) Zinsen 2,5% 85 400 612,50 Kapital 3 400 16 000 24 500 KESt (25% der Zinsen) 21,25 100 153,13 Zinsen effektive (2,5 Zinsen
Tilgungsrechnung. (K n + R n = ln. / ln(q) (nachschüssig) + R. / ln(q) (vorschüssig)
 (K n + R n = ln n = ln q 1 K 0 + R q 1 (K n q + R q 1 K 0 q + R q 1 ) / ln(q) (nachschüssig) ) / ln(q) (vorschüssig) Eine einfache Formel, um q aus R,n,K n und K 0 auszurechnen, gibt es nicht. Tilgungsrechnung
(K n + R n = ln n = ln q 1 K 0 + R q 1 (K n q + R q 1 K 0 q + R q 1 ) / ln(q) (nachschüssig) ) / ln(q) (vorschüssig) Eine einfache Formel, um q aus R,n,K n und K 0 auszurechnen, gibt es nicht. Tilgungsrechnung
Finanzwirtschaft. Teil II: Bewertung
 Sparpläne und Kreditverträge 1 Finanzwirtschaft Teil II: Bewertung Sparpläne und Kreditverträge Agenda Sparpläne und Kreditverträge 2 Endliche Laufzeit Unendliche Laufzeit Zusammenfassung Sparpläne und
Sparpläne und Kreditverträge 1 Finanzwirtschaft Teil II: Bewertung Sparpläne und Kreditverträge Agenda Sparpläne und Kreditverträge 2 Endliche Laufzeit Unendliche Laufzeit Zusammenfassung Sparpläne und
2. Ein Unternehmer muss einen Kredit zu 8,5 % aufnehmen. Nach einem Jahr zahlt er 1275 Zinsen. Wie hoch ist der Kredit?
 Besuchen Sie auch die Seite http://www.matheaufgaben-loesen.de/ dort gibt es viele Aufgaben zu weiteren Themen und unter Hinweise den Weg zu den Lösungen. Aufgaben zu Zinsrechnung 1. Wie viel Zinsen sind
Besuchen Sie auch die Seite http://www.matheaufgaben-loesen.de/ dort gibt es viele Aufgaben zu weiteren Themen und unter Hinweise den Weg zu den Lösungen. Aufgaben zu Zinsrechnung 1. Wie viel Zinsen sind
Download. Klassenarbeiten Mathematik 8. Zinsrechnung. Jens Conrad, Hardy Seifert. Downloadauszug aus dem Originaltitel:
 Download Jens Conrad, Hardy Seifert Klassenarbeiten Mathematik 8 Downloadauszug aus dem Originaltitel: Klassenarbeiten Mathematik 8 Dieser Download ist ein Auszug aus dem Originaltitel Klassenarbeiten
Download Jens Conrad, Hardy Seifert Klassenarbeiten Mathematik 8 Downloadauszug aus dem Originaltitel: Klassenarbeiten Mathematik 8 Dieser Download ist ein Auszug aus dem Originaltitel Klassenarbeiten
Klassische Finanzmathematik (Abschnitt KF.1 )
 Die Finanzatheatik ist eine Disziplin der angewandten Matheatik, die sich insbesondere it der Analyse und de Vergleich von Zahlungsströen und die theoretisch Erittlung des Geldwertes von Finanzprodukten.
Die Finanzatheatik ist eine Disziplin der angewandten Matheatik, die sich insbesondere it der Analyse und de Vergleich von Zahlungsströen und die theoretisch Erittlung des Geldwertes von Finanzprodukten.
A n a l y s i s Finanzmathematik
 A n a l y s i s Finanzmathematik Die Finanzmathematik ist eine Disziplin der angewandten Mathematik, die sich mit Themen aus dem Bereich von Finanzdienstleistern, wie etwa Banken oder Versicherungen, beschäftigt.
A n a l y s i s Finanzmathematik Die Finanzmathematik ist eine Disziplin der angewandten Mathematik, die sich mit Themen aus dem Bereich von Finanzdienstleistern, wie etwa Banken oder Versicherungen, beschäftigt.
XONTRO Newsletter. Makler. Nr. 16
 XONTRO Newsletter Makler Nr. 16 Seite 1 In XONTRO werden zum 24. Januar 2005 folgende Änderungen eingeführt: Inflationsindexierte Anleihen Stückzinsberechnung für französische und italienische Staatsanleihen
XONTRO Newsletter Makler Nr. 16 Seite 1 In XONTRO werden zum 24. Januar 2005 folgende Änderungen eingeführt: Inflationsindexierte Anleihen Stückzinsberechnung für französische und italienische Staatsanleihen
XONTRO Newsletter. Kreditinstitute. Nr. 18
 XONTRO Newsletter Kreditinstitute Nr. 18 Seite 1 In XONTRO werden zum 24. Januar 2005 folgende Änderungen eingeführt: Inflationsindexierte Anleihen Stückzinsberechnung für französische und italienische
XONTRO Newsletter Kreditinstitute Nr. 18 Seite 1 In XONTRO werden zum 24. Januar 2005 folgende Änderungen eingeführt: Inflationsindexierte Anleihen Stückzinsberechnung für französische und italienische
1. Wie viel EUR betragen die Kreditzinsen? Kredit (EUR) Zinsfuß Zeit a) 28500,00 7,5% 1 Jahr, 6 Monate. b) 12800,00 8,75 % 2 Jahre, 9 Monate
 1. Wie viel EUR betragen die Kreditzinsen? Kredit (EUR) Zinsfuß Zeit a) 28500,00 7,5% 1 Jahr, 6 Monate b) 12800,00 8,75 % 2 Jahre, 9 Monate c) 4560,00 9,25 % 5 Monate d) 53400,00 5,5 % 7 Monate e) 1 080,00
1. Wie viel EUR betragen die Kreditzinsen? Kredit (EUR) Zinsfuß Zeit a) 28500,00 7,5% 1 Jahr, 6 Monate b) 12800,00 8,75 % 2 Jahre, 9 Monate c) 4560,00 9,25 % 5 Monate d) 53400,00 5,5 % 7 Monate e) 1 080,00
Zinsrechner. Bedienungsanleitung
 Zinsrechner Bedienungsanleitung Medcontroller Dragonerstraße 35 30163 Hannover Telefon: 0511 397 0990 kundenservice@medcontroller.de www.medcontroller.de Inhaltsverzeichnis Hintergrund... 2 Nutzungsbedingungen
Zinsrechner Bedienungsanleitung Medcontroller Dragonerstraße 35 30163 Hannover Telefon: 0511 397 0990 kundenservice@medcontroller.de www.medcontroller.de Inhaltsverzeichnis Hintergrund... 2 Nutzungsbedingungen
Berechnung des Grundwertes 27. Zinsrechnung
 Berechnung des Grundwertes 27 Das Rechnen mit Zinsen hat im Wirtschaftsleben große Bedeutung. Banken vergüten Ihnen Zinsen, wenn Sie Geld anlegen oder berechnen Zinsen, wenn Sie einen Kredit beanspruchen.
Berechnung des Grundwertes 27 Das Rechnen mit Zinsen hat im Wirtschaftsleben große Bedeutung. Banken vergüten Ihnen Zinsen, wenn Sie Geld anlegen oder berechnen Zinsen, wenn Sie einen Kredit beanspruchen.
Anwendungen in der elementaren Zinsrechnung. Kapitalwert zum Zeitpunkt j (nach j Zinsperioden) Bsp. 1. 0 1 2 3 4 Zeitpunkte
 Anwendungen in der elementaren Zinsrechnung Zinssatz (Rendite) je Zinsperiode i = p% p= Prozentpunkte Zinsfaktor (Aufzinsungsfaktor) q =1+i Diskontfaktor (Abzinsungsfaktor) v =1/(1 + i) =q 1 Laufzeit n
Anwendungen in der elementaren Zinsrechnung Zinssatz (Rendite) je Zinsperiode i = p% p= Prozentpunkte Zinsfaktor (Aufzinsungsfaktor) q =1+i Diskontfaktor (Abzinsungsfaktor) v =1/(1 + i) =q 1 Laufzeit n
, und wie zuvor. 2. Einmalanlage mehrjährig mit festen Zinssatz (Kapitalentwicklung): mit Endkapital, Anfangskapital und 1 %
 Themenerläuterung Das Thema verlangt von dir die Berechnung von Zinsen bzw. Zinseszinsen, Anfangskapital, Endkapital und Sparraten. In seltenen Fällen wird auch einmal die Berechnung eines Kleinkredites
Themenerläuterung Das Thema verlangt von dir die Berechnung von Zinsen bzw. Zinseszinsen, Anfangskapital, Endkapital und Sparraten. In seltenen Fällen wird auch einmal die Berechnung eines Kleinkredites
Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer
 Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer Allgemein: Das RSA-Verschlüsselungsverfahren ist ein häufig benutztes Verschlüsselungsverfahren, weil es sehr sicher ist. Es gehört zu der Klasse der
Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer Allgemein: Das RSA-Verschlüsselungsverfahren ist ein häufig benutztes Verschlüsselungsverfahren, weil es sehr sicher ist. Es gehört zu der Klasse der
Universität Duisburg-Essen
 T U T O R I U M S A U F G A B E N z u r I N V E S T I T I O N u n d F I N A N Z I E R U N G Einführung in die Zinsrechnung Zinsen sind die Vergütung für die zeitweise Überlassung von Kapital; sie kommen
T U T O R I U M S A U F G A B E N z u r I N V E S T I T I O N u n d F I N A N Z I E R U N G Einführung in die Zinsrechnung Zinsen sind die Vergütung für die zeitweise Überlassung von Kapital; sie kommen
Kapitalerhöhung - Verbuchung
 Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
Wachstum 2. Michael Dröttboom 1 LernWerkstatt-Selm.de
 1. Herr Meier bekommt nach 3 Jahren Geldanlage 25.000. Er hatte 22.500 angelegt. Wie hoch war der Zinssatz? 2. Herr Meiers Vorfahren haben bei der Gründung Roms (753. V. Chr.) 1 Sesterze auf die Bank gebracht
1. Herr Meier bekommt nach 3 Jahren Geldanlage 25.000. Er hatte 22.500 angelegt. Wie hoch war der Zinssatz? 2. Herr Meiers Vorfahren haben bei der Gründung Roms (753. V. Chr.) 1 Sesterze auf die Bank gebracht
5. Finanzwirtschaft 5.1 Inhalt und Aufgaben
 5. Finanzwirtschaft 5.1 Inhalt und Aufgaben Die Funktionalbereiche der Unternehung und die Eingliederung der Finanzwirtschaft: Finanzwirtschaft Beschaffung Produktion Absatz Märkte für Produktionsfaktoren
5. Finanzwirtschaft 5.1 Inhalt und Aufgaben Die Funktionalbereiche der Unternehung und die Eingliederung der Finanzwirtschaft: Finanzwirtschaft Beschaffung Produktion Absatz Märkte für Produktionsfaktoren
Bedienungsanleitung Rückabwicklungsrechner
 1 Eingaben Zelle C2 Auszahlungsbetrag Hier muss der erste Auszahlungsbetrag eingegeben werden. Weitere Auszahlungen siehe Weiter unten. Zelle C3 Zeitpunkt der Auszahlung Datum der ersten Auszahlung Zelle
1 Eingaben Zelle C2 Auszahlungsbetrag Hier muss der erste Auszahlungsbetrag eingegeben werden. Weitere Auszahlungen siehe Weiter unten. Zelle C3 Zeitpunkt der Auszahlung Datum der ersten Auszahlung Zelle
Microsoft Excel 2010 Mehrfachoperation
 Hochschulrechenzentrum Justus-Liebig-Universität Gießen Microsoft Excel 2010 Mehrfachoperation Mehrfachoperationen in Excel 2010 Seite 1 von 6 Inhaltsverzeichnis Einleitung... 2 Mehrfachoperation mit
Hochschulrechenzentrum Justus-Liebig-Universität Gießen Microsoft Excel 2010 Mehrfachoperation Mehrfachoperationen in Excel 2010 Seite 1 von 6 Inhaltsverzeichnis Einleitung... 2 Mehrfachoperation mit
Korrigenda Handbuch der Bewertung
 Korrigenda Handbuch der Bewertung Kapitel 3 Abschnitt 3.5 Seite(n) 104-109 Titel Der Terminvertrag: Ein Beispiel für den Einsatz von Future Values Änderungen In den Beispielen 21 und 22 ist der Halbjahressatz
Korrigenda Handbuch der Bewertung Kapitel 3 Abschnitt 3.5 Seite(n) 104-109 Titel Der Terminvertrag: Ein Beispiel für den Einsatz von Future Values Änderungen In den Beispielen 21 und 22 ist der Halbjahressatz
Das große ElterngeldPlus 1x1. Alles über das ElterngeldPlus. Wer kann ElterngeldPlus beantragen? ElterngeldPlus verstehen ein paar einleitende Fakten
 Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
Gratis Excel SVERWEIS Funktions-Anleitung, Tutorial, ebook, PDF-E-Book
 Gratis Excel SVERWEIS Funktions-Anleitung, Tutorial, ebook, PDF-E-Book Wir wollen wissen wieviel Umsatz Vertreter Müller im Juni gemacht hat? Dazu klicken wir irgendwo in ein Feld und geben ein: =SVERWEIS
Gratis Excel SVERWEIS Funktions-Anleitung, Tutorial, ebook, PDF-E-Book Wir wollen wissen wieviel Umsatz Vertreter Müller im Juni gemacht hat? Dazu klicken wir irgendwo in ein Feld und geben ein: =SVERWEIS
1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage:
 Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Lebensversicherung. http://www.konsument.at/cs/satellite?pagename=konsument/magazinartikel/printma... OBJEKTIV UNBESTECHLICH KEINE WERBUNG
 Seite 1 von 6 OBJEKTIV UNBESTECHLICH KEINE WERBUNG Lebensversicherung Verschenken Sie kein Geld! veröffentlicht am 11.03.2011, aktualisiert am 14.03.2011 "Verschenken Sie kein Geld" ist der aktuelle Rat
Seite 1 von 6 OBJEKTIV UNBESTECHLICH KEINE WERBUNG Lebensversicherung Verschenken Sie kein Geld! veröffentlicht am 11.03.2011, aktualisiert am 14.03.2011 "Verschenken Sie kein Geld" ist der aktuelle Rat
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Gehen wir einmal davon aus, dass die von uns angenommenen
 geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
Übungsaufgaben Tilgungsrechnung
 1 Zusatzmaterialien zu Finanz- und Wirtschaftsmathematik im Unterricht, Band 1 Übungsaufgaben Tilgungsrechnung Überarbeitungsstand: 1.März 2016 Die grundlegenden Ideen der folgenden Aufgaben beruhen auf
1 Zusatzmaterialien zu Finanz- und Wirtschaftsmathematik im Unterricht, Band 1 Übungsaufgaben Tilgungsrechnung Überarbeitungsstand: 1.März 2016 Die grundlegenden Ideen der folgenden Aufgaben beruhen auf
Handbuch Fischertechnik-Einzelteiltabelle V3.7.3
 Handbuch Fischertechnik-Einzelteiltabelle V3.7.3 von Markus Mack Stand: Samstag, 17. April 2004 Inhaltsverzeichnis 1. Systemvorraussetzungen...3 2. Installation und Start...3 3. Anpassen der Tabelle...3
Handbuch Fischertechnik-Einzelteiltabelle V3.7.3 von Markus Mack Stand: Samstag, 17. April 2004 Inhaltsverzeichnis 1. Systemvorraussetzungen...3 2. Installation und Start...3 3. Anpassen der Tabelle...3
Verschenken Sie kein Geld!
 20 Verschenken Sie kein Geld! einschlägigen Börsenplätzen hat zudem die Kaufprovisionen der Fonds spürbar nach unten gedrückt. Trotzdem sind die Kosten nach wie vor ein wichtiges Bewertungskriterium dafür,
20 Verschenken Sie kein Geld! einschlägigen Börsenplätzen hat zudem die Kaufprovisionen der Fonds spürbar nach unten gedrückt. Trotzdem sind die Kosten nach wie vor ein wichtiges Bewertungskriterium dafür,
Persönliche Zukunftsplanung mit Menschen, denen nicht zugetraut wird, dass sie für sich selbst sprechen können Von Susanne Göbel und Josef Ströbl
 Persönliche Zukunftsplanung mit Menschen, denen nicht zugetraut Von Susanne Göbel und Josef Ströbl Die Ideen der Persönlichen Zukunftsplanung stammen aus Nordamerika. Dort werden Zukunftsplanungen schon
Persönliche Zukunftsplanung mit Menschen, denen nicht zugetraut Von Susanne Göbel und Josef Ströbl Die Ideen der Persönlichen Zukunftsplanung stammen aus Nordamerika. Dort werden Zukunftsplanungen schon
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Fritz verlangt einen Zins von 257.14% (Jahreszins. das ist übelster Wucher ) b) k = CHF 150.--, Zeit: 2 Monate, zm = CHF 10.
 Seite 8 1 Zinssatz Bruttozins am 31.12. Verrechnungssteuer Nettozins am 31.12. Kapital k Saldo am 31.12. a) 3.5% 2436 852.60 1583.4 69 600 71 183.40 b) 2.3% 4046 1416.10 2629.90 175 913.05 178'542.95 c)
Seite 8 1 Zinssatz Bruttozins am 31.12. Verrechnungssteuer Nettozins am 31.12. Kapital k Saldo am 31.12. a) 3.5% 2436 852.60 1583.4 69 600 71 183.40 b) 2.3% 4046 1416.10 2629.90 175 913.05 178'542.95 c)
Wertpapiere in den Augen der Vorarlberger. Eine Studie von IMAS International im Auftrag von Erste Bank & Sparkassen
 Wertpapiere in den Augen der Vorarlberger Eine Studie von IMAS International im Auftrag von Erste Bank & Sparkassen Studiendesign Auftraggeber: Erste Bank der oesterreichischen Sparkassen Durchführungszeitraum:
Wertpapiere in den Augen der Vorarlberger Eine Studie von IMAS International im Auftrag von Erste Bank & Sparkassen Studiendesign Auftraggeber: Erste Bank der oesterreichischen Sparkassen Durchführungszeitraum:
Inhalt 1. Was wird gefördert? Bausparverträge
 Inhalt 1. Was wird gefördert? 2. Wie viel Prozent bringt das? 3. In welchem Alter ist das sinnvoll? 4. Wie viel muss man sparen? 5. Bis zu welchem Einkommen gibt es Förderung? 6. Wie groß sollten die Verträge
Inhalt 1. Was wird gefördert? 2. Wie viel Prozent bringt das? 3. In welchem Alter ist das sinnvoll? 4. Wie viel muss man sparen? 5. Bis zu welchem Einkommen gibt es Förderung? 6. Wie groß sollten die Verträge
Was ist clevere Altersvorsorge?
 Was ist clevere Altersvorsorge? Um eine gute Altersvorsorge zu erreichen, ist es clever einen unabhängigen Berater auszuwählen Angestellte bzw. Berater von Banken, Versicherungen, Fondsgesellschaften und
Was ist clevere Altersvorsorge? Um eine gute Altersvorsorge zu erreichen, ist es clever einen unabhängigen Berater auszuwählen Angestellte bzw. Berater von Banken, Versicherungen, Fondsgesellschaften und
Sparen in Deutschland - mit Blick über die Ländergrenzen
 Sparen in Deutschland - mit Blick über die Ländergrenzen Die wichtigsten Ergebnisse Allianz Deutschland AG, Marktforschung, September 2010 1 1 Sparverhalten allgemein 2 Gründe für das Geldsparen 3 Geldanlageformen
Sparen in Deutschland - mit Blick über die Ländergrenzen Die wichtigsten Ergebnisse Allianz Deutschland AG, Marktforschung, September 2010 1 1 Sparverhalten allgemein 2 Gründe für das Geldsparen 3 Geldanlageformen
Tilgungsplan im NTCS Controlling
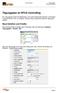 im Der bietet die Möglichkeit, neue oder bestehende Darlehen und Kredite in übersichtlicher Form zu erfassen. Ebenso können gewährte Darlehen dargestellt werden. Neue Darlehen und Kredite Der Einstieg
im Der bietet die Möglichkeit, neue oder bestehende Darlehen und Kredite in übersichtlicher Form zu erfassen. Ebenso können gewährte Darlehen dargestellt werden. Neue Darlehen und Kredite Der Einstieg
Prof. Dr. Arnd Wiedemann Methodische Grundlagen des Controlling und Risikomanagements
 Prof. Dr. Arnd Wiedemann Methodische Grundlagen des Controlling und Risikomanagements Prof. Dr. Arnd Wiedemann Methoden CRM / WS 12-13 1 Agenda Teil A: Teil B: Teil C: Finanzmathematisches Basiswissen
Prof. Dr. Arnd Wiedemann Methodische Grundlagen des Controlling und Risikomanagements Prof. Dr. Arnd Wiedemann Methoden CRM / WS 12-13 1 Agenda Teil A: Teil B: Teil C: Finanzmathematisches Basiswissen
Das Persönliche Budget in verständlicher Sprache
 Das Persönliche Budget in verständlicher Sprache Das Persönliche Budget mehr Selbstbestimmung, mehr Selbstständigkeit, mehr Selbstbewusstsein! Dieser Text soll den behinderten Menschen in Westfalen-Lippe,
Das Persönliche Budget in verständlicher Sprache Das Persönliche Budget mehr Selbstbestimmung, mehr Selbstständigkeit, mehr Selbstbewusstsein! Dieser Text soll den behinderten Menschen in Westfalen-Lippe,
Anleitung über den Umgang mit Schildern
 Anleitung über den Umgang mit Schildern -Vorwort -Wo bekommt man Schilder? -Wo und wie speichert man die Schilder? -Wie füge ich die Schilder in meinen Track ein? -Welche Bauteile kann man noch für Schilder
Anleitung über den Umgang mit Schildern -Vorwort -Wo bekommt man Schilder? -Wo und wie speichert man die Schilder? -Wie füge ich die Schilder in meinen Track ein? -Welche Bauteile kann man noch für Schilder
Die Zinsrechnung ist eine Anwendung der Prozentrechnung mit speziellen Begriffen. Frau Mayer erhält nach einem Jahr 8,40 Zinsen.
 Zinsen berechnen Die Zinsrechnung ist eine Anwendung der Prozentrechnung mit speziellen Begriffen. Grundwert G Kapital K Prozentwert P Zinsen Z Prozentsatz p Zinssatz p Frau Mayer hat ein Guthaben von
Zinsen berechnen Die Zinsrechnung ist eine Anwendung der Prozentrechnung mit speziellen Begriffen. Grundwert G Kapital K Prozentwert P Zinsen Z Prozentsatz p Zinssatz p Frau Mayer hat ein Guthaben von
Download. Führerscheine Zinsrechnung. Schnell-Tests zur Lernstandserfassung. Jens Conrad, Hardy Seifert. Downloadauszug aus dem Originaltitel:
 Download Jens Conrad, Hardy Seifert Führerscheine Zinsrechnung Schnell-Tests zur Lernstandserfassung Downloadauszug aus dem Originaltitel: Führerscheine Zinsrechnung Schnell-Tests zur Lernstandserfassung
Download Jens Conrad, Hardy Seifert Führerscheine Zinsrechnung Schnell-Tests zur Lernstandserfassung Downloadauszug aus dem Originaltitel: Führerscheine Zinsrechnung Schnell-Tests zur Lernstandserfassung
8. Berechnung der kalkulatorischen Zinsen
 8. Berechnung der kalkulatorischen Zinsen 8.1. Allgemeines In der laufenden Rechnung werden im Konto 322.00 Zinsen nur die ermittelten Fremdkapitalzinsen erfasst. Sobald aber eine Betriebsabrechnung erstellt
8. Berechnung der kalkulatorischen Zinsen 8.1. Allgemeines In der laufenden Rechnung werden im Konto 322.00 Zinsen nur die ermittelten Fremdkapitalzinsen erfasst. Sobald aber eine Betriebsabrechnung erstellt
Finanzmathematik. Dr. Bommhardt. Das Vervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.
 Finanzmathematik Dr. Bommhardt. Das Vervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.de Das Tilgungsrechnen Für Kredite gibt es drei unterschiedliche
Finanzmathematik Dr. Bommhardt. Das Vervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.de Das Tilgungsrechnen Für Kredite gibt es drei unterschiedliche
Finanzmathematik. Zinsrechnung I 1.)
 Finanzmathematik Zinsrechnung I 1.) Ein Vater leiht seinem Sohn am 1.1. eines Jahres 1.000.- DM. Es wird vereinbart, dass der Sohn bei einfacher Verzinsung von 8% das Kapital einschließlich der Zinsen
Finanzmathematik Zinsrechnung I 1.) Ein Vater leiht seinem Sohn am 1.1. eines Jahres 1.000.- DM. Es wird vereinbart, dass der Sohn bei einfacher Verzinsung von 8% das Kapital einschließlich der Zinsen
Senkung des technischen Zinssatzes und des Umwandlungssatzes
 Senkung des technischen Zinssatzes und des Umwandlungssatzes Was ist ein Umwandlungssatz? Die PKE führt für jede versicherte Person ein individuelles Konto. Diesem werden die Beiträge, allfällige Einlagen
Senkung des technischen Zinssatzes und des Umwandlungssatzes Was ist ein Umwandlungssatz? Die PKE führt für jede versicherte Person ein individuelles Konto. Diesem werden die Beiträge, allfällige Einlagen
Der Leverage-Effekt wirkt sich unter verschiedenen Umständen auf die Eigenkapitalrendite aus.
 Anhang Leverage-Effekt Leverage-Effekt Bezeichnungs- Herkunft Das englische Wort Leverage heisst Hebelwirkung oder Hebelkraft. Zweck Der Leverage-Effekt wirkt sich unter verschiedenen Umständen auf die
Anhang Leverage-Effekt Leverage-Effekt Bezeichnungs- Herkunft Das englische Wort Leverage heisst Hebelwirkung oder Hebelkraft. Zweck Der Leverage-Effekt wirkt sich unter verschiedenen Umständen auf die
Andreas Rühl. Investmentfonds. verstehen und richtig nutzen. Strategien für die optimale Vermögensstruktur. FinanzBuch Verlag
 Andreas Rühl Investmentfonds verstehen und richtig nutzen Strategien für die optimale Vermögensstruktur FinanzBuch Verlag 1. Kapitel Wollen Sie Millionär werden? Kennen Sie die Formel zur ersten Million?
Andreas Rühl Investmentfonds verstehen und richtig nutzen Strategien für die optimale Vermögensstruktur FinanzBuch Verlag 1. Kapitel Wollen Sie Millionär werden? Kennen Sie die Formel zur ersten Million?
Finanzwirtschaft. Teil II: Bewertung. Zinssätze und Renten
 Zinssätze und Renten 1 Finanzwirtschaft Teil II: Bewertung Zinssätze und Renten Agenda Zinssätze und Renten 2 Effektivzinsen Spot-Zinsen Forward-Zinsen Bewertung Kennziffern Zusammenfassung Zinssätze und
Zinssätze und Renten 1 Finanzwirtschaft Teil II: Bewertung Zinssätze und Renten Agenda Zinssätze und Renten 2 Effektivzinsen Spot-Zinsen Forward-Zinsen Bewertung Kennziffern Zusammenfassung Zinssätze und
Derivate und Bewertung
 . Dr. Daniel Sommer Marie-Curie-Str. 30 60439 Franfurt am Main Klausur Derivate und Bewertung.......... Wintersemester 2008/09 Klausur Derivate und Bewertung Wintersemester 2008/09 Aufgabe 1: Zinsurven,
. Dr. Daniel Sommer Marie-Curie-Str. 30 60439 Franfurt am Main Klausur Derivate und Bewertung.......... Wintersemester 2008/09 Klausur Derivate und Bewertung Wintersemester 2008/09 Aufgabe 1: Zinsurven,
Lösungshinweise zur Einsendearbeit 2 SS 2011
 Lösungshinweise zur Einsendearbeit 2 zum Kurs 41500, Finanzwirtschaft: Grundlagen, SS2011 1 Lösungshinweise zur Einsendearbeit 2 SS 2011 Finanzwirtschaft: Grundlagen, Kurs 41500 Aufgabe Finanzierungsbeziehungen
Lösungshinweise zur Einsendearbeit 2 zum Kurs 41500, Finanzwirtschaft: Grundlagen, SS2011 1 Lösungshinweise zur Einsendearbeit 2 SS 2011 Finanzwirtschaft: Grundlagen, Kurs 41500 Aufgabe Finanzierungsbeziehungen
Anhand des bereits hergeleiteten Models erstellen wir nun mit der Formel
 Ausarbeitung zum Proseminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn zum Thema Simulation des Anlagenpreismodels von Simon Uphus im WS 09/10 Zusammenfassung
Ausarbeitung zum Proseminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn zum Thema Simulation des Anlagenpreismodels von Simon Uphus im WS 09/10 Zusammenfassung
Leichte-Sprache-Bilder
 Leichte-Sprache-Bilder Reinhild Kassing Information - So geht es 1. Bilder gucken 2. anmelden für Probe-Bilder 3. Bilder bestellen 4. Rechnung bezahlen 5. Bilder runterladen 6. neue Bilder vorschlagen
Leichte-Sprache-Bilder Reinhild Kassing Information - So geht es 1. Bilder gucken 2. anmelden für Probe-Bilder 3. Bilder bestellen 4. Rechnung bezahlen 5. Bilder runterladen 6. neue Bilder vorschlagen
Bei der Ermittlung der Zinstage wird der erste Tag nicht, der letzte Tag aber voll mitgerechnet.
 Zinsrechnung Sofern nicht ausdrücklich erwähnt, werden die Zinsen nach der deutschen Zinsmethode berechnet. Bei der deutschen Zinsmethode wird das Zinsjahr mit 360 Tagen und der Monat mit 30 Tagen gerechnet:
Zinsrechnung Sofern nicht ausdrücklich erwähnt, werden die Zinsen nach der deutschen Zinsmethode berechnet. Bei der deutschen Zinsmethode wird das Zinsjahr mit 360 Tagen und der Monat mit 30 Tagen gerechnet:
Austausch- bzw. Übergangsprozesse und Gleichgewichtsverteilungen
 Austausch- bzw. Übergangsrozesse und Gleichgewichtsverteilungen Wir betrachten ein System mit verschiedenen Zuständen, zwischen denen ein Austausch stattfinden kann. Etwa soziale Schichten in einer Gesellschaft:
Austausch- bzw. Übergangsrozesse und Gleichgewichtsverteilungen Wir betrachten ein System mit verschiedenen Zuständen, zwischen denen ein Austausch stattfinden kann. Etwa soziale Schichten in einer Gesellschaft:
ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN
 ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN CHRISTIAN HARTFELDT. Zweiter Mittelwertsatz Der Mittelwertsatz Satz VI.3.4) lässt sich verallgemeinern zu Satz.. Seien f, g : [a, b] R auf [a,
ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN CHRISTIAN HARTFELDT. Zweiter Mittelwertsatz Der Mittelwertsatz Satz VI.3.4) lässt sich verallgemeinern zu Satz.. Seien f, g : [a, b] R auf [a,
Hochschule Rhein-Main. Sommersemester 2015
 Vorlesung Hochschule Rhein-Main Sommersemester 2015 Dr. Roland Stamm 29. Juni 2015 Erinnerung Bewertung eines Bonds mit Kupon k, Nominal N, Laufzeit t n: n Π(t) = N k δ(t i 1, t i ) P (t, t i ) + N P (t,
Vorlesung Hochschule Rhein-Main Sommersemester 2015 Dr. Roland Stamm 29. Juni 2015 Erinnerung Bewertung eines Bonds mit Kupon k, Nominal N, Laufzeit t n: n Π(t) = N k δ(t i 1, t i ) P (t, t i ) + N P (t,
Zinssätze. Georg Wehowar. 4. Dezember 2007
 4. Dezember 2007 Grundlagen der Zinsrechnung Verschiedene Anleihen Forward Rate Agreement Forward Zinsen Allgemeines Allgemeine Grundlagen K 0... Anfangskapital K t... Kapital nach einer Zeitspanne t Z
4. Dezember 2007 Grundlagen der Zinsrechnung Verschiedene Anleihen Forward Rate Agreement Forward Zinsen Allgemeines Allgemeine Grundlagen K 0... Anfangskapital K t... Kapital nach einer Zeitspanne t Z
Zinsrechnung Z leicht 1
 Zinsrechnung Z leicht 1 Berechne die Jahreszinsen im Kopf! a) Kapital: 500 Zinssatz: 1 % b) Kapital: 1 000 Zinssatz: 1,5 % c) Kapital: 20 000 Zinssatz: 4 % d) Kapital: 5 000 Zinssatz: 2 % e) Kapital: 10
Zinsrechnung Z leicht 1 Berechne die Jahreszinsen im Kopf! a) Kapital: 500 Zinssatz: 1 % b) Kapital: 1 000 Zinssatz: 1,5 % c) Kapital: 20 000 Zinssatz: 4 % d) Kapital: 5 000 Zinssatz: 2 % e) Kapital: 10
40-Tage-Wunder- Kurs. Umarme, was Du nicht ändern kannst.
 40-Tage-Wunder- Kurs Umarme, was Du nicht ändern kannst. Das sagt Wikipedia: Als Wunder (griechisch thauma) gilt umgangssprachlich ein Ereignis, dessen Zustandekommen man sich nicht erklären kann, so dass
40-Tage-Wunder- Kurs Umarme, was Du nicht ändern kannst. Das sagt Wikipedia: Als Wunder (griechisch thauma) gilt umgangssprachlich ein Ereignis, dessen Zustandekommen man sich nicht erklären kann, so dass
Was ist eine Aktie? Detlef Faber
 Was ist eine Aktie? Wenn eine Firma hohe Investitionskosten hat, kann sie eine Aktiengesellschaft gründen und bei privaten Geldgebern Geld einsammeln. Wer eine Aktie hat, besitzt dadurch ein Stück der
Was ist eine Aktie? Wenn eine Firma hohe Investitionskosten hat, kann sie eine Aktiengesellschaft gründen und bei privaten Geldgebern Geld einsammeln. Wer eine Aktie hat, besitzt dadurch ein Stück der
Mathematik 1 für Wirtschaftsinformatik
 Mathematik 1 für Wirtschaftsinformatik Wintersemester 2012/13 Hochschule Augsburg Äquivalenzprinzip der Finanzmathematik Das Äquivalenzprinzip der Finanzmathematik für Vergleich von Zahlungen, welche
Mathematik 1 für Wirtschaftsinformatik Wintersemester 2012/13 Hochschule Augsburg Äquivalenzprinzip der Finanzmathematik Das Äquivalenzprinzip der Finanzmathematik für Vergleich von Zahlungen, welche
b) Wie hoch ist der Betrag nach Abschluss eines Studiums von sechs Jahren?
 Fachhochschule Köln Fakultät für Wirtschaftswissenschaften Prof. Dr. Arrenberg Raum 221, Tel. 39 14 jutta.arrenberg@fh-koeln.de Übungen zur Mathematik für Prüfungskandidaten und Prüfungskandidatinnen Unterjährliche
Fachhochschule Köln Fakultät für Wirtschaftswissenschaften Prof. Dr. Arrenberg Raum 221, Tel. 39 14 jutta.arrenberg@fh-koeln.de Übungen zur Mathematik für Prüfungskandidaten und Prüfungskandidatinnen Unterjährliche
Anspar-Darlehensvertrag
 Anspar-Darlehensvertrag Zwischen Name: Straße: PLZ, Ort: Tel.: Mobil: E-Mail: Personalausweisnummer: - nachfolgend Gläubiger genannt und der Wilms, Ingo und Winkels, Friedrich, Florian GbR vertreten durch:
Anspar-Darlehensvertrag Zwischen Name: Straße: PLZ, Ort: Tel.: Mobil: E-Mail: Personalausweisnummer: - nachfolgend Gläubiger genannt und der Wilms, Ingo und Winkels, Friedrich, Florian GbR vertreten durch:
Übungen zur Vorlesung QM II Unterjährliche Renten Aufgabe 8.1 Ein Auto wird auf Leasingbasis zu folgenden Bedingungen erworben:
 Technische Hochschule Köln Fakultät für Wirtschafts- und Rechtswissenschaften Prof. Dr. Arrenberg Raum 22, Tel. 394 jutta.arrenberg@th-koeln.de Übungen zur Vorlesung QM II Unterjährliche Renten Aufgabe
Technische Hochschule Köln Fakultät für Wirtschafts- und Rechtswissenschaften Prof. Dr. Arrenberg Raum 22, Tel. 394 jutta.arrenberg@th-koeln.de Übungen zur Vorlesung QM II Unterjährliche Renten Aufgabe
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA)
 Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2014/15 Hochschule Augsburg Grundlagentest Ungleichungen! Testfrage: Ungleichungen 1 Die Lösungsmenge
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2014/15 Hochschule Augsburg Grundlagentest Ungleichungen! Testfrage: Ungleichungen 1 Die Lösungsmenge
Lineare Gleichungssysteme
 Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Gleichungen Lösen. Ein graphischer Blick auf Gleichungen
 Gleichungen Lösen Was bedeutet es, eine Gleichung zu lösen? Was ist überhaupt eine Gleichung? Eine Gleichung ist, grundsätzlich eine Aussage über zwei mathematische Terme, dass sie gleich sind. Ein Term
Gleichungen Lösen Was bedeutet es, eine Gleichung zu lösen? Was ist überhaupt eine Gleichung? Eine Gleichung ist, grundsätzlich eine Aussage über zwei mathematische Terme, dass sie gleich sind. Ein Term
einfache Rendite 0 145 85 1 160 90 2 135 100 3 165 105 4 190 95 5 210 110
 Übungsbeispiele 1/6 1) Vervollständigen Sie folgende Tabelle: Nr. Aktie A Aktie B Schlusskurs in Schlusskurs in 0 145 85 1 160 90 2 135 100 3 165 105 4 190 95 5 210 110 Arithmetisches Mittel Standardabweichung
Übungsbeispiele 1/6 1) Vervollständigen Sie folgende Tabelle: Nr. Aktie A Aktie B Schlusskurs in Schlusskurs in 0 145 85 1 160 90 2 135 100 3 165 105 4 190 95 5 210 110 Arithmetisches Mittel Standardabweichung
Carsten Roth. Schritt für Schritt zur persönlich abgestimmten Geldanlage. Eine Einführung. interna. Ihr persönlicher Experte
 Carsten Roth Schritt für Schritt zur persönlich abgestimmten Geldanlage Eine Einführung interna Ihr persönlicher Experte Inhalt Einführung.......................................... 7 1. Weshalb sollten
Carsten Roth Schritt für Schritt zur persönlich abgestimmten Geldanlage Eine Einführung interna Ihr persönlicher Experte Inhalt Einführung.......................................... 7 1. Weshalb sollten
