Raumtiefe in Malerei und Computergrafik
|
|
|
- Martha Ursler
- vor 8 Jahren
- Abrufe
Transkript
1 Raumtiefe in Malerei und Computergrafik Peter Deuflhard, Hans-Christian Hege 1. Juni 2012 Inhaltsverzeichnis Einführung 1 1 Raumdarstellung in der Malerei 1 2 Raumdarstellung in der Computergrafik 9 Literatur 19 1
2 Einführung Die Tiefenwirkung dreidimensionaler Räume in einem zweidimensionalen Bild einzufangen, ist ein Faszinosum nahezu aller Kulturen der Menschheitsgeschichte. Der vorliegende Aufsatz folgt den Spuren dieses Faszinosums, vergleichend in der Malerei und der mathematisierten Computergrafik. Die Entdeckung der Zentralperspektive in der italienischen Renaissance zeigt bereits den engen Zusammenhang von Malerei und Mathematik. Auf der Suche nach Maltechniken, mit denen Raumtiefe bildnerisch dargestellt werden kann, beginnen wir in Kap. 1 mit einem chronologischen Gang durch verschiedene Epochen der europäischen Malerei. Hieraus abgeleitete Prinzipien, soweit sie im Rechner realisierbar scheinen, stellen wir in Kap. 2 am Beispiel moderner Methoden der mathematischen Visualisierung vor. 1 Raumdarstellung in der Malerei Um verschiedene Methoden der Darstellung von Raumtiefe kennenzulernen, wandern wir zunächst durch eine kleine Galerie von wenigen, aber mit Bedacht ausgewählten Bildern, beginnend in einer Zeit vor der Entdeckung der Zentralperspektive bis hin zu einer Zeit, in der die Zentralperspektive ihre herrschende Rolle als Maltechnik verloren hatte. Stefan Lochner: Madonna im Rosenhag (Abb. 1). Obwohl vor der Einführung der Zentralperspektive in die europäische Kunst entstanden, zeigt dieses Tafelbild die Madonna ganz offensichtlich vor einem goldenen Hintergrund. Der räumliche Eindruck entsteht durch drei Elemente: (a) Das blaue Gewand tritt durch seine bloße Farbe vor dem goldenen Hintergrund und dem pflanzenfarbenen Boden optisch in den Vordergrund, unterstützt durch die Schatten des Faltenwurfs. (b) Der Rosenhag 1 ist mit schrägen Linien als Vorahnung der Zentralperspektive gezeichnet. Allerdings ist auf den ersten Blick nicht klar, ob diese Linien nach vorne offen oder nach hinten offen verlaufen, es scheint ein Vexierbild vorzuliegen. Man erkennt jedoch eindeutig, dass die Aureole der Madonna die horizontalen Stäbe des Rosenhags partiell verdeckt, dass also die Madonna vor dem bewachsenen Gitter sitzt. (c) Im Mittelgrund wird der Boden begrenzt durch zwei nach hinten über Eck verlaufende Hecken, partiell verdeckt, die wie ein Koordinatensystem Raum aufspannen. Rein konstruktiv gesehen, ist das Gitter in den Hecken verankert. So ergibt sich schließlich auf den zweiten Blick doch 1 Rosenhag ist eine rosenbewachsene Pergola 1
3 Abbildung 1: Stefan Lochner: Madonna im Rosenhag (etwa 1448), Wallraf- Richartz-Museum, Köln. Mischtechnik auf Holz. Maße: 51 x 40 cm. noch, dass sich das Gitter nach vorne öffnet. Der Vexiercharakter lässt sich somit auflösen. Eine echte Perspektive ist allerdings nicht gelungen: man muss zu lange hinschauen und nachdenken, um die räumliche Anordnung zweifelsfrei sehen zu können. Albrecht Dürer: Zentralperspektive (Abb. 2 und 3). Auf seiner Italienreise hatte Albrecht Dürer die Zentralperspektive studiert. Der Holzschnitt in Abb. 2 diente als Illustration zu Dürers Buch Underweysung der Messung mit dem Zirckel und Richtscheyt (veröffentlicht 1538, posthum). Obwohl doch eigentlich die didaktische Darstellung einer Zeichen- und Maltechnik, erschließt sich dem unbefangenen Betrachter unmittelbar der Widerspruch zwischen dem im wörtlichen Sinne verklemmt sitzenden Zeichner und dem atmenden Leben auf der anderen Seite des vertikal aufgestellten Netzrahmens, bei Alberti [4] in seinem 1435 erschienenen Werk De Pictura als velum bezeichnet. Sollte Dürer, der in seinem Kupferstich Melencolia I schöpferisch tief in die Depression eingetaucht ist, die Zentralperspektive 2
4 Abbildung 2: Albrecht Dürer: Der Zeichner des liegenden Weibes ( ). Holzschnitt, veröffentlicht 1538, posthum. Maße: 7.5 x 21.5 cm Abbildung 3: Albrecht Dürer: Der Zeichner der Laute (1525). Holzschnitt. Maße: 13.1 x 18.8 cm mit humorvollem Abstand betrachtet haben, im Sinne von hier die Technik, dort das sinnliche Leben? Im Aphilia-Forum [1] heißt es dazu: Die Illustration mit der Größe von nur 7,5 auf 21,5 cm vereint Sujets, die eigentlich nicht zueinander passen. Es geht gleichermaßen um Voyeurismus wie um eine Zeichentechnik: Und Dürers Coup gelingt prächtig. Das Motiv hätte als großes Ölgemälde vermutlich einen großen Skandal ausgelöst. Die posthume Veröffentlichung, erst für die zweite Auflage autorisiert durch Dürers Frau, erhält so eine besondere Bedeutung. Zu Lebzeiten, in der ersten Auflage, erschien ein funktionell vergleichbares Bild, siehe Abb. 3, diesmal ohne die Zweideutigkeit des Ausdrucks. Eine humorvolle Distanz zur vielleicht allzu technischen Maltechnik ist allerdings auch hier zu spüren. 3
5 Abbildung 4: Francisco de Goya: El Coloso ( ). Aquatinta. Maße: 28.7 x 20.8 cm. Francisco de Goya: El Coloso (Abb. 4). Dieses Bild eines Riesen ist erstaunlich klein. Es befindet sich heute im Prado in Madrid. Die räumliche Plastizität der Gestalt erwächst hier durch keinerlei spezielle Perspektive, sondern eindeutig aus dem Effekt von Licht und Schatten. Die vorgestellte Größe der Figur entsteht, bei tiefliegendem Augenpunkt, assoziativ durch die geniale Hinzukomposition der Mondsichel. Als Experiment versuche man nur, die Mondsichel abzudecken, sodann die Augen zu schließen und wieder zu öffnen: Jetzt lässt sich dem Riesen keine Größe mehr zuordnen, er kann sowohl groß als auch klein sein! Zum Vergleich: Es gibt ein Gemälde gleichen Namens, das jedoch vermutlich nicht von Goya selbst stammt. Es benutzt ebenfalls Licht und Schatten zur Raumdarstellung des Riesen, jedoch Menschen als Größenvergleich (einen Heereszug über ein Schlachtfeld), also eine eher traditionelle Technik zur Darstellung räumlicher Proportionen. Caspar David Friedrich: Felsenlandschaft (Abb. 5). In den meisten Quellen wird dieses Ölgemälde als Felsenlandschaft im Elbsandsteingebirge bezeichnet, in manchen auch als Felsenschlucht im Harz (Friedrich 4
6 Abbildung 5: Caspar David Friedrich: Felsenlandschaft im Elbsandsteingebirge (1822/1823). Öl auf Leinwand, Österreichische Galerie, Wien. Maße: 91 x 74 cm. selbst hat seine Bilder nur selten mit Titeln versehen). In der Tat existieren Felsen mit der markanten Wollsackverwitterung in beiden Mittelgebirgen. Die suggestive Tiefenwirkung gründet sich hier auf zwei Techniken: (a) schneidende Linien (z. B. umgestürzter Baum), die ein klares vorne und hinten definieren, (b) frische Farben im Vordergrund, blaugetönte Farben im Hintergrund, die frequenzabhängige Lichtstreuung im Dunst darstellend. Ernst Barlach: Stürzende Frau (Abb. 6). Die hier ausgewählte Lithographie zeigt klar, dass Ernst Barlach wohl eher ein Bildhauer war, weniger ein Zeichner. Sie ist das 27. Blatt aus der Begleitmappe zu seinem symbolisch-schwülstigen Drama Der tote Tag, das 1912 im Druck (bei Paul Cassirer, Berlin) erschienen ist, siehe Fromm/Thiem [10]. Die Frauengestalt ist durch gekrümmte Schraffurlinien plastisch modelliert, wodurch bereits eine räumliche Form entsteht. Die emotionale Wucht des Bildes ergibt sich aus zwei Kompositionselementen: (a) der Bewegung, die sich im 5
7 Abbildung 6: Ernst Barlach: Stürzende Frau (1910/11). Lithographie. Maße: 26.0 x 30.0 cm auf 51.5 x 67.5 cm. Stürzen der Gestalt und im Fallen des Messers ausdrückt, wodurch Raum durch Bewegung ausgeschöpft wird, (b) der Korrespondenz der beiden Schattenflächen, derjenigen auf der Unterseite der Frau und derjenigen am Boden, die den Raum dazwischen aufspannen. Das Licht kommt von hinten oben, wobei allerdings der Effekt verfremdet ist durch einen dunklen Hintergrundstreifen. Die Frau stürzt quasi in ihren Schatten, was die Assoziation zum Suizid auslöst. 2 August Macke: Blick in eine Gasse (Abb. 7). Auf der berühmten Tunisreise gemeinsam mit Paul Klee und Louis Moilliet hat August Macke eine Fülle von Aquarellen erstellt, vergleiche Moeller [19]. Das ausgewählte ist eines der ersten. Die atmosphärische Dichte, die geniale farbliche Komposition, mit der die Szene in flirrender Sonnenhitze eingefangen ist, steht hier nicht im Fokus. Stattdessen interessieren wir uns für die äußerst ungewöhnliche Raumdarstellung. Bei Moeller [19, S. 12] heisst es dazu: Ein starker Tiefenzug, eine ausgeprägte Perspektive ist gegeben, die allerdings durch die Rückenfigur im Vordergrund gebremst wird. Die Gebäude, die ku- 2 In der Tat begeht die Mutter im letzten Akt von Barlachs Drama Selbstmord. 6
8 Abbildung 7: August Macke: Blick in eine Gasse (1914). Aquarell. Maße: 29 x 22.5 cm bisch aufgefassten Blo cke wie die fu r die tunesische Architektur typischen Bogenelemente betonen den raumbildenden Charakter. Bei genauerer Betrachtung zeigt sich, dass der Eindruck von Raumtiefe durch drei Elemente erzeugt wird: (a) Schra g nach hinten verlaufende Kantenlinien kubischer Geba ude deuten eine ra umliche Perspektive an, die Linien haben jedoch keinen gemeinsamen Fluchtpunkt. Auch hier liegt, wie schon weiter oben in Abb. 1, wieder ein Vexierbildcharakter vor. Seine Auflo sung gelingt auch hier nur durch weitere Details: (b) Die Kantenlinien des zentral gesetzten Torbogens schneiden farblich nur wenig abgesetzte kubische Geba udefla chen, was aber dennoch mit (a) sowie den von links einfallenden schra gen Schattenlinien einen klaren Bezug von vorne und hinten herstellt. (c) Die große Ru ckenfigur im Vordergrund, mit gelbem Gewand und rotem Schal, stellt einen klaren Proportionsbezug zu den beiden kleinen Hintergrundfiguren mit rotem Gewand her, die dadurch als entfernt wirken (hier ist Moeller [19] eindeutig zu widersprechen). Die Proportionen stehen als Ersatz fu r die Zentralperspektive, auch hier vergleichbar den mittelalterlichen Maltechniken, womit sich ein Kreis schließt. 7
9 Zusammenfassung (Kap. 1) Aus der Betrachtung der ausgewählten Bilder können wir eine Reihe von Elementen herausfiltern, durch die Maler räumliche Tiefe darstellen: Schneiden von Linien, z.b. Aureole der Madonna vor Rosenhag (Stefan Lochner), umgestürzter Baum vor Felsenlandschaft (Caspar David Friedrich), Torbogen vor kubischen Häusern (August Macke); Licht und Schatten, z.b. Faltenwurf des Gewandes der Madonna (bei Stefan Lochner), Plastizität des Riesen (bei Francisco de Goya), zwei Schatten bei stürzender Frau (bei Ernst Barlach), manchmal auch durch Schraffur (ebenfalls bei Ernst Barlach); Zentralperspektive, z.b. in penibler Ausführung (bei Albrecht Dürer) oder auch in nur ungefährer Ausführung (bei Stefan Lochner und August Macke); Dunst und Farbverschiebung in der Distanz, z.b. Felsenlandschaft (bei Caspar David Friedrich); angedeutete Bewegung, z.b. die Venus von Sandro Botticelli, siehe etwa Deuflhard [9], oder die Stürzende Frau (bei Ernst Barlach). Im Zusammenhang mit dem zweiten oben genannten Punkt (Licht und Schatten) sei ausdrücklich darauf hingewiesen, dass sich die visuelle Wahrnehmung des Menschen nicht an Linien, sondern an Flächen und Schattenfeldern orientiert, siehe dazu etwa die Untersuchung von Mahr [15] zur Physik des Sehens. Diese neurologisch fixierte Mustererkennung hat sich wohl evolutionär entwickelt, damit wir Gesichter rasch erkennen; in der Tat scheinen wir Gesichtsbereiche wie tektonische Platten wahrzunehmen, siehe etwa McNeill [17, S. 122]. Von besonderer Bedeutung ist dabei, dass wir als natürlich gegeben annehmen, dass Licht von oben kommt; beleuchtet man ein bekanntes Gesicht von unten, wird es in vielen Fällen nicht mehr spontan erkannt (siehe ebenfalls McNeill [17]). 8
10 2 Raumdarstellung in der Computergrafik Mathematik als historisch gewachsene Wissenschaftsdisziplin ist erst im letzten Jahrhundert im Zuge ihrer Globalisierung kulturunabhängig geworden. Allerdings gilt dies auch heute nicht, sobald sie auf die Herstellung von Bildern angewendet wird, also in der Computergrafik: Auf dem Weg über das grafische Design und die Ästhetik entsteht zwangsläufig eine Kulturabhängigkeit. Es gibt jedoch weiterhin kulturunabhängige Elemente. So scheinen etwa globale Prinzipien der Raumwahrnehmung zu existieren, die evolutionsbedingt der Menschheit als Ganzes zu eigen sind. Die Gestalttheorie, siehe Metzger [18], stellt einen ersten Versuch dar, solche Prinzipien axiomatisch zu fassen. In Weiterentwicklung dieses Entwurfs hat sich in jüngster Zeit eine Mathematisierung der Gestalttheorie entwickelt, siehe Desolneux/Moisan/Morel [8]. Diese Theorien passen in ihrer Abstraktheit gut zur Abstraktheit der Mathematik. Zur Zeit stellen sie allerdings eher ein Programm für die Zukunft dar, vorzugsweise für die algorithmische Bildanalyse. Im nun folgenden Kapitel wählen wir eine etwas konkretere Sicht auf die Bildsynthese, wie sie sich in der gegenwärtigen Computergrafik etabliert hat. Abbildung 8: Raumszene in Euklidischer Geometrie und Bildentstehung in einer Kamera oder alternativ im Auge des Beobachters, durch Lichtstrahlen die von einer Lichtquelle ausgehen. 9
11 Vorab sei der zur Malerei sehr unterschiedliche Prozess der Bilderzeugung angesprochen: Mathematische Bilderzeugung ist immer Bildberechnung. In der heutigen Computergrafik hat sich deshalb im Wesentlichen das in Abb. 8 dargestellte Paradigma etabliert. Jede Raumszene ist charakterisiert durch geometrische Objekte, die im virtuellen Raum positioniert sind, Lichtquellen, die ebenfalls im virtuellen Raum positioniert werden müssen, die optischen Eigenschaften der Objekte und eine virtuelle Kamera, mit der die Szene abgebildet wird. Unter Geometrie ist meist die Euklidische Geometrie zu verstehen, da sie unserer alltäglichen Wahrnehmung entspricht. Es sind jedoch auch andere Geometrien denkbar, wie wir weiter unten unter dem Stichwort Nichteuklidische Geometrien ausführen. Jede denkbare Geometrie lässt sich in mathematische Formeln fassen und als solche algorithmisch im Zuge der Bilderzeugung realisieren. Die Wirkung der Lichtquellen auf die Objekte wird durch Beleuchtungsmodelle festgelegt, die mit der geometrischen Beschreibung der Objekte unmittelbar verknüpft sind. Positionierung von Lichtquellen, Definition der optischen Eigenschaften aller Objekte sowie die Positionierung und Einstellung der Kamera sind die ersten Festlegungen, die ein Computergrafiker vorab zu treffen hat. Euklidische Geometrie Darstellungsmethoden. Die Objekte werden alternativ durch Oberflächen- oder Volumenbeschreibungen im Rechner repräsentiert. Zur Bildberechnung wird die Szene auf die gerasterte Bildebene in der virtuellen Kamera projiziert. Dabei ist das Problem der Verdeckung zu lösen. Dies geschieht in moderner Grafikhardware mit dem Tiefenpuffer-Verfahren, das zeitgleich von dem Deutschen Wolfgang Straßer [23] und dem Amerikaner Edwin Catmull [7] erfunden wurde. Im Fall von Objekten, die durch ihre Oberflächen repräsentiert sind, sind eventuell auftretende schneidende Linien algorithmisch zu identifizieren. Bei halbtransparenten, volumenhaften Objekten, wie Wolken, Dunst oder Rauch, die typischerweise durch räumliche Dichtefunktionen repräsentiert werden, werden einzelne Volumenelemente 10
12 auf die Bildebene projiziert, die sich wechselseitig jedoch nicht vollständig überdecken (volume rendering). Geometrisch ist die 3D-Szene auf eine 2D-Abbildung zu reduzieren, die trotzdem für den Betrachter räumlich wirkt. Mathematisch gesprochen, wird dies durch Projektionsverfahren geleistet, die in der Bildwissenschaft meist mit dem Ausdruck Perspektiven bezeichnet werden. Die Zentralperspektive ist nur eine von vielen Möglichkeiten. Daneben gibt es noch Parallelprojektionen, deren Spezialfall isometrische Projektion in der Architektur und Bauplanung gerne verwendet wird, weil sie winkel- und längentreu ist. Leidlich bekannt ist auch die sphärische Projektion bzw. Fischaugenprojektion. Abbildung 9: Virtueller Patient in der Mund-Kiefer-Gesichts-Chirurgie [24]. Operationsplanung in der MKG-Chirurgie (Abb. 9). Dieses Bild stammt aus dem Kontext einer Operationsplanung in der Mund-Kiefer- Gesichts-Chirurgie, siehe Zachow/Hege/Deuflhard [24]. Algorithmisch wurde die Zentralperspektive festgelegt. Der Kopf ist aufgebaut aus Dreiecksgittern für Oberflächen und innere Grenzflächen zwischen unterschiedlichen Materialien sowie Tetraedergittern im Volumen. Der Raumeffekt ergibt sich hier im Wesentlichen aus zwei geometrischen Aspekten: (a) der krümmungsabhängigen Dichte der gezeigten Gitterpunkte (sog. adaptive Gitter), (b) schneidenden Linien am Rand der Öffnung ins Innere des Schädels. Bei ge- 11
13 nauerem Hinsehen beobachtet man eine Schattierung der Oberflächen, die von einer virtuellen Lichtquelle oberhalb des Kopfes erzeugt ist dies bringt uns direkt zum nächsten Abschnitt. Beleuchtung Globale Beleuchtungsmodelle. Kehren wir zurück zu Abb. 8 und verfolgen den Weg von Lichtstrahlen in der schematisch dargestellten Raumszene. Ausgehend von der Lichtquelle fallen Strahlen auf die geometrischen Objekte und werden von diesen absorbiert, reflektiert oder transmittiert (abhängig von der Oberflächenbeschaffenheit der Körper). Mehrfache Reflexionen sind möglich, bis das Licht schließlich die Szene verlässt oder in die Kamera fällt. Rendering-Gleichung. Zum tieferen Verständnis gestatten wir uns einen Exkurs für mathematisch/physikalisch interessierte Leser: Eine sorgfältige mathematische Modellierung dieser physikalischen Phänomene führt auf die folgende lineare Transportgleichung, siehe Krüger [13] und, in genauerer Ausarbeitung, Hege/Höllerer/Stalling[11], n I = (κ+σ)i+q+ 1 4π σ(x, n, ν ) p(x, n, n, ν, ν )I(x, n, ν )dω dν. Hierin bezeichnet x die Raumvariable, n die Richtung der Lichtstrahlen und ν deren Frequenz, I(x, n, ν) die Lichtintensität, κ(x, n, ν) den materialabhängigen Absorptionskoeffizienten, σ(x, n, ν) den Streukoeffizienten des durchstrahlten Materials sowie schließlich p(x, n, n, ν, ν ) die Phasenfunktion, die Frequenz- und Richtungsänderungen durch Streuung beschreibt. Mathematisch gesprochen handelt es sich hierbei um eine Integro-Differentialgleichung. Sie wird erst durch zusätzliche Randbedingungen formal lösbar, die wir hier jedoch nicht eigens entwickeln. Im Spezialfall frequenzunabhängiger Streuung (was etwa die Blaufärbung durch Dunst ausschließt) lassen sich die Randbedingungen zu einer einzigen Integralgleichung zusammenfassen: I(x, n) = E(x, n) + k(x, n, n )I in (x, n )dω, x S, worin k den Oberflächenstreuungskern, S die Oberfläche aller geometrischen Objekte und E die vorgegebene Intensität am Rand S bezeichnet. Dies ist die sogenannte rendering equation von Kajiya [12]. 12
14 Die volle numerische Simulation dieser Gleichungen fu hrt auf globale Beleuchtungsmodelle, die allerdings a ußerst rechenaufwendig sind. Es gilt also, einen fu r den jeweiligen Zweck vertretbaren Kompromiss zu finden zwischen algorithmischer Komplexita t und verfu gbarer Computerhardware auf der einen Seite sowie erwu nschter optischer Wirkung auf der anderen Seite. Daraus ergibt sich eine Hierarchie von sukzessive weniger rechenaufwendigen globalen Beleuchtungsmodellen. Die derzeit popula rste Mo glichkeit der na herungsweisen Lo sung der obigen Transportgleichung ist die sogenannte ray tracing - Methode (zu deutsch: Strahlverfolgungsmethode ). Bei dieser wird ein große Zahl von einzelnen Lichtstrahlen durch die Szene algorithmisch verfolgt, d.h. es werden alle ihre Auftreffpunkte auf Ko rpern und die unter Umsta nden mehrfache Reflexion an Ko rperoberfla chen unter Beru cksichtigung ihrer Verdeckung durch andere Ko rperoberfla chen berechnet. Anschließend werden deren ortsabha ngige Intensita ten in jedem Raumpunkt aufsummiert, gerade so, wie es in Abb. 8 skizziert ist. Derartige Methoden sind heute auf hochparallelen, extrem schnellen Grafikprozessoren implementiert und werden zum Beispiel in der Filmindustrie standardma ßig verwendet. Abbildung 10: Turbulente Stro mung. Links: Leonardo da Vinci ( ), siehe Zo llner [26, S. 523]. Rechts: Visualisierung durch beleuchtete Stromlinien (ZIB, Software Amira [22, 2]). Lokale Beleuchtungsmodelle. Weniger rechenaufwendig und fu r wissenschaftliche Visualisierungen in der Regel ausreichend sind sogenannte lokale Beleuchtungsmodelle, bei denen keine Mehrfachreflektionen beru cksichtigt werden. Eine dieser Methoden, die sich weltweiter Popularita t erfreut, sei im Folgenden na her dargestellt: die Methode der beleuchteten Linien. In 13
15 Abb. 10 sind zwei Darstellungen einer turbulenten Strömung nebeneinandergestellt, deren Entstehungszeit um fünf Jahrhunderte differiert. Wie in der linken Abbildung gezeigt, hatte Leonardo da Vinci die bahnbrechende Idee, eine von ihm beobachtete Strömung durch Strömungslinien zu charakterisieren; allerdings weist dieses Bild keine räumliche Tiefe auf. Im rechten Bild wurde der bei Zöckler/Stalling/Hege [25] beschriebene besonders effiziente Algorithmus FastLIC zur Darstellung von Strömungslinien angewendet; hier entsteht ganz offenbar ein räumlicher Eindruck durch die Lichteffekte auf den Linien. Die Technik, einzelne beleuchtete Linien zu malen und so einen Raumeindruck zu erzeugen, beherrschte Leonardo da Vinci durchaus und verwendete sie etwa, um gelocktes Haar darzustellen. Ein Beispiel hierfür ist das berühmte Gemälde Madonna in der Felsengrotte ( ), siehe die beiden Versionen bei Zöllner [26, S. 65/66] sowie die Ausschnittsvergrößerung auf S. 63 im gleichen Band. Nichteuklidische Geometrien Die Euklidische Geometrie ist, physikalisch gesprochen, die lokale Geometrie des Raumes, in dem wir leben. Was die genaue geometrische Struktur des Weltalls betrifft, ist das Tor für mathematische Spekulation noch offen. Zur Illustration geben wir zwei Beispiele. Abbildung 11: Pflasterung eines regulären Dodekaeders im hyperbolischen Raum. Bild erzeugt von Levy (National Center for Supercomputing Applications, Urbana-Champaign) und Munzner (damals Stanford University, jetzt UBC Vancouver) für den Artikel [6]. 14
16 Hyperbolische Geometrie. In Abb. 11 ist eine typische hyperbolische Geometrie gezeigt, siehe Levy/Munzner [3] und Bucher/Spergel [6]. Es handelt sich um eine Pflasterung eines regulären Dodekaeders. Im Euklidischen Raum wäre eine solche Pflasterung nicht möglich. Die Größe der Zellen harmoniert mit der Skala der Krümmung. Obwohl lokal Euklidische Geometrie vorliegt, fällt die Winkelgröße mit wachsender Distanz der Objekte exponentiell ab, wie die Abbildung zeigt. Lorentzgeometrie. In der Speziellen Relativitätstheorie gilt Invarianz unter Lorentztransformation, d.h. die Geometrie ist vierdimensional, zu den drei Raumdimensionen x, y, z kommt noch die zeitartige Dimension ict hinzu, wobei i die imaginäre Einheit mit i 2 = 1 bezeichnet, c die Lichtgeschwindigkeit und t die Zeit. Die veränderte Geometrie wird erst sichtbar, wenn sich Objekte mit einer Geschwindigkeit nahe der Lichtgeschwindigkeit bewegen. Die Physiker und Computergrafiker Ruder und Weiskopf [21] haben einen Film gedreht, der einen Flug durchs Brandenburger Tor von West nach Ost mit einer Geschwindigkeit 0.99 c beschreibt. In Abb.12 stellen wir vier Schnappschüsse aus diesem Film vor. Abbildung 12: Relativistischer Flug durch das Brandenburger Tor, nach Ruder/Weiskopf [21]. Links oben: Annäherung von Westen, Straße des 17. Juni. Rechts oben: Kurz vor Durchflug von Westen. Links unten: Im Tor während des Durchflugs. Rechts unten: Rückblick bei Entfernung nach Osten, Unter den Linden. 15
17 Zusammenfassung (Kap. 2) Wir kehren zurück zu den vier grundsätzlichen Methoden der Raumdarstellung, die wir in Kap. 1 genannt haben. Schneiden von Linien: dies führt auf das algorithmisch durchaus anspruchsvolle geometrische Verdeckungsproblem, das auf heutigen Rechnern einfach lösbar ist; Licht und Schatten: diese Thematik wird mit Beleuchtungsmodellen unterschiedlicher Komplexität behandelt, wobei das Hauptproblem in der realistischen Modellierung und Simulation optischer Eigenschaften von Oberflächen besteht; Perspektive: alle Arten von Perspektiven unter Einschluss der Zentralperspektive lassen sich quasi per Knopfdruck algorithmisch durch Projektionsmethoden realisieren; Dunst und Farbverschiebung in der Distanz 3 : Je nach angestrebter Realitätsnähe kann diese Methodik sehr rechenaufwendig werden, siehe etwa Krueger[14], Max [16], Preetham/Peter/Smits [20] oder Bruneton/Peyret [5]; angedeutete Bewegung: diese Methodik ist wie in der Malerei mit dem Motiv immanent verknüpft. Zusammenschau Malerei und Computergrafik haben sehr unterschiedliche technische Voraussetzungen. Der Zugang der Computergrafik ist dabei eher mathematisch als intuitiv. Wie in den obigen Zusammenfassungen zu Kap. 1 und Kap. 2 ausgeführt, ist die heutige Computergrafik durchaus in der Lage, Methoden der Raumdarstellung nachzuahmen, die in der Malerei entstanden sind. Darstellungen in nichteuklidischer Geometrie gehen sogar weit über das in der Malerei Denkbare hinaus. Es muss jedoch betont werden, dass unsere ganzheitliche Raumwahrnehmung vor der Bilderstellung sowohl von der Malerei als auch von der Computergrafik einen je eigenen schöpferischen Akt der Bildkomposition verlangt; die Auswahl von Farben, Kontrasten, Formen und Proportionen mit Blick auf die angestrebte Wirkung auf den Betrachter [15]. 3 Dieser Zusammenhang findet sich bereits bei Alberti 1435 [4], siehe Abb. 7 in Mahr 16
18 geschieht mit völlig unterschiedlichen Techniken. Verglichen mit den Jahrhunderten Entwicklung in der Malerei befindet sich die Computergrafik hierbei noch in ihren Anfängen. Und doch liefert sie uns schon vollständig im Computer berechnete Filme mit synthetischen Schauspielern auch wenn bisher noch menschliche Schauspieler den künstlichen ihre Mimik, Gestik und Statur verleihen. Literatur [1] [2] (Software). [3] [4] Alberti, Leon Baptista: De Pictura, [5] Bruneton, E. und F. Neyret: Precomputed atmospheric scattering. Computer Graphics Forum, 27(4): , [6] Bucher, M.A. und D.N. Spergel: Inflation in a low-density universe. Scientific American, 280:42 49, [7] Catmull, E.: A subdivision algorithm for computer display of curved surfaces. Doktorarbeit, Utah University, Salt Lake City, UT, [8] Desolneux, A., L. Moisan und J.-M. Morel: From Gestalt Theory to Image Analysis, Band 34 der Reihe Interdisciplinary Applied Mathematics. Springer, [9] Deuflhard, P.: Was ist ein schönes Gesicht? Auf der Suche nach Kriterien. Zeitschrift für Literaturwissenschaft und Linguistik (LiLi), 38:42 71, [10] Fromm, A. und H. Thiem (Herausgeber): Barlach auf der Bühne: Inszenierungen Ernst Barlach Haus, Hamburg, und Ernst Barlach Stiftung, Güstrow, [11] Hege, Hans-Christian, Tobias Höllerer und Detlev Stalling: Volume Rendering Mathematical Models and Algorithmic Aspects. ZIB Technical Report TR 93-7, Zuse Institute Berlin (ZIB), Berlin, Germany, June pp. 17
19 [12] Kajiya, J.T. und B.P. Von Herzen: Ray tracing volume densities. In: ACM SIGGRAPH Computer Graphics, Band 18:3, Seiten ACM, [13] Krueger, W.: The application of transport theory to visualization of 3-D scalar data fields. Computers in Physics, 5: , [14] Krueger, Wolfgang: Volume rendering and data feature enhancement. SIGGRAPH Computer Graphics, 24:21 26, [15] Mahr, B.: Zur Perspektivität des Objektbezugs. Alberti s Definition des Bildes und Frege s Objektivität des Sinns. In: Lepper, V., C. Markschies und P. Deuflhard (Herausgeber): Arbeitstitel: Perspektiven, Seite??? Akademie-Verlag, [16] Max, Nelson: Optical Models for Direct Volume Rendering. IEEE Transactions on Visualization and Computer Graphics, 1:99 108, June [17] McNeill, D.: Das Gesicht: Eine Kulturgeschichte. Magnus-Verlag, [18] Metzger, W.: Die Gesetze des Sehens. Die Lehre vom Sehen der Formen und Dinge des Raumes und der Bewegung. Verlag Dietmar Klotz, 3. Auflage, [19] Moeller, M. M.: August Macke. Die Tunisreise. Prestel, 3. Auflage, [20] Preetham, A. J., Peter Shirley und Brian Smits: A practical analytic model for daylight. In: Proceedings of the 26th annual conference on Computer graphics and interactive techniques, SIGGRAPH 99, Seiten , New York, NY, USA, ACM Press/Addison- Wesley Publishing Co. [21] Ruder, H. und D. Weiskopf: Simulation und Visualisierung in der Astrophysik oder die wundersame Reise des Christoph Zenger mit der U.S.S. Enterprise. In: Bungartz, H.J. und S. Zimmer (Herausgeber): Numerische Simulation als interdisziplinäre Herausforderung: Beiträge zum 60. Geburtstag von C. Zenger, Band 3 der Reihe Texte, die die Wissenschaft nicht braucht, Seiten Springer,
20 [22] Stalling, D., M. Westerhoff und H.-C. Hege: Amira: A highly interactive system for visual data analysis. In: Hansen, C.D. und C.R. Johnson (Herausgeber): The Visualization Handbook, Kapitel 38, Seiten Elsevier, [23] Straßer, W.: Schnelle Kurven-und Flächendarstellung auf grafischen Sichtgeräten. Doktorarbeit, Institut für Informationsverarbeitung, Technische Universität Berlin, [24] Zachow, S., H.-C. Hege und P. Deuflhard: Computer Assisted Planning in Cranio-Maxillofacial Surgery. J. Computing and Information Technology, 14:53 64, [25] Zöckler, M., D. Stalling und H.-C. Hege: Interactive visualization of 3D-vector fields using illuminated streamlines. In: IEEE Visualization 1996, Seiten , [26] Zöllner, F.: Leonardo da Vinci. Sämtliche Gemälde und Zeichnungen. Verlag Taschen, Köln,
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
3.2 Spiegelungen an zwei Spiegeln
 3 Die Theorie des Spiegelbuches 45 sehen, wenn die Person uns direkt gegenüber steht. Denn dann hat sie eine Drehung um die senkrechte Achse gemacht und dabei links und rechts vertauscht. 3.2 Spiegelungen
3 Die Theorie des Spiegelbuches 45 sehen, wenn die Person uns direkt gegenüber steht. Denn dann hat sie eine Drehung um die senkrechte Achse gemacht und dabei links und rechts vertauscht. 3.2 Spiegelungen
Die Übereckperspektive mit zwei Fluchtpunkten
 Perspektive Perspektive mit zwei Fluchtpunkten (S. 1 von 8) / www.kunstbrowser.de Die Übereckperspektive mit zwei Fluchtpunkten Bei dieser Perspektivart wird der rechtwinklige Körper so auf die Grundebene
Perspektive Perspektive mit zwei Fluchtpunkten (S. 1 von 8) / www.kunstbrowser.de Die Übereckperspektive mit zwei Fluchtpunkten Bei dieser Perspektivart wird der rechtwinklige Körper so auf die Grundebene
Praktikum Schau Geometrie
 Praktikum Schau Geometrie Intuition, Erklärung, Konstruktion Teil 1 Sehen auf intuitive Weise Teil 2 Formale Perspektive mit Aufriss und Grundriss Teil 3 Ein niederländischer Maler zeigt ein unmögliches
Praktikum Schau Geometrie Intuition, Erklärung, Konstruktion Teil 1 Sehen auf intuitive Weise Teil 2 Formale Perspektive mit Aufriss und Grundriss Teil 3 Ein niederländischer Maler zeigt ein unmögliches
Und was uns betrifft, da erfinden wir uns einfach gegenseitig.
 Freier Fall 1 Der einzige Mensch Der einzige Mensch bin ich Der einzige Mensch bin ich an deem ich versuchen kann zu beobachten wie es geht wenn man sich in ihn hineinversetzt. Ich bin der einzige Mensch
Freier Fall 1 Der einzige Mensch Der einzige Mensch bin ich Der einzige Mensch bin ich an deem ich versuchen kann zu beobachten wie es geht wenn man sich in ihn hineinversetzt. Ich bin der einzige Mensch
Lineare Funktionen. 1 Proportionale Funktionen 3 1.1 Definition... 3 1.2 Eigenschaften... 3. 2 Steigungsdreieck 3
 Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Optik: Teilgebiet der Physik, das sich mit der Untersuchung des Lichtes beschäftigt
 -II.1- Geometrische Optik Optik: Teilgebiet der, das sich mit der Untersuchung des Lichtes beschäftigt 1 Ausbreitung des Lichtes Das sich ausbreitende Licht stellt einen Transport von Energie dar. Man
-II.1- Geometrische Optik Optik: Teilgebiet der, das sich mit der Untersuchung des Lichtes beschäftigt 1 Ausbreitung des Lichtes Das sich ausbreitende Licht stellt einen Transport von Energie dar. Man
Lichtbrechung an Linsen
 Sammellinsen Lichtbrechung an Linsen Fällt ein paralleles Lichtbündel auf eine Sammellinse, so werden die Lichtstrahlen so gebrochen, dass sie durch einen Brennpunkt der Linse verlaufen. Der Abstand zwischen
Sammellinsen Lichtbrechung an Linsen Fällt ein paralleles Lichtbündel auf eine Sammellinse, so werden die Lichtstrahlen so gebrochen, dass sie durch einen Brennpunkt der Linse verlaufen. Der Abstand zwischen
Eigenen Farbverlauf erstellen
 Diese Serie ist an totale Neulinge gerichtet. Neu bei PhotoLine, evtl. sogar komplett neu, was Bildbearbeitung betrifft. So versuche ich, hier alles einfach zu halten. Ich habe sogar PhotoLine ein zweites
Diese Serie ist an totale Neulinge gerichtet. Neu bei PhotoLine, evtl. sogar komplett neu, was Bildbearbeitung betrifft. So versuche ich, hier alles einfach zu halten. Ich habe sogar PhotoLine ein zweites
4. Jeder Knoten hat höchstens zwei Kinder, ein linkes und ein rechtes.
 Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
Grundlagen der Theoretischen Informatik, SoSe 2008
 1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Lernwerkstatt für die Klassen 7 bis 9: Linsen und optische Geräte
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Lernwerkstatt für die Klassen 7 bis 9: Linsen und optische Geräte Das komplette Material finden Sie hier: Download bei School-Scout.de
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Lernwerkstatt für die Klassen 7 bis 9: Linsen und optische Geräte Das komplette Material finden Sie hier: Download bei School-Scout.de
Wie Sie mit Mastern arbeiten
 Wie Sie mit Mastern arbeiten Was ist ein Master? Einer der großen Vorteile von EDV besteht darin, dass Ihnen der Rechner Arbeit abnimmt. Diesen Vorteil sollten sie nutzen, wo immer es geht. In PowerPoint
Wie Sie mit Mastern arbeiten Was ist ein Master? Einer der großen Vorteile von EDV besteht darin, dass Ihnen der Rechner Arbeit abnimmt. Diesen Vorteil sollten sie nutzen, wo immer es geht. In PowerPoint
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Approximation durch Taylorpolynome
 TU Berlin Fakultät II - Mathematik und Naturwissenschaften Sekretariat MA 4-1 Straße des 17. Juni 10623 Berlin Hochschultag Approximation durch Taylorpolynome Im Rahmen der Schülerinnen- und Schüler-Uni
TU Berlin Fakultät II - Mathematik und Naturwissenschaften Sekretariat MA 4-1 Straße des 17. Juni 10623 Berlin Hochschultag Approximation durch Taylorpolynome Im Rahmen der Schülerinnen- und Schüler-Uni
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Ist Fernsehen schädlich für die eigene Meinung oder fördert es unabhängig zu denken?
 UErörterung zu dem Thema Ist Fernsehen schädlich für die eigene Meinung oder fördert es unabhängig zu denken? 2000 by christoph hoffmann Seite I Gliederung 1. In zu großen Mengen ist alles schädlich. 2.
UErörterung zu dem Thema Ist Fernsehen schädlich für die eigene Meinung oder fördert es unabhängig zu denken? 2000 by christoph hoffmann Seite I Gliederung 1. In zu großen Mengen ist alles schädlich. 2.
Paper Computer Science Experiment. Computation (NP-Vollständigkeit) Steinerbäume
 Paper Computer Science Experiment Great Principles of Computing Computation (NP-Vollständigkeit) Thema Steinerbäume Unterrichtsform Entdeckendes Lernen, Einzelarbeit, Lernen am Modell Voraussetzung Bäume
Paper Computer Science Experiment Great Principles of Computing Computation (NP-Vollständigkeit) Thema Steinerbäume Unterrichtsform Entdeckendes Lernen, Einzelarbeit, Lernen am Modell Voraussetzung Bäume
FELIX REIDENBACH illustration 2d3d4d. Making Of. Illustration für das LTU-Motiv Bodemuseum
 FELIX REIDENBACH illustration 2d3d4d Making Of Illustration für das LTU-Motiv Bodemuseum Für den Stil der Illustration ließen wir uns von Architektur- Entwürfen der 60er Jahre inspirieren. Diese Bilder
FELIX REIDENBACH illustration 2d3d4d Making Of Illustration für das LTU-Motiv Bodemuseum Für den Stil der Illustration ließen wir uns von Architektur- Entwürfen der 60er Jahre inspirieren. Diese Bilder
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Gehen wir einmal davon aus, dass die von uns angenommenen
 geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
Inhalt. Thema: Energie. Gedanke. Experiment/Spiel. Thema. Batterietests. Batterie. Batterien haben zwei Pole. Strom erzeugen
 Inhalt Experiment/Spiel Thema Gedanke Batterietests Batterie Batterien haben zwei Pole. Experiment Elektrizität herstellen Strom erzeugen Elektrizität kann durch Bewegung erzeugt werden. Experiment Stromkreis
Inhalt Experiment/Spiel Thema Gedanke Batterietests Batterie Batterien haben zwei Pole. Experiment Elektrizität herstellen Strom erzeugen Elektrizität kann durch Bewegung erzeugt werden. Experiment Stromkreis
1 topologisches Sortieren
 Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Info zum Zusammenhang von Auflösung und Genauigkeit
 Da es oft Nachfragen und Verständnisprobleme mit den oben genannten Begriffen gibt, möchten wir hier versuchen etwas Licht ins Dunkel zu bringen. Nehmen wir mal an, Sie haben ein Stück Wasserrohr mit der
Da es oft Nachfragen und Verständnisprobleme mit den oben genannten Begriffen gibt, möchten wir hier versuchen etwas Licht ins Dunkel zu bringen. Nehmen wir mal an, Sie haben ein Stück Wasserrohr mit der
1. Sichtbarkeitsproblem beim Rendern einer dreidimensionalen Szene auf einer zweidimensionalen
 3D-Rendering Ulf Döring, Markus Färber 07.03.2011 1. Sichtbarkeitsproblem beim Rendern einer dreidimensionalen Szene auf einer zweidimensionalen Anzeigefläche (a) Worin besteht das Sichtbarkeitsproblem?
3D-Rendering Ulf Döring, Markus Färber 07.03.2011 1. Sichtbarkeitsproblem beim Rendern einer dreidimensionalen Szene auf einer zweidimensionalen Anzeigefläche (a) Worin besteht das Sichtbarkeitsproblem?
Lineare Gleichungssysteme
 Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Optik. Optik. Optik. Optik. Optik
 Nenne das Brechungsgesetz! Beim Übergang von Luft in Glas (Wasser, Kunststoff) wird der Lichtstrahl zum Lot hin gebrochen. Beim Übergang von Glas (Wasser...) in Luft wird der Lichtstrahl vom Lot weg gebrochen.
Nenne das Brechungsgesetz! Beim Übergang von Luft in Glas (Wasser, Kunststoff) wird der Lichtstrahl zum Lot hin gebrochen. Beim Übergang von Glas (Wasser...) in Luft wird der Lichtstrahl vom Lot weg gebrochen.
Basis und Dimension. Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren.
 Basis und Dimension Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren. Definition. Sei V ein K-Vektorraum und (v i ) i I eine Familie von Vektoren
Basis und Dimension Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren. Definition. Sei V ein K-Vektorraum und (v i ) i I eine Familie von Vektoren
Speicher in der Cloud
 Speicher in der Cloud Kostenbremse, Sicherheitsrisiko oder Basis für die unternehmensweite Kollaboration? von Cornelius Höchel-Winter 2013 ComConsult Research GmbH, Aachen 3 SYNCHRONISATION TEUFELSZEUG
Speicher in der Cloud Kostenbremse, Sicherheitsrisiko oder Basis für die unternehmensweite Kollaboration? von Cornelius Höchel-Winter 2013 ComConsult Research GmbH, Aachen 3 SYNCHRONISATION TEUFELSZEUG
Advanced Rendering Interior Szene
 Advanced Rendering Interior Szene in Cinema 4D 11-11.5 Als erstes, sollten Sie ihre Szene in Cinema 4D öffnen. vergewissern sie sich, ob alle Licht quellen die evtl. mit importiert wurden, aus der Szene
Advanced Rendering Interior Szene in Cinema 4D 11-11.5 Als erstes, sollten Sie ihre Szene in Cinema 4D öffnen. vergewissern sie sich, ob alle Licht quellen die evtl. mit importiert wurden, aus der Szene
Akt die Treppe herabsteigend Nr.2
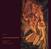 Dokumentation Akt die Treppe herabsteigend Nr.2 im Fach 3D Animation im WS 04/05 von Christian Kerl, Sonja Schoett Marcel Duchamp Die Vorlage zu unserem Film liefert das Bild Akt die Treppe herabsteigend
Dokumentation Akt die Treppe herabsteigend Nr.2 im Fach 3D Animation im WS 04/05 von Christian Kerl, Sonja Schoett Marcel Duchamp Die Vorlage zu unserem Film liefert das Bild Akt die Treppe herabsteigend
Im Original veränderbare Word-Dateien
 Computergrafik Bilder, Grafiken, Zeichnungen etc., die mithilfe von Computern hergestellt oder bearbeitet werden, bezeichnet man allgemein als Computergrafiken. Früher wurde streng zwischen Computergrafik
Computergrafik Bilder, Grafiken, Zeichnungen etc., die mithilfe von Computern hergestellt oder bearbeitet werden, bezeichnet man allgemein als Computergrafiken. Früher wurde streng zwischen Computergrafik
OECD Programme for International Student Assessment PISA 2000. Lösungen der Beispielaufgaben aus dem Mathematiktest. Deutschland
 OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
PTV VISWALK TIPPS UND TRICKS PTV VISWALK TIPPS UND TRICKS: VERWENDUNG DICHTEBASIERTER TEILROUTEN
 PTV VISWALK TIPPS UND TRICKS PTV VISWALK TIPPS UND TRICKS: VERWENDUNG DICHTEBASIERTER TEILROUTEN Karlsruhe, April 2015 Verwendung dichte-basierter Teilrouten Stellen Sie sich vor, in einem belebten Gebäude,
PTV VISWALK TIPPS UND TRICKS PTV VISWALK TIPPS UND TRICKS: VERWENDUNG DICHTEBASIERTER TEILROUTEN Karlsruhe, April 2015 Verwendung dichte-basierter Teilrouten Stellen Sie sich vor, in einem belebten Gebäude,
5.2 Neue Projekte erstellen
 5.2 Neue Projekte erstellen Das Bearbeiten von bestehenden Projekten und Objekten ist ja nicht schlecht wie aber können Sie neue Objekte hinzufügen oder gar völlig neue Projekte erstellen? Die Antwort
5.2 Neue Projekte erstellen Das Bearbeiten von bestehenden Projekten und Objekten ist ja nicht schlecht wie aber können Sie neue Objekte hinzufügen oder gar völlig neue Projekte erstellen? Die Antwort
Austausch- bzw. Übergangsprozesse und Gleichgewichtsverteilungen
 Austausch- bzw. Übergangsrozesse und Gleichgewichtsverteilungen Wir betrachten ein System mit verschiedenen Zuständen, zwischen denen ein Austausch stattfinden kann. Etwa soziale Schichten in einer Gesellschaft:
Austausch- bzw. Übergangsrozesse und Gleichgewichtsverteilungen Wir betrachten ein System mit verschiedenen Zuständen, zwischen denen ein Austausch stattfinden kann. Etwa soziale Schichten in einer Gesellschaft:
Raytracing. Schlussbericht. Jonas Lauener 1995, Áedán Christie 1997 Melvin Ott 1997, Timon Stampfli 1997
 Raytracing Schlussbericht Jonas Lauener 1995, Áedán Christie 1997 Melvin Ott 1997, Timon Stampfli 1997 bei Betreuer Marco Manzi, Institut für Informatik und angewandte Mathematik Inhalt Fragestellung...
Raytracing Schlussbericht Jonas Lauener 1995, Áedán Christie 1997 Melvin Ott 1997, Timon Stampfli 1997 bei Betreuer Marco Manzi, Institut für Informatik und angewandte Mathematik Inhalt Fragestellung...
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Farbtypen. Bedeutung von Farben 1. Drucken. Arbeiten mit Farben. Papierhandhabung. Wartung. Problemlösung. Verwaltung. Index
 Bedeutung von Farben 1 Ihr Drucker bietet Ihnen die Möglichkeit, Farben als Kommunikationsmittel einzusetzen. Farben wecken die Aufmerksamkeit, schaffen Respekt und verleihen Ihren Ausdrucken oder sonstigen
Bedeutung von Farben 1 Ihr Drucker bietet Ihnen die Möglichkeit, Farben als Kommunikationsmittel einzusetzen. Farben wecken die Aufmerksamkeit, schaffen Respekt und verleihen Ihren Ausdrucken oder sonstigen
Das große ElterngeldPlus 1x1. Alles über das ElterngeldPlus. Wer kann ElterngeldPlus beantragen? ElterngeldPlus verstehen ein paar einleitende Fakten
 Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
Basteln und Zeichnen
 Titel des Arbeitsblatts Seite Inhalt 1 Falte eine Hexentreppe 2 Falte eine Ziehharmonika 3 Die Schatzinsel 4 Das Quadrat und seine Winkel 5 Senkrechte und parallele Linien 6 Ein Scherenschnitt 7 Bastle
Titel des Arbeitsblatts Seite Inhalt 1 Falte eine Hexentreppe 2 Falte eine Ziehharmonika 3 Die Schatzinsel 4 Das Quadrat und seine Winkel 5 Senkrechte und parallele Linien 6 Ein Scherenschnitt 7 Bastle
Wie löst man Mathematikaufgaben?
 Wie löst man Mathematikaufgaben? Manfred Dobrowolski Universität Würzburg Wie löst man Mathematikaufgaben? 1 Das Schubfachprinzip 2 Das Invarianzprinzip 3 Das Extremalprinzip Das Schubfachprinzip Verteilt
Wie löst man Mathematikaufgaben? Manfred Dobrowolski Universität Würzburg Wie löst man Mathematikaufgaben? 1 Das Schubfachprinzip 2 Das Invarianzprinzip 3 Das Extremalprinzip Das Schubfachprinzip Verteilt
Und im Bereich Lernschwächen kommen sie, wenn sie merken, das Kind hat Probleme beim Rechnen oder Lesen und Schreiben.
 5.e. PDF zur Hördatei und Herr Kennedy zum Thema: Unsere Erfahrungen in der Kennedy-Schule Teil 2 Herr Kennedy, Sie haben eine Nachhilfeschule in der schwerpunktmäßig an Lernschwächen wie Lese-Rechtschreibschwäche,
5.e. PDF zur Hördatei und Herr Kennedy zum Thema: Unsere Erfahrungen in der Kennedy-Schule Teil 2 Herr Kennedy, Sie haben eine Nachhilfeschule in der schwerpunktmäßig an Lernschwächen wie Lese-Rechtschreibschwäche,
Partitionieren in Vista und Windows 7/8
 Partitionieren in Vista und Windows 7/8 Windows Vista und Windows 7 können von Haus aus Festplatten partitionieren. Doch die Funktion ist etwas schwer zu entdecken, denn sie heißt "Volume verkleinern".
Partitionieren in Vista und Windows 7/8 Windows Vista und Windows 7 können von Haus aus Festplatten partitionieren. Doch die Funktion ist etwas schwer zu entdecken, denn sie heißt "Volume verkleinern".
Erstellen von x-y-diagrammen in OpenOffice.calc
 Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
Der Leverage-Effekt wirkt sich unter verschiedenen Umständen auf die Eigenkapitalrendite aus.
 Anhang Leverage-Effekt Leverage-Effekt Bezeichnungs- Herkunft Das englische Wort Leverage heisst Hebelwirkung oder Hebelkraft. Zweck Der Leverage-Effekt wirkt sich unter verschiedenen Umständen auf die
Anhang Leverage-Effekt Leverage-Effekt Bezeichnungs- Herkunft Das englische Wort Leverage heisst Hebelwirkung oder Hebelkraft. Zweck Der Leverage-Effekt wirkt sich unter verschiedenen Umständen auf die
Die Online-Meetings bei den Anonymen Alkoholikern. zum Thema. Online - Meetings. Eine neue Form der Selbsthilfe?
 Die Online-Meetings bei den Anonymen Alkoholikern zum Thema Online - Meetings Eine neue Form der Selbsthilfe? Informationsverhalten von jungen Menschen (Quelle: FAZ.NET vom 2.7.2010). Erfahrungen können
Die Online-Meetings bei den Anonymen Alkoholikern zum Thema Online - Meetings Eine neue Form der Selbsthilfe? Informationsverhalten von jungen Menschen (Quelle: FAZ.NET vom 2.7.2010). Erfahrungen können
Die Übertragung der Tonalität auf den Bildstil
 Bildstil der Marke Niederösterreich Die Bildwelt einer Marke gliedert sich in zwei Komponenten die Bildsprache und den Bildstil. Dabei beschreibt die Bildsprache den Inhalt der Bilder, also das, was dargestellt
Bildstil der Marke Niederösterreich Die Bildwelt einer Marke gliedert sich in zwei Komponenten die Bildsprache und den Bildstil. Dabei beschreibt die Bildsprache den Inhalt der Bilder, also das, was dargestellt
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Wir gehen aus von euklidischen Anschauungsraum bzw. von der euklidischen Zeichenebene. Parallele Geraden schneiden einander nicht.
 2 Ein wenig projektive Geometrie 2.1 Fernpunkte 2.1.1 Projektive Einführung von Fernpunkten Wir gehen aus von euklidischen Anschauungsraum bzw. von der euklidischen Zeichenebene. Parallele Geraden schneiden
2 Ein wenig projektive Geometrie 2.1 Fernpunkte 2.1.1 Projektive Einführung von Fernpunkten Wir gehen aus von euklidischen Anschauungsraum bzw. von der euklidischen Zeichenebene. Parallele Geraden schneiden
ONLINE-AKADEMIE. "Diplomierter NLP Anwender für Schule und Unterricht" Ziele
 ONLINE-AKADEMIE Ziele Wenn man von Menschen hört, die etwas Großartiges in ihrem Leben geleistet haben, erfahren wir oft, dass diese ihr Ziel über Jahre verfolgt haben oder diesen Wunsch schon bereits
ONLINE-AKADEMIE Ziele Wenn man von Menschen hört, die etwas Großartiges in ihrem Leben geleistet haben, erfahren wir oft, dass diese ihr Ziel über Jahre verfolgt haben oder diesen Wunsch schon bereits
Fotos verkleinern mit Paint
 Fotos verkleinern mit Paint Warum Paint? Sicher, es gibt eine Menge kostenloser guter Programme und Möglichkeiten im Netz zum Verkleinern von Fotos. Letztendlich ist es Geschmackssache, aber meine Erfahrungen
Fotos verkleinern mit Paint Warum Paint? Sicher, es gibt eine Menge kostenloser guter Programme und Möglichkeiten im Netz zum Verkleinern von Fotos. Letztendlich ist es Geschmackssache, aber meine Erfahrungen
Charakteristikum des Gutachtenstils: Es wird mit einer Frage begonnen, sodann werden die Voraussetzungen Schritt für Schritt aufgezeigt und erörtert.
 Der Gutachtenstil: Charakteristikum des Gutachtenstils: Es wird mit einer Frage begonnen, sodann werden die Voraussetzungen Schritt für Schritt aufgezeigt und erörtert. Das Ergebnis steht am Schluß. Charakteristikum
Der Gutachtenstil: Charakteristikum des Gutachtenstils: Es wird mit einer Frage begonnen, sodann werden die Voraussetzungen Schritt für Schritt aufgezeigt und erörtert. Das Ergebnis steht am Schluß. Charakteristikum
7 Rechnen mit Polynomen
 7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
Virtuelle Fotografie (CGI)
 (CGI) Vorteile und Beispiele Das ist (k)ein Foto. Diese Abbildung ist nicht mit einer Kamera erstellt worden. Was Sie sehen basiert auf CAD-Daten unserer Kunden. Wir erzeugen damit Bilder ausschließlich
(CGI) Vorteile und Beispiele Das ist (k)ein Foto. Diese Abbildung ist nicht mit einer Kamera erstellt worden. Was Sie sehen basiert auf CAD-Daten unserer Kunden. Wir erzeugen damit Bilder ausschließlich
Comenius Schulprojekt The sun and the Danube. Versuch 1: Spannung U und Stom I in Abhängigkeit der Beleuchtungsstärke E U 0, I k = f ( E )
 Blatt 2 von 12 Versuch 1: Spannung U und Stom I in Abhängigkeit der Beleuchtungsstärke E U 0, I k = f ( E ) Solar-Zellen bestehen prinzipiell aus zwei Schichten mit unterschiedlichem elektrischen Verhalten.
Blatt 2 von 12 Versuch 1: Spannung U und Stom I in Abhängigkeit der Beleuchtungsstärke E U 0, I k = f ( E ) Solar-Zellen bestehen prinzipiell aus zwei Schichten mit unterschiedlichem elektrischen Verhalten.
4 Aufzählungen und Listen erstellen
 4 4 Aufzählungen und Listen erstellen Beim Strukturieren von Dokumenten und Inhalten stellen Listen und Aufzählungen wichtige Werkzeuge dar. Mit ihnen lässt sich so ziemlich alles sortieren, was auf einer
4 4 Aufzählungen und Listen erstellen Beim Strukturieren von Dokumenten und Inhalten stellen Listen und Aufzählungen wichtige Werkzeuge dar. Mit ihnen lässt sich so ziemlich alles sortieren, was auf einer
Falten regelmäßiger Vielecke
 Blatt 1 Gleichseitige Dreiecke Ausgehend von einem quadratischen Stück Papier kann man ohne weiteres Werkzeug viele interessante geometrische Figuren nur mit den Mitteln des Papierfaltens (Origami) erzeugen.
Blatt 1 Gleichseitige Dreiecke Ausgehend von einem quadratischen Stück Papier kann man ohne weiteres Werkzeug viele interessante geometrische Figuren nur mit den Mitteln des Papierfaltens (Origami) erzeugen.
sm@rt-tan plus Flickerfeld bewegt sich nicht
 Technischer Hintergrund Um die Verwendung des Verfahrens Sm@rt-TAN plus des neuen sicheren TAN- Verfahrens so komfortabel wie möglich zu gestalten, wurde eine Möglichkeit geschaffen, die Angaben einer
Technischer Hintergrund Um die Verwendung des Verfahrens Sm@rt-TAN plus des neuen sicheren TAN- Verfahrens so komfortabel wie möglich zu gestalten, wurde eine Möglichkeit geschaffen, die Angaben einer
impact ordering Info Produktkonfigurator
 impact ordering Info Copyright Copyright 2013 veenion GmbH Alle Rechte vorbehalten. Kein Teil der Dokumentation darf in irgendeiner Form ohne schriftliche Genehmigung der veenion GmbH reproduziert, verändert
impact ordering Info Copyright Copyright 2013 veenion GmbH Alle Rechte vorbehalten. Kein Teil der Dokumentation darf in irgendeiner Form ohne schriftliche Genehmigung der veenion GmbH reproduziert, verändert
1 C H R I S T O P H D R Ö S S E R D E R M A T H E M A T I K V E R F Ü H R E R
 C H R I S T O P H D R Ö S S E R D E R M A T H E M A T I K V E R F Ü H R E R L Ö S U N G E N Seite 7 n Wenn vier Menschen auf einem Quadratmeter stehen, dann hat jeder eine Fläche von 50 mal 50 Zentimeter
C H R I S T O P H D R Ö S S E R D E R M A T H E M A T I K V E R F Ü H R E R L Ö S U N G E N Seite 7 n Wenn vier Menschen auf einem Quadratmeter stehen, dann hat jeder eine Fläche von 50 mal 50 Zentimeter
Programm 4: Arbeiten mit thematischen Karten
 : Arbeiten mit thematischen Karten A) Anteil der ausländischen Wohnbevölkerung an der Wohnbevölkerung insgesamt 2001 in Prozent 1. Inhaltliche und kartographische Beschreibung - Originalkarte Bei dieser
: Arbeiten mit thematischen Karten A) Anteil der ausländischen Wohnbevölkerung an der Wohnbevölkerung insgesamt 2001 in Prozent 1. Inhaltliche und kartographische Beschreibung - Originalkarte Bei dieser
Einstein-Wellen-Mobil
 Arbeitsvorschlag für interaktive Station Relativistische Fahrradfahrt Bebachten Sie die Szenerie beim Anfahren und Beschleunigen. Bewegen Sie sich tatsächlich zunächst rückwärts? Wie können Sie das feststellen?
Arbeitsvorschlag für interaktive Station Relativistische Fahrradfahrt Bebachten Sie die Szenerie beim Anfahren und Beschleunigen. Bewegen Sie sich tatsächlich zunächst rückwärts? Wie können Sie das feststellen?
Additional Cycle Index (ACIX) Thomas Theuerzeit
 Additional Cycle Index (ACIX) Thomas Theuerzeit Der nachfolgende Artikel über den ACIX stammt vom Entwickler des Indikators Thomas Theuerzeit. Weitere Informationen über Projekte von Thomas Theuerzeit
Additional Cycle Index (ACIX) Thomas Theuerzeit Der nachfolgende Artikel über den ACIX stammt vom Entwickler des Indikators Thomas Theuerzeit. Weitere Informationen über Projekte von Thomas Theuerzeit
3D GLASBILD AUS IHREM LIEBLINGSFOTO. Fotogeschenke in Glas
 3D GLASBILD AUS IHREM LIEBLINGSFOTO. Fotogeschenke in Glas Wie kommt mein Bild ins Glas? Die Glasinnengravur mittels Laser ist technisch sehr anspruchsvoll, bietet aber gleichzeitig hohes kreatives Potential.
3D GLASBILD AUS IHREM LIEBLINGSFOTO. Fotogeschenke in Glas Wie kommt mein Bild ins Glas? Die Glasinnengravur mittels Laser ist technisch sehr anspruchsvoll, bietet aber gleichzeitig hohes kreatives Potential.
2.1 Präsentieren wozu eigentlich?
 2.1 Präsentieren wozu eigentlich? Gute Ideen verkaufen sich in den seltensten Fällen von allein. Es ist heute mehr denn je notwendig, sich und seine Leistungen, Produkte etc. gut zu präsentieren, d. h.
2.1 Präsentieren wozu eigentlich? Gute Ideen verkaufen sich in den seltensten Fällen von allein. Es ist heute mehr denn je notwendig, sich und seine Leistungen, Produkte etc. gut zu präsentieren, d. h.
Berechnung der Erhöhung der Durchschnittsprämien
 Wolfram Fischer Berechnung der Erhöhung der Durchschnittsprämien Oktober 2004 1 Zusammenfassung Zur Berechnung der Durchschnittsprämien wird das gesamte gemeldete Prämienvolumen Zusammenfassung durch die
Wolfram Fischer Berechnung der Erhöhung der Durchschnittsprämien Oktober 2004 1 Zusammenfassung Zur Berechnung der Durchschnittsprämien wird das gesamte gemeldete Prämienvolumen Zusammenfassung durch die
Pädagogik. Melanie Schewtschenko. Eingewöhnung und Übergang in die Kinderkrippe. Warum ist die Beteiligung der Eltern so wichtig?
 Pädagogik Melanie Schewtschenko Eingewöhnung und Übergang in die Kinderkrippe Warum ist die Beteiligung der Eltern so wichtig? Studienarbeit Inhaltsverzeichnis 1. Einleitung.2 2. Warum ist Eingewöhnung
Pädagogik Melanie Schewtschenko Eingewöhnung und Übergang in die Kinderkrippe Warum ist die Beteiligung der Eltern so wichtig? Studienarbeit Inhaltsverzeichnis 1. Einleitung.2 2. Warum ist Eingewöhnung
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
 50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
Lernerfolge sichern - Ein wichtiger Beitrag zu mehr Motivation
 Lernerfolge sichern - Ein wichtiger Beitrag zu mehr Motivation Einführung Mit welchen Erwartungen gehen Jugendliche eigentlich in ihre Ausbildung? Wir haben zu dieser Frage einmal die Meinungen von Auszubildenden
Lernerfolge sichern - Ein wichtiger Beitrag zu mehr Motivation Einführung Mit welchen Erwartungen gehen Jugendliche eigentlich in ihre Ausbildung? Wir haben zu dieser Frage einmal die Meinungen von Auszubildenden
Bilder Schärfen und Rauschen entfernen
 Bilder Schärfen und Rauschen entfernen Um alte Bilder, so wie die von der Olympus Camedia 840 L noch dazu zu bewegen, Farben froh und frisch daherzukommen, bedarf es einiger Arbeit und die habe ich hier
Bilder Schärfen und Rauschen entfernen Um alte Bilder, so wie die von der Olympus Camedia 840 L noch dazu zu bewegen, Farben froh und frisch daherzukommen, bedarf es einiger Arbeit und die habe ich hier
M03a Lernstraße für den Unterricht in Sekundarstufe I
 M03a Lernstraße für den Unterricht in Sekundarstufe I 1. Station: Der Taufspruch Jedem Täufling wird bei der Taufe ein Taufspruch mit auf den Weg gegeben. Dabei handelt es sich um einen Vers aus der Bibel.
M03a Lernstraße für den Unterricht in Sekundarstufe I 1. Station: Der Taufspruch Jedem Täufling wird bei der Taufe ein Taufspruch mit auf den Weg gegeben. Dabei handelt es sich um einen Vers aus der Bibel.
Tipps und Tricks für CATIA V5
 DMU-NAVIGATOR Laden großer Baugruppen im DMU-Navigator In einigen Branchen wie dem Flugzeugbau wird der DMU-Navigator als Viewer eingesetzt. Leider kann es auch hier dauern, bis die komplette Geometrie
DMU-NAVIGATOR Laden großer Baugruppen im DMU-Navigator In einigen Branchen wie dem Flugzeugbau wird der DMU-Navigator als Viewer eingesetzt. Leider kann es auch hier dauern, bis die komplette Geometrie
Einführung. Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit (3) Vorlesungen zur Komplexitätstheorie. K-Vollständigkeit (1/5)
 Einführung 3 Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit (3) Univ.-Prof. Dr. Christoph Meinel Hasso-Plattner-Institut Universität Potsdam, Deutschland Hatten den Reduktionsbegriff
Einführung 3 Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit (3) Univ.-Prof. Dr. Christoph Meinel Hasso-Plattner-Institut Universität Potsdam, Deutschland Hatten den Reduktionsbegriff
Histogramm Mit dem Histogramm zu besseren Bildern?!
 Seite 1 Mit dem zu besseren Bildern?! Eine Einführung in die funktion von Digitalkameras - 13. Eppsteiner Fototage - Seite 2 - Begriffserklärung - Ein (Säulendiagramm) ist die grafische Darstellung der
Seite 1 Mit dem zu besseren Bildern?! Eine Einführung in die funktion von Digitalkameras - 13. Eppsteiner Fototage - Seite 2 - Begriffserklärung - Ein (Säulendiagramm) ist die grafische Darstellung der
Erste-Schritte VP 5.1
 In diesem Dokument werden wichtige Einstellungen beschrieben, die vorgenommen werden müssen, wenn mit einer leeren Planung begonnen wird. Inhaltsverzeichnis Erstellung einer leeren Planung...1 Wichtige
In diesem Dokument werden wichtige Einstellungen beschrieben, die vorgenommen werden müssen, wenn mit einer leeren Planung begonnen wird. Inhaltsverzeichnis Erstellung einer leeren Planung...1 Wichtige
Access [basics] Rechnen in Berichten. Beispieldatenbank. Datensatzweise berechnen. Berechnung im Textfeld. Reporting in Berichten Rechnen in Berichten
![Access [basics] Rechnen in Berichten. Beispieldatenbank. Datensatzweise berechnen. Berechnung im Textfeld. Reporting in Berichten Rechnen in Berichten Access [basics] Rechnen in Berichten. Beispieldatenbank. Datensatzweise berechnen. Berechnung im Textfeld. Reporting in Berichten Rechnen in Berichten](/thumbs/30/14319702.jpg) Berichte bieten die gleichen Möglichkeit zur Berechnung von Werten wie Formulare und noch einige mehr. Im Gegensatz zu Formularen bieten Berichte die Möglichkeit, eine laufende Summe zu bilden oder Berechnungen
Berichte bieten die gleichen Möglichkeit zur Berechnung von Werten wie Formulare und noch einige mehr. Im Gegensatz zu Formularen bieten Berichte die Möglichkeit, eine laufende Summe zu bilden oder Berechnungen
Kulturelle Evolution 12
 3.3 Kulturelle Evolution Kulturelle Evolution Kulturelle Evolution 12 Seit die Menschen Erfindungen machen wie z.b. das Rad oder den Pflug, haben sie sich im Körperbau kaum mehr verändert. Dafür war einfach
3.3 Kulturelle Evolution Kulturelle Evolution Kulturelle Evolution 12 Seit die Menschen Erfindungen machen wie z.b. das Rad oder den Pflug, haben sie sich im Körperbau kaum mehr verändert. Dafür war einfach
Gitterherstellung und Polarisation
 Versuch 1: Gitterherstellung und Polarisation Bei diesem Versuch wollen wir untersuchen wie man durch Überlagerung von zwei ebenen Wellen Gttterstrukturen erzeugen kann. Im zweiten Teil wird die Sichtbarkeit
Versuch 1: Gitterherstellung und Polarisation Bei diesem Versuch wollen wir untersuchen wie man durch Überlagerung von zwei ebenen Wellen Gttterstrukturen erzeugen kann. Im zweiten Teil wird die Sichtbarkeit
Ein Spiel für 2-3 goldhungrige Spieler ab 8 Jahren.
 Ein Spiel für 2-3 goldhungrige Spieler ab 8 Jahren. Gold! Gold! Nichts als Gold, soweit das Auge reicht. So ein Goldesel ist schon was Praktisches. Doch Vorsicht: Die störrischen Viecher können einem auch
Ein Spiel für 2-3 goldhungrige Spieler ab 8 Jahren. Gold! Gold! Nichts als Gold, soweit das Auge reicht. So ein Goldesel ist schon was Praktisches. Doch Vorsicht: Die störrischen Viecher können einem auch
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
EM-Wellen. david vajda 3. Februar 2016. Zu den Physikalischen Größen innerhalb der Elektrodynamik gehören:
 david vajda 3. Februar 2016 Zu den Physikalischen Größen innerhalb der Elektrodynamik gehören: Elektrische Stromstärke I Elektrische Spannung U Elektrischer Widerstand R Ladung Q Probeladung q Zeit t Arbeit
david vajda 3. Februar 2016 Zu den Physikalischen Größen innerhalb der Elektrodynamik gehören: Elektrische Stromstärke I Elektrische Spannung U Elektrischer Widerstand R Ladung Q Probeladung q Zeit t Arbeit
Was ist eine Systemkamera?
 Kapitel 1 Was ist eine Systemkamera? 1 Was ist eine Systemkamera? Die spiegellose Systemkamera ist eine inzwischen eigenständige Klasse von Kameras, die sich zwischen Kompaktkameras und digitalen Spiegelreflexkameras
Kapitel 1 Was ist eine Systemkamera? 1 Was ist eine Systemkamera? Die spiegellose Systemkamera ist eine inzwischen eigenständige Klasse von Kameras, die sich zwischen Kompaktkameras und digitalen Spiegelreflexkameras
Informationen zum neuen Studmail häufige Fragen
 1 Stand: 15.01.2013 Informationen zum neuen Studmail häufige Fragen (Dokument wird bei Bedarf laufend erweitert) Problem: Einloggen funktioniert, aber der Browser lädt dann ewig und zeigt nichts an Lösung:
1 Stand: 15.01.2013 Informationen zum neuen Studmail häufige Fragen (Dokument wird bei Bedarf laufend erweitert) Problem: Einloggen funktioniert, aber der Browser lädt dann ewig und zeigt nichts an Lösung:
Schülervorstellungen zum Sehen und Möglichkeiten ihrer Erhebung Stand: 12.10.2015
 Schülervorstellungen zum Sehen und Möglichkeiten ihrer Erhebung Stand: 12.10.2015 Fakultativ kann vor Durchführung der Unterrichtseinheiten eine Erhebung zu den Schülervorstellungen zum Sehvorgang stattfinden,
Schülervorstellungen zum Sehen und Möglichkeiten ihrer Erhebung Stand: 12.10.2015 Fakultativ kann vor Durchführung der Unterrichtseinheiten eine Erhebung zu den Schülervorstellungen zum Sehvorgang stattfinden,
P1-41 AUSWERTUNG VERSUCH GEOMETRISCHE OPTIK
 P1-41 AUSWERTUNG VERSUCH GEOMETRISCHE OPTIK GRUPPE 19 - SASKIA MEIßNER, ARNOLD SEILER 1 Bestimmung der Brennweite 11 Naives Verfahren zur Bestimmung der Brennweite Es soll nur mit Maÿstab und Schirm die
P1-41 AUSWERTUNG VERSUCH GEOMETRISCHE OPTIK GRUPPE 19 - SASKIA MEIßNER, ARNOLD SEILER 1 Bestimmung der Brennweite 11 Naives Verfahren zur Bestimmung der Brennweite Es soll nur mit Maÿstab und Schirm die
Die reellen Lösungen der kubischen Gleichung
 Die reellen Lösungen der kubischen Gleichung Klaus-R. Löffler Inhaltsverzeichnis 1 Einfach zu behandelnde Sonderfälle 1 2 Die ganzrationale Funktion dritten Grades 2 2.1 Reduktion...........................................
Die reellen Lösungen der kubischen Gleichung Klaus-R. Löffler Inhaltsverzeichnis 1 Einfach zu behandelnde Sonderfälle 1 2 Die ganzrationale Funktion dritten Grades 2 2.1 Reduktion...........................................
Proportionen am Buch. Einige Standard-Blatt-Formate
 Proportionen am Buch Mittelalter / Renaissance: Asien versus Westeuropa. Blattästhetik. Umblättern. Japan oft nur oben/unten, Westeuropa rund herum Freiraum. Satzspiegel: übliche Konstruktionen. Siehe
Proportionen am Buch Mittelalter / Renaissance: Asien versus Westeuropa. Blattästhetik. Umblättern. Japan oft nur oben/unten, Westeuropa rund herum Freiraum. Satzspiegel: übliche Konstruktionen. Siehe
Gefahr erkannt Gefahr gebannt
 Ihre Unfallversicherung informiert Toter Winkel Gefahr erkannt Gefahr gebannt Gesetzliche Unfallversicherung Die Situation Liebe Eltern! Immer wieder kommt es zu schweren Verkehrsunfällen, weil LKW-Fahrer
Ihre Unfallversicherung informiert Toter Winkel Gefahr erkannt Gefahr gebannt Gesetzliche Unfallversicherung Die Situation Liebe Eltern! Immer wieder kommt es zu schweren Verkehrsunfällen, weil LKW-Fahrer
Datensicherung. Beschreibung der Datensicherung
 Datensicherung Mit dem Datensicherungsprogramm können Sie Ihre persönlichen Daten problemlos Sichern. Es ist möglich eine komplette Datensicherung durchzuführen, aber auch nur die neuen und geänderten
Datensicherung Mit dem Datensicherungsprogramm können Sie Ihre persönlichen Daten problemlos Sichern. Es ist möglich eine komplette Datensicherung durchzuführen, aber auch nur die neuen und geänderten
Satzhilfen Publisher Seite Einrichten
 Satzhilfen Publisher Seite Einrichten Es gibt verschiedene Möglichkeiten die Seite einzurichten, wir fangen mit der normalen Version an, Seite einrichten auf Format A5 Wählen Sie zunächst Datei Seite einrichten,
Satzhilfen Publisher Seite Einrichten Es gibt verschiedene Möglichkeiten die Seite einzurichten, wir fangen mit der normalen Version an, Seite einrichten auf Format A5 Wählen Sie zunächst Datei Seite einrichten,
ADFC Hessen HessenForum 20.-22. November 2015 Frankfurt am Main. Workshop: Gute Fotos für ADFC-Medien
 ADFC Hessen HessenForum 20.-22. November 2015 Frankfurt am Main Workshop: Gute Fotos für ADFC-Medien Sammlung gelungener und weniger gelungener Beispiele mit Kommentaren aus dem Workshop Workshop-Leitung:
ADFC Hessen HessenForum 20.-22. November 2015 Frankfurt am Main Workshop: Gute Fotos für ADFC-Medien Sammlung gelungener und weniger gelungener Beispiele mit Kommentaren aus dem Workshop Workshop-Leitung:
Leichte-Sprache-Bilder
 Leichte-Sprache-Bilder Reinhild Kassing Information - So geht es 1. Bilder gucken 2. anmelden für Probe-Bilder 3. Bilder bestellen 4. Rechnung bezahlen 5. Bilder runterladen 6. neue Bilder vorschlagen
Leichte-Sprache-Bilder Reinhild Kassing Information - So geht es 1. Bilder gucken 2. anmelden für Probe-Bilder 3. Bilder bestellen 4. Rechnung bezahlen 5. Bilder runterladen 6. neue Bilder vorschlagen
Die besten Tipps für eindrucksvolle Schwarz-Weiss Aufnahmen
 Die besten Tipps für eindrucksvolle Schwarz-Weiss Aufnahmen Digitale Fotografie für Einsteiger und Fortgeschrittene www.fotoschule-kleinewaltraud.de Schöne Fotos leicht gelernt 1 Schule deinen Blick 2
Die besten Tipps für eindrucksvolle Schwarz-Weiss Aufnahmen Digitale Fotografie für Einsteiger und Fortgeschrittene www.fotoschule-kleinewaltraud.de Schöne Fotos leicht gelernt 1 Schule deinen Blick 2
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Portfolio: "Die Ratten" von Gerhart Hauptmann
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Portfolio: "Die Ratten" von Gerhart Hauptmann Das komplette Material finden Sie hier: Download bei School-Scout.de Titel: man zum
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Portfolio: "Die Ratten" von Gerhart Hauptmann Das komplette Material finden Sie hier: Download bei School-Scout.de Titel: man zum
Übungen zur Experimentalphysik 3
 Übungen zur Experimentalphysik 3 Prof. Dr. L. Oberauer Wintersemester 2010/2011 7. Übungsblatt - 6.Dezember 2010 Musterlösung Franziska Konitzer (franziska.konitzer@tum.de) Aufgabe 1 ( ) (8 Punkte) Optische
Übungen zur Experimentalphysik 3 Prof. Dr. L. Oberauer Wintersemester 2010/2011 7. Übungsblatt - 6.Dezember 2010 Musterlösung Franziska Konitzer (franziska.konitzer@tum.de) Aufgabe 1 ( ) (8 Punkte) Optische
Was ist Sozial-Raum-Orientierung?
 Was ist Sozial-Raum-Orientierung? Dr. Wolfgang Hinte Universität Duisburg-Essen Institut für Stadt-Entwicklung und Sozial-Raum-Orientierte Arbeit Das ist eine Zusammen-Fassung des Vortrages: Sozialräume
Was ist Sozial-Raum-Orientierung? Dr. Wolfgang Hinte Universität Duisburg-Essen Institut für Stadt-Entwicklung und Sozial-Raum-Orientierte Arbeit Das ist eine Zusammen-Fassung des Vortrages: Sozialräume
EINMALEINS BEZIEHUNGSREICH
 EINMALEINS BEZIEHUNGSREICH Thema: Übung des kleinen Einmaleins; operative Beziehungen erkunden Stufe: ab 2. Schuljahr Dauer: 2 bis 3 Lektionen Materialien: Kleine Einmaleinstafeln (ohne Farben), Punktefelder
EINMALEINS BEZIEHUNGSREICH Thema: Übung des kleinen Einmaleins; operative Beziehungen erkunden Stufe: ab 2. Schuljahr Dauer: 2 bis 3 Lektionen Materialien: Kleine Einmaleinstafeln (ohne Farben), Punktefelder
3D-Ultraschall-Aufnahmen. Eine Fachinformation Ihrer Abteilung für Geburtshilfe
 3D-Ultraschall-Aufnahmen Eine Fachinformation Ihrer Abteilung für Geburtshilfe 2 Hufeland Klinikum Da werden Hände sein, die Dich tragen, und Arme, in denen Du sicher bist, und Menschen, die Dir ohne Fragen
3D-Ultraschall-Aufnahmen Eine Fachinformation Ihrer Abteilung für Geburtshilfe 2 Hufeland Klinikum Da werden Hände sein, die Dich tragen, und Arme, in denen Du sicher bist, und Menschen, die Dir ohne Fragen
http://www.nervepreserve.com/quick3dcover/scrshot.html
 Quick 3D Cover Manche haben sich sicher gefragt, wo die 3D-Abbildungen mit Schattierungen und Spiegelungen auf vielen Webseiten herkommen. Es gibt im Freeware und Open Source - Bereich viele kleinere Lösungen,
Quick 3D Cover Manche haben sich sicher gefragt, wo die 3D-Abbildungen mit Schattierungen und Spiegelungen auf vielen Webseiten herkommen. Es gibt im Freeware und Open Source - Bereich viele kleinere Lösungen,
