Physik für Bauingenieure
|
|
|
- Juliane Adenauer
- vor 8 Jahren
- Abrufe
Transkript
1 Fachbereich Physik Prof. Dr. Rudolf Feile Dipl. Phys. Markus Domschke Sommersemster April 2010 Physik für Bauingenieure Übungsblatt 2 Gruppenübungen 1. Springende Kugeln Die nebenstehende Abbildung zeigt die Momentaufnahme eines Versuchs aus der Vorlesung, bei dem kleine Kugeln durch Stöße in einem Rohr auf unterschiedliche Höhen katapultiert werden. Das Rohr kann nun in Höhenstreifen der Höhe [h:h + dh] 1 cm unterteilt werden. a) Lesen Sie ab, wie viele Kugeln sich jeweils in den Abschnitten h bis h + dh befinden. b) Wieviele Kugeln befinden sich in dem Rohr? c) Was ist die mittlere Höhe der Kugeln? a) Die Tabelle gibt an, wie viele Kugeln sich im jeweiligen Abschnitt befinden Höhe / cm Anzahl h b) Um die Anzahl zu erlangen muss über die Höhen summiert werden N 5 Anzahl h 95Kugeln h c) Die mittlere Höhe ist gegeben durch H N 5 1 i Anzahl h h (was für h gewählt wird muss definiert werden; hier wird die Mitte gewählt) h 1 N 5 Anzahl h h i 1 26Kugeln 1,5cm+ 14Kugeln 2,5cm+1Kugeln 3,5cm+2Kugeln 4,5cm] 95Kugeln [52Kugeln 0,5cm+ 1,2cm Für die untere Grenze ergibt sich h low 0,7 cm, für die obere Grenze h up 1,7 cm. Wie groß ist also der Fehler? War die Wahl der Höhe geschickt?
2 2. Eine Wagenladung Hohlblocksteine Gegeben ist die abgebildete Verteilungsfunktion n(m). n gibt die Anzahl der Steine mit der Masse m im Bereich m und m+dm1 kg an. n(m) / kg -1 a) Geben Sie die abschnittsweise definierte Funktion n(m) an. b) Wieviele Hohlblocksteine umfasst die Wagenladung? 100 c) Was ist die mittlere Masse eines Hohlblocksteins? a) Die abschnittsweise definierte Funktion n(m) ist: m / kg n 1 (m)0kg 1 n 2 (m) 100kg 1 0kg 1 n 3 (m)100kg 1 + 0kg 1 100kg 1 n 4 (m)0kg 1 1 (m )20kg 2 m 200kg m [,] 17kg 1 (m ) 50kg 2 m+850kg m [,17kg] m m 17kg b) Um die Anzahl zu erlangen muss immer über die Funktion n(m) integriert werden mit N b n(m) dm 17kg N n 2 (m) dm + n 3 (m) dm 20kg 2 m 200kg 1 17kg dm + 50kg 2 m+850kg 1 dm 2 m 2 200kg 1 m + 25kg 2 m kg 1 m 17kg Steine a c) Die mittlere Masse ist gegeben durch M 1 N b a m n(m) dm M 1 17kg m n N 2 (m) dm + m n 3 (m) dm 1 20kg 2 m 2 200kg 1 m 17kg dm N + 50kg 2 m kg 1 m dm 1 20 N kg 2 m 3 100kg 1 m kg 2 m kg 1 m 2 17kg ( ( ) kg 2 ) kg kg 3. Ausdehnung des Eiffelturms Um wieviel länger ist der Eiffelturm (Höhe h 324, 82 m bei 10 C) im Sommer bei Temperaturen von T Sommer 35 C im Vergleich zum Winter mit Temperaturen von T Winter 15 C? Hinweis: Den Ausdehnungskoeffizienten von Stahl liegt beiα1, K 1.
3 Man berechnet die Längenänderungen des Eiffelturms mit der Formel h h α(t T 0). Es gilt: h ges α (T Sommer T 0 ) (T Winter T 0 ) α T Sommer T Winter 1, K 1 50K6, h h 0,211m 4. Thermische Ausdehnung der Öresundbrücke Die Öresundbrücke zwischen Dänemark und Schweden ist 7845 m lang (bei 20 C) und aus Spannbeton hergestellt worden. Da sich der Beton bei Temperaturänderungen ausdehnt, bzw. zusammenzieht, mussten auf beiden Seiten der Brücke Ausgleichselemente angebracht werden, die die Temperaturausdehnung ausgleichen. a) Welche Längenänderung müssen die Ausgleichselemente jeweils kompensieren können, wenn der erwartete Temperaturbereich von 50 C im Sommer bis zu 40 C im Winter reichen kann? Die Zufahrtsrampen werden nicht berücksichtigt, der thermische Ausdehnungskoeffizient von Spannbeton istα K 1. b) Welchen Ausdehnungskoeffizient müssen die Stahlseile, mit denen das mittlere Brückenteil aufgehängt ist, haben, damit sich die Fahrbahn mit wechselnder Temperatur nicht krümmt? Die Pfeiler, an denen die Stahlseile befestigt sind, sind aus dem selben Spannbeton hergestellt, wie die Fahrbahn. a) Für die maximale Ausdehnung die die Ausgleichselemente kompensieren müssen, muss gelten: l ges l Sommer + l Winter Man berechne als die beiden Längenänderungen mit der Formel l l Für den Sommer ergibt sich also: l Sommer l Für den Winter folgt analog: α(t T 0 ). α(t Sommer T 0 ) K 1 (323,15K 293,15K) l Sommer 0,235m l Winter l α(t Winter T 0 ) K 1 (233,15K 293,15K) l Winter 0,471m Insgesamt ergibt das l ges l Sommer + l Winter 0,235m+0,471m0,706m b) Die Ausdehnung der Fahrbahn und der Brückenpfeiler sind gleich. Daher muss der Ausdehnungskoeffizient der Stahlseile den Wert des Spannbetons haben. Bildlich kann man sich einen massiven Quader aus Spannbeton vorstellen (Fahrbahn und Pfeiler sind die Seitenflächen). Erfährt ein solcher Quader eine Temperaturänderung, dehnt er sich linear in alle Richtungen aus. Insbesondere dehnt er sich auch auf der Diagonalen (also in Richtung des Seils) genau so aus, wie in Richtung der Seitenflächen. Das kann man auch rechnen - wen es interessiert (beachte Skizze): Damit folgt: x x α Beton T bzw. y y α Beton T und l l+ l (x+ x) 2 +(y+ y) 2 l+ l (α Seil T) (x+x (α Beton T)) 2 +(y+ y (α Beton T)) 2 l (1+α Seil T) (x (1+α Beton T)) 2 +(y (1+α Beton T)) 2 l (1+α Seil T) x 2 (1+α Beton T) 2 + y 2 (1+α Beton T) 2 l (1+α Seil T)(1+α Beton T) x 2 + y 2 (1+α Seil T)(1+α Beton T) α Seil α Beton x 2 + y 2 α Seil T
4 5. Für den USA Aufenthalt Anfang des 18. Jahrhunderts entwickelte Daniel Gabriel Fahrenheit eine Temperaturskala, die noch heute in einigen englischsprachigen Ländern (vor allem dem USA) der hierzulande üblichen Celsius Temperaturskala vorgezogen wird. Die Fahrenheit Temperaturskala lässt sich folgendermaßen in die Celsius Temperaturskala umrechnen: C ( T Fahrenheit 32) 5 F 9 a) Geben Sie die umgekehrte Umrechnungsformel von Grad Celsius in Grad Fahrenheit an. Für den Nullpunkt seiner Temperaturskala (0 F) wählte Fahrenheit die tiefste Temperatur des strengen Winters 1708/1709 in seiner Heimatstadt Danzig. Den anderen Fixpunkt seiner Skala wählte er bei 100 F. b) Berechnen Sie diese Temperaturen in Grad Celsius. Was könnte Fahrenheit für seine 100 F verwendet haben? c) Rechnen Sie die fehlenden Werte aus: / C , T Fahrenheit / F a) Die Umrechnung erfolgt duch Umstellung der Gleichung b) T Fahrenheit F 1,8 TCelsius C F 17,78 C 100 F37,78 C Fahrenheit wählte die Körpertemperatur eines Menschen als zweiten Fixpunkt (leider hatte er etwas erhöhte Temperatur). Übrigens: Manche Quellen behaupten auch, das Fahrenheit die tiefste Temperatur, die er mit einer Eis-Salz- Kältemischung erzeugen konnte, als 0 F wählte, da diese gerade 17,8 C entspricht. c) Die Tabelle: / C , ,44 T Fahrenheit / F , A. Dichte von Sand Hausübungen Ein Betonwerk führt Buch über die Dichte der angelieferten LKW-Ladungen Sand. Die Häufigkeitsverteilung wird folgendermaßen beschrieben: n(ρ) n 0 (ρ ) 2 (ρ ρ max ) 2 mit den Parametern 1200 kg,ρ m 3 max 1600 kg und n m ( cm3 g )5. a) Skizzieren Sie den Verlauf der Häufigkeitsverteilung (Nullstellen und Maximalwert) im Bereich ρ ρ max. b) Wieviele LKW-Ladungen wurden in die Statistik aufgenommen (wurden geliefert)? c) Was ist die mittlere Dichte des angelieferten Sandes? d) Der Preis einer LKW-Ladung Sand hängt von der Dichte wie folgt ab: P(ρ) P 0 + A 1 (ρ ) mit P 0 20 und A LKW 1 25 LKW cm3 g Was sind die Gesamtausgaben für den Sand? Hinweis: Bei dieser Aufgabe ist auch die korrekte Rechnung mit den Maßeinheiten wichtig.
5 a) Der Verlauf sieht wie folgt aus: Die Nullstellen der Funktion sind beiρ max und. Das Maximum liegt beiρ 1400 kg m 3. Wichtig: n ( cm3 g ) ( m3 kg )5 n(ρ) ρ [kg/m 3 ] b) Man berechne N n(ρ) dρ n 0 (ρ ) 2 (ρ ρ max ) 2 dρ n 0 (ρ 2 2ρ +ρ 2 min )(ρ2 2ρρ max +ρ 2 max ) dρ. 512 Ladungen c) Die mittlere Dichte errechnet sich analog zur mittleren Masse ρ 1 N 1 N n 0 N. 1, kg m 3 ρn(ρ) dρ n 0 ρ(ρ ) 2 (ρ ρ max ) 2 dρ ρ(ρ 2 2ρ +ρ 2 min )(ρ2 2ρρ max +ρ 2 max ) dρ d) Die Ausgaben werden mit der Formel P(ρ) P 0 + A 1 (ρ ) errrechnet. Ausgaben P(ρ)n(ρ) dρ P0 + A 1 (ρ ) n(ρ) dρ P0 A 1 n(ρ)+a1 ρ n(ρ) dρ ρ max P 0 A 1 n(ρ) dρ+a 1 ρ n(ρ) dρ } {{ } N P 0 A 1 N+ A1 N ρ uro } {{ } N ρ
6 B. Thermische Ausdehnung einer Kugel Eine Messingkugel (linearer thermischer Ausdehnungskoeffizientα K 1 ) hat bei der Temperatur T 1 20 C den Durchmesser d 1 20 mm. a) Auf welche Temperatur T 2 muss die Kugel mindestens erwärmt werden, damit sie in einem Ring mit dem Innendurchmesser d 2 20, 03 mm stecken bleibt? b) Wie hat sich das Kugelvolumen bei der Erwärmung von T 1 auf T 2 relativ verändert ( V V )? a) Es muss die Temperatur errechnet werden, bei der der Durchmesser der Kugel gerade größer als d 2 ist. Für die Ausdehung des Durchmessers gilt die lineare Längenausdehnung d α(t T d 0). Somit folgt: d(t) d 1 α (T T 1 ) Gesucht ist nun die Temperatur T 2 bei der d(t)0,03 m ist. 0,03m d(t 2 ) d 1 α (T 2 T 1 ) T 2 T 1 + d(t 2) d 1 α 98,95 C b) Für das Volumen einer Kugel gilt: V Kugel (T) 4π 3 R(T)3 4π d(t) Die Volumenänderung errechnet man mit V Kugel (T) V Kugel (T 1 ) 3α(T T 1 ). V Kugel (T 1 )4,189cm 1 und V Kugel (T 2 )0,019cm 1 führen zu V V 0,0045 C. Fremde Temperaturskalen Auf seiner 80-tägigen Reise um die Welt stößt der Brite Phileas Fog in Siam auf ein Dorf, in dem der Siedepunkt von Wasser mit 33ℵbezeichnet wird. Die Körperwärme eines Menschen (37 C) mit 12ℵ. 0 ℵ ist die kälteste Temperatur, die der Dorfälteste jemals erlebt hat. Phileas notiert sich diese Angaben und überträgt sie linear in die Celsiusskala, die er gewohnt ist. a) Geben Sie eine Umrechnungsformel zwischen den Temperaturskalen an. b) Welche Temperatur in Grad Celsius musste der Dorfälteste ertragen? a) Die Umrechnung hat einen linearen Verlauf, das heißt a Tℵ + b C ℵ Verwende die beiden Umrechnungen um die Koeffizienten a, b zu errechnen. (Siedepunkt von Wasser) 100 C C 33ℵ a ℵ + b (Körperwärme eines Menschen) 37 C 12ℵ a C ℵ + b a3 und b 1 Die Umrechnungsformel vonℵ in Grad Celsius ist also: C 3 Tℵ ℵ + 1 b) Mit der Umrechnungsformel aus a) erhält man für die niedrigste Temperatur die der Dorfälteste je erlebt hat C 3 Tℵ ℵ ℵ ℵ + 11 T 0ℵ 1 C
Die Größe von Flächen vergleichen
 Vertiefen 1 Die Größe von Flächen vergleichen zu Aufgabe 1 Schulbuch, Seite 182 1 Wer hat am meisten Platz? Ordne die Figuren nach ihrem Flächeninhalt. Begründe deine Reihenfolge. 1 2 3 4 zu Aufgabe 2
Vertiefen 1 Die Größe von Flächen vergleichen zu Aufgabe 1 Schulbuch, Seite 182 1 Wer hat am meisten Platz? Ordne die Figuren nach ihrem Flächeninhalt. Begründe deine Reihenfolge. 1 2 3 4 zu Aufgabe 2
Physik für Bauingenieure
 Fachbereich Physik Prof. Dr. Ruolf Feile Dipl. Phys. Markus Domschke Sommersemester 00 4. 8. Juni 00 Physik für Bauingenieure Übungsblatt 9 Gruppenübungen. Konensator Zwei quaratische Metallplatten mit
Fachbereich Physik Prof. Dr. Ruolf Feile Dipl. Phys. Markus Domschke Sommersemester 00 4. 8. Juni 00 Physik für Bauingenieure Übungsblatt 9 Gruppenübungen. Konensator Zwei quaratische Metallplatten mit
Info zum Zusammenhang von Auflösung und Genauigkeit
 Da es oft Nachfragen und Verständnisprobleme mit den oben genannten Begriffen gibt, möchten wir hier versuchen etwas Licht ins Dunkel zu bringen. Nehmen wir mal an, Sie haben ein Stück Wasserrohr mit der
Da es oft Nachfragen und Verständnisprobleme mit den oben genannten Begriffen gibt, möchten wir hier versuchen etwas Licht ins Dunkel zu bringen. Nehmen wir mal an, Sie haben ein Stück Wasserrohr mit der
Administratives BSL PB
 Administratives Die folgenden Seiten sind ausschliesslich als Ergänzung zum Unterricht für die Schüler der BSL gedacht (intern) und dürfen weder teilweise noch vollständig kopiert oder verbreitet werden.
Administratives Die folgenden Seiten sind ausschliesslich als Ergänzung zum Unterricht für die Schüler der BSL gedacht (intern) und dürfen weder teilweise noch vollständig kopiert oder verbreitet werden.
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lösung. Prüfungsteil 1: Aufgabe 1
 Zentrale Prüfung 01 Lösung Diese Lösung wurde erstellt von Cornelia Sanzenbacher. Sie ist keine offizielle Lösung des Ministeriums für Schule und Weiterbildung des Landes. Prüfungsteil 1: Aufgabe 1 a)
Zentrale Prüfung 01 Lösung Diese Lösung wurde erstellt von Cornelia Sanzenbacher. Sie ist keine offizielle Lösung des Ministeriums für Schule und Weiterbildung des Landes. Prüfungsteil 1: Aufgabe 1 a)
2.8 Grenzflächeneffekte
 - 86-2.8 Grenzflächeneffekte 2.8.1 Oberflächenspannung An Grenzflächen treten besondere Effekte auf, welche im Volumen nicht beobachtbar sind. Die molekulare Grundlage dafür sind Kohäsionskräfte, d.h.
- 86-2.8 Grenzflächeneffekte 2.8.1 Oberflächenspannung An Grenzflächen treten besondere Effekte auf, welche im Volumen nicht beobachtbar sind. Die molekulare Grundlage dafür sind Kohäsionskräfte, d.h.
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Prozentrechnung. Wir können nun eine Formel für die Berechnung des Prozentwertes aufstellen:
 Prozentrechnung Wir beginnen mit einem Beisiel: Nehmen wir mal an, ein Handy kostet 200 und es gibt 5% Rabatt (Preisnachlass), wie groß ist dann der Rabatt in Euro und wie viel kostet dann das Handy? Wenn
Prozentrechnung Wir beginnen mit einem Beisiel: Nehmen wir mal an, ein Handy kostet 200 und es gibt 5% Rabatt (Preisnachlass), wie groß ist dann der Rabatt in Euro und wie viel kostet dann das Handy? Wenn
Der monatliche Tarif für ein Handy wurde als lineare Funktion der Form f(x) = k x + d modelliert (siehe Grafik).
 1) Handytarif Der monatliche Tarif für ein Handy wurde als lineare Funktion der Form f(x) = k x + d modelliert (siehe Grafik). Euro Gesprächsminuten Tragen Sie in der folgenden Tabelle ein, welche Bedeutung
1) Handytarif Der monatliche Tarif für ein Handy wurde als lineare Funktion der Form f(x) = k x + d modelliert (siehe Grafik). Euro Gesprächsminuten Tragen Sie in der folgenden Tabelle ein, welche Bedeutung
Ideale und Reale Gase. Was ist ein ideales Gas? einatomige Moleküle mit keinerlei gegenseitiger WW keinem Eigenvolumen (punktförmig)
 Ideale und Reale Gase Was ist ein ideales Gas? einatomige Moleküle mit keinerlei gegenseitiger WW keinem Eigenvolumen (punktförmig) Wann sind reale Gase ideal? Reale Gase verhalten sich wie ideale Gase
Ideale und Reale Gase Was ist ein ideales Gas? einatomige Moleküle mit keinerlei gegenseitiger WW keinem Eigenvolumen (punktförmig) Wann sind reale Gase ideal? Reale Gase verhalten sich wie ideale Gase
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
Praktikum Physik. Protokoll zum Versuch 1: Viskosität. Durchgeführt am 26.01.2012. Gruppe X
 Praktikum Physik Protokoll zum Versuch 1: Viskosität Durchgeführt am 26.01.2012 Gruppe X Name 1 und Name 2 (abc.xyz@uni-ulm.de) (abc.xyz@uni-ulm.de) Betreuerin: Wir bestätigen hiermit, dass wir das Protokoll
Praktikum Physik Protokoll zum Versuch 1: Viskosität Durchgeführt am 26.01.2012 Gruppe X Name 1 und Name 2 (abc.xyz@uni-ulm.de) (abc.xyz@uni-ulm.de) Betreuerin: Wir bestätigen hiermit, dass wir das Protokoll
6. Übungsblatt zur Experimentalphysik 1
 6. Übungsblatt zur Experimentalphysik (Besprechung ab dem 3. Dezember 2006) Aufgabe 6. Loch in der Regentonne Eine h 2m hohe, voll gefüllte Regentonne steht ebenerdig. Versehentlich wird nun die Regentonne
6. Übungsblatt zur Experimentalphysik (Besprechung ab dem 3. Dezember 2006) Aufgabe 6. Loch in der Regentonne Eine h 2m hohe, voll gefüllte Regentonne steht ebenerdig. Versehentlich wird nun die Regentonne
Aufgaben. 2.1. Leiten Sie die Formeln (9) und (10) her! Vorbetrachtungen. Der High-Fall
 Aufgaben 2.1. Leiten Sie die Formeln (9) und (10) her! Vorbetrachtungen I. Die open-collector-gatter auf der "in"-seite dürfen erst einen High erkennen, wenn alle open-collector-gatter der "out"-seite
Aufgaben 2.1. Leiten Sie die Formeln (9) und (10) her! Vorbetrachtungen I. Die open-collector-gatter auf der "in"-seite dürfen erst einen High erkennen, wenn alle open-collector-gatter der "out"-seite
7 Rechnen mit Polynomen
 7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
Lichtbrechung an Linsen
 Sammellinsen Lichtbrechung an Linsen Fällt ein paralleles Lichtbündel auf eine Sammellinse, so werden die Lichtstrahlen so gebrochen, dass sie durch einen Brennpunkt der Linse verlaufen. Der Abstand zwischen
Sammellinsen Lichtbrechung an Linsen Fällt ein paralleles Lichtbündel auf eine Sammellinse, so werden die Lichtstrahlen so gebrochen, dass sie durch einen Brennpunkt der Linse verlaufen. Der Abstand zwischen
LU-Zerlegung. Zusätze zum Gelben Rechenbuch. Peter Furlan. Verlag Martina Furlan. Inhaltsverzeichnis. 1 Definitionen.
 Zusätze zum Gelben Rechenbuch LU-Zerlegung Peter Furlan Verlag Martina Furlan Inhaltsverzeichnis Definitionen 2 (Allgemeine) LU-Zerlegung 2 3 Vereinfachte LU-Zerlegung 3 4 Lösung eines linearen Gleichungssystems
Zusätze zum Gelben Rechenbuch LU-Zerlegung Peter Furlan Verlag Martina Furlan Inhaltsverzeichnis Definitionen 2 (Allgemeine) LU-Zerlegung 2 3 Vereinfachte LU-Zerlegung 3 4 Lösung eines linearen Gleichungssystems
1 C H R I S T O P H D R Ö S S E R D E R M A T H E M A T I K V E R F Ü H R E R
 C H R I S T O P H D R Ö S S E R D E R M A T H E M A T I K V E R F Ü H R E R L Ö S U N G E N Seite 7 n Wenn vier Menschen auf einem Quadratmeter stehen, dann hat jeder eine Fläche von 50 mal 50 Zentimeter
C H R I S T O P H D R Ö S S E R D E R M A T H E M A T I K V E R F Ü H R E R L Ö S U N G E N Seite 7 n Wenn vier Menschen auf einem Quadratmeter stehen, dann hat jeder eine Fläche von 50 mal 50 Zentimeter
P = U eff I eff. I eff = = 1 kw 120 V = 1000 W
 Sie haben für diesen 50 Minuten Zeit. Die zu vergebenen Punkte sind an den Aufgaben angemerkt. Die Gesamtzahl beträgt 20 P + 1 Formpunkt. Bei einer Rechnung wird auf die korrekte Verwendung der Einheiten
Sie haben für diesen 50 Minuten Zeit. Die zu vergebenen Punkte sind an den Aufgaben angemerkt. Die Gesamtzahl beträgt 20 P + 1 Formpunkt. Bei einer Rechnung wird auf die korrekte Verwendung der Einheiten
B 2. " Zeigen Sie, dass die Wahrscheinlichkeit, dass eine Leiterplatte akzeptiert wird, 0,93 beträgt. (genauerer Wert: 0,933).!:!!
 Das folgende System besteht aus 4 Schraubenfedern. Die Federn A ; B funktionieren unabhängig von einander. Die Ausfallzeit T (in Monaten) der Federn sei eine weibullverteilte Zufallsvariable mit den folgenden
Das folgende System besteht aus 4 Schraubenfedern. Die Federn A ; B funktionieren unabhängig von einander. Die Ausfallzeit T (in Monaten) der Federn sei eine weibullverteilte Zufallsvariable mit den folgenden
Aufgabe 1 (Fundamentum)
 Aufgabe 1 (Fundamentum) a) Kreuze an, wie viele Minuten du ungefähr seit deiner Geburt gelebt hast. 80.000.000 8.000.000 800.000 80.000 8.000 b) Bei einer Durchschnittsgeschwindigkeit von 80 km / h benötigt
Aufgabe 1 (Fundamentum) a) Kreuze an, wie viele Minuten du ungefähr seit deiner Geburt gelebt hast. 80.000.000 8.000.000 800.000 80.000 8.000 b) Bei einer Durchschnittsgeschwindigkeit von 80 km / h benötigt
- 2 - AP WS 10M. 1 Finanzmathematik Punkte
 - 2 - AP WS 10M 1 Finanzmathematik Punkte Frau Werner hat vor einigen Jahren bei einer Versicherungsgesellschaft einen Vertrag für eine Lebensversicherung abgeschlossen. Am Ende der Laufzeit dieser Versicherung
- 2 - AP WS 10M 1 Finanzmathematik Punkte Frau Werner hat vor einigen Jahren bei einer Versicherungsgesellschaft einen Vertrag für eine Lebensversicherung abgeschlossen. Am Ende der Laufzeit dieser Versicherung
Anleitung über den Umgang mit Schildern
 Anleitung über den Umgang mit Schildern -Vorwort -Wo bekommt man Schilder? -Wo und wie speichert man die Schilder? -Wie füge ich die Schilder in meinen Track ein? -Welche Bauteile kann man noch für Schilder
Anleitung über den Umgang mit Schildern -Vorwort -Wo bekommt man Schilder? -Wo und wie speichert man die Schilder? -Wie füge ich die Schilder in meinen Track ein? -Welche Bauteile kann man noch für Schilder
von: Oktay Arslan Kathrin Steiner Tamara Hänggi Marco Schweizer GIB-Liestal Mühlemattstrasse 34 4410 Liestal ATG
 von: Oktay Arslan Kathrin Steiner Tamara Hänggi Marco Schweizer GIB-Liestal Mühlemattstrasse 34 4410 Liestal ATG 20.03.2009 1 Inhaltsverzeichnis 1. Zusammenfassung S. 3 2. Aufgabestellung S. 3 3. Lösungsansätze
von: Oktay Arslan Kathrin Steiner Tamara Hänggi Marco Schweizer GIB-Liestal Mühlemattstrasse 34 4410 Liestal ATG 20.03.2009 1 Inhaltsverzeichnis 1. Zusammenfassung S. 3 2. Aufgabestellung S. 3 3. Lösungsansätze
Physik für Bauingenieure
 Fachbereich Physik Prof. Dr. Rudolf Feile Dipl. Phys. Markus Domschke Sommersemster 010 10. 14. Mai 010 Physik für Bauingenieure Übungsblatt 4 1. Wie viele Luftmoleküle befinden sich im Hörsaal Gruppenübungen
Fachbereich Physik Prof. Dr. Rudolf Feile Dipl. Phys. Markus Domschke Sommersemster 010 10. 14. Mai 010 Physik für Bauingenieure Übungsblatt 4 1. Wie viele Luftmoleküle befinden sich im Hörsaal Gruppenübungen
OECD Programme for International Student Assessment PISA 2000. Lösungen der Beispielaufgaben aus dem Mathematiktest. Deutschland
 OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
Wachstum 2. Michael Dröttboom 1 LernWerkstatt-Selm.de
 1. Herr Meier bekommt nach 3 Jahren Geldanlage 25.000. Er hatte 22.500 angelegt. Wie hoch war der Zinssatz? 2. Herr Meiers Vorfahren haben bei der Gründung Roms (753. V. Chr.) 1 Sesterze auf die Bank gebracht
1. Herr Meier bekommt nach 3 Jahren Geldanlage 25.000. Er hatte 22.500 angelegt. Wie hoch war der Zinssatz? 2. Herr Meiers Vorfahren haben bei der Gründung Roms (753. V. Chr.) 1 Sesterze auf die Bank gebracht
Statistische Thermodynamik I Lösungen zur Serie 1
 Statistische Thermodynamik I Lösungen zur Serie Zufallsvariablen, Wahrscheinlichkeitsverteilungen 4. März 2. Zwei Lektoren lesen ein Buch. Lektor A findet 2 Druckfehler, Lektor B nur 5. Von den gefundenen
Statistische Thermodynamik I Lösungen zur Serie Zufallsvariablen, Wahrscheinlichkeitsverteilungen 4. März 2. Zwei Lektoren lesen ein Buch. Lektor A findet 2 Druckfehler, Lektor B nur 5. Von den gefundenen
Handbuch. NAFI Online-Spezial. Kunden- / Datenverwaltung. 1. Auflage. (Stand: 24.09.2014)
 Handbuch NAFI Online-Spezial 1. Auflage (Stand: 24.09.2014) Copyright 2016 by NAFI GmbH Unerlaubte Vervielfältigungen sind untersagt! Inhaltsangabe Einleitung... 3 Kundenauswahl... 3 Kunde hinzufügen...
Handbuch NAFI Online-Spezial 1. Auflage (Stand: 24.09.2014) Copyright 2016 by NAFI GmbH Unerlaubte Vervielfältigungen sind untersagt! Inhaltsangabe Einleitung... 3 Kundenauswahl... 3 Kunde hinzufügen...
EXPEDITION Mathematik 3 / Übungsaufgaben
 1 Berechne das Volumen und die Oberfläche eines Prismas mit der Höhe h = 20 cm. Die Grundfläche ist ein a) Parallelogramm mit a 12 cm; b 8 cm; ha 6 cm b) gleichschenkliges Dreieck mit a b 5 cm; c 60 mm;
1 Berechne das Volumen und die Oberfläche eines Prismas mit der Höhe h = 20 cm. Die Grundfläche ist ein a) Parallelogramm mit a 12 cm; b 8 cm; ha 6 cm b) gleichschenkliges Dreieck mit a b 5 cm; c 60 mm;
Bruchrechnung Wir teilen gerecht auf
 Bruchrechnung Wir teilen gerecht auf Minipizzen auf Personen. Bruchrechnung Wir teilen gerecht auf Minipizzen auf Personen. : (+) : + Wir teilen einen Teil Eine halbe Minipizza auf Personen. :? Wir teilen
Bruchrechnung Wir teilen gerecht auf Minipizzen auf Personen. Bruchrechnung Wir teilen gerecht auf Minipizzen auf Personen. : (+) : + Wir teilen einen Teil Eine halbe Minipizza auf Personen. :? Wir teilen
Festigkeit von FDM-3D-Druckteilen
 Festigkeit von FDM-3D-Druckteilen Häufig werden bei 3D-Druck-Filamenten die Kunststoff-Festigkeit und physikalischen Eigenschaften diskutiert ohne die Einflüsse der Geometrie und der Verschweißung der
Festigkeit von FDM-3D-Druckteilen Häufig werden bei 3D-Druck-Filamenten die Kunststoff-Festigkeit und physikalischen Eigenschaften diskutiert ohne die Einflüsse der Geometrie und der Verschweißung der
Vermessung und Verständnis von FFT Bildern
 Vermessung und Verständnis von FFT Bildern Viele Auswertungen basieren auf der "Fast Fourier Transformation" FFT um die (ungewünschten) Regelmäßigkeiten im Schliffbild darzustellen. Die Fourier-Transformation
Vermessung und Verständnis von FFT Bildern Viele Auswertungen basieren auf der "Fast Fourier Transformation" FFT um die (ungewünschten) Regelmäßigkeiten im Schliffbild darzustellen. Die Fourier-Transformation
Simulation LIF5000. Abbildung 1
 Simulation LIF5000 Abbildung 1 Zur Simulation von analogen Schaltungen verwende ich Ltspice/SwitcherCAD III. Dieses Programm ist sehr leistungsfähig und wenn man weis wie, dann kann man damit fast alles
Simulation LIF5000 Abbildung 1 Zur Simulation von analogen Schaltungen verwende ich Ltspice/SwitcherCAD III. Dieses Programm ist sehr leistungsfähig und wenn man weis wie, dann kann man damit fast alles
PTV VISWALK TIPPS UND TRICKS PTV VISWALK TIPPS UND TRICKS: VERWENDUNG DICHTEBASIERTER TEILROUTEN
 PTV VISWALK TIPPS UND TRICKS PTV VISWALK TIPPS UND TRICKS: VERWENDUNG DICHTEBASIERTER TEILROUTEN Karlsruhe, April 2015 Verwendung dichte-basierter Teilrouten Stellen Sie sich vor, in einem belebten Gebäude,
PTV VISWALK TIPPS UND TRICKS PTV VISWALK TIPPS UND TRICKS: VERWENDUNG DICHTEBASIERTER TEILROUTEN Karlsruhe, April 2015 Verwendung dichte-basierter Teilrouten Stellen Sie sich vor, in einem belebten Gebäude,
Lineare Funktionen. 1 Proportionale Funktionen 3 1.1 Definition... 3 1.2 Eigenschaften... 3. 2 Steigungsdreieck 3
 Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
R. Brinkmann http://brinkmann-du.de Seite 1 23.02.2013
 R. Brinkmann http://brinkmann-du.de Seite 1 23.02.2013 SEK I Lösungen zur Zinseszinsrechnung I Ergebnisse und ausführliche Lösungen zum nblatt SEK I Rechnen mit Zinseszinsen I. Zinseszins Rechenaufgaben
R. Brinkmann http://brinkmann-du.de Seite 1 23.02.2013 SEK I Lösungen zur Zinseszinsrechnung I Ergebnisse und ausführliche Lösungen zum nblatt SEK I Rechnen mit Zinseszinsen I. Zinseszins Rechenaufgaben
HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN
 HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN Zinsen haben im täglichen Geschäftsleben große Bedeutung und somit auch die eigentliche Zinsrechnung, z.b: - Wenn Sie Ihre Rechnungen zu spät
HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN Zinsen haben im täglichen Geschäftsleben große Bedeutung und somit auch die eigentliche Zinsrechnung, z.b: - Wenn Sie Ihre Rechnungen zu spät
DOWNLOAD. Arbeiten im Baumarkt. Mathe-Aufgaben aus dem. Pools, Pumpen, Wassermengen. Karin Schwacha. Downloadauszug aus dem Originaltitel:
 DOWNLOAD Karin Schwacha Arbeiten im Baumarkt Mathe-Aufgaben aus dem Berufsalltag: Pools, Pumpen, Wassermengen Mathe-Aufgaben aus dem Berufsalltag Klasse 8 10 auszug aus dem Originaltitel: Aus vielen Berufen
DOWNLOAD Karin Schwacha Arbeiten im Baumarkt Mathe-Aufgaben aus dem Berufsalltag: Pools, Pumpen, Wassermengen Mathe-Aufgaben aus dem Berufsalltag Klasse 8 10 auszug aus dem Originaltitel: Aus vielen Berufen
Lösungsmethoden gewöhnlicher Differentialgleichungen (Dgl.)
 Lösungsmethoden gewöhnlicher Dierentialgleichungen Dgl) Allgemeine und partikuläre Lösung einer gewöhnlichen Dierentialgleichung Eine Dierentialgleichung ist eine Gleichung! Zum Unterschied von den gewöhnlichen
Lösungsmethoden gewöhnlicher Dierentialgleichungen Dgl) Allgemeine und partikuläre Lösung einer gewöhnlichen Dierentialgleichung Eine Dierentialgleichung ist eine Gleichung! Zum Unterschied von den gewöhnlichen
15.3 Bedingte Wahrscheinlichkeit und Unabhängigkeit
 5.3 Bedingte Wahrscheinlichkeit und Unabhängigkeit Einführendes Beispiel ( Erhöhung der Sicherheit bei Flugreisen ) Die statistische Wahrscheinlichkeit, dass während eines Fluges ein Sprengsatz an Bord
5.3 Bedingte Wahrscheinlichkeit und Unabhängigkeit Einführendes Beispiel ( Erhöhung der Sicherheit bei Flugreisen ) Die statistische Wahrscheinlichkeit, dass während eines Fluges ein Sprengsatz an Bord
Die reellen Lösungen der kubischen Gleichung
 Die reellen Lösungen der kubischen Gleichung Klaus-R. Löffler Inhaltsverzeichnis 1 Einfach zu behandelnde Sonderfälle 1 2 Die ganzrationale Funktion dritten Grades 2 2.1 Reduktion...........................................
Die reellen Lösungen der kubischen Gleichung Klaus-R. Löffler Inhaltsverzeichnis 1 Einfach zu behandelnde Sonderfälle 1 2 Die ganzrationale Funktion dritten Grades 2 2.1 Reduktion...........................................
Fit in Mathe. Juni 2014 Klassenstufe 9. Lineare Funktionen
 Thema Musterlösungen Juni 0 Klassenstufe 9 Lineare Funktionen a) Vervollständige die Tabelle mit den Funktionswerten: x 6 8 0 6 0 x 5 6 7 8 9 0 b) Gib die Funktionsgleichung an x 6 8 0 6 0 8 x,5,75,5 0,5-0,5
Thema Musterlösungen Juni 0 Klassenstufe 9 Lineare Funktionen a) Vervollständige die Tabelle mit den Funktionswerten: x 6 8 0 6 0 x 5 6 7 8 9 0 b) Gib die Funktionsgleichung an x 6 8 0 6 0 8 x,5,75,5 0,5-0,5
AGROPLUS Buchhaltung. Daten-Server und Sicherheitskopie. Version vom 21.10.2013b
 AGROPLUS Buchhaltung Daten-Server und Sicherheitskopie Version vom 21.10.2013b 3a) Der Daten-Server Modus und der Tresor Der Daten-Server ist eine Betriebsart welche dem Nutzer eine grosse Flexibilität
AGROPLUS Buchhaltung Daten-Server und Sicherheitskopie Version vom 21.10.2013b 3a) Der Daten-Server Modus und der Tresor Der Daten-Server ist eine Betriebsart welche dem Nutzer eine grosse Flexibilität
Sichere E-Mail Anleitung Zertifikate / Schlüssel für Kunden der Sparkasse Germersheim-Kandel. Sichere E-Mail. der
 Sichere E-Mail der Nutzung von Zertifikaten / Schlüsseln zur sicheren Kommunikation per E-Mail mit der Sparkasse Germersheim-Kandel Inhalt: 1. Voraussetzungen... 2 2. Registrierungsprozess... 2 3. Empfang
Sichere E-Mail der Nutzung von Zertifikaten / Schlüsseln zur sicheren Kommunikation per E-Mail mit der Sparkasse Germersheim-Kandel Inhalt: 1. Voraussetzungen... 2 2. Registrierungsprozess... 2 3. Empfang
Mathematik. Prüfung zum mittleren Bildungsabschluss 2008. Saarland. Schriftliche Prüfung Pflichtaufgaben. Name: Vorname: Klasse:
 Prüfung zum mittleren Bildungsabschluss 2008 Schriftliche Prüfung Pflichtaufgaben Mathematik Saarland Ministerium für Bildung, Familie, Frauen und Kultur Name: Vorname: Klasse: Bearbeitungszeit: 120 Minuten
Prüfung zum mittleren Bildungsabschluss 2008 Schriftliche Prüfung Pflichtaufgaben Mathematik Saarland Ministerium für Bildung, Familie, Frauen und Kultur Name: Vorname: Klasse: Bearbeitungszeit: 120 Minuten
Korrelation (II) Korrelation und Kausalität
 Korrelation (II) Korrelation und Kausalität Situation: Seien X, Y zwei metrisch skalierte Merkmale mit Ausprägungen (x 1, x 2,..., x n ) bzw. (y 1, y 2,..., y n ). D.h. für jede i = 1, 2,..., n bezeichnen
Korrelation (II) Korrelation und Kausalität Situation: Seien X, Y zwei metrisch skalierte Merkmale mit Ausprägungen (x 1, x 2,..., x n ) bzw. (y 1, y 2,..., y n ). D.h. für jede i = 1, 2,..., n bezeichnen
Arbeitspunkt einer Diode
 Arbeitspunkt einer Diode Liegt eine Diode mit einem Widerstand R in Reihe an einer Spannung U 0, so müssen sich die beiden diese Spannung teilen. Vom Widerstand wissen wir, dass er bei einer Spannung von
Arbeitspunkt einer Diode Liegt eine Diode mit einem Widerstand R in Reihe an einer Spannung U 0, so müssen sich die beiden diese Spannung teilen. Vom Widerstand wissen wir, dass er bei einer Spannung von
Musterlösungen zur Linearen Algebra II Blatt 5
 Musterlösungen zur Linearen Algebra II Blatt 5 Aufgabe. Man betrachte die Matrix A := über dem Körper R und über dem Körper F und bestimme jeweils die Jordan- Normalform. Beweis. Das charakteristische
Musterlösungen zur Linearen Algebra II Blatt 5 Aufgabe. Man betrachte die Matrix A := über dem Körper R und über dem Körper F und bestimme jeweils die Jordan- Normalform. Beweis. Das charakteristische
Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer
 Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer Allgemein: Das RSA-Verschlüsselungsverfahren ist ein häufig benutztes Verschlüsselungsverfahren, weil es sehr sicher ist. Es gehört zu der Klasse der
Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer Allgemein: Das RSA-Verschlüsselungsverfahren ist ein häufig benutztes Verschlüsselungsverfahren, weil es sehr sicher ist. Es gehört zu der Klasse der
1. Einführung. 2. Alternativen zu eigenen Auswertungen. 3. Erstellen eigener Tabellen-Auswertungen
 1. Einführung Über die Tabellen-Auswertungen können Sie eigene Auswertungen nach Ihren Wünschen erstellen. Diese Auswertungen werden immer anhand der aktuellen Daten aus orgamax ermittelt, Sie können also
1. Einführung Über die Tabellen-Auswertungen können Sie eigene Auswertungen nach Ihren Wünschen erstellen. Diese Auswertungen werden immer anhand der aktuellen Daten aus orgamax ermittelt, Sie können also
Lineare Algebra und Lösung linearer zeitinvarianter Differentialgleichungssysteme
 Übung Lineare Algebra und Lösung linearer zeitinvarianter Differentialgleichungssysteme Diese Übung beschäftigt sich mit Grundbegriffen der linearen Algebra. Im Speziellen werden lineare Abbildungen, sowie
Übung Lineare Algebra und Lösung linearer zeitinvarianter Differentialgleichungssysteme Diese Übung beschäftigt sich mit Grundbegriffen der linearen Algebra. Im Speziellen werden lineare Abbildungen, sowie
Übungen zur Experimentalphysik 3
 Übungen zur Experimentalphysik 3 Prof. Dr. L. Oberauer Wintersemester 2010/2011 7. Übungsblatt - 6.Dezember 2010 Musterlösung Franziska Konitzer (franziska.konitzer@tum.de) Aufgabe 1 ( ) (8 Punkte) Optische
Übungen zur Experimentalphysik 3 Prof. Dr. L. Oberauer Wintersemester 2010/2011 7. Übungsblatt - 6.Dezember 2010 Musterlösung Franziska Konitzer (franziska.konitzer@tum.de) Aufgabe 1 ( ) (8 Punkte) Optische
Praktikum Physik. Protokoll zum Versuch: Geometrische Optik. Durchgeführt am 24.11.2011
 Praktikum Physik Protokoll zum Versuch: Geometrische Optik Durchgeführt am 24.11.2011 Gruppe X Name1 und Name 2 (abc.xyz@uni-ulm.de) (abc.xyz@uni-ulm.de) Betreuerin: Wir bestätigen hiermit, dass wir das
Praktikum Physik Protokoll zum Versuch: Geometrische Optik Durchgeführt am 24.11.2011 Gruppe X Name1 und Name 2 (abc.xyz@uni-ulm.de) (abc.xyz@uni-ulm.de) Betreuerin: Wir bestätigen hiermit, dass wir das
A Lösungen zu Einführungsaufgaben zu QueueTraffic
 A Lösungen zu Einführungsaufgaben zu QueueTraffic 1. Selber Phasen einstellen a) Wo im Alltag: Baustelle, vor einem Zebrastreifen, Unfall... 2. Ankunftsrate und Verteilungen a) poissonverteilt: b) konstant:
A Lösungen zu Einführungsaufgaben zu QueueTraffic 1. Selber Phasen einstellen a) Wo im Alltag: Baustelle, vor einem Zebrastreifen, Unfall... 2. Ankunftsrate und Verteilungen a) poissonverteilt: b) konstant:
WinVetpro im Betriebsmodus Laptop
 WinVetpro im Betriebsmodus Laptop Um Unterwegs Daten auf einem mobilen Gerät mit WinVetpro zu erfassen, ohne den Betrieb in der Praxis während dieser Zeit zu unterbrechen und ohne eine ständige Online
WinVetpro im Betriebsmodus Laptop Um Unterwegs Daten auf einem mobilen Gerät mit WinVetpro zu erfassen, ohne den Betrieb in der Praxis während dieser Zeit zu unterbrechen und ohne eine ständige Online
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
13. Lineare DGL höherer Ordnung. Eine DGL heißt von n-ter Ordnung, wenn Ableitungen y, y, y,... bis zur n-ten Ableitung y (n) darin vorkommen.
 13. Lineare DGL höherer Ordnung. Eine DGL heißt von n-ter Ordnung, wenn Ableitungen y, y, y,... bis zur n-ten Ableitung y (n) darin vorkommen. Sie heißt linear, wenn sie die Form y (n) + a n 1 y (n 1)
13. Lineare DGL höherer Ordnung. Eine DGL heißt von n-ter Ordnung, wenn Ableitungen y, y, y,... bis zur n-ten Ableitung y (n) darin vorkommen. Sie heißt linear, wenn sie die Form y (n) + a n 1 y (n 1)
Abiturprüfung Mathematik 2008 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe Für jedes t f t () + t R ist die Funktion f t gegeben durch = mit R. Das Schaubild von f t heißt K t.. (6 Punkte)
Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe Für jedes t f t () + t R ist die Funktion f t gegeben durch = mit R. Das Schaubild von f t heißt K t.. (6 Punkte)
Repetitionsaufgaben Wurzelgleichungen
 Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Spielanleitung. Art.-Nr.: 60 610 4539 Spieleautoren: Arno Steinwender und Christoph Puhl
 Spielanleitung Art.-Nr.: 60 610 4539 Spieleautoren: Arno Steinwender und Christoph Puhl Spielangaben Spieler: 2-4 Alter: ab 10 Jahre / Erwachsene Spieleautoren: Arno Steinwender und Christoph Puhl Inhalt:
Spielanleitung Art.-Nr.: 60 610 4539 Spieleautoren: Arno Steinwender und Christoph Puhl Spielangaben Spieler: 2-4 Alter: ab 10 Jahre / Erwachsene Spieleautoren: Arno Steinwender und Christoph Puhl Inhalt:
Outlook. sysplus.ch outlook - mail-grundlagen Seite 1/8. Mail-Grundlagen. Posteingang
 sysplus.ch outlook - mail-grundlagen Seite 1/8 Outlook Mail-Grundlagen Posteingang Es gibt verschiedene Möglichkeiten, um zum Posteingang zu gelangen. Man kann links im Outlook-Fenster auf die Schaltfläche
sysplus.ch outlook - mail-grundlagen Seite 1/8 Outlook Mail-Grundlagen Posteingang Es gibt verschiedene Möglichkeiten, um zum Posteingang zu gelangen. Man kann links im Outlook-Fenster auf die Schaltfläche
n 0 1 2 3 4 5 6 7 8 9 10 11 12 S n 1250 1244, 085 1214, 075 1220, 136 1226, 167 Nach einem Jahr beträgt der Schuldenstand ca. 1177,09.
 Gymnasium Leichlingen 10a M Lö 2007/08.2 2/2 Aufgaben/Lösungen der Klassenarbeit Nr. 4 von Fr., 2008-04-25 2 45 Aufgabe 1: Die A-Bank bietet Kredite zu einem Zinssatz von 6% pro Jahr an. Ein privater Keditvermittler
Gymnasium Leichlingen 10a M Lö 2007/08.2 2/2 Aufgaben/Lösungen der Klassenarbeit Nr. 4 von Fr., 2008-04-25 2 45 Aufgabe 1: Die A-Bank bietet Kredite zu einem Zinssatz von 6% pro Jahr an. Ein privater Keditvermittler
Checkliste. zur Gesprächsvorbereitung Mitarbeitergespräch. Aktivität / Frage Handlungsbedarf erledigt
 Checkliste zur Gesprächsvorbereitung Mitarbeitergespräch Aktivität / Frage Handlungsbedarf erledigt Wissen des Mitarbeiters zu Führen mit Zielen Reicht es aus? Nein? Was muß vorbereitend getan werden?
Checkliste zur Gesprächsvorbereitung Mitarbeitergespräch Aktivität / Frage Handlungsbedarf erledigt Wissen des Mitarbeiters zu Führen mit Zielen Reicht es aus? Nein? Was muß vorbereitend getan werden?
Modellbildungssysteme: Pädagogische und didaktische Ziele
 Modellbildungssysteme: Pädagogische und didaktische Ziele Was hat Modellbildung mit der Schule zu tun? Der Bildungsplan 1994 formuliert: "Die schnelle Zunahme des Wissens, die hohe Differenzierung und
Modellbildungssysteme: Pädagogische und didaktische Ziele Was hat Modellbildung mit der Schule zu tun? Der Bildungsplan 1994 formuliert: "Die schnelle Zunahme des Wissens, die hohe Differenzierung und
Übungsaufgaben Klasse 7
 Übungsaufgaben Klasse 7 2. Oktober 2006 Dreieckskonstruktion Versuche erst, alle Aufgaben zu lösen. Die Lösungen findest du ab Montag auf: http://www.hagener-berg.de/serdar/ unter dem Punkt Schulinfos.
Übungsaufgaben Klasse 7 2. Oktober 2006 Dreieckskonstruktion Versuche erst, alle Aufgaben zu lösen. Die Lösungen findest du ab Montag auf: http://www.hagener-berg.de/serdar/ unter dem Punkt Schulinfos.
Abschlussprüfung Realschule Bayern II / III: 2009 Haupttermin B 1.0 B 1.1
 B 1.0 B 1.1 L: Wir wissen von, dass sie den Scheitel hat und durch den Punkt läuft. Was nichts bringt, ist beide Punkte in die allgemeine Parabelgleichung einzusetzen und das Gleichungssystem zu lösen,
B 1.0 B 1.1 L: Wir wissen von, dass sie den Scheitel hat und durch den Punkt läuft. Was nichts bringt, ist beide Punkte in die allgemeine Parabelgleichung einzusetzen und das Gleichungssystem zu lösen,
Euch fällt mit Sicherheit noch viel mehr ein!
 MEMOBOARD Dieses Memoboard ist vielseitig einsetzbar. Es passt in dein persönliches Nähzimmer, denn du kannst daran alle deine Ideen und Bilder sammeln. Es passt in das Büro deines Liebsten, denn er kann
MEMOBOARD Dieses Memoboard ist vielseitig einsetzbar. Es passt in dein persönliches Nähzimmer, denn du kannst daran alle deine Ideen und Bilder sammeln. Es passt in das Büro deines Liebsten, denn er kann
Rente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren Rentenperiode = Zeitabstand zwischen zwei Rentenzahlungen
 5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
Tag der Mathematik 2012
 Gruppenwettbewerb Einzelwettbewerb Mathematische Hürden Aufgaben mit en und Bepunktung Allgemeine Hinweise: Als Hilfsmittel dürfen nur Schreibzeug, Geodreieck und Zirkel benutzt werden. Taschenrechner
Gruppenwettbewerb Einzelwettbewerb Mathematische Hürden Aufgaben mit en und Bepunktung Allgemeine Hinweise: Als Hilfsmittel dürfen nur Schreibzeug, Geodreieck und Zirkel benutzt werden. Taschenrechner
Daten sammeln, darstellen, auswerten
 Vertiefen 1 Daten sammeln, darstellen, auswerten zu Aufgabe 1 Schulbuch, Seite 22 1 Haustiere zählen In der Tabelle rechts stehen die Haustiere der Kinder aus der Klasse 5b. a) Wie oft wurden die Haustiere
Vertiefen 1 Daten sammeln, darstellen, auswerten zu Aufgabe 1 Schulbuch, Seite 22 1 Haustiere zählen In der Tabelle rechts stehen die Haustiere der Kinder aus der Klasse 5b. a) Wie oft wurden die Haustiere
Formung einer Brustzugabe
 Formung einer Brustzugabe 1 Formung einer Brustzugabe Wenn du eine große Oberweite hast (in deutschen Größen etwa ab C-Körbchen), macht es Sinn, bei einem Oberteil zusätzliches Gestrick als Brustzugabe
Formung einer Brustzugabe 1 Formung einer Brustzugabe Wenn du eine große Oberweite hast (in deutschen Größen etwa ab C-Körbchen), macht es Sinn, bei einem Oberteil zusätzliches Gestrick als Brustzugabe
Korrigenda Handbuch der Bewertung
 Korrigenda Handbuch der Bewertung Kapitel 3 Abschnitt 3.5 Seite(n) 104-109 Titel Der Terminvertrag: Ein Beispiel für den Einsatz von Future Values Änderungen In den Beispielen 21 und 22 ist der Halbjahressatz
Korrigenda Handbuch der Bewertung Kapitel 3 Abschnitt 3.5 Seite(n) 104-109 Titel Der Terminvertrag: Ein Beispiel für den Einsatz von Future Values Änderungen In den Beispielen 21 und 22 ist der Halbjahressatz
6.2 Scan-Konvertierung (Scan Conversion)
 6.2 Scan-Konvertierung (Scan Conversion) Scan-Konvertierung ist die Rasterung von einfachen Objekten (Geraden, Kreisen, Kurven). Als Ausgabemedium dient meist der Bildschirm, der aus einem Pixelraster
6.2 Scan-Konvertierung (Scan Conversion) Scan-Konvertierung ist die Rasterung von einfachen Objekten (Geraden, Kreisen, Kurven). Als Ausgabemedium dient meist der Bildschirm, der aus einem Pixelraster
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen
 Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Stationsunterricht im Physikunterricht der Klasse 10
 Oranke-Oberschule Berlin (Gymnasium) Konrad-Wolf-Straße 11 13055 Berlin Frau Dr. D. Meyerhöfer Stationsunterricht im Physikunterricht der Klasse 10 Experimente zur spezifischen Wärmekapazität von Körpern
Oranke-Oberschule Berlin (Gymnasium) Konrad-Wolf-Straße 11 13055 Berlin Frau Dr. D. Meyerhöfer Stationsunterricht im Physikunterricht der Klasse 10 Experimente zur spezifischen Wärmekapazität von Körpern
Aufgabe 1. Zunächst wird die allgemeine Tangentengleichung in Abhängigkeit von a aufgestellt:
 Aufgabe 1 1.1. Bestimmung von D max : 1. Bedingung: x >0 ; da ln(x) nur für x > 0 definiert ist. 2. Bedingung: Somit ist die Funktion f a nur für x > 0 definiert und sie besitzt eine Definitionslücke an
Aufgabe 1 1.1. Bestimmung von D max : 1. Bedingung: x >0 ; da ln(x) nur für x > 0 definiert ist. 2. Bedingung: Somit ist die Funktion f a nur für x > 0 definiert und sie besitzt eine Definitionslücke an
1 Aufgabe: Absorption von Laserstrahlung
 1 Aufgabe: Absorption von Laserstrahlung Werkstoff n R n i Glas 1,5 0,0 Aluminium (300 K) 25,3 90,0 Aluminium (730 K) 36,2 48,0 Aluminium (930 K) 33,5 41,9 Kupfer 11,0 50,0 Gold 12,0 54,7 Baustahl (570
1 Aufgabe: Absorption von Laserstrahlung Werkstoff n R n i Glas 1,5 0,0 Aluminium (300 K) 25,3 90,0 Aluminium (730 K) 36,2 48,0 Aluminium (930 K) 33,5 41,9 Kupfer 11,0 50,0 Gold 12,0 54,7 Baustahl (570
Bauhinweise Dampfbad Selbstbau:
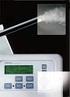 Bauhinweise Dampfbad Selbstbau: Kaiser Wellness +43 660 68 60 599 www.dampfgenerator.at office@kaiser-wellness.at Dampfbad Selbstbau Bauhinweise - Dampfbad Selbstbau: Das eigene Dampfbad, einfach selbst
Bauhinweise Dampfbad Selbstbau: Kaiser Wellness +43 660 68 60 599 www.dampfgenerator.at office@kaiser-wellness.at Dampfbad Selbstbau Bauhinweise - Dampfbad Selbstbau: Das eigene Dampfbad, einfach selbst
Die Näherung durch die Sekante durch die Punkte A und C ist schlechter, da der Punkt C weiter von A entfernt liegt.
 LÖSUNGEN TEIL 1 Arbeitszeit: 50 min Gegeben ist die Funktion f mit der Gleichung. Begründen Sie, warum die Steigung der Sekante durch die Punkte A(0 2) und C(3 11) eine weniger gute Näherung für die Tangentensteigung
LÖSUNGEN TEIL 1 Arbeitszeit: 50 min Gegeben ist die Funktion f mit der Gleichung. Begründen Sie, warum die Steigung der Sekante durch die Punkte A(0 2) und C(3 11) eine weniger gute Näherung für die Tangentensteigung
Installation OMNIKEY 3121 USB
 Installation OMNIKEY 3121 USB Vorbereitungen Installation PC/SC Treiber CT-API Treiber Einstellungen in Starke Praxis Testen des Kartenlesegeräts Vorbereitungen Bevor Sie Änderungen am System vornehmen,
Installation OMNIKEY 3121 USB Vorbereitungen Installation PC/SC Treiber CT-API Treiber Einstellungen in Starke Praxis Testen des Kartenlesegeräts Vorbereitungen Bevor Sie Änderungen am System vornehmen,
Leseprobe. Wilhelm Kleppmann. Versuchsplanung. Produkte und Prozesse optimieren ISBN: 978-3-446-42033-5. Weitere Informationen oder Bestellungen unter
 Leseprobe Wilhelm Kleppmann Versuchsplanung Produkte und Prozesse optimieren ISBN: -3-44-4033-5 Weitere Informationen oder Bestellungen unter http://www.hanser.de/-3-44-4033-5 sowie im Buchhandel. Carl
Leseprobe Wilhelm Kleppmann Versuchsplanung Produkte und Prozesse optimieren ISBN: -3-44-4033-5 Weitere Informationen oder Bestellungen unter http://www.hanser.de/-3-44-4033-5 sowie im Buchhandel. Carl
Physik1. Physik der Wärme. WS 15/16 1. Sem. B.Sc. Oec. und B.Sc. CH
 3 Physik1. Physik der Wärme. WS 15/16 1. Sem. B.Sc. Oec. und B.Sc. CH Physik Wärme 5 Themen Begriffsklärung Anwendungen Temperaturskalen Modellvorstellung Wärmeausdehnung Thermische Ausdehnung Phasenübergänge
3 Physik1. Physik der Wärme. WS 15/16 1. Sem. B.Sc. Oec. und B.Sc. CH Physik Wärme 5 Themen Begriffsklärung Anwendungen Temperaturskalen Modellvorstellung Wärmeausdehnung Thermische Ausdehnung Phasenübergänge
So gehts Schritt-für-Schritt-Anleitung
 So gehts Schritt-für-Schritt-Anleitung Software WISO Mein Büro Thema Eigene Auswertungen, Tabellenauswertungen Version/Datum V 13.00.05.101 Über die Tabellen-Auswertungen ist es möglich eigene Auswertungen
So gehts Schritt-für-Schritt-Anleitung Software WISO Mein Büro Thema Eigene Auswertungen, Tabellenauswertungen Version/Datum V 13.00.05.101 Über die Tabellen-Auswertungen ist es möglich eigene Auswertungen
= i (V) = d 2. v = d! p! n da v 1 = v 2 gilt auch d 1 ÿ p ÿ n 1 = d 2 ÿ p ÿ n 2 (III) p kürzen (Division durch p) d 1 ÿ n 1 = d 2 ÿ n 2 (IV) oder
 v = d! p! n da v 1 = v 2 (I) (II) gilt auch d 1 ÿ p ÿ n 1 = d 2 ÿ p ÿ n 2 (III) p kürzen (Division durch p) d 1 ÿ n 1 = d 2 ÿ n 2 (IV) oder i = Übersetzungsverhältnis n 1 n 2 = d 2 d 1 = i (V) Beispiel
v = d! p! n da v 1 = v 2 (I) (II) gilt auch d 1 ÿ p ÿ n 1 = d 2 ÿ p ÿ n 2 (III) p kürzen (Division durch p) d 1 ÿ n 1 = d 2 ÿ n 2 (IV) oder i = Übersetzungsverhältnis n 1 n 2 = d 2 d 1 = i (V) Beispiel
Erster Prüfungsteil: Aufgabe 1
 Erster Prüfungsteil: Aufgabe Kriterien: Der Prüfling Lösung: Punkte: a) entscheidet sich für passenden Wert 8 000 000 b) wählt ein geeignetes Verfahren zur z. B. Dreisatz Berechnung gibt das richtige Ergebnis
Erster Prüfungsteil: Aufgabe Kriterien: Der Prüfling Lösung: Punkte: a) entscheidet sich für passenden Wert 8 000 000 b) wählt ein geeignetes Verfahren zur z. B. Dreisatz Berechnung gibt das richtige Ergebnis
Download. Mathematik üben Klasse 8 Funktionen. Differenzierte Materialien für das ganze Schuljahr. Jens Conrad, Hardy Seifert
 Download Jens Conrad, Hard Seifert Mathematik üben Klasse 8 Funktionen Differenzierte Materialien für das ganze Schuljahr Downloadauszug aus dem Originaltitel: Mathematik üben Klasse 8 Funktionen Differenzierte
Download Jens Conrad, Hard Seifert Mathematik üben Klasse 8 Funktionen Differenzierte Materialien für das ganze Schuljahr Downloadauszug aus dem Originaltitel: Mathematik üben Klasse 8 Funktionen Differenzierte
Umfrage der Klasse 8c zum Thema "Smartphones"
 Umfrage der Klasse 8c zum Thema "Smartphones" Gruppe Aylin, Antonia, Lisa, Vanessa Wir haben in den Wochen der Projektarbeit eine Umfrage gemacht, bei der wir insgesamt 25 Leute befragt haben. Zuvor hatten
Umfrage der Klasse 8c zum Thema "Smartphones" Gruppe Aylin, Antonia, Lisa, Vanessa Wir haben in den Wochen der Projektarbeit eine Umfrage gemacht, bei der wir insgesamt 25 Leute befragt haben. Zuvor hatten
!(0) + o 1("). Es ist damit möglich, dass mehrere Familien geschlossener Orbits gleichzeitig abzweigen.
 Bifurkationen an geschlossenen Orbits 5.4 167 der Schnittabbldung konstruiert. Die Periode T (") der zugehörigen periodischen Lösungen ergibt sich aus =! + o 1 (") beziehungsweise Es ist also t 0 = T (")
Bifurkationen an geschlossenen Orbits 5.4 167 der Schnittabbldung konstruiert. Die Periode T (") der zugehörigen periodischen Lösungen ergibt sich aus =! + o 1 (") beziehungsweise Es ist also t 0 = T (")
Güte von Tests. die Wahrscheinlichkeit für den Fehler 2. Art bei der Testentscheidung, nämlich. falsch ist. Darauf haben wir bereits im Kapitel über
 Güte von s Grundlegendes zum Konzept der Güte Ableitung der Gütefunktion des Gauss im Einstichprobenproblem Grafische Darstellung der Gütefunktionen des Gauss im Einstichprobenproblem Ableitung der Gütefunktion
Güte von s Grundlegendes zum Konzept der Güte Ableitung der Gütefunktion des Gauss im Einstichprobenproblem Grafische Darstellung der Gütefunktionen des Gauss im Einstichprobenproblem Ableitung der Gütefunktion
Meinungen zur Altersvorsorge
 Meinungen zur Altersvorsorge Datenbasis: 1.003 Befragte ab 18 Jahren, die nicht in Rente sind Erhebungszeitraum: 19. bis 22. März 2007 statistische Fehlertoleranz: +/- 3 Prozentpunkte Auftraggeber: komm.passion
Meinungen zur Altersvorsorge Datenbasis: 1.003 Befragte ab 18 Jahren, die nicht in Rente sind Erhebungszeitraum: 19. bis 22. März 2007 statistische Fehlertoleranz: +/- 3 Prozentpunkte Auftraggeber: komm.passion
TYPO3 Tipps und Tricks
 TYPO3 Tipps und Tricks Seiten als Shortcut. Hiermit ist gemeint, dass eine Oberseite direkt auf eine tiefere Unterseite verlinkt. Dies kann bei Themen ohne gesonderte Übersichtsseite hilfreich sein. Zum
TYPO3 Tipps und Tricks Seiten als Shortcut. Hiermit ist gemeint, dass eine Oberseite direkt auf eine tiefere Unterseite verlinkt. Dies kann bei Themen ohne gesonderte Übersichtsseite hilfreich sein. Zum
Kapitel 4 Die Datenbank Kuchenbestellung Seite 1
 Kapitel 4 Die Datenbank Kuchenbestellung Seite 1 4 Die Datenbank Kuchenbestellung In diesem Kapitel werde ich die Theorie aus Kapitel 2 Die Datenbank Buchausleihe an Hand einer weiteren Datenbank Kuchenbestellung
Kapitel 4 Die Datenbank Kuchenbestellung Seite 1 4 Die Datenbank Kuchenbestellung In diesem Kapitel werde ich die Theorie aus Kapitel 2 Die Datenbank Buchausleihe an Hand einer weiteren Datenbank Kuchenbestellung
STATISTIK. Erinnere dich
 Thema Nr.20 STATISTIK Erinnere dich Die Stichprobe Drei Schüler haben folgende Noten geschrieben : Johann : 4 6 18 7 17 12 12 18 Barbara : 13 13 12 10 12 3 14 12 14 15 Julia : 15 9 14 13 10 12 12 11 10
Thema Nr.20 STATISTIK Erinnere dich Die Stichprobe Drei Schüler haben folgende Noten geschrieben : Johann : 4 6 18 7 17 12 12 18 Barbara : 13 13 12 10 12 3 14 12 14 15 Julia : 15 9 14 13 10 12 12 11 10
Thema: Winkel in der Geometrie:
 Thema: Winkel in der Geometrie: Zuerst ist es wichtig zu wissen, welche Winkel es gibt: - Nullwinkel: 0 - spitzer Winkel: 1-89 (Bild 1) - rechter Winkel: genau 90 (Bild 2) - stumpfer Winkel: 91-179 (Bild
Thema: Winkel in der Geometrie: Zuerst ist es wichtig zu wissen, welche Winkel es gibt: - Nullwinkel: 0 - spitzer Winkel: 1-89 (Bild 1) - rechter Winkel: genau 90 (Bild 2) - stumpfer Winkel: 91-179 (Bild
Grundlagen der Theoretischen Informatik, SoSe 2008
 1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
der Eingabe! Haben Sie das Ergebnis? Auf diesen schwarzen Punkt kommen wir noch zu sprechen.
 Medizintechnik MATHCAD Kapitel. Einfache Rechnungen mit MATHCAD ohne Variablendefinition In diesem kleinen Kapitel wollen wir die ersten Schritte mit MATHCAD tun und folgende Aufgaben lösen: 8 a: 5 =?
Medizintechnik MATHCAD Kapitel. Einfache Rechnungen mit MATHCAD ohne Variablendefinition In diesem kleinen Kapitel wollen wir die ersten Schritte mit MATHCAD tun und folgende Aufgaben lösen: 8 a: 5 =?
Labor Optische Messtechnik
 Fachbereich MN Fachhochschule Darmstadt Studiengang Optotechnik und Bildverarbeitung Labor Optische Messtechnik Versuch: Michelson Interferometer durchgeführt am: 30. April 003 Gruppe: Tobias Crößmann,
Fachbereich MN Fachhochschule Darmstadt Studiengang Optotechnik und Bildverarbeitung Labor Optische Messtechnik Versuch: Michelson Interferometer durchgeführt am: 30. April 003 Gruppe: Tobias Crößmann,
