Versuchsplanung. Grundlagen. Extrapolieren unzulässig! Beobachtungsbereich!
|
|
|
- Jörn Beck
- vor 8 Jahren
- Abrufe
Transkript
1 Versuchsplnung 22 CRGRAPH Grundlgen Die Aufgbe ist es Versuche so zu kombinieren, dss die Zusmmenhänge einer Funktion oder eines Prozesses bestmöglich durch eine spätere Auswertung wiedergegeben werden können. Es gibt Einflussgrößen, die gezielt vriiert werden können, ber uch oft Störgrößen, die zumindest im Versuchsumfeld kontrolliert einstellbr sein müssen. Die Wirklichkeit soll durch ein vereinfchtes Modell beschrieben werden. Dbei sind unter Umständen Nichtlinieritäten und Wechselwirkungen zu berücksichtigen. Die vereinfchten Modelle mit qudrtischen und kubischen Ansätzen können jedoch oft den relen Verluf nicht vollständig wiedergeben. Es ist im Versuchspln deshlb vorher genu zu überlegen, für welchen Extrpolieren unzulässig! Beobchtungsbereich ds Modell gelten soll. Für ein Feder-Msse-System, wie im Bild rechts drgestellt, reicht im vorderen Bereich ein qudrtischer Anstz: y ω + b ω² konst Der weitere Kurvenverluf ist dmit ber nicht gültig. Ein Extrpolieren würde völlig flsche Ergebnisse liefern. Dieses Problem ist llzu oft der Grund für ds Scheitern einer DoE Zielgröße Y Beobchtungsbereich! F m ω o 3 β 6 y^ Y m 2 f 2 ω o ( ω, , ω... 2 β 2 n ) Einflussgrößen F
2 Versuchsplnung 22 CRGRAPH Für die weitere Einführung der Versuchskombintionen soll zunächst ein linerer Zusmmenhng ngenommen werden. Zur Bestimmung nur der Einzeleinflüsse (Effekte) wird zuerst ein Versuch bei unterer Stufe jedes Fktors ls Bsis- oder Ausgngsmessung benötigt. Dnch wird jeder Fktor lleine vriiert (obere Stufe des Beobchtungsbereiches). Diese Vorgehensweise wird uch One fctor t the time" gennnt. Nebenstehendes Bild soll dies verdeutlichen. Der vordere Punkt ist die Bsismessung, die nderen stellen die obere Stufe der Fktoren A, B und C dr. Mit dieser Versuchsnordnung ist es nicht möglich, heruszufinden, wie ds System regiert, wenn mehrere Fktoren zu gleichen Zeit verändert werden. Ergibt sich z.b. bei A und B uf oberer Stufe eine überproportionle Veränderung der Zielgröße gegenüber der Summe der Einzeleffekte, so liegt eine Wechselwirkung vor. Diese Wechselwirkungen lssen sich nur mit zusätzlichen Versuchen bestimmen. Neben der fehlenden Möglichkeit hier Wechselwirkungen uswerten zu können, besteht ußerdem den Nchteil, dss eine Ungleichgewicht der Versuchsnordnung vorliegt. Die Tbelle der Versuchseinstellungen führt zu einer unerwünschten Korreltion der Fktoren. Ziel der Versuchsplnung ist es uch dies zu vermeiden, um dmit sicherzustellen, dss die Fktoren voneinnder unbhängig sind. Neben den klssischen Versuchsplänen, wie den voll- und teilfktoriellen wird in der Prxis oft ein sogennnter D- Optimler Versuchspln ngewendet. A C B D-Optimle Versuchspläne Ds Ziel von D-Optimlen Plänen ist mit minimlem Aufwnd Versuchspläne zu erstellen, die die gewünschten Effekte und Wechselwirkungen eindeutig bbilden. Dies ist ein entscheidender Vorteil gegenüber teilfktoriellen Plänen, bei denen Wechselwirkungen z.t. miteinnder vermengt sind. Mit p Anzhl Fktoren berechnet sich die Anzhl der einfchen Wechselwirkungen: p p*(p-)/2 Die höheren Wechselwirkungen (z.b. ABC, ABD, ACD, usw.) werden in der Regel nicht berücksichtigt, d ihr Einfluss gegenüber den einfchen meist geringer ist. Sie würden uch den Umfng der Versuche sprengen. Insgesmt wird für einen Versuchspln mit zwei Einstellungen folgende Anzhl Versuche benötigt: Konstnte : Hupteffekte (Fktoren) : p Wechselwirkungen : p*(p-)/2 Σ : p+ p*(p-)/2+
3 Versuchsplnung 22 CRGRAPH Im Flle eines qudrtischen Modells kommen noch einml p Versuche hinzu (mit mittlerer Einstellung). Weiterhin werden c. Versuche benötigt, um genügend Informtion über die Streuungen zu erhlten (Signifiknzen der Fktoren). Ein D-Optimler Pln wird nicht mit einem festem Schem generiert, sondern itertiv ufgebut. Er ht u.. folgende wichtige Eigenschften: T Mximierung der Determinnte Det( ) (Kennzhl für Auswertbrkeit) Minimierung der Korreltionen und Vertruensbereiche Möglichst gute Ausblncierung, d.h. gleiche Anzhl von Stufen (gilt nur für Rndbereiche - und +, nicht für Zwischenwerte) Insbesondere ufgrund der Zielsetzung, dss lle Wechselwirkungen bei geringer Versuchsnzhl erknnt werden sollen, verhindert dss diese Pläne vollständig orthogonl sind. D.h. gewisse Korreltionen lssen sich nicht vollständig beseitigen. In der Auswertung über Multiple Regression ist dies jedoch ein untergeordneter Nchteil. Vorteile- und Nchteile der D-optimlen Versuchspläne + Freie Whl für die Zhl der Stufen pro Einflussfktor. Die Stufenzhl knn von Fktor zu Fktor unterschiedlich gewählt werden. + Freie Whl der Stufenbstände, die äquidistnt oder nicht äquidistnt gewählt werden können. + Freie Whl für die Verteilung der Versuchspunkte im n-dimensionlen Versuchsrum + Freie Whl des mthemtischen Modells + Erweiterungsmöglichkeit durch neue Einflussfktoren Drehmoment nicht erreichbr Begrenzung + Bestimmte Einstellungen und Kombintionen können usgeschlossen werden, die nicht erreichbr sind (siehe Beispiel einer Drehmomentkurve) Drehzhl
4 Versuchsplnung 22 CRGRAPH - Der Versuchspln ist nicht orthogonl, die Abweichungen sind ber meist nur klein - Die Erstellung der Pläne ist nur mit entsprechenden Rechenlgorithmen möglich C Hinweise: Der drgestellte Grundversuchspln zur Bestimmung der Fktoren und Wechselwirkungen ist hier der Ausgngspunkt, bevor über die Determinnte weitere Versuche hinzugefügt werden. In der Litertur findet mn zur Bestimmung eines Grundversuchsplnes uch ndere Vorgehensweisen uf die hier nicht weiter eingegngen werden soll. A - B Erzeugung eines D-Optimle Versuchsplnes Es gibt verschiedene Verfhren für die Erzeugung von D- Optimlen Versuchsplänen. Diese sind insbesondere die gennnten Exchnge-Algorithmen beschrieben in /6/ und //. Eine ndere Möglichkeit ist die hier gezeigte Methode der Rndomisierung. Der Grundpln wird zunächst so ngelegt, dss die Anzhl der Stufen möglichst gut usblnciert ist (siehe Beispiel mit 3 Fktoren rechts). Bei qudrtischen, kubischen oder höherwertigeren Plänen werden die inneren Stufen (hier die ) weniger oft belegt, d die Determinnte stärker durch die ußen liegenden Einstellungen erhöht werden knn. Dnch erfolgt itertiv ein Tuschen der Positionen der Stufen uf ihren Plätzen. Dies ist besser, ls wenn durch den Zufllsgenertor der Wert der Stufen direkt festgelegt wird. Denn hierdurch wird erreicht, dss die Anzhl der unteren, oberen und mittleren Stufen erhlten bleibt. Dieser Rndomtusch wird solnge wiederholt, bis die Determinnte mximl und die Korreltion miniml ist, oder eine weitere Itertion keine nennenswerten Verbesserungen mehr bringt. A - - A - - B - - B - - C - - C - - usw Ein D-Optimlen Pln knn uch vereinfcht durch einen Grundpln mit Zustzversuchen ufgebut werden. In diesem Grundpln ist zunächst jeder Fktor lleine uf hoher Stufe. Hinzu kommen dnn noch die Kombintion der Wechselwirkungen (jeweils prweise Fktoren uf hoher Stufe). Ddurch sollen die Wechselwirkungen eindeutig bestimmbr sein. Die Zustzversuche werden uch hier über Rndomuswhl solnge usgetuscht, bis die Determinnte optiml ist. Im Folgenden soll ein nchvollziehbres Beispiel für einen einfchen D-Optimlen Pln gezeigt werden. Dieser ist zwr streng genommen nicht gnz der optimle, soll ber ds Prinzip verdeutlichen:
5 Versuchsplnung 22 CRGRAPH Beispiel: Für den Fll einer 3x3 Mtrix berechnet sich die Determinnte nch Srrus nch dem drgestellten Schem: Huptdigonle Nebendigonle Die Splten und 2 werden nochmls n die rechte Seite gesetzt. Die Determinnte D errechnet sich dnn mit: D Gesucht wird ein D-Optimler Pln mit Versuchen zur Bestimmung von 3 Huptfktoren und einer Wechselwirkung AB (Vollfktoriell Versuche). A B C A B C Vollfktorieller Versuchspln Kndidtenstz Nummer im Kndidtenstz Grundpln D-Optiml (lle Huptfktoren + Wechselwirkung AB) Gesucht: optimler Zustzversuch Im Grundpln sind bereits die Versuche 2,3,4 und us dem Kndidtenstz enthlten. Es sind nun der Reihe nch die verbleibenden Versuche,6,7 und 8 ncheinnder einzusetzen, bis die bestmöglichste Determinnte entsteht. Erster Versuch mit Kndidt : T
6 Versuchsplnung 22 CRGRAPH T ' wird Wert für Wert über folgende Formel berechnet: n k k j T i k i j x x x, ) (,, ' mit j Spltenindex, i Zeilenindex T Det( T ) ()()() + ()(-)(-) + (-)()(-) - (-)()(-) - ()(-)(-) - ()()() 2 Nächster Versuch mit Kndidt 6: 6 6 T T Det( T ) 6 ()()() + (-)(-3)(-) + (-)(-)(-3) - (-)()(-) - ()(-3)(-3) - (-)(- )() 64 Ws ein erheblich schlechterer Wert ist, ls mit Kndidt. Insgesmt errechnen sich für die weiteren Kndidten folgende Determinnten: Kndidt Det( T ) Somit bildet entweder Kndidt oder 8 die optimle Determinnte. Hinweis: Im Grundpln müsste eigentlich ein weiterer Versuch zur Bestimmung der Konstnten enthlten sein. Dieser wurde hier unterschlgen. In Hinblick uf einen möglichst einfchen Aufbu um Umfng wurde dieses Beispiel bewusst reduziert gehlten. Zur Auswertung der Mtrix siehe uch Kpitel Multiple Regression.
7 Versuchsplnung 22 CRGRAPH Anwendung in Visul-Sel 2. In Visul-Sel gibt es unterschiedliche Möglichkeiten einen Versuchspln zu erstellen oder zu importieren. Im folgendem wird die direkte Eingbe von Fktoren beschrieben. Die weiteren Optionen sind in der Beschreibung der Systemnlyse ufgeführt.
8 Versuchsplnung 22 CRGRAPH Versuchspläne (Experimente) erstellt mn direkt im Dilogfenster unter dem Menüpunkt Dten/Versuchspläne im Huptfenster oder über die Ikone der Einstiegsmske. Eine empfehlenswerte Vorgehensweise ist jedoch über die Verwendung eines Wirkdigrmms, siehe Systemnlyse. Unter der Rubrik Fktoren werden die gewünschten unbhängigen Prmeter oder Fktoren definiert. Diese können entweder Quntittiv oder Ktegoril sein. Quntittive Fktoren können beliebige Zhlenwerte innerhlb einer festzulegenden unteren und oberen Grenze hben, die neben den Nmen einzugeben sind. Ktegorile Fktoren sind textliche Bezeichnungen für bestimmte Vorgänge oder Buteile, z.b. Liefernt A und B usw. Es können bis zu 7 ktegorile Bezeichnungen je Fktor definiert werden. Für linere Beziehungen reichen 2 Einstellungen für quntittive Größen. Für nichtlinere Zusmmenhänge müssen mindestens drei Einstellungen verwendet werden (qudrtisches Modell). Siehe hierzu uch Kpitel D-Optimle Versuchspläne. Es wird ber zunächst nur die obere und untere Stufe jedes Fktors benötigt. Durch die spätere Whl des qudrtischen Modells kommen utomtisch die Zwischenwerte hinzu. Die untere Stufe mit der kleinsten Zhl ist die Grundstellung. Alle weiteren Einstellungen kommen mindestens einml im Versuchspln vor. Sie müssen nicht gleiche Abstände hben. Nchdem die unbhängigen Fktoren bennnt wurden, ist noch die Zielgröße zu definieren. Wird diese nicht eingegeben, so erhält diese utomtisch die Bezeichnung Y. Im späteren Versuchspln wird eine leere Splte mit diesem Nmen ngefügt, in die die Ergebnisse der Versuche eingetrgen werden. Einzelne Fktoren können uch wieder gelöscht werden (Pfeiltste oberhlb Quntittiv). Zu bechten ist, dss die Anzhl der Versuche insbesondere bei vollfktoriellen Versuchsplänen mit der Anzhl der Fktoren erheblich zunimmt. In der ersten Splte des Versuchplnes steht später die Nummerierung der Versuchsreihenfolgen. Unter Umständen erfordert die Vrition einer oder mehrerer
9 Versuchsplnung 22 CRGRAPH Fktoren einen zu großen Aufwnd (z.b. wegen Mschineneinstellungen). Es sind dnn bestimmte Kombintionen hintereinnder durchzuführen. Dies erreicht mn, indem der Fktor uf schwierig einzustellen gesetzt wird. Im nächsten Schritt (Tste Weiter oder Rubrik Design) wird ds Design oder der Typ des Versuchsplnes festgelegt. Als Modell steht Liner, Wechselwirkungen, Qudrtisch und Kubisch zur Verfügung. Entsprechend der Auswhl, werden in einer Auswhlliste links die benötigten Terme hinzugefügt. Einzelne können uch wieder gelöscht werden (Pfeiltste), z.b. wenn beknnt ist, dss bestimmte Wechselwirkungen nicht vorkommen. Als Typ knn Vollfktoriell, Teilfktoriell, Tguchi, zentrl zusmmengesetzt und D-Optiml, sowie Mischung-D-Opt. gewählt werden. Weiter unten wird gleichzeitig mit der Modell- und Typuswhl die Anzhl der so gennnten Kndidten und die Anzhl der benötigten Versuche ngezeigt. Die Kndidten entsprechen immer denen des vollfktoriellen Versuchsplnes. Für ein qudrtisches Modell mit 4 Fktoren werden lso Versuche benötigt. Zusätzlich können uch noch Zentrlpunkte mit den mittleren Werten und Wiederholungen gewählt werden. Siehe hierzu Optionen. Für rein linere Beziehungen werden die orthogonlen Versuchspläne nch Tguchi empfohlen. Unter der Rubrik Anordnung können zunächst die Versuchsnordnungen für jeweils zwei Fktoren ngezeigt werden. Dbei lssen sich uch Einschränkungen (Constrins) definieren, die in der Versuchsdurchführung nicht erreichbr sind. Hierzu ist rechts eine Auswhl zu treffen, über den Bereich der nicht verwendet werden soll, (dunkelgruer Bereich). Unterhlb der Fktorennmen können die konkreten Zhlenwerte hierfür eingegeben werden. Die Stndrdvorgbe ist der jeweilige Mittelwert. Auch ktegorile Fktoren können usgeschlossen werden (letzte Auswhl unter Einschränkungen). Dies mcht jedoch nur Sinn, wenn diese zusmmen mit bedingten Einschränkungen nderer Fktoren nicht mit ufgenommen werden sollen. Ansonsten würde mn diese ktegorile Vrinte unter Fktoren erst gr nicht ufnehmen. Bedingte Einschränkungen gelten ber uch für quntittive Fktoren. Z.B. knn es sein, dss physiklisch ein Bereich eines Fktors nur nicht erreichbr ist, wenn gleichzeitig die Einstellung eines nderen Fktors dies verhindert. Nch diesen Eingben ist die Tste Neu zu drücken, um diese Einschränkungen für den Versuchspln festzuhlten. In der Liste unten links können Sie lle gemchten Einschränkungen sehen und wieder löschen. Zum Ändern vorhndener Definitionen ist eine Auswhl in der Liste nzuklicken. Dnch können Zhlenwerte oder Bereiche geändert werden. Zum Abspeichern ist die Tste Übernehmen zu drücken. Für ein und dieselbe Fktorkombintion lssen sich mehrere Einschränkungen ncheinnder definieren, z.b. Abschneiden der linken oberen und rechten unteren
10 Versuchsplnung 22 CRGRAPH Ecke. Unter der Rubrik Optionen gibt es noch eine Reihe von Einstellungen, die bei Bedrf gewählt werden können. Zusätzlich knn die untere Einstellung der Fktoren wiederholt werden. Die obere Einstellung ist im Grundversuchspln nicht enthlten und knn hinzugenommen werden. Ist zu erwrten, dss sich die Streuungen des Systems bei unterer und oberer Einstellung strk unterscheiden, so sind in beiden Wiederholungen sinnvoll. Ohne Wiederholungen mindestens einer Zustzuswhl ist keine Auswertung über den pure Error und über ein evtl. Lck of Fit möglich (siehe ANOVA in multipler Regression). Für D-Optimle Pläne gibt es weiterhin Zustzversuche zu dem Grundversuchspln. Diese sind stndrdmäßig. Siehe hierzu Kpitel D-Optimle Versuchspläne. Für ds Modell Liner und Wechselwirkungen sollte die Anzhl nicht betrgen, d sonst zu wenig Freiheitsgrde für die Bestimmung der p-vlues vorhnden sein können. Wurden bereits Versuche durchgeführt, die einbezogen werden sollen, so sind diese uf der Tbellenseite unter der Angbe Fixpunkte (Inclusions) einzugeben. In dieser Tbellenseite müssen die Fktornmen in der ersten Zeile in der Reihenfolge stehen, wie sie unter der Liste Fktoren stehen. Bei der Erstellung des Versuchsplnes wird geprüft, ob diese schon vorhnden sind. Wenn nicht, werden diese einzeln dem Versuchspln hinzugefügt. Dieses Vorgehen knn uch dzu benutzt werden, bestimmte Einstellungskombintionen explizit mit ufzunehmen. Soll zu einem bereits durchgeführten Versuchspln, ein Fktor neu hinzukommen, so ist in der Tbelle, definiert unter Fixpunkte, eine weitere Splte mit diesen Fktornmen ufzunehmen. Die Einstellung entspricht der bei den vorherigen Versuchen. D dieser Fktor bisher nicht vriiert wurde, sind in llen Zeilen ntürlich die gleichen Werten einzutrgen. Für D-Optimle Versuchspläne gibt es die Möglichkeit nstelle des Kndidtensets us dem vollfktoriellen Pln eine eigene Auswhl vorzugeben. Dmit lssen sich z.b. uch Versuchsplnvrinten kombinieren. Ist nfänglich ein zentrl zusmmengesetzter Versuchspln gewünscht, dieser ber in der Anzhl der Versuche zu groß, so knn im zweitem Schritt ein D-Optimler Pln mit Kndidtenset eines zentrl zusmmengesetzten ufgebut werden. Dieser benötigt evtl. erheblich weniger Versuche. Die Zieltbelle für den neuen Pln ist unter Allgemein dnn uf z.b. T2 zu setzen. Mn knn uch komplexere Einschränkungen und Selektionen, die mnuell us einem vollfktoriellen Versuchspln berbeitet wurden, hier verwenden. Der Nchteil ist, dss mn hierbei nicht mehr sicherstellen knn, dss die Auswertbrkeit zu % möglich ist. Demgegenüber erstellt mn einen neuen Pln unter Einbeziehung einer vorhndenen Tbelle mit Fixpunkte immer ls optimlen Versuchspln und es werden evtl. notwendig Versuche zu den vorhndenen ergänzt.
11 Versuchsplnung 22 CRGRAPH Unter Wiederholungen ist es möglich jeden Versuch in der Tbelle mehrfch drzustellen. Dies ist sinnvoll, wenn eine entsprechende Streuung der Ergebnisse erwrtet wird. In diesen Fll sind ntürlich unter Zusätzlich keine Werte > notwendig. Bei D-Optimlen Plänen knn es dbei jedoch zu Scheinkorreltionen kommen. Es empfiehlt sich die Wiederholungen in verschiedene Splten zu schreiben. Ausgewertet wird dnn der Mittelwert ym hierus und z.b. die Stndrdbweichung s bzw. ds S/N-Verhältnis nch Tguchi. Dies ermöglicht insbesondere robuste Systeme zu erstellen (siehe Beispiel..\6_Dtenuswertung\ Beispiel_Tguchi.vxg). Anstelle der Erzeugung von ym, s und S/N über Formeln, knn uch die Funktion Sttistik/Sttistic Summry verwendet werden. Der Tbellenbereich F-I8 muss dvor mrkiert sein. Besteht die Befürchtung, dss die Reihenfolge der Versuche über der Zeit (z.b. wegen Umwelteinflüsse) einen Einfluss uf die Ergebnisse ht, so ist uf jeden Fll die Einstellung der Fktoren bei Beginn der Versuche m Ende nochmls zu wiederholen. Bei der Auswertung knn evtl. uch die Splte der Versuchsreihenfolge ls Pseudofktor mit usgewertet werden. Hierzu ist in der. Splte ein Titel zu schreiben (z.b. VNr) Nch Betätigung der Tste Ok wird der Versuchspln in die unter Allgemein ngegebene Tbellenseite geschrieben. Stndrdmäßig ist dies die Tbellenseite Experiment. Ds mehrmlige Erzeugen von D-Optimlen Plänen ergibt unterschiedliche Pläne, die weitgehend gleichwertig sind. Voll- oder teilfktorielle Pläne sind immer gleich. Im Kpitel Systemnlyse wird zur Erstellung von Versuchsplänen ein nderer Weg vorgeschlgen. Hier werden die Fktoren zunächst grfisch ls Mindmp erstellt. Ist zunächst nicht klr, welche Fktoren uszuwählen sind, ist diese Vorgehensweise zu empfehlen. Nch Durchführung der Versuche und Eingbe der Ergebnisse in die letzte Splte, knn die Multiple Regression ufgerufen werden, um die Dten uszuwerten.
Vorlesung. Einführung in die mathematische Sprache und naive Mengenlehre
 Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
1KOhm + - y = x LED leuchtet wenn Schalter x gedrückt ist
 . Ohm = LED leuchtet wenn chlter gedrückt ist 2. Ohm = NICH ( = NO ) LED leuchtet wenn chlter nicht gedrückt ist = ist die Negtion von? Gibt es so einen kleinen chlter (Mikrotster)? 2. Ohm = UND LED leuchtet
. Ohm = LED leuchtet wenn chlter gedrückt ist 2. Ohm = NICH ( = NO ) LED leuchtet wenn chlter nicht gedrückt ist = ist die Negtion von? Gibt es so einen kleinen chlter (Mikrotster)? 2. Ohm = UND LED leuchtet
SPSS Clementine. Auswertung von offenen Fragen mit TextMining für Clementine. Beispiel: Haustiere
 V1.1 Auswertung von offenen Frgen mit TextMining für Clementine Beispiel: Hustiere Im Dezember 2005 ht SPSS (Schweiz) AG im Auftrg von NZZ Folio eine Online-Umfrge unter den Lesern und Leserinnen durchgeführt.
V1.1 Auswertung von offenen Frgen mit TextMining für Clementine Beispiel: Hustiere Im Dezember 2005 ht SPSS (Schweiz) AG im Auftrg von NZZ Folio eine Online-Umfrge unter den Lesern und Leserinnen durchgeführt.
Exportmodul Artikel-Nr.: 20208
 Seite 1 / 5 V5.32 Exportmodul Artikel-Nr.: 20208 Erweiterungsmodul für ds ELV-TimeMster Komplettsystem Hndbuch und Beschreibungen Ab der Version 5 befinden sich die Kurznleitung und ds gesmte Hndbuch ls
Seite 1 / 5 V5.32 Exportmodul Artikel-Nr.: 20208 Erweiterungsmodul für ds ELV-TimeMster Komplettsystem Hndbuch und Beschreibungen Ab der Version 5 befinden sich die Kurznleitung und ds gesmte Hndbuch ls
Mathematik. Name, Vorname:
 Kntonsschule Zürich Birch Fchmittelschule Aufnhmeprüfung 2007 Nme, Vornme: Nr.: Zeit: 90 Minuten erlubte Hilfsmittel: Tschenrechner us der Sekundrschule, lso weder progrmmierbr noch grfik- oder lgebrfähig
Kntonsschule Zürich Birch Fchmittelschule Aufnhmeprüfung 2007 Nme, Vornme: Nr.: Zeit: 90 Minuten erlubte Hilfsmittel: Tschenrechner us der Sekundrschule, lso weder progrmmierbr noch grfik- oder lgebrfähig
A1 Web Presence Service
 1 Im Bestellen Sie Ihr Service nächsten Schritt muss dem Web Presence Service eine zugewiesen werden. Sie können entweder eine neue registrieren, Ihre bestehende zu uns trnsferieren oder mit Ihrer extern
1 Im Bestellen Sie Ihr Service nächsten Schritt muss dem Web Presence Service eine zugewiesen werden. Sie können entweder eine neue registrieren, Ihre bestehende zu uns trnsferieren oder mit Ihrer extern
Teilfachprüfung Mathematik Studiengang: Wirtschaft Neue Diplomprüfungsordnung (NPO)
 Fchhochschule Düsseldorf SS 2007 Teilfchprüfung Mthemtik Studiengng: Wirtschft Neue Diplomprüfungsordnung (NPO) Prüfungsdtum: 29..2007 Prüfer: Prof. Dr. Horst Peters / Dipl. Volkswirt Lothr Schmeink Prüfungsform:
Fchhochschule Düsseldorf SS 2007 Teilfchprüfung Mthemtik Studiengng: Wirtschft Neue Diplomprüfungsordnung (NPO) Prüfungsdtum: 29..2007 Prüfer: Prof. Dr. Horst Peters / Dipl. Volkswirt Lothr Schmeink Prüfungsform:
Mathe Warm-Up, Teil 1 1 2
 Mthe Wrm-Up, Teil 1 1 2 HEUTE: 1. Elementre Rechenopertionen: Brüche, Potenzen, Logrithmus, Wurzeln 2. Summen- und Produktzeichen 3. Gleichungen/Ungleichungen 1 orientiert sich n den Kpiteln 3,4,6,8 des
Mthe Wrm-Up, Teil 1 1 2 HEUTE: 1. Elementre Rechenopertionen: Brüche, Potenzen, Logrithmus, Wurzeln 2. Summen- und Produktzeichen 3. Gleichungen/Ungleichungen 1 orientiert sich n den Kpiteln 3,4,6,8 des
Die Regelungen zu den Einsendeaufgaben (Einsendeschluss, Klausurzulassung) finden Sie in den Studien- und Prüfungsinformationen Heft Nr. 1.
 Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN. 7. Übung/Lösung Mathematik für Studierende der Biologie 25.11.2015
 LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR BIOLOGIE Prof. Anres Herz, Dr. Stefn Häusler emil: heusler@biologie.uni-muenchen.e Deprtment Biologie II Telefon: 089-280-74800 Großhernerstr. 2 Fx:
LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR BIOLOGIE Prof. Anres Herz, Dr. Stefn Häusler emil: heusler@biologie.uni-muenchen.e Deprtment Biologie II Telefon: 089-280-74800 Großhernerstr. 2 Fx:
Großübung zu Kräften, Momenten, Äquivalenz und Gleichgewicht
 Großübung u Kräften, omenten, Äuivlen und Gleichgewicht Der Körper Ein mterielles Teilgebiet des Universums beeichnet mn ls Körper. Im llgemeinen sind Körper deformierbr. Sonderfll strrer Körper (odellvorstellung)
Großübung u Kräften, omenten, Äuivlen und Gleichgewicht Der Körper Ein mterielles Teilgebiet des Universums beeichnet mn ls Körper. Im llgemeinen sind Körper deformierbr. Sonderfll strrer Körper (odellvorstellung)
Mathematik schriftlich
 WS KV Chur Abschlussprüfungen 00 für die Berufsmtur kufmännische Richtung Mthemtik schriftlich LÖSUNGEN Kndidtennummer Nme Vornme Dtum der Prüfung Bewertung mögliche erteilte Punkte Punkte. Aufgbe 0. Aufgbe
WS KV Chur Abschlussprüfungen 00 für die Berufsmtur kufmännische Richtung Mthemtik schriftlich LÖSUNGEN Kndidtennummer Nme Vornme Dtum der Prüfung Bewertung mögliche erteilte Punkte Punkte. Aufgbe 0. Aufgbe
1. Voraussetzung. 2. Web-Account anlegen. 3. Einloggen. 4. Kunden-Portal verwenden 5. Sub-Accounts 5.1Sub-Account anlegen. 5.2 Sub-Account bearbeiten
 Anleitung DER WEG ZUM TOLL COLLECT KUNDEN-PORTAL Inhlt 1. Vorussetzung 2. Web-Account nlegen 3. Einloggen 4. Kunden-Portl verwenden 5. Sub-Accounts 5.1Sub-Account nlegen 5.2 Sub-Account berbeiten 5.3 Sub-Account
Anleitung DER WEG ZUM TOLL COLLECT KUNDEN-PORTAL Inhlt 1. Vorussetzung 2. Web-Account nlegen 3. Einloggen 4. Kunden-Portl verwenden 5. Sub-Accounts 5.1Sub-Account nlegen 5.2 Sub-Account berbeiten 5.3 Sub-Account
Einführung in Mathcad 14.0 2011 H.
 Einführung in Mthc. H. Glvnik Eitieren von Termen Tet schreiben mit Shift " + + Nvigtion mit Leertste un Cursor + Löschen mit Shift + Entf + + 5 sin( ) + Arten von Gleichheitszeichen Definition eines Terms
Einführung in Mthc. H. Glvnik Eitieren von Termen Tet schreiben mit Shift " + + Nvigtion mit Leertste un Cursor + Löschen mit Shift + Entf + + 5 sin( ) + Arten von Gleichheitszeichen Definition eines Terms
Domäne und Bereich. Relationen zwischen Mengen/auf einer Menge. Anmerkungen zur Terminologie. r Relationen auf/in einer Menge.
 Reltionen zwischen Mengen/uf einer Menge! Eine Reltion R A B (mit A B) ist eine Reltion zwischen der Menge A und der Menge B, oder uch: von A nch B. Drstellung: c A! Wenn A = B, d.h. R A A, heißt R eine
Reltionen zwischen Mengen/uf einer Menge! Eine Reltion R A B (mit A B) ist eine Reltion zwischen der Menge A und der Menge B, oder uch: von A nch B. Drstellung: c A! Wenn A = B, d.h. R A A, heißt R eine
Canon Nikon Sony. Deutschland 55 45 25. Österreich 40 35 35. Schweiz 30 30 20. Resteuropa 60 40 30 55 45 25 40 35 35 J 30 30 20 60 40 30
 15 Mtrizenrechnung 15 Mtrizenrechnung 15.1 Mtrix ls Zhlenschem Eine Internetfirm verkuft über einen eigenen Shop Digitlkmers. Es wird jeweils nur ds Topmodel der Firmen Cnon, Nikon und Sony ngeboten. Verkuft
15 Mtrizenrechnung 15 Mtrizenrechnung 15.1 Mtrix ls Zhlenschem Eine Internetfirm verkuft über einen eigenen Shop Digitlkmers. Es wird jeweils nur ds Topmodel der Firmen Cnon, Nikon und Sony ngeboten. Verkuft
Dehnungsmessstreifen E3d
 Dehnungsmessstreifen E3d Dehnungsmessstreifen E3d Physiklisches Prktikum für Mschinenbuer Lehrstuhl für Messtechnik und Sensorik 1 Aufgbenstellung Der Versuch soll zunächst mit den grundsätzlichen Problemen
Dehnungsmessstreifen E3d Dehnungsmessstreifen E3d Physiklisches Prktikum für Mschinenbuer Lehrstuhl für Messtechnik und Sensorik 1 Aufgbenstellung Der Versuch soll zunächst mit den grundsätzlichen Problemen
Nutzung der Abwärme aus Erneuerbare-Energie-Anlagen
 5 2014 Sonderdruck us BWK 5-2014 Wichtige Kennzhlen und effiziente Plnung für die dezentrle Wärmewende Nutzung der Abwärme us Erneuerbre-Energie-Anlgen Wichtige Kennzhlen und effiziente Plnung für die
5 2014 Sonderdruck us BWK 5-2014 Wichtige Kennzhlen und effiziente Plnung für die dezentrle Wärmewende Nutzung der Abwärme us Erneuerbre-Energie-Anlgen Wichtige Kennzhlen und effiziente Plnung für die
3 Wiederholung des Bruchrechnens
 3 Wiederholung des Bruchrechnens Ein Bruch entsteht, wenn ein Gnzes in mehrere gleiche Teile zerlegt wird. Jeder Bruch besteht us dem Zähler, der Zhl über dem Bruchstrich, und dem Nenner, der Zhl unter
3 Wiederholung des Bruchrechnens Ein Bruch entsteht, wenn ein Gnzes in mehrere gleiche Teile zerlegt wird. Jeder Bruch besteht us dem Zähler, der Zhl über dem Bruchstrich, und dem Nenner, der Zhl unter
Dein Trainingsplan. sportmannschaft. ... und was sonst noch wichtig ist. Deine Zähne sind wie deine. und du bist der Trainer!
 hben Freunde Deine Zähne sind wie deine sportmnnschft und du bist der Triner! Und jeder Triner weiß, wie wichtig jeder einzelne Spieler ist eine wichtige und schöne Aufgbe! Drum sei nett zu deinen Zähnen
hben Freunde Deine Zähne sind wie deine sportmnnschft und du bist der Triner! Und jeder Triner weiß, wie wichtig jeder einzelne Spieler ist eine wichtige und schöne Aufgbe! Drum sei nett zu deinen Zähnen
Leitfaden für die Berechnung des Netzentgeltes bei der Rhein-Ruhr Verteilnetz GmbH
 Leitfden für die Berechnung des Netzentgeltes bei der Rhein-Ruhr Verteilnetz GmbH Stnd: 20.01.2012 Gültig b: 01.01.2012 Inhltsverzeichnis 1 Benötigte Dten... 3 2 Netzentgelte... 4 2.1 Entgelt für Entnhme
Leitfden für die Berechnung des Netzentgeltes bei der Rhein-Ruhr Verteilnetz GmbH Stnd: 20.01.2012 Gültig b: 01.01.2012 Inhltsverzeichnis 1 Benötigte Dten... 3 2 Netzentgelte... 4 2.1 Entgelt für Entnhme
1 Kurvendiskussion /40
 009 Herbst, (Mthemtik) Aufgbenvorschlg B Kurvendiskussion /0 Gegeben ist eine Funktion f mit der Funktionsgleichung: f ( ) 0 6 = ; mit.. Untersuchen Sie ds Verhlten der Funktionswerte von f im Unendlichen.
009 Herbst, (Mthemtik) Aufgbenvorschlg B Kurvendiskussion /0 Gegeben ist eine Funktion f mit der Funktionsgleichung: f ( ) 0 6 = ; mit.. Untersuchen Sie ds Verhlten der Funktionswerte von f im Unendlichen.
Unterrichts- und Prüfungsplanung M306 Modulverantwortlicher: Beat Kündig Modulpartner: R. Rubin
 Dokument Dtum (Version) Gültig für 200 / 0 Seite von 7 Unterrichts- und Prüfungsplnung M306 Modulverntwortlicher: Bet Kündig Modulprtner: R. Rubin Lernschritt-Nr. Hndlungsziele Zielsetzung unter Berücksichtigung
Dokument Dtum (Version) Gültig für 200 / 0 Seite von 7 Unterrichts- und Prüfungsplnung M306 Modulverntwortlicher: Bet Kündig Modulprtner: R. Rubin Lernschritt-Nr. Hndlungsziele Zielsetzung unter Berücksichtigung
Definition Suffixbaum
 Suffix-Bäume Definition Suche nch einer Menge von Mustern Längste gemeinsme Zeichenkette Pltzreduktion Suffixbäume für Muster Alle Pre Suffix-Präfix Übereinstimmung Sich wiederholende Strukturen Definition
Suffix-Bäume Definition Suche nch einer Menge von Mustern Längste gemeinsme Zeichenkette Pltzreduktion Suffixbäume für Muster Alle Pre Suffix-Präfix Übereinstimmung Sich wiederholende Strukturen Definition
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Dental-CT bei Kindern Technische Vorgehensweise und exemplarische Befunde
 Corneli Schröder, Alexnder Schumm Dentl-CT ei Kindern Technische Vorgehensweise und exemplrische Befunde Die Computertomogrphie der Zhnreihen (Dentl-CT) wird ei Kindern und Jugendlichen selten eingesetzt,
Corneli Schröder, Alexnder Schumm Dentl-CT ei Kindern Technische Vorgehensweise und exemplrische Befunde Die Computertomogrphie der Zhnreihen (Dentl-CT) wird ei Kindern und Jugendlichen selten eingesetzt,
Fallbeispiel: Eintragen einer Behandlung
 Fallbeispiel: Eintragen einer Behandlung Im ersten Beispiel gelernt, wie man einen Patienten aus der Datenbank aussucht oder falls er noch nicht in der Datenbank ist neu anlegt. Im dritten Beispiel haben
Fallbeispiel: Eintragen einer Behandlung Im ersten Beispiel gelernt, wie man einen Patienten aus der Datenbank aussucht oder falls er noch nicht in der Datenbank ist neu anlegt. Im dritten Beispiel haben
Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* aller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt:
 8. Grundlgen der Informtionstheorie 8.1 Informtionsgehlt, Entropie, Redundnz Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* ller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt: 1.
8. Grundlgen der Informtionstheorie 8.1 Informtionsgehlt, Entropie, Redundnz Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* ller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt: 1.
BÜrO HYPER aufgebautes BÜrOsYsteM
 5 JAHRE NACHKAUFGARANTIE BÜrO HYPER UFGeBUtes BÜrOsYsteM Gerundete ecken und Knten nch din-fchbericht 147 schreibtisch und ergonomische Mße nch din En 527-1 sthl-orgzrge mit verdeckter Führung, Präzisionsuszüge
5 JAHRE NACHKAUFGARANTIE BÜrO HYPER UFGeBUtes BÜrOsYsteM Gerundete ecken und Knten nch din-fchbericht 147 schreibtisch und ergonomische Mße nch din En 527-1 sthl-orgzrge mit verdeckter Führung, Präzisionsuszüge
- 1 - VB Inhaltsverzeichnis
 - - VB Inhltsverzeichnis Inhltsverzeichnis... Die Inverse einer Mtrix.... Definition der Einheitsmtrix.... Bedingung für die inverse Mtrix.... Berechnung der Inversen Mtrix..... Ds Verfhren nch Guß mit
- - VB Inhltsverzeichnis Inhltsverzeichnis... Die Inverse einer Mtrix.... Definition der Einheitsmtrix.... Bedingung für die inverse Mtrix.... Berechnung der Inversen Mtrix..... Ds Verfhren nch Guß mit
Musterlösungen (ohne Gewähr) Aufgabe 1 ( 7 Punkte) Geben Sie die Koordinaten des Flächenschwerpunktes des dargestellten Querschnitts an!
 Seite 1/15 Aufgbe 1 ( 7 Punkte) Geben Sie die Koordinten des lächenschwerpunktes des drgestellten Querschnitts n! 2 Gegeben:. 4 ΣA i = y 2 x Σx i A i = x s = Σy i A i = y s = ΣA i = 8 2 Σx i A i = 13 3
Seite 1/15 Aufgbe 1 ( 7 Punkte) Geben Sie die Koordinten des lächenschwerpunktes des drgestellten Querschnitts n! 2 Gegeben:. 4 ΣA i = y 2 x Σx i A i = x s = Σy i A i = y s = ΣA i = 8 2 Σx i A i = 13 3
Abitur - Leistungskurs Mathematik. Sachsen-Anhalt 1999
 Abitur - Leistungskurs Mthemtik Schsen-Anhlt 999 Gebiet L - Anlysis Augbe.. y, D, R,. Die Funktionenschr sei gegeben durch Die Grphen der Funktionen der Schr werden mit G bezeichnet. ) Ermitteln Sieden
Abitur - Leistungskurs Mthemtik Schsen-Anhlt 999 Gebiet L - Anlysis Augbe.. y, D, R,. Die Funktionenschr sei gegeben durch Die Grphen der Funktionen der Schr werden mit G bezeichnet. ) Ermitteln Sieden
Kreis und Kreisteile. - Aufgaben Teil 2 -
 - Aufgben Teil - Am Ende der Aufgbensmmlung finden Sie eine Formelübersicht 61. Bestimme den Inhlt 6. Bestimme den Inhlt Abhängigkeit von r. Abhängigkeit von. 63. Berechne r in Abhängigkeit von 64. Berechne
- Aufgben Teil - Am Ende der Aufgbensmmlung finden Sie eine Formelübersicht 61. Bestimme den Inhlt 6. Bestimme den Inhlt Abhängigkeit von r. Abhängigkeit von. 63. Berechne r in Abhängigkeit von 64. Berechne
Abwesenheitsnotiz im Exchange Server 2010
 Abwesenheitsnotiz im Exchange Server 2010 1.) Richten Sie die Abwesenheitsnotiz in Outlook 2010 ein und definieren Sie, an welche Absender diese gesendet werden soll. Klicken Sie dazu auf Datei -> Informationen
Abwesenheitsnotiz im Exchange Server 2010 1.) Richten Sie die Abwesenheitsnotiz in Outlook 2010 ein und definieren Sie, an welche Absender diese gesendet werden soll. Klicken Sie dazu auf Datei -> Informationen
1 topologisches Sortieren
 Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Beispiel-Abiturprüfung
 Mthemtik BeispielAbiturprüfung Prüfungsteile A und B Bewertungsschlüssel und Lösungshinweise (nicht für den Prüfling bestimmt) Die Bewertung der erbrchten Prüfungsleistungen ht sich für jede Aufgbe nch
Mthemtik BeispielAbiturprüfung Prüfungsteile A und B Bewertungsschlüssel und Lösungshinweise (nicht für den Prüfling bestimmt) Die Bewertung der erbrchten Prüfungsleistungen ht sich für jede Aufgbe nch
Erstellen von x-y-diagrammen in OpenOffice.calc
 Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
Excel Pivot-Tabellen 2010 effektiv
 7.2 Berechnete Felder Falls in der Datenquelle die Zahlen nicht in der Form vorliegen wie Sie diese benötigen, können Sie die gewünschten Ergebnisse mit Formeln berechnen. Dazu erzeugen Sie ein berechnetes
7.2 Berechnete Felder Falls in der Datenquelle die Zahlen nicht in der Form vorliegen wie Sie diese benötigen, können Sie die gewünschten Ergebnisse mit Formeln berechnen. Dazu erzeugen Sie ein berechnetes
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl. Sommersemester 2009
 UNIVERSIÄ KARLSRUHE Institut für Anlysis HDoz. Dr. P. C. Kunstmnn Dipl.-Mth. M. Uhl Sommersemester 9 Höhere Mthemti II für die Fchrichtungen Eletroingenieurwesen, Physi und Geodäsie inlusive Komplexe Anlysis
UNIVERSIÄ KARLSRUHE Institut für Anlysis HDoz. Dr. P. C. Kunstmnn Dipl.-Mth. M. Uhl Sommersemester 9 Höhere Mthemti II für die Fchrichtungen Eletroingenieurwesen, Physi und Geodäsie inlusive Komplexe Anlysis
Hausaufgabe 2 (Induktionsbeweis):
 Prof. Dr. J. Giesl Formle Sprhen, Automten, Prozesse SS 2010 Üung 3 (Age is 12.05.2010) M. Brokshmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden
Prof. Dr. J. Giesl Formle Sprhen, Automten, Prozesse SS 2010 Üung 3 (Age is 12.05.2010) M. Brokshmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden
Limit Texas Hold em. Meine persönlichen Erfahrungen
 Limit Texs Hold em Meine persönlichen Erfhrungen Dominic Dietiker c Drft dte 21. September 2010 Inhltsverzeichnis 1. Spielnleitung...................................... 1 1.1 Der Spielverluf....................................
Limit Texs Hold em Meine persönlichen Erfhrungen Dominic Dietiker c Drft dte 21. September 2010 Inhltsverzeichnis 1. Spielnleitung...................................... 1 1.1 Der Spielverluf....................................
Einrichtung Schritte:
 Einrichtung Schritte: - Installation der erforderlichen Ausstellerzertifikate Die Ausstellerzertifikate (Fehler! Verweisquelle konnte nicht gefunden werden., Fehler! Verweisquelle konnte nicht gefunden
Einrichtung Schritte: - Installation der erforderlichen Ausstellerzertifikate Die Ausstellerzertifikate (Fehler! Verweisquelle konnte nicht gefunden werden., Fehler! Verweisquelle konnte nicht gefunden
LU-Zerlegung. Zusätze zum Gelben Rechenbuch. Peter Furlan. Verlag Martina Furlan. Inhaltsverzeichnis. 1 Definitionen.
 Zusätze zum Gelben Rechenbuch LU-Zerlegung Peter Furlan Verlag Martina Furlan Inhaltsverzeichnis Definitionen 2 (Allgemeine) LU-Zerlegung 2 3 Vereinfachte LU-Zerlegung 3 4 Lösung eines linearen Gleichungssystems
Zusätze zum Gelben Rechenbuch LU-Zerlegung Peter Furlan Verlag Martina Furlan Inhaltsverzeichnis Definitionen 2 (Allgemeine) LU-Zerlegung 2 3 Vereinfachte LU-Zerlegung 3 4 Lösung eines linearen Gleichungssystems
Massenversand Dorfstrasse 143 CH - 8802 Kilchberg Telefon 01 / 716 10 00 Telefax 01 / 716 10 05 info@hp-engineering.com www.hp-engineering.
 Massenversand Massenversand Seite 1 Massenversand Seite 2 Inhaltsverzeichnis 1. WICHTIGE INFORMATIONEN ZUR BEDIENUNG VON CUMULUS 4 2. STAMMDATEN FÜR DEN MASSENVERSAND 4 2.1 ALLGEMEINE STAMMDATEN 4 2.2
Massenversand Massenversand Seite 1 Massenversand Seite 2 Inhaltsverzeichnis 1. WICHTIGE INFORMATIONEN ZUR BEDIENUNG VON CUMULUS 4 2. STAMMDATEN FÜR DEN MASSENVERSAND 4 2.1 ALLGEMEINE STAMMDATEN 4 2.2
3 Hyperbolische Geometrie
 Ausgewählte Kpitel der Geometrie 3 Hperbolische Geometrie [... ] Im Folgenden betrchten wir nun spezielle gebrochen-linere Abbildungen, nämlich solche, für die (mit den Bezeichnungen ϕ,b,c,d wie oben die
Ausgewählte Kpitel der Geometrie 3 Hperbolische Geometrie [... ] Im Folgenden betrchten wir nun spezielle gebrochen-linere Abbildungen, nämlich solche, für die (mit den Bezeichnungen ϕ,b,c,d wie oben die
Datenexport aus JS - Software
 Datenexport aus JS - Software Diese Programm-Option benötigen Sie um Kundendaten aus der JS-Software in andere Programme wie Word, Works oder Excel zu exportieren. Wählen Sie aus dem Programm-Menu unter
Datenexport aus JS - Software Diese Programm-Option benötigen Sie um Kundendaten aus der JS-Software in andere Programme wie Word, Works oder Excel zu exportieren. Wählen Sie aus dem Programm-Menu unter
Anleitung zum GUI Version 2.x
 GUI (Graphical User Interface) für PC-DMIS V3.x 4.x Seite 1 von 7 Anleitung zum GUI Version 2.x Einsatzziel des Programms: Über ein grafisches Menü PC-DMIS Messprogramme starten. Empfehlenswert für Anwender
GUI (Graphical User Interface) für PC-DMIS V3.x 4.x Seite 1 von 7 Anleitung zum GUI Version 2.x Einsatzziel des Programms: Über ein grafisches Menü PC-DMIS Messprogramme starten. Empfehlenswert für Anwender
Word 2010 Schnellbausteine
 WO.001, Version 1.0 02.04.2013 Kurzanleitung Word 2010 Schnellbausteine Word 2010 enthält eine umfangreiche Sammlung vordefinierter Bausteine, die sogenannten "Schnellbausteine". Neben den aus den früheren
WO.001, Version 1.0 02.04.2013 Kurzanleitung Word 2010 Schnellbausteine Word 2010 enthält eine umfangreiche Sammlung vordefinierter Bausteine, die sogenannten "Schnellbausteine". Neben den aus den früheren
Streuungsmaße. Grundbegriffe
 Grundbegriffe Untersuchungseinheiten U,...,U n Merkml X Urliste x,...,x n geordnete Urliste x (),...,x (n) Es gilt i.llg.: xi x() i, i, Κ, n In einer westdeutschen Großstdt gibt es insgesmt drei Träger
Grundbegriffe Untersuchungseinheiten U,...,U n Merkml X Urliste x,...,x n geordnete Urliste x (),...,x (n) Es gilt i.llg.: xi x() i, i, Κ, n In einer westdeutschen Großstdt gibt es insgesmt drei Träger
1 Einleitung. Lernziele. automatische Antworten bei Abwesenheit senden. Einstellungen für automatische Antworten Lerndauer. 4 Minuten.
 1 Einleitung Lernziele automatische Antworten bei Abwesenheit senden Einstellungen für automatische Antworten Lerndauer 4 Minuten Seite 1 von 18 2 Antworten bei Abwesenheit senden» Outlook kann während
1 Einleitung Lernziele automatische Antworten bei Abwesenheit senden Einstellungen für automatische Antworten Lerndauer 4 Minuten Seite 1 von 18 2 Antworten bei Abwesenheit senden» Outlook kann während
Reinigung 146. Reinigen des Hindernissensors. Reinigung der Projektoroberfläche. Reinigen des Projektionsfensters. Warnung. Warnung.
 Reinigung 146 Bei Verschmutzung oder Bildverschlechterung muss der Projektor gereinigt werden. Schlten Sie den Projektor vor der Reinigung us. Reinigung der Projektoroberfläche Reinigen Sie die Projektoroberfläche
Reinigung 146 Bei Verschmutzung oder Bildverschlechterung muss der Projektor gereinigt werden. Schlten Sie den Projektor vor der Reinigung us. Reinigung der Projektoroberfläche Reinigen Sie die Projektoroberfläche
LEITFADEN ZUR SCHÄTZUNG DER BEITRAGSNACHWEISE
 STOTAX GEHALT UND LOHN Stollfuß Medien LEITFADEN ZUR SCHÄTZUNG DER BEITRAGSNACHWEISE Stand 09.12.2009 Seit dem Januar 2006 hat der Gesetzgeber die Fälligkeit der SV-Beiträge vorgezogen. So kann es vorkommen,
STOTAX GEHALT UND LOHN Stollfuß Medien LEITFADEN ZUR SCHÄTZUNG DER BEITRAGSNACHWEISE Stand 09.12.2009 Seit dem Januar 2006 hat der Gesetzgeber die Fälligkeit der SV-Beiträge vorgezogen. So kann es vorkommen,
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Lehrer: Einschreibemethoden
 Lehrer: Einschreibemethoden Einschreibemethoden Für die Einschreibung in Ihren Kurs gibt es unterschiedliche Methoden. Sie können die Schüler über die Liste eingeschriebene Nutzer Ihrem Kurs zuweisen oder
Lehrer: Einschreibemethoden Einschreibemethoden Für die Einschreibung in Ihren Kurs gibt es unterschiedliche Methoden. Sie können die Schüler über die Liste eingeschriebene Nutzer Ihrem Kurs zuweisen oder
M@school Software- und Druckerzuweisung Selbstlernmaterialien
 Bildung und Sport M@school Software- und Druckerzuweisung Selbstlernmaterialien Hinweise zum Skript: LMK = Linker Mausklick RMK = Rechter Mausklick LMT = Linke Maustaste RMT = Rechte Maustaste Um die Lesbarkeit
Bildung und Sport M@school Software- und Druckerzuweisung Selbstlernmaterialien Hinweise zum Skript: LMK = Linker Mausklick RMK = Rechter Mausklick LMT = Linke Maustaste RMT = Rechte Maustaste Um die Lesbarkeit
Boole'sche Algebra. Inhaltsübersicht. Binäre Funktionen, Boole'sche Algebren, Schaltalgebra. Verknüpfungen der mathematischen Logik
 Boole'sche Algebr Binäre Funktionen, Boole'sche Algebren, Schltlgebr Inhltsübersicht Verknüpfungen der mthemtischen Logik Boole sche Algebren Grundelemente der Schltlgebr Regeln der Schltlgebr Normlformen
Boole'sche Algebr Binäre Funktionen, Boole'sche Algebren, Schltlgebr Inhltsübersicht Verknüpfungen der mthemtischen Logik Boole sche Algebren Grundelemente der Schltlgebr Regeln der Schltlgebr Normlformen
Mathematik PM Rechenarten
 Rechenrten.1 Addition Ds Pluszeichen besgt, dss mn zur Zhl die Zhl b hinzuzählt oder ddiert. Aus diesem Grunde heisst diese Rechenrt uch Addition. + b = c Summnd plus Summnd gleich Summe Kommuttivgesetz
Rechenrten.1 Addition Ds Pluszeichen besgt, dss mn zur Zhl die Zhl b hinzuzählt oder ddiert. Aus diesem Grunde heisst diese Rechenrt uch Addition. + b = c Summnd plus Summnd gleich Summe Kommuttivgesetz
1. Adressen für den Serienversand (Briefe Katalogdruck Werbung/Anfrage ) auswählen. Die Auswahl kann gespeichert werden.
 Der Serienversand Was kann man mit der Maske Serienversand machen? 1. Adressen für den Serienversand (Briefe Katalogdruck Werbung/Anfrage ) auswählen. Die Auswahl kann gespeichert werden. 2. Adressen auswählen,
Der Serienversand Was kann man mit der Maske Serienversand machen? 1. Adressen für den Serienversand (Briefe Katalogdruck Werbung/Anfrage ) auswählen. Die Auswahl kann gespeichert werden. 2. Adressen auswählen,
6. Quadratische Gleichungen
 6. Qudrtische Gleichungen 6. Vorbemerkungen Potenzieren und Wurzelziehen, somit uch Qudrieren und Ziehen der Qudrtwurzel, sind entgegengesetzte Opertionen. Sie heben sich gegenseitig uf. qudrieren Qudrtwurzel
6. Qudrtische Gleichungen 6. Vorbemerkungen Potenzieren und Wurzelziehen, somit uch Qudrieren und Ziehen der Qudrtwurzel, sind entgegengesetzte Opertionen. Sie heben sich gegenseitig uf. qudrieren Qudrtwurzel
Mit dem sogenannten Seriendruck können Etiketten und Briefe mit einer Adressdatei (z. B. Excel) verknüpft werden.
 WORD 2010 Etiketten drucken Mit dem sogenannten Seriendruck können Etiketten und Briefe mit einer Adressdatei (z. B. Excel) verknüpft werden. Diese Anwendung erfolgt über die Registerkarte Sendungen 1
WORD 2010 Etiketten drucken Mit dem sogenannten Seriendruck können Etiketten und Briefe mit einer Adressdatei (z. B. Excel) verknüpft werden. Diese Anwendung erfolgt über die Registerkarte Sendungen 1
HANDBUCH PHOENIX II - DOKUMENTENVERWALTUNG
 it4sport GmbH HANDBUCH PHOENIX II - DOKUMENTENVERWALTUNG Stand 10.07.2014 Version 2.0 1. INHALTSVERZEICHNIS 2. Abbildungsverzeichnis... 3 3. Dokumentenumfang... 4 4. Dokumente anzeigen... 5 4.1 Dokumente
it4sport GmbH HANDBUCH PHOENIX II - DOKUMENTENVERWALTUNG Stand 10.07.2014 Version 2.0 1. INHALTSVERZEICHNIS 2. Abbildungsverzeichnis... 3 3. Dokumentenumfang... 4 4. Dokumente anzeigen... 5 4.1 Dokumente
OECD Programme for International Student Assessment PISA 2000. Lösungen der Beispielaufgaben aus dem Mathematiktest. Deutschland
 OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
Schriftliche Prüfungsarbeit zum mittleren Schulabschluss 2007 im Fach Mathematik
 Sentsverwltung für Bildung, Wissenschft und Forschung Schriftliche Prüfungsrbeit zum mittleren Schulbschluss 007 im Fch Mthemtik 30. Mi 007 Arbeitsbeginn: 10.00 Uhr Berbeitungszeit: 10 Minuten Zugelssene
Sentsverwltung für Bildung, Wissenschft und Forschung Schriftliche Prüfungsrbeit zum mittleren Schulbschluss 007 im Fch Mthemtik 30. Mi 007 Arbeitsbeginn: 10.00 Uhr Berbeitungszeit: 10 Minuten Zugelssene
Installations und Bedienungsanleitung
 Instlltions und Bedienungsnleitung EKRUCBS Instlltions und Bedienungsnleitung Deutsch Inhltsverzeichnis Inhltsverzeichnis Für den Benutzer 2 1 Schltflächen 2 2 Sttussymole 2 Für den Instllteur 3 3 Üersicht:
Instlltions und Bedienungsnleitung EKRUCBS Instlltions und Bedienungsnleitung Deutsch Inhltsverzeichnis Inhltsverzeichnis Für den Benutzer 2 1 Schltflächen 2 2 Sttussymole 2 Für den Instllteur 3 3 Üersicht:
Aufgaben zur Vorlesung Analysis II Prof. Dr. Holger Dette SS 2012 Lösungen zu Blatt 6
 Aufgben zur Vorlesung Anlysis II Prof. Dr. Holger Dette SS 0 Lösungen zu Bltt 6 Aufgbe. Die Funktion f : [, ) R sei in jedem endlichen Teilintervll von [, ) Riemnnintegrierbr. Für n N sei I n := f() d.
Aufgben zur Vorlesung Anlysis II Prof. Dr. Holger Dette SS 0 Lösungen zu Bltt 6 Aufgbe. Die Funktion f : [, ) R sei in jedem endlichen Teilintervll von [, ) Riemnnintegrierbr. Für n N sei I n := f() d.
Windows. Workshop Internet-Explorer: Arbeiten mit Favoriten, Teil 1
 Workshop Internet-Explorer: Arbeiten mit Favoriten, Teil 1 Wenn der Name nicht gerade www.buch.de oder www.bmw.de heißt, sind Internetadressen oft schwer zu merken Deshalb ist es sinnvoll, die Adressen
Workshop Internet-Explorer: Arbeiten mit Favoriten, Teil 1 Wenn der Name nicht gerade www.buch.de oder www.bmw.de heißt, sind Internetadressen oft schwer zu merken Deshalb ist es sinnvoll, die Adressen
1.5 Umsatzsteuervoranmeldung
 1.5 Umsatzsteuervoranmeldung In diesem Abschnitt werden die Arbeitschritte zum Erstellen des MwSt Abrechnungsschemas erläutert. Es wird gezeigt, wie die Werte für die monatliche Umsatzsteuervoranmeldung
1.5 Umsatzsteuervoranmeldung In diesem Abschnitt werden die Arbeitschritte zum Erstellen des MwSt Abrechnungsschemas erläutert. Es wird gezeigt, wie die Werte für die monatliche Umsatzsteuervoranmeldung
Whitepaper. Produkt: combit Relationship Manager 7. combit Relationship Manager email-rückläufer Script. combit GmbH Untere Laube 30 78462 Konstanz
 combit GmbH Untere Laube 30 78462 Konstanz Whitepaper Produkt: combit Relationship Manager 7 combit Relationship Manager email-rückläufer Script Inhalt Einleitung 3 Notwendige Anpassungen 3 crm Solution
combit GmbH Untere Laube 30 78462 Konstanz Whitepaper Produkt: combit Relationship Manager 7 combit Relationship Manager email-rückläufer Script Inhalt Einleitung 3 Notwendige Anpassungen 3 crm Solution
16.3 Unterrichtsmaterialien
 16.3 Unterrichtsmterilien Vness D.l. Pfeiffer, Christine Glöggler, Stephnie Hhn und Sven Gembll Mteril 1: Alignieren von Nukleotidsequenzen für die Verwndtschftsnlyse Für eine Verwndtschftsnlyse vergleicht
16.3 Unterrichtsmterilien Vness D.l. Pfeiffer, Christine Glöggler, Stephnie Hhn und Sven Gembll Mteril 1: Alignieren von Nukleotidsequenzen für die Verwndtschftsnlyse Für eine Verwndtschftsnlyse vergleicht
Dokumentation IBIS Monitor
 Dokumentation IBIS Monitor Seite 1 von 16 11.01.06 Inhaltsverzeichnis 1. Allgemein 2. Installation und Programm starten 3. Programmkonfiguration 4. Aufzeichnung 4.1 Aufzeichnung mitschneiden 4.1.1 Inhalt
Dokumentation IBIS Monitor Seite 1 von 16 11.01.06 Inhaltsverzeichnis 1. Allgemein 2. Installation und Programm starten 3. Programmkonfiguration 4. Aufzeichnung 4.1 Aufzeichnung mitschneiden 4.1.1 Inhalt
Whitepaper. Produkt: combit factura manager. Mehrwertsteuererhöhung durchführen. combit GmbH Untere Laube 30 78462 Konstanz
 combit GmbH Untere Laube 30 78462 Konstanz Whitepaper Produkt: combit factura manager Mehrwertsteuererhöhung durchführen Mehrwertsteuererhöhung durchführen - 2 - Inhalt Aufgabenstellung 3 Allgemeine Hinweise
combit GmbH Untere Laube 30 78462 Konstanz Whitepaper Produkt: combit factura manager Mehrwertsteuererhöhung durchführen Mehrwertsteuererhöhung durchführen - 2 - Inhalt Aufgabenstellung 3 Allgemeine Hinweise
teischl.com Software Design & Services e.u. office@teischl.com www.teischl.com/booknkeep www.facebook.com/booknkeep
 teischl.com Software Design & Services e.u. office@teischl.com www.teischl.com/booknkeep www.facebook.com/booknkeep 1. Erstellen Sie ein neues Rechnungsformular Mit book n keep können Sie nun Ihre eigenen
teischl.com Software Design & Services e.u. office@teischl.com www.teischl.com/booknkeep www.facebook.com/booknkeep 1. Erstellen Sie ein neues Rechnungsformular Mit book n keep können Sie nun Ihre eigenen
Ungleichungen. Jan Pöschko. 28. Mai Einführung
 Ungleichungen Jn Pöschko 8. Mi 009 Inhltsverzeichnis Einführung. Ws sind Ungleichungen?................................. Äquivlenzumformungen..................................3 Rechnen mit Ungleichungen...............................
Ungleichungen Jn Pöschko 8. Mi 009 Inhltsverzeichnis Einführung. Ws sind Ungleichungen?................................. Äquivlenzumformungen..................................3 Rechnen mit Ungleichungen...............................
1. Einführung 2. 2. Erstellung einer Teillieferung 2. 3. Erstellung einer Teilrechnung 6
 Inhalt 1. Einführung 2 2. Erstellung einer Teillieferung 2 3. Erstellung einer Teilrechnung 6 4. Erstellung einer Sammellieferung/ Mehrere Aufträge zu einem Lieferschein zusammenfassen 11 5. Besonderheiten
Inhalt 1. Einführung 2 2. Erstellung einer Teillieferung 2 3. Erstellung einer Teilrechnung 6 4. Erstellung einer Sammellieferung/ Mehrere Aufträge zu einem Lieferschein zusammenfassen 11 5. Besonderheiten
FuxMedia Programm im Netzwerk einrichten am Beispiel von Windows 7
 FuxMedia Programm im Netzwerk einrichten am Beispiel von Windows 7 Die Installation der FuxMedia Software erfolgt erst NACH Einrichtung des Netzlaufwerks! Menüleiste einblenden, falls nicht vorhanden Die
FuxMedia Programm im Netzwerk einrichten am Beispiel von Windows 7 Die Installation der FuxMedia Software erfolgt erst NACH Einrichtung des Netzlaufwerks! Menüleiste einblenden, falls nicht vorhanden Die
Erweiterung der Aufgabe. Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen:
 VBA Programmierung mit Excel Schleifen 1/6 Erweiterung der Aufgabe Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen: Es müssen also 11 (B L) x 35 = 385 Zellen berücksichtigt
VBA Programmierung mit Excel Schleifen 1/6 Erweiterung der Aufgabe Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen: Es müssen also 11 (B L) x 35 = 385 Zellen berücksichtigt
Text Formatierung in Excel
 Text Formatierung in Excel Das Aussehen des Textes einer oder mehrerer Zellen kann in Excel über verschiedene Knöpfe beeinflusst werden. Dazu zuerst die betroffenen Zelle(n) anwählen und danach den entsprechenden
Text Formatierung in Excel Das Aussehen des Textes einer oder mehrerer Zellen kann in Excel über verschiedene Knöpfe beeinflusst werden. Dazu zuerst die betroffenen Zelle(n) anwählen und danach den entsprechenden
1 Räumliche Darstellung in Adobe Illustrator
 Räumliche Drstellung in Adobe Illustrtor 1 1 Räumliche Drstellung in Adobe Illustrtor Dieses Tutoril gibt Tips und Hinweise zur räumlichen Drstellung von einfchen Objekten, insbesondere Bewegungspfeilen.
Räumliche Drstellung in Adobe Illustrtor 1 1 Räumliche Drstellung in Adobe Illustrtor Dieses Tutoril gibt Tips und Hinweise zur räumlichen Drstellung von einfchen Objekten, insbesondere Bewegungspfeilen.
Dokumentation. estat Version 2.0
 Dokumentation estat Version 2.0 Installation Die Datei estat.xla in beliebiges Verzeichnis speichern. Im Menü Extras AddIns... Durchsuchen die Datei estat.xla auswählen. Danach das Auswahlhäkchen beim
Dokumentation estat Version 2.0 Installation Die Datei estat.xla in beliebiges Verzeichnis speichern. Im Menü Extras AddIns... Durchsuchen die Datei estat.xla auswählen. Danach das Auswahlhäkchen beim
Kurzanleitung fu r Clubbeauftragte zur Pflege der Mitgliederdaten im Mitgliederbereich
 Kurzanleitung fu r Clubbeauftragte zur Pflege der Mitgliederdaten im Mitgliederbereich Mitgliederbereich (Version 1.0) Bitte loggen Sie sich in den Mitgliederbereich mit den Ihnen bekannten Zugangsdaten
Kurzanleitung fu r Clubbeauftragte zur Pflege der Mitgliederdaten im Mitgliederbereich Mitgliederbereich (Version 1.0) Bitte loggen Sie sich in den Mitgliederbereich mit den Ihnen bekannten Zugangsdaten
Menü Macro. WinIBW2-Macros unter Windows7? Macros aufnehmen
 Menü Macro WinIBW2-Macros unter Windows7?... 1 Macros aufnehmen... 1 Menübefehle und Schaltflächen in Macros verwenden... 4 Macros bearbeiten... 4 Macros löschen... 5 Macro-Dateien... 5 Macros importieren...
Menü Macro WinIBW2-Macros unter Windows7?... 1 Macros aufnehmen... 1 Menübefehle und Schaltflächen in Macros verwenden... 4 Macros bearbeiten... 4 Macros löschen... 5 Macro-Dateien... 5 Macros importieren...
Stammdatenanlage über den Einrichtungsassistenten
 Stammdatenanlage über den Einrichtungsassistenten Schritt für Schritt zur fertig eingerichteten Hotelverwaltung mit dem Einrichtungsassistenten Bitte bereiten Sie sich, bevor Sie starten, mit der Checkliste
Stammdatenanlage über den Einrichtungsassistenten Schritt für Schritt zur fertig eingerichteten Hotelverwaltung mit dem Einrichtungsassistenten Bitte bereiten Sie sich, bevor Sie starten, mit der Checkliste
Serienbrieferstellung in Word mit Kunden-Datenimport aus Excel
 Sehr vielen Mitarbeitern fällt es schwer, Serienbriefe an Kunden zu verschicken, wenn sie die Serienbrieffunktion von Word nicht beherrschen. Wenn die Kunden mit Excel verwaltet werden, genügen nur ein
Sehr vielen Mitarbeitern fällt es schwer, Serienbriefe an Kunden zu verschicken, wenn sie die Serienbrieffunktion von Word nicht beherrschen. Wenn die Kunden mit Excel verwaltet werden, genügen nur ein
123 Familienausgleichskasse
 1 Fmilienzulgen: Anmeldung für Arbeitnehmende eines nicht beitrgspflichtigen Arbeitgebers (Anobg) Antrgstellerin / Antrgsteller Abrechnungsnummer (xxx.xxx) 123 Fmilienusgleichsksse Sozilversicherungsnstlt
1 Fmilienzulgen: Anmeldung für Arbeitnehmende eines nicht beitrgspflichtigen Arbeitgebers (Anobg) Antrgstellerin / Antrgsteller Abrechnungsnummer (xxx.xxx) 123 Fmilienusgleichsksse Sozilversicherungsnstlt
iphone- und ipad-praxis: Kalender optimal synchronisieren
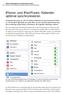 42 iphone- und ipad-praxis: Kalender optimal synchronisieren Die Synchronisierung von ios mit anderen Kalendern ist eine elementare Funktion. Die Standard-App bildet eine gute Basis, für eine optimale
42 iphone- und ipad-praxis: Kalender optimal synchronisieren Die Synchronisierung von ios mit anderen Kalendern ist eine elementare Funktion. Die Standard-App bildet eine gute Basis, für eine optimale
Lineare Algebra und Numerische Mathematik für D-BAUG
 R Käppeli L Herrmnn W Wu Herbstsemester 206 Linere Algebr und Numerische Mthemtik für D-BAUG Beispiellösung für Serie 5 ETH Zürich D-MATH Aufgbe 5 5) Seien u und v Lösungen des LGS Ax = b mit n Unbeknnten
R Käppeli L Herrmnn W Wu Herbstsemester 206 Linere Algebr und Numerische Mthemtik für D-BAUG Beispiellösung für Serie 5 ETH Zürich D-MATH Aufgbe 5 5) Seien u und v Lösungen des LGS Ax = b mit n Unbeknnten
Lineare Funktionen. 1 Proportionale Funktionen 3 1.1 Definition... 3 1.2 Eigenschaften... 3. 2 Steigungsdreieck 3
 Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
2. Im Admin Bereich drücken Sie bitte auf den roten Button Webseite bearbeiten, sodass Sie in den Bearbeitungsbereich Ihrer Homepage gelangen.
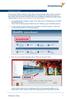 Bildergalerie einfügen Wenn Sie eine Vielzahl an Bildern zu einem Thema auf Ihre Homepage stellen möchten, steht Ihnen bei Schmetterling Quadra das Modul Bildergalerie zur Verfügung. Ihre Kunden können
Bildergalerie einfügen Wenn Sie eine Vielzahl an Bildern zu einem Thema auf Ihre Homepage stellen möchten, steht Ihnen bei Schmetterling Quadra das Modul Bildergalerie zur Verfügung. Ihre Kunden können
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
Ihr Ideen- & Projektmanagement-Tool
 Planungsbox 2.9 Ihr Ideen- & Projektmanagement-Tool Planungsbox verknüpft Notizen, Termine, Dateien, email- & Internetadressen, ToDo-Listen und Auswertungen Planungsbox verwaltet ToDo-Listen, Termine und
Planungsbox 2.9 Ihr Ideen- & Projektmanagement-Tool Planungsbox verknüpft Notizen, Termine, Dateien, email- & Internetadressen, ToDo-Listen und Auswertungen Planungsbox verwaltet ToDo-Listen, Termine und
Erstellen und Bearbeiten von Inhalten (Assets)
 Wichtig! Beachten Sie die Designrichtlinien im Kapitel Darstellung und Vorgaben zur Erstellung der Inhalte Ein Linkset erstellen Sie, wenn Sie mehrere Links gruppiert ausgeben möchten. Sie sollten diesem
Wichtig! Beachten Sie die Designrichtlinien im Kapitel Darstellung und Vorgaben zur Erstellung der Inhalte Ein Linkset erstellen Sie, wenn Sie mehrere Links gruppiert ausgeben möchten. Sie sollten diesem
Satz 6.5 (Mittelwertsatz der Integralrechnung) Sei f : [a, b] R stetig. Dann gibt es ein ξ [a, b], so dass. b a. f dx = (b a)f(ξ) f dx (b a)m.
![Satz 6.5 (Mittelwertsatz der Integralrechnung) Sei f : [a, b] R stetig. Dann gibt es ein ξ [a, b], so dass. b a. f dx = (b a)f(ξ) f dx (b a)m. Satz 6.5 (Mittelwertsatz der Integralrechnung) Sei f : [a, b] R stetig. Dann gibt es ein ξ [a, b], so dass. b a. f dx = (b a)f(ξ) f dx (b a)m.](/thumbs/74/70413961.jpg) Stz 6.5 (Mittelwertstz der Integrlrechnung) Sei f : [, b] R stetig. Dnn gibt es ein ξ [, b], so dss 9:08.06.2015 gilt. f dx = (b )f(ξ) Lemm 6.6 Sei f : [, b] R stetig und m f(x) M für lle x [, b]. Dnn
Stz 6.5 (Mittelwertstz der Integrlrechnung) Sei f : [, b] R stetig. Dnn gibt es ein ξ [, b], so dss 9:08.06.2015 gilt. f dx = (b )f(ξ) Lemm 6.6 Sei f : [, b] R stetig und m f(x) M für lle x [, b]. Dnn
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
AGROPLUS Buchhaltung. Daten-Server und Sicherheitskopie. Version vom 21.10.2013b
 AGROPLUS Buchhaltung Daten-Server und Sicherheitskopie Version vom 21.10.2013b 3a) Der Daten-Server Modus und der Tresor Der Daten-Server ist eine Betriebsart welche dem Nutzer eine grosse Flexibilität
AGROPLUS Buchhaltung Daten-Server und Sicherheitskopie Version vom 21.10.2013b 3a) Der Daten-Server Modus und der Tresor Der Daten-Server ist eine Betriebsart welche dem Nutzer eine grosse Flexibilität
Einfache Varianzanalyse für abhängige
 Einfache Varianzanalyse für abhängige Stichproben Wie beim t-test gibt es auch bei der VA eine Alternative für abhängige Stichproben. Anmerkung: Was man unter abhängigen Stichproben versteht und wie diese
Einfache Varianzanalyse für abhängige Stichproben Wie beim t-test gibt es auch bei der VA eine Alternative für abhängige Stichproben. Anmerkung: Was man unter abhängigen Stichproben versteht und wie diese
Hilfe zum Warenkorb des Elektronischen Katalogs 2007 Version 1.0
 Nutzen Sie die vielfältigen Möglichkeiten des Warenkorbes, um Ihre Bestellung/Anfrage an das für Sie zuständige Moeller-Haus zu senden, oder senden Sie den Warenkorb an den Lieferanten Ihrer Moeller-Produkte.
Nutzen Sie die vielfältigen Möglichkeiten des Warenkorbes, um Ihre Bestellung/Anfrage an das für Sie zuständige Moeller-Haus zu senden, oder senden Sie den Warenkorb an den Lieferanten Ihrer Moeller-Produkte.
Leseprobe. Wilhelm Kleppmann. Versuchsplanung. Produkte und Prozesse optimieren ISBN: 978-3-446-42033-5. Weitere Informationen oder Bestellungen unter
 Leseprobe Wilhelm Kleppmann Versuchsplanung Produkte und Prozesse optimieren ISBN: -3-44-4033-5 Weitere Informationen oder Bestellungen unter http://www.hanser.de/-3-44-4033-5 sowie im Buchhandel. Carl
Leseprobe Wilhelm Kleppmann Versuchsplanung Produkte und Prozesse optimieren ISBN: -3-44-4033-5 Weitere Informationen oder Bestellungen unter http://www.hanser.de/-3-44-4033-5 sowie im Buchhandel. Carl
teamsync Kurzanleitung
 1 teamsync Kurzanleitung Version 4.0-19. November 2012 2 1 Einleitung Mit teamsync können Sie die Produkte teamspace und projectfacts mit Microsoft Outlook synchronisieren.laden Sie sich teamsync hier
1 teamsync Kurzanleitung Version 4.0-19. November 2012 2 1 Einleitung Mit teamsync können Sie die Produkte teamspace und projectfacts mit Microsoft Outlook synchronisieren.laden Sie sich teamsync hier
Präfixcodes und der Huffman Algorithmus
 Präfixcodes und der Huffmn Algorithmus Präfixcodes und Codebäume Im Folgenden werden wir Codes untersuchen, die in der Regel keine Blockcodes sind. In diesem Fll können Codewörter verschiedene Länge hben
Präfixcodes und der Huffmn Algorithmus Präfixcodes und Codebäume Im Folgenden werden wir Codes untersuchen, die in der Regel keine Blockcodes sind. In diesem Fll können Codewörter verschiedene Länge hben
