Limit Texas Hold em. Meine persönlichen Erfahrungen
|
|
|
- Andrea Kurzmann
- vor 8 Jahren
- Abrufe
Transkript
1 Limit Texs Hold em Meine persönlichen Erfhrungen Dominic Dietiker c Drft dte 21. September 2010
2 Inhltsverzeichnis 1. Spielnleitung Der Spielverluf Die Limit-Struktur Rnk of Hnds Royl Flush Stright Flush Four of Kind Full House Flush Stright Three of Kind Two Pir One Pir High Crd A. Sttistiken A.1 Overpir Tbelle B. Nützliche Formeln B.1 Prozent zu Odds Formel B.2 Odds zu Prozent Formel B. Odds zu Bruch B.4 Bruch zu Odds Formel ii
3 Abbildungsverzeichnis 1.1 Rnk of Hnds iii
4 Tbellenverzeichnis 1.1 Fixierte Einsätze bei $5-$10 Limit Hold em Gängige Limit-Strukturen in U.S. Crdrooms & Csinos A.1 Preflop Overpir Whrscheinlichkeiten bei N Gegnern iv
5 Spielnleitung In diesem Kpitel Der Spielverluf Die Limit-Struktur Rnk of Hnds Royl Flush Stright Flush Four of Kind Full House Flush Stright Three of Kind Two Pir One Pir High Crd Wie funktioniert Limit Hold em? Ws bedeutet ds Wörtchen Limit? Ws ist der Unterschied zwischen No-Limit Hold em und Limit Hold em?... diesen und weitere Frgen wollen wir uns in diesem Kpitel widmen und uns mit x vertrut mchen. 1
6 Kpitel 1: Spielnleitung 1.1 Der Spielverluf Der Del Zuerst bestimmt mn einen Deler (weißer Deler-Button). Bevor die Krten usgeteilt werden zhlen die beiden nächsten Spieler links vom Deler den Smll Blind und den Big Blind. Dnn bekommen lle Spieler zwei Krten. Die erste Wettrunde (Pre-Flop) Der Spieler links vom Big Blind ist UTG (under the gun) und ht die Optionen check, bet oder fold. Nchdem jemnd gewettet ht, ht der nächste Spieler die Optionen fold, cll oder rise. Wenn die Wetten eglisiert sind, teilt der Deler eine Burn-Crd 1 us und die nächsten drei Krten für den Flop. Die zweite Wettrunde (Post-Flop) Der Spieler links vom Deler ist jetzt für die weiteren drei Wettrunden UTG und ht die Optionen check oder bet. Nchdem jemnd gewettet ht, ht der nächste Spieler die Optionen fold, cll oder rise. Wenn die Wetten eglisiert sind, teilt der Deler eine Burn-Crd us und die nächste Krte für den Turn. Die dritte Wettrunde (Turn) Der Spieler links vom Deler ist UTG. Nchdem jemnd gewettet ht, ht der nächste Spieler die Optionen fold, cll oder rise. Achtung: Die Einsätze sind jetzt bei der Lrge Bet Size. Sind die Wetten eglisiert, teilt der Deler eine Burn-Crd us und die nächste Krte für den River. Die vierte Wettrunde (River) Der Spieler links vom Deler ist UTG. Flls Wetten eglisiert sind, deckt der Mnn der gewettet oder den letzten Rise gebrcht ht, die Krten beim Showdown zuerst uf, weitere Teilnehmer im Uhrzeigersinn. Die nächste Spielrunde Der Spieler links vom Deler wird zum Deler. 1 Eine Krte zu burnen bedeutet, diese nicht zu verwenden 1.1. Der Spielverluf 2
7 Kpitel 1: Spielnleitung 1.2 Die Limit-Struktur Die Limit-Struktur fixiert die Höhe der Wetteinsätze in den 4 Wettrunden Pre-Flop, Post-Flop, Turn & River. Angenommen wir spielen $5-$10 Limit Hold em, dnn sind die Einsätze wie folgt: Wettrunde Bezeichnung Bet Size 1 Pre-Flop $5 2 Post-Flop $5 Turn $10 4 River $10 Tbelle 1.1: Fixierte Einsätze bei $5-$10 Limit Hold em Weitere Limit-Strukturen sind hier: Struktur Smll Bet Lrge Bet Smll Blind Big Blind $0.25-$0.50 $0.25 $0.50 $0.10 $0.25 $1-$2 $1 $2 $0.50 $1 $2-$4 $2 $4 $1 $2 $-$6 $ $6 $1 $ $5-$10 $5 $10 $2 $5 $10-$20 $10 $20 $5 $10 $15-$0 $15 $0 $10 $15 $40-$80 $40 $80 $20 $40 $75-$150 $75 $150 $50 $75 Tbelle 1.2: Gängige Limit-Strukturen in U.S. Crdrooms & Csinos 1.2. Die Limit-Struktur
8 Kpitel 1: Spielnleitung 1. Rnk of Hnds Der Wert einer us 5 Krten bestehenden Poker-Hnd bsiert uf deren mthemtischer Häufigkeit, wobei der höhere Krtenwert entscheidend ist. Frben sind gleichwertig. Ds Ass ist die höchste Krte, gefolgt von K,Q,J,T,9,8,7,6,5,4,,2. Beim Five-High-Stright (z.b A ) und beim Five-High-Stright-Flush (z.b A), knn mn ds Ass ls niederste Krte benutzen. Von der wertvollsten Kombintion zur Häufigsten ist die Reihenfolge: Royl Flush, Stright Flush, Four of Kind, Full House, Flush, Stright, Three of Kind, Two Pir, One Pir und High Crd. Royl Flush Stright Flush Four of Kind Full House Flush Stright Three of Kind Two Pir One Pir High Crd Abbildung 1.1: Rnk of Hnds Nchfolgend möchte ich die jeweiligen Rnkings mit möglichen Strting-Hnds und deren Whrscheinlichkeit, sich uf dem Flop zu relisieren, näher vorstellen. Mit diesem Anstz möchte ich Ihnen eine erste Idee vermitteln, ws die Qulität einer Strting-Hnd usmcht. 1.. Rnk of Hnds 4
9 Kpitel 1: Spielnleitung 1..1 Royl Flush Ds Royl Flush ist die höchste Strße in gleicher Frbe eigentlich ein Ace- High-Stright-Flush. Aus den Kombintionen, 5 Krten us 52 uszuwählen, ergeben genu 4 ein Royl Flush. Diese Ttsche mcht ds Royl Flush zur seltensten und somit wertvollsten Kombintion. Angenommen Sie hlten K J. Wie hoch ist dnn die Whrscheinlichkeit ein Royl Flush zu floppen? Es gibt Kombintionen Krten us den restlichen 50 Krten uszuwählen zwei Krten kennen Sie j schon. D die Frbe Spdes in unserem Beispiel schon gegeben ist, hben Sie nur die er-kombintion A Q T, welche Ihnen zum Royl Flush verhilft. Die Chncen stehen 19599:1 (0.0051%). 1 ) = 1 = % = : 1 Ds bedeutet, dß Sie mit den Hole-Crds K J von Fällen einml ein Royl Flush floppen Stright Flush Ds Stright Flush ist eine Strsse in gleicher Frbe, dessen höchste Krte kein Ass ist. Angenommen Sie hlten Suited Three-Gppers im Bereich ATs-5As wie z.b. T 6. Wieviele Flops verhelfen Ihnen dnn zu einem Stright Flush? D Ihnen in diesem Fll nur helfen, genu ein Flop us möglichen Flops: 1.. Rnk of Hnds 5
10 Kpitel 1: Spielnleitung 1 ) = 1 = % = : 1 Angenommen Sie hlten Suited Two-Gppers im Bereich KTs-52s wie z.b. T 7, dnn hben Sie bereits 2 Flops, die Ihnen zu einem Stright Flush verhelfen: J 9 8 und Die Chncen stehen 9799:1 (0.01%). 2 ) = 2 = 0.01% = 9799 : 1 Wenn Sie Suited One-Gppers im Bereich QTs-5s hlten wie z.b. 9 7, dnn hben Sie bereits Flops, die Ihnen zu einem Stright Flush helfen: J T 8, T 8 6 und Die Chncen mit 9 7 ein Stright Flush zu floppen stehen bei 65:1 (0.015%). ) = = 0.015% = to 65 : 1 Bei Suited Connectors im Bereich JTs-54s, z.b. 9 8, ergeben sich bereits 4 Flops zu einem Stright Flush: Q J T, J T 7, T 7 6 und Die Chncen mit 9 8 ein Stright Flush zu floppen stehen 4899:1 (0.02%). 4 ) = 4 = 0.02% = 4899 : 1 Fzit: Suited Connectors hben Flops mehr zum Stright-Flush ls Suited Three- Gppers. Ds mg eine pedntische Feststellung sein, ber beim Stright wird ersichtlich wieweit Connectors Gppers überlegen sind. 1.. Rnk of Hnds 6
11 Kpitel 1: Spielnleitung 1.. Four of Kind Four of Kind sind 4 Krten mit gleichem Wert und eine beliebige Krte. Angenommen Sie hlten K K. Wieviele Flops verhelfen Ihnen dnn zu Four of Kind? Es sind noch 2 Könige im restlichen Deck und wenn Sie sich frgen uf wieviele Arten mn K K mit den restlichen 48 Krten kombinieren knn, dnn hben Sie bereits die Lösung. Es gibt 48 Flops von den möglichen Flops, welche Ihnen zu Four of Kind verhelfen. Die Chncen mit K K Four of Kind zu floppen stehen bei 407:1 (0.25%). ( 2 )( 48 ) 2 1 ) = 48 = 0.25% = 407 : 1 Angenommen Sie hlten A K. Dnn helfen Ihnen nur noch 2 Flops zu Four of Kind: A A A und K K K. Die Chncen mit A K Four of Kind zu floppen stehen bei 9799:1 (0.01%). 2 ( ) ) = 2 = 0.01% = 9799 : Rnk of Hnds 7
12 Kpitel 1: Spielnleitung 1..4 Full House Ein Full House sind Krten mit gleichem Wert und ein beliebiges Pr. Angenommen Sie hlten J J. Wieviele Flops verhelfen Ihnen dnn zu einem Full House? Einer der beiden restlichen Jcks in Kombintion mit einem beliebigen Pärchen (144 Flops) oder drei gleiche Krten us den restlichen 12 Werten (48 Flops), ergeben 192 Flops. Die Chncen mit J J ein Full House zu floppen stehen bei 101:1 (1%). ( 2 )( )( 4 ) ( )( 4 ) ) = 192 = 1% = 101 : 1 Angenommen Sie hlten J 7. Dnn verhelfen Ihnen nur noch 18 Flops zu einem Full House: Zwei Krten us J J J in Kombintion mit einer Krte us oder nders herum. Die Chncen mit J 7 ein Full House zu floppen stehen bei 1088:1 (0.09%). 2 ( ) 2)( 1 ) = 18 = 0.09% = 1088 : Rnk of Hnds 8
13 Kpitel 1: Spielnleitung 1..5 Flush Ein Flush sind 5 Krten der gleichen Frbe, wobei die Reihenfolge keine Rolle spielt. Angenommen Sie hlten Suited One-Gppers wie z.b. Q T. Wieviele Flops verhelfen Ihnen dnn zu einem Flush? Jeder Flop, der lles in Clubs bringt weniger die Flops A K J, K J 9 und J 9 8 zum Stright Flush. Ds wären dnn 165 Flops - Flops. Die Chncen mit Q T ein Flush zu floppen stehen bei 120:1 (0.8%). ( 11 ) ) = 162 = 0.8% = 120 : 1 Angenommen Sie hlten A K. Dnn hben Sie genu 2 Flops mehr zum Flush ls bei Q T : Jeder Flop, der lles in Clubs bringt weniger der eine Flop Q J T zum Stright Flush. Ds wären dnn 165 Flops - 1 Flop. Die Chncen mit A K ein Flush zu floppen stehen bei 118.5:1 (0.84%). ( 11 ) 1 ) = 164 = 0.84% = : 1 A K ergibt 164 Flops und Q T 162 Flops zum Flush, d Q T mehr Stright Flush Kombintionen ht. Die Chncen uf ein Flush oder Stright Flush ist bei beiden gleich. Wenn Sie mit A K ein Flush floppen, dnn hben Sie ds Nut-Flush. Mit Q T hben Sie llerdings mehr Flops zu einem Stright: A K ht nur 6 Flops zum Stright, Q T 189 Flops. 1.. Rnk of Hnds 9
14 Kpitel 1: Spielnleitung 1..6 Stright Ein Stright ist eine Strsse in unterschiedlicher Frbe. Angenommen Sie hlten Unsuited Connectors im Bereich JT-54, z.b. J T. Wieviele Flops verhelfen Ihnen dnn zu einem Stright? Die er-kombintionen AKQ, KQ9, Q98 und 987. D jeder Krtenwert in 4 Frben vorhnden ist, knn mn jede er-kombintion uf := 4 = 64 Arten uswählen. Ds wären dnn 64 4 = 256 Flops. Die Chncen mit J T ein Stright zu floppen stehen bei 75:1 (1.%). ( 4 )( 4 1( 1) 50 ) = 256 = 1.% = 75 : Rnk of Hnds 10
15 Kpitel 1: Spielnleitung 1..7 Three of Kind Three of Kind sind drei Krten mit selbem Wert kombiniert mit zwei Krten unterschiedlichen Wertes. Angenommen Sie hlten ein Pocket-Pir z.b. T T. Dnn helfen Ihnen 2112 Flops zu Three of Kind. Die Chncen mit einem Pocket-Pir Three of Kind zu floppen stehen bei 8.:1 (10.8%). ( 2 )( )( 4 2 ) 1) = 2112 = 10.8% = 8. : 1 Angenommen Sie hlten A T. Dnn helfen Ihnen zwei Asse und jede ndere Krte usser die Zehn oder nders herum. Ds sind 264 Flops. Die Chncen mit A T Three of Kind zu floppen stehen bei 7:1 (1.5%). 2 ( 11 )( 4 ) 2)( 1 1 ) = 264 = 1.5% = 7 : Rnk of Hnds 11
16 Kpitel 1: Spielnleitung 1..8 Two Pir Two Pir sind zwei Pre. Angenommen Sie hlten Q 8. Wieviele Flops verhelfen Ihnen dnn zu Two Pir? Entweder eine Queen mit einer 8 und einer Krten von nderem Wert, oder eine Queen mit einem Pr (ber nicht 8ten) oder eine 8 mit einem Pr (ber nicht Queens). Ds sind 792 Flops. Die Chncen mit Q 8 Two Pir zu floppen stehen bei 2.7:1 (4%). ( )( )( )( 4 ) ( )( 11 )( ) 2) = 792 = 4% = 2.7 : 1 Angenommen Sie floppen entweder eine Queen oder eine 8 in Kombintion mit einem Pir uf dem Bord, dnn teilen Sie ds Bord-Pir mit den nderen Spielern. Die Chncen mit Q 8 ein Flop mit einer Queen, einer 8 und einer beliebigen Krte us den restlichen 11 Werten zu bekommen, stehen bei 48.5:1 (2%). 96 Flops. ( )( )( 11 )( ) 1) = 96 = 2% = 48.5 : Rnk of Hnds 12
17 Kpitel 1: Spielnleitung 1..9 One Pir One Pir ist ein Pr mit drei beliebigen nderen Krten. Angenommen Sie hlten 7 4. Wieviele Flops verhelfen Ihnen dnn zu einem Pr? Entweder eine 7 mit zwei nderen Krten nders 4 oder nders herum, oder ein nderes Pr in Kombintion mit einer Krte der restlichen 10 Werte Flops. Die Chncen mit 7 4 One Pir zu floppen stehen bei 1.47:1 (40.4%). 2 ( 11 )( 4 2 ( 1)( 2 1) + 11 )( 4 10 )( 4 ) 1 2)( 1 1 ) = 7920 = 40.4% = 1.47 : 1 Angenommen Sie hlten A K. Dnn ist die Whrscheinlichkeit reltiv hoch, dss Sie uf dem Flop zumindest ein Ass oder einen König treffen. Ds bedeutet: Entweder mchen Sie Top-Pir, Top-Two-Pir, ein Set, ein Full-House oder Four-of--Kind. Die Chncen: 2.08:1 (2.4%). 656 Flops 2 ( 44 ) ( 1)( )( 4 ( 2)( 1 1) + 2 ( 2)( 1) )( 4 ( 1)( 1)( 1 1) + 2 ) ) = ( 44 ) 1 ) = 656 = 2.4% = 2.08 : Rnk of Hnds 1
18 Kpitel 1: Spielnleitung High Crd Wenn Sie weder ein Pocket-Pir noch den Flop getroffen hben, dnn hben Sie High Crd. Angenommen Sie hlten A T. Dnn stehen die Chncen, dß Sie den Flop überhupt nicht treffen bei 0.87:1 (5.5%). Ds heisst: Ein Flop mit Krten von unterschiedlichem Wert, weder Ass noch Zehn, weniger die Kombintion KQJ. ) [ ( ) ( 11 1] 4 1 ) = = 5.5% = 0.87 : 1 Zusmmenfssung Im diesem Kpitel hben Sie den Spielverluf, gängige Limits und die Wertung der Hände in Limit Hold em kennengelernt. Sie wissen jetzt, dss der Turn vor dem River kommt, dss sich die Bet-Size nch dem Flop verdoppelt und ds ein Stright höher ist ls Three of Kind. 1.. Rnk of Hnds 14
19 Anhng A: Sttistiken In diesem Anhng... A.1 Overpir Tbelle
20 Anhng A: Sttistiken A.1 Overpir Tbelle Wie hoch ist die Whrscheinlichkeit, dss jemnd bei N Spielern Preflop ein Over-Pir ht, wenn Sie ein beliebiges Pocket-Pir hlten? Pocket-Pir Anzhl Gegner KK 0.49% 0.98% 1.47% 1.96% 2.44% 2.9%.4%.92% 4.40% QQ 0.98% 1.95% 2.94%.92% 4.90% 5.88% 6.86% 7.8% 8.81% JJ 1.47% 2.94% 4.41% 5.87% 7.4% 8.82% 10.28% 11.75% 1.20% TT 1.96%.92% 5.88% 7.84% 9.80% 11.74% 1.70% 15.65% 17.60% % 4.89% 7.4% 9.80% 12.2% 14.68% 17.11% 19.5% 21.95% % 5.88% 8.81% 11.74% 14.67% 17.59% 20.50% 2.9% 26.26% 77.4% 6.85% 10.28% 1.70% 17.11% 20.50% 2.87% 27.22% 0.54% 66.92% 7.84% 11.75% 15.65% 19.54% 2.9% 27.2% 1.01% 4.76% % 8.81% 1.21% 17.60% 21.96% 26.28% 0.55% 4.76% 8.91% % 9.80% 14.68% 19.54% 24.7% 29.14%.85% 8.46% 42.98% 5.9% 10.77% 16.15% 21.48% 26.78% 1.99% 7.10% 42.10% 46.95% % 11.49% 17.61% 2.42% 29.17% 4.81% 40.% 45.67% 50.81% Tbelle A.1: Preflop Overpir Whrscheinlichkeiten bei N Gegnern A.1. Overpir Tbelle 16
21 Anhng B: Nützliche Formeln In diesem Anhng... B.1 Prozent zu Odds Formel B.2 Odds zu Prozent Formel B. Odds zu Bruch B.4 Bruch zu Odds Formel
22 Anhng B: Nützliche Formeln B.1 Prozent zu Odds Formel 100 P P = : b Beispiel: Wieviel ist 27.8% in Odds? (P = 27.8) = : 1 B.2 Odds zu Prozent Formel 100 ( /b) + 1 = P Wobei der ersten und b der zweiten Zhl der Odds (odds ginst) entspricht. Beispiel: Wieviel ist 2.597:1 in Prozent? ( = 2.597, b = 1) 100 ( /1) + 1 = 27.8% B. Odds zu Bruch : b = b + b Wobei der ersten und b der zweiten Zhl der Odds (odds ginst) entspricht. b wird zum Zähler, + b zum Nenner. Beispiele: Wieviel ist 5: ls Bruch? ( = 5, b = ) 5 + = 8 Wieviel ist 2:1 ls Bruch? ( = 2, b = 1) = 1 B.1. Prozent zu Odds Formel 18
23 Anhng B: Nützliche Formeln B.4 Bruch zu Odds Formel b = (b ) : Wobei dem Zähler und b dem Nenner entspricht. Nenner minus Zähler ergibt die erste Zhl der Odds, wobei der Zähler der Zweiten entspricht. Beispiele: Wieviel ist /8 in Odds? ( =, b = 8) (8 ) : = 5 : Wieviel ist 2 / in Odds? ( = 2, b = ) ( 2) : 2 = 1 : 2 B.4. Bruch zu Odds Formel 19
24 Index C cheese siehe us goud brie R Rnk of Hnds Royl Flush Flush Four of Kind Full House One Pir Stright Stright Flush Three of Kind Two Pir
Spielerklärung. Poker. Poker
 Spielerklärung Poker Poker Herzlich willkommen bei WestSpiel Poker ist sicherlich das populärste und auch eines der spannendsten Kartenspiele der Welt. Glück allein reicht allerdings nicht, um beim Pokern
Spielerklärung Poker Poker Herzlich willkommen bei WestSpiel Poker ist sicherlich das populärste und auch eines der spannendsten Kartenspiele der Welt. Glück allein reicht allerdings nicht, um beim Pokern
Spielerklärung Ultimate Texas Hold em
 Spielerklärung Ultimate Texas Hold em Ultimate Texas Hold em ist ein spannendes Poker-Spiel mit verdeckten- und Gemeinschaftskarten. Bei dieser Pokervariante spielen die Gäste gegen die Spielbank und nicht
Spielerklärung Ultimate Texas Hold em Ultimate Texas Hold em ist ein spannendes Poker-Spiel mit verdeckten- und Gemeinschaftskarten. Bei dieser Pokervariante spielen die Gäste gegen die Spielbank und nicht
Schritte international im Beruf
 1 Ws mchen die Leute uf dem Foto? Kreuzen Sie n. Die Leute sind ei der Berufsertung. mchen zusmmen ein Seminr. hen gerde Puse. pnthermedi / Werner H. Wer sind die Leute? Ergänzen Sie. die Referentin /
1 Ws mchen die Leute uf dem Foto? Kreuzen Sie n. Die Leute sind ei der Berufsertung. mchen zusmmen ein Seminr. hen gerde Puse. pnthermedi / Werner H. Wer sind die Leute? Ergänzen Sie. die Referentin /
Die Verteidigung des Big Blind
 Die Verteidigung des Big Blind Skript zum Coaching von cjheigl 11.9.2012 In diesem Coaching: Angriff auf die Blinds: Steals und Non-Steals Typische Ranges der Angreifer nach Position Ermitteln der gegnerischen
Die Verteidigung des Big Blind Skript zum Coaching von cjheigl 11.9.2012 In diesem Coaching: Angriff auf die Blinds: Steals und Non-Steals Typische Ranges der Angreifer nach Position Ermitteln der gegnerischen
Domäne und Bereich. Relationen zwischen Mengen/auf einer Menge. Anmerkungen zur Terminologie. r Relationen auf/in einer Menge.
 Reltionen zwischen Mengen/uf einer Menge! Eine Reltion R A B (mit A B) ist eine Reltion zwischen der Menge A und der Menge B, oder uch: von A nch B. Drstellung: c A! Wenn A = B, d.h. R A A, heißt R eine
Reltionen zwischen Mengen/uf einer Menge! Eine Reltion R A B (mit A B) ist eine Reltion zwischen der Menge A und der Menge B, oder uch: von A nch B. Drstellung: c A! Wenn A = B, d.h. R A A, heißt R eine
Therapiebegleiter Kopfschmerztagebuch
 Vornme & Nchnme Therpieegleiter Kopfschmerztgeuch Liee Ptientin, lieer Ptient, Wie Können sie helfen? Bitte führen Sie regelmäßig euch m esten täglich. Trgen Sie in die Splten die jeweiligen Informtionen
Vornme & Nchnme Therpieegleiter Kopfschmerztgeuch Liee Ptientin, lieer Ptient, Wie Können sie helfen? Bitte führen Sie regelmäßig euch m esten täglich. Trgen Sie in die Splten die jeweiligen Informtionen
Mathematik. Name, Vorname:
 Kntonsschule Zürich Birch Fchmittelschule Aufnhmeprüfung 2007 Nme, Vornme: Nr.: Zeit: 90 Minuten erlubte Hilfsmittel: Tschenrechner us der Sekundrschule, lso weder progrmmierbr noch grfik- oder lgebrfähig
Kntonsschule Zürich Birch Fchmittelschule Aufnhmeprüfung 2007 Nme, Vornme: Nr.: Zeit: 90 Minuten erlubte Hilfsmittel: Tschenrechner us der Sekundrschule, lso weder progrmmierbr noch grfik- oder lgebrfähig
Vorlesung. Einführung in die mathematische Sprache und naive Mengenlehre
 Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Funktionen und Mächtigkeiten
 Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Dein Trainingsplan. sportmannschaft. ... und was sonst noch wichtig ist. Deine Zähne sind wie deine. und du bist der Trainer!
 hben Freunde Deine Zähne sind wie deine sportmnnschft und du bist der Triner! Und jeder Triner weiß, wie wichtig jeder einzelne Spieler ist eine wichtige und schöne Aufgbe! Drum sei nett zu deinen Zähnen
hben Freunde Deine Zähne sind wie deine sportmnnschft und du bist der Triner! Und jeder Triner weiß, wie wichtig jeder einzelne Spieler ist eine wichtige und schöne Aufgbe! Drum sei nett zu deinen Zähnen
123 Familienausgleichskasse
 1 Fmilienzulgen: Anmeldung für Arbeitnehmende eines nicht beitrgspflichtigen Arbeitgebers (Anobg) Antrgstellerin / Antrgsteller Abrechnungsnummer (xxx.xxx) 123 Fmilienusgleichsksse Sozilversicherungsnstlt
1 Fmilienzulgen: Anmeldung für Arbeitnehmende eines nicht beitrgspflichtigen Arbeitgebers (Anobg) Antrgstellerin / Antrgsteller Abrechnungsnummer (xxx.xxx) 123 Fmilienusgleichsksse Sozilversicherungsnstlt
3 Wiederholung des Bruchrechnens
 3 Wiederholung des Bruchrechnens Ein Bruch entsteht, wenn ein Gnzes in mehrere gleiche Teile zerlegt wird. Jeder Bruch besteht us dem Zähler, der Zhl über dem Bruchstrich, und dem Nenner, der Zhl unter
3 Wiederholung des Bruchrechnens Ein Bruch entsteht, wenn ein Gnzes in mehrere gleiche Teile zerlegt wird. Jeder Bruch besteht us dem Zähler, der Zhl über dem Bruchstrich, und dem Nenner, der Zhl unter
Mathe Warm-Up, Teil 1 1 2
 Mthe Wrm-Up, Teil 1 1 2 HEUTE: 1. Elementre Rechenopertionen: Brüche, Potenzen, Logrithmus, Wurzeln 2. Summen- und Produktzeichen 3. Gleichungen/Ungleichungen 1 orientiert sich n den Kpiteln 3,4,6,8 des
Mthe Wrm-Up, Teil 1 1 2 HEUTE: 1. Elementre Rechenopertionen: Brüche, Potenzen, Logrithmus, Wurzeln 2. Summen- und Produktzeichen 3. Gleichungen/Ungleichungen 1 orientiert sich n den Kpiteln 3,4,6,8 des
http://de.pokertips.org/rules/ by PP2000 / 2009 Seite 1
 http://de.pokertips.org/rules/ by PP2000 / 2009 Seite 1 Inhalt Die Karten... 3 Rangfolge der Pokerblätter... 4 Texas Hold em Regeln... 6 Ohama Regeln... 8 7-Card Stud Regeln... 10 Grundlagen des Bietens...
http://de.pokertips.org/rules/ by PP2000 / 2009 Seite 1 Inhalt Die Karten... 3 Rangfolge der Pokerblätter... 4 Texas Hold em Regeln... 6 Ohama Regeln... 8 7-Card Stud Regeln... 10 Grundlagen des Bietens...
1KOhm + - y = x LED leuchtet wenn Schalter x gedrückt ist
 . Ohm = LED leuchtet wenn chlter gedrückt ist 2. Ohm = NICH ( = NO ) LED leuchtet wenn chlter nicht gedrückt ist = ist die Negtion von? Gibt es so einen kleinen chlter (Mikrotster)? 2. Ohm = UND LED leuchtet
. Ohm = LED leuchtet wenn chlter gedrückt ist 2. Ohm = NICH ( = NO ) LED leuchtet wenn chlter nicht gedrückt ist = ist die Negtion von? Gibt es so einen kleinen chlter (Mikrotster)? 2. Ohm = UND LED leuchtet
Sichere E-Mail Anleitung Zertifikate / Schlüssel für Kunden der Sparkasse Germersheim-Kandel. Sichere E-Mail. der
 Sichere E-Mail der Nutzung von Zertifikaten / Schlüsseln zur sicheren Kommunikation per E-Mail mit der Sparkasse Germersheim-Kandel Inhalt: 1. Voraussetzungen... 2 2. Registrierungsprozess... 2 3. Empfang
Sichere E-Mail der Nutzung von Zertifikaten / Schlüsseln zur sicheren Kommunikation per E-Mail mit der Sparkasse Germersheim-Kandel Inhalt: 1. Voraussetzungen... 2 2. Registrierungsprozess... 2 3. Empfang
DIE IEDLE VON CATAN THEMEN-SET ZUM ARTENSPIE FÜR ZWEI SPIELER WIND & WETTER. Stefan Strohschneider Stephan Leinhäuser
 K S DIE IEDLE VON CATAN R THEMEN-SET ZUM ARTENSPIE FÜR ZWEI SPIELER L WIND & WETTER www.das-leinhaus.de Stefan Strohschneider Stephan Leinhäuser Das Themenset Wind & Wetter Idee Stefan Strohschneider hatte
K S DIE IEDLE VON CATAN R THEMEN-SET ZUM ARTENSPIE FÜR ZWEI SPIELER L WIND & WETTER www.das-leinhaus.de Stefan Strohschneider Stephan Leinhäuser Das Themenset Wind & Wetter Idee Stefan Strohschneider hatte
Schriftliche Prüfungsarbeit zum mittleren Schulabschluss 2007 im Fach Mathematik
 Sentsverwltung für Bildung, Wissenschft und Forschung Schriftliche Prüfungsrbeit zum mittleren Schulbschluss 007 im Fch Mthemtik 30. Mi 007 Arbeitsbeginn: 10.00 Uhr Berbeitungszeit: 10 Minuten Zugelssene
Sentsverwltung für Bildung, Wissenschft und Forschung Schriftliche Prüfungsrbeit zum mittleren Schulbschluss 007 im Fch Mthemtik 30. Mi 007 Arbeitsbeginn: 10.00 Uhr Berbeitungszeit: 10 Minuten Zugelssene
Erfahrungen mit Hartz IV- Empfängern
 Erfahrungen mit Hartz IV- Empfängern Ausgewählte Ergebnisse einer Befragung von Unternehmen aus den Branchen Gastronomie, Pflege und Handwerk Pressegespräch der Bundesagentur für Arbeit am 12. November
Erfahrungen mit Hartz IV- Empfängern Ausgewählte Ergebnisse einer Befragung von Unternehmen aus den Branchen Gastronomie, Pflege und Handwerk Pressegespräch der Bundesagentur für Arbeit am 12. November
Sparen in Deutschland - mit Blick über die Ländergrenzen
 Sparen in Deutschland - mit Blick über die Ländergrenzen Die wichtigsten Ergebnisse Allianz Deutschland AG, Marktforschung, September 2010 1 1 Sparverhalten allgemein 2 Gründe für das Geldsparen 3 Geldanlageformen
Sparen in Deutschland - mit Blick über die Ländergrenzen Die wichtigsten Ergebnisse Allianz Deutschland AG, Marktforschung, September 2010 1 1 Sparverhalten allgemein 2 Gründe für das Geldsparen 3 Geldanlageformen
Hardware - Software - Net zwerke
 Komprimierung der Ortho-Daten als ZIP-Archiv Dieses Dokument beschreibt die Archivierung aller Ortho-Daten als ZIP-Archiv über die MS- DOS-Eingabe-Aufforderung. Diese Information kann Ihnen zum Sichern
Komprimierung der Ortho-Daten als ZIP-Archiv Dieses Dokument beschreibt die Archivierung aller Ortho-Daten als ZIP-Archiv über die MS- DOS-Eingabe-Aufforderung. Diese Information kann Ihnen zum Sichern
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
Mathematik schriftlich
 WS KV Chur Abschlussprüfungen 00 für die Berufsmtur kufmännische Richtung Mthemtik schriftlich LÖSUNGEN Kndidtennummer Nme Vornme Dtum der Prüfung Bewertung mögliche erteilte Punkte Punkte. Aufgbe 0. Aufgbe
WS KV Chur Abschlussprüfungen 00 für die Berufsmtur kufmännische Richtung Mthemtik schriftlich LÖSUNGEN Kndidtennummer Nme Vornme Dtum der Prüfung Bewertung mögliche erteilte Punkte Punkte. Aufgbe 0. Aufgbe
Häufig gestellte Fragen (FAQ)
 An wen wende ich mich im Schadensfall? Egal für welche Versicherungsgesellschaft Sie sich entschieden haben, Sie wenden sich bitte immer an uns. Wir leiten Ihre Schadensmeldung sofort an die zuständige
An wen wende ich mich im Schadensfall? Egal für welche Versicherungsgesellschaft Sie sich entschieden haben, Sie wenden sich bitte immer an uns. Wir leiten Ihre Schadensmeldung sofort an die zuständige
1. Voraussetzung. 2. Web-Account anlegen. 3. Einloggen. 4. Kunden-Portal verwenden 5. Sub-Accounts 5.1Sub-Account anlegen. 5.2 Sub-Account bearbeiten
 Anleitung DER WEG ZUM TOLL COLLECT KUNDEN-PORTAL Inhlt 1. Vorussetzung 2. Web-Account nlegen 3. Einloggen 4. Kunden-Portl verwenden 5. Sub-Accounts 5.1Sub-Account nlegen 5.2 Sub-Account berbeiten 5.3 Sub-Account
Anleitung DER WEG ZUM TOLL COLLECT KUNDEN-PORTAL Inhlt 1. Vorussetzung 2. Web-Account nlegen 3. Einloggen 4. Kunden-Portl verwenden 5. Sub-Accounts 5.1Sub-Account nlegen 5.2 Sub-Account berbeiten 5.3 Sub-Account
Serienbrieferstellung in Word mit Kunden-Datenimport aus Excel
 Sehr vielen Mitarbeitern fällt es schwer, Serienbriefe an Kunden zu verschicken, wenn sie die Serienbrieffunktion von Word nicht beherrschen. Wenn die Kunden mit Excel verwaltet werden, genügen nur ein
Sehr vielen Mitarbeitern fällt es schwer, Serienbriefe an Kunden zu verschicken, wenn sie die Serienbrieffunktion von Word nicht beherrschen. Wenn die Kunden mit Excel verwaltet werden, genügen nur ein
SCHRITT 1: Öffnen des Bildes und Auswahl der Option»Drucken«im Menü»Datei«...2. SCHRITT 2: Angeben des Papierformat im Dialog»Drucklayout«...
 Drucken - Druckformat Frage Wie passt man Bilder beim Drucken an bestimmte Papierformate an? Antwort Das Drucken von Bildern ist mit der Druckfunktion von Capture NX sehr einfach. Hier erklären wir, wie
Drucken - Druckformat Frage Wie passt man Bilder beim Drucken an bestimmte Papierformate an? Antwort Das Drucken von Bildern ist mit der Druckfunktion von Capture NX sehr einfach. Hier erklären wir, wie
Meinungen zur Altersvorsorge
 Meinungen zur Altersvorsorge Datenbasis: 1.003 Befragte ab 18 Jahren, die nicht in Rente sind Erhebungszeitraum: 19. bis 22. März 2007 statistische Fehlertoleranz: +/- 3 Prozentpunkte Auftraggeber: komm.passion
Meinungen zur Altersvorsorge Datenbasis: 1.003 Befragte ab 18 Jahren, die nicht in Rente sind Erhebungszeitraum: 19. bis 22. März 2007 statistische Fehlertoleranz: +/- 3 Prozentpunkte Auftraggeber: komm.passion
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Die SPD und die Grünen machen im Niedersächsischen Landtag. Alle Menschen sollen in der Politik mitmachen können.
 Antrag Die SPD und die Grünen machen im Niedersächsischen Landtag einen Vorschlag: Alle Menschen sollen in der Politik mitmachen können. Menschen mit Behinderung und Menschen ohne Behinderung. Der Niedersächsische
Antrag Die SPD und die Grünen machen im Niedersächsischen Landtag einen Vorschlag: Alle Menschen sollen in der Politik mitmachen können. Menschen mit Behinderung und Menschen ohne Behinderung. Der Niedersächsische
Aufgaben zur Vorlesung Analysis II Prof. Dr. Holger Dette SS 2012 Lösungen zu Blatt 6
 Aufgben zur Vorlesung Anlysis II Prof. Dr. Holger Dette SS 0 Lösungen zu Bltt 6 Aufgbe. Die Funktion f : [, ) R sei in jedem endlichen Teilintervll von [, ) Riemnnintegrierbr. Für n N sei I n := f() d.
Aufgben zur Vorlesung Anlysis II Prof. Dr. Holger Dette SS 0 Lösungen zu Bltt 6 Aufgbe. Die Funktion f : [, ) R sei in jedem endlichen Teilintervll von [, ) Riemnnintegrierbr. Für n N sei I n := f() d.
Statuten in leichter Sprache
 Statuten in leichter Sprache Zweck vom Verein Artikel 1: Zivil-Gesetz-Buch Es gibt einen Verein der selbstbestimmung.ch heisst. Der Verein ist so aufgebaut, wie es im Zivil-Gesetz-Buch steht. Im Zivil-Gesetz-Buch
Statuten in leichter Sprache Zweck vom Verein Artikel 1: Zivil-Gesetz-Buch Es gibt einen Verein der selbstbestimmung.ch heisst. Der Verein ist so aufgebaut, wie es im Zivil-Gesetz-Buch steht. Im Zivil-Gesetz-Buch
Vorgestellt vom mexikanischen Rat für Fremdenverkehr
 Vorgestellt vom mexikanischen Rat für Fremdenverkehr Willkommen bei Explore México, die Kartenfunktion von Visitmexico.com. Unser Ziel ist es, Ihnen die Möglichkeit zu geben, sowohl den kulturellen Reichtum
Vorgestellt vom mexikanischen Rat für Fremdenverkehr Willkommen bei Explore México, die Kartenfunktion von Visitmexico.com. Unser Ziel ist es, Ihnen die Möglichkeit zu geben, sowohl den kulturellen Reichtum
Mathematik PM Rechenarten
 Rechenrten.1 Addition Ds Pluszeichen besgt, dss mn zur Zhl die Zhl b hinzuzählt oder ddiert. Aus diesem Grunde heisst diese Rechenrt uch Addition. + b = c Summnd plus Summnd gleich Summe Kommuttivgesetz
Rechenrten.1 Addition Ds Pluszeichen besgt, dss mn zur Zhl die Zhl b hinzuzählt oder ddiert. Aus diesem Grunde heisst diese Rechenrt uch Addition. + b = c Summnd plus Summnd gleich Summe Kommuttivgesetz
Installation der Demoversion vom M-Doc AutoSigner
 Mentana-Claimsoft AG Seite 1 Installation der Demoversion vom M-Doc AutoSigner Version 1.0 Mentana-Claimsoft AG Seite 2 Inhaltsverzeichnis 1 Installation der Demoversion von M-Doc AutoSigner... 3 2 Installation
Mentana-Claimsoft AG Seite 1 Installation der Demoversion vom M-Doc AutoSigner Version 1.0 Mentana-Claimsoft AG Seite 2 Inhaltsverzeichnis 1 Installation der Demoversion von M-Doc AutoSigner... 3 2 Installation
Dazu stellen Sie den Cursor in die Zeile, aus der eine Überschrift werden soll, und klicken auf die gewünschte Überschrift.
 Überschriften mit Zahlen Wenn Sie ein Stück Text als Überschrift formatieren möchten, weisen Sie diesem Text einfach das Format Überschrift 1 oder Überschrift 2 usw. zu. Dazu klicken Sie auf das Symbol
Überschriften mit Zahlen Wenn Sie ein Stück Text als Überschrift formatieren möchten, weisen Sie diesem Text einfach das Format Überschrift 1 oder Überschrift 2 usw. zu. Dazu klicken Sie auf das Symbol
Abschlussprüfung Realschule Bayern II / III: 2009 Haupttermin B 1.0 B 1.1
 B 1.0 B 1.1 L: Wir wissen von, dass sie den Scheitel hat und durch den Punkt läuft. Was nichts bringt, ist beide Punkte in die allgemeine Parabelgleichung einzusetzen und das Gleichungssystem zu lösen,
B 1.0 B 1.1 L: Wir wissen von, dass sie den Scheitel hat und durch den Punkt läuft. Was nichts bringt, ist beide Punkte in die allgemeine Parabelgleichung einzusetzen und das Gleichungssystem zu lösen,
Bestandesaufnahme und Bedürfnisanalyse
 Bestandesaufnahme und Bedürfnisanalyse Bestandesaufnahme: Wie bist du auf Nachhilfe aufmerksam gemacht worden? Wie stehst du selber hinter Nachhilfe-Unterricht? 100 % 50 % 0 % Voll und ganz, weil ich aus
Bestandesaufnahme und Bedürfnisanalyse Bestandesaufnahme: Wie bist du auf Nachhilfe aufmerksam gemacht worden? Wie stehst du selber hinter Nachhilfe-Unterricht? 100 % 50 % 0 % Voll und ganz, weil ich aus
LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN. 7. Übung/Lösung Mathematik für Studierende der Biologie 25.11.2015
 LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR BIOLOGIE Prof. Anres Herz, Dr. Stefn Häusler emil: heusler@biologie.uni-muenchen.e Deprtment Biologie II Telefon: 089-280-74800 Großhernerstr. 2 Fx:
LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR BIOLOGIE Prof. Anres Herz, Dr. Stefn Häusler emil: heusler@biologie.uni-muenchen.e Deprtment Biologie II Telefon: 089-280-74800 Großhernerstr. 2 Fx:
Leichte-Sprache-Bilder
 Leichte-Sprache-Bilder Reinhild Kassing Information - So geht es 1. Bilder gucken 2. anmelden für Probe-Bilder 3. Bilder bestellen 4. Rechnung bezahlen 5. Bilder runterladen 6. neue Bilder vorschlagen
Leichte-Sprache-Bilder Reinhild Kassing Information - So geht es 1. Bilder gucken 2. anmelden für Probe-Bilder 3. Bilder bestellen 4. Rechnung bezahlen 5. Bilder runterladen 6. neue Bilder vorschlagen
Kriterien für die Auszeichnung einer Abbaustelle
 Stnd Mi 2015 Kriterien Seite 1/2 Kriterien für die Auszeichnung einer Abbustelle GRUNDSATZ Mit dem Zertifikt werden Abbustellen usgezeichnet, die durch ihre besondere ökologische Qulität einen wichtigen
Stnd Mi 2015 Kriterien Seite 1/2 Kriterien für die Auszeichnung einer Abbustelle GRUNDSATZ Mit dem Zertifikt werden Abbustellen usgezeichnet, die durch ihre besondere ökologische Qulität einen wichtigen
Wie melde ich meinen Verein bei BOOKANDPLAY an?
 Wie melde ich meinen Verein bei BOOKANDPLAY an? Geben Sie in Ihrem Internet-Browser (bitte benutzen Sie immer Mozilla Firefox) als Adresse www.bookandplay.de ein. Anmerkung: Wir empfehlen Ihnen auch allgemein
Wie melde ich meinen Verein bei BOOKANDPLAY an? Geben Sie in Ihrem Internet-Browser (bitte benutzen Sie immer Mozilla Firefox) als Adresse www.bookandplay.de ein. Anmerkung: Wir empfehlen Ihnen auch allgemein
Stellvertretenden Genehmiger verwalten. Tipps & Tricks
 Tipps & Tricks INHALT SEITE 1. Grundlegende Informationen 3 2.1 Aktivieren eines Stellvertretenden Genehmigers 4 2.2 Deaktivieren eines Stellvertretenden Genehmigers 11 2 1. Grundlegende Informationen
Tipps & Tricks INHALT SEITE 1. Grundlegende Informationen 3 2.1 Aktivieren eines Stellvertretenden Genehmigers 4 2.2 Deaktivieren eines Stellvertretenden Genehmigers 11 2 1. Grundlegende Informationen
Der Tag hat 24 Stunden. Bitte schreibt in die linke Spalte alles auf, was ihr gestern getan habt und euch noch einfällt: War es ein stressiger
 Workshop pädagogische Tage JCBS in Sechselberg 2011 Zeitmanagement in der Schule I. Zeit- wo gehst du hin? Der Tag hat 24 Stunden. Bitte schreibt in die linke Spalte alles auf, was ihr gestern getan habt
Workshop pädagogische Tage JCBS in Sechselberg 2011 Zeitmanagement in der Schule I. Zeit- wo gehst du hin? Der Tag hat 24 Stunden. Bitte schreibt in die linke Spalte alles auf, was ihr gestern getan habt
Evangelisieren warum eigentlich?
 Predigtreihe zum Jahresthema 1/12 Evangelisieren warum eigentlich? Ich evangelisiere aus Überzeugung Gründe, warum wir nicht evangelisieren - Festes Bild von Evangelisation - Negative Erfahrungen von und
Predigtreihe zum Jahresthema 1/12 Evangelisieren warum eigentlich? Ich evangelisiere aus Überzeugung Gründe, warum wir nicht evangelisieren - Festes Bild von Evangelisation - Negative Erfahrungen von und
Teilfachprüfung Mathematik Studiengang: Wirtschaft Neue Diplomprüfungsordnung (NPO)
 Fchhochschule Düsseldorf SS 2007 Teilfchprüfung Mthemtik Studiengng: Wirtschft Neue Diplomprüfungsordnung (NPO) Prüfungsdtum: 29..2007 Prüfer: Prof. Dr. Horst Peters / Dipl. Volkswirt Lothr Schmeink Prüfungsform:
Fchhochschule Düsseldorf SS 2007 Teilfchprüfung Mthemtik Studiengng: Wirtschft Neue Diplomprüfungsordnung (NPO) Prüfungsdtum: 29..2007 Prüfer: Prof. Dr. Horst Peters / Dipl. Volkswirt Lothr Schmeink Prüfungsform:
Daten-Synchronisation zwischen dem ZDV-Webmailer und Outlook (2002-2007) Zentrum für Datenverarbeitung der Universität Tübingen
 Daten-Synchronisation zwischen dem ZDV-Webmailer und Outlook (2002-2007) Zentrum für Datenverarbeitung der Universität Tübingen Inhalt 1. Die Funambol Software... 3 2. Download und Installation... 3 3.
Daten-Synchronisation zwischen dem ZDV-Webmailer und Outlook (2002-2007) Zentrum für Datenverarbeitung der Universität Tübingen Inhalt 1. Die Funambol Software... 3 2. Download und Installation... 3 3.
Hinweise in Leichter Sprache zum Vertrag über das Betreute Wohnen
 Hinweise in Leichter Sprache zum Vertrag über das Betreute Wohnen Sie möchten im Betreuten Wohnen leben. Dafür müssen Sie einen Vertrag abschließen. Und Sie müssen den Vertrag unterschreiben. Das steht
Hinweise in Leichter Sprache zum Vertrag über das Betreute Wohnen Sie möchten im Betreuten Wohnen leben. Dafür müssen Sie einen Vertrag abschließen. Und Sie müssen den Vertrag unterschreiben. Das steht
Was meinen die Leute eigentlich mit: Grexit?
 Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
IT-SICHERHEIT IM UNTERNEHMEN Mehr Sicherheit für Ihre Entscheidung
 IT-SICHERHEIT IM UNTERNEHMEN Mehr Sicherheit für Ihre Entscheidung IT-SICHERHEIT IM UNTERNEHMEN Mehr Sicherheit für ihre Entscheidung Entdecken Sie was IT Sicherheit im Unternehmen bedeutet IT Sicherheit
IT-SICHERHEIT IM UNTERNEHMEN Mehr Sicherheit für Ihre Entscheidung IT-SICHERHEIT IM UNTERNEHMEN Mehr Sicherheit für ihre Entscheidung Entdecken Sie was IT Sicherheit im Unternehmen bedeutet IT Sicherheit
Wärmebildkamera. Arbeitszeit: 15 Minuten
 Wärmebildkamera Arbeitszeit: 15 Minuten Ob Menschen, Tiere oder Gegenstände: Sie alle senden unsichtbare Wärmestrahlen aus. Mit sogenannten Wärmebildkameras können diese sichtbar gemacht werden. Dadurch
Wärmebildkamera Arbeitszeit: 15 Minuten Ob Menschen, Tiere oder Gegenstände: Sie alle senden unsichtbare Wärmestrahlen aus. Mit sogenannten Wärmebildkameras können diese sichtbar gemacht werden. Dadurch
Abitur - Leistungskurs Mathematik. Sachsen-Anhalt 1999
 Abitur - Leistungskurs Mthemtik Schsen-Anhlt 999 Gebiet L - Anlysis Augbe.. y, D, R,. Die Funktionenschr sei gegeben durch Die Grphen der Funktionen der Schr werden mit G bezeichnet. ) Ermitteln Sieden
Abitur - Leistungskurs Mthemtik Schsen-Anhlt 999 Gebiet L - Anlysis Augbe.. y, D, R,. Die Funktionenschr sei gegeben durch Die Grphen der Funktionen der Schr werden mit G bezeichnet. ) Ermitteln Sieden
ANLEITUNG - WIE UNTERSTÜTZE ICH AUF STARTNEXT?
 ANLEITUNG - WIE UNTERSTÜTZE ICH AUF STARTNEXT? Wenn Sie das Projekt DIE ANFÄNGERIN unterstützen wollen, können Sie das mit oder ohne Registrierung auf www.startnext.com tun. Sie können also als Gast unterstützen
ANLEITUNG - WIE UNTERSTÜTZE ICH AUF STARTNEXT? Wenn Sie das Projekt DIE ANFÄNGERIN unterstützen wollen, können Sie das mit oder ohne Registrierung auf www.startnext.com tun. Sie können also als Gast unterstützen
4.1 Wie bediene ich das Webportal?
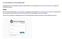 4.1 Wie bediene ich das Webportal? Die Bedienung ist durch ein Redaktionssystem sehr einfach möglich. Das Tutorial zeigt Ihnen wie Sie SMS-News und Top-News erstellen und veröffentlichen können. Schritt
4.1 Wie bediene ich das Webportal? Die Bedienung ist durch ein Redaktionssystem sehr einfach möglich. Das Tutorial zeigt Ihnen wie Sie SMS-News und Top-News erstellen und veröffentlichen können. Schritt
Die richtigen Partner finden, Ressourcen finden und zusammenführen
 Kongress Kinder.Stiften.Zukunft Workshop Willst Du mit mir gehen? Die richtigen Partner finden, Ressourcen finden und zusammenführen Dr. Christof Eichert Unsere Ziele: Ein gemeinsames Verständnis für die
Kongress Kinder.Stiften.Zukunft Workshop Willst Du mit mir gehen? Die richtigen Partner finden, Ressourcen finden und zusammenführen Dr. Christof Eichert Unsere Ziele: Ein gemeinsames Verständnis für die
TYPO3 Tipps und Tricks
 TYPO3 Tipps und Tricks Seiten als Shortcut. Hiermit ist gemeint, dass eine Oberseite direkt auf eine tiefere Unterseite verlinkt. Dies kann bei Themen ohne gesonderte Übersichtsseite hilfreich sein. Zum
TYPO3 Tipps und Tricks Seiten als Shortcut. Hiermit ist gemeint, dass eine Oberseite direkt auf eine tiefere Unterseite verlinkt. Dies kann bei Themen ohne gesonderte Übersichtsseite hilfreich sein. Zum
Mind Mapping am PC. für Präsentationen, Vorträge, Selbstmanagement. von Isolde Kommer, Helmut Reinke. 1. Auflage. Hanser München 1999
 Mind Mapping am PC für Präsentationen, Vorträge, Selbstmanagement von Isolde Kommer, Helmut Reinke 1. Auflage Hanser München 1999 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 446 21222 0 schnell
Mind Mapping am PC für Präsentationen, Vorträge, Selbstmanagement von Isolde Kommer, Helmut Reinke 1. Auflage Hanser München 1999 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 446 21222 0 schnell
Definition und Begriffe
 Merkblatt: Das Dreieck Definition und Begriffe Das Dreieck ist ein Vieleck. In der Ebene ist es die einfachste Figur, die von geraden Linien begrenzt wird. Ecken: Jedes Dreieck hat drei Ecken, die meist
Merkblatt: Das Dreieck Definition und Begriffe Das Dreieck ist ein Vieleck. In der Ebene ist es die einfachste Figur, die von geraden Linien begrenzt wird. Ecken: Jedes Dreieck hat drei Ecken, die meist
Rente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren Rentenperiode = Zeitabstand zwischen zwei Rentenzahlungen
 5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
Dow Jones am 13.06.08 im 1-min Chat
 Dow Jones am 13.06.08 im 1-min Chat Dieser Ausschnitt ist eine Formation: Wechselstäbe am unteren Bollinger Band mit Punkt d über dem 20-er GD nach 3 tieferen Hoch s. Wenn ich einen Ausbruch aus Wechselstäben
Dow Jones am 13.06.08 im 1-min Chat Dieser Ausschnitt ist eine Formation: Wechselstäbe am unteren Bollinger Band mit Punkt d über dem 20-er GD nach 3 tieferen Hoch s. Wenn ich einen Ausbruch aus Wechselstäben
Eigentlich sollte es ein Wanderpokal werden.
 Eigentlich sollte es ein Wanderpokal werden. Umso mehr freuen wir uns, ihn erneut entgegennehmen zu dürfen. Denn die DWS ist zum 11. Mal in Folge Deutschlands beste Fondsgesellschaft. Dies ist das Ergebnis
Eigentlich sollte es ein Wanderpokal werden. Umso mehr freuen wir uns, ihn erneut entgegennehmen zu dürfen. Denn die DWS ist zum 11. Mal in Folge Deutschlands beste Fondsgesellschaft. Dies ist das Ergebnis
AW: AW: AW: AW: Kooperationsanfrage anwalt.de
 Seite 1 von 5 AW: AW: AW: AW: Kooperationsanfrage anwalt.de Di 13.08.2013 08:31 An:'Rene Meier' ; ich freue mich, dass alles noch so gut funktioniert hat. Die Logointegration
Seite 1 von 5 AW: AW: AW: AW: Kooperationsanfrage anwalt.de Di 13.08.2013 08:31 An:'Rene Meier' ; ich freue mich, dass alles noch so gut funktioniert hat. Die Logointegration
Lizenzierung von StarMoney 10 bzw. StarMoney Business 7 durchführen
 Lizenzierung von StarMoney 10 bzw. StarMoney Business 7 durchführen In dieser Anleitung möchten wir Ihnen die Lizenzierung der StarMoney 10 bzw. StarMoney Business 7 erläutern. In dieser Anleitung beziehen
Lizenzierung von StarMoney 10 bzw. StarMoney Business 7 durchführen In dieser Anleitung möchten wir Ihnen die Lizenzierung der StarMoney 10 bzw. StarMoney Business 7 erläutern. In dieser Anleitung beziehen
Wir machen neue Politik für Baden-Württemberg
 Wir machen neue Politik für Baden-Württemberg Am 27. März 2011 haben die Menschen in Baden-Württemberg gewählt. Sie wollten eine andere Politik als vorher. Die Menschen haben die GRÜNEN und die SPD in
Wir machen neue Politik für Baden-Württemberg Am 27. März 2011 haben die Menschen in Baden-Württemberg gewählt. Sie wollten eine andere Politik als vorher. Die Menschen haben die GRÜNEN und die SPD in
Dokumentenverwaltung im Internet
 Dokumentenverwaltung im Internet WS 09/10 mit: Thema: Workflow und Rollenverteilung im Backend Gruppe: DVI 10 Patrick Plaum und Kay Hofmann Inhalt 1. Benutzer und Benutzergruppen erstellen...2 1.1. Benutzergruppen...2
Dokumentenverwaltung im Internet WS 09/10 mit: Thema: Workflow und Rollenverteilung im Backend Gruppe: DVI 10 Patrick Plaum und Kay Hofmann Inhalt 1. Benutzer und Benutzergruppen erstellen...2 1.1. Benutzergruppen...2
Subpostfächer und Vertretungen für Unternehmen
 SCHRITT-FÜR-SCHRITT Seite 1 von 7 Subpostfächer und Vertretungen für Unternehmen Organisationsstruktur 1:1 abbilden Individuelle Postfächer für Abteilungen und/oder Mitarbeiter Unterschiedliche Berechtigungen
SCHRITT-FÜR-SCHRITT Seite 1 von 7 Subpostfächer und Vertretungen für Unternehmen Organisationsstruktur 1:1 abbilden Individuelle Postfächer für Abteilungen und/oder Mitarbeiter Unterschiedliche Berechtigungen
Hinweise zum elektronischen Meldeformular
 Paul-Ehrlich-Institut Postfach 63207 Langen Jochen Halbauer Referat Pharmakovigilanz 2 Tel. +49 (0) 6103 77 3114 Fax +49 (0) 6103 77 1268 E-Mail pharmakovigilanz2@pei.de 22.06.2015 Hinweise zum elektronischen
Paul-Ehrlich-Institut Postfach 63207 Langen Jochen Halbauer Referat Pharmakovigilanz 2 Tel. +49 (0) 6103 77 3114 Fax +49 (0) 6103 77 1268 E-Mail pharmakovigilanz2@pei.de 22.06.2015 Hinweise zum elektronischen
Keil Telecom Homepage - Hersteller von Isdn Tk Anlagen und Türsprechsystemen für Heim und Bü...
 Keil Telecom Homepge - Hersteller von Isdn Tk Anlgen und Türsprechsystemen für Heim und Bü... Seite 1 von 1 Einutürlutsprecher esonders kleine und kompkte Buform Einu üerll dort wo Pltz knpp ist Briefkästen,
Keil Telecom Homepge - Hersteller von Isdn Tk Anlgen und Türsprechsystemen für Heim und Bü... Seite 1 von 1 Einutürlutsprecher esonders kleine und kompkte Buform Einu üerll dort wo Pltz knpp ist Briefkästen,
Das sogenannte Beamen ist auch in EEP möglich ohne das Zusatzprogramm Beamer. Zwar etwas umständlicher aber es funktioniert
 Beamen in EEP Das sogenannte Beamen ist auch in EEP möglich ohne das Zusatzprogramm Beamer. Zwar etwas umständlicher aber es funktioniert Zuerst musst du dir 2 Programme besorgen und zwar: Albert, das
Beamen in EEP Das sogenannte Beamen ist auch in EEP möglich ohne das Zusatzprogramm Beamer. Zwar etwas umständlicher aber es funktioniert Zuerst musst du dir 2 Programme besorgen und zwar: Albert, das
FuxMedia Programm im Netzwerk einrichten am Beispiel von Windows 7
 FuxMedia Programm im Netzwerk einrichten am Beispiel von Windows 7 Die Installation der FuxMedia Software erfolgt erst NACH Einrichtung des Netzlaufwerks! Menüleiste einblenden, falls nicht vorhanden Die
FuxMedia Programm im Netzwerk einrichten am Beispiel von Windows 7 Die Installation der FuxMedia Software erfolgt erst NACH Einrichtung des Netzlaufwerks! Menüleiste einblenden, falls nicht vorhanden Die
Erfolg beginnt im Kopf
 Erfolg beginnt im Kopf Wie Sie ausgeglichen bleiben und Ihre Ziele einfacher erreichen 8. VR-Unternehmerforum AGRAR Die Ausgangslage Am Markt 6 49406 Barnstorf Am Markt 6 49406 Barnstorf Alles verändert
Erfolg beginnt im Kopf Wie Sie ausgeglichen bleiben und Ihre Ziele einfacher erreichen 8. VR-Unternehmerforum AGRAR Die Ausgangslage Am Markt 6 49406 Barnstorf Am Markt 6 49406 Barnstorf Alles verändert
Professionelle Seminare im Bereich MS-Office
 Gegenüber PowerPoint 2003 hat sich in PowerPoint 2007 gerade im Bereich der Master einiges geändert. Auf Handzettelmaster und Notizenmaster gehe ich in diesen Ausführungen nicht ein, die sind recht einfach
Gegenüber PowerPoint 2003 hat sich in PowerPoint 2007 gerade im Bereich der Master einiges geändert. Auf Handzettelmaster und Notizenmaster gehe ich in diesen Ausführungen nicht ein, die sind recht einfach
Waggonbeleuchtung. Stützkondensatoren
 Waggonbeleuchtung Hier finden Sie alle Informationen, wie Sie Ihre Waggons eindrucksvoll beleuchten können. Diese Anleitung basiert auf die Verwendung von PCB-Streifen als Leiterbahn und SMD zur Beleuchtung.
Waggonbeleuchtung Hier finden Sie alle Informationen, wie Sie Ihre Waggons eindrucksvoll beleuchten können. Diese Anleitung basiert auf die Verwendung von PCB-Streifen als Leiterbahn und SMD zur Beleuchtung.
Outlook. sysplus.ch outlook - mail-grundlagen Seite 1/8. Mail-Grundlagen. Posteingang
 sysplus.ch outlook - mail-grundlagen Seite 1/8 Outlook Mail-Grundlagen Posteingang Es gibt verschiedene Möglichkeiten, um zum Posteingang zu gelangen. Man kann links im Outlook-Fenster auf die Schaltfläche
sysplus.ch outlook - mail-grundlagen Seite 1/8 Outlook Mail-Grundlagen Posteingang Es gibt verschiedene Möglichkeiten, um zum Posteingang zu gelangen. Man kann links im Outlook-Fenster auf die Schaltfläche
Hamburg Kernfach Mathematik Zentralabitur 2013 Erhöhtes Anforderungsniveau Analysis 2
 Hmburg Kernfch Mhemik Zenrlbiur 2013 Erhöhes Anforderungsniveu Anlysis 2 Smrphones Die Mrkeinführung eines neuen Smrphones vom Elekronikherseller PEAR wird ses ufgereg erwre. Zur Modellierung der Enwicklung
Hmburg Kernfch Mhemik Zenrlbiur 2013 Erhöhes Anforderungsniveu Anlysis 2 Smrphones Die Mrkeinführung eines neuen Smrphones vom Elekronikherseller PEAR wird ses ufgereg erwre. Zur Modellierung der Enwicklung
Die Regelungen zu den Einsendeaufgaben (Einsendeschluss, Klausurzulassung) finden Sie in den Studien- und Prüfungsinformationen Heft Nr. 1.
 Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
Prozentrechnung. Wir können nun eine Formel für die Berechnung des Prozentwertes aufstellen:
 Prozentrechnung Wir beginnen mit einem Beisiel: Nehmen wir mal an, ein Handy kostet 200 und es gibt 5% Rabatt (Preisnachlass), wie groß ist dann der Rabatt in Euro und wie viel kostet dann das Handy? Wenn
Prozentrechnung Wir beginnen mit einem Beisiel: Nehmen wir mal an, ein Handy kostet 200 und es gibt 5% Rabatt (Preisnachlass), wie groß ist dann der Rabatt in Euro und wie viel kostet dann das Handy? Wenn
Internet online Update (Mozilla Firefox)
 Um Ihr Consoir Beta immer schnell und umkompliziert auf den aktuellsten Stand zu bringen, bieten wir allen Kunden ein Internet Update an. Öffnen Sie Ihren Mozilla Firefox und gehen auf unsere Internetseite:
Um Ihr Consoir Beta immer schnell und umkompliziert auf den aktuellsten Stand zu bringen, bieten wir allen Kunden ein Internet Update an. Öffnen Sie Ihren Mozilla Firefox und gehen auf unsere Internetseite:
Das Festkomitee hat die Abi-Seite neu konzipiert, die nun auf einem (gemieteten) Share Point Server
 Hallo Leute Das Festkomitee hat die Abi-Seite neu konzipiert, die nun auf einem (gemieteten) Share Point Server (= echtes - zeug ) liegt! Die neue Form hat insbesondere folgende Vorteile: Du bekommst einen
Hallo Leute Das Festkomitee hat die Abi-Seite neu konzipiert, die nun auf einem (gemieteten) Share Point Server (= echtes - zeug ) liegt! Die neue Form hat insbesondere folgende Vorteile: Du bekommst einen
Canon Nikon Sony. Deutschland 55 45 25. Österreich 40 35 35. Schweiz 30 30 20. Resteuropa 60 40 30 55 45 25 40 35 35 J 30 30 20 60 40 30
 15 Mtrizenrechnung 15 Mtrizenrechnung 15.1 Mtrix ls Zhlenschem Eine Internetfirm verkuft über einen eigenen Shop Digitlkmers. Es wird jeweils nur ds Topmodel der Firmen Cnon, Nikon und Sony ngeboten. Verkuft
15 Mtrizenrechnung 15 Mtrizenrechnung 15.1 Mtrix ls Zhlenschem Eine Internetfirm verkuft über einen eigenen Shop Digitlkmers. Es wird jeweils nur ds Topmodel der Firmen Cnon, Nikon und Sony ngeboten. Verkuft
Kreativ visualisieren
 Kreativ visualisieren Haben Sie schon einmal etwas von sogenannten»sich selbst erfüllenden Prophezeiungen«gehört? Damit ist gemeint, dass ein Ereignis mit hoher Wahrscheinlichkeit eintritt, wenn wir uns
Kreativ visualisieren Haben Sie schon einmal etwas von sogenannten»sich selbst erfüllenden Prophezeiungen«gehört? Damit ist gemeint, dass ein Ereignis mit hoher Wahrscheinlichkeit eintritt, wenn wir uns
Arbeitsblätter. Sinnvolle Finanzberichte. Seite 19
 Seite 19 Arbeitsblätter Seite 20 Dieses Arbeitsblatt wird Sie Schritt für Schritt durch das Verfahren von Finanzanalysen geleiten. Sie gehen von Ihren Finanzberichten aus egal wie einfach oder hoch entwickelt
Seite 19 Arbeitsblätter Seite 20 Dieses Arbeitsblatt wird Sie Schritt für Schritt durch das Verfahren von Finanzanalysen geleiten. Sie gehen von Ihren Finanzberichten aus egal wie einfach oder hoch entwickelt
Datenbank LAP - Chefexperten Detailhandel
 AJR Informatique Conseil Datenbank LAP - Chefexperten Detailhandel Kurzanleitung Version 01-17 Februar 2009 1 Zugang zur Datenbank Zugang zur Datenbank erhalten Sie unter www.dblap.ch. Zum Training können
AJR Informatique Conseil Datenbank LAP - Chefexperten Detailhandel Kurzanleitung Version 01-17 Februar 2009 1 Zugang zur Datenbank Zugang zur Datenbank erhalten Sie unter www.dblap.ch. Zum Training können
Poker. Spielregeln. www.worldstoreofpoker.de
 Poker Spielregeln www.worldstoreofpoker.de Poker-Glossar Add-On All-In Ante Bet Big Blind Buy-In Burn-Card Call Check Chip-Race Community- Cards Dealer-Button Flop Fold Freeze Out Heads Up Hole Cards Kicker
Poker Spielregeln www.worldstoreofpoker.de Poker-Glossar Add-On All-In Ante Bet Big Blind Buy-In Burn-Card Call Check Chip-Race Community- Cards Dealer-Button Flop Fold Freeze Out Heads Up Hole Cards Kicker
Welche Gedanken wir uns für die Erstellung einer Präsentation machen, sollen Ihnen die folgende Folien zeigen.
 Wir wollen mit Ihnen Ihren Auftritt gestalten Steil-Vorlage ist ein österreichisches Start-up mit mehr als zehn Jahren Erfahrung in IT und Kommunikation. Unser Ziel ist, dass jede einzelne Mitarbeiterin
Wir wollen mit Ihnen Ihren Auftritt gestalten Steil-Vorlage ist ein österreichisches Start-up mit mehr als zehn Jahren Erfahrung in IT und Kommunikation. Unser Ziel ist, dass jede einzelne Mitarbeiterin
Studienplatzbeschaffung
 Studienplatzbeschaffung - Einklagen www.asta.haw-hamburg.de Hintergrund Alle Unis und Hochschulen unterliegen dem Kapazitätsausschöpfungsgebot Sie müssen alle ihnen zur Verfügung stehenden Plätze vergeben!
Studienplatzbeschaffung - Einklagen www.asta.haw-hamburg.de Hintergrund Alle Unis und Hochschulen unterliegen dem Kapazitätsausschöpfungsgebot Sie müssen alle ihnen zur Verfügung stehenden Plätze vergeben!
Kapitel 4 Die Datenbank Kuchenbestellung Seite 1
 Kapitel 4 Die Datenbank Kuchenbestellung Seite 1 4 Die Datenbank Kuchenbestellung In diesem Kapitel werde ich die Theorie aus Kapitel 2 Die Datenbank Buchausleihe an Hand einer weiteren Datenbank Kuchenbestellung
Kapitel 4 Die Datenbank Kuchenbestellung Seite 1 4 Die Datenbank Kuchenbestellung In diesem Kapitel werde ich die Theorie aus Kapitel 2 Die Datenbank Buchausleihe an Hand einer weiteren Datenbank Kuchenbestellung
FRAGEBOGEN Webseite. Ihre Daten helfen uns und Ihnen bei der Erfüllung unseres Auftrages. Bitte nehmen Sie sich etwas
 1 Ihre Daten helfen uns und Ihnen bei der Erfüllung unseres Auftrages. Bitte nehmen Sie sich etwas Zeit und beantworten Sie so viele Fragen, wie möglich. Dabei gibt es kein richtig oder falsch. Je detaillierter
1 Ihre Daten helfen uns und Ihnen bei der Erfüllung unseres Auftrages. Bitte nehmen Sie sich etwas Zeit und beantworten Sie so viele Fragen, wie möglich. Dabei gibt es kein richtig oder falsch. Je detaillierter
Studio d A2-05 Medien über Medien sprechen
 über sprechen über sprechen Wählen Sie vier bzw. Geräte. Warum benutzen Sie diese bzw. Geräte? Wie oft? Notieren Sie. die bzw. Geräte Warum? Wie oft? Fragen Sie auch Ihren / Ihre Partner(in) und notieren
über sprechen über sprechen Wählen Sie vier bzw. Geräte. Warum benutzen Sie diese bzw. Geräte? Wie oft? Notieren Sie. die bzw. Geräte Warum? Wie oft? Fragen Sie auch Ihren / Ihre Partner(in) und notieren
Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* aller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt:
 8. Grundlgen der Informtionstheorie 8.1 Informtionsgehlt, Entropie, Redundnz Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* ller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt: 1.
8. Grundlgen der Informtionstheorie 8.1 Informtionsgehlt, Entropie, Redundnz Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* ller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt: 1.
Auswertung des Jahresabschlusses Bilanzanalyse 2
 KA11 Unternehmensergebnisse aufbereiten, bewerten und nutzen Auswertung des Jahresabschlusses Bilanzanalyse 2 Kennzahlen zur Bilanzanalyse Die aufbereitete Bilanz kann mit Hilfe unterschiedlicher Kennzahlen
KA11 Unternehmensergebnisse aufbereiten, bewerten und nutzen Auswertung des Jahresabschlusses Bilanzanalyse 2 Kennzahlen zur Bilanzanalyse Die aufbereitete Bilanz kann mit Hilfe unterschiedlicher Kennzahlen
Verarbeitung von ZV-Dateien im Internetbanking. Inhalt. 1. Datei einlesen... 2. 2. Datei anzeigen, ändern, löschen... 4. 3. Auftrag ausführen...
 Inhalt 1. Datei einlesen... 2 2. Datei anzeigen, ändern, löschen... 4 3. Auftrag ausführen... 5 4. Hinweise... 7 Seite 1 Im Internetbanking haben Sie die Möglichkeit, Zahlungsverkehrsdateien (DTA-Dateien,
Inhalt 1. Datei einlesen... 2 2. Datei anzeigen, ändern, löschen... 4 3. Auftrag ausführen... 5 4. Hinweise... 7 Seite 1 Im Internetbanking haben Sie die Möglichkeit, Zahlungsverkehrsdateien (DTA-Dateien,
Das Modul ARTIKEL-BARCODE ermöglicht den Druck von Barcode-Etiketten der EAN-Codes 8 und 13.
 FAKTURA Artikel-Barcode 1 Modul ARTIKEL-BARCODE Das Modul ARTIKEL-BARCODE ermöglicht den Druck von Barcode-Etiketten der EAN-Codes 8 und 13. Es können Etiketten aller gängigen Standard-Größen verwendet
FAKTURA Artikel-Barcode 1 Modul ARTIKEL-BARCODE Das Modul ARTIKEL-BARCODE ermöglicht den Druck von Barcode-Etiketten der EAN-Codes 8 und 13. Es können Etiketten aller gängigen Standard-Größen verwendet
1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage:
 Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Tutorium zur Mikroökonomie II WS 02/03 Universität Mannheim Tri Vi Dang. Aufgabenblatt 3 (KW 44) (30.10.02)
 Tutorium zur Mikroökonomie II WS 02/03 Universität Mannheim Tri Vi Dang Aufgabenblatt 3 (KW 44) (30.10.02) Aufgabe 1: Preisdiskriminierung dritten Grades (20 Punkte) Ein innovativer Uni-Absolvent plant,
Tutorium zur Mikroökonomie II WS 02/03 Universität Mannheim Tri Vi Dang Aufgabenblatt 3 (KW 44) (30.10.02) Aufgabe 1: Preisdiskriminierung dritten Grades (20 Punkte) Ein innovativer Uni-Absolvent plant,
Begrüßung mit Schwung und Begeisterung. Die Teilnehmer müssen spüren, dass die Aufgabe Spaß macht.
 Begrüßung mit Schwung und Begeisterung. Die Teilnehmer müssen spüren, dass die Aufgabe Spaß macht. Wenn Sie die Teilnehmer kennen, ein paar persönliche Worte... oder Alternativ eine Frage zum aktuellen
Begrüßung mit Schwung und Begeisterung. Die Teilnehmer müssen spüren, dass die Aufgabe Spaß macht. Wenn Sie die Teilnehmer kennen, ein paar persönliche Worte... oder Alternativ eine Frage zum aktuellen
SPIELBESCHREIBUNGEN DART RADIKAL SYSTEM
 SPIELBESCHREIBUNGEN DART RADIKAL SYSTEM X01: 301, 501, 701 oder 901 Rundenbegrenzungen: 301 (15); 501 (20); 701 (25); 901 (30) In diesem Spiel beginnen alle Spieler mit 301, 501, 701 oder 901 Punkten.
SPIELBESCHREIBUNGEN DART RADIKAL SYSTEM X01: 301, 501, 701 oder 901 Rundenbegrenzungen: 301 (15); 501 (20); 701 (25); 901 (30) In diesem Spiel beginnen alle Spieler mit 301, 501, 701 oder 901 Punkten.
Schrittweise Anleitung zur Erstellung einer Angebotseite 1. In Ihrem Dashboard klicken Sie auf Neu anlegen, um eine neue Seite zu erstellen.
 Schrittweise Anleitung zur Erstellung einer Angebotseite 1. In Ihrem Dashboard klicken Sie auf Neu anlegen, um eine neue Seite zu erstellen. Klicken Sie auf Neu anlegen, um Ihre neue Angebotseite zu erstellen..
Schrittweise Anleitung zur Erstellung einer Angebotseite 1. In Ihrem Dashboard klicken Sie auf Neu anlegen, um eine neue Seite zu erstellen. Klicken Sie auf Neu anlegen, um Ihre neue Angebotseite zu erstellen..
