Ermittlung von Leistungsgrenzen verschiedener Lagerstrategien unter Berücksichtigung zentraler Einflussgrößen
|
|
|
- Ina Geier
- vor 7 Jahren
- Abrufe
Transkript
1 Ermilung von Leiunggrenzen verchiedener Lagerraegien uner Berücichigung zenraler Einflugrößen Dipl.-Wir.-Ing. (FH) Anne Piepenburg, Prof. Dr.-Ing. Rainer Brun Helmu-Schmid-Univeriä, Hamburg Lehruhl für Machinenelemene und Techniche Logii Abrac: Am Lehruhl für Machinenelemene und Techniche Logii der Helmu- Schmid-Univeriä wurde ein neuer Modellierunganaz zur Leiungberechnung von Lageryemen enwicel. Da Modell baier auf der mahemaich analyichen Berechnung der mileren Spielzei und ermöglich die Berücichigung weigehend beliebiger Lagerraegien. Bei der Modellenwiclung wurden der loale Aulaunggrad owie die loale Verweildauer der einzelnen Lagerfächer al zenrale Einflugrößen auf die Syemleiung idenifizier. Da Modell ermöglich eral die Einflüe dieer beiden grundlegenden Größen analyich zu bechreiben und dami iefere Einichen in die weenlichen Wirzuammenhänge zu gewinnen. Einleiung Auomaiiere Lageryeme verurachen hohe Koen durch den Lagerberieb aber auch durch die Abchreibung der Inveiion. Dehalb wird ei langem veruch die logiiche Syemleiung nich nur durch eine Seigerung der Leiungfähigei der eingeezen Techni, ondern inbeondere durch augefeile Lagerraegien d.h. durch eine inelligene Zuordnung der Lagereinheien zu den Lagerfächern zu erhöhen. Die Auwahl der für den jeweiligen Anwendungfall richigen Lagerraegie i einerei von großer Bedeuung für die Wirchaflichei de Lageryem und andererei einefall rivial. Vorauezung hierfür i die Möglichei, verchiedene Lagerraegien objeiv vergleichen und beweren zu önnen. Diee ann mihilfe von Compuerimulaionen uner definieren Einazzenarien gechehen. Tiefere Einichen in die weenlichen Zuammenhänge zwichen den Einfluparameern und der Zielgröße Umchlagleiung laen ich dabei jedoch nur chwer gewinnen. Da in dieem Zuammenhang enwicele Modell oll im folgenden Beirag vorgeell werden. Grundlagen zum Lager. Sochaiche Einflugrößen im Lager Einige der in einem Lager aufreenden Parameer önnen durch Wahrcheinlicheivereilungen bechrieben werden. Im vorliegenden Beirag ind da inbeondere die Fahrzeivereilung und die Verweildauervereilung. Logiic Journal : Proceeding ISSN Seie
2 Die Dichefunion der Fahrzeivereilung gib die Wahrcheinlichei an, mi welcher eine beimme Spielzei bei einem Einzelpiel einri. Die Wahrcheinlichei nimm bei chaoicher Lagerung mi eigendem linear zu (vgl. Abb. ), weil die Anzahl von Lagerfächern mi gleicher Spielzei mi zunehmendem Aband vom Übergabepun wäch. Vorauezung hierfür i, da da Verhälni von Lagerhöhe zu Lagerbreie dem Verhälni von Hubgechwindigei zu Fahrgechwindigei gleich. Die Verweildauer eine Ariel i bei beimmen Lagerraegien Encheidunggrundlage, in welche Lagerfach (LF) der Ariel eingelager wird. Da die Verweildauer de Ariel jedoch zum Einlagerungzeipun unbeann i, lieg die Verweildauervereilung idealerweie aufgrund von Erfahrungweren vor. Die Verweildauervereilung gib an, mi welcher Wahrcheinlichei eine beimme Verweildauer einri, oda abhängig von der verwendeen Lagerraegie der Einlagerungor für die Lagereinhei (LE) beimm werden ann. Die Inerpreaion der Verweildauervereilung oll im Folgenden anhand einer gleichvereilen Verweildauer erfolgen. Abbildung : Dichefunion der Fahrzeivereilung Abbildung : Unerchiedliche Gleichvereilungen der Verweildauer Wenn eine Zufallgröße (in dieem Fall die Verweildauer) gleichvereil i, beeh für jede mögliche Verweildauer die gleiche Einriwahrcheinlichei. Abbildung zeig drei Dichefunionen einer Gleichvereilung. Lieg eine Gleichvereilung wie bei vor, o unercheiden ich die Verweildauern im Sorimen aum. Bei ar unerchiedlichen Verweildauern ha die Dichefunion der Gleichvereilung den Verlauf 3.. Lagerraegien Al Lagerraegien werden Verfahren bezeichne, nach denen ein Lagerfach für die Einlagerung augewähl wird. Gängige Lagerraegien ind beipielweie die chaoiche Lagerung, die Kürzee-Fahrzei-Sraegie oder die ABC-Zonierung. Bei der chaoichen Lagerung werden anommende Ladeeinheien zufällig Lagerfächern Logiic Journal : Proceeding ISSN Seie
3 zugewieen, oda für jede Lagerfach die gleiche Wahrcheinlichei beeh, angefahren zu werden. Die Kürzee-Fahrzei-Sraegie (KFZ) hingegen wähl unabhängig vom einzulagernden Ariel immer den Lageror mi dem ürzeen Fahrweg au. Wird da Lager in Zonen eingeeil, prich man ofmal von einer ABC-Zonierung. Innerhalb einer Zone werden nur Ladeeinheien mi definieren Aribuauprägungen eingelager [Ho8]. Eine weiere Lagerraegie, die in der Praxi bilang aum Anwendung finde, i die dynamiche Zonierung. Die dynamiche Zonierung wurde von Michael Gla enwicel. Gla geh davon au, da die Verweildauervereilung der Ariel owie die Fahrzeivereilung im Lager vor Einlagerung beann ind. Um den Lageror eine anommenden Ariel zu beimmen wird deen Verweildauerquanil mi dem Quanil in der Fahrzeivereilung gleichgeez. Über die Invere der Fahrzeivereilungfunion lä ich chließlich die Fahrzei zu dem geuchen Lageror für den Ariel berechnen (vgl. Abb. 3 und Gl..) [Gla8]: F ( F ( )) (.) F F V V Abbildung 3: Verweildauervereilung de Ariel (lin) und die Fahrzeivereilung de Lager (rech) In dem vorliegenden Beirag finden die chaoiche Lagerung und die dynamiche Zonierung nach Gla Anwendung. 3 Modell zur Leiungberechnung 3. Vorauezung und Annahmen zur Modellbildung Die Leiung eine Lager wird durch die milere Spielzei charaeriier. Die Spielzei eine Lagerfache i die Zeidauer, die für die Auführung eine Arbeipiel, d.h. einer Au- oder Einlagerung benöig wird. Da Arbeipiel i dabei eine zyliche Wiederholung von einzelnen Arbeioperaionen. Werden die für die Arbeioperaionen benöigen Zeianeile addier, ergib ich die Spielzei für ein beimme Arbeipiel. Diee Zeianeile werden in wegabhängige und wegunabhängige Zeianeile unerchieden. Die Spielzei häng im Weenlichen von der Länge de beim Tranporvorgang zurüczulegenden Wege ab. Somi i die Spielzei für jede Lagerfach unerchiedlich, ie wird al pezielle Spielzei bezeichne [Bru9]. Logiic Journal : Proceeding ISSN Seie 3
4 In dem enwicelen Modell önnen zeiliche Schwanungen nich berache werden. Bei den in dem Modell verwendeen Größen handel e ich um zeiliche Mielwere, oda nur aionäre Zuände durch da Modell bechrieben werden önnen. Zunäch wird nur eine einzelne Regalfläche modellier. Da Modell ann jedoch auf mehrere Regalflächen erweier werden. Die modelliere Regalfläche beeh au M x N gleichgroßen Lagerfächern (vgl. Abb. 4). Abbildung 4: modelliere Regalfläche Abbildung 5: Zyluzei eine Lagerfach Jede Lagerfach i eindeuig durch eine Indize i, j geennzeichne. Für jede Lagerfach ei die Spielzei, die Verweildauer v und der Aulaunggrad beann. Der Aulaunggrad bechreib da Verhälni der Zwichenanunfzei A (Zyluzei) und der Verweildauer v ν (3.) A Die Zwichenanunfzei ez ich dabei au der Verweildauer einer Lagereinhei und der Zeidauer leer, in der da Lagerfach leer i, zuammen. Abbildung 5 zeig den ypichen Zylu, den jede Lagerfach durchläuf. Die Zeianeile zwichen Einlagerung und Aulagerung owie die Leerzei önnen bei jedem Zylu variieren. E gil alo: + (3.) A ν leer Hierau folg durch Umellen von Gl. 3. und anchließende Einezen in Gl. 3.: A ν und leer ν (3.3) + (3.4) Um die Anfahrwahrcheinlichei P eine Lagerfache zu beimmen, wird die Regalfläche al eine Parallelchalung vieler (genauer M x N) Bedienaionen aufgefa (vgl. Abb. 6). Logiic Journal : Proceeding ISSN Seie 4
5 Abbildung 6: Regalfläche al Bedienaion Die Wahrcheinlichei, da eine anommende LE in Lagerfach LF eingelager wird, ergib ich au dem relaiven Durchaz de Lagerfache. E gil alo: ge P (3.5) ge Der zeilich gemiele Durchaz i der Kehrwer der Zwichenanunfzei A de Lagerfache (3.6) A Durch da Aufummieren aller Einzeldurchäze erhäl man den Geamdurchaz durch die geame Lagerfläche ge zu ab (3.7) i j Der örlich gemiele Durchaz m ergib ich, wenn man den Geamdurchaz auf die Anzahl M x N der Lagerfächer in der Lagerfläche bezieh. m E( ) ge M N (3.8) 3. Leiungberechnung mi einem direen Modell Die milere Spielzei i ein Mielwer für die beim Einzelpiel benöige Zeidauer. Sie i der Erwarungwer der peziellen Spielzeien für die einzelnen Lagerfächer: P (3.9) j i Mi Gleichung 3.5 folg: Logiic Journal : Proceeding ISSN Seie 5
6 M N i j ge (3.) Mi Gleichung 3.8 folg weier: M N MN i j m (3.) Der Quoien m ann al lagerfachabhängiger Einflufaor gedeue werden. Durch Rücführung der Lagerfachdurchäze auf die Urprunggrößen v und (vgl. Gl. 3.3 und 3.6) erhäl man: M N i j ν M N i j ν (3.) 3.3 Leiungberechnung mi einem eigen Modell Durch den Grenzübergang zu unendlich vielen Lagerfächern ( N, M ) ann eine Koninuierung de Problem durchgeführ werden. Somi werden die Lagerfächer bei gleichbleibender Regalfläche infinieimal lein. Uner der Annahme, da alle Lagerfächer gleich groß ind, ergib ich die Breie eine Lagerfache au der Länge L dividier durch die Anzahl M der Lagerfächer in x Richung: L Δ x, lim M Δ x dx (3.3)+(3.4) M Enprechende gil für die Höhe eine Lagerfache: H Δ y, lim y dy N N Δ (3.5)+(3.6) Δx Δy (3.7) MN L H Durch Einezen in (3.) und Koninuierung von und erhäl man: ( x, y), ( x, y) ( xy, ) x y dxdy LH LH (, ) x y (3.8) m au (3.) folg chließlich: Logiic Journal : Proceeding ISSN Seie 6
7 S LH x y ( xy, ) S ( x, y ) dxdy v( x, y) ( xy, ) dxdy ( x, y) LH x y mi ( x, y), ( x, y) v ν ν (3.9) 3.4 Leiungberechnung mi einem laier direen Modell In jedem Lager gib e Klaen von Lagerfächern die hinichlich der relevanen Größen gleiche Were aufweien. Diee Fächer liegen auf einer gemeinamen Linie, der ogenannen Iolinie. Eine Iolinie verbinde alle Pune (bzw. LF), für die man von einem beimmen Pun au (z.b. der Übergabepun in einem Lager) die gleiche pezielle Einzelpielzei benöig [Arn9]. E werden daher M Teilmengen K von Lagerfächern gebilde. Für alle Elemene einer Klae ind die Were der Aulaung, der Verweildauer v und der Spielzei gleich groß. E gil: v v [, M ] i j, K Die Anzahl der Lagerfächer (Elemene) der Klae K ei die Häufigei h. Die relaive Häufigei der Klaen i dann: h rel, h MN (3.) Mi Gleichung (3.) erhäl man durch die Klaierung: h rel, h rel, v v (3.) 3.5 Leiungberechnung mi einem laier oninuierlichen Modell Nimm man eine weiere oninuierliche Verfeinerung der Klaierung bi zum Grenzfall M vor, o ann die Zuordnung der Klaen nich mehr durch den Index erfolgen. Hierfür wird ein eiger Parameer benöig. Da die Klaierung üblicher Weie anhand der Spielzei erfolg, biee e ich an, die relevanen Parameer in Abhängigei von der Spielzei darzuellen: Logiic Journal : Proceeding ISSN Seie 7
8 ( ), ( ) ν ν Bei wachendem M reb die Klaenhäufigei h bzw. h,rel gegen null. Diee mu daher auf die Klaenbreie bezogen werden: h rel, lim ( ) M Δ Im Grenzübergang f M reb der Quoien h, rel Δ (3.) gegen die Dichefunion der Spielzeivereilung bei chaoicher Lagerung. Der Quoien wird im Folgenden al geomericher Spielzeifaor bezeichne. Der geomeriche Spielzeifaor lä ich mi Hilfe der Dichefunion der Spielzeivereilung (vgl. Abb. 7) bei chaoicher Lagerung beimmen. E gil: f ( ) f [, ] in max in ax ax in (3.3) f ax wird mi Hilfe der Bedingung beimm, da die Fläche uner der Dichefunion ein mu: fax ( ax in) (3.4) fax ( ) ax in Dami ergib ich für die Dichefunion: (3.5) f ( ) ( ) in ( ax in ) (3.6) Für die weieren Berechnungen mi dem Leiungodell wird eine Variablenubiuion mi der Hilfvariablen durchgeführ. Die Subiuion ermöglich eine Inegraion im Werebereich τ. Die Dichefunion wird dami in den Urprung verchoben und normier (vgl. Abb. 7). Die Dichefunion in Abhängigei der Hilfvariablen zeig Gleichung 3.7. Logiic Journal : Proceeding ISSN Seie 8
9 f ( τ ) ax τ (3.7) in Abbildung 7: Geomeriche Vereilung der Spielzei Mi den dargeellen Übergängen für (3.): max min max min ( ) f ( ) d ν ( ) ( ) f ( ) d ν ( ) M folg au der Beimmunggleichung (3.8) in ax in und ax ind die obere und unere Grenze de Werebereich der Spielzei. Nach der Variablenubiuion erhäl man: τ ( ) f ( τ) ( +Δ τ) dτ ( τ ) in ν τ ( ) f ( τ) dτ ν ( τ ) mi τ ax in in (3.9)+(3.3) 3.6 Modellvalidierung anhand der chaoichen Lagerung Die Modellvalidierung erfolg anhand der chaoichen Lagerung. Für die Berechnung der mileren Einzelpielzei bei chaoicher Lagerung lieg eine analyiche Formel vor, die die Spielzei in Abhängigei der Bewegunggrößen de Fördermiel bei parallelem Bewegungablauf owie onanen Zeianeilen für die Laaufnahme und Laabgabe und der Lagerauaße beimm. Bei Güligei de Modell zur Leiungbeimmung mu da Ergebni für die milere Spielzei mi dem Ergebni der beannen analyichen Formel übereinimmen. Die analyiche Formel für die milere Einzelpielzei bei chaoicher Lagerung laue: KA + KE 4 L + + (3.3) 3 u mi KA onaner Zeianeil für da Aulagern Logiic Journal : Proceeding ISSN Seie 9
10 KE onaner Zeianeil für da Einlagern Zeianeil für x Bechleunigen und Abbremen L u Lagerlänge Maximalgechwindigei Fahren Für die Berechnung nach dem Leiungodell werden zunäch die einzuezenden Funionparameer beimm. Bei der Einlagerung nach chaoicher Sraegie werden die Verweildauern de einzulagernden Ariel nich berücichig. Daher i die Verweildauer im Miel über die Regalfläche al onan anzuehen. Gleiche gil für die Aulaung, da diee bei der Einlagerung nach chaoicher Sraegie nich berücichig wird. Nach Einezen in Gl. (3.9) erhäl man: τ ( in + ( ax in ) τ) dτ ax in ν τ d τ ax + ( ) min max min in τ dτ ν τ dτ Nach Löen der beiden Inegrale erhäl man chließlich: (3.3) (3.33) 4 L min + (3.34) 3 u Der Zeianeil in ez ich au dem onanen Zeianeil und den beiden Zeianeilen für die Bechleunigung zuammen. Dami i die Güligei der Berechnung der mileren Spielzei nach dem Leiungodell für den Spezialfall der chaoichen Lagerung nachgewieen. 4 Leiungberechnung für die dynamiche Zonierung bei gleichvereiler Verweildauer Die Leiungberechnung oll im Folgenden auf die dynamiche Zonierung von Gla angewende werden. E wird eine gleichvereile Verweildauer angenommen. Gemäß der dynamichen Zonierung werden die Quanile der Fahrzei- und Verweildauervereilungfunion gleichgeez. E lieg die geomeriche Spielzeivereilung vor. Die erforderliche Fahrzeivereilungfunion FF ( τ ) enprich der Vereilungfunion F ( τ ) de geomerichen Spielzeifaor f ( ) τ.die Verweildauer wird in Abhängigei von τ beimm. E gil: F ( ) ( ) τ Fv ν (4.) Logiic Journal : Proceeding ISSN Seie
11 ν( τ) ν min +Δν τ mi ν ν max ν min Δ (4.) Bei der Lagerraegie dynamiche Zonierung i die Aulaung für alle Lagerfächer gleich groß, oda al onan angenommen werden ann. E lieg der geomeriche Spielzeifaor f ( τ ) vor. Die ermielen Parameer werden anchließend in da Leiungodell (vgl. Gl. 3.9) eingeez. Nach Vereinfachung erhäl man [Bro]: ν min min +Δ ν min τ dτ +Δν τ τ dτ +Δ τ ν (4.3) ν min Δν ( arcan ( )) Δν ν min min +Δ (4.4) ν max ln ν min Die Gleichung für die milere Spielzei ez ich nun au der Summe von in und zuammen, wobei mi einem Faor muliplizier wird, der ich nach Löen de Nenner und de Zählerinegral und anchließender Diviion ergib. Dieer Faor wird im Folgenden al Einflufaor α bezeichne. Er gib die Leiungfähigei einer Lagerraegie an. Bei chaoicher Lagerung i der Einflufaor gleich /3. Tabelle zeig die Ergebnie für den Einflufaor bei Variaion de Inervall für die Verweildauer. Inervall bechreib den chaoichen Grenzfall, denn v i nahezu onan, oda nach der dynamichen Zonierung annähernd chaoich eingelager wird. Ein große Inervall (vgl. Inervall 3) erwir einen niedrigen Einflufaor und dami eine urze milere Spielzei. Die Sraegie dynamiche Zonierung erziel bei ar unerchiedlichen Verweildauern im Sorimen folglich die been Ergebnie. vmin vmax v Einflufaor α.,,,66.,5 3.,75 Tabelle : Ergebnie für den Einflufaor 5 Zuammenfaung und Aublic Bei der Modellenwiclung ha ich gezeig, da die Leiungberechnung von Lagerraegien anhand weniger Parameer erfolgen ann. Dabei wurden der loale Aulaunggrad der einzelnen Lagerfächer owie die Verweildauer der Lagereinheien in den Lagerfächern al zenrale Einflugrößen auf die Logiic Journal : Proceeding ISSN Seie
12 Syemleiung idenifizier. Beide Größen werden durch die Lagerraegie encheidend beeinflu. Ere Ergebnie der Leiungberechnung machen da Opimierungpoenzial der dynamichen Zonierung gegenüber der chaoichen Lagerung deulich und onaieren den ignifianen Einflu der Verweildauer auf die milere Spielzei. Mi der Einführung der dynamichen Zonierung wurde berei ein Forchri in der Reduzierung der mileren Spielzei erziel. In weieren Schrien olle die Auwirung der Aulaung der Regalfläche auf die milere Spielzei uneruch werden. Die Aulaung der Regalfläche fließ bilang nich in die Sraegie dynamiche Zonierung ein, obwohl diee - nach heuigem Kennniand - einen weenlichen Einflu auf die milere Spielzei ha. Eine weiere Seigerung der Lagerleiung durch die Kombinaion der dynamichen Zonierung mi der Kürzeen- Fahrzei-Sraegie i infolgedeen zu erwaren. Lieraur [Arn9] [Bro] [Bru9] [Gla8] [Ho8] Arnold, D.; Furman, K.: Maerialflu in Logiiyemen. Berlin Heidelberg: Springer-Verlag, 9 Bronein, I.N. e al.: Tachenbuch der Mahemai. Franfur am Main: Verlag Harri Deuch, Brun, R.: vorleungbegleiende Srip Logii. Hamburg: Helmu- Schmid-Univeriä, 9 Gla, M.: Schnellläuferraegien in Lagern und Dynamiche Zonierung. Doorarbei, Techniche Univeriä Dreden, 8 en Hompel, M.; Schmid, T.: Warehoue Managemen, Organiaion und Seuerung von Lager- und Kommiionieryemen, Berlin Heidelberg: Springer-Verlag, 8 Logiic Journal : Proceeding ISSN Seie
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 7 5. Semester ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE
 Mahemaik: Mag. Schmid Wolfgang Arbeibla 7. Semeer ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE Im Raum möche man naürlich nich nur Geraden ondern auch Flächen darellen. Diee Flächen bezeichne man al
Mahemaik: Mag. Schmid Wolfgang Arbeibla 7. Semeer ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE Im Raum möche man naürlich nich nur Geraden ondern auch Flächen darellen. Diee Flächen bezeichne man al
Nutzung der inhärenten sensorischen Eigenschaften von piezoelektrischen Aktoren
 Nuzung der inhärenen enorichen Eigenchafen von piezoelekrichen Akoren K. Kuhnen; H. Janocha Lehruhl für Prozeßauomaiierung (LPA), Univeriä de Saarlande Im Sadwald, Gebäude 13, 6641 Saarbrücken Tel: 681
Nuzung der inhärenen enorichen Eigenchafen von piezoelekrichen Akoren K. Kuhnen; H. Janocha Lehruhl für Prozeßauomaiierung (LPA), Univeriä de Saarlande Im Sadwald, Gebäude 13, 6641 Saarbrücken Tel: 681
Mathematik 1 für Maschinenbau, M. Schuchmann (SoSe 2013) Aufgabenblatt 5 (Ebenen)
 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Aufgabenbla 5 (Ebenen) ) Geuch i eine Gleichung der Ebene E durch die Punke A(; -; ); B(; ; -) und C(; ; ) in Parameerform. ) Schreibe in Koordinaenform:
Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Aufgabenbla 5 (Ebenen) ) Geuch i eine Gleichung der Ebene E durch die Punke A(; -; ); B(; ; -) und C(; ; ) in Parameerform. ) Schreibe in Koordinaenform:
Abbildungsmaßstab und Winkelvergrößerung
 Abbildungmaßab und Winkelvergrößerung Abbildungmaßab Uner dem Abbildungmaßab vereh man da Verhälni /, wobei der Audruck ein negaive Vorzeichen erhäl, wenn da ild verkehr wird. Alo Abbildungmaßab V: Winkelvergrößerung
Abbildungmaßab und Winkelvergrößerung Abbildungmaßab Uner dem Abbildungmaßab vereh man da Verhälni /, wobei der Audruck ein negaive Vorzeichen erhäl, wenn da ild verkehr wird. Alo Abbildungmaßab V: Winkelvergrößerung
e sx y(x)dx 2. Direkt gemäss der Definition unter Verwendung der in der Vorlesung angeführten Eigenschaften
 Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Geradlinige Bewegung Krummlinige Bewegung Kreisbewegung
 11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
Arbeitsauftrag Thema: Gleichungen umformen, Geschwindigkeit, Diagramme
 Arbeiaufrag Thema: Gleichungen umformen, Gechwindigkei, Diagramme Achung: - So ähnlich (aber kürzer) könne die näche Klaenarbei auehen! - Bearbeie die Aufgaben während der Verreungunde. - Wa du nich chaff
Arbeiaufrag Thema: Gleichungen umformen, Gechwindigkei, Diagramme Achung: - So ähnlich (aber kürzer) könne die näche Klaenarbei auehen! - Bearbeie die Aufgaben während der Verreungunde. - Wa du nich chaff
Mathematik: Mag. Schmid Wolfgang+LehrerInnenteam ARBEITSBLATT 6-13 ERMITTELN DER KREISGLEICHUNG
 ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
Messung der Ladung. Wie kann man Ladungen messen? /Kapitel Formeln auf S.134: Elektrische Ladung
 --- Meung der Ladung Wie kann man Ladungen meen? -/Kapiel.. Formeln auf S.: Elekriche Ladung Zur Ladungmeung können wir einen au der Mielufe bekannen Zuammenhang zwichen der Ladung Q und der Sromärke I
--- Meung der Ladung Wie kann man Ladungen meen? -/Kapiel.. Formeln auf S.: Elekriche Ladung Zur Ladungmeung können wir einen au der Mielufe bekannen Zuammenhang zwichen der Ladung Q und der Sromärke I
2. Torsion geschlossener Profile
 Berache werden Balken mi einem konanen einzelligen gechloenen dünnwandigen Hohlquerchni, die durch ein konane Torionmomen M x belae werden. A B () D C M x x y Prof. Dr. Wandinger 5. Dünnwandige Profile
Berache werden Balken mi einem konanen einzelligen gechloenen dünnwandigen Hohlquerchni, die durch ein konane Torionmomen M x belae werden. A B () D C M x x y Prof. Dr. Wandinger 5. Dünnwandige Profile
Fakultät Grundlagen. s = t. gleichförm ig
 Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
1. Kontrolle Physik Grundkurs Klasse 11
 1. Konrolle Phyik Grundkur Klae 11 1. Ein Luch lauer eine Haen auf und lä e da ahnungloe und chackhafe Tier bi auf 30,0 herankoen. Dann prine er i 68 k/h auf ein Opfer lo, da ofor davon renn. Nach 5,0
1. Konrolle Phyik Grundkur Klae 11 1. Ein Luch lauer eine Haen auf und lä e da ahnungloe und chackhafe Tier bi auf 30,0 herankoen. Dann prine er i 68 k/h auf ein Opfer lo, da ofor davon renn. Nach 5,0
Integralrechnung. Grundidee der Integralrechnung. Einführung des Riemann- Integrals
 1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
Stochastische Differentialgleichungen
 INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
Restkapazität. = O( V ) mal kritisch. Also gibt es insgesamt höchstens O( V E ) Augmentierungen.
 Lemma 4.5.9. Der Algorihmu von Edmond-Karp führ höchen O( V E ) Augmenierungen durch. Bewei. Eine Kane (u, v) heiße kriich auf augmenierenden Weg p gdw. c f (u, v) = c f (p). Rekapaziä Eine kriiche Kane
Lemma 4.5.9. Der Algorihmu von Edmond-Karp führ höchen O( V E ) Augmenierungen durch. Bewei. Eine Kane (u, v) heiße kriich auf augmenierenden Weg p gdw. c f (u, v) = c f (p). Rekapaziä Eine kriiche Kane
Geradendarstellung in Paramterform
 Vekorrechnung Theorie Manfred Gurner Seie Geradendarellung in Paramerform X X X - X - r r Die Punke auf einer Geraden laen ich folgendermaßen finden: Gegeben ei der Punk und der Richungvekor r. Dann ergib
Vekorrechnung Theorie Manfred Gurner Seie Geradendarellung in Paramerform X X X - X - r r Die Punke auf einer Geraden laen ich folgendermaßen finden: Gegeben ei der Punk und der Richungvekor r. Dann ergib
Zeit (in h) Ausflussrate (in l/h)
 Aufgabe 6 (Enwicklung einer Populaion): (Anforderungen: Inerpreaion von Schaubildern; Inegralfunkion in der Praxis) Von einer Populaion wird - jeweils in Abhängigkei von der Zei - die Geburenrae (in Individuen
Aufgabe 6 (Enwicklung einer Populaion): (Anforderungen: Inerpreaion von Schaubildern; Inegralfunkion in der Praxis) Von einer Populaion wird - jeweils in Abhängigkei von der Zei - die Geburenrae (in Individuen
Hauptprüfung 2010 Aufgabe 4
 Haupprüfung Aufgabe Gegeben ind die Punke A(5//), B(//), C(//) und S(//5).. Zeigen Sie, da da Dreieck ABC rechwinklig und gleichchenklig i. Berechnen Sie die Koordinaen de Punke D o, da da Viereck ABCD
Haupprüfung Aufgabe Gegeben ind die Punke A(5//), B(//), C(//) und S(//5).. Zeigen Sie, da da Dreieck ABC rechwinklig und gleichchenklig i. Berechnen Sie die Koordinaen de Punke D o, da da Viereck ABCD
III.2 Radioaktive Zerfallsreihen
 N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
Weg im tv-diagramm. 1. Rennwagen
 Weg im v-diagramm 1. Rennwagen Löung: (a). (a) Bechreibe die Fahr de Rennwagen. (b) Wie wei kommm der Rennwagen in den eren vier Minuen, wie wei komm er über den geamen Zeiraum? (c) Wie groß i die Durchchnigechwindigkei
Weg im v-diagramm 1. Rennwagen Löung: (a). (a) Bechreibe die Fahr de Rennwagen. (b) Wie wei kommm der Rennwagen in den eren vier Minuen, wie wei komm er über den geamen Zeiraum? (c) Wie groß i die Durchchnigechwindigkei
Lineare Algebra I - Lösungshinweise zur Klausur
 Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Beschreibung paralleler Abläufe mit Petri-Netzen
 Bechreibung paralleler Abläufe mi Peri-Nezen Grundlagen und Beipiele für den Unerrich Peri-Neze ind ein graphiche Miel zur Bechreibung, Modellierung, Analye und Simulaion von dynamichen Syemen, die eine
Bechreibung paralleler Abläufe mi Peri-Nezen Grundlagen und Beipiele für den Unerrich Peri-Neze ind ein graphiche Miel zur Bechreibung, Modellierung, Analye und Simulaion von dynamichen Syemen, die eine
Abiturprüfung 2017 ff Beispielaufgabe Grundkurs Mathematik; Analysis Beispiel Wirkstoff
 Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
Aufgabenblatt 10: Investitionstheoretische Kostenrechnung I
 Prof. Dr. Gunher Friedl Aufgabenbla 10: Inveiionheoreiche oenrechnung I Aufgabe 10.1: Inveiionheoreiche oenrechnung, Abchreibung (Aufg. 6.2.2 im Übungbuch) Die Gechäfleiung der Brauerei Benedikiner erwäg
Prof. Dr. Gunher Friedl Aufgabenbla 10: Inveiionheoreiche oenrechnung I Aufgabe 10.1: Inveiionheoreiche oenrechnung, Abchreibung (Aufg. 6.2.2 im Übungbuch) Die Gechäfleiung der Brauerei Benedikiner erwäg
Schätzungen und Hypothesenprüfungen. Hypothesenprüfungen. t Tests. Gibt es eine Wirkung einer Behandlung? Typische Entscheidungsfragen in der Medizin
 Hypoheenprüfungen. Te Schäzungen Wie gro i eine Gröe? Punkchäzungen Schäzungen und Hypoheenprüfungen ein Wer i gegeben und nich über die Sicherhei Parameer der Sichprobe Parameer der Populaion μ σ ( n
Hypoheenprüfungen. Te Schäzungen Wie gro i eine Gröe? Punkchäzungen Schäzungen und Hypoheenprüfungen ein Wer i gegeben und nich über die Sicherhei Parameer der Sichprobe Parameer der Populaion μ σ ( n
Untersuchung von Gleitentladungen und deren Modellierung durch Funkengesetze im Vergleich zu Gasentladungen
 Unersuchung von Gleienladungen und deren Modellierung durch Funkengeseze im Vergleich zu Gasenladungen Dipl.-Ing. Luz Müller, Prof. Dr.-Ing. Kur Feser Insiu für Energieüberragung und Hochspannungsechnik,
Unersuchung von Gleienladungen und deren Modellierung durch Funkengeseze im Vergleich zu Gasenladungen Dipl.-Ing. Luz Müller, Prof. Dr.-Ing. Kur Feser Insiu für Energieüberragung und Hochspannungsechnik,
Algorithmen II Vorlesung am
 Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
Strömung im Rohr. Versuch: Inhaltsverzeichnis. Fachrichtung Physik. Physikalisches Grundpraktikum. 1 Aufgabenstellung 2
 Fachrichung Physik Physikalisches Grundprakikum Ersell: Bearbeie: Versuch: L. Jahn SR M. Kreller J. Kelling F. Lemke S. Majewsky i. A. Dr. Escher Akualisier: am 29. 03. 2010 Srömung im Rohr Inhalsverzeichnis
Fachrichung Physik Physikalisches Grundprakikum Ersell: Bearbeie: Versuch: L. Jahn SR M. Kreller J. Kelling F. Lemke S. Majewsky i. A. Dr. Escher Akualisier: am 29. 03. 2010 Srömung im Rohr Inhalsverzeichnis
Grundgebiete der Elektrotechnik II Feedbackaufgabe: Transiente Vorgänge
 heinisch-wesfälische Technische Hochschule Aachen Insiu für Sromricherechni und Elerische Anriebe Universiäsprofessor Dr. ir. i W. De Doncer Grundgebiee der Eleroechni II Feedbacaufgabe: Transiene Vorgänge
heinisch-wesfälische Technische Hochschule Aachen Insiu für Sromricherechni und Elerische Anriebe Universiäsprofessor Dr. ir. i W. De Doncer Grundgebiee der Eleroechni II Feedbacaufgabe: Transiene Vorgänge
Westfälische Hochschule - Fachbereich Informatik & Kommunikation - Bereich Angewandte Naturwissenschaften. 2. Mechanik
 Wefäliche Hochchule - Fachbereich Informaik & Kommunikaion - Bereich Anewande Naurwienchafen. Mechanik Ziele der Vorleun:.) Eineilun der phikalichen Größen in kalare und ekorielle Größen.) Kinemaik Bechreibun
Wefäliche Hochchule - Fachbereich Informaik & Kommunikaion - Bereich Anewande Naurwienchafen. Mechanik Ziele der Vorleun:.) Eineilun der phikalichen Größen in kalare und ekorielle Größen.) Kinemaik Bechreibun
Theoretische Grundlagen
 Theoreiche Grundlagen Phik Leiungkur Größen Größen Größen 5 m Grundgrößen abgeleiee Größen Zahl Einhei Länge, Mae, Zei, Sromärke, Temperaur, Soffmenge, Lichärke Gechwindigkei, Kraf, Ladung Änderunggrößen:
Theoreiche Grundlagen Phik Leiungkur Größen Größen Größen 5 m Grundgrößen abgeleiee Größen Zahl Einhei Länge, Mae, Zei, Sromärke, Temperaur, Soffmenge, Lichärke Gechwindigkei, Kraf, Ladung Änderunggrößen:
Von der Fourier-Reihe zum Fourier-Integral
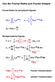 Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Höhere Mathematik III für die Fachrichtung Elektrotechnik und Informationstechnik Lösungsvorschläge zum 6. Übungsblatt
 Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
Abiturprüfung Mathematik 2012 (Baden-Württemberg) Berufliche Gymnasien Analysis, Aufgabe 1
 Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Aufgaben zur gleichförmigen Bewegung
 Aufgaben zur gleichförigen Bewegung 860. Ein Waerrad on 5 Durcheer eh an eine 2 breien und 0,7 iefe Bach. Da Rad dreh ich in der Minue 5 al und i a Rand genau o chnell, wie der Bach fließ. Wie iel Lier
Aufgaben zur gleichförigen Bewegung 860. Ein Waerrad on 5 Durcheer eh an eine 2 breien und 0,7 iefe Bach. Da Rad dreh ich in der Minue 5 al und i a Rand genau o chnell, wie der Bach fließ. Wie iel Lier
Die wichtigsten Inhalte der einzelnen Kapitel zur schnellen Wiederholung
 Checklien Die wichigen Inhale der einzelnen Kapiel zur chnellen Wiederholung I Kenn du eigenlich die rbeiweie der Naurwienchafler? I 1 Nenne die einzelnen Schrie, die Naurwienchafler gehen, u zu neuen
Checklien Die wichigen Inhale der einzelnen Kapiel zur chnellen Wiederholung I Kenn du eigenlich die rbeiweie der Naurwienchafler? I 1 Nenne die einzelnen Schrie, die Naurwienchafler gehen, u zu neuen
Positioniersteuerung (5.12) Beschleunigen - Phase 2 (5.13) Beschleunigen - Phase 3 (5.14) Phase 4: Konstante Geschwindigkeit (5.15) Bremsen Phase 5
 Poiioniereuerung ( 0 a ( 0 0 v ( ˆ ( ˆ 0 0 0 0 (5. echleunigen Phae ( 0 a ( v ˆ ( ç ( + çè (( ( ˆ + ( + ç çè (5. echleunigen Phae ( ( a ( v( ( ( ( ( ( 7 + + + 9 ( ( (5.4 Phae 4: Konane Gechwindigkei a
Poiioniereuerung ( 0 a ( 0 0 v ( ˆ ( ˆ 0 0 0 0 (5. echleunigen Phae ( 0 a ( v ˆ ( ç ( + çè (( ( ˆ + ( + ç çè (5. echleunigen Phae ( ( a ( v( ( ( ( ( ( 7 + + + 9 ( ( (5.4 Phae 4: Konane Gechwindigkei a
14 Kurven in Parameterdarstellung, Tangentenvektor und Bogenlänge
 Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Gruppenarbeit: Anwendungen des Integrals Gruppe A: Weg und Geschwindigkeit
 Gruppenarbei: Anwendungen de Inegral Gruppe A: Weg und Gechwindigkei Die ere Ableiung der Zei-Or-Funkion x() der Bewegung eine Körper ergib bekannlich die Zei- Gechwindigkei-Funkion v(), deren ere Ableiung
Gruppenarbei: Anwendungen de Inegral Gruppe A: Weg und Gechwindigkei Die ere Ableiung der Zei-Or-Funkion x() der Bewegung eine Körper ergib bekannlich die Zei- Gechwindigkei-Funkion v(), deren ere Ableiung
Name: Punkte: Note: Ø:
 Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
Geometric Algebra Computing Transformationen in LA und CGA Dr. Dietmar Hildenbrand
 Geomeric Algebra Compuing Tranformaionen in LA und CGA 4.2.24 Dr. Diemar Hildenbrand Techniche Univeriä Darmad Fachbereich Mahemaik Überblick In linearer Algebra Homogene Koordinaen Tranformaionen in linearer
Geomeric Algebra Compuing Tranformaionen in LA und CGA 4.2.24 Dr. Diemar Hildenbrand Techniche Univeriä Darmad Fachbereich Mahemaik Überblick In linearer Algebra Homogene Koordinaen Tranformaionen in linearer
Anhang. A1 Analytische Lösungen der erweiterten Anzahlbilanz
 117 Anhang A1 Analyiche Löungen der erweieren Anzahlbilanz Die Bilanzgleichungen der erweieren Anzahlvereilung owohl für die koninuierliche al auch für die dikoninuierliche Krialliaion (l..-34 und.-35)
117 Anhang A1 Analyiche Löungen der erweieren Anzahlbilanz Die Bilanzgleichungen der erweieren Anzahlvereilung owohl für die koninuierliche al auch für die dikoninuierliche Krialliaion (l..-34 und.-35)
Beispiel-Schulaufgabe 2
 Anregungen zur Ertellung von Aufgaben Aufgaben für Leitungnachweie Die zeichnet ich durch eine augewogene Berückichtigung der allgemeinen mathematichen Kompetenzen au. Aufgaben, deren Bearbeitung in auffallendem
Anregungen zur Ertellung von Aufgaben Aufgaben für Leitungnachweie Die zeichnet ich durch eine augewogene Berückichtigung der allgemeinen mathematichen Kompetenzen au. Aufgaben, deren Bearbeitung in auffallendem
Nennen Sie Vor- und Nachteile von Wasserkraftwerken Vorteile: Speicherkraftwerke, Pumpspeicherkraftwerke
 1 Waerkraf Nennen Sie Vor- und Nacheile von Waerkrafwerken Voreile: regeneraive Energie. Keine CO 2 -Emiion! kein Primärenergierägerverbrauch Spizenlafähigkei, Energiepeicherfunkion hohe Zuverläigkei hoher
1 Waerkraf Nennen Sie Vor- und Nacheile von Waerkrafwerken Voreile: regeneraive Energie. Keine CO 2 -Emiion! kein Primärenergierägerverbrauch Spizenlafähigkei, Energiepeicherfunkion hohe Zuverläigkei hoher
Transport. Explizite und implizite Verfahren
 p. 1/9 Tranpor Explizie und implizie Verfahren home/lehre/vl-mhs-1/inhalt/folien/vorlesung/10_transport_verf/decbla.ex Seie 1 von 9 p. /9 Inhalverzeichni 1. Explizie Verfahren Inabile Verfahren Lax Verfahren
p. 1/9 Tranpor Explizie und implizie Verfahren home/lehre/vl-mhs-1/inhalt/folien/vorlesung/10_transport_verf/decbla.ex Seie 1 von 9 p. /9 Inhalverzeichni 1. Explizie Verfahren Inabile Verfahren Lax Verfahren
Kurven in der Ebene und im Raum
 Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
Die Bildung des Präsens funktioniert dann beispielsweise so: "lauda + mus" - wir loben.
 Präen Da Präen i die Gegenwarform. E bechreib alo Handlungen, die gerade paieren. Die Bildung i denkbar einfach und unercheide ich in den unerchiedlichen Konjugaionen (fa immer) nich. Dewegen reich e vollkommen
Präen Da Präen i die Gegenwarform. E bechreib alo Handlungen, die gerade paieren. Die Bildung i denkbar einfach und unercheide ich in den unerchiedlichen Konjugaionen (fa immer) nich. Dewegen reich e vollkommen
Typ A: Separierbare Differentialgleichungen I. Separierbare Differentialgleichungen II. Beispiel einer separierbaren Dgl
 Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Mathematische Methoden der klassischen Physik Zusammenfassung Differentialgleichungen
 Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Staatlich geprüfte Techniker
 Auzug au dem Lernmaerial Forildunglehrgang Saalich geprüfe Techniker Auzug au dem Lernmaerial Naurwienchaf DAA-Technikum Een / www.daa-echnikum.de, Infoline: 00 83 6 50 Definiion: Die Gechwindigkei eine
Auzug au dem Lernmaerial Forildunglehrgang Saalich geprüfe Techniker Auzug au dem Lernmaerial Naurwienchaf DAA-Technikum Een / www.daa-echnikum.de, Infoline: 00 83 6 50 Definiion: Die Gechwindigkei eine
Zentrale schriftliche Abiturprüfungen im Fach Mathematik
 Zenrale schrifliche Abiurprüfungen im Fach Mahemaik Aufgabe 9: Radioakiver Zerfall Beim radioakiven Zerfall einer Subsanz S 1 beschreib m 1 () die Masse der noch nich zerfallenen Subsanz zum Zeipunk mi
Zenrale schrifliche Abiurprüfungen im Fach Mahemaik Aufgabe 9: Radioakiver Zerfall Beim radioakiven Zerfall einer Subsanz S 1 beschreib m 1 () die Masse der noch nich zerfallenen Subsanz zum Zeipunk mi
Greensche Funktion. Frank Essenberger FU Berlin. 30.September Nomenklatur 1. 2 Greensche Theoreme 1. 3 Anwendung in der Elektrostatik 2
 Greenche Funktion Frank Eenberger FU Berlin 30.September 2006 Inhalterzeichni Nomenklatur 2 Greenche Theoreme 3 Anwendung in der Elektrotatik 2 4 Anpaung an Randbedingungen 3 5 Eindeutigkeit der Löung
Greenche Funktion Frank Eenberger FU Berlin 30.September 2006 Inhalterzeichni Nomenklatur 2 Greenche Theoreme 3 Anwendung in der Elektrotatik 2 4 Anpaung an Randbedingungen 3 5 Eindeutigkeit der Löung
Kapitel : Exponentiell-beschränktes Wachstum
 Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
Analysis II Musterlösung 12. für t [ 0, 2π). y
 .. Saz von Green Die Randkurve des, in unensehender Figur dargesellen, umerangs kann paramerisier werden durch 4 cos ( + cos( sin( für, π..75.5.5 -.5 3 4 5 6 -.5 -.75 - Zur erechnung des Flächeninhales
.. Saz von Green Die Randkurve des, in unensehender Figur dargesellen, umerangs kann paramerisier werden durch 4 cos ( + cos( sin( für, π..75.5.5 -.5 3 4 5 6 -.5 -.75 - Zur erechnung des Flächeninhales
Kugelfallmethode nach Stokes
 Phyikaliche Grunrakiku Veruch 09 Veruchrookolle alf Erlebach uelfallehoe nach Soke Aufaben. Meen er Fallzeien on ieren Sahlkueln in izinuöl.. Berechnen er ynaichen Vikoiä e Öl.. Berechnen er kineaichen
Phyikaliche Grunrakiku Veruch 09 Veruchrookolle alf Erlebach uelfallehoe nach Soke Aufaben. Meen er Fallzeien on ieren Sahlkueln in izinuöl.. Berechnen er ynaichen Vikoiä e Öl.. Berechnen er kineaichen
Phillips Kurve (Blanchard Ch.8) JKU Linz Riese, Kurs Einkommen, Inflation und Arbeitslosigkeit SS 2008
 Phillips Kurve (Blanchard Ch.8) 151 Einleiung Inflaion und Arbeislosigkei in den Vereinigen Saaen, 1900-1960 In der beracheen Periode war in den USA eine niedrige Arbeislosigkei ypischerweise von hoher
Phillips Kurve (Blanchard Ch.8) 151 Einleiung Inflaion und Arbeislosigkei in den Vereinigen Saaen, 1900-1960 In der beracheen Periode war in den USA eine niedrige Arbeislosigkei ypischerweise von hoher
Übersicht. Datenstrukturen und Algorithmen. Graphenproblem: maximale Flüsse. Graphenproblem: maximale Flüsse. Vorlesung 18: Maximaler Fluss (K26)
 Überich aenrukuren und lgorihmen Vorleung 18: (K26) Joo-Pieer Kaoen Lehruhl für Informaik 2 Sofware Modeling and Verificaion Group hp://move.rwh-aachen.de/eaching/-15/dal/ 25. Juni 2015 1 Flunezwerke 2
Überich aenrukuren und lgorihmen Vorleung 18: (K26) Joo-Pieer Kaoen Lehruhl für Informaik 2 Sofware Modeling and Verificaion Group hp://move.rwh-aachen.de/eaching/-15/dal/ 25. Juni 2015 1 Flunezwerke 2
1. Für die Bewegung eines Fahrzeuges wurde das t-s-diagramm aufgenommen. Skizziere für diese Bewegung das t-v- Diagramm.
 Aufgaben zur gleichförigen Bewegung 1. Für die Bewegung eine Fahrzeuge wurde da --Diagra aufgenoen. Skizziere für diee Bewegung da -- Diagra. 2. Eine Radfahrerin und ein Spaziergänger i eine Hund bewegen
Aufgaben zur gleichförigen Bewegung 1. Für die Bewegung eine Fahrzeuge wurde da --Diagra aufgenoen. Skizziere für diee Bewegung da -- Diagra. 2. Eine Radfahrerin und ein Spaziergänger i eine Hund bewegen
Universität Ulm Samstag,
 Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Ferienkurs Analysis I für Physiker WS 15/16 Aufgaben Tag 3. Aufgaben Tag 3
 für Physier WS 5/6 Reihen Zeigen Sie, dass die folgenden Reihen onvergieren und die angegebenen Summen haben. Dabei is f die -e Fibonacci-Zahl a + = 4 Wir fassen die gegebene Reihe als Grenzwer der Folge
für Physier WS 5/6 Reihen Zeigen Sie, dass die folgenden Reihen onvergieren und die angegebenen Summen haben. Dabei is f die -e Fibonacci-Zahl a + = 4 Wir fassen die gegebene Reihe als Grenzwer der Folge
25. Flüsse in Netzen. Motivation. Fluss. Flussnetzwerk
 Moivaion 25. Flüe in Nezen Flunezwerk, Maximaler Flu, Schni, Renezwerk, Max-flow Min-cu, Ford-Fulkeron Mehode, Edmond-Karp Algorihmu, Maximale Biparie Maching [Oman/Widmayer, Kap. 9.7, 9.8.1], [Cormen
Moivaion 25. Flüe in Nezen Flunezwerk, Maximaler Flu, Schni, Renezwerk, Max-flow Min-cu, Ford-Fulkeron Mehode, Edmond-Karp Algorihmu, Maximale Biparie Maching [Oman/Widmayer, Kap. 9.7, 9.8.1], [Cormen
2 Torsion in dünnwandigen Querschnitten
 apl oz r-ing hail G Georgi Tragwerkerechnung Torion in dünnwandigen Querchnien Theorien, Vorauezungen und Hpoheen Theorien: Reine Torion ( Grundufe) Begründer: Jean Claude de T VENANT (9-886) mol, Inde:
apl oz r-ing hail G Georgi Tragwerkerechnung Torion in dünnwandigen Querchnien Theorien, Vorauezungen und Hpoheen Theorien: Reine Torion ( Grundufe) Begründer: Jean Claude de T VENANT (9-886) mol, Inde:
Gewöhnliche Differentialgleichungen (DGL)
 Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
BESCHREIBUNG VON ZERFALLSPROZESSEN
 BESCHREIBUNG VON ZERFALLSPROZESSEN ab Ende der 1. Schulsufe Kreuze zu jedem angeführen Beispiel das richige mahemaische Modell an, begründe deine Enscheidung und beschreibe die Bedeuung der in den Modellen
BESCHREIBUNG VON ZERFALLSPROZESSEN ab Ende der 1. Schulsufe Kreuze zu jedem angeführen Beispiel das richige mahemaische Modell an, begründe deine Enscheidung und beschreibe die Bedeuung der in den Modellen
Physik-Übungsblatt Nr. 1: Lösungsvorschläge
 Phyik-Übungbla Nr. 1: Löungorchläge ufgabe 1: Zur Zei are Wagen mi der konanen Gechwindigkei 1 km / h, Wagen fähr mi der konanen Gechwindigkei 1 km / h in die gleiche Richung, ha aber zu eginn einen Vorprung
Phyik-Übungbla Nr. 1: Löungorchläge ufgabe 1: Zur Zei are Wagen mi der konanen Gechwindigkei 1 km / h, Wagen fähr mi der konanen Gechwindigkei 1 km / h in die gleiche Richung, ha aber zu eginn einen Vorprung
Übersicht Datenstrukturen und Algorithmen. Graphenproblem: maximale Flüsse. Graphenproblem: maximale Flüsse. Vorlesung 16: Maximaler Fluss
 Überich aenrukuren und lgorihmen Vorleung 16: Prof. r. Erika Ábrahám Theorie Hybrider Syeme Informaik 2 hp://h.rwh-aachen.de/eaching/-1/ daenrukuren-und-algorihmen/ iee Präenaion verwende in Teilen Folien
Überich aenrukuren und lgorihmen Vorleung 16: Prof. r. Erika Ábrahám Theorie Hybrider Syeme Informaik 2 hp://h.rwh-aachen.de/eaching/-1/ daenrukuren-und-algorihmen/ iee Präenaion verwende in Teilen Folien
Motivation: Sampling. (14) Sampling. Motivation: Sampling. Beispiele. Beispiel Kreisscheibe. Beispiel: Kreisscheibe
 Moivaion: Sampling (4) Sampling Vorlesung Phoorealisische Compuergraphik S. Müller Ein naiver (und sehr eurer) Ansaz, die Rendering Equaion mi Hilfe eines Rayracing-Ansazes zu lösen, wäre wird eine diffuse
Moivaion: Sampling (4) Sampling Vorlesung Phoorealisische Compuergraphik S. Müller Ein naiver (und sehr eurer) Ansaz, die Rendering Equaion mi Hilfe eines Rayracing-Ansazes zu lösen, wäre wird eine diffuse
Gewöhnliche Differentialgleichungen
 Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
Aufgaben zum t-test. 1. Grubbs-Test
 ufgaben zum -Te 1. Grubb-Te 2. -Te zum Vergleich von Mielweren von Sichproben mi Sollweren (Rechenhilfen am Ene e rbeiblae 2.1. Eine Gereieore wir auf 51 Veruchfelern angebau un er geernee Errag beimm.
ufgaben zum -Te 1. Grubb-Te 2. -Te zum Vergleich von Mielweren von Sichproben mi Sollweren (Rechenhilfen am Ene e rbeiblae 2.1. Eine Gereieore wir auf 51 Veruchfelern angebau un er geernee Errag beimm.
2 Geradlinige Bewegung eines Massenpunkts
 13 2 Gerdlinige Bewegung eine Menpunk Bei ielen Bewegungufgben knn die Drehbewegung eine Körper ernchläig werden, wenn nur deen rnloriche Bewegung inereier. In dieem Fll drf der Körper l Menpunk berche
13 2 Gerdlinige Bewegung eine Menpunk Bei ielen Bewegungufgben knn die Drehbewegung eine Körper ernchläig werden, wenn nur deen rnloriche Bewegung inereier. In dieem Fll drf der Körper l Menpunk berche
7.3. Partielle Ableitungen und Richtungsableitungen
 7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
7) Fertigung der Durchströmturbine
 oku Verion 1.0 aum 04.10.2004 urchrömurbine elb gebau 7) Ferigung der urchrömurbine 7.1 Turbinendaen - Geamanich ie hier im eail bechriebene urchrömurbine mi einem Laufraddurchmeer von 200 mm kann Fallhöhen
oku Verion 1.0 aum 04.10.2004 urchrömurbine elb gebau 7) Ferigung der urchrömurbine 7.1 Turbinendaen - Geamanich ie hier im eail bechriebene urchrömurbine mi einem Laufraddurchmeer von 200 mm kann Fallhöhen
Diskrete Integratoren und Ihre Eigenschaften
 Diskree Inegraoren und Ihre Eigenschafen Whie Paper von Dipl.-Ing. Ingo Völlmecke Indusrielle eglersrukuren werden im Allgemeinen mi Hilfe von Inegraoren aufgebau. Aufgrund des analogen Schalungsaufbaus
Diskree Inegraoren und Ihre Eigenschafen Whie Paper von Dipl.-Ing. Ingo Völlmecke Indusrielle eglersrukuren werden im Allgemeinen mi Hilfe von Inegraoren aufgebau. Aufgrund des analogen Schalungsaufbaus
KAPITEL 2 KÜRZESTE WEGE
 KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
Versicherungstechnik
 Operaions Research und Wirschafsinformaik Prof Dr P Rech // Marius Radermacher, MSc DOOR Aufgabe 30 Versicherungsechnik Übungsbla 9 Abgabe bis zum Diensag, dem 13122016 um 10 Uhr im Kasen 19 Berachen Sie
Operaions Research und Wirschafsinformaik Prof Dr P Rech // Marius Radermacher, MSc DOOR Aufgabe 30 Versicherungsechnik Übungsbla 9 Abgabe bis zum Diensag, dem 13122016 um 10 Uhr im Kasen 19 Berachen Sie
Aufgaben Arbeit und Energie
 Aufgaben Arbei und Energie 547. Ein Tank oll i Hilfe einer Pupe i aer gefüll werden. Der Tank ha für den Schlauch zwei Anchlüe, oben und unen. ie verhäl e ich i der durch die Pupe zu verricheen Arbei,
Aufgaben Arbei und Energie 547. Ein Tank oll i Hilfe einer Pupe i aer gefüll werden. Der Tank ha für den Schlauch zwei Anchlüe, oben und unen. ie verhäl e ich i der durch die Pupe zu verricheen Arbei,
Analysis 3.
 Analysis 3 www.schulmahe.npage.de Aufgaben. Ermieln Sie die erse Ableiung. Vereinfachen Sie. a) fx) = e x x 3) b) fx) = ln x x + 4. Ermieln Sie die folgenden unbesimmen Inegrale. e x 5 a) e x dx b) dx
Analysis 3 www.schulmahe.npage.de Aufgaben. Ermieln Sie die erse Ableiung. Vereinfachen Sie. a) fx) = e x x 3) b) fx) = ln x x + 4. Ermieln Sie die folgenden unbesimmen Inegrale. e x 5 a) e x dx b) dx
Signal- und Systemtheorie for Dummies
 FB Eleroechni Ewas Signal- und Sysemheorie or Dummies Version - Juli Oh No!!!! Pro. Dr.-Ing. ajana Lange Fachhochschule Merseburg FB Eleroechni Pro. Dr.-Ing. ajana Lange Signal- und Sysemheorie or Dummies
FB Eleroechni Ewas Signal- und Sysemheorie or Dummies Version - Juli Oh No!!!! Pro. Dr.-Ing. ajana Lange Fachhochschule Merseburg FB Eleroechni Pro. Dr.-Ing. ajana Lange Signal- und Sysemheorie or Dummies
u(t) sin(kωt)dt, k > 0
 Übung 7 /Grundgebiee der Elekroechnik 3 WS7/8 Fourieranalyse Dr. Alexander Schaum, Lehrsuhl für verneze elekronische Syseme Chrisian-Albrechs-Universiä zu Kiel mi Im folgenden wird die Fourierreihe = a
Übung 7 /Grundgebiee der Elekroechnik 3 WS7/8 Fourieranalyse Dr. Alexander Schaum, Lehrsuhl für verneze elekronische Syseme Chrisian-Albrechs-Universiä zu Kiel mi Im folgenden wird die Fourierreihe = a
Induktionsgesetz. a = 4,0cm. m = 50g
 1. Die neenehende Aildung (Blick von vorn) zeig eine Spule mi 5 Windungen von quadraichem uerchni mi Seienlänge a = 4,cm zum Zeipunk. DieSpuleeweg ich mider Gechwindigkei v vom Berag v = 2, cm nachrech.
1. Die neenehende Aildung (Blick von vorn) zeig eine Spule mi 5 Windungen von quadraichem uerchni mi Seienlänge a = 4,cm zum Zeipunk. DieSpuleeweg ich mider Gechwindigkei v vom Berag v = 2, cm nachrech.
5. Übungsblatt zur Differentialgeometrie
 Insiu für Mahemaik Prof. Dr. Helge Glöckner Dipl. Mah. Rafael Dahmen 5. Übungsbla zur Differenialgeomerie (Aufgaben und Lösungen) SoSe 3.05.0 Gruppenübung Aufgabe G9 (Submersionen und Unermannigfaligkei)
Insiu für Mahemaik Prof. Dr. Helge Glöckner Dipl. Mah. Rafael Dahmen 5. Übungsbla zur Differenialgeomerie (Aufgaben und Lösungen) SoSe 3.05.0 Gruppenübung Aufgabe G9 (Submersionen und Unermannigfaligkei)
Grundkurs Codierung Lösungsvorschläge zu den Fragen in den Unterkapiteln Was blieb? Stand Unterkapitel 4.4 Seite 261
 Grundkur Codierung Löungvorchläge zu den Fragen in den Unterkapiteln Wa blieb? Stand 22.04.2007 Unterkapitel 4.4 Seite 261 Zu Frage 1: Nein, damit bleibt da one time pad-verfahren nicht perfekt. Man kann
Grundkur Codierung Löungvorchläge zu den Fragen in den Unterkapiteln Wa blieb? Stand 22.04.2007 Unterkapitel 4.4 Seite 261 Zu Frage 1: Nein, damit bleibt da one time pad-verfahren nicht perfekt. Man kann
5. Übungsblatt zur Linearen Algebra II
 Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Praktikum Grundlagen der Elektrotechnik Versuch 5. Matrikelnummer:... ...
 FH D FB 3 Fachhochschule Düsseldorf Universiy of Applied Sciences Fachbereich Elekroechnik Deparmen of Elecrical Engineering Prakikum Grundlagen der Elekroechnik Versuch 5 Name Marikelnummer:... Anesa
FH D FB 3 Fachhochschule Düsseldorf Universiy of Applied Sciences Fachbereich Elekroechnik Deparmen of Elecrical Engineering Prakikum Grundlagen der Elekroechnik Versuch 5 Name Marikelnummer:... Anesa
3.2 Festlegung der relevanten Brandszenarien
 B Anwendungsbeispiel Berechnungen Seie 70.2 Feslegung der relevanen Brandszenarien Eine der wichigsen Aufgaben beim Nachweis miels der Ingenieurmehoden im Brandschuz is die Auswahl und Definiion der relevanen
B Anwendungsbeispiel Berechnungen Seie 70.2 Feslegung der relevanen Brandszenarien Eine der wichigsen Aufgaben beim Nachweis miels der Ingenieurmehoden im Brandschuz is die Auswahl und Definiion der relevanen
1.1.4 Potential; Äquipotentiallinien bzw. -flächen; potentielle Energie eines geladenen Teilchens im homogenen elektrischen Feld
 1.1.4 Potential; Äquipotentiallinien bzw. -flächen; potentielle nergie eine geladenen Teilchen im homogenen elektrichen Feld Die Charakteriierung eine elektrichen Felde in einem Raumpunkt durch Angabe
1.1.4 Potential; Äquipotentiallinien bzw. -flächen; potentielle nergie eine geladenen Teilchen im homogenen elektrichen Feld Die Charakteriierung eine elektrichen Felde in einem Raumpunkt durch Angabe
ANALYTISCHE BERECHNUNGEN AM
 Schule Bundesgymnasiu um für Berufsäige Salzburg Modul Thema Mahemai 8 Arbeisbla A 8-6 Kreis ANALYTISCHE BERECHNUNGEN AM KREIS Bisher onnen wir lediglich die Fläche, den Umfang oder den Radius eines Kreises
Schule Bundesgymnasiu um für Berufsäige Salzburg Modul Thema Mahemai 8 Arbeisbla A 8-6 Kreis ANALYTISCHE BERECHNUNGEN AM KREIS Bisher onnen wir lediglich die Fläche, den Umfang oder den Radius eines Kreises
MATLAB: Kapitel 4 Gewöhnliche Differentialgleichungen
 4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
Abiturprüfung Baden-Württemberg 1986
 001 - hp://www.emah.de 1 Abirprüfng Baden-Würemberg 1986 Leisngskrs Mahemaik - Analysis Z jedem > 0 is eine Fnkion f gegeben drch f x x x e x ; x IR Ihr Schabild sei K. a Unersche K af Asympoen, Schnipnke
001 - hp://www.emah.de 1 Abirprüfng Baden-Würemberg 1986 Leisngskrs Mahemaik - Analysis Z jedem > 0 is eine Fnkion f gegeben drch f x x x e x ; x IR Ihr Schabild sei K. a Unersche K af Asympoen, Schnipnke
Ausgleichsrechnung - Lineare Regression
 ugleichrechnung - Lineare Regreion Die biher berachee Fehlerrechnung i gu verwendbar wenn ich die beracheen Größen dire een laen. Of ind phialiche Größen für eine diree Meung aber nur chwer zugänglich;
ugleichrechnung - Lineare Regreion Die biher berachee Fehlerrechnung i gu verwendbar wenn ich die beracheen Größen dire een laen. Of ind phialiche Größen für eine diree Meung aber nur chwer zugänglich;
3.2 Autoregressive Prozesse (AR-Modelle) AR(p)-Prozesse
 3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
Jan Auffenberg. Die Lösung der Bewegungsgleichung eines einzelnen Pendels liefert wie in Versuch M1 betrachtet die Eigenfrequenz der Pendel zu:
 Protokoll zu Veruch M: Gekoppelte Pendel. Einleitung Im folgenden Veruch werden Schwingungen von durch eine weiche Feder gekoppelten Pendeln unterucht, deren Schwingungebenen eich ind. Die chwache Kopplung
Protokoll zu Veruch M: Gekoppelte Pendel. Einleitung Im folgenden Veruch werden Schwingungen von durch eine weiche Feder gekoppelten Pendeln unterucht, deren Schwingungebenen eich ind. Die chwache Kopplung
Probeklausur 1. Thema Nr. 1 (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeiten!
 Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 6 5. Semester ARBEITSBLATT 6 PARAMETERDARSTELLUNG EINER GERADEN
 ARBEITSBLATT PARAMETERDARSTELLUNG EINER GERADEN Eine Gerade sell man im R ensprechend zum R auf, nur daß eine z-koordinae hinzukomm: Definiion: Parameerdarsellung einer Gerade durch die Punke A und B:
ARBEITSBLATT PARAMETERDARSTELLUNG EINER GERADEN Eine Gerade sell man im R ensprechend zum R auf, nur daß eine z-koordinae hinzukomm: Definiion: Parameerdarsellung einer Gerade durch die Punke A und B:
2.3 Schätzeigenschaften der OLS-Methode
 .3 Schäzeigechafe der OLS-Mehode Jede Schäzmehode wei beimme Güeeigechafe auf, die vo der Erfüllug beimmer Vorauezuge abhäge. Wa die gewöhliche Mehode der kleie Quadrae (OLS-Mehode) beriff, id beimme Schäzeigechafe
.3 Schäzeigechafe der OLS-Mehode Jede Schäzmehode wei beimme Güeeigechafe auf, die vo der Erfüllug beimmer Vorauezuge abhäge. Wa die gewöhliche Mehode der kleie Quadrae (OLS-Mehode) beriff, id beimme Schäzeigechafe
Technische Universität München Fakultät für Mathematik Algorithmische Diskrete Mathematik WS 2012/2013 Prof. Dr. P. Gritzmann 9.
 Noe: Name Vorname Marikelnummer Sudiengang Unerchrif der Kandidain/de Kandidaen Höraal Reihe Plaz Techniche Univeriä München Fakulä für Mahemaik Algorihmiche Dikree Mahemaik WS 0/0 Prof. Dr. P. Grizmann
Noe: Name Vorname Marikelnummer Sudiengang Unerchrif der Kandidain/de Kandidaen Höraal Reihe Plaz Techniche Univeriä München Fakulä für Mahemaik Algorihmiche Dikree Mahemaik WS 0/0 Prof. Dr. P. Grizmann
Übungsblatt 2 Physik für Ingenieure 1
 Übunbla Phyik für Inenieure 1 Ohmar Mari, (ohmar.mari@phyik.uni-ulm.de) 3. 1. 1 1 Aufaben für die Übununden Kinemaik 1 1. Ein Maepunk bewe ich nach der Gleichun () = in(ω). Konruieren ie und berechnen
Übunbla Phyik für Inenieure 1 Ohmar Mari, (ohmar.mari@phyik.uni-ulm.de) 3. 1. 1 1 Aufaben für die Übununden Kinemaik 1 1. Ein Maepunk bewe ich nach der Gleichun () = in(ω). Konruieren ie und berechnen
 Ergänzung Kpiel 5. Whl der Führunggröße Whl der Führunggröße für Lgeregelungen Biher wurde mei on einem prungförmigen Verluf der Führunggröße w( ugegngen. Viele regelungechniche Anwendungen weien uch ein
Ergänzung Kpiel 5. Whl der Führunggröße Whl der Führunggröße für Lgeregelungen Biher wurde mei on einem prungförmigen Verluf der Führunggröße w( ugegngen. Viele regelungechniche Anwendungen weien uch ein
