Inhalt, Formelsammlung:
|
|
|
- Irmgard Schneider
- vor 7 Jahren
- Abrufe
Transkript
1 Inlt, Fomelsmmlung: Geometie Ds llgemeine Deiek Spezielle Deieke Vieeke Regelmäßige Vieleke Keisfläen Pismen Pymien un Kegel 5 Pymien- un Kegelstümpfe 6 Kugel 6 Zentise Stekung un ie Stlensätze 6 Stz es Pytgos, Kteten- un Höenstz 7 Tigonometie, Winkelfunktionen 7 lge Die Reengesetze e ition un Sutktion 7 Renen mit negtiven Zlen 7 Klmmeenung 8 Renen mit Vilen 8 Die inomisen Fomeln 8 uenung 8 Linee Gleiungen 9 Linee Gleiungssysteme 9 Qutise Gleiungen 0 Linee un qutise Funktionen 0 Deistzenung 0 Pozentenung 0 Zinsenung Qut- un Kuikwuzeln Potenzen Logitmen Mittelwete Umenen von Eineiten Stostik Dten efssen Wseinlikeitsenung opyigt 0 Mtemtik-Velg, wwwmtevelgom
2 Fomelsmmlung Geometie Seite Ds llgemeine Deiek ezeinungen: γ Gleiseitiges Deiek: lle ei Seiten sin glei lng Jee Höe ist zuglei Winkel- un Seitenlieene 60 Summe e Innenwinkel: γ Höe: Fläeninlt: Fläeninlt un Umfng: Gleisenkliges Deiek: Zwei Seiten, ie eien Senkel, sin glei lng Die itte Seite ist ie sis Die Höe liet en Winkel g un ie Seite Fläeninlt: Umfng: U γ γ Fläeninlt: Umfng: U Retwinkliges Deiek: Spezielle Deieke In einem etwinkligen Deiek wi ie Seite gegenüe em eten Winkel ls Hypotenuse ezeinet Die eien Seiten, ie en eten Winkel ilen, sin ie Kteten Fläeninlt: Umfng: U Stz es Tles: Ṁ ' γ 90 Jee Punkt uf em Keis um M (mit M M) ilet mit en Punkten un ein etwinkliges Deiek Vieeke Retek: lle Innenwinkel etgen 90 Die eien Digonlen sin glei lng un lieen si M Fläeninlt: Umfng: U ( ) Digonle: Qut: lle Innenwinkel etgen 90 lle Seiten sin glei lng Die eien Digonlen steen senket ufeinne, sie sin glei lng un lieen si Fläeninlt: Digonle: M Umfng: U opyigt 0 Mtemtik-Velg, wwwmtevelgom
3 Fomelsmmlung Geometie Seite Pllelogmm: Die gegenüeliegenen Seiten sin zueinne pllel un glei lng Die gegenüeliegenen Winkel sin glei goß Die Digonlen e un f lieen si e f M Fläeninlt: Umfng: U ( ) Tpez: Minestens zwei Seiten sin pllel ( ) Fläeninlt: m ( ) m ist ie Mittelpllele Umfng: U m Den: Jeweils zwei ente Seiten sin glei lng Minestens zwei gegenüeliegene Winkel sin glei goß Die sen e un f steen senket ufeinne Regelmäßige Vieleke (n-eke) Ein Vielek eißt egelmäßig, wenn lle Seiten glei lng zw lle Innenwinkel glei goß sin Regelmäßiges Fünfek: Umkeisius, i Inkeisius i u Regelmäßiges Sesek: Fläeninlt: 5 Umfng: U 5 u Umkeisius, i Inkeisius i u u, i Fläeninlt: Umfng: U 6 i Regelmäßiges n-ek: D f e Fläeninlt: e f Umfng: U ( ) 60 n Fläeninlt: n i Umfng: U n Die Summe e Innenwinkel eines n-eks etägt (n ) 80 Keisfläen Rute (Romus): lle Seiten sin glei lng Die gegenüeliegenen Innenwinkel sin jeweils glei goß Die eien Digonlen steen senket ufeinne Keis: M Mittelpunkt, Rius, Dumesse e f Fläeninlt: Umfng: U e f M Fläeninlt: π π Umfng: U π π Die Summe e Innenwinkel von Vieeken ist 60 π, opyigt 0 Mtemtik-Velg, wwwmtevelgom
4 Fomelsmmlung Geometie Seite Keising: ußenius, i Innenius, Ringeite Gleiseitige Deieksäule: M Keisussnitt: M i i Fläeninlt: π ( i ) π ogenlänge: 60 ussnittsfläe: oe π 60 liegen Gunfläe: G steen Mntel: M Volumen: V G Oefläe: O ( 6) Pismen (gee Köpe) Tpezsäule: Pismen: In jeem Pism git es zwei gleie Seitenfläen, ie pllel zueinne steen G Gunfläe, Höe, Volumen: V G Mntel: M u (u Umfng e Gunfläe) Wüfel: Gunfläe: G, Volumen: V Oefläe: O 6, Mntel: M Digonle: liegen Gunfläe: G Volumen: V G steen ( ) Oefläe: O G () Mntel: M ( ) Que: Zyline: π Mntel M Gunfläe: G, Volumen: V Oefläe: O ( ), Mntel: M ( ) Digonle: Gunfläe: G π ( Keis) Volumen: V π Mntel: M π Oefläe: O G M π π π ( ) opyigt 0 Mtemtik-Velg, wwwmtevelgom
5 Fomelsmmlung Geometie Seite 5 Holzyline (Ro): äußee Rius, i Gunfläe: G π ( i ) i innee Rius Volumen: V G π ( i ) Äußee Mntel: M π Innee Mntel: M i π i Oefläe: O G M M i π äußee Mntel M G ( Keising) Pymien un Kegel G Gunfläe, llg Volumen: V G, Höe Qutise Pymie: Tetee: lle vie Seitenfläen sin gleiseitige Deieke Gunfläe: G ( gleiseitiges Deiek) Volumen: V G, mit 6 folgt: V Mntel: M G Sesseitige Pymie: s Gunfläe: G, Oefläe: O G ( egelmäßiges Sesek) Volumen: V G Mntel: M s Oefläe: O G M s s Gunfläe: G, Volumen: V G Oefläe: O G M s Mntel: M s s mit s Kegel: s 0,5 (mit ) s π Mntel M s s Gunfläe: G π Volumen: V G π Mntel: M π s π s 60, mit s 60 Oefläe: O G M π ( s) opyigt 0 Mtemtik-Velg, wwwmtevelgom
6 Fomelsmmlung Geometie Seite 6 Pymien- un Kegelstümpfe G Gunfläe, D Dekelfläe llgemeines Volumen: V (G G D D) Qutise Pymienstumpf: Gunfläe: G Dekelfläe: D Volumen: V ( ) Mntel: M ( ) Oefläe: O G D M ( ) Zentise Stekung un Stlensätze Zentise Stekung: ei eine zentisen Stekung (mit em Stekzentum Z un em Stekfkto k) leien lle Winkelgößen elten Jee ilsteke ist k -ml so goß wie ie Oiginlsteke Z Es gilt: k Z' Z γ Z' Z ' Z' Z, un γ γ Die Fläe e ilfigu ist um en Fkto k göße: k γ' ' ' ' ' Kegelstumpf: s s π s π Mntel M Die Stlensätze: e f f e D Z g T Q g Z S R Figu Figu Gunfläe: G π Dekelfläe: D π Stlenstz: Zwei snitte uf einem Stl velten si zueinne wie ie entspeenen snitte uf em neen Stl: Volumen: V π ( ) Mntel: M π s ( ) Oefläe: O G D M π π π s ( ) In Figu gilt: In Figu gilt: Z Z ZR ZT Z ZD ZS ZQ Kugel Stlenstz: Die snitte uf en Pllelen velten si zueinne wie ie (von Z gemessenen) entspeenen snitte uf en Stlen: M In Figu gilt: In Figu gilt: D RS QT Z un Z D ZR un ZT RS QT Z ZD ZS ZQ Volumen: V π Oefläe: O π opyigt 0 Mtemtik-Velg, wwwmtevelgom
7 Fomelsmmlung Geometie / lge Seite 7 Stz es Pytgos, Kteten- un Höenstz In einem etwinkligen Deiek wi ie Seite gegenüe em eten Winkel ls Hypotenuse ezeinet Die eien Seiten, ie en eten Winkel ilen, sin ie Kteten p un q sin ie Hypotenusensnitte q γ 90 p Stz es Pytgos: Höenstz: p q Die Reengesetze e ition un Multipliktion Ds Kommuttivgesetz (Vetusungsgesetz): ition: Multipliktion: Ds ssozitivgesetz (Veinungsgesetz): ition: ( ) ( ) Multipliktion: ( ) ( ) Ds Distiutivgesetz (Veteilungsgesetz): ( ) Ktetenstz: p un q un ( ) Tigonometie, Winkelfunktionen Vom Winkel us ettet wi in einem etwinkligen Deiek iejenige Seite ls Gegen ktete ezeinet, ie em Winkel gegenüeliegt Die Ktete, ie m Winkel n liegt, nennt mn n ktete Gegenktete γ 90 Die Winkelfunktionen: sin Gegenktete Hypotenuse os Gegenktete nktete nktete Hypotenuse tn Gegenktete nktete esonee Wete: sin 0 0,5 os 0,5 0 tn 0 Renen mit negtiven Zlen Negtive un positive Zlen uf em Zlenstl: Negtive Zlen Positive Zlen - Die negtiven Zlen liegen uf em Zlenstl links vom Uspung 0 Die positiven Zlen liegen ets vom Uspung De etg eine Zl: De etg eine Zl entspit em stn iese Zl vom Uspung 0 uf em Zlenstl Z : oe ition un Sutktion uf em Zlenstl: ( stet fü en etg eine eellen Zl) Mn iet zu e Zl Z ie Zl, inem mn von Z us um -Längeneineiten n ets get Mn sutiet von e Zl Z ie Zl, inem mn von Z us um -Längeneineiten n links get Die itions- un Sutktionsegeln: ( un steen fü ie etäge eelle Zlen) Die Summen zw Diffeenzen:,,, ween n folgenen Regeln eenet: ei gleien Vozeien iet mn ie etäge un Die Summe eält s gemeinsme Vozeien Z : 5 8 oe ei untesielien Vozeien sutiet mn en kleineen etg vom gößeen Die Diffeenz eält s Vozeien, s vo em gößeen etg stet Z : 6 9 oe 8 opyigt 0 Mtemtik-Velg, wwwmtevelgom
8 Fomelsmmlung lge Seite 8 Multipliktion un Division: Mn multipliziet zwei Zlen mit gleiem Vozeien, inem mn ie etäge multipliziet Ds Poukt eält s positive Vozeien Mn multipliziet zwei Zlen mit untesielien Vozeien, inem mn ie etäge multipliziet Ds Poukt eält s negtive Vozeien ml ml ml ml u u u u Klmmeenung uflösen von Plus -Klmmen: Es gilt: () () ( ) ( ) uflösen von Minus -Klmmen: Es gilt: ( ) () () ( ) usmultiplizieen (vgl Distiutivgesetz): un ( ± ± ) ± ± ( ± ± ) ± ± Multiplizieen von Summen un Diffeenzen: In Summen un Diffeenzen ween gleitige Teme zusmmengefsst, inem mn ie Summe zw Diffeenz e Koeffizienten eenet ete: De Mlpunkt wi eim Renen mit Vilen meist weggelssen Es eeutet: x x Summen un Diffeenzen mit vesieentigen Temen: x y x y ( )x ( )y In Summen un Diffeenzen us vesieentigen Temen können nu ie gleitigen Teme zusmmengefsst ween Z : x y x 7y 5x y Multipliktion un Division: (x) ( )x, z : 5x 0x x y ( )xy, z : 7x 5y 5xy (x) : ( : )x, z : 8x : 6 (8 : 6)x x Die inomisen Fomeln ( ) ( ) ( ) ( ) u: uenung Jee Quotient : (, Z, mit 0) knn ls u gesieen ween Din ist e Zäle un e Nenne uteile: Mit einem u wi ein uteil von etws Gnzem esieen De Nenne es us git n, in wie viele Teile s Gnze geteilt ween soll De Zäle es us git n, wie viele von iesen Teilen gemeint sin eispiele: ( ) ( ) oe ( ) ( ) Renen mit Vilen,,, x, y R, x un y sin ie Vilen,, un ween Koeffizienten gennnt ition un Sutktion: x x x ( ) x, z : x 5x x 0x x x x ( ) x, z : 7x x 8x x Kewet: Mn eält en Kewet (zw Keu oe Rezipokes) eines us, inem mn Zäle un Nenne vetust Es gilt: opyigt 0 Mtemtik-Velg, wwwmtevelgom
9 Fomelsmmlung lge Seite 9 Eweiten: üe ween eweitet, inem mn Zäle un Nenne mit e gleien Zl multipliziet Es gilt: mit 0 Küzen: üe ween geküzt, inem mn Zäle un Nenne u ie gleie Zl iviiet Ein u knn nu nn mit geküzt ween, wenn un u teil sin Es gilt: : :, mit 0 ition un Sutktion gleinmige üe: üe mit gleiem Nenne eißen gleinmig Gleinmige üe ween iet zw sutiet, inem mn ie Zäle iet zw sutiet un en Nenne eieält: un ition un Sutktion ungleinmige üe: Ungleinmige üe ween iet zw sutiet, inem mn sie uf enselen Nenne, en Huptnenne, eweitet De Huptnenne ist ein gemeinsmes Vielfes e eien Nenne nsließen vefät mn wie ei gleinmigen üen Es gilt: un Multipliktion un Division: Zwei üe ween miteinne multipliziet, inem mn Zäle mit Zäle un Nenne mit Nenne multipliziet Mn iviiet u einen u, inem mn mit seinem Kewet multipliziet : : llgemeine Fom: Linee Gleiungssysteme ( Gleiungen, Vilen) x y x y (I) (II) mit en Konstnten,,,,, R un en Vilen x un y Lösungsvefen: Einsetzungsvefen: Mn löst eine Gleiung n eine Vilen uf (z n y) un setzt en entspeenen Tem in ie zweite Gleiung ein Gleisetzungsvefen: Mn löst eie Gleiungen n eselen Vilen uf (z n y) un setzt ie eien Teme fü y glei itionsvefen: Mn fomt eie Gleiungen so um, ss eim ieen zw Sutieen eie Gleiungen eine Vile eusfällt ei llen ei Vefen eält mn eine Gleiung mit nu no eine Vilen, ie u uflösen eenet ween knn Die zweite Vile eält mn u Einsetzen e eeneten esten Vile in eine e eien usgngsgleiungen Gfise Lösung: Mn löst eie Gleiungen n y uf un zeinet jeweils ie Gee zu Funktionsgleiung y mx in ein Suil Die Koointen es Snittpunkts S(x s y s ) eie Geen sin ie Lösungsmenge eispiel: g: y x, : y x,5 y g S(,5) Die Koointen es Snittpunkts sin S(,5) Dmit ist ie Lösungsmenge L { (;,5) } x Linee Gleiungen Zwei Gleiungen sin äquivlent, wenn sie ie gleie Lösungsmenge en Die Lösungsmenge eine Gleiung änet si nit, wenn mn uf eien Seiten enselen Tem iet oe sutiet, eie Seiten mit eine Zl ( 0) zw einem Tem multipliziet oe iviiet eispiel: x 0 x : x L { } mit 0 opyigt 0 Mtemtik-Velg, wwwmtevelgom
10 Fomelsmmlung lge Seite 0 Qutise Gleiungen llgemeine Fom: x x 0 mit en Konstnten,, R un 0 Lösung: x, ± mit e Diskiminnten D Nomlfom: x px q 0 mit en Konstnten p, q R p p Lösung: x ± ( ) q, p mit e Diskiminnten D ( ) q Zl e Lösungen: (ei llgemeine Fom un Nomlfom) genu eine Lösung fü D 0 zwei Lösungen fü D > 0 keine Lösung fü D < 0 Linee un qutise Funktionen Linee Funktionen: y m x, m ist ie Steigung, ist e y-sensnitt y x y mx y y m x x Deistzenung Popotionle Zuonungen: eispiel: Ein uto veut Lite Kftstoff uf 6 km Wie weit knn mn (ei konstntem Veu) mit 0 Liten fen? : 0 Lite ^ 6 km Lite ^,5 km 0 Lite ^ 70 km : 0 Umgeket popotionle Zuonungen: eispiel: 8 Pfee fessen in 5 Tgen eine estimmte Menge Hfe Wie lnge wüe ie gleie Menge Hfe fü 0 Pfee eien? : Pfee ^ 5 Tge Pfe ^ 0 Tge 0 Pfee ^ Tge Pozentenung 8 : 0 Die Gungleiung e Pozentenung: p Pozentstz, G Gunwet, p G 00 p % P w p Pw p G Pozentsätze im Keisigmm: P w Pozentwet 00 Pw G p Qutise Funktionen: ) llgemeine Fom: y x px q ) Seitelfom: y (x ) De Seitelfom knn mn ie Seitelkoointen e Pel iekt lesen: S ( ) y Es gilt: % å,6 eispiel: p % 0 % p % 5 % p % 5 % 5 % 0 % % ei negtivem -Wet ist ie Nomlpel n links vesoen ei negtivem -Wet ist ie Nomlpel n unten vesoen x Vemete un veingete Gunwet: G Gunwet, W neu neue Wet vemete (veingete) Gunwet Es gilt: q G W neu p mit q ( 00) p un q ( ) ei Eöung es Gunwets ei Veingeung es Gunwets 00 opyigt 0 Mtemtik-Velg, wwwmtevelgom
11 Fomelsmmlung lge Seite Zinsenung K Sttkpitl, Keit oe Dleen, Z Zinsen, p % Zinsstz, n nzl e Je, m nzl e Monte, t nzl e Tge Jeszinsen: Montszinsen: Tgeszinsen: K p Z 00 K p m Z m 00 K p t Z t Mont t in e Zinsenung imme 0 Tge J t in e Zinsenung imme 60 Tge Zinseszins (ei konstntem Zinsstz p) : K 0 Sttkpitel, K n Kpitl n n Jen n Es gilt: K n K 0 q p, mit q ( ) 00 Qut- un Kuikwuzeln Qutwuzel (spi: Wuzel ) mit R 0 ist e Rikn ± ist ie Lösung e Gleiung x Logitmen Seiweise: log (spi: Logitmus zu sis ) mit, R un x log ist ie Lösung e Gleiung x log un log 0 Spezielle sen: Zenelogitmus: log 0 lg Ntülie Logitmus: log e ln e (mit e Eulesen Zl e,788 ) Logitmengesetze: log (u v) log u log v log u v log u log v log u log u ( R) Mittelwete itmetises Mittel: M x x x n n Geometises Mittel: G n x x x n Es gilt: un un fü, > 0 Umenen von Eineiten Rtionlmen es Nennes: Mn knn einen Nenne tionl men, inem mn en u mit e Wuzel es Nennes eweitet: Kuikwuzel (spi: -te Wuzel von ) mit R 0 ist ie Lösung e Gleiung x Seiweise: Potenzen n n Fktoen mit R \ {0} ; n N Potenz n (spi: o n ), sis, n Exponent Spezielle Potenzen: (spi: -Qut ),, 0, n Potenzgesetze: ei > 0 fü m, n R un ei R \ {0} fü m, n Z gleie sis: m n m n un m n m n gleie Exponent: n n ( ) n un n n n ( ) Potenzieen: ( n ) m n m un ( s ) n n s n n Länge: km m m m mm Fläe: m m m mm Volumen: m m m mm (Lite) Msse: t kg g mg Zeit: Tg min s opyigt 0 Mtemtik-Velg, wwwmtevelgom
12 Fomelsmmlung Stostik Seite Dten efssen Mekml X: De eotete Wet eine Dteneie Zum eispiel ie Köpegöße e Jugenlien eine Sulklsse Uliste: Ungeonete Zusmmenstellung e eoteten Mekmle zw Egenisse Zum eispiel Köpegöße von 5 Jugenlien:,65 m;,78 m;,6 m;,8 m;,59 m Rngliste oe geonete Uliste: N e Göße geonete Uliste Zum eispiel:,59 m;,6 m;,65 m;,78 m;,8 m solute Häufigkeit: Die Zl, ie ngit, wie oft ein Mekmlswet in eine Häufigkeitsliste vokommt Reltive Häufigkeit: solute Häufigkeit Gesmtzl lle Wete Minimum x min : De kleinste Wet eine Liste Mximum x mx : De gößte Wet eine Liste Mittelwet oe Dusnitt: Wenn jee Mekmlswet nu einml vokommt, eenet mn en Mittelwet mit x x x x n n De Mittelwet knn u mit en eltiven Häufigkeiten i eine Häufigkeitstelle eenet ween Dnn gilt: x x x n x n Molwet x*: Dejenige Wet in e Uliste, e m äufigsten vokommt Meee Molwete sin mögli Zentlwet x ~ ( Mein): Wi mitilfe eine geoneten Uliste zw Rngliste estimmt ei eine ungeen nzl n Weten gilt: ~ x ist e mittlee Wet e Rngliste ei eine geen nzl n Weten gilt: ~ x ist e Mittelwet e eien in e Mitte steenen Wete Untees Qutil q u : Mn multipliziet ie nzl e Wete e Uliste mit ¼ Ist s Egenis nit gnzzlig nimmt mn en näst öeen Rngpltz De Mekmlswet ieses Rngpltzes ist q u ei gnzzligem Egenis ist q u e Mittelwet us em Wet ieses un es näst öeen Rngpltzes Wseinlikeitsenung Zufllsexpeiment: Ein Vesu, essen usgng ungewiss ist Zum eispiel s Wefen eines Wüfels Eeignis: lle usgänge mit eine estimmten Eigensft ilen ein Eeignis Zum eispiel geöen eim Wüfeln ie ugenzlen ; un 5 zum Eeignis ungee ugenzlen Lple-Expeiment: Sin lle möglien usgänge eines Zufllsexpeiments glei wseinli, spit mn von einem Lple-Expeiment Lple-Wseinlikeit: Sin lle usgänge eines Zufllsexpeiments glei wseinli, gilt fü ie Wseinlikeit P() eines Eeignisses : P() nzl e usgänge,ei enen eintitt nzl lle möglien usgänge Gegeneeignis: Zu jeem Eeignis git es ein Gegeneeignis, s genu s Gegenteil eseit Die Summe e Wseinlikeiten eines Eeignisses un seines Gegeneeignisses ist imme Es gilt: P( ) P() Mestufige Zufllsexpeimente: Ist ein Zufllsvesu, ei em meee neinne lufene Zufllsvesue zu einem einzigen Zufllsvesu zusmmengefsst ween Zum eispiel s eimlige Wefen eine Münze mit en Teilegenissen Wppen (W) oe Zl (Z) umigmm: Jees mestufige Zufllsexpeiment knn in einem umigmm vensulit ween Din esiftet mn ie Knoten mit en Teileegenissen (eim Münzwuf mit Z oe W) Die Wseinlikeiten e Teilegenisse seit mn uf ie Äste eim Wefen Teilexpeiment Z W Teilexpeiment eine ielen Münze ist iese Wseinlikeit ½ Pfegel: Die Wseinlikeit eines Vesususgngs in einem mestufigen Zufllsexpeiment ist glei em Poukt e Wseinlikeiten entlng es entspeenen Pfes Z (Z; Z) W (Z; W) Z (W; Z) W (W; W) Oees Qutil q o : Wi wie s untee Qutil estimmt, nu ss mn ie nzl e Wete e Uliste mit ¾ multipliziet oxplot: Ist ein Säulen- oe lkenigmm, in s mn x min, x mx, q u un q o eintägt Die ox zwisen en eien Qutilen umfsst 50% lle Wete opyigt 0 Mtemtik-Velg, wwwmtevelgom Summenegel: Die Wseinlikeit eines Eeignisses in einem mestufigen Zufllsexpeiment ist glei e Summe e Wseinlikeiten lle zu iesem Eeignis geöenen Pfe
Vierecke. 1. Parallelogramm Ein Viereck heißt Parallelogramm, wenn die Gegenseiten jeweils parallel sind.
 Vieeke. Pllelogmm Ein Vieek eißt Pllelogmm, wenn ie egenseiten jeweils pllel sin. D C Stz: Ein Vieek ist genu nn punktsymmetis (zum Digonlensnittpunkt), wenn es ein Pllelogmm ist. Ein Vieek ist genu nn
Vieeke. Pllelogmm Ein Vieek eißt Pllelogmm, wenn ie egenseiten jeweils pllel sin. D C Stz: Ein Vieek ist genu nn punktsymmetis (zum Digonlensnittpunkt), wenn es ein Pllelogmm ist. Ein Vieek ist genu nn
Zehnerpotenz Bezeichnung Vorsilbe Symbol Zehnerpotenz Bezeichnung Vorsilbe Symbol = Billion tera T
 Fomelsmmlung Fomelsmmlung ieise Busten α Α Alp η Η Et ν Ν Ny τ Τ Tu β Β Bet ϑ Θ Tet ξ Ξ Xi υ Υ Ypsilon γ Γ mm ι Ι Iot ο Ο Omikon φ Φ Pi δ Δ Delt κ Κ Kpp π Π Pi χ Χ Ci ε Ε Epsilon λ Λ Lm ϱ Ρ Ro ψ Ψ Psi
Fomelsmmlung Fomelsmmlung ieise Busten α Α Alp η Η Et ν Ν Ny τ Τ Tu β Β Bet ϑ Θ Tet ξ Ξ Xi υ Υ Ypsilon γ Γ mm ι Ι Iot ο Ο Omikon φ Φ Pi δ Δ Delt κ Κ Kpp π Π Pi χ Χ Ci ε Ε Epsilon λ Λ Lm ϱ Ρ Ro ψ Ψ Psi
Formeln zu Mathematik für die Fachhochschulreife
 Fomeln zu Mtemtik fü die Fcocsculeife Beeitet von B. Gimm und B. Sciemnn 3. Auflge VERLAG EUROPA-LEHRMITTEL Nouney, Vollme GmH & Co. KG Düsselege Stße 3 4781 Hn-Guiten Euop-N.: 8519 Autoen: Bend Gimm Bend
Fomeln zu Mtemtik fü die Fcocsculeife Beeitet von B. Gimm und B. Sciemnn 3. Auflge VERLAG EUROPA-LEHRMITTEL Nouney, Vollme GmH & Co. KG Düsselege Stße 3 4781 Hn-Guiten Euop-N.: 8519 Autoen: Bend Gimm Bend
Formelsammlung Mathematik
 Formelsmmlung Mthemtik Inhlt Mßumwnlungen... Längenmße... Flähenmße... Rum- un Hohlmße... Zeitmße... Rehtek... Qurt... llgemeines Dreiek... 4 Rehtwinkeliges Dreiek... 4 Gleihshenkliges Dreiek... 5 Gleihseitiges
Formelsmmlung Mthemtik Inhlt Mßumwnlungen... Längenmße... Flähenmße... Rum- un Hohlmße... Zeitmße... Rehtek... Qurt... llgemeines Dreiek... 4 Rehtwinkeliges Dreiek... 4 Gleihshenkliges Dreiek... 5 Gleihseitiges
Abiturprüfung Mathematik 2017 Merkhilfe S. 1/8. Dreieck Flächeninhalt: 1 2. Mindestens zwei Seiten sind gleich lang.
 Aitupüfung Mthemtik 07 Mekhilfe S. /8 Eene Figuen Deieck Flächeninhlt: A g h g gleichschenkliges Deieck Mindestens zwei Seiten sind gleich lng. gleichseitiges Deieck Alle dei Seiten sind gleich lng. Flächeninhlt:
Aitupüfung Mthemtik 07 Mekhilfe S. /8 Eene Figuen Deieck Flächeninhlt: A g h g gleichschenkliges Deieck Mindestens zwei Seiten sind gleich lng. gleichseitiges Deieck Alle dei Seiten sind gleich lng. Flächeninhlt:
Kleine Algebra-Formelsammlung
 Immnuel-Knt-Gymnsium Heiligenhus Gierhrt Kleine Alger-Formelsmmlung Mittelstufe (is Klsse 0) Drgestellt sin ie wichtigsten Fkten un Gesetze, woei iverse Ausnhmeregeln wie z.b. s Verot er Division urch
Immnuel-Knt-Gymnsium Heiligenhus Gierhrt Kleine Alger-Formelsmmlung Mittelstufe (is Klsse 0) Drgestellt sin ie wichtigsten Fkten un Gesetze, woei iverse Ausnhmeregeln wie z.b. s Verot er Division urch
Wert eines Terms berechnen
 gnz kl: Mthemtik 3 - Ds Feienheft mit Efolgsnzeige 3 Wet eines Tems eechnen Teme sind sinnvolle Rechenusdücke, die us Zhlen, Vilen, Rechenzeichen und Klmmen estehen können. Sinnlose Rechenusdücke (z. B.:
gnz kl: Mthemtik 3 - Ds Feienheft mit Efolgsnzeige 3 Wet eines Tems eechnen Teme sind sinnvolle Rechenusdücke, die us Zhlen, Vilen, Rechenzeichen und Klmmen estehen können. Sinnlose Rechenusdücke (z. B.:
Größter gemeinsamer Teiler und kleinstes gemeinsames Vielfaches
 Größter gemeinsmer Teiler un kleinstes gemeinsmes Vielfhes 1 Der größte gemeinsme Teiler (ggt) Zu jeer Zhl knn mn ihre Teilermenge ngeen. Τ0 {1; 2; ; 5; 6; 10; 15; 0} Τ {1; 2; ; ; 6; } Die gemeinsmen Teiler
Größter gemeinsmer Teiler un kleinstes gemeinsmes Vielfhes 1 Der größte gemeinsme Teiler (ggt) Zu jeer Zhl knn mn ihre Teilermenge ngeen. Τ0 {1; 2; ; 5; 6; 10; 15; 0} Τ {1; 2; ; ; 6; } Die gemeinsmen Teiler
Formelsammlung. x 2 + px + q = 0 ax 2 + bx + c = 0 x 1,2. = p 2 ± p². Fläche eines rechtwinkligen Dreiecks: Fläche eines Dreiecks: A = 1 2 g h
 Fomelsmmlung p q Fomel: c Fomel x 2 + px + q = 0 x 2 + x + c = 0 x 1,2 = p 2 ± p² 4 q x 1,2 = ± ² 4c 2 Fläce eines Deiecks: Fläce eines ectwinkligen Deiecks: A = 1 2 g A = 1 2 g Fläce eines Qudts: A =
Fomelsmmlung p q Fomel: c Fomel x 2 + px + q = 0 x 2 + x + c = 0 x 1,2 = p 2 ± p² 4 q x 1,2 = ± ² 4c 2 Fläce eines Deiecks: Fläce eines ectwinkligen Deiecks: A = 1 2 g A = 1 2 g Fläce eines Qudts: A =
Mathematik: Mag. Wolfgang Schmid Arbeitsblatt Semester ARBEITSBLATT 11 EXTREMWERTAUFGABEN
 Mtemtik: Mg. Wolfgng Smid beitsbltt 11 6. Semeste BEITSBLTT 11 EXTEMWETUFGBEN In diesem beitsbltt befssen wi uns mit ufgben, bei denen einem gegebenen Köpe ein ndee Köpe eingesieben ode umsieben wid. Beispiel:
Mtemtik: Mg. Wolfgng Smid beitsbltt 11 6. Semeste BEITSBLTT 11 EXTEMWETUFGBEN In diesem beitsbltt befssen wi uns mit ufgben, bei denen einem gegebenen Köpe ein ndee Köpe eingesieben ode umsieben wid. Beispiel:
Grundwissen l Klasse 5
 Grundwissen l Klsse 5 1 Zhlenmengen und Punktmengen {1; 2; 3; 4; 5; 6;... } Die Menge der ntürlichen Zhlen. 0 {0; 1; 2; 3; 4; 5;... } Die Menge der ntürlichen Zhlen mit Null. M {; ; C;... } Die Menge der
Grundwissen l Klsse 5 1 Zhlenmengen und Punktmengen {1; 2; 3; 4; 5; 6;... } Die Menge der ntürlichen Zhlen. 0 {0; 1; 2; 3; 4; 5;... } Die Menge der ntürlichen Zhlen mit Null. M {; ; C;... } Die Menge der
Mathe lernen mit Paul
 Mte lernen mit Pul Die kleine Formelsmmlung Mit Gutscein für 2 kostenlose Unterrictsstunden 2 Mte lernen mit Pul Inlt Algebr Mße und Gewicte 4 Grundrecenrten 5 Brucrecnung 6 Potenzen und Wurzeln 7 Prozentrecnung
Mte lernen mit Pul Die kleine Formelsmmlung Mit Gutscein für 2 kostenlose Unterrictsstunden 2 Mte lernen mit Pul Inlt Algebr Mße und Gewicte 4 Grundrecenrten 5 Brucrecnung 6 Potenzen und Wurzeln 7 Prozentrecnung
Schülerkurs. Mathematik > Lineare Algebra > Lineare Gleichungen Lineare Gleichungssysteme > Teil I: Theorie. Michael Buhlmann
 Michel Buhlmnn Schülekus Mthemtik > Linee Alge > Linee Gleichungen Linee Gleichungssysteme > Teil I: Theoie Linee Gleichungen und linee Gleichungssysteme duchziehen den Mthemtikunteicht in llen Schulfomen
Michel Buhlmnn Schülekus Mthemtik > Linee Alge > Linee Gleichungen Linee Gleichungssysteme > Teil I: Theoie Linee Gleichungen und linee Gleichungssysteme duchziehen den Mthemtikunteicht in llen Schulfomen
Inhalt: Die vorliegenden Folienvorlagen enthalten folgende Elemente:
 Stzgruppe des Pytgors Inlt: 1 Der Stz des Pytgors Pytgors im Rum 3 ufstellen von Formeln 4 Prktise nwendungen 5 Der Ktetenstz 6 Der Höenstz 7 Exkurs: Konstruktion retwinkliger Dreieke 8 ekliste 9 Hinweise
Stzgruppe des Pytgors Inlt: 1 Der Stz des Pytgors Pytgors im Rum 3 ufstellen von Formeln 4 Prktise nwendungen 5 Der Ktetenstz 6 Der Höenstz 7 Exkurs: Konstruktion retwinkliger Dreieke 8 ekliste 9 Hinweise
Dreiecke können einerseits nach den Eigenschaften ihrer Seiten und andererseits nach ihren Winkeln benannt werden. Einteilung nach den Seiten:
 gnz klr: Mthemtik 2 - s Ferienheft mit Erfolgsnzeiger 3 Rettungsring Eigenshften von reieken & Viereken Eigenshften von reieken Ein reiek ht immer 3 Ekpunkte, 3 Seiten un 3 Innenwinkel. ie eshriftung eines
gnz klr: Mthemtik 2 - s Ferienheft mit Erfolgsnzeiger 3 Rettungsring Eigenshften von reieken & Viereken Eigenshften von reieken Ein reiek ht immer 3 Ekpunkte, 3 Seiten un 3 Innenwinkel. ie eshriftung eines
Lineare Algebra. Übungsblatt November Aufgabe 1. (4=2+2 Punkte) Sei V ein K-Vektorraum und seien v 1,..., v n V.
 Goethe-Univesität Fnkfut Institut fü Mthemtik Linee Alge Wintesemeste 28/9 Pof. D. Jko Sti Mtin Lütke Üungsltt 5 3. Noveme 28 Aufge. (42+2 Punkte) Sei V ein K-Vektoum un seien v... v n V. () Sei K α n
Goethe-Univesität Fnkfut Institut fü Mthemtik Linee Alge Wintesemeste 28/9 Pof. D. Jko Sti Mtin Lütke Üungsltt 5 3. Noveme 28 Aufge. (42+2 Punkte) Sei V ein K-Vektoum un seien v... v n V. () Sei K α n
Der Kosinussatz. So erhalten wir: und. Um beide Formeln miteinander vereinen zu können, stellen wir die zweite Formel nach h 2 um, und erhalten:
 Der Kosinusstz Dreieke lssen si mit drei ngen zu irer Figur, vollständig zeinen. D er die zeinerise Lösung eines Dreieks nit so genu und zudem ret ufwendig ist, muss es u einen renerisen Weg geen, die
Der Kosinusstz Dreieke lssen si mit drei ngen zu irer Figur, vollständig zeinen. D er die zeinerise Lösung eines Dreieks nit so genu und zudem ret ufwendig ist, muss es u einen renerisen Weg geen, die
1. Ableitung von Funktionen mit einer Veränderlichen
 . Ableitung von Funktionen mit einer Veränerlichen. Algebrische Interprettion Die Ableitung einer Funktion f f f+ f = lim. 0 = ist efiniert ls In Worten usgerückt ist ie Ableitung er Grenzwert er Änerungsrte
. Ableitung von Funktionen mit einer Veränerlichen. Algebrische Interprettion Die Ableitung einer Funktion f f f+ f = lim. 0 = ist efiniert ls In Worten usgerückt ist ie Ableitung er Grenzwert er Änerungsrte
R. Brinkmann http://brinkmann-du.de Seite 1 17.11.2010
 R. rinkmnn http://rinkmnn-du.de Seite 7..2 Grundegriffe der Vektorrehnung Vektor und Sklr Ein Teil der in Nturwissenshft und Tehnik uftretenden Größen ist ei festgelegter Mßeinheit durh die nge einer Mßzhl
R. rinkmnn http://rinkmnn-du.de Seite 7..2 Grundegriffe der Vektorrehnung Vektor und Sklr Ein Teil der in Nturwissenshft und Tehnik uftretenden Größen ist ei festgelegter Mßeinheit durh die nge einer Mßzhl
x a 2 (b 2 c 2 ) (a + b 4 + a + weil Klammern nicht geschlossen oder Operationszeichen keine Terme verbinden.
 Termnlyse Mthemtik. Klsse Ivo Blöhliger Terme Ein wihtiger Teil es mthemtishen Hnwerks esteht rin, Terme umzuformen. Dzu müssen einerseits ie Rehengesetze er reellen Zhlen verinnerliht sein, un nererseits
Termnlyse Mthemtik. Klsse Ivo Blöhliger Terme Ein wihtiger Teil es mthemtishen Hnwerks esteht rin, Terme umzuformen. Dzu müssen einerseits ie Rehengesetze er reellen Zhlen verinnerliht sein, un nererseits
. - Verwandle das Rechteck in ein flächeninhaltsgleiches Rechteck mit der neuen Breite x1. und der neuen Länge y. = und neuer zugehöriger Länge
 Wirserg-Gymnsium Grundwissen temtik 9. rgngsstufe Lerninlte Fkten-Regeln-Beisiele Reelle Zlen Defintion der Qudrtwurzeln: Für 0 ist diejenige nit negtive Zl, deren Qudrt ergit. eißt Rdiknd. Es git Zlen,
Wirserg-Gymnsium Grundwissen temtik 9. rgngsstufe Lerninlte Fkten-Regeln-Beisiele Reelle Zlen Defintion der Qudrtwurzeln: Für 0 ist diejenige nit negtive Zl, deren Qudrt ergit. eißt Rdiknd. Es git Zlen,
Volumen und Oberfläche von Prismen und Zylindern: Das Volumen und die Oberfläche sind für alle geraden Prismen und Zylinder wie folgt zu berechnen:
 Körpererehnungen Grunwissen Grunwissen Viele mthemtishe Körper lssen sih us en eknnten geometrishen Grunkörpern zusmmensetzen: us geren Prismen, Zylinern, Kegeln, Pyrmien un Kugeln. Hinsihtlih er Oerflähen-
Körpererehnungen Grunwissen Grunwissen Viele mthemtishe Körper lssen sih us en eknnten geometrishen Grunkörpern zusmmensetzen: us geren Prismen, Zylinern, Kegeln, Pyrmien un Kugeln. Hinsihtlih er Oerflähen-
EBENE GEOMETRIE. 1) Kollineare Punkte: liegen alle auf einer Geraden. 6) Parallele Geraden: schneiden sich nicht: g 2. 7) Einteilung der Dreiecke:
 N GOTRI 1) Kollinee Punkte: lieen lle uf eine Geden 6) Pllele Geden: sneiden si nit: ) u denselen Punkt eende Geden: 7) inteilun de eieke: n den eiten: O uneelmäßi: lle eiten vesieden ln 3) Winkeleinteilun:
N GOTRI 1) Kollinee Punkte: lieen lle uf eine Geden 6) Pllele Geden: sneiden si nit: ) u denselen Punkt eende Geden: 7) inteilun de eieke: n den eiten: O uneelmäßi: lle eiten vesieden ln 3) Winkeleinteilun:
Großdruck. ohne Beispiele. (a + b) = a + 2ab + b. (a - b) = a - 2ab + b. (a + b) (a - b) = a - b. Zeitspannen: erste binomische Formel:
 16 7 8 9 4 5 6 1 2 3 1 2 13 14 15 5 6 1 2 3 4 b c A B 3 4 5 6 7 8 9 10 11 12 17 18 19 20 21 22 23 24 25 C 13 14 15 16 9 10 11 12 7 8 2 2 2 erste binomische Formel: ( + b) + 2b + b 2 2 2 zweite binomische
16 7 8 9 4 5 6 1 2 3 1 2 13 14 15 5 6 1 2 3 4 b c A B 3 4 5 6 7 8 9 10 11 12 17 18 19 20 21 22 23 24 25 C 13 14 15 16 9 10 11 12 7 8 2 2 2 erste binomische Formel: ( + b) + 2b + b 2 2 2 zweite binomische
7. VEKTORRECHNUNG, ANALYTISCHE GEOMETRIE
 Vektoechnung Anltische Geometie 7. VEKTORRECHNUNG ANALYTISCHE GEOMETRIE 7.1. Vektoen () Definition Schiet mn einen Punkt P 1 im Koodintensstem in eine ndee Lge P so ist diese Schieung duch Ange des Upunktes
Vektoechnung Anltische Geometie 7. VEKTORRECHNUNG ANALYTISCHE GEOMETRIE 7.1. Vektoen () Definition Schiet mn einen Punkt P 1 im Koodintensstem in eine ndee Lge P so ist diese Schieung duch Ange des Upunktes
Vorkurs Mathematik Fachhochschule Frankfurt, Fachbereich 2. Fachhochschule Frankfurt am Main Fachbereich Informatik und Ingenieurwissenschaften
 Vorkurs Mthemtik Fchhochschule Frnkfurt, Fchereich Fchhochschule Frnkfurt m Min Fchereich Informtik und Ingenieurwissenschften Vorkurs Mthemtik Sie finden lle Mterilien sowie ergänzende Informtionen unter
Vorkurs Mthemtik Fchhochschule Frnkfurt, Fchereich Fchhochschule Frnkfurt m Min Fchereich Informtik und Ingenieurwissenschften Vorkurs Mthemtik Sie finden lle Mterilien sowie ergänzende Informtionen unter
Grundwissen Mathematik 8.Klasse Gymnasium SOB. Darstellung im Koordinatensystem: Der Kreisumfang ist direkt proportional zu seinem Radius.
 Gymso 1 Grundwissen Mthemtik 8.Klsse Gymnsium SOB 1.Funktionle Zusmmenhänge 1.1.Proportionlität Ändern sih ei einer Zuordnung die eiden Größen im gleihen Verhältnis, so spriht mn von einer direkten Proportionlität.
Gymso 1 Grundwissen Mthemtik 8.Klsse Gymnsium SOB 1.Funktionle Zusmmenhänge 1.1.Proportionlität Ändern sih ei einer Zuordnung die eiden Größen im gleihen Verhältnis, so spriht mn von einer direkten Proportionlität.
Lösungen zu den Wiederholungsaufgaben zum Grundwissenkatalog Mathematik der 7. Jahrgangsstufe. c) 5x ( 2 3 = 17 3
 Gymnsium Stein Lösungen zu den Wiederholungsufgen zum Grundwissenktlog Mthemtik der. Jhrgngsstufe ) ) ❶: keine; ❷: ; ❸: ; ❹: ; ❺: keine; ❻: ; ❼: ; ❽: ; ❾: ) ❶; ❷; ❹; ❾ ) ) ( 0,x ) 0,x ( 0,x ) = = 0,0x
Gymnsium Stein Lösungen zu den Wiederholungsufgen zum Grundwissenktlog Mthemtik der. Jhrgngsstufe ) ) ❶: keine; ❷: ; ❸: ; ❹: ; ❺: keine; ❻: ; ❼: ; ❽: ; ❾: ) ❶; ❷; ❹; ❾ ) ) ( 0,x ) 0,x ( 0,x ) = = 0,0x
Formelsammlung Mathematik 4. Klasse
 Formelsmmlung Mthemtik 4. Klsse Inhlt Rehtek... Qurt... llgemeines Dreiek... Rehtwinkeliges Dreiek... Gleihshenkliges Dreiek... 4 Gleihseitiges Dreiek... 4 Trpez... 5 Prllelogrmm... 5 Rute Rhomus... 6
Formelsmmlung Mthemtik 4. Klsse Inhlt Rehtek... Qurt... llgemeines Dreiek... Rehtwinkeliges Dreiek... Gleihshenkliges Dreiek... 4 Gleihseitiges Dreiek... 4 Trpez... 5 Prllelogrmm... 5 Rute Rhomus... 6
Volumen von Rotationskörpern, Bogenlänge und Mantelfläche
 Modul Integle 3 Volumen von Rottionsköpen, Bogenlänge und Mntelfläche In diesem Modul geht es um einige spezielle Anwendungen de Integlechnung, und Volumin, Längen und Flächen zu estimmen. Fngen wi mit
Modul Integle 3 Volumen von Rottionsköpen, Bogenlänge und Mntelfläche In diesem Modul geht es um einige spezielle Anwendungen de Integlechnung, und Volumin, Längen und Flächen zu estimmen. Fngen wi mit
Lösen einer Gleichung 3. Grades
 Lösen eine Gleichung Gdes We sich uf dieses Abenteue einlssen will, bucht einige Kenntnisse übe komlee Zhlen Es eicht be, wenn mn folgende Schvehlte kennt und kochezettig (mn nehme) nwenden knn: Es gibt
Lösen eine Gleichung Gdes We sich uf dieses Abenteue einlssen will, bucht einige Kenntnisse übe komlee Zhlen Es eicht be, wenn mn folgende Schvehlte kennt und kochezettig (mn nehme) nwenden knn: Es gibt
ist ein Punkt im 2-dimensionalen karthesischen Koordinatensystem, früher hieß stumpfer gestreckter Winkel 180 o
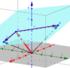 Geometie Punkt ist ein Punkt im -dimensionlen ktesisen Koodintensystem, füe ieß P x p y P szisse eute x-koodinte x p Odinte eute y-koodinte y P stnd de Punkte und d(, ) = = (x x ) + (y y ) Die Steke t
Geometie Punkt ist ein Punkt im -dimensionlen ktesisen Koodintensystem, füe ieß P x p y P szisse eute x-koodinte x p Odinte eute y-koodinte y P stnd de Punkte und d(, ) = = (x x ) + (y y ) Die Steke t
Ü b u n g s b l a t t 13. Organisatorisches:
 MATHEMATIK FÜ INFOMATIKE I WINTESEMESTE 7/8 POF. D. FIEDICH EISENBAND D. KAI GEHS Ü b u n g s b l t t 13 Orgnistorisches: Dieses Übungsbltt wir nicht mehr korrigiert. D ie Aufgben ennoch klusurrelevnt
MATHEMATIK FÜ INFOMATIKE I WINTESEMESTE 7/8 POF. D. FIEDICH EISENBAND D. KAI GEHS Ü b u n g s b l t t 13 Orgnistorisches: Dieses Übungsbltt wir nicht mehr korrigiert. D ie Aufgben ennoch klusurrelevnt
Kapitel 3: Deckabbildungen von Figuren - Symmetrie. 3.1 Die Gruppe (K,o) aller Kongruenzabbildungen einer Ebene
 Gruppe er Kongruenzilungen 1 Gruppe er Kongruenzilungen 2 Kpitel 3: ekilungen von Figuren - Symmetrie 3.1 ie Gruppe (K,o) ller Kongruenzilungen einer Eene K ist ie Menge ller Kongruenzilungen E E; o ist
Gruppe er Kongruenzilungen 1 Gruppe er Kongruenzilungen 2 Kpitel 3: ekilungen von Figuren - Symmetrie 3.1 ie Gruppe (K,o) ller Kongruenzilungen einer Eene K ist ie Menge ller Kongruenzilungen E E; o ist
Magnetismus EM 48. fh-pw
 Mgnetismus Hll Effekt 9 Hll Effekt (Anwenungen) 5 Dehmoment eine eiteschleife 5 eispiel: Dehmoment eine Spule 5 iot-svt Gesetz 55 Mgnetfel im nneen eine eiteschleife 56 Mgnetfel eines stomfühenen eites
Mgnetismus Hll Effekt 9 Hll Effekt (Anwenungen) 5 Dehmoment eine eiteschleife 5 eispiel: Dehmoment eine Spule 5 iot-svt Gesetz 55 Mgnetfel im nneen eine eiteschleife 56 Mgnetfel eines stomfühenen eites
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt Semester ARBEITSBLATT 14 MULTIPLIKATION EINES VEKTORS MIT EINEM SKALAR
 Mthemtik: Mg. Schmid Wolfgng Areitsltt. Semester ARBEITSBLATT MULTIPLIKATION EINES VEKTORS MIT EINEM SKALAR Zunächst einml müssen wir den Begriff Sklr klären. Definition: Unter einem Sklr ersteht mn eine
Mthemtik: Mg. Schmid Wolfgng Areitsltt. Semester ARBEITSBLATT MULTIPLIKATION EINES VEKTORS MIT EINEM SKALAR Zunächst einml müssen wir den Begriff Sklr klären. Definition: Unter einem Sklr ersteht mn eine
Grundwissen Mathematik 7I
 Winkel m Kreis Grundwissen themtik 7I Rndwinkelstz Der Winkel heißt ittelpunktswinkel über der Sehne []. Die Winkel n sind die Rndwinkel über der Sehne []. lle Rndwinkel über einer Sehne eines Kreises
Winkel m Kreis Grundwissen themtik 7I Rndwinkelstz Der Winkel heißt ittelpunktswinkel über der Sehne []. Die Winkel n sind die Rndwinkel über der Sehne []. lle Rndwinkel über einer Sehne eines Kreises
LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN. 7. Übung/Lösung Mathematik für Studierende der Biologie
 LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR BIOLOGIE Pof. Anes Hez, D. Stefn Häusle emil: heusle@biologie.uni-muenchen.e Deptment Biologie II Telefon: 89-8-748 Goßhenest. Fx: 89-8-7483 85 Plnegg-Mtinsie
LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR BIOLOGIE Pof. Anes Hez, D. Stefn Häusle emil: heusle@biologie.uni-muenchen.e Deptment Biologie II Telefon: 89-8-748 Goßhenest. Fx: 89-8-7483 85 Plnegg-Mtinsie
a) Behauptung: Es gibt die folgenden drei stabilen Matchings:
 Musterlösung - ufgenltt 1 ufge 1 ) ehuptung: Es git ie folgenen rei stilen Mthings: ies knn mn ntürlih für ein so kleines eispiel urh etrhten ller möglihen 3! = 6 Mthings eweisen. Mn knn er uh strukturierter
Musterlösung - ufgenltt 1 ufge 1 ) ehuptung: Es git ie folgenen rei stilen Mthings: ies knn mn ntürlih für ein so kleines eispiel urh etrhten ller möglihen 3! = 6 Mthings eweisen. Mn knn er uh strukturierter
Regiomontanus - Gymnasium Haßfurt - Grundwissen Mathematik Jahrgangsstufe 9
 Regiomontnus - Gymnsium Hßfurt - Grundwissen Mthemtik Jhrgngsstufe 9 Wissen und Können Zhlenmengen N Z Q R ntürliche gnze rtionle reelle Aufgen, Beispiele, Erläuterungen N, Z, Q, R Wurzeln (Qudrtwurzel)
Regiomontnus - Gymnsium Hßfurt - Grundwissen Mthemtik Jhrgngsstufe 9 Wissen und Können Zhlenmengen N Z Q R ntürliche gnze rtionle reelle Aufgen, Beispiele, Erläuterungen N, Z, Q, R Wurzeln (Qudrtwurzel)
Grundwissen 8 Klasse. y = c x ist, das x-y-diagramm eine Ursprungsgerade ist.
 Grundwissen 8 Klsse Direkt proportionle Größen x und y sind direkt proportionl, wenn zum n-en Wert ür x der n-e Wert ür y eört, die Wertepre quotientenlei y y2 sind:, x x2 y x ist, ds x-y-dirmm eine Ursprunserde
Grundwissen 8 Klsse Direkt proportionle Größen x und y sind direkt proportionl, wenn zum n-en Wert ür x der n-e Wert ür y eört, die Wertepre quotientenlei y y2 sind:, x x2 y x ist, ds x-y-dirmm eine Ursprunserde
Großdruck. mit Beispielen. (a + b) = a + 2ab + b. (a - b) = a - 2ab + b. (a + b) (a - b) = a - b. Zeitspannen: erste binomische Formel:
 16 7 8 9 4 5 6 1 2 3 1 2 13 14 15 5 6 1 2 3 4 b c A B 3 4 5 6 7 8 9 10 11 12 17 18 19 20 21 22 23 24 25 C 13 14 15 16 9 10 11 12 7 8 2 2 2 erste binomische Formel: ( + b) + 2b + b 2 2 2 zweite binomische
16 7 8 9 4 5 6 1 2 3 1 2 13 14 15 5 6 1 2 3 4 b c A B 3 4 5 6 7 8 9 10 11 12 17 18 19 20 21 22 23 24 25 C 13 14 15 16 9 10 11 12 7 8 2 2 2 erste binomische Formel: ( + b) + 2b + b 2 2 2 zweite binomische
Kürzeste Wege. möglich ist 6. Füge v zu S hinzu und setze d[v] d [v] (u,v) E. Datenstrukturen und Algorithmen 14. Elementare Graphalgorithmen
![Kürzeste Wege. möglich ist 6. Füge v zu S hinzu und setze d[v] d [v] (u,v) E. Datenstrukturen und Algorithmen 14. Elementare Graphalgorithmen Kürzeste Wege. möglich ist 6. Füge v zu S hinzu und setze d[v] d [v] (u,v) E. Datenstrukturen und Algorithmen 14. Elementare Graphalgorithmen](/thumbs/71/64497347.jpg) Algorithmus von Dijkstr: 1. Es sei S ie Menge er enteckten Knoten. Invrinte: Merke optimle Lösung für S: Für lle v S sei [v] = δ(s,v) ie Länge es kürzesten Weges von s nch v 3. Zu Beginn: S={s} un [s]=
Algorithmus von Dijkstr: 1. Es sei S ie Menge er enteckten Knoten. Invrinte: Merke optimle Lösung für S: Für lle v S sei [v] = δ(s,v) ie Länge es kürzesten Weges von s nch v 3. Zu Beginn: S={s} un [s]=
für beliebige Mengen A, B, C
 1.1 Mengenlehre A A A B B A A B B C A C für elieige Mengen A, B, C (Reflexivität) (Symmetrie) (Trnsitivität) (1) (2) (3) A B = B A A B = B A (Kommuttivgesetze) (4) (A B) C = A (B C) (A B) C = A (B C) (Assozitivgesetze)
1.1 Mengenlehre A A A B B A A B B C A C für elieige Mengen A, B, C (Reflexivität) (Symmetrie) (Trnsitivität) (1) (2) (3) A B = B A A B = B A (Kommuttivgesetze) (4) (A B) C = A (B C) (A B) C = A (B C) (Assozitivgesetze)
Eigenschaften mathematischer Körper
 Rettungsing Köpe gnz kl: temtik 4 - Ds Feieneft mit Efolgsnzeige Eigenscften mtemtisce Köpe Eigenscften von Pismen Ein gedes Pism t imme eine und- und eine Deckfläce, die deckungsgleic und pllel zueinnde
Rettungsing Köpe gnz kl: temtik 4 - Ds Feieneft mit Efolgsnzeige Eigenscften mtemtisce Köpe Eigenscften von Pismen Ein gedes Pism t imme eine und- und eine Deckfläce, die deckungsgleic und pllel zueinnde
Wir wählen einen Punkt O des zwei- bzw. dreidimensionalen euklidischen Raums als Ursprung oder Nullpunkt. b 3 c. b 2
 IV. Teilung und Teilverhältnis im Punktrum ================================================================ 4.1 Der Punktrum Wir wählen einen Punkt O des zwei- zw. dreidimensionlen euklidischen Rums ls
IV. Teilung und Teilverhältnis im Punktrum ================================================================ 4.1 Der Punktrum Wir wählen einen Punkt O des zwei- zw. dreidimensionlen euklidischen Rums ls
n n n
 mthbu.ch9+ Repetition mthbu.ch9+ LU 901 1. Die Route de Steetpde in Züich ist 3.8 km lng. Wie lnge ist sie uf eine Kte mit dem Mssstb 1 : 5 000? 15. cm. Auf eine Kte des Mssstbs 1 : 5 000 misst du einen
mthbu.ch9+ Repetition mthbu.ch9+ LU 901 1. Die Route de Steetpde in Züich ist 3.8 km lng. Wie lnge ist sie uf eine Kte mit dem Mssstb 1 : 5 000? 15. cm. Auf eine Kte des Mssstbs 1 : 5 000 misst du einen
1. Grundlagen. 2. Summenzeichen, Produktzeichen. 3. Fakultät, Binomialkoeffizient. 4. Potenzen, Wurzeln, Logarithmen. 5. Elementare Funktionen
 Inhlte Brückenkurs Mthemtik Fchhochschule Hnnover SS 00 Dipl.-Mth. Corneli Reiterger. Grundlgen. Summenzeichen, Produktzeichen. Fkultät, Binomilkoeffizient. Potenzen, Wurzeln, Logrithmen. Elementre Funktionen
Inhlte Brückenkurs Mthemtik Fchhochschule Hnnover SS 00 Dipl.-Mth. Corneli Reiterger. Grundlgen. Summenzeichen, Produktzeichen. Fkultät, Binomilkoeffizient. Potenzen, Wurzeln, Logrithmen. Elementre Funktionen
Begriffe: Addition Subtraktion Multiplikation Division. Summe Differenz Produkt Quotient a + b a b a b a : b
 Grundlgen 0.0. Zhlbereiche ntürliche Zhlen: N = {0; ; 2;...} (nch DIN 547) N = N \ {0} gnze Zhlen: Z = {... 2; ; 0; ; 2;...} rtionle Zhlen: Q = { p p, q Z, q 0} q Q besteht us llen Bruchzhlen. reelle Zhlen:
Grundlgen 0.0. Zhlbereiche ntürliche Zhlen: N = {0; ; 2;...} (nch DIN 547) N = N \ {0} gnze Zhlen: Z = {... 2; ; 0; ; 2;...} rtionle Zhlen: Q = { p p, q Z, q 0} q Q besteht us llen Bruchzhlen. reelle Zhlen:
Nullstellen quadratischer Gleichungen
 Nullstellen qudrtischer Gleichungen Rolnd Heynkes 5.11.005, Achen Nch y ufgelöst hen qudrtische Gleichungen die Form y = x +x+c. Zeichnet mn für jedes x uf der rechten Seite und ds drus resultierende y
Nullstellen qudrtischer Gleichungen Rolnd Heynkes 5.11.005, Achen Nch y ufgelöst hen qudrtische Gleichungen die Form y = x +x+c. Zeichnet mn für jedes x uf der rechten Seite und ds drus resultierende y
ARBEITSBLATT 5L-8 FLÄCHE ZWISCHEN FUNKTION UND X-ACHSE
 Mthemtik: Mg. Schmid WolfgngLehrerInnentem RBEITSBLTT 5L-8 FLÄCHE ZWISCHEN FUNKTION UND X-CHSE Wie wir die Fläche zwischen einer Funktion und der -chse erechnen, hen wir rechentechnische ereits geklärt.
Mthemtik: Mg. Schmid WolfgngLehrerInnentem RBEITSBLTT 5L-8 FLÄCHE ZWISCHEN FUNKTION UND X-CHSE Wie wir die Fläche zwischen einer Funktion und der -chse erechnen, hen wir rechentechnische ereits geklärt.
Analysis II. Uneigentliche Integrale
 Pof D H Benne Osnbück SS 204 Anlysis II Volesung 3 In diese Volesung entwickeln wi die Integtionstheoie weite, und zw untesuchen wi die Fge, ws pssiet, wenn wi in einem Integl b die Intevllgenzen gegen
Pof D H Benne Osnbück SS 204 Anlysis II Volesung 3 In diese Volesung entwickeln wi die Integtionstheoie weite, und zw untesuchen wi die Fge, ws pssiet, wenn wi in einem Integl b die Intevllgenzen gegen
Download. Mathematik üben Klasse 8 (Un-)regelmäßige Vierecke. Differenzierte Materialien für das ganze Schuljahr. Jens Conrad, Hardy Seifert
 ownlo Jens onr, Hry Seifert Mthemtik üen Klsse 8 (Un-)regelmäßige Vierecke ifferenzierte Mterilien für s gnze Schuljhr ownlouszug us em Originltitel: Mthemtik üen Klsse 8 (Un-)regelmäßige Vierecke ifferenzierte
ownlo Jens onr, Hry Seifert Mthemtik üen Klsse 8 (Un-)regelmäßige Vierecke ifferenzierte Mterilien für s gnze Schuljhr ownlouszug us em Originltitel: Mthemtik üen Klsse 8 (Un-)regelmäßige Vierecke ifferenzierte
Formelsammlung Mathematik Fachoberschule Jahrgangsstufe 12 Hochtaunusschule Oberursel. Philipp Maurer in Zusammenarbeit mit StR A.
 Fomelsmmlung Mtemtik Fcoescule Jgngsstufe 12 Hoctunusscule Oeusel Pilipp Mue in Zusmmeneit mit StR A. Käme Stnd: 20. Feu 2014 Fomelsmmlung Mtemtik Fcoescule Jgngsstufe 12 Inltsvezeicnis 1 Mtemtisce Gundlgen
Fomelsmmlung Mtemtik Fcoescule Jgngsstufe 12 Hoctunusscule Oeusel Pilipp Mue in Zusmmeneit mit StR A. Käme Stnd: 20. Feu 2014 Fomelsmmlung Mtemtik Fcoescule Jgngsstufe 12 Inltsvezeicnis 1 Mtemtisce Gundlgen
Teil 1. Prisma - Zylinder Pyramide - Kegel Pyramidenstumpf - Kegelstumpf Kugel - Kugelteile. Datei Nr Friedrich Buckel. Stand: 30.
 Teil 1 Prism - Zylinder Pyrmide - Kegel Pyrmidenstumpf - Kegelstumpf Kugel - Kugelteile Dtei Nr. 11610 Stnd: 0. April 016 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK Geometrie Körperberenungen Demo-Text für
Teil 1 Prism - Zylinder Pyrmide - Kegel Pyrmidenstumpf - Kegelstumpf Kugel - Kugelteile Dtei Nr. 11610 Stnd: 0. April 016 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK Geometrie Körperberenungen Demo-Text für
Satz 6.5 (Mittelwertsatz der Integralrechnung) Sei f : [a, b] R stetig. Dann gibt es ein ξ [a, b], so dass. b a. f dx = (b a)f(ξ) f dx (b a)m.
![Satz 6.5 (Mittelwertsatz der Integralrechnung) Sei f : [a, b] R stetig. Dann gibt es ein ξ [a, b], so dass. b a. f dx = (b a)f(ξ) f dx (b a)m. Satz 6.5 (Mittelwertsatz der Integralrechnung) Sei f : [a, b] R stetig. Dann gibt es ein ξ [a, b], so dass. b a. f dx = (b a)f(ξ) f dx (b a)m.](/thumbs/74/70413961.jpg) Stz 6.5 (Mittelwertstz der Integrlrechnung) Sei f : [, b] R stetig. Dnn gibt es ein ξ [, b], so dss 9:08.06.2015 gilt. f dx = (b )f(ξ) Lemm 6.6 Sei f : [, b] R stetig und m f(x) M für lle x [, b]. Dnn
Stz 6.5 (Mittelwertstz der Integrlrechnung) Sei f : [, b] R stetig. Dnn gibt es ein ξ [, b], so dss 9:08.06.2015 gilt. f dx = (b )f(ξ) Lemm 6.6 Sei f : [, b] R stetig und m f(x) M für lle x [, b]. Dnn
Formeln Informationsund Systemtechnik
 EUROA-ACHBUCHREIHE fü elekoecnice un elekonice Beufe omeln Infomionun Syemecnik Auoen Monik Bugmie Suieniekoin Sug Ulic G.. eye Dipl.-Ing., Anly fü Meienecnik Kln Ben Gimm Oeuien Leoneg, Sinelfingen Gego
EUROA-ACHBUCHREIHE fü elekoecnice un elekonice Beufe omeln Infomionun Syemecnik Auoen Monik Bugmie Suieniekoin Sug Ulic G.. eye Dipl.-Ing., Anly fü Meienecnik Kln Ben Gimm Oeuien Leoneg, Sinelfingen Gego
LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN. 7. Übung/Lösung Mathematik für Studierende der Biologie 25.11.2015
 LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR BIOLOGIE Prof. Anres Herz, Dr. Stefn Häusler emil: heusler@biologie.uni-muenchen.e Deprtment Biologie II Telefon: 089-280-74800 Großhernerstr. 2 Fx:
LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR BIOLOGIE Prof. Anres Herz, Dr. Stefn Häusler emil: heusler@biologie.uni-muenchen.e Deprtment Biologie II Telefon: 089-280-74800 Großhernerstr. 2 Fx:
2.2. Aufgaben zu Figuren
 2.2. Aufgen zu Figuren Aufge 1 Zeichne ds Dreieck ABC in ein Koordintensystem. Bestimme die Innenwinkel, und und erechne ihre Summe. Ws stellst Du fest? ) A(1 2), B(8 3) und C(3 7) ) A(0 3), B(10 1) und
2.2. Aufgen zu Figuren Aufge 1 Zeichne ds Dreieck ABC in ein Koordintensystem. Bestimme die Innenwinkel, und und erechne ihre Summe. Ws stellst Du fest? ) A(1 2), B(8 3) und C(3 7) ) A(0 3), B(10 1) und
Abschlussprüfungen an den Bezirksschulen 2001 Mathematik 1.S
 bschlusspüfungen n den eziksschulen 00 Mthemtik.S ) Veeinfche soweit ls möglich: n + 4n + 4 : n + 4 - n b) Löse die folgende Gleichung nch uf: + + ) estimme die vie gössten gnzzhligen Lösungen: 0 4 7 +
bschlusspüfungen n den eziksschulen 00 Mthemtik.S ) Veeinfche soweit ls möglich: n + 4n + 4 : n + 4 - n b) Löse die folgende Gleichung nch uf: + + ) estimme die vie gössten gnzzhligen Lösungen: 0 4 7 +
(a) Entscheide, ob aus der angegebenen Stellung Spieler A gewinnen kann. (Der Index gibt jeweils die Zugnummer an.)
 Detment Mthemtik Tg de Mthemtik 31. Oktobe 2009 Klssenstufen 9, 10 Aufgbe 1 (6+7+7 Punkte). Zwei Siele A und B sielen uf einem 2 9- Kästchen-Sielfeld. Sie ziehen bwechselnd, Siele A beginnt. Ein Zug besteht
Detment Mthemtik Tg de Mthemtik 31. Oktobe 2009 Klssenstufen 9, 10 Aufgbe 1 (6+7+7 Punkte). Zwei Siele A und B sielen uf einem 2 9- Kästchen-Sielfeld. Sie ziehen bwechselnd, Siele A beginnt. Ein Zug besteht
RESULTATE UND LÖSUNGEN
 TG TECHNOLOGISCHE GRUNDLAGEN Kpitel 3 Mthemtik Kpitel 3.2 Alger Grundrechenrten RESULTATE UND LÖSUNGEN Verfsser: Hns-Rudolf Niedererger Elektroingenieur FH/HTL Vordergut 1, 8772 Nidfurn 055-654 12 87 Ausge:
TG TECHNOLOGISCHE GRUNDLAGEN Kpitel 3 Mthemtik Kpitel 3.2 Alger Grundrechenrten RESULTATE UND LÖSUNGEN Verfsser: Hns-Rudolf Niedererger Elektroingenieur FH/HTL Vordergut 1, 8772 Nidfurn 055-654 12 87 Ausge:
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt Semester ARBEITSBLATT 15 ORTHOGONALITÄT
 Mthemtik: Mg. Schmid Wolfgng Areitsltt 5. Semester ARBEITSBLATT 5 ORTHOGONALITÄT Ws versteht mn zunächst einml unter orthogonl? Dies ist nur ein nderes Wort für norml oder im rechten Winkel. Ws uns hier
Mthemtik: Mg. Schmid Wolfgng Areitsltt 5. Semester ARBEITSBLATT 5 ORTHOGONALITÄT Ws versteht mn zunächst einml unter orthogonl? Dies ist nur ein nderes Wort für norml oder im rechten Winkel. Ws uns hier
Der Begriff der Stammfunktion
 Lernunterlgen Integrlrehnung Der Begriff der Stmmfunktion Wir gehen von folgender Frgestellung us: welhe Funktion F x liefert ls Aleitung eine gegeene Funktion f x. Wir suhen lso eine Umkehrung der Aleitung
Lernunterlgen Integrlrehnung Der Begriff der Stmmfunktion Wir gehen von folgender Frgestellung us: welhe Funktion F x liefert ls Aleitung eine gegeene Funktion f x. Wir suhen lso eine Umkehrung der Aleitung
Übungen: Extremwertaufgaben
 Übungen: Extemwetufgben.0 Eine Stenwte ht meist die Fom eines Zylindes (Rdius, Höhe h) mit eine oben ufgesetzten Hlbkugel (siehe z. B. die im Bild unten gezeigte Fitz-Weiths-Stenwte in Neumkt). Die gesmte
Übungen: Extemwetufgben.0 Eine Stenwte ht meist die Fom eines Zylindes (Rdius, Höhe h) mit eine oben ufgesetzten Hlbkugel (siehe z. B. die im Bild unten gezeigte Fitz-Weiths-Stenwte in Neumkt). Die gesmte
Vorkurs Mathematik Frankfurt University Of Applied Sciences, Fachbereich 2 1
 Vorkurs Mthemtik Frnkfurt University Of Applied Sciences, Fchbereich 1 Rechnen mit Potenzen N bezeichnet die Menge der ntürlichen Zhlen, Q die Menge der rtionlen Zhlen und R die Menge der reellen Zhlen.
Vorkurs Mthemtik Frnkfurt University Of Applied Sciences, Fchbereich 1 Rechnen mit Potenzen N bezeichnet die Menge der ntürlichen Zhlen, Q die Menge der rtionlen Zhlen und R die Menge der reellen Zhlen.
Musterlösung zur Probeklausur zur Geometrie
 UNIVERSITÄT ULM Institut für Zhlentheorie un Whrsheinlihkeitstheorie Musterlösung zur Proeklusur zur Geometrie Prof. Dr. Helmut Mier, Hns- Peter Rek Gesmtpunktzhl: 3 Punkte, Punkte= % keine Age. Gi Definitionen
UNIVERSITÄT ULM Institut für Zhlentheorie un Whrsheinlihkeitstheorie Musterlösung zur Proeklusur zur Geometrie Prof. Dr. Helmut Mier, Hns- Peter Rek Gesmtpunktzhl: 3 Punkte, Punkte= % keine Age. Gi Definitionen
Grundwissen. 9. Jahrgangsstufe. Mathematik
 Gundwissen 9. Jahgangsstufe Mathematik Seite 1 1 Reelle Zahlen 1.1 Rechnen mit Quadatwuzeln a ist diejenige nicht negative Zahl, die zum Quadat a egibt. d.h.: ist keine Wuzel aus 4. Eine Wuzel kann nicht
Gundwissen 9. Jahgangsstufe Mathematik Seite 1 1 Reelle Zahlen 1.1 Rechnen mit Quadatwuzeln a ist diejenige nicht negative Zahl, die zum Quadat a egibt. d.h.: ist keine Wuzel aus 4. Eine Wuzel kann nicht
Dreiecke und Vierecke
 reieke un Viereke Viereke Welhe esoneren Viereke sin eknnt, ws zeihnet esonere Viereke us? Impuls uf Seiten, Winkel, Symmetrie!.) s Qurt: Ein Qurt esitzt folgene Eigenshften: lle Seiten sin gleihlng. (
reieke un Viereke Viereke Welhe esoneren Viereke sin eknnt, ws zeihnet esonere Viereke us? Impuls uf Seiten, Winkel, Symmetrie!.) s Qurt: Ein Qurt esitzt folgene Eigenshften: lle Seiten sin gleihlng. (
2. Das Rechnen mit ganzen Zahlen (Rechnen in )
 . Ds Rechnen mit gnzen Zhlen (Rechnen in ).1 Addition und Subtrktion 5 + = 7 Summnd Summnd Summe 5 - = Minuend Subtrhend Differenz In Aussgen mit Vriblen lssen sich nur gleiche Vriblen ddieren bzw. subtrhieren.
. Ds Rechnen mit gnzen Zhlen (Rechnen in ).1 Addition und Subtrktion 5 + = 7 Summnd Summnd Summe 5 - = Minuend Subtrhend Differenz In Aussgen mit Vriblen lssen sich nur gleiche Vriblen ddieren bzw. subtrhieren.
Grundwissen Mathematik 7II-III
 Grundwissen themtik 7II-III ultipliktion und ivision in QI Rechenregeln c c c d : b d b d b d b c Vorzeichenregeln + + + + + + + : + + : + : + + : Potenzgesetze. Potenzgesetz n m n m + eispiel: 7 + Ü:
Grundwissen themtik 7II-III ultipliktion und ivision in QI Rechenregeln c c c d : b d b d b d b c Vorzeichenregeln + + + + + + + : + + : + : + + : Potenzgesetze. Potenzgesetz n m n m + eispiel: 7 + Ü:
Strahl Eine gerade Linie, die auf einer Seite von einem Punkt begrenzt wird, (Anfangspunkt) heißt Strahl.
 1. 1. 2. Strecke B B Gerde Eine gerde, von zwei Punkten begrenzte Linie heißt Strecke. Eine gerde Linie, die nicht begrenzt ist, heißt Gerde. D.h. eine Gerde ht keine Endpunkte! 2. 3. 3. g Strhl Eine gerde
1. 1. 2. Strecke B B Gerde Eine gerde, von zwei Punkten begrenzte Linie heißt Strecke. Eine gerde Linie, die nicht begrenzt ist, heißt Gerde. D.h. eine Gerde ht keine Endpunkte! 2. 3. 3. g Strhl Eine gerde
Formelsammlung für berufliche Gymnasien Mathematik
 Mit zugelssener Merkhilfe ohner Ott Deush Formelsmmlung für eruflihe Gymnsien Mthemtik Ds Werk und seine Teile sind urheerrehtlih geshützt. Jede Nutzung in nderen ls den gesetzlih zugelssenen Fällen edrf
Mit zugelssener Merkhilfe ohner Ott Deush Formelsmmlung für eruflihe Gymnsien Mthemtik Ds Werk und seine Teile sind urheerrehtlih geshützt. Jede Nutzung in nderen ls den gesetzlih zugelssenen Fällen edrf
Lösung: a) 1093 1100 b) 1093 1090
 OvTG Guting, Grundwissen Mthemtik 5. Klsse 1. Ntürliche Zhlen Dezimlsystem Mn nennt die Zhlen, die mn zum Zählen verwendet, 10963 = 1 10000+ 0 1000+ 9 100+ 6 10 + 3 1 ntürliche Zhlen. Der Stellenwert der
OvTG Guting, Grundwissen Mthemtik 5. Klsse 1. Ntürliche Zhlen Dezimlsystem Mn nennt die Zhlen, die mn zum Zählen verwendet, 10963 = 1 10000+ 0 1000+ 9 100+ 6 10 + 3 1 ntürliche Zhlen. Der Stellenwert der
II Orientieren und Bewegen im Raum
 Schüleruchseiten II Orientieren und ewegen im Rum Erkundungen Seite Seite ( ), ( ), D ( ), E ( ), F ( ), G ( ), H ( ) Ich sehe ws, ws Du nicht siehst Individuelle Lösungen Rechnen mit Vektoren uftrg )
Schüleruchseiten II Orientieren und ewegen im Rum Erkundungen Seite Seite ( ), ( ), D ( ), E ( ), F ( ), G ( ), H ( ) Ich sehe ws, ws Du nicht siehst Individuelle Lösungen Rechnen mit Vektoren uftrg )
G1 Trigonometrie. G1 Trigonometrie. G1.1 Die trigonometrischen Grundfunktionen und ihre wichtigsten Eigenschaften
 G1.1 Die trigonometrischen Grundfunktionen und ihre wichtigsten Eigenschften Seitenverhältnisse und Winkel in rechtwinkligen Dreiecken Beispiel: Wenn in einem Dreieck ABC zum Beispiel die Seite genu so
G1.1 Die trigonometrischen Grundfunktionen und ihre wichtigsten Eigenschften Seitenverhältnisse und Winkel in rechtwinkligen Dreiecken Beispiel: Wenn in einem Dreieck ABC zum Beispiel die Seite genu so
Grundzüge DS & Alg (WS14/15) Lösungsvorschlag zu Aufgabenblatt 7. Aufgabe 1
 Aufge 1 () Anmerkung: Der Punkt in den Bäumen t keinerlei Bedeutung und ist nur d, um drstellen zu können, ws linkes und retes Kind eines Elternteils sein soll Einfügen von,,,,,,, 0, 17 : : : Rottion :
Aufge 1 () Anmerkung: Der Punkt in den Bäumen t keinerlei Bedeutung und ist nur d, um drstellen zu können, ws linkes und retes Kind eines Elternteils sein soll Einfügen von,,,,,,, 0, 17 : : : Rottion :
Grundlagen der Algebra
 PH Bern, Vorbereitungskurs MATHEMATIK Vorkenntnisse 0 Grundlgen der Algebr Einleitung Auf den nchfolgenden Seiten werden grundlegende Begriffe und Ttschen der Algebr erläutert: Zhlenmengen, Rechenopertionen,
PH Bern, Vorbereitungskurs MATHEMATIK Vorkenntnisse 0 Grundlgen der Algebr Einleitung Auf den nchfolgenden Seiten werden grundlegende Begriffe und Ttschen der Algebr erläutert: Zhlenmengen, Rechenopertionen,
MW-E Mathematikwettbewerb der Einführungsphase
 MW-E Mthemtikwettewer der Einführungsphse.Ferur 08 MW-E Mthemtikwettewer der Einführungsphse Hinweis: Von jeder Schülerin zw. jedem Schüler werden fünf Aufgen gewertet. Werden mehr ls fünf Aufgen ereitet,
MW-E Mthemtikwettewer der Einführungsphse.Ferur 08 MW-E Mthemtikwettewer der Einführungsphse Hinweis: Von jeder Schülerin zw. jedem Schüler werden fünf Aufgen gewertet. Werden mehr ls fünf Aufgen ereitet,
V O R K U R S M A T H E M A T I K
 Fchbereich - Informtik und Ingenieurwissenschften V O R K U R S M A T H E M A T I K 100 = 16765060089401496700576 u v u v u v u v uv /(u v) u v u v ( + b ) 5 = 5 + 5 4 b + 10 b +10 b + 5 b 4 + b 5 Die
Fchbereich - Informtik und Ingenieurwissenschften V O R K U R S M A T H E M A T I K 100 = 16765060089401496700576 u v u v u v u v uv /(u v) u v u v ( + b ) 5 = 5 + 5 4 b + 10 b +10 b + 5 b 4 + b 5 Die
Diagnostiktest Mathematik
 Dignostiktest Mthemtik Sie bebsichtigen b em nächsten Schuljhr ie Srlänische Meister- un Technikerschule, Führungskemie es Hnwerks zu besuchen. Herzlichen Glückwunsch zu Ihrem Vorhben. Dmit Sie zielgerichtet
Dignostiktest Mthemtik Sie bebsichtigen b em nächsten Schuljhr ie Srlänische Meister- un Technikerschule, Führungskemie es Hnwerks zu besuchen. Herzlichen Glückwunsch zu Ihrem Vorhben. Dmit Sie zielgerichtet
Bruchrechnung. W. Kippels 6. Dezember Inhaltsverzeichnis. 1 Vorwort 2. 2 Einleitung 3
 Bruchrechnung W. Kippels 6. Dezemer 08 Inhltsverzeichnis Vorwort Einleitung Die Bruchrechenregeln. Addition gleichnmiger Brüche........................ Addition ungleichnmiger Brüche.......................
Bruchrechnung W. Kippels 6. Dezemer 08 Inhltsverzeichnis Vorwort Einleitung Die Bruchrechenregeln. Addition gleichnmiger Brüche........................ Addition ungleichnmiger Brüche.......................
Relationen: Äquivalenzrelationen, Ordnungsrelationen
 TH Mittelhessen, Sommersemester 202 Lösungen zu Üungsltt 9 Fchereich MNI, Diskrete Mthemtik 2. Juni 202 Prof. Dr. Hns-Rudolf Metz Reltionen: Äquivlenzreltionen, Ordnungsreltionen Aufge. Welche der folgenden
TH Mittelhessen, Sommersemester 202 Lösungen zu Üungsltt 9 Fchereich MNI, Diskrete Mthemtik 2. Juni 202 Prof. Dr. Hns-Rudolf Metz Reltionen: Äquivlenzreltionen, Ordnungsreltionen Aufge. Welche der folgenden
15. Kürzeste Wege. SS 2017 DuA - Kapitel 15 1
 5. Kürzeste Wege t s SS DuA - Kpitel 5 Gewichtete Grphen Ein gewichteter Grph G ist ein Pr (V,E) zusmmen mit einer Gewichtsfunktion w, woei E V V un w: E IR. Für e E heißt w(e) s Gewicht von e. Für einen
5. Kürzeste Wege t s SS DuA - Kpitel 5 Gewichtete Grphen Ein gewichteter Grph G ist ein Pr (V,E) zusmmen mit einer Gewichtsfunktion w, woei E V V un w: E IR. Für e E heißt w(e) s Gewicht von e. Für einen
B Figuren und Körper
 B Figuen und Köpe 1 Keis und Keisteile Ein Keis mit dem Rdius ht den Flächen inhlt A = p 2 und den Umfng U = 2p. Die Keiszhl p = 3,14159 ist eine itionle Zhl. Als Nähe ungswete fü p benutzt mn oftmls p
B Figuen und Köpe 1 Keis und Keisteile Ein Keis mit dem Rdius ht den Flächen inhlt A = p 2 und den Umfng U = 2p. Die Keiszhl p = 3,14159 ist eine itionle Zhl. Als Nähe ungswete fü p benutzt mn oftmls p
Vorbereitung auf (3. Mai 2012) NAME: 5. Schularbeit: MATHEMATIK KL.: M3/I. - S.1
 Vorereitung uf (3. Mi 01) NME: 5. Sulreit: MTHEMTIK KL.: M3/I. - S.1 Netze versieener Prismen zeinen (Grunfläe: Dreiek, Vierek, regelmäßiges Sesek). Ds Netz eines Prisms estet us Grunfläe + Dekfläe + Mntel.
Vorereitung uf (3. Mi 01) NME: 5. Sulreit: MTHEMTIK KL.: M3/I. - S.1 Netze versieener Prismen zeinen (Grunfläe: Dreiek, Vierek, regelmäßiges Sesek). Ds Netz eines Prisms estet us Grunfläe + Dekfläe + Mntel.
Mathematik PM Rationale Zahlen. Ist a kein Vielfaches von b, so entsteht eine neue Zahl, Bruch oder rationale Zahl genannt. Sie bilden die Menge Q.
 Mthetik PM Rtionle Zhlen Rtionle Zhlen. Einführung Die Gleihung = 9 ht ie Lösung. Z 9 9 Die Gleihung = ht ie Lösung. Z Definition Die Gleihung =, it, Z un 0, ht ie Ist kein Vielfhes von, so entsteht eine
Mthetik PM Rtionle Zhlen Rtionle Zhlen. Einführung Die Gleihung = 9 ht ie Lösung. Z 9 9 Die Gleihung = ht ie Lösung. Z Definition Die Gleihung =, it, Z un 0, ht ie Ist kein Vielfhes von, so entsteht eine
6 Tiefensuche in ungerichteten Graphen: Zweifache Zusammenhangskomponenten
 66 6 ZWEIFACHE ZUSAMMENHANGSKOMPONENEN 6 iefenshe in ngerihteten Grphen: Zeifhe Zsmmenhngskomponenten Der Algorithms ist gnz gen ersele ie im gerihteten Fll! Ailng 1 zeigt noh einml en gerihtete Fll n
66 6 ZWEIFACHE ZUSAMMENHANGSKOMPONENEN 6 iefenshe in ngerihteten Grphen: Zeifhe Zsmmenhngskomponenten Der Algorithms ist gnz gen ersele ie im gerihteten Fll! Ailng 1 zeigt noh einml en gerihtete Fll n
Teilbarkeitsregeln. 6.1 Grundwissen Mathematik Algebra Klasse 6. Teilbarkeit durch 2: Eine Zahl ist durch 2 teilbar, wenn die Endziffer gerade ist.
 6.1 Grundwissen Mthemtik Algebr Klsse 6 Teilbrkeitsregeln Definition und Regeln Teilbrkeit durch 2: Eine Zhl ist durch 2 teilbr, wenn die Endziffer gerde ist. Teilbrkeit durch 3: Eine Zhl ist durch 3 teilbr,
6.1 Grundwissen Mthemtik Algebr Klsse 6 Teilbrkeitsregeln Definition und Regeln Teilbrkeit durch 2: Eine Zhl ist durch 2 teilbr, wenn die Endziffer gerde ist. Teilbrkeit durch 3: Eine Zhl ist durch 3 teilbr,
Die Dreiecke ADM A und BCM C sind kongruent aufgrund
 Westfälische Wilhelms-Universität Münster Mthemtisches Institut pl. Prof. Dr. Lutz Hille Dr. Krin Hlupczok Üungen zur Vorlesung Elementre Geometrie Sommersemester 010 Musterlösung zu ltt 4 vom 3. Mi 010
Westfälische Wilhelms-Universität Münster Mthemtisches Institut pl. Prof. Dr. Lutz Hille Dr. Krin Hlupczok Üungen zur Vorlesung Elementre Geometrie Sommersemester 010 Musterlösung zu ltt 4 vom 3. Mi 010
Übungsbeispiele Dreiecke Mag. Thomas Höfferer. Aufgaben DREIECKE
 Übungsbeispiele Deiecke Mg. Toms Höffee ufgben DREIECKE Fläce von Deiecken: D 1. Gegeben sin ie ei Seiten eines llgemeinen Deiecks. estimme ie Fläce un ie ei Höen e einzelnen Deiecke. b c b c.) 1 1 15
Übungsbeispiele Deiecke Mg. Toms Höffee ufgben DREIECKE Fläce von Deiecken: D 1. Gegeben sin ie ei Seiten eines llgemeinen Deiecks. estimme ie Fläce un ie ei Höen e einzelnen Deiecke. b c b c.) 1 1 15
Der Goldene Schnitt. III. Der Goldene Schnitt in der Mathematik
 Der Goldene Schnitt III. Der Goldene Schnitt in der Mthemtik 1. Herleitung des Goldenen Schnitt Per Definition des Goldenen Schnitt gilt: b = b. (>b>0) Nch der Drstellung (s.o.) gilt, wenn S (der mittlere
Der Goldene Schnitt III. Der Goldene Schnitt in der Mthemtik 1. Herleitung des Goldenen Schnitt Per Definition des Goldenen Schnitt gilt: b = b. (>b>0) Nch der Drstellung (s.o.) gilt, wenn S (der mittlere
Menge der natürlichen Zahlen. ℕ = ℕ {0} Menge der ganzen Zahlen ℤ = ℤ {0} ℝ. Menge der reellen Zahlen. ℝ = ℝ {0} ℝ+ = { x ℝ x 0}
 Mekhilfe Mthemtik fü Bildugsgäge die zu FHSR fühe Zhlemege ℕ = { ; ; ; ;...} Mege de tüliche Zhle ℕ = ℕ {} ℤ = {... ; ; ; ; ; ;...} Mege de gze Zhle ℤ = ℤ {} ℝ Mege de eelle Zhle ℝ = ℝ {} ℝ+ = { ℝ } Mege
Mekhilfe Mthemtik fü Bildugsgäge die zu FHSR fühe Zhlemege ℕ = { ; ; ; ;...} Mege de tüliche Zhle ℕ = ℕ {} ℤ = {... ; ; ; ; ; ;...} Mege de gze Zhle ℤ = ℤ {} ℝ Mege de eelle Zhle ℝ = ℝ {} ℝ+ = { ℝ } Mege
Einige Formeln zum Goldenen Schnitt
 Einige Formeln zum Goldenen Schnitt Eine Strecke wird im Verhältnis geteilt, wenn ds Verhältnis der Gesmtstrecke m+m zur längeren Teilstrecke M gleich dem Verhältnis der längeren Teilstrecke M zur kürzeren
Einige Formeln zum Goldenen Schnitt Eine Strecke wird im Verhältnis geteilt, wenn ds Verhältnis der Gesmtstrecke m+m zur längeren Teilstrecke M gleich dem Verhältnis der längeren Teilstrecke M zur kürzeren
Bruchrechnen. Faßt man zwei Drittel eines Ganzen zusammen, so schreibt man 3. Bezeichnungen bei Brüchen: Der Bruch als Quotient:
 Bruhrehnen Zerlegt mn ein Gnzes (einen Li Brot, eine Torte, einen Apfel, einen Geletrg, eine Kreisflähe, ein Rehtek, eine Streke,... ) in,,... gleihe Teile, so heißt ein solher Teil (Bruhteil es Gnzen)
Bruhrehnen Zerlegt mn ein Gnzes (einen Li Brot, eine Torte, einen Apfel, einen Geletrg, eine Kreisflähe, ein Rehtek, eine Streke,... ) in,,... gleihe Teile, so heißt ein solher Teil (Bruhteil es Gnzen)
3. Ganzrationale Funktionen
 3. Gnzrtionle Funktionen ) Definitionen und Beispiele Definition: Eine gnzrtionle Funktion n-ten Grdes ht ls Definitionsterm ein Polynom n-ten Grdes, d.h. y = f() = n n n-1 n-1 1 0. n 0, i ( i = 1, n)
3. Gnzrtionle Funktionen ) Definitionen und Beispiele Definition: Eine gnzrtionle Funktion n-ten Grdes ht ls Definitionsterm ein Polynom n-ten Grdes, d.h. y = f() = n n n-1 n-1 1 0. n 0, i ( i = 1, n)
Grundwissen. 9. Jahrgangsstufe. Mathematik
 Gundwissen 9. Jahgangsstufe Mathematik Seite Reelle Zahlen. Rechnen mit Quadatwuzeln a ist diejenige nicht negative Zahl, die zum Quadat a egibt. d.h.: ist keine Wuzel aus. Eine Wuzel kann nicht negativ
Gundwissen 9. Jahgangsstufe Mathematik Seite Reelle Zahlen. Rechnen mit Quadatwuzeln a ist diejenige nicht negative Zahl, die zum Quadat a egibt. d.h.: ist keine Wuzel aus. Eine Wuzel kann nicht negativ
MATHEMATIK GRUNDWISSEN KLASSE 5
 MATHEMATIK GRUNDWISSEN KLASSE 5 Them NATÜRLICHE ZAHLEN Zählen und Ordnen Ntürliche Zhlen werden zum Zählen und Ordnen verwendet Stefn ist beim 100m-Luf ls 2. ins Ziel gekommen. Große Zhlen und Zehnerpotenzen
MATHEMATIK GRUNDWISSEN KLASSE 5 Them NATÜRLICHE ZAHLEN Zählen und Ordnen Ntürliche Zhlen werden zum Zählen und Ordnen verwendet Stefn ist beim 100m-Luf ls 2. ins Ziel gekommen. Große Zhlen und Zehnerpotenzen
