Röntgen Computertomographie (CT) Hounsfield, W.A. Kalender: Computertomographie Publicis MCD Verlag, 2000
|
|
|
- Swen Hafner
- vor 7 Jahren
- Abrufe
Transkript
1 Hounsfield, 1969 Zusätzliche Literatur: W.A. Kalender: Computertomographie Publicis MCD Verlag, 2000
2 Entwicklung der CT im historischen Überblick 1895 W.C. Röntgen entdeckt eine 'neue Art von Strahlen', die später nach ihm als Röntgenstrahlen benannt werden 1917 J.H. Radon entwickelt die mathematischen Grundlagen zur Errechnung von Querschnittsbildern aus Transmissionsmessungen 1960/1970 Verbesserung der Computertechnologie 1972 G.N. Hounsfield und J. Ambrose führen erste klinische Untersuchungen mit Computertomographie durch 1975 erster Ganzkörpertomograph im klinischen Einsatz 1979 Verleihung des Nobelpreises an Hounsfield und Cormack 1989 erste klinische Untersuchungen mit Spiral-CT 1998 erste klinische Untersuchungen mit Mehrzeilen-Spiral-CT 2000 ca klinische Spiral-CT- Installationen weltweit
3
4 1974 Bildmatrix: 80 x Bildmatrix: 512 x 512 Spiral-CT
5 Hounsfield, 1969 moderner CT-Scanner
6 Probleme der Projektionsradiographie: Röntgenbild: - modulierte Verteilung der durch Gewebe transmittierten Röntgenquanten - 2D Projektion der Schwächungseigenschaften des Gewebes - Überlagerungsbild: alle durchstrahlten Volumenelemente tragen zur Schwächung bei? - Linienintegral der Abschwächung: = µ( x, y, z JD J0 e )dl - Kontrast: Strukturen mit großem µ (Knochen) bzw. Dickenunterschiede; Weichteilgewebe nicht darstellbar - Projektionsradiographie ist nicht tomographisch
7 homogenes Objekt; mono-chromatische Strahlung J D = J 0 e µ d P = ln J J 0 D = µ d J 0 µ = 1 d ln J J 0 D J D P = Projektionswert
8 inhomogenes Objekt; mono-chromatische Strahlung?? ln = = = = = = i i i i D ds d d d d d J J P e J e J e J J d i i i µ µ µ µ µ µ µ D J 0 J D
9 inhomogenes Objekt; poly-chromatische Strahlung J 0 J D P µ ( x, y) = = = E max 0 J J ln J?? 0 0 D ( E) e d 0 µ d s de J D
10 Prinzipien der Röntgen-Computertomographie
11 Prinzip der Computertomographie: - messe räumliche Verteilung einer physikalischen Eigenschaft [µ(x,y)] des zu untersuchenden Objekts - errechne aus Meßwerten überlagerungsfreie Bilder (Radon-Transformation und Fourier-Scheiben-Theorem)
12 Idee: Aufnahme einzelner Schichten betrachte menschlicher Körper als ein aus endlich vielen diskreten Volumenelementen zusammengesetztes Objekt in grober Auflösung: - einzelne transversale Schichten der Dicke s - Schichten zusammengesetzt aus diskreten quaderförmigen Volumenelementen x Volumenelement: Bildelement: Voxel (volume element) Pixel (picture element)
13 Messung von Schichtbildern und inverses Problem Inverses Problem: Gegeben eine Menge N p von Messungen (Schichtbilder) außerhalb eines Objektes, bestimme die Verteilung der physikalischen Kenngröße µ innerhalb des Objektes J. Radon (1917): Die 2D-Verteilung einer Objekteigenschaft kann exakt beschrieben werden, wenn eine unendliche Anzahl von Linienintegralen vorliegt. Durch eine endliche Anzahl N p von Messungen kann die Verteilung µ(x,y) ausreichend approximiert werden Vorwärtsproblem: gegeben µ(x,y) innerhalb des Objekts, bestimme Ergebnis der Messung außerhalb des Objekts.
14 Einfachstes Meßprinzip der CT Mit Radon Vorgabe: erst Translation (ergibt Projektion) dann Rotation (min. 180 ) Nadelstrahl Moderne CT-Scanner: Projektionen mit ca Meßwerten pro Projektion
15 Radon-Transformation (I) J. Radon (1917): Die 2D-Verteilung einer Objekteigenschaft kann exakt beschrieben werden, wenn eine unendliche Anzahl von Linienintegralen vorliegt. sei f(x,y) beliebige integrierbare Funktion beschreibe f(x,y) durch alle geraden Linienintegrale durch Definitionsgebiet von f(x,y): + ( x( l), y( l ) f ) dl
16 Radon-Transformation (II) naiver Ansatz: integriere nacheinander durch alle Punkte über alle Richtungen einige Linienintegrale sind identisch wähle geeignetes Ordnungsschema, so dass alle Linienintegrale nur einmal vorkommen (Hesse Normalform) r r e = s r e = Θ = f ( x, y) dl = p( Θ, s) Θ Einheitsve ktor in Richtung Winkel zwischen Integrationslinie undnormalen durchnull
17 Radon-Transformation (III) mit Θ [0,180 ] und mit allen s: (s min < s < s max ) alle möglichen Linienintegrale p(θ,s) über Funktion f(x,y) Radon-Transformation: Übertragung der Werte der Linienintegrale in p(q,s)-diagramm Eine Linie in der Radontransformierten mit Θ =const nennt man Projektion p Θ (s) p Θ (s) = Zahlenfolge aller Linienintegrale über f(x,y) mit Θ =const und variablem Abstand s zum Koordinatenursprung
18 Radon-Transformation (III- 1) Berechnung der Radontransformierten für Θ=0
19 Radon-Transformation (III- 2) Berechnung der Radontransformierten für Θ 0
20 Fourier-Scheiben-Theorem (I) - Messung mit Nadelstrahl für gegebenen Winkel Θ und Abstand s vom Koordinatenursprung (Projektionswerte p Θ (s)) entspricht der Radontransformierten des Bildes. - Mit Hilfe des Fourier-Scheiben-Theorems läßt sich aus der Radontransformierten die Funktion f(x,y) bestimmen (d.h. µ(x,y)) Zusammenhang zwischen Radon- und Fourier-Transformation (Projektionssatz oder Fourier -Scheiben-Theorem): r sei Rf(e, s) = G( α) = F( u, v) für mit G( α) = F1 F( u, v) = F { RΘ f ( s) } { f ( x, y) } 2 r r e r r f ( ) d Radontransformierte des Objekts ( u, v) = α (cosθ,sin Θ) µ(x,y) durch inverse 2D-FT f
21 Fourier-Scheiben-Theorem (Bew e i s f ü r Q =0) Projektion zum Winkel Θ=0
22 Fourier-Scheiben-Theorem (Bew e i s f ü r Q =0) Def.: 1D-FT(p Θ=0 (s)) ergibt Werte der 2D-FT von f(x,y) auf der u-achse
23 Fourier-Scheiben-Theorem (Bew e i s f ü r Q 0) Projektion für Θ 0
24 Fourier-Scheiben-Theorem (Bew e i s f ü r Q 0) Projektion p Θ (s) kann als Projektion auf der x -Achse eines gedrehten Koordinatensystems aufgefaßt werden. Es gilt die gleiche Herleitung wie für Θ=0: 1D-FT(p Θ (s)) ergibt Werte der 2D-FT von f(x,y) auf der u -Achse Allgemein gilt: Die FT einer um den Winkel Θ gedrehten Funktion f(x,y) ist um den genau den gleichen Winkel Θ gegenüber der FT F(u,v) verdreht q.e.d.
25 Fourier-Scheiben-Theorem (II) Θ=0 Θ 0
26 Fourier-Scheiben-Theorem (III) Sei eine Funktion f(x,y) gegeben und F(u,v) deren 2D-Fouriertransformierte Sei weiter p Θ (s) eine Projektion von f(x,y) und P Θ (w) deren 1D-Fouriertransformierte Dann beschreibt P Θ (w) die Werte von F(u,v) auf einem Radialstrahl zum Winkel Θ.
27 Rekonstruktion von f(x,y) = µ(x,y) aus Radon-Transformation
28 Radon-Transformation und Computertomographie Durchgang eines nadelförmigen Rö.-Strahls durch Körper
29 Radon-Transformation und Computertomographie
30 Radon-Transformation und Computertomographie Caveat: - Daten liegen als Werte auf Radialstrahlen vor! - Schnelle Fouriertransformation (FFT) benötigt Uminterpolation auf quadratisches Gitter (Polarkoordinaten kartesische Koordinaten) - Uminterpolation kann zu schwerwiegenden Artefakten führen! (moderne Scanner ermöglichen Abtastung im kartesischen Raster)
31 Iterative CT- Rekonstruktion (I) - gesuchte Verteilung µ(x,y) liegt nach Messung nur in Form der Projektionswerte (Radon-Transformierte) vor. - finde Rücktransformation um µ(x,y) zu erhalten einfachster Ansatz: gesucht: N x N Bildpunkte der Matrix: N 2 Werte gegeben: M = N p x N d = Anzahl Projektionen x Anzahl Werte/Projektion wenn M N: über-bestimmtes Problem lösbar!
32 Iterative CT- Rekonstruktion (II) Allgemeiner Fall: sei f(x,y) = µ(x,y) Für digitale Verarbeitung: Hintereinandersetzen der Zeilen der Bildmatrix ergibt Zahlenfolge mit einzelnem Index: f i Messung mit Nadelstrahl j liefert Integral über Werte f i, die auf dem Strahl liegen: - Funktionswerte f i werden mit Gewichtsfaktor w ij multipliziert u. addiert - w ij gibt Flächenanteil vom Nadelstrahl j zum Pixel i an (wg. Nadelstrahl sind die meisten w ij =0)
33 Iterative CT- Rekonstruktion (III) N MN M M M N N N N f w f w f w p f w f w f w p f w f w f w p = = = L M L L Meßwerte p i (Linienintegrale) lassen sich darstellen als: lineare Abbildung!! Beispiel: Bildgröße: 512x512 N = gegeben: 1000 Projektionen mit jeweils 800 Detektoren M = 1000 x 800 = (über-bestimmtes Problem) Gleichungen mit Unbekannten!!
34 Iterative CT- Rekonstruktion (IV) Lösen des linearen Gleichungssystems: (1) direkte Methoden z.b. Gauß-Elimination unpraktikabel bei großen Matrizen (2) iterative Methoden:
35
36
37 Iterative CT- Rekonstruktion (V) - Verfahren konvergiert immer - Verfahren wird bei der Röntgen-CT heute nicht mehr verwendet - Verfahren findet jedoch bei PET/SPECT immer mehr Anwendung
38 C T -Rekonstruktion mit gefilterter Rückprojektion Wiederholung: Messung mit Nadelstrahl für gegebenen Winkel Θ und Abstand s vom Koordinatenursprung (Projektionswerte p Θ (s)) entspricht der Radon- Transformierten des Bildes µ(x,y). Mit Fourier-Scheiben-Theorem gilt: - durch 1D-FT der gemessenen Projektion erhält man die 2D-FT von µ(x,y) auf einer Geraden in Richtung Θ. - Rekonstruktion von µ(x,y) durch inverse 2D-FT möglich Problem: Daten liegen in Polarkoordinaten vor; FFT benötigt kartesische Koordinaten
39 C T -Rekonstruktion mit gefilterter Rückprojektion (I) Rückprojektion: Messwerte (Projektionswerte p Θ (s)) sind Linienintegrale von µ(x,y). Jedoch: Integralwert = Summe aller Beiträge und ohne Ortsinformation Ansatz: R ückprojektion: gleichmäßige Verteilung des Integralwerts entlang des ursprünglichen Integrationsweges Überlagerung aller Projektionsgeraden im Punkt (x,y) µ(x,y) näherungsweise
40 C T -Rekonstruktion mit gefilterter Rückprojektion (II) Rückprojektion: 0. Rückprojektion 1. Rückprojektion 3. Rückprojektion Schwächungsprofil: µ(x) N. Rückprojektion x Schwächungsprofil nach N Rückprojektionen
41 C T -Rekonstruktion mit gefilterter Rückprojektion (III) Rückprojektion: Durch Rückprojektion entsteht eine Punktbildfunktion (PBF) der Form 1/r 1/r Jedem Bildpunkt kann eine derartige PBF zugeordnet werden, gewichtet mit dem lokalen µ(x,y) Rückprojektion = 1/r * µ(x,y) (Faltung) Rückprojektion führt zu Verwischung, dadurch keine Kontrastunterschiede und keine Feinstrukturen erkennbar
42 C T -Rekonstruktion mit gefilterter Rückprojektion (IV) Gefilterte Rückprojektion: Idee: Modifiziere Punktbildfunktion derart, dass Verwischung minimiert (ideal: verhindert) wird. Ansatz: Faltung des Schwächungsprofils mit geeignetem Filter (Faltungskern)
43 C T -Rekonstruktion mit gefilterter Rückprojektion (V) Gefilterte Rückprojektion: Originalprofil Faltungskern = gefiltertes Profil
44 C T -Rekonstruktion mit gefilterter Rückprojektion (VI) Gefilterte Rückprojektion: 0. Rückprojektion 1. Rückprojektion 3. Rückprojektion Schwächungsprofil: µ(x) N. Rückprojektion x Schwächungsprofil nach N Rückprojektionen
45 Einfluß des Faltungskerns glättend Standard Kanten betonend
46 Einfluß des Faltungskerns glättend soft Standard Kanten betonend bone
47 C T -Rekonstruktion mit gefilterter Rückprojektion (VII) Gesucht: f(x,y) = µ(x,y) aus der inversen 2D-FT von F(u,v) mit Zylinderkoordinaten im Fourierraum u = w. cos Θ v = w. sin Θ dudv = w. dw. dθ folgt
48 C T -Rekonstruktion mit gefilterter Rückprojektion (VIII) Reduktion der Integrationsfläche auf [0,π] (w.g. Hesse Normalform) Absolutbetrag von w, da in dieser Form negative Radien vorkommen.
49 C T -Rekonstruktion mit gefilterter Rückprojektion (IX) Ersetze Wäre w nicht im Integral enthalten, bräuchte nur die inverse FT angewendet werden, um die Originale Projektion p Θ (s) zu erhalten. Durch Multiplikation im Fourierraum mit w wird die Projektion p Θ (s) gefiltert ~ p Θ (s) ist gefilterte Projektion (Faltung im Ortsraum = Multiplikation im Fourierraum). h(s) ist Impulsantwort des Filters (=Faltungskern)
50 C T -Rekonstruktion mit gefilterter Rückprojektion (X) Welche Funktion h(s) gehört zur FT von w? Problem: h(s) nur im Grenzübergang definierbar Ansatz: w w. exp(-ε w ) Inverse FT von w. exp(-ε w ) hierfür gilt: Betrachte Übergang ε 0: rhs geht über in w lhs geht über in -1/2πs 2 peak bei s=0 wird umso schmaler und höher je kleiner ε
51 C T -Rekonstruktion mit gefilterter Rückprojektion (XI) Was bedeutet das Integral über Θ? Rückprojektion: Um den Wert von f(x,y)=µ(x,y) an einem gegebenen Punkt (x,y) zu erhalten, nimm von allen gefilterten Projektionen ~ p Q (s) an der Stelle xcosq + ysinq und summiere diese Werte auf.
52 C T -Rekonstruktion mit gefilterter Rückprojektion (XII)
53 C T -Rekonstruktion mit gefilterter Rückprojektion (XIII)
54 C T -Rekonstruktion mit gefilterter Rückprojektion (XIV) Bei der Rückprojektion trifft der Projektionsstrahl nicht immer auf die Mitte der quadratisch angeordneten Pixel. Rückwärts vorgehen: ziele vom Zentrum des Pixels unter Winkel Θ auf die gefilterte Projektion Dann: lineare Interpolation zwischen benachbarten Werten, um Meßort des Detektors zu approximieren.
55 C T -Rekonstruktion mit gefilterter Rückprojektion (XV) Einhalten des Abtast-Theorems und Rauschen: durch digitales Abtasten gibt es in den Projektionen p Θ (s) eine maximale Frequenz w max = 1/2 S, wobei S= Detektor-Abstand Da Raumfrequenzen oberhalb w max nicht bekannt sind, kann Projektionsverfahren in der Praxis nur schlechter sein (Überbewertung hoher Raumfrequenzen). Bei Raumfrequenzen w< w max wird das Spektrum P Θ (w) meist von Rauschen dominiert. Durch Multiplikation mit w wird Rauschen zusätzlich verstärkt
56 C T -Rekonstruktion mit gefilterter Rückprojektion (XV) Einhalten des Abtast-Theorems und Rauschen:
57 C T -Rekonstruktion mit gefilterter Rückprojektion (XVI) Alternative Filterfunktionen nach Shepp & Logan und Ramachandran & Lakshminarayan
58 C T -Rekonstruktion mit gefilterter Rückprojektion (XVI) Alternative Filterfunktionen nach Shepp & Logan und Ramachandran & Lakshminarayan
59 C T -Rekonstruktion mit gefilterter Rückprojektion (XVII) analoge und digitale Filterung:
60 C T -Rekonstruktion mit gefilterter Rückprojektion (XVII) analoge und digitale Rückprojektion: M = Zahl der Projektionen
61 Was wird im CT-Bild dargestellt?
62 Hounsfield -Skala Absorptions- oder Schwächungskoeffizient in der Kernphysik: [ µ ] = cm 1 µ abh. von Rö.-Energie!! in der Medizin: relative Hounsfield-Skala (CT-Zahl) µ rel = µ µ µ Wasser Wasser Mensch besteht zu mehr als 60 % aus Wasser - die meisten körper-eigenen Substanzen unterscheiden sich nur wenig von µ Wasser, daher Darstellung der Abweichung in Promille
63 Hounsfield -Skala CT-Zahl
64 Hounsfield -Skala 70 50
65 Hounsfield -Skala Werte-Bereich: bis (entspricht 4096 Graustufen) in erster Näherung proportional zu Dichte der Gewebe: Luft/Gase ~-1000 Fett ~ -90 Wasser ~ 0 Weichteile ~ +20 Knochen > +250 Unterschiede Lunge bis Knochen groß Unterschiede bei Weichteilen, Fettgewebe, Wasser nur gering (typische Differenzierung durch Betrachtung: Graustufen) Fenstertechnik
66 Hounsfield -Skala + Fenstertechnik Grauwertdarstellung Verbesserte Beurteilbarkeit der Bilder W C z.b. mit: Knochenfenster: C/W = 1000/2500 Mediastinalfenster: C/W = -50/ 400 Lungenfenster: C/W = -625/1250 C Fenstermitte (center) W Fensterbreite (width)
67 Hounsfield -Skala + Fenstertechnik
68 Hounsfield -Skala + Zwei-Spektren CT CT-Zahlen meist eindeutig interpretierbar (beachte: Addition aller Materialien und chemischen Elemente pro Voxel!!) Unklare Befunde (Beispiel): Beobachtung: Areal mit erhöhter Schwächung im Weichteilgewebe Frage: frischer Prozess (Blutung) oder alter Prozess (Kalkeinlagerung) Ausnutzung der ordnungszahlbedingten Energieabhängigkeit von µ µ = f(e,z) Zwei-Spektren CT: - zwei Aufnahmen mit unterschiedlichen Rö.-Energien - Subtraktion liefert materialselektive Bilder
69 Hounsfield -Skala + Zwei-Spektren CT
70 Homogenitätsbestimmung Toleranz: + 4HU vom Sollwert (Wasser: 0 HU)
71 Projektionsradiographie und Computertomographie: Beide Verfahren: - Bildgebung mit Röntgenstrahlen - vergleichbare Dosis (neuere CT-Geräte geringere Dosis) Projektionsradiographie: - Kontrast = Summe der Signalbeiträge (µ) entlang der Transmission - Kontrast abhängig von Z und Dosis Computertomographie - Kontrast = Werte benachbarter Voxel (nicht durch Summenoder Linienintegrale); lokale Zusammensetzung des Gewebes - kein Einfluß angrenzender oder überlappender Strukturen
72 CT-Bild Röntgen-Bild CT-Bild: hoher lokaler Kontrast K K = CT=J 1 -J 2 ~ 50 % Röntgen-Bild: niedriger Weichgewebekontrast K=(J 1 -J 2 )/((J 1 +J 2 )/2) ~ 0,23 %
Grundlagen der Computer-Tomographie
 Grundlagen der Computer-Tomographie Quellenangabe Die folgenden Folien sind zum Teil dem Übersichtsvortrag: imbie.meb.uni-bonn.de/epileptologie/staff/lehnertz/ct1.pdf entnommen. Als Quelle für die mathematischen
Grundlagen der Computer-Tomographie Quellenangabe Die folgenden Folien sind zum Teil dem Übersichtsvortrag: imbie.meb.uni-bonn.de/epileptologie/staff/lehnertz/ct1.pdf entnommen. Als Quelle für die mathematischen
Grundlagen der Computertomographie. Dr. Stephan Scheidegger, 2006
 Grundlagen der Computertomographie Dr. Stephan Scheidegger, 2006 Computertomographie Inhalt Technik der Computertomographie Bild-Rekonstruktion Scanning-Methoden Dentale Volumentomographie ROENTGENTECHNIK
Grundlagen der Computertomographie Dr. Stephan Scheidegger, 2006 Computertomographie Inhalt Technik der Computertomographie Bild-Rekonstruktion Scanning-Methoden Dentale Volumentomographie ROENTGENTECHNIK
Computertomographie (CT), Magnetresonanztomographie (MRT) und Ultraschall (US)
 Computertomographie (CT), Magnetresonanztomographie (MRT) und Ultraschall (US) Prof. Dr. Willi Kalender, Ph.D. Institut für Medizinische Physik Universität Erlangen-Nürnberg www.imp.uni-erlangen,de 3D
Computertomographie (CT), Magnetresonanztomographie (MRT) und Ultraschall (US) Prof. Dr. Willi Kalender, Ph.D. Institut für Medizinische Physik Universität Erlangen-Nürnberg www.imp.uni-erlangen,de 3D
Computer Tomographie. Angiographie. Ein Vortrag im Rahmen des Seminars Hydrodynamik des Blutes. Sabrina Pospich. TU Dortmund - Fakultät Physik
 Computer Tomographie Ein Vortrag im Rahmen des Seminars Hydrodynamik des Blutes TU Dortmund - Fakultät Physik CT Inhaltsverzeichnis 1 Funktionsweise der CT Einleitung 2 Iterative Rekonstruktion Radon-Transformation
Computer Tomographie Ein Vortrag im Rahmen des Seminars Hydrodynamik des Blutes TU Dortmund - Fakultät Physik CT Inhaltsverzeichnis 1 Funktionsweise der CT Einleitung 2 Iterative Rekonstruktion Radon-Transformation
Magnetresonanztomographie (MRT) Grundlagen der Tomographie
 Gegeben: Körper in einem starken B 0 -Feld - Folge von HF-Pulsen erzeugt rotierende Quermagnetisierung M T - M T variiert je nach Gewebetyp ortsabhängige Observable: M T (x,y,z) - kleine Volumenelemente
Gegeben: Körper in einem starken B 0 -Feld - Folge von HF-Pulsen erzeugt rotierende Quermagnetisierung M T - M T variiert je nach Gewebetyp ortsabhängige Observable: M T (x,y,z) - kleine Volumenelemente
Lineare Gleichungen mit 2 Variablen
 Lineare Gleichungen mit 2 Variablen Lineare Gleichungen mit 2 Variablen sind sehr eng verwandt mit linearen Funktionen. Die Funktionsgleichung einer linearen Funktion f(x) = m x+q m: Steigung, q: y Achsenabschnitt
Lineare Gleichungen mit 2 Variablen Lineare Gleichungen mit 2 Variablen sind sehr eng verwandt mit linearen Funktionen. Die Funktionsgleichung einer linearen Funktion f(x) = m x+q m: Steigung, q: y Achsenabschnitt
Systemtheorie abbildender Systeme
 Bandbegrenzung Bild in (b) nicht band-begrenzt: scharfe Kanten = Dirac-Funktionen = weißes Spektrum Erfordert Tapering vor Digitalisierung (Multiplikation mit geeigneter Fensterfunktion; auf Null drücken
Bandbegrenzung Bild in (b) nicht band-begrenzt: scharfe Kanten = Dirac-Funktionen = weißes Spektrum Erfordert Tapering vor Digitalisierung (Multiplikation mit geeigneter Fensterfunktion; auf Null drücken
Computertomographie (CT) Prof. Dr.-Ing. Georgios Sakas
 (CT) Prof. Dr.-Ing. Georgios Sakas 31.10.07 Danksagung Diese Folien beinhalten Beiträge von Dr. Ronald Blechschmidt-Trapp, Braun GmbH, Kronberg (ehemals Institut elektromechanische Konstruktionen, TUD)
(CT) Prof. Dr.-Ing. Georgios Sakas 31.10.07 Danksagung Diese Folien beinhalten Beiträge von Dr. Ronald Blechschmidt-Trapp, Braun GmbH, Kronberg (ehemals Institut elektromechanische Konstruktionen, TUD)
Bildgebende Systeme in der Medizin
 10/27/2011 Page 1 Hochschule Mannheim Bildgebende Systeme in der Medizin Computer-Tomographie Faculty of Medicine Mannheim University of Heidelberg Theodor-Kutzer-Ufer 1-3 D-68167 Mannheim, Germany Friedrich.Wetterling@MedMa.Uni-Heidelberg.de
10/27/2011 Page 1 Hochschule Mannheim Bildgebende Systeme in der Medizin Computer-Tomographie Faculty of Medicine Mannheim University of Heidelberg Theodor-Kutzer-Ufer 1-3 D-68167 Mannheim, Germany Friedrich.Wetterling@MedMa.Uni-Heidelberg.de
4.5 Überbestimmte Gleichungssysteme, Gauß sche Ausgleichrechnung
 4.5 Überbestimmte Gleichungssysteme, Gauß sche Ausgleichrechnung In vielen Anwendungen treten lineare Gleichungssysteme auf, die eine unterschiedliche Anzahl von Gleichungen und Unbekannten besitzen: Ax
4.5 Überbestimmte Gleichungssysteme, Gauß sche Ausgleichrechnung In vielen Anwendungen treten lineare Gleichungssysteme auf, die eine unterschiedliche Anzahl von Gleichungen und Unbekannten besitzen: Ax
Bilderzeugung und Bildrekonstruktion
 Medizinische Bilder werden auf vielerlei Arten erstellt. Wir stellen einige kurz vor. In der Tomographie werden die gemessenen Signale einem Rekonstruktionsschritt unterworfen, bevor ein Bild entsteht.
Medizinische Bilder werden auf vielerlei Arten erstellt. Wir stellen einige kurz vor. In der Tomographie werden die gemessenen Signale einem Rekonstruktionsschritt unterworfen, bevor ein Bild entsteht.
Bilderzeugung und Bildrekonstruktion
 und Bildrekonstruktion Medizinische Bilder werden auf vielerlei Arten erstellt. Wir stellen einige kurz vor. In der Tomographie werden die gemessenen Signale einem Rekonstruktionsschritt unterworfen, bevor
und Bildrekonstruktion Medizinische Bilder werden auf vielerlei Arten erstellt. Wir stellen einige kurz vor. In der Tomographie werden die gemessenen Signale einem Rekonstruktionsschritt unterworfen, bevor
Vektoren. Kapitel 3. 3.1 Skalare, Vektoren, Tensoren. 3.2 Vektoren
 Kapitel 3 Vektoren 31 Skalare, Vektoren, Tensoren Viele physikalische Größen lassen sich bei bekannter Maßeinheit durch Angabe ihres Betrages als reelle Zahl vollständig angeben Solche Größen nennt man
Kapitel 3 Vektoren 31 Skalare, Vektoren, Tensoren Viele physikalische Größen lassen sich bei bekannter Maßeinheit durch Angabe ihres Betrages als reelle Zahl vollständig angeben Solche Größen nennt man
Funktionsweise und Rekonstruktionsverfahren SPECT & SPECT/CT. C. Schütze
 Funktionsweise und Rekonstruktionsverfahren SPECT & SPECT/CT C. Schütze Gammakamera und SPECT-Systeme http://www.healthcare.siemens.com, http://www.healthcare.philips.com, http://www.miegermany.de Grundprinzip
Funktionsweise und Rekonstruktionsverfahren SPECT & SPECT/CT C. Schütze Gammakamera und SPECT-Systeme http://www.healthcare.siemens.com, http://www.healthcare.philips.com, http://www.miegermany.de Grundprinzip
Computergrafik 2: Filtern im Frequenzraum
 Computergrafik 2: Filtern im Frequenzraum Prof. Dr. Michael Rohs, Dipl.-Inform. Sven Kratz michael.rohs@ifi.lmu.de MHCI Lab, LMU München Folien teilweise von Andreas Butz, sowie von Klaus D. Tönnies (Grundlagen
Computergrafik 2: Filtern im Frequenzraum Prof. Dr. Michael Rohs, Dipl.-Inform. Sven Kratz michael.rohs@ifi.lmu.de MHCI Lab, LMU München Folien teilweise von Andreas Butz, sowie von Klaus D. Tönnies (Grundlagen
Vektoren und Matrizen
 Vektoren und Matrizen Einführung: Wie wir gesehen haben, trägt der R 2, also die Menge aller Zahlenpaare, eine Körperstruktur mit der Multiplikation (a + bi(c + di ac bd + (ad + bci Man kann jedoch zeigen,
Vektoren und Matrizen Einführung: Wie wir gesehen haben, trägt der R 2, also die Menge aller Zahlenpaare, eine Körperstruktur mit der Multiplikation (a + bi(c + di ac bd + (ad + bci Man kann jedoch zeigen,
Mehrfachintegrale 1-E1. Ma 2 Lubov Vassilevskaya
 Mehrfachintegrale 1-E1 1-E2 Mehrfachintegrale c Die Erweiterung des Integralbegriffs führt zu den Mehrfachintegralen, die in den naturwissenschaftlich-technischen Anwendungen u.a. bei der Berechnung der
Mehrfachintegrale 1-E1 1-E2 Mehrfachintegrale c Die Erweiterung des Integralbegriffs führt zu den Mehrfachintegralen, die in den naturwissenschaftlich-technischen Anwendungen u.a. bei der Berechnung der
Computertomographie. Grundlagen, Gerätetechnologie, Bildqualität, Anwendungen. Uli A. Kalender. Publicis MCD Verlag
 Computertomographie Grundlagen, Gerätetechnologie, Bildqualität, Anwendungen Uli A. Kalender Publicis MCD Verlag Vorwort 5 Inhaltsverzeichnis 9 Historischer Überblick 13 1 Grundlagen der Computertomographie
Computertomographie Grundlagen, Gerätetechnologie, Bildqualität, Anwendungen Uli A. Kalender Publicis MCD Verlag Vorwort 5 Inhaltsverzeichnis 9 Historischer Überblick 13 1 Grundlagen der Computertomographie
Höhere Mathematik III WS 05/06 Lösungshinweis Aufgabe G 11 Blatt 2
 Höhere Mathematik III WS 5/6 Lösungshinweis Aufgabe G 11 Blatt Die zu optimierende Zielfunktion ist der Abstand zum Ursprung. Ein bekannter Trick (Vereinfachung der Rechnung) besteht darin, das Quadrat
Höhere Mathematik III WS 5/6 Lösungshinweis Aufgabe G 11 Blatt Die zu optimierende Zielfunktion ist der Abstand zum Ursprung. Ein bekannter Trick (Vereinfachung der Rechnung) besteht darin, das Quadrat
Mathematik I+II. für FT, LOT, PT, WT im WS 2015/2016 und SS 2016
 Mathematik I+II für FT, LOT, PT, WT im WS 2015/2016 und SS 2016 I. Wiederholung Schulwissen 1.1. Zahlbereiche 1.2. Rechnen mit reellen Zahlen 1.2.1. Bruchrechnung 1.2.2. Betrag 1.2.3. Potenzen 1.2.4. Wurzeln
Mathematik I+II für FT, LOT, PT, WT im WS 2015/2016 und SS 2016 I. Wiederholung Schulwissen 1.1. Zahlbereiche 1.2. Rechnen mit reellen Zahlen 1.2.1. Bruchrechnung 1.2.2. Betrag 1.2.3. Potenzen 1.2.4. Wurzeln
Hänsch-Frequenzkamm (Nobelpreis 2005, Theodor W. Hänsch, LMU)
 Hänsch-Frequenzkamm (Nobelpreis 2005, Theodor W. Hänsch, LMU) http://nobelprize.org/physics/laureates/2005/hansch-slides.pdf.../info.html (Dank an Thomas Udem) Ziel: Messung v. "optischen Frequenzen" mit
Hänsch-Frequenzkamm (Nobelpreis 2005, Theodor W. Hänsch, LMU) http://nobelprize.org/physics/laureates/2005/hansch-slides.pdf.../info.html (Dank an Thomas Udem) Ziel: Messung v. "optischen Frequenzen" mit
Aufgabe 1 - Tricks mit linearen Gleichungen
 Institut für Informatik Visual Computing Prof. Dr. Michael Wand & M.Sc. Sebastian Brodehl Sommersemester 2018 Modellierung I Übungsblatt 4: LGS, Vektorräume und Inverse Probleme Letzte Änderung: 10:20
Institut für Informatik Visual Computing Prof. Dr. Michael Wand & M.Sc. Sebastian Brodehl Sommersemester 2018 Modellierung I Übungsblatt 4: LGS, Vektorräume und Inverse Probleme Letzte Änderung: 10:20
F CT1 Verschiedene Abtastverfahren in der Computertomographie
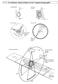 F CT1 Verschiedene Abtastverfahren in der Computertomographie AB CT1 Prinzip der Computertomographie AB CT1 Prinzip der Computertomographie - Musterlösung Kollimatoren blenden ein etwa bleistiftdickes
F CT1 Verschiedene Abtastverfahren in der Computertomographie AB CT1 Prinzip der Computertomographie AB CT1 Prinzip der Computertomographie - Musterlösung Kollimatoren blenden ein etwa bleistiftdickes
Mathematik in der Medizintechnik
 Mathematik in der Medizintechnik Prof. Dr. Bastian von Harrach http://numerical.solutions Institut für Mathematik, Goethe-Universität Frankfurt am Main NIGHT of SCIENCE 2016 Goethe-Universität Frankfurt
Mathematik in der Medizintechnik Prof. Dr. Bastian von Harrach http://numerical.solutions Institut für Mathematik, Goethe-Universität Frankfurt am Main NIGHT of SCIENCE 2016 Goethe-Universität Frankfurt
Rekonstruktion dynamischer Kardio-CT-Daten
 Seminar Kardiologie Dipl.-Phys. Stefan Wesarg Rekonstruktion dynamischer Kardio-CT-Daten Vortrag von Florian Nöll Überblick 1. Die Bedeutung der Computertomographie und wie man eine CT durchführt 2. Evolution
Seminar Kardiologie Dipl.-Phys. Stefan Wesarg Rekonstruktion dynamischer Kardio-CT-Daten Vortrag von Florian Nöll Überblick 1. Die Bedeutung der Computertomographie und wie man eine CT durchführt 2. Evolution
Element: Skalarprodukt: Standardbasis: Allgemeine Basis: Orthonormalität: Entwicklung: Koeffizienten: Vollständigkeit:
 C6.4 Konzeptionelle Grundlage der Fourier-Entwicklung Kernaussage: Fourier-Entwicklung ist Basiswechsel im Funktionenraum Zur Erinnerung: Eigenschaften einer Basis in Element: Skalarprodukt: Invariante
C6.4 Konzeptionelle Grundlage der Fourier-Entwicklung Kernaussage: Fourier-Entwicklung ist Basiswechsel im Funktionenraum Zur Erinnerung: Eigenschaften einer Basis in Element: Skalarprodukt: Invariante
Lineare Algebra und Computer Grafik
 Lineare Algebra und Computer Grafik Kurze Zusammenfassung (Stand: 3 Juli 2) Prof Dr V Stahl Copyright 28 by Volker Stahl All rights reserved V Stahl Lineare Algebra und Computer Grafik Zusammenfassung
Lineare Algebra und Computer Grafik Kurze Zusammenfassung (Stand: 3 Juli 2) Prof Dr V Stahl Copyright 28 by Volker Stahl All rights reserved V Stahl Lineare Algebra und Computer Grafik Zusammenfassung
Einleitung 2. 1 Koordinatensysteme 2. 2 Lineare Abbildungen 4. 3 Literaturverzeichnis 7
 Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Grundlagen der Computertomographie
 Grundlagen der Computertomographie André Liebing Fachmann für med.-techn. Radiologie (Chefarzt: Prof. Dr. med. J. Link) Spital Lachen AG RadiologieKongressRuhr 13.10.2011 Bochum Einleitung 1 Projektions-
Grundlagen der Computertomographie André Liebing Fachmann für med.-techn. Radiologie (Chefarzt: Prof. Dr. med. J. Link) Spital Lachen AG RadiologieKongressRuhr 13.10.2011 Bochum Einleitung 1 Projektions-
Methode der kleinsten Quadrate
 1. Phase: Methode der kleinsten Quadrate Einführung Im Vortrag über das CT-Verfahren hat Herr Köckler schon auf die Methode der kleinsten Quadrate hingewiesen. Diese Lösungsmethode, welche bei überbestimmten
1. Phase: Methode der kleinsten Quadrate Einführung Im Vortrag über das CT-Verfahren hat Herr Köckler schon auf die Methode der kleinsten Quadrate hingewiesen. Diese Lösungsmethode, welche bei überbestimmten
) (1 BE) 1 2 ln 2. und somit
 1 Aufgaben aus dem Aufgabenpool 1 1.1 Analysis A1_1 Eine Funktion f ist durch 1 x f(x) e 1, x IR, gegeben. Ermitteln Sie die Nullstelle der Funktion f. ( ) b) Die Tangente an den Graphen von f im Punkt
1 Aufgaben aus dem Aufgabenpool 1 1.1 Analysis A1_1 Eine Funktion f ist durch 1 x f(x) e 1, x IR, gegeben. Ermitteln Sie die Nullstelle der Funktion f. ( ) b) Die Tangente an den Graphen von f im Punkt
Aufgabensammlung aus Mathematik 2 UMIT, SS 2010, Version vom 7. Mai 2010
 Aufgabensammlung aus Mathematik 2 UMIT, SS 2, Version vom 7. Mai 2 I Aufgabe I Teschl / K 3 Zerlegen Sie die Zahl 8 N in ihre Primfaktoren. Aufgabe II Teschl / K 3 Gegeben sind die natürliche Zahl 7 und
Aufgabensammlung aus Mathematik 2 UMIT, SS 2, Version vom 7. Mai 2 I Aufgabe I Teschl / K 3 Zerlegen Sie die Zahl 8 N in ihre Primfaktoren. Aufgabe II Teschl / K 3 Gegeben sind die natürliche Zahl 7 und
Was bisher geschah. digitale Bilder: Funktion B : pos col Matrix B col pos. Punktoperationen f : col 1 col 2
 Was bisher geschah digitale Bilder: Funktion B : pos col Matrix B col pos statistische Merkmale Punktoperationen f : col 1 col 2 (Bildanalyse) (Farbtransformation) Geometrische Operationen f : pos 1 pos
Was bisher geschah digitale Bilder: Funktion B : pos col Matrix B col pos statistische Merkmale Punktoperationen f : col 1 col 2 (Bildanalyse) (Farbtransformation) Geometrische Operationen f : pos 1 pos
Seminar WS 1999/2000: Robotik in der Medizin. Computer Tomographie. Matthias Bonn
 Seminar WS 1999/2000: Robotik in der Medizin Computer Tomographie Matthias Bonn Allgemeines 1. Allgemeines 1.1 Medizinische Motivation Bei der Computertomographie handelt es sich um ein spezielles Röntgenverfahren
Seminar WS 1999/2000: Robotik in der Medizin Computer Tomographie Matthias Bonn Allgemeines 1. Allgemeines 1.1 Medizinische Motivation Bei der Computertomographie handelt es sich um ein spezielles Röntgenverfahren
Lineare Gleichungssysteme
 Fakultät Grundlagen Juli 2015 Fakultät Grundlagen Übersicht Lineare Gleichungssystem mit 2 Variablen 1 Lineare Gleichungssystem mit 2 Variablen Beispiele 2 Fakultät Grundlagen Folie: 2 Beispiel I Lineare
Fakultät Grundlagen Juli 2015 Fakultät Grundlagen Übersicht Lineare Gleichungssystem mit 2 Variablen 1 Lineare Gleichungssystem mit 2 Variablen Beispiele 2 Fakultät Grundlagen Folie: 2 Beispiel I Lineare
Verbindung Aspekte der Analysis und der Linearen Algebra!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 1
 Aspekte der Analysis und der Linearen Algebra!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 1 Aspekte der Analysis und der Linearen Algebra!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 2 Arbeitsauftrag für Gruppenarbeit
Aspekte der Analysis und der Linearen Algebra!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 1 Aspekte der Analysis und der Linearen Algebra!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 2 Arbeitsauftrag für Gruppenarbeit
1 Fraktale Eigenschaften der Koch-Kurve
 Anhang Inhaltsverzeichnis Fraktale Eigenschaften der Koch-Kurve iii. Einführung.................................. iii.2 Defintion.................................... iii.3 Gesamtlänge der Koch-Kurve........................
Anhang Inhaltsverzeichnis Fraktale Eigenschaften der Koch-Kurve iii. Einführung.................................. iii.2 Defintion.................................... iii.3 Gesamtlänge der Koch-Kurve........................
VOM RÖNTGENBILD ZUM COMPUTERTOMOGRAMM
 VOM RÖNTGENBILD ZUM COMPUTERTOMOGRAMM REFERAT IM RAHMEN DES FACHSEMINARS WS2009/10 AUSARBEITUNG BEI PROF. KARL-OTTO LINN BJÖRN SAßMANNSHAUSEN 1 0. INHALT 1. Vorwort... 3 2. Geschichte Der Computertomogrphie...
VOM RÖNTGENBILD ZUM COMPUTERTOMOGRAMM REFERAT IM RAHMEN DES FACHSEMINARS WS2009/10 AUSARBEITUNG BEI PROF. KARL-OTTO LINN BJÖRN SAßMANNSHAUSEN 1 0. INHALT 1. Vorwort... 3 2. Geschichte Der Computertomogrphie...
Mathematische Erfrischungen III - Vektoren und Matrizen
 Signalverarbeitung und Musikalische Akustik - MuWi UHH WS 06/07 Mathematische Erfrischungen III - Vektoren und Matrizen Universität Hamburg Vektoren entstanden aus dem Wunsch, u.a. Bewegungen, Verschiebungen
Signalverarbeitung und Musikalische Akustik - MuWi UHH WS 06/07 Mathematische Erfrischungen III - Vektoren und Matrizen Universität Hamburg Vektoren entstanden aus dem Wunsch, u.a. Bewegungen, Verschiebungen
1. Filterung im Ortsbereich 1.1 Grundbegriffe 1.2 Lineare Filter 1.3 Nicht-Lineare Filter 1.4 Separabele Filter 1.
 . Filterung im Ortsbereich. Grundbegriffe. Lineare Filter.3 Nicht-Lineare Filter.4 Separabele Filter.5 Implementierung. Filterung im Frequenzbereich. Fouriertransformation. Hoch-, Tief- und Bandpassfilter.3
. Filterung im Ortsbereich. Grundbegriffe. Lineare Filter.3 Nicht-Lineare Filter.4 Separabele Filter.5 Implementierung. Filterung im Frequenzbereich. Fouriertransformation. Hoch-, Tief- und Bandpassfilter.3
oder A = (a ij ), A =
 Matrizen 1 Worum geht es in diesem Modul? Definition und Typ einer Matrix Spezielle Matrizen Rechenoperationen mit Matrizen Rang einer Matrix Rechengesetze Erwartungswert, Varianz und Kovarianz bei mehrdimensionalen
Matrizen 1 Worum geht es in diesem Modul? Definition und Typ einer Matrix Spezielle Matrizen Rechenoperationen mit Matrizen Rang einer Matrix Rechengesetze Erwartungswert, Varianz und Kovarianz bei mehrdimensionalen
Motivation. Diskretisierung. Überblick. Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen. Diskretisierung und Quantisierung
 Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen Motivation Analoge Aufnahme von Sprache, Bildern Digitale Speicherung durch Diskretisierung + Quantisierung Informationsverlust
Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen Motivation Analoge Aufnahme von Sprache, Bildern Digitale Speicherung durch Diskretisierung + Quantisierung Informationsverlust
Tutorium: Diskrete Mathematik
 Tutorium: Diskrete Mathematik Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Definition Als lineare Gleichungssysteme bezeichnet man in der linearen Algebra Gleichungssysteme der folgenden
Tutorium: Diskrete Mathematik Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Definition Als lineare Gleichungssysteme bezeichnet man in der linearen Algebra Gleichungssysteme der folgenden
Mathematik, Signale und moderne Kommunikation
 Natur ab 4 - PH Baden Mathematik, Signale und moderne Kommunikation 1 monika.doerfler@univie.ac.at 29.4.2009 1 NuHAG, Universität Wien monika.doerfler@univie.ac.at Mathematik, Signale und moderne Kommunikation
Natur ab 4 - PH Baden Mathematik, Signale und moderne Kommunikation 1 monika.doerfler@univie.ac.at 29.4.2009 1 NuHAG, Universität Wien monika.doerfler@univie.ac.at Mathematik, Signale und moderne Kommunikation
Mathematische Grundbegriffe. Eindimensionale Funktionen
 Mathematische Grundbegriffe Eindimensionale Funktionen f ( )»1 Rechteckfunktion f ( ) 1 < 0,5 rect( ) = 0 sonst Dirac-Funktion f ( ) 1 δ ( ) = lim rect( ) p 0 p p»2 Ausblendung f ( ) + f ( ') = f ( ) δ
Mathematische Grundbegriffe Eindimensionale Funktionen f ( )»1 Rechteckfunktion f ( ) 1 < 0,5 rect( ) = 0 sonst Dirac-Funktion f ( ) 1 δ ( ) = lim rect( ) p 0 p p»2 Ausblendung f ( ) + f ( ') = f ( ) δ
Transformation - 3. Für "übliche" Anwendungen in der Geometrie ist es sinnvoll, bei Transformationen eine gleiche
 Transformation - 3 Wiederholung und spezielle Angaben im Zusammenhang mit Kreis-Berechnungen 1. Problemstellung Im Zusammenhang mit der Berechnung von Schnittflächen kann es sinnvoll sein, die Berechnung
Transformation - 3 Wiederholung und spezielle Angaben im Zusammenhang mit Kreis-Berechnungen 1. Problemstellung Im Zusammenhang mit der Berechnung von Schnittflächen kann es sinnvoll sein, die Berechnung
Übung zur Vorlesung 2D Grafik Wintersemester 05/06. Otmar Hilliges
 Übung zur Vorlesung 2D Grafik Wintersemester 05/06 Übungsblatt 5 Musterlösung auf der Übungsseite. https://wiki.medien.ifi.lmu.de/pub/main/uebung2dgrafikws 0506/FFT_LSG.jar Page 2 transform() for (y =
Übung zur Vorlesung 2D Grafik Wintersemester 05/06 Übungsblatt 5 Musterlösung auf der Übungsseite. https://wiki.medien.ifi.lmu.de/pub/main/uebung2dgrafikws 0506/FFT_LSG.jar Page 2 transform() for (y =
Bildverarbeitung: Filterung. D. Schlesinger () Bildverarbeitung: Filterung 1 / 17
 Bildverarbeitung: Filterung D. Schlesinger () Bildverarbeitung: Filterung 1 / 17 Allgemeines Klassische Anwendung: Entrauschung (Fast) jeder Filter basiert auf einem Modell (Annahme): Signal + Rauschen
Bildverarbeitung: Filterung D. Schlesinger () Bildverarbeitung: Filterung 1 / 17 Allgemeines Klassische Anwendung: Entrauschung (Fast) jeder Filter basiert auf einem Modell (Annahme): Signal + Rauschen
Mathematik für Ingenieure mit Maple
 Thomas Westermann Mathematik für Ingenieure mit Maple Band 2: Differential- und Integralrechnung für Funktionen mehrerer Variablen, gewöhnliche und partielle Differentialgleichungen, Fourier-Analysis Mit
Thomas Westermann Mathematik für Ingenieure mit Maple Band 2: Differential- und Integralrechnung für Funktionen mehrerer Variablen, gewöhnliche und partielle Differentialgleichungen, Fourier-Analysis Mit
CT Methoden. Lernziele. Röntgen / CT Das Arbeitspferd. Computertomographie- Wie alles begann. Computertomographie: Prinzip Rohdaten.
 Lernziele CT Methoden Vergleich zum konventionellen Röntgen CT Inkremental- / Spiraltechnik Bildnachverarbeitung Florian Vogt Intravenöse und orale Kontrastmittel Unterschiedliche KM-Phasen Röntgen / CT
Lernziele CT Methoden Vergleich zum konventionellen Röntgen CT Inkremental- / Spiraltechnik Bildnachverarbeitung Florian Vogt Intravenöse und orale Kontrastmittel Unterschiedliche KM-Phasen Röntgen / CT
Computertomographie. Die Idee
 Computertomographie Außermathematische Anwendungen im Mathematikunterricht WS 202/3 Franz Embacher, Universität Wien Die Idee Die Idee der Computertomographie besteht darin, aus der Abschwächung (Absorption)
Computertomographie Außermathematische Anwendungen im Mathematikunterricht WS 202/3 Franz Embacher, Universität Wien Die Idee Die Idee der Computertomographie besteht darin, aus der Abschwächung (Absorption)
Matrizen, Determinanten, lineare Gleichungssysteme
 Matrizen, Determinanten, lineare Gleichungssysteme 1 Matrizen Definition 1. Eine Matrix A vom Typ m n (oder eine m n Matrix, A R m n oder A C m n ) ist ein rechteckiges Zahlenschema mit m Zeilen und n
Matrizen, Determinanten, lineare Gleichungssysteme 1 Matrizen Definition 1. Eine Matrix A vom Typ m n (oder eine m n Matrix, A R m n oder A C m n ) ist ein rechteckiges Zahlenschema mit m Zeilen und n
Inhaltsverzeichnis. Daniel von Grünigen. Digitale Signalverarbeitung. mit einer Einführung in die kontinuierlichen Signale und Systeme
 Inhaltsverzeichnis Daniel von Grünigen Digitale Signalverarbeitung mit einer Einführung in die kontinuierlichen Signale und Systeme ISBN (Buch): 978-3-446-44079-1 ISBN (E-Book): 978-3-446-43991-7 Weitere
Inhaltsverzeichnis Daniel von Grünigen Digitale Signalverarbeitung mit einer Einführung in die kontinuierlichen Signale und Systeme ISBN (Buch): 978-3-446-44079-1 ISBN (E-Book): 978-3-446-43991-7 Weitere
Graphische Datenverarbeitung und Bildverarbeitung
 Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Fourier-Transformation Graphische DV und BV, Regina Pohle, 8. Fourier-Transformation 1 Einordnung in die Inhalte der Vorlesung Einführung
Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Fourier-Transformation Graphische DV und BV, Regina Pohle, 8. Fourier-Transformation 1 Einordnung in die Inhalte der Vorlesung Einführung
Das Wort Vektor kommt aus dem lateinischen und heißt so viel wie "Träger" oder "Fahrer".
 Was ist ein Vektor? Das Wort Vektor kommt aus dem lateinischen und heißt so viel wie "Träger" oder "Fahrer". Vektoren sind Listen von Zahlen. Man kann einen Vektor darstellen, indem man seine Komponenten
Was ist ein Vektor? Das Wort Vektor kommt aus dem lateinischen und heißt so viel wie "Träger" oder "Fahrer". Vektoren sind Listen von Zahlen. Man kann einen Vektor darstellen, indem man seine Komponenten
5 Lineare Gleichungssysteme und Determinanten
 5 Lineare Gleichungssysteme und Determinanten 51 Lineare Gleichungssysteme Definition 51 Bei einem linearen Gleichungssystem (LGS) sind n Unbekannte x 1, x 2,, x n so zu bestimmen, dass ein System von
5 Lineare Gleichungssysteme und Determinanten 51 Lineare Gleichungssysteme Definition 51 Bei einem linearen Gleichungssystem (LGS) sind n Unbekannte x 1, x 2,, x n so zu bestimmen, dass ein System von
Bildpunkt auf dem Gitter: Pixel (picture element) (manchmal auch Pel)
 4. Digitalisierung und Bildoperationen 4.1 Digitalisierung (Sampling, Abtastung) Rasterung auf 2D-Bildmatrix mathematisch: Abb. einer 2-dim. Bildfunktion mit kontinuierlichem Definitionsbereich auf digitales
4. Digitalisierung und Bildoperationen 4.1 Digitalisierung (Sampling, Abtastung) Rasterung auf 2D-Bildmatrix mathematisch: Abb. einer 2-dim. Bildfunktion mit kontinuierlichem Definitionsbereich auf digitales
ELEMENTAR-MATHEMATIK
 WILLERS ELEMENTAR-MATHEMATIK Ein Vorkurs zur Höheren Mathematik 13., durchgesehene Auflage von Dr.-Ing. G. Opitz und Dr. phil. H. Wilson Mit 189 Abbildungen VERLAG THEODOR STEINKOPFF DRESDEN 1968 Inhaltsverzeichnis
WILLERS ELEMENTAR-MATHEMATIK Ein Vorkurs zur Höheren Mathematik 13., durchgesehene Auflage von Dr.-Ing. G. Opitz und Dr. phil. H. Wilson Mit 189 Abbildungen VERLAG THEODOR STEINKOPFF DRESDEN 1968 Inhaltsverzeichnis
Vektoralgebra Anwendungen der Vektorrechnung VEKTORRECHNUNG. Prof. Dr. Dan Eugen Ulmet. Hochschule Esslingen 1/64
 1/64 VEKTORRECHNUNG Prof. Dr. Dan Eugen Ulmet Hochschule Esslingen März 2011 2/64 Overview Vektoralgebra 1 Vektoralgebra 2 Was sind Vektoren? 3/64 Vektoren werden geometrisch definiert als Pfeilklassen:
1/64 VEKTORRECHNUNG Prof. Dr. Dan Eugen Ulmet Hochschule Esslingen März 2011 2/64 Overview Vektoralgebra 1 Vektoralgebra 2 Was sind Vektoren? 3/64 Vektoren werden geometrisch definiert als Pfeilklassen:
Transformation Allgemeines Die Lage eines Punktes kann durch einen Ortsvektor (ausgehend vom Ursprung des Koordinatensystems
 Transformation - 1 1. Allgemeines 2. Zwei durch eine Translation verknüpfte gleichartige Basissysteme 3. Zwei durch eine Translation verknüpfte verschiedenartige Basissysteme (noch gleiche Orientierung)
Transformation - 1 1. Allgemeines 2. Zwei durch eine Translation verknüpfte gleichartige Basissysteme 3. Zwei durch eine Translation verknüpfte verschiedenartige Basissysteme (noch gleiche Orientierung)
Schülerworkshop Computertomographie Mathematik als Schlüsseltechnologie
 Schülerworkshop Computertomographie Mathematik als Schlüsseltechnologie Norbert Köckler 1. und 2. Juni 2007 Computertomographie und lineare Gleichungssysteme Überblick zum CT-Vortrag 1. Einleitung Wer
Schülerworkshop Computertomographie Mathematik als Schlüsseltechnologie Norbert Köckler 1. und 2. Juni 2007 Computertomographie und lineare Gleichungssysteme Überblick zum CT-Vortrag 1. Einleitung Wer
5 Interpolation und Approximation
 5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
03. Vektoren im R 2, R 3 und R n
 03 Vektoren im R 2, R 3 und R n Unter Verwendung eines Koordinatensystems kann jedem Punkt der Ebene umkehrbar eindeutig ein Zahlenpaar (x, y) zugeordnet werden P (x, y) Man nennt x und y die kartesischen
03 Vektoren im R 2, R 3 und R n Unter Verwendung eines Koordinatensystems kann jedem Punkt der Ebene umkehrbar eindeutig ein Zahlenpaar (x, y) zugeordnet werden P (x, y) Man nennt x und y die kartesischen
Vorkurs: Mathematik für Informatiker
 Vorkurs: Mathematik für Informatiker Teil 4 Wintersemester 2017/18 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2017 Steven Köhler Wintersemester 2017/18 Inhaltsverzeichnis Teil 1 Teil
Vorkurs: Mathematik für Informatiker Teil 4 Wintersemester 2017/18 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2017 Steven Köhler Wintersemester 2017/18 Inhaltsverzeichnis Teil 1 Teil
bzw. eine obere Dreiecksmatrix die Gestalt (U: upper)
 bzw. eine obere Dreiecksmatrix die Gestalt (U: upper) U = u 11 u 12 u 1n 1 u nn 0 u 22 u 2n 1 u 2n 0......... 0 0 u n 1n 1 u n 1n 0 0 0 u nn Eine nicht notwendig quadratische Matrix A = (a ij ) heißt obere
bzw. eine obere Dreiecksmatrix die Gestalt (U: upper) U = u 11 u 12 u 1n 1 u nn 0 u 22 u 2n 1 u 2n 0......... 0 0 u n 1n 1 u n 1n 0 0 0 u nn Eine nicht notwendig quadratische Matrix A = (a ij ) heißt obere
7 Integralrechnung für Funktionen einer Variablen
 7 Integralrechnung für Funktionen einer Variablen In diesem Kapitel sei stets D R, und I R ein Intervall. 7. Das unbestimmte Integral (Stammfunktion) Es sei f : I R eine Funktion. Eine differenzierbare
7 Integralrechnung für Funktionen einer Variablen In diesem Kapitel sei stets D R, und I R ein Intervall. 7. Das unbestimmte Integral (Stammfunktion) Es sei f : I R eine Funktion. Eine differenzierbare
Digitale Bildverarbeitung - Rechnerübung 3
 Digitale Bildverarbeitung - Rechnerübung 3 1. Khoros Zur Durchführung der Rechnerübung wird das Programmpaket KHOROS mit seiner Benutzerschnittstelle Cantata verwendet. Nach der Anmeldung am Rechner durch
Digitale Bildverarbeitung - Rechnerübung 3 1. Khoros Zur Durchführung der Rechnerübung wird das Programmpaket KHOROS mit seiner Benutzerschnittstelle Cantata verwendet. Nach der Anmeldung am Rechner durch
Element: Skalarprodukt: Standardbasis: Allgemeine Basis: Orthonormalität: Entwicklung: Koeffizienten: Vollständigkeit:
 C6.4 Konzeptionelle Grundlage der Fourier-Entwicklung Kernaussage: Fourier-Entwicklung ist Basiswechsel im Funktionenraum Zur Erinnerung: Eigenschaften einer Basis in Element: Skalarprodukt: Invariante
C6.4 Konzeptionelle Grundlage der Fourier-Entwicklung Kernaussage: Fourier-Entwicklung ist Basiswechsel im Funktionenraum Zur Erinnerung: Eigenschaften einer Basis in Element: Skalarprodukt: Invariante
Transformation - Homogene Koordinaten. y + b )
 Transformation - Homogene Koordinaten In der "üblichen" Behandlung werden für die Verschiebung (Translation) und die Drehung (Rotation) verschiedene Rechenvorschriften benutzt - einmal Addition von Vektoren
Transformation - Homogene Koordinaten In der "üblichen" Behandlung werden für die Verschiebung (Translation) und die Drehung (Rotation) verschiedene Rechenvorschriften benutzt - einmal Addition von Vektoren
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil... Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analysis 3... 5 Wahlteil Analytische Geometrie... Wahlteil Analytische Geometrie... Lösungen: 00 Pflichtteil Lösungen zur Prüfung 00: Pflichtteil
Pflichtteil... Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analysis 3... 5 Wahlteil Analytische Geometrie... Wahlteil Analytische Geometrie... Lösungen: 00 Pflichtteil Lösungen zur Prüfung 00: Pflichtteil
Lösbarkeit linearer Gleichungssysteme
 Lösbarkeit linearer Gleichungssysteme Lineares Gleichungssystem: Ax b, A R m n, x R n, b R m L R m R n Lx Ax Bemerkung b 0 R m Das Gleichungssystem heißt homogen a A0 0 Das LGS ist stets lösbar b Wenn
Lösbarkeit linearer Gleichungssysteme Lineares Gleichungssystem: Ax b, A R m n, x R n, b R m L R m R n Lx Ax Bemerkung b 0 R m Das Gleichungssystem heißt homogen a A0 0 Das LGS ist stets lösbar b Wenn
Übung: Computergrafik 1
 Prof. Dr. Andreas Butz Prof. Dr. Ing. Axel Hoppe Dipl.-Medieninf. Dominikus Baur Dipl.-Medieninf. Sebastian Boring Übung: Computergrafik 1 Fouriertransformation Organisatorisches Neue Abgabefrist für Blatt
Prof. Dr. Andreas Butz Prof. Dr. Ing. Axel Hoppe Dipl.-Medieninf. Dominikus Baur Dipl.-Medieninf. Sebastian Boring Übung: Computergrafik 1 Fouriertransformation Organisatorisches Neue Abgabefrist für Blatt
Vorkurs: Mathematik für Informatiker
 Vorkurs: Mathematik für Informatiker Teil 4 Wintersemester 2018/19 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2018 Steven Köhler Wintersemester 2018/19 Inhaltsverzeichnis Teil 1 Teil
Vorkurs: Mathematik für Informatiker Teil 4 Wintersemester 2018/19 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2018 Steven Köhler Wintersemester 2018/19 Inhaltsverzeichnis Teil 1 Teil
03. Vektoren im R 2, R 3 und R n
 03 Vektoren im R 2, R 3 und R n Unter Verwendung eines Koordinatensystems kann jedem Punkt der Ebene umkehrbar eindeutig ein Zahlenpaar (x, y) zugeordnet werden P (x, y) Man nennt x und y die kartesischen
03 Vektoren im R 2, R 3 und R n Unter Verwendung eines Koordinatensystems kann jedem Punkt der Ebene umkehrbar eindeutig ein Zahlenpaar (x, y) zugeordnet werden P (x, y) Man nennt x und y die kartesischen
5. Geraden und Ebenen im Raum 5.1. Lineare Abhängigkeit und Unabhängigkeit von Vektoren
 5 Geraden und Ebenen im Raum 5 Lineare Abhängigkeit und Unabhängigkeit von Vektoren Definition: Die Vektoren a,a,,a n heißen linear abhängig, wenn mindestens einer dieser Vektoren als Linearkombination
5 Geraden und Ebenen im Raum 5 Lineare Abhängigkeit und Unabhängigkeit von Vektoren Definition: Die Vektoren a,a,,a n heißen linear abhängig, wenn mindestens einer dieser Vektoren als Linearkombination
Diskrete Signalverarbeitung und diskrete Systeme
 Diskrete Signalverarbeitung und diskrete Systeme Computer- basierte Verarbeitung von Signalen und Realisierung von Systemverhalten erfordern diskrete Signale und diskrete Systembeschreibungen. Wegen der
Diskrete Signalverarbeitung und diskrete Systeme Computer- basierte Verarbeitung von Signalen und Realisierung von Systemverhalten erfordern diskrete Signale und diskrete Systembeschreibungen. Wegen der
Mischungsverhältnisse: Nehmen wir an, es stehen zwei Substanzen (zum Beispiel Flüssigkeiten) mit spezifischen Gewicht a = 2 kg/l bzw.
 Kapitel 5 Lineare Algebra 51 Lineare Gleichungssysteme und Matrizen Man begegnet Systemen von linearen Gleichungen in sehr vielen verschiedenen Zusammenhängen, etwa bei Mischungsverhältnissen von Substanzen
Kapitel 5 Lineare Algebra 51 Lineare Gleichungssysteme und Matrizen Man begegnet Systemen von linearen Gleichungen in sehr vielen verschiedenen Zusammenhängen, etwa bei Mischungsverhältnissen von Substanzen
Digitalisierung. Vorlesung FH-Hagenberg DSB
 Digitalisierung Vorlesung FH-Hagenberg DSB Abbildungssysteme Camera obscura einfachstes Abbildungssystem bekannt seit dem Altertum Licht fällt durch eine Lochblende in das Innere einer abgedunkelten Kammer
Digitalisierung Vorlesung FH-Hagenberg DSB Abbildungssysteme Camera obscura einfachstes Abbildungssystem bekannt seit dem Altertum Licht fällt durch eine Lochblende in das Innere einer abgedunkelten Kammer
Vektoren, Vektorräume
 Vektoren, Vektorräume Roman Wienands Sommersemester 2010 Mathematisches Institut der Universität zu Köln Roman Wienands (Universität zu Köln) Mathematik II für Studierende der Chemie Sommersemester 2010
Vektoren, Vektorräume Roman Wienands Sommersemester 2010 Mathematisches Institut der Universität zu Köln Roman Wienands (Universität zu Köln) Mathematik II für Studierende der Chemie Sommersemester 2010
Lineare Algebra 1. Roger Burkhardt
 Lineare Algebra 1 Roger Burkhardt roger.burkhardt@fhnw.ch Fachhochschule Nordwestschweiz Hochschule für Technik Institut für Geistes- und Naturwissenschaft HS 2010/11 2 Rechenoperationen und Gesetze Gleichheit
Lineare Algebra 1 Roger Burkhardt roger.burkhardt@fhnw.ch Fachhochschule Nordwestschweiz Hochschule für Technik Institut für Geistes- und Naturwissenschaft HS 2010/11 2 Rechenoperationen und Gesetze Gleichheit
Basiswissen Matrizen
 Basiswissen Matrizen Mathematik GK 32 Definition (Die Matrix) Eine Matrix A mit m Zeilen und n Spalten heißt m x n Matrix: a a 2 a 4 A a 2 a 22 a 24 a 4 a 42 a 44 Definition 2 (Die Addition von Matrizen)
Basiswissen Matrizen Mathematik GK 32 Definition (Die Matrix) Eine Matrix A mit m Zeilen und n Spalten heißt m x n Matrix: a a 2 a 4 A a 2 a 22 a 24 a 4 a 42 a 44 Definition 2 (Die Addition von Matrizen)
Digitale Signalverarbeitung
 Daniel Ch. von Grünigen Digitale Signalverarbeitung mit einer Einführung in die kontinuierlichen Signale und Systeme 4. Auflage Mit 222 Bildern, 91 Beispielen, 80 Aufgaben sowie einer CD-ROM mit Lösungen
Daniel Ch. von Grünigen Digitale Signalverarbeitung mit einer Einführung in die kontinuierlichen Signale und Systeme 4. Auflage Mit 222 Bildern, 91 Beispielen, 80 Aufgaben sowie einer CD-ROM mit Lösungen
Matrizen. a12 a1. a11. a1n a 21. a 2 j. a 22. a 2n. A = (a i j ) (m, n) = i te Zeile. a i 1. a i 2. a i n. a i j. a m1 a m 2 a m j a m n] j te Spalte
![Matrizen. a12 a1. a11. a1n a 21. a 2 j. a 22. a 2n. A = (a i j ) (m, n) = i te Zeile. a i 1. a i 2. a i n. a i j. a m1 a m 2 a m j a m n] j te Spalte Matrizen. a12 a1. a11. a1n a 21. a 2 j. a 22. a 2n. A = (a i j ) (m, n) = i te Zeile. a i 1. a i 2. a i n. a i j. a m1 a m 2 a m j a m n] j te Spalte](/thumbs/71/64996309.jpg) Mathematik I Matrizen In diesem Kapitel werden wir lernen was Matrizen sind und wie man mit Matrizen rechnet. Matrizen ermöglichen eine kompakte Darstellungsform vieler mathematischer Strukturen. Zum Darstellung
Mathematik I Matrizen In diesem Kapitel werden wir lernen was Matrizen sind und wie man mit Matrizen rechnet. Matrizen ermöglichen eine kompakte Darstellungsform vieler mathematischer Strukturen. Zum Darstellung
Bildbeispiele Physikalisches Prinzip Hounsfield-Einheiten Bilderzeugung. Strahlenbelastung Bildbeispiele. Hirn - Weichteilfenster
 Prof. Dr. med. P. Schramm Röntgen- Computer-Tomografie Magnet-Resonanz-Tomografie Physikalisches Prinzip Dr. rer. nat. Uwe H. Melchert Röntgen - Computer-Tomografie Bildbeispiele Physikalisches Prinzip
Prof. Dr. med. P. Schramm Röntgen- Computer-Tomografie Magnet-Resonanz-Tomografie Physikalisches Prinzip Dr. rer. nat. Uwe H. Melchert Röntgen - Computer-Tomografie Bildbeispiele Physikalisches Prinzip
IRIS CT-Dosisreduktion durch iterative Rekonstruktion
 14. Fortbildungsseminar der Arbeitsgemeinschaft Physik und Technik Münster 18. 19.6. 2010 IRIS CT-Dosisreduktion durch iterative Rekonstruktion Dr. Stefan Ulzheimer Siemens AG Healthcare Forchheim Übersicht
14. Fortbildungsseminar der Arbeitsgemeinschaft Physik und Technik Münster 18. 19.6. 2010 IRIS CT-Dosisreduktion durch iterative Rekonstruktion Dr. Stefan Ulzheimer Siemens AG Healthcare Forchheim Übersicht
Rechenmethoden der Physik
 May-Britt Kallenrode Rechenmethoden der Physik Mathematischer Begleiter zur Experimentalphysik Mit 47 Abbildungen, 297 Aufgaben und Lösungen Springer Teil I Erste Schritte Rechnen in der Mechanik Rechnen
May-Britt Kallenrode Rechenmethoden der Physik Mathematischer Begleiter zur Experimentalphysik Mit 47 Abbildungen, 297 Aufgaben und Lösungen Springer Teil I Erste Schritte Rechnen in der Mechanik Rechnen
Vorkurs: Mathematik für Informatiker
 Vorkurs: Mathematik für Informatiker Teil 4 Wintersemester 018/19 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de c 018 Steven Köhler Wintersemester 018/19 Inhaltsverzeichnis Teil 1 Teil Teil
Vorkurs: Mathematik für Informatiker Teil 4 Wintersemester 018/19 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de c 018 Steven Köhler Wintersemester 018/19 Inhaltsverzeichnis Teil 1 Teil Teil
Vorlesung Mathematik 2 für Informatik
 Vorlesung Mathematik für Informatik Inhalt: Lineare Algebra Rechnen mit Vektoren und Matrizen Lineare Gleichungssysteme, GauÿAlgorithmus Vektorräume, Lineare Abbildungen Eigenwerte und Eigenvektoren Literatur
Vorlesung Mathematik für Informatik Inhalt: Lineare Algebra Rechnen mit Vektoren und Matrizen Lineare Gleichungssysteme, GauÿAlgorithmus Vektorräume, Lineare Abbildungen Eigenwerte und Eigenvektoren Literatur
Lineares Gleichungssystem - Vertiefung
 Lineares Gleichungssystem - Vertiefung Die Lösung Linearer Gleichungssysteme ist das "Gauß'sche Eliminationsverfahren" gut geeignet - schon erklärt unter Z02. Alternativ kann mit einem Matrixformalismus
Lineares Gleichungssystem - Vertiefung Die Lösung Linearer Gleichungssysteme ist das "Gauß'sche Eliminationsverfahren" gut geeignet - schon erklärt unter Z02. Alternativ kann mit einem Matrixformalismus
3. Übungsblatt Aufgaben mit Lösungen
 . Übungsblatt Aufgaben mit Lösungen Aufgabe 6: Gegeben seien die Ebene E : 4x + x + 8 =, der Punkt P = ( und die Gerade H : x(λ = (4,, + λ(,,, λ R. (a Bestimmen Sie eine Gerade durch den Punkt P, die senkrecht
. Übungsblatt Aufgaben mit Lösungen Aufgabe 6: Gegeben seien die Ebene E : 4x + x + 8 =, der Punkt P = ( und die Gerade H : x(λ = (4,, + λ(,,, λ R. (a Bestimmen Sie eine Gerade durch den Punkt P, die senkrecht
2 Rationale und reelle Zahlen
 2 reelle Es gibt Mathematik mit Grenzwert (Analysis) und Mathematik ohne Grenzwert (z.b Algebra). Grenzwerte existieren sicher nur dann, wenn der Zahlbereich vollständig ist, also keine Lücken aufweist
2 reelle Es gibt Mathematik mit Grenzwert (Analysis) und Mathematik ohne Grenzwert (z.b Algebra). Grenzwerte existieren sicher nur dann, wenn der Zahlbereich vollständig ist, also keine Lücken aufweist
9 Lineare Gleichungssysteme
 9 Lineare Gleichungssysteme Eine der häufigsten mathematischen Aufgaben ist die Lösung linearer Gleichungssysteme In diesem Abschnitt beschäftigen wir uns zunächst mit Lösbarkeitsbedingungen und mit der
9 Lineare Gleichungssysteme Eine der häufigsten mathematischen Aufgaben ist die Lösung linearer Gleichungssysteme In diesem Abschnitt beschäftigen wir uns zunächst mit Lösbarkeitsbedingungen und mit der
Lineare Transformationen und Determinanten. 10-E Ma 1 Lubov Vassilevskaya
 Lineare Transformationen und Determinanten 10-E Ma 1 Lubov Vassilevskaya Lineare Transformation cc Definition: V und W sind zwei Vektorräume. Eine Funktion T nennt man eine lineare Transformation von V
Lineare Transformationen und Determinanten 10-E Ma 1 Lubov Vassilevskaya Lineare Transformation cc Definition: V und W sind zwei Vektorräume. Eine Funktion T nennt man eine lineare Transformation von V
Lineare Algebra. Mathematik II für Chemiker. Daniel Gerth
 Lineare Algebra Mathematik II für Chemiker Daniel Gerth Überblick Lineare Algebra Dieses Kapitel erklärt: Was man unter Vektoren versteht Wie man einfache geometrische Sachverhalte beschreibt Was man unter
Lineare Algebra Mathematik II für Chemiker Daniel Gerth Überblick Lineare Algebra Dieses Kapitel erklärt: Was man unter Vektoren versteht Wie man einfache geometrische Sachverhalte beschreibt Was man unter
Dentale Volumentomographie (DVT) Grundlagen
 Dentale Volumentomographie (DVT) Grundlagen Priv.-Doz. Dr. Ralf Schulze Dentale Volumentomographie (DVT) Grundlagen Priv.-Doz. Dr. Ralf Schulze c 2009 1 / 28 Dentale Volumentomographie Definition Bei der
Dentale Volumentomographie (DVT) Grundlagen Priv.-Doz. Dr. Ralf Schulze Dentale Volumentomographie (DVT) Grundlagen Priv.-Doz. Dr. Ralf Schulze c 2009 1 / 28 Dentale Volumentomographie Definition Bei der
3 Invertierbare Matrizen Die Inverse einer (2 2)-Matrix Eigenschaften invertierbarer Matrizen... 18
 Wirtschaftswissenschaftliches Zentrum Universität Basel Mathematik 2 Dr. Thomas Zehrt Vektoren und Matrizen Inhaltsverzeichnis Vektoren(Wiederholung bzw. Selbststudium 2. Linearkombinationen..............................
Wirtschaftswissenschaftliches Zentrum Universität Basel Mathematik 2 Dr. Thomas Zehrt Vektoren und Matrizen Inhaltsverzeichnis Vektoren(Wiederholung bzw. Selbststudium 2. Linearkombinationen..............................
