2.6.2 Die zehn Punktgruppen-Symmetrieoperationen
|
|
|
- Angela Reuter
- vor 7 Jahren
- Abrufe
Transkript
1 Spiegelung an einer Ebene Ebene u( r r 0 ) = 0 Ax + By + Cz + D = 0 Für P (P (( x))) : x = x + ( 1) u u 2a, dabei ist a der Abstand zwischen der Ebene und dem Punkt P ( x) a = ( Ax+By+Cz+D ) A x = x 2a u 2 +B 2 +C 2 u Inversion J = (2.15) Drehinversion I = A z n J = cos(ϕ) sin(ϕ) 0 sin(ϕ) cos(ϕ) (2.16) Die zehn Punktgruppen-Symmetrieoperationen Dies sind die 1-, 2-, 3-, 4- und 6-zähligen Drehachsen und ihre zugehörigen Drehinversionsachsen Alle in einem Kristall vorhandenen Symmetrieoperationen bilden eine mathematische Gruppe, eine so genannte Symmetriegruppe. Aus diesen zehn Symmetrieoperationen ergeben sich 31
2 32 mögliche Symmetriegruppen, die im Falle von Kristallen als Kristallklassen bezeichnet werden Objekte mit den fünf kubischen kristallographischen Punktgruppen Links oben ist die Schönflies-Nomenklatur der Symmetriegruppe und rechts unten die internationale Nomenklatur (1, 2, 3, 4...p p-zählige Drehachse; 1, 2, 3, 4... p p-zählige Inversionsachse; m Spiegelebene; p/m p-zählige Drehachse mit senkrechter Spiegelebene). Die verdeckten Seiten ergeben sich durch eine Rotation um 120 an der im ersten Bild eingezeichneten Raumdiagonalen Die Nomenklatur der kubischen kristallographischen Punktgruppen nach Schönflies unechte Operation Diese führt ein rechtshändiges System in ein linkshändiges über und umgekehrt. O h ist die volle Punktsymmetriegruppe eines Würfels einschließlich der unechten Operationen, welche die horizontale Spiegelebene zulässt (4 drei- und 3 vier-zählige Drehachsen, wie beim Oktaeder, zusätzlich eine horizontale Spiegelebene) O ist die volle Punktsymmetriegruppe eines Oktaeders einschließlich der unechten Operationen (4 drei- und 3 vier-zählige Drehachsen, wie beim Oktaeder). T d ist die volle Punktsymmetriegruppe eines Tetraeders einschließlich der unechten Operationen (4 drei- und 3 zwei-zählige Drehachsen, wie beim Tetraeder, zusätzlich eine diagonale Spiegelebene). T ist die volle Punktsymmetriegruppe eines Oktaeders ohne die unechten Operationen (4 drei- und 3 zwei-zählige Drehachsen, wie beim Tetraeder). 32
3 T h umfasst neben den Operationen von T auch noch Inversionsoperationen (4 drei- und 3 zwei-zählige Drehachsen, wie beim Tetraeder, zusätzlich eine horizontale Spiegelebene) Die Nomenklatur der nicht-kubischen kristallographischen Punktgruppen nach Schönflies C n Diese Punktgruppe enthält nur n-zählige Rotationsachsen. C nv Zusätzlich zu den n-zähligen Rotationsachsen besitzen diese Punktgruppen auch noch v Spiegelebenen, in denen die Rotationsachse liegt (verikal). C nh Diese Punktgruppe enthält neben der n-zähligen Rotationsachse auch noch eine Spiegelebene senkrecht zur Rotationsachse (horizontal). S n Diese Punktgruppen enthalten nur eine n-zählige Rotations-Reflexions-Achse. D n Zusätzlich zu einer n-zähligen Rotationsachse n zwei-zählige Rotationsachsen senkrecht zu der n-zähligen Achse. D nh Diese Punktgruppe weist die höchste Symmetrie auf. Neben den D n Symmetrien besitzt sie noch jeweils eine Spiegelebene senkrecht zu den Rotationsachsen (horizontal). D nd Diese Punktgruppe enthält neben den Elementen von D n noch zusätzlich Spiegelebenen, in der die n-zählige Rotationsachse liegt, und die den Winkel zwischen zwei zwei-zähligen Rotationsachsen halbiert (diagonal). 33
4 2.6.6 Die 27 nicht-kubischen kristallographischen Punktgruppen Die Seiten auf der Rückseite lassen sich durch eine Rotation um die n-zählige Rotationsachse erzeugen, die bei allen Darstellungen vertikal steht. 34
5 2.6.7 Die 32 Kristallklassen Nr. Kristallsystem Schönflies Hermann und Laue-Symmetrie Mauguin 1 Triklin C C i Monoklin C C s m 5 C 2h 2/m 6 Orthorhombisch D C 2v mm2 8 D 2h mmm mmm 9 Tetragonal C S C 4h 4/m 4/m 12 D C 4v 4mm 14 D 2d 42m 15 D 4h 4/mmm 4/mmm 16 Trigonal C C 3i D C 3v 3m 20 D 3d 3m 3m 21 Hexagonal C C 3h 6 23 C 6h 6/m 6/m 24 D C 6v 6mm 26 D 3h 62m 27 D 6h 6/mmm 6/mmm 28 Kubisch T T h m3 m3 30 O T d 43m 32 O h m3m m3m 1, 2, 3, 4...p p-zählige Drehachse; 1, 2, 3, 4... p p-zählige Inversionsachse; m Spiegelebene; p/m p-zählige Drehachse mit senkrechter Spiegelebene Einführung von zusätzlichen Translationssymmetrieelementen Die Gleitspiegelebene Hierbei wird zu einer Spiegelung an einer Ebene auch noch eine Verschiebung entlang dieser Ebene durchgeführt. 35
6 Die Schraubenachse In diesem Fall kommt zu einer Drehung um eine n-zählige Achse noch eine Verschiebung entlang der Drehachse. Dabei muss zwischen den beiden Drehrichtungen unterschieden werden. Damit ergeben sich 230 Raumgruppen 36
7 Konzept der Kristallsymmetrien und deren Beschreibung Hierarchie der Kristallsymmetrien So lässt sich nun eine Hierarchie der Kristallsymmetrien für die sieben Kristallsysteme angeben: 37
8 Das kubische Gitter weist die höchste Symmetrie auf. Die Symmetrie nimmt in der Reihe zum triklinen Gitter hin ab, welches die niedrigste Symmetrie aufweist. Das hexagonale und das trigonal (rhomboedrische) Gitter spielen eine gewisse Sonderrolle Punktgruppen und Raumgruppen Die vorher angesprochenen Raumgruppen lassen sich wie folgt zusammensetzen: Punktgruppen aus den sieben Kristallsystemen Gitteranzahl Gitter Punktgruppen gesamte Punktgruppen 1 Triklin Monoklin Orthorhombisch Tetragonal Hexagonal Rhomboedrisch Kubisch Bravais-Gitter Durch hinzufügen der Gleitspiegelebenen und der Schraubenachsen ergeben sich dann die 230 Raumgruppen. 2.7 Beugung an periodische Strukturen reziprokes Gitter Allgemeine Betrachtungen Allgemeine Methoden zur Strukturanalyse: durch abbildende Methoden hochaufgelöste Elektronenmikroskopie Gitterstörungen in YBCO durch Ionenbeschuss Metallnanopartikel 38
9 Feldionenemission (FIE) FIE-Aufnahme eines BCC-Kristalls FIE-Aufnahme eines BCC-Kristalls Rastertunnel- und Rasterkraftmikroskopie STM-Aufnahme von Si(111) AFM-Aufnahme von Graphit durch Beugungserscheinungen Röntgenstrahlung Elektronenstrahl Neutronenstrahl Atom-/Ionenstrahl In Beugungsexperimenten hängen die Mechanismen, welche die Streuung verursachen von der Strahlung ab, die verwendet wird: Neutronen werden so gut wie nicht nicht an den geladenen aber sehr leichten Elektronen gestreut, sondern an den schweren Kernen (10 15 m) näherungsweise Punktstreuer. γ-quanten und Elektronen wechselwirken mit der Ladung der Elektronenhülle (10 10 m) 10 5 mal größer. Die Masse der im Strahl verwendeten Teilchen spielt ebenfalls eine wichtige Rolle, da hierdurch der Impulsübertrag bei gegebener Energie bestimmt wird. Wechselwirkungsmechanismus ist auch von Bedeutung (elastische oder inelastische Streuung) 39
10 Gemeinsame Theorie für alle genannten Beugungsprozesse (Quasiklassisch, allerdings Teilchen als Welle) Die Auflösung der Methode wird durch die de Broglie-Wellenlänge der eingesetzten Strahlung bestimmt: γ-quanten: E = ω; ω = 2πc λ 12,4Å E/keV E = 2π c λ λ γ = 2π c E λ γ = 6, W s m/s E/1, AsV = Neutronen / Elektronen / Atome: E = p2 2m ; mit p = k und k = 2π λ ergibt sich λ = h p E = 2 2m Elektronen m E = 9, kg λ E = 12,3Å E/eV Neutronen m N = 1, kg λ N = 0,29Å E/eV Heliumkerne m He = 6, kg λ He = 0,14Å E/eV 1 2mE λ 2 λ h Energieabhängigkeit des Probenstrahls zur Strukturanalyse Benötigte Energie um eine Auflösung von 1Å zu erreichen: Helium: 20meV (300K) Stickstoff: 100meV (1200K) Elektronen: 200eV γ-quanten 20keV 40
11 2.7.3 Beschreibung der Beugung Eine Kugelwelle geht von Q aus und ist bei R r näherungsweise eine ebene Welle mit der Amplitude A (z.b. elektrische Feldstärke) und der Intensität A A = I im streuenden Medium an der Position p gilt: A p ( p, t) = A 0 e (i k 0 ( R+ r) iω 0 t) (2.17) Das streuende Medium an der Position p streut die Welle an der komplexen Streudichte ρ( r) und verursacht eine Änderung der Welle. Von dem Streuzentrum geht eine Kugelwelle aus, die durch die einfallende Welle angeregt wird: A B ( B, t) = A p ( r, t)ρ( r) eik R r R r (2.18) Für ein festen Ort p hat k die Richtung von R + r somit kann man auch schreiben: A B ( B, t) = A p ( r, t)ρ( r) e(i k ( R r)) R r Im Fall großer Entfernungen lässt sich nähern: A B ( B, t) = A p ( r, t)ρ( r) 1 R e(i k ( R r)) (2.19) (2.20) mit der gleichen Richtung für alle Orte p. Durch einsetzen von Gl. (2.17) in Gl. (2.20) ergibt sich: A B ( B, t) = A 0 e (i k 0 ( R+ r) iω 0 t) ρ( r) 1 R ei k ( R r r) (2.21) = A 0 R ei( k 0 R+ k R ) e iω 0t ρ( r)e i r ( k 0 k) Um nun die gesamte Welle am Ort des Beobachters zu erhalten, muss man über das gesamte streuende Volumen integrieren: A B ( B, t) = A 0 R ei( k 0 R+ k R ) e iω 0t ρ( r)e i r ( k 0 k) d r (2.22) Ist ρ( r) zeitunabhängig und die Zeitabhängigkeit enthält ausschließlich ω 0, dann handelt es sich um einen elastischen Prozess und es gilt Energieerhaltung. Im Allgemeinen ist ρ( r, t) 41
12 nicht nur orts- sondern auch zeitabhängig, wenn z.b. eine Anregung des streuenden Mediums stattfindet. Dies hat zur Folge, dass auch Frequenzen ω ω 0 auftreten. Der Beobachter misst nicht Amplituden, sondern Intensitäten, für die gilt: I( K) A B 2 ρ( r)e i r K d r 2 (2.23) mit dem Streuvektor K = k k 0.Dies kann als Fouriertransformierte der Streudichte ρ( r) bezüglich des Streuvektors K angesehen werden. Das hat folgende Konsequenzen: Je kleiner die Strukturen in ρ( r), desto größer muss K gewählt werden, z.b. durch Vergrößerung k 0. Die Unmöglichkeit, die Amplitude als Funktion von Ort und Zeit zu messen, macht die wesentliche Schwierigkeit der Strukturanalyse aus. Aus der Amplitude ließe sich durch inverse Fouriertransformation direkt die Streudichteverteilung ρ( r) bestimmen. Wegen der Nicht-Eindeutigkeit zwischen Intensität und ρ( r) ist man darauf angewiesen, Annahmen für die Strukturen oder weitere Messungen zu benutzen, um einen Ausgangspunkt für die Struktur zu haben, die dann durch die Messergebnisse angepasst werden kann Periodische Strukturen und reziprokes Gitter Wiederholt sich die Streudichte periodisch mit einer Periode von a, so gilt (zunächst in einer Dimension): ρ(x) = ρ(x + na) mit n = 0, ±1, ±2,.... (2.24) Damit lautet die Entwicklung in eine Fourier-Reihe: ρ(x) = n n2π ρ n e i( a )x (2.25) und die Erweiterung auf drei Dimensionen: ρ( r) = G ρ G e i G r. (2.26) Dabei muss G bestimmte Bedingungen erfüllen, damit eine Translationsinvarianz bezüglich aller Gittervektoren r n = n 1 a 1 + n 2 a 2 + n 3 a 3 (2.27) gegeben ist. Somit muss für G gelten: G r n = 2πm. (2.28) Wobei m ganze Zahlen für n 1, n 2 und n 3 darstellt. Nun lässt sich der Vektor G nach einer Basis g zerlegen: G = h g 1 + k g 2 + l g 3 (2.29) 42
13 mit den ganzen Zahlen h, k, l. Die Bedingung (2.28) bedeutet im Fall n 2 = n 3 = 0: Mit beliebigem n 1 kann dies nur erfüllt sein, wenn ist. Allgemein muss gelten: (h g 1 + k g 2 + l g 3 ) n 1 a 1 = 2πm. (2.30) g 1 a 1 = 2π und g 2 a 1 = g 3 a 1 = 0 (2.31) g i a j = 2πδ ij. (2.32) Die dadurch definierte Basis g 1, g 2, g 3 spannt das so genannte reziproke Gitter auf. Es ist jedem Gitter eindeutig zugeordnet und seine Gitterpunkte werden mit den Zahlen h, k, l beschrieben. Die Konstruktionsvorschrift lässt sich unmittelbar aus Gl. (2.32) ableiten. So steht der Vektor g 1 senkrecht auf der von den Vektoren a 2 und a 3 aufgespannten Ebene und dessen Betrag ist gegeben 2π a 1 cos ( g 1, a 1 ). g 1 = a 2 a 3 2π a 1 ( a 2 a 3 ) g 2 = a 3 a 1 2π a 2 ( a 3 a 1 ) g 3 = a 1 a 2 2π a 3 ( a 1 a 2 ) (2.33) Streuung an periodischen Strukturen Die Fourier-Entwicklung der Streudichteverteilung ρ( r) wird in die Gleichung (2.23) für die Streuintensität eingesetzt, wobei wieder der Streuvektor K = k k 0 verwendet wird: I( K) A 0 2 R 2 ρ G G e i( G K) r d r 2. (2.34) 43
14 Für einen ausgedehnten Kristall, bestehend aus vielen Elementarzellen, liefert das Integral nur für G = K einen von Null verschiedenen Beitrag, da es in Komponenten ausgeschrieben die δ-funktion darstellt. Sein Wert entspricht dann dem Streuvolumen V. Das bedeutet: { e i( G K) r V für G = K d r = 0 sonst (2.35) Somit ergeben sich nur dann Beugungsreflexe, wenn die Differenz k k 0 zwischen einfallendem und auslaufendem Strahl gerade Gleich G ist. Daher ergibt sich für die Intensität: I( K = G) A 0 2 R 2 ρ G 2 V 2 (2.36) Die Intensität ist somit proportional dem Quadrat des Streuvolumens. Allerdings nimmt die Breite der Reflexe mit der Größe des Streuvolumens V 1 ab. Damit nimmt die integrale Streuintensität pro Reflex linear mit dem Streuvolumen zu wie es zu erwarten ist. Jeder Reflex lässt sich über die Zahlen h, k, l ( G = h g 1 +k g 2 +l g 3 ) eindeutig identifizieren, sie werden daher zur Identifikation benutzt. Für negative Werte wird dann h, k, l verwendet. Es lässt sich so formulieren: I hkl = ρ hkl 2 (2.37) Für den Fall, dass keine Absorption stattfindet, ist die Streudichte ρ( r) eine reellwertige Funktion und somit ergibt sich wegen Gl. (2.26): ρ hkl = ρ h k l. (2.38) Für die Intensitäten folgt: I hkl = I h k l (Friedelsche Regel) (2.39) Dies hat die Konsequenz, dass das Beugungsbild ein Inversionszentrum aufweist, selbst wenn die ursprüngliche Kristallstruktur diese Symmetrie nicht aufweist. Betrachtet man die Bedingung, G = K, (2.40) die auch als Laue-Bedingung bekannt ist, etwas genauer, so lässt sich daraus direkt die Ewald-Konstruktion ableiten. 44
15 Die Konstruktion: 1. k0 wird vom Ursprung aus in das reziproke Gitter eingezeichnet. 2. Unter der Voraussetzung, dass die Beugung elastisch stattfindet ( k = k 0 = 2π/λ), sind alle Punkte, die auf einer Kugel um den Ursprung von k 0 mit Radius k 0 = k liegen, mögliche Endpunkte eines Vektors K = k k 0. Dies ist gleichbedeutend damit, dass die Bedingung G = K erfüllt ist. 3. Der Vektor k wird dann mit der Spitze an den Vektor k 0 angeschlossen. 4. Es ergibt sich ein Beugungsreflex mit den Indizes (hkl) Es sind also die folgenden Bedingungen zu erfüllen, um einen Reflex in eine bestimmte Richtung zu bekommen: Der Vektor K muss so liegen, dass er vom Ursprung aus einen Punkt im reziproken Gitter erreicht. Dies hat zur Folge, dass sowohl 1. die Wellenlänge als auch 2. die Richtung des einfallenden Strahls richtig gewählt werden müssen. 3. Die ausfallenden Reflexe können nur in bestimmte Richtungen entstehen, in denen die Ewald-Kugel Punkte des reziproken Gitters trifft. Entsprechend muss natürlich auch ein Detektor positioniert sein. Um diese Bedingungen zu erfüllen, gibt es verschiedene experimentelle Methoden. 45
16 2.7.6 Millersche Indizes Drei Punkte des Gitters definieren eine Ebene. Die ganzen Zahlen m, n, o bezeichnen die Achsenabschnitte der Ebene in Einheiten der Basisvektoren. Um die Ebene anzugeben, verwendet man die so genannten Millerschen Indizes. Diese werden auf folgende Weise bestimmt: 1. Bestimme die Achsenabschnitte m, n, o. 2. Bilde den Kehrwert der Achsenabschnitte 1/m, 1/n, 1/o. 3. Multipliziere sie mit einer ganzen Zahl p, so dass ein Tripel ganzer und teilerfreier Zahlen (hkl) entsteht. Hier sind die Achsenabschnitte 3a, 2b und 2c. Die Kehrwerte sind 1/3, 1/2 und 1/2. Mit p = 6 lauten die Millerschen Indizes (233). Zusammenhang der Millerschen Indizes und des reziproken Gittervektors: Die Gittervektoren G hkl stehen senkrecht auf der Ebene mit den Miller-Indizes (hkl). 46
17 Die Länge des Vektors G hkl ist gleich dem 2π-fachen des reziproken Abstandes der Netzebenen (hkl). Millersche Indizes des hexagonalen Gitters Im hexagonalen Gitter ist es nicht sinnvoll, die kartesische Definition der Miller-Indizes zu verwenden, da einige unterschiedlich bezeichnete Ebenen äquivalent sind und andererseits vorhandene Ebenen nicht charakterisiert werden können. Deshalb verwendet man im hexagonalen Gitter vier Indizes: Im linken Bild sind die mit (100) und (1 10) Ebenen äquivalente Prismenebenen dargestellt. Die vier Indizes werden mit (hkil) bezeichnet, wobei i = (h + k) (2.41) gelten muss, da vier Indizes in drei Dimensionen überbestimmt sind. Um diese Gleichung zu erfüllen, wird die a 1 Richtung nicht mit (1000) bezeichnet, sondern mit (2 1 10) Braggsche Deutung der Röntgenbeugung Bragg nahm an, dass Kristalle aus parallelen Ebenen aufgebaut ist und Röntgenlicht von unterschiedlichen Ebenen im Kristall reflektiert wird. Annahmen: 1. Das einfallende Röntgenlicht wird von den Ionen einer jeden Ebene reflektiert (Einfallswinkel = Ausfallswinkel). 2. Um einen Reflex zu erhalten, muss das Röntgenlicht von den unterschiedlichen Ebenen kommend konstruktiv interferieren. 47
18 Mit der Bedingung, dass für konstruktive Interferenz der Gangunterschied zwischen zwei Strahlen ganzzahlige Vielfache der Wellenlänge sein müssen, ergibt sich: nλ = 2d sin(θ) (2.42) Der Bragg-Winkel ist gerade der halbe Winkel, um den der einfallende Strahl gebeugt wird. 48
19 2.7.8 von Laue Formulierung der Röntgenbeugung Die Deutung von Laue unterscheidet sich in zwei wesentlichen Punkten: 1. es werden keine speziellen Gitterebenen angenommen 2. es werden keine Annahmen zur Reflexion gemacht Vielmehr betrachtet Laue: 1. einen Kristall zusammengesetzt aus identischen mikroskopischen Objekten, die an jedem Ort des Bravais-Gitters sitzen. 2. jedes dieser Objekte als Ausgangspunkt einer Kugelwelle. 3. die Entstehung der Reflexe als eine konstruktive Interferenz dieser Kugelwellen. Um die Bedingung für konstruktive Interferenz zu finden nehmen wir: Der Wegunterschied ergibt sich zu: nur zwei Streuzentren im Abstand d, ein Röntgenstrahl von einer fernen Röntgenquelle, entlang einer Richtung n, mit einer Wellenlänge λ, mit einem Wellenvektor k = 2π n/λ, einem in Richtung n gestreuten Strahl, mit unveränderten Wellenlänge λ (elastische Streuung) und und dem Wellenvektor k = 2π n /λ. d cos(θ) + d cos(θ ) = d ( n n ). (2.43) Und somit ist die Bedingung für konstruktive Interferenz: d ( n n ) = mλ mit der ganzen Zahl m (2.44) Werden beide Seiten mit 2π/λ multipliziert, ergibt sich: d ( k k ) = 2πm (2.45) 49
20 Nun werden nicht nur zwei Streuzentren angenommen, sondern ein ganzes Bravais-Gitter von Streuzentren. Diese sitzen wieder auf Gitterpunkten, die durch den Gittervektor r n (siehe Gl. (2.27)) erreicht werden. Somit ergibt sich für die konstruktive Interferenz: r n ( k k ) = r n K = 2πm mit der ganzen Zahl m und allen Bravais-Vektoren R (2.46) Vergleicht man dieses Resultat mit Gl. (2.28), so folgt daraus, dass nur dann Reflexe durch konstruktive Interferenz auftreten, wenn G = K ist Die Brillouin-Zone Die Bedingung für einen Bragg-Reflex K = k k 0 = G hkl hat zur Konsequenz, dass die Endpunkte der Vektoren k und k, welche die Streubedingung erfüllen, auf den Mittelsenkrechten- Ebenen der G hkl liegen. Das kleinste Volumen, das diese Mittelsenkrechten-Ebenen einschließen, lässt sich in analoger Weise konstruieren wie die Wigner-Seitz-Zelle. Dieses Volumen im reziproken Gitter wird Brillouin-Zone (1. Brillouin-Zone) genannt. 1. Verbinde die Punkte des reziproken Gitters in der Umgebung eines beliebigen Punktes durch Linien 2. errichte senkrecht zu jeder dieser Verbindungslinien eine Ebene, so dass die Linie in zwei Hälften geteilt wird 3. das Volumen, in dem sich der ursprünglich gewählte Punkt befindet und welches durch die innersten Flächen begrenzt wird, ist die Brillouin-Zone In drei Dimensionen haben die ersten Brillouin-Zonen folgendes Aussehen 50
21 Der Strukturfaktor Nach der Gleichung (2.35) ist zwar gegeben, wo die Reflexe liegen, aber nicht, wie stark ihre Intensität ist. Um Information hierüber zu erlangen, ist es notwendig, die Fourier- Transformierte der Streudichte ρ hkl zu berechnen: ρ hkl = 1 V Z Zelle ρ( r)e i G r d r. (2.47) Hierbei wird über die Einheitszelle integriert. Da sich der größte Teil der Elektronen in der Nähe des Atomkerns aufhalten, lässt sich das Integral in Einzelintegrale aufspalten, die phasenrichtig überlagert werden. Hier soll nun der Ortsvektor r in drei Teile aufgespalten werden: 1. den Vektor r n, der zum Ursprung der Einheitszelle weist 2. den Vektor r α, der vom Ursprung der Einheitszelle zur jeweiligen Position des Atoms weist 3. und den Vektor r, der vom Zentrum des Atoms in den Umgebenden Raum weist. Damit lässt sich mit der Fourier-Entwicklung von ρ( r) (siehe Gl. (2.26)) schreiben: ρ hkl = 1 ρ G e i G r α ρ α ( r V )e i G r dr. (2.48) Z α Wobei sich nun das Integral über ein Atom erstreckt, weshalb es auch als Atomfaktor bezeichnet wird. Da man meist von einer kugelförmigen Verteilung um ein Atom ausgehen kann, ist es naheliegend, zu Kugelkoordinaten überzugehen: f α = ρ α ( r )e i G r dr 2π π r b = ρ α ( r )e igr cos(θ) r 2 dr d(cos(θ))dϕ (2.49) ϕ=0 θ=0 0 Durch Integration über die beiden Winkel erhält man: f α = 4π ρ α (r )r 2 sin(gr ) Gr dr. (2.50) Sei Θ der Winkel zwischen k und k 0, wobei bei keiner Streuung Θ = 0 gelte, dann lässt sich schreiben: G = 2k 0 sin(θ) (2.51) ( ) sin 4πr sin(θ) f α = 4π ρ α (r 2 λ )r dr (2.52) 4πr sin(θ) λ 51
22 ( ) Der Atomfaktor ist somit eine Funktion von f sin(θ) λ, wobei die Vorwärtsstreuung den größten Wert hierfür liefert. So ergibt sich für Θ = 0: f α = 4π ρ α (r )r 2 dr, (2.53) die über das Atom integrierte Streudichte, die im Fall von Röntgenstrahlung proportional zu Kernladungszahl Z ist. Die Summe aus Gl. (2.48) beschreibt die Interferenzen zwischen den Streuwellen und der verschiedenen Atome der Einheitszelle und ergeben den so genannten Strukturfaktor: S hkl = α f α e i G hkl r α. (2.54) Da primitive Gitter nur ein Atom pro Einheitszelle enthalten, gilt hier S hkl = f α. Wird der Vektor r α in den Basisvektoren des Gitter geschrieben: r α = u α a 1 + v α a 2 + w α a 3, (2.55) sind die Faktoren u, v und w kleiner als 1 und es ergibt sich für den Strukturfaktor: S hkl = α f α e 2πi(huα+kvα+lwα). (2.56) Im Falle des kubisch-raumzentrierten Gitters sitzen die Atome auf den Positionen [0,0,0] und [1/2,1/2,1/2] und beide haben den gleichen Atomfaktor f α, damit folgt für S: ( S hkl = f 1 + e iπ(h+k+l)) { 0 (h + k + l) ungerade = (2.57) 2f (h + k + l) gerade Es gehen bestimmte Reflexe durch destruktive Interferenz verloren. So is der (100)-Reflex nicht zu beobachten, sofern Zentral- und Eckatome identisch sind. 2.8 Experimentelle Methoden der Strukturanalyse und deren Darstellung in der Ewald-Konstruktion Die Laue-Methode Bei dieser Methode verwendet man: 1. einen Einkristall 2. eine feste Orientierung des Kristalls bezüglich des einfallenden Analysestrahls (meist Röntgenstrahlung) 3. eine Strahlquelle, die nicht monochromatisch ist es sind Wellenlängen in einem Bereich λ 1 bis λ 2 vorhanden. 52
23 Hierdurch wird die Bedingung, dass ein Punkt des reziproken Gitters auf der Oberfläche der Ewald-Kugel liegen muss, dahingehend aufgeweicht, dass hier ein ganzer Bereich (zwischen k1 = 2π r 0 /λ 1 und k 2 = 2π r 0 /λ 2, dabei ist r 0 die feste Einfallsrichtung) erlaubt ist. Die Laue-Methode ist die Beste, um die Orientierung eines Kristalls bekannter Struktur zu bestimmen. Liegt der einfallende Strahl entlang einer Symmetrie-Achse, so wird das Reflexmuster dieselbe Symmetrie aufweisen. Der Aufbau beim Laue-Verfahren 53
24 Beispiele, die mit dem Laue-Verfahren aufgenommen wurden Laue-Aufnahme eines Quasikristalls aus Al6 CuLi3. Es ist deutlich die fu nf-za hlige Symmetrie zu erkennen. Laue-Aufnahme von Kalialaun (KAl(SO4 )2 12H2 O); es ist deutlich zu sehen, dass der Kristall nicht eine vier sondern eine zwei-za hlige Symmetrie aufweist Die Drehkristall-Methode Die Methode zeichnet sich durch folgende Eigenschaften aus: 1. ein Einkristall 2. eine monochrome Strahlquelle 3. die Orientierung des Kristalls bezu glich des einfallenden Analysestrahls wird systematisch vera ndert 54
k.com Vorlesung Geomaterialien 2. Doppelstunde Kristallographische Grundlagen Prof. Dr. F.E. Brenker
 k.com Vorlesung Geomaterialien 2. Doppelstunde Kristallographische Grundlagen Prof. Dr. F.E. Brenker Institut für Geowissenschaften FE Mineralogie JWG-Universität Frankfurt Netzebene Translation: Verschiebung,
k.com Vorlesung Geomaterialien 2. Doppelstunde Kristallographische Grundlagen Prof. Dr. F.E. Brenker Institut für Geowissenschaften FE Mineralogie JWG-Universität Frankfurt Netzebene Translation: Verschiebung,
3. Struktur idealer Kristalle
 3. Struktur idealer Kristalle 3.1 Raumgitter - 3-D-periodische Anordnungen - Raumgitter und Basis - primitive Translationen - Elementarzelle - Dreh- und Spiegelsymmetrien - Einheitszelle - 7 Kristallsysteme,
3. Struktur idealer Kristalle 3.1 Raumgitter - 3-D-periodische Anordnungen - Raumgitter und Basis - primitive Translationen - Elementarzelle - Dreh- und Spiegelsymmetrien - Einheitszelle - 7 Kristallsysteme,
3. Struktur idealer Kristalle
 3. Struktur idealer Kristalle 3.1 Raumgitter - 3-D-periodische Anordnungen - Raumgitter und Basis - primitive Translationen - Elementarzelle - Dreh- und Spiegelsymmetrien - Einheitszelle - 7 Kristallsysteme,
3. Struktur idealer Kristalle 3.1 Raumgitter - 3-D-periodische Anordnungen - Raumgitter und Basis - primitive Translationen - Elementarzelle - Dreh- und Spiegelsymmetrien - Einheitszelle - 7 Kristallsysteme,
Anorganische Chemie III - Festkörperchemie
 Mathematisch-Naturwissenschaftliche Fakultät Institut für Chemie Abteilung Anorganische Chemie/Festkörperchemie Prof. Dr. Martin Köckerling Vorlesung Anorganische Chemie III - Festkörperchemie 1 Wiederholung
Mathematisch-Naturwissenschaftliche Fakultät Institut für Chemie Abteilung Anorganische Chemie/Festkörperchemie Prof. Dr. Martin Köckerling Vorlesung Anorganische Chemie III - Festkörperchemie 1 Wiederholung
Allgemeine Mineralogie - Kristallographie. Diamant
 Allgemeine Mineralogie - Kristallographie Diamant Bravaisgitter Aus den fünf 2-D Gittern können durch Translation in die dritte Dimension insgesamt 14 Bravaisgitter erzeugt werden Einteilung der Bravais
Allgemeine Mineralogie - Kristallographie Diamant Bravaisgitter Aus den fünf 2-D Gittern können durch Translation in die dritte Dimension insgesamt 14 Bravaisgitter erzeugt werden Einteilung der Bravais
Kristallstruktur und Mikrostruktur Teil I Vorlesung 3
 Kristallstruktur und Mikrostruktur Teil I Vorlesung 3 1 Wiederholung Punktsymmetrie - Erkennung 1/ Eine Punktsymmetrie-Gruppe {G} mit Ordnung N hat N Punktsymmetrieoperationen G i, i = 1,2, N. aber nur
Kristallstruktur und Mikrostruktur Teil I Vorlesung 3 1 Wiederholung Punktsymmetrie - Erkennung 1/ Eine Punktsymmetrie-Gruppe {G} mit Ordnung N hat N Punktsymmetrieoperationen G i, i = 1,2, N. aber nur
Hexagonal dichtest gepackte Struktur
 Hexagonal dichtest gepackte Struktur Auch diese Struktur ist sehr wichtig, da sie von sehr vielen Systemen angenommen wird (kein Bravaisgitter). Das einfach hexagonale Bravais-Gitter (in 3-dim): zwei-dim:
Hexagonal dichtest gepackte Struktur Auch diese Struktur ist sehr wichtig, da sie von sehr vielen Systemen angenommen wird (kein Bravaisgitter). Das einfach hexagonale Bravais-Gitter (in 3-dim): zwei-dim:
2.1 Translationssymmetrie
 2.1 Translationssymmetrie Die periodische Anordnung eines Kristalls entspricht mathematisch einer Translationssymmetrie. Diese wird mit Hilfe von drei fundamentalen Translationsvektoren beschrieben: T
2.1 Translationssymmetrie Die periodische Anordnung eines Kristalls entspricht mathematisch einer Translationssymmetrie. Diese wird mit Hilfe von drei fundamentalen Translationsvektoren beschrieben: T
Röntgenstrukturanalyse von Einkristallen
 Strukturmethoden: Röntgenstrukturanalyse von Einkristallen Sommersemester 2017 Christoph Wölper Institut für Anorganische Chemie der Universität Duisburg-Essen Wiederholung Was bisher geschah Symmetrie,
Strukturmethoden: Röntgenstrukturanalyse von Einkristallen Sommersemester 2017 Christoph Wölper Institut für Anorganische Chemie der Universität Duisburg-Essen Wiederholung Was bisher geschah Symmetrie,
Physikalisches Fortgeschrittenenpraktikum Strukturbestimmung. Vorbereitung. 1 Kristallstrukturen. 1.1 Gittertranslationsvektoren
 Physikalisches Fortgeschrittenenpraktikum Strukturbestimmung Vorbereitung Armin Burgmeier Robert Schittny Wir wollen uns in diesem Versuch mit der Bestimmung der Kristallstruktur einer Pulverprobe aus
Physikalisches Fortgeschrittenenpraktikum Strukturbestimmung Vorbereitung Armin Burgmeier Robert Schittny Wir wollen uns in diesem Versuch mit der Bestimmung der Kristallstruktur einer Pulverprobe aus
II.3. Primitive Elementarzellen und Basisvektoren
 II.3. Primitive Elementarzellen und Basisvektoren Elementarzelle (EZ): lückenlose Überdeckung des Raumes, Beispiel: Würfel für kubische Gitter, Primitive EZ: enthält 1 Gitterpunkt Beispiel: kubische bcc-struktur
II.3. Primitive Elementarzellen und Basisvektoren Elementarzelle (EZ): lückenlose Überdeckung des Raumes, Beispiel: Würfel für kubische Gitter, Primitive EZ: enthält 1 Gitterpunkt Beispiel: kubische bcc-struktur
Übungen Festkörper (WS 2018/2019) (wird im Laufe des Semesters vervollständigt)
 Übungen Festkörper (WS 2018/2019) (wird im Laufe des Semesters vervollständigt) Aufgabe 0) (a0) Es sollen aus folgenden Einheitszellen in allen Raumrichtungen unendlich periodisch fortgesetzte Festkörper
Übungen Festkörper (WS 2018/2019) (wird im Laufe des Semesters vervollständigt) Aufgabe 0) (a0) Es sollen aus folgenden Einheitszellen in allen Raumrichtungen unendlich periodisch fortgesetzte Festkörper
Department Chemie. Röntgenbeugung. ISP-Methodenkurs. Dr. Frank Hoffmann
 Department Chemie Röntgenbeugung ISP-Methodenkurs Dr. Frank Hoffmann 22.01.2008 Ergebnis einer RSA Ä Atomsorten und deren Koordinaten in der asymmetrischen Einheit Ä Bindungslängen und -winkel Ä Elementarzelle
Department Chemie Röntgenbeugung ISP-Methodenkurs Dr. Frank Hoffmann 22.01.2008 Ergebnis einer RSA Ä Atomsorten und deren Koordinaten in der asymmetrischen Einheit Ä Bindungslängen und -winkel Ä Elementarzelle
Kristallographie und Röntgenbeugung
 16.04.2009 Gliederung 1 Grundlagen der Kristallographie 2 Röntgenstrahlung Laue-Bedingung Bragg-Bedingung Ewaldsche Konstruktion Röntgenverfahren zur Strukturanalyse von Kristallen 3 4 Festkörper kristalliner
16.04.2009 Gliederung 1 Grundlagen der Kristallographie 2 Röntgenstrahlung Laue-Bedingung Bragg-Bedingung Ewaldsche Konstruktion Röntgenverfahren zur Strukturanalyse von Kristallen 3 4 Festkörper kristalliner
Strukturmethoden: Röntgenstrukturanalyse von Einkristallen. Sommersemester Christoph Wölper
 Strukturmethoden: Röntgenstrukturanalyse von Einkristallen Sommersemester 2012 Christoph Wölper Christoph Wölper christoph.woelper@uni-due.de http://www.uni-due.de/~adb297b Vorlesungs-Script unter: http://www.uni-due.de/~adb297b/ss2012/strukturmethoden_vorlesung.pdf
Strukturmethoden: Röntgenstrukturanalyse von Einkristallen Sommersemester 2012 Christoph Wölper Christoph Wölper christoph.woelper@uni-due.de http://www.uni-due.de/~adb297b Vorlesungs-Script unter: http://www.uni-due.de/~adb297b/ss2012/strukturmethoden_vorlesung.pdf
Übungen zur Experimentalphysik 3
 Übungen zur Experimentalphysik 3 Prof. Dr. L. Oberauer Wintersemester 2010/2011 9. Übungsblatt - 20.Dezember 2010 Musterlösung Franziska Konitzer (franziska.konitzer@tum.de) Aufgabe 1 ( ) (5 Punkte) Mit
Übungen zur Experimentalphysik 3 Prof. Dr. L. Oberauer Wintersemester 2010/2011 9. Übungsblatt - 20.Dezember 2010 Musterlösung Franziska Konitzer (franziska.konitzer@tum.de) Aufgabe 1 ( ) (5 Punkte) Mit
Masterstudiengang Chemie Vorlesung Struktur und Funktion (WS 2014/15) Struktur und Funktion: (Kap. 2)
 Masterstudiengang Chemie Vorlesung Struktur und Funktion (WS 2014/15) Übersicht 2 Beugung von Röntgenstrahlen an Kristallen 2.1 Erzeugung von Röntgenstrahlen 2.2 Streuung an Elektronen 2.3 Streuung an
Masterstudiengang Chemie Vorlesung Struktur und Funktion (WS 2014/15) Übersicht 2 Beugung von Röntgenstrahlen an Kristallen 2.1 Erzeugung von Röntgenstrahlen 2.2 Streuung an Elektronen 2.3 Streuung an
Kristallstruktur und Mikrostruktur Teil I Vorlesung 2
 Kristallstruktur und Mikrostruktur Teil I Vorlesung 2 1 Kristallstruktur und Teil I Scripte Mikrostruktur http://www.uni-stuttgart.de/mawi/aktuelles_lehrangebot/lehrangebot.html 2 Wiederholung Koordinatensysteme
Kristallstruktur und Mikrostruktur Teil I Vorlesung 2 1 Kristallstruktur und Teil I Scripte Mikrostruktur http://www.uni-stuttgart.de/mawi/aktuelles_lehrangebot/lehrangebot.html 2 Wiederholung Koordinatensysteme
Praktikumsversuch B2.1 Zwei röntgenografische Verfahren der Festkörperphysik
 Praktikumsversuch B2.1 Zwei röntgenografische Verfahren der Festkörperphysik Alexander Komarek, Sebastian Bleikamp, Martin Valldor Raum 326 im II. Physikalischen Institut der Universität zu Köln 1 Einleitung
Praktikumsversuch B2.1 Zwei röntgenografische Verfahren der Festkörperphysik Alexander Komarek, Sebastian Bleikamp, Martin Valldor Raum 326 im II. Physikalischen Institut der Universität zu Köln 1 Einleitung
Kristallstruktur und Mikrostruktur Teil I Vorlesung 2
 Kristallstruktur und Mikrostruktur Teil I Vorlesung 2 1 Kristallstruktur und Teil I Scripte Mikrostruktur http://www.uni-stuttgart.de/mawi/aktuelles_lehrangebot/lehrangebot.html 2 Wiederholung Koordinatensysteme
Kristallstruktur und Mikrostruktur Teil I Vorlesung 2 1 Kristallstruktur und Teil I Scripte Mikrostruktur http://www.uni-stuttgart.de/mawi/aktuelles_lehrangebot/lehrangebot.html 2 Wiederholung Koordinatensysteme
Vorlesung Festkörperphysik. WS 2014/2015 Vorlesungen Universität Rostock Heinrich Stolz
 Vorlesung Festkörperphysik WS 2014/2015 Vorlesungen 28.10.14 Universität Rostock Heinrich Stolz 1 2. Das Reziproke Gitter Wichtige mathematische Objekt in der Physik mit periodischer Struktur? ebene Welle
Vorlesung Festkörperphysik WS 2014/2015 Vorlesungen 28.10.14 Universität Rostock Heinrich Stolz 1 2. Das Reziproke Gitter Wichtige mathematische Objekt in der Physik mit periodischer Struktur? ebene Welle
Kristallographie. Walter Borchardt-Ott. Eine Einführung für Naturwissenschaftler. Springer. Sechste, überarbeitete und erweiterte Auflage
 Walter Borchardt-Ott Kristallographie Eine Einführung für Naturwissenschaftler Sechste, überarbeitete und erweiterte Auflage Mit 290 Abbildungen und 44 Tabellen Springer Inhaltsverzeichnis 1 Einleitung
Walter Borchardt-Ott Kristallographie Eine Einführung für Naturwissenschaftler Sechste, überarbeitete und erweiterte Auflage Mit 290 Abbildungen und 44 Tabellen Springer Inhaltsverzeichnis 1 Einleitung
Festk0203_ /11/2002. Neben Translationen gibt es noch weitere Deckoperationen die eine Struktur in sich überführen können:
 Festk234 37 11/11/22 2.9. Drehungen und Drehinversionen Bereits kennen gelernt: Translationssymmetrie. Neben Translationen gibt es noch weitere Deckoperationen die eine Struktur in sich überführen können:
Festk234 37 11/11/22 2.9. Drehungen und Drehinversionen Bereits kennen gelernt: Translationssymmetrie. Neben Translationen gibt es noch weitere Deckoperationen die eine Struktur in sich überführen können:
19.Juni Strukturbestimmung. Gruppe 36. Simon Honc Christian Hütter
 19.Juni 2005 Strukturbestimmung Gruppe 36 Simon Honc shonc@web.de Christian Hütter christian.huetter@gmx.de 1 I. Theoretische Grundlagen 1. Struktur idealer Kristalle Generell kann man bei Kristallen vom
19.Juni 2005 Strukturbestimmung Gruppe 36 Simon Honc shonc@web.de Christian Hütter christian.huetter@gmx.de 1 I. Theoretische Grundlagen 1. Struktur idealer Kristalle Generell kann man bei Kristallen vom
Vorlesung "Molekülphysik/Festkörperphysik" Sommersemester 2012 Prof. Dr. F. Kremer
 Vorlesung "Molekülphysik/Festkörperphysik" Sommersemester 202 Prof. Dr. F. Kremer Übersicht der Vorlesung am 6.4.202 Der kristalline Zustand Das Raumgitter Die Millerschen Indices Das reziproke Gitter
Vorlesung "Molekülphysik/Festkörperphysik" Sommersemester 202 Prof. Dr. F. Kremer Übersicht der Vorlesung am 6.4.202 Der kristalline Zustand Das Raumgitter Die Millerschen Indices Das reziproke Gitter
Übungen Festkörper (WS 2017/2018) (wird im Laufe des Semesters vervollständigt)
 Übungen Festkörper (WS 2017/2018) (wird im Laufe des Semesters vervollständigt) Aufgabe 0) (a0a) Es sollen aus folgenden kubischen Einheitszellen in allen Raumrichtungen unendlich periodisch fortgesetzte
Übungen Festkörper (WS 2017/2018) (wird im Laufe des Semesters vervollständigt) Aufgabe 0) (a0a) Es sollen aus folgenden kubischen Einheitszellen in allen Raumrichtungen unendlich periodisch fortgesetzte
Grundlagen der Kristallographie
 Grundlagen der Kristallographie Motivation Reflektionsbedingungen g Begriffsdefinitionen und internationale Konvention Kristall Einheitszelle Quasikristalle Penrose Tiling Die 7 Kristallsysteme Kristallographische
Grundlagen der Kristallographie Motivation Reflektionsbedingungen g Begriffsdefinitionen und internationale Konvention Kristall Einheitszelle Quasikristalle Penrose Tiling Die 7 Kristallsysteme Kristallographische
Struktur von Einkristallen
 Struktur von Einkristallen Beschreibung des einkristallinen Festkörpers Am einfachsten zu beschreiben sind atomare Kristalle bei denen an jedem Punkt des Raumgitters sich genau ein Atom befindet. Man wählt
Struktur von Einkristallen Beschreibung des einkristallinen Festkörpers Am einfachsten zu beschreiben sind atomare Kristalle bei denen an jedem Punkt des Raumgitters sich genau ein Atom befindet. Man wählt
Grundlagen-Vertiefung PW3. Kristalle und Kristallstrukturen Version von 15. Oktober 2013
 Grundlagen-Vertiefung PW3 Kristalle und Kristallstrukturen Version von 15. Oktober 2013 Kristalle besitzen einen geordneten und periodischen Gitteraufbau. Die überwiegende Mehrzahl der anorganischen Festkörper
Grundlagen-Vertiefung PW3 Kristalle und Kristallstrukturen Version von 15. Oktober 2013 Kristalle besitzen einen geordneten und periodischen Gitteraufbau. Die überwiegende Mehrzahl der anorganischen Festkörper
Methoden der Chemie III Teil 1 Modul M.Che.1101 WS 2010/11 3 Moderne Methoden der Anorganischen Chemie Mi 10:15-12:00, Hörsaal II George Sheldrick
 Methoden der Chemie III Teil 1 Modul M.Che.1101 WS 2010/11 3 Moderne Methoden der Anorganischen Chemie Mi 10:15-12:00, Hörsaal II George Sheldrick gsheldr@shelx.uni-ac.gwdg.de Das Gitter Kristalle bestehen
Methoden der Chemie III Teil 1 Modul M.Che.1101 WS 2010/11 3 Moderne Methoden der Anorganischen Chemie Mi 10:15-12:00, Hörsaal II George Sheldrick gsheldr@shelx.uni-ac.gwdg.de Das Gitter Kristalle bestehen
Übungen Festkörper (WS 2018/2019) (wird im Laufe des Semesters vervollständigt)
 Übungen Festkörper (WS 2018/2019) (wird im Laufe des Semesters vervollständigt) Aufgabe 0) (a0) Es sollen aus folgenden Einheitszellen in allen Raumrichtungen unendlich periodisch fortgesetzte Festkörper
Übungen Festkörper (WS 2018/2019) (wird im Laufe des Semesters vervollständigt) Aufgabe 0) (a0) Es sollen aus folgenden Einheitszellen in allen Raumrichtungen unendlich periodisch fortgesetzte Festkörper
Wiederholung der letzten Vorlesungsstunde
 Wiederholung der letzten Vorlesungsstunde Festkörper, ausgewählte Beispiele spezieller Eigenschaften von Feststoffen, Kohlenstoffmodifikationen, Nichtstöchiometrie, Unterscheidung kristalliner und amorpher
Wiederholung der letzten Vorlesungsstunde Festkörper, ausgewählte Beispiele spezieller Eigenschaften von Feststoffen, Kohlenstoffmodifikationen, Nichtstöchiometrie, Unterscheidung kristalliner und amorpher
Matura2016-Lösung. Problemstellung 1
 Matura-Lösung Problemstellung. Die Funktion f( = + 9k + müsste bei = den Wert annehmen, also gilt + 9k + = k =. Wir betrachten den Bereich mit positiven Werten. Dann gilt: f ( = 8 + 8 = = ; = Bei liegt
Matura-Lösung Problemstellung. Die Funktion f( = + 9k + müsste bei = den Wert annehmen, also gilt + 9k + = k =. Wir betrachten den Bereich mit positiven Werten. Dann gilt: f ( = 8 + 8 = = ; = Bei liegt
Physik IV Einführung in die Atomistik und die Struktur der Materie
 Physik IV Einführung in die Atomistik und die Struktur der Materie Sommersemester 2011 Vorlesung 21 30.06.2011 Physik IV - Einführung in die Atomistik Vorlesung 21 Prof. Thorsten Kröll 30.06.2011 1 H 2
Physik IV Einführung in die Atomistik und die Struktur der Materie Sommersemester 2011 Vorlesung 21 30.06.2011 Physik IV - Einführung in die Atomistik Vorlesung 21 Prof. Thorsten Kröll 30.06.2011 1 H 2
Werkstoffe und Sensorik
 1 1. Kristall-Strukturen Kristalline Materialien bestehen aus regelmäßigen Anordnungen von Atomen in 3 Dimensionen. Einheitszelle: Kleinste, sich wiederholende Einheit, die die volle Symmetrie der Kristallstruktur
1 1. Kristall-Strukturen Kristalline Materialien bestehen aus regelmäßigen Anordnungen von Atomen in 3 Dimensionen. Einheitszelle: Kleinste, sich wiederholende Einheit, die die volle Symmetrie der Kristallstruktur
P 2 - Piezoelektrizität
 56 P2 Piezoelektrizität P 2 - Piezoelektrizität Ein Kristall, dessen Punktgruppe (Kristallklasse) kein Symmetriezentrum (Z) aufweist, kann prinzipiell piezoelektrisch sein Das heißt, der auf den Kristall
56 P2 Piezoelektrizität P 2 - Piezoelektrizität Ein Kristall, dessen Punktgruppe (Kristallklasse) kein Symmetriezentrum (Z) aufweist, kann prinzipiell piezoelektrisch sein Das heißt, der auf den Kristall
Methoden der Chemie III Teil 1 Modul M.Che.1101 WS 2010/11 6 Moderne Methoden der Anorganischen Chemie Mi 10:15-12:00, Hörsaal II George Sheldrick
 Methoden der Chemie III Teil 1 Modul M.Che.1101 WS 2010/11 6 Moderne Methoden der Anorganischen Chemie Mi 10:15-12:00, Hörsaal II George Sheldrick gsheldr@shelx.uni-ac.gwdg.de Röntgenbeugung und das reziproke
Methoden der Chemie III Teil 1 Modul M.Che.1101 WS 2010/11 6 Moderne Methoden der Anorganischen Chemie Mi 10:15-12:00, Hörsaal II George Sheldrick gsheldr@shelx.uni-ac.gwdg.de Röntgenbeugung und das reziproke
Nachbesprechung. Übung 3
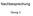 Nachbesprechung Übung 3 Form (a) Pinakoid, (b) allgemeine Fläche (Pfeil) wird durch eine Spiegelebene in ein Doma überführt, (c) Sphenoid (Pfeil), generiert durch die Wirkung einer 2-zähligen Achse, (d)
Nachbesprechung Übung 3 Form (a) Pinakoid, (b) allgemeine Fläche (Pfeil) wird durch eine Spiegelebene in ein Doma überführt, (c) Sphenoid (Pfeil), generiert durch die Wirkung einer 2-zähligen Achse, (d)
Kristallographie I. Inhalt von Kapitel 5
 88 Inhalt von Kapitel 5 5 Untersuchung von Kristallen... 89 5.1 Lichtoptik... 89 5.2 Röntgenographische Untersuchung von Kristallen... 93 5.2.1 Beugung von Röntgenstrahlung am Kristallgitter... 94 5.2.2
88 Inhalt von Kapitel 5 5 Untersuchung von Kristallen... 89 5.1 Lichtoptik... 89 5.2 Röntgenographische Untersuchung von Kristallen... 93 5.2.1 Beugung von Röntgenstrahlung am Kristallgitter... 94 5.2.2
Kurs Röntgenstrukturanalyse, Teil 1: Der kristalline Zustand
 Kurs Röntgenstrukturanalyse, Teil 1: Der kristalline Zustand Beispiel 1: Difluoramin M. F. Klapdor, H. Willner, W. Poll, D. Mootz, Angew. Chem. 1996, 108, 336. Gitterpunkt, Gitter, Elementarzelle, Gitterkonstanten,
Kurs Röntgenstrukturanalyse, Teil 1: Der kristalline Zustand Beispiel 1: Difluoramin M. F. Klapdor, H. Willner, W. Poll, D. Mootz, Angew. Chem. 1996, 108, 336. Gitterpunkt, Gitter, Elementarzelle, Gitterkonstanten,
Crystal Diffraction. Günter Krois Markus Kurz
 Günter Krois Markus Kurz Inhalt 1. Einleitung... 3 2. Doppelspalt Experiment... 3 2.1. Das Experiment... 3 2.2. Der Detektor... 3 2.3. Welle Teilchen Terminologie... 4 3. Beugung am Kristallgitter... 4
Günter Krois Markus Kurz Inhalt 1. Einleitung... 3 2. Doppelspalt Experiment... 3 2.1. Das Experiment... 3 2.2. Der Detektor... 3 2.3. Welle Teilchen Terminologie... 4 3. Beugung am Kristallgitter... 4
Typisch metallische Eigenschaften:
 Typisch metallische Eigenschaften: hohe elektrische Leitfähigkeit hohe thermische Leitfähigkeit bei Energiezufuhr (Wärme, elektromagnetische Strahlung) können Elektronen emittiert werden metallischer Glanz
Typisch metallische Eigenschaften: hohe elektrische Leitfähigkeit hohe thermische Leitfähigkeit bei Energiezufuhr (Wärme, elektromagnetische Strahlung) können Elektronen emittiert werden metallischer Glanz
Vorbemerkung. [disclaimer]
![Vorbemerkung. [disclaimer] Vorbemerkung. [disclaimer]](/thumbs/55/36733836.jpg) Vorbemerkung Dies ist ein korrigierter Übungszettel aus dem Modul physik411. Dieser Übungszettel wurde von einem Tutor korrigiert. Dies bedeutet jedoch nicht, dass es sich um eine Musterlösung handelt.
Vorbemerkung Dies ist ein korrigierter Übungszettel aus dem Modul physik411. Dieser Übungszettel wurde von einem Tutor korrigiert. Dies bedeutet jedoch nicht, dass es sich um eine Musterlösung handelt.
Struktur von Festkörpern
 Struktur von Festkörpern Wir wollen uns zunächst mit der Struktur von Festkörpern, daß heißt mit der Geometrie in der sie vorliegen beschäftigen Kovalent gebundene Festkörper haben wir bereits in Form
Struktur von Festkörpern Wir wollen uns zunächst mit der Struktur von Festkörpern, daß heißt mit der Geometrie in der sie vorliegen beschäftigen Kovalent gebundene Festkörper haben wir bereits in Form
Kristallstruktur und Mikrostruktur Teil I Vorlesung 5
 Kristallstruktur und Mikrostruktur Teil I Vorlesung 5 Wiederholung # 2D Muster haben keine Spiegelebene in der Projektionebene # Der Verschiebungsvektor v einer Gleitspiegelebene, parallel zur Achse t
Kristallstruktur und Mikrostruktur Teil I Vorlesung 5 Wiederholung # 2D Muster haben keine Spiegelebene in der Projektionebene # Der Verschiebungsvektor v einer Gleitspiegelebene, parallel zur Achse t
ISP-Methodenkurs. Pulverdiffraktometrie. Prof. Dr. Michael Fröba, AC Raum 114, Tel: 040 /
 ISP-Methodenkurs Pulverdiffraktometrie Prof. Dr. Michael Fröba, AC Raum 4, Tel: 4 / 4838-337 www.chemie.uni-hamburg.de/ac/froeba/ Röntgenstrahlung (I) Wilhelm Conrad Röntgen (845-93) 879-888 Professor
ISP-Methodenkurs Pulverdiffraktometrie Prof. Dr. Michael Fröba, AC Raum 4, Tel: 4 / 4838-337 www.chemie.uni-hamburg.de/ac/froeba/ Röntgenstrahlung (I) Wilhelm Conrad Röntgen (845-93) 879-888 Professor
Einführung in die Kristallographie
 WILL KLEBER Einführung in die Kristallographie 18., stark bearbeitete Auflage von Hans-Joachim Bautsch und Joachim Böhm Verlag Technik Berlin Inhaltsverzeichnis Einleitung 11 1. Kristallstrukturlehre und
WILL KLEBER Einführung in die Kristallographie 18., stark bearbeitete Auflage von Hans-Joachim Bautsch und Joachim Böhm Verlag Technik Berlin Inhaltsverzeichnis Einleitung 11 1. Kristallstrukturlehre und
Übungen zur Experimentalphysik 3
 Übungen zur Experimentalphysik 3 Prof. Dr. L. Oberauer Wintersemester 2010/2011 10. Übungsblatt - 10. Januar 2011 Musterlösung Franziska Konitzer (franziska.konitzer@tum.de) Aufgabe 1 ( ) (6 Punkte) a)
Übungen zur Experimentalphysik 3 Prof. Dr. L. Oberauer Wintersemester 2010/2011 10. Übungsblatt - 10. Januar 2011 Musterlösung Franziska Konitzer (franziska.konitzer@tum.de) Aufgabe 1 ( ) (6 Punkte) a)
Praktikum Instrumentelle Analytik
 Praktikum Instrumentelle Analytik Sommersemester 2004 Kristallographie/Röntgenbeugung Aufgabenteil 2 Korrektur Gruppe 1 Vera Eulenberg Alexandra Huber Jasmin Fischer 1 Ziel dieser Aufgabe ist es, anhand
Praktikum Instrumentelle Analytik Sommersemester 2004 Kristallographie/Röntgenbeugung Aufgabenteil 2 Korrektur Gruppe 1 Vera Eulenberg Alexandra Huber Jasmin Fischer 1 Ziel dieser Aufgabe ist es, anhand
Kristallstrukturen. Kapitel Beugung an periodischen Strukturen
 Kapitel 2 Kristallstrukturen Festkörper bestehen aus einer Ansammlung von Atomen, die durch chemische Bindungen miteinander verbunden sind. Im thermodynamischen Gleichgewicht werden sich die Atome geometrisch
Kapitel 2 Kristallstrukturen Festkörper bestehen aus einer Ansammlung von Atomen, die durch chemische Bindungen miteinander verbunden sind. Im thermodynamischen Gleichgewicht werden sich die Atome geometrisch
Gefüge und Eigenschaften metallischer Werkstoffe WS 17/18
 Gefüge und Eigenschaften metallischer Werkstoffe WS 7/8 Übung 5 Musterlösung 0..07 Aufgabe Welche Bravais-Gittertypen gibt es? Welche Modifikationen besitzen Sie? Nennen Sie Materialbeispiele zu jedem
Gefüge und Eigenschaften metallischer Werkstoffe WS 7/8 Übung 5 Musterlösung 0..07 Aufgabe Welche Bravais-Gittertypen gibt es? Welche Modifikationen besitzen Sie? Nennen Sie Materialbeispiele zu jedem
Allgemeine Chemie Symmetrie von Molekülen
 Allgemeine Chemie Symmetrie von Molekülen AC_Molekuelsymmetrie.doc Seite 1 von 23 Fck / 12.10.05 Inhaltsverzeichnis 1 Einleitung...3 1.1 Anwendungsbereiche der Molekülsymmetrie...3 1.2 Sinn und Zweck der
Allgemeine Chemie Symmetrie von Molekülen AC_Molekuelsymmetrie.doc Seite 1 von 23 Fck / 12.10.05 Inhaltsverzeichnis 1 Einleitung...3 1.1 Anwendungsbereiche der Molekülsymmetrie...3 1.2 Sinn und Zweck der
Besprechung am
 PN2 Einführung in die Physik für Chemiker 2 Prof. J. Lipfert SS 2016 Übungsblatt 10 Übungsblatt 10 Besprechung am 27.6.2016 Aufgabe 1 Interferenz an dünnen Schichten. Weißes Licht fällt unter einem Winkel
PN2 Einführung in die Physik für Chemiker 2 Prof. J. Lipfert SS 2016 Übungsblatt 10 Übungsblatt 10 Besprechung am 27.6.2016 Aufgabe 1 Interferenz an dünnen Schichten. Weißes Licht fällt unter einem Winkel
Anhang Häufig verwendete Symbole
 68 Anhang Häufig verwendete Symbole Anhang Häufig verwendete Symbole θ B exakter Braggwinkel θ B Abweichung vom Braggwinkel λ Wellenlänge d Netzebenenabstand π & σ Parallel- & Senkrechtkomponente der Polarisation
68 Anhang Häufig verwendete Symbole Anhang Häufig verwendete Symbole θ B exakter Braggwinkel θ B Abweichung vom Braggwinkel λ Wellenlänge d Netzebenenabstand π & σ Parallel- & Senkrechtkomponente der Polarisation
Abitur 2016 Mathematik Geometrie V
 Seite http://www.abiturloesung.de/ Seite Abitur Mathematik Geometrie V Betrachtet wird der abgebildete Würfel A B C D E F G H. Die Eckpunkte D, E, F und H dieses Würfels besitzen in einem kartesischen
Seite http://www.abiturloesung.de/ Seite Abitur Mathematik Geometrie V Betrachtet wird der abgebildete Würfel A B C D E F G H. Die Eckpunkte D, E, F und H dieses Würfels besitzen in einem kartesischen
Die Bragg sche Beugungsbedingung. θ θ θ θ Ebene hkl
 Die Bragg sche Beugungsbedingung Eintr effender Strahl Austretender Str ahl Gebeugter Strahl θ θ θ θ Ebene hkl d hkl x x Ebene hkl Wegdifferenz: 2 x = 2 d hkl sin θ Konstruktive Interferenz: n λ = 2 d
Die Bragg sche Beugungsbedingung Eintr effender Strahl Austretender Str ahl Gebeugter Strahl θ θ θ θ Ebene hkl d hkl x x Ebene hkl Wegdifferenz: 2 x = 2 d hkl sin θ Konstruktive Interferenz: n λ = 2 d
Kristallstruktur und Mikrostruktur Teil I Vorlesung 5
 Kristallstruktur und Mikrostruktur Teil I Vorlesung 5 Wiederholung 2/m 2/m 2/m {1 i 2 x 2 y 2 z m x m y m z } Ordnung 8! m 2 i 2 Wiederholung Spezielle Lagen # spezielle Lagen in zentrierten Raumgruppen
Kristallstruktur und Mikrostruktur Teil I Vorlesung 5 Wiederholung 2/m 2/m 2/m {1 i 2 x 2 y 2 z m x m y m z } Ordnung 8! m 2 i 2 Wiederholung Spezielle Lagen # spezielle Lagen in zentrierten Raumgruppen
Beugung niederenergetischer Elektronen an Oberächen (LEED)
 Freie Universität Berlin Sommersemester 2007 Arnimallee 4 495 Berlin Fortgeschrittenenpraktikum Vorbereitung Beugung niederenergetischer Elektronen an Oberächen (LEED) Erik Streb 20. Juni 2007 Betreuer:
Freie Universität Berlin Sommersemester 2007 Arnimallee 4 495 Berlin Fortgeschrittenenpraktikum Vorbereitung Beugung niederenergetischer Elektronen an Oberächen (LEED) Erik Streb 20. Juni 2007 Betreuer:
Einführung in die Kristallographie
 Einführung in die Kristallographie Gerhard Heide Institut für Mineralogie Professur für Allgemeine und Angewandte Mineralogie Brennhausgasse 14 03731-39-2665 oder -2628 gerhard.heide@mineral.tu-freiberg.de
Einführung in die Kristallographie Gerhard Heide Institut für Mineralogie Professur für Allgemeine und Angewandte Mineralogie Brennhausgasse 14 03731-39-2665 oder -2628 gerhard.heide@mineral.tu-freiberg.de
Kristallographie I. Inhalt von Kapitel 3
 62 Kristallographie I Inhalt von Kapitel 3 3 Der Kristall als Diskontinuum... 63 3.1 Zweidimensionale Raumgruppen... 63 3.1.1 Elementarmaschen... 63 3.1.2 Die zweidimensionalen Punkt- und Raumgruppen...
62 Kristallographie I Inhalt von Kapitel 3 3 Der Kristall als Diskontinuum... 63 3.1 Zweidimensionale Raumgruppen... 63 3.1.1 Elementarmaschen... 63 3.1.2 Die zweidimensionalen Punkt- und Raumgruppen...
2. Kristallstrukturen 2.1 Bindungsarten
 2. Kristallstrukturen 2.1 Bindungsarten Bindungskräfte zwischen den Atomen ermöglichen systematische und geordnete Anlagerung der Atome Entstehung von Kristallstrukturen Metall-Ion (+) Metallische Bindung
2. Kristallstrukturen 2.1 Bindungsarten Bindungskräfte zwischen den Atomen ermöglichen systematische und geordnete Anlagerung der Atome Entstehung von Kristallstrukturen Metall-Ion (+) Metallische Bindung
Achim Kittel. Energie- und Halbleiterforschung Fakultät 5, Institut für Physik Büro: W1A Tel.:
 Festkörperphysik Achim Kittel Energie- und Halbleiterforschung Fakultät 5, Institut für Physik Büro: W1A 1-102 Tel.: 0441-798 3539 email: kittel@uni-oldenburg.de Sommersemester 2005 Inhaltsverzeichnis
Festkörperphysik Achim Kittel Energie- und Halbleiterforschung Fakultät 5, Institut für Physik Büro: W1A 1-102 Tel.: 0441-798 3539 email: kittel@uni-oldenburg.de Sommersemester 2005 Inhaltsverzeichnis
Kristallstruktur und Mikrostruktur Teil I Vorlesung 6
 Kristallstruktur und Mikrostruktur Teil I Vorlesung 6 Teil I: Zotov 1 Koordinatensysteme, Das Raumgitter, Das reziproke Gitter, Der Metrik-Tensor 2 Abstrakte Gruppen, Symmetrieoperationen, Punktsymmetrie
Kristallstruktur und Mikrostruktur Teil I Vorlesung 6 Teil I: Zotov 1 Koordinatensysteme, Das Raumgitter, Das reziproke Gitter, Der Metrik-Tensor 2 Abstrakte Gruppen, Symmetrieoperationen, Punktsymmetrie
Fortgeschrittenen-Praktikum
 Fortgeschrittenen-Praktikum Versuch 12: Beugung langsamer Elektronen (LEED) Lehrstuhl für Festkörperphysik (Prof. Fauster) Programm Oberflächen und niederenergetische Elektronen Prinzip und Informationsgehalt
Fortgeschrittenen-Praktikum Versuch 12: Beugung langsamer Elektronen (LEED) Lehrstuhl für Festkörperphysik (Prof. Fauster) Programm Oberflächen und niederenergetische Elektronen Prinzip und Informationsgehalt
 Übungen zu Experimentalphysik 4 - Lösungsvorschläge Prof. S. Paul Sommersemester 005 Dr. Jan Friedrich Nr. 5 16.05.005 Email Jan.Friedrich@ph.tum.de Telefon 089/89-1586 Physik Department E18, Raum 3564
Übungen zu Experimentalphysik 4 - Lösungsvorschläge Prof. S. Paul Sommersemester 005 Dr. Jan Friedrich Nr. 5 16.05.005 Email Jan.Friedrich@ph.tum.de Telefon 089/89-1586 Physik Department E18, Raum 3564
Kristallstruktur und Mikrostruktur Teil I Vorlesung 6
 Kristallstruktur und Mikrostruktur Teil I Vorlesung 6 g Wiederholung g 2 Verschiedene Ellementarzellen möglich 2 2 2 m g 2 P4g (p4gm) m 2 m Wiederholung 2 2 2 Verschiedene Ellementarzellen möglich m 2
Kristallstruktur und Mikrostruktur Teil I Vorlesung 6 g Wiederholung g 2 Verschiedene Ellementarzellen möglich 2 2 2 m g 2 P4g (p4gm) m 2 m Wiederholung 2 2 2 Verschiedene Ellementarzellen möglich m 2
Kristallstruktur und Mikrostruktur Teil I Vorlesung 4
 Kristallstruktur und Mikrostruktur Teil I Vorlesung 4 Wiederholung - Gleitspiegelebene A B 2 Symmetrieoperationen - Zusammenfassung Fixed Point No fixed Point Drehachsen Translationen keine Translationen
Kristallstruktur und Mikrostruktur Teil I Vorlesung 4 Wiederholung - Gleitspiegelebene A B 2 Symmetrieoperationen - Zusammenfassung Fixed Point No fixed Point Drehachsen Translationen keine Translationen
Fortgeschrittenenpraktikum. 2. Praktikumsversuch aus Halbleiterphysik. Röntgenbeugung
 2. Praktikumsversuch aus Halbleiterphysik Röntgenbeugung, 0555150 (Autor), 0555342 Gruppe I/1 1 Inhaltsverzeichnis 1 Theoretische Grundlagen 3 1.1 Bragg-Bedingung.............................................
2. Praktikumsversuch aus Halbleiterphysik Röntgenbeugung, 0555150 (Autor), 0555342 Gruppe I/1 1 Inhaltsverzeichnis 1 Theoretische Grundlagen 3 1.1 Bragg-Bedingung.............................................
Gliederung der Vorlesung im SS
 Gliederung der Vorlesung im SS A. Struktureller Aufbau von Werkstoffen. Atomare Struktur.. Atomaufbau und Periodensystem der Elemente.2. Interatomare Bindungen.3. Aggregatzustände 2. Struktur des Festkörpers
Gliederung der Vorlesung im SS A. Struktureller Aufbau von Werkstoffen. Atomare Struktur.. Atomaufbau und Periodensystem der Elemente.2. Interatomare Bindungen.3. Aggregatzustände 2. Struktur des Festkörpers
Kristallstruktur und Mikrostruktur Teil I Vorlesung 4
 Kristallstruktur und Mikrostruktur Teil I Vorlesung 4 Symmetrieoperationen - Zusammenfassung Fixed Point No fixed Point Drehachsen Translationen keine Translationen Drehinversionsachsen Schraubenachsen
Kristallstruktur und Mikrostruktur Teil I Vorlesung 4 Symmetrieoperationen - Zusammenfassung Fixed Point No fixed Point Drehachsen Translationen keine Translationen Drehinversionsachsen Schraubenachsen
Einleitung 2. 1 Koordinatensysteme 2. 2 Lineare Abbildungen 4. 3 Literaturverzeichnis 7
 Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Röntgenographische Charakterisierung der hergestellten Feststoffe mittels Pulverdiffraktion, sowie Auswertung der erhaltenen Pulverdiffraktogramme
 Röntgenographische Charakterisierung der hergestellten Feststoffe mittels Pulverdiffraktion, sowie Auswertung der erhaltenen Pulverdiffraktogramme Vorbemerkung: Wegen der umfassenden Theorie von kristallographischen
Röntgenographische Charakterisierung der hergestellten Feststoffe mittels Pulverdiffraktion, sowie Auswertung der erhaltenen Pulverdiffraktogramme Vorbemerkung: Wegen der umfassenden Theorie von kristallographischen
Ulrich Schwarz Experimentelle Sensorik Institut für Physik, TU Chemnitz. Sommersemeser Physik der kondensierten Materie
 Ulrich Schwarz Experimentelle Sensorik Institut für Physik, TU Chemnitz In Vertretung von Carsten Deibel Optik & Photonik Kondensierter Materie Institut für Physik, TU Chemnitz Sommersemeser 2018 Strukturbestimmung
Ulrich Schwarz Experimentelle Sensorik Institut für Physik, TU Chemnitz In Vertretung von Carsten Deibel Optik & Photonik Kondensierter Materie Institut für Physik, TU Chemnitz Sommersemeser 2018 Strukturbestimmung
1.4 Gradient, Divergenz und Rotation
 .4 Gradient, Divergenz und Rotation 5.4 Gradient, Divergenz und Rotation Die Begriffe Gradient, Divergenz und Rotation erfordern die partiellen Ableitung aus Abschnitt.. sowie das Konzept des Differentialoperators.
.4 Gradient, Divergenz und Rotation 5.4 Gradient, Divergenz und Rotation Die Begriffe Gradient, Divergenz und Rotation erfordern die partiellen Ableitung aus Abschnitt.. sowie das Konzept des Differentialoperators.
Übungen zur Experimentalphysik 3
 Übungen zur Experimentalphysik 3 Prof. Dr. L. Oberauer Wintersemester 2010/2011 4. Übungsblatt - 15.November 2010 Musterlösung Franziska Konitzer (franziska.konitzer@tum.de) Aufgabe 1 ( ) (3 Punkte) Welche
Übungen zur Experimentalphysik 3 Prof. Dr. L. Oberauer Wintersemester 2010/2011 4. Übungsblatt - 15.November 2010 Musterlösung Franziska Konitzer (franziska.konitzer@tum.de) Aufgabe 1 ( ) (3 Punkte) Welche
2. METALLISCHE WERKSTOFFE
 2. METALLISCHE WERKSTOFFE Metalle sind kristallin aufgebaut Bindung wischen den Atomen = Metallbindung Jedes Atom gibt ~ 1 Elektron aus äußerster Schale ab positiv geladene Metallionen negativ geladene
2. METALLISCHE WERKSTOFFE Metalle sind kristallin aufgebaut Bindung wischen den Atomen = Metallbindung Jedes Atom gibt ~ 1 Elektron aus äußerster Schale ab positiv geladene Metallionen negativ geladene
Protokoll zum Versuch Debye - Scherrer - Verfahren. Tina Clauß, Jan Steinhoff Betreuer: Dr. Uschmann
 Protokoll zum Versuch Debye - Scherrer - Verfahren Tina Clauß, Jan Steinhoff Betreuer: Dr. Uschmann 6. März 2005 3 Inhaltsverzeichnis 1 Aufgabenstellung 4 2 Theoretische Grundlagen 4 2.1 Röntgenstrahlung.................................
Protokoll zum Versuch Debye - Scherrer - Verfahren Tina Clauß, Jan Steinhoff Betreuer: Dr. Uschmann 6. März 2005 3 Inhaltsverzeichnis 1 Aufgabenstellung 4 2 Theoretische Grundlagen 4 2.1 Röntgenstrahlung.................................
Bericht zum Versuch Strukturanalyse mittels Röntgenstrahlung
 Bericht zum Versuch Strukturanalyse mittels Röntgenstrahlung Michael Goerz, Anton Haase 9. Februar 2007 Freie Universität Berlin Fortgeschrittenenpraktikum Teil A Tutor: C. Rüdt Inhalt 1 Einführung 2 1.1
Bericht zum Versuch Strukturanalyse mittels Röntgenstrahlung Michael Goerz, Anton Haase 9. Februar 2007 Freie Universität Berlin Fortgeschrittenenpraktikum Teil A Tutor: C. Rüdt Inhalt 1 Einführung 2 1.1
Thema heute: Chemische Bindungen - Ionenbindung
 Wiederholung der letzten Vorlesungsstunde: Chemische Bindungen, Doppelbindungsregel, VSEPR-Theorie Thema heute: Chemische Bindungen - Ionenbindung Vorlesung Allgemeine Chemie, Prof. Dr. Martin Köckerling
Wiederholung der letzten Vorlesungsstunde: Chemische Bindungen, Doppelbindungsregel, VSEPR-Theorie Thema heute: Chemische Bindungen - Ionenbindung Vorlesung Allgemeine Chemie, Prof. Dr. Martin Köckerling
8. Übungsblatt zur Mathematik I für Maschinenbau
 Fachbereich Mathematik Prof. Dr. M. Joswig Dr. habil. Sören Kraußhar Dipl.-Math. Katja Kulas 8. Übungsblatt zur Mathematik I für Maschinenbau Gruppenübung WS / 6..-.. Aufgabe G (Matrixinversion mit Gauß-Algorithmus
Fachbereich Mathematik Prof. Dr. M. Joswig Dr. habil. Sören Kraußhar Dipl.-Math. Katja Kulas 8. Übungsblatt zur Mathematik I für Maschinenbau Gruppenübung WS / 6..-.. Aufgabe G (Matrixinversion mit Gauß-Algorithmus
Reflexion - Teil Formel unter Verwendung von Vektoren
 Reflexion - Teil 1 1. Formel unter Verwendung von Vektoren (1. - 7. in R 2 ) 2. Fallunterscheidung: Beispiele zu 1. 3. Beispiel - Reflexionspunkt bekannt 4. Muss zur Berechnung von r der Reflexionspunkt
Reflexion - Teil 1 1. Formel unter Verwendung von Vektoren (1. - 7. in R 2 ) 2. Fallunterscheidung: Beispiele zu 1. 3. Beispiel - Reflexionspunkt bekannt 4. Muss zur Berechnung von r der Reflexionspunkt
Experimentalphysik V Gehört bei Prof. Dr. Löhneysen. KIT - Karlsruher Institut für Technologie Wintersemester 2012/13
 Experimentalphysik V Gehört bei Prof. Dr. Löhneysen KIT - Karlsruher Institut für Technologie Wintersemester 2012/13 Mitschriebe ausgearbeitet von Philipp Basler, Nils Braun, Larissa Bauer Überprüft von
Experimentalphysik V Gehört bei Prof. Dr. Löhneysen KIT - Karlsruher Institut für Technologie Wintersemester 2012/13 Mitschriebe ausgearbeitet von Philipp Basler, Nils Braun, Larissa Bauer Überprüft von
Grundlagen der Chemie Ionenradien
 Ionenradien Prof. Annie Powell KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Ionenradien In einem Ionenkristall halten benachbarte
Ionenradien Prof. Annie Powell KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Ionenradien In einem Ionenkristall halten benachbarte
2. Struktur von Festkörpern
 2. Struktur von Festkörpern 2.1 Kristallisation von Festkörpern Bevor es einen Festkörper gibt, muss es zur Kristallbildung kommen. Bis auf einige Ausnahmen (Gläser, amorphe Substanzen, Polymere, Zufallslegierungen)
2. Struktur von Festkörpern 2.1 Kristallisation von Festkörpern Bevor es einen Festkörper gibt, muss es zur Kristallbildung kommen. Bis auf einige Ausnahmen (Gläser, amorphe Substanzen, Polymere, Zufallslegierungen)
Kreissektoren und Bogenmaß
 M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius Mittelpunktswinkel : Länge des Kreisbogens gilt für einen Kreissektor mit Fläche des Kreissektors Das Bogenmaß eines Winkels ist die Länge des
M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius Mittelpunktswinkel : Länge des Kreisbogens gilt für einen Kreissektor mit Fläche des Kreissektors Das Bogenmaß eines Winkels ist die Länge des
Strukturmethoden: Röntgenstrukturanalyse von Einkristallen. Sommersemester Christoph Wölper. Universität Duisburg-Essen
 Strukturmethoden: Röntgenstrukturanalyse von Einkristallen Sommersemester 2014 Christoph Wölper Universität Duisburg-Essen Christoph Wölper christoph.woelper@uni-due.de http://www.uni-due.de/~adb297b Vorlesungs-Skript
Strukturmethoden: Röntgenstrukturanalyse von Einkristallen Sommersemester 2014 Christoph Wölper Universität Duisburg-Essen Christoph Wölper christoph.woelper@uni-due.de http://www.uni-due.de/~adb297b Vorlesungs-Skript
Mathematischer Vorkurs für Physiker WS 2011/12 Vorlesung 3
 TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2011/12 Vorlesung 3 Differenziation und Integration von Vektorfunktionen Der Ortsvektor: Man kann einen Punkt P im Raum eindeutig durch die
TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2011/12 Vorlesung 3 Differenziation und Integration von Vektorfunktionen Der Ortsvektor: Man kann einen Punkt P im Raum eindeutig durch die
Auswirkungen der Symmetrien auf physikalische Effekte
 Auswirkungen der Symmetrien auf physikalische Effekte Teil 1 Elektrische Polarisation 1. Elektrische Polarisation In einem elektrisch nicht leitenden Körper also in einem Dielektrikum verschieben sich
Auswirkungen der Symmetrien auf physikalische Effekte Teil 1 Elektrische Polarisation 1. Elektrische Polarisation In einem elektrisch nicht leitenden Körper also in einem Dielektrikum verschieben sich
Basisvokabular zur Strukturchemie (F. Kubel)
 Basisvokabular zur Strukturchemie (F. Kubel) Ångström Längenmaßeinheit in der Kristallographie 1Å=10-8 cm=100pm Anisotropie Richtungsabhängigkeit einer (vektoriellen) Eigenschaft Apolar Kristallstruktur
Basisvokabular zur Strukturchemie (F. Kubel) Ångström Längenmaßeinheit in der Kristallographie 1Å=10-8 cm=100pm Anisotropie Richtungsabhängigkeit einer (vektoriellen) Eigenschaft Apolar Kristallstruktur
Hexagonales Kristallsystem und Honigwabenstruktur von Graphen
 Kapitel 2 Hexagonales Kristallsystem und Honigwabenstruktur von Graphen Die Diskussion der kristallographischen Begriffe in diesem Kapitel folgt [?]. 2. Kristallgitter 2.. Definitionen Periodische Anordnung
Kapitel 2 Hexagonales Kristallsystem und Honigwabenstruktur von Graphen Die Diskussion der kristallographischen Begriffe in diesem Kapitel folgt [?]. 2. Kristallgitter 2.. Definitionen Periodische Anordnung
Einführung in die Physik II für Studierende der Naturwissenschaften und Zahnheilkunde. Sommersemester 2007
 Einführung in die Physik II für Studierende der Naturwissenschaften und Zahnheilkunde Sommersemester 2007 VL #45 am 18.07.2007 Vladimir Dyakonov Erzeugung von Interferenzen: 1) Durch Wellenfrontaufspaltung
Einführung in die Physik II für Studierende der Naturwissenschaften und Zahnheilkunde Sommersemester 2007 VL #45 am 18.07.2007 Vladimir Dyakonov Erzeugung von Interferenzen: 1) Durch Wellenfrontaufspaltung
Anorganische Chemie III - Festkörperchemie
 Mathematisch-Naturwissenschaftliche Fakultät Institut für Chemie Abteilung Anorganische Chemie/Festkörperchemie Prof. Dr. Martin Köckerling Vorlesung Anorganische Chemie III - Festkörperchemie 1 Wiederholung
Mathematisch-Naturwissenschaftliche Fakultät Institut für Chemie Abteilung Anorganische Chemie/Festkörperchemie Prof. Dr. Martin Köckerling Vorlesung Anorganische Chemie III - Festkörperchemie 1 Wiederholung
Übung (5) 4x 2y +2u 3v =1 3x 2u + v =0 2x +3y u +2v =0
 Übung (5). Lösen Sie folgendes lineare Gleichungssystem - sagen Sie zuvor, wie die Lösungsmenge aussehen sollte bzw. geometrisch zu interpretieren wäre: 4x y +u 3v = 3x u + v =0 x +3y u +v =0. Sagen Sie
Übung (5). Lösen Sie folgendes lineare Gleichungssystem - sagen Sie zuvor, wie die Lösungsmenge aussehen sollte bzw. geometrisch zu interpretieren wäre: 4x y +u 3v = 3x u + v =0 x +3y u +v =0. Sagen Sie
Lernmaterialblatt Mathematik. Vektorrechnung eine Einführung. Anwendung Mathematik I. Einleitung:
 Vektorrechnung eine Einführung Einleitung: Um beispielsweise das Dreieck ABC in der Abbildung an die Position A'B'C' zu verschieben, muss jeder Punkt um sieben Einheiten nach rechts und drei nach oben
Vektorrechnung eine Einführung Einleitung: Um beispielsweise das Dreieck ABC in der Abbildung an die Position A'B'C' zu verschieben, muss jeder Punkt um sieben Einheiten nach rechts und drei nach oben
Ferienkurs Experimentalphysik 3
 Ferienkurs Experimentalphysik 3 Wintersemester 2014/2015 Thomas Maier, Alexander Wolf Lösung 3 Beugung und Interferenz Aufgabe 1: Seifenblasen a) Erklären Sie, warum Seifenblasen in bunten Farben schillern.
Ferienkurs Experimentalphysik 3 Wintersemester 2014/2015 Thomas Maier, Alexander Wolf Lösung 3 Beugung und Interferenz Aufgabe 1: Seifenblasen a) Erklären Sie, warum Seifenblasen in bunten Farben schillern.
Fortgeschrittenen Praktikum, SS 2008
 Röntgenbeugung (RBE) Fortgeschrittenen Praktikum, SS 2008 Alexander Seizinger, Michael Ziller, Philipp Buchegger, Tobias Müller Betreuer: Prof. Jörg Ihringer Tübingen, den 15. Juli 2008 1 Theorie 1.1 Erzeugung
Röntgenbeugung (RBE) Fortgeschrittenen Praktikum, SS 2008 Alexander Seizinger, Michael Ziller, Philipp Buchegger, Tobias Müller Betreuer: Prof. Jörg Ihringer Tübingen, den 15. Juli 2008 1 Theorie 1.1 Erzeugung
6 Elektromagnetische Schwingungen und Wellen. E y. E(z=0) Polarisation Richtung des E-Vektors gibt die Polarisation an.
 6 Elektromagnetische Schwingungen und Wellen E y E(z=0) E 0 z E y E 0 t Abbildung 6.10: (a) E(z, t = t 1 ): Momentaufnahme für t = t 1. (b) E(z = z 1, t): Zeitabhängigkeit an festem Ort z = z 1. Polarisation
6 Elektromagnetische Schwingungen und Wellen E y E(z=0) E 0 z E y E 0 t Abbildung 6.10: (a) E(z, t = t 1 ): Momentaufnahme für t = t 1. (b) E(z = z 1, t): Zeitabhängigkeit an festem Ort z = z 1. Polarisation
Photonische Kristalle
 Kapitel 2 Photonische Kristalle 2.1 Einführung In den letzten 20 Jahren entwickelten sich die Photonischen Kristalle zu einem bevorzugten Gegenstand der Grundlagenforschung aber auch der angewandten Forschung
Kapitel 2 Photonische Kristalle 2.1 Einführung In den letzten 20 Jahren entwickelten sich die Photonischen Kristalle zu einem bevorzugten Gegenstand der Grundlagenforschung aber auch der angewandten Forschung
