Integrale und Grenzwerte
|
|
|
- Achim Hartmann
- vor 7 Jahren
- Abrufe
Transkript
1 Prof. Dr. Michael Eisermann Höhere Mathematik 3 WiSe 22/3 Inhalt dieses Kapitels S.2 Kapitel D Integrale und Grenzwerte Then I come along and try differentiating under the integral sign, and often it worked. So I got a great reputation for doing integrals, only because my box of tools was different from everybody else s, and they had tried all their tools on it before giving the problem to me. (ichard Feynman, , Surely ou re Joking, Mr. Feynman!) Vertauschen von Integral und Summe Beispiel und Gegenbeispiel Absolut summierbare Familien und ihre Summe Vertauschung von Integral und Summe 2 Vertauschen von Integral und Grenzwert Punktweise Konvergenz Majorisierte Konvergenz Anwendung auf die Stirling Formel 3 Vertauschen von Integral und Ableitung Parameterabhängige Integrale Kompakte Integrationsbereiche Beliebige Integrationsbereiche Stand. Februar 23, 4:29 Wann vertauschen Integral und Grenzwert? S.2 Vorgehensweise S.22 Überblick Integration einer eihe: Unter welchen Voraussetzungen gilt f k f k? Stetigkeit des Integrals: Unter welchen Voraussetzungen gilt lim f k lim f k? k k Ableiten des Integrals: Unter welchen Voraussetzungen gilt f(x, y) dy f(x, y) dy? Diese echentechniken sind häufig sehr nützlich.! Die Gleichungen gelten leider nicht immer, wie Beispiele zeigen. Es gibt einfache Kriterien. Diese müssen wir kennen und beachten. In Anwendung treten diese Umformungen häufig auf. Leider werden sie oft blind oder nach Gefühl angewendet, oder gar so getan, als gälten sie immer. Das ist nicht richtig, wie wir an Beispielen sehen. Die Gleichungen gelten aber doch häufig genug, um nützlich zu sein, und zahlreiche Beispiele illustrieren die Kraft dieser Methoden. Zur korrekten Anwendung brauchen wir also geeignete Kriterien! Wir wollen daher in diesem Kapitel die Voraussetzungen erläutern und die ersehnten echenregeln ableiten. Als Mahnung zur Sorgfalt illustrieren einfache Gegenbeispiele, wann die Formeln nicht gelten. Wir beginnen mit einer Wiederholung von Summen und eihen, die die Analogie zu Treppenfunktionen und Integralen hervorhebt. Vertauschung von Integral und Summe ist dann eine Folgerung wie der Satz von Fubini zur Vertauschung von Integralen.
2 Beispiel: Integration von Potenzreihen D., S.23 Ein warnendes Gegenbeispiel D., S.24 Zu integrieren sei f : ] ρ, ρ[, gegeben als reelle Potenzreihe f(x) a k x k k k + k + 2 mit Konvergenzradius ρ >. Für die Integralfunktion gilt F (x) x f(t) dt x ( x ) a k t k dt ( ) a k t k dt a k k + xk+ k a k k xk Probe mit HDI: Wir dürfen Potenzreihen termweise ableiten. Die Vertauschung gilt hier dank absoluter Konvergenz der eihe. Dieses nützliche Kriterium wollen wir möglichst allgemein formulieren. Für k N sei f k I [k,k+] I [k+,k+2]. Offenbar gilt f k(x) dx. Auch für f + f ist das Integral Null. Ein warnendes Gegenbeispiel D., S.25 Ein warnendes Gegenbeispiel D., S.26 Graph zu f + f + f 2 : n + n + 2 Graph zu f + f + f 2 + f 3 : Für n N haben wir die Teleskopsumme n f k I [,] I [n+,n+2]. Für n erhalten wir deshalb punktweise Konvergenz gegen f k I [,], das heißt f k (x) I [,] (x) für jedes x. Hier vertauschen eihe und Integral nicht: ( ) ( ) f k (x) dx f k (x) dx. Anschaulich: Masse verschwindet nach Unendlich.
3 Von endlichen zu unendlichen Summen D.2, S.27 echenregeln in [, ] D.2, S.28 Um obigem Problem auf den Grund zu gehen, betrachten wir genauer den Übergang von endlichen Summen zu unendlichen eihen. Zur Wiederholung siehe Kimmerle Stroppel, Analysis,.8.9. Sei I eine Indexmenge, etwa I {,,..., n} oder N oder Z. Sei (a i ) i I eine Familie in, also eine Abbildung a: I. Das heißt, jedem Index i I wird eine reelle Zahl a i zugeordnet. Ist I {i, i 2,..., i n } endlich, so definieren wir die Summe a i : a i + a i2 + + a in. i I Dank Assoziativität und Kommutativität ist diese Summe wohldefiniert, das heißt unabhängig von Klammerung und eihenfolge der Addition. Ziel: Wie kann man unendliche Summen definieren? Da hierbei auch unendliche Werte auftreten können, betrachten wir Summen in [, ]. Wir betrachten die erweiterte Zahlengerade (, +,, <). Die reellen Zahlen (, +,, <) sind ein vollständiger angeordneter Körper. Die Erweiterung um ± macht + zum größten und zum kleinsten Element in (, <). Ein wesentlicher Vorteil ist: Jede Teilmenge M hat ein Supremum und ein Infimum in. Allerdings ist (, +, ) kein Körper; z.b. ist die Addition nicht assoziativ: (+ + ) ( + ). Man muss also aufpassen! Zur Vereinfachung beschränken wir uns auf ([, ], +,, <). Dies ist zwar kein Körper, aber immerhin ein Halbring: Die Addition ist assoziativ und kommutativ. Neutrales Element für die Addition ist. Die üblichen echenreglen gelten also bis auf Inverse! Die Multiplikation ist assoziativ und kommutativ. Neutrales Element für die Multiplikation ist. Die Multiplikation ist distributiv über die Addition. Summation einer Familie in [, ] D.2, S.29 Eigenschaften der Summation in [, ] D.2, S.22 Wir betrachten eine Famile (a i ) i I mit a i [, ] für alle i I. Ist I {i, i 2,..., i n } endlich, so definieren wir die Summe a i : a i + a i2 + + a in. i I Dank Assoziativität und Kommutativität ist diese Summe wohldefiniert, das heißt, unabhängig von Klammerung und eihenfolge der Addition. Im allgemeinen Fall einer beliebigen Indexmenge definieren wir die Summe über i I als Supremum aller endlichen Teilsummen: { } a i : sup a i J I endlich i I i J Eine besondere Summationsreihenfolge wird hier nicht benötigt! Die Summe in [, ] verhält sich genauso wie ein Integral. Normierung: Gilt a i für alle i I {j}, so folgt i I a i a j. Ebenso gelten Linearität, Monotonie, Einschachtelung, Ausschöpfung. Fubini und Transformationssatz für Summen sind enthalten in: Satz DA (Umordnungssatz) Sei (a i ) i I eine Familie in [, ]. Für jede Zerlegung I j J I j gilt a i a i. i I j J i I j Hierbei bedeutet I j J I j eine Zerlegung der Indexmenge I in disjunkte Teilmengen I j I, also I j I k für j k und I j J I j. Der Satz besagt, dass man bei der Summierung in [, ] auf diese Weise beliebig umgruppieren und umordnen darf. Der Umordnungssatz folgt unmittelbar aus der geschickten Konstruktion: Dank Assoziativität und Kommutativität in ([, ], +) gilt die Gleichung für endliche Summen in [, ]. Durch Übergang zum Supremum gilt die Gleichung dann auch für beliebige Familien in [, ]. (Die Ausformulierung des Beweises ist nicht schwer aber länglich. Wir lassen Sie hier aus.) Beispiel: Für jede Familie (a i ) i N mit a i [, ] gilt (a 2k + a 4k+ + a 4k+3 ). i N a i j N(a 2j + a 2j+ ) k N
4 Beispiel: geometrische eihe in [, ] D.2, S.22 Absolut summierbare Familien in D.2, S.222 Sei I N. Für q < und summieren wir (q i ) i N. Es gilt q + q + + q n qn+ q Hieraus folgt die bekannte Summenformel i N q i q q. Wir wollen als nächstes auch negative Summanden zulassen. Wir summieren dann Positiv- und Negativteil getrennt. Zu summieren sei eine Familie (a i ) i I reeller Zahlen a i. Wir zerlegen a i a + i a i mit a ± i max(, ±a i ). Für den Absolutbetrag gilt dann a i a + i + a i. Definition DB Für jede Familie (a i ) i I reeller Zahlen a i gilt a i i I i I a + i + a i. i I Ist dieser Wert endlich, so nennen wir (a i ) i I absolut summierbar. In diesem Falle können wir die Summe von (a i ) i I definieren durch a i : i I i I a + i a i. i I Absolut summierbare Familien in C D.2, S.223 Anwendung: Potenzreihen D.2, S.224 Jede Familie (c i ) i I komplexer Zahlen c i C können wir zerlegen in ealteil a i e c i und Imaginärteil b i Im c i. Hieraus lässt sich c i zusammensetzen gemäß c i a i + ib i. Definition DC Wir nennen (c i ) i I absolut summierbar, wenn i I c i < gilt. In diesem Falle können wir die Summe definieren durch c i : a i + i b i. i I i I i I Satz DD (Majorantenkriterium) Aus c i q i folgt i I c i i I q i dank Monotonie. Ist die zweite Summe endlich, so auch die erste, und (c i ) i I ist absolut summierbar. Satz DE (Majoration durch geometrische eihe) Sei (c k ) k N eine Folge komplexer Zahlen. Sei M und q <. Gilt c k Mq k für alle k N, so ist (c k ) k N absolut summierbar, und c k c k M/( q). k N k N Satz DF (Konvergenzradius einer Potenzreihe) Für jede Potenzreihe a kz k definieren wir den Konvergenzradius ρ : / lim sup k a k. Für z < ρ konvergiert die eihe absolut, für z > ρ divergiert sie. Beweis: Angenommen ρ <. Es gilt a k ρ k M für ein M und alle k N. Für z qρ mit q < folgt a k z k a k ρ k q k Mq k, also k N a kz k M/( q). Beispiel: exp(z) zk /k! konvergiert absolut für alle z C.
5 Der Umordnungssatz D.2, S.225 Der Umordnungssatz D.2, S.226 Satz DG (großer Umordnungssatz) Sei (a i ) i I eine Familie in C. Für jede Zerlegung I j J I j gilt a i a i. i I j J i I j Ist dieser Wert endlich, so ist (a i ) i I absolut summierbar, und es gilt a i a i. i I j J i I j Beweis: Die erste Gleichung ist der obige Umordnungssatz für Familien in [, ]. Für absolut summierbare Familien in folgt die zweite Gleichung aus der ersten durch Zerlegung in Positiv- und Negativteil. Für absolut summierbare Familien in C schließlich folgt die Gleichung durch Zerlegung in eal- und Imaginärteil. Analog zum Transformationssatz für Integrale erhalten wir: Satz DH (kleiner Umordnungssatz) Sei (a i ) i I eine Familie in C. Für jede Bijektion ϕ: J I gilt a i ϕ(j). j J a i I Ist dieser Wert endlich, so ist (a i ) i I absolut summierbar, und es gilt a i a ϕ(j). i I j J Beweis: Der kleine Umordnungssatz folgt aus dem großen mittels I j {ϕ(j)}. Der Umordnungssatz D.2, S.227 Anwendung: komplexe Exponentialfunktion D.2, S.228 Eine Doppelfolge (a ij ) i,j N in C ist eine Abbildung N N C. Jedem Indexpaar (i, j) N N wird eine Zahl a ij C zugeordnet. Analog zum Satz von Fubini für Integrale erhalten wir: Satz DI (Cauchy Umordnungssatz) Für jede Doppelfolge (a ij ) i,j N in C gilt ij (i,j) N N a ij i N j N a ij j N i N a k N i+jk a ij Ist dieser Wert endlich, so ist (a ij ) absolut summierbar, und es gilt a ij a ij a ij (i,j) N N i N j N j N i N k N i+jk Beweis: Der Cauchy Umordnungssatz folgt aus dem großen Umordnungssatz mittels der offensichtlichen Zerlegungen der Indexmenge N N. a ij. Aus der Exponentialreihe folgt die Funktionalgleichung exp(z + w) exp(z) exp(w) für alle z, w C. Dank binomischer Formel und Umordnungssatz gilt nämlich: ( ) ( z k ) w l z k w l exp(z) exp(w) k! l! k! l! n n! n ( n k l ) z k w n k n k+ln n n! (z + w)n exp(z + w). Dies entspricht dem Potenzgesetz, daher die Kurzschreibweise e z : exp(z). Die Funktionalgleichung besagt e z+w e z e w. Aus der Euler Formel e iz cos z + sin z erhält man die Additionstheoreme für sin und cos.
6 Summierbare Folgen D.2, S.229 Summierbare und absolut summierbare Folgen D.2, S.23 Die Indexmenge N {,, 2, 3,... } hat eine besondere Ordnung! Sei (a k ) k N eine Folge in. Wir definieren die Partialsummen s n n a k : a + a + + a n. Falls die Folge (s n ) n N für n konvergiert, so definieren wir a k : lim n n a k. Beispiel: Dank Leibniz Kriterium konvergiert die alternierende eihe ( ) k k Diese eihe konvergiert nicht absolut, denn k N k. Das entspricht absoluter / uneigentlicher Integrierbarkeit [S.36]. Wir haben zwei verschiedene Summationsverfahren, nämlich a k : lim Satz DJ n a k n und k N a k : k N a + k k N Ist (a k ) k N absolut summierbar, so konvergieren beide Summationsverfahren und stimmen überein. Das heißt, es gilt a k k N a k. Für n gilt nämlich n a± k k N a± k, also n a k n n a + k a k k N a + k k N a k k N a k. a k. Gegenbeispiel zur Umordnung D.2, S.23 Gegenbeispiel zur Umordnung D.2, S.232 Absolut konvergente eihen haben viele nützliche Eigenschaften. Leider ist nicht jede konvergente eihe auch absolut konvergent. Man muss dann aufpassen, z.b. gilt der Umordnungssatz nicht mehr! Übung: Sei f : N N definiert durch f(i, i) und f(i, i + ), sowie f(i, j) sonst. Skizze als Matrix: Hier gilt i j f(i, j) und j i Nachrechnen und staunen! Es kommt noch toller... f(i, j) Satz DK (iemannscher Umordnungssatz) Sei n a n konvergent aber nicht absolut konvergent. Zu jeder Zahl r existiert dann eine Umordnung ϕ: N N mit a ϕ(k) r. Als konkretes Beispiel betrachten wir ln(2) n ( ) n n Umordnung nach dem Muster (a 2k + a 4k+ ) + a 4k+3 liefert ( ) ( ) ( ) ln(2) Auch jeder andere Grenzwert lässt sich durch Umordnung herstellen. Fazit: Absolute Konvergenz ist die beste Grundlage.
7 Vertauschung von Summe und Integral Dank Linearität gilt n f k n f k für jedes n N. Nehmen wir zunächst f k : [, ] an. Es gilt dann n f k f k. Hieraus folgt die monotone Konvergenz des Integrals n f k f k. Aus f k folgt die monotone Konvergenz der eihe n f k f k. Für jede Folge messbarer Funktionen f k : [, ] gilt daher f k f k. D.3, S.233 Vertauschung von Summe und Integral Satz DL (absolut konvergente eihen in L ()) Sei (f k ) k N eine Folge messbarer Funktionen f k : C. Dann gilt f k f k. Ist dieser Wert endlich, so ist f k in fast allen Punkten x absolut konvergent, zudem über absolut integrierbar, und es gilt f k f k. D.3, S.234 Die erste Gleichung haben wir zuvor gezeigt. Die Punkte x mit f k(x) + bilden eine Nullmenge N. Für alle x N gilt f k(x) < +, und wir definieren f(x) f k(x) durch die absolut konvergente eihe. Für x N setzen wir f(x). Die zweite Gleichung gilt für f k : [, ]. Sie folgt für reelle Funktionen durch Zerlegung f f + f, und sodann für komplexe Funktionen durch Zerlegung f e f + i Im f. Beispiel: Die Wallis eihe für π/2 D.3, S.235 Fazit: Wann gilt Vertauschbarkeit? D.3, S.236 Wir wollen die Kreiszahl π durch die Wallis eihe darstellen: π 2 2 k 3 5 (2k + ) Zwei raffinierte echnungen: Einerseits gilt dank Substitution π/2 2 sin(t) π/2 2 sin(t) 2 dt 2 sin(t) [ ] π/2 + cos 2 t dt 2 arctan(cos t) π 2. Andererseits gilt dank absoluter Konvergenz der geometrischen eihe: π/2 2 sin(t) π/2 2 sin(t) 2 dt sin(t) dt 2 sin(t)2 π/2 2 k sin(t) 2k+ dt π/2 2 k sin(t) 2k+ dt 2 3 k (2k + ) Letzteres berechnet man rekursiv durch partielle Integration [S.]. Für f f k möchten wir Integral und Summe vertauschen: ( ) f k (x) dx? ( ) f k (x) dx Hierfür haben wir folgende hinreichende Kriterien: Gleichheit gilt für f k (monotone Konvergenz). Gleichheit gilt für f k < bzw. f k <, z.b. für konvergente Potenzreihen, f k (x) a k x k.! Andernfalls ist Vorsicht geboten: Vertauschbarkeit gilt nicht immer! Im folgenden warnenden Beispiel gilt f k f k. Die Konvergenz ist nicht monoton, denn f k hat einen positiven und einen negativen Teil. Zudem gilt f k f n. Unsere einfachen Kriterien lassen also für dieses Beispiel keinen Schluss zu. Wir müssen daher fk und f k getrennt ausrechnen, um sie dann vergleichen zu können.! Diese Kriterien sind hinreichend aber i.a. nicht notwendig [S.257].
8 Punktweise Konvergenz D2., S.237 Punktweise Konvergenz D2., S.238 Definition D2A Eine Funktionenfolge f k : konvergiert punktweise für k gegen eine Funktion f :, wenn f k (x) f(x) für jedes x gilt Beispiel: Für k N sei f k : definiert durch f k (x) e (x k)2. Für jedes x und k + gilt f k (x). Aber für die Integrale gilt lim f k(x) dx lim f k (x) dx π k + k + Die anschauliche Ursache: Die Masse verschwindet nach Unendlich. Gleiches gilt für jede integrierbare Funktion f : n mit f(x) für x, zum Beispiel f I Q für einen endlichen Quader Q, und ihre Verschiebungen f k (x) f(x kv). In vielen echnungen stehen wie vor der Frage: Wie verhalten sich die Integrale f k und f unter punktweiser Konvergenz f k f? Messbarkeit ist unkaputtbar! Sind alle f k messbar und konvergiert f k f punktweise, dann ist auch die Grenzfunktion f messbar. Stetigkeit und Integrierbarkeit hingegen können verloren gehen! Monotone Konvergenz funktioniert! Aus f k f folgt f k Im Allgemeinen folgt aus f k f jedoch nicht f k Typisches Problem: Masse verschwindet nach Unendlich. f. f. Unter welchen Voraussetzungen können wir f k f schließen? Stetigkeit und Integrierbarkeit sind zerbrechlich! D2., S.239 Grenzwert und Integral vertauschen nicht! D2., S.24! Sind alle Funktionen f k stetig bzw. integrierbar, so kann man nicht auf die Stetigkeit bzw. Integrierbarkeit der Grenzfunktion f schließen! k /k Für k sei f k : [, ] definiert durch { k 2 x für x f k (x) k, x für k x. Für jedes x ], ] gilt lim k f k(x) x. Jede der Funktionen f k ist stetig und somit integrierbar. Die Grenzfunktion f(x) x ist nicht stetig und auch nicht integrierbar.! Selbst wenn alle f k und die Grenzfunktion f integrierbar sind, gilt im Allgemeinen nicht die Konvergenz der Integralfolge! r /r r Für r > definieren wir die Dreiecksfunktion { für x r, r : durch r (x) r x für x r. r 2 Es gilt r(x) dx für alle r >. Für jedes x gilt lim r(x) (x) : r { für x, für x. Für die Grenzfunktion gilt (x) dx. Also lim r r (x) dx lim r r(x) dx. Die Ursache auch hier: Die Masse verschwindet nach Unendlich.
9 Grenzwert und Integral vertauschen nicht! D2., S.24 Dreiecksfunktionen ( r ) r D2.2, S.242 /r 2 r r r Für jedes x gilt lim r(x). r Die Grenzfunktion hat daher Integral. Also r (x) dx lim r lim r(x) dx. r Die Ursache auch hier: Die Masse verschwindet nach Unendlich Hüllfunktion zu ( r ) r D2.2, S.243 Majorisierte Integrierbarkeit: Definition D2.2, S r h(x) 4 x Definition D2B (majorisiert integrierbare Familien) Sei (f i ) i I eine Familie messbarer Funktionen f i :. Wir nennen h: [, ] Majorante, wenn f i h für alle i I gilt. Die Familie heißt majorisiert integrierbar, wenn eine integrierbare Majorante existiert, also h: [, ] mit f i h und h < Bemerkung: Dank f i h gilt f i h <, also ist jede Funktion f i integrierbar. Die Funktion h ist eine Majorante für die gesamte Familie (f i ) i I : Ihre Integrierbarkeit garantiert anschaulich, dass keine Masse nach Unendlich verschwindet. Angenommen, g sup i I f i ist messbar. Das ist immer der Fall, wenn I abzählbar ist und alle f i messbar sind. In diesem Fall ist g die kleinste Majorante, auch Hüllfunktion genannt, und die Familie (f i ) i I ist genau dann majorisiert integrierbar, wenn g < gilt. Beispiel: Zu ( r ) r > ist h(x) 4 x eine Majorante. Dies ist die kleinste Majorante, die sog. Hüllfunktion, denn 2 x (x) h(x). Die Familie ( r ) r > ist nicht majorisiert integrierbar. Ebensowenig die Familie (f k ) k N der wandernden Glockenkurven.
10 Majorisierte Integrierbarkeit: Beispiel D2.2, S.245 Majorisierte Integrierbarkeit: Beispiel D2.2, S.246 f f 4 f 9 f 6 Die Funktionen f n scheinen zu konvergieren... Wogegen? Aufgabe: Für jedes t und n gilt f n (t) e t2 /2. Genauer: f n (t) e t2 /2 für t, und f n (t) e t2 /2 für t Wir untersuchen die Funktionenfolge f n : mit ( ( ( f n (t) exp n ln + t ) t ) ) n n Hieraus gewinnen wir die Hüllfunktion h(t) : sup f n (t) n { t e t für t, e t2 /2 für t. Diese Funktion h: ist absolut integrierbar. Also ist die Familie (f n ) n N majorisiert integrierbar. für t > n, sowie f n (t) für t n. Majorisierte Integrierbarkeit: Beispiel D2.2, S.247 Lösung Majorisierte Integrierbarkeit: Beispiel D2.2, S.248 Lösung Lösung: Für < s < nutzen wir die Potenzreihenentwicklung ln( + s) s s2 2 + s3 3 s Für s t/ n mit n < t < n gilt also ( ( n ln + t ) t ) t2 n n 2 + t3 3 n t4 4n +... Für n konvergiert dies gegen t 2 /2, also f n (t) e t2 /2. Per Kurvendiskussion findet man genauer: Für t gilt f n (t) e t2 /2. Für t gilt f n (t) e t2 /2. ln( + s) s ln( + s) s s 2 s
11 Der Satz von der majorisierten Konvergenz Satz D2C (majorisierte Konvergenz) Sei f, f, f 2,... : eine Folge messbarer Funktionen. D2.2, S.249 Angenommen f n konvergiert punktweise gegen f :. 2 Es existiert eine Majorante h: mit f n h und h <. Dann ist f integrierbar und f n f, somit f n f. Die integrierbare Mojarante verhindert, dass die Funktionenfolge f n nach Unendlich entkommt. In den obigen Gegenbeispielen war genau das die Ursache des Problems! Unter dieser Vorsichtsmaßnahme gilt also die schöne Formel lim f n (x) dx lim f n(x) dx f(x) dx. n n Dies ist eine starke und nützliche Stetigkeitseigenschaft des Integrals! Sei h: [, ] integrierbar. Auf der Menge aller messbaren Funktion f : mit f h ist die Abbildung f f stetig, in dem Sinne, dass aus f n f stets f n f folgt.! Die majorisierte Integrierbarkeit ist hier wesentlich. Beweis der majorisierten Konvergenz Wir beginnen wir folgender Betragsabschätzung: f n f f n f f n f Wir zeigen nun, dass die rechte Seite f n f für n gegen Null strebt. Die folgende echnung ist etwas technisch, aber jeder einzelne Schritt ist leicht. Lemma von Fatou: Sind f n : [, ] messbar, dann gilt lim inf f n lim inf f n. Beweis des Lemmas: Für g n : inf k n f k gilt g n f n und g n g lim inf f n, also MK! lim inf f n lim g n lim g n lim inf g n lim inf f n. Beweis des Satzes der majorisierten Konvergenz: D2.2, S.25 Aus f n h folgt f h (fast überall), somit f f n f + f n 2h. Mit Fatou folgt: ( ) ( ) 2h lim inf 2h f n f lim inf 2h f n f ( ) lim inf 2h f n f 2h lim sup f n f Da der Wert 2h endlich ist, können wir ihn auf beiden Seiten subtrahieren. Wir erhalten lim sup f n f. Mit f n f folgt lim f n f. Nochmal Integral und Summe Sei (g k ) k N eine Folge messbarer Funktionen g k : mit g k g k <. Dank majorisierter Konvergenz erhalten wir erneut g k g k. Für n gilt (fast überall) punktweise Konvergenz n f n g k f g k. Zudem ist h g k eine Majorante für (f n ) n N, und somit n f n f g k. g k D2.2, S.25 Nochmal Integral und Summe Die absolute Konvergenz g k < ist hinreichend aber nicht notwendig für die Gleichung g k g k. Als einfaches und erhellendes Beispiel berechnen wir: ( ) ( ) k e (k+)x dx ( ) k k + ln(2) ( ) ( ) k e (k+)x e x dx ln(2) + e x Absolute Konvergenz gilt hier nicht: ( ) e (k+)x dx ( ) e (k+)x dx k + + e x + e x D2.2, S.252 Doch gilt majorisierte Konvergenz, denn n ( )k e (k+)x e x.
12 Fazit: Wann gilt Vertauschbarkeit? D2.2, S.253 Anwendung: Stirling Formel D2.3, S.254 Für f n f möchten wir Integral und Limes vertauschen:? f n (x) dx lim f n(x) dx n lim n Dies ist eine starke und nützliche Stetigkeitseigenschaft des Integrals! Hierfür haben wir folgende Kriterien: Gleichheit gilt bei monotoner Konvergenz f n f, bei majorisierter Konvergenz f n f mit f n h und h <, insbesondere, wenn vol() < und f n M für alle n N. Dies verhindert, dass Masse nach Unendlich verschwindet.! Andernfalls ist Vorsicht geboten: Vertauschbarkeit gilt nicht immer! 7 n! 2 3 n Anwendung: Stirling Formel D2.3, S.255 Anwendung: Stirling Formel D2.3, S.256 Aufgabe: Man berechne n!/ n(n/e) n für n. Lösung: Wir wissen bereits n! x n e x dx. Im Vergleich zu n ( ) n n e erhalten wir n! ( ( ( x n(n/e) n exp n ln + n) x ) ) dx n n Substitution x n t + n bedeutet dx n dt und x n + t n, also n! ( ( ( n(n/e) n exp n ln + t ) t ) ) dt n n n Zu integrieren ist hier die Funktion ( ( ( f n (t) exp n ln + t ) t ) ) I n n [ n,+ [ (t). Uns interessiert das Verhalten für n. Wir haben oben die punktweise Konvergenz gefunden: f n (t) e t2 /2. Zudem ist die Familie (f n ) n N majorisiert integrierbar. Wir dürfen also Limes und Integral vertauschen: f n (t) dt lim f n(t) dt e t2 /2 dt 2π n lim n Satz D2D (Stirling Formel) Für n gilt n! n(n/e) n f n (t) dt e t2 /2 dt 2π Damit haben wir schließlich das Wachstumsverhalten der Fakultät n n! durch die Stirling Formel als asymptotische Näherungsformel ausdrücken können [S.].
13 Parameterabhängige Integrale D3., S.257 Ableitung von Parameterintegralen (echtecke) D3.2, S.258 Ein parameterabhängiges Integral ist von der Form F : X C mit F (x) f(x, y) dy. Beispiele: Wir kennen bereits die Gamma Funktion Γ: > > mit Γ(x) y y x e y dy. Die Fourier Transformierte einer Funktion f : C ist f : C mit f(x) 2π + y f(y) e ixy dy. Das Newton Potential einer Massenverteilung ρ: 3 ist F : 3 ρ(y) mit F (x) y x dy. y 3 Ist F stetig? differenzierbar? Wann gilt Ableitung unter dem Integral? f(x, y) dy? f(x, y) dy Für Integrale über echtecken erhalten wir folgenden Spezialfall: Satz D3A (Ableitungsregel für Integrale über echtecken) Sei f : [x, x ] [y, y ] stetig. Dann ist die Funktion F : [x, x ] mit F (x) : y y f(x, y) dy stetig. Ist zudem f stetig diff bar bezüglich x, so auch F, und es gilt Kurzum: F (x) y y d y y f(x, y) dy dx y y f(x, y) dy. x f(x, y) dy x Statt [x, x ] können wir offene Mengen X p betrachten. Statt [y, y ] können wir über kompakte q integrieren. Ableitung von Parameterintegralen (kompakt) D3.2, S.259 Ableitung von Parameterintegralen (kompakt) D3.2, S.26 Wann dürfen wir unter dem Integral ableiten? Wir brauchen praktische Kriterien! Der folgende Satz gibt ein besonders einfaches Kriterium für den wichtigen Spezialfall, dass der Integrationsbereich kompakt ist. Wir heben diesen besonders schönen Fall hervor. Satz D3B (Ableitungsregel für Integrale über Kompakta) Sei X p offen, q kompakt, f : X stetig. Dann ist F : X mit F (x) : f(x, y) dy stetig. Ist zudem f stetig diff bar bezüglich x j, so auch F, und es gilt F (x) f(x, y) dy. Kurzum: f(x, y) dy f(x, y) dy! Kompaktheit von und Stetigkeit von f bzw. f sind wesentlich! Beweis: Stetigkeit gilt dank majorisierter Konvergenz. Sei p und x [a, b] X. Dank HDI und Fubini berechnen wir F (x) F (a) lin f(x, y) f(a, y) dy x HDI f(t, y) dt dy ta t Fubini f(t, y) d(t, y) t Fubini [a,x] x ta f(t, y) dy dt t Nochmals dank HDI und Stetigkeit folgt hieraus F (x) HDI f(x, y) dy. x : Die Vertauschung von Ableitung und Integral führen wir dank HDI zurück auf die Vertauschung von zwei Integralen. Der Satz von Fubini lässt sich anwenden, da f stetig ist und somit absolut integrierbar auf [a, b]. Der HDI lässt sich anwenden dank Stetigkeit.
14 Anwendung: Newton Potential D3.2, S.26 Anwendung: Newton Potential D3.2, S.262 Ergänzung Das Newton Potential einer Masse m im Punkt y 3 ist F : 3 {y} mit F (x) m y x (bis auf Konstanten&Vorzeichen). Das zugehörige Gravitationsfeld ist f : 3 {y} 3 mit f(x) grad F (x) m y x y x 3. Für K 3 kompakt und Dichte ρ: K haben wir entsprechend F : 3 ρ(y) K mit F (x) y x dy. Das zugehörige Gravitationsfeld ist dann f : 3 K 3 mit f(x) grad F (x) K K y x ρ(y) dy. y x 3 Übung: Man prüfe die echnung für grad F sorgfältig nach. Aus f grad F folgt für die Divergenz div f f x + f 2 x 2 + f 3 x 3 2 F x 2 F. + 2 F x F x 2 3 Man nennt div grad den Laplace Operator. x 2 x 2 2 x 2 3 Eine Funktion F mit der Eigenschaft F heißt harmonisch. Übung: Das Newton Potential F : 3 {y} mit F (x) m y x ist harmonisch, ebenso F : 3 K mit ρ(y) F (x) y x dy. K Leibniz egel für Integrale über Normalbereiche D3.2, S.263 Ergänzung Leibniz egel für Integrale über Normalbereiche D3.2, S.264 Ergänzung Satz D3C (Leibniz egel für Integrale über Normalbereiche) Sei X p offen und g, h: X stetig mit g h sowie B { (x, y) p+ x X, g(x) y h(x) }. Sei f : B stetig. Dann ist die Funktion F : X mit F (x) : h(x) g(x) f(x, y) dy stetig. Sind zudem f, g, h stetig diff bar bezüglich x, so auch F, und F h(x) f (x) (x, y) dy f(x, g(x)) g (x) + f(x, h(x)) h (x). g(x) Der HDI ist ein Spezialfall: d dx x a f(y) dy f(x). Wie zuvor dürfen wir unter dem Integral ableiten, jetzt aber kommen zusätzlich die Ableitungen der Intervallgrenzen hinzu. Der Einfachheit halber denken wir uns f fortgesetzt zu einer stetig differenzierbaren Funktion f : X. Beweis: Für x X und u, v betrachten wir die Funktion G(x, u, v) v u f(x, y) dy Diese ist stetig in x, u, v. Also ist F (x) G(x, g(x), h(x)) stetig in x. Für die Ableitung finden wir dank Kettenregel und HDI: F (x) G x h(x) g(x) (x) + G u g (x) + G v h (x) f (x, y) dy f(x, g(x)) g (x) + (x, h(x)) h (x)f
15 Gegenbeispiel zur Stetigkeit des Integrals D3.2, S.265 Nachrechnen des Gegenbeispiels D3.2, S.266 Lösung Für g : mit g(t) e t2 haben wir g(t) dt π gezeigt. Die Funktion f : mit f(x, y) x g(xy) ist stetig. f(x, y) xe (xy)2 y Das parameterabhängige Integral F (x) f(x, y) dy ist nicht stetig: π für x >, F (x) für x, π für x <. Die Funktion g(t) e t2 dient als schönes und konkretes Beispiel. Das Phänomen besteht jedoch für jede stetige Funktion g :. Das Integral a : g(t) dt erfülle für das Folgende < a <. Die Funktion f : mit f(x, y) x g(xy) ist stetig. Dennoch ist das Parameterintegral F (x) f(x, y) dy unstetig: F (x) f(x, y) dy x g(xy) dy sign(x) g(xy) x dy Substitution t xy und dt x dy: sign(x) g(t) dt sign(x) a Das Umklappen des Vorzeichens ist in der Skizze gut zu erkennen. Gegenbeispiel zur Ableitung unter dem Integral D3.2, S.267 Nachrechnen des Gegenbeispiels D3.2, S.268 Lösung Für g : mit g(t) e t2 haben wir g(t) dt π gezeigt. Die Funktion f : mit f(x, y) x x g(xy) ist stetig diff bar. f(x, y) x x e (xy)2 Wir finden F (x) f(x, y) dy x π, also F (x) π, aber { π f für x, (x, y) dy x für x. Aufgabe: Man prüfe diese echnung sorgfältig nach. y Lösung: Dank Substitution t xy und dt x dy gilt F (x) f(x, y) dy x x g(xy) dy x g(t) dt x π. Also F (x) π. Ableiten unter dem Integral liefert f(x, y) dy 2 x g(xy) + xy x g (xy) dy. x Das verschwindet für x. Für x substituieren wir erneut: f(x, y) dy 2 x g(xy) + xy x g (xy) dy x 2 g(t) dt 2 t 2 g(t) dt 2 π π π (Siehe unten, Momente der Normalverteilung.) In x gilt also d f(x, y) dy π f(x, y) dy. dx x
16 Ableitung von Parameterintegralen (allgemein) D3.3, S.269 Stetigkeit von Parameterintegralen (allgemein) D3.3, S.27 Im den vorangegangenen Sätzen war der Integrationsbereich kompakt. Was tun, wenn über einen nicht-kompakten Bereich integriert wird, etwa oder n? Wie zuvor müssen wir verhindern, dass Masse nach Unendlich verschwindet. Das gelingt am besten wie folgt: Satz D3D (Ableitung von Parameterintegralen) Sei f : X mit X p offen und q. Ist für jedes x X die Abbildung y f(x, y) über integrierbar, so erhalten wir F : X mit F (x) : f(x, y) dy. Ist f bezüglich x stetig und majorisiert int bar über, also f(x, y) h(y) mit h(y) dy <, so ist F stetig. 2 f Ist : X stetig bezüglich x j und majorisiert int bar über, so ist auch F stetig diff bar bezüglich x j, und es gilt F (x) f(x, y) dy. Ableitung von Parameterintegralen (allgemein) Sei p und x [a, b] X. F (x) F (a) lin f(x, y) f(a, y) dy x HDI f(t, y) dt dy ta t Fubini f(t, y) d(t, y) t Fubini [a,x] x ta f(t, y) dy dt t Nochmals dank HDI und Stetigkeit folgt hieraus F (x) HDI f(x, y) dy. x D3.3, S.27 : Die Vertauschung von Ableitung und Integral führen wir dank HDI zurück auf die Vertauschung von zwei Integralen. Der Satz von Fubini lässt sich hier anwenden, da f majorisiert integrierbar ist und somit absolut integrierbar auf [a, b]. Die Stetigkeit wird im letzten Schritt für den HDI gebraucht! Wir rechnen als erstes die Stetigkeit von F nach: Für x a in X gilt lim F (x) lim f(x, y) dy x a x a () (2) lim f(x, y) dy f(a, y) dy F (a) x a : Man sieht hieraus, dass für die Stetigkeit von F im Punkt a X genügen: () Für alle x X, oder zumindest alle x in einer Umgebung von a, ist die Abbildung f(x, ): : y f(x, y) majorisiert integrierbar. (2) Für jedes y ist die Abbildung f(, y): X : x f(x, y) in a stetig. Das bedeutet lim x a f(x, y) f(a, y) für alle x a und y. Diese Bedingungen sind automatisch erfüllt, wenn f : X stetig und kompakt ist: Als Majorante wählen wir die Konstante M sup { f(x, y) x B(a, r), y }. Hier ist B(a, r) X der kompakte Ball mit Mittelpunkt a und adius < r <. Im zweiten Teil leiten wir bezüglich x j ab und halten dabei x,..., x j, x j+,..., x p fest. Wir fordern dann die Bedingungen () und (2) für die Ableitung f : X. Zur einfacheren Schreibweise reicht es, den Fall einer Variablen zu betrachten, also p. Ableitung von Parameterintegralen (allgemein) Als alternativen Beweis der Ableitungsformel weisen wir folgende Gleichungen nach: F (x) () F (x + he j ) F (x) lim h h (2) f(x + he j, y) f(x, y) lim h (3) h dy f(x + he j, y) f(x, y) lim dy (4) h h f(x, y) dy Gleichung () und (4) ist die Definition der partiellen Ableitung, (2) gilt dank Linearität des Integrals, also bleibt (3) zu zeigen. Dank der vorausgesetzten majorisierten Integrierbarkeit existiert eine Funktion h: [, ] mit h < und f(x, y) h(y). x Nach dem (eindimensionalen) Mittelwertsatz der Differentialrechnung gilt f(x + he j, y) f(x, y) h f (x + ηe j, y) für ein η [, h]. Durch Übergang zum Betrag folgt hieraus f(x + he j, y) f(x, y) h f (x + ηe j, y) h(y). Somit gilt (3) dank majorisierter Konvergenz. D3.3, S.272
17 Anwendung: Gamma Funktion D3.3, S.273 Anwendung: Gamma Funktion D3.3, S.274 Aufgabe: Durch Ableiten unter dem Integral berechne man (erneut) x n e x dx n! Diese Gleichung haben wir bereits durch partielle Integration gewonnen [S.24]. Das war auch nicht wirklich schwierig, aber doch etwas mühsamer. Differenzieren ist leichter. Lösung: Für t > betrachten wir das Integral e tx dx. Integriert wird hier über x, wobei t ein fester Parameter ist: e tx dx [ e tx t ] t. Die Ableitung unter dem Integral xe tx ist majorisiert integrierbar: Für < t < t gilt xe tx xe t x, und letzteres ist integrierbar. Wir dürfen daher unter dem Integral nach t ableiten: xe tx dx t 2, also Nochmaliges Ableiten nach t liefert x 2 e tx dx 2 t 3, also Nochmaliges Ableiten nach t liefert x 3 e tx dx 3! t 4, Per Induktion erhalten wir: also x n e tx dx n! t n+ xe tx dx t 2. x 2 e tx dx 2 t 3. x 3 e tx dx 3! t 4. Anwendung: Momente der Normalverteilung D3.3, S.275 Anwendung: Momente der Normalverteilung D3.3, S.276 Aufgabe: Durch Ableiten unter dem Integral berechne man { x n e x2 /2 3 5 (n ) falls n gerade, dx 2π falls n ungerade. Die Funktion ϕ(x) e x2 /2 / 2π ist die Dichte der Standardnormalverteilung, die in der Wahrscheinlichkeitsrechnung eine zentrale olle spielt. Das Integral über xϕ(x) ist ihr Mittelwert (Schwerpunkt), hier aus Symmetriegründen. Das Integral über x 2 ϕ(x) ist ihre Varianz (Trägheitsmoment). Allgemein nennt man das Integral über x n ϕ(x) das n te Moment. Lösung: Wir wissen bereits e y2 dy π. Substitution y x t/2 mit t > und dy dx t/2 ergibt e tx2 /2 dx t 2 2π. Wir dürfen unter dem Integral nach t ableiten und erhalten x2 2 e tx2 /2 dx 2 t 3 2 2π, also x 2 e tx2 /2 dx t 3 2 2π. Nochmaliges Ableiten nach t liefert x4 2 e tx2 /2 dx 3 2 t 5 2 2π, also x 4 e tx2 /2 dx 3 t 5 2 2π. Nochmaliges Ableiten nach t liefert x 6 e tx2 /2 dx 3 5 t 7 2 2π. Dieses Muster setzt sich fort. Per Induktion erhalten wir x 2k e tx2 /2 dx 3 5 (2k ) t 2k+ 2 2π.
18 Anwendung: Ein erstes Fourier Integral D3.3, S.277 Anwendung: Ein erstes Fourier Integral D3.3, S.278 Aufgabe: Man berechne das parameterabhängige Integral F : mit F (x) + y x 4 e y2 cos(xy) dy. e y2 cos(xy) x Existiert das Integral für jedes x? Ja, denn e y2 cos(xy) e y2. Ist F stetig? Ja, denn e y2 cos(xy) ist bzgl. y majorisiert integrierbar. Ist F differenzierbar? Ja, dank majorisierter Int barkeit der Ableitung: f e x y 2 ( y) sin(xy) y e y2. Fazit: Wann gilt Vertauschbarkeit? y S.279 Lösung: Ableiten unter dem Integral und partielle Integration: + F (x) d e y2 cos(xy) dy dx y [ + sin(xy)] 2 e y2 y 2 + y + y Wir kommen so auf die Differentialgleichung F (x) 2 x F (x). Diese wird gelöst durch F (x) c e x2 /4 mit c. e y2 ( y) sin(xy) dy e y2 x cos(xy) dy x 2 F (x). Wir kennen zudem den Anfangswert F () π. Daraus folgt F (x) πe x2 /4. Man rechnet leicht nach, dass u(x) c e x2 /4 die Gleichung u (x) x u(x) erfüllt. 2 Wir werden später sehen, dass dies wirklich alle Lösungen der Differentialgleichung sind. Anders gesagt, der Anfangswert u() legt die Lösung eindeutig fest, hier u(x) πe x2 /4. Fazit: Wann gilt Vertauschbarkeit? S.28 Sei f : X mit X p offen und q. Ist für jedes x X die Abbildung y f(x, y) über integrierbar, so erhalten wir F : X mit F (x) : f(x, y) dy. Für die Stetigkeit von F haben wir folgende Kriterien: Stetigkeit gilt, wenn f stetig und kompakt ist, oder allgemeiner, wenn f bezüglich x stetig ist und majorisiert integrierbar über. In diesem Fall gilt die schöne Formel lim f(x, y) dy lim f(x, y) dy x x x x f(x, y) dy.! Andernfalls ist Vorsicht geboten: Stetigkeit gilt nicht immer! Wir wollen unter dem Integral ableiten gemäß? F (x) f(x, y) dy F (x) f (x, y) dy Für die Gültigkeit dieser Gleichung haben wir folgende Kriterien: Sie gilt, wenn f stetig und kompakt ist, oder allgemeiner, wenn f bezüglich x j stetig ist und majorisiert int bar über. In diesem Fall gilt die schöne Formel f(x, y) dy f(x, y) dy.! Andernfalls ist Vorsicht geboten: Vertauschbarkeit gilt nicht immer!
Kapitel C. Integrale und Grenzwerte
 Kapitel C Integrale und Grenzwerte Inhalt dieses Kapitels C000 1 Der Satz von Fubini 2 Der Transformationssatz 1 Vertauschen von Integral und eihe 2 Vertauschen von Integral und Limes 3 Vertauschen von
Kapitel C Integrale und Grenzwerte Inhalt dieses Kapitels C000 1 Der Satz von Fubini 2 Der Transformationssatz 1 Vertauschen von Integral und eihe 2 Vertauschen von Integral und Limes 3 Vertauschen von
Integrale und Grenzwerte
 Prof. Dr. Michael Eisermann Höhere Mathematik 3 (vertieft) Kapitel D Integrale und Grenzwerte h ε δ 0 k ε δ 0 Then I come along and try differentiating under the integral sign, and often it worked. So
Prof. Dr. Michael Eisermann Höhere Mathematik 3 (vertieft) Kapitel D Integrale und Grenzwerte h ε δ 0 k ε δ 0 Then I come along and try differentiating under the integral sign, and often it worked. So
Integrale und Grenzwerte
 Prof. Dr. Michael Eisermann Höhere Mathematik 3 (vertieft) Kapitel D Integrale und Grenzwerte h ε δ 0 k ε δ 0 Then I come along and try differentiating under the integral sign, and often it worked. So
Prof. Dr. Michael Eisermann Höhere Mathematik 3 (vertieft) Kapitel D Integrale und Grenzwerte h ε δ 0 k ε δ 0 Then I come along and try differentiating under the integral sign, and often it worked. So
Integrale und Grenzwerte
 Prof. Dr. Michael Eisermann Höhere Mathematik 3 (vertieft) Kapitel D Integrale und Grenzwerte h ε δ k ε δ Then I come along and try differentiating under the integral sign, and often it worked. So I got
Prof. Dr. Michael Eisermann Höhere Mathematik 3 (vertieft) Kapitel D Integrale und Grenzwerte h ε δ k ε δ Then I come along and try differentiating under the integral sign, and often it worked. So I got
Mehrdimensionale Integration
 Kapitel C Mehrdimensionale Integration h s r h h r h r Inhalt dieses Kapitels C000 1 Der Satz von Fubini 3 Aufgaben und Anwendungen 1 Vertauschen von Integral und Reihe Mehrdimensionale Integration #Der
Kapitel C Mehrdimensionale Integration h s r h h r h r Inhalt dieses Kapitels C000 1 Der Satz von Fubini 3 Aufgaben und Anwendungen 1 Vertauschen von Integral und Reihe Mehrdimensionale Integration #Der
3 Reihen. 3.1 Konvergenz und Divergenz. Die Eindeutigkeit nach Satz 13 ergibt schließlich (5). (6) folgt aus (2) und (1) wegen. 1 a +log ba.
 Die Eindeutigkeit nach Satz 3 ergibt schließlich (5). (6) folgt aus (2) und () wegen Aussage (7) ergibt sich aus () und (6). 0 = log b = log b ( a a) = log b a +log ba. 3 Reihen 3. Konvergenz und Divergenz
Die Eindeutigkeit nach Satz 3 ergibt schließlich (5). (6) folgt aus (2) und () wegen Aussage (7) ergibt sich aus () und (6). 0 = log b = log b ( a a) = log b a +log ba. 3 Reihen 3. Konvergenz und Divergenz
1 Reihen von Zahlen. Inhalt:
 5 Kapitel 3 Reihen Reihen von Zahlen Inhalt: Konvergenz und Divergenz von Reihen reeller oder komplexer Zahlen, geometrische Reihe, harmonische Reihe, alternierende Reihen. Cauchy-Kriterium, absolute Konvergenz,
5 Kapitel 3 Reihen Reihen von Zahlen Inhalt: Konvergenz und Divergenz von Reihen reeller oder komplexer Zahlen, geometrische Reihe, harmonische Reihe, alternierende Reihen. Cauchy-Kriterium, absolute Konvergenz,
Kapitel 4. Reihen 4.1. Definition und Beispiele
 Kapitel 4. Reihen 4.1. Definition und Beispiele Ist (a n ) eine Folge von Zahlen, so heißt der formale Ausdruck a ν = a 0 + a 1 + a 2 +... eine Reihe; die einzelnen a ν sind die Glieder dieser Reihe. Um
Kapitel 4. Reihen 4.1. Definition und Beispiele Ist (a n ) eine Folge von Zahlen, so heißt der formale Ausdruck a ν = a 0 + a 1 + a 2 +... eine Reihe; die einzelnen a ν sind die Glieder dieser Reihe. Um
Konvergenz von Folgen
 6 Konvergenz von Folgen Definition 6.1 Eine Folge in C (oder R) ist eine Abbildung f : N C (oder R). Schreibweise: (a n ) n N, (a n ), a 1, a 2... wobei a n = f(n). Beispiele: 1) (1 + 2 n ) n N, 3 2, 5
6 Konvergenz von Folgen Definition 6.1 Eine Folge in C (oder R) ist eine Abbildung f : N C (oder R). Schreibweise: (a n ) n N, (a n ), a 1, a 2... wobei a n = f(n). Beispiele: 1) (1 + 2 n ) n N, 3 2, 5
INGENIEURMATHEMATIK. 8. Reihen. Sommersemester Prof. Dr. Gunar Matthies
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
Analysis I. 3. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 3. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine Abbildung F von einer Menge L in eine
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 3. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine Abbildung F von einer Menge L in eine
Ferienkurs Analysis 1, SoSe Unendliche Reihen. Florian Beye August 15, 2008
 Ferienkurs Analysis 1, SoSe 2008 Unendliche Reihen Florian Beye August 15, 2008 1 Reihen und deren Konvergenz Definition 1.1. Eine reelle bzw. komplexe Reihe ist eine unendliche Summe über die Glieder
Ferienkurs Analysis 1, SoSe 2008 Unendliche Reihen Florian Beye August 15, 2008 1 Reihen und deren Konvergenz Definition 1.1. Eine reelle bzw. komplexe Reihe ist eine unendliche Summe über die Glieder
Mathematik I. Vorlesung 25. Der große Umordnungssatz
 Prof. Dr. H. Brenner Osnabrück WS 009/010 Mathematik I Vorlesung 5 Der große Umordnungssatz Satz 5.1. (Großer Umordnungssatz) Es sei a i, i I, eine summierbare Familie von komplexen Zahlen mit der Summe
Prof. Dr. H. Brenner Osnabrück WS 009/010 Mathematik I Vorlesung 5 Der große Umordnungssatz Satz 5.1. (Großer Umordnungssatz) Es sei a i, i I, eine summierbare Familie von komplexen Zahlen mit der Summe
Folgen und Reihen. Thomas Blasi
 Folgen und Reihen Thomas Blasi 02.03.2009 Inhaltsverzeichnis Folgen und Grenzwerte 2. Definitionen und Bemerkungen............................. 2.2 Konvergenz und Beschränktheit.............................
Folgen und Reihen Thomas Blasi 02.03.2009 Inhaltsverzeichnis Folgen und Grenzwerte 2. Definitionen und Bemerkungen............................. 2.2 Konvergenz und Beschränktheit.............................
Reihen, Exponentialfunktion Vorlesung
 Reihen, Exponentialfunktion Vorlesung Marcus Jung 5.03.20 Inhaltsverzeichnis Inhaltsverzeichnis Reihen 3. Denition.................................... 3.2 Konvergenzkriterien für Reihen........................
Reihen, Exponentialfunktion Vorlesung Marcus Jung 5.03.20 Inhaltsverzeichnis Inhaltsverzeichnis Reihen 3. Denition.................................... 3.2 Konvergenzkriterien für Reihen........................
Analysis I. 6. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 6. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine Relation zwischen den Mengen X und Y.
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 6. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine Relation zwischen den Mengen X und Y.
2 Folgen und Reihen. 2.1 Folgen in C Konvergenz von Folgen. := f(n)
 2 Folgen und Reihen 2.1 Folgen in C 2.1.1 Konvergenz von Folgen Eine Folge komplexer Zahlen ist eine Funktion f : N C. Mit a n schreibt man (a n ) n=1, (a n ) oder auch a 1, a 2,.... := f(n) (a n ) heißt
2 Folgen und Reihen 2.1 Folgen in C 2.1.1 Konvergenz von Folgen Eine Folge komplexer Zahlen ist eine Funktion f : N C. Mit a n schreibt man (a n ) n=1, (a n ) oder auch a 1, a 2,.... := f(n) (a n ) heißt
SS 2016 Höhere Mathematik für s Studium der Physik 21. Juli Probeklausur. Die Antworten zu den jeweiligen Fragen sind in blauer Farbe notiert.
 SS 6 Höhere Mathematik für s Studium der Physik. Juli 6 Probeklausur Die Antworten zu den jeweiligen Fragen sind in blauer Farbe notiert. Fragen Sei (X, d) ein metrischer Raum. Beantworten Sie die nachfolgenden
SS 6 Höhere Mathematik für s Studium der Physik. Juli 6 Probeklausur Die Antworten zu den jeweiligen Fragen sind in blauer Farbe notiert. Fragen Sei (X, d) ein metrischer Raum. Beantworten Sie die nachfolgenden
Vorlesungsprüfung Differential- und Integralrechnung (PHY.C30) Fragenkatalog
 Vorlesungsprüfung Differential- und Integralrechnung (PHY.C30) Fragenkatalog Im folgenden finden Sie eine Liste von typischen Prüfungsfragen für die Vorlesungsprüfung Differential- und Integralrechnung
Vorlesungsprüfung Differential- und Integralrechnung (PHY.C30) Fragenkatalog Im folgenden finden Sie eine Liste von typischen Prüfungsfragen für die Vorlesungsprüfung Differential- und Integralrechnung
Übungsklausur Höhere Mathematik I für die Fachrichtung Physik
 Karlsruher Institut für Technologie (KIT) Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning WS /3 6..3 Übungsklausur Höhere Mathematik I für die Fachrichtung Physik Aufgabe ((3++5) Punkte)
Karlsruher Institut für Technologie (KIT) Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning WS /3 6..3 Übungsklausur Höhere Mathematik I für die Fachrichtung Physik Aufgabe ((3++5) Punkte)
4 Reihen und Finanzmathematik
 4 Reihen und Finanzmathematik 4. Reihen Aus Folgen lassen sich durch Aufaddieren weitere Folgen konstruieren. Das sind die sogenannten Reihen, sie spielen in der Finanzmathematik eine wichtige Rolle. Sei
4 Reihen und Finanzmathematik 4. Reihen Aus Folgen lassen sich durch Aufaddieren weitere Folgen konstruieren. Das sind die sogenannten Reihen, sie spielen in der Finanzmathematik eine wichtige Rolle. Sei
1.1 Vorbemerkung: Konvergenz von Reihen. g = lim. n=0. n=0 a n sei konvergent und schreibt. a n = g. (2) n=0
 1 Taylor-Entwicklung 1.1 Vorbemerkung: Konvergenz von Reihen Gegeben sei eine unendliche Folge a 0,a 1,a,... reeller Zahlen a n R. Hat der Grenzwert g = lim k a n (1) einen endlichen Wert g R, so sagt
1 Taylor-Entwicklung 1.1 Vorbemerkung: Konvergenz von Reihen Gegeben sei eine unendliche Folge a 0,a 1,a,... reeller Zahlen a n R. Hat der Grenzwert g = lim k a n (1) einen endlichen Wert g R, so sagt
Vorlesung Analysis I WS 07/08
 Vorlesung Analysis I WS 07/08 Erich Ossa Vorläufige Version 07/12/04 Ausdruck 8. Januar 2008 Inhaltsverzeichnis 1 Grundlagen 1 1.1 Elementare Logik.................................. 1 1.1.A Aussagenlogik................................
Vorlesung Analysis I WS 07/08 Erich Ossa Vorläufige Version 07/12/04 Ausdruck 8. Januar 2008 Inhaltsverzeichnis 1 Grundlagen 1 1.1 Elementare Logik.................................. 1 1.1.A Aussagenlogik................................
3 Folgen, Reihen, Grenzwerte 3.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die
 3 Folgen, Reihen, Grenzwerte 3.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die eindeutig den natürlichen Zahlen zugeordnet sind ( n N, auch
3 Folgen, Reihen, Grenzwerte 3.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die eindeutig den natürlichen Zahlen zugeordnet sind ( n N, auch
ANALYSIS I FÜR TPH WS 2018/19 3. Übung Übersicht
 ANALYSIS I FÜR TPH WS 208/9 3. Übung Übersicht Aufgaben zu Kapitel 5 und 6 Aufgabe : Konvergenz von Reihen (i) Aufgabe 2: Konvergenz von Reihen (ii) Aufgabe 3: ( ) Konvergenz von Reihen (iii) Aufgabe 4:
ANALYSIS I FÜR TPH WS 208/9 3. Übung Übersicht Aufgaben zu Kapitel 5 und 6 Aufgabe : Konvergenz von Reihen (i) Aufgabe 2: Konvergenz von Reihen (ii) Aufgabe 3: ( ) Konvergenz von Reihen (iii) Aufgabe 4:
Die alternierende harmonische Reihe.
 Die alternierende harmonische Reihe Beispiel: Die alternierende harmonische Reihe k k + = 2 + 3 4 + konvergiert nach dem Leibnizschen Konvergenzkriterium, und es gilt k k + = ln2 = 06934 für den Grenzwert
Die alternierende harmonische Reihe Beispiel: Die alternierende harmonische Reihe k k + = 2 + 3 4 + konvergiert nach dem Leibnizschen Konvergenzkriterium, und es gilt k k + = ln2 = 06934 für den Grenzwert
Kapitel 5 Reihen 196
 Kapitel 5 Reihen 96 Kapitel 5. Definition und Beispiele 97 Das Material dieses Kapitels können Sie nachlesen in: MICHAEL SPIVAK, Calculus, Kapitel 22 DIRK HACHENBERGER, Mathematik für Informatiker, Kapitel
Kapitel 5 Reihen 96 Kapitel 5. Definition und Beispiele 97 Das Material dieses Kapitels können Sie nachlesen in: MICHAEL SPIVAK, Calculus, Kapitel 22 DIRK HACHENBERGER, Mathematik für Informatiker, Kapitel
Lösungsvorschlag zur Übungsklausur zur Analysis I
 Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 NWF I - Mathematik 9..9 Universität Regensburg Lösungsvorschlag zur Übungsklausur zur Analysis I Frage 1 Vervollständigen Sie die folgenden
Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 NWF I - Mathematik 9..9 Universität Regensburg Lösungsvorschlag zur Übungsklausur zur Analysis I Frage 1 Vervollständigen Sie die folgenden
Ferienkurs Analysis 1
 Skript Ferienkurs Analysis 1 Fabian Hafner und Thomas Baldauf TUM Wintersemester 2016/17 04.04.2017 Das Skript wurde teilweise übernommen vom Skript des Ferienkurses WS 2014, verfasst von Andreas Wörfel.
Skript Ferienkurs Analysis 1 Fabian Hafner und Thomas Baldauf TUM Wintersemester 2016/17 04.04.2017 Das Skript wurde teilweise übernommen vom Skript des Ferienkurses WS 2014, verfasst von Andreas Wörfel.
θ für alle n n 0, 0, dann divergiert a n. θ n, also die mit a n0 θ n 0
 6 REIHEN 6. Konvergenzkriterien - 19 - Wenn man im Majorantenkriterium die geometrische Reihe als Majorante nimmt, erhält man das (6..18) Quotientenkriterium : Sei (a n ) n N0 eine Folge in C. Es gebe
6 REIHEN 6. Konvergenzkriterien - 19 - Wenn man im Majorantenkriterium die geometrische Reihe als Majorante nimmt, erhält man das (6..18) Quotientenkriterium : Sei (a n ) n N0 eine Folge in C. Es gebe
Folgen und Reihen. Beschränkte Folge: Es gibt eine Zahl c = const.
 Folgen und Reihen Folgen: Def.: Eine Abbildung a N K, n a(n) := a n (K = R C) wird Zahlenfolge genannt. Sie heißt reelle (komplexe) Zahlenfolge, falls K = R(C) ist. Symbole: a n K: Elemente der Folge,
Folgen und Reihen Folgen: Def.: Eine Abbildung a N K, n a(n) := a n (K = R C) wird Zahlenfolge genannt. Sie heißt reelle (komplexe) Zahlenfolge, falls K = R(C) ist. Symbole: a n K: Elemente der Folge,
Folgen, Reihen, Potenzreihen, Exponentialfunktion
 Ferienkurs Seite 1 Technische Universität München Ferienkurs Analysis 1 Hannah Schamoni Wintersemester 2011/12 Folgen, Reihen, Potenzreihen, Exponentialfunktion 20.03.2012 Inhaltsverzeichnis 1 Folgen 2
Ferienkurs Seite 1 Technische Universität München Ferienkurs Analysis 1 Hannah Schamoni Wintersemester 2011/12 Folgen, Reihen, Potenzreihen, Exponentialfunktion 20.03.2012 Inhaltsverzeichnis 1 Folgen 2
Übungen Analysis I WS 03/04
 Blatt Abgabe: Mittwoch, 29.0.03 Aufgabe : Beweisen Sie, daß für jede natürliche Zahl n gilt: n ( ) n (x + y) n = x i y n i, i (b) n ν 2 = ν= i=0 n(n + )(2n + ), 6 (c) 2 3n ist durch 7 teilbar. Aufgabe
Blatt Abgabe: Mittwoch, 29.0.03 Aufgabe : Beweisen Sie, daß für jede natürliche Zahl n gilt: n ( ) n (x + y) n = x i y n i, i (b) n ν 2 = ν= i=0 n(n + )(2n + ), 6 (c) 2 3n ist durch 7 teilbar. Aufgabe
Lösungen zur Klausur zur Analysis 1, WiSe 2016/17
 BERGISCHE UNIVERSITÄT WUPPERTAL..7 Fakultät 4 - Mathematik und Naturwissenschaften Prof. N. V. Shcherbina Dr. T. P. Pawlaschyk www.kana.uni-wuppertal.de Lösungen zur Klausur zur Analysis, WiSe 6/7 Klausureinsicht:
BERGISCHE UNIVERSITÄT WUPPERTAL..7 Fakultät 4 - Mathematik und Naturwissenschaften Prof. N. V. Shcherbina Dr. T. P. Pawlaschyk www.kana.uni-wuppertal.de Lösungen zur Klausur zur Analysis, WiSe 6/7 Klausureinsicht:
10 Aus der Analysis. Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit
 10 Aus der Analysis Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit Zahlenfolgen Ein unendliche Folge reeller Zahlen heißt Zahlenfolge. Im Beispiel 2, 3, 2, 2 2, 2
10 Aus der Analysis Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit Zahlenfolgen Ein unendliche Folge reeller Zahlen heißt Zahlenfolge. Im Beispiel 2, 3, 2, 2 2, 2
10 Kriterien für absolute Konvergenz von Reihen
 10 Kriterien für absolute Konvergenz von Reihen 10.1 Majoranten- und Minorantenkriterium 10.3 Wurzelkriterium 10.4 Quotientenkriterium 10.9 Riemannscher Umordnungssatz 10.10 Äquivalenzen zur absoluten
10 Kriterien für absolute Konvergenz von Reihen 10.1 Majoranten- und Minorantenkriterium 10.3 Wurzelkriterium 10.4 Quotientenkriterium 10.9 Riemannscher Umordnungssatz 10.10 Äquivalenzen zur absoluten
Tutorium: Analysis und lineare Algebra. Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen
 Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
2.6 Stetigkeit und Grenzwerte
 2.6 Stetigkeit und Grenzwerte Anschaulich gesprochen ist eine Funktion stetig, wenn ihr Graph sich zeichnen lässt, ohne den Stift abzusetzen. Das ist natürlich keine präzise mathematische Definition und
2.6 Stetigkeit und Grenzwerte Anschaulich gesprochen ist eine Funktion stetig, wenn ihr Graph sich zeichnen lässt, ohne den Stift abzusetzen. Das ist natürlich keine präzise mathematische Definition und
Die komplexe Exponentialfunktion und die Winkelfunktionen
 Die komplexe Exponentialfunktion und die Winkelfunktionen In dieser Zusammenfassung werden die für uns wichtigsten Eigenschaften der komplexen und reellen Exponentialfunktion sowie der Winkelfunktionen
Die komplexe Exponentialfunktion und die Winkelfunktionen In dieser Zusammenfassung werden die für uns wichtigsten Eigenschaften der komplexen und reellen Exponentialfunktion sowie der Winkelfunktionen
Analysis I - Ferienkurs
 TU-München, Dienstag, der 6.03.200 Analysis I - Ferienkurs Andreas Schindewolf 5. März 200 Inhaltsverzeichnis. Folgen 3.. Konvergenz und Cauchy-Folgen..................... 3.2. Konvergenz-Kriterien für
TU-München, Dienstag, der 6.03.200 Analysis I - Ferienkurs Andreas Schindewolf 5. März 200 Inhaltsverzeichnis. Folgen 3.. Konvergenz und Cauchy-Folgen..................... 3.2. Konvergenz-Kriterien für
2.6 Der Satz von Fubini
 1 2.6 Der Satz von Fubini Unser Ziel ist der Beweis des folgenden Ergebnisses. 6.1. Satz von Fubini Sei f : R n+m R integrierbar. Dann gibt es eine Nullmenge N R m, so dass gilt: 1. Für alle y R m \ N
1 2.6 Der Satz von Fubini Unser Ziel ist der Beweis des folgenden Ergebnisses. 6.1. Satz von Fubini Sei f : R n+m R integrierbar. Dann gibt es eine Nullmenge N R m, so dass gilt: 1. Für alle y R m \ N
Analysis I (HS 2016): SUMMIERBARE FAMILIEN
 Analysis I (HS 2016: SUMMIERBARE FAMILIEN Dietmar A. Salamon ETH-Zürich 26. Oktober 2016 Zusammenfassung Dieses Manuskript enthält eine Einführung in den Begriff einer summierbaren Familie reeller oder
Analysis I (HS 2016: SUMMIERBARE FAMILIEN Dietmar A. Salamon ETH-Zürich 26. Oktober 2016 Zusammenfassung Dieses Manuskript enthält eine Einführung in den Begriff einer summierbaren Familie reeller oder
Vorlesung: Analysis I für Ingenieure
 Vorlesung: Analysis I für Ingenieure Dozent: Dr. Michael Karow Thema: unendliche Reihen Definition. Eine unendliche Reihe ist der Grenzwert einer Folge von Summen: a k = lim k a k, wobei a k C. Falls der
Vorlesung: Analysis I für Ingenieure Dozent: Dr. Michael Karow Thema: unendliche Reihen Definition. Eine unendliche Reihe ist der Grenzwert einer Folge von Summen: a k = lim k a k, wobei a k C. Falls der
sign: R R, sign(x) := 0 falls x = 0 1 falls x < 0 Diese ist im Punkt x 0 = 0 nicht stetig, denn etwa zu ε = 1 finden wir kein δ > 0
 ANALYSIS FÜR PHYSIK UND VERWANDTE FÄCHER I 81 3. Stetigkeit 3.1. Stetigkeit. Im Folgenden sei D R eine beliebige nichtleere Teilmenge. Typischerweise wird D ein allgemeines Intervall sein, siehe Abschnitt
ANALYSIS FÜR PHYSIK UND VERWANDTE FÄCHER I 81 3. Stetigkeit 3.1. Stetigkeit. Im Folgenden sei D R eine beliebige nichtleere Teilmenge. Typischerweise wird D ein allgemeines Intervall sein, siehe Abschnitt
Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13)
 1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 5: Konvergenz Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 15. Dezember 2011) Folgen Eine Folge x 0, x 1,
1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 5: Konvergenz Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 15. Dezember 2011) Folgen Eine Folge x 0, x 1,
Tutorium: Analysis und lineare Algebra
 Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
Analysis I. Guofang Wang Universität Freiburg
 Universität Freiburg 31.1.2017 Definition 2.2 (uneigentliches Riemann-Integral) Sei I = [a, b) mit a < b. Die Funktion f : I R sei Riemann-integrierbar auf [a, b ] für alle b < b. Falls x lim x b a f(ξ)
Universität Freiburg 31.1.2017 Definition 2.2 (uneigentliches Riemann-Integral) Sei I = [a, b) mit a < b. Die Funktion f : I R sei Riemann-integrierbar auf [a, b ] für alle b < b. Falls x lim x b a f(ξ)
Kapitel 3. Reihen und ihre Konvergenz
 Kapitel 3 Reihen und ihre Konvergenz Abschnitt 3.1 Der Reihenbegri und erste Beispiele Denitionen zu Reihen, 1 Denition. Sei (a n ) n N0 eine Folge reeller Zahlen. Für n N 0 heiÿt dann die Zahl s n :=
Kapitel 3 Reihen und ihre Konvergenz Abschnitt 3.1 Der Reihenbegri und erste Beispiele Denitionen zu Reihen, 1 Denition. Sei (a n ) n N0 eine Folge reeller Zahlen. Für n N 0 heiÿt dann die Zahl s n :=
15. Bereichsintegrale
 H.J. Oberle Analysis III WS 212/13 15. Bereichsintegrale 15.1 Integrale über uadern Ziel ist die Berechnung des Volumens unterhalb des Graphen einer Funktion f : R n D R, genauer zwischen dem Graphen von
H.J. Oberle Analysis III WS 212/13 15. Bereichsintegrale 15.1 Integrale über uadern Ziel ist die Berechnung des Volumens unterhalb des Graphen einer Funktion f : R n D R, genauer zwischen dem Graphen von
Übungen zu Analysis, SS 2015
 Übungen zu Analysis, SS 215 Ulisse Stefanelli 15. Juni 215 1 Wiederholung 1. Untersuchen Sie das Verhalten der folgenden Folgen a n = n 2 cosh(1/n), b n = ln(ln(n))/n, c n = (2 n n 2 )/n!, 2. Stellen Sie
Übungen zu Analysis, SS 215 Ulisse Stefanelli 15. Juni 215 1 Wiederholung 1. Untersuchen Sie das Verhalten der folgenden Folgen a n = n 2 cosh(1/n), b n = ln(ln(n))/n, c n = (2 n n 2 )/n!, 2. Stellen Sie
ANALYSIS I FÜR TPH WS 2016/17 3. Übung Übersicht
 ANALYSIS I FÜR TPH WS 206/7 3. Übung Übersicht Aufgaben zu Kapitel 5 und 6 Aufgabe : Untersuchung von Reihen mittels Konvergenzkriterien Aufgabe 2: Konvergenz und Berechnung von Reihen I Aufgabe 3: ( )
ANALYSIS I FÜR TPH WS 206/7 3. Übung Übersicht Aufgaben zu Kapitel 5 und 6 Aufgabe : Untersuchung von Reihen mittels Konvergenzkriterien Aufgabe 2: Konvergenz und Berechnung von Reihen I Aufgabe 3: ( )
Höhere Mathematik für Physiker II
 Universität Heidelberg Sommersemester 2013 Wiederholungsblatt Übungen zur Vorlesung Höhere Mathematik für Physiker II Prof Dr Anna Marciniak-Czochra Dipl Math Alexandra Köthe Fragen Machen Sie sich bei
Universität Heidelberg Sommersemester 2013 Wiederholungsblatt Übungen zur Vorlesung Höhere Mathematik für Physiker II Prof Dr Anna Marciniak-Czochra Dipl Math Alexandra Köthe Fragen Machen Sie sich bei
HM I Tutorien 6 und 7
 HM I Tutorien 6 und 7 Lucas Kunz. Dezember 207 und 8. Dezember 207 Inhaltsverzeichnis Vorwort 2 2 Theorie 2 2. Definition einer Reihe.............................. 2 2.2 Absolute Konvergenz..............................
HM I Tutorien 6 und 7 Lucas Kunz. Dezember 207 und 8. Dezember 207 Inhaltsverzeichnis Vorwort 2 2 Theorie 2 2. Definition einer Reihe.............................. 2 2.2 Absolute Konvergenz..............................
Vorlesung Mathematik 1 für Ingenieure (Wintersemester 2015/16)
 1 Vorlesung Mathematik 1 für Ingenieure (Wintersemester 2015/16) Kapitel 7: Konvergenz und Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
1 Vorlesung Mathematik 1 für Ingenieure (Wintersemester 2015/16) Kapitel 7: Konvergenz und Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
Stetige Funktionen. Definition. Seien (X, d) und (Y, ϱ) metrische Räume und f : X Y eine Abbildung. D(f) X sei der Definitionsbereich von f.
 Stetige Funktionen Abbildungen f : X Y, wobei X und Y strukturierte Mengen sind (wie z.b. Vektorräume oder metrische Räume), spielen eine zentrale Rolle in der Mathematik. In der Analysis sind Abbildungen
Stetige Funktionen Abbildungen f : X Y, wobei X und Y strukturierte Mengen sind (wie z.b. Vektorräume oder metrische Räume), spielen eine zentrale Rolle in der Mathematik. In der Analysis sind Abbildungen
Analysis I. 5. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 5. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Die Umkehrabbildung zu einer bijektiven Abbildung
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 5. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Die Umkehrabbildung zu einer bijektiven Abbildung
Höhere Mathematik für Ingenieure 2
 Höhere Mathematik für Ingenieure 2 Prof. Dr. Swanhild Bernstein Sommersemester 218 Institut für Angewandte Analysis Kurven- und Parameterintegrale Parameterintegrale Typische Beispiele für Parameterintegrale
Höhere Mathematik für Ingenieure 2 Prof. Dr. Swanhild Bernstein Sommersemester 218 Institut für Angewandte Analysis Kurven- und Parameterintegrale Parameterintegrale Typische Beispiele für Parameterintegrale
Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie. Tobias Ried
 Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie Tobias Ried. März 2 2 Aufgabe (Messbarkeit der Komposition zweier Abbildungen). Seien (X, A), (Y, B) und (Z, C) Messräume und f : (X,
Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie Tobias Ried. März 2 2 Aufgabe (Messbarkeit der Komposition zweier Abbildungen). Seien (X, A), (Y, B) und (Z, C) Messräume und f : (X,
Musterlösung Klausur zu Analysis II. Verständnisteil
 Technische Universität Berlin SS 2009 Institut für Mathematik 20.07.2009 Prof. Dr. R. Schneider Fritz Krüger Sebastian Holtz Musterlösung Klausur zu Analysis II Verständnisteil 1. (a) Sei D R n konvex
Technische Universität Berlin SS 2009 Institut für Mathematik 20.07.2009 Prof. Dr. R. Schneider Fritz Krüger Sebastian Holtz Musterlösung Klausur zu Analysis II Verständnisteil 1. (a) Sei D R n konvex
k=1 {S n } n N konvergiert, so schreibt man: a n n=1 und spricht dann von Konvergenz oder Divergenz der unendlichen Reihe
 7 Reihen sind spezielle Folgen, die durch Summation entstehen. Definition 7. : {a n } n N sei Folge in C; S n := n Folge {S n } n N unendliche Reihe. Falls a k statt lim S n. a k heißt {S n } n N konvergiert,
7 Reihen sind spezielle Folgen, die durch Summation entstehen. Definition 7. : {a n } n N sei Folge in C; S n := n Folge {S n } n N unendliche Reihe. Falls a k statt lim S n. a k heißt {S n } n N konvergiert,
Beispiele zur Konvergenzuntersuchung bei Reihen.
 Beispiele zur Konvergenzuntersuchung bei Reihen Beispiel: Wir untersuchen die Konvergenz der Exponentialreihe z k k! für z C Anwendung des Quotientenkriteriums ergibt z k+1 (k + 1! z k = z k+1 k! z k (k
Beispiele zur Konvergenzuntersuchung bei Reihen Beispiel: Wir untersuchen die Konvergenz der Exponentialreihe z k k! für z C Anwendung des Quotientenkriteriums ergibt z k+1 (k + 1! z k = z k+1 k! z k (k
Kapitel 4 Folgen, Reihen & Funktionen
 Kapitel 4 Folgen, Reihen & Funktionen Inhaltsverzeichnis FOLGEN REELLER ZAHLEN... 3 DEFINITION... 3 GRENZWERT... 3 HÄUFUNGSPUNKT... 4 MONOTONIE... 4 BESCHRÄNKTHEIT... 4 SÄTZE... 4 RECHNEN MIT GRENZWERTEN...
Kapitel 4 Folgen, Reihen & Funktionen Inhaltsverzeichnis FOLGEN REELLER ZAHLEN... 3 DEFINITION... 3 GRENZWERT... 3 HÄUFUNGSPUNKT... 4 MONOTONIE... 4 BESCHRÄNKTHEIT... 4 SÄTZE... 4 RECHNEN MIT GRENZWERTEN...
Aufgabe 1 Zeigen Sie mittels vollständiger Induktion, dass für alle n N. n(n + 1)(2n + 1) 6. j 2 = gilt.
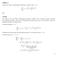 Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Analysis I. 2. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Die Produktmenge aus zwei Mengen L und M.
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Die Produktmenge aus zwei Mengen L und M.
Analysis I. 8. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 8. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine Ordnungsrelation auf einer Menge I. (2)
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 8. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine Ordnungsrelation auf einer Menge I. (2)
Aufgabensammlung zur Analysis 1
 Analysis 1 18.12.2017 Prof. Dr. H. Koch Dr. F. Gmeineder Abgabe: Keine Abgabe. Aufgabensammlung zur Analysis 1 Anmerkungen: Das vorliegende Blatt enthält eine Auswahl von Aufgaben, die auf Klausuren zur
Analysis 1 18.12.2017 Prof. Dr. H. Koch Dr. F. Gmeineder Abgabe: Keine Abgabe. Aufgabensammlung zur Analysis 1 Anmerkungen: Das vorliegende Blatt enthält eine Auswahl von Aufgaben, die auf Klausuren zur
c < 1, (1) c k x k0 c k = x k0
 4.14 Satz (Quotientenkriterium). Es sei (x k ) Folge in K. Falls ein k 0 existiert, so dass für k k 0 gilt x k 0 und x k+1 x k c < 1, (1) so ist x k absolut konvergent. Beweis. Aus (1) folgt mit vollständiger
4.14 Satz (Quotientenkriterium). Es sei (x k ) Folge in K. Falls ein k 0 existiert, so dass für k k 0 gilt x k 0 und x k+1 x k c < 1, (1) so ist x k absolut konvergent. Beweis. Aus (1) folgt mit vollständiger
Klausur Höhere Mathematik I für die Fachrichtung Physik
 Karlsruher Institut für Technologie (KIT Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning WS /3 4.3.3 Klausur Höhere Mathematik I für die Fachrichtung Physik Aufgabe ((4+3+3 Punkte a Welche
Karlsruher Institut für Technologie (KIT Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning WS /3 4.3.3 Klausur Höhere Mathematik I für die Fachrichtung Physik Aufgabe ((4+3+3 Punkte a Welche
Analyis I - Reihen und Potenzreihen
 Analyis I - Reihen und January 13, 2009 Analyis I - Reihen und Definition (Reihen) Reihen Sei (a k ) k N eine Folge und n N. Dann heißt (s k ) k N mit s n = n k=1 die Partialsummenfolge von (a k ) k N.
Analyis I - Reihen und January 13, 2009 Analyis I - Reihen und Definition (Reihen) Reihen Sei (a k ) k N eine Folge und n N. Dann heißt (s k ) k N mit s n = n k=1 die Partialsummenfolge von (a k ) k N.
Wiederholungsklausur zur Analysis I
 Wiederholungsklausur zur Analysis I Prof. Dr. C. Löh/M. Blank 5. Oktober 2011 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie, ob Sie alle Seiten erhalten
Wiederholungsklausur zur Analysis I Prof. Dr. C. Löh/M. Blank 5. Oktober 2011 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie, ob Sie alle Seiten erhalten
Höhere Mathematik für die Fachrichtung Physik
 Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Dipl.-Math. Sebastian Schwarz Höhere Mathematik für die Fachrichtung Physik Lösungsvorschläge zum 6. Übungsblatt Aufgabe
Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Dipl.-Math. Sebastian Schwarz Höhere Mathematik für die Fachrichtung Physik Lösungsvorschläge zum 6. Übungsblatt Aufgabe
L 2 -Theorie und Plancherel-Theorem
 L -Theorie und Plancherel-Theorem Seminar Grundideen der Harmonischen Analysis bei Porf Dr Michael Struwe HS 007 Vortrag von Manuela Dübendorfer 1 Wiederholung aus der L 1 -Theorie Um die Fourier-Transformation
L -Theorie und Plancherel-Theorem Seminar Grundideen der Harmonischen Analysis bei Porf Dr Michael Struwe HS 007 Vortrag von Manuela Dübendorfer 1 Wiederholung aus der L 1 -Theorie Um die Fourier-Transformation
Nachklausur zur Analysis 2, SoSe 2017
 BERGISCHE UNIVERSITÄT WUPPERTAL 18.9.17 Fakultät 4 - Mathematik und Naturwissenschaften Prof. N. V. Shcherbina Dr. T. P. Pawlaschyk www.kana.uni-wuppertal.de Nachklausur zur Analysis 2, SoSe 217 Aufgabe
BERGISCHE UNIVERSITÄT WUPPERTAL 18.9.17 Fakultät 4 - Mathematik und Naturwissenschaften Prof. N. V. Shcherbina Dr. T. P. Pawlaschyk www.kana.uni-wuppertal.de Nachklausur zur Analysis 2, SoSe 217 Aufgabe
Vorlesung Mathematik 2 für Ingenieure (Sommersemester 2016)
 1 Vorlesung Mathematik 2 für Ingenieure (Sommersemester 216) Kapitel 11: Potenzreihen und Fourier-Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
1 Vorlesung Mathematik 2 für Ingenieure (Sommersemester 216) Kapitel 11: Potenzreihen und Fourier-Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
Analysis I. Guofang Wang Universität Freiburg
 Universität Freiburg 22.11.2016 3. Mächtigkeit und die komplexe Zahlen Komplexe Zahlen Definition Die komplexe Zahlen sind definiert als C = R 2 = R R, mit (x 1, y 1 ) + (x 2, y 2 ) = (x 1 + x 2, y 1 +
Universität Freiburg 22.11.2016 3. Mächtigkeit und die komplexe Zahlen Komplexe Zahlen Definition Die komplexe Zahlen sind definiert als C = R 2 = R R, mit (x 1, y 1 ) + (x 2, y 2 ) = (x 1 + x 2, y 1 +
20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen
 20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
Analysis für Informatiker und Statistiker Nachklausur
 Prof. Dr. Peter Otte Wintersemester 213/14 Tom Bachmann, Sebastian Gottwald 14.3.214 Analysis für Informatiker und Statistiker Nachklausur Lösungsvorschlag Name:.......................................................
Prof. Dr. Peter Otte Wintersemester 213/14 Tom Bachmann, Sebastian Gottwald 14.3.214 Analysis für Informatiker und Statistiker Nachklausur Lösungsvorschlag Name:.......................................................
Analysis I. 7. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 7. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine surjektive Abbildung f: L M. () Ein archimedisch
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 7. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine surjektive Abbildung f: L M. () Ein archimedisch
Höhere Mathematik III für die Fachrichtung Physik Wintersemester 2016/17. Lösungsvorschlag zu Übungsblatt 5
 Institut für Analysis Dr. Christoph Schmoeger M.Sc. Jonathan Wunderlich Höhere Mathematik III für die Fachrichtung Physik Wintersemester 6/7..7 Lösungsvorschlag zu Übungsblatt 5 Aufgabe 6: Zeigen Sie mit
Institut für Analysis Dr. Christoph Schmoeger M.Sc. Jonathan Wunderlich Höhere Mathematik III für die Fachrichtung Physik Wintersemester 6/7..7 Lösungsvorschlag zu Übungsblatt 5 Aufgabe 6: Zeigen Sie mit
Vorbereitungskurs Mathematik zum Sommersemester 2015 Folgen und Reihen
 Vorbereitungskurs Mathematik zum Sommersemester 2015 Folgen und Reihen Susanna Pohl Vorkurs Mathematik TU Dortmund 12.03.2015 Folgen und Reihen Folgen und Grenzwerte Rechenregeln für konvergente Folgen
Vorbereitungskurs Mathematik zum Sommersemester 2015 Folgen und Reihen Susanna Pohl Vorkurs Mathematik TU Dortmund 12.03.2015 Folgen und Reihen Folgen und Grenzwerte Rechenregeln für konvergente Folgen
HM I Tutorium 5. Lucas Kunz. 21. November 2018
 HM I Tutorium 5 Lucas Kunz 2. November 208 Inhaltsverzeichnis Theorie 2. Definition.................................... 2.2 Wichtige Reihen................................. 2.3 Absolute Konvergenz..............................
HM I Tutorium 5 Lucas Kunz 2. November 208 Inhaltsverzeichnis Theorie 2. Definition.................................... 2.2 Wichtige Reihen................................. 2.3 Absolute Konvergenz..............................
Staatsexamen Herbst 2017 Differential- und Integralrechnung, Thema I
 Staatsexamen Herbst 17 Differential- und Integralrechnung, Thema I 1. a) Die Aussage ist wahr! Sei s R der Reihenwert der Reihe k=1 Da a n = s n s n 1 für n, ist also b) Die Aussage ist falsch! a k, also
Staatsexamen Herbst 17 Differential- und Integralrechnung, Thema I 1. a) Die Aussage ist wahr! Sei s R der Reihenwert der Reihe k=1 Da a n = s n s n 1 für n, ist also b) Die Aussage ist falsch! a k, also
Lösungen zu Übungsblatt 9
 Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
Analysis I. Vorlesung 16. Funktionenfolgen
 Prof. Dr. H. Brenner Osnabrück WS 2014/2015 Analysis I Vorlesung 16 Funktionenfolgen Eine (vertikal gestauchte) Darstellung der ersten acht polynomialen Approximationen der reellen Exponentialfunktion
Prof. Dr. H. Brenner Osnabrück WS 2014/2015 Analysis I Vorlesung 16 Funktionenfolgen Eine (vertikal gestauchte) Darstellung der ersten acht polynomialen Approximationen der reellen Exponentialfunktion
Die Fakultät. Thomas Peters Thomas Mathe-Seiten 2. Mai 2010
 Die Fakultät Thomas Peters Thomas Mathe-Seiten www.mathe-seiten.de 2. Mai 200 Dieser Artikel gibt die Definition der klassischen Fakultät und führt von dort aus zunächst zu der Anwendung in Taylor-Reihen
Die Fakultät Thomas Peters Thomas Mathe-Seiten www.mathe-seiten.de 2. Mai 200 Dieser Artikel gibt die Definition der klassischen Fakultät und führt von dort aus zunächst zu der Anwendung in Taylor-Reihen
Leitfaden a tx t
 Leitfaden -0.7. Potenz-Reihen. Definition: Es sei (a 0, a, a 2,...) eine Folge reeller Zahlen (wir beginnen hier mit dem Index t 0). Ist x R, so kann man die Folge (a 0, a x, a 2 x 2, a 3 x 3,...) und
Leitfaden -0.7. Potenz-Reihen. Definition: Es sei (a 0, a, a 2,...) eine Folge reeller Zahlen (wir beginnen hier mit dem Index t 0). Ist x R, so kann man die Folge (a 0, a x, a 2 x 2, a 3 x 3,...) und
Folgen und Grenzwerte
 Wintersemester 2015/201 Folgen und Grenzwerte von Sven Grützmacher Dieser Vortrag wurde für den (von der Fachschaft organisierten) Vorkurs für die Studienanfänger an der Fakultät für Mathematik und Informatik
Wintersemester 2015/201 Folgen und Grenzwerte von Sven Grützmacher Dieser Vortrag wurde für den (von der Fachschaft organisierten) Vorkurs für die Studienanfänger an der Fakultät für Mathematik und Informatik
Folgen und Reihen von Funktionen
 Folgen und Reihen von Funktionen Sehr häufig treten in der Mathematik Folgen bzw. Reihen von Funktionen auf. Ist etwa (f n ) eine Folge von Funktionen, dann können wir uns für ein festes x fragen, ob die
Folgen und Reihen von Funktionen Sehr häufig treten in der Mathematik Folgen bzw. Reihen von Funktionen auf. Ist etwa (f n ) eine Folge von Funktionen, dann können wir uns für ein festes x fragen, ob die
Mathematik II für Studierende der Informatik (Analysis und lineare Algebra) im Sommersemester 2018
 (Analysis und lineare Algebra) im Sommersemester 2018 2. Juli 2018 1/1 Wir geben einige wesentliche Sätze über bestimmte Integrale an, deren Beweise man in den Standardlehrbüchern der Analysis findet.
(Analysis und lineare Algebra) im Sommersemester 2018 2. Juli 2018 1/1 Wir geben einige wesentliche Sätze über bestimmte Integrale an, deren Beweise man in den Standardlehrbüchern der Analysis findet.
HM I Tutorium 6. Lucas Kunz. 28. November 2018
 HM I Tutorium 6 Lucas Kunz 28. November 208 Inhaltsverzeichnis Theorie 2. Exponentialfunktion.............................. 2.2 Trigonometrische Funktionen......................... 2.3 Potenzreihen...................................
HM I Tutorium 6 Lucas Kunz 28. November 208 Inhaltsverzeichnis Theorie 2. Exponentialfunktion.............................. 2.2 Trigonometrische Funktionen......................... 2.3 Potenzreihen...................................
HM I Tutorium 5. Lucas Kunz. 24. November 2016
 HM I Tutorium 5 Lucas Kunz 24. November 206 Inhaltsverzeichnis Theorie 2. Definition einer Reihe.............................. 2.2 Wichtige Reihen................................. 2.3 Limites inferior
HM I Tutorium 5 Lucas Kunz 24. November 206 Inhaltsverzeichnis Theorie 2. Definition einer Reihe.............................. 2.2 Wichtige Reihen................................. 2.3 Limites inferior
Analysis I. 11. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 11. Beispielklausur mit en Aufgabe 1. Definiere die folgenden kursiv gedruckten) Begriffe. 1) Ein angeordneter Körper. ) Eine Folge in
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 11. Beispielklausur mit en Aufgabe 1. Definiere die folgenden kursiv gedruckten) Begriffe. 1) Ein angeordneter Körper. ) Eine Folge in
Aufgaben zur Analysis I aus dem Wiederholungskurs
 Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 Hilfskräfte: A. Weiß, W. Thumann 6.3.29 NWF I - Mathematik Universität Regensburg Aufgaben zur Analysis I aus dem Wiederholungskurs Die folgenden
Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 Hilfskräfte: A. Weiß, W. Thumann 6.3.29 NWF I - Mathematik Universität Regensburg Aufgaben zur Analysis I aus dem Wiederholungskurs Die folgenden
Unendliche Reihen. D.h. Die Summe einer unendlichen Reihe ist der Grenzwert der Folge der Partialsummen.
 Unendliche Reihen Wegen der elementaren Eigenschaften der Zahlen ist lar, was unter einer endlichen Summe von Zahlen a + a 2 +... + zu verstehen ist. Vorderhand ist noch nicht erlärt, was unter einer unendlichen
Unendliche Reihen Wegen der elementaren Eigenschaften der Zahlen ist lar, was unter einer endlichen Summe von Zahlen a + a 2 +... + zu verstehen ist. Vorderhand ist noch nicht erlärt, was unter einer unendlichen
Lebesgue-Integral und L p -Räume
 Lebesgue-Integral und L p -Räume Seminar Integraltransformationen, WS 2012/13 1 Treppenfunktionen Grundlage jedes Integralbegriffs ist das geometrisch definierte Integral von Treppenfunktionen. Für A R
Lebesgue-Integral und L p -Räume Seminar Integraltransformationen, WS 2012/13 1 Treppenfunktionen Grundlage jedes Integralbegriffs ist das geometrisch definierte Integral von Treppenfunktionen. Für A R
Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript
 Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript Janko Latschev Fachbereich Mathematik Universität Hamburg www.math.uni-hamburg.de/home/latschev Hamburg,
Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript Janko Latschev Fachbereich Mathematik Universität Hamburg www.math.uni-hamburg.de/home/latschev Hamburg,
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
2 Rationale und reelle Zahlen
 2 reelle Es gibt Mathematik mit Grenzwert (Analysis) und Mathematik ohne Grenzwert (z.b Algebra). Grenzwerte existieren sicher nur dann, wenn der Zahlbereich vollständig ist, also keine Lücken aufweist
2 reelle Es gibt Mathematik mit Grenzwert (Analysis) und Mathematik ohne Grenzwert (z.b Algebra). Grenzwerte existieren sicher nur dann, wenn der Zahlbereich vollständig ist, also keine Lücken aufweist
