Kapitel 7. Reihen. Konvergenz unendlicher Reihen. Konvergenzkriterien. Potenzreihen und Taylorreihen. Anwendungen
|
|
|
- Günther Peters
- vor 7 Jahren
- Abrufe
Transkript
1 Kapitel 7 Reihen Konvergenz unendlicher Reihen Konvergenzkriterien Potenzreihen und Taylorreihen Anwendungen
2 Reihen Konvergenz unendlicher Reihen Konvergenz unendlicher Reihen Betrachtet man die unendliche Reihe , so stellt man fest, dass jeder Summand stets um die Hälfte kleiner ist als sein Vorgänger. Die auf der Zahlengeraden hinzukommenden Stücke werden also immer kleiner, bis sie wegen ihrer Winzigkeit nicht mehr sichtbar sind. Je länger man den Additionsvorgang fortsetzt, desto näher kommt man der Eins, sie wird aber in der Summe nie übersprungen werden. 0 1/2 1/ 4 1/8 1/16 1/ IR Mathematik kompakt 1
3 Mathematik kompakt 2 Untersuchung einer Reihe Untersuchen wir andererseits die Reihe , so gilt - Glieder 1 bis 2 der Reihe: > = 1 2, - Glieder 3 bis 6 der Reihe: > 4 18 = 1 2, usw. Eine bestimmte Anzahl von Summanden, die wir Teilsumme nennen wollen, ergibt stets einen Summenwert größer als 1/2: } {{ } > } {{ } > } {{ } > = } {{ } > Die Summe wird also unendlich groß, obwohl wie im ersten Beispiel die einzelnen Summanden auch hier immer kleiner werden. Reihen Konvergenz unendlicher Reihen
4 Reihen Konvergenz unendlicher Reihen Unendliche Reihe, Partialsumme Definition Ist (a n ) n IN = a 0, a 1, a 2, eine Zahlenfolge, dann heißt die durch die Vorschrift s n := n 1 a k = a 0 + a a n 1, n IN +, neu gebildete Folge (s n ) n IN+ (die aus (a n ) gebildete) unendliche Reihe. Statt lim n s n schreibt man a k. Die Glieder s n dieser Folge werden Partialsummen genannt. Man beachte, dass die n-te Partialsumme gemäß unserer Definition stets aus n Summanden besteht: usw. s 1 = a 0, s 2 = a 0 + a 1, s 3 = a 0 + a 1 + a 2, Mathematik kompakt 3
5 Reihen Konvergenz unendlicher Reihen Beispiel Der Reihe liegt die Folge ( ) 1 2 n+1 n IN zugrunde. Die Partialsummen ergeben sich zu s n = 2n 1 2 n. Anstelle der Grenzwertnotation schreibt man lim n 2 n 1 2 n 1 2 k+1. Mathematik kompakt 4
6 Reihen Konvergenz unendlicher Reihen Übung Durch welche Folge wird die Reihe definiert? Mathematik kompakt 5
7 Reihen Konvergenz unendlicher Reihen Lösung Die unendliche Reihe wird durch die Folge ( 1 n + 2 n IN definiert. Man kann sie in der Form schreiben. n 1 ( 1 ) k + 2 ) n IN + Mathematik kompakt 6
8 Reihen Konvergenz unendlicher Reihen Konvergenz und Divergenz unendlicher Reihen Definition Eine unendliche Reihe (s n ) n IN+ heißt konvergent, wenn die Folge ihrer Partialsummen konvergent ist, d.h. wenn a k = lim n s n = s gilt. Der Grenzwert s heißt Summe oder Summenwert der unendlichen Reihe. Existiert s nicht, so nennt man die Reihe divergent. Eigentlich steht das Symbol a k für die Summe einer konvergenten Reihe. Man benutzt es aber auch zur Bezeichnung der (nicht notwendigerweise konvergenten) Folge von Partialsummen (s n = n 1 a k) n IN+ selbst. Mathematik kompakt 7
9 Reihen Konvergenz unendlicher Reihen Beispiel a) Zu untersuchen ist, ob die Reihe ( 1) k konvergent ist. Für die Folge der Partialsummen erhält man s 1 = ( 1) 0 = 1, s 2 = s 1 + ( 1) 1 = 0, s 3 = s 2 + ( 1) 2 = 1, usw., d.h. diese ist alternierend: 1, 0, 1, 0,... Daher divergiert die Reihe. b) Die sog. harmonische Reihe 1 k+1 stimmt bis auf den ersten Summanden mit der Reihe 1 k+2 überein. Letztere wird unendlich groß, was wir bereits festgestellt haben. Dies trifft natürlich auch für die harmonische Reihe zu. Man sagt, sie ist divergent gegen und schreibt 1 k + 1 =. Mathematik kompakt 8
10 Reihen Konvergenz unendlicher Reihen Übung Bestimmen Sie 1 2 k+1. Mathematik kompakt 9
11 Reihen Konvergenz unendlicher Reihen Lösung Man erhält 1 = lim 2k+1 n = lim n 2 n 1 2 n (1 12 n ) = 1. Mathematik kompakt 10
12 Reihen Konvergenz unendlicher Reihen Unendliche geometrische Reihe Wir kennen endliche geometrische Reihen der Form n 1 i=0 a 0 q i n 1 = a 0 i=0 Jetzt können wir die Konvergenz der unendlichen geometrischen Reihe q k untersuchen: Dazu betrachten wir die Partialsummen q i. s n = 1 + q + q q n 1. Für q = 1 ist s n = n. Wegen lim n n = hat man bestimmte Divergenz mit dem uneigentlichen Grenzwert. Für q 1 ergibt sich aus der Formel für die endliche geometrische Reihe s n = qn 1 q 1. Daraus folgt lim n s q n 1 n = lim n q 1 = lim n q n 1. q 1 Für q < 1 konvergiert die Reihe mit dem Summenwert 1 1 q, da bekanntlich lim n q n = 0. Für q > 1 hat man wegen lim n q n = ± Divergenz. Mathematik kompakt 11
13 Reihen Konvergenz unendlicher Reihen Unendliche geometrische Reihe Zusammenfassend halten wir fest: Falls q < 1, dann gilt für die geometrische Reihe a 0 (1 + q + q 2 + q ) = a 0 qk = a q. In allen anderen Fällen liegt Divergenz vor. Mathematik kompakt 12
14 Reihen Konvergenz unendlicher Reihen Beispiel Die bereits bekannte Reihe n k+1 n IN + ist natürlich eine geometrische Reihe mit a 0 = 1/2 und dem konstanten Quotienten q = 1/2. Es ergibt sich damit: 1 2 k+1 = 1 2 = 1 2 ( ) 1 k /2 = 1. Mathematik kompakt 13
15 Reihen Konvergenz unendlicher Reihen Übung Berechnen Sie die Summe der geom. Reihe Mathematik kompakt 14
16 Reihen Konvergenz unendlicher Reihen Lösung Für diese geometrische Reihe gilt a 0 = 1 und q = 3/4. Obige Formel liefert somit ( 3 4 )k = 1 1 ( 3/4) = 4 7. Mathematik kompakt 15
17 Reihen Konvergenz unendlicher Reihen Rechenregeln für konvergente Reihen Da eine Reihe lediglich eine in besonderer Weise geschriebene Folge ist, gelten zu den Folgen analoge Rechenregeln: Ist a k = a, so gilt: b k = b und c = const, (a k + b k ) = a + b, c a k = c a k = c a. Wegen des Kommutativgesetzes ist die Summe endlich vieler Zahlen immer unabhängig von der Reihenfolge der Summanden. Die Summe einer konvergenten unendlichen Reihe ist mittels der Folge ihrer Partialsummen definiert. In diese geht aber die Reihenfolge der Summanden wesentlich ein, so dass man i.allg. die Unabhängigkeit des Summenwertes von der Summationsreihenfolge nicht erwarten kann. Mathematik kompakt 16
18 Mathematik kompakt 17 Abhängigkeit von Summationsreihenfolge Bekanntlich konvergiert die sog. alternierende harmonische Reihe gegen den Grenzwert ln 2: ( 1) k k + 1 = = ln 2. Wenn wir diese Reihe nun so umordnen, dass auf einen positiven Summanden stets zwei negative folgen, so ergibt sich: (1 1 2 ) ( ) ( ) ( )... = = ( )... = 1 ln 2. 2 Die umgeordnete Reihe hat also einen anderen Wert (ln 2 ln 2 2 ). Reihen Konvergenz unendlicher Reihen
19 Reihen Konvergenz unendlicher Reihen Absolut konvergente Reihe Definition Die Reihe a k heißt absolut konvergent, wenn die Reihe der absoluten Summanden a k konvergiert. Bei absolut konvergenten Reihen darf man die Summanden beliebig umordnen, die Reihe konvergiert dann immer noch gegen denselben Summenwert. Die Reihe ( 1) k k + 1 ist nicht absolut konvergent, da die zugehörige Reihe mit den absoluten Summanden auf die harmonische Reihe führt und diese divergiert. 1 k + 1 Mathematik kompakt 18
20 Reihen Konvergenzkriterien Notwendiges Konvergenzkriterium Bildet man aus der Folge (a n ) die Reihe a k, so lässt sich jedes Folgenglied auch als Differenz zweier aufeinander folgender Partialsummen s n+1, s n schreiben: a n = n a k n 1 a k = s n+1 s n. Wenn man nun annimmt, dass die Reihe gegen die Summe s konvergiert, dann muss natürlich gelten: lim n a n = lim s n n+1 lim s n n = s s = 0. Wenn eine Reihe a k konvergiert, dann ist die Folge der einzelnen Summanden (a k ) eine Nullfolge. Umgekehrt: Wenn lim k a k 0, dann divergiert die Reihe a k. Kriterium ist nicht hinreichend! Z.B. harmonische Reihe: Glieder a k = k+1 1 bilden zwar Nullfolge, die Reihe ist aber divergent. Mathematik kompakt 19
21 Reihen Konvergenzkriterien Beispiel a) Die Reihe ( 1) k divergiert, da die a k entweder 1 oder 1 sind, also keine Nullfolge bilden. b) Die Summanden der Reihe 1 2 k+1 bilden eine Nullfolge. Da das Kriterium aber nicht hinreichend ist, kann man nicht entscheiden, ob die Reihe konvergiert oder nicht. Hierzu sind andere Kriterien nötig. Mathematik kompakt 20
22 Reihen Konvergenzkriterien Leibniz-Kriterium Dem notwendigen Kriterium sehr ähnlich ist ein hinreichendes Kriterium für sog. alternierende Reihen, deren Summanden abwechselndes Vorzeichen haben (a 2k > 0, a 2k+1 < 0 oder umgekehrt). Eine alternierende Reihe ist konvergent, wenn die Absolutbeträge der Summanden eine monoton fallende Nullfolge bilden. Mit Hilfe der Abbildung kann man sich das Leibniz- Kriterium plausibel machen: Man sieht, wie die Partialsummenfolge s n immer weniger alterniert und gegen einen Grenzwert s konvergiert. s 1 = a 0 s 2 =a 0 -a 1 s 3 = a 0 - a 1 + a 2 s 4 s 6 s 5 s Mathematik kompakt 21
23 Reihen Konvergenzkriterien Beispiel Die alternierende harmonische Reihe ( 1) k k + 1 konvergiert nach Leibniz-Kriterium, da ( 1 k + 1 eine monoton fallende Nullfolge ist. ) Mathematik kompakt 22
24 Reihen Konvergenzkriterien Übung Konvergiert die Reihe ? Mathematik kompakt 23
25 Reihen Konvergenzkriterien Lösung Es handelt sich hier um die sog. Leibniz sche Reihe Da ( ( 1) k 2k k + 1 eine monotone Nullfolge ist, konvergiert diese nach Leibniz-Kriterium. ) Ihr Summenwert, den wir hier aber nicht ermitteln wollen, ergibt sich interessanterweise zu π 4. Mathematik kompakt 24
26 Reihen Konvergenzkriterien Vergleichskriterium, Majorantenkriterium Wichtig sind Kriterien für die absolute Konvergenz einer Reihe a k. Die Summanden der Reihe a k sind alle nichtnegativ, daher bilden die zugehörigen Partialsummen eine monoton wachsende Folge. Diese Partialsummenfolge und damit a k konvergiert also, falls sie nach oben beschränkt ist. Ist die Reihe c k absolut konvergent und gilt für fast alle Summanden der Reihe a k a k c k, dann ist auch diese absolut konvergent. Die absolute Konvergenz von a k ergibt sich sofort:die monoton wachsende Partialsummenfolge n 1 ( a k ) n IN+ ist ja durch c k nach oben beschränkt. Mathematik kompakt 25
27 Reihen Konvergenzkriterien Beispiel Wir untersuchen die Konvergenz von 3 k 4 k + 5. Zunächst stellen wir fest, dass für alle Summanden a k := 3k 4 k + 5 < 3k 4 k = ( 3 4 ) k := c k gilt. Für die geometrische Reihe c k gilt aber ( 3 4 ) k = 1 1 3/4 = 4. Da diese absolut konvergiert, folgt nach dem Majorantenkriterium auch die absolute Konvergenz unserer zu untersuchenden Reihe. Mathematik kompakt 26
28 Reihen Konvergenzkriterien Vergleichskriterium, Minorantenkriterium Da die Reihe c k quasi so etwas wie eine obere Schranke für die Reihe a k ist, nennt man erstere auch Majorante, entsprechend das Kriterium eben Majorantenkriterium. Nun kann man umgekehrt auch untere Schranken für gewisse Reihen angeben, so genannte Minoranten. Mit diesen erhält man ein ähnliches Vergleichskriterium, das Minorantenkriterium: Ist die Reihe c k divergent und gilt für fast alle k die Abschätzung a k c k 0, dann ist auch die Reihe a k divergent. Mathematik kompakt 27
29 Reihen Konvergenzkriterien Übung Ist die Reihe konvergent? Mathematik kompakt 28
30 Reihen Konvergenzkriterien Lösung Wegen k k 0 folgt sofort a k := 1 k 1 k =: c k. Deshalb ist k=1 c k = k=1 1 k eine divergente Minorante für k=1 1 k. Diese Reihe divergiert also ebenfalls. Mathematik kompakt 29
31 Reihen Konvergenzkriterien Wurzelkriterium Besonders hilfreich als Vergleichsreihe ist die geometrische Reihe. Sie liefert das Wurzelkriterium: Die Reihe a k ist absolut konvergent, wenn für ein positives q < 1 gilt: k a k q für fast alle k. Gilt hingegen k a k 1 bzw. a k 1 für fast alle k, so divergiert die Reihe. Da aus k a k q sofort a k q k folgt, ist die geometrische Reihe q k offenbar eine Majorante für a k. Diese konvergiert absolut, weil für q < 1 die geometrische Reihe absolut konvergent ist. Die Divergenzaussage ist offensichtlich. Mathematik kompakt 30
32 Reihen Konvergenzkriterien Beispiel Für die Reihe 1 (3 + ( 1) k ) k = gilt mit k 1 k a k = ( 1) k 1 (=: q). 2 Nach dem Wurzelkriterium ist die Reihe daher konvergent. Mathematik kompakt 31
33 Reihen Konvergenzkriterien Übung Ist die Reihe konvergent? 5 k (3 + ( 1) k ) k Mathematik kompakt 32
34 Reihen Konvergenzkriterien Lösung Mit k 1 gilt die Abschätzung k a k = ( 1) k Also ist die Reihe nach dem Wurzelkriterium divergent. Mathematik kompakt 33
35 Reihen Konvergenzkriterien Quotientenkriterium Aus dem Wurzelkriterium kann man ein weiteres Kriterium folgern, das Quotientenkriterium: Die Reihe a k ist absolut konvergent, wenn für ein positives q < 1 gilt: a k+1 a k Gilt hingegen q für fast alle k. a k+1 a k divergiert die Reihe. 1 für fast alle k, so Mathematik kompakt 34
36 Reihen Konvergenzkriterien Beispiel Um die Konvergenz der Reihe k=1 2 k k 5 = zu bestimmen, ermittelt man den Quotienten a k+1 a k = 2 k+1 k 5 ( k (k + 1) 5 2 k = 2 k + 1 Für fast alle k, nämlich für k 7, gilt aber 2 ( k k + 1 Somit ist die Reihe divergent. ) ) 5. Mathematik kompakt 35
37 Reihen Konvergenzkriterien Übung Entscheiden Sie mit dem Quotientenkriterium, ob die Reihe konvergent ist. 1 k! Mathematik kompakt 36
38 Reihen Konvergenzkriterien Lösung Es gilt für k > 0. a k+1 a k = k! (k + 1)! = 1 k Damit folgt die Konvergenz der Reihe. Mathematik kompakt 37
39 Reihen Konvergenzkriterien Quotientenkriterium einfache Version In beiden Kriterien ist die Bedingung q < 1 sehr wichtig. Gilt für fast alle k nur k a k 1 bzw. a k+1 a k 1, dann kann man keine Entscheidung treffen (z.b. Konvergenz: k=1 1 k 2, Divergenz: k=1 1 k ). Leichter zu handhaben als das Wurzelkriterium, dafür aber nicht so weitreichend, ist das Quotientenkriterium. Ist speziell die Folge ( a ) k+1 a k k IN konvergent, so genügt eine Grenzwertuntersuchung: Die Reihe a k ist dann absolut konvergent, wenn gilt: lim k a k+1 a k bzw. divergent, wenn gilt: lim k a k+1 a k = q < 1 = q > 1. Mathematik kompakt 38
40 Reihen Potenz- und Taylorreihen Potenzreihen Die geometrische Reihe q k konvergiert für beliebige q < 1 gegen 1 1 q. Anders ausgedrückt kann man statt q verwenden wir jetzt x IR sagen, dass für x < 1 die Funktion f(x) = 1 x 1 durch eine unendliche Reihe dargestellt wird. Es gilt schließlich 1 1 x = x k für x < 1. Die Summanden dieser Reihe sind Potenzen von x. Man nennt solche Reihen daher Potenzreihen. Definition Gegeben seien eine Folge (a k ) und eine fixe reelle Zahl x 0. Dann bezeichnet man für x IR die Reihe a k(x x 0 ) k als Potenzreihe. Die a k heißen Koeffizienten und x 0 nennt man Entwicklungspunkt. Mathematik kompakt 39
41 Reihen Potenz- und Taylorreihen Konvergenzradius und -intervall Mit Hilfe der bekannten Konvergenzkriterien kann man nun überprüfen, für welche x-werte eine Reihe konvergiert: Es gibt Potenzreihen, die für alle x IR konvergieren, solche die nur im Punkt x 0 konvergieren und andere, die dann konvergieren, wenn x Werte aus einem Intervall der Form (x 0 r, x 0 +r) mit reellem r > 0 annimmt. Für jede Potenzreihe, die nicht nur im Entwicklungspunkt x 0 konvergiert, existiert eine reelle Zahl r > 0, so dass die Potenzreihe überall im Intervall x x 0 < r (Konvergenzintervall) konvergiert und für x x 0 > r divergiert. Die Zahl r nennt man Konvergenzradius. Konvergiert die Reihe für alle x IR, so setzt man r =. Mathematik kompakt 40
42 Reihen Potenz- und Taylorreihen Konvergenzbereich von Potenzreihen Ob eine Potenzreihe auch an den Randstellen des Konvergenzintervalls, d.h. für x = x 0 ± r, konvergiert, muss jeweils gesondert untersucht werden. Die Abbildung veranschaulicht das Konvergenzverhalten von Potenzreihen: Divergenz (?? Konvergenz ( Divergenz x 0 x0- r x + r 0 Der Begriff Konvergenzradius kommt übrigens aus der Komplexen Analysis : Man kann in einer Potenzreihe anstelle der reellen Variablen x auch eine komplexe Variable z C zulassen. In diesem Falle ist der Konvergenzbereich dann ein Kreis mit Radius r. Mathematik kompakt 41
43 Reihen Potenz- und Taylorreihen Beispiel a) Die Potenzreihe x k hat den Entwicklungspunkt x 0 = 0 und den Konvergenzradius r = 1. Das Konvergenzintervall ergibt sich zu ( 1, +1). In den Rändern divergiert die Reihe bekanntlich. b) Gegeben sei die Potenzreihe x k k!. Mit a k = gilt für festes, aber beliebiges x x k k! lim k a k+1 a k = lim k = lim k x k+1 (k + 1)! k! x k x k + 1 = 0 < 1. Aus der einfachen Version des Quotientenkriteriums folgt daher die Konvergenz der Reihe für beliebige reelle x. Die Reihe hat den Konvergenzradius r = und das Konvergenzintervall (, ). Mathematik kompakt 42
44 Reihen Potenz- und Taylorreihen Übung a) Welchen Konvergenzradius hat ( 1) k x 2k+1 (2k + 1)!? b) Bestimmen Sie Konvergenzintervall und Konvergenzradius der Reihe k! x k. Mathematik kompakt 43
45 Mathematik kompakt 44 Lösung a) Es ist lim k x 2k+3 (2k + 3)! / x 2k+1 (2k + 1)! = lim k x 2 (2k + 2)(2k + 3) = 0, also kleiner 1 für festes, aber beliebiges x. Die Reihe konvergiert damit nach Quotientenkriterium für alle reellen x. Man sagt, dass sie den Konvergenzradius r = hat. b) Wir setzen a k := k! x k und benutzen das Quotientenkriterium: lim k a k+1 a k k = lim (k + 1)! x k+1 k! x k = lim k (k + 1)x = für beliebige x 0. Die Reihe konvergiert nur für x = 0. Das Konvergenzintervall besteht damit lediglich aus dem Punkt x = 0. Man sagt, dass die Reihe den Konvergenzradius r = 0 hat. Reihen Potenz- und Taylorreihen
46 Reihen Potenz- und Taylorreihen Taylorreihen Betrachten wir eine beliebig oft differenzierbare Funktion y = f(x) und deren Taylorentwicklung um x 0 vom Grad n, (R n (x) ist das Lagrange sche Restglied) f(x) = n f (k) (x 0 ) (x x 0 ) k + R n (x), k! so können wir den Grenzübergang n vornehmen und erhalten eine spezielle Potenzreihe: Definition Die Taylorreihe der Funktion y = f(x) bzgl. der Stelle x 0 ist definiert durch T (x) = f (k) (x 0 ) (x x 0 ) k. k! Mathematik kompakt 45
47 Reihen Potenz- und Taylorreihen Übereinstimmungs-Kriterium Auch Taylorreihen haben einen Konvergenzradius. Es stellt sich allerdings die Frage, ob die Funktion T (x), die durch sie definiert wird, im Konvergenzintervall mit der Ausgangsfunktion f(x) übereinstimmt. Da die n-te Partialsumme der Taylorreihe das n-te Taylorpolynom ist, erhält man aus der Taylorformel sofort: Eine notwendige und hinreichende Bedingung dafür, dass f(x) durch die zugehörige Taylorreihe T (x) im Konvergenzintervall dargestellt wird, ist: lim n R n(x) = = 0 lim n f (n+1) (ξ) (n + 1)! (x x 0) n+1 mit x 0 < ξ < x bzw. x < ξ < x 0. Mathematik kompakt 46
48 Reihen Potenz- und Taylorreihen Beispiel Für f(x) = e x gilt und somit f (k) (x) = e x f (k) (0) = 1 für k IN. Daher ergibt sich die Taylorreihe der Exponentialfunktion bzgl. x 0 = 0 zu T (x) = x k k!. Diese Reihe hat den Konvergenzradius r =. Fraglich ist noch, ob sie mit der e-funktion übereinstimmt. Mit geeignetem ξ und e ξ M (x fest!) gilt lim n R n(x) = lim e ξ n x n+1 (n + 1)! x n+1 M lim n (n + 1)! = 0, da natürlich auch die Reihe x k+1 überall (k+1)! konvergiert, deren Summanden also notwendigerweise eine Nullfolge bilden. Mathematik kompakt 47
49 Reihen Potenz- und Taylorreihen Potenzreihenentwicklung von e x Die Taylorreihe stimmt daher mit der Exponentialfunktion überein: e x = x k k! = 1 + x + x2 2! + x3 3! + x4 4! +... Obige Gleichung wird auch als Potenzreihenentwicklung der Exponentialfunktion bezeichnet. Mathematik kompakt 48
50 Reihen Potenz- und Taylorreihen Übung Ermitteln Sie die Taylorreihe T (x) der Funktion in x 0 = 0. y = sin x Für welche Werte von x konvergiert diese Reihe? Mathematik kompakt 49
51 Reihen Potenz- und Taylorreihen Lösung Für die Funktion f(x) = sin x und deren Ableitungen gilt: f(x) = sin x, f(0) = 0, f (1) (x) = cos x, f (1) (0) = 1, f (2) (x) = sin x, f (2) (0) = 0, f (3) (x) = cos x, f (3) (0) = 1, f (4) (x) = sin x, f (4) (0) = 0, usw. Die Ableitungswerte von f(x) in x 0 = 0 ergeben sich also zyklisch zu 0, 1, 0, 1. Somit gilt: T (x) = 0+1 x+ 0 2! x ! x ! x ! x Man erwartet folgende Potenzreihenentwicklung von sin x: sin x = x2k+1 ( 1)k (2k + 1)! = x x3 3! + x5 5! x7 7! ±... Mathematik kompakt 50
52 Reihen Potenz- und Taylorreihen y(x) = sin xund zugeh. Taylorpolynome Diese Vermutung lässt sich leicht verifizieren: Bekannt ist, dass das Konvergenzintervall dieser Reihe (, ) ist. Zudem stellt sie f(x) = sin x dar, da mit geeignetem ξ unter Beachtung von f (n+1) (ξ) 1 folgt: lim n R n(x) lim n x n+1 (n + 1)! = 0. Die Abbildung zeigt die Sinus-Funktion und ihre zugehörigen Taylorpolynome der ungeraden Ordnungen n = 3, 5,..., n= n= Mathematik kompakt 51
53 Reihen Potenz- und Taylorreihen Potenzreihenentwicklung von cos x Auf ähnliche Weise erhält man auch die Potenzreihenentwicklung von f(x) = cos x: Definition cos x = x2k ( 1)k (2k)! = 1 x2 2! + x4 4! x6 6! ±... Mathematik kompakt 52
54 Anwendung Achilles und die Schildkröte Zenons berühmtestes Paradoxon Im 5. vorchristlichen Jahrhundert lebte im damals griechischen Süditalien Zenon von Elea, der durch die nach ihm benannten Paradoxien viel Verwirrung stiftete. Zenons berühmtestes Paradoxon ist das von Achilles und der Schildkröte: Der Held Achilles war als besonders schneller Läufer bekannt und gab deshalb einer (10-mal langsameren) Schildkröte einen Vorsprung von 10 m. Zenon überlegte nun, dass Achilles die Schildkröte niemals einholen werde. Warum? Nun, wenn Achilles den anfänglichen Vorsprung der Schildkröte durchlaufen hat, ist diese 1 m vorgerückt. Wenn Achilles diesen 1 m zurücklegt, ist die Schildkröte wiederum ein Stück (nämlich 10 cm) weiter. Und wenn Achilles auch diesen Vorsprung einholt, so hat die Schildkröte 1 cm gut gemacht. Usw. Mathematik kompakt 53
55 Anwendung Achilles und die Schildkröte Achilles und die Schildkröte Immer dann wenn Achilles den vorigen Vorsprung der Schildkröte eingeholt hat, ist diese wieder ein kleines Stückchen weiter. Also holt er sie nie ein. 1.) Achilles 10 m Schildkröte 2.) 11 m 10 m Schildkröte Achilles 3.) 11.1 m 11 m Schildkröte Achilles 4.) m 11.1 m Schildkröte Achilles Das klingt sehr logisch! Dennoch widerspricht es jeglicher Alltagserfahrung: Schnellere Läufer überholen langsamere, auch wenn diese einen Vorsprung hatten. Der heranpreschende Porsche wird auf der Autobahn am langsameren Polo ohne Probleme vorbeiziehen. Mathematik kompakt 54
56 Anwendung Achilles und die Schildkröte Konvergente geometrische Reihe Wenn wir die oben genannten Strecken des Achilles zusammenzählen, so erhalten wir die konvergente geometrische Reihe = 10+ = 10 + n= /10 = = ( 1 10 ) n Den Wert 11.1 erhalten wir auch durch folgende einfache Überlegung. Wenn die Geschwindigkeit der Schildkröte v beträgt, dann ist die Geschwindigkeit von Achilles 10v. Der Weg s, den Achilles bzw. die Schildkröte in der Zeit t zurücklegen, ist s Achilles = 10v t bzw. s Schildkröte = v t Die beiden Läufer treffen einander, wenn beide Wege gleich sind: 10v t = v t Mathematik kompakt 55
57 Anwendung Achilles und die Schildkröte Treffpunkt der Läufer 10v t = v t Diese einfache Gleichung ergibt 9vt = 10 bzw. nach t aufgelöst: t = 10 9v. In eine der beiden Strecken s Achilles oder s Schildkröte eingesetzt erhalten wir: s = 10v 10 9v = = = Also: Bei der Marke 11.1 m hat Achilles die Schildkröte eingeholt. Dies ist gerade die (endliche) Summe obiger konvergenter geometrischer Reihe. Es gibt übrigens noch eine subtilere Form der Paradoxie von Achilles und der Schildkröte: Danach kann Achilles überhaupt nicht starten. Denn bevor er den Vorsprung der Schildkröte zurückgelegt hätte, müsste er ja erst die halbe Strecke durchlaufen haben, vor der Hälfte müsse er ein Viertel passiert haben, davor ein Achtel, davor ein Sechzehntel... Also käme er überhaupt nicht zum Loslaufen! Mathematik kompakt 56
58 Anwendung Taschenrechner und e-funktion Wie wertet der Taschenrechner z.b. die e-funktion aus? Grob gesagt sind mathematisch und für den Taschenrechner die genannten Funktionen über ihre Taylorreihe definiert und werden durch Auswertung eines Taylor-Polynoms mit kleinem Restglied näherungsweise berechnet. Für die e-funktion wird etwa die folgende Taylorreihenentwicklung benutzt: e x = bzw. x k k! = 1 + x + x2 2! + x3 3! + x4 4! +... e x = 1 + x + x2 2! + x3 3! xn n! Taylorpolynom } {{ } mit dem Lagrange schen Restglied R n (x) = mit 0 < ξ < x bzw. x < ξ < 0. eξ (n + 1)! xn+1 + R n (x) } {{ } Restglied Mathematik kompakt 57
59 Anwendung Taschenrechner und e-funktion Rechengenauigkeit Ein üblicher Taschenrechner hat etwa 8 Stellen im Display und rechnet intern mit 10 Stellen Genauigkeit. Um also dem vom Taschenrechner berechneten Wert trauen zu können, muss eine Genauigkeit von ɛ = (wegen Auf- bzw. Abrunden) erzielt werden, d.h. das Restglied R n (x) muss kleiner als ɛ werden. Dazu betrachten wir zunächst den Bereich 0.1 < x < 0.1. Das Restglied können wir dann mit R n e0.1 (n + 1)! 0.1n+1 abschätzen. Für n = 5 ergibt sich für das Restglied R und bereits für n = 6 erhalten wir R < ɛ. D.h. wir sind auf der sicheren Seite, wenn wir im Bereich von 0.1 < x < 0.1 die e-funktion durch das Taylorpolynom 6-ten Grades annähern: 1 + x + x2 2! + x3 3! + x4 4! + x5 5! + x6 6!. Mathematik kompakt 58
60 Anwendung Taschenrechner und e-funktion Genauigkeits-Probleme I Wir haben nun das Problem der Annäherung der e- Funktion im Bereich 0.1 < x < 0.1, also nahe am Entwicklungspunkt 0 der Potenzreihe, gelöst. Wollten wir mit der gleichen Genauigkeit (10 Stellen) im Bereich 1 < x < 1 rechnen, so müssten wir insgesamt ganze 13 Terme auswerten. Und im Bereich 10 < x < 10 könnten wir bei der geforderten Genauigkeit ɛ erst beim Taylorpolynom 36-ten Grades sicher sein. Ein weiteres Problem stellt die Auswertung der Taylorreihe für x < 0 dar. Dieses Problem kann man aber ganz elegant durch die Formel e x = 1 e x umgehen und sozusagen die Auswertung für negative x auf die Auswertung für positive x und Kehrwertbildung zurückführen. Mathematik kompakt 59
61 Anwendung Taschenrechner und e-funktion Genauigkeits-Probleme II Was passiert aber nun für x >> 0? Hier gibt es mehrere Möglichkeiten. Man kann z.b. die x-werte mit x > 0.1 in den Bereich 0 < x < 0.1 transformieren. Wegen ( e x 2 m ) 2 m = e x suche man zunächst eine Zahl m, so dass x = x 2 m < 0.1, werte e x aus über das Taylorpolynom 6-ten Grades, dann quadriere man m-mal (wegen hoch 2 m ). Eine andere Möglichkeit wäre es, die Zahl x > 0.1 in einen ganzzahligen Anteil, in einen Anteil zwischen 0.1 und 1 und in einen Anteil kleiner 0.1 zu zerlegen, also etwa = Dann ist e = e 23 e 0.4 e Die Auswertung von e erfolgt über das Taylorpolynom 6-ten Grades, e 0.4 entnehme man einer Tabelle mit allen Werten von e 0.1, e 0.2,... bis e 0.9. Auch für e 23 kann man Tabellen benutzen, etwa solche mit Werten e 1, e 2, e 5, e 10 etc. Mathematik kompakt 60
62 Mathematik kompakt 61 Auswertungs-Alternativen Auch für das Taylorpolynom 6-ten Grades lassen sich noch Verbesserungen finden. Zunächst sollte man es mit dem Horner-Schema auswerten: ((((( x + x2 2! + x3 3! + x4 4! + +x5 5! + x6 6! ) ) = 6! x + 1 x + 1 x + 1 x + 1 x + 1 x ! 4! 3! 2! Die Fakultäten kann man wiederum als Konstanten im Speicher ablegen. Es werden dann für die Auswertung obigen Polynoms nur 6 Multiplikationen (und 6 Additionen) benötigt. Aber selbst hier kann man die Zahl der benötigten Multiplikationen/Divisionen noch reduzieren. Man kann obiges Taylorpolynom auch durch eine rationale Funktion approximieren: 1 + x + x2 2! + x3 3! + x4 4! + +x5 5! + x6 6! ) ) x3 + 12x x x x 2 60x ) Anwendung Taschenrechner und e-funktion
63 Mathematik kompakt 62 Padé-Approximation Man gewinnt diesen Ausdruck durch die so genannte Padé-Approximation, einer Erweiterung der Taylor schen Polynomnäherung auf rationale Funktionen. Den erhaltenen Bruch kann man dann noch durch sukzessive Polynomdivision in einen Kettenbruch überführen im obigen Beispiel erhielte man: x x x x x 2 60x = x x + 10 x Der Vorteil bei der Auswertung dieses Kettenbruchs liegt darin, dass hier nur noch 3 Divisionen (und einige Additionen) auszuführen sind. Es geht also doppelt so schnell wie beim Einsetzen in obiges Horner-Polynom. Anwendung Taschenrechner und e-funktion
INGENIEURMATHEMATIK. 8. Reihen. Sommersemester Prof. Dr. Gunar Matthies
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
3 Reihen. 3.1 Konvergenz und Divergenz. Die Eindeutigkeit nach Satz 13 ergibt schließlich (5). (6) folgt aus (2) und (1) wegen. 1 a +log ba.
 Die Eindeutigkeit nach Satz 3 ergibt schließlich (5). (6) folgt aus (2) und () wegen Aussage (7) ergibt sich aus () und (6). 0 = log b = log b ( a a) = log b a +log ba. 3 Reihen 3. Konvergenz und Divergenz
Die Eindeutigkeit nach Satz 3 ergibt schließlich (5). (6) folgt aus (2) und () wegen Aussage (7) ergibt sich aus () und (6). 0 = log b = log b ( a a) = log b a +log ba. 3 Reihen 3. Konvergenz und Divergenz
Kapitel 4. Reihen 4.1. Definition und Beispiele
 Kapitel 4. Reihen 4.1. Definition und Beispiele Ist (a n ) eine Folge von Zahlen, so heißt der formale Ausdruck a ν = a 0 + a 1 + a 2 +... eine Reihe; die einzelnen a ν sind die Glieder dieser Reihe. Um
Kapitel 4. Reihen 4.1. Definition und Beispiele Ist (a n ) eine Folge von Zahlen, so heißt der formale Ausdruck a ν = a 0 + a 1 + a 2 +... eine Reihe; die einzelnen a ν sind die Glieder dieser Reihe. Um
Vorlesung: Analysis I für Ingenieure
 Vorlesung: Analysis I für Ingenieure Dozent: Dr. Michael Karow Thema: unendliche Reihen Definition. Eine unendliche Reihe ist der Grenzwert einer Folge von Summen: a k = lim k a k, wobei a k C. Falls der
Vorlesung: Analysis I für Ingenieure Dozent: Dr. Michael Karow Thema: unendliche Reihen Definition. Eine unendliche Reihe ist der Grenzwert einer Folge von Summen: a k = lim k a k, wobei a k C. Falls der
4 Reihen und Finanzmathematik
 4 Reihen und Finanzmathematik 4. Reihen Aus Folgen lassen sich durch Aufaddieren weitere Folgen konstruieren. Das sind die sogenannten Reihen, sie spielen in der Finanzmathematik eine wichtige Rolle. Sei
4 Reihen und Finanzmathematik 4. Reihen Aus Folgen lassen sich durch Aufaddieren weitere Folgen konstruieren. Das sind die sogenannten Reihen, sie spielen in der Finanzmathematik eine wichtige Rolle. Sei
3 Folgen, Reihen, Grenzwerte 3.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die
 3 Folgen, Reihen, Grenzwerte 3.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die eindeutig den natürlichen Zahlen zugeordnet sind ( n N, auch
3 Folgen, Reihen, Grenzwerte 3.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die eindeutig den natürlichen Zahlen zugeordnet sind ( n N, auch
Kapitel 5 Reihen 196
 Kapitel 5 Reihen 96 Kapitel 5. Definition und Beispiele 97 Das Material dieses Kapitels können Sie nachlesen in: MICHAEL SPIVAK, Calculus, Kapitel 22 DIRK HACHENBERGER, Mathematik für Informatiker, Kapitel
Kapitel 5 Reihen 96 Kapitel 5. Definition und Beispiele 97 Das Material dieses Kapitels können Sie nachlesen in: MICHAEL SPIVAK, Calculus, Kapitel 22 DIRK HACHENBERGER, Mathematik für Informatiker, Kapitel
Wenn man eine Folge gegeben hat, so kann man auch versuchen, eine Summe. a 0 + a 1 + a 2 +
 8 Reihen 38 8 Reihen Wenn man eine Folge gegeben hat, so kann man auch versuchen, eine Summe a 0 + a + a 2 + zu bilden. Wir wollen nun erklären, was wir darunter verstehen wollen. Zunächst kann man die
8 Reihen 38 8 Reihen Wenn man eine Folge gegeben hat, so kann man auch versuchen, eine Summe a 0 + a + a 2 + zu bilden. Wir wollen nun erklären, was wir darunter verstehen wollen. Zunächst kann man die
Tutorium: Analysis und lineare Algebra. Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen
 Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
Tutorium: Analysis und lineare Algebra
 Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
Ferienkurs Analysis 1, SoSe Unendliche Reihen. Florian Beye August 15, 2008
 Ferienkurs Analysis 1, SoSe 2008 Unendliche Reihen Florian Beye August 15, 2008 1 Reihen und deren Konvergenz Definition 1.1. Eine reelle bzw. komplexe Reihe ist eine unendliche Summe über die Glieder
Ferienkurs Analysis 1, SoSe 2008 Unendliche Reihen Florian Beye August 15, 2008 1 Reihen und deren Konvergenz Definition 1.1. Eine reelle bzw. komplexe Reihe ist eine unendliche Summe über die Glieder
Folgen und Reihen. Beschränkte Folge: Es gibt eine Zahl c = const.
 Folgen und Reihen Folgen: Def.: Eine Abbildung a N K, n a(n) := a n (K = R C) wird Zahlenfolge genannt. Sie heißt reelle (komplexe) Zahlenfolge, falls K = R(C) ist. Symbole: a n K: Elemente der Folge,
Folgen und Reihen Folgen: Def.: Eine Abbildung a N K, n a(n) := a n (K = R C) wird Zahlenfolge genannt. Sie heißt reelle (komplexe) Zahlenfolge, falls K = R(C) ist. Symbole: a n K: Elemente der Folge,
REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert
![REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert](/thumbs/55/37057337.jpg) Reihenentwicklungen Herbert Paukert 1 REIHENENTWICKLUNGEN Eine kurze Einführung Herbert Paukert [1] Reihen mit konstanten Gliedern [2] Potenzreihen [3] Reihenentwicklung von Funktionen Reihenentwicklungen
Reihenentwicklungen Herbert Paukert 1 REIHENENTWICKLUNGEN Eine kurze Einführung Herbert Paukert [1] Reihen mit konstanten Gliedern [2] Potenzreihen [3] Reihenentwicklung von Funktionen Reihenentwicklungen
Folgen und Reihen. Folgen. Inhalt. Mathematik für Chemiker Teil 1: Analysis. Folgen und Reihen. Reelle Funktionen. Vorlesung im Wintersemester 2014
 Inhalt Mathematik für Chemiker Teil 1: Analysis Vorlesung im Wintersemester 2014 Kurt Frischmuth Institut für Mathematik, Universität Rostock Rostock, Oktober 2014... Folgen und Reihen Reelle Funktionen
Inhalt Mathematik für Chemiker Teil 1: Analysis Vorlesung im Wintersemester 2014 Kurt Frischmuth Institut für Mathematik, Universität Rostock Rostock, Oktober 2014... Folgen und Reihen Reelle Funktionen
Folgen. Eine (unendliche) (Zahlen)folge ist eine Abbildung. dann als. notiert, und das wird abgekürzt mit. nennt man die Folgenglieder.
 Folgen Eine (unendliche) (Zahlen)folge ist eine Abbildung Statt dann als schreibt man auch oder ähnlich, die Folge wird notiert, und das wird abgekürzt mit. Die nennt man die Folgenglieder. Mathematik
Folgen Eine (unendliche) (Zahlen)folge ist eine Abbildung Statt dann als schreibt man auch oder ähnlich, die Folge wird notiert, und das wird abgekürzt mit. Die nennt man die Folgenglieder. Mathematik
Man schreibt dann lim. = bzw. lim
 Die Funktion f : R R geht für x nach (bzw. ), fallses für allem R + ein t(ε) R + gibt, so dass gilt ist x > t(ε), dann folgt f(x) > M bzw. ist x > t(ε), dann folgt f(x) < M. Man schreibt dann lim x = bzw.
Die Funktion f : R R geht für x nach (bzw. ), fallses für allem R + ein t(ε) R + gibt, so dass gilt ist x > t(ε), dann folgt f(x) > M bzw. ist x > t(ε), dann folgt f(x) < M. Man schreibt dann lim x = bzw.
Kap. 10: Folgen und Reihen. Eine Funktion a : N Ñ R
 Definition: Zahlenfolge Kap. 10: Folgen und Reihen 10.1 Definition: Zahlenfolge Eine Funktion a : N Ñ R poder Cq heißt reelle (oder komplexe) Zahlenfolge. Man nennt a n apnq das n-te Folgenglied und schreibt
Definition: Zahlenfolge Kap. 10: Folgen und Reihen 10.1 Definition: Zahlenfolge Eine Funktion a : N Ñ R poder Cq heißt reelle (oder komplexe) Zahlenfolge. Man nennt a n apnq das n-te Folgenglied und schreibt
Mathematik I Herbstsemester 2018 Kapitel 6: Potenzreihen
 Mathematik I Herbstsemester 208 Kapitel 6: Potenzreihen Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas / 58 6. Potenzreihen Reihen (Zahlenreihen) Konvergenzkriterien für Reihen Notwendiges
Mathematik I Herbstsemester 208 Kapitel 6: Potenzreihen Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas / 58 6. Potenzreihen Reihen (Zahlenreihen) Konvergenzkriterien für Reihen Notwendiges
Folgen und Reihen. Thomas Blasi
 Folgen und Reihen Thomas Blasi 02.03.2009 Inhaltsverzeichnis Folgen und Grenzwerte 2. Definitionen und Bemerkungen............................. 2.2 Konvergenz und Beschränktheit.............................
Folgen und Reihen Thomas Blasi 02.03.2009 Inhaltsverzeichnis Folgen und Grenzwerte 2. Definitionen und Bemerkungen............................. 2.2 Konvergenz und Beschränktheit.............................
Mathematik I - Woche 10
 Mathematik I - Woche 0 Philip Müller Reihen. Was ist eine Reihe Wir hatten bis jetzt Folgen. Eine Folge (a n ) n N ist eine Vorschrift, die von den natürlichen Zahlen, in die reellen Zahlen abbildet. Ein
Mathematik I - Woche 0 Philip Müller Reihen. Was ist eine Reihe Wir hatten bis jetzt Folgen. Eine Folge (a n ) n N ist eine Vorschrift, die von den natürlichen Zahlen, in die reellen Zahlen abbildet. Ein
Folgen und Reihen. 1 Konvergenz
 Folgen und Reihen Man betrachte viele Zahlen hintereinander geschrieben. Solche Folgen von Zahlen können durch nummeriert werden. Es entsteht eine Zuordnung der natürlichen Zahlen zu den Gliedern der Folge.
Folgen und Reihen Man betrachte viele Zahlen hintereinander geschrieben. Solche Folgen von Zahlen können durch nummeriert werden. Es entsteht eine Zuordnung der natürlichen Zahlen zu den Gliedern der Folge.
Die Taylorreihe einer Funktion
 Kapitel 6 Die Taylorreihe einer Funktion Dieser Abschnitt beschäftigt sich mit Taylorreihen, Taylorpolynomen und der Restgliedabschätzung für Taylorpolynome. Die Taylorreihe einer reellen Funktion ist
Kapitel 6 Die Taylorreihe einer Funktion Dieser Abschnitt beschäftigt sich mit Taylorreihen, Taylorpolynomen und der Restgliedabschätzung für Taylorpolynome. Die Taylorreihe einer reellen Funktion ist
Numerische Verfahren und Grundlagen der Analysis
 Numerische Verfahren und Grundlagen der Analysis Rasa Steuding Hochschule RheinMain Wiesbaden Wintersemester 20/2 R. Steuding (HS-RM) NumAna Wintersemester 20/2 / 20 2. Reihen R. Steuding (HS-RM) NumAna
Numerische Verfahren und Grundlagen der Analysis Rasa Steuding Hochschule RheinMain Wiesbaden Wintersemester 20/2 R. Steuding (HS-RM) NumAna Wintersemester 20/2 / 20 2. Reihen R. Steuding (HS-RM) NumAna
Kapitel 3. Reihen und ihre Konvergenz
 Kapitel 3 Reihen und ihre Konvergenz Abschnitt 3.1 Der Reihenbegri und erste Beispiele Denitionen zu Reihen, 1 Denition. Sei (a n ) n N0 eine Folge reeller Zahlen. Für n N 0 heiÿt dann die Zahl s n :=
Kapitel 3 Reihen und ihre Konvergenz Abschnitt 3.1 Der Reihenbegri und erste Beispiele Denitionen zu Reihen, 1 Denition. Sei (a n ) n N0 eine Folge reeller Zahlen. Für n N 0 heiÿt dann die Zahl s n :=
Ferienkurs Analysis 1
 Skript Ferienkurs Analysis 1 Fabian Hafner und Thomas Baldauf TUM Wintersemester 2016/17 04.04.2017 Das Skript wurde teilweise übernommen vom Skript des Ferienkurses WS 2014, verfasst von Andreas Wörfel.
Skript Ferienkurs Analysis 1 Fabian Hafner und Thomas Baldauf TUM Wintersemester 2016/17 04.04.2017 Das Skript wurde teilweise übernommen vom Skript des Ferienkurses WS 2014, verfasst von Andreas Wörfel.
Unendliche Reihen. D.h. Die Summe einer unendlichen Reihe ist der Grenzwert der Folge der Partialsummen.
 Unendliche Reihen Wegen der elementaren Eigenschaften der Zahlen ist lar, was unter einer endlichen Summe von Zahlen a + a 2 +... + zu verstehen ist. Vorderhand ist noch nicht erlärt, was unter einer unendlichen
Unendliche Reihen Wegen der elementaren Eigenschaften der Zahlen ist lar, was unter einer endlichen Summe von Zahlen a + a 2 +... + zu verstehen ist. Vorderhand ist noch nicht erlärt, was unter einer unendlichen
= (n 2 ) 1 (Kurzschreibweise: a n = n 2 ) ergibt die Zahlenfolge 1, 4, 9, 16, 25, 36,.
 2 Folgen, Reihen, Grenzwerte 2.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die eindeutig den natürlichen Zahlen zugeordnet sind (n N; auch
2 Folgen, Reihen, Grenzwerte 2.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die eindeutig den natürlichen Zahlen zugeordnet sind (n N; auch
1 Reihen von Zahlen. Inhalt:
 5 Kapitel 3 Reihen Reihen von Zahlen Inhalt: Konvergenz und Divergenz von Reihen reeller oder komplexer Zahlen, geometrische Reihe, harmonische Reihe, alternierende Reihen. Cauchy-Kriterium, absolute Konvergenz,
5 Kapitel 3 Reihen Reihen von Zahlen Inhalt: Konvergenz und Divergenz von Reihen reeller oder komplexer Zahlen, geometrische Reihe, harmonische Reihe, alternierende Reihen. Cauchy-Kriterium, absolute Konvergenz,
k=1 {S n } n N konvergiert, so schreibt man: a n n=1 und spricht dann von Konvergenz oder Divergenz der unendlichen Reihe
 7 Reihen sind spezielle Folgen, die durch Summation entstehen. Definition 7. : {a n } n N sei Folge in C; S n := n Folge {S n } n N unendliche Reihe. Falls a k statt lim S n. a k heißt {S n } n N konvergiert,
7 Reihen sind spezielle Folgen, die durch Summation entstehen. Definition 7. : {a n } n N sei Folge in C; S n := n Folge {S n } n N unendliche Reihe. Falls a k statt lim S n. a k heißt {S n } n N konvergiert,
1.1 Vorbemerkung: Konvergenz von Reihen. g = lim. n=0. n=0 a n sei konvergent und schreibt. a n = g. (2) n=0
 1 Taylor-Entwicklung 1.1 Vorbemerkung: Konvergenz von Reihen Gegeben sei eine unendliche Folge a 0,a 1,a,... reeller Zahlen a n R. Hat der Grenzwert g = lim k a n (1) einen endlichen Wert g R, so sagt
1 Taylor-Entwicklung 1.1 Vorbemerkung: Konvergenz von Reihen Gegeben sei eine unendliche Folge a 0,a 1,a,... reeller Zahlen a n R. Hat der Grenzwert g = lim k a n (1) einen endlichen Wert g R, so sagt
4 Reihen. s n = a 1 + a 2 + + a n = Die Folge (s n ) n N der Partialsummen heißt eine (unendliche) Reihe und wird auch als a k. k=1. )n N geschrieben.
 4 Reihen Aus Folgen lassen sich durch Aufaddieren weitere Folgen konstruieren. Das sind die sogenannten Reihen, sie spielen in der Finanzmathematik eine wichtige Rolle. Sei (a k ) k N eine Folge. Wir definieren
4 Reihen Aus Folgen lassen sich durch Aufaddieren weitere Folgen konstruieren. Das sind die sogenannten Reihen, sie spielen in der Finanzmathematik eine wichtige Rolle. Sei (a k ) k N eine Folge. Wir definieren
5. Unendliche Reihen [Kö 6]
![5. Unendliche Reihen [Kö 6] 5. Unendliche Reihen [Kö 6]](/thumbs/92/110553245.jpg) 25 5. Unendliche Reihen [Kö 6] 5.1 Grundbegriffe Definition 1. Es sei k Z und (a i ) i k eine (komplexe) Folge. Unter der unendlichen Reihe a i versteht man die Folge (s n ) n k der Partialsummen s n :=
25 5. Unendliche Reihen [Kö 6] 5.1 Grundbegriffe Definition 1. Es sei k Z und (a i ) i k eine (komplexe) Folge. Unter der unendlichen Reihe a i versteht man die Folge (s n ) n k der Partialsummen s n :=
Analysis I. Vorlesung 9. Reihen
 Prof. Dr. H. Brenner Osnabrück WS 20/204 Analysis I Vorlesung 9 Reihen Wir haben in der siebten Vorlesung gesagt, dass man eine Dezimalentwicklung, also eine (unendliche) Ziffernfolge mit Ziffern zwischen
Prof. Dr. H. Brenner Osnabrück WS 20/204 Analysis I Vorlesung 9 Reihen Wir haben in der siebten Vorlesung gesagt, dass man eine Dezimalentwicklung, also eine (unendliche) Ziffernfolge mit Ziffern zwischen
7 KONVERGENTE FOLGEN 35. inf M = Infimum von M. bezeichnet haben. Definition. Sei (a n ) n N eine beschränkte Folge in R. Dann heißt.
 7 KONVERGENTE FOLGEN 35 und die größe untere Schranke mit bezeichnet haben. inf M = Infimum von M Definition. Sei (a n ) n N eine beschränkte Folge in R. Dann heißt der Limes superior der Folge, und lim
7 KONVERGENTE FOLGEN 35 und die größe untere Schranke mit bezeichnet haben. inf M = Infimum von M Definition. Sei (a n ) n N eine beschränkte Folge in R. Dann heißt der Limes superior der Folge, und lim
Reihen, Exponentialfunktion Vorlesung
 Reihen, Exponentialfunktion Vorlesung Marcus Jung 5.03.20 Inhaltsverzeichnis Inhaltsverzeichnis Reihen 3. Denition.................................... 3.2 Konvergenzkriterien für Reihen........................
Reihen, Exponentialfunktion Vorlesung Marcus Jung 5.03.20 Inhaltsverzeichnis Inhaltsverzeichnis Reihen 3. Denition.................................... 3.2 Konvergenzkriterien für Reihen........................
n=1 a n mit reellen Zahlen a n einen
 4 Unendliche Reihen 4. Definition und Beispiele Ein altes Problem der Analysis ist es, einer Reihe mit reellen Zahlen einen Wert zuzuordnen. Ein typisches Beispiel ist die unendliche Reihe + +..., die
4 Unendliche Reihen 4. Definition und Beispiele Ein altes Problem der Analysis ist es, einer Reihe mit reellen Zahlen einen Wert zuzuordnen. Ein typisches Beispiel ist die unendliche Reihe + +..., die
Folgen und Reihen. Christoph Laabs, n s k und ist Grenzwert dieser Reihe.
 Folgen und Reihen Christoph Laabs, christoph.laabs@tu-dresden.de Grundlagen Eine Reihe ist darstellbar durch z. B. = a 0 + a + a 2 + a + a 4 +... Ausgesprochen wird das als Summe von von k bis Unendlich.
Folgen und Reihen Christoph Laabs, christoph.laabs@tu-dresden.de Grundlagen Eine Reihe ist darstellbar durch z. B. = a 0 + a + a 2 + a + a 4 +... Ausgesprochen wird das als Summe von von k bis Unendlich.
Konvergenz und Divergenz einer unendlichen Reihe. 5-E Ma 2 Lubov Vassilevskaya
 Konvergenz und Divergenz einer unendlichen Reihe 5-E Ma 2 Lubov Vassilevskaya Folgen und Reihen: Beispiele Unter dem Bildungsgesetz einer unendlichen Reihe n i= versteht man einen funktionalen Zusammenhang
Konvergenz und Divergenz einer unendlichen Reihe 5-E Ma 2 Lubov Vassilevskaya Folgen und Reihen: Beispiele Unter dem Bildungsgesetz einer unendlichen Reihe n i= versteht man einen funktionalen Zusammenhang
HM I Tutorien 6 und 7
 HM I Tutorien 6 und 7 Lucas Kunz. Dezember 207 und 8. Dezember 207 Inhaltsverzeichnis Vorwort 2 2 Theorie 2 2. Definition einer Reihe.............................. 2 2.2 Absolute Konvergenz..............................
HM I Tutorien 6 und 7 Lucas Kunz. Dezember 207 und 8. Dezember 207 Inhaltsverzeichnis Vorwort 2 2 Theorie 2 2. Definition einer Reihe.............................. 2 2.2 Absolute Konvergenz..............................
HM I Tutorium 5. Lucas Kunz. 21. November 2018
 HM I Tutorium 5 Lucas Kunz 2. November 208 Inhaltsverzeichnis Theorie 2. Definition.................................... 2.2 Wichtige Reihen................................. 2.3 Absolute Konvergenz..............................
HM I Tutorium 5 Lucas Kunz 2. November 208 Inhaltsverzeichnis Theorie 2. Definition.................................... 2.2 Wichtige Reihen................................. 2.3 Absolute Konvergenz..............................
KAPITEL 9. Funktionenreihen
 KAPITEL 9 Funktionenreihen 9. TaylorReihen............................ 28 9.2 Potenzreihen............................ 223 9.3 Grenzfunktionen von Funktionenfolgen bzw. reihen........ 230 9.4 Anwendungen............................
KAPITEL 9 Funktionenreihen 9. TaylorReihen............................ 28 9.2 Potenzreihen............................ 223 9.3 Grenzfunktionen von Funktionenfolgen bzw. reihen........ 230 9.4 Anwendungen............................
Kapitel 4 Folgen und Reihen
 Kapitel 4 Folgen und Reihen Inhalt 4.1 4.1 Konvergenzkriterien für für Folgen 4.2 4.2 Reihen 4.3 4.3 Achilles und und die die Schildkröte Seite 2 4.1 Konvergenzkriterien für Folgen Wiederholung (vgl. (vgl.
Kapitel 4 Folgen und Reihen Inhalt 4.1 4.1 Konvergenzkriterien für für Folgen 4.2 4.2 Reihen 4.3 4.3 Achilles und und die die Schildkröte Seite 2 4.1 Konvergenzkriterien für Folgen Wiederholung (vgl. (vgl.
2 Folgen und Reihen. 2.1 Folgen in C Konvergenz von Folgen. := f(n)
 2 Folgen und Reihen 2.1 Folgen in C 2.1.1 Konvergenz von Folgen Eine Folge komplexer Zahlen ist eine Funktion f : N C. Mit a n schreibt man (a n ) n=1, (a n ) oder auch a 1, a 2,.... := f(n) (a n ) heißt
2 Folgen und Reihen 2.1 Folgen in C 2.1.1 Konvergenz von Folgen Eine Folge komplexer Zahlen ist eine Funktion f : N C. Mit a n schreibt man (a n ) n=1, (a n ) oder auch a 1, a 2,.... := f(n) (a n ) heißt
Häufungspunkte und Satz von Bolzano und Weierstraß.
 Häufungspunkte und Satz von Bolzano und Weierstraß. Definition: Sei (a nk ) k N eine konvergente Teilfolge der Folge (a n ) n N.Dannwirdder Grenzwert der Teilfolge (a nk ) k N als Häufungspunkt der Folge
Häufungspunkte und Satz von Bolzano und Weierstraß. Definition: Sei (a nk ) k N eine konvergente Teilfolge der Folge (a n ) n N.Dannwirdder Grenzwert der Teilfolge (a nk ) k N als Häufungspunkt der Folge
eine reelle oder komplexe Folge ist, kann man daraus eine neue Folge {s n } n=0 konstruieren durch s n = a 0 + a a n, s n = a k.
 Analysis, Woche 7 Reihen I A 7. Folgen aus Folgen Wenn a n eine reelle oder komplexe Folge ist, kann man daraus eine neue Folge s n konstruieren durch s n = a 0 + a + + a n, oder netter geschrieben s n
Analysis, Woche 7 Reihen I A 7. Folgen aus Folgen Wenn a n eine reelle oder komplexe Folge ist, kann man daraus eine neue Folge s n konstruieren durch s n = a 0 + a + + a n, oder netter geschrieben s n
Folgen und Reihen. Kapitel Zahlenfolgen
 Kapitel 2 Folgen und Reihen 2. Zahlenfolgen Definition. Eine Folge reeller Zahlen a 0,a,a 2,..., die gewonnen wird durch eine Vorschrift, die jeder natürlichen Zahl n N genau eine reelle Zahl a n zuordnet,
Kapitel 2 Folgen und Reihen 2. Zahlenfolgen Definition. Eine Folge reeller Zahlen a 0,a,a 2,..., die gewonnen wird durch eine Vorschrift, die jeder natürlichen Zahl n N genau eine reelle Zahl a n zuordnet,
x k = s k=1 y k = y konvergent. Dann folgt (cx k ) = cx für c K. Partialsummenfolge konvergiert
 4 Reihen Im Folgenden sei K R oder K C. 4. Definition. Es sei (x k ) Folge in K. Wir schreiben x k s und sagen, die Reihe x k konvergiere, falls die sogenannte Partialsummen-Folge s n x k n, 2,... in K
4 Reihen Im Folgenden sei K R oder K C. 4. Definition. Es sei (x k ) Folge in K. Wir schreiben x k s und sagen, die Reihe x k konvergiere, falls die sogenannte Partialsummen-Folge s n x k n, 2,... in K
Analysis I. Guofang Wang Universität Freiburg
 Universität Freiburg 22.11.2016 3. Mächtigkeit und die komplexe Zahlen Komplexe Zahlen Definition Die komplexe Zahlen sind definiert als C = R 2 = R R, mit (x 1, y 1 ) + (x 2, y 2 ) = (x 1 + x 2, y 1 +
Universität Freiburg 22.11.2016 3. Mächtigkeit und die komplexe Zahlen Komplexe Zahlen Definition Die komplexe Zahlen sind definiert als C = R 2 = R R, mit (x 1, y 1 ) + (x 2, y 2 ) = (x 1 + x 2, y 1 +
6 - Unendliche Reihen
 Kapitel 2 Folgen und Reihen Seite 1 6 Unendliche Reihen Definition 6.1 (Unendliche Reihen) Sei eine Folge aus C. Unter der unendlichen Reihe mit den Gliedern versteht man das Symbol oder Die Zahl heißt
Kapitel 2 Folgen und Reihen Seite 1 6 Unendliche Reihen Definition 6.1 (Unendliche Reihen) Sei eine Folge aus C. Unter der unendlichen Reihe mit den Gliedern versteht man das Symbol oder Die Zahl heißt
10 Aus der Analysis. Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit
 10 Aus der Analysis Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit Zahlenfolgen Ein unendliche Folge reeller Zahlen heißt Zahlenfolge. Im Beispiel 2, 3, 2, 2 2, 2
10 Aus der Analysis Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit Zahlenfolgen Ein unendliche Folge reeller Zahlen heißt Zahlenfolge. Im Beispiel 2, 3, 2, 2 2, 2
Folgen, Reihen, Grenzwerte u. Stetigkeit
 Folgen, Reihen, Grenzwerte u. Stetigkeit Josef F. Bürgler Abt. Informatik HTA Luzern, FH Zentralschweiz HTA.MA+INF Josef F. Bürgler (HTA Luzern) Einf. Infinitesimalrechnung HTA.MA+INF 1 / 33 Inhalt 1 Folgen
Folgen, Reihen, Grenzwerte u. Stetigkeit Josef F. Bürgler Abt. Informatik HTA Luzern, FH Zentralschweiz HTA.MA+INF Josef F. Bürgler (HTA Luzern) Einf. Infinitesimalrechnung HTA.MA+INF 1 / 33 Inhalt 1 Folgen
Höhere Mathematik II. (Vorlesungskript)
 Fakultät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Universität der Bundeswehr München Höhere Mathematik II (Vorlesungskript) Univ. Prof. Dr. sc. math. Kurt Marti 2 2 L
Fakultät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Universität der Bundeswehr München Höhere Mathematik II (Vorlesungskript) Univ. Prof. Dr. sc. math. Kurt Marti 2 2 L
1 k = = Sie ist also gerade der Grenzwert der zur Folge (r k 10 k ) k N0 gehörenden Reihe( n
 Die zur Folge ( k ) k N gehörende Reihe ( n k ) n N ist divergent, genauer k =. 2. Dezimalzahlen: Eine Zahl r = r 0,r r 2 r 3 mit r 0 N 0 und r n {0,...,9} für n hat den Wert r = r 0 +r 0 +r 2 00 +...
Die zur Folge ( k ) k N gehörende Reihe ( n k ) n N ist divergent, genauer k =. 2. Dezimalzahlen: Eine Zahl r = r 0,r r 2 r 3 mit r 0 N 0 und r n {0,...,9} für n hat den Wert r = r 0 +r 0 +r 2 00 +...
Wirtschaftsmathematik
 Hochschule Darmstadt FB Mathematik und Naturwissenschaften Wirtschaftsmathematik für die Betriebswirtschaftslehre (B.Sc.) Sommersemester 207 Adam Georg Balogh Dr. rer. nat. habil. Adam Georg Balogh E-mail:
Hochschule Darmstadt FB Mathematik und Naturwissenschaften Wirtschaftsmathematik für die Betriebswirtschaftslehre (B.Sc.) Sommersemester 207 Adam Georg Balogh Dr. rer. nat. habil. Adam Georg Balogh E-mail:
HM I Tutorium 5. Lucas Kunz. 24. November 2016
 HM I Tutorium 5 Lucas Kunz 24. November 206 Inhaltsverzeichnis Theorie 2. Definition einer Reihe.............................. 2.2 Wichtige Reihen................................. 2.3 Limites inferior
HM I Tutorium 5 Lucas Kunz 24. November 206 Inhaltsverzeichnis Theorie 2. Definition einer Reihe.............................. 2.2 Wichtige Reihen................................. 2.3 Limites inferior
KAPITEL 2. Folgen und Reihen
 KAPITEL 2 Folgen und Reihen 1. Konvergenz und Divergenz Definition 2.1 (Folgen). Eine Abbildung a : N R (bzw. a : N 0 R) nennt man Folge. Statt a : N R schreibt man meist (a n ) n N und a n statt a(n).
KAPITEL 2 Folgen und Reihen 1. Konvergenz und Divergenz Definition 2.1 (Folgen). Eine Abbildung a : N R (bzw. a : N 0 R) nennt man Folge. Statt a : N R schreibt man meist (a n ) n N und a n statt a(n).
Folgen und Reihen. Bernhard Ganter. Institut für Algebra TU Dresden D Dresden
 Folgen und Reihen Bernhard Ganter Institut für Algebra TU Dresden D-0062 Dresden bernhard.ganter@tu-dresden.de Folgen Eine (unendliche) (Zahlen)folge ist eine Abbildung f : N R. Statt f (n) schreibt man
Folgen und Reihen Bernhard Ganter Institut für Algebra TU Dresden D-0062 Dresden bernhard.ganter@tu-dresden.de Folgen Eine (unendliche) (Zahlen)folge ist eine Abbildung f : N R. Statt f (n) schreibt man
eine reelle oder komplexe Folge ist, kann man daraus eine neue Folge {s n } n=0 konstruieren durch s n = a 0 + a a n, a k.
 Analysis, Woche 7 Reihen I 7. Folgen aus Folgen Wenn a n eine reelle oder komplexe Folge ist, kann man daraus eine neue Folge s n konstruieren durch s n = a 0 + a + + a n, oder netter geschrieben s n =
Analysis, Woche 7 Reihen I 7. Folgen aus Folgen Wenn a n eine reelle oder komplexe Folge ist, kann man daraus eine neue Folge s n konstruieren durch s n = a 0 + a + + a n, oder netter geschrieben s n =
Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13)
 1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 5: Konvergenz Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 15. Dezember 2011) Folgen Eine Folge x 0, x 1,
1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 5: Konvergenz Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 15. Dezember 2011) Folgen Eine Folge x 0, x 1,
Analyis I - Reihen und Potenzreihen
 Analyis I - Reihen und January 13, 2009 Analyis I - Reihen und Definition (Reihen) Reihen Sei (a k ) k N eine Folge und n N. Dann heißt (s k ) k N mit s n = n k=1 die Partialsummenfolge von (a k ) k N.
Analyis I - Reihen und January 13, 2009 Analyis I - Reihen und Definition (Reihen) Reihen Sei (a k ) k N eine Folge und n N. Dann heißt (s k ) k N mit s n = n k=1 die Partialsummenfolge von (a k ) k N.
10 Kriterien für absolute Konvergenz von Reihen
 10 Kriterien für absolute Konvergenz von Reihen 10.1 Majoranten- und Minorantenkriterium 10.3 Wurzelkriterium 10.4 Quotientenkriterium 10.9 Riemannscher Umordnungssatz 10.10 Äquivalenzen zur absoluten
10 Kriterien für absolute Konvergenz von Reihen 10.1 Majoranten- und Minorantenkriterium 10.3 Wurzelkriterium 10.4 Quotientenkriterium 10.9 Riemannscher Umordnungssatz 10.10 Äquivalenzen zur absoluten
Folgen, Reihen, Potenzreihen, Exponentialfunktion
 Ferienkurs Seite 1 Technische Universität München Ferienkurs Analysis 1 Hannah Schamoni Wintersemester 2011/12 Folgen, Reihen, Potenzreihen, Exponentialfunktion 20.03.2012 Inhaltsverzeichnis 1 Folgen 2
Ferienkurs Seite 1 Technische Universität München Ferienkurs Analysis 1 Hannah Schamoni Wintersemester 2011/12 Folgen, Reihen, Potenzreihen, Exponentialfunktion 20.03.2012 Inhaltsverzeichnis 1 Folgen 2
Folgen und Reihen. Mathematik-Repetitorium
 Folgen und Reihen 1.1 Vollständige Induktion 1.2 Zahlenfolgen 1.3 Eigenschaften konvergenter Zahlenfolgen 1.4 Konvergenzkriterien 1.5 Unendliche Reihen 1.6 Eigenschaften unendlicher Reihen 1.7 Rechnen
Folgen und Reihen 1.1 Vollständige Induktion 1.2 Zahlenfolgen 1.3 Eigenschaften konvergenter Zahlenfolgen 1.4 Konvergenzkriterien 1.5 Unendliche Reihen 1.6 Eigenschaften unendlicher Reihen 1.7 Rechnen
Vorbereitungskurs Mathematik zum Sommersemester 2015 Folgen und Reihen
 Vorbereitungskurs Mathematik zum Sommersemester 2015 Folgen und Reihen Susanna Pohl Vorkurs Mathematik TU Dortmund 12.03.2015 Folgen und Reihen Folgen und Grenzwerte Rechenregeln für konvergente Folgen
Vorbereitungskurs Mathematik zum Sommersemester 2015 Folgen und Reihen Susanna Pohl Vorkurs Mathematik TU Dortmund 12.03.2015 Folgen und Reihen Folgen und Grenzwerte Rechenregeln für konvergente Folgen
Konvergenz von Folgen
 6 Konvergenz von Folgen Definition 6.1 Eine Folge in C (oder R) ist eine Abbildung f : N C (oder R). Schreibweise: (a n ) n N, (a n ), a 1, a 2... wobei a n = f(n). Beispiele: 1) (1 + 2 n ) n N, 3 2, 5
6 Konvergenz von Folgen Definition 6.1 Eine Folge in C (oder R) ist eine Abbildung f : N C (oder R). Schreibweise: (a n ) n N, (a n ), a 1, a 2... wobei a n = f(n). Beispiele: 1) (1 + 2 n ) n N, 3 2, 5
D-INFK Analysis I FS 2017 Prof. Dr. Özlem Imamoglu. MC-Fragen Serie 1. Einsendeschluss: Freitag, der :00 Uhr
 D-INFK Analysis I FS 2017 Prof. Dr. Özlem Imamoglu MC-Fragen Serie 1 Einsendeschluss: Freitag, der 26.09.2014 12:00 Uhr 1. Welche der folgenden Aussagen sind richtig? (a) Eine divergente Folge ist nicht
D-INFK Analysis I FS 2017 Prof. Dr. Özlem Imamoglu MC-Fragen Serie 1 Einsendeschluss: Freitag, der 26.09.2014 12:00 Uhr 1. Welche der folgenden Aussagen sind richtig? (a) Eine divergente Folge ist nicht
REIHEN. 1. Definition und Konvergenz. Definition (unendliche) Reihe
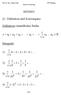 REIHEN 1. Definition und Konvergenz Definition (unendliche) Reihe 1 2 3, s = a + a + a + + a + = a a Beispiele 1) = 1+ 2+ 3+ 4 +... 2) 1 1 1 = 1 + + +... 2 3 3) 1 1 1 1 = 1 + + + +... 10 2 3 10 10 10 4)
REIHEN 1. Definition und Konvergenz Definition (unendliche) Reihe 1 2 3, s = a + a + a + + a + = a a Beispiele 1) = 1+ 2+ 3+ 4 +... 2) 1 1 1 = 1 + + +... 2 3 3) 1 1 1 1 = 1 + + + +... 10 2 3 10 10 10 4)
1 Einleitung. 2 Reelle Zahlen. 3 Konvergenz von Folgen
 1 Einleitung Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis 1 aus dem Wintersemester 2008/09
1 Einleitung Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis 1 aus dem Wintersemester 2008/09
3. Folgen und Reihen. 3.1 Folgen und Grenzwerte. Denition 3.1 (Folge) Kapitelgliederung
 Kapitelgliederung 3. Folgen und Reihen 3.1 Folgen und Grenzwerte 3.2 Rechenregeln für konvergente Folgen 3.3 Monotone Folgen und Teilfolgen 3.4 Ein Algorithmus zur Wurzelberechnung 3.5 Reihen 3.6 Absolut
Kapitelgliederung 3. Folgen und Reihen 3.1 Folgen und Grenzwerte 3.2 Rechenregeln für konvergente Folgen 3.3 Monotone Folgen und Teilfolgen 3.4 Ein Algorithmus zur Wurzelberechnung 3.5 Reihen 3.6 Absolut
ANALYSIS 1 Kapitel 5: Unendliche Reihen
 ANALYSIS 1 Kapitel 5: Unendliche Reihen MAB.01012UB MAT.101UB Vorlesung im WS 2017/18 Günter LETTL Institut für Mathematik und wissenschaftliches Rechnen Karl-Franzens-Universität Graz 5.1 Grundbegrie
ANALYSIS 1 Kapitel 5: Unendliche Reihen MAB.01012UB MAT.101UB Vorlesung im WS 2017/18 Günter LETTL Institut für Mathematik und wissenschaftliches Rechnen Karl-Franzens-Universität Graz 5.1 Grundbegrie
Aufgabe 1 Zeigen Sie mittels vollständiger Induktion, dass für alle n N. n(n + 1)(2n + 1) 6. j 2 = gilt.
 Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
2.6 Stetigkeit und Grenzwerte
 2.6 Stetigkeit und Grenzwerte Anschaulich gesprochen ist eine Funktion stetig, wenn ihr Graph sich zeichnen lässt, ohne den Stift abzusetzen. Das ist natürlich keine präzise mathematische Definition und
2.6 Stetigkeit und Grenzwerte Anschaulich gesprochen ist eine Funktion stetig, wenn ihr Graph sich zeichnen lässt, ohne den Stift abzusetzen. Das ist natürlich keine präzise mathematische Definition und
Technische Universität München Zentrum Mathematik. Übungsblatt 7
 Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 7 Hausaufgaben Aufgabe 7. Berechnen Sie die folgenden unbestimmten Integrale.
Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 7 Hausaufgaben Aufgabe 7. Berechnen Sie die folgenden unbestimmten Integrale.
LS Informatik 4 & Folgen und Reihen. Buchholz / Rudolph: MafI 2 38
 3. Folgen und Reihen Buchholz / Rudolph: MafI 2 38 Kapitelgliederung 3.1 Folgen und Grenzwerte 3.2 Rechenregeln für konvergente Folgen 3.3 Monotone Folgen und Teilfolgen 3.4 Ein Algorithmus zur Wurzelberechnung
3. Folgen und Reihen Buchholz / Rudolph: MafI 2 38 Kapitelgliederung 3.1 Folgen und Grenzwerte 3.2 Rechenregeln für konvergente Folgen 3.3 Monotone Folgen und Teilfolgen 3.4 Ein Algorithmus zur Wurzelberechnung
Lösungshinweise zu den Hausaufgaben:
 P. Engel, T. Pfrommer S. Poppitz, Dr. I. Rybak 3. Gruppenübung zur Vorlesung Höhere Mathematik 2 Sommersemester 2009 Prof. Dr. M. Stroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe
P. Engel, T. Pfrommer S. Poppitz, Dr. I. Rybak 3. Gruppenübung zur Vorlesung Höhere Mathematik 2 Sommersemester 2009 Prof. Dr. M. Stroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe
Mathematische Anwendersysteme Einführung in MuPAD
 Mathematische Anwendersysteme Einführung in MuPAD Tag 6 Folgen Konvergenzkriterien Reihen Potenzreihen 2322004 Gerd Rapin grapin@mathuni-goettingende Gerd Rapin Mathematische Anwendersysteme: Einführung
Mathematische Anwendersysteme Einführung in MuPAD Tag 6 Folgen Konvergenzkriterien Reihen Potenzreihen 2322004 Gerd Rapin grapin@mathuni-goettingende Gerd Rapin Mathematische Anwendersysteme: Einführung
Konvergenz einer Folge. 1-E1 Ma 1 Lubov Vassilevskaya
 Konvergenz einer Folge 1-E1 Ma 1 Lubov Vassilevskaya Konvergenz einer Folge: Inhalt Drei Verhaltensmuster von Folgen. Beispiele 1 ) = 1 n, = n n +1, 2 ) = ( 1)n n +1 n und ihre graphischen Darstellungen.,
Konvergenz einer Folge 1-E1 Ma 1 Lubov Vassilevskaya Konvergenz einer Folge: Inhalt Drei Verhaltensmuster von Folgen. Beispiele 1 ) = 1 n, = n n +1, 2 ) = ( 1)n n +1 n und ihre graphischen Darstellungen.,
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger. Lösung - Serie 1
 D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie. Frage Welche der Aussagen sind richtig? Eine divergente Folge ist nicht beschränkt. Falsch. Z.B. ist {( ) n } n N beschränkt und divergent.
D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie. Frage Welche der Aussagen sind richtig? Eine divergente Folge ist nicht beschränkt. Falsch. Z.B. ist {( ) n } n N beschränkt und divergent.
11. Folgen und Reihen.
 - Funktionen Folgen und Reihen Folgen Eine Folge reeller Zahlen ist eine Abbildung a: N R Statt a(n) für n N schreibt man meist a n ; es handelt sich also bei einer Folge um die Angabe der Zahlen a, a
- Funktionen Folgen und Reihen Folgen Eine Folge reeller Zahlen ist eine Abbildung a: N R Statt a(n) für n N schreibt man meist a n ; es handelt sich also bei einer Folge um die Angabe der Zahlen a, a
TECHNISCHE UNIVERSITÄT MÜNCHEN
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathemati PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Höhere Mathemati für Informatier II (Sommersemester 00) Lösungen zu Aufgabenblatt
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathemati PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Höhere Mathemati für Informatier II (Sommersemester 00) Lösungen zu Aufgabenblatt
Folgen und Reihen. Katharina Brazda 9. März 2007
 Katharina Brazda 9. März 2007 Inhaltsverzeichnis 1 Folgen 2 1.1 Definition von Folgen - explizite und rekursive Darstellung.............. 2 1.2 Wachstumsverhalten von Folgen - Monotonie und Beschränktheit..........
Katharina Brazda 9. März 2007 Inhaltsverzeichnis 1 Folgen 2 1.1 Definition von Folgen - explizite und rekursive Darstellung.............. 2 1.2 Wachstumsverhalten von Folgen - Monotonie und Beschränktheit..........
Der Satz von Taylor. Kapitel 7
 Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
Funktionenfolgen, Potenzreihen, Exponentialfunktion
 Kapitel 8 Funktionenfolgen, Potenzreihen, Exponentialfunktion Der in Definition 7. eingeführte Begriff einer Folge ist nicht auf die Betrachtung reeller Zahlen eingeschränkt und das Beispiel {a n } = {x
Kapitel 8 Funktionenfolgen, Potenzreihen, Exponentialfunktion Der in Definition 7. eingeführte Begriff einer Folge ist nicht auf die Betrachtung reeller Zahlen eingeschränkt und das Beispiel {a n } = {x
Vorlesung Mathematik 1 für Ingenieure (Wintersemester 2015/16)
 1 Vorlesung Mathematik 1 für Ingenieure (Wintersemester 2015/16) Kapitel 7: Konvergenz und Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
1 Vorlesung Mathematik 1 für Ingenieure (Wintersemester 2015/16) Kapitel 7: Konvergenz und Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
Mathematik I. Vorlesung 25. Der große Umordnungssatz
 Prof. Dr. H. Brenner Osnabrück WS 009/010 Mathematik I Vorlesung 5 Der große Umordnungssatz Satz 5.1. (Großer Umordnungssatz) Es sei a i, i I, eine summierbare Familie von komplexen Zahlen mit der Summe
Prof. Dr. H. Brenner Osnabrück WS 009/010 Mathematik I Vorlesung 5 Der große Umordnungssatz Satz 5.1. (Großer Umordnungssatz) Es sei a i, i I, eine summierbare Familie von komplexen Zahlen mit der Summe
Grundlagen: Folgen u. endliche Reihen Unendliche Reihen Potenzreihen. Reihen. Fakultät Grundlagen. März 2015
 Fakultät Grundlagen März 015 Fakultät Grundlagen Grundlagen: und endliche Beispiele Geometrische Reihe, Konvergenzkriterien Fakultät Grundlagen Folie: Übersicht Grundlagen: und endliche Artithmetische
Fakultät Grundlagen März 015 Fakultät Grundlagen Grundlagen: und endliche Beispiele Geometrische Reihe, Konvergenzkriterien Fakultät Grundlagen Folie: Übersicht Grundlagen: und endliche Artithmetische
Absolute Konvergenz. Definition 3.8. Beispiel 3.9. Eine Reihe. a n. konvergent ist. Die alternierende harmonische Reihe aber nicht absolut konvergent.
 Definition 3.8 Eine Reihe n=1 a n heißt absolut konvergent, wenn die Reihe konvergent ist. a n n=1 Beispiel 3.9 Die alternierende harmonische Reihe aber nicht absolut konvergent. n=1 ( 1)n 1 n ist zwar
Definition 3.8 Eine Reihe n=1 a n heißt absolut konvergent, wenn die Reihe konvergent ist. a n n=1 Beispiel 3.9 Die alternierende harmonische Reihe aber nicht absolut konvergent. n=1 ( 1)n 1 n ist zwar
Ferienkurs Analysis 1 - Wintersemester 2014/15. 1 Aussage, Mengen, Induktion, Quantoren
 Ferienkurs Analysis 1 - Wintersemester 2014/15 Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis
Ferienkurs Analysis 1 - Wintersemester 2014/15 Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis
Analysis I. 3. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 3. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine Abbildung F von einer Menge L in eine
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 3. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine Abbildung F von einer Menge L in eine
ANALYSIS I FÜR TPH WS 2018/19 3. Übung Übersicht
 ANALYSIS I FÜR TPH WS 208/9 3. Übung Übersicht Aufgaben zu Kapitel 5 und 6 Aufgabe : Konvergenz von Reihen (i) Aufgabe 2: Konvergenz von Reihen (ii) Aufgabe 3: ( ) Konvergenz von Reihen (iii) Aufgabe 4:
ANALYSIS I FÜR TPH WS 208/9 3. Übung Übersicht Aufgaben zu Kapitel 5 und 6 Aufgabe : Konvergenz von Reihen (i) Aufgabe 2: Konvergenz von Reihen (ii) Aufgabe 3: ( ) Konvergenz von Reihen (iii) Aufgabe 4:
2 Folgen und Reihen. 2.1 Folgen. Definition 2.1 (Zahlenfolge). Betrachten Sie folgende Liste von Zahlen:
 2 Folgen und Reihen 2. Folgen Betrachten Sie folgende Liste von Zahlen:,, 2, 3, 5, 8, 3, 2... Erkennen Sie ein Gesetz, mit dem man die Liste sinnvoll fortsetzen kann? Offenbar können Sie mit diesem Gesetz
2 Folgen und Reihen 2. Folgen Betrachten Sie folgende Liste von Zahlen:,, 2, 3, 5, 8, 3, 2... Erkennen Sie ein Gesetz, mit dem man die Liste sinnvoll fortsetzen kann? Offenbar können Sie mit diesem Gesetz
Die Fakultät. Thomas Peters Thomas Mathe-Seiten 2. Mai 2010
 Die Fakultät Thomas Peters Thomas Mathe-Seiten www.mathe-seiten.de 2. Mai 200 Dieser Artikel gibt die Definition der klassischen Fakultät und führt von dort aus zunächst zu der Anwendung in Taylor-Reihen
Die Fakultät Thomas Peters Thomas Mathe-Seiten www.mathe-seiten.de 2. Mai 200 Dieser Artikel gibt die Definition der klassischen Fakultät und führt von dort aus zunächst zu der Anwendung in Taylor-Reihen
Anleitung zu Blatt 2, Analysis II
 Fachbereich Mathematik der Universität Hamburg Dr. H. P. Kiani Anleitung zu Blatt 2, Analysis II SoSe 202 Funktionenfolgen, Potenzreihen I Die ins Netz gestellten Kopien der Anleitungsfolien sollen nur
Fachbereich Mathematik der Universität Hamburg Dr. H. P. Kiani Anleitung zu Blatt 2, Analysis II SoSe 202 Funktionenfolgen, Potenzreihen I Die ins Netz gestellten Kopien der Anleitungsfolien sollen nur
Angewandte Mathematik und Programmierung
 Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu wissenschaftlichen Rechnens mit C++ und Matlab SS2013 Inhalt Bis jetzt : Die grundlegende Aspekte
Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu wissenschaftlichen Rechnens mit C++ und Matlab SS2013 Inhalt Bis jetzt : Die grundlegende Aspekte
Kapitel 3: Folgen und Reihen
 Kapitel 3: und Reihen Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz Stefan Ruzika (KO) Kapitel 3: und Reihen 1 / 29 Gliederung 1 Grundbegriffe 2 Abbildungen und elementare
Kapitel 3: und Reihen Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz Stefan Ruzika (KO) Kapitel 3: und Reihen 1 / 29 Gliederung 1 Grundbegriffe 2 Abbildungen und elementare
Die alternierende harmonische Reihe.
 Die alternierende harmonische Reihe Beispiel: Die alternierende harmonische Reihe k k + = 2 + 3 4 + konvergiert nach dem Leibnizschen Konvergenzkriterium, und es gilt k k + = ln2 = 06934 für den Grenzwert
Die alternierende harmonische Reihe Beispiel: Die alternierende harmonische Reihe k k + = 2 + 3 4 + konvergiert nach dem Leibnizschen Konvergenzkriterium, und es gilt k k + = ln2 = 06934 für den Grenzwert
5. Reihen. k=1 x k = s. Oft startet man die Folge/Reihe auch bei k =0oder einem anderen Wert. Für Konvergenzfragen macht das keinen Unterschied.
 5 5. Reihen Im Folgenden sei X K n oder ein beliebiger K-Vektorraum mit Norm. 5.. Definition. Es sei (x k ) Folge in X. DieFolge n s n x k n,,... der Partialsummen heißt (unendliche) Reihe und wird mit
5 5. Reihen Im Folgenden sei X K n oder ein beliebiger K-Vektorraum mit Norm. 5.. Definition. Es sei (x k ) Folge in X. DieFolge n s n x k n,,... der Partialsummen heißt (unendliche) Reihe und wird mit
Folgen und Reihen. Kapitel Folgen und Grenzwerte
 Kapitel 3 Folgen und Reihen Wie bereits in der Einleitung angedeutet, beschäftigt sich die Analysis sehr stark mit Grenzprozessen. Wir werden in diesem Kapitel die wichtigsten Grenzprozesse, nämlich die
Kapitel 3 Folgen und Reihen Wie bereits in der Einleitung angedeutet, beschäftigt sich die Analysis sehr stark mit Grenzprozessen. Wir werden in diesem Kapitel die wichtigsten Grenzprozesse, nämlich die
Spickzettel Mathe C1
 Spickzettel Mathe C1 1 Mengenlehre 1.1 Potenzmenge Die Potenzmenge P (Ω) einer Menge Ω ist die Menge aller Teilmengen von Ω. Dabei gilt: P (Ω) := {A A Ω} card P (Ω) = 2 card Ω P (Ω) 1.2 Mengenalgebra Eine
Spickzettel Mathe C1 1 Mengenlehre 1.1 Potenzmenge Die Potenzmenge P (Ω) einer Menge Ω ist die Menge aller Teilmengen von Ω. Dabei gilt: P (Ω) := {A A Ω} card P (Ω) = 2 card Ω P (Ω) 1.2 Mengenalgebra Eine
