Setze = oder ein. a) b) c) Berechne im Kopf. a) =... b) =... c) =...
|
|
|
- Sophie Ackermann
- vor 7 Jahren
- Abrufe
Transkript
1 A Grundrechnungsarten 2. Multiplizieren und Dividieren MULTIPLIZIEREN NATÜRLICHER ZAHLEN 1 Multipliziere. Finde das Lösungswort. 1) 3 4 = 9) 3 8 = 2) 8 8 = 10) 9 4 = 3) 6 6 = 11) 2 6 = 4) 5 8 = 12) 4 10 = 5) 4 8 = 13) 9 7 = 6) 6 4 = 14) 9 2 = 7) 3 6 = 15) 3 9 = 8) 8 9 = 16) 7 8 = Z 32 U 63 T 40 S 12 P 64 N 18 L 72 I 36 G 27 E 24! Setze = oder ein. a) b) c) Berechne im Kopf. a) =... b) =... c) =... d) =... e) =... f) =... g) =... h) =... i) =... 4 Vervollständige die Rechnung. a) 5. = 250 b) 7.. = 490 c) 9.. = 540 d).. 50 = 200 e). 80 = 480 f). 60 = 360 1
2 5 Male die Felder mit den richtigen Lösungen färbig an. Wenn deine Lösungen richtig sind, ergibt sich ein Tier = = = = = = = = = = = = Multipliziere. a) 4 5 b) Schülerinnen und Schüler fahren mit dem Bus ins Kino. Eine Kinokarte für die Sondervorstellung kostet 8 Euro. Der Bus kostet pro Kind 5 Euro. Wie viel Geld muss für die 90 Schülerinnen und Schüler eingesammelt werden? 2
3 8 In der Zeichnung sind alle richtigen Lösungen enthalten. Findest du deine Lösung nicht, dann überprüfe deine Rechnung auf Fehler. a) b) c) d) e) f) g) h) i) Berechne a) b) c) d) ÜBERSCHLAGSRECHNUNG Mit vereinfachten Zahlen bekommst du einen Näherungswert. 10 Runde beide Teile der Multiplikation. Abrunden bei 0, 1, 2, 3, 4. Aufrunden bei 5, 6, 7, 8, a) b) c) Runde beide Teile der Multiplikation und berechne a) b) c) =
4 12 Multipliziere mit einer zweistelligen Zahl. Gehe so vor: ) Führe die Multiplikation mit der Zehnerzahl durch ) Vergiss nicht die 0 anzuhängen. 4) 3) Addiere Multipliziere zum Schluss nun mit die der beiden Einerzahl. Teilergebnisse der Multiplikation. a) b) Kreuze die richtige Lösung an. Führe eine Überschlagsrechnung durch. a) b) Male die Felder mit den richtigen Lösungen färbig an. Wenn deine Lösungen richtig sind, ergibt sich ein Tier
5 DIVIDIEREN NATÜRLICHER ZAHLEN 15 Rechne im Kopf. a) 56 : 8 =... b) 72 : 8 =... c) 45 : 5 =... d) 81 : 9 =... e) 49 : 7 =... f) 30 : 6 =... g) 42 : 7 =... h) 64 : 8 =... i) 63 : 9 = Vervollständige die Rechnungen. a) b) c) d).. 4 = = = = = = = = = = = = Mit welcher Multiplikation ergibt sich die Zahl? a) 72 = b) 45 = c) 32 = d) 63 = e) 42 = f) 81 = Bestimme zuerst den Stellenwert. Zeichne für die 1. Stelle einen Bogen ein. Stellenwert: Mache einen Punkt für jede deiner Lösungsziffern. ) 915 : 4 =... 9 H kann man durch 4 teilen, darum nimm für jede Stelle einen Punkt. 3 Stellen ) 428 : 6 =.. 4 H kann man nicht durch 6 teilen, darum rechne mit 42 Z durch 6. 2 Stellen a) 575 : 5 = b) 279 : 6 = c) 349 : 5 = d) 745 : 8 = 5
6 19 SCHRIFTLICHES DIVIDIEREN Dividiere Gehe so vor: 8 2 : 2 = 4 1 1) Bestimme den Stellenwert. 2) Beginne mit dem Zehner. (8 : 2 = 4) 0 2 3) Überprüfe: 4 2 = 8 und 0 ist 8 4) Nächste Stelle 2 herab; 2 : 2 = 1 5) Überprüfe: 1 2 = 2 und 0 ist 2 0 R 6) 0 Rest. ) a) 93 : 3 = b) 128 : 4 = DIVIDIEREN DURCH 10, 100, Schau auf die Nullen. Bei der Division durch 10, 100 und kannst du bei beiden Zahlen der Division die gleiche Anzahl der Nullen wegstreichen : 10 = 600 a) : 10 =... b) : 10 = : 100 = : 100 = : 100 = : 1000 = : = : = Vereinfache zuerst die gegebene Division. 540 : 60 = a) : 700 = b) : 80 = c) : 800 = 54 : 6 = Rechne im Kopf. a) 450 : 30 = b) 360 : 90 = c) 660 : 60 = d) 810 : 90 = DIVIDIEREN MIT REST Der Rest muss immer kleiner sein, als die Zahl durch die dividiert wird. 23 Rechne im Kopf. 11 : 5 = 2 R (Rest) 1 a) 25 : 6 =... b) 27 : 4 =... c) 49 : 6 = Kopfrechnungen a) 65 : 9 =... b) 31 : 8=... c) 58 : 8 =... 6
7 25 In der Zeichnung sind alle richtigen Lösungen enthalten. Findest du deine Lösung nicht, dann überprüfe deine Rechnung auf Fehler. 132 : 3 = : 4 = : 3 = : 4 = : 7 = : 4 = : 7 = : 8 = : 5 = : 8 = : 9 = : 6 = : 2 = : 6 = : 7 = : 5 = : 5 = : 8 = : 6 = : 3 = : 2 = : 8 = : 9 = : 4 = : 6 = : 4 = : 7 = : 4 = : 9 =
8 26 Berechne und führe die Probe durch. 8 6 : 2 = 4 3 Probe: R ) Gehe so vor: 1) Bestimme den Stellenwert. Führe die Division durch. 2) Die Probe zur Division ist eine Multiplikation. (43 2 = 86) a) 96 : 8 = b) 98 : 7 = c) 78 : 2 = d) 60 : 4 = Berechne Hinweis: Es kann auch ein Rest übrig bleiben. a) 69 : 5 = b) 83 : 4 = c) 57 : 6 = d) 111 : 2 = e) 809 : 4 = Dividiere. a) : 50 = b) : 70 = c) : 60 = 29 Bestimme den Stellenwert und dividiere. Führe auch eine Überschlagsrechnung mit gerundeten Zahlen durch : 6 2 = 4 2 Ü: : 60 = : Gehe so vor: R 1) Bestimme den Stellenwert. 2) Überlege: Wie oft ist 62 in 260 enthalten? 3) Multipliziere 62 mit 4 und schreibe das Ergebnis an. 4) Subtrahiere. ( = 12) 5) Nächste Stelle 4 herab. 6) Überlege: Wie oft ist 62 in 124 enthalten? Tipp: Wie oft ist 6 in 12 enthalten? (2-mal) 7) Multipliziere (62 2 = 124) 8) Subtrahiere ( = 0 Rest) Tipp: Wie oft ist 6 in 26 enthalten? (4-mal) a) 308 : 22 = b) 656 : 41 = c) 972 : 81 = d) : 42 = e) : 32 = f) : 51 = 8
9 30 Male die Felder mit den richtigen Lösungen färbig an. Wenn deine Lösungen richtig sind, ergibt sich ein Wort. a) 789 : 4 =.... b) 226 : 20 =.... c) 757 : 21 = : 9 = : 30 = : 32 = : 7 = : 40 = : 46 = : 8 = : 50 = : 55 = : 3 = : 60 = : 96 = R2 45 R8 36 R R1 62 R R9 31 R3 63 R11 69 R8 451 R3 11 R6 52 R30 48 R62 31 R2 49 R5 124 R5 36 R52 36 R1 49 R6 812 R1 31 Wie viel kostet eine Zeitschrift? In einer Trafik werden 27 Stück einer Zeitschrift verkauft. Die Trafikantin nimmt 81 ein. 32 In der Zeichnung sind alle richtigen Lösungen enthalten. Findest du deine Lösung nicht, dann überprüfe deine Rechnung auf Fehler. Führe auch eine Überschlagsrechnung durch. 708 : 59 = 944 : 59 = : 18 = 968 : 88 = 928 : 29 = 897 : 69 =
Rechnen mit natürlichen Zahlen
 D Rechnen mit natürlichen Zahlen 15. Dividieren natürlicher Zahlen 1 Führe die Divisionen mit den Bohnen durch. (Material: trockene Bohnen Teile 2 Bohnen auf 8 Schülerinnen auf. Teile 20 Bohnen auf 4 Schüler
D Rechnen mit natürlichen Zahlen 15. Dividieren natürlicher Zahlen 1 Führe die Divisionen mit den Bohnen durch. (Material: trockene Bohnen Teile 2 Bohnen auf 8 Schülerinnen auf. Teile 20 Bohnen auf 4 Schüler
Begriffe, die auf eine Multiplikation oder Division hinweisen
 Fachbegriffe der Addition und Subtraktion Bei der Addition werden Zahlen zusammengezählt: 2 + 4 = 6 1. Summand 2. Summand Summe Bei der Subtraktion wird eine Zahl von einer anderen abgezogen. 7 2 = 5 Minuend
Fachbegriffe der Addition und Subtraktion Bei der Addition werden Zahlen zusammengezählt: 2 + 4 = 6 1. Summand 2. Summand Summe Bei der Subtraktion wird eine Zahl von einer anderen abgezogen. 7 2 = 5 Minuend
Addition und Subtraktion Addieren heißt zusammenzählen, plus rechnen oder die Summe bilden.
 1 Grundwissen Rechenarten Addition und Subtraktion Addieren heißt zusammenzählen, plus rechnen oder die Summe bilden. 418 + 2 987 = 3 405 + 2 987 418 Umkehraufgabe 3 405 Summe Ergebnis der Summe 2 987
1 Grundwissen Rechenarten Addition und Subtraktion Addieren heißt zusammenzählen, plus rechnen oder die Summe bilden. 418 + 2 987 = 3 405 + 2 987 418 Umkehraufgabe 3 405 Summe Ergebnis der Summe 2 987
Dividieren durch zweistellige Zahlen - reine Übungssache! Für diese schwierigen Rechnungen musst
 Elisabeth Fuchs Dividieren durch zweistellige Zahlen - reine Übungssache! Und wir sind immer mit dabei! Für diese schwierigen Rechnungen musst du viele verschiedene Teilrechnungen gut beherrschen. layout:
Elisabeth Fuchs Dividieren durch zweistellige Zahlen - reine Übungssache! Und wir sind immer mit dabei! Für diese schwierigen Rechnungen musst du viele verschiedene Teilrechnungen gut beherrschen. layout:
Grundrechnungsarten mit Brüchen
 ganz klar: Mathematik - Das Ferienheft mit Erfolgsanzeiger Unechte Brüche gemischte Zahlen, 9_,,... unechte Brüche (Zähler > Nenner) _, _,,... gemischte Zahlen Unechte Brüche kann man immer in eine gemischte
ganz klar: Mathematik - Das Ferienheft mit Erfolgsanzeiger Unechte Brüche gemischte Zahlen, 9_,,... unechte Brüche (Zähler > Nenner) _, _,,... gemischte Zahlen Unechte Brüche kann man immer in eine gemischte
Aufgaben zu Lambacher Schweizer 6 Hessen
 Aufgaben zu Kapitel I Erweitern und Kürzen Erweitere im Kopf. a) mit ; 6; b) å mit ; 6; 7 c) mit ; ; d) å mit ; ; e) mit ; ; 7 f) mit ; ; Erweitere auf den angegebenen Nenner. a) 0: ; ; ; 0 ; 0 ; 0 b)
Aufgaben zu Kapitel I Erweitern und Kürzen Erweitere im Kopf. a) mit ; 6; b) å mit ; 6; 7 c) mit ; ; d) å mit ; ; e) mit ; ; 7 f) mit ; ; Erweitere auf den angegebenen Nenner. a) 0: ; ; ; 0 ; 0 ; 0 b)
Darstellen, Ordnen und Vergleichen
 Darstellen, Ordnen und Vergleichen negative Zahlen positive Zahlen 1_ 6 < 3,5 3 < +2 +1 2 < +5 Um negative Zahlen darstellen zu können, wird der Zahlenstrahl zu einer Zahlengeraden erweitert. Wenn zwei
Darstellen, Ordnen und Vergleichen negative Zahlen positive Zahlen 1_ 6 < 3,5 3 < +2 +1 2 < +5 Um negative Zahlen darstellen zu können, wird der Zahlenstrahl zu einer Zahlengeraden erweitert. Wenn zwei
Terme, Rechengesetze, Gleichungen
 Terme, Rechengesetze, Gleichungen Ein Junge kauft sich eine CD zu 15 und eine DVD zu 23. Er bezahlt mit einem 50 - Schein. Wie viel erhält er zurück? Schüler notieren mögliche Rechenwege: (1) 15 + 23 =
Terme, Rechengesetze, Gleichungen Ein Junge kauft sich eine CD zu 15 und eine DVD zu 23. Er bezahlt mit einem 50 - Schein. Wie viel erhält er zurück? Schüler notieren mögliche Rechenwege: (1) 15 + 23 =
Schriftliches Rechnen bis zur Million
 1. Addieren (Zusammenzählen), 3 Seiten Schriftliches Rechnen bis zur Million Inhaltsverzeichnis 2.1. Subtrahieren (Abziehen) Abziehverfahren 1 *, 4 Seiten ###### 7 1 6 #82473-34915 #47558 2.2. Subtrahieren
1. Addieren (Zusammenzählen), 3 Seiten Schriftliches Rechnen bis zur Million Inhaltsverzeichnis 2.1. Subtrahieren (Abziehen) Abziehverfahren 1 *, 4 Seiten ###### 7 1 6 #82473-34915 #47558 2.2. Subtrahieren
Dividieren durch zweistellige Zahlen - reine Übungssache! Für diese schwierigen Rechnungen musst
 Elisabeth Fuchs Dividieren durch zweistellige Zahlen - reine Übungssache! Und wir sind immer mit dabei! Für diese schwierigen Rechnungen musst du viele verschiedene Teilrechnungen gut beherrschen. layout:
Elisabeth Fuchs Dividieren durch zweistellige Zahlen - reine Übungssache! Und wir sind immer mit dabei! Für diese schwierigen Rechnungen musst du viele verschiedene Teilrechnungen gut beherrschen. layout:
Mathematik für Klasse 6 Rechnen mit Dezimalzahlen
 Mathematik für Klasse 6 Rechnen mit Dezimalzahlen 16 Trainingseinheiten zum Unterricht Dazu gehört auch eine Einführung in die Anfänge der Prozentrechnung. Datei Nr. 10310 Friedrich W. Buckel Stand: Stand
Mathematik für Klasse 6 Rechnen mit Dezimalzahlen 16 Trainingseinheiten zum Unterricht Dazu gehört auch eine Einführung in die Anfänge der Prozentrechnung. Datei Nr. 10310 Friedrich W. Buckel Stand: Stand
Vorrangregeln der Grundrechnungsarten
 Vorrangregeln der Grundrechnungsarten Wenn verschiedene Rechenzeichen in einer Rechnung vorkommen, so gelten folgende Regeln:. Klammerrechnung. Punktrechnungen von links nach rechts ( ) vor vor +. Strichrechnungen
Vorrangregeln der Grundrechnungsarten Wenn verschiedene Rechenzeichen in einer Rechnung vorkommen, so gelten folgende Regeln:. Klammerrechnung. Punktrechnungen von links nach rechts ( ) vor vor +. Strichrechnungen
9 = c) a) = b) = c) = d) =
 A Grundrechnungsarten. Rechnen mit Brüchen Addieren und Subtrahieren von Brüchen Addiere und subtrahiere die Brüche. a) 0 0 0 b) - 0...... Brüche mit gleichem Nenner werden addiert, indem du die Zähler
A Grundrechnungsarten. Rechnen mit Brüchen Addieren und Subtrahieren von Brüchen Addiere und subtrahiere die Brüche. a) 0 0 0 b) - 0...... Brüche mit gleichem Nenner werden addiert, indem du die Zähler
Vorrangregeln der Grundrechnungsarten
 Vorrangregeln der Grundrechnungsarten Wenn verschiedene Rechenzeichen in einer Rechnung vorkommen, so gelten folgende Regeln:. Klammerrechnung. Punktrechnungen von links nach rechts ( ) vor vor +. Strichrechnungen
Vorrangregeln der Grundrechnungsarten Wenn verschiedene Rechenzeichen in einer Rechnung vorkommen, so gelten folgende Regeln:. Klammerrechnung. Punktrechnungen von links nach rechts ( ) vor vor +. Strichrechnungen
Stellenwerttafel und Quersumme
 6 Stellenwerttafel und Quersumme Trage die Zahlen in die Stellenwerttafel ein. HT ZT T H Z E a) 7 T + 4 H + Z + 8 E b) HT + 4 H + Z + E c) ZT + 9 T + 6 H + Z d) 5 ZT + 5 T + 9 H + Z e) 4 HT + ZT + 5 T
6 Stellenwerttafel und Quersumme Trage die Zahlen in die Stellenwerttafel ein. HT ZT T H Z E a) 7 T + 4 H + Z + 8 E b) HT + 4 H + Z + E c) ZT + 9 T + 6 H + Z d) 5 ZT + 5 T + 9 H + Z e) 4 HT + ZT + 5 T
(13+ 46) 4= (51+ 19) 6= (13+ 22) 6= (53+ 3) 5= Summe der Ergebnisse: 3 530 Summe der Ergebnisse: 3 259
 Klammerrechnung Lösungen 1. Löse die Aufgaben wie im Beispiel. (+ 38) = 90 = 360 (9+ 31) 3= 60 3= 180 (3+ 36) 6= 70 6= 0 (63+ 17) 3= 80 3= 0 (19+ 1) 6= 0 6= 0 (7+ 16) 9= 90 9= 810 (36+ ) 8= 80 8= 60 (8+
Klammerrechnung Lösungen 1. Löse die Aufgaben wie im Beispiel. (+ 38) = 90 = 360 (9+ 31) 3= 60 3= 180 (3+ 36) 6= 70 6= 0 (63+ 17) 3= 80 3= 0 (19+ 1) 6= 0 6= 0 (7+ 16) 9= 90 9= 810 (36+ ) 8= 80 8= 60 (8+
1. Definition von Dezimalzahlen
 . Definition von Dezimalzahlen Definition: Dezimalzahlen sind Zahlen mit einem Komma, wobei die Ziffern nach dem Komma die Zehntel, Hundertstel, Tausendstel, usw. entsprechend dem -er Zahlensystem anzeigen.
. Definition von Dezimalzahlen Definition: Dezimalzahlen sind Zahlen mit einem Komma, wobei die Ziffern nach dem Komma die Zehntel, Hundertstel, Tausendstel, usw. entsprechend dem -er Zahlensystem anzeigen.
Rechnen mit natürlichen Zahlen
 Addieren und Subtrahieren einer Zahl Fachausdrücke bei der Addition und Subtraktion: Addition (+) 52 + 27 = 79 1. Summand + 2. Summand = Summe Rechnen mit natürlichen Zahlen Subtraktion ( - ) Strichrechnungen
Addieren und Subtrahieren einer Zahl Fachausdrücke bei der Addition und Subtraktion: Addition (+) 52 + 27 = 79 1. Summand + 2. Summand = Summe Rechnen mit natürlichen Zahlen Subtraktion ( - ) Strichrechnungen
Schriftliche Addition 1. Schriftliche Subtraktion 2
 Schriftliche Addition Addiere folgende Zahlen und rechne die Probe! 0 99 / 0 0 5 05 / 55 09 0 9 / 0 0 0 00 / 9 590 0 / 05 9 / 0 90 90 / 0 0 5 0 / 509 0 0 / 9 Schriftliche Subtraktion Subtrahiere folgende
Schriftliche Addition Addiere folgende Zahlen und rechne die Probe! 0 99 / 0 0 5 05 / 55 09 0 9 / 0 0 0 00 / 9 590 0 / 05 9 / 0 90 90 / 0 0 5 0 / 509 0 0 / 9 Schriftliche Subtraktion Subtrahiere folgende
Dezimal. Dezimal. 6 Dezimalzahlen multiplizieren 7 8 Periodische Dezimalzahlen 9. Addition. Multiplikation. Algebra
 Brüche und zahlen zahlen vergleichen zahlen runden 4 Addieren & subtrahieren Multiplizieren & dividieren mit Zehnerzahlen zahlen multiplizieren 7 8 Periodische zahlen 9 + Addition Z E z h t 4,4 9,9 4,4
Brüche und zahlen zahlen vergleichen zahlen runden 4 Addieren & subtrahieren Multiplizieren & dividieren mit Zehnerzahlen zahlen multiplizieren 7 8 Periodische zahlen 9 + Addition Z E z h t 4,4 9,9 4,4
1 Grundwissen 6 2 Dezimalbrüche (Dezimalzahlen) 9 3 Brüche 11 4 Rationale Zahlen 16 5 Potenzen und Wurzeln 20 6 Größen und Schätzen 24
 Inhalt A Grundrechenarten Grundwissen 6 Dezimalbrüche (Dezimalzahlen) 9 Brüche Rationale Zahlen 6 5 Potenzen und Wurzeln 0 6 Größen und Schätzen B Zuordnungen Proportionale Zuordnungen 8 Umgekehrt proportionale
Inhalt A Grundrechenarten Grundwissen 6 Dezimalbrüche (Dezimalzahlen) 9 Brüche Rationale Zahlen 6 5 Potenzen und Wurzeln 0 6 Größen und Schätzen B Zuordnungen Proportionale Zuordnungen 8 Umgekehrt proportionale
R. Brinkmann Seite
 R. Brinkmann http//brinkmann-du.de Seite 1 09.02.2013 SEK I Lösungen zu rechnen mit Brüchen I Ergebnisse und ausführliche Lösungen zum nblatt SEK I Bruchrechnung I Einfache Bruchaufgaben zur Vorbereitung
R. Brinkmann http//brinkmann-du.de Seite 1 09.02.2013 SEK I Lösungen zu rechnen mit Brüchen I Ergebnisse und ausführliche Lösungen zum nblatt SEK I Bruchrechnung I Einfache Bruchaufgaben zur Vorbereitung
Schriftliches Rechnen bis zur Million
 Schriftliches Rechnen bis zur Million Inhaltsverzeichnis 1. Addieren (Zusammenzählen), 3 Seiten 2. Subtrahieren (Abziehen) Abziehverfahren *, 4 Seiten ###### 7 1 6 #82473-34915 #47558 3. Subtrahieren (Abziehen)
Schriftliches Rechnen bis zur Million Inhaltsverzeichnis 1. Addieren (Zusammenzählen), 3 Seiten 2. Subtrahieren (Abziehen) Abziehverfahren *, 4 Seiten ###### 7 1 6 #82473-34915 #47558 3. Subtrahieren (Abziehen)
1 Mein Wissen aus der Volksschule
 E1 E2 E3 Ich gehe in eine neue Schule. Sie heißt: In meiner neuen Klasse sind Mädchen und Buben, insgesamt sind wir Kinder. Mit diesen Kindern war ich schon in der Volksschule in einer Klasse: digi.schule/gmk1k1e1
E1 E2 E3 Ich gehe in eine neue Schule. Sie heißt: In meiner neuen Klasse sind Mädchen und Buben, insgesamt sind wir Kinder. Mit diesen Kindern war ich schon in der Volksschule in einer Klasse: digi.schule/gmk1k1e1
Wenn ich z. B. auf Zehner (Rundungsstelle) runden will, unterstreiche ich die Einerzahl. Beispielzahl 1: 54
 LM Grundrechenarten/ Kopfrechnen S. 7 Übergang Schule - Betrieb Beispiel 1: Runden auf die Zehnerstelle Wenn ich z. B. auf Zehner (Rundungsstelle) runden will, unterstreiche ich die Einerzahl. Beispielzahl
LM Grundrechenarten/ Kopfrechnen S. 7 Übergang Schule - Betrieb Beispiel 1: Runden auf die Zehnerstelle Wenn ich z. B. auf Zehner (Rundungsstelle) runden will, unterstreiche ich die Einerzahl. Beispielzahl
a) 71,45 + 25,07 44,91 = d) 63,8 + 40,03 35,94 = c) 3,604 1,28 0,45 = f) 230,05 79,602 + 51,4 =
 Name: 1) SUBTRAHIERE DIE KLEINERE ZAHL VON DER GRÖßEREN: a) 43,86 521,43 b) 15864,2 85,8 c) 0,8 0,643 2) RECHNE VORTEILHAFT! a) 1,45 + 25,0 44,1 d) 63,8 + 40,03 35,4 b) 0,85 + 1,0835 0,084 e),6 30,04 +
Name: 1) SUBTRAHIERE DIE KLEINERE ZAHL VON DER GRÖßEREN: a) 43,86 521,43 b) 15864,2 85,8 c) 0,8 0,643 2) RECHNE VORTEILHAFT! a) 1,45 + 25,0 44,1 d) 63,8 + 40,03 35,4 b) 0,85 + 1,0835 0,084 e),6 30,04 +
Zehntausenderschritte ZR 100 000 1
 Zehntausenderschritte ZR 100 000 1 Ordne folgende Zahlen der Größe nach! Beginne bei der kleinsten Zahl! a) 30 000, 50 000, 20 000, 40 000, 60 000 b) 40 000, 60 000, 50 000, 20 000, 30 000 c) 90 000, 100
Zehntausenderschritte ZR 100 000 1 Ordne folgende Zahlen der Größe nach! Beginne bei der kleinsten Zahl! a) 30 000, 50 000, 20 000, 40 000, 60 000 b) 40 000, 60 000, 50 000, 20 000, 30 000 c) 90 000, 100
DOWNLOAD. Vertretungsstunde Mathematik Klasse: Dezimalbrüche. Marco Bettner/Erik Dinges. Downloadauszug aus dem Originaltitel:
 DOWNLOAD Marco Bettner/Erik Dinges Vertretungsstunde Mathematik 8 6. Klasse: auszug aus dem Originaltitel: ordnen 1 3,9 3,7 4,1 3,95 3,65 4,2 3,55 4 3,8 Sortiere die von klein nach groß. Zeichne dazu die
DOWNLOAD Marco Bettner/Erik Dinges Vertretungsstunde Mathematik 8 6. Klasse: auszug aus dem Originaltitel: ordnen 1 3,9 3,7 4,1 3,95 3,65 4,2 3,55 4 3,8 Sortiere die von klein nach groß. Zeichne dazu die
Einführung in die Bruchrechnung
 - Seite 1 Einführung in die Bruchrechnung 1. Der Bruchbegriff Die Tafel unter drei Kindern aufteilen! Die Schokoladentafel wird zer"brochen" Jedes Kind erhält einen "Bruchteil". Wenn die Tafel aus 15 Stücken
- Seite 1 Einführung in die Bruchrechnung 1. Der Bruchbegriff Die Tafel unter drei Kindern aufteilen! Die Schokoladentafel wird zer"brochen" Jedes Kind erhält einen "Bruchteil". Wenn die Tafel aus 15 Stücken
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 6 1. Semester ARBEITSBLATT 6 VERBINDUNG DER VIER GRUNDRECHNUNGSARTEN IN Q
 ARBEITSBLATT 6 VERBINDUNG DER VIER GRUNDRECHNUNGSARTEN IN Q Dieser Punkt fällt in der Erklärung besonders leicht. Zusammengefasst kann man sagen, dass alles beim Alten bleibt. Es bleiben also sämtliche
ARBEITSBLATT 6 VERBINDUNG DER VIER GRUNDRECHNUNGSARTEN IN Q Dieser Punkt fällt in der Erklärung besonders leicht. Zusammengefasst kann man sagen, dass alles beim Alten bleibt. Es bleiben also sämtliche
Lerninhalte ALFONS Lernwelt Mathematik 4. Klasse Seite 1
 Lerninhalte ALFONS Lernwelt Mathematik 4. Klasse Seite 1 1. Zahlenstrahl 1. Zehnerschritte bis 1000: Wie heißen die Zahlen? 2. Zehnerschritte bis 1000: Von wo bis wo? 3. Zehnerschritte bis 1000: Wo ist
Lerninhalte ALFONS Lernwelt Mathematik 4. Klasse Seite 1 1. Zahlenstrahl 1. Zehnerschritte bis 1000: Wie heißen die Zahlen? 2. Zehnerschritte bis 1000: Von wo bis wo? 3. Zehnerschritte bis 1000: Wo ist
Übungsaufgaben Klasse 4/5
 Mathestunde 4 Übungsaufgaben Klasse 4/5 Das musst du können! Mathematik Übungsheft für die 4./5. Klasse Dieses Heft gehört: Mathestunde 4 - Übungsaufgaben Klasse 4/5 Das musst du können! Mathematik Übungsheft
Mathestunde 4 Übungsaufgaben Klasse 4/5 Das musst du können! Mathematik Übungsheft für die 4./5. Klasse Dieses Heft gehört: Mathestunde 4 - Übungsaufgaben Klasse 4/5 Das musst du können! Mathematik Übungsheft
Würfelbauten Geometrie. Perspektiven Ansichten von Körpern malen. Würfelbauten. Geometrie
 Wiederholung (S. 4 9) Der Zahlenraum Seite (S. 10 23) Schätzen und zählen Zahlen Zahlen vergleichen () Das Hunderterfeld Zehnerzahlen Zehner und Einer Zahlen Zahlbilder erkennen Zahlbilder Zahlen Zahlbilder
Wiederholung (S. 4 9) Der Zahlenraum Seite (S. 10 23) Schätzen und zählen Zahlen Zahlen vergleichen () Das Hunderterfeld Zehnerzahlen Zehner und Einer Zahlen Zahlbilder erkennen Zahlbilder Zahlen Zahlbilder
Kartei. Halbschriftliche Multiplikation und Division. Überlege aus welchen Reihen die Ausschnitte. gehören und setze die Reihe nach beiden Seiten
 Halbschriftliche Multiplikation und Division / Karte 00 Kartei Halbschriftliche Multiplikation und Division Halbschriftliche Multiplikation und Division / Karte 01 Schriftliche Multiplikation und Division
Halbschriftliche Multiplikation und Division / Karte 00 Kartei Halbschriftliche Multiplikation und Division Halbschriftliche Multiplikation und Division / Karte 01 Schriftliche Multiplikation und Division
Rechentraining. 4 a) b) c) d) e) f) g) h)
 Rechentraining Kopfrechenaufgaben 1 a) 27 + 13 b) 45 + 25 c) 78 + 22 d) 64 + 36 e) 205 + 95 f) 909 + 91 g) 487 + 23 h) 630 + 470 i) 777 + 333 j) 34 23 k) 42 33 l) 177 78 m) 555 444 n) 1010 101 o) 808 88
Rechentraining Kopfrechenaufgaben 1 a) 27 + 13 b) 45 + 25 c) 78 + 22 d) 64 + 36 e) 205 + 95 f) 909 + 91 g) 487 + 23 h) 630 + 470 i) 777 + 333 j) 34 23 k) 42 33 l) 177 78 m) 555 444 n) 1010 101 o) 808 88
Voransicht. Grundrechen Führerschein: Aufwärmtraining
 Grundrechen Führerschein: Aufwärmtraining Mit dieser Seite kannst du dich auf den Grundrechen Führerschein vorbereiten. 1 Additionspuzzle. Zerschneide das Bild rechts, rechne die Aufgabe links in deinem
Grundrechen Führerschein: Aufwärmtraining Mit dieser Seite kannst du dich auf den Grundrechen Führerschein vorbereiten. 1 Additionspuzzle. Zerschneide das Bild rechts, rechne die Aufgabe links in deinem
inhaltsbezogene Kompetenzen Die SuS... Kapitel I: Rationale Zahlen
 prozessbezogene Kompetenzen Die SuS... Kapitel I: Rationale Zahlen inhaltsbezogene Kompetenzen Die SuS... Kapitel I: Rationale Zahlen konkrete Umsetzung zur Zielerreichung Die SuS können... Kapitel I:
prozessbezogene Kompetenzen Die SuS... Kapitel I: Rationale Zahlen inhaltsbezogene Kompetenzen Die SuS... Kapitel I: Rationale Zahlen konkrete Umsetzung zur Zielerreichung Die SuS können... Kapitel I:
1 Strichlisten und Diagramme Die Schülerinnen und Schüler fertigen Strichlisten an und beantworten Fragen mithilfe eines Diagramms.
 Inklusionsmaterial Nummer Titel Beschreibung 1 Strichlisten und Diagramme Die Schülerinnen und Schüler fertigen Strichlisten an und beantworten Fragen mithilfe eines Diagramms. 2 Säulendiagramme Die Schülerinnen
Inklusionsmaterial Nummer Titel Beschreibung 1 Strichlisten und Diagramme Die Schülerinnen und Schüler fertigen Strichlisten an und beantworten Fragen mithilfe eines Diagramms. 2 Säulendiagramme Die Schülerinnen
Lerninhalte ALFONS Lernwelt Mathematik 4. Klasse
 Seite 1 Turmzimmer 1: Zahlenstrahl 1. Zehnerschritte bis 1000: Wie heißen die Zahlen? 7. Hunderterschritte bis 10000: Wo ist die Zahl? 2. Zehnerschritte bis 1000: Von wo bis wo? 8. Hunderterschritte bis
Seite 1 Turmzimmer 1: Zahlenstrahl 1. Zehnerschritte bis 1000: Wie heißen die Zahlen? 7. Hunderterschritte bis 10000: Wo ist die Zahl? 2. Zehnerschritte bis 1000: Von wo bis wo? 8. Hunderterschritte bis
36 Schriftliches Rechnen
 36 Schriftliches Rechnen Mit bayerischem Abziehverfahren (gültig seit 2015) Subtrahieren ohne Zehnerüberschreitung Du sollst schriftlich rechnen: 3 765 2 512 = 3 7 6 5 Beginne immer mit den Einern, und
36 Schriftliches Rechnen Mit bayerischem Abziehverfahren (gültig seit 2015) Subtrahieren ohne Zehnerüberschreitung Du sollst schriftlich rechnen: 3 765 2 512 = 3 7 6 5 Beginne immer mit den Einern, und
Vorbereitung auf den Hauptschulabschluss Mathematik
 Katrin Hiemer/Elisabeth Vogt Vorbereitung auf den Hauptschulabschluss Mathematik MANZ VERLAG Das Werk und seine Teile sind urheberrechtlich geschützt. Jede Nutzung in anderen als den gesetzlich zugelassenen
Katrin Hiemer/Elisabeth Vogt Vorbereitung auf den Hauptschulabschluss Mathematik MANZ VERLAG Das Werk und seine Teile sind urheberrechtlich geschützt. Jede Nutzung in anderen als den gesetzlich zugelassenen
1. Grundlagen der Arithmetik
 1. Grundlagen der Arithmetik Die vier Grundrechenarten THEORIE Addition (plus-rechnen, addieren, zusammenzählen): Summand + Summand = Summe Subtraktion (minus-rechnen, subtrahieren, wegzählen): Minuend
1. Grundlagen der Arithmetik Die vier Grundrechenarten THEORIE Addition (plus-rechnen, addieren, zusammenzählen): Summand + Summand = Summe Subtraktion (minus-rechnen, subtrahieren, wegzählen): Minuend
Natürliche Zahlen Lösungen
 1) Du hörst Zahlen. Schreibe diese in Ziffernschreibweise auf. a) 158 b) 1 274 c) 5 026 d) 253 613 e) 305 580 2) Eine Zahl ist mit Kugeln in der Stellenwerttafel dargestellt. An der Hunderterstelle wird
1) Du hörst Zahlen. Schreibe diese in Ziffernschreibweise auf. a) 158 b) 1 274 c) 5 026 d) 253 613 e) 305 580 2) Eine Zahl ist mit Kugeln in der Stellenwerttafel dargestellt. An der Hunderterstelle wird
1F Wintersemester 2012/2013 Unterlagen: LehrerInnenteam GFB
 Mathematik -Arbeitsblatt -: Rechnen in Q F Wintersemester 0/0 Unterlagen: LehrerInnenteam GFB VERBINDUNG DER VIER GRUNDRECHNUNGSARTEN IN Q Dieser Punkt fällt in der Erklärung besonders leicht. Zusammengefasst
Mathematik -Arbeitsblatt -: Rechnen in Q F Wintersemester 0/0 Unterlagen: LehrerInnenteam GFB VERBINDUNG DER VIER GRUNDRECHNUNGSARTEN IN Q Dieser Punkt fällt in der Erklärung besonders leicht. Zusammengefasst
Grundwissen 5. Klasse
 Grundwissen 5. Klasse 1/5 1. Zahlenmengen Grundwissen 5. Klasse Natürliche Zahlen ohne Null: N 1;2;3;4;5;... mit der Null: N 0 0;1;2;3;4;... Ganze Zahlen: Z... 3; 2; 1;0;1;2;3;.... 2. Die Rechenarten a)
Grundwissen 5. Klasse 1/5 1. Zahlenmengen Grundwissen 5. Klasse Natürliche Zahlen ohne Null: N 1;2;3;4;5;... mit der Null: N 0 0;1;2;3;4;... Ganze Zahlen: Z... 3; 2; 1;0;1;2;3;.... 2. Die Rechenarten a)
Aufgabe 8: Runden, schriftliches Rechnen
 Schüler/in Aufgabe 8: Runden, schriftliches Rechnen LERNZIELE: Zahlen runden und Resultate schätzen Die schriftlichen Verfahren kennen Achte darauf: 1. Du hältst dich beim Runden an die Rundungsregel (Aufgabe
Schüler/in Aufgabe 8: Runden, schriftliches Rechnen LERNZIELE: Zahlen runden und Resultate schätzen Die schriftlichen Verfahren kennen Achte darauf: 1. Du hältst dich beim Runden an die Rundungsregel (Aufgabe
25 29 KV : Nr. 1. KV 1; 7: Nr. 1; ; 12: Nr. 1 3; 26: Nr. 1 und 2. 20: Nr. 1; 21: Nr. 3. Zahlen am Zahlenstrahl 18; 19;
 für Kinder mit gehobenen Anforderungen für Kinder mit mittleren Anforderungen Thema Themenheft 1 6 17 KV 2 6; 9; 10 KV 2 4; 5: Nr. 1 und 2; 7; 8; 10 KV 1; 7: Nr. 1; 8 6 11; 12: Nr. 1 3; 13: Nr. 1 und 2;
für Kinder mit gehobenen Anforderungen für Kinder mit mittleren Anforderungen Thema Themenheft 1 6 17 KV 2 6; 9; 10 KV 2 4; 5: Nr. 1 und 2; 7; 8; 10 KV 1; 7: Nr. 1; 8 6 11; 12: Nr. 1 3; 13: Nr. 1 und 2;
Illustrierende Aufgaben zum LehrplanPLUS
 Division mit Rest Jahrgangsstufe 4 Fach Mathematik Kompetenzerwartungen M 3/4 1 M 3/4 1.2 Zahlen und Operationen Im Zahlenraum bis zur Million rechnen und Strukturen nutzen Die Schülerinnen und Schüler
Division mit Rest Jahrgangsstufe 4 Fach Mathematik Kompetenzerwartungen M 3/4 1 M 3/4 1.2 Zahlen und Operationen Im Zahlenraum bis zur Million rechnen und Strukturen nutzen Die Schülerinnen und Schüler
Gib die richtigen Fachbegriffe an. Welche Information gibt der Nenner eines Bruches an?
 1 6/1 Gib die richtigen Fachbegriffe an. 2 6/1 Welche Information gibt der Nenner eines Bruches an? 3 6/1 Welcher Bruchteil ist markiert? 4 6/1 Welcher Bruchteil ist markiert? 5 6/1 Welcher Bruchteil ist
1 6/1 Gib die richtigen Fachbegriffe an. 2 6/1 Welche Information gibt der Nenner eines Bruches an? 3 6/1 Welcher Bruchteil ist markiert? 4 6/1 Welcher Bruchteil ist markiert? 5 6/1 Welcher Bruchteil ist
(53+ 3) 5 = = Summe der Ergebnisse: 3.530 Summe der Ergebnisse: 3.259
 Klammerrechnung 1. Löse die Aufgaben wie im Beispiel. (+ 38) = 90 = 360 (9+ 31) 3 = = (3+ 36) 6 = = (63+ 17) 3 = = (19+ 1) 6 = = (7+ 16) 9 = = (36+ ) 8 = = (8+ 7) 8 = = (3+ 8) 3 = = (13+ 6) = = (8+ 76)
Klammerrechnung 1. Löse die Aufgaben wie im Beispiel. (+ 38) = 90 = 360 (9+ 31) 3 = = (3+ 36) 6 = = (63+ 17) 3 = = (19+ 1) 6 = = (7+ 16) 9 = = (36+ ) 8 = = (8+ 7) 8 = = (3+ 8) 3 = = (13+ 6) = = (8+ 76)
Aufgaben zu Lambacher Schweizer 5 Hessen
 Aufgaben zu Kapitel I Kopfrechenaufgaben 1 Berechne im Kopf. a) 60 + 32 b) 57 + 41 c) 130 + 72 d) 504 + 91 e) 75 + 47 f) 76 + 85 g) 124 + 127 h) 295 + 76 i) 129 + 396 j) 747 + 239 2 a) 3800 + 4600 b) 5700
Aufgaben zu Kapitel I Kopfrechenaufgaben 1 Berechne im Kopf. a) 60 + 32 b) 57 + 41 c) 130 + 72 d) 504 + 91 e) 75 + 47 f) 76 + 85 g) 124 + 127 h) 295 + 76 i) 129 + 396 j) 747 + 239 2 a) 3800 + 4600 b) 5700
Rechnen mit rationalen Zahlen
 Rechnen mit rationalen Zahlen a ist die Gegenzahl von a und ( a) a Subtraktionsregel: Statt eine rationale Zahl zu subtrahieren, addiert man ihre Gegenzahl. ( 8) ( ) ( 8) + ( + ) 8 + 7, (,6) 7, + ( +,6)
Rechnen mit rationalen Zahlen a ist die Gegenzahl von a und ( a) a Subtraktionsregel: Statt eine rationale Zahl zu subtrahieren, addiert man ihre Gegenzahl. ( 8) ( ) ( 8) + ( + ) 8 + 7, (,6) 7, + ( +,6)
Brüche. 3 Zä hler Bruchstrich Nenner. Wie kann man einen Bruch erkennen / ablesen? Beispiel:
 8 Brüche Zä hler Bruchstrich Nenner Wie kann man einen Bruch erkennen / ablesen? Zähle zuerst alle Bruchstücke cke eines Ganzen. Die Anzahl sagt dir, wie der Nenner heißt. Jetzt zählst z du alle gefärbten
8 Brüche Zä hler Bruchstrich Nenner Wie kann man einen Bruch erkennen / ablesen? Zähle zuerst alle Bruchstücke cke eines Ganzen. Die Anzahl sagt dir, wie der Nenner heißt. Jetzt zählst z du alle gefärbten
36 Schriftliches Rechnen
 36 Schriftliches Rechnen Mit bayerischem Abziehverfahren (gültig seit 2015) Du sollst schriftlich rechnen: 3 765 2 512 = 3 7 6 5 Subtrahieren ohne Zehnerüberschreitung Beginne immer mit den Einern, und
36 Schriftliches Rechnen Mit bayerischem Abziehverfahren (gültig seit 2015) Du sollst schriftlich rechnen: 3 765 2 512 = 3 7 6 5 Subtrahieren ohne Zehnerüberschreitung Beginne immer mit den Einern, und
Grundrechnungsarten mit Dezimalzahlen
 Grundrechnungsarten mit Dezimalzahlen Vorrangregeln Die Rechnungsarten zweiter Stufe haben Vorrang vor den Rechnungsarten erster Stufe. Man sagt: "Punktrechnung geht vor Strichrechnung" Treten in einer
Grundrechnungsarten mit Dezimalzahlen Vorrangregeln Die Rechnungsarten zweiter Stufe haben Vorrang vor den Rechnungsarten erster Stufe. Man sagt: "Punktrechnung geht vor Strichrechnung" Treten in einer
Tausenderschritte ZR 10 000 1
 Tausenderschritte ZR 10 000 1 Ordne folgende Zahlen der Größe nach! Beginne bei der kleinsten Zahl! a) 3 000, 5 000, 2 000, 4 000, 6 000 b) 4 000, 6 000, 5 000, 2 000, 3 000 c) 9 000, 10 000, 3 000, 5
Tausenderschritte ZR 10 000 1 Ordne folgende Zahlen der Größe nach! Beginne bei der kleinsten Zahl! a) 3 000, 5 000, 2 000, 4 000, 6 000 b) 4 000, 6 000, 5 000, 2 000, 3 000 c) 9 000, 10 000, 3 000, 5
Lernkontrolle 6 / 4. Schuljahr / Aufgabenangebot
 Lernkontrolle 6 / 4. Schuljahr / Aufgabenangebot Thema: Vertiefung, Ergänzung und Ausblick Kontrollaufgaben ZB 4: S. 88-106 1. Arithmetik: TILL-Zahlen S. 88 / 89 O/B 6 6 1 3 8 4 1 1 4 4 1 7 8 9 3 3 + 1
Lernkontrolle 6 / 4. Schuljahr / Aufgabenangebot Thema: Vertiefung, Ergänzung und Ausblick Kontrollaufgaben ZB 4: S. 88-106 1. Arithmetik: TILL-Zahlen S. 88 / 89 O/B 6 6 1 3 8 4 1 1 4 4 1 7 8 9 3 3 + 1
die ganze Zahl die rationale Zahl
 die ganze Zahl Beispiele für ganze Zahlen:..., 3, 2, 1, 0, 1, 2, 3,... Ganze Zahlen sind die natürlichen Zahlen und die negativen Zahlen (Minuszahlen). Z = {..., 3, 2, 1, 0, 1, 2, 3, } die rationale Zahl
die ganze Zahl Beispiele für ganze Zahlen:..., 3, 2, 1, 0, 1, 2, 3,... Ganze Zahlen sind die natürlichen Zahlen und die negativen Zahlen (Minuszahlen). Z = {..., 3, 2, 1, 0, 1, 2, 3, } die rationale Zahl
r587c2 Name: Klasse: Datum:
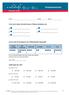 Testen und Fördern r587c2 Lösungen Audio Audio Lösungen r587c2 Name: Klasse: Datum: 1) Du hörst Zahlen. Schreibe diese in Ziffernschreibweise auf. a) d) b) e) c) 2) Eine Zahl ist mit Kugeln in der Stellenwerttafel
Testen und Fördern r587c2 Lösungen Audio Audio Lösungen r587c2 Name: Klasse: Datum: 1) Du hörst Zahlen. Schreibe diese in Ziffernschreibweise auf. a) d) b) e) c) 2) Eine Zahl ist mit Kugeln in der Stellenwerttafel
Bilde die Quersumme! Wie heißen die Nachbarzehner? Wie heißen Nachbarhunderter? Wie heißen Nachbartausender?
 Arbeit mit der gelegten Zahl Bilde die Quersumme! Wie heißen die Nachbarzehner? Wie heißen Nachbarhunderter? Wie heißen Nachbartausender? Wie heißen Nachbarzehntausender? Wie heißen die Nachbarzahlen?
Arbeit mit der gelegten Zahl Bilde die Quersumme! Wie heißen die Nachbarzehner? Wie heißen Nachbarhunderter? Wie heißen Nachbartausender? Wie heißen Nachbarzehntausender? Wie heißen die Nachbarzahlen?
3074 : 7 = 439 1Rest
 4.2 Division I1 213 214 H1, digi.schule/gm1b213 Rechne vorteilhaft! a) 800 : 20 c) 4 200 : 70 e) 4 800 : 60 g) 45 000 : 500 b) 600 : 50 d) 81 000 : 900 f) 56 000 : 70 h) 72 000 : 80 digi.schule/gm1b214
4.2 Division I1 213 214 H1, digi.schule/gm1b213 Rechne vorteilhaft! a) 800 : 20 c) 4 200 : 70 e) 4 800 : 60 g) 45 000 : 500 b) 600 : 50 d) 81 000 : 900 f) 56 000 : 70 h) 72 000 : 80 digi.schule/gm1b214
Wiederholen und vertiefen
 Wiederholen und vertiefen 350 + 20 480 60 910 70 470 + 90 230 + 80 840 70 370 420 840 560 310 770 370 760 230 610 720 710 510 460 + 150 380 150 570 + 140 920 160 430 + 290 740 370 610 230 710 760 720 370
Wiederholen und vertiefen 350 + 20 480 60 910 70 470 + 90 230 + 80 840 70 370 420 840 560 310 770 370 760 230 610 720 710 510 460 + 150 380 150 570 + 140 920 160 430 + 290 740 370 610 230 710 760 720 370
Lerneinheit 3: Mit Euro und Cent rechnen
 LM Maßeinheiten S. 11 Übergang Schule - Betrieb Lerneinheit 3: Mit Euro und Cent rechnen A: Werden mehrere Größen addiert (+) oder voneinander subtrahiert (-), muss man alle Größen zuvor in die gleiche
LM Maßeinheiten S. 11 Übergang Schule - Betrieb Lerneinheit 3: Mit Euro und Cent rechnen A: Werden mehrere Größen addiert (+) oder voneinander subtrahiert (-), muss man alle Größen zuvor in die gleiche
Rechnen mit Variablen
 E Rechnen mit Variablen 5. Gleichungen 1 Rätselrechnungen Welches Streichholz muss umgelegt werden, damit die Rechnung stimmt? (Material: Streichhölzer) a) b) Berechne den Wert der Variablen. Eine Gleichung
E Rechnen mit Variablen 5. Gleichungen 1 Rätselrechnungen Welches Streichholz muss umgelegt werden, damit die Rechnung stimmt? (Material: Streichhölzer) a) b) Berechne den Wert der Variablen. Eine Gleichung
Mathematik-Arbeitsblatt Klasse:
 Mathematik-Arbeitsblatt Klasse: 23.10.2012 Aufgabe 1 (5A1.01-031-m) Martin, Michael und Max möchten für die Mama zu Weihnachten gemeinsam ein Buch als Geschenk kaufen. Es kostet 27. Jeder der drei hat
Mathematik-Arbeitsblatt Klasse: 23.10.2012 Aufgabe 1 (5A1.01-031-m) Martin, Michael und Max möchten für die Mama zu Weihnachten gemeinsam ein Buch als Geschenk kaufen. Es kostet 27. Jeder der drei hat
Gleichungen. 1. 3 x = 12. 2. 5 x = 40. 3. 3 x+11 = 32. 4. 8 x 9 = 31. 5. 9 x 13 = 23. 6. 5 (x 2) = 20. 7. 6 (x+5) = 42. 8.
 Gleichungen. x = 2 2. x = 40. x+ = 2 4. 8 x 9 =. 9 x = 2 6. (x 2) = 20 7. 6 (x+) = 42 8. 4 x+ x = 2 9. x x = 4 0. 2 (x+)+ (x ) = 9. (x+2)+ (x ) = 2 2. 9+4 (x ) = 7. 4+2 (x+) = 20 4. 2 (9 x) =. (x+2) =
Gleichungen. x = 2 2. x = 40. x+ = 2 4. 8 x 9 =. 9 x = 2 6. (x 2) = 20 7. 6 (x+) = 42 8. 4 x+ x = 2 9. x x = 4 0. 2 (x+)+ (x ) = 9. (x+2)+ (x ) = 2 2. 9+4 (x ) = 7. 4+2 (x+) = 20 4. 2 (9 x) =. (x+2) =
In s Ziel treffen - durch Multiplizieren und Dividieren
 In s Ziel treffen - durch Multiplizieren und Dividieren Multipliziere oder dividiere so, dass du mit möglichst wenigen Versuchen ins Zielgebiet triffst. Jeder Versuch kostet einen Punkt. Notiere die Anzahl
In s Ziel treffen - durch Multiplizieren und Dividieren Multipliziere oder dividiere so, dass du mit möglichst wenigen Versuchen ins Zielgebiet triffst. Jeder Versuch kostet einen Punkt. Notiere die Anzahl
1 Basiswissen aus der Sekundarstufe 1
 1 Basiswissen aus der Sekundarstufe 1 Check-in Methode M1 Finde den Fehler und erkläre, wie du vorgehst! Stelle das Beispiel richtig! 3 569,22 278,18 3 391,14 So rechne ich: Meine Erklärung: M2 So verschiebe
1 Basiswissen aus der Sekundarstufe 1 Check-in Methode M1 Finde den Fehler und erkläre, wie du vorgehst! Stelle das Beispiel richtig! 3 569,22 278,18 3 391,14 So rechne ich: Meine Erklärung: M2 So verschiebe
VORSCHAU. zur Vollversion. Inhalt. Stellenwerte I Schriftliches Subtrahieren IV Stellenwerte II Rechenturm I...
 Inhalt Stellenwerte I..................... 1 Stellenwerte II..................... 2 Schriftliches Subtrahieren IV........ 28 Rechenturm I..................... 29 enstrahl I..................... 3 enstrahl
Inhalt Stellenwerte I..................... 1 Stellenwerte II..................... 2 Schriftliches Subtrahieren IV........ 28 Rechenturm I..................... 29 enstrahl I..................... 3 enstrahl
nachsehen, ob zwei etwas ausrechnen Dinge gleich sind oder ob es Unterschiede gibt etwas aussieht richtig ist Arbeitsanweisungen - Quartett berechnen
 Arbeitsanweisungen - Quartett nachsehen, ob zwei Dinge gleich sind oder ob es vergleichen - etwas ausrechnen - nachsehen, ob alles richtig ist - genau sagen, wie etwas aussieht etwas ausrechnen berechnen
Arbeitsanweisungen - Quartett nachsehen, ob zwei Dinge gleich sind oder ob es vergleichen - etwas ausrechnen - nachsehen, ob alles richtig ist - genau sagen, wie etwas aussieht etwas ausrechnen berechnen
Mein Mathebild Arbeiten in der mathewerkstatt
 Seite MB 1 Mein Mathebild Arbeiten in der mathewerkstatt Seite im Materialblock: Wissensspeicher Seite MB 2 MB 2 Wissensspeicher Dreiecke und Vielecke Flächen 1 Wissensspeicher Dreiecke und Vielecke Wenn
Seite MB 1 Mein Mathebild Arbeiten in der mathewerkstatt Seite im Materialblock: Wissensspeicher Seite MB 2 MB 2 Wissensspeicher Dreiecke und Vielecke Flächen 1 Wissensspeicher Dreiecke und Vielecke Wenn
Rechentrainer 3. Schroedel. Herausgegeben von Prof. Dr. Hans-Dieter Rinkens Kurt Hönisch Gerhild Träger
 Rechentrainer Herausgegeben von Prof. Dr. Hans-Dieter Rinkens Kurt Hönisch Gerhild Träger Erarbeitet von Nadine Franke-Binder, Kurt Hönisch, Claudia Neuburg, Dr. Thomas Rottmann, Michaela Schmitz, Gerhild
Rechentrainer Herausgegeben von Prof. Dr. Hans-Dieter Rinkens Kurt Hönisch Gerhild Träger Erarbeitet von Nadine Franke-Binder, Kurt Hönisch, Claudia Neuburg, Dr. Thomas Rottmann, Michaela Schmitz, Gerhild
Vorbereitung auf die 1. Schularbeit: MATHEMATIK KL.: M3/I. - S.1 L E R N Z I E L H I L F E N
 . Schularbeit: MTHEMTIK KL.: M/I. - S. Kommen in einer Rechnung mehrere Rechnungsarten bzw. Klammern vor, so muss folgende Reihenfolge eingehalten werden: ) Rechne zuerst den Wert einer Klammer aus! )
. Schularbeit: MTHEMTIK KL.: M/I. - S. Kommen in einer Rechnung mehrere Rechnungsarten bzw. Klammern vor, so muss folgende Reihenfolge eingehalten werden: ) Rechne zuerst den Wert einer Klammer aus! )
14:30 Uhr. 17:30 Uhr. 18:30 Uhr. 15:30 Uhr. 16:30 Uhr
 So fit BIST du 1 Trage die Uhrzeiten ein! Du kannst daneben auch eine Uhr zeichnen. 1) 2 30 14:30 Uhr 2) 5 30 17:30 Uhr 3) 6 30 18:30 Uhr 4) 3 30 15:30 Uhr 5) 4 30 16:30 Uhr 68 So fit BIST du 1 1) Trage
So fit BIST du 1 Trage die Uhrzeiten ein! Du kannst daneben auch eine Uhr zeichnen. 1) 2 30 14:30 Uhr 2) 5 30 17:30 Uhr 3) 6 30 18:30 Uhr 4) 3 30 15:30 Uhr 5) 4 30 16:30 Uhr 68 So fit BIST du 1 1) Trage
Mathematik-Aufgabenpool > Grundrechnen mit Dezimalzahlen
 Michael Buhlmann Mathematik-Aufgabenpool > Grundrechnen mit Dezimalzahlen Einleitung: Dezimalzahlen (Dezimalbrüch sind (rational Zahlen von der Form Vorkommastellen-Komma- Nachkommastellen. Gerechnet wird
Michael Buhlmann Mathematik-Aufgabenpool > Grundrechnen mit Dezimalzahlen Einleitung: Dezimalzahlen (Dezimalbrüch sind (rational Zahlen von der Form Vorkommastellen-Komma- Nachkommastellen. Gerechnet wird
4.0 Skala Mathematik 1. Klasse
 Skala Mathematik 1. Klasse Dekadisches Zahlensystem: 1.SA Natürliche Zahlen & Statistik übertroffen Die SuS können komplexere Aufgabenstellungen im Bereich dekadischen Zahlensystem. (K3) Die SuS können
Skala Mathematik 1. Klasse Dekadisches Zahlensystem: 1.SA Natürliche Zahlen & Statistik übertroffen Die SuS können komplexere Aufgabenstellungen im Bereich dekadischen Zahlensystem. (K3) Die SuS können
LERNSTANDSERFASSUNG. Name: Datum: Copyright by ILV-H
 LERNSTANDSERFASSUNG Name: Datum: Wie gut kannst du schätzen? a) Wie viele Meter lang misst unser Schulzimmer?... b) Wie viele Menschen leben auf der Welt?... c) Wie schwer sind alle SchülerInnen zusammen?...
LERNSTANDSERFASSUNG Name: Datum: Wie gut kannst du schätzen? a) Wie viele Meter lang misst unser Schulzimmer?... b) Wie viele Menschen leben auf der Welt?... c) Wie schwer sind alle SchülerInnen zusammen?...
Mathematik. Begriffe und Aufgaben
 Mathematik Begriffe und Zahlen Zahlen, Ziffern und Stellenwerte Definitionen Zahlen Zahlen, Ziffern und Stellenwerte Begriff Erklärung/Definition Beispiele Ziffern sind die Bausteine der Zahlenschreibweise
Mathematik Begriffe und Zahlen Zahlen, Ziffern und Stellenwerte Definitionen Zahlen Zahlen, Ziffern und Stellenwerte Begriff Erklärung/Definition Beispiele Ziffern sind die Bausteine der Zahlenschreibweise
Aufgabensammlung Klasse 8
 Aufgabensammlung Klasse 8 Inhaltsverzeichnis 1 Potenzen mit natürlichen Hochzahlen 3 1.1 Rechenregeln für das Rechnen mit Potenzen..................... 3 1.1.1 Addition und Subtraktion von Potenzen...................
Aufgabensammlung Klasse 8 Inhaltsverzeichnis 1 Potenzen mit natürlichen Hochzahlen 3 1.1 Rechenregeln für das Rechnen mit Potenzen..................... 3 1.1.1 Addition und Subtraktion von Potenzen...................
Download. Mathematik Üben Klasse 5 Multiplikation und Division. Differenzierte Materialien für das ganze Schuljahr.
 Download Martin Gehstein Mathematik Üben Klasse 5 Multiplikation und Division Differenzierte Materialien für das ganze Schuljahr Downloadauszug aus dem Originaltitel: Mathematik üben Klasse 5 Multiplikation
Download Martin Gehstein Mathematik Üben Klasse 5 Multiplikation und Division Differenzierte Materialien für das ganze Schuljahr Downloadauszug aus dem Originaltitel: Mathematik üben Klasse 5 Multiplikation
Förderkurs: Arbeiten mit Größen, Modellieren und Problemlösen Umgang mit Sachaufgaben, Festigung der Grundrechnungsarten, Arbeiten mit Zahlen
 Förderkurs im Schuljahr 2016/17 VS Großarl Förderkurs: Arbeiten mit Größen, Modellieren und Problemlösen Umgang mit, Festigung der Grundrechnungsarten, Arbeiten mit Zahlen Zielgruppe: GS II 3. Klasse Verantwortliche:
Förderkurs im Schuljahr 2016/17 VS Großarl Förderkurs: Arbeiten mit Größen, Modellieren und Problemlösen Umgang mit, Festigung der Grundrechnungsarten, Arbeiten mit Zahlen Zielgruppe: GS II 3. Klasse Verantwortliche:
Dorothee Raab. Mathematik 4. Klasse. Einfach lernen mit Rabe Linus. Extra: 100 Belohnungssticker
 Dorothee Raab Mathematik 4. Klasse Mathematik 4. Klasse Einfach lernen mit Rabe Linus Extra: 100 Belohnungssticker Vorwort Liebe(r) (dein Name), in diesem Buch kannst du alles lernen, üben und wiederholen,
Dorothee Raab Mathematik 4. Klasse Mathematik 4. Klasse Einfach lernen mit Rabe Linus Extra: 100 Belohnungssticker Vorwort Liebe(r) (dein Name), in diesem Buch kannst du alles lernen, üben und wiederholen,
Gruber I Neumann. Erfolg in VERA-8. Vergleichsarbeit Mathematik Klasse 8 Gymnasium
 Gruber I Neumann Erfolg in VERA-8 Vergleichsarbeit Mathematik Klasse 8 Gymnasium . Zahlen Zahlen Tipps ab Seite, Lösungen ab Seite 0. Zahlen und Zahlenmengen Es gibt verschiedene Zahlenarten, z.b. ganze
Gruber I Neumann Erfolg in VERA-8 Vergleichsarbeit Mathematik Klasse 8 Gymnasium . Zahlen Zahlen Tipps ab Seite, Lösungen ab Seite 0. Zahlen und Zahlenmengen Es gibt verschiedene Zahlenarten, z.b. ganze
Orientieren im Zahlenraum bis 1 Million
 Inhalt A Orientieren im Zahlenraum bis 1 Million 1 Stellentafel und Zahlenstrahl 6 2 Nachbarzahlen und Runden 8 3 Anordnen 10 B Addieren und Subtrahieren 1 Mündliches Addieren und Subtrahieren 12 2 Schriftliches
Inhalt A Orientieren im Zahlenraum bis 1 Million 1 Stellentafel und Zahlenstrahl 6 2 Nachbarzahlen und Runden 8 3 Anordnen 10 B Addieren und Subtrahieren 1 Mündliches Addieren und Subtrahieren 12 2 Schriftliches
Gleiche Zahlen gleicher Rahmen. Immer drei gehören zusammen. Male die Rahmen passend an. 6HT + 1T + 7H + 4Z + 4E E
 l Zahlen bis 000 000 einander zuordnen Gleiche Zahlen gleicher Rahmen. Immer drei gehören zusammen. Male die Rahmen passend an. 94 785 900000 + 0000 + 4000 + 700 + 80 + 5 78 90 78 09 60 744 600000 + 0000
l Zahlen bis 000 000 einander zuordnen Gleiche Zahlen gleicher Rahmen. Immer drei gehören zusammen. Male die Rahmen passend an. 94 785 900000 + 0000 + 4000 + 700 + 80 + 5 78 90 78 09 60 744 600000 + 0000
Multiplikation und Division - Division
 Multiplikation und Division - Division Qualifizierungseinheit Multiplikation und Division Lernziele: Wenn Sie diese Qualifizierungseinheit bearbeitet haben, können Sie ganze Zahlen multiplizieren und dividieren
Multiplikation und Division - Division Qualifizierungseinheit Multiplikation und Division Lernziele: Wenn Sie diese Qualifizierungseinheit bearbeitet haben, können Sie ganze Zahlen multiplizieren und dividieren
In Arbeit! Bruchungleichungen. Aufgaben mit Lösungsweg zur Webseite 2008 by Josef Raddy. 1
 In Arbeit! Bruchungleichungen Aufgaben mit Lösungsweg zur Webseite www.mathematik.net 8 by Josef Raddy Version:..8 6.5 Uhr www.mathematik.net Aufgaben. Bruchungleichungen mit einem Bruch: Lösen durch Fallunterscheidung
In Arbeit! Bruchungleichungen Aufgaben mit Lösungsweg zur Webseite www.mathematik.net 8 by Josef Raddy Version:..8 6.5 Uhr www.mathematik.net Aufgaben. Bruchungleichungen mit einem Bruch: Lösen durch Fallunterscheidung
3. Schulaufgabe aus der Mathematik Lösungshinweise
 3. Schulaufgabe aus der Mathematik Lösungshinweise Gruppe A Aufgabe 1 Die Gesamtzahl der Schüler ist 2 + 4 + 7 + 9 + 3 + 0 = 25. Zählt man alle Noten zusammen, dann bekommt man: 2 1 + 4 2 + 7 3 + 9 4 +
3. Schulaufgabe aus der Mathematik Lösungshinweise Gruppe A Aufgabe 1 Die Gesamtzahl der Schüler ist 2 + 4 + 7 + 9 + 3 + 0 = 25. Zählt man alle Noten zusammen, dann bekommt man: 2 1 + 4 2 + 7 3 + 9 4 +
Inhalt. 1. Addition und Subtraktion bis 100. 3. Die Zahlen bis 1000. 4. Rechnen bis 1000. 2. Multiplikation und Division bis 100. Lehrerteil...
 Inhalt 1. Addition und Subtraktion bis 100 Lehrerteil................................. 6 Hallo! Mein Name ist Hase!................... 12 Hallo! Ich bin der Igel!....................... 13 Wie viele Hasen
Inhalt 1. Addition und Subtraktion bis 100 Lehrerteil................................. 6 Hallo! Mein Name ist Hase!................... 12 Hallo! Ich bin der Igel!....................... 13 Wie viele Hasen
1. Schularbeit Mathematik Oktober 2015
 1. Schularbeit Mathematik 3 14. Oktober 2015 Name: Klasse: Wichtige Anmerkungen: Rechne OHNE Taschenrechner! Schreibe alle Rechenwege oder Nebenrechnungen übersichtlich auf! Ergebnisse ohne Nebenrechnung,
1. Schularbeit Mathematik 3 14. Oktober 2015 Name: Klasse: Wichtige Anmerkungen: Rechne OHNE Taschenrechner! Schreibe alle Rechenwege oder Nebenrechnungen übersichtlich auf! Ergebnisse ohne Nebenrechnung,
Aufgabe 5: Einspluseins, Einmaleins
 Schüler/in Aufgabe 5: Einspluseins, Einmaleins LERNZIEL: Rechenoperationen mit einfachen ganzen Zahlen im Kopf lösen Achte darauf: 1. Du rechnest das kleine Einmaleins sicher (ohne Fehler) und schnell
Schüler/in Aufgabe 5: Einspluseins, Einmaleins LERNZIEL: Rechenoperationen mit einfachen ganzen Zahlen im Kopf lösen Achte darauf: 1. Du rechnest das kleine Einmaleins sicher (ohne Fehler) und schnell
Es spielen 2 bis 4 Schüler/innen. Benötigt wird mindestens 1 Zehnerwürfel und jedes Kind braucht. einen Farbstift.
 Einmaleinszahlen würfeln_spiel_anleitung Es spielen 2 bis 4 Schüler/innen einen Farbstift. 2 3 4 Benötigt wird mindestens Zehnerwürfel und jedes Kind braucht 5 6 7 8 9 0 2 4 5 6 8 20 2 24 25 helfen sich
Einmaleinszahlen würfeln_spiel_anleitung Es spielen 2 bis 4 Schüler/innen einen Farbstift. 2 3 4 Benötigt wird mindestens Zehnerwürfel und jedes Kind braucht 5 6 7 8 9 0 2 4 5 6 8 20 2 24 25 helfen sich
Entnimm die Lösungsbuchstaben der Tabelle. Wie heißt das Lösungswort?...
 A Grundrechnungsarten 1. Addieren und Subtrahieren ADDIEREN NATÜRLICHER ZAHLEN 1 Ausflug Zwei Klassen besuchen mit drei Lehrerinnen eine Ausstellung. In der ersten Klasse sind 22 Schülerinnen und Schüler,
A Grundrechnungsarten 1. Addieren und Subtrahieren ADDIEREN NATÜRLICHER ZAHLEN 1 Ausflug Zwei Klassen besuchen mit drei Lehrerinnen eine Ausstellung. In der ersten Klasse sind 22 Schülerinnen und Schüler,
Aufgabe 2: Welche Brüche sind auf dem Zahlenstrahl durch die Pfeile gekennzeichnet? Schreibe die Brüche in die Kästen.
 Grundwissen Klasse 6 - Lösungen I. Bruchzahlen. Sicheres Umgehen mit Bruchzahlen Brüche als Anteil verstehen Brüche am Zahlenstrahl darstellen Brüche erweitern / kürzen können (Mathehelfer: S.6/7) Aufgabe
Grundwissen Klasse 6 - Lösungen I. Bruchzahlen. Sicheres Umgehen mit Bruchzahlen Brüche als Anteil verstehen Brüche am Zahlenstrahl darstellen Brüche erweitern / kürzen können (Mathehelfer: S.6/7) Aufgabe
Aufgaben mit zwei Rechenzeichen nebeneinander zum Beispiel: 5 (+ 3) Es gilt:
 Hilfe Addition und Subtraktion von Rationalen Zahlen Rechnen mit rationalen Zahlen, also Rechnen im negativen Bereich ist nicht immer so einfach. Ich kann mir das eigentlich ganz gut mit Schulden oder
Hilfe Addition und Subtraktion von Rationalen Zahlen Rechnen mit rationalen Zahlen, also Rechnen im negativen Bereich ist nicht immer so einfach. Ich kann mir das eigentlich ganz gut mit Schulden oder
Mathe-Wortschatz für Textaufgaben 4. Klasse bis 6. Klasse
 netzwerk sims Sprachförderung in mehrsprachigen Schulen 1 von 11 Mathe-Wortschatz für Textaufgaben 4. Klasse bis 6. Klasse à Zusatzmaterial zum Dokument «Mathe-Wortschatz für Textaufgaben 2. Klasse bis
netzwerk sims Sprachförderung in mehrsprachigen Schulen 1 von 11 Mathe-Wortschatz für Textaufgaben 4. Klasse bis 6. Klasse à Zusatzmaterial zum Dokument «Mathe-Wortschatz für Textaufgaben 2. Klasse bis
Lerninhalte ALFONS Lernwelt Mathematik 3. Klasse
 Seite 1 Turmzimmer 1: Zahlenstrahl 1. Zehnerschritte: Wie heißt die Zahl? 7. Einerschritte: Wie heißt die Zahl? 2. Zehnerschritte: Wie heißen die Zahlen? 1 8. Einerschritte: Wie heißen die Zahlen? 1 3.
Seite 1 Turmzimmer 1: Zahlenstrahl 1. Zehnerschritte: Wie heißt die Zahl? 7. Einerschritte: Wie heißt die Zahl? 2. Zehnerschritte: Wie heißen die Zahlen? 1 8. Einerschritte: Wie heißen die Zahlen? 1 3.
1 Rätselrechnungen Welches Streichholz muss umgelegt werden, damit die Rechnung stimmt? (Material: Streichhölzer) a) b)
 1 Rätselrechnungen Welches Streichholz muss umgelegt werden, damit die Rechnung stimmt? (Material: Streichhölzer) a) b) Berechne den Wert der Variablen. Eine Gleichung kannst du dir als eine Balkenwaage
1 Rätselrechnungen Welches Streichholz muss umgelegt werden, damit die Rechnung stimmt? (Material: Streichhölzer) a) b) Berechne den Wert der Variablen. Eine Gleichung kannst du dir als eine Balkenwaage
Einführung in die Bruchrechnung Station Welcher Anteil ist gefärbt? Formuliere einen vollständigen Antwortsatz. Verwende die Bruchschreibweise.
 Seite Einführung in die Bruchrechnung Station. Welcher Anteil ist gefärbt? Formuliere einen vollständigen Antwortsatz. Verwende die Bruchschreibweise.. Berechne die Anteile an den folgenden Größen: a)
Seite Einführung in die Bruchrechnung Station. Welcher Anteil ist gefärbt? Formuliere einen vollständigen Antwortsatz. Verwende die Bruchschreibweise.. Berechne die Anteile an den folgenden Größen: a)
Operieren mit rationalen Zahlen 4
 1 7 Anteile beschreiben Käseexport 01 In den ersten sechs Monaten des Jahres 201 wurden insgesamt rund 2 000 t Schweizer Käse exportiert: 18 000 t Hartkäse, 8 000 t Halbhartkäse, 500 t Weichkäse und 1
1 7 Anteile beschreiben Käseexport 01 In den ersten sechs Monaten des Jahres 201 wurden insgesamt rund 2 000 t Schweizer Käse exportiert: 18 000 t Hartkäse, 8 000 t Halbhartkäse, 500 t Weichkäse und 1
