1 Elemente der Wahrscheinlichkeitstheorie
|
|
|
- Samuel Förstner
- vor 7 Jahren
- Abrufe
Transkript
1 H.-J. Starkloff Unendlichdimensionale Stochastik Kap Oktober Elemente der Wahrscheinlichkeitstheorie 1.1 Messbare Räume Gegeben seien eine nichtleere Menge Ω und eine Menge A von Teilmengen von Ω. Definition 1 A heißt σ Algebra auf Ω falls (i) Ω A; (ii) A n A, n N A n A und A n A; (iii) A A Ω \ A A. In diesem Fall heißt (Ω, A) ein messbarer Raum oder Messraum und die Elemente der σ Algebra A heißen messbare Mengen oder (zufällige) Ereignisse. Es gibt eine ganze Reihe unterschiedlicher Formulierungen der Definition einer σ Algebra auf Ω, die zueinander äquivalent sind, insbesondere braucht man nicht beide Forderungen in (ii) zu stellen, sondern nur eine. Es folgen einige Beispiele für σ Algebren, bei denen die messbaren Mengen direkt charakterisiert werden können. Beispiele 2 (i) Ω nichtleer, A = {, Ω}. (ii) Ω nichtleer, A = {A : A Ω} Potenzmenge, Menge aller Teilmengen. (iii) Ω = R, A = {A R : A symmetrisch, d.h. A = A}. (iv) Ω nichtleer, A = {A Ω : A oder Ω \ A ist höchstens abzählbar}. (v) Ω nichtleer, Γ nichtleere Indexmenge, Ω = Ω γ disjunkte Zerlegung der Grundmenge, A = {A Ω : A Ω γ Ω γ A γ Γ}. Häufiger werden jedoch σ Algebren verwendet, bei denen keine einfachen Charakterisierungen aller Elemente der σ Algebra angebbar sind und die (nur) durch eine erzeugende Menge bestimmt werden. Grundlage dazu ist die folgende Behauptung. Behauptung 3 Es seien Ω und Γ nichtleere Mengen und für jedes γ Γ sei A γ σ Algebra auf Ω. Dann ist der Durchschnitt A γ eine σ Algebra auf Ω. eine Folgerung 4 Ist A 0 eine beliebige Menge von Teilmengen der nichtleeren Menge Ω, dann existiert eine kleinste σ Algebra auf Ω, die A 0 enthält. Diese σ Algebra heißt die von A 0 erzeugte σ Algebra und sie wird mit σ(a 0 ) bezeichnet. Beweis Die gesuchte σ Algebra ist der Durchschnitt aller σ Algebren auf Ω, die A 0 enthalten. Dabei gibt es mindestens eine σ Algebra auf Ω, die A 0 enthält und zwar die Potenzmenge der Grundmenge Ω. Ist A 0 schon eine σ Algebra auf Ω, dann fällt natürlich die von A 0 erzeugte σ Algebra mit A 0 zusammen, d. h. es gilt σ(a 0 ) = A 0.
2 H.-J. Starkloff Unendlichdimensionale Stochastik Kap Oktober Beispiele 5 (i) Ω nichtleer, A 0 = σ(a 0 ) = {, Ω}. (ii) Ω = R, A 0 = {0} σ(a 0 ) = {, {0}, R \ {0}, R}. (iii) Ω nichtleer, A 0 = {{ω} : ω Ω} (die Menge aller einelementigen Teilmengen) σ(a 0 ) = {A Ω : A oder Ω \ A ist höchstens abzählbar}. Ein wichtigeres konkretes Beispiel einer σ Algebra auf der Menge der reellen Zahlen R ist die σ Algebra der Borel-Mengen auf R. Definition 6 Die σ Algebra auf der Menge der reellen Zahlen, die vom System der offenen Teilmengen der reellen Zahlengeraden erzeugt wird, heißt die Borelsche σ Algebra auf R oder die σ Algebra der Borel-Mengen auf R, sie wird mit B(R) bezeichnet. Ein und diesselbe σ Algebra auf einer Grundmenge Ω kann von ganz unterschiedlichen Mengen A 0 erzeugt werden, relevante Beispiele dazu werden im Kontext der Vorlesung später behandelt. Für die σ Algebra der Borel-Mengen auf R sei schon jetzt die folgende einfache Behauptung angegeben. Behauptung 7 Jedes der folgenden Teilmengensysteme der Menge der reellen Zahlen erzeugt die Borelsche σ Algebra: 1. die Menge aller abgeschlossenen Teilmengen von R; 2. die Menge aller offenen Intervalle; 3. die Menge aller endlichen offenen Intervalle; 4. die Menge aller endlichen offenen Intervalle mit rationalen Endpunkten; 5. die Menge aller offenen Intervalle der Form (, a) mit a R; 6. die Menge aller offenen Intervalle der Form (, a) mit a Q, d.h. die Menge der halbunendlichen Intervalle mit rationalen Endpunkten; 7. die Menge aller abgeschlossenen Intervalle der Form (, a] mit a R; 8. die Menge aller abgeschlossenen Intervalle der Form (, a] mit a Q. Definition 8 Es sei (Ω, A) ein messbarer Raum. Die σ Algebra A heißt höchstens abzählbar erzeugt, falls ein höchstens abzählbares Mengensystem A 0 mit σ(a 0 ) = A existiert. Behauptung 9 Die Kardinalzahl einer höchstens abzählbar erzeugten σ Algebra ist nicht größer als die Kardinalzahl der Menge der reellen Zahlen. Der Beweis dieser Behauptung ist z.b. in Michel[1] Nr. 4.10, S.31, zu finden. Folgerung 10 Es gibt nicht Borel-messbare Teilmengen in der Menge der reellen Zahlen. Beweis Die Menge aller endlichen offenen Intervalle in R mit rationalen Endpunkten bilden ein Erzeugendensystem für die σ Algebra der Borel-Mengen auf R. Diese Menge ist abzählbar unendlich, folglich ist die Mächtigkeit der σ Algebra der Borel-Mengen auf R gleich der Mächtigkeit von R. (Da jede einelementige Menge eine abgeschlossene Menge und folglich ein Element von B(R) ist, kann die Mächtigkeit von B(R) nicht kleiner als die Mächtigkeit von R sein.) Die Potenzmenge von R besitzt aber eine größere Mächtigkeit als R selbst, also muss es Teilmengen von R geben, die nicht in B(R) liegen.
3 H.-J. Starkloff Unendlichdimensionale Stochastik Kap Oktober Maßräume Definition 1 Gegeben sei ein messbarer Raum (Ω, A). Die Abbildung µ : A [0, ] heißt Maß auf (Ω, A), wenn die folgenden Bedingungen gelten: (i) µ( ) = 0 and (ii) (A n ) A ( mit A ) i A j = für i j ist die Eigenschaft der σ Additivität erfüllt, d.h. µ A n = µ(a n ). In diesem Fall heißt das Tripel (Ω, A, µ) Maßraum. Das Maß µ heißt σ endlich, wenn eine Folge (A n ) von messbaren Mengen existiert mit Ω = A n und µ(a n ) < für alle n N. Das Maß µ heißt endlich, falls µ(ω) < gilt. Gilt sogar µ(ω) = 1, dann heißt das Maß ein normiertes Maß oder Wahrscheinlichkeitsmaß oder kurz Wahrscheinlichkeit und das Tripel (Ω, A, µ) Wahrscheinlichkeitsraum. Wahrscheinlichkeitsmaße werden häufig (so auch hier) durch P bezeichnet. Gelten für eine Abbildung µ : A R (oder µ : A [, ) oder µ : A (, ]) die obigen Eigenschaften (i) und (ii), dann heißt µ ein signiertes Maß. Beispiel 2 Ein äußerst wichtiges Beispiel für einen konkreten Wahrscheinlichkeitsraum ist die Menge der reellen Zahlen zwischen 0 und 1, d.h. Ω = (0, 1), ausgestattet mit der σ Algebra der Borel-Mengen B((0, 1)) und dem Lebesgue-Maß P = λ als Wahrscheinlichkeitsmaß. Bei Bedarf kann natürlich auch eine der Mengen (0, 1], [0, 1) oder [0, 1] betrachtet werden. Im Folgenden werden wir Stetigkeitseigenschaften von Wahrscheinlichkeitsmaßen benötigen, die zur σ Additivität des Maßes äquivalent sind. Die entsprechende Behauptung sei hier ohne Beweis angeführt (der Beweis ist in den Lehrbüchern der Maß-und Integrationstheorie zu finden), eine entsprechende Aussage gilt auch für allgemeine endliche Maße und unter geeigneten Zusatzbedingungen für unendliche Maße. Behauptung 3 Es sei (Ω, A, P) ein Wahrscheinlichkeitsraum. (i) Ist (A n ) eine monoton fallende Folge von messbaren Mengen, d.h. es gelten A n A und A n+1 A n n N, dann folgt daraus ( ) lim P(A n) = P A n. n (ii) Ist (A n ) eine monoton wachsende Folge von messbaren Mengen, d.h. es gelten A n A und A n A n+1 n N, dann folgt daraus ( ) lim P(A n) = P A n. n Bei bestimmten Fragestellungen ist es bequem mit vollständigen Wahrscheinlichkeitsräumen zu arbeiten. Die dazu notwendigen Begriffe und grundlegenden Aussagen sollen nun folgen.
4 H.-J. Starkloff Unendlichdimensionale Stochastik Kap Oktober Definition 4 Gegeben sei ein Wahrscheinlichkeitsraum (Ω, A, P). Eine Teilmenge B von Ω (die nicht in A liegen muss) heißt P Nullmenge oder Nullmenge bezüglich P, falls es eine Menge A A mit B A und P(A) = 0 gibt. Die Menge aller P Nullmengen werde mit N P bezeichnet. Mit A P werde die folgende Menge von Teilmengen Ω bezeichnet: A P := A N P := { A Ω : A = A 1 B mit A 1 A und B N P}. Behauptung 5 Die Menge A P ist eine σ Algebra auf Ω mit A A P und das Wahrscheinlichkeitsmaß P auf A kann zu einem Wahrscheinlichkeitsmaß P auf A P durch die Definition P(A) = P(A 1 ) falls A = A 1 B mit A 1 A und B N P fortgesetzt werden. Behauptung 6 Die σ Algebra A P und das Wahrscheinlichkeitsmaß P lassen sich auch folgendermaßen charakterisieren: A P = σ ( A N P) oder A P = {A Ω : A 1, A 2 A mit A 1 A A 2 und P(A 1 ) = P(A 2 ) } P(A) = P(A 1 ) = P(A 2 ) falls A 1 A A 2 mit A 1, A 2 A und P(A 1 ) = P(A 2 ) Definition 7 Die σ Algebra A in einem Wahrscheinlichkeitsraum (Ω, A, P) heißt vollständig, wenn A = A P und folglich auch P = P gelten. Genau in diesem Fall heißt auch der Wahrscheinlichkeitsraum (Ω, A, P) vollständig. Nicht jeder Wahrscheinlichkeitsraum ist automatisch vollständig, aber es gilt die folgende Aussage. Behauptung 8 Jeder Wahrscheinlichkeitsraum kann vervollständigt werden. Wir werden im Folgenden immer angeben, wenn wir einen vollständigen Wahrscheinlichkeitsraum voraussetzen. 1.3 Messbare Abbildungen Es gibt verschiedene Möglichkeiten, messbare Abbildungen zu definieren. Wir wählen hier die üblichste und behandeln später den Zusammenhang zu anderen Varianten in speziellen Situationen. Zuerst vermerken wir einige grundlegende Eigenschaften von inversen Abbildungen (als Abbildungen von Mengensystemen). Definition 1 Gegeben seien zwei nichtleere Mengen Ω, X und eine Abbildung ξ : Ω X, d.h. für jedes ω Ω ist ξ(ω) X eindeutig definiert. Dann heißt für eine beliebige Teilmenge B X von X die Menge ξ 1 (B) := {ω Ω : ξ(ω) B} das (volle) Urbild von B unter der Abbildung ξ. Behauptung 2 Gegeben seien nichtleere Mengen Ω, X und eine Abbildung ξ : Ω X.
5 H.-J. Starkloff Unendlichdimensionale Stochastik Kap Oktober (i) Wird ξ 1 als Abbildung der Potenzmenge von X in die Potenzmenge von Ω betrachtet, erhält sie alle mengentheoretischen Operationen, d.h. für beliebige nichtleere Indexmengen Γ und Mengen B X, B γ X, γ Γ, gelten ( ) ξ 1 B γ = ξ 1 (B γ ) ; ξ 1 ( B γ ) = ξ 1 (B γ ) ; ξ 1 (X \ B) = Ω \ ξ 1 (B). (ii) Ist auf Ω eine σ Algebra A gegeben, so ist das Mengensystem { B X : ξ 1 (B) A } eine σ Algebra auf X. (iii) Ist auf X eine σ Algebra A X gegeben, so das Mengensystem ξ 1 (A X ) := { A Ω : A = ξ 1 (B) für ein B A X } = {ξ 1 (B) : B A X } eine σ Algebra auf Ω. Die beiden letzten Punkte obiger Behauptung geben Wege an, wie mit Hilfe einer Abbildung eine gegebene σ Algebra in einen anderen Raum transportiert werden kann. Definition 3 Gegeben seien eine nichtleere Menge Ω, ein messbarer Raum (X, A X ) und eine Abbildung ξ : Ω X. Die in obiger Behauptung (iii) definierte σ Algebra ξ 1 (A X ) wird die von ξ erzeugte σ Algebra genannt und mit σ(ξ) bezeichnet: σ(ξ) = ξ 1 (A X ). Nun kommen wir zum grundlegenden Begriff einer messbaren Abbildung. Man vergleiche diese Definition mit der Definition einer stetigen Funktion eines metrischen (oder topologischen) Raumes in einen metrischen (oder topologischen) Raum. Definition 4 Gegeben seien zwei messbare Räume (Ω, A) und (X, A X ) und eine Abbildung ξ : Ω X. Die Abbildung ξ heißt messbar oder X-wertige Zufallsvariable oder Zufallsvariable in X oder Zufallselement in X falls ξ 1 (A X ) = σ(ξ) A gilt. Genauer kann die Messbarkeit auch als A A X Messbarkeit charakterisiert werden. Häufig genutzt werden die folgenden Eigenschaften. Behauptung 5 Gegeben seien die messbaren Räume (Ω, A), (X, A X ) und (Y, A Y ), sowie die Abbildungen ξ : Ω X und f : X Y. Ist die Abbildung ξ A A X messbar und die Abbildung f A X A Y messbar, dann ist die Komposition η : Ω Y, η(ω) := f(ξ(ω)) eine A A Y messbare Abbildung. Behauptung 6 Gegeben seien die messbaren Räume (Ω, A) und (X, A X ), wobei A X durch eine Menge A 0 erzeugt werde, d.h. A X = σ(a 0 ). Dann ist eine Abbildung ξ : Ω X genau dann A A X messbar, wenn für jede Menge B A 0 gilt: ξ 1 (B) A.
6 H.-J. Starkloff Unendlichdimensionale Stochastik Kap Oktober Behauptung 7 Gegeben seien die messbaren Räume (Ω, A), (X, A X ) und (Y γ, A γ ), γ Γ, wobei die σ Algebra A X durch die Menge von Abbildungen f γ : X Y γ, γ Γ, erzeugt werde, d.h. A X = σ(f γ, γ Γ). Dann ist eine Abbildung ξ : Ω X genau dann A A X messbar, wenn für jedes γ Γ die Abbildung ω f γ (ξ(ω)) A A γ messbar ist. Ein weiteres fundamentales mathematisches Objekt, welches bei der Untersuchung von Zufallsvariablen in einer Menge X eigentlich immer eine Rolle spielt, ist die Verteilung der X-wertigen Zufallsvariablen. Definition 8 Gegeben seien ein Wahrscheinlichkeitsraum (Ω, A, P), ein messbarer Raum (X, A X ) und eine X-wertige Zufallsvariable ξ : Ω X. Die Abbildung Pξ 1 : A X [0, 1], Pξ 1 (B) = P ( ξ 1 (B) ) = P (ω Ω : ξ(ω) B) =: P(ξ B) ist ein Wahrscheinlichkeitsmaß auf dem messbaren Raum (X, A X ), welches Verteilung oder Wahrscheinlichkeitsverteilung der Zufallsvariable ξ genannt und mit P ξ bezeichnet wird, d.h. P ξ (B) = P(ξ B), B A X. Die nächste Behauptung zeigt, dass jedes Wahrscheinlichkeitsmaß auf einem messbaren Raum als die Verteilung einer entsprechenden Zufallsvariable aufgefasst werden kann (obwohl dieses Maß auch direkt gegeben sein kann, d.h. ohne Bezug auf eine Zufallsvariable). Andererseits haben im Allgemeinen viele unterschiedliche Zufallsvariablen ein und dieselbe Verteilung, d.h. durch die Verteilung wird eine erzeugende Zufallsvariable nicht eindeutig definiert. Behauptung 9 Gegeben seien ein messbarer Raum (X, A X ) und ein Wahrscheinlichkeitsmaß P X auf (X, A X ). Dann existiert ein Wahrscheinlichkeitsraum (Ω, A, P) und darauf eine X-wertige Zufallsvariable ξ : Ω X, so dass P X die Verteilung von ξ ist, d.h. P ξ = P X. Beweis Man nehme (Ω, A, P) = (X, A X, P X ) und die X-wertige Zufallsvariable ξ, welche durch ξ(x) = x, x X = Ω definiert wird. Für Integrale von reellwertigen messbaren Abbildungen gilt die bekannte Substitutionsformel. Behauptung 10 Gegeben seien ein Wahrscheinlichkeitsraum (Ω, A, P), ein messbarer Raum (X, A X ), eine X-wertige Zufallsvariable ξ : Ω X und eine messbare reellwertige Abbildung f : (X, A X ) (R, B(R)). Dann gilt Ef(ξ) := f(ξ(ω))p(dω) = f(x)p X (dx) Ω in dem Sinne, dass wenn eines der Integrale existiert auch das andere existiert (jeweils als abstraktes Lebesgue-Integral auf dem entsprechenden Maßraum) und deren Werte übereinstimmen. X Literatur [1] H. Michel. Maß- und Integrationstheorie. Dt. Verl. d. Wissenschaften, Berlin, 1978.
Im gesamten Kapitel sei Ω eine nichtleere Menge. Wir bezeichnen die Potenzmenge
 1 Mengensysteme Ein Mengensystem ist eine Familie von Teilmengen einer Grundmenge und damit eine Teilmenge der Potenzmenge der Grundmenge. In diesem Kapitel untersuchen wir Mengensysteme, die unter bestimmten
1 Mengensysteme Ein Mengensystem ist eine Familie von Teilmengen einer Grundmenge und damit eine Teilmenge der Potenzmenge der Grundmenge. In diesem Kapitel untersuchen wir Mengensysteme, die unter bestimmten
Zufallsvariablen: Die allgemeine Definition
 KAPITEL 8 Zufallsvariablen: Die allgemeine Definition 8.1. Zufallsvariablen Bis zu diesem Zeitpunkt haben wir ausschließlich Zufallsvariablen mit endlich oder abzählbar vielen Werten (also diskrete Zufallsvariablen)
KAPITEL 8 Zufallsvariablen: Die allgemeine Definition 8.1. Zufallsvariablen Bis zu diesem Zeitpunkt haben wir ausschließlich Zufallsvariablen mit endlich oder abzählbar vielen Werten (also diskrete Zufallsvariablen)
Zufallsvariable, Verteilung, Verteilungsfunktion
 Kapitel 5 Zufallsvariable, Verteilung, Verteilungsfunktion 5.1 Zufallsvariable Sei (Ω, A, P ) ein beliebiger Wahrscheinlichkeitsraum. Häufig interessiert nicht ω selbst, sondern eine Kennzahl X(ω), d.h.
Kapitel 5 Zufallsvariable, Verteilung, Verteilungsfunktion 5.1 Zufallsvariable Sei (Ω, A, P ) ein beliebiger Wahrscheinlichkeitsraum. Häufig interessiert nicht ω selbst, sondern eine Kennzahl X(ω), d.h.
Kapitel II - Wahrscheinlichkeitsraum
 Universität Karlsruhe (TH) Institut für Statistik und Mathematische Wirtschaftstheorie Wahrscheinlichkeitstheorie Kapitel II - Wahrscheinlichkeitsraum Markus Höchstötter Lehrstuhl für Statistik, Ökonometrie
Universität Karlsruhe (TH) Institut für Statistik und Mathematische Wirtschaftstheorie Wahrscheinlichkeitstheorie Kapitel II - Wahrscheinlichkeitsraum Markus Höchstötter Lehrstuhl für Statistik, Ökonometrie
Messbare Vektorräume
 Messbare Vektorräume Hans-Jörg Starkloff TU Bergakademie Freiberg Westsächsische Hochschule Zwickau Dezember 2010 / Januar 2011 Hans-Jörg Starkloff Messbare Vektorräume 1 1. Definition Geg. X linearer
Messbare Vektorräume Hans-Jörg Starkloff TU Bergakademie Freiberg Westsächsische Hochschule Zwickau Dezember 2010 / Januar 2011 Hans-Jörg Starkloff Messbare Vektorräume 1 1. Definition Geg. X linearer
Kapitel II - Wahrscheinlichkeitsraum
 Institut für Volkswirtschaftslehre (ECON) Lehrstuhl für Ökonometrie und Statistik Kapitel II - Wahrscheinlichkeitsraum Wahrscheinlichkeitstheorie Prof. Dr. W.-D. Heller Hartwig Senska Carlo Siebenschuh
Institut für Volkswirtschaftslehre (ECON) Lehrstuhl für Ökonometrie und Statistik Kapitel II - Wahrscheinlichkeitsraum Wahrscheinlichkeitstheorie Prof. Dr. W.-D. Heller Hartwig Senska Carlo Siebenschuh
Grundbegriffe der Wahrscheinlichkeitstheorie
 KAPITEL 1 Grundbegriffe der Wahrscheinlichkeitstheorie 1. Zufallsexperimente, Ausgänge, Grundmenge In der Stochastik betrachten wir Zufallsexperimente. Die Ausgänge eines Zufallsexperiments fassen wir
KAPITEL 1 Grundbegriffe der Wahrscheinlichkeitstheorie 1. Zufallsexperimente, Ausgänge, Grundmenge In der Stochastik betrachten wir Zufallsexperimente. Die Ausgänge eines Zufallsexperiments fassen wir
Zufallsvariable in separablen Banach- und Hilbert-Räumen
 Zufallsvariable in separablen Banach- und Hilbert-Räumen Hans-Jörg Starkloff TU Bergakademie Freiberg Westsächsische Hochschule Zwickau Januar 2011 Hans-Jörg Starkloff Zufallsvariable in separablen Banach-
Zufallsvariable in separablen Banach- und Hilbert-Räumen Hans-Jörg Starkloff TU Bergakademie Freiberg Westsächsische Hochschule Zwickau Januar 2011 Hans-Jörg Starkloff Zufallsvariable in separablen Banach-
Lineare Algebra 1. Detlev W. Hoffmann. WS 2013/14, TU Dortmund
 Lineare Algebra 1 Detlev W. Hoffmann WS 2013/14, TU Dortmund 1 Mengen und Zahlen 1.1 Mengen und Abbildungen Eine Menge ist eine Zusammenfassung wohlunterscheidbarer Objekte unserer Anschauung/unseres Denkens/unserer
Lineare Algebra 1 Detlev W. Hoffmann WS 2013/14, TU Dortmund 1 Mengen und Zahlen 1.1 Mengen und Abbildungen Eine Menge ist eine Zusammenfassung wohlunterscheidbarer Objekte unserer Anschauung/unseres Denkens/unserer
Musterlösung Analysis 3 - Maßtherorie
 Musterlösung Analysis 3 - Maßtherorie 10. März 2011 Aufgabe 1: Zum Aufwärmen (i) Zeige, dass die Mengensysteme {, X} und P(X) σ-algebren sind. Es sind jeweils nur die Charakteristika nachzuweisen. (1)
Musterlösung Analysis 3 - Maßtherorie 10. März 2011 Aufgabe 1: Zum Aufwärmen (i) Zeige, dass die Mengensysteme {, X} und P(X) σ-algebren sind. Es sind jeweils nur die Charakteristika nachzuweisen. (1)
Aufgaben zu Kapitel 0
 Aufgaben zu Kapitel 0 0.1. Seien A und B zwei Mengen. Wie kann man paarweise disjunkte Mengen A 1, A 2 und A 3 so wählen, dass A 1 A 2 A 3 = A B gilt? 0.2. Seien E ein Menge und A eine Teilmengen von E.
Aufgaben zu Kapitel 0 0.1. Seien A und B zwei Mengen. Wie kann man paarweise disjunkte Mengen A 1, A 2 und A 3 so wählen, dass A 1 A 2 A 3 = A B gilt? 0.2. Seien E ein Menge und A eine Teilmengen von E.
Inhaltsverzeichnis (Ausschnitt)
 8 Messbarkeit und Bildwahrscheinlichkeit Inhaltsverzeichnis (Ausschnitt) 8 Messbarkeit und Bildwahrscheinlichkeit Messbare Abbildungen Bildwahrscheinlichkeit Deskriptive Statistik und Wahrscheinlichkeitsrechnung
8 Messbarkeit und Bildwahrscheinlichkeit Inhaltsverzeichnis (Ausschnitt) 8 Messbarkeit und Bildwahrscheinlichkeit Messbare Abbildungen Bildwahrscheinlichkeit Deskriptive Statistik und Wahrscheinlichkeitsrechnung
Mathematik III. Topologische Räume
 Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 63 Wir beschäftigen uns weiter mit der Frage, welchen Teilmengen des R n man ein sinnvolles Volumen zuordnen kann. Es wird sich herausstellen,
Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 63 Wir beschäftigen uns weiter mit der Frage, welchen Teilmengen des R n man ein sinnvolles Volumen zuordnen kann. Es wird sich herausstellen,
Definition: Ein endlicher Ergebnisraum ist eine nichtleere Menge, deren. wird als Ereignis, jede einelementige Teilmenge als Elementarereignis
 Stochastische Prozesse: Grundlegende Begriffe bei zufälligen Prozessen In diesem Abschnitt beschäftigen wir uns mit den grundlegenden Begriffen und Definitionen von Zufallsexperimenten, also Prozessen,
Stochastische Prozesse: Grundlegende Begriffe bei zufälligen Prozessen In diesem Abschnitt beschäftigen wir uns mit den grundlegenden Begriffen und Definitionen von Zufallsexperimenten, also Prozessen,
Stetige Funktionen. Definition. Seien (X, d) und (Y, ϱ) metrische Räume und f : X Y eine Abbildung. D(f) X sei der Definitionsbereich von f.
 Stetige Funktionen Abbildungen f : X Y, wobei X und Y strukturierte Mengen sind (wie z.b. Vektorräume oder metrische Räume), spielen eine zentrale Rolle in der Mathematik. In der Analysis sind Abbildungen
Stetige Funktionen Abbildungen f : X Y, wobei X und Y strukturierte Mengen sind (wie z.b. Vektorräume oder metrische Räume), spielen eine zentrale Rolle in der Mathematik. In der Analysis sind Abbildungen
σ-algebren, Definition des Maßraums
 σ-algebren, Definition des Maßraums Ziel der Maßtheorie ist es, Teilmengen einer Grundmenge X auf sinnvolle Weise einen Inhalt zuzuordnen. Diese Zuordnung soll so beschaffen sein, dass dabei die intuitiven
σ-algebren, Definition des Maßraums Ziel der Maßtheorie ist es, Teilmengen einer Grundmenge X auf sinnvolle Weise einen Inhalt zuzuordnen. Diese Zuordnung soll so beschaffen sein, dass dabei die intuitiven
Definitionen und Aussagen zur Maßtheorie
 Definitionen und Aussagen zur Maßtheorie Man möchte den Teilmengen eines Raumes ein Gewicht zuordnen. Wir werden sehen, daß dies in sinnvoller Weise häufig nicht für alle Teilmengen möglich ist, sondern
Definitionen und Aussagen zur Maßtheorie Man möchte den Teilmengen eines Raumes ein Gewicht zuordnen. Wir werden sehen, daß dies in sinnvoller Weise häufig nicht für alle Teilmengen möglich ist, sondern
Stochastik I. Vorlesungsmitschrift
 Stochastik I Vorlesungsmitschrift Ulrich Horst Institut für Mathematik Humboldt-Universität zu Berlin Inhaltsverzeichnis 1 Grundbegriffe 1 1.1 Wahrscheinlichkeitsräume..................................
Stochastik I Vorlesungsmitschrift Ulrich Horst Institut für Mathematik Humboldt-Universität zu Berlin Inhaltsverzeichnis 1 Grundbegriffe 1 1.1 Wahrscheinlichkeitsräume..................................
Kap 1: VEKTORRÄUME. (c) (λµ) v = λ (µ v) (b) λ (v + w) = (λ v) + (λ w) (d) 1 v = v
 Kap 1: VEKTORRÄUME Es sei X eine Menge. Eine Familie von Elementen von X ist eine Abbildung ϕ : I X, i ϕ(i) = x i, wobei die Menge I in diesem Zusammenhang auch Indexmenge genannt wird. Man schreibt vereinfacht
Kap 1: VEKTORRÄUME Es sei X eine Menge. Eine Familie von Elementen von X ist eine Abbildung ϕ : I X, i ϕ(i) = x i, wobei die Menge I in diesem Zusammenhang auch Indexmenge genannt wird. Man schreibt vereinfacht
Analysis III. Vorlesung 61
 Prof. Dr. H. Brenner Osnabrück WS 2014/2015 Analysis III Vorlesung 61 In diesem Kurs beschäftigen wir uns mit dem Flächeninhalt von ebenen Gebilden und den Volumina von räumlichen Gebilden. Für ein Rechteck
Prof. Dr. H. Brenner Osnabrück WS 2014/2015 Analysis III Vorlesung 61 In diesem Kurs beschäftigen wir uns mit dem Flächeninhalt von ebenen Gebilden und den Volumina von räumlichen Gebilden. Für ein Rechteck
Mathematik III. Prof. Dr. H. Brenner Osnabrück WS 2010/2011. Vorlesung 62 In diesem Kurs beschäftigen wir uns mit dem
 Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 62 In diesem Kurs beschäftigen wir uns mit dem Flächeninhalt von ebenen Gebilden und den Volumina von räumlichen Gebilden. Für ein Rechteck
Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 62 In diesem Kurs beschäftigen wir uns mit dem Flächeninhalt von ebenen Gebilden und den Volumina von räumlichen Gebilden. Für ein Rechteck
4 Messbare Funktionen
 4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
Topologische Grundbegriffe I. 1 Offene und Abgeschlossene Mengen
 Topologische Grundbegriffe I Vortrag zum Proseminar Analysis, 26.04.2010 Nina Neidhardt und Simon Langer Im Folgenden soll gezeigt werden, dass topologische Konzepte, die uns schon für die Reellen Zahlen
Topologische Grundbegriffe I Vortrag zum Proseminar Analysis, 26.04.2010 Nina Neidhardt und Simon Langer Im Folgenden soll gezeigt werden, dass topologische Konzepte, die uns schon für die Reellen Zahlen
Analysis III, WS 2011/2012 Montag $Id: masse.tex,v /10/31 15:48:07 hk Exp $
 $Id: masse.tex,v 1.8 2011/10/31 15:48:07 hk Exp $ 2 Maßräume 2.2 Meßbare Abbildungen Der nächste Grundbegriff sind die meßbaren Abbildungen. Erinnern Sie sich daran das wir eigentlich einen Integralbegriff
$Id: masse.tex,v 1.8 2011/10/31 15:48:07 hk Exp $ 2 Maßräume 2.2 Meßbare Abbildungen Der nächste Grundbegriff sind die meßbaren Abbildungen. Erinnern Sie sich daran das wir eigentlich einen Integralbegriff
Übungsrunde 9, Gruppe 2 LVA 107.369, Übungsrunde 8, Gruppe 2, 12.12. Markus Nemetz, TU Wien, 12/2006
 3.75. Angabe Übungsrunde 9, Gruppe 2 LVA 07.369, Übungsrunde 8, Gruppe 2, 2.2. Markus Nemetz, markus.nemetz@tuwien.ac.at, TU Wien, 2/2006 X sei eine stetige sg mit Dichte f(x), x R. Ermitteln Sie einen
3.75. Angabe Übungsrunde 9, Gruppe 2 LVA 07.369, Übungsrunde 8, Gruppe 2, 2.2. Markus Nemetz, markus.nemetz@tuwien.ac.at, TU Wien, 2/2006 X sei eine stetige sg mit Dichte f(x), x R. Ermitteln Sie einen
Skriptbausteine zur Vorlesung Maßtheorie
 Skriptbausteine zur Vorlesung Maßtheorie Vorlesender: Prof. Dr. Bernd Hofmann Der folgende Text soll die Nacharbeit der Vorlesung erleichtern und dabei an Definitionen, Sätze und Beispiele erinnern. Das
Skriptbausteine zur Vorlesung Maßtheorie Vorlesender: Prof. Dr. Bernd Hofmann Der folgende Text soll die Nacharbeit der Vorlesung erleichtern und dabei an Definitionen, Sätze und Beispiele erinnern. Das
Abbildungseigenschaften
 Abbildungseigenschaften.5. Injektivität Injektivität (injektiv, linkseindeutig) ist eine Eigenschaft einer mathematischen Funktion. Sie bedeutet, dass jedes Element der Zielmenge höchstens einmal als Funktionswert
Abbildungseigenschaften.5. Injektivität Injektivität (injektiv, linkseindeutig) ist eine Eigenschaft einer mathematischen Funktion. Sie bedeutet, dass jedes Element der Zielmenge höchstens einmal als Funktionswert
Lehrstuhl IV Stochastik & Analysis. Stochastik II. Wahrscheinlichkeitstheorie I. Skriptum nach einer Vorlesung von Hans-Peter Scheffler
 Fachschaft Mathematik Uni Dortmund Lehrstuhl IV Stochastik & Analysis Stochastik II Wahrscheinlichkeitstheorie I Skriptum nach einer Vorlesung von Hans-Peter Scheffler Letzte Änderung: 26. November 2002
Fachschaft Mathematik Uni Dortmund Lehrstuhl IV Stochastik & Analysis Stochastik II Wahrscheinlichkeitstheorie I Skriptum nach einer Vorlesung von Hans-Peter Scheffler Letzte Änderung: 26. November 2002
Lemma (Eigenschaften elementarer Mengen) 1. Jede elementare Menge lässt sich als disjunkte Vereinigung halboffener Intervalle schreiben.
 12.3. DIE LEBESGUE ALGEBRA 19 Bemerkung 12.3.2 (Bezeichnungen) Im Buch von Bauer [2] werden elementare Mengen als Figuren bezeichnet. Wir folgen mit unserer Nomenklatur Rudin [15]. Natürlich kann man auf
12.3. DIE LEBESGUE ALGEBRA 19 Bemerkung 12.3.2 (Bezeichnungen) Im Buch von Bauer [2] werden elementare Mengen als Figuren bezeichnet. Wir folgen mit unserer Nomenklatur Rudin [15]. Natürlich kann man auf
Reelle Analysis. Vorlesungsskript. Enno Lenzmann, Universität Basel. 11. Oktober 2013
 Reelle Analysis Vorlesungsskript Enno Lenzmann, Universität Basel 11. Oktober 2013 3 Fortsetzung von Prämassen zu Massen Der Begriff des Prämasses ist nicht ausreichend, um eine geschmeidige Integrationstheorie
Reelle Analysis Vorlesungsskript Enno Lenzmann, Universität Basel 11. Oktober 2013 3 Fortsetzung von Prämassen zu Massen Der Begriff des Prämasses ist nicht ausreichend, um eine geschmeidige Integrationstheorie
3 Bedingte Erwartungswerte
 3 Bedingte Erwartungswerte 3.3 Existenz und Eindeutigkeit des bedingten Erwartungswertes E A 0(X) 3.6 Konvexitätsungleichung für bedingte Erwartungswerte 3.9 Konvergenzsätze von Levi, Fatou und Lebesgue
3 Bedingte Erwartungswerte 3.3 Existenz und Eindeutigkeit des bedingten Erwartungswertes E A 0(X) 3.6 Konvexitätsungleichung für bedingte Erwartungswerte 3.9 Konvergenzsätze von Levi, Fatou und Lebesgue
Kapitel II Kontinuierliche Wahrscheinlichkeitsräume
 Kapitel II Kontinuierliche Wahrscheinlichkeitsräume 1. Einführung 1.1 Motivation Interpretation der Poisson-Verteilung als Grenzwert der Binomialverteilung. DWT 1.1 Motivation 211/476 Beispiel 85 Wir betrachten
Kapitel II Kontinuierliche Wahrscheinlichkeitsräume 1. Einführung 1.1 Motivation Interpretation der Poisson-Verteilung als Grenzwert der Binomialverteilung. DWT 1.1 Motivation 211/476 Beispiel 85 Wir betrachten
3. Übungsblatt - Lösungsskizzen. so, dass f tatsächlich eine Wahrscheinlichkeitsdichte
 Einführung in die Wahrscheinlichkeitstheorie und Statistik Prof. Dr. Jan Johannes Sandra Schluttenhofer Wintersemester 208/9 3. Übungsblatt - Lösungsskizzen Aufgabe 9 Stetige Verteilungen, 4 =.5 +.5 +
Einführung in die Wahrscheinlichkeitstheorie und Statistik Prof. Dr. Jan Johannes Sandra Schluttenhofer Wintersemester 208/9 3. Übungsblatt - Lösungsskizzen Aufgabe 9 Stetige Verteilungen, 4 =.5 +.5 +
TECHNISCHE UNIVERSITÄT MÜNCHEN
 Prof. Dr. D. Castrigiano Dr. M. Prähofer Zentralübung 38. Einschränkung eines Maßes TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Mathematik für Physiker 4 (Analysis 3) http://www.ma.tum.de/hm/ma9204
Prof. Dr. D. Castrigiano Dr. M. Prähofer Zentralübung 38. Einschränkung eines Maßes TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Mathematik für Physiker 4 (Analysis 3) http://www.ma.tum.de/hm/ma9204
I Grundbegriffe 1 1 Wahrscheinlichkeitsräume Bedingte Wahrscheinlichkeiten und Unabhängigkeit Reellwertige Zufallsvariablen...
 Inhaltsverzeichnis I Grundbegriffe 1 1 Wahrscheinlichkeitsräume......................... 1 2 Bedingte Wahrscheinlichkeiten und Unabhängigkeit........... 7 3 Reellwertige Zufallsvariablen........................
Inhaltsverzeichnis I Grundbegriffe 1 1 Wahrscheinlichkeitsräume......................... 1 2 Bedingte Wahrscheinlichkeiten und Unabhängigkeit........... 7 3 Reellwertige Zufallsvariablen........................
2 Rationale und reelle Zahlen
 2 reelle Es gibt Mathematik mit Grenzwert (Analysis) und Mathematik ohne Grenzwert (z.b Algebra). Grenzwerte existieren sicher nur dann, wenn der Zahlbereich vollständig ist, also keine Lücken aufweist
2 reelle Es gibt Mathematik mit Grenzwert (Analysis) und Mathematik ohne Grenzwert (z.b Algebra). Grenzwerte existieren sicher nur dann, wenn der Zahlbereich vollständig ist, also keine Lücken aufweist
Wahrscheinlichkeitstheorie
 Wahrscheinlichkeitstheorie Peter Eichelsbacher Wintersemester 2008/09 Inhaltsverzeichnis 1 σ-algebren und Maße 3 2 Fortsetzung von Prämaßen zu Maßen 17 3 Messbare Abbildungen und das Lebesgue-Borel-Maß
Wahrscheinlichkeitstheorie Peter Eichelsbacher Wintersemester 2008/09 Inhaltsverzeichnis 1 σ-algebren und Maße 3 2 Fortsetzung von Prämaßen zu Maßen 17 3 Messbare Abbildungen und das Lebesgue-Borel-Maß
Stochastik Wiederholung von Teil 1
 Stochastik Wiederholung von Teil 1 Andrej Depperschmidt Sommersemester 2016 Wahrscheinlichkeitsraum Definition Das Tripple (Ω, A, P) heißt Wahrscheinlichkeitsraum, falls gilt: (i) A ist eine σ-algebra,
Stochastik Wiederholung von Teil 1 Andrej Depperschmidt Sommersemester 2016 Wahrscheinlichkeitsraum Definition Das Tripple (Ω, A, P) heißt Wahrscheinlichkeitsraum, falls gilt: (i) A ist eine σ-algebra,
Analysis I: Übungsblatt 1 Lösungen
 Analysis I: Übungsblatt 1 Lösungen Verständnisfragen 1. Was ist Mathematik? Mathematik ist eine Wissenschaft, die selbstgeschaffene, abstrakte Strukturen auf ihre Eigenschaften und Muster hin untersucht.
Analysis I: Übungsblatt 1 Lösungen Verständnisfragen 1. Was ist Mathematik? Mathematik ist eine Wissenschaft, die selbstgeschaffene, abstrakte Strukturen auf ihre Eigenschaften und Muster hin untersucht.
1 falls x 2. falls x = 1 und. 0 falls x > 1. eine Lebesgue-integrierbare Majorante. Somit können wir den Satz von Lebesgue anwenden:
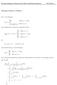 Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
3 Reihen. 3.1 Konvergenz und Divergenz. Die Eindeutigkeit nach Satz 13 ergibt schließlich (5). (6) folgt aus (2) und (1) wegen. 1 a +log ba.
 Die Eindeutigkeit nach Satz 3 ergibt schließlich (5). (6) folgt aus (2) und () wegen Aussage (7) ergibt sich aus () und (6). 0 = log b = log b ( a a) = log b a +log ba. 3 Reihen 3. Konvergenz und Divergenz
Die Eindeutigkeit nach Satz 3 ergibt schließlich (5). (6) folgt aus (2) und () wegen Aussage (7) ergibt sich aus () und (6). 0 = log b = log b ( a a) = log b a +log ba. 3 Reihen 3. Konvergenz und Divergenz
Wahrscheinlichkeitsrechnung
 Grundstudium Mathematik Wahrscheinlichkeitsrechnung Bearbeitet von Dominique Foata, Aime Fuchs 1. Auflage 1999. Taschenbuch. xv, 383 S. Paperback ISBN 978 3 7643 6169 3 Format (B x L): 17 x 24,4 cm Gewicht:
Grundstudium Mathematik Wahrscheinlichkeitsrechnung Bearbeitet von Dominique Foata, Aime Fuchs 1. Auflage 1999. Taschenbuch. xv, 383 S. Paperback ISBN 978 3 7643 6169 3 Format (B x L): 17 x 24,4 cm Gewicht:
8 Konvergenzkriterien und Häufungswerte von Folgen in R
 8 Konvergenzkriterien und Häufungswerte von Folgen in R 8.1 Konvergenz monotoner Folgen 8.2 Die Zahl e 8.3 Existenz monotoner Teilfolgen 8.4 Auswahlprinzip von Bolzano-Weierstraß 8.5 Konvergenzkriterium
8 Konvergenzkriterien und Häufungswerte von Folgen in R 8.1 Konvergenz monotoner Folgen 8.2 Die Zahl e 8.3 Existenz monotoner Teilfolgen 8.4 Auswahlprinzip von Bolzano-Weierstraß 8.5 Konvergenzkriterium
Grundlagen Mengenlehre, Maßtheorie
 Grundlagen Mengenlehre, Maßtheorie 12. März 2011 1 Grundlagen der Mengenlehre - Rechnen mit Mengen Im folgenden bezeichnen wir mit P(X) die Menge aller Teilmengen von X, die sogenannte Potenzmenge von
Grundlagen Mengenlehre, Maßtheorie 12. März 2011 1 Grundlagen der Mengenlehre - Rechnen mit Mengen Im folgenden bezeichnen wir mit P(X) die Menge aller Teilmengen von X, die sogenannte Potenzmenge von
KAPITEL 5 ZUFALLSVARIABLE
 KAPITEL 5 ZUFALLSVARIABLE Das in den vorangegangenen Kapiteln beschriebene Modell reicht nicht mehr aus, wenn es darum geht, solche vom Zufall abhängige Grössen oder Zustände zufälliger Systeme zu beschreiben,
KAPITEL 5 ZUFALLSVARIABLE Das in den vorangegangenen Kapiteln beschriebene Modell reicht nicht mehr aus, wenn es darum geht, solche vom Zufall abhängige Grössen oder Zustände zufälliger Systeme zu beschreiben,
1 Grundlagen der Maßtheorie
 1 Grundlagen der Maßtheorie In diesem Kapitel führen wir die Mengensysteme ein, die eine systematische Betrachtung von Ereignissen und zufälligen Beobachtungen in der Wahrscheinlichkeitstheorie erlauben.
1 Grundlagen der Maßtheorie In diesem Kapitel führen wir die Mengensysteme ein, die eine systematische Betrachtung von Ereignissen und zufälligen Beobachtungen in der Wahrscheinlichkeitstheorie erlauben.
Satz Eine Teilmenge U von M ist genau dann offen, wenn jeder Punkt von U innerer Punkt ist. U x, und U ist als Vereinigung offener Mengen offen.
 Ergänzungen zu offenen und abgeschlossenen Mengen Definition Ist L Teilmenge eines topologischen Raums M, so heißt x L innerer Punkt von L, wenn es eine offene Umgebung von x gibt, die ganz in L liegt.
Ergänzungen zu offenen und abgeschlossenen Mengen Definition Ist L Teilmenge eines topologischen Raums M, so heißt x L innerer Punkt von L, wenn es eine offene Umgebung von x gibt, die ganz in L liegt.
Universität Leipzig, SoSo 2013
 Vorlesung Wahrscheinlichkeitstheorie I Universität Leipzig, SoSo 2013 Prof. Dr. Max v. Renesse renesse@uni-leipzig.de Sprechstunde: Di 13.15-14.45, A 337 Übungen: Mo 11.15 -- 12.45 A 314 K. Zimmermann
Vorlesung Wahrscheinlichkeitstheorie I Universität Leipzig, SoSo 2013 Prof. Dr. Max v. Renesse renesse@uni-leipzig.de Sprechstunde: Di 13.15-14.45, A 337 Übungen: Mo 11.15 -- 12.45 A 314 K. Zimmermann
8. Formelsammlung. Pr[ ] = 0. 0 Pr[A] 1. Pr[Ā] = 1 Pr[A] A B = Pr[A] Pr[B] DWT 8.1 Gesetze zum Rechnen mit Ereignissen 203/467 Ernst W.
![8. Formelsammlung. Pr[ ] = 0. 0 Pr[A] 1. Pr[Ā] = 1 Pr[A] A B = Pr[A] Pr[B] DWT 8.1 Gesetze zum Rechnen mit Ereignissen 203/467 Ernst W. 8. Formelsammlung. Pr[ ] = 0. 0 Pr[A] 1. Pr[Ā] = 1 Pr[A] A B = Pr[A] Pr[B] DWT 8.1 Gesetze zum Rechnen mit Ereignissen 203/467 Ernst W.](/thumbs/69/59978031.jpg) 8. Formelsammlung 8.1 Gesetze zum Rechnen mit Ereignissen Im Folgenden seien A und B, sowie A 1,..., A n Ereignisse. Die Notation A B steht für A B und zugleich A B = (disjunkte Vereinigung). A 1... A
8. Formelsammlung 8.1 Gesetze zum Rechnen mit Ereignissen Im Folgenden seien A und B, sowie A 1,..., A n Ereignisse. Die Notation A B steht für A B und zugleich A B = (disjunkte Vereinigung). A 1... A
Das Lebesgue-Maß im R p
 Das Lebesgue-Maß im R p Wir werden nun im R p ein metrisches äußeres Maß definieren, welches schließlich zum Lebesgue-Maß führen wird. Als erstes definieren wir das Volumen von Intervallen des R p. Seien
Das Lebesgue-Maß im R p Wir werden nun im R p ein metrisches äußeres Maß definieren, welches schließlich zum Lebesgue-Maß führen wird. Als erstes definieren wir das Volumen von Intervallen des R p. Seien
Wissenschaftliches Arbeiten Quantitative Methoden
 Wissenschaftliches Arbeiten Quantitative Methoden Prof. Dr. Stefan Nickel WS 2008 / 2009 Gliederung I. Motivation II. III. IV. Lesen mathematischer Symbole Wissenschaftliche Argumentation Matrizenrechnung
Wissenschaftliches Arbeiten Quantitative Methoden Prof. Dr. Stefan Nickel WS 2008 / 2009 Gliederung I. Motivation II. III. IV. Lesen mathematischer Symbole Wissenschaftliche Argumentation Matrizenrechnung
Eine Aussage kann eine Eigenschaft für ein einzelnes, konkretes Objekt behaupten:
 Aussagen Aussagen Eine Aussage kann eine Eigenschaft für ein einzelnes, konkretes Objekt behaupten: verbale Aussage formale Aussage Wahrheitswert 1) 201 ist teilbar durch 3 3 201 wahre Aussage (w.a.) 2)
Aussagen Aussagen Eine Aussage kann eine Eigenschaft für ein einzelnes, konkretes Objekt behaupten: verbale Aussage formale Aussage Wahrheitswert 1) 201 ist teilbar durch 3 3 201 wahre Aussage (w.a.) 2)
Universität Basel Wirtschaftswissenschaftliches Zentrum. Zufallsvariablen. Dr. Thomas Zehrt
 Universität Basel Wirtschaftswissenschaftliches Zentrum Zufallsvariablen Dr. Thomas Zehrt Inhalt: 1. Einführung 2. Zufallsvariablen 3. Diskrete Zufallsvariablen 4. Stetige Zufallsvariablen 5. Erwartungswert
Universität Basel Wirtschaftswissenschaftliches Zentrum Zufallsvariablen Dr. Thomas Zehrt Inhalt: 1. Einführung 2. Zufallsvariablen 3. Diskrete Zufallsvariablen 4. Stetige Zufallsvariablen 5. Erwartungswert
Statistik für Ingenieure Vorlesung 3
 Statistik für Ingenieure Vorlesung 3 Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut für Stochastik 14. November 2017 3. Zufallsgrößen 3.1 Zufallsgrößen und ihre Verteilung Häufig sind
Statistik für Ingenieure Vorlesung 3 Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut für Stochastik 14. November 2017 3. Zufallsgrößen 3.1 Zufallsgrößen und ihre Verteilung Häufig sind
Kapitel II Kontinuierliche Wahrscheinlichkeitsraume
 Kapitel II Kontinuierliche Wahrscheinlichkeitsraume 1. Einfuhrung 1.1 Motivation Interpretation der Poisson-Verteilung als Grenzwert der Binomialverteilung. DWT 1.1 Motivation 195/460 Beispiel 78 Wir betrachten
Kapitel II Kontinuierliche Wahrscheinlichkeitsraume 1. Einfuhrung 1.1 Motivation Interpretation der Poisson-Verteilung als Grenzwert der Binomialverteilung. DWT 1.1 Motivation 195/460 Beispiel 78 Wir betrachten
Meßbare Funktionen. bilden die Grundlage der Integrationstheorie. Definition 24.1 :
 24 Meßbare Funktionen bilden die Grundlage der Integrationstheorie. Definition 24. : Sei X eine beliebige Menge, Y ein topologischer Raum, λ ein Maß auf X. f : X Y heißt λ-messbar, falls f (Ω) λ-messbar
24 Meßbare Funktionen bilden die Grundlage der Integrationstheorie. Definition 24. : Sei X eine beliebige Menge, Y ein topologischer Raum, λ ein Maß auf X. f : X Y heißt λ-messbar, falls f (Ω) λ-messbar
Maß und Wahrscheinlichkeit
 Klaus D. Schmidt Maß und Wahrscheinlichkeit Springer Einleitung 1 Teil I Mengensysteme und Abbildungen 1 Mengensysteme 7 1.1 Topologien 8 1.2 er-algebren 14 1.3 Dynkin-Systeme 16 1.4 n-stabile Mengensysteme
Klaus D. Schmidt Maß und Wahrscheinlichkeit Springer Einleitung 1 Teil I Mengensysteme und Abbildungen 1 Mengensysteme 7 1.1 Topologien 8 1.2 er-algebren 14 1.3 Dynkin-Systeme 16 1.4 n-stabile Mengensysteme
Übungsblatt 5 zur Vorlesung Wahrscheinlichkeitstheorie
 Dr. Christoph Luchsinger Übungsblatt 5 zur Vorlesung Wahrscheinlichkeitstheorie Allgemeine Masse Herausgabe des Übungsblattes: Woche 13, Abgabe der Lösungen: Woche 14 (bis Freitag, 16.15 Uhr), Besprechung:
Dr. Christoph Luchsinger Übungsblatt 5 zur Vorlesung Wahrscheinlichkeitstheorie Allgemeine Masse Herausgabe des Übungsblattes: Woche 13, Abgabe der Lösungen: Woche 14 (bis Freitag, 16.15 Uhr), Besprechung:
Maß und Wahrscheinlichkeit
 Springer-Lehrbuch Maß und Wahrscheinlichkeit Bearbeitet von Klaus D. Schmidt 1. Auflage 2011. Taschenbuch. xii, 484 S. Paperback ISBN 978 3 642 21025 9 Format (B x L): 15,5 x 23,5 cm Gewicht: 775 g Weitere
Springer-Lehrbuch Maß und Wahrscheinlichkeit Bearbeitet von Klaus D. Schmidt 1. Auflage 2011. Taschenbuch. xii, 484 S. Paperback ISBN 978 3 642 21025 9 Format (B x L): 15,5 x 23,5 cm Gewicht: 775 g Weitere
Skript zur Vorlesung MASS- UND INTEGRATIONSTHEORIE
 Skript zur Vorlesung MASS- UND INTEGRATIONSTHEORIE Jürgen Gärtner Sommer 2008 Inhaltsverzeichnis Vorbemerkungen 5 1. Motivation. Inhaltliche Bedeutung des Maßbegriffs 7 2. Das Lebesguesche Maß ebener
Skript zur Vorlesung MASS- UND INTEGRATIONSTHEORIE Jürgen Gärtner Sommer 2008 Inhaltsverzeichnis Vorbemerkungen 5 1. Motivation. Inhaltliche Bedeutung des Maßbegriffs 7 2. Das Lebesguesche Maß ebener
Metrische äußere Maße, Borel-Maße
 Metrische äußere Maße, Borel-Maße Zum einen haben wir mit dem Fortsetzungssatz gesehen, dass man mit einem äußeren Maß (auf P(X) ) stets eine σ-algebra und ein Maß auf dieser bekommt. Liegt nun ein metrischer
Metrische äußere Maße, Borel-Maße Zum einen haben wir mit dem Fortsetzungssatz gesehen, dass man mit einem äußeren Maß (auf P(X) ) stets eine σ-algebra und ein Maß auf dieser bekommt. Liegt nun ein metrischer
Einführung in die Wahrscheinlichkeitstheorie Lösungsvorschläge zu Übungsblatt 4
 TUM, Zentrum Mathematik Lehrstuhl für Mathematische Physik WS 3/4 Prof. Dr. Silke Rolles Thomas Höfelsauer Felizitas Weidner Tutoraufgaben: Einführung in die Wahrscheinlichkeitstheorie Lösungsvorschläge
TUM, Zentrum Mathematik Lehrstuhl für Mathematische Physik WS 3/4 Prof. Dr. Silke Rolles Thomas Höfelsauer Felizitas Weidner Tutoraufgaben: Einführung in die Wahrscheinlichkeitstheorie Lösungsvorschläge
Stochastik. 1. Wahrscheinlichkeitsräume
 Stochastik 1. Wahrscheinlichkeitsräume Ein Zufallsexperiment ist ein beliebig oft und gleichartig wiederholbarer Vorgang mit mindestens zwei verschiedenen Ergebnissen, bei dem der Ausgang ungewiß ist.
Stochastik 1. Wahrscheinlichkeitsräume Ein Zufallsexperiment ist ein beliebig oft und gleichartig wiederholbarer Vorgang mit mindestens zwei verschiedenen Ergebnissen, bei dem der Ausgang ungewiß ist.
Wahrscheinlichkeitsrechnung und Statistik
 1. und 2. Vorlesung - 2017 Im Alltag... Laut den meteorologischen Vorhersagen wird es morgen regnen. Ob ich riskiere und die Wette verlieren werde? Ich werde mit Sicherheit gewinnen! Ist das wirklich unmöglich?
1. und 2. Vorlesung - 2017 Im Alltag... Laut den meteorologischen Vorhersagen wird es morgen regnen. Ob ich riskiere und die Wette verlieren werde? Ich werde mit Sicherheit gewinnen! Ist das wirklich unmöglich?
Stochastik. Stand: 19. Juli 2015, 14:02
 Stochastik Dominik Bullach Hannes F. Funk Stand: 19. Juli 2015, 14:02 Dies ist eine Mitschrift der Vorlesung von Prof. Dr. Peter Pickl im Sommersemester 2015. Sie stellt den Versuch dar, den Vorlesungsstoff
Stochastik Dominik Bullach Hannes F. Funk Stand: 19. Juli 2015, 14:02 Dies ist eine Mitschrift der Vorlesung von Prof. Dr. Peter Pickl im Sommersemester 2015. Sie stellt den Versuch dar, den Vorlesungsstoff
2. Vorlesung. Die Theorie der schwarz-weissen Ketten.
 2. Vorlesung. Die Theorie der schwarz-weissen Ketten. Die Theorie der schwarzen Steinchen haben wir jetzt halbwegs vertanden. Statt mit schwarzen Steinen wie die Griechen, wollen wir jetzt mit schwarzen
2. Vorlesung. Die Theorie der schwarz-weissen Ketten. Die Theorie der schwarzen Steinchen haben wir jetzt halbwegs vertanden. Statt mit schwarzen Steinen wie die Griechen, wollen wir jetzt mit schwarzen
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Eine Auswahl wichtiger Definitionen und Aussagen zur Vorlesung»Stochastik für Informatiker und Regelschullehrer«
 Eine Auswahl wichtiger Definitionen und Aussagen zur Vorlesung»Stochastik für Informatiker und Regelschullehrer«Werner Linde WS 2008/09 Inhaltsverzeichnis 1 Wahrscheinlichkeiten 2 1.1 Wahrscheinlichkeitsräume...........................
Eine Auswahl wichtiger Definitionen und Aussagen zur Vorlesung»Stochastik für Informatiker und Regelschullehrer«Werner Linde WS 2008/09 Inhaltsverzeichnis 1 Wahrscheinlichkeiten 2 1.1 Wahrscheinlichkeitsräume...........................
13 Mehrdimensionale Zufallsvariablen Zufallsvektoren
 3 Mehrdimensionale Zufallsvariablen Zufallsvektoren Bisher haben wir uns ausschließlich mit Zufallsexperimenten beschäftigt, bei denen die Beobachtung eines einzigen Merkmals im Vordergrund stand. In diesem
3 Mehrdimensionale Zufallsvariablen Zufallsvektoren Bisher haben wir uns ausschließlich mit Zufallsexperimenten beschäftigt, bei denen die Beobachtung eines einzigen Merkmals im Vordergrund stand. In diesem
Wahrscheinlichkeitstheorie und Maßtheorie
 KAPITEL 7 Wahrscheinlichkeitstheorie und Maßtheorie 7.1. Vorüberlegungen Die folgenden drei Beispiele sind Spezialfälle des Oberbegriffs Maß. Beispiel 7.1.1 (Verteilung der Ladung oder der Masse). Man
KAPITEL 7 Wahrscheinlichkeitstheorie und Maßtheorie 7.1. Vorüberlegungen Die folgenden drei Beispiele sind Spezialfälle des Oberbegriffs Maß. Beispiel 7.1.1 (Verteilung der Ladung oder der Masse). Man
Wichtige Begriffe und Sätze aus der Wahrscheinlichkeitsrechnung
 Wichtige Begriffe und Sätze aus der Wahrscheinlichkeitsrechnung Version: 22. September 2015 Evelina Erlacher 1 Mengen Es sei Ω eine Menge (die Universalmenge ) und A, B seien Teilmengen von Ω. Dann schreiben
Wichtige Begriffe und Sätze aus der Wahrscheinlichkeitsrechnung Version: 22. September 2015 Evelina Erlacher 1 Mengen Es sei Ω eine Menge (die Universalmenge ) und A, B seien Teilmengen von Ω. Dann schreiben
PD Dr. R. Schätzle 1.11.1999. Maßtheoretische Methoden WS 1999/00
 ETH Zürich Departement für Mathematik PD Dr. R. Schätzle 1.11.1999 Maßtheoretische Methoden WS 1999/00 1.Übung AUFGABE 1: Es sei µ ein borelreguläres Maß auf einem metrischen Raum X und X = j=1 V j, wobei
ETH Zürich Departement für Mathematik PD Dr. R. Schätzle 1.11.1999 Maßtheoretische Methoden WS 1999/00 1.Übung AUFGABE 1: Es sei µ ein borelreguläres Maß auf einem metrischen Raum X und X = j=1 V j, wobei
6. Stochastische Modelle II: Stetige Wahrscheinlichkeitsverteilungen, insbesondere Normalverteilungen
 6. Stochastische Modelle II: Stetige Wahrscheinlichkeitsverteilungen, insbesondere Normalverteilungen Dr. Antje Kiesel Institut für Angewandte Mathematik WS 2011/2012 Bisher: Diskrete Zufallsvariablen,
6. Stochastische Modelle II: Stetige Wahrscheinlichkeitsverteilungen, insbesondere Normalverteilungen Dr. Antje Kiesel Institut für Angewandte Mathematik WS 2011/2012 Bisher: Diskrete Zufallsvariablen,
Grundlagen. Kapitel Mengen
 Kapitel 1 Grundlagen 1.1 Mengen Grundobjekte mathematischer Theorien sind Mengen. Zwar stellt man sich darunter Gesamtheiten von gewissen Dingen (den Elementen der Menge) vor, doch führt die uneingeschränkte
Kapitel 1 Grundlagen 1.1 Mengen Grundobjekte mathematischer Theorien sind Mengen. Zwar stellt man sich darunter Gesamtheiten von gewissen Dingen (den Elementen der Menge) vor, doch führt die uneingeschränkte
Übungen zur Analysis 3
 Mathematisches Institut der Universität München Prof. Dr. Franz Merkl Wintersemester 013/01 Blatt 17.10.013 Übungen zur Analysis 3.1ε σ-subadditivität. a Es sei µ ein Inhalt auf einer Mengenalgebra A.
Mathematisches Institut der Universität München Prof. Dr. Franz Merkl Wintersemester 013/01 Blatt 17.10.013 Übungen zur Analysis 3.1ε σ-subadditivität. a Es sei µ ein Inhalt auf einer Mengenalgebra A.
2. Integration. {x : f(x) <a+ 1 n }
 9 2.1. Definition. 2. Integration in Maß ist eine nichtnegative, abzählbar additive Mengenfunktion. in Maßraum ist ein Tripel (X,,µ) bestehend aus einem messbaren Raum X mit der -lgebra und einem auf definierten
9 2.1. Definition. 2. Integration in Maß ist eine nichtnegative, abzählbar additive Mengenfunktion. in Maßraum ist ein Tripel (X,,µ) bestehend aus einem messbaren Raum X mit der -lgebra und einem auf definierten
Topologische Räume und stetige Abbildungen Teil 2
 TU Dortmund Mathematik Fakultät Proseminar zur Linearen Algebra Ausarbeitung zum Thema Topologische Räume und stetige Abbildungen Teil 2 Anna Kwasniok Dozent: Prof. Dr. L. Schwachhöfer Vorstellung des
TU Dortmund Mathematik Fakultät Proseminar zur Linearen Algebra Ausarbeitung zum Thema Topologische Räume und stetige Abbildungen Teil 2 Anna Kwasniok Dozent: Prof. Dr. L. Schwachhöfer Vorstellung des
Kapitel II. Konvergenz von Folgen und Reihen
 Kapitel II Konvergenz von Folgen und Reihen 7 Einführende Beispiele und Rechenregeln für konvergente Folgen 8 Konvergenzkriterien und Häufungswerte von Folgen in R 9 Konvergenz und absolute Konvergenz
Kapitel II Konvergenz von Folgen und Reihen 7 Einführende Beispiele und Rechenregeln für konvergente Folgen 8 Konvergenzkriterien und Häufungswerte von Folgen in R 9 Konvergenz und absolute Konvergenz
Teil II. Wahrscheinlichkeitsrechnung
 Teil II Wahrscheinlichkeitsrechnung Deskriptive Statistik und Wahrscheinlichkeitsrechnung (SS 2014) Folie 129 5 Zufallsexperimente Inhaltsverzeichnis (Ausschnitt) 5 Zufallsexperimente Ergebnisse Ereignisse
Teil II Wahrscheinlichkeitsrechnung Deskriptive Statistik und Wahrscheinlichkeitsrechnung (SS 2014) Folie 129 5 Zufallsexperimente Inhaltsverzeichnis (Ausschnitt) 5 Zufallsexperimente Ergebnisse Ereignisse
Teil II. Wahrscheinlichkeitsrechnung. Deskriptive Statistik und Wahrscheinlichkeitsrechnung (SS 2015) Folie 129
 Teil II Wahrscheinlichkeitsrechnung Deskriptive Statistik und Wahrscheinlichkeitsrechnung (SS 2015) Folie 129 5 Zufallsexperimente Inhaltsverzeichnis (Ausschnitt) 5 Zufallsexperimente Ergebnisse Ereignisse
Teil II Wahrscheinlichkeitsrechnung Deskriptive Statistik und Wahrscheinlichkeitsrechnung (SS 2015) Folie 129 5 Zufallsexperimente Inhaltsverzeichnis (Ausschnitt) 5 Zufallsexperimente Ergebnisse Ereignisse
Teil II. Wahrscheinlichkeitsrechnung. Inhaltsverzeichnis (Ausschnitt) Zufallsexperimente (Zufallsvorgänge) Ergebnisse
 5 Zufallsexperimente Inhaltsverzeichnis (Ausschnitt) Teil II Wahrscheinlichkeitsrechnung 5 Zufallsexperimente Ergebnisse Ereignisse Wahrscheinlichkeiten Deskriptive Statistik und Wahrscheinlichkeitsrechnung
5 Zufallsexperimente Inhaltsverzeichnis (Ausschnitt) Teil II Wahrscheinlichkeitsrechnung 5 Zufallsexperimente Ergebnisse Ereignisse Wahrscheinlichkeiten Deskriptive Statistik und Wahrscheinlichkeitsrechnung
Analysis II (FS 2015): ZUSAMMENHÄNGENDE METRISCHE RÄUME
 Analysis II (FS 2015): ZUSAMMENHÄNGENDE METRISCHE RÄUME Dietmar A. Salamon ETH-Zürich 23. Februar 2015 1 Topologische Grundbegriffe Sei (X, d) ein metrischer Raum, d.h. X ist eine Menge und d : X X R ist
Analysis II (FS 2015): ZUSAMMENHÄNGENDE METRISCHE RÄUME Dietmar A. Salamon ETH-Zürich 23. Februar 2015 1 Topologische Grundbegriffe Sei (X, d) ein metrischer Raum, d.h. X ist eine Menge und d : X X R ist
Statistik I für Betriebswirte Vorlesung 3
 Statistik I für Betriebswirte Vorlesung 3 Dr. Andreas Wünsche TU Bergakademie Freiberg Institut für Stochastik 20. April 2017 Dr. Andreas Wünsche Statistik I für Betriebswirte Vorlesung 3 Version: 18.
Statistik I für Betriebswirte Vorlesung 3 Dr. Andreas Wünsche TU Bergakademie Freiberg Institut für Stochastik 20. April 2017 Dr. Andreas Wünsche Statistik I für Betriebswirte Vorlesung 3 Version: 18.
Einführung in die angewandte Stochastik
 Einführung in die angewandte Stochastik Fabian Meyer 5. April 2018 Inhaltsverzeichnis 1 Wahrscheinlichkeitsrechnung 3 1.1 Definitionen................................... 3 1.2 Wahrscheinlichkeitsmaß, Wahrscheinlichkeitsverteilung,
Einführung in die angewandte Stochastik Fabian Meyer 5. April 2018 Inhaltsverzeichnis 1 Wahrscheinlichkeitsrechnung 3 1.1 Definitionen................................... 3 1.2 Wahrscheinlichkeitsmaß, Wahrscheinlichkeitsverteilung,
Einführung in die Mengenlehre
 Einführung in die Mengenlehre Kevin Kaatz, Lern-Online.net im Mai 2009 Lern-Online.net Mathematik-Portal 1 Inhaltsverzeichnis 1 Vorwort und 3 1.1 Vorwort und Literaturempfehlungen............................
Einführung in die Mengenlehre Kevin Kaatz, Lern-Online.net im Mai 2009 Lern-Online.net Mathematik-Portal 1 Inhaltsverzeichnis 1 Vorwort und 3 1.1 Vorwort und Literaturempfehlungen............................
B Grundbegriffe zu Mengen und Abbildungen
 B Grundbegriffe zu Mengen und Abbildungen Die Sprache der Mengen und Abbildungen hat sich als Basissprache in der modernen Mathematik durchgesetzt. Da sie sehr praktisch ist, wird sie auch in diesem Buch
B Grundbegriffe zu Mengen und Abbildungen Die Sprache der Mengen und Abbildungen hat sich als Basissprache in der modernen Mathematik durchgesetzt. Da sie sehr praktisch ist, wird sie auch in diesem Buch
8 Verteilungsfunktionen und Dichten
 8 Verteilungsfunktionen und Dichten 8.1 Satz und Definition (Dichten) Eine Funktion f : R R heißt Dichtefunktion, kurz Dichte, wenn sie (Riemann-) integrierbar ist mit f(t) 0 für alle t R und Setzt man
8 Verteilungsfunktionen und Dichten 8.1 Satz und Definition (Dichten) Eine Funktion f : R R heißt Dichtefunktion, kurz Dichte, wenn sie (Riemann-) integrierbar ist mit f(t) 0 für alle t R und Setzt man
Konvergenz von Folgen
 6 Konvergenz von Folgen Definition 6.1 Eine Folge in C (oder R) ist eine Abbildung f : N C (oder R). Schreibweise: (a n ) n N, (a n ), a 1, a 2... wobei a n = f(n). Beispiele: 1) (1 + 2 n ) n N, 3 2, 5
6 Konvergenz von Folgen Definition 6.1 Eine Folge in C (oder R) ist eine Abbildung f : N C (oder R). Schreibweise: (a n ) n N, (a n ), a 1, a 2... wobei a n = f(n). Beispiele: 1) (1 + 2 n ) n N, 3 2, 5
Mathematik I. Vorlesung 8. Cauchy-Folgen
 Prof. Dr. H. Brenner Osnabrück WS 2009/2010 Mathematik I Vorlesung 8 Cauchy-Folgen Ein Problem des Konvergenzbegriffes ist, dass zur Formulierung der Grenzwert verwendet wird, den man unter Umständen noch
Prof. Dr. H. Brenner Osnabrück WS 2009/2010 Mathematik I Vorlesung 8 Cauchy-Folgen Ein Problem des Konvergenzbegriffes ist, dass zur Formulierung der Grenzwert verwendet wird, den man unter Umständen noch
Einführung in die Stochastik 6. Übungsblatt
 Einführung in die Stochastik 6. Übungsblatt Fachbereich Mathematik SS M. Kohler 3. Mai A. Fromkorth D. Furer Gruppen und Hausübung Aufgabe (a) Die Wahrscheinlichkeit, dass eine S Bahn Verspätung hat, betrage.3.
Einführung in die Stochastik 6. Übungsblatt Fachbereich Mathematik SS M. Kohler 3. Mai A. Fromkorth D. Furer Gruppen und Hausübung Aufgabe (a) Die Wahrscheinlichkeit, dass eine S Bahn Verspätung hat, betrage.3.
KONSTRUKTION VON MASSEN
 KONSTRUKTION VON MASSEN MARCUS HEITEL 1. Einleitung Wir wollen im Folgenden das Lebesguemaß konstruieren. Dieses soll die Eigenschaft λ ( [a, b = b a für a, b R besitzen. Nun ist ein Maß aber auf einer
KONSTRUKTION VON MASSEN MARCUS HEITEL 1. Einleitung Wir wollen im Folgenden das Lebesguemaß konstruieren. Dieses soll die Eigenschaft λ ( [a, b = b a für a, b R besitzen. Nun ist ein Maß aber auf einer
01145 Maß- und Integrationstheorie
 01145 Maß- und Integrationstheorie Eine Einführung Prof. Dr. Werner Kirsch Wissenschaftliche Mitarbeit: Dr. Tobias Mühlenbruch Lehrgebiet Stochastik FernUniversität in Hagen LG.Stochastik@fernuni-hagen.de
01145 Maß- und Integrationstheorie Eine Einführung Prof. Dr. Werner Kirsch Wissenschaftliche Mitarbeit: Dr. Tobias Mühlenbruch Lehrgebiet Stochastik FernUniversität in Hagen LG.Stochastik@fernuni-hagen.de
Lineare Algebra II 9. Übungsblatt
 Lineare Algebra II 9. Übungsblatt Fachbereich Mathematik SS Prof. Dr. Kollross 5./6. Juni Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G (Minitest: ohne Benutzung des Skripts und innerhalb von Minuten!)
Lineare Algebra II 9. Übungsblatt Fachbereich Mathematik SS Prof. Dr. Kollross 5./6. Juni Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G (Minitest: ohne Benutzung des Skripts und innerhalb von Minuten!)
1. Topologische Räume
 1. Topologische Räume 5 1. Topologische Räume Wie schon in der Einleitung erwähnt wollen wir uns in dieser Vorlesung mit stetigen Abbildungen beschäftigen. Als Erstes müssen wir uns daher fragen, welche
1. Topologische Räume 5 1. Topologische Räume Wie schon in der Einleitung erwähnt wollen wir uns in dieser Vorlesung mit stetigen Abbildungen beschäftigen. Als Erstes müssen wir uns daher fragen, welche
Stochastische Prozesse
 INSTITUT FÜR STOCHASTIK SS 2009 UNIVERSITÄT KARLSRUHE Blatt 9 Priv.-Doz. Dr. D. Kadelka Dipl.-Math. W. Lao Übungen zur Vorlesung Stochastische Prozesse Musterlösungen Aufgabe 40: Es sei (X t ) t 0 ein
INSTITUT FÜR STOCHASTIK SS 2009 UNIVERSITÄT KARLSRUHE Blatt 9 Priv.-Doz. Dr. D. Kadelka Dipl.-Math. W. Lao Übungen zur Vorlesung Stochastische Prozesse Musterlösungen Aufgabe 40: Es sei (X t ) t 0 ein
Analysis I - Stetige Funktionen
 Kompaktheit und January 13, 2009 Kompaktheit und Funktionengrenzwert Definition Seien X, d X ) und Y, d Y ) metrische Räume. Desweiteren seien E eine Teilmenge von X, f : E Y eine Funktion und p ein Häufungspunkt
Kompaktheit und January 13, 2009 Kompaktheit und Funktionengrenzwert Definition Seien X, d X ) und Y, d Y ) metrische Räume. Desweiteren seien E eine Teilmenge von X, f : E Y eine Funktion und p ein Häufungspunkt
