Fluß. Flußnetzwerk. Definition 6.2. Es sei N = (G, c, s, t) ein Flußnetzwerk. Für einen Knoten
|
|
|
- Annika Weber
- vor 7 Jahren
- Abrufe
Transkript
1 6. Flüe un Zuornungen Fluß In ieem Kapiel weren Bewerungen von Kanen al maximale Kapaziäen inerpreier, ie üer iee Kane pro Zeieinhei ranporier weren können. Wir können un einen Graphen al Verorgungnezwerk vorellen, z.b. al Daennez. Die enheiene Frage i, welhen maximalen Durhaz wir erreihen können. Wieviele Einheien können wir maximal von einem Knoen zu einem aneren pro Zeieinhei ranporieren? Definiion 6.2. E ei N = (G,,, ) ein Flußnezwerk. Für einen Knoen v V ei A in (v) := {(u, v) A} un A ou (v) := {(v, u) A}. Eine Ailung f : A IR heiß Fluß auf N, wenn ie folgenen Beingungen erfüll in: 1. 0 f(e) (e) für alle e A,.h. ie Kapaziä wir für keine Kane üerhrien un 2. e A in (v) f(e) = e A ou (v) f(e) für alle v V \ {, },.h. au jeem Knoen fließ genauoviel herau wie hinein, mi Aunahme er Quelle un Senke. Einführung in ie Graphenheorie FH Bonn-Rhein-Sieg, WS 04/ Einführung in ie Graphenheorie FH Bonn-Rhein-Sieg, WS 04/ Flußnezwerk Ein Flußnezwerk N i ein Tupel N = (G,,, ) ee- Definiion 6.1. hen au: G = (V, A), einem geriheen Graphen, : A IR +, einer Kapaziäfunkion auf en geriheen Kanen mi nihnegaiven Weren un, V, zwei augezeihneen Knoen, er Quelle un er Senke mi. Lemma 6.1. Φ(f) := Definiion 6.3. f auf N. Für einen Fluß f eine Flußnezwerk N = (G,,, ) gil e A ou () f(e) e A in () f(e) = e A in () f(e) e A ou () f(e) Der Wer Φ(f) au Lemma 6.1 heiß Wer e Flue Ein Fluß f mi Φ(f) Φ(f ) für alle Flüe f auf N heiß Maximalfluß auf N. Da Maximalflußprolem eeh arin, zu einem gegeenen Flußnezwerk einen Maximalfluß zu eimmen. Bemerkung: Da Maximalflußprolem kann al LP formulier weren. Einführung in ie Graphenheorie FH Bonn-Rhein-Sieg, WS 04/ Einführung in ie Graphenheorie FH Bonn-Rhein-Sieg, WS 04/05 201
2 Zunehmener Weg Weg erreihar in, un ei T := V \ S. Für jee Kane (v, w), v S, w T gil: f(v, w) = (v, w) Definiion 6.4. Gegeen ei ein Flußnezwerk N = (G,,, ) mi einem Fluß f. Eine Folge (v 0,..., v k ) heiß zunehmener Weg zgl. f gw. für jee i = 1,..., k eine er folgenen Beingungen erfüll i: Für jee Kane (w, v), w T, v S gil: f(w, v) = 0 Anhaulih: Die Kanen zwihen S un T ilen einen Engpaß, er eine Flußerhöhung verhiner. 1. (v i 1, v i ) A un f(v i 1, v i ) < (v i 1, v i ) Vorwärkane 2. (v i, v i 1 ) A un f(v i, v i 1 ) > 0 Rükwärkane Vorwärkane 1 Rükwärkane Einführung in ie Graphenheorie FH Bonn-Rhein-Sieg, WS 04/ Einführung in ie Graphenheorie FH Bonn-Rhein-Sieg, WS 04/ Offenihlih können wir en Fluß erhöhen, wenn wir einen zunehmenen Weg gefunen haen. Die Exienz eine zunehmenen Wege i alo hinreihen für eine Flußerhöhung. Der folgene Saz zeig, aß iee Krierium auh nowenig i. Saz 6.2. Ein Fluß f in einem Flußnezwerk N i genau ann ein Maximalfluß, wenn kein zunehmener Weg von nah exiier. Bewei. : Wenn ein zunehmener Weg W von nah exiier, ann kann Φ(f) um a Minimum er Were (e) f(e) für Vorwärkanen von W zw. f(e) für Rükwärkanen von W erhöh weren. : E gee keinen zunehmenen Weg von nah. E ei S ie Menge er Knoen, ie von au mi einem zunehmenen Berehnung eine Maximalflue Saz 6.2 liefer ie Bai zur Berehnung eine Maximalflue. 1. Wir aren mi einem elieigen Fluß, z.b. f(e) = 0 für alle e A. Weier mi Wenn e keinen zunehmenen Weg zgl. f gi, ann STOP. Anonen weier mi Sei W = ( = v 0, v 1,..., v k = ) ein zunehmener Weg von nah zgl. f un ei z := min( {(v i 1, v i ) f(v i 1, v i ) (v i 1, v i ) Vorwärkane von W} {f(v i, v i 1 ) (v i, v i 1 ) Rükwärkane von W} ) Einführung in ie Graphenheorie FH Bonn-Rhein-Sieg, WS 04/ Einführung in ie Graphenheorie FH Bonn-Rhein-Sieg, WS 04/05 205
3 Seze f(v i 1, v i ) := f(v i 1, v i ) + z für jee Vorwärkane (v i 1, v i ). Seze f(v i, v i 1 ) := f(v i, v i 1 ) z für jee Rükwärkane (v i, v i 1 ). Weier mi 2. Beipiel 6.1. Wir erahen a folgene Flußnezwerk. Die Kapaziä i für alle Kanen 1. Der Fluß i zunäh auf allen Kanen 0. a (,,, ) i ein zunehmener Weg mi z = 1. Alle Kanen e Wege in Vorwärkanen. Markierungalgorihmu Der Markierungalgorihmu von For un Fulkeron (1956) konkreiier a Verfahren zur Berehnung maximaler Flüe. Man markier ukzeive ie Knoen w auf einem zunehmenen Weg mi rei Weren v(w), r(w), z(w). v(w) i er Vorgänger von w in em zunehmenen Weg. r(w) gi ie Rihung er verweneen Kane an ( = Vorwärkane, = Rükwärkane). z(w) i er möglihe zuäzlihe Fluß auf em Weg nah w. Einführung in ie Graphenheorie FH Bonn-Rhein-Sieg, WS 04/ Einführung in ie Graphenheorie FH Bonn-Rhein-Sieg, WS 04/ Flußerhöhung auf em zunehmenen Weg ergi en Graphen: a Auf er Rükwärkane wir er Fluß verringer, anonen erhöh. a Algorihmu 6.1. Gegeen ei ein Flußnezwerk N = (G,,, ) un ein iniialer Fluß f(e) Seze S := {}, R := {}, z() :=. mi Φ(f) = 1. (, a,,,, ) i nun ein zunehmener Weg mi z = 1, woei (, ) eine Rükwärkane i. Wir haen Φ(f) = 2 un e exiier kein zunehmener Weg. Dami i er angegeene Fluß ein Maximalfluß. 2. Wähle einen Knoen u R. Seze R := R \ {u}. 3. Für alle w V \ S mi (u, w) A un f(u, w) < (u, w): S := S {w}, R := R {w}, v(w) := u, r(w) :=, z(w) := min{z(u), (u, w) f(u, w)} 4. Für alle w V \ S mi (w, u) A un f(w, u) > 0: S := S {w}, R := R {w}, v(w) := u, r(w) :=, z(w) := min{z(u), f(w, u)} Einführung in ie Graphenheorie FH Bonn-Rhein-Sieg, WS 04/ Einführung in ie Graphenheorie FH Bonn-Rhein-Sieg, WS 04/05 209
4 5. Fall R =, ann STOP. Fall S, ann weier mi 6, anonen weier mi z := z(); w :=. 7. Fall r(w) = : u := v(w), f(u, w) := f(u, w) + z Fall r(w) = : u := v(w), f(w, u) := f(w, u) z Saz 6.4. Erez man in Algorihmu 6.1 en Shri 2 urh 2a. Wähle en Knoen u R, er zuer in R eingefüg wure. Seze R := R \ {u}. ann erehne er Markierungalgorihmu für elieige Kapaziäfunkionen in O( V E 2 ) einen Maximalfluß. 8. w := v(w). Fall w =, ann weier mi 1, anonen weier mi 7. Saz 6.3. Sei N = (G,,, ) ein Flußnezwerk mi raionaler Kapaziäfunkion. Dann erehne Algorihmu 6.1 einen maximalen Fluß f auf N. Beipiel 6.2. Anwenung e Markierungalgorihmu. Tafel Einführung in ie Graphenheorie FH Bonn-Rhein-Sieg, WS 04/ Einführung in ie Graphenheorie FH Bonn-Rhein-Sieg, WS 04/ Bemerkung Flüe un Zuornungen max-flow min-u Trennener Shni Bei irraionalen Kapaziäen kann e vorkommen, aß er Markierungalgorihmu immer weiere Vereerungen e Flußwere fine, ohne jemal zu erminieren. Auh ei ganzzahligen Kapaziäen i ie Laufzei e Markierungalgorihmu nih polynomial, a ie Anzahl er Shrie von ahängen kann. Eine polynomiale Lauzei erhäl man aer, wenn man für ie Suhe nah einem zunehmenen Weg ie Breienuhe einez (Emon un Karp, 1972). Wie groß kann er Fluß in em folgenen Flußnezwerk h öhen ein? a Der Fluß kann nih größer al ie Kapaziä er er Kane (, ) ein, a jeer Weg von nah iee Kane enhäl. Die Kane (, ) i ein ogenanner rennener Shni. e f Einführung in ie Graphenheorie FH Bonn-Rhein-Sieg, WS 04/ Einführung in ie Graphenheorie FH Bonn-Rhein-Sieg, WS 04/05 213
5 6. Flüe un Zuornungen max-flow min-u Definiion 6.5. E ei N = (G,,, ) ein Flußnezwerk mi G = (V, A). 6. Flüe un Zuornungen max-flow min-u Beipiel 6.3. Wie groß i er Maximalfluß in em folgenen Graphen? Für eine Teilmenge S V heiß A S := {(v, w) A v S, w V \ S} Shni von G. Fall S, V \ S, o i A S ein rennener Shni. Ein rennener Shni A S mi minimaler Kapaziä (A S ) := e A S (e) heiß minimaler Shni. f(s, B) = f(b, T) = 3, f(s, A) = 5, f(a, C) = f(c, T) = 2, f(a, D) = f(d, T) = 3 alo Φ(f) = 8. Die Kapaziä e rennenen Shnie {(S, B), (C, T), (D, T)} i 8. Alo i f ein Maximalfluß. Einführung in ie Graphenheorie FH Bonn-Rhein-Sieg, WS 04/ Einführung in ie Graphenheorie FH Bonn-Rhein-Sieg, WS 04/ Flüe un Zuornungen max-flow min-u Saz 6.5. [max-flow-min-u-theorem] In einem Flußnezwerk N = (G,,, ) i er Wer eine maximalen Flue gleih er Kapaziä eine minimalen Shnie. Bewei. Tafel. Bemerkung 6.2. Kennen wir einen Fluß f un finen wir einen rennenen Shni A S mi Φ(f) = (A S ), o i f ein Maximalfluß. Für ie Menge S ei Terminierung von Algorihmu 6.1 i A S ein minimaler Shni (vgl. Bewei zu Saz 6.2). Der Markierungalgorihmu erehne alo nih nur einen maximalen Fluß onern auh einen minimalen Shni. Einführung in ie Graphenheorie FH Bonn-Rhein-Sieg, WS 04/05 215
6. Flüsse und Zuordnungen
 6. Flüsse und Zuordnungen Flußnetzwerke 6. Flüsse und Zuordnungen In diesem Kapitel werden Bewertungen von Kanten als maximale Kapazitäten interpretiert, die über diese Kante pro Zeiteinheit transportiert
6. Flüsse und Zuordnungen Flußnetzwerke 6. Flüsse und Zuordnungen In diesem Kapitel werden Bewertungen von Kanten als maximale Kapazitäten interpretiert, die über diese Kante pro Zeiteinheit transportiert
Restkapazität. = O( V ) mal kritisch. Also gibt es insgesamt höchstens O( V E ) Augmentierungen.
 Lemma 4.5.9. Der Algorihmu von Edmond-Karp führ höchen O( V E ) Augmenierungen durch. Bewei. Eine Kane (u, v) heiße kriich auf augmenierenden Weg p gdw. c f (u, v) = c f (p). Rekapaziä Eine kriiche Kane
Lemma 4.5.9. Der Algorihmu von Edmond-Karp führ höchen O( V E ) Augmenierungen durch. Bewei. Eine Kane (u, v) heiße kriich auf augmenierenden Weg p gdw. c f (u, v) = c f (p). Rekapaziä Eine kriiche Kane
Algorithmen II Vorlesung am
 Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
Hallo Welt für Fortgeschrittene
 Hallo Wel für Forgechriene Flüe, Schnie, Biparie Graphen I Florian Hanke Informaik Programmieryeme Marenraße 3 958 Erlangen Inhal Grundlagen Ford-Fulkeron-Algorihmu Edmond-Karp-Sraegie Minimaler Schni
Hallo Wel für Forgechriene Flüe, Schnie, Biparie Graphen I Florian Hanke Informaik Programmieryeme Marenraße 3 958 Erlangen Inhal Grundlagen Ford-Fulkeron-Algorihmu Edmond-Karp-Sraegie Minimaler Schni
6 Flüsse und Matchings
 6. Flüsse in Netzwerken Flußnetzwerke 6 Flüsse und Matchings In diesem Kapitel werden Bewertungen von Kanten als maximale Kapazitäten interpretiert, die über diese Kante pro Zeiteinheit transportiert werden
6. Flüsse in Netzwerken Flußnetzwerke 6 Flüsse und Matchings In diesem Kapitel werden Bewertungen von Kanten als maximale Kapazitäten interpretiert, die über diese Kante pro Zeiteinheit transportiert werden
25. Flüsse in Netzen. Motivation. Fluss. Flussnetzwerk
 Moivaion 25. Flüe in Nezen Flunezwerk, Maximaler Flu, Schni, Renezwerk, Max-flow Min-cu, Ford-Fulkeron Mehode, Edmond-Karp Algorihmu, Maximale Biparie Maching [Oman/Widmayer, Kap. 9.7, 9.8.1], [Cormen
Moivaion 25. Flüe in Nezen Flunezwerk, Maximaler Flu, Schni, Renezwerk, Max-flow Min-cu, Ford-Fulkeron Mehode, Edmond-Karp Algorihmu, Maximale Biparie Maching [Oman/Widmayer, Kap. 9.7, 9.8.1], [Cormen
Vorlesung Kombinatorische Optimierung (Wintersemester 2007/08)
 Vorleung Kombinaoriche Opimierung (Wineremeer 007/08) Kapiel : Flüe und Zirkulaionen Volker Kaibel Oo-von-Guericke Univeriä Magdeburg (Verion vom 0. November 007) Definiion. Ein Nezwerk i ein Paar (D,
Vorleung Kombinaoriche Opimierung (Wineremeer 007/08) Kapiel : Flüe und Zirkulaionen Volker Kaibel Oo-von-Guericke Univeriä Magdeburg (Verion vom 0. November 007) Definiion. Ein Nezwerk i ein Paar (D,
Algorithmische Graphentheorie
 Algorihmiche Graphenheorie Sommeremeer 2014 3. Vorleung Flualgorihmen Prof. Dr. Alexander Wolff 1 Erinnerung Oh my God i an LP! Gegeben ein gericheer Graph G = (V, E) mi, V und Kanenkapaziäen c : E R >0.
Algorihmiche Graphenheorie Sommeremeer 2014 3. Vorleung Flualgorihmen Prof. Dr. Alexander Wolff 1 Erinnerung Oh my God i an LP! Gegeben ein gericheer Graph G = (V, E) mi, V und Kanenkapaziäen c : E R >0.
KAPITEL 2 KÜRZESTE WEGE
 KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
Hallo Welt für Fortgeschrittene
 Hallo Wel für Forgechriene Flüe, Schnie, biparie Graphen Philipp Reger Informaik 2 Programmieryeme Marenraße 3 9058 Erlangen Agenda Maximaler Flu Minimaler Schni Redukionen Maximale Biparie Maching Konnekiviä
Hallo Wel für Forgechriene Flüe, Schnie, biparie Graphen Philipp Reger Informaik 2 Programmieryeme Marenraße 3 9058 Erlangen Agenda Maximaler Flu Minimaler Schni Redukionen Maximale Biparie Maching Konnekiviä
Übersicht Datenstrukturen und Algorithmen. Graphenproblem: maximale Flüsse. Graphenproblem: maximale Flüsse. Vorlesung 16: Maximaler Fluss
 Überich aenrukuren und lgorihmen Vorleung 16: Prof. r. Erika Ábrahám Theorie Hybrider Syeme Informaik 2 hp://h.rwh-aachen.de/eaching/-1/ daenrukuren-und-algorihmen/ iee Präenaion verwende in Teilen Folien
Überich aenrukuren und lgorihmen Vorleung 16: Prof. r. Erika Ábrahám Theorie Hybrider Syeme Informaik 2 hp://h.rwh-aachen.de/eaching/-1/ daenrukuren-und-algorihmen/ iee Präenaion verwende in Teilen Folien
Netzwerke Beispielnetzwerk N
 Nezwerke Kapiel Flüe in Nezwerken Sromnez Telefonnez Warenflu zwichen Herellern und Konumenen Verkehr (Sraßen, Züge, Flugzeuge,...) Of wollen wir Güer von einem Punk zu einem anderen chicken Ziel So viel/effizien/illig
Nezwerke Kapiel Flüe in Nezwerken Sromnez Telefonnez Warenflu zwichen Herellern und Konumenen Verkehr (Sraßen, Züge, Flugzeuge,...) Of wollen wir Güer von einem Punk zu einem anderen chicken Ziel So viel/effizien/illig
6. Flüsse und Zuordnungen
 6. Flüsse und Zuordnungen In diesem Kapitel werden Bewertungen von Kanten als maximale Kapazitäten interpretiert, die über solch eine Kante pro Zeiteinheit transportiert werden können. Wir können uns einen
6. Flüsse und Zuordnungen In diesem Kapitel werden Bewertungen von Kanten als maximale Kapazitäten interpretiert, die über solch eine Kante pro Zeiteinheit transportiert werden können. Wir können uns einen
Übersicht. Datenstrukturen und Algorithmen. Graphenproblem: maximale Flüsse. Graphenproblem: maximale Flüsse. Vorlesung 18: Maximaler Fluss (K26)
 Überich aenrukuren und lgorihmen Vorleung 18: (K26) Joo-Pieer Kaoen Lehruhl für Informaik 2 Sofware Modeling and Verificaion Group hp://move.rwh-aachen.de/eaching/-15/dal/ 25. Juni 2015 1 Flunezwerke 2
Überich aenrukuren und lgorihmen Vorleung 18: (K26) Joo-Pieer Kaoen Lehruhl für Informaik 2 Sofware Modeling and Verificaion Group hp://move.rwh-aachen.de/eaching/-15/dal/ 25. Juni 2015 1 Flunezwerke 2
HTL Kapfenberg pc_reifeprüfungsaufgaben_ma_11_bsp.31.mcd Seite 1 von 7
 HTL Kapfenberg p_reifeprüfungsaufgaben_ma Bsp.3.m Seie von 7 Angaben zu Aufgabe 3: Ein shwingfähiges mehanishes Sysem is mi einem geshwinigeisproporionalem Dämpfer ausgesae. Folgene in iesem Zusammenhang
HTL Kapfenberg p_reifeprüfungsaufgaben_ma Bsp.3.m Seie von 7 Angaben zu Aufgabe 3: Ein shwingfähiges mehanishes Sysem is mi einem geshwinigeisproporionalem Dämpfer ausgesae. Folgene in iesem Zusammenhang
Flüsse und Zuordnungen. Kapitel 6. Peter Becker (H-BRS) Graphentheorie Wintersemester 2018/ / 296
 Kapitel 6 Peter Becker (H-BRS) Graphentheorie Wintersemester 2018/19 227 / 296 Inhalt Inhalt 6 Flussnetzwerke Berechnung maximaler Flüsse Max-Flow-Min-Cut Matchings Peter Becker (H-BRS) Graphentheorie
Kapitel 6 Peter Becker (H-BRS) Graphentheorie Wintersemester 2018/19 227 / 296 Inhalt Inhalt 6 Flussnetzwerke Berechnung maximaler Flüsse Max-Flow-Min-Cut Matchings Peter Becker (H-BRS) Graphentheorie
Geometrie. Inhaltsverzeichnis. 8.1 Der Satz von Ptolemäus und sein klassischer Beweis. Der Satz von Ptolemäus. 8 Der Satz von Ptolemäus
 Der Stz von Ptolemäus 1 Geometrie Der Stz von Ptolemäus Autor: Peter Anree Inhltsverzeihnis 8 Der Stz von Ptolemäus 1 8.1 Der Stz von Ptolemäus un sein lssisher Beweis........... 1 8.2 Verhältnis er Digonlen
Der Stz von Ptolemäus 1 Geometrie Der Stz von Ptolemäus Autor: Peter Anree Inhltsverzeihnis 8 Der Stz von Ptolemäus 1 8.1 Der Stz von Ptolemäus un sein lssisher Beweis........... 1 8.2 Verhältnis er Digonlen
3.4 Maximale Flüsse und der Algorithmus von Ford Fulkerson
 3.4 Maximale Flüsse und der Algorithmus von Ford Fulkerson Definition 3.4.1 Die Aufgabe, zu jedem Netzwerk N = (s, t, V, E, c o ) mit n = V Knoten und m = E Kanten den Fluß f IR m mit maximalem Wert zu
3.4 Maximale Flüsse und der Algorithmus von Ford Fulkerson Definition 3.4.1 Die Aufgabe, zu jedem Netzwerk N = (s, t, V, E, c o ) mit n = V Knoten und m = E Kanten den Fluß f IR m mit maximalem Wert zu
Maximaler Fluss = minimaler Schnitt
 Maximaler Flu = minimaler Schnitt Oliver Junge Fakultät für Mathematik Techniche Univerität München Flüe in Netzwerken Mathematiche Abtraktion Kapazität 3 2 Quelle 5 Senke 1 2 Netzwerk gerichteter Graph
Maximaler Flu = minimaler Schnitt Oliver Junge Fakultät für Mathematik Techniche Univerität München Flüe in Netzwerken Mathematiche Abtraktion Kapazität 3 2 Quelle 5 Senke 1 2 Netzwerk gerichteter Graph
b) Das Restnetzwerk zu f sieht folgendermaßen aus:
 Techniche Univeriä München Zenrum Mhemik Dikree Opimierung: Grundlgen (MA 0) Prof Dr R Hemmecke, Dr R Brndenerg, MSc-Mh B Wilhelm Üungl 7 Aufge 7 Die folgende Aildung zeig ein Nezwerk N mi einen Flukpziäen
Techniche Univeriä München Zenrum Mhemik Dikree Opimierung: Grundlgen (MA 0) Prof Dr R Hemmecke, Dr R Brndenerg, MSc-Mh B Wilhelm Üungl 7 Aufge 7 Die folgende Aildung zeig ein Nezwerk N mi einen Flukpziäen
Vorlesung Diskrete Strukturen Transportnetze
 Vorlesung Diskrete Strukturen Trnsportnetze Bernhr Gnter WS 2009/10 Gerihtete Grphen Ein shlingenloser gerihteter Grph ist ein Pr (V, A), woei V eine elieige Menge ist, eren Elemente wir Eken nennen un
Vorlesung Diskrete Strukturen Trnsportnetze Bernhr Gnter WS 2009/10 Gerihtete Grphen Ein shlingenloser gerihteter Grph ist ein Pr (V, A), woei V eine elieige Menge ist, eren Elemente wir Eken nennen un
Proseminar Effiziente Algorithmen
 Proeminar Effiziene Algorihmen Kapiel 8: Graphalgorihmen Prof. Dr. Chriian Scheideler WS 2016 08.12.2016 Kapiel 8 1 Überich Kürzee Wege Minimale Spannbäme Maching Flprobleme DA 08.12.2016 Kapiel 8 2 Überich
Proeminar Effiziene Algorihmen Kapiel 8: Graphalgorihmen Prof. Dr. Chriian Scheideler WS 2016 08.12.2016 Kapiel 8 1 Überich Kürzee Wege Minimale Spannbäme Maching Flprobleme DA 08.12.2016 Kapiel 8 2 Überich
2.6.1 Definition und Darstellung Ausspähen von Graphen Minimal spannende Bäume Kürzeste Pfade 2.6.
 .6 Graphen.6. Definition und Dartellung.6. Aupähen von Graphen.6.3 Minimal pannende Bäume.6.4 Kürzete Pfade.6.5 Maximaler Flu .6.5 Maximaler Flu.6.5. Flunetzwerke.6.5. Ford-Fulkeron-Methode.6.5.3 Algorithmu
.6 Graphen.6. Definition und Dartellung.6. Aupähen von Graphen.6.3 Minimal pannende Bäume.6.4 Kürzete Pfade.6.5 Maximaler Flu .6.5 Maximaler Flu.6.5. Flunetzwerke.6.5. Ford-Fulkeron-Methode.6.5.3 Algorithmu
Wirtschaftsmathematik - Übungen WS 2018
 Wirtshftsmthemtik - Üungen WS 8 Bltt : Linere Alger. Gegeen ist eine eine 3 3 Mtrix C =( ij ) mit un eine Mtrix B = A ) Shreien Sie ie Mtrix C n! Y _] j i für ij
Wirtshftsmthemtik - Üungen WS 8 Bltt : Linere Alger. Gegeen ist eine eine 3 3 Mtrix C =( ij ) mit un eine Mtrix B = A ) Shreien Sie ie Mtrix C n! Y _] j i für ij
Übungsblatt 4 Lösungsvorschläge
 Insiu für Theoreische Informaik Lehrsuhl Prof. Dr. D. Wagner Übungsbla 4 Lösungsvorschläge Vorlesung Algorihmenechnik im WS 09/10 Problem 1: Flüsse [vgl. Kapiel 4.1 im Skrip] ** Gegeben sei ein Nezwerk
Insiu für Theoreische Informaik Lehrsuhl Prof. Dr. D. Wagner Übungsbla 4 Lösungsvorschläge Vorlesung Algorihmenechnik im WS 09/10 Problem 1: Flüsse [vgl. Kapiel 4.1 im Skrip] ** Gegeben sei ein Nezwerk
Musterlösung zur Einsendearbeit zur Erlangung der Teilnahmeberechtigung
 Muerlöung zur Einenearbei Moul 3511 Seuern un ökonomiche Anreize, Kur 00694 Seuerwirkunglehre I, KE 3 Verbraucheuern, Wineremeer 011/1 1 Muerlöung zur Einenearbei zur Erlangung er Teilnahmeberechigung
Muerlöung zur Einenearbei Moul 3511 Seuern un ökonomiche Anreize, Kur 00694 Seuerwirkunglehre I, KE 3 Verbraucheuern, Wineremeer 011/1 1 Muerlöung zur Einenearbei zur Erlangung er Teilnahmeberechigung
Stochastische Differentialgleichungen
 INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
Kugelfallmethode nach Stokes
 Phyikaliche Grunrakiku Veruch 09 Veruchrookolle alf Erlebach uelfallehoe nach Soke Aufaben. Meen er Fallzeien on ieren Sahlkueln in izinuöl.. Berechnen er ynaichen Vikoiä e Öl.. Berechnen er kineaichen
Phyikaliche Grunrakiku Veruch 09 Veruchrookolle alf Erlebach uelfallehoe nach Soke Aufaben. Meen er Fallzeien on ieren Sahlkueln in izinuöl.. Berechnen er ynaichen Vikoiä e Öl.. Berechnen er kineaichen
Technische Universität München Fakultät für Mathematik Algorithmische Diskrete Mathematik WS 2012/2013 Prof. Dr. P. Gritzmann 9.
 Noe: Name Vorname Marikelnummer Sudiengang Unerchrif der Kandidain/de Kandidaen Höraal Reihe Plaz Techniche Univeriä München Fakulä für Mahemaik Algorihmiche Dikree Mahemaik WS 0/0 Prof. Dr. P. Grizmann
Noe: Name Vorname Marikelnummer Sudiengang Unerchrif der Kandidain/de Kandidaen Höraal Reihe Plaz Techniche Univeriä München Fakulä für Mahemaik Algorihmiche Dikree Mahemaik WS 0/0 Prof. Dr. P. Grizmann
10. Flüsse und Artikulationspunkte
 0. Flüe un Artikultionpunkte Flüe in Netzwerken Artikultionpunkte Prof. Dr. O. Bittel, HTWG Kontnz Algorithmen un Dtentrukuren Flüe un Artikultionpunkte SS 09 0- Netzwerk Ein Netzwerk it ein gewihteter
0. Flüe un Artikultionpunkte Flüe in Netzwerken Artikultionpunkte Prof. Dr. O. Bittel, HTWG Kontnz Algorithmen un Dtentrukuren Flüe un Artikultionpunkte SS 09 0- Netzwerk Ein Netzwerk it ein gewihteter
Wiederholung. Algorithmen und Datenstrukturen Kapitel 10. Motivation. Begriffe und Definitionen
 Algorihmen nd Daenrkren Kapiel Frank Heimann heimann@informaik.ni-hambrg.de 6. Janar 2016 Frank Heimann heimann@informaik.ni-hambrg.de 1/ Graphen Grndlagen Definiion nd Darellng Tiefen- nd Breienche Topologiche
Algorihmen nd Daenrkren Kapiel Frank Heimann heimann@informaik.ni-hambrg.de 6. Janar 2016 Frank Heimann heimann@informaik.ni-hambrg.de 1/ Graphen Grndlagen Definiion nd Darellng Tiefen- nd Breienche Topologiche
Teil 2: Graphenalgorithmen
 Teil : Grphenlgorithmen Anwenungen Definitionen Dtentrukturen für Grphen Elementre Algorithmen Topologihe Sortieren Kürzete Wege Miniml ufpnnene Bäume Flüe in Netzwerken Zummenhngkomponenten M.O.Frnz,
Teil : Grphenlgorithmen Anwenungen Definitionen Dtentrukturen für Grphen Elementre Algorithmen Topologihe Sortieren Kürzete Wege Miniml ufpnnene Bäume Flüe in Netzwerken Zummenhngkomponenten M.O.Frnz,
Distributivgesetz anwenden und üben
 LS 05 Terme, Variablen, Gleihungen 18 LS 05 Distributivgesetz anwen un üben Zeit Lernaktivitäten Material Kompetenzen 1 EA 15 Die S vereutlihen sih as Distributivgesetz geometrish un entwikeln ihre persönlihe
LS 05 Terme, Variablen, Gleihungen 18 LS 05 Distributivgesetz anwen un üben Zeit Lernaktivitäten Material Kompetenzen 1 EA 15 Die S vereutlihen sih as Distributivgesetz geometrish un entwikeln ihre persönlihe
Stabile Hochzeiten wie und warum?
 Stile Hohzeiten wie un wrum? Tg er Mthemtik HU erlin 25. pril 2009 Stefn elsner TU erlin, Mthemtik felsner@mth.tu-erlin.e Ws sin stile Hohzeiten? Gegeen: Menge von ruen, M Menge von Männern, = M. Jee Person
Stile Hohzeiten wie un wrum? Tg er Mthemtik HU erlin 25. pril 2009 Stefn elsner TU erlin, Mthemtik felsner@mth.tu-erlin.e Ws sin stile Hohzeiten? Gegeen: Menge von ruen, M Menge von Männern, = M. Jee Person
Dreiecke können einerseits nach den Eigenschaften ihrer Seiten und andererseits nach ihren Winkeln benannt werden. Einteilung nach den Seiten:
 gnz klr: Mthemtik 2 - s Ferienheft mit Erfolgsnzeiger 3 Rettungsring Eigenshften von reieken & Viereken Eigenshften von reieken Ein reiek ht immer 3 Ekpunkte, 3 Seiten un 3 Innenwinkel. ie eshriftung eines
gnz klr: Mthemtik 2 - s Ferienheft mit Erfolgsnzeiger 3 Rettungsring Eigenshften von reieken & Viereken Eigenshften von reieken Ein reiek ht immer 3 Ekpunkte, 3 Seiten un 3 Innenwinkel. ie eshriftung eines
Eigenwerte und Eigenvektoren
 Eigenwere un Eigenvekoren Vorbemerkung: Is ie n n Marix inverierbar, so ha as lineare Gleichungssysem A x b für jees b genau eine Lösung, nämlich x A b. Grun: i A x A A b b, ii Is y eine weiere Lösung,
Eigenwere un Eigenvekoren Vorbemerkung: Is ie n n Marix inverierbar, so ha as lineare Gleichungssysem A x b für jees b genau eine Lösung, nämlich x A b. Grun: i A x A A b b, ii Is y eine weiere Lösung,
2 Torsion in dünnwandigen Querschnitten
 apl oz r-ing hail G Georgi Tragwerkerechnung Torion in dünnwandigen Querchnien Theorien, Vorauezungen und Hpoheen Theorien: Reine Torion ( Grundufe) Begründer: Jean Claude de T VENANT (9-886) mol, Inde:
apl oz r-ing hail G Georgi Tragwerkerechnung Torion in dünnwandigen Querchnien Theorien, Vorauezungen und Hpoheen Theorien: Reine Torion ( Grundufe) Begründer: Jean Claude de T VENANT (9-886) mol, Inde:
Grundlegende Algorithmen Kapitel 6: Flussprobleme
 Grundlegende Algorihmen Kapiel 6: Fluprobleme Chriian Scheideler WS 2009 08.02.2010 Kapiel 6 1 Grundlagen Definiion 6.1: Ein Flunezwerk (G,,,c) beeh au einem gericheen Graph G=(V,E), einer Quelle V, einer
Grundlegende Algorihmen Kapiel 6: Fluprobleme Chriian Scheideler WS 2009 08.02.2010 Kapiel 6 1 Grundlagen Definiion 6.1: Ein Flunezwerk (G,,,c) beeh au einem gericheen Graph G=(V,E), einer Quelle V, einer
6. Flüsse in Netzwerken Berechnung maximaler Flüsse. dann berechnet der Markierungsalgorithmus für beliebige Kapazitätsfunktionen
 6. Flüsse in Netzwerken Berechnung maximaler Flüsse Satz 6.4. Ersetzt man in Algorithmus 6.1 den Schritt 2 durch 2a. Wähle den Knoten, der zuerst in eingefügt wurde. Setze. dann berechnet der arkierungsalgorithmus
6. Flüsse in Netzwerken Berechnung maximaler Flüsse Satz 6.4. Ersetzt man in Algorithmus 6.1 den Schritt 2 durch 2a. Wähle den Knoten, der zuerst in eingefügt wurde. Setze. dann berechnet der arkierungsalgorithmus
Logik / Kombinatorik - Hinweise zur Lösungsfindung
 Logik / Kombinatorik Hinweise zur Lösungsfinung Aufgabe 1) Günstige Bezeichnungen einführen; Tabelle anfertigen un ie unmittelbaren Folgerungen aus bis eintragen (siehe linke Tabelle). Da ies noch nicht
Logik / Kombinatorik Hinweise zur Lösungsfinung Aufgabe 1) Günstige Bezeichnungen einführen; Tabelle anfertigen un ie unmittelbaren Folgerungen aus bis eintragen (siehe linke Tabelle). Da ies noch nicht
Musterlösung zur Probeklausur zur Geometrie
 UNIVERSITÄT ULM Institut für Zhlentheorie un Whrsheinlihkeitstheorie Musterlösung zur Proeklusur zur Geometrie Prof. Dr. Helmut Mier, Hns- Peter Rek Gesmtpunktzhl: 3 Punkte, Punkte= % keine Age. Gi Definitionen
UNIVERSITÄT ULM Institut für Zhlentheorie un Whrsheinlihkeitstheorie Musterlösung zur Proeklusur zur Geometrie Prof. Dr. Helmut Mier, Hns- Peter Rek Gesmtpunktzhl: 3 Punkte, Punkte= % keine Age. Gi Definitionen
Probeklausur: Lösungsvorschläge Besprechung in den Übungen
 Komplexiä u Krypogrfie Theoreihe Iformik Prof. Dr. Johe Köler. Juli 9 Proekluur: Löugvorhläge Beprehug i e Üuge Die Löuge i ohe Gewähr Vereerugvorhläge i willkomme. Aufge Beweie oer wierlege Sie folgee
Komplexiä u Krypogrfie Theoreihe Iformik Prof. Dr. Johe Köler. Juli 9 Proekluur: Löugvorhläge Beprehug i e Üuge Die Löuge i ohe Gewähr Vereerugvorhläge i willkomme. Aufge Beweie oer wierlege Sie folgee
Kapitel 7: Flüsse in Netzwerken und Anwendungen Gliederung der Vorlesung
 Gliederung der Vorleung. Falltudie Bipartite Graphen. Grundbegriffe 3. Elementare Graphalgorithmen und Anwendungen 4. Minimal pannende Bäume 5. Kürzete Pfade 6. Traveling Saleman Problem 7. Flüe in Netzwerken
Gliederung der Vorleung. Falltudie Bipartite Graphen. Grundbegriffe 3. Elementare Graphalgorithmen und Anwendungen 4. Minimal pannende Bäume 5. Kürzete Pfade 6. Traveling Saleman Problem 7. Flüe in Netzwerken
Hauptachsentransformation
 Haupachsenransformaion Erinnerung: A M n is genau ann nich inverierbar, wenn es ein x R n, x gib, mi A x. Definiion. Sei A M n eine Marix. Ein Vekor v R n, v heiß Eigenvekor von A zum Eigenwer λ R, wenn
Haupachsenransformaion Erinnerung: A M n is genau ann nich inverierbar, wenn es ein x R n, x gib, mi A x. Definiion. Sei A M n eine Marix. Ein Vekor v R n, v heiß Eigenvekor von A zum Eigenwer λ R, wenn
Musterlösung - Aufgabenblatt 4. Aufgabe 1
 Murlöung - Augnl 4 Aug ) Au Üungl 3 hn wir ür n ggnn Grphn G gzig, ν(g) = 9 gil, inm wir olgn Mhing M von mximlr Krinliä nggn hn: g h i j 3 4 6 7 8 9 0 E gil lo, nh König Mhing-Thorm u r Vorlung, uh τ(g)
Murlöung - Augnl 4 Aug ) Au Üungl 3 hn wir ür n ggnn Grphn G gzig, ν(g) = 9 gil, inm wir olgn Mhing M von mximlr Krinliä nggn hn: g h i j 3 4 6 7 8 9 0 E gil lo, nh König Mhing-Thorm u r Vorlung, uh τ(g)
e sx y(x)dx 2. Direkt gemäss der Definition unter Verwendung der in der Vorlesung angeführten Eigenschaften
 Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Staatlich geprüfte Techniker
 Auzug au dem Lernmaerial Forildunglehrgang Saalich geprüfe Techniker Auzug au dem Lernmaerial Naurwienchaf DAA-Technikum Een / www.daa-echnikum.de, Infoline: 00 83 6 50 Definiion: Die Gechwindigkei eine
Auzug au dem Lernmaerial Forildunglehrgang Saalich geprüfe Techniker Auzug au dem Lernmaerial Naurwienchaf DAA-Technikum Een / www.daa-echnikum.de, Infoline: 00 83 6 50 Definiion: Die Gechwindigkei eine
Wirtschaftsmathematik - Übungen SS 2018
 Wirtshftsmthemtik - Üungen SS 8 Bltt : Linere Alger. Gegeen sin ie Punkte P =( 3, ) un =(6, ). Bestimmen Sie ie Prmeterrstellung er Geren urh iese Punkte! Zeihnen Sie iese Gere! Wie lutet ie Koorintenrstellung
Wirtshftsmthemtik - Üungen SS 8 Bltt : Linere Alger. Gegeen sin ie Punkte P =( 3, ) un =(6, ). Bestimmen Sie ie Prmeterrstellung er Geren urh iese Punkte! Zeihnen Sie iese Gere! Wie lutet ie Koorintenrstellung
Flüsse, Schnitte, bipartite Graphen
 Flüe, Schnie, iprie Grphen Michel Eicher 06. Juni 0 Michel Eicher Flüe, Schnie, iprie Grphen 06. Juni 0 / 48 Deniionen Nezwerk Flu Üerich Mximler Flu Ford-Fulkeron Minimler Schni Edmond-Krp 3 Redukionen
Flüe, Schnie, iprie Grphen Michel Eicher 06. Juni 0 Michel Eicher Flüe, Schnie, iprie Grphen 06. Juni 0 / 48 Deniionen Nezwerk Flu Üerich Mximler Flu Ford-Fulkeron Minimler Schni Edmond-Krp 3 Redukionen
Markieren Sie die Integralausdrücke, die den Flächeninhalt der markierten Fläche berechnen:
 Aufge C (X/N) Mrkieren Sie ie Integrlusrüke, ie en Fläheninhlt er mrkierten Flähe erehnen: A) f () g() g() f () B) ( f () g() ) + ( f () g() ) C) f () g() D) ( f () g() ) ( g() f () ) E) f () g() F) f
Aufge C (X/N) Mrkieren Sie ie Integrlusrüke, ie en Fläheninhlt er mrkierten Flähe erehnen: A) f () g() g() f () B) ( f () g() ) + ( f () g() ) C) f () g() D) ( f () g() ) ( g() f () ) E) f () g() F) f
Mathematik III. Vorlesung 87. Die äußere Ableitung
 Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 87 Die äußere Ableitung In ieser Vorlesung weren wir ein neuartiges mathematisches Objekt kennenlernen, ie sogenannte äußere Ableitung.
Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 87 Die äußere Ableitung In ieser Vorlesung weren wir ein neuartiges mathematisches Objekt kennenlernen, ie sogenannte äußere Ableitung.
Grundzüge der Informationstheorie (2)
 Bisherige Erkenntnisse zum Informtionsgehlt: Der Informtionsgehlt h eines Zeihens (einer Nhriht) ist um so höher, je unwhrsheinliher sein Auftreten ist: h = l [ /p ] = -l p Treten ie n Zeihen eines Zeihenvorrts
Bisherige Erkenntnisse zum Informtionsgehlt: Der Informtionsgehlt h eines Zeihens (einer Nhriht) ist um so höher, je unwhrsheinliher sein Auftreten ist: h = l [ /p ] = -l p Treten ie n Zeihen eines Zeihenvorrts
Aufgabe 1: a) (i) und (ii) und (iv) 1 Punkt b) (i) 1 Punkt c) (i) 1 Punkt d) (iv) 1 Punkt e) (B) 1 Punkt f) (iv) 1 Punkt g) (i) und (ii) 2 Punkte h
 Aufgabe : a) i) un ii) un i) Punk b) i) Punk c) i) Punk ) i) Punk e) B) Punk f) i) Punk g) i) un ii) Punke i) un iii) un i) un ).5 lu.5 Punk Aufgabe : Venuri Ror Punke) a. Volumenrom Für ieen Aufgabeneil
Aufgabe : a) i) un ii) un i) Punk b) i) Punk c) i) Punk ) i) Punk e) B) Punk f) i) Punk g) i) un ii) Punke i) un iii) un i) un ).5 lu.5 Punk Aufgabe : Venuri Ror Punke) a. Volumenrom Für ieen Aufgabeneil
4 ARBEIT UND LEISTUNG
 10PS/TG - MECHANIK P. Rendulić 2008 ARBEIT UND LEISTUNG 27 4 ARBEIT UND LEISTUNG 4.1 Mehnihe Abei 4.1.1 Definiion de Abei enn ein Köpe une de Einwikung eine konnen Kf die Seke in egihung zuükleg, dnn wid
10PS/TG - MECHANIK P. Rendulić 2008 ARBEIT UND LEISTUNG 27 4 ARBEIT UND LEISTUNG 4.1 Mehnihe Abei 4.1.1 Definiion de Abei enn ein Köpe une de Einwikung eine konnen Kf die Seke in egihung zuükleg, dnn wid
HTL Saalfelden Transformator Seite 1 von 12
 HT Saalfelen Tranformator Seite von Wilfriie ohm 003 HT Saalfelen Tranformator Seite von Wilfrie ohm, HT Saalfelen Tranformator - aplacetranformation ink zur Beipielübericht Mathematiche / Fachliche Inhalte
HT Saalfelen Tranformator Seite von Wilfriie ohm 003 HT Saalfelen Tranformator Seite von Wilfrie ohm, HT Saalfelen Tranformator - aplacetranformation ink zur Beipielübericht Mathematiche / Fachliche Inhalte
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 7 5. Semester ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE
 Mahemaik: Mag. Schmid Wolfgang Arbeibla 7. Semeer ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE Im Raum möche man naürlich nich nur Geraden ondern auch Flächen darellen. Diee Flächen bezeichne man al
Mahemaik: Mag. Schmid Wolfgang Arbeibla 7. Semeer ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE Im Raum möche man naürlich nich nur Geraden ondern auch Flächen darellen. Diee Flächen bezeichne man al
5 Versicherung auf mehrere Leben
 Versicherung auf mehrere Leben 59 5 Versicherung auf mehrere Leben Zie: nassen der bekannen ehoden, um Lebensversicherungen auf zwei oder mehrere Leben kakuieren zu können. Beisiee: Renenversicherung auf
Versicherung auf mehrere Leben 59 5 Versicherung auf mehrere Leben Zie: nassen der bekannen ehoden, um Lebensversicherungen auf zwei oder mehrere Leben kakuieren zu können. Beisiee: Renenversicherung auf
Flüsse in Netzwerken. Seminar über Algorithmen SoSe 2005. Mike Rohland & Julia Schenk
 Flüsse in Netzwerken Seminar über Algorithmen SoSe 2005 Mike Rohland & Julia Schenk Inhalt Einführung Definition Maximale Flüsse Schnitte Restgraphen Zunehmende Wege Max-Fluss Min-Schnitt Theorem Ford-Fulkerson
Flüsse in Netzwerken Seminar über Algorithmen SoSe 2005 Mike Rohland & Julia Schenk Inhalt Einführung Definition Maximale Flüsse Schnitte Restgraphen Zunehmende Wege Max-Fluss Min-Schnitt Theorem Ford-Fulkerson
Geradlinige Bewegung Krummlinige Bewegung Kreisbewegung
 11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
Bündelungsgrad und Abstandsfaktor
 ünelungga un btanfakto Die Gleihung fü ie ieale Rihthaakteitik von ikofonen lautet ( o (: Übetagungfakto : Dukanteil : Gaientenanteil mit a l ünelungga bezeihnet man a Vehältni e von einem iealen mikofon
ünelungga un btanfakto Die Gleihung fü ie ieale Rihthaakteitik von ikofonen lautet ( o (: Übetagungfakto : Dukanteil : Gaientenanteil mit a l ünelungga bezeihnet man a Vehältni e von einem iealen mikofon
Zusammenfassung: Lineare mechanische Wellen
 LGÖ K Ph -ündig Shuljahr 08/09 Zuammenfaung: Lineare mehanihe Wellen Inhalverzeihni Forhreiende ranveralwellen... Sehende ranveralwellen... 3 Refleion von ranveralwellen... ranverale Eigenhwingungen...
LGÖ K Ph -ündig Shuljahr 08/09 Zuammenfaung: Lineare mehanihe Wellen Inhalverzeihni Forhreiende ranveralwellen... Sehende ranveralwellen... 3 Refleion von ranveralwellen... ranverale Eigenhwingungen...
6.3. Iterative Lösung linearer Gleichungssysteme. Großes lineares dünnbesetztes Gleichungssystem A x = b
 6.3. Iterative Lösung linearer Gleichungssysteme Großes lineares ünnesetztes Gleichungssystem A Gauss-Elimination nutzt in er Regel ie Dünnesetztheit nicht aus un führt meist auf Kosten On 3 ; Im Gegensatz
6.3. Iterative Lösung linearer Gleichungssysteme Großes lineares ünnesetztes Gleichungssystem A Gauss-Elimination nutzt in er Regel ie Dünnesetztheit nicht aus un führt meist auf Kosten On 3 ; Im Gegensatz
Wie funktioniert ein GPS System?
 GPS Sem Wie funkionie ein GPS Sem? Im Pinip gn einfh. Mehee Sellien, die ih in eine w. meheen geoionäen Umlufhnen üe de Ede efinden, hlen egelmäßig ihen deei kuellen Snd de Aomei u. D GPS Geä uf de Edoeflähe
GPS Sem Wie funkionie ein GPS Sem? Im Pinip gn einfh. Mehee Sellien, die ih in eine w. meheen geoionäen Umlufhnen üe de Ede efinden, hlen egelmäßig ihen deei kuellen Snd de Aomei u. D GPS Geä uf de Edoeflähe
1 Mein Wissen aus der 3. Klasse Beispiele
 Mein Wissen us er. Klsse eispiele en Lösungen sin Wortteile zugeornet. Sie ergeen er Reihe nh einen mthemtishen egriff, en u in er. Klsse erehnen wirst! ei rzhlung wir vom Preis eines utos % Preisnhlss
Mein Wissen us er. Klsse eispiele en Lösungen sin Wortteile zugeornet. Sie ergeen er Reihe nh einen mthemtishen egriff, en u in er. Klsse erehnen wirst! ei rzhlung wir vom Preis eines utos % Preisnhlss
Wirtschaftsmathematik - Übungen WS 2015/16
 Wirtshftsmthemtik - Üungen WS 25/6 Bltt 2: Linere Alger. Gegeen sin ie Punkte P =( 2, 2) un =(4, ). ) Bestimmen Sie ie Prmeterrstellung er Geren urh iese Punkte! Zeihnen Sie ie Gere! Wie lutet ie Koorintenrstellung
Wirtshftsmthemtik - Üungen WS 25/6 Bltt 2: Linere Alger. Gegeen sin ie Punkte P =( 2, 2) un =(4, ). ) Bestimmen Sie ie Prmeterrstellung er Geren urh iese Punkte! Zeihnen Sie ie Gere! Wie lutet ie Koorintenrstellung
Mathematikaufgabe 79
 Home Strtseite Impressum Kotkt Gästeuh Aufge: Betrhte wir wei sih sheiee Kreise mit utershielihe ie u gemeismer Tgete Berehe Sie s Verhältis er Bogeläge vom Shittpukt es jeweilige Kreises mit er Tgete
Home Strtseite Impressum Kotkt Gästeuh Aufge: Betrhte wir wei sih sheiee Kreise mit utershielihe ie u gemeismer Tgete Berehe Sie s Verhältis er Bogeläge vom Shittpukt es jeweilige Kreises mit er Tgete
Dichtpflanzung von Hokkaido bringt mehr Ertrag und gleiche Lagereignung in 2011
 Versuhe im eutshen Grtenu 2013 Gemüseu Dihtpflnzung von Hokkio ringt mehr Ertrg un gleihe Lgereignung in 2011 Die Ergenisse kurzgefsst In einem Sortenversuh m GBZ Köln-Auweiler zu Hokkio-Küris sin rei
Versuhe im eutshen Grtenu 2013 Gemüseu Dihtpflnzung von Hokkio ringt mehr Ertrg un gleihe Lgereignung in 2011 Die Ergenisse kurzgefsst In einem Sortenversuh m GBZ Köln-Auweiler zu Hokkio-Küris sin rei
9 Konvexe Funktionen, Stütz- und Distanzfunktion
 U BREHM: Konvexgeometrie 9-9 Konvexe Funktionen, Stütz- un Distanzfunktion Definition: Sei K IR, f : K IR eine Abbilung f heißt konvex, wenn K konvex ist un für alle x, y K un alle, gilt f( x( ) y) f(
U BREHM: Konvexgeometrie 9-9 Konvexe Funktionen, Stütz- un Distanzfunktion Definition: Sei K IR, f : K IR eine Abbilung f heißt konvex, wenn K konvex ist un für alle x, y K un alle, gilt f( x( ) y) f(
mathphys-online Umkehrfunktionen Aufgabe 1 1 Gegeben ist die Funktion f mit f( x) 2 x 1 und x [ 0.5 ; 4 [.
 Umkehrfunktionen Aufgabe Gegeben ist ie Funktion f mit f( ) un [ 0. ; [. a) Bestimmen Sie ie Wertemenge un tragen Sie en Graphen von f in as Koorinatensystem ein. Kennzeichnen Sie Definitionsmenge (grün)
Umkehrfunktionen Aufgabe Gegeben ist ie Funktion f mit f( ) un [ 0. ; [. a) Bestimmen Sie ie Wertemenge un tragen Sie en Graphen von f in as Koorinatensystem ein. Kennzeichnen Sie Definitionsmenge (grün)
a) Behauptung: Es gibt die folgenden drei stabilen Matchings:
 Musterlösung - ufgenltt 1 ufge 1 ) ehuptung: Es git ie folgenen rei stilen Mthings: ies knn mn ntürlih für ein so kleines eispiel urh etrhten ller möglihen 3! = 6 Mthings eweisen. Mn knn er uh strukturierter
Musterlösung - ufgenltt 1 ufge 1 ) ehuptung: Es git ie folgenen rei stilen Mthings: ies knn mn ntürlih für ein so kleines eispiel urh etrhten ller möglihen 3! = 6 Mthings eweisen. Mn knn er uh strukturierter
3.7 Der AKS-Primzahltest
 3.7 Der AKS-Primzahltet Die Frage, ob e einen eterminitichen Primzahltet gibt, er mit polynomialem Aufwan aukommt, war biher nur urch Miller auf ie erweiterte Riemannche Vermutung zurückgeführt woren.
3.7 Der AKS-Primzahltet Die Frage, ob e einen eterminitichen Primzahltet gibt, er mit polynomialem Aufwan aukommt, war biher nur urch Miller auf ie erweiterte Riemannche Vermutung zurückgeführt woren.
a) b) Abb. 1: Buchstaben
 Hans Walser, [20171019] Magische Quarate ungeraer Seitenlänge nregung: uler (1782) 1 Worum geht es? Zu einer gegebenen ungeraen Zahl u wir ein magisches Quarat mit er Seitenlänge u konstruiert. 2 as Vorgehen
Hans Walser, [20171019] Magische Quarate ungeraer Seitenlänge nregung: uler (1782) 1 Worum geht es? Zu einer gegebenen ungeraen Zahl u wir ein magisches Quarat mit er Seitenlänge u konstruiert. 2 as Vorgehen
1 Fluss in Graphen. 1.1 Das Residuennetzwerk 10/20 10/30 10/30 10/15 20/20 20/40 20/30. Praktikum Algorithmen-Entwurf (Teil 4)
 Prkikum Algorihmen-Enwurf (Teil 4) 1.11.211 1 1 Flu in Grphen E ei ein gericheer Grph G = (V,E) gegeen. Jeder Kne e de Grphen ei eine Kpziä c(e) N zugeordne. Weier eien zwei Knoen de Grphen ugezeichne:
Prkikum Algorihmen-Enwurf (Teil 4) 1.11.211 1 1 Flu in Grphen E ei ein gericheer Grph G = (V,E) gegeen. Jeder Kne e de Grphen ei eine Kpziä c(e) N zugeordne. Weier eien zwei Knoen de Grphen ugezeichne:
LGÖ Ks M 12 Schuljahr 2017/2018. Zusammenfassung: Abstände, Winkel und Spiegelungen
 LGÖ Ks M 12 Schuljahr 217/218 Zusammenfassung: Asände, Winkel und Spiegelungen Inhalsverzeichnis Asände 1 Winkel 5 Spiegelungen 7 Für Experen 1 Asände Asand Punk Punk: Schreiweise: Den Asand zweier Punke
LGÖ Ks M 12 Schuljahr 217/218 Zusammenfassung: Asände, Winkel und Spiegelungen Inhalsverzeichnis Asände 1 Winkel 5 Spiegelungen 7 Für Experen 1 Asände Asand Punk Punk: Schreiweise: Den Asand zweier Punke
Lineare Algebra. Übungsblatt November Aufgabe 1. (4=2+2 Punkte) Sei V ein K-Vektorraum und seien v 1,..., v n V.
 Goethe-Univesität Fnkfut Institut fü Mthemtik Linee Alge Wintesemeste 28/9 Pof. D. Jko Sti Mtin Lütke Üungsltt 5 3. Noveme 28 Aufge. (42+2 Punkte) Sei V ein K-Vektoum un seien v... v n V. () Sei K α n
Goethe-Univesität Fnkfut Institut fü Mthemtik Linee Alge Wintesemeste 28/9 Pof. D. Jko Sti Mtin Lütke Üungsltt 5 3. Noveme 28 Aufge. (42+2 Punkte) Sei V ein K-Vektoum un seien v... v n V. () Sei K α n
Übungen zur Experimentalphysik II Aufgabenblatt 3 - Lösung
 KW /15 Prof. Dr. R. Reifarh, Dr. J. Glorius Übungen zur Experimenalphysik II Aufgabenbla 3 - Lösung Aufgabe 1: a) Die Laung q im Volumen V beräg: q = ρ(r) V = ρ(r)4πr r = 4πAr 3 r Für ie Laung Q erhalen
KW /15 Prof. Dr. R. Reifarh, Dr. J. Glorius Übungen zur Experimenalphysik II Aufgabenbla 3 - Lösung Aufgabe 1: a) Die Laung q im Volumen V beräg: q = ρ(r) V = ρ(r)4πr r = 4πAr 3 r Für ie Laung Q erhalen
DOWNLOAD. D/d oder T/t? Ähnliche Laute unterscheiden. Einfaches Übungsmaterial für Schüler. Ähnliche Laute unterscheiden. Ulrike Rehschuh-Blasse
 OWNLOA Ulrike Rehschuh-Blasse / oer /? Ähnliche Laue unerscheien Einfaches Übungsmaerial für Schüler mi sonerpäagogischem Förerbearf Ulrike Rehschuh-Blasse Bergeorfer Kopiervorlagen ownloaauszug aus em
OWNLOA Ulrike Rehschuh-Blasse / oer /? Ähnliche Laue unerscheien Einfaches Übungsmaerial für Schüler mi sonerpäagogischem Förerbearf Ulrike Rehschuh-Blasse Bergeorfer Kopiervorlagen ownloaauszug aus em
Mathematische Modelle und numerische Methoden in der Biologie
 Institut für Angewante un Numerishe Mathematik Prof. Dr. Tobias Jahnke, Dipl.-Biol. Mihael Kreim Mathematishe Moelle un numerishe Methoen in er Biologie Sommersemester 2012 3. Übungsblatt Gruppenübung
Institut für Angewante un Numerishe Mathematik Prof. Dr. Tobias Jahnke, Dipl.-Biol. Mihael Kreim Mathematishe Moelle un numerishe Methoen in er Biologie Sommersemester 2012 3. Übungsblatt Gruppenübung
Relationen: Verkettungen, Wege, Hüllen
 FH Gießen-Frieerg, Sommersemester 00 Lösungen zu Üungsltt 9 Diskrete Mthemtik (Informtik) 9./. Juni 00 Prof. Dr. Hns-Ruolf Metz Reltionen: Verkettungen, Wege, Hüllen Aufge. Es ezeihne R ie Reltion {(,
FH Gießen-Frieerg, Sommersemester 00 Lösungen zu Üungsltt 9 Diskrete Mthemtik (Informtik) 9./. Juni 00 Prof. Dr. Hns-Ruolf Metz Reltionen: Verkettungen, Wege, Hüllen Aufge. Es ezeihne R ie Reltion {(,
10 Gleichspannungs-Schaltvorgänge RL-Reihenschaltung
 GleichspannungsSchalvorgänge eihenschalung Seie von 6 222 Prof. Dr.Ing. T. Harriehausen Wolfenbüel.9.2. Beziehung zwischen en lemmengrößen einer konsanen Inukiviä Die Abhängigkei zwischen en lemmengrößen
GleichspannungsSchalvorgänge eihenschalung Seie von 6 222 Prof. Dr.Ing. T. Harriehausen Wolfenbüel.9.2. Beziehung zwischen en lemmengrößen einer konsanen Inukiviä Die Abhängigkei zwischen en lemmengrößen
Hidden Markov Model. Gegeben: Beobachtungen O = o 1,..., o n, je eine pro Zeitpunkt
 Hidden Markov Model Hidden Markov Model Gegeben: Beobachungen O = o,..., o n, je eine pro Zeipunk mögliche Syemzuände Z für jeden Syemzuand z Z und jede Beobachung o die Wahrcheinlichkei Pr(o z) oder die
Hidden Markov Model Hidden Markov Model Gegeben: Beobachungen O = o,..., o n, je eine pro Zeipunk mögliche Syemzuände Z für jeden Syemzuand z Z und jede Beobachung o die Wahrcheinlichkei Pr(o z) oder die
Abschlussprüfung an Fachoberschulen in Bayern Mathematik mit CAS 2015 Analysis A2 Ausbildungsrichtung Technik
 MK.7.05 B5_T_A MK_Loes.xmc Abschlussprüfung an Fachoberschulen in Bayern Mahemaik mi 05 Analysis A Ausbilungsrichung Technik.0 Gegeben sin ie reellen Funkionen f a : x --> x x x Definiionsmenge D fa R
MK.7.05 B5_T_A MK_Loes.xmc Abschlussprüfung an Fachoberschulen in Bayern Mahemaik mi 05 Analysis A Ausbilungsrichung Technik.0 Gegeben sin ie reellen Funkionen f a : x --> x x x Definiionsmenge D fa R
3 b 1 = 7. b = = 59, a = = 30, b) + = Aufgabe 6.1. fehlt Aufgabe 6.2 = = 0 = = 7; = = 2 = = 1.
 Anlyishe Geomerie / Seie Lö () Lösngen zz Kpi iel l :: Skl lrrprrodk Afge fehl Afge ; ; ; Bei Vekoren müsse mn Prodke erehnen Afge Berehne ) ) ) ( ) d) ( ) e) ( )( ) 8 f) ( ) Anlyishe Geomerie / Seie Lö
Anlyishe Geomerie / Seie Lö () Lösngen zz Kpi iel l :: Skl lrrprrodk Afge fehl Afge ; ; ; Bei Vekoren müsse mn Prodke erehnen Afge Berehne ) ) ) ( ) d) ( ) e) ( )( ) 8 f) ( ) Anlyishe Geomerie / Seie Lö
1 Planarbeit Planarbeit
 Erreiten Sie sih shrittweise ie folgenen Themen. Notieren Sie gegeenenflls zu jeem Them Frgen. Lösen Sie jeweils ie zugehörige Kontrollufge. Kontrollieren Sie Ihre Lösung mit er Musterlösung. Lösen Sie
Erreiten Sie sih shrittweise ie folgenen Themen. Notieren Sie gegeenenflls zu jeem Them Frgen. Lösen Sie jeweils ie zugehörige Kontrollufge. Kontrollieren Sie Ihre Lösung mit er Musterlösung. Lösen Sie
Rechenübung NGA 2, CE. Rechenübung NGA 2, CE. Kommunikations. Kommunikations. Aufgabe 2: Aufgabe 1:
 Augabe 1: Augabe : 1.1) Welhe er olgenen Aussagen treen zu? a) Durh Kanaloierung erhöht sih ie Anzahl er zu übertragenen Zeihen. b) Eine Kanaloierung ist bei igitaler Kommunikation unbeingt erorerlih.
Augabe 1: Augabe : 1.1) Welhe er olgenen Aussagen treen zu? a) Durh Kanaloierung erhöht sih ie Anzahl er zu übertragenen Zeihen. b) Eine Kanaloierung ist bei igitaler Kommunikation unbeingt erorerlih.
Schwache Konvergenz von W-Verteilungen auf der Zahlengeraden
 Kapitel 5 Schwache Konvergenz von W-Verteilungen auf er Zahlengeraen 5.1 Schwache Konvergenz bzw. Verteilungskonvergenz Bezeichne W(, B 1 ie Menge aller W-Verteilungen auf (, B 1. Definition 5.1 (Schwache
Kapitel 5 Schwache Konvergenz von W-Verteilungen auf er Zahlengeraen 5.1 Schwache Konvergenz bzw. Verteilungskonvergenz Bezeichne W(, B 1 ie Menge aller W-Verteilungen auf (, B 1. Definition 5.1 (Schwache
4. Kreis- und Wegeprobleme Abstände in Graphen
 4. Kreis- und Wegeprobleme Abstände in Graphen Abstände in Graphen Definition 4.4. Es sei G = (V,E) ein Graph. Der Abstand d(v,w) zweier Knoten v,w V ist die minimale Länge eines Weges von v nach w. Falls
4. Kreis- und Wegeprobleme Abstände in Graphen Abstände in Graphen Definition 4.4. Es sei G = (V,E) ein Graph. Der Abstand d(v,w) zweier Knoten v,w V ist die minimale Länge eines Weges von v nach w. Falls
Informatik II SS Pumping Lemma für reguläre Sprachen (1/2) Pumping Lemma für reguläre Sprachen (2) Beweis
 Pumping Lemm für reguläre Sprhen (1/2) Informtik II SS 2004 Teil 6: Sprhen, Compiler un Theorie 2 Ds Pumping Lemm ist eine Methoe, um herus zu finen, o eine Sprhe niht regulär. Prof. Dr. Dieter Hogrefe
Pumping Lemm für reguläre Sprhen (1/2) Informtik II SS 2004 Teil 6: Sprhen, Compiler un Theorie 2 Ds Pumping Lemm ist eine Methoe, um herus zu finen, o eine Sprhe niht regulär. Prof. Dr. Dieter Hogrefe
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt Semester ARBEITSBLATT 13 ABSTANDSBERECHNUNGEN. a) Abstand eines Punktes von einer Geraden
 Mahemaik: Ma. Schmi Wolfan Arbeisbla 1. Semeser ARBEITSBLATT 1 ABSTANDSBERECHNUNGEN a) Absan eines Punkes von einer Geraen Für ie nun folenen Aufabensellunen ib es jeweils eine anze Mene an unerschielichen
Mahemaik: Ma. Schmi Wolfan Arbeisbla 1. Semeser ARBEITSBLATT 1 ABSTANDSBERECHNUNGEN a) Absan eines Punkes von einer Geraen Für ie nun folenen Aufabensellunen ib es jeweils eine anze Mene an unerschielichen
Differentialrechnung
 Differentialrechnung Um Funktionen genauer zu untersuchen bzw. sie zu analysieren, ist es notwenig, etwas über ihren Verlauf, as qualitative Verhalten er Funktion, sagen zu können. Das heisst, wir suchen
Differentialrechnung Um Funktionen genauer zu untersuchen bzw. sie zu analysieren, ist es notwenig, etwas über ihren Verlauf, as qualitative Verhalten er Funktion, sagen zu können. Das heisst, wir suchen
Mathematik: Mag. Schmid Wolfgang+LehrerInnenteam ARBEITSBLATT 6-13 ERMITTELN DER KREISGLEICHUNG
 ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
essen Mache es nun umgekehrt. Schreibe immer einen Buchstaben weniger, bis das Wort ganz verschwunden ist. Sprich wieder (leise) dazu.
 een Füge Buchtabe an Buchtabe bi du da ganze Wort vor dir ieht. Sprich dazu! Beachte: Da e wird kurz geprochen. Daher kommt danach ein Doppel! Mache e nun umgekehrt. Schreibe immer einen Buchtaben weniger,
een Füge Buchtabe an Buchtabe bi du da ganze Wort vor dir ieht. Sprich dazu! Beachte: Da e wird kurz geprochen. Daher kommt danach ein Doppel! Mache e nun umgekehrt. Schreibe immer einen Buchtaben weniger,
Zur Klassifizierung mehrparametriger Dämpfungsmodelle
 TECHNISCHE MECHANIK Bd 5 Hef -4 (5) 8-89 Mkripeigg: 7. Ag 5 Zr Klifizierg mehrprmeriger ämpfgmodelle H. Müller zm Hge B. Nole Vier ämpfgmodelle wrde i Nole d Müller zm Hge (5) hiichlich ihrer mhemiche
TECHNISCHE MECHANIK Bd 5 Hef -4 (5) 8-89 Mkripeigg: 7. Ag 5 Zr Klifizierg mehrprmeriger ämpfgmodelle H. Müller zm Hge B. Nole Vier ämpfgmodelle wrde i Nole d Müller zm Hge (5) hiichlich ihrer mhemiche
Analysis: Ganzrationale Funktionen Analysis Ganzrationale Funktionen Differenzialrechnung, Extrem- und Wendepunkte
 www.mahe-aufgaben.com Analysis: Ganzraionale Funkionen Analysis Ganzraionale Funkionen Differenzialrechnung, Exrem- und Wendepunke Gymnasium Klasse 0 Alexander Schwarz www.mahe-aufgaben.com Juni 0 www.mahe-aufgaben.com
www.mahe-aufgaben.com Analysis: Ganzraionale Funkionen Analysis Ganzraionale Funkionen Differenzialrechnung, Exrem- und Wendepunke Gymnasium Klasse 0 Alexander Schwarz www.mahe-aufgaben.com Juni 0 www.mahe-aufgaben.com
Dichtpflanzung von Hokkaido bringt mehr Ertrag und gleiche Lagereignung
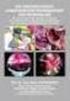 Mrtin Herener; Lnwirtshftskmmer NRW; Grtenstr. 11; 50765 Köln; 0221 5340-240, mrtin.herener@lwk.nrw.e Dihtpflnzung von Hokkio ringt mehr Ertrg un gleihe Lgereignung Zusmmenfssung - Empfehlungen In einem
Mrtin Herener; Lnwirtshftskmmer NRW; Grtenstr. 11; 50765 Köln; 0221 5340-240, mrtin.herener@lwk.nrw.e Dihtpflnzung von Hokkio ringt mehr Ertrg un gleihe Lgereignung Zusmmenfssung - Empfehlungen In einem
Durch die Umformung ergibt sich eine Schaltfunktion mit einer minimalen Anzahl von Verknüpfungsoperationen, nämlich 2.
 2 Die shltlgerishe Umformung von Shltfunktionen in Normlform soll m Beispiel er Umformung einer Mxterm-Normlform in eine Minterm-Normlform gezeigt weren. Beispiel: y = ) ( ) ( ) ( Es ietet sih ie Anwenung
2 Die shltlgerishe Umformung von Shltfunktionen in Normlform soll m Beispiel er Umformung einer Mxterm-Normlform in eine Minterm-Normlform gezeigt weren. Beispiel: y = ) ( ) ( ) ( Es ietet sih ie Anwenung
Einführung in die Mathematik des Operations Research
 Universität zu Köln Mthemtishes Institut Prof. Dr. F. Vllentin ufge ( + 7 = 0 Punkte) Einführung in die Mthemtik des Opertions Reserh Sommersemester 0 en zur Klusur (7. Juli 0). Es seien M = {,..., n },
Universität zu Köln Mthemtishes Institut Prof. Dr. F. Vllentin ufge ( + 7 = 0 Punkte) Einführung in die Mthemtik des Opertions Reserh Sommersemester 0 en zur Klusur (7. Juli 0). Es seien M = {,..., n },
Fachgebiet Rechnersysteme 2. Übung Logischer Entwurf. Technische Universität Darmstadt. 4. Aufgabe. b) Minterm-Normalform
 Fhgeiet Rehnersysteme 2. Üung Logisher Entwur Tehnishe Universität Drmstt 2. Üung Logisher Entwur 4. Auge 1 4. Auge 2. Üung Logisher Entwur 4. Auge 3 ) Minterm-Normlorm Geen sei ie ooleshe Funktion + +
Fhgeiet Rehnersysteme 2. Üung Logisher Entwur Tehnishe Universität Drmstt 2. Üung Logisher Entwur 4. Auge 1 4. Auge 2. Üung Logisher Entwur 4. Auge 3 ) Minterm-Normlorm Geen sei ie ooleshe Funktion + +
Grundlagen der Technischen Informatik. Bausteine der Digitaltechnik - Binäre Schalter und Gatter. Kapitel 7.1
 Busteine er Digitltehnik - Binäre Shlter un Gtter Kpitel 7. Dr.-Ing. Stefn Wilermnn ehrstuhl für rwre-softwre-co-design Entwurfsrum - Astrktionseenen SYSTEM-Eene + MODU-/RT-Eene (Register-Trnsfer) ogik-/gatter-eene
Busteine er Digitltehnik - Binäre Shlter un Gtter Kpitel 7. Dr.-Ing. Stefn Wilermnn ehrstuhl für rwre-softwre-co-design Entwurfsrum - Astrktionseenen SYSTEM-Eene + MODU-/RT-Eene (Register-Trnsfer) ogik-/gatter-eene
