Darstellende Geometrie (DG) Schule: HTBLuVA St. Pölten Abteilung: Elektronik Lehrperson: Dipl.-Ing. Wolfgang Lenz Jahrgang: 2002 / 03 Klasse: 1AT
|
|
|
- Guido Diefenbach
- vor 7 Jahren
- Abrufe
Transkript
1 Darstellende Geometrie (DG) Schule: HTBLuVA St. Pölten Abteilung: Elektronik Lehrperson: Dipl.-Ing. Wolfgang Lenz Jahrgang: 2002 / 03 Klasse: 1AT
2 1 Anmerkung Prof. Lenz ist bereits pensioniert. Im Unterricht wurde folgendes Lehrbuch verwendet: Frischherz, Piegler, Technisches Zeichnen Fachzeichnen 1. Teil, 2002, Verlag Jugend & Volk, Wien ISBN: Die Zeichnungen sind durch den Scanvorgang, das Einfügen in den Texteditor sowie Konvertierungsvorgänge nicht mehr in Originalgröße. 2 Inhaltsverzeichnis 1 Anmerkung Inhaltsverzeichnis Linienarten Die wichtigsten Bezeichnungen, gebräuchliche Symbole Einleitung Hauptrisse Maßstäbliche Risse Normalriss und Schrägriss Die Bildebene Der Normalriss Der Schrägriss Der Kavalierriss (auch Frontalriss genannt) Angabe eines Kavalierrisses (Frontalriss) Näherungsweise Kavalierrissdarstellung von Kreisen die nicht parallel zur Bildebene liegen Konstruktion und Anwendung des Verkürzungswinkels α (nur für Tiefenstrecken (x-richtung)) Grund- und Aufriss Abbildung eines Raumpunktes P Zweckmäßige Angabe eines Raumpunktes P Seitenrisse Der 13-Seitenriss Der 23-Seitenriss Punkt, Gerade Der Punkt Die Gerade Die projizierenden Geraden Die Profilgeraden Spezielle Lagen von Geraden Satz vom Winkel, Satz vom rechten Winkel Spurpunkte einer Geraden Neigungswinkel einer Geraden gegen eine Bildebene Die Ebene Angabestücke einer Ebene Hauptgeraden in einer Ebene Paralleldrehen einer Ebene Konstruktionsaufgaben Projizierendmachen einer Ebene HTL / DG 1AT Seite 2 / 53
3 14.6 Normalgerade zu einer Ebene Normalgerade γ zu einer Geraden g Die Ellipse Scheitelkrümmungskreise einer Ellipse Weitere Beispiele HTL / DG 1AT Seite 3 / 53
4 3 Linienarten Breite Volllinie 0,6mm weich (F, HB) Strichlierte Linie 0,3mm hart oder weich Schmale Linie 0,15mm hart (4H, 3H) Strich 4-6mm Abstand 1mm langer Strich 8-15mm kurzer Strich 1mm Abstand 1mm Alle Striche gleich lang! Nie mit einem Abstand beginnen! 4 Die wichtigsten Bezeichnungen, gebräuchliche Symbole Um rasch miteinander kommunizieren zu können, sind einige gebräuchliche Symbole sinnvoll. Punkte... (Großbuchstaben, röm. Ziffern, arab. Ziffern) Geraden, Strecken, Kurven...(Kleinbuchstaben) Ebenen und andere Flächen... (griech. Buchstaben (z.b.: π, ε, ν, )) Winkel...(griech. Kleinbuchstaben (z.b.: α, β, δ, φ, ψ, )) Länge der Strecke A B... AB Länge des Bogens A B... AB Parallelzeichen...// Normalzeichen.... Rechtwinkelzeichen... Winkelzeichen... Ist Element von... Ist nicht Element von... Durch... Nicht durch... Und... Oder... Durchschnitt, geschnitten mit... HTL / DG 1AT Seite 4 / 53
5 Beispiele: 1) Gerade g durch die Punkte A, B g A g B ( g A, B) 2) Gerade g parallel zu g und g durch P g // g g P 3) Gerade n normal auf g und n durch P n g n P 4) Ebene ε durch die Punkte A, B, C ε A ε B ε C ( ε A, B, C) 5 Einleitung Die DARSTELLENDE GEOMETRIE ist die Lehre von den gesetzmäßigen Abbildungen räumlicher Objekte auf eine Ebene (Zeichenebene). Betrachten wir irgendein Raumobjekt, so sehen wir sein Bild ähnlich einer Fotografie. Die Sehstrahlen sammeln sich im Auge und liefern das uns allen wohlbekannte Bild unserer dreidimensionalen Umwelt. Umgekehrt könnte man ein Raumobjekt aus einem Punkt (Projektionszentrum) projizieren und erhielte auf diese Art und Weise auf einer Leinwand (Zeichenebene) sein ebenes Bild. Dieses Bild bezeichnet man als RISS. Liegt das Projektionszentrum in messbarer Entfernung von dem abzubildenden Objekt, so spricht man von einem ZENTRALRISS (= ebenes Bild des Objektes bei Zentralprojektionen) HTL / DG 1AT Seite 5 / 53
6 Liegt das Projektionszentrum jedoch unendlich weit vom Objekt entfernt, so spricht man von einem PARALLELRISS. (=ebenes Bild des Objekts bei Parallelprojektion) Die Projektionsstrahlen sind parallel und kommen aus dem unendlich fernen Projektionszentrum. Da das (unendlich ferne) Projektionszentrum zeichnerisch nicht erfasst werden kann, ist es bei Parallelprojektionen üblich, die s.g. BLICKRICHTUNG (= Projektionsstrahlrichtung) anzugeben. (Blickrichtung = Richtung, in der das unendlich ferne Projektionszentrum zu suchen ist) 6 Hauptrisse Den meisten Objekten lassen sich in zwangloser Weise die Begriffe BREITE, TIEFE, HÖHE zuordnen, analog dazu kennen wir in der Darstellenden Geometrie drei Hauptblickrichtungen dazugehörend drei Hauptrisse. Grundriss... (Projektionszentrum unendlich weit oben) Aufriss... (Projektionszentrum unendlich weit vorne) Kreuzriss... (Projektionszentrum unendlich weit links) HTL / DG 1AT Seite 6 / 53
7 Oberhalb des Grundrisses wird der Aufriss angeordnet Grund- und Aufriss einer Ecke (eines Punktes) liegen auf einer senkrechten Hilfsgeraden einem 12-Ordner. Rechte neben dem Aufriss wird der Kreuzriss angeordnet Auf- und Kreuzriss einer Ecke (eines Punktes) liegen auf einer waagrechten Hilfsgeraden einem 23-Ordner. 7 Maßstäbliche Risse Die meisten Gegenstände können nicht in ihrer natürlichen Größe abgebildet werden, da ihre Bilder entweder zu groß (Haus) oder zu klein (Uhrteile) werden würden. Man zeichnet daher die meisten Gegenstände in einem bestimmten Maßstab. z.b.: M 1:10 bedeutet: ein Zentimeter in der Zeichnung entspricht 10 Zentimeter Wirklichkeit (Verkleinerung) oder M 2:1 bedeutet: zwei Zentimeter in der Zeichnung entsprechen 1 Zentimeter Wirklichkeit (Vergrößerung) HTL / DG 1AT Seite 7 / 53
8 8 Normalriss und Schrägriss 8.1 Die Bildebene Beim Parallelriss werden Punkte des Gegenstandes durch parallele Projektionsstrahlen auf die sog. Bildebene (= Ebene in der das ebene Bild des Körpers entsteht) projiziert. Beim Parallelriss sind alle Projektionsstrahlen parallel, also zur Bildebene gleich geneigt. 8.2 Der Normalriss Ein Parallelriss heißt Normalriss, wenn die Blickrichtung (Projektionsstahlrichtung) zur Bildebene normal steht. 8.3 Der Schrägriss Ein Parallelriss heißt Schrägriss, wenn die Blickrichtung (Projektionsstrahlrichtung) zur Bildebene nicht normal steht. 9 Der Kavalierriss (auch Frontalriss genannt) = spezifischer Schrägriss, bei dem senkrechte Körperseitenflächen parallel zu einer senkrechten (frontalen) Bildebene (sie liegt wie eine Aufrissebene) angenommen werden. 1, 2, 3, 4 Vorderseite 5, 6, 7, 8 Rückseite b n = x s HTL / DG 1AT Seite 8 / 53
9 Für beliebige Parallelrisse (Schräg- und Normalrisse) gilt der wichtige Satz: LIEGT EINE EBENE FIGUR PARALLEL ZU EINER BILDEBENE; SO BILDET SICH DIESE EBENE UNVERZERRT AB. Also: Alle Längen bzw. alle Winkel die parallel zu einer Bildebene liegen, erscheinen unverzerrt. Alle tiefen Strecken (z.b.: 5-1, 6-2, 7-3, 8-4) bilden sich in Richtung b n = x s ab. 9.1 Angabe eines Kavalierrisses (Frontalriss) 1) Körper durch Grund- und Aufriss oder Auf- und Kreuzriss oder Grund-, Auf- und Kreuzriss 2) Normalprojektion b n (b n = x s ) der Blickrichtung b auf die Bildebene π (b n = Aufriss von b) Möglichkeiten: 0 < φ < 90 Ansicht von links oben 90 < φ < 180 Ansicht von rechts oben 180 < φ < 270 Ansicht von rechts unten 270 < φ < 360 Ansicht von links unten 3) Verzerrung V x der Strecken in Tiefenrichtung (also in x-richtung) z.b.: Vx = 2 : 3 Bildstrecke Urstrecke speziell: Vx = 1:1 Keine Verzerrungen der Strecken in Tiefenrichtung: Isometrischer Kavalierriss Bemerkung: Aus rein optischen Gründen verzichtet man auf eine Verlängerung der Strecken in Tiefenrichtung. HTL / DG 1AT Seite 9 / 53
10 9.2 Näherungsweise Kavalierrissdarstellung von Kreisen die nicht parallel zur Bildebene liegen Die Parallelprojektion eines Kreises ist im Allgemeinen eine Elypse. Prinzip: Man umschreibt dem Kreis ein Hauptrichtungsquadrat. Dieses geht vermöge einer Kavalierrissprojektion über in ein Hauptrichtungsparallelogramm, in das die Bildebene passen muss. Bemerkung: Hauptrichtungen sind die x-, y- und z-richtungen. Geg.: Körper durch Auf und Kreuzriss, b n = 30 Ges.: Isometrischer Kavalierriss (V x = 1:1) HTL / DG 1AT Seite 10 / 53
11 Zur Verkürzung von Strecken in Tiefenrichtung (x-richtung): Verkürzungswinkel α. Bemerkung: Strecken in y- und z-richtung sind bei jedem Kavalierriss unversehrt. 9.3 Konstruktion und Anwendung des Verkürzungswinkels α (nur für Tiefenstrecken (x-richtung)) z.b.: V x = 2:3 (Bildstrecke : Urstrecke) e beliebige Einheit Die verkürzte Bildstrecke wird mit dem Zirkel berührend an den zweiten Winkelschenkel abgegriffen (und sofort in den Kavalierriss übertragen). HTL / DG 1AT Seite 11 / 53
12 10 Grund- und Aufriss Definiton: Zwei Normalrisse, deren Blickrichtungen zueinander normal sind, heißen zugeordnete Normalrisse. Grund- und Aufriss sind zugeordnete Normalrisse mit den Blickrichtungen: 1) Blickrichtung von oben 1. Rissebene π 1 (Grundrissebene) waagrecht 2) Blickrichtung von vorne 2. Rissebene π 2 (Aufrissebene) senkrecht (frontal) Grund- und Aufrissebene schneiden sich längs einer Geraden 12 (12 Rissachse ) Abbildung eines Raumpunktes P Sehstrahl 1 von oben durch P P in π 1 ( P = 1 π1) Sehstrahl 2 von vorne durch P P in π 2 ( P = 2 π 2 ) Die Sehstrahlen 1 und 2 bilden eine Ebene σ, die zu π 1 und π 2 normal steht. HTL / DG 1AT Seite 12 / 53
13 Die Darstellende Geometrie hat die Aufgabe, Gegenstände des Raumes in einer Zeichenebene darzustellen und konstruktiv zu beherrschen. Man vereinigt daher Grund- und Aufriss in einer Zeichenebene und zwar so: Wir denken uns π 2 in unsere Zeichenebene gelegt und die Grundrissebene π 1 um die Rissachse 12 um 90 in die Zeichenebene geklappt. Zeichenebene geklappt: π 1 (π 1 ) Der Punkt P beschreibt beim Drehen um 12 einen Viertelkreisbogen p P ( P ) s ( s ) Wir erkennen weiters: (s ) und s s fallen nach der Drehung in die Verbindungsgerade [( P ), P ] 12 zusammen. Eine solche Gerade [( P ), P ] 12 nennt man 12-Ordner. Von nun an wollen wir uns die Drehung π1 in die Zeichenebene bereits ausgeführt denken und schreiben daher statt (P ) nur noch P. Entsprechende Punkte ( P, P ) liegen stets auf einem 12- Ordner senkrecht zur Rissachse 12. Von dieser Ordnerbedingung gibt es keine Ausnahmen! HTL / DG 1AT Seite 13 / 53
14 11 Zweckmäßige Angabe eines Raumpunktes P Durch 3 Zahlen (Koordinaten): z.b.: P(3 / 2 / 4) P(xp / yp / zp) Der Punkt P liegt 2e rechts von 0, 3e vor π2, 4e über π1 y-koordinate x-koordinate z-koordinate HTL / DG 1AT Seite 14 / 53
15 Beispiele: P(3/-7/2), Q(4/-5/0), R(0/-3/5), S(0/-1/0), T(-2/2/4), U(3/5/-5), V(-2/7/-3) Der Punkt P liegt 7e links von 0, 3e vor π 2, 2e über π 1. Der Punkt Q liegt 5e links von 0, 4e vor π 2, 0e über π 1. Der Punkt R liegt 3e links von 0, 0e vor π 2, 5e über π 1. Der Punkt S liegt 1e links von 0, 0e vor π 2, 0e über π 1 also auf 12. Der Punkt T liegt 2e rechts von 0, 2e hinter π 2, 4e über π 1. Der Punkt U liegt 5e rechts von 0, 3e vor π 2, 5e unter π 1. Der Punkt V liegt 7e rechts von 0, 2e hinter π 2, 3e unter π Seitenrisse 12.1 Der 13-Seitenriss Einführung einer neuen Bildebene π 3 normal auf π 1 Sehstrahlrichtung 3 normal zur Bildebene. (Der 13-Seitenriss ist also auch ein Normalriss.) Wozu: 1) Das 3. Bild eines Körpers wird anschaulicher. 2) Das 3. Bild eines Körpers wird einfacher Konstruktionen sich einfach durchführbar. HTL / DG 1AT Seite 15 / 53
16 Wie beim Grund- und Aufrissverfahren wird nun π3 um die Rissachse 13 um 90 in die Zeichenebene geklappt. P beschreibt dabei einen Viertelkreisbogen um die neue Rissachse 13 und gelangt nach (P ). P und (P ) liegen auf einem 13-Ordner senkrecht zur Rissachse 13. Statt (P ) schreiben wir wiederum nur P. Wichtige Erkenntnis: P hat von 13 den gleichen Abstand wie P von 12! Geg.: P, P,12, 13 Geg.: A, A, B, B,12, 13 Ges.: P Ges.: A, B Achtung: Die Abstände müssen dabei orientiert abgetragen werden! HTL / DG 1AT Seite 16 / 53
17 Geg.: Recheckiges Prisma mit schrägem Schnitt Ges.: 13-Seitenriss bei geg. Rissachse 13 HTL / DG 1AT Seite 17 / 53
18 Geg.: Regelmäßige fünfseitige Pyramide mit schrägem Schnitt Ges.: 13-Seitenriss bei geg. Rissachse 13 HTL / DG 1AT Seite 18 / 53
19 A(0/6/3), B(-2/4/2), C(-3/2/-4), D(3/0/-3), E(2/-2/0), F(2/-4/3), G(4/-6/3), H(0/-8/6) Der Punkt A liegt 6e rechts von 0, in π 2, 3e über π 1 B liegt 4e rechts von 0, 2e hinter π 2, 2e über π 1 C liegt 2e rechts von 0, 3e hinter π 2, 4e unter π 1 D liegt auf 0, 3e vor π 2, auf 12 E liegt 2e links von 0, 2e vor π 2, auf 12 F liegt 4e links von 0, 2e vor π 2, 3e über π 1 G liegt 6e links von 0, 4e vor π 2, 3e über π 1 H liegt 8e links von 0, in π 2, auf 12 HTL / DG 1AT Seite 19 / 53
20 Geg.: Körperkombination Ges.: 13-Seitenriss HTL / DG 1AT Seite 20 / 53
21 12.2 Der 23-Seitenriss Einführung einer neuen Bildebene π 3, normal auf π 2. Sehstrahlrichtung 3 normal zu π 3. (Der 23-Seitenriss ist also auch ein Normalriss!) π3 wird um die Rissachse 23 um 90 in die Zeichenebene geklappt. P beschreibt dabei einen Viertelkreisbogen um die neue Rissachse 23 und gelangt nach (P ). P und P liegen auf einem 23-Ordner, senkrecht zur Rissachse 23. Wichtige Erkenntnis: P hat von 23 den gleichen Abstand wir P von 12. Geg.: P, P,12, 23 Ges.: P HTL / DG 1AT Seite 21 / 53
22 Geg.: A, A, B, B,12, 23 Ges.: A, B Achtung: Die Abstände müssen dabei wiederum abgetragen werden! Geg.: Körperkombination, 12, 13 Ges.: 23-Seitenriss HTL / DG 1AT Seite 22 / 53
23 13 Punkt, Gerade 13.1 Der Punkt Wir alle wissen, was man unter einem Punkt versteht, aber trotzdem lässt er sich nicht sinnvoll definieren. Ein Punkt ist dimensionslos. Hilfsvorstellung: Körperecke, Kreismittelpunkt, Schnittpunkt zweier Geraden, usw Die Gerade Eindimensional, vorstellbar als kürzeste Verbindung zweier Punkte jedoch unendlich lang. Angabe einer Geraden: Durch zwei Punkte: g[a,b] Grund und Aufriss einer Geraden, allgemeine Lage Die projizierenden Geraden Definition: Unter einer projizierenden Geraden versteht man eine Gerade, die normal auf eine Bildebene steht. Eine erstprojizierende Gerade steht normal auf π1, ihr Grundriss ist ein Punkt, ihr Aufriss steht senkrecht auf die Rissachse 12. Aus g π1 folgt: g //π 2 g ist also automatisch eine 2. Hauptgerade (g = h 2 ) z.b.: AB = A B HTL / DG 1AT Seite 23 / 53
24 Eine zweitprojizierende Gerade steht normal auf π2, ihr Aufriss ist ein Punkt, ihr Grundriss steht senkrecht auf die Rissachse 12. Aus g π 2 folgt: g //π 1 g ist also automatisch eine 1. Hauptgerade (g = h 1 ) z.b.: AB = A B Die Profilgeraden Definition: Geraden für die Grund- und Aufriss in Ordnerrichtung fallen, heißen Profilgeraden. Achtung: Eine Profilgerade muss stets durch 2 Punkte gegeben sein! Bemerkung: Wahre Längen von Strecken sind jetzt nicht direkt ersichtlich Spezielle Lagen von Geraden Die Hauptgeraden Definition: Unter einer Hauptgeraden versteht man eine Gerade, die parallel zu einer Bildebene liegt. Eine 1. Hauptgerade (h 1 ) liegt parallel zu π 1, ihr Aufriss ( h 1 ) ist parallel zur Rissachse 12. (Der Grundriss hat beliebige Lage.) Wir wissen bereits: Aus h 1 // π 1 folgt: Strecken auf h 1 können im Grundriss unverzerrt gemessen werden. z.b.: AB = A B Umkehrung: Liegt der Aufriss einer Geraden parallel zur Rissachse 12, so handelt es sich automatisch um eine 1. Hauptgerade (g = h 1 ) HTL / DG 1AT Seite 24 / 53
25 Eine 2. Hauptgerade (h 2 ) liegt parallel zu π2, ihr Grundriss ( h 2 ) ist parallel zur Rissachse 12 (Der Aufriss hat beliebige Lage.) Wir wissen bereits: Aus h 2 // π 2 folgt: Strecken auf h 2 können im Aufriss unverzerrt gemessen werden. z.b.: AB = A B Umkehrung: Liegt der Grundriss einer Geraden parallel zur Rissachse, so handelt es sich automatisch um eine 2. Hauptgerade. (g = h 2 ) Vervollständigungsaufgabe für Profilgerade Geg.: Profilgerade g[a,b], C mit C eg Ges.: C Zur 1. Methode: Direkte Teilverhältnisübertragung mit dem Strahlensatz. Zur 2. Methode: 2-fache Parallelprojektion zur Teilverhältnisübertragung Die Hilfsstrahlen sind beliebig, die Entsprechenden jedoch zueinander parallel. Achtung: g ~ muss konstruiert werden! HÜ: Geg.: Profilgerade g[a,b], C mit C eg Ges.: C HTL / DG 1AT Seite 25 / 53
26 Länge einer Strecke ( Wahre Länge einer Strecke )(w.l.) Wir wissen bereits: Für alle Parallelprojektionen (Schräg- und Normalrisse) gilt: Liegt eine ebene Figur parallel zu einer Bildebene (oder in einer Bildebene), so erscheint sie in der jeweiligen Projektion unverzerrt. (Eine Strecke ist sicher die einfachste ebene Figur.) Bestimmung der wahren Länge einer Strecke (w.l.): 1. Methode: Seitenriss Man legt durch die Strecke s eine 13- oder 23- Seitenrissebene ( s = 13 oder s = 23). Die Strecke s liegt dann in der jeweiligen Seitenrissebene und erscheint im entsprechenden 3. Riss unverzerrt (also in wahrer Länge) Bemerkung: Die Seitenrissmethode erfordert viel Platz. 2. Methode: Differenzendreieck Aus der ersten Methode entwickelt sich die 2. Methode, indem hier bloß die Differenz der Abstände abgetragen wird. (selbes Ergebnis, jedoch weniger Platzbedarf) Bemerkung: Die Methode des Differenzendreiecks wird in der DG gerne angewandt. HTL / DG 1AT Seite 26 / 53
27 Abtragen einer Strecke auf einer Geraden Diese Methode ist die Umkehrung der Ermittlung der wahren Länge. Problem: Von A g sollen nach rechts 7cm abgetragen werden. Prinzip: Sieht man auf einer Geraden irgendeine Strecke in wahrer Länge (auf g 0 ), so sind dort alle Strecken in wahrer Länge ersichtlich (also auch unserer 7cm). Praxis: 1. Wahl eines beliebigen Hilfspunktes auf g um irgendeine Strecke zu erhalten. 2. Wahre Länge von A 1 (auf g 0 ) 3. Dort 7cm abtragen und Ergebnis zurückbringen. Bemerkung: Hilfspunkte (zum Beispiel 1) können auf einer Geraden außer auf Profilgeraden stets problemlos gewählt werden. Sonderfall: Das Abtragen einer Strecke auf einer Profilgeraden Problem: Auf der Profilgeraden g[a,b] sollen von A in Richtung B 5cm abgetragen werden. Anleitung: Hier bietet die 1. Methode (Seitenrissmethode) zur Bestimmung der wahren Länge gewisse Vorteile (keine Vervollständigungsaufgabe für Profilgerade notwendig). HÜ: Schmierpapier! Wahre Größe des Dreiecks [A,B,C] HTL / DG 1AT Seite 27 / 53
28 Lage von Geraden zueinander Zwei Gerade können: 1. zueinander parallel sein (Fig. 1) 2. sich schneiden (Fig. 2) 3. sich kreuzen ( Windschief liegen ) (Fig. 3) Die Bilder paralleler Geraden sind zueinander wiederum parallel ( parallelentreu der Parallelprojektion ). zu 1) d.h. a // b a // b und a // b + zu 2) Schneidende Geraden haben einen Schnittpunkt. Dieser genügt der Ordnerbedingung. zu 3) Kreuzende Geraden haben keinen Schnittpunkt. Sichtbarkeitsbestimmung mittels Deckpunkten (scheinbare Schnittpunkte) ( 1 = 2 bzw. 3 = 4 ) HTL / DG 1AT Seite 28 / 53
29 Geg.: Halbstrahlen a, b, c durch s Ges.: Dreiseitige Pyramide (s. Skizze) mit SA = 8 cm, SB = 10cm, SC = 9cm 12 HTL / DG 1AT Seite 29 / 53
30 13.3 Satz vom Winkel, Satz vom rechten Winkel Ein Winkel erscheint genau dann in wahrer Größe, wenn beide Schenkel zu ein und derselben Bildebene parallel liegen. (Nach dem Satz: Liegt eine Ebene Figur parallel zu einer Bildebene, so erscheint sie in der Parallelprojektion auf diese Bildebene unverzerrt.) Ein rechter Winkel erscheint genau dann in wahrer Größe, wenn mindestens ein Schenkel parallel zu einer Bildebene liegt. (Also auf einer Hauptgeraden) 13.4 Spurpunkte einer Geraden Unter einem Spurpunkt einer Geraden versteht man den Durchstoßpunkt einer Geraden durch eine Bildebene. (durch π 1, π 2, ) Man bezeichnet: G 1 1. Spurpunkt von g ( G1 = g π1) G 2 2. Spurpunkt von g G = g ) ( 2 π 2 Geg.: Gerade G Ges.: 1. und 2. Spurpunkt (G 1 und G 2 ) HTL / DG 1AT Seite 30 / 53
31 Geg.: g Ges.: G 1, G 2 Man beachte: G 1 hat keinen z-abstand (z = 0) G 2 hat keinen x-abstand (x = 0) 13.5 Neigungswinkel einer Geraden gegen eine Bildebene Der 1. Neigungswinkel α 1 einer Geraden g gegen π 1 ist definitionsgemäß gleich dem Winkel zwischen den Geraden g und ihrem Grundriss g, wobei der Scheitel der 1. Spurpunkt G 1 von g ist. Analog: 2. Neigungswinkel α 2 Also: α1 = gπ1 def. g g = g g Scheitel G 1 α = g def. g g = g g Scheitel G 2 2 π 2 Geg.: Gerade g Ges.: 1. und 2. Neigungswinkel (α 1 und α 2 ) 1 bel. Hilfspunkt auf g HTL / DG 1AT Seite 31 / 53
32 Geg.: g Ges.: α 1, α 2 14 Die Ebene 14.1 Angabestücke einer Ebene 1) Durch drei Punkte, die nicht auf einer Geraden liegen: ε[a,b,c] Geg.: X mit Ges.: X X ε Lösung: Beliebige Hilfsgerade p durch X, die ganz in der Ebene liegt Bemerkung: Dieses Verfahren wird angittern eines Punktes in einer Ebene genannt HTL / DG 1AT Seite 32 / 53
33 2) Durch eine Gerade und einen Punkt, der nicht auf der Geraden liegt: ε[g,p] Geg.: X mit X ε Ges.: X Lösung: Hilfsgerade p durch X und P 2a) Bei ungünstiger Lage des Punktes X: Ebenenangabe ε[g,p] in eine Dreiecksangabe ε[1, 2 beliebig auf g, P] verwandeln. HTL / DG 1AT Seite 33 / 53
34 3) Durch zwei parallele Geraden: ε[a//b] Geg.: X mit Ges.: X X ε Lösung: Beliebige Hilfsgerade p durch X jedoch p nicht parallel a,b 4) Durch zwei sich schneidende Geraden: ε[ a b = s ] Geg.: X mit X ε Ges.: X Lösung: Beliebige Hilfsgerade p durch X, jedoch p nicht durch s HTL / DG 1AT Seite 34 / 53
35 14.2 Hauptgeraden in einer Ebene Wir erkennen: Die Hauptgeraden in einer Ebene der gleichen Art sind zueinander parallel d.h.: Alle h 1 sind zueinander parallel Alle h 2 sind zueinander parallel für {h 1 },{h 2 } in ε Geg.: ε[a,b,c] Ges.: h 1 durch C, h 2 durch A Lässt sich das Problem nicht direkt lösen, so sind Hilfshauptgerade zu verwenden h 1 h1 h 1 h 1 // h Paralleldrehen einer Ebene Die Ebene wird auf eine 1. Hauptgerade (h 1 ) parallel zu π 1 oder eine 2. Hauptgerade (h 2 ) parallel zu π 2 gedreht. Dabei beschreiben alle Punkte, die nicht auf der Hauptgerade liegen, Kreisbögen, deren Trägerebenen normal auf die jeweilige Hauptgerade liegen. Alle Punkte auf der Hauptgeraden bleiben fest, sie heißen Fixpunkte. Beachte: Als Drehachse eignet sich ausschließlich eine Hauptgerade!!! wozu: 1) Alle Figuren dieser Ebene erscheinen in der parallel gedrehten Lage unverzerrt. 2) Konstruktionen können in der parallel gedrehten Lagen unverzerrt durchgeführt werden. HTL / DG 1AT Seite 35 / 53
36 Bsp.: Wahre Größe des Winkels α Bsp.: Wahre Größe des Winkels α HTL / DG 1AT Seite 36 / 53
37 14.4 Konstruktionsaufgaben Vorgang: 1) Skizze des gelösten Problems, Angabestücke eintragen und unterstreichen 2) Konstruktion anhand der Skizze überlegen 3) Ebene paralleldrehen und Konstruktion dort unverzerrt ausführen 4) Ergebnis zurückdrehen Bsp.: Von einem gleichseitigen Dreieck kennt man die Trägergerade g einer Seite, sowie die gegenüber liegende Ecke A. HTL / DG 1AT Seite 37 / 53
38 Bsp.: Wahre Größe des Dreiecks [A(6/16/4), B(8/10/8), C(2/3/2] Das Zurückdrehen von Punkten die nicht direkt auf einer Geraden liegen Voraussetzungen: 1) Hauptgerade h 2) Mindestens ein bereit bekanntes Punktepaar (z.b.: A+A 0 ) Geg.: Hauptgerade h, A+A 0, X 0, Y 0 Ges.: X, Y HTL / DG 1AT Seite 38 / 53
39 Bsp.: Geg.: M(5/8/5), p[i(4/2/0), II(0/15/6)] Ges.: Regelm. Fünfeck (siehe Skizze) HÜ: regelm. Sechseck HTL / DG 1AT Seite 39 / 53
40 14.5 Projizierendmachen einer Ebene Um eine Ebene projizierend zu machen, benötigt man einen Seitenriss. 13 h 1 oder 23 h 2 Geg.: ε[a,b,c] Ges.: ε projizierend Geg.: ε[g,p] Ges.: ε projizierend HTL / DG 1AT Seite 40 / 53
41 14.6 Normalgerade zu einer Ebene Eine Gerade, welche normal auf eine Ebene steht, heißt Normalgerade zur Ebene. Durch jeden Punkt des Raumes gibt es genau eine Gerade, welche auf eine gewisse Ebene normal steht. Achtung: Die Normalgerade n z einer Ebene liegt nicht in der Ebene und kann daher dort nicht angegittert werden! Zeichnen der Normalgeraden n Nach dem Satz vom rechten Winkel gilt: n h 1 und n h 2. Geg.: ε[g,p] Ges.: n ε n P HTL / DG 1AT Seite 41 / 53
42 Man richte über dem Dreieck [A(2/6/1), B(4/4/3), C(1/11/5)] ein gerades dreiseitiges Prisma mit der Höhe h = 7cm. HTL / DG 1AT Seite 42 / 53
43 Man errichte über dem Dreieck [A(5/3/3), B(4/13/0), C(1/8/6)] eine dreiseitige Pyramide so, dass die Spitze S 9cm über dem Höhenschnittpunkt H des Dreiecks liegt. HTL / DG 1AT Seite 43 / 53
44 1. Fall: kein Winkel größer als Fall: ein Winkel größer als 90 S Schwerpunkt I Inkreismittelpunkt H Höhenschnittpunkt U Umkreismittelpunkt sc Schwerlinie Schwerpunkt nicht parallel drehen immer im Dreieck Seite halbieren mit Ecke verbinden Schnittpunkt = S Inkreismittelpunkt auch im Dreieck parallel drehen! Winkelsymetralen zeichnen Schnittpunkt I Höhenschnittpunkt Beim 2. Fall außerhalb HTL / DG 1AT Seite 44 / 53
45 Man errichte über dem Dreieck [A(4/6/2), B(6/15/4), C(2/11/7)] eine dreiseitige Pyramide so, dass die Spitze S 10cm über den Inkreismittelpunkt des Dreiecks liege. HTL / DG 1AT Seite 45 / 53
46 HTL / DG 1AT Seite 46 / 53
47 14.7 Normalgerade γ zu einer Geraden g Eine Ebene, welche normal zu einer Geraden steht, heißt Normalebene zu der Geraden. Durch jeden Punkt des Raumes gibt es genau eine Ebene, die auf eine gewisse Gerade normal steht. Aufspannen der Ebene γ: Die Normalebene γ wird aufgespannt durch 2 Hauptgeraden, wobei: γ[h 1,h 2 ] h g 1 h g 2 Geg.: g, P g Geg.: g, P g Ges.: γ g γ P Ges.: γ g γ P Anwendung: Symmetrieebene σ (= γ im Streckenmittelpunkt) der Strecke AB Beachte: Die Symmetrieebene σ ist die Menge aller Punkte, die von den Punkten A,B den gleichen Abstand haben. Geg.: Strecke AB Ges.: Symmetrieebene HTL / DG 1AT Seite 47 / 53
48 15 Die Ellipse Definition: Die Ellipse ist definiert als Menge aller Punkte in einer Ebene, die von 2 festen Punkte F1, F2 (Brennpunkte) konstante Abstandssumme 2a haben. Konstruktion nach Definition: Man bezeichnet: A,B Hauptscheitel der Ellipse C,D Nebenscheitel der Ellipse M Mittelpunkt der Ellipse F1,F2 Brennpunkt der Ellipse P allg. Ellipsenpunkt a...halbe Hauptachse der Ellipse b...halbe Nebenachse der Ellipse e lineare Exzentrität der Ellipse x,y Brennstrahlen x + y = 2a = konstant 2 e = a + b 2 Variation von x liefert weitere Ellipsenpunkte HTL / DG 1AT Seite 48 / 53
49 15.1 Scheitelkrümmungskreise einer Ellipse Mit Hilfe der Scheitelkrümmungskreise ist das Zeichnen einer Ellipse besonders bequem. Gärtnerkonstruktion einer Ellipse: 16 Weitere Beispiele Geg.: Profilgerade g[a,b], C mit Ges.: C C g HTL / DG 1AT Seite 49 / 53
50 HTL / DG 1AT Seite 50 / 53
51 DG-Hausübung Geg.: Isometrischer Kavalierriss eines Körpers Ges.: Grund- Auf- und Kreuzriss in der genormten Anordnung mit unsichtbaren Kanten, jedoch ohne Abmessungen einzutragen HTL / DG 1AT Seite 51 / 53
52 Geg.: Isometrischer Kavalierriss eines Körpers Ges.: Grund- Auf- und Kreuzriss in der genormten Anordnung mit unsichtbaren Kanten, jedoch ohne Abmessungen einzutragen HTL / DG 1AT Seite 52 / 53
53 Geg.: Körper durch Auf- und Kreuzriss Ges.: Kavalierriss Gr. A b n (= x s ) = 150, V x = 2:3 Gr. B b n (= x s ) = 30, V x = 3:4 HTL / DG 1AT Seite 53 / 53
Elemente der Zweitafelprojektion
 Teil I Elemente der Zweitafelprojektion 1 Einleitung Darstellende Geometrie: Eindeutige Darstellung der Geometrie des Raumes auf einer Zeichenebene ohne primäre Anschaulichkeit. Eine DG-Zeichnung muss
Teil I Elemente der Zweitafelprojektion 1 Einleitung Darstellende Geometrie: Eindeutige Darstellung der Geometrie des Raumes auf einer Zeichenebene ohne primäre Anschaulichkeit. Eine DG-Zeichnung muss
Normalprojektion. Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion.
 4. Der dreidimensionale Raum 4.5 Hauptrisse Normalprojektion Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion. Zum Beispiel:
4. Der dreidimensionale Raum 4.5 Hauptrisse Normalprojektion Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion. Zum Beispiel:
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 29. Februar 2016 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Prüfungsfach: Darstellende Geometrie Termin: 29. Februar 2016 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
9"+#5(00(),(& 7(8.(5+%(
 !"#$%"&'%()*"+, 9"+#5(00(),(& 7(8.(5+%( -%)&'(*+.%/(0&12+&,"#&34(%5"1(06(+1"*+() Inhaltsverzeichnis Vorwort...5 1. Darstellung im Zweitafelverfahren...7 2. Darstellung des Punktes...9 3. Darstellung der
!"#$%"&'%()*"+, 9"+#5(00(),(& 7(8.(5+%( -%)&'(*+.%/(0&12+&,"#&34(%5"1(06(+1"*+() Inhaltsverzeichnis Vorwort...5 1. Darstellung im Zweitafelverfahren...7 2. Darstellung des Punktes...9 3. Darstellung der
Grundrissebene und Aufrissebene
 Grundrissebene und Aufrissebene x 3 (bzw. z) - Höhe Aufrissebene 2 (bzw. yz-ebene) Rissachse x 12 O x 2 (bzw. y) - Breite Grundrissebene 1 (bzw. xy-ebene) x 1 (bzw. x) - Tiefe Grund- / Aufrissverfahren
Grundrissebene und Aufrissebene x 3 (bzw. z) - Höhe Aufrissebene 2 (bzw. yz-ebene) Rissachse x 12 O x 2 (bzw. y) - Breite Grundrissebene 1 (bzw. xy-ebene) x 1 (bzw. x) - Tiefe Grund- / Aufrissverfahren
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 5. März 2018 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 5. März 2018 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Grundsätzliche Konstruktionshilfen:
 Grundsätzliche Konstruktionshilfen: Konstruktion des Netzes Seite 1 Wahre Größe von Flächen und Geraden Seite 1 Drehen in Hauptlage Seite 2 Wahre Größe durch weiteren Riss Seite 4 Sichtbarkeit Seite 5
Grundsätzliche Konstruktionshilfen: Konstruktion des Netzes Seite 1 Wahre Größe von Flächen und Geraden Seite 1 Drehen in Hauptlage Seite 2 Wahre Größe durch weiteren Riss Seite 4 Sichtbarkeit Seite 5
Darstellende Geometrie
 Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
Kapitel 4: Zeichnerische Darstellung von Körpern. Darstellung von Körpern in der Ebene. Ziel bei der Darstellung von räumlichen Figuren (Körpern):
 Kapitel 4: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung von räumlichen Figuren (Körpern):
Kapitel 4: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung von räumlichen Figuren (Körpern):
Darstellende Geometrie
 Darstellende Geometrie für Architekten und Bauingenieure Skript und Präsenzübungen WS 2010/11 Institut Computational Mathematics Technische Universität Braunschweig Inhaltsverzeichnis 1 Projektionsarten
Darstellende Geometrie für Architekten und Bauingenieure Skript und Präsenzübungen WS 2010/11 Institut Computational Mathematics Technische Universität Braunschweig Inhaltsverzeichnis 1 Projektionsarten
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Termin: 14. September 2012 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten vor Beginn der
Prüfungsfach: Termin: 14. September 2012 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten vor Beginn der
Projektionen:
 Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 25. Februar 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.00 Uhr 11.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Prüfungsfach: Darstellende Geometrie Termin: 25. Februar 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.00 Uhr 11.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
KOP1_1_28. Lüftungsschacht
 Titel Relevante(r) Deskriptor(en) Lehrstoff Ausbildungsinhalte Methodisch/Didaktische Hinweise Hilfsmittel Quelle weitere Beispiele Lüftungsschacht Die Schülerinnen und Schüler können normgerechte Zeichnungen
Titel Relevante(r) Deskriptor(en) Lehrstoff Ausbildungsinhalte Methodisch/Didaktische Hinweise Hilfsmittel Quelle weitere Beispiele Lüftungsschacht Die Schülerinnen und Schüler können normgerechte Zeichnungen
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Methoden der Darstellung Termin: 13. September 2013 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.30 Uhr 11.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
Prüfungsfach: Methoden der Darstellung Termin: 13. September 2013 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.30 Uhr 11.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
Technische Darstellung
 Fakultät Maschinenwesen Institut für Festkörpermechanik Professur für Getriebelehre Prof. Dr. rer. nat. habil. Dr. h. c. Karl-Heinz Modler Bearbeiter: Dr.-Ing. Kerstin Becker Telefon: +49 351 463-32732
Fakultät Maschinenwesen Institut für Festkörpermechanik Professur für Getriebelehre Prof. Dr. rer. nat. habil. Dr. h. c. Karl-Heinz Modler Bearbeiter: Dr.-Ing. Kerstin Becker Telefon: +49 351 463-32732
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 31. August 2016 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 31. August 2016 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
7) Normale Axonometrie
 7) In der 7.Klasse haben wir (allgemeine) axonometrische Risse technischer Objekte hergestellt; dabei haben wir die Eigenschaften von Parallelrissen ausgenützt. Nun wollen wir axonometrische Angaben so
7) In der 7.Klasse haben wir (allgemeine) axonometrische Risse technischer Objekte hergestellt; dabei haben wir die Eigenschaften von Parallelrissen ausgenützt. Nun wollen wir axonometrische Angaben so
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 25. August 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 16.00 Uhr 17.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 25. August 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 16.00 Uhr 17.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 30. August 2017 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 30. August 2017 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Projektionen:
 Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Durchstoßpunkt Gerade Ebene. Vorkurs Darstellende Geometrie. Erstprojizierende Hilfsebene ν durch g. Teil I. Lösung mit erstprojizierender Hilfsebene
 Durchstoßpunkt Gerade Ebene Vorkurs Darstellende Geometrie Durchstoßpunkt Gerade Ebene Bestimmen Sie den Durchstoßpunkt D der Geraden g mit der Ebene ε. Hans-Peter Schröcker Arbeitsbereich Geometrie und
Durchstoßpunkt Gerade Ebene Vorkurs Darstellende Geometrie Durchstoßpunkt Gerade Ebene Bestimmen Sie den Durchstoßpunkt D der Geraden g mit der Ebene ε. Hans-Peter Schröcker Arbeitsbereich Geometrie und
G1.02 In jedes der drei Muster hat sich ein Fehler eingeschlichen. Kennzeichne diesen, indem du den Bereich mit roter Farbe einringelst!
 1 Muster (Teil 1) G1.01 Vervollständige das Muster, sodass der gesamte Raster ausgefüllt ist! Verwende dazu ein Geodreieck und einen gespitzten Bleistift oder einen Druckbleistift mit einer 0,5 mm HB-Mine
1 Muster (Teil 1) G1.01 Vervollständige das Muster, sodass der gesamte Raster ausgefüllt ist! Verwende dazu ein Geodreieck und einen gespitzten Bleistift oder einen Druckbleistift mit einer 0,5 mm HB-Mine
Termin: 8. September zugel. Hilfsmittel:
 Technische Universität München Lehrstuhl für Holzbau und Baukonstruktion Prof. Dr.-Ing. Stefan Winter Methoden der Darstellung Prüfung Herbst 2010 Name: Matrikelnummer: Prüfungsfach: Methoden der Darstellung
Technische Universität München Lehrstuhl für Holzbau und Baukonstruktion Prof. Dr.-Ing. Stefan Winter Methoden der Darstellung Prüfung Herbst 2010 Name: Matrikelnummer: Prüfungsfach: Methoden der Darstellung
Termin: 9. September zugel. Hilfsmittel:
 Technische Universität München Lehrstuhl für Holzbau und Baukonstruktion Univ.-Prof. Dr.-Ing. Mike Sieder Univ.-Prof. Dr.-Ing. Stefan Winter Methoden der Darstellung Prüfung Herbst 2011 Name: Matrikelnummer:
Technische Universität München Lehrstuhl für Holzbau und Baukonstruktion Univ.-Prof. Dr.-Ing. Mike Sieder Univ.-Prof. Dr.-Ing. Stefan Winter Methoden der Darstellung Prüfung Herbst 2011 Name: Matrikelnummer:
D C. Man unterscheidet in der Geometrie zwischen Körpern, Flächen, Linien und Punkten.
 V. Körper, Flächen und Punkte ================================================================= 5.1 Körper H G E F D C A B Man unterscheidet in der Geometrie zwischen Körpern, Flächen, Linien und Punkten.
V. Körper, Flächen und Punkte ================================================================= 5.1 Körper H G E F D C A B Man unterscheidet in der Geometrie zwischen Körpern, Flächen, Linien und Punkten.
4.22 Buch XI der Elemente
 4.22 Buch XI der Elemente In Buch XI werden die Grundbegriffe der räumlichen Geometrie eingeführt und für viele Propositionen aus den Büchern I und VI die entsprechende dreidimensionale Aussagen bewiesen.
4.22 Buch XI der Elemente In Buch XI werden die Grundbegriffe der räumlichen Geometrie eingeführt und für viele Propositionen aus den Büchern I und VI die entsprechende dreidimensionale Aussagen bewiesen.
Geometrie 1. 1.)Geometrische Grundkonstruktionen. Halbierung einer Strecke, Mittelsenkrechte. Teilung einer Strecke. Winkelhalbierung.
 Geometrie 1 1.)Geometrische Grundkonstruktionen Halbierung einer Strecke, Mittelsenkrechte Teilung einer Strecke Winkelhalbierung Thaleskreis Konstruktion von Dreiecken Kongruenzsätze: SSS-Satz, SWS-Satz,
Geometrie 1 1.)Geometrische Grundkonstruktionen Halbierung einer Strecke, Mittelsenkrechte Teilung einer Strecke Winkelhalbierung Thaleskreis Konstruktion von Dreiecken Kongruenzsätze: SSS-Satz, SWS-Satz,
Parallelprojektion. Das Projektionszentrum liegt im Unendlichen. Projektionsebene. Projektionsrichtung. Quader. Bild des Quaders
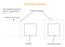 Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Ziel bei der Darstellung von räumlichen Figuren (Körpern): Startseite
 Startseite Zentralprojektion 1 Kapitel 3: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung
Startseite Zentralprojektion 1 Kapitel 3: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung
Darstellende Geometrie Übungen. Tutorial. Übungsblatt: Perspektive Rekonstruktion - FSI
 Darstellende Geometrie Übungen Institut für 0Irchitektur und IIIedien Tutorial Übungsblatt: Perspektive Rekonstruktion - FSI Gegeben sind ein Foto ( mit lotrechter Bildebene ) von einem quaderförmigen
Darstellende Geometrie Übungen Institut für 0Irchitektur und IIIedien Tutorial Übungsblatt: Perspektive Rekonstruktion - FSI Gegeben sind ein Foto ( mit lotrechter Bildebene ) von einem quaderförmigen
KOP1_1_8. Die Schülerinnen und Schüler können normgerechte Zeichnungen lesen.
 Titel Risszeichnen Die Schülerinnen und Schüler können normgerechte Zeichnungen lesen. Relevante(r) Deskriptor(en) Die Schülerinnen und Schüler können Konstruktionsaufgaben mittels geeigneter Abbildungsverfahren
Titel Risszeichnen Die Schülerinnen und Schüler können normgerechte Zeichnungen lesen. Relevante(r) Deskriptor(en) Die Schülerinnen und Schüler können Konstruktionsaufgaben mittels geeigneter Abbildungsverfahren
Der Hauptsatz der Axonometrie, Aufbauverfahren
 Axonometrie Der Hauptsatz der Axonometrie, Aufbauverfahren Gegeben seien ein kartesisches Rechtssystem (U, E x, E y, E z ) und eine Bildebene π derart, daÿ bezüglich einer Parallelprojektion p keine Koordinatenebene
Axonometrie Der Hauptsatz der Axonometrie, Aufbauverfahren Gegeben seien ein kartesisches Rechtssystem (U, E x, E y, E z ) und eine Bildebene π derart, daÿ bezüglich einer Parallelprojektion p keine Koordinatenebene
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 20. März 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 20. März 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
DARSTELLENDE GEOMETRIE I
 DARSTELLENDE GEOMETRIE I VON DR. RUDOLF BEREIS Professor und Direktor des Instituts für Geometrie an der Technischen Universität Dresden Mit 361 Abbildungen AKADEMIE-VERLAG BERLIN 1964 h. INHALT Hinweise
DARSTELLENDE GEOMETRIE I VON DR. RUDOLF BEREIS Professor und Direktor des Instituts für Geometrie an der Technischen Universität Dresden Mit 361 Abbildungen AKADEMIE-VERLAG BERLIN 1964 h. INHALT Hinweise
iek Institut für Entwerfen und Konstruieren
 Darstellende Geometrie Institut für Entwerfen und Konstruieren Prof. José Luis Moro Matthias Rottner Heiko Stachel 1 Modul Grundlagen der Darstellung und Konstruktion Termine Grundlagen der Darstellung
Darstellende Geometrie Institut für Entwerfen und Konstruieren Prof. José Luis Moro Matthias Rottner Heiko Stachel 1 Modul Grundlagen der Darstellung und Konstruktion Termine Grundlagen der Darstellung
Hans Walser. Raumgeometrie. Modul 4 Die Ebene Lernumgebung Teil 2
 Hans Walser Raumgeometrie Modul 4 Die Ebene Lernumgebung Teil 2 Hans Walser: Modul 4, Die Ebene. Lernumgebung. Teil 2 ii Inhalt 1 Abstand Punkt / Ebene... 1 2 Abstand... 2 3 Neigungswinkel... 3 4 Neigungswinkel...
Hans Walser Raumgeometrie Modul 4 Die Ebene Lernumgebung Teil 2 Hans Walser: Modul 4, Die Ebene. Lernumgebung. Teil 2 ii Inhalt 1 Abstand Punkt / Ebene... 1 2 Abstand... 2 3 Neigungswinkel... 3 4 Neigungswinkel...
Wo viel Licht ist, ist starker Schatten.
 Wo viel Licht ist, ist starker Schatten. (Goethe; Götz von Berlichingen) Perspektive & Schatten Die senkrechte Parallelprojektion (Normalperspektive) Aufriss (Vorderansicht Blick von vorne) Seitenriss
Wo viel Licht ist, ist starker Schatten. (Goethe; Götz von Berlichingen) Perspektive & Schatten Die senkrechte Parallelprojektion (Normalperspektive) Aufriss (Vorderansicht Blick von vorne) Seitenriss
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 2. September 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 9.00 Uhr 10.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Prüfungsfach: Darstellende Geometrie Termin: 2. September 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 9.00 Uhr 10.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Geometrische Grundlagen der Architekturdarstellung
 Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
Computational Geometry, MU Leoben
 Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Methoden der Darstellung Termin: 7. März 2013 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 11.30 Uhr 12.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Methoden der Darstellung Termin: 7. März 2013 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 11.30 Uhr 12.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Die Zentralprojektion
 Perspektive Perspektivmodell (S. 1 von 6) / www.kunstbrowser.de Die Zentralprojektion Die Zentralprojektion eines Gegenstandes auf eine ebene Bildfläche ist das Grundprinzip, aus dem sich alle zentralperspektivischen
Perspektive Perspektivmodell (S. 1 von 6) / www.kunstbrowser.de Die Zentralprojektion Die Zentralprojektion eines Gegenstandes auf eine ebene Bildfläche ist das Grundprinzip, aus dem sich alle zentralperspektivischen
Hans Walser. Raumgeometrie. Modul 4 Die Ebene
 Hans Walser Raumgeometrie Modul 4 Die Ebene Hans Walser: Modul 4, Die Ebene ii Modul 4 für die Lehrveranstaltung Raumgeometrie Sommer 2000 Erstausgabe Sommer 2002 Überarbeitung Sommer 2003 Fehlerkorrekturen,
Hans Walser Raumgeometrie Modul 4 Die Ebene Hans Walser: Modul 4, Die Ebene ii Modul 4 für die Lehrveranstaltung Raumgeometrie Sommer 2000 Erstausgabe Sommer 2002 Überarbeitung Sommer 2003 Fehlerkorrekturen,
Seite 1 Einleitung Elemente der Darstellenden Geometrie 13. Lernkontrolle A 1 15
 Inhaltsverzeichnis Seite 1 Einleitung 13 2 Elemente der Darstellenden Geometrie 13 Lernkontrolle A 1 15 3 Projektionsarten und Verfahren 15 3.1 Projektionsvorgang 15 3.2 Projektionsarten 16 3.2.1 Zentralprojektion
Inhaltsverzeichnis Seite 1 Einleitung 13 2 Elemente der Darstellenden Geometrie 13 Lernkontrolle A 1 15 3 Projektionsarten und Verfahren 15 3.1 Projektionsvorgang 15 3.2 Projektionsarten 16 3.2.1 Zentralprojektion
Lösungen. Christian Haas. Durchdringungen. Ausbildungseinheit für Anlagen- und Apparatebauer/innen. Reform Lernziele:
 Durchdringungen Ausbildungseinheit für Anlagen- und Apparatebauer/innen EFZ Reform 2013 13 Lösungen Lernziele: Durchdringungen im Zusammenhang mit den Abwicklungen konstruieren Christian Haas Zeichnungstechnik
Durchdringungen Ausbildungseinheit für Anlagen- und Apparatebauer/innen EFZ Reform 2013 13 Lösungen Lernziele: Durchdringungen im Zusammenhang mit den Abwicklungen konstruieren Christian Haas Zeichnungstechnik
Inhaltsverzeichnis. geometrischer Objekte auszufüllen. Die Liste der Lösungen kann auch eine ABC Liste zu diesen Themen sein.
 Lückentexte 1 zu den Themen: I. Der Kreis als Figur in der Ebene II. Der Kreis als Figur im Raum III. Die Kugel Multiple Choice Aufgabe zum Thema IV. Ebene Schnitte einer Kugel Kreuzworträtsel zu den Themen:
Lückentexte 1 zu den Themen: I. Der Kreis als Figur in der Ebene II. Der Kreis als Figur im Raum III. Die Kugel Multiple Choice Aufgabe zum Thema IV. Ebene Schnitte einer Kugel Kreuzworträtsel zu den Themen:
Abbildung 1.5: Streckensymmetrale
 Abbildung 1.5: Streckensymmetrale Abbildung 1.6: Winkelsymmetrale Abbildung 1.7: Höhenschnittpunkt Abbildung 1.8: Umkreismittelpunkt Abbildung 1.9: Inkreismittelpunkt Abbildung 1.10: Schwerpunkt Abbildung
Abbildung 1.5: Streckensymmetrale Abbildung 1.6: Winkelsymmetrale Abbildung 1.7: Höhenschnittpunkt Abbildung 1.8: Umkreismittelpunkt Abbildung 1.9: Inkreismittelpunkt Abbildung 1.10: Schwerpunkt Abbildung
2.6. Aufgaben zu Kongruenzabbildungen
 Aufgabe.6. Aufgaben zu Kongruenzabbildungen Gegeben sind die Dreiecke ABC mit A(0 ), B( 0) und C(3 0) sowie A B C mit A ( ), B (3 ) und C ( ). Beschreibe die Abbildung, die das Dreieck ABC auf das Dreieck
Aufgabe.6. Aufgaben zu Kongruenzabbildungen Gegeben sind die Dreiecke ABC mit A(0 ), B( 0) und C(3 0) sowie A B C mit A ( ), B (3 ) und C ( ). Beschreibe die Abbildung, die das Dreieck ABC auf das Dreieck
Einige Fragen aus den Elementen der Darstellenden Geometrie,
 Einige Fragen aus den Elementen der Darstellenden Geometrie, Von A. KIEFER (Zürich). (Als Manuskript eingegangen am 4. März 1929.) I. Wenn P', P" in dem System der vereinigten Bildebenen der Grund und
Einige Fragen aus den Elementen der Darstellenden Geometrie, Von A. KIEFER (Zürich). (Als Manuskript eingegangen am 4. März 1929.) I. Wenn P', P" in dem System der vereinigten Bildebenen der Grund und
Rotation eines Punktes um eine Achse allgemeiner Lage
 Rotation eines Punktes um eine chse allgemeiner Lage Es gibt eine allgemein, in der arstellenden Geometrie übliche Methode, dieses eispiele zu lösen: 1) chse in Wahrer Größe darstellen - ein weiterer Seitenriss
Rotation eines Punktes um eine chse allgemeiner Lage Es gibt eine allgemein, in der arstellenden Geometrie übliche Methode, dieses eispiele zu lösen: 1) chse in Wahrer Größe darstellen - ein weiterer Seitenriss
1) ie Linien der abgebildeten Bauteile entsprechen den Linienarten nach DIN EN ISO
 1) ie Linien der abgebildeten Bauteile entsprechen den Linienarten nach DIN EN ISO 128-24. Ordnen Sie den gekennzeichneten Linien die korrekten Linienarten zu! A B C D F G J K Verwenden Sie dazu die in
1) ie Linien der abgebildeten Bauteile entsprechen den Linienarten nach DIN EN ISO 128-24. Ordnen Sie den gekennzeichneten Linien die korrekten Linienarten zu! A B C D F G J K Verwenden Sie dazu die in
Computational Geometry, MU Leoben
 Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
GEOMETRIE (4a) Kurzskript
 GEOMETRIE (4a) Kurzskript Dieses Kurzskript ist vor allem eine Sammlung von Sätzen und Definitionen und sollte ausdrücklich nur zusammen mit weiteren Erläuterungen in der Veranstaltung genutzt werden.
GEOMETRIE (4a) Kurzskript Dieses Kurzskript ist vor allem eine Sammlung von Sätzen und Definitionen und sollte ausdrücklich nur zusammen mit weiteren Erläuterungen in der Veranstaltung genutzt werden.
2.3.1 Rechtshändiges und linkshändiges Koordinatensystem
 2.3. Rechtshändiges und linkshändiges Koordinatensstem Die Koordinatenachsen im dreidimensionalen Raum lassen sich auf wei verschieden Arten anordnen: Linkshändig und Rechtshändig (s. Abbildung 2.9). Um
2.3. Rechtshändiges und linkshändiges Koordinatensstem Die Koordinatenachsen im dreidimensionalen Raum lassen sich auf wei verschieden Arten anordnen: Linkshändig und Rechtshändig (s. Abbildung 2.9). Um
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt Semester ARBEITSBLATT 14 DIE MERKWÜRDIGEN PUNKTE DES DREIECKS
 REITSLTT 14 1) Der Höhenschnittpunkt DIE MERKWÜRDIGEN PUNKTE DES DREIECKS Definition: Unter einer Höhe versteht man eine Normale auf eine Seite zum gegenüberliegenden Eckpunkt. Die Höhe h c steht also
REITSLTT 14 1) Der Höhenschnittpunkt DIE MERKWÜRDIGEN PUNKTE DES DREIECKS Definition: Unter einer Höhe versteht man eine Normale auf eine Seite zum gegenüberliegenden Eckpunkt. Die Höhe h c steht also
Lösungen IV ) β = 54,8 ; γ = 70,4 106) a) 65 b) 65 (115?) d) 57,5
 (Stark 7 S. 6ff) Lösungen IV. a) gleichschenklig 0) a) () α = β = 6,7 () β = 7,8 ; γ = 4,4 () α = 4 ; γ = (4) α = β = (80 γ)/ b) 79,6 und 0,8 oder 0, und 0, c) α = β = 64 ; γ = d) gleichschenklig; zwei
(Stark 7 S. 6ff) Lösungen IV. a) gleichschenklig 0) a) () α = β = 6,7 () β = 7,8 ; γ = 4,4 () α = 4 ; γ = (4) α = β = (80 γ)/ b) 79,6 und 0,8 oder 0, und 0, c) α = β = 64 ; γ = d) gleichschenklig; zwei
2.3 Linienarten und Linienbreiten nach DIN 15 T1
 Angebots- Zeichnung Fundament- Zeichnung Zeichnung zur Erläuterung einer Ausschreibung oder zur Abgabe eines Angebotes Enthält Angaben über die Fertigung des Fundamentes für die Aufstellung der Maschine
Angebots- Zeichnung Fundament- Zeichnung Zeichnung zur Erläuterung einer Ausschreibung oder zur Abgabe eines Angebotes Enthält Angaben über die Fertigung des Fundamentes für die Aufstellung der Maschine
Zweidimensionale Vektorrechnung:
 Zweidimensionale Vektorrechnung: Gib jeweils den Vektor AB und seine Länge an! (a A(, B(6 5 (b A(, B( 4 (c A(, B( 0 (d A(0 0, B(4 (e A(0, B( 0 (f A(, B( Gib jeweils die Summe a + b und die Differenz a
Zweidimensionale Vektorrechnung: Gib jeweils den Vektor AB und seine Länge an! (a A(, B(6 5 (b A(, B( 4 (c A(, B( 0 (d A(0 0, B(4 (e A(0, B( 0 (f A(, B( Gib jeweils die Summe a + b und die Differenz a
Perspektive Vertiefung
 Perspektive Vertiefung Hans-Peter Schröcker Arbeitsbereich Geometrie und CAD, Universität Innsbruck Wintersemester 2007/08 Teil I Einleitung Organisatorisches Perspektive Vertiefung Seminar, 2 Std. Donnerstag,
Perspektive Vertiefung Hans-Peter Schröcker Arbeitsbereich Geometrie und CAD, Universität Innsbruck Wintersemester 2007/08 Teil I Einleitung Organisatorisches Perspektive Vertiefung Seminar, 2 Std. Donnerstag,
Seiten 7 / 8 Aufgaben Punktmengen (Die Lösungen sind verkleinert gezeichnet) 1 a) Problemanalyse
 Seiten 7 / 8 Aufgaben Punktmengen (Die Lösungen sind verkleinert gezeichnet) 1 a) Problemanalyse k mam 1. näher bei M als bei A (Entfernung von 2 Punkten) 2. weniger als 35mm von A entfernt (Entf. von
Seiten 7 / 8 Aufgaben Punktmengen (Die Lösungen sind verkleinert gezeichnet) 1 a) Problemanalyse k mam 1. näher bei M als bei A (Entfernung von 2 Punkten) 2. weniger als 35mm von A entfernt (Entf. von
Axonometrie. 11 Axonometrien. Grundrissaxonometrie x : y : z = 1 : 1 : 1
 11 n Grundrissaonometrie : : = 1 : 1 : 1 Übersicht "... sstematisch abgewandelt, wird eine Einelfrage in Form möglichst vieler Variationen vorgetragen. Der Betrachter sieht sich in die Position eines Voeurs
11 n Grundrissaonometrie : : = 1 : 1 : 1 Übersicht "... sstematisch abgewandelt, wird eine Einelfrage in Form möglichst vieler Variationen vorgetragen. Der Betrachter sieht sich in die Position eines Voeurs
Examen Kurzfragen (sortiert) VI. Dreiecke. 24. Juni 2014
 Examen Kurzfragen (sortiert) VI. Dreiecke 24. Juni 2014 VI. Dreiecke Frage 1 Wie werden im rechtwinkligen Dreieck die beiden Seiten genannt, die dem rechten Winkel anliegen? VI. Dreiecke Frage 1 Wie werden
Examen Kurzfragen (sortiert) VI. Dreiecke 24. Juni 2014 VI. Dreiecke Frage 1 Wie werden im rechtwinkligen Dreieck die beiden Seiten genannt, die dem rechten Winkel anliegen? VI. Dreiecke Frage 1 Wie werden
Josef Vogelmann Darstellende Geometrie
 Josef Vogelmann Darstellende Geometrie Kamprath-Reihe Technik Dipl.-Ing. (FH) Josef Vogelmann Darstellende Geometrie Die Lehre vom richtigen Zeichnen eine Grundlage des technischen Zeichnens 5. Auflage
Josef Vogelmann Darstellende Geometrie Kamprath-Reihe Technik Dipl.-Ing. (FH) Josef Vogelmann Darstellende Geometrie Die Lehre vom richtigen Zeichnen eine Grundlage des technischen Zeichnens 5. Auflage
Grundwissen JS 7: Geometrie 17. Juli (a) Wann heißt eine Figur achsensymmetrisch? Welche Bedeutung hat die Symmetrieachse anschaulich
 GYMNASIUM MIT SCHÜLERHEIM EGNITZ math-technolog u sprachl Gymnasium WILHELM-VON-HUMBOLDT-STRASSE 7 91257 EGNITZ FERNRUF 09241/48333 FAX 09241/2564 Grundwissen JS 7: Geometrie 17 Juli 2007 1(a) Wann heißt
GYMNASIUM MIT SCHÜLERHEIM EGNITZ math-technolog u sprachl Gymnasium WILHELM-VON-HUMBOLDT-STRASSE 7 91257 EGNITZ FERNRUF 09241/48333 FAX 09241/2564 Grundwissen JS 7: Geometrie 17 Juli 2007 1(a) Wann heißt
Projektion. FG Borrego - TU Berlin Architekturdarstellung und Gestaltung Collaborative Design Laboratory
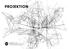 Projektion Unterscheidung nach Lage des Projektionszentrums im Unendlichen im Endlichen Parallelprojektion Zentralprojektion Projektionszentrum Z R R Q Q R P R Z' P Q Q Bildebene P Bildebene P Parallelität
Projektion Unterscheidung nach Lage des Projektionszentrums im Unendlichen im Endlichen Parallelprojektion Zentralprojektion Projektionszentrum Z R R Q Q R P R Z' P Q Q Bildebene P Bildebene P Parallelität
Normalprojektion. Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion.
 4. Der dreidimensionale Raum 4.5 Hauptrisse Normalprojektion Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion. Zum Beispiel:
4. Der dreidimensionale Raum 4.5 Hauptrisse Normalprojektion Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion. Zum Beispiel:
mentor Lernhilfe: Mathematik 7. Klasse Baumann
 mentor Lernhilfen mentor Lernhilfe: Mathematik 7. Klasse Geometrie: Achsen- und Punktspiegelung, Drehung, Verschiebung, Winkelgesetze von Rolf Baumann 1. Auflage mentor Lernhilfe: Mathematik 7. Klasse
mentor Lernhilfen mentor Lernhilfe: Mathematik 7. Klasse Geometrie: Achsen- und Punktspiegelung, Drehung, Verschiebung, Winkelgesetze von Rolf Baumann 1. Auflage mentor Lernhilfe: Mathematik 7. Klasse
Lösungen zum Thema Geometrie. Lösungen zur Aufg. 0: a) Gib an, um welche besondere Linie im Dreieck es sich jeweils handelt.
 Lösungen zum Thema Geometrie Lösungen zur Aufg. 0: a) Gib an, um welche besondere Linie im Dreieck es sich jeweils handelt. Höhe h c Winkelhalbierende w α Mittelsenkrechte ms c Seitenhalbierende s c b)
Lösungen zum Thema Geometrie Lösungen zur Aufg. 0: a) Gib an, um welche besondere Linie im Dreieck es sich jeweils handelt. Höhe h c Winkelhalbierende w α Mittelsenkrechte ms c Seitenhalbierende s c b)
Aufgabenstellung zur Wahlfachübung 4
 Darstellende Geometrie für Architekten III Institut für Geometrie und Prakt. Mathematik RWTH Aachen 4.2 Prismen Geometrie der Formen Übung 4 Seite 1 Aufgabenstellung zur Wahlfachübung 4 Hausübung zum Thema
Darstellende Geometrie für Architekten III Institut für Geometrie und Prakt. Mathematik RWTH Aachen 4.2 Prismen Geometrie der Formen Übung 4 Seite 1 Aufgabenstellung zur Wahlfachübung 4 Hausübung zum Thema
Dipl, ng (FH) Darstellende
 Kamprath-Reihe Technik Dipl, ng (FH) Darstellende Josef Vogelmann Die Lehre vom richtigen Zeichnen eine Grundlage des technischen Zeichnens 6. Auflage Vogel Buchverlag Inhaltsverzeichnis 1. Einleitung
Kamprath-Reihe Technik Dipl, ng (FH) Darstellende Josef Vogelmann Die Lehre vom richtigen Zeichnen eine Grundlage des technischen Zeichnens 6. Auflage Vogel Buchverlag Inhaltsverzeichnis 1. Einleitung
Geometrische Grundlagen der Architekturdarstellung
 Geometrische Grundlagen der Architekturdarstellung von Cornelie Leopold 1. Auflage Springer Vieweg Wiesbaden 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 8348 1838 6 schnell und portofrei
Geometrische Grundlagen der Architekturdarstellung von Cornelie Leopold 1. Auflage Springer Vieweg Wiesbaden 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 8348 1838 6 schnell und portofrei
1 Kartesische Normalkoordinatensysteme 5
 Inhaltsverzeichnis 1 Kartesische Normalkoordinatensysteme 5 2 SchrÄagrisse 7 3 Zugeordnete Normalrisse 13 3.1 Hauptrisse....................................... 13 3.2 Grundriss eines Punktes...............................
Inhaltsverzeichnis 1 Kartesische Normalkoordinatensysteme 5 2 SchrÄagrisse 7 3 Zugeordnete Normalrisse 13 3.1 Hauptrisse....................................... 13 3.2 Grundriss eines Punktes...............................
DREIECKSFORMEN 1. Station 1 (H1) Gib an, um welche Form von Dreieck es sich jeweils handelt! Teile dabei nach Winkel und nach Seiten ein!
 Station 1 (H1) DREIECKSFORMEN 1 Gib an, um welche Form von Dreieck es sich jeweils handelt! Teile dabei nach Winkel und nach Seiten ein! Station 1 LÖSUNG a) Spitzwinkliges Dreieck und gleichschenkliges
Station 1 (H1) DREIECKSFORMEN 1 Gib an, um welche Form von Dreieck es sich jeweils handelt! Teile dabei nach Winkel und nach Seiten ein! Station 1 LÖSUNG a) Spitzwinkliges Dreieck und gleichschenkliges
Achtung: Die Aufgabenkarten werden nacheinander ausgegeben! 1
 Achtung: Die Aufgabenkarten werden nacheinander ausgegeben! 1 Aufgabe 1 Zeichne in Geogebra ein beliebiges Dreieck und konstruiere den Umkreismittelpunkt U, den Schwerpunkt S und den Höhenschnittpunkt
Achtung: Die Aufgabenkarten werden nacheinander ausgegeben! 1 Aufgabe 1 Zeichne in Geogebra ein beliebiges Dreieck und konstruiere den Umkreismittelpunkt U, den Schwerpunkt S und den Höhenschnittpunkt
Gundlagen Klasse 5/6 Geometrie. nach oben. Inhaltsverzeichnis
 Inhaltsverzeichnis Grundbegriffe der Geometrie Geometrische Abbildungen Das Koordinatensystem Schnittpunkt von Geraden Symmetrien Orthogonale Geraden Abstände Parallele Geraden Vierecke Diagonalen in Vielecken
Inhaltsverzeichnis Grundbegriffe der Geometrie Geometrische Abbildungen Das Koordinatensystem Schnittpunkt von Geraden Symmetrien Orthogonale Geraden Abstände Parallele Geraden Vierecke Diagonalen in Vielecken
KOP1_3_5. Rohrverbindungen. Die Schülerinnen und Schüler können normgerechte Zeichnungen lesen.
 Titel Rohrverbindungen Die Schülerinnen und Schüler können normgerechte Zeichnungen lesen. Relevante(r) Deskriptor(en) Lehrstoff Ausbildungsinhalte Methodisch/Didaktische Hinweise Hilfsmittel Quelle weitere
Titel Rohrverbindungen Die Schülerinnen und Schüler können normgerechte Zeichnungen lesen. Relevante(r) Deskriptor(en) Lehrstoff Ausbildungsinhalte Methodisch/Didaktische Hinweise Hilfsmittel Quelle weitere
Computational Geometry, MU Leoben
 Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Die Kapitel 1 und 2.1 haben wir im Jahr 2012 behandelt. Im Zirkel am haben wir mit Kapitel 2.2 begonnen.
 Das vorliegende Skript beschäftigt sich mit dem Thema Elementargeometrie. Das Skript entsteht entlang einer Unterrichtsreihe in der Mathematischen Schülergesellschaft(MSG) im Schuljahr 2012/2013. Die vorliegende
Das vorliegende Skript beschäftigt sich mit dem Thema Elementargeometrie. Das Skript entsteht entlang einer Unterrichtsreihe in der Mathematischen Schülergesellschaft(MSG) im Schuljahr 2012/2013. Die vorliegende
Klausur zur Einführung in die Geometrie im SS 2002
 Klausur zur Einführung in die Geometrie im SS 2002 Name, Vorname... Matr.Nr.... Semester-Anzahl im SS 2002:... Studiengang GH/R/S Tutor/in:... Aufg.1 Aufg,2 Aufg.3 Aufg.4 Aufg.5 Aufg.6 Aufg.7 Aufg.8 Gesamt
Klausur zur Einführung in die Geometrie im SS 2002 Name, Vorname... Matr.Nr.... Semester-Anzahl im SS 2002:... Studiengang GH/R/S Tutor/in:... Aufg.1 Aufg,2 Aufg.3 Aufg.4 Aufg.5 Aufg.6 Aufg.7 Aufg.8 Gesamt
Geometrische Grundlagen der. Architekturdarstellung
 Cornelie Leopold Geometrische Grundlagen der. Architekturdarstellung 4. Auflage Mit 469 Abbildungen unter Mitwirkung von Andreas Matievits STUDIUM 11 VIEWEG+ TEUBNER INHALTSVERZEICHNIS Vorwort 1 EINFÜHRUNG
Cornelie Leopold Geometrische Grundlagen der. Architekturdarstellung 4. Auflage Mit 469 Abbildungen unter Mitwirkung von Andreas Matievits STUDIUM 11 VIEWEG+ TEUBNER INHALTSVERZEICHNIS Vorwort 1 EINFÜHRUNG
Einerseits: Zentralperspektive
 VOM RAUM IN DIE EBENE UND ZURÜCK Ebene Figuren wie Dreiecke, Vierecke, andere Vielecke, Kreise lassen sich auf einem Zeichenblatt entweder in wahrer Größe oder unter Beibehaltung ihrer Form! maßstäblich
VOM RAUM IN DIE EBENE UND ZURÜCK Ebene Figuren wie Dreiecke, Vierecke, andere Vielecke, Kreise lassen sich auf einem Zeichenblatt entweder in wahrer Größe oder unter Beibehaltung ihrer Form! maßstäblich
Kanten ergänzen. Lisa hat Schrägrisse von Pyramiden gezeichnet. Dabei sind ihr Fehler passiert. Ergänze die fehlenden Kanten. Möglicher Lösungsweg
 Kanten ergänzen Lisa hat Schrägrisse von Pyramiden gezeichnet. Dabei sind ihr Fehler passiert. Ergänze die fehlenden Kanten. Möglicher Lösungsweg Einrichtungshaus 1. Hier siehst du zwei Bilder eines Einrichtungshauses:
Kanten ergänzen Lisa hat Schrägrisse von Pyramiden gezeichnet. Dabei sind ihr Fehler passiert. Ergänze die fehlenden Kanten. Möglicher Lösungsweg Einrichtungshaus 1. Hier siehst du zwei Bilder eines Einrichtungshauses:
Sekundarschulabschluss für Erwachsene. Geometrie A b) Strecken Sie das Dreieck ABC (Streckfaktor: -1/ Streckzentrum Z) (3 Punkte)
 SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2013 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2013 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
Themenbereich: Besondere Dreiecke Seite 1 von 6
 Themenbereich: Besondere Dreiecke Seite 1 von 6 Lernziele: - Kenntnis der Bezeichnungen für besondere Dreiecke - Kenntnis der Seiten- und Winkelbezeichnungen bei besonderen Dreiecken - Kenntnis der Eigenschaften
Themenbereich: Besondere Dreiecke Seite 1 von 6 Lernziele: - Kenntnis der Bezeichnungen für besondere Dreiecke - Kenntnis der Seiten- und Winkelbezeichnungen bei besonderen Dreiecken - Kenntnis der Eigenschaften
Konstruktionen am Dreieck
 Winkelhalbierende Die Winkelhalbierende halbiert den jeweiligen Innenwinkel des Dreiecks. Sie agieren als Symmetrieachse. Dadurch ist jeder Punkt der Winkelhalbierenden gleich weit von den beiden Schenkeln
Winkelhalbierende Die Winkelhalbierende halbiert den jeweiligen Innenwinkel des Dreiecks. Sie agieren als Symmetrieachse. Dadurch ist jeder Punkt der Winkelhalbierenden gleich weit von den beiden Schenkeln
Geometrische Grundlagen der Architekturdarstellung
 Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
Sekundarschulabschluss für Erwachsene
 SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2011 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2011 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
r a t u Parametergleichung der Geraden durch den Punkt A mit dem Richtungsvektor u t R heisst Parameter
 8 3. Darstellung der Geraden im Raum 3.. Parametergleichung der Geraden Die naheliegende Vermutung, dass eine Gerade des Raumes durch eine Gleichung der Form ax + by + cz +d = 0 beschrieben werden kann
8 3. Darstellung der Geraden im Raum 3.. Parametergleichung der Geraden Die naheliegende Vermutung, dass eine Gerade des Raumes durch eine Gleichung der Form ax + by + cz +d = 0 beschrieben werden kann
Darstellende Geometrie Übungen. Tutorial 09. CAD 2 - Archimedische Körper
 Tutorial 09 CAD 2 - Archimedische Körper Achtung: In diesem Tutorial wird die Konstruktion eines Pentagondodekaeders erklärt. Diese ist der Konstruktion des Fußballes aus der Übung 09 sehr ähnlich und
Tutorial 09 CAD 2 - Archimedische Körper Achtung: In diesem Tutorial wird die Konstruktion eines Pentagondodekaeders erklärt. Diese ist der Konstruktion des Fußballes aus der Übung 09 sehr ähnlich und
2.5. Aufgaben zu Dreieckskonstruktionen
 2.5. Aufgaben zu Dreieckskonstruktionen Aufgabe 1 Zeichne das Dreieck AC mit A( 1 2), (5 0) und C(3 6) und konstruiere seinen Umkreis. Gib den Radius und den Mittelpunkt des Umkreises an. Aufgabe 2 Konstruiere
2.5. Aufgaben zu Dreieckskonstruktionen Aufgabe 1 Zeichne das Dreieck AC mit A( 1 2), (5 0) und C(3 6) und konstruiere seinen Umkreis. Gib den Radius und den Mittelpunkt des Umkreises an. Aufgabe 2 Konstruiere
Winkel zeichnen. Hilfe. ACHTUNG! Achte immer genau darauf
 Hilfe Winkel zeichnen 1. Zeichne einen Schenkel (die rote Linie) S 2. Lege das Geodreieck mit der Null am Scheitelpunkt an. (Dort wo der Winkel hinkommen soll) S 3. Möchtest du zum Beispiel einen Winkel
Hilfe Winkel zeichnen 1. Zeichne einen Schenkel (die rote Linie) S 2. Lege das Geodreieck mit der Null am Scheitelpunkt an. (Dort wo der Winkel hinkommen soll) S 3. Möchtest du zum Beispiel einen Winkel
Figuren Lösungen. 1) Welche Art Dreieck hat die beschriebene Eigenschaft? Ordne die Eigenschaften den Dreiecken zu. Alle Winkel betragen 60.
 1) Welche Art Dreieck hat die beschriebene Eigenschaft? Ordne die Eigenschaften den Dreiecken zu. Alle Winkel betragen 60. Es gibt drei Symmetrieachsen. Gleichseitiges Dreieck Zwei Seiten stehen normal.
1) Welche Art Dreieck hat die beschriebene Eigenschaft? Ordne die Eigenschaften den Dreiecken zu. Alle Winkel betragen 60. Es gibt drei Symmetrieachsen. Gleichseitiges Dreieck Zwei Seiten stehen normal.
37 II.1. Abbildungen
 37 II.1. Abbildungen "Abbildung" und "Funktion" sind verschiedene Namen für denselben Begriff, der charakterisiert ist durch die Angabe der Definitionsmenge ("Was wird abgebildet?"), der Wertemenge ("Wohin
37 II.1. Abbildungen "Abbildung" und "Funktion" sind verschiedene Namen für denselben Begriff, der charakterisiert ist durch die Angabe der Definitionsmenge ("Was wird abgebildet?"), der Wertemenge ("Wohin
Die Strahlensätze machen eine Aussage über Streckenverhältnisse, nämlich:
 Elementargeometrie Der. Strahlensatz Geschichte: In den Elementen des Euklid wird im 5.Buch die Proportionenlehre behandelt, d.h. die geometrische Theorie aller algebraischen Umformungen der Proportion.
Elementargeometrie Der. Strahlensatz Geschichte: In den Elementen des Euklid wird im 5.Buch die Proportionenlehre behandelt, d.h. die geometrische Theorie aller algebraischen Umformungen der Proportion.
Klausur zur Akademischen Teilprüfung, Modul 2,
 PH Heidelberg, Fach Mathematik Klausur zur Akademischen Teilprüfung, Modul, GHPO I vom.7.00, RPO vom 4.08.00 Einführung in die Geometrie Wintersemester 1/1, 1. Februar 01 Klausur zur ATP, Modul, Einführung
PH Heidelberg, Fach Mathematik Klausur zur Akademischen Teilprüfung, Modul, GHPO I vom.7.00, RPO vom 4.08.00 Einführung in die Geometrie Wintersemester 1/1, 1. Februar 01 Klausur zur ATP, Modul, Einführung
Figur in der Bildfläche bzw. Bildebene
 2 ABBILDUNGSMETHODEN 2.1 Projektionsarten Um dreidimensionale Objekte wie Gebäude, Stadträume oder Bauteile darzustellen, werden diese auf eine Bildfläche bzw. eine Bildebene abgebildet. Der hierbei verwendete
2 ABBILDUNGSMETHODEN 2.1 Projektionsarten Um dreidimensionale Objekte wie Gebäude, Stadträume oder Bauteile darzustellen, werden diese auf eine Bildfläche bzw. eine Bildebene abgebildet. Der hierbei verwendete
