Informatik II. Registermaschinen. Registermaschinen. Registermaschinen. Rainer Schrader. 7. Dezember 2005
|
|
|
- Philipp Althaus
- vor 7 Jahren
- Abrufe
Transkript
1 Informatik II Rainer Schrader Zentrum für Angewandte Informatik Köln 7. Dezember 25 / 82 2 / 82 Gliederung Aufbau und Eigenschaften universelle RAM s RAM-Berechenbarkeit Nichtentscheidbarkeit Reduzierbarkeit Aufzählbarkeit wir vereinfachen das Modell eines von-neumann-rechners eine Registermaschine (Random Access Maschine = RAM) stellt eine Abstraktion des von-neumann-rechners dar sie besteht aus (i) einer zentralen Recheneinheit (ii) einem Speicher (iii) einem Programm (iv) einem Eingabe- und einem Ausgabeband 3 / 82 4 / 82
2 Eingabeband Register Befehlszähler Programm Ausgabeband Die einzelnen Teile der Registermaschine haben folgende Eigenschaften: Speicher: abzählbar unendlich viele Speicherzellen (Register) mit den Adressen,, 2,..., jedes Register kann eine Zahl aus N aufnehmen der Inhalt eines Registers ist entweder eine Zahl aus N oder nicht definiert. Recheneinheit: enthält Befehlszähler und Akkumulator ( b= Register ). beide Register können natürliche Zahlen speichern Programm: endliche numerische Folge von Befehlen, aus der weiter unten spezifizierten Befehlsmenge. Ein-/Ausgabeband: zwei unbeschränkt lange Bänder, unterteilt in Zellen jede Zelle kann ein Element aus {,, 2} aufnehmen 5 / 82 6 / 82 zu Beginn der Rechnung steht eine Eingabe (x,... x n ) {,, 2} auf dem Eingabeband alle Register sind undefiniert Bezeichnungen: c(i) aktueller Inhalt der Registers i der Befehlszähler enthält den Wert in einem Schritt wird der durch den Inhalt des Befehlszählers spezifizierte Befehl des Programms ausgeführt er verändert den Akku, die Register, den Befehlszähler und evtl. das Ausgabeband. b aktueller Inhalt des Befehlszählers e, a aktueller Inhalt des Ein-/Ausgabeband e i und a j die aktuellen Positionen des Ein- bzw. Ausgabebands 2 Trennzeichen zwischen {, }-Folgen 22 EOF auf den Bändern ε undefiniert Die folgenden Befehle werden jeweils nur ausgeführt, wenn die Registerinhalte definiert sind 7 / 82 8 / 82
3 Befehlsliste. read c() e i, Lesekopf rückt eins weiter 2. write a j c(), Schreibkopf rückt eins weiter 3. c-load k c() k, 4. load k c() c(k ) 5. i-load k c() c(c(k )) 6. store k c(k ) c() 7. i-store k c(c(k )) c() 8. goto k b k 9. jumpzero k if c() = then b k else b b +. end Programm hält. add k c() c() + c(k ) 2. sub k c() max{c() c(k ), } 3. shift c() c() 2 Beispiel Lies eine Binärzahl ein und wandle diese in eine Dezimalzahl um: () c-load 2 (2) store /* 2 Register (3) c-load (4) store 3 /* Register 3 (5) read (6) store 2 /* x i Register 2 (7) load /* 2 Register (8) sub 2 /* 2 x i Register (9) jumpzero 5 /* 2 gefunden, Ende der Eingabe () load 3 /* lade Dezimalzahl () add /* 2 Register Register (2) add 2 /* Register + x i Register (3) store 3 /* speichere zurück (4) goto 5 /* lies nächste Binärstelle (5) end 9 / 82 / 82 um die Berechnungen einer RAM beschreiben zu können, frieren wir die Maschine in jedem Rechenschritt ein der aktuelle Zustand einer RAM wird durch die Inhalte von Registern, Bändern und des Befehlszählers beschrieben dies führt auf den Begriff Zustand bzw. Konfiguration einer RAM wir benötigen dazu den Begriff einer partiellen Funktion f : X Y heißt partiell, wenn f nicht in jedem x X definiert sein muss Eine Konfiguration K einer RAM ist ein Tupel (b, c, e, a) mit b N (Inhalt des Befehlszählers) c : N part. N (Speicherinhaltsfunktion) a, e {,, 2} {ε} (Beschriftung der Ein-/Ausgabebänder). K bezeichne die Menge aller Konfigurationen wir zeichnen folgende Konfigurationen aus: Anfang Ende die jeweils nächste / 82 2 / 82
4 Startkonfiguration S = {start(x ) = (,nd, x, ε) : x {,, 2} } nd bedeutet, dass die Registerinhalte nicht definiert sind Endkonfiguration E = {(b, c, e, a) : Befehl mit Nummer b ist end } Nachfolgekonfiguration sei K = (b, c, e, a) sei K die Konfiguration ist, die aus K durch Anwendung des Befehls b hervorgeht, falls er und seine Operanden definiert sind j K, falls b wohldefiniert δ(k ) = ε, sonst. dadurch wird eine partielle Funktion δ : K part. K definiert Sei K eine Konfiguration δ(k ) heißt die direkte Nachfolgekonfiguration sei δ = δ und δ m = δ(δ m ) δ m (K ) heißt die m-te Nachfolgekonfiguration, K ist (indirekte) Nachfolgekonfiguration von K, falls K = δ m (K ) für ein m δ (K ) := {δ m (K ) : m N, δ m (K ) definiert} 3 / 82 4 / 82 Eine RAM M berechnet folgende partielle Funktion: eine RAM M berechnet eine partielle Funktion, die intuitiv wie folgt definiert ist: 8 < a, falls die Berechnung mit a endet f M (x ) = Fehler, falls ein Fehler auftritt, : undefiniert, falls M in eine Endlosschleife gerät etwas formaler: 8 >< f M (x ) = >: a Fehler f M : {,, 2} part {,, 2} {Fehler} es existiert K = (b, c, e, a) δ (start(x )) E es existiert K δ (start(x ))\E, δ (K ) nicht definiert ε es existiert kein K δ (start(x )) E, aber mit jedem erreichten k K ist auch δ(k ) definiert 5 / 82 6 / 82
5 Gliederung Aufbau und Eigenschaften Einschub: Turing-Maschinen universelle RAM s RAM-Berechenbarkeit Nichtentscheidbarkeit Reduzierbarkeit Aufzählbarkeit Eine (deterministische) Turingmaschine besteht aus: Turingmaschinen einer Recheneinheit einem zweiseitig unbeschränkten Band (= Speicher) einem Schreib-/Lesekopf einer Übergangstabelle (Programm) # # # # # # Band Zustand z 3 Schreib /Lesekopf Übergangstabelle δ z z 2 z 3 # 7 / 82 8 / 82 Eine (deterministische) Turingmaschine besteht aus: Turingmaschinen einer Recheneinheit einem zweiseitig unbeschränkten Band (= Speicher) einem Schreib-/Lesekopf einer Übergangstabelle (Programm) ist stets in einem von endlich vielen Zuständen z Z hält (wenn sie hält) in einer Menge E Z von Endzuständen ist zu Beginn in einem Zustand z (Startzustand) Turingmaschinen das Band besteht aus Feldern, die mit den Zahlen i Z durchnumeriert sind jedes Feld enthält einen Buchstaben aus dem Alphabet A = {, } #, wobei # = blank zu Beginn steht die Eingabe x,..., x n mit x i # auf den Feldern i =,..., n alle anderen Felder enthalten # der Kopf steht über dem Feld in jedem Schritt liest der Kopf auf dem Feld, über dem er steht, einen Buchstaben 9 / 82 2 / 82
6 das Programm besteht aus der Übergangstabelle die Tabelle hat Z E Zeilen und drei Spalten Turingmaschinen für jeden Zustand und für jedes mögliche Zeichen auf dem Band beschreibt die Tabelle die nächste Aktion 8 >< δ(q, a) = >: (z, a, L) überschreibe a durch a, nimm Zustand z ein und gehe nach links (z, a, N) wie oben, bleibe stehen (z, a, R) wie oben, gehe nach rechts nd der Rechner stoppt mit einer Fehlermeldung Turingmaschinen wenn der Rechner ohne Fehlermeldung stoppt, so steht das Ergebnis rechts vom Kopf eine Konfiguration besteht aus einem Element αzβ aus A Z A mit α A, β A, wobei gilt: auf dem Band steht αβ, der Kopf steht über dem. Element von β, der Zustand ist z. die Tabelle definiert eine partielle Übergangsfunktion δ : Z E A part Z A {L, R, N} 2 / / 82 Turingmaschinen α z β ist direkte Nachfolgekonfiguration von αzβ, wenn diese Konfiguration durch einen Rechenschritt aus αzβ hervorgeht (indirekte) Nachfolgekonfigurationen sind entsprechend definiert F = A E A ist die Menge der Endkonfigurationen eine Turingmaschine M berechnet die partielle Funktion part f M : {, } {, } mit 8 < y, falls es eine Nachfolgekonfiguration f M (x ) = K = αzy von z x mit z E gibt : nd, sonst Turingmaschinen Beispiel Die folgende Maschine liest eine Binärzahl x, addiert eine und schreibt das Ergebnis wieder auf das Band: Lesezustand δ(z,) = (z,,r) δ(z,) = (z,,r) δ(z,#) = (z,#,l) /* lies die Zahl Übertragszustand δ(z,) = (z 2,,L) /* addiere δ(z,) = (z,,l) δ(z,#) = (e,,n) kein Übertrag δ(z 2,) = (z 2,,L) δ(z 2,) = (z 2,,L) δ(z 2,#) = (e,#,r) 23 / / 82
7 Gliederung Aufbau und Eigenschaften Einschub: Turing-Maschinen universelle RAM s RAM-Berechenbarkeit Nichtentscheidbarkeit Reduzierbarkeit Aufzählbarkeit RAM-Programmierung bisher ist das Programm in einer RAM fest installiert bei von-neumann-rechnern wird das Programm jedoch wie die Daten eingelesen und vom Rechner interpretiert wir wollen also versuchen, eine RAM zu konstruieren, die programmierbar ist. 25 / / 82 ein Programm besteht aus Befehlen B i der Befehlsliste jeder Befehl wird durch seine Nummer und einen Parameter kodiert. Befehle Anzahl der Parameter Bedeutung 3 7,, 2 Registeradresse 8, 9 Sprungadresse alle anderen ignorieren wie früher identifizieren wir das Alphabet über {,, 2} mit dem Alphabet über {, } dabei setzen wir = = = 2. die binäre Kodierung eines Programmes M bezeichnen wir mit G (M) sei M = (B, B 2,..., B l ) ein Programm die Kodierung G(M) von M ist das Tupel G(M) = (k, Nummer(B ), Parameter(B ),..., Nummer(B k ), Parameter(B k ), 2, 2) alle Zahlen sind binär kodiert und durch Zweien getrennt 27 / / 82
8 der erste Schritt beim Ablauf eines Programms könnte eine Syntaxanalyse sein die Eingabe besteht dann aus zwei Teilen: dem Programm gefolgt vom Input für das Programm verläuft die Syntaxanalyse erfolgreich, wird danach das Programm gestartet Lemma Es gibt eine RAM, die bei Eingabe von x {, } entscheidet, ob x die Kodierung eines Programms ist. Beweisskizze: a) Berechne aus x die dargestellten Dezimalzahlen x,..., x n und deren Anzahl n b) speichere sie in den ersten Registern,..., n + ab. die Syntaxanalyse kann mit einer RAM durchgeführt werden: Lemma Es gibt eine RAM, die bei Eingabe von x {, } entscheidet, ob x die Kodierung eines Programms ist. c) Teste, ob n = 2x + d) Teste, ob jedes x i, i gerade, aus {,..., 3} ist. e) Teste, ob für jedes x i, i gerade, gilt: (x i {, 2,, 3} x i+ = ) Wir werden im weiteren eine RAM mit ihrem Programm identifizieren. 29 / 82 3 / 82 sei M eine RAM M heißt universell oder programmierbar, falls: für jedes Programm M und jeden Input x = (x,..., x n ) {,, 2} gilt: M simuliert M, d.h. M gefüttert mit der Kodierung von M gefolgt von x liefert M(x ) f M (G(M), x ) = f M (x ) Beweisidee: das Programm von M besteht aus drei Teilen: dem Hauptprogramm einer Syntaxanalyse einem Simulationsprogramm für jeden Befehlsytyp zuerst wird eine Syntaxanalyse durchgeführt danach wird jeder Befehl von M per Unterprogramm simuliert Satz Es existiert eine universelle RAM M. 3 / / 82
9 Satz Es existiert eine universelle RAM M. Beweisskizze: Wir bezeichnen die Größen, die sich auf die Maschine M beziehen, mit dem Index. führe auf M eine Syntaxanalyse durch. (a) falls der erste Teil des Inputs kein Programm ist, gib eine Fehlermeldung aus und stoppe (b) andernfalls sei der Input G(M) = (k, B, P, B 2, P 2,...) in den ersten Registern (,..., 2k + ). 2. teile die M -Register auf in die mit geradem und mit ungeradem Index die geraden simulieren die M-Register (identifiziere i 2i + 2) die ungeraden werden als Arbeitsspeicher und zur Speicherung des Programms G(M) genutzt 3. kopiere G(M) in die Register (3, 5,..., 4k + 3), setze c () = 5 4. simuliere M auf M. Es soll stets gelten: ist M nach t Schritten in Konfiguration (b, c, e, a), dann gilt für M nach t Simulationsschritten: c () = b, e = e, a = a (c (3),..., c (4k + 3)) = G(M) c (2i + 2) = c(i), i =,... b = erster Befehl des Simulationsprogramms 33 / / simuliere M auf M. Es soll stets gelten: sei M nach t Schritten in Konfiguration (b, c, e, a) dann gilt für M nach t Simulationsschritten: c () = b, e = e, a = a (c (3),..., c (4l + 3)) = G(M) c (2i + 2) = c(i), i =,... b = erster Befehl des Simulationsprogramms 5. Simulation a) für jeden Befehl besitzt M ein Unterprogramm, das ihn simuliert b) schreibe die Nummer und den Parameter des Befehls in die Register 3 und 5 Beispiel: goto k c-load /* lade die Konstante */ store 7 /* speichere im Register 7 */ load 5 /* Sprungadresse */ sub 7 /* Akku = k */ add /* Akku = 2(k ) */ add /* Akku = 4(k ) */ store 9 /* speichere 4(k ) im Register 9 */ c-load 5 /* lade die Konstante 5 */ add 9 /* Akku = 5 + 4(k ) */ store /* c () enthält nächsten Befehl */ c) führe den Befehl mit Nummer c (3) und Parameter c (5) aus 35 / / 82
10 Beispiel: store k c-load /* c () = */ add 5 /* c () = k + */ add /* c () = 2k + 2 berechne neue Adresse */ store 7 /* c (7) = 2k + 2 speichere neue Adresse */ load 2 /* c () = c()(= c (2)) lade Akku von M in den Akku von M */ i-store 7 /* c (c (7)) = c (2k + 2) = c() speichere */ Gliederung Aufbau und Eigenschaften universelle RAM s RAM-Berechenbarkeit Nichtentscheidbarkeit Reduzierbarkeit Aufzählbarkeit 37 / / 82 sei f : {,, 2} part {,, 2} eine partielle Funktion f heißt berechenbar (genauer: RAM-berechenbar), falls es eine Registermaschine M gibt mit f M = f, d.h. ist f (x ) definiert, so schreibt M f (x ) auf das Ausgabeband ist f (x ) nicht definiert, so hält M nicht (gerät in den Fehlermodus oder in den nicht definierten Zustand). insbesondere ist die nirgends definierte Funktion nd durch die RAM M nd, die nie hält, berechenbar. der Begriff Berechenbarkeit ist mit verschiedenen Konzepten formuliert worden wir werden im nächsten Kapitel die Berechenbarkeit mittels Turing-Maschinen untersuchen es hat sich herausgestellt, dass all diese Konzepte äquivalent sind obwohl sie alle Abstraktionen von existierenden Maschinen sind, hat Church die Vermutung geäußert, dass diese Abstraktionen nicht mächtiger sind als die realen Maschinen: 39 / 82 4 / 82
11 Church sche These: Die in einem intuitiven Sinne berechenbaren Funktionen sind genau die berechenbaren Funktionen. wir haben bisher RAM-Programme mit ihrer Kodierung identifiziert wir können ein solches Wort über {, } auch als Binärdarstellung einer Dezimalzahl auffassen dazu benutzen wir die folgende Abbildung: dies ist keine Aussage im Sinne der Mathematik insbesondere ist der unpräzise Begriff intuitiv berechenbar nicht definiert er soll ausdrücken, dass alles, was auf einem abstrakten Rechnermodell berechnet werden kann, auch auf realen Maschinen berechnet werden kann sei x = (x n,..., x ) {, } sei d : {, } N\{} definiert durch j, d (x ) = P n i= 2i x i + 2 n+, d (G (M)) heißt Gödelnummer von M. für x = ε sonst 4 / / 82 j, für x = ε d (x ) = P n i= 2i x i + 2 n+, sonst d berechnet nicht die von x definierte Dezimalzahl d (x ) = 2 n+ + (x n,..., x ) 2 so kann zwischen () und () unterschieden werden 43 / 82 Lemma d : {, } N {} ist bijektiv und RAM-berechenbar. Beweisskizze: die Berechenbarkeit ergibt sich analog zur Umrechnung einer Binärzahl in die Dezimalzahl seien x = (x m,..., x ), y = (y n,..., y ) {, } mit x y dann ist entweder m n oder (x m,..., x ) 2 (y n,..., y ) 2 sei umgekehrt k N {} sei n die größte natürliche Zahl mit 2 n+ k dann ist k 2 n+ < 2 n+ sei x = (x n,..., x ) die Binärdarstellung von k 2 n+, evtl. mit führenden Nullen aufgefüllt dann ist d (x ) = k daraus folgt die Bijektivität. 44 / 82
12 Wir können somit RAM-Programme M identifizieren mit: ihrer binären Kodierung G(M) {, } ihrer Gödelnummer d (G (M)) N {} ebenso können wir jede Folge x {, } mit ihrer Gödelnummer identifizieren wir sagen: k N {} oder x {, } ist eine RAM damit können wir den Input für eine universelle RAM als Paar (k, l) auffassen k N {} ist die Gödelnummer des Programms l N {} ist die Gödelnummer des Inputs Gliederung Aufbau und Eigenschaften universelle RAM s RAM-Berechenbarkeit Nichtentscheidbarkeit Reduzierbarkeit Aufzählbarkeit 45 / / 82 Bemerkung nach der Church schen These sind die berechenbaren Funktionen genau die Funktionen, die wir auf realen Rechnern berechnen können was lässt sich also RAM-berechnen? wir werden zeigen, dass es Funktionen gibt, die auf keiner RAM berechnet werden können um die Beweisidee klar zu machen, betrachten wir folgende Analogie: Es gibt Funktionen f : {, } {, }, die nicht durch ein C-Programm berechenbar sind. Beweis: Wir benutzen zwei Eigenschaften: ) Jedes C-Programm ist ein endlicher Text über einem endlichen Alphabet A. 2) Jedes C-Programm berechnet eine Funktion f : A A {Programm hält nicht}. 47 / / 82
13 ) Jedes C-Programm ist ein endlicher Text über einem endlichen Alphabet A. 2) Jedes C-Programm berechnet eine Funktion f : A A {Programm hält nicht}. aus der ersten Eigenschaft folgt, dass die Menge P aller C-Programme abzählbar ist sei P P die Teilmenge aller Programme, die eine Funktion f : {, } {, } berechnen (also halten und einen Output in {, } erzeugen) enthält P zwei Programme, die dieselbe Funktion berechnen, so entfernen wir jeweils eines dieser Programme dann ist P ebenfalls abzählbar wir identifizieren P mit den Funktionen, die von P berechnet werden sei {f, f 2,... } eine Aufzählung von P wir stellen uns jetzt die f i (x j ) in Matrixform aufgeschrieben vor: f f f f f x x x x x x x ebenso ist die Menge {, } aufzählbar sei x =, x 2 =, x 3 =, x 4 =, x 5 =,... eine solche Aufzählung 49 / 82 5 / 82 betrachte die aus der Diagonalen abgeleitete Funktion: f f f f f x x x x x x x sowie die invertierte Funktion f : etwas formaler: f (x ) f (x 2 ) f (x 3 )... f 2 (x ) f 2 (x 2 ) f 2 (x 3 )... f 3 (x ) f 3 (x 2 ) f 3 (x 3 ) betrachte die aus der Diagonalen abgeleitete Funktion: zu jedem x {, } existiert genau ein j mit x = x j setze f (x ) = f j (x j ). angenommen f P dann existiert ein i mit f = f i an der Stelle x = x i gilt f (x i ) = f i (x i ) f i (x i ) = f (x i ) damit kann f nicht von einem C-Programm berechnet werden f kann in der Tabelle nicht vorkommen. 5 / / 82
14 wir haben bei den berechenbaren Funktionen stets Abbildungen {, } {, } betrachtet wie bei den C-Programmen vereinfachen wir die Fragestellung wir betrachten jetzt Abbildungen {, } {, } es reicht sicherlich, unter diesen Abbildungen eine als nicht berechenbar nachzuweisen anschaulich interessiert uns im weiteren das folgende Problem: ist die Antwort auf eine gegebene Frage ja oder nein? genauer gesagt: können wir entscheiden, ob die Antwort auf eine kodierte Frage x {, } oder ist? äquivalent dazu ist: gegeben x {, } entscheide, ob x f () sei L = f () der Urbilder der L ist als Menge von Wörtern eine Sprache wir fragen also, ob das Spracherkennungsproblem: gegeben L {, } und x {, }, ist x L? mittels einer RAM beantwortet werden kann. 53 / / 82 sei L eine Sprache die charakteristische Funktion χ L von L ist gegeben durch: χ L (x ) = x L L heißt entscheidbar, wenn χ L (x ) berechenbar ist Eine RAM akzeptiert L, falls sie χ L berechnet wir haben gesehen, dass wir mit Hilfe der Syntaxanalyse entscheiden können, ob k die Gödelnummer eines syntaktisch korrekten RAM-Programms ist wir wenden uns jetzt der Frage zu, ob wir einem RAM-Programm ansehen können, ob es bei gegebenem Input hält seien (k, l) (N {}) (N {}) sei H = {(k, l) : k ist eine RAM M und M mit Input l hält } 55 / / 82
15 Satz (Halteproblem) H ist nicht entscheidbar. Beweis: wir führen wieder den Diagonalisierungstrick durch angenommen, es existiert eine solche RAM M, die H entscheidet dann lässt sich eine zweite RAM M konstruieren mit j M, falls M(n, n) = (n, n) = nd, sonst im zweiten Fall hält M also nicht j M, falls M(n, n) = (n, n) = nd, sonst da M eine RAM ist, existiert eine Gödelnummer k von M was passiert, wenn wir M mit (k, k ) starten? M(k, k ) = M mit Input k hält M (k, k ) = M(k, k ) = d.h. M kann nicht existieren. 57 / / 82 Gliederung Aufbau und Eigenschaften universelle RAM s RAM-Berechenbarkeit Nichtentscheidbarkeit Reduzierbarkeit Aufzählbarkeit mit dem Halteproblem haben wir ein erstes Problem als unentscheidbar erkannt das folgende Konzept wird uns helfen, weitere Probleme zu finden: seien L und L zwei Sprachen über dem Alphabet A L heißt reduzierbar auf L, wenn es eine berechenbare Funktion f : A A gibt mit x L f (x ) L Notation: L L L L L L, denn: die Umkehrfunktion muss nicht existieren wenn sie existiert, muss sie nicht berechenbar sein 59 / 82 6 / 82
16 Lemma (i) ist transitiv (ii) L L, L nicht entscheidbar = L nicht entscheidbar. Beweis: (i) sei L reduzierbar auf L mittels der berechenbaren Funktion f sei L reduzierbar auf L mittels der berechenbaren Funktion g dann gilt: x L f (x ) L und y L g(y ) L damit ist x L g(f (x )) L. g f ist berechenbar (schalte die beiden Programme hintereinander) damit folgt L L. Lemma (i) ist transitiv. (ii) L L, L nicht entscheidbar = L nicht entscheidbar. Beweis: (ii) ist L L mittels einer berechenbaren Funktion f, so ist χ L (x ) = x L f (x ) L χ L (f (x )) =, d.h. χ L = χ L f wäre L entscheidbar, so wäre per Definition χ L berechenbar da auch f berechenbar ist, folgt χ L f berechenbar somit wäre auch χ L berechenbar und damit L entscheidbar. 6 / / 82 Satz Die folgenden Sprachen sind nicht entscheidbar: (i) H = {k : k ist eine RAM, die bei Input hält} (ii) H = {k : k ist eine RAM, die immer hält} Beweis: (i) wir zeigen H H wir müssen dazu eine berechenbare Funktion f konstruieren, so dass (k, l) H f (k, l) H sei k die Gödelnummer einer RAM und l die Gödelnummer eines Inputs wir konstruieren eine zweite RAM mit Gödelnummer k wie folgt: bei Eingabe einer Null verhält sich k wie k mit Eingabe l wird keine Null eingegeben, so geht k in eine Endlosschleife sei k die Gödelnummer einer RAM und l die Gödelnummer eines Inputs wir konstruieren eine zweite RAM mit Gödelnummer k wie folgt: bei Eingabe einer Null verhält sich k wie k mit Eingabe l wird keine Null eingegeben, so geht k in eine Endlosschleife wir behaupten, dass die folgende Funktion f : N {} N {} N {} eine Reduktionsfunktion ist: j k f (k, l) =, falls k Gödelnummer einer RAM (k, l), sonst f ist berechenbar: führe Syntaxanalyse von k durch falls positiv, gib Kodierung von k aus, andernfalls (k, l) (k, l) H k ist eine RAM, die bei Input l hält f (k, l) = k und k mit Input hält f (k, l) H. 63 / / 82
17 Satz Die folgenden Sprachen sind nicht entscheidbar: (i) H = {k : k ist eine RAM, die bei Input hält} (ii) H = {k : k ist eine RAM, die immer hält} Bemerkung: mit L ist auch L = {, } L entscheidbar, denn χ L = χ L. Beweis: (ii) Wir zeigen H H. sei dazu k die Gödelnummer einer RAM sei k die Gödelnummer einer RAM, die sich für jeden Input wie k gestartet mit verhält. folgende Funktion ist berechenbar wir haben gesehen, dass eine RAM einer anderen nicht ansehen kann, ob sie hält oder an der Stelle definiert ist wir wollen zeigen, dass wir überhaupt keine speziellen Eigenschaften testen können j k f (k ) =, k, falls k eine RAM sonst k H k ist eine RAM, die bei Input hält f (k ) = k und k hält immer f (k ) H. 65 / / 82 zwei RAM-Programme heißen äquivalent, wenn sie dieselbe partielle Funktion berechnen eine semantische Eigenschaft eines Programms ist eine Eigenschaft, die allen äquivalenten Programmen gemein ist Beispiele: bei Eingabe halten immer halten zieht die Wurzel aus dem Input berechnet die Funktion f nicht semantische Eigenschaften: verwendet keinen Sprungbefehl enthält mehr als 9 Anweisungen Satz (Rice) Eine semantische Eigenschaft von RAMs ist genau dann entscheidbar, wenn alle RAMs diese Eigenschaft haben oder keine. Beweis: sei E eine semantische Eigenschaft sei E = {k : k ist eine RAM mit Eigenschaft E} haben alle RAMs die Eigenschaft E, so ist E mittels Syntaxanalyse zu entscheiden hat keine RAM die Eigenschaft E, so ist E = und einfach zu entscheiden. 67 / / 82
18 sei umgekehrt E eine Eigenschaft, die eine nichttriviale Teilmenge aller RAMs besitzen sei nd die überall nicht definierte Funktion nd ist berechenbar (nach einer früheren Beobachtung) wir unterscheiden zwei Fälle: a) nd hat Eigenschaft E oder b) nd hat Eigenschaft E nicht wir unterscheiden zwei Fälle: a) nd hat Eigenschaft E oder b) nd hat Eigenschaft E nicht im ersten Fall zeigen wir H E nach früheren Lemma ist dann E nicht entscheidbar damit ist auch E nicht entscheidbar im zweiten Fall zeigt man analog H E wir beschränken uns im folgenden auf den ersten Fall. 69 / 82 7 / 82 sei k eine RAM, die die Eigenschaft E nicht besitzt zu einer beliebigen RAM m bauen wir eine RAM m, die bei Input l folgendes leistet: m verhält sich wie m mit Input falls m mit Input hält, verhält sich m wie k mit Input l j k (l), falls m d.h. m H (l) = undefiniert, sonst als Reduktionsfunktion wählen wir j m, falls m H f (m) = undefiniert, sonst j k (l), falls m d.h. m H (l) = undefiniert, sonst als Reduktionsfunktion wählen wir j m, falls m H f (m) = undefiniert, sonst ) f ist berechenbar (lass M mit Input laufen, wenn M hält, gib M aus) 2a) m H m hält an der Stelle f (m) = m und m mit Input l berechnet k (l) f (m) ist eine RAM ohne Eigenschaft E f (m) E 2b) m H m hält an der Stelle nicht f (m) = nd E 7 / / 82
19 bisher haben wir Probleme betrachtet, die nach dem Halten oder Nichthalten von fragen unter den nichtentscheidbaren Problemen gibt es auch natürlichere Fragestellungen Postsches Korrespondenzproblem gegeben: eine Menge von Paaren binärer Wörter {(x, y ), (x 2, y 2 ),..., (x n, y n )} gesucht: Indices i j, j =,... k mit i j n, so dass x i x i2... x ik = y i y i2... y ik Bemerkungen: es ist zugelassen, dass Indizes der Eingabefolge mehrmals auftauchen die Anzahl k der zu bestimmenden Paare ist a priori nicht beschränkt es sind Umsortierungen erlaubt, d.h. i j+ < i j Beispiel: die Paare (, ), (, ), (, ) haben die Lösung 2,,, 3 das Korrespondenzproblem, das in der Theorie formaler Sprachen eine Rolle spielt, ist nicht entscheidbar 73 / / 82 bisher haben wir Probleme betrachtet, die nach dem Halten oder Nichthalten von fragen unter den nichtentscheidbaren Problemen gibt es auch natürlichere Fragestellungen Postsches Korrespondenzproblem gegeben: eine Menge von Paaren binärer Wörter {(x, y ), (x 2, y 2 ),..., (x n, y n )} gesucht: Indices i j, j =,... k mit i j n, so dass x i x i2... x ik = y i y i2... y ik Gliederung Aufbau und Eigenschaften universelle RAM s RAM-Berechenbarkeit Nichtentscheidbarkeit Reduzierbarkeit Aufzählbarkeit das Korrespondenzproblem, das in der Theorie formaler Sprachen eine Rolle spielt, ist nicht entscheidbar 75 / / 82
20 ein untauglicher Versuch für das Halteproblem: gegeben (k, l), führe die RAM k mit Input l aus wenn k hält, ist die Antwort auf das Halteproblem klar, andernfalls können wir k nicht einfach abbrechen und behaupten, k halte nicht diese Beobachtung führt auf das folgende Konzept es hat zur Strukturierung nichtentscheidbarer Probleme beigetragen sei L {, } ein Sprache L ist (rekursiv) aufzählbar, wenn es eine total berechenbare Funktion f : {, } {, } gibt mit f ({, } ) = L identifizieren wir {, } mit N, dann zählt f : N {, } alle Elemente von L auf (eventuell mit Wiederholungen) schwächer als Berechenbarkeit: wir füttern f nacheinander mit, 2, 3,... f erzeugt eine Liste f (), f (2), f (3),... ist x L, so wird x irgendwann in der Liste erscheinen d.h., ist x L, so liefert f einen Nachweis dafür der Nachweis versagt jedoch, falls x / L. 77 / / 82 Vorsicht vor Verwechslungen von aufzählbar mit abzählbar wir haben gesehen, dass die partiell berechenbaren Funktionen aufzählbar sind: erzeuge nacheinander alle {, }-Folgen interpretiere jede {, }-Folge als Kodierung eines RAM-Programms entferne die Folgen, die die Syntaxanalyse nicht passieren die total berechenbaren Funktionen sind jedoch nicht aufzählbar: angenommen f, f 2,... wäre eine solche Aufzählung sei g(n) = f n (n) + dann ist g total und berechenbar aber g ist nicht in der Aufzählung enthalten. dies ist wieder der Diagonalisierungstrick er versagt bei den partiellen Funktionen, weil diese auf der Diagonale nicht definiert sein müssen 79 / 82 8 / 82
21 Satz Eine Sprache L ist genau dann entscheidbar, wenn L und L aufzählbar sind. Beweisskizze: (i) sei M eine RAM, die L akzeptiert baue zwei RAMs M, M, die das folgende leisten: für einen gegeben Input x lassen beide M laufen gibt M eine aus, so schreiben M x und M ε auf ihr Ausgabeband gibt M eine aus, so schreiben M x und M ε auf ihr Ausgabeband dann gilt: f M = L und f M = L. Satz Eine Sprache L ist genau dann entscheidbar, wenn L und L aufzählbar sind. Beweisskizze: (ii) seien umgekehrt M und M 2 zwei RAM s, die L bzw. L aufzählen baue eine neue RAM M, die zu einem gegeben Input x das folgende leistet: für i =, 2,... füttert sie M und M 2 abwechselnd mit i M vergleicht die beiden Outputs mit x ist der Output von M gleich x, so gibt M eine aus und hält ist der Output von M 2 gleich x, so gibt M eine aus und hält andernfalls wird i erhöht dann ist f M = L. 8 / / 82
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik 0 KIT 17.05.2010 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik nationales Forschungszentrum Vorlesung in am
Theoretische Grundlagen der Informatik 0 KIT 17.05.2010 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik nationales Forschungszentrum Vorlesung in am
Informatik II. Turingmaschinen. Turingmaschinen. Turingmaschinen. Rainer Schrader. 14. Dezember 2005
 Informatik II Rainer Schrader Zentrum für Angewandte Informatik Köln 14. Dezember 2005 1 / 76 2 / 76 Gliederung Aufbau und Eigenschaften Maße für Zeit- und Platzbedarf Simulation RAM/Turingmaschine nichtdeterministische
Informatik II Rainer Schrader Zentrum für Angewandte Informatik Köln 14. Dezember 2005 1 / 76 2 / 76 Gliederung Aufbau und Eigenschaften Maße für Zeit- und Platzbedarf Simulation RAM/Turingmaschine nichtdeterministische
Theoretische Informatik. 1. Turingmaschinen. Rainer Schrader. 16. April Institut für Informatik. Turingmaschinen.
 Theoretische Informatik Rainer Schrader. Institut für Informatik 6. April 202 / 97 2 / 97 die Kapitelüberschrift leitet sich ab von Gliederung Aufbau und Eigenschaften Maße für Zeit- und Platzbedarf Programmierung
Theoretische Informatik Rainer Schrader. Institut für Informatik 6. April 202 / 97 2 / 97 die Kapitelüberschrift leitet sich ab von Gliederung Aufbau und Eigenschaften Maße für Zeit- und Platzbedarf Programmierung
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik 0 KIT 07.11.2014 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik nationales Forschungszentrum Vorlesung in am
Theoretische Grundlagen der Informatik 0 KIT 07.11.2014 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik nationales Forschungszentrum Vorlesung in am
Halteproblem/Kodierung von Turing-Maschinen
 Halteproblem/Kodierung von Turing-Maschinen Unser Ziel ist es nun zu zeigen, dass das sogenannte Halteproblem unentscheidbar ist. Halteproblem (informell) Eingabe: Turing-Maschine M mit Eingabe w. Frage:
Halteproblem/Kodierung von Turing-Maschinen Unser Ziel ist es nun zu zeigen, dass das sogenannte Halteproblem unentscheidbar ist. Halteproblem (informell) Eingabe: Turing-Maschine M mit Eingabe w. Frage:
Informatik III. Christian Schindelhauer Wintersemester 2006/ Vorlesung
 Informatik III Christian Schindelhauer Wintersemester 2006/07 13. Vorlesung 07.12.2006 1 Überblick: Die Church- Turing-These Turing-Maschinen 1-Band Turing-Maschine Mehrband-Turing-Maschinen Nichtdeterministische
Informatik III Christian Schindelhauer Wintersemester 2006/07 13. Vorlesung 07.12.2006 1 Überblick: Die Church- Turing-These Turing-Maschinen 1-Band Turing-Maschine Mehrband-Turing-Maschinen Nichtdeterministische
Berechenbarkeit und Komplexität: Probleme, Sprachen, Maschinen
 Berechenbarkeit und Komplexität: Probleme, Sprachen, Maschinen Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität 25. Oktober 2006 Was ist ein Problem? Informelle Umschreibung
Berechenbarkeit und Komplexität: Probleme, Sprachen, Maschinen Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität 25. Oktober 2006 Was ist ein Problem? Informelle Umschreibung
1 Einführung. 2 Typ-0- und Typ-1-Sprachen. 3 Berechnungsmodelle. 4 Unentscheidbarkeit. 5 Unentscheidbare Probleme. 6 Komplexitätstheorie
 1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie WS 11/12 155 Überblick Zunächst einmal definieren wir formal den Begriff
1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie WS 11/12 155 Überblick Zunächst einmal definieren wir formal den Begriff
Kontextsensitive und Typ 0 Sprachen Slide 2. Die Turingmaschine
 Kontextsensitive und Typ 0 Sprachen Slide 2 Die Turingmaschine DTM = Deterministische Turingmaschine NTM = Nichtdeterministische Turingmaschine TM = DTM oder NTM Intuitiv gilt: DTM = (DFA + dynamischer
Kontextsensitive und Typ 0 Sprachen Slide 2 Die Turingmaschine DTM = Deterministische Turingmaschine NTM = Nichtdeterministische Turingmaschine TM = DTM oder NTM Intuitiv gilt: DTM = (DFA + dynamischer
Random Access Machine (RAM) Berechenbarkeit und Komplexität Random Access Machines
 Random Access Machine (RAM) Berechenbarkeit und Komplexität Random Access Machines Wolfgang Schreiner Wolfgang.Schreiner@risc.jku.at Research Institute for Symbolic Computation (RISC) Johannes Kepler University,
Random Access Machine (RAM) Berechenbarkeit und Komplexität Random Access Machines Wolfgang Schreiner Wolfgang.Schreiner@risc.jku.at Research Institute for Symbolic Computation (RISC) Johannes Kepler University,
1 Einführung. 2 Typ-0- und Typ-1-Sprachen. 3 Berechnungsmodelle. 4 Unentscheidbarkeit. 5 Unentscheidbare Probleme. 6 Komplexitätstheorie
 1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie 139 Unentscheidbarkeit Überblick Zunächst einmal definieren wir formal
1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie 139 Unentscheidbarkeit Überblick Zunächst einmal definieren wir formal
Informatik III. Arne Vater Wintersemester 2006/ Vorlesung
 Informatik III Arne Vater Wintersemester 2006/07 11. Vorlesung 30.11.2006 1 Beziehungen zwischen den Sprachen Jede reguläre Sprache ist eine kontextfreie Sprache. Jede kontextfreie Sprache ist eine entscheidbare
Informatik III Arne Vater Wintersemester 2006/07 11. Vorlesung 30.11.2006 1 Beziehungen zwischen den Sprachen Jede reguläre Sprache ist eine kontextfreie Sprache. Jede kontextfreie Sprache ist eine entscheidbare
Das Halteproblem für Turingmaschinen
 Das Halteproblem für Turingmaschinen Das Halteproblem für Turingmaschinen ist definiert als die Sprache H := { T w : T ist eine TM, die bei Eingabe w {0, 1} hält }. Behauptung: H {0, 1} ist nicht entscheidbar.
Das Halteproblem für Turingmaschinen Das Halteproblem für Turingmaschinen ist definiert als die Sprache H := { T w : T ist eine TM, die bei Eingabe w {0, 1} hält }. Behauptung: H {0, 1} ist nicht entscheidbar.
Einführung in die Theoretische Informatik
 Einführung in die Theoretische Informatik Johannes Köbler Institut für Informatik Humboldt-Universität zu Berlin WS 2011/12 Die Registermaschine (random access machine, RAM) 0 I 0 1 I 1 2 I 2 m I m Programm
Einführung in die Theoretische Informatik Johannes Köbler Institut für Informatik Humboldt-Universität zu Berlin WS 2011/12 Die Registermaschine (random access machine, RAM) 0 I 0 1 I 1 2 I 2 m I m Programm
Theoretische Informatik. nichtdeterministische Turingmaschinen NDTM. Turingmaschinen. Rainer Schrader. 29. April 2009
 Theoretische Informatik Rainer Schrader nichtdeterministische Turingmaschinen Zentrum für Angewandte Informatik Köln 29. April 2009 1 / 33 2 / 33 Turingmaschinen das Konzept des Nichtdeterminismus nahm
Theoretische Informatik Rainer Schrader nichtdeterministische Turingmaschinen Zentrum für Angewandte Informatik Köln 29. April 2009 1 / 33 2 / 33 Turingmaschinen das Konzept des Nichtdeterminismus nahm
Falls H die Eingabe verwirft, so wissen wir, dass M bei Eingabe w nicht hält. M hält im verwerfenden Haltezustand. Beweis:
 1 Unentscheidbarkeit 2 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 #include char *s="include
1 Unentscheidbarkeit 2 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 #include char *s="include
Entscheidungsprobleme
 Entscheidungsprobleme übliche Formulierung gegeben: Eingabe x aus einer Grundmenge U Frage: Hat x eine bestimmte Eigenschaft P? Beispiel: gegeben: Frage: n N Ist n eine Primzahl? Formalisierung: Grundmenge
Entscheidungsprobleme übliche Formulierung gegeben: Eingabe x aus einer Grundmenge U Frage: Hat x eine bestimmte Eigenschaft P? Beispiel: gegeben: Frage: n N Ist n eine Primzahl? Formalisierung: Grundmenge
2.5 Halteproblem und Unentscheidbarkeit
 38 25 Halteproblem und Unentscheidbarkeit Der Berechenbarkeitsbegriff ist auf Funktionen zugeschnitten Wir wollen nun einen entsprechenden Begriff für Mengen einführen Definition 255 Eine Menge A Σ heißt
38 25 Halteproblem und Unentscheidbarkeit Der Berechenbarkeitsbegriff ist auf Funktionen zugeschnitten Wir wollen nun einen entsprechenden Begriff für Mengen einführen Definition 255 Eine Menge A Σ heißt
Theoretische Informatik für Wirtschaftsinformatik und Lehramt
 Theoretische Informatik für Wirtschaftsinformatik und Lehramt Entscheidungsprobleme Priv.-Doz. Dr. Stefan Milius stefan.milius@fau.de Theoretische Informatik Friedrich-Alexander Universität Erlangen-Nürnberg
Theoretische Informatik für Wirtschaftsinformatik und Lehramt Entscheidungsprobleme Priv.-Doz. Dr. Stefan Milius stefan.milius@fau.de Theoretische Informatik Friedrich-Alexander Universität Erlangen-Nürnberg
Ein formales Berechnungsmodell: Turingmaschinen. Turingmaschinen 26 / 62
 Ein formales Berechnungsmodell: Turingmaschinen Turingmaschinen 26 / 62 Ein formales Rechnermodell Bisher haben wir abstrakt von Algorithmen bzw. Programmen gesprochen und uns dabei JAVA- oder C++-Programme
Ein formales Berechnungsmodell: Turingmaschinen Turingmaschinen 26 / 62 Ein formales Rechnermodell Bisher haben wir abstrakt von Algorithmen bzw. Programmen gesprochen und uns dabei JAVA- oder C++-Programme
Theoretische Informatik Mitschrift
 Theoretische Informatik Mitschrift 9. Berechenbarkeit, Entscheidbarkeit, Aufzählbarkeit 9.1 Grundbegriffe bereits gezeigt: Spracherkennung durch Turingmaschine = Berechnung der semi-charakteristischen
Theoretische Informatik Mitschrift 9. Berechenbarkeit, Entscheidbarkeit, Aufzählbarkeit 9.1 Grundbegriffe bereits gezeigt: Spracherkennung durch Turingmaschine = Berechnung der semi-charakteristischen
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Turingmaschinen und rekursiv aufzählbare Sprachen (V) 7.07.2016 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik Turingmaschinen und rekursiv aufzählbare Sprachen (V) 7.07.2016 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Berechenbarkeit und Komplexität: Rekursive Aufzählbarkeit und die Technik der Reduktion
 Berechenbarkeit und Komplexität: Rekursive Aufzählbarkeit und die Technik der Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität 26. November 2007 Semi-Entscheidbarkeit
Berechenbarkeit und Komplexität: Rekursive Aufzählbarkeit und die Technik der Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität 26. November 2007 Semi-Entscheidbarkeit
Theoretische Informatik und Logik Übungsblatt 1 (2016S) Lösung
 Theoretische Informatik und Logik Übungsblatt (26S) en Aufgabe. Sei L = {w#w r w {, } }. Geben Sie eine deterministische Turingmaschine M an, welche die Sprache L akzeptiert. Wählen Sie mindestens einen
Theoretische Informatik und Logik Übungsblatt (26S) en Aufgabe. Sei L = {w#w r w {, } }. Geben Sie eine deterministische Turingmaschine M an, welche die Sprache L akzeptiert. Wählen Sie mindestens einen
Reduktionen. Formalisierung von Sprache A ist nicht schwerer als Sprache B.
 Reduktionen Formalisierung von Sprache A ist nicht schwerer als Sprache B. Idee: Algorithmus/DTM für B kann genutzt werden, um A zu entscheiden/akzeptieren. WS 2018/19 Reduktionen 1 Zwei einfache Sprachen
Reduktionen Formalisierung von Sprache A ist nicht schwerer als Sprache B. Idee: Algorithmus/DTM für B kann genutzt werden, um A zu entscheiden/akzeptieren. WS 2018/19 Reduktionen 1 Zwei einfache Sprachen
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 17.November 2011 INSTITUT FÜR THEORETISCHE 0 KIT 17.11.2011 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Theoretische Grundlagen der Informatik Vorlesung am 17.November 2011 INSTITUT FÜR THEORETISCHE 0 KIT 17.11.2011 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Theoretische Grundlagen der Informatik. Vorlesung am 07. November INSTITUT FÜR THEORETISCHE INFORMATIK
 Theoretische Grundlagen der Informatik 0 07.11.2017 Torsten Ueckerdt - Theoretische Grundlagen der Informatik KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Frage Frage: Ist der
Theoretische Grundlagen der Informatik 0 07.11.2017 Torsten Ueckerdt - Theoretische Grundlagen der Informatik KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Frage Frage: Ist der
1.5 Turing-Berechenbarkeit
 A.M. Turing (1937): Maschinenmodell zur exakten Beschreibung des Begriffs effektiv berechenbar Stift Mensch a c b b Rechenblatt a b b c Lese-/Schreibkopf endliche Kontrolle Turingmaschine Eine Turingmaschine
A.M. Turing (1937): Maschinenmodell zur exakten Beschreibung des Begriffs effektiv berechenbar Stift Mensch a c b b Rechenblatt a b b c Lese-/Schreibkopf endliche Kontrolle Turingmaschine Eine Turingmaschine
Berechenbarkeit. Script, Kapitel 2
 Berechenbarkeit Script, Kapitel 2 Intuitiver Berechenbarkeitsbegriff Turing-Berechenbarkeit WHILE-Berechenbarkeit Church sche These Entscheidungsprobleme Unentscheidbarkeit des Halteproblems für Turingmaschinen
Berechenbarkeit Script, Kapitel 2 Intuitiver Berechenbarkeitsbegriff Turing-Berechenbarkeit WHILE-Berechenbarkeit Church sche These Entscheidungsprobleme Unentscheidbarkeit des Halteproblems für Turingmaschinen
Unentscheidbarkeitssätze der Logik
 Unentscheidbarkeitssätze der Logik Elmar Eder () Unentscheidbarkeitssätze der Logik 1 / 30 Die Zahlentheorie ist nicht formalisierbar Satz (Kurt Gödel) Zu jedem korrekten formalen System der Zahlentheorie
Unentscheidbarkeitssätze der Logik Elmar Eder () Unentscheidbarkeitssätze der Logik 1 / 30 Die Zahlentheorie ist nicht formalisierbar Satz (Kurt Gödel) Zu jedem korrekten formalen System der Zahlentheorie
1.5 Turing-Berechenbarkeit
 A.M. Turing (1937): Maschinenmodell zur exakten Beschreibung des Begriffs effektiv berechenbar Stift Mensch a c b b Rechenblatt a b b c Lese-/Schreibkopf endliche Kontrolle Turingmaschine Eine Turingmaschine
A.M. Turing (1937): Maschinenmodell zur exakten Beschreibung des Begriffs effektiv berechenbar Stift Mensch a c b b Rechenblatt a b b c Lese-/Schreibkopf endliche Kontrolle Turingmaschine Eine Turingmaschine
6.4 Entscheidbarkeit. nein sein müssen, ist klar. THEO 6.4 Entscheidbarkeit 205/307 c Ernst W. Mayr
 6.4 Entscheidbarkeit Wortproblem Leerheit Äquivalenz Schnittproblem Typ 3 ja ja ja ja DCFL ja ja ja nein (*) Typ 2 ja ja nein (*) nein Typ 1 ja nein (*) nein nein Typ 0 nein (*) nein nein nein (*) Diese
6.4 Entscheidbarkeit Wortproblem Leerheit Äquivalenz Schnittproblem Typ 3 ja ja ja ja DCFL ja ja ja nein (*) Typ 2 ja ja nein (*) nein Typ 1 ja nein (*) nein nein Typ 0 nein (*) nein nein nein (*) Diese
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Turingmaschinen und rekursiv aufzählbare Sprachen (III) 8.07.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik Turingmaschinen und rekursiv aufzählbare Sprachen (III) 8.07.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Mächtigkeit von WHILE-Programmen
 Mächtigkeit von WHILE-Programmen Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 23 Turingmaschine (TM) M = (Q, Σ, Γ, B, q 0, q, δ) Unendliches Band... 0 c
Mächtigkeit von WHILE-Programmen Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 23 Turingmaschine (TM) M = (Q, Σ, Γ, B, q 0, q, δ) Unendliches Band... 0 c
Übungsblatt 3. Vorlesung Theoretische Grundlagen der Informatik im WS 17/18
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 3 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 21. November 2017 Abgabe 5. Dezember 2017, 11:00 Uhr
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 3 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 21. November 2017 Abgabe 5. Dezember 2017, 11:00 Uhr
Turing-Maschine. Berechenbarkeit und Komplexität Turing-Maschinen. Turing-Maschine. Beispiel
 Berechenbarkeit und Komplexität Turing-Maschinen Wolfgang Schreiner Wolfgang.Schreiner@risc.jku.at Research Institute for Symbolic Computation (RISC) Johannes Kepler University, Linz, Austria http://www.risc.jku.at
Berechenbarkeit und Komplexität Turing-Maschinen Wolfgang Schreiner Wolfgang.Schreiner@risc.jku.at Research Institute for Symbolic Computation (RISC) Johannes Kepler University, Linz, Austria http://www.risc.jku.at
Berechenbarkeit und Komplexität: Rekursive Aufzählbarkeit und die Technik der Reduktion
 Berechenbarkeit und Komplexität: Rekursive Aufzählbarkeit und die Technik der Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität 7. Dezember 2006 Rekursiv vs. rekursiv
Berechenbarkeit und Komplexität: Rekursive Aufzählbarkeit und die Technik der Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität 7. Dezember 2006 Rekursiv vs. rekursiv
Turing Maschinen II Wiederholung
 Organisatorisches VL-03: Turing Maschinen II (Berechenbarkeit und Komplexität, WS 2017) Gerhard Woeginger Nächste Vorlesung: Mittwoch, Oktober 25, 14:15 15:45 Uhr, Roter Hörsaal Webseite: http://algo.rwth-aachen.de/lehre/ws1718/buk.php
Organisatorisches VL-03: Turing Maschinen II (Berechenbarkeit und Komplexität, WS 2017) Gerhard Woeginger Nächste Vorlesung: Mittwoch, Oktober 25, 14:15 15:45 Uhr, Roter Hörsaal Webseite: http://algo.rwth-aachen.de/lehre/ws1718/buk.php
Registermaschine (RAM), Church-Turing-These
 Registermaschine (RAM), Church-Turing-These Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 21. Oktober 2010 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Registermaschine (RAM), Church-Turing-These Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 21. Oktober 2010 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
VL-03: Turing Maschinen II. (Berechenbarkeit und Komplexität, WS 2017) Gerhard Woeginger
 VL-03: Turing Maschinen II (Berechenbarkeit und Komplexität, WS 2017) Gerhard Woeginger WS 2017, RWTH BuK/WS 2017 VL-03: Turing Maschinen II 1/27 Organisatorisches Nächste Vorlesung: Mittwoch, Oktober
VL-03: Turing Maschinen II (Berechenbarkeit und Komplexität, WS 2017) Gerhard Woeginger WS 2017, RWTH BuK/WS 2017 VL-03: Turing Maschinen II 1/27 Organisatorisches Nächste Vorlesung: Mittwoch, Oktober
Unentscheidbarkeit. 1. Wann sind Sprachen unentscheidbar? 1, A 0, A } = {
 Unentscheidbarkeit 1. Wann sind Sprachen unentscheidbar? Eine Menge A heisst entscheidbar, falls die charakteristische Funktion von A, nämlich A : {0,1}, berechenbar ist, d.h. gilt: A = { 1, A 0, A } Eine
Unentscheidbarkeit 1. Wann sind Sprachen unentscheidbar? Eine Menge A heisst entscheidbar, falls die charakteristische Funktion von A, nämlich A : {0,1}, berechenbar ist, d.h. gilt: A = { 1, A 0, A } Eine
GTI. Hannes Diener Juli. ENC B-0123,
 GTI Hannes Diener ENC B-0123, diener@math.uni-siegen.de 4.-9. Juli 1 / 29 Entscheidungsprobleme und Halteproblem In diesem Kapitel wollen wir uns an Stelle von Berechenbarkeit von Funktion, welche bei
GTI Hannes Diener ENC B-0123, diener@math.uni-siegen.de 4.-9. Juli 1 / 29 Entscheidungsprobleme und Halteproblem In diesem Kapitel wollen wir uns an Stelle von Berechenbarkeit von Funktion, welche bei
Berechenbarkeitstheorie 14. Vorlesung
 1 Berechenbarkeitstheorie Dr. Institut für Mathematische Logik und Grundlagenforschung WWU Münster WS 15/16 Alle Folien unter Creative Commons Attribution-NonCommercial 3.0 Unported Lizenz. Erinnerung
1 Berechenbarkeitstheorie Dr. Institut für Mathematische Logik und Grundlagenforschung WWU Münster WS 15/16 Alle Folien unter Creative Commons Attribution-NonCommercial 3.0 Unported Lizenz. Erinnerung
Berechenbarkeit und Komplexität Vorlesung 10
 Berechenbarkeit und Komplexität Vorlesung 10 Prof. Dr. Wolfgang Thomas Lehrstuhl Informatik 7 RWTH Aachen 27. November 2014 Wolfgang Thomas, Informatik 7 () Vorlesung Berechenbarkeit und Komplexität 27.
Berechenbarkeit und Komplexität Vorlesung 10 Prof. Dr. Wolfgang Thomas Lehrstuhl Informatik 7 RWTH Aachen 27. November 2014 Wolfgang Thomas, Informatik 7 () Vorlesung Berechenbarkeit und Komplexität 27.
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2011 Lösungsblatt 9 25. Juli 2011 Einführung in die Theoretische Informatik
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2011 Lösungsblatt 9 25. Juli 2011 Einführung in die Theoretische Informatik
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Turing-Maschine, Berechenbarkeit INSTITUT FÜR THEORETISCHE INFORMATIK 0 KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
Theoretische Grundlagen der Informatik Turing-Maschine, Berechenbarkeit INSTITUT FÜR THEORETISCHE INFORMATIK 0 KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Turingmaschinen und rekursiv aufzählbare Sprachen (II) 2.07.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik Turingmaschinen und rekursiv aufzählbare Sprachen (II) 2.07.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Turingmaschinen und rekursiv aufzählbare Sprachen (V) 15.07.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik Turingmaschinen und rekursiv aufzählbare Sprachen (V) 15.07.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Registermaschine (RAM), Church-Turing-These. Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen
 Registermaschine (RAM), Church-Turing-These Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 22 Registermaschinen (RAM) Programm b c(0) c(1) c(2) c(3) c(4)...
Registermaschine (RAM), Church-Turing-These Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 22 Registermaschinen (RAM) Programm b c(0) c(1) c(2) c(3) c(4)...
Turing Maschine. Thorsten Timmer. SS 2005 Proseminar Beschreibungskomplexität bei Prof. D. Wotschke. Turing Maschine SS 2005 p.
 Thorsten Timmer SS 2005 Proseminar Beschreibungskomplexität bei Prof. D. Wotschke Turing Maschine SS 2005 p. 1/35 Inhalt Einführung Formale Definition Berechenbare Sprachen und Funktionen Berechnung ganzzahliger
Thorsten Timmer SS 2005 Proseminar Beschreibungskomplexität bei Prof. D. Wotschke Turing Maschine SS 2005 p. 1/35 Inhalt Einführung Formale Definition Berechenbare Sprachen und Funktionen Berechnung ganzzahliger
Fragen 1. Muss eine DTM ein Wort zu Ende gelesen haben, um es zu akzeptieren? a) Ja! b) Nein!
 4 Turingmaschinen Eingabeband nicht nur lesen, sondern auch schreiben kann und die zudem mit ihrem Lese-Schreib-Kopf (LSK) nach links und rechts gehen kann. Das Eingabeband ist zudem in beide Richtungen
4 Turingmaschinen Eingabeband nicht nur lesen, sondern auch schreiben kann und die zudem mit ihrem Lese-Schreib-Kopf (LSK) nach links und rechts gehen kann. Das Eingabeband ist zudem in beide Richtungen
Wie man eine Sprache versteht
 Aufzählbarkeit Formale Grundlagen der Informatik 1 Kapitel 10 Aufzählbarkeit und (Un-)Entscheidbarkeit Frank Heitmann heitmann@informatik.uni-hamburg.de 11. Mai 2015 Definition 1 Eine Menge M Σ heißt (rekursiv)
Aufzählbarkeit Formale Grundlagen der Informatik 1 Kapitel 10 Aufzählbarkeit und (Un-)Entscheidbarkeit Frank Heitmann heitmann@informatik.uni-hamburg.de 11. Mai 2015 Definition 1 Eine Menge M Σ heißt (rekursiv)
Der Satz von Rice. Dann ist C(S) eine unentscheidbare Menge.
 Der Satz von Rice Satz: Sei R die Klasse der (Turing-) berechenbaren Funktionen, S eine nichttriviale Teilmenge von R und C(S) ={w Mw berechnet eine Funktion aus S}. Dann ist C(S) eine unentscheidbare
Der Satz von Rice Satz: Sei R die Klasse der (Turing-) berechenbaren Funktionen, S eine nichttriviale Teilmenge von R und C(S) ={w Mw berechnet eine Funktion aus S}. Dann ist C(S) eine unentscheidbare
Einführung in Berechenbarkeit, Komplexität und Formale Sprachen
 Einführung in Berechenbarkeit, Komplexität und Formale Sprachen V7, 3.11.09 Willkommen zur Vorlesung Einführung in Berechenbarkeit, Komplexität und Formale Sprachen Friedhelm Meyer auf der Heide 1 Rückblick
Einführung in Berechenbarkeit, Komplexität und Formale Sprachen V7, 3.11.09 Willkommen zur Vorlesung Einführung in Berechenbarkeit, Komplexität und Formale Sprachen Friedhelm Meyer auf der Heide 1 Rückblick
11. Woche: Turingmaschinen und Komplexität Rekursive Aufzählbarkeit, Entscheidbarkeit Laufzeit, Klassen DTIME und P
 11 Woche: Turingmaschinen und Komplexität Rekursive Aufzählbarkeit, Entscheidbarkeit Laufzeit, Klassen DTIME und P 11 Woche: Turingmaschinen, Entscheidbarkeit, P 239/ 333 Einführung in die NP-Vollständigkeitstheorie
11 Woche: Turingmaschinen und Komplexität Rekursive Aufzählbarkeit, Entscheidbarkeit Laufzeit, Klassen DTIME und P 11 Woche: Turingmaschinen, Entscheidbarkeit, P 239/ 333 Einführung in die NP-Vollständigkeitstheorie
Rekursive Aufzählbarkeit Die Reduktion
 Rekursive Aufzählbarkeit Die Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen November 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Rekursive Aufzählbarkeit Die Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen November 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Übungsblatt 1. Lorenz Leutgeb. 30. März 2015
 Übungsblatt Lorenz Leutgeb 30. März 205 Aufgabe. Annahmen ohne Einschränkungen: P Σ und P Γ. Per Definitionem der Reduktion: P P 2 f : Σ Γ wobei f total und berechenbar, genau so, dass: w Σ : w P f(w)
Übungsblatt Lorenz Leutgeb 30. März 205 Aufgabe. Annahmen ohne Einschränkungen: P Σ und P Γ. Per Definitionem der Reduktion: P P 2 f : Σ Γ wobei f total und berechenbar, genau so, dass: w Σ : w P f(w)
Theoretische Informatik. Probabilistische Turingmaschinen PTM PTM. Rainer Schrader. 10. Juni 2009
 Theoretische Informatik Rainer Schrader Probabilistische Turingmaschinen Institut für Informatik 10. Juni 009 1 / 30 / 30 Gliederung probabilistische Turingmaschinen Beziehungen zwischen und NDTM es stellt
Theoretische Informatik Rainer Schrader Probabilistische Turingmaschinen Institut für Informatik 10. Juni 009 1 / 30 / 30 Gliederung probabilistische Turingmaschinen Beziehungen zwischen und NDTM es stellt
Einführung in Berechenbarkeit, Komplexität und Formale Sprachen
 Einführung in Berechenbarkeit, Komplexität und Formale Sprachen V8, 5.11.09 Willkommen zur Vorlesung Einführung in Berechenbarkeit, Komplexität und Formale Sprachen Friedhelm Meyer auf der Heide 1 Rückblick
Einführung in Berechenbarkeit, Komplexität und Formale Sprachen V8, 5.11.09 Willkommen zur Vorlesung Einführung in Berechenbarkeit, Komplexität und Formale Sprachen Friedhelm Meyer auf der Heide 1 Rückblick
VL-06: Unentscheidbarkeit II. (Berechenbarkeit und Komplexität, WS 2017) Gerhard Woeginger
 VL-06: Unentscheidbarkeit II (Berechenbarkeit und Komplexität, WS 2017) Gerhard Woeginger WS 2017, RWTH BuK/WS 2017 VL-06: Unentscheidbarkeit II 1/37 Organisatorisches Nächste Vorlesung: Mittwoch, November
VL-06: Unentscheidbarkeit II (Berechenbarkeit und Komplexität, WS 2017) Gerhard Woeginger WS 2017, RWTH BuK/WS 2017 VL-06: Unentscheidbarkeit II 1/37 Organisatorisches Nächste Vorlesung: Mittwoch, November
Definition 98 Eine Turingmaschine heißt linear beschränkt (kurz: LBA), falls für alle q Q gilt:
 5.2 Linear beschränkte Automaten Definition 98 Eine Turingmaschine heißt linear beschränkt (kurz: LBA), falls für alle q Q gilt: (q, c, d) δ(q, ) = c =. Ein Leerzeichen wird also nie durch ein anderes
5.2 Linear beschränkte Automaten Definition 98 Eine Turingmaschine heißt linear beschränkt (kurz: LBA), falls für alle q Q gilt: (q, c, d) δ(q, ) = c =. Ein Leerzeichen wird also nie durch ein anderes
Klausur: Berechenbarkeit und Komplexität (Niedermeier/Chen/Froese/Sorge, Sommersemester 2016)
 Technische Universität Berlin, Berlin, 28.07.2016 Name:... Matr.-Nr.:... Klausur: Berechenbarkeit und Komplexität (Niedermeier/Chen/Froese/Sorge, Sommersemester 2016) Einlesezeit: Bearbeitungszeit: Max.
Technische Universität Berlin, Berlin, 28.07.2016 Name:... Matr.-Nr.:... Klausur: Berechenbarkeit und Komplexität (Niedermeier/Chen/Froese/Sorge, Sommersemester 2016) Einlesezeit: Bearbeitungszeit: Max.
Auffrischung Einige (wenige) Grundlagen der Theoretischen Informatik
 Logik, Berechenbarkeit und Komplexität Sommersemester 2008 Fachhochschule Wiesbaden Prof. Dr. Steffen Reith Auffrischung Einige (wenige) Grundlagen der Theoretischen Informatik 1 Turingmaschinen - Ein
Logik, Berechenbarkeit und Komplexität Sommersemester 2008 Fachhochschule Wiesbaden Prof. Dr. Steffen Reith Auffrischung Einige (wenige) Grundlagen der Theoretischen Informatik 1 Turingmaschinen - Ein
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier. Henning Fernau Universität Trier
 Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2010 Lösungsblatt 11 15. Juli 2010 Einführung in die Theoretische
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2010 Lösungsblatt 11 15. Juli 2010 Einführung in die Theoretische
Berechenbarkeit. Script, Kapitel 2
 Berechenbarkeit Script, Kapitel 2 Intuitiver Berechenbarkeitsbegriff Turing-Berechenbarkeit WHILE-Berechenbarkeit Church sche These Entscheidungsprobleme Unentscheidbarkeit des Halteproblems für Turingmaschinen
Berechenbarkeit Script, Kapitel 2 Intuitiver Berechenbarkeitsbegriff Turing-Berechenbarkeit WHILE-Berechenbarkeit Church sche These Entscheidungsprobleme Unentscheidbarkeit des Halteproblems für Turingmaschinen
Universelle Turingmaschinen
 Universelle Turingmaschinen bisher: zum Erkennen einer rekursiven Sprache L wurde jeweils eine spezielle dtm M L angegeben jetzt: konstruieren feste dtm ( universelle Turingmaschine ), die als Eingabe
Universelle Turingmaschinen bisher: zum Erkennen einer rekursiven Sprache L wurde jeweils eine spezielle dtm M L angegeben jetzt: konstruieren feste dtm ( universelle Turingmaschine ), die als Eingabe
2.4 Kontextsensitive und Typ 0-Sprachen
 Definition 2.43 Eine Typ 1 Grammatik ist in Kuroda Normalform, falls alle Regeln eine der folgenden 4 Formen haben: Dabei: A, B, C, D V und a Σ. Satz 2.44 A a, A B, A BC, AB CD. Für jede Typ 1 Grammatik
Definition 2.43 Eine Typ 1 Grammatik ist in Kuroda Normalform, falls alle Regeln eine der folgenden 4 Formen haben: Dabei: A, B, C, D V und a Σ. Satz 2.44 A a, A B, A BC, AB CD. Für jede Typ 1 Grammatik
Komplexitätstheorie WiSe 2011/12 in Trier. Henning Fernau Universität Trier
 Komplexitätstheorie WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Komplexitätstheorie Gesamtübersicht Organisatorisches / Einführung Motivation / Erinnerung / Fragestellungen
Komplexitätstheorie WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Komplexitätstheorie Gesamtübersicht Organisatorisches / Einführung Motivation / Erinnerung / Fragestellungen
Unentscheidbarkeit. Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: Komplexitätstheorie und effiziente Algorithmen
 Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: und effiziente Algorithmen Wintersemester 2011/12 Prof. Barbara König Übungsleitung: Henning Kerstan & Jan Stückrath Worum geht
Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: und effiziente Algorithmen Wintersemester 2011/12 Prof. Barbara König Übungsleitung: Henning Kerstan & Jan Stückrath Worum geht
1 Einführung. 2 Typ-0- und Typ-1-Sprachen. 3 Berechnungsmodelle. 4 Unentscheidbarkeit. 5 Unentscheidbare Probleme. 6 Komplexitätstheorie
 1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie 15 Ziele vgl. AFS: Berechnungsmodelle für Typ-0- und Typ-1-Sprachen (Nicht-)Abschlußeigenschaften
1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie 15 Ziele vgl. AFS: Berechnungsmodelle für Typ-0- und Typ-1-Sprachen (Nicht-)Abschlußeigenschaften
Unentscheidbarkeit von Problemen mittels Turingmaschinen
 Unentscheidbarkeit von Problemen mittels Turingmaschinen Daniel Roßberg 0356177 Roland Schatz 0355521 2. Juni 2004 Zusammenfassung In dieser Arbeit befassen wir uns mit der Unentscheidbarkeit von Problemen
Unentscheidbarkeit von Problemen mittels Turingmaschinen Daniel Roßberg 0356177 Roland Schatz 0355521 2. Juni 2004 Zusammenfassung In dieser Arbeit befassen wir uns mit der Unentscheidbarkeit von Problemen
Grundlagen der Theoretischen Informatik Musterlösungen zu ausgewählten Übungsaufgaben
 Dieses Dokument soll mehr dazu dienen, Beispiele für die formal korrekt mathematische Bearbeitung von Aufgaben zu liefern, als konkrete Hinweise auf typische Klausuraufgaben zu liefern. Die hier gezeigten
Dieses Dokument soll mehr dazu dienen, Beispiele für die formal korrekt mathematische Bearbeitung von Aufgaben zu liefern, als konkrete Hinweise auf typische Klausuraufgaben zu liefern. Die hier gezeigten
Satz von Rice. Lemma 39
 Unentscheidbarkeit Satz von Rice Das nächste Resultat zeigt, dass jede Eigenschaft der von einer Turing-Maschine berechneten Funktion unentscheidbar ist. Das bedeutet, es gibt keine Methode, mit der man
Unentscheidbarkeit Satz von Rice Das nächste Resultat zeigt, dass jede Eigenschaft der von einer Turing-Maschine berechneten Funktion unentscheidbar ist. Das bedeutet, es gibt keine Methode, mit der man
Algorithmentheorie 8. Vorlesung
 Algorithmentheorie 8. Vorlesung Martin Dietzfelbinger 1. Juni 2006 1.7 Die Churchsche These Der intuitive Berechenbarkeitsbegriff wird durch die Formalisierung TM-Berechenbarkeit, also Rekursivität von
Algorithmentheorie 8. Vorlesung Martin Dietzfelbinger 1. Juni 2006 1.7 Die Churchsche These Der intuitive Berechenbarkeitsbegriff wird durch die Formalisierung TM-Berechenbarkeit, also Rekursivität von
11. Übungsblatt. x y(top(push(x, y)) = y)
 Logik, Berechenbarkeit und Komplexität Sommersemester 2012 Hochschule RheinMain Prof. Dr. Steffen Reith 11. Übungsblatt 1. Ein Keller (engl. stack) ist eine bekannte Datenstruktur. Sei die Signatur S =
Logik, Berechenbarkeit und Komplexität Sommersemester 2012 Hochschule RheinMain Prof. Dr. Steffen Reith 11. Übungsblatt 1. Ein Keller (engl. stack) ist eine bekannte Datenstruktur. Sei die Signatur S =
Wir haben eine Beziehung zwischen entscheidbar und rekursiv aufzählbar hergeleitet.
 Rückschau 12.11.04 Wir haben eine Beziehung zwischen entscheidbar und rekursiv aufzählbar hergeleitet. Wir haben das Prinzip der Diagonalisierung eingeführt und mit DIAG eine erste nicht rek. aufz. Sprache
Rückschau 12.11.04 Wir haben eine Beziehung zwischen entscheidbar und rekursiv aufzählbar hergeleitet. Wir haben das Prinzip der Diagonalisierung eingeführt und mit DIAG eine erste nicht rek. aufz. Sprache
Theoretische Informatik 1
 Theoretische Informatik 1 Die Komplexitätsklasse P David Kappel Institut für Grundlagen der Informationsverarbeitung TU Graz SS 2012 Übersicht Äquivalenz von RM und TM Äquivalenz, Sätze Simulation DTM
Theoretische Informatik 1 Die Komplexitätsklasse P David Kappel Institut für Grundlagen der Informationsverarbeitung TU Graz SS 2012 Übersicht Äquivalenz von RM und TM Äquivalenz, Sätze Simulation DTM
a b b a Vom DFA zur TM Formale Grundlagen der Informatik 1 Kapitel 9 Turing-Maschinen Der Lese-/Schreibkopf Bedeutung der TM
 Vom DFA zur TM Formale der Informatik 1 Kapitel 9 Frank Heitmann heitmann@informatik.uni-hamburg.de a b b a z 0 a z 1 a z 2 b 2. Mai 2016 Wir wollen auf dem Band nach rechts und links gehen können und
Vom DFA zur TM Formale der Informatik 1 Kapitel 9 Frank Heitmann heitmann@informatik.uni-hamburg.de a b b a z 0 a z 1 a z 2 b 2. Mai 2016 Wir wollen auf dem Band nach rechts und links gehen können und
Informatik III. Christian Schindelhauer Wintersemester 2006/ Vorlesung
 Informatik III Christian Schindelhauer Wintersemester 2006/07 15. Vorlesung 14.12.2006 1 Reduktionen Unentscheidbare Probleme Das Halteproblem Das Leerheitsproblem einer Turingmaschine Ein einfaches nicht
Informatik III Christian Schindelhauer Wintersemester 2006/07 15. Vorlesung 14.12.2006 1 Reduktionen Unentscheidbare Probleme Das Halteproblem Das Leerheitsproblem einer Turingmaschine Ein einfaches nicht
Das Postsche Korrespondenzproblem
 Das Postsche Korrespondenzproblem Eine Instanz des PKP ist eine Liste von Paaren aus Σ Σ : (v 1, w 1 ),..., (v n, w n ) Eine Lösung ist eine Folge i 1,..., i k von Indizes 1 i j n mit v i1... v ik = w
Das Postsche Korrespondenzproblem Eine Instanz des PKP ist eine Liste von Paaren aus Σ Σ : (v 1, w 1 ),..., (v n, w n ) Eine Lösung ist eine Folge i 1,..., i k von Indizes 1 i j n mit v i1... v ik = w
Beispiel: NTM. M = ({q 0,q 1,q 2 }, {0, 1}, {0, 1, #},δ, q 0, #, {q 2 }) q 2
 Beispiel: NTM M = ({q 0,q 1,q 2 }, {0, 1}, {0, 1, #},δ, q 0, #, {q 2 }) 0,1,R 0,0,R q0 1,0,R q1 #,#,R q2 0,0,L Zustand 0 1 # q 0 {(1, R, q 0 )} {(0, R, q 1 )} q 1 {(0, R, q 1 ),(0, L, q 0 )} {(1, R, q
Beispiel: NTM M = ({q 0,q 1,q 2 }, {0, 1}, {0, 1, #},δ, q 0, #, {q 2 }) 0,1,R 0,0,R q0 1,0,R q1 #,#,R q2 0,0,L Zustand 0 1 # q 0 {(1, R, q 0 )} {(0, R, q 1 )} q 1 {(0, R, q 1 ),(0, L, q 0 )} {(1, R, q
Semi-Entscheidbarkeit und rekursive Aufzählbarkeit
 Semi-Entscheidbarkeit und rekursive Aufzählbarkeit Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 9. November 2009 Berthold Vöcking, Informatik 1 () Vorlesung
Semi-Entscheidbarkeit und rekursive Aufzählbarkeit Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 9. November 2009 Berthold Vöcking, Informatik 1 () Vorlesung
LOOP-Programme: Syntaktische Komponenten
 LOOP-Programme: Syntaktische Komponenten LOOP-Programme bestehen aus folgenden Zeichen (syntaktischen Komponenten): Variablen: x 0 x 1 x 2... Konstanten: 0 1 2... Operationssymbole: + Trennsymbole: ; :=
LOOP-Programme: Syntaktische Komponenten LOOP-Programme bestehen aus folgenden Zeichen (syntaktischen Komponenten): Variablen: x 0 x 1 x 2... Konstanten: 0 1 2... Operationssymbole: + Trennsymbole: ; :=
Grundlagen der Theoretischen Informatik: Übung 10
 Grundlagen der Theoretischen Informatik: Übung 10 Joachim Selke Fachgebiet Theoretische Informatik Universität Hannover 20. Januar 2005 Turing-Maschinen als Rechenmaschinen gegeben sei eine Funktion f
Grundlagen der Theoretischen Informatik: Übung 10 Joachim Selke Fachgebiet Theoretische Informatik Universität Hannover 20. Januar 2005 Turing-Maschinen als Rechenmaschinen gegeben sei eine Funktion f
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier. Henning Fernau Universität Trier
 Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Einführung in die mathematische Logik
 Prof. Dr. H. Brenner Osnabrück SS 2014 Einführung in die mathematische Logik Vorlesung 19 Entscheidbarkeit und Berechenbarkeit In der letzten Vorlesung haben wir verschiedene mathematische Operationen
Prof. Dr. H. Brenner Osnabrück SS 2014 Einführung in die mathematische Logik Vorlesung 19 Entscheidbarkeit und Berechenbarkeit In der letzten Vorlesung haben wir verschiedene mathematische Operationen
Universelle Maschinen und universelle Funktionen
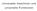 Universelle Maschinen und universelle Funktionen UNIVERSELLE FUNKTIONEN DEFINITION. Sei F eine Klasse von partiellen Funktionen über N. Eine partielle Funktion ϕ (n+1) ist n-universell für F, wenn (i)
Universelle Maschinen und universelle Funktionen UNIVERSELLE FUNKTIONEN DEFINITION. Sei F eine Klasse von partiellen Funktionen über N. Eine partielle Funktion ϕ (n+1) ist n-universell für F, wenn (i)
Entscheidungsprobleme
 Entscheidungsprobleme übliche Formulierung gegeben: Eingabe x aus einer Grundmenge M Frage: Hat x eine bestimmte Eigenschaft P? Beispiel: gegeben: Frage: n N Ist n eine Primzahl? Formalisierung: Grundmenge
Entscheidungsprobleme übliche Formulierung gegeben: Eingabe x aus einer Grundmenge M Frage: Hat x eine bestimmte Eigenschaft P? Beispiel: gegeben: Frage: n N Ist n eine Primzahl? Formalisierung: Grundmenge
Rekursiv aufzählbare Sprachen
 Kapitel 4 Rekursiv aufzählbare Sprachen 4.1 Grammatiken und die Chomsky-Hierarchie Durch Zulassung komplexer Ableitungsregeln können mit Grammatiken größere Klassen als die kontextfreien Sprachen beschrieben
Kapitel 4 Rekursiv aufzählbare Sprachen 4.1 Grammatiken und die Chomsky-Hierarchie Durch Zulassung komplexer Ableitungsregeln können mit Grammatiken größere Klassen als die kontextfreien Sprachen beschrieben
Turing-Maschinen: Ein abstrakes Maschinenmodell
 Wann ist eine Funktion (über den natürlichen Zahlen) berechenbar? Intuitiv: Wenn es einen Algorithmus gibt, der sie berechnet! Was heißt, eine Elementaroperation ist maschinell ausführbar? Was verstehen
Wann ist eine Funktion (über den natürlichen Zahlen) berechenbar? Intuitiv: Wenn es einen Algorithmus gibt, der sie berechnet! Was heißt, eine Elementaroperation ist maschinell ausführbar? Was verstehen
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier. Henning Fernau Universität Trier
 Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
1 Eine Menge M Σ heißt (rekursiv) aufzählbar genau. 2 Die Familie aller aufzählbaren Mengen wird mit RE
 Aufzählbarkeit Formale Grundlagen der Informatik 1 Kapitel 9 Entscheidbarkeit und Aufzählbarkeit Frank Heitmann heitmann@informatik.uni-hamburg.de 5. Mai 2014 Definition 1 Eine Menge M Σ heißt (rekursiv)
Aufzählbarkeit Formale Grundlagen der Informatik 1 Kapitel 9 Entscheidbarkeit und Aufzählbarkeit Frank Heitmann heitmann@informatik.uni-hamburg.de 5. Mai 2014 Definition 1 Eine Menge M Σ heißt (rekursiv)
Diskrete Mathematik II
 Diskrete Mathematik II Alexander May Fakultät für Mathematik Ruhr-Universität Bochum Sommersemester 2011 DiMa II - Vorlesung 01-04.04.2011 1 / 252 Organisatorisches Vorlesung: Mo 12-14 in HZO 70, Di 09-10
Diskrete Mathematik II Alexander May Fakultät für Mathematik Ruhr-Universität Bochum Sommersemester 2011 DiMa II - Vorlesung 01-04.04.2011 1 / 252 Organisatorisches Vorlesung: Mo 12-14 in HZO 70, Di 09-10
Unentscheidbare Probleme: Diagonalisierung
 Unentscheidbare Probleme: Diagonalisierung Prof Dr Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen Oktober 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Unentscheidbare Probleme: Diagonalisierung Prof Dr Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen Oktober 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Mehrband-Turingmaschinen und die universelle Turingmaschine
 Mehrband-Turingmaschinen und die universelle Turingmaschine Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 15 Turingmaschinen mit mehreren Bändern k-band
Mehrband-Turingmaschinen und die universelle Turingmaschine Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 15 Turingmaschinen mit mehreren Bändern k-band
Einführung in die Informatik Turing Machines
 Einführung in die Informatik Turing Machines Eine abstrakte Maschine zur Präzisierung des Algorithmenbegriffs Wolfram Burgard 1 Motivation und Einleitung Bisher haben wir verschiedene Programmiersprachen
Einführung in die Informatik Turing Machines Eine abstrakte Maschine zur Präzisierung des Algorithmenbegriffs Wolfram Burgard 1 Motivation und Einleitung Bisher haben wir verschiedene Programmiersprachen
Turingmaschinen Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: Komplexitätstheorie und effiziente Algorithmen
 Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: und effiziente Algorithmen Wintersemester 2011/12 Schematische Darstellung einer Turing-Maschine: Kopf kann sich nach links und
Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: und effiziente Algorithmen Wintersemester 2011/12 Schematische Darstellung einer Turing-Maschine: Kopf kann sich nach links und
