Formelsammlung Mathematik Fachoberschule Jahrgangsstufe 12 Hochtaunusschule Oberursel. Philipp Maurer in Zusammenarbeit mit StR A.
|
|
|
- Laura Abel
- vor 7 Jahren
- Abrufe
Transkript
1 Fomelsmmlung Mtemtik Fcoescule Jgngsstufe 12 Hoctunusscule Oeusel Pilipp Mue in Zusmmeneit mit StR A. Käme Stnd: 20. Feu 2014
2 Fomelsmmlung Mtemtik Fcoescule Jgngsstufe 12 Inltsvezeicnis 1 Mtemtisce Gundlgen Potenzgesetze Binomisce Fomeln Beecnung n Deiecken Tigonometie Stz des Pytgos Gnztionle Funktionen Geden Nomlfom Steigungsdeieck und Steigungswinkel Funktionen zweiten Gdes Sceitelpunktfom Qudtisce Egänzung zu Bestimmung de Sceitelpunktfom pq-fomel Fomel Vogeensweise Sustitution: Lösen iqudtisce Gleicungen Kuvendiskussion Steen gegen ± Symmetien Aleitungsegeln (Potenzegel, Poduktegel, Quotientenegel, Kettenegel) Extemwete Wendepunkte Tngenten Nomle Steigungswinkel Scnittwinkel Astnd zwiscen zwei Punkten Rekonstuktion 6 5 Extemwetufgen 6 6 Integlecnung Integieen Vogeensweise Fläce zwiscen zwei Funktionen Geometisce Figuen Inlt und Umfng eene Figuen Volumen und Oefläce von Köpen Pilipp Mue in Zusmmeneit mit StR A. Käme Seite 1
3 Fomelsmmlung Mtemtik Fcoescule Jgngsstufe 12 1 Mtemtisce Gundlgen 1.1 Potenzgesetze x 0 = 1 x = 1 x x 1 = x x x = x + x = x x = x x (x ) = x (x y) = x y ( x y ) = x y 1.2 Binomisce Fomeln 1. inomisce Fomel: (+) 2 = inomisce Fomel: ( ) 2 = inomisce Fomel: (+) ( ) = Beecnung n Deiecken A α c C. B 2.1 Tigonometie Sinus sin(α) = Gegenktete Hypotenuse = c Kosinus cos(α) = Anktete Hypotenuse = c Tngens tn(α) = Gegenktete Anktete = 2.2 Stz des Pytgos = c 2 Pilipp Mue in Zusmmeneit mit StR A. Käme Seite 2
4 Fomelsmmlung Mtemtik Fcoescule Jgngsstufe 12 3 Gnztionle Funktionen 3.1 Geden Nomlfom f(x) = m x Steigungsdeieck und Steigungswinkel P 2 P 1 x 2-x 1 y 2-y 1 Steigung: m = y x = y2 y1 x 2 x 1 Steigungswinkel: α = ctn(m) 3.2 Funktionen zweiten Gdes Sceitelpunktfom f(x) = (x x s ) 2 +y s Steckung/Stucung x s x-wet des Sceitelpunktes y s y-wet des Sceitelpunktes Qudtisce Egänzung zu Bestimmung de Sceitelpunktfom Gegeene qudtisce Funktion y = x 2 +x+c Ausklmmen des Leitkoeffizienten y = ( ( x 2 + x) +c Qudtisce Egänzung y = x 2 + x+( ) 2 ( 2 ) 2 ) 2 +c (x+ ) 2 ( Bildung des Qudts y = [ 2 ) 2 ] 2 +c Ausmultiplizieen y = ( ) x c 2 Sceitelpunktfom de Funktion y = ( ) ) x+ 2 + (c 2 ( ) 4 Alesen des Sceitelpunkts S 2 2 c pq-fomel Fomel 0 = x 2 +p x+q x 1/2 = p 2 ± (p 2) 2 q Vogeensweise Funktion zweiten Gdes f(x) = x 2 +x+c Esten Fkto duc teilen f(x) = x 2 + x+ c f(x) = 0 setzen 0 = x 2 + x+ c ( In pq-fomel einsetzen x 1/2 = ) 2 2 ± 2 c 3.4 Sustitution: Lösen iqudtisce Gleicungen Funktion vieten Gedes f(x) = x 4 + x 2 +c z estimmen z = x 2 in f(x) einsetzen f(z) = z 2 + z +c Nullsetzen und mit pq-fomel weite ecnen f(z) = 0 Wuzel de Egenisse de pq-fomel zieen x 1/2 = ± z 1 x 3/4 = ± z 2 Pilipp Mue in Zusmmeneit mit StR A. Käme Seite 3
5 Fomelsmmlung Mtemtik Fcoescule Jgngsstufe Kuvendiskussion Steen gegen ± Betctet wid ieei nu de öcste Exponent und sein Vofkto x n positiv negtiv n gede fü x gegen + f(x) get gegen + fü x gegen + f(x) get gegen fü x gegen f(x) get gegen + fü x gegen f(x) get gegen n ungede fü x gegen + f(x) get gegen + fü x gegen + f(x) get gegen fü x gegen f(x) get gegen fü x gegen f(x) get gegen Symmetien Acsensymmetie: Alle Exponenten gede f(x) = f(-x) Punktsymmetie: Alle Exponenten ungede f(x) = -f(-x) Aleitungsegeln (Potenzegel, Poduktegel, Quotientenegel, Kettenegel) Potenzegel f(x) = x n f (x) = n x n 1 Poduktegel f(x) = u(x) v(x) f (x) = u (x) v(x)+u(x) v (x) Quotientenegel f(x) = u(x) v(x) f (x) = u (x) v(x) u(x) v (x) (v(x)) 2 Kettenegel f(x) = u(v(x)) f (x) = u (v(x)) v (x) Pilipp Mue in Zusmmeneit mit StR A. Käme Seite 4
6 Fomelsmmlung Mtemtik Fcoescule Jgngsstufe Extemwete Bilde f (x) Nullstelle(n) von f (x) sucen f (x) = 0 x 0 =... notwendige Bedingung: ( Steigung = 0) Nullstelle(n) von f (x) in f(x) einsetzen, um die y-wete de Extemwete zu estimmen (f(x 0 ) =...) ineicende Bedingung: f (x) 0 Emitteln o x 0 ein Hoc- ode Tiefpunkt ist, indem x 0 in f (x) eingesetzt wid: 1. f (x) > 0 Tiefpunkt (lokles Minimum) 2. f (x) < 0 Hocpunkt (lokles Mximum) 3. f (x) = 0 Sttelpunkt Wendepunkte Vogeen wie ei Extemweten. Bedingungen sind lledings etws geändet: notwendige Bedingung: f (x) = 0 ineicende Bedingung: f (x) 0 1. Aleitungen ilden (is f (x)) 2. Nullstellen sucen notwendige Bedingung Wendepunkt f (x) = 0 x 1/2/3/ Einsetzen de Nullstellen in f(x) y 1/2/3/ ineicende Bedingung x 1/2/3/... einsetzen 5. Einzeicnen 6. uf Plusiilität püfen Pilipp Mue in Zusmmeneit mit StR A. Käme Seite 5
7 Fomelsmmlung Mtemtik Fcoescule Jgngsstufe Tngenten Definition: Gede die im Beüpunkt die identisce Steigung wie die Funktion t Nomlfom eine Geden y = m x+ 1. Aleitung ilden und x einsetzen m = f (x) Punkt (duc den die Tngente get) in Nomlfom einsetzen y p = m x p + = y p m x p 3.7 Nomle Definition: Gede, die im Scnittpunkt die Funktion im Recten Winkel (90 ) scneidet Est die Tngente estimmen (siee Tngente) und dnn mit m 2 = 1 m 1 die Nomle estimmen. 3.8 Steigungswinkel m = f (x) fü x den Punkt einsetzen m = tnα α = ctnm 3.9 Scnittwinkel m estimmen wie eim Steigungswinkel α = ctnm 1 ctnm Astnd zwiscen zwei Punkten 2 = ( x) 2 +( y) 2 2 = (x 2 x 1 ) 2 +(y 2 y 1 ) 2 4 Rekonstuktion Funktionsnstz vom Gd n ufstellen f(x) = x n + x n Aleitungen emitteln f (x) und f (x) Bedingung fomulieen i.d.r. n+1 Bedingungen f(x) fü Funktionswete f (x) fü Steigung und Extem f (x) fü Kümmung und Wendepunkte Wete einsetzen Gleicungssystem ufstellen Gleicungssystem lösen z.b. Einsetzvefen ode Guss-Jodn 5 Extemwetufgen HB Huptedingung ufstellen Funktion fü zu optimieende Göße fomulieen NB Neenedingung ufstellen Rndedingung / Einscänkung Zielfunktion emitteln NB in HB einsetzen, so dss diese nu von eine Vile ängt Extemwet estimmen f (x) = 0 und f (x) 0 lle gesucten Gößen emitteln einsetzen in HB / NB Kontolle des Egenisses 6 Integlecnung 6.1 Integieen f(x) = x n F(x) = n+1 xn Vogeensweise f(x)dx = [F(x)] = F() F() 6.3 Fläce zwiscen zwei Funktionen f 1(x)dx f 2(x)dx = [f 1(x) f 2 (x)]dx Hinweis: Integtion de Teilfläce duc scittweise Integtion üe die Scnittpunkte von f 1 und f 2 Pilipp Mue in Zusmmeneit mit StR A. Käme Seite 6
8 Fomelsmmlung Mtemtik Fcoescule Jgngsstufe 12 7 Geometisce Figuen 7.1 Inlt und Umfng eene Figuen Qudt Recteck Deieck Pllelogmm g Inlt: A = 2 Inlt: A = Inlt: A = 1 2 g Inlt: A = Umfng: U = 4 Umfng: U = 2+2 Umfng: U = ++c Umfng: U = 2+2 Keis Keisusscnitt Tpez gleicseitiges Deieck α Inlt: A = π 2 Inlt: A = π 2 α 360 Inlt: A = + 2 Höe: = 1 2 g 3 α Umfng: U = 2π Bogen: = 2π Volumen und Oefläce von Köpen Wüfel Qude Zylinde c Volumen: V = 3 Volumen: V = c Volumen: V = π 2 Oefläce: O = 6 2 Oefläce: O = 2 (+c+c) Oefläce: O = 2π( +) Pymide Kegel Kugel g g g G Volumen: V = 1 3 G Volumen: V = 1 3 π2 Volumen: V = 4 3 π 3 Oefläce: Summe de Inlte de Oefläce: O = π( +s) Oefläce: O = 4π 2 Gundfläce und de Seitenfläce Pilipp Mue in Zusmmeneit mit StR A. Käme Seite 7
Formelsammlung. x 2 + px + q = 0 ax 2 + bx + c = 0 x 1,2. = p 2 ± p². Fläche eines rechtwinkligen Dreiecks: Fläche eines Dreiecks: A = 1 2 g h
 Fomelsmmlung p q Fomel: c Fomel x 2 + px + q = 0 x 2 + x + c = 0 x 1,2 = p 2 ± p² 4 q x 1,2 = ± ² 4c 2 Fläce eines Deiecks: Fläce eines ectwinkligen Deiecks: A = 1 2 g A = 1 2 g Fläce eines Qudts: A =
Fomelsmmlung p q Fomel: c Fomel x 2 + px + q = 0 x 2 + x + c = 0 x 1,2 = p 2 ± p² 4 q x 1,2 = ± ² 4c 2 Fläce eines Deiecks: Fläce eines ectwinkligen Deiecks: A = 1 2 g A = 1 2 g Fläce eines Qudts: A =
Eigenschaften mathematischer Körper
 Rettungsing Köpe gnz kl: temtik 4 - Ds Feieneft mit Efolgsnzeige Eigenscften mtemtisce Köpe Eigenscften von Pismen Ein gedes Pism t imme eine und- und eine Deckfläce, die deckungsgleic und pllel zueinnde
Rettungsing Köpe gnz kl: temtik 4 - Ds Feieneft mit Efolgsnzeige Eigenscften mtemtisce Köpe Eigenscften von Pismen Ein gedes Pism t imme eine und- und eine Deckfläce, die deckungsgleic und pllel zueinnde
Formeln zu Mathematik für die Fachhochschulreife
 Fomeln zu Mtemtik fü die Fcocsculeife Beeitet von B. Gimm und B. Sciemnn 3. Auflge VERLAG EUROPA-LEHRMITTEL Nouney, Vollme GmH & Co. KG Düsselege Stße 3 4781 Hn-Guiten Euop-N.: 8519 Autoen: Bend Gimm Bend
Fomeln zu Mtemtik fü die Fcocsculeife Beeitet von B. Gimm und B. Sciemnn 3. Auflge VERLAG EUROPA-LEHRMITTEL Nouney, Vollme GmH & Co. KG Düsselege Stße 3 4781 Hn-Guiten Euop-N.: 8519 Autoen: Bend Gimm Bend
Abiturprüfung Mathematik 2017 Merkhilfe S. 1/8. Dreieck Flächeninhalt: 1 2. Mindestens zwei Seiten sind gleich lang.
 Aitupüfung Mthemtik 07 Mekhilfe S. /8 Eene Figuen Deieck Flächeninhlt: A g h g gleichschenkliges Deieck Mindestens zwei Seiten sind gleich lng. gleichseitiges Deieck Alle dei Seiten sind gleich lng. Flächeninhlt:
Aitupüfung Mthemtik 07 Mekhilfe S. /8 Eene Figuen Deieck Flächeninhlt: A g h g gleichschenkliges Deieck Mindestens zwei Seiten sind gleich lng. gleichseitiges Deieck Alle dei Seiten sind gleich lng. Flächeninhlt:
Formeln zu Mathematik für die Fachhochschulreife
 Fomeln zu Mtemtik fü die Fcocsculeife Beeitet von B. Gimm und B. Sciemnn 3. Auflge VERLAG EUROPA-LEHRMITTEL Nouney, Vollme GmH & Co. KG Düsselege Stße 3 4781 Hn-Guiten Euop-N.: 8519 Autoen: Bend Gimm Bend
Fomeln zu Mtemtik fü die Fcocsculeife Beeitet von B. Gimm und B. Sciemnn 3. Auflge VERLAG EUROPA-LEHRMITTEL Nouney, Vollme GmH & Co. KG Düsselege Stße 3 4781 Hn-Guiten Euop-N.: 8519 Autoen: Bend Gimm Bend
x 8x 2 x 3 x Anwendungsorientierte Mathematik für Techniker Lösungen der Aufgaben zu Kapitel
 Anwendungsoientiete Mtemtik ü Tecnike Lösungen de Augen zu Kpitel 8 8. 8. 5 8. 8 8. 7² 8. 5 ² + 0 8. 6 ³ + ² 8. 7 8. 8 8. 8. 0 8. 6 Duckele: Die Auge sollte luten 6 7 8. " 8 0.5 0 0 6 8 Wi estimmen die
Anwendungsoientiete Mtemtik ü Tecnike Lösungen de Augen zu Kpitel 8 8. 8. 5 8. 8 8. 7² 8. 5 ² + 0 8. 6 ³ + ² 8. 7 8. 8 8. 8. 0 8. 6 Duckele: Die Auge sollte luten 6 7 8. " 8 0.5 0 0 6 8 Wi estimmen die
Aufgabe 9: Prisma mit maximalem Volumen
 Lösungen de Extemwetpoleme im Skipt, Ascnitt 86 Aufgae 9: Pisma mit maximalem olumen Wete > 0 sind natülic sinnlos! ( x ) ( 00 x ) ( 60 x) x 0 50 0 0 0 ( ) 0 0 0 0 0 5 0 5 0 5 0 5 0 5 50 olumenfunktion:
Lösungen de Extemwetpoleme im Skipt, Ascnitt 86 Aufgae 9: Pisma mit maximalem olumen Wete > 0 sind natülic sinnlos! ( x ) ( 00 x ) ( 60 x) x 0 50 0 0 0 ( ) 0 0 0 0 0 5 0 5 0 5 0 5 0 5 50 olumenfunktion:
Wir teilen das Intervall [a,b] in n Teilintervalle der Breite x (Skizze: n = 5). Wir ersetzen die im k-ten Teilintervall f x und der
![Wir teilen das Intervall [a,b] in n Teilintervalle der Breite x (Skizze: n = 5). Wir ersetzen die im k-ten Teilintervall f x und der Wir teilen das Intervall [a,b] in n Teilintervalle der Breite x (Skizze: n = 5). Wir ersetzen die im k-ten Teilintervall f x und der](/thumbs/97/132649618.jpg) olumen von Rotationsköpen Die Fläce zwiscen de stetigen Kuve y = f(x), de x-acse und den Paallelen x = a und x = b ezeugt bei Rotation um die x-acse einen sogenannten Rotationsköpe. Gesuct ist das olumen
olumen von Rotationsköpen Die Fläce zwiscen de stetigen Kuve y = f(x), de x-acse und den Paallelen x = a und x = b ezeugt bei Rotation um die x-acse einen sogenannten Rotationsköpe. Gesuct ist das olumen
P eine waagrechte Tangente besitzt.
 Mtemtik MB Üungsltt Temen: unktionsuntesucungen, Etem mit und one Neenedingungen DHBW STUTTGART MB MATHEMATI SEITE VON Aufge A: Gegeen ist die unktion, in impliite om ) Bestimmen Sie die Tngentensteigung
Mtemtik MB Üungsltt Temen: unktionsuntesucungen, Etem mit und one Neenedingungen DHBW STUTTGART MB MATHEMATI SEITE VON Aufge A: Gegeen ist die unktion, in impliite om ) Bestimmen Sie die Tngentensteigung
Merkhilfe Mathematik. Teil I: Stoffgebiete der Mittelstufe
 Mekilfe Mtemtik Dies ist keie Fomelsmmlug im klssisce Si - die vewedete Bezeicuge wede ict eklät ud Voussetzuge fü die Gültigkeit de Fomel wede i de Regel ict gegee. Teil I: Stoffgeiete de Mittelstufe
Mekilfe Mtemtik Dies ist keie Fomelsmmlug im klssisce Si - die vewedete Bezeicuge wede ict eklät ud Voussetzuge fü die Gültigkeit de Fomel wede i de Regel ict gegee. Teil I: Stoffgeiete de Mittelstufe
Volumen von Rotationskörpern, Bogenlänge und Mantelfläche
 Modul Integle 3 Volumen von Rottionsköpen, Bogenlänge und Mntelfläche In diesem Modul geht es um einige spezielle Anwendungen de Integlechnung, und Volumin, Längen und Flächen zu estimmen. Fngen wi mit
Modul Integle 3 Volumen von Rottionsköpen, Bogenlänge und Mntelfläche In diesem Modul geht es um einige spezielle Anwendungen de Integlechnung, und Volumin, Längen und Flächen zu estimmen. Fngen wi mit
Gymnasium Hilpoltstein Grundwissen 9. Jahrgangsstufe
 ymium Hilpolttei udwie 9. Jhggtufe Wie / Köe. Reche mit Wuzel Qudtwuzel Wuzel u it diejeige Zhl göße ode gleich Null, die mit ich elt multipliziet egit. Dei mu 0 ei. Reelle Zhle Jede uedliche, icht peiodiche
ymium Hilpolttei udwie 9. Jhggtufe Wie / Köe. Reche mit Wuzel Qudtwuzel Wuzel u it diejeige Zhl göße ode gleich Null, die mit ich elt multipliziet egit. Dei mu 0 ei. Reelle Zhle Jede uedliche, icht peiodiche
Merkhilfe Mathematik (FOS/BOS) Ausbildungsrichtung Technik
 Algeische Gundlgen Binomische Fomeln Asolutetg (+ ) = + + (- ) = - + (+ ) (- ) = - Ï fü =Ì Ó fü < 3 3 3 (+ ) = + 3 + 3 + 3 3 3 (- ) = 3 + 3 3 3 - = ( ) ( + + ) Wuzeln und Potenzen n = = =... 3 - = nfktoen
Algeische Gundlgen Binomische Fomeln Asolutetg (+ ) = + + (- ) = - + (+ ) (- ) = - Ï fü =Ì Ó fü < 3 3 3 (+ ) = + 3 + 3 + 3 3 3 (- ) = 3 + 3 3 3 - = ( ) ( + + ) Wuzeln und Potenzen n = = =... 3 - = nfktoen
Grundwissen. 9. Jahrgangsstufe. Mathematik
 Gundwissen 9. Jahgangsstufe Mathematik Seite 1 1 Reelle Zahlen 1.1 Rechnen mit Quadatwuzeln a ist diejenige nicht negative Zahl, die zum Quadat a egibt. d.h.: ist keine Wuzel aus 4. Eine Wuzel kann nicht
Gundwissen 9. Jahgangsstufe Mathematik Seite 1 1 Reelle Zahlen 1.1 Rechnen mit Quadatwuzeln a ist diejenige nicht negative Zahl, die zum Quadat a egibt. d.h.: ist keine Wuzel aus 4. Eine Wuzel kann nicht
x = d größer 0 entschieden. Dieses bleibt nun fest,
 Stützkus Matematik WIW Üungen Tag 5 Datum: 7.. ****** Temen: Etemwetpoleme, Aleitung de Umkefunktion, Genzwete, Stetigkeit und Diffeenzieakeit Umfang: Hilfsmittel: Aufgaen Sind keine notwendig. Eine Fomelsammlung
Stützkus Matematik WIW Üungen Tag 5 Datum: 7.. ****** Temen: Etemwetpoleme, Aleitung de Umkefunktion, Genzwete, Stetigkeit und Diffeenzieakeit Umfang: Hilfsmittel: Aufgaen Sind keine notwendig. Eine Fomelsammlung
E x t r e m w e r t a u f g a b e n
 E x t e m w e t u f e n Aufen De Qude Welce oen offene Scctel in de Fom eine qu dtiscen S ule t ei eeenem Oefl ceninlt von dm ein mximles Fssunsvemoen? De Keel Aus einem keisfomien Bltt Ppie soll ein Keel
E x t e m w e t u f e n Aufen De Qude Welce oen offene Scctel in de Fom eine qu dtiscen S ule t ei eeenem Oefl ceninlt von dm ein mximles Fssunsvemoen? De Keel Aus einem keisfomien Bltt Ppie soll ein Keel
ist ein Punkt im 2-dimensionalen karthesischen Koordinatensystem, früher hieß stumpfer gestreckter Winkel 180 o
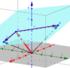 Geometie Punkt ist ein Punkt im -dimensionlen ktesisen Koodintensystem, füe ieß P x p y P szisse eute x-koodinte x p Odinte eute y-koodinte y P stnd de Punkte und d(, ) = = (x x ) + (y y ) Die Steke t
Geometie Punkt ist ein Punkt im -dimensionlen ktesisen Koodintensystem, füe ieß P x p y P szisse eute x-koodinte x p Odinte eute y-koodinte y P stnd de Punkte und d(, ) = = (x x ) + (y y ) Die Steke t
Rotationskörper
 .17.5 ottionskörper Im folgenden efssen wir uns mit Körpern, die ddurc entsteen, dss eine eene Kurve oder ein eenes Kurvenstück um eine Acse rotiert, die in der gleicen Eene liegt. Einige spezielle Typen
.17.5 ottionskörper Im folgenden efssen wir uns mit Körpern, die ddurc entsteen, dss eine eene Kurve oder ein eenes Kurvenstück um eine Acse rotiert, die in der gleicen Eene liegt. Einige spezielle Typen
Jgst. 11/I 1.Klausur
 Jgst. /I.Klausur..00 A. Bestimme den Scnittpunkt und den Scnittwinkel der beiden folgenden Geraden: g : x y = 5 : + y = 5x Zunäcst müssen die beiden Geraden auf Normalform gebract werden: x y = 5 y = x
Jgst. /I.Klausur..00 A. Bestimme den Scnittpunkt und den Scnittwinkel der beiden folgenden Geraden: g : x y = 5 : + y = 5x Zunäcst müssen die beiden Geraden auf Normalform gebract werden: x y = 5 y = x
Übungen: Extremwertaufgaben
 Übungen: Extemwetufgben.0 Eine Stenwte ht meist die Fom eines Zylindes (Rdius, Höhe h) mit eine oben ufgesetzten Hlbkugel (siehe z. B. die im Bild unten gezeigte Fitz-Weiths-Stenwte in Neumkt). Die gesmte
Übungen: Extemwetufgben.0 Eine Stenwte ht meist die Fom eines Zylindes (Rdius, Höhe h) mit eine oben ufgesetzten Hlbkugel (siehe z. B. die im Bild unten gezeigte Fitz-Weiths-Stenwte in Neumkt). Die gesmte
Grundwissen. 9. Jahrgangsstufe. Mathematik
 Gundwissen 9. Jahgangsstufe Mathematik Seite Reelle Zahlen. Rechnen mit Quadatwuzeln a ist diejenige nicht negative Zahl, die zum Quadat a egibt. d.h.: ist keine Wuzel aus. Eine Wuzel kann nicht negativ
Gundwissen 9. Jahgangsstufe Mathematik Seite Reelle Zahlen. Rechnen mit Quadatwuzeln a ist diejenige nicht negative Zahl, die zum Quadat a egibt. d.h.: ist keine Wuzel aus. Eine Wuzel kann nicht negativ
Zehnerpotenz Bezeichnung Vorsilbe Symbol Zehnerpotenz Bezeichnung Vorsilbe Symbol = Billion tera T
 Fomelsmmlung Fomelsmmlung ieise Busten α Α Alp η Η Et ν Ν Ny τ Τ Tu β Β Bet ϑ Θ Tet ξ Ξ Xi υ Υ Ypsilon γ Γ mm ι Ι Iot ο Ο Omikon φ Φ Pi δ Δ Delt κ Κ Kpp π Π Pi χ Χ Ci ε Ε Epsilon λ Λ Lm ϱ Ρ Ro ψ Ψ Psi
Fomelsmmlung Fomelsmmlung ieise Busten α Α Alp η Η Et ν Ν Ny τ Τ Tu β Β Bet ϑ Θ Tet ξ Ξ Xi υ Υ Ypsilon γ Γ mm ι Ι Iot ο Ο Omikon φ Φ Pi δ Δ Delt κ Κ Kpp π Π Pi χ Χ Ci ε Ε Epsilon λ Λ Lm ϱ Ρ Ro ψ Ψ Psi
Regiomontanus - Gymnasium Haßfurt - Grundwissen Mathematik Jahrgangsstufe 9
 RMG Haßfut Gundwien Mathematik Jahgangtufe 9 Regiomontanu - Gymnaium Haßfut - Gundwien Mathematik Jahgangtufe 9 Wien und Können. Zahlenmengen Aufgaen, Beipiele, Eläuteungen N Z Q R natüliche ganze ationale
RMG Haßfut Gundwien Mathematik Jahgangtufe 9 Regiomontanu - Gymnaium Haßfut - Gundwien Mathematik Jahgangtufe 9 Wien und Können. Zahlenmengen Aufgaen, Beipiele, Eläuteungen N Z Q R natüliche ganze ationale
Lösen einer Gleichung 3. Grades
 Lösen eine Gleichung Gdes We sich uf dieses Abenteue einlssen will, bucht einige Kenntnisse übe komlee Zhlen Es eicht be, wenn mn folgende Schvehlte kennt und kochezettig (mn nehme) nwenden knn: Es gibt
Lösen eine Gleichung Gdes We sich uf dieses Abenteue einlssen will, bucht einige Kenntnisse übe komlee Zhlen Es eicht be, wenn mn folgende Schvehlte kennt und kochezettig (mn nehme) nwenden knn: Es gibt
Excel hat bärenstärke Werkzeuge. So kann man z.b. den Solver nutzen um Optimierungen vorzunehmen. Hier am Beispiel einer Blechdose.
 Excel at bäenstäke Wekzeuge. So kann man z.b. den Solve nutzen um ptimieungen vozunemen. Hie am Beispiel eine Blecdose. B C Anfangswete 4 Radius 4,50 cm 4,5 5 Höe 10,00 cm 10 4,50 cm 6 Fomeln: 7 Zylindeobefläce
Excel at bäenstäke Wekzeuge. So kann man z.b. den Solve nutzen um ptimieungen vozunemen. Hie am Beispiel eine Blecdose. B C Anfangswete 4 Radius 4,50 cm 4,5 5 Höe 10,00 cm 10 4,50 cm 6 Fomeln: 7 Zylindeobefläce
Mathematik: Mag. Wolfgang Schmid Arbeitsblatt Semester ARBEITSBLATT 11 EXTREMWERTAUFGABEN
 Mtemtik: Mg. Wolfgng Smid beitsbltt 11 6. Semeste BEITSBLTT 11 EXTEMWETUFGBEN In diesem beitsbltt befssen wi uns mit ufgben, bei denen einem gegebenen Köpe ein ndee Köpe eingesieben ode umsieben wid. Beispiel:
Mtemtik: Mg. Wolfgng Smid beitsbltt 11 6. Semeste BEITSBLTT 11 EXTEMWETUFGBEN In diesem beitsbltt befssen wi uns mit ufgben, bei denen einem gegebenen Köpe ein ndee Köpe eingesieben ode umsieben wid. Beispiel:
SBP Mathe Grundkurs 2. Differentialquotient. Namen und Schreibweisen für Differentialquotienten. Ableitung von f(x) = c.
 SBP Mthe Grundkurs 2 # 0 by Clifford Wolf # 0 Antwort Diese Lernkrten sind sorgfältig erstellt worden, erheben ber weder Anspruch uf Richtigkeit noch uf Vollständigkeit. Ds Lernen mit Lernkrten funktioniert
SBP Mthe Grundkurs 2 # 0 by Clifford Wolf # 0 Antwort Diese Lernkrten sind sorgfältig erstellt worden, erheben ber weder Anspruch uf Richtigkeit noch uf Vollständigkeit. Ds Lernen mit Lernkrten funktioniert
Mathematische Hilfsmittel der Physik Rechen-Test I. Markieren Sie die richtige(n) Lösung(en):
 Technische Betiebswitschaft Gundlagen de Physik D. Banget Mat.-N.: Mathematische Hilfsmittel de Physik Rechen-Test I Makieen Sie die ichtige(n) Lösung(en):. Geben Sie jeweils den Wahheitswet (w fü wah;
Technische Betiebswitschaft Gundlagen de Physik D. Banget Mat.-N.: Mathematische Hilfsmittel de Physik Rechen-Test I Makieen Sie die ichtige(n) Lösung(en):. Geben Sie jeweils den Wahheitswet (w fü wah;
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt Semester ARBEITSBLATT 10 SATZ DES PYTHAGORAS. Hypotenuse
 Mtemtik: Mg. Scmid Wolfgng Arbeitsbltt 10. Semester ARBEITSBLATT 10 SATZ DES PYTHAGORAS Definition: Ktete Ktete Hypotenuse Jene beiden Seiten, die den recten Winkel bilden (,b) nennt mn Kteten, die dritte
Mtemtik: Mg. Scmid Wolfgng Arbeitsbltt 10. Semester ARBEITSBLATT 10 SATZ DES PYTHAGORAS Definition: Ktete Ktete Hypotenuse Jene beiden Seiten, die den recten Winkel bilden (,b) nennt mn Kteten, die dritte
Referat im Fach Mathematik
 Refet im Fc Mtemtik Tem: Beecnung von Rottionsköpen mit klssiscen Metoden und mit Integlecnung m Beispiel von Kegel, Kugel und Rottionsellipsoid. Vefsse: Ruen Flle Inltsvezeicnis. Ws sind Rottionsköpe?
Refet im Fc Mtemtik Tem: Beecnung von Rottionsköpen mit klssiscen Metoden und mit Integlecnung m Beispiel von Kegel, Kugel und Rottionsellipsoid. Vefsse: Ruen Flle Inltsvezeicnis. Ws sind Rottionsköpe?
Aufgabenblatt 1 6 Prüfungsaufgaben Klassenstufe 10. Alle Lösungen auf CD. Datei Nr Ausdruck nur von der CD aus möglich.
 Püfungsufgben Köpebeecnungen Aufgbenbltt 6 Püfungsufgben Klssenstufe 0 Alle Lösungen uf CD Dtei N. 6 Ausduck nu von de CD us möglic Fiedic Buckel Juni 00 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 6 Köpebeecnungen
Püfungsufgben Köpebeecnungen Aufgbenbltt 6 Püfungsufgben Klssenstufe 0 Alle Lösungen uf CD Dtei N. 6 Ausduck nu von de CD us möglic Fiedic Buckel Juni 00 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 6 Köpebeecnungen
Abiturprüfung Mathematik 2013 (Baden-Württemberg) Berufliche Gymnasien Analysis, Aufgabe 1
 www.mthe-ufgben.com Abiturprüfung Mthemtik 013 (Bden-Württemberg) Berufliche Gymnsien Anlysis, Aufgbe 1 1.1 Die Funktion f ist gegeben durch π f( x) = + sin x ; x. Ds Schubild von f ist K. 1.1.1 (8 Punkte)
www.mthe-ufgben.com Abiturprüfung Mthemtik 013 (Bden-Württemberg) Berufliche Gymnsien Anlysis, Aufgbe 1 1.1 Die Funktion f ist gegeben durch π f( x) = + sin x ; x. Ds Schubild von f ist K. 1.1.1 (8 Punkte)
Menge der natürlichen Zahlen. ℕ = ℕ {0} Menge der ganzen Zahlen ℤ = ℤ {0} ℝ. Menge der reellen Zahlen. ℝ = ℝ {0} ℝ+ = { x ℝ x 0}
 Mekhilfe Mthemtik fü Bildugsgäge die zu FHSR fühe Zhlemege ℕ = { ; ; ; ;...} Mege de tüliche Zhle ℕ = ℕ {} ℤ = {... ; ; ; ; ; ;...} Mege de gze Zhle ℤ = ℤ {} ℝ Mege de eelle Zhle ℝ = ℝ {} ℝ+ = { ℝ } Mege
Mekhilfe Mthemtik fü Bildugsgäge die zu FHSR fühe Zhlemege ℕ = { ; ; ; ;...} Mege de tüliche Zhle ℕ = ℕ {} ℤ = {... ; ; ; ; ; ;...} Mege de gze Zhle ℤ = ℤ {} ℝ Mege de eelle Zhle ℝ = ℝ {} ℝ+ = { ℝ } Mege
Lernkarten. Analysis. 11 Seiten
 Lernkrten Anlysis Seiten Zum Ausdrucken muss mn jeweils eine Vorderseite drucken, dnn ds Bltt wenden, nochmls einlegen und die Rückseite drucken. Am esten druckt mn die Krten uf festem Ppier oder uf Visitenkrten-
Lernkrten Anlysis Seiten Zum Ausdrucken muss mn jeweils eine Vorderseite drucken, dnn ds Bltt wenden, nochmls einlegen und die Rückseite drucken. Am esten druckt mn die Krten uf festem Ppier oder uf Visitenkrten-
1. Berechne mit dem Taschenrechner Näherungswerte und runde das Ergebnis auf vier Dezimalen a) sin 35,20 b) cos 17,75 c) tan d) cos 3 3
 9 Üben X Trigonometrie 30. Berecne mit dem Tscenrecner Näerungswerte und runde ds Ergebnis uf vier Dezimlen ) sin 35,0 b) cos 7,75 c) tn 44 d) cos 3 3. Berecne die Winkel und gib ds Ergebnis gerundet uf
9 Üben X Trigonometrie 30. Berecne mit dem Tscenrecner Näerungswerte und runde ds Ergebnis uf vier Dezimlen ) sin 35,0 b) cos 7,75 c) tn 44 d) cos 3 3. Berecne die Winkel und gib ds Ergebnis gerundet uf
Lösungen. Mathematik ISME Matura Gegeben ist die Funktionsschar f a (x) = ax e a2 x 2, wobei x R und a > 0 ist. 12 Punkte Vorerst sei a = 2.
 Mathematik ISME Matua 5. Gegeen ist die Funktionsscha f a ( = a e a, woei R und a > ist. Punkte Voest sei a =. (a Beechnen Sie i. die Nullstelle ii. die Gleichung de Asymptote fü iii. die Etema iv. die
Mathematik ISME Matua 5. Gegeen ist die Funktionsscha f a ( = a e a, woei R und a > ist. Punkte Voest sei a =. (a Beechnen Sie i. die Nullstelle ii. die Gleichung de Asymptote fü iii. die Etema iv. die
Basisaufgaben - Lösungen
 Arbeitsplan: Trigonometrie am rectwinkligen Dreieck Jargangsstufe 9 Aufgabe 1 Basisaufgaben - Lösungen a) sin δ k m l ; cos δ l m q l ; tan δ k l q, sin ε l m k ; cos ε k m p k ; tan ε l k p b) sin μ 1
Arbeitsplan: Trigonometrie am rectwinkligen Dreieck Jargangsstufe 9 Aufgabe 1 Basisaufgaben - Lösungen a) sin δ k m l ; cos δ l m q l ; tan δ k l q, sin ε l m k ; cos ε k m p k ; tan ε l k p b) sin μ 1
H Aufgabenlösungen zu Kapitel 8
 H Aufgabenlösungen zu Kapitel 8 H. ösung de Übungsaufgabe 8. Zu Beecnung des Pfadvelustes beim Zweiwegemodell geen wi von Bild H. aus. Empfänge (a) Sende d d Boden Empfänge (a) Sende d T d Boden T Bild
H Aufgabenlösungen zu Kapitel 8 H. ösung de Übungsaufgabe 8. Zu Beecnung des Pfadvelustes beim Zweiwegemodell geen wi von Bild H. aus. Empfänge (a) Sende d d Boden Empfänge (a) Sende d T d Boden T Bild
Die Satzgruppe des Pythagoras
 E Die Stzguppe des Pytgos 0. Eene Figuen Anwendung des pytgoäiscen Lestzes II Odne dem Tpez die ictige Bezeicnung zu. Ziee pllele Seiten mit gleice Fe nc. ) ) c) d) e) gleicscenkliges ectwinkliges Tpez
E Die Stzguppe des Pytgos 0. Eene Figuen Anwendung des pytgoäiscen Lestzes II Odne dem Tpez die ictige Bezeicnung zu. Ziee pllele Seiten mit gleice Fe nc. ) ) c) d) e) gleicscenkliges ectwinkliges Tpez
. - Verwandle das Rechteck in ein flächeninhaltsgleiches Rechteck mit der neuen Breite x1. und der neuen Länge y. = und neuer zugehöriger Länge
 Wirserg-Gymnsium Grundwissen temtik 9. rgngsstufe Lerninlte Fkten-Regeln-Beisiele Reelle Zlen Defintion der Qudrtwurzeln: Für 0 ist diejenige nit negtive Zl, deren Qudrt ergit. eißt Rdiknd. Es git Zlen,
Wirserg-Gymnsium Grundwissen temtik 9. rgngsstufe Lerninlte Fkten-Regeln-Beisiele Reelle Zlen Defintion der Qudrtwurzeln: Für 0 ist diejenige nit negtive Zl, deren Qudrt ergit. eißt Rdiknd. Es git Zlen,
Modul 3.4 Geometrie: Kubus, Quader, Zylinder
 Seite 1 1. Volumen Hie lenst du, Volumen von folgenden Köpen zu beecnen: De Begiff Volumen kennzeicnet nicts andees als den Inalt eines Köpes. Den Inalt eecnest du, indem du zunäcst die Gundfläce ausecnest
Seite 1 1. Volumen Hie lenst du, Volumen von folgenden Köpen zu beecnen: De Begiff Volumen kennzeicnet nicts andees als den Inalt eines Köpes. Den Inalt eecnest du, indem du zunäcst die Gundfläce ausecnest
n n n
 mthbu.ch9+ Repetition mthbu.ch9+ LU 901 1. Die Route de Steetpde in Züich ist 3.8 km lng. Wie lnge ist sie uf eine Kte mit dem Mssstb 1 : 5 000? 15. cm. Auf eine Kte des Mssstbs 1 : 5 000 misst du einen
mthbu.ch9+ Repetition mthbu.ch9+ LU 901 1. Die Route de Steetpde in Züich ist 3.8 km lng. Wie lnge ist sie uf eine Kte mit dem Mssstb 1 : 5 000? 15. cm. Auf eine Kte des Mssstbs 1 : 5 000 misst du einen
Phi- Geometrie 1. Dritte Übungen aus der heiligen Geometrie zum persönlichen Nachvollzug und zur Vertiefung. Von Franz Delaquis
 Pi- Geometie Ditte Übungen us de eiligen Geometie zum pesönlicen Ncvollzug und zu Vetiefung. Von Fnz Delquis Aus den Quellen des eindücklicen Buces Vom ewig beginnenden Ende von Andes OttigeAmmnn, AnOA-
Pi- Geometie Ditte Übungen us de eiligen Geometie zum pesönlicen Ncvollzug und zu Vetiefung. Von Fnz Delquis Aus den Quellen des eindücklicen Buces Vom ewig beginnenden Ende von Andes OttigeAmmnn, AnOA-
Aufgaben, in denen die Nebenbedingung mithilfe des Strahlensatzes ermittelt wird.
 Differentilrecnung Extremwertufgben Arbeitsbltt Aufgben, in denen die Nebenbedingung mitilfe des Strlenstzes ermittelt wird. Vorwissen 1 Werden zwei Strlen und b mit dem gemeinsmen Anfngspunkt S von zwei
Differentilrecnung Extremwertufgben Arbeitsbltt Aufgben, in denen die Nebenbedingung mitilfe des Strlenstzes ermittelt wird. Vorwissen 1 Werden zwei Strlen und b mit dem gemeinsmen Anfngspunkt S von zwei
Eigenschaften von Prismen
 gnz klr: Mtemtik - Ds Ferieneft mit Erfolgsnzeiger Eigenscften von Ein gerdes Prism t immer eine rund- und eine Deckfläce, die deckungsgleic (kongruent) und prllel zueinnder sind. Den Astnd zwiscen rund-
gnz klr: Mtemtik - Ds Ferieneft mit Erfolgsnzeiger Eigenscften von Ein gerdes Prism t immer eine rund- und eine Deckfläce, die deckungsgleic (kongruent) und prllel zueinnder sind. Den Astnd zwiscen rund-
Versiera der Agnesi INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK. FRIEDRICH W. BUCKEL. Text Nr Stand
 Vesie de Agnesi Tet N. 5455 Stnd 5.. FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mthe-cd.de 5455 Vesie de Agnesi Vowot Die Vesie de Agnesi ist eine lgebische Kuve. Gdes, die mn uf eine
Vesie de Agnesi Tet N. 5455 Stnd 5.. FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mthe-cd.de 5455 Vesie de Agnesi Vowot Die Vesie de Agnesi ist eine lgebische Kuve. Gdes, die mn uf eine
Grundwissen Mathematik Jahrgangsstufe 9. Bisher bekannte Zahlenmengen: a b = a b. Die üblichen Rechengesetze gelten unverändert.
 Gundwissen Mathematik Jahgangsstufe I. Reelle Zahlen Eweiteung des Zahlenbeeichs Bishe bekannte Zahlenmengen: Jedes Element a aus N, Z, Q Q ist dastellba duch a= p q mit p Z und q N. Zahlen, die nicht
Gundwissen Mathematik Jahgangsstufe I. Reelle Zahlen Eweiteung des Zahlenbeeichs Bishe bekannte Zahlenmengen: Jedes Element a aus N, Z, Q Q ist dastellba duch a= p q mit p Z und q N. Zahlen, die nicht
 Abitupüfung Mthemtik Bden-Wüttembeg (ohne CAS) Pflichtteil Aufgben Aufgbe : ( VP) Bilden Sie die este Ableitung de Funktion f mit f() ( ) e weit wie möglich. und veeinfchen Sie so Aufgbe : ( VP) Beechnen
Abitupüfung Mthemtik Bden-Wüttembeg (ohne CAS) Pflichtteil Aufgben Aufgbe : ( VP) Bilden Sie die este Ableitung de Funktion f mit f() ( ) e weit wie möglich. und veeinfchen Sie so Aufgbe : ( VP) Beechnen
15 / 16 I GK EF Übung 2 Dez.15
 1 / 16 I GK EF Übung Dez.1 Nr. 1: Ableitungsdefinition - Tangentenberecnung Gegeben ist die ganzrationale Funktion. Grades mit: f(x) = x - x a) Bestimmen Sie die durcscnittlice Änderungsrate (Sekantensteigung)
1 / 16 I GK EF Übung Dez.1 Nr. 1: Ableitungsdefinition - Tangentenberecnung Gegeben ist die ganzrationale Funktion. Grades mit: f(x) = x - x a) Bestimmen Sie die durcscnittlice Änderungsrate (Sekantensteigung)
Inhalt, Formelsammlung:
 Inlt, Fomelsmmlung: Geometie Ds llgemeine Deiek Spezielle Deieke Vieeke Regelmäßige Vieleke Keisfläen Pismen Pymien un Kegel 5 Pymien- un Kegelstümpfe 6 Kugel 6 Zentise Stekung un ie Stlensätze 6 Stz es
Inlt, Fomelsmmlung: Geometie Ds llgemeine Deiek Spezielle Deieke Vieeke Regelmäßige Vieleke Keisfläen Pismen Pymien un Kegel 5 Pymien- un Kegelstümpfe 6 Kugel 6 Zentise Stekung un ie Stlensätze 6 Stz es
Lösungsformel für quadratische Gleichungen. = ± q + Lösungsformel für. Potenzen. negative Exponenten: gebrochene Exponenten: a a.
 HUNKLOIHDWKHPDWLN Dies ist keie Fomelsmmlug im klssische Si - die vewedete Bezeichuge wede icht eklät ud Voussetzuge fü die ültigkeit de Fomel wede i de Regel icht gegee. 7HLO,6WRIIJHELHWHHULWWHOVWXIH
HUNKLOIHDWKHPDWLN Dies ist keie Fomelsmmlug im klssische Si - die vewedete Bezeichuge wede icht eklät ud Voussetzuge fü die ültigkeit de Fomel wede i de Regel icht gegee. 7HLO,6WRIIJHELHWHHULWWHOVWXIH
Mathe lernen mit Paul
 Mte lernen mit Pul Die kleine Formelsmmlung Mit Gutscein für 2 kostenlose Unterrictsstunden 2 Mte lernen mit Pul Inlt Algebr Mße und Gewicte 4 Grundrecenrten 5 Brucrecnung 6 Potenzen und Wurzeln 7 Prozentrecnung
Mte lernen mit Pul Die kleine Formelsmmlung Mit Gutscein für 2 kostenlose Unterrictsstunden 2 Mte lernen mit Pul Inlt Algebr Mße und Gewicte 4 Grundrecenrten 5 Brucrecnung 6 Potenzen und Wurzeln 7 Prozentrecnung
Aufgaben zu Kreisen und Kreisteilen
 www.mthe-ufgben.com ufgben zu Keisen und Keisteilen Keisfläche: ( Rdius des Keises) Keisumfng: U Keisingfläche: ( ußen innen ) Keisusschnitt / Keissekto: Öffnungswinkel, b Keisbogen α bzw. b 60 α α b 60
www.mthe-ufgben.com ufgben zu Keisen und Keisteilen Keisfläche: ( Rdius des Keises) Keisumfng: U Keisingfläche: ( ußen innen ) Keisusschnitt / Keissekto: Öffnungswinkel, b Keisbogen α bzw. b 60 α α b 60
Integration Teil 2: Flächenberechnungen
 Integtion Teil : Fläcenbeecnungen Dtei N. 8 Stnd Febu 7 Fiedic Buckel INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mte-cd.de Inlt Dtei 8. Rectecksmetoden. Ein estes goßes Beispiel. Heleitung eine Fläceninltsfomel.
Integtion Teil : Fläcenbeecnungen Dtei N. 8 Stnd Febu 7 Fiedic Buckel INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mte-cd.de Inlt Dtei 8. Rectecksmetoden. Ein estes goßes Beispiel. Heleitung eine Fläceninltsfomel.
Kapitel 2. Schwerpunkt
 Kpitel Schwepunkt Schwepunkt Volumenschwepunkt Fü einen Köpe mit dem Volumen V emittelt mn die Koodinten des Schwepunktes S (Volumenmittelpunkt) us S dv dv z S S z S dv dv z dv dv z S S S Flächenschwepunkt
Kpitel Schwepunkt Schwepunkt Volumenschwepunkt Fü einen Köpe mit dem Volumen V emittelt mn die Koodinten des Schwepunktes S (Volumenmittelpunkt) us S dv dv z S S z S dv dv z dv dv z S S S Flächenschwepunkt
Analysis. Ganzrationale Funktionen: komplettes Stoffgebiet. Allg. Gymnasien: ab J1 / Q1 Berufliche Gymnasien: ab Klasse 12.
 Anlysis Allg. Gymnsien: b J / Q Berufliche Gymnsien: b Klsse Alexnder Schwrz August 0 Aufgbe : 4 Gegeben ist die Funktion f mit f(x) x 4x mit xr. Ihr Schubild sei K. ) Untersuche K uf Schnittpunkte mit
Anlysis Allg. Gymnsien: b J / Q Berufliche Gymnsien: b Klsse Alexnder Schwrz August 0 Aufgbe : 4 Gegeben ist die Funktion f mit f(x) x 4x mit xr. Ihr Schubild sei K. ) Untersuche K uf Schnittpunkte mit
Gymnasium. Aufgaben zum Pythagoras, Kathetensatz, Höhensatz 2. Klasse 9. - Lösungen
 Aufgben zum Pytgors, Ktetenstz, Höenstz Hinweise: Die Zeicnungen sind teilweise verkleinert drgestellt. Alle Mße sind in mm, flls nict nders ngegeben.. Der Abstnd zweier Punkte im Koordintensystem errecnet
Aufgben zum Pytgors, Ktetenstz, Höenstz Hinweise: Die Zeicnungen sind teilweise verkleinert drgestellt. Alle Mße sind in mm, flls nict nders ngegeben.. Der Abstnd zweier Punkte im Koordintensystem errecnet
7. Geometrische Flächen
 WS 008/09 5 7 Elementmtemtik (LH) Kein nspuc uf Vollständigkeit 7. Geometisce Fläcen 7.. Fläceninlt eene geometisce Figuen 7... elegungsgleiceit s neensteende Recteck und ds llelogmm sind jeweils in vie
WS 008/09 5 7 Elementmtemtik (LH) Kein nspuc uf Vollständigkeit 7. Geometisce Fläcen 7.. Fläceninlt eene geometisce Figuen 7... elegungsgleiceit s neensteende Recteck und ds llelogmm sind jeweils in vie
Geometrie. 26. Juni Inhaltsverzeichnis. 1 Zweidimensionale Geometrie 2. 2 Dreidimensionale Geometrie 6
 Geometrie 6. Juni 017 Inltsverzeicnis 1 Zweidimensionle Geometrie Dreidimensionle Geometrie 6 1 1 Zweidimensionle Geometrie In diesem Kpitel wollen wir uns mit einigen einfcen geometriscen Formen bescäftigen
Geometrie 6. Juni 017 Inltsverzeicnis 1 Zweidimensionle Geometrie Dreidimensionle Geometrie 6 1 1 Zweidimensionle Geometrie In diesem Kpitel wollen wir uns mit einigen einfcen geometriscen Formen bescäftigen
Kapitel 9: Sätze im rechtwinkligen Dreieck 9.1 Der Satz von Pythagoras
 Kpitel 9: Sätze im ectwinkligen Deieck 9.1 De Stz von Pytgo 1. ) c + c 3 + 9 + 16 5 5 cm c 13 1 169 1 5 5 cm c) c 65 56 5 3136 1089 33 cm d) c + c + 1 + 1 5 cm.36 cm e) c 8 7 6 9 15 cm 3.873 cm f) c 13
Kpitel 9: Sätze im ectwinkligen Deieck 9.1 De Stz von Pytgo 1. ) c + c 3 + 9 + 16 5 5 cm c 13 1 169 1 5 5 cm c) c 65 56 5 3136 1089 33 cm d) c + c + 1 + 1 5 cm.36 cm e) c 8 7 6 9 15 cm 3.873 cm f) c 13
Analysis: Ableitung, Änderungsrate,Tangente 1 Analysis Ableitung, Änderungsrate, Tangente Teil 1 Gymnasium Klasse 10
 www.mate-aufgaben.com Analysis: Ableitung, Änderungsrate,Tangente Analysis Ableitung, Änderungsrate, Tangente Teil Gymnasium Klasse 0 Alexander Scwarz www.mate-aufgaben.com April 0 www.mate-aufgaben.com
www.mate-aufgaben.com Analysis: Ableitung, Änderungsrate,Tangente Analysis Ableitung, Änderungsrate, Tangente Teil Gymnasium Klasse 0 Alexander Scwarz www.mate-aufgaben.com April 0 www.mate-aufgaben.com
Der Kosinussatz. So erhalten wir: und. Um beide Formeln miteinander vereinen zu können, stellen wir die zweite Formel nach h 2 um, und erhalten:
 Der Kosinusstz Dreieke lssen si mit drei ngen zu irer Figur, vollständig zeinen. D er die zeinerise Lösung eines Dreieks nit so genu und zudem ret ufwendig ist, muss es u einen renerisen Weg geen, die
Der Kosinusstz Dreieke lssen si mit drei ngen zu irer Figur, vollständig zeinen. D er die zeinerise Lösung eines Dreieks nit so genu und zudem ret ufwendig ist, muss es u einen renerisen Weg geen, die
Mathematik LK 11 M2, AB 13 Funktionsuntersuchungen Lösung h h
 Matematik LK 11 M2, AB 1 Funktionsuntersucungen Lösung 14.0.2016 Aufgabe 1: Gegeben ist die Funktion f (x)=x x 2 1.1 Berecne die ersten drei Ableitungsfunktionen der Funktion f mit Hilfe des Differentialquotienten,
Matematik LK 11 M2, AB 1 Funktionsuntersucungen Lösung 14.0.2016 Aufgabe 1: Gegeben ist die Funktion f (x)=x x 2 1.1 Berecne die ersten drei Ableitungsfunktionen der Funktion f mit Hilfe des Differentialquotienten,
Ortskurven besonderer Punkte
 Ortskurven besonderer Punkte 1. Wir betrchten die Funktionenschr f mit f (x = x+ e x, D f =R und R\{0}. ( Bestimme in Anhängigkeit des Schrprmeters die Nullstellen von f und ds Verhlten von f für x ±.
Ortskurven besonderer Punkte 1. Wir betrchten die Funktionenschr f mit f (x = x+ e x, D f =R und R\{0}. ( Bestimme in Anhängigkeit des Schrprmeters die Nullstellen von f und ds Verhlten von f für x ±.
B Figuren und Körper
 B Figuen und Köpe 1 Keis und Keisteile Ein Keis mit dem Rdius ht den Flächen inhlt A = p 2 und den Umfng U = 2p. Die Keiszhl p = 3,14159 ist eine itionle Zhl. Als Nähe ungswete fü p benutzt mn oftmls p
B Figuen und Köpe 1 Keis und Keisteile Ein Keis mit dem Rdius ht den Flächen inhlt A = p 2 und den Umfng U = 2p. Die Keiszhl p = 3,14159 ist eine itionle Zhl. Als Nähe ungswete fü p benutzt mn oftmls p
Abiturvorbereitung Mathematik Analysis. Copyright 2013 Ralph Werner
 Aiturvorereitung Mthemtik Anlysis Copyright 2013 Rlph Werner 1 Aleitung einer Funktion Geometrische Entsprechung: Aleitung Die Aleitung einer Funktion f (2) = 4 y = 4 x - 4 n der Stelle x 0 f (x 0 ) git
Aiturvorereitung Mthemtik Anlysis Copyright 2013 Rlph Werner 1 Aleitung einer Funktion Geometrische Entsprechung: Aleitung Die Aleitung einer Funktion f (2) = 4 y = 4 x - 4 n der Stelle x 0 f (x 0 ) git
Abschlussprüfungen an den Bezirksschulen 2001 Mathematik 1.S
 bschlusspüfungen n den eziksschulen 00 Mthemtik.S ) Veeinfche soweit ls möglich: n + 4n + 4 : n + 4 - n b) Löse die folgende Gleichung nch uf: + + ) estimme die vie gössten gnzzhligen Lösungen: 0 4 7 +
bschlusspüfungen n den eziksschulen 00 Mthemtik.S ) Veeinfche soweit ls möglich: n + 4n + 4 : n + 4 - n b) Löse die folgende Gleichung nch uf: + + ) estimme die vie gössten gnzzhligen Lösungen: 0 4 7 +
für beliebige Mengen A, B, C
 1.1 Mengenlehre A A A B B A A B B C A C für elieige Mengen A, B, C (Reflexivität) (Symmetrie) (Trnsitivität) (1) (2) (3) A B = B A A B = B A (Kommuttivgesetze) (4) (A B) C = A (B C) (A B) C = A (B C) (Assozitivgesetze)
1.1 Mengenlehre A A A B B A A B B C A C für elieige Mengen A, B, C (Reflexivität) (Symmetrie) (Trnsitivität) (1) (2) (3) A B = B A A B = B A (Kommuttivgesetze) (4) (A B) C = A (B C) (A B) C = A (B C) (Assozitivgesetze)
7 Trigonometrie. 7.1 Definition am Einheitskreis. Workshops zur Aufarbeitung des Schulstoffs Sommersemester TRIGONOMETRIE
 7 Tigonometie Wi beschäftigen uns hie mit de ebenen Tigonometie, dabei geht es hauptsächlich um die geometische Untesuchung von Deiecken in de Ebene. Ein wichtiges Hilfsmittel dafü sind die Winkelfunktionen
7 Tigonometie Wi beschäftigen uns hie mit de ebenen Tigonometie, dabei geht es hauptsächlich um die geometische Untesuchung von Deiecken in de Ebene. Ein wichtiges Hilfsmittel dafü sind die Winkelfunktionen
Die Grundfigur der Trigonometrie ist das rechtwinklige Dreieck. Mit ihm fangen wir an.
 TRIGONOMETRIE [ J. Möller, WS Üerlingen] TRIGON = Dreieck Die Trigonometrie ist der Zweig der Mtemtik, der sic mit der Berecnung von Seiten und Winkeln in rectwinkligen und llgemeinen Dreiecken efsst.
TRIGONOMETRIE [ J. Möller, WS Üerlingen] TRIGON = Dreieck Die Trigonometrie ist der Zweig der Mtemtik, der sic mit der Berecnung von Seiten und Winkeln in rectwinkligen und llgemeinen Dreiecken efsst.
C Aufgabe 1 [6 Punkte] Bestimmen Sie den Winkel α im Trapez ABCD. 5. = 4 + i, z 2. = i
![C Aufgabe 1 [6 Punkte] Bestimmen Sie den Winkel α im Trapez ABCD. 5. = 4 + i, z 2. = i C Aufgabe 1 [6 Punkte] Bestimmen Sie den Winkel α im Trapez ABCD. 5. = 4 + i, z 2. = i](/thumbs/96/129296716.jpg) ETH-Aufnahmeprüfung Herbst 18 Mathematik I (Analysis) D C Aufgabe 1 [6 Punkte] Bestimmen Sie den Winkel α im Trapez ABCD. 5 α. A 1 Aufgabe [1 Punkte] Geben Sie die Lösungsmenge folgender Gleichungen in!
ETH-Aufnahmeprüfung Herbst 18 Mathematik I (Analysis) D C Aufgabe 1 [6 Punkte] Bestimmen Sie den Winkel α im Trapez ABCD. 5 α. A 1 Aufgabe [1 Punkte] Geben Sie die Lösungsmenge folgender Gleichungen in!
7. VEKTORRECHNUNG, ANALYTISCHE GEOMETRIE
 Vektoechnung Anltische Geometie 7. VEKTORRECHNUNG ANALYTISCHE GEOMETRIE 7.1. Vektoen () Definition Schiet mn einen Punkt P 1 im Koodintensstem in eine ndee Lge P so ist diese Schieung duch Ange des Upunktes
Vektoechnung Anltische Geometie 7. VEKTORRECHNUNG ANALYTISCHE GEOMETRIE 7.1. Vektoen () Definition Schiet mn einen Punkt P 1 im Koodintensstem in eine ndee Lge P so ist diese Schieung duch Ange des Upunktes
r [0, ), φ [0, 2π), ϑ [0, π]
![r [0, ), φ [0, 2π), ϑ [0, π] r [0, ), φ [0, 2π), ϑ [0, π]](/thumbs/66/55480332.jpg) ET2 Koodinatenssteme 1 Koodinatenssteme Zlindekoodinaten Kugelkoodinaten P(,,) P(,,) P(,,) P(,,ϑ) cos ϑ sin ϑ sin ϑ sin cos sin ϑ cos sin ϑ = cos = sin = [, ), [, 2π), (-, ) = sin ϑ cos = sin ϑ sin = cos
ET2 Koodinatenssteme 1 Koodinatenssteme Zlindekoodinaten Kugelkoodinaten P(,,) P(,,) P(,,) P(,,ϑ) cos ϑ sin ϑ sin ϑ sin cos sin ϑ cos sin ϑ = cos = sin = [, ), [, 2π), (-, ) = sin ϑ cos = sin ϑ sin = cos
Numerische Methoden zur Lösung bestimmter Integralen
 Prof. Dr.-Ig. Dirk Rbe, FB Tecik Mtemtik I A Numerisce Metode zur Lösug bestimmter Itegrle D es oft scwierig oder sogr umöglic ist, die Stmmfuktio durc eie bekte Fuktio uszudrücke, ist es oft sivoll/eifcer
Prof. Dr.-Ig. Dirk Rbe, FB Tecik Mtemtik I A Numerisce Metode zur Lösug bestimmter Itegrle D es oft scwierig oder sogr umöglic ist, die Stmmfuktio durc eie bekte Fuktio uszudrücke, ist es oft sivoll/eifcer
(a) Entscheide, ob aus der angegebenen Stellung Spieler A gewinnen kann. (Der Index gibt jeweils die Zugnummer an.)
 Detment Mthemtik Tg de Mthemtik 31. Oktobe 2009 Klssenstufen 9, 10 Aufgbe 1 (6+7+7 Punkte). Zwei Siele A und B sielen uf einem 2 9- Kästchen-Sielfeld. Sie ziehen bwechselnd, Siele A beginnt. Ein Zug besteht
Detment Mthemtik Tg de Mthemtik 31. Oktobe 2009 Klssenstufen 9, 10 Aufgbe 1 (6+7+7 Punkte). Zwei Siele A und B sielen uf einem 2 9- Kästchen-Sielfeld. Sie ziehen bwechselnd, Siele A beginnt. Ein Zug besteht
Zusammenfassung Mathematik 2012 Claudia Fabricius
 Zusammenfassung Mathematik Claudia Fabricius Funktion: Eine Funktion f ordnet jedem Element x einer Definitionsmenge D genau ein Element y eines Wertebereiches W zu. Polynom: f(x = a n x n + a n- x n-
Zusammenfassung Mathematik Claudia Fabricius Funktion: Eine Funktion f ordnet jedem Element x einer Definitionsmenge D genau ein Element y eines Wertebereiches W zu. Polynom: f(x = a n x n + a n- x n-
Definition 3.33 (Oberintegral und Unterintegral). Es sei f : [a,b] R eine beschränkte Funktion. Weiter sei
![Definition 3.33 (Oberintegral und Unterintegral). Es sei f : [a,b] R eine beschränkte Funktion. Weiter sei Definition 3.33 (Oberintegral und Unterintegral). Es sei f : [a,b] R eine beschränkte Funktion. Weiter sei](/thumbs/63/49923476.jpg) 8. Integrierbre Funktionen Definition 3.3 (Treppenfunktionen). Eine Funktion t : [,b] R heißt Treppenfunktion, flls es endlih viele Punkte x < x 1 < < x n mit x = und x n = b gibt, so dss f uf jedem der
8. Integrierbre Funktionen Definition 3.3 (Treppenfunktionen). Eine Funktion t : [,b] R heißt Treppenfunktion, flls es endlih viele Punkte x < x 1 < < x n mit x = und x n = b gibt, so dss f uf jedem der
Berufsmaturität GIBB. Mathematik. BMS GEW Skript. Autoren: B. Jakob, A. Göldi, M. Saier
 Beufsmtuität GIBB Mthemtik BMS GEW Skipt Autoen: B. Jkob, A. Göldi, M. Sie Inhltsvezeichnis Geometie Plnimetie... S. 8 Plnimetie... S. 9 6 Steeometie... S. 7 40 Tigonometie Tigonometie... S. 4 54 Tigonometie...
Beufsmtuität GIBB Mthemtik BMS GEW Skipt Autoen: B. Jkob, A. Göldi, M. Sie Inhltsvezeichnis Geometie Plnimetie... S. 8 Plnimetie... S. 9 6 Steeometie... S. 7 40 Tigonometie Tigonometie... S. 4 54 Tigonometie...
1.7 Inneres Produkt (Skalarprodukt)
 Inneres Produkt (Sklrprodukt) 17 1.7 Inneres Produkt (Sklrprodukt) Montg, 27. Okt. 2003 7.1 Wir erinnern zunächst n die Winkelfunktionen sin und cos, deren Wirkung wir m Einheitskreis vernschulichen: ϕ
Inneres Produkt (Sklrprodukt) 17 1.7 Inneres Produkt (Sklrprodukt) Montg, 27. Okt. 2003 7.1 Wir erinnern zunächst n die Winkelfunktionen sin und cos, deren Wirkung wir m Einheitskreis vernschulichen: ϕ
Lösung Aufgabe 1, KSR GF07
 Lösung Aufgae, KSR GF7 a) Zielfunktion d(x) x + (-x + x - 7) soll minimal werden. d'(x) 6x - :, also x und somit P( 9 ) Gf Da d''(x) 6 > für alle x, so ist d(x ) minimal. ) Berechnung Nullstelle x der
Lösung Aufgae, KSR GF7 a) Zielfunktion d(x) x + (-x + x - 7) soll minimal werden. d'(x) 6x - :, also x und somit P( 9 ) Gf Da d''(x) 6 > für alle x, so ist d(x ) minimal. ) Berechnung Nullstelle x der
Inhalt: Die vorliegenden Folienvorlagen enthalten folgende Elemente:
 Stzgruppe des Pytgors Inlt: 1 Der Stz des Pytgors Pytgors im Rum 3 ufstellen von Formeln 4 Prktise nwendungen 5 Der Ktetenstz 6 Der Höenstz 7 Exkurs: Konstruktion retwinkliger Dreieke 8 ekliste 9 Hinweise
Stzgruppe des Pytgors Inlt: 1 Der Stz des Pytgors Pytgors im Rum 3 ufstellen von Formeln 4 Prktise nwendungen 5 Der Ktetenstz 6 Der Höenstz 7 Exkurs: Konstruktion retwinkliger Dreieke 8 ekliste 9 Hinweise
EBENE GEOMETRIE. 1) Kollineare Punkte: liegen alle auf einer Geraden. 6) Parallele Geraden: schneiden sich nicht: g 2. 7) Einteilung der Dreiecke:
 N GOTRI 1) Kollinee Punkte: lieen lle uf eine Geden 6) Pllele Geden: sneiden si nit: ) u denselen Punkt eende Geden: 7) inteilun de eieke: n den eiten: O uneelmäßi: lle eiten vesieden ln 3) Winkeleinteilun:
N GOTRI 1) Kollinee Punkte: lieen lle uf eine Geden 6) Pllele Geden: sneiden si nit: ) u denselen Punkt eende Geden: 7) inteilun de eieke: n den eiten: O uneelmäßi: lle eiten vesieden ln 3) Winkeleinteilun:
Vektorrechnung. In der Physik unterscheiden wir grundsätzlich zwei verschiedene Typen physikalischer Einheiten: Skalare und Vektoren.
 Kntonsschule Solothun Vektoechung RYS Vektoechnung. Gundlgen. Skl / Vekto In de Phsik untescheiden wi gundsätlich wei veschiedene Tpen phsiklische Einheiten: Skle und Vektoen. Ein Skl ist eine elle Zhl.
Kntonsschule Solothun Vektoechung RYS Vektoechnung. Gundlgen. Skl / Vekto In de Phsik untescheiden wi gundsätlich wei veschiedene Tpen phsiklische Einheiten: Skle und Vektoen. Ein Skl ist eine elle Zhl.
α Winkel der Schrägen
 Glechföge Bewegung eg Gechwndgket t π d n t Glechföge echleungte Bewegung Bewegung ohne nfng- t gechwndgket t t t d n t eg Gechwndgket et Duchee Dehhl eg Bechleungung et Gechwndgket - n - - - chefe Eene
Glechföge Bewegung eg Gechwndgket t π d n t Glechföge echleungte Bewegung Bewegung ohne nfng- t gechwndgket t t t d n t eg Gechwndgket et Duchee Dehhl eg Bechleungung et Gechwndgket - n - - - chefe Eene
Aufgaben zur Bestimmung des Tangentenwinkels von Spiralen
 Aufgabenblatt-Spialen Tangentenwinkel.doc 1 Aufgaben zu Bestimmung des Tangentenwinkels von Spialen Gegeben ist die Spiale mit de Gleichung = 0,5 φ, φ im Bogenmaß. (a) Geben Sie die Gleichung fü Winkel
Aufgabenblatt-Spialen Tangentenwinkel.doc 1 Aufgaben zu Bestimmung des Tangentenwinkels von Spialen Gegeben ist die Spiale mit de Gleichung = 0,5 φ, φ im Bogenmaß. (a) Geben Sie die Gleichung fü Winkel
N a c h s c h r e i b k l a u s u r
 N a c s c r e i b k l a u s u r Aufgabe Bestimmen Sie die Ableitung der Funktion f (x) an der Stelle x 0, indem Sie den Grenzwert des Differenzenquotienten berecnen. a) f (x) = 4 x 2 x 2 x 0 = 4 b) f (x)
N a c s c r e i b k l a u s u r Aufgabe Bestimmen Sie die Ableitung der Funktion f (x) an der Stelle x 0, indem Sie den Grenzwert des Differenzenquotienten berecnen. a) f (x) = 4 x 2 x 2 x 0 = 4 b) f (x)
Kapitel 9 Integralrechnung für Funktionen einer Veränderlichen 9.6 Volumen von Rotationskörpern
 Wolte/Dhn: Anlsis Individuell c Spinge 75 Kpitel 9 Integlechnung fü Funktionen eine Veändelichen 9.6 Volumen von Rottionsköpen Wi wenden uns jetzt de Bestimmung des Volumens eines sogennnten Rottionsköpes
Wolte/Dhn: Anlsis Individuell c Spinge 75 Kpitel 9 Integlechnung fü Funktionen eine Veändelichen 9.6 Volumen von Rottionsköpen Wi wenden uns jetzt de Bestimmung des Volumens eines sogennnten Rottionsköpes
Mathematikaufgaben > Analysis > Funktionenscharen
 Michel Buhlmnn Mthemtikugen > Anlysis > Funktionenschren Auge: Gegeen ist die Funktionenschr t t t mit reellen Prmeter t >. Die zugehörigen Schuilder heißen K t. Skizziere die Schuilder K,5, K und K jeweils
Michel Buhlmnn Mthemtikugen > Anlysis > Funktionenschren Auge: Gegeen ist die Funktionenschr t t t mit reellen Prmeter t >. Die zugehörigen Schuilder heißen K t. Skizziere die Schuilder K,5, K und K jeweils
Regiomontanus - Gymnasium Haßfurt - Grundwissen Mathematik Jahrgangsstufe 9
 Regiomontanus - Gymnasium Haßfurt - Grundwissen Mathematik Jahrgangsstufe 9 Wissen und Können. Zahlenmengen Aufgaen, Beispiele, Erläuterungen N Z Q R natürliche ganze rationale reelle Zahlen Zahlen Zahlen
Regiomontanus - Gymnasium Haßfurt - Grundwissen Mathematik Jahrgangsstufe 9 Wissen und Können. Zahlenmengen Aufgaen, Beispiele, Erläuterungen N Z Q R natürliche ganze rationale reelle Zahlen Zahlen Zahlen
Regiomontanus - Gymnasium Haßfurt - Grundwissen Mathematik Jahrgangsstufe 9
 Regiomontnus - Gymnsium Hßfurt - Grundwissen Mthemtik Jhrgngsstufe 9 Wissen und Können Zhlenmengen N Z Q R ntürliche gnze rtionle reelle Aufgen, Beispiele, Erläuterungen N, Z, Q, R Wurzeln (Qudrtwurzel)
Regiomontnus - Gymnsium Hßfurt - Grundwissen Mthemtik Jhrgngsstufe 9 Wissen und Können Zhlenmengen N Z Q R ntürliche gnze rtionle reelle Aufgen, Beispiele, Erläuterungen N, Z, Q, R Wurzeln (Qudrtwurzel)
TRIGONOMETRISCHE 1 FUNKTIONEN
 IGONOMEISCHE FUNKIONEN Bse en w uns n enem Dek mt den Seten, den Höen, den Sätzen des Eukld und Pytgos, dem Bogenmß üe ene Deeksete, und ds nu uf Spezlfälle esänkt, usenndesetzen müssen De snd jedo dekte
IGONOMEISCHE FUNKIONEN Bse en w uns n enem Dek mt den Seten, den Höen, den Sätzen des Eukld und Pytgos, dem Bogenmß üe ene Deeksete, und ds nu uf Spezlfälle esänkt, usenndesetzen müssen De snd jedo dekte
Übungsbeispiele Dreiecke Mag. Thomas Höfferer. Aufgaben DREIECKE
 Übungsbeispiele Deiecke Mg. Toms Höffee ufgben DREIECKE Fläce von Deiecken: D 1. Gegeben sin ie ei Seiten eines llgemeinen Deiecks. estimme ie Fläce un ie ei Höen e einzelnen Deiecke. b c b c.) 1 1 15
Übungsbeispiele Deiecke Mg. Toms Höffee ufgben DREIECKE Fläce von Deiecken: D 1. Gegeben sin ie ei Seiten eines llgemeinen Deiecks. estimme ie Fläce un ie ei Höen e einzelnen Deiecke. b c b c.) 1 1 15
Analysis: Klausur Analysis
 Analysis Klausur zu Ableitung, Extrem- und Wendepunkten, Interpretation von Grapen von Ableitungsfunktionen, Tangenten und Normalen (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Scwarz www.mate-aufgaben.com
Analysis Klausur zu Ableitung, Extrem- und Wendepunkten, Interpretation von Grapen von Ableitungsfunktionen, Tangenten und Normalen (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Scwarz www.mate-aufgaben.com
ÜBUNG 4.: GEKRÜMMTE STÄBE
 ÜUG 4: GEKÜTE STÄE ufgbe 1: Schnittgößen und Spnnungveteilung gekümmte Stäbe y Löung: K Gegeben: bmeungen und eltung eine im ild dgetellten m uechnitt eingepnnten Stbe mit Keiquechnitt: d ufgbe: ) etimmung
ÜUG 4: GEKÜTE STÄE ufgbe 1: Schnittgößen und Spnnungveteilung gekümmte Stäbe y Löung: K Gegeben: bmeungen und eltung eine im ild dgetellten m uechnitt eingepnnten Stbe mit Keiquechnitt: d ufgbe: ) etimmung
MC-Serie 12 - Integrationstechniken
 Anlysis D-BAUG Dr. Meike Akveld HS 15 MC-Serie 1 - Integrtionstechniken 1. Die Formel f(x) dx = xf(x) xf (x) dx i) ist im Allgemeinen flsch. ii) folgt us der Sustitutionsregel. iii) folgt us dem Huptstz
Anlysis D-BAUG Dr. Meike Akveld HS 15 MC-Serie 1 - Integrtionstechniken 1. Die Formel f(x) dx = xf(x) xf (x) dx i) ist im Allgemeinen flsch. ii) folgt us der Sustitutionsregel. iii) folgt us dem Huptstz
Mathematik Trigonometrie Einführung
 Mthemtik Trigonometrie Einführung Ws edeutet ds Wort Trigonometrie und mit ws eshäftigt sih die Trigonometrie? Eine kleine Wortkunde: tri edeutet 'drei' Beispiel: Trithlon,... gon edeutet 'Winkel'/'Ek'
Mthemtik Trigonometrie Einführung Ws edeutet ds Wort Trigonometrie und mit ws eshäftigt sih die Trigonometrie? Eine kleine Wortkunde: tri edeutet 'drei' Beispiel: Trithlon,... gon edeutet 'Winkel'/'Ek'
DEMO für Trigonometrie. Teil 1. Geometrie Sinus, Kosinus und Tangens im rechtwinkligen Dreieck INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
 Gemetrie Sinus, Ksinus und Tngens im retwinkligen Dreiek Text Nr. 16001 Stnd 8. pril 010 Friedri ukel Trignmetrie DEM für www.mte-d.de INTERNETILITHEK FÜR SHULMTHEMTIK Teil 1 www.mte-d.de 16001 Trignmetrie
Gemetrie Sinus, Ksinus und Tngens im retwinkligen Dreiek Text Nr. 16001 Stnd 8. pril 010 Friedri ukel Trignmetrie DEM für www.mte-d.de INTERNETILITHEK FÜR SHULMTHEMTIK Teil 1 www.mte-d.de 16001 Trignmetrie
Uneigentliche Integrale & mehrdim. Differenzialrechnung
 Mthemtik I für Biologen, Geowissenschftler und Geoökologen Uneigentliche Integrle & mehrdimensionle Differenzilrechnung 25. Jnur 2010 Uneigentliche Integrle Unendlich Integrnd divergiert Grenze Prtielle
Mthemtik I für Biologen, Geowissenschftler und Geoökologen Uneigentliche Integrle & mehrdimensionle Differenzilrechnung 25. Jnur 2010 Uneigentliche Integrle Unendlich Integrnd divergiert Grenze Prtielle
