2. Exkurs: Spaziergang durch die Gruppentheorie!"#$
|
|
|
- Stefan Fuchs
- vor 7 Jahren
- Abrufe
Transkript
1 2. Exkurs: Spaziergang durch die Gruppentheorie $ Gruppentheorie ein durchaus kompliziertes Teilgebiet der Mathematik!" Gegenstand: systematische Behandlung von Symmetrie!" Bei Verzicht auf mathematische Strenge (Beweise): Wichtiges Werkzeug für Chemiker; anhand sehr anschaulicher Symmetrieüberlegungen lassen sich wichtige Einblicke in den Aufbau von Molekülen zu gewinnen!" Konstruktion von Molekülorbitalen!" Vereinfachung der Diskussion elektronischer Strukturen und von Molekülschwingungen!" Literatur Hollemann & Wiberg: Anorganische Chemie, de Gruyter 2007 (S. 180 ff) Engelke: Aufbau der Moleküle, 3. Aufl., Teubner 1996 Kettle: Symmetrie und Struktur, Teubner 1985 Gade: Koordinationschemie, Wiley-VCH 1998 (S.127 ff) Atkins: Physikalische Chemie, Wiley-VCH 1987 (S. 415 ff) Shriver & Atkins: Inorganic Chemistry, 3 rd Edition, Oxford Univ. Press 1999 (S. 117 ff) Housecroft & Sharpe: Anorganische Chemie, 2. Aufl., Pearson Studium 2006 (S. 85 ff)
2 2. Exkurs: Spaziergang durch die Gruppentheorie!"%$ Symmetrieelemente und Symmetrieoperationen Welche Gestalt müsste das Symbol an achter Stelle haben? 8? Quelle: Hollemann-Wiberg S. 180 Durch jedes Zeichen verläuft in der Mitte von oben nach unten eine Spiegelebene Die rechten Hälften bilden die Zahlenreihe 1-7 Das nächste Symbol ist demnach eine vertikal gespiegelte 8 Symmetrieelement: Spiegelebene, Symmetrieoperation: Spiegelung
3 2. Exkurs: Spaziergang durch die Gruppentheorie!"&$ Spielregeln!" Die Symmetrie eines Moleküls ist durch Operationen charakterisiert, durch die die Atompositionen so vertauscht werden, dass die resultierende Anordnung von der ursprünglichen nicht zu unterscheiden ist.!" Diese Transformationen haben (also) keinen Einfluss auf die physikalischen Eigenschaften des Moleküls! " #!!" Transformationen: Drehung, Spiegelung, Drehspiegelung, Inversion (Zeitumkehr ignoriert) Definitionen!" Operatoren: Symbole, die angeben, was mit der darauffolgenden Funktion zu tun ist Beispiel: Der -Operator schreibt vor, die Ableitung einer Funktion nach x zu bilden Entsprechend schreibt das Operatorprodukt vor, zunächst die Ableitung einer Funktion nach y zu bilden, dann das Ergebnis nach x abzuleiten
4 2. Exkurs: Spaziergang durch die Gruppentheorie!#-$!" Symmetrieoperation: Operation (lineare Transformation, also Koordinatentransformation), durch die ein Objekt in eine neue Position gebracht wird, die zur ersten äquivalent ist (1)! ' : Drehung um eine n -zählige Symmetrieachse, Drehwinkel=360 /n (n=1,2,3,4 ) (2) ": Identitätsoperation, erzeugt ein unverändertes Molekül (darstellbar als Drehung um 360,!! -Operation). An jedem Molekül durchführbar, unabhängig von seiner Symmetrie (3)! : Spiegelung an einer Ebene (4) #$: Inversion an einem Punkt (5) % ' : Drehspiegelung, Drehung um 360 /n gefolgt von einer Spiegelung an einer senkrecht zur Drehachse angeordneten Ebene (engl.: improper rotation) (%! $($!)$% * $($#$... warum?) % +,$
5 2. Exkurs: Spaziergang durch die Gruppentheorie!#!$!" Symmetrieelemente: Punkte, Linien und Flächen als Bezug für Symmetrieoperationen. Hat ein Molekül mehr als eine Drehachse, so wird diejenige mit dem größten n als Hauptdrehachse (engl.: principal axis) bezeichnet dies ist die Achse höchster Molekülsymmetrie (C 3 -Achse im BF 3 ) Liegt eine Spiegelebene senkrecht zu einer Hauptdrehachse, so wird sie mit dem Symbol!. gekennzeichnet (Index h für horizontal, Beispiel BF 3 ). Beinhaltet die Ebene die Hauptdrehachse, so wird sie mit! v gekennzeichnet (Index v für vertikal). Beinhaltet ein Molekül mehrere Spiegelebenen, so werden sie zur Unterscheidung als! v,! v,! v usw. bezeichnet (Beispiel H 2 O).
6 2. Exkurs: Spaziergang durch die Gruppentheorie!#*$ Sonderfall! d -Spiegelebene (Index d für diedrisch), z. B. im XeF 4 (Punktgruppe D 4h ): " Halbiert Winkel zwischen zwei benachbarten zweizähligen Achsen " Enthält gleichzeitig die Hauptdrehachse
7 2. Exkurs: Spaziergang durch die Gruppentheorie!#:$!" Punktgruppen: Jedes Molekül lässt sich einer Gruppe zuordnen, die aus nacheinander auszuführenden Symmetrieoperationen gebildet wird Die Symmetrie des Wassermoleküls ist durch die vier Symmetrieoperationen ",$! *,! / und! / 0 vollständig definiert Eine Punktgruppe umfasst die Zahl der erlaubten Symmetrieoperationen (in jedem Molekül gibt es einen Punkt, der unter allen SymOps unverändert bleibt) Um eine Gruppe zu bilden, müssen die jeweiligen Operationen vier Bedingungen erfüllen (1) Die Eindeutigkeitsoperation (") muss definiert sein (2) Das Produkt zweier Operationen muss zur Gruppe gehören (3) Assoziativität muss gelten $$$$$$$! * $!$2! * $!$! / 3$($$2! * $!$! * 3$!$! / $ (4) Das Reziproke jeder Operation muß existieren $$$$$$$&!$& '( $($"$$2.456,$! * $!$! * $($"$57893 Multiplikationstabelle $$$$$$$$$"$$$$$! * $$$$! / $$$$! / 1 $ "$$$$$$$"$$$$$! * $$$$! / $$$$! / 1$! * $$$$$! *$$$$$$ "$$$$$! / 1$$$! / $! / $$$$$! /$ $$$! / 1$$$"$$$$$! * $$! / 1$$$! / 1$$$! /$$$$$$! *$$$$$$ "$ $
8 2. Exkurs: Spaziergang durch die Gruppentheorie!#+$!" Punktgruppen: Verwendung des Kurzsymbols C 2v anstelle umständlicher Auflistung der Symmetrieoperationen Man spricht von der C 2v -Symmtrie des Wassermoleküls. Für bestimmte (Abelsche) Punktgruppen spielt die Reihenfolge der Symmetrieoperationen keine Rolle, die Ausführung zweier Symmetrieoperationen nacheinander liefert das gleiche Ergebnis wie die Ausführung einer anderen Operation der Gruppe! / $!$! * $($! *$! $! /$ ($! /$ $%& $ % + $!$! / $;$! /$! $ % +$$ 2<3$ Hausaufgabe: Zeigen Sie dies für Methan (Punktgruppe ) = )$
9 Lösung Hausaufgabe!#>$!" S 4 = C 4!! h!!"!" S 4!! v = #S 4!!"!"!"! v! S 4 = S 4!!"!"!"
10 2. Exkurs: Spaziergang durch die Gruppentheorie!#"$ Beispiele (Schönfließ-Nomenklatur)
11 2. Exkurs: Spaziergang durch die Gruppentheorie!##$
12 2. Exkurs: Spaziergang durch die Gruppentheorie!#%$
13 Flussdiagramm zur Bestimmung molekularer Punktgruppen!#&$ ).' *.' ( 2 ' &'$&# ( 3 ' &'$&# +.' % -.' ) ' * ' + 4' ( -/' &'$&# $# $# &'$&# ( 2 ' &'$&# ( 3' &'$&#!! &'$&# + ' $%&#' #()$*+,' &'$&# 50'( ) 6' )'5'7' * &'$&# ( ) ' &'$&#!' &'$&# $' &'$&# ( 0' ' )5' )! 5' $%&$#! 2' $%&$# (' 70 ''''8 ''''4 )' # '( 1' '( (' ) 0)' ) 0)' $%&$# $%&$# ' )2'! 2' $%&$# )! 3' $%&$# ( )' * 2 oder mehr C n -Achsen mit n > 2? # Suche Hauptachse C n ; gibt es dazu senkrechte C 2? ' )' ( )2' ( )3'
14 Flussdiagramm zur Bestimmung molekularer Punktgruppen!%-$ &.$ /.$! + $! > $ ).$, F.$ & $ / $ ) =$! F/$ #$ #$! + $! >$!! ) $?@A5BCA$ A4'5D6E$ H!$! ' )$ '$H$*$ *! ' $!$ #$!!$! * $$$$I '$ #! G$! 4$ * 2 oder mehr C n -Achsen mit n > 2 # Suche Hauptachse C n ; gibt es dazu senkrechte C 2?
15 Flussdiagramm zur Bestimmung molekularer Punktgruppen!%!$ Punktgruppe H 2? &.$ /.$ J$ J$ #$! + $! > $ ).$, F.$ & $ / $ ) =$! F/$ #$ #$! + $! >$!! ) $?@A5BCA$ A4'5D6E$ H!$! ' )$ '$H$*$ *! ' $!$ #$!!$! * $$$$I '$ #! G$! 4$ * 2 oder mehr C n -Achsen mit n > 2 # Suche Hauptachse C n ; gibt es dazu senkrechte C 2?
16 Flussdiagramm zur Bestimmung molekularer Punktgruppen!%*$ Punktgruppe HNO 3? &.$ /.$! + $! > $ ).$!", F.$ & $ / $ ) =$! F/$ #$ #$! + $! >$!! ) $?@A5BCA$ A4'5D6E$ H!$! ' )$ '$H$*$ *! ' $!$ #$!!$! * $$$$I '$ #! G$! 4$ * 2 oder mehr C n -Achsen mit n > 2? # Suche Hauptachse C n ; gibt es dazu senkrechte C 2?
17 Flussdiagramm zur Bestimmung molekularer Punktgruppen!%:$ Punktgruppe B(OH) 3? &.$ C 3! /.$! + $! > $ ).$, F.$ & $ / $ ) =$! F/$ #$ #$! + $! >$!! ) $?@A5BCA$ A4'5D6E$ H!$! ' )$ '$H$*$ *! ' $!$ #$!!$! * $$$$I '$ #! G$! 4$ * 2 oder mehr C n -Achsen mit n > 2?
18 Flussdiagramm zur Bestimmung molekularer Punktgruppen!%+$ Punktgruppe B(OH) 3? C 3!?@A5BCA$ A4'5D6E$ H!$! ' )$ '$H$*$ *! ' $! '/$ '! /$!.$! * $$$$I '$ # $ $ $
19 Flussdiagramm zur Bestimmung molekularer Punktgruppen!%>$ Punktgruppe B(OH) 3? C 3! S! 3! h! # Suche Hauptachse C n ; gibt es dazu senkrechte C 2??@A5BCA$ A4'5D6E$ H!$! ' )$ '$H$*$ *! ' $! '/$ '! /$!.$! * $$$$I '$ # # Suche Hauptachse C n ; gibt es dazu senkrechte C 2? % *'$ % *'$! '.$!.$ '! =$, '$ (H$KL'B7M6LNN5$! :.$! '$, '.$, '=$
20 Punktgruppenbestimmung für molekulare Strukturen!%"$ Weitere Hausaufgaben: Punktgruppenbestimmung BH 3 Methan Benzol Ferrocen (ekliptische Konformation) mit Hilfe des Flussdiagramms oben, oder der Website Weitere graphisch schön aufbereitete Informationen finden sich unter:
21 2. Exkurs: Spaziergang durch die Gruppentheorie!%#$ Multiplikation von Symmetrieoperationen! " Definition Symmetrieoperation: Effekt jeder Operation der Punktgruppe C 2v bei Anwendung auf das Wassermolekül besteht darin, das Molekül in sich selbst zu überführen (Äquivalent zur Multiplikation mit der Zahl 1) z! " Dies lässt sich mit Hilfe der folgenden Tabelle darstellen Operation E C 2 " v " v Effekt " v (xz)! " Für das Wassermolekül als Ganzes erscheint das erst einmal sinnlos " v '(yz)! " Anders für assoziierte Größen, etwa das 2p y -Orbital des Sauerstoffatoms Operation E C 2 " v " v Effekt (2p y )
22 2. Exkurs: Spaziergang durch die Gruppentheorie!%%$! " Achtung! Problem bei Konvention: C 2 ist z-achse, Spiegelebenen nicht festgelegt!! " Mulliken-Konvention: planares Molekül liegt in der yz-ebene! " Betrachtung des 2p x -Orbitals z Operation E C 2 " v " v Effekt (2p x ) ! " Betrachtung des 2p z -Orbitals " v (xz) Operation E C 2 " v " v " v '(yz) Effekt (2p z ) ! " Betrachtung eines 3d xy -Orbitals Operation E C 2 " v " v Effekt (3d xy )
23 2. Exkurs: Spaziergang durch die Gruppentheorie!%&$ Charaktertafeln! " Zusammenstellung der C 2v -Symmetrieoperationen auf die O-AOs im H 2 O C 2v E C 2 " v " v 2p z d xy p y p x ! " Jede Zeile der Tabelle entspricht einer irreduziblen Darstellung der Symmetrieoperationen der Punktgruppe " v (xz) z " v '(yz)! " Die Tabelleneinträge (1,-1) zeigen, wie sich einzelne Objekte (z.b. Orbitale) unter den einzelnen Operationen verhalten, sie charakterisieren die jeweiligen Wirkungen und werden als Charaktere bezeichnet! " Anmerkung: der Charakter einer Matrix ist als ihre Spur gegeben (Summe Diagonalelemente)
24 2. Exkurs: Spaziergang durch die Gruppentheorie!&-$ Die Mulliken-Symbolik Konventionen für die Bezeichnung irreduzibler Darstellungen z Symbol Eigenschaft A: symmetrisch unter n-facher Drehung B: antisymmetrisch "- E: zweidimensional ( später ) T: dreidimensional ( ) " v (xz) Index Position Eigenschaft 1 tief symm. unter " v oder C 2 senkrecht zu C n 2 tief antisymm. -"- g tief symm. unter i u tief antisymm. unter i ' hoch symm. unter " h wenn nicht i vorhanden " hoch antisymm. -"- + hoch symm. unter " v in D!h wenn - hoch antisymm. -"- " v '(yz)
25 2. Exkurs: Spaziergang durch die Gruppentheorie!&!$ Orthogonalitätseigenschaften irreduzibler Darstellungen! " Betrachtet man das Produkt zweier irreduzibler Darstellungen der Charaktertafel, also die Summe der Charakterprodukte, so gilt: A 2 B 1 = (1 1) + (1-1) + (-1 1) + (-1-1) = 0 dies gilt für alle Produkte unterschiedlicher irreduzibler Darstellungen (ID)! " Multiplikationen der gleichen IDs liefern dagegen die Zahl der Operationen einer Punktgruppe A 1 A 1 = 4, B 1 B 1 = 4 dies ist kein Zufall, die Zahl der Operationen heißt Ordnung einer Gruppe die Punktgruppe C 2v hat also die Ordnung 4.
26 2. Exkurs: Spaziergang durch die Gruppentheorie!&*$ Transformationseigenschaften der AOs in H 2 O z Die Darstellung der Bindungssituation in H 2 O kann durch Verwendung der C 2v -Charaktertafel erheblich vereinfacht werden Valenzorbitale: O: 2s, 2p, H: 2 x 1s " v (xz) Die O-AOs haben wir schon betrachtet: " v '(yz) 2s, 2p z! A 1 2p y! B 2 2p x! B 1 nun zu den s-orbitalen der H-Atome soll man die H-Atome einzeln oder gemeinsam betrachten?! wann immer eine (oder mehrere) Operation(en) der Punktgruppe zur Vertauschung oder Mischung von Orbitalen führt, müssen diese Orbitale gemeinsam betrachtet werden!
27 2. Exkurs: Spaziergang durch die Gruppentheorie!&:$ Verhalten der 1s (H) -Orbitale unter Symmetrieoperationen der C 2v PG: "$ ! *$ ! v ! v Betrachtet man die Transformation mehrerer Objekte gemeinsam, so ist der Charakter, den sie unter einer Symmetrieopertation erzeugen gleich der Summe der Charaktere, den sie als Einzelobjekte erzeugen: E: H 1 und H 2 unverändert, Charakter 1, Gesamtcharakter 2 " v : 0 Symmetrieoperationen, die zur Vertauschung führen, ergeben den Gesamtcharkter 0 C 2 : H 1 und H 2 verschwinden von ihrer ursprünglichen Position: Charkter 0 " v : 2 Damit ergibt sich der Charaktersatz "! *! v! v => nicht in der Charaktertafel C 2v enthalten, => Reduzible Darstellung!
28 2. Exkurs: Spaziergang durch die Gruppentheorie!&+$ E C 2 " v " v => entspricht der Summe zweier IDs (A 1 und B 2 ) A 1 : B 2 : A 1 +B 2 : Zerlegung von reduziblen Darstellungen in irreduzible möglich (eindeutig)! Beziehung zwischen reduziblen und irreduziblen Darstellungen: Multiplikation mit A 1 : (2 1) + (0 1) + (0 1) + (2 1) = 4 Multiplikation mit B 1 : (2 1) + (0-1) + (0 1) + (2-1) = 0 Multiplikation mit A 2 : (2 1) + (0 1) + (0-1) + (2-1) = 0 Multiplikation mit B 2 : (2 1) + (0-1) + (0-1) + (2 1) = 4 => Multiplikation ergibt nur dann von 0 verschiedene Ergebnisse, wenn man aus der Charaktertafel diejenigen ID auswählt, die in der reduziblen Darstellung enthalten sind!
29 2. Exkurs: Spaziergang durch die Gruppentheorie!&>$ Allgemeine Vorschrift zur Reduktion reduzibler Darstellungen (a) Reduzible Darstellung aufschreiben E C 2 " v " v (b) Irreduzible Darstellung aufschreiben (B 2 ) (c) Multiplikation der Charaktere (Spalten) (d) Addition der Produkte, Division durch Ordnung der Gruppe 4 / 4 = 1 => Die reduzible Darstellung enthält B 2 (sonst 0) => Analog für A 1 => Ist B 2 mehrfach enthalten, ergibt sich 2 etc.
30 2. Exkurs: Spaziergang durch die Gruppentheorie!&"$ Beispiel: Reduktion in C 2v E C2 "v "v A 1 : (Summe = 0) A 2 : (Summe = 4, /h = 1) (h: Gruppenordnung) B 1 : (Summe = 0) B 2 : (Summe = 4, /h = 1) A 2 : B 2 : A 2 + B 2 : => es gibt viele reduzible Darstellungen zum gleichen Symmetrieverhalten => Begriff der Basis
31 2. Exkurs, Beispiel: Bindungsbildung im Wassermolekül!&#$ Molekülorbitalaufbau aus Atomorbitalen Vorteil der Darstellung in der neuen Basis: Orbitalwechselwirkungen müssen nur zwischen Basisfunktionen gleicher Symmetrie betrachtet werden. " qualitative Betrachtungen zum Aufbau von MO-Schemata vereinfacht " Explizite Berechnungen erheblich vereinfacht (z. B. treten Überlappungsintegrale nur für Orbitale in einer gemeinsamen irreduziblen Darstellung auf)
32 3. Exkurs, Beispiel: Bindungsbildung im Wassermolekül!&%$ Qualitative Konstruktion des MO-Diagramms
33 2. Exkurs, Beispiel: Bindungsbildung im Wassermolekül!&&$ Beispiel: HF/STO-3G-Rechnung am H 2 O (Gaussian03) Molekülebene in YZ
34 2. Exkurs, Beispiel: Bindungsbildung im Wassermolekül *--$ z " v (xz) " v '(yz)
35 Exkurs Ende *-!$
ACF-Vorkurs: Symmetrie in der Anorganischen Chemie
 ACF-Vorkurs: Symmetrie in der Anorganischen Chemie Stichworte: - Symmetrielemente - Punktgruppen - Charaktertafeln - Anwendung in der MO-Theorie I.1 Zur qualitativen Beschreibung genügt es oft, die Form
ACF-Vorkurs: Symmetrie in der Anorganischen Chemie Stichworte: - Symmetrielemente - Punktgruppen - Charaktertafeln - Anwendung in der MO-Theorie I.1 Zur qualitativen Beschreibung genügt es oft, die Form
Klausur zur Vorlesung Symmetrie in Chemie und Spektroskopie
 Klausur zur Vorlesung Symmetrie in Chemie und Spektroskopie Zulässige Hilfsmittel: Charakterentafeln, Schema Hierarchie der Punktgruppen SS 6 Prof. Dr. B. Dick Aufgabe 1 (15P): Finden Sie die Punktgruppe
Klausur zur Vorlesung Symmetrie in Chemie und Spektroskopie Zulässige Hilfsmittel: Charakterentafeln, Schema Hierarchie der Punktgruppen SS 6 Prof. Dr. B. Dick Aufgabe 1 (15P): Finden Sie die Punktgruppe
Absorptionsspektrum von PTCDA und DiMe-PTCDI
 3. Gruppentheorie Absorption coefficient *10 5 6 4 2 0 Absorptionsspektrum von PTCDA und DiMe-PTCDI PTCDA Wavelength / nm 800 700 600 500 400 HOMO-LUMO Übergang S 0 -S 1 transition S 0 -S 2 transition
3. Gruppentheorie Absorption coefficient *10 5 6 4 2 0 Absorptionsspektrum von PTCDA und DiMe-PTCDI PTCDA Wavelength / nm 800 700 600 500 400 HOMO-LUMO Übergang S 0 -S 1 transition S 0 -S 2 transition
= {e} U (1) U (2) U (3) = {e,a,b,c} 4 : e a b e e a b a a c e b b e c
 KONZEPT DER GRUPPE 6.7 Untergruppen U ist eine Gruppe mit derselben Gruppenoperation wie G und der Ordnung h U h G U ist dann eine Untergruppe von G, wenn alle u i G sind. Beispiel 9: Untergruppen von
KONZEPT DER GRUPPE 6.7 Untergruppen U ist eine Gruppe mit derselben Gruppenoperation wie G und der Ordnung h U h G U ist dann eine Untergruppe von G, wenn alle u i G sind. Beispiel 9: Untergruppen von
Gruppentheorie und Symmetrie in der Chemie
 Gruppentheorie und Symmetrie in der Chemie Martin Schütz Institut für theoretische Chemie, Universität Stuttgart Pfaffenwaldring 55, D-70569 Stuttgart Stuttgart, 3. Mai 00 Stabilizers von Atomen Ein Operator
Gruppentheorie und Symmetrie in der Chemie Martin Schütz Institut für theoretische Chemie, Universität Stuttgart Pfaffenwaldring 55, D-70569 Stuttgart Stuttgart, 3. Mai 00 Stabilizers von Atomen Ein Operator
Gruppentheorie und Symmetrie in der Chemie
 Gruppentheorie und Symmetrie in der Chemie Martin Schütz Institut für theoretische Chemie, Universität Stuttgart Pfaffenwaldring 55, D-70569 Stuttgart Stuttgart, 26. April 2002 Mathematische Definition
Gruppentheorie und Symmetrie in der Chemie Martin Schütz Institut für theoretische Chemie, Universität Stuttgart Pfaffenwaldring 55, D-70569 Stuttgart Stuttgart, 26. April 2002 Mathematische Definition
Ausarbeitung zum Vortrag Symmetrie in der Molekülphysik
 WWU Münster Institut für Theoretische Physik Seminar zur Theorie der Atome, Kerne und kondensierten Materie Ausarbeitung zum Vortrag Symmetrie in der Molekülphysik Marcel Hahn, m hahn07@uni-muenster.de
WWU Münster Institut für Theoretische Physik Seminar zur Theorie der Atome, Kerne und kondensierten Materie Ausarbeitung zum Vortrag Symmetrie in der Molekülphysik Marcel Hahn, m hahn07@uni-muenster.de
Allgemeine Chemie Symmetrie von Molekülen
 Allgemeine Chemie Symmetrie von Molekülen AC_Molekuelsymmetrie.doc Seite 1 von 23 Fck / 12.10.05 Inhaltsverzeichnis 1 Einleitung...3 1.1 Anwendungsbereiche der Molekülsymmetrie...3 1.2 Sinn und Zweck der
Allgemeine Chemie Symmetrie von Molekülen AC_Molekuelsymmetrie.doc Seite 1 von 23 Fck / 12.10.05 Inhaltsverzeichnis 1 Einleitung...3 1.1 Anwendungsbereiche der Molekülsymmetrie...3 1.2 Sinn und Zweck der
Anorganische Chemie III
 Seminar zur Vorlesung Anorganische Chemie III Wintersemester 2015/16 Christoph Wölper Institut für Anorganische Chemie der Universität Duisburg-Essen Wiederholung Was bisher geschah # Darstellungen für
Seminar zur Vorlesung Anorganische Chemie III Wintersemester 2015/16 Christoph Wölper Institut für Anorganische Chemie der Universität Duisburg-Essen Wiederholung Was bisher geschah # Darstellungen für
O ist gegenüber C 2. invariant. Allgemein bezeichnet man mit C n. ist symmetrisch gegenüber, das JCl Ion gegenüber C 4
 107 KAPITEL J Symmetrien 1. Einleitung a) Warum Symmetriebetrachtungen? Je komplizierter die Probleme, desto mehr spielen Symmetriebetrachtungen eine Rolle. Die Symmetriebetrachtungen in der Molekülphysik
107 KAPITEL J Symmetrien 1. Einleitung a) Warum Symmetriebetrachtungen? Je komplizierter die Probleme, desto mehr spielen Symmetriebetrachtungen eine Rolle. Die Symmetriebetrachtungen in der Molekülphysik
Seminar zum Praktikum Anorganische Chemie III III
 Seminar zum Praktikum Anorganische Chemie III III Metallorganische Chemie Dr. J. Wachter IR-Teil3 www.chemie.uni-regensburg.de/anorganische_chemie/scheer/lehre.html www.chemie.uniregensburg.de/anorganische_chemie/wachter/lehre.html
Seminar zum Praktikum Anorganische Chemie III III Metallorganische Chemie Dr. J. Wachter IR-Teil3 www.chemie.uni-regensburg.de/anorganische_chemie/scheer/lehre.html www.chemie.uniregensburg.de/anorganische_chemie/wachter/lehre.html
2 Symmetrieoperationen und -elemente. 1.8 Klassen 2 SYMMETRIEOPERATIONEN UND -ELEMENTE 7
 SYMMETRIEOPERATIONEN UND -ELEMENTE 7.8 Klassen Zweck: Zusammenfassen zueinander ähnlicher (konjugierter) Elemente einer Gruppe. Durch Bestimmung aller Klassen ergibt sich eine eindeutige Zerlegung on G:
SYMMETRIEOPERATIONEN UND -ELEMENTE 7.8 Klassen Zweck: Zusammenfassen zueinander ähnlicher (konjugierter) Elemente einer Gruppe. Durch Bestimmung aller Klassen ergibt sich eine eindeutige Zerlegung on G:
PC II Kinetik und Struktur. Kapitel 5. Symmetrie
 PC II Kinetik und Struktur Kapitel 5 Symmetrie Symmetrie Wozu? Symmetrieoperationen, Punktgruppen, Charakterentafeln Symmetrie von Molekülen, Orbitalen, Schwingungen 1 Was ist Symmetrie? 2 Symmetrie -
PC II Kinetik und Struktur Kapitel 5 Symmetrie Symmetrie Wozu? Symmetrieoperationen, Punktgruppen, Charakterentafeln Symmetrie von Molekülen, Orbitalen, Schwingungen 1 Was ist Symmetrie? 2 Symmetrie -
PC II Kinetik und Struktur. Kapitel 5. Symmetrie
 PC II Kinetik und Struktur Kapitel 5 Symmetrie Symmetrie Wozu? Symmetrieoperationen, Punktgruppen, Charakterentafeln Symmetrie von Molekülen, Orbitalen, Schwingungen 1 Was ist Symmetrie? 2 Symmetrie -
PC II Kinetik und Struktur Kapitel 5 Symmetrie Symmetrie Wozu? Symmetrieoperationen, Punktgruppen, Charakterentafeln Symmetrie von Molekülen, Orbitalen, Schwingungen 1 Was ist Symmetrie? 2 Symmetrie -
3.1 Gruppen, Untergruppen und Gruppen-Homomorphismen
 TEIL II: GRUPPEN In der modernen Algebra versucht man die Zahlen (Z, Q, R, ) durch die Konzentration auf Rechenoperationen (+,,... ), oder allgemeiner auf strukturelle Eigenschaften dieser Operationen,
TEIL II: GRUPPEN In der modernen Algebra versucht man die Zahlen (Z, Q, R, ) durch die Konzentration auf Rechenoperationen (+,,... ), oder allgemeiner auf strukturelle Eigenschaften dieser Operationen,
Symmetrie und Struktur
 Symmetrie und Struktur Eine Einführung in die Gruppentheorie Von Prof. Sidney RA. Kettle University of East Anglia, Norwich Aus dem Englischen übersetzt von Dr. Elke Buchholz, Aachen Mit 167 Bildern und
Symmetrie und Struktur Eine Einführung in die Gruppentheorie Von Prof. Sidney RA. Kettle University of East Anglia, Norwich Aus dem Englischen übersetzt von Dr. Elke Buchholz, Aachen Mit 167 Bildern und
Metallorganische Chemie und Katalyse der Übergangsmetalle
 etallorganische Chemie und Katalyse der Übergangsmetalle Nadia C. ösch-zanetti Institut für Anorganische Chemie der Universität Göttingen Inhalt indestens eine etall-kohlenstoffbindung n CR 3 n CR 2 n
etallorganische Chemie und Katalyse der Übergangsmetalle Nadia C. ösch-zanetti Institut für Anorganische Chemie der Universität Göttingen Inhalt indestens eine etall-kohlenstoffbindung n CR 3 n CR 2 n
Gruppentheorie und Symmetrie in der Chemie
 Gruppentheorie und Symmetrie in der Chemie Martin Schütz Institut für theoretische Chemie, Universität Stuttgart Pfaffenwaldring 55, D-7569 Stuttgart Stuttgart, 8. Mai M. Schütz, Vorlesung Gruppentheorie
Gruppentheorie und Symmetrie in der Chemie Martin Schütz Institut für theoretische Chemie, Universität Stuttgart Pfaffenwaldring 55, D-7569 Stuttgart Stuttgart, 8. Mai M. Schütz, Vorlesung Gruppentheorie
1 Konzept der Gruppe. 1.1 Allgemeine Nomenklatur. 1.2 Gruppenaxiome 1 KONZEPT DER GRUPPE 1
 1 KONZEPT DER GRUPPE 1 In dieser Vorlesung sollen spektroskopische Auswahlregeln, die auf der Symmetrie von Molekülen basieren, vorgestellt werden. Mit Hilfe dieser Regeln lassen sich optische und Schwingungs-Spektren
1 KONZEPT DER GRUPPE 1 In dieser Vorlesung sollen spektroskopische Auswahlregeln, die auf der Symmetrie von Molekülen basieren, vorgestellt werden. Mit Hilfe dieser Regeln lassen sich optische und Schwingungs-Spektren
Kristallstruktur und Mikrostruktur Teil I Vorlesung 2
 Kristallstruktur und Mikrostruktur Teil I Vorlesung 2 1 Kristallstruktur und Teil I Scripte Mikrostruktur http://www.uni-stuttgart.de/mawi/aktuelles_lehrangebot/lehrangebot.html 2 Wiederholung Koordinatensysteme
Kristallstruktur und Mikrostruktur Teil I Vorlesung 2 1 Kristallstruktur und Teil I Scripte Mikrostruktur http://www.uni-stuttgart.de/mawi/aktuelles_lehrangebot/lehrangebot.html 2 Wiederholung Koordinatensysteme
Gruppentheorie ERNST MORITZ ARNDT UNIVERSITÄT GREIFSWALD. Mathematisch-Naturwissenschaftliche Fakultät INSTITUT FÜR BIOCHEMIE
 ERNST MORITZ ARNDT UNIVERSITÄT GREIFSWALD Mathematisch-Naturwissenschaftliche Fakultät INSTITUT FÜR BIOCHEMIE Arbeitskreis Physikalische Chemie Prof. Dr. Walter Langel Gruppentheorie Molekülschwingungen
ERNST MORITZ ARNDT UNIVERSITÄT GREIFSWALD Mathematisch-Naturwissenschaftliche Fakultät INSTITUT FÜR BIOCHEMIE Arbeitskreis Physikalische Chemie Prof. Dr. Walter Langel Gruppentheorie Molekülschwingungen
Musterlösungen Blatt Mathematischer Vorkurs. Sommersemester Dr. O. Zobay. Matrizen
 Musterlösungen Blatt 8 34007 Mathematischer Vorkurs Sommersemester 007 Dr O Zobay Matrizen Welche Matrixprodukte können mit den folgenden Matrizen gebildet werden? ( 4 5 A, B ( 0 9 7, C 8 0 5 4 Wir können
Musterlösungen Blatt 8 34007 Mathematischer Vorkurs Sommersemester 007 Dr O Zobay Matrizen Welche Matrixprodukte können mit den folgenden Matrizen gebildet werden? ( 4 5 A, B ( 0 9 7, C 8 0 5 4 Wir können
Gruppentheorie und Symmetrie in der Chemie
 Gruppentheorie und Symmetrie in der Chemie Martin Schütz Institut für theoretische Chemie, Universität Stuttgart Pfaffenwaldring 55, D-70569 Stuttgart Stuttgart, 0. April 00 M. Schütz, Vorlesung Gruppentheorie
Gruppentheorie und Symmetrie in der Chemie Martin Schütz Institut für theoretische Chemie, Universität Stuttgart Pfaffenwaldring 55, D-70569 Stuttgart Stuttgart, 0. April 00 M. Schütz, Vorlesung Gruppentheorie
Symmetrieelemente C 3 C 2 C 3 O H H N H H H
 Symmetrieelemente Ein Symmetrielement liegt vor, wenn ein Objekt (hier: Molekül) durch eine Symmetrieoperation mit sich selbst zur Deckung gebracht werden kann. neue und alter Orientierung nicht unterscheidbar
Symmetrieelemente Ein Symmetrielement liegt vor, wenn ein Objekt (hier: Molekül) durch eine Symmetrieoperation mit sich selbst zur Deckung gebracht werden kann. neue und alter Orientierung nicht unterscheidbar
4 Matrixdarstellung von Symmetrieoperationen
 4 MATRIXDARSTELLUNG VON SYMMETRIEOPERATIONEN 4 Konsistenz der minimalen Symmetrieanalyse: fehlende Symmetrieelemente? Beispiel 3: Punktgruppe D h Im Schema (3.1) wird die Punktgruppe D h durch Auffinden
4 MATRIXDARSTELLUNG VON SYMMETRIEOPERATIONEN 4 Konsistenz der minimalen Symmetrieanalyse: fehlende Symmetrieelemente? Beispiel 3: Punktgruppe D h Im Schema (3.1) wird die Punktgruppe D h durch Auffinden
Kristallstruktur und Mikrostruktur Teil I Vorlesung 2
 Kristallstruktur und Mikrostruktur Teil I Vorlesung 2 1 Kristallstruktur und Teil I Scripte Mikrostruktur http://www.uni-stuttgart.de/mawi/aktuelles_lehrangebot/lehrangebot.html 2 Wiederholung Koordinatensysteme
Kristallstruktur und Mikrostruktur Teil I Vorlesung 2 1 Kristallstruktur und Teil I Scripte Mikrostruktur http://www.uni-stuttgart.de/mawi/aktuelles_lehrangebot/lehrangebot.html 2 Wiederholung Koordinatensysteme
3. Gruppentheorie für Fußgänger
 3. Gruppentheorie für Fußgänger Methan als Beispiel Methan als Beispiel Raumgruppen 230 Raumgruppen in 3d Symmetrie-Elemente Weitere wichtige Definitionen Untergruppe Konjugationsklasse Abelsche Gruppen:
3. Gruppentheorie für Fußgänger Methan als Beispiel Methan als Beispiel Raumgruppen 230 Raumgruppen in 3d Symmetrie-Elemente Weitere wichtige Definitionen Untergruppe Konjugationsklasse Abelsche Gruppen:
Outline. 1 Vektoren im Raum. 2 Komponenten und Koordinaten. 3 Skalarprodukt. 4 Vektorprodukt. 5 Analytische Geometrie. 6 Lineare Räume, Gruppentheorie
 Outline 1 Vektoren im Raum 2 Komponenten und Koordinaten 3 Skalarprodukt 4 Vektorprodukt 5 Analytische Geometrie 6 Lineare Räume, Gruppentheorie Roman Wienands (Universität zu Köln) Mathematik II für Studierende
Outline 1 Vektoren im Raum 2 Komponenten und Koordinaten 3 Skalarprodukt 4 Vektorprodukt 5 Analytische Geometrie 6 Lineare Räume, Gruppentheorie Roman Wienands (Universität zu Köln) Mathematik II für Studierende
Theoretische Chemie II. (Gruppentheorie)
 Theoretische Chemie II (Gruppentheorie) Modul BCh 4.4 Sommersemester 2016 i Vorwort Dieses Skript enthält die wesentlichen Inhalte, mathematischen Formeln und Abbildungen der Vorlesung Theoretische Chemie
Theoretische Chemie II (Gruppentheorie) Modul BCh 4.4 Sommersemester 2016 i Vorwort Dieses Skript enthält die wesentlichen Inhalte, mathematischen Formeln und Abbildungen der Vorlesung Theoretische Chemie
Schrödinger-Gleichung
 Schrödinger-Gleichung abgeleitet aus Teilchen-Welle-Dualismus (de Broglie) Ψ = Ε Ψ Der amiltonian enthält kinetische und potentielle Energie aller Teilchen wirkt auf die Wellenfunktion Ψ. Ψ 2 beschreibt
Schrödinger-Gleichung abgeleitet aus Teilchen-Welle-Dualismus (de Broglie) Ψ = Ε Ψ Der amiltonian enthält kinetische und potentielle Energie aller Teilchen wirkt auf die Wellenfunktion Ψ. Ψ 2 beschreibt
3.1 Gruppen, Untergruppen und Gruppen-Homomorphismen
 Inhaltsverzeichnis Teil II: Gruppen 2 3.1 Gruppen, Untergruppen und Gruppen-Homomorphismen.................. 2 3.1.1 Gruppen.......................................... 2 3.1.2 Untergruppen.......................................
Inhaltsverzeichnis Teil II: Gruppen 2 3.1 Gruppen, Untergruppen und Gruppen-Homomorphismen.................. 2 3.1.1 Gruppen.......................................... 2 3.1.2 Untergruppen.......................................
Vektoren - Die Basis
 Vektoren - Die Basis Motivation (Als Vereinfachung - der Schreibarbeit - wählen wir meistens Vektoren in R 2.) Eigentlich ist ja Alles klar! Für einen Vektor a gilt a = ( a x a y )! Am Ende werden wir
Vektoren - Die Basis Motivation (Als Vereinfachung - der Schreibarbeit - wählen wir meistens Vektoren in R 2.) Eigentlich ist ja Alles klar! Für einen Vektor a gilt a = ( a x a y )! Am Ende werden wir
Kristallstruktur und Mikrostruktur Teil I Vorlesung 3
 Kristallstruktur und Mikrostruktur Teil I Vorlesung 3 1 Wiederholung Punktsymmetrie - Erkennung 1/ Eine Punktsymmetrie-Gruppe {G} mit Ordnung N hat N Punktsymmetrieoperationen G i, i = 1,2, N. aber nur
Kristallstruktur und Mikrostruktur Teil I Vorlesung 3 1 Wiederholung Punktsymmetrie - Erkennung 1/ Eine Punktsymmetrie-Gruppe {G} mit Ordnung N hat N Punktsymmetrieoperationen G i, i = 1,2, N. aber nur
Verknüpfung zweier C 2 Drehachsen
 Phsikalische und Theoretische Methoden der Anorganischen Chemie, WS 2009/10 Verknüpfung zweier Drehachsen 2 C (360 /2) = C 360 /2 D (360 /2) Phsikalische und Theoretische Methoden der Anorganischen Chemie,
Phsikalische und Theoretische Methoden der Anorganischen Chemie, WS 2009/10 Verknüpfung zweier Drehachsen 2 C (360 /2) = C 360 /2 D (360 /2) Phsikalische und Theoretische Methoden der Anorganischen Chemie,
Matrizen. a12 a1. a11. a1n a 21. a 2 j. a 22. a 2n. A = (a i j ) (m, n) = i te Zeile. a i 1. a i 2. a i n. a i j. a m1 a m 2 a m j a m n] j te Spalte
![Matrizen. a12 a1. a11. a1n a 21. a 2 j. a 22. a 2n. A = (a i j ) (m, n) = i te Zeile. a i 1. a i 2. a i n. a i j. a m1 a m 2 a m j a m n] j te Spalte Matrizen. a12 a1. a11. a1n a 21. a 2 j. a 22. a 2n. A = (a i j ) (m, n) = i te Zeile. a i 1. a i 2. a i n. a i j. a m1 a m 2 a m j a m n] j te Spalte](/thumbs/71/64996309.jpg) Mathematik I Matrizen In diesem Kapitel werden wir lernen was Matrizen sind und wie man mit Matrizen rechnet. Matrizen ermöglichen eine kompakte Darstellungsform vieler mathematischer Strukturen. Zum Darstellung
Mathematik I Matrizen In diesem Kapitel werden wir lernen was Matrizen sind und wie man mit Matrizen rechnet. Matrizen ermöglichen eine kompakte Darstellungsform vieler mathematischer Strukturen. Zum Darstellung
LCAO-Ansatz und Punktsymmetrie
 LCAO-Ansatz und Punktsymmetrie Quantenchemische Rechenmethoden: Grundlagen und Anwendungen M+K-Kurs, 3.2015 Nutzen von Symmetrie bei quantenchemischen Rechnungen (LCAO-Ansatz) Wiederholung Punktgruppen
LCAO-Ansatz und Punktsymmetrie Quantenchemische Rechenmethoden: Grundlagen und Anwendungen M+K-Kurs, 3.2015 Nutzen von Symmetrie bei quantenchemischen Rechnungen (LCAO-Ansatz) Wiederholung Punktgruppen
Symmetrie und Anwendungen
 PC II Kinetik und Struktur Kapitel 6 Symmetrie und Anwendungen Symmetrie von Schwingungen und Orbitalen, Klassifizierung von Molekülschwingungen Auswahlregeln: erlaubte verbotene Übergänge IR-, Raman-,
PC II Kinetik und Struktur Kapitel 6 Symmetrie und Anwendungen Symmetrie von Schwingungen und Orbitalen, Klassifizierung von Molekülschwingungen Auswahlregeln: erlaubte verbotene Übergänge IR-, Raman-,
Gruppentheorie und Symmetrie in der Chemie
 Gruppentheorie und Symmetrie in der Chemie Martin Schütz Institut für theoretische Chemie, Universität Stuttgart Pfaffenwaldring, D-709 Stuttgart Stuttgart, 8. Juli 00 M. Schütz, Vorlesung Gruppentheorie
Gruppentheorie und Symmetrie in der Chemie Martin Schütz Institut für theoretische Chemie, Universität Stuttgart Pfaffenwaldring, D-709 Stuttgart Stuttgart, 8. Juli 00 M. Schütz, Vorlesung Gruppentheorie
In den vorigen Abschnitten wurden die globalen kartesischen Koordinaten der Atome eines Moleküls transformiert.
 4 MATRXDARSTELLUNG VON SYMMETREOPERATONEN 33 4.8 Lokale Koordinatenachsen m Gegensat um globalen Koordinatensstem, das für das gesamte Molekül gilt, sind lokale Koordinatenachsen individuell für jedes
4 MATRXDARSTELLUNG VON SYMMETREOPERATONEN 33 4.8 Lokale Koordinatenachsen m Gegensat um globalen Koordinatensstem, das für das gesamte Molekül gilt, sind lokale Koordinatenachsen individuell für jedes
g g 1 = g 1 g = e. (79)
 B Anhang B B.1 Kristallographische Symmetriegruppen B.1.1 Definition Eine Menge G = {g 1, g 2,...,g k,... } von Elementen g k nennt man eine Gruppe, wenn die Verknüpfung (Operator: ) der Elemente g k die
B Anhang B B.1 Kristallographische Symmetriegruppen B.1.1 Definition Eine Menge G = {g 1, g 2,...,g k,... } von Elementen g k nennt man eine Gruppe, wenn die Verknüpfung (Operator: ) der Elemente g k die
KAPITEL 6. Algebra Gruppen
 KAPITEL 6 Algebra 6.. Gruppen Bekannt sind die Kongruenzklassen, bijektive Abbildungen, Permutationen. Wir hatten in diesen Fällen eine Verknüpfung auf einer Menge. (Addition bzw. Multiplikation bei den
KAPITEL 6 Algebra 6.. Gruppen Bekannt sind die Kongruenzklassen, bijektive Abbildungen, Permutationen. Wir hatten in diesen Fällen eine Verknüpfung auf einer Menge. (Addition bzw. Multiplikation bei den
LCAO-Ansatz und Punktsymmetrie
 LCAO-Ansatz und Punktsymmetrie Quantenchemische Rechenmethoden: Grundlagen und Anwendungen M+K-Kurs, 3.2017 Nutzen von Symmetrie bei quantenchemischen Rechnungen (LCAO-Ansatz) Wiederholung Punktgruppen
LCAO-Ansatz und Punktsymmetrie Quantenchemische Rechenmethoden: Grundlagen und Anwendungen M+K-Kurs, 3.2017 Nutzen von Symmetrie bei quantenchemischen Rechnungen (LCAO-Ansatz) Wiederholung Punktgruppen
2.3.4 Drehungen in drei Dimensionen
 2.3.4 Drehungen in drei Dimensionen Wir verallgemeinern die bisherigen Betrachtungen nun auf den dreidimensionalen Fall. Für Drehungen des Koordinatensystems um die Koordinatenachsen ergibt sich 1 x 1
2.3.4 Drehungen in drei Dimensionen Wir verallgemeinern die bisherigen Betrachtungen nun auf den dreidimensionalen Fall. Für Drehungen des Koordinatensystems um die Koordinatenachsen ergibt sich 1 x 1
Das Schwingungsspektrum von Wasser
 Das Schwingungsspektrum von Wasser Vortrag im Rahmen des Seminars zum anorganisch-chemischen Fortgeschrittenenpraktikum Institut für Anorganische Chemie Universität Karlsruhe Matthias Ernst Freitag, 29.6.2006
Das Schwingungsspektrum von Wasser Vortrag im Rahmen des Seminars zum anorganisch-chemischen Fortgeschrittenenpraktikum Institut für Anorganische Chemie Universität Karlsruhe Matthias Ernst Freitag, 29.6.2006
Hexagonal dichtest gepackte Struktur
 Hexagonal dichtest gepackte Struktur Auch diese Struktur ist sehr wichtig, da sie von sehr vielen Systemen angenommen wird (kein Bravaisgitter). Das einfach hexagonale Bravais-Gitter (in 3-dim): zwei-dim:
Hexagonal dichtest gepackte Struktur Auch diese Struktur ist sehr wichtig, da sie von sehr vielen Systemen angenommen wird (kein Bravaisgitter). Das einfach hexagonale Bravais-Gitter (in 3-dim): zwei-dim:
9 WOODWARD-HOFFMANN-REGELN 92
 9 WOODWARD-HOFFMANN-REGELN 92 Die SMOs des Reaktanden und der Produkte (die nach Idealisierung nicht mehr unterschieden werden) müssen konstruiert und nach ihrer Knotenstruktur energetisch klassifiziert
9 WOODWARD-HOFFMANN-REGELN 92 Die SMOs des Reaktanden und der Produkte (die nach Idealisierung nicht mehr unterschieden werden) müssen konstruiert und nach ihrer Knotenstruktur energetisch klassifiziert
UE Einführung in die Algebra und Diskrete Mathematik KV Algebra und Diskrete Mathematik
 UE Einführung in die Algebra und Diskrete Mathematik KV Algebra und Diskrete Mathematik 6. Übungszettel, 30. April 2013 Lösungen 1. Zeigen Sie detailliert: Das homomorphe Bild einer zyklischen Gruppe ist
UE Einführung in die Algebra und Diskrete Mathematik KV Algebra und Diskrete Mathematik 6. Übungszettel, 30. April 2013 Lösungen 1. Zeigen Sie detailliert: Das homomorphe Bild einer zyklischen Gruppe ist
Transformation - 3. Für "übliche" Anwendungen in der Geometrie ist es sinnvoll, bei Transformationen eine gleiche
 Transformation - 3 Wiederholung und spezielle Angaben im Zusammenhang mit Kreis-Berechnungen 1. Problemstellung Im Zusammenhang mit der Berechnung von Schnittflächen kann es sinnvoll sein, die Berechnung
Transformation - 3 Wiederholung und spezielle Angaben im Zusammenhang mit Kreis-Berechnungen 1. Problemstellung Im Zusammenhang mit der Berechnung von Schnittflächen kann es sinnvoll sein, die Berechnung
a 2β... a n ω alle Permutationen von α β γ... ω a 3 γ ( 1) k a 1α
 Mathematik 1 - Übungsblatt 7 Lösungshinweise Tipp: Verwenden Sie zur Kontrolle Scilab, wo immer es möglich ist. Aufgabe 1 (Definitionsformel für Determinanten) Determinanten quadratischer Matrizen sind
Mathematik 1 - Übungsblatt 7 Lösungshinweise Tipp: Verwenden Sie zur Kontrolle Scilab, wo immer es möglich ist. Aufgabe 1 (Definitionsformel für Determinanten) Determinanten quadratischer Matrizen sind
4.4. Rang und Inversion einer Matrix
 44 Rang und Inversion einer Matrix Der Rang einer Matrix ist die Dimension ihres Zeilenraumes also die Maximalzahl linear unabhängiger Zeilen Daß der Rang sich bei elementaren Zeilenumformungen nicht ändert
44 Rang und Inversion einer Matrix Der Rang einer Matrix ist die Dimension ihres Zeilenraumes also die Maximalzahl linear unabhängiger Zeilen Daß der Rang sich bei elementaren Zeilenumformungen nicht ändert
Vektorräume. 1. v + w = w + v (Kommutativität der Vektoraddition)
 Vektorräume In vielen physikalischen Betrachtungen treten Größen auf, die nicht nur durch ihren Zahlenwert charakterisiert werden, sondern auch durch ihre Richtung Man nennt sie vektorielle Größen im Gegensatz
Vektorräume In vielen physikalischen Betrachtungen treten Größen auf, die nicht nur durch ihren Zahlenwert charakterisiert werden, sondern auch durch ihre Richtung Man nennt sie vektorielle Größen im Gegensatz
2. Linear Combination of Atomic Orbitals
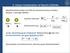 . Linear Combination of Atomi Orbitals Molekülorbitale werden mit ilfe des Variationsansatzes erhalten. Beispiel: -atomiges Molekül Atom, ϕ Atom, ϕ amilton-operator: Orthonormierung: ˆ ϕ El. Atom ϕ = =
. Linear Combination of Atomi Orbitals Molekülorbitale werden mit ilfe des Variationsansatzes erhalten. Beispiel: -atomiges Molekül Atom, ϕ Atom, ϕ amilton-operator: Orthonormierung: ˆ ϕ El. Atom ϕ = =
Inhalt.
 Inhalt 1 Grundlagen 13 1.1 Einfuhrung 13 1.1.1 Notwendigkeit der Quantentheorie 13 1.1.2 Historie I 16 1.1.3 Klassisches Eigenwertproblem - Die schwingende Saite 18 1.1.4 Die zeitunabhängige Schrödinger-Gleichung
Inhalt 1 Grundlagen 13 1.1 Einfuhrung 13 1.1.1 Notwendigkeit der Quantentheorie 13 1.1.2 Historie I 16 1.1.3 Klassisches Eigenwertproblem - Die schwingende Saite 18 1.1.4 Die zeitunabhängige Schrödinger-Gleichung
Lösung 2: Relationen, Abbildungen, Mächtigkeit, Gruppen
 D-MATH Lineare Algebra I HS 2016 Dr. Meike Akveld Lösung 2: Relationen, Abbildungen, Mächtigkeit, Gruppen 1. Gegeben n, m Z schreiben wir m n k Z : n = km Wir sagen m teilt n. Eine Zahl n Z ist gerade,
D-MATH Lineare Algebra I HS 2016 Dr. Meike Akveld Lösung 2: Relationen, Abbildungen, Mächtigkeit, Gruppen 1. Gegeben n, m Z schreiben wir m n k Z : n = km Wir sagen m teilt n. Eine Zahl n Z ist gerade,
Wiederholungsblatt zur Gruppentheorie
 Wiederholungsblatt zur Gruppentheorie von Christian Elsholtz, TU Clausthal, WS 1999/2000 Um Ihnen zu helfen, die Gruppentheorie zu wiederholen, stelle ich hier einige wichtige Beispiele und einige Lösungen
Wiederholungsblatt zur Gruppentheorie von Christian Elsholtz, TU Clausthal, WS 1999/2000 Um Ihnen zu helfen, die Gruppentheorie zu wiederholen, stelle ich hier einige wichtige Beispiele und einige Lösungen
1 Lineare Gleichungssysteme und Matrizen
 1 Lineare Gleichungssysteme und Matrizen Das Studium linearer Gleichungssysteme und ihrer Lösungen ist eines der wichtigsten Themen der linearen Algebra. Wir werden zunächst einige grundlegende Begriffe
1 Lineare Gleichungssysteme und Matrizen Das Studium linearer Gleichungssysteme und ihrer Lösungen ist eines der wichtigsten Themen der linearen Algebra. Wir werden zunächst einige grundlegende Begriffe
Symmetrische Figuren von Prof. Dr. Frank
 Symmetrische Figuren von Prof. Dr. Frank Eckhard Großmann November 3, 2009 1 Mathematische Formeln und Darstellungen vorweggegriffen Dieses Kapitel soll nochmal alle notwendigen mathematischen Grundlagen
Symmetrische Figuren von Prof. Dr. Frank Eckhard Großmann November 3, 2009 1 Mathematische Formeln und Darstellungen vorweggegriffen Dieses Kapitel soll nochmal alle notwendigen mathematischen Grundlagen
5. Raum-Zeit-Symmetrien: Erhaltungssätze
 5. Raum-Zeit-Symmetrien: Erhaltungssätze Unter Symmetrie versteht man die Invarianz unter einer bestimmten Operation. Ein Objekt wird als symmetrisch bezeichnet, wenn es gegenüber Symmetrieoperationen
5. Raum-Zeit-Symmetrien: Erhaltungssätze Unter Symmetrie versteht man die Invarianz unter einer bestimmten Operation. Ein Objekt wird als symmetrisch bezeichnet, wenn es gegenüber Symmetrieoperationen
13. ABBILDUNGEN EUKLIDISCHEN VEKTORRÄUMEN
 13. ABBILDUNGEN in EUKLIDISCHEN VEKTORRÄUMEN 1 Orthogonale Abbildungen im R 2 und R 3. Eine orthogonale Abbildung ist eine lineare Abbildung, die Längen und Orthogonalität erhält. Die zugehörige Matrix
13. ABBILDUNGEN in EUKLIDISCHEN VEKTORRÄUMEN 1 Orthogonale Abbildungen im R 2 und R 3. Eine orthogonale Abbildung ist eine lineare Abbildung, die Längen und Orthogonalität erhält. Die zugehörige Matrix
Anhang 1 Gruppen und Klassen: Definitionen und Beispiele
 Anhang Gruppen und Klassen: Definitionen und Beispiele AI.I Gruppen In Kapitel 2 wurde eine Definition der Gruppe gegeben, die zwar für unsere Zwecke ausreichend, doch unvollständig war; nicht alle Forderungen
Anhang Gruppen und Klassen: Definitionen und Beispiele AI.I Gruppen In Kapitel 2 wurde eine Definition der Gruppe gegeben, die zwar für unsere Zwecke ausreichend, doch unvollständig war; nicht alle Forderungen
Historisches zur Gruppentheorie
 Historisches zur Gruppentheorie Dipl.-Inform. Wolfgang Globke Institut für Algebra und Geometrie Arbeitsgruppe Differentialgeometrie Universität Karlsruhe 1 / 20 Gruppen: Abstrakte Definition Eine Gruppe
Historisches zur Gruppentheorie Dipl.-Inform. Wolfgang Globke Institut für Algebra und Geometrie Arbeitsgruppe Differentialgeometrie Universität Karlsruhe 1 / 20 Gruppen: Abstrakte Definition Eine Gruppe
Anorganische Chemie 3 (3.1) Teil 1 - Symmetrie. Was ist Symmetrie?
 Anorganische Chemie 3 (3.1) Teil 1 - Symmetrie Was ist Symmetrie? AC3 WS 2011/12 1 Symmetrie (griechisch = Ebenmaß, Gleichmaß) bedeutet die gesetzmäßige Wiederholung eines Motivs und damit die Übereinstimmung
Anorganische Chemie 3 (3.1) Teil 1 - Symmetrie Was ist Symmetrie? AC3 WS 2011/12 1 Symmetrie (griechisch = Ebenmaß, Gleichmaß) bedeutet die gesetzmäßige Wiederholung eines Motivs und damit die Übereinstimmung
Transformation Allgemeines Die Lage eines Punktes kann durch einen Ortsvektor (ausgehend vom Ursprung des Koordinatensystems
 Transformation - 1 1. Allgemeines 2. Zwei durch eine Translation verknüpfte gleichartige Basissysteme 3. Zwei durch eine Translation verknüpfte verschiedenartige Basissysteme (noch gleiche Orientierung)
Transformation - 1 1. Allgemeines 2. Zwei durch eine Translation verknüpfte gleichartige Basissysteme 3. Zwei durch eine Translation verknüpfte verschiedenartige Basissysteme (noch gleiche Orientierung)
3.4 Algebraische Strukturen
 3.4 Algebraische Strukturen 9 3.4 Algebraische Strukturen Man sagt, eine Menge hat eine algebraische Struktur, wenn in ihr eine Operation definiert ist, d.h. eine Verknüpfung von zwei Elementen der Menge,
3.4 Algebraische Strukturen 9 3.4 Algebraische Strukturen Man sagt, eine Menge hat eine algebraische Struktur, wenn in ihr eine Operation definiert ist, d.h. eine Verknüpfung von zwei Elementen der Menge,
Lineare Algebra. Mathematik II für Chemiker. Daniel Gerth
 Lineare Algebra Mathematik II für Chemiker Daniel Gerth Überblick Lineare Algebra Dieses Kapitel erklärt: Was man unter Vektoren versteht Wie man einfache geometrische Sachverhalte beschreibt Was man unter
Lineare Algebra Mathematik II für Chemiker Daniel Gerth Überblick Lineare Algebra Dieses Kapitel erklärt: Was man unter Vektoren versteht Wie man einfache geometrische Sachverhalte beschreibt Was man unter
Affine Koordinatentransformationen
 Affine Koordinatentransformationen Medieninformatik IL Andreas Unterweger Vertiefung Medieninformatik Studiengang ITS FH Salzburg Wintersemester 017/18 Andreas Unterweger (FH Salzburg) Affine Koordinatentransformationen
Affine Koordinatentransformationen Medieninformatik IL Andreas Unterweger Vertiefung Medieninformatik Studiengang ITS FH Salzburg Wintersemester 017/18 Andreas Unterweger (FH Salzburg) Affine Koordinatentransformationen
Gruppen und Kryptographie. Hagen Knaf, März 2018
 Gruppen und Kryptographie Hagen Knaf, März 2018 Überblick 1. 2. Potenzen 3. Diskrete Logarithmen 4. Schlüsseltausch nach Diffie-Hellman Kreislimit I, 1958 Kleiner und kleiner I, 1956 Welches der beiden
Gruppen und Kryptographie Hagen Knaf, März 2018 Überblick 1. 2. Potenzen 3. Diskrete Logarithmen 4. Schlüsseltausch nach Diffie-Hellman Kreislimit I, 1958 Kleiner und kleiner I, 1956 Welches der beiden
4.1. Vektorräume und lineare Abbildungen
 4.1. Vektorräume und lineare Abbildungen Mengen von Abbildungen Für beliebige Mengen X und Y bezeichnet Y X die Menge aller Abbildungen von X nach Y (Reihenfolge beachten!) Die Bezeichnungsweise erklärt
4.1. Vektorräume und lineare Abbildungen Mengen von Abbildungen Für beliebige Mengen X und Y bezeichnet Y X die Menge aller Abbildungen von X nach Y (Reihenfolge beachten!) Die Bezeichnungsweise erklärt
Matrizen und Drehungen
 Matrizen und Drehungen 20. Noember 2003 Diese Ausführungen sind im wesentlichen dem Skript zur Vorlesung Einführung in die Theoretische Physik I und II on PD Dr. Horst Fichtner entnommen. Dieses entstand
Matrizen und Drehungen 20. Noember 2003 Diese Ausführungen sind im wesentlichen dem Skript zur Vorlesung Einführung in die Theoretische Physik I und II on PD Dr. Horst Fichtner entnommen. Dieses entstand
D-MATH Tommaso Goldhirsch. Serie 3
 Serie 3 Aufgabe 1 Sei G eine Gruppe und X eine Teilmenge von G. Die von X erzeugte Untergruppe von G ist die kleinste Untergruppe von G die X enthält. (Dass es eindeutig eine "kleinste" gibt wird in der
Serie 3 Aufgabe 1 Sei G eine Gruppe und X eine Teilmenge von G. Die von X erzeugte Untergruppe von G ist die kleinste Untergruppe von G die X enthält. (Dass es eindeutig eine "kleinste" gibt wird in der
Analogie- bzw. Symmetriebetrachtungen zum arithmetischen und harmonischen Mittel *
 Otto Hamborg 4. November 995 Bismarckstraße 06 065 Berlin Tel. 030-33 67 65 hamborg-berlin@t-online.de Analogie- bzw. Symmetriebetrachtungen zum arithmetischen und harmonischen Mittel * Den folgenden Ausführungen
Otto Hamborg 4. November 995 Bismarckstraße 06 065 Berlin Tel. 030-33 67 65 hamborg-berlin@t-online.de Analogie- bzw. Symmetriebetrachtungen zum arithmetischen und harmonischen Mittel * Den folgenden Ausführungen
3 Lineare Abbildungen und Matrizen
 3 Lineare Abbildungen und Matrizen Definition 3.1. Es seien V und W zwei Vektorräume über demselben Zahlkörper k. Eine Abbildung heisst linear, falls gilt i) [ λ k ] [ v V ] [ f (λ v) = λ f ( v) ] ii)
3 Lineare Abbildungen und Matrizen Definition 3.1. Es seien V und W zwei Vektorräume über demselben Zahlkörper k. Eine Abbildung heisst linear, falls gilt i) [ λ k ] [ v V ] [ f (λ v) = λ f ( v) ] ii)
B Grundbegriffe zu Mengen und Abbildungen
 B Grundbegriffe zu Mengen und Abbildungen Die Sprache der Mengen und Abbildungen hat sich als Basissprache in der modernen Mathematik durchgesetzt. Da sie sehr praktisch ist, wird sie auch in diesem Buch
B Grundbegriffe zu Mengen und Abbildungen Die Sprache der Mengen und Abbildungen hat sich als Basissprache in der modernen Mathematik durchgesetzt. Da sie sehr praktisch ist, wird sie auch in diesem Buch
3.3. Drehungen und Spiegelungen
 3.3. Drehungen und Spiegelungen Drehungen und Spiegelungen in der Ebene Die Multiplikation einer komplexen Zahl z = x + i y (aufgefaßt als Punkt oder Ortsvektor der Ebene) mit der Zahl w = e ( ) = i φ
3.3. Drehungen und Spiegelungen Drehungen und Spiegelungen in der Ebene Die Multiplikation einer komplexen Zahl z = x + i y (aufgefaßt als Punkt oder Ortsvektor der Ebene) mit der Zahl w = e ( ) = i φ
Lineare Abbildungen. De nition Seien V, W Vektorräume. Eine Abbildung f : V! W heißt linear, wenn gilt
 Lineare Abbildungen Lineare Abbildungen De nition Seien V, W Vektorräume. Eine Abbildung f : V! W heißt linear, wenn gilt (L. ) f ist homogen; d.h. f( ~v) = f(~v) für alle 2 R, ~v 2 V, (L. ) f ist additiv;
Lineare Abbildungen Lineare Abbildungen De nition Seien V, W Vektorräume. Eine Abbildung f : V! W heißt linear, wenn gilt (L. ) f ist homogen; d.h. f( ~v) = f(~v) für alle 2 R, ~v 2 V, (L. ) f ist additiv;
Logische Grundlagen der Mathematik, WS 2014/15
 Logische Grundlagen der Mathematik, WS 2014/15 Thomas Timmermann 26. November 2014 Was kommt nach den natürlichen Zahlen? Mehr als die natürlichen Zahlen braucht man nicht, um einige der schwierigsten
Logische Grundlagen der Mathematik, WS 2014/15 Thomas Timmermann 26. November 2014 Was kommt nach den natürlichen Zahlen? Mehr als die natürlichen Zahlen braucht man nicht, um einige der schwierigsten
Anorganische Chemie III - Festkörperchemie
 Mathematisch-Naturwissenschaftliche Fakultät Institut für Chemie Abteilung Anorganische Chemie/Festkörperchemie Prof. Dr. Martin Köckerling Vorlesung Anorganische Chemie III - Festkörperchemie 1 Wiederholung
Mathematisch-Naturwissenschaftliche Fakultät Institut für Chemie Abteilung Anorganische Chemie/Festkörperchemie Prof. Dr. Martin Köckerling Vorlesung Anorganische Chemie III - Festkörperchemie 1 Wiederholung
Spezielle Matrixformen
 Definition B57 (Transposition) Eine einfache aber wichtige Operation auf Matrizen ist die Transposition, die aus einer (m n) Matrix A eine (n m) Matrix B = A T macht Hierbei gilt β i j = α j i, so daß
Definition B57 (Transposition) Eine einfache aber wichtige Operation auf Matrizen ist die Transposition, die aus einer (m n) Matrix A eine (n m) Matrix B = A T macht Hierbei gilt β i j = α j i, so daß
täglich einmal Scilab!
 Mathematik 1 - Übungsblatt 7 täglich einmal Scilab! Aufgabe 1 (Definitionsformel für Determinanten) Determinanten quadratischer Matrizen sind skalare Größen (=einfache Zahlen im Gegensatz zu vektoriellen
Mathematik 1 - Übungsblatt 7 täglich einmal Scilab! Aufgabe 1 (Definitionsformel für Determinanten) Determinanten quadratischer Matrizen sind skalare Größen (=einfache Zahlen im Gegensatz zu vektoriellen
Verschiedenes. Exponieren einer Matrix. Wir betrachten als Beispiel folgende Matrix: 0 1 A = 1 0
 Verschiedenes Exponieren einer Matrix Wir betrachten als Beispiel folgende Matrix: A = Man kann die Funktion f(a) einer Matrix A so berechnen, indem man auf die Reihendarstellung der Funktion f(x) zurückgeht.
Verschiedenes Exponieren einer Matrix Wir betrachten als Beispiel folgende Matrix: A = Man kann die Funktion f(a) einer Matrix A so berechnen, indem man auf die Reihendarstellung der Funktion f(x) zurückgeht.
Mathematisches Kaleidoskop II Materialien Teil 3. Dr. Hermann Dürkop
 Mathematisches Kaleidoskop II Materialien Teil 3 Dr. Hermann Dürkop E-Mail: info@ermanus.de .3.3 Noch zwei Isomorphie-Beispiele Beispiel : Wir betrachten die Symmetrien eines nichtquadratischen Rechtecks.
Mathematisches Kaleidoskop II Materialien Teil 3 Dr. Hermann Dürkop E-Mail: info@ermanus.de .3.3 Noch zwei Isomorphie-Beispiele Beispiel : Wir betrachten die Symmetrien eines nichtquadratischen Rechtecks.
Methoden der Chemie III Teil 1 Modul M.Che.1101 WS 2010/11 1 Moderne Methoden der Anorganischen Chemie Mi 10:15-12:00, Hörsaal II George Sheldrick
 Methoden der Chemie III Teil 1 Modul M.Che.1101 WS 2010/11 1 Moderne Methoden der Anorganischen Chemie Mi 10:15-12:00, Hörsaal II George Sheldrick gsheldr@shelx.uni-ac.gwdg.de Teil. 1. Kristallstrukturbestimmung
Methoden der Chemie III Teil 1 Modul M.Che.1101 WS 2010/11 1 Moderne Methoden der Anorganischen Chemie Mi 10:15-12:00, Hörsaal II George Sheldrick gsheldr@shelx.uni-ac.gwdg.de Teil. 1. Kristallstrukturbestimmung
WS 20013/14. Diskrete Strukturen
 WS 20013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
WS 20013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
Lineare Algebra I 5. Tutorium Die Restklassenringe /n
 Lineare Algebra I 5. Tutorium Die Restklassenringe /n Fachbereich Mathematik WS 2010/2011 Prof. Dr. Kollross 19. November 2010 Dr. Le Roux Dipl.-Math. Susanne Kürsten Aufgaben In diesem Tutrorium soll
Lineare Algebra I 5. Tutorium Die Restklassenringe /n Fachbereich Mathematik WS 2010/2011 Prof. Dr. Kollross 19. November 2010 Dr. Le Roux Dipl.-Math. Susanne Kürsten Aufgaben In diesem Tutrorium soll
Lineare Algebra I. Prof. Dr. M. Rost. Übungen Blatt 2 (WS 2010/2011) Abgabetermin: Donnerstag, 28. Oktober.
 Lineare Algebra I Prof. Dr. M. Rost Übungen Blatt 2 (WS 2010/2011) Abgabetermin: Donnerstag, 28. Oktober http://www.math.uni-bielefeld.de/~rost/la1 Erinnerungen und Ergänzungen zur Vorlesung: Im Folgenden
Lineare Algebra I Prof. Dr. M. Rost Übungen Blatt 2 (WS 2010/2011) Abgabetermin: Donnerstag, 28. Oktober http://www.math.uni-bielefeld.de/~rost/la1 Erinnerungen und Ergänzungen zur Vorlesung: Im Folgenden
Das Schwingungsspektrum von H 2 O
 zum Vortrag Das Schwingungsspektrum von 2 O im ahmen des Seminars zum OC-F-Praktikums Allein aus der Kenntnis der Symmetrie eines Moleküls können ückschlüsse auf und Voraussagen über das Verhalten des
zum Vortrag Das Schwingungsspektrum von 2 O im ahmen des Seminars zum OC-F-Praktikums Allein aus der Kenntnis der Symmetrie eines Moleküls können ückschlüsse auf und Voraussagen über das Verhalten des
} Symmetrieachse von A und B.
 5 Symmetrieachsen Seite 1 von 6 5 Symmetrieachsen Gleicher Abstand von zwei Punkten Betrachtet man zwei fest vorgegebene Punkte A und B, drängt sich im Zusammenhang mit dem Abstandsbegriff eine Frage auf,
5 Symmetrieachsen Seite 1 von 6 5 Symmetrieachsen Gleicher Abstand von zwei Punkten Betrachtet man zwei fest vorgegebene Punkte A und B, drängt sich im Zusammenhang mit dem Abstandsbegriff eine Frage auf,
(Man sagt dafür auch, dass die Teilmenge U bezüglich der Gruppenoperationen abgeschlossen sein muss.)
 3. Untergruppen 19 3. Untergruppen Nachdem wir nun einige grundlegende Gruppen kennengelernt haben, wollen wir in diesem Kapitel eine einfache Möglichkeit untersuchen, mit der man aus bereits bekannten
3. Untergruppen 19 3. Untergruppen Nachdem wir nun einige grundlegende Gruppen kennengelernt haben, wollen wir in diesem Kapitel eine einfache Möglichkeit untersuchen, mit der man aus bereits bekannten
Brückenkurs Mathematik
 Brückenkurs Mathematik 6.10. - 17.10. Vorlesung 3 Geometrie Doris Bohnet Universität Hamburg - Department Mathematik Mi 8.10.2008 1 Geometrie des Dreiecks 2 Vektoren Länge eines Vektors Skalarprodukt Kreuzprodukt
Brückenkurs Mathematik 6.10. - 17.10. Vorlesung 3 Geometrie Doris Bohnet Universität Hamburg - Department Mathematik Mi 8.10.2008 1 Geometrie des Dreiecks 2 Vektoren Länge eines Vektors Skalarprodukt Kreuzprodukt
Städtewettbewerb Frühjahr 2008
 Städtewettbewerb Frühjahr 2008 Lösungsvorschläge Hamburg 5. März 2008 [Version 7. April 2008] M Mittelstufe Aufgabe M.1 (3 P.). Die gegenüberliegenden Seiten eines konvexen Sechsecks ABCDEF seien jeweils
Städtewettbewerb Frühjahr 2008 Lösungsvorschläge Hamburg 5. März 2008 [Version 7. April 2008] M Mittelstufe Aufgabe M.1 (3 P.). Die gegenüberliegenden Seiten eines konvexen Sechsecks ABCDEF seien jeweils
Kristallographie. Walter Borchardt-Ott. Eine Einführung für Naturwissenschaftler. Springer. Sechste, überarbeitete und erweiterte Auflage
 Walter Borchardt-Ott Kristallographie Eine Einführung für Naturwissenschaftler Sechste, überarbeitete und erweiterte Auflage Mit 290 Abbildungen und 44 Tabellen Springer Inhaltsverzeichnis 1 Einleitung
Walter Borchardt-Ott Kristallographie Eine Einführung für Naturwissenschaftler Sechste, überarbeitete und erweiterte Auflage Mit 290 Abbildungen und 44 Tabellen Springer Inhaltsverzeichnis 1 Einleitung
Lösungen zum Übungsblatt 10
 Lösungen zum Übungsblatt 10 Aufgabe 1 a) vierbeiniger, rechteckiger Tisch C 2 -Achse senkrecht zur Tischplatte in der Tischmitte zwei Spiegelebenen σ v, die die C 2 -Achse enthalten und je zwei Seiten
Lösungen zum Übungsblatt 10 Aufgabe 1 a) vierbeiniger, rechteckiger Tisch C 2 -Achse senkrecht zur Tischplatte in der Tischmitte zwei Spiegelebenen σ v, die die C 2 -Achse enthalten und je zwei Seiten
Anorganische Chemie I A. Mezzetti Musterlösung VI
 Anorganische Chemie I O-LCAO A. ezzetti usterlösung VI π-bindungen in quadratisch-planaren Kompleen (a) Schreiben Sie die reduzible Darstellung Γπ für die π-ligandengruppenorbitale auf und bestimmen Sie
Anorganische Chemie I O-LCAO A. ezzetti usterlösung VI π-bindungen in quadratisch-planaren Kompleen (a) Schreiben Sie die reduzible Darstellung Γπ für die π-ligandengruppenorbitale auf und bestimmen Sie
Mathematik II Frühjahrssemester 2013
 Mathematik II Frühjahrssemester 2013 Prof Dr Erich Walter Farkas Kapitel 7: Lineare Algebra 71 Reelle Matrizen Prof Dr Erich Walter Farkas Mathematik I+II, 71 Reelle Matrizen 1 / 31 1 2 3 4 Prof Dr Erich
Mathematik II Frühjahrssemester 2013 Prof Dr Erich Walter Farkas Kapitel 7: Lineare Algebra 71 Reelle Matrizen Prof Dr Erich Walter Farkas Mathematik I+II, 71 Reelle Matrizen 1 / 31 1 2 3 4 Prof Dr Erich
3.1 Gruppen, Untergruppen und Gruppen-Homomorphismen
 TEIL II: GRUPPEN In der modernen Algebra versucht man die Zahlen (Z, Q, R, ) durch die Konzentration auf Rechenoperationen (+,,... ), oder allgemeiner auf strukturelle Eigenschaften dieser Operationen,
TEIL II: GRUPPEN In der modernen Algebra versucht man die Zahlen (Z, Q, R, ) durch die Konzentration auf Rechenoperationen (+,,... ), oder allgemeiner auf strukturelle Eigenschaften dieser Operationen,
Mathematik I Herbstsemester 2014 Kapitel 8: Lineare Algebra 8.1 Reelle Matrizen
 Mathematik I Herbstsemester 2014 Kapitel 8: Lineare Algebra 81 Reelle Matrizen Prof Dr Erich Walter Farkas http://wwwmathethzch/ farkas 1 / 31 1 2 3 4 2 / 31 Transponierte einer Matrix 1 Transponierte
Mathematik I Herbstsemester 2014 Kapitel 8: Lineare Algebra 81 Reelle Matrizen Prof Dr Erich Walter Farkas http://wwwmathethzch/ farkas 1 / 31 1 2 3 4 2 / 31 Transponierte einer Matrix 1 Transponierte
2. Verzerrungszustand
 2. Verzerrungszustand Ein Körper, der belastet wird, verformt sich. Dabei ändern die Punkte des Körpers ihre Lage. Die Lageänderung der Punkte des Körpers wird als Verschiebung bezeichnet. Ist die Verschiebung
2. Verzerrungszustand Ein Körper, der belastet wird, verformt sich. Dabei ändern die Punkte des Körpers ihre Lage. Die Lageänderung der Punkte des Körpers wird als Verschiebung bezeichnet. Ist die Verschiebung
5. Äquivalenzrelationen
 5. Äquivalenzrelationen 35 5. Äquivalenzrelationen Wenn man eine große und komplizierte Menge (bzw. Gruppe) untersuchen will, so kann es sinnvoll sein, zunächst kleinere, einfachere Mengen (bzw. Gruppen)
5. Äquivalenzrelationen 35 5. Äquivalenzrelationen Wenn man eine große und komplizierte Menge (bzw. Gruppe) untersuchen will, so kann es sinnvoll sein, zunächst kleinere, einfachere Mengen (bzw. Gruppen)
