Prof. Dr. Günter Hellmig. Aufgabenskript Induktive Statistik
|
|
|
- Marie Glöckner
- vor 7 Jahren
- Abrufe
Transkript
1 rof. Dr. Günter Hellmig Aufgabenskript Induktive Statistik
2 Inhalt:.Kombinatorik: Variation und Kombination, jeweils ohne Wiederholung 2.Rechnen mit Wahrscheinlichkeiten: Additions- und Multiplikationssätze 3.Rechnen mit Wahrscheinlichkeiten: Vierfeldertafel, bedingte Wahrscheinlichkeit 4.Allgemeine Verteilungen: Wahrscheinlichkeitsfunktion, Wahrscheinlichkeitssummenfunktion, Erwartungswert, Varianz 5.Binomialverteilung und oissonverteilung: Berechnung von Wahrscheinlichkeiten 6.Normalverteilung: Berechnung von Wahrscheinlichkeiten, die zu einem bestimmten Intervall gehören 7.Normalverteilung: Berechnung von Ereignissen, die zu einer bestimmten Wahrscheinlichkeit gehören 8.Normalverteilung: Berechnung von Intervallen, die zu einer bestimmten Wahrscheinlichkeit gehören 9.Schätzverfahren: Berechnung des Zufallsstreubereichs für einen Mittelwert 0.Schätzverfahren: Berechnung des Vertrauensbereichs für einen Mittelwert.Schätzverfahren: Berechnung des Vertrauensbereichs für einen Anteilswert und dessen Umrechnung 2.Schätzverfahren: Berechnung des Vertrauensbereichs für einen Mittelwert und Verwendung der t-verteilung *** Das vorliegende Aufgabenskript gehört zur Teil-Lehrveranstaltung Induktive Statistik und ist gemäß dem Vorlesungsablauf thematisch geordnet. Das Skript resultiert aus Klausuraufgaben der letzten Jahre. Bei der rüfungsvorbereitung wird empfohlen, die Aufgaben blind zu bearbeiten, d.h. ohne ständigen Blick auf die Musterlösung. Die Bearbeitungszeit für die Aufgaben ist im Durchschnitt mit 5 Minuten zu veranschlagen; im Einzelnen sind es - je nach Anzahl der Unterfragen und je nach Schwierigkeitsgrad 0 bis 20 Minuten.
3 . An einem ferderennen nehmen 0 ferde teil. Wie hoch ist die Wahrscheinlichkeit (rozent), dass man wenn man keine Kenntnis über die Stärken der einzelnen ferde hat folgende Ergebnisse richtig voraussagt: a) Siegendes ferd b) Die ersten drei ferde in der Reihenfolge des Einlaufs c) Die ersten drei ferde ohne Berücksichtigung der Reihenfolge d) Wie hoch wären die drei Wahrscheinlichkeiten zu a) bis c), wenn man Kenntnis hat, dass ein bestimmtes ferd siegen wird (und von dieser Kenntnis bei der Voraussage Gebrauch macht)? e) Wie hoch wären die drei Wahrscheinlichkeiten zu a) bis c), wenn man Kenntnis hat, dass ein bestimmtes ferd nicht siegen wird (und von dieser Kenntnis bei der Voraussage Gebrauch macht)? n(a) a) r( A) 0 (rozent) n(i) 0 n! 0! b) Vk(n) (n k)! (0 3)! r( A) 0,0039 0,39 (rozent) 720 c) n Ck(n) 20 k r( A) 0, ,833 (rozent) 20 n(a) d)() r( A) n(i) 00 (rozent) n! 9! (2) Vk(n) (n k)! (9 2)! r( A) 0, ,389 (rozent) n (3) Ck(n) k r( A) 0, ,778 (rozent) n(a) e)() r( A) n(i) 9, (rozent) n! 9! (2) Vk(n) (n k)! (9 3)! r( A) 504 0,0098 0,98 (rozent) n (3) Ck(n) k r( A) 0,090 84,90 (rozent)
4 2. Die Wahrscheinlichkeit (bei einem älteren Ehepaar), dass der Mann noch in 20 Jahren lebt, sei 30 %, und dass die Frau noch in 20 Jahren lebt, sei 40 %. a) Wie groß ist die Wahrscheinlichkeit (rozent), dass () beide noch in 20 Jahren leben, (2) mindestens eine erson noch in 20 Jahren lebt, (3) nur der Mann noch in 20 Jahren lebt, (4) beide in 20 Jahren nicht mehr leben? b) Welche Annahme liegt den Berechnungen zugrunde? (Annahme kurz benennen und erläutern!) a)() ( A B) p p(a) p(b ) 0,3 0,4 0,2 2 (rozent) p p(a) + p(b) p(a) p(b ) 0,3+0,4-0,3 0,4 0,58 58 (rozent) (2) ( A B) p p(a) p(a) p(b ) 0,3-0,3 0,4 0,8 8 (rozent) (3) ( A \ A B) (4) ( A B) p p(a) p(b ) (-0,3) (-0,4) 0,42 42 (rozent) b) Unabhängigkeit Die Überlebenswahrscheinlichkeit des einen Ehepartners ändert sich nicht, wenn der andere Ehepartner stirbt.
5 3. Zur Herstellung eines Artikels werden drei Maschinen X, Y und Z eingesetzt, die unabhängig voneinander arbeiten. Maschine X, die 60 rozent der Gesamtproduktion herstellt, hat eine Ausschuss-Quote von 0,0; für Maschine Y lauten die entsprechenden Werte 30 rozent und 0,04; für Maschine Z sind es 0 rozent und 0,07. a) Erstellen Sie eine (vollständige) Mehrfeldertafel! b) Wie groß ist bei Zufallsauswahl die Wahrscheinlichkeit (rozent), dass () ein mangelhaftes Stück von Maschine X stammt, (2) ein mangelfreies Stück von Maschine Y stammt, (3) ein von Maschine Y stammendes Stück mangelfrei ist, (4) ein von Maschine Z stammendes Stück mangelfrei ist? a) B mangelfrei B mangelhaft X 0,594 0,0 0,6 0,006 0,6 Y 0,288 0,04 0,3 0,02 0,3 Z 0,093 0,07 0, 0,007 0, 0,975 0,025,0 b)() p ( X B) ( X B) p( B) p 0,006 0, % 0,025 (2) p ( Y B) (3) p ( B Y) (4) p ( B Z) ( Y B) pb ( ) p 0,288 0, ,54 % 0,975 ( B Y) py ( ) p 0,288 0, % 0,3 ( B Z) pz ( ) p 0,093 0, % 0,
6 4. Ein Handwerksbetrieb kalkuliert, dass die Arbeitszeit für einen bestimmten Auftrag zwischen 30 und 40 Stunden dauern wird, und zwar: 30 Stunden mit einer Wahrscheinlichkeit von 5 rozent 32 Stunden mit einer Wahrscheinlichkeit von 45 rozent Stunden mit einer Wahrscheinlichkeit von 30 rozent 40 Stunden mit einer Wahrscheinlichkeit von 0 rozent a) Erstellen Sie grafisch die Wahrscheinlichkeitsfunktion und die Wahrscheinlichkeitssummenfunktion! b) Berechnen Sie den Erwartungswert und die Varianz! a),00 j 0,50 0,40 0,30 0,20 0,0 p j 0,90 0,80 0,70 0,60 0,50 0,40 0,30 0,20 0, xj xj b) j x j p j x j p j x j - µ ( xj µ ) 2 2 ( xj µ ) 30 0,5 4, , ,45 4,4-2 4,8 3 0,30, , ,0 4, , , ,5 p j µ k x 34 j j p j 2 k 2 ( xj µ ) pj j 0,5
7 5. Bei einem Glücksspiel ( Roulette ) gibt es bekanntlich Zahlen; eine Zahl wird vom Spieler gewählt; und eine Zahl wird zufällig und unabhängig als Gewinnzahl benannt. Der Spieler hat gewonnen, wenn seine gewählte Zahl mit der benannten Gewinnzahl übereinstimmt. - Ein Spieler unternimmt Spielversuche, wobei er jeweils dieselbe Zahl wählt. Wie groß ist die Wahrscheinlichkeit (rozent), dass er a) kein einziges Mal gewinnt (Berechnung auf zwei Arten!) b) genau einmal gewinnt (Berechnung auf zwei Arten!) c) mindestens einmal gewinnt (Berechnung auf zwei Arten!) n x n x a) B( x n, ) Q ( ) ( ) B 0, ( ) x 0 B ( 0, ) ( ) 0, ,29 % x 36 0 µ µ ( x µ ) e ( 0 ) e x! ( 0 ) e 0, ,79 % n x n x b) B( x n, ) Q B(, ) ( ) ( ) B x (, ) ( ) x ,29,29 % µ µ ( x µ ) e ( ) e x! ( ) e 0! 0, ,79 %! 36 n x n x c) B( x n, ) Q B( 0, ) ( ) 0 ( ) x (, ) ( ) B 0 x 36 0, ,7 % 0 µ µ ( x µ ) e ( 0 ) e x! ( 0 ) e 0, ,2 % 0!
8 6. Der Lagerabgang (Mengeneinheiten) in einem Firmenlager ist normalverteilt mit Erwartungswert 5 und Standardabweichung 2. Wie hoch ist die Wahrscheinlichkeit, dass der Lagerabgang a) weniger als 6 Mengeneinheiten beträgt (Antwortsatz!) b) mehr als 8 Mengeneinheiten beträgt (Antwortsatz!) a) u x µ 6 5 u 0,5 2 (0,5) Fe 0,695 Wahrscheinlichkeit 69,5 % b) u x µ 8 5 u,5 2 Fe (,5) 0,9332 Wahrscheinlichkeit 6,68 %
9 7. Ein Bäckereibetrieb kauft für Vorratszwecke 70 akete Zucker (Sollgewicht 500 Gramm, Standardabweichung 0 Gramm, Normalverteilung). Wie viele akete werden voraussichtlich a) zwischen 495 Gramm und 505 Gramm wiegen (Antwortsatz!) b) weniger als 55 Gramm wiegen (Antwortsatz!) c) genau 500 Gramm wiegen (Antwortsatz!) (Hinweis: Bestimmen Sie bei allen Teilfragen zunächst die Wahrscheinlichkeit, dass das jeweilige Gewichtsintervall bzw. Gewicht für ein aket zutrifft.) a) b) u x µ u 0 Fz (0,5) X N 0,3829 X N X 70 0,3829 0,5 65,093 Anzahl der akete 65 u x µ u 0 Fe (,5) X N 0,9332 X N X 70 0,9332,5 58,644 Anzahl der akete 59 x µ c) u 0 0 Fz (0) 0 X X N 70 0 N Anzahl der akete 0 0
10 8. In einem Sägewerk werden rohe Holzbretter zugeschnitten. Die Länge der Bretter soll 90 cm betragen, die Standardabweichung beträgt,5 cm; es liegt näherungsweise Normalverteilung vor. a) In welchem Intervall wird die Länge eines zufällig ausgewählten Brettes bei einer Sicherheitswahrscheinlichkeit von 95 % liegen? (Antwortsatz!) b) Welche Obergrenze wird die Länge bei einer Irrtumswahrscheinlichkeit von % haben? (Antwortsatz!) a) u x µ Fz (u) 0,95 uz ±,96 x 90 ±,96,5 92,94 xo xu 87,06 Intervall zwischen 87,06 und 92,94 cm b) u x µ Fe (u) 0,99 ue + 2,33 x ,33,5 93,495 xo Obergrenze bei 93,495 cm
11 9. In einer repräsentativen Studie wurde festgestellt, dass Frauen im Durchschnitt eine Körpergröße von 75 Zentimetern haben bei einer Standardabweichung von 3 Zentimetern. Bei der Nachprüfung dieses Ergebnisses werden 70 Frauen untersucht. - In welchem Intervall liegt deren durchschnittliche Körpergröße, wenn eine Irrtumswahrscheinlichkeit a) von 4,55 % angenommen wird? (Antwortsatz!) b) von 0,27 % angenommen wird? (Antwortsatz!) a) r µ u n x µ + u n α Fz r x ,0455 ( 75 0,72 x ,72) 0, 9545 r ( 74,28 x 75,72) 0, 9545 r Intervall zwischen 74,28 und 75,72 cm b) r µ u n x µ + u n α Fz r x ,0027 ( 75,08 x 75 +,08) 0, 9973 r ( 73,92 x 76,08) 0, 9973 r Intervall zwischen 73,92 und 76,08 cm
12 0.Ein Marktforschungsinstitut befragt 500 zufällig ausgewählte ersonen in Deutschland nach einem bestimmten Waschmittel; davon erklären 80 %, dass sie das betreffende Waschmittel kennen. In welchem Intervall wird dann der entsprechende rozentsatz in der Gesamtbevölkerung liegen, wenn eine Aussagewahrscheinlichkeit a) von 90 % angenommen wird (Antwortsatz!) b) von 98 % angenommen wird (Antwortsatz!) p q p q a) r p uz p + uz α n n 0,80 0,20 0,80 0,20 r 0,80,64 0,80 +, ,90 ( 0,80 0,0293 0,80 + 0,0293 ) 0, 90 r ( 0,7707 0,8293 ) 0, 90 r Zwischen 77,07 % und 82,93 % p q p q b) r p uz p + uz α n n 0,80 0,20 0,80 0,20 r 0,80 2,33 0,80 2, ,98 ( 0,80 0,047 0,80 + 0,047 ) 0, 98 r ( 0,7583 0,847 ) 0, 98 r Zwischen 75,83 % und 84,7 %
13 .Bei 200 Studierenden der Hochschule Bochum wurde eine Befragung durchgeführt. Dabei gaben 0 Studierende an, dass sie regelmäßig mit öffentlichen Verkehrsmitteln zur Fachhochschule kommen. a) Wie lautet der Anteilswert bei den Befragten? b) Berechnen Sie das Schätzintervall für den Anteilswert bei allen Studierenden, wenn eine Sicherheitswahrscheinlichkeit von 90 % angenommen wird! (Antwortsatz!) c) Wie lautet das entsprechende Schätzintervall für die Gesamtzahl der Studierenden, wenn die Hochschule Bochum 4500 Studierende hat? (Antwortsatz!) a) x p n 0 p 200 0,55 b) r p p q p q uz p + uz n n α 0,55 0,45 0,55 0,45 r 0,55,64 0,55 +, ,90 ( 0,55 0,0577 0,55 + 0,0577 ) 0, 90 r ( 0,4923 0,6077 ) 0, 90 r Intervall zwischen 49,23 % und 60,77 % der Studierenden c) X N X N Xu 0, Xo 0, Intervall zwischen 225 und 2735 Studierende
14 2.In einem Finanzamt wurden sämtliche Einkommensteuerbescheide und Steuerrückzahlungen einer Nachprüfung unterzogen. Die Steuerrückzahlungen waren normalverteilt; anhand einer Stichprobe wurde ein durchschnittlicher Rückzahlungsbetrag von 500 Euro bei einer Standardabweichung von 00 Euro ermittelt. Innerhalb welcher Grenzen wird der durchschnittliche Rückzahlungsbetrag sämtlicher Einkommensteuerbescheide bei einer Sicherheitswahrscheinlichkeit von 99 % liegen, wenn die betreffende Stichprobe a) einen Umfang von 400 gehabt hat (Antwortsatz!) b) einen Umfang von 6 gehabt hat (Antwortsatz!) s s a) r x uz µ x + uz α n n r 500 2,58 µ , ,99 ( 487, µ 52,9 ) 0, 99 r Rückzahlungsbetrag zwischen 487,0 und 52,90 Euro s ν s b) r x tz ν µ x + tz α n n r 500 2,95 µ , ,99 ( 426,25 µ 573,75 ) 0, 99 r Rückzahlungsbetrag zwischen 426,25 und 573,75 Euro
Vorlesungsskript. Induktive Statistik. Prof. Dr. Günter Hellmig
 Vorlesungsskript Induktive Statistik Prof. Dr. Günter Hellmig Prof. Dr. Günter Hellmig Vorlesungsskript Induktive Statistik Erstes Kapitel Das erste Kapitel beschäftigt sich mit einem Einstieg in die Wahrscheinlichkeitslehre,
Vorlesungsskript Induktive Statistik Prof. Dr. Günter Hellmig Prof. Dr. Günter Hellmig Vorlesungsskript Induktive Statistik Erstes Kapitel Das erste Kapitel beschäftigt sich mit einem Einstieg in die Wahrscheinlichkeitslehre,
Dr. H. Grunert Schließende Statistik Vorlesungscharts. Vorlesung 7. Schätzverfahren
 Vorlesungscharts Vorlesung 7 Schätzverfahren Konstruktion von Konfidenzintervallen Konfidenzintervalle für den Erwartungswert normalverteilter Grundgesamtheiten Konfidenzintervalle für Anteilswerte Seite
Vorlesungscharts Vorlesung 7 Schätzverfahren Konstruktion von Konfidenzintervallen Konfidenzintervalle für den Erwartungswert normalverteilter Grundgesamtheiten Konfidenzintervalle für Anteilswerte Seite
Übungsaufgaben zu Statistik II
 Übungsaufgaben zu Statistik II Prof. Dr. Irene Prof. Dr. Albrecht Ungerer Die Kapitel beziehen sich auf das Buch: /Ungerer (2016): Statistik für Wirtschaftswissenschaftler Springer Gabler 4 Übungsaufgaben
Übungsaufgaben zu Statistik II Prof. Dr. Irene Prof. Dr. Albrecht Ungerer Die Kapitel beziehen sich auf das Buch: /Ungerer (2016): Statistik für Wirtschaftswissenschaftler Springer Gabler 4 Übungsaufgaben
Stichproben Parameterschätzung Konfidenzintervalle:
 Stichproben Parameterschätzung Konfidenzintervalle: Beispiel Wahlprognose: Die Grundgesamtheit hat einen Prozentsatz p der Partei A wählt. Wenn dieser Prozentsatz bekannt ist, dann kann man z.b. ausrechnen,
Stichproben Parameterschätzung Konfidenzintervalle: Beispiel Wahlprognose: Die Grundgesamtheit hat einen Prozentsatz p der Partei A wählt. Wenn dieser Prozentsatz bekannt ist, dann kann man z.b. ausrechnen,
7. Übung: Aufgabe 1. b), c), e) Aufgabe 2. a), c), e) Aufgabe 3. c), e) Aufgabe 4. Aufgabe 5. Aufgabe 6. Aufgabe 7. Aufgabe 8. Aufgabe 9.
 7. Übung: Aufgabe 1 b), c), e) Aufgabe a), c), e) Aufgabe 3 c), e) Aufgabe 4 b) Aufgabe 5 a) Aufgabe 6 b) Aufgabe 7 e) Aufgabe 8 c) Aufgabe 9 a), c), e) Aufgabe 10 b), d) Aufgabe 11 a) Aufgabe 1 b) Aufgabe
7. Übung: Aufgabe 1 b), c), e) Aufgabe a), c), e) Aufgabe 3 c), e) Aufgabe 4 b) Aufgabe 5 a) Aufgabe 6 b) Aufgabe 7 e) Aufgabe 8 c) Aufgabe 9 a), c), e) Aufgabe 10 b), d) Aufgabe 11 a) Aufgabe 1 b) Aufgabe
Klausur zur Vorlesung
 Institut für Mathematische Stochastik WS 2006/2007 Universität Karlsruhe 12. Februar 2007 Priv.-Doz. Dr. D. Kadelka Dipl.-Math. W. Lao Aufgabe 1 (15 Punkte) Klausur zur Vorlesung Statistik für Biologen
Institut für Mathematische Stochastik WS 2006/2007 Universität Karlsruhe 12. Februar 2007 Priv.-Doz. Dr. D. Kadelka Dipl.-Math. W. Lao Aufgabe 1 (15 Punkte) Klausur zur Vorlesung Statistik für Biologen
Bestimmte Zufallsvariablen sind von Natur aus normalverteilt. - naturwissenschaftliche Variablen: originär z.b. Intelligenz, Körpergröße, Messfehler
 6.6 Normalverteilung Die Normalverteilung kann als das wichtigste Verteilungsmodell der Statistik angesehen werden. Sie wird nach ihrem Entdecker auch Gaußsche Glockenkurve genannt. Die herausragende Stellung
6.6 Normalverteilung Die Normalverteilung kann als das wichtigste Verteilungsmodell der Statistik angesehen werden. Sie wird nach ihrem Entdecker auch Gaußsche Glockenkurve genannt. Die herausragende Stellung
A3.Die Lebensdauer eines elektronischen Gerätes werde als normalverteilt angenommen. Der Erwartungswert betrage
 Aufgaben ~ Beispiele A1. Wir spielen Roulette mit einem Einsatz von 5 mit der Glückszahl 15. Die Wahrscheinlichkeiten und Auszahlungen beim Roulette sind in folgender Tabelle zusammengefasst: Ereignis
Aufgaben ~ Beispiele A1. Wir spielen Roulette mit einem Einsatz von 5 mit der Glückszahl 15. Die Wahrscheinlichkeiten und Auszahlungen beim Roulette sind in folgender Tabelle zusammengefasst: Ereignis
Handelt es sich bei den folgenden um diskrete oder stetige Zufallsvariablen?
 1. Handelt es sich bei den folgenden um diskrete oder stetige Zufallsvariablen? a.) Anzahl der Kunden, die an der Kasse in der Schlange stehen. b.) Die Menge an Energie, die pro Tag von einem Energieversorgungsunternehmen
1. Handelt es sich bei den folgenden um diskrete oder stetige Zufallsvariablen? a.) Anzahl der Kunden, die an der Kasse in der Schlange stehen. b.) Die Menge an Energie, die pro Tag von einem Energieversorgungsunternehmen
Biomathematik für Mediziner, Klausur WS 1999/2000 Seite 1
 Biomathematik für Mediziner, Klausur WS 1999/2000 Seite 1 Aufgabe 1: Wieviele der folgenden Variablen sind quantitativ stetig? Schulnoten, Familienstand, Religion, Steuerklasse, Alter, Reaktionszeit, Fahrzeit,
Biomathematik für Mediziner, Klausur WS 1999/2000 Seite 1 Aufgabe 1: Wieviele der folgenden Variablen sind quantitativ stetig? Schulnoten, Familienstand, Religion, Steuerklasse, Alter, Reaktionszeit, Fahrzeit,
(8 + 2 Punkte) = = 0.75
 Aufgabe 1 (8 + 2 Punkte) Von 20 Teilnehmern einer Bergwanderung geben 8 Personen an Knieschmerzen zu haben. 6 Teilnehmer leiden an Sonnenbrand. 8 Teilnehmer blieben unversehrt. a) Wie groß ist die Wahrscheinlichkeit,
Aufgabe 1 (8 + 2 Punkte) Von 20 Teilnehmern einer Bergwanderung geben 8 Personen an Knieschmerzen zu haben. 6 Teilnehmer leiden an Sonnenbrand. 8 Teilnehmer blieben unversehrt. a) Wie groß ist die Wahrscheinlichkeit,
Aufgabe 8: Stochastik (WTR)
 Abitur Mathematik: Nordrhein-Westfalen 2013 Aufgabe 8 a) (1) WAHRSCHEINLICHKEIT FÜR KEINE ANGABE ERMITTELN Nach der Laplace Formel ist Anzahl der Personen, die keine Angabe machten keine Angabe Gesamtzahl
Abitur Mathematik: Nordrhein-Westfalen 2013 Aufgabe 8 a) (1) WAHRSCHEINLICHKEIT FÜR KEINE ANGABE ERMITTELN Nach der Laplace Formel ist Anzahl der Personen, die keine Angabe machten keine Angabe Gesamtzahl
Institut für Biometrie und klinische Forschung. WiSe 2012/2013
 Klinische Forschung WWU Münster Pflichtvorlesung zum Querschnittsfach Epidemiologie, Biometrie und Med. Informatik Praktikum der Medizinischen Biometrie (3) Überblick. Deskriptive Statistik I 2. Deskriptive
Klinische Forschung WWU Münster Pflichtvorlesung zum Querschnittsfach Epidemiologie, Biometrie und Med. Informatik Praktikum der Medizinischen Biometrie (3) Überblick. Deskriptive Statistik I 2. Deskriptive
Übungsaufgaben zu Kapitel 5
 Übungsaufgaben zu Kapitel 5 Lösungen zu den Übungsaufgaben ab Seite 9. Aufgabe 9 Bei der Herstellung von Schokoladentafeln interessiert a) das durchschnittliche Abfüllgewicht einer Tafel Schokolade. b)
Übungsaufgaben zu Kapitel 5 Lösungen zu den Übungsaufgaben ab Seite 9. Aufgabe 9 Bei der Herstellung von Schokoladentafeln interessiert a) das durchschnittliche Abfüllgewicht einer Tafel Schokolade. b)
Beschreibende Statistik Deskriptive Statistik. Schließende Statistik Inferenzstatistik. Schluss von der Stichprobe auf die Grundgesamtheit
 Beschreibende Statistik Deskriptive Statistik Schließende Statistik Inferenzstatistik Beschreibung der Stichprobe Schluss von der Stichprobe auf die Grundgesamtheit Keine Voraussetzungen Voraussetzung:
Beschreibende Statistik Deskriptive Statistik Schließende Statistik Inferenzstatistik Beschreibung der Stichprobe Schluss von der Stichprobe auf die Grundgesamtheit Keine Voraussetzungen Voraussetzung:
Wahrscheinlichkeitsrechnung und schließende Statistik
 Günther Bourier Wahrscheinlichkeitsrechnung und schließende Statistik Praxisorientierte Einführung Mit Aufgaben und Lösungen 3. F überarbeitete Auflage GABLER Inhaltsverzeichnis Vorwort Inhaltsverzeichnis
Günther Bourier Wahrscheinlichkeitsrechnung und schließende Statistik Praxisorientierte Einführung Mit Aufgaben und Lösungen 3. F überarbeitete Auflage GABLER Inhaltsverzeichnis Vorwort Inhaltsverzeichnis
Konfidenzintervalle Grundlegendes Prinzip Erwartungswert Bekannte Varianz Unbekannte Varianz Anteilswert Differenzen von Erwartungswert Anteilswert
 Konfidenzintervalle Grundlegendes Prinzip Erwartungswert Bekannte Varianz Unbekannte Varianz Anteilswert Differenzen von Erwartungswert Anteilswert Beispiel für Konfidenzintervall Im Prinzip haben wir
Konfidenzintervalle Grundlegendes Prinzip Erwartungswert Bekannte Varianz Unbekannte Varianz Anteilswert Differenzen von Erwartungswert Anteilswert Beispiel für Konfidenzintervall Im Prinzip haben wir
2. Lösung weitere Übungsaufgaben Statistik II WiSe 2016/2017
 . Lösung weitere Übungsaufgaben Statistik II WiSe 016/017 1. Aufgabe: Bei der Produktion eines Werkstückes wurde die Bearbeitungszeit untersucht. Für die als normalverteilt angesehene zufällige Bearbeitungszeit
. Lösung weitere Übungsaufgaben Statistik II WiSe 016/017 1. Aufgabe: Bei der Produktion eines Werkstückes wurde die Bearbeitungszeit untersucht. Für die als normalverteilt angesehene zufällige Bearbeitungszeit
= 3. Kapitel 4: Normalverteilung.. und Standardnormalverteilung und: das Konfidenzintervall..
 Kapitel : Normalverteilung.. und Standardnormalverteilung und: das Konfidenzintervall.. Mittelwert = Summe aller Einzelwerte / n = durchschnittliche Ausprägung, wenn alle gleich viel hätten. Streuung =
Kapitel : Normalverteilung.. und Standardnormalverteilung und: das Konfidenzintervall.. Mittelwert = Summe aller Einzelwerte / n = durchschnittliche Ausprägung, wenn alle gleich viel hätten. Streuung =
p = h n (K)= Juli vl smart vp qk notebook Praktische Lösung des Problems: mit den Werten
 I. Eigenschaften von Schätzfunktionen Wir wollen den unbekannten Anteil p von Autos ermitteln, die mit Katalysator fahren. Mathematisch können wir das Problem wie folgt beschreiben: Sei X der Autotyp eines
I. Eigenschaften von Schätzfunktionen Wir wollen den unbekannten Anteil p von Autos ermitteln, die mit Katalysator fahren. Mathematisch können wir das Problem wie folgt beschreiben: Sei X der Autotyp eines
Fit for Abi & Study Stochastik
 Fit for Abi & Study Stochastik Prof. Dr. Tilla Schade Hochschule Harz 15. und 16. April 2014 No. 1 Stochastik besteht aus: Wahrscheinlichkeitsrechnung Statistik No. 2 Gliederung Grundlagen Zufallsgrößen
Fit for Abi & Study Stochastik Prof. Dr. Tilla Schade Hochschule Harz 15. und 16. April 2014 No. 1 Stochastik besteht aus: Wahrscheinlichkeitsrechnung Statistik No. 2 Gliederung Grundlagen Zufallsgrößen
Prüfung aus Statistik 1 für SoziologInnen. Musterlösung
 Prüfung aus Statistik 1 für SoziologInnen Gesamtpunktezahl =80 1) Wissenstest (maximal 20 Punkte) Prüfungsdauer: 2 Stunden Musterlösung Kreuzen ( ) Sie die jeweils richtige Antwort an. Jede richtige Antwort
Prüfung aus Statistik 1 für SoziologInnen Gesamtpunktezahl =80 1) Wissenstest (maximal 20 Punkte) Prüfungsdauer: 2 Stunden Musterlösung Kreuzen ( ) Sie die jeweils richtige Antwort an. Jede richtige Antwort
Stochastik (BSc D-MAVT / BSc D-MATH / BSc D-MATL)
 Prof. Dr. M. Maathuis ETH Zürich Winter 2010 Stochastik (BSc D-MAVT / BSc D-MATH / BSc D-MATL) Schreiben Sie für Aufgabe 2-4 stets alle Zwischenschritte und -rechnungen sowie Begründungen auf. Aufgabe
Prof. Dr. M. Maathuis ETH Zürich Winter 2010 Stochastik (BSc D-MAVT / BSc D-MATH / BSc D-MATL) Schreiben Sie für Aufgabe 2-4 stets alle Zwischenschritte und -rechnungen sowie Begründungen auf. Aufgabe
Webinar Induktive Statistik. - Wahrscheinlichkeitsrechnung - Stichprobentheorie
 Webinar Induktive Statistik - Wahrscheinlichkeitsrechnung - Stichprobentheorie Wahrscheinlichkeitstheorie Aufgabe : Zwei Lieferanten decken den Bedarf eines PKW-Herstellers von 00.000 Einheiten pro Monat.
Webinar Induktive Statistik - Wahrscheinlichkeitsrechnung - Stichprobentheorie Wahrscheinlichkeitstheorie Aufgabe : Zwei Lieferanten decken den Bedarf eines PKW-Herstellers von 00.000 Einheiten pro Monat.
Auswertung und Lösung
 Dieses Quiz soll Ihnen helfen, Kapitel 4.6 und 4.7 besser zu verstehen. Auswertung und Lösung Abgaben: 59 / 265 Maximal erreichte Punktzahl: 8 Minimal erreichte Punktzahl: 0 Durchschnitt: 4.78 1 Frage
Dieses Quiz soll Ihnen helfen, Kapitel 4.6 und 4.7 besser zu verstehen. Auswertung und Lösung Abgaben: 59 / 265 Maximal erreichte Punktzahl: 8 Minimal erreichte Punktzahl: 0 Durchschnitt: 4.78 1 Frage
SozialwissenschaftlerInnen II
 Statistik für SozialwissenschaftlerInnen II Henning Best best@wiso.uni-koeln.de Universität zu Köln Forschungsinstitut für Soziologie Statistik für SozialwissenschaftlerInnen II p.1 Wahrscheinlichkeitsfunktionen
Statistik für SozialwissenschaftlerInnen II Henning Best best@wiso.uni-koeln.de Universität zu Köln Forschungsinstitut für Soziologie Statistik für SozialwissenschaftlerInnen II p.1 Wahrscheinlichkeitsfunktionen
Übungsblatt 9 (25. bis 29. Juni)
 Statistik 2 Dr. Andrea Beccarini Dipl.-Vw. Dipl.-Kffr. Heike Bornewasser-Hermes Sommersemester 2012 Übungsblatt 9 (25. bis 29. Juni) Stetiges Verteilungsmodell und Gemeinsame Verteilung Stetiges Verteilungsmodell
Statistik 2 Dr. Andrea Beccarini Dipl.-Vw. Dipl.-Kffr. Heike Bornewasser-Hermes Sommersemester 2012 Übungsblatt 9 (25. bis 29. Juni) Stetiges Verteilungsmodell und Gemeinsame Verteilung Stetiges Verteilungsmodell
Klausur Statistik Lösungshinweise
 Klausur Statistik Lösungshinweise Prüfungsdatum: 21. Januar 2016 Prüfer: Etschberger, Heiden, Jansen Studiengang: IM und BW Punkte: 15, 15, 12, 14, 16, 18 ; Summe der Punkte: 90 Aufgabe 1 15 Punkte Bei
Klausur Statistik Lösungshinweise Prüfungsdatum: 21. Januar 2016 Prüfer: Etschberger, Heiden, Jansen Studiengang: IM und BW Punkte: 15, 15, 12, 14, 16, 18 ; Summe der Punkte: 90 Aufgabe 1 15 Punkte Bei
5. Schließende Statistik (Inferenzstatistik, konfirmatorische Verfahren)
 5. Schließende Statistik (Inferenzstatistik, konfirmatorische Verfahren) 5.1. Einführung Schätzen unbekannter Parameter im Modell, z.b. Wahrscheinlichkeiten p i (Anteile in der Gesamtmenge), Erwartungswerte
5. Schließende Statistik (Inferenzstatistik, konfirmatorische Verfahren) 5.1. Einführung Schätzen unbekannter Parameter im Modell, z.b. Wahrscheinlichkeiten p i (Anteile in der Gesamtmenge), Erwartungswerte
Statistik-Klausur vom 6. Februar 2007
 Statistik-Klausur vom 6. Februar 2007 Bearbeitungszeit: 90 Minuten Aufgabe 1 Bei einer Besucherumfrage in zwei Museen wurden die Besuchsdauern (gemessen in Stunden) festgestellt: Besuchsdauer Anteil der
Statistik-Klausur vom 6. Februar 2007 Bearbeitungszeit: 90 Minuten Aufgabe 1 Bei einer Besucherumfrage in zwei Museen wurden die Besuchsdauern (gemessen in Stunden) festgestellt: Besuchsdauer Anteil der
Statistik Übungen WS 2017/18
 Statistik Übungen WS 2017/18 Blatt 2: Wahrscheinlichkeitsrechnung 1. Die nach dem französischen Mathematiker Pierre-Simon de Laplace benannten Laplace- Experimente beruhen auf der Annahme, dass bei einem
Statistik Übungen WS 2017/18 Blatt 2: Wahrscheinlichkeitsrechnung 1. Die nach dem französischen Mathematiker Pierre-Simon de Laplace benannten Laplace- Experimente beruhen auf der Annahme, dass bei einem
Statistik und Wahrscheinlichkeit
 Statistik und Wahrscheinlichkeit 1) Eine Schülergruppe hat an einem Mathematikwettbewerb teilgenommen. a) Die 12 Burschen der Schülergruppe haben folgende Punktezahlen erreicht: 32; 38; 40; 52; 53; 54;
Statistik und Wahrscheinlichkeit 1) Eine Schülergruppe hat an einem Mathematikwettbewerb teilgenommen. a) Die 12 Burschen der Schülergruppe haben folgende Punktezahlen erreicht: 32; 38; 40; 52; 53; 54;
Wahrscheinlichkeit und Statistik: Zusammenfassung
 HSR Hochschule für Technik Rapperswil Wahrscheinlichkeit und Statistik: Zusammenfassung beinhaltet Teile des Skripts von Herrn Hardy von Lukas Wilhelm lwilhelm.net 12. Januar 2007 Inhaltsverzeichnis 1
HSR Hochschule für Technik Rapperswil Wahrscheinlichkeit und Statistik: Zusammenfassung beinhaltet Teile des Skripts von Herrn Hardy von Lukas Wilhelm lwilhelm.net 12. Januar 2007 Inhaltsverzeichnis 1
Wahrscheinlichkeitstheorie und Statistik vom
 INSTITUT FÜR STOCHASTIK SS 2007 UNIVERSITÄT KARLSRUHE Priv.-Doz. Dr. D. Kadelka Dipl.-Math. oec. W. Lao Klausur (Maschineningenieure) Wahrscheinlichkeitstheorie und Statistik vom 2.9.2007 Musterlösungen
INSTITUT FÜR STOCHASTIK SS 2007 UNIVERSITÄT KARLSRUHE Priv.-Doz. Dr. D. Kadelka Dipl.-Math. oec. W. Lao Klausur (Maschineningenieure) Wahrscheinlichkeitstheorie und Statistik vom 2.9.2007 Musterlösungen
2 Aufgaben aus [Teschl, Band 2]
![2 Aufgaben aus [Teschl, Band 2] 2 Aufgaben aus [Teschl, Band 2]](/thumbs/58/42404853.jpg) 20 2 Aufgaben aus [Teschl, Band 2] 2.1 Kap. 25: Beschreibende Statistik 25.3 Übungsaufgabe 25.3 a i. Arithmetisches Mittel: 10.5 ii. Median: 10.4 iii. Quartile: x 0.25 Y 4 10.1, x 0.75 Y 12 11.1 iv. Varianz:
20 2 Aufgaben aus [Teschl, Band 2] 2.1 Kap. 25: Beschreibende Statistik 25.3 Übungsaufgabe 25.3 a i. Arithmetisches Mittel: 10.5 ii. Median: 10.4 iii. Quartile: x 0.25 Y 4 10.1, x 0.75 Y 12 11.1 iv. Varianz:
Aufgabe 1 (8= Punkte) 13 Studenten haben die folgenden Noten (ganze Zahl) in der Statistikklausur erhalten:
 Aufgabe 1 (8=2+2+2+2 Punkte) 13 Studenten haben die folgenden Noten (ganze Zahl) in der Statistikklausur erhalten: Die Zufallsvariable X bezeichne die Note. 1443533523253. a) Wie groß ist h(x 5)? Kreuzen
Aufgabe 1 (8=2+2+2+2 Punkte) 13 Studenten haben die folgenden Noten (ganze Zahl) in der Statistikklausur erhalten: Die Zufallsvariable X bezeichne die Note. 1443533523253. a) Wie groß ist h(x 5)? Kreuzen
5. Spezielle stetige Verteilungen
 5. Spezielle stetige Verteilungen 5.1 Stetige Gleichverteilung Eine Zufallsvariable X folgt einer stetigen Gleichverteilung mit den Parametern a und b, wenn für die Dichtefunktion von X gilt: f x = 1 für
5. Spezielle stetige Verteilungen 5.1 Stetige Gleichverteilung Eine Zufallsvariable X folgt einer stetigen Gleichverteilung mit den Parametern a und b, wenn für die Dichtefunktion von X gilt: f x = 1 für
Prüfungsteil 2, Aufgabe 8 Stochastik
 Prüfung Mathematik Nordrhein-Westfalen 2013 (LK) Aufgabe 8: (WTR) Abitur Mathematik: Prüfungsteil 2, Aufgabe 8 Nordrhein-Westfalen 2012 LK Aufgabe a (1) und (2) 1. SCHRITT: VERTEILUNG ANGEBEN Da die Anzahl
Prüfung Mathematik Nordrhein-Westfalen 2013 (LK) Aufgabe 8: (WTR) Abitur Mathematik: Prüfungsteil 2, Aufgabe 8 Nordrhein-Westfalen 2012 LK Aufgabe a (1) und (2) 1. SCHRITT: VERTEILUNG ANGEBEN Da die Anzahl
Lösungen zur Klausur GRUNDLAGEN DER WAHRSCHEINLICHKEITSTHEORIE UND STATISTIK
 Institut für Stochastik Dr. Steffen Winter Lösungen zur Klausur GRUNDLAGEN DER WAHRSCHEINLICHKEITSTHEORIE UND STATISTIK für Studierende der INFORMATIK vom 17. Juli 01 (Dauer: 90 Minuten) Übersicht über
Institut für Stochastik Dr. Steffen Winter Lösungen zur Klausur GRUNDLAGEN DER WAHRSCHEINLICHKEITSTHEORIE UND STATISTIK für Studierende der INFORMATIK vom 17. Juli 01 (Dauer: 90 Minuten) Übersicht über
Einführung in die Statistik I BA VM, 45 Minuten, Probeklausur
 Gesamtpunktzahl der Statistik I-Klausur: 12 Einführung in die Statistik I BA VM, 45 Minuten, Probeklausur 03.07.2015 Name, Vorname: Matrikelnr.: Um die volle Punktzahl zu erhalten, müssen Sie bei den Berechnungen
Gesamtpunktzahl der Statistik I-Klausur: 12 Einführung in die Statistik I BA VM, 45 Minuten, Probeklausur 03.07.2015 Name, Vorname: Matrikelnr.: Um die volle Punktzahl zu erhalten, müssen Sie bei den Berechnungen
Willkommen zur Vorlesung Statistik (Master)
 Willkommen zur Vorlesung Statistik (Master) Thema dieser Vorlesung: Punkt- und Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische Fakultät, Seminar für Sozialwissenschaften Prof. Dr.
Willkommen zur Vorlesung Statistik (Master) Thema dieser Vorlesung: Punkt- und Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische Fakultät, Seminar für Sozialwissenschaften Prof. Dr.
Wirtschaftsstatistik-Klausur am
 Wirtschaftsstatistik-Klausur am 03.07.208 Aufgabe Statistik-Dozent K.R. lehrt an einer privaten FH in Köln, wohnt aber in Frankfurt am Main. Er hat - wegen möglicher saisonaler Schwankungen - zwei Semester
Wirtschaftsstatistik-Klausur am 03.07.208 Aufgabe Statistik-Dozent K.R. lehrt an einer privaten FH in Köln, wohnt aber in Frankfurt am Main. Er hat - wegen möglicher saisonaler Schwankungen - zwei Semester
2.3 Intervallschätzung
 2.3.1 Motivation und Hinführung Bsp. 2.15. [Wahlumfrage] Der wahre Anteil der rot-grün Wähler unter allen Wählern war 2009 auf eine Nachkommastelle gerundet genau 33.7%. Wie groß ist die Wahrscheinlichkeit,
2.3.1 Motivation und Hinführung Bsp. 2.15. [Wahlumfrage] Der wahre Anteil der rot-grün Wähler unter allen Wählern war 2009 auf eine Nachkommastelle gerundet genau 33.7%. Wie groß ist die Wahrscheinlichkeit,
Zeigen Sie mittles vollständiger Induktion, dass für jede natürliche Zahl n 1 gilt: n (2k 1) = n 2.
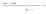 Aufgabe 1. (5 Punkte) Zeigen Sie mittles vollständiger Induktion, dass für jede natürliche Zahl n 1 gilt: n k=1 (2k 1) = n 2. Aufgabe 2. (7 Punkte) Gegeben sei das lineare Gleichungssystem x + 2z = 0 ay
Aufgabe 1. (5 Punkte) Zeigen Sie mittles vollständiger Induktion, dass für jede natürliche Zahl n 1 gilt: n k=1 (2k 1) = n 2. Aufgabe 2. (7 Punkte) Gegeben sei das lineare Gleichungssystem x + 2z = 0 ay
Binomialverteilung. Häufigkeit, mit der Ereignis A bei n unabhängigen Versuchen eintritt. Träger von X : X = {0, 1, 2,..., n}.
 Binomialverteilung Konstruktionsprinzip: Ein Zufallsexperiment wird n mal unabhängig durchgeführt. Wir interessieren uns jeweils nur, ob ein bestimmtes Ereignis A eintritt oder nicht. X = Häufigkeit, mit
Binomialverteilung Konstruktionsprinzip: Ein Zufallsexperiment wird n mal unabhängig durchgeführt. Wir interessieren uns jeweils nur, ob ein bestimmtes Ereignis A eintritt oder nicht. X = Häufigkeit, mit
Zeit zum Kochen [in min] [10, 20[ [20, 30[ [30, 40[ [40, 50[ [50,60[ [60, 100] Hi
![Zeit zum Kochen [in min] [10, 20[ [20, 30[ [30, 40[ [40, 50[ [50,60[ [60, 100] Hi Zeit zum Kochen [in min] [10, 20[ [20, 30[ [30, 40[ [40, 50[ [50,60[ [60, 100] Hi](/thumbs/48/24644287.jpg) 1. Susi und Fritzi bereiten ein Faschingsfest vor, dazu gehört natürlich ein Faschingsmenü. Ideen haben sie genug, aber sie möchten nicht zu viel Zeit fürs Kochen aufwenden. In einer Zeitschrift fanden
1. Susi und Fritzi bereiten ein Faschingsfest vor, dazu gehört natürlich ein Faschingsmenü. Ideen haben sie genug, aber sie möchten nicht zu viel Zeit fürs Kochen aufwenden. In einer Zeitschrift fanden
Heute. Die Binomialverteilung. Poissonverteilung. Approximation der Binomialverteilung durch die Normalverteilung
 Heute Die Binomialverteilung Poissonverteilung Approximation der Binomialverteilung durch die Normalverteilung Arbeiten mit Wahrscheinlichkeitsverteilungen Die Binomialverteilung Man werfe eine Münze n
Heute Die Binomialverteilung Poissonverteilung Approximation der Binomialverteilung durch die Normalverteilung Arbeiten mit Wahrscheinlichkeitsverteilungen Die Binomialverteilung Man werfe eine Münze n
Teil VIII. Zentraler Grenzwertsatz und Vertrauensintervalle. Woche 6: Zentraler Grenzwertsatz und Vertrauensintervalle. Lernziele. Typische Situation
 Woche 6: Zentraler Grenzwertsatz und Vertrauensintervalle Patric Müller ETHZ Teil VIII Zentraler Grenzwertsatz und Vertrauensintervalle WBL 17/19, 29.05.2017 Wahrscheinlichkeit
Woche 6: Zentraler Grenzwertsatz und Vertrauensintervalle Patric Müller ETHZ Teil VIII Zentraler Grenzwertsatz und Vertrauensintervalle WBL 17/19, 29.05.2017 Wahrscheinlichkeit
Die Normalverteilung. Mathematik W30. Mag. Rainer Sickinger LMM, BR. v 0 Mag. Rainer Sickinger Mathematik W30 1 / 51
 Mathematik W30 Mag. Rainer Sickinger LMM, BR v 0 Mag. Rainer Sickinger Mathematik W30 1 / 51 Einführung Heute nehmen wir uns die Normalverteilung vor. Bis jetzt konnte unsere Zufallsvariable (das X in
Mathematik W30 Mag. Rainer Sickinger LMM, BR v 0 Mag. Rainer Sickinger Mathematik W30 1 / 51 Einführung Heute nehmen wir uns die Normalverteilung vor. Bis jetzt konnte unsere Zufallsvariable (das X in
Stoffverteilungsplan Mathematik Leistungskurs. Lambacher Schweizer Stochastik ISBN Klassenarbeit
 Lambacher Schweizer Q3.1 Grundlegende Begriffe der Grundlagen der Wahrscheinlichkeitstheorie: Beschreiben von Zufallsexperimenten (Laplace-Experimente) unter Verwendung der Begriffe Ergebnis, Ergebnismenge,
Lambacher Schweizer Q3.1 Grundlegende Begriffe der Grundlagen der Wahrscheinlichkeitstheorie: Beschreiben von Zufallsexperimenten (Laplace-Experimente) unter Verwendung der Begriffe Ergebnis, Ergebnismenge,
Abiturvorbereitung Alkoholsünder, bedingte Wahrscheinlichkeit, Hypothesentest Aufgabenblatt
 R. Brinkmann http://brinkmann-du.de Seite 2.05.2009 Abiturvorbereitung Alkoholsünder, bedingte Wahrscheinlichkeit, Hypothesentest Aufgabenblatt Aufgabe 0 0. In einer bestimmten Stadt an einer bestimmten
R. Brinkmann http://brinkmann-du.de Seite 2.05.2009 Abiturvorbereitung Alkoholsünder, bedingte Wahrscheinlichkeit, Hypothesentest Aufgabenblatt Aufgabe 0 0. In einer bestimmten Stadt an einer bestimmten
4.1. Nullhypothese, Gegenhypothese und Entscheidung
 rof. Dr. Roland Füss Statistik II SS 8 4. Testtheorie 4.. Nullhypothese, Gegenhypothese und Entscheidung ypothesen Annahmen über die Verteilung oder über einzelne arameter der Verteilung eines Merkmals
rof. Dr. Roland Füss Statistik II SS 8 4. Testtheorie 4.. Nullhypothese, Gegenhypothese und Entscheidung ypothesen Annahmen über die Verteilung oder über einzelne arameter der Verteilung eines Merkmals
WTheorie: Verteilungen. Aufgabe 54
 Aufgabe 54 WTheorie: Verteilungen Die Gesamtdauer X eines Projektes wird als normalverteilt mit dem Parameter D 10 (Wochen) angenommen. Ferner wird für die Wahrscheinlichkeit P.8 X 12/ der Wert 0;8 geschätzt.
Aufgabe 54 WTheorie: Verteilungen Die Gesamtdauer X eines Projektes wird als normalverteilt mit dem Parameter D 10 (Wochen) angenommen. Ferner wird für die Wahrscheinlichkeit P.8 X 12/ der Wert 0;8 geschätzt.
Prüfungsteil 2, Aufgabe 8 Stochastik
 Prüfung Mathematik Nordrhein-Westfalen 2013 (LK) Aufgabe 7: (WTR) Abitur Mathematik: Prüfungsteil 2, Aufgabe 8 Nordrhein-Westfalen 2012 GK Aufgabe a (1) und (2) 1. SCHRITT: VERTEILUNG ANGEBEN Da die Anzahl
Prüfung Mathematik Nordrhein-Westfalen 2013 (LK) Aufgabe 7: (WTR) Abitur Mathematik: Prüfungsteil 2, Aufgabe 8 Nordrhein-Westfalen 2012 GK Aufgabe a (1) und (2) 1. SCHRITT: VERTEILUNG ANGEBEN Da die Anzahl
Schließende Statistik
 Schließende Statistik [statistical inference] Sollen auf der Basis von empirischen Untersuchungen (Daten) Erkenntnisse gewonnen und Entscheidungen gefällt werden, sind die Methoden der Statistik einzusetzen.
Schließende Statistik [statistical inference] Sollen auf der Basis von empirischen Untersuchungen (Daten) Erkenntnisse gewonnen und Entscheidungen gefällt werden, sind die Methoden der Statistik einzusetzen.
Willkommen zur Vorlesung Statistik (Master)
 Willkommen zur Vorlesung Statistik (Master) Thema dieser Vorlesung: Punkt- und Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische Fakultät, Seminar für Sozialwissenschaften Prof. Dr.
Willkommen zur Vorlesung Statistik (Master) Thema dieser Vorlesung: Punkt- und Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische Fakultät, Seminar für Sozialwissenschaften Prof. Dr.
Biomathematik für Mediziner
 Institut für Medizinische Biometrie, Informatik und Epidemiologie der Universität Bonn (Direktor: Prof. Dr. Max P. Baur) Biomathematik für Mediziner Klausur SS 2002 Aufgabe 1: Franz Beckenbauer will, dass
Institut für Medizinische Biometrie, Informatik und Epidemiologie der Universität Bonn (Direktor: Prof. Dr. Max P. Baur) Biomathematik für Mediziner Klausur SS 2002 Aufgabe 1: Franz Beckenbauer will, dass
Statistik Zusätzliche Beispiele WS 2018/19
 Statistik Zusätzliche Beispiele WS 208/9 Blatt 2: Wahrscheinlichkeitsrechnung. Erstellen Sie zur Zufallsgröße Augensumme von drei fairen Würfeln eine Tabelle der Wahrscheinlichkeitsfunktion und vergleichen
Statistik Zusätzliche Beispiele WS 208/9 Blatt 2: Wahrscheinlichkeitsrechnung. Erstellen Sie zur Zufallsgröße Augensumme von drei fairen Würfeln eine Tabelle der Wahrscheinlichkeitsfunktion und vergleichen
Abitur 2013 Mathematik Stochastik IV
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 201 Mathematik Stochastik IV In einer Großstadt steht die Wahl des Oberbürgermeisters bevor. 12% der Wahlberechtigten sind Jungwähler, d. h. Personen
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 201 Mathematik Stochastik IV In einer Großstadt steht die Wahl des Oberbürgermeisters bevor. 12% der Wahlberechtigten sind Jungwähler, d. h. Personen
Grundlegende Eigenschaften von Punktschätzern
 Grundlegende Eigenschaften von Punktschätzern Worum geht es in diesem Modul? Schätzer als Zufallsvariablen Vorbereitung einer Simulation Verteilung von P-Dach Empirische Lage- und Streuungsparameter zur
Grundlegende Eigenschaften von Punktschätzern Worum geht es in diesem Modul? Schätzer als Zufallsvariablen Vorbereitung einer Simulation Verteilung von P-Dach Empirische Lage- und Streuungsparameter zur
Verteilungen eindimensionaler stetiger Zufallsvariablen Stetige Verteilungen. Chi-Quadrat-Verteilung Studentverteilung Fisher-Verteilung
 Verteilungen eindimensionaler stetiger Zufallsvariablen Stetige Verteilungen Chi-Quadrat-Verteilung Studentverteilung Fisher-Verteilung Typisierung der stetigen theoretischen Verteilungen Bibliografie:
Verteilungen eindimensionaler stetiger Zufallsvariablen Stetige Verteilungen Chi-Quadrat-Verteilung Studentverteilung Fisher-Verteilung Typisierung der stetigen theoretischen Verteilungen Bibliografie:
1. Einführung in die induktive Statistik
 Wichtige Begriffe 1. Einführung in die induktive Statistik Grundgesamtheit: Statistische Masse, die zu untersuchen ist, bzw. über die Aussagen getroffen werden soll Stichprobe: Teil einer statistischen
Wichtige Begriffe 1. Einführung in die induktive Statistik Grundgesamtheit: Statistische Masse, die zu untersuchen ist, bzw. über die Aussagen getroffen werden soll Stichprobe: Teil einer statistischen
Biomathematik für Mediziner
 Institut für Medizinische Biometrie, Informatik und Epidemiologie der Universität Bonn (Direktor: Prof. Dr. Max P. Baur) Biomathematik für Mediziner Klausur WS 2002/2003 Aufgabe 1: Man gehe davon aus,
Institut für Medizinische Biometrie, Informatik und Epidemiologie der Universität Bonn (Direktor: Prof. Dr. Max P. Baur) Biomathematik für Mediziner Klausur WS 2002/2003 Aufgabe 1: Man gehe davon aus,
Wahrscheinlichkeitstheorie und Statistik vom
 INSTITUT FÜR STOCHASTIK SS 2010 Karlsruher Institut für Technologie Priv.-Doz. Dr. D. Kadelka Klausur Wahrscheinlichkeitstheorie und Statistik vom 14.9.2010 Musterlösungen Aufgabe 1: Gegeben sei eine Urliste
INSTITUT FÜR STOCHASTIK SS 2010 Karlsruher Institut für Technologie Priv.-Doz. Dr. D. Kadelka Klausur Wahrscheinlichkeitstheorie und Statistik vom 14.9.2010 Musterlösungen Aufgabe 1: Gegeben sei eine Urliste
Anpassungstests VORGEHENSWEISE
 Anpassungstests Anpassungstests prüfen, wie sehr sich ein bestimmter Datensatz einer erwarteten Verteilung anpasst bzw. von dieser abweicht. Nach der Erläuterung der Funktionsweise sind je ein Beispiel
Anpassungstests Anpassungstests prüfen, wie sehr sich ein bestimmter Datensatz einer erwarteten Verteilung anpasst bzw. von dieser abweicht. Nach der Erläuterung der Funktionsweise sind je ein Beispiel
Nachklausur Mathematik für Biologen WS 08/09
 Aufgabe 1: (5 Punkte) In einer diploiden Population beobachten wir die Ausprägung eines bestimmten Gens, das zwei Allele V und W annimmt. Somit besitzt jedes Individuum V V, V W oder W W als Genotyp. Die
Aufgabe 1: (5 Punkte) In einer diploiden Population beobachten wir die Ausprägung eines bestimmten Gens, das zwei Allele V und W annimmt. Somit besitzt jedes Individuum V V, V W oder W W als Genotyp. Die
Statistik Übungen SS 2018
 Statistik Übungen SS 2018 Blatt 2: Wahrscheinlichkeitsrechnung 1. Die nach dem französischen Mathematiker Pierre-Simon de Laplace benannten Laplace- Experimente beruhen auf der Annahme, dass bei einem
Statistik Übungen SS 2018 Blatt 2: Wahrscheinlichkeitsrechnung 1. Die nach dem französischen Mathematiker Pierre-Simon de Laplace benannten Laplace- Experimente beruhen auf der Annahme, dass bei einem
Stetige Verteilungen. A: Beispiele Beispiel 1: a) In den folgenden Abbildungen sind die Dichtefunktionen von drei bekannten Verteilungen graphisch
 6 Stetige Verteilungen 1 Kapitel 6: Stetige Verteilungen A: Beispiele Beispiel 1: a) In den folgenden Abbildungen sind die Dichtefunktionen von drei bekannten Verteilungen graphisch dargestellt. 0.2 6
6 Stetige Verteilungen 1 Kapitel 6: Stetige Verteilungen A: Beispiele Beispiel 1: a) In den folgenden Abbildungen sind die Dichtefunktionen von drei bekannten Verteilungen graphisch dargestellt. 0.2 6
ˆ Die Verluste der einzelnen Perioden sind in den ersten zehn Perioden stochastisch
 Technische Hochschule Köln Fakultät für Wirtschafts- und Rechtswissenschaften Prof. Dr. Arrenberg Raum 221, Tel. 39 14 jutta.arrenberg@th-koeln.de Übungen zu QM III (Wirtschaftsstatistik) Binomialverteilung
Technische Hochschule Köln Fakultät für Wirtschafts- und Rechtswissenschaften Prof. Dr. Arrenberg Raum 221, Tel. 39 14 jutta.arrenberg@th-koeln.de Übungen zu QM III (Wirtschaftsstatistik) Binomialverteilung
1.1.1 Ergebnismengen Wahrscheinlichkeiten Formale Definition der Wahrscheinlichkeit Laplace-Experimente...
 Inhaltsverzeichnis 0 Einführung 1 1 Zufallsvorgänge und Wahrscheinlichkeiten 5 1.1 Zufallsvorgänge.......................... 5 1.1.1 Ergebnismengen..................... 6 1.1.2 Ereignisse und ihre Verknüpfung............
Inhaltsverzeichnis 0 Einführung 1 1 Zufallsvorgänge und Wahrscheinlichkeiten 5 1.1 Zufallsvorgänge.......................... 5 1.1.1 Ergebnismengen..................... 6 1.1.2 Ereignisse und ihre Verknüpfung............
GRUPPE B Prüfung aus Statistik 1 für SoziologInnen
 GRUPPE B Prüfung aus Statistik 1 für SoziologInnen 16. Oktober 2015 Gesamtpunktezahl =80 Prüfungsdauer: 2 Stunden Name in Blockbuchstaben: Matrikelnummer: 1) Wissenstest (maximal 20 Punkte) Kreuzen ( )
GRUPPE B Prüfung aus Statistik 1 für SoziologInnen 16. Oktober 2015 Gesamtpunktezahl =80 Prüfungsdauer: 2 Stunden Name in Blockbuchstaben: Matrikelnummer: 1) Wissenstest (maximal 20 Punkte) Kreuzen ( )
13. Jgst. 2. Kursarbeit Datum:
 13. Jgst. 2. Kursarbeit Datum: 23.11.2017 Klasse: GY LK 2 Fach: Mathematik (Leistungsfach) Thema: edingte W keit & Vierfeldertafel; inomial- & Normalverteilung; Sigma-Intervalle Name: Punkte: Note: Aufgabe
13. Jgst. 2. Kursarbeit Datum: 23.11.2017 Klasse: GY LK 2 Fach: Mathematik (Leistungsfach) Thema: edingte W keit & Vierfeldertafel; inomial- & Normalverteilung; Sigma-Intervalle Name: Punkte: Note: Aufgabe
Auswertung von Messungen Teil II
 Auswertung von Messungen Teil II 1. Grundgesamtheit und Stichprobe. Modellverteilungen.1 Normalverteilung. Binominalverteilung.3 Poissonverteilung.4 Näherungen von Binominal- und Poissonverteilung 3. Zentraler
Auswertung von Messungen Teil II 1. Grundgesamtheit und Stichprobe. Modellverteilungen.1 Normalverteilung. Binominalverteilung.3 Poissonverteilung.4 Näherungen von Binominal- und Poissonverteilung 3. Zentraler
Klausurnachbesprechung
 Klausurnachbesprechung 8.0.006 nicht bestanden bestanden sehr gut gut befriedigend ausreichend 0 5 0 5 0 5 Aufgabe B Aufgabe : 0 Punkte Der Anteil an Grundwasserneubildung (GWN in %) an der Gesamtabflussbildung
Klausurnachbesprechung 8.0.006 nicht bestanden bestanden sehr gut gut befriedigend ausreichend 0 5 0 5 0 5 Aufgabe B Aufgabe : 0 Punkte Der Anteil an Grundwasserneubildung (GWN in %) an der Gesamtabflussbildung
f(x) = P (X = x) = 0, sonst heißt Poisson-verteilt mit Parameter (oder Rate) λ > 0, kurz X P o(λ). Es gilt x x! 1 Wahrscheinlichkeitsrechnung 212
 1.6.2 Poisson Verteilung Eine weitere wichtige diskrete Verteilung ist die Poisson-Verteilung. Sie modelliert die Anzahl (eher seltener) Ereignisse in einem Zeitintervall (Unfälle, Todesfälle; Sozialkontakte,
1.6.2 Poisson Verteilung Eine weitere wichtige diskrete Verteilung ist die Poisson-Verteilung. Sie modelliert die Anzahl (eher seltener) Ereignisse in einem Zeitintervall (Unfälle, Todesfälle; Sozialkontakte,
Statistische Tests (Signifikanztests)
 Statistische Tests (Signifikanztests) [testing statistical hypothesis] Prüfen und Bewerten von Hypothesen (Annahmen, Vermutungen) über die Verteilungen von Merkmalen in einer Grundgesamtheit (Population)
Statistische Tests (Signifikanztests) [testing statistical hypothesis] Prüfen und Bewerten von Hypothesen (Annahmen, Vermutungen) über die Verteilungen von Merkmalen in einer Grundgesamtheit (Population)
Einführung in Quantitative Methoden
 Einführung in Quantitative Methoden Karin Waldherr & Pantelis Christodoulides 11. Mai 2011 Waldherr / Christodoulides Einführung in Quantitative Methoden- 8.VO 1/40 Poisson-Verteilung Diese Verteilung
Einführung in Quantitative Methoden Karin Waldherr & Pantelis Christodoulides 11. Mai 2011 Waldherr / Christodoulides Einführung in Quantitative Methoden- 8.VO 1/40 Poisson-Verteilung Diese Verteilung
Statistik Zusätzliche Beispiele SS 2018 Blatt 3: Schließende Statistik
 Statistik Zusätzliche Beispiele SS 2018 Blatt 3: Schließende Statistik 1. I Ein Personalchef führt so lange Vorstellungsgespräche durch bis der erste geeignete Bewerber darunter ist und stellt diesen an.
Statistik Zusätzliche Beispiele SS 2018 Blatt 3: Schließende Statistik 1. I Ein Personalchef führt so lange Vorstellungsgespräche durch bis der erste geeignete Bewerber darunter ist und stellt diesen an.
Statistik I für Betriebswirte Vorlesung 14
 Statistik I für Betriebswirte Vorlesung 14 Dr. Andreas Wünsche TU Bergakademie Freiberg Institut für Stochastik 13. Juli 017 Dr. Andreas Wünsche Statistik I für Betriebswirte Vorlesung 14 Version: 8. Juli
Statistik I für Betriebswirte Vorlesung 14 Dr. Andreas Wünsche TU Bergakademie Freiberg Institut für Stochastik 13. Juli 017 Dr. Andreas Wünsche Statistik I für Betriebswirte Vorlesung 14 Version: 8. Juli
So berechnen Sie einen Schätzer für einen Punkt
 htw saar 1 EINFÜHRUNG IN DIE STATISTIK: SCHÄTZEN UND TESTEN htw saar 2 Schätzen: Einführung Ziel der Statistik ist es, aus den Beobachtungen eines Merkmales in einer Stichprobe Rückschlüsse über die Verteilung
htw saar 1 EINFÜHRUNG IN DIE STATISTIK: SCHÄTZEN UND TESTEN htw saar 2 Schätzen: Einführung Ziel der Statistik ist es, aus den Beobachtungen eines Merkmales in einer Stichprobe Rückschlüsse über die Verteilung
Deckblatt. Name der Kursleiterin/des Kursleiters, bei der Sie angemeldet sind: Annelie Gebert. Nur einen Studiengang ankreuzen!!!
 Deckblatt Name Vorname Matrikelnr. Name in Druckbuchstaben Name der Kursleiterin/des Kursleiters, bei der Sie angemeldet sind: Annelie Gebert Nur einen Studiengang ankreuzen!!! Bachelorstudiengang Sozialökonomie
Deckblatt Name Vorname Matrikelnr. Name in Druckbuchstaben Name der Kursleiterin/des Kursleiters, bei der Sie angemeldet sind: Annelie Gebert Nur einen Studiengang ankreuzen!!! Bachelorstudiengang Sozialökonomie
Wirtschaftsstatistik-Klausur am
 Wirtschaftsstatistik-Klausur am 0.07.017 Aufgabe 1 Ein Handy- und PC-Hersteller verfügt über ein exklusives Filialnetz von 900 Filialen. Der Gewinn (in GE) der Filialen ist in der folgenden Tabelle nach
Wirtschaftsstatistik-Klausur am 0.07.017 Aufgabe 1 Ein Handy- und PC-Hersteller verfügt über ein exklusives Filialnetz von 900 Filialen. Der Gewinn (in GE) der Filialen ist in der folgenden Tabelle nach
Mathematik 2 Probeprüfung 1
 WWZ Wirtschaftswissenschaftliche Fakultät der Universität Basel Dr. Thomas Zehrt Bitte in Druckbuchstaben ausfüllen: Name Vorname Mathematik 2 Probeprüfung 1 Zeit: 90 Minuten, Maximale Punktzahl: 72 Zur
WWZ Wirtschaftswissenschaftliche Fakultät der Universität Basel Dr. Thomas Zehrt Bitte in Druckbuchstaben ausfüllen: Name Vorname Mathematik 2 Probeprüfung 1 Zeit: 90 Minuten, Maximale Punktzahl: 72 Zur
2.3 Intervallschätzung
 2.3.1 Motivation und Hinführung Bsp. 2.11. [Wahlumfrage] Der wahre Anteil der rot-grün Wähler 2009 war genau 33.7%. Wie groß ist die Wahrscheinlichkeit, in einer Zufallsstichprobe von 1000 Personen genau
2.3.1 Motivation und Hinführung Bsp. 2.11. [Wahlumfrage] Der wahre Anteil der rot-grün Wähler 2009 war genau 33.7%. Wie groß ist die Wahrscheinlichkeit, in einer Zufallsstichprobe von 1000 Personen genau
SS 2017 Torsten Schreiber
 173 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Wird die Anordnung von unterschiedlichen Objekten eines Experiments untersucht, so handelt es sich um eine. Möchte man die Anzahl der möglichen
173 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Wird die Anordnung von unterschiedlichen Objekten eines Experiments untersucht, so handelt es sich um eine. Möchte man die Anzahl der möglichen
Übungen mit dem Applet
 Übungen mit dem Applet 1. Visualisierung der Verteilungsform... 1.1. Normalverteilung... 1.. t-verteilung... 1.3. χ -Verteilung... 1.4. F-Verteilung...3. Berechnung von Wahrscheinlichkeiten...3.1. Visualisierung
Übungen mit dem Applet 1. Visualisierung der Verteilungsform... 1.1. Normalverteilung... 1.. t-verteilung... 1.3. χ -Verteilung... 1.4. F-Verteilung...3. Berechnung von Wahrscheinlichkeiten...3.1. Visualisierung
Statistik I für Betriebswirte Vorlesung 14
 Statistik I für Betriebswirte Vorlesung 14 Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut für Stochastik 11. Juli 016 Prof. Dr. Hans-Jörg Starkloff Statistik I für Betriebswirte Vorlesung
Statistik I für Betriebswirte Vorlesung 14 Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut für Stochastik 11. Juli 016 Prof. Dr. Hans-Jörg Starkloff Statistik I für Betriebswirte Vorlesung
Erstellen Sie eine Vierfeldertafel, die diese Situation wiedergibt.
 Bei der Bearbeitung der Aufgabe dürfen alle Funktionen des Taschenrechners genutzt werden. Aufgabe 4: Stochastik Vorbemerkung: Führen Sie stets geeignete Zufallsvariablen und Namen für Ereignisse ein.
Bei der Bearbeitung der Aufgabe dürfen alle Funktionen des Taschenrechners genutzt werden. Aufgabe 4: Stochastik Vorbemerkung: Führen Sie stets geeignete Zufallsvariablen und Namen für Ereignisse ein.
mathphys-online Abiturprüfung Berufliche Oberschule 2012 Mathematik 13 Technik - Aufgabe B I - Lösung
 Abiturprüfung Berufliche Oberschule 2012 Mathematik 13 Technik - Aufgabe B I - Lösung Während der Fußballweltmeisterschaft 2010 in Südafrika gelangte der Krake Paul aus dem Aquarium in Oberhausen zu großer
Abiturprüfung Berufliche Oberschule 2012 Mathematik 13 Technik - Aufgabe B I - Lösung Während der Fußballweltmeisterschaft 2010 in Südafrika gelangte der Krake Paul aus dem Aquarium in Oberhausen zu großer
Wahrscheinlichkeitsverteilungen
 Universität Bielefeld 3. Mai 2005 Wahrscheinlichkeitsrechnung Wahrscheinlichkeitsrechnung Das Ziehen einer Stichprobe ist die Realisierung eines Zufallsexperimentes. Die Wahrscheinlichkeitsrechnung betrachtet
Universität Bielefeld 3. Mai 2005 Wahrscheinlichkeitsrechnung Wahrscheinlichkeitsrechnung Das Ziehen einer Stichprobe ist die Realisierung eines Zufallsexperimentes. Die Wahrscheinlichkeitsrechnung betrachtet
Mathematik 3 für Informatik
 Gunter Ochs Wintersemester 20/6 Mathematik 3 für Informatik Lösungen zum Hausaufgabenblatt 4 Lösungshinweise (ohne Ganantie auf Fehlerfreiheit. Wenn man beim Roulette auf Rot oder Schwarz setzt, erhält
Gunter Ochs Wintersemester 20/6 Mathematik 3 für Informatik Lösungen zum Hausaufgabenblatt 4 Lösungshinweise (ohne Ganantie auf Fehlerfreiheit. Wenn man beim Roulette auf Rot oder Schwarz setzt, erhält
Biomathematik für Mediziner, Klausur WS 2000/2001 Seite 1
 Biomathematik für Mediziner, Klausur WS 2000/2001 Seite 1 Aufgabe 1: Von 2 gleichartigen Maschinen eines pharmazeutischen Betriebes stellt die erste 40% und die zweite 60% der Produkte her. Dabei verursacht
Biomathematik für Mediziner, Klausur WS 2000/2001 Seite 1 Aufgabe 1: Von 2 gleichartigen Maschinen eines pharmazeutischen Betriebes stellt die erste 40% und die zweite 60% der Produkte her. Dabei verursacht
Statistik-Klausur vom
 Statistik-Klausur vom 27.09.2010 Bearbeitungszeit: 60 Minuten Aufgabe 1 Ein international tätiges Unternehmen mit mehreren Niederlassungen in Deutschland und dem übrigen Europa hat seine überfälligen Forderungen
Statistik-Klausur vom 27.09.2010 Bearbeitungszeit: 60 Minuten Aufgabe 1 Ein international tätiges Unternehmen mit mehreren Niederlassungen in Deutschland und dem übrigen Europa hat seine überfälligen Forderungen
Statistik für NichtStatistiker
 Statistik für NichtStatistiker Zufall und Wahrscheinlichkeit von Prof. Dr. Karl Bosch 5., verbesserte Auflage R. Oldenbourg Verlag München Wien Inhaltsverzeichnis 1. ZufalLsexperimente und zufällige Ereignisse
Statistik für NichtStatistiker Zufall und Wahrscheinlichkeit von Prof. Dr. Karl Bosch 5., verbesserte Auflage R. Oldenbourg Verlag München Wien Inhaltsverzeichnis 1. ZufalLsexperimente und zufällige Ereignisse
Klausur zu Methoden der Statistik II (mit Kurzlösung) Sommersemester Aufgabe 1
 Lehrstuhl für Statistik und Ökonometrie der Otto-Friedrich-Universität Bamberg Prof. Dr. Susanne Rässler Klausur zu Methoden der Statistik II (mit Kurzlösung) Sommersemester 2010 Aufgabe 1 Die Inhaberin
Lehrstuhl für Statistik und Ökonometrie der Otto-Friedrich-Universität Bamberg Prof. Dr. Susanne Rässler Klausur zu Methoden der Statistik II (mit Kurzlösung) Sommersemester 2010 Aufgabe 1 Die Inhaberin
5. Schließende Statistik (Inferenzstatistik, konfirmatorische Verfahren)
 5. Schließende Statistik (Inferenzstatistik, konfirmatorische Verfahren) 5.1. Einführung Schätzen unbekannter Parameter im Modell, z.b. Wahrscheinlichkeiten p i (Anteile in der Gesamtmenge), Erwartungswerte
5. Schließende Statistik (Inferenzstatistik, konfirmatorische Verfahren) 5.1. Einführung Schätzen unbekannter Parameter im Modell, z.b. Wahrscheinlichkeiten p i (Anteile in der Gesamtmenge), Erwartungswerte
Binomialverteilung Vertrauensbereich für den Anteil
 Übungen mit dem Applet Binomialverteilung Vertrauensbereich für den Anteil Binomialverteilung Vertrauensbereich für den Anteil 1. Statistischer Hintergrund und Darstellung.... Wie entsteht der Vertrauensbereich?...
Übungen mit dem Applet Binomialverteilung Vertrauensbereich für den Anteil Binomialverteilung Vertrauensbereich für den Anteil 1. Statistischer Hintergrund und Darstellung.... Wie entsteht der Vertrauensbereich?...
