Die absolut kleinsten Diskriminanten der biquadratischen Zahlkörper
|
|
|
- Bernd Maus
- vor 7 Jahren
- Abrufe
Transkript
1 Akademie d. Wissenschaften Wien; download unter Die absolut kleinsten Diskriminanten der biquadratischen Zahlkörper Von Josef Mayer (Vorgelegt in der Sitzung am 14. Novem ber 1929) Herr Ph. F u rtw ä n g le r bestimmt in einer Abhandlung1 die absolut kleinsten Diskriminanten der kubischen Zahlkörper. Die hiebei benützte Methode besteht in einer Anwendung der Reduktionstheorie der definiten quadratischen Formen und bildet auch die wesentliche Grundlage der folgenden Bestimmung der absolut kleinsten Diskriminanten der biquadratischen Zahlkörper. Vor dieser allgemeinen Betrachtung sollen zunächst die absolut kleinsten Diskriminanten jener speziellen biquadratischen Körper bestimmt werden, welche einen quadratischen Unterkörper besitzen. I. Die absolut kleinsten Diskriminanten der Relativkörper. Bedeutet [j. eine ganze quadratfreie Zahl aus dem quadratischen Körper k ('s/m ), dann ist der Körper K (v V > \/w ) e^n Körper vierten Grades, der relativ quadratisch in bezug auf k ist. Für den Körper k (\ /m ) ist immer h ~ 1 als Klassenzahl vorausgesetzt, da nur solche Körper für die folgende Untersuchung notwendig sind. Bedeuten D und d die Diskriminanten des Oberkörpers K und des Unterkörpers li und bezeichnet n (Dk) die Norm der Relativdiskriminante Dk, genommen im Körper k, so ist D dk n (Dk). Je nach dem Verhalten der Primzahl 2 im Körper k (v / 7^) und je nach der Wahl der Zahl a aus k sind nun verschiedene Fälle zu unterscheiden, die in der folgenden Übersicht zusammengestellt sind: 1. Die Zahl 2 bleibt im Körper k Primideal. ct) Ist j. primär, so ist I) d2. 7z (jx). ß) Ist [J. nicht primär, dann ist D IQ d 2.n(\)).? Die Zahl 2 zerfällt im Körper k in zwei verschiedene Primideale 2 = XL. X2. 1 Zur Theorie der in Linearfaktoren zerlegbaren, ganzzahligen ternären kubischen Formen. Göttingen, Hilbert, Theorie der algebraischen Zahlkörper, Bericht der Deutschen Mathematikerver., 4. Bd. Sitzungsberichte d. mathem.-naturw. Kl., Abt. Ila, 138. Bd., lieft. 48
2 734 Akademie d. Wissenschaften J. Wien; Mayer, download unter a) Ist ;x primär, so ist I ) d -. n (\x). ß) Ist \xnicht primär, aber jj, = v2(x;), so ist D 4.d-.u(\x). 7) Ist fx nicht primär und auch v2 (Xi), so ist D 16.d -. u (\x). Die Zahl 2 wird im Körper k Quadrat eines Primideales, a) Ist j, primär, so ist D =. d -. n ß) Ist J, nicht primär, aber x= v2(2), so ist D ~ A.d-.n(\x). Y) Ist [jl nicht primär und auch a^ev2 (2), dann ist D 16. d -. n (ix). Um [x als primäre Zahl im Körper (\ /m ) leicht zu erkennen, werden hier die entsprechenden Bedingungen aufgestellt: J. m = 1(4), Minimalbasis in k 1, co = m. Aus (a + b co) = (x + y co) 2 (4) folgt das System der Kongruenzen 2 xy y - = &(4), _ in 1 a;2 H _y == a (4). Damit ergeben sich in diesem Falle folgende Bedingungen für primäre Zahlen: d) b = 0 (4), a = 1 (4), ra < / i\ lj) ^ = 1 ( 4 ), a (4), 7) * = 3(4), «eee^ - V ). m = 3(4), Minimalbasis in ß (\ /m ) :1, \/77/. Soll [x = a + b \ f m primär sein, so muß das System der Kongruenzen: 2 xy = b (4), x- + niy2 = ci (4) lösbar sein. Dies ist der Fall, wenn a) b = 0 (4), a = 1 (2), ß) * = 2(4), a = 0(4). m = 2(4), Minimalbasis in k (\ Jm ) In analoger W eise ergeben sich folgende Bedingungen für primäre Zahlen: 7.) b == 0 (4), a (4), ß) b = 0 (4), a = 2 (4), y) b = 2(4), a = 3 (4).
3 Absolut Akademie kleinste d. Wissenschaften Diskriminanten Wien; download der biquadratischen unter Zahlkörper. 735 Bei der Bestimmung der absolut kleinsten Diskriminanten sind je nach der Art der konjugierten Körper drei Fälle zu unterscheiden. A. V ie r re e lle k o n ju g ie r te K örp er. Wir betrachten zunächst den Körper K [ \ f \Jb). Er ist relativ quadratisch in bezug auf den reellen quadratischen Körper k ( \ f 5); seine Diskriminante ist D = = 725, da die Zahl [x \ / 5 im Körper k ( \ / 5) primär ist und ihre Norm n (\x) = 29 beträgt. D 725 ist in diesem Falle die kleinste Diskriminante eines Relativkörpers. Aus der Annahme D 725 folgt zunächst, daß nur jene reellen quadratischen Körper als Unterkörper auftreten können, deren Diskriminante d ^ \ j 7 25 ist; es sind dies die quadratischen Körper li (\ f m), für welche beziehungsweise ist. 111 = 6, , 13, 3, 2, 5, d 24, 21, 17, 13, 12, 8, 5 Weiters ergibt sich für die ganze Zahl \x aus k die Ungleichung d -.f. 11 ( J.) rss 725, wtobei für den Faktor / je nach der zahlentheoretischen Natur der Zahl x und der Zahl 2, wie bereits gezeigt wurde, die Werte 1, oder 16 zu setzen sind. Von den zu (j, assoziierten Zahlen sind nu jene zu berücksichtigen, die durch Multiplikation der Zahl \x mit einer quadratfreien Einheit des Körpers li entstehen. Da die vier konjugierten Körper reell sein sollen, muß \x außerdem total positiv sein. Eine einfache Untersuchung zeigt jedoch, daß keine Zahl der in Betracht kommenden quadratischen Körper alle diese Bedingungen erfüllt. B. Z w ei re e lle und zw ei im a g in ä re k o n ju g ie r te K ö rp er. In diesem Falle besitzt der Körper K (\/3 + 2 \Jo) die absolut kleinste Diskriminante. Der Beweis hiefür ist analog dem vorgehenden Falle zu führen. Für die Diskriminanten der quadratischen Unterkörper, die wieder reell sein müssen, ergibt sich r/ ^ \ / Die Zahl jj. müßte nun so bestimmt werden, daß neben der Ungleichung j d -. f n (\x) fg 275 auch die Bedingung 11 ( jj.) < 0 erfüllt ist, was nicht möglich ist.
4 736 Akademie d. Wissenschaften J. Wien; Maj'er, download unter C. V ie r im a g in ä re k o n ju g ie r te K örp er. Gleich den beiden früheren Fällen kann gezeigt werden, der Körper K ( \/ \ / 3) die kleinste Diskriminante D 117 besitzt, wobei zu beachten ist, daß die quadratischen Unterkörper, für welche d < L \ /ll7 gilt, reell oder imaginär sein können und im Falle eines reellen Unterkörpers total negativ sein muß. daß II. Die absolut kleinsten Diskriminanten der allgemeinen biquadratischen Körper. Ein Satz über quaternäre quadratische Formen, der für die folgende Betrachtung notwendig ist, soll zunächst dargestellt werden. Nach M in k o w sk i1 ist eine positiv definite quaternäre quadratische Form cp( ^ x, x3,,r4) = V bik. Xj xk, (/, k 1, 2, 3, 4; bil( ~ bki) wenn sie den Un dann und nur dann eine reduzierte Form, gleichungen und einer Reihe von Ungleichungen bn ^ b 22^ b 33^ b ( 1)? (e n e ä,s 8>s4)^ Z 7,,A (2) genügt, wobei e7/= 1 ist und die anderen Größen sk (k h) die W erte 0, + 1 und 1 annehmen können. Für jede reduzierte quaternäre quadratische Form gilt die Ungleichung bn h 2 b 3 3 K ± ^ 4 D ('?)> (3) wenn D (cp) die Diskriminante der Form bedeutet. M in k o w s k i2 beweist zunächst die allgemeine Ungleichung \ubn b22 b n t=i=d (cp) für reduzierte quadratische Formen; hiebei ist X/;, eine gewisse positive nur von n abhängige Konstante. Die Frage nach dem präzisen Werte von \n führt auf die extremen Formen, die zuerst von K o rk in e und Z o lo ta r e ff3 definiert und untersucht wurden. Mit Hilfe dieser extremen Formen kann durch Betrachtung eines 1 Sur la reduction des formes quadratiques positives quaternaires. Ges. Abhandlungen von M inkowski, 1911, I. Bd., p Diskontinuitätsbereich für arithmetische Äquivalenz. Ges. Abhandlg. M inkowski, 1911, II. Bd., p Sur les formes quadratiques. Math. Ann., Bd. VI und Bd. XI.
5 Absolut Akademie kleinste d. Wissenschaften Diskriminanten Wien; download der biquadratischen unter Zahlkörper. 737 vierdimensionalen Punktgitters die oben behauptete Ungleichung (3) nachgewiesen werden. A. V ier r e e lle k o n ju g ie r te K örp er. Die quadratische Form / (x1, x2,x3,x j (xx + co2 x%+ w3 x3 + co4 x4)2 + (xt + (Oa x2 + x3 + wi x j (X^ + (tio Xt) + X3 + Ü X ^)2 (x^ + X2 + 0)3 / X, + x±) - ' =?! +?t + fs +?4 enthalte in jeder Klammer eine Basisform je eines der vier reellen konjugierten Körper. Sie ist positiv definit, ihre Diskriminante ist gleich der Diskriminante des biquadratischen Körpers K und das Minimum der Form ist 4. Für ganzzahlige xv x2,x3,xi sind v2, "f3, selbst vier konjugierte ganze algebraische Zahlen, die einer Gleichung vierten Grades genügen, deren letzter Koeffizient i? 1? 2? 3? 4.; unbedingt ^ 1 sein muß, so daß auch für die positive Quadratwurzel aus I'-Pj cp2. cp3 cp4 die Ungleichung \ / cpt rp2 <p3 cp4 j ^ 1 gilt. Aus dieser Ungleichung aber folgt nach dem Satze über das geometrische und arithmetische Mittel sofort die Ungleichung?i +?l +?Ü +?I = 4- Bestimmen wir zu der quadratischen Form f (xv x2, x3,,i4) eine äquivalente reduzierte Form, so bleibt zunächst das Minimum der Form als Invariante der Klasse erhalten; auch die einzelnen Basisformen in den Klammerausdrücken bleiben Basisformen derselben algebraischen Zahlkörper, denn die Substitutionen des Reduktionsprozesses haben alle die Determinante + 1. Die so erhaltene reduzierte quadratische Form? ( X l >X2 X$ x i ) (X1 1 2 X2 + Ps Xn + P i X± ) ~ + ( X 1 + P* X2 + p'i X3 + P * X± ) '+ + ( x i + [Mx 2 + f>:)x3 + p i x 4) 2 + rj* X% p'l'-^i)1 = t = V b ikxixk (4) is k 1 ist der ursprünglichen Form ganz ähnlich. Die in den einzelnen Klammerausdrücken nun erscheinenden Minimalbasen werden nach F u r tw ä n g le r reduzierte Minimalbasen genannt. Ihre Existenz folgt unmittelbar aus der Existenz der reduzierten Form. W ir betrachten nun den Zahlkörper K (p2). Da die Relativkörper bereits untersucht wurden, kann vorausgesetzt werden, daß dieser Zahlkörper keinen quadratischen Unterkörper besitze. p2 ist demnach sicher eine Irrationalzahl vierten Grades; sie genüge der irreduziblen Gleichung X 1 f- Cl] x^ CI.) X~ -f- Cln X - - CI^ 0.
6 738 Akademie d. Wissenschaften J. Wien; Mayer, download unter Die Diskriminante D des biquadratischen Körpers sei gegeben. Da D zugleich die Diskriminante der obigen reduzierten Form ist, so lassen sich aus den Reduktionsbedingungen (1), (2) und aus der Ungleichung (3) Grenzen für die elementarsymmetrischen Funktionen von (j2 und seinen Konjugierten gewinnen. E s ergeben sich folgende Ungleichungen für die Gleichungskoeffizienten: a x\ ^ c, (c = 0, 1, 2), 4 (< '- \ /D ) ^ «2 ~ {c 4), wenn < 0 und a2 =}= 0. Damit ist die Möglichkeit gegeben, zu jedem Werte I) jene biquadratischen Zahlkörper aufzusuchen, die eine Diskriminante ^ I) besitzen. Setzen wir D = 725, so nehmen die Ungleichungen (5) folgende Gestalt an: 0, 4 ^ a 2 ^ 2, 1.7,1 ^ 2, \at = 1, 1, = 2, - 2 ^ a 2 ^ 0, 0, a 0 = : 0 j a.ä \ ^ (3, a2 0 : 1a3 j ^ 6, 0, a., =j= 0 : i as rg 9. Von den vielen Gleichungen, deren Koeffizienten obigen B e dingungen genügen, kann eine stattliche Menge ausgeschaltet werden. Zunächst fällt die Hälfte jener Gleichungen weg, die durch die Substitution * -» - ineinander übergehen. E s sind demnach für den ersten Koeffizienten ax nur die Werte 0, 1, 2 zu nehmen und im Falle a x ~ 0 für den dritten Koeffizienten nur die positiven Werte zu berücksichtigen. Ferner müssen die Koeffizienten ax und a2 der Bedingung 4 ^ a i 2 a2 ^ 8 (ti) genügen, wie sich aus den Reduktionsbedingungen (1), (2) und der Ungleichung (3) leicht ergibt. Weitere Bedingungen, die für die Ausschaltung besonders günstig wirken, können mittels des Sturmsehen Satzes hergeleitet werden. Aus der Ungleichung (6) folgt,
7 Absolut Akademie kleinste d. Wissenschaften Diskriminanten Wien; download der biquadratischen unter Zahlkörper daß die Wurzeln der in Betracht kommenden Gleichungen in dem Intervalle ( 3, + 3 ) liegen müssen. Da nun die Gleichungen vier reelle Wurzeln haben sollen, so muß die Sturm sche Kette für die Werte 3, + 3 vier Zeichenwechsel verlieren, was folgendes Schema gibt: 3 + o / (X) + + A (X) + /> (.r) + + fs {x) + t\ (^) + + Jede Funktion dieser Kette liefert zwei Bedingungen für die Gleichungskoeffizienten. Besonders die Funktion f 3 (x) wirkt durch die aus dem Schem a sich ergebenden Ungleichungen f ( 3) < 0, /»( + 3 ) > 0 derart günstig, daß nur mehr wenige Gleichungen für die weitere Untersuchung übrig bleiben. Von diesem Reste besitzt der größere Teil der Gleichungen negative Diskriminanten. Schaltet man überdies die reduziblen Gleichungen aus, so verbleiben nur noch die folgenden fünf Gleichungen: a t a -> a s Cl^ Gleichungsdisk Die Gleichungsdiskriminanten sind in allen fünf Fällen zugleich die Körperdiskriminanten der entsprechenden Zahlkörper. Die beiden letzten Gleichungen x i - h x 3 3 x 2.r+ 1 rr 0 und xi + 2 x 3 2 x2 3 x-h 1 0 sind algebraisch abhängig. Sie zerfallen im quadratischen Körper * ( V A ) in zwei Faktoren '2 + o (1 \ / O ) X ---1 ö 'O + V / 5 ) * i = 0, (3 + \ / 5 ) x 2+ x ^ (3 \ / 5 ) = 0.
8 740 Akademie d. Wissenschaften J. Wien; Mayer, download unter Aus den Wurzeln ergeben sich die beiden Zahlkörper K { \ /7 + 2 v/ö) und k ( \ J 7 2 y/ö), die einzigen biquadratischen Zahlkörper, welche in diesem Falle die kleinste Diskriminante 725 besitzen. B. 2 r e e lle und 2 im a g in ä re k o n ju g ie r te K örp er. Es seien (l, w2, o)3, oo4), (1, (4, 0)3, W4) Minimalbasen der zwei reellen und (1, w", w3, 0)4), (1, co"', w"', Minimalbasen der zwei imaginären Körper. W ir betrachten die quadratische Form f (xv X2,X5,Xi ) r= (xt + C02 X2 + W3 X3 + X4)2 + (x\ + (O9X2 + lügx3 + W4x4) (x^ + OJ2,T2 + (0 ;/^ 3 + (O4 A-'^) + C0'";l'2 + 0)3*X.j + Diese Form ist positiv definit, ihre Diskriminante ist bis auf das Vorzeichen gleich der Diskriminante des biquadratischen Zahlkörpers und ihr Minimum beträgt 4. Die dieser Form entsprechende reduzierte Form ist analog gebaut; es ist bloß der Bezeichnung wegen in der obigen Form an Stelle der 0h überall p{- zu setzen. An diese reduzierte Form schließt die weitere Betrachtung an. Der Körper isf(p2) besitze keinen quadratischen Unterkörper, so daß p2 sicher Wurzel einer irreduziblen Gleichung vierten Grades x f- ci2x~ -f- ci^x -f- ci^ 0 ist. Aus den Reduktionsbedingungen (1), (2) und aus der Ungleichung (3) ergeben sich sofort jp + p'+j/'+p/"! ^ 2 und 4 ^ ( p 2 + p/2 + p"2 + p///2) ^ \ J^ T J oder p + p' + 2 o c, 4 rsjj (p2 + p/2 + 2 a2 + 2 t 2) ^ d, wenn wir für p ^zro + n, rj" o h, \ / I) d setzen und für c nur die W erte d= 2, dt 1, 0 zulassen. Die Gleichungskoeffizienten a 2, a 3 und sind Funktionen der Größen p, p', a, t. Durch die beiden Bedingungen 2 o = c p [J und o2 + t 2 = \y{fl p2 p/2) lassen sich noch zwei Veränderliche eliminieren, wobei für c nur die W erte dz 2, dr 1, 0 in Betracht kommen und für d der größte W ert d \ f D zu nehmen ist. Aus einer geometrischen B e trachtung dieser Funktionen gewinnt man wieder Grenzen für die Gleichungskoeffizienten. Für D = 275 ergeben sich folgende Intervalle
9 Absolut Akademie kleinste d. Diskriminanten Wissenschaften Wien; download der biquadratischen unter Zahlkörper. 7 4 t ( = 0 : 3 ^ a 2 ^ 3, 0 ^ a3 ^ 3, 0 ^ a 1^ 2,la 1= \ 2 ^ a 2^ 3, 4 ^ a 3 ^ 3, < * J^ 2 ; {ax 2 1 ^ a 2 ^ 4, 4 ^ ö3 ^ 4, hiebei ist schon berücksichtigt, daß von zwei Gleichungen, die durch die Substitution x-+ x ineinander übergehen, nur eine im Bereiche vorkommt. Die Untersuchung liefert die beiden Gleichungen xi + 2 x 3 x 1 rr 0 und x4-hx3 2 x 1 rr 0, die durch die Substitution x-+ ineinander übergehen. Aus den x Wurzeln dieser Gleichungen ist zu erkennen, daß der reelle Körper 7v(\/3 + 2 \ J5 ) und der imaginäre Körper k { \ / 3 2 v/ö) die absolut kleinste Diskriminante 275 besitzen. Die vorher bestimmten Grenzen der Gleichungskoeffizienten bleiben auch für D 283 erhalten, so daß also in diesem B e reiche auch alle Körper mit einer Diskriminante Z) 5^283 vertreten sein müssen. Außer D rr 275 existiert jedoch keine absolut kleinere Diskriminante. Die Körper mit der Diskriminante D r r 283 sind definiert durch die Gleichungen: xi 2 x 2+ x + 1 rr 0, xa + x3 2,r2+ l = o, xi + x 1 0,,T4+ X3 1 rr 0, die voneinander algebraisch abhängig sind. C. V ie r im a g in ä re k o n ju g ie r te K örp er. Die quadratische Form / (xt, x2, x,}, x±) rr (xl + coä x2 + co3 ;r3 4- C0 x±) (xx+ coix2 + co3^3 4- co^r4) + + (x x + CO9 x 9 -f- co"x :, (ji'l,t4) (x x + co"7*, -+ to3'x 3 + co^7x^j enthalte in jedem Klammerausdrucke eine Basisform eines der vier konjugierten Körper. Die Form ist wieder positiv definit, hat das Minimum 2 und ihre Diskriminante wobei D die Diskriminante des biquadratischen Körpers bedeutet. Aus der entsprechenden reduzierten Form lassen sich wieder Grenzen für die Gleichungskoeffizienten gewinnen, die in diesem Falle, für D 117 gesetzt, folgende Gestalt annehmen: k i ^ 2, 2 5g 4, c73 <^4, a± 1.
10 7 4 2 J. Mayer, Akademie Absolut d. Wissenschaften kleinste Diskriminanlen Wien; download unter fler biquadratischen usw. Die weitere Untersuchung gestaltet sich analog den vorhergehenden Fällen und ergibt die imaginären Körper k [ \ / \ + 2 s/ ^ ) und k { \ / 1 2 s /~ s) mit der kleinsten möglichen Diskriminante Die absolut kleinsten Diskriminanten der biquadratischen Zahlkörper sind 725, 275, 117, je nachdem von den vier konjugierten Körpern alle vier reell, zwei reell und zwei imaginär oder alle vier imaginär sind. Die folgende Übersicht gibt die entsprechenden Zahlkörper an: D Zahlkörper 725 i k (s/ ^ /S ), j Ä-(\/3 + 2 v/5), ( v /3-2 V 5 '), 117 I * ' ( ^ ), Ä ' ( V - l - 2 V - " 3 ). Die Zahlkörper einer jeden Zeile sind einander konjugiert aber nicht identisch. Es ist bemerkenswert, daß diese biquadratischen Körper quadratische Relativkörper über den quadratischen Körpern mit absolut kleinster Diskriminante sind.
Analytische Lösung algebraischer Gleichungen dritten und vierten Grades
 Analytische Lösung algebraischer Gleichungen dritten und vierten Grades Inhaltsverzeichnis 1 Einführung 1 2 Gleichungen dritten Grades 3 3 Gleichungen vierten Grades 7 1 Einführung In diesem Skript werden
Analytische Lösung algebraischer Gleichungen dritten und vierten Grades Inhaltsverzeichnis 1 Einführung 1 2 Gleichungen dritten Grades 3 3 Gleichungen vierten Grades 7 1 Einführung In diesem Skript werden
Lösungen - Serie 4 zu den Übungsaufgaben zur Vorlesung Algebraische Zahlentheorie
 Lösungen - Serie 4 zu den Übungsaufgaben zur Vorlesung Algebraische Zahlentheorie Aufgabe 1: Betrachten Sie Zahlkörper. a) Untersuchen Sie, wie viele ganze Ideale a mit festgelegter Norm N(a) = a es in
Lösungen - Serie 4 zu den Übungsaufgaben zur Vorlesung Algebraische Zahlentheorie Aufgabe 1: Betrachten Sie Zahlkörper. a) Untersuchen Sie, wie viele ganze Ideale a mit festgelegter Norm N(a) = a es in
Zur Berechnung ganzer Punkte auf Mordellkurven über globalen Körpern
 Zur Berechnung ganzer Punkte auf Mordellkurven über globalen Körpern Michael E. Pohst Institut für Mathematik Technische Universität Berlin 4. Februar, 2015 Mordells Gleichung ist y 2 = x 3 + κ mit einer
Zur Berechnung ganzer Punkte auf Mordellkurven über globalen Körpern Michael E. Pohst Institut für Mathematik Technische Universität Berlin 4. Februar, 2015 Mordells Gleichung ist y 2 = x 3 + κ mit einer
Einführung in die Zahlentheorie
 Einführung in die Zahlentheorie Jörn Steuding Uni Wü, SoSe 2015 I Zahlen II Modulare Arithmetik III Quadratische Reste IV Diophantische Gleichungen V Quadratische Formen Wir behandeln die wesentliche Zahlentheorie
Einführung in die Zahlentheorie Jörn Steuding Uni Wü, SoSe 2015 I Zahlen II Modulare Arithmetik III Quadratische Reste IV Diophantische Gleichungen V Quadratische Formen Wir behandeln die wesentliche Zahlentheorie
Nürnberg. Augsburg. München
 IT T OIT-- @ ß 77 T -13- Fx-111 : F 121 : 121 -: 221 : 221 32 73 T -3- Tx: - I ö - L L T ä F ö F : x : - y - OIT (ß -F O- -- O: 3 : 1 ( y Jö J 2 OIT 3 L! T F: ß: : : : : I 1 x 22 ( x ö 1 - : F * F : @
IT T OIT-- @ ß 77 T -13- Fx-111 : F 121 : 121 -: 221 : 221 32 73 T -3- Tx: - I ö - L L T ä F ö F : x : - y - OIT (ß -F O- -- O: 3 : 1 ( y Jö J 2 OIT 3 L! T F: ß: : : : : I 1 x 22 ( x ö 1 - : F * F : @
Über die Bestimmung der linearen Teiler einer algebraischen Form.
 Über die Bestimmung der linearen Teiler einer algebraischen Form. Von F. HOCEVAR aus Graz. In den zahlreichen Arbeiten über die linearen Teiler der Formen beschäftigte man sich bisher in der Regel nur
Über die Bestimmung der linearen Teiler einer algebraischen Form. Von F. HOCEVAR aus Graz. In den zahlreichen Arbeiten über die linearen Teiler der Formen beschäftigte man sich bisher in der Regel nur
DIE ZERLEGUNG VON PRIMZAHLEN IN ALGEBRAISCHEN ZAHL- KÖRPERN*
 DIE ZERLEGUNG VON PRIMZAHLEN IN ALGEBRAISCHEN ZAHL- KÖRPERN* VON ANDREAS SPEISER In den folgenden Zeilen wird gezeigt, dass das Problem der Zerlegung einer Primzahl in einem algebraischen Körper identisch
DIE ZERLEGUNG VON PRIMZAHLEN IN ALGEBRAISCHEN ZAHL- KÖRPERN* VON ANDREAS SPEISER In den folgenden Zeilen wird gezeigt, dass das Problem der Zerlegung einer Primzahl in einem algebraischen Körper identisch
Über die Resultante einer Covariante und einer Grundform
 Akademie d. Wissenschaften Wien; download unter www.biologiezentrum.at 1 0 1 3 Über die Resultante einer Covariante und einer Grundform von Dr. Gustav Kohn, Prioaldocent a n d er lc, U niversität in 'Wie».
Akademie d. Wissenschaften Wien; download unter www.biologiezentrum.at 1 0 1 3 Über die Resultante einer Covariante und einer Grundform von Dr. Gustav Kohn, Prioaldocent a n d er lc, U niversität in 'Wie».
Lösen von Gleichungen mittels Ungleichungen
 Lösen von Gleichungen mittels Ungleichungen. März 00 Die Aufgaben sind mit Schwierigkeitsstufen leicht, mittel, schwer markiert. Aufgabe (leicht) Ermittle alle nichtnegativen reellen Zahlen a, b, c, für
Lösen von Gleichungen mittels Ungleichungen. März 00 Die Aufgaben sind mit Schwierigkeitsstufen leicht, mittel, schwer markiert. Aufgabe (leicht) Ermittle alle nichtnegativen reellen Zahlen a, b, c, für
Algebra II, SS September 2011 Aufgaben zur Körpertheorie. (+1 + i), x 2 = 1 2. ( 1 + i), x 4 = 1 2
 1. Zeige, dass Q(, i) Zerfällungskörper von X 4 + 1 Q[X] ist. Lösung: Die vier Nullstellen von X 4 + 1 über Q sind x 1 = 1 (+1 + i), x = 1 (+1 i), x 3 = 1 ( 1 + i), x 4 = 1 ( 1 i). Damit ist ein Zerfällungskörper
1. Zeige, dass Q(, i) Zerfällungskörper von X 4 + 1 Q[X] ist. Lösung: Die vier Nullstellen von X 4 + 1 über Q sind x 1 = 1 (+1 + i), x = 1 (+1 i), x 3 = 1 ( 1 + i), x 4 = 1 ( 1 i). Damit ist ein Zerfällungskörper
Geometrische Darstellung der Theorie gruppen.
 Akademie d. Wissenschaften Wien; download unter www.biologiezentrum.at 418 der Polar Geometrische Darstellung der Theorie gruppen. Von Emil Waelsch, ord. H örer an der deutschen technischen Huchschule
Akademie d. Wissenschaften Wien; download unter www.biologiezentrum.at 418 der Polar Geometrische Darstellung der Theorie gruppen. Von Emil Waelsch, ord. H örer an der deutschen technischen Huchschule
B. Vorträge der Sektionssitzungen.
 B. Vorträge der Sektionssitzungen. 1. Sektion: Arithmetik und Algebra. Über die Genera in algebraischen Zahlkörpern. Von H. WEBER in Strafsburg. Indem ich. der ehrenvollen Aufforderung des Komites nachkomme,
B. Vorträge der Sektionssitzungen. 1. Sektion: Arithmetik und Algebra. Über die Genera in algebraischen Zahlkörpern. Von H. WEBER in Strafsburg. Indem ich. der ehrenvollen Aufforderung des Komites nachkomme,
Kleingruppen zur Service-Veranstaltung Mathematik I fu r Ingenieure bei Prof. Dr. G. Herbort im WS12/13 Dipl.-Math. T. Pawlaschyk,
 Lo sungen zu den U bungsaufgaben, Blatt Kleingruppen zur Service-Veranstaltung Mathematik I fu r Ingenieure bei Prof. Dr. G. Herbort im WS/ Dipl.-Math. T. Pawlaschyk,.0. Themen: Wurzeln, Gleichungen, Ungleichungen
Lo sungen zu den U bungsaufgaben, Blatt Kleingruppen zur Service-Veranstaltung Mathematik I fu r Ingenieure bei Prof. Dr. G. Herbort im WS/ Dipl.-Math. T. Pawlaschyk,.0. Themen: Wurzeln, Gleichungen, Ungleichungen
Gleichungen und Ungleichungen
 Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme. Kapitel 3 Gleichungen und Ungleichungen linke Seite = rechte Seite Grundmenge: Menge aller Zahlen, die wir als Lösung der Gleichung
Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme. Kapitel 3 Gleichungen und Ungleichungen linke Seite = rechte Seite Grundmenge: Menge aller Zahlen, die wir als Lösung der Gleichung
Gleichungen und Ungleichungen
 Kapitel 3 Gleichungen und Ungleichungen Josef Leydold Auffrischungskurs Mathematik WS 2017/18 3 Gleichungen und Ungleichungen 1 / 58 Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme.
Kapitel 3 Gleichungen und Ungleichungen Josef Leydold Auffrischungskurs Mathematik WS 2017/18 3 Gleichungen und Ungleichungen 1 / 58 Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme.
Gleichungen und Ungleichungen
 Kapitel 3 Gleichungen und Ungleichungen Josef Leydold Auffrischungskurs Mathematik WS 2017/18 3 Gleichungen und Ungleichungen 1 / 58 Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme.
Kapitel 3 Gleichungen und Ungleichungen Josef Leydold Auffrischungskurs Mathematik WS 2017/18 3 Gleichungen und Ungleichungen 1 / 58 Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme.
ein Polynom n-ten Grades und (x) sei ein Polynom vom höchstens -1 teu Grade, welches zu f(x) teilerfremd ist. Es seien ferner,,
 104 [Ser. 3, Vol. 2, U ber Entwickelungskoeffizienten der rationalen Funktion. Matsusaburo F*JIWARA. [VORGELEGT AM 1. APRIL 1920] 1. Es sei ein Polynom n-ten Grades und (x) sei ein Polynom vom höchstens
104 [Ser. 3, Vol. 2, U ber Entwickelungskoeffizienten der rationalen Funktion. Matsusaburo F*JIWARA. [VORGELEGT AM 1. APRIL 1920] 1. Es sei ein Polynom n-ten Grades und (x) sei ein Polynom vom höchstens
Inhaltsverzeichnis. Arithmetische Untersuchungen. Seite
 Inhaltsverzeichnis. Arithmetische Untersuchungen. Erster Abschnitt Von der Congruenz der Zahlen im Allgemeinen. 1 Congruente Zahlen, Modulu, Reste und Nichtreste. Artikel 1 3. Kleinste Reste. Artikel 4.
Inhaltsverzeichnis. Arithmetische Untersuchungen. Erster Abschnitt Von der Congruenz der Zahlen im Allgemeinen. 1 Congruente Zahlen, Modulu, Reste und Nichtreste. Artikel 1 3. Kleinste Reste. Artikel 4.
Mittel aus Dirichlet-Reihen mit reellen Restcharakteren.
 Mittel aus Dirichlet-Reihen mit reellen Restcharakteren. Von MAX GUT (Zürich). (AIs Manuskript eingegangen am 0. April 940.) In einer Note ) habe ich gezeigt, dass wenn q eine beliebige Primzahl ist, und
Mittel aus Dirichlet-Reihen mit reellen Restcharakteren. Von MAX GUT (Zürich). (AIs Manuskript eingegangen am 0. April 940.) In einer Note ) habe ich gezeigt, dass wenn q eine beliebige Primzahl ist, und
Komplexe Zahlen. Allgemeines. Definition. Darstellungsformen. Umrechnungen
 Komplexe Zahlen Allgemeines Definition Eine komplexe Zahl z x + y i besteht aus einem Realteil Re(z) x und einem Imaginärteil Im(z) y. Der Imaginärteil wird mit der Imaginären-Einheit i multipliziert.
Komplexe Zahlen Allgemeines Definition Eine komplexe Zahl z x + y i besteht aus einem Realteil Re(z) x und einem Imaginärteil Im(z) y. Der Imaginärteil wird mit der Imaginären-Einheit i multipliziert.
8.5 Symmetrische Polynome, Diskriminate und Resultante
 332 85 Symmetrische Polynome, Diskriminate und Resultante Ein weiteres Verfahren zur Feststellung, ob mehrfache Wurzeln vorliegen, ist die Betrachtung der Diskriminante, deren Einführung jetzt vorbereitet
332 85 Symmetrische Polynome, Diskriminate und Resultante Ein weiteres Verfahren zur Feststellung, ob mehrfache Wurzeln vorliegen, ist die Betrachtung der Diskriminante, deren Einführung jetzt vorbereitet
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 22 Algebraische Körpererweiterung Satz 1. Sei K L eine Körpererweiterung und sei f L ein Element. Dann sind folgende Aussagen
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 22 Algebraische Körpererweiterung Satz 1. Sei K L eine Körpererweiterung und sei f L ein Element. Dann sind folgende Aussagen
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 23 Die Gradformel Satz 1. Seien K L und L M endliche Körperweiterungen. Dann ist auch K M eine endliche Körpererweiterung und
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 23 Die Gradformel Satz 1. Seien K L und L M endliche Körperweiterungen. Dann ist auch K M eine endliche Körpererweiterung und
Grundlagen komplexe Zahlen. natürliche Zahlen
 Grundlagen komplexe Zahlen Die Zahlenbereichserweiterungen von den natürlichen Zahlen hin zu den reellen Zahlen waren dadurch motiviert, bestimmte Rechenoperationen uneingeschränkt ausführen zu können.
Grundlagen komplexe Zahlen Die Zahlenbereichserweiterungen von den natürlichen Zahlen hin zu den reellen Zahlen waren dadurch motiviert, bestimmte Rechenoperationen uneingeschränkt ausführen zu können.
Übungsblatt 6 zur Algebra I
 Universität Augsburg Sommersemester 2013 Lehrstuhl für Algebra und Zahlentheorie Ingo Blechschmidt Prof. Marc Nieper-Wißkirchen Robert Gelb Übungsblatt 6 zur Algebra I Abgabe bis 27. Mai 2013, 17:00 Uhr
Universität Augsburg Sommersemester 2013 Lehrstuhl für Algebra und Zahlentheorie Ingo Blechschmidt Prof. Marc Nieper-Wißkirchen Robert Gelb Übungsblatt 6 zur Algebra I Abgabe bis 27. Mai 2013, 17:00 Uhr
Naturwiss.-med. Ver. Innsbruck; download unter
 lieber die geometrische Bedeutung der complexen Elemente der analytischen Geometrie. (Auszug aus dem Vortrage in der Sitzung v. 20. Februar 1890) von Prof. Dr. 0. Stolz. Genügen zweien algebraischen Gleichungen
lieber die geometrische Bedeutung der complexen Elemente der analytischen Geometrie. (Auszug aus dem Vortrage in der Sitzung v. 20. Februar 1890) von Prof. Dr. 0. Stolz. Genügen zweien algebraischen Gleichungen
Polynomgleichungen. Gesetzmäßigkeiten
 Polynomgleichungen Gesetzmäßigkeiten Werden zwei Terme durch ein Gleichheitszeichen miteinander verbunden, so entsteht eine Gleichung. Enthält die Gleichung die Variable x nur in der 1. Potenz, so spricht
Polynomgleichungen Gesetzmäßigkeiten Werden zwei Terme durch ein Gleichheitszeichen miteinander verbunden, so entsteht eine Gleichung. Enthält die Gleichung die Variable x nur in der 1. Potenz, so spricht
Vorkurs: Mathematik für Informatiker
 Vorkurs: Mathematik für Informatiker Teil 3 Wintersemester 2017/18 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2017 Steven Köhler Wintersemester 2017/18 Inhaltsverzeichnis Teil 1 Teil
Vorkurs: Mathematik für Informatiker Teil 3 Wintersemester 2017/18 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2017 Steven Köhler Wintersemester 2017/18 Inhaltsverzeichnis Teil 1 Teil
Kapitel II. Algebraische Grundbegriffe
 Kapitel II. Algebraische Grundbegriffe 1 Ringe und Körper Für das Rechnen in Z haben wir in Kap. I, 1 Regeln aufgestellt, welche auch in Q und R gelten. Damit werden Z, Q und R zu Ringen im folgenden Sinn:
Kapitel II. Algebraische Grundbegriffe 1 Ringe und Körper Für das Rechnen in Z haben wir in Kap. I, 1 Regeln aufgestellt, welche auch in Q und R gelten. Damit werden Z, Q und R zu Ringen im folgenden Sinn:
Vorkurs: Mathematik für Informatiker
 Vorkurs: Mathematik für Informatiker Teil 3 Wintersemester 2017/18 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2017 Steven Köhler Wintersemester 2017/18 Inhaltsverzeichnis Teil 1 Teil
Vorkurs: Mathematik für Informatiker Teil 3 Wintersemester 2017/18 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2017 Steven Köhler Wintersemester 2017/18 Inhaltsverzeichnis Teil 1 Teil
. Dann hat die Gleichung [X 2 ] p k = [a] p k in ( Z/p k Z )
![. Dann hat die Gleichung [X 2 ] p k = [a] p k in ( Z/p k Z ) . Dann hat die Gleichung [X 2 ] p k = [a] p k in ( Z/p k Z )](/thumbs/62/46609231.jpg) Aufgabe 57 a) Seien p Primzahl, p 2, k N und [a] p k ( Z/p k Z ). Dann hat die Gleichung [X 2 ] p k = [a] p k in ( Z/p k Z ) genau zwei oder gar keine Lösung. Beweis: Sei [x] p k ( Z/p k Z ) eine Lösung
Aufgabe 57 a) Seien p Primzahl, p 2, k N und [a] p k ( Z/p k Z ). Dann hat die Gleichung [X 2 ] p k = [a] p k in ( Z/p k Z ) genau zwei oder gar keine Lösung. Beweis: Sei [x] p k ( Z/p k Z ) eine Lösung
3.3 Reduzierte Basen nach Lenstra, Lenstra und Lovász
 Gitter und Codes c Rudolf Scharlau 15. Juni 2009 221 3.3 Reduzierte Basen nach Lenstra, Lenstra und Lovász Alternativ zu klassischen Konzepten wie dem von Minkowski gibt es seit gut 25 Jahren den Reduktionsbegriff
Gitter und Codes c Rudolf Scharlau 15. Juni 2009 221 3.3 Reduzierte Basen nach Lenstra, Lenstra und Lovász Alternativ zu klassischen Konzepten wie dem von Minkowski gibt es seit gut 25 Jahren den Reduktionsbegriff
Algebraische Zahlentheorie
 III-11 9. Der Satz von Kronecker-Weber. Ein Zahlkörper K heißt abelsch, wenn K : Q eine galois sche Körpererweiterung ist und die Galois-Gruppe Gal(K : Q) abelsch ist. Ist die Galois-Gruppe sogar zyklisch,
III-11 9. Der Satz von Kronecker-Weber. Ein Zahlkörper K heißt abelsch, wenn K : Q eine galois sche Körpererweiterung ist und die Galois-Gruppe Gal(K : Q) abelsch ist. Ist die Galois-Gruppe sogar zyklisch,
Lineare Algebra II 3. Übungsblatt
 Lineare Algebra II 3. Übungsblatt Fachbereich Mathematik SS 2011 Prof. Dr. Kollross 27./28. April 2011 Susanne Kürsten Tristan Alex Minitest Aufgabe M1 (Formale Polynome) Betrachten Sie die folgenden Polynome
Lineare Algebra II 3. Übungsblatt Fachbereich Mathematik SS 2011 Prof. Dr. Kollross 27./28. April 2011 Susanne Kürsten Tristan Alex Minitest Aufgabe M1 (Formale Polynome) Betrachten Sie die folgenden Polynome
Übungsaufgaben zur Zahlentheorie (Holtkamp)
 Ruhr-Universität Bochum Fakultät für Mathematik Sommersemester 2005 Übungsaufgaben zur Zahlentheorie (Holtkamp) Sonderregelung: Zur vollständigen Lösung jeder Aufgabe gehört die Kennzeichnung der (maximal
Ruhr-Universität Bochum Fakultät für Mathematik Sommersemester 2005 Übungsaufgaben zur Zahlentheorie (Holtkamp) Sonderregelung: Zur vollständigen Lösung jeder Aufgabe gehört die Kennzeichnung der (maximal
15ab 21bc 9b = 3b 5a 7c 3
 4 4.1 Einführung Haben alle Summanden einer algebraischen Summe einen gemeinsamen Faktor, so kann man diesen gemeinsamen Faktor ausklammern. Die Summe wird dadurch in ein Produkt umgewandelt. Tipp: Kontrolle
4 4.1 Einführung Haben alle Summanden einer algebraischen Summe einen gemeinsamen Faktor, so kann man diesen gemeinsamen Faktor ausklammern. Die Summe wird dadurch in ein Produkt umgewandelt. Tipp: Kontrolle
6 Polynomielle Gleichungen und Polynomfunktionen
 6 Polynomielle Gleichungen und Polynomfunktionen Lineare Gleichungen Eine lineare Gleichung in einer Variablen ist eine Gleichung der Form ax + b = cx + d mit festen Zahlen a und c mit a c. Dies kann man
6 Polynomielle Gleichungen und Polynomfunktionen Lineare Gleichungen Eine lineare Gleichung in einer Variablen ist eine Gleichung der Form ax + b = cx + d mit festen Zahlen a und c mit a c. Dies kann man
15 Auflösbarkeit durch Radikale
 Chr.Nelius: Algebra (SS 2006) 1 15 Auflösbarkeit durch Radikale f [T] sei ein normiertes Polynom vom Grade 1. Wir wollen die Frage untersuchen, ob sich die Nullstellen von f formelmäßig berechnen lassen.
Chr.Nelius: Algebra (SS 2006) 1 15 Auflösbarkeit durch Radikale f [T] sei ein normiertes Polynom vom Grade 1. Wir wollen die Frage untersuchen, ob sich die Nullstellen von f formelmäßig berechnen lassen.
Overview of Stuttgart s Suburbs
 Ovv V V Cy C V V T + ( ) X* ( F) Z (),X*,, +,, +,X*,X* () vv L Fä F O T IC,C F V v V öv öv, +,X* F/ T / T L () L T O + T VVT * VVT F F/ T F X* / O C ö I O ö O ä I F I L I I F L F V I ä L L L ö C O L L
Ovv V V Cy C V V T + ( ) X* ( F) Z (),X*,, +,, +,X*,X* () vv L Fä F O T IC,C F V v V öv öv, +,X* F/ T / T L () L T O + T VVT * VVT F F/ T F X* / O C ö I O ö O ä I F I L I I F L F V I ä L L L ö C O L L
Algebraische Zahlentheorie. Teil II. Die Diskriminante.
 II-1 Algebraische Zahlentheorie Teil II Die Diskriminante Sei K ein Zahlkörper vom Grad n (also [K : Q] = n) Es gibt genau n Körper- Homomorphismen σ i : K C (siehe Merkzettel Separabilität) Stellen wir
II-1 Algebraische Zahlentheorie Teil II Die Diskriminante Sei K ein Zahlkörper vom Grad n (also [K : Q] = n) Es gibt genau n Körper- Homomorphismen σ i : K C (siehe Merkzettel Separabilität) Stellen wir
Kapitel 6: Das quadratische Reziprozitätsgesetz
 Kapitel 6: Das quadratische Reziprozitätsgesetz Ziel dieses Kapitels: die Untersuchung der Lösbarkeit der Kongruenzgleichung X also die Frage, ob die ganze Zahl Z eine Quadratwurzel modulo P besitzt. Im
Kapitel 6: Das quadratische Reziprozitätsgesetz Ziel dieses Kapitels: die Untersuchung der Lösbarkeit der Kongruenzgleichung X also die Frage, ob die ganze Zahl Z eine Quadratwurzel modulo P besitzt. Im
Körper- und Galoistheorie
 Prof. Dr. H. Brenner Osnabrück SS 2011 Körper- und Galoistheorie Vorlesung 3 Es sei K L eine endliche Körpererweiterung und x L ein Element. Dann sind die Potenzen x i, i N, linear abhängig, und das bedeutet,
Prof. Dr. H. Brenner Osnabrück SS 2011 Körper- und Galoistheorie Vorlesung 3 Es sei K L eine endliche Körpererweiterung und x L ein Element. Dann sind die Potenzen x i, i N, linear abhängig, und das bedeutet,
Algebra. 1 = a u + b,
 Fachbereich Mathematik Prof. Dr. Nils Scheithauer Walter Reußwig TECHNISCHE UNIVERSITÄT DARMSTADT WS 08/09 11. November 2008 Algebra 5. Übung mit Lösungshinweisen Aufgabe 23 Es sei R ein euklidischer Integritätsbereich.
Fachbereich Mathematik Prof. Dr. Nils Scheithauer Walter Reußwig TECHNISCHE UNIVERSITÄT DARMSTADT WS 08/09 11. November 2008 Algebra 5. Übung mit Lösungshinweisen Aufgabe 23 Es sei R ein euklidischer Integritätsbereich.
Lösungsvorschläge zu den Aufgaben auf Übungsblatt 07. x Dy y x
 Lösungsvorschläge zu den Aufgaben auf Übungsblatt 07 Aufgabe 1. Es seien R ein kommutativer Ring mit 1 und D R. Wir schreiben { ) x Dy QR, D) = x, y R}. y x Dann ist QR, D) abgeschlossen bezüglich der
Lösungsvorschläge zu den Aufgaben auf Übungsblatt 07 Aufgabe 1. Es seien R ein kommutativer Ring mit 1 und D R. Wir schreiben { ) x Dy QR, D) = x, y R}. y x Dann ist QR, D) abgeschlossen bezüglich der
Sitzungsberichte. der. mathematisch-naturwissenschaftlichen Abteilung. der. Bayerischen Akademie der Wissenschaften zu München.
 Sitzungsberichte der mathematisch-naturwissenschaftlichen Abteilung der Bayerischen Akademie der Wissenschaften zu München Jahrgang 1943 München 1944 aii'j syrischen Akademie der Wissenschaften Komiöfs^ion
Sitzungsberichte der mathematisch-naturwissenschaftlichen Abteilung der Bayerischen Akademie der Wissenschaften zu München Jahrgang 1943 München 1944 aii'j syrischen Akademie der Wissenschaften Komiöfs^ion
Aufgaben zu den ganzrationalen Funktionen
 Aufgaben zu den ganzrationalen Funktionen 1. Bestimmen Sie die Nullstellen folgender ganzrationaler Funktionen. a) y = x + x 6 b) y = x 3 3x + x c) y = (x + 4)(x + x ) d) y = x 4 5x + 4 e) y = x 3 + x
Aufgaben zu den ganzrationalen Funktionen 1. Bestimmen Sie die Nullstellen folgender ganzrationaler Funktionen. a) y = x + x 6 b) y = x 3 3x + x c) y = (x + 4)(x + x ) d) y = x 4 5x + 4 e) y = x 3 + x
2 Polynome und rationale Funktionen
 Gleichungen spielen auch in der Ingenieurmathematik eine große Rolle. Sie beschreiben zum Beispiel Bedingungen, unter denen Vorgänge ablaufen, Gleichgewichtszustände, Punktmengen. Gleichungen für eine
Gleichungen spielen auch in der Ingenieurmathematik eine große Rolle. Sie beschreiben zum Beispiel Bedingungen, unter denen Vorgänge ablaufen, Gleichgewichtszustände, Punktmengen. Gleichungen für eine
12 3 Komplexe Zahlen. P(x y) z = x + jy
 2 3 Komplexe Zahlen 3 Komplexe Zahlen 3. Grundrechenoperationen Definition Die Menge C = {z = a + jb a, b IR; j 2 = } heißt Menge der komplexen Zahlen; j heißt imaginäre Einheit. (andere Bezeichnung: i)
2 3 Komplexe Zahlen 3 Komplexe Zahlen 3. Grundrechenoperationen Definition Die Menge C = {z = a + jb a, b IR; j 2 = } heißt Menge der komplexen Zahlen; j heißt imaginäre Einheit. (andere Bezeichnung: i)
6 Gleichungen und Gleichungssysteme
 03.05.0 6 Gleichungen und Gleichungssysteme Äquivalente Gleichungsumformungen ( ohne Änderung der Lösungsmenge ).) a = b a c = b c Addition eines beliebigen Summanden c.) a = b a - c = b - c Subtraktion
03.05.0 6 Gleichungen und Gleichungssysteme Äquivalente Gleichungsumformungen ( ohne Änderung der Lösungsmenge ).) a = b a c = b c Addition eines beliebigen Summanden c.) a = b a - c = b - c Subtraktion
Quadratische Funktion
 Quadratische Funktion 1. Übliche Formen 1) Allgemeine Form: y = f(x) = a x 2 + b x + c a, b, c Konstanten Grundlegender Fall a = 1, b = 0, c = 0, also y = x 2 : "Normalparabel" Vorteil: Keine Brüche für
Quadratische Funktion 1. Übliche Formen 1) Allgemeine Form: y = f(x) = a x 2 + b x + c a, b, c Konstanten Grundlegender Fall a = 1, b = 0, c = 0, also y = x 2 : "Normalparabel" Vorteil: Keine Brüche für
ANALYSIS 2 VERSION 26. Juni 2018
 ANALYSIS VERSION 6 Juni 018 LISIBACH ANDRÉ 6 Potenzreihenentwicklung 61 Einleitung Die Linearisierung einer Funktion f(x an der Stelle x ist die Funktion L(x f( + df dx ((x Die Linearisierung ist ein Polynom
ANALYSIS VERSION 6 Juni 018 LISIBACH ANDRÉ 6 Potenzreihenentwicklung 61 Einleitung Die Linearisierung einer Funktion f(x an der Stelle x ist die Funktion L(x f( + df dx ((x Die Linearisierung ist ein Polynom
Arbeitsblatt Gleichungen höheren Grades
 Mathematik-Service Dr. Fritsch www.math-service.de Tel. 061/776 Arbeitsblatt Gleichungen höheren Grades 1. Lösen Sie folgenden quadratischen Gleichungen mittels quadratischer Ergänzung! (a) x x + = 0 (b)
Mathematik-Service Dr. Fritsch www.math-service.de Tel. 061/776 Arbeitsblatt Gleichungen höheren Grades 1. Lösen Sie folgenden quadratischen Gleichungen mittels quadratischer Ergänzung! (a) x x + = 0 (b)
Vortrag 4 - Primärzerlegung
 Vortrag 4 - Primärzerlegung von Christian Straßberger Beispiel 4.1: Primfaktorzerlegung als Primärzerlegung Sei n Z : n = ±p d1 1 pd2 2 pdr r, wobei p i Primzahlen, d i N. Dann ist (n) = (p d1 1 ) (pdr
Vortrag 4 - Primärzerlegung von Christian Straßberger Beispiel 4.1: Primfaktorzerlegung als Primärzerlegung Sei n Z : n = ±p d1 1 pd2 2 pdr r, wobei p i Primzahlen, d i N. Dann ist (n) = (p d1 1 ) (pdr
DIE KUBISCHE RESOLVENTE
 DIE KUBISCHE RESOLVENTE ANNA FLÖTOTTO Bachelorarbeit vorgelegt von Anna Flötotto Fakultät für Mathematik Universität Bielefeld Oktober 2007 Inhaltsverzeichnis 1. Einleitung 1 2. Voraussetzungen 3 3. Die
DIE KUBISCHE RESOLVENTE ANNA FLÖTOTTO Bachelorarbeit vorgelegt von Anna Flötotto Fakultät für Mathematik Universität Bielefeld Oktober 2007 Inhaltsverzeichnis 1. Einleitung 1 2. Voraussetzungen 3 3. Die
Polynome Teil VI: Die Potenzsummenformeln von NEWTON
 Die WURZEL Werkstatt Mathematik Polynome Teil VI: Die Potenzsummenformeln von NEWTON In der letzten Ausgabe der Werkstatt haben wir gesehen, dass sich Potenzsummen, etwa die symmetrischen Funktionen p
Die WURZEL Werkstatt Mathematik Polynome Teil VI: Die Potenzsummenformeln von NEWTON In der letzten Ausgabe der Werkstatt haben wir gesehen, dass sich Potenzsummen, etwa die symmetrischen Funktionen p
Entscheidungsverfahren mit Anwendungen in der Softwareverifikation
 Entscheidungsverfahren mit Anwendungen in der Softwareverifikation XII: Quantoren-Elimination Carsten Sinz Institut für Theoretische Informatik 23.01.2019 Foliensatz basiert z.t. auf Folien von Erika Abraham
Entscheidungsverfahren mit Anwendungen in der Softwareverifikation XII: Quantoren-Elimination Carsten Sinz Institut für Theoretische Informatik 23.01.2019 Foliensatz basiert z.t. auf Folien von Erika Abraham
Die Unlösbarkeit der Gleichung fünften Grades durch Radikale. Teilnehmer: Gruppenleiter:
 Die Unlösbarkeit der Gleichung fünften Grades durch adikale Teilnehmer: Max Bender Marcus Gawlik Anton Milge Leonard Poetzsch Gabor adtke Miao Zhang Gruppenleiter: Jürg Kramer Andreas-Oberschule Georg-Forster-Oberschule
Die Unlösbarkeit der Gleichung fünften Grades durch adikale Teilnehmer: Max Bender Marcus Gawlik Anton Milge Leonard Poetzsch Gabor adtke Miao Zhang Gruppenleiter: Jürg Kramer Andreas-Oberschule Georg-Forster-Oberschule
11. Übung zur Vorlesung. Zahlentheorie. im Wintersemester 2015/16
 11. Übung zur Vorlesung Aufgabe 41. Zeige, dass das Polynom (X 2 13)(X 2 17)(X 2 13 17) Z[X] modulo jeder natürlichen Zahl n N eine Nullstelle hat, aber keine Nullstelle in Z besitzt. Aufgabe 42. Sei p
11. Übung zur Vorlesung Aufgabe 41. Zeige, dass das Polynom (X 2 13)(X 2 17)(X 2 13 17) Z[X] modulo jeder natürlichen Zahl n N eine Nullstelle hat, aber keine Nullstelle in Z besitzt. Aufgabe 42. Sei p
QUADRATISCHE GLEICHUNGENN
 Schule Bundesgymnasium für Berufstätige Salzburg Thema Mathematik Arbeitsblatt A -.: Quadratische Gleichungen LehrerInnenteam m/ Mag Wolfgang Schmid Unterlagen QUADRATISCHE GLEICHUNGENN Definition: Eine
Schule Bundesgymnasium für Berufstätige Salzburg Thema Mathematik Arbeitsblatt A -.: Quadratische Gleichungen LehrerInnenteam m/ Mag Wolfgang Schmid Unterlagen QUADRATISCHE GLEICHUNGENN Definition: Eine
Tutorium Mathematik II M WM
 Tutorium Mathematik II M WM 9.6.7 Lösungen Lösen Sie folgende Systeme von Differentialgleichungen der Form x = A x + b mit. A = 6 und b = et. e t Hinweis: Die Eigenwerte und -vektoren der Matrix A lauten:
Tutorium Mathematik II M WM 9.6.7 Lösungen Lösen Sie folgende Systeme von Differentialgleichungen der Form x = A x + b mit. A = 6 und b = et. e t Hinweis: Die Eigenwerte und -vektoren der Matrix A lauten:
Mathematischer Vorkurs NAT-ING II
 Mathematischer Vorkurs NAT-ING II (02.09.2013 20.09.2013) Dr. Jörg Horst WS 2013-2014 Mathematischer Vorkurs TU Dortmund Seite 1 / 252 Kapitel 15 Komplexe Zahlen Mathematischer Vorkurs TU Dortmund Seite
Mathematischer Vorkurs NAT-ING II (02.09.2013 20.09.2013) Dr. Jörg Horst WS 2013-2014 Mathematischer Vorkurs TU Dortmund Seite 1 / 252 Kapitel 15 Komplexe Zahlen Mathematischer Vorkurs TU Dortmund Seite
11. Übung zur Vorlesung Zahlentheorie. im Wintersemester 2016/17. Untersuche mit dem Lucas-Lehmer-Test, ob die Zahl n = prim ist.
 11. Übung zur Vorlesung Aufgabe 41. Untersuche mit dem Lucas-Lehmer-Test, ob die Zahl n = 2 11 1 prim ist. Aufgabe 42. Beweise das folgende Kriterium von Proth mit dem Pocklington-Test: Sei n > 1 gegeben.
11. Übung zur Vorlesung Aufgabe 41. Untersuche mit dem Lucas-Lehmer-Test, ob die Zahl n = 2 11 1 prim ist. Aufgabe 42. Beweise das folgende Kriterium von Proth mit dem Pocklington-Test: Sei n > 1 gegeben.
Algebraische Gleichungen
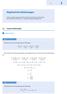 13 Algebraische Gleichungen H.Ra,J.M.Ra,Übungsbuch Mathematik für Fachschule Technik und Berufskolleg, OI 10.1007/978-3-658-07788-4_, Sringer Fachmedien Wiesbaden 015.1 Lineare Gleichungen >Lehrbuch Kaitel
13 Algebraische Gleichungen H.Ra,J.M.Ra,Übungsbuch Mathematik für Fachschule Technik und Berufskolleg, OI 10.1007/978-3-658-07788-4_, Sringer Fachmedien Wiesbaden 015.1 Lineare Gleichungen >Lehrbuch Kaitel
Zahlentheoretische Variationen zum Satz des Pythagoras
 Zahlentheoretische zum Satz des nstitut für Mathematik Humboldt-Universität zu Berlin 17. Januar 2017 Aus Die Pythagoreer von Bartel L. van der Waerden Satz. Ein rechtwinkliges Dreieck mit den Katheten
Zahlentheoretische zum Satz des nstitut für Mathematik Humboldt-Universität zu Berlin 17. Januar 2017 Aus Die Pythagoreer von Bartel L. van der Waerden Satz. Ein rechtwinkliges Dreieck mit den Katheten
Summen aufeinander folgender Quadrate, die ein Quadrat ergeben
 Elem Math 60 (2005) 66 71 001-6018/05/020066-6 c Swiss Mathematical Society, 2005 Elemente der Mathematik Summen aufeinander folgender Quadrate, die ein Quadrat ergeben Josef Rung und Johann Werner Josef
Elem Math 60 (2005) 66 71 001-6018/05/020066-6 c Swiss Mathematical Society, 2005 Elemente der Mathematik Summen aufeinander folgender Quadrate, die ein Quadrat ergeben Josef Rung und Johann Werner Josef
Symmetrische Polynome,Diskriminante und Resultante, Fermatscher Satz für Polynome
 Proseminar Lineare Algebra SS10 Symmetrische Polynome,Diskriminante und Resultante, Fermatscher Satz für Polynome Natalja Shesterina Heinrich-Heine-Universität ASymmetrische Polynome Definition 1 Sei n
Proseminar Lineare Algebra SS10 Symmetrische Polynome,Diskriminante und Resultante, Fermatscher Satz für Polynome Natalja Shesterina Heinrich-Heine-Universität ASymmetrische Polynome Definition 1 Sei n
2015, MNZ. Jürgen Schmidt. 2.Tag. Vorkurs. Mathematik WS 2015/16
 Vorkurs Mathematik WS 2015/16 2.Tag Arten von Gleichungen Lineare Gleichungen (und Funktionen) 0 = ax + b (oft als Funktion: y = mx + n) a,b R Parameter m Anstieg, n Achsenabschnitt Quadratische Gleichungen
Vorkurs Mathematik WS 2015/16 2.Tag Arten von Gleichungen Lineare Gleichungen (und Funktionen) 0 = ax + b (oft als Funktion: y = mx + n) a,b R Parameter m Anstieg, n Achsenabschnitt Quadratische Gleichungen
22. Ermitteln Sie die Lösungsmengen der folgenden Gleichungssysteme mit dem Additionsverfahren:
 Aufgaben zur Selbstüberprüfung: 20. Ermitteln Sie die Lösungsmengen der folgenden linearen Gleichungssysteme mit dem Gleichsetzung verfahren: a) I) 2x) - X2 = 5 b) 3x) - 6X2 = 9 c) 4x) + 2x2 = 8 TI) 3x)
Aufgaben zur Selbstüberprüfung: 20. Ermitteln Sie die Lösungsmengen der folgenden linearen Gleichungssysteme mit dem Gleichsetzung verfahren: a) I) 2x) - X2 = 5 b) 3x) - 6X2 = 9 c) 4x) + 2x2 = 8 TI) 3x)
Analysis 1, Woche 3. Komplexe Zahlen I. 3.1 Etwas Imaginäres
 Analysis, Woche 3 Komplexe Zahlen I A 3. Etwas Imaginäres Zusätzlich zu den reellen Zahlen führen wir das Symbol i ein und wir vereinbaren: i. Wir möchten die reellen Zahlen erweitern mit i. Das heißt,
Analysis, Woche 3 Komplexe Zahlen I A 3. Etwas Imaginäres Zusätzlich zu den reellen Zahlen führen wir das Symbol i ein und wir vereinbaren: i. Wir möchten die reellen Zahlen erweitern mit i. Das heißt,
L-Funktionen in Geometrie und Arithmetik
 Fachbereich Mathematik Technische Universität Darmstadt bruinier@mathematik.tu-darmstadt.de 30. Januar 2008 Leonhard Euler (1707 1783) Bernhard Riemann (1826-1866) Die rationalen Zahlen Prinzahlen Die
Fachbereich Mathematik Technische Universität Darmstadt bruinier@mathematik.tu-darmstadt.de 30. Januar 2008 Leonhard Euler (1707 1783) Bernhard Riemann (1826-1866) Die rationalen Zahlen Prinzahlen Die
Übung ln(p) x aus dem Primzahlsatz π(x) x/ ln(x) folgt. Gehen Sie dabei wie folgt vor: i) p x
 Übung 0 Übung 0 Zeigen Sie, dass der Primzahlsatz π(x) x/ ln(x) aus p x ln(p) x folgt Übung 02 Zeigen Sie, dass p x ln(p) x aus dem Primzahlsatz π(x) x/ ln(x) folgt Gehen Sie dabei wie folgt vor: i) p
Übung 0 Übung 0 Zeigen Sie, dass der Primzahlsatz π(x) x/ ln(x) aus p x ln(p) x folgt Übung 02 Zeigen Sie, dass p x ln(p) x aus dem Primzahlsatz π(x) x/ ln(x) folgt Gehen Sie dabei wie folgt vor: i) p
Algebra. (b) Der Beweis funktioniert analog zu Teil (a), nur daß wir in der Argumentation Z durch R und 2 durch c ersetzen müssen.
 Fachbereich Mathematik Prof. Dr. Nils Scheithauer Walter Reußwig TECHNISCHE UNIVERSITÄT DARMSTADT WS 08/09 2. Dezember 2008 Algebra 8. Übung mit Lösungshinweisen Aufgabe 36 (a) Zeige, daß Z[X] kein Hauptidealring
Fachbereich Mathematik Prof. Dr. Nils Scheithauer Walter Reußwig TECHNISCHE UNIVERSITÄT DARMSTADT WS 08/09 2. Dezember 2008 Algebra 8. Übung mit Lösungshinweisen Aufgabe 36 (a) Zeige, daß Z[X] kein Hauptidealring
sie ist also eine Lösung der Differenzialgleichung y 0 = Ay. Bei x = 0 sind diese n Spalten auch linear unabhängig, da ja
 Lineare Systeme mit konstanten Koeffizienten 44 63 Zusammenhang mit Fundamentalsystemen Für die Matrix-Exponenzialfunkton e Ax gilt (e Ax ) = Ae Ax Für jede Spalte '(x) der Matrix e Ax Matrixmultpiplikation
Lineare Systeme mit konstanten Koeffizienten 44 63 Zusammenhang mit Fundamentalsystemen Für die Matrix-Exponenzialfunkton e Ax gilt (e Ax ) = Ae Ax Für jede Spalte '(x) der Matrix e Ax Matrixmultpiplikation
Theorie 3: Graphische Veranschaulichung der Fallunterscheidung
 Die Formel von Cardano - mit grahischer Lösung Theorie : Grahische Veranschaulichung der Fallunterscheidung Gegeben ist eine kubische Gleichung in reduzierter Form: x x = 0 mit 0 IR. Definieren Sie einen
Die Formel von Cardano - mit grahischer Lösung Theorie : Grahische Veranschaulichung der Fallunterscheidung Gegeben ist eine kubische Gleichung in reduzierter Form: x x = 0 mit 0 IR. Definieren Sie einen
Numerische Lineare Algebra
 Numerische Lineare Algebra Vorlesung 5 Prof. Dr. Klaus Höllig Institut für Mathematischen Methoden in den Ingenieurwissenschaften, Numerik und Geometrische Modellierung SS 21 Prof. Dr. Klaus Höllig (IMNG)
Numerische Lineare Algebra Vorlesung 5 Prof. Dr. Klaus Höllig Institut für Mathematischen Methoden in den Ingenieurwissenschaften, Numerik und Geometrische Modellierung SS 21 Prof. Dr. Klaus Höllig (IMNG)
Erste Schularbeit Mathematik Klasse 7D WIKU am
 Erste Schularbeit Mathematik Klasse 7D WIKU am 12.11.2014 ANTWORTVORLAGE Achtung: Teil 2 war noch in einem anderen Modus, daher muss man die Punkte umrechnen P unkte wirkliche P unkte =. Kompensationspunkte
Erste Schularbeit Mathematik Klasse 7D WIKU am 12.11.2014 ANTWORTVORLAGE Achtung: Teil 2 war noch in einem anderen Modus, daher muss man die Punkte umrechnen P unkte wirkliche P unkte =. Kompensationspunkte
1 Lineare Gleichungssysteme und Matrizen
 1 Lineare Gleichungssysteme und Matrizen Das Studium linearer Gleichungssysteme und ihrer Lösungen ist eines der wichtigsten Themen der linearen Algebra. Wir werden zunächst einige grundlegende Begriffe
1 Lineare Gleichungssysteme und Matrizen Das Studium linearer Gleichungssysteme und ihrer Lösungen ist eines der wichtigsten Themen der linearen Algebra. Wir werden zunächst einige grundlegende Begriffe
Vorkurs Mathematik 2016
 Vorkurs Mathematik 2016 Vorkurs Mathematik Grad n p(x) =a n x n + a n 1 x n 1 +...+ a 1 x + a 0 führender Koeffizient Absolutglied a n, a n 1,..., a 1, a 0... Koeffizienten a n = 1... normiertes Polynom
Vorkurs Mathematik 2016 Vorkurs Mathematik Grad n p(x) =a n x n + a n 1 x n 1 +...+ a 1 x + a 0 führender Koeffizient Absolutglied a n, a n 1,..., a 1, a 0... Koeffizienten a n = 1... normiertes Polynom
Faktorisierung von Polynomen
 Faktorisierung von Polynomen Ein Polynom p vom Grad n besitzt, einschließlich Vielfachheiten, genau n komplexe Nullstellen z k und lässt sich somit als Produkt der entsprechenden Linearfaktoren schreiben:
Faktorisierung von Polynomen Ein Polynom p vom Grad n besitzt, einschließlich Vielfachheiten, genau n komplexe Nullstellen z k und lässt sich somit als Produkt der entsprechenden Linearfaktoren schreiben:
Mathematischer Vorbereitungskurs für Ökonomen
 Mathematischer Vorbereitungskurs für Ökonomen Dr. Thomas Zehrt Wirtschaftswissenschaftliches Zentrum Universität Basel Ungleichungen Inhalt: 1. Grundlegendes 2. Lineare Ungleichungen 3. Ungleichungen mit
Mathematischer Vorbereitungskurs für Ökonomen Dr. Thomas Zehrt Wirtschaftswissenschaftliches Zentrum Universität Basel Ungleichungen Inhalt: 1. Grundlegendes 2. Lineare Ungleichungen 3. Ungleichungen mit
Gewöhnliche Differentialgleichungen. Teil II: Lineare DGLs mit konstanten Koeffizienten
 - 1 - Gewöhnliche Differentialgleichungen Teil II: Lineare DGLs mit konstanten Koeffizienten Wir wenden uns jetzt einer speziellen, einfachen Klasse von DGLs zu, die allerdings in der Physik durchaus beträchtliche
- 1 - Gewöhnliche Differentialgleichungen Teil II: Lineare DGLs mit konstanten Koeffizienten Wir wenden uns jetzt einer speziellen, einfachen Klasse von DGLs zu, die allerdings in der Physik durchaus beträchtliche
Armin Leutbecher. Zahlentheorie. Eine Einführung in die Algebra. Mit 9 Abbildungen, 6 Tabellen und 1 Falttafel. SJ Springer
 Armin Leutbecher Zahlentheorie Eine Einführung in die Algebra Mit 9 Abbildungen, 6 Tabellen und 1 Falttafel SJ Springer Inhaltsverzeichnis Einleitung 1 Häufig verwendete Abkürzungen 9 1 Der Fundamentalsatz
Armin Leutbecher Zahlentheorie Eine Einführung in die Algebra Mit 9 Abbildungen, 6 Tabellen und 1 Falttafel SJ Springer Inhaltsverzeichnis Einleitung 1 Häufig verwendete Abkürzungen 9 1 Der Fundamentalsatz
Anwendungen der Differentialrechnung
 KAPITEL 3 Anwendungen der Differentialrechnung 3.1 Lokale Maxima und Minima Definition 16: Sei f : D R eine Funktion von n Veränderlichen. Ein Punkt x heißt lokale oder relative Maximalstelle bzw. Minimalstelle
KAPITEL 3 Anwendungen der Differentialrechnung 3.1 Lokale Maxima und Minima Definition 16: Sei f : D R eine Funktion von n Veränderlichen. Ein Punkt x heißt lokale oder relative Maximalstelle bzw. Minimalstelle
Algebraische Gleichungen. Martin Brehm February 2, 2007
 Algebraische Gleichungen Martin Brehm February, 007 1. Der Begriff Algebra Algebraische Gleichungen Durch das herauskristalisieren von mehreren Teilgebieten der Algebra ist es schwer geworden eine einheitliche
Algebraische Gleichungen Martin Brehm February, 007 1. Der Begriff Algebra Algebraische Gleichungen Durch das herauskristalisieren von mehreren Teilgebieten der Algebra ist es schwer geworden eine einheitliche
Theorie der reell abgeschlossenen Körper (RCF)
 Theorie der reell abgeschlossenen Körper (RCF) 1 Einführung Die im Vortrag betrachteten Modelle verwenden die Sprache L ORing ={0,1,+,-,,
Theorie der reell abgeschlossenen Körper (RCF) 1 Einführung Die im Vortrag betrachteten Modelle verwenden die Sprache L ORing ={0,1,+,-,,
3 Gewöhnliche Differentialgleichungen 23.4.
 3 Gewöhnliche Differentialgleichungen 23.4. 3.1 Differentialgleichungen erster Ordnung 3.1.1 Fundamentalsätze Definition 3.1. Es sei Ω R d eine offene Menge und V : Ω R d eine Vektorfunktion. Eine Kurve
3 Gewöhnliche Differentialgleichungen 23.4. 3.1 Differentialgleichungen erster Ordnung 3.1.1 Fundamentalsätze Definition 3.1. Es sei Ω R d eine offene Menge und V : Ω R d eine Vektorfunktion. Eine Kurve
Konstruktion der reellen Zahlen
 Konstruktion der reellen Zahlen Zur Wiederholung: Eine Menge K (mit mindestens zwei Elementen) heißt Körper, wenn für beliebige Elemente x, y K eindeutig eine Summe x+y K und ein Produkt x y K definiert
Konstruktion der reellen Zahlen Zur Wiederholung: Eine Menge K (mit mindestens zwei Elementen) heißt Körper, wenn für beliebige Elemente x, y K eindeutig eine Summe x+y K und ein Produkt x y K definiert
Körper- und Galoistheorie
 Prof. Dr. H. Brenner Osnabrück SS 2011 Körper- und Galoistheorie Vorlesung 11 Zerfällungskörper Wir wollen zu einem Polynom F K[X] einen Körper konstruieren, über dem F in Linearfaktoren zerfällt. Dies
Prof. Dr. H. Brenner Osnabrück SS 2011 Körper- und Galoistheorie Vorlesung 11 Zerfällungskörper Wir wollen zu einem Polynom F K[X] einen Körper konstruieren, über dem F in Linearfaktoren zerfällt. Dies
Über konvexe Matrixfunktionen.*)
 Wegener, Untersuchungen download unter www.biologiezentrum.at über Finslersche Räume. 7 III. Zwei- und dreidimensionale Finslersche Räume mit 3 der Grundform: L = ] / aiklx' x 'k x '1 Im zweidimensionalen
Wegener, Untersuchungen download unter www.biologiezentrum.at über Finslersche Räume. 7 III. Zwei- und dreidimensionale Finslersche Räume mit 3 der Grundform: L = ] / aiklx' x 'k x '1 Im zweidimensionalen
Lösung zu Serie [Aufgabe] Faktorisieren Sie die folgenden Polynome so weit wie möglich:
![Lösung zu Serie [Aufgabe] Faktorisieren Sie die folgenden Polynome so weit wie möglich: Lösung zu Serie [Aufgabe] Faktorisieren Sie die folgenden Polynome so weit wie möglich:](/thumbs/67/57409595.jpg) Lineare Algebra D-MATH, HS 04 Prof. Richard Pink Lösung zu Serie. [Aufgabe] Faktorisieren Sie die folgenden Polynome so weit wie möglich: a) F (X) := X 5 X in R[X] und C[X]. b) F (X) := X 4 +X 3 +X in
Lineare Algebra D-MATH, HS 04 Prof. Richard Pink Lösung zu Serie. [Aufgabe] Faktorisieren Sie die folgenden Polynome so weit wie möglich: a) F (X) := X 5 X in R[X] und C[X]. b) F (X) := X 4 +X 3 +X in
D-MATH, D-PHYS, D-CHAB Analysis I HS 2017 Prof. Manfred Einsiedler. Lösung 4
 D-MATH, D-PHYS, D-CHAB Analysis I HS 017 Prof. Manfred Einsiedler Lösung 4 Hinweise 1. Zeigen Sie, dass inf X die kleinste obere Schranke von X ist.. Dass z 1, z Lösungen sind, kann man durch Einsetzen
D-MATH, D-PHYS, D-CHAB Analysis I HS 017 Prof. Manfred Einsiedler Lösung 4 Hinweise 1. Zeigen Sie, dass inf X die kleinste obere Schranke von X ist.. Dass z 1, z Lösungen sind, kann man durch Einsetzen
beschrieben. Von unten betrachtet, werden die ganzen Zahlen als Erweiterung der natürlichen Zahlen eingeführt, um uneingeschränkt die Gleichung
 4 Komplexe Zahlen Wir haben bisher das Zahlengebäude N Z Q R beschrieben. Von unten betrachtet, werden die ganzen Zahlen als Erweiterung der natürlichen Zahlen eingeführt, um uneingeschränkt die Gleichung
4 Komplexe Zahlen Wir haben bisher das Zahlengebäude N Z Q R beschrieben. Von unten betrachtet, werden die ganzen Zahlen als Erweiterung der natürlichen Zahlen eingeführt, um uneingeschränkt die Gleichung
Minkowski-Theorie & die Klassenzahl
 Minkowski-Theorie & die Klassenzahl David Müßig Seminar zur Kommutativen Algebra Bemerkung 1. Wir betrachten im Folgenden stets endliche Körpererweiterungen K Q vom Grade n (K ist also ein algebraischer
Minkowski-Theorie & die Klassenzahl David Müßig Seminar zur Kommutativen Algebra Bemerkung 1. Wir betrachten im Folgenden stets endliche Körpererweiterungen K Q vom Grade n (K ist also ein algebraischer
( ) ( ) Schnittpunkt mit der y Achse P 0 y : Bedingung: y = f 0. y s s
 R. Brinkmann http://brinkmann-du.de Seite 07.0.0 Achsenschnittpunkte ganzrationaler Funktionen Schnittpunkt mit der y Achse P 0 y : Bedingung: y = f 0 y s s f = f 0 = 0 0 = 0 0 = P ( 0 ) oder P ( 0 f(0)
R. Brinkmann http://brinkmann-du.de Seite 07.0.0 Achsenschnittpunkte ganzrationaler Funktionen Schnittpunkt mit der y Achse P 0 y : Bedingung: y = f 0 y s s f = f 0 = 0 0 = 0 0 = P ( 0 ) oder P ( 0 f(0)
2. Reelle und komplexe Zahlen [Sch-St ]
![2. Reelle und komplexe Zahlen [Sch-St ] 2. Reelle und komplexe Zahlen [Sch-St ]](/thumbs/76/73697648.jpg) 7 2. Reelle und komplexe Zahlen [Sch-St 6.4-6.5] 2.1 Körperstruktur und Anordnung von R [Kö 2.1-2.2] Für (beliebige) reelle Zahlen a, b, c R gelten die folgenden (algebraischen) Körperaxiome: (K1) a +
7 2. Reelle und komplexe Zahlen [Sch-St 6.4-6.5] 2.1 Körperstruktur und Anordnung von R [Kö 2.1-2.2] Für (beliebige) reelle Zahlen a, b, c R gelten die folgenden (algebraischen) Körperaxiome: (K1) a +
Mathematikaufgaben zur Vorbereitung auf das Studium
 Hochschule für Technik und Wirtschaft Dresden (FH) Fachbereich Informatik/Mathematik Mathematikaufgaben zur Vorbereitung auf das Studium Studiengänge Allgemeiner Maschinenbau Fahrzeugtechnik Dresden 2002
Hochschule für Technik und Wirtschaft Dresden (FH) Fachbereich Informatik/Mathematik Mathematikaufgaben zur Vorbereitung auf das Studium Studiengänge Allgemeiner Maschinenbau Fahrzeugtechnik Dresden 2002
Einführung in die Zahlentheorie
 Einführung in die Zahlentheorie Jörn Steuding Uni Wü, SoSe 2015 I Zahlen II Modulare Arithmetik III Quadratische Reste IV Diophantische Gleichungen V Quadratische Formen Wir behandeln die wesentliche Zahlentheorie
Einführung in die Zahlentheorie Jörn Steuding Uni Wü, SoSe 2015 I Zahlen II Modulare Arithmetik III Quadratische Reste IV Diophantische Gleichungen V Quadratische Formen Wir behandeln die wesentliche Zahlentheorie
m 1 Die Bewegung der drei Kugeln wird beschrieben durch das folgende Differentialgleichungssystem x 1 (t) x 2 (t) x 3 (t) k 12 k 12 k 12 k k 23
 Kapitel 5 Eigenwerte 5. Definition und Beispiele Wir sehen uns ein System dreier schwingender Kugeln der Massen m, m und m 3 an, die durch Federn aneinander gekoppelt sein sollen. m k m k 3 m 3 x ( t x
Kapitel 5 Eigenwerte 5. Definition und Beispiele Wir sehen uns ein System dreier schwingender Kugeln der Massen m, m und m 3 an, die durch Federn aneinander gekoppelt sein sollen. m k m k 3 m 3 x ( t x
