M_G7 EF Pvn Klausurvorbereitung: Lösungen 13. Oktober Klausurvorbereitung. Lösungen
|
|
|
- Josef Schmidt
- vor 7 Jahren
- Abrufe
Transkript
1 Klausurvorbereitung Lösungen I. Funktionen Funktionen und ihre Eigenschaften S. 14 Aufg. 2 f(-2)=0,5 f(0,1)=-10 f(78)= 1 78 g(-2)=-7 g(0,1)=-2,8 g(78)=153 h(-2)=57 h(0,1)=23,82 h(78)=11257 D f = R/{0} D g = R D h = R Wertetabellen und Graphen zu den Funktionen f, g und h siehe Abbildungen 1 und 2. W f = R/{0} W g = R W h = [7; ) d) Es gelten f(1) = 1 und f(5, 5) 0, 18, d.h. dass Punkt P auf dem Graphen von f liegt, Punkt Q aber nicht. Es gelten g(1) = 1 und g(5, 5) = 8, d.h. Punkte P und Q liegen beide auf dem Graphen von g. Es gelten h(1) = 15 und h(5, 5) = 19, 5, d.h. Punkte P und Q liegen beide nicht auf dem Graphen von h. 1
2 Abbildung 1: Wertetabelle zu den Funktionen f, g und h Abbildung 2: Graphen zu den Funktionen f (blau), g (rot) und h (grün) 2
3 S. 14 Aufg. 3 u(-2)=-46 u(0,1)=-12,82 u(78)= v(-2)=0,5 v(0,1) 0,24 v(78) 0,012 w(-2) -0,33 w(0,1) -1,11 w(78) 0,013 D u = R D v = R/{-4} D w = R/{1} Wertetabellen und Graphen zu den Funktionen u, v und w siehe Abbildungen 3 und 4. W u = ( ; 4] W v = R/{0} W w = R/{0} d) Es gelten u(1) = 4 und u(5, 5) = 8, 5 sowie v(1) = 0, 2 und v(5, 5) 0, 11. Ferner ist w(1) nicht definiert und w(5, 5) 0, 22. Diese Ergebnisse bedeuten, dass keiner der Punkte P und Q auf den Graphen der Funktionen u, v und w liegen. 3
4 Abbildung 3: Wertetabellen zu den Funktionen u, v und w Abbildung 4: Graphen zu den Funktionen u (blau), v (rot) und w (grün) 4
5 S. 15 Aufg. 1 Die Lösung dieser Aufgabe finden Sie im Buch auf der Seite 255. Lineare und quadratische Funktionen Bitte beachten Sie hier die Aufgabenzettel, die Sie im Unterricht bekommen haben und die Lösungen, die Sie erarbeitet und besprochen haben. Potenzfunktionen S. 21 Aufg. 2 Im Folgenden sind in den Abbildungen 5 bis 7 die Wertetabellen bzw. die Funktionsplots für die Graphen von,, und d) aufgeführt. Abbildung 5: Wertetabelle für in blau und in rot 5
6 Abbildung 6: Wertetabelle für in grün und d) in lila Abbildung 7: Graphen zu Funktionen in in blau, in rot, in grün und d) in lila 6
7 S. 21 Aufg. 3 Zur Funktion f gehört der Graph C. Da der Exponent gerade ist, haben alle Funktionswerte das gleiche Vorzeichen. Hier sind sie immer positiv. Es gibt nur zwei Funktionsgleichungen mit geradem Exponenten. Der Graph der Funktion j mit j(x) = x 1 0 verläuft wesentlich steiler als der Graph zu f mit f(x) = 0, 01x 4, weshalb C zur Funktion f gehört. Zur Funktion g gehört der Graph D. Da der Exponent ungerade ist, wechseln die Funktionswerte das Vorzeichen bei x = 0. Hier sind sie für x < 0 negativ und für x > 0 positiv. Es kommen daher nur die Graphen B und D infrage. Eine Punktprobe für x = 2 ergibt: g(x) = 4. Dies ist nur beim Graphen D richtig. Zur Funktion h gehört der Graph B. Siehe Begründung zum Aufgabenteil. d) Zur Funktion j gehört der Graph A. Siehe Begründung zum Aufgabenteil. S. 22 Aufg. 5 Abbildung 8: Funktionsplots zu f (blau), g (rot), h (grün) und j (lil 7
8 Gemeinsamkeiten: Alle Graphen verlaufen durch den Ursprung, weil es sich um Potenzfunktionen handelt. Die Graphen von den Funktionen f und h haben nur positive Funktionswerte, weil der Exponent jeweils gerade ist und der Vorfaktor mit 0,1 positiv ist. Die Funktionswerte von den Funktionen g und j wechseln bei x = 0 ihr Vorzeichen. Hier sind sie für x < 0 negativ und x > 0 positiv, weil der Vorfaktor mit 0,1 positiv ist. Unterschiede: Je höher der Exponent in der Funktionsgleichung ist, desto steiler verläuft der Graph. S. 22 Aufg. 7 Setzt man den Punkt P in f(x) = a x n ein, ergibt sich: 0, 5 = a 1 n Da 1 n = 1 für alle n R gilt, egal was man für n einsetzt, ist a = 0, 5. Es folgt: 32 = 0, 5 ( 2) n 64 = ( 2) n 64 = ( 2) 6 So ist n = 6. Man hat nun n und a gefunden und es ergibt sich für die Funktionsgleichung: y = 0, 5 x 6 Mit derselben Methode wie in ergibt sich für die Funktionsgleichung y = 0, 25 x 7. Mit derselben Methode wie in ergibt sich für die Funktionsgleichung y = 2 x 4. d) Mit derselben Methode wie in ergibt sich für die Funktionsgleichung y = 0, 4 x 3. e) Mit derselben Methode wie in ergibt sich für die Funktionsgleichung y = 3 x 5. f) Mit derselben Methode wie in ergibt sich für die Funktionsgleichung y = 7 x 4. 8
9 S. 22 Aufg. 11 Für das Volumen V eines Würfels gilt V = x 3, wobei x die Kantenlänge des Würfels darstellt. Diese Formel kann man in der Formelsammlung nachschlagen, falls sie nicht mehr parat ist. Ein Würfel mit der Kantenlänge x = 3 cm wiegt 3 g. Die allgemeine Form einer Potenzfunktion ist y = a x n. Das bedeutet für den Würfel mathematisch: 3 = a 1, 5 3 Man setzt also für y = 3, da sich nach dem Wiegen des Würfels das Gewicht gleich 3 ergeben soll. Die Kantenlänge ist x, also x = 1, 5. Dies setzt man auch in die allgemeine Form der Potenzfunktion ein. Den Faktor a kennt man nicht, man muss es nun ermitteln: 3 = a 1, = a = a a = Setzt man nun a in die allgemeine Form, so ergibt sich die endgültige Gleichung für das Gewicht des Würfels: y = x3 Berechne nun das Gewicht für die Kantenlänge 1,5 cm und zusätzlich die für 3 cm und 1,5 cm: y = , 53 = 3 y = = 24 y = = Antwort: Der Würfel mit der Kantenlänge 1,5 cm wiegt 3 g, wie in der Aufgabe vorgegeben. Der Würfel mit der Kantenlänge 3 cm wiegt 24 g und der Würfel mit der Kantenlänge 150 cm wiegt g bzw kg. 9
10 Ganzrationale Funktionen S. 26 Aufg. 4 Es gelten lim Es gelten lim Es gelten lim d) Es gelten lim x f(x) = und lim x x f(x) = und lim x x f(x) = und lim x x f(x) = und lim x f(x) =. f(x) =. f(x) =. f(x) =. e) Es gelten lim f(x) = und lim f(x) =. x x f) Es gelten lim f(x) = und lim f(x) =. x x S. 26 Aufg. 6 Der Graph der Funktion g gehört zum Graphen in Fig. 1, da der y-achsenabschnitt bei 2 liegt und dies der einzige Graph ist, bei dem dies gilt. Es gelten außerdem lim g(x) = x und lim g(x) =. x Der Graph der Funktion f gehört zum Graphen in Fig. 2, da der Graph durch den Ursprung verläuft. Es gelten außerdem lim f(x) = und lim f(x) =. x x Der Graph der Funktion k gehört zum Graphen in Fig. 3, da der y-achsenabschnitt bei 1 liegt und dies der einzige Graph ist, bei dem dies gilt. Es gelten außerdem lim k(x) = x und lim k(x) =. x Der Graph der Funktion h gehört zum Graphen in Fig. 4, da der Graph durch den Ursprung verläuft. Es gelten außerdem lim h(x) = und lim h(x) =. x x S. 26 Aufg. 7 Die Funktion h mit h(t) = 8t 3 +60t 2 +50t+600 gibt an, in welcher Höhe sich die Gondel zum Zeitpunkt t befindet. Hier ist t die Variable und wird in Minuten angegeben. h wird in Metern angegeben. Möchte man die Berghöhe ermitteln, muss man die Zeit betrachten, die die Gondel bis zur Berghöhe braucht. Dies sind 5 Minuten und 20 Sekunden. Umgerechnet in Minuten 10
11 folgt: Daraus folgt für die Höhe: = 16 3 h(t) = 8t t t h( 16 3 ) = 8 ( ) ( 16 3 ) Antwort: Die Bergstation befindet sich in ungefähr 1360 Meter Höhe. Möchte man die Zeit für die 2000-m-Grenze ermitteln, setzt man für h(t) = 2000 ein und berechnet t. Es folgt: h(t) = 8t t t = 8t t t = 8t t t = t t t Man löse diese Gleichung mit dem ClassPad. (Erinnerung: Definieren Sie sich eine Funktion mit dem Befehl define und lösen Sie diese mit dem Befehl solve). Diese Gleichung hat nur eine Lösung (dreifache Lösung), nämlich t 4, 15 Eine negative Zeit ergibt keinen Sinn, sodass man mit der Funktion h folgern kann, dass die Gondel nie bis in die 2000 Meter Höhe fährt. Vergleicht man den Graphen der Funktion (s. Abb. 9) mit dieser Vermutung, dann findet man eine Bestätigung. Die Gondel fährt maximal nur bis in die 1361 Meter Höhe. Antwort: Die Gondel durchbricht nie die 2000-m-Grenze! Da die Gondel bei 600 Meter Höhe startet und nur bis ungefähr 1361 Meter Höhe fährt, ist eine sinnvolle Definitionsmenge D f = {x R 0 < x < 8}. Auf die 8 Minuten kommt man, weil der Graph für den Wert 600 zwei x-werte hat, nämlich die 0 und ungefähr 8. Man kann in der Abbildung 9 beobachten, dass bei 0 Metern die Gondel an der 11
12 Abbildung 9: Der Graph der Funktion h. Talstation startet und bei 5,39 Minuten an der Bergstation ist und nach 8 Minuten wieder unten an der Talstation. Die Gondel fährt somit schneller abwärts als aufwärts. Auch diesen Bereich (bis x = 8) muss man also berücksichtigen. Somit ist die Eingrenzung der Bewegung der Gondel auf den Definitionsbereich D f = {x R 0 < x < 8} sinnvoll. S. 27 Aufg. 1 Die Lösung finden Sie im Buch auf der Seite 255. S. 27 Aufg. 8 lim f(x) = und lim f(x) = x x lim f(x) = und lim f(x) = x x lim f(x) = und lim f(x) = x x d) lim f(x) = und lim f(x) = x x 12
13 Symmetrie S. 29 Aufg. 2 Es gelten die Bedingungen f( x) = f(x) für Achsensymmetrie zur y-achse und weiter f( x) = f(x) für Punktsymmetrie zum Ursprung (0 0). f ist gerade, der Graph von f verläuft achsensymmetrisch zur y-achse. Es gilt: f( x) = ( x) 4 = x 4 = f(x) f ist weder gerade noch ungerade, der Graph von f verläuft weder achsensymmetrisch zur y-achse noch punktsymmetrisch zum Ursprung. Es gelten: f( x) = 2( x) + 3 = 2x + 3 f(x) f( x) f hat nur gerade Exponenten und ist gerade, der Graph von f verläuft achsensymmetrisch zur y-achse. Es gilt: f( x) = 7 ( x) 4 + 2( x) 6 = 7 x 4 + 2x 6 = f(x) d) f ist weder gerade noch ungerade, der Graph von f verläuft weder achsensymmetrisch zur y-achse noch punktsymmetrisch zum Ursprung. Es gelten: f( x) = 4( x) = 4x f(x) f(x) e) f hat nur gerade Exponenten und ist gerade, der Graph von f verläuft achsensymmetrisch zur y-achse. Es gilt: f( x) = 1 6 ( x)6 ( x) = 1 6 x6 x = f(x) f) f hat nur ungerade Exponenten und ist ungerade, der Graph von f verläuft punktsymmetrisch zum Ursprung. Es gilt: f( x) = ( x) 3 ( x + 1)( x 1) = x 3 ( x + 1)( x 1) = [x 3 (x + 1)(x 1)] = f(x) S. 29 Aufg. 4 Diese Aufgabe muss rechnerisch und graphisch gelöst werden. Zu der Graphischen Lösung schauen Sie bitte in den Abbildungen 10 und 11 nach. 13
14 f ist ungerade, der Graph von f verläuft punktsymmetrisch zum Ursprung. Es gilt: f( x) = 1 x = 1 x = f(x) f ist gerade, der Graph von f verläuft achsensymmetrisch zur y-achse. Es gilt: f( x) = 1 ( x) 2 = 1 x 2 = f(x) f ist weder gerade noch ungerade, der Graph von f verläuft weder achsensymmetrisch zur y-achse noch punktsymmetrisch zum Ursprung. Es gilt: f( x) = 1 f(x) f(x) x + 1 Abbildung 10: Graphen zu den Funktionen in blau, rot und grün d) f ist gerade, der Graph von f ist achsensymmetrisch zur y-achse. Es gilt: f( x) = 1 ( x) 2 = 1 x 2 = f(x) 14
15 e) f ist ungerade, der Graph von f verläuft punktsymmetrisch zum Ursprung. Es gilt: x f( x) = ( x) = x x = [ x x ] = f(x) d) f ist gerade, der Graph von f ist achsensymmetrisch zur y-achse. Es gilt: 5 f( x) = ( x) 4 + ( x) = 5 2 x 4 + x = f(x) 2 Abbildung 11: Graphen zu den Funktionen in d) lila, e) schwarz und f) blau S. 30 Aufg. 2 Die Lösung zu dieser Aufgabe finden Sie im Buch auf der Seite 256. S. 30 Aufg. 7 Aussagen 1) und 5) treffen für die Funktion f zu. Aussagen 2); 3); 4) und 5) treffen für die Funktion g zu. 15
16 S. 30 Aufg. 9 Um die Symmetrie zu überprüfen, muss man die Symmetrieeigenschaften rechnerisch überprüfen. Überprüfen, ob punktsymmetrisch Es soll überprüft werden, wann f( x) = f(x) ist, damit Punktsymmetrie nachgewiesen werden kann. Es gelten: und Diese sollen gleich sein, also: f( x) = ( x) 3 + 2t( x) 2 + t( x) = x 3 + 2tx 2 tx f(x) = x 3 2tx 2 tx x 3 + 2tx 2 tx = x 3 2tx 2 tx Diese Gleichung stimmt nur, wenn t = 0 ist. Somit ist die Funktion f(x) punktsymmetrisch für t = 0. Überprüfen, ob achsensymmetrisch Nun muss man noch die Achsensymmetrie überprüfen, also f( x) = f(x). Es gelten: und Diese sollen gleich sein, also: f( x) = ( x) 3 + 2t( x) 2 + t( x) = x 3 + 2tx 2 tx f(x) = x 3 + 2tx 2 + tx x 3 + 2tx 2 tx = x 3 + 2tx 2 + tx Diese Gleichung ist nicht einmal gleich, wenn t = 0 ist, d.h. die Funktion f(x) kann nie achsensymmetrisch zur y-achse sein. Antwort: Die Funktion f(x) ist punktsymmetrisch zum Ursprung für t = 0. Sie ist aber nicht achsensymmetrisch zur y-achse. Mit der gleichen Methode wie in folgt: f ist achsensymmetrisch zur y-achse für t = 1. Mit der gleichen Methode wie in folgt: f ist punktsymmetrisch zum Ursprung für alle ungeraden t. d) Mit der gleichen Methode wie in folgt: f ist achsensymmetrisch zur y-achse für t = 2. 16
17 Transformationen: Verschiebung und Streckung von Graphen S. 39 Aufg. 1 Die Funktion g erhält man aus der Funktion f, wenn man f mit dem Faktor 2 streckt. Es gilt: g(x) = 2 f(x). Die Funktion g erhält man aus der Funktion f, wenn man f mit dem Faktor 3 2 streckt: Es gilt: g(x) = 3 2 f(x). Die Funktion g erhält man aus der Funktion f, wenn man f mit dem Faktor 1 6 staucht. Es gilt g(x) = 1 6 f(x). d) Die Funktion g erhält man aus der Funktion f, wenn man f an der x-achse spiegelt und dann mit dem Faktor 1 2 staucht. Es gilt: g(x) = 1 2 f(x). S. 40 Aufg. 1 Die Lösung dieser Aufgabe finden Sie im Buch auf der Seite 256. S. 40 Aufg. 2 (Mitte) Die Lösung dieser Aufgabe finden Sie im Buch auf der Seite 257. S. 40 Aufg. 4 Gegeben ist die Funktion f(x) mit f(x) = x 4 2x 2. g(x) = 2 f(x) 1 = 2(x 4 2x 2 ) 1 = 2x 4 4x 2 1 g(x) = f(x 1) = (x 1) 4 + 2(x 1) 2 = x 4 + 4x 3 4x Zu den Graphen der Funktion g für und siehe Abbildungen 12 bzw
18 Abbildung 12: Graphen zu den Funktionen f (blau) und g (rot) in Aufgabe Abbildung 13: Graphen zu den Funktionen f (blau) und g (grün) in Aufgabe 18
19 S. 40 Aufg. 5 Gegeben ist die Funktion f(x) = x 3 2x 2. Abbildung 14: Graph der Funktion f (blau) und g (rot) Der Graph der Funktion g ist um 2 nach rechts und 3 nach oben verschoben, also sind a = 2 und b = 3. Somit ist g(x) = (x 2) 3 2(x 2)
20 Abbildung 15: Graph der Funktion f (blau) und g (grün) Der Graph der Funktion g ist um 1 nach links und 4 nach oben verschoben, also sind a = 1 und b = 4. Somit ist g(x) = (x + 1) 3 2(x + 1)
21 Abbildung 16: Graph der Funktion f (blau) und g (lil Der Graph der Funktion g ist um 2 nach links und 2 nach unten verschoben, also sind a = 2 und b = 2. Somit ist g(x) = (x + 2) 3 2(x + 2)
22 d) Abbildung 17: Graph der Funktion f (blau) und g (schwarz) Der Graph der Funktion g ist um 1 nach rechts und 1 nach oben verschoben, also sind a = 1 und b = 1. Somit ist g(x) = (x 1) 3 2(x 1) Wiederholen - Vertiefen - Vernetzen S. 41 Aufg. 1 D f = R lim x D f = R lim x f(x) = und lim x f(x) = und lim x D f = R/{0} lim x f(x) = f(x) = f(x) = 0 und lim x f(x) = 0 22
23 Abbildung 18: Graph der Funktion f in Aufgabe Abbildung 19: Graph der Funktion f in Aufgabe 23
24 Abbildung 20: Graph der Funktion f in Aufgabe S. 41 Aufg. 5 f(x) = x 3 Es gilt: g(x) = f(x 1) + 2 = (x 1) Der Graph der Funktion f wurde um 1 nach rechts und 2 nach oben verschoben. Der Graph g ist somit nicht mehr punktsymmetrisch zum Ursprung, aber punktsymmetrisch zum Punkt P (0 2). Gegeben ist die Funktion h mit h(x) = x 4 + 8x x x + 5. Es soll gezeigt werden, dass h symmetrisch zur Geraden x = 2 ist. Um dies zu zeigen, soll gezeigt werden, dass wenn man den Graphen von h um 2 nach rechts verschiebt, sich eine Achsensymmetrie zur y-achse ergibt. Der um 2 nach rechts verschobene Graph von h soll z heißen. Dann gilt: z(x) = h(x 2) = (x 2) 4 + 8(x 2) (x 2) (x 2) + 5 Damit eine Achsensymmetrie zur y-achse vorliegt, muss die Bedingung z( x) = z(x) 24
25 gelten. Bilden Sie z( x): z( x) = ( x 2) 4 + 8( x 2) ( x 2) ( x 2) + 5 = ( (x + 2)) 4 + 8( (x + 2)) ( (x + 2)) ( (x + 2)) + 5 = (x + 2) 4 8(x + 2) (x + 2) 2 20(x + 2) + 5 = z(x) Der letzte Schritt, dass am Ende tatsächlich z(x) kann eventuell nicht sofort erkennbar sein. Zeichnen Sie in diesem Fall die beiden Graphen von z( x) und z(x). Sie sind tatsächlich gleich! Somit ist die Bedingung z( x) = z(x) wahr und die Achsensymmetrie zur y-achse ist gezeigt. S. 41 Aufg. 6 Der Graph der Funktion f ist achsensymmetrisch zur y-achse. Es gilt: f( x) = 1 8 ( x)4 ( x) = 1 8 x4 x = f(x) Folgende Schnittpunkte ergeben sich nach einer graphischen Lösung: Schnittpunkt mit der y-achse: S y (0 9 ). Graphische Lösung hierzu in der Abbildung Schnittpunkte mit der x-achse: S 1 ( 3 0) und S 2 (3 0). Graphische Lösungen hierzu in den Abbildungen 22 und 23. Man muss den Graphen um 9 8 sich dann: nach oben verschieben. Folgende Koordinaten ergeben S 1 ( 2 2 0), S 2 (0 0), S 3 (2 2 0) Graphische Lösung in der Abbildung
26 Abbildung 21: y-achsenabschnitt Abbildung 22: Schnittpunkt von f an der x-achse 26
27 Abbildung 23: Schnittpunkt von f an der x-achse Abbildung 24: Funktion f verschoben um 9 8 nach oben 27
28 Training S. 47 Aufg. 4 Die Lösung zu dieser Aufgabe finden Sie im Buch auf der Seite 258. S. 47 Aufg. 5 Die Lösung zu dieser Aufgabe finden Sie im Buch auf der Seite 258. S. 47 Aufg. 6 Die Lösung zu dieser Aufgabe finden Sie im Buch auf der Seite
Ganzrationale Funktionen
 Ganzrationale Funktionen Eine Metallwerkstatt möchte aus 60 cm langen und 40 cm breiten Metallblechen kleine Schachteln herstellen (siehe Skizze). Die Schachteln sollen möglichst groß sein. Stellen Sie
Ganzrationale Funktionen Eine Metallwerkstatt möchte aus 60 cm langen und 40 cm breiten Metallblechen kleine Schachteln herstellen (siehe Skizze). Die Schachteln sollen möglichst groß sein. Stellen Sie
Aufgabe Was wissen Sie über die Symmetrie ganzrationaler Funktionen?
 R. Brinkmann http://brinkmann-du.de Seite 0.0.0 Lösungen VBKA Ganzrationale Funktionen I Zur Vorbereitung einer Klassenarbeit en: A A A A A A A4 A4 n n Was bedeutet: f(x) = a x + a x +... + a x + a x +
R. Brinkmann http://brinkmann-du.de Seite 0.0.0 Lösungen VBKA Ganzrationale Funktionen I Zur Vorbereitung einer Klassenarbeit en: A A A A A A A4 A4 n n Was bedeutet: f(x) = a x + a x +... + a x + a x +
Diese Funktion ist mein Typ!
 Diese Funktion ist mein Typ! Überblick über die wichtigsten Funktionstypen der 10.Jgst.: Lineare Funktionen Quadratische Funktionen Ganzrationale Funktionen Gebrochen-rationale Funktionen Trigonometrische
Diese Funktion ist mein Typ! Überblick über die wichtigsten Funktionstypen der 10.Jgst.: Lineare Funktionen Quadratische Funktionen Ganzrationale Funktionen Gebrochen-rationale Funktionen Trigonometrische
Regel Die Steigung einer Funktion kann rechnerisch ermittelt werden, wenn mindestens zwei Punkte gegeben sind.
 Funktionen Station 1 Bestimmung der Steigung einer Geraden durch zwei Punkte Die Steigung einer Funktion kann rechnerisch ermittelt werden, wenn mindestens zwei Punkte gegeben sind. m = f(x 2 ) f(x 1 )
Funktionen Station 1 Bestimmung der Steigung einer Geraden durch zwei Punkte Die Steigung einer Funktion kann rechnerisch ermittelt werden, wenn mindestens zwei Punkte gegeben sind. m = f(x 2 ) f(x 1 )
R. Brinkmann Seite Klassenarbeit Mathematik Bearbeitungszeit 90 min. Di SG10 D Gruppe A NAME: Lösungen
 R. Brinkmann http://brinkmann-du.de Seite 8..0 Klassenarbeit Mathematik Bearbeitungszeit 90 min. Di.06. SG0 D Gruppe A NAME: Lösungen Hilfsmittel: Taschenrechner Alle Ergebnisse sind soweit möglich durch
R. Brinkmann http://brinkmann-du.de Seite 8..0 Klassenarbeit Mathematik Bearbeitungszeit 90 min. Di.06. SG0 D Gruppe A NAME: Lösungen Hilfsmittel: Taschenrechner Alle Ergebnisse sind soweit möglich durch
Aufgabensammlung zum Üben Blatt 1
 Aufgabensammlung zum Üben Blatt 1 Seite 1 Lineare Funktionen ohne Parameter: 1. Die Gerade g ist durch die Punkte A ( 3 4 ) und B( 2 1 ) festgelegt, die Gerade h durch die Punkte C ( 5 3 ) und D ( -2-2
Aufgabensammlung zum Üben Blatt 1 Seite 1 Lineare Funktionen ohne Parameter: 1. Die Gerade g ist durch die Punkte A ( 3 4 ) und B( 2 1 ) festgelegt, die Gerade h durch die Punkte C ( 5 3 ) und D ( -2-2
Aufstellen der Funktionsgleichung aus gegebenen Bedingungen
 R. Brinkmann http://brinkmann-du.de Seite..0 Aufstellen der Funktionsgleichung aus gegebenen Bedingungen Wir erinnern uns, um die Funktionsgleichung einer Parabel zu bestimmen waren die Koordinaten von
R. Brinkmann http://brinkmann-du.de Seite..0 Aufstellen der Funktionsgleichung aus gegebenen Bedingungen Wir erinnern uns, um die Funktionsgleichung einer Parabel zu bestimmen waren die Koordinaten von
Exponentialfunktionen. Eigenschaften, graphische Darstellungen 1-E1 Vorkurs, Mathematik
 e Exponentialfunktionen Eigenschaften, graphische Darstellungen 1-E1 Vorkurs, Mathematik Exponentialfunktionen Potenzfunktion: y = x 9 Exponentialfunktion: y = 9 x Die Potenz- und die Exponentialfunktionen
e Exponentialfunktionen Eigenschaften, graphische Darstellungen 1-E1 Vorkurs, Mathematik Exponentialfunktionen Potenzfunktion: y = x 9 Exponentialfunktion: y = 9 x Die Potenz- und die Exponentialfunktionen
Die gebrochenrationale Funktion
 Die gebrochenrationale Funktion Definition: Unter einer gebrochenrationalen Funktion versteht man den Quotienten zweier ganzrationaler Funktionen, d.h. Funktionen der Form f :x! a n xn + a n 1 x n 1 +...+
Die gebrochenrationale Funktion Definition: Unter einer gebrochenrationalen Funktion versteht man den Quotienten zweier ganzrationaler Funktionen, d.h. Funktionen der Form f :x! a n xn + a n 1 x n 1 +...+
Gebrochen-rationale Funktionen
 Definition Eine gebrochen-rationale Funktion ist eine Funktion, bei der sich im Zähler und Nenner eine ganzrationale Funktion (Polynom) befindet: Eigenschaften f(x) = g(x) h(x) Echt gebrochen-rationale
Definition Eine gebrochen-rationale Funktion ist eine Funktion, bei der sich im Zähler und Nenner eine ganzrationale Funktion (Polynom) befindet: Eigenschaften f(x) = g(x) h(x) Echt gebrochen-rationale
Grundwissen Mathematik JS 11
 GYMNASIUM MIT SCHÜLERHEIM PEGNITZ math-naturw u neusprachl Gymnasium WILHELM-VON-HUMBOLDT-STRASSE 7 957 PEGNITZ FERNRUF 94/48 FAX 94/564 Grundwissen Mathematik JS Was versteht man allgemein unter einer
GYMNASIUM MIT SCHÜLERHEIM PEGNITZ math-naturw u neusprachl Gymnasium WILHELM-VON-HUMBOLDT-STRASSE 7 957 PEGNITZ FERNRUF 94/48 FAX 94/564 Grundwissen Mathematik JS Was versteht man allgemein unter einer
Gerade, ungerade oder weder noch? Algebraische und graphische Beweise. 4-E1 Vorkurs, Mathematik
 Gerade, ungerade oder weder noch? Algebraische und graphische Beweise 4-E1 Symmetrie einer Funktion: Aufgabe 3 Bestimmen Sie algebraisch und graphisch, ob die Funktionen gerade oder ungerade sind, oder
Gerade, ungerade oder weder noch? Algebraische und graphische Beweise 4-E1 Symmetrie einer Funktion: Aufgabe 3 Bestimmen Sie algebraisch und graphisch, ob die Funktionen gerade oder ungerade sind, oder
4.5. Ganzrationale Funktionen
 .5. Ganzrationale Funktionen Definition Eine Funktion der Gestalt f(x) = a n x n a n 1 x n 1... a 2 x 2 a 1 x a 0 mit reellen Koeffizienten a n, a n 1,... und a n 0 heißt ganzrationale Funktion n-ten Grades
.5. Ganzrationale Funktionen Definition Eine Funktion der Gestalt f(x) = a n x n a n 1 x n 1... a 2 x 2 a 1 x a 0 mit reellen Koeffizienten a n, a n 1,... und a n 0 heißt ganzrationale Funktion n-ten Grades
Aufgaben zu den ganzrationalen Funktionen
 Aufgaben zu den ganzrationalen Funktionen 1. Bestimmen Sie die Nullstellen folgender ganzrationaler Funktionen. a) y = x + x 6 b) y = x 3 3x + x c) y = (x + 4)(x + x ) d) y = x 4 5x + 4 e) y = x 3 + x
Aufgaben zu den ganzrationalen Funktionen 1. Bestimmen Sie die Nullstellen folgender ganzrationaler Funktionen. a) y = x + x 6 b) y = x 3 3x + x c) y = (x + 4)(x + x ) d) y = x 4 5x + 4 e) y = x 3 + x
Differenzialrechnung
 Mathe Differenzialrechnung Differenzialrechnung 1. Grenzwerte von Funktionen Idee: Gegeben eine Funktion: Gesucht: y = f(x) lim f(x) = g s = Wert gegen den die Funktion streben soll (meist 0 oder ) g =
Mathe Differenzialrechnung Differenzialrechnung 1. Grenzwerte von Funktionen Idee: Gegeben eine Funktion: Gesucht: y = f(x) lim f(x) = g s = Wert gegen den die Funktion streben soll (meist 0 oder ) g =
Abschlussprüfung Fachoberschule 2016 Mathematik
 Abschlussprüfung Fachoberschule 06 Aufgabenvorschlag A Funktionsuntersuchung /6 Gegeben ist die Funktion f mit der Funktionsgleichung f ( x) = x + x; x IR. Berechnen Sie die Funktionswerte f( x ) für folgende
Abschlussprüfung Fachoberschule 06 Aufgabenvorschlag A Funktionsuntersuchung /6 Gegeben ist die Funktion f mit der Funktionsgleichung f ( x) = x + x; x IR. Berechnen Sie die Funktionswerte f( x ) für folgende
f. y = 0,2x g. y = 1,5x + 5 h. y = 4 6x i. y = 4 + 5,5x j. y = 0,5x + 3,5
 11. Lineare Funktionen Übungsaufgaben: 11.1 Zeichne jeweils den Graphen der zugehörigen Geraden a. y = 0,5x 0,25 b. y = 0,1x + 2 c. y = 2x 2 d. 2x + 4y 5 = 0 e. y = x f. y = 0,2x g. y = 1,5x + 5 h. y =
11. Lineare Funktionen Übungsaufgaben: 11.1 Zeichne jeweils den Graphen der zugehörigen Geraden a. y = 0,5x 0,25 b. y = 0,1x + 2 c. y = 2x 2 d. 2x + 4y 5 = 0 e. y = x f. y = 0,2x g. y = 1,5x + 5 h. y =
Mathematisches Thema Quadratische Funktionen 1. Art Anwenden. Klasse 10. Schwierigkeit x. Klasse 10. Mathematisches Thema
 Quadratische Funktionen 1 1.) Zeige, dass die Funktion in der Form f() = a 2 + b +c geschrieben werden kann und gebe a, b und c an. a) f() = ( -5) ( +7) b) f() = ( -1) ( +1) c) f() = 3 ( - 4) 2.) Wie heißen
Quadratische Funktionen 1 1.) Zeige, dass die Funktion in der Form f() = a 2 + b +c geschrieben werden kann und gebe a, b und c an. a) f() = ( -5) ( +7) b) f() = ( -1) ( +1) c) f() = 3 ( - 4) 2.) Wie heißen
Arbeitsblätter zur Vergleichsklausur EF. Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf.
 Arbeitsblätter zur Vergleichsklausur EF Arbeitsblatt I.1 Nullstellen Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der
Arbeitsblätter zur Vergleichsklausur EF Arbeitsblatt I.1 Nullstellen Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der
Einführung. Ablesen von einander zugeordneten Werten
 Einführung Zusammenhänge zwischen Größen wie Temperatur, Geschwindigkeit, Lautstärke, Fahrstrecke, Preis, Einkommen, Steuer etc. werden mit beschrieben. Eine Zuordnung f, die jedem x A genau ein y B zuweist,
Einführung Zusammenhänge zwischen Größen wie Temperatur, Geschwindigkeit, Lautstärke, Fahrstrecke, Preis, Einkommen, Steuer etc. werden mit beschrieben. Eine Zuordnung f, die jedem x A genau ein y B zuweist,
Einführungsphase Mathematik. Thema: Quadratische Funktionen. quadratische Gleichungen
 Thema: Quadratische Funktionen quadratische Gleichungen Normalform einer linearen Funktion Normalform einer quadratischen Funktion Handelt es sich um quadratische Funktionen??? Ja, denn a = 3, b = 0, c
Thema: Quadratische Funktionen quadratische Gleichungen Normalform einer linearen Funktion Normalform einer quadratischen Funktion Handelt es sich um quadratische Funktionen??? Ja, denn a = 3, b = 0, c
R. Brinkmann Seite
 R. Brinkmann http://brinkmann-du.de Seite 1 1.08.016 Kurvendiskussion Vorbetrachtungen Um den Graphen einer Funktion zeichnen und interpretieren zu können, ist es erforderlich einiges über markante Punkte
R. Brinkmann http://brinkmann-du.de Seite 1 1.08.016 Kurvendiskussion Vorbetrachtungen Um den Graphen einer Funktion zeichnen und interpretieren zu können, ist es erforderlich einiges über markante Punkte
Ganzrationale Funktionen
 Eine Dokumentation von Sandro Antoniol Klasse 3f Mai 2003 Inhaltsverzeichnis: 1. Einleitung...3 2. Grundlagen...4 2.1. Symmetrieeigenschaften von Kurven...4 2.1.1. gerade Exponenten...4 2.1.2. ungerade
Eine Dokumentation von Sandro Antoniol Klasse 3f Mai 2003 Inhaltsverzeichnis: 1. Einleitung...3 2. Grundlagen...4 2.1. Symmetrieeigenschaften von Kurven...4 2.1.1. gerade Exponenten...4 2.1.2. ungerade
Funktionen lassen sich durch verschiedene Eigenschaften charakterisieren. Man nennt die Untersuchung von Funktionen auch Kurvendiskussion.
 Tutorium Mathe 1 MT I Funktionen: Funktionen lassen sich durch verschiedene Eigenschaften charakterisieren Man nennt die Untersuchung von Funktionen auch Kurvendiskussion 1 Definitionsbereich/Wertebereich
Tutorium Mathe 1 MT I Funktionen: Funktionen lassen sich durch verschiedene Eigenschaften charakterisieren Man nennt die Untersuchung von Funktionen auch Kurvendiskussion 1 Definitionsbereich/Wertebereich
B Anwendungen der Differenzialrechnung
 B Anwendungen der Differenzialrechnung Kurvendiskussionen Um den Verlauf eines Funktionsgraphen zu bestimmen, kann eine Wertetabelle aufgestellt werden. Dies kann jedoch sehr mühselig sein und es ist nicht
B Anwendungen der Differenzialrechnung Kurvendiskussionen Um den Verlauf eines Funktionsgraphen zu bestimmen, kann eine Wertetabelle aufgestellt werden. Dies kann jedoch sehr mühselig sein und es ist nicht
WWG Grundwissen Mathematik 10. Klasse
 WWG Grundwissen Mathematik 10. Klasse I. Kreiszahl 1. Kreis: Fläche des Kreissektors: = Länge des Kreisbogens: = Im Einheitskreis gilt: = 2 = 2. Kugel: Oberflächeninhalt: = 4 Volumen: = II. Geometrische
WWG Grundwissen Mathematik 10. Klasse I. Kreiszahl 1. Kreis: Fläche des Kreissektors: = Länge des Kreisbogens: = Im Einheitskreis gilt: = 2 = 2. Kugel: Oberflächeninhalt: = 4 Volumen: = II. Geometrische
Merksatz Begriff der Funktion
 Der Begriff Funktion Um uns klar zu machen, was eine Funktion (lateinisch functio) ist, betrachten wir uns die Gegenüberstellung nachfolgender Situationen. Die Temperatur eines Gewässers wird in verschiedenen
Der Begriff Funktion Um uns klar zu machen, was eine Funktion (lateinisch functio) ist, betrachten wir uns die Gegenüberstellung nachfolgender Situationen. Die Temperatur eines Gewässers wird in verschiedenen
Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf.
 I. Nullstellen Arbeitsblatt I.1 Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der Faktoren null wird, sonst nicht. Beispiele:
I. Nullstellen Arbeitsblatt I.1 Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der Faktoren null wird, sonst nicht. Beispiele:
Lizenziert für: Seite 8 Aufgabe 3 Exercise-ID Ex
 : Funktionen und ihre Graphen Im Kapitel Funktionen und ihre Graphen lernst du, verschiedene Eigenschaften einer Funktion zu bestimmen. Mit den ausführlichen Lösungswegen von MatheScout siehst du, wie
: Funktionen und ihre Graphen Im Kapitel Funktionen und ihre Graphen lernst du, verschiedene Eigenschaften einer Funktion zu bestimmen. Mit den ausführlichen Lösungswegen von MatheScout siehst du, wie
1. Gegeben sind die Scheitelpunkte von Parabeln. Gib die Funktionsgleichungen an. a) S(-3/5) b) S(-1/-8) c) S(1/-0,5) d) S(0,5/0,2)
 Vermischte Übungen (1) Verschiebung der Normalparabel 1. Gegeben sind die Scheitelpunkte von Parabeln. Gib die Funktionsgleichungen an. a) S(-3/5) b) S(-1/-8) c) S(1/-0,5) d) S(0,5/0,). In der Abbildung
Vermischte Übungen (1) Verschiebung der Normalparabel 1. Gegeben sind die Scheitelpunkte von Parabeln. Gib die Funktionsgleichungen an. a) S(-3/5) b) S(-1/-8) c) S(1/-0,5) d) S(0,5/0,). In der Abbildung
Lineare Funktionen y = m x + n Sekundarstufe I u. II Funktion ist monoton fallend, verläuft vom II. in den IV.
 LINEARE FUNKTIONEN heißt Anstieg oder Steigung heißt y-achsenabschnitt Graphen linearer Funktionen sind stets Geraden Konstante Funktionen Spezialfall Graphen sind waagerechte Geraden (parallel zur x-achse)
LINEARE FUNKTIONEN heißt Anstieg oder Steigung heißt y-achsenabschnitt Graphen linearer Funktionen sind stets Geraden Konstante Funktionen Spezialfall Graphen sind waagerechte Geraden (parallel zur x-achse)
Wahrscheinlichkeitsrechnung. Trigonometrie Sinus und Kosinus
 Gymnasium Neutraubling Grundwissen Mathematik 10. Jahrgangsstufe Wissen und Können Aufgaben, Beispiele und Erläuterungen 1. Bedingte Wahrscheinlichkeit Bezeichnungen: P(A): Wahrscheinlichkeit des Ereignisses
Gymnasium Neutraubling Grundwissen Mathematik 10. Jahrgangsstufe Wissen und Können Aufgaben, Beispiele und Erläuterungen 1. Bedingte Wahrscheinlichkeit Bezeichnungen: P(A): Wahrscheinlichkeit des Ereignisses
Abitur 2013 Mathematik Infinitesimalrechnung II
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 213 Mathematik Infinitesimalrechnung II Teilaufgabe Teil 1 1 (5 BE) Geben Sie für die Funktion f mit f(x) = ln(213 x) den maximalen Definitionsbereich
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 213 Mathematik Infinitesimalrechnung II Teilaufgabe Teil 1 1 (5 BE) Geben Sie für die Funktion f mit f(x) = ln(213 x) den maximalen Definitionsbereich
Urs Wyder, 4057 Basel Funktionen. f x x x x 2
 Urs Wyder, 4057 Basel Urs.Wyder@edubs.ch Funktionen f 3 ( ) = + f ( ) = sin(4 ) Inhaltsverzeichnis DEFINITION DES FUNKTIONSBEGRIFFS...3. NOTATION...3. STETIGKEIT...3.3 ABSCHNITTSWEISE DEFINIERTE FUNKTIONEN...4
Urs Wyder, 4057 Basel Urs.Wyder@edubs.ch Funktionen f 3 ( ) = + f ( ) = sin(4 ) Inhaltsverzeichnis DEFINITION DES FUNKTIONSBEGRIFFS...3. NOTATION...3. STETIGKEIT...3.3 ABSCHNITTSWEISE DEFINIERTE FUNKTIONEN...4
Funktionsgraphen (Aufgaben)
 Gymnasium Pegnitz JS 9 August 2007 Funktionsgraphen (Aufgaben) 1. Betrachte die beiden linearen Funktionen f(x) = x + 2 und g(x) = x 3 und die quadratische Funktion p(x) = f(x) g(x) (a) Zeichne die Graphen
Gymnasium Pegnitz JS 9 August 2007 Funktionsgraphen (Aufgaben) 1. Betrachte die beiden linearen Funktionen f(x) = x + 2 und g(x) = x 3 und die quadratische Funktion p(x) = f(x) g(x) (a) Zeichne die Graphen
Schwerpunktaufgaben zur Vorbereitung auf die Leistungsfeststellung
 Schwerpunktaufgaben zur Vorbereitung auf die Leistungsfeststellung 1. Lösen Sie folgendes Gleichungssystem mit Hilfe des Gauß-Verfahrens. Überprüfen Sie Ihr Ergebnis mit dem Taschenrechner. ganzzahlig
Schwerpunktaufgaben zur Vorbereitung auf die Leistungsfeststellung 1. Lösen Sie folgendes Gleichungssystem mit Hilfe des Gauß-Verfahrens. Überprüfen Sie Ihr Ergebnis mit dem Taschenrechner. ganzzahlig
Logarithmusfunktion zur Basis 2, Aufgaben. 7-E Vorkurs, Mathematik
 Logarithmusfunktion zur Basis 2, Aufgaben 7-E Vorkurs, Mathematik Logarithmusfunktion zur Basis 2: Aufgaben 7-9 Aufgabe 7: Bestimmen Sie eine vertikale Asymptote für die folgenden Funktionen: f ( x) =
Logarithmusfunktion zur Basis 2, Aufgaben 7-E Vorkurs, Mathematik Logarithmusfunktion zur Basis 2: Aufgaben 7-9 Aufgabe 7: Bestimmen Sie eine vertikale Asymptote für die folgenden Funktionen: f ( x) =
Lösungen zu Aufgabenblatt 4. Ganzrationale Funktionen Alle Aufgaben mit reelen Zahlen!! assume(type::real) Aufgabe 1:
 Lösungen zu Aufgabenblatt 4 Ganzrationale Funktionen Alle Aufgaben mit reelen Zahlen!! assume(type::real) R Aufgabe 1: a) Die angegebene Funktion ist eine ganzrationale Funktion, da die Summanden in dem
Lösungen zu Aufgabenblatt 4 Ganzrationale Funktionen Alle Aufgaben mit reelen Zahlen!! assume(type::real) R Aufgabe 1: a) Die angegebene Funktion ist eine ganzrationale Funktion, da die Summanden in dem
F u n k t i o n e n Potenzfunktionen
 F u n k t i o n e n Potenzfunktionen Die Kathedrale von Brasilia steht in der brasilianischen Hauptstadt Brasilia wurde von Oscar Niemeyer (*907 in Rio de Janeiro). Die Kathedrale von Brasilia besteht
F u n k t i o n e n Potenzfunktionen Die Kathedrale von Brasilia steht in der brasilianischen Hauptstadt Brasilia wurde von Oscar Niemeyer (*907 in Rio de Janeiro). Die Kathedrale von Brasilia besteht
a) Begründen Sie, dass der Graph von f symmetrisch zum Punkt S 0 2 f) Ermitteln Sie eine Gleichung der Tangente im Punkt B
 I. Wendepunkte 1. Bestimmen Sie Art und Lage der Extrempunkte sowie die Wendepunkte des Graphen der Funktion f mit der angegebenen Funktionsgleichung. a) f(x) 1 b) 12 (x + 1) (x 2) (x + 6) f(x) 1 4 x4
I. Wendepunkte 1. Bestimmen Sie Art und Lage der Extrempunkte sowie die Wendepunkte des Graphen der Funktion f mit der angegebenen Funktionsgleichung. a) f(x) 1 b) 12 (x + 1) (x 2) (x + 6) f(x) 1 4 x4
4.1. Aufgaben zu linearen Funktionen
 .. Aufgaben zu linearen Funktionen Aufgabe : Koordinatensystem a) Gib die Koordinaten der Punkte P - P 8 in dem rechts abgebildeten Koordinatensystem an. b) Markiere die Punkte A( ); B( ); C( ); D( );
.. Aufgaben zu linearen Funktionen Aufgabe : Koordinatensystem a) Gib die Koordinaten der Punkte P - P 8 in dem rechts abgebildeten Koordinatensystem an. b) Markiere die Punkte A( ); B( ); C( ); D( );
Wertetabelle : x 0 0,5 1 2 3 4 0,5 1. y = f(x) = x 2 0 0,25 1 4 9 16 0,25 1. Graph der Funktion :
 Quadratische Funktionen ================================================================= 1. Die Normalparabel Die Funktion f : x y = x, D = R, heißt Quadratfunktion. Wertetabelle : x 0 0,5 1 3 4 0,5 1
Quadratische Funktionen ================================================================= 1. Die Normalparabel Die Funktion f : x y = x, D = R, heißt Quadratfunktion. Wertetabelle : x 0 0,5 1 3 4 0,5 1
Kreissektoren und Bogenmaß
 M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius r gilt für einen Kreissektor mit Mittelpunktswinkel α: Länge des Kreisbogens Fläche des Kreissektors b = α α 2rπ A = 360 360 πr2 Das Bogenmaß
M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius r gilt für einen Kreissektor mit Mittelpunktswinkel α: Länge des Kreisbogens Fläche des Kreissektors b = α α 2rπ A = 360 360 πr2 Das Bogenmaß
Arbeitsblätter Förderplan EF
 Arbeitsblätter Förderplan EF I.1 Nullstellen bestimmen Lösungen I.2 Parabeln: Nullstellen, Scheitelpunkte,Transformationen Lösungen I.3 Graphen und Funktionsterme zuordnen Lösungen II.1 Transformationen
Arbeitsblätter Förderplan EF I.1 Nullstellen bestimmen Lösungen I.2 Parabeln: Nullstellen, Scheitelpunkte,Transformationen Lösungen I.3 Graphen und Funktionsterme zuordnen Lösungen II.1 Transformationen
QUADRATISCHE FUNKTIONEN (Funktionen des 2 e Grades)
 QUADRATISCHE FUNKTIONEN (Funktionen des 2 e Grades) I. Einführung: Allgemeine Funktionsgleichung: y = ax 2 + px + q Aufgabe 2 1 (Westermann EK, S.14) II. Terminologie: a.) Abhängige Variable (erklärte
QUADRATISCHE FUNKTIONEN (Funktionen des 2 e Grades) I. Einführung: Allgemeine Funktionsgleichung: y = ax 2 + px + q Aufgabe 2 1 (Westermann EK, S.14) II. Terminologie: a.) Abhängige Variable (erklärte
3.6 Verhalten an den Polstellen
 44 Kapitel 3. Gebrochen-rationale Funktionen Beispiel 3.5.3. f(x) = 2x2 + 5 2x 1 f(0) = 2 02 + 5 2 0 1 = 5 1 = 5 3.6 Verhalten an den Polstellen Die Polstellen teilen den Graph in mehrere Teile. Da der
44 Kapitel 3. Gebrochen-rationale Funktionen Beispiel 3.5.3. f(x) = 2x2 + 5 2x 1 f(0) = 2 02 + 5 2 0 1 = 5 1 = 5 3.6 Verhalten an den Polstellen Die Polstellen teilen den Graph in mehrere Teile. Da der
Zusammenfassung der Kurvendiskussion
 Zusammenfassung der Kurvendiskussion Diskussionspunkte 1 Größtmögliche Definitionsmenge D f 2 Symmetrieeigenschaften des Graphen G f 3 Nullstellen, Polstellen, Schnittpunkte mit der y-achse, Vielfachheit
Zusammenfassung der Kurvendiskussion Diskussionspunkte 1 Größtmögliche Definitionsmenge D f 2 Symmetrieeigenschaften des Graphen G f 3 Nullstellen, Polstellen, Schnittpunkte mit der y-achse, Vielfachheit
Bayern Teil 1. Aufgabe 1. Abitur Mathematik: Musterlösung. Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten:
 Abitur Mathematik: Bayern 2013 Teil 1 Aufgabe 1 a) 1. SCHRITT: DEFINITIONSMENGE BESTIMMEN Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten: 3x + 9 0 x 3 2. SCHRITT: NULLSTELLEN
Abitur Mathematik: Bayern 2013 Teil 1 Aufgabe 1 a) 1. SCHRITT: DEFINITIONSMENGE BESTIMMEN Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten: 3x + 9 0 x 3 2. SCHRITT: NULLSTELLEN
eine Musteraufgabe Wir betrachten die Funktion f mit f(x) = x3 + 3x 2-6x + 2.
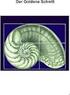 Wir betrachten die Funktion f mit f(x) = - 1 3 x3 + 3x 2-6x + 2. a) Zeigen Sie, dass das Schaubild von f symmetrisch zum Punkt Z(3 2) ist. b) Bestimmen Sie die Koordinaten der Achsenschnittpunkte des Schaubilds
Wir betrachten die Funktion f mit f(x) = - 1 3 x3 + 3x 2-6x + 2. a) Zeigen Sie, dass das Schaubild von f symmetrisch zum Punkt Z(3 2) ist. b) Bestimmen Sie die Koordinaten der Achsenschnittpunkte des Schaubilds
Ableitung und Steigung. lim h
 Ableitung und Steigung Aufgabe 1 Bestimme die Ableitung der Funktion f(x) = x über den Differentialquotienten. f (x f '(x ) lim h h) f (x h ) (x lim h h) h x x lim h hx h h x h(x lim h h h) lim x h h x
Ableitung und Steigung Aufgabe 1 Bestimme die Ableitung der Funktion f(x) = x über den Differentialquotienten. f (x f '(x ) lim h h) f (x h ) (x lim h h) h x x lim h hx h h x h(x lim h h h) lim x h h x
Gleichsetzungsverfahren
 Funktion Eine Funktion ist eine Zuordnung, bei der zu jeder Größe eines ersten Bereichs (Ein gabegröße) genau eine Größe eines zweiten Bereichs (Ausgabegröße) gehört. Eine Funktion wird durch eine Funktionsvorschrift
Funktion Eine Funktion ist eine Zuordnung, bei der zu jeder Größe eines ersten Bereichs (Ein gabegröße) genau eine Größe eines zweiten Bereichs (Ausgabegröße) gehört. Eine Funktion wird durch eine Funktionsvorschrift
Illustrierende Aufgaben zum LehrplanPLUS. Ganzrationale Funktionen
 Fach- und Berufsoberschule, Mathematik, Jahrgangsstufen und Ganzrationale Funktionen Stand: 8.0.08 Jahrgangsstufen FOS, BOS Fach/Fächer Mathematik Übergreifende Bildungs- und Erziehungsziele Zeitrahmen
Fach- und Berufsoberschule, Mathematik, Jahrgangsstufen und Ganzrationale Funktionen Stand: 8.0.08 Jahrgangsstufen FOS, BOS Fach/Fächer Mathematik Übergreifende Bildungs- und Erziehungsziele Zeitrahmen
Lineare Funktionen Arbeitsblatt 1
 Lineare Funktionen Arbeitsblatt 1 Eine Funktion mit der Gleichung y = m x + b heißt lineare Funktion. Ihr Graph ist eine Gerade mit der Steigung m. Die Gerade schneidet die y-achse im Punkt P(0 b). Man
Lineare Funktionen Arbeitsblatt 1 Eine Funktion mit der Gleichung y = m x + b heißt lineare Funktion. Ihr Graph ist eine Gerade mit der Steigung m. Die Gerade schneidet die y-achse im Punkt P(0 b). Man
Illustrierende Aufgaben zum LehrplanPLUS. Graphen ganzrationaler Funktionen
 Graphen ganzrationaler Funktionen Stand: 29.09.2017 Jahrgangsstufen FOS 11, BOS 12 Fach/Fächer Mathematik Übergreifende Bildungs- und Erziehungsziele Zeitrahmen Benötigtes Material 45 Minuten Die Aufgabe
Graphen ganzrationaler Funktionen Stand: 29.09.2017 Jahrgangsstufen FOS 11, BOS 12 Fach/Fächer Mathematik Übergreifende Bildungs- und Erziehungsziele Zeitrahmen Benötigtes Material 45 Minuten Die Aufgabe
a) Prüfen Sie, ob die Graphen der Funktionen f und g orthogonal sind: f(x) = 1,5x 1; g(x) =
 50 Kapitel 2: Rationale Funktionen und ihre Anwendungen 2.2.5 Orthogonale Geraden Geraden, die senkrecht aufeinander stehen, werden als zueinander orthogonale Geraden bezeichnet. Der Graph von g entsteht
50 Kapitel 2: Rationale Funktionen und ihre Anwendungen 2.2.5 Orthogonale Geraden Geraden, die senkrecht aufeinander stehen, werden als zueinander orthogonale Geraden bezeichnet. Der Graph von g entsteht
Die Steigung m ist ein Quotient zweier Differenzen und heißt daher Differenzenquotient.
 Seite Definition lineare Funktion Eine Funktion f mit dem Funktionsterm f(x) = m x + b, also der Funktionsgleichung y = m x + b, heißt lineare Funktion. Ihr Graph G f ist eine Gerade mit der Steigung m
Seite Definition lineare Funktion Eine Funktion f mit dem Funktionsterm f(x) = m x + b, also der Funktionsgleichung y = m x + b, heißt lineare Funktion. Ihr Graph G f ist eine Gerade mit der Steigung m
Lösungen ==================================================================
 Lösungen ================================================================== Aufgabe Bestimme f '(x) a) f(x) = e x f '(x) = e x ( ) = 4 e c x b) f(x) = x e x f '(x) = e x ( ) = + e x c) f(x) = 3 e (x+)
Lösungen ================================================================== Aufgabe Bestimme f '(x) a) f(x) = e x f '(x) = e x ( ) = 4 e c x b) f(x) = x e x f '(x) = e x ( ) = + e x c) f(x) = 3 e (x+)
Aufgabe zum Thema: Gebrochen - rationale Funktionen
 Aufgabe zum Thema: Gebrochen - rationale Funktionen Eine gebrochen-rationale Funktion Z (x) hat als Zähler- N (x) funktion Z (x) eine lineare Funktion und als Nennerfunktion N (x) eine ganz-rationale Funktion
Aufgabe zum Thema: Gebrochen - rationale Funktionen Eine gebrochen-rationale Funktion Z (x) hat als Zähler- N (x) funktion Z (x) eine lineare Funktion und als Nennerfunktion N (x) eine ganz-rationale Funktion
Kurvendiskussion. Gesetzmäßigkeiten. Lineare Funktionen. Funktionsgleichung
 Kurvendiskussion Gesetzmäßigkeiten Lineare Funktionen Funktionsgleichung y = mx + c m: Steigung c: y-achsenabschnitt (Funktionswert für y, bei dem der Graph die y-achse schneidet Beispiel : y = x 3 mit
Kurvendiskussion Gesetzmäßigkeiten Lineare Funktionen Funktionsgleichung y = mx + c m: Steigung c: y-achsenabschnitt (Funktionswert für y, bei dem der Graph die y-achse schneidet Beispiel : y = x 3 mit
Definition des Begriffs Funktion
 Definition des Begriffs Funktion In der Mathematik ist eine Funktion (lateinisch functio) oder Abbildung eine Beziehung (Relation) zwischen zwei Mengen, die jedem Element der Definitionsmenge (Funktionsargument,
Definition des Begriffs Funktion In der Mathematik ist eine Funktion (lateinisch functio) oder Abbildung eine Beziehung (Relation) zwischen zwei Mengen, die jedem Element der Definitionsmenge (Funktionsargument,
Analysis 1. Einführung. 22. März Mathe-Squad GbR. Einführung 1
 Analysis 1 Einführung Mathe-Squad GbR 22. März 2017 Einführung 1 y 10 9 8 7 6 5 4 3 2 1 10 9 8 7 6 5 4 3 2 1 1 2 3 4 5 6 7 8 910 2 x /* */ Einführung Allgemeines 2 Allgemeines Funktion f(x) bildet jeden
Analysis 1 Einführung Mathe-Squad GbR 22. März 2017 Einführung 1 y 10 9 8 7 6 5 4 3 2 1 10 9 8 7 6 5 4 3 2 1 1 2 3 4 5 6 7 8 910 2 x /* */ Einführung Allgemeines 2 Allgemeines Funktion f(x) bildet jeden
Symmetrie zum Ursprung
 Symmetrie zum Ursprung Um was geht es? Betrachten wir das Schaubild einer ganzrationalen Funktion mit ungeradem Grad, z.b.: f : R R x f x = 2 15 x3 23 15 x Wertetabelle x f(x) -3 1,0-2 2,0-1 1,4 0 0 1-1,4
Symmetrie zum Ursprung Um was geht es? Betrachten wir das Schaubild einer ganzrationalen Funktion mit ungeradem Grad, z.b.: f : R R x f x = 2 15 x3 23 15 x Wertetabelle x f(x) -3 1,0-2 2,0-1 1,4 0 0 1-1,4
Mathematik 9. Quadratische Funktionen
 Mathematik 9 Funktionen Eine Zuordnung f, die jedem x einer Menge D (Definitionsmenge) genau ein Element y = f(x) einer Menge Z (Zielmenge) zuordnet, heißt Funktion. Dabei heißt y = f(x) Funktionswert
Mathematik 9 Funktionen Eine Zuordnung f, die jedem x einer Menge D (Definitionsmenge) genau ein Element y = f(x) einer Menge Z (Zielmenge) zuordnet, heißt Funktion. Dabei heißt y = f(x) Funktionswert
Expertenpuzzle Quadratische Funktionen
 Phase 1 Lösung für die Expertengruppe I Im Folgenden sollen die in IR definierten Funktionen a : x x, b : x x 0,5, c : x x und d: x x 3 untersucht werden. Die Abbildung zeigt den Graphen G a von a, also
Phase 1 Lösung für die Expertengruppe I Im Folgenden sollen die in IR definierten Funktionen a : x x, b : x x 0,5, c : x x und d: x x 3 untersucht werden. Die Abbildung zeigt den Graphen G a von a, also
Die allgemeine Sinusfunktion
 Die allgemeine Sinusfunktion 1. Die Tageslänge(Zeitdauer zwischen Sonnenaufgang und Sonnenuntergang) an einem festen Ort verändert sich im Lauf eines Jahres. Die Graphik zeigt diese Veränderung für München.
Die allgemeine Sinusfunktion 1. Die Tageslänge(Zeitdauer zwischen Sonnenaufgang und Sonnenuntergang) an einem festen Ort verändert sich im Lauf eines Jahres. Die Graphik zeigt diese Veränderung für München.
α π r² Achtung: Das Grundwissen steht im Lehrplan! 1. Kreis und Kugel
 Achtung: Das Grundwissen steht im Lehrplan! Tipps zum Grundwissen Mathematik Jahrgangsstufe 10 Folgende Begriffe und Aufgaben solltest Du nach der 10. Klasse kennen und können: (Falls Du Lücken entdeckst,
Achtung: Das Grundwissen steht im Lehrplan! Tipps zum Grundwissen Mathematik Jahrgangsstufe 10 Folgende Begriffe und Aufgaben solltest Du nach der 10. Klasse kennen und können: (Falls Du Lücken entdeckst,
Kreissektoren und Bogenmaß
 M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius gilt für einen Kreissektor mit Mittelpunktswinkel : Länge des Kreisbogens Fläche des Kreissektors = = 360 360 Das Bogenmaß eines Winkels ist
M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius gilt für einen Kreissektor mit Mittelpunktswinkel : Länge des Kreisbogens Fläche des Kreissektors = = 360 360 Das Bogenmaß eines Winkels ist
Kreissektoren und Bogenmaß
 M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius gilt für einen Kreissektor mit Mittelpunktswinkel : Länge des Kreisbogens Fläche des Kreissektors = 2 = 360 360 Das Bogenmaß eines Winkels ist
M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius gilt für einen Kreissektor mit Mittelpunktswinkel : Länge des Kreisbogens Fläche des Kreissektors = 2 = 360 360 Das Bogenmaß eines Winkels ist
Mathematik im Berufskolleg I
 1 Bohner Ott Deusch Mathematik im Berufskolleg I Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab 6. Auflage 2016 ISBN 978-3-8120-0234-9 Das Werk und seine Teile sind urheberrechtlich geschützt.
1 Bohner Ott Deusch Mathematik im Berufskolleg I Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab 6. Auflage 2016 ISBN 978-3-8120-0234-9 Das Werk und seine Teile sind urheberrechtlich geschützt.
Quadratische Funktion
 Quadratische Funktion sind Funktionen die nur eine Variable enthalten, deren Exponent 2 ist und keine Variable die einen Exponenten enthält, der größer ist als 2. Zum Beispiel die quadratische Funktion
Quadratische Funktion sind Funktionen die nur eine Variable enthalten, deren Exponent 2 ist und keine Variable die einen Exponenten enthält, der größer ist als 2. Zum Beispiel die quadratische Funktion
Mathematik LK M2, 2. KA Eigenschaften ganzr. Funktionen Lösung
 Aufgabe 1: Grenzwerte 2 x 3 1.1 Berechne unter Anwendung der 3( +12 x 10 Grenzwertsätze für Funktionen: lim x 3 x 3 +2 x+10 2 x 2 x 3 +12 x 10 1+ 6 lim x 3 x 3 +2 x+10 = lim x 10 3) 2 x 2 x 2 3 x 3( 1
Aufgabe 1: Grenzwerte 2 x 3 1.1 Berechne unter Anwendung der 3( +12 x 10 Grenzwertsätze für Funktionen: lim x 3 x 3 +2 x+10 2 x 2 x 3 +12 x 10 1+ 6 lim x 3 x 3 +2 x+10 = lim x 10 3) 2 x 2 x 2 3 x 3( 1
Tiefpunkt = relatives Minimum hinreichende Bedingung:
 R. Brinkmann http://brinkmann-du.de Seite 1 0.0.01 Kurvendiskussion Vorbetrachtungen Um den Graphen einer Funktion zeichnen und interpretieren zu können, ist es erforderlich einiges über markante Punkte
R. Brinkmann http://brinkmann-du.de Seite 1 0.0.01 Kurvendiskussion Vorbetrachtungen Um den Graphen einer Funktion zeichnen und interpretieren zu können, ist es erforderlich einiges über markante Punkte
( ) 6 eine. 1. Führen Sie für die Funktion f mit vollständige Kurvendiskussion durch. eine. 5. Führen Sie für die Funktion f mit f ( x) = 2x
 . Führen Sie für die Funktion f mit vollständige Kurvendiskussion durch. Berücksichtigen Sie dabei die folgenden Punkte: f( ) 0 7 eine -Definitionsmenge; -Symmetrie; -Grenzwertverhalten; -Schnittpunkt
. Führen Sie für die Funktion f mit vollständige Kurvendiskussion durch. Berücksichtigen Sie dabei die folgenden Punkte: f( ) 0 7 eine -Definitionsmenge; -Symmetrie; -Grenzwertverhalten; -Schnittpunkt
Mathematik-Lexikon. Abszisse Die x-koordinate eines Punktes -> Ordinate
 Mathematik-Lexikon HM00 Abszisse Die x-koordinate eines Punktes -> Ordinate Aufstellen von Funktionstermen Gesucht: Ganzrationale Funktion n-ten Grades: ƒ(x) = a n x n + a n-1 x n-1 + a n- x n- +... +
Mathematik-Lexikon HM00 Abszisse Die x-koordinate eines Punktes -> Ordinate Aufstellen von Funktionstermen Gesucht: Ganzrationale Funktion n-ten Grades: ƒ(x) = a n x n + a n-1 x n-1 + a n- x n- +... +
g 2 g 1 15/16 I Übungen 2 EF Be Sept. 15 p 1 p 2
 15/16 I Übungen EF Be Sept. 15 Nr. 1: a) Funktion oder Relation? Welcher Graph gehört zu einer Funktion, welcher nicht? Begründe Deine Antwort kurz. a) und d) sind keine Funktionen, da die Zuordnungen
15/16 I Übungen EF Be Sept. 15 Nr. 1: a) Funktion oder Relation? Welcher Graph gehört zu einer Funktion, welcher nicht? Begründe Deine Antwort kurz. a) und d) sind keine Funktionen, da die Zuordnungen
Einiges zu den Potenzfunktionen. Exponentialfunktionen
 Einiges zu den Potenzfunktionen Es sind zunächst zwei Arten der Potenzfunktionen zu unterscheiden. Erstens die eigentlichen Potenzfunktionen, bei denen die Variable x als Basis von Potenzen vorkommt. Diese
Einiges zu den Potenzfunktionen Es sind zunächst zwei Arten der Potenzfunktionen zu unterscheiden. Erstens die eigentlichen Potenzfunktionen, bei denen die Variable x als Basis von Potenzen vorkommt. Diese
Gebrochen-rationale Funktionen
 Definition Eine gebrochen-rationale Funktion ist eine Funktion, bei der sich im Nenner befindet. f() = a h() Beispiel 1: f() = 1 Beispiel 2: f() = 1 ² Definitionsbereich und Definitionslücken Bei einer
Definition Eine gebrochen-rationale Funktion ist eine Funktion, bei der sich im Nenner befindet. f() = a h() Beispiel 1: f() = 1 Beispiel 2: f() = 1 ² Definitionsbereich und Definitionslücken Bei einer
)e2 (3 x2 ) a) Untersuchen Sie den Graphen auf Symmetrie, ermitteln Sie die Nullstellen von f und bestimmen Sie das Verhalten von f für x.
 Analysis Aufgabe aus Abiturprüfung Bayern GK (abgeändert). Gegeben ist die Funktion f(x) = ( x )e ( x ). a) Untersuchen Sie den Graphen auf Symmetrie, ermitteln Sie die Nullstellen von f und bestimmen
Analysis Aufgabe aus Abiturprüfung Bayern GK (abgeändert). Gegeben ist die Funktion f(x) = ( x )e ( x ). a) Untersuchen Sie den Graphen auf Symmetrie, ermitteln Sie die Nullstellen von f und bestimmen
Abitur 2017 Mathematik Infinitesimalrechnung I
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion g : x 2 4 + x 1 mit maximaler Definitionsmenge D g. Der Graph von g wird mit G g bezeichnet.
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion g : x 2 4 + x 1 mit maximaler Definitionsmenge D g. Der Graph von g wird mit G g bezeichnet.
Kreissektoren und Bogenmaß
 M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius Mittelpunktswinkel : Länge des Kreisbogens gilt für einen Kreissektor mit Fläche des Kreissektors Das Bogenmaß eines Winkels ist die Länge des
M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius Mittelpunktswinkel : Länge des Kreisbogens gilt für einen Kreissektor mit Fläche des Kreissektors Das Bogenmaß eines Winkels ist die Länge des
Arbeitsblatt 4: Kurvendiskussion - Von Skizzen zu Extremstellen-Bedingungen
 Arbeitsblatt 4: Kurvendiskussion - Von Skizzen zu Etremstellen-Bedingungen Häufig sind Ableitungsfunktionsterme leichter zu handhaben als die Terme der Ausgangsfunktonen, weil sie niedrigere Eponenten
Arbeitsblatt 4: Kurvendiskussion - Von Skizzen zu Etremstellen-Bedingungen Häufig sind Ableitungsfunktionsterme leichter zu handhaben als die Terme der Ausgangsfunktonen, weil sie niedrigere Eponenten
Abitur 2015 Mathematik Infinitesimalrechnung I
 Seite 1 Abiturloesung.de - Abituraufgaben Abitur 215 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion f : x ( x 3 8 ) (2 + ln x) mit maximalem Definitionsbereich D. Teilaufgabe Teil A 1a (1
Seite 1 Abiturloesung.de - Abituraufgaben Abitur 215 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion f : x ( x 3 8 ) (2 + ln x) mit maximalem Definitionsbereich D. Teilaufgabe Teil A 1a (1
Beschränktheit, Monotonie & Symmetrie
 Beschränktheit, Monotonie & Symmetrie ein Referat Dies ist eine Beilage zum Gruppen-SOL - Projekt Potenz- & Exponentialfunktionen Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch November 2015 Inhaltsverzeichnis
Beschränktheit, Monotonie & Symmetrie ein Referat Dies ist eine Beilage zum Gruppen-SOL - Projekt Potenz- & Exponentialfunktionen Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch November 2015 Inhaltsverzeichnis
Funktionenklassen. Einiges, was wir bisher über Funktionen gelernt haben kann auf alle Funktionen übertragen werden.
 R. Brinkmann http://brinkmann-du.de Seite 0.0.008 Einführung: Funktionenklassen Bisher haben wir nur ganzrationale Funktionen kennen gelernt. Sie gehören zu der Klasse der Rationalen Funktionen. In der
R. Brinkmann http://brinkmann-du.de Seite 0.0.008 Einführung: Funktionenklassen Bisher haben wir nur ganzrationale Funktionen kennen gelernt. Sie gehören zu der Klasse der Rationalen Funktionen. In der
Mathemathik-Prüfungen
 M. Arend Stand Juni 2005 Seite 1 1980: Mathemathik-Prüfungen 1980-2005 1. Eine zur y-achse symmetrische Parabel 4.Ordnung geht durch P 1 (0 4) und hat in P 2 (-1 1) einen Wendepunkt. 2. Diskutieren Sie
M. Arend Stand Juni 2005 Seite 1 1980: Mathemathik-Prüfungen 1980-2005 1. Eine zur y-achse symmetrische Parabel 4.Ordnung geht durch P 1 (0 4) und hat in P 2 (-1 1) einen Wendepunkt. 2. Diskutieren Sie
Symmetrien, gerade und ungerade Funktionen
 Symmetrien, gerade und ungerade Funktionen Wir Menschen fühlen uns von Symmetrien angezogen. 1-E1 1-E2 Vorausgesetzte Kenntnisse Definition einer Funktion, einer Relation, des Definitionsbereiches einer
Symmetrien, gerade und ungerade Funktionen Wir Menschen fühlen uns von Symmetrien angezogen. 1-E1 1-E2 Vorausgesetzte Kenntnisse Definition einer Funktion, einer Relation, des Definitionsbereiches einer
1.2 Weisen Sie rechnerisch nach, dass das Schaubild der Funktion mit 4P! bei 1 einen Sattelpunkt aufweist.
 Aufgabe A1 1.1 Erläutere anhand einer Skizze, ob das Integral 3P größer, kleiner oder gleich Null ist. 1.2 Für eine Funktion gilt: (1) 0 für 2 und 1 (2) 23 (3) 13 (4) 2 (5) 1 6 Welche Aussagen lassen sich
Aufgabe A1 1.1 Erläutere anhand einer Skizze, ob das Integral 3P größer, kleiner oder gleich Null ist. 1.2 Für eine Funktion gilt: (1) 0 für 2 und 1 (2) 23 (3) 13 (4) 2 (5) 1 6 Welche Aussagen lassen sich
+ 2. Bruchgleichungen
 Bruchgleichungen Gleichungen mit einer Lösungsvariablen im Nenner eines Bruchs heißen Bruchgleichungen. Definitionsmenge: Nenner 0 Lösungsweg: 1. Multiplikation mit dem Hauptnenner 2. Äquivalenzumformungen
Bruchgleichungen Gleichungen mit einer Lösungsvariablen im Nenner eines Bruchs heißen Bruchgleichungen. Definitionsmenge: Nenner 0 Lösungsweg: 1. Multiplikation mit dem Hauptnenner 2. Äquivalenzumformungen
Kantonsschule Solothurn RYS SS11/ Nach welcher Vorschrift wird der Funktionswert y aus x berechnet? Welcher Definitionsbereich ID ist sinnvoll?
 RYS SS11/1 - Übungen 1. Nach welcher Vorschrift wird der Funktionswert y aus berechnet? Welcher Definitionsbereich ID ist sinnvoll? a) : Seitenlänge eines Quadrates (in cm) y: Flächeninhalt des Quadrates
RYS SS11/1 - Übungen 1. Nach welcher Vorschrift wird der Funktionswert y aus berechnet? Welcher Definitionsbereich ID ist sinnvoll? a) : Seitenlänge eines Quadrates (in cm) y: Flächeninhalt des Quadrates
Analysis. A1 Funktionen/Funktionsklassen. 1 Grundbegriffe. 2 Grundfunktionen
 A1 Funktionen/Funktionsklassen 1 Grundbegriffe Analysis A 1.1 Gegeben sei die Funktion f mit f(x) = 2 x 2 + x. a) Bestimme, wenn möglich, die Funktionswerte an den Stellen 0, 4 und 2. b) Gib die maximale
A1 Funktionen/Funktionsklassen 1 Grundbegriffe Analysis A 1.1 Gegeben sei die Funktion f mit f(x) = 2 x 2 + x. a) Bestimme, wenn möglich, die Funktionswerte an den Stellen 0, 4 und 2. b) Gib die maximale
Analysis f(x) = x 2 1. (x D f )
 Analysis 15 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f mit f(x) = x3 x 1 (x D f ) a) Geben Sie den maximalen Definitionsbereich der Funktion f an. Zeigen Sie, dass der Graph der Funktion
Analysis 15 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f mit f(x) = x3 x 1 (x D f ) a) Geben Sie den maximalen Definitionsbereich der Funktion f an. Zeigen Sie, dass der Graph der Funktion
SYMMETRIE FRANZ LEMMERMEYER
 SYMMETRIE FRANZ LEMMERMEYER Symmetrie ist ein außerordentlich wichtiges Konzept in der Mathematik und der Physik. Ist beispielsweise (x, y) eine Lösung des Gleichungssystems x + y = 5, xy = 1, so muss
SYMMETRIE FRANZ LEMMERMEYER Symmetrie ist ein außerordentlich wichtiges Konzept in der Mathematik und der Physik. Ist beispielsweise (x, y) eine Lösung des Gleichungssystems x + y = 5, xy = 1, so muss
1 Benenne Gemeinsamkeiten und Unterschiede der beiden Graphen und gib die zugehörigen Funktionsgleichungen an.
 Teste dich! - (/6) Benenne Gemeinsamkeiten und Unterschiede der beiden Graphen und gib die zugehörigen Funktionsgleichungen an. 0 Cornelsen Verlag, Berlin. Alle Rechte vorbehalten. Gemeinsamkeiten: Beide
Teste dich! - (/6) Benenne Gemeinsamkeiten und Unterschiede der beiden Graphen und gib die zugehörigen Funktionsgleichungen an. 0 Cornelsen Verlag, Berlin. Alle Rechte vorbehalten. Gemeinsamkeiten: Beide
Pflichtteilaufgaben zu Funktionenkompetenz. Baden-Württemberg
 Pflichtteilaufgaben zu Funktionenkompetenz Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com September 016 1 Übungsaufgaben: Ü1: Die Abbildung zeigt
Pflichtteilaufgaben zu Funktionenkompetenz Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com September 016 1 Übungsaufgaben: Ü1: Die Abbildung zeigt
Nur für die Lehrkraft
 Senatsverwaltung für Bildung, Jugend und Wissenschaft Fach Abschlussprüfung an der Fachoberschule im Schuljahr 05/6 (A) Nur für die Lehrkraft Prüfungstag 9. Mai 06 Prüfungszeit Zugelassene Hilfsmittel
Senatsverwaltung für Bildung, Jugend und Wissenschaft Fach Abschlussprüfung an der Fachoberschule im Schuljahr 05/6 (A) Nur für die Lehrkraft Prüfungstag 9. Mai 06 Prüfungszeit Zugelassene Hilfsmittel
x 2 x 1.Untersuchen Sie die Schaubilder der Funktion auf ihre Symmetrieeigenschaften. (Achsensymmetrie/ Punktsymmetrie)
 I. Grenzverhalten von Funktionen. Verhalten einer Funktion für bzw.. Bestimmen Sie den Grenzwert a) b) ) ( + ( ) c) ( + ) ( ) II. Symmetrie.Untersuchen Sie die Schaubilder der Funktion auf ihre Symmetrieeigenschaften.
I. Grenzverhalten von Funktionen. Verhalten einer Funktion für bzw.. Bestimmen Sie den Grenzwert a) b) ) ( + ( ) c) ( + ) ( ) II. Symmetrie.Untersuchen Sie die Schaubilder der Funktion auf ihre Symmetrieeigenschaften.
Kurvendiskussion. Mag. Mone Denninger 10. Oktober Extremwerte (=Lokale Extrema) 2. 5 Monotonieverhalten 3. 6 Krümmungsverhalten 4
 Mag. Mone Denninger 10. Oktober 2004 Inhaltsverzeichnis 1 Definitionsmenge 2 1.1 Verhalten am Rand und an den Lücken des Definitionsbereichs............................ 2 2 Nullstellen 2 3 Extremwerte
Mag. Mone Denninger 10. Oktober 2004 Inhaltsverzeichnis 1 Definitionsmenge 2 1.1 Verhalten am Rand und an den Lücken des Definitionsbereichs............................ 2 2 Nullstellen 2 3 Extremwerte
