Mathematik für Wirtschaftswissenschaften I Wintersemester 2015/16 Universität Leipzig. Lösungvorschläge Präsenzaufgaben Serien 1-10
|
|
|
- Inken Ritter
- vor 7 Jahren
- Abrufe
Transkript
1 Mathematik für Wirtschaftswissenschaften I Wintersemester 05/6 Universität Leipzig Lösungvorschläge Präsenzaufgaben Serien -0 Inhaltsverzeichnis Serie Serie 5 3 Serie 8 4 Serie 9 5 Serie 3 6 Serie 6 7 Serie 9 8 Serie 9 Serie 5 0 Serie 8
2 Serie. Aufgabe Zeigen Sie, dass die folgenden Aussageformen Tautologien sind.. (A B) (B C) (A C),. (A B) (B C) (A C). Lösung: Wir stellen die Wahrheitstabelle für die Aussageformen auf:. Teilaufgabe A W W W F W F F F B W W F W F W F F C W F W W F F W F A B W W F F F F W W B C W F F W W F F W (A B) (B C) W F F F F F F W (A C) W F W F F W F W (A B) (B C) (A C) W W W W W W W W Da die Formel für jede beliebige Belegung der Variablen A, B, C wahr ist, ist es eine Tautologie.. Teilaufgabe A W W W F W F F F B W W F W F W F F C W F W W F F W F A B W W F W F W W W B C W F W W W F W W (A B) (B C) W F F W F F W W (A C) W F W W F W W W (A B) (B C) (A C) W W W W W W W W. Aufgabe Stellen Sie die Aussageform für das umgangssprachliche entweder... oder... auf. Diese wird mitunter durch die Symbole oder XOR gekennzeichnet. Lösung: entweder A oder B bedeutet, dass immer genau eine der Variablen wahr sein muss und die jeweils andere nicht. Dies wird z.b. durch die Aussageform (A B) ( A B) ausgedrückt wie die Wahrheitstabelle zeigt:
3 .3 Aufgabe A W W F F B W F W F A B F W F F A B F F W F (A B) ( A B) F W W F Stellen Sie die folgenden Aussageformen als logische Schaltungen dar.. A B,. (A B) C, 3. A B. Lösung:. A B ist äquivalent zu (A B) ( A B).. Eine mögliche Schaltung ist 3. A B ist äquivalent zu (A B) ( A B). 3
4 .4 Aufgabe Betrachten Sie folgendes Gespräche zwischen einem Professor der Aussagenlogik und einem Studenten. Student: Können Sie mir sagen, wieso ich durchgefallen bin, obwohl ich so viel gelernt habe. Professor: Alle schlechten Studenten sind durchgefallen. Student: Seien Sie nicht so gemein, ich bin doch gar kein schlechter Student. Professor: Offensichtlicher Weise sind Sie es doch. Begründen Sie den Schluss des Professors. Lösung: Die Aussage Alle schlechten Studenten sind durchgefallen des Professors ist lediglich eine logische Implikation Student schlecht fällt durch. Der Student denkt, dies wäre die gleiche Aussage wie Fällt durch Student schlecht. Damit beweist er, dass er die Grundlagen der Aussagenlogik nicht verstanden hat, was dem Professor wiederum zeigt, dass der Student in der Tat schlecht ist. 4
5 Serie. Aufgabe Seien Mengen A, B und C gegeben. Zeigen Sie die Gleichungen Lösung:. Es gilt (A B) C = (A C) (B C) () (A B) (A C) = A (B C) () x (A B) C x A B x C (x A x B) x C (x A x C) (x B x C) x A C x B C x (A C) (B C) Also folgt x (A B) C x (A C) (B C), d.h. (A B) C = (A C) (B C).. Es gilt (x, y) (A B) (A C) (x, y) (A B) (x, y) (A C) x A y B x A y C x A y B y C x A y B C (x, y) A (B C) Damit folgt (A B) (A C) = A (B C).. Aufgabe Seien zwei endliche Mengen A und B gegeben. Zeigen Sie, dass #A B = #A #B. Lösung: Sei A = {a,..., a n }. Dann gilt ( n ) #(A B) = # {(a k, b) : b B} = k= n #{(a k, b) : b B} = k= n #B = n #B = #A #B k= 5
6 .3 Aufgabe a) Geben Sie auf der Grundmenge M = {,, 3, 4, 5} jeweils ein Beispiel mit Skizze einer Relation R M M an, die genau zwei der Eigenschaften der Transitivität, der Symmetrie bzw. der Reflexivität hat. b) Zeigen Sie: Der Durchschnitt R R zweier transitiver Relationen R, R ist erneut transitiv. Lösung: a). Symmetrisch und reflexiv, aber nicht transitiv: X X X X 3 X X 4 X 5 X X (Es gilt (5, ), (, 3) R aber (5, 3) / R). Symmetrisch und transitiv, nicht reflexiv: X X X X Reflexiv und transitiv, nicht symmetrisch: X X X X X X X X X 3 X X X 4 X X 5 X b) Seien (x, y), (y, z) R R. (x, y), (y, z) R und (x, y), (y, z) R. Da R und R transitiv sind, folgt (x, z) R und (x, z) R. (x, z) R R. Somit ist R R transitiv. 6
7 .4 Aufgabe Zeigen Sie die Gültigkeit des Assoziativitätsgesetzes und Kommutativgesetzes der rationalen Zahlen bzgl. der Addition: für alle q, q, q 3 Q. Lösung: (q + q ) + q 3 = q + (q + q 3 ) q + q = q + q. Seien q, q, q 3 Q mit q i = z i /n i, z i, n i Z. Wir benutzen nur die Definition der Addition in Q und die Gültigkeit des Assoziativitätsgesetzes der Addition in Z: (q + q ) + q 3 = ( z n + z n ) + z 3 n 3 = z n + z n n n + z 3 n 3 = (z n + z n )n 3 + n n z 3 = (z n n 3 + z n n 3 ) + n n z 3 n n n 3 n n n 3 = z n n 3 + (z n n 3 + n n z 3 ) = z n n 3 + n (z n 3 + n z 3 ) n n n 3 = z n + z n 3 + n z 3 n n 3 = z n +. Analog wie in. sei q i = z i /n i. Dann gilt ( z n + z 3 n 3 n n n ) 3 = q + (q + q 3 ) q + q = z + z = z n + n z = n z + z n = z n + n z n n n n n n n n = z + z = q + q n n 7
8 3 Serie 3. Aufgabe Geben Sie jeweils die Lösungsmenge L für x an:. 5x 3x +, L = (, 4 ]. 7 x, L = (0, 49] 3. x+, L = (, ) [, ) 3. Aufgabe Geben Sie jeweils die Lösungsmenge L für x an:. x + 4 3, L = [ 7, ]. 3x, L = (, 3 ] [, ) 3.3 Aufgabe Skizzieren Sie jeweils auf dem Zahlenstrahl die Lösungsmengen L für x:. 3x 6 < 9. x + 4 < 3 Lösung:. Umstellen liefert x < 3. Lösungsmenge:. Lösungsmenge: Aufgabe Berechnen Sie eine Approximation der Zahl 6, indem Sie die ersten 4 Schritte einer zulässigen Intervallschachtelung durchführen. Lösung: x = 6 < x < 3, setze I := (, 3) m = +3 = 5. m = 5 4 = > 6 I = (, 5 ) m = +5/ = 9 4 m = 8 6 = < 6 I 3 = ( 9 4, 5 ) m 3 = 9/4+5/ = 9 8 m 3 = = < 6 I 4 = ( 9 8, 5 ) m 4 = 9/8+5/ =.4375 (Es gilt ) 8
9 4 Serie 4. Aufgabe Zeigen Sie gemäß der Definition von Grenzwerten, dass (7 + ( ) n n ) 3 = 7. lim n Lösung: Zu zeigen ist: Für alle ε > 0 existiert ein n 0 N, s.d. 7 + ( )n n 3 7 < ε n N : n n 0. Beweis. Sei nun ε > 0 gegeben. Aus der Vorlesung ist bekannt, dass die Folge n n eine Nullfolge ist. Somit existiert ein n 0 N, s.d. n < ε n N : n n 0. Dann gilt für alle n N mit n n ( )n n 3 7 = ( )n n 3 = n 3 n ε. 4. Aufgabe Überprüfen Sie, ob die folgenden Folgen konvergieren und bestimmen Sie ggf. den Grenzwert: Lösung: Die erste Folge a n := ( )n n + 4 n +, b n := 5n4 n 4 + 7n. a n = ( )n n + 4 n + kann nicht konvergieren, da sie sich für n wie die alternierende Folge n ( ) n verhält. 9
10 Beweis. Betrachte nun die Differenz zwischen der Folge a n und der alternierenden Folge: d n := ( )n n + 4 n + ( ) n = ( )n n + 4 ( )n ( ) n n + = 4 ( )n n +. Offensichtlich ist d n eine Nullfolge. Falls a n konvergieren würde, so würde nach den Rechenregeln für Konvergenz auch die Summe a n + d n = ( ) n konvergieren. Dies wäre aber ein Widerspruch. Für die Folge geht man standardmäßig vor: b n = 5n4 n 4 + 7n b n = 5n4 n 4 + 7n = 5 n n Der Zähler konvergiert gegen fünf und der Nenner gegen zwei. Aus den Rechenregeln für Konvergenz folgt also 4.3 Aufgabe lim b 5 n n = lim 4 n n + 7 n ( ) lim 5 n n = ( 4 ) + 7 n lim n = 5. Zeigen Sie mithilfe von Induktion für alle n N die Summenformel Lösung: Induktionsanfang: n = : + + n = n(n + )(n + ). 6 = = 6 6 = ( + ). 6 0
11 Induktionsvoraussetzung: Es gilt für ein n N Induktionsbehauptung: n = n(n + )(n + ). 6 Beweis (n + ) = (n + )(n + )(n + 3) (n + ) =(n + ) n I.V. = (n + ) + n(n + )(n + ) 6 =n(n + ) + (n + ) + n(n + )(n + ) 6 = (n(n + ) n)(n + ) 6 = 6 (n + 7n + 6)(n + ) = (n + )(n + 3)(n + ) Aufgabe Zeigen Sie, dass die folgende rekursiv definierte Folge konvergiert und bestimmen Sie den Grenzwert: Lösung: a :=, a n+ := a n. Schritt (Beschränktheit) Per Induktion zeigen, dass 0 < a n < n N. Induktionsanfang ist in Aufgabenstellung gegeben durch 0 < a <. Induktionsvoraussetzung: n N : 0 < a n < 0 < a n < 0 < a n < 0 < a n < 0 < a n = a n+ < (3)
12 Schritt (Monotonie) Da 0 < a n < gilt, gilt auch an > a n a n < ( a n ) a n+ = (4) a n < ( a n ) = a n Daher ist a n streng monoton fallend. Schritt 3 (Der Grenzwert) Da a n durch 0 nach unten beschränkt und monoton fallend ist, muss der Grenzwert lim a n =: a R existieren. Damit n gilt also: lim a n+ = a = lim a n = a n n a = a a = ( a) = a + a 0 = a + a a = a a = 0 oder a = (5) Da a < und a n streng monoton fallend ist, kann nur a = 0 gelten.
13 5 Serie 5. Aufgabe Berechnen Sie den Zahlwert der angegebenen Summe:. 4 n= (4n 3) = = 8. 0 n= (n n) = = ( ) n k= k k+ = ( ( ) + ) ( ) n n+ = n+ 5. Aufgabe Entscheiden Sie mithilfe des Wurzelkriteriums, ob die nachfolgende Reihe konvergiert oder nicht. ( (5937) n ) n n n=0 Lösung: Es ist a n = (5937) n n n und n an = (5937) n n n n = n (5937) n n = 5937 n n n Damit gilt mit ε = /5938 für alle n 5938 n an = 5937 n = ε. Nach dem Wurzelkriterium aus der Vorlesung konvergiert die Reihe also. 5.3 Aufgabe Entscheiden Sie mithilfe des Quotientenkriteriums, für welche x R die nachfolgende Reihe konvergiert. Lösung: Es ist a n = a n+ a n xn (n )! und n=0 = xn+ 4 n+ (n + )! x n (n )! 4n (n )! x n 4 n = 4 x (n + ) n. Da x /(n(n+)) für jedes x R gegen 0 konvergiert, existiert also ein ε > 0, sodass für schließlich alle n a n+ ε a n gilt. Also konvergiert die Reihe nach dem Quotientenkriterium für alle x R. 3
14 5.4 Aufgabe Herr Fuchs schlägt uns folgenden Deal zum einmaligen Preis von 60 Euro vor: Er zahlt uns sofort und weitere 0 Jahre lang jeweils 6 Euro. Benutzen Sie einen Taschenrechner um mithilfe einer Intervallschachtelung approximativ festzustellen für welchen jährlichen Diskontsatz p (0, 00) dies ein fairer Deal ist. Lösung: Der Barwert der künftigen Zahlungen beträgt 0 n=0 6 (+ ( ) + p n = 6 00) p 00 + p 00 = 6 Der Deal ist also fair, falls (00+p) 00 (00+p) p 00+p 60 = 6 (00 + p) 00 p(00 + p) 0 0p(00 + p) 0 = (00 + p) 00 = 6 00 (00+p) p = 6 (00 + p) 00 p(00 + p) 0 0 = (00 + p) 0 (0p (00 + p)) = (00 + p) 0 (9p 00) + 00 Nun suchen wir mit einer Intervallschachtelung eine Nullstelle in (0, 00) der stetigen Funktion f(p) = (00 + p) 0 (9p 00) Dazu setzen wir einfach testweise Werte für p ein und nähern uns so immer weiter einer Nullstelle an, z.b. so: p f(p)
15 Also hat f in der Nähe von p =.963 eine Nullstelle, d.h. es handelt sich um einen fairen Deal, wenn ein Diskontsatz von ca..963% p.a. vorausgesetzt wird. 5
16 6 Serie 6. Aufgabe Zeigen Sie, dass für r, s R, m Q, r, s, m > 0 gilt. r < s r m < s m Lösung: Wir zeigen zunächst per vollständiger Induktion, dass r < s r m < s m für alle m N gilt. m = : r < s r = r < s = s m > : r < s r m < s m r m = r m r < s m r < s m s = s m Nehmen wir nun an, dass r m < s m für ein bel. m N gilt. Dann gibt es nur 3 Fälle:. r = s,. r > s, 3. r < s. Aus Fall folgt r m = s m und aus Fall nach obiger Induktion r m > s m, also in beiden Fällen ein Widerspruch. Demnach muss Fall 3 gelten, nämlich r < s. Also haben wir für m N insgesamt r < s r m < s m Sei nun m = p q Q, m > 0, p, q N. Dann gilt (rm ) q = r p q q = r p und analog (s m ) q = s p. Nach obiger Aussage haben wir damit 6. Aufgabe r < s r p < s p (r m ) q < (s m ) q r m < s m Leiten Sie die Rechenregel her. log b (a) = ln(a) ln(b) Lösung: ( b ln(a) ln(a) ln(b) = e ln(b)) ln(b) ln(a) ln(b) = e ln(b) = e ln(a) = a ln(a) ln(b) = log b ) (b ln(a) ln(b) = log b (a) 6
17 6.3 Aufgabe Lösen Sie die folgenden Gleichungen nach x auf.. (x + 6) 3 4 = 8. 3 x+5 7 = x+ = 5 x 3 Lösung:. (x + 6) 3 4 = 8 x + 6 = = 4 = 6 x = 0. 0 = 3 x+5 7 = 3 x = 3 3 (3 x+ ) 0 = 3 x+ 9 = 3x x = log 3 (/9) = log 3 (9) = x+ = 5 x 3 = (5 ) x 3 = 5 4x 6 = 55x+ 5 4x 6 = 5 (5x+) (4x 6) = 5 x+7 x = Aufgabe Zwei Versicherungen A und B bieten Ihnen zum gleichen Preis folgendes Paket zur privaten Altersvorsorge an. Sie zahlen einmalig einen Festbetrag S 0 ein, welcher dann jährlich verzinst wird, bis Sie den Vertrag auflösen. Versicherung A bietet Ihnen einen Zinssatz von % p.a. und zusätzlich eine Zahlung von S 0 / bei Vertragsende. Versicherung B bietet Ihnen hingegen einen Zinssatz von 4, 04% p.a. Stellen Sie Gleichungen für die Auszahlung R A (t) bzw. R B (t) nach t Jahren Laufzeit auf. Nach wie vielen Jahren lohnt sich die Altersvorsorge von Versicherung B mehr als die von A? Lösung: Es gilt R A (t) = S 0.0 t + / S 0 = S 0 (.0 t + /) R B (t) = S t Man beachte, dass.0 =.0404, weswegen für x =.0 t. Lösen nach x ergibt R A (t) = R B (t).0404 t.0 t / = 0 x x / = 0 x = ± 3 7
18 wobei x = ( 3) < 0, was wegen der Substitution x =.0 t nicht zulässig ist. Also ist die einzige Lösung bzw..0 t = x = ( + 3) ( t = log.0 ( + ) 3) = ln ( ( + 3) ) ln(.0) Also lohnt sich Versicherung B aber 6 Jahren mehr als Versicherung A. 8
19 7 Serie 7. Aufgabe Seien zwei surjektive Funktionen f : X Y und g : Y Z gegeben. Zeigen Sie, dass dann die Funktion g f, gegeben durch ebenfalls surjektiv ist. g f(x) = g(f(x)), Lösung: Sei z Z. Da g surjektiv ist, existiert ein y Y mit g(y) = z. Da f surjektiv ist, existiert ein x X mit f(x) = y. Also gilt g f(x) = g(f(x)) = g(y) = z. Also haben wir gezeigt, dass es für jedes z Z ein x X gibt mit g f(x) = z. Damit ist g f surjektiv. 7. Aufgabe Bestimmen Sie den Scheitelpunkt der quadratischen Funktion f : R R f(x) = x 6x + 0 und zerlegen Sie die reellen Zahlen in zwei disjunkte Intervalle, s.d. f auf diesen jeweils injektiv ist. Bestimmen Sie die Umkehrfunktion der jeweiligen Einschränkungen von f. Lösung: Durch quadratische Ergänzgung erhalten wir f(x) = x 6x + 0 = x 6x = (x 3) + Damit ist der Scheitelpunkt S(3 ). Also ist f auf (, 3) und [3, + ) jeweils injektiv. Lösen wir die Gleichung y = f(x) bzw. y = (x 3) + nach x auf, erhalten wir x = 3 ± y also sind die Umkehrfunktionen der Einschränkungen von f auf (, 3) bzw. [3, + ) gegeben durch (f (, 3)) (y) = 3 y und (f [3, + )) (y) = 3 + y 9
20 7.3 Aufgabe Zeigen Sie: Falls f : R D R eine streng monoton wachsende Funktion ist (d.h. x < y f(x) < f(y) für alle x, y D), so ist f injektiv. Lösung: Zu zeigen: Falls f(x) = f(x ), so folgt x = x. Seien also x, x D mit f(x) = f(x ). Für zwei reelle Zahlen gibt es genau 3 Möglichkeiten:. x < x,. x > x, 3. x = x.. Fall: x < x. Wegen der strengen Monotonie von f folgt dann f(x) < f(x ). Dies ist ein Widerspruch zu f(x) = f(x )!. Fall: x > x. Wegen der strengen Monotonie von f folgt f(x) > f(x ). Auch dies ist ein Widerspruch zu f(x) = f(x )! Da einer der 3 oben beschriebenen Fälle vorliegen muss und Fall und zu Widersprüchen führen, muss zwangsläufig Fall 3 vorliegen. Also gilt x = x. Damit ist f injektiv. 7.4 Aufgabe Betrachten Sie die Funktion f : R >0 [, ] f(x) = sin(ln(x)). Untersuchen Sie nun, ob Funktionen g, h : [, ] R >0 existieren, s.d. Lösung: f g(x) = x x [, ], h f(x) = x x R >0.. Aus der Schule sollte bekannt sein, dass es eine Funktion arcsin : [, ] [ π, π ] gibt mit sin(arcsin(x)) = x x [, ] wobei arcsin(sin(x)) = x für beliebiges x R im allgemeinen falsch ist (z.b. ist arcsin(sin(π)) = arcsin(0) = 0). Definieren wir also g durch haben wir für alle x [, ] g(x) = e arcsin x f g(x) = sin(ln(e arcsin(x) )) = sin(arcsin(x)) = x.. Da f nicht injektiv ist, kann es die gesuchte Funktion h nicht geben: Nehmen wir an, es gäbe h mit h f(x) = x für alle x > 0. Dann folgt aber wegen 0 = sin(0) = sin(ln()) = f() 0
21 und dass 0 = sin(π) = sin(ln(e π )) = f(e π ) = h(f()) = h(f(e π )) = e π. Das ist offensichtlich ein Widerspruch, weshalb die Annahme, dass ein solches h existiere falsch ist.
22 8 Serie 8. Aufgabe Zeigen Sie, dass die Funktion f : R R { x 4, x 3 f(x) = x x, x > 3 an der Stelle x = 3 unstetig ist. Lösung: Betrachte die Folgen a n = 3 n und b n = 3+ n. Dann gilt lim n a n = lim n b n = 3 und ( ( lim f(a n) = lim 3 ) ) 4 = 3 4 = n n und lim f(b n) = lim n ( ( 3 + n ) ) 3 = 3 3 = 6 n Es gibt also zwei Folgen a n 3 und b n 3 mit lim f(a n ) lim f(b n ). Damit ist f unstetig in x = Aufgabe Benutzen Sie den Folgen-Grenzwertsatz um zu zeigen, dass die Funktion f : R R f(x) = 5x 3x stetig auf ganz R ist. Lösung: Sei x R und (x n ) eine beliebige Folge mit x n x. Dann gilt nach dem Folgen-Grenzwertsatz lim f(x ( ) ( ) n) = lim 5 x n 3 x n = lim 5 x n lim (3 x n) n n n n ( ) ( ) ( ) ( ) = lim 5 lim x n x n lim 3 lim x n n n n n ( ) = 5 lim x n lim x n 3 x = 5 x x 3x = 5x 3x = f(x) n n Demnach gilt für jedes x R und jede Folge x n x, dass lim n f(x n ) = f(x). Damit ist f stetig auf ganz R. 8.3 Aufgabe Berechnen Sie die ersten Ableitungen der folgenden Funktionen.. f(x) = sin(3x + 4x )
23 . g(x) = ln(x) sin(x) 3. h(x) = ex ln(x ) Lösung:. f (x) = sin (3x + 4x ) (3 + 8x) = cos(3x + 4x ) (8x + 3). 3. g (x) = ln(x) sin(x) (ln (x) sin(x)+ln(x) sin (x)) = sin(x) x + ln(x) cos(x) ln(x) sin(x) h (x) = ex ln(x ) e x x x ln(x ) = e x ln(x ) x ln(x ) = e x x ln(x ) x ln(x ) 8.4 Aufgabe Bestimmen Sie für die Funktion f : R R die Gleichung der Tangente an den Funktionsgraph an der Stelle x = 3 und fertigen Sie eine Skizze an. f(x) = 3 x3 x Lösung: Die Steigung der Tangente ist gleich des Wertes der ersten Ableitung von f in x = 3. Es gilt und f ( ) 3 f = ( ) 3 = 3 ( ) 3 = 5 4 ( ) = = 3 8 Wir ( suchen also eine Funktion der Form T (x) = 5 4x + b, die durch den Punkt 3, f ( ( 3 )) = 3, 8) 3 geht. Es muss also gelten, dass 3 8 = T ( 3 ) = b = b b = 8 8 Skizze: T (x) = 5 4 x 8 8 3
24 4 y f(x) T (x) x
25 9 Serie 9. Aufgabe Zeigen Sie, dass die Funktion f : R R { x sin ( ) f(x) = x, x 0 0, x = 0 überall differenzierbar ist und bestimmen Sie f. Ist f stetig? Lösung: Nach den Rechenregeln des Differenzierens erhalten wir für x 0 f (x) = x sin In x = 0 gilt ( ) + x cos x f f(0 + h) f(0) (0) = lim = lim h 0 h ( ) ( x ) x = x sin ( h sin h) h 0 h ( ) cos x = lim h 0 h sin Insgesamt haben wir also { f x sin ( ( (x) = x) cos ) x, x 0 0, x = 0 Da lim x 0 x 0 f (x) nicht existiert, ist f nicht stetig in x = Aufgabe ( ) x ( ) = 0 h Zeigen Sie mit den Regeln von L Hospital, dass ( ). lim n ln(+a n) a n = für jede Folge (a n) n N mit a n 0 und ( ). lim n a n ln = für jede Folge (a n ) n N mit a n. a n+ a n Warum sind die L Hospital schen Regeln in beiden Fällen anwendbar? Lösung:. Wir benutzen die L Hospital sche Regel an Stellen: lim n ln( + a n ) a n ln( + a n ) = lim a n n a n ln( + a n ) = lim x ln( + x) x 0 x ln( + x) LH = lim +x x 0 ln( + x) + x = lim x 0 = +x x x + ( + x) ln( + x) = lim x 0 x +x ln( + x) + x +x LH = lim x 0 + ln( + x) + 5
26 . Es gilt lim a n ln n 9.3 Aufgabe ( ) an + ln = lim a n n ( + ) an an a n b n= ln an = lim n x LH +x ( x) (+x) ( ) ( x) = lim x 0 = lim x 0 x = ( ) +b n b n b n = lim x 0 x + x ln = lim x 0 ( +x x x ( x) Berechnen Sie für die folgenden Funktionen die Ableitung der Umkehrfunktion:. f :] π, π [ R, f(x) = tan(x). g :] π, π [ [, ], g(x) = sin(x). Lösung:. Zunächst berechnen wir tan (x) = d sin(x) dx cos(x) = cos(x) sin(x) ( sin(x)) cos (x) Nun gilt x = tan(arctan(x)) und durch Ableiten erhalten wir = cos (x) + sin (x) cos (x) ) = +tan (x) = tan (arctan(x)) arctan (x) = (+tan (arctan x)) arctan (x) = (+x ) arctan (x) Damit folgt arctan (x) = + x. Es gilt x = sin(arcsin(x)). Durch Ableiten erhalten wir = cos(arcsin(x)) arcsin (x) Wir wollen cos möglichst durch sin ausdrücken, damit sich das arcsin x aufhebt. Generell gilt die Formel also cos x + sin x = cos x = sin x. Zusätzlich gilt für x ( π, π ), dass cos x > 0. Daher folgt cos x = sin x. Setzen wir dies oben ein, erhalten wir = sin (arcsin(x)) arcsin (x) = x arcsin (x) Umstellen ergibt arcsin (x) = x 6
27 9.4 Aufgabe Bestimmen Sie das Taylor-Polynom der Ordnung 5 zur Funktion f : R >0 R, x f(x) = x ln x mit Entwicklungspunkt x 0 = und berechnen Sie damit näherungsweise f(.3). Lösung: Wir berechnen die ersten fünf Ableitungen von f und deren Wert an der Stelle x 0 = :. f (x) = ln x +, f () =. f (x) = x, f () = 3. f (3) (x) = x, f (3) () = 4. f (4) (x) = x 3, f (4) () = 5. f (5) (x) = 6 x 4, f (5) () = 6 Nach Definition ist das Taylorpolynom der 5. Ordnung dann (T 5 f)(x) = 5 f (n) () (x ) n = 0 + (x ) + n! (x ) + 6 (x )3 + 4 (x )4 + 6 (x )5 0 n=0 = (x ) + (x ) 6 (x )3 + (x )4 (x )5 0 Der Verlauf der Funktionsgraphen sieht so aus: 4 y f(x) (T 5 f)(x) 3 4 x Damit gilt näherungsweise f(.3) (T 5 f)(.3) = =
28 0 Serie 0. Aufgabe Fertigen Sie eine Skizze an, die die Graphen der Funktion f k (x) = x k für k {,,, } im Intervall [, ] enthält. Lösung: 4 x x x x 4 0. Aufgabe Untersuchen Sie die Graphen der folgenden Funktionen auf Symmetrie bezüglich des Koordinatenursprungs bzw. der y-achse. Bestimmen Sie weiter die jeweiligen Grenzwerte für x ±.. f(x) = 3x 5 + x 3 + 9x. g(x) = +x 3. h(x) = sin(x) + e x Lösung: Eine Funktion f ist genau dann punktsymmetrisch zum Koordinatenursprung, falls f( x) = f(x) für alle x R gilt. Sie ist achsensymmetrisch zur y-achse, falls f( x) = f(x) für alle x R gilt.. Es gilt f( x) = 3( x) 5 + ( x) 3 + 9( x) = 3x 5 x 3 9x = ( 3x 5 + x 3 + 9x) = f(x) 8
29 Damit ist f punktsymmetrisch zum Ursprung. Wegen f( ) = 3 3 = f(), ist f nicht achsensymmetrisch zur y-achse. Weiter gilt lim f(x) = x 3x5 + x 3 + 9x = lim x x5 ( 3 + x + 9 x ) 4 = Wegen f( x) = f(x), ist. Es gilt lim f(x) = lim f( x) = lim f(x) = + x x x g( x) = + ( x) = + x = g(x) Damit ist g achsensymmetrisch zur y-achse. Wegen g( ) = / / = g() ist g nicht punktsymmetrisch zum Ursprung. Weiter gilt lim x Wegen g( x) = g(x), ist damit auch + x = 0 lim g(x) = lim g( x) = lim g(x) = 0 x x x 3. h ist weder achsen- noch punktsymmetrisch, da mit ( h π ) = + e π/ gilt, dass < h( π/) < 0 und ( π ) h = + e π/ > Es kann also weder h( x) = h(x) noch h( x) = h(x) gelten. Da lim x e x = 0, gilt lim h(x) = lim sin(x). x x Dieser Grenzwert existiert nicht. Wegen sin(x) und e x + für x + folgt lim h(x) = + x 9
30 0.3 Aufgabe Untersuchen Sie auf welchen Intervallen die Funktion f konvex bzw. konkav ist. Lösung: Es gilt f(x) = x 4 7x 3 + 4x 5 f (x) = 8x 3 x + 4 f (x) = 4x 4x Es gilt also f (x) = 0 genau dann wenn x = 0 oder x = 7/4. Da f eine nach oben geöffnete Parabel ist (oder durch Testeinsetzungen überprüfen), gilt f (x) < 0 für 0 < x < 7/4 und f (x) > 0 für x < 0 bzw. 7/4 < x. Also ist f auf (, 0) (7/4, + ) konvex und auf (0, 7/4) konkav. 0.4 Aufgabe Führen Sie eine vollständige Kurvendiskussion der Funktion f durch. { x ln x, x 0 f(x) = 0, x = 0 Hinweis: ln x ist eine Kurzschreibweise für ln( x ). Lösung:. Definitionsbereich: D(f) = R. Stetigkeit: Die Funktion x ln x ist als Produkt und Verkettung stetiger Funktionen in allen x R \ {0} stetig. Es bleibt zu prüfen ob f stetig in x = 0 ist. Dazu benutzen wir die Regel von L Hospital: ln x lim x 0 x ln x = lim x 0 x LH = lim x 0 x x 3 = lim x x x 0 x = 0 }{{} =± 3. Schnittpunkte mit der y-achse ist (0, f(0)) = (0, 0). 4. Nullstellen: Damit f(x) = 0 gilt, muss entweder x = 0 oder ln x = 0 gelten. Wie schon oben gesehen, ist x = 0 eine Nullstelle. Weiter sind x = ± Nullstellen, da ln() = 0. Es gilt also N(f) = {, 0, }. 5. Symmetrie: f ist symmetrisch zur y-achse, da für alle x 0. f( x) = ( x) ln x = x ln x 30
31 6. Ableitungen: Es gilt für x 0 f (x) = x ln x + x und d.h. f f(0 + h) f(0) (0) = lim = lim h ln h LH = 0 h 0 h h 0 f (x) = { x ln x + x, x 0 0, x = 0 Weiter gilt für x 0 f (x) = ln x + 3 und f f (h) f (0) (0) = lim = lim ln h + = h 0 h h 0 f ist also nur für x 0 zweimal differenzierbar. 7. Extrempunkte: Betrachten wir zunächst x 0. Dann gilt f (0) = 0 genau dann, wenn x ln x = x ln(x ) = x = e x = ± e Einsetzen in die zweite Ableitung liefert f (±/ e) = ln(e / ) + 3 = > 0. Damit hat f bei x = ± e lokale Minima. Es gilt weiter f (0) = 0, f ( e 5 ) = e 5 ( 5) e 5 = 9e 5 > 0 und f (e 5 ) = e 5 ( 5) + e 5 = 9e 5 < 0 Damit liegt ein Vorzeichenwechsel von f vom Positiven ins Negative vor. Das bedeutet, dass die Funktion links von x = 0 steigt und rechts fällt. Also hat f in x = 0 ein Maximum. x e 0 e EP Minimum Maximum Minimum 3
32 8. Wendestellen: Es ist f (x) = 0 für x = ±e 3/ Weiter gilt e < e 3/ < e < e 3/ < e. Einsetzen in f liefert f ( e ) = > 0 f (e ) = < 0 f (e ) = > 0 Also wechselt f bei x = ±e 3/ das Vorzeichen. Damit hat f dort Wendestellen. Noch genauer ist f auf (, e 3/ ) (e 3/, + ) konvex und auf ( e 3/, e 3/ ) konkav. 9. Verhalten im Unendlichen: Da f achsensymmetrisch zur y-achse ist, reicht es x zu betrachten: lim f(x) = lim f(x) = lim x x x x ln x = + 3
Klausurenkurs zum Staatsexamen (WS 2016/17): Differential und Integralrechnung 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 206/7): Differential und Integralrechnung 3 3. (Herbst 20, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 206/7): Differential und Integralrechnung 3 3. (Herbst 20, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende
Klausurenkurs zum Staatsexamen (WS 2015/16): Differential und Integralrechnung 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 25/6): Differential und Integralrechnung 3 3. (Herbst 2, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende Tatsachen
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 25/6): Differential und Integralrechnung 3 3. (Herbst 2, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende Tatsachen
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger. Lösung - Serie 6. (n+1)!. Daraus folgt, dass e 1/x < (n+
 D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger Lösung - Serie 6 1. MC-Aufgaben (Online-Abgabe) 1. Für alle ganzen Zahlen n 1 gilt... (a) e 1/x = o(x n ) für x 0 + (b) e 1/x = o(x n ) für x 0 + (c)
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger Lösung - Serie 6 1. MC-Aufgaben (Online-Abgabe) 1. Für alle ganzen Zahlen n 1 gilt... (a) e 1/x = o(x n ) für x 0 + (b) e 1/x = o(x n ) für x 0 + (c)
Übungsklausur Höhere Mathematik I für die Fachrichtung Physik
 Karlsruher Institut für Technologie (KIT) Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning WS /3 6..3 Übungsklausur Höhere Mathematik I für die Fachrichtung Physik Aufgabe ((3++5) Punkte)
Karlsruher Institut für Technologie (KIT) Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning WS /3 6..3 Übungsklausur Höhere Mathematik I für die Fachrichtung Physik Aufgabe ((3++5) Punkte)
Übersicht. 1. Motivation. 2. Grundlagen
 Übersicht 1. Motivation 2. Grundlagen 3. Analysis 3.1 Folgen, Reihen, Zinsen 3.2 Funktionen 3.3 Differentialrechnung 3.4 Extremwertbestimmung 3.5 Nichtlineare Gleichungen 3.6 Funktionen mehrerer Variabler
Übersicht 1. Motivation 2. Grundlagen 3. Analysis 3.1 Folgen, Reihen, Zinsen 3.2 Funktionen 3.3 Differentialrechnung 3.4 Extremwertbestimmung 3.5 Nichtlineare Gleichungen 3.6 Funktionen mehrerer Variabler
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger. Lösung - Serie 5. x 1 2x 3 = lim 6x
 D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie 5. MC-Aufgaben Online-Abgabe. Durch zweifache Anwendung der Regel von Bernoulli-de l Hôpital folgt Stimmt diese Überlegung? lim x x 3 +
D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie 5. MC-Aufgaben Online-Abgabe. Durch zweifache Anwendung der Regel von Bernoulli-de l Hôpital folgt Stimmt diese Überlegung? lim x x 3 +
(1 + z 2j ) = 1 z2n+2. 1 z. (1 + z)(1 z) 1 z. 1 z. (1 + z 2j ) = 1 z. 1 z 1 z
 Aufgabe Zeigen Sie mit vollständiger Induktion: Für alle n N gilt (8 Punkte) n ( + z 2j ) = 2n+, wobei z C, z, eine komplexe Zahl ist Lösung [8 Punkte] Induktionsanfang: n = : ( + z 2j ) = ( + z 2 ) =
Aufgabe Zeigen Sie mit vollständiger Induktion: Für alle n N gilt (8 Punkte) n ( + z 2j ) = 2n+, wobei z C, z, eine komplexe Zahl ist Lösung [8 Punkte] Induktionsanfang: n = : ( + z 2j ) = ( + z 2 ) =
Mathematischer Vorbereitungskurs für das MINT-Studium
 Mathematischer Vorbereitungskurs für das MINT-Studium Dr. B. Hallouet b.hallouet@mx.uni-saarland.de SS 2017 Vorlesung 7 MINT Mathkurs SS 2017 1 / 25 Vorlesung 7 (Lecture 7) Differentialrechnung differential
Mathematischer Vorbereitungskurs für das MINT-Studium Dr. B. Hallouet b.hallouet@mx.uni-saarland.de SS 2017 Vorlesung 7 MINT Mathkurs SS 2017 1 / 25 Vorlesung 7 (Lecture 7) Differentialrechnung differential
Klausur Analysis für Informatiker Musterlösung
 Prof. Dr. Torsten Wedhorn WS 9/ Dr. Ralf Kasprowitz Elena Fink Klausur Analysis für Informatiker Musterlösung 9.2.2 Name, Vorname Studienfach Matrikelnummer Semester Übungsgruppe Zugelassene Hilfsmittel:
Prof. Dr. Torsten Wedhorn WS 9/ Dr. Ralf Kasprowitz Elena Fink Klausur Analysis für Informatiker Musterlösung 9.2.2 Name, Vorname Studienfach Matrikelnummer Semester Übungsgruppe Zugelassene Hilfsmittel:
Mathematik für Studierende der Biologie Wintersemester 2017/18. Grundlagentutorium 4 Lösungen
 Mathematik für Studierende der Biologie Wintersemester 207/8 Grundlagentutorium 4 Lösungen Sebastian Groß Termin Mittwochs 5:45 7:45 Großer Hörsaal Biozentrum (B00.09) E-Mail gross@bio.lmu.de Sprechzeiten
Mathematik für Studierende der Biologie Wintersemester 207/8 Grundlagentutorium 4 Lösungen Sebastian Groß Termin Mittwochs 5:45 7:45 Großer Hörsaal Biozentrum (B00.09) E-Mail gross@bio.lmu.de Sprechzeiten
Analysis für Informatiker und Statistiker Nachklausur
 Prof. Dr. Peter Otte Wintersemester 213/14 Tom Bachmann, Sebastian Gottwald 14.3.214 Analysis für Informatiker und Statistiker Nachklausur Lösungsvorschlag Name:.......................................................
Prof. Dr. Peter Otte Wintersemester 213/14 Tom Bachmann, Sebastian Gottwald 14.3.214 Analysis für Informatiker und Statistiker Nachklausur Lösungsvorschlag Name:.......................................................
Höhere Mathematik II. Variante A
 Lehrstuhl II für Mathematik Prof Dr E Triesch Höhere Mathematik II SoSe 5 Variante A Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind zehn handbeschriebene DinA4-Blätter (Vorder- und Rückseite
Lehrstuhl II für Mathematik Prof Dr E Triesch Höhere Mathematik II SoSe 5 Variante A Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind zehn handbeschriebene DinA4-Blätter (Vorder- und Rückseite
Übungen zu Einführung in die Analysis
 Übungen zu Einführung in die Analysis (Nach einer Zusammengestellung von Günther Hörmann) Sommersemester 2011 Vor den folgenden Aufgaben werden in den ersten Wochen der Übungen noch jene zur Einführung
Übungen zu Einführung in die Analysis (Nach einer Zusammengestellung von Günther Hörmann) Sommersemester 2011 Vor den folgenden Aufgaben werden in den ersten Wochen der Übungen noch jene zur Einführung
Vorlesung Analysis I WS 07/08
 Vorlesung Analysis I WS 07/08 Erich Ossa Vorläufige Version 07/12/04 Ausdruck 8. Januar 2008 Inhaltsverzeichnis 1 Grundlagen 1 1.1 Elementare Logik.................................. 1 1.1.A Aussagenlogik................................
Vorlesung Analysis I WS 07/08 Erich Ossa Vorläufige Version 07/12/04 Ausdruck 8. Januar 2008 Inhaltsverzeichnis 1 Grundlagen 1 1.1 Elementare Logik.................................. 1 1.1.A Aussagenlogik................................
13. Übungsblatt zur Mathematik I für Maschinenbau
 Fachbereich Mathematik Prof. Dr. M. Joswig Dr. habil. Sören Kraußhar Dipl.-Math. Katja Kulas 3. Übungsblatt zur Mathematik I für Maschinenbau Gruppenübung WS 00/ 07.0.-.0. Aufgabe G Stetigkeit) a) Gegeben
Fachbereich Mathematik Prof. Dr. M. Joswig Dr. habil. Sören Kraußhar Dipl.-Math. Katja Kulas 3. Übungsblatt zur Mathematik I für Maschinenbau Gruppenübung WS 00/ 07.0.-.0. Aufgabe G Stetigkeit) a) Gegeben
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
6 Di erentialrechnung, die Exponentialfunktion
 6 Di erentialrechnung, die Exonentialfunktion 6. Exonentialfunktion Wir führen die Exonentialfunktion ein, die eine stetige Funktion mit folgenden Eigenschaften ist: ex(x + y) =ex(x)ex(y) (8) ex(0) =,
6 Di erentialrechnung, die Exonentialfunktion 6. Exonentialfunktion Wir führen die Exonentialfunktion ein, die eine stetige Funktion mit folgenden Eigenschaften ist: ex(x + y) =ex(x)ex(y) (8) ex(0) =,
Teil I Auswahlfragen
 UNIVERSITÄT KOBLENZ LANDAU INSTITUT FÜR MATHEMATIK Dr. Dominik Faas Grundlagen der Analysis Sommersemester 010 Klausur vom 07.09.010 Teil I Auswahlfragen Name: Hinweise: Bei den folgenden Auswahlfragen
UNIVERSITÄT KOBLENZ LANDAU INSTITUT FÜR MATHEMATIK Dr. Dominik Faas Grundlagen der Analysis Sommersemester 010 Klausur vom 07.09.010 Teil I Auswahlfragen Name: Hinweise: Bei den folgenden Auswahlfragen
g(x) := (x 2 + 2x + 4) sin(x) für z 1 := 1 + 3i und z 2 := 1 + i. Geben Sie das Ergebnis jeweils
 . Aufgabe Punkte a Berechnen Sie den Grenzwert n + n + 3n. b Leiten Sie die folgenden Funktionen ab. Dabei ist a R eine Konstante. fx : lnx e a, gx : x + x + 4 sinx c Berechnen Sie z z und z z in der Form
. Aufgabe Punkte a Berechnen Sie den Grenzwert n + n + 3n. b Leiten Sie die folgenden Funktionen ab. Dabei ist a R eine Konstante. fx : lnx e a, gx : x + x + 4 sinx c Berechnen Sie z z und z z in der Form
Musterlösung zur Klausur Analysis I für Lehramt Gymnasium Wintersemester 2017/18, am
 Musterlösung zur Klausur Analysis I für Lehramt Gymnasium Wintersemester 07/8, am 9.3.08 Aufgabe : Zeigen Sie, dass für alle n N gilt: n n+ n ( ) (8 Punte) Beweis mittels vollständiger Indution n : ( )
Musterlösung zur Klausur Analysis I für Lehramt Gymnasium Wintersemester 07/8, am 9.3.08 Aufgabe : Zeigen Sie, dass für alle n N gilt: n n+ n ( ) (8 Punte) Beweis mittels vollständiger Indution n : ( )
6.2 Die Regeln von de l Hospital. Ausgangsfrage: Wie berechnet man den Grenzwert. Beispiel: Sei f(x) = x 2 und g(x) = x. Dann gilt. lim.
 6.2 Die Regeln von de l Hospital Ausgangsfrage: Wie berechnet man den Grenzwert falls g(x), beide Funktionen gegen Null konvergieren, d.h. = g(x) = 0 beide Funktionen gegen Unendlich konvergieren, d.h.
6.2 Die Regeln von de l Hospital Ausgangsfrage: Wie berechnet man den Grenzwert falls g(x), beide Funktionen gegen Null konvergieren, d.h. = g(x) = 0 beide Funktionen gegen Unendlich konvergieren, d.h.
Mathematik für Sicherheitsingenieure I A
 Prof. Dr. J. Ruppenthal Wuppertal, 3.8.8 Dr. T. Pawlaschyk Mathematik für Sicherheitsingenieure I A Aufgabe. (5+5+5+5 Punkte) a) Geben Sie für jede der folgenden Aussagen an, ob sie WAHR oder FALSCH ist.
Prof. Dr. J. Ruppenthal Wuppertal, 3.8.8 Dr. T. Pawlaschyk Mathematik für Sicherheitsingenieure I A Aufgabe. (5+5+5+5 Punkte) a) Geben Sie für jede der folgenden Aussagen an, ob sie WAHR oder FALSCH ist.
1. Aufgabe (6 Punkte) Zeigen Sie mit Hilfe der vollständigen Induktion, dass folgende Gleichheit gilt für alle n N, n 2. k (k + 1)! = 1 1 n!.
 . Aufgabe (6 Punte) Zeigen Sie mit Hilfe der vollständigen Indution, dass folgende Gleichheit gilt für alle n N, n 2 n ( + )! n!. [6P] Ind. Anfang: n 2 oder l.s. ( + )! 2 r.s. 2! 2. ( + )! 2! 2! 2 2 2
. Aufgabe (6 Punte) Zeigen Sie mit Hilfe der vollständigen Indution, dass folgende Gleichheit gilt für alle n N, n 2 n ( + )! n!. [6P] Ind. Anfang: n 2 oder l.s. ( + )! 2 r.s. 2! 2. ( + )! 2! 2! 2 2 2
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger. Lösung - Serie 1
 D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie. Frage Welche der Aussagen sind richtig? Eine divergente Folge ist nicht beschränkt. Falsch. Z.B. ist {( ) n } n N beschränkt und divergent.
D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie. Frage Welche der Aussagen sind richtig? Eine divergente Folge ist nicht beschränkt. Falsch. Z.B. ist {( ) n } n N beschränkt und divergent.
Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1
![Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1 Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1](/thumbs/91/105628768.jpg) Abitur Mathematik: Bayern 2012 Teil 1 Aufgabe 1 a) DEFINITIONSMENGE f(x) = ln(x + 3) x + 3 > 0 x > 3 D f =] 3; + [ ABLEITUNG Kettenregel liefert f (x) = 1 x + 3 1 = 1 x + 3 b) DEFINITIONSMENGE 3 g(x) =
Abitur Mathematik: Bayern 2012 Teil 1 Aufgabe 1 a) DEFINITIONSMENGE f(x) = ln(x + 3) x + 3 > 0 x > 3 D f =] 3; + [ ABLEITUNG Kettenregel liefert f (x) = 1 x + 3 1 = 1 x + 3 b) DEFINITIONSMENGE 3 g(x) =
Zusammenfassung An1I HS2012 Analysis für Informatiker 1
 Zusammenfassung An1I HS2012 Analysis für Informatiker 1 Emanuel Duss emanuel.duss@gmail.com 19. November 2012 Analysis für Informatiker 1 Inhaltsverzeichnis Inhaltsverzeichnis 1 Grundlagen der Lehre von
Zusammenfassung An1I HS2012 Analysis für Informatiker 1 Emanuel Duss emanuel.duss@gmail.com 19. November 2012 Analysis für Informatiker 1 Inhaltsverzeichnis Inhaltsverzeichnis 1 Grundlagen der Lehre von
8 Reelle Funktionen. 16. Januar
 6. Januar 9 54 8 Reelle Funktionen 8. Reelle Funktion: Eine reelle Funktion f : D f R ordnet jedem Element x D f der Menge D f R eine reelle Zahl y R zu, und man schreibt y = f(x), x D. Die Menge D f heißt
6. Januar 9 54 8 Reelle Funktionen 8. Reelle Funktion: Eine reelle Funktion f : D f R ordnet jedem Element x D f der Menge D f R eine reelle Zahl y R zu, und man schreibt y = f(x), x D. Die Menge D f heißt
Mathematik I HM I A. SoSe Variante A
 Prof. Dr. E. Triesch Mathematik I SoSe 08 Variante A Hinweise zur Bearbeitung: Benutzen Sie zur Beantwortung aller Aufgaben ausschließlich das in der Klausur ausgeteilte Papier! Es werden nur die Antworten
Prof. Dr. E. Triesch Mathematik I SoSe 08 Variante A Hinweise zur Bearbeitung: Benutzen Sie zur Beantwortung aller Aufgaben ausschließlich das in der Klausur ausgeteilte Papier! Es werden nur die Antworten
Mathematik für Studierende der Biologie Wintersemester 2018/19. Grundlagentutorium 4 Lösungen
 Mathematik für Studierende der Biologie Wintersemester 2018/19 Grundlagentutorium Lösungen Sebastian Groß Termin Mittwochs 15:5 17:5 Großer Hörsaal Biozentrum (B00.019) E-Mail gross@bio.lmu.de Sprechzeiten
Mathematik für Studierende der Biologie Wintersemester 2018/19 Grundlagentutorium Lösungen Sebastian Groß Termin Mittwochs 15:5 17:5 Großer Hörsaal Biozentrum (B00.019) E-Mail gross@bio.lmu.de Sprechzeiten
9. Übungsblatt zur Vorlesung Mathematik I für Informatik
 Fachbereich Mathematik Prof. Dr. Thomas Streicher Dr. Sven Herrmann Dipl.-Math. Susanne Pape 9. Übungsblatt zur Vorlesung Mathematik I für Informatik Wintersemester 2009/2010 8./9. Dezember 2009 Gruppenübung
Fachbereich Mathematik Prof. Dr. Thomas Streicher Dr. Sven Herrmann Dipl.-Math. Susanne Pape 9. Übungsblatt zur Vorlesung Mathematik I für Informatik Wintersemester 2009/2010 8./9. Dezember 2009 Gruppenübung
Höhere Mathematik I für Ingenieurinnen und Ingenieure Beispiele zur 11. Übung
 TU Bergakademie Freiberg Vorl. Frau Prof. Dr. Swanhild Bernstein Übung Dipl.-Math. Daniel Lorenz Freiberg, 06. Dezember 06 Höhere Mathematik I für Ingenieurinnen und Ingenieure Beispiele zur. Übung In
TU Bergakademie Freiberg Vorl. Frau Prof. Dr. Swanhild Bernstein Übung Dipl.-Math. Daniel Lorenz Freiberg, 06. Dezember 06 Höhere Mathematik I für Ingenieurinnen und Ingenieure Beispiele zur. Übung In
x e x sin(x) lim oder lim bestimmen lassen.
 Es folgt nun noch ein Nachtrag zum Thema Grenzwerte von Funktionen. Wir hatten in Abschnitt 2.6 Beispiele von Funktionen gesehen, bei denen die üblichen Grenzwertregeln nicht weiterhelfen, etwa bei Quotienten
Es folgt nun noch ein Nachtrag zum Thema Grenzwerte von Funktionen. Wir hatten in Abschnitt 2.6 Beispiele von Funktionen gesehen, bei denen die üblichen Grenzwertregeln nicht weiterhelfen, etwa bei Quotienten
Abitur 2011 G8 Musterabitur Mathematik Infinitesimalrechnung
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 211 G8 Musterabitur Mathematik Infinitesimalrechnung I Teilaufgabe 1 (3 BE) Bestimmen Sie die Nullstellen der Funktion f : x (e x 2) (x 3 2x ) mit Definitionsbereich
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 211 G8 Musterabitur Mathematik Infinitesimalrechnung I Teilaufgabe 1 (3 BE) Bestimmen Sie die Nullstellen der Funktion f : x (e x 2) (x 3 2x ) mit Definitionsbereich
Tutorium: Analysis und Lineare Algebra
 Tutorium: Analysis und Lineare Algebra Vorbereitung der Bonusklausur am 25.06.2018 20. Juni 2018 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2018 Steven Köhler 20. Juni 2018 Konvergenz
Tutorium: Analysis und Lineare Algebra Vorbereitung der Bonusklausur am 25.06.2018 20. Juni 2018 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2018 Steven Köhler 20. Juni 2018 Konvergenz
Lösung zur Serie 8. x + 2x 2 sin(1/x), falls x 0, f(x) := 0, falls x = 0. = lim
 Lösung zur Serie 8 Aufgabe 40 Wir zeigen in dieser Aufgabe, dass die Voraussetzung dass die Funktion in einer kleinen Umgebung injektiv sein muss, beim Satz über die Umkehrfunktion notwendig ist. Hierzu
Lösung zur Serie 8 Aufgabe 40 Wir zeigen in dieser Aufgabe, dass die Voraussetzung dass die Funktion in einer kleinen Umgebung injektiv sein muss, beim Satz über die Umkehrfunktion notwendig ist. Hierzu
Analysis I. 6. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 6. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine Relation zwischen den Mengen X und Y.
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 6. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine Relation zwischen den Mengen X und Y.
Mathematik für Sicherheitsingenieure I A
 Priv.-Doz. Dr. J. Ruppenthal Wuppertal, 9.0.08 Dr. T. Pawlaschyk Mathematik für Sicherheitsingenieure I A Aufgabe. (5+5+6+4 Punkte) a) Geben Sie für jede der folgenden Aussagen an, ob sie WAHR oder FALSCH
Priv.-Doz. Dr. J. Ruppenthal Wuppertal, 9.0.08 Dr. T. Pawlaschyk Mathematik für Sicherheitsingenieure I A Aufgabe. (5+5+6+4 Punkte) a) Geben Sie für jede der folgenden Aussagen an, ob sie WAHR oder FALSCH
Analysis 1 für Informatiker (An1I)
 Hochschule für Technik Rapperswil Analysis 1 für Informatiker (An1I) Stand: 2012-11-13 Inhaltsverzeichnis 1 Funktionen 3 1.1 Gerade, ungerade und periodische Funktionen..................... 3 1.2 Injektive,
Hochschule für Technik Rapperswil Analysis 1 für Informatiker (An1I) Stand: 2012-11-13 Inhaltsverzeichnis 1 Funktionen 3 1.1 Gerade, ungerade und periodische Funktionen..................... 3 1.2 Injektive,
Lösung - Serie 3. D-MAVT/D-MATL Analysis I HS 2018 Dr. Andreas Steiger. MC-Aufgaben (Online-Abgabe)
 D-MAVT/D-MATL Analysis I HS 018 Dr. Andreas Steiger Lösung - Serie 3 MC-Aufgaben (Online-Abgabe) 1. Es sei die Funktion f : [0, ) [0, ) definiert durch f(x) = ln(x + 1), wobei der Logarithmus ln zur Basis
D-MAVT/D-MATL Analysis I HS 018 Dr. Andreas Steiger Lösung - Serie 3 MC-Aufgaben (Online-Abgabe) 1. Es sei die Funktion f : [0, ) [0, ) definiert durch f(x) = ln(x + 1), wobei der Logarithmus ln zur Basis
Wiederholungsklausur zur Analysis I
 Wiederholungsklausur zur Analysis I Prof. Dr. C. Löh/M. Blank 5. Oktober 2011 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie, ob Sie alle Seiten erhalten
Wiederholungsklausur zur Analysis I Prof. Dr. C. Löh/M. Blank 5. Oktober 2011 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie, ob Sie alle Seiten erhalten
Nachklausur Analysis I
 SS 008 Prof. Dr. John M. Sullivan Kerstin Günther Technische Universität Berlin Fakultät II Institut für Mathematik Nachklausur Analysis I 07.0.008 Name: Vorname: Matr.-Nr.: Studiengang: Mit der Veröffentlichung
SS 008 Prof. Dr. John M. Sullivan Kerstin Günther Technische Universität Berlin Fakultät II Institut für Mathematik Nachklausur Analysis I 07.0.008 Name: Vorname: Matr.-Nr.: Studiengang: Mit der Veröffentlichung
Aufgaben und Lösungen Ausarbeitung der Übungsstunde zur Vorlesung Analysis I
 Aufgaben und en Ausarbeitung der Übungsstunde zur Vorlesung Analysis I Wintersemester 2008/2009 Übung 6 Einleitung Eventuell auftretende Fragen zum Übungsblatt sollen beantwortet werden. Dazu ist es erforderlich,
Aufgaben und en Ausarbeitung der Übungsstunde zur Vorlesung Analysis I Wintersemester 2008/2009 Übung 6 Einleitung Eventuell auftretende Fragen zum Übungsblatt sollen beantwortet werden. Dazu ist es erforderlich,
Differenzialrechnung
 Mathe Differenzialrechnung Differenzialrechnung 1. Grenzwerte von Funktionen Idee: Gegeben eine Funktion: Gesucht: y = f(x) lim f(x) = g s = Wert gegen den die Funktion streben soll (meist 0 oder ) g =
Mathe Differenzialrechnung Differenzialrechnung 1. Grenzwerte von Funktionen Idee: Gegeben eine Funktion: Gesucht: y = f(x) lim f(x) = g s = Wert gegen den die Funktion streben soll (meist 0 oder ) g =
Univariate Analysis. Analysis und nichtlineare Modelle Sommersemester
 Analysis und nichtlineare Modelle Sommersemester 9 5 Univariate Analysis C. Berechnen Sie ohne Taschenrechner(!). Runden Sie die Ergebnisse auf ganze Zahlen. (a) 7 :, (b) 795 :.. Berechnen Sie ohne Taschenrechner(!):
Analysis und nichtlineare Modelle Sommersemester 9 5 Univariate Analysis C. Berechnen Sie ohne Taschenrechner(!). Runden Sie die Ergebnisse auf ganze Zahlen. (a) 7 :, (b) 795 :.. Berechnen Sie ohne Taschenrechner(!):
Aufgabe 1 Zeigen Sie mittels vollständiger Induktion, dass für alle n N. n(n + 1)(2n + 1) 6. j 2 = gilt.
 Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Stetigkeit. Definitionen. Beispiele
 Stetigkeit Definitionen Stetigkeit Sei f : D mit D eine Funktion. f heißt stetig in a D, falls für jede Folge x n in D (d.h. x n D für alle n ) mit lim x n a gilt: lim f x n f a. Die Funktion f : D heißt
Stetigkeit Definitionen Stetigkeit Sei f : D mit D eine Funktion. f heißt stetig in a D, falls für jede Folge x n in D (d.h. x n D für alle n ) mit lim x n a gilt: lim f x n f a. Die Funktion f : D heißt
LMU MÜNCHEN. Mathematik für Studierende der Biologie Wintersemester 2016/17. GRUNDLAGENTUTORIUM 5 - Lösungen. Anmerkung
 LMU MÜNCHEN Mathematik für Studierende der Biologie Wintersemester 2016/17 GRUNDLAGENTUTORIUM 5 - Lösungen Anmerkung Es handelt sich hierbei um eine Musterlösung so wie es von Ihnen in einer Klausur erwartet
LMU MÜNCHEN Mathematik für Studierende der Biologie Wintersemester 2016/17 GRUNDLAGENTUTORIUM 5 - Lösungen Anmerkung Es handelt sich hierbei um eine Musterlösung so wie es von Ihnen in einer Klausur erwartet
Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann
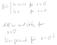 Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann heißt f (x) = (f ) (x) die zweite Ableitung von f
Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann heißt f (x) = (f ) (x) die zweite Ableitung von f
Übungsaufgaben Folgen und Reihen
 Kallenrode, www.sotere.uos.de Übungsaufgaben Folgen und Reihen. Untersuchen Sie die folgenden Folgen auf Monotonie, Beschränktheit und Konvergenz (geben Sie gegebenenfalls den Grenzwert an): inverse Fakultäten:,,
Kallenrode, www.sotere.uos.de Übungsaufgaben Folgen und Reihen. Untersuchen Sie die folgenden Folgen auf Monotonie, Beschränktheit und Konvergenz (geben Sie gegebenenfalls den Grenzwert an): inverse Fakultäten:,,
Misterlösung zur Klausur zur Vorlesung Analysis I, WS08/09, Samstag, (Version C)
 Misterlösung zur Klausur zur Vorlesung Analysis I, WS08/09, Samstag, 14..009 (Version C Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen aus der Vorlesung
Misterlösung zur Klausur zur Vorlesung Analysis I, WS08/09, Samstag, 14..009 (Version C Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen aus der Vorlesung
Lösungsvorschlag zur Übungsklausur zur Analysis I
 Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 NWF I - Mathematik 9..9 Universität Regensburg Lösungsvorschlag zur Übungsklausur zur Analysis I Frage 1 Vervollständigen Sie die folgenden
Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 NWF I - Mathematik 9..9 Universität Regensburg Lösungsvorschlag zur Übungsklausur zur Analysis I Frage 1 Vervollständigen Sie die folgenden
3 Folgen, Reihen und stetige Funktionen
 Höhere Mathematik 101 3 Folgen, Reihen und stetige Funktionen 3.1 Folgen und Reihen: Definitionen und Beispiele Eine reelle oder komplexe Zahlenfolge ist eine Abbildung, die jeder natürlichen Zahl n eine
Höhere Mathematik 101 3 Folgen, Reihen und stetige Funktionen 3.1 Folgen und Reihen: Definitionen und Beispiele Eine reelle oder komplexe Zahlenfolge ist eine Abbildung, die jeder natürlichen Zahl n eine
11 Spezielle Funktionen und ihre Eigenschaften
 78 II. ANALYSIS 11 Spezielle Funktionen und ihre Eigenschaften In diesem Abschnitt wollen wir wichtige Eigenschaften der allgemeinen Exponentialund Logarithmusfunktion sowie einiger trigonometrischer Funktionen
78 II. ANALYSIS 11 Spezielle Funktionen und ihre Eigenschaften In diesem Abschnitt wollen wir wichtige Eigenschaften der allgemeinen Exponentialund Logarithmusfunktion sowie einiger trigonometrischer Funktionen
( ) Dann gilt f(x) g(x) in der Nähe von x 0, das heisst. Für den Fehler r(h) dieser Näherung erhält man unter Verwendung von ( )
 64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
Analysis I. 3. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 3. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine Abbildung F von einer Menge L in eine
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 3. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine Abbildung F von einer Menge L in eine
Analysis1-Klausuren in den ET-Studiengängen (Ba) ab 2007
 Analysis-Klausuren in den ET-Studiengängen (Ba) ab 7 Im Folgenden finden Sie die Aufgabenstellungen der bisherigen Klausuren Analysis im Bachelorstudium der ET-Studiengänge sowie knapp gehaltene Ergebnisangaben.
Analysis-Klausuren in den ET-Studiengängen (Ba) ab 7 Im Folgenden finden Sie die Aufgabenstellungen der bisherigen Klausuren Analysis im Bachelorstudium der ET-Studiengänge sowie knapp gehaltene Ergebnisangaben.
Differential- und Integralrechnung
 Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Anwendungen der Differentialrechnung
 KAPITEL 5 Anwendungen der Differentialrechnung 5.1 Maxima und Minima einer Funktion......................... 80 5.2 Mittelwertsatz.................................... 82 5.3 Kurvendiskussion..................................
KAPITEL 5 Anwendungen der Differentialrechnung 5.1 Maxima und Minima einer Funktion......................... 80 5.2 Mittelwertsatz.................................... 82 5.3 Kurvendiskussion..................................
Tutorium Mathematik I M WM Lösungen
 Tutorium Mathematik I M WM Lösungen 3... Durch mehrmaliges Anwenden der Regel von de l Hospital ergibt sich: e e sin() e cos()e sin() sin() cos() e + sin()e sin() cos ()e sin() sin() e + cos()e sin() +
Tutorium Mathematik I M WM Lösungen 3... Durch mehrmaliges Anwenden der Regel von de l Hospital ergibt sich: e e sin() e cos()e sin() sin() cos() e + sin()e sin() cos ()e sin() sin() e + cos()e sin() +
Thema 5 Differentiation
 Thema 5 Differentiation Definition 1 Sei f : D R. Dann ist f im Punkt x 0 differenzierbar, falls f(x) f(x 0 ) x x 0 x x 0 auf der Menge D \ {x 0 } existiert. Der Limes ist dann die Ableitung von f im Punkt
Thema 5 Differentiation Definition 1 Sei f : D R. Dann ist f im Punkt x 0 differenzierbar, falls f(x) f(x 0 ) x x 0 x x 0 auf der Menge D \ {x 0 } existiert. Der Limes ist dann die Ableitung von f im Punkt
Skripten für die Oberstufe. Kurvendiskussion. f (x) f (x)dx = e x.
 Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
Anwendungen der Differentialrechnung
 KAPITEL 7 Anwendungen der Differentialrechnung 7.1 Maxima und Minima einer Funktion................. 141 7.2 Mittelwertsatz............................ 144 7.3 Kurvendiskussion..........................
KAPITEL 7 Anwendungen der Differentialrechnung 7.1 Maxima und Minima einer Funktion................. 141 7.2 Mittelwertsatz............................ 144 7.3 Kurvendiskussion..........................
Mathematik zum Mitnehmen
 Mathematik zum Mitnehmen Zusammenfassungen und Übersichten aus Arens et al., Mathematik Bearbeitet von Tilo Arens, Frank Hettlich, Christian Karpfinger, Ulrich Kockelkorn, Klaus Lichtenegger, Hellmuth
Mathematik zum Mitnehmen Zusammenfassungen und Übersichten aus Arens et al., Mathematik Bearbeitet von Tilo Arens, Frank Hettlich, Christian Karpfinger, Ulrich Kockelkorn, Klaus Lichtenegger, Hellmuth
Technische Universität München Zentrum Mathematik. Übungsblatt 4
 Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 4 Hausaufgaben Aufgabe 4. Gegeben sei die Funktion f : D R mit f(x) :=
Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 4 Hausaufgaben Aufgabe 4. Gegeben sei die Funktion f : D R mit f(x) :=
Ferienkurs Stetigkeit und Konvergenz Seite 1. Technische Universität München Ferienkurs Analysis 1. Musterlösung = lim.
 Ferienkurs Stetigkeit und Konvergenz Seite Technische Universität München Ferienkurs Analysis Hannah Schamoni Stetigkeit und Konvergenz Musterlösung 6.03.20. Grenzwerte I Berechnen Sie lim f(), lim f()
Ferienkurs Stetigkeit und Konvergenz Seite Technische Universität München Ferienkurs Analysis Hannah Schamoni Stetigkeit und Konvergenz Musterlösung 6.03.20. Grenzwerte I Berechnen Sie lim f(), lim f()
I. Verfahren mit gebrochen rationalen Funktionen:
 I. Verfahren mit gebrochen rationalen Funktionen: 1. Definitionslücken bestimmen: Nenner wird gleich 0 gesetzt! 2. Prüfung ob eine hebbare Definitionslücke vorliegt: Eine hebbare Definitionslücke liegt
I. Verfahren mit gebrochen rationalen Funktionen: 1. Definitionslücken bestimmen: Nenner wird gleich 0 gesetzt! 2. Prüfung ob eine hebbare Definitionslücke vorliegt: Eine hebbare Definitionslücke liegt
Analysis I. 6. Übungsstunde. Steven Battilana. battilana.uk/teaching
 Analysis I 6. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching April 26, 2017 1 Erinnerung Eine Abbildung f : X Y heisst injektiv, falls 1, 2 X : 1 2 f( 1 ) f( 2 ). (In Worten:
Analysis I 6. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching April 26, 2017 1 Erinnerung Eine Abbildung f : X Y heisst injektiv, falls 1, 2 X : 1 2 f( 1 ) f( 2 ). (In Worten:
2) Gegeben sei die Menge. Bei welchen der gegebenen Zerlegungen handelt es sich um eine Klasseneinteilung?
 00 0 000 0 000 000 0 000 000 0 0 0 0 0 000 000 0 000 00 000 0 0 0 00 0 0 0 0 000 000 000 00 000 0 0 0 0 0 0 0 0 000 0 0 0 Themenkatalog Mengenlehre Aussagenlogik Relationen Funktionen Vollständige Induktion
00 0 000 0 000 000 0 000 000 0 0 0 0 0 000 000 0 000 00 000 0 0 0 00 0 0 0 0 000 000 000 00 000 0 0 0 0 0 0 0 0 000 0 0 0 Themenkatalog Mengenlehre Aussagenlogik Relationen Funktionen Vollständige Induktion
4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion.
 4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion. Definition 4.3. Es sei f : R D R eine auf D erklarte Funktion. Die Funktion f hat in a D eine globales oder
4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion. Definition 4.3. Es sei f : R D R eine auf D erklarte Funktion. Die Funktion f hat in a D eine globales oder
Kapitel 5: Differentialrechnung
 Kapitel 5: Differentialrechnung Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz Stefan Ruzika (KO) Kapitel 5: Differentialrechnung 1 / 23 Gliederung 1 Grundbegriffe 2 Abbildungen
Kapitel 5: Differentialrechnung Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz Stefan Ruzika (KO) Kapitel 5: Differentialrechnung 1 / 23 Gliederung 1 Grundbegriffe 2 Abbildungen
Lösungen zur Probeklausur zur Vorlesung Analysis I, WS08/09, Samstag, (Version A)
 Lösungen zur Probeklausur zur Vorlesung Analysis I, WS08/09, Samstag, 10.1.009 (Version A) Kennwort: Übungsgruppe: (Sie können ein beliebiges Kennwort wählen, um Ihre Anonymität zu wahren! Da die Probeklausur
Lösungen zur Probeklausur zur Vorlesung Analysis I, WS08/09, Samstag, 10.1.009 (Version A) Kennwort: Übungsgruppe: (Sie können ein beliebiges Kennwort wählen, um Ihre Anonymität zu wahren! Da die Probeklausur
D-BAUG Analysis I HS 2015 Dr. Meike Akveld. Clicker Fragen
 D-BAUG Analysis I HS 05 Dr. Meike Akveld Clicker Fragen Frage Der Satz: Dieser Satz ist falsch ist wahr ist richtig weiss ich nicht Es handelt hier um eine sogenannte Paradoxie. Die Paradoxie dieses Satzes
D-BAUG Analysis I HS 05 Dr. Meike Akveld Clicker Fragen Frage Der Satz: Dieser Satz ist falsch ist wahr ist richtig weiss ich nicht Es handelt hier um eine sogenannte Paradoxie. Die Paradoxie dieses Satzes
Technische Universität Berlin. Klausur Analysis I
 SS 2008 Prof. Dr. John M. Sullivan Kerstin Günther Technische Universität Berlin Fakultät II Institut für Mathematik Klausur Analysis I 4.07.2008 Name: Vorname: Matr.-Nr.: Studiengang: Mit der Veröffentlichung
SS 2008 Prof. Dr. John M. Sullivan Kerstin Günther Technische Universität Berlin Fakultät II Institut für Mathematik Klausur Analysis I 4.07.2008 Name: Vorname: Matr.-Nr.: Studiengang: Mit der Veröffentlichung
Monotonie, Konkavität und Extrema
 Kapitel 8 Monotonie, Konkavität und Extrema Josef Leydold Auffrischungskurs Mathematik WS 2017/18 8 Monotonie, Konkavität und Extrema 1 / 55 Monotonie Eine Funktion f heißt monoton steigend, falls x 1
Kapitel 8 Monotonie, Konkavität und Extrema Josef Leydold Auffrischungskurs Mathematik WS 2017/18 8 Monotonie, Konkavität und Extrema 1 / 55 Monotonie Eine Funktion f heißt monoton steigend, falls x 1
Monotonie, Konkavität und Extrema
 Kapitel 8 Monotonie, Konkavität und Extrema Josef Leydold Auffrischungskurs Mathematik WS 2017/18 8 Monotonie, Konkavität und Extrema 1 / 55 Monotonie Eine Funktion f heißt monoton steigend, falls x 1
Kapitel 8 Monotonie, Konkavität und Extrema Josef Leydold Auffrischungskurs Mathematik WS 2017/18 8 Monotonie, Konkavität und Extrema 1 / 55 Monotonie Eine Funktion f heißt monoton steigend, falls x 1
Klausur zur Analysis I WS 01/02
 Klausur zur Analysis I WS 0/0 Prof. Dr. E. Kuwert. Februar 00 Aufgabe (4 Punkte) Berechnen Sie unter a) und b) jeweils die Ableitung von f für x (0, ): a) f(x) = e sin x b) f(x) = x α log x a) f (x) =
Klausur zur Analysis I WS 0/0 Prof. Dr. E. Kuwert. Februar 00 Aufgabe (4 Punkte) Berechnen Sie unter a) und b) jeweils die Ableitung von f für x (0, ): a) f(x) = e sin x b) f(x) = x α log x a) f (x) =
LS Informatik 4 & Funktionen. Buchholz / Rudolph: MafI 2 88
 4. Funktionen Buchholz / Rudolph: MafI 2 88 Kapitelgliederung 4.1 Grundlegende Denitionen 4.2 Polynome und rationale Funktionen 4.3 Beschränkte und monotone Funktionen 4.4 Grenzwerte von Funktionen 4.5
4. Funktionen Buchholz / Rudolph: MafI 2 88 Kapitelgliederung 4.1 Grundlegende Denitionen 4.2 Polynome und rationale Funktionen 4.3 Beschränkte und monotone Funktionen 4.4 Grenzwerte von Funktionen 4.5
Höhere Mathematik II. Variante A
 Lehrstuhl II für Mathematik Prof. Dr. E. Triesch Höhere Mathematik II SoSe 01 Variante A Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind zehn handbeschriebene DinA-Blätter Vorder- und Rückseite
Lehrstuhl II für Mathematik Prof. Dr. E. Triesch Höhere Mathematik II SoSe 01 Variante A Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind zehn handbeschriebene DinA-Blätter Vorder- und Rückseite
11. Übungsblatt zur Mathematik I für Maschinenbau
 Fachbereich Mathematik Prof. Dr. M. Joswig Dr. habil. Sören Kraußhar Dipl.-Math. Katja Kulas. Übungsblatt zur Mathematik I für Maschinenbau Gruppenübung WS 200/ 2.0.-28.0. Aufgabe G (Grenzwertberechnung)
Fachbereich Mathematik Prof. Dr. M. Joswig Dr. habil. Sören Kraußhar Dipl.-Math. Katja Kulas. Übungsblatt zur Mathematik I für Maschinenbau Gruppenübung WS 200/ 2.0.-28.0. Aufgabe G (Grenzwertberechnung)
Lösungen Klausur. k k (n + 1) n. für alle n N. Lösung: IA: Für n = 1 ist 1. k k + (n + 1) n+1. k k = k=1. k=1 kk = 1 1 = 1 2 = 2 1.
 Lösungen Klausur Aufgabe (3 Punkte) Zeigen Sie, dass n k k (n + ) n k für alle n N. IA: Für n ist k kk 2 2. IV: Es gilt n k kk (n + ) n für ein n N. IS: Wir haben n+ k k k n k k + (n + ) n+ k IV (n + )
Lösungen Klausur Aufgabe (3 Punkte) Zeigen Sie, dass n k k (n + ) n k für alle n N. IA: Für n ist k kk 2 2. IV: Es gilt n k kk (n + ) n für ein n N. IS: Wir haben n+ k k k n k k + (n + ) n+ k IV (n + )
Vorlesung Mathematik für Ingenieure 1 (Wintersemester 2008/09)
 Vorlesung Mathematik für Ingenieure (Wintersemester 2008/09) Kapitel 6: Differenzialrechnung einer Veränderlichen Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 9. November 2008) Die
Vorlesung Mathematik für Ingenieure (Wintersemester 2008/09) Kapitel 6: Differenzialrechnung einer Veränderlichen Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 9. November 2008) Die
Klausur zur Vorlesung Analysis I für Lehramtskandidaten. (Sommersemester 2008) Dr. C. Lange, J. Schütz
 Klausur zur Vorlesung Analysis I für Lehramtskandidaten (Sommersemester 008) Dr. C. Lange, J. Schütz Beginn: 17. Juli 008, 10:00 Uhr Ende: 17. Juli 008, 11:30 Uhr Name: Matrikelnummer: Ich studiere: Bachelor
Klausur zur Vorlesung Analysis I für Lehramtskandidaten (Sommersemester 008) Dr. C. Lange, J. Schütz Beginn: 17. Juli 008, 10:00 Uhr Ende: 17. Juli 008, 11:30 Uhr Name: Matrikelnummer: Ich studiere: Bachelor
Staatsexamen Herbst 2017 Differential- und Integralrechnung, Thema I
 Staatsexamen Herbst 17 Differential- und Integralrechnung, Thema I 1. a) Die Aussage ist wahr! Sei s R der Reihenwert der Reihe k=1 Da a n = s n s n 1 für n, ist also b) Die Aussage ist falsch! a k, also
Staatsexamen Herbst 17 Differential- und Integralrechnung, Thema I 1. a) Die Aussage ist wahr! Sei s R der Reihenwert der Reihe k=1 Da a n = s n s n 1 für n, ist also b) Die Aussage ist falsch! a k, also
Prof. Dr. Stefan Luckhaus WS 2013/14. Übungsserie 1. Mathematik für Wirtschaftswissenschaftler
 Prof. Dr. Stefan Luckhaus WS 203/4 Übungsserie Aufgabe. Seien f : R R, g : R R Funktionen, die wie folgt definiert sind: fx) =, gx) = x +. + x2 Stellen Sie die Funktionen als Quotienten von Polynomen dar.
Prof. Dr. Stefan Luckhaus WS 203/4 Übungsserie Aufgabe. Seien f : R R, g : R R Funktionen, die wie folgt definiert sind: fx) =, gx) = x +. + x2 Stellen Sie die Funktionen als Quotienten von Polynomen dar.
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Prof. Dr. Oliver Matte Max Lein Zentralübung Mathematik für Physiker 2 Analysis ) Wintersemester 200/20 Lösungsblatt 5 2..200) 32. Häufungspunkte Sei a
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Prof. Dr. Oliver Matte Max Lein Zentralübung Mathematik für Physiker 2 Analysis ) Wintersemester 200/20 Lösungsblatt 5 2..200) 32. Häufungspunkte Sei a
Analysis I Lösung von Serie 9
 FS 07 9.. MC Fragen: Ableitungen (a) Die Figur zeigt den Graphen einer zweimal differenzierbaren Funktion f. Was lässt sich über f, f und f sagen? Nichts Die Funktion f ist positiv. Die Funktion f ist
FS 07 9.. MC Fragen: Ableitungen (a) Die Figur zeigt den Graphen einer zweimal differenzierbaren Funktion f. Was lässt sich über f, f und f sagen? Nichts Die Funktion f ist positiv. Die Funktion f ist
Höhere Mathematik 1 Übung 9
 Aufgaben, die in der Präsenzübung nicht besprochen wurden, können in der darauf folgenden übung beim jeweiligen übungsleiter bzw. bei der jeweiligen übungsleiterin abgegeben werden. Diese Abgabe ist freiwillig
Aufgaben, die in der Präsenzübung nicht besprochen wurden, können in der darauf folgenden übung beim jeweiligen übungsleiter bzw. bei der jeweiligen übungsleiterin abgegeben werden. Diese Abgabe ist freiwillig
1. Aufgabe 8 Punkte. f (x) = (x 2 + 1) e x2. Es gilt. f (x) = 2xe x2 + ( x ) e x2 ( 2x) = 2x 3 e x2.
 1. Aufgabe 8 Punkte Geben Sie die Bereiche, auf denen die Funktion f : R R mit f (x) = (x + 1) e x monoton wachsend oder fallend ist, an, und untersuchen Sie die Funktion auf lokale und globale Extrema.
1. Aufgabe 8 Punkte Geben Sie die Bereiche, auf denen die Funktion f : R R mit f (x) = (x + 1) e x monoton wachsend oder fallend ist, an, und untersuchen Sie die Funktion auf lokale und globale Extrema.
Ferienkurs Analysis 1 - Wintersemester 2014/15. 1 Aussage, Mengen, Induktion, Quantoren
 Ferienkurs Analysis 1 - Wintersemester 2014/15 Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis
Ferienkurs Analysis 1 - Wintersemester 2014/15 Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis
Mathematik I Herbstsemester 2018 Kapitel 4: Anwendungen der Differentialrechnung
 Mathematik I Herbstsemester 2018 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 55 4. Anwendungen der Differentialrechnung Monotonie Krümmung Linearisierung einer Funktion Extremwerte
Mathematik I Herbstsemester 2018 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 55 4. Anwendungen der Differentialrechnung Monotonie Krümmung Linearisierung einer Funktion Extremwerte
Kapitel 5. Differenzialrechnung für Funktionen einer Variablen
 Kapitel 5. Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen
Kapitel 5. Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen
10 Differenzierbare Funktionen
 10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
Lösungsvorschlag zur Nachklausur zur Analysis
 Prof Dr H Garcke, D Depner SS 09 NWF I - Mathematik 080009 Universität Regensburg Lösungsvorschlag zur Nachklausur zur Analysis Aufgabe Untersuchen Sie folgende Reihen auf Konvergenz und berechnen Sie
Prof Dr H Garcke, D Depner SS 09 NWF I - Mathematik 080009 Universität Regensburg Lösungsvorschlag zur Nachklausur zur Analysis Aufgabe Untersuchen Sie folgende Reihen auf Konvergenz und berechnen Sie
Karlsruher Institut für Technologie (KIT) WS 2012/13 Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning
 Karlsruher Institut für Technologie (KIT) WS 202/3 Institut für Analysis 26..202 Prof. Dr. Tobias Lamm Dr. Patrick Breuning Höhere Mathematik I für die Fachrichtung Physik 7. Übungsblatt Aufgabe Untersuchen
Karlsruher Institut für Technologie (KIT) WS 202/3 Institut für Analysis 26..202 Prof. Dr. Tobias Lamm Dr. Patrick Breuning Höhere Mathematik I für die Fachrichtung Physik 7. Übungsblatt Aufgabe Untersuchen
KLAUSUR. Analysis (E-Technik/Mechatronik/W-Ing) Prof. Dr. Werner Seiler Dr. Matthias Fetzer, Dominik Wulf
 KLAUSUR Analysis (E-Technik/Mechatronik/W-Ing).9.7 Prof. Dr. Werner Seiler Dr. Matthias Fetzer, Dominik Wulf Name: Vorname: Matr. Nr./Studiengang: Versuch Nr.: Unterschrift: In der Klausur können Sie insgesamt
KLAUSUR Analysis (E-Technik/Mechatronik/W-Ing).9.7 Prof. Dr. Werner Seiler Dr. Matthias Fetzer, Dominik Wulf Name: Vorname: Matr. Nr./Studiengang: Versuch Nr.: Unterschrift: In der Klausur können Sie insgesamt
Mathematischer Vorkurs NAT-ING II
 Mathematischer Vorkurs NAT-ING II (02.09.2013 20.09.2013) Dr. Jörg Horst WS 2013-2014 Mathematischer Vorkurs TU Dortmund Seite 1 / 252 Kapitel 7 Differenzierbarkeit Mathematischer Vorkurs TU Dortmund Seite
Mathematischer Vorkurs NAT-ING II (02.09.2013 20.09.2013) Dr. Jörg Horst WS 2013-2014 Mathematischer Vorkurs TU Dortmund Seite 1 / 252 Kapitel 7 Differenzierbarkeit Mathematischer Vorkurs TU Dortmund Seite
