1 Die natürliche Exponentialfunktion und ihre Ableitung
|
|
|
- Magdalena Berg
- vor 7 Jahren
- Abrufe
Transkript
1 Schülerbuchseite 5 5 Lösungen vorläuig VI Natürliche Eponential- und Logarithmusunktion Die natürliche Eponentialunktion und ihre Ableitung S. 5 Durch Ausprobieren erkennt man, dass < a <, bzw. sogar,5 < a <,8., Für a =,7 hat man schon ast die Gerade, als Tangente., 0,9 0,8 a 0,7 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,5 0, S. 5 = e ; e 5,598; e 0,5,80; e 0,5; e ,55; e, 0,0; e e 5,5; e ,008; e,7,00 a) () = e + entsteht aus dem,8 Graphen von () = e durch Verschiebung um nach oben.,,, b) () = e ist eine Streckung des Graphen von () = e mit,8, dem Faktor., c) () = e ist eine Spiegelung an, der -Achse. 0,8 d) () = e ist eine Verschiebung 0, um nach rechts. 0, 0, 0, 0, 0, 0,8 Ein DIN-A-Blatt ist cm breit und 9,7 cm hoch. a) Gesucht ist so, dass e 9,7; durch Probieren mit dem TR: e,9 9,7 Der Graph passt bis =,9 au das Blatt. b) e = 8857 cm 000 km Das Blatt müsste rund 000 km hoch sein. 5 a) () = e ; ( ) = e 0,5 b) () = e ; (0,5) = e 0,5,95 c) () = e e; () = e e =,5 e d) () = e e e (0) = Ernst Klett Verlag GmbH, Stuttgart 00 Lambacher Schweizer, Ausgabe Baern, Lösungen und Materialien Klasse ISBN VI Natürliche Eponentialund Logarithmusunktion 5
2 Schülerbuchseite 5 Lösungen vorläuig a) () = e ; Ansatz ür g: = m + t, wobei m A = () und m B = ( ) () = e; e = e + t t = 0; t A : = e ( ) = e ; e = e + t t = e ; t B: = e + e b) m N = m A bzw. m N = m B Steigung der Normalen in A: m N = e ; Steigung der Normalen in B: m N = e 7 Parallele Tangenten haben dieselbe Steigung, also () = g () a) () = e ; g () = e = P (0 ); Q (0 0) b) () = e ; g () = e = keine Lösung möglich c) () = e ; g () = e e = e P ( e ) ; Q ( e ) 8 c () = c e ; Schnittpunkt mit der -Achse: c e 0 = c (0 c) c () = c e ; c (0) = c = 0, 0, () = 0, e 9 a) Gleichung der Tangente im Punkt P (a e a ) m P = (a) = e a ; e a = e a a + t t = e a ( a) t: = e a + ( a) e a Q: e a + ( a) e a = 0 = a b) Die -Koordinate des Punktes Q ist um kleiner als die -Koordinate des Punktes P. c) tan α = e a tan α = ea P Q e a = ea P Q P Q = oder Q = P d) Zu jedem Punkt P (a (a)) indet man immer einen. Punkt Q (a 0), der auch au der Tangente liegt. Die Verbindungsgerade PQ stellt die Tangente dar. 0 Vgl. Augabe 9. Wenn die Tangente durch (0 0) geht, hat der Berührpunkt die Koordinaten ( e). Die Tangente hat die Gleichung = e. a) Der Graph von () wird an der -Achse gespiegelt und um nach oben verschoben. b) Der Graph von () verschiebt sich um nach links. c) Der Graph von () wird an der - und der -Achse gespiegelt. d) Der Graph von () verschiebt sich um nach links und wird an der -Achse gespiegelt. () gehört zu dem lilaarbigen Graphen; (0) = 0 () gehört zu dem blauen Graphen; (0) = () gehört zu dem orangearbigen Graphen; Spiegelung von = e an der -Achse und Verschiebung um nach oben. () gehört zu dem roten Graphen; () = 0; es handelt sich um eine um nach rechts verschobene und mit dem Faktor 0,5 gestauchte Normalparabel. a) () = c e + a =, a = c e () = c e + c e ; also keine eindeutige Lösung möglich. Bsp.: c = a = e () = e + e b) (0) = c e 0 + a =, a = c (0) = c e 0 = c = () = e a = a) 8 b) 57, c) d) 5 e), ) 8,5 g) 80 h) 7 i) 57,8 k) 50 Ernst Klett Verlag GmbH, Stuttgart 00 Lambacher Schweizer, Ausgabe Baern, Lösungen und Materialien Klasse ISBN VI Natürliche Eponentialund Logarithmusunktion
3 Schülerbuchseite Lösungen vorläuig Die natürliche Logarithmusunktion und ihre Ableitung S a) F zugeordnet wird. b) g () = () e = e ür = g (e) = e = e ür = g (e ) = g stellt den Graph einer Funktion dar, da zu jedem * R + genau ein -Wert B e = e ür = g (e ) = g E e = e ür = g ( e ) = D C F' b E' c) g ordnet jeder positiven Zahl ihren A 5 Logarithmus zur Basis e zu. D' C' a S. 57 Teilaugabe b), Fehler im Schülerbuch? a) Schätzung: + = ln = ln 8 = ln + ln 8,0 +,08 =,8 b) Schätzung: : = ln = ln 8 = 0,9 c) Schätzung: + = ln 7 = ln 8 + ln 9 = ln 8 + ln =,8 d) Schätzung: = ln 0,75 = ln 8 = ln ln 8,0,08 = 0,98 e) Schätzung: ln = ln ln = ln,0 ) Schätzung: = 0,7 ln 8 = ln,08 = 0,9 a) ohne TR nicht lösbar b) ln (e ) = ln e = c) ln (e ) = ln e = d) ln ( e ) = ln e = e) ohne TR nicht lösbar ) ohne TR nicht lösbar g) [ln (e )] = [ ln e] = = 8 h) [ln (e ) 5 ] = ln e 0 = 0 i) ohne TR nicht lösbar a) D = R + ; () = b) D = R + ; () = c) D = R + ; () = d) D = R + ; () = e) D = R ; () = ) D = R + ; () = 5 () = gelbes Kärtchen g () = + lila Kärtchen h () = + rotes Kärtchen k () = grünes Kärtchen u () = gelbes Kärtchen v () = blaues Kärtchen Das Kärtchen 8 gehört zu keiner gegebenen Funktion. a) F () = ln + c > 0 b) F () = ln + c > 0 F () = ln ( ) + c < 0 F () = ln ( ) + c < 0 c) F () = + ln + c > 0 d) F () = 5 ln + c > 0 F () = + ln ( ) + c < 0 F () = 5 ln ( ) + c < 0 7 a) > 0: F () = 0,5 ln ; F () = = () < 0: F () = 0,5 ln ( ); F () = ( ) = = () b) > : F () = ln ( ); F () = = () < : F () = ln ( ); F () = ( ) = = () Ernst Klett Verlag GmbH, Stuttgart 00 Lambacher Schweizer, Ausgabe Baern, Lösungen und Materialien Klasse ISBN VI Natürliche Eponentialund Logarithmusunktion 7
4 Schülerbuchseite 57 Lösungen vorläuig 8 a) (0,5) = ; () = ; () = 0,5; () = 0,5 b) abgelesen: (,75) (,75) mit TR: (,7) 0,58; (,7) 0,55 9 Ansatz: = m + t a) m = (e ) = e (e = e ) = e + t t = t P: = e + b) Tangentengleichung an einem beliebigen Punkt P ( P ln P ) * G : Steigung: ( P ) = P ln P = P P + t t = ln P t P : = P + ln P A * t: = P 0 + ln P = ln P P = e t A : = e + c) Tangentengleichung siehe b): t: = P + ln P B (0 n) * t: n = P 0 + ln P n + = ln P P = e n + t B : = e (n + ) + n 0 a) Vermutung: g () ist eine Tangente an G mit g() Berührpunkt bei e b) Schnittpunkt (graphisch): A (e ) A Rechnerisch muss gelten: ln = e 5 ür = e: ln e = e e () = w. A. Tangente an G in (e ): = e a) b) P ( P ln (k P )); m = ( P ) = P 5 7 c) () = ln b p () q () h () g () () () ln (k P ) = P P + t t = ln (k P ) t P : = P + ln (k P ) A * t P : = P 0 + ln (k P ) = ln (k P ) e = k P P = e k Zu jedem k gibt es einen Berühr- punkt P ( e k ). Die Tangente durch P verläut auch durch A. Steigung der Normale in P ( P ln P ): m = P Gleichung der Normale durch 0: = P Da P Schnittpunkt von Normale und Graph () ist, gilt: ln P = P Diese Gleichung wird erüllt von P 0,5. a Ernst Klett Verlag GmbH, Stuttgart 00 Lambacher Schweizer, Ausgabe Baern, Lösungen und Materialien Klasse ISBN VI Natürliche Eponentialund Logarithmusunktion 8
5 Schülerbuchseite 58 Lösungen vorläuig S. 58 = ln ( + ) violetter Graph, da Nullstelle bei = = ln + blauer Graph, Verschiebung von ln um + in -Richtung = ln ( ) gelber Graph, da Nullstelle bei = = + + roter Graph, Nullstelle bei = Keine Graphen ür = ln, = , = ln + ln a) = ln + b) = ln ( + ) c) = ln d) = ln ( ) e) Individuelle Lösungen a) c) ln () d) b) violett: = + ln ; Verschiebung in -Richtung um nach oben blau: = ln ( +,5); Verschiebung in -Richtung um,5 nach links gelb: = ln ; Streckung in -Richtung mit Faktor rot: = ln ( ) ; Streckung in -Richtung mit Faktor 5 Für die Schnittstelle 0 muss gelten: () ln 0 = a 0 + c () 0 a 0 = (orthogonal) a = ln () alle Parabeln mit = schneiden orthogonal. Schnittpunkt au -Achse: ln 0 = 0 0 = c = also: ür = = 0,5 + 0,5 = 0,5 a) = ln nicht lösbar keine Nullstelle () = ; = 0 ür = Minimum ür T ( ), da () < 0 ür < und () > 0 ür > b) () = e ür = e = + e 5 P ( + e + e + ln ( + e) ) (0,7,58) () = e ür = e = e < 0 da + D gibt es keinen solchen Punkt. c) Berührpunkt: ( B B ln B ) Tangente durch Ursprung mit Steigung m = ( B ): B ln B = ( B ) B ln B =, also B = e B (e e ) T 5 Ernst Klett Verlag GmbH, Stuttgart 00 Lambacher Schweizer, Ausgabe Baern, Lösungen und Materialien Klasse ISBN VI Natürliche Eponentialund Logarithmusunktion 9
6 Schülerbuchseite 58 0 Lösungen vorläuig 7 a) D = R + b) () = ln = ( ln ) Etremwert ür ( ln ) = 0 ln =, also = e; da () > 0 ür < e und () < 0 ür > 0 H ( e e ) c) () ür 0, da () > 0 ür < e und einzige Nullstelle bei = 8 Sei J = Junge; D = Note J J D 9 D a) P (D) = 0, % b) P ( J D) = 9 0 = 0 % c) P J (D) = = 50 % d) P D ( J) = 9 9, % Ableiten zusammengesetzter Funktionen S. 59 a) h () = + e = u () (); h () = ( + ) ln = u () g () h () = e + = (u()); h () = + ln = u () g () h 5 () = (e ) + = u ( ()); h () = g (u ()) b) h 5 () = e ; h () = (Anwendung der Kettenregel) + S. 0 a) () = e b) () = e c) () = = d) () = e + e) () = + = + ) () = e g) () = e + = e + h) () = ) ( = oder () = ln ln ; () = a) ist Stammunktion von g () = () = = b) g ist Stammunktion von () = g () = ln ln = a) D = R; () = e + e = e ( + ) b) D = R + ; () = ln + = ln + c) D = R; () = e + e ( ) = e ( ) d) D = R + ; () = = oder () = ln () = e) D = R + ; () = ln = ln = ( ln + ) ) D = R; () = e ; () = e + e = e ( + ) g) D = R \[0; ]; () = ( ( ) ) ( ) = ( ) ( ) = ( ) h) D = R \{ }; () = ( + ) e e ( + ) = ( e ( + ) ) ( + ) = ( e + ) ( + ) 5 a) richtig: () = e cos + e ( sin ) = e ( cos sin ) Vorzeichenehler bei der Ableitung von cos! b) richtig: () = e ln + e = e ( ln + ) Fehler bei der Ableitung von e : Richtig ist (e ) = e Ernst Klett Verlag GmbH, Stuttgart 00 Lambacher Schweizer, Ausgabe Baern, Lösungen und Materialien Klasse ISBN VI Natürliche Eponentialund Logarithmusunktion 0
7 Schülerbuchseite 0 Lösungen vorläuig Summe: s () = e + + ; s () = e + Dierenz: d () = e ; d () = e ; d () = + e ; d () = e Produkt: p () = e ( + ); p () = e ( + ) + e = e ( + + ) Quotient : q () = e + ; q () = ( + ) e e ( + ) = e ( + ) ( + ) Quotient : q () = + e ; q () = e ( + ) e 9 e = e ( ) 9 e = e ( + ) Verkettung: Verkettung: (g ()) = e ( + ) = e + ; (g ()) = e + = e + g ( ()) = ( e ) + = 9 e + ; g ( ()) = e 7 a) () = e ; () = e b) () = ln ln ( + ); ( > 0); () = + Kontrolle: Jeweils Etremstellen von mit Nullstellen von c) () = ( ln + ln ) ; () = vergleichen. Ebenso Steigungsverhalten von d) () = e + e = e ( + ); () = e und Vorzeichen. zu a) zu b) ' A 5 B ' zu c) zu d) ' 5 5 ' 5 5 Ernst Klett Verlag GmbH, Stuttgart 00 Lambacher Schweizer, Ausgabe Baern, Lösungen und Materialien Klasse ISBN VI Natürliche Eponentialund Logarithmusunktion
8 Schülerbuchseite 0 Lösungen vorläuig 8 v () = 0 ür = 0 und =, v () > 0 ür < 0 und > ; v () < 0 ür 0 < < Somit gilt ür v (): v hat bei = 0 einen Hochpunkt und bei = einen Tiepunkt. Ebenso gilt ür () = e v () : hat Hochpunkt bei und Tiepunkt bei. () 5 v () v() 9 waagrechte Tangente, wenn () = 0. a) () = e ; e = 0 wenn = e = 0 P (0 ) b) () = e + e = e ( + ); e ( + ) = 0 wenn + = 0 = P ( e ) c) () = ln ln = ; ln = 0 wenn ln = = e P ( e e ) d) () = e + + e + = e + ( + ); e + ( + ) = 0 wenn + = 0 = P ( ) 0 () F () = = () F () = = () F () = (ln + ) + ln ( + ) = ln + + ln ln = ln + ln + () F () = ln + = ln + = ln F () = ln ist Stammunktion von () = ln Graph der Funktion: schwarz; Graph der Ableitung: grün; Graph der Stammunktion: blau Grad von = ; die beiden Etremwerte sind Nullstellen der Ableitung (). Nullstellen von () sind die Etremwerte der Stammunktionen F (). Ebenso möglich: Prüen des jeweiligen Monotonieverhaltens. a) e + > 0 ür alle * R D = R c) b) F () = e + e = e e +,5,5 F 0,5 5 () = e + Gleichung einer Tangente: = m + t T P : m = ( ) = e 8 P ( e 8 e ) 8 = e 8 ( ) + t t = e e 8 = 9 e 8 ; T P : = e e 8 T P : m = () = e 8 P ( e 8 e ) 8 = e 8 + t t = e e 8 = 9 e 8 ; T P : = e e 8 Schnittpunkt: T P = T P : e e = e e 8 = 0; S (0 9 e 8 ) Ernst Klett Verlag GmbH, Stuttgart 00 Lambacher Schweizer, Ausgabe Baern, Lösungen und Materialien Klasse ISBN VI Natürliche Eponentialund Logarithmusunktion
9 Schülerbuchseite 0 Lösungen vorläuig () = g (); = m + m + = 0 m 0: / = ± m m Es gibt genau eine Lösung, wenn + m = 0, g S( ) also ür m =. Dann gilt ür S: = = ( ± 0 = S ( ) ) 5 m = 0 = S ( ) Eponentialunktionen und Eponentialgleichungen S. Zu lösen ist die Gleichung,85 Mrd. = 0,99 e 0,09 t Mrd. Durch Probieren (z. B. ür t = 0, t = 0, t = 0, t = 0) erkennt man, dass 0 < t < 0 sein muss. Genaueres Anhähern ergibt 5 < t <. Der genaue (gerundete) Wert ergibt t 5,87, d. h. im Jahr 0 hat sich die Zahl der Einwohner Indiens verdoppelt. Rechnet man mit doppelt so viel, ist e 0,09 t, also t =,. Aus der Deinition von ln olgt e ln =. Also: = e ln k = ln. S. a) b) e ln = ln = c) d) e) e ln = (e ln ) = 8 ) ln ( e ) = ln + ln e = ln ln + = ln g) ln ( e ) = ln ln + ln e = ln h) e ln = ( e ln ) = = i) ln e = ln ar a) ln a s = r ln a s ln a = r s c) a ln a = e ln ( a ln a ) = e ln a ln a = e b) a b ln a = e ln ( a b ln a ) = e ln b ln a ln a = e ln b = b 5 a) richtig; Anwendung der Potenzgesetze: () = e e + = e + + = e + b) alsch; () = e = e ln e = e ln + a) richtig; () = = (e ln ) = e ln = e ln a) e = ln e = ln = ln b) e = 000 ln e = ln 000 = ln 000 c) e 0,5 = hat keine Lösung d) ln ( ) ln = ln ( ) = e ln ( ) = e = e e) e + = 5 e + =,5 ln e + = ln,5 = ln,5 ) ln ( ) + ln ( ) = ln + ln = ln = e ln = e = e 7 () = e = e ; () = e = e = ln e = ln somit = ln 8 a) = ln = ln = ln ln b) = = ln = ln = ln ln c) = = = ln = ln = ln ln d) = = = hat keine Lösung Ernst Klett Verlag GmbH, Stuttgart 00 Lambacher Schweizer, Ausgabe Baern, Lösungen und Materialien Klasse ISBN VI Natürliche Eponentialund Logarithmusunktion
10 Schülerbuchseite Lösungen vorläuig 9 a) e = e = Eponentenvergleich b) e = e = Eponentenvergleich c) e (e ) = 0 e = = ln ; e > 0, Produktwert = 0, wenn mindestens Faktor = 0 d) (e ) (ln ) = 0 e = oder ln =, also = 0 oder = e e) e e = 0 e (e ) = 0 e Begründung wie = = ln ) ln (ln ) = 0 ln = 0 oder ln = = oder = e bei Teilaugabe c) 0 a) u = e ; u 7 u + = 0; u / = 7 ± ; u = ; u = e = = ln ; e = = ln b) u = e ; u u + = 0 (u ) = 0 u = e = = 0 c) (e ) e 5 = 0 e = u; u u 5 = 0; u / = ± ; u = 5; u = e = 5 = ln 5 (e = nicht lösbar) d) e = u; u u 0 = 0; u / = ; u = 5; u = e = 5 = ln 5 (e = nicht lösbar) a) b) e = e = = ln 5 D B ( ln ) B c) e = 5 e = 5 = ln 5,5 0,5 0,5,5 C C ( ln 5 5 ) d) () = e ; e = e = = = ln = ln D ( ln ) a) () = (e ln ) = e ln ; () = ln e ln = ln,8 F () = ln e ln = ln b) () = e ln ( ) ; () = ln ( ) e ln ( ) = ln ( ) ( ) 0,055 ( ) F () = ln ( ) e ln ( ) = ln ( ( ) ) c) () = e ( ) ln ; () = ln e ( ) ln = ln 0,9 F () = e ( ) ln = ln e d) () = 0,5 = ( ) = = e ( ) ln ; () = ln e ( ) ln = ln,8 F () = ln e( ) ln = ln 0,5 Ernst Klett Verlag GmbH, Stuttgart 00 Lambacher Schweizer, Ausgabe Baern, Lösungen und Materialien Klasse ISBN VI Natürliche Eponentialund Logarithmusunktion
11 Schülerbuchseite Lösungen vorläuig a) b) B (,5,5) A (,8 0,) a A(,7 0,57) 5 5 g,8;,5,7 c) d) 5 B(,7 5,5) a A(,0,0) g A(0,0,0) 5 5 h 0,0;,7,0;, a) 5 ( ) = b) ( ) ( + ) ( ) + = ( ) ( + ) ( ) + = ( ) c) a + b ( a b ) = a + b ( a ab + b ) = ab 5 Eponential- und Logarithmusunktionen und ihre Graphen S. g = 0 e ; Vermutung: lim 0 e = 0 g = 0 e ; Vermutung: lim 0 e = g = e 0 ; Vermutung: lim e 0 = + a) () = e + gehört zum gelben Graph; (0) = ; lim () = + ± b) g () = + e gehört zum blauen Graph; (0) = 0; lim () = + ; lim () = 0 + c) h () = ln ( 0,5) gehört zum schwarzen Graph; (,5) = 0; lim () = 0 d) k () = e gehört zum roten Graph; (0) = ; () < 0 ür alle * D lim () = 0 ± Ernst Klett Verlag GmbH, Stuttgart 00 Lambacher Schweizer, Ausgabe Baern, Lösungen und Materialien Klasse ISBN VI Natürliche Eponentialund Logarithmusunktion 5
12 Schülerbuchseite 5 Lösungen vorläuig S. 5 a) lim + ( e 7 ) = 7; lim ( e 7 ) = + Asmptote: = 7 lim b) lim + ( 5 e ) = 0; ( 5 e ) = Asmptote: = 0 c) lim + ( 8 ln ) = 0; lim ( 8 ln 0 ) = Asmptote: = 0 d) lim ( e ) = ; lim ( + e ) = e) lim ( e 7 ) = + ; lim + ( e 7 ) = + keine Asmptoten ) lim + ln ( ) = 0; lim ln ( ) = 0 Asmptote: = 0 g) lim 5 ln = + ; lim 5 ln = 0 keine Asmptote + 0 h) lim e = 0; lim e = 0 Asmptote: = i) lim + ( + ln ) = 0; lim 0 ( + ln ) = Asmptote: = 0 k) lim + e = + ; lim e = 0 Asmptote: = b e 8 g 0 k 5 c i g d 0 a 5 h Vorgehensweise ür alle Teilaugaben: Man bestimmt spezielle Funktionswerte und das Verhalten ür lim. ± a) () = e ; (0) = e ; () = lim e = 0, also -Achse ist Asmptote + b) g () = 0,5 e + ; (0) =,5 lim ( 0,5 e + ) = ; lim + ( 0,5 e + ) = + c) h () = 0,5 e ; (0) = ; lim ( 0,5 e ) = ; lim + ( 0,5 e ) = ; Asmptote: = 0,5 d) k () = + e ; k (0) = lim ( + e ) = +, lim + ( + e ) = ; Asmptote: = 0 8 k() () 8 h() g() Ernst Klett Verlag GmbH, Stuttgart 00 Lambacher Schweizer, Ausgabe Baern, Lösungen und Materialien Klasse ISBN VI Natürliche Eponentialund Logarithmusunktion
13 Schülerbuchseite 5 Lösungen vorläuig 5 a) lim + e = 0 richtig (Satz); lim 0 e = + alsch; richtig: lim 0 e = 0 b) lim + 0 e = lim ( 0 e + e ) = 0 richtig; lim + + e = 0 richtig; (e wächst stärker als ) c) lim ln = alsch; 0 richtig: lim ln = 0; 0 lim ln = + richtig d) lim 0 + = 0 richtig; ln lim + + = 0 alsch; ln richtig: lim + + ln = + e) lim e = + alsch; richtig: lim < e = ; (ln steigt langsamer als + ) lim > e = + richtig d) 8 e) b) c) a) d) e) ) Individuelle Lösungen S. a) D = R; lim + e = 0; Asmptote: = 0 b) D = R + ; lim ln + = ; lim ln 0 = 0 keine Asmptote c) D = R \{0}; lim + e = ; lim e = ; Asmptote: = lim e = + ; 0 Asmptote: = 0 > 0 d) D = R; lim + ( + ) e = 0; Asmptote: = 0 7 Die drei Graphen sind achsensmmetrisch zur -Achse. () Es gilt: lim () = + ür alle ± drei Funktionen. 5 g() 5 7 Die -Achse ist senkrechte Asmptote. D = R \{0} ür und g. D h = R \[ ; ] 5 h() Ernst Klett Verlag GmbH, Stuttgart 00 Lambacher Schweizer, Ausgabe Baern, Lösungen und Materialien Klasse ISBN VI Natürliche Eponentialund Logarithmusunktion 7
14 Schülerbuchseite Lösungen vorläuig 8 a) () = e ; () = 0 ür = ln ; (ln ) = ln E (ln 0,) () > 0 ür < < ln ; () < 0 ür ln < < + E ist Maimum. W = ] ; ln ] keine Nullstelle b) () = 0,5 e ; () = 0 ür = ln ; ( ln ) = ln E ( ln 0,) () < 0 ür < < ln ; () > 0 ür ln < < + E ist Minimum. W = [ ln + ; + [ keine Nullstelle c) () = e e ; () = 0 ür = 0; (0) = E (0 ) () < 0 ür < < 0; () > 0 ür 0 < < + E ist Minimum. W = [ ; + [ keine Nullstelle d) () = ln ; () = 0 ür = e; (e) = e E (e e) (ln ) () < 0 ür 0 < < e; () > 0 ür e < < + E ist Minimum. W = ] ; 0 [, [ e ; [ keine Nullstelle 9 a) () = 5 e ; D = R einzige Nullstelle: = 0 () = 5 e + 5 e = 5 e ( + ) () = 0 ür = () < 0 ür < < ; () > 0 ür < < + Minimum ( 5 e ) lim 5 e = 0; = 0 ist Asmptote. 8 c) () = e + ; D = R einzige Nullstelle ür = 0 () = e + + e + ( ) = e + ( ) () = 0 ür = () > 0 ür < < ; () < 0 ür < < + Maimum ( ) lim + e + = 0; = 0 ist Asmptote. 8 8 b) () = ( + ) e ; D = R einzige Nullstelle ür = () = e + ( + ) e = e ( + ) () = 0 ür = () < 0 ür < < ; () > 0 ür < < + Minimum ( e ) lim ( + ) e = 0; = 0 ist Asmptote. 8 d) () = ln ( ); D = ] ; + [ einzige Nullstelle ür = () = ; kein Etremwert; () > 0 ür * D G steigt monoton. 8 lim ln ( ) = + ; lim ln ( ) = + (keine Asmptoten) 8 8 Ernst Klett Verlag GmbH, Stuttgart 00 Lambacher Schweizer, Ausgabe Baern, Lösungen und Materialien Klasse ISBN VI Natürliche Eponentialund Logarithmusunktion 8
15 Schülerbuchseite Lösungen vorläuig e) () = e ; D = R einzige (doppelte) Nullstelle ür = 0 () = e e = e ( ) () = 0 ür = 0 oder = () < 0 ür < < 0; () > 0 ür 0 < < () < 0 ür < < + Minimum (0 0); Maimum ( 8 e ) lim + e = 0; = 0 ist Asmptote. ) () = sin ( π ) ; D = R Nullstellen ür = π ( k + ) k * Z Etremstellen: () = cos ( π ) ; () = 0 = π (k + ) Hochpunkte ür k gerade Tiepunkte ür k ungerade keine Asmptoten g) () = + ; D = R \{ } einzige doppelte Nullstelle ür = 0 () = + ( + ) = ( + ) ( + ) ; () = 0 ür = 0 oder = () > 0 ür < < ; () < 0 ür < < ; Maimum ( ) () < 0 ür < < 0; () > 0 ür 0 < < ; Minimum (0 0) = ist senkrechte Asmptote. = ist schräge Asmptote ( + = + + ). 8 h) () = 5 ln ; D = R + einzige Nullstelle ür = () = 0 ln + 5 = 5 ( ln + ) () = 0 ür = e () < 0 ür 0 < < e ; () > 0 ür e < < + Minimum ( e,5 e ) keine Asmptoten Ernst Klett Verlag GmbH, Stuttgart 00 Lambacher Schweizer, Ausgabe Baern, Lösungen und Materialien Klasse ISBN VI Natürliche Eponentialund Logarithmusunktion 9
16 Schülerbuchseite Lösungen vorläuig 0 G = G v ; v (0) = ; G v ist achsensmmetrisch zur -Achse; v () 0,07; v ( ) 0,07 G = G p ; p (0) = ; G p ist achsensmmetrisch zur -Achse; G p ist eine Parabel. G = G h ; h (0) = ; h () = 0; lim h () = ; lim h () = + + G = G k ; k (0) = ; keine Nullstellen; G k ist achsensmmetrisch zur -Achse; k () = ; k ( ) = G 5 = G u ; u (0) = ; G u hat Minimum bei (0 ). G = G ; (0) = 0; G ist achsensmmetrisch zur -Achse; W = R 0 + a) () = e ; F () = e + + c c * R b) () = e 0,5 ; F () = e 0,5 + c c * R c) () = ln e ( + ) ln = + ln ; F () = ln e ( + ) ln = ln + + c c * R d) () = ln 0, e ln 0, = 0, ln 0,; F () = ln 0, e ln 0, + + c = ln 0, 0, + + c c * R () = ( ) e a) hat bei = eine doppelte Nullstelle, somit hat G im Punkt P ( 0) einen Etrempunkt; der linke Graph gehört zu G. b) Der rechte Graph ist der an der -Achse gespiegelte G ; also g: ( + ) e a) h () = ln ; D h = R + ; lim h () = ; lim h () = b) h () = ln ; D h = R + ; lim h () = 0; lim h () = + c) h () = ln ; D h = R + ; lim h () = + ; lim h () = d) h () = ln ; D h = R + \{}; lim h () = 0; lim () = ; lim/ > h () = + ; lim h () = 0 < h + e) h () = ln ( ) ; D h = R + ; lim h () = ; lim h () = ) h () = ln () ; D h = [ ; + [; lim h () = + 7 b) a) d) c) ) e) d) () = a e k ; () = k a e k I. () = e e = a e k II. (0) = = a k a = ; k = Ernst Klett Verlag GmbH, Stuttgart 00 Lambacher Schweizer, Ausgabe Baern, Lösungen und Materialien Klasse ISBN VI Natürliche Eponentialund Logarithmusunktion 0
17 Schülerbuchseite 7 Lösungen vorläuig S. 7 5 () = (ln ) ; doppelte Nullstelle ür = a) () = ln ; () = 0 ür = ; () < 0 ür 0 < < ; () > 0 ür < < + ; P ( 0) ist Minimum. b) Gleichung der Ursprungsgeraden: = m ; m = () = ln Für Berührpunkt B ( B (ln B ) ) * Ursprungsgeraden (ln B ) = B ln B B (ln B ) = ln B ln B = 0 oder ln B = B = oder B = e Tangenten: = 0 oder = e c) F () = (ln ) + ln ln + = (ln ) + ln ln + = (ln ) a) z. B. () = ln ( ) [() = ln ( + )] b) z. B. () = e + [() = e ] c) z. B. () = e + [() = ln ] d) z. B. () = e + e 7 a) () = 0 ür =, also Schnittpunkt mit der -Achse ( 0). (0) =, also Schnittpunkt mit der -Achse (0 ). (Lage der -Achse und Einheiten siehe Graphik) b) () = e + ( ) e = e ( ); () = 0 ür = () < 0 ür < < () > 0 ür < < + P ( e) ist Tiepunkt. 5 8 a) Erkennbare Merkmale: 5. Achsensmmetrie zur -Achse: ( ) = e + e ( ) = (). Nullstelle bei (0 0): (0) = e 0 + e 0 = 0. Tiepunkt bei (0 0): () = e e b) g () = + a + b; g () = + a g (0) = (0) = 0 b = 0 g (0) = (0) = 0 a = 0 gesuchte Funktion: g () = () = 0 wenn e = e bzw. = somit Etremstelle bei (0 0) () < 0 ür < < 0 () > 0 ür 0 < < + Tiepunkt bei (0 0) 9 L = 0 lg Ø Ø 0 ; Flüstern: Einsetzen von L = 0 ergibt = lg ( Ø 0 Ø0 ), also Ø 0 = 0 Ø 0 oder Ø 0 = 00 Ø 0 ; Normale Unterhaltung: Einsetzen von L = 0 ergibt = lg ( Ø 0 Ø0 ), also Ø 0 = 0 Ø 0 oder Ø 0 = 0000 Ø 0. Damit ist Ø 0 = 00 Ø 0, d. h. die Schallintensität ist beim normalen Reden 00-mal größer gegenüber der beim Flüstern. 0 a; c () = a c ( e c + e c ) a) a; c ( ) = a c ( e c + e c ( ) ) = a c ( e c + e c ) = a; c (); Achsensmmetrie zur -Achse b) a; c () = a c ( e c e c ) ; a; c () = 0 ür e c = e c, also c = c, somit = 0 Minimum ( 0 a c ) Ernst Klett Verlag GmbH, Stuttgart 00 Lambacher Schweizer, Ausgabe Baern, Lösungen und Materialien Klasse ISBN VI Natürliche Eponentialund Logarithmusunktion
18 Schülerbuchseite 7 9 Lösungen vorläuig c) Es muss gelten: I. c (0) = a c = 5 aus I: a = 5 c eingesetzt in II: II. c (00) = a c ( e 00 c + e 00 c ) = 0 5 ( e 00 c + e 00 c ) = 0 e 00 c + e 00 c = 0 Substitution u = e 00 c : u + u = 0 u u + = 0; u = ,9; u = ,089 u = e 00 c olgt c 0,07789 oder c 0,07789 Damit erhält man in beiden Fällen dieselbe Funktion: () =,5 ( e 0, e 0,0779 ) d) () = 0,097 ( e 0, e 0,0779 ) (00) = 0,798; tan φ = 0,798 ergibt ein Geälle von ca. 7 %. φ, e) Bedingung: () = 5, also,5 ( e 0, e 0,0779 ) = 5 Substitution: u = e 0,0779 : u + u = 0 u u + = 0; u = ,88 u = ,757 u = e 0,0779 olgt: 7, Die Seilhöhe beträgt im Abstand von ca. 7 m, gemessen von der tiesten Stelle, 5 m. ) Bedingung: () = 0,, also 0,097 ( e 0,0779 e 0,0779 ) = 0, Daraus erhält man 50,7 Ein Stuntman könnte das Seil au einer Strecke von gut 00 m beahren. a) Jeder Repräsentant von g liegt parallel zur Geraden g. Somit gibt g die Richtung der Geraden g an. g: Ein Steigungsdreieck von g hat die Katheten und, also gibt = + t der Vektor ( ) die Richtung von g an. t g = ( ) Wegen g. ( b) n: = + t; n = ( ) ; n g = ( ) = ( ) gilt dies auch ür ) ( ) = + ( ) = = 0 Die Vektoren n und g stehen senkrecht aueinander, somit ist auch die Gerade n senkrecht zur Geraden g. Die Euler sche Zahl e S. 9 a) K 0 = K 0 ( + p 00 ) 0 = K = ( + p 00 ) 0 = ( + p 00 ) 0 p = 00 ( ),5 Der Jahreszinssatz beträgt etwa,5 %. b) K 0 = K 0,05 0 = 0000,05 0 5,98 c) K 0 = K 0 ( ) 700 = ( ) ,9 a) t 0 = 0 n (t 0 + 0) = n (t); n (t 0 ) = n (0) = 000 n (t) = n (0) +,75 t n (0) = t = 000 ( +,75 t) b) n (5) = 000 ( +,75 t 5) = 7 50 Es muss gelten: s n + s n = (n + )! < 0. Dies ist ab n = 9 der Fall. Ernst Klett Verlag GmbH, Stuttgart 00 Lambacher Schweizer, Ausgabe Baern, Lösungen und Materialien Klasse ISBN VI Natürliche Eponentialund Logarithmusunktion
1 Verhalten in der Umgebung der Definitionslücken
 Schülerbuchseite 8 Lösungen vorläuig S. 8 I Graphen gebrochen rationaler Funktionen Verhalten in der Umgebung der Deinitionslücken : 0 + 0,6 g: 0 + 0,6 (Gesamtpreis in ) (Durchschnittspreis pro Liter in
Schülerbuchseite 8 Lösungen vorläuig S. 8 I Graphen gebrochen rationaler Funktionen Verhalten in der Umgebung der Deinitionslücken : 0 + 0,6 g: 0 + 0,6 (Gesamtpreis in ) (Durchschnittspreis pro Liter in
1 Die zweite Ableitung
 Schülerbuchseite 5 Lösungen vorläuig und deren Graphen Die zweite Ableitung S. Um den Graphen der Ableitung zu skizzieren, sucht man zuerst die Punkte mit waagrechten Tangenten. so erhält man die Nullstellen
Schülerbuchseite 5 Lösungen vorläuig und deren Graphen Die zweite Ableitung S. Um den Graphen der Ableitung zu skizzieren, sucht man zuerst die Punkte mit waagrechten Tangenten. so erhält man die Nullstellen
1 Differenzenquotient und mittlere Änderungsrate
 Schülerbuchseite 8 9 Lösungen vorläufig Differenzenquotient und mittlere Änderungsrate S. 8 a) Da der dargestellte Graph keine Gerade ist, verläuft die Temperaturzunahme nicht gleichmäßig. Temperaturzunahme
Schülerbuchseite 8 9 Lösungen vorläufig Differenzenquotient und mittlere Änderungsrate S. 8 a) Da der dargestellte Graph keine Gerade ist, verläuft die Temperaturzunahme nicht gleichmäßig. Temperaturzunahme
1 Exponentielles Wachstum
 Schülerbuchseite 56 58 Lösungen vorläufig VI Anwendungen der Differential- und Integralrechnung Exponentielles Wachstum S. 56 S. 58 a) H (t) = 4000,0 t b),0 t = e k t,0 = e k k = ln,0 0,0 H (t) = 4000
Schülerbuchseite 56 58 Lösungen vorläufig VI Anwendungen der Differential- und Integralrechnung Exponentielles Wachstum S. 56 S. 58 a) H (t) = 4000,0 t b),0 t = e k t,0 = e k k = ln,0 0,0 H (t) = 4000
Natürliche Exponential- und Logarithmusfunktion. Kapitel 5
 Natürliche Eponential- und Logarithmusfunktion Kapitel . Die natürliche Eponentialfunktion und ihre Ableitung 48 Arbeitsaufträge. Individuelle Lösungen Jahr 908 90 90 930 90 960 970 990 000 00 in Sekunden
Natürliche Eponential- und Logarithmusfunktion Kapitel . Die natürliche Eponentialfunktion und ihre Ableitung 48 Arbeitsaufträge. Individuelle Lösungen Jahr 908 90 90 930 90 960 970 990 000 00 in Sekunden
Weitere Ableitungsregeln. Kapitel 4
 Weitere Ableitungsregeln Kapitel . Die Kettenregel L f() = u(v()) g() = v(u()) a) + + b) cos [( + ) ] (cos + ) c) sin ( ) [sin ()] d) e) ( = _ ) _ ( f) cos [π( + )] cos (π) + g) ( ) = h) ( + ) + = + +
Weitere Ableitungsregeln Kapitel . Die Kettenregel L f() = u(v()) g() = v(u()) a) + + b) cos [( + ) ] (cos + ) c) sin ( ) [sin ()] d) e) ( = _ ) _ ( f) cos [π( + )] cos (π) + g) ( ) = h) ( + ) + = + +
Hauptprüfung Fachhochschulreife Baden-Württemberg
 Hauptprüung Fachhochschulreie 204 Baden-Württemberg Augabe 2 Analysis Hilsmittel: graikähiger Taschenrechner Beruskolleg Alexander Schwarz www.mathe-augaben.com September 204 Gegeben ist die Funktion mit
Hauptprüung Fachhochschulreie 204 Baden-Württemberg Augabe 2 Analysis Hilsmittel: graikähiger Taschenrechner Beruskolleg Alexander Schwarz www.mathe-augaben.com September 204 Gegeben ist die Funktion mit
1 Ergänzen Sie für die Funktionen u, v und w mit u (x) = cos (2 x), v (x) = 2 x 2 und w (x) = 9 x 1
 Neue Funktionen aus alten Funktionen: Produkt, Quotient, Verkettung Sind die Funktionen u mit u () = und v mit v () = cos () gegeben, so erhält man die Verkettung u v () = u v () dieser beiden Funktionen,
Neue Funktionen aus alten Funktionen: Produkt, Quotient, Verkettung Sind die Funktionen u mit u () = und v mit v () = cos () gegeben, so erhält man die Verkettung u v () = u v () dieser beiden Funktionen,
Funktionenlehre. Grundwissenskatalog G8-Lehrplanstandard
 GRUNDWISSEN MATHEMATIK Funktionenlehre Grundwissenskatalog G8-Lehrplanstandard Basierend auf den Grundwissenskatalogen des Rhöngmnasiums Bad Neustadt und des Kurt-Huber-Gmnasiums Gräfelfing J O H A N N
GRUNDWISSEN MATHEMATIK Funktionenlehre Grundwissenskatalog G8-Lehrplanstandard Basierend auf den Grundwissenskatalogen des Rhöngmnasiums Bad Neustadt und des Kurt-Huber-Gmnasiums Gräfelfing J O H A N N
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil... Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analysis 3... 5 Wahlteil Analytische Geometrie... Wahlteil Analytische Geometrie... Lösungen: 00 Pflichtteil Lösungen zur Prüfung 00: Pflichtteil
Pflichtteil... Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analysis 3... 5 Wahlteil Analytische Geometrie... Wahlteil Analytische Geometrie... Lösungen: 00 Pflichtteil Lösungen zur Prüfung 00: Pflichtteil
9 Funktionen und ihre Graphen
 57 9 Funktionen und ihre Graphen Funktionsbegriff Eine Funktion ordnet jedem Element aus einer Menge D f genau ein Element aus einer Menge W f zu. mit = f(), D f Die Menge aller Funktionswerte nennt man
57 9 Funktionen und ihre Graphen Funktionsbegriff Eine Funktion ordnet jedem Element aus einer Menge D f genau ein Element aus einer Menge W f zu. mit = f(), D f Die Menge aller Funktionswerte nennt man
Pflichtteilaufgaben zu Elemente der Kurvendiskussion. Baden-Württemberg
 Pflichtteilaufgaben zu Elemente der Kurvendiskussion Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com September 6 Übungsaufgaben: Ü: Gegeben ist
Pflichtteilaufgaben zu Elemente der Kurvendiskussion Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com September 6 Übungsaufgaben: Ü: Gegeben ist
Bayern Teil 1. Aufgabe 1. Abitur Mathematik: Musterlösung. Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten:
 Abitur Mathematik: Bayern 2013 Teil 1 Aufgabe 1 a) 1. SCHRITT: DEFINITIONSMENGE BESTIMMEN Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten: 3x + 9 0 x 3 2. SCHRITT: NULLSTELLEN
Abitur Mathematik: Bayern 2013 Teil 1 Aufgabe 1 a) 1. SCHRITT: DEFINITIONSMENGE BESTIMMEN Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten: 3x + 9 0 x 3 2. SCHRITT: NULLSTELLEN
13 3. a) Uhrzeit Wasseranstieg (in cm pro Stunde)
 1 Funktionen als mathematische Modelle Noch it in Dierenzialrechnung? 1 1. a) Höhenänderung zwischen 0 m und 1 00 m (in der Horizontalen): ca. 800 m 600 m = 00 m durchschnittliche Änderungsrate im Intervall
1 Funktionen als mathematische Modelle Noch it in Dierenzialrechnung? 1 1. a) Höhenänderung zwischen 0 m und 1 00 m (in der Horizontalen): ca. 800 m 600 m = 00 m durchschnittliche Änderungsrate im Intervall
I Funktionen und ihre Graphen
 Schülerbuchseite 7 Erkundung Seite 7 Autrag Die Aussage au Kärtchen Nr. ist als achsensmmetrisch zur -Achse zu verstehen, Kärtchen Nr. 6 als punktsmmetrisch zum Ursprung und Kärtchen Nr. als ür beliebige
Schülerbuchseite 7 Erkundung Seite 7 Autrag Die Aussage au Kärtchen Nr. ist als achsensmmetrisch zur -Achse zu verstehen, Kärtchen Nr. 6 als punktsmmetrisch zum Ursprung und Kärtchen Nr. als ür beliebige
4.4. Aufgaben zu Potenzfunktionen
 .. Aufgaben zu Potenzfunktionen Definition: Eine Funktion der Form f() = c z mit z Z\{;} heißt Potenzfunktion. Aufgabe : Potenzfunktionen mit positiven Eponenten (Parabeln). Ergänze: 9 8 7 6 - - - - -
.. Aufgaben zu Potenzfunktionen Definition: Eine Funktion der Form f() = c z mit z Z\{;} heißt Potenzfunktion. Aufgabe : Potenzfunktionen mit positiven Eponenten (Parabeln). Ergänze: 9 8 7 6 - - - - -
Bayern Musterlösung zu Klausur Analysis, Aufgabengruppe I
 Diese Lösung wurde erstellt von Tanja Reimbold. Sie ist keine offizielle Lösung des Bayerischen Staatsministeriums für Unterricht und Kultus. Teil 1 Aufgabe 1 Definitionsbereich: Bestimmung der Nullstelle
Diese Lösung wurde erstellt von Tanja Reimbold. Sie ist keine offizielle Lösung des Bayerischen Staatsministeriums für Unterricht und Kultus. Teil 1 Aufgabe 1 Definitionsbereich: Bestimmung der Nullstelle
Optimale Vorbereitung auf die Mathematik-Prüfung zur Fachhochschulreife (am Berufskolleg) Verständliche Zusammenfassungen und Basisübungen
 Ott Rosner Optimale Vorbereitung au die Mathematik-Prüung zur Fachhochschulreie (am Beruskolleg) Verständliche Zusammenassungen und Basisübungen Merkur Verlag Rinteln Wirtschatswissenschatliche Bücherei
Ott Rosner Optimale Vorbereitung au die Mathematik-Prüung zur Fachhochschulreie (am Beruskolleg) Verständliche Zusammenassungen und Basisübungen Merkur Verlag Rinteln Wirtschatswissenschatliche Bücherei
1 Ableitungen. Hinweise und Lösungen:
 Hinweise und Lösungen: http://mathemathemathe.de/analsis/analsis-grundagen Ableitungen Übung.: Einfache Ableitungen - Bestimme die ersten Ableitungen a) f() = 7 + + 8 b) f() = a + a a K(t) = t t + 0 Übung.:
Hinweise und Lösungen: http://mathemathemathe.de/analsis/analsis-grundagen Ableitungen Übung.: Einfache Ableitungen - Bestimme die ersten Ableitungen a) f() = 7 + + 8 b) f() = a + a a K(t) = t t + 0 Übung.:
. Ihr Schaubild sei &. a) Geben Sie die Asymptoten von & an. b) Bestimmen Sie den Schnittpunkt der Tangente an & im Punkt 1 1 mit der Achse.
 Aufgabe A4/04 Gegeben ist die Funktion mit 2; 0. Das Schaubild von hat im Punkt 1 die Tangente. Ermitteln Sie eine Gleichung von. Die Tangente schneidet die Achse im Punkt. Bestimmen Sie die Koordinaten
Aufgabe A4/04 Gegeben ist die Funktion mit 2; 0. Das Schaubild von hat im Punkt 1 die Tangente. Ermitteln Sie eine Gleichung von. Die Tangente schneidet die Achse im Punkt. Bestimmen Sie die Koordinaten
Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf.
 I. Nullstellen Arbeitsblatt I.1 Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der Faktoren null wird, sonst nicht. Beispiele:
I. Nullstellen Arbeitsblatt I.1 Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der Faktoren null wird, sonst nicht. Beispiele:
Abiturprüfung Mathematik 2012 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen
 Abiturprüfung Mathematik 202 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen klaus_messner@web.de www.elearning-freiburg.de Pflichtteil 202 2 Aufgabe : Bilden Sie die erste Ableitung
Abiturprüfung Mathematik 202 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen klaus_messner@web.de www.elearning-freiburg.de Pflichtteil 202 2 Aufgabe : Bilden Sie die erste Ableitung
Zentrale schriftliche Abiturprüfungen im Fach Mathematik
 Zentrale schritliche Abiturprüungen im Fach Mathematik Augabe : Schibau Au einer Hamburger Wert wird eine Hochgeschwindigkeitsähre als Doppelrumpschi (Katamaran) geplant. Der mittlere Teil des Schisrumpes
Zentrale schritliche Abiturprüungen im Fach Mathematik Augabe : Schibau Au einer Hamburger Wert wird eine Hochgeschwindigkeitsähre als Doppelrumpschi (Katamaran) geplant. Der mittlere Teil des Schisrumpes
Vorkurs Mathematik für Ingenieur Innen WS 2018/2019 Übung 7
 Prof. Dr. J. Pannek Dynamics in Logistics Vorkurs Mathematik für Ingenieur Innen WS 018/019 Übung 7 Aufgabe 1 : Etremwerte Der Ellipse + y = 1 ist ein Rechteck mit Seitenlängen p, q, dessen Seiten parallel
Prof. Dr. J. Pannek Dynamics in Logistics Vorkurs Mathematik für Ingenieur Innen WS 018/019 Übung 7 Aufgabe 1 : Etremwerte Der Ellipse + y = 1 ist ein Rechteck mit Seitenlängen p, q, dessen Seiten parallel
Vorkurs Mathematik für Ingenieure WS 2015/2016 Übung 6
 Prof. Dr. J. Pannek Dynamics in Logistics Vorkurs Mathematik für Ingenieure WS 015/016 Übung 6 Aufgabe 1 : Differentialrechnung (a Berechnen Sie die Ableitung nachstehender Funktionen an der Stelle 0 und
Prof. Dr. J. Pannek Dynamics in Logistics Vorkurs Mathematik für Ingenieure WS 015/016 Übung 6 Aufgabe 1 : Differentialrechnung (a Berechnen Sie die Ableitung nachstehender Funktionen an der Stelle 0 und
MATHE KLASSE 11. Funktionen Extremwerte lineare Funktionen WOLFGANG STILLER
 MATHE KLASSE Funktionen Etremwerte lineare Funktionen FUNKTION Def.: Funktionen sind eindeutige Zuordnungen. (Mathe eine Menge X [Definitionsbereich] wird einer Menge Y [Wertebereich] zugeordnet. Jedem
MATHE KLASSE Funktionen Etremwerte lineare Funktionen FUNKTION Def.: Funktionen sind eindeutige Zuordnungen. (Mathe eine Menge X [Definitionsbereich] wird einer Menge Y [Wertebereich] zugeordnet. Jedem
Skripten für die Oberstufe. Kurvendiskussion. f (x) f (x)dx = e x.
 Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
Trigonometrische Funktionen
 Trigonometrische Funktionen. Gegeben ist die Funktion f() = (sin( π )) Ihr Graph sei K. a) Skizzieren Sie K im Intervall [0,]. Geben Sie die Periode von f an. Geben Sie alle Hoch- und Tiefpunkte von K
Trigonometrische Funktionen. Gegeben ist die Funktion f() = (sin( π )) Ihr Graph sei K. a) Skizzieren Sie K im Intervall [0,]. Geben Sie die Periode von f an. Geben Sie alle Hoch- und Tiefpunkte von K
Abitur 2014 Mathematik Infinitesimalrechnung I
 Seite http://www.abiturloesung.de/ Seite 2 Abitur 204 Mathematik Infinitesimalrechnung I Die Abbildung zeigt den Graphen einer Funktion f. Teilaufgabe Teil A (5 BE) Gegeben ist die Funktion f : x x ln
Seite http://www.abiturloesung.de/ Seite 2 Abitur 204 Mathematik Infinitesimalrechnung I Die Abbildung zeigt den Graphen einer Funktion f. Teilaufgabe Teil A (5 BE) Gegeben ist die Funktion f : x x ln
Inhalt der Lösungen zur Prüfung 2011:
 Inhalt der Lösungen zur Prüfung : Pflichtteil Wahlteil Analysis 7 Wahlteil Analysis Wahlteil Analysis 6 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 6 Pflichtteil Lösungen zur Prüfung
Inhalt der Lösungen zur Prüfung : Pflichtteil Wahlteil Analysis 7 Wahlteil Analysis Wahlteil Analysis 6 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 6 Pflichtteil Lösungen zur Prüfung
43.1 Beispiel und Hinführung Ein Körper bewegt sich mit einer konstanten Geschwindigkeit von. . Zum Zeitpunkt t 0s beschleunigt er mit a 0,5
 4 Umkehrunktion 4. Beispiel und Hinührung Ein Körper bewegt sich mit einer konstanten Geschwindigkeit von v m s. Zum m Zeitpunkt t s beschleunigt er mit a,5. Der Beschleunigungsvorgang dauert 6 Sekunden.
4 Umkehrunktion 4. Beispiel und Hinührung Ein Körper bewegt sich mit einer konstanten Geschwindigkeit von v m s. Zum m Zeitpunkt t s beschleunigt er mit a,5. Der Beschleunigungsvorgang dauert 6 Sekunden.
Diskussion einzelner Funktionen
 Diskussion einzelner Funktionen. Wir betrachten die Funktion f mit f() = cos sin (a) Berechne f() für { π, π, π, π, } 5π und zeichne den Grafen von f im - Intervall [ π, ] 5π. Einheiten: cm auf der y-achse,
Diskussion einzelner Funktionen. Wir betrachten die Funktion f mit f() = cos sin (a) Berechne f() für { π, π, π, π, } 5π und zeichne den Grafen von f im - Intervall [ π, ] 5π. Einheiten: cm auf der y-achse,
Arbeitsblätter zur Vergleichsklausur EF. Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf.
 Arbeitsblätter zur Vergleichsklausur EF Arbeitsblatt I.1 Nullstellen Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der
Arbeitsblätter zur Vergleichsklausur EF Arbeitsblatt I.1 Nullstellen Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der
Optimale Vorbereitung auf die Mathematik-Prüfung
 Ott Rosner Optimale Vorbereitung auf die Mathematik-Prüfung zur Fachhochschulreife (am Berufskolleg) Verständliche Zusammenfassungen und Basisübungen Merkur Verlag Rinteln Wirtschaftswissenschaftliche
Ott Rosner Optimale Vorbereitung auf die Mathematik-Prüfung zur Fachhochschulreife (am Berufskolleg) Verständliche Zusammenfassungen und Basisübungen Merkur Verlag Rinteln Wirtschaftswissenschaftliche
a) Im Berührungspunkt müssen die y-werte und die Steigungen übereinstimmen:
 . ANALYSIS Gegeben ist die kubische Parabel f: y = x 3 6x + 8x + a) Die Gerade g: y = k x + berührt die Parabel an der Stelle x = x 0 > 0. Bestimmen Sie den Parameter k. b) Berechnen Sie den Inhalt der
. ANALYSIS Gegeben ist die kubische Parabel f: y = x 3 6x + 8x + a) Die Gerade g: y = k x + berührt die Parabel an der Stelle x = x 0 > 0. Bestimmen Sie den Parameter k. b) Berechnen Sie den Inhalt der
Gebrochen rationale Funktion f(x) = x2 +1
 Gebrochen rationale Funktion f() = +. Der Graph der Funktion f ist punktsmmetrisch, es gilt: f( ) = ( ) + f() = f( ) = + = + = f(). An der Stelle = 0 ist f nicht definiert, an dieser Stelle liegt ein Pol
Gebrochen rationale Funktion f() = +. Der Graph der Funktion f ist punktsmmetrisch, es gilt: f( ) = ( ) + f() = f( ) = + = + = f(). An der Stelle = 0 ist f nicht definiert, an dieser Stelle liegt ein Pol
Arbeitsblätter Förderplan EF
 Arbeitsblätter Förderplan EF I.1 Nullstellen bestimmen Lösungen I.2 Parabeln: Nullstellen, Scheitelpunkte,Transformationen Lösungen I.3 Graphen und Funktionsterme zuordnen Lösungen II.1 Transformationen
Arbeitsblätter Förderplan EF I.1 Nullstellen bestimmen Lösungen I.2 Parabeln: Nullstellen, Scheitelpunkte,Transformationen Lösungen I.3 Graphen und Funktionsterme zuordnen Lösungen II.1 Transformationen
Die Steigung m ist ein Quotient zweier Differenzen und heißt daher Differenzenquotient.
 Seite Definition lineare Funktion Eine Funktion f mit dem Funktionsterm f(x) = m x + b, also der Funktionsgleichung y = m x + b, heißt lineare Funktion. Ihr Graph G f ist eine Gerade mit der Steigung m
Seite Definition lineare Funktion Eine Funktion f mit dem Funktionsterm f(x) = m x + b, also der Funktionsgleichung y = m x + b, heißt lineare Funktion. Ihr Graph G f ist eine Gerade mit der Steigung m
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil Wahlteil Analysis 7 Wahlteil Analysis Wahlteil Analysis 7 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 8 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Pflichtteil Wahlteil Analysis 7 Wahlteil Analysis Wahlteil Analysis 7 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 8 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Mathematik im Berufskolleg I
 1 Bohner Ott Deusch Mathematik im Berufskolleg I Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab 6. Auflage 2016 ISBN 978-3-8120-0234-9 Das Werk und seine Teile sind urheberrechtlich geschützt.
1 Bohner Ott Deusch Mathematik im Berufskolleg I Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab 6. Auflage 2016 ISBN 978-3-8120-0234-9 Das Werk und seine Teile sind urheberrechtlich geschützt.
Inhalt der Lösungen zur Prüfung 2012:
 Inhalt der Lösungen zur Prüfung : Pflichtteil... Wahlteil Analsis... 8 Wahlteil Analsis... Wahlteil Analsis... 4 Wahlteil Analtische Geometrie... 8 Wahlteil Analtische Geometrie... Pflichtteil Lösungen
Inhalt der Lösungen zur Prüfung : Pflichtteil... Wahlteil Analsis... 8 Wahlteil Analsis... Wahlteil Analsis... 4 Wahlteil Analtische Geometrie... 8 Wahlteil Analtische Geometrie... Pflichtteil Lösungen
Abschlussprüfung Berufliche Oberschule 2017 Mathematik 12 Technik - A II - Lösung mit CAS. e 2x mit der maximalen Definitionsmenge D f = IR.
 Abschlussprüfung Berufliche Oberschule 07 Mathematik Technik - A II - Lösung mit Teilaufgabe.0 Gegeben ist die reelle Funktion f mit f( ) e mit der maimalen Definitionsmenge D f IR. Teilaufgabe. ( BE)
Abschlussprüfung Berufliche Oberschule 07 Mathematik Technik - A II - Lösung mit Teilaufgabe.0 Gegeben ist die reelle Funktion f mit f( ) e mit der maimalen Definitionsmenge D f IR. Teilaufgabe. ( BE)
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil... Wahlteil Analysis... 7 Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analytische Geometrie... 9 Wahlteil Analytische Geometrie... 008 Pflichtteil Lösungen zur Prüfung 008: Pflichtteil
Pflichtteil... Wahlteil Analysis... 7 Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analytische Geometrie... 9 Wahlteil Analytische Geometrie... 008 Pflichtteil Lösungen zur Prüfung 008: Pflichtteil
Mathematik > Analysis > Kurvendiskussion/Funktionsuntersuchung > Polynome
 Michael Buhlmann Schülerkurs Mathematik > Analsis > Kurvendiskussion/Funktionsuntersuchung > Polnome Kurvendiskussionen/Funktionsuntersuchungen gehören zum Standard der Mathematik an den Oberstuen der
Michael Buhlmann Schülerkurs Mathematik > Analsis > Kurvendiskussion/Funktionsuntersuchung > Polnome Kurvendiskussionen/Funktionsuntersuchungen gehören zum Standard der Mathematik an den Oberstuen der
Quadratische Funktionen Arbeitsblatt 1
 Quadratische Funktionen Arbeitsblatt 1 Spezielle quadratische Funktion Die Funktionsgleichung einer speziellen quadratischen Funktion hat die Form y = 3 x 2. Der dazugehörige Graph heißt Parabel. Bei einer
Quadratische Funktionen Arbeitsblatt 1 Spezielle quadratische Funktion Die Funktionsgleichung einer speziellen quadratischen Funktion hat die Form y = 3 x 2. Der dazugehörige Graph heißt Parabel. Bei einer
Lösungen IV.1. 1) a) F b) F c) Z d) F e) R f) Z g) Z h) F i) Z j) F
 Lösungen IV. ) a) F b) F c) Z d) F e) R f) Z g) Z h) F i) Z j) F ) a) () a () a + () a () a () a + () a b) () W = {,, } () W = {,, } () W = {,, 9} () W = {,, } () W = {,, } () W = {,, 8} ) a) b) Jost Gabi
Lösungen IV. ) a) F b) F c) Z d) F e) R f) Z g) Z h) F i) Z j) F ) a) () a () a + () a () a () a + () a b) () W = {,, } () W = {,, } () W = {,, 9} () W = {,, } () W = {,, } () W = {,, 8} ) a) b) Jost Gabi
Abitur 2012 Mathematik Infinitesimalrechnung I
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 212 Mathematik Infinitesimalrechnung I Geben Sie zu den Funktionstermen jeweils den maximalen Definitionsbereich sowie einen Term der Ableitungsfunktion
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 212 Mathematik Infinitesimalrechnung I Geben Sie zu den Funktionstermen jeweils den maximalen Definitionsbereich sowie einen Term der Ableitungsfunktion
Diese Funktion ist mein Typ!
 Diese Funktion ist mein Typ! Überblick über die wichtigsten Funktionstypen der 10.Jgst.: Lineare Funktionen Quadratische Funktionen Ganzrationale Funktionen Gebrochen-rationale Funktionen Trigonometrische
Diese Funktion ist mein Typ! Überblick über die wichtigsten Funktionstypen der 10.Jgst.: Lineare Funktionen Quadratische Funktionen Ganzrationale Funktionen Gebrochen-rationale Funktionen Trigonometrische
Funktionen ) W(t) = 105 l 15 l. 3) 7 Minuten; Werte von 0 bis 7 Minuten; Definitionsmenge 4) Werte von 0 bis 105 l 6) Der Graph ist eine Gerade.
 Funktionen. ) W(t) = l l min t ) W l ) t min W(t) l 9 ) Minuten; Werte von bis Minuten; Definitionsmenge ) Werte von bis l ) Der Graph ist eine Gerade. t min. a) ) ) ) - - - - - - - - - Funktion. Die Funktions-
Funktionen. ) W(t) = l l min t ) W l ) t min W(t) l 9 ) Minuten; Werte von bis Minuten; Definitionsmenge ) Werte von bis l ) Der Graph ist eine Gerade. t min. a) ) ) ) - - - - - - - - - Funktion. Die Funktions-
Wurzelfunktionen Aufgaben
 Wurzelfunktionen Aufgaben. Für jedes k (k > 0) ist die Funktion f k (x) = 8 (x k ) kx, 0 x gegeben. a) Untersuchen Sie die Funktion f k auf Nullstellen und Extrema. Ermitteln Sie lim f k(x) sowie für 0
Wurzelfunktionen Aufgaben. Für jedes k (k > 0) ist die Funktion f k (x) = 8 (x k ) kx, 0 x gegeben. a) Untersuchen Sie die Funktion f k auf Nullstellen und Extrema. Ermitteln Sie lim f k(x) sowie für 0
Mathematik-Lexikon. Abszisse Die x-koordinate eines Punktes -> Ordinate
 Mathematik-Lexikon HM00 Abszisse Die x-koordinate eines Punktes -> Ordinate Aufstellen von Funktionstermen Gesucht: Ganzrationale Funktion n-ten Grades: ƒ(x) = a n x n + a n-1 x n-1 + a n- x n- +... +
Mathematik-Lexikon HM00 Abszisse Die x-koordinate eines Punktes -> Ordinate Aufstellen von Funktionstermen Gesucht: Ganzrationale Funktion n-ten Grades: ƒ(x) = a n x n + a n-1 x n-1 + a n- x n- +... +
PFLICHTTEIL NT = e x (x+2) = x+2 Oder Umschreiben: f(x) = 1. = (x 2 e x ) 1, und dann Kettenregel
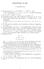 PFLICHTTEIL NT 26 F. LEMMERMEYER (1 Quotientenregel: f (x = x2 e x 2xe x x = e x (x+2 4 x = x+2 3 x 3 e. x Oder Umschreiben: f(x = 1 x 2 e = (x 2 e x 1, und dann Kettenregel x f (x = (x 2 e x 2 (2xe x
PFLICHTTEIL NT 26 F. LEMMERMEYER (1 Quotientenregel: f (x = x2 e x 2xe x x = e x (x+2 4 x = x+2 3 x 3 e. x Oder Umschreiben: f(x = 1 x 2 e = (x 2 e x 1, und dann Kettenregel x f (x = (x 2 e x 2 (2xe x
I Alte und neue Funktionen und ihre Ableitung
 Schülerbuchseiten 8 I Alte und neue Funktionen und ihre Ableitung Erkundungen Seite Ableitung von Eponentialfunktionen Eponentialfunktionen und Ableitungsgraphen f G ; Begründung: f (0) = ; f () = ; f
Schülerbuchseiten 8 I Alte und neue Funktionen und ihre Ableitung Erkundungen Seite Ableitung von Eponentialfunktionen Eponentialfunktionen und Ableitungsgraphen f G ; Begründung: f (0) = ; f () = ; f
Mathe-Abitur ab 2004: Fundus für den Pflichtbereich Lösungen (1)
 Mathe-Abitur ab 24: Fundus für den Pflichtbereich Lösungen () Die Autoren übernehmen keine Garantie für die Richtigkeit der Lösungen. Auch wurde sicher nicht immer der kürzeste und eleganteste Lösungsweg
Mathe-Abitur ab 24: Fundus für den Pflichtbereich Lösungen () Die Autoren übernehmen keine Garantie für die Richtigkeit der Lösungen. Auch wurde sicher nicht immer der kürzeste und eleganteste Lösungsweg
Schaubilderanalyse. Teil 1 ab Klassenstufe 10.
 Schaubilderanalyse Teil ab Klassenstufe 0 Erkennen von Funktionen der Typen: Ganzrational, gebrochen rational, eponentiell, Logarithmusund Wurzelfunktionen, Sinus und Kosinus Große Aufgabensammlung Hinweis:
Schaubilderanalyse Teil ab Klassenstufe 0 Erkennen von Funktionen der Typen: Ganzrational, gebrochen rational, eponentiell, Logarithmusund Wurzelfunktionen, Sinus und Kosinus Große Aufgabensammlung Hinweis:
Jahrgangsstufe 11. f(x) = 1 12 x4 1 3 x3 3 2 x2 nach allen Regeln der Kunst und zeichnen Sie ihren Graphen.
 Jahrgangsstufe. Diskutieren Sie die Funktion f mit der Gleichung f) = 3 3 3 nach allen Regeln der Kunst und zeichnen Sie ihren Graphen. Lösung: NS: 0 =,69, 0 = 0, 03 = + 6,69 lim f) = + ± f ) = 3 3 3 f
Jahrgangsstufe. Diskutieren Sie die Funktion f mit der Gleichung f) = 3 3 3 nach allen Regeln der Kunst und zeichnen Sie ihren Graphen. Lösung: NS: 0 =,69, 0 = 0, 03 = + 6,69 lim f) = + ± f ) = 3 3 3 f
Analysis. Ganzrationale Funktionen: Nullstellen, Extrempunkte, Monotonie, Verhalten im Unendlichen, Tangente. Gymnasium Klasse 10
 Analysis Ganzrationale Funktionen: Nullstellen, Extrempunkte, Monotonie, Verhalten im Unendlichen, Tangente Gymnasium Klasse 1 Hilfsmittel: wissenschaftlicher Taschenrechner Alexander Schwarz März 18 1
Analysis Ganzrationale Funktionen: Nullstellen, Extrempunkte, Monotonie, Verhalten im Unendlichen, Tangente Gymnasium Klasse 1 Hilfsmittel: wissenschaftlicher Taschenrechner Alexander Schwarz März 18 1
Mathematik 3 für Informatik
 Gunter Ochs Sommersemester 0 Mathematik 3 für Informatik Hausaufgabenblatt Lösungshinweise ohne Garantie auf Fehlerfeiheit). Seien f ) = { {, falls, falls und f ) =. ln, falls a) Skizzieren
Gunter Ochs Sommersemester 0 Mathematik 3 für Informatik Hausaufgabenblatt Lösungshinweise ohne Garantie auf Fehlerfeiheit). Seien f ) = { {, falls, falls und f ) =. ln, falls a) Skizzieren
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil Wahlteil Analysis 8 Wahlteil Analysis Wahlteil Analysis 9 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 9 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Pflichtteil Wahlteil Analysis 8 Wahlteil Analysis Wahlteil Analysis 9 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 9 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
1 Lineare Funktionen. 1 Antiproportionale Funktionen
 Funktion Eine Funktion ist eine Zuordnung, bei der zu jeder Größe eines ersten Bereichs (Ein gabegröße) genau eine Größe eines zweiten Bereichs (Ausgabegröße) gehört. Eine Funktion wird durch eine Funktionsvorschrift
Funktion Eine Funktion ist eine Zuordnung, bei der zu jeder Größe eines ersten Bereichs (Ein gabegröße) genau eine Größe eines zweiten Bereichs (Ausgabegröße) gehört. Eine Funktion wird durch eine Funktionsvorschrift
Alle zu orthogonalen Tangenten müssen die Steigung 4,32 1 haben. 0, ,2723* 1,2** 6 Punktprobe mit %&1,2'1,2( 2* 3,6* 64,272 4,272 2* 3,6* 1,7280
 Lösung A1 6 3 a) 1,21,2 64,272 1,23 1,2 4,32 1,2 1,21,2 4,32 1,24,2724,329,456 b) Alle Tangenten zu parallel müssen die Steigung 4,32 haben. 4,323 :3 1,44, 1,2 Für 1,2 siehe Aufgabenteil a). 1,21,2 67,728
Lösung A1 6 3 a) 1,21,2 64,272 1,23 1,2 4,32 1,2 1,21,2 4,32 1,24,2724,329,456 b) Alle Tangenten zu parallel müssen die Steigung 4,32 haben. 4,323 :3 1,44, 1,2 Für 1,2 siehe Aufgabenteil a). 1,21,2 67,728
Zusammenfassung: Differenzialrechnung 2
 LGÖ Ks M 11 Schuljahr 17/18 Zusammenfassung: Differenzialrechnung Inhaltsverzeichnis Etrem- und Wendepunkte... 1 Etremwertprobleme... 8 Etrem- und Wendepunkte Definition: Ist eine reelle Zahl, dann heißt
LGÖ Ks M 11 Schuljahr 17/18 Zusammenfassung: Differenzialrechnung Inhaltsverzeichnis Etrem- und Wendepunkte... 1 Etremwertprobleme... 8 Etrem- und Wendepunkte Definition: Ist eine reelle Zahl, dann heißt
Korrigendum Lambacher Schweizer 9/10, 1. Auflage 2011
 Korrigendum Lambacher Schweizer 9/,. Auflage Klett und Balmer Verlag, Baar. April. Seite, Aufgabe Tipp: Suche dir Punkte auf dem Kreis, die du zur Bestimmung heranziehen kannst Bestimme das Streckzentrum
Korrigendum Lambacher Schweizer 9/,. Auflage Klett und Balmer Verlag, Baar. April. Seite, Aufgabe Tipp: Suche dir Punkte auf dem Kreis, die du zur Bestimmung heranziehen kannst Bestimme das Streckzentrum
Abschlussprûfung Berufskolleg. (Fachhochschulreife) DEMO. Prüfungsaufgaben aus Baden-Württemberg. Analysis
 Abschlussprûfung Berufskolleg (Fachhochschulreife) Prüfungsaufgaben aus Baden-Württemberg Analysis Ganzrationale Funktionen Eponentialfunktionen Trigonometrische Funktionen Jahrgänge bis Tet Nr. 73 Stand
Abschlussprûfung Berufskolleg (Fachhochschulreife) Prüfungsaufgaben aus Baden-Württemberg Analysis Ganzrationale Funktionen Eponentialfunktionen Trigonometrische Funktionen Jahrgänge bis Tet Nr. 73 Stand
Funktionen-Katalog. I. Geraden. f(x) = 1 oder y = 1. x = 1. eine Gerade parallel zur x-achse. Gerade parallel zur y- Achse (keine Funktion) f(x) = - x
 Funktionen-Katalog I. Geraden II. Ganzrationale Funktion: Parabeln -ten Grades 3-ten Grades Parabeln höheren Grades III. Gebrochenrationale Funktionen: Asymptoten, Polstellen... IV. Eponentialfunktionen
Funktionen-Katalog I. Geraden II. Ganzrationale Funktion: Parabeln -ten Grades 3-ten Grades Parabeln höheren Grades III. Gebrochenrationale Funktionen: Asymptoten, Polstellen... IV. Eponentialfunktionen
4 x x kleinste6 Funktionswert für alle x aus einer Umgebung von x 1 ist.
 Differenzialrechnung 51 1.2.2 Etrempunkte Die Funktion f mit f () = 1 12 3 7 4 2 + 10 + 17 3 beschreibt näherungsweise die wöch entlichen Verkaufszahlen von Rasenmähern. Dabei ist die Zeit in Wochen nach
Differenzialrechnung 51 1.2.2 Etrempunkte Die Funktion f mit f () = 1 12 3 7 4 2 + 10 + 17 3 beschreibt näherungsweise die wöch entlichen Verkaufszahlen von Rasenmähern. Dabei ist die Zeit in Wochen nach
Abiturprüfung Mathematik 2007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
Ü b u n g s a r b e i t
 Ü b u n g s a r b e i t Aufgabe. a) Die Querschnittsfläche eines Abwasserkanals ist im unteren Teil von einer Parabel k begrenzt, an die sich nach oben die beiden Geraden g und h anschließen. Bestimmen
Ü b u n g s a r b e i t Aufgabe. a) Die Querschnittsfläche eines Abwasserkanals ist im unteren Teil von einer Parabel k begrenzt, an die sich nach oben die beiden Geraden g und h anschließen. Bestimmen
Inhaltsverzeichnis. Beispiel einer Abiturprüfung 18
 VB 004 Inhaltsverzeichnis Kurvendiskussion Einführung Ableitungen einer Funktion 3 Monotonieverhalten der Funktion 3 Wie bekommen wir nun raus, wo eine Funktion steigt oder fällt? 3 Symmetrieverhalten
VB 004 Inhaltsverzeichnis Kurvendiskussion Einführung Ableitungen einer Funktion 3 Monotonieverhalten der Funktion 3 Wie bekommen wir nun raus, wo eine Funktion steigt oder fällt? 3 Symmetrieverhalten
Ganzrationale Funktionen 1.) Parabeln 2-ten Grades f(x) = x² (Parabel) I. Geraden. f(x) = -x². f(x) = 1 oder y = 1. x = 2
 Mathematik in der Kursstufe: Analysis () Mathematik in der Kursstufe: Analysis () Analysis (): Funktionen-Katalog I. Geraden II. Ganzrationale Funktion: Parabeln -ten Grades 3-ten Grades Parabeln höheren
Mathematik in der Kursstufe: Analysis () Mathematik in der Kursstufe: Analysis () Analysis (): Funktionen-Katalog I. Geraden II. Ganzrationale Funktion: Parabeln -ten Grades 3-ten Grades Parabeln höheren
Funktionen mehrerer Variabler
 Funktionen mehrerer Variabler Fakultät Grundlagen Juli 2015 Fakultät Grundlagen Funktionen mehrerer Variabler Übersicht Funktionsbegriff 1 Funktionsbegriff Beispiele Darstellung Schnitte 2 Partielle Ableitungen
Funktionen mehrerer Variabler Fakultät Grundlagen Juli 2015 Fakultät Grundlagen Funktionen mehrerer Variabler Übersicht Funktionsbegriff 1 Funktionsbegriff Beispiele Darstellung Schnitte 2 Partielle Ableitungen
Technische Universität Dresden, Fakultät Mathematik Prof. Dr. F. Schuricht, Dr. M. Herrich. der Übungsaufgaben zum Brückenkurs Mathematik 2018
 Technische Universität Dresden, Fakultät Mathematik Prof. Dr. F. Schuricht, Dr. M. Herrich E R G E B N I S S E der Übungsaufgaben zum Brückenkurs Mathematik 08 Ergebnisse zur. Übung am.09.08 Thema: Logik,
Technische Universität Dresden, Fakultät Mathematik Prof. Dr. F. Schuricht, Dr. M. Herrich E R G E B N I S S E der Übungsaufgaben zum Brückenkurs Mathematik 08 Ergebnisse zur. Übung am.09.08 Thema: Logik,
Tutorium Mathematik ITB1(B), WI1(B)
 Tutorium Mathematik ITB(B), WI(B) Aufgabenblatt D Differenzialrechnung Prof Dr Peter Plappert Fachbereich Grundlagen Die Aufgaben dieses Aufgabenblattes sollen ohne die Benutzung von Taschenrechnern bearbeitet
Tutorium Mathematik ITB(B), WI(B) Aufgabenblatt D Differenzialrechnung Prof Dr Peter Plappert Fachbereich Grundlagen Die Aufgaben dieses Aufgabenblattes sollen ohne die Benutzung von Taschenrechnern bearbeitet
Matur-/Abituraufgaben Analysis
 Matur-/Abituraufgaben Analysis 1. Tropfen Die folgende Skizze zeigt die Kurve k mit der Gleichung y = (1 ) im Intervall 1. Die Kurve k bildet zusammen mit ihrem Spiegelbild k eine zur -Achse symmetrische
Matur-/Abituraufgaben Analysis 1. Tropfen Die folgende Skizze zeigt die Kurve k mit der Gleichung y = (1 ) im Intervall 1. Die Kurve k bildet zusammen mit ihrem Spiegelbild k eine zur -Achse symmetrische
Funktionsgraphen (Aufgaben)
 Gymnasium Pegnitz JS 9 August 2007 Funktionsgraphen (Aufgaben) 1. Betrachte die beiden linearen Funktionen f(x) = x + 2 und g(x) = x 3 und die quadratische Funktion p(x) = f(x) g(x) (a) Zeichne die Graphen
Gymnasium Pegnitz JS 9 August 2007 Funktionsgraphen (Aufgaben) 1. Betrachte die beiden linearen Funktionen f(x) = x + 2 und g(x) = x 3 und die quadratische Funktion p(x) = f(x) g(x) (a) Zeichne die Graphen
Hauptprüfung Abiturprüfung 2015 (ohne CAS) Baden-Württemberg
 Baden-Württemberg: Abitur 01 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 01 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Baden-Württemberg: Abitur 01 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 01 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Mathematik 12. Jahrgangsstufe - Hausaufgaben
 Version:. November Mathematik. Jahrgangsstufe - Hausaufgaben Inhaltsverzeichnis Integralrechnung.5 Kurvendiskussion und Integralrechnung................... Flächenberechnung. Stammfunktionen..................................
Version:. November Mathematik. Jahrgangsstufe - Hausaufgaben Inhaltsverzeichnis Integralrechnung.5 Kurvendiskussion und Integralrechnung................... Flächenberechnung. Stammfunktionen..................................
www.mathe-aufgaben.com
 Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit sin() f() =. Aufgabe : ( VP) Berechnen Sie das Integral ( )
Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit sin() f() =. Aufgabe : ( VP) Berechnen Sie das Integral ( )
( 0 ( x) d) Die Funktionsgleichung der Funktion 1 lautet: f( Für x 2 = 0 : Wähle die Werte -1 und 1. Überprüfe x1 = 1,
 Differentialrechnung IV (Wendepunkte) (Kap 7) (Haben Sie Probleme bei der Bearbeitung dieser Aufgaben versuchen Sie diese in Ihrer Kleingruppe mit Hilfe des Arbeitsbuchs Mathematik zu klären Führt dies
Differentialrechnung IV (Wendepunkte) (Kap 7) (Haben Sie Probleme bei der Bearbeitung dieser Aufgaben versuchen Sie diese in Ihrer Kleingruppe mit Hilfe des Arbeitsbuchs Mathematik zu klären Führt dies
Mathematischer Vorbereitungskurs für das MINT-Studium
 Mathematischer Vorbereitungskurs für das MINT-Studium Dr. B. Hallouet b.hallouet@m.uni-saarland.de SS 07 Vorlesung 5 MINT Mathkurs SS 07 / 8 Vorlesung 5 (Lecture 5) Reelle Funktionen einer reellen Veränderlichen
Mathematischer Vorbereitungskurs für das MINT-Studium Dr. B. Hallouet b.hallouet@m.uni-saarland.de SS 07 Vorlesung 5 MINT Mathkurs SS 07 / 8 Vorlesung 5 (Lecture 5) Reelle Funktionen einer reellen Veränderlichen
Abitur 2017 Mathematik Infinitesimalrechnung I
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion g : x 2 4 + x 1 mit maximaler Definitionsmenge D g. Der Graph von g wird mit G g bezeichnet.
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion g : x 2 4 + x 1 mit maximaler Definitionsmenge D g. Der Graph von g wird mit G g bezeichnet.
Pflichtteil - Exponentialfunktion
 Pflichtteil - Eponentialfunktion Aufgabe (Ableiten) Bestimme die. und. Ableitung der folgenden Funktionen: a) f() = ln() + b) g() = e Aufgabe (Integrieren) Berechnen Sie die Integrale: a) e d b) c) h()
Pflichtteil - Eponentialfunktion Aufgabe (Ableiten) Bestimme die. und. Ableitung der folgenden Funktionen: a) f() = ln() + b) g() = e Aufgabe (Integrieren) Berechnen Sie die Integrale: a) e d b) c) h()
Abitur 2011 G8 Musterabitur Mathematik Infinitesimalrechnung
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 211 G8 Musterabitur Mathematik Infinitesimalrechnung I Teilaufgabe 1 (3 BE) Bestimmen Sie die Nullstellen der Funktion f : x (e x 2) (x 3 2x ) mit Definitionsbereich
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 211 G8 Musterabitur Mathematik Infinitesimalrechnung I Teilaufgabe 1 (3 BE) Bestimmen Sie die Nullstellen der Funktion f : x (e x 2) (x 3 2x ) mit Definitionsbereich
Hauptprüfung Abiturprüfung 2016 (ohne CAS) Baden-Württemberg
 Baden-Württemberg: Abitur 06 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 06 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com
Baden-Württemberg: Abitur 06 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 06 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com
Anwendungen der Differentialrechnung Optimieren und Modellieren. Kapitel 7
 Anwendungen der Differentialrechnung ptimieren und Modellieren Kapitel 7 7. Etremwertprobleme 9 Arbeitsaufträge. a) Seitenlängen: cm; cm mit + = 9, also = 9 (und > 0; > 0),5 5 6 7 8 8 7 6 5,5 A (in cm
Anwendungen der Differentialrechnung ptimieren und Modellieren Kapitel 7 7. Etremwertprobleme 9 Arbeitsaufträge. a) Seitenlängen: cm; cm mit + = 9, also = 9 (und > 0; > 0),5 5 6 7 8 8 7 6 5,5 A (in cm
4.8. Prüfungsaufgaben zu trigonometrischen Funktionen
 .8. Prüfungsaufgaben zu trigonometrischen Funktionen Aufgabe : Schaubilder der trigonomtrischen Funktionen (8) a) Zeichne den Graphen der Sinusfunktion im Bereich π und gib fünf verschiedene Funktionswerte
.8. Prüfungsaufgaben zu trigonometrischen Funktionen Aufgabe : Schaubilder der trigonomtrischen Funktionen (8) a) Zeichne den Graphen der Sinusfunktion im Bereich π und gib fünf verschiedene Funktionswerte
 Abiturprüfung Mathematik 0 Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f() = ( sin() + 7) 5. Aufgabe : ( VP) Berechnen Sie eine Stammfunktion
Abiturprüfung Mathematik 0 Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f() = ( sin() + 7) 5. Aufgabe : ( VP) Berechnen Sie eine Stammfunktion
Klasse Dozent. Musteraufgaben. f(x) = g(x) = Bestimme die zu den abgebildeten Graphen. gehörenden Funktionsgleichungen!0.
 Fach: Mathematik - Quadratische Funktionen Anzahl Aufgaben: 51 Musteraufgaben Diese Aufgabensammlung wurde mit KlasseDozent erstellt. Sie haben diese Aufgaben zusätzlich als KlasseDozent-Importdatei (.xml)
Fach: Mathematik - Quadratische Funktionen Anzahl Aufgaben: 51 Musteraufgaben Diese Aufgabensammlung wurde mit KlasseDozent erstellt. Sie haben diese Aufgaben zusätzlich als KlasseDozent-Importdatei (.xml)
Analysis: Exponentialfunktionen Analysis
 www.mathe-aufgaben.com Analysis: Eponentialfunktionen Analysis Klausur zu Eponentialfunktionen ohne Wachstum (Ableitung, Stammfunktion, Fläche, Rotationsvolumen, Etremwertaufgabe) Gymnasium ab J Aleander
www.mathe-aufgaben.com Analysis: Eponentialfunktionen Analysis Klausur zu Eponentialfunktionen ohne Wachstum (Ableitung, Stammfunktion, Fläche, Rotationsvolumen, Etremwertaufgabe) Gymnasium ab J Aleander
Mathematik Übungsklausur 2013 Ausführliche Lösungen
 Mathematik Übungsklausur 0 Ausführliche Lösungen Analysis Aufgabe Die Nullstellen einer Funktion f mit Definitionsbereich D f sind die Lösungen der Gleichung f(x) = 0 in D f. Damit erhält man: a) f: x
Mathematik Übungsklausur 0 Ausführliche Lösungen Analysis Aufgabe Die Nullstellen einer Funktion f mit Definitionsbereich D f sind die Lösungen der Gleichung f(x) = 0 in D f. Damit erhält man: a) f: x
a) Der Graph von g entsteht durch Verschiebung des Graphen von f um nach. Es gilt also: g(x) = f(x)
 Vertikale Verschiebung a) Der Graph von g entsteht durch Verschiebung des Graphen von f um nach. Es gilt also: g() = f() b) Zeichne den Graphen der Funktion h mit h() = f() ein. Oben oder unten? f() +
Vertikale Verschiebung a) Der Graph von g entsteht durch Verschiebung des Graphen von f um nach. Es gilt also: g() = f() b) Zeichne den Graphen der Funktion h mit h() = f() ein. Oben oder unten? f() +
Aufgaben zum Aufstellen von Funktionen aus gegebenen Bedingungen
 Augaben zum Austellen von Funktionen aus gegebenen Bedingungen 1. Die Parabel Gp ist der Graph der quadratischen Funktion p(. Diese Parabel schneidet die x-achse im Punkt N(6/0). Ihr Scheitelpunkt S(/yS)
Augaben zum Austellen von Funktionen aus gegebenen Bedingungen 1. Die Parabel Gp ist der Graph der quadratischen Funktion p(. Diese Parabel schneidet die x-achse im Punkt N(6/0). Ihr Scheitelpunkt S(/yS)
3 Differenzialrechnung
 Differenzialrechnung 3 Differenzialrechnung 3.1 Ableitungsregeln Übersicht Beispiel Vorgehen Potenzfunktionen f(x) = x 4 f (x) = 4 x 3 f(x) = x f (x) = 1 x 0 = 1 f(x) = x Hochzahl f (x) = Hochzahl x Hochzahl
Differenzialrechnung 3 Differenzialrechnung 3.1 Ableitungsregeln Übersicht Beispiel Vorgehen Potenzfunktionen f(x) = x 4 f (x) = 4 x 3 f(x) = x f (x) = 1 x 0 = 1 f(x) = x Hochzahl f (x) = Hochzahl x Hochzahl
ARBEITSUNTERLAGEN. zum STARTERKURS an der UNIVERSITÄT DES SAARLANDES
 ARBEITSUNTERLAGEN zum STARTERKURS an der UNIVERSITÄT DES SAARLANDES Vorbemerkung Ziel des Propädeutikums ist es, die Schulmathematik wieder ins Gedächtnis zu rufen und eine gemeinsame Grundlage für die
ARBEITSUNTERLAGEN zum STARTERKURS an der UNIVERSITÄT DES SAARLANDES Vorbemerkung Ziel des Propädeutikums ist es, die Schulmathematik wieder ins Gedächtnis zu rufen und eine gemeinsame Grundlage für die
Inhalt der Lösungen zur Prüfung 2015:
 Inhalt der Lösungen zur Prüfung : Pflichtteil... Wahlteil Analysis... 8 Wahlteil Analysis... Wahlteil Analytische Geometrie/Stochastik... Wahlteil Analytische Geometrie/Stochastik... 9 Pflichtteil Lösungen
Inhalt der Lösungen zur Prüfung : Pflichtteil... Wahlteil Analysis... 8 Wahlteil Analysis... Wahlteil Analytische Geometrie/Stochastik... Wahlteil Analytische Geometrie/Stochastik... 9 Pflichtteil Lösungen
Abitur Mathematik Baden-Württemberg 2012
 Abitur Mathematik: Baden-Württemberg 2012 Im sind keine Hilfsmittel zugelassen. Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist die Verkettung der Potenzfunktion g(x)
Abitur Mathematik: Baden-Württemberg 2012 Im sind keine Hilfsmittel zugelassen. Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist die Verkettung der Potenzfunktion g(x)
