FORMALE SYSTEME. 6. Vorlesung: Reguläre Ausdrücke. TU Dresden, 27. Oktober Markus Krötzsch
|
|
|
- Helmuth Bayer
- vor 7 Jahren
- Abrufe
Transkript
1 FORMALE SYSTEME 6. Vorlesung: Reguläre Ausdrücke Mrkus Krötzsch TU Dresden, 27. Oktober 2016
2 Rückblick Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 2 von 29
3 Wiederholung: Opertionen uf Automten A B 1 C D 1 E = A B 1 C D 1 E 0 A B 0 C 0 0, 1 = A, C B, C D 1 A, D 1 B, D A B 0 1 = A B 1 ɛ A B 1 C D 1 E = A B 0 1 C ɛ D 1 E 0 1 A B 1 C 0 = A 1 B 1 C q f ɛ Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 3 von 29
4 NFAs mit Wortübergängen Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 4 von 29
5 Drstellungen von Typ-3-Sprchen reguläre Grmmtik q 1 q 2 q 1 q2 DFA NFA NFA ɛ-nfa DFA NFA ɛ-nfa konstr. ɛ-elim. duler Grph Potenzm.- Syntxdigrmm Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 5 von 29
6 Reguläre Ausdrücke Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 6 von 29
7 Endliche Sprchen Eine einfche Beobchtung: Stz: Jede endliche Sprche ist regulär. Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 7 von 29
8 Endliche Sprchen Eine einfche Beobchtung: Stz: Jede endliche Sprche ist regulär. Beweis: Mn knn eine beliebige endliche Sprche {w 1,..., w n } durch einen NFA mit Wortübergängen erkennen: w 1 w 2 A... w n B Wie in der letzten Vorlesung gezeigt, knn dieser in einen NFA umgeformt werden. Jeder NFA kzeptiert eine reguläre Sprche. Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 7 von 29
9 Sprchen konstruieren? Wir hben gesehen: Jede endliche Sprche ist regulär. Durch Anwendung von,,, und entstehen us regulären Sprchen immer wieder reguläre Sprchen. Eine ntürliche Frge ist lso: Welche regulären Sprchen knn mn durch Anwendung von,,, und us endlichen Sprchen konstruieren? Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 8 von 29
10 Sprchen konstruieren? Wir hben gesehen: Jede endliche Sprche ist regulär. Durch Anwendung von,,, und entstehen us regulären Sprchen immer wieder reguläre Sprchen. Eine ntürliche Frge ist lso: Welche regulären Sprchen knn mn durch Anwendung von,,, und us endlichen Sprchen konstruieren? Alle! Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 8 von 29
11 Die kleinste (,, )-bgeschlossene Klsse Überrschender Weise sind und nicht einml nötig! Stz: Alle regulären Sprchen können durch Anwendung von, und us endlichen Sprchen konstruiert werden. Mit und knn mn jede endliche Sprche leicht us den Sprchen, {ɛ} und {} ( Σ) konstruieren. Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 9 von 29
12 Die kleinste (,, )-bgeschlossene Klsse Überrschender Weise sind und nicht einml nötig! Stz: Alle regulären Sprchen können durch Anwendung von, und us endlichen Sprchen konstruiert werden. Mit und knn mn jede endliche Sprche leicht us den Sprchen, {ɛ} und {} ( Σ) konstruieren. Mit den beknnten Abschlusseigenschften erhält mn lso: Stz: Die Klsse der regulären Sprchen ist die kleinste Klsse von Sprchen mit den folgenden Eigenschften: Sie enthält die Sprchen, {ɛ} und {} für lle Σ Sie ist bgeschlossen unter den Opertoren, und Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 9 von 29
13 Die kleinste (,, )-bgeschlossene Klsse Überrschender Weise sind und nicht einml nötig! Stz: Alle regulären Sprchen können durch Anwendung von, und us endlichen Sprchen konstruiert werden. Mit und knn mn jede endliche Sprche leicht us den Sprchen, {ɛ} und {} ( Σ) konstruieren. Mit den beknnten Abschlusseigenschften erhält mn lso: Stz: Die Klsse der regulären Sprchen ist die kleinste Klsse von Sprchen mit den folgenden Eigenschften: Sie enthält die Sprchen, {ɛ} und {} für lle Σ Sie ist bgeschlossen unter den Opertoren, und Beweispln: Definiere diese Klsse syntktisch: reguläre Ausdrücke Zeige, dss diese genu die regulären Sprchen drstellen Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 9 von 29
14 Reguläre Ausdrücke Ds motiviert die Einführung einer eigenen Syntx: Die Menge der regulärer Ausdrücke über einem Alphbet Σ ist induktiv wie folgt definiert: ist ein regulärer Ausdruck ɛ ist ein regulärer Ausdruck ist ein regulärer Ausdruck für jedes Σ Wenn α und β reguläre Ausdrücke sind, dnn sind uch (αβ), (α β) und (α) reguläre Ausdrücke D.h. die Menge der regulären Ausdrücke ist die kleinste Menge, welche die Bedingungen erfüllt. Anmerkung: Mnchml werden (α + β) sttt (α β) und (α β) oder (α β) sttt (αβ) verwendet Beispiele regulärer Ausdrücke sind ((b) ) oder uch (((ɛ ɛ)) ). Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 10 von 29
15 Reguläre Ausdrücke ls formle Sprche Mn knn die Menge der regulären Ausdrücke über dem Alphbet Σ = {σ 1,..., σ n } uch ls kontextfreie Grmmtik über dem Alphbet Σ {, ɛ, (, ),, } beschreiben: S ɛ A (SS) (S S) (S) A σ 1... σ n Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 11 von 29
16 Reguläre Ausdrücke ls formle Sprche Mn knn die Menge der regulären Ausdrücke über dem Alphbet Σ = {σ 1,..., σ n } uch ls kontextfreie Grmmtik über dem Alphbet Σ {, ɛ, (, ),, } beschreiben: S ɛ A (SS) (S S) (S) A σ 1... σ n Solche Nottionen werden in der Prxis oft weiter vereinfcht: Endliche Mengen ls Nichtterminle: S ɛ Σ (SS) (S S) (S) Mehrere Nichtterminle ls Hinweis uf unterschiedliche Ausdrücke: α ɛ Σ (αβ) (α β) (α) Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 11 von 29
17 Semntik regulärer Ausdrücke Reguläre Ausdrücke beschreiben die erwrteten Sprchen: Die Sprche eines regulären Ausdrucks α wird mit L(α) bezeichnet und rekursiv definiert: L( ) = L(ɛ) = {ɛ} L() = {} für jedes Σ L((αβ)) = L(α) L(β) L((α β)) = L(α) L(β) L((α) ) = L(α) Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 12 von 29
18 Semntik regulärer Ausdrücke Reguläre Ausdrücke beschreiben die erwrteten Sprchen: Die Sprche eines regulären Ausdrucks α wird mit L(α) bezeichnet und rekursiv definiert: L( ) = L(ɛ) = {ɛ} L() = {} für jedes Σ L((αβ)) = L(α) L(β) L((α β)) = L(α) L(β) L((α) ) = L(α) Beispiel: L(((b)) ) = (L((b))) = (L() L(b)) = ({} {b}) = {b} Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 12 von 29
19 Vereinfchte Klmmerung Reguläre Ausdrücke können durch Klmmerungsregeln vereinfcht werden: bindet stärker ls Konktention bindet stärker ls Beispiel: b bc ist kurz für (((b) ) (bc)) Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 13 von 29
20 Vereinfchte Klmmerung Reguläre Ausdrücke können durch Klmmerungsregeln vereinfcht werden: bindet stärker ls Konktention bindet stärker ls Beispiel: b bc ist kurz für (((b) ) (bc)) Konktention und Alterntive sind ssozitiv: L((α(βγ))) = L(((αβ)γ)) L((α (β γ))) = L(((α β) γ)) Dher ist es unproblemtisch, dss die Klmmerregeln die Reihenfolge nicht spezifizieren. Beispiel: könnte für genu 42 verschiedene reguläre Ausdrücke stehen, unter nderem für (((((10)1)0)1)0), ((10)((10)(10))) und (1((0((10)1))0)). Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 13 von 29
21 Kurzschreibweisen für reguläre Ausdrücke Mn knn eine Reihe von Kurzschreibweisen definieren: α + ist kurz für α(α) α? ist kurz für (α ɛ) α{n, m} mit 0 n m ist kurz für (α } {{... } α... α } {{... } α) n-ml m-ml Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 14 von 29
22 Kurzschreibweisen für reguläre Ausdrücke Mn knn eine Reihe von Kurzschreibweisen definieren: α + ist kurz für α(α) α? ist kurz für (α ɛ) α{n, m} mit 0 n m ist kurz für (α } {{... } α... α } {{... } α) n-ml m-ml Implementierungen regulärer Ausdrücke bieten uch Kurzformen für Alterntiven einzelner Symbole ( Chrcter Clsses ):.: beliebiges Symbol, d.h. σ 1... σ n flls Σ = {σ 1,..., σ n } [θ 1 θ l ]: beliebiges Symbol us einer Liste, d.h. θ 1... θ l [ˆθ 1 θ l ]: beliebiges Symbol nicht us einer Liste, d.h. σ 1... σ l mit {σ 1,..., σ l } = Σ \ {θ 1,..., θ l } Weitere Kurzformen für prktisch wichtige Fälle, z.b. \s oder [:blnk:] für Leerzeichen, \d oder [:digit:] für Ziffern Theoretiker meiden Kurzformen (mehr Formen = mehr Fälle in Beweisen und Definitionen) Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 14 von 29
23 Regexps in der Prxis Reguläre Ausdrücke sind von großer prktischer Bedeutung Mustererkennung in Texten (Pttern Mtching) Lexer/Tokenizer Suche nch Muster in Dtenbnken... Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 15 von 29
24 Regexps in der Prxis Reguläre Ausdrücke sind von großer prktischer Bedeutung Mustererkennung in Texten (Pttern Mtching) Lexer/Tokenizer Suche nch Muster in Dtenbnken... Unterschiede zur reinen Lehre: Pttern Mtching: (1) spezifiziere eine Sprche (Suchwörter) und (2) finde deren Vorkommen (Mtches) in einem längeren Wort (Text) Möglichkeiten zur Steuerung des zweiten Teils nötig (z.b. greedy vs. lzy mtching) Referenzen: prktische Implementierungen erluben es meist, Teile eines Mtches im Muster wieder zu verwenden keine reguläre Sprche mehr Escping: Unterscheidung von Steuerzeichen (Metzeichen) und Alphbetssymbolen ist prktisch ufwändig Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 15 von 29
25 Äquivlenz regulärer Ausdrücke Zwei reguläre Ausdrücke α und β sind äquivlent, in Symbolen α β, wenn L(α) = L(β). Typische Rechenregeln der Sprchopertionen gelten nlog: α β β α ɛα αɛ α α(β γ) αβ αγ α α (β γ)α βα γα α α α ɛ ɛ ɛ Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 16 von 29
26 Von Regulären Ausdrücken zu Automten Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 17 von 29
27 Zielstellung Behuptung: Eine Sprche L ist genu dnn regulär, wenn es einen regulären Ausdruck α gibt mit L(α) = L. Beweis (Pln): Teilbehuptung 1: Für jeden regulären Ausdruck α gibt es einen NFA M, so dss L(α) = L(M) Zwei mögliche Beweismethoden: (1) Kompositionelle Methode (2) Explizite Konstruktion Teilbehuptung 2: Für jeden NFA M gibt es einen regulären Ausdruck α, so dss L(α) = L(M) Zwei mögliche Beweismethoden: (1) Ersetzungsmethode (2) Dynmische Progrmmierung Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 18 von 29
28 Drstellungen von Typ-3-Sprchen reguläre Grmmtik q 1 q 2 q 1 q2 regulärer Ausdruck 1) Ersetzung 2) Dyn. Prog. 1) komposit. 2) explizit DFA NFA NFA ɛ-nfa DFA NFA ɛ-nfa konstr. ɛ-elim. duler Grph Potenzm.- Syntxdigrmm Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 19 von 29
29 Drstellungen von Typ-3-Sprchen reguläre Grmmtik q 1 q 2 q 1 q2 regulärer Ausdruck 1) Ersetzung 2) Dyn. Prog. 1) komposit. 2) explizit DFA NFA NFA ɛ-nfa DFA NFA ɛ-nfa konstr. ɛ-elim. duler Grph Potenzm.- Syntxdigrmm Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 19 von 29
30 Rekursive Komposition von ɛ-nfa Die Struktur regulärer Ausdrücke knn mit Opertionen uf Automten direkt bgebildet werden. Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 20 von 29
31 Rekursive Komposition von ɛ-nfa Die Struktur regulärer Ausdrücke knn mit Opertionen uf Automten direkt bgebildet werden. Für einen Ausdruck α definieren wir rekursiv den ɛ-nfa M(α): Grundfälle: Wenn α = dnn M(α) = A Wenn α = ɛ dnn M(α) = Wenn α = dnn M(α) = A B A Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 20 von 29
32 Rekursive Komposition von ɛ-nfa Die Struktur regulärer Ausdrücke knn mit Opertionen uf Automten direkt bgebildet werden. Für einen Ausdruck α definieren wir rekursiv den ɛ-nfa M(α): Grundfälle: Wenn α = dnn M(α) = A Wenn α = ɛ dnn M(α) = Wenn α = dnn M(α) = A B Rekursive Fälle: Wir bezeichnen mit elim ɛ (M) den NFA, der us einem ɛ-nfa M durch Eliminierung der ɛ-übergänge entsteht. Wenn α = (βγ) dnn M(α) = elim ɛ (M(β) M(γ)) Wenn α = (β γ) dnn M(α) = M(β) M(γ) Wenn α = (β) dnn M(α) = elim ɛ (M(β) ) Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 20 von 29 A
33 Beispiel Regulärer Ausdruck: b Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 21 von 29
34 Beispiel Regulärer Ausdruck: b 1 2 Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 21 von 29
35 Beispiel Regulärer Ausdruck: b 1 2 b b 3 4 Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 21 von 29
36 Beispiel Regulärer Ausdruck: b 1 2 b b Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 21 von 29
37 Beispiel Regulärer Ausdruck: b 1 2 b b 3 4 ɛ 5 6 q f Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 21 von 29
38 Beispiel Regulärer Ausdruck: b 1 2 b b 3 4 ɛ ɛ ɛ 5 6 q f b Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 21 von 29
39 Beispiel Regulärer Ausdruck: b b b b 1 2 b 3 4 b b ɛ ɛ ɛ 5 6 q f Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 21 von 29
40 Korrektheit der Kompositionsmethode Stz: Für jeden regulären Ausdruck α gilt L(α) = L(M(α)). Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 22 von 29
41 Korrektheit der Kompositionsmethode Stz: Für jeden regulären Ausdruck α gilt L(α) = L(M(α)). Beweis: Die Gleichheit folgt us der Definition von L(α) und der Korrektheit der Opertionen uf Automten und der ɛ-eliminierung. Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 22 von 29
42 Korrektheit der Kompositionsmethode Stz: Für jeden regulären Ausdruck α gilt L(α) = L(M(α)). Beweis: Die Gleichheit folgt us der Definition von L(α) und der Korrektheit der Opertionen uf Automten und der ɛ-eliminierung. Forml ist der Beweis eine strukturelle Induktion: wir konstruieren unsere Argumenttion entlng der Struktur regulärer Ausdrücke. Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 22 von 29
43 Korrektheit der Kompositionsmethode Stz: Für jeden regulären Ausdruck α gilt L(α) = L(M(α)). Beweis: Die Gleichheit folgt us der Definition von L(α) und der Korrektheit der Opertionen uf Automten und der ɛ-eliminierung. Forml ist der Beweis eine strukturelle Induktion: wir konstruieren unsere Argumenttion entlng der Struktur regulärer Ausdrücke. Induktionsnfng: Für die Grundfälle α =, α = ɛ und α = ist die Behuptung leicht zu sehen Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 22 von 29
44 Korrektheit der Kompositionsmethode Stz: Für jeden regulären Ausdruck α gilt L(α) = L(M(α)). Beweis: Die Gleichheit folgt us der Definition von L(α) und der Korrektheit der Opertionen uf Automten und der ɛ-eliminierung. Forml ist der Beweis eine strukturelle Induktion: wir konstruieren unsere Argumenttion entlng der Struktur regulärer Ausdrücke. Induktionsnfng: Für die Grundfälle α =, α = ɛ und α = ist die Behuptung leicht zu sehen Induktionshypothese (IH): Die Behuptung wurde bereits für β und γ gezeigt, d.h. L(β) = L(M(β)) und L(γ) = L(M(γ)) Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 22 von 29
45 Korrektheit der Kompositionsmethode Stz: Für jeden regulären Ausdruck α gilt L(α) = L(M(α)). Beweis: Die Gleichheit folgt us der Definition von L(α) und der Korrektheit der Opertionen uf Automten und der ɛ-eliminierung. Forml ist der Beweis eine strukturelle Induktion: wir konstruieren unsere Argumenttion entlng der Struktur regulärer Ausdrücke. Induktionsnfng: Für die Grundfälle α =, α = ɛ und α = ist die Behuptung leicht zu sehen Induktionshypothese (IH): Die Behuptung wurde bereits für β und γ gezeigt, d.h. L(β) = L(M(β)) und L(γ) = L(M(γ)) Induktionsschritt: Im Fll α = (βγ) gilt: L(α) Def. = L(β) L(γ) IH = L(M(β)) L(M(γ)) (1) = L(M(β) M(γ)) (2) = L(elim ɛ (M(β) M(γ))) Def. = L(M(α)). (1) Korrektheit der Opertion ; (2) Korrektheit der ɛ-eliminierung Die Fälle α = (β γ) und α = (β) sind nlog. Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 22 von 29
46 Drstellungen von Typ-3-Sprchen reguläre Grmmtik q 1 q 2 q 1 q2 regulärer Ausdruck 1) Ersetzung 2) Dyn. Prog. 1) komposit. 2) explizit DFA NFA NFA ɛ-nfa DFA NFA ɛ-nfa konstr. ɛ-elim. duler Grph Potenzm.- Syntxdigrmm Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 23 von 29
47 Explizite Konstruktion des NFA Idee: Beginne mit einem NFA mit RegExp-Übergängen, bei dem Knten mit regulären Ausdrücken beschriftet sind Eliminiere diese Übergänge schrittweise, ähnlich wie beim Eliminieren von Wortübergängen Es ist einfcher, ds für reguläre Ausdrücke zu tun, die kein enthlten Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 24 von 29
48 Eliminierung von Der folgende einfche Algorithmus erzeugt reguläre Ausdrücke ohne innere Vorkommen von : Eingbe: regulärer Ausdruck α Ausgbe: äquivlenter regulärer Ausdruck β ohne (flls L(α) ) oder (flls L(α) = ) Wende die folgenden Ersetzungsregeln erschöpfend uf Teilusdrücke von α n: (γ ) γ und ( γ) γ (γ ) und ( γ) ( ) ɛ Gib ds Ergebnis dieser Ersetzungen us. Die Korrektheit des Algorithmus folgt us der Korrektheit der ngewendeten Ersetzungsregeln Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 25 von 29
49 Explizite Konstruktion von NFAs Für den Ausdruck können wir einen NFA direkt ngeben (wie vorn); ndernflls gehen wir wie folgt vor: Gegeben: regulärer Ausdruck α ohne Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 26 von 29
50 Explizite Konstruktion von NFAs Für den Ausdruck können wir einen NFA direkt ngeben (wie vorn); ndernflls gehen wir wie folgt vor: Gegeben: regulärer Ausdruck α ohne α Initilisierung: M α = A B Solnge es in M α Übergänge q β p gibt, die mit einem Ausdruck β {ɛ} Σ beschriftet sind, wende eine der folgenden Regeln n: Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 26 von 29
51 Explizite Konstruktion von NFAs Für den Ausdruck können wir einen NFA direkt ngeben (wie vorn); ndernflls gehen wir wie folgt vor: Gegeben: regulärer Ausdruck α ohne α Initilisierung: M α = A B Solnge es in M α Übergänge q β p gibt, die mit einem Ausdruck β {ɛ} Σ beschriftet sind, wende eine der folgenden Regeln n: (γ 1 γ 2 ) Ersetze q p γ 1 γ 2 durch q r p Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 26 von 29
52 Explizite Konstruktion von NFAs Für den Ausdruck können wir einen NFA direkt ngeben (wie vorn); ndernflls gehen wir wie folgt vor: Gegeben: regulärer Ausdruck α ohne α Initilisierung: M α = A B Solnge es in M α Übergänge q β p gibt, die mit einem Ausdruck β {ɛ} Σ beschriftet sind, wende eine der folgenden Regeln n: (γ 1 γ 2 ) Ersetze q p γ 1 γ 2 durch q r p (γ 1 γ 2 ) Ersetze q p γ 1 durch q γ 2 p Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 26 von 29
53 Explizite Konstruktion von NFAs Für den Ausdruck können wir einen NFA direkt ngeben (wie vorn); ndernflls gehen wir wie folgt vor: Gegeben: regulärer Ausdruck α ohne α Initilisierung: M α = A B Solnge es in M α Übergänge q β p gibt, die mit einem Ausdruck β {ɛ} Σ beschriftet sind, wende eine der folgenden Regeln n: (γ 1 γ 2 ) Ersetze q p γ 1 γ 2 durch q r p (γ 1 γ 2 ) Ersetze q p γ 1 durch q γ 2 p γ (γ) ɛ ɛ Ersetze q p durch q r p Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 26 von 29
54 Beispiel Regulärer Ausdruck: b Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 27 von 29
55 Beispiel Regulärer Ausdruck: b b 1 2 Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 27 von 29
56 Beispiel Regulärer Ausdruck: b 1 2 b Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 27 von 29
57 Beispiel Regulärer Ausdruck: b 1 2 b 3 Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 27 von 29
58 Beispiel Regulärer Ausdruck: b 1 2 b ɛ 3 4 ɛ Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 27 von 29
59 Beispiel Regulärer Ausdruck: b 1 2 b b ɛ b 3 ɛ 4 ɛ-übergänge können wie gewohnt eliminiert werden, um einen NFA zu erhlten Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 27 von 29
60 Vergleich NFA-Konstruktionen Ausdruck: b Kompositioneller Anstz Expliziter Anstz 1 2 b 3 4 b b 2 b 3 4 b b q f Liner viele Zustände Meist etws größer Korrektheitsbeweis us Abschlusseigenschften Fst ohne Löschen (ußer ɛ-übergänge) Liner viele Zustände Meist etws kleiner Korrektheitsbeweis erfordert neue Argumenttion Übergänge werden oft gelöscht ) Bzgl. Länge des reg. Ausdrucks bzw. bzgl. Anzhl seiner Opertionen Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 28 von 29
61 Zusmmenfssung und Ausblick Reguläre Ausdrücke sind eine prktisch wichtige Methode zur Beschreibung (beliebiger) regulärer Sprchen Die kompositionelle Methode wendet Automten-Opertionen n, um us einem regulären Ausdruck einen NFA zu erzeugen Die explizite Methode verwendet Übergänge mit regulären Ausdrücken, die schrittweise expndiert werden Offene Frgen: Wie kommt mn zurück von NFA zu regulärem Ausdruck? Welche Sprchen sind nicht regulär? Wie knn mn Automten systemtisch vereinfchen? Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 29 von 29
FORMALE SYSTEME. 7. Vorlesung: Reguläre Ausdrücke. TU Dresden, 2. November Markus Krötzsch
FORMALE SYSTEME 7. Vorlesung: Reguläre Ausdrücke Mrkus Krötzsch TU Dresden, 2. November 2017 Rndll Munroe, https://xkcd.com/851_mke_it_better/, CC-BY-NC 2.5 Mrkus Krötzsch, 2. November 2017 Formle Systeme
FORMALE SYSTEME. Kleene s Theorem. Wiederholung: Reguläre Ausdrücke. 7. Vorlesung: Reguläre Ausdrücke. TU Dresden, 2.
FORMALE SYSTEME 7. Vorlesung: Reguläre Ausdrücke Mrkus Krötzsch Rndll Munroe, https://xkcd.com/851_mke_it_etter/, CC-BY-NC 2.5 TU Dresden, 2. Novemer 2017 Mrkus Krötzsch, 2. Novemer 2017 Formle Systeme
2 2 Reguläre Sprachen. 2.6 Minimale DFAs und der Satz von Myhill-Nerode. Übersicht
Formle Systeme, Automten, Prozesse Übersicht 2 2.1 Reguläre Ausdrücke 2.2 Endliche Automten 2.3 Nichtdeterministische endliche Automten 2.4 Die Potenzmengenkonstruktion 2.5 NFAs mit ɛ-übergängen 2.7 Berechnung
Einführung in die theoretische Informatik Sommersemester 2017 Übungsblatt Lösungsskizze 3
Prof. J. Esprz Technische Universität München S. Sickert, J. Krämer KEINE ABGABE Einführung in die theoretische Informtik Sommersemester 27 Üungsltt 3 Üungsltt Wir unterscheiden zwischen Üungs- und Agelättern.
Berechenbarkeitstheorie 4. Vorlesung
1 Berechenbrkeitstheorie Dr. Institut für Mthemtische Logik und Grundlgenforschung WWU Münster WS 15/16 Alle Folien unter Cretive Commons Attribution-NonCommercil 3.0 Unported Lizenz. Reguläre Ausdrücke
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2011
Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 011 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Snder Bruggink Automten und Formle Sprchen 1 Reguläre Sprchen Wir eschäftigen uns
Automaten und formale Sprachen Notizen zu den Folien
3 Endliche Automten Automten und formle Sprchen Notizen zu den Folien Üerführungsfunktion eines NFA (Folien 107 und 108) Wie sieht die Üerführungsfunktion us? δ : Z Σ P(Z) Ds heißt, jedem Pr us Zustnd
Finite-State Technology
Finite-Stte Technology Teil IV: Automten (2. Teil) 1 Definition eines -NEA Ein -NEA ist ein Quintupel A = (Q,, δ, q0, F), wobei Q = eine endliche Menge von Zuständen = eine endliche Menge von Eingbesymbolen
Einführung in die Theoretische Informatik
Technische Universität München Fkultät für Informtik Prof. Tois Nipkow, Ph.D. Ssch Böhme, Lrs Noschinski Sommersemester 2011 Lösungsltt 4 20. Juni 2011 Einführung in die Theoretische Informtik Hinweis:
Minimalautomat. Wir stellen uns die Frage nach dem. kleinsten DFA für eine reguläre Sprache L, d.h. nach einem DFA mit möglichst wenigen Zuständen.
Rechtslinere Sprchen Minimlutomt Es git lso sehr verschiedene endliche Beschreiungen einer regulären Sprche (DFA, NFA, rechtslinere Grmmtiken, reguläre Ausdrücke). Diese können ineinnder üersetzt werden.
Minimierung von DFAs. Minimierung 21 / 98
Minimierung von DFAs Minimierung 21 / 98 Ein Beispiel: Die reguläre Sprche L({, } ) Wie stellt mn fest, o ein Wort ds Suffix esitzt? Ein erster Anstz: Speichere im ktuellen Zustnd die eiden zuletzt gelesenen
Automaten und formale Sprachen Notizen zu den Folien
3 Endliche Automten Automten und formle Sprchen Notizen zu den Folien DFA Reguläre Grmmtik (Folie 89) Stz. Jede von einem endlichen Automten kzeptierte Sprche ist regulär. Beweis. Nch Definition, ist eine
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester Kurzer Einschub: das Schubfachprinzip.
Reguläre Sprchen Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 0 Ds Pumping-Lemm Wir hen is jetzt vier Formlismen kennengelernt, mit denen wir eine reguläre Sprche ngeen können:
Automaten und formale Sprachen Notizen zu den Folien
3 Endliche Automten Automten und formle Sprchen Notizen zu den Folien Üerführungsfunction eines DFA (Folie 92) Wie sieht die Üerführungfunktion us? δ : Z Σ Z Ds heißt: Ein Pr us Zustnd und Alphetsymol
Vorname: Nachname: Matrikelnummer: Studiengang (bitte ankreuzen): Technik-Kommunikation M.A.
Formle Systeme, Automten, Prozesse SS 2010 Musterlösung - Klusur 23.09.2010 Prof. Dr. J. Giesl M. Brockschmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder Vornme: Nchnme: Mtrikelnummer: Studiengng (itte nkreuzen):
Theoretische Informatik WS 2014/2015
Prof. Dr. Andres Podelski Mtthis Heizmnn Alexnder Nutz Christin Schilling Probeklusur zur Vorlesung Theoretische Informtik WS 2014/2015 Die Klusur besteht us diesem Deckbltt und sieben Blättern mit je
a q 0 q 1 a M q 1 q 3 q 2
Prof Dr J Giesl Formle Systeme, Automten, Prozesse SS 2010 Musterlösung - Üung 4 M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden us dem
Frank Heitmann 2/71. 1 Betrachten wir Σ für ein Alphabet Σ, so ist Σ die Menge
Formle Grundlgen der Informtik Kpitel 2 und reguläre Sprchen Frnk Heitmnn heitmnn@informtik.uni-hmurg.de 7. April 24 Frnk Heitmnn heitmnn@informtik.uni-hmurg.de /7 Alphet und Wörter - Zusmmengefsst Die
Automaten und formale Sprachen Notizen zu den Folien
5 Ds Pumping Lemm Schufchprinzip (Folie 144) Automten und formle Sprchen Notizen zu den Folien Im Block Ds Schufchprinzip für endliche Automten steht m n (sttt m > n), weil die Länge eines Pfdes die Anzhl
Übungsblatt 1. Vorlesung Theoretische Grundlagen der Informatik im WS 17/18
Institut für Theoretische Informtik Lehrstuhl Prof. Dr. D. Wgner Üungsltt Vorlesung Theoretische Grundlgen der Informtik im WS 78 Ausge 9. Oktoer 27 Age 7. Novemer 27, : Uhr (im Ksten im UG von Geäude
Formale Systeme, Automaten, Prozesse SS 2010 Musterlösung - Übung 6 M. Brockschmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder
Prof Dr J Giesl Formle ysteme, utomten, Prozesse 2010 M rockschmidt, F Emmes, C Fuhs, C Otto, T tröder Hinweise: Die Husufgben sollen in Gruppen von je 2 tudierenden us dem gleichen Tutorium berbeitet
Formale Systeme, Automaten, Prozesse SS 2010 Musterlösung - Übung 2 M. Brockschmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder
Prof Dr J Giesl Formle Systeme, Automten, Prozesse SS 2010 Musterlösung - Üung 2 M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden us dem
Klausur Formale Sprachen und Automaten Grundlagen des Compilerbaus
Klusur Formle Sprchen und Automten Grundlgen des Compilerus 25. Novemer 2014 Nme: Unterschrift: Mtrikelnummer: Kurs: Note: Aufge erreichre erreichte Nr. Punkte Punkte 1 10 2 10 3 12 4 11 5 9 6 6 7 11 8
Reguläre Sprachen. Reguläre Ausdrücke NFAs
Reguläre Sprchen Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 0 Dr Snder Bruggink Üungsleitung: Jn Stückrth Wir eschäftigen uns jetzt einige Wochen mit regulären Sprchen deterministische
Grundlagen der Theoretischen Informatik
Grundlgen der Theoretischen Informtik 3. Endliche Automten (II) 28.04.2016 Vioric Sofronie-Stokkermns e-mil: sofronie@uni-koblenz.de 1 Übersicht 1. Motivtion 2. Terminologie 3. Endliche Automten und reguläre
Einführung in die Theoretische Informatik
Einführung in die Theoretische Informtik Johnnes Köler Institut für Informtik Humoldt-Universität zu Berlin WS 011/1 Inhlt der Vorlesung Themen dieser VL: Welche Rechenmodelle sind däqut? Welche Proleme
Sind Tokens erst einmal klassifiziert, kann man die Teilwörter vorverarbeiten:
Sind Tokens erst einml klssifiziert, knn mn die Teilwörter vorverreiten: Wegwerfen irrelevnter Teile wie Leerzeichen, Kommentren, Aussondern von Prgms, dh Direktiven n den Compiler, die nicht Teil des
Vorkurs Theoretische Informatik
Vorkurs Theoretische Informtik Einführung in reguläre Sprchen Areitskreis Theoretische Informtik Freitg, 05.10.2018 Fchgruppe Informtik Üersicht 1. Chomsky-Hierchie 2. Automten NEA DEA 3. Grmmtik und Automten
LR(k)-Parser. CYK-Algorithmus ist zu langsam.
LR(k)-Prser Ziele: Effizienter (und deterministischer) Test, ob ein gegebenes Wort w in der Sprche L(G) enthlten ist. Flls j: Konstruktion des Syntxbums Flls nein: Hinweise zum Fehler CYK-Algorithmus ist
Endliche Automaten 7. Endliche Automaten
Endliche Automten 7 Endliche Automten Einfches Modellierungswekzeug (z.b. UML-Sttechrts) Verrbeiten Wörter/Ereignisfolgen Erkennen Sprchen Erluben schnelle Sprcherkennung Anwendungsbereiche: Objektorientierte
RWTH Aachen Lehrgebiet Theoretische Informatik Rossmanith Dreier Hark Kuinke. SS 2017 Blatt
RWTH Achen Lehrgeiet Theoretische Informtik Rossmnith Dreier Hrk Kuinke SS 2017 Bltt 4 22.5.2017 Lösungsvorschlg zur Vorlesung Formle Sprchen, Automten und Prozesse Aufge T11 1. L, d L, er / L. L, d für
Minimalität des Myhill-Nerode Automaten
inimlität des yhill-nerode Automten Wir wollen zeigen, dss der im Beweis zum yhill-nerode Stz konstruierte DEA für die reguläre Sprche L immer der DEA mit den wenigsten Zuständen für L ist. Sei 0 der konstruierte
vollständig (Vervollständigung) deterministisch, DFA (Potenzmengenkonstruktion) Minimalautomat: minimaler vollständiger DFA
Ws isher geschh NFA A = (X, Q, δ, I, F ) vollständig (Vervollständigung) deterministisch, DFA (Potenzmengenkonstruktion) Minimlutomt: minimler vollständiger DFA Für jede Sprche L X sind die folgenden Aussgen
Grundbegriffe der Informatik Aufgabenblatt 6
Mtr.nr.: Nchnme: Vornme: Grundbegriffe der Informtik Aufgbenbltt 6 Tutorium: Nr. Nme des Tutors: Ausgbe: 2. Dezember 2015 Abgbe: 11. Dezember 2015, 12:30 Uhr im GBI-Briefksten im Untergeschoss von Gebäude
1.5. Abbildung. DEFINITION injektiv, surjektiv, bijektiv Eine Abbildung f ist injektiv, falls es zu jedem y Y höchstens ein x X gibt mit
CHAPTER. MENGEN UND R ELATIONEN.5. ABBILDUNG.5. Abbildung Eine Abbildung (oder Funktion ist eine Reltion f über X Y mit der Eigenschft: für jedes x us X gibt es genu ein y Y mit (x,y f. Die übliche Schreibweise
2.6 Reduktion endlicher Automaten
Endliche Automten Jörg Roth 153 2.6 Reduktion endlicher Automten Motivtion: Wir sind n Automten interessiert, die mit möglichst wenigen Zuständen uskommen. Automten, die eine Sprche mit einem Minimum n
Nichtdeterministische endliche Automaten. Nichtdetermistische Automaten J. Blömer 1/12
Nichtdeterministische endliche Automten Nichtdetermistische Automten J. Blömer 1/12 Nichtdeterministische endliche Automten In mnchen Modellierungen ist die Forderung, dss δ eine Funktion von Q Σ Q ist,
Formale Sprachen. Endliche Automaten - Kleene. Reguläre Sprachen. Rudolf FREUND, Marion OSWALD. Endliche Automaten. Endliche Automaten: Beispiel
Formle Sprchen Reguläre Sprchen Endliche Automten - Kleene STEPHEN KLEENE (99-994) Rudolf FREUND, Mrion OSWALD 956: Representtion of events in nerve nets nd finite utomt. In: C.E. Shnnon und J. McCrthy
... in unserem Fall: Scanner. Generator. Spezifikation. Spezifikation von Token-Klassen: Reguläre Ausdrücke;
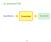in unserem Fll: Speziiktion Genertor Scnner Speziiktion von Token-Klssen: Reguläre Ausdrücke; Generierte Implementierung: Endliche Automten + X :-) 11 in unserem Fll: 0[1-9][0-9]* Genertor 0 [1 9] [0 9]
Scheinklausur: Theoretische Informatik I
+//+ Scheinklusur: Theoretische Informtik I WS / Hinweise: Hlten Sie die Klusur geschlossen, is der Beginn durch die Aufsichtspersonen ngezeigt wird Betrugsversuche oder Stören hen sofortigen Ausschluss
Formale Sprachen und Automaten. Schriftlicher Test
Formle Sprchen und Automten Prof. Dr. Uwe Nestmnn - 23. Ferur 2017 Schriftlicher Test Studentenidentifiktion: NACHNAME VORNAME MATRIKELNUMMER S TUDIENGANG Informtik Bchelor, Aufgenüersicht: AUFGABE S EITE
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2012. Sprachen. Grammatiken (Einführung)
Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Automaten und Formale Sprachen 7. Vorlesung
Automten und Formle Sprchen 7. Vorlesung Mrtin Dietzfelinger Bis nächste Woche: Folien studieren. Detils, Beispiele im Skript, Seiten 70 99. Definitionen lernen, Beispiele nsehen, Frgen vorereiten. Üungsufgen
Lösungen zum Ergänzungsblatt 4
en zum Ergänzungsltt 4 Letzte Änderung: 23. Novemer 2018 Theoretische Informtik I WS 2018 Crlos Cmino Vorereitungsufgen Vorereitungsufge 1 Sei M = ({p, q, r}, {, }, δ, p, {q, r}) ein DEA mit folgender
Universität Karlsruhe Institut für Theoretische Informatik. Klausur: Informatik III
Nme Vornme Mtrikelnummer Lösungsvorschlg Universität Krlsruhe Institut für Theoretische Informtik o. Prof. Dr. P. Snders 8. März 2006 Klusur: Informtik III Aufgbe 1. Multiple Choice 10 Punkte Aufgbe 2.
Einführung in die Theoretische Informatik
Einführung in die Theoretische Informtik Johnnes Köler Institut für Informtik Humoldt-Universität zu Berlin WS 2011/12 Minimierung von DFAs Frge Wie können wir feststellen, o ein DFA M = (Z, Σ, δ, q 0,
Ergänzungsblatt 6. Letzte Änderung: 24. November 2018
Ergänzungsltt 6 Letzte Änderung: 24. Novemer 2018 Theoretische Informtik I WS 2018 Crlos Cmino Erinnerung: Die Besprechungstermine für die Ergänzungen 7 is 10 fllen is uf Weiteres us. Aufgen, Lösungen
Formale Methoden 1. Gerhard Jäger 16. Januar Uni Bielefeld, WS 2007/2008 1/19
1/19 Formale Methoden 1 Gerhard Jäger Gerhard.Jaeger@uni-bielefeld.de Uni Bielefeld, WS 2007/2008 16. Januar 2008 2/19 Reguläre Ausdrücke vierte Art (neben Typ-3-Grammatiken, deterministischen und nicht-deterministischen
Lösung zur Klausur. Grundlagen der Theoretischen Informatik. 1. Zeigen Sie, dass die folgende Sprache regulär ist: w {a, b} w a w b 0 (mod 3) }.
Lösung zur Klusur Grundlgen der Theoretischen Informtik 1. Zeigen Sie, dss die folgende Sprche regulär ist: { w {, } w w 0 (mod 3) }. Lösung: Wir nennen die Sprche L. Eine Sprche ist genu dnn regulär,
Einführung in den Compilerbau
Einführung in den Compileru Lexiklische Anlyse II Dr. Armin Wolf 3. Vorlesung SoSe 2010, Universität Potsdm Einführung in den Compileru 1 Lexiklische Anlyse Beispiel Geg.: T mit T = {0,1,2,4,7} (vom Strtzustnd
Technische Universität München Sommer 2016 Prof. J. Esparza / Dr. M. Luttenberger, S. Sickert 11. Juli HA-Lösung. TA-Lösung
Technische Universität München Sommer 26 Prof. J. Esparza / Dr. M. Luttenberger, S. Sickert. Juli 26 HA-Lösung TA-Lösung Einführung in die theoretische Informatik Aufgabenblatt 3 Beachten Sie: Soweit nicht
Was nicht bewertet werden soll, streichen Sie bitte durch. Werden Täuschungsversuche beobachtet, so wird die Präsenzübung mit 0 Punkten bewertet.
Prof Dr Dr hc W Thoms Formle Systeme, Automten, Prozesse SS 2011 Musterlösung - Präsenzüung Dniel Neider, Crsten Otto Vornme: Nchnme: Mtrikelnummer: Studiengng (itte nkreuzen): Informtik Bchelor Informtik
FORMALE SYSTEME. 8. Vorlesung: Minimale Automaten. TU Dresden, 6. November Markus Krötzsch Lehrstuhl Wissensbasierte Systeme
FORMALE SYSTEME 8. Vorlesung: Minimale Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme TU Dresden, 6. November 2017 Rückblick Markus Krötzsch, 6. November 2017 Formale Systeme Folie 2 von 26
Vorlesung Theoretische Informatik Sommersemester 2018 Dr. B. Baumgarten
Vorlesung Theoretische Informtik Sommersemester 28 Dr. B. Bumgrten Üungen zur Wiederholung quer durch den Stoff Mit Lösungseispielen Vollständigkeit wird nicht grntiert, und einige sind klusuruntypisch
Mitschrift Repetitorium Theoretische Informatik und Logik
Mitschrift Repetitorium Theoretische Informtik und Logik Teil 1: Formle Sprchen, 15.01.2010, 1. Edit Allgemeine Hinweise für die Prüfung Ds Pumping-Lemm für kontextfreie Sprchen kommt nicht (sehr wohl
ist ein regulärer Ausdruck.
Dr. Sebastian Bab WiSe 12/13 Theoretische Grlagen der Informatik für TI Termin: VL 11 vom 22.11.2012 Reguläre Ausdrücke Reguläre Ausdrücke sind eine lesbarere Notation für Sprachen Denition 1 (Regulärer
Satz 6.5 (Mittelwertsatz der Integralrechnung) Sei f : [a, b] R stetig. Dann gibt es ein ξ [a, b], so dass. b a. f dx = (b a)f(ξ) f dx (b a)m.
![Satz 6.5 (Mittelwertsatz der Integralrechnung) Sei f : [a, b] R stetig. Dann gibt es ein ξ [a, b], so dass. b a. f dx = (b a)f(ξ) f dx (b a)m.](/thumbs/74/70413961.jpg "Satz 6.5 (Mittelwertsatz der Integralrechnung) Sei f : [a, b] R stetig. Dann gibt es ein ξ [a, b], so dass. b a. f dx = (b a)f(ξ) f dx (b a)m.")
Stz 6.5 (Mittelwertstz der Integrlrechnung) Sei f : [, b] R stetig. Dnn gibt es ein ξ [, b], so dss 9:08.06.2015 gilt. f dx = (b )f(ξ) Lemm 6.6 Sei f : [, b] R stetig und m f(x) M für lle x [, b]. Dnn
Übungen zur Linearen Algebra 1
Übungen zur Lineren Algebr Lösungen Wintersemester 9/ Universität Heidelberg Mthemtisches Institut Lösungen Bltt Dr. D. Vogel Michel Mier Aufgbe 44. b 4 b b 4 ( )b Fll : = ( )b 4 b ( ) b ( ) ( )(b ) b
Automaten, Spiele, und Logik
Automten, Spiele, und Logik Woche 9 13. Juni 2014 Inhlt der heutigen Vorlesung Büchi Automten co-büchi Automten Komplementierung für deterministische Büchi Automten Ein Ziel: den Stz von Büchi-Elgot-Trkhtenrot
Grundbegriffe der Informatik Aufgabenblatt 5
Grundegriffe der Informtik Aufgenltt 5 Mtr.nr.: Nchnme: Vornme: Tutorium: Nr. Nme des Tutors: Ausge: 20. Novemer 2013 Age: 29. Novemer 2013, 12:30 Uhr im GBI-Briefksten im Untergeschoss von Geäude 50.34
1 Metrische Räume. Sei X eine nichtleere Menge. Definition 1.1. Eine Abbildung: d : X X R heißt Metrik auf X, falls für alle x, y, z X gilt
Metrische Räume Sei X eine nichtleere Menge. Definition.. Eine Abbildung: d : X X R heißt Metrik uf X, flls für lle x, y, z X gilt (i) d(x, y) 0, (ii) d(x, y) = d(y, x), (iii) d(x, y) d(x, z) + d(z, y)
DEA1 Deterministische Version
Endliche Automten 4 Deterministische endliche Automten Zu dem nichtdeterministischen Automten EA git es eine deterministische Version. EA Akzeptor für Wörter üer X = { } mit mindestens einem führenden.
Inhalt. Endliche Automaten. Automaten und Formale Sprachen. Franz Binder. Endliche Automaten. Deterministische Automaten
Formle Inhlt Reguläre Reguläre Formle Zustndsdigrmm Reguläre δ: Σ (Q Q Ω) Beispiel δ 0 δ 0 1 2 1 2 0 1 2 δ Formle Automt Reguläre Definition Ein nicht-deterministischer, endlicher Automt esteht us einer
Gliederung. Kapitel 1: Endliche Automaten
Gliederung 0. Motivtion und Einordnung 1. Endliche Automten 2. Formle Sprchen 3. Berechnungstheorie 4. Komplexitätstheorie 1.1. 1.2. Minimierungslgorithmus 1.3. Grenzen endlicher Automten 1/1, S. 1 2017
1.1 Grundlagen: Reguläre Ausdrücke
11 Grundlgen: Reguläre Ausdrücke Progrmmtext enutzt ein endliches Alphet Σ von Einge-Zeichen, zb ASCII :-) Die Menge der Textschnitte einer Token-Klsse ist i regulär Reguläre Sprchen knn mn mithile regulärer
R := {((a, b), (c, d)) a + d = c + b}. Die Element des Quotienten M/R sind die Klassen
Die ntürlichen Zhlen (zusmmen mit der Addition und der Multipliktion) wurden in Kpitel 3 xiomtisch eingeführt. Aus den ntürlichen Zhlen knn mn nun die gnzen Zhlen Z = {..., 2, 1, 0, 1, 2,...} die rtionlen
Franz Binder. Vorlesung im 2006W
Formle Reguläre und Formle Institut für Alger Johnnes Kepler Universität Linz Vorlesung im 2006W http://www.lger.uni-linz.c.t/students/win/ml Formle Inhlt Reguläre Reguläre Formle Zustndsdigrmm δ: Σ (Q
Endliche Automaten können wahlweise graphisch oder tabellarisch angegeben werden.
Aufgensmmlung GTI Hinweise. Dies ist eine Aufgensmmlung zum Lernen für die Klusur, keine Proeklusur. Die Zeitduer, die für die Lösung vorgesehen ist, ist lso nicht uf drei Stunden normiert. Für die Klusur
FORMALE SYSTEME. Wiederholung. Beispiel: NFA. Wiederholung: NFA. 4. Vorlesung: Nichtdeterministische Endliche Automaten. TU Dresden, 19.
Wiederholung FORMALE SYSTEME 4. Vorlesung: Nichtdeterministische Endliche Automaten Markus Krötzsch Professur für Wissensbasierte Systeme Grammatiken können Sprachen beschreiben und sie grob in Typen unterteilen
Übungen zur Wiederholung quer durch den Stoff Vollständigkeit wird nicht garantiert, und einige sind umfangreicher als klausurtypisch.
Vorlesung Theoretische Informtik Sommersemester 2017 Dr. B. Bumgrten Üungen zur Wiederholung quer durch den Stoff Vollständigkeit wird nicht grntiert, und einige sind umfngreicher ls klusurtypisch. 1.
FORMALE SYSTEME. Wiederholung. Beispiel: NFA. Wiederholung: NFA. 4. Vorlesung: Nichtdeterministische Endliche Automaten. TU Dresden, 20.
Wiederholung FORMALE SYSTEME 4. Vorlesung: Nichtdeterministische Endliche Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme Grammatiken können Sprachen beschreiben und sie grob in Typen unterteilen
Ungleichungen. Jan Pöschko. 28. Mai Einführung
Ungleichungen Jn Pöschko 8. Mi 009 Inhltsverzeichnis Einführung. Ws sind Ungleichungen?................................. Äquivlenzumformungen..................................3 Rechnen mit Ungleichungen...............................
Hausaufgabe 2 (Induktionsbeweis):
Prof. Dr. J. Giesl Formle Sprhen, Automten, Prozesse SS 2010 Üung 3 (Age is 12.05.2010) M. Brokshmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden
Ergänzungsblatt 7. Letzte Änderung: 30. November Vorbereitungsaufgaben
Theoretische Informtik I WS 2018 Crlos Cmino Ergänzungsltt 7 Letzte Änderung: 30. Novemer 2018 Vorereitungsufgen Vorereitungsufge 1 Wiederholen Sie die Begriffe us Üungsltt 0, Aschnitt 4. 1. Welche der
Umwandlung von endlichen Automaten in reguläre Ausdrücke
Umwndlung von endlichen Automten in reguläre Ausdrücke Wir werden sehen, wie mn us einem endlichen Automten M einen regulären Ausdruck γ konstruieren knn, der genu die von M kzeptierte Sprche erzeugt.
dem Verfahren aus dem Beweis zu Satz 2.20 erhalten wir zunächst die folgenden beiden ε-ndeas für die Sprachen {a} {b} und {ε} {a} +
Lösungen zu Üungsltt 3 Aufge 1. Es gilt L(( ) ) = ({} {}) {} = ({} {}) ({} {} + ). Mit dem Verfhren us dem Beweis zu Stz 2.20 erhlten wir zunächst die folgenden eiden -NDEAs für die Sprchen {} {} und {}
Automaten und formale Sprachen Notizen zu den Folien
5 Ds Pumping Lemm Shufhprinzip (Folie 137) Automten und formle Sprhen Notizen zu den Folien Im Blok Ds Shufhprinzip für endlihe Automten steht m n (sttt m > n), weil die Länge eines Pfdes die Anzhl von
1.2 Eigenschaften der reellen Zahlen
12 Kpitel 1 Mthemtisches Hndwerkszeug 12 Eigenschften der reellen Zhlen Alle Rechenregeln der Grundrechenrten der reellen Zhlen lssen sich uf einige wenige Rechengesetze zurückführen, die in der folgenden
6. Übungsblatt. (i) Von welchem Typ ist die Grammatik G? Begründen Sie Ihre Antwort kurz.
Vorlesung Theoretische Informtik Sommersemester 2015 Prof. S. Lnge 6. Üungsltt 1. Aufge Es sei die folgende Grmmtik G = [Σ, V, S, R] gegeen. Dei seien Σ = {, } und V = {S, B}, woei S ds Strtsymol ist.
Klausur zur Vorlesung Grundbegriffe der Informatik 10. März 2009 mit Lösungsvorschlägen
Klusur zur Vorlesung Grundegriffe der Informtik 10. März 2009 mit Lösungsvorschlägen Klusurnummer Nme: Vornme: Mtr.-Nr.: Aufge 1 2 3 4 5 6 7 mx. Punkte 4 2 7 8 8 8 9 tts. Punkte Gesmtpunktzhl: Note: Aufge
Hauptklausur zur Vorlesung Theoretische Grundlagen der Informatik Wintersemester 2011/2012
Institut für Theoretische Informtik Lehrstuhl Prof. Dr. D. Wgner Huptklusur zur Vorlesung Theoretische Grundlgen der Informtik Wintersemester 2011/2012 Hier Aufkleber mit Nme und Mtrikelnr. nbringen Vornme:
Automaten, Spiele, und Logik
Automten, Spiele, und Logik Woche 1 15. April 2014 Inhlt der gnzen Vorlesung Automten uf endlichen Wörtern uf undendlichen Wörtern uf endlichen Bäumen Spiele Erreichrkeitsspiele Ehrenfeucht-Frïssé Spiele
Informatik I WS 07/08 Tutorium 24
Info I Tutorium 24 Informtik I WS 07/08 Tutorium 24 10.01.08 Bstin Molkenthin E-Mil: infotut@sunshine2k.de Web: http://infotut.sunshine2k.de Anmeldung IPK Eine inoffizielle Info-1 Probeklusur findet m
Präsenz-Aufgaben = i. (a) i 15 = i 14 i = (i 2 ) 7 i = ( 1) 7 i = i i 15 = 0 + ( 1)i, i (i i) = i 1 = i i 15 = 0 + 1i,
Präsenz-Aufgben 1. 1. Schreiben Sie z in der Form z α + βi mit α,β R. Aus der Vorlesung ist beknnt: i i i 1, i 1 1 i i i i i 1 i. () i 15 i 1 i (i ) 7 i ( 1) 7 i i i 15 + ( 1)i, (b) i 15 1 i 15 () 1 i
2.6 Unendliche Reihen
2.6 Unendliche Reihen In normierten Räumen steht ds wichtige Werkzeug der Bildung von unendlichen Reihen zur Verfügung. Mn denke in diesem Zusmmenhng drn, dss mn in der Anlysis Potenz- und Fourierreihen
Grundlagen des Maschinellen Lernens Kap 3: Lernverfahren in anderen Domänen
. Motivtion 2. Lernmodelle Teil I 2.. Lernen im Limes 2.2. Fllstudie: Lernen von Ptternsprchen 3. Lernverfhren in nderen Domänen 3.. 3.2. Entscheidungsbäume 3.3. Entscheidungsbäume über regulären Ptterns
Algorithmen und Datenstrukturen (Th. Ottmann und P. Widmayer) Folien: Editierdistanz Autor: Sven Schuierer
Algorithmen und Dtenstrukturen (Th. Ottmnn und P. Widmyer) Folien: Editierdistnz Autor: Sven Schuierer Institut für Informtik Georges-Köhler-Allee Albert-Ludwigs-Universität Freiburg 1 Editier-Distnz Gegeben:
Mathematische Probleme, SS 2018 Donnerstag 7.6. $Id: dreieck.tex,v /06/07 14:52:59 hk Exp $
$Id: dreieck.tex,v 1.45 2018/06/07 14:52:59 hk Exp $ 2 Dreiecke 2.2 Ähnliche Dreiecke Wir htten zwei Dreiecke kongruent gennnt wenn sie sich durch eine ewegung der Ebene ineinnder überführen lssen und
Einführung in die Theoretische Informatik
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2 Lösungsblatt 2 3. Mai 2 Einführung in die Theoretische Informatik Hinweis:
Aufge 4 Die Grmmtik G 2 CFG(f; g) in Chomsky-Normlform sei gegeen wie folgt: S! AB j A! AS j B! SB j ) Stellen Sie mit Hilfe des Cocke-Younger-Ksmi-Al
RHEINISCH- WESTFÄLISCHE TECHNISCHE HOCHSCHULE AACHEN LEHRSTUHL FÜR INFORMATIK II RWTH Achen D-52056 Achen GERMANY http://www-i2.informtik.rwth-chen.de 2i Klusur für den Leistungsnchweis zur Vorlesung Automtentheorie
Grundlagen der Theoretischen Informatik
Grundlgen der Theoretischen Informtik 3. Endliche Automten 6.05.2015 Vioric Sofronie-Stokkermns e-mil: sofronie@uni-kolenz.de 1 Üersicht 1. Motivtion 2. Terminologie 3. Endliche Automten und reguläre Sprchen
Übungsblatt Nr. 1. Lösungsvorschlag
Institut für Kryptogrphie und Sicherheit Prof. Dr. Jörn Müller-Qude Nico Döttling Dirk Achench Tois Nilges Vorlesung Theoretische Grundlgen der Informtik Üungsltt Nr. svorschlg Aufge (K) (4 Punkte): Semi-Thue-Systeme
Vorname: Nachname: Matrikelnummer: Studiengang (bitte ankreuzen): Technik-Kommunikation M.A.
Formle Systeme, Automten, Prozesse SS 2011 Musterlösung - Klusur 09082011 Prof Dr Dr hc W Thoms Dniel Neider, Crsten Otto Vornme: Nchnme: Mtrikelnummer: Studiengng (itte nkreuzen): Informtik Bchelor Informtik
Endliche Automaten. S. Kuske: Endliche Automaten; 6.Novenber 2006
1 Endliche Automten Einfches Modellierungswekzeug (z.b. UML-Sttechrts) Verrbeiten Wörter/Ereignisfolgen Erkennen Sprchen Erluben schnelle Sprcherkennung Anwendungsbereiche: Objektorientierte Modellierung,
Lineare Algebra I 5. Tutorium mit Lösungshinweisen
Fchbereich Mthemtik Prof Dr JH Bruinier Mrtin Fuchssteiner Ky Schwieger TECHNISCHE UNIVERSITÄT DARMSTADT AWS 07/08 0607 (T ) Linere Algebr I 5 Tutorium mit Lösungshinweisen Welche Gruppen kennen Sie? Welche
Potenzautomat. Gegeben: A = (Z, I, d, s 0, F ) P(A) = (P(Z), I, D, {s 0 }, F P ) P(Z) = {S S Z}: Potenzmenge von Z; D : P(Z) I P(Z) mit
1 Potenzutomt Gegeben: A = (Z, I, d, s 0, F ) P(A) = (P(Z), I, D, {s 0 }, F P ) P(Z) = {S S Z}: Potenzmenge von Z; D : P(Z) I P(Z) mit D(S, x) = d(s, x) s S für lle S P(Z), x I; F P = {S P(Z) S F }. Potenzutomt
Satz (Abschluß unter der Stern-Operation)
Satz (Abschluß unter der Stern-Operation) Wenn L eine reguläre Sprache ist, dann ist auch L regulär. Beweis: Es gibt einen NFA M = (Z, Σ, S, δ, S, E) mit L(M) = L. Wir bauen aus diesem NFA nun wie folgt
1 Σ endliches Terminalalphabet, 2 V endliche Menge von Variablen (mit V Σ = ), 3 P (V (Σ ΣV )) {(S, ε)} endliche Menge von Regeln,
Theorie der Informatik 8. März 25 8. Reguläre Sprachen I Theorie der Informatik 8. Reguläre Sprachen I 8. Reguläre Grammatiken Malte Helmert Gabriele Röger 8.2 DFAs Universität Basel 8. März 25 8.3 NFAs