Reguläre Sprachen Slide 1. Reguläre Sprachen. Hans U. Simon (RUB) Homepage:
|
|
|
- Erika Förstner
- vor 7 Jahren
- Abrufe
Transkript
1 Reguläre Sprachen Slide 1 Reguläre Sprachen Hans U. Simon (RUB) simon@lmi.rub.de Homepage:
2 Reguläre Sprachen Slide 2 Merkmale endlicher Automaten: Endliche Automaten Speicher, genannt Zustandsmenge (oder auch endliche Kontrolle), hat konstante Größe (d.h., er wächst nicht mit der Länge der Eingabe). Eingabewort wird zeichenweise von links nach rechts abgearbeitet. Pro Zeichen erfolgt ein Zustandswechsel. Nach Abarbeitung wird die Eingabe akzeptiert oder verworfen. Menge der akzeptierten Eingabeworte bildet die Sprache des Automaten. Bezeichnungen: DFA = Deterministic Finite Automaton = deterministischer endlicher Automat NFA = Nondeterministic Finite Automaton = nicht deterministischer endlicher Automat
3 Reguläre Sprachen Slide 3 Veranschaulichung i... n a a... a... a 1 2 i n Lesekopf z aktueller Zustand... Eingabeband endliche Kontrolle Z Abbildung 1: DFA mit Eingabeband (in Zellen unterteilt), Lesekopf und endlicher Kontrolle. Nach Verarbeitung von a i erfolgt ein Zustandswechsel und der Lesekopf rückt eine Position nach rechts.
4 Reguläre Sprachen Slide 4 DFA (formale Definition) Ein DFA M besteht aus den folgenden Komponenten: Z, die Zustandsmenge Σ, das Eingabealphabet δ : Z Σ Z, die Überführungsfunktion z 0 Z, der Startzustand E Z, die Menge der Endzustände Arbeitsweise: Anfangs befindet sich M im Startzustand z 0. Nach Verarbeitung des Zeichens a im Zustand z geht M in den Zustand z = δ(z,a) über. Nach Verarbeitung des letzten Zeichens der Eingabe wird diese genau dann akzeptiert wenn M sich in einem Endzustand befindet.
5 Reguläre Sprachen Slide 5 Beispiel Betrachte den DFA M mit den folgenden Komponenten: Z = {z 0,z 1,z 2,z 3 }. Σ = {a,b}. Startzustand ist z 0. E = {z 3 }. δ ist gegeben durch folgende Tabelle: δ z 0 z 1 z 2 z 3 a z 1 z 2 z 3 z 0 b z 3 z 0 z 1 z 2 Eingabe aaabbaaab führt zur Zustandsfolge z 0,z 1,z 2,z 3,z 2,z 1,z 2,z 3,z 0,z 3. Akzeptiere! Eingabe bbabb führt zur Zustandsfolge z 0,z 3,z 2,z 3,z 2,z 1. Verwerfe!
6 Reguläre Sprachen Slide 6 a z 3 Visualisierung am Zustandsgraphen z b b z2 Schema: z 0 1 a a b b a c z z Startzustand Endzustand Zustandswechsel Abbildung 2: der Zustandsgraph G M zum Beispiel DFA M. Rechnungen an Eingaben wie zum Beispiel aaabbaaab oder bbabb entsprechen Pfaden im Zustandsgraphen. Merke wohl: Da δ : Z Σ Z den Folgezustand eindeutig festlegt, gibt es zu jeder Eingabe w einen eindeutigen (von z 0 startenden) Pfad P w in G M.
7 Reguläre Sprachen Slide 7 Die von einem DFA akzeptierte Sprache Die vom DFA M akzeptierte Sprache ist gegeben durch T(M) := {w Σ Pfad P w durch G M endet in einem Endzustand}. Scharfes Hinsehen beim Zustandsgraph liefert für den Beispiel DFA: T(M) := {w {a,b} w a w b 3 (mod 4)}.
8 Reguläre Sprachen Slide 8 Die Funktion delta Hut Intuition: ˆδ(z,w) soll der Zustand sein, in dem der DFA sich befindet, wenn er gestartet im Zustand z das Wort w (zeichenweise) abgearbeitet hat. Induktive Definition: Für alle z Z, a Σ, x Σ : 1. ˆδ(z,ε) := z. 2. ˆδ(z,ax) := ˆδ(δ(z,a),x). Auf Z Σ stimmt ˆδ mit δ überein: ˆδ(z,a) = ˆδ(δ(z,a),ε) = δ(z,a) Es gilt: T(M) = {w Σ ˆδ(z 0,w) E}
9 Reguläre Sprachen Slide 9 Elegantere Notation Definiere für z Z und w Σ : z w := ˆδ(z,w) Dann gilt eine Art Assoziativgesetz für alle z Z,x,y Σ : z (x y) = (z x) y z (x y) ist der Zustand, den der DFA erreicht, wenn er gestartet in z das Wort xy (Konkatenation von x und y) zeichenweise abarbeitet. Der Ausdruck (z x) y liefert dasselbe Ergebnis, wobei z x der Zwischenzustand ist, den der DFA nach Verarbeitung von x (aber noch vor der Verarbeitung von y) innehat.
10 Reguläre Sprachen Slide 10 Vom DFA zur regulären Grammatik Satz: Jeder DFA M = (Z,Σ,δ,z 0,E) lässt sich in eine reguläre Grammatik G = (V,Σ,P,S) mit L(G) = T(M) transformieren. Folgerung: Jede von einem DFA akzeptierte Sprache ist regulär. Technische Vereinfachung: Wir setzen im Beweis des Satzes z 0 / E (gleichbedeutend zu ε / T(M) voraus. Randnotiz: Im Falle z 0 E müsste die im Beweis enthaltene Konstruktion von G um die Regel z 0 ε erweitert werden.
11 Reguläre Sprachen Slide 11 Vom DFA zur regulären Grammatik (fortgesetzt) Konstruktiver Beweis: Setze V := Z, S := z 0 und definiere P wie folgt. Für jede Transition δ(z,a) = z nimm in P die Regel z az auf. Falls dabei z E, dann nimm zusätzlich die Regel z a in P auf. Für alle w = a 1 a n Σ + (mit a i Σ) sind die folgenden Aussagen äquivalent: 1. w T(M). 2. Es gibt eine Folge z 0,...,z n von Zuständen mit Startzustand z 0, z n E und z i = δ(z i 1,a i ). 3. Es gibt eine Folge z 0,...,z n 1 von Variablen mit Startvariable z 0 und z 0 G a 1 z 1 G a 1 a 2 z 2 G G a 1 a n 1 z n 1 G a 1 a 2 a n 1 a n. 4. w L(G).
12 Reguläre Sprachen Slide 12 Nicht-deterministische Zustandswechsel Bei NFA s kann der Zustandsgraph folgenden Ausschnitt enthalten: z a a z z Abbildung 3: Wer die Wahl hat, hat die Qual. I.A. existieren mehrere mögliche Zustandswechsel pro Rechenschritt (und auch mehrere Startzustände). Zu einer Eingabe gibt es i.a. viele korrespondierende Pfade durch den Zustandsgraphen. Die Eingabe gilt als akzeptiert, wenn mindestens einer der korrespondierenden Pfad in einem Endzustand endet (in Analogie dazu, dass bei Grammatiken eine erfolgreiche Ableitung genügt).
13 Reguläre Sprachen Slide 13 NFA (formale Definition) P(Z) bezeichnet die Potenzmenge von Z (Menge aller Teilmengen von Z). Ein NFA M besteht aus den folgenden Komponenten: Z, die Zustandsmenge Σ, das Eingabealphabet δ : Z Σ P(Z), die Überführungsfunktion S Z, die Menge der Startzustände E Z, die Menge der Endzustände
14 Reguläre Sprachen Slide 14 Arbeitsweise des NFA Anfangs befindet sich M (wahlweise) in einem der Startzustände. Nach Verarbeitung des Zeichens a im Zustand z kann M (wahlweise) in einen Zustand z δ(z,a) übergehen. Die Eingabe wird akzeptiert genau dann, wenn M durch geeignete Wahl eines Startzustandes und durch geeignete Zustandswechsel nach Abarbeitung der Eingabe einen Endzustand erreichen kann. Beachte: Falls δ(z, a) =, dann ergeben sich im Zustand z bei Verarbeitung von a keine möglichen Folgezustände.
15 Reguläre Sprachen Slide 15 Die von einem NFA akzeptierte Sprache Der Zustandsgraph G M zu einem NFA M ist völlig analog definiert wie bei DFAs. Die vom NFA M akzeptierte Sprache besteht(per Definition) aus allen Wörtern w Σ mit folgender Eigenschaft: Es existiert ein von einem Startzustand ausgehender Pfad in G M, dessen Kanten (in der korrekten Reihenfolge) mit den Buchstaben von w beschriftet sind und der in einem Endzustand endet.
16 Reguläre Sprachen Slide 16 Beispiel 0,1 0 0 z z z Abbildung 4: NFA M gegeben durch seinen Zustandsgraphen G M. Scharfes Hinsehen ergibt: T(M) = {w {0,1} w = 0 oder w endet mit 00}
17 Reguläre Sprachen Slide 17 Die Funktion delta Hut Intuition: Für eine Teilmenge Q Z der Zustände soll ˆδ(Q,w) die Menge der Zustände sein, welche sich ausgehend von einem der Zustände in Q erreichen lassen, wenn w zeichenweise abgearbeitet wird. Induktive Definition: Für alle Q Z, a Σ, x Σ : 1. ˆδ(Q,ε) := Q. 2. ˆδ(Q,ax) := ˆδ( z Q δ(z,a),x). Dann gilt: T(M) = {w Σ ˆδ(S,w) E }
18 Reguläre Sprachen Slide 18 Vom NFA zum DFA Satz: Jeder NFA M = (Z,Σ,δ,S,E) lässt sich in einen DFA M = (Z,Σ,δ,z 0,E ) mit T(M ) = T(M) transformieren. Beweis (Potenzmengenkonstruktion): Wir wählen Z = P(Z), d.h., jeder Makrozustand von M ist eine Teilmenge der Zustände von M. M soll M in folgendem Sinn simulieren: ( ) Zu jedem Zeitpunkt der Rechnung soll M in dem Makrozustand sein, der übereinstimmt mit der Menge der gegenwärtig von M erreichbaren Zustände.
19 Reguläre Sprachen Slide 19 Vom NFA zum DFA (fortgesetzt) Hierzu definieren wir die restlichen Komponenten von M wie folgt: 1. z 0 = S. (Damit gilt ( ) zu Anfang.) 2. δ (Q,a) = z Qδ(z,a). (Damit bleibt ( ) während Verarbeitung des nächsten Zeichens richtig). 3. E = {Q Z Q E }. Die gewünschte Bedingung ( ) ergibt sich induktiv aus 1. und 2. Aus ( ) und 3. folgt schließlich T(M ) = T(M).
20 Reguläre Sprachen Slide 20 Beispiel z 0,1 0 0 z 1 0 z 2 z 0 z 1 z 2 0 vom Startzustand aus nicht erreichbarer Zustand NFA M z 0 z z 0 z 2 1 vom Startzustand aus nicht erreich bare Komponente z 1 z z 1 0 Zustand zur leeren Menge 1 z 1 0 0,1 z 2 1 0,1 simulierender DFA M
21 Reguläre Sprachen Slide 21 Die kombinatorische Explosion... Potenzmengenkonstruktion NFA DFA Frage: Gibt es effizientere Simulationen? Antwort: i.a. Nein!
22 Reguläre Sprachen Slide 22 Eine Sprache mit kleinem NFA... Die Sprache L n = {w {0,1} w n und das n letzte Zeichen von w ist 0 } kann von einem NFA mit n+1 Zuständen erkannt werden: 0,1 0 0,1 0,1 0,1 0,1 Abbildung 5: Ein NFA für L 5.
23 Reguläre Sprachen Slide die große DFAs benötigt Angenommen es gäbe einen DFA M für L n mit weniger als 2 n Zuständen? Widerspruch (in 5 Schritten): 1. Dann gibt es 2 verschiedene Wörter x,y {0,1} n mit z 0 x = z 0 y (Schubfachprinzip). 2. Betrachte eine Bit-Position i, in der x und y sich unterscheiden. Sagen wir: Bit i von x ist 0 und Bit i von y ist Betrachte x = x0 i 1 und y = y0 i 1. Bit i von x (bzw. von y) ist das n-letzte Bit von x (bzw. von y ). Daher ist x L n und y / L n. 4. Wegen z 0 (x 0 i 1 ) = (z 0 x) 0 i 1 = (z 0 y) 0 i 1 = z 0 (y 0 i 1 ) gelangt M bei den Eingaben x und y zum gleichen Zustand. 5. M macht also entweder auf Eingabe x oder auf Eingabe y einen Fehler.
24 Reguläre Sprachen Slide 24 Kleines Gedächtnis, große Fehler Beim Widerspruchsbeweis wurde ausgenutzt: Wenn ein DFA zwei Eingaben x,y identifiziert (im Sinne von z 0 x = z 0 y), dann kann er auch Eingaben der Form xu und yu nicht auseinander halten. Wenn ein DFA ein zu kleines Gedächtnis (= Zustandsmenge) hat, dann identifiziert er evtl. Eingaben, die er besser unterscheiden können sollte.
25 Reguläre Sprachen Slide 25 Vom NFA zum DFA: Zusammenfassung Jeder NFA mit n Zuständen lässt sich in einen äquivalenten DFA mit 2 n Zuständen transformieren. Wir haben Sprachen L n, n 1, angegeben, die von einem NFA mit n+1 Zuständen erkannt werden können, aber nicht von einem DFA mit weniger als 2 n Zuständen. Andererseits kann man zeigen, dass L n von einem DFA mit 2 n Zuständen erkannt werden kann (s. Übung).
26 Reguläre Sprachen Slide 26 Von der regulären Grammatik zum NFA Satz: Jede reguläre Grammatik G = (V,Σ,P,S) lässt sich in einen NFA M = (Z,Σ,δ,S,E) mit T(M) = L(G) transformieren. Zusammen mit den früheren Ergebnissen erhalten wir den Zirkelschluss Es ergibt sich die DFA reguläre Grammatik NFA DFA. Folgerung: Die Klasse der regulären Sprachen kann wahlweise durch DFAs, NFAs oder reguläre Grammatiken repräsentiert werden. Im folgenden Beweis des Satzes dürfen wir voraussetzen, dass P entweder keine ε-transition enthält oder nur die ε-transition S ε, wobei in letzterem Falle S auf keiner rechten Seite einer Regel aus P auftritt.
27 Reguläre Sprachen Slide 27 Konstruktiver Beweis: Wähle die Komponenten von M wie folgt: Z = V {X} und S = {S}. Falls S ε / P, dann setze E = {X}; andernfalls E = {S,X}. Für jede Regel der Form A ab in P nimm B in δ(a,a) auf. Für jede Regel der Form A a in P nimm X in δ(a,a) auf. Für alle w = a 1 a n Σ + (mit a i Σ) sind die folgenden Aussagen äquivalent: 1. w L(G). 2. Es gibt eine Folge A 1,...,A n 1 von Variablen mit S G a 1 A 1 G a 1 a 2 A 2 G G a 1 a 2 a n 1 A n 1 G a 1 a 2 a n 1 a n. 3. Es gibt eine Folge von Zuständen A 1,...,A n 1 mit A 1 δ(s,a 1 ), A 2 δ(a 1,a 2 ),..., A n 1 δ(a n 2,a n 1 ), X δ(a n 1,a n ). 4. w T(M).
28 Reguläre Sprachen Slide 28 Reguläre Ausdrücke Induktive Definition der Syntax regulärer Ausdrücke: 1., ε und a für jedes a Σ sind reguläre Ausdrücke. 2. Wenn α und β reguläre Ausdrücke sind, dann sind auch (α β), (α β) und (α ) reguläre Ausdrücke. Die Regel geht vor und geht vor (in Analogie zu Punktrechnung geht vor Strichrechnung ) hilft Klammern einzusparen. Konkatenationszeichen darf auch weggelassen werden.
29 Reguläre Sprachen Slide 29 Die von regulären Ausdrücken dargestellte Sprache L(α) bezeichne die durch den regulären Ausdruck α repräsentierte Sprache im Sinne der folgenden Definition. Induktive Definition der Semantik regulärer Ausdrücke: 1. L( ) = ; L(ε) = {ε}; L(a) = {a}. 2. L(α β) = L(α) L(β); L(α β) = L(α) L(β); L(α ) = L(α).,ε,a,, haben also die offensichtliche Interpretation; Zeichen wird als Vereinigung interpretiert.
30 Reguläre Sprachen Slide 30 Beispiele Die uns schon bekannte Sprache {w {0,1} w = 0 oder w endet mit 00} ist mit regulären Ausdrücken traumhaft elegant beschreibbar: 0 (0 1) 00. Jede endliche Sprache ist durch einen regulären Ausdruck beschreibbar. Denn: 1. Jedes einzelne Wort ergibt sich als Konkatenation seiner (endlich vielen) Zeichen. 2. Jede endliche Sprache ist eine Vereinigung ihrer (endlich vielen) Wörter. 3. Konkatenation und Vereinigung sind Operatoren, die regulären Ausdrücken zur Verfügung stehen.
31 Reguläre Sprachen Slide 31 Ankündigung Strukturelle Induktion kommt zum Einsatz!
32 Reguläre Sprachen Slide 32 Von regulären Ausdrücken zu NFAs Satz: Jeder reguläre Ausdruck γ kann in einen NFA M mit T(M) = L(γ) transformiert werden. Beweis: (Induktion nach der Struktur regulärer Ausdrücke) Zu zeigen: 1. Zu den einfachen regulären Ausdrücken,ε,a mit a Σ finden wir jeweils einen passenden NFA. 2. Aus passenden NFAs M 1 und M 2 für reguläre Ausdrücke α und β können wir jeweils einen passenden NFA für α β, α β und α zusammenbasteln (ein Syntheseproblem ).
33 Reguläre Sprachen Slide 33 Passende NFAs für einfache reguläre Ausdrücke Endlich mal eine babyleichte Aufgabe: a (a) (b) (c) Abbildung 6: (a) ein NFA für (b) ein NFA für {ε} (c) ein NFA für {a}
34 Reguläre Sprachen Slide 34 Syntheseproblem bei den Operationen, Grundidee in folgender Abbildung: M 1 a a M M 1 2 M M als Parallelschaltung 2 von M 1, M (a) 2 M als Serienschaltung von M, M 1 (b) 2 Abbildung 7: (a) ein NFA für T(M 1 ) T(M 2 ) (b) ein NFA für T(M 1 ) T(M 2 )
35 Reguläre Sprachen Slide 35 Lösung des Syntheseproblems für Vereinigung Voraussetzung: T(M 1 ) = L(α), T(M 2 ) = L(β); M i = (Z i,σ,δ i,s i,e i ). Synthese eines Automaten M für L(α) L(β): M := {Z 1 Z 2,Σ,δ,S 1 S 2,E 1 E 2 } δ 1 (z,a) falls z Z 1 δ(z,a) := δ 2 (z,a) falls z Z 2
36 Reguläre Sprachen Slide 36 Lösung des Syntheseproblems für Konkatenation Synthese eines Automaten M = (Z,Σ,δ,S,E) für L(α) L(β): Z := Z 1 Z 2 δ 1 (z 1,a) falls δ 1 (z 1,a) E 1 = δ(z 1,a) := δ 1 (z 1,a) S 2 falls δ 1 (z 1,a) E 1 δ(z 2,a) := δ 2 (z 2,a) S 1 falls ε / T(M 1 ) S := S 1 S 2 falls ε T(M 1 ) E := E 2
37 Reguläre Sprachen Slide 37 Syntheseproblem bei der Operation Grundidee in folgender Abbildung: a M a M (M erweitert um Ruckkopplungen) Abbildung 8: ein NFA M für T(M)
38 Reguläre Sprachen Slide 38 Lösung des Syntheseproblems für Operation Voraussetzung: T(M) = L(α); M = (Z,Σ,δ,S,E). Synthese eines Automaten M = (Z,Σ,δ,S,E ) für L(α) für den Fall ε T(M): Z := Z δ (z,a) := δ(z,a) falls δ(z,a) E = δ(z,a) S falls δ(z,a) E S := S E := E Falls ε / T(M), dann wird darüberhinaus ein neuer Zustand z 0 in die Mengen Z, S und E aufgenommen.
39 Reguläre Sprachen Slide 39 Von DFAs zu regulären Ausdrücken Satz: Jeder DFA M = {{z 1,...,z n },Σ,δ,z 1,E) kann in einen regulären Ausdruck γ mit L(γ) = T(M) transformiert werden. Beweisidee: Verwende Hilfssprachen, die sich mit Hilfe der Operationen,, aus einzelnen Zeichen zusammenbasteln lassen, so dass T(M) sich als Vereinigung (geeignet ausgewählter) Hilfssprachen darstellen lässt.
40 Reguläre Sprachen Slide 40 Umsetzung der Beweisidee die Hilfssprachen Ri,j k sei die Menge aller Wörter x Σ mit: 1. M gestartet in z i ist nach Abarbeitung von x im Zustand z j. 2. Dabei werden nur Zwischenzustände aus {z 1,...,z k } angenommen. Beachte: Im Falle k = 0 sind keine Zwischenzustände erlaubt (Übergang von z i nach z j durch maximal einen Zustandswechsel).
41 Reguläre Sprachen Slide 41 Umsetzung der Beweisidee (fortgesetzt) Die Hilfssprachen haben die gewünschten Eigenschaften: T(M) = j:z j E R n 1,j R 0 i,j = {a Σ {ε} ˆδ(z i,a) = z j } R k i,j = R k 1 i,j R k 1 i,k (Rk 1 k,k ) R k 1 k,j Die letzte Gleichung gilt, da die Wörter aus R k i,j in zwei Klassen zerfallen: Wörter, deren Berechnungspfad von z i nach z j nur die Zwischenknoten aus {z 1,...,z k 1 } verwendet (also Wörter aus R k 1 i,j ) Wörter der Form x = uvw, wobei u einen Berechnungspfad von z i nach z k mit Zwischenknoten aus {z 1,...,z k 1 } besitzt (also u R k 1 i,k ), v einen Berechnungspfad, der iteriert von z k nach z k führt (also v (R k 1 k,k ) ), und w einen Berechnungspfad von z k nach z j mit Zwischenknoten aus {z 1,...,z k 1 } (also w R k 1 k,j ).
42 Reguläre Sprachen Slide 42 Das Pumping Lemma (uvw Theorem) Satz: Für jede reguläre Sprache L Σ gilt: n 1, x L mit x n, u,v,w Σ mit x = uvw,1 v uv n, i 0 : uv i w L.
43 Reguläre Sprachen Slide 43 Beweis Benutze einen DFA M = (Z,Σ,δ,z 0,E), der L erkennt, und wähle n := Z. Zu einem Wort x = a 1 a s L mit a i Σ und s n betrachte den resultierenden Berechnungspfad P im Zustandsgraphen G M : z 0 a 1 z a 2 a s 1 1 z s 1 a s z s wobei z 0 = z 0 und z s E. Es muss zwei Indizes 0 j < k n mit z j = z k geben (Schubfachprinzip). Berechnugspfad P enthält daher den Zyklus z j a j+1 z j+1 a j+2 ak 1 z k 1 a k z k. Da der Zyklus im Berechnungspfad P iteriert durchlaufen (oder auch weggelassen) werden kann, hat die Zerlegung x = uvw mit u = a 1 a j, v = a j+1 a k, w = a k+1 a s die gewünschten Eigenschaften 1 v uv n und i 0 : uv i w L.
44 Reguläre Sprachen Slide 44 Anwendung: Nachweis der Nichtregularität Folgerung: Falls für eine Sprache L Σ die Bedingung n 1, x L mit x n, u,v,w Σ mit x = uvw,1 v uv n, i 0 : uv i w / L erfüllt ist, dann ist L nicht regulär.
45 Reguläre Sprachen Slide 45 Beispiele für nicht reguläre Sprachen Die folgende Sprache L {a,b} ist nicht regulär: Begründung: L = {a m b m m 1} 1. Zu beliebig vorgegebenem n 1 wähle x = a n b n. Offensichtlich gilt x L und x n. 2. Zu beliebig vorgegebener Zerlegung x = uvw mit 1 v uv n wähle i = 0. Beachte, dass uv das Zeichen b nicht enthält (wegen uv n). Nun gilt uv 0 w = uw = a n v b n / L, da uw a < uw b.
46 Reguläre Sprachen Slide 46 Beispiele für nicht reguläre Sprachen (fortgesetzt) Die folgende Sprache L {0} ist nicht regulär: L = {0 m m ist eine Quadratzahl} Begründung: 1. Zu beliebig vorgegebenem n 1 wähle x = 0 n2. Offensichtlich gilt x L und x n. 2. Zu beliebig vorgegebener Zerlegung x = uvw mit 1 v uv n wähle i = 2. Nun gilt da n 2 + v wegen uv 2 w = 0 n2 + v / L, n 2 < n 2 + v n 2 +n < n 2 +2n+1 = (n+1) 2 keine Quadratzahl ist.
47 Reguläre Sprachen Slide 47 Beispiele für nicht reguläre Sprachen (fortgesetzt) Die folgende Sprache L {0} ist nicht regulär: Begründung: L = {0 p p ist eine Primzahl} 1. Zu beliebig vorgegebenem n 1 wähle x = 0 p für eine Primzahl p n+2. Offensichtlich gilt x L und x n. 2. Zu beliebig vorgegebener Zerlegung x = uvw mit 1 v uv n wähle i = uw. Beachte, dass uw = p v (n+2) n = 2. Nun gilt uv uw w = 0 uw ( v +1) / L, da uw ( v + 1) offensichtlich keine Primzahl ist.
48 Reguläre Sprachen Slide 48 Zwei Relationen auf Wörtern Definition: M sei ein DFA mit Startzustand z 0. xr M y gdw z 0 x = z 0 y. intuitiv: M identifiziert die Wörter x und y: nach Verarbeitung von x erreicht er denselben Zustand wie nach Verarbeitung von y. Definition (Nerode Relation) L Σ sei eine formale Sprache. Suff L (x) := {w Σ : xw L} sei die Menge der Suffixe, die x Σ zu einem Wort aus L fortsetzen. Wir definieren: xr L y gdw Suff L (x) = Suff L (y). Wir sagen Suffix w unterscheidet zwischen x und y, wenn entweder xw L und yw / L oder xw / L und yw in L. Beobachtung: xr L y gdw Es gibt keinen Suffix, der zwischen x und y unterscheidet.
49 Reguläre Sprachen Slide 49 Eigenschaften dieser Relationen Bemerkungen 1. Beide Relationen sind Äquivalenzrelationen, d.h., sie sind reflexiv, symmetrisch und transitiv. 2. Darüberhinaus gilt: xr M y = xvr M yv xr L y = xvr L yv
50 Reguläre Sprachen Slide 50 Exkurs: Index, Verfeinerung, Vergröberung R,R 1,R 2 seien Äquivalenzrelationen. Index von R = Anzahl der Äquivalenzklassen von R (evtl. ). R 1 heißt Verfeinerung von R 2 (und R 2 Vergröberung von R 1 ) gdw ar 1 b ar 2 b. In diesem Fall zerfällt jede Äquivalenzklasse von R 2 in Äquivalenzklassen von R 1 und somit gilt: Index von R 2 Index von R 1.
51 Reguläre Sprachen Slide 51 Der Satz von Myhill und Nerode Satz: L ist regulär gdw R L hat einen endlichen Index. Der Beweis zerfällt in zwei Teile.
52 Reguläre Sprachen Slide Beweisrichtung Lemma: Wenn L regulär ist, dann hat R L einen endlichen Index. Beweis in 5 Teilschritten: Wähle einen DFA M, der L erkennt (und nur Zustände besitzt, die vom Startzustand z 0 aus erreichbar sind). Index von R M = Z, da jeder Zustand z Z genau eine Äquivalenzklasse, nämlich {x z 0 x = z}, induziert. z 0 x = z 0 y = Suff L (x) = Suff L (y). Ansonsten gäbe es einen Suffix w, der zwischen x und y unterscheidet, und M würde auf einer der Eingaben xw und yw einen Fehler machen. R L ist Vergröberung von R M : xr M y = z 0 x = z 0 y = Suff L (x) = Suff L (y) = xr L y Index von R L Index von R M = Z <.
53 Reguläre Sprachen Slide Beweisrichtung Lemma: Wenn R L einen endlichen Index hat, dann ist L regulär. Für ein Wort x bezeichne [x] die zugehörige Äquivalenzklasse bez. R L. Bei endlichem Index von R L, sagen wir Index k, gibt es k Äquivalenzklassen, sagen wir [x 1 ],...,[x k ]. BeweiserfolgtdurchAngabeeinesDFA(Nerode Automat)M = (Z,Σ,δ,z 0,E): 1. Z = {[x 1 ],...,[x k ]}. 2. z 0 = [ε]. 3. E = {[x] x L}. 4. δ([x],a) = [xa]. Das Problem der Wohldefiniertheit wird an der Tafel diskutiert! M gestartet in Zustand [ε] ist nach Verarbeitung eines Wortes x (gemäß der Definition von δ) im Zustand [x]. Aus der Definition von E folgt nun T(M) = L.
54 Reguläre Sprachen Slide 54 Betrachte die Sprache Beispiel L = {x {0,1} x endet mit 00}. R L hat 3 Äquivalenzklassen: [ε] = {x x endet nicht mit 0} [0] = {x x endet mit 0 aber nicht mit 00} [00] = {x x endet mit 00} Der Nerode Automat mit Zuständen z 0 = [ε],z 1 = [0],z 2 = [00] ist dann durch folgenden Zustandsgraphen gegeben: z z z
55 Reguläre Sprachen Slide 55 Minimierung eines gegebenen DFA Eingabe: DFA M = (Z,Σ,δ,z 0,E), bei dem jeder Zustand vom Startzustand aus erreichbar ist Ausgabe: Minimalautomat M 0 zu M: der DFA mit möglichst wenigen Zuständen, der dieselbe Sprache wie M erkennt Methode: Verschmelzung äquivalenter Zustände (Details folgen)
56 Reguläre Sprachen Slide 56 Äquivalente und inäquivalente Zustände T M (z) := {w Σ : z w E} sei die Menge aller Wörter, die z in einen Endzustand überführen. Zwei Zustände z 1,z 2 Z heißen äquivalent, notiert als z 1 z 2, gdw T M (z 1 ) = T M (z 2 ). [z] bezeichnet im Folgenden die Äquivalenzklasse zum Zustand z. Wir sagen w unterscheidet zwischen z 1 und z 2 gdw entweder z 1 w E und z 2 w / E oder z 1 w / E und z 2 w E. Somit gilt z 1 z 2 gdw es kein Wort gibt, das zwischen z 1 und z 2 unterscheidet. Beobachtung Genaudann,wennz 1 z 2,könnenz 1 undz 2 zueinemzustand verschmolzen werden, ohne die Sprache T(M) abzuändern.
57 Reguläre Sprachen Slide 57 Auffinden von inäquivalenten Zustandspaaren Falls z 1 E und z 2 / E (oder umgekehrt), dann sind z 1,z 2 inäquivalent. Begründung: Das leere Wort ε unterscheidet zwischen z 1 und z 2. Falls z 1,z 2 inäquivalent sind, und z 1 = z 1 a,z 2 = z 2 a für ein a Σ, dann sind auch z 1,z 2 inäquivalent. Begründung: Wenn w zwischen z 1 und z 2 unterscheidet, dann unterscheidet aw zwischen z 1 und z 2.
58 Reguläre Sprachen Slide 58 Resultierende Minimierungsprozedur Markierung aller Paare inäquivalenter Zustände kann wie folgt geschehen: Initialisierung: Markiere alle Paare (z 1,z 2 ) mit z 1 E und z 2 / E sowie alle Paare mit z 1 / E und z 2 E. Iteration: SolangeeinunmarkiertesPaar(z 1,z 2 ),eina Σundeinmarkiertes Paar (z 1,z 2) mit z 1 = z 1 a,z 2 = z 2 a existieren, markiere (z 1,z 2 ) ebenfalls. Äquivalente Zustandspaare sind gerade die unmarkierten Paare. Berechnung des Minimalautomaten: Transformiere G M zu einem gröberen Zustandsgraphen, bei welchem jede Äquivalenzklasse von Knoten durch einen einzigen Superknoten repräsentiert ist. Eine mit a markierte Kante von z nach z wird dann zu einer mit a markierten Kante von [z] nach [z ]. Startknoten ist nun [z 0 ], Endknoten sind die Superknoten [z] mit z E.
59 Reguläre Sprachen Slide 59 Beispiel Links der DFA M, rechts der Minimalautomat M 0 : z z z 4 0,1 1 0 z2 z3 0 [z ] = {z,z } [z ] = {z,z } z z z z 0 z ,1 Die folgende Tabelle gibt die markierten Paare inäquivalenter Knoten an: z 0 z 1 z 2 z 3 z 1 * z 2 * z 3 * * z 4 * * * *
60 Reguläre Sprachen Slide 60 Abschlusseigenschaften Satz: Die Klasse der regulären Sprachen ist abgeschlossen unter den Operationen,,,,. Beweis: Abschluss unter., ist offensichtlich: Reguläre Sprachen sind durch reguläre Ausdrücke repräsentierbar. Abschluss unter ist einfach nachzuweisen: Falls T(M) = L mit DFA M = (Z,Σ,δ,z 0,E) so folgt T( M) = L mit DFA M := (Z,Σ,δ,z 0,Z \E). Abschluss unter ergibt sich jetzt mit de Morgan : L 1 L 2 = L 1 L 2 = L 1 L 2
61 Reguläre Sprachen Slide 61 Der Produktautomat Produktautomat liefert einen alternativen Beweis für den Abschluss unter Vereinigung und Durchschnitt. Zu gegeben DFAs M 1 = (Z 1,Σ,δ 1,z 01,E 1 ) und M 2 = (Z 2,Σ,δ 2,z 02,E 2 ) betrachte den DFA M = (Z 1 Z 2,Σ,δ,(z 01,z 02 ),E) mit δ((z 1,z 2 ),a) = (δ 1 (z 1,a),δ 2 (z 2,a)). Intuition: M führt die Rechnungen von M 1 und M 2 parallel aus. Mit E = E 1 E 2 folgt T(M) = T(M 1 ) T(M 2 ). Mit E = (E 1 Z 2 ) (Z 1 E 2 ) folgt T(M) = T(M 1 ) T(M 2 ).
62 Reguläre Sprachen Slide 62 Das Wortproblem Eingabe: x Σ Frage: x L? Spezielles Wortproblem für eine reguläre Sprache L Σ Komplexität: lösbar in Realzeit (n = x Rechenschritte) Methode: Benutze einen DFA M mit T(M) = L. Gestartet auf Eingabe x liefert er die Antwort in x Rechenschritten.
63 Reguläre Sprachen Slide 63 Das Leerheitsproblem Eingabe: DFA M gegeben durch seinen Zustandsgraphen G M Frage: T(M) =? Komplexität: lösbar in Linearzeit Methode: Verwende eine Graphexplorationstechnik (wie DFS oder BFS): T(M) von z 0 ist ein Zustand aus E erreichbar Bemerkung: Eine analoge Methode ist auch bei gegebenem NFA verwendbar.
64 Reguläre Sprachen Slide 64 Das Endlichkeitsproblem Eingabe: DFA M gegeben durch seinen Zustandsgraphen G M Frage: T(M) <? Komplexität: lösbar in Linearzeit Methode: Verwende eine Graphexplorationstechnik (wie DFS oder BFS): Markiere alle Zustände, die von z 0 aus erreichbar sind und von denen ausgehend sich ein Zustand aus E erreichen lässt. Es bezeichne G M von markierten Knoten induzierten Untergraphen von G M. Nutze aus: T(M) = G M enthält einen Zyklus Bemerkung: Eine analoge Methode ist auch bei gegebenem NFA verwendbar.
65 Reguläre Sprachen Slide 65 Das Schnittproblem Eingabe: DFAs M 1,M 2 gegeben durch ihre Zustandsgraphen G M1,G M2 Frage: T(M 1 ) T(M 2 ) =? Komplexität: lösbar mit quadratischem Zeitaufwand Methode: Berechne den Produktautomaten M mit T(M) = T(M 1 ) T(M 2 ) und löse für M das Leerheitsproblem. Bemerkung: Eine analoge Methode ist auch bei gegebenen NFAs verwendbar.
66 Reguläre Sprachen Slide 66 Das Inklusionsproblem Eingabe: DFAs M 1,M 2 gegeben durch ihre Zustandsgraphen G M1,G M2 Frage: T(M 1 ) T(M 2 )? Komplexität: lösbar mit quadratischem Zeitaufwand Methode: Nutze aus, dass A B A B =. Berechne aus M 2 den DFA M 2 mit T( M 2 ) = T(M 2 ). Löse für M 1 und M 2 das Schnittproblem.
67 Reguläre Sprachen Slide 67 Das Äquivalenzproblem Eingabe: DFAs M 1,M 2 gegeben durch ihre Zustandsgraphen G M1,G M2 Frage: T(M 1 ) = T(M 2 )? Komplexität: lösbar mit quadratischem Zeitaufwand Methode: Offensichtliche Reduktion auf das Inklusionsproblem wegen A = B (A B und B A)
68 Reguläre Sprachen Slide 68 Lernziele Kenntnis der wesentlichen Konzepte und Resultate auf dem Level der regulären Sprachen besitzen und Zusammenhänge verstehen aus DFA bzw. NFA den Zustandsgraphen ablesen und umgekehrt zu einer regulären Sprache einen passende(n) reguläre Grammatik, DFA, NFA, bzw. regulären Ausdruck angeben können und umgekehrt wechselseitige Transformationen zwischen den Repräsentationsformen (reguläre Grammatik, DFA, NFA, regulärer Ausdruck) durchführen können Nachweis der Nicht Regularität einer Sprache mit Hilfe des Pumping Lemmas führen können Nerode Relation zu einer Sprache bestimmen können den Minimalautomaten zu einem gegebenen DFA konstruieren können zu einem gegebenen DFA die besprochenen Entscheidungsprobleme lösen können
2.2 Reguläre Sprachen Endliche Automaten
 2.2.1 Endliche Automaten E I N G A B E Lesekopf endliche Kontrolle Signal für Endzustand Ein endlicher Automat liest ein Wort zeichenweise und akzeptiert oder verwirft. endlicher Automat Sprache der akzeptierten
2.2.1 Endliche Automaten E I N G A B E Lesekopf endliche Kontrolle Signal für Endzustand Ein endlicher Automat liest ein Wort zeichenweise und akzeptiert oder verwirft. endlicher Automat Sprache der akzeptierten
Reguläre Sprachen. R. Stiebe: Theoretische Informatik für ING-IF und Lehrer,
 Reguläre Sprachen Reguläre Sprachen (Typ-3-Sprachen) haben große Bedeutung in Textverarbeitung und Programmierung (z.b. lexikalische Analyse) besitzen für viele Entscheidungsprobleme effiziente Algorithmen
Reguläre Sprachen Reguläre Sprachen (Typ-3-Sprachen) haben große Bedeutung in Textverarbeitung und Programmierung (z.b. lexikalische Analyse) besitzen für viele Entscheidungsprobleme effiziente Algorithmen
1 Σ endliches Terminalalphabet, 2 V endliche Menge von Variablen (mit V Σ = ), 3 P (V (Σ ΣV )) {(S, ε)} endliche Menge von Regeln,
 Theorie der Informatik 9. März 24 7. Reguläre Sprachen I Theorie der Informatik 7. Reguläre Sprachen I Malte Helmert Gabriele Röger Universität Basel 9. März 24 7. Reguläre Grammatiken 7.2 DFAs 7.3 NFAs
Theorie der Informatik 9. März 24 7. Reguläre Sprachen I Theorie der Informatik 7. Reguläre Sprachen I Malte Helmert Gabriele Röger Universität Basel 9. März 24 7. Reguläre Grammatiken 7.2 DFAs 7.3 NFAs
Theorie der Informatik
 Theorie der Informatik 8. Reguläre Sprachen II Malte Helmert Gabriele Röger Universität Basel 24. März 24 Pumping Lemma Pumping Lemma: Motivation Man kann zeigen, dass eine Sprache regulär ist, indem man
Theorie der Informatik 8. Reguläre Sprachen II Malte Helmert Gabriele Röger Universität Basel 24. März 24 Pumping Lemma Pumping Lemma: Motivation Man kann zeigen, dass eine Sprache regulär ist, indem man
Endliche Automaten. δ : Z Σ Z die Überführungsfunktion, z 0 Z der Startzustand und F Z die Menge der Endzustände (Finalzustände).
 Endliche Automaten Endliche Automaten Definition Ein deterministischer endlicher Automat (kurz DFA für deterministic finite automaton ) ist ein Quintupel M = (Σ, Z, δ, z 0, F), wobei Σ ein Alphabet ist,
Endliche Automaten Endliche Automaten Definition Ein deterministischer endlicher Automat (kurz DFA für deterministic finite automaton ) ist ein Quintupel M = (Σ, Z, δ, z 0, F), wobei Σ ein Alphabet ist,
Definition (Reguläre Ausdrücke) Sei Σ ein Alphabet, dann gilt: (ii) ε ist ein regulärer Ausdruck über Σ.
 Reguläre Ausdrücke Definition (Reguläre Ausdrücke) Sei Σ ein Alphabet, dann gilt: (i) ist ein regulärer Ausdruck über Σ. (ii) ε ist ein regulärer Ausdruck über Σ. (iii) Für jedes a Σ ist a ein regulärer
Reguläre Ausdrücke Definition (Reguläre Ausdrücke) Sei Σ ein Alphabet, dann gilt: (i) ist ein regulärer Ausdruck über Σ. (ii) ε ist ein regulärer Ausdruck über Σ. (iii) Für jedes a Σ ist a ein regulärer
1 Σ endliches Terminalalphabet, 2 V endliche Menge von Variablen (mit V Σ = ), 3 P (V (Σ ΣV )) {(S, ε)} endliche Menge von Regeln,
 Theorie der Informatik 8. März 25 8. Reguläre Sprachen I Theorie der Informatik 8. Reguläre Sprachen I 8. Reguläre Grammatiken Malte Helmert Gabriele Röger 8.2 DFAs Universität Basel 8. März 25 8.3 NFAs
Theorie der Informatik 8. März 25 8. Reguläre Sprachen I Theorie der Informatik 8. Reguläre Sprachen I 8. Reguläre Grammatiken Malte Helmert Gabriele Röger 8.2 DFAs Universität Basel 8. März 25 8.3 NFAs
Theoretische Informatik Mitschrift
 5 Eigenschaften regulärer Sprachen 51: Die Nerode-Relation Theoretische Informatik Mitschrift Definition 51: Sei L * L * * mit L :={u, v * * w *:uw L v w L }heißt Nerode-Relation von L Sei ={0,1}, L= *{00}
5 Eigenschaften regulärer Sprachen 51: Die Nerode-Relation Theoretische Informatik Mitschrift Definition 51: Sei L * L * * mit L :={u, v * * w *:uw L v w L }heißt Nerode-Relation von L Sei ={0,1}, L= *{00}
Satz (Abschluß unter der Stern-Operation)
 Satz (Abschluß unter der Stern-Operation) Wenn L eine reguläre Sprache ist, dann ist auch L regulär. Beweis: Es gibt einen NFA M = (Z, Σ, S, δ, S, E) mit L(M) = L. Wir bauen aus diesem NFA nun wie folgt
Satz (Abschluß unter der Stern-Operation) Wenn L eine reguläre Sprache ist, dann ist auch L regulär. Beweis: Es gibt einen NFA M = (Z, Σ, S, δ, S, E) mit L(M) = L. Wir bauen aus diesem NFA nun wie folgt
Das Pumping Lemma: Ein Anwendungsbeispiel
 Das Pumping Lemma: Ein Anwendungsbeispiel Beispiel: Die Palindromsprache ist nicht regulär. L = { } w {0, 1} w ist ein Palindrom Beweis: Angenommen, L ist doch regulär. Gemäß Pumping Lemma gibt es dann
Das Pumping Lemma: Ein Anwendungsbeispiel Beispiel: Die Palindromsprache ist nicht regulär. L = { } w {0, 1} w ist ein Palindrom Beweis: Angenommen, L ist doch regulär. Gemäß Pumping Lemma gibt es dann
Die Nerode-Relation und der Index einer Sprache L
 Die Nerode-Relation und der Index einer Sprache L Eine zweite zentrale Idee: Sei A ein vollständiger DFA für die Sprache L. Repäsentiere einen beliebigen Zustand p von A durch die Worte in Σ, die zu p
Die Nerode-Relation und der Index einer Sprache L Eine zweite zentrale Idee: Sei A ein vollständiger DFA für die Sprache L. Repäsentiere einen beliebigen Zustand p von A durch die Worte in Σ, die zu p
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Wintersemester 2007 / 2008 Prof. Dr. Heribert Vollmer Institut für Theoretische Informatik 29.10.2007 Reguläre Sprachen Ein (deterministischer) endlicher Automat
Grundlagen der Theoretischen Informatik Wintersemester 2007 / 2008 Prof. Dr. Heribert Vollmer Institut für Theoretische Informatik 29.10.2007 Reguläre Sprachen Ein (deterministischer) endlicher Automat
Informatik IV Theoretische Informatik
 Informatik IV Theoretische Informatik Kapitel 2 Sommersemester 29 Dozent: Prof. Dr. J. Rothe J. Rothe (HHU Düsseldorf) Informatik IV / 7 Endliche Automaten Beispiel Abbildung: TCP J. Rothe (HHU Düsseldorf)
Informatik IV Theoretische Informatik Kapitel 2 Sommersemester 29 Dozent: Prof. Dr. J. Rothe J. Rothe (HHU Düsseldorf) Informatik IV / 7 Endliche Automaten Beispiel Abbildung: TCP J. Rothe (HHU Düsseldorf)
FORMALE SYSTEME. 10. Vorlesung: Grenzen regulärer Sprachen / Probleme für Automaten. TU Dresden, 14. November 2016.
 FORMALE SYSTEME 10. Vorlesung: Grenzen regulärer Sprachen / Probleme für Automaten Markus Krötzsch TU Dresden, 14. November 2016 Rückblick Markus Krötzsch, 14. November 2016 Formale Systeme Folie 2 von
FORMALE SYSTEME 10. Vorlesung: Grenzen regulärer Sprachen / Probleme für Automaten Markus Krötzsch TU Dresden, 14. November 2016 Rückblick Markus Krötzsch, 14. November 2016 Formale Systeme Folie 2 von
Theoretische Informatik für Wirtschaftsinformatik und Lehramt
 Theoretische Informatik für Wirtschaftsinformatik und Lehramt Eigenschaften regulärer Sprachen Priv.-Doz. Dr. Stefan Milius stefan.milius@fau.de Theoretische Informatik Friedrich-Alexander Universität
Theoretische Informatik für Wirtschaftsinformatik und Lehramt Eigenschaften regulärer Sprachen Priv.-Doz. Dr. Stefan Milius stefan.milius@fau.de Theoretische Informatik Friedrich-Alexander Universität
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2013
 Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2013 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Reguläre Ausdrücke Wozu
Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2013 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Reguläre Ausdrücke Wozu
q 0 q gdw. nicht (q A) (q A) q i+1 q gdw. q i q oder ( a Σ) δ(q, a) i δ(q, a) L = {a n b n : n N} für a, b Σ, a b
 Kap. 2: Endliche Automaten Myhill Nerode 2.4 Minimalautomat für reguläre Sprache Abschnitt 2.4.3 L Σ regulär der Äuivalenzklassen-Automat zu L ist ein DFA mit minimaler Zustandszahl (= index( L )) unter
Kap. 2: Endliche Automaten Myhill Nerode 2.4 Minimalautomat für reguläre Sprache Abschnitt 2.4.3 L Σ regulär der Äuivalenzklassen-Automat zu L ist ein DFA mit minimaler Zustandszahl (= index( L )) unter
Die mathematische Seite
 Kellerautomaten In der ersten Vorlesung haben wir den endlichen Automaten kennengelernt. Mit diesem werden wir uns in der zweiten Vorlesung noch etwas eingängiger beschäftigen und bspw. Ansätze zur Konstruktion
Kellerautomaten In der ersten Vorlesung haben wir den endlichen Automaten kennengelernt. Mit diesem werden wir uns in der zweiten Vorlesung noch etwas eingängiger beschäftigen und bspw. Ansätze zur Konstruktion
Äquivalenzrelation R A zu DFA A. Rechtsinvarianz. Relation R L zur Sprache L
 Rechtsinvarianz Definition T4.2.8: Eine Äquivalenzrelation R auf Σ* heißt rechtsinvariant, wenn x R y z Σ*: xz R yz. Index von R: Anzahl der Äquivalenzklassen von R. Notation: ind(r) Im Folgenden: 2 rechtsinvariante
Rechtsinvarianz Definition T4.2.8: Eine Äquivalenzrelation R auf Σ* heißt rechtsinvariant, wenn x R y z Σ*: xz R yz. Index von R: Anzahl der Äquivalenzklassen von R. Notation: ind(r) Im Folgenden: 2 rechtsinvariante
2 2 Reguläre Sprachen. 2.2 Endliche Automaten. Übersicht
 Formale Systeme, Automaten, Prozesse Übersicht 2 2. Reguläre Ausdrücke 2.3 Nichtdeterministische endliche Automaten 2.4 Die Potenzmengenkonstruktion 2.5 NFAs mit ɛ-übergängen 2.6 Minimale DFAs und der
Formale Systeme, Automaten, Prozesse Übersicht 2 2. Reguläre Ausdrücke 2.3 Nichtdeterministische endliche Automaten 2.4 Die Potenzmengenkonstruktion 2.5 NFAs mit ɛ-übergängen 2.6 Minimale DFAs und der
Formale Grundlagen der Informatik 1 Kapitel 5 Abschlusseigenschaften
 Formale Grundlagen der Informatik 1 Kapitel 5 Frank Heitmann heitmann@informatik.uni-hamburg.de 18. April 2016 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/64 NFAs - Grundlagen DFAs vs. NFAs Der
Formale Grundlagen der Informatik 1 Kapitel 5 Frank Heitmann heitmann@informatik.uni-hamburg.de 18. April 2016 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/64 NFAs - Grundlagen DFAs vs. NFAs Der
Kapitel 2: Formale Sprachen Gliederung
 Gliederung. Einleitung und Grundbegriffe. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.. Chomsky-Grammatiken 2.2. Reguläre Sprachen Reguläre Grammatiken, ND-Automaten
Gliederung. Einleitung und Grundbegriffe. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.. Chomsky-Grammatiken 2.2. Reguläre Sprachen Reguläre Grammatiken, ND-Automaten
DisMod-Repetitorium Tag 4
 DisMod-Repetitorium Tag 4 Endliche Automaten, Reguläre Sprachen und Kontextfreie Grammatiken 22. März 2018 1 Endliche Automaten Definition DFA Auswertungen Äquivalenzrelationen Verschmelzungsrelation und
DisMod-Repetitorium Tag 4 Endliche Automaten, Reguläre Sprachen und Kontextfreie Grammatiken 22. März 2018 1 Endliche Automaten Definition DFA Auswertungen Äquivalenzrelationen Verschmelzungsrelation und
FORMALE SYSTEME. 8. Vorlesung: Minimale Automaten. TU Dresden, 6. November Markus Krötzsch Lehrstuhl Wissensbasierte Systeme
 FORMALE SYSTEME 8. Vorlesung: Minimale Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme TU Dresden, 6. November 2017 Rückblick Markus Krötzsch, 6. November 2017 Formale Systeme Folie 2 von 26
FORMALE SYSTEME 8. Vorlesung: Minimale Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme TU Dresden, 6. November 2017 Rückblick Markus Krötzsch, 6. November 2017 Formale Systeme Folie 2 von 26
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier. Henning Fernau Universität Trier
 Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
Automaten und Formale Sprachen SoSe 2007 in Trier. Henning Fernau Universität Trier
 Automaten und Formale Sprachen SoSe 2007 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche Automaten und
Automaten und Formale Sprachen SoSe 2007 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche Automaten und
Kontextsensitive und Typ 0 Sprachen Slide 2. Die Turingmaschine
 Kontextsensitive und Typ 0 Sprachen Slide 2 Die Turingmaschine DTM = Deterministische Turingmaschine NTM = Nichtdeterministische Turingmaschine TM = DTM oder NTM Intuitiv gilt: DTM = (DFA + dynamischer
Kontextsensitive und Typ 0 Sprachen Slide 2 Die Turingmaschine DTM = Deterministische Turingmaschine NTM = Nichtdeterministische Turingmaschine TM = DTM oder NTM Intuitiv gilt: DTM = (DFA + dynamischer
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Übung am 3..2 INSTITUT FÜR THEORETISCHE KIT 7..2 Universität des Andrea Landes Schumm Baden-Württemberg - Theoretische und Grundlagen der Informatik INSTITUT FÜR
Theoretische Grundlagen der Informatik Übung am 3..2 INSTITUT FÜR THEORETISCHE KIT 7..2 Universität des Andrea Landes Schumm Baden-Württemberg - Theoretische und Grundlagen der Informatik INSTITUT FÜR
Informatik IV. Pingo Sommersemester Dozent: Prof. Dr. J. Rothe. J. Rothe (HHU Düsseldorf) Informatik IV 1 / 13
 Informatik IV Sommersemester 2019 Dozent: Prof. Dr. J. Rothe J. Rothe (HHU Düsseldorf) Informatik IV 1 / 13 Website http://pingo.upb.de/ Code: 1869 J. Rothe (HHU Düsseldorf) Informatik IV 2 / 13 Frage
Informatik IV Sommersemester 2019 Dozent: Prof. Dr. J. Rothe J. Rothe (HHU Düsseldorf) Informatik IV 1 / 13 Website http://pingo.upb.de/ Code: 1869 J. Rothe (HHU Düsseldorf) Informatik IV 2 / 13 Frage
Theorie der Informatik
 Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen Malte Helmert Gabriele Röger Universität Basel 7. April 2014 Kontextsensitive und allgemeine Grammatiken Wiederholung: (kontextsensitive)
Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen Malte Helmert Gabriele Röger Universität Basel 7. April 2014 Kontextsensitive und allgemeine Grammatiken Wiederholung: (kontextsensitive)
Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden kann.
 Der Satz von Kleene Wir haben somit Folgendes bewiesen: Der Satz von Kleene Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden
Der Satz von Kleene Wir haben somit Folgendes bewiesen: Der Satz von Kleene Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden
Übung Theoretische Grundlagen
 Übung Theoretische Grundlagen Nico Döttling October 25, 22 Automatenminimierung Konstruktion des Äquivalenzklassenautomaten Aus der Vorlesung bekannt Überflüssige Zustände lassen sich effizient erkennen
Übung Theoretische Grundlagen Nico Döttling October 25, 22 Automatenminimierung Konstruktion des Äquivalenzklassenautomaten Aus der Vorlesung bekannt Überflüssige Zustände lassen sich effizient erkennen
Vorlesungsmitschrift zur Vorlesung Theoretische Informatik I vom 23. Juni Christian Franz
 Vorlesungsmitschrift zur Vorlesung Theoretische Informatik I vom 23. Juni 2 Christian Franz Inhaltsverzeichnis Wiederholung: Vorlesung vom 9.6.2... Beispiele für Äquivalenzklassen... 4.5. Minimierung
Vorlesungsmitschrift zur Vorlesung Theoretische Informatik I vom 23. Juni 2 Christian Franz Inhaltsverzeichnis Wiederholung: Vorlesung vom 9.6.2... Beispiele für Äquivalenzklassen... 4.5. Minimierung
Frank Heitmann 2/47. 1 Ein PDA beginnt im Startzustand z 0 und mit im Keller. 2 Ist der Automat
 Formale Grundlagen der Informatik 1 Kapitel 5 Über reguläre Sprachen hinaus und (Teil 2) Frank Heitmann heitmann@informatik.uni-hamburg.de 21. April 2015 Der Kellerautomat - Formal Definition (Kellerautomat
Formale Grundlagen der Informatik 1 Kapitel 5 Über reguläre Sprachen hinaus und (Teil 2) Frank Heitmann heitmann@informatik.uni-hamburg.de 21. April 2015 Der Kellerautomat - Formal Definition (Kellerautomat
Formale Methoden 1. Gerhard Jäger 9. Januar Uni Bielefeld, WS 2007/2008 1/23
 1/23 Formale Methoden 1 Gerhard Jäger Gerhard.Jaeger@uni-bielefeld.de Uni Bielefeld, WS 2007/2008 9. Januar 2008 2/23 Automaten (informell) gedachte Maschine/abstraktes Modell einer Maschine verhält sich
1/23 Formale Methoden 1 Gerhard Jäger Gerhard.Jaeger@uni-bielefeld.de Uni Bielefeld, WS 2007/2008 9. Januar 2008 2/23 Automaten (informell) gedachte Maschine/abstraktes Modell einer Maschine verhält sich
5.2 Endliche Automaten
 114 5.2 Endliche Automaten Endliche Automaten sind Turingmaschinen, die nur endlichen Speicher besitzen. Wie wir bereits im Zusammenhang mit Turingmaschinen gesehen haben, kann endlicher Speicher durch
114 5.2 Endliche Automaten Endliche Automaten sind Turingmaschinen, die nur endlichen Speicher besitzen. Wie wir bereits im Zusammenhang mit Turingmaschinen gesehen haben, kann endlicher Speicher durch
Für jede Sprache L X sind die folgenden Aussagen äquivalent:
 Was bisher geschah Für jede Sprache L X sind die folgenden Aussagen äquivalent: Es existiert ein NFA A mit L = L(A) (L REC(NFA)). Es existiert ein vollständiger NFA B mit L = L(B). Es existiert ein ε-nfa
Was bisher geschah Für jede Sprache L X sind die folgenden Aussagen äquivalent: Es existiert ein NFA A mit L = L(A) (L REC(NFA)). Es existiert ein vollständiger NFA B mit L = L(B). Es existiert ein ε-nfa
Automaten und Formale Sprachen SoSe 2013 in Trier
 Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Das Pumping-Lemma Formulierung
 Das Pumping-Lemma Formulierung Sei L reguläre Sprache. Dann gibt es ein n N mit: jedes Wort w L mit w n kann zerlegt werden in w = xyz, so dass gilt: 1. xy n 2. y 1 3. für alle k 0 ist xy k z L. 59 / 162
Das Pumping-Lemma Formulierung Sei L reguläre Sprache. Dann gibt es ein n N mit: jedes Wort w L mit w n kann zerlegt werden in w = xyz, so dass gilt: 1. xy n 2. y 1 3. für alle k 0 ist xy k z L. 59 / 162
11.1 Kontextsensitive und allgemeine Grammatiken
 Theorie der Informatik 7. April 2014 11. Kontextsensitive und Typ-0-Sprachen Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen 11.1 Kontextsensitive und allgemeine Grammatiken Malte Helmert
Theorie der Informatik 7. April 2014 11. Kontextsensitive und Typ-0-Sprachen Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen 11.1 Kontextsensitive und allgemeine Grammatiken Malte Helmert
FORMALE SYSTEME. Der Satz von Myhill und Nerode. Automaten verkleinern mit Quotientenbildung. Verschiedene Äquivalenzrelationen
 Automaten verkleinern mit Quotientenbildung Wir betrachten DFAs mit totaler Übergangsfunktion. FORMALE SYSTEME 9. Vorlesung: Minimale Automaten (2) Markus Krötzsch TU Dresden, 9. November 207 C 0 A 0 [A]
Automaten verkleinern mit Quotientenbildung Wir betrachten DFAs mit totaler Übergangsfunktion. FORMALE SYSTEME 9. Vorlesung: Minimale Automaten (2) Markus Krötzsch TU Dresden, 9. November 207 C 0 A 0 [A]
Formale Sprachen und endliche Automaten
 Formale Sprachen und endliche Automaten Formale Sprachen Definition: 1 (Alphabet) Ein Alphabet Σ ist eine endliche, nichtleere Menge von Zeichen oder Symbolen. Ein Wort über dem Alphabet Σ ist eine endliche
Formale Sprachen und endliche Automaten Formale Sprachen Definition: 1 (Alphabet) Ein Alphabet Σ ist eine endliche, nichtleere Menge von Zeichen oder Symbolen. Ein Wort über dem Alphabet Σ ist eine endliche
Worterkennung in Texten speziell im Compilerbau 20. April Frank Heitmann 2/64
 Grenzen regulärer Sprachen? Formale Grundlagen der Informatik 1 Kapitel 4 Über reguläre Sprachen hinaus und Pumping Lemma Frank Heitmann heitmann@informatik.uni-hamburg.de Wir haben mittlerweile einiges
Grenzen regulärer Sprachen? Formale Grundlagen der Informatik 1 Kapitel 4 Über reguläre Sprachen hinaus und Pumping Lemma Frank Heitmann heitmann@informatik.uni-hamburg.de Wir haben mittlerweile einiges
Kurz-Skript zur Theoretischen Informatik I
 Kurz-Skript zur Theoretischen Informatik I Inhaltsverzeichnis 1 Grundlagen 2 2 Reguläre Ausdrücke 4 3 Endliche Automaten 5 3.1 Vollständige endliche Automaten................................... 6 3.2 ε
Kurz-Skript zur Theoretischen Informatik I Inhaltsverzeichnis 1 Grundlagen 2 2 Reguläre Ausdrücke 4 3 Endliche Automaten 5 3.1 Vollständige endliche Automaten................................... 6 3.2 ε
Informatik III. Christian Schindelhauer Wintersemester 2006/07 8. Vorlesung
 Informatik III Christian Schindelhauer Wintersemester 2006/07 8. Vorlesung 17.11.2006 schindel@informatik.uni-freiburg.de 1 Prinzip des Kellerautomats Push-Down-Automaton (PDA) Ein Kellerautomat vereinigt
Informatik III Christian Schindelhauer Wintersemester 2006/07 8. Vorlesung 17.11.2006 schindel@informatik.uni-freiburg.de 1 Prinzip des Kellerautomats Push-Down-Automaton (PDA) Ein Kellerautomat vereinigt
Suche nach einem solchen Kreis. Endlichkeitstest. Vereinigung und Durchschnitt. Abschlusseigenschaften
 Endlichkeitstest Eingabe: DFA/NFA M. Frage: Ist die von M akzeptierte Sprache endlich? Nahe liegende Beobachtung: In einem DFA/NFA, der eine unendliche Sprache akzeptiert, muss es einen Kreis geben, der
Endlichkeitstest Eingabe: DFA/NFA M. Frage: Ist die von M akzeptierte Sprache endlich? Nahe liegende Beobachtung: In einem DFA/NFA, der eine unendliche Sprache akzeptiert, muss es einen Kreis geben, der
Homomorphismen. Defnition: Σ und Γ seien zwei endliche Alphabete, und h sei eine Abbildung h : Σ Γ. Wir definieren die folgenden Sprachen:
 Homomorphismen Σ und Γ seien zwei endliche Alphabete, und h sei eine Abbildung h : Σ Γ. Wir definieren die folgenden Sprachen: h(l) := {h(u) : u L} Γ, für jede Sprache L Σ, h 1 (M) := {u Σ : h(u) M} Σ,
Homomorphismen Σ und Γ seien zwei endliche Alphabete, und h sei eine Abbildung h : Σ Γ. Wir definieren die folgenden Sprachen: h(l) := {h(u) : u L} Γ, für jede Sprache L Σ, h 1 (M) := {u Σ : h(u) M} Σ,
FORMALE SYSTEME. Wiederholung. Beispiel: NFA. Wiederholung: NFA. 4. Vorlesung: Nichtdeterministische Endliche Automaten. TU Dresden, 19.
 Wiederholung FORMALE SYSTEME 4. Vorlesung: Nichtdeterministische Endliche Automaten Markus Krötzsch Professur für Wissensbasierte Systeme Grammatiken können Sprachen beschreiben und sie grob in Typen unterteilen
Wiederholung FORMALE SYSTEME 4. Vorlesung: Nichtdeterministische Endliche Automaten Markus Krötzsch Professur für Wissensbasierte Systeme Grammatiken können Sprachen beschreiben und sie grob in Typen unterteilen
Endliche Automaten. Endliche Automaten 1 / 102
 Endliche Automaten Endliche Automaten 1 / 102 Endliche Automaten Endliche Automaten erlauben eine Beschreibung von Handlungsabläufen: Wie ändert sich ein Systemzustand in Abhängigkeit von veränderten Umgebungsbedingungen?
Endliche Automaten Endliche Automaten 1 / 102 Endliche Automaten Endliche Automaten erlauben eine Beschreibung von Handlungsabläufen: Wie ändert sich ein Systemzustand in Abhängigkeit von veränderten Umgebungsbedingungen?
Automaten und Formale Sprachen ε-automaten und Minimierung
 Automaten und Formale Sprachen ε-automaten und Minimierung Ralf Möller Hamburg Univ. of Technology Literatur Gottfried Vossen, Kurt-Ulrich Witt: Grundkurs Theoretische Informatik, Vieweg Verlag 2 Danksagung
Automaten und Formale Sprachen ε-automaten und Minimierung Ralf Möller Hamburg Univ. of Technology Literatur Gottfried Vossen, Kurt-Ulrich Witt: Grundkurs Theoretische Informatik, Vieweg Verlag 2 Danksagung
Informatik III. Christian Schindelhauer Wintersemester 2006/07 3. Vorlesung
 Informatik III Christian Schindelhauer Wintersemester 2006/07 3. Vorlesung 02.11.2006 schindel@informatik.uni-freiburg.de 1 Kapitel III Reguläre Sprachen Reguläre Sprachen und Ausdrücke Informatik III
Informatik III Christian Schindelhauer Wintersemester 2006/07 3. Vorlesung 02.11.2006 schindel@informatik.uni-freiburg.de 1 Kapitel III Reguläre Sprachen Reguläre Sprachen und Ausdrücke Informatik III
... = für δ(z, a i ) = z. Abbildung 4.4: Interpretation der Arbeitsweise eines endlichen Automaten
 3 Reguläre Sprachen 63 3 Reguläre Sprachen In diesem Kapitel beschäftigen wir uns etwas näher mit den regulären Sprachen, insbesondere mit der Möglichkeit verschiedener Charakterisierungen und den Eigenschaften
3 Reguläre Sprachen 63 3 Reguläre Sprachen In diesem Kapitel beschäftigen wir uns etwas näher mit den regulären Sprachen, insbesondere mit der Möglichkeit verschiedener Charakterisierungen und den Eigenschaften
Induktionsprinzipien für andere Bereiche. falscher Induktionsbeweis über N Übung Beispiele. Reguläre Σ-Sprachen Abschnitt 2.
 Kap 1: Grundegriffe Induktion 1.2.3 Induktionsprinzipien für andere Bereiche Beispiele Bereich M M 0 M erzeugende Operationen N 0} S: n n + 1 Σ ε} ( w wa ) für a Σ, c}-terme c} (t 1, t 2 ) (t 1 t 2 ) endl.
Kap 1: Grundegriffe Induktion 1.2.3 Induktionsprinzipien für andere Bereiche Beispiele Bereich M M 0 M erzeugende Operationen N 0} S: n n + 1 Σ ε} ( w wa ) für a Σ, c}-terme c} (t 1, t 2 ) (t 1 t 2 ) endl.
äußere Klammern können entfallen, ebenso solche, die wegen Assoziativität von + und Konkatenation nicht notwendig sind:
 3. Reguläre Sprachen Bisher wurden Automaten behandelt und Äquivalenzen zwischen den verschiedenen Automaten gezeigt. DEAs erkennen formale Sprachen. Gibt es formale Sprachen, die nicht erkannt werden?
3. Reguläre Sprachen Bisher wurden Automaten behandelt und Äquivalenzen zwischen den verschiedenen Automaten gezeigt. DEAs erkennen formale Sprachen. Gibt es formale Sprachen, die nicht erkannt werden?
2.2 Nichtdeterministische endliche Automaten
 2 Endliche Automaten arbeiten und hier kann dann ggf. auch wieder auf die Konstruktion verwiesen werden. Fragen 1. Wie viele Informationen kann man in einem DFA speichern? a) beliebig viele b) endlich
2 Endliche Automaten arbeiten und hier kann dann ggf. auch wieder auf die Konstruktion verwiesen werden. Fragen 1. Wie viele Informationen kann man in einem DFA speichern? a) beliebig viele b) endlich
Typ-3-Sprachen. Das Pumping-Lemma
 Das Pumping-Lemma Typ-3-Sprachen Um zu zeigen, daß eine Sprache L regulär ist, kannman einen NFA M angeben mit L(M) = L, oder eine rechtslineare Grammatik G angeben mit L(G) =L, oder einen regulären Ausdruck
Das Pumping-Lemma Typ-3-Sprachen Um zu zeigen, daß eine Sprache L regulär ist, kannman einen NFA M angeben mit L(M) = L, oder eine rechtslineare Grammatik G angeben mit L(G) =L, oder einen regulären Ausdruck
Seien M 1,M 2 NFAs f. die Sprachen L 1 und L 2. Konstruktion eines NFAs für L 1 L 2 : Erzeuge Kopien von M 1 und M 2. p 1
 Beispiel Produktautomat p Vereinfachte Konstruktion f. NFAs Seien M,M 2 NFAs f. die Sprachen L und L 2. Konstruktion eines NFAs für L L 2 : Erzeuge Kopien von M und M 2. p q q p 2 Erzeuge neuen Startzustand
Beispiel Produktautomat p Vereinfachte Konstruktion f. NFAs Seien M,M 2 NFAs f. die Sprachen L und L 2. Konstruktion eines NFAs für L L 2 : Erzeuge Kopien von M und M 2. p q q p 2 Erzeuge neuen Startzustand
Formale Sprachen und Komplexität, SS 18, Prof. Dr. Volker Heun. Übungsblatt 4. Abgabe: bis Mo Uhr
 Formale Sprachen und Komplexität, SS 18, Prof. r. Volker Heun Übungsblatt 4 bgabe: bis Mo. 28.5.218 8 Uhr Institut für Informatik Prof. r. Volker Heun Ludwig-Maximilians-Universität München Formale Sprachen
Formale Sprachen und Komplexität, SS 18, Prof. r. Volker Heun Übungsblatt 4 bgabe: bis Mo. 28.5.218 8 Uhr Institut für Informatik Prof. r. Volker Heun Ludwig-Maximilians-Universität München Formale Sprachen
FoSAP-Panikzettel. Caspar Zecha, Philipp Schröer, Fabian Meyer, Christoph von Oy, Tobias Polock 5. April Grundlagen 2
 FoSAP-Panikzettel Caspar Zecha, Philipp Schröer, Fabian Meyer, Christoph von Oy, Tobias Polock 5. April 2018 Inhaltsverzeichnis 1 Grundlagen 2 2 DFAs 2 2.1 Produktkonstruktion..............................
FoSAP-Panikzettel Caspar Zecha, Philipp Schröer, Fabian Meyer, Christoph von Oy, Tobias Polock 5. April 2018 Inhaltsverzeichnis 1 Grundlagen 2 2 DFAs 2 2.1 Produktkonstruktion..............................
c) {abcde, abcfg, bcade, bcafg} d) {ade, afg, bcde, bcfg} c) {abcabc} d) {abcbc, abc, a} c) {aa, ab, ba, bb} d) {{aa}, {ab}, {ba}, {bb}}
 2 Endliche Automaten Fragen 1. Was ergibt sich bei {a, bc} {de, fg}? a) {abc, defg} b) {abcde, abcfg} c) {abcde, abcfg, bcade, bcafg} d) {ade, afg, bcde, bcfg} 2. Was ergibt sich bei {abc, a} {bc, λ}?
2 Endliche Automaten Fragen 1. Was ergibt sich bei {a, bc} {de, fg}? a) {abc, defg} b) {abcde, abcfg} c) {abcde, abcfg, bcade, bcafg} d) {ade, afg, bcde, bcfg} 2. Was ergibt sich bei {abc, a} {bc, λ}?
Informatik III. Christian Schindelhauer Wintersemester 2006/ Vorlesung
 Informatik III Christian Schindelhauer Wintersemester 2006/07 13. Vorlesung 07.12.2006 1 Überblick: Die Church- Turing-These Turing-Maschinen 1-Band Turing-Maschine Mehrband-Turing-Maschinen Nichtdeterministische
Informatik III Christian Schindelhauer Wintersemester 2006/07 13. Vorlesung 07.12.2006 1 Überblick: Die Church- Turing-These Turing-Maschinen 1-Band Turing-Maschine Mehrband-Turing-Maschinen Nichtdeterministische
Kontextfreie Sprachen werden von PDAs akzeptiert
 Kontextfreie Sprachen werden von PDAs akzeptiert Sei G = (Σ, V, S, P) eine kontextfreie Grammatik. Dann gibt es einen PDA A mit L(A) = L(G). Der PDA A arbeitet mit nur einem Zustand q 0, besitzt das Kelleralphabet
Kontextfreie Sprachen werden von PDAs akzeptiert Sei G = (Σ, V, S, P) eine kontextfreie Grammatik. Dann gibt es einen PDA A mit L(A) = L(G). Der PDA A arbeitet mit nur einem Zustand q 0, besitzt das Kelleralphabet
Lösung zur Klausur. Grundlagen der Theoretischen Informatik im WiSe 2003/2004
 Lösung zur Klausur Grundlagen der Theoretischen Informatik im WiSe 2003/2004 1. Geben Sie einen deterministischen endlichen Automaten an, der die Sprache aller Wörter über dem Alphabet {0, 1} akzeptiert,
Lösung zur Klausur Grundlagen der Theoretischen Informatik im WiSe 2003/2004 1. Geben Sie einen deterministischen endlichen Automaten an, der die Sprache aller Wörter über dem Alphabet {0, 1} akzeptiert,
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Release 1.0 Daniel Schmidt 13. 11. 2013 Inhaltsverzeichnis 1 Vorlesungsverzeichnis: 1 1.1 Vorlesungen............................................... 1 2 Definitionsverzeichnis:
Theoretische Grundlagen der Informatik Release 1.0 Daniel Schmidt 13. 11. 2013 Inhaltsverzeichnis 1 Vorlesungsverzeichnis: 1 1.1 Vorlesungen............................................... 1 2 Definitionsverzeichnis:
Abschlusseigenschaften
 Abschlusseigenschaften Die Klasse der regulären Sprachen hat eine große Zahl nützlicher Eigenschaften, insbesondere die folgenden Abschlusseigenschaften: Satz: Die Klasse der regulären Sprachen ist abgeschlossen
Abschlusseigenschaften Die Klasse der regulären Sprachen hat eine große Zahl nützlicher Eigenschaften, insbesondere die folgenden Abschlusseigenschaften: Satz: Die Klasse der regulären Sprachen ist abgeschlossen
Beispiel Produktautomat
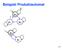 Beispiel Produktautomat 0 1 p 0 p 1 p 2 q 0 q 1 445 Vereinfachte Konstruktion f. NFAs Seien M 1,M 2 NFAs f. die Sprachen L 1 und L 2. Konstruktion eines NFAs für L 1 L 2 : Erzeuge Kopien von M 1 und M
Beispiel Produktautomat 0 1 p 0 p 1 p 2 q 0 q 1 445 Vereinfachte Konstruktion f. NFAs Seien M 1,M 2 NFAs f. die Sprachen L 1 und L 2. Konstruktion eines NFAs für L 1 L 2 : Erzeuge Kopien von M 1 und M
10 Kellerautomaten. Kellerautomaten
 10 Kellerautomaten Bisher hatten wir kontextfreie Sprachen nur mit Hilfe von Grammatiken charakterisiert. Wir haben gesehen, dass endliche Automaten nicht in der Lage sind, alle kontextfreien Sprachen
10 Kellerautomaten Bisher hatten wir kontextfreie Sprachen nur mit Hilfe von Grammatiken charakterisiert. Wir haben gesehen, dass endliche Automaten nicht in der Lage sind, alle kontextfreien Sprachen
FORMALE SYSTEME. Wiederholung. Beispiel: NFA. Wiederholung: NFA. 4. Vorlesung: Nichtdeterministische Endliche Automaten. TU Dresden, 20.
 Wiederholung FORMALE SYSTEME 4. Vorlesung: Nichtdeterministische Endliche Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme Grammatiken können Sprachen beschreiben und sie grob in Typen unterteilen
Wiederholung FORMALE SYSTEME 4. Vorlesung: Nichtdeterministische Endliche Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme Grammatiken können Sprachen beschreiben und sie grob in Typen unterteilen
Ogden s Lemma: Der Beweis (1/5)
 Ogden s Lemma: Der Beweis (1/5) Wir betrachten zuerst die Rahmenbedingungen : Laut dem auf der vorhergehenden Folie zitierten Satz gibt es zur kontextfreien Sprache L eine Grammatik G = (Σ, V, S, P) in
Ogden s Lemma: Der Beweis (1/5) Wir betrachten zuerst die Rahmenbedingungen : Laut dem auf der vorhergehenden Folie zitierten Satz gibt es zur kontextfreien Sprache L eine Grammatik G = (Σ, V, S, P) in
Kapitel 2: Formale Sprachen Gliederung. 0. Grundbegriffe 1. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie
 Gliederung. Grundbegriffe. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.. Chomsky-Grammatiken 2.2. Reguläre Sprachen (noch weiter) 2.3. Kontextfreie Sprachen 2/4,
Gliederung. Grundbegriffe. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.. Chomsky-Grammatiken 2.2. Reguläre Sprachen (noch weiter) 2.3. Kontextfreie Sprachen 2/4,
Technische Universität München Sommer 2016 Prof. J. Esparza / Dr. M. Luttenberger, S. Sickert 2. Mai HA-Lösung. TA-Lösung
 Technische Universität München Sommer 2016 Prof. J. Esparza / Dr. M. Luttenberger, S. Sickert 2. Mai 2016 HA-Lösung TA-Lösung Einführung in die theoretische Informatik Aufgabenblatt 2 Beachten Sie: Soweit
Technische Universität München Sommer 2016 Prof. J. Esparza / Dr. M. Luttenberger, S. Sickert 2. Mai 2016 HA-Lösung TA-Lösung Einführung in die theoretische Informatik Aufgabenblatt 2 Beachten Sie: Soweit
Minimalautomaten. Minimalautomaten. Frage: Ist der Äquivalenzautomat A der kleinste Automat ( Minimalautomat ) der die Sprache L(A) erkennt?
 Minimalautomaten Frage: Ist der Äquivalenzautomat A der kleinste Automat ( Minimalautomat ) der die Sprache L(A) erkennt? 1 Minimalautomaten Satz: Falls A keine unerreichbaren Zustände hat, ist A der kleinste
Minimalautomaten Frage: Ist der Äquivalenzautomat A der kleinste Automat ( Minimalautomat ) der die Sprache L(A) erkennt? 1 Minimalautomaten Satz: Falls A keine unerreichbaren Zustände hat, ist A der kleinste
Algorithmen mit konstantem Platzbedarf: Die Klasse REG
 Algorithmen mit konstantem Platzbedarf: Die Klasse REG Sommerakademie Rot an der Rot AG 1 Wieviel Platz brauchen Algorithmen wirklich? Daniel Alm Institut für Numerische Simulation Universität Bonn August
Algorithmen mit konstantem Platzbedarf: Die Klasse REG Sommerakademie Rot an der Rot AG 1 Wieviel Platz brauchen Algorithmen wirklich? Daniel Alm Institut für Numerische Simulation Universität Bonn August
Theoretische Informatik Mitschrift
 3. Endliche Automaten endliche Zustandsübergangssysteme Theoretische Informatik Mitschrift Beispiel: 2-Bit-Ringzähler: ={Inc} L R ={IncInc Inc,Inc 7, Inc 11,...} n ' mod ' 4=3 ={Inc n k 0.n=4 k3 } 2-Bit-Ringzähler
3. Endliche Automaten endliche Zustandsübergangssysteme Theoretische Informatik Mitschrift Beispiel: 2-Bit-Ringzähler: ={Inc} L R ={IncInc Inc,Inc 7, Inc 11,...} n ' mod ' 4=3 ={Inc n k 0.n=4 k3 } 2-Bit-Ringzähler
Automaten und Formale Sprachen SoSe 2013 in Trier
 Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
liefern eine nicht maschinenbasierte Charakterisierung der regulären
 Reguläre Ausdrücke 1 Ziel: L=L M für NFA M L=L(r) für einen regulären Ausdruck r Reguläre Ausdrücke über einem Alphabet Σ Slide 1 liefern eine nicht maschinenbasierte Charakterisierung der regulären Sprachen
Reguläre Ausdrücke 1 Ziel: L=L M für NFA M L=L(r) für einen regulären Ausdruck r Reguläre Ausdrücke über einem Alphabet Σ Slide 1 liefern eine nicht maschinenbasierte Charakterisierung der regulären Sprachen
20. REGULÄRE SPRACHEN
 20. REGULÄRE SPRACHEN Zum Abschluss betrachten wir die kleinste der Chomsky-Klassen, die Klasse der rechtslinearen Sprachen, die auch als reguläre Sprachen bezeichnet werden. Wir führen zunächst eine Normalform
20. REGULÄRE SPRACHEN Zum Abschluss betrachten wir die kleinste der Chomsky-Klassen, die Klasse der rechtslinearen Sprachen, die auch als reguläre Sprachen bezeichnet werden. Wir führen zunächst eine Normalform
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2 Lösungsblatt 2. Mai 2 Einführung in die Theoretische Informatik
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2 Lösungsblatt 2. Mai 2 Einführung in die Theoretische Informatik
Theoretische Grundlagen der Informatik. Vorlesung am 02. November INSTITUT FÜR THEORETISCHE INFORMATIK
 Theoretische Grundlagen der Informatik Vorlesung am 2. November 27 2..27 Dorothea Wagner - Theoretische Grundlagen der Informatik KIT Die Forschungsuniversität in der Vorlesung am 2. November 27 Helmholtz-Gemeinschaft
Theoretische Grundlagen der Informatik Vorlesung am 2. November 27 2..27 Dorothea Wagner - Theoretische Grundlagen der Informatik KIT Die Forschungsuniversität in der Vorlesung am 2. November 27 Helmholtz-Gemeinschaft
Deterministische und nichtdeterministische Turing-Maschinen, Typ1- und Typ0-Sprachen
 Dr. Sebastian Bab WiSe 12/13 Theoretische Grundlagen der Informatik für TI Termin: VL 15 + 16 vom 17.12.2012 und 20.12.2012 Deterministische und nichtdeterministische Turing-Maschinen, Typ1- und Typ0-Sprachen
Dr. Sebastian Bab WiSe 12/13 Theoretische Grundlagen der Informatik für TI Termin: VL 15 + 16 vom 17.12.2012 und 20.12.2012 Deterministische und nichtdeterministische Turing-Maschinen, Typ1- und Typ0-Sprachen
Endliche Automaten. Endliche Automaten 1 / 115
 Endliche Automaten Endliche Automaten 1 / 115 Endliche Automaten Endliche Automaten erlauben eine Beschreibung von Handlungsabläufen: Wie ändert sich ein Systemzustand in Abhängigkeit von veränderten Umgebungsbedingungen?
Endliche Automaten Endliche Automaten 1 / 115 Endliche Automaten Endliche Automaten erlauben eine Beschreibung von Handlungsabläufen: Wie ändert sich ein Systemzustand in Abhängigkeit von veränderten Umgebungsbedingungen?
Grundlagen der Informatik. Prof. Dr. Stefan Enderle NTA Isny
 Grundlagen der Informatik Prof. Dr. Stefan Enderle NTA Isny 1. Automaten und Sprachen 1.1 Endlicher Automat Einen endlichen Automaten stellen wir uns als Black Box vor, die sich aufgrund einer Folge von
Grundlagen der Informatik Prof. Dr. Stefan Enderle NTA Isny 1. Automaten und Sprachen 1.1 Endlicher Automat Einen endlichen Automaten stellen wir uns als Black Box vor, die sich aufgrund einer Folge von
Grundlagen der theoretischen Informatik
 Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 30.04.2013 Grenzen regulärer Sprachen Wie beweist man, dass eine Sprache nicht regulär
Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 30.04.2013 Grenzen regulärer Sprachen Wie beweist man, dass eine Sprache nicht regulär
Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit. Zugangsnummer: 3288
 Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit Wiederholung Kapitel 2 http://pingo.upb.de Zugangsnummer: 3288 Dozent: Jun.-Prof. Dr. D. Baumeister
Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit Wiederholung Kapitel 2 http://pingo.upb.de Zugangsnummer: 3288 Dozent: Jun.-Prof. Dr. D. Baumeister
Automaten und Formale Sprachen SoSe 2007 in Trier. Henning Fernau Universität Trier
 Automaten und Formale Sprachen SoSe 2007 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche Automaten und
Automaten und Formale Sprachen SoSe 2007 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche Automaten und
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 18. Januar 2018 INSTITUT FÜR THEORETISCHE 0 18.01.2018 Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE KIT Die Forschungsuniversität
Theoretische Grundlagen der Informatik Vorlesung am 18. Januar 2018 INSTITUT FÜR THEORETISCHE 0 18.01.2018 Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE KIT Die Forschungsuniversität
Grundlagen der theoretischen Informatik
 Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 04.06.2013 An den Transitionen sieht man zunächst, dass nur die folgenden Zustandsübergänge
Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 04.06.2013 An den Transitionen sieht man zunächst, dass nur die folgenden Zustandsübergänge
Beweisidee: 1 Verwende den Keller zur Simulation der Grammatik. Leite ein Wort. 2 Problem: der Keller darf nicht beliebig verwendet werden, man kann
 Automaten und Formale prachen alias Theoretische Informatik ommersemester 2011 Dr. ander Bruggink Übungsleitung: Jan tückrath Wir beschäftigen uns ab jetzt einige Wochen mit kontextfreien prachen: Kontextfreie
Automaten und Formale prachen alias Theoretische Informatik ommersemester 2011 Dr. ander Bruggink Übungsleitung: Jan tückrath Wir beschäftigen uns ab jetzt einige Wochen mit kontextfreien prachen: Kontextfreie
Potenzmengenkonstruktion. Vergleich DFAs NFAs. NFA DFA ohne überflüssige Zust. Ansatz nicht praktikabel
 Vergleich DFAs NFAs Frage: Können NFAs nichtreguläre Sprachen erkennen? NEIN Potenzmengenkonstruktion Gegeben: NFA (Q,Σ,q 0,δ,F), konstruiere DFA: Q =P (Q), q 0 = {q 0 }, F ={q q F } Satz T4.4.5: Zu jedem
Vergleich DFAs NFAs Frage: Können NFAs nichtreguläre Sprachen erkennen? NEIN Potenzmengenkonstruktion Gegeben: NFA (Q,Σ,q 0,δ,F), konstruiere DFA: Q =P (Q), q 0 = {q 0 }, F ={q q F } Satz T4.4.5: Zu jedem
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2012
 Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Abgeschlossenheit (Definition)
Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Abgeschlossenheit (Definition)
Automaten und Formale Sprachen SoSe 2013 in Trier
 Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2 Lösungsblatt 2 3. Mai 2 Einführung in die Theoretische Informatik Hinweis:
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2 Lösungsblatt 2 3. Mai 2 Einführung in die Theoretische Informatik Hinweis:
Formale Sprachen. Formale Grundlagen (WIN) 2008S, F. Binder. Vorlesung im 2008S
 Formale Grundlagen (WIN) Franz Binder Institut für Algebra Johannes Kepler Universität Linz Vorlesung im 2008S http://www.algebra.uni-linz.ac.at/students/win/fg Inhalt Das Alphabet Σ sei eine endliche
Formale Grundlagen (WIN) Franz Binder Institut für Algebra Johannes Kepler Universität Linz Vorlesung im 2008S http://www.algebra.uni-linz.ac.at/students/win/fg Inhalt Das Alphabet Σ sei eine endliche
Übersicht. 3 3 Kontextfreie Sprachen
 Formale Systeme, Automaten, Prozesse Übersicht 3 3.1 Kontextfreie Sprachen und Grammatiken 3.2 Ableitungsbäume 3.3 Die pre -Operation 3.4 Entscheidungsprobleme für CFGs 3.5 Normalformen für CFGs 3.6 Chomsky-Normalform
Formale Systeme, Automaten, Prozesse Übersicht 3 3.1 Kontextfreie Sprachen und Grammatiken 3.2 Ableitungsbäume 3.3 Die pre -Operation 3.4 Entscheidungsprobleme für CFGs 3.5 Normalformen für CFGs 3.6 Chomsky-Normalform
Diskrete Mathematik. Anna-Lena Rädler Christina Kohl Georg Moser Christian Sternagel Vincent van Oostrom
 Diskrete Mathematik Anna-Lena Rädler Christina Kohl Georg Moser Christian Sternagel Vincent van Oostrom Zusammenfassung der letzten LVA Definition Ein ɛ-nea N = (Q, Σ, δ, S, F) ist gegeben durch eine endliche
Diskrete Mathematik Anna-Lena Rädler Christina Kohl Georg Moser Christian Sternagel Vincent van Oostrom Zusammenfassung der letzten LVA Definition Ein ɛ-nea N = (Q, Σ, δ, S, F) ist gegeben durch eine endliche
Grundlagen der Theoretischen Informatik, SoSe 2008
 2. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 1 Einelementiges Alphabet (4 Punkte) (a) Geben
2. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 1 Einelementiges Alphabet (4 Punkte) (a) Geben
Technische Universität München Sommer 2016 Prof. J. Esparza / Dr. M. Luttenberger, S. Sickert 11. Juli HA-Lösung. TA-Lösung
 Technische Universität München Sommer 26 Prof. J. Esparza / Dr. M. Luttenberger, S. Sickert. Juli 26 HA-Lösung TA-Lösung Einführung in die theoretische Informatik Aufgabenblatt 3 Beachten Sie: Soweit nicht
Technische Universität München Sommer 26 Prof. J. Esparza / Dr. M. Luttenberger, S. Sickert. Juli 26 HA-Lösung TA-Lösung Einführung in die theoretische Informatik Aufgabenblatt 3 Beachten Sie: Soweit nicht
WS07/08 Automaten und Formale Sprachen 5. Vorlesung
 WS7/8 Automaten und Formale Sprachen 5. Vorlesung Martin Dietzfelbinger 3. November 27 FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/8 3..27 Stichworte Induktive Definitionen: (i) Basisobjekte,
WS7/8 Automaten und Formale Sprachen 5. Vorlesung Martin Dietzfelbinger 3. November 27 FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/8 3..27 Stichworte Induktive Definitionen: (i) Basisobjekte,
Formale Sprachen. Reguläre Sprachen. Rudolf FREUND, Marian KOGLER
 Formale Sprachen Reguläre Sprachen Rudolf FREUND, Marian KOGLER Endliche Automaten - Kleene STEPHEN KLEENE (99-994) 956: Representation of events in nerve nets and finite automata. In: C.E. Shannon und
Formale Sprachen Reguläre Sprachen Rudolf FREUND, Marian KOGLER Endliche Automaten - Kleene STEPHEN KLEENE (99-994) 956: Representation of events in nerve nets and finite automata. In: C.E. Shannon und
7 Endliche Automaten. 7.1 Deterministische endliche Automaten
 7 Endliche Automaten 7.1 Deterministische endliche Automaten 7.2 Nichtdeterministische endliche Automaten 7.3 Endliche Automaten mit g-übergängen Endliche Automaten 1 7.1 Deterministische endliche Automaten
7 Endliche Automaten 7.1 Deterministische endliche Automaten 7.2 Nichtdeterministische endliche Automaten 7.3 Endliche Automaten mit g-übergängen Endliche Automaten 1 7.1 Deterministische endliche Automaten
