REFERAT FÜR INNOVATIVE ARCHIKETUREN
|
|
|
- Lieselotte Schuler
- vor 7 Jahren
- Abrufe
Transkript
1 REFERAT FÜR INNOVATIVE ARCHIKETUREN THEMA CHAOSTHEORIE REFERENTEN TIMO BÖLLINGER & DOMINIC ECKART DATUM 9. NOVEMBER 2004 FACHRICHTUNG INFORMATIONSTECHNIK NETZWERK UND SOFTWARETECHNIK AN DER BERUFSAKADEMIE MANNHEIM
2 2 Inhaltsverzeichnis 1. Was versteht man unter Chaostheorie Bedeutende Namen der Chaostheorie Benoit B. Mandelbrot Jules Henri Poincaré Mitchell Feigenbaum Edward N. Lorenz Bedeutende Begriffe der Chaostheorie Selbstähnlichkeit Fraktale Phasenraum Attraktor Rössler-Attraktor Lorenz-Attraktor Schmetterlingseffekt Beispiele Mandelbrotmenge Sierpinski-Dreieck Feigenbaum Szenario Mephisto Walzer Fazit Literaturverzeichnis...17
3 3 1. Was versteht man unter Chaostheorie Unter der Chaos-Theorie versteht man die Theorie des deterministischen Chaos oder die Theorie Nichtlinearer Dynamischer Systeme, einem Teilgebiet der nichtlinearen Dynamik innerhalb von Mathematik und Physik. Sie geht u.a. auf die Arbeiten von Henri Poincaré, Edward N. Lorenz, Mitchell Feigenbaum und Benoit Mandelbrot zurück. Chaotisches Verhalten äußert sich dadurch, dass schon geringste Änderungen der Anfangsbedingungen zu sehr unterschiedlichen Ergebnissen führen können (Schmetterlingseffekt). Systeme, die chaotisches Verhalten zeigen, sind zum Beispiel: Wetter und Klima Plattentektonik Turbulenz Wirtschaftskreisläufe Internet Bevölkerungswachstum Merkmale chaotischer Systeme sind: Irreguläre Bewegung Begrenzte Vorhersagbarkeit Selbstähnlichkeit
4 4 2. Bedeutende Namen der Chaostheorie 2.1. Benoit B. Mandelbrot Der französische Mathematiker wurde am in Warschau, Polen, geboren. Er besuchte Universitäten in Frankreich und den USA und erlangte 1952 seinen Doktortitel an der Universität von Paris. Werdegang: Wirtschaftswissenschaften in Harvard Technik in Yale Physiologie am Albert Einstein College of Quelle: Medicine Mathematik in Paris und Genf 1958 arbeitete er als IBM-Fellow 1 am Thomas B. Watson Research Center in New York. Er entwickelte die Geometrie der Fraktale zu einen separaten Zweig der Mathematik. Die fraktale Geometrie unterscheidet sich durch eine abstraktere Behandlung der Dimension von der herkömmlichen Geometrie. Sie wird in wachsendem Maß auf vielen verschiedenen Gebieten der Wissenschaft und Technik angewandt. Die nach ihm benannte Mandelbrot-Menge kann mit Hilfe von Computern visualisiert werden (Mandelbrotberechnung, auch bekannt als Apfelmännchen ) Quelle: 1 Ein IBM Fellow ist eine hervorgehobene Person. Der Titel geht auf Thomas J. Watson, Jr. zurück, seit 1962 erhalten pro Jahr 4 bis 5 Personen diesen höchsten Ehrentitel, im Technologie-Bereich, bei IBM. Quelle:
5 Jules Henri Poincaré Quelle: Der französischische Mathematiker und theoretische Physiker Jules Henri Poincaré wurde am in Nancy geboren und verstarb am in Paris. Werdegang: 1879 Promotion in Caën Ordinarius für mathematische Physik an der Sorbonne in Paris 1887 Mitglied der Akademie der Wissenschaften 1906 Präsident der Akademie der Wissenschaften 1909 Mitglied der Académie française Poincaré lieferte grundlegende Beiträge zu den unterschiedlichsten Teilgebieten der Mathematik. Ein wesentlicher Beitrag zur Entwicklung der speziellen Relativitätstheorie war seine Arbeit über die Dynamik der Elektronen (1906). Er veröffentlichte etwa 250 Werke, z.b. den Gebieten Topologie (Poincaré-Vermutung), Funktionentheorie, Differentialgleichungen, Wahrscheinlichkeitstheorie, Chaostheorie, Optik, Himmelsmechanik, Elektromagnetismus und Relativitätstheorie. In seinen Arbeiten hinterfragte er bereits erbrachte Beweise wie die Lagrange- und Laplace-Theorie. Henri Poincare beschäftigte sich als Erster mit dem Prinzip von Chaos in deterministischen Systemen, diese Arbeit erhielt aber erst viel später, 1963, die Anerkennung der wissenschaftlichen Welt. Neben seinen wissenschaftlichen Arbeiten, verfasste er auch diverse populär wissenschaftliche Werke wie "Science and Method" und "The Value of Science".
6 Mitchell Feigenbaum Der amerikanische Physiker Mitchell Feigenbaum erkannte bestimmte übereinstimmende Muster in chaotischen Systemen, woraus er Kenngrößen ableitete, die man heute Feigenbaum-Konstanten nennt. Diese werden mit der Geometrie der Fraktale in Zusammenhang gebracht. Quelle: Entwickler des einfachsten chaotischen Systems (Feigenbaum Szenario) Edward N. Lorenz Der Meteorologe war Professor am MIT (Massachusetts Institute of Technology) entdeckte er durch vermeintlich fehlerhafte Computerauswertungen von Wetterdaten den sogenannten Schmetterlingseffekt. Quelle:
7 7 3. Bedeutende Begriffe der Chaostheorie 3.1. Selbstähnlichkeit Der Begriff Selbstähnlichkeit beschreibt die Eigenschaft eines Objektes, wonach ein kleiner Ausschnitt dem gesamten Objekt ähnelt. Beispielsweise ähnelt die Struktur eines vergrößerten Ausschnittes eines Berggipfels dem gesamten Gebirge selbst, während sich der Ausschnitt einer Kugeloberfläche bei starker Vergrößerung immer weiter einer Fläche nähert. Ein Gebilde wird selbstähnlich oder skaleninvariant genannt, wenn ein Teil ähnlich dem Gesamtobjekt ist. Eine erstaunliche Konsequenz der Selbstähnlichkeit stellt die Tatsache dar, dass sich ein Teil von der Gesamtfigur nur in der Größe unterscheidet, egal wie stark man diesen verkleinert. Beim hineinzoomen in eine selbstähnliche Figur findet sich unbegrenzt immer wieder die selbe Struktur. Eine triviale Ausnahme stellt eine einfache Strecke dar, die bei Verkleinerung ebenfalls in einen Teil von sich selbst übergeht, also auch selbstähnlich ist. Es lässt sich also auch in einem chaotischen System eine gewisse Ordnung feststellen Fraktale Um komplexere Gebilde als Geraden, Kreise, Würfel oder Kugeln zu beschreiben bedarf es einer besonderen Geometrie. Benoit B. Mandelbrot hat dazu die Begriffe "Fraktal" und "fraktale Geometrie" in den siebziger Jahren eingeführt. In der Natur kommen häufig Formen vor, die sich mit Hilfe fraktaler Geometrien beschreiben lassen, wie z.b. Berge oder Küstenlinien. Beispiele für künstliche Fraktale sind das sogenannte Sierpinski-Dreieck oder die Mandelbrotmenge. Fraktale sind wie andere Formen oder Gebilde definierte Mengen im n-dimensionalen metrischen Raum, jedoch muss bei der mathematischen Behandlung von einer fraktalen Dimension ausgegangen werden. Die Hausdorff-Dimension eines Fraktals ist stets größer als ihre topologische Dimension. Die topologische Dimension entspricht der Anzahl der für die Parameter-
8 8 darstellung der Kurve benötigte Variablen und kann nur ganzzahlige Werte annehmen ( normale Geometrie ), während die Hausdorff-Dimension D (oder fraktale Dimension) beliebige positive reelle Werte annehmen kann. Man spricht daher auch von gebrochenen Dimensionen. Intuitiv betrachtet kann D als Meßzahl für die "Komplexität" bzw. "Rauheit" der Kurve aufgefasst werden. Beispielsweise erscheint ein Fraktal der Dimension D = 1,125 "einfacher" und "glatter" als ein Fraktal der Dimension D = 1,837. Man unterscheidet zwischen deterministischen und stochastischen Fraktalen. Bei stochastischen Fraktalen wird der Generierungsprozess durch zufällige Schwankungen mitbestimmt, während deterministische Fraktale (wie z.b. das Sierpinski- Dreieck) eine sehr reguläre Struktur aufweisen. Allen Fraktalen gleich ist ihre interessanteste Eigenschaft, ihre Vergrößerungsinvarianz, also die Tatsache, dass ein Fraktal unabhängig von der Vergrößerungsstufe stets die gleiche Struktur aufweist (Selbstähnlichkeit). Da Selbstähnlichkeit auch in der Natur häufig vorkommt (Pflanzen, Küstenlinien, Berge, Wolken etc.), sind stochastische Fraktale besonders gut für die künstliche Genierung von komplexen Naturszenen, sowie für die Modellierung von Naturvorgängen geeignet. Fraktale haben ebenfalls eine Bedeutung bei der fraktalen Kompression (Komprimierung von Dateien). Fraktale werden zwar in der Regel sehr einfach definiert und nur durch kleine Datenmengen beschrieben, allerdings erfordert die hohe Anzahl der iterativ auf die anfallenden Daten angewandte Definitionsvorschrift einen enormen Rechenaufwand. Deshalb wurden die bereits entdeckten und beschriebenen Fraktale auch erst durch moderne Computeranlagen visualisiert und populär.
9 Phasenraum Der Phasenraum wird von zeitlich veränderlichen Variablen, die zu einem System von Differentialgleichungen (DGL) und ihren zeitlichen Ableitungen gehören, aufgespannt. Die grafische Darstellung nennt man Phasenraumportrait oder einfach Phasenportrait. Das Phasenraumportrait kann zur graphisch Lösung dieser Funktionen verwendet werden, ohne die eigentliche Lösungsfunktion der DGL s und deren Ableitungen zu kennen. Das Phasenportrait kann nicht die rechnerische Lösung des Systems ersetzen, bietet aber für bestimmte Fragestellungen eine Lösung. Aus der Darstellung können Eigenschaften wie Stabilität oder die Gleichgewichtspunkte abgelesen werden, aber auch die Kritischen Punkte. Diese spielen eine sehr wichtige Rolle, denn an diesen Punkten sind alle zeitlichen Ableitungen null. Wenn man nun die DGL s um die Kritischen Punkte linearisiert, kann das Verhalten der DGL s um die Punkte näher betrachtet werden. Dieses Verfahren wird allgemein als lineare Stabilitätsanalyse bezeichnet. Mathematisch lässt sich beweisen, dass die Punkte im Phasenraum das durch die DGL s und die Ableitung aufgespannte System eindeutig charakterisieren. Gerade im Bereichen, in denen mit komplexen Systemen gearbeitet wird, Quelle: hat der Phasenraum eine hohe Bedeutung erlangt. Ein Beispiel für die Anwendung ist zum Beispiel in der Biologie, das Räuber-Beute-Modell. Dieses spiegelt die Populationsbestände wieder. Andere Beispiele kommen z.b. aus der Physik: dort werden Phasenraumportraits überwiegend um die Entwicklung von Systemen (Oszillatoren, Entropie 2 von Vielteilchensystemen) zu veranschaulichen. 2 Die Entropie (zu altgr. entrépein, "umkehren") ist ein Maß für die Unordnung oder Zufälligkeit eines Systems (Quelle: de.wikipedia.org )
10 Attraktor Ein Attraktor ist eine klar erkennbare Struktur in einem Phasenraum. Dieser zeigt die Zustände, auf die sich ein System im Laufe der Zeit hinbewegt. Die Attraktoren können in zwei Gruppen aufgeteilt werden: Attraktoren mit ganzzahliger Dimension: Diese beschreiben nichtchaotische Systeme. (Punkt-Attraktoren, Grenzzyklen) Attraktoren mit nicht ganzzahliger Dimension: Diese beschreiben oft chaotische Systeme: sie werden auch seltsame Attraktoren genannt. Zwei Beispiele für Seltsame Attraktoren sind die von Lorenz und Rössler Rössler-Attraktor Der Rössler-Attraktor ist nach Prof. Dr. Otto E. Rössler genannt. Er lehrt am Institut für Physikalische und Theoretische Chemie in Tübingen. Der Attraktor ist durch das folgende Differentialgleichungssystem definiert: Die numerische Lösung sieht für Parameter a=0.15, b=0.20, c=10.0, Schritte, dt=0.5, so aus: Quelle: de.wikipedia.org
11 Lorenz-Attraktor Der Lorenz-Attraktor wurde nach dem Meteorologen Edward N. Lorenz genannt. Er dient zur Lösung eines Systems von drei gekoppelten, nichtlinearen Differenzialgleichungen. Als einfaches Modell zur Lösung von Konvektionsströmungen in der Erdatmosphäre wurde dieses Modell von Edward N. Lorenz erstellt. Im Laufe der Zeit hat sich herausgestellt, dass dieses Verfahren auch im Bereich der Modellierung von Lasern eingesetzt werden kann. In der numerischen Lösung des betrachteten Systems erkennt man ein bestimmtes chaotisches Verhalten der Parameter. Wie schon beim Rössler-Aktraktor wird das Runge-Kutta-Verfahren zur numerischen Lösung herangezogen. In der folgenden 3D-Grafik sind die gezeichneten Ergebnisse einer solchen Berechnung abgebildet. Quelle: de.wikipedia.org
12 Schmetterlingseffekt Der Schmetterlingseffekt ist eine zufällige Entdeckung des Meteorologen Edward Lorenz, der 1963 Wetterdaten mit dem Computer berechnete um Vorhersagen zu erstellen. Er rundete die Werte auf drei Stellen hinter dem Komma, da die Maschinen dieser Zeit noch sehr langsam arbeiteten. Lorenz misstraute den erhaltenen Ergebnissen, nicht zuletzt weil die Computer auch unzuverlässig arbeiteten. So gab er als Startmenge nicht die Daten des Vortages, sondern Zwischenwerte ein, berechnete damit also einen gewissen Zeitraum doppelt. Lorenz überlegte sich, dass ein Fehler vorliegen musste, wenn die doppelt berechneten Szenarien voneinander abweichen würden. Die beiden Kurven hatten in der Tat nichts mehr gemeinsam. Als Lorenz die gleichen Anfangswerte eingab, stellte er überrascht fest, dass der Computer identische Ergebnisse lieferte, also in Ordnung sein musste. Bald fand er heraus, dass der Computer mit mehreren Stellen hinter dem Komma rechnete als er eingegeben hatte. Dieser Unterschied von einem hundertstel Prozent hatte die Vorhersage komplett durcheinander gebracht, obwohl es nur einem zusätzlichen leichten Windhauch entsprach! Also konnte der Flügelschlag eines Schmetterlings theoretisch einen Orkan auslösen. So ging dieses Phänomen als "Schmetterlingseffekt" in die Wissenschaftsgeschichte ein.
13 13 4. Beispiele 4.1. Mandelbrotmenge Wie bereits weiter oben erwähnt, wird die Mandelbrotmenge umgangssprachlich auch "Apfelmännchen" genannt. Diese Menge geht auf Benoit Mandelbrot zurück, der dieses Fraktal im Jahre 1980 entdeckte. Die Mandelbrot-Menge spielt auch heute noch eine wichtige Rolle in der Chaostheorie. Es ist wohl nicht übertrieben wenn man behauptet, dass die Mandelbromenge die höchste geometrische Formenvielfalt besitzt. Diese Aussage lässt sich relativ einfach veranschaulichen, indem man dem Kritiker den Rand näher bringt. Das Anwendungsgebiet der Mandelbrotmenge: Die Mandelbrotmenge wird im Zusammenhang mit der Julia-Menge eingesetzt, sie ist genauer gesagt die beschränkte Form der Julia-Menge, da ihr Anfangswert auf z0 = 0 gesetzt wir. Die Julia- bzw. Mandelbrot- Menge hat folgendes Bildungsgesetz für die Zahlenfolge z,..., z 0, z1 z n : = z c n + 1 n ² + c C Die grafische Darstellung erfolgt in einer komplexen Ebene, wobei ein Punkt der Mandelbrotmenge schwarz gezeichnet wird. Die anderen Punkte werden je nach ihrem Divergenzgrad mit unterschiedlichen Farben gezeichnet. Jeder Punkt c in der komplexen Ebene entspricht einer Julia-Menge. Über die Position des Punktes c im komplexen Raum und im Bezug auf die Mandelbrotmenge kann nun auf die Eigenschaften der Julia-Menge geschlossen werden: Ist c ein Teil der Mandelbrot-Menge, so ist die Julia-Menge zusammenhängend. Ist dies nicht der Fall, so ist die Julia-Menge eine Cantormenge 3 unzusammenhängender Punkte. Ist c am Rand der Mandelbrotmenge, so ist die Juliamenge in kleinen Umgebungen um c der Mandelbrot-Menge ähnlich. 3 Unter einer Cantor-Menge, auch Cantor-Staub oder Wischmenge genannt, versteht man eine Menge, die überabzählbar unendlich viele Elemente enthält, gleichzeitig aber ein Maß von Null (im Sinne des Riemannschen Integrals) besitzt. Quelle:
14 Sierpinski-Dreieck Das Sierpinski-Dreieck wurde nach dem polnischen Mathematiker Waclaw Sierpinski (* ) genannt. Es wird in das Gebiet der Fraktalen-Geometrie eingeordnet. Man kann das Dreieck auf verschiedenste Weisen konstruieren, auch die Dimension ist beliebig. In diesem Referat beschränken wir uns auf eine Konstruktion in der zweiten Dimension. Die Grundlage bildet ein gleichseitiges Dreieck, in diesem werden einfach die Seitenmittelpunkte bestimmt und anschließend mit Linien verbunden. Das Verfahren wird nun wiederum auf die drei äußeren der insgesamt vier entstanden Dreiecke angewendet. Dieses Verfahren kann beliebig oft durchgeführt werden. Theoretisch gesehen erhält man als Ergebnis eine Figur von endlicher Fläche, die aber einen Umfang von unendlicher Länge hat. Das Sierpinski-Dreieck hat die gebrochene Dimension von 1,2618 und erscheint dadurch einfach und glatt. Schritt 1... Schritt 2... Schritt 3... Quelle:
15 Feigenbaum Szenario Eines der einfachsten und bekanntesten Systeme der Chaosforschung ist das Feigenbaumszenario, das durch folgende Formel beschrieben wird: X (t+1) = X (t) r(1 - X (t) ) Der Parameter t repräsentiert einen Zeitpunkt, der Parameter r kann frei gewählt werden. Das Feigenbaumszenario zeigt eindrucksvoll den Übergang von einem deterministischen Zustand in einen chaotischen, unvorhersagbaren Zustand eines Systems. Ob die Lösung determiniert hängt allein von der Wahl des Parameters r ab! Wird dieser größer als 3, gewählt, springt die Lösung völlig unvorhersagbar zwischen den Extremwerten 0 und 1 hin und her (unterer Teil der Abbildung). Quelle:
16 Mephisto Walzer Ein Experiment der Uni Potsdam zeigt beeindruckend, dass durchaus auch Ordnung im Chaos gefunden werden kann. Die Abbildung zeigt die kontinuierliche Signalreihe eines Experiments mit einem Wasserboiler. Es kann eine Mittelwertfunktion gebildet werden. Darauf wird ein neues Verfahren angewandt, welches die Zeitreihe in eine Zeichenfolge umwandelt: Liegt ein Messwert über dem berechneten Mittelwert wird eine 1 gesetzt, liegt ein Wert darunter eine 0. Für das durchgeführte Experiment erhält man eine erstaunliche Folge: Wird die erhaltene Zeichenfolge nun auf innere Symmetrien und Gesetzmäßigkeiten untersucht, stellt man Folgendes fest: Auf die erste 0 folgt eine 1, auf das Paket 01 folgt 10, auf die ersten vier Zeichen 0110 folgt wiederum die Negation 1001 usw. Diese Zeichenfolge wird auch mit dem prosaischen Namen "Mephisto-Walzer" betitelt: "...der Geist, der stets verneint."
17 17 5. Fazit Die Chaostheorie hat in weiten Bereichen der Wissenschaft Einzug erhalten, da viele Probleme sich nicht durch einfache mathematische oder physikalische Modelle abbilden lassen. Die vorgestellten Methoden zeigen grundlegende Ansätze, die dann auf die jeweiligen Problemstellungen angepasst werden müssen. Dadurch können chaotische Systeme wie z.b.: Wetter und Klima Plattentektonik Turbulenz Wirtschaftskreisläufe Internet Populationswachstum Herzrhythmusstörungen Modellierung unregelmäßiger Naturformen in mathematisch fassbare Systeme überführt und/oder berechnet werden. Die Chaostheorie erlangte zunehmend durch die Weiterentwicklung leistungsfähigerer Computersysteme an Relevanz. Erst Computer versetzten die Wissenschaftler in die Lage die rechenintensiven Nichtlinearen Dynamischen Systeme zu berechnen. 6. Literaturverzeichnis
Die Chaostheorie a) Geschichtliche Betrachtung Die Chaostheorie Quellenverzeichnis
 Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften
Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften
Mathematik erzeugt grafische Kunstwerke und zauberhafte Videos: Was sind Fraktale?
 Mathematik erzeugt grafische Kunstwerke und zauberhafte Videos: Was sind Fraktale? Klaus Kusche Frühjahr 2019 Inhalt Unser Ziel Was ist ein Fraktal? Von linearen geometrischen Abbildungen zu iterierten
Mathematik erzeugt grafische Kunstwerke und zauberhafte Videos: Was sind Fraktale? Klaus Kusche Frühjahr 2019 Inhalt Unser Ziel Was ist ein Fraktal? Von linearen geometrischen Abbildungen zu iterierten
Deterministisches Chaos
 Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
Fraktale und Beispiele aus der Physik
 Fraktale und Beispiele aus der Physik Anschauung Warum beschäftigen Fraktale (auch) Naturwissenschaftler? kurze Wiederholung Konkretes Beispiel: Magnetpendel Das Experiment Mathematische Beschreibung Trajektorien
Fraktale und Beispiele aus der Physik Anschauung Warum beschäftigen Fraktale (auch) Naturwissenschaftler? kurze Wiederholung Konkretes Beispiel: Magnetpendel Das Experiment Mathematische Beschreibung Trajektorien
HARMONIK ZWISCHEN ORDNUNG UND CHAOS
 HARMONIK ZWISCHEN ORDNUNG UND CHAOS Grundstrukturen der Natur und ihre Wahrnehmung durch den Hörenden Menschen Vortrag auf dem Harmonik-Symposion 2010 am 2. Mai 2010 Hans G. Weidinger 1. Was ist Harmonik?
HARMONIK ZWISCHEN ORDNUNG UND CHAOS Grundstrukturen der Natur und ihre Wahrnehmung durch den Hörenden Menschen Vortrag auf dem Harmonik-Symposion 2010 am 2. Mai 2010 Hans G. Weidinger 1. Was ist Harmonik?
6.1 Beispiele dissipativer Systeme. Der Duffing Ozillator. Bewegungsgleichung: Nichtlinearität
 6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
Die Chaostheorie und Fraktale in der Natur
 Hallertau-Gymnasium Wolnzach Abiturjahrgang 2009/2011 Facharbeit aus dem Leistungskurs Physik Die Chaostheorie und Fraktale in der Natur Eine physikalisch-philosophische Abhandlung über das Wesen der Natur
Hallertau-Gymnasium Wolnzach Abiturjahrgang 2009/2011 Facharbeit aus dem Leistungskurs Physik Die Chaostheorie und Fraktale in der Natur Eine physikalisch-philosophische Abhandlung über das Wesen der Natur
Chaotische Systeme. ViLab. Marian Panten
 Chaotische Systeme ViLab Marian Panten Einleitung Geschichte Übersicht Merkmale und Eigenschaften Beispiele und Anwendungen Schluss 26. November 2003 - = Marian Panten - Chaotische Systeme = - 2 Einleitung
Chaotische Systeme ViLab Marian Panten Einleitung Geschichte Übersicht Merkmale und Eigenschaften Beispiele und Anwendungen Schluss 26. November 2003 - = Marian Panten - Chaotische Systeme = - 2 Einleitung
Fraktale. Mathe Fans an die Uni. Sommersemester 2009
 Fraktale Mathe Fans an die Uni Ein Fraktal ist ein Muster, das einen hohen Grad Selbstähnlichkeit aufweist. Das ist beispielsweise der Fall, wenn ein Objekt aus mehreren verkleinerten Kopien seiner selbst
Fraktale Mathe Fans an die Uni Ein Fraktal ist ein Muster, das einen hohen Grad Selbstähnlichkeit aufweist. Das ist beispielsweise der Fall, wenn ein Objekt aus mehreren verkleinerten Kopien seiner selbst
FC3 - Duffing Oszillator
 FC3 - Duffing Oszillator 4. Oktober 2007 Universität Paderborn - Theoretische Physik leer Autor: Stephan Blankenburg, Björn Lange Datum: 4. Oktober 2007 FC3 - Duffing Oszillator 3 1 Theorie komplexer Systeme
FC3 - Duffing Oszillator 4. Oktober 2007 Universität Paderborn - Theoretische Physik leer Autor: Stephan Blankenburg, Björn Lange Datum: 4. Oktober 2007 FC3 - Duffing Oszillator 3 1 Theorie komplexer Systeme
Wie lang ist die Küste Großbritanniens?
 Wie lang ist die Küste Großbritanniens? Vortrag am 16.01.2009 Fach: Physik Deterministisches Chaos Ein Vortrag von Tina Rosner und Florian Sachs Werner-von-Siemens-Gymnasium Magdeburg Gliederung 1 Das
Wie lang ist die Küste Großbritanniens? Vortrag am 16.01.2009 Fach: Physik Deterministisches Chaos Ein Vortrag von Tina Rosner und Florian Sachs Werner-von-Siemens-Gymnasium Magdeburg Gliederung 1 Das
Herbert Zeitler Wolfgang Neidhardt. Fraktale und Chaos. Eine Einführung. Wissenschaftliche Buchgesellschaft Darmstadt
 Herbert Zeitler Wolfgang Neidhardt Fraktale und Chaos Eine Einführung Wissenschaftliche Buchgesellschaft Darmstadt f INHALT Einleitung 1 I. Iteration reeller Funktionen und Chaos in dynamischen Systemen.
Herbert Zeitler Wolfgang Neidhardt Fraktale und Chaos Eine Einführung Wissenschaftliche Buchgesellschaft Darmstadt f INHALT Einleitung 1 I. Iteration reeller Funktionen und Chaos in dynamischen Systemen.
7. Systeme mit drei (und mehr) Spezies: chaotische Systeme
 7. Systeme mit drei (und mehr) Spezies: chaotische Systeme Dies kann z.b. Ein System mit mehreren verschiedenen Räubern sein, die die selben Beutetiere jagen. Auch ein nicht autonomes System mit zwei Spezies
7. Systeme mit drei (und mehr) Spezies: chaotische Systeme Dies kann z.b. Ein System mit mehreren verschiedenen Räubern sein, die die selben Beutetiere jagen. Auch ein nicht autonomes System mit zwei Spezies
8. Deterministisches Chaos
 8. Deterministisches Chaos Widerspruch: deterministisch chaotisch Schmetterlingseffekt: Der Flügelschlag eines Schmetterlings entscheidet über die Entwicklung eines Sturms. Allgemein: kleinste Änderungen
8. Deterministisches Chaos Widerspruch: deterministisch chaotisch Schmetterlingseffekt: Der Flügelschlag eines Schmetterlings entscheidet über die Entwicklung eines Sturms. Allgemein: kleinste Änderungen
Chaos Oder Mandelbrot und Peitsche
 Chaos Oder Mandelbrot und Peitsche Warum kann man das Wetter nicht genau vorhersagen? Du kennst sicher das Problem: du planst mit deiner Familie ein Picknick, dass in letzter Minute abgesagt werden muss,
Chaos Oder Mandelbrot und Peitsche Warum kann man das Wetter nicht genau vorhersagen? Du kennst sicher das Problem: du planst mit deiner Familie ein Picknick, dass in letzter Minute abgesagt werden muss,
Seltsame Attraktoren
 1 Seltsame Attraktoren Proseminar: Theoretische Physik Jonas Haferkamp 9. Juli 2014 Abbildung: Poincaré-Schnitt der Duffing-Gleichungen 2 3 Gliederung 1 Motivation 2 Was ist ein (seltsamer) Attraktor?
1 Seltsame Attraktoren Proseminar: Theoretische Physik Jonas Haferkamp 9. Juli 2014 Abbildung: Poincaré-Schnitt der Duffing-Gleichungen 2 3 Gliederung 1 Motivation 2 Was ist ein (seltsamer) Attraktor?
Algorithmen für Chaos und Fraktale
 Dietmar Herrmann Algorithmen für Chaos und Fraktale A... :.., ADDISON-WESLEY PUBLISHING COMPANY Bonn Paris Reading, Massachusetts Menlo Park, California New York. Don Mills, Ontario Wokingham, ; England
Dietmar Herrmann Algorithmen für Chaos und Fraktale A... :.., ADDISON-WESLEY PUBLISHING COMPANY Bonn Paris Reading, Massachusetts Menlo Park, California New York. Don Mills, Ontario Wokingham, ; England
2. Fraktale Geometrie
 2. Fraktale Geometrie Komplexe Systeme ohne charakteristische Längenskala z.b. Risse in festen Materialien, Küstenlinien, Flussläufe und anderes.. Skaleninvariante Systeme Gebrochene Dimensionen Fraktale
2. Fraktale Geometrie Komplexe Systeme ohne charakteristische Längenskala z.b. Risse in festen Materialien, Küstenlinien, Flussläufe und anderes.. Skaleninvariante Systeme Gebrochene Dimensionen Fraktale
Thema: Visualisierung mit MAPLE
 Ostervortrag zum Linux-Stammtisch am 07.04.2017 Thema: Visualisierung mit MAPLE Sybille Handrock 1 Computeralgebrasysteme Computeralgebra beschäftigt sich mit Methoden zum Lösen mathematischer Probleme
Ostervortrag zum Linux-Stammtisch am 07.04.2017 Thema: Visualisierung mit MAPLE Sybille Handrock 1 Computeralgebrasysteme Computeralgebra beschäftigt sich mit Methoden zum Lösen mathematischer Probleme
Dynamisches Chaos. 1. Einleitung: Determinismus und Chaos
 Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen
 Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen Auf dem Weg zu einem neuen Verständnis der Naturwissenschaften Deutsche Ausgabe bearbeitet von Eckhard Rebhan Mit 110 Abbildungen T) Piper
Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen Auf dem Weg zu einem neuen Verständnis der Naturwissenschaften Deutsche Ausgabe bearbeitet von Eckhard Rebhan Mit 110 Abbildungen T) Piper
Kantengraphen und Planare Graphen. Seminararbeit
 Kantengraphen und Planare Graphen Seminararbeit in Mathematisches Seminar für LAK 621.378 SS 2018 vorgelegt von Anna Maria Gärtner bei: Baur, Karin, Univ.-Prof. Dr.phil. Graz, 2018 Inhaltsverzeichnis 1
Kantengraphen und Planare Graphen Seminararbeit in Mathematisches Seminar für LAK 621.378 SS 2018 vorgelegt von Anna Maria Gärtner bei: Baur, Karin, Univ.-Prof. Dr.phil. Graz, 2018 Inhaltsverzeichnis 1
FRAKTALE. Eine Dokumentation von Dominik Assmann, Philipp Gewessler und Paul Maier
 FRAKTALE Eine Dokumentation von Dominik Assmann, Philipp Gewessler und Paul Maier I. Fraktale allgemein a. Mathematischer Algorithmus i. Komplexe Zahlen b. Konvergieren und Divergieren i. Bei Mandelbrotmengen
FRAKTALE Eine Dokumentation von Dominik Assmann, Philipp Gewessler und Paul Maier I. Fraktale allgemein a. Mathematischer Algorithmus i. Komplexe Zahlen b. Konvergieren und Divergieren i. Bei Mandelbrotmengen
Kunst und Wissenschaft
 Kunst und Wissenschaft HS 8 Visualisierung von Newton-Fraktalen Inhalt 1. Ist Schönheit Harmonie? Mathematik in Musik und Malerei 2. Warum heissen Fraktale Fraktale? oder: was ist hier zerbrochen? 3. Was
Kunst und Wissenschaft HS 8 Visualisierung von Newton-Fraktalen Inhalt 1. Ist Schönheit Harmonie? Mathematik in Musik und Malerei 2. Warum heissen Fraktale Fraktale? oder: was ist hier zerbrochen? 3. Was
Partielle Differentialgleichungen
 http://www.free background wallpaper.com/background wallpaper water.php Partielle Differentialgleichungen 1 E Partielle Differentialgleichungen Eine partielle Differentialgleichung (Abkürzung PDGL) ist
http://www.free background wallpaper.com/background wallpaper water.php Partielle Differentialgleichungen 1 E Partielle Differentialgleichungen Eine partielle Differentialgleichung (Abkürzung PDGL) ist
Mathematik 2 für Nichtmathematiker
 Mathematik 2 für Nichtmathematiker Funktionen - Folgen und Reihen - Differential- und Integralrechnung - Differentialgleichungen - Ordnung und Chaos von Professor Dr. Manfred Precht Dipl.-Math. Karl Voit
Mathematik 2 für Nichtmathematiker Funktionen - Folgen und Reihen - Differential- und Integralrechnung - Differentialgleichungen - Ordnung und Chaos von Professor Dr. Manfred Precht Dipl.-Math. Karl Voit
GRUNDLEGENDE MODELLE. Caroline Herbek
 GRUNDLEGENDE MODELLE Caroline Herbek Lineares Wachstum Charakteristikum: konstante absolute Zunahme d einer Größe N t in einem Zeitschritt Differenzengleichung: N t -N t-1 =d => N t = N t-1 +d (Rekursion)
GRUNDLEGENDE MODELLE Caroline Herbek Lineares Wachstum Charakteristikum: konstante absolute Zunahme d einer Größe N t in einem Zeitschritt Differenzengleichung: N t -N t-1 =d => N t = N t-1 +d (Rekursion)
1 Nicht-lineare dynamische Systeme
 1 Nicht-lineare dynamische Systeme 1.1 Charakteristika linerarer Systeme Superpositionsprinzip: Sind x 1 und x Lösungen eines linearen Systems, dann ist auch α 1 x 1 + α x eine Lösung. Berühmte Beispiele:
1 Nicht-lineare dynamische Systeme 1.1 Charakteristika linerarer Systeme Superpositionsprinzip: Sind x 1 und x Lösungen eines linearen Systems, dann ist auch α 1 x 1 + α x eine Lösung. Berühmte Beispiele:
Bedeutende Theorien des 20. Jahrhunderts
 Bedeutende Theorien des 20. Jahrhunderts Ein Vorstoß zu den Grenzen von Berechenbarkeit und Erkenntnis Quantenmechanik - Relativitätstheorie - Gravitation - Kosmologie - Chaostheorie - Prädikatenlogik
Bedeutende Theorien des 20. Jahrhunderts Ein Vorstoß zu den Grenzen von Berechenbarkeit und Erkenntnis Quantenmechanik - Relativitätstheorie - Gravitation - Kosmologie - Chaostheorie - Prädikatenlogik
Chaos im getriebenen nicht-linearen Pendel
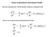 Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
Chaos - Nichtlineare Dynamik
 Äg Chaos - Nichtlineare Dynamik Renate Thies Universität Dortmund - Fachbereich Informatik Lehrstuhl für Systemanalyse (LS11) Sommersemester 2004 Chaos - Nichtlineare Dynamik 1/102 Inhaltsverzeichnis Äg
Äg Chaos - Nichtlineare Dynamik Renate Thies Universität Dortmund - Fachbereich Informatik Lehrstuhl für Systemanalyse (LS11) Sommersemester 2004 Chaos - Nichtlineare Dynamik 1/102 Inhaltsverzeichnis Äg
Vortragsthemen. Reelle Dynamik
 Vortragsthemen Jede Teilnehmende ist für ein Thema verantwortlich, das sie im Kurs vorstellen wird. Es gibt also insgesamt 15 Vorträge, 4 aus den Gebieten Reelle bzw. Komplexe Dynamik und 7 aus dem Gebiet
Vortragsthemen Jede Teilnehmende ist für ein Thema verantwortlich, das sie im Kurs vorstellen wird. Es gibt also insgesamt 15 Vorträge, 4 aus den Gebieten Reelle bzw. Komplexe Dynamik und 7 aus dem Gebiet
9 Fraktale. Dabei hängt das Ergebnis vom Maßstab der Karte und von der eingestellten Weite des Stechzirkels
 79 9 Fraktale Problemstellung Im Jahr 1967 veröffentlichte der Mathematiker Benoit Mandelbrot 3 eine Arbeit mit dem Titel How long is the coast of Britain? Statistical self-similarity and fractional dimension.
79 9 Fraktale Problemstellung Im Jahr 1967 veröffentlichte der Mathematiker Benoit Mandelbrot 3 eine Arbeit mit dem Titel How long is the coast of Britain? Statistical self-similarity and fractional dimension.
Jan Henrik Sylvester. 10. Februar 2003
 Seminar über gewöhnliche Differentialgleichungen Chaos in eindimensionalen diskreten dynamischen Systemen: Das Feigenbaum-Szenario Die logistische Abbildung Jan Henrik Sylvester 10. Februar 2003 1 Die
Seminar über gewöhnliche Differentialgleichungen Chaos in eindimensionalen diskreten dynamischen Systemen: Das Feigenbaum-Szenario Die logistische Abbildung Jan Henrik Sylvester 10. Februar 2003 1 Die
Von der Schönheit des mathematischen Chaos. Eine Einführung in Seltsame Attraktoren mit jreality
 Von der Schönheit des mathematischen Chaos Eine Einführung in Seltsame Attraktoren mit jreality Inhalt Physikalische Grundlagen Definition Eigenschaften Beispiele Implementierung Demonstration Physikalische
Von der Schönheit des mathematischen Chaos Eine Einführung in Seltsame Attraktoren mit jreality Inhalt Physikalische Grundlagen Definition Eigenschaften Beispiele Implementierung Demonstration Physikalische
Spezielle Kinetik MC 1.3. Prof. Dr. B. Dietzek. Friedrich-Schiller-Universität Jena, Institut für Physikalische Chemie. Wintersemester 2016/2017
 Spezielle Kinetik MC 1.3 Prof. Dr. B. Dietzek Friedrich-Schiller-Universität Jena, Institut für Physikalische Chemie Wintersemester 2016/2017 B. Dietzek/D. Bender Spezielle Kinetik 1 Physikalische Chemie//Master
Spezielle Kinetik MC 1.3 Prof. Dr. B. Dietzek Friedrich-Schiller-Universität Jena, Institut für Physikalische Chemie Wintersemester 2016/2017 B. Dietzek/D. Bender Spezielle Kinetik 1 Physikalische Chemie//Master
Mathematische Grundlagen der dynamischen Simulation
 Mathematische Grundlagen der dynamischen Simulation Dynamische Systeme sind Systeme, die sich verändern. Es geht dabei um eine zeitliche Entwicklung und wie immer in der Informatik betrachten wir dabei
Mathematische Grundlagen der dynamischen Simulation Dynamische Systeme sind Systeme, die sich verändern. Es geht dabei um eine zeitliche Entwicklung und wie immer in der Informatik betrachten wir dabei
Newton-Verfahren und komplexe Dynamik. Jonathan Clausing
 Newton-Verfahren und komplexe Dynamik Jonathan Clausing Newton-Verfahren und komplexe Dynamik Von nutzloser und nützlicher Mathematik Iteration komplexer Polynome Die gefüllte Julia-Menge Die Mandelbrotmenge
Newton-Verfahren und komplexe Dynamik Jonathan Clausing Newton-Verfahren und komplexe Dynamik Von nutzloser und nützlicher Mathematik Iteration komplexer Polynome Die gefüllte Julia-Menge Die Mandelbrotmenge
( ) Diskretes dynamisches Chaos. 1. Einleitung: Diskrete dynamische Systeme
 Diskretes dynamisches Chaos. Einleitung: Diskrete dynamische Systeme Verschiedene Problemstellungen können zu zeitlich diskreten Systemen (Differenzengleichungen) führen: Zinseszinsrechnung: x(n+) = x(n)
Diskretes dynamisches Chaos. Einleitung: Diskrete dynamische Systeme Verschiedene Problemstellungen können zu zeitlich diskreten Systemen (Differenzengleichungen) führen: Zinseszinsrechnung: x(n+) = x(n)
Abbildung 1: Feigenbaum-Diagramm
 Kursübersicht Im folgenden findet Ihr Zusammenfassungen zu jedem der drei Teilgebiete, die wir im Kurs behandeln möchten. Die genaue Gewichtung der drei Gebiete ist noch nicht festgelegt und hängt von
Kursübersicht Im folgenden findet Ihr Zusammenfassungen zu jedem der drei Teilgebiete, die wir im Kurs behandeln möchten. Die genaue Gewichtung der drei Gebiete ist noch nicht festgelegt und hängt von
Systemanalyse und Modellbildung
 Systemanalyse und Modellbildung Universität Koblenz-Landau Fachbereich 7: Natur- und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) 7. Zeitdiskrete Modelle 7.1
Systemanalyse und Modellbildung Universität Koblenz-Landau Fachbereich 7: Natur- und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) 7. Zeitdiskrete Modelle 7.1
SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle
 Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
Dr. Robert Strich Dr. Ysette Weiss Pidstrygach
 Kinder Uni 2008 Geheimnis Mathematik oder wo sich Mathematik verstecken kann Dr. Robert Strich Dr. Ysette Weiss Pidstrygach Mathebrille Wir begeben uns in eine ideale Welt. Unsere Expeditionsausrüstung
Kinder Uni 2008 Geheimnis Mathematik oder wo sich Mathematik verstecken kann Dr. Robert Strich Dr. Ysette Weiss Pidstrygach Mathebrille Wir begeben uns in eine ideale Welt. Unsere Expeditionsausrüstung
Fraktale und Julia-Mengen
 Uutner, J. Roser, A. Unseld, F. Fraktale und Julia-Mengen mit 77 Abbildungen Verlag Harri Deutsch Inhalt I Klassische Fraktale l 1 Cantor-Menge 2 1.1 Konstruktion und Eigenschaften 2 1.2 Triadische Darstellung
Uutner, J. Roser, A. Unseld, F. Fraktale und Julia-Mengen mit 77 Abbildungen Verlag Harri Deutsch Inhalt I Klassische Fraktale l 1 Cantor-Menge 2 1.1 Konstruktion und Eigenschaften 2 1.2 Triadische Darstellung
Sind Märkte prognostizierbar? Wie setzen wir im Berufshandel die Möglichkeiten der Erwartungshaltung im Trading ein?
 Sind Märkte prognostizierbar? Wie setzen wir im Berufshandel die Möglichkeiten der Erwartungshaltung im Trading ein? Handel Dienstleistungsgeschäft Verwaltung Worin besteht die Motivation und Notwendigkeit,
Sind Märkte prognostizierbar? Wie setzen wir im Berufshandel die Möglichkeiten der Erwartungshaltung im Trading ein? Handel Dienstleistungsgeschäft Verwaltung Worin besteht die Motivation und Notwendigkeit,
Fraktale und Chaos. Wir beschftigten uns mit Fraktalen, die aus dem Studium komplexer dynamischer
 Fraktale und Chaos Teilnehmer: Markus Auricht (Heinrich-Hertz-Oberschule) Martin Czudra (Andreas-Oberschule) Robert Foellmer (Heinrich-Hertz-Oberschule) Aser Hage-Ali (Heinrich-Hertz-Oberschule) Alexej
Fraktale und Chaos Teilnehmer: Markus Auricht (Heinrich-Hertz-Oberschule) Martin Czudra (Andreas-Oberschule) Robert Foellmer (Heinrich-Hertz-Oberschule) Aser Hage-Ali (Heinrich-Hertz-Oberschule) Alexej
Oberstufe Mathematik - Fraktale Annika Maier, Anja Schmid; Abitur 2004. Fraktale
 Fraktale 1 Einleitung : Um solche grafischen Gebilde handelt es sich in unserem mathematischen Referat Wir werden in möglichst nicht-mathematischer Sprache, also für jedermann zugänglich, beschreiben,
Fraktale 1 Einleitung : Um solche grafischen Gebilde handelt es sich in unserem mathematischen Referat Wir werden in möglichst nicht-mathematischer Sprache, also für jedermann zugänglich, beschreiben,
I N T E R M I T T E N Z U N D S T R U K T U R F U N K T I O N E N
 Lars Knapik Geophysikalisch-Meteorologisches Seminar Zusammenfassung des Vortrags vom 26.06.2008 I N T E R M I T T E N Z U N D S T R U K T U R F U N K T I O N E N Selbstähnlichkeit Um Intermittenz zu erklären
Lars Knapik Geophysikalisch-Meteorologisches Seminar Zusammenfassung des Vortrags vom 26.06.2008 I N T E R M I T T E N Z U N D S T R U K T U R F U N K T I O N E N Selbstähnlichkeit Um Intermittenz zu erklären
BERÜHMTE KURVEN Logarithmische Spirale. Die Logarithmische Spirale wird durch eine Gleichung in Polarkoordinaten angegeben: r(φ)=a*e k φ
 BERÜHMTE KURVEN Gruppenleiter: Jürgen Appell, Kristina Appell, Anna Martellotti Hilfskräfte: Alison Cross, Ruth Smith Teilnehmer(innen): Ann-Christin Gerstner, Matthias Geuder, Michael Kierstein, Lukas
BERÜHMTE KURVEN Gruppenleiter: Jürgen Appell, Kristina Appell, Anna Martellotti Hilfskräfte: Alison Cross, Ruth Smith Teilnehmer(innen): Ann-Christin Gerstner, Matthias Geuder, Michael Kierstein, Lukas
Juliamengen und Mandelbrotmenge
 Xin Xu Florian Pausinger 18. Januar 2008 Inhaltsverzeichnis 1 Mathematische Grundlagen Komplexe Zahlen Über Iterationen und beschränkte Folgen 2 Quadratische Familie Bildbeispiele 3 Charakterisierung Über
Xin Xu Florian Pausinger 18. Januar 2008 Inhaltsverzeichnis 1 Mathematische Grundlagen Komplexe Zahlen Über Iterationen und beschränkte Folgen 2 Quadratische Familie Bildbeispiele 3 Charakterisierung Über
Rückblick. Dynamische Systeme. Reiner Lauterbach. Fakultät für Mathematik, Informatik und Naturwissenschaften Universität Hamburg
 Fakultät für Mathematik, Informatik und Naturwissenschaften Universität Hamburg 5. Vorlesung Ergänzungen 14.05.2012 Satz. Die C [0, 1] ist gegeben durch C = c [0, 1] c = c j 3 j, c j {0, 2}. j=1 Beweis.
Fakultät für Mathematik, Informatik und Naturwissenschaften Universität Hamburg 5. Vorlesung Ergänzungen 14.05.2012 Satz. Die C [0, 1] ist gegeben durch C = c [0, 1] c = c j 3 j, c j {0, 2}. j=1 Beweis.
Darstellung von Kurven und Flächen
 Darstellung von Kurven und Flächen Proseminar Computergraphik, 10. Juni 2008 Christoph Dähne Seite 1 Inhalt Polygonnetze 3 Knotenliste 3 Kantenliste 3 Parametrisierte kubische Kurven 4 Definition 4 Stetigkeit
Darstellung von Kurven und Flächen Proseminar Computergraphik, 10. Juni 2008 Christoph Dähne Seite 1 Inhalt Polygonnetze 3 Knotenliste 3 Kantenliste 3 Parametrisierte kubische Kurven 4 Definition 4 Stetigkeit
Nichtlinearität in der klassischen Physik
 Nichtlinearität in der klassischen Physik Dr. Peter Schlagheck Vorlesung an der Uni Regensburg im Wintersemester 25/26 Inhaltsverzeichnis Klassische Mechanik 2. Lagrange-Formalismus........................................
Nichtlinearität in der klassischen Physik Dr. Peter Schlagheck Vorlesung an der Uni Regensburg im Wintersemester 25/26 Inhaltsverzeichnis Klassische Mechanik 2. Lagrange-Formalismus........................................
2 Selbstähnlichkeit, Selbstähnlichkeitsdimension
 9 2 Selbstähnlichkeit, Selbstähnlichkeitsdimension und Fraktale 2.1 Selbstähnlichkeit Bei den Betrachtungen zur Dimension in Kapitel 1 haben wir ähnliche (im geometrischen Sinn) Figuren miteinander verglichen.
9 2 Selbstähnlichkeit, Selbstähnlichkeitsdimension und Fraktale 2.1 Selbstähnlichkeit Bei den Betrachtungen zur Dimension in Kapitel 1 haben wir ähnliche (im geometrischen Sinn) Figuren miteinander verglichen.
Nichtlineare Phänomene und Selbstorganisation
 Nichtlineare Phänomene und Selbstorganisation Von Dr. rer i.. ibü: Rein*»i M ce Doz. Dr. rer. nat. nabii. Jürn Schmelzer Prof. Dr. rer. nat. habil. Gerd Röpke Universität Rostock Mit zahlreichen Figuren
Nichtlineare Phänomene und Selbstorganisation Von Dr. rer i.. ibü: Rein*»i M ce Doz. Dr. rer. nat. nabii. Jürn Schmelzer Prof. Dr. rer. nat. habil. Gerd Röpke Universität Rostock Mit zahlreichen Figuren
Die Darstellung nichtlinearer Bewegungsabläufe
 Die Darstellung nichtlinearer Bewegungsabläufe Die Darstellung linearer Bewegungsabläufe Manchmal sind die Dinge mehr, als sie auf den ersten Blick zu sein scheinen. Auch chaotische Systeme offenbaren
Die Darstellung nichtlinearer Bewegungsabläufe Die Darstellung linearer Bewegungsabläufe Manchmal sind die Dinge mehr, als sie auf den ersten Blick zu sein scheinen. Auch chaotische Systeme offenbaren
Motivation der Vorlesung Analysis IV
 Motivation der Vorlesung Analysis IV B. Ammann 1 1 Universität Regensburg Vorlesung Analysis IV im SS 2015 Geometrie von Untermannigfaltigkeiten Ziel: Verständnis von Kurven in der Ebene Kurven im Raum
Motivation der Vorlesung Analysis IV B. Ammann 1 1 Universität Regensburg Vorlesung Analysis IV im SS 2015 Geometrie von Untermannigfaltigkeiten Ziel: Verständnis von Kurven in der Ebene Kurven im Raum
Iteriertes Funktionensystem. Martin Aigner Rainer Brodinger Martin Rieger
 Iteriertes Funktionensystem Martin Aigner Rainer Brodinger Martin Rieger Agenda Einleitendes Beispiel Definition und Beschreibung Einsatzgebiete / Anwendungen weitere Beispiele Sierpinski-Dreieck "Das
Iteriertes Funktionensystem Martin Aigner Rainer Brodinger Martin Rieger Agenda Einleitendes Beispiel Definition und Beschreibung Einsatzgebiete / Anwendungen weitere Beispiele Sierpinski-Dreieck "Das
Mengenlehre 1-E1. M-1, Lubov Vassilevskaya
 Mengenlehre 1-E1 M-1, Lubov Vassilevskaya Abb.: Schloss (Fragment), Fulda 1-E2 M-1, Lubov Vassilevskaya Abb.: Glöcken, Darstellung einer Menge Ohne es zu wissen begegnet jedes Kleinkind dem Prinzip der
Mengenlehre 1-E1 M-1, Lubov Vassilevskaya Abb.: Schloss (Fragment), Fulda 1-E2 M-1, Lubov Vassilevskaya Abb.: Glöcken, Darstellung einer Menge Ohne es zu wissen begegnet jedes Kleinkind dem Prinzip der
Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2.
 Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) Geschwindigkeit:
Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) Geschwindigkeit:
Martin-Anderson-Nexö-Gymnasium, Dresden
 Fraktale Wechselspiel zwischen Chaos und Ordnung Teilnehmer: David Burgschweiger Tim Gabriel Welf Garkisch Anne Kell Leonard König Erik Lorenz Sofie Martins Niklas Schelten Heinrich-Hertz-Oberschule, Berlin
Fraktale Wechselspiel zwischen Chaos und Ordnung Teilnehmer: David Burgschweiger Tim Gabriel Welf Garkisch Anne Kell Leonard König Erik Lorenz Sofie Martins Niklas Schelten Heinrich-Hertz-Oberschule, Berlin
Experimente, Ideen und Entwicklung der Chaostheorie
 Experimente, Ideen und Entwicklung der Chaostheorie Stephan Lück Ursprünge der Chaostheorie Edward Lorenz (1917-2008) Meteorologe einfaches Atmosphärenmodell (ca. 1960) basierend auf Konvektion Modellexperiment
Experimente, Ideen und Entwicklung der Chaostheorie Stephan Lück Ursprünge der Chaostheorie Edward Lorenz (1917-2008) Meteorologe einfaches Atmosphärenmodell (ca. 1960) basierend auf Konvektion Modellexperiment
Die Entdeckung des Chaos
 Die Entdeckung des Chaos Dieser Artikel beschreibt das sogenannte deterministische Chaos, das in berechenbaren Rückkopplungssystemen zutage tritt. Das per Emailkontakt verfügbare Programm Feigenbaum ermöglicht
Die Entdeckung des Chaos Dieser Artikel beschreibt das sogenannte deterministische Chaos, das in berechenbaren Rückkopplungssystemen zutage tritt. Das per Emailkontakt verfügbare Programm Feigenbaum ermöglicht
Chaos Seminar Wetter und Klima. Dominik Fröschl
 Chaos Seminar Wetter und Klima Dominik Fröschl 05.02.2010 1 Inhaltsverzeichnis 1 Einleitung 3 1.1 Vorbemerkungen......................... 3 1.2 Begriffsklärung.......................... 3 1.3 Entstehung
Chaos Seminar Wetter und Klima Dominik Fröschl 05.02.2010 1 Inhaltsverzeichnis 1 Einleitung 3 1.1 Vorbemerkungen......................... 3 1.2 Begriffsklärung.......................... 3 1.3 Entstehung
Nichtlineare Dynamik Einführung
 Nichtlineare Dynamik Einführung Tobias Kerscher gekürzte Internetversion (ohne fremde Bilder) Sommerakademie Ftan 2004, 13. August Gliederung 1. Def: Nichtlineare Physik 2. Typische Beispiele 3. Dynamische
Nichtlineare Dynamik Einführung Tobias Kerscher gekürzte Internetversion (ohne fremde Bilder) Sommerakademie Ftan 2004, 13. August Gliederung 1. Def: Nichtlineare Physik 2. Typische Beispiele 3. Dynamische
Kenneth J. Falconer. Fraktale Geometrie. Mathematische Grundlagen und Anwendungen. Aus dem Englischen von Jens Meyer. Mit 98 Abbildungen
 Kenneth J. Falconer Fraktale Geometrie Mathematische Grundlagen und Anwendungen Aus dem Englischen von Jens Meyer Mit 98 Abbildungen Spektrum Akademischer Verlag Heidelberg Berlin Oxford Inhalt Vorwort
Kenneth J. Falconer Fraktale Geometrie Mathematische Grundlagen und Anwendungen Aus dem Englischen von Jens Meyer Mit 98 Abbildungen Spektrum Akademischer Verlag Heidelberg Berlin Oxford Inhalt Vorwort
Jahrbuch 2003/2004 Baues, Hans-Joachim; Jibladze, Mamuka Abbildungen zwischen Sphären
 Abbildungen zwischen Sphären Maps between spheres Baues, Hans-Joachim; Jibladze, Mamuka Max-Planck-Institut für Mathematik, Bonn Korrespondierender Autor E-Mail: baues@mpim-bonn.mpg.de Zusammenfassung
Abbildungen zwischen Sphären Maps between spheres Baues, Hans-Joachim; Jibladze, Mamuka Max-Planck-Institut für Mathematik, Bonn Korrespondierender Autor E-Mail: baues@mpim-bonn.mpg.de Zusammenfassung
Brückenkurs Mathematik. Jörn Steuding (Uni Würzburg), 25. November 2017
 Brückenkurs Mathematik Jörn Steuding (Uni Würzburg), 25. November 2017 unser Programm 11. November: 1. Zahlen und einfache Gleichungen Zahlen, Rechengesetze, lineare u. quadratische Gleichungen, Dezimalbrüche,
Brückenkurs Mathematik Jörn Steuding (Uni Würzburg), 25. November 2017 unser Programm 11. November: 1. Zahlen und einfache Gleichungen Zahlen, Rechengesetze, lineare u. quadratische Gleichungen, Dezimalbrüche,
MATHE-BRIEF. Juni 2017 Nr. 80. Die Mandelbrotmenge
 MATHE-BRIEF Juni 2017 Nr. 80 Herausgegeben von der Österreichischen Mathematischen Gesellschaft http: // www.oemg.ac.at / Mathe Brief mathe brief@oemg.ac.at Die Mandelbrotmenge Komplexe Zahlen werden im
MATHE-BRIEF Juni 2017 Nr. 80 Herausgegeben von der Österreichischen Mathematischen Gesellschaft http: // www.oemg.ac.at / Mathe Brief mathe brief@oemg.ac.at Die Mandelbrotmenge Komplexe Zahlen werden im
Theorie und Numerik von Differentialgleichungen mit MATLAB und SIMULINK. K. Taubert Universität Hamburg SS08
 Theorie und Numerik von Differentialgleichungen mit MATLAB und SIMULINK K. Taubert Universität Hamburg SS8 Linearisierung 2 LINEARISIERUNG und das VERHALTEN VON LÖSUNGEN NICHTLINEARER DIFFERENTIALGLEICHUNGEN
Theorie und Numerik von Differentialgleichungen mit MATLAB und SIMULINK K. Taubert Universität Hamburg SS8 Linearisierung 2 LINEARISIERUNG und das VERHALTEN VON LÖSUNGEN NICHTLINEARER DIFFERENTIALGLEICHUNGEN
1 Die Mandelbrotmenge
 1 Die Mandelbrotmenge In diesem Abschnitt wollen wir mathematische Aspekte der sogenannten Mandelbrotmenge beleuchten, die wir im Folgenden mit M bezeichnen wollen. 1 Ihr Name ist ihrem Entdecker Benoît
1 Die Mandelbrotmenge In diesem Abschnitt wollen wir mathematische Aspekte der sogenannten Mandelbrotmenge beleuchten, die wir im Folgenden mit M bezeichnen wollen. 1 Ihr Name ist ihrem Entdecker Benoît
Serie 13: Online Test
 D-ERDW, D-HEST, D-USYS Mathematik I HS 13 Dr. Ana Cannas Serie 13: Online Test Einsendeschluss: 31. Januar 214 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung verwenden.
D-ERDW, D-HEST, D-USYS Mathematik I HS 13 Dr. Ana Cannas Serie 13: Online Test Einsendeschluss: 31. Januar 214 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung verwenden.
Algebraische Topologie
 Kurzbeschreibung des Zyklus Algebraische Topologie Thomas Schick 22. Juni 2012 1 Studienobjekte (beispielsweise) (1) topologische Räume (2) Mannigfaltigkeiten, z.b. Flächen (3) Knoten in R 3 (4) Beziehungen
Kurzbeschreibung des Zyklus Algebraische Topologie Thomas Schick 22. Juni 2012 1 Studienobjekte (beispielsweise) (1) topologische Räume (2) Mannigfaltigkeiten, z.b. Flächen (3) Knoten in R 3 (4) Beziehungen
Gewöhnliche Differentialgleichungen: Einleitung
 Gewöhnliche Differentialgleichungen: Einleitung Die Sprache des Universums ist die Sprache der Differentialgleichungen. 1-E1 Faszinierender Anwendungsreichtum cc 1-E2 Wie verstanden die Alten das Naturgesetz?
Gewöhnliche Differentialgleichungen: Einleitung Die Sprache des Universums ist die Sprache der Differentialgleichungen. 1-E1 Faszinierender Anwendungsreichtum cc 1-E2 Wie verstanden die Alten das Naturgesetz?
C7 Differentgleichungen (DG) C7.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: Ort: Geschwindigkeit:
 C7 Differentgleichungen (DG) C7.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) [Stoffgliederung im Skript für Kapitel
C7 Differentgleichungen (DG) C7.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) [Stoffgliederung im Skript für Kapitel
Seminar Fraktale. Kapitel 13 Dynamical Systems. Von Dirk Simon
 Seminar Fraktale Kapitel 13 Dynamical Systems Von Dirk Simon Übersicht Einführung und Definitionen Dynamische Systeme Attraktoren Chaos Ein paar Beispiele Anwendungen Einführung Anwendung für f r Dynamische
Seminar Fraktale Kapitel 13 Dynamical Systems Von Dirk Simon Übersicht Einführung und Definitionen Dynamische Systeme Attraktoren Chaos Ein paar Beispiele Anwendungen Einführung Anwendung für f r Dynamische
Wiederholung: Gravitation in der klassischen Physik
 Gravitation II Wiederholung: Gravitation in der klassischen Physik Eigenschaften: Intrinsische (ladungsartige) Eigenschaft der schweren Masse (Gravitationsladung) Es gibt nur positive Gravitationsladungen
Gravitation II Wiederholung: Gravitation in der klassischen Physik Eigenschaften: Intrinsische (ladungsartige) Eigenschaft der schweren Masse (Gravitationsladung) Es gibt nur positive Gravitationsladungen
Mathematischer Vorkurs für Physiker WS 2012/13 Vorlesung 8
 TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 212/1 Vorlesung 8 Integration über ebene Bereiche Wir betrachten einen regulären Bereich in der x-y Ebene, der einfach zusammenhängend ist.
TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 212/1 Vorlesung 8 Integration über ebene Bereiche Wir betrachten einen regulären Bereich in der x-y Ebene, der einfach zusammenhängend ist.
Systemtheorie. Vorlesung 6: Lösung linearer Differentialgleichungen. Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann
 Systemtheorie Vorlesung 6: Lösung linearer Differentialgleichungen Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann Einführung Viele technischen Anwendungen lassen sich zumindest näherungsweise
Systemtheorie Vorlesung 6: Lösung linearer Differentialgleichungen Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann Einführung Viele technischen Anwendungen lassen sich zumindest näherungsweise
Euler-Verfahren. exakte Lösung. Euler-Streckenzüge. Folie 1
 exakte Lösung Euler-Verfahren Folie 1 Euler-Streckenzüge Ein paar grundlegende Anmerkungen zur Numerik Die Begriffe Numerik bzw. Numerische Mathematik bezeichnen ein Teilgebiet der Mathematik, welches
exakte Lösung Euler-Verfahren Folie 1 Euler-Streckenzüge Ein paar grundlegende Anmerkungen zur Numerik Die Begriffe Numerik bzw. Numerische Mathematik bezeichnen ein Teilgebiet der Mathematik, welches
Überlegungen zum Visualisieren
 Überlegungen zum Visualisieren und Modellieren Vortrag am Samstag, 18. Juli 2009 Bei der T3-Tagung in Freiburg Michael Bürker, Universität Freiburg 16.07.09 Michael Bürker, Uni Freiburg 1 Überblick Grundsätzliche
Überlegungen zum Visualisieren und Modellieren Vortrag am Samstag, 18. Juli 2009 Bei der T3-Tagung in Freiburg Michael Bürker, Universität Freiburg 16.07.09 Michael Bürker, Uni Freiburg 1 Überblick Grundsätzliche
Station Figurierte Zahlen Teil 2. Arbeitsheft. Teilnehmercode
 Station Figurierte Zahlen Teil 2 Arbeitsheft Teilnehmercode Mathematik-Labor Station Figurierte Zahlen Liebe Schülerinnen und Schüler! Schon die alten Griechen haben Zahlen mit Hilfe von Zählsteinen dargestellt:
Station Figurierte Zahlen Teil 2 Arbeitsheft Teilnehmercode Mathematik-Labor Station Figurierte Zahlen Liebe Schülerinnen und Schüler! Schon die alten Griechen haben Zahlen mit Hilfe von Zählsteinen dargestellt:
Kantonsschule Ausserschwyz. Physik. Kantonsschule Ausserschwyz 95
 Kantonsschule Ausserschwyz Kantonsschule Ausserschwyz 95 Bildungsziele Für das Grundlagenfach Die Schülerinnen und Schüler sollen grundlegende physikalische Gebiete und Phänomene kennen lernen; Terminologie,
Kantonsschule Ausserschwyz Kantonsschule Ausserschwyz 95 Bildungsziele Für das Grundlagenfach Die Schülerinnen und Schüler sollen grundlegende physikalische Gebiete und Phänomene kennen lernen; Terminologie,
Hamilton-Systeme. J. Struckmeier
 Invarianten für zeitabhängige Hamilton-Systeme J. Struckmeier Vortrag im Rahmen des Winterseminars des Instituts für Angewandte Physik der Johann-Wolfgang-Goethe-Universität Frankfurt a.m. Hirschegg, 04.
Invarianten für zeitabhängige Hamilton-Systeme J. Struckmeier Vortrag im Rahmen des Winterseminars des Instituts für Angewandte Physik der Johann-Wolfgang-Goethe-Universität Frankfurt a.m. Hirschegg, 04.
Gewöhnliche Differentialgleichungen. Teil II: Lineare DGLs mit konstanten Koeffizienten
 - 1 - Gewöhnliche Differentialgleichungen Teil II: Lineare DGLs mit konstanten Koeffizienten Wir wenden uns jetzt einer speziellen, einfachen Klasse von DGLs zu, die allerdings in der Physik durchaus beträchtliche
- 1 - Gewöhnliche Differentialgleichungen Teil II: Lineare DGLs mit konstanten Koeffizienten Wir wenden uns jetzt einer speziellen, einfachen Klasse von DGLs zu, die allerdings in der Physik durchaus beträchtliche
Proseminar über multimediale Lineare Algebra und Analytische Geometrie
 Proseminar über multimediale Lineare Algebra und Analytische Geometrie Aufgabensteller: Dr. M. Kaplan Josef Lichtinger Montag, 1. Dezember 008 Proseminar WS0809 Inhaltsverzeichnis 1 Aufgabenstellung 3
Proseminar über multimediale Lineare Algebra und Analytische Geometrie Aufgabensteller: Dr. M. Kaplan Josef Lichtinger Montag, 1. Dezember 008 Proseminar WS0809 Inhaltsverzeichnis 1 Aufgabenstellung 3
Topologische Räume und stetige Abbildungen Teil 2
 TU Dortmund Mathematik Fakultät Proseminar zur Linearen Algebra Ausarbeitung zum Thema Topologische Räume und stetige Abbildungen Teil 2 Anna Kwasniok Dozent: Prof. Dr. L. Schwachhöfer Vorstellung des
TU Dortmund Mathematik Fakultät Proseminar zur Linearen Algebra Ausarbeitung zum Thema Topologische Räume und stetige Abbildungen Teil 2 Anna Kwasniok Dozent: Prof. Dr. L. Schwachhöfer Vorstellung des
Wie bügle ich ein Tischtuch? Prof. Dr. Uwe Jannsen
 Auflösungen von Singularitäten, oder: Wie bügle ich ein Tischtuch? Prof. Dr. Uwe Jannsen (Universität Regensburg) Vortrag 10.12.2010 Bayerische Akademie der Wissenschaften Prof. Dr. Uwe Jannsen (Regensburg)
Auflösungen von Singularitäten, oder: Wie bügle ich ein Tischtuch? Prof. Dr. Uwe Jannsen (Universität Regensburg) Vortrag 10.12.2010 Bayerische Akademie der Wissenschaften Prof. Dr. Uwe Jannsen (Regensburg)
Beispiele. Strecke A R 1 (genauso für R d ):
 Definition 6.1.1 (fraktale Dimension). Sei A R d beschränkt und für ε > 0 sei N A (ε) die minimale Anzahl der d-dimensionalen Kugeln vom Radius ε, mit denen A überdeckt werden kann. Die fraktale Dimension
Definition 6.1.1 (fraktale Dimension). Sei A R d beschränkt und für ε > 0 sei N A (ε) die minimale Anzahl der d-dimensionalen Kugeln vom Radius ε, mit denen A überdeckt werden kann. Die fraktale Dimension
Theoretische Biophysik - Statistische Physik
 Theoretische Biophysik - Statistische Physik 10. Vorlesung Pawel Romanczuk Wintersemester 2018 http://lab.romanczuk.de/teaching/ 1 Brownsche Bewegung Zusammenfassung letzte VL Formulierung über Newtonsche
Theoretische Biophysik - Statistische Physik 10. Vorlesung Pawel Romanczuk Wintersemester 2018 http://lab.romanczuk.de/teaching/ 1 Brownsche Bewegung Zusammenfassung letzte VL Formulierung über Newtonsche
Differenzialgleichungen erster Ordnung
 Differenzialgleichungen erster Ordnung Fakultät Grundlagen Mai 2011 Fakultät Grundlagen Differenzialgleichungen erster Ordnung Übersicht Grundsätzliches 1 Grundsätzliches Geometrische Deutung Numerik 2
Differenzialgleichungen erster Ordnung Fakultät Grundlagen Mai 2011 Fakultät Grundlagen Differenzialgleichungen erster Ordnung Übersicht Grundsätzliches 1 Grundsätzliches Geometrische Deutung Numerik 2
Das wissen Sie: 6. Welche Möglichkeiten zur Darstellung periodischer Funktionen (Signalen) kennen Sie?
 Das wissen Sie: 1. Wann ist eine Funktion (Signal) gerade, ungerade, harmonisch, periodisch (Kombinationsbeispiele)? 2. Wie lassen sich harmonische Schwingungen mathematisch beschreiben und welche Beziehungen
Das wissen Sie: 1. Wann ist eine Funktion (Signal) gerade, ungerade, harmonisch, periodisch (Kombinationsbeispiele)? 2. Wie lassen sich harmonische Schwingungen mathematisch beschreiben und welche Beziehungen
Computergrafik SS 2016 Oliver Vornberger. Vorlesung vom Kapitel 11: Fraktale
 Computergrafik SS 2016 Oliver Vornberger Vorlesung vom 03.05.2016 Kapitel 11: Fraktale 1 Selbstähnlichkeit 2 Koch'sche Schneeflocke a+(x-a) cos(60 ) - (y-b) sin(60 ) b+(y-b) cos(60 ) + (x-a) sin(60 ) a,b
Computergrafik SS 2016 Oliver Vornberger Vorlesung vom 03.05.2016 Kapitel 11: Fraktale 1 Selbstähnlichkeit 2 Koch'sche Schneeflocke a+(x-a) cos(60 ) - (y-b) sin(60 ) b+(y-b) cos(60 ) + (x-a) sin(60 ) a,b
Eine Einführung in die Differentialgeometrie
 Eine Einführung in die Differentialgeometrie Nach einer Vorlesung von Prof. Helga Baum 1 Getippt haben Luise Fehlinger und Carsten Falk 4. Mai 2006 1 Der Inhalt dieses Skriptes beruht auf den Vorlesungen
Eine Einführung in die Differentialgeometrie Nach einer Vorlesung von Prof. Helga Baum 1 Getippt haben Luise Fehlinger und Carsten Falk 4. Mai 2006 1 Der Inhalt dieses Skriptes beruht auf den Vorlesungen
Kurze Geschichte der linearen Algebra
 Kurze Geschichte der linearen Algebra Dipl.-Inform. Wolfgang Globke Institut für Algebra und Geometrie Arbeitsgruppe Differentialgeometrie Universität Karlsruhe 1 / 20 Entwicklung Die Historische Entwicklung
Kurze Geschichte der linearen Algebra Dipl.-Inform. Wolfgang Globke Institut für Algebra und Geometrie Arbeitsgruppe Differentialgeometrie Universität Karlsruhe 1 / 20 Entwicklung Die Historische Entwicklung
AUFGABEN ZUR FUNKTIONENTHEORIE. von. Prof. Dr. H.-W. Burmann
 AUFGABEN ZUR FUNKTIONENTHEORIE von Prof. Dr. H.-W. Burmann Bei den folgenden Aufgaben handelt es sich um Reste, die bei der Erstellung der Aufgabenblätter übriggeblieben sind. Der Schwierigkeitsgrad der
AUFGABEN ZUR FUNKTIONENTHEORIE von Prof. Dr. H.-W. Burmann Bei den folgenden Aufgaben handelt es sich um Reste, die bei der Erstellung der Aufgabenblätter übriggeblieben sind. Der Schwierigkeitsgrad der
Versuchsprotokoll. Mathematisch-Naturwissenschaftliche Fakultät I Institut für Physik. Versuch O10: Linsensysteme Arbeitsplatz Nr.
 Mathematisch-Naturwissenschaftliche Fakultät I Institut für Physik Physikalisches Grundpraktikum I Versuchsprotokoll Versuch O10: Linsensysteme Arbeitsplatz Nr. 1 0. Inhaltsverzeichnis 1. Einleitung 2.
Mathematisch-Naturwissenschaftliche Fakultät I Institut für Physik Physikalisches Grundpraktikum I Versuchsprotokoll Versuch O10: Linsensysteme Arbeitsplatz Nr. 1 0. Inhaltsverzeichnis 1. Einleitung 2.
DAS VORHERGESAGTE CHAOS
 DAS VORHERGESAGTE CHAOS Vorhersagen sind schwierig, besonders wenn sie die Zukunft betreffen, in erster Linie dann, wenn es sich um Wettervorhersagen handelt ein Zitat, das Berühmtheiten wie Nils Bohr
DAS VORHERGESAGTE CHAOS Vorhersagen sind schwierig, besonders wenn sie die Zukunft betreffen, in erster Linie dann, wenn es sich um Wettervorhersagen handelt ein Zitat, das Berühmtheiten wie Nils Bohr
