Studienarbeit. Modellierung des Skineffekts im Zeitbereich für die Beschreibung von Verbindungsstrukturen in der Schaltungssimulation

Transkript

1 Otto-von-Guericke-Universität Magdeburg Fakultät für Elektrotechnik und Informationstechnik Institut für Grundlagen der Elektrotechnik und Elektromagnetische Verträglichkeit Studienarbeit Modellierung des Skineffekts im Zeitbereich für die Beschreibung von Verbindungsstrukturen in der Schaltungssimulation eingereicht: 30. Oktober 2007 von: Mathias Magdowski geboren am 09. April 1984 in Wolmirstedt

2 Kurzreferat Der Skineffekt, die Verringerung des wirksamen Leiterquerschnitts bei höheren Frequenzen, ist ein wichtiger Verlustmechanismus innerhalb von elektrischen Verbindungsstrukturen. Für die Beschreibung im Frequenzbereich existieren viele wohlbekannte Lösungen. Basierend auf der Methode des Full Spectrum Convolution Macromodeling wird in dieser Arbeit ein neues Skineffekt-Modell entwickelt, das eine effektive Zeitbereichsbeschreibung ermöglicht. Anhand von Beispielen wird die Integration des Modells in diskrete Leitungsmodelle und in PEEC-Modelle untersucht, um den Einfluss des Skineffekts bei der Simulation von Leiterstrukturen mit transienten Strom- und Spannungsverläufen adäquat erfassen zu können. Abstract The skin effect is characterized by a reduction of a conductor s effective cross-sectional area and is of great importance for the losses in electrical interconnection systems. Many well-known solutions exist for its modeling in the frequency domain. Based on the method of Full Spectrum Convolution Macromodeling in this seminar paper a new skin effect model is developed for effective time domain analysis. The integration of this model into the transmission line model and into the PEEC model is studied in two examples. Thereby the influence of skin effect on the simulation of interconnection systems with transient current and voltage progressions is investigated. i

3 Inhaltsverzeichnis 1 Einführung Ursachen und Auswirkungen des Skineffekts Bedeutung des Skineffekts Beschreibung des Skineffekts im Frequenzbereich Skineffekt im Leiter mit rundem Querschnitt Skineffekt im Leiter mit rechteckigem Querschnitt Genäherte analytische Lösung Numerische Berechnung mittels FIT Skineffekt im Mikrostreifenleiter Allgemeine Eigenschaften der Frequenzgänge Modellierung des Skineffekts im Zeitbereich Zustand der Forschung Modellierung des Skineffekts mittels FSCM Anwendung des FSCM-Modells zur Modellierung von Verbindungsstrukturen Leitungsmodelle mit Skineffekt Modellierung des Skineffekts in PEEC Simulationsergebnisse Zusammenfassung 46 A Diagramme 50 A.1 Stromverteilung im Leiter mit rundem Querschnitt A.2 Stromverteilung im Leiter mit rechteckigem Querschnitt A.3 Testpulse und Stromantworten für die Validierung des FSCM-Modells im Zeitbereich

4 Abbildungsverzeichnis 2.1 Abschnitt eines Leiters mit rundem Querschnitt in Zylinderkoordinaten Längenbezogene Impedanz in Abhängigkeit der Frequenz für einen Kupferdraht mit 1 mm Radius Längenbezogene Impedanz in Abhängigkeit der Frequenz für einen Kupferdraht mit 1 mm Radius (doppelt logarithmische Darstellung) Längenbezogener Widerstand und innere Induktivität in Abhängigkeit der Frequenz für einen Kupferdraht mit 1 mm Radius Abschnitt eines Leiters mit rechteckigem Querschnitt Längenbezogene Impedanz in Abhängigkeit der Frequenz für einen Kupferleiter mit 1 mm 1 mm Querschnitt Längenbezogener Widerstand und innere Induktivität in Abhängigkeit der Frequenz für einen Kupferleiter mit 1 mm 1 mm Querschnitt Stromverteilung für einen Kupferleiter mit rechteckigem Querschnitt von 1 mm 1 mm bei 100 khz Längenbezogener Widerstand und innere Induktivität in Abhängigkeit der Frequenz für einen Kupferleiter mit 1 mm 1 mm Querschnitt (Vergleich von analytischer Lösung und FIT-Lösung) Querschnitt eines Mikrostreifenleiters Schematische Stromverteilung über den Querschnitt des Mikrostreifenleiters bei verschiedenen Frequenzen Längenbezogener Widerstand und innere Induktivität in Abhängigkeit der Frequenz für einen typischen Mikrostreifenleiter Schematische Darstellung einiger möglicher Querschnittsdiskretisierungen für PEEC-Modelle Stufennetzwerke für die Approximation der Impedanzverläufe Längenbezogene Admittanz in Abhängigkeit der Frequenz für einen Kupferdraht mit 1 mm Radius Vergleich von Modell und exakter Lösung der Admittanz in Abhängigkeit der Frequenz für einen Kupferdraht mit 1 mm Radius Zeitverlauf und Spektrum für einen rechteckigen Puls mit 1 µs Breite

5 Abbildungsverzeichnis 3.6 Antwortfunktion des Stromes auf einen rechteckigen Puls mit 1 µs Breite Zugeordnetes Ersatzschaltbild einer Induktivität für Netzwerksimulatoren Zugeordnetes diskretes Ersatzschaltbild des FSCM-Skineffekt-Modells für Netzwerksimulatoren Allgemeines Ersatzschaltbild eines differentiellen Leitungsstückes Schematische Darstellung einer Doppelleitung Ersatzschaltbild der Leitung Ersatzschaltbild einer PEEC-Volumenzelle k, einer Oberflächenzelle i und einer weiteren Oberflächenzelle modifizierte PEEC-Volumenzelle mit FSCM-Skineffekt-Modell Unendlich langer, gerader Stromfaden über einer ideal leitenden Ebene Vergleich zwischen exaktem und modelliertem Verlauf des längenbezogenen Widerstandes und der inneren Induktivität für einen Mikrostreifenleiter Schematischer Programmablaufplan eines Netzwerksimulators Spannung am Lastwiderstand am Ende der Doppelleitung Generatorspannung und Spannung am Lastwiderstand der Mikrostreifenleitung bei verschiedenen Flankensteilheiten A.1 Stromdichte in Abhängigkeit vom Radius bei 50 Hz (kein Skineffekt) A.2 Stromdichte in Abhängigkeit vom Radius bei 5 khz (sehr gering ausgeprägter Skineffekt) A.3 Stromdichte in Abhängigkeit vom Radius bei 500 khz (Skineffekt wird bedeutend) A.4 Stromdichte in Abhängigkeit vom Radius bei 50 MHz (Skineffekt ist sehr stark) A.5 Stromdichte über den Querschnitt bei 1 khz (kaum Skineffekt) A.6 Stromdichte über den Querschnitt bei 100 khz (Skineffekt wird sichtbar). 53 A.7 Stromdichte über den Querschnitt bei 1 MHz (Skineffekt ist bedeutend).. 54 A.8 Stromdichte über den Querschnitt bei 100 MHz (Skineffekt ist sehr ausgeprägt) 54 A.9 Zeitverlauf und Spektrum für einen dreieckigen Puls mit 1 µs Anstiegszeit. 55 A.10 Antwortfunktion des Stromes auf einen dreieckigen Puls mit 1 µs Anstiegszeit 55 A.11 Zeitverlauf und Spektrum für einen trapezförmigen Puls mit 0,25 µs Anstiegszeit A.12 Antwortfunktion des Stromes auf einen trapezförmigen Puls mit 0,25 µs Anstiegszeit

6 Tabellenverzeichnis 2.1 Beispiele für die Skintiefe in Kupfer Abmaße eines Mikrostreifenleiters

7 1 Einführung 1.1 Ursachen und Auswirkungen des Skineffekts Bei Gleichstrom ist der in einem Leiter fließende Strom gleichmäßig über den Querschnitt verteilt. Die Stromdichte ist über den Querschnitt konstant. Das durch den Stromfluss induzierte Magnetfeld bleibt konstant. Bei Wechselstrom mit steigenden Frequenzen verändert sich das Magnetfeld und erzeugt im Inneren des Leiters zunehmend Wirbelströme, die dem ursprünglichen Strom entgegengerichtet sind und diesen abschwächen. Der in einem Leiter fließende Strom wird immer stärker aus der Mitte verdrängt und fließt verstärkt in den Randbereichen des Leiters. Die Stromdichte ändert sich über den Querschnitt. Bei sehr hohen Frequenzen fließt der Strom nur noch in einer dünnen Haut auf der Oberfläche des Leiters. Diese Erscheinung wird deshalb Skineffekt genannt. Beim Leiter mit rechteckigem Querschnitt konzentriert sich der Strom hauptsächlich an den Kanten. Durch die Verringerung der für den Stromfluss wirksamen Querschnittsfläche wird der Wirk- und Blindwiderstand des Leiters erhöht. Dadurch steigen natürlich auch die Verluste im Leiter an. Außerdem wird auch die Flankensteilheit digitaler Signale beeinflusst. 1.2 Bedeutung des Skineffekts Die Entwicklung innovativer elektronischer Schaltungen ist neben der fortschreitenden Miniaturisierung durch eine ständige Zunahme der Arbeitsfrequenzen gekennzeichnet. Gründe dafür sind unter anderem die Forderung nach immer schnelleren Taktfrequenzen in der Informationselektronik, nach höheren Datenübertragungsraten in der Kommunikationstechnik und auch zu höheren Schaltfrequenzen in der Leistungselektronik. Durch diese Steigerung der Arbeitsfrequenzen tritt der Skineffekt immer stärker in Erscheinung und ist neben den Verlusten durch Abstrahlung und dielektrischen Verlusten zu einem der dominierenden Verlustmechanismen in Verbindungsstrukturen innerhalb elektronischer Baugruppen geworden. Deshalb ist es wichtig, den Skineffekt schon in der elektromagnetischen Simulation bei der Entwicklung elektronischer Geräte adäquat erfassen zu können. 5

8 2 Beschreibung des Skineffekts im Frequenzbereich 2.1 Skineffekt im Leiter mit rundem Querschnitt Der runde Leiter in Luft, also ohne ein umgebendes Dielektrikum, ist ein guter Anfang für eine weitere Betrachtung. Viele reale Leiter haben einen runden Querschnitt, z. B. in Zweidrahtleitungen oder Koaxialkabeln. Außerdem ist die mathematische Beschreibung übersichtlich und auf analytischem Wege möglich. Eine recht ausführliche Herleitung der Stromdichteverteilung im Leiter mit rundem Querschnitt ist in [Phi75] angegeben. Für die Herleitung bietet sich die Beschreibung in Zylinderkoordinaten r, α und z an. Der Leiter wird dabei als gerade und unendlich lang angenommen. Der Außenradius des Leiters ist r 0. Ein Ausschnitt aus diesem Leiter ist in Abbildung 2.1 dargestellt. Der Strom fließt dabei nur in Richtung von z und wird als rotationssymmetrisch angenommen. Die Stromdichte J hat dann nur eine Komponente in Richtung von z und hängt nur vom Radius r ab. Die für die Herleitung wichtigen Materialkonstanten sind die Leitfähigkeit γ, die Permeabilität µ und die Permittivität ε. Die Stromdichte J und die elektrische Feldstärke E sind über die Leitfähigkeit γ miteinander verknüpft. J = γ E (2.1) r 0 H r A z, I d s d A Abbildung 2.1: Abschnitt eines Leiters mit rundem Querschnitt in Zylinderkoordinaten 6

9 2 Beschreibung des Skineffekts im Frequenzbereich Aus der 1. Maxwellschen Gleichung in Integralform, s H d s = D J + da t (2.2) A kann die Ableitung der elektrischen Verschiebungsflussdichte D vernachlässigt werden, t wenn ω γ ist. Es folgt eine Gleichung, die einen Zusammenhang zwischen der Stromdichte ε J und der magnetischen Feldstärke H herstellt, s H d s = A J d A (2.3) Nach der Integration über einen Kreisring aus dem Querschnitt des Leiters erhält man: H α 2πr = 2π J z rdr (2.4) Durch die Ableitung des Ausdrucks nach r erhält man eine erste Differentialgleichung (DGL): H α r r = H α r r + H α = J z r (2.5) H α r + H α r = J z = γe z (2.6) Diese DGL enthält noch die magnetische und elektrische Feldstärke, weshalb es nötig ist eine weitere Gleichung zu finden, um eine Größe durch die andere zu ersetzen. Das gelingt durch die Nutzung der 2. Maxwellschen Gleichung: rot E = B t und B = µ H (2.7) Durch Einsetzen in Zylinderkoordinaten erhält man: rote = 1 r e r r e α e z r α z 0 0 E z = 1 r e E z r α e E z α r = 0 Ez r 0 (2.8) Daraus folgt, dass die örtliche Ableitung der elektrischen Feldstärke der zeitlichen Ableitung der magnetischen Feldstärke entspricht. E z r = µ H α t (2.9) 7

10 2 Beschreibung des Skineffekts im Frequenzbereich Nachdem man die Gleichung (2.6) nach t ableitet, kann man die Gleichung (2.9) einsetzen und erhält eine DGL, die nur noch von der elektrischen Feldstärke abhängt. 1 µ 2 H α r t + 1 r H α t 2 E z r 2 = γ E z t + 1 µr E z r = γ E z t (2.10) (2.11) Beim Übergang vom Zeitbereich in den Frequenzbereich ersetzt man die Ableitung nach t durch eine Multiplikation mit jω. 2 E z r r E z r jωµγe z = 0 (2.12) Die Form entspricht der Besselschen DGL 0. Ordnung. 2 J z r r J z r + k2 J z = 0 mit k 2 = jωµγ (2.13) Für diese DGL ist die entsprechende allgemeine Lösung in vielen mathematischen Nachschlagewerken, z. B. in [Bar76], angegeben. J z (r) = A J 0 (kr) + B N 0 (kr) (2.14) Dabei ist J 0 die Besselsche Funktion 0. Ordnung und N 0 die Neumannsche Funktion 0. Ordnung. Aufgrund der endlichen Stromdichte im Zentrum des Leiters bei r = 0 muss auch B = 0 sein, weil N 0 im Ursprung eine Polstelle besitzt. Die spezielle Lösung der Besselschen DGL sieht dann folgendermaßen aus: J z (r) = A J 0 (kr) mit k = jωµγ (2.15) Nun muss noch der Faktor A bestimmt werden. Dazu kann man die bekannte magnetische Feldstärke an der Oberfläche des Leiters ausnutzen. H α (r 0 ) = I z 2πr 0 (2.16) Außerdem folgt aus Gleichung (2.9): H α = 1 E z jωµ r = 1 J z jωµγ r = A J 0 (kr) jωµγ r (2.17) 8

11 2 Beschreibung des Skineffekts im Frequenzbereich Frequenz Skintiefe 50 Hz 9,3 mm 100 Hz 6,6 mm 5 khz 0,93 mm 10 khz 0,66 mm 500 khz 93 µm 1 MHz 66 µm 50 MHz 9,3 µm 100 MHz 6,6 µm Tabelle 2.1: Beispiele für die Skintiefe in Kupfer Durch das Ausnutzen der Beziehung J 0(kr) = J 1 (kr)k kann man weiter umstellen zu: H α = Ak jωµγ J 1(kr) (2.18) Damit kann man durch Gleichsetzen von (2.16) sowie (2.18) und Umstellen den Faktor A bestimmen. A = jωµγi Z 2πr 0 k 1 J 1 (kr 0 ) (2.19) Damit ergibt sich schließlich die vom Radius und der Frequenz abhängige Stromdichte zu: J z (r) = jωµγi Z 2πr 0 k J0(kr) J 1 (kr 0 ) = I Zk 2πr 0 J0(kr) J 1 (kr 0 ) (2.20) Diese beschreibende Gleichung entspricht einer Diffusionsgleichung. Sie beschreibt, wie das Feld außerhalb des Leiters in den Leiter hineindiffundiert. Die Stromdichte ist dabei eine komplexe Größe. Sie ändert mit dem Radius nicht nur ihren Betrag, sondern auch die Phase. Um den Ausdruck etwas verständlicher zu machen, kann man das k = jωµγ umformen zu: ωµγ k = (1 j) 2 = 1 j δ Das δ wird Skintiefe genannt und entspricht der Eindringtiefe des äußeren Feldes. δ = (2.21) 2 ωµγ = 1 πfµγ (2.22) Das heißt, dass nach δ das äußere Feld auf 1/ e abgefallen ist (wenn δ r 0 ). Der Strom kann nur bis zu dieser Tiefe effektiv in den Leiter eindringen. Innerhalb dieses Bereiches fließt nur noch ein geringer Teil des Stromes. In Tabelle 2.1 sind einige Beispielwerte der Skintiefe für Kupfer angegeben. Einige Beispiele der Stromdichteverteilung sind im Anhang A.1 dargestellt. 9

12 2 Beschreibung des Skineffekts im Frequenzbereich Re[Z (j ω)] und Im[Z (j ω)] in Ω/m Realteil Imaginärteil f in Hz Abbildung 2.2: Längenbezogene Impedanz in Abhängigkeit der Frequenz für einen Kupferdraht mit 1 mm Radius Für die weitere Beschreibung ist nun die längenbezogene Impedanz des Leiters mit rundem Querschnitt wichtig. Die Impedanz Z ergibt sich aus: Z = U I = E zl I z = J zl γi z (2.23) Um zur längenbezogenen Impedanz Z zu gelangen, muss man durch die Länge l teilen: Z (jω) = J z(jω) γi z = jωµγ 2πr 0 γ J0( jωµγr 0 ) J 1 ( jωµγr 0 ) (2.24) Die Größe kann man in den Realteil R (jω) = R {Z (jω)} und den Imaginärteil X (jω) = ωl (jω) = I {Z (jω)} aufteilen. Der Realteil entspricht dem längenbezogenen Wirkwiderstand, der Imaginärteil dem längenbezogenen Blindwiderstand. In Abbildung 2.2 sind Wirkwiderstand und Blindwiderstand exemplarisch dargestellt. Man erkennt, dass der Wirkwiderstand bei tiefen Frequenzen konstant bleibt und ab einer bestimmten Frequenz, die im folgenden Knickfrequenz genannt wird, ansteigt. Der Anstieg verläuft dann bei großen Frequenzen proportional zu ω. Der Blindwiderstand steigt bei tiefen Frequenzen bis zur Knickfrequenz proportional zu ω, bei hohen Frequenzen über der Knickfrequenz dann ebenfalls proportional zu ω. Das kann man besonders gut in der doppelt logarithmischen Darstellung in Abbildung 2.3 erkennen. 10

13 2 Beschreibung des Skineffekts im Frequenzbereich Re[Z (j ω)] und Im[Z (j ω)] in Ω/m Realteil Imaginärteil f in Hz Abbildung 2.3: Längenbezogene Impedanz in Abhängigkeit der Frequenz für einen Kupferdraht mit 1 mm Radius (doppelt logarithmische Darstellung) Teilt man den längenbezogenen Blindwiderstand durch die Kreisfrequenz ω, so erhält man die längenbezogenen innere Induktivität L (jω) des Leiters. Die frequenzabhängigen Verläufe von L (jω) und R (jω) sind in Abbildung 2.4 dargestellt. Die längenbezogene innere Induktivität bleibt bei tiefen Frequenzen konstant. Ab der Knickfrequenz fällt die Induktivität dann proportional zu 1/ ω. 2.2 Skineffekt im Leiter mit rechteckigem Querschnitt Einige reale Leiter haben einen rechteckigen Querschnitt, z. B. Leiterzüge auf PCBs oder Stromsammelschienen. In diesen Fällen kann der Leiter erstmal nicht mit rundem Querschnitt angenommen werden. Eine neue Beschreibung für den rechteckigen Querschnitt wird nötig. Diese wird aber natürlich mathematisch anspruchsvoller, weil z. B. nicht mehr in den praktischen Zylinderkoordinaten gerechnet werden kann und die Stromdichte jetzt außerdem von zwei Variablen x und y abhängt. Dem Problem des Skineffekts im Leiter mit rechteckigem Querschnitt kann man sich auf verschiedenen Wegen nähern. Eine genäherte analytische Lösung der frequenzabhängigen längenbezogenen Impedanz findet sich in [Gia96]. Außerdem kann man für die Stromverteilung auch numerische Lösungen finden. In dieser Arbeit wird die Finite-Integral-Methode (engl. Finite Integration 11

14 2 Beschreibung des Skineffekts im Frequenzbereich Induktivität L (j ω) in nh/m R (j ω) in Ω/m Widerstand f in Hz Abbildung 2.4: Längenbezogener Widerstand und innere Induktivität in Abhängigkeit der Frequenz für einen Kupferdraht mit 1 mm Radius y b, z a x Abbildung 2.5: Abschnitt eines Leiters mit rechteckigem Querschnitt Technique, FIT) nach [Wei77] benutzt, ebenso wäre aber z. B. auch die Finite-Elemente- Methode (FEM) geeignet Genäherte analytische Lösung Ein Abschnitt eines Leiters mit rechteckigem Querschnitt ist in Abbildung 2.5 dargestellt. Die Querschnittsabmessungen sind a und b. Die Herleitung der frequenzabhängigen Impedanz des Leiters in [Gia96] erfolgt über eine Laplace-Transformation der Maxwellschen Gleichungen und einen Reihenansatz zur Lösung der Differentialgleichung. Es ergibt sich 12

15 2 Beschreibung des Skineffekts im Frequenzbereich für die längenbezogene Impedanz: Z (jω) = R 0 2 k=1 tanh ζ k (a/b) + ζ k (a/b) η k 1 tanh ζ k (b/a) k=1 ζ k (b/a) η k (2.25) Die verwendeten Hilfsgrößen werden in Gleichung (2.26) definiert. Es zeigt sich, dass die unendliche Summe recht schnell konvergiert. Deshalb genügt es für die effiziente numerische Auswertung nur wenige Summenglieder zu berechnen. In dieser Arbeit werden 100 Glieder summiert. ( ) 2 (2k 1)πx ζ k (x) = + jxω 2 ω c (2.26a) ( ) 2 (2k 1)π η k = 2 (2.26b) ω c = 4 µγab (2.26c) R 0 = 1 abγ (2.26d) Die Impedanz kann man auch hier wieder in Realteil und Imaginärteil aufteilen. Sie entsprechen auch hier dem Wirkwiderstand und Blindwiderstand. In Abbildung 2.6 sind Wirkwiderstand und Blindwiderstand exemplarisch für einen Kupferleiter mit 1 mm x 1 mm Querschnittsfläche dargestellt. Man erkennt, dass der Wirkwiderstand bei tiefen Frequenzen auch hier konstant bleibt und ab der Knickfrequenz ω c proportional zu ω ansteigt. Der Blindwiderstand steigt bei Frequenzen unterhalb von ω c wieder proportional zu ω, bei Frequenzen über ω c dann ebenfalls proportional zu ω. Auch die längenbezogene innere Induktivität bleibt bei tiefen Frequenzen konstant. Ab der Knickfrequenz ω c fällt die Induktivität dann ebenso proportional zu 1/ ω. Dieser Zusammenhang ist in Abbildung 2.7 dargestellt Numerische Berechnung mittels FIT Die Finite-Integral-Methode ist ein numerisches Verfahren zur Lösung der Maxwellschen Gleichungen. Dabei wird das Simulationsgebiet in sogenannte FIT-Zellen unterteilt, die ein elementares und ein duales Gitter bilden. Die Größe einer FIT-Zelle wird durch die Schrittweite h festgelegt. Das Strömungsfeld im rechteckigen Leiter kann durch eine TM- Welle beschrieben werden. Das E-Feld hat dann nur eine Komponente in z-richtung entlang des Leiters. Das H-Feld verläuft nur tangential zur Stromrichtung und hat nur Komponenten in x- und y-richtung. Die Feldgrößen ändern sich entlang z nicht, damit 13

16 2 Beschreibung des Skineffekts im Frequenzbereich 0.14 Re[Z (j ω)] und Im[Z (j ω)] in Ω/m Realteil Imaginärteil f in Hz Abbildung 2.6: Längenbezogene Impedanz in Abhängigkeit der Frequenz für einen Kupferleiter mit 1 mm 1 mm Querschnitt Induktivität 0.2 L (j ω) in nh/m R (j ω) in Ω/m Widerstand f in Hz Abbildung 2.7: Längenbezogener Widerstand und innere Induktivität in Abhängigkeit der Frequenz für einen Kupferleiter mit 1 mm 1 mm Querschnitt 14

17 2 Beschreibung des Skineffekts im Frequenzbereich sind die Ableitungen / z nicht vorhanden. Damit kann man im leitenden Medium die Maxwellschen Gleichungen in integraler Form im Frequenzbereich umschreiben zu: H xy ds = J z da = γ E z da (2.27) s A A E z ds = jω B x da (2.28) s A E z ds = jω B y da (2.29) s Das 2-dimensionale Simulationsgebiet in x und y-richtung wird in i und j diskretisiert. Nun wird jede Gleichung entsprechend dem FIT-Algorithmus für das Gitter diskretisiert und als Ergebnis eine Matrix A gebildet. Als Randbedingung kann man eine eingeprägte Spannung pro Längeneinheit U am Rand des Leiters benutzen und erhält den Vektor der diskreten Randbedingungen B. Nun kann man das Gleichungssystem AX g = B nach dem Vektor der Unbekannten X g umstellen. Dieser Vektor X g enthält die gesuchten elektrischen und magnetischen Spannungen auf den Kanten des elementaren und dualen Gitters. Damit kann man die Stromdichte in allen Gitterpunkten i und j aus dem E-Feld berechnen. Den gesamten Strom erhält man durch das Integral über die Stromdichte und in diskreter Form als die Summe über die Stromdichte in den Gitterpunkten. I z = J z da I = h 2 J z (i, j) (2.30) A i j A Damit lässt sich mit dem Ohmschen Gesetz (2.31) die längenbezogene Impedanz des Leiters berechnen. Der Realteil von Z(jω) entspricht wieder dem Wirkwiderstand, der Imaginärteil dem Blindwiderstand. Teilt man den Blindwiderstand durch die Frequenz, so erhält man die innere Induktivität. Z (jω) = U I(jω) (2.31) Die ausführliche Vorgehensweise mit der Darstellung des elementaren und dualen Gitters ist in [Koc07] dargestellt. Das Ergebnis der Simulation, die Stromverteilung für einen rechteckigen Kupferleiter bei einer Frequenz von 100 khz, ist in Abbildung 2.8 dargestellt. Der 1 mm 1 mm große Leiter ist dabei in FIT-Zellen unterteilt worden. Der Wirkwiderstand ist dabei auf das 1,541-fache des Gleichstromwiderstandes R 0 angestiegen. Die innere Induktivität ist auf das 0,727-fache der Gleichstrominduktivität L 0 abgesunken. Die Stromdichte ist in den Ecken besonders hoch. Sie ist 2,945-mal so groß wie die Stromdichte im Zentrum des Leiters. Die Stromdichteverteilungen für weitere Frequenzen sind im Anhang A.2 dargestellt. Wiederholt man das Verfahren in einer Iteration für verschiedene Frequenzen, kann man 15

18 2 Beschreibung des Skineffekts im Frequenzbereich J z (x,y) in A/m 2 x x x x in m y in m x Abbildung 2.8: Stromverteilung für einen Kupferleiter mit rechteckigem Querschnitt von 1 mm 1 mm bei 100 khz den Frequenzgang der längenbezogenen Impedanz darstellen. Der 1 mm 1 mm große Kupferleiter wurde dabei in FIT-Zellen unterteilt. Der Frequenzgang für R(jω) und L(jω) ist in Abbildung 2.9 dargestellt. Als Referenz ist auch die genäherte analytische Lösung aus Abschnitt dargestellt. Wie man sieht, stimmen beide Lösungen für R(jω) bei niedrigen Frequenzen sehr gut überein. Die Abweichungen bei höheren Frequenzen resultieren aus der ungenügenden Diskretisierung. Je höher die Frequenz, desto geringer wird die Skintiefe und desto feiner muss man diskretisieren. Beim Frequenzgang der Induktivität L(jω) ist zu sehen, dass die FIT-Lösung immer etwas höhere Werte zeigt als die analytische Lösung. Außerdem gibt es auch hier Abweichungen bei hohen Frequenzen, die analytische Lösung strebt gegen Null, die FIT-Lösung nicht. Auch hier müsste man allgemein noch feiner diskretisieren. 2.3 Skineffekt im Mikrostreifenleiter Die Mikrostreifenleitung ist eine Art Wellenleiter, der aus einem metallischen Leiter über einer Masseebene besteht. Beide sind durch ein dielektrisches Substrat voneinander getrennt. Ein Querschnitt durch einen Mikrostreifenleiter ist in Abbildung 2.10 dargestellt. Die verwendeten Abmaße sind in Tabelle 2.2 benannt. 16

19 2 Beschreibung des Skineffekts im Frequenzbereich 50 FIT Lösung für R(j ω) analytische Lösung für R(j ω) L (j ω) in nh/m FIT Lösung für L(j ω) analytische Lösung für L(j ω) R (j ω) in Ω/m f in Hz Abbildung 2.9: Längenbezogener Widerstand und innere Induktivität in Abhängigkeit der Frequenz für einen Kupferleiter mit 1 mm 1 mm Querschnitt (Vergleich von analytischer Lösung und FIT-Lösung) w t h t g Abbildung 2.10: Querschnitt eines Mikrostreifenleiters Variable w g h t Bedeutung Breite des Streifens Breite der Masseebene Höhe des dielektrischen Substrats Höhe der Metallisierung Tabelle 2.2: Abmaße eines Mikrostreifenleiters 17

20 2 Beschreibung des Skineffekts im Frequenzbereich Abbildung 2.11: Schematische Stromverteilung über den Querschnitt des Mikrostreifenleiters bei verschiedenen Frequenzen Mikrostreifenleiter werden vor allem in der HF-Technik als Leitungsstrukturen zur Weiterleitung, Kopplung und Filterung hoher Signalfrequenzen eingesetzt. Die Vorteile liegen in der gänzlich planaren und materialsparenden Struktur. Diese ist in einem lithografischen Prozess sowie durch Ätzen und Fräsen besonders einfach automatisierbar und damit kostengünstig und reproduzierbar herzustellen. Ein weiterer Vorteil ist die geringe Ausbreitung des Feldes außerhalb der planaren Struktur. Dadurch tritt nur eine geringe Abstrahlung von Wellen in den Raum auf. Nachteilig ist die relativ hohe Dämpfung, weshalb Mikrostreifenleiter meist nur für kurze Entfernungen innerhalb von Baugruppen eingesetzt werden. Ein weiterer Nachteil liegt in der komplexen mathematischen Beschreibung. Eine Welle breitet sich einerseits im Substrat zwischen Streifen und Masseebene aus, sie tritt aber andererseits auch in den mit Luft gefüllten Raum über dem Streifen über. Deshalb muss man das Dielektrikum als inhomogen betrachten und die effektive Permittivität ε eff benutzen, die in [Mis01] beschrieben wird. Dort wird auch die Berechnung der für die HF-Technik wichtigen Wellenimpedanz Z c beschrieben. Um den Skineffekt zu verdeutlichen, ist die Stromverteilung über den Querschnitt des Mikrostreifenleiters in Abbildung 2.11 dargestellt. Obwohl diese Abbildung nur beispielhaft und stark vereinfacht ist, verdeutlicht sie doch recht gut die wirkenden Mechanismen. Bei Gleichstrom ist die Stromverteilung gleichmäßig über den Querschnitt. Bei mittleren Frequenzen wirkt der Proximity-Effekt und der Strom sammelt sich in der Masseebene unterhalb des Streifens. Durch die Verringerung des wirksamen Querschnitts kommt es zu Verlusten. Der Proximity-Effekt ist hier der entscheidende Verlustmechanismus. Mit weiter steigenden Frequenzen kommt es zusätzlich zu Stromverdrängung und der 18

21 2 Beschreibung des Skineffekts im Frequenzbereich Strom fließt nun verstärkt in den Randbereichen des Leiters. Bei noch höheren Frequenzen fließt der Strom nur noch in einer dünnen Haut auf der Oberfläche des Streifens sowie der Masseebene unterhalb des Streifens und es kommt zum charakteristischen Skineffekt. Der Wirkwiderstand und die Verluste steigen nun stark an. In diesem Frequenzbereich bestimmt der Skineffekt maßgeblich die Verluste. Bei noch höheren Frequenzen werden weitere Verlustmechanismen wirksam, die in [Bye03] und [Sle07] besprochen werden. Diese werden vor allem durch die Oberflächenrauhigkeit der Metallisierung und durch dielektrische Verluste im Substrat hervorgerufen. Möchte man diese Verluste nun nicht nur qualitativ, sondern auch quantitativ beschreiben, so ist auch hier der Ansatz über die längenbezogene Impedanz Z (jω) des Mikrostreifenleiters sinnvoll. Diese Impedanz lässt sich aber aufgrund der komplexen Struktur nicht für alle Frequenzen analytisch herleiten, sondern nur numerisch berechnen. Ein Versuch, diese numerischen Ergebnisse der Momentenmethode wieder in geschlossene Formeln zu überführen, findet sich in [DS94]. Diese Interpolationsformel wird nun benutzt, um die längenbezogene Impedanz eines typischen Mikrostreifenleiters mit folgenden Abmaßen und Eigenschaften zu berechnen. w = 0,2 mm g = 2,0 mm h = 0,1 mm t = 10 µm γ = S m ε eff = 4 (2.32a) (2.32b) (2.32c) (2.32d) (2.32e) (2.32f) Die charakteristische Impedanz dieses Mikrostreifenleiters beträgt Z c = 50 Ω. Die längenbezogene Impedanz, aufgeteilt in Wirkwiderstand und innere Induktivität, ist in Abbildung 2.12 dargestellt. Man erkennt auch hier, dass der Wirkwiderstand bei niedrigen Frequenzen zunächst konstant bleibt. Ab einer Frequenz von etwa 500 khz steigt der Widerstand zunächst an, bleibt dann aber auf diesem Niveau konstant. Dies lässt sich auf den Proximity-Effekt zurückführen. Erst ab einer Frequenz von etwa 100 MHz steigt der Widerstand aufgrund des Skineffekts stark an, der Anstieg ist nun proportional zu ω. Auch die innere Induktivität bleibt bei tiefen Frequenzen zunächst konstant. Ab etwa 500 khz sinkt die innere Induktivität dann ab. Was hier gegenüber den Frequenzgängen der Impedanzen von rundem und rechteckigem Leiter auffällt, ist die unterschiedliche Knickfrequenz für Widerstand und Induktivität. Die innere Induktivität strebt schon bei niedrigeren Frequenzen gegen Null, der Widerstand steigt erst bei höheren Frequenzen überproportional an. 19

22 2 Beschreibung des Skineffekts im Frequenzbereich Induktivität Widerstand L (j ω) in nh/m R (j ω) in Ω/m f in Hz Abbildung 2.12: Längenbezogener Widerstand und innere Induktivität in Abhängigkeit der Frequenz für einen typischen Mikrostreifenleiter 2.4 Allgemeine Eigenschaften der Frequenzgänge Allen betrachteten Frequenzgängen der längenbezogenen Impedanz, bzw. des längenbezogenen Widerstandes und der längenbezogenen inneren Induktivität ist folgendes gemeinsam: Widerstand und Induktivität sind für niedrige Frequenzen konstant ab einer bestimmten Knickfrequenz steigt der Widerstand an und die innere Induktivität fällt ab oberhalb der Knickfrequenz steigt der Widerstand proportional zu ω und die Induktivität sinkt proportional zu 1/ ω ab Unterschiede zwischen den Frequenzgängen gibt es besonders im Bereich der Knickfrequenz. Beim Mikrostreifenleiter gibt es außerdem offensichtlich zwei verschiedene Knickfrequenzen für Induktivität und Widerstand. Zusätzlich ist dort auch der Einfluss des Proximity- Effektes sichtbar. 20

23 3 Modellierung des Skineffekts im Zeitbereich 3.1 Zustand der Forschung Die bisherige Beschreibung im Frequenzbereich ist besonders dort sinnvoll, wo auch im Frequenzbereich berechnet und simuliert wird. Das trifft z. B. für die Nachrichtentechnik zu, bei der häufig Frequenzmultiplexing (engl. Frequency Division Multiple Access, FDMA) zum Einsatz kommt. Die Signale dort haben eine sehr geringe spektrale Breite und eine relative Bandbreite von nur wenigen Prozent. Anders sieht es z. B. in der Informationstechnik oder Leistungselektronik aus. Dort wird häufig mit pulsförmigen Signalen, mit rampenförmigen Verläufen, mit steigenden und fallenden Flanken, allgemein also mit transienten Verläufen von Strom und Spannung gearbeitet. Deshalb ist es sinnvoll, den Skineffekt auch im Zeitbereich beschreiben zu können. Diese Beschreibung kann dann z. B. in diskrete Leitungsmodelle oder in die Methode der partielle Elemente (PEEC-Methode) integriert werden. Ein weiterer Vorteil gegenüber den Beschreibungen im Frequenzbereich liegt darin, das Verhalten nichtlinearer Komponenten berücksichtigen zu können. Im Folgenden soll der bisherige Stand der Forschung innerhalb der PEEC-Methode zu diesem Thema kurz darstellt werden. Eine kurze Einführung in die Methode der partiellen Elemente findet man in Abschnitt D-Diskretisierung Die 3D-Diskretisierung wird schon in [Rue74] vorgeschlagen und in [CR00] näher erläutert. Dabei wird ein Leiter nicht nur in tangentialer Richtung, sondern auch innerhalb der Querschnittsfläche in PEEC-Zellen unterteilt. Mögliche Diskretisierungsmuster sind in Abbildung 3.1 gezeigt. Diese Methode ist recht intuitiv und bietet recht genaue Simulationsergebnisse auch im Zeitbereich. Außerdem kann auch ohne weiteres der Proximity-Effekt betrachtet werden. Von sehr großem Nachteil ist aber, dass die Anzahl der PEEC-Zellen durch die Querschnittsdiskretisierung stark ansteigt. Dadurch steigt auch die Ordnung der Systemmatrix stark an und die benötigte Rechenzeit steigt um Größenordnungen. 21

24 3 Modellierung des Skineffekts im Zeitbereich a) runder Leiter b) rechteckiger Leiter, c) rechteckiger Leiter, gleichmäßig diskretisiert angepasst diskretisiert Abbildung 3.1: Schematische Darstellung einiger möglicher Querschnittsdiskretisierungen für PEEC-Modelle Nach [Gör02] ist die Analyse der Verbindungsstrukturen einer gesamten Schaltung damit leider unmöglich. Näherung durch Stufennetzwerke Um die Nachteile der 3D-Diskretisierung zu umgehen und den Skineffekt trotzdem zu berücksichtigen, wurden Lösungen gesucht, die eine näherungsweise Modellierung erlauben. Dabei soll die frequenzabhängige Änderung des Wirkwiderstandes und der inneren Induktivität durch Ersatznetzwerke (sog. Stufennetzwerke oder Kettenleiter-Schaltungen) aus Widerständen und Induktivitäten nachgebildet werden. Diese Widerstände und Induktivitäten bilden die konstanten und frequenzunabhängigen Parameter des Modells. Sie erlauben eine aufwandsärmere netzwerkorientierte Modellierung des Skineffekts im Zeitbereich. Für die Parametrierung sind verschiedene Verfahren möglich. Ein Verfahren ist in [KN96] dargestellt und berechnet die Parameter des Stufennetzwerks durch geometrische Staffelung der Widerstands- und Induktivitätswerte. Ein zweites Verfahren ist in [GW98] erläutert und beschreibt die Approximation der Impedanzverläufe durch Ausgleichsrechnung. Ein drittes Verfahren, bei dem der Skineffekt durch eine angepasste frequenzabhängige mittlere Oberflächenimpedanz (engl. MSI, Mean Surface Impedance) berücksichtigt wird, ist in [WK03] vorgestellt. Bei korrekter Parametrierung schlängelt sich bei allen Verfahren der frequenzabhängige Impedanzverlauf des Stufennetzwerks um den exakten Verlauf, der in Kapitel 2 hergeleitet wurde. Zwei Möglichkeiten des Stufennetzwerks sind in Abbildung 3.2 dargestellt. In der Praxis benutzt man meist 4 bis 8 Stufen. Der Vorteil dieser Methode ist, dass sie eine näherungsweise Modellierung des Skineffekts im Zeitbereich gestattet. Nachteilig ist, dass das Modell erst durch eine Optimierung der Parameter der 4 bis 8 Stufen an den exakten Impedanzverlauf angepasst werden muss. Diese Näherung stimmt dann auch nur für einen bestimmten Frequenzbereich. Außerdem fügt man zusätzliche Bauelemente in das PEEC-Modell ein. Dadurch steigen die Anzahl 22

25 3 Modellierung des Skineffekts im Zeitbereich L 1 L 2 L n R 1 R 2 R n R 1 R 2 R 3 R n 1 L 1 L 2 L n a) Ersatzschaltbild für geometrische Staffelung der Parameter [KN96] b) Ersatzschaltbild für Ausgleichsrechnung [GW98] Abbildung 3.2: Stufennetzwerke für die Approximation der Impedanzverläufe der Knoten und damit auch die Ordnung der Systemmatrix an. Die benötigte Rechenzeit steigt auch hier stark an. 3.2 Modellierung des Skineffekts mittels FSCM Der in dieser Arbeit vorgestellte neue Ansatz zur Beschreibung des Skineffekts im Zeitbereich benutzt das sog. Full Spectrum Convolution Macromodeling. Dabei wird allgemein eine über den gesamten Frequenzbereich (engl. full spectrum) gültige frequenzabhängige Größe über inverse Fouriertransformation in den Zeitbereich überführt und dann über ein Faltungsintegral (convolution) ausgewertet. Weil für die frequenzabhängigen Verläufe die inverse Fouriertransformation häufig nicht direkt möglich ist, müssen diese durch einfachere und transformierbare Verläufe angenähert werden (macromodeling). Eine beispielhafte Anwendung, in der FSCM ebenfalls genutzt wird, ist in [KW07] oder [KWL07] zu finden. Ein erster Ansatz wäre also die frequenzabhängige Impedanz (2.24) von Seite 10 über die inverse Fouriertransformation in den Zeitbereich zu überführen: z(t) = 1 2π + Z(jω) e jtω dω (3.1) Wie aber aus allen Impedanzverläufen aus Kapitel 2 ersichtlich ist, gilt lim ω Z(jω). Das bedeutet, der Integrand strebt für hohe Frequenzen gegen unendlich. Das Integral konvergiert nicht und eine Transformation ist in dieser Form nicht möglich. Deshalb ist es sinnvoll, die längenbezogene Impedanz in eine Admittanz umzuwandeln. Für den Leiter mit rundem Querschnitt ist das in Formel (3.2) gezeigt. Die Admittanz ist ebenfalls eine komplexe Größe. Ihr Realteil entspricht dem Wirkleitwert (Konduktanz), der Imaginärteil dem Blindleitwert (Suszeptanz). Der beispielhafte frequenzabhängige Verlauf der Admittanz für einen runden Kupferleiter ist in Abbildung 3.3 dargestellt. Der Vorteil der Admittanzdarstellung ist, dass lim ω Y (jω) 0. Das bedeutet, der Integrand in Gleichung (3.3) strebt für hohe Frequenzen gegen Null und das Transformationsintegral 23

26 3 Modellierung des Skineffekts im Zeitbereich 200 Re[Y (j ω)] und Im[Y (j ω)] in Sm Realteil Imaginärteil f in Hz Abbildung 3.3: Längenbezogene Admittanz in Abhängigkeit der Frequenz für einen Kupferdraht mit 1 mm Radius konvergiert. Leider ist aber aufgrund der Besselschen Funktionen mit der Wurzel der Frequenz im Argument eine analytische Transformation in dieser Form nicht möglich. Y (jω) = y(t) = 1 2π 1 Z (jω) = + 2πr 0γ J1( jωµγr 0 ) jωµγ J 0 ( jωµγr 0 ) (3.2) Y (jω) e jtω dω (3.3) Deshalb ist es nötig, die Admittanz zu modellieren. Das Modell soll den exakten Verlauf von Y (jω) nachbilden und es muss eine inverse Fouriertransformation für das Modell existieren. Ein solches Modell wurde gefunden und ist in Gleichung (3.4) angegeben. Es hängt nur von zwei Parametern ab, einem Gleichstromwiderstand R 0 und einer Knickfrequenz ω c. Y modell (jω) = 1 R 0 1 = 1 1 (3.4) 1 + j ω R ω jωτc c Weil das Modell später im Zeitbereich genutzt werden soll, ist es sinnvoll, die Knickfrequenz in eine Knickzeitkonstante τ c umzuwandeln. Die Parametrierung kann einerseits über eine Optimierungsroutine erfolgen, welche die Summe der quadratischen Abweichungen zwischen dem exakten und modellierten Admittanzverlauf minimiert. Diese nichtlineare Optimierung 24

27 3 Modellierung des Skineffekts im Zeitbereich findet in einem bestimmten Frequenzbereich ω [ω min, ω max ] auf folgende Art statt: ω max ω min [Y (jω) Y modell (jω, τ c )] 2 dω τ c min (3.5) Dabei ist Y (jω) die exakte Lösung der Admittanz und τ c die zu optimierende Knickzeitkonstante. Der Wert des Gleichstromwiderstandes R 0 muss nicht durch eine Optimierung bestimmt werden, sondern ergibt sich aus der Grenzwertbetrachtung Y (0) = Y modell (0) zu R 0 = 1. Andererseits hat sich für den runden Leiter auch folgende Parametrierung Y (0) bewährt: Gleichstromwiderstand R 0 = l γπr 2 0 Gleichstrominduktivität L 0 = µ 8π Knickfrequenz ω c = R 0 2L 0 = 50 nh Knickzeitkonstante τ c = 1 ω c Damit ergeben sich für den im Beispiel verwendeten Kupferdraht die Werte R 0 = 5,48 mω und τ c = 1, s. Der Vergleich des Admittanzverlaufs zwischen exakter Lösung und Modell ist in Abbildung 3.4 dargestellt. Man erkennt, dass Modell und exakte Lösung für kleine und große Frequenzen sehr gut übereinstimmen und nur im Bereich der Knickfrequenz kleine Abweichungen zu verzeichnen sind. Welchen Einfluss diese frequenzabhängigen Abweichungen für Berechnungen im Zeitbereich darstellen, soll später untersucht werden. Um nun zur Zeitbereichsdarstellung des Modells zu gelangen, muss man die inverse Fouriertransformation durchführen. y modell (t) = 1 2π + Y modell (jω) e jtω dω (3.6) t y modell (t) = g(t) = 1 e τc h(t) (3.7) R 0 πtτc Die Lösung der inversen Fouriertransformation entspricht der Impulsantwort. Der Ausdruck h(t) ist dabei der Heaviside-Sprung. Zur Bewertung des Modells im Zeitbereich kann nun die Antwort des Stromes i modell (t) auf einen bestimmten Spannungspuls u(t) an der Admittanz über das sogenannte Duhamel-Integral berechnet werden. i modell (t) = s(0) u(t) + t 0 y modell (t τ)u(τ) dτ (3.8) 25

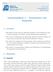
28 3 Modellierung des Skineffekts im Zeitbereich 200 Re[Y (j ω)] und Im[Y (j ω)] in Sm Realteil (exakte Lösung) Imaginärteil (exakte Lösung) Realteil (Modell) Imaginärteil (Modell) f in Hz Abbildung 3.4: Vergleich von Modell und exakter Lösung der Admittanz in Abhängigkeit der Frequenz für einen Kupferdraht mit 1 mm Radius Dabei ergibt sich die Anfangsbedingung aus der Multiplikation der Sprungantwort s(0) mit der Anregung u(t). Die Sprungantwort lässt sich allgemein durch eine Faltung der Impulsantwort mit dem Heaviside-Sprung h(t) berechnen: s(t) = g(t) h(t) = + g(τ)h(t τ) dτ = t g(τ) dτ (3.9) Setzt man y modell für die Impulsantwort g zum Zeitpunkt t = 0 ein, so ergibt sich s(0) = 0. Das beschriebene Modell ist also nicht sprungfähig. Damit fällt die Anfangsbedingung weg und es verbleibt das einfache Faltungsintegral zur Berechnung der Stromantwort des Skineffekt-Modells im Zeitbereich: i modell (t) = t 0 y modell (t τ)u(τ) dτ (3.10) Als Referenz zur Bewertung des Modells wird nun das Spektrum U(jω) des Pulses im Frequenzbereich mit der exakten Lösung Y (jω) multipliziert und über eine inverse FFT (Fast Fourier Transformation) ebenfalls in den Zeitbereich überführt. Zur analytischen Auswertung der Ausdrücke wird das Computer-Algebra-System Maple benutzt, die numerische Berechnung erfolgt mit MATLAB. Als Testfunktion kann z. B. ein rechteckiger Puls 26

29 3 Modellierung des Skineffekts im Zeitbereich Abbildung 3.5: Zeitverlauf und Spektrum für einen rechteckigen Puls mit 1 µs Breite mit der Breite τ r für die Spannung benutzt werden. u(t) = u 0 [h(t) h(t τ r )] (3.11) U(jω) = u 0 j e jωτr 1 ω (3.12) Zeitverlauf und Spektrum für einen solchen Puls sind in Abbildung 3.5 dargestellt. Die Antwortfunktionen des Stromes sind in Abbildung 3.6 gezeigt. Die FFT erfolgte dabei mit 4096 Werten. Weitere Testpulse und die entsprechenden Antworten sind im Anhang A.3 dargestellt. Wie man erkennt, zeigt das Modell nicht nur im Frequenzbereich, sondern auch im Zeitbereich gute Übereinstimmung mit der exakten Lösung. Für die weiteren Ziele, die Integration des Skineffekt-Modells in Leitung- und PEEC- Modelle sowie die Erstellung eines Skineffekt-Modells für Netzwerksimulatoren, ist es nötig, das analytische Modell für numerische Berechnungen zu diskretisieren. Viele Netzwerksimulatoren, z. B. auch das sehr verbreitete SPICE, benutzen die modifizierte Knotenspannungsmethode (MNA - modified nodal analysis). Dieses Verfahren basiert auf der einfachen Knotenspannungsanalyse gemäß Y U = I, besitzt aber weiterhin einige Vorteile, z. B. können auch ideale Spannungsquellen behandelt werden. Innerhalb der MNA-Methode muss für jedes Bauelement, das eine Zeitabhängigkeit besitzt, ein diskretes zugeordnetes Ersatzschaltbild erstellt werden. Dabei wird zuerst die kontinuierliche Zeit und damit auch alle zeitabhängigen Verläufe in diskrete Schritte unterteilt. Es werden folgende vereinfachten Schreibweisen definiert: Zeitschritt: t Diskretisierung der Zeit: n t = t n Diskretisierung des Spannungsverlaufs: u(t n ) = u n Diskretisierung des Stromverlaufs: i(t n ) = i n 27

30 3 Modellierung des Skineffekts im Zeitbereich i(t) in A exakte Lösung (mit Multiplikation im Frequenzbereich und FFT) Lösung des Modells (mit Faltung im Zeitbereich) t in s x 10 6 Abbildung 3.6: Antwortfunktion des Stromes auf einen rechteckigen Puls mit 1 µs Breite Strom und Spannung an einem Bauelement werden nur noch zu bestimmten Zeitpunkten berechnet. Zwischen den Zeitpunkten werden die Verläufe durch Geraden genähert. Ein Integral kann dann z. B. einfach als ein Trapez berechnet werden. Bei der Erstellung des zugeordneten Ersatzschaltbildes, z. B. einer Induktivität, wird folgende Vorgehensweise benutzt: t n+1 t n u(t) = L di(t) dt (3.13) di(t) = 1 t n+1 u(t) dt L t n (3.14) i n+1 i n = 1 L un+1 + u n 2 i n+1 = t 2L }{{} g t (3.15) u n+1 + t 2L u n + i n }{{} J n+1 (3.16) Die entstehenden Terme können als ein Leitwert g und eine Stromquelle J n+1 interpretiert werden. Damit ist aus der Induktivität ein diskretes zugeordnetes Ersatzschaltbild entstanden, das in Abbildung 3.7 dargestellt ist. Die gleiche Vorgehensweise kann nun für das FSCM-Skineffekt-Modell wiederholt werden. 28

31 3 Modellierung des Skineffekts im Zeitbereich u t u n 1 L i t g i n 1 Abbildung 3.7: Zugeordnetes Ersatzschaltbild einer Induktivität für Netzwerksimulatoren J n 1 Dazu muss das Faltungsintegral (3.10) diskretisiert werden. i n+1 = t n+1 0 y(t n+1 τ)u(τ) dτ für τ = 0... t n+1 (3.17) Weiter kann man das Integral entlang der Zeitachse in mehrere Integrale aufteilen, die jeweils einen Integrationsschritt t lang sind. Diese Teilintegrale werden dann aufsummiert: i n+1 = n k=0 t k+1 t k y(t n+1 τ)u(τ) dτ für τ = t k... t k+1 (3.18) Nun kann man das Eingangssignal u(t) stückweise durch Geraden annähern (Newton- Approximation). Für jeden Zeitschritt erhält man einen Anstieg a k = u k+1 u k t Offset b k = u k. Das Eingangssignal kann jetzt umgeschrieben werden: und einen u(τ) = a k τ + b k für τ = t k... t k+1 (3.19) Setzt man dies in das Faltungsintegral ein und verschiebt die Grenzen des Integrals, so erhält man: i n+1 = i n+1 = i n+1 = n k=0 n k=0 n k=0 0 t k+1 t k y(t n+1 τ)(a k (τ t k ) + b k ) dτ für τ = t k... t k+1 (3.20) t k+1 t k t k t k y(t n+1 (τ + t k ))(a k (τ + t k t k ) + b k ) dτ (3.21) t y(t n+1 t k τ)(a k τ + b k ) dτ für τ = 0... t (3.22) Die erreichte Form hat den Vorteil, dass die Grenzen des Integrals unabhängig vom Zeitpunkt sind. Damit kann man das Integral nun einmal analytisch lösen und die erlangte 29

32 3 Modellierung des Skineffekts im Zeitbereich Lösung wieder in die Summe einsetzen. Die analytische Lösung des Integrals lautet: t 0 y(t n+1 t k τ)(a k τ + b k ) dτ = + 1 τc T n+1,k a k Ψ n+1,k + R 0 π 1 R 0 a k τc T n,k π Ψ n,k + ( a k T n+1,k + b k a ) k 2 τ c ( a k T n+1,k + b k a ) k 2 τ c Φ n,k Φ n+1,k (3.23) Ψ n,k = e T n,k τc Φ n,k = erf Tn,k τc (3.24) (3.25) T n,k = t n t k = (n k) t (3.26) Die analytische Lösung des Integrals kann man nun in die Summe einsetzen und alle Anstiege a k und Offsets b k ersetzen: i n+1 = i n+1 = + n 1 k=0 R 0 n τc T n+1,k a k Ψ n+1,k + π ( a k T n+1,k + b k a ) k 2 τ c ( 1 τc T n,k a k k=0 R 0 π Ψ n,k + a k T n+1,k + b k a ) k 2 τ c n 1 τc T n+1,k (u k+1 u k ) Ψ n+1,k k=0 R 0 t π n [( 1 (u k+1 u k )T n+1,k + tu k u k+1 u k k=0 R 0 t 2 n 1 τc T n,k (u k+1 u k ) k=0 R 0 t π Ψ n,k n [( 1 (u k+1 u k )T n+1,k + tu k u k+1 u k R 0 t 2 k=0 Φ n,k Φ n+1,k τ c ) Φ n+1,k ] τ c ) Φ n,k ] (3.27) (3.28) Nun können alle u k ausgeklammert werden. Der Rest des Ausdrucks wird als neue Variable Ω k zusammengefasst. Dadurch wird aus dem Faltungsintegral eine Summe. i(t n+1 ) = t n+1 0 y modell (t n+1 τ)u(τ) dτ i n+1 = n+1 k=0 Ω k u k (3.29) Die gesamte Intelligenz der Berechnung steckt nun in den Koeffizienten Ω k, die wie folgt 30

33 3 Modellierung des Skineffekts im Zeitbereich berechnet werden: τct n+1,k Ψ π n+1,k + ( ) T n,k + τc Φn+1,k 2 τct + n,k Ψ π n,k ( ) T n,k + τc Φn,k k = 0 2 Ω k = 1 R 0 t τct + n+1,k 1 Ψ π n+1,k 1 + ( ) T n+1,k 1 τc Φn+1,k 1 2 τct n,k 1 Ψ π n,k 1 ( ) T n+1,k 1 τc Φn,k 1 k = n (3.30) τct n+1,k π Ψ n+1,k + ( T n,k + τc 2 ) Φn+1,k + τct n,k π Ψ n,k ( T n,k + τc 2 ) Φn,k τct + n+1,k 1 Ψ π n+1,k 1 + ( ) T n+1,k 1 τc Φn+1,k 1 2 τct n,k 1 Ψ π n,k 1 ( ) T n+1,k 1 τc Φn,k 1 sonst 2 Für das weitere Ziel, die Erstellung eines zugeordneten Ersatzschaltbildes für Netzwerksimulatoren wie SPICE, ist es praktisch, die Summenformel aufzutrennen: n+1 n i n+1 = Ω k u k = Ω k u k + Ω n+1 u n+1 (3.31) }{{} k=0 k=0 }{{} g n+1 J n+1 Die aus dem Faltungsintegral hervorgegangene Summenformel kann nun ebenfalls als eine Parallelschaltung aus einer Stromquelle J n+1 und einem Leitwert g n+1 interpretiert werden. Diese Elemente müssen in jedem Zeitschritt neu berechnet werden: i n+1 = J n+1 + g n+1 u n+1 (3.32) n J n+1 = Ω k u k (3.33) k=0 g n+1 = Ω n+1 (3.34) Das zugeordnete Ersatzschaltbild des Skineffekt-Modells, das sehr große Ähnlichkeiten mit dem Ersatzschaltbild der Induktivität aufweist (vergleiche Abbildung 3.7 auf Seite 29), ist in Abbildung 3.8 gezeigt. Dieses Ersatzschaltbild kann nun in jeden Netzwerksimulator, der nach der MNA-Methode funktioniert, implementiert werden. Damit kann man z. B. eine Spule mit Skineffekt simulieren, oder den Skineffekt in diskrete Leitungsmodelle oder PEEC-Modelle integrieren. Das neue FSCM-Skineffekt-Modell besitzt gegenüber den anderen vorgestellten Modellvarianten folgende Vorteile: 31