Eigenschaften kompakter Operatoren
|
|
|
- Josef Neumann
- vor 7 Jahren
- Abrufe
Transkript
1 Eigenschaften kompakter Operatoren Denition Seien X, Y normierte Räume und sei A : X Y linear. Dann heiÿt A kompakt (vollstetig), wenn für jede beschränkte Menge B X die Menge A(B) kompakt ist.
2 Eigenschaften kompakter Operatoren Denition Seien X, Y normierte Räume und sei A : X Y linear. Dann heiÿt A kompakt (vollstetig), wenn für jede beschränkte Menge B X die Menge A(B) kompakt ist. Theorem Seinen X, Y, Z Hilberträume und sei A : X Y linear. Dann gilt: 1. A ist genau dann kompakt, wenn für jede beschränkte Folge (x n ) n in X die Folge (Ax n ) n eine konvergente Teilfolge besitzt. 2. Ist A kompakt, so ist A beschränkt (also stetig) und damit A L(X, Y ). 3. Linearkombinationen kompakter linearer Operatoren sind kompakt. 4. Sei A 1 L(X, Y ), A 2 L(Y, Z). Dann ist A 1 A 2 kompakt, falls A 1 oder A 2 kompakt ist.
3 5. Sei Y ein Banachraum und für alle n N sei A n : X Y linear und kompakt. Es gelte lim n A A n = 0. Dann ist A kompakt. 6. Sei A beschränkt und dim(r(a)) <, dann ist A kompakt.
4 5. Sei Y ein Banachraum und für alle n N sei A n : X Y linear und kompakt. Es gelte lim n A A n = 0. Dann ist A kompakt. 6. Sei A beschränkt und dim(r(a)) <, dann ist A kompakt. Sei (x n ) n X beschränkt mit sup n N x n Y C. Da A 1 kompakt die Folge (A 1 x m ) m N eine konvergente Teilfolge (A 1 x m1 (k)) k N Da A 2 kompakt die Folge (A 2 x m1 (k)) k N eine konvergente Teilfolge (A 2 x m2 (k)) k N... (vollst. Induktion) (x mi (k)) k N T.F. von (x m ) m N, (x mi 1 (k)) k N Teilfolge von (x mi (k)) k N ist für alle i N jeweils (K i x mi (k)) k N konvergiert. (insb. ist dann auch für alle j i die Folge K i (x mj (k)) k N konvergent). Sei nun y i := x mi (i) die Diagonalfolge, Teilfolge von x m.
5 Zu zeigen: (Ky i ) ist konvergent. Wegen lim n A A n = 0 ex. für jedes ɛ > 0 ein n N so dass A A n ɛ 3C. Aus der Konstruktion von y i folgt, dass A n y i konvergiert (endl. viele Elemente spielen keine Rolle), sei also i 0 N so dass für i, j > i 0 gilt A n y i A n y j ɛ 3.
6 Damit gilt für i, j > i 0 Ay i Ay j Ay i A n y i + A n y i A n y j + A n y j Ay i (1) A A n ( y i + y j ) + ɛ 3 < ɛ 3C 2C + ɛ 3 = ɛ. (2) (Ay i ) ist Cauchy-Folge. Da Y Banachraum (vollständig) (Ay i ) konvergiert. Da x n bel. war A ist kompakt. 6.: Folg aus dem Satz von Heine-Borel, das danach der Abschluss der beschränkten Teilmengen von R(A) kompakt ist.
7 Denition Sei A : X X linear und kompakt. A selbstadjungiert, falls (Ax, y) = (x, Ay) x, y X
8 Denition Sei A : X X linear und kompakt. A selbstadjungiert, falls (Ax, y) = (x, Ay) x, y X Theorem Sei A L(X, X ) kompakt und selbstadjungiert. Dann sind alle Eigenwerte von A reell. Weiterhin sind Eigenfunktionen zu unterschiedlichen Eigenwerten orthogonal. Theorem Sei A L(X, X ) kompakt und selbstadjungiert. Dann sind A X,X oder ( A X,X ) Eigenwerte von A. Theorem Sei A L(X, X ) kompakt und selbstadjungiert. Dann existiert eine Hilbertbasis aus Eigenvektoren von A und für jedes f X gilt die Darstellung f = i (f, φ i )φ i + f 0, mit Af 0 = 0.
9 Beweis. Sei (λ n ) n 1 die Folge aller nicht verschwindenden Eigenwerte von A. Setze λ 0 = 0, E 0 = N(A), und E n = N(A λ n I ). Es gilt (s.o.) 0 dim(e 0 ) und 0 < dim(e n ) <. Zu zeigen: H = n 0 E n. Die Räume (E n ) n 0 sind orthogonal: Sei u E n, v E m, n m, dann gilt λ m (u, v) = (Au, v) = (u, Av) = λ n (u, v), und da λ n λ m folgt (u, v) = 0.
10 Sei F der Raum aufgespannt von den Räumen (E n ) n 0. Zu zeigen: F ist Dicht in H (i.e. F = 0, bzgl. H). Es ist klar, dass A(F ) F. Sei nun u F dann gilt (Au, v) = (}{{} u, }{{} Av ) = 0, v F, F F und daher A(F ) F und somit A(F ) F. Sei T 0 := T F. T 0 ist wieder selbstadjungiert und kompakt. Wir zeigen nun per Widerspruch dass σ(t 0 ) = 0 und damit T 0 = 0: Nehme also an, es ex. λ 0 mit T 0 u = λu. Damit ist λ aber auch einer der Eigenwerte von T, o.b.d.a. λ n mit n 1. Daher ist u E n F. Da aber u F F folgt, dass u = 0, also ein Widerspruch und daher T 0 = 0. Damit folgt schlieÿlich F N(T ). Da auf der anderen Seite gilt aber N(T ) F und damit F F. Daraus folgt F = 0 und F dicht in H.
11 Theorem Sei W der Eigenraum eines kompakten Operators zum Eigenwert µ 0. Dann ist W endlichdimensional. Theorem Sei A L(X, Y ) kompakt und selbstadjungiert. Dann häufen sich die Eigenwerte von A höchstens bei 0, d.h. wenn λ n eine Folge von Eigenwerten von A ist, so dass dann ist λ = 0. λ n λ wenn n
12 Theorem Sei W der Eigenraum eines kompakten Operators zum Eigenwert µ 0. Dann ist W endlichdimensional. Theorem Sei A L(X, Y ) kompakt und selbstadjungiert. Dann häufen sich die Eigenwerte von A höchstens bei 0, d.h. wenn λ n eine Folge von Eigenwerten von A ist, so dass dann ist λ = 0. λ n λ wenn n Theorem (Spektralsatz für kompakte, selbstadjungierte Operatoren) Sei A L kompakt, selbstadjungiert. Sei λ n die Folge der Eigenwerte und x n die zugehörigen, normalisierten Eigenvektoren. Dann gilt Ax = λ n x n (x, x n ) X n=1
Beispiele. Grundlagen. Kompakte Operatoren. Regularisierungsoperatoren
 Beispiele Grundlagen Kompakte Operatoren Regularisierungsoperatoren Transportgleichung Dierenzieren ( nx ) (f δ n ) (x) = f (x) + n cos, x [0, 1], δ Regularisierung!! Inverse Wärmeleitung Durc f (f δ n
Beispiele Grundlagen Kompakte Operatoren Regularisierungsoperatoren Transportgleichung Dierenzieren ( nx ) (f δ n ) (x) = f (x) + n cos, x [0, 1], δ Regularisierung!! Inverse Wärmeleitung Durc f (f δ n
Kompakte Operatoren in Hilberträumen
 Kompakte Operatoren in Hilberträumen 1 Vorbemerkungen Im Folgenden bezeichne H immer einen seperablen Hilbertraum über C Mit B(H 1, H 2 ) bezeichnen wir die Menge aller beschränkten linearen Operatoren
Kompakte Operatoren in Hilberträumen 1 Vorbemerkungen Im Folgenden bezeichne H immer einen seperablen Hilbertraum über C Mit B(H 1, H 2 ) bezeichnen wir die Menge aller beschränkten linearen Operatoren
Lösungsvorschlag zu den Hausaufgaben der 8. Übung
 FAKULTÄT FÜR MATHEMATIK Prof Dr Patrizio Ne Frank Osterbrink Johannes Lankeit 9503 Lösungsvorschlag zu den Hausaufgaben der 8 Übung Hausaufgabe : Beweise den Satz über die Parallelogrammgleichung Sei H
FAKULTÄT FÜR MATHEMATIK Prof Dr Patrizio Ne Frank Osterbrink Johannes Lankeit 9503 Lösungsvorschlag zu den Hausaufgaben der 8 Übung Hausaufgabe : Beweise den Satz über die Parallelogrammgleichung Sei H
4 Kompakte Operatoren
 4.1 Kompakte Op. auf dem Hilbertraum 57 4 Kompakte Operatoren 4.1 Kompakte Operatoren auf dem Hilbertraum 4.1.1 Folg. (id H kompakt H endlichdim.) Die identische Abbildung eines Prähilbertraumes X ist
4.1 Kompakte Op. auf dem Hilbertraum 57 4 Kompakte Operatoren 4.1 Kompakte Operatoren auf dem Hilbertraum 4.1.1 Folg. (id H kompakt H endlichdim.) Die identische Abbildung eines Prähilbertraumes X ist
also ist Sx m eine Cauchyfolge und somit konvergent. Zusammen sagen die Sätze 11.1 und 11.2, dass B (X) ein abgeschlossenes zweiseitiges
 11. Kompakte Operatoren Seien X, Y Banachräume, und sei T : X Y ein linearer Operator. Definition 11.1. T heißt kompakt, enn T (B) eine kompakte Teilmenge von Y ist für alle beschränkten Mengen B X. Wir
11. Kompakte Operatoren Seien X, Y Banachräume, und sei T : X Y ein linearer Operator. Definition 11.1. T heißt kompakt, enn T (B) eine kompakte Teilmenge von Y ist für alle beschränkten Mengen B X. Wir
Funktionalanalysis II. Carsten Schütt SS 2012
 1. Jeder Filter ist in einem Ultrafilter enthalten. 2. Es sei X ein topologischer Hausdor Raum. X ist genau dann kompakt, wenn jeder Ultrafilter konvergiert. 3. (Skript) (i) {0, 1} [0,1] mit der Produkttopologie
1. Jeder Filter ist in einem Ultrafilter enthalten. 2. Es sei X ein topologischer Hausdor Raum. X ist genau dann kompakt, wenn jeder Ultrafilter konvergiert. 3. (Skript) (i) {0, 1} [0,1] mit der Produkttopologie
1 Hilbertraum. 1.1 Denition und einführende Beispiele. Im Folgenden sei K {R, C}.
 1 1 Hilbertraum Im Folgenden sei K {R, C}. 1.1 Denition und einführende Beispiele Denition 1.1 (inneres Produkt, Skalarprodukt) Ein inneres Produkt auf einem K-Vektorraum V ist eine positiv denite hermitesche
1 1 Hilbertraum Im Folgenden sei K {R, C}. 1.1 Denition und einführende Beispiele Denition 1.1 (inneres Produkt, Skalarprodukt) Ein inneres Produkt auf einem K-Vektorraum V ist eine positiv denite hermitesche
Wiederholung. Wir wiederholen einige Begriffe und Sätze der Analysis, die in der Maßtheorie eine wichtige Rolle spielen.
 Wiederholung Wir wiederholen einige Begriffe und Sätze der Analysis, die in der Maßtheorie eine wichtige Rolle spielen. Definition. Sei X eine Menge und d : X X R eine Abbildung mit den Eigenschaften 1.
Wiederholung Wir wiederholen einige Begriffe und Sätze der Analysis, die in der Maßtheorie eine wichtige Rolle spielen. Definition. Sei X eine Menge und d : X X R eine Abbildung mit den Eigenschaften 1.
Differentialgleichungen und Hilberträume Sommersemester 2014 Übungsblatt 11
 Institut für Analysis Prof. Dr. Wolfgang Reichel Dipl.-Math. Anton Verbitsky Aufgabe 1 Differentialgleichungen und Hilberträume Sommersemester 14 Übungsblatt 11 5 Punkte In dieser Aufgabe geht es um die
Institut für Analysis Prof. Dr. Wolfgang Reichel Dipl.-Math. Anton Verbitsky Aufgabe 1 Differentialgleichungen und Hilberträume Sommersemester 14 Übungsblatt 11 5 Punkte In dieser Aufgabe geht es um die
Höhere Funktionalanalysis WS2016/17 Übungsblatt
 Höhere Funktionalanalysis WS2016/17 Übungsblatt 1 11.10.2016 Aufgabe 1. Berechne die Normen der Operatoren (a) f L [0, 1], M f : L 2 [0, 1] L 2 [0, 1], (M f g)(x) = f(x)g(x). (b) g C[0, 1], T g : C[0,
Höhere Funktionalanalysis WS2016/17 Übungsblatt 1 11.10.2016 Aufgabe 1. Berechne die Normen der Operatoren (a) f L [0, 1], M f : L 2 [0, 1] L 2 [0, 1], (M f g)(x) = f(x)g(x). (b) g C[0, 1], T g : C[0,
Schauderbasen und das Beispiel der Riesz-Basen auf Hilberträumen
 Schauderbasen und das Beispiel der Riesz-Basen auf ilberträumen Bernhard Stiftner 0. Dezember 0 Inhaltsverzeichnis Allgemeines zu Schauderbasen Spezielle Schauderbasen auf ilberträumen 8 3 Literatur 8
Schauderbasen und das Beispiel der Riesz-Basen auf ilberträumen Bernhard Stiftner 0. Dezember 0 Inhaltsverzeichnis Allgemeines zu Schauderbasen Spezielle Schauderbasen auf ilberträumen 8 3 Literatur 8
Vollständiger Raum, Banachraum
 Grundbegriffe beschränkte Menge Cauchyfolge Vollständiger Raum, Banachraum Kriterium für die Vollständigkeit Präkompakte Menge Kompakte Menge Entropiezahl Eigenschaften kompakter und präkompakter Mengen
Grundbegriffe beschränkte Menge Cauchyfolge Vollständiger Raum, Banachraum Kriterium für die Vollständigkeit Präkompakte Menge Kompakte Menge Entropiezahl Eigenschaften kompakter und präkompakter Mengen
Variante A. Hinweise
 Lehrstuhl C für Mathematik (Analysis Prof Dr Holger Rauhut Aachen, den 373 Wiederholungsklausur zur Höheren Mathematik I SoSe 3 Variante A Hinweise Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind
Lehrstuhl C für Mathematik (Analysis Prof Dr Holger Rauhut Aachen, den 373 Wiederholungsklausur zur Höheren Mathematik I SoSe 3 Variante A Hinweise Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind
Optimale Steuerung, Prof.Dr. L. Blank 1. II Linear-quadratische elliptische Steuerungsprobleme
 Optimale Steuerung, Prof.Dr. L. Blank 1 II Linear-quadratische elliptische Steuerungsprobleme Zuerst: Zusammenstellung einiger Begriffe und Aussagen aus der Funktionalanalysis (FA), um dann etwas über
Optimale Steuerung, Prof.Dr. L. Blank 1 II Linear-quadratische elliptische Steuerungsprobleme Zuerst: Zusammenstellung einiger Begriffe und Aussagen aus der Funktionalanalysis (FA), um dann etwas über
4. Kompakte Operatoren im Hilbertraum.
 4. Kompakte Operatoren im Hilbertraum. Die einfachste Klasse von Operatoren bilden die Operatoren mit endlichem Rang, Af = N f, x j y j, f H, j=1 mit N N und (fest gewählten) x j, y j H, j = 1,...,N; dabei
4. Kompakte Operatoren im Hilbertraum. Die einfachste Klasse von Operatoren bilden die Operatoren mit endlichem Rang, Af = N f, x j y j, f H, j=1 mit N N und (fest gewählten) x j, y j H, j = 1,...,N; dabei
Rechenoperationen mit Folgen. Rekursion und Iteration.
 Rechenoperationen mit Folgen. Die Menge aller Folgen in V bildet einen Vektorraum, V N, für den die Addition und skalare Multiplikation wie folgt definiert sind. (a n ) n N + (b n ) n N := (a n + b n )
Rechenoperationen mit Folgen. Die Menge aller Folgen in V bildet einen Vektorraum, V N, für den die Addition und skalare Multiplikation wie folgt definiert sind. (a n ) n N + (b n ) n N := (a n + b n )
Lineare Algebra II (SS 13)
 Lineare Algebra II (SS 13) Bernhard Hanke Universität Augsburg 03.07.2013 Bernhard Hanke 1 / 16 Selbstadjungierte Endomorphismen und der Spektralsatz Definition Es sei (V,, ) ein euklidischer oder unitärer
Lineare Algebra II (SS 13) Bernhard Hanke Universität Augsburg 03.07.2013 Bernhard Hanke 1 / 16 Selbstadjungierte Endomorphismen und der Spektralsatz Definition Es sei (V,, ) ein euklidischer oder unitärer
7.3 Unitäre Operatoren
 Wir können jeden Operator T wie folgt schreiben: Dabei gilt T = 1 2 (T + T ) + i( 1 2 i (T T )) (T + T ) = T + T sowie ( 1 2 i (T T )) = 1 2 i (T T) = 1 2 i (T T ). Wir können T also in zwei lineare Operatoren
Wir können jeden Operator T wie folgt schreiben: Dabei gilt T = 1 2 (T + T ) + i( 1 2 i (T T )) (T + T ) = T + T sowie ( 1 2 i (T T )) = 1 2 i (T T) = 1 2 i (T T ). Wir können T also in zwei lineare Operatoren
Analysis I für Studierende der Ingenieurwissenschaften
 Analysis I für Studierende der Ingenieurwissenschaften Ingenuin Gasser Department Mathematik Universität Hamburg Technische Universität Hamburg Harburg Wintersemester 2008/2009 1 Definition: Sei M R, alsom
Analysis I für Studierende der Ingenieurwissenschaften Ingenuin Gasser Department Mathematik Universität Hamburg Technische Universität Hamburg Harburg Wintersemester 2008/2009 1 Definition: Sei M R, alsom
Kapitel 3. Konvergenz von Folgen und Reihen
 Kapitel 3. Konvergenz von Folgen und Reihen 3.1. Normierte Vektorräume Definition: Sei V ein Vektorraum (oder linearer Raum) über (dem Körper) R. Eine Abbildung : V [0, ) heißt Norm auf V, falls die folgenden
Kapitel 3. Konvergenz von Folgen und Reihen 3.1. Normierte Vektorräume Definition: Sei V ein Vektorraum (oder linearer Raum) über (dem Körper) R. Eine Abbildung : V [0, ) heißt Norm auf V, falls die folgenden
10. Unbeschränkte selbstadjungierte. Operatoren
 10. Unbeschränkte selbstadjungierte 10.1. Motivation Operatoren Observable hermitescher Operator, quadratische Form mit reellen Erwartungswerten Erzeugende einer Gruppe von Transformationen (z. B. Schrödinger
10. Unbeschränkte selbstadjungierte 10.1. Motivation Operatoren Observable hermitescher Operator, quadratische Form mit reellen Erwartungswerten Erzeugende einer Gruppe von Transformationen (z. B. Schrödinger
Vorlesung Lineare Funktionale LINEARE FUNKTIONALE 69
 13.1. LINEARE FUNKTIONALE 69 Vorlesung 13 13.1 Lineare Funktionale Der Begriff der schwachen Konvergenz wird klarer, wenn man lineare Funktionale betrachtet. Das Skalarprodukt f, g in Hilberträumenkann
13.1. LINEARE FUNKTIONALE 69 Vorlesung 13 13.1 Lineare Funktionale Der Begriff der schwachen Konvergenz wird klarer, wenn man lineare Funktionale betrachtet. Das Skalarprodukt f, g in Hilberträumenkann
ist reelles lineares Funktional. x(t) ϕ(t) dt ist reelles lineares Funktional für alle ϕ L 2 (0, 1).
 Kapitel 4 Stetige lineare Funktionale 4.1 Der Satz von Hahn - Banach Definition 4.1. Sei X ein linearer normierter Raum über dem Körper K (R oder C). Ein linearer Operator f : X K heißt (reelles oder komplexes)
Kapitel 4 Stetige lineare Funktionale 4.1 Der Satz von Hahn - Banach Definition 4.1. Sei X ein linearer normierter Raum über dem Körper K (R oder C). Ein linearer Operator f : X K heißt (reelles oder komplexes)
Ein Crashkurs zum Spektralsatz
 Ein Crashkurs zum Spektralsatz Zum Seminar partielle Differentialgleichungen 1 2 (WS 1999/2000) 17. Oktober 1999 1 Fragen an sick@math.uni-bonn.de oder mueller@math.uni-bonn.de 2 Dieses Skript ist auch
Ein Crashkurs zum Spektralsatz Zum Seminar partielle Differentialgleichungen 1 2 (WS 1999/2000) 17. Oktober 1999 1 Fragen an sick@math.uni-bonn.de oder mueller@math.uni-bonn.de 2 Dieses Skript ist auch
Karhunen-Loeve Entwicklung stochastischer Prozesse
 Karhunen-Loeve Entwicklung stochastischer Prozesse Wintersemester 2015/16 Erstellt von Manuel Summer Inhaltsverzeichnis 1 Einleitung 3 2 Kompakte Operatoren 4 2.1 Hilbert-Schmidt Operator..........................
Karhunen-Loeve Entwicklung stochastischer Prozesse Wintersemester 2015/16 Erstellt von Manuel Summer Inhaltsverzeichnis 1 Einleitung 3 2 Kompakte Operatoren 4 2.1 Hilbert-Schmidt Operator..........................
p = 0 Nun zur eigentlichen Aufgabe. Wie wir wissen, ist {1, X, X 2 } eine Basis von V, die wir nun mit Gram-Schmidt orthogonalisieren.
 Aufgabe 1 Es sei V = {p R[X] Grad p 2} und a, b, c R fest gewählt Überzeugen Sie sich davon, dass die Abbildung, : V V R, deniert durch p, q := p(a)q(a) + p (b)q (b) + p (c)q (c) ein Skalarprodukt ist
Aufgabe 1 Es sei V = {p R[X] Grad p 2} und a, b, c R fest gewählt Überzeugen Sie sich davon, dass die Abbildung, : V V R, deniert durch p, q := p(a)q(a) + p (b)q (b) + p (c)q (c) ein Skalarprodukt ist
FUNKTIONALANALYSIS. Carsten Schütt WS 2006/7
 1. Eine Teilmenge K eines topologischen Raumes heißt folgenkompakt, wenn jede Folge in K eine Teilfolge enthält, die in K konvergiert. Die Menge K heißt abzählbar kompakt, wenn jede unendliche Teilmenge
1. Eine Teilmenge K eines topologischen Raumes heißt folgenkompakt, wenn jede Folge in K eine Teilfolge enthält, die in K konvergiert. Die Menge K heißt abzählbar kompakt, wenn jede unendliche Teilmenge
Merkblatt zur Funktionalanalysis
 Merkblatt zur Funktionalanalysis Literatur: Hackbusch, W.: Theorie und Numerik elliptischer Differentialgleichungen. Teubner, 986. Knabner, P., Angermann, L.: Numerik partieller Differentialgleichungen.
Merkblatt zur Funktionalanalysis Literatur: Hackbusch, W.: Theorie und Numerik elliptischer Differentialgleichungen. Teubner, 986. Knabner, P., Angermann, L.: Numerik partieller Differentialgleichungen.
Lösungen der Aufgaben zu Kapitel 11
 Lösungen der Aufgaben zu Kapitel Vorbemerkung: Zur Bestimmung der Eigenwerte (bzw. des charakteristischen Polynoms) einer (, )-Matrix verwenden wir stets die Regel von Sarrus (Satz..) und zur Bestimmung
Lösungen der Aufgaben zu Kapitel Vorbemerkung: Zur Bestimmung der Eigenwerte (bzw. des charakteristischen Polynoms) einer (, )-Matrix verwenden wir stets die Regel von Sarrus (Satz..) und zur Bestimmung
Zusammenfassung Analysis 2
 Zusammenfassung Analysis 2 1.2 Metrische Räume Die Grundlage metrischer Räume bildet der Begriff des Abstandes (Metrik). Definition 1.1 Ein metrischer Raum ist ein Paar (X, d), bestehend aus einer Menge
Zusammenfassung Analysis 2 1.2 Metrische Räume Die Grundlage metrischer Räume bildet der Begriff des Abstandes (Metrik). Definition 1.1 Ein metrischer Raum ist ein Paar (X, d), bestehend aus einer Menge
7 Lineare Abbildungen und Skalarprodukt
 Mathematik II für inf/swt, Sommersemester 22, Seite 121 7 Lineare Abbildungen und Skalarprodukt 71 Vorbemerkungen Standard Skalarprodukt siehe Kap 21, Skalarprodukt abstrakt siehe Kap 34 Norm u 2 u, u
Mathematik II für inf/swt, Sommersemester 22, Seite 121 7 Lineare Abbildungen und Skalarprodukt 71 Vorbemerkungen Standard Skalarprodukt siehe Kap 21, Skalarprodukt abstrakt siehe Kap 34 Norm u 2 u, u
6 Kompakte Operatoren
 6 Kompakte Operatoren 6.1 Definition. X, Y seien Banachräume. A 2L(X, Y ) heißt kompakt, falls das Bild jeder beschränkten Menge in einer kompakten Menge enthalten ist (relativ kompakt ist), mit anderen
6 Kompakte Operatoren 6.1 Definition. X, Y seien Banachräume. A 2L(X, Y ) heißt kompakt, falls das Bild jeder beschränkten Menge in einer kompakten Menge enthalten ist (relativ kompakt ist), mit anderen
ist ein n-dimensionaler, reeller Vektorraum (vgl. Lineare Algebra). Wir definieren auf diesem VR ein Skalarprodukt durch i y i i=1
 24 14 Metrische Räume 14.1 R n als euklidischer Vektorraum Die Menge R n = {(x 1,..., x n ) x i R} versehen mit der Addition und der skalaren Multiplikation x + y = (x 1 + y 1,..., x n + y n ) λx = (λx
24 14 Metrische Räume 14.1 R n als euklidischer Vektorraum Die Menge R n = {(x 1,..., x n ) x i R} versehen mit der Addition und der skalaren Multiplikation x + y = (x 1 + y 1,..., x n + y n ) λx = (λx
Funktionalanalysis. Wintersemester 2010/2011 Dr. Tomáš Dohnal, Universität Stuttgart. Inhalt der Vorlesung im Detail
 Funktionalanalysis Wintersemester 21/211 Dr. Tomáš Dohnal, Universität Stuttgart Inhalt der Vorlesung im Detail 1. Metrische Räume, normierte Räume und Innenprodukträume; Funktionenräume Metrische Räume
Funktionalanalysis Wintersemester 21/211 Dr. Tomáš Dohnal, Universität Stuttgart Inhalt der Vorlesung im Detail 1. Metrische Räume, normierte Räume und Innenprodukträume; Funktionenräume Metrische Räume
Inhaltsverzeichnis. 6 Topologische Grundlagen. 6.1 Normierte Räume
 Inhaltsverzeichnis 6 Topologische Grundlagen 1 6.1 Normierte Räume................................ 1 6.2 Skalarprodukte................................. 2 6.3 Metrische Räume................................
Inhaltsverzeichnis 6 Topologische Grundlagen 1 6.1 Normierte Räume................................ 1 6.2 Skalarprodukte................................. 2 6.3 Metrische Räume................................
Matrix-Potenzen und größter Eigenwert
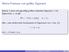 Matrix-Potenzen und größter Eigenwert Besitzt A einen betragsmäßig größten einfachen Eigenwert λ mit Eigenvektor v, so gilt A n x = λ n (cv + o(1)), n, falls x eine nichttriviale Komponente im Eigenraum
Matrix-Potenzen und größter Eigenwert Besitzt A einen betragsmäßig größten einfachen Eigenwert λ mit Eigenvektor v, so gilt A n x = λ n (cv + o(1)), n, falls x eine nichttriviale Komponente im Eigenraum
([0, 1]) und int K = p 1
![([0, 1]) und int K = p 1 ([0, 1]) und int K = p 1](/thumbs/76/74234111.jpg) 126 III. Der Satz von Hahn-Banach und seine Konsequenzen wie man durch Einsetzen unmittelbar erkennt. Zeigen wir noch die Halbstetigkeit von f: Sei(x n ) eine Folge in L p (R) mitx n x in L p (R) und f(x
126 III. Der Satz von Hahn-Banach und seine Konsequenzen wie man durch Einsetzen unmittelbar erkennt. Zeigen wir noch die Halbstetigkeit von f: Sei(x n ) eine Folge in L p (R) mitx n x in L p (R) und f(x
Universität des Saarlandes Seminar der Fachrichtung Mathematik Rudolf Umla
 Universität des Saarlandes Seminar der Fachrichtung Mathematik Rudolf Umla Sätze über Konvexität von Kapitel 4.7 bis 4.10 Theorem 4.7-1. Sei U ein konvexer Unterraum eines normierten Vektorraums. Dann
Universität des Saarlandes Seminar der Fachrichtung Mathematik Rudolf Umla Sätze über Konvexität von Kapitel 4.7 bis 4.10 Theorem 4.7-1. Sei U ein konvexer Unterraum eines normierten Vektorraums. Dann
45 Hilberträume. v = 2 <v, v>.
 45 Hilberträume Zusammenfassung Unter dem Begriff Hilbertraum werden solche euklidische oder unitäre Vektorräume zusammengefasst, die auch noch vollständig sind. Damit werden die in 41, 42 und in 43, 44
45 Hilberträume Zusammenfassung Unter dem Begriff Hilbertraum werden solche euklidische oder unitäre Vektorräume zusammengefasst, die auch noch vollständig sind. Damit werden die in 41, 42 und in 43, 44
Universität Stuttgart Fakultät Mathematik und Physik Institut für Analysis, Dynamik und Modellierung. Lösungen zur Probeklausur 2.
 Adµ Universität Stuttgart Fakultät Mathematik und Physik Institut für Analysis, Dynamik und Modellierung Blatt Probeklausur 2 Lösungen zur Probeklausur 2 Aufgabe 1 1. Formulieren Sie den Satz von Taylor
Adµ Universität Stuttgart Fakultät Mathematik und Physik Institut für Analysis, Dynamik und Modellierung Blatt Probeklausur 2 Lösungen zur Probeklausur 2 Aufgabe 1 1. Formulieren Sie den Satz von Taylor
4 Funktionenfolgen und normierte Räume
 $Id: norm.tex,v 1.9 2011/06/01 15:13:45 hk Exp $ $Id: jordan.tex,v 1.3 2011/06/01 15:30:12 hk Exp hk $ 4 Funktionenfolgen und normierte Räume 4.5 Normierte Räume In der letzten Sitzung hatten wir den Begriff
$Id: norm.tex,v 1.9 2011/06/01 15:13:45 hk Exp $ $Id: jordan.tex,v 1.3 2011/06/01 15:30:12 hk Exp hk $ 4 Funktionenfolgen und normierte Räume 4.5 Normierte Räume In der letzten Sitzung hatten wir den Begriff
7.2 Die adjungierte Abbildung
 7.2 Die adjungierte Abbildung Definition 7.2.1 Eine lineare Abbildung f : V K heißt lineares Funktional oder Linearform. (Diese Definition gilt für beliebige K-Vektorräume, nicht nur für innere Produkträume.)
7.2 Die adjungierte Abbildung Definition 7.2.1 Eine lineare Abbildung f : V K heißt lineares Funktional oder Linearform. (Diese Definition gilt für beliebige K-Vektorräume, nicht nur für innere Produkträume.)
Fachbereich Mathematik/Informatik 16. Juni 2012 Prof. Dr. H. Brenner. Mathematik für Anwender II. Testklausur mit Lösungen
 Fachbereich Mathematik/Informatik 6. Juni 0 Prof. Dr. H. Brenner Mathematik für Anwender II Testklausur mit Lösungen Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Ein Skalarprodukt
Fachbereich Mathematik/Informatik 6. Juni 0 Prof. Dr. H. Brenner Mathematik für Anwender II Testklausur mit Lösungen Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Ein Skalarprodukt
10 Unitäre Vektorräume
 10 Unitäre Vektorräume Pink: Lineare Algebra 2014/15 Seite 98 10 Unitäre Vektorräume Die Theorie komplexer Vektorräume mit Skalarprodukt folgt denselben Linien wie die Theorie reeller Vektorräume mit Skalarprodukt;
10 Unitäre Vektorräume Pink: Lineare Algebra 2014/15 Seite 98 10 Unitäre Vektorräume Die Theorie komplexer Vektorräume mit Skalarprodukt folgt denselben Linien wie die Theorie reeller Vektorräume mit Skalarprodukt;
10 Hilberträume. (b) λx,y = λ x,y für x,y X, λ K. (c) x, y = y, x für x, y X (Komplexe Konjugation nur im Falle K = C)
 10 Hilberträume 10.1. Definition. Sei X ein Vektorraum über K. Eine Abbildung, : X X K heißt Skalarprodukt, falls (a) x 1 + x,y = x 1,y + x,y für x 1,x,y X (b) λx,y = λ x,y für x,y X, λ K (c) x, y = y,
10 Hilberträume 10.1. Definition. Sei X ein Vektorraum über K. Eine Abbildung, : X X K heißt Skalarprodukt, falls (a) x 1 + x,y = x 1,y + x,y für x 1,x,y X (b) λx,y = λ x,y für x,y X, λ K (c) x, y = y,
x, y 2 f(x)g(x) dµ(x). Es ist leicht nachzuprüfen, dass die x 2 setzen. Dann liefert (5.1) n=1 x ny n bzw. f, g = Ω
 5. Hilberträume Definition 5.1. Sei H ein komplexer Vektorraum. Eine Abbildung, : H H C heißt Skalarprodukt (oder inneres Produkt) auf H, wenn für alle x, y, z H, α C 1) x, x 0 und x, x = 0 x = 0; ) x,
5. Hilberträume Definition 5.1. Sei H ein komplexer Vektorraum. Eine Abbildung, : H H C heißt Skalarprodukt (oder inneres Produkt) auf H, wenn für alle x, y, z H, α C 1) x, x 0 und x, x = 0 x = 0; ) x,
Ausgewählte Lösungen zu den Übungsblättern 9-10
 Fakultät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Vorlesung: Lineare Algebra (ME), Prof. Dr. J. Gwinner Dezember Ausgewählte Lösungen zu den Übungsblättern 9- Übungsblatt
Fakultät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Vorlesung: Lineare Algebra (ME), Prof. Dr. J. Gwinner Dezember Ausgewählte Lösungen zu den Übungsblättern 9- Übungsblatt
Lineare Algebra II 8. Übungsblatt
 Lineare Algebra II 8. Übungsblatt Fachbereich Mathematik SS 11 Prof. Dr. Kollross 1./9. Juni 11 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minitest) Sei V ein euklidischer oder unitärer Vektorraum.
Lineare Algebra II 8. Übungsblatt Fachbereich Mathematik SS 11 Prof. Dr. Kollross 1./9. Juni 11 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minitest) Sei V ein euklidischer oder unitärer Vektorraum.
Lineare Algebra II 6. Übungsblatt
 Lineare Algebra II 6 Übungsblatt Fachbereich Mathematik SS 2011 Prof Dr Kollross 18/19 Mai 2011 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minimalpolynom) Bestimmen Sie das Minimalpolynom der
Lineare Algebra II 6 Übungsblatt Fachbereich Mathematik SS 2011 Prof Dr Kollross 18/19 Mai 2011 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minimalpolynom) Bestimmen Sie das Minimalpolynom der
ANALYSIS 1 Kapitel 4: Folgen von (reellen und komplexen) Zahlen
 ANALYSIS 1 Kapitel 4: Folgen von (reellen und komplexen) Zahlen MAB.01012UB MAT.101UB Vorlesung im WS 2017/18 Günter LETTL Institut für Mathematik und wissenschaftliches Rechnen Karl-Franzens-Universität
ANALYSIS 1 Kapitel 4: Folgen von (reellen und komplexen) Zahlen MAB.01012UB MAT.101UB Vorlesung im WS 2017/18 Günter LETTL Institut für Mathematik und wissenschaftliches Rechnen Karl-Franzens-Universität
6 Hauptachsentransformation
 6 Hauptachsentransformation A Diagonalisierung symmetrischer Matrizen (6.1) Satz: Sei A M(n n, R) symmetrisch. Dann gibt es eine orthogonale n n-matrix U mit U t AU = D Diagonalmatrix Es folgt: Die Spalten
6 Hauptachsentransformation A Diagonalisierung symmetrischer Matrizen (6.1) Satz: Sei A M(n n, R) symmetrisch. Dann gibt es eine orthogonale n n-matrix U mit U t AU = D Diagonalmatrix Es folgt: Die Spalten
Definition 3.1. Sei A X. Unter einer offenen Überdeckung von A versteht man eine Familie (U i ) i I offener Mengen U i X mit U i
 3 Kompaktheit In der Analysis I zeigt man, dass stetige Funktionen f : [a, b] R auf abgeschlossenen, beschränkten Intervallen [a, b] gleichmäßig stetig und beschränkt sind und dass sie ihr Supremum und
3 Kompaktheit In der Analysis I zeigt man, dass stetige Funktionen f : [a, b] R auf abgeschlossenen, beschränkten Intervallen [a, b] gleichmäßig stetig und beschränkt sind und dass sie ihr Supremum und
Orthogonalreihendarstellung eines zentrierten Gauß-Prozesses
 Orthogonalreihendarstellung eines zentrierten Gauß-Prozesses Thomas Steinle Seminar Zufällige Felder Universität Ulm 18. November, 2008 Einleitung Inhalt Einleitung Wiederholung und Themenvorstellung Wichtiges
Orthogonalreihendarstellung eines zentrierten Gauß-Prozesses Thomas Steinle Seminar Zufällige Felder Universität Ulm 18. November, 2008 Einleitung Inhalt Einleitung Wiederholung und Themenvorstellung Wichtiges
Spektralsatz für denisierbare lineare Relationen in Kreinräumen
 Spektralsatz für denisierbare lineare Relationen in n Diplomarbeit - Raphael Pruckner Technische Universität Wien 1.Oktober 2014 FWF (I 1536-N25) :: Joint Project :: RFBR (13-01-91002-ANF) Satz (Spektralsatz
Spektralsatz für denisierbare lineare Relationen in n Diplomarbeit - Raphael Pruckner Technische Universität Wien 1.Oktober 2014 FWF (I 1536-N25) :: Joint Project :: RFBR (13-01-91002-ANF) Satz (Spektralsatz
10.2. SELBSTADJUNGIERTE OPERATOREN 67
 10.2. SELBSTADJUNGIERTE OPERATOREN 67 10. Spektralsatz 10.1. Spektrum. Sei K entweder R oder C. Definition 10.1.1. Sei X ein Banachraum und T L(X,X) L(X). (i) Die Menge ρ(t) K aller rellen oder komplexen
10.2. SELBSTADJUNGIERTE OPERATOREN 67 10. Spektralsatz 10.1. Spektrum. Sei K entweder R oder C. Definition 10.1.1. Sei X ein Banachraum und T L(X,X) L(X). (i) Die Menge ρ(t) K aller rellen oder komplexen
2.3 Eigenschaften linearer Operatoren
 2.3. LINEARE OPERATOREN 47 2.3 Eigenschaften linearer Operatoren Es seien V, W normierte Räume. Die Elemente von L(V ; W ) werden oft als lineare Operatoren bezeichnet. Wir hatten gesehen, dass die Stetigkeit
2.3. LINEARE OPERATOREN 47 2.3 Eigenschaften linearer Operatoren Es seien V, W normierte Räume. Die Elemente von L(V ; W ) werden oft als lineare Operatoren bezeichnet. Wir hatten gesehen, dass die Stetigkeit
Lineare Algebra und Geometrie II, Übungen
 Lineare Algebra und Geometrie II, Übungen Gruppe (9 9 45 ) Sei A 2 Bestimmen Sie A und A Finden Sie weiters Vektoren u, v R 2 mit u und Au A, beziehungsweise v und Av A Zunächst die Berechnung der Norm
Lineare Algebra und Geometrie II, Übungen Gruppe (9 9 45 ) Sei A 2 Bestimmen Sie A und A Finden Sie weiters Vektoren u, v R 2 mit u und Au A, beziehungsweise v und Av A Zunächst die Berechnung der Norm
Die reellen Zahlen als Äquivalenzklassen rationaler Cauchy-Folgen. Steven Klein
 Die reellen Zahlen als Äquivalenzklassen rationaler Cauchy-Folgen Steven Klein 04.01.017 1 In dieser Ausarbeitung konstruieren wir die reellen Zahlen aus den rationalen Zahlen. Hierzu denieren wir zunächst
Die reellen Zahlen als Äquivalenzklassen rationaler Cauchy-Folgen Steven Klein 04.01.017 1 In dieser Ausarbeitung konstruieren wir die reellen Zahlen aus den rationalen Zahlen. Hierzu denieren wir zunächst
4 Fehlerabschätzungen und Konvergenz der FEM
 4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
3 Bilinearform, Basen und Matrizen
 Lineare Algebra II 2. Oktober 2013 Mitschrift der Vorlesung Lineare Algebra II im SS 2013 bei Prof. Peter Littelmann von Dario Antweiler an der Universität zu Köln. Kann Fehler enthalten. Veröentlicht
Lineare Algebra II 2. Oktober 2013 Mitschrift der Vorlesung Lineare Algebra II im SS 2013 bei Prof. Peter Littelmann von Dario Antweiler an der Universität zu Köln. Kann Fehler enthalten. Veröentlicht
Lineare Algebra für Physiker 11. Übungsblatt
 Lineare Algebra für Physiker 11. Übungsblatt Fachbereich Mathematik SS 01 Prof. Dr. Matthias Schneider./. Juli 01 Dr. Silke Horn Dipl.-Math. Dominik Kremer Gruppenübung Aufgabe G1 (Minitest) (a) Welche
Lineare Algebra für Physiker 11. Übungsblatt Fachbereich Mathematik SS 01 Prof. Dr. Matthias Schneider./. Juli 01 Dr. Silke Horn Dipl.-Math. Dominik Kremer Gruppenübung Aufgabe G1 (Minitest) (a) Welche
1. Übungsblatt: Lineare Algebra II Abgabe: 8./ in den Übungsgruppen
 Hannover, den 7. Februar 2002 Aufgabe. Übungsblatt: Lineare Algebra II Abgabe: 8./9.4.2002 in den Übungsgruppen (2, 2, 3 Punkte) Der Vektorraum V = C[, ] sei mit dem üblichen Skalarprodukt f, g = f(t)g(t)
Hannover, den 7. Februar 2002 Aufgabe. Übungsblatt: Lineare Algebra II Abgabe: 8./9.4.2002 in den Übungsgruppen (2, 2, 3 Punkte) Der Vektorraum V = C[, ] sei mit dem üblichen Skalarprodukt f, g = f(t)g(t)
2. Dezember Lineare Algebra II. Christian Ebert & Fritz Hamm. Skalarprodukt, Norm, Metrik. Matrizen. Lineare Abbildungen
 Algebra und Algebra 2. Dezember 2011 Übersicht Algebra und Algebra I Gruppen & Körper Vektorräume, Basis & Dimension Algebra Norm & Metrik Abbildung & Algebra I Eigenwerte, Eigenwertzerlegung Singulärwertzerlegung
Algebra und Algebra 2. Dezember 2011 Übersicht Algebra und Algebra I Gruppen & Körper Vektorräume, Basis & Dimension Algebra Norm & Metrik Abbildung & Algebra I Eigenwerte, Eigenwertzerlegung Singulärwertzerlegung
Grundlagen der Mathematik 2 Nachklausur
 Andreas Gathmann und Yue Ren Sommersemester 6 Grundlagen der Mathematik Nachklausur Bearbeitungszeit: 8 Minuten Aufgabe (6 Punkte): Es sei f : R R, (x,y) xye (x+y). (a) Bestimme alle lokalen Maxima und
Andreas Gathmann und Yue Ren Sommersemester 6 Grundlagen der Mathematik Nachklausur Bearbeitungszeit: 8 Minuten Aufgabe (6 Punkte): Es sei f : R R, (x,y) xye (x+y). (a) Bestimme alle lokalen Maxima und
i=1 i=1,...,n x K f(x).
 2. Normierte Räume und Banachräume Ein normierter Raum ist ein Vektorraum, auf dem wir Längen messen können. Genauer definieren wir: Definition 2.1. Sei X ein Vektorraum über C. Eine Abbildung : X [0,
2. Normierte Räume und Banachräume Ein normierter Raum ist ein Vektorraum, auf dem wir Längen messen können. Genauer definieren wir: Definition 2.1. Sei X ein Vektorraum über C. Eine Abbildung : X [0,
9 Metrische und normierte Räume
 9 Metrische und normierte Räume Idee: Wir wollen Abstände zwischen Punkten messen. Der Abstand soll eine reelle Zahl 0 sein (ohne Dimensionsangabe wie Meter...). 9.1 Definition Sei X eine Menge. Eine Metrik
9 Metrische und normierte Räume Idee: Wir wollen Abstände zwischen Punkten messen. Der Abstand soll eine reelle Zahl 0 sein (ohne Dimensionsangabe wie Meter...). 9.1 Definition Sei X eine Menge. Eine Metrik
4 Fehlerabschätzungen und Konvergenz der FEM
 4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
Lösungen der Übungsaufgaben von Kapitel 3
 Analysis I Ein Lernbuch für den sanften Wechsel von der Schule zur Uni 1 Lösungen der Übungsaufgaben von Kapitel 3 zu 3.1 3.1.1 Bestimmen Sie den Abschluss, den offenen Kern und den Rand folgender Teilmengen
Analysis I Ein Lernbuch für den sanften Wechsel von der Schule zur Uni 1 Lösungen der Übungsaufgaben von Kapitel 3 zu 3.1 3.1.1 Bestimmen Sie den Abschluss, den offenen Kern und den Rand folgender Teilmengen
Lösungsvorschlag Klausur MA9801
 Lehrstuhl für Numerische Mathematik Garching, den 03.08.2012 Prof. Dr. Herbert Egger Dr. Matthias Schlottbom Lösungsvorschlag Klausur MA9801 Aufgabe 1 [4 Punkte] Seien M, N Mengen und f : M N eine Abbildung.
Lehrstuhl für Numerische Mathematik Garching, den 03.08.2012 Prof. Dr. Herbert Egger Dr. Matthias Schlottbom Lösungsvorschlag Klausur MA9801 Aufgabe 1 [4 Punkte] Seien M, N Mengen und f : M N eine Abbildung.
Universität Ulm Abgabe: Mittwoch,
 Universität Ulm Abgabe: Mittwoch, 8.5.23 Prof. Dr. W. Arendt Jochen Glück Sommersemester 23 Punktzahl: 36+4* Lösungen Halbgruppen und Evolutionsgleichungen: Blatt 2. Sei X ein Banachraum und (T (t)) t
Universität Ulm Abgabe: Mittwoch, 8.5.23 Prof. Dr. W. Arendt Jochen Glück Sommersemester 23 Punktzahl: 36+4* Lösungen Halbgruppen und Evolutionsgleichungen: Blatt 2. Sei X ein Banachraum und (T (t)) t
3. Folgen und Reihen. 3.1 Folgen und Grenzwerte. Denition 3.1 (Folge) Kapitelgliederung
 Kapitelgliederung 3. Folgen und Reihen 3.1 Folgen und Grenzwerte 3.2 Rechenregeln für konvergente Folgen 3.3 Monotone Folgen und Teilfolgen 3.4 Ein Algorithmus zur Wurzelberechnung 3.5 Reihen 3.6 Absolut
Kapitelgliederung 3. Folgen und Reihen 3.1 Folgen und Grenzwerte 3.2 Rechenregeln für konvergente Folgen 3.3 Monotone Folgen und Teilfolgen 3.4 Ein Algorithmus zur Wurzelberechnung 3.5 Reihen 3.6 Absolut
Sommer 2017 Musterlösung
 Sommer 7 Musterlösung. (5 Punkte) a) Sei V ein Vektorraum über K und sei T End(V ). Geben Sie die Definition eines Eigenwertes von T und zeigen Sie für endlichdimensionales V, dass λ K genau dann ein Eigenwert
Sommer 7 Musterlösung. (5 Punkte) a) Sei V ein Vektorraum über K und sei T End(V ). Geben Sie die Definition eines Eigenwertes von T und zeigen Sie für endlichdimensionales V, dass λ K genau dann ein Eigenwert
a b Q = b a 0 ) existiert ein Element p Q, so dass gilt: q 1 q 2 = 2 b 1 b 2 a 1 b 2 a 2 b 1 a 1 a 2 b 1 b 2 a 1 b 2 a 2 b 1 a b p = 1 det(q) C 2 2,
 Aufgabe I Es sei Q die folgende Teilmenge von C 2 2 : { ( ) a b Q a, b C b a Hier bezeichnet der Querstrich die komplexe Konjugation Zeigen Sie: (a) Mit den üblichen Verknüpfungen + und für Matrizen ist
Aufgabe I Es sei Q die folgende Teilmenge von C 2 2 : { ( ) a b Q a, b C b a Hier bezeichnet der Querstrich die komplexe Konjugation Zeigen Sie: (a) Mit den üblichen Verknüpfungen + und für Matrizen ist
35 Stetige lineare Abbildungen
 171 35 Stetige lineare Abbildungen Lernziele: Konzepte: Lineare Operatoren und ihre Normen Resultate: Abschätzungen für Matrizennormen Kompetenzen: Abschätzung von Operatornormen 35.1 Lineare Abbildungen.
171 35 Stetige lineare Abbildungen Lernziele: Konzepte: Lineare Operatoren und ihre Normen Resultate: Abschätzungen für Matrizennormen Kompetenzen: Abschätzung von Operatornormen 35.1 Lineare Abbildungen.
Seminar: Integralgleichungen (WS 06/07)
 Seminar: Integralgleichungen (WS 06/07) Numerische Behandlung der Fredholmschen Integralgleichung - Teil 1 Melanie Seifried Erik Ivar Fredholm (1866-1927) Schwedischer Mathematiker, der große Beiträge
Seminar: Integralgleichungen (WS 06/07) Numerische Behandlung der Fredholmschen Integralgleichung - Teil 1 Melanie Seifried Erik Ivar Fredholm (1866-1927) Schwedischer Mathematiker, der große Beiträge
LS Informatik 4 & Folgen und Reihen. Buchholz / Rudolph: MafI 2 38
 3. Folgen und Reihen Buchholz / Rudolph: MafI 2 38 Kapitelgliederung 3.1 Folgen und Grenzwerte 3.2 Rechenregeln für konvergente Folgen 3.3 Monotone Folgen und Teilfolgen 3.4 Ein Algorithmus zur Wurzelberechnung
3. Folgen und Reihen Buchholz / Rudolph: MafI 2 38 Kapitelgliederung 3.1 Folgen und Grenzwerte 3.2 Rechenregeln für konvergente Folgen 3.3 Monotone Folgen und Teilfolgen 3.4 Ein Algorithmus zur Wurzelberechnung
Wiederholungsserie II
 Lineare Algebra II D-MATH, FS 205 Prof. Richard Pink Wiederholungsserie II. Zeige durch Kopfrechnen, dass die folgende reelle Matrix invertierbar ist: 205 2344 234 990 A := 224 423 990 3026 230 204 9095
Lineare Algebra II D-MATH, FS 205 Prof. Richard Pink Wiederholungsserie II. Zeige durch Kopfrechnen, dass die folgende reelle Matrix invertierbar ist: 205 2344 234 990 A := 224 423 990 3026 230 204 9095
D-Math/Phys Lineare Algebra II FS 2017 Dr. Meike Akveld. Clicker Fragen
 D-Math/Phys Lineare Algebra II FS 2017 Dr. Meike Akveld Clicker Fragen Frage 1 Wenn eine reelle Matrix einen Eigenvektor hat, so hat es unendlich viele Eigenvektoren Sei u K n einen Eigenvektor von A M
D-Math/Phys Lineare Algebra II FS 2017 Dr. Meike Akveld Clicker Fragen Frage 1 Wenn eine reelle Matrix einen Eigenvektor hat, so hat es unendlich viele Eigenvektoren Sei u K n einen Eigenvektor von A M
Technische Universität München. Aufgaben Mittwoch SS 2012
 Technische Universität München Andreas Wörfel Ferienkurs Analysis 2 für Physiker Aufgaben Mittwoch SS 2012 Aufgabe 1 Äquivalente Aussagen für Stetigkeit( ) Beweisen Sie folgenden Satz: Seien X und Y metrische
Technische Universität München Andreas Wörfel Ferienkurs Analysis 2 für Physiker Aufgaben Mittwoch SS 2012 Aufgabe 1 Äquivalente Aussagen für Stetigkeit( ) Beweisen Sie folgenden Satz: Seien X und Y metrische
Seminar Spektraltheorie und Riemannsche Geometrie. Satz von Peter-Weyl
 Seminar Spektraltheorie und Riemannsche eometrie Satz von Peter-Weyl Seminar im Sommersemester 2003 zur Vorlesung lobale Analysis II bei Prof. Werner Müller Jens Putzka Bonn, den 25. Juli 2003 1 Das Peter-Weyl-Theorem
Seminar Spektraltheorie und Riemannsche eometrie Satz von Peter-Weyl Seminar im Sommersemester 2003 zur Vorlesung lobale Analysis II bei Prof. Werner Müller Jens Putzka Bonn, den 25. Juli 2003 1 Das Peter-Weyl-Theorem
5 Stetigkeit und Differenzierbarkeit
 5 Stetigkeit und Differenzierbarkeit 5.1 Stetigkeit und Grenzwerte von Funktionen f(x 0 ) x 0 Graph einer stetigen Funktion. Analysis I TUHH, Winter 2006/2007 Armin Iske 127 Häufungspunkt und Abschluss.
5 Stetigkeit und Differenzierbarkeit 5.1 Stetigkeit und Grenzwerte von Funktionen f(x 0 ) x 0 Graph einer stetigen Funktion. Analysis I TUHH, Winter 2006/2007 Armin Iske 127 Häufungspunkt und Abschluss.
Musterlösungen zur Linearen Algebra II Übungsklausur
 Musterlösungen zur Linearen Algebra II Übungsklausur Aufgabe. Sei A R 3 3. Welche der folgenden Aussagen sind richtig? a Ist det(a =, dann ist A eine orthogonale Matrix. b Ist A eine orthogonale Matrix,
Musterlösungen zur Linearen Algebra II Übungsklausur Aufgabe. Sei A R 3 3. Welche der folgenden Aussagen sind richtig? a Ist det(a =, dann ist A eine orthogonale Matrix. b Ist A eine orthogonale Matrix,
Spickzettel Mathe C1
 Spickzettel Mathe C1 1 Mengenlehre 1.1 Potenzmenge Die Potenzmenge P (Ω) einer Menge Ω ist die Menge aller Teilmengen von Ω. Dabei gilt: P (Ω) := {A A Ω} card P (Ω) = 2 card Ω P (Ω) 1.2 Mengenalgebra Eine
Spickzettel Mathe C1 1 Mengenlehre 1.1 Potenzmenge Die Potenzmenge P (Ω) einer Menge Ω ist die Menge aller Teilmengen von Ω. Dabei gilt: P (Ω) := {A A Ω} card P (Ω) = 2 card Ω P (Ω) 1.2 Mengenalgebra Eine
B) Lineare Operatoren 7. Algebra, Norm, Konvergenzen, Strukturen
 B) Lineare Operatoren 7. Algebra, Norm, Konvergenzen, Strukturen 7.1. Def: Linearer Operator: Lineare Abbildung zwischen Vektorräumen A( ) AA A: V W Spezieller: zwischen normierten Räumen, Banachräumen
B) Lineare Operatoren 7. Algebra, Norm, Konvergenzen, Strukturen 7.1. Def: Linearer Operator: Lineare Abbildung zwischen Vektorräumen A( ) AA A: V W Spezieller: zwischen normierten Räumen, Banachräumen
2 k k 1 k(k + 1) = 2n+1. n = 0 = k(k + 1) = 2n+1 n n. = 2 n+1 n + 2 (n + 1)(n + 2) + n. (n + 1)(n + 2)
 Prof. Hesse Höhere Mathematik I und II Musterlösung 7. 0. 0, 80min Aufgabe (3 Punkte) Zeigen Sie mit vollständiger Induktion: Für alle n N gilt n k= k k k(k + ) = n+ n +. Induktionsanfang: k= Induktionsschluss
Prof. Hesse Höhere Mathematik I und II Musterlösung 7. 0. 0, 80min Aufgabe (3 Punkte) Zeigen Sie mit vollständiger Induktion: Für alle n N gilt n k= k k k(k + ) = n+ n +. Induktionsanfang: k= Induktionsschluss
22 KAPITEL 1. GRUNDLAGEN. Um zu zeigen, dass diese Folge nicht konvergent ist, betrachten wir den punktweisen Limes und erhalten die Funktion
 KAPITEL 1. GRUNDLAGEN Um zu zeigen, dass diese Folge nicht konvergent ist, betrachten wir den punktweisen Limes und erhalten die Funktion 1 für 0 x < 1 g 0 (x) = 1 1 für < x 1. Natürlich gibt dies von
KAPITEL 1. GRUNDLAGEN Um zu zeigen, dass diese Folge nicht konvergent ist, betrachten wir den punktweisen Limes und erhalten die Funktion 1 für 0 x < 1 g 0 (x) = 1 1 für < x 1. Natürlich gibt dies von
Musterlösung Klausur zu Analysis II. Verständnisteil
 Technische Universität Berlin SS 2009 Institut für Mathematik 20.07.2009 Prof. Dr. R. Schneider Fritz Krüger Sebastian Holtz Musterlösung Klausur zu Analysis II Verständnisteil 1. (a) Sei D R n konvex
Technische Universität Berlin SS 2009 Institut für Mathematik 20.07.2009 Prof. Dr. R. Schneider Fritz Krüger Sebastian Holtz Musterlösung Klausur zu Analysis II Verständnisteil 1. (a) Sei D R n konvex
Häufungspunkte und Satz von Bolzano und Weierstraß.
 Häufungspunkte und Satz von Bolzano und Weierstraß. Definition: Sei (a nk ) k N eine konvergente Teilfolge der Folge (a n ) n N.Dannwirdder Grenzwert der Teilfolge (a nk ) k N als Häufungspunkt der Folge
Häufungspunkte und Satz von Bolzano und Weierstraß. Definition: Sei (a nk ) k N eine konvergente Teilfolge der Folge (a n ) n N.Dannwirdder Grenzwert der Teilfolge (a nk ) k N als Häufungspunkt der Folge
Das Newton Verfahren.
 Das Newton Verfahren. Ziel: Bestimme eine Nullstelle einer differenzierbaren Funktion f :[a, b] R. Verwende die Newton Iteration: x n+1 := x n f x n) f x n ) für f x n ) 0 mit Startwert x 0. Das Verfahren
Das Newton Verfahren. Ziel: Bestimme eine Nullstelle einer differenzierbaren Funktion f :[a, b] R. Verwende die Newton Iteration: x n+1 := x n f x n) f x n ) für f x n ) 0 mit Startwert x 0. Das Verfahren
Mathematisches Institut der Universität Heidelberg Prof. Dr. E. Freitag /Thorsten Heidersdorf. Probeklausur
 Mathematisches Institut der Universität Heidelberg Prof. Dr. E. Freitag /Thorsten Heidersdorf Probeklausur Diese Probeklausur soll a) als Test für euch selber dienen, b) die Vorbereitung auf die Klausur
Mathematisches Institut der Universität Heidelberg Prof. Dr. E. Freitag /Thorsten Heidersdorf Probeklausur Diese Probeklausur soll a) als Test für euch selber dienen, b) die Vorbereitung auf die Klausur
Mathematisches Argumentieren und Beweisen Beweisarten Besipiele. Hagen Knaf, WS 2014/15
 Mathematisches Argumentieren und Beweisen Beweisarten Besipiele Hagen Knaf, WS 2014/15 Im Folgenden sind einige der in der Vorlesung besprochenen Beispielbeweise für die verschiedenen Beweisarten aufgeführt
Mathematisches Argumentieren und Beweisen Beweisarten Besipiele Hagen Knaf, WS 2014/15 Im Folgenden sind einige der in der Vorlesung besprochenen Beispielbeweise für die verschiedenen Beweisarten aufgeführt
4 Funktionenfolgen und normierte Räume
 $Id: norm.tex,v 1.57 2018/06/08 16:27:08 hk Exp $ $Id: jordan.tex,v 1.34 2018/07/12 20:08:29 hk Exp $ 4 Funktionenfolgen und normierte Räume 4.7 Kompakte Mengen Am Ende der letzten Sitzung hatten wir zwei
$Id: norm.tex,v 1.57 2018/06/08 16:27:08 hk Exp $ $Id: jordan.tex,v 1.34 2018/07/12 20:08:29 hk Exp $ 4 Funktionenfolgen und normierte Räume 4.7 Kompakte Mengen Am Ende der letzten Sitzung hatten wir zwei
Topologien auf B(H) Bachelorarbeit. am Fachbereich Mathematik und Informatik der Westfälischen Wilhelms-Universität. 16.
 Topologien auf B(H) Bachelorarbeit 16. August 2016 am Fachbereich Mathematik und Informatik der Westfälischen Wilhelms-Universität Name: Yannick Overesch Matrikelnummer: 395 526 Studiengang: Mathematik
Topologien auf B(H) Bachelorarbeit 16. August 2016 am Fachbereich Mathematik und Informatik der Westfälischen Wilhelms-Universität Name: Yannick Overesch Matrikelnummer: 395 526 Studiengang: Mathematik
Ferienkurs Analysis 3. Ari Wugalter März 2011
 Ari Wugalter 07. - 08. März 2011 1 1 Hilberträume Im ersten Kapitel wollen wir uns mit den grundlegenden Eigenschaften von Hilberträumen beschäfitgen. Hilberträume habe die herausragende Eigenschaft, dass
Ari Wugalter 07. - 08. März 2011 1 1 Hilberträume Im ersten Kapitel wollen wir uns mit den grundlegenden Eigenschaften von Hilberträumen beschäfitgen. Hilberträume habe die herausragende Eigenschaft, dass
fj 2 = f n f n+1. fj 2 = 0 2 = 0 = 0 1 = f 0 f 1. f 2 j = f n f n+1 +fn+1 = (f n +f n+1 )f n+1 = f n+2 f n+1 = f n+1 f (n+1)+1.
 Stroppel Musterlösung 4..4, 8min Aufgabe 3 Punkte) Sei f n ) n N die Fibonacci-Folge, die durch f :=, f := und f n+ := f n +f n definiert ist. Beweisen Sie durch vollständige Induktion, dass für alle n
Stroppel Musterlösung 4..4, 8min Aufgabe 3 Punkte) Sei f n ) n N die Fibonacci-Folge, die durch f :=, f := und f n+ := f n +f n definiert ist. Beweisen Sie durch vollständige Induktion, dass für alle n
α + x x 1 F c y + x 1 F (y) c z + x 1 F (z) für alle y, z M. Dies folgt aus
 4. Dualräume und schwache Topologien Den Begriff des Dualraums hatten wir bereits in Kapitel 2 definiert. Der Dualraum X eines Banachraums X ist X = B(X, C). X ist mit der Abbildungsnorm F = sup x =1 F
4. Dualräume und schwache Topologien Den Begriff des Dualraums hatten wir bereits in Kapitel 2 definiert. Der Dualraum X eines Banachraums X ist X = B(X, C). X ist mit der Abbildungsnorm F = sup x =1 F
7 Orthogonale und unitäre Matrizen
 $Id: orthogonal.tex,v.6 2/7/ 4::3 hk Exp $ $Id: mdiffb.tex,v.3 2/7/ 4::5 hk Exp hk $ 7 Orthogonale und unitäre Matrizen 7.2 Drehungen Wir wollen uns jetzt mit Drehungen im dreidimensionalen Raum beschäftigen.
$Id: orthogonal.tex,v.6 2/7/ 4::3 hk Exp $ $Id: mdiffb.tex,v.3 2/7/ 4::5 hk Exp hk $ 7 Orthogonale und unitäre Matrizen 7.2 Drehungen Wir wollen uns jetzt mit Drehungen im dreidimensionalen Raum beschäftigen.
Lineare Algebra und analytische Geometrie II
 Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Vorlesung 53 Norm von Endomorphismen und Matrizen Definition 53.1. Es seien V und W endlichdimensionale normierte K-
Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Vorlesung 53 Norm von Endomorphismen und Matrizen Definition 53.1. Es seien V und W endlichdimensionale normierte K-
Blatt 5. , womit (U jk ) n k=0
 Übungen zur Topologie, G. Favi 7. März 009 Blatt 5 Abgabe: 3. April 008, 1:00 Uhr Aufgabe 1. Zeige, daÿ für alle n N die n-sphäre S n in R n+1 kompakt ist. Beweis. Wir schreiben d(x, y) := y x für die
Übungen zur Topologie, G. Favi 7. März 009 Blatt 5 Abgabe: 3. April 008, 1:00 Uhr Aufgabe 1. Zeige, daÿ für alle n N die n-sphäre S n in R n+1 kompakt ist. Beweis. Wir schreiben d(x, y) := y x für die
Definition Eine Metrik d auf der Menge X ist eine Abbildung d : X X IR
 0 Inhaltsverzeichnis 1 Metrik 1 1.1 Definition einer Metrik............................. 1 1.2 Abstand eines Punktes von einer Menge................... 1 1.3 Einbettung eines metrischen Raumes in einen
0 Inhaltsverzeichnis 1 Metrik 1 1.1 Definition einer Metrik............................. 1 1.2 Abstand eines Punktes von einer Menge................... 1 1.3 Einbettung eines metrischen Raumes in einen
