Mathematik Übungsaufgaben mit Lösungen Berlin
|
|
|
- Marielies Sternberg
- vor 7 Jahren
- Abrufe
Transkript
1 7 Mathematik Übungsaufgaben mit Lösungen Berlin
2 Rechnen mit natürlichen und gebrochenen Zahlen Rechnen mit natürlichen und gebrochenen Zahlen. Rechne vorteilhaft. a) b) c) 6 + ( + 7) d) + ( + 7) e) f) 7 : g) 68 0 h) 8 ( + ) i) 8 : (7 ) j) (7 + 9) : k) (70 ) : 9 l) 8 : 9 m) ( ) ( ) n) 8 9 ( ) o) ( + ) p) : 7. Löse die Aufgaben. a),7 b),,7 c) 0,, d), 0, e),6 : 9 f), : g) 9,8 : h) 7, : i),8 0 j),8 00 k) 0,7 00 l), 00 m) 6, : 0 n) 6, : 00 o), : 0 p), : 00. Gib an, welchen Bruchteil von der gesamten Fläche der gefärbte Teil einnimmt. a) b) c) d) e) f). Vergleiche. Setze <, > oder = ein. a) 6 0 b),,0 c) 0, 0,0 d),0,000 e) 0, 0,0 f) g) 9 7 h) 6. Ordne. Beginne jeweils mit der kleinsten Zahl. a),7, 0,,8 0,089 b) 7 c) a) Erweitere die Brüche. b) Kürze die Brüche. = 9 ; = ; 7 = ; ; 00 ; Berechne. a) b) 7 + c) + d) e) + + f) 6 + g) h) Löse die Aufgabenketten. Was stellst du fest? a) b) 8 c) 6 : d) : 6 : : 6 : : 6 : 6 : : :
3 Rationale Zahlen 9. Belege die Leerstelle mit einer Zahl, sodass richtig gelöste Aufgaben entstehen. a) + = b) = 6 = + = = 7 + = 6 c), + =, 7,8 =, +, = 6, : 9 = = 9 0 d), = 0, e), : = 0,,6 : = 0. Berechne. = = = : 0, = 8 = 9 f), =,0 : = 7 : = 0 7 : = : = a) e) i) von b) von 7 c) von 6 d) von von 0 f) von 9 g) von von j) von k) von 7 0 h) von 6 l) 9 von 8 Rationale Zahlen Positive und negative Zahlen. Zeichne eine Zahlengerade, die von 0 bis +0 reicht. Kennzeichne dort die Punkte, die zu den folgenden Zahlen gehören: A = 9,; B = + 8,; C = 7,; D = + 6,; E =,; F = +,7. Setze das richtige Relationszeichen (<; =; >). a) 0 b) c) d) e) 0,9 0,09 f) 6 i) j) 0 g),7 h) 0,,9 6 6 k) ( ) l),, m) n) o) 0 p) 7 0. Trage die folgenden Punkte in ein Koordinatensystem und versuche, durch Verbinden der Punkte eine Figur zu erkennen: a) A ( ); A ( 0); A ( 6 ); A ( ); A ( 6); A 6 (0 ); A 7 ( ); A 8 (0 0) b) B ( ); B (0 ); B ( ); B ( 0); B ( ); B 6 (0 ); B 7 ( ); B 8 ( 0)
4 Rationale Zahlen Addition und Subtraktion Löse die Aufgaben.. a) (+ 7) + (+ 8) b) (+ 7) + (+ 8) c) (+ 6) + (+77) d) (+ 6) + (+ 68) e) (+ 9) + (+ 9) f) (+ 6) + (+ 7) g) (+ 9) + (+ 8) h) (+ 88) + (+ ) i) (+76) + (+ 69). a) (+,) + (+7,8) b) (+,) + (+ 8,9) c) (+,) + (+ 9,) d) (+,) + (+,6) e) (+,6) + (+ 6,) f) (+,) + (+,6) g) (+,) + (+ 7,9) h) (+ 8,6) + (+ 6,) i) (+7,8) + (+,8). a) (+,7) + (+,8) b) (+7,) + (+ 69,7) c) (+ 8,6) + (+7,79) d) (+ 6,8) + (+ 79,6) e) (+,) + (+8,76) f) (+ 6,789) + (+,) g) (+,6) + (+,0) h) (+ 890,) + (+ 9,) i) (+,6) + (+,8). a) ( ) + ( 7) b) ( ) + ( 69) c) ( 67) + ( 8) d) ( 79) + ( 96) e) ( 8) + ( 8) f) ( 9) + ( 76) g) ( 6) + ( 7) h) ( 9) + ( 8) i) ( ) + ( 89). a) ( ) + ( 676) b) ( ) + ( 8) c) ( 67) + ( 9) d) ( 789) + ( 0) e) ( 90) + ( ) f) ( 6) + ( 67) g) ( 68) + ( ) h) ( 80) + ( 879) i) ( 6) + ( 6) 6. a) ( 7,) + (,7) b) ( 6,) + (,8) c) (,) + ( 6,9) d) ( 8,6) + (,) e) (,) + ( 7,) f) (,) + (,6) g) (,6) + ( 78,9) h) (,9) + ( 7,) i) ( 7,8) + (,9) 7. a) (,6) + (,) b) ( 67,8) + ( 8,) c) ( 9,) + ( 97,9) d) ( 6,7) + ( 68,6) e) ( 6,) + ( 7,6) f) (,) + (,8) g) (,679) + ( 66,9) h) ( 8,06) + ( 7,097) i) ( 7,) + (,) 8. a) (+ 67) + ( 87) b) ( 8) + (+ 9) c) (+76) + ( ) d) ( 8) + (+ ) e) (+ 9) + ( 9) f) ( 9) + (+) g) (+ ) + ( 9) h) ( ) + (+ 9) i) (+7) + ( 7) 9. a) ( 7) + (+7) b) (+ 7) + ( 8) c) ( 7) + (+ 87) d) (+7) + ( 976) e) ( 7) + (+7) f) (+ 7) + ( 8) g) ( 9) + (+ 8) h) (+ 9) + ( 8) i) ( 9) + (+8) 0. a) (+7,) + (,) b) (,7) + (+,) c) (+,8) + ( 9,9) d) ( 8,) + (+ 8,) e) (+,) + (,7) f) (,) + (+7,) g) (+ 6,) + ( 8,6) h) (,6) + (+ 6,8) i) (+ 9,) + ( 8,7). a) (,) + (+,) b) (+,) + (,6) c) (,) + (+,) d) (+,) + (,9) e) (,) + (+,6) f) (+,) + (,6) g) ( 7,) + (+ 7,8) h) (+ 7,) + ( 7,) i) (,7) + (+ 6,). a) (+7) (+6) b) (+7) ( 6) c) ( 8) ( 97) d) ( 8) (+79) e) (,6) (+,7) f) ( 6,) ( 7,) g) (+6,) (+7,) h) (+0,7) ( 7,0) i) (,7) (+,)
5 Rationale Zahlen. a) (+ 96) ( 7) b) (+ ) (+ 89) c) (+ 8) ( 7) d) (+ 6 7) (+ 76) e) ( 6) ( 6) f) ( 6 98) ( 986) g) (+ 87) ( 9) h) ( 08) (+ 69) i) (+ 7) ( 67). a) (+ 0,7) ( 8,0) b) ( 7,9) (,8) c) ( 87,) (+,6) d) (,) (+ 7,9) e) (,7) ( 6,8) f) (+ 8,6) (+ 7,7) g) (+,6) (,) h) (+7,) (,) i) (+ 6,) (+ 8,6). a) b) c) d) a) b) c) d) Multiplikation. Berechne. a) 0, 0,6 7 0, 0, 0, b) 0,, 6, 9,,8 c) 0, 0,, ( ),6 0 0,8 ( ) d) 0 0,0 0, 0,,7 ( ), 00. Berechne. Lege zuerst das Vorzeichen des Ergebnisses fest. a) ( ) 7 ( ) 6 ( 8) ( ) ( ) b), ( ) (,),, ( ) 0,0 ( 00) c) 7 ( ) 0 ( 8) ( ) ( 0,7) d) ( 0,6) 0,6 0,7 6, ( 0) 6 0,0. Löse folgende Aufgaben. Bestimme zunächst das Vorzeichen des Produkts. a) ( ) 6 ( ) 0 0, ( ) 7 ( ) ( ) ( ) ( ) ( ) b) ( ) 6 0 ( ) 0, 8 ( ) ( ) 6 0 ( ) ( ) ( 0) ( ) ( ) c) ( ) ( ) ( 0) ( 0) ( ) 0 ( 0,) 6 ( ) ( ) 8 ( ). Bestimme x jeweils so, dass wahre Aussagen entstehen. a) x = b) x ( ) = 60 c) 0 x = d) x = 8 x = 8 9 x = 0 x = 8 x = 6 9 x = 8 x 8 = 8 0 x = x = 6. Übertrage ins Heft und ergänze die Tabellen. a) 7 0, b) 0, 0 0, 0,
6 6 Rationale Zahlen 6. Bestimme das Vorzeichen und rechne dann schriftlich. Führe eine Überschlagsrechnung durch. a) 8, (,) b) 08 ( 88) c) 7, ( 0,8) d) 6 8 e) 7, ( 8) 7. Übetrage die folgende Tabelle in dein Heft und löse die Aufgaben: x ,7 +,8 7, +,9 y ,6 0, 0,7 +, x y ( x) y ( x) ( y) x ( y) (x y) Division. Berechne. a) 6 : : 6 : 0, 60 : 0,7 : b) 8 : ( 6) 9 : ( 9) 00 : ( ) : ( ) 0 : ( 0,) c) 0 : ( ) 000 : ( 0),8 : ( ) : (,) 99 : ( 00). Bestimme zunächst das Vorzeichen und rechne dann schriftlich. Führe eine Überschlagsrechnung durch. a) 0 : ( 0) b) 08 : ( 78) c) 77, : ( 0,) d) 6, : e) 87, : ( 88) f) 0,8 : ( 0,8). Welches Vorzeichen hat das Ergebnis? Bestimme den Quotienten der Beträge beider Zahlen durch schriftliches Rechnen. a) 66 : ( ) b) 78, : ( 0,6) c) 0,08 : ( 0,) d) 76 : ( ) e) 97, : (,8) f) 0,8 : (,) g) 87 : h) : ( 7). Übernimm die Tabellen ins Heft und rechne. a) : 6 b) : 6, ,6 0,8 6. Ermittle jeweils, für welches a eine wahre Aussage entsteht. a) 96 : a = b) : a = c) a : ( 90) = d) a : ( ) = 8 e) a : ( ) = f) 0,9 : ( a) = 0, 6. Berechne. a) ( ) : 7 b) : (6,,) c) (7 ) : ( 8 + ) d) ( ) : e) ( 88 + ) : f) ( 7 8) : ( )
7 Variablen, Terme, Gleichungen 7 7. Berechne. a) (+ ) : ( 7) b) (+9) : ( 7) c) ( 7) : ( 8) d) (+ 9) : (+ ) e) ( 96) : (+) f) ( 08) : ( 8) g) ( 6) : (+6) h) ( 0) : (+ ) i) (,8) : ( 0,8) j) (,8) : (7,) k) (+,7) : ( 0,) l) (,9) : ( ) m) ( + ) : ( ) n) ( + 8 ) : ( 8 ) o) ( 9 ) : ( 0 ) p) ( 6 ) : ( 8. Übernimm die Tabelle ins Heft und rechne. a),6 b) 6,6 x x : 0 x : 00 0 x 00 x c) 00 d) ) Variablen, Terme, Gleichungen. Übertrage die Tabelle in dein Heft und berechne die Werte der verschiedenen Terme. Setze dabei für die Variablen die angegebenen Zahlen ein. a) x + b) y c), (a + ) d) d d e), s f) w + w,6 0. Berechne jeweils den Wert des Terms. a) x für x = b) a + für a =, c) (s,) für s = 8, d) r : 6 für r = e) (z + ) für z = 9 f),(y + ) für y =. Welchen Wert bekommen die Terme für a =? a) a + b) a c) a d) a a e) a f) a + g) a a + a h) a a. Setze für die Variablen eine Zahl so ein, dass wahre Aussagen entstehen. a) 7 x = 9 b) 0 : y = c) 8 z = d) (6 + 8) : u = e) a a 8 = 7 f) w + 8 = 8 : g) 6t = 0 t h) (0,s + ) = 0
8 8 Variablen, Terme, Gleichungen. Fasse möglichst weit zusammen. a) x + x b) a + a + a + a c) s + s + s d) a + a + a + b + b + b + b e) 0k r + r k f) + x + y g) ab + ab ab h) k + k k + k i) ( ) + ( x) + ( y) 6. Fasse zusammen. a) x + x b) s + s + s c) e e d) 0,a,a e) 96d + 9d f),f +,7f g) k 9k h),x,8x + x i) c c + 9c j) 7,y + 0,y k) 7j j l) y y 7. Fasse zusammen. Achte dabei auf die nicht sichtbare Eins. a) 8m m b) a + 89a c) p + 7p +p d) 0,7x x e) b 6b f) d + d 7d g) n + n n h) w + w + w 8. Fasse zusammen. a) a 7b + a + 7b b) 7g + d d g + d c) x + y 67x + x d) s + + s 6s e) 6, v 8,9 v 0,u 8,u f) u + 8t + u u + 9t g) e + 9e 6 + e h),x + 9, x 7 + y i) r t 8r + t + t 9. Bestimme die Lösungsmenge. a) 6x = b) 8x = 0 c) e) x = 0 f) = y x 6 = d) 0 = x g), = a h) b = 6 0. Löse folgende Gleichungen durch Anwenden der Umformungsregeln. Gib die Lösungsmenge an. Führe eine Probe durch. a) 0x 6 = b) x + 8 = 8 c) x + = d) + x = e) + x = f) a = g) + y = 0 h) 8 = 7y i) = x + j) x = k) + a = 0 l),x 6 = 9. Ermittle diejenige rationale Zahl, die die Gleichung erfüllt. Fasse dazu, wenn möglich, entsprechende Terme zuerst zusammen. Führe eine Probe durch. a) x + x = x + b) x 6x 0 = x 6 x c) x x + 8 = x 7 d) 6 a = 7a 6a + 0 e) 0y y + 8 = f) = b b + 8 g) 6z z = h) x + x + 6 = 7x x. Bestimme die Lösungsmenge. Kontrolliere deine Lösungen. Beachte die Grundmenge. a) x + x x + 8 x + 7x = x G = Q b) 9 + y 7y y = 7y + 8 y 6 G = N c) a + 6 a + + 8a 0 = a 0 a + 6a 0 G = Q d) 8d +, = 7d + 7, 8d d +, + d G = Z e) + 7x 8 6x x + + 8x x = 0 G = Q. Löse folgende Gleichungen: a) x + 6 = b) x 7 = c) 9 + x = 6 d) = 6 + x e) + x = f) a, =, g) + b = 6 h),8 = z,6 i),8 =, + y
9 Zuordnungen, Proportionalitäten 9 Zuordnungen, Proportionalitäten. Untersuche, ob zwischen den Zahlen für x und y eine proportionale oder antiproportionale Zuordnung besteht und gib, wenn möglich, den Proportionalitätsfaktor an. a) x 0,,0,,0,,0 b) x y,,0 7, 0,0,,0 y 6, c) x 6 d) x 0, 0, 0,6 0,8 0,9, y y 0,,0,,0,,0. Ergänze so, dass eine proportionale Zuordnung entsteht. a) a b) s 7,7 b 6,8 7 0 t,,9. Ergänze so, dass eine antiproportionale Zuordnung entsteht. a) b 8 0, b) s 0, 0, 0,8 c t 0,6. Berechne jeweils den Wert für x, wenn die Zuordnungen proportional sind. a) Masse Preis b) Anzahl Preis c) Länge Preis d) Benzinmenge t 70 8 Stück 7 90 dm 6 t x Stück x x dm 8 Preis e) Strecke Zeit f) Arbeitszeit Lohn l, 7 km min h 6 8 l x km x min 66 h x. Berechne jeweils den Wert für x, wenn die Zuordnungen antiproportional sind. c) Anzahl der Kühe a) Arbeiter Arbeitszeit b) Baumaschinen Arbeitszeit Futtervorrat 6 Arbeiter h Bagger 8 h Kühe 0 Tage Arbeiter x h x Bagger 6 h 8 Kühe x Tage d) Personenzahl Buspreis je Person e) Arbeiter Arbeitszeit f) Baumaschinen Arbeitszeit Personen 8 7 Arbeiter 8 h 6 Bagger 0 h x Personen 6 x Arbeiter 8 h Bagger x h
10 0 Zuordnungen, Proportionalitäten 6. Bei den folgenden Beispielen handelt es sich um proportionale Zusammenhänge. Löse die Aufgaben. Erkläre dein Vorgehen. a) kg Äpfel kosten. Wie viel Euro kostet kg Äpfel? b) 6 Flaschen Mineralwasser kosten,0. Wie viel Euro kostet eine Flasche? c) 0 Eier kosten,0. Wie viel Cent kostet ein Ei? d) In, Stunden legt ein Radfahrer eine Strecke von 0 km zurück. Wie viel Kilometer schafft er in einer Stunde? e) Ein m langer Holzbalken hat eine Masse von kg. Welche Masse hat ein entsprechender Balken von m Länge? f) 800 g Schweinefleisch kosten,0. Wie viel Euro kosten 00 g Schweinefleisch? g) Eine Seilbahn überwindet auf einer Strecke von 0 m einen Höhenunterschied von 60 m. Auf welcher Strecke beträgt der Höhenunterschied 00 m? h) kg Tomaten kostet,. Wie viel Euro kosten kg Tomaten? i) Flasche Saft kostet,0. Wie viel Euro kosten 6 Flaschen? j) Ein Ei kostet 9 Cent. Wie viel Euro kosten Eier? k) Ein Dampfer fährt in einer Stunde 0 km. Wie weit kommt er in, Stunden? l) m Holz wiegt, t. Wie schwer sind m Holz? m) Eine Straße steigt auf einer Länge von 00 m um 8 m. Wie groß ist der Höhenunterschied bei einer Länge von 900 m? n) kg Rindfleisch kostet 6,6. Wie viel Euro kosten 00 g Rindfleisch? 7. Bei den folgenden Beispielen handelt es sich um antiproportionale Zusammenhänge. Löse die Aufgaben. Erkläre dein Vorgehen. a) Arbeiter brauchen für eine bestimmte Arbeit Stunden. Wie lange braucht ein Arbeiter für die gleiche Arbeit? b) gleich starke Pumpen füllen ein Schwimmbecken in 7 Stunden. Wie lange braucht eine Pumpe dafür? c) Wenn sich Personen den Preis für eine Taxifahrt teilen, muss jeder 7,0 bezahlen. Wie viel Euro muss eine Person allein bezahlen? d) Wenn man eine Klasse in Dreiergruppen teilt, entstehen 8 Gruppen. Wie groß ist die gesamte Klasse? e) Wenn Gerd pro Tag ausgibt, reicht sein Urlaubsgeld Tage. Wie lange reicht es, wenn er pro Tag ausgibt? f) Wenn Frau Krause es schafft, in jeder Woche 800 g abzunehmen, hat sie ihr Idealgewicht in 6 Wochen erreicht. Wie lange dauert es, wenn sie 00 g pro Woche abnimmt? g) Bei einer Geschwindigkeit von 0 km braucht man mit dem Auto bis zum Bahnhof 0 min. h Wie lange braucht man dafür bei einer Geschwindigkeit von 0 km h? h) Ein Maler braucht zum Streichen eines Zauns 9 Stunden. Wie lange brauchen Maler für die gleiche Arbeit bei gleichem Tempo? i) Eine Pumpe pumpt ein Becken in 7 Stunden leer. Wie lange brauchen Pumpen? j) Eine Klasse besteht aus Schülern. Wie viele Möglichkeiten gibt es, sie in Gruppen gleicher Größe einzuteilen? k) Wenn sich Gerd jeden Tag ein Softeis kauft, reicht sein Taschengeld 0 Tage. Wie lange reicht es, wenn er jeden Tag drei Softeis kauft?
11 Prozentrechnung Prozentrechnung Prozentwerte. Gib von den folgenden Schülerzahlen % an: a) 700 b) 00 c) 0 d) 0 e) 000 f) 00 g) 0 h) 70 i) 0 j) 60 k) 7 80 l) Berechne von 600 km die gegebenen Anteile. a) % b) % c) % d), % e) 0 % f) 0 % g) % h) 0 % i) 00 % j) 0, %. Berechne. a) % von 70 b) 7 % von c), % von 780 d) 0 % von 89, e) 7, % von 8 f) 0 % von 800 g), % von 00 h) % von 8 i) 6 % von 0. Berechne und vergleiche die Ergebnisse der folgenden Aufgaben: a) 0 % von 00 b) 9 % von 0 c) 8 % von 0 d) 7 % von 0 e) 6 % von 0 f) % von 0. Vergleiche. Setze das richtige Zeichen (<; =; >). a) 7 % von 0 und % von 60 b) 0 % von 6 und 6 % von 0 c) 6,6 % von 7 und, % von 96 d),7 % von 0 und 7 % von Prozentsätze. Wie viel Prozent von 00 km entsprechen folgende Längenangaben? a) 80 km b) 0 km c) 600 km d) 8 km e) 70 km f) km. Wie viel Prozent sind m von den folgenden Längenangaben? a) 0 m b) 0 m c) 7, m d) m e) 000 m f) m. Wie viel Prozent sind a) 6 von ; b) 7 von 0; c) von,; d),8 von 8; e) von 70; f) 6 von 60; g) 7 von 7; h) von 0,?. Berechne jeweils den Prozentsatz. a) 69, m von 70 m b) 7,9 g von, g c) 7, t von 8 t d) 0 m von 7 00 m. Gib in Prozent an. a) g von kg b) ha von km c) mm von cm d) min von h e) h von Tag f) Tag von Jahr 6. Berechne die Prozentsätze. Runde das Ergebnis auf eine Dezimalstelle. a),7 von, b) 8 von 8 c) 6, von 70, d) 0,6 von e) 7 von 7 f) 8,6 von 0 g) 9 von h) 9, von 6 i) von,
12 Prozentrechnung Grundwerte. Die folgenden Figuren sind jeweils Teil einer Gesamtfigur. Wie könnte diese aussehen? a) b) c) 7% % 60%. Gib jeweils an, wie viel 00 % sind. a) 0 % sind 8 kg b) 0 % sind 8 kg c) 00 % sind 8 kg d) 60 % sind 8 kg e) 0, % sind 8 kg f) % sind 8 kg. Gib jeweils den Grundwert an. a) 8 t sind 80 % b) 6 t sind 80 % c) t sind 80 % d) 6 t sind 7 % e),6 t sind 7 % f) 6 t sind 7 %. Berechne jeweils 00 %. Runde die Ergebnisse auf Ganze. a) 7,9 % sind 00 cm b),7 % sind cm c) 8,6 % sind cm d) 0 % sind 7 00 cm e) 0, % sind,0 cm f) 6 % sind 80 cm Prozentuale Veränderungen. Vermehre die folgenden Größenangaben jeweils um % bzw. auf %. a) 00 m b) 0 dt c) 8 g d) 9,6 cm e),0 km. Vermindere die folgenden Größenangaben jeweils um % bzw. auf 78 %. a) 00 m b) 0 dt c) 96 g d) 9, m e) 0,60 km. Vermehre. a) 0 um 0 % b) auf % c) 8 um % d) 0 auf 9 %. Die folgenden Preise werden um % gesenkt. Wie viel Euro kosten die Waren dann? a) 0,00 b) 6,00 c),00 d) 7,0 e) 99,90 f) 999,00. Die folgenden Angaben sind Preise nach einer Preissenkung um %. Wie viel Euro kosteten die Waren vor der Preissenkung? a) 0,00 b) 6,00 c),00 d) 7,0 e) 99,90 f) 999,00 6. Auf Waren wird eine Mehrwertsteuer von 9 % bzw. 7 % des Grundbetrags erhoben. Berechne die jeweiligen Mehrwertsteuern in Euro und den Preis (Grundbetrag + Mehrwertsteuer). a) 0,00 b) 7 c) 900,00 d) 0, e) 8,0 f) Auf wie viel Prozent (um wie viel Prozent) wurden die Zahlen verkleinert? a) b) c) d) e) f) ursprüngliche Zahl verkleinerte Zahl
13 Knobelei Knobelei. Kreuzzahlrätsel waagerecht: a 79 c 7 e 8, 8 f g 0 : h 8 i 6 n o 0 p 6 senkrecht: a 0 0 b c 0, d 00 f 80 : 0 k l 6 6 m 8 0 n 7 8 a e g m o b c d f h i k l n p. Wenn du von einer rationalen Zahl 0 subtrahierst, die Differenz verdoppelst und dann 0 addierst, dieses Ergebnis halbierst und nun noch dazu rechnest, so erhälst du deine ursprüngliche wieder. Prüfe die Aussage mit der Zahl 0 nach.. Hier stimmt was nicht? Lege jeweils nur ein Hölzchen um, so erhältst du wahre Aussagen. a) b) c) d). Alexander behauptet, dass er Gedanken lesen kann. Er lässt Daniela folgende Rechnung ausführen: Denke dir eine natürliche Zahl, multipliziere ihren Nachfolger mit, vermindere dieses Ergebnis um und subtrahiere deine gedachte Zahl. Dividiere nun durch und nenne mir das Ergebnis deiner Rechnung. Als Daniela ihm die Zahl 0 nennt, sagt er ihr die gedachte Zahl. Wie heißt diese?. Hinter einer der Türen liegt ein Goldschatz, hinter den anderen lauert das Verderben. Welche musst du öffnen, um an den Schatz zu gelangen? Ich gebe dir eine Hilfe. Viel Glück. Rätsel: = + 6 ( ) = ( ) 6 = 6 Öffne. 6. Robert und Steffen spielen Zahlenraten. Robert: Denke dir eine Zahl, addiere. Verdopple die Summe und addiere zu ihr die gedachte Zahl. Von dem Ergebnis subtrahiere 8. Als Steffen das Ergebnis 9 nennt, weiß Robert, dass er sich die gedacht hat. Erkläre, wieso er das weiß. 7. Der Empfangschef des Hotels sagt: Wir können % der Gruppe bei uns unterbringen. Antwortet der Reiseleiter: Prima, dann können ja alle hierbleiben, wir sind nur. Hat der Reiseleiter recht?
14 Rechnen mit natürlichen und gebrochenen Zahlen Lösungen Rechnen mit natürlichen und gebrochenen Zahlen. a) (7 + ) + (6 + 8) = 00 b) (87 7) + ( + 9) = 0 c) (6 + ) + 7 = 67 d) + 0 = 7 e) = 00 f) : 7 = g) 0 h) 8 0 = 0 i) 8 : = 7 j) 8 : = 7 k) 70 : 9 : 9 = l) 8 : 9 = 06 m) = 0 n) 6 o) 8 00 = 800 p) : 7 = 9. a) 0,8 b),77 c) 0,7 d) 0,88 e) 0, f),8 g),8 h), i) 8, j) 8 k) 7, l) 0 m),6 n) 0,6 o) 0, p) 0,0. a) b) 0 c) d) e) 0 f) 7. a) < b) > c) > d) = e) > f) < g) < h) <. a) 0,089 < 0, <,7 <,8 <, b) < < < 7 c) < 9 < 7 < < 6. a) 6 9 ; 0 ; 0 b) ; ; ; a) e) 6 = 77 7 = 7 b) f) i), j) 6 = c) = 7 0 = 0 g) k) l) d) 8 = 8 h) 0 = = 0 = 0 8. a) ; 8; ; ; ; Halbieren eines Faktors führt zum Halbieren des Produkts. b) ; ; ; ; 8 ; 6 Halbieren eines Faktors führt zum Halbieren des Produkts. c) ; ; 6; ; ; 8 Halbieren des Divisors führt zum Verdoppeln des Produkts. d) 8; ; ; ; ; Halbieren des Dividenden führt zum Verdoppeln des Quotienten. 9. a) 9 + = 0 = 6 = : 9 = 6 b) + = = = = 9 0 c), +, =, 7,8, =,,6 +, = 6,, 0,7 =,0 d), 0, = 0,, : = 0,,6 :, = 0,8 : 0, = e) f) = 6 0 : 7 = 9 7 = : = 0 0. a) 6 b) 9 c) g) 0 h) i) 6 = 7 : = = 9 9 : 9 = d) e) f) j) k) 0 l) 6
15 Rationale Zahlen Rationale Zahlen Positive und negative Zahlen. individuelle Lösung. a) < b) > c) < d) > e) < f) = g) < h) < i) = j) = k) = l) > m) > n) > o) > p) < Lösungen. a) Stern b) Stern Addition und Subtraktion. a) + b) + c) + d) + e) + f) + 79 g) + 6 h) + i) +7. a) + 9,0 b) +, c) +,7 d) +7, e) +, f) + 7,9 g) + 0,99 h) +7, i) + 0,6. a) + 9, b) +767,0 c) + 87,9 d) +, e) + 9,6 f) + 7,989 g) + 6,9 h) + 99,7 i) +,6. a) 7 b) c) d) 7 e) 9 f) 80 g) 0 h) 0 i) 90. a) 799 b) 90 c) 06 d) 09 e) f) 90 g) 70 h) 68 i) 7 6. a),9 b), c), d),0 e) 9,9 f) 7, g) 8, h), i) 6,99 7. a) 7,0 b),0 c) 0, d) 0, e),96 f) 8,78 g) 6,79 h) 6,7 i) 779, 8. a) 0 b) + c) + d) 0 e) + f) 7 g) 0 h) + i) 0 9. a) 6 b) + 89 c) + d) e) f) + g) 0 h) +0 i) + 0. a) +,8 b) +,8 c), d) 0, e), f) +, g), h) +, i) + 0,. a) + 8, b) 00, c) +99,9 d) 00,6 e) + 00, f) 09, g) +, h) 6,9 i) + 0,7. a) 6 b) +08 c) + d) 7 e) 6, f) +, g), h),8 i) 9,9
16 6 Rationale Zahlen Lösungen. a) + 8 b) + c) d) + 68 e) + 07 f) g) + 6 h) 6 77 i) a) +,8 b) +,9 c) 99,8 d) 9, e),9 f) +0,9 g) + 66,8 h) + 8,7 i),. a) + b) 88 c) 09 d) a) + b) 789 c) 79 d) + Multiplikation. a) 0,,, b) 8,9,,6 c),,,8 0 d) 0, 0, 6,8. a) b) ,, + 9,6 + c) ,7 d) + + 0, 9, +0 0,6. a) b) c) a) x = b) x = c) x =, d) x =, x = x = 0 x = 7 x = x = 9 x = 6 x = 0, x =. a) 7 0, b) 0, 0, 0, 0,0, 0, 6 0,0 6. a),7 b) 78 6 c) 8,868 d) 0 68 e) 08,6 7. x ,7 +,8 7, +,9 y ,6 0, 0,7 +, x y , 0,7 +,0 +,9 ( x) y , + 0,7,0,9 ( x) ( y) , 0,7 +,0 +,9 x ( y) , + 0,7,0,9 (x y) , + 0,7,0,9
17 Variablen, Terme, Gleichungen 7 Division. a) 0 0, b) 7 60 c) 0 0,9 0 0,99. a) 0, b) 6 c),87 d),9 8 e) 9,9 f). a) + b) 0, c) 0, d) e), f) +, g) 7 h) + 6 Lösungen. a) : 6 b) : 6, ,6 0,06 0,0 0,09 0, 0,8 0,0 0, 0,0 0, a) a = 8 b) a = 7 c) a = 70 d) a = 96 e) a = 60 f) a = 6. a) b) c) d) e) f) 0 7. a) 6 b) 7 c) + 9 d) + e) 8 f) + 6 g) h) i) + j) m) n) 6 9 = 9 o) = p) + 6 = + 7 k) l) + 0, 8. zeilenweise: a) ; 0,; 0,0; 0; 00 b),6; 0,6; 0,06; 6; 60 c) 6;,66; 0,66; 66; 660 d) 0; ; 0,; 00; 000 e) 00; 0; ; 000; Variablen, Terme, Gleichungen.,6 0 a) x +,8 7 6 b) y 0 0,8 6 8 c), (a + ) 0 0,6,, 6 0, d) d d,6 0 0 e), s 8, 0, 8,8 6,,,6,6 7,6 f) w + w,6 0. a) 0 b) 0, c) d) e) 6 f),6. a) b) c) d) e) f) 0 g) h)
18 8 Zuordnungen, Proportionalitäten Lösungen. a) x = 7 b) x = c) z = d) u = e) a = ; f) w = g) t = h) s =. a) x b) a c) s + 9 d) a + b e) k + r f) ( + x + y) g) 6ab h) 0k i) ( + x + y) 6. a) 7x b) 66s c) e d),7a e) 87d f) 9,f g) k h),9x i) 8c j) 6,9y k) j l) y 7. a) 7m b) 88a c) p d) 0,x e) 6b f) d g) n h) w 8. a) 9a + 66b b) 8g 0d c) x + y d) s + e),v 88u f) u + 7t g) e + 9 h) 0,x + y 7,8 i) r 9. a) L = { b) L = { c) L = {7 d) L = { e) L = {0 f) L = { g) L = {, h) L = {, 0. a) L = { b) L = {0 c) L = { d) L = {0 e) L = { f) L = {8 g) L = { 6 h) L = {7 i) L = {0 j) L = { k) L = { l) L = {. a) x = b) x = c) x = d) a = e) y = f) b = g) z = h) x =. a) L = { b) L = { c) L = { ; a = d) L = {6 e) L = Q. a) x = b) x = c) x = d) x = 6 e) x = 8 f) a = 8, g) b = h) z = 9, i) y = 6,9 Zuordnungen, Proportionalitäten. a) Vermutung: y x y und x wachsen in gleicher Weise (Verdopplung von y führt zur Verdopplung von x) x y =, 0, =,0,0 = = y = x k = proportionale Zuordnung b) Vermutung: y x y und x wachsen in unterschiedliche Richtungen. Die Paare sind produktgleich. x y = = 6 = = y k = antiproportionale Zuordnung x c) keine Proportionalität: keine Quotientengleichheit, keine Produktgleichheit d) y x Quotientengleichheit k =,; y =, x proportionale Zuordnung. a) a b) s 0 7,7, b 6,, t 9, 6,,,,9
19 Prozentrechnung 9. a) b 8 0 9, b) s 0, 0, 0, 0,8, c,6 9 t 6,8 0,6. a) x = 70 = 000 b) x = 7 : 6 = c) x = 90 dm : = 0 dm d) x =, 9 = 8, e) x = : = 7 f) x = 6 = 88. a) 6 h = x h x = 6 b) 8 h = x 6 h x = c) 0 Tage = 8 x Tage x = d) 8 = x 6 x = 7 e) 7 8 h = x 8 h x = f) 6 0 h = x h x = Lösungen 6. a),00 b) 0,0 c) Cent d) 0 km e) 0, kg f) 0,0 g) 00 m h),70 i) 6, j),08 k) km l),8 t m) 7 m n), 7. a) 6 Stunden b) Stunden c) 8,0 d) Schüler e) 0 Tage f) Wochen g) 0 min h) Stunden i), Stunden j) Anzahl der Gruppen 6 8 Anzahl der Schüler pro Gruppe 8 6 k) 0 Tage, wenn er nichts anderes kauft. Prozentrechnung Prozentwerte. a) b) 6 c) d) 9 e) 0 f) g) 0,6 h), i) 7 j), k) 7 l) 6. a) km b) 7 km c) 67 km d) 7,0 km e) 70 km f) 80 km g) km h) 0 km i) 00 km j), km. a) b) c) 89, d) 7,8 e) 0,0 f) 70 g) 6, h) 6, i) 6,. a) 60 b) 8,9 c) 7,6 d) 6, e), f), f) < e) < d) < c) < b) < a). 0, > 0 b) 79, = 79, c),9 < d),9 =,9 Prozentsätze. a) 0 % b) 0 % c) 0 % d) % e), % f) 0, %. a) 0 % b) 0 % c) 00 % d) % e) 0, % f) 00 %. a) 0 % b) % c) 00 % d) % e) 60 % f) % g) 7, % h) 0 %. a) 6 % b) 8 % c) 0 % d) %
20 0 Prozentrechnung Lösungen. a) 0, % b) % c) 0 % d), 6 % e), 6 % f) 0,7 % 6. a),8 % b) 9, % c) 6,7 % d),0 % e) 08,0 % f) 69,7 % g) 0, % h), % i) 8, % Grundwerte. a) b) c) Vorgabe Ergänzung zu 00%. a) 80 kg b) 6 kg c) 9 kg d) 0 kg e) 600 kg f) kg. a), t b) 0, t c), t d) 0 t e) 7,8 t f) 77,8 t. a) 99 cm b) 6 08 cm c) 6 6 cm d) 7 08 cm e) 7 67 cm f) cm Prozentuale Veränderungen. + % a) m b), dt c),76 g d) 0,7 cm e) 7,6 km + % a) m b) 6, dt c) 8,6 g d),7 cm e) 8,666 km. % a) m b), dt c) 8,8 g d) 6,896 cm e) 6,98 km % a) m b) 87, dt c) 7,88 g d),976 cm e),868 km. a) 6 b) 9 86 c),8 d),6. a),0 b),60 c), d),88 e) 69,9 f) 89,. a),9 b) 8,8 c) 60,00 d) 0,9 e),8 f) 7,9 6. a) b) c) d) e) f) 7 %,0 9, 0, G + 7 %,0 9, 0 0,8 7, %,70, 6 0,0, 7 00 G + 9 %,70 7, 6 0,6, a) b) c) d) e) f) auf wie viel Prozent 90 % 0,6 % 7 % 9,6 % 9,6 % 99,6 % um wie viel Prozent 0 % 9, % % 7, %, % 0, %
21 Knobelei Knobelei. waagerecht: a 6; c 8; e 68; f 6; g 80; h ; i ; n 8; o 90; p 96 senkrecht: a 68; b 80; c ; d 86; f ; k 70; l 6; m 99; n 89. [( 0 0) + 0] : + = 0 allgemein: [(a 0) + 0] : + = a = a. a) b) c) d). gedachte Zahl: 9 allgemein: {[(n + ) ] n : = n + n gedachte Zahl Lösungen. = = =. Tür öffnen 6. (n + ) + n 8 = n Genannte Zahl durch dividieren, um die gedachte Zahl (n) zu erhalten. 7. % von Personen sind 6 Personen; der Reiseleiter hat nicht recht.
7 Mathematik. Übungsaufgaben mit Lösungen Brandenburg
 7 Mathematik Übungsaufgaben mit Lösungen Brandenburg 2 Natürliche und gebrochene Zahlen Natürliche und gebrochene Zahlen Rechne vorteilhaft. a) 75 + 6 + 25 + 84 b) 87 + 2 7 + 9 c) 6 + (4 + 7) d) + (2 +
7 Mathematik Übungsaufgaben mit Lösungen Brandenburg 2 Natürliche und gebrochene Zahlen Natürliche und gebrochene Zahlen Rechne vorteilhaft. a) 75 + 6 + 25 + 84 b) 87 + 2 7 + 9 c) 6 + (4 + 7) d) + (2 +
Mathematik für Gymnasien
 Mathematik für Gymnasien Übungsaufgaben- LÖSUNGEN -Jahrgangsstufe I. Brüche. Allgemein: a) Zähler, Bruchstrich, Nenner b) Der Nenner gibt die Anzahl der gleichen Teile an, in die das Ganze zerlegt werden
Mathematik für Gymnasien Übungsaufgaben- LÖSUNGEN -Jahrgangsstufe I. Brüche. Allgemein: a) Zähler, Bruchstrich, Nenner b) Der Nenner gibt die Anzahl der gleichen Teile an, in die das Ganze zerlegt werden
Mathematik für Gymnasien Übungsaufgaben - Jahrgangsstufe 6
 Mathematik für Gymnasien Übungsaufgaben - Jahrgangsstufe I. Brüche. Allgemein: a) Aus welchen Bestandteilen besteht ein Bruch? b) Was besagt der Nenner? c) Was besagt der Zähler? d) In welchen Diagrammen
Mathematik für Gymnasien Übungsaufgaben - Jahrgangsstufe I. Brüche. Allgemein: a) Aus welchen Bestandteilen besteht ein Bruch? b) Was besagt der Nenner? c) Was besagt der Zähler? d) In welchen Diagrammen
Darstellen, Ordnen und Vergleichen
 Darstellen, Ordnen und Vergleichen negative Zahlen positive Zahlen 1_ 6 < 3,5 3 < +2 +1 2 < +5 Um negative Zahlen darstellen zu können, wird der Zahlenstrahl zu einer Zahlengeraden erweitert. Wenn zwei
Darstellen, Ordnen und Vergleichen negative Zahlen positive Zahlen 1_ 6 < 3,5 3 < +2 +1 2 < +5 Um negative Zahlen darstellen zu können, wird der Zahlenstrahl zu einer Zahlengeraden erweitert. Wenn zwei
Aufgaben zu Lambacher Schweizer 6 Hessen
 Aufgaben zu Kapitel I Erweitern und Kürzen Erweitere im Kopf. a) mit ; 6; b) å mit ; 6; 7 c) mit ; ; d) å mit ; ; e) mit ; ; 7 f) mit ; ; Erweitere auf den angegebenen Nenner. a) 0: ; ; ; 0 ; 0 ; 0 b)
Aufgaben zu Kapitel I Erweitern und Kürzen Erweitere im Kopf. a) mit ; 6; b) å mit ; 6; 7 c) mit ; ; d) å mit ; ; e) mit ; ; 7 f) mit ; ; Erweitere auf den angegebenen Nenner. a) 0: ; ; ; 0 ; 0 ; 0 b)
Rechentraining. 4 a) b) c) d) e) f) g) h)
 Rechentraining Kopfrechenaufgaben 1 a) 27 + 13 b) 45 + 25 c) 78 + 22 d) 64 + 36 e) 205 + 95 f) 909 + 91 g) 487 + 23 h) 630 + 470 i) 777 + 333 j) 34 23 k) 42 33 l) 177 78 m) 555 444 n) 1010 101 o) 808 88
Rechentraining Kopfrechenaufgaben 1 a) 27 + 13 b) 45 + 25 c) 78 + 22 d) 64 + 36 e) 205 + 95 f) 909 + 91 g) 487 + 23 h) 630 + 470 i) 777 + 333 j) 34 23 k) 42 33 l) 177 78 m) 555 444 n) 1010 101 o) 808 88
1 Grundwissen 6 2 Dezimalbrüche (Dezimalzahlen) 9 3 Brüche 11 4 Rationale Zahlen 16 5 Potenzen und Wurzeln 20 6 Größen und Schätzen 24
 Inhalt A Grundrechenarten Grundwissen 6 Dezimalbrüche (Dezimalzahlen) 9 Brüche Rationale Zahlen 6 5 Potenzen und Wurzeln 0 6 Größen und Schätzen B Zuordnungen Proportionale Zuordnungen 8 Umgekehrt proportionale
Inhalt A Grundrechenarten Grundwissen 6 Dezimalbrüche (Dezimalzahlen) 9 Brüche Rationale Zahlen 6 5 Potenzen und Wurzeln 0 6 Größen und Schätzen B Zuordnungen Proportionale Zuordnungen 8 Umgekehrt proportionale
Grundwissenskatalog der 6. Jahrgangsstufe G8 - Mathematik Friedrich-Koenig-Gymnasium Würzburg
 Grundwissenskatalog der. Jahrgangsstufe G8 - Mathematik Friedrich-Koenig-Gymnasium Würzburg. Brüche und Dezimalzahlen Bruchteile Berechnung von Bruchteilen Bruchzahlen als Quotient Gemischte Zahlen Erweitern
Grundwissenskatalog der. Jahrgangsstufe G8 - Mathematik Friedrich-Koenig-Gymnasium Würzburg. Brüche und Dezimalzahlen Bruchteile Berechnung von Bruchteilen Bruchzahlen als Quotient Gemischte Zahlen Erweitern
Umgekehrter Dreisatz Der umgekehrte Dreisatz ist ein Rechenverfahren, das man bei umgekehrt proportionalen Zuordnungen anwenden kann.
 Dreisatz Der Dreisatz ist ein Rechenverfahren, das man bei proportionalen Zuordnungen anwenden kann. 3 Tafeln Schokolade wiegen 5 g. Wie viel Gramm wiegen 5 Tafeln? 1. Satz: 3 Tafeln wiegen 5 g.. Satz:
Dreisatz Der Dreisatz ist ein Rechenverfahren, das man bei proportionalen Zuordnungen anwenden kann. 3 Tafeln Schokolade wiegen 5 g. Wie viel Gramm wiegen 5 Tafeln? 1. Satz: 3 Tafeln wiegen 5 g.. Satz:
Sachkompetenz Zahlen. Zahlen lesen und schreiben. zählen, Zahlen ordnen. Zahlen erfassen. Zahlen als Operatoren verwenden
 Zahlen Zahlen lesen und schreiben Zahlen und Zahlwörter lesen und schreiben Zahlen und Zahlwörter bis 20 lesen und schreiben Zahlen bis 100 lesen und schreiben große Zahlen lesen und schreiben die Bedeutung
Zahlen Zahlen lesen und schreiben Zahlen und Zahlwörter lesen und schreiben Zahlen und Zahlwörter bis 20 lesen und schreiben Zahlen bis 100 lesen und schreiben große Zahlen lesen und schreiben die Bedeutung
Bruchrechnen ohne Variablen Anwendungen 11
 Bruchrechnen ohne Variablen Anwendungen Addieren/Subtrahieren gleichnamiger Brüche Addition gleichnamiger Brüche: Nenner übernehmen; Zähler addieren: Subtraktion gleichnamiger Brüche: Nenner übernehmen;
Bruchrechnen ohne Variablen Anwendungen Addieren/Subtrahieren gleichnamiger Brüche Addition gleichnamiger Brüche: Nenner übernehmen; Zähler addieren: Subtraktion gleichnamiger Brüche: Nenner übernehmen;
Bruchrechnen ohne Variablen Anwendungen 11 - Lösungen
 Bruchrechnen ohne Variablen Anwendungen - Addieren/Subtrahieren gleichnamiger Brüche Addition gleichnamiger Brüche: Nenner übernehmen; Zähler addieren: Subtraktion gleichnamiger Brüche: Nenner übernehmen;
Bruchrechnen ohne Variablen Anwendungen - Addieren/Subtrahieren gleichnamiger Brüche Addition gleichnamiger Brüche: Nenner übernehmen; Zähler addieren: Subtraktion gleichnamiger Brüche: Nenner übernehmen;
1 Rechnen. Addition rationaler Zahlen gleicher Vorzeichen Summand + Summand = Summe
 Rationale Zahlen Die ganzen Zahlen zusammen mit allen positiven und negativen Bruchzahlen heißen rationale Zahlen. Die Menge der rationalen Zahlen wird mit Q bezeichnet. Je weiter links eine Zahl auf dem
Rationale Zahlen Die ganzen Zahlen zusammen mit allen positiven und negativen Bruchzahlen heißen rationale Zahlen. Die Menge der rationalen Zahlen wird mit Q bezeichnet. Je weiter links eine Zahl auf dem
Aufgaben mit zwei Rechenzeichen nebeneinander zum Beispiel: 5 (+ 3) Es gilt:
 Hilfe Addition und Subtraktion von Rationalen Zahlen Rechnen mit rationalen Zahlen, also Rechnen im negativen Bereich ist nicht immer so einfach. Ich kann mir das eigentlich ganz gut mit Schulden oder
Hilfe Addition und Subtraktion von Rationalen Zahlen Rechnen mit rationalen Zahlen, also Rechnen im negativen Bereich ist nicht immer so einfach. Ich kann mir das eigentlich ganz gut mit Schulden oder
sfg Brüche Brüche beschreiben Bruchteile bzw. Anteile M 6.1 Die Schokoladentafel hat 14 Stückchen, d.h. ein Stückchen entspricht dem Anteil
 M 6. Brüche Brüche beschreiben Bruchteile bzw. Anteile 3 4 von 00kg = 4 von 00kg 3 = (00kg 4) 3 = kg 3 = 7kg (s. auch 6.0) Die Schokoladentafel hat 4 Stückchen, d.h. ein Stückchen entspricht dem Anteil
M 6. Brüche Brüche beschreiben Bruchteile bzw. Anteile 3 4 von 00kg = 4 von 00kg 3 = (00kg 4) 3 = kg 3 = 7kg (s. auch 6.0) Die Schokoladentafel hat 4 Stückchen, d.h. ein Stückchen entspricht dem Anteil
9 = c) a) = b) = c) = d) =
 A Grundrechnungsarten. Rechnen mit Brüchen Addieren und Subtrahieren von Brüchen Addiere und subtrahiere die Brüche. a) 0 0 0 b) - 0...... Brüche mit gleichem Nenner werden addiert, indem du die Zähler
A Grundrechnungsarten. Rechnen mit Brüchen Addieren und Subtrahieren von Brüchen Addiere und subtrahiere die Brüche. a) 0 0 0 b) - 0...... Brüche mit gleichem Nenner werden addiert, indem du die Zähler
LERNSTANDSERFASSUNG. Name: Datum: Copyright by ILV-H
 LERNSTANDSERFASSUNG Name: Datum: Wie gut kannst du schätzen? a) Wie viele Meter lang misst unser Schulzimmer?... b) Wie viele Menschen leben auf der Welt?... c) Wie schwer sind alle SchülerInnen zusammen?...
LERNSTANDSERFASSUNG Name: Datum: Wie gut kannst du schätzen? a) Wie viele Meter lang misst unser Schulzimmer?... b) Wie viele Menschen leben auf der Welt?... c) Wie schwer sind alle SchülerInnen zusammen?...
Stoffverteilungsplan Mathematik Klasse 5
 Stoffverteilungsplan Mathematik Klasse 5 Lehrwerk: Mathematik heute; Schroedel Zeitraum Themen/Inhalte Begriffe/Bemerkungen Lehrbuch/KA Leitidee/Kompetenzen Weitere Hinweise 6 Wochen Natürliche Zahlen
Stoffverteilungsplan Mathematik Klasse 5 Lehrwerk: Mathematik heute; Schroedel Zeitraum Themen/Inhalte Begriffe/Bemerkungen Lehrbuch/KA Leitidee/Kompetenzen Weitere Hinweise 6 Wochen Natürliche Zahlen
Kurs 1 Grundlagen EBBR Vollzeit (1 von 2)
 Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 72 A 2895 Bremen Kurs Grundlagen EBBR Vollzeit ( von 2) Name: Ich So schätze ich meinen Lernzuwachs ein. Kapitel im Buch kann ich
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 72 A 2895 Bremen Kurs Grundlagen EBBR Vollzeit ( von 2) Name: Ich So schätze ich meinen Lernzuwachs ein. Kapitel im Buch kann ich
Schulinternes Curriculum Mathematik Jahrgangsstufe 7
 Schulinternes Curriculum Mathematik Jahrgangsstufe 7 Unterrichtsvorhaben I: Rationale Zahlen Arithmetik / Algebra Ordnen Operieren rationale Zahlen ordnen und vergleichen Grundrechenarten für rationale
Schulinternes Curriculum Mathematik Jahrgangsstufe 7 Unterrichtsvorhaben I: Rationale Zahlen Arithmetik / Algebra Ordnen Operieren rationale Zahlen ordnen und vergleichen Grundrechenarten für rationale
Große Anzahlen schätzen. 1 Da sind ja viele Menschen! Schätze, wie viele Menschen auf dem Bild zu sehen sind.
 Große Anzahlen schätzen 1 Da sind ja viele Menschen! Schätze, wie viele Menschen auf dem Bild zu sehen sind. Ich schätze, es sind Menschen. Wie weiß man, wie viele Menschen das ungefähr sind? Kennst du
Große Anzahlen schätzen 1 Da sind ja viele Menschen! Schätze, wie viele Menschen auf dem Bild zu sehen sind. Ich schätze, es sind Menschen. Wie weiß man, wie viele Menschen das ungefähr sind? Kennst du
Voransicht. Grundrechen Führerschein: Aufwärmtraining
 Grundrechen Führerschein: Aufwärmtraining Mit dieser Seite kannst du dich auf den Grundrechen Führerschein vorbereiten. 1 Additionspuzzle. Zerschneide das Bild rechts, rechne die Aufgabe links in deinem
Grundrechen Führerschein: Aufwärmtraining Mit dieser Seite kannst du dich auf den Grundrechen Führerschein vorbereiten. 1 Additionspuzzle. Zerschneide das Bild rechts, rechne die Aufgabe links in deinem
Ganze und rationale Zahlen:
 Ganze und rationale Zahlen: 1.1 Beantworte die Fragen. Welche Temperatur wird angezeigt? -2 C 2 C -0,2 C - C Um wieviel müsste es wärmer werden, damit es 10 C hat? 2 C 7 C 12 C 18 C Die Temperatur steigt
Ganze und rationale Zahlen: 1.1 Beantworte die Fragen. Welche Temperatur wird angezeigt? -2 C 2 C -0,2 C - C Um wieviel müsste es wärmer werden, damit es 10 C hat? 2 C 7 C 12 C 18 C Die Temperatur steigt
Serie 1 Klasse Vereinfache. a) 2(4a 5b) b) 3. Rechne um. a) 456 m =... km b) 7,24 t =... kg
 Serie 1 Klasse 10 1. Berechne. 1 a) 4 3 b) 0,64 : 8 c) 4 6 d) ³. Vereinfache. 1x²y a) (4a 5b) b) 4xy 3. Rechne um. a) 456 m =... km b) 7,4 t =... kg 4. Ermittle. a) 50 % von 30 sind... b) 4 kg von 480
Serie 1 Klasse 10 1. Berechne. 1 a) 4 3 b) 0,64 : 8 c) 4 6 d) ³. Vereinfache. 1x²y a) (4a 5b) b) 4xy 3. Rechne um. a) 456 m =... km b) 7,4 t =... kg 4. Ermittle. a) 50 % von 30 sind... b) 4 kg von 480
Positiven Zahlen haben ein Pluszeichen (+) oder gar kein Zeichen vor der Zahl. Negative Zahlen erkennt man am Minuszeichen (-) vor der Zahl.
 Hilfe RATIONALE ZAHLEN Q Positiven Zahlen haben ein Pluszeichen (+) oder gar kein Zeichen vor der Zahl. Negative Zahlen erkennt man am Minuszeichen (-) vor der Zahl. Alle positiven und negativen Zahlen
Hilfe RATIONALE ZAHLEN Q Positiven Zahlen haben ein Pluszeichen (+) oder gar kein Zeichen vor der Zahl. Negative Zahlen erkennt man am Minuszeichen (-) vor der Zahl. Alle positiven und negativen Zahlen
Rechnen mit Variablen
 E Rechnen mit Variablen 5. Gleichungen 1 Rätselrechnungen Welches Streichholz muss umgelegt werden, damit die Rechnung stimmt? (Material: Streichhölzer) a) b) Berechne den Wert der Variablen. Eine Gleichung
E Rechnen mit Variablen 5. Gleichungen 1 Rätselrechnungen Welches Streichholz muss umgelegt werden, damit die Rechnung stimmt? (Material: Streichhölzer) a) b) Berechne den Wert der Variablen. Eine Gleichung
Mathematik 4 Primarstufe
 Mathematik 4 Primarstufe Handlungs-/Themenaspekte Bezüge zum Lehrplan 21 Die Übersicht zeigt die Bezüge zwischen den Themen des Lehrmittels und den Kompetenzen des Lehrplans 21. Es ist jeweils diejenige
Mathematik 4 Primarstufe Handlungs-/Themenaspekte Bezüge zum Lehrplan 21 Die Übersicht zeigt die Bezüge zwischen den Themen des Lehrmittels und den Kompetenzen des Lehrplans 21. Es ist jeweils diejenige
Vorbereitung auf die 1. Schularbeit: MATHEMATIK KL.: M3/I. - S.1 Mi,
 . Schularbeit: MATHEMATIK KL.: M/I. - S. Mi,.0.0 ) Welche Zahl kann eingesetzt werden, damit die Gleichung stimmt? Suche die Lösung durch Probieren oder durch Umkehrung! ( + ) - = ( - ) - ) Gib für b jeweils
. Schularbeit: MATHEMATIK KL.: M/I. - S. Mi,.0.0 ) Welche Zahl kann eingesetzt werden, damit die Gleichung stimmt? Suche die Lösung durch Probieren oder durch Umkehrung! ( + ) - = ( - ) - ) Gib für b jeweils
b) Notieren Sie hier die Brüche aus der Tabelle, die sich noch kürzen lassen und kürzen Sie diese soweit als möglich: 1 2
 Addieren und Subtrahieren gleichnamiger Brüche Addition gleichnamiger Brüche: Nenner übernehmen; Zähler addieren: Subtraktion gleichnamiger Brüche: Nenner übernehmen; Zähler subtrahieren. Füllen Sie die
Addieren und Subtrahieren gleichnamiger Brüche Addition gleichnamiger Brüche: Nenner übernehmen; Zähler addieren: Subtraktion gleichnamiger Brüche: Nenner übernehmen; Zähler subtrahieren. Füllen Sie die
Kapitel im Fokus. Ich kann / kenne. 5. Klasse Stand Juni **Anzahl der KA: 6 pro Schuljahr** Daten und Zufall. Größen messen
 Daten und Zufall Sammeln und Auswerten von Daten Strichliste Absolute Häufigkeit Säulendiagramm Daten erfassen (Strichlisten, Tabellen). gesammelte Daten auswerten. Daten mithilfe von Diagrammen darstellen.
Daten und Zufall Sammeln und Auswerten von Daten Strichliste Absolute Häufigkeit Säulendiagramm Daten erfassen (Strichlisten, Tabellen). gesammelte Daten auswerten. Daten mithilfe von Diagrammen darstellen.
Stoffverteilungsplan Mathematik Klasse 7 RS,
 Stoffverteilungsplan Mathematik Klasse 7 RS, 04.12.2006 Inhalte Prozessbezogene Kompetenzen Inhaltsbezogene Kompetenzen Methoden 1 Rationale Zahlen Unter Null 1 Ganze Zahlen 2 Rationale Zalen 3 Anordnung
Stoffverteilungsplan Mathematik Klasse 7 RS, 04.12.2006 Inhalte Prozessbezogene Kompetenzen Inhaltsbezogene Kompetenzen Methoden 1 Rationale Zahlen Unter Null 1 Ganze Zahlen 2 Rationale Zalen 3 Anordnung
1. Schularbeit Mathematik Oktober 2015
 1. Schularbeit Mathematik 3 14. Oktober 2015 Name: Klasse: Wichtige Anmerkungen: Rechne OHNE Taschenrechner! Schreibe alle Rechenwege oder Nebenrechnungen übersichtlich auf! Ergebnisse ohne Nebenrechnung,
1. Schularbeit Mathematik 3 14. Oktober 2015 Name: Klasse: Wichtige Anmerkungen: Rechne OHNE Taschenrechner! Schreibe alle Rechenwege oder Nebenrechnungen übersichtlich auf! Ergebnisse ohne Nebenrechnung,
mein grosses übungsbuch mathematik
 königs lernhilfen mein grosses übungsbuch mathematik 5. / 6. klasse 1. Auflage 2019 ISBN: 978-3-8044-1231-6 PDF: 978-3-8044-5331-9 Genehmigte Lizenzausgabe für den C. Bange Verlag, 96142 Hollfeld Alle
königs lernhilfen mein grosses übungsbuch mathematik 5. / 6. klasse 1. Auflage 2019 ISBN: 978-3-8044-1231-6 PDF: 978-3-8044-5331-9 Genehmigte Lizenzausgabe für den C. Bange Verlag, 96142 Hollfeld Alle
1.1 Bruchteile und Bruchzahlen Bruchteile von Ganzen lassen sich mit Hilfe von Bruchzahlen darstellen: 6 3 = Schraffiert:
 Zahlen. Bruchteile und Bruchzahlen Bruchteile von Ganzen lassen sich mit Hilfe von Bruchzahlen darstellen: Gelb: 6 = Schraffiert: 20 0 Bruchteile gibt man häufig in Prozent (%) an. Prozent = Hundertstel
Zahlen. Bruchteile und Bruchzahlen Bruchteile von Ganzen lassen sich mit Hilfe von Bruchzahlen darstellen: Gelb: 6 = Schraffiert: 20 0 Bruchteile gibt man häufig in Prozent (%) an. Prozent = Hundertstel
M-Beispiele samt Lösungen
 HS Pians M-Beispiele samt Lösungen M-Beispiele zur Vorbereitung auf die. Schularbeit Termin: Fr.,..00 Köck Erstellt..00 . Schularbeit aus MATHEMATIK KL.: M/I. - S...00 ) Berechne den Mittelwert! Gib das
HS Pians M-Beispiele samt Lösungen M-Beispiele zur Vorbereitung auf die. Schularbeit Termin: Fr.,..00 Köck Erstellt..00 . Schularbeit aus MATHEMATIK KL.: M/I. - S...00 ) Berechne den Mittelwert! Gib das
Serie W1, Kl Wie viele Flächen, Ecken und Kanten hat ein Quader? F: E: K:
 Serie W1, Kl. 5 1. 89 + 32 = 2. 17 8 = 3. 120 : 5 = 4. 123 42 = 5. Wie viele Flächen, Ecken und Kanten hat ein Quader? F: E: K: 6. 165 cm = dm 7. 48 000 g = kg 8. Skizziere das abgebildete Würfelnetz.
Serie W1, Kl. 5 1. 89 + 32 = 2. 17 8 = 3. 120 : 5 = 4. 123 42 = 5. Wie viele Flächen, Ecken und Kanten hat ein Quader? F: E: K: 6. 165 cm = dm 7. 48 000 g = kg 8. Skizziere das abgebildete Würfelnetz.
Grundwissen. 6. Jahrgangsstufe. Mathematik
 Grundwissen 6. Jahrgangsstufe Mathematik 1 Brüche Grundwissen Mathematik 6. Jahrgangsstufe Seite 1 1.1 Bruchteil 1.2 Erweitern und Kürzen Erweitern: Zähler und Nenner mit der selben Zahl multiplizieren
Grundwissen 6. Jahrgangsstufe Mathematik 1 Brüche Grundwissen Mathematik 6. Jahrgangsstufe Seite 1 1.1 Bruchteil 1.2 Erweitern und Kürzen Erweitern: Zähler und Nenner mit der selben Zahl multiplizieren
1 Natürliche Zahlen und ihre Erweiterung zu den ganzen Zahlen
 Natürliche Zahlen darstellen das Zehnersystem Natürliche Zahlen und ihre Erweiterung zu den ganzen Zahlen Trage die fehlenden Zahlen in die Tabelle ein. Vorgänger 7 Zahl 6 87 6 87 Nachfolger 8 7 6 900
Natürliche Zahlen darstellen das Zehnersystem Natürliche Zahlen und ihre Erweiterung zu den ganzen Zahlen Trage die fehlenden Zahlen in die Tabelle ein. Vorgänger 7 Zahl 6 87 6 87 Nachfolger 8 7 6 900
fwg Brüche Brüche beschreiben Bruchteile bzw. Anteile M 6.1 (s. auch 6.10) Stückchen, d.h. ein Stückchen entspricht dem Anteil
 M 6.1 Brüche Brüche beschreiben Bruchteile bzw. Anteile (s. auch 6.10) Die Schokoladentafel hat Stückchen, d.h. ein Stückchen entspricht dem Anteil M 6.2 Prozentschreibweise Anteile werden häufig in Prozent
M 6.1 Brüche Brüche beschreiben Bruchteile bzw. Anteile (s. auch 6.10) Die Schokoladentafel hat Stückchen, d.h. ein Stückchen entspricht dem Anteil M 6.2 Prozentschreibweise Anteile werden häufig in Prozent
KGS-Stoffverteilungsplan RS-Zweig Mathematik 7 (Grundlage Kerncurricula) Lehrbuch: Schnittpunkt 7, Klett
 erläutern die Notwendigkeit der Zahlbereichserweiterung auf die rationalen Zahlen anhand von Beispielen besitzen Vorstellungen negativer Zahlen als Abstraktion verschiedener Sachverhalte des täglichen
erläutern die Notwendigkeit der Zahlbereichserweiterung auf die rationalen Zahlen anhand von Beispielen besitzen Vorstellungen negativer Zahlen als Abstraktion verschiedener Sachverhalte des täglichen
1 Rätselrechnungen Welches Streichholz muss umgelegt werden, damit die Rechnung stimmt? (Material: Streichhölzer) a) b)
 1 Rätselrechnungen Welches Streichholz muss umgelegt werden, damit die Rechnung stimmt? (Material: Streichhölzer) a) b) Berechne den Wert der Variablen. Eine Gleichung kannst du dir als eine Balkenwaage
1 Rätselrechnungen Welches Streichholz muss umgelegt werden, damit die Rechnung stimmt? (Material: Streichhölzer) a) b) Berechne den Wert der Variablen. Eine Gleichung kannst du dir als eine Balkenwaage
2. Erstelle einen Term, der den Flächeninhalt beschreibt (Alle Maße in cm).
 A Grundwissen (Beispiele) a) (63 5 2) 3 11 8 c) 10 7 + (17 +169 : 13) 2 b) 60 : 4 + (9 + 15) : 3 d) 12² (4 4² 3) : 4 B Äquivalenzumformungen und Äquivalenz von Termen 1. Welche der Terme sind äquivalent?
A Grundwissen (Beispiele) a) (63 5 2) 3 11 8 c) 10 7 + (17 +169 : 13) 2 b) 60 : 4 + (9 + 15) : 3 d) 12² (4 4² 3) : 4 B Äquivalenzumformungen und Äquivalenz von Termen 1. Welche der Terme sind äquivalent?
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Mathematik ganz einfach mit Lösungsbeispielen 7-8
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Mathematik ganz einfach mit Lösungsbeispielen 7-8 Das komplette Material finden Sie hier: School-Scoutde Inhaltsverzeichnis Klasse
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Mathematik ganz einfach mit Lösungsbeispielen 7-8 Das komplette Material finden Sie hier: School-Scoutde Inhaltsverzeichnis Klasse
Grundwissen. 6. Jahrgangsstufe. Mathematik
 Grundwissen 6. Jahrgangsstufe Mathematik Brüche Grundwissen Mathematik 6. Jahrgangsstufe Seite. Bruchteil 3 4 von 00kg =75 kg NR: 00kg :4 3=25 kg 3=75 kg 3 4 heißt Anteil ; 75kg heißt Bruchteil.2 Erweitern
Grundwissen 6. Jahrgangsstufe Mathematik Brüche Grundwissen Mathematik 6. Jahrgangsstufe Seite. Bruchteil 3 4 von 00kg =75 kg NR: 00kg :4 3=25 kg 3=75 kg 3 4 heißt Anteil ; 75kg heißt Bruchteil.2 Erweitern
Mit symbolischen, formalen und technischen Elementen der Mathematik umgehen Wertetabellen zur Bearbeitung linearer Zusammenhänge nutzen.
 MAT 07-01 Zuordnungen 14 DS Leitidee: Funktionaler Zusammenhang Thema im Buch: Unterwegs Werte aus Schaubildern ablesen und ihre Bedeutung erklären. entscheiden und begründen, ob es sich um eine nicht
MAT 07-01 Zuordnungen 14 DS Leitidee: Funktionaler Zusammenhang Thema im Buch: Unterwegs Werte aus Schaubildern ablesen und ihre Bedeutung erklären. entscheiden und begründen, ob es sich um eine nicht
6. Klasse. Rechnen und Sachaufgaben. Mathe. Rechnen und Sachaufgaben. in 15 Minuten
 Rechnen und Sachaufgaben 6. Klasse Mathe Rechnen und Sachaufgaben in Minuten Klasse Mathe Duden in Minuten Rechnen und Sachaufgaben 6. Klasse., aktualisierte Auflage Dudenverlag Mannheim Zürich Inhalt
Rechnen und Sachaufgaben 6. Klasse Mathe Rechnen und Sachaufgaben in Minuten Klasse Mathe Duden in Minuten Rechnen und Sachaufgaben 6. Klasse., aktualisierte Auflage Dudenverlag Mannheim Zürich Inhalt
Matheheft 7. Klasse. Kurz geübt & schnell kapiert. Matheheft. 7. Klasse. Matheheft 7. Klasse
 Matheheft 7. Klasse Matheheft 7. Klasse Kurz geübt & schnell kapiert Matheheft 7. Klasse Kurz geübt & schnell kapiert Matheheft 7. Klasse Lernplan von 1 Seite Prozent- und Zinsrechnung bearbeiten am Anteile
Matheheft 7. Klasse Matheheft 7. Klasse Kurz geübt & schnell kapiert Matheheft 7. Klasse Kurz geübt & schnell kapiert Matheheft 7. Klasse Lernplan von 1 Seite Prozent- und Zinsrechnung bearbeiten am Anteile
Probeunterricht 2008 an Wirtschaftsschulen in Bayern
 an Wirtschaftsschulen in Bayern Mathematik 7. Jahrgangsstufe Arbeitszeit Teil I (Zahlenrechnen): Arbeitszeit Teil II (Textrechnen): 45 Minuten 45 Minuten Name.. Vorname.. Bewertung (Erstkorrektor) Bewertung
an Wirtschaftsschulen in Bayern Mathematik 7. Jahrgangsstufe Arbeitszeit Teil I (Zahlenrechnen): Arbeitszeit Teil II (Textrechnen): 45 Minuten 45 Minuten Name.. Vorname.. Bewertung (Erstkorrektor) Bewertung
Begriffe, die auf eine Multiplikation oder Division hinweisen
 Fachbegriffe der Addition und Subtraktion Bei der Addition werden Zahlen zusammengezählt: 2 + 4 = 6 1. Summand 2. Summand Summe Bei der Subtraktion wird eine Zahl von einer anderen abgezogen. 7 2 = 5 Minuend
Fachbegriffe der Addition und Subtraktion Bei der Addition werden Zahlen zusammengezählt: 2 + 4 = 6 1. Summand 2. Summand Summe Bei der Subtraktion wird eine Zahl von einer anderen abgezogen. 7 2 = 5 Minuend
JAHRGANGSSTUFE 5 Prozessbezogene Kompetenzen Inhaltsbezogene Kompetenzen
 JAHRGANGSSTUFE 5 Prozessbezogene Kompetenzen Inhaltsbezogene Kompetenzen ELEMENTE DER MATHEMATIK 5 Schroedel Verlag Argumentieren Problemlösen Modellieren Werkzeuge Arithmetik/ Algebra Funktionen Geometrie
JAHRGANGSSTUFE 5 Prozessbezogene Kompetenzen Inhaltsbezogene Kompetenzen ELEMENTE DER MATHEMATIK 5 Schroedel Verlag Argumentieren Problemlösen Modellieren Werkzeuge Arithmetik/ Algebra Funktionen Geometrie
Erzbischöfliche Liebfrauenschule Köln. Schulinternes Curriculum Fach: Mathematik Jg. 7
 Erzbischöfliche Liebfrauenschule Köln Schulinternes Curriculum Fach: Mathematik Jg. 7 Reihen -folge Buchabschnit t Themen Inhaltsbezogene Kompetenzen Prozessbezogene Kompetenzen 1 1.1 1.9 Zuordnungen -
Erzbischöfliche Liebfrauenschule Köln Schulinternes Curriculum Fach: Mathematik Jg. 7 Reihen -folge Buchabschnit t Themen Inhaltsbezogene Kompetenzen Prozessbezogene Kompetenzen 1 1.1 1.9 Zuordnungen -
2. Was ist der größere Preisnachlass? Erläutere kurz mit Worten. Alle Hosen um 30% reduziert! oder Alle Hosen um 30 Euro reduziert!
 Mathematik 7b Übungsblatt Nr.1 11.10.2006 Rechne so oft es geht ohne TR. Kontrolliere anschließend mit dem TR. 1. a) Schreibe in Prozent: 3 5 0, 23 247 1000 b) Gib den Anteil in Prozent an: 340kg von 625
Mathematik 7b Übungsblatt Nr.1 11.10.2006 Rechne so oft es geht ohne TR. Kontrolliere anschließend mit dem TR. 1. a) Schreibe in Prozent: 3 5 0, 23 247 1000 b) Gib den Anteil in Prozent an: 340kg von 625
Inhalt. 1 Bruchteile und Bruchzahlen. 2 Dezimalzahlen. 3 Addition und Subtraktion rationaler Zahlen. 4 Multiplikation und Division rationaler Zahlen
 Inhalt 1 Bruchteile und Bruchzahlen 1.1 Veranschaulichen von Bruchteilen............................. 1.2 Erkennen und Berechnen von Bruchteilen........................ 8 1.3 Erweitern und Kürzen von Brüchen.............................
Inhalt 1 Bruchteile und Bruchzahlen 1.1 Veranschaulichen von Bruchteilen............................. 1.2 Erkennen und Berechnen von Bruchteilen........................ 8 1.3 Erweitern und Kürzen von Brüchen.............................
Mathematik. Begriffe und Aufgaben
 Mathematik Begriffe und Zahlen Zahlen, Ziffern und Stellenwerte Definitionen Zahlen Zahlen, Ziffern und Stellenwerte Begriff Erklärung/Definition Beispiele Ziffern sind die Bausteine der Zahlenschreibweise
Mathematik Begriffe und Zahlen Zahlen, Ziffern und Stellenwerte Definitionen Zahlen Zahlen, Ziffern und Stellenwerte Begriff Erklärung/Definition Beispiele Ziffern sind die Bausteine der Zahlenschreibweise
Grundwissen 5. Klasse
 Grundwissen 5. Klasse 1/5 1. Zahlenmengen Grundwissen 5. Klasse Natürliche Zahlen ohne Null: N 1;2;3;4;5;... mit der Null: N 0 0;1;2;3;4;... Ganze Zahlen: Z... 3; 2; 1;0;1;2;3;.... 2. Die Rechenarten a)
Grundwissen 5. Klasse 1/5 1. Zahlenmengen Grundwissen 5. Klasse Natürliche Zahlen ohne Null: N 1;2;3;4;5;... mit der Null: N 0 0;1;2;3;4;... Ganze Zahlen: Z... 3; 2; 1;0;1;2;3;.... 2. Die Rechenarten a)
Selbstüberprüfungsbogen Bruchrechnung
 Selbstüberprüfungsbogen Bruchrechnung Modul: Bruchrechnung Name: SINUS.NRW 00 ) Vorstellung zu Brüchen r f Übungen a) Notiere die zugehörigen Brüche. b) Wie groß ist der Anteil der Fläche mit der? c) Wie
Selbstüberprüfungsbogen Bruchrechnung Modul: Bruchrechnung Name: SINUS.NRW 00 ) Vorstellung zu Brüchen r f Übungen a) Notiere die zugehörigen Brüche. b) Wie groß ist der Anteil der Fläche mit der? c) Wie
Rationale Zahlen. Vergleichen und Ordnen rationaler Zahlen
 Rationale Zahlen Vergleichen und Ordnen rationaler Zahlen Von zwei rationalen Zahlen ist die die kleinere Zahl, die auf der Zahlengeraden weiter links liegt.. Setze das richtige Zeichen. a) -3 4 b) - -3
Rationale Zahlen Vergleichen und Ordnen rationaler Zahlen Von zwei rationalen Zahlen ist die die kleinere Zahl, die auf der Zahlengeraden weiter links liegt.. Setze das richtige Zeichen. a) -3 4 b) - -3
Lösungen zum Selbstüberprüfungsbogen Bruchrechnung
 Lösungen zum Selbstüberprüfungsbogen Bruchrechnung Modul: Bruchrechnung Name: SINUS.NRW 00 ) Vorstellung zu Brüchen r f Übungen a) Notiere die zugehörigen Brüche. b) Wie groß ist der Anteil der Fläche
Lösungen zum Selbstüberprüfungsbogen Bruchrechnung Modul: Bruchrechnung Name: SINUS.NRW 00 ) Vorstellung zu Brüchen r f Übungen a) Notiere die zugehörigen Brüche. b) Wie groß ist der Anteil der Fläche
Fragen und Aufgaben zum Grundwissen Mathematik JGST. 7
 Fragen und Aufgaben zum Grundwissen Mathematik JGST. 7 LÖSUNGEN. Gib die Primfaktorzerlegung der Zahlen 0 und an. 0 0 7 7 7. Erkläre, wie man zwei ganze Zahlen addiert bzw. multipliziert. Bei gleichem
Fragen und Aufgaben zum Grundwissen Mathematik JGST. 7 LÖSUNGEN. Gib die Primfaktorzerlegung der Zahlen 0 und an. 0 0 7 7 7. Erkläre, wie man zwei ganze Zahlen addiert bzw. multipliziert. Bei gleichem
M 5. Inhaltsverzeichnis Grundwissen M 5.1. Diagramme. Tabelle: (Beispiel: Klassensprecherwahl) Säulendiagramm: Balkendiagramm:
 M 5 Inhaltsverzeichnis Grundwissen M 5.1 Diagramme M 5.2 Natürliche Zahlen M 5.3 Terme (Rechenausdrücke) M 5.4 Vorrangregeln M 5.5 Ganze Zahlen M 5.6 Addition und Subtraktion in Z M 5.7 Koordinatensystem
M 5 Inhaltsverzeichnis Grundwissen M 5.1 Diagramme M 5.2 Natürliche Zahlen M 5.3 Terme (Rechenausdrücke) M 5.4 Vorrangregeln M 5.5 Ganze Zahlen M 5.6 Addition und Subtraktion in Z M 5.7 Koordinatensystem
Brüche. Brüche beschreiben Bruchteile. M 6.1. Die Schokoladentafel hat 14 Stückchen, d.h. ein Stückchen entspricht dem Anteil
 M 6. Brüche Brüche beschreiben Bruchteile. 3 4 von 00kg = ( von 00kg) 3 = (00kg 4) 3 = kg 3 = 7kg 4 Die Schokoladentafel hat 4 Stückchen, d.h. ein Stückchen entspricht dem Anteil 4 M 6. Prozentschreibweise
M 6. Brüche Brüche beschreiben Bruchteile. 3 4 von 00kg = ( von 00kg) 3 = (00kg 4) 3 = kg 3 = 7kg 4 Die Schokoladentafel hat 4 Stückchen, d.h. ein Stückchen entspricht dem Anteil 4 M 6. Prozentschreibweise
10. Berechne den Wert des Decksteins in der Multiplikationsmauer. 4 0,5 6 0,5
 6. Berechne den Wert der Terme. 4 P. a) 63 + ( 73) b) 93 + ( 67) 7. Berechne den Wert des Decksteins in der Additionsmauer. 14 24 25 46 8. Berechne den Wert der Terme. 4 P. a) 25 (+ 9) b) 17 ( 7) 9. Berechne
6. Berechne den Wert der Terme. 4 P. a) 63 + ( 73) b) 93 + ( 67) 7. Berechne den Wert des Decksteins in der Additionsmauer. 14 24 25 46 8. Berechne den Wert der Terme. 4 P. a) 25 (+ 9) b) 17 ( 7) 9. Berechne
KGS-Stoffverteilungsplan RS-Zweig Mathematik 7 Lehrbuch: Schnittpunkt 7, Klett
 formulieren Fragen zu unterschiedlichen Aspekten von interpretieren das Ergebnis in Bezug auf die Realsituation nutzen systematische Probierverfahren gliedern das Problem in Teilprobleme auf beurteilen
formulieren Fragen zu unterschiedlichen Aspekten von interpretieren das Ergebnis in Bezug auf die Realsituation nutzen systematische Probierverfahren gliedern das Problem in Teilprobleme auf beurteilen
Ein Bruchteil vom Ganzen lässt sich mit Hilfe von Bruchzahlen darstellen. Bsp.: Ganzes: 20 Kästchen
 Grundwissen Mathematik G8 6. Klasse Zahlen. Brüche.. Bruchteile und Bruchzahlen Ein Bruchteil vom Ganzen lässt sich mit Hilfe von Bruchzahlen darstellen. Ganzes: 0 Kästchen 6 6 graue Kästchen, also: 0
Grundwissen Mathematik G8 6. Klasse Zahlen. Brüche.. Bruchteile und Bruchzahlen Ein Bruchteil vom Ganzen lässt sich mit Hilfe von Bruchzahlen darstellen. Ganzes: 0 Kästchen 6 6 graue Kästchen, also: 0
4 Liter! Wie ist die Einheitsstrecke sinnvoller Weise zu wählen, damit man die gegebenen Zahlen möglichst genau auf der Zahlengeraden markieren kann?
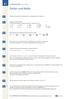 Zahlen und Maße Welche Zahlen haben den Betrag? Gib mindestens zwei Zahlen an! Gegeben ist die Zahl 0,. Welche Darstellungen entsprechen dieser Zahl? Kreuze an! % 0 % 0 00 0 0 0,0 0,00 Markiere auf dem
Zahlen und Maße Welche Zahlen haben den Betrag? Gib mindestens zwei Zahlen an! Gegeben ist die Zahl 0,. Welche Darstellungen entsprechen dieser Zahl? Kreuze an! % 0 % 0 00 0 0 0,0 0,00 Markiere auf dem
Serie W1 Klasse 8 RS. 1. 7,4 dm³ = cm³ 2. 5 (13-6) = 3. Berechne für a = - 4,5 b = - 3
 Serie W1 Klasse 8 RS 1. 7,4 dm³ = cm³ 2. 5 (13-6) = 3. Berechne für a = - 4,5 b = - 3 3 c = 4 2a - b; a + b; b : c 4. 36:0,4 = 5. Vergleiche. 30+2 10+5 30+2 (10+5) 6. Kürze 12 44 7. Berechne a 8a - 28
Serie W1 Klasse 8 RS 1. 7,4 dm³ = cm³ 2. 5 (13-6) = 3. Berechne für a = - 4,5 b = - 3 3 c = 4 2a - b; a + b; b : c 4. 36:0,4 = 5. Vergleiche. 30+2 10+5 30+2 (10+5) 6. Kürze 12 44 7. Berechne a 8a - 28
Kompetenzen am Ende der Einheit GRUNDWISSEN
 Kompetenzen am Ende der Einheit GRUNDWISSEN A) Grundrechenarten mit - 1.Natürlichen Zahlen : Berechne ohne Taschenrechner : a) 6438 + 64742 b) 8633 5877 c) 28 * 36 d) 7884 : 9-2. Brüchen : Berechne ohne
Kompetenzen am Ende der Einheit GRUNDWISSEN A) Grundrechenarten mit - 1.Natürlichen Zahlen : Berechne ohne Taschenrechner : a) 6438 + 64742 b) 8633 5877 c) 28 * 36 d) 7884 : 9-2. Brüchen : Berechne ohne
Grundwissen Mathematik für die Jahrgangsstufe 6 - Lösungen
 Grundwissen Mathematik für die Jahrgangsstufe 6 - Lösungen 1. Gib mindestens drei Eigenschaften der natürlichen Zahlen an. Jede natürliche Zahl hat einen Nachfolger und jede natürliche Zahl außer 1 hat
Grundwissen Mathematik für die Jahrgangsstufe 6 - Lösungen 1. Gib mindestens drei Eigenschaften der natürlichen Zahlen an. Jede natürliche Zahl hat einen Nachfolger und jede natürliche Zahl außer 1 hat
gebrochene Zahl gekürzt mit 9 sind erweitert mit 8 sind
 Vorbereitungsaufgaben Mathematik. Bruchrechnung.. Grundlagen: gebrochene Zahl gemeiner Bruch Zähler Nenner Dezimalbruch Ganze, Zehntel Hundertstel Tausendstel Kürzen: Zähler und Nenner durch dieselbe Zahl
Vorbereitungsaufgaben Mathematik. Bruchrechnung.. Grundlagen: gebrochene Zahl gemeiner Bruch Zähler Nenner Dezimalbruch Ganze, Zehntel Hundertstel Tausendstel Kürzen: Zähler und Nenner durch dieselbe Zahl
Rechnen mit Brüchen PRÜFUNG 10. Ohne Formelsammlung! Name: Klasse: Datum: Punkte: Note: Klassenschnitt/ Maximalnote : Ausgabe: 15.
 MATHEMATIK PRÜFUNGSVORBEREITUNG Rechnen mit Brüchen Name: Klasse: Datum: PRÜFUNG 0 : Note: Ausgabe:. September 0 Klassenschnitt/ Maximalnote : Selbsteinschätzung: / (freiwillig) Für alle Berechnungsaufgaben
MATHEMATIK PRÜFUNGSVORBEREITUNG Rechnen mit Brüchen Name: Klasse: Datum: PRÜFUNG 0 : Note: Ausgabe:. September 0 Klassenschnitt/ Maximalnote : Selbsteinschätzung: / (freiwillig) Für alle Berechnungsaufgaben
7 a) 80 r s r s b) 8 x y 2 48 x y c) 75 x x 150 x y y d) 20 b a b + 20 a + 25 b
 Lösungen der Kapitel Rechnen mit Termen Standpunkt, Seite Addition x + Summe vermehrt um fünf Multiplikation x Produkt das Fünffache Subtraktion x Differenz vermindert um fünf Division x : Quotient der
Lösungen der Kapitel Rechnen mit Termen Standpunkt, Seite Addition x + Summe vermehrt um fünf Multiplikation x Produkt das Fünffache Subtraktion x Differenz vermindert um fünf Division x : Quotient der
Rechnen und Sachaufgaben. Mathe. Rechnen und Sachaufgaben. in 15 Minuten. 5. Klasse
 Rechnen und Sachaufgaben 5. Klasse Mathe Rechnen und Sachaufgaben in 15 Minuten Klasse Mathe Duden in 15 Minuten Rechnen und Sachaufgaben 5. Klasse 2., aktualisierte Auflage Dudenverlag Mannheim Zürich
Rechnen und Sachaufgaben 5. Klasse Mathe Rechnen und Sachaufgaben in 15 Minuten Klasse Mathe Duden in 15 Minuten Rechnen und Sachaufgaben 5. Klasse 2., aktualisierte Auflage Dudenverlag Mannheim Zürich
Stoffverteilungsplan Von den Rahmenvorgaben des Kerncurriculums zum Schulcurriculum für das 7. Schuljahr
 Von den Rahmenvorgaben des Kerncurriculums zum Schulcurriculum für das 7. Schuljahr Anregungen für Mathematik in der Hauptschule Niedersachsen auf der Grundlage von Maßstab 7 Der Stoffverteilungsplan geht
Von den Rahmenvorgaben des Kerncurriculums zum Schulcurriculum für das 7. Schuljahr Anregungen für Mathematik in der Hauptschule Niedersachsen auf der Grundlage von Maßstab 7 Der Stoffverteilungsplan geht
Jahrgangsstufenarbeit Mathematik. für die Jahrgangsstufe 6 an den bayerischen Hauptschulen. 30. September Aufgaben. Arbeitszeit: 45 Minuten
 Jahrgangsstufenarbeit Mathematik für die Jahrgangsstufe 6 an den bayerischen Hauptschulen 30. September 010 Aufgaben Arbeitszeit: 45 Minuten Name: Klasse: Schule: Lernbereich/Lehrplanthema Aufgaben maximale
Jahrgangsstufenarbeit Mathematik für die Jahrgangsstufe 6 an den bayerischen Hauptschulen 30. September 010 Aufgaben Arbeitszeit: 45 Minuten Name: Klasse: Schule: Lernbereich/Lehrplanthema Aufgaben maximale
Probeunterricht 2012 an Wirtschaftsschulen in Bayern
 an Wirtschaftsschulen in Bayern Mathematik 8. Jahrgangsstufe Arbeitszeit Teil I (Zahlenrechnen) Seiten 1 bis 4: Arbeitszeit Teil II (Textrechnen) Seiten 5 bis 8: 45 Minuten 45 Minuten Name:.... Vorname:.
an Wirtschaftsschulen in Bayern Mathematik 8. Jahrgangsstufe Arbeitszeit Teil I (Zahlenrechnen) Seiten 1 bis 4: Arbeitszeit Teil II (Textrechnen) Seiten 5 bis 8: 45 Minuten 45 Minuten Name:.... Vorname:.
Aufgaben zu Lambacher Schweizer 5 Hessen
 Aufgaben zu Kapitel I Kopfrechenaufgaben 1 Berechne im Kopf. a) 60 + 32 b) 57 + 41 c) 130 + 72 d) 504 + 91 e) 75 + 47 f) 76 + 85 g) 124 + 127 h) 295 + 76 i) 129 + 396 j) 747 + 239 2 a) 3800 + 4600 b) 5700
Aufgaben zu Kapitel I Kopfrechenaufgaben 1 Berechne im Kopf. a) 60 + 32 b) 57 + 41 c) 130 + 72 d) 504 + 91 e) 75 + 47 f) 76 + 85 g) 124 + 127 h) 295 + 76 i) 129 + 396 j) 747 + 239 2 a) 3800 + 4600 b) 5700
Treffpunkte für die kantonale Vergleichsarbeit der 6. Klassen. Mathematik
 Treffpunkte für die kantonale Vergleichsarbeit der 6. Klassen Mathematik Solothurn, 21. Mai 2012 1 Arithmetik 1.1 Natürliche Zahlen 1.1.1 Die Sch können natürliche Zahlen lesen und schreiben. S. 6/7 S.
Treffpunkte für die kantonale Vergleichsarbeit der 6. Klassen Mathematik Solothurn, 21. Mai 2012 1 Arithmetik 1.1 Natürliche Zahlen 1.1.1 Die Sch können natürliche Zahlen lesen und schreiben. S. 6/7 S.
Brüche. Brüche beschreiben Bruchteile. M 6.1. von 100 kg) 3 = (100 kg 4) 3 = 25 kg 3 = 75 kg
 M 6. Brüche Brüche beschreiben Bruchteile. 3 4 von 00 kg = ( 4 von 00 kg) 3 = (00 kg 4) 3 = kg 3 = 7 kg Die Schokoladentafel hat 4 Stückchen, d.h. ein Stückchen entspricht dem Anteil 4 Carina Kahoun (08)
M 6. Brüche Brüche beschreiben Bruchteile. 3 4 von 00 kg = ( 4 von 00 kg) 3 = (00 kg 4) 3 = kg 3 = 7 kg Die Schokoladentafel hat 4 Stückchen, d.h. ein Stückchen entspricht dem Anteil 4 Carina Kahoun (08)
Gruber I Neumann. Erfolg in VERA-8. Vergleichsarbeit Mathematik Klasse 8 Gymnasium
 Gruber I Neumann Erfolg in VERA-8 Vergleichsarbeit Mathematik Klasse 8 Gymnasium . Zahlen Zahlen Tipps ab Seite, Lösungen ab Seite 0. Zahlen und Zahlenmengen Es gibt verschiedene Zahlenarten, z.b. ganze
Gruber I Neumann Erfolg in VERA-8 Vergleichsarbeit Mathematik Klasse 8 Gymnasium . Zahlen Zahlen Tipps ab Seite, Lösungen ab Seite 0. Zahlen und Zahlenmengen Es gibt verschiedene Zahlenarten, z.b. ganze
Stoffverteilungsplan Klasse 7
 Stoffverteilungsplan Klasse 7 Rahmenlehrplan Im Blickpunkt: Mathematische Kompetenzen 6 Viel Erfolg im neuen Schuljahr 1 Zahlen und Operationen 30 Basiswissen: Brüche und Dezimalzahlen Kapitel 1: Rationale
Stoffverteilungsplan Klasse 7 Rahmenlehrplan Im Blickpunkt: Mathematische Kompetenzen 6 Viel Erfolg im neuen Schuljahr 1 Zahlen und Operationen 30 Basiswissen: Brüche und Dezimalzahlen Kapitel 1: Rationale
1. Grundlagen der Arithmetik
 1. Grundlagen der Arithmetik Die vier Grundrechenarten THEORIE Addition (plus-rechnen, addieren, zusammenzählen): Summand + Summand = Summe Subtraktion (minus-rechnen, subtrahieren, wegzählen): Minuend
1. Grundlagen der Arithmetik Die vier Grundrechenarten THEORIE Addition (plus-rechnen, addieren, zusammenzählen): Summand + Summand = Summe Subtraktion (minus-rechnen, subtrahieren, wegzählen): Minuend
Schularbeitsstoff zur 2. Schularbeit am
 Schularbeitsstoff zur. Schularbeit am 19.1.016 Flächeninhalt 8 Flächeninhalt 1 9 Flächeninhalt 1 14 Flächeninhalt Bruchzahlen 10 Bruchzahlen Potenzen Potenzen 11 Potenzen 1 Potenzen Variable und Funktionen
Schularbeitsstoff zur. Schularbeit am 19.1.016 Flächeninhalt 8 Flächeninhalt 1 9 Flächeninhalt 1 14 Flächeninhalt Bruchzahlen 10 Bruchzahlen Potenzen Potenzen 11 Potenzen 1 Potenzen Variable und Funktionen
Die ganzen Zahlen. zwölf Billionen zweihundertvier Milliarden achtzig Millionen vierhunderteinundfünfzigtausendelf
 Die ganzen Zahlen Große Zahlen lesen und schreiben (bis Billion) Stellentafel Die Stufenzahlen im Zehnersystem sind zwölf Billionen zweihundertvier Milliarden achtzig Millionen vierhunderteinundfünfzigtausendelf
Die ganzen Zahlen Große Zahlen lesen und schreiben (bis Billion) Stellentafel Die Stufenzahlen im Zehnersystem sind zwölf Billionen zweihundertvier Milliarden achtzig Millionen vierhunderteinundfünfzigtausendelf
inhaltsbezogene Kompetenzbereiche/Kompetenzen Ordnen und vergleichen Zahlen
 Arithmetik/Algebra 1. Rechnen mit Brüchen Vergleichen und bewerten Lösungswege Argumentationen und Darstellungen Erkunden Untersuchen Muster und Beziehungen bei Zahlen und Figuren und stellen Vermutungen
Arithmetik/Algebra 1. Rechnen mit Brüchen Vergleichen und bewerten Lösungswege Argumentationen und Darstellungen Erkunden Untersuchen Muster und Beziehungen bei Zahlen und Figuren und stellen Vermutungen
PDF created with pdffactory Pro trial version
 1. Berechne: a) - 311 185 b) - 176 + 213 c) 234 865 d) 195 (- 523) e) (- 324) (- 267) f) 165 + (- 316) g) (-23) 18 h) (- 17) (- 54) i) 35 (- 78) j) 314 1234 k) (- 8) 4 l) (- 11) 3 m) (- 2) 9 n) (- 2) 10
1. Berechne: a) - 311 185 b) - 176 + 213 c) 234 865 d) 195 (- 523) e) (- 324) (- 267) f) 165 + (- 316) g) (-23) 18 h) (- 17) (- 54) i) 35 (- 78) j) 314 1234 k) (- 8) 4 l) (- 11) 3 m) (- 2) 9 n) (- 2) 10
Jahrgangsstufenarbeit Mathematik. für die Jahrgangsstufe 6 an den bayerischen Hauptschulen. 30. September Aufgaben. Arbeitszeit: 45 Minuten
 Jahrgangsstufenarbeit Mathematik für die Jahrgangsstufe 6 an den bayerischen Hauptschulen 30. September Aufgaben Arbeitszeit: 45 Minuten Name: Klasse: Schule: Lernbereich/Lehrplanthema Aufgaben maximale
Jahrgangsstufenarbeit Mathematik für die Jahrgangsstufe 6 an den bayerischen Hauptschulen 30. September Aufgaben Arbeitszeit: 45 Minuten Name: Klasse: Schule: Lernbereich/Lehrplanthema Aufgaben maximale
1 Rationale Zahlen. Versuche, in das Koordinatensystem ein Rechteck zu zeichnen, bei dem die Summe aller Koordinaten 20 ergibt!
 1 Das Bild des Wasserfalls ist im Frühjahr bei 13 C entstanden. Welche Auswirkungen kann ein Temperaturrückgang im Winter um 20 C haben? 2 Carola hat eine Frage: Wenn ich von einer Zahl eine andere Zahl
1 Das Bild des Wasserfalls ist im Frühjahr bei 13 C entstanden. Welche Auswirkungen kann ein Temperaturrückgang im Winter um 20 C haben? 2 Carola hat eine Frage: Wenn ich von einer Zahl eine andere Zahl
Einführung KV 32 Kopfrechnen leicht gemacht (1) 6/7 KV 33 Kopfrechnen leicht gemacht (2) 6/7 KV 34 Vorlage zur Rückmeldung 9
 Inhaltsverzeichnis zur Schülerbuchseite Karteikarten KV Karteikarten zum Nachschlagen () 6/7, 6, 22 25, 56 60 KV 2 Karteikarten zum Nachschlagen (2) 24/25, 57, 43 KV 3 Karteikarten zum Nachschlagen (3)
Inhaltsverzeichnis zur Schülerbuchseite Karteikarten KV Karteikarten zum Nachschlagen () 6/7, 6, 22 25, 56 60 KV 2 Karteikarten zum Nachschlagen (2) 24/25, 57, 43 KV 3 Karteikarten zum Nachschlagen (3)
Grundwissen Klasse 6
 Zahlenmengen = {; 2; ; 4; ; 6;... } Die Menge der natürlichen Zahlen. = {... ; 2; ; 0; ; 2; ;...} Die Menge der ganzen Zahlen. 0 Die Menge der positiven rationalen Zahlen mit Null. ddition und Subtraktion
Zahlenmengen = {; 2; ; 4; ; 6;... } Die Menge der natürlichen Zahlen. = {... ; 2; ; 0; ; 2; ;...} Die Menge der ganzen Zahlen. 0 Die Menge der positiven rationalen Zahlen mit Null. ddition und Subtraktion
MEMO Brüche 1 Zähler, Nenner, Stammbruch, einfache und gemischte Brüche
 MEMO Brüche Zähler, Nenner, Stammbruch, einfache und gemischte Brüche )Brüche: Grundbegriffe a) Zähler und Nenner die obere Zahl heisst Zähler die untere Zahl heisst Nenner Der Nenner Der Zähler ist der
MEMO Brüche Zähler, Nenner, Stammbruch, einfache und gemischte Brüche )Brüche: Grundbegriffe a) Zähler und Nenner die obere Zahl heisst Zähler die untere Zahl heisst Nenner Der Nenner Der Zähler ist der
Stoffverteilungsplan Mathematik 7 auf der Grundlage des Lehrplans Schnittpunkt 7 Klettbuch
 K5: Symbolische und formale Sprache in natürliche Sprache übersetzen und umgekehrt K4: Verschiedene Formen der Darstellung von mathematischen Objekten und Situationen anwenden und interpretieren K6: Die
K5: Symbolische und formale Sprache in natürliche Sprache übersetzen und umgekehrt K4: Verschiedene Formen der Darstellung von mathematischen Objekten und Situationen anwenden und interpretieren K6: Die
Bilde die Quersumme! Wie heißen die Nachbarzehner? Wie heißen Nachbarhunderter? Wie heißen Nachbartausender?
 Arbeit mit der gelegten Zahl Bilde die Quersumme! Wie heißen die Nachbarzehner? Wie heißen Nachbarhunderter? Wie heißen Nachbartausender? Wie heißen Nachbarzehntausender? Wie heißen die Nachbarzahlen?
Arbeit mit der gelegten Zahl Bilde die Quersumme! Wie heißen die Nachbarzehner? Wie heißen Nachbarhunderter? Wie heißen Nachbartausender? Wie heißen Nachbarzehntausender? Wie heißen die Nachbarzahlen?
( 3) = Sektor. Mittelpunktswinkel. Brüche. Begriffe Zähler. Welcher Teil des Ganzen ist dunkel gefärbt? Bruch = Nenner
 Brüche Begriffe Zähler Bruch Nenner Beachte: Der Bruchstrich steht immer auf der gleichen Höhe wie die Rechenzeichen! Q: Menge der rationalen Zahlen. Sie enthält alle Brüche (Quotienten). Welcher Teil
Brüche Begriffe Zähler Bruch Nenner Beachte: Der Bruchstrich steht immer auf der gleichen Höhe wie die Rechenzeichen! Q: Menge der rationalen Zahlen. Sie enthält alle Brüche (Quotienten). Welcher Teil
2.2 Quadratwurzeln. e) f) 8
 I. Quadratwurzeln Rechne im Kopf und erkläre, wie du vorgegangen bist!, H a) 7 8 b) 5 6 c) 9 d) 6 9 e) 0 _ f) 8 _ g) 7 _ 00 h) 5 _ 69 Teilweises Wurzelziehen ist dann möglich, wenn sich eine Zahl so zerlegen
I. Quadratwurzeln Rechne im Kopf und erkläre, wie du vorgegangen bist!, H a) 7 8 b) 5 6 c) 9 d) 6 9 e) 0 _ f) 8 _ g) 7 _ 00 h) 5 _ 69 Teilweises Wurzelziehen ist dann möglich, wenn sich eine Zahl so zerlegen
perfekt für Klassenarbeiten Videos zu jeder Übungsaufgabe alle Themen sehr übersichtlich alle Anforderungsbereiche StrandMathe GbR
 perfekt für Klassenarbeiten Videos zu jeder Übungsaufgabe alle Themen sehr übersichtlich alle Anforderungsbereiche Unsere Übungshefte sind für alle Schülerinnen und Schüler, die keine Lust auf 300-seitige
perfekt für Klassenarbeiten Videos zu jeder Übungsaufgabe alle Themen sehr übersichtlich alle Anforderungsbereiche Unsere Übungshefte sind für alle Schülerinnen und Schüler, die keine Lust auf 300-seitige
