Die Chomsky Hierarchie
|
|
|
- Helmut Bieber
- vor 7 Jahren
- Abrufe
Transkript
1 Die Chomsky Hierarchie Slide 1 Die Chomsky Hierarchie Hans U. Simon (RUB) mit Modifikationen von Maike Buchin (RUB) Lehrstuhl Mathematik und Informatik Homepage:
2 Die Chomsky Hierarchie Slide 2 Vorgeplänkel: Mathematische Grundlagen Voraussetzung: Wissen aus mathematischen Grundvorlesungen hier: weitere Grundlagen zu Wörtern, Sprachen und Relationen
3 Die Chomsky Hierarchie Slide 3 Alphabet und Zeichen Alphabet = nichtleere, endliche Menge Die Elemente eines Alphabets Σ werden als Zeichen, Symbole oder Buchstaben bezeichnet. Beispiele: 1. Σ = {a,...,z} {A,...,Z} {0,...,9}. 2. Σ = {a,b}. 3. Σ = {0,1}.
4 Die Chomsky Hierarchie Slide 4 Zeichenfolgen Σ + = Menge der nicht leeren Zeichenfolgen über Alphabet Σ. Die Elemente von Σ + werden auch als Wörter, Sätze oder Strings bezeichnet. Die Länge eines Strings w ist gegeben durch w = Anzahl der Zeichen (mit Vielfachheit) in w. Für ein Zeichen a Σ schreiben wir w a = Anzahl der Vorkommen von a in w. Beispiel: {a,b} + = {a,b,aa,ab,ba,bb,aaa,...}. a = ba a = 1, ba = 2, aaa = 3. inf ormatik = 10.
5 Die Chomsky Hierarchie Slide 5 Zeichenfolgen (fortgesetzt) Das leere Wort der Länge 0 wird mit ε bezeichnet. (Spielt eine ähnliche Rolle wie die Null beim Addieren.) Σ = Σ + {ε} bezeichnet dann die Menge aller Strings (inklusive dem leeren) über Alphabet Σ.
6 Die Chomsky Hierarchie Slide 6 Konkatenation von Wörtern Wörter konkateniert (= aneinandergehängt) ergeben wieder Wörter: Sei u = σ 1...σ m und v = τ 1...τ n, dann ist uv = σ 1...σ m τ 1...τ n, Es gilt: uv = u + v Beispiel: Für u = ab und v = aab gilt uv = abaab und uv = 2+3 = 5. Die n fache Konkatenation eines Wortes w mit sich selbst notieren wir mit w n. Es gilt w n = n w. Beispiel: Für w = ab gilt w 3 = ababab und w 3 = 3 2 = 6.
7 Die Chomsky Hierarchie Slide 7 Formale Sprachen Eine Menge A Σ heißt (formale) Sprache über Alphabet Σ. Beispiele: 1. L = {p {0,1} p ist Binärdarstellung einer Primzahl}. 2. L = {ε,0,1,001}. 3. L = {alle gültigen JAVA-Programme}.
8 Die Chomsky Hierarchie Slide 8 Formale Sprachen (fortgesetzt) Neben den üblichen Mengenoperationen (Vereinigung, Durchschnitt, Komplement, Mengendifferenz,...) sind auf Sprachen die folgenden Operationen von Interesse: Konkatenation AB := {uv u A,v B}. Potenz A n := A A }{{}, wobei A 0 = {ε} und A 1 = A. n mal Kleenescher Abschluss A + = n 1 A n und A = n 0 A n.
9 Die Chomsky Hierarchie Slide 9 Formale Sprachen (fortgesetzt) Beispiel Betrachte die Sprachen A = {w {a,b} w = 5} und B = {w {a,b} w = 7}. Dann gilt AB = {w {a,b} w = 12} A 20 = {w {a,b} w = 100} A = {w {a,b} 5 ist Teiler von w }
10 Die Chomsky Hierarchie Slide 10 Relationen Wir betrachten Relationen R über einer Grundmenge M. Formal: R M M. Statt (x,y) R schreiben wir oft xry. Statt (x,y) R und (y,z) R schreiben wir mitunter xryrz. Zur Erinnerung: eine Relation R heisst: 1. reflexiv, wenn x M : xrx 2. transitiv, wenn x,y,z M : xryrz xrz 3. symmetrisch, wenn x,y M : xry yrx
11 Die Chomsky Hierarchie Slide 11 Verknüpfung von Relationen Ähnlich wie bei formalen Sprachen betrachten wir folgende Operationen: Konkatenation RS := {(x,y) M M z M : xrz und zsy}. Potenz R n := R R }{{}, wobei R 0 = {(x,x) x M} und R 1 = R. n mal (reflexive) transitive Hülle R + = n 1 R n und R = n 0 R n. Es gilt: 1. R n = {(x,y) M M z 1,...,z n 1 : xrz 1 Rz 2 Rz n 1 Ry} für n R + ist die kleinste transitive R umfassende Relation. 3. R ist die kleinste reflexive und transitive R umfassende Relation.
12 Die Chomsky Hierarchie Slide 12 Beispiele M = Menge von Personen R = die Relation ist Schwester von S = die Relation ist Vater oder Mutter von Dann gilt: RS = die Relation ist Tante von S 2 S + = die Relation ist Großvater oder Großmutter von = die Relation ist (echter) Vorfahr von
13 Die Chomsky Hierarchie Slide 13 Jetzt gehts zur Sache!
14 Die Chomsky Hierarchie Slide 14 Grammatiken Eine Grammatik besteht aus vier Komponenten G = (V,Σ,P,S): V, die Menge der Variablen Σ, das Terminalalphabet P (V Σ) + (V Σ), das Regel oder Produktionensystem S V, die Startvariable Dabei sind V,Σ,P endliche Mengen und V Σ =. Ein Paar (y,y ) aus P notieren wir meist in der Form y y. Intuition: In einer grammatischen Ableitung darf y durch y ersetzt werden. Strings über Σ heißen Sätze; Strings über V Σ heißen Satzformen. Schreibweise: Wir verwenden i.d.r. Grossbuchstaben für Variablen und Kleinbuchstaben für Terminale.
15 Die Chomsky Hierarchie Slide 15 Grammatische Ableitungen Die Notation u G v bedeutet, dass Satzform u unter einer Regelanwendung der Grammatik G in Satzform v übergehen kann: u,v haben die Form u = xyz, v = xy z, und y y P. Es ist also G eine Relation auf (V Σ). Mit Hilfe von Relation G können folgende Relationen gebildet werden: n G + G G = n fache Potenz von G = transitive Hülle von G = reflexive transitive Hülle von G
16 Die Chomsky Hierarchie Slide 16 Grammatische Ableitungen (fortgesetzt) u n Gv bedeutet, dass Satzform u unter n Anwendungen von Regeln der Grammatik G in Satzform v übergehen kann. u + Gv bedeutet, dass Satzform u unter einer iterierten Anwendung (mindestens einmal) von Regeln der Grammatik G in Satzform v übergehen kann. u Gv bedeutet, dass Satzform u unter einer iterierten Anwendung (auch null-mal) von Regeln der Grammatik G in Satzform v übergehen kann.
17 Die Chomsky Hierarchie Slide 17 Grammatische Ableitungen (fortgesetzt) Eine Folge w 0,w 1,...,w n von Satzformen mit w 0 = S, w n Σ und w i G w i+1 heißt Ableitung (von w n mit Regeln aus G). Die von G erzeugte Sprache ist die Menge aller aus Startsymbol S ableitbaren Wörter über Terminalalphabet Σ: L(G) := {w Σ S Gw}
18 Die Chomsky Hierarchie Slide 18 Beispiel: Korrekt geklammerte Rechenausdrücke Betrachte die Grammatik G mit den Komponenten V = {E,T,F}. Σ = {(,),a,+, }. P enthalte die Regeln E T, E E +T, T F, T T F, F a, F (E). S = E, d.h., E ist die Startvariable. Intuition: E steht für EXPRESSION (arithmetischer Ausdruck), T für TERM und F für FACTOR. Terminalzeichen a repräsentiert einen atomaren Ausdruck (etwa eine Konstante oder eine Variable). Die Grammatik soll gerade die korrekt geklammerten Rechenausdrücke erzeugen.
19 Die Chomsky Hierarchie Slide 19 Beispiel (fortgesetzt) Es gilt a (a+a)+a L(G) wie folgende Ableitung zeigt: E E +T T +T T F +T F F +T a F +T a (E)+T a (E +T)+T a (T +T)+T a (F +T)+T a (a+t)+t a (a+f)+t a (a+a)+t a (a+a)+f a (a+a)+a Es wurde in jedem Schritt die am weitesten links stehende Variable ersetzt: wir sprechen von einer Linksableitung.
20 Die Chomsky Hierarchie Slide 20 Chomsky Hierarchie ohne Sonderregeln für ε Typ 0: Eine Grammatik mit Regeln der allgemeinen Form w w mit w (V Σ) + und w (V Σ) heißt Grammatik vom Typ 0. Typ 1: Eine Grammatik mit Regeln der Form w w mit w,w (V Σ) + und w w heißt kontextsensitive (oder auch Typ 1) Grammatik. Typ 2: Eine Grammatik mit Regeln der Form X w mit X V und w (V Σ) + heißt kontextfreie (oder auch Typ 2) Grammatik. Typ 3: Eine Grammatik mit Regeln der Form X a oder X ay mit X,Y V und a Σ heißt reguläre (oder auch Typ 3) Grammatik. Wir übertragen diese Bezeichnungen auch auf die von den Grammatiken generierten Sprachen. Offensichtlich gilt: regulär kontextfrei kontextsensitiv Typ 0 formale Sprache
21 Die Chomsky Hierarchie Slide 21 Sonderregeln für das leere Wort Jetzige Definition von Typ 1,2,3 Grammatiken G erlaubt nicht die Generierung des leeren Wortes ε (schlecht, falls ε L(G) erwünscht ist). Daher folgende Regelung: Typ 1: Wir erlauben auch die Regel S ε, S Startsymbol. In diesem Falle darf aber S auf keiner rechten Seite einer Regel auftreten. Typ 2 bzw. 3: Wir erlauben beliebige ε-regeln der Form A ε, A V.
22 Die Chomsky Hierarchie Slide 22 Sonderregeln für das leere Wort (fortgesetzt) Satz: L ist vom Typ 1 (bzw. 2 oder 3) unter Einsatz der Sonderregeln dund L\{ε} ist vom Typ 1 (bzw. 2 oder 3) ohne Einsatz der Sonderregeln. Beweis für Typ 1: : folgt sofort, denn sei G Grammatik mit Sonderregeln, dann ist G mit P = P\{(S,ε)} Grammatik für L(G)\{ε} : Sei G Grammatik ohne Sonderregeln und ε L erwünscht. Dann füge die Regeln S S,S ε hinzu und verwende S als neue Startvariable. Beweis für Typ 2: später.
23 Die Chomsky Hierarchie Slide 23 Sonderregeln für das leere Wort (fortgesetzt) Folgerung: Für formale Sprachen bleibt die Inklusionskette regulär kontextfrei kontextsensitiv Typ 0 gültig, auch wenn Sonderregeln für das leere Wort eingesetzt werden dürfen.
24 Die Chomsky Hierarchie Slide 24 Echtheit der Chomsky Hierarchie (Übersicht) 1. Die Sprache {a n b n n 1} ist kontextfrei aber nicht regulär. 2. Die Sprache {a n b n c n n 1} ist kontextsensitiv aber nicht kontextfrei. 3. Es gibt Sprachen vom Typ 0, die nicht kontextsensitiv sind (Beweis später). 4. Es gibt überabzählbar viele formale Sprachen, aber nur abzählbar viele vom Typ 0. Daher sind alle Inklusionen der Chomsky Hierarchie echt.
25 Die Chomsky Hierarchie Slide 25 Echtheit der Chomsky Hierarchie (fortgesetzt) Die kontextfreien Regeln erzeugen die Sprache S ab, S asb {a n b n n 1}. Wir werden später sehen, dass diese Sprache nicht regulär ist. Beispiel: Die reguläre Sprache {a n b m n,m 1} wird erzeugt durch die Regeln S as, S ab, B b, B bb.
26 Die Chomsky Hierarchie Slide 26 Echtheit der Chomsky Hierarchie (fortgesetzt) Satz: Die kontextsensitive Grammatik mit den Regeln S asbc, S abc, CB BC ab ab, bb bb, bc bc, cc cc erzeugt die Sprache {a n b n c n n 1} Beweis: : Ein Wort an b n c n lässt sich ableiten durch S n 1 G n 1 G an 1 S(BC) n 1 G a n (BC) n n(n 1)/2 G a n b n C n G a n b n cc n 1 n 1 G a n b n c n. : folgt aus für Satzform w mit S G w gilt: w a = w Bb = w Cc für Satz w mit S G w gilt: a s vor b s vor c s. a n B n C n G a n bb n 1 C n Wir werden später sehen, dass diese Sprache nicht kontextfrei ist.
27 Die Chomsky Hierarchie Slide 27 Das Wortproblem Das Wortproblem für eine Sprache L Σ ist folgendes Problem: Eingabe: w Σ Frage: w L? Es heißt entscheidbar, wenn ein Algorithmus existiert, der für jede Eingabe w die richtige Antwort liefert. Satz: Das Wortproblem für eine kontextsensitive Sprache L ist stets entscheidbar. Idee: Verwende eine kontextsensitive Grammatik G, die L generiert. Wegen der Monotonie Eigenschaft rechte Seite einer Regel ist nicht kürzer als die linke Seite sind nur die endlich vielen Satzformen mit einer Maximallänge von n = w für die Ableitung von w relevant.
28 Die Chomsky Hierarchie Slide 28 Implementierung der Idee: 1. Setze n := w. Das Wortproblem (fortgesetzt) 2. Berechne die Menge Abl n aller Satzformen der Maximallänge n, die sich aus S ableiten lassen: Abl n := {w (V Σ) w n und S Gw} 3. Falls w Abl n, dann akzeptiere w; andernfalls verwerfe w. Dabei kann Abl n iterativ berechnet werden wie folgt: Initialisierung Abl := {S}. Iteration Solange ein Wort w / Abl mit w n, u Abl : u G w existiert, nimm auch w in Abl auf.
29 Die Chomsky Hierarchie Slide 29 Das Wortproblem (fortgesetzt) Skizze der Korrektheit: In jedem Schritt der Iteration, enthält Abl nur Satzformen, die sich aus S ableiten lassen. Da es nur endlich (exponentiell) viele Wörter der Länge n über Σ V gibt, stoppt die Iteration. Jeder Iterationsschritt dauert endliche Zeit, da endlich viele Teilwörter auf endlich viele Regeln geprüft werden. Beispiel: Um zu prüfen, ob aabb und abbb in der von S ab, S asb erzeugten Sprache liegen, berechnen wir iterativ Abl 4 = {S,ab,aSb,aabb}, und stellen fest, dass aabb L(G) und abbb / L(G).
30 Die Chomsky Hierarchie Slide 30 Syntaxbäume Betrachte wieder eine kontextfreie Grammatik G = (V, Σ, P, S). Jede Regel B A 1 A k kann durch eine Verzweigung visualisiert werden: B A1 A2.... A A k-1 k Abbildung 1: Visualisierung einer Regel B A 1 A k.
31 Die Chomsky Hierarchie Slide 31 Syntaxbäume (fortgesetzt) Ein Syntaxbaum zur kontextfreien Grammatik G mit Beschriftung w ist ein geordneter Wurzelbaum mit folgenden Eigenschaften: 1. Die Wurzel ist mit dem Startsymbol S markiert. 2. Die inneren Knoten sind mit Variablen aus V markiert. 3. Jede Verzweigung entspricht einer Regel aus P. 4. Die Blätter sind mit Terminalzeichen aus Σ (oder mit ε) markiert. 5. Von links nach rechts gelesen ergeben die Blattmarkierungen das Wort w.
32 Die Chomsky Hierarchie Slide 32 Beispiel E E T F E E T T T T F F F F a * ( a + a ) + a Abbildung 2: Der Syntaxbaum zur Ableitung von a (a+a)+a mit der Grammatik für korrekt geklammerte Rechenausdrücke.
33 Die Chomsky Hierarchie Slide 33 Syntaxbäume (fortgesetzt) Folgende Aussagen sind äquivalent: 1. Es gibt eine Ableitung von w mit Regeln aus G. 2. Es gibt einen Syntaxbaum zu G mit Beschriftung w. 3. Es gibt eine Linksableitung von w mit Regeln aus G. Ein formaler Beweis könnte durch einen Ringschluss erfolgen.
34 Die Chomsky Hierarchie Slide 34 Eindeutige und mehrdeutige Grammatiken Eine kontextfreie Grammatik G heißt mehrdeutig, wenn sie verschiedene Syntaxbäume mit derselben Beschriftung zulässt; andernfalls heißt sie eindeutig. Eine kontextfreie Sprache L heißt eindeutig, wenn eine L generierende eindeutige kontextfreie Grammatik G existiert; andernfalls heißt sie inhärent mehrdeutig. Programmiersprachen sollten eindeutig sein, damit jedes Programm eindeutig interpretiert werden kann.
35 Die Chomsky Hierarchie Slide 35 Illustration an einem abschreckenden Beispiel Die Grammatik mit den Regeln E a, E E +E, E E E erzeugt Rechenausdrücke mit den Operationen + und. Sie ist mehrdeutig: E E E E E E a + a * a a + a * a Abbildung 3: Zwei verschiedene Syntaxbäume für den Rechenausdruck a+a a.
36 Die Chomsky Hierarchie Slide 36 Fortsetzung des abschreckenden Beispiels Der linke Syntaxbaum berechnet a + (a a); der rechte berechnet (a+a) a. Die Mehrdeutigkeit führt zu unterschiedlichen Berechnungen (schlecht!) Die eindeutige Grammatik, die wir früher für Rechenausdrücke eingeführt hatten, ist daher vorzuziehen.
37 Die Chomsky Hierarchie Slide 37 Eine weitere mehrdeutige Beispiel-Grammatik Die Regeln P 1 K ε, K KK, K (K) erzeugen die Sprache L der korrekten Klammerausdrücke. Diese können auch durch den Klammerniveautest erkannt werden: Für jedes Vorkommen von ( zähle das Niveau um 1 hoch. Für jedes Vorkommen von ) zähle das Niveau um 1 runter. Korrekte Klammerausdrücke durchlaufen nicht-negative Niveaus und führen am Ende zu Niveau 0. Ein atomarer Klammerausdruck ist einer der erst am Ende, aber nicht zwischendurch, Niveau 0 erreicht. Jeder Klammerausdruck zerfällt eindeutig in eine Konkatenation atomarer Klammerausdrücke.
38 Die Chomsky Hierarchie Slide 38 Beispiele für (korrekte und falsche) Klammerausdrücke Korrekt geklammerte Ausdrücke: ( ) ( ( ) ( ) ) ( ) Niveau Falsch geklammerte Ausdrücke: ( ( ) ) ( Niveau
39 Die Chomsky Hierarchie Slide 39 Korrektheit der Grammatik Behauptung: Die Grammatik G 1 mit den Regeln P 1 erzeugt L. Beweis: Wir zeigen L(G 1 ) = L in zwei Schritten. : Induktion (#Ableitungsschritte): n = 1: K ε liefert korrekten Klammerausdruck. n > 1: K KK sowie K (K) führen nach I.V. zu korrekten Ausdrücken. : Induktion ( w ): n = 0: w = ε lässt sich durch K ε ableiten. n > 1: betrachte erste Verzweigung im Syntaxbaum: falls w aus nur einem atomaren Klammerausdruck besteht, muss diese der Regel K (K) entsprechen; andernfalls der Regel K KK. Die Behauptung folgt dann mit I.V.
40 Die Chomsky Hierarchie Slide 40 Demonstration der Mehrdeutigkeit K K K K Abbildung 4: Zwei verschiedene Syntaxbäume für den leeren Klammerausdruck.
41 Die Chomsky Hierarchie Slide 41 Eindeutige Grammatik für dieselbe Sprache K ε,k (K)K Behauptung: Die Grammatik G 2 mit obigen Regeln ist eindeutig. Beweis: Sei w L(G 2 ) beliebig. Induktion ( w ): n = 0: w = ε hat eindeutigen Syntaxbaum entsprechend der Regel K ε. n > 1: w hat die Gestalt w = (α)β. Die erste Verzweigung im Syntaxbaum muss also der Regel K (K)K entsprechen. Die Behauptung folgt dann mit I.V. angewandt auf α,β.
42 Die Chomsky Hierarchie Slide 42 Beispiel einer inhärent mehrdeutigen Sprache Die Sprache L = {a i b j c k i = j oder j = k} ist inhärent mehrdeutig (ohne Beweis).
43 Die Chomsky Hierarchie Slide 43 Kontextfreiheit und Programmiersprachen Klammerausdrücke: Als Bestandteil von Rechenausdrücken (oder auch durch die mit begin und end angezeigte Blockstruktur) kommen sie in Programmen vor. Die Sprache der Klammerausdrücke ist kontextfrei (wie wir wissen). Wortduplikate: Die Sprache {w$w : w Σ } kommt als Muster in Programmieprachen vor, bei denen Variable deklariert werden müssen (1. Vorkommen im Deklarationsteil; 2. Vorkommen bei der ersten Wertzuweisung). Sie ist aber, wie wir später sehen werden, nicht kontextfrei. Bemerkung: Obwohl Programmiersprachen i.a. nicht vollständig kontextfrei sind, sind sie im Wesentlichen kontextfrei.
44 Die Chomsky Hierarchie Slide 44 Backus Naur Form Backus Naur Form (BNF) erlaubt flexiblere Formen von kontextfreien Regeln: 1. Die Metaregel A β 1 β 2 β n (unter Verwendung des Metasymbols ) steht für A β 1 A β 2 A β n Dadurch lassen sich alle A-Regeln in einer Zeile zusammenfassen. 2. A α[β]γ steht für A αγ αβγ: man darf β zwischen α und γ einfügen, muss es aber nicht. 3. A α{β}γ steht für A αγ αbγ,b β βb: das Wort β kann zwischen α und γ iteriert (auch null mal) eingefügt werden.
45 Die Chomsky Hierarchie Slide 45 Beispiel zur Backus Naur Form Die Regeln E T, E E +T, T F, T T F, F a, F (E) für korrekt geklammerte Rechenausdrücke können in BNF kompakt notiert werden wie folgt: Oder noch kompakter: bzw. in der Form: E T E +T, T F T F, F a (E) E [E+]T, T [T ]F, F a (E) E {T+}T, T {F }F, F a (E)
46 Die Chomsky Hierarchie Slide 46 Exemplarische Lernziele zur Chomsky Hierarchie Grundbegriffe kennen (Vokabeln lernen!) und intellektuell beherrschen bei Operationen auf Sprachen die Ergebnissprache beschreiben bei Operationen auf Relationen die Ergebnisrelation beschreiben zu einer gegebenen Sprache eine passende Grammatik finden zu einer gegebenen Grammatik die davon erzeugte Sprache intelligent erraten zu einem Wort aus einer Sprache die passende grammatische Ableitung (im kontextfreien Fall auch den Syntaxbaum) finden Mehrdeutigkeit einer kontextfreien Grammatik erkennen und, sofern möglich, vermeiden können
Die Chomsky Hierarchie
 Die Chomsky Hierarchie Slide 1 Die Chomsky Hierarchie Hans U. Simon (RUB) Email: simon@lmi.rub.de Homepage: http://www.ruhr-uni-bochum.de/lmi Die Chomsky Hierarchie Slide 2 Vorgeplänkel: Mathematische
Die Chomsky Hierarchie Slide 1 Die Chomsky Hierarchie Hans U. Simon (RUB) Email: simon@lmi.rub.de Homepage: http://www.ruhr-uni-bochum.de/lmi Die Chomsky Hierarchie Slide 2 Vorgeplänkel: Mathematische
Lemma Für jede monotone Grammatik G gibt es eine kontextsensitive
 Lemma Für jede monotone Grammatik G gibt es eine kontextsensitive Grammatik G mit L(G) = L(G ). Beweis im Beispiel (2.): G = (V,Σ, P, S) : P = {S asbc, S abc, CB BC, ab ab, bb bb, bc bc, cc cc}. (i) G
Lemma Für jede monotone Grammatik G gibt es eine kontextsensitive Grammatik G mit L(G) = L(G ). Beweis im Beispiel (2.): G = (V,Σ, P, S) : P = {S asbc, S abc, CB BC, ab ab, bb bb, bc bc, cc cc}. (i) G
2.1 Allgemeines. Was ist eine Sprache? Beispiele:
 Was ist eine Sprache? Beispiele: (a) Deutsch, Japanisch, Latein, Esperanto,...: Natürliche Sprachen (b) Pascal, C, Java, Aussagenlogik,...: Formale Sprachen Wie beschreibt man eine Sprache? (i) Syntax
Was ist eine Sprache? Beispiele: (a) Deutsch, Japanisch, Latein, Esperanto,...: Natürliche Sprachen (b) Pascal, C, Java, Aussagenlogik,...: Formale Sprachen Wie beschreibt man eine Sprache? (i) Syntax
Definition 4 (Operationen auf Sprachen) Beispiel 5. Seien A, B Σ zwei (formale) Sprachen. Konkatenation: AB = {uv ; u A, v B} A + = n 1 An
 Definition 4 (Operationen auf Sprachen) Seien A, B Σ zwei (formale) Sprachen. Konkatenation: AB = {uv ; u A, v B} A 0 = {ɛ}, A n+1 = AA n A = n 0 An A + = n 1 An Beispiel 5 {ab, b}{a, bb} = {aba, abbb,
Definition 4 (Operationen auf Sprachen) Seien A, B Σ zwei (formale) Sprachen. Konkatenation: AB = {uv ; u A, v B} A 0 = {ɛ}, A n+1 = AA n A = n 0 An A + = n 1 An Beispiel 5 {ab, b}{a, bb} = {aba, abbb,
Grammatiken. Eine Grammatik G mit Alphabet Σ besteht aus: Variablen V. Startsymbol S V. Kurzschreibweise G = (V, Σ, P, S)
 Grammatiken Eine Grammatik G mit Alphabet Σ besteht aus: Variablen V Startsymbol S V Produktionen P ( (V Σ) \ Σ ) (V Σ) Kurzschreibweise G = (V, Σ, P, S) Schreibweise für Produktion (α, β) P: α β 67 /
Grammatiken Eine Grammatik G mit Alphabet Σ besteht aus: Variablen V Startsymbol S V Produktionen P ( (V Σ) \ Σ ) (V Σ) Kurzschreibweise G = (V, Σ, P, S) Schreibweise für Produktion (α, β) P: α β 67 /
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 15.01.2015 INSTITUT FÜR THEORETISCHE 0 KIT 15.01.2015 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik Vorlesung am 15.01.2015 INSTITUT FÜR THEORETISCHE 0 KIT 15.01.2015 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Mehrdeutige Grammatiken
 Mehrdeutige Grammatiken Wir haben gesehen, dass es auch mehr als eine Linksableitung, d.h. mehr als einen Syntaxbaum geben kann, um das selbe Terminalwort zu erzeugen. Eine Grammatik, die für mindestens
Mehrdeutige Grammatiken Wir haben gesehen, dass es auch mehr als eine Linksableitung, d.h. mehr als einen Syntaxbaum geben kann, um das selbe Terminalwort zu erzeugen. Eine Grammatik, die für mindestens
1 Automatentheorie und Formale Sprachen
 Sanders: TGI October 29, 2015 1 1 Automatentheorie und Formale Sprachen 1.1 Allgemeines Sanders: TGI October 29, 2015 2 Beispiel: Arithmetische Ausdrücke:EXPR Σ={1,a,+,,,(,)} a ist Platzhalter für Konstanten
Sanders: TGI October 29, 2015 1 1 Automatentheorie und Formale Sprachen 1.1 Allgemeines Sanders: TGI October 29, 2015 2 Beispiel: Arithmetische Ausdrücke:EXPR Σ={1,a,+,,,(,)} a ist Platzhalter für Konstanten
Kapitel IV Formale Sprachen und Grammatiken
 Kapitel IV Formale Sprachen und Grammatiken 1. Begriffe und Notationen Sei Σ ein (endliches) Alphabet. Dann Definition 42 1 ist Σ das Monoid über Σ, d.h. die Menge aller endlichen Wörter über Σ; 2 ist
Kapitel IV Formale Sprachen und Grammatiken 1. Begriffe und Notationen Sei Σ ein (endliches) Alphabet. Dann Definition 42 1 ist Σ das Monoid über Σ, d.h. die Menge aller endlichen Wörter über Σ; 2 ist
Grammatiken. Grammatiken sind regelbasierte Kalküle zur Konstruktion von Systemen und Sprachen Überprüfung von Systemen und Sprachen
 Grammatiken Grammatiken sind regelbasierte Kalküle zur Konstruktion von Systemen und Sprachen Überprüfung von Systemen und Sprachen Grammatiken eignen sich besonders zur Modellierung beliebig tief geschachtelter,
Grammatiken Grammatiken sind regelbasierte Kalküle zur Konstruktion von Systemen und Sprachen Überprüfung von Systemen und Sprachen Grammatiken eignen sich besonders zur Modellierung beliebig tief geschachtelter,
Formale Sprachen. Grammatiken und die Chomsky-Hierarchie. Rudolf FREUND, Marian KOGLER
 Formale Sprachen Grammatiken und die Chomsky-Hierarchie Rudolf FREUND, Marian KOGLER Grammatiken Das fundamentale Modell zur Beschreibung von formalen Sprachen durch Erzeugungsmechanismen sind Grammatiken.
Formale Sprachen Grammatiken und die Chomsky-Hierarchie Rudolf FREUND, Marian KOGLER Grammatiken Das fundamentale Modell zur Beschreibung von formalen Sprachen durch Erzeugungsmechanismen sind Grammatiken.
Theoretische Informatik Mitschrift
 Theoretische Informatik Mitschrift 2. Grammatiken und die Chomsky-Hierarchie Beispiel: Syntaxdefinition in BNF :=
Theoretische Informatik Mitschrift 2. Grammatiken und die Chomsky-Hierarchie Beispiel: Syntaxdefinition in BNF :=
Theorie der Informatik. Theorie der Informatik. 6.1 Einführung. 6.2 Alphabete und formale Sprachen. 6.3 Grammatiken. 6.4 Chomsky-Hierarchie
 Theorie der Informatik 17. März 2014 6. Formale Sprachen und Grammatiken Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 6.1 Einführung
Theorie der Informatik 17. März 2014 6. Formale Sprachen und Grammatiken Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 6.1 Einführung
Formale Sprachen. Grammatiken. Grammatiken und die Chomsky-Hierarchie. Rudolf FREUND, Marion OSWALD. Grammatiken: Ableitung
 Formale Sprachen rammatiken und die Chomsky-Hierarchie Rudolf FREUND, Marion OSWALD rammatiken Das fundamentale Modell zur Beschreibung von formalen Sprachen durch Erzeugungsmechanismen sind rammatiken.
Formale Sprachen rammatiken und die Chomsky-Hierarchie Rudolf FREUND, Marion OSWALD rammatiken Das fundamentale Modell zur Beschreibung von formalen Sprachen durch Erzeugungsmechanismen sind rammatiken.
Formale Sprachen. Script, Kapitel 4. Grammatiken
 Formale Sprachen Grammatiken Script, Kapitel 4 erzeugen Sprachen eingeführt von Chomsky zur Beschreibung natürlicher Sprache bedeutend für die Syntaxdefinition und -analyse von Programmiersprachen Automaten
Formale Sprachen Grammatiken Script, Kapitel 4 erzeugen Sprachen eingeführt von Chomsky zur Beschreibung natürlicher Sprache bedeutend für die Syntaxdefinition und -analyse von Programmiersprachen Automaten
Theoretische Informatik I (Grundzüge der Informatik I)
 Theoretische Informatik I (Grundzüge der Informatik I) Literatur: Buch zur Vorlesung: Uwe Schöning, Theoretische Informatik - kurzgefasst. Spektrum Akademischer Verlag, Heidelberg/Berlin, 4. Auflage, 2001.
Theoretische Informatik I (Grundzüge der Informatik I) Literatur: Buch zur Vorlesung: Uwe Schöning, Theoretische Informatik - kurzgefasst. Spektrum Akademischer Verlag, Heidelberg/Berlin, 4. Auflage, 2001.
Automaten und formale Sprachen Klausurvorbereitung
 Automaten und formale Sprachen Klausurvorbereitung Rami Swailem Mathematik Naturwissenschaften und Informatik FH-Gießen-Friedberg Inhaltsverzeichnis 1 Definitionen 2 2 Altklausur Jäger 2006 8 1 1 Definitionen
Automaten und formale Sprachen Klausurvorbereitung Rami Swailem Mathematik Naturwissenschaften und Informatik FH-Gießen-Friedberg Inhaltsverzeichnis 1 Definitionen 2 2 Altklausur Jäger 2006 8 1 1 Definitionen
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 17. Januar 2012 INSTITUT FÜR THEORETISCHE 0 KIT 18.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Theoretische Grundlagen der Informatik Vorlesung am 17. Januar 2012 INSTITUT FÜR THEORETISCHE 0 KIT 18.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Kapitel: Die Chomsky Hierarchie. Die Chomsky Hierarchie 1 / 14
 Kapitel: Die Chomsky Hierarchie Die Chomsky Hierarchie 1 / 14 Allgemeine Grammatiken Definition Eine Grammatik G = (Σ, V, S, P) besteht aus: einem endlichen Alphabet Σ, einer endlichen Menge V von Variablen
Kapitel: Die Chomsky Hierarchie Die Chomsky Hierarchie 1 / 14 Allgemeine Grammatiken Definition Eine Grammatik G = (Σ, V, S, P) besteht aus: einem endlichen Alphabet Σ, einer endlichen Menge V von Variablen
Grundbegriffe. Grammatiken
 Grammatiken Grammatiken in der Informatik sind ähnlich wie Grammatiken für natürliche Sprachen ein Mittel, um alle syntaktisch korrekten Sätze (hier: Wörter) einer Sprache zu erzeugen. Beispiel: Eine vereinfachte
Grammatiken Grammatiken in der Informatik sind ähnlich wie Grammatiken für natürliche Sprachen ein Mittel, um alle syntaktisch korrekten Sätze (hier: Wörter) einer Sprache zu erzeugen. Beispiel: Eine vereinfachte
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Sommersemester 2016 20.04.2016 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt 1. Terminologie 2. Endliche Automaten und reguläre Sprachen
Grundlagen der Theoretischen Informatik Sommersemester 2016 20.04.2016 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt 1. Terminologie 2. Endliche Automaten und reguläre Sprachen
Umformung NTM DTM. Charakterisierung rek. aufz. Spr. Chomsky-3-Grammatiken (T5.3) Chomsky-0-Grammatik Rek. Aufz.
 Chomsky-0-Grammatik Rek. Aufz. Satz T5.2.2: Wenn L durch eine Chomsky-0- Grammatik G beschrieben wird, gibt es eine NTM M, die L akzeptiert. Beweis: Algo von M: Schreibe S auf freie Spur. Iteriere: Führe
Chomsky-0-Grammatik Rek. Aufz. Satz T5.2.2: Wenn L durch eine Chomsky-0- Grammatik G beschrieben wird, gibt es eine NTM M, die L akzeptiert. Beweis: Algo von M: Schreibe S auf freie Spur. Iteriere: Führe
Was bisher geschah Chomsky-Hierarchie für Sprachen: L 0 Menge aller durch (beliebige) Grammatiken beschriebenen Sprachen L 1 Menge aller monotonen
 Was bisher geschah Chomsky-Hierarchie für Sprachen: L 0 Menge aller durch (beliebige) Grammatiken beschriebenen Sprachen L 1 Menge aller monotonen (Kontextsensitive) Sprachen L 2 Menge aller kontextfreien
Was bisher geschah Chomsky-Hierarchie für Sprachen: L 0 Menge aller durch (beliebige) Grammatiken beschriebenen Sprachen L 1 Menge aller monotonen (Kontextsensitive) Sprachen L 2 Menge aller kontextfreien
q 0 q gdw. nicht (q A) (q A) q i+1 q gdw. q i q oder ( a Σ) δ(q, a) i δ(q, a) L = {a n b n : n N} für a, b Σ, a b
 Kap. 2: Endliche Automaten Myhill Nerode 2.4 Minimalautomat für reguläre Sprache Abschnitt 2.4.3 L Σ regulär der Äuivalenzklassen-Automat zu L ist ein DFA mit minimaler Zustandszahl (= index( L )) unter
Kap. 2: Endliche Automaten Myhill Nerode 2.4 Minimalautomat für reguläre Sprache Abschnitt 2.4.3 L Σ regulär der Äuivalenzklassen-Automat zu L ist ein DFA mit minimaler Zustandszahl (= index( L )) unter
I.5. Kontextfreie Sprachen
 I.5. Kontextfreie prachen Zieht man in Betracht, dass BNF-yteme gerade so beschaffen sind, dass auf der linken eite immer genau ein Nichtterminal steht, so sind das also gerade die Ableitungsregeln einer
I.5. Kontextfreie prachen Zieht man in Betracht, dass BNF-yteme gerade so beschaffen sind, dass auf der linken eite immer genau ein Nichtterminal steht, so sind das also gerade die Ableitungsregeln einer
kontextfreie Grammatiken Theoretische Informatik kontextfreie Grammatiken kontextfreie Grammatiken Rainer Schrader 14. Juli 2009 Gliederung
 Theoretische Informatik Rainer Schrader Zentrum für Angewandte Informatik Köln 14. Juli 2009 1 / 40 2 / 40 Beispiele: Aus den bisher gemachten Überlegungen ergibt sich: aus der Chomsky-Hierarchie bleiben
Theoretische Informatik Rainer Schrader Zentrum für Angewandte Informatik Köln 14. Juli 2009 1 / 40 2 / 40 Beispiele: Aus den bisher gemachten Überlegungen ergibt sich: aus der Chomsky-Hierarchie bleiben
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Sommersemester 2015 22.04.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt 1. Terminologie 2. Endliche Automaten und reguläre Sprachen
Grundlagen der Theoretischen Informatik Sommersemester 2015 22.04.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt 1. Terminologie 2. Endliche Automaten und reguläre Sprachen
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Sommersemester 2015 23.04.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt 1. Terminologie 2. Endliche Automaten und reguläre Sprachen
Grundlagen der Theoretischen Informatik Sommersemester 2015 23.04.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt 1. Terminologie 2. Endliche Automaten und reguläre Sprachen
Programmiersprachen und Übersetzer
 Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Sommersemester 2015 29.04.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt 1. Motivation 2. Terminologie 3. Endliche Automaten und reguläre
Grundlagen der Theoretischen Informatik Sommersemester 2015 29.04.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt 1. Motivation 2. Terminologie 3. Endliche Automaten und reguläre
Alphabet, formale Sprache
 n Alphabet Alphabet, formale Sprache l nichtleere endliche Menge von Zeichen ( Buchstaben, Symbole) n Wort über einem Alphabet l endliche Folge von Buchstaben, die auch leer sein kann ( ε leere Wort) l
n Alphabet Alphabet, formale Sprache l nichtleere endliche Menge von Zeichen ( Buchstaben, Symbole) n Wort über einem Alphabet l endliche Folge von Buchstaben, die auch leer sein kann ( ε leere Wort) l
Theorie der Informatik
 Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 Einführung Beispiel: Aussagenlogische Formeln Aus dem Logikteil: Definition (Syntax
Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 Einführung Beispiel: Aussagenlogische Formeln Aus dem Logikteil: Definition (Syntax
7. Formale Sprachen und Grammatiken
 7. Formale Sprachen und Grammatiken Computer verwenden zur Verarbeitung von Daten und Informationen künstliche, formale Sprachen (Maschinenspr., Assemblerspachen, Programmierspr., Datenbankspr., Wissensrepräsentationsspr.,...)
7. Formale Sprachen und Grammatiken Computer verwenden zur Verarbeitung von Daten und Informationen künstliche, formale Sprachen (Maschinenspr., Assemblerspachen, Programmierspr., Datenbankspr., Wissensrepräsentationsspr.,...)
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Dank. Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I. Reguläre Ausdrücke als Suchmuster für grep
 Dank Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Diese Vorlesungsmaterialien basieren ganz wesentlich auf den Folien zu den Vorlesungen
Dank Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Diese Vorlesungsmaterialien basieren ganz wesentlich auf den Folien zu den Vorlesungen
Übungsblatt 6. Vorlesung Theoretische Grundlagen der Informatik im WS 17/18
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 6 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 10. Januar 2018 Abgabe 23. Januar 2018, 11:00 Uhr (im
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 6 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 10. Januar 2018 Abgabe 23. Januar 2018, 11:00 Uhr (im
Übungsblatt 7. Vorlesung Theoretische Grundlagen der Informatik im WS 16/17
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 7 Vorlesung Theoretische Grundlagen der Informatik im W 16/17 Ausgabe 17. Januar 2017 Abgabe 31. Januar 2017, 11:00 Uhr (im
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 7 Vorlesung Theoretische Grundlagen der Informatik im W 16/17 Ausgabe 17. Januar 2017 Abgabe 31. Januar 2017, 11:00 Uhr (im
Deterministischer Kellerautomat (DPDA)
 Deterministische Kellerautomaten Deterministischer Kellerautomat (DPDA) Definition Ein Septupel M = (Σ,Γ, Z,δ, z 0,#, F) heißt deterministischer Kellerautomat (kurz DPDA), falls gilt: 1 M = (Σ,Γ, Z,δ,
Deterministische Kellerautomaten Deterministischer Kellerautomat (DPDA) Definition Ein Septupel M = (Σ,Γ, Z,δ, z 0,#, F) heißt deterministischer Kellerautomat (kurz DPDA), falls gilt: 1 M = (Σ,Γ, Z,δ,
Automatentheorie und formale Sprachen
 Automatentheorie und formale Sprachen VL 8 Chomsky-Grammatiken Kathrin Hoffmann 23. Mai 2012 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 23.5. 2012 250 Wortproblem Wortproblem ist das
Automatentheorie und formale Sprachen VL 8 Chomsky-Grammatiken Kathrin Hoffmann 23. Mai 2012 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 23.5. 2012 250 Wortproblem Wortproblem ist das
Was bisher geschah: Formale Sprachen
 Was bisher geschah: Formale Sprachen Alphabet, Wort, Sprache Operationen und Relationen auf Wörtern und Sprachen Darstellung unendlicher Sprachen durch reguläre Ausdrücke (Syntax, Semantik, Äquivalenz)
Was bisher geschah: Formale Sprachen Alphabet, Wort, Sprache Operationen und Relationen auf Wörtern und Sprachen Darstellung unendlicher Sprachen durch reguläre Ausdrücke (Syntax, Semantik, Äquivalenz)
Kontextfreie Grammatiken
 Kontextfreie Grammatiken Bisher haben wir verschiedene Automatenmodelle kennengelernt. Diesen Automaten können Wörter vorgelegt werden, die von den Automaten gelesen und dann akzeptiert oder abgelehnt
Kontextfreie Grammatiken Bisher haben wir verschiedene Automatenmodelle kennengelernt. Diesen Automaten können Wörter vorgelegt werden, die von den Automaten gelesen und dann akzeptiert oder abgelehnt
Einführung in die Theoretische Informatik
 Einführung in die Theoretische Informatik Woche 7 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 Zusammenfassung Zusammenfassung der letzten LV 1 Wir betrachten die folgende Signatur
Einführung in die Theoretische Informatik Woche 7 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 Zusammenfassung Zusammenfassung der letzten LV 1 Wir betrachten die folgende Signatur
FORMALE SYSTEME. Sprachen beschreiben. Wiederholung. Wie kann man Sprachen beschreiben? 2. Vorlesung: Grammatiken und die Chomsky-Hierarchie
 Wiederholung FORMALE SYSTEME 2. Vorlesung: Grammatiken und die Chomsky-Hierarchie Markus Krötzsch Formale Sprachen sind in Praxis und Theorie sehr wichtig Ein Alphabet ist eine nichtleere, endliche Menge
Wiederholung FORMALE SYSTEME 2. Vorlesung: Grammatiken und die Chomsky-Hierarchie Markus Krötzsch Formale Sprachen sind in Praxis und Theorie sehr wichtig Ein Alphabet ist eine nichtleere, endliche Menge
Kontextfreie Sprachen
 Kontextfreie Sprachen Bedeutung: Programmiersprachen (Compilerbau) Syntaxbäume Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung
Kontextfreie Sprachen Bedeutung: Programmiersprachen (Compilerbau) Syntaxbäume Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung
Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit
 Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit Sommersemester 2011 Dozent: Prof. Dr. J. Rothe, Prof. Dr. M. Leuschel J. Rothe (HHU Düsseldorf)
Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit Sommersemester 2011 Dozent: Prof. Dr. J. Rothe, Prof. Dr. M. Leuschel J. Rothe (HHU Düsseldorf)
Kontextfreie Sprachen
 Kontextfreie Sprachen besitzen große Bedeutung im Compilerbau Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung durch
Kontextfreie Sprachen besitzen große Bedeutung im Compilerbau Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung durch
1 Formale Sprachen, reguläre und kontextfreie Grammatiken
 Praktische Informatik 1, WS 2001/02, reguläre Ausdrücke und kontextfreie Grammatiken 1 1 Formale Sprachen, reguläre und kontextfreie Grammatiken Ein Alphabet A ist eine endliche Menge von Zeichen. Die
Praktische Informatik 1, WS 2001/02, reguläre Ausdrücke und kontextfreie Grammatiken 1 1 Formale Sprachen, reguläre und kontextfreie Grammatiken Ein Alphabet A ist eine endliche Menge von Zeichen. Die
Zusammenfassung. Beispiel. 1 Wir betrachten die folgende Signatur F = {,, +, 0, 1} sodass. 3 Wir betrachten die Identitäten E. 4 Dann gilt E 1 + x = 1
 Zusammenfassung Zusammenfassung der letzten LVA Einführung in die Theoretische Informatik Christina Kohl Alexander Maringele eorg Moser Michael Schaper Institut für Informatik @ UIBK Wintersemester 2016
Zusammenfassung Zusammenfassung der letzten LVA Einführung in die Theoretische Informatik Christina Kohl Alexander Maringele eorg Moser Michael Schaper Institut für Informatik @ UIBK Wintersemester 2016
Formale Grundlagen der Informatik
 Formale Grundlagen der Informatik / 2015 1 Reguläre Ausdrücke Kommen in der Praxis immer dann vor, wenn standardisierte Eingaben erforderlich sind: Telefonnummern: +Land (0) Ort Anschluß Dateinamen: (A-Z,
Formale Grundlagen der Informatik / 2015 1 Reguläre Ausdrücke Kommen in der Praxis immer dann vor, wenn standardisierte Eingaben erforderlich sind: Telefonnummern: +Land (0) Ort Anschluß Dateinamen: (A-Z,
Normalformen für kontextfreie Grammatiken. Noam CHOMSKY, Sheila GREIBACH. Bäume. Ableitungen in kontextfreien Grammatiken. Grammatik G = (N,T,P,S)
 Noam CHOMSKY, Sheila GREIBACH Normalformen für kontextfreie Grammatiken Noam CHOMSKY (*1928 ) Sheila GREIBACH (*1939) Grammatik G = (N,T,P,S) GREIBACH Normalform: A aw, w N* Erweiterte GREIBACH Normalform:
Noam CHOMSKY, Sheila GREIBACH Normalformen für kontextfreie Grammatiken Noam CHOMSKY (*1928 ) Sheila GREIBACH (*1939) Grammatik G = (N,T,P,S) GREIBACH Normalform: A aw, w N* Erweiterte GREIBACH Normalform:
Reguläre Sprachen. R. Stiebe: Theoretische Informatik für ING-IF und Lehrer,
 Reguläre Sprachen Reguläre Sprachen (Typ-3-Sprachen) haben große Bedeutung in Textverarbeitung und Programmierung (z.b. lexikalische Analyse) besitzen für viele Entscheidungsprobleme effiziente Algorithmen
Reguläre Sprachen Reguläre Sprachen (Typ-3-Sprachen) haben große Bedeutung in Textverarbeitung und Programmierung (z.b. lexikalische Analyse) besitzen für viele Entscheidungsprobleme effiziente Algorithmen
Motivation natürliche Sprachen
 Motivation natürliche Sprachen (Satz) (Substantivphrase)(Verbphrase) (Satz) (Substantivphrase)(Verbphrase)(Objektphrase) (Substantivphrase) (Artikel)(Substantiv) (Verbphrase) (Verb)(Adverb) (Substantiv)
Motivation natürliche Sprachen (Satz) (Substantivphrase)(Verbphrase) (Satz) (Substantivphrase)(Verbphrase)(Objektphrase) (Substantivphrase) (Artikel)(Substantiv) (Verbphrase) (Verb)(Adverb) (Substantiv)
Automaten und Formale Sprachen
 Automaten und Formale Sprachen Prof. Dr. Dietrich Kuske FG Theoretische Informatik, TU Ilmenau Wintersemester 2011/12 WS 11/12 1 Organisatorisches zur Vorlesung Informationen, aktuelle Version der Folien
Automaten und Formale Sprachen Prof. Dr. Dietrich Kuske FG Theoretische Informatik, TU Ilmenau Wintersemester 2011/12 WS 11/12 1 Organisatorisches zur Vorlesung Informationen, aktuelle Version der Folien
Definition (Reguläre Ausdrücke) Sei Σ ein Alphabet, dann gilt: (ii) ε ist ein regulärer Ausdruck über Σ.
 Reguläre Ausdrücke Definition (Reguläre Ausdrücke) Sei Σ ein Alphabet, dann gilt: (i) ist ein regulärer Ausdruck über Σ. (ii) ε ist ein regulärer Ausdruck über Σ. (iii) Für jedes a Σ ist a ein regulärer
Reguläre Ausdrücke Definition (Reguläre Ausdrücke) Sei Σ ein Alphabet, dann gilt: (i) ist ein regulärer Ausdruck über Σ. (ii) ε ist ein regulärer Ausdruck über Σ. (iii) Für jedes a Σ ist a ein regulärer
Grundlagen der theoretischen Informatik
 Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 09.04.2013 Inhalt der Vorlesung Teil I: Automaten und formale Sprachen (Kurt Sieber)
Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 09.04.2013 Inhalt der Vorlesung Teil I: Automaten und formale Sprachen (Kurt Sieber)
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (I) 3.06.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Organisatorisches 1. Teilklausur: Mittwoch,
Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (I) 3.06.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Organisatorisches 1. Teilklausur: Mittwoch,
Grundlagen Theoretischer Informatik 2 WiSe 2009/10 in Trier. Henning Fernau Universität Trier
 Grundlagen Theoretischer Informatik 2 WiSe 2009/10 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; inführung rsetzungsverfahren:
Grundlagen Theoretischer Informatik 2 WiSe 2009/10 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; inführung rsetzungsverfahren:
Dank. 1 Ableitungsbäume. 2 Umformung von Grammatiken. 3 Normalformen. 4 Pumping-Lemma für kontextfreie Sprachen. 5 Pushdown-Automaten (PDAs)
 ank Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert iese Vorlesungsmaterialien basieren ganz wesentlich auf den Folien zu den Vorlesungen
ank Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert iese Vorlesungsmaterialien basieren ganz wesentlich auf den Folien zu den Vorlesungen
Grundlagen der Theoretischen Informatik
 1 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 2 Kontextfreie Grammatiken Definition: Eine Grammatik G
1 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 2 Kontextfreie Grammatiken Definition: Eine Grammatik G
Kontextfreie Grammatiken. Kontextfreie Grammatiken 1 / 45
 Kontextfreie Grammatiken Kontextfreie Grammatiken 1 / 45 Was kann man mit kontextfreien Grammatiken anfangen? Kontextfreie Grammatiken, kurz: werden zur Modellierung von KFGs beliebig tief geschachtelten
Kontextfreie Grammatiken Kontextfreie Grammatiken 1 / 45 Was kann man mit kontextfreien Grammatiken anfangen? Kontextfreie Grammatiken, kurz: werden zur Modellierung von KFGs beliebig tief geschachtelten
Abschluss gegen Substitution. Wiederholung. Beispiel. Abschluss gegen Substitution
 Wiederholung Beschreibungsformen für reguläre Sprachen: DFAs NFAs Reguläre Ausdrücke:, {ε}, {a}, und deren Verknüpfung mit + (Vereinigung), (Konkatenation) und * (kleenescher Abschluss) Abschluss gegen
Wiederholung Beschreibungsformen für reguläre Sprachen: DFAs NFAs Reguläre Ausdrücke:, {ε}, {a}, und deren Verknüpfung mit + (Vereinigung), (Konkatenation) und * (kleenescher Abschluss) Abschluss gegen
FORMALE SYSTEME. 3. Vorlesung: Endliche Automaten. TU Dresden, 17. Oktober Markus Krötzsch
 FORMALE SYSTEME 3. Vorlesung: Endliche Automaten Markus Krötzsch TU Dresden, 17. Oktober 2016 Rückblick Markus Krötzsch, 17. Oktober 2016 Formale Systeme Folie 2 von 31 Wiederholung Mit Grammatiken können
FORMALE SYSTEME 3. Vorlesung: Endliche Automaten Markus Krötzsch TU Dresden, 17. Oktober 2016 Rückblick Markus Krötzsch, 17. Oktober 2016 Formale Systeme Folie 2 von 31 Wiederholung Mit Grammatiken können
Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen 19
 Inhalt 1 inführung 2 Automatentheorie und ormale prachen Grammatiken Reguläre prachen und endliche Automaten Kontextfreie prachen und Kellerautomaten Kontextsensitive und yp 0-prachen 3 Berechenbarkeitstheorie
Inhalt 1 inführung 2 Automatentheorie und ormale prachen Grammatiken Reguläre prachen und endliche Automaten Kontextfreie prachen und Kellerautomaten Kontextsensitive und yp 0-prachen 3 Berechenbarkeitstheorie
Formalismen für REG. Formale Grundlagen der Informatik 1 Kapitel 7 Kontextfreie Sprachen. Das Pumping Lemma. Abschlusseigenschaften
 Formalismen für RE Formale rundlagen der Informatik 1 Kapitel 7 Kontextfreie Sprachen Frank Heitmann heitmann@informatik.uni-hamburg.de Satz Zu jeder regulären Sprache L gibt es einen DFA A mit L(A) =
Formalismen für RE Formale rundlagen der Informatik 1 Kapitel 7 Kontextfreie Sprachen Frank Heitmann heitmann@informatik.uni-hamburg.de Satz Zu jeder regulären Sprache L gibt es einen DFA A mit L(A) =
11.1 Kontextsensitive und allgemeine Grammatiken
 Theorie der Informatik 7. April 2014 11. Kontextsensitive und Typ-0-Sprachen Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen 11.1 Kontextsensitive und allgemeine Grammatiken Malte Helmert
Theorie der Informatik 7. April 2014 11. Kontextsensitive und Typ-0-Sprachen Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen 11.1 Kontextsensitive und allgemeine Grammatiken Malte Helmert
Theorie der Informatik
 Theorie der Informatik 8. Reguläre Sprachen II Malte Helmert Gabriele Röger Universität Basel 24. März 24 Pumping Lemma Pumping Lemma: Motivation Man kann zeigen, dass eine Sprache regulär ist, indem man
Theorie der Informatik 8. Reguläre Sprachen II Malte Helmert Gabriele Röger Universität Basel 24. März 24 Pumping Lemma Pumping Lemma: Motivation Man kann zeigen, dass eine Sprache regulär ist, indem man
Endliche Sprachen. Folgerung: Alle endlichen Sprachen sind regulär. Beweis: Sei L={w 1,,w n } Σ*. Dann ist w 1 +L+w n ein regulärer Ausdruck für
 Endliche Sprachen Folgerung: Alle endlichen Sprachen sind regulär. Beweis: Sei L={w 1,,w n } Σ*. Dann ist w 1 +L+w n ein regulärer Ausdruck für L. 447 Zusammenfassung Beschreibungsformen für reguläre Sprachen:
Endliche Sprachen Folgerung: Alle endlichen Sprachen sind regulär. Beweis: Sei L={w 1,,w n } Σ*. Dann ist w 1 +L+w n ein regulärer Ausdruck für L. 447 Zusammenfassung Beschreibungsformen für reguläre Sprachen:
Grammatik Prüfung möglich, ob eine Zeichenfolge zur Sprache gehört oder nicht
 Zusammenhang: Formale Sprache Grammatik Formale Sprache kann durch Grammatik beschrieben werden. Zur Sprache L = L(G) gehören nur diejenigen Kombinationen der Zeichen des Eingabealphabets, die durch die
Zusammenhang: Formale Sprache Grammatik Formale Sprache kann durch Grammatik beschrieben werden. Zur Sprache L = L(G) gehören nur diejenigen Kombinationen der Zeichen des Eingabealphabets, die durch die
Theorie der Informatik
 Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen Malte Helmert Gabriele Röger Universität Basel 7. April 2014 Kontextsensitive und allgemeine Grammatiken Wiederholung: (kontextsensitive)
Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen Malte Helmert Gabriele Röger Universität Basel 7. April 2014 Kontextsensitive und allgemeine Grammatiken Wiederholung: (kontextsensitive)
Sprachen sind durch folgenden Aufbau gekennzeichnet:
 BNF UND SYNTAXDIAGRAMME 1. Allgemeines 1.1 Aufbau von Sprachen BNF und Syntaxdiagramme werden verwendet, um die Syntax einer Sprache darzustellen und graphisch zu veranschaulichen. Mit ihnen können entweder
BNF UND SYNTAXDIAGRAMME 1. Allgemeines 1.1 Aufbau von Sprachen BNF und Syntaxdiagramme werden verwendet, um die Syntax einer Sprache darzustellen und graphisch zu veranschaulichen. Mit ihnen können entweder
Ein Satz der deutschen Sprache besitzt ein Subjekt, ein Prädikat und ein Objekt (SPO).
 1 Grammatiken Autor: Tilman Blumenbach Letzte Änderung: 28. Juni 2012 18:15 Ziel von Grammatiken Wollen die Struktur von Sprachen modellieren und charakterisieren. Beispiel Ein Satz der deutschen Sprache
1 Grammatiken Autor: Tilman Blumenbach Letzte Änderung: 28. Juni 2012 18:15 Ziel von Grammatiken Wollen die Struktur von Sprachen modellieren und charakterisieren. Beispiel Ein Satz der deutschen Sprache
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (II) 11.06.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (II) 11.06.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Informatik. Prof. Dr. Stefan Enderle NTA Isny
 Grundlagen der Informatik Prof. Dr. Stefan Enderle NTA Isny 1. Automaten und Sprachen 1.1 Endlicher Automat Einen endlichen Automaten stellen wir uns als Black Box vor, die sich aufgrund einer Folge von
Grundlagen der Informatik Prof. Dr. Stefan Enderle NTA Isny 1. Automaten und Sprachen 1.1 Endlicher Automat Einen endlichen Automaten stellen wir uns als Black Box vor, die sich aufgrund einer Folge von
Grundbegriffe der Informatik Tutorium 7
 Grundbegriffe der Informatik Tutorium 7 Tutorium Nr. 16 Philipp Oppermann 16. Dezember 2014 KARLSRUHER INSTITUT FÜR TECHNOLOGIE KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum
Grundbegriffe der Informatik Tutorium 7 Tutorium Nr. 16 Philipp Oppermann 16. Dezember 2014 KARLSRUHER INSTITUT FÜR TECHNOLOGIE KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum
Beschreibungskomplexität von Grammatiken Definitionen
 Beschreibungskomplexität von Grammatiken Definitionen Für eine Grammatik G = (N, T, P, S) führen wir die folgenden drei Komplexitätsmaße ein: Var(G) = #(N), Prod(G) = #(P ), Symb(G) = ( α + β + 1). α β
Beschreibungskomplexität von Grammatiken Definitionen Für eine Grammatik G = (N, T, P, S) führen wir die folgenden drei Komplexitätsmaße ein: Var(G) = #(N), Prod(G) = #(P ), Symb(G) = ( α + β + 1). α β
Formale Sprachen und Grammatiken
 Formale Sprachen und Grammatiken Jede Sprache besitzt die Aspekte Semantik (Bedeutung) und Syntax (formaler Aufbau). Die zulässige und korrekte Form der Wörter und Sätze einer Sprache wird durch die Syntax
Formale Sprachen und Grammatiken Jede Sprache besitzt die Aspekte Semantik (Bedeutung) und Syntax (formaler Aufbau). Die zulässige und korrekte Form der Wörter und Sätze einer Sprache wird durch die Syntax
Theoretische Informatik 2
 Theoretische Informatik 2 Johannes Köbler Institut für Informatik Humboldt-Universität zu Berlin WS 2009/10 Die Chomsky-Hierarchie Definition Sei G = (V, Σ, P, S) eine Grammatik. 1 G heißt vom Typ 3 oder
Theoretische Informatik 2 Johannes Köbler Institut für Informatik Humboldt-Universität zu Berlin WS 2009/10 Die Chomsky-Hierarchie Definition Sei G = (V, Σ, P, S) eine Grammatik. 1 G heißt vom Typ 3 oder
Theoretische Informatik. Grammatiken. Grammatiken. Grammatiken. Rainer Schrader. 9. Juli 2009
 Theoretische Informatik Rainer Schrader Institut für Informatik 9. Juli 2009 1 / 41 2 / 41 Gliederung die Chomsky-Hierarchie Typ 0- Typ 3- Typ 1- Die Programmierung eines Rechners in einer höheren Programmiersprache
Theoretische Informatik Rainer Schrader Institut für Informatik 9. Juli 2009 1 / 41 2 / 41 Gliederung die Chomsky-Hierarchie Typ 0- Typ 3- Typ 1- Die Programmierung eines Rechners in einer höheren Programmiersprache
Kapitel 2: Formale Sprachen Gliederung. 0. Grundbegriffe 1. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie
 Gliederung 0. Grundbegriffe 1. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.1. 2.2. Reguläre Sprachen 2.3. Kontextfreie Sprachen 2/1, Folie 1 2015 Prof. Steffen
Gliederung 0. Grundbegriffe 1. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.1. 2.2. Reguläre Sprachen 2.3. Kontextfreie Sprachen 2/1, Folie 1 2015 Prof. Steffen
WS06/07 Referentin: Katharina Blinova. Formale Sprachen. Hauptseminar Intelligente Systeme Dozent: Prof. Dr. J. Rolshoven
 WS06/07 Referentin: Katharina Blinova Formale Sprachen Hauptseminar Intelligente Systeme Dozent: Prof. Dr. J. Rolshoven 1. Allgemeines 2. Formale Sprachen 3. Formale Grammatiken 4. Chomsky-Hierarchie 5.
WS06/07 Referentin: Katharina Blinova Formale Sprachen Hauptseminar Intelligente Systeme Dozent: Prof. Dr. J. Rolshoven 1. Allgemeines 2. Formale Sprachen 3. Formale Grammatiken 4. Chomsky-Hierarchie 5.
1 Σ endliches Terminalalphabet, 2 V endliche Menge von Variablen (mit V Σ = ), 3 P (V (Σ ΣV )) {(S, ε)} endliche Menge von Regeln,
 Theorie der Informatik 9. März 24 7. Reguläre Sprachen I Theorie der Informatik 7. Reguläre Sprachen I Malte Helmert Gabriele Röger Universität Basel 9. März 24 7. Reguläre Grammatiken 7.2 DFAs 7.3 NFAs
Theorie der Informatik 9. März 24 7. Reguläre Sprachen I Theorie der Informatik 7. Reguläre Sprachen I Malte Helmert Gabriele Röger Universität Basel 9. März 24 7. Reguläre Grammatiken 7.2 DFAs 7.3 NFAs
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 8: kontextfreie Grammatiken Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2009/2010 1/37 Überblick Kontextfreie Grammatiken
Grundbegriffe der Informatik Einheit 8: kontextfreie Grammatiken Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2009/2010 1/37 Überblick Kontextfreie Grammatiken
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2011
 Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2011 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Wir beschäftigen uns ab
Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2011 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Wir beschäftigen uns ab
Motivation. Formale Grundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen. Informales Beispiel. Informales Beispiel.
 Kontextfreie Kontextfreie Motivation Formale rundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen Bisher hatten wir Automaten, die Wörter akzeptieren Frank Heitmann heitmann@informatik.uni-hamburg.de
Kontextfreie Kontextfreie Motivation Formale rundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen Bisher hatten wir Automaten, die Wörter akzeptieren Frank Heitmann heitmann@informatik.uni-hamburg.de
Übungsaufgaben zu Formalen Sprachen und Automaten
 Universität Freiburg PD Dr. A. Jakoby Sommer 27 Übungen zum Repetitorium Informatik III Übungsaufgaben zu Formalen Sprachen und Automaten. Untersuchen Sie das folgende Spiel: A B x x 2 x 3 C D Eine Murmel
Universität Freiburg PD Dr. A. Jakoby Sommer 27 Übungen zum Repetitorium Informatik III Übungsaufgaben zu Formalen Sprachen und Automaten. Untersuchen Sie das folgende Spiel: A B x x 2 x 3 C D Eine Murmel
Grundlagen der Informatik II. Teil I: Formale Modelle der Informatik
 Grundlagen der Informatik II Teil I: Formale Modelle der Informatik 1 Einführung GdInfoII 1-2 Ziele/Fragestellungen der Theoretischen Informatik 1. Einführung abstrakter Modelle für informationsverarbeitende
Grundlagen der Informatik II Teil I: Formale Modelle der Informatik 1 Einführung GdInfoII 1-2 Ziele/Fragestellungen der Theoretischen Informatik 1. Einführung abstrakter Modelle für informationsverarbeitende
7. Syntax: Grammatiken, EBNF
 7. Syntax: Grammatiken, EBNF Teil 1 Sehr schönes Beispiel für Notwendigkeit der Theoretischen Informatik für Belange der Praktischen Informatik Vertiefung in: Einführung in die Theoretische Informatik
7. Syntax: Grammatiken, EBNF Teil 1 Sehr schönes Beispiel für Notwendigkeit der Theoretischen Informatik für Belange der Praktischen Informatik Vertiefung in: Einführung in die Theoretische Informatik
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (III) 17.06.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (III) 17.06.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Zusammenfassung. 1 Wir betrachten die folgende Signatur F = {+,,, 0, 1} sodass. 3 Wir betrachten die Gleichungen E. 4 Dann gilt E 1 + x 1
 Zusammenfassung Zusammenfassung der letzten LV Einführung in die Theoretische Informatik Woche 7 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 1 Wir betrachten die folgende Signatur
Zusammenfassung Zusammenfassung der letzten LV Einführung in die Theoretische Informatik Woche 7 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 1 Wir betrachten die folgende Signatur
Rekursiv aufzählbare Sprachen
 Kapitel 4 Rekursiv aufzählbare Sprachen 4.1 Grammatiken und die Chomsky-Hierarchie Durch Zulassung komplexer Ableitungsregeln können mit Grammatiken größere Klassen als die kontextfreien Sprachen beschrieben
Kapitel 4 Rekursiv aufzählbare Sprachen 4.1 Grammatiken und die Chomsky-Hierarchie Durch Zulassung komplexer Ableitungsregeln können mit Grammatiken größere Klassen als die kontextfreien Sprachen beschrieben
Informales Beispiel. Formale Grundlagen der Informatik 1 Kapitel 6 Eigenschaften kontextfreier Sprachen. Grammatiken. Anmerkungen
 Informales Beispiel Formale Grundlagen der Informatik 1 Kapitel 6 Eigenschaften kontextfreier Sprachen Frank Heitmann heitmann@informatik.uni-hamburg.de 22. April 2014 I L IL ID L a b c D 0 1 2 3 4 Eine
Informales Beispiel Formale Grundlagen der Informatik 1 Kapitel 6 Eigenschaften kontextfreier Sprachen Frank Heitmann heitmann@informatik.uni-hamburg.de 22. April 2014 I L IL ID L a b c D 0 1 2 3 4 Eine
1 Σ endliches Terminalalphabet, 2 V endliche Menge von Variablen (mit V Σ = ), 3 P (V (Σ ΣV )) {(S, ε)} endliche Menge von Regeln,
 Theorie der Informatik 8. März 25 8. Reguläre Sprachen I Theorie der Informatik 8. Reguläre Sprachen I 8. Reguläre Grammatiken Malte Helmert Gabriele Röger 8.2 DFAs Universität Basel 8. März 25 8.3 NFAs
Theorie der Informatik 8. März 25 8. Reguläre Sprachen I Theorie der Informatik 8. Reguläre Sprachen I 8. Reguläre Grammatiken Malte Helmert Gabriele Röger 8.2 DFAs Universität Basel 8. März 25 8.3 NFAs
(Prüfungs-)Aufgaben zu formale Sprachen
 (Prüfungs-)Aufgaben zu formale Sprachen (siehe auch bei den Aufgaben zu endlichen Automaten) 1) Eine Grammatik G sei gegeben durch: N = {S, A}, T = {a, b, c, d}, P = { (S, Sa), (S, ba), (A, ba), (A, c),
(Prüfungs-)Aufgaben zu formale Sprachen (siehe auch bei den Aufgaben zu endlichen Automaten) 1) Eine Grammatik G sei gegeben durch: N = {S, A}, T = {a, b, c, d}, P = { (S, Sa), (S, ba), (A, ba), (A, c),
Satz (Abschluß unter der Stern-Operation)
 Satz (Abschluß unter der Stern-Operation) Wenn L eine reguläre Sprache ist, dann ist auch L regulär. Beweis: Es gibt einen NFA M = (Z, Σ, S, δ, S, E) mit L(M) = L. Wir bauen aus diesem NFA nun wie folgt
Satz (Abschluß unter der Stern-Operation) Wenn L eine reguläre Sprache ist, dann ist auch L regulär. Beweis: Es gibt einen NFA M = (Z, Σ, S, δ, S, E) mit L(M) = L. Wir bauen aus diesem NFA nun wie folgt
Kontextfreie (Typ-2) Sprachen
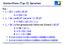 Kontextfreie (Typ-2) prachen Bsp.: L 1 = { n 1 n n>} с {,1}* 1 1 L 2 = {w wє{,1}* und w=w rev } с {,1}* 11 1 ε L 3 = {w w hat genausoviele Nullen wie Einsen} с {,1}* B 1 ε 1 B 1 1 BB 1 11 11 11 11B 111
Kontextfreie (Typ-2) prachen Bsp.: L 1 = { n 1 n n>} с {,1}* 1 1 L 2 = {w wє{,1}* und w=w rev } с {,1}* 11 1 ε L 3 = {w w hat genausoviele Nullen wie Einsen} с {,1}* B 1 ε 1 B 1 1 BB 1 11 11 11 11B 111
Hochschule Bonn-Rhein-Sieg University of Applied Sciences Grantham-Allee Sankt Augustin
 Hochschule Bonn-Rhein-Sieg Uniersity of Applied Sciences Grantham-Allee 20 53757 Sankt Augustin Director b-it Applied Science Institute Fachbereich Informatik Prof. Dr. Kurt-Ulrich Witt Mathematische und
Hochschule Bonn-Rhein-Sieg Uniersity of Applied Sciences Grantham-Allee 20 53757 Sankt Augustin Director b-it Applied Science Institute Fachbereich Informatik Prof. Dr. Kurt-Ulrich Witt Mathematische und
Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I
 Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Institut für Informatik Sommersemester 2007 B. Beckert Grundlagen d. Theoretischen Informatik:
Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Institut für Informatik Sommersemester 2007 B. Beckert Grundlagen d. Theoretischen Informatik:
Kapitel 0: Grundbegriffe Gliederung
 Gliederung 0. Grundbegriffe 1. Endliche Automaten 2. Formale Sprachen 3. Berechenbarkeitstheorie 4. Komplexitätstheorie 5. Kryptographie 0/2, Folie 1 2009 Prof. Steffen Lange - HDa/FbI - Theoretische Informatik
Gliederung 0. Grundbegriffe 1. Endliche Automaten 2. Formale Sprachen 3. Berechenbarkeitstheorie 4. Komplexitätstheorie 5. Kryptographie 0/2, Folie 1 2009 Prof. Steffen Lange - HDa/FbI - Theoretische Informatik
Berechenbarkeitstheorie 7. Vorlesung
 1 Berechenbarkeitstheorie Dr. Institut für Mathematische Logik und Grundlagenforschung WWU Münster W 15/16 Alle Folien unter Creative Commons Attribution-NonCommercial 3.0 Unported Lizenz. Das Pumpinglemma
1 Berechenbarkeitstheorie Dr. Institut für Mathematische Logik und Grundlagenforschung WWU Münster W 15/16 Alle Folien unter Creative Commons Attribution-NonCommercial 3.0 Unported Lizenz. Das Pumpinglemma
Formale Sprachen. Formale Grundlagen (WIN) 2008S, F. Binder. Vorlesung im 2008S
 Formale Grundlagen (WIN) Franz Binder Institut für Algebra Johannes Kepler Universität Linz Vorlesung im 2008S http://www.algebra.uni-linz.ac.at/students/win/fg Inhalt Das Alphabet Σ sei eine endliche
Formale Grundlagen (WIN) Franz Binder Institut für Algebra Johannes Kepler Universität Linz Vorlesung im 2008S http://www.algebra.uni-linz.ac.at/students/win/fg Inhalt Das Alphabet Σ sei eine endliche
