Versicherungstechnik
|
|
|
- Johannes Schräder
- vor 7 Jahren
- Abrufe
Transkript
1 Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Marius Radermacher, M.Sc. DOOR Aufgabe 20 Versicherungstechnik Übungsblatt 6 Abgabe bis zum Dienstag, dem um 10 Uhr im Kasten 19 Der 60-Jährige Herr Vogt besitzt eine lebenslange Todesfallversicherung. Die Leistungshöhe beträgt L = Euro. Herr Vogt ist seit kurzem pensioniert, hat keine Rücklagen gebildet und verfügt monatlich nur über sehr geringes Einkommen. Daher möchte er seine Situation durch eine sofortbeginnende Rentenversicherung verbessern. Da er über keine finanziellen Mittel verfügt, um die Beiträge dafür zahlen zu können, möchte er die Arme-Leute-Versicherung abschließen. Bei dieser speziellen Versicherung dient die Leistung seiner Todesfallversicherung als Einmalbeitrag für die sofortbeginnende Rentenversicherung. Natürlich wird der Beitrag erst im Todesfall bezahlt. a) Stellen Sie bitte eine Gleichung nach dem schwachen versicherungstechnischen Äquivalenzprinzip auf. Geben Sie dazu eplizit den Beitrags- und Leistungsbarwert an. b) Mit welcher jährlichen Rente kann Herr Vogt zusätzlich rechnen? Geben Sie bitte eine Formel für die Rentenhöhe R an und drücken Sie diese durch Kommutationswerte aus. (2 Punkte) Lösungsvorschlag: Das versicherungstechnische Äquivalenzprinzip fordert die Gleichheit des Beitrags- und Leistungsbarwerts: BB 0 = LB 0. Der Beitrag fällt in diesem Fall als Einmalbeitrag an und beträgt Euro. Die Zahlung findet jedoch erst im Todesfall statt. Damit entspricht der Beitragsbarwert dem Leistungsbarwert der lebenslangen Todesfallversicherung, die Herr Vogt bereits abgeschlossen hat. ω BB 0 = t=0 tp q +t v t = Ä = M D. Der Leistungsbarwert einer sofortbeginnenden Rente ergibt sich aus n 1 LB 0 = R ä, n = R tp v t. Aus a) folgt über die Gleichung LB 0 = BB 0 : t= Ä = R ä, n R = Ä ä, n R = M N.
2 Aufgabe 21 Geben Sie eine allgemeine Formel an, um aus der Jahresnettoprämie N P einer n-jährigen Risikolebensversicherung die Jahresnettoprämie NP a einer um m Jahre aufgeschobenen n-jährigen Risikolebensversicherung (Beginn der Aufschubzeit im Alter ) abzuleiten. Nehmen Sie dabei an, dass die Beitragszahlung in beiden Fällen identisch ist. Lösungsvorschlag: Gleiche Beitragszahlungsweise in den ersten n Jahren. Dann gilt für die Beitragsbarwerte: Und für die Leistungsbarwerte: NP ä, n = BB 0, bzw. NP a ä, n = BB0. a LB 0 = V S n A und LB a 0 = V S m n A mit n A = n 1 bzw. m n A = Da LB 0 = BB 0 und LB a 0 = BBa 0 folgt t=0 n 1 tp q +t v t+1 t=0 t+mp q +t+m v t+m+1 ä, n ä, n V S n A NP = V S n A NP = V S m n A NP α = V S m n A NP α NP a = NP m n A na und = NP M+m M +m+n M M +n (1,5 Punkte) Aufgabe 22 a) Was versteht man unter dem Begriff Deckungskapital bzw. Deckungsrückstellung in der Versicherungstechnik? Was unterscheidet das prospektive vom retrospektiven Deckungskapital? b) Wie verändert sich das Deckungskapital bei verschiedenen Versicherungstypen im Zeitablauf? Skizzieren Sie bitte (schematisch) den Verlauf des prospektiven Deckungskapitals (Nettobetrachtung) für eine reine Todesfallversicherung (mit konstanter Leistung), Kapitallebensversicherung (mit konstanter Leistung),
3 sofort beginnende Leibrente gegen (sofortige) Einmalzahlung, aufgeschobene Leibrente mit abgekürzter Beitragszahlung und sofort beginnende (lebenslange) Leibrente mit lebenslanger Beitragszahlung! c) Was verstehen Sie unter natürlicher Beitragszahlungsweise? Wie großist das Deckungskapital bei Vereinbarung dieser Zahlungsweise? d) Geben Sie bitte ein Beispiel einer Versicherung an, aus dem klar wird, weshalb natürliche Beiträge i. Allg. nicht verwendet werden. e) Interpretieren Sie die Fälle, falls t V pro > 0 bzw. t V pro Beiträge und Leistungen. Warum ist der Fall t V pro gewünscht? Lösungsvorschlag: < 0 für 0 < t n hinsichtlich der < 0 für Lebensversicherungen nicht Merke: Hat der VN in der Vergangenheit mehr bezahlt, so darf das VU diese Überschüsse nicht als Gewinne einstreichen, sondern muss sie als Guthaben des VN auf dessen Konto verbuchen. Der am Jahresbeginn auf dem Konto befindliche Betrag heißt Deckungsrückstellung bzw. Reserve oder Deckungskapital a) Deckungskapital (Nettobetrachtung): Für t = 0,1,2,..., n 1 seien bzw. BB t = n t 1 k=0 kp +t B k+t v (t+k) t sowie n t LB t = k=0 kp +t L k+t v (t+k) t BE t = t 1 k=0 kp B k r (k) t tp und definiert. Man unterscheidet: LE t = t 1 k=0 kp L k r (k) t tp Prospektives Deckungskapital: Beim prospektiven DK wird wie der Name sagt in die Zukunft geblickt. = LB t BB t tv pro Es wird gefragt: Was wird noch geleistet? Was wird noch eingezahlt?
4 Retrospektives Deckungskapital: Hier wird im Gegensatz zum prospektiven Deckungskapital in die Vergangenheit geschaut. tv retro = BE t LE t Die Fragen lauten: Was wurde bereits eingezahlt? Was wurde bereits geleistet? Mit LE t Leistungsendwert nach t Jahren und BE t Beitragsendwert nach t Jahren. Es gilt folgender Zusammenhang: (bei gleichen Rechnungsgrundlagen) tv pro = t V retro =: t V Achtung: Eine Unterscheidung zwischen den beiden Größen ist jedoch in der Realität nicht ohne Sinn: Im prospektiven DK gehen Schätzungen über das zukünftige Zinsniveau ein, die sich von Jahr zu Jahr ändern können (und insbesondere im Vorfeld falsch sein könnten). Im retrospektiven DK gehen nur fie, d. h. bekannte Größen ein. Dadurch kann es zu unterschiedlichen Deckungskapitalen bei den beiden Betrachtungsweisen kommen, wodurch die verschiedenen Begriffe gerechtfertigt sind. Anmerkung: in der privaten Krankenversicherung (PKV) wird das Deckungskapital Alterungsrückstellung genannt! b) Darstellung des Deckungskapitals im Zeitverlauf für verschiedene Versicherungstypen: reine Todesfallversicherung (mit konstanter Leistung) Kapitallebensversicherung - gemischte Versicherung (mit konstanter Leistung) VS n
5 sofort beginnende Leibrente gegen (sofortige) Einmalzahlung X um l Jahre aufgeschobene Leibrente mit auf k Jahre abgekürzter Beitragszahlung n k l n k l
6 l k n sofort beginnende (lebenslange) Leibrente mit lebenslanger Beitragszahlung tv = 0 t, denn L t = L und B t = B für alle t. Wegen LB 0 = BB 0 ist dann L = B und daher LB t = BB t für alle t. c) Natürliche Beitragszahlungsweise (Strenges Äquivalenzprinzip): Prämien B t, die zu Beginn von Periode t + 1 gezahlt werden, entsprechen stets den zu erwartenden diskontierten Leistungen für die entsprechende Periode. w t V = LB t BB t = 0 t Damit gilt das strenge Äquivalenzprinzip!, d.h. LB t = BB t Behauptung: Dies gilt genau dann, wenn t. B t = { Lt t < n 1 L n 1 + p +n 1 L n v n t = n 1 Hierbei entspricht L n genau der Ablaufleistung! Beweis: Übung! d) Weshalb werden natürliche Beiträge im Allgemeinen nicht verwendet: Beispiel: Risikoversicherung: V S = 1, Alter, Laufzeit n Jahre natürlicher Beitrag für VS 1 im 1. Jahr: B 0 = q v natürlicher Beitrag für VS 1 im t-ten Jahr B t = q +t v
7 natürlicher Beitrag ist proportional zur Sterblichkeit wegen Anstieg der Sterblichkeit im Alter impliziert das starken Anstieg der Beiträge hin zum Versicherungsende. (z.b. = 30, n = 35 B n 1 15 B 0 ) Dies ist unerwünscht! Beispiel: Erlebensfallversicherung: V S = S, = 30, n = 35 natürliche Beiträge haben zur Folge: B t = L t = 0, t = 0,1,..., n 2 L n 1 = 0 B n 1 = p +n 1 L n v n = p +n 1 S v n Im letzten Jahr ist die abgezinste erwartete VS als Beitrag aufzubringen! Versicherungscharakter geht hier verloren! Beispiel: Krankenversicherung hier: wegen steigenden Krankheitskosten im Alter ergeben sich steigende Beiträge über gesamte Laufzeit (d.h. i.d.r. bis zum Lebensende) Beiträge eplodieren. e) Fall 1: t V pro > 0 LB t > BB t, d.h. Deckungsrückstellung ist derjenige Teil des Leistungsbarwertes nach t Jahren, der nicht durch erwartete zukünftige Beiträge gedeckt wird. in Vergangenheit wurden mehr Beiträge an VU geleistet als zur Deckung der Risiken in den ersten t Jahren notwendig war. Fall 2: t V pro < 0 BB t > LB t, d.h. VN muss in den letzten (n t)-jahren noch Beiträge nachträglich für Leistungen bezahlen, die das VU in den ersten t Jahren bereits erbrachte. Achtung: t V pro < 0 nicht gewünscht, weil sogenannte Unterdeckung entsteht! Kündigt der VN den Vertrag, hat das VU Verlust in dieser Höhe! (3,5 Punkte) Aufgabe 23 Gegeben sei ein Versicherungstarif zu dessen Abschluss ein -Jähriger bei einer Laufzeit von n Jahren die über die gesamte Laufzeit gleich bleibende Nettoprämie P zu entrichten hat. Die Nettoprämie eines +t-jährigen, der in den Versicherungstarif nach t Jahren einsteigt, betrage P +t. Zeigen Sie für 0 < t n 1 die Gültigkeit der sog. Beitragsdifferenzformel, die besagt, dass folgender Zusammenhang für die Deckungsrückstellung im (t + 1)-ten Versicherungsjahr gilt: tv = (P +t P ) ä +t, n t.
8 Lösungsvorschlag: tv = LB t BB t Sei LB 0 der Leistungsbarwert eines -Jährigen, dann gilt tv = LBt BBt +t = LB0 P ä +t, n t +t = BB 0 P ä +t, n t = P +t ä +t, n m P ä +t, n t LB +t BB +t 0 auf den Beitrags- bzw. Leistungsbarwert in der Ver- Dabei beziehen sich 0 und sicherung des + t-jährigen. (1 Punkt)
Versicherungstechnik
 Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Marius Radermacher, M.Sc. DOOR Aufgabe 16 Versicherungstechnik Übungsblatt 5 Abgabe bis zum Dienstag, dem 22.11.2016 um 10 Uhr im Kasten
Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Marius Radermacher, M.Sc. DOOR Aufgabe 16 Versicherungstechnik Übungsblatt 5 Abgabe bis zum Dienstag, dem 22.11.2016 um 10 Uhr im Kasten
Versicherungstechnik
 Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Marius Radermacher, M.Sc. DOOR Aufgabe 37 Versicherungstechnik Übungsblatt 11 Abgabe bis zum Dienstag, dem 10.01.2017 um 10 Uhr im Kasten
Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Marius Radermacher, M.Sc. DOOR Aufgabe 37 Versicherungstechnik Übungsblatt 11 Abgabe bis zum Dienstag, dem 10.01.2017 um 10 Uhr im Kasten
Versicherungstechnik
 Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Marius Radermacher, M.Sc. DOOR Aufgabe 9 Versicherungstechnik Übungsblatt 3 Abgabe bis Dienstag, dem 08.11.2016 um 10 Uhr im Kasten 19
Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Marius Radermacher, M.Sc. DOOR Aufgabe 9 Versicherungstechnik Übungsblatt 3 Abgabe bis Dienstag, dem 08.11.2016 um 10 Uhr im Kasten 19
Übungen zur Versicherungsmathematik
 Übungen zur Versicherungsmathematik I Lebensversicherungsmathematik Vervollständige die folgende Tabelle, wobei jedes der Symbole durch die anderen ausgedrückt werden soll i d i d v r i i d +i v v +i r
Übungen zur Versicherungsmathematik I Lebensversicherungsmathematik Vervollständige die folgende Tabelle, wobei jedes der Symbole durch die anderen ausgedrückt werden soll i d i d v r i i d +i v v +i r
Zinseszins- und Rentenrechnung
 Zinseszins- und Rentenrechnung 1 Berechnen Sie den Zeitpunkt, an dem sich das Einlagekapital K bei a) jährlicher b) monatlicher c) stetiger Verzinsung verdoppelt hat, wobei i der jährliche nominelle Zinssatz
Zinseszins- und Rentenrechnung 1 Berechnen Sie den Zeitpunkt, an dem sich das Einlagekapital K bei a) jährlicher b) monatlicher c) stetiger Verzinsung verdoppelt hat, wobei i der jährliche nominelle Zinssatz
1 Einleitung Wesen der Versicherung Versicherungssparten Formen der Lebensversicherung Geschäftsverbindung...
 1 Einleitung... 1 1.1 Wesen der Versicherung... 1 1.2 Versicherungssparten... 2 1.3 Formen der Lebensversicherung... 4 1.4 Geschäftsverbindung... 5 1.5 Bedeutung der Lebensversicherung... 7 1.6 Historischer
1 Einleitung... 1 1.1 Wesen der Versicherung... 1 1.2 Versicherungssparten... 2 1.3 Formen der Lebensversicherung... 4 1.4 Geschäftsverbindung... 5 1.5 Bedeutung der Lebensversicherung... 7 1.6 Historischer
Deckungskapital. Proseminar Versicherungsmathematik. TU Graz. 11. Dezember 2007
 Deckungskapital Gülnur Adanç Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 1 Inhaltsverzeichnis 1 Deckungskapital 2 1.1 Prospektive und Retrospektive Methode.................... 3 1.1.1
Deckungskapital Gülnur Adanç Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 1 Inhaltsverzeichnis 1 Deckungskapital 2 1.1 Prospektive und Retrospektive Methode.................... 3 1.1.1
Cashflows von Versicherungsverträgen in der Lebensversicherung
 Cashflows von Versicherungsverträgen in der Lebensversicherung 5. Juni 2015 1 / 37 Inhalt Geschäftsmodell der Lebensversicherung Produkte der Lebensversicherung Zahlungsströme unter Unsicherheit Deckungsrückstellung
Cashflows von Versicherungsverträgen in der Lebensversicherung 5. Juni 2015 1 / 37 Inhalt Geschäftsmodell der Lebensversicherung Produkte der Lebensversicherung Zahlungsströme unter Unsicherheit Deckungsrückstellung
Lebensversicherungsmathematik. Vorbemerkungen, Literaturhinweise und Symbolverzeichnis
 Lebensversicherungsmathematik Vorbemerkungen, Literaturhinweise und Symbolverzeichnis Inhalt Datum 24.Apr 8.Mai 29.Mai!! 12.Jun 26.Jun 10.Jul 26. Jul Themen KE 1: Modellierung von Sterblichkeit KE 2: Modellierung
Lebensversicherungsmathematik Vorbemerkungen, Literaturhinweise und Symbolverzeichnis Inhalt Datum 24.Apr 8.Mai 29.Mai!! 12.Jun 26.Jun 10.Jul 26. Jul Themen KE 1: Modellierung von Sterblichkeit KE 2: Modellierung
Versicherungstechnik
 Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Dipl.-Math. Rolf Wendt DOOR Aufgabe 5 Versicherungstechnik Übungsblatt 2 Abgabe bis zum Dienstag, dem 27.0.205 um 0 Uhr im Kasten 9 Die
Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Dipl.-Math. Rolf Wendt DOOR Aufgabe 5 Versicherungstechnik Übungsblatt 2 Abgabe bis zum Dienstag, dem 27.0.205 um 0 Uhr im Kasten 9 Die
Lebensversicherungsmathematik. Kurseinheit 4 Prospektive Kalkulation (Aktuarielles Standardverfahren)
 Lebensversicherungsmathematik Kurseinheit 4 (Aktuarielles Standardverfahren) Inhalt Topic Leistungsbarwert und Nettoeinmalprämie Lernziel Grundidee der prospektiven Kalkulation (mit Vor- und Nachteilen)
Lebensversicherungsmathematik Kurseinheit 4 (Aktuarielles Standardverfahren) Inhalt Topic Leistungsbarwert und Nettoeinmalprämie Lernziel Grundidee der prospektiven Kalkulation (mit Vor- und Nachteilen)
vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist.
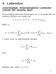 4. Leibrenten vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist. NEP ä x : Y = 1 + v + v 2 + + v K = ä
4. Leibrenten vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist. NEP ä x : Y = 1 + v + v 2 + + v K = ä
Mitschrift zur Vorlesung. von Jurgen Behne. Martin R. Elsner
 Mitschrift zur Vorlesung Versicherungsmathematik von Jurgen Behne im Wintersemester 1997/98, Sommersemester 1998 Martin R. Elsner " 4. Januar 1999 Inhaltsverzeichnis A Lebensversicherung 5 I Der Zins als
Mitschrift zur Vorlesung Versicherungsmathematik von Jurgen Behne im Wintersemester 1997/98, Sommersemester 1998 Martin R. Elsner " 4. Januar 1999 Inhaltsverzeichnis A Lebensversicherung 5 I Der Zins als
Zinseszins- und Rentenrechnung
 Zinseszins- und Rentenrechnung 1 Berechnen Sie den Zeitpunkt, an dem sich das Einlagekapital K bei a) jährlicher b) monatlicher c) stetiger Verzinsung verdoppelt hat, wobei i der jährliche nominelle Zinssatz
Zinseszins- und Rentenrechnung 1 Berechnen Sie den Zeitpunkt, an dem sich das Einlagekapital K bei a) jährlicher b) monatlicher c) stetiger Verzinsung verdoppelt hat, wobei i der jährliche nominelle Zinssatz
Renditeaspekte in der Rentenzahlungsphase
 watsonwyatt.com Renditeaspekte in der Rentenzahlungsphase Vergleich von marktrendite und biometrischer Rendite Alexander Schalk q x -Club, Berlin 12. März 2007 Agenda 1. Einleitung 2. Prinzip der lebenslangen
watsonwyatt.com Renditeaspekte in der Rentenzahlungsphase Vergleich von marktrendite und biometrischer Rendite Alexander Schalk q x -Club, Berlin 12. März 2007 Agenda 1. Einleitung 2. Prinzip der lebenslangen
Leseprobe. Wolfgang Eichholz, Eberhard Vilkner. Taschenbuch der Wirtschaftsmathematik. ISBN (Buch):
 Leseprobe Wolfgang Eichholz, Eberhard Vilkner Taschenbuch der Wirtschaftsmathematik ISBN Buch): 978-3-446-43535-3 ISBN E-Book): 978-3-446-43574- Weitere Informationen oder Bestellungen unter http://www.hanser-fachbuch.de/978-3-446-43535-3
Leseprobe Wolfgang Eichholz, Eberhard Vilkner Taschenbuch der Wirtschaftsmathematik ISBN Buch): 978-3-446-43535-3 ISBN E-Book): 978-3-446-43574- Weitere Informationen oder Bestellungen unter http://www.hanser-fachbuch.de/978-3-446-43535-3
Lebensversicherungsmathematik. Vorbemerkungen, Literaturhinweise und Symbolverzeichnis
 Lebensversicherungsmathematik Vorbemerkungen, Literaturhinweise und Symbolverzeichnis Inhalt Datum Themen 14.Okt KE 1: Modellierung von Sterblichkeit KE 2: Modellierung von Todesfall-Versicherungen 28.Okt
Lebensversicherungsmathematik Vorbemerkungen, Literaturhinweise und Symbolverzeichnis Inhalt Datum Themen 14.Okt KE 1: Modellierung von Sterblichkeit KE 2: Modellierung von Todesfall-Versicherungen 28.Okt
Condor Lebensversicherungs-AG Stand Seite 1 von 5
 Stand 01.01.2015 Seite 1 von 5 Besondere Bedingungen der für die Direktversicherung - Förderung nach 3 Nr. 63 Einkommensteuergesetz (EStG) - (9Y03) Stand: 01.01.2015 Inhaltsverzeichnis Welche Leistungen
Stand 01.01.2015 Seite 1 von 5 Besondere Bedingungen der für die Direktversicherung - Förderung nach 3 Nr. 63 Einkommensteuergesetz (EStG) - (9Y03) Stand: 01.01.2015 Inhaltsverzeichnis Welche Leistungen
Versicherungstechnik
 Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Dipl.-Math. Rolf Wendt DOOR Aufgabe 49 Versicherungstechnik Übungsblatt 15 Abgabe bis zum Dienstag, dem 02.02.2016 um 10 Uhr im Kasten
Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Dipl.-Math. Rolf Wendt DOOR Aufgabe 49 Versicherungstechnik Übungsblatt 15 Abgabe bis zum Dienstag, dem 02.02.2016 um 10 Uhr im Kasten
33) (bzw. 6) ) p = 7(%), K 0 = 0, 100(Euro) werden am Ersten des Monats eingezahlt, also vorschüssige Zahlung.
 1 Lösungsvorschläge zu der Zinsaufgaben 33 37 (bzw. 6 10): 33) (bzw. 6) ) p = 7(%), K 0 = 0, 100(Euro) werden am Ersten des Monats eingezahlt, also vorschüssige Zahlung. I) monatliche Zinsgutschrift: m
1 Lösungsvorschläge zu der Zinsaufgaben 33 37 (bzw. 6 10): 33) (bzw. 6) ) p = 7(%), K 0 = 0, 100(Euro) werden am Ersten des Monats eingezahlt, also vorschüssige Zahlung. I) monatliche Zinsgutschrift: m
III. Grundlagen der Lebensversicherungsmathematik III.5. Deckungskapital für Lebensversicherungsprodukte
 III. Grundlagen der Lebensversicherungsmathematik III.5. Deckungskapital für Lebensversicherungsprodukte Universität Basel Herbstsemester 2015 Dr. Ruprecht Witzel ruprecht.witzel@aktuariat-witzel.ch www.aktuariat-witzel.ch
III. Grundlagen der Lebensversicherungsmathematik III.5. Deckungskapital für Lebensversicherungsprodukte Universität Basel Herbstsemester 2015 Dr. Ruprecht Witzel ruprecht.witzel@aktuariat-witzel.ch www.aktuariat-witzel.ch
Muss man erst 100 werden, damit sich eine Rentenversicherung lohnt?
 Muss man erst 100 werden, damit sich Dr. Johannes Lörper Presse-Workshop, Berlin 26.1.17 Versicherer rechnen mit eigenen Sterbetafeln Lebenserwartung eines heute 60-jährigen Mannes Statistisches Bundesamt*
Muss man erst 100 werden, damit sich Dr. Johannes Lörper Presse-Workshop, Berlin 26.1.17 Versicherer rechnen mit eigenen Sterbetafeln Lebenserwartung eines heute 60-jährigen Mannes Statistisches Bundesamt*
ERGÄNZENDE BEDINGUNGEN FÜR AUFGESCHOBENE LEIBRENTENVERSICHERUNGEN
 Ausgabe 2014 ERGÄNZENDE BEDINGUNGEN FÜR AUFGESCHOBENE LEIBRENTENVERSICHERUNGEN INHALT 1. Begriffe 2 1.1 Rentenperiode 2 1.2 Inventar-Deckungskapital 2 1.3 Ausreichendes Deckungskapital 2 1.4 Rückkaufswert
Ausgabe 2014 ERGÄNZENDE BEDINGUNGEN FÜR AUFGESCHOBENE LEIBRENTENVERSICHERUNGEN INHALT 1. Begriffe 2 1.1 Rentenperiode 2 1.2 Inventar-Deckungskapital 2 1.3 Ausreichendes Deckungskapital 2 1.4 Rückkaufswert
Im Sinne einer besseren Lesbarkeit verwenden wir im Geschäftsbericht durchgängig die Begriffe Mitarbeiter und Vertreter.
 Allianz Versicherungs-AG Anhangangabe der Überschussanteilsätze Geschäftsbericht 2015 Im Sinne einer besseren Lesbarkeit verwenden wir im Geschäftsbericht durchgängig die Begriffe Mitarbeiter und Vertreter.
Allianz Versicherungs-AG Anhangangabe der Überschussanteilsätze Geschäftsbericht 2015 Im Sinne einer besseren Lesbarkeit verwenden wir im Geschäftsbericht durchgängig die Begriffe Mitarbeiter und Vertreter.
Wirtschaftsmathematik
 Einführung in einige Teilbereiche der Wintersemester 2016 Prof. Dr. Stefan Etschberger HSA m+1 re = r m + i 2 Äquivalenzprinzip der Finanzmathematik Das Äquivalenzprinzip der Finanzmathematik für Vergleich
Einführung in einige Teilbereiche der Wintersemester 2016 Prof. Dr. Stefan Etschberger HSA m+1 re = r m + i 2 Äquivalenzprinzip der Finanzmathematik Das Äquivalenzprinzip der Finanzmathematik für Vergleich
Kostenausweis mylife Nettotarife 2017 Stand
 Kostenausweis mylife Nettotarife 2017 Stand 03.2017 Inhaltsverzeichnis Seite Private Rente 1. mylife Classic (sofortbeginnend), Tarif LSN 2 2. mylife Fonds-Rente (auch als Direktversicherung) / mylife
Kostenausweis mylife Nettotarife 2017 Stand 03.2017 Inhaltsverzeichnis Seite Private Rente 1. mylife Classic (sofortbeginnend), Tarif LSN 2 2. mylife Fonds-Rente (auch als Direktversicherung) / mylife
Ein Unternehmen der R+V Versicherungsgruppe Mit Sicherheit besser unterwegs
 Ein Unternehmen der R+V Versicherungsgruppe Mit Sicherheit besser unterwegs Performance-Rente Wir leben länger und können uns nicht auf die gesetzliche Rente verlassen Wir Deutschen werden immer älter
Ein Unternehmen der R+V Versicherungsgruppe Mit Sicherheit besser unterwegs Performance-Rente Wir leben länger und können uns nicht auf die gesetzliche Rente verlassen Wir Deutschen werden immer älter
Lebensversicherungsmathematik Prüfungsbeispiele Termine 22.10.2004-25.6.2007 nach Themen geordnet
 Lebensversicherungsmathematik Prüfungsbeispiele Termine 22.10.2004-25.6.2007 nach Themen geordnet R. Kainhofer, Inst. f. Wirtschaftsmathematik, FAM, TU Wien Inhaltsverzeichnis 1 Prüfungsbeispiele der schriftlichen
Lebensversicherungsmathematik Prüfungsbeispiele Termine 22.10.2004-25.6.2007 nach Themen geordnet R. Kainhofer, Inst. f. Wirtschaftsmathematik, FAM, TU Wien Inhaltsverzeichnis 1 Prüfungsbeispiele der schriftlichen
Taschenbuch der Wirtschaftsmathematik
 Taschenbuch der Wirtschaftsmathematik Bearbeitet von Wolfgang Eichholz, Eberhard Vilkner 6., aktualisierte Auflage 013. Buch. 396 S. Kartoniert ISBN 978 3 446 43535 3 Format B x L): 1,7 x 19,5 cm Gewicht:
Taschenbuch der Wirtschaftsmathematik Bearbeitet von Wolfgang Eichholz, Eberhard Vilkner 6., aktualisierte Auflage 013. Buch. 396 S. Kartoniert ISBN 978 3 446 43535 3 Format B x L): 1,7 x 19,5 cm Gewicht:
III. Grundlagen der Lebensversicherungsmathematik III.3. Grundlagen der Theorie der Personengesamtheiten
 III. Grundlagen der Lebensversicherungsmathematik III.3. Grundlagen der Theorie der Personengesamtheiten Universität Basel Herbstsemester 2015 Dr. Ruprecht Witzel ruprecht.witzel@aktuariat-witzel.ch www.aktuariat-witzel.ch
III. Grundlagen der Lebensversicherungsmathematik III.3. Grundlagen der Theorie der Personengesamtheiten Universität Basel Herbstsemester 2015 Dr. Ruprecht Witzel ruprecht.witzel@aktuariat-witzel.ch www.aktuariat-witzel.ch
ANTWORTENKATALOG MVB RENTE PLUS / RIESTER
 ANTWORTENKATALOG MVB RENTE PLUS / RIESTER TEIL D: AUSZAHLPHASE INHALTSVERZEICHNIS STAND: 29.03.2017 Seite 1. Wann und in welcher Form erhalte ich Rentenzahlungen aus meinem MVB-RentePlus- Vertrag? 2. Was
ANTWORTENKATALOG MVB RENTE PLUS / RIESTER TEIL D: AUSZAHLPHASE INHALTSVERZEICHNIS STAND: 29.03.2017 Seite 1. Wann und in welcher Form erhalte ich Rentenzahlungen aus meinem MVB-RentePlus- Vertrag? 2. Was
Lebensversicherungsmathematik. Kurseinheit 5 Rentenversicherungen
 Lebensversicherungsmathematik Kurseinheit 5 1 Inhalt Topic Lernziel Sofortbeginnende Renten Ökonomische Grundlage für Rentenversicherung Rentengarantiezeiten Konzept der Vererbung Thielsche Gleichung für
Lebensversicherungsmathematik Kurseinheit 5 1 Inhalt Topic Lernziel Sofortbeginnende Renten Ökonomische Grundlage für Rentenversicherung Rentengarantiezeiten Konzept der Vererbung Thielsche Gleichung für
Anhang Überschussverteilung 2016
 39 Überschussverteilung 2016 Überschussbeteiligung der Versiche rungsnehmer/-innen in 2016 Für die Zuteilungen in 2016 werden die im Folgenden bestimmten laufenden Überschussanteile, für Fälligkeiten in
39 Überschussverteilung 2016 Überschussbeteiligung der Versiche rungsnehmer/-innen in 2016 Für die Zuteilungen in 2016 werden die im Folgenden bestimmten laufenden Überschussanteile, für Fälligkeiten in
Stochas(sche Unternehmensmodelle Op#onspreistheorie bei den LV/KV
 Stochas(sche Unternehmensmodelle Op#onspreistheorie bei den LV/KV Inhalt Op#onen und Garan#en in LV- /KV- Policen Produkte der LV/KV mit deren enthaltenen Opionalitäten und Garan#en Risiken der LV/KV Lebensversicherung
Stochas(sche Unternehmensmodelle Op#onspreistheorie bei den LV/KV Inhalt Op#onen und Garan#en in LV- /KV- Policen Produkte der LV/KV mit deren enthaltenen Opionalitäten und Garan#en Risiken der LV/KV Lebensversicherung
GARANTIE INVESTMENT RENTE
 GARANTIE INVESTMENT RENTE MEHR RENDITE = MEHR RENTE EINE DER HÖCHSTEN GARANTIERTEN RENTEN AM MARKT Schaffen Sie sich für das Alter genug finanzielle Freiheit, um Ihr Leben individuell und aktiv zu gestalten.
GARANTIE INVESTMENT RENTE MEHR RENDITE = MEHR RENTE EINE DER HÖCHSTEN GARANTIERTEN RENTEN AM MARKT Schaffen Sie sich für das Alter genug finanzielle Freiheit, um Ihr Leben individuell und aktiv zu gestalten.
GARANTIE INVESTMENT RENTE MEHR RENDITE = MEHR RENTE
 GARANTIE INVESTMENT RENTE MEHR RENDITE = MEHR RENTE EINE DER HÖCHSTEN GARANTIERTEN RENTEN AM MARKT Schaffen Sie sich für das Alter genug finanzielle Freiheit, um Ihr Leben individuell und aktiv zu gestalten.
GARANTIE INVESTMENT RENTE MEHR RENDITE = MEHR RENTE EINE DER HÖCHSTEN GARANTIERTEN RENTEN AM MARKT Schaffen Sie sich für das Alter genug finanzielle Freiheit, um Ihr Leben individuell und aktiv zu gestalten.
Alterseinkünftegesetz
 Die Rente ist sicher! Die Rente ist sicher! 1 Glauben Sie das wirklich? 2 Und was ist wenn Sie in Rente gehen? 69,5 48,2 55,8 Dann gibt es mit Sicherheit weniger 46,0 50,8 Rentenniveau 2000 2040 Rentenniveau
Die Rente ist sicher! Die Rente ist sicher! 1 Glauben Sie das wirklich? 2 Und was ist wenn Sie in Rente gehen? 69,5 48,2 55,8 Dann gibt es mit Sicherheit weniger 46,0 50,8 Rentenniveau 2000 2040 Rentenniveau
Zinsen, Zinseszins, Rentenrechnung und Tilgung
 Zinsen, Zinseszins, Rentenrechnung und Tilgung 1. Zinsen, Zinseszins 2. Rentenrechnung 3. Tilgung Nevzat Ates, Birgit Jacobs Zinsrechnen mit dem Dreisatz 1 Zinsen Zinsrechnen mit den Formeln Zinseszins
Zinsen, Zinseszins, Rentenrechnung und Tilgung 1. Zinsen, Zinseszins 2. Rentenrechnung 3. Tilgung Nevzat Ates, Birgit Jacobs Zinsrechnen mit dem Dreisatz 1 Zinsen Zinsrechnen mit den Formeln Zinseszins
Lebensversicherungsmathematik. Kurseinheit 3 Thielsche Gleichung und gemischte Versicherungen
 Lebensversicherungsmathematik Kurseinheit 3 und gemischte Versicherungen 1 Inhalt Topic Gemischte Lebensversicherung (Endowment) Lernziel Ökonomie der gemischten Lebensversicherung Prämien und Reservekalkulation
Lebensversicherungsmathematik Kurseinheit 3 und gemischte Versicherungen 1 Inhalt Topic Gemischte Lebensversicherung (Endowment) Lernziel Ökonomie der gemischten Lebensversicherung Prämien und Reservekalkulation
Bericht zur Prüfung im Oktober 2003 über Mathematik der Lebensversicherung (Grundwissen)
 Bericht zur Prüfung im Oktober 2003 über Mathematik der Lebensversicherung Grundwissen) Jürgen Strobel Köln) und Hans-Jochen Bartels Mannheim) Am 04.10.2003 wurde in Köln die zehnte Prüfung über Mathematik
Bericht zur Prüfung im Oktober 2003 über Mathematik der Lebensversicherung Grundwissen) Jürgen Strobel Köln) und Hans-Jochen Bartels Mannheim) Am 04.10.2003 wurde in Köln die zehnte Prüfung über Mathematik
Pensions- und Hinterbliebenenversicherung
 08. Jänner 2008 Überblick 1 Modell von Schärtlin Personengesamtheiten Übergangswahrscheinlichkeiten 2 Pension Überblick Modell von Schärtlin Personengesamtheiten Übergangswahrscheinlichkeiten Pension:
08. Jänner 2008 Überblick 1 Modell von Schärtlin Personengesamtheiten Übergangswahrscheinlichkeiten 2 Pension Überblick Modell von Schärtlin Personengesamtheiten Übergangswahrscheinlichkeiten Pension:
NÜRNBERGER DAX -Rente mit Sicherheitsplus.
 NÜRNBERGER DAX -Rente mit Sicherheitsplus. Die NÜRNBERGER DAX -Rente ist eine konventionelle Rentenversicherung, die Sie an der Wertentwicklung des DAX teilhaben lässt (Indexpartizipation). Vorsorge mit
NÜRNBERGER DAX -Rente mit Sicherheitsplus. Die NÜRNBERGER DAX -Rente ist eine konventionelle Rentenversicherung, die Sie an der Wertentwicklung des DAX teilhaben lässt (Indexpartizipation). Vorsorge mit
NÜRNBERGER DAX -Rente mit Sicherheitsplus.
 NÜRNBERGER DAX -Rente mit Sicherheitsplus. Die NÜRNBERGER DAX -Rente ist eine konventionelle Rentenversicherung, die Sie an der Wertentwicklung des DAX teilhaben lässt (Indexpartizipation). Vorsorge mit
NÜRNBERGER DAX -Rente mit Sicherheitsplus. Die NÜRNBERGER DAX -Rente ist eine konventionelle Rentenversicherung, die Sie an der Wertentwicklung des DAX teilhaben lässt (Indexpartizipation). Vorsorge mit
Cashflows in Versicherungsverträgen der KV
 Cashflows in Versicherungsverträgen der KV Sarah Dempwolf 5. Juni 2015 Universität zu Köln Gliederung 1. Vergleich von privaten und gesetzlichen Krankenversicherungen 2. Allgemeines zur PKV 3. Kostenerstattungsprinzip
Cashflows in Versicherungsverträgen der KV Sarah Dempwolf 5. Juni 2015 Universität zu Köln Gliederung 1. Vergleich von privaten und gesetzlichen Krankenversicherungen 2. Allgemeines zur PKV 3. Kostenerstattungsprinzip
Todesfallversicherungen
 Todesfallversicherungen Unsere Todesfallversicherungen mit garantiertem Kapital bieten Familien, Paaren, Eigenheimbesitzern und Geschäftspartnern finanzielle Sicherheit. Ein gutes Gefühl! Finanzielle Sicherheit
Todesfallversicherungen Unsere Todesfallversicherungen mit garantiertem Kapital bieten Familien, Paaren, Eigenheimbesitzern und Geschäftspartnern finanzielle Sicherheit. Ein gutes Gefühl! Finanzielle Sicherheit
Überschussbeteiligung der Versicherungsnehmer
 Überschussbeteiligung der Versicherungsnehmer Die Sicherung der dauernden Erfüllbarkeit der Verträge mit garantierten Leistungen machen vorsichtige Annahmen bezüglich der versicherten Risiken und der Zinserwartung
Überschussbeteiligung der Versicherungsnehmer Die Sicherung der dauernden Erfüllbarkeit der Verträge mit garantierten Leistungen machen vorsichtige Annahmen bezüglich der versicherten Risiken und der Zinserwartung
Der Unterschied zwischen gesetzlicher und privater Krankenversicherung
 Der Unterschied zwischen gesetzlicher und privater Krankenversicherung Rainer Voss AOK Rheinland/Hamburg, Regionaldirektion Essen Mülheim an der Ruhr In der gesetzlichen Krankenversicherung sind Arbeitnehmer
Der Unterschied zwischen gesetzlicher und privater Krankenversicherung Rainer Voss AOK Rheinland/Hamburg, Regionaldirektion Essen Mülheim an der Ruhr In der gesetzlichen Krankenversicherung sind Arbeitnehmer
Im Sinne einer besseren Lesbarkeit verwenden wir im Geschäftsbericht durchgängig die Begriffe Mitarbeiter und Vertreter.
 Allianz Versicherungs-AG Anhangangabe der Überschussanteilsätze Geschäftsbericht 2016 Im Sinne einer besseren Lesbarkeit verwenden wir im Geschäftsbericht durchgängig die Begriffe Mitarbeiter und Vertreter.
Allianz Versicherungs-AG Anhangangabe der Überschussanteilsätze Geschäftsbericht 2016 Im Sinne einer besseren Lesbarkeit verwenden wir im Geschäftsbericht durchgängig die Begriffe Mitarbeiter und Vertreter.
Steuer Allgemein. Versicherteninformation mylife Steuer Allgemein. www.mylife-leben.de
 Steuer Allgemein Versicherteninformation mylife Steuer Allgemein www.mylife-leben.de Merkblatt Steuerinformation allgemein Steuerrechtliche Rahmenbedingungen Die folgenden Informationen geben Ihnen einen
Steuer Allgemein Versicherteninformation mylife Steuer Allgemein www.mylife-leben.de Merkblatt Steuerinformation allgemein Steuerrechtliche Rahmenbedingungen Die folgenden Informationen geben Ihnen einen
Zinsratentheorie in der Versicherung
 Zinsratentheorie in der Versicherung Julia Eisenberg 04.05.2010 Gliederung 1 Bewertung durch Diversifikation Gesetz der großen Zahl Zinssatz, Aufzinsungs- und Diskontierungsfaktoren Verluste und Äquivalenzprinzip
Zinsratentheorie in der Versicherung Julia Eisenberg 04.05.2010 Gliederung 1 Bewertung durch Diversifikation Gesetz der großen Zahl Zinssatz, Aufzinsungs- und Diskontierungsfaktoren Verluste und Äquivalenzprinzip
Altersvorsorgevertrag für das geförderte Sparen in weiteren Geschäftsanteilen an Wohnungsgenossenschaften
 Altersvorsorgevertrag für das geförderte Sparen in weiteren Geschäftsanteilen an Wohnungsgenossenschaften Muster des GdW Bundesverband deutscher Wohnungs- und Immobilienunternehmen e.v. zwischen (Mitglied)
Altersvorsorgevertrag für das geförderte Sparen in weiteren Geschäftsanteilen an Wohnungsgenossenschaften Muster des GdW Bundesverband deutscher Wohnungs- und Immobilienunternehmen e.v. zwischen (Mitglied)
Die Lösung für Ihre Pläne. BasiAL, die Basisrente der ALTE LEIPZIGER. Private Altersvorsorge BASISRENTE
 Private Altersvorsorge BASISRENTE Optionale Sicherheitsbausteine: n Berufsunfähigkeitsschutz n Hinterbliebenenschutz Die Lösung für Ihre Pläne. BasiAL, die Basisrente der ALTE LEIPZIGER. Finanzielle Sicherheit
Private Altersvorsorge BASISRENTE Optionale Sicherheitsbausteine: n Berufsunfähigkeitsschutz n Hinterbliebenenschutz Die Lösung für Ihre Pläne. BasiAL, die Basisrente der ALTE LEIPZIGER. Finanzielle Sicherheit
6. Übungsblatt zur Einführung in die Stochastik
 Fachbereich Mathematik Prof. Dr. Michael Kohler Dipl.-Math. Andreas Fromkorth Dipl.-Inf. Jens Mehnert SS 9 1.6.29 6. Übungsblatt zur Einführung in die Stochastik Aufgabe 22 Sei P ein auf der Borelschen
Fachbereich Mathematik Prof. Dr. Michael Kohler Dipl.-Math. Andreas Fromkorth Dipl.-Inf. Jens Mehnert SS 9 1.6.29 6. Übungsblatt zur Einführung in die Stochastik Aufgabe 22 Sei P ein auf der Borelschen
Mit Sicherheit ein Leben lang
 Ein Unternehmen der R+V Versicherungsgruppe Mit Sicherheit ein Leben lang Sofort-Rente Jetzt mit einer Einmalzahlung ein Leben lang versorgt sein und entspannt in die Zukunft blicken Wir Deutschen werden
Ein Unternehmen der R+V Versicherungsgruppe Mit Sicherheit ein Leben lang Sofort-Rente Jetzt mit einer Einmalzahlung ein Leben lang versorgt sein und entspannt in die Zukunft blicken Wir Deutschen werden
Grundbegriffe Gegenstand der Tilgungsrechnung ist ein von einem Gläubiger (z. B. Bank) an einen Schuldner ausgeliehener Geldbetrag S;
 1 5.3. Tilgungsrechnung Grundbegriffe Gegenstand der Tilgungsrechnung ist ein von einem Gläubiger (z. B. Bank) an einen Schuldner ausgeliehener Geldbetrag S; Bezeichnung: S... Schuld, Darlehen, Kredit
1 5.3. Tilgungsrechnung Grundbegriffe Gegenstand der Tilgungsrechnung ist ein von einem Gläubiger (z. B. Bank) an einen Schuldner ausgeliehener Geldbetrag S; Bezeichnung: S... Schuld, Darlehen, Kredit
Überschussbeteiligung 2016
 Seite 1 Überschussbeteiligung 2016 für die für das Neugeschäft geöffneten Tarife Barmenia BasisRente Classic... 2 Barmenia BasisRente Invest... 3 Barmenia BasisRente Sofort... 4 Barmenia FörderRente Classic...
Seite 1 Überschussbeteiligung 2016 für die für das Neugeschäft geöffneten Tarife Barmenia BasisRente Classic... 2 Barmenia BasisRente Invest... 3 Barmenia BasisRente Sofort... 4 Barmenia FörderRente Classic...
Helvetia PayPlan. Das flexible Rentenkonto für die Generation 50 plus.
 Helvetia PayPlan Das flexible Rentenkonto für die Generation 50 plus. 1 Zitat Früher sprach man bei Bundesschatzbriefen von einer risikolosen Rendite, nun sollte man von einem renditelosem Risiko reden.
Helvetia PayPlan Das flexible Rentenkonto für die Generation 50 plus. 1 Zitat Früher sprach man bei Bundesschatzbriefen von einer risikolosen Rendite, nun sollte man von einem renditelosem Risiko reden.
Vertrieb Leben (02/2011)
 1 Basis der Garantiemodelle n Hauptunterscheidung der Garantien n Festverzinsliche Wertpapiere n Optionen 2 Übersicht von Garantiemodellen regelbasierte Modelle Statisches 2-Topf-Hybrid Statisches 2-Topf-Hybrid
1 Basis der Garantiemodelle n Hauptunterscheidung der Garantien n Festverzinsliche Wertpapiere n Optionen 2 Übersicht von Garantiemodellen regelbasierte Modelle Statisches 2-Topf-Hybrid Statisches 2-Topf-Hybrid
Ein Unternehmen der R+V Versicherungsgruppe Chancen ohne Risiko
 Ein Unternehmen der R+V Versicherungsgruppe Chancen ohne Risiko INDEX-Rente Jetzt für das Alter vorsorgen und entspannt in die Zukunft blicken Wir Deutschen werden immer älter und können so unseren längsten
Ein Unternehmen der R+V Versicherungsgruppe Chancen ohne Risiko INDEX-Rente Jetzt für das Alter vorsorgen und entspannt in die Zukunft blicken Wir Deutschen werden immer älter und können so unseren längsten
Kräftig Steuern sparen mit BasisRente. Die Altersvorsorge, von der ich schon heute profitiere.
 Kräftig Steuern sparen mit. Die Altersvorsorge, von der ich schon heute profitiere. Die Rente ist sicher. Auch für mich? Irgendwann haben Sie das Rentenalter erreicht. Aber reicht dann auch Ihre Rente?
Kräftig Steuern sparen mit. Die Altersvorsorge, von der ich schon heute profitiere. Die Rente ist sicher. Auch für mich? Irgendwann haben Sie das Rentenalter erreicht. Aber reicht dann auch Ihre Rente?
Rente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren Rentenperiode = Zeitabstand zwischen zwei Rentenzahlungen
 5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
Mathematik 1 für Wirtschaftsinformatik
 Mathematik 1 für Wirtschaftsinformatik Wintersemester 2012/13 Hochschule Augsburg Äquivalenzprinzip der Finanzmathematik Das Äquivalenzprinzip der Finanzmathematik für Vergleich von Zahlungen, welche
Mathematik 1 für Wirtschaftsinformatik Wintersemester 2012/13 Hochschule Augsburg Äquivalenzprinzip der Finanzmathematik Das Äquivalenzprinzip der Finanzmathematik für Vergleich von Zahlungen, welche
Übungsaufgaben zu Kapitel 6: Finanzmärkte und Erwartungen
 Kapitel 6 Übungsaufgaben zu Kapitel 6: Finanzmärkte und Erwartungen Übungsaufgabe 6-1a 6-1a) Welche Typen von Zinsstrukturkurven kennen Sie? Stellen Sie die Typen graphisch dar und erläutern Sie diese.
Kapitel 6 Übungsaufgaben zu Kapitel 6: Finanzmärkte und Erwartungen Übungsaufgabe 6-1a 6-1a) Welche Typen von Zinsstrukturkurven kennen Sie? Stellen Sie die Typen graphisch dar und erläutern Sie diese.
Übungen zur Vorlesung QM II Unterjährliche Renten Aufgabe 8.1 Ein Auto wird auf Leasingbasis zu folgenden Bedingungen erworben:
 Technische Hochschule Köln Fakultät für Wirtschafts- und Rechtswissenschaften Prof. Dr. Arrenberg Raum 221, Tel. 39 14 jutta.arrenberg@th-koeln.de Übungen zur Vorlesung QM II Unterjährliche Renten Aufgabe
Technische Hochschule Köln Fakultät für Wirtschafts- und Rechtswissenschaften Prof. Dr. Arrenberg Raum 221, Tel. 39 14 jutta.arrenberg@th-koeln.de Übungen zur Vorlesung QM II Unterjährliche Renten Aufgabe
2013 Generali Rente Chance Plus Chance aber bitte mit Garantie!
 Nur zur internen Verwendung! 2013 Generali Rente Chance Plus Chance aber bitte mit Garantie! Vorstellung bei der Mertens & Ludwig GbR Dortmund, 30.04.2013 Chance mit Garantie Nur zur internen Verwendung!
Nur zur internen Verwendung! 2013 Generali Rente Chance Plus Chance aber bitte mit Garantie! Vorstellung bei der Mertens & Ludwig GbR Dortmund, 30.04.2013 Chance mit Garantie Nur zur internen Verwendung!
Wirtschaftsmathematik
 Einführung in einige Teilbereiche der Sommersemester 2015 Prof. Dr. Stefan Etschberger HSA Rentenrechnung Definition Rente: Zahlungsstrom mit Zahlungen in gleichen zeitlichen Abständen und (meistens) in
Einführung in einige Teilbereiche der Sommersemester 2015 Prof. Dr. Stefan Etschberger HSA Rentenrechnung Definition Rente: Zahlungsstrom mit Zahlungen in gleichen zeitlichen Abständen und (meistens) in
3.3. Tilgungsrechnung
 3.3. Tilgungsrechnung Grundbegriffe Gegenstand der Tilgungsrechnung ist ein von einem Gläubiger (z. B. Bank) an einen Schuldner ausgeliehener Geldbetrag S; Bezeichnung: S... Schuld, Darlehen, Kredit Es
3.3. Tilgungsrechnung Grundbegriffe Gegenstand der Tilgungsrechnung ist ein von einem Gläubiger (z. B. Bank) an einen Schuldner ausgeliehener Geldbetrag S; Bezeichnung: S... Schuld, Darlehen, Kredit Es
= = x 2 = 2x x 2 1 = x 3 = 2x x 2 2 =
 1 Lösungsvorschläge zu den Aufgaben 28, 29, 30 b), 31, 32, 33, 35, 36 i) und 37 a) von Blatt 4: 28) a) fx) := x 3 10! = 0 Wir bestimmen eine Näherungslösung mit dem Newtonverfahren: Als Startwert wählen
1 Lösungsvorschläge zu den Aufgaben 28, 29, 30 b), 31, 32, 33, 35, 36 i) und 37 a) von Blatt 4: 28) a) fx) := x 3 10! = 0 Wir bestimmen eine Näherungslösung mit dem Newtonverfahren: Als Startwert wählen
Überlegungen zur transparenten Gestaltung einer Lebensversicherung
 Überlegungen zur transparenten Gestaltung einer Lebensversicherung 1 Transparenz ist zielorientiert ist kein Selbstzweck hat Grenzen 2 Produkttransparenz Markttransparenz Klarheit über die Leistung Vertragsmacht
Überlegungen zur transparenten Gestaltung einer Lebensversicherung 1 Transparenz ist zielorientiert ist kein Selbstzweck hat Grenzen 2 Produkttransparenz Markttransparenz Klarheit über die Leistung Vertragsmacht
Anlage zum Geschäftsbericht IDUNA Vereinigte Lebensversicherung ag für Handwerk, Handel und Gewerbe
 Anlage zum Geschäftsbericht 205 IDUNA Vereinigte Lebensversicherung ag für Handwerk, Handel und Gewerbe Überschussanteile Überschussanteile für die Versicherungsnehmer 206 Auf den nachfolgenden Seiten
Anlage zum Geschäftsbericht 205 IDUNA Vereinigte Lebensversicherung ag für Handwerk, Handel und Gewerbe Überschussanteile Überschussanteile für die Versicherungsnehmer 206 Auf den nachfolgenden Seiten
PiL-Gutachten. Wichtiger Risikoschutz. Bestellnummer: 8428
 PiL-Gutachten Wichtiger Risikoschutz Bestellnummer: 8428 27.06.2014 Sehr geehrter Herr Muster, Sie besitzen einen Vertrag mit ausgeprägtem Risikoschutz. Aus diesem Grund konzentrieren wir uns zunächst
PiL-Gutachten Wichtiger Risikoschutz Bestellnummer: 8428 27.06.2014 Sehr geehrter Herr Muster, Sie besitzen einen Vertrag mit ausgeprägtem Risikoschutz. Aus diesem Grund konzentrieren wir uns zunächst
Tarif 30 Swiss Life BUZ / BUZ plus
 Produktleistung Tarif 30 Swiss Life BUZ / BUZ plus Kurzbeschreibung Berufsunfähigkeits-Zusatzversicherung (BUZ) Swiss Life BUZ plus: Berufsunfähigkeits-Zusatzversicherung mit Rente bei Arbeitsunfähigkeit
Produktleistung Tarif 30 Swiss Life BUZ / BUZ plus Kurzbeschreibung Berufsunfähigkeits-Zusatzversicherung (BUZ) Swiss Life BUZ plus: Berufsunfähigkeits-Zusatzversicherung mit Rente bei Arbeitsunfähigkeit
Lebensversicherungsmathematik. Kurseinheit 2 Modellierung von Todesfallversicherungen. Modellierung von Todesfallversicherungen 1
 Lebensversicherungsmathematik Kurseinheit 2 Modellierung von Todesfallversicherungen 1 Inhalt Topic Technisch einjährige Todesfall-Versicherung (yearly renewalbe term YRT ) Risikoprämie in der Fondsgebundenen
Lebensversicherungsmathematik Kurseinheit 2 Modellierung von Todesfallversicherungen 1 Inhalt Topic Technisch einjährige Todesfall-Versicherung (yearly renewalbe term YRT ) Risikoprämie in der Fondsgebundenen
FAQs zu»albärt«dem Kindervorsorge-Konzept
 Geschäftspartner FAQs zu»albärt«dem Kindervorsorge-Konzept Juli 2016 INFOS & FAKTEN FAQs zu»albärt«dem Kindervorsorge-Konzept Um Sie bestmöglich bei der Beratung zu unserem Kindervorsorge-Konzept»ALbärt«zu
Geschäftspartner FAQs zu»albärt«dem Kindervorsorge-Konzept Juli 2016 INFOS & FAKTEN FAQs zu»albärt«dem Kindervorsorge-Konzept Um Sie bestmöglich bei der Beratung zu unserem Kindervorsorge-Konzept»ALbärt«zu
Die Altersvorsorge, von der ich schon heute profitiere.
 Die Altersvorsorge, von der ich schon heute profitiere. Die Rente ist sicher. Auch für mich? Irgendwann haben Sie das Rentenalter erreicht. Aber reicht dann auch Ihre Rente? Wer sich heute darauf freut,
Die Altersvorsorge, von der ich schon heute profitiere. Die Rente ist sicher. Auch für mich? Irgendwann haben Sie das Rentenalter erreicht. Aber reicht dann auch Ihre Rente? Wer sich heute darauf freut,
GEGENÜBERSTELLUNG PRODUKTINFORMATIONSBLATT
 GEGENÜBERSTELLUNG PRODUKTINFORMATIONSBLATT Gesamtverband der Deutschen Versicherungswirtschaft (GDV) / Prof. Hans-Peter SCHWINTOWSKI, Humboldt-Universität (beide Berlin) Produktinformationsblatt GDV Formulierungsvorschlag
GEGENÜBERSTELLUNG PRODUKTINFORMATIONSBLATT Gesamtverband der Deutschen Versicherungswirtschaft (GDV) / Prof. Hans-Peter SCHWINTOWSKI, Humboldt-Universität (beide Berlin) Produktinformationsblatt GDV Formulierungsvorschlag
Einführung in die Stochastik 6. Übungsblatt
 Einführung in die Stochastik 6. Übungsblatt Fachbereich Mathematik SS M. Kohler 3. Mai A. Fromkorth D. Furer Gruppen und Hausübung Aufgabe (a) Die Wahrscheinlichkeit, dass eine S Bahn Verspätung hat, betrage.3.
Einführung in die Stochastik 6. Übungsblatt Fachbereich Mathematik SS M. Kohler 3. Mai A. Fromkorth D. Furer Gruppen und Hausübung Aufgabe (a) Die Wahrscheinlichkeit, dass eine S Bahn Verspätung hat, betrage.3.
Vorsorgeaufwendungen Rentenbesteuerung Kapitallebensversicherungen Neuerungen ab dem 01.01.2005
 Vorsorgeaufwendungen Rentenbesteuerung Kapitallebensversicherungen Neuerungen ab dem 01.01.2005 Kompetenz beweisen. Vertrauen verdienen. Durch das Alterseinkünftegesetz (AltEinkG) wurde die Beitragsfreistellung
Vorsorgeaufwendungen Rentenbesteuerung Kapitallebensversicherungen Neuerungen ab dem 01.01.2005 Kompetenz beweisen. Vertrauen verdienen. Durch das Alterseinkünftegesetz (AltEinkG) wurde die Beitragsfreistellung
Lebensversicherungs - Mathematik
 Die Prinzipien der Lebensversicherungs - Mathematik von P. Sdiouten, Associate of the Institute of Actuaries in London. Aus dem Holländischen übersetzt von Т. Chr. F. Reach. Vorwort von Corneille L. Landre..0.
Die Prinzipien der Lebensversicherungs - Mathematik von P. Sdiouten, Associate of the Institute of Actuaries in London. Aus dem Holländischen übersetzt von Т. Chr. F. Reach. Vorwort von Corneille L. Landre..0.
Individueller Vorschlag für Herrn Muster Hans vom
 Individueller Vorschlag 1601080009 für Herrn Muster Hans vom 16.11.2012 Dieser Vorschlag wurde Ihnen überreicht von Ihrem IDEAL Partner: MAV-Versicherungsmakler Martin Alberer Schleißheimer Str. 207 80809
Individueller Vorschlag 1601080009 für Herrn Muster Hans vom 16.11.2012 Dieser Vorschlag wurde Ihnen überreicht von Ihrem IDEAL Partner: MAV-Versicherungsmakler Martin Alberer Schleißheimer Str. 207 80809
Generali 3-Phasen-Rente Bunt wie das Leben
 Generali 3-Phasen-Rente Bunt wie das Leben Die neue Generali 3-Phasen-Rente Konventionelle Rentenversicherung mit sensationeller Verfügbarkeit Einmalanlagen bereits ab 10.000 Option bei Pflege ohne Gesundheitsfragen
Generali 3-Phasen-Rente Bunt wie das Leben Die neue Generali 3-Phasen-Rente Konventionelle Rentenversicherung mit sensationeller Verfügbarkeit Einmalanlagen bereits ab 10.000 Option bei Pflege ohne Gesundheitsfragen
Gesetz zur Neuordnung der einkommensteuerrechtlichen Behandlung von Altersvorsorgeaufwendungen und Altersbezügen (Alterseinkünftegesetz - AltEinkG)
 Gesetz zur Neuordnung der einkommensteuerrechtlichen Behandlung von und Altersbezügen (Alterseinkünftegesetz - AltEinkG) Die wichtigsten Änderungen im Überblick Inhalt: Änderungen bei Kapitalversicherungen
Gesetz zur Neuordnung der einkommensteuerrechtlichen Behandlung von und Altersbezügen (Alterseinkünftegesetz - AltEinkG) Die wichtigsten Änderungen im Überblick Inhalt: Änderungen bei Kapitalversicherungen
Sterbegeld-Police ohne Gesundheitsprüfung Information. Das Leben genießen. Weil alles geregelt ist. Einmal kümmern. Nie mehr darüber nachdenken.
 Sterbegeld-Police ohne Gesundheitsprüfung Information Das Leben genießen. Weil alles geregelt ist. Einmal kümmern. Nie mehr darüber nachdenken. Ihre Vorsorge ein Zeichen der Fürsorge. Es gibt Dinge, die
Sterbegeld-Police ohne Gesundheitsprüfung Information Das Leben genießen. Weil alles geregelt ist. Einmal kümmern. Nie mehr darüber nachdenken. Ihre Vorsorge ein Zeichen der Fürsorge. Es gibt Dinge, die
IDEAL Versicherung. IDEAL PflegeRente. Tarif und Verkauf - Stand 04/2013. Der Spezialist für Senioren.
 IDEAL Versicherung IDEAL PflegeRente Tarif und Verkauf - Stand 04/2013 Der Spezialist für Senioren. Ihr Referent 2 Birger Mählmann Leitender Vertriebstrainer der IDEAL Versicherungsgruppe Agenda 3 Warum
IDEAL Versicherung IDEAL PflegeRente Tarif und Verkauf - Stand 04/2013 Der Spezialist für Senioren. Ihr Referent 2 Birger Mählmann Leitender Vertriebstrainer der IDEAL Versicherungsgruppe Agenda 3 Warum
Kapitel 4. Folgen und Reihen. Josef Leydold Auffrischungskurs Mathematik WS 2017/18 4 Folgen und Reihen 1 / 38
 Kapitel 4 Folgen und Reihen Josef Leydold Auffrischungskurs Mathematik WS 2017/18 4 Folgen und Reihen 1 / 38 Folgen Eine Folge ist eine Anordnung von reellen Zahlen. Die einzelnen Zahlen heißen Glieder
Kapitel 4 Folgen und Reihen Josef Leydold Auffrischungskurs Mathematik WS 2017/18 4 Folgen und Reihen 1 / 38 Folgen Eine Folge ist eine Anordnung von reellen Zahlen. Die einzelnen Zahlen heißen Glieder
TU Kaiserslautern, SS 2012 von Dr. Hans-Otto Herr
 Praxis der Lebensversicherungs- mathematik TU Kaiserslautern, SS 2012 von Dr. Hans-Otto Herr 1 Über mich 56 Jahre alt Mathematikstudium in Mainz Diplom 1983, Promotion 1988 Wissenschaftlicher Mitarbeiter
Praxis der Lebensversicherungs- mathematik TU Kaiserslautern, SS 2012 von Dr. Hans-Otto Herr 1 Über mich 56 Jahre alt Mathematikstudium in Mainz Diplom 1983, Promotion 1988 Wissenschaftlicher Mitarbeiter
Beitragserhöhung? Tarif wechseln!
 Beitragserhöhung? Tarif wechseln! Vielen privat Krankenversicherten wird Jahr für Jahr die Erhöhung ihres Beitrags mitgeteilt, teils spürbar. Was tun? Mit einem Tarifwechsel innerhalb der bestehenden Versicherung
Beitragserhöhung? Tarif wechseln! Vielen privat Krankenversicherten wird Jahr für Jahr die Erhöhung ihres Beitrags mitgeteilt, teils spürbar. Was tun? Mit einem Tarifwechsel innerhalb der bestehenden Versicherung
Geben Sie Ihrem Ruhestand eine sichere Basis!
 ds:basis Die steuerlich geförderte Altersvorsorge mit fl exibler Beitragszahlung Geben Sie Ihrem Ruhestand eine sichere Basis! Hohe lebenslange Garantierente Steigende Steuerförderung in der Ansparphase
ds:basis Die steuerlich geförderte Altersvorsorge mit fl exibler Beitragszahlung Geben Sie Ihrem Ruhestand eine sichere Basis! Hohe lebenslange Garantierente Steigende Steuerförderung in der Ansparphase
Die Kosten einer garantierten, lebenslangen Rente
 Die Kosten einer garantierten, lebenslangen Rente Berlin, 16. März 2016 Herzlich Willkommen Prof. Michael Hauer Institut für Vorsorge und Finanzplanung Übersicht 1 Einstieg: Warum Altersvorsorge? 2 Vorstellung
Die Kosten einer garantierten, lebenslangen Rente Berlin, 16. März 2016 Herzlich Willkommen Prof. Michael Hauer Institut für Vorsorge und Finanzplanung Übersicht 1 Einstieg: Warum Altersvorsorge? 2 Vorstellung
Unser Vorschlag im Überblick FiskAL Klassische Riester-Rente (HRV50) im Rahmen des Honorartarifes
 Unser Vorschlag im Überblick FiskAL Klassische Riester-Rente (HRV50) im Rahmen des Honorartarifes Persönliche Daten Versicherter Herr Wertpapier Forum Geburtsdatum 01.06.1984 Jährlicher Beitrag Versicherungsbeginn
Unser Vorschlag im Überblick FiskAL Klassische Riester-Rente (HRV50) im Rahmen des Honorartarifes Persönliche Daten Versicherter Herr Wertpapier Forum Geburtsdatum 01.06.1984 Jährlicher Beitrag Versicherungsbeginn
Die Altersvorsorge, von der ich schon heute profitiere.
 Die Altersvorsorge, von der ich schon heute profitiere. Kräftig Steuern sparen mit. Die Rente ist sicher. Auch für mich? Irgendwann haben Sie das Rentenalter erreicht. Aber reicht dann auch Ihre Rente?
Die Altersvorsorge, von der ich schon heute profitiere. Kräftig Steuern sparen mit. Die Rente ist sicher. Auch für mich? Irgendwann haben Sie das Rentenalter erreicht. Aber reicht dann auch Ihre Rente?
F-Mathe-Klausur am
 F-Mathe-Klausur am 19.07.2017 Aufgabe 1 Jemand zahlt bei 4% Zinsen p.a. im Zeitraum vom 01.01.2010 bis 31.12.2015 jeweils zu Beginn eines Monats 200 und im Zeitraum vom 01.01.2016 bis 31.12.2018 jeweils
F-Mathe-Klausur am 19.07.2017 Aufgabe 1 Jemand zahlt bei 4% Zinsen p.a. im Zeitraum vom 01.01.2010 bis 31.12.2015 jeweils zu Beginn eines Monats 200 und im Zeitraum vom 01.01.2016 bis 31.12.2018 jeweils
BASISRENTE FÜRS ALTER VORSORGEN UND DABEI STEUERN SPAREN
 BASISRENTE FÜRS ALTER VORSORGEN UND DABEI STEUERN SPAREN 03 INHALT AUCH SELBSTSTÄNDIGE MÜSSEN VORSORGEN 04 WAS IST EINE BASISRENTENVERSICHERUNG? 06 DER STAAT UNTERSTÜTZT SIE 08 DIE RENTE VOLL VERSTEUERN?
BASISRENTE FÜRS ALTER VORSORGEN UND DABEI STEUERN SPAREN 03 INHALT AUCH SELBSTSTÄNDIGE MÜSSEN VORSORGEN 04 WAS IST EINE BASISRENTENVERSICHERUNG? 06 DER STAAT UNTERSTÜTZT SIE 08 DIE RENTE VOLL VERSTEUERN?
Praktische Lebensversicheru ngsmathematik
 Karl MichaelOrtmann Praktische Lebensversicheru ngsmathematik Mit zahlreichen Beispielen, Abbildungen und Anwendungen STUDIUM 11 VIEWEG+ TEUBNER Inhaltsverzeichnis 1 Einleitung 1 1.1 Wesen der Versicherung
Karl MichaelOrtmann Praktische Lebensversicheru ngsmathematik Mit zahlreichen Beispielen, Abbildungen und Anwendungen STUDIUM 11 VIEWEG+ TEUBNER Inhaltsverzeichnis 1 Einleitung 1 1.1 Wesen der Versicherung
Langfristige Bedeutung des Rechnungszinses für Versorgungswerke
 Langfristige Bedeutung des Rechnungszinses für Versorgungswerke Dr. Richard Herrmann, Köln 16. Juni 2006 Langfristige Bedeutung des Rechnungszins für Versorgungswerke Gliederung 1. Garantien in der Altersversorgung
Langfristige Bedeutung des Rechnungszinses für Versorgungswerke Dr. Richard Herrmann, Köln 16. Juni 2006 Langfristige Bedeutung des Rechnungszins für Versorgungswerke Gliederung 1. Garantien in der Altersversorgung
Absicherung. Frischer Wind für Ihre Altersvorsorge. Mit der Basis Rente auf Kurs. Verwandeln Sie Ihre Steuer in Ihre Altersvorsorge.
 Absicherung Frischer Wind für Ihre Altersvorsorge. Mit der Basis Rente auf Kurs. Verwandeln Sie Ihre Steuer in Ihre Altersvorsorge. Starker Rückenwind: Hohe Steuervorteile für Ihre Altersvorsorge. Wer
Absicherung Frischer Wind für Ihre Altersvorsorge. Mit der Basis Rente auf Kurs. Verwandeln Sie Ihre Steuer in Ihre Altersvorsorge. Starker Rückenwind: Hohe Steuervorteile für Ihre Altersvorsorge. Wer
NÜRNBERGER Konzept-Tarife. Produktförderung Leben, Stand 12/2015 Keine Weitergabe an Kunden und Dritte - nur für interne Zwecke unverbindlich.
 Chancen im Verkauf Sparverhalten der Deutschen: Sicherheit geht vor Rendite Chancen im Verkauf Der Kapitalmarkt aktuelle Situation Die Umlaufrendite* liegt bei 0,40% (Stand 18.12.2015) * Die Umlaufrendite
Chancen im Verkauf Sparverhalten der Deutschen: Sicherheit geht vor Rendite Chancen im Verkauf Der Kapitalmarkt aktuelle Situation Die Umlaufrendite* liegt bei 0,40% (Stand 18.12.2015) * Die Umlaufrendite
Übungen zur Vorlesung Funktionentheorie Sommersemester Musterlösung zu Blatt 10. f(z) f(z) dz
 UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6. MATHEMATIK Prof. Dr. Roland Speicher M.Sc. Tobias Mai Übungen zur Vorlesung Funktionentheorie Sommersemester 0 Musterlösung zu Blatt 0 Aufgabe. Berechnen Sie
UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6. MATHEMATIK Prof. Dr. Roland Speicher M.Sc. Tobias Mai Übungen zur Vorlesung Funktionentheorie Sommersemester 0 Musterlösung zu Blatt 0 Aufgabe. Berechnen Sie
NÜRNBERGER Konzept-Renten
 NÜRNBERGER Konzept-Renten NÜRNBERGER Konzept-Renten 1. Ausgangssituation 2. Zielgruppen 3. Produkte 4. Verkaufsunterstützung 2 Das Sparverhalten der Deutschen: Sicherheit geht vor Rendite 3 Die ideale
NÜRNBERGER Konzept-Renten NÜRNBERGER Konzept-Renten 1. Ausgangssituation 2. Zielgruppen 3. Produkte 4. Verkaufsunterstützung 2 Das Sparverhalten der Deutschen: Sicherheit geht vor Rendite 3 Die ideale
