Einführung in Simulationen mit Monte Carlo und Brownscher Dynamik. Martin Oettel Johannes Bleibel
|
|
|
- Ewald Geisler
- vor 7 Jahren
- Abrufe
Transkript
1 Einführung in Simulationen mit Monte Carlo und Brownscher Dynamik Martin Oettel Johannes Bleibel
2 Die Monte Carlo-Methode 1. Beispiel Bestimmung von π 1 1 π = 1 1 dx 1 dy G(x, y) G (x, y) = θ(1 x 2 + y 2 ) θ(x) = { 1 (x>0) 0 (sonst) (physikalische Größe) Würfeln x j y j = RANDOM_NUMBER ([ 1,1]) = RANDOM_NUMBER ([ 1,1]) π 1 M j=1 M θ(1 x j 2 + y j 2 ) Übersetzung: Welcher Anteil der Zufallspunkte liegt im Kreis?
3 Die Monte Carlo-Methode 1. Beispiel - Programmieraufgabe im VM Physik für Nanoscience Schreiben Sie ein MC-Programm für π Unterteilen Sie die Gesamtzahl der Messungen : N = N samples N meas In jedem sample haben Sie N meas Messungen, bilden Sie den Mittelwert in jedem sample. Berechnen Sie den Mittelwert über alle samples. Berechnen Sie die Standardabweichung und die Unsicherheit des Mittelwertes über alle samples. Veranschaulichen Sie dies entsprechend, vor allem als Funktion von N samples
4 N meas = 1000, Fehlerbalken: σ mean = N samples (πi i=1 π) N samples (N samples 1), π i = 1 N meas N j=1 meas πij π 100 = N samples
5 Statistische Theorie der physikalischen Eigenschaften (Statistische Mechanik) Beispiel: Verteilung der Moleküle in einer Flüssigkeit jedes Teilchen kann sich im gesamten Raum aufhalten, ist aber mit allen anderen Teilchen korreliert N Teilchen Verteilung wird beschrieben durch eine Verteilungsfunktion = Wahrscheinlichkeitsdichte f ( r 1,..., r N ) Integral über alle Teilchenpositionen ist 1: Verteilungfunktion ist normiert d 3 r 1... d 3 r N f ( r 1,..., r N ) = 1 Eine physikalische Größe sei Funktion der Teilchenkoordinaten: Der Erwartungswert dieser Größe ist dann: G = G ( r i ) G = d 3 r 1... d 3 r N G ( r i ) f ( r 1,..., r N ) Einfaches Beispiel: Schwerpunkt N G ( r i ) 1 N i=1 r i Selbst wenn f bekannt ist, dann erfordert die Berechnung des Erwartungswert einer physikalischen Größe (wie der Schwerpunkt) im Prinzip eine 3N-dimensionale Integration!
6 Statistische Theorie der physikalischen Eigenschaften Strategien zur Lösung des Integrals G = d 3 r 1... d 3 r N G ( r i ) f ( r 1,..., r N ) 1. Molekulardynamik N Teilchen zum Zeitpunkt t Man löst die Bewegungsgleichungen von N Teilchen näherungsweise numerisch, erhält also r i (t) Dann: 1 G lim T T T 0 dt G ( r i (t)) Was steckt dahinter? Für lange Zeiten strebt ein System ins Gleichgewicht. N Teilchen zum Zeitpunkt t+δt Ergodenhypothese: Die zeitlich gemittelte Verteilung der Teilchen im Raum (aufgrund der Lösung r i (t) ), strebt der Gleichgewichtsverteilung f eq ( r 1,..., r N ) zu. G = d 3 r 1... d 3 r N G ( r i ) f eq ( r 1,..., r N ) 1 M j=1 M G ( ri (t j )) M Zeitschritte, t j = j Δ t
7 Statistische Theorie der physikalischen Eigenschaften Strategien zur Lösung des Integrals G = d 3 r 1... d 3 r N G ( r i ) f ( r 1,..., r N ) 2. Monte Carlo Boltzmann-Faktor : Die Gleichgewichtsverteilung ist bekannt und lautet f eq ( r 1,..., r n ) = 1 Z e E pot ( r 1,..., r n ) k T k J/K Boltzmann-Konstante Z heißt Konfigurationsintegral und normiert f eq Z = d 3 r 1... d 3 r N e E pot ( r 1,..., r n ) k T E pot ist die gesamte potentielle Energie der Moleküle Beispiel: Flüssigkeit an einer Wand externes Potential (Wand) Paarpotential u N E pot = i=1 j<i u( r i r j ) + i=1 N V ext ( r i )
8 Statistische Theorie der physikalischen Eigenschaften Strategien zur Lösung des Integrals G = d 3 r 1... d 3 r N G ( r i ) f ( r 1,..., r N ) 2. Monte Carlo (MC) Anstatt 3N Integrale zu lösen, würfeln wir auf eine geschickte Art und Weise M mal unsere Koordinaten: r i r i, j ( j=1... M ) G = d 3 r 1... d 3 r N G ( r i ) f eq ( r 1,..., r N ) 1 M j=1 M G ( r i, j ) Man beachte die formale Ähnlichkeit zu Molekulardynamik: r i (t j ) r i, j MD: Lösen der Bewegungsgleichung in M Schritten MC: Würfeln der Koordinaten M mal Die genauen Würfel regeln (importance sampling) kommen später.
9 Die Monte Carlo-Methode 1. Beispiel noch einmal Bestimmung von π 1 1 π = 1 1 dx 1 dy f ( x, y) G ( x, y) f ( x, y) = 1 (Gleichverteilung) G (x, y) = θ(1 x 2 + y 2 ) θ(x) = { 1 (x>0) 0 (sonst) (physikalische Größe) Würfeln x j y j = RANDOM_NUMBER ([ 1,1]) = RANDOM_NUMBER ([ 1,1]) π 1 M j=1 M θ(1 x j 2 + y j 2 ) Übersetzung: Welcher Anteil der Zufallspunkte liegt im Kreis?
10 Die Monte Carlo-Methode 2. Ein Beispiel von Daan Frenkel: Durchschnittstiefe des Nils Niltiefe = dx dy f ( x, y) G(x, y) Nil f ( x, y) = { 1 (Punkt im Nil) 0 (sonst) G (x, y) = z ( x, y) Naives Monte Carlo: Zufallspunkte auf quadratischer Karte M Niltiefe = 1 M j=1 f (x j, y j )G(x j, y j ) ist meistens 0! Das ist nicht das, was wir wollen!
11 Die Monte Carlo-Methode 3. Importance sampling und Metropolis-Algorithmus Wir wollen: und nicht: G = d 3 r 1... d 3 r N G ( r i ) f eq ( r 1,..., r N ) 1 M j=1 M G 1 M j=1 ( f eq ( r 1,..., r n ) = 1 Z e M G ( r i, j ) G ( r i, j ) f eq ( r 1, j,..., r N, j ) E pot ( r 1,..., r n ) k T ) Wir wollen also Zufallszahlen r i, j erzeugen, deren Verteilung mit dem Boltzmann-Faktor f eq gewichtet sind.
12 Die Monte Carlo-Methode 3. Importance sampling und Metropolis-Algorithmus Der Algorithmus: 1. Starte mit einer beliebigen Anfangskonfiguration: 2. Für jedes Teilchen: Berechne potentielle Energie vor Verrückung r i = r i, 0 E pot,vor = E pot ( r 1,..., r N ) Verrücke Position zufällig: ( x'i ) y ' = ( xi ) i y i z ' i z i + Δ x ( r 1 r 2 r 3) r 1, r 2, r 3...Zufallszahlen zwischen -1 und 1 Berechne Energieänderung: Δ E pot = E pot ( r 1,..., r ' i,..., r N ) E pot,vor Akzeptiere oder verwerfe die neuen Koordinaten: Δ E pot < 0 : r i = r ' i Δ E pot > 0 : r i = r ' i nur mit Wahrscheinlichkeit e Δ E pot k T Wiederhole die Schritte unter 2. für jedes Teilchen. Benutze immer die aktuellen Koordinaten der Teilchen. 3. Berechne die physikalische Größe G 1 = G ( r 1,..., r N ) 4. Wiederhole Schritte 2 und 3 M-1 mal 5. Endresultat: M G = 1 M j=1 G j
13 Die Monte Carlo-Methode 3. Importance sampling und Metropolis-Algorithmus Warum funktioniert dieser Algorithmus? Der Monte Carlo-Schritt (2.) würfelt uns eine neue Konfiguration. Minimale Bedingung: Haben wir schon Konfigurationen erreicht, die mit bleiben die neuen Konfigurationen auch mit f eq verteilt sind, so verteilt. f eq Gedankenexperiment: - Konfigurationen seien numerierbar: (z.b. durch Diskretisierung des Raumes) c k = { r 1,..., r N } k - sehr viele Monte Carlo-Schritte, angewandt auf sehr viele Konfigurationen - Monte Carlo-Schritt definiert uns eine Übergangsrate = Übergangswahrscheinlichkeit pro Schritt zwischen den Konfigurationen p k l = p(c k c l ) - Gleichgewicht: Es gilt für alle Konfigurationen c l k l f eq (c l ) p l k = k l f eq (c k ) p k l Rate, mit der c l verlassen wird Rate, mit der c l erreicht wird balance
14 Die Monte Carlo-Methode 3. Importance sampling und Metropolis-Algorithmus Warum funktioniert dieser Algorithmus? Gedankenexperiment: - Gleichgewicht, stärkere Bedingung: Es gilt für alle Paare von Konfigurationen f eq (c l ) p l k = f eq (c k ) p k l c k, c l detailed balance Wenn detailed balance, dann auch balance! - Also: p l k = f E E pot,l pot, k eq(c k ) p k l f eq (c l ) = e k T - Check Metropolis-Algorithmus: dies wird genau erfüllt! Entwicklung zum Gleichgewicht: Wir haben gesehen, dass Metropolis uns im Gleichgewicht lässt. Aber kommen wir auch dahin, wenn wir mit einer beliebigen Konfiguration beginnen? Das ist nicht einfach zu beantworten, muss in jedem Fall praktisch getestet werden.
15 Die Monte Carlo-Methode 4. Praktische Hinweise zur Implementierung von Metropolis Harte Potentiale und MC move (Verrückung) : kein Überlapp mit anderen Teilchen Akzeptanz Überlapp Ablehnung periodische Randbedingungen: bei move und Überlappsbestimmung beachten! acceptance ratio : (Bedingung an Δ x!) Observable (Messgrößen) als unabhängige Funktionen definieren. Maximal einmal pro sweep ( attempted move for all particles ) messen!
16 Die Monte Carlo-Methode 5. Eine Observable: Paarkorrelationsfunktion r Δ V g (r) = lim Δ V 0 ( N Δ V Δ V ) 1 (N /V ) normierte Wahrscheinlichkeit dafür, im Abstand r zu einem Testteilchen andere Teilchen zu finden
17 Monte-Carlo Mehode Beispiel: Paarkorrelationsfunktionen für harte Kugeln Programmieraufgabe im VM Physik für Nanoscience Bestimmen Sie die Paarkorrelationsfunktion mit Fehlerbalken für harte Kugeln: Teilchenzahlen N = O(100) Dichten ρ* = 0.2, 0.5 und 0.94 ( ρ* = ρσ 3, σ = 2 R: Hartkugeldurchmesser )
18 N= 340, 10 samples mit 100 sweeps ρ = 0.2 σ 2 σ 3σ
19 N= 340, 10 samples mit 100 sweeps ρ = 0.5 σ 2 σ 3σ
20 Part II Brownian Dynamics
21 Reminder: Statistical Mechanics Beispiel: Verteilung der Moleküle in einer Flüssigkeit jedes Teilchen kann sich im gesamten Raum aufhalten, ist aber mit allen anderen Teilchen korreliert N Teilchen Verteilung wird beschrieben durch eine Verteilungsfunktion = Wahrscheinlichkeitsdichte f ( r 1,..., r N ) Integral über alle Teilchenpositionen ist 1: Verteilungfunktion ist normiert d 3 r 1... d 3 r N f ( r 1,..., r N ) = 1 Eine physikalische Größe sei Funktion der Teilchenkoordinaten: Der Erwartungswert dieser Größe ist dann: G = G ( r i ) G = d 3 r 1... d 3 r N G ( r i ) f ( r 1,..., r N ) Einfaches Beispiel: Schwerpunkt N G ( r i ) 1 N i=1 r i Selbst wenn f bekannt ist, dann erfordert die Berechnung des Erwartungswert einer physikalischen Größe (wie der Schwerpunkt) im Prinzip eine 3N-dimensionale Integration!
22 Die Molekulardynamik-Methode 1. Übersicht Ziel: Berechnung von gemittelten physikalischen Größen: man benötigt r i (t) 1 G lim T T T 0 dt G ( r i (t)) d.h. ausgehend von einer Anfangsverteilung der Teilchen im Raum, werden die Bewegungsgleichungen integriert: m ri = F i 2. zeitliche Ableitung 2 mal integrieren! gesamte Kraft auf Teilchen i Schwierigkeiten: - F i : im allgemeinen schwierig zu bestimmen (WW zwischen N Teilchen!) Ansatz: berücksichtige nur paarweise Wechselwirkungen N F i = j=1, j i F ij mit F ij = V ( r i, r j ) - zweifache numerische Integration
23 Die Molekulardynamik-Methode 2. Integration mittels Euler-Verfahren Betrachte x-komponente eines Teilchens: ẍ=f x /m bzw. dv x dt =F x/ m Taylor-Entwicklung der Geschwindigkeit: v x (t )=v x, 0 + dv x dt t=t 0 (t t 0 ) v x (t ) v x, 0 = dv x dt t=t 0 Δ t Δ v x = F m Δ t diskreter Zeitschritt Änderung der Geschwindigkeit des Teilchens (zweite Integration für die Position analog) Vorteile: - einfaches Verfahren - unaufwendige Implementierung Nachteile: - benötigt kleine Zeitschritte - Stabilität
24 Die Molekulardynamik-Methode 3. Der Algorithmus (Prinzip) Initialisierung (Position, Geschwindigkeit) Berechnug der Kräfte ein Durchlauf Integration der Bewegungsgleichungen (neue Position, neue Geschwindigkeit) ein Zeitschritt Ende Berechnung von Observablen integriere n Zeitschritte, mittle über m Durchläufe
25 Die Molekulardynamik-Methode 4. Brown'sche Dynamik (Teilchen in Flüssigkeiten) Moleküle der Flüssigkeit sind klein gegen die Teilchengröße Explizite Beschreibung aller Flüssigkeitsmoleküle und Teilchen ist aufwändig - viele Stöße pro Zeitintervall - im Prinzip deterministisch, praktisch aber zufällig - Brown'sche Bewegung - Idee: Füge eine zufällige Kraft in die Bewegungsgleichungen ein Newton'sche Dynamik Langevin Dynamik
26 Die Molkulardynamik-Methode 5. Überdämpfte Bewegung kleine Reynoldszahl Re= ρv d η Verhältnis von Trägheitskräften zu Zähigkeitskräften Starke Dämpfung (hohe Reibungskraft) Trägheit wird vernachlässigbar d.h. Teilchen bewegen sich nur unter Einwirkung einer Kraft! Die Dynamik wird reversibel! Bewegungsgleichung (übergedämpfter Grenzfall): v i =Γ F i sehr einfache Bewegungsgleichung nur eine Integration nötig Mobilität Γ= 1 6 π ηd
27 Die Molekulardynamik-Methode 5. Überdämpfte Bewegung Bewegungsgleichung (übergedämpfter Grenzfall): v i =Γ F i Gesamtkraft enthält Zufallskraft: F i = V + F rand v i =Γ( V )+Γ F rand konservative Kräfte zufällige Geschwindigkeit Mit Euler Verfahren: Δ r i =(Γ( V )+Γ F rand )Δ t Δ r i =Γ ( V )Δ t + r rand Änderung der Position konservative Kräfte (Drift) zufällige Verschiebung Position-Langevin Gleichung: r=γ F + r rand
28 Die Molekulardynamik-Methode r 2 6. Mittleres Verschiebungsquadrat - Diffusion Einstein (1905) und Smoluchowski (1906): D=Γ k B T Diffusionskonstante Boltzmann Konstante Messung der Diffusion: Mittleres Verschiebungsquadrat r 2 (t ) = r (t) r (t=0) 2 (gemittelt über alle Teilchen) damit: D= 1 4t r2 (t ) bzw. r 2 (t ) =4Dt (2D) 1. Ziel der Brown'schen Dynamik: korrekte Beschreibung der Diffusion! Steuerung des MSD über die zufälligen Verschiebungen Breite der Zufalssverteilung soll von Temperatur und Mobilität abhängen r rand =0 σ= 2 Γ k B T Δ t= 2 D Δ t
29 Die Molekulardynamik-Methode 7. Details zur Implementierung Einheiten, Potentiale Abstände als Vielfache des Teilchendurchmessers: r= r σ Energie als Vielfaches von damit: F= V = σ k B T V = Ṽ k B T Ṽ k B T üblich: k B T =1 Zeiteinheit entsprechend wählen! Potential muss stetig sein! V V V (r) = {4 ϵ (( σ r ) 12 ( σ r ) 6 ) +c (r< r c ) 0 (sonst) Harte Kugeln unmöglich! weiche Kugeln σ r r
30 Die Molekulardynamik-Methode 7. Details zur Implementierung Zufallskräfte, zufällige Verschiebung Zufällige Verschiebung: r rand =0 σ= 2 Γ k B T Δ t= 2 D Δ t Gauß gleichförmig Varianz: 1 σ 2 Varianz: 12 (b a)2 a b gleichförmige Verteilung: Zeitschrittweitensteuerung leicht möglich!
31 Die Molekulardynamik-Methode Beispiel: Programmieraufgabe aus dem VM Nanoscience Schreiben Sie ein Programm zur Simulation einer Brown'schen Dynamik - Berechnen sie das mittlere Verschiebungsquadrat a) ohne Wechselwirkung b) mit einer rein repulsiven Wechselwirkung *(c) mit einer zusätzlich attraktiven Wechselwirkung) - Berechnen Sie die Paarkorrelationsfunktion g(r) für den Fall b) und vergleichen Sie das Ergebnis mit Ihren MC-Resultaten (gleiche Dichte, gleiche Teilchenanzahl) - Erstellen Sie Snapshots des Systems zur Visualisierung der Brown'sche Bewegung
32 Die Molekulardynamik-Methode Trajektorie eines einzelnen Brownschen Teilchens in 3D
33 Die Molekulardynamik-Methode Mean square displacement eines idealen Gases ind 3D: r 2 (t ) 6Dt
34 Die Molekulardynamik-Methode Vergleich MC (Dieter, 500 Teilchen) BD (Malte, 800 Teilchen), weiches repulsives Potential
Moleküldynamik. Modell: Klassische Mechanik Newtonsche Bewegungsgleichungen. = m a i
 Mikroskopische Simulation der Molekülbewegungen Moleküldynamik Statistische Mechanik Modell: Klassische Mechanik Newtonsche Bewegungsgleichungen Makroskopische igenschaften des Systems (nergie, Temp, Druck,
Mikroskopische Simulation der Molekülbewegungen Moleküldynamik Statistische Mechanik Modell: Klassische Mechanik Newtonsche Bewegungsgleichungen Makroskopische igenschaften des Systems (nergie, Temp, Druck,
Brownsche Bewegung Seminar - Weiche Materie
 Brownsche Bewegung Seminar - Weiche Materie Simon Schnyder 11. Februar 2008 Übersicht Abbildung: 3 Realisationen des Weges eines Brownschen Teilchens mit gl. Startort Struktur des Vortrags Brownsches Teilchen
Brownsche Bewegung Seminar - Weiche Materie Simon Schnyder 11. Februar 2008 Übersicht Abbildung: 3 Realisationen des Weges eines Brownschen Teilchens mit gl. Startort Struktur des Vortrags Brownsches Teilchen
2.1 Importance sampling: Metropolis-Algorithmus
 Kapitel 2 Simulationstechniken 2.1 Importance sampling: Metropolis-Algorithmus Eine zentrale Fragestellung in der statistischen Physik ist die Bestimmung von Erwartungswerten einer Observablen O in einem
Kapitel 2 Simulationstechniken 2.1 Importance sampling: Metropolis-Algorithmus Eine zentrale Fragestellung in der statistischen Physik ist die Bestimmung von Erwartungswerten einer Observablen O in einem
6. Boltzmann Gleichung
 6. Boltzmann Gleichung 1 6.1 Herleitung der Boltzmann Gleichung 2 6.2 H-Theorem 3 6.3 Transportphänomene G. Kahl (Institut für Theoretische Physik) Statistische Physik II Kapitel 6 3. Juni 2013 1 / 23
6. Boltzmann Gleichung 1 6.1 Herleitung der Boltzmann Gleichung 2 6.2 H-Theorem 3 6.3 Transportphänomene G. Kahl (Institut für Theoretische Physik) Statistische Physik II Kapitel 6 3. Juni 2013 1 / 23
V5: Klassische statistische Mechanik thermodynamische Ensembles
 V5: Klassische statistische Mechanik thermodynamische Ensembles Die statistische Mechanik behandelt Systeme mit vielen (im Grunde unendlich vielen) Freiheitsgraden. Diese sollen durch wenige Makrovariablen
V5: Klassische statistische Mechanik thermodynamische Ensembles Die statistische Mechanik behandelt Systeme mit vielen (im Grunde unendlich vielen) Freiheitsgraden. Diese sollen durch wenige Makrovariablen
4. Verteilungen von Funktionen von Zufallsvariablen
 4. Verteilungen von Funktionen von Zufallsvariablen Allgemeine Problemstellung: Gegeben sei die gemeinsame Verteilung der ZV en X 1,..., X n (d.h. bekannt seien f X1,...,X n bzw. F X1,...,X n ) Wir betrachten
4. Verteilungen von Funktionen von Zufallsvariablen Allgemeine Problemstellung: Gegeben sei die gemeinsame Verteilung der ZV en X 1,..., X n (d.h. bekannt seien f X1,...,X n bzw. F X1,...,X n ) Wir betrachten
ν und λ ausgedrückt in Energie E und Impuls p
 phys4.011 Page 1 8.3 Die Schrödinger-Gleichung die grundlegende Gleichung der Quantenmechanik (in den bis jetzt diskutierten Fällen) eine Wellengleichung für Materiewellen (gilt aber auch allgemeiner)
phys4.011 Page 1 8.3 Die Schrödinger-Gleichung die grundlegende Gleichung der Quantenmechanik (in den bis jetzt diskutierten Fällen) eine Wellengleichung für Materiewellen (gilt aber auch allgemeiner)
Monte-Carlo-Methode. mit Pseudo- und Quasizufallszahlen
 Gott würfelt nicht Monte-Carlo-Methode mit Pseudo- und Quasizufallszahlen Inhaltsverzeichnis Pseudo- und Quasizufallszahlen Monte-Carlo- Monte-Carlo- Monte-Carlo-Methode Bekannt nach Stadt Monte Carlo
Gott würfelt nicht Monte-Carlo-Methode mit Pseudo- und Quasizufallszahlen Inhaltsverzeichnis Pseudo- und Quasizufallszahlen Monte-Carlo- Monte-Carlo- Monte-Carlo-Methode Bekannt nach Stadt Monte Carlo
Winter-Semester 2017/18. Moderne Theoretische Physik IIIa. Statistische Physik
 Winter-Semester 2017/18 Moderne Theoretische Physik IIIa Statistische Physik Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie Do 11:30-13:00, Lehmann Raum 022, Geb 30.22 http://www.tkm.kit.edu/lehre/
Winter-Semester 2017/18 Moderne Theoretische Physik IIIa Statistische Physik Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie Do 11:30-13:00, Lehmann Raum 022, Geb 30.22 http://www.tkm.kit.edu/lehre/
BZQ II: Stochastikpraktikum
 BZQ II: Stochastikpraktikum Block 5: Markov-Chain-Monte-Carlo-Verfahren Randolf Altmeyer February 1, 2017 Überblick 1 Monte-Carlo-Methoden, Zufallszahlen, statistische Tests 2 Nichtparametrische Methoden
BZQ II: Stochastikpraktikum Block 5: Markov-Chain-Monte-Carlo-Verfahren Randolf Altmeyer February 1, 2017 Überblick 1 Monte-Carlo-Methoden, Zufallszahlen, statistische Tests 2 Nichtparametrische Methoden
Theoretische Physik 1 Mechanik
 Technische Universität München Fakultät für Physik Ferienkurs Theoretische Physik 1 Mechanik Skript zu Vorlesung 2: konservative Kräfte, Vielteilchensysteme und ausgedehnte Körper gehalten von: Markus
Technische Universität München Fakultät für Physik Ferienkurs Theoretische Physik 1 Mechanik Skript zu Vorlesung 2: konservative Kräfte, Vielteilchensysteme und ausgedehnte Körper gehalten von: Markus
Thermodynamik (Wärmelehre) III kinetische Gastheorie
 Physik A VL6 (07.1.01) Thermodynamik (Wärmelehre) III kinetische Gastheorie Thermische Bewegung Die kinetische Gastheorie Mikroskopische Betrachtung des Druckes Mawell sche Geschwindigkeitserteilung gdes
Physik A VL6 (07.1.01) Thermodynamik (Wärmelehre) III kinetische Gastheorie Thermische Bewegung Die kinetische Gastheorie Mikroskopische Betrachtung des Druckes Mawell sche Geschwindigkeitserteilung gdes
I.1.3 b. (I.7a) I.1 Grundbegriffe der Newton schen Mechanik 9
 I. Grundbegriffe der Newton schen Mechanik 9 I..3 b Arbeit einer Kraft Wird die Wirkung einer Kraft über ein Zeitintervall oder genauer über die Strecke, welche das mechanische System in diesem Zeitintervall
I. Grundbegriffe der Newton schen Mechanik 9 I..3 b Arbeit einer Kraft Wird die Wirkung einer Kraft über ein Zeitintervall oder genauer über die Strecke, welche das mechanische System in diesem Zeitintervall
4 Thermodynamik mikroskopisch: kinetische Gastheorie makroskopisch: System:
 Theorie der Wärme kann auf zwei verschiedene Arten behandelt werden. mikroskopisch: Bewegung von Gasatomen oder -molekülen. Vielzahl von Teilchen ( 10 23 ) im Allgemeinen nicht vollständig beschreibbar
Theorie der Wärme kann auf zwei verschiedene Arten behandelt werden. mikroskopisch: Bewegung von Gasatomen oder -molekülen. Vielzahl von Teilchen ( 10 23 ) im Allgemeinen nicht vollständig beschreibbar
13 Mehrdimensionale Zufallsvariablen Zufallsvektoren
 3 Mehrdimensionale Zufallsvariablen Zufallsvektoren Bisher haben wir uns ausschließlich mit Zufallsexperimenten beschäftigt, bei denen die Beobachtung eines einzigen Merkmals im Vordergrund stand. In diesem
3 Mehrdimensionale Zufallsvariablen Zufallsvektoren Bisher haben wir uns ausschließlich mit Zufallsexperimenten beschäftigt, bei denen die Beobachtung eines einzigen Merkmals im Vordergrund stand. In diesem
Der Erwartungswert E[g(X)] von g(x) ist definiert. g(x k )w(x = x k ),
![Der Erwartungswert E[g(X)] von g(x) ist definiert. g(x k )w(x = x k ), Der Erwartungswert E[g(X)] von g(x) ist definiert. g(x k )w(x = x k ),](/thumbs/74/71302796.jpg) 2.5 Parameter einer Verteilung 2.5. Erwartungswert X eine Zufallsvariable, g : R R stetig. Der Erwartungswert E[g(X)] von g(x) ist definiert durch: E[g(X)] := k g(x k )w(x = x k ), falls X diskret ist
2.5 Parameter einer Verteilung 2.5. Erwartungswert X eine Zufallsvariable, g : R R stetig. Der Erwartungswert E[g(X)] von g(x) ist definiert durch: E[g(X)] := k g(x k )w(x = x k ), falls X diskret ist
Wahrscheinlichkeitsrechnung und Statistik
 5. Vorlesung Verteilungsfunktion (VF) Definition 9 Die Verteilungsfunktion (VF) einer Zufallsgröße X ist F : R R definiert als F (x) := P({ω Ω : X (ω) x}) = P( X x ) für jedes x R. Satz 9 - Eigenschaften
5. Vorlesung Verteilungsfunktion (VF) Definition 9 Die Verteilungsfunktion (VF) einer Zufallsgröße X ist F : R R definiert als F (x) := P({ω Ω : X (ω) x}) = P( X x ) für jedes x R. Satz 9 - Eigenschaften
Stochastik Praktikum Markov Chain Monte Carlo Methoden
 Stochastik Praktikum Markov Chain Monte Carlo Methoden Humboldt-Universität zu Berlin 14.10.2010 Problemstellung Wie kann eine Zufallsstichprobe am Computer simuliert werden, deren Verteilung aus einem
Stochastik Praktikum Markov Chain Monte Carlo Methoden Humboldt-Universität zu Berlin 14.10.2010 Problemstellung Wie kann eine Zufallsstichprobe am Computer simuliert werden, deren Verteilung aus einem
7 Die Hamilton-Jacobi-Theorie
 7 Die Hamilton-Jacobi-Theorie Ausgearbeitet von Rolf Horn und Bernhard Schmitz 7.1 Einleitung Um die Hamilton schen Bewegungsgleichungen q k = H(q, p) p k ṗ k = H(p, q) q k zu vereinfachen, führten wir
7 Die Hamilton-Jacobi-Theorie Ausgearbeitet von Rolf Horn und Bernhard Schmitz 7.1 Einleitung Um die Hamilton schen Bewegungsgleichungen q k = H(q, p) p k ṗ k = H(p, q) q k zu vereinfachen, führten wir
Woche 2: Zufallsvariablen
 Woche 2: Zufallsvariablen Patric Müller ETHZ WBL 17/19, 24.04.2017 Wahrscheinlichkeit und Statistik Patric Müller WBL 2017 Teil III Zufallsvariablen Wahrscheinlichkeit
Woche 2: Zufallsvariablen Patric Müller ETHZ WBL 17/19, 24.04.2017 Wahrscheinlichkeit und Statistik Patric Müller WBL 2017 Teil III Zufallsvariablen Wahrscheinlichkeit
Wahrscheinlichkeitsrechnung und Quantentheorie
 Physikalische Chemie II: Atombau und chemische Bindung Winter 2013/14 Wahrscheinlichkeitsrechnung und Quantentheorie Messergebnisse können in der Quantenmechanik ganz prinzipiell nur noch mit einer bestimmten
Physikalische Chemie II: Atombau und chemische Bindung Winter 2013/14 Wahrscheinlichkeitsrechnung und Quantentheorie Messergebnisse können in der Quantenmechanik ganz prinzipiell nur noch mit einer bestimmten
Mathematik für Biologen
 Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 1. Dezember 21 1 Integralrechnung Flächeninhalt Stammfunktion Rechenregeln 2 Dichten von Erwartungswert und Varianz
Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 1. Dezember 21 1 Integralrechnung Flächeninhalt Stammfunktion Rechenregeln 2 Dichten von Erwartungswert und Varianz
4.1 Stichproben, Verteilungen und Schätzwerte. N(t) = N 0 e λt, (4.1)
 Kapitel 4 Stichproben und Schätzungen 4.1 Stichproben, Verteilungen und Schätzwerte Eine physikalische Messung ist eine endliche Stichprobe aus einer Grundgesamtheit, die endlich oder unendlich sein kann.
Kapitel 4 Stichproben und Schätzungen 4.1 Stichproben, Verteilungen und Schätzwerte Eine physikalische Messung ist eine endliche Stichprobe aus einer Grundgesamtheit, die endlich oder unendlich sein kann.
Einführung in die Boltzmann-Gleichung. Flavius Guiaş Universität Dortmund
 Einführung in die Boltzmann-Gleichung Flavius Guiaş Universität Dortmund Antrittsvorlesung, 19.04.2007 INHALT 1 Herleitung der Boltzmann-Gleichung 2 Boltzmann-Ungleichung und Maxwell-Verteilung 3 H-Theorem
Einführung in die Boltzmann-Gleichung Flavius Guiaş Universität Dortmund Antrittsvorlesung, 19.04.2007 INHALT 1 Herleitung der Boltzmann-Gleichung 2 Boltzmann-Ungleichung und Maxwell-Verteilung 3 H-Theorem
f) Ideales Gas - mikroskopisch
 f) Ideales Gas - mikroskopisch i) Annahmen Schon gehabt: Massenpunkte ohne Eigenvolumen Nur elastische Stöße, keine Wechselwirkungen Jetzt dazu: Wände vollkommen elastisch, perfekte Reflektoren Zeitliches
f) Ideales Gas - mikroskopisch i) Annahmen Schon gehabt: Massenpunkte ohne Eigenvolumen Nur elastische Stöße, keine Wechselwirkungen Jetzt dazu: Wände vollkommen elastisch, perfekte Reflektoren Zeitliches
Rechnernutzung in der Physik Teil 3 Statistische Methoden der Datenanalyse
 Rechnernutzung in der Physik Teil 3 Statistische Methoden der Datenanalyse Karlsruher Institut für Technologie Ulrich Husemann Institut für Experimentelle Kernphysik, Karlsruher Institut für Technologie
Rechnernutzung in der Physik Teil 3 Statistische Methoden der Datenanalyse Karlsruher Institut für Technologie Ulrich Husemann Institut für Experimentelle Kernphysik, Karlsruher Institut für Technologie
Stetige Verteilungen Rechteckverteilung
 Stetige Verteilungen Rechteckverteilung Die Längenabweichungen X produzierter Werkstücke von der Norm seien gleichmäßig verteilt zwischen a = mm und b = 4mm. Die Dichtefunktion lautet also f(x) = für a
Stetige Verteilungen Rechteckverteilung Die Längenabweichungen X produzierter Werkstücke von der Norm seien gleichmäßig verteilt zwischen a = mm und b = 4mm. Die Dichtefunktion lautet also f(x) = für a
Zufallsvariablen [random variable]
![Zufallsvariablen [random variable] Zufallsvariablen [random variable]](/thumbs/52/29710821.jpg) Zufallsvariablen [random variable] Eine Zufallsvariable (Zufallsgröße) X beschreibt (kodiert) die Versuchsausgänge ω Ω mit Hilfe von Zahlen, d.h. X ist eine Funktion X : Ω R ω X(ω) Zufallsvariablen werden
Zufallsvariablen [random variable] Eine Zufallsvariable (Zufallsgröße) X beschreibt (kodiert) die Versuchsausgänge ω Ω mit Hilfe von Zahlen, d.h. X ist eine Funktion X : Ω R ω X(ω) Zufallsvariablen werden
Mathematik des Hybriden Monte-Carlo. Marcus Weber. Zuse Institute Berlin
 Mathematik des Hybriden Monte-Carlo Marcus Weber Zuse Institute Berlin Statistische Thermodynamik Ziel: Am Computer ein Ensemble samplen. Messung im Gleichgewicht (zeitunabhängige Verteilung π der Systemzustände
Mathematik des Hybriden Monte-Carlo Marcus Weber Zuse Institute Berlin Statistische Thermodynamik Ziel: Am Computer ein Ensemble samplen. Messung im Gleichgewicht (zeitunabhängige Verteilung π der Systemzustände
Computer Vision: Kalman Filter
 Computer Vision: Kalman Filter D. Schlesinger TUD/INF/KI/IS D. Schlesinger () Computer Vision: Kalman Filter 1 / 8 Bayesscher Filter Ein Objekt kann sich in einem Zustand x X befinden. Zum Zeitpunkt i
Computer Vision: Kalman Filter D. Schlesinger TUD/INF/KI/IS D. Schlesinger () Computer Vision: Kalman Filter 1 / 8 Bayesscher Filter Ein Objekt kann sich in einem Zustand x X befinden. Zum Zeitpunkt i
4. Gemeinsame Verteilung und Grenzwertsätze
 4. Gemeinsame Verteilung und Grenzwertsätze Häufig in der Praxis: Man muss mehrere (n) ZV en gleichzeitig betrachten (vgl. Statistik I, Kapitel 6) Zunächst Vereinfachung: Betrachte n = 2 Zufallsvariablen
4. Gemeinsame Verteilung und Grenzwertsätze Häufig in der Praxis: Man muss mehrere (n) ZV en gleichzeitig betrachten (vgl. Statistik I, Kapitel 6) Zunächst Vereinfachung: Betrachte n = 2 Zufallsvariablen
4. Gemeinsame Verteilung und Grenzwertsätze
 4. Gemeinsame Verteilung und Grenzwertsätze Häufig in der Praxis: Man muss mehrere (n) ZV en gleichzeitig betrachten (vgl. Statistik I, Kapitel 6) Zunächst Vereinfachung: Betrachte n = 2 Zufallsvariablen
4. Gemeinsame Verteilung und Grenzwertsätze Häufig in der Praxis: Man muss mehrere (n) ZV en gleichzeitig betrachten (vgl. Statistik I, Kapitel 6) Zunächst Vereinfachung: Betrachte n = 2 Zufallsvariablen
Bioinformatik für Biochemiker
 Bioinformatik für Biochemiker Oliver Kohlbacher WS 2009/2010 13. Ab-initio-Vorhersage Abt. Simulation biologischer Systeme WSI/ZBIT, Eberhard Karls Universität Tübingen Gliederung Ab-Initio-Vorhersage
Bioinformatik für Biochemiker Oliver Kohlbacher WS 2009/2010 13. Ab-initio-Vorhersage Abt. Simulation biologischer Systeme WSI/ZBIT, Eberhard Karls Universität Tübingen Gliederung Ab-Initio-Vorhersage
Mehrdimensionale Verteilungen und Korrelation
 Vorlesung: Computergestützte Datenauswertung Mehrdimensionale Verteilungen und Korrelation Günter Quast Fakultät für Physik Institut für Experimentelle Kernphysik SS '17 KIT Die Forschungsuniversität in
Vorlesung: Computergestützte Datenauswertung Mehrdimensionale Verteilungen und Korrelation Günter Quast Fakultät für Physik Institut für Experimentelle Kernphysik SS '17 KIT Die Forschungsuniversität in
Grundlagen der Monte Carlo Simulation
 Grundlagen der Monte Carlo Simulation 10. Dezember 2003 Peter Hofmann Inhaltsverzeichnis 1 Monte Carlo Simulation.................... 2 1.1 Problemstellung.................... 2 1.2 Lösung durch Monte
Grundlagen der Monte Carlo Simulation 10. Dezember 2003 Peter Hofmann Inhaltsverzeichnis 1 Monte Carlo Simulation.................... 2 1.1 Problemstellung.................... 2 1.2 Lösung durch Monte
Differentialgleichungen
 Differentialgleichungen Viele physikalische Probleme können mathematisch als gewöhnliche Differentialgleichungen formuliert werden nur eine unabhängige Variable (meist t), z.b. Bewegungsgleichungen: gleichmäßig
Differentialgleichungen Viele physikalische Probleme können mathematisch als gewöhnliche Differentialgleichungen formuliert werden nur eine unabhängige Variable (meist t), z.b. Bewegungsgleichungen: gleichmäßig
Ausgewählte Kapitel der Klassischen Statistischen Physik. Transport in Ratschen
 Ausgewählte Kapitel der Klassischen Statistischen Physik Transport in Ratschen Paul Egetmeyer Steffen Nothelfer August 4, 2010 Gliederung Einleitung und Wiederholung Bedingungen Übedämpfte Theorie An-
Ausgewählte Kapitel der Klassischen Statistischen Physik Transport in Ratschen Paul Egetmeyer Steffen Nothelfer August 4, 2010 Gliederung Einleitung und Wiederholung Bedingungen Übedämpfte Theorie An-
Theoretische Chemie (TC II) Computational Chemistry
 Theoretische Chemie (TC II) Computational Chemistry Irene Burghardt (burghardt@chemie.uni-frankfurt.de) Praktikumsbetreuung: Dr. Matthias Ruckenbauer (matruc@theochem.uni-frankfurt.de) Dr. Haleh Hashemi
Theoretische Chemie (TC II) Computational Chemistry Irene Burghardt (burghardt@chemie.uni-frankfurt.de) Praktikumsbetreuung: Dr. Matthias Ruckenbauer (matruc@theochem.uni-frankfurt.de) Dr. Haleh Hashemi
70 Wichtige kontinuierliche Verteilungen
 70 Wichtige kontinuierliche Verteilungen 70. Motivation Zufallsvariablen sind nicht immer diskret, sie können oft auch jede beliebige reelle Zahl in einem Intervall [c, d] einnehmen. Beispiele für solche
70 Wichtige kontinuierliche Verteilungen 70. Motivation Zufallsvariablen sind nicht immer diskret, sie können oft auch jede beliebige reelle Zahl in einem Intervall [c, d] einnehmen. Beispiele für solche
Maxwell-Boltzmann Verteilung. Mykola Zotko Frankfurt am Main
 Maxwell-Boltzmann Verteilung James Clerk Maxwell 1831-1879 Ludwig Boltzmann 1844-1906 Maxwell-Boltzmann Verteilung 1860 Geschwindigkeitsverteilung - eine Verteilungsfunktion, die angibt, mit welcher relativen
Maxwell-Boltzmann Verteilung James Clerk Maxwell 1831-1879 Ludwig Boltzmann 1844-1906 Maxwell-Boltzmann Verteilung 1860 Geschwindigkeitsverteilung - eine Verteilungsfunktion, die angibt, mit welcher relativen
8.1. Kinetische Theorie der Wärme
 8.1. Kinetische Theorie der Wärme Deinition: Ein ideales Gas ist ein System von harten Massenpunkten, die untereinander und mit den Wänden elastische Stöße durchühren und keiner anderen Wechselwirkung
8.1. Kinetische Theorie der Wärme Deinition: Ein ideales Gas ist ein System von harten Massenpunkten, die untereinander und mit den Wänden elastische Stöße durchühren und keiner anderen Wechselwirkung
Kapitel 3. Statistische Definition der Entropie. 3.1 Ensemble aus vielen Teilchen
 Kapitel 3 Statistische Definition der Entropie 3.1 Ensemble aus vielen Teilchen Die Überlegungen dieses Abschnitts werden für klassische Teilchen formuliert, gelten sinngemäß aber genauso auch für Quantensysteme.
Kapitel 3 Statistische Definition der Entropie 3.1 Ensemble aus vielen Teilchen Die Überlegungen dieses Abschnitts werden für klassische Teilchen formuliert, gelten sinngemäß aber genauso auch für Quantensysteme.
Die Maximum-Likelihood-Methode
 Vorlesung: Computergestützte Datenauswertung Die Maximum-Likelihood-Methode Günter Quast Fakultät für Physik Institut für Experimentelle Kernphysik SS '17 KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft
Vorlesung: Computergestützte Datenauswertung Die Maximum-Likelihood-Methode Günter Quast Fakultät für Physik Institut für Experimentelle Kernphysik SS '17 KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft
: Quantenmechanische Lösung H + 2. Molekülion und. Aufstellen der Schrödingergleichung für das H + 2
 H + 2 Die molekulare Bindung : Quantenmechanische Lösung Aufstellen der Schrödingergleichung für das H + 2 Molekülion und Lösung Wichtige Einschränkung: Die Kerne sind festgehalten H Ψ(r) = E Ψ(r) (11)
H + 2 Die molekulare Bindung : Quantenmechanische Lösung Aufstellen der Schrödingergleichung für das H + 2 Molekülion und Lösung Wichtige Einschränkung: Die Kerne sind festgehalten H Ψ(r) = E Ψ(r) (11)
1.3. DAS COULOMBSCHE GESETZ, ELEKTROSTATISCHES FELD 9
 8 KAPITEL. ELEKTROSTATIK.3 Das Coulombsche Gesetz, elektrostatisches Feld Zur Einführung verschiedener Grundbegriffe betrachten wir zunächst einmal die Kraft, die zwischen zwei Ladungen q an der Position
8 KAPITEL. ELEKTROSTATIK.3 Das Coulombsche Gesetz, elektrostatisches Feld Zur Einführung verschiedener Grundbegriffe betrachten wir zunächst einmal die Kraft, die zwischen zwei Ladungen q an der Position
Brahe Kepler. Bacon Descartes
 Newton s Mechanics Stellar Orbits! Brahe Kepler Gravity! Actio = Reactio F = d dt p Gallilei Galilei! Bacon Descartes Leibnitz Leibniz! 1 Statistical Mechanics Steam Engine! Energy Conservation Kinematic
Newton s Mechanics Stellar Orbits! Brahe Kepler Gravity! Actio = Reactio F = d dt p Gallilei Galilei! Bacon Descartes Leibnitz Leibniz! 1 Statistical Mechanics Steam Engine! Energy Conservation Kinematic
Grundlagen der Wahrscheinlichkeitstheorie
 Priv.-Doz. Dr. H. Steinacker Wintersemester 2013/2014 Grundlagen der Wahrscheinlichkeitstheorie betrachte Wiederholungen eines Experimentes, gleicher Vorbereitung (z.b. Würfeln, Dart werfen, Doppelspaltexperiment,...)
Priv.-Doz. Dr. H. Steinacker Wintersemester 2013/2014 Grundlagen der Wahrscheinlichkeitstheorie betrachte Wiederholungen eines Experimentes, gleicher Vorbereitung (z.b. Würfeln, Dart werfen, Doppelspaltexperiment,...)
DWT 1.4 Rechnen mit kontinuierlichen Zufallsvariablen 234/467 Ernst W. Mayr
 1.4.2 Kontinuierliche Zufallsvariablen als Grenzwerte diskreter Zufallsvariablen Sei X eine kontinuierliche Zufallsvariable. Wir können aus X leicht eine diskrete Zufallsvariable konstruieren, indem wir
1.4.2 Kontinuierliche Zufallsvariablen als Grenzwerte diskreter Zufallsvariablen Sei X eine kontinuierliche Zufallsvariable. Wir können aus X leicht eine diskrete Zufallsvariable konstruieren, indem wir
2.4 Kinetische Gastheorie - Druck und Temperatur im Teilchenmodell
 2.4 Kinetische Gastheorie - Druck und Temperatur im Teilchenmodell Mit den drei Zustandsgrößen Druck, Temperatur und Volumen konnte der Zustand von Gasen makroskopisch beschrieben werden. So kann zum Beispiel
2.4 Kinetische Gastheorie - Druck und Temperatur im Teilchenmodell Mit den drei Zustandsgrößen Druck, Temperatur und Volumen konnte der Zustand von Gasen makroskopisch beschrieben werden. So kann zum Beispiel
Simulation von Brownscher Dynamik und Assoziationsraten von PP-Komplexen. Alexander Baldauf Montag
 Simulation von Brownscher Dynamik und Assoziationsraten von PP-Komplexen Alexander Baldauf Montag 25.04.2005 Motivation Typen von Interaktionen Verschiedene Methoden zur Vorhersage Wie kommen die beiden
Simulation von Brownscher Dynamik und Assoziationsraten von PP-Komplexen Alexander Baldauf Montag 25.04.2005 Motivation Typen von Interaktionen Verschiedene Methoden zur Vorhersage Wie kommen die beiden
Thermodynamik. Christian Britz
 Hauptsätze der Klassische nanoskaliger Systeme 04.02.2013 Inhalt Einleitung Hauptsätze der Klassische nanoskaliger Systeme 1 Einleitung 2 Hauptsätze der 3 4 Klassische 5 6 7 nanoskaliger Systeme 8 Hauptsätze
Hauptsätze der Klassische nanoskaliger Systeme 04.02.2013 Inhalt Einleitung Hauptsätze der Klassische nanoskaliger Systeme 1 Einleitung 2 Hauptsätze der 3 4 Klassische 5 6 7 nanoskaliger Systeme 8 Hauptsätze
Einführung in die Wahrscheinlichkeitstheorie Lösungsvorschläge zu Übungsblatt 4
 TUM, Zentrum Mathematik Lehrstuhl für Mathematische Physik WS 3/4 Prof. Dr. Silke Rolles Thomas Höfelsauer Felizitas Weidner Tutoraufgaben: Einführung in die Wahrscheinlichkeitstheorie Lösungsvorschläge
TUM, Zentrum Mathematik Lehrstuhl für Mathematische Physik WS 3/4 Prof. Dr. Silke Rolles Thomas Höfelsauer Felizitas Weidner Tutoraufgaben: Einführung in die Wahrscheinlichkeitstheorie Lösungsvorschläge
Wahrscheinlichkeitsrechnung und stochastische Prozesse
 Kapitel 7 Wahrscheinlichkeitsrechnung und stochastische Prozesse Zufallsvariable, Wahrscheinlichkeitsdichte, Markov-Prozess ( Zukunft hängt von der Vergangenheit nur über die Gegenwart ab. 7. Einführung
Kapitel 7 Wahrscheinlichkeitsrechnung und stochastische Prozesse Zufallsvariable, Wahrscheinlichkeitsdichte, Markov-Prozess ( Zukunft hängt von der Vergangenheit nur über die Gegenwart ab. 7. Einführung
7.5 Erwartungswert, Varianz
 7.5 Erwartungswert, Varianz Def. 7.5.: a) X sei eine diskrete ZV, die bei unendl. vielen Werten x k folgende Zusatzbedingung erfüllt: x k p k
7.5 Erwartungswert, Varianz Def. 7.5.: a) X sei eine diskrete ZV, die bei unendl. vielen Werten x k folgende Zusatzbedingung erfüllt: x k p k
5 Interpolation und Approximation
 5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
Theorie Parameterschätzung Ausblick. Schätzung. Raimar Sandner. Studentenseminar "Statistische Methoden in der Physik"
 Studentenseminar "Statistische Methoden in der Physik" Gliederung 1 2 3 Worum geht es hier? Gliederung 1 2 3 Stichproben Gegeben eine Beobachtungsreihe x = (x 1, x 2,..., x n ): Realisierung der n-dimensionalen
Studentenseminar "Statistische Methoden in der Physik" Gliederung 1 2 3 Worum geht es hier? Gliederung 1 2 3 Stichproben Gegeben eine Beobachtungsreihe x = (x 1, x 2,..., x n ): Realisierung der n-dimensionalen
Computersimulationen in der Astronomie
 Computersimulationen in der Astronomie Fabian Heimann Universität Göttingen, Fabian.Heimann@stud.uni-goettingen.de Astronomisches Sommerlager 2013 Inhaltsverzeichnis 1 Differentialgleichungen 3 1.1 Beispiele.....................................
Computersimulationen in der Astronomie Fabian Heimann Universität Göttingen, Fabian.Heimann@stud.uni-goettingen.de Astronomisches Sommerlager 2013 Inhaltsverzeichnis 1 Differentialgleichungen 3 1.1 Beispiele.....................................
Wahrscheinlichkeit und Statistik: Zusammenfassung
 HSR Hochschule für Technik Rapperswil Wahrscheinlichkeit und Statistik: Zusammenfassung beinhaltet Teile des Skripts von Herrn Hardy von Lukas Wilhelm lwilhelm.net 12. Januar 2007 Inhaltsverzeichnis 1
HSR Hochschule für Technik Rapperswil Wahrscheinlichkeit und Statistik: Zusammenfassung beinhaltet Teile des Skripts von Herrn Hardy von Lukas Wilhelm lwilhelm.net 12. Januar 2007 Inhaltsverzeichnis 1
3. Gemeinsame und bedingte Verteilung, stochastische Unabhängigkeit
 3. Gemeinsame und bedingte Verteilung, stochastische Unabhängigkeit Lernziele dieses Kapitels: Mehrdimensionale Zufallsvariablen (Zufallsvektoren) (Verteilung, Kenngrößen) Abhängigkeitsstrukturen Multivariate
3. Gemeinsame und bedingte Verteilung, stochastische Unabhängigkeit Lernziele dieses Kapitels: Mehrdimensionale Zufallsvariablen (Zufallsvektoren) (Verteilung, Kenngrößen) Abhängigkeitsstrukturen Multivariate
Modell der Punktmasse
 Kinematik Die Kinematik (kinema, griech., Bewegung) ist die Lehre von der Bewegung von Punkten und Körpern im Raum, beschrieben durch die Größen Weg (Änderung der Ortskoordinate) s, Geschwindigkeit v und
Kinematik Die Kinematik (kinema, griech., Bewegung) ist die Lehre von der Bewegung von Punkten und Körpern im Raum, beschrieben durch die Größen Weg (Änderung der Ortskoordinate) s, Geschwindigkeit v und
Vorlesung Physikalische Chemie IV Statistische Thermodynamik realer chemischer Systeme"
 Vorlesung Physikalische Chemie IV Statistische Thermodynamik realer chemischer Systeme" Dietmar Paschek SS 016 Gittermodell für Mischungen Grenzen der Bragg-Williams Näherung Das Ising Modell Quasi-Chemische
Vorlesung Physikalische Chemie IV Statistische Thermodynamik realer chemischer Systeme" Dietmar Paschek SS 016 Gittermodell für Mischungen Grenzen der Bragg-Williams Näherung Das Ising Modell Quasi-Chemische
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
Schweredruck von Flüssigkeiten
 Schweredruck von Flüssigkeiten Flüssigkeiten sind nahezu inkompressibel. Kompressibilität κ: Typische Werte: Wasser: 4.6 10-5 1/bar @ 0ºC Quecksilber: 4 10-6 1/bar @ 0ºC Pentan: 4. 10-6 1/bar @ 0ºC Dichte
Schweredruck von Flüssigkeiten Flüssigkeiten sind nahezu inkompressibel. Kompressibilität κ: Typische Werte: Wasser: 4.6 10-5 1/bar @ 0ºC Quecksilber: 4 10-6 1/bar @ 0ºC Pentan: 4. 10-6 1/bar @ 0ºC Dichte
Statistik - Fehlerrechnung - Auswertung von Messungen
 Statistik - Fehlerrechnung - Auswertung von Messungen TEIL II Vorbereitungskurs F-Praktikum B (Physik), RWTH Aachen Thomas Hebbeker Eindimensionaler Fall: Parameterbestimmung - Beispiele [Übung] Mehrdimensionaler
Statistik - Fehlerrechnung - Auswertung von Messungen TEIL II Vorbereitungskurs F-Praktikum B (Physik), RWTH Aachen Thomas Hebbeker Eindimensionaler Fall: Parameterbestimmung - Beispiele [Übung] Mehrdimensionaler
Grundlagen der Diffusion Ein kurzes Tutorial. basierend auf Unterlagen von Peter Stüber, Felix Roosen-Runge und Frank Schreiber
 Grundlagen der Diffusion Ein kurzes Tutorial basierend auf Unterlagen von Peter Stüber, Felix Roosen-Runge und Frank Schreiber Begriffserklärung: Kolloide In Lösungsmittel gelöste Teilchen (1nm-1µm) Klein
Grundlagen der Diffusion Ein kurzes Tutorial basierend auf Unterlagen von Peter Stüber, Felix Roosen-Runge und Frank Schreiber Begriffserklärung: Kolloide In Lösungsmittel gelöste Teilchen (1nm-1µm) Klein
Blatt 05.2: Green sche Funktionen
 Fakultät für Physik T: Klassische Mechanik, SoSe 05 Dozent: Jan von Delft Übungen: Katharina Stadler, Frauke Schwarz, Dennis Schimmel, Lukas Weidinger http://homepages.physik.uni-muenchen.de/~vondelft/lehre/5t/
Fakultät für Physik T: Klassische Mechanik, SoSe 05 Dozent: Jan von Delft Übungen: Katharina Stadler, Frauke Schwarz, Dennis Schimmel, Lukas Weidinger http://homepages.physik.uni-muenchen.de/~vondelft/lehre/5t/
Grundlagen der Physik 2 Schwingungen und Wärmelehre
 Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti othmar.marti@uni-ulm.de Institut für Experimentelle Physik 14. 06. 2007 Othmar Marti (Universität Ulm) Schwingungen und Wärmelehre 14. 06.
Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti othmar.marti@uni-ulm.de Institut für Experimentelle Physik 14. 06. 2007 Othmar Marti (Universität Ulm) Schwingungen und Wärmelehre 14. 06.
Seminar Level Set Methoden
 Seminar Level Set Methoden Geometric Flows and Variational Methods Michael Möller Institut für Numerische und Angewandte Mathematik Fachbereich Mathematik und Informatik WWU Münster SS 2007 1. Einführung
Seminar Level Set Methoden Geometric Flows and Variational Methods Michael Möller Institut für Numerische und Angewandte Mathematik Fachbereich Mathematik und Informatik WWU Münster SS 2007 1. Einführung
Grundlagen der Physik 2 Schwingungen und Wärmelehre
 Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti othmar.marti@uni-ulm.de Institut für Experimentelle Physik 14. 06. 2007 Othmar Marti (Universität Ulm) Schwingungen und Wärmelehre 14. 06.
Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti othmar.marti@uni-ulm.de Institut für Experimentelle Physik 14. 06. 2007 Othmar Marti (Universität Ulm) Schwingungen und Wärmelehre 14. 06.
Statistische Physik - Theorie der Wärme (PD Dr. M. Falcke)
 Freie Universität Berlin WS 2006/2007 Fachbereich Physik 0..2006 Statistische Physik - Theorie der Wärme (PD Dr. M. Falcke) Übungsblatt 3: Zentraler Grenzwertsatz, Mikrokanonisches Ensemble, Entropie Aufgabe
Freie Universität Berlin WS 2006/2007 Fachbereich Physik 0..2006 Statistische Physik - Theorie der Wärme (PD Dr. M. Falcke) Übungsblatt 3: Zentraler Grenzwertsatz, Mikrokanonisches Ensemble, Entropie Aufgabe
1 Vorbemerkungen 1. 2 Zufallsexperimente - grundlegende Begriffe und Eigenschaften 2. 3 Wahrscheinlichkeitsaxiome 4. 4 Laplace-Experimente 6
 Inhaltsverzeichnis Vorbemerkungen 2 Zufallsexperimente - grundlegende Begriffe und Eigenschaften 2 3 Wahrscheinlichkeitsaxiome 4 4 Laplace-Experimente 6 5 Hilfsmittel aus der Kombinatorik 7 6 Bedingte
Inhaltsverzeichnis Vorbemerkungen 2 Zufallsexperimente - grundlegende Begriffe und Eigenschaften 2 3 Wahrscheinlichkeitsaxiome 4 4 Laplace-Experimente 6 5 Hilfsmittel aus der Kombinatorik 7 6 Bedingte
0 für t < für 1 t < für 2 t < für 3 t < für 4 t < 5 1 für t 5
 4 Verteilungen und ihre Kennzahlen 1 Kapitel 4: Verteilungen und ihre Kennzahlen A: Beispiele Beispiel 1: Eine diskrete Zufallsvariable X, die nur die Werte 1,, 3, 4, 5 mit positiver Wahrscheinlichkeit
4 Verteilungen und ihre Kennzahlen 1 Kapitel 4: Verteilungen und ihre Kennzahlen A: Beispiele Beispiel 1: Eine diskrete Zufallsvariable X, die nur die Werte 1,, 3, 4, 5 mit positiver Wahrscheinlichkeit
Numerische Methoden und Algorithmen in der Physik
 Numerische Methoden und Algorithmen in der Physik Hartmut Stadie, Christian Autermann 15.01.2009 Numerische Methoden und Algorithmen in der Physik Christian Autermann 1/ 47 Methode der kleinsten Quadrate
Numerische Methoden und Algorithmen in der Physik Hartmut Stadie, Christian Autermann 15.01.2009 Numerische Methoden und Algorithmen in der Physik Christian Autermann 1/ 47 Methode der kleinsten Quadrate
Zur Erinnerung. Stichworte aus der 14. Vorlesung: Grenzflächenphänomene: Oberflächenspannung. Grenzflächenspannung. Kapillarität
 Zur Erinnerung Stichworte aus der 14. Vorlesung: Grenzflächenphänomene: Oberflächenspannung Grenzflächenspannung Kapillarität Makroskopische Gastheorie: Gesetz on Boyle-Mariotte Luftdruck Barometrische
Zur Erinnerung Stichworte aus der 14. Vorlesung: Grenzflächenphänomene: Oberflächenspannung Grenzflächenspannung Kapillarität Makroskopische Gastheorie: Gesetz on Boyle-Mariotte Luftdruck Barometrische
Moderne Methoden der Datenverarbeitung in der Physik I
 Moderne Methoden der Datenverarbeitung in der Physik I Prof. Dr. Stefan Schael / Dr. Thomas Kirn I. Physikalisches Institut MAPLE II, Krypthographie Wahrscheinlichkeit Zufallszahlen, Wahrscheinlichkeitsdichten,
Moderne Methoden der Datenverarbeitung in der Physik I Prof. Dr. Stefan Schael / Dr. Thomas Kirn I. Physikalisches Institut MAPLE II, Krypthographie Wahrscheinlichkeit Zufallszahlen, Wahrscheinlichkeitsdichten,
Spezielle Verteilungen einer Variablen
 Kapitel 2 Spezielle Verteilungen einer Variablen In diesem Kapitel werden wir einige häufig benutzte Verteilungen, die von einer Variablen abhängen, vorstellen. 2.1 Binomial-Verteilung Binomial-Verteilungen
Kapitel 2 Spezielle Verteilungen einer Variablen In diesem Kapitel werden wir einige häufig benutzte Verteilungen, die von einer Variablen abhängen, vorstellen. 2.1 Binomial-Verteilung Binomial-Verteilungen
Teil VI. Gemeinsame Verteilungen. Lernziele. Beispiel: Zwei Würfel. Gemeinsame Verteilung
 Zusammenfassung: diskrete und stetige Verteilungen Woche 4: Verteilungen Patric Müller diskret Wahrscheinlichkeitsverteilung p() stetig Wahrscheinlichkeitsdichte f ()
Zusammenfassung: diskrete und stetige Verteilungen Woche 4: Verteilungen Patric Müller diskret Wahrscheinlichkeitsverteilung p() stetig Wahrscheinlichkeitsdichte f ()
Moderne Theoretische Physik WS 2013/2014
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik WS 23/24 Prof. Dr. A. Shnirman Blatt 2:Lösungen Dr. B. Narozhny Besprechung 8..23. Gauß scher
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik WS 23/24 Prof. Dr. A. Shnirman Blatt 2:Lösungen Dr. B. Narozhny Besprechung 8..23. Gauß scher
1. Wärmelehre 1.1. Temperatur. Physikalische Grundeinheiten : Die Internationalen Basiseinheiten SI (frz. Système international d unités)
 1. Wärmelehre 1.1. Temperatur Physikalische Grundeinheiten : Die Internationalen Basiseinheiten SI (frz. Système international d unités) 1. Wärmelehre 1.1. Temperatur Ein Maß für die Temperatur Prinzip
1. Wärmelehre 1.1. Temperatur Physikalische Grundeinheiten : Die Internationalen Basiseinheiten SI (frz. Système international d unités) 1. Wärmelehre 1.1. Temperatur Ein Maß für die Temperatur Prinzip
Hydrodynamische Wechselwirkung und Stokes Reibung
 Hydrodynamische Wechselwirkung und Stokes Reibung 9. Februar 2008 Problemstellung Kolloidsuspension aus Teilchen und Lösungsmittel Teilchen bewegen sich aufgrund von externen Kräften Schwerkraft Äußere
Hydrodynamische Wechselwirkung und Stokes Reibung 9. Februar 2008 Problemstellung Kolloidsuspension aus Teilchen und Lösungsmittel Teilchen bewegen sich aufgrund von externen Kräften Schwerkraft Äußere
Verteilungen mehrerer Variablen
 Kapitel 3 Verteilungen mehrerer Variablen 3. Eigenschaften von Verteilungen mehrerer Variablen Im allgemeinen muss man Wahrscheinlichkeiten für mehrere Variable, die häufig auch voneinander abhängen, gleichzeitig
Kapitel 3 Verteilungen mehrerer Variablen 3. Eigenschaften von Verteilungen mehrerer Variablen Im allgemeinen muss man Wahrscheinlichkeiten für mehrere Variable, die häufig auch voneinander abhängen, gleichzeitig
Kleine Schwingungen vieler Freiheitsgrade
 Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: ) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung: Bei fortgeschrittenen
Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: ) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung: Bei fortgeschrittenen
Einführung in die Stochastik für Informatiker Übungsaufgaben mit Lösungen
 Einführung in die Stochastik für Informatiker Übungsaufgaben mit Lösungen David Geier und Sven Middelberg RWTH Aachen, Sommersemester 27 Inhaltsverzeichnis Information 2 Aufgabe 4 Aufgabe 2 6 4 Aufgabe
Einführung in die Stochastik für Informatiker Übungsaufgaben mit Lösungen David Geier und Sven Middelberg RWTH Aachen, Sommersemester 27 Inhaltsverzeichnis Information 2 Aufgabe 4 Aufgabe 2 6 4 Aufgabe
Atomistische Modellierung
 Atomistische Modellierung Heptan Feuer (Sandia) Gerolf Ziegenhain TU Kaiserslautern Übersicht Kurzer Abriß der Geschichte Warum Computersimulationen? Beispiele: Verschiedene Längenskalen Genauer: Molekulardynamik
Atomistische Modellierung Heptan Feuer (Sandia) Gerolf Ziegenhain TU Kaiserslautern Übersicht Kurzer Abriß der Geschichte Warum Computersimulationen? Beispiele: Verschiedene Längenskalen Genauer: Molekulardynamik
Chaos im getriebenen nicht-linearen Pendel
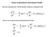 Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
5. Spezielle stetige Verteilungen
 5. Spezielle stetige Verteilungen 5.1 Stetige Gleichverteilung Eine Zufallsvariable X folgt einer stetigen Gleichverteilung mit den Parametern a und b, wenn für die Dichtefunktion von X gilt: f x = 1 für
5. Spezielle stetige Verteilungen 5.1 Stetige Gleichverteilung Eine Zufallsvariable X folgt einer stetigen Gleichverteilung mit den Parametern a und b, wenn für die Dichtefunktion von X gilt: f x = 1 für
Lösung von Optimierungsproblemen mit Monte Carlo Methoden
 Lösung von Optimierungsproblemen mit Monte Carlo Methoden Am Beispiel des Problem des Handlungsreisenden Vortragende: Alexandra Vosseler Inhaltsverzeichnis I. Einleitung II. Optimierung mit MCM II.i Vom
Lösung von Optimierungsproblemen mit Monte Carlo Methoden Am Beispiel des Problem des Handlungsreisenden Vortragende: Alexandra Vosseler Inhaltsverzeichnis I. Einleitung II. Optimierung mit MCM II.i Vom
15.5 Stetige Zufallsvariablen
 5.5 Stetige Zufallsvariablen Es gibt auch Zufallsvariable, bei denen jedes Elementarereignis die Wahrscheinlich keit hat. Beispiel: Lebensdauer eines radioaktiven Atoms Die Lebensdauer eines radioaktiven
5.5 Stetige Zufallsvariablen Es gibt auch Zufallsvariable, bei denen jedes Elementarereignis die Wahrscheinlich keit hat. Beispiel: Lebensdauer eines radioaktiven Atoms Die Lebensdauer eines radioaktiven
Fortgeschrittene MD/MC Methoden Wie man die freie Energie berechnet. Andreas Irmler
 Fortgeschrittene MD/MC Methoden Wie man die freie Energie berechnet Andreas Irmler 22. März 2010 Inhaltsverzeichnis 1 Freie Energie 2 1.1 Motivation............................................... 2 1.2
Fortgeschrittene MD/MC Methoden Wie man die freie Energie berechnet Andreas Irmler 22. März 2010 Inhaltsverzeichnis 1 Freie Energie 2 1.1 Motivation............................................... 2 1.2
Zufallsgrößen. Vorlesung Statistik für KW 29.04.2008 Helmut Küchenhoff
 Zufallsgrößen 2.5 Zufallsgrößen 2.5.1 Verteilungsfunktion einer Zufallsgröße 2.5.2 Wahrscheinlichkeits- und Dichtefunktion Wahrscheinlichkeitsfunktion einer diskreten Zufallsgröße Dichtefunktion einer
Zufallsgrößen 2.5 Zufallsgrößen 2.5.1 Verteilungsfunktion einer Zufallsgröße 2.5.2 Wahrscheinlichkeits- und Dichtefunktion Wahrscheinlichkeitsfunktion einer diskreten Zufallsgröße Dichtefunktion einer
2 Grundgrößen und -gesetze der Elektrodynamik
 Grundgrößen und -gesetze der Elektrodynamik. Grundgrößen der Elektrodynamik.. Ladung und die dreidimensionale δ-distribution Ladung Q, q Ladungen treten in zwei Variationen auf: positiv und negativ Einheit:
Grundgrößen und -gesetze der Elektrodynamik. Grundgrößen der Elektrodynamik.. Ladung und die dreidimensionale δ-distribution Ladung Q, q Ladungen treten in zwei Variationen auf: positiv und negativ Einheit:
5. Numerische Differentiation. und Integration
 5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
Klassische Theoretische Physik: Elektrodynamik
 Klassische Theoretische Physik: Elektrodynamik Kaustuv Basu (Deutsche Übersetzung: Jens Erler) Argelander-Institut für Astronomie Auf dem Hügel 71 kbasu@astro.uni-bonn.de Website: www.astro.uni-bonn.de/tp-l
Klassische Theoretische Physik: Elektrodynamik Kaustuv Basu (Deutsche Übersetzung: Jens Erler) Argelander-Institut für Astronomie Auf dem Hügel 71 kbasu@astro.uni-bonn.de Website: www.astro.uni-bonn.de/tp-l
Mathematischer Vorkurs für Physiker WS 2011/12 Vorlesung 3
 TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2011/12 Vorlesung 3 Differenziation und Integration von Vektorfunktionen Der Ortsvektor: Man kann einen Punkt P im Raum eindeutig durch die
TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2011/12 Vorlesung 3 Differenziation und Integration von Vektorfunktionen Der Ortsvektor: Man kann einen Punkt P im Raum eindeutig durch die
Wichtige Definitionen und Aussagen
 Wichtige Definitionen und Aussagen Zufallsexperiment, Ergebnis, Ereignis: Unter einem Zufallsexperiment verstehen wir einen Vorgang, dessen Ausgänge sich nicht vorhersagen lassen Die möglichen Ausgänge
Wichtige Definitionen und Aussagen Zufallsexperiment, Ergebnis, Ereignis: Unter einem Zufallsexperiment verstehen wir einen Vorgang, dessen Ausgänge sich nicht vorhersagen lassen Die möglichen Ausgänge
Wiederholung Film Brownsche Bewegung in Milch (Fettröpfchen in Wasser)
 2.Vorlesung Wiederholung Film Brownsche Bewegung in Milch (Fettröpfchen in Wasser) P.F.: Man weiß heute, dass das Brownsche Teilchen ein Perpetuum mobile zweiter Art ist, und dass sein Vorhandensein den
2.Vorlesung Wiederholung Film Brownsche Bewegung in Milch (Fettröpfchen in Wasser) P.F.: Man weiß heute, dass das Brownsche Teilchen ein Perpetuum mobile zweiter Art ist, und dass sein Vorhandensein den
DWT 2.1 Maximum-Likelihood-Prinzip zur Konstruktion von Schätzvariablen 330/467 Ernst W. Mayr
 2.1 Maximum-Likelihood-Prinzip zur Konstruktion von Schätzvariablen Wir betrachten nun ein Verfahren zur Konstruktion von Schätzvariablen für Parameter von Verteilungen. Sei X = (X 1,..., X n ). Bei X
2.1 Maximum-Likelihood-Prinzip zur Konstruktion von Schätzvariablen Wir betrachten nun ein Verfahren zur Konstruktion von Schätzvariablen für Parameter von Verteilungen. Sei X = (X 1,..., X n ). Bei X
Wechselkurse und Finanzmarkt-Indizes
 8. Mai 2008 Inhaltsverzeichnis 1 Wechselkurse Einführung Wechselkurs US Dollar - Deutsche Mark Statistischer Prozess 2 Reinjektion Eigenschaften der Fluktuationen von x(τ) 3 Diffusion auf Finanzmärkten
8. Mai 2008 Inhaltsverzeichnis 1 Wechselkurse Einführung Wechselkurs US Dollar - Deutsche Mark Statistischer Prozess 2 Reinjektion Eigenschaften der Fluktuationen von x(τ) 3 Diffusion auf Finanzmärkten
