Musterableitung Relativsätze als Hilfestellung zur Lösung von Aufgaben in den Übungen und der Klausur
|
|
|
- Friedrich Jörn Gerber
- vor 7 Jahren
- Abrufe
Transkript
1 eminar: Formale emantik Modul : Grammatikorie eminarleiter: Anke Assmann Institut für Linguistik Universität Leipzig Musterableitung Relativsätze als Hilfestellung zur Lösung von Aufgaben in den Übungen und der Klausur 1 Regeln (1) Terminale Knoten (TK) Wenn α ein terminaler Knoten ist, dann ist α im Definitionsbereich von, wenn α im Lexikon spezifiziert ist. (2) Nicht-verzweigende Knoten (NK) Wenn α ein nicht-verzweigender Knoten ist und β sein Tochterknoten ist, dann ist α im Definitionsbereich von, wenn β im Definitionsbereich von ist. Dann ist α = β. (3) Funktionale Applikation (FA) Wenn α ein verzweigender Knoten ist, {β, γ} die Menge von α s Tochterknoten ist, dann ist α im Definitionsbereich von, wenn sowohl β als auch γ im Definitionsbereich von sind und β eine Funktion ist, deren Definitionsbereich γ ist. Dann ist α = β(γ). (4) Prädikatmodifikation (PM) Wenn α ein verzweigender Knoten ist, {β, γ} die Menge von α s Tochterknoten ist, dann ist α im Definitionsbereich von, wenn sowohl β als auch γ im Definitionsbereich von sind und wenn β, γ D <e,t>. Dann ist α = λx D e. β(x) = γ(x) = 1. (5) Prädikatabstraktion (PA) Wenn α ein verzweigender Knoten ist, dessen Tochterknoten β i und γ sind, wobei β ein Relativpronomen oder such ist, und i IN, dann gilt für eine beliebige Zuweisungsfunktion a, α a = λx : x D e und γ ist im Definitionsbereich von ax/i. γ ax/i. (6) Zuweisungsunabhängige Denotation (assignment-independent denotation: AID) Für jeden Baum α gilt, α ist im Definitionsbereich von, gdw für alle Zuweisungen a und b, α a = α b. Wenn α im Definitionsbereich von, dann gilt für alle Zuweisungen a, α = α a. (7) puren/pronomen-regel (P) Wenn α eine pur oder ein Pronomen ist, a eine Zuweisungsfunktion und i dom(a), dann α i a = a(i). (8) mod. Zuweisung (MZ) ei a eine Zuweisungsfunktion, i IN und x D. Dann ist a x/i die einzige Zuweisung, die folgende Bedingungen erfüllt: a. dom(a x/i ) = dom(a) {i}, b. a x/i (i) = x und c. für jedes j dom(a x/i ), wobei j i: a x/i (j) = a(j). (9) Konvention für leere Zuweisungen (LZ) Für jeden Baum α gilt, α := α. 2 Aufgabe Bestimme die Denotation des folgenden Ausdrucks. 1
2 (10) such 2 wh 1 3 Ausführliche Ableitung Hinweis: Im folgenden ist wieder erst ein sehr detaillierter Beweis gegeben. o etwas ist in den Übungen und der Klausur nicht gefordert. Der Beweis soll lediglich dem Verständnis dienen. Im Anschluss an den Beweis gibt es eine legitime Kurzform des Beweises. chrit: Dem atz eine syntaktische truktur zuweisen (11) AP such 2 chritt 2: Denotationen der terminalen Knoten bestimmen chritt 3: Ableitung (12) a. = b. = [λx D e. [λy D e. y begutachtet x]] c. = [λf : f D <e,t> und es gibt genau ein x, so dass f(x) = 1. das einzige y, so dass f(y) = 1] d. = [λx D e. x ist ein Buch] e. = [λx D e. [λy D e. y schrieb x]] ist semantisch leer, such 2 /wh 1 sind synkategorematisch, / sind Variablen. 2
3 AP such 2 = (wegen LZ) 3
4 AP such 2 = (wegen PA) [λx D e. x/2 ] 4
5 = (wegen MZ) [λx D e. [] ] = (wegen sem. Leere ) [λx D e. [] ] = (wegen FA) 5
6 [λx D e. [] [] ] = (wegen NK) [λx D e. [] ( [] )] = (wegen AID) 6
7 [λx D e. [] ()] = (wegen FA) [λx D e. [] [] ()] = (wegen AID) 7
8 [λx D e. [] ()] = (wegen FA) [λx D e. ( [] [] ) ()] = (wegen AID) [λx D e. ( [] ) ()] = (wegen PM) 8
9 [λx D e. (([λy D e. [] (y) = [] (y) = 1])) ()] = (wegen NK) [λx D e. (([λy D e. [] (y) = [] (y) = 1])) ()] = (wegen AID) [λx D e. (([λy D e. (y) = [] (y) = 1])) ()] = (wegen PA) 9
10 [λx D e. (([λy D e. (y) = [λz D e. C [] z/1 ](y) = 1])) ()] = (wegen sem. Leere ) [λx D e. (([λy D e. (y) = [λz D e. [] z/1 ](y) = 1])) ()] [λx D e. (([λy D e. (y) = [] y/1 = 1])) ()] = (wegen MZ) [λx D e. (([λy D e. (y) = = 1])) ()] = (wegen FA) [λx D e. (([λy D e. (y) = ()] = 1])) 10
11 = (wegen NK) [λx D e. (([λy D e. (y) = = (wegen P) ( ) = 1])) ()] [λx D e. (([λy D e. (y) = = (wegen FA) (x) = 1])) ()] [λx D e. (([λy D e. (y) = = (wegen AID) (x) = 1])) ()] [λx D e. (([λy D e. (y) = = (wegen NK) (x) = 1])) ()] [λx D e. (([λy D e. (y) = ( = (wegen P) ) (x) = 1])) ()] [λx D e. (([λy D e. (y) = (y)(x) = 1])) ()] = (wegen (12-a)) [λx D e. (([λy D e. (y) = (y)(x) = 1])) ()] = (wegen (12-d)) [λx D e. (([λy D e. [λx D e. x ist ein Buch](y) = (y)(x) = 1])) ()] [λx D e. (([λy D e. y ist ein Buch und (y)(x) = 1])) ()] 11
12 = (wegen (12-e)) [λx D e. (([λy D e. y ist ein Buch und [λx D e. [λy D e. y schrieb x ]](y)(x) = 1])) ()] [λx D e. (([λy D e. y ist ein Buch und [λy D e. y schrieb y](x) = 1])) ()] [λx D e. (([λy D e. y ist ein Buch und x schrieb y])) ()] = (wegen (12-c)) [λx D e. ([λf : f D <e,t> und es gibt genau ein x, so dass f(x ) = 1. das einzige z, so dass f(z) = 1]([λy D e. y ist ein Buch und x schrieb y])) ()] [λx D e. (das einzige z, so dass [λy D e. y ist ein Buch und x schrieb y](z) = 1) ()] [λx D e. (das einzige z, so dass gilt z ist ein Buch und x schrieb z) ()] = (wegen (12-b)) [λx D e. [λx D e. [λy D e. y begutachtet x ]](das einzige z, so dass gilt z ist ein Buch und x schrieb z) ()] [λx D e. [λy D e. y begutachtet das einzige z, so dass gilt z ist ein Buch und x schrieb z]()] [λx D e. begutachtet das einzige z, so dass gilt z ist ein Buch und x schrieb z] 4 Kurzform chrit: Dem atz eine syntaktische truktur zuweisen 12
13 (13) AP 3 such chritt 2: Denotationen der terminalen Knoten bestimmen (14) a. = b. = [λx D e. [λy D e. y begutachtet x]] c. = [λf : f D <e,t> und es gibt genau ein x, so dass f(x) = 1. das einzige y, so dass f(y) = 1] d. = [λx D e. x ist ein Buch] e. = [λx D e. [λy D e. y schrieb x]] ist semantisch leer, such 2 /wh 1 sind synkategorematisch, / sind Variablen. chritt 3: Ableitung (Hinweise: ) Labels und Indizes sind unsere Freunde. Man kann sie anstelle von ganzen trukturbäumen einsetzen. Auch wenn man mehrere chritte auf einmal unternimmt, sollte man genau auflisten, welche Regeln angewendet werden, um auf den nächsten chritt zu kommen. Eine andere Möglichkeit den Beweis zu führen, besteht darin, zuerst die Denotationen einiger Teilbäume zu ermitteln (z.b. von 1, 6, 7, PP 1 etc.), und diese dann direkt einzusetzen. 13
14 AP 3 = (wegen LZ angew. auf AP 3, PA angew. auf AP 3, MZ, sem. Leere ) [λx D e. 3 [] ] = (wegen FA angew. auf 3, NK angew. auf 3, AID angew. auf ) [λx D e. 3 [] ()] = (wegen FA angew. auf 3, AID angew. auf ) [λx D e. ( 4 [] )()] = (wegen FA angew. auf 4, AID angew. auf ) [λx D e. (( 3 [] )) ()] = (wegen PM angew. auf 3, NK angew. auf 4, AID angewendet auf ) [λx D e. (([λy D e. (y) = 4 [] (y) = 1])) ()] = (wegen PA angew. auf 4, sem. Leere ) [λx D e. (([λy D e. (y) = [λz D e. 4 []z/1 ](y) = 1])) ()] [λx D e. (([λy D e. (y) = 4 []y/1 = 1])) ()] = (wegen MZ) [λx D e. (([λy D e. (y) = 4 = (wegen FA angew. auf 4, NK angew. auf 5 ) [λx D e. (([λy D e. (y) = 4 = (wegen P angew. auf ) [λx D e. (([λy D e. (y) = 4 = (wegen FA angew. auf 4, AID angew. auf, NK angew. auf 6 ) = 1])) ()] ( (x) = 1])) ()] ) = 1])) ()] 14
15 [λx D e. (([λy D e. (y) = ( = (wegen P angew. auf ) ) (x) = 1])) ()] [λx D e. (([λy D e. (y) = (y)(x) = 1])) ()] = (wegen (14-a)) [λx D e. (([λy D e. (y) = (y)(x) = 1])) ()] = (wegen (14-d), Def. λ-notation) [λx D e. (([λy D e. y ist ein Buch und (y)(x) = 1])) ()] = (wegen (14-e), Def. λ-notation) [λx D e. (([λy D e. y ist ein Buch und x schrieb y])) ()] = (wegen (14-c), Def. λ-notation) [λx D e. (das einzige z, so dass gilt z ist ein Buch und x schrieb z) ()] = (wegen (14-b), Def. λ-notation) [λx D e. begutachtet das einzige z, so dass gilt z ist ein Buch und x schrieb z] 15
Musterlösung Übungsblatt 3 ( ) 1 Prädikatmodifikation 40 Punkte
 Seminar: Formale Semantik Modul 04-006-1006: Grammatiktheorie Seminarleiter: Anke Assmann Musterlösung Übungsblatt 3 (14.05.2013) Abgabe bis 22.05.2013 Institut für Linguistik Universität Leipzig 1 Prädikatmodifikation
Seminar: Formale Semantik Modul 04-006-1006: Grammatiktheorie Seminarleiter: Anke Assmann Musterlösung Übungsblatt 3 (14.05.2013) Abgabe bis 22.05.2013 Institut für Linguistik Universität Leipzig 1 Prädikatmodifikation
Musterlösung Übungsblatt 6 ( )
 Seminar: Formale Semantik Modul 04-006-1006: Grammatikorie Seminarleiter: Anke Assmann Musterlösung Übungsblatt 6 (05.06.2013) Abgabe bis 14.06.2013 Institut für Linguistik Universität Leipzig Hinweis:
Seminar: Formale Semantik Modul 04-006-1006: Grammatikorie Seminarleiter: Anke Assmann Musterlösung Übungsblatt 6 (05.06.2013) Abgabe bis 14.06.2013 Institut für Linguistik Universität Leipzig Hinweis:
Linguistische Grundlagen 6. Semantik
 Linguistische Grundlagen 6. Semantik Gereon Müller Institut für Linguistik Universität Leipzig www.uni-leipzig.de/ muellerg Gereon Müller (Institut für Linguistik) 04-006-1001: Linguistische Grundlagen
Linguistische Grundlagen 6. Semantik Gereon Müller Institut für Linguistik Universität Leipzig www.uni-leipzig.de/ muellerg Gereon Müller (Institut für Linguistik) 04-006-1001: Linguistische Grundlagen
Formale Semantik. Anke Assmann Heim & Kratzer 1998, Kap. 3. Universität Leipzig, Institut für Linguistik
 1 / 30 Formale Semantik Heim & Kratzer 1998, Kap. 3 Anke Assmann anke.assmann@uni-leipzig.de Universität Leipzig, Institut für Linguistik 23.04.2013 2 / 30 Vorbemerkung Bisher gab es für jede syntaktische
1 / 30 Formale Semantik Heim & Kratzer 1998, Kap. 3 Anke Assmann anke.assmann@uni-leipzig.de Universität Leipzig, Institut für Linguistik 23.04.2013 2 / 30 Vorbemerkung Bisher gab es für jede syntaktische
Musterlösung Übungsblatt 1 ( )
 Seminar: Formale Semantik Modul 04-006-1006: Grammatiktheorie Seminarleiter: Anke Assmann Musterlösung Übungsblatt 1 (16.04.2013) Abgabe bis 26.04.2013 Institut für Linguistik Universität Leipzig 1 Funktionen
Seminar: Formale Semantik Modul 04-006-1006: Grammatiktheorie Seminarleiter: Anke Assmann Musterlösung Übungsblatt 1 (16.04.2013) Abgabe bis 26.04.2013 Institut für Linguistik Universität Leipzig 1 Funktionen
Formale Semantik. Anke Assmann Heim & Kratzer 1998, Kap. 2. Universität Leipzig, Institut für Linguistik
 1 / 52 Formale Semantik Heim & Kratzer 1998, Kap. 2 Anke Assmann anke.assmann@uni-leipzig.de Universität Leipzig, Institut für Linguistik 09.04.2013 2 / 52 Inhalt 1 Ein sanfter Einstieg 2 Ermittlung von
1 / 52 Formale Semantik Heim & Kratzer 1998, Kap. 2 Anke Assmann anke.assmann@uni-leipzig.de Universität Leipzig, Institut für Linguistik 09.04.2013 2 / 52 Inhalt 1 Ein sanfter Einstieg 2 Ermittlung von
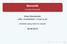
Musterlösung. [8 Punkte] Vereinfachen Sie folgende λ-ausdrücke so weit wie möglich Schritt für Schritt, d.h. nur eine λ-konversion pro Schritt.
![Musterlösung. [8 Punkte] Vereinfachen Sie folgende λ-ausdrücke so weit wie möglich Schritt für Schritt, d.h. nur eine λ-konversion pro Schritt. Musterlösung. [8 Punkte] Vereinfachen Sie folgende λ-ausdrücke so weit wie möglich Schritt für Schritt, d.h. nur eine λ-konversion pro Schritt.](/thumbs/98/137149256.jpg) Modulprüfung Grammatiktheorie, 2013 10.07.2013 Institut für Linguistik, Universität Leipzig Probeklausur: Formale emantik ([105] Punkte insgesamt.) Prüfer: Anke Assmann Hinweis: Unterstrichene Punktzahlen
Modulprüfung Grammatiktheorie, 2013 10.07.2013 Institut für Linguistik, Universität Leipzig Probeklausur: Formale emantik ([105] Punkte insgesamt.) Prüfer: Anke Assmann Hinweis: Unterstrichene Punktzahlen
3.4 Direkte vs. indirekte Interpretation
 3 Theorie der λ -Repräsentation 3.4 Direkte vs. indirekte Interpretation In unserer semantischen Analyse natürlichsprachlicher Ausdrücke haben wir bisher die Methode der indirekten Interpretation zugrunde
3 Theorie der λ -Repräsentation 3.4 Direkte vs. indirekte Interpretation In unserer semantischen Analyse natürlichsprachlicher Ausdrücke haben wir bisher die Methode der indirekten Interpretation zugrunde
Typengetriebene Interpretation. Arnim von Stechow Einführung in die Semantik
 Typengetriebene Interpretation Arnim von Stechow Einführung in die Semantik arnim.stechow@uni-tuebingen.de Programm Logische Typen Typengesteuerte Interpretation λ-schreibweise Prädikatsmodifikation (PM)
Typengetriebene Interpretation Arnim von Stechow Einführung in die Semantik arnim.stechow@uni-tuebingen.de Programm Logische Typen Typengesteuerte Interpretation λ-schreibweise Prädikatsmodifikation (PM)
Semantik. Anke Himmelreich Formale Semantik. Universität Leipzig, Institut für Linguistik 1 / 47
 1 / 47 Semantik Formale Semantik Anke Himmelreich anke.assmann@uni-leipzig.de Universität Leipzig, Institut für Linguistik 09.06.2016 2 / 47 Inhaltsverzeichnis 1 Vorbemerkungen 2 Wahrheitskonditionale
1 / 47 Semantik Formale Semantik Anke Himmelreich anke.assmann@uni-leipzig.de Universität Leipzig, Institut für Linguistik 09.06.2016 2 / 47 Inhaltsverzeichnis 1 Vorbemerkungen 2 Wahrheitskonditionale
Musterlösung Übungsblatt 2 ( ) 1 Prädikatmodifikation 23 Punkte
 eminar: Formale emanik Modul 04-006-1006: Grammaikheorie eminarleier: Anke Assmann Muserlösung Übungsbla 2 (07.05.2013) Abgabe bis 14.05.2013 Insiu für Linguisik Universiä Leipzig 1 Prädikamodifikaion
eminar: Formale emanik Modul 04-006-1006: Grammaikheorie eminarleier: Anke Assmann Muserlösung Übungsbla 2 (07.05.2013) Abgabe bis 14.05.2013 Insiu für Linguisik Universiä Leipzig 1 Prädikamodifikaion
Formale Semantik. Anke Assmann Zusammenfassung. Universität Leipzig, Institut für Linguistik 1 / 100
 1 / 100 Formale Semantik Zusammenfassung Anke Assmann anke.assmann@uni-leipzig.de Universität Leipzig, Institut für Linguistik 09.07.2013 2 / 100 Warnung Die folgende Zusammenfassung ersetzt nicht die
1 / 100 Formale Semantik Zusammenfassung Anke Assmann anke.assmann@uni-leipzig.de Universität Leipzig, Institut für Linguistik 09.07.2013 2 / 100 Warnung Die folgende Zusammenfassung ersetzt nicht die
EF Semantik: Musterlösung zu Aufgabenblatt 2
 EF Semantik: Musterlösung zu Aufgabenblatt 2 Magdalena Schwager magdalena@schwager.at Sommersemester 2010, Universität Wien Lösen Sie folgende Aufgaben (1)-(4) und geben Sie sie zusammengetackert bei András,
EF Semantik: Musterlösung zu Aufgabenblatt 2 Magdalena Schwager magdalena@schwager.at Sommersemester 2010, Universität Wien Lösen Sie folgende Aufgaben (1)-(4) und geben Sie sie zusammengetackert bei András,
Einführung in das λ-kalkül
 Einführung in das λ-kalkül Max Wagner IPD Snelting 1 3.11.2017 Max Wagner - Einführung in das λ-kalkül IPD KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Syntax Abstrakte Syntax:
Einführung in das λ-kalkül Max Wagner IPD Snelting 1 3.11.2017 Max Wagner - Einführung in das λ-kalkül IPD KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Syntax Abstrakte Syntax:
Funktionale Programmierung Einführung
 Einführung Prof. Dr. Oliver Braun Fakultät für Informatik und Mathematik Hochschule München Letzte Änderung: 13.09.2017 15:29 Inhaltsverzeichnis Was ist imperative Programmierung.......................
Einführung Prof. Dr. Oliver Braun Fakultät für Informatik und Mathematik Hochschule München Letzte Änderung: 13.09.2017 15:29 Inhaltsverzeichnis Was ist imperative Programmierung.......................
2 Theorie der semantischen Typen
 2 Theorie der semantischen Typen 2 Theorie der semantischen Typen [ Dowty 83-97, Gamut 75-9, Partee 338-34] 2. Typen Eine mögliche Erweiterung von PL ist die Prädikatenlogik der 2. Stufe (PL2). In PL2
2 Theorie der semantischen Typen 2 Theorie der semantischen Typen [ Dowty 83-97, Gamut 75-9, Partee 338-34] 2. Typen Eine mögliche Erweiterung von PL ist die Prädikatenlogik der 2. Stufe (PL2). In PL2
Schriftliche Hausaufgaben SoSe 2009 Musterlösung
 Schriftliche Hausaufgaben SoSe 2009 Musterlösung 1. Lexikalische Semantik I: Merkmalsanalyse & Prototypen (6 Punkte) i. Bestimmen Sie gemeinsame und unterscheidende Merkmale der beiden durch die Substantive
Schriftliche Hausaufgaben SoSe 2009 Musterlösung 1. Lexikalische Semantik I: Merkmalsanalyse & Prototypen (6 Punkte) i. Bestimmen Sie gemeinsame und unterscheidende Merkmale der beiden durch die Substantive
Höhere Mathematik für die Fachrichtung Physik
 Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Michael Hott, M. Sc. WS 5/6..6 Höhere Mathematik für die Fachrichtung Physik Lösungsvorschläge zum. Übungsblatt Aufgabe
Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Michael Hott, M. Sc. WS 5/6..6 Höhere Mathematik für die Fachrichtung Physik Lösungsvorschläge zum. Übungsblatt Aufgabe
Formale Methoden 1. Gerhard Jäger 12. Dezember Uni Bielefeld, WS 2007/2008 1/22
 1/22 Formale Methoden 1 Gerhard Jäger Gerhard.Jaeger@uni-bielefeld.de Uni Bielefeld, WS 2007/2008 12. Dezember 2007 2/22 Bäume Baumdiagramme Ein Baumdiagramm eines Satzes stellt drei Arten von Information
1/22 Formale Methoden 1 Gerhard Jäger Gerhard.Jaeger@uni-bielefeld.de Uni Bielefeld, WS 2007/2008 12. Dezember 2007 2/22 Bäume Baumdiagramme Ein Baumdiagramm eines Satzes stellt drei Arten von Information
4.3 NPn als Objekte oder als Prädikative [Chierchia , Lohnstein ]
![4.3 NPn als Objekte oder als Prädikative [Chierchia , Lohnstein ] 4.3 NPn als Objekte oder als Prädikative [Chierchia , Lohnstein ]](/thumbs/61/45932266.jpg) 4 Semantik von Nominalphrasen 4.3 NPn als Objekte oder als Prädikative [Chierchia 147-168, Lohnstein 185-196] 4.3.1 Quantifizierende NPn in Objektposition Steht eine quantifizierende NP nicht in Subjekt-,
4 Semantik von Nominalphrasen 4.3 NPn als Objekte oder als Prädikative [Chierchia 147-168, Lohnstein 185-196] 4.3.1 Quantifizierende NPn in Objektposition Steht eine quantifizierende NP nicht in Subjekt-,
Funktionale Programmierung - Grundlagen -
 Funktionale Programmierung - Grundlagen - λ Logische und funktionale Programmierung - Universität Potsdam - M. Thomas - Funkt. Programmierung Gundlagen - IX.1 λ-ausdrücke 1) Variablen: x, y, z,...v,v 1,...
Funktionale Programmierung - Grundlagen - λ Logische und funktionale Programmierung - Universität Potsdam - M. Thomas - Funkt. Programmierung Gundlagen - IX.1 λ-ausdrücke 1) Variablen: x, y, z,...v,v 1,...
Grundkurs Semantik. Sitzung 6: Prädikation, Modifikation, Referenz. Andrew Murphy
 Grundkurs Semantik Sitzung 6: Prädikation, Modifikation, Referenz Andrew Murphy andrew.murphy@uni-leizpig.de Grundkurs Semantik HU Berlin, Sommersemester 2015 http://www.uni-leipzig.de/ murphy/semantik15
Grundkurs Semantik Sitzung 6: Prädikation, Modifikation, Referenz Andrew Murphy andrew.murphy@uni-leizpig.de Grundkurs Semantik HU Berlin, Sommersemester 2015 http://www.uni-leipzig.de/ murphy/semantik15
AM3: Differenzial- und Integralrechnung im R n. 1 Begriffe. 2 Norm, Konvergenz und Stetigkeit. x 1. x 2. f : x n. aus Platzgründen schreibt man:
 AM3: Differenzial- und Integralrechnung im R n 1 Begriffe f : x 1 f 1 (x 1, x 2,..., x n ) x 2... f 2 (x 1, x 2,..., x n )... x n f m (x 1, x 2,..., x n ) }{{}}{{} R n R m aus Platzgründen schreibt man:
AM3: Differenzial- und Integralrechnung im R n 1 Begriffe f : x 1 f 1 (x 1, x 2,..., x n ) x 2... f 2 (x 1, x 2,..., x n )... x n f m (x 1, x 2,..., x n ) }{{}}{{} R n R m aus Platzgründen schreibt man:
Theoretische Informatik II
 Theoretische Informatik II Dr. Eva Richter / Holger Arnold Universität Potsdam, Theoretische Informatik, Sommersemester 2008 Übungsblatt 3 (Version 4) Abgabetermin: 13.5.2008, 12.00 Uhr Der λ-kalkül Da
Theoretische Informatik II Dr. Eva Richter / Holger Arnold Universität Potsdam, Theoretische Informatik, Sommersemester 2008 Übungsblatt 3 (Version 4) Abgabetermin: 13.5.2008, 12.00 Uhr Der λ-kalkül Da
2.2.2 Semantik von TL. Menge der Domänen. Zu jedem Typ gibt es eine Menge von möglichen Denotationen der Ausdrücke dieses Typs.
 2.2.2 Semantik von TL Menge der Domänen Zu jedem Typ gibt es eine Menge von möglichen Denotationen der Ausdrücke dieses Typs. Diese Menge wird Domäne des betreffenden Typs genannt. Johannes Dölling: Formale
2.2.2 Semantik von TL Menge der Domänen Zu jedem Typ gibt es eine Menge von möglichen Denotationen der Ausdrücke dieses Typs. Diese Menge wird Domäne des betreffenden Typs genannt. Johannes Dölling: Formale
Aufgaben für die 14. Übung zur Vorlesung Mathematik 2 für Informatiker: Analysis Sommersemester 2010
 Aufgaben für die 4. Übung zur Vorlesung Mathematik für Informatiker: Analysis Sommersemester 4. Bestimmen Sie den Flächeninhalt der dreiblättrigen Kleeblattkurve γ für ein Kleeblatt. Die Polarkoordinaten-
Aufgaben für die 4. Übung zur Vorlesung Mathematik für Informatiker: Analysis Sommersemester 4. Bestimmen Sie den Flächeninhalt der dreiblättrigen Kleeblattkurve γ für ein Kleeblatt. Die Polarkoordinaten-
Formale Semantik. Anke Assmann Heim & Kratzer 1998, Kap. 1. Universität Leipzig, Institut für Linguistik
 1 / 20 Formale Semantik Heim & Kratzer 1998, Kap. 1 Anke Assmann anke.assmann@uni-leipzig.de Universität Leipzig, Institut für Linguistik 09.04.2013 2 / 20 Inhalt 1 Vorbemerkungen 2 Wahrheitskonditionale
1 / 20 Formale Semantik Heim & Kratzer 1998, Kap. 1 Anke Assmann anke.assmann@uni-leipzig.de Universität Leipzig, Institut für Linguistik 09.04.2013 2 / 20 Inhalt 1 Vorbemerkungen 2 Wahrheitskonditionale
Technische Universität München. Probeklausur Lösung SS 2012
 Technische Universität München Andreas Wörfel & Carla Zensen Ferienkurs Analysis für Physiker Probeklausur Lösung SS Aufgabe Differenzierbarkeit / Punkte: [4,, 3, 4] Es sei f(x, y) = sin(x3 + y 3 ) x +
Technische Universität München Andreas Wörfel & Carla Zensen Ferienkurs Analysis für Physiker Probeklausur Lösung SS Aufgabe Differenzierbarkeit / Punkte: [4,, 3, 4] Es sei f(x, y) = sin(x3 + y 3 ) x +
1 0, x C X (A). = 1 χ A(x).
 Aufgabe 1 a) Wir müssen nur zeigen, dass χ A B (x) = χ A (x) χ B (x) für alle x X gilt. (Dass χ A χ B Abbildung von X in {0, 1} ist, ist klar.) Sei also x X beliebig. Fall 1: x A B. Dies bedeutet x A und
Aufgabe 1 a) Wir müssen nur zeigen, dass χ A B (x) = χ A (x) χ B (x) für alle x X gilt. (Dass χ A χ B Abbildung von X in {0, 1} ist, ist klar.) Sei also x X beliebig. Fall 1: x A B. Dies bedeutet x A und
Extensionale Semantik I
 Einheiten: 29.04. 13.05. HS/OS Satzsemantik SoSe 2015 Eberhard Karls Universität Tübingen Sarah Zobel, sarah.zobel@ds.uni-tuebingen.de Extensionale Semantik I Inhaltsverzeichnis 1 Konzeptueller Hintergrund
Einheiten: 29.04. 13.05. HS/OS Satzsemantik SoSe 2015 Eberhard Karls Universität Tübingen Sarah Zobel, sarah.zobel@ds.uni-tuebingen.de Extensionale Semantik I Inhaltsverzeichnis 1 Konzeptueller Hintergrund
Extensionale Semantik II
 Einheiten: 20.05. 10.06. HS/OS Satzsemantik SoSe 2015 Eberhard Karls Universität Tübingen Sarah Zobel, sarah.zobel@ds.uni-tuebingen.de Extensionale Semantik II Inhaltsverzeichnis 1 Non-verbale Prädikate:
Einheiten: 20.05. 10.06. HS/OS Satzsemantik SoSe 2015 Eberhard Karls Universität Tübingen Sarah Zobel, sarah.zobel@ds.uni-tuebingen.de Extensionale Semantik II Inhaltsverzeichnis 1 Non-verbale Prädikate:
Einführung in die Formale Semantik (Block II) Wiederholung und Zusammenfassung. Magdalena Schwager
 Einführung in die Formale Semantik (Block II) Magdalena Schwager magdalena@schwager.at Sommersemester 2010, Universität Wien (folgt Heim & Kratzer, Ch.4) Wiederholung und Zusammenfassung Ziel der formalen
Einführung in die Formale Semantik (Block II) Magdalena Schwager magdalena@schwager.at Sommersemester 2010, Universität Wien (folgt Heim & Kratzer, Ch.4) Wiederholung und Zusammenfassung Ziel der formalen
Kontextfreie Sprachen Kontextfreie Sprachen und Grammatiken. Satzformen sind die Wörter aus (N T ). Notation: Wir verwenden oft
 und Grammatiken (Folie 119, eite 202 im kript) atzformen sind die Wörter aus (N T ). Notation: Wir verwenden oft a, b, c,... für Terminalsymbole A, B, C,... für Nonterminale u, v, w,... für Terminalwörter
und Grammatiken (Folie 119, eite 202 im kript) atzformen sind die Wörter aus (N T ). Notation: Wir verwenden oft a, b, c,... für Terminalsymbole A, B, C,... für Nonterminale u, v, w,... für Terminalwörter
10 Extremwerte mit Nebenbedingungen
 10 Extremwerte mit Nebenbedingungen 49 10 Extremwerte mit Nebenbedingungen Wir betrachten nun Extremwertaufgaben, bei denen nach dem Extremwert einer fx 1,, x n gesucht wird, aber die Menge der zulässigen
10 Extremwerte mit Nebenbedingungen 49 10 Extremwerte mit Nebenbedingungen Wir betrachten nun Extremwertaufgaben, bei denen nach dem Extremwert einer fx 1,, x n gesucht wird, aber die Menge der zulässigen
Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler
 Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler Sommersemester 7 (7.8.7). Gegeben ist die Matrix A 3 3 3 (a) Bestimmen Sie sämtliche Eigenwerte sowie die zugehörigen Eigenvektoren.
Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler Sommersemester 7 (7.8.7). Gegeben ist die Matrix A 3 3 3 (a) Bestimmen Sie sämtliche Eigenwerte sowie die zugehörigen Eigenvektoren.
AM3: Differenzial- und Integralrechnung im R n. 1 Begriffe. 2 Norm, Konvergenz und Stetigkeit. x 1. x 2. f : x n. aus Platzgründen schreibt man:
 AM3: Differenzial- und Integralrechnung im R n 1 Begriffe f : x 1 f 1 x 1, x 2,..., x n ) x 2... f 2 x 1, x 2,..., x n )... x n f m x 1, x 2,..., x n ) }{{}}{{} R n R m aus Platzgründen schreibt man: f
AM3: Differenzial- und Integralrechnung im R n 1 Begriffe f : x 1 f 1 x 1, x 2,..., x n ) x 2... f 2 x 1, x 2,..., x n )... x n f m x 1, x 2,..., x n ) }{{}}{{} R n R m aus Platzgründen schreibt man: f
1. Allgemeine Konstruktionsanweisung
 1. Allgemeine Konstruktionsanweisung Zur Konstruktion der emantik eines atzes nach den bekannten Mechanismen wird zunächst das Erstellen eines syntaktischen Ableitungsbaumes empfohlen, an dem sich auch
1. Allgemeine Konstruktionsanweisung Zur Konstruktion der emantik eines atzes nach den bekannten Mechanismen wird zunächst das Erstellen eines syntaktischen Ableitungsbaumes empfohlen, an dem sich auch
D-MATH, D-PHYS, D-CHAB Analysis II FS 2018 Prof. Manfred Einsiedler. Übungsblatt 6. f(x, y, z) = xyz + 3e x y
 D-MATH, D-PHYS, D-CHAB Analysis II FS 2018 Prof. Manfred Einsiedler Übungsblatt 6 1. Es seien f : R 2 R 3 und g : R 3 R 3 die Funktionen definiert durch x cos(y) 2 y 2 f(x, y) = x sin(y) und g(x, y, z)
D-MATH, D-PHYS, D-CHAB Analysis II FS 2018 Prof. Manfred Einsiedler Übungsblatt 6 1. Es seien f : R 2 R 3 und g : R 3 R 3 die Funktionen definiert durch x cos(y) 2 y 2 f(x, y) = x sin(y) und g(x, y, z)
Funktionen und sprachliche Bedeutungen
 Einführung in die Semantik,4. Sitzung Mehr zu Funktionen / Mengen, Relationen, Göttingen 1. November 2006 Mengen und sprachliche Bedeutungen Abstraktion und Konversion Rekursion Charakteristische Funktionen
Einführung in die Semantik,4. Sitzung Mehr zu Funktionen / Mengen, Relationen, Göttingen 1. November 2006 Mengen und sprachliche Bedeutungen Abstraktion und Konversion Rekursion Charakteristische Funktionen
Mathematik für Informatiker I Mitschrift zur Vorlesung vom
 Mathematik für Informatiker I Mitschrift zur Vorlesung vom 18.11.2004 Zur Wiederholung: Das Kartesische Produkt dient dem Ordnen von Mengen. A B = {(a, b) : a A, b B)} Spezialfall A = Äquivalenzrelation
Mathematik für Informatiker I Mitschrift zur Vorlesung vom 18.11.2004 Zur Wiederholung: Das Kartesische Produkt dient dem Ordnen von Mengen. A B = {(a, b) : a A, b B)} Spezialfall A = Äquivalenzrelation
DisMod-Repetitorium Tag 1
 DisMod-Repetitorium Tag 1 Aussagenlogik, Mengen 19. März 2018 1 Organisatorisches 2 Tipps zur Klausur 3 Aussagenlogik Was gehört in die Aussagenlogik, was nicht? Notationen für viele Terme Belegungen,
DisMod-Repetitorium Tag 1 Aussagenlogik, Mengen 19. März 2018 1 Organisatorisches 2 Tipps zur Klausur 3 Aussagenlogik Was gehört in die Aussagenlogik, was nicht? Notationen für viele Terme Belegungen,
Wichtige Klassen reeller Funktionen
 0 Wichtige Klassen reeller Funktionen Monotone Funktionen sind i.a. unstetig, aber man kann etwas über das Grenzwertverhalten aussagen, wenn man nur einseitige Grenzwerte betrachtet. Definition 0. : Sei
0 Wichtige Klassen reeller Funktionen Monotone Funktionen sind i.a. unstetig, aber man kann etwas über das Grenzwertverhalten aussagen, wenn man nur einseitige Grenzwerte betrachtet. Definition 0. : Sei
Analysis I. 7. Übungsstunde. Steven Battilana. battilana.uk/teaching
 Analysis I 7. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching April 26, 207 Erinnerung Satz. (Zwischenwertsatz) Sei f : [a, b] R stetig mit f(a) f(b). Dann gibt es zu jedem
Analysis I 7. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching April 26, 207 Erinnerung Satz. (Zwischenwertsatz) Sei f : [a, b] R stetig mit f(a) f(b). Dann gibt es zu jedem
Lambda-Notation. Semantik und Pragmatik. Lambda-Notation. Lambda-Notation. Lambda-Notation. Lambda-Notation
 emantik und Pragmatik 22. Mai 2006 Gerard Jäger mit Angabe des Definitionsbereics Funktionen aben Definitionsbereic: { x, x 2 x N} { x, x 2 x R} Notation λx.x 2 desalb unvollständig vollständige Notation:
emantik und Pragmatik 22. Mai 2006 Gerard Jäger mit Angabe des Definitionsbereics Funktionen aben Definitionsbereic: { x, x 2 x N} { x, x 2 x R} Notation λx.x 2 desalb unvollständig vollständige Notation:
Übungen zum Ferienkurs Analysis II 2014
 Übungen zum Ferienkurs Analysis II 4 Probeklausur Allgemein Hinweise: Die Arbeitszeit beträgt 9 Minuten. Falls nicht anders angegeben, sind alle en ausführlich und nachvollziehbar zu begründen. Schreiben
Übungen zum Ferienkurs Analysis II 4 Probeklausur Allgemein Hinweise: Die Arbeitszeit beträgt 9 Minuten. Falls nicht anders angegeben, sind alle en ausführlich und nachvollziehbar zu begründen. Schreiben
4.3 NPn als Objekte oder als Prädikative
 4.3 NPn als Objekte oder als Prädikative 4.3.1 Quantifizierende NPn in Objektposition Steht eine quantifizierende NP nicht in Subjekt-, sondern in Objektposition, ist unter den bisher angenommenen Voraussetzungen
4.3 NPn als Objekte oder als Prädikative 4.3.1 Quantifizierende NPn in Objektposition Steht eine quantifizierende NP nicht in Subjekt-, sondern in Objektposition, ist unter den bisher angenommenen Voraussetzungen
Übungsblatt 1. Analysis II SS
 Übungsblatt 1 Aufgabe 1 (Die Jensen Ungleichung) (i) Sei f : (a, b) R eine zwei mal stetig differenzierbare Funktion. In Notation: f C 2 (a, b). Wir nehmen an, daß f konvex ist, d.h. f 0. Beweisen Sie
Übungsblatt 1 Aufgabe 1 (Die Jensen Ungleichung) (i) Sei f : (a, b) R eine zwei mal stetig differenzierbare Funktion. In Notation: f C 2 (a, b). Wir nehmen an, daß f konvex ist, d.h. f 0. Beweisen Sie
Der einfach getypter Lambda-Kalkül
 Der einfach getypter Lambda-Kalkül Typprüfung und Typinferenz Tobias Nipkow und Steffen Smolka Technische Universität München 1 Einleitung 2 Explizit getypter λ-kalkül 3 Implizit getypter λ-kalkül Statische
Der einfach getypter Lambda-Kalkül Typprüfung und Typinferenz Tobias Nipkow und Steffen Smolka Technische Universität München 1 Einleitung 2 Explizit getypter λ-kalkül 3 Implizit getypter λ-kalkül Statische
7 Intensionale Semantik
 7 Intensionale Semantik 7.1 Intension und Extension Bisher wurde eine extensionale Semantik verfolgt. D.h. als Denotationen von Sätzen wurden Wahrheitswerte, als Denotationen von Individuenausdrücken Individuen
7 Intensionale Semantik 7.1 Intension und Extension Bisher wurde eine extensionale Semantik verfolgt. D.h. als Denotationen von Sätzen wurden Wahrheitswerte, als Denotationen von Individuenausdrücken Individuen
Formale Methoden der Softwaretechnik 1 Vorlesung vom : Grundlage von Isabelle
 1 Formale Methoden der Softwaretechnik 1 Vorlesung vom 16.11.09: Grundlage von Isabelle Christoph Lüth, Lutz Schröder Universität Bremen Wintersemester 2009/10 2 Fahrplan Teil I: Grundlagen der Formalen
1 Formale Methoden der Softwaretechnik 1 Vorlesung vom 16.11.09: Grundlage von Isabelle Christoph Lüth, Lutz Schröder Universität Bremen Wintersemester 2009/10 2 Fahrplan Teil I: Grundlagen der Formalen
Name Vorname Fachrichtg. Matrikelnr. Punkte Klausur Aufgabe max. Punkte Punkte. Bitte beachten!
 Fakultät für Mathematik Institut für Algebra und Geometrie Prof. Dr. Martin Henk, Dr. Michael Höding Modulprüfung Mathematik III Fachrichtung: Computer Science in Engineering, Computervisualistik, Informatik,
Fakultät für Mathematik Institut für Algebra und Geometrie Prof. Dr. Martin Henk, Dr. Michael Höding Modulprüfung Mathematik III Fachrichtung: Computer Science in Engineering, Computervisualistik, Informatik,
Musterlösung. TECHNISCHE UNIVERSITÄT MÜNCHEN Fakultät für Mathematik. Klausur Mathematik für Physiker 3 (Analysis 2) I... II...
 ................ Note I II Name Vorname 1 Matrikelnummer Studiengang (Hauptfach) Fachrichtung (Nebenfach) 2 3 Unterschrift der Kandidatin/des Kandidaten 4 TECHNISCHE UNIVERSITÄT MÜNCHEN Fakultät für Mathematik
................ Note I II Name Vorname 1 Matrikelnummer Studiengang (Hauptfach) Fachrichtung (Nebenfach) 2 3 Unterschrift der Kandidatin/des Kandidaten 4 TECHNISCHE UNIVERSITÄT MÜNCHEN Fakultät für Mathematik
9 Differentialrechnung für Funktionen in n Variablen
 $Id: diff.tex,v.7 29/7/2 3:4:3 hk Exp $ $Id: ntaylor.tex,v.2 29/7/2 3:26:42 hk Exp $ 9 Differentialrechnung für Funktionen in n Variablen 9.6 Lagrange Multiplikatoren Die Berechnung von Maxima und Minima
$Id: diff.tex,v.7 29/7/2 3:4:3 hk Exp $ $Id: ntaylor.tex,v.2 29/7/2 3:26:42 hk Exp $ 9 Differentialrechnung für Funktionen in n Variablen 9.6 Lagrange Multiplikatoren Die Berechnung von Maxima und Minima
Nichtklassische Logiken
 Nichtklassische Logiken Peter H. Schmitt pschmitt@ira.uka.de UNIVERSITÄT KARLSRUHE Sommersemester 2004 P. H. Schmitt: Nichtklassische Logiken p.1 Inhalt Wiederholung P. H. Schmitt: Nichtklassische Logiken
Nichtklassische Logiken Peter H. Schmitt pschmitt@ira.uka.de UNIVERSITÄT KARLSRUHE Sommersemester 2004 P. H. Schmitt: Nichtklassische Logiken p.1 Inhalt Wiederholung P. H. Schmitt: Nichtklassische Logiken
Fortgeschrittene Funktionale Programmierung
 Fortgeschrittene Funktionale Programmierung 13. Vorlesung Janis Voigtländer Universität Bonn Wintersemester 2015/16 Erweiterung um Datentypen Typen: τ := Bool [τ] Terme: t := False True [ ] τ t : t case
Fortgeschrittene Funktionale Programmierung 13. Vorlesung Janis Voigtländer Universität Bonn Wintersemester 2015/16 Erweiterung um Datentypen Typen: τ := Bool [τ] Terme: t := False True [ ] τ t : t case
5 Potenzreihenansatz und spezielle Funktionen
 5 Potenzreihenansatz und spezielle Funktionen In diesem Kapitel betrachten wir eine Methode zur Lösung linearer Differentialgleichungen höherer Ordnung, die sich anwenden läßt, wenn sich alle Koeffizienten
5 Potenzreihenansatz und spezielle Funktionen In diesem Kapitel betrachten wir eine Methode zur Lösung linearer Differentialgleichungen höherer Ordnung, die sich anwenden läßt, wenn sich alle Koeffizienten
Inferenzmethoden. Einheit 18. Logik höherer Stufe
 Inferenzmethoden Einheit 18 Logik höherer Stufe 1. Syntax und Semantik 2. Simulation mathematischer Konstrukte 3. Beweisführung in Logik höherer Stufe Logik höherer Stufe Logik erster Stufe hat nur einfache
Inferenzmethoden Einheit 18 Logik höherer Stufe 1. Syntax und Semantik 2. Simulation mathematischer Konstrukte 3. Beweisführung in Logik höherer Stufe Logik höherer Stufe Logik erster Stufe hat nur einfache
Diskursrepräsentationstheorie. Th H
 Diskursrepräsentationstheorie Th H Einführung in die Diskursrepräsentationstheorie Zentraler Gegenstand der Diskursrepräsentationstheorie (DRT) sind sog. Diskurse Abfolgen von Deklarativsätzen. Die DRT
Diskursrepräsentationstheorie Th H Einführung in die Diskursrepräsentationstheorie Zentraler Gegenstand der Diskursrepräsentationstheorie (DRT) sind sog. Diskurse Abfolgen von Deklarativsätzen. Die DRT
Lineare Differentialgleichungen höherer Ordnung
 Lineare Differentialgleichungen höherer Ordnung I. Grundlegendes Eine homogene lineare Differentialgleichung n-ter Ordnung besitzt die Form y (n) + a n 1 (x)y (n 1) +... + a 1 (x)y + a 0 (x)y = 0 Eine
Lineare Differentialgleichungen höherer Ordnung I. Grundlegendes Eine homogene lineare Differentialgleichung n-ter Ordnung besitzt die Form y (n) + a n 1 (x)y (n 1) +... + a 1 (x)y + a 0 (x)y = 0 Eine
Fortgeschrittene Funktionale Programmierung
 Fortgeschrittene Funktionale Programmierung 12. Vorlesung Janis Voigtländer Universität Bonn Wintersemester 2015/16 Motivation Auf http://www-ps.iai.uni-bonn.de/ft: 1 Motivation 1 Betrachtungen zu Polymorphie
Fortgeschrittene Funktionale Programmierung 12. Vorlesung Janis Voigtländer Universität Bonn Wintersemester 2015/16 Motivation Auf http://www-ps.iai.uni-bonn.de/ft: 1 Motivation 1 Betrachtungen zu Polymorphie
Diskrete Strukturen Nachholklausur
 Technische Universität München Winter 0/7 Prof. H. J. Bungartz / Dr. M. Luttenberger, J. Bräckle, K. Röhner HA- Diskrete Strukturen Nachholklausur.04.07 Beachten Sie: Soweit nicht anders angegeben, ist
Technische Universität München Winter 0/7 Prof. H. J. Bungartz / Dr. M. Luttenberger, J. Bräckle, K. Röhner HA- Diskrete Strukturen Nachholklausur.04.07 Beachten Sie: Soweit nicht anders angegeben, ist
Lösung - Serie 25. D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger
 D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger Lösung - Serie 25 1. Wie lautet die charakteristische Gleichung der Differentialgleichung y + 2y + y = 0? (a) λ 3 + 2λ + 1 = 0 (b) λ 3 + 2λ = 0 (c)
D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger Lösung - Serie 25 1. Wie lautet die charakteristische Gleichung der Differentialgleichung y + 2y + y = 0? (a) λ 3 + 2λ + 1 = 0 (b) λ 3 + 2λ = 0 (c)
Lineare Algebra und Analytische Geometrie
 Fakultät Mathematik und Naturwissenschaften, Fachrichtung Mathematik, Institut für Algebra Prof. Dr. Stefan Schmidt Name, Vorname: erreichte Punktzahl: Teil 1: Teil 2: Note: Klausur zur Vorlesung: Lineare
Fakultät Mathematik und Naturwissenschaften, Fachrichtung Mathematik, Institut für Algebra Prof. Dr. Stefan Schmidt Name, Vorname: erreichte Punktzahl: Teil 1: Teil 2: Note: Klausur zur Vorlesung: Lineare
Mathematische Grundlagen
 Prof. Dr. Peter Becker Fachbereich Informatik Mathematische Grundlagen Klausur Sommersemester 2016 16. September 2016, 1:00 14:0 Uhr Name: Vorname: Matrikelnr.: Unterschrift: Aufgabe 1 2 4 5 6 Summe Punkte
Prof. Dr. Peter Becker Fachbereich Informatik Mathematische Grundlagen Klausur Sommersemester 2016 16. September 2016, 1:00 14:0 Uhr Name: Vorname: Matrikelnr.: Unterschrift: Aufgabe 1 2 4 5 6 Summe Punkte
Programmierkurs Python II
 Programmierkurs Python II Michaela Regneri & tefan Thater FR 4.7 Allgemeine Linguistik (Computerlinguistik) Universität des aarlandes ommersemester 2010 (Charniak, 1997) the dog biscuits N V N V the dog
Programmierkurs Python II Michaela Regneri & tefan Thater FR 4.7 Allgemeine Linguistik (Computerlinguistik) Universität des aarlandes ommersemester 2010 (Charniak, 1997) the dog biscuits N V N V the dog
Höhere Mathematik II für BWIW, BNC, BAI, BGIP, GTB, Ma Hausaufgaben zum Übungsblatt 5 - Lösung
 TU Bergakademie Freiberg Sommersemester Dr. Gunter Semmler Dr. Anja Kohl Höhere Mathematik II für BWIW, BNC, BAI, BGIP, GTB, Ma Hausaufgaben zum Übungsblatt 5 - Lösung Differentialrechnung für Funktionen
TU Bergakademie Freiberg Sommersemester Dr. Gunter Semmler Dr. Anja Kohl Höhere Mathematik II für BWIW, BNC, BAI, BGIP, GTB, Ma Hausaufgaben zum Übungsblatt 5 - Lösung Differentialrechnung für Funktionen
Klausur zur Mathematik III. Variante A
 Lehrstuhl C für Mathematik (Analysis) Prof. Dr. Oliver Schaudt Aachen, den 21.02.2018 Klausur zur Mathematik III WS 2017/18 Variante A Name Matrikelnr. Hinweise Zugelassene Hilfsmittel: Als Hilfsmittel
Lehrstuhl C für Mathematik (Analysis) Prof. Dr. Oliver Schaudt Aachen, den 21.02.2018 Klausur zur Mathematik III WS 2017/18 Variante A Name Matrikelnr. Hinweise Zugelassene Hilfsmittel: Als Hilfsmittel
Klassische Extremwerttheorie Seien (X k ), k IN, nicht degenerierte i.i.d. ZV mit Verteilungsfunktion. Für n 1 definiere S n := n
 Klassische Extremwerttheorie Seien (X k ), k IN, nicht degenerierte i.i.d. ZV mit Verteilungsfunktion F. Für n 1 definiere S n := n i=1 X i, M n := max{x i :1 i n} Frage: Welche sind die möglichen (nicht
Klassische Extremwerttheorie Seien (X k ), k IN, nicht degenerierte i.i.d. ZV mit Verteilungsfunktion F. Für n 1 definiere S n := n i=1 X i, M n := max{x i :1 i n} Frage: Welche sind die möglichen (nicht
Klausur zur Mathematik III. Variante B
 Lehrstuhl C für Mathematik (Analysis) Prof. Dr. Oliver Schaudt Aachen, den 21.02.2018 Klausur zur Mathematik III WS 2017/18 Variante B Name Matrikelnr. Hinweise Zugelassene Hilfsmittel: Als Hilfsmittel
Lehrstuhl C für Mathematik (Analysis) Prof. Dr. Oliver Schaudt Aachen, den 21.02.2018 Klausur zur Mathematik III WS 2017/18 Variante B Name Matrikelnr. Hinweise Zugelassene Hilfsmittel: Als Hilfsmittel
Sprachanalyse. Fachseminar WS 08/09 Dozent: Prof. Dr. Helmut Weber Referentin: Nadia Douiri
 Sprachanalyse WS 08/09 Dozent: Prof. Dr. Helmut Weber Referentin: Inhalt 1. Formale Sprachen 2. Chomsky-Hierarchie 2 FORMALE SPRACHE 1. WAS IST EINE SPRACHE? 2. WIE BESCHREIBT MAN EINE SPRACHE? 3. WAS
Sprachanalyse WS 08/09 Dozent: Prof. Dr. Helmut Weber Referentin: Inhalt 1. Formale Sprachen 2. Chomsky-Hierarchie 2 FORMALE SPRACHE 1. WAS IST EINE SPRACHE? 2. WIE BESCHREIBT MAN EINE SPRACHE? 3. WAS
Übungen zur Ingenieur-Mathematik I WS 2017/2018 Blatt Aufgabe 33: Zeigen Sie, dass für die Funktionen
 Übungen zur Ingenieur-Mathematik I WS 7/8 Blatt 8..7 Aufgabe : Zeigen Sie, dass für die Funktionen a b gilt: cosh x = (ex + e x und sinh x = (ex e x a (cosh x = sinh x, b (sinh x = cosh x, c cosh x sinh
Übungen zur Ingenieur-Mathematik I WS 7/8 Blatt 8..7 Aufgabe : Zeigen Sie, dass für die Funktionen a b gilt: cosh x = (ex + e x und sinh x = (ex e x a (cosh x = sinh x, b (sinh x = cosh x, c cosh x sinh
9. Woche: Elliptische Kurven - Gruppenarithmetik. 9. Woche: Elliptische Kurven - Gruppenarithmetik 187/ 238
 9 Woche: Elliptische Kurven - Gruppenarithmetik 9 Woche: Elliptische Kurven - Gruppenarithmetik 187/ 238 Elliptische Kurven Ḋefinition Elliptische Kurve Eine elliptische Kurve E über dem Körper K ist eine
9 Woche: Elliptische Kurven - Gruppenarithmetik 9 Woche: Elliptische Kurven - Gruppenarithmetik 187/ 238 Elliptische Kurven Ḋefinition Elliptische Kurve Eine elliptische Kurve E über dem Körper K ist eine
Formale Systeme. Prof. Dr. Bernhard Beckert, WS 2017/ KIT Die Forschungsuniversita t in der Helmholtz-Gemeinschaft
 Formale Systeme Prof. Dr. Bernhard Beckert, WS 2017/2018 Pra dikatenlogik: Tableaukalku l (ohne Gleichheit) KIT I NSTITUT F U R T HEORETISCHE I NFORMATIK www.kit.edu KIT Die Forschungsuniversita t in der
Formale Systeme Prof. Dr. Bernhard Beckert, WS 2017/2018 Pra dikatenlogik: Tableaukalku l (ohne Gleichheit) KIT I NSTITUT F U R T HEORETISCHE I NFORMATIK www.kit.edu KIT Die Forschungsuniversita t in der
Formale Systeme. Prof. Dr. Bernhard Beckert, WS 2016/ KIT Die Forschungsuniversita t in der Helmholtz-Gemeinschaft
 Formale Systeme Prof. Dr. Bernhard Beckert, WS 2016/2017 Pra dikatenlogik: Tableaukalku l (ohne Gleichheit) KIT I NSTITUT F U R T HEORETISCHE I NFORMATIK www.kit.edu KIT Die Forschungsuniversita t in der
Formale Systeme Prof. Dr. Bernhard Beckert, WS 2016/2017 Pra dikatenlogik: Tableaukalku l (ohne Gleichheit) KIT I NSTITUT F U R T HEORETISCHE I NFORMATIK www.kit.edu KIT Die Forschungsuniversita t in der
Funktionale Programmierung ALP I. λ Kalkül WS 2012/2013. Prof. Dr. Margarita Esponda. Prof. Dr. Margarita Esponda
 ALP I λ Kalkül WS 2012/2013 Berechenbarkeit - inspiriert durch Hilbert's Frage - im Jahr 1900, Paris - Internationaler Mathematikerkongress Gibt es ein System von Axiomen, aus denen alle Gesetze der Mathematik
ALP I λ Kalkül WS 2012/2013 Berechenbarkeit - inspiriert durch Hilbert's Frage - im Jahr 1900, Paris - Internationaler Mathematikerkongress Gibt es ein System von Axiomen, aus denen alle Gesetze der Mathematik
Konvexe Mengen und konvexe Funktionen
 Technische Universität Dortmund Fakultät für Mathematik Lehrstuhl I: Analysis Ausarbeitung Analysis III Seminar Konvexe Mengen und konvexe Funktionen Name: Jessica Prang Datum: 14.04.2015 Seminarleiter:
Technische Universität Dortmund Fakultät für Mathematik Lehrstuhl I: Analysis Ausarbeitung Analysis III Seminar Konvexe Mengen und konvexe Funktionen Name: Jessica Prang Datum: 14.04.2015 Seminarleiter:
Programmierung 1 (Wintersemester 2015/16) Lösungsblatt: Aufgaben für die Übungsgruppen: 8 (Kapitel 9)
 Fachrichtung 6. Informatik Universität des Saarlandes Tutorenteam der Vorlesung Programmierung Programmierung (Wintersemester 5/6) Lösungsblatt: Aufgaben für die Übungsgruppen: 8 (Kapitel 9) Hinweis: Dieses
Fachrichtung 6. Informatik Universität des Saarlandes Tutorenteam der Vorlesung Programmierung Programmierung (Wintersemester 5/6) Lösungsblatt: Aufgaben für die Übungsgruppen: 8 (Kapitel 9) Hinweis: Dieses
A1: Diplomvorprüfung HM II/III WS 2007/
 A: Diplomvorprüfung HM II/III WS 7/8 6..8 Aufgabe. (+68 Punkte) a) Ist die Reihe k+ k k 5k konvergent oder divergent? Begründen Sie ihre Aussage! b) Führen Sie eine Partialbruchzerlegung für n+ durch und
A: Diplomvorprüfung HM II/III WS 7/8 6..8 Aufgabe. (+68 Punkte) a) Ist die Reihe k+ k k 5k konvergent oder divergent? Begründen Sie ihre Aussage! b) Führen Sie eine Partialbruchzerlegung für n+ durch und
Musterlösung Klausur zu Analysis II. Verständnisteil
 Technische Universität Berlin SS 2009 Institut für Mathematik 20.07.2009 Prof. Dr. R. Schneider Fritz Krüger Sebastian Holtz Musterlösung Klausur zu Analysis II Verständnisteil 1. (a) Sei D R n konvex
Technische Universität Berlin SS 2009 Institut für Mathematik 20.07.2009 Prof. Dr. R. Schneider Fritz Krüger Sebastian Holtz Musterlösung Klausur zu Analysis II Verständnisteil 1. (a) Sei D R n konvex
Probeklausur. 1 Stetigkeit [7 Punkte] 2 Differenzierbarkeit [10 Punkte] Ferienkurs Analysis 2 für Physiker SS Karolina Stoiber Aileen Wolf
![Probeklausur. 1 Stetigkeit [7 Punkte] 2 Differenzierbarkeit [10 Punkte] Ferienkurs Analysis 2 für Physiker SS Karolina Stoiber Aileen Wolf Probeklausur. 1 Stetigkeit [7 Punkte] 2 Differenzierbarkeit [10 Punkte] Ferienkurs Analysis 2 für Physiker SS Karolina Stoiber Aileen Wolf](/thumbs/76/73718518.jpg) Karolina Stoiber Aileen Wolf Ferienkurs Analysis 2 für Physiker SS 26 A Probeklausur Allgemein Hinweise: Die Arbeitszeit beträgt 9 Minuten. Falls nicht anders angegeben, sind alle en ausführlich und nachvollziehbar
Karolina Stoiber Aileen Wolf Ferienkurs Analysis 2 für Physiker SS 26 A Probeklausur Allgemein Hinweise: Die Arbeitszeit beträgt 9 Minuten. Falls nicht anders angegeben, sind alle en ausführlich und nachvollziehbar
Einführung in die mathematische Logik
 Prof. Dr. H. Brenner Osnabrück SS 2014 Einführung in die mathematische Logik Vorlesung 4 Die Ableitungsbeziehung Definition 4.1. Es sei Γ L V eine Ausdrucksmenge in der Sprache der Aussagenlogik zu einer
Prof. Dr. H. Brenner Osnabrück SS 2014 Einführung in die mathematische Logik Vorlesung 4 Die Ableitungsbeziehung Definition 4.1. Es sei Γ L V eine Ausdrucksmenge in der Sprache der Aussagenlogik zu einer
Musterlösung zu Blatt 1
 Musterlösung zu Blatt Analysis III für Lehramt Gymnasium Wintersemester 0/4 Überprüfe zunächst die notwendige Bedingung Dfx y z = 0 für die Existenz lokaler Extrema Mit x fx y z = 8x und y fx y z = + z
Musterlösung zu Blatt Analysis III für Lehramt Gymnasium Wintersemester 0/4 Überprüfe zunächst die notwendige Bedingung Dfx y z = 0 für die Existenz lokaler Extrema Mit x fx y z = 8x und y fx y z = + z
MIA Analysis einer reellen Veränderlichen WS 06/07. Kapitel VI. Differenzierbare Funktionen in einer Veränderlichen
 Version 01.02. Januar 2007 MIA Analysis einer reellen Veränderlichen WS 06/07 Kurzfassung Martin Schottenloher Kapitel VI. Differenzierbare Funktionen in einer Veränderlichen In diesem Kapitel werden differenzierbare
Version 01.02. Januar 2007 MIA Analysis einer reellen Veränderlichen WS 06/07 Kurzfassung Martin Schottenloher Kapitel VI. Differenzierbare Funktionen in einer Veränderlichen In diesem Kapitel werden differenzierbare
Aufgabe Bonus.1. Aufgabe Bonus.2. Aufgabe Bonus.3. Aufgabe Bonus.4. HTWK Leipzig, Fakultät IMN Prof. Dr. Sibylle Schwarz
 HTWK Leipzig, Fakultät IMN Prof. Dr. Sibylle Schwarz sibylle.schwarz@htwk-leipzig.de Bonus. Übung zur Vorlesung Modellierung Wintersemester 2017/18 Lösungen bis 3. Januar 2018 einzusenden im Opal-Kurs
HTWK Leipzig, Fakultät IMN Prof. Dr. Sibylle Schwarz sibylle.schwarz@htwk-leipzig.de Bonus. Übung zur Vorlesung Modellierung Wintersemester 2017/18 Lösungen bis 3. Januar 2018 einzusenden im Opal-Kurs
Formale Systeme. Aussagenlogik: Sequenzenkalkül. Prof. Dr. Bernhard Beckert WS 2010/2011 KIT INSTITUT FÜR THEORETISCHE INFORMATIK
 Formale Systeme Prof. Dr. Bernhard Beckert WS 2010/2011 KIT INSTITUT FÜR THEORETISCHE INFORMATIK KIT University of the State of Baden-Württemberg and National Large-scale Research Center of the Helmholtz
Formale Systeme Prof. Dr. Bernhard Beckert WS 2010/2011 KIT INSTITUT FÜR THEORETISCHE INFORMATIK KIT University of the State of Baden-Württemberg and National Large-scale Research Center of the Helmholtz
2.1 Grundlagen: Kontextfreie Grammatiken
 2.1 Grundlagen: Kontextfreie Grammatiken Programme einer Programmiersprache können unbeschränkt viele Tokens enthalten, aber nur endlich viele Token-Klassen :-) Als endliches Terminal-Alphabet T wählen
2.1 Grundlagen: Kontextfreie Grammatiken Programme einer Programmiersprache können unbeschränkt viele Tokens enthalten, aber nur endlich viele Token-Klassen :-) Als endliches Terminal-Alphabet T wählen
Algebra II. Prof. Dr. M. Rost. Übungen Blatt 3 (SS 2016) 1. Abgabetermin: Freitag, 6. Mai.
 Algebra II Prof. Dr. M. Rost Übungen Blatt 3 (SS 2016) 1 Abgabetermin: Freitag, 6. Mai http://www.math.uni-bielefeld.de/~rost/a2 Erinnerungen an die Vorlesung: Im Folgenden werden manchmal einige Definitionen
Algebra II Prof. Dr. M. Rost Übungen Blatt 3 (SS 2016) 1 Abgabetermin: Freitag, 6. Mai http://www.math.uni-bielefeld.de/~rost/a2 Erinnerungen an die Vorlesung: Im Folgenden werden manchmal einige Definitionen
Fachhochschule Nordwestschweiz (FHNW) Hochschule Technik Lösungen Serie 10 (Lineare Abbildungen)
 Fachhochschule Nordwestschweiz (FHNW) Hochschule Technik Lösungen Serie (Lineare Abbildungen) Dozent/in: R. Burkhardt Büro:.6 Klasse: Semester: Datum: HS 8/9. Aufgabe Zeige, dass die folgenden Abbildungen
Fachhochschule Nordwestschweiz (FHNW) Hochschule Technik Lösungen Serie (Lineare Abbildungen) Dozent/in: R. Burkhardt Büro:.6 Klasse: Semester: Datum: HS 8/9. Aufgabe Zeige, dass die folgenden Abbildungen
Klausur: Höhere Mathematik III
 Prof. Dr. Josef Bemelmans Templergraben 55 5262 Aachen Raum 11 111 (Hauptgebäude) Klausur: Höhere Mathematik III Tel.: +49 241 8 94889 Sekr.: +49 241 8 94921 Fax: +49 241 8 92323 bemelmans@instmath.rwth-aachen.de
Prof. Dr. Josef Bemelmans Templergraben 55 5262 Aachen Raum 11 111 (Hauptgebäude) Klausur: Höhere Mathematik III Tel.: +49 241 8 94889 Sekr.: +49 241 8 94921 Fax: +49 241 8 92323 bemelmans@instmath.rwth-aachen.de
Proseminar Mathematik. Ungleichungen I Betreuung: Natalia Grinberg. Karlsruher Institut für Technologie
 Proseminar Mathematik Ungleichungen I 12.6.215 Betreuung: Natalia Grinberg Karlsruher Institut für Technologie Inhaltsverzeichnis 1 Young-Ungleichung 2 2 Hölder-Ungleichung 4 3 Minkowski-Ungleichung 5
Proseminar Mathematik Ungleichungen I 12.6.215 Betreuung: Natalia Grinberg Karlsruher Institut für Technologie Inhaltsverzeichnis 1 Young-Ungleichung 2 2 Hölder-Ungleichung 4 3 Minkowski-Ungleichung 5
2 Mengen, Abbildungen und Relationen
 Vorlesung WS 08 09 Analysis 1 Dr. Siegfried Echterhoff 2 Mengen, Abbildungen und Relationen Definition 2.1 (Mengen von Cantor, 1845 1918) Eine Menge M ist eine Zusammenfassung von wohlbestimmten und wohl
Vorlesung WS 08 09 Analysis 1 Dr. Siegfried Echterhoff 2 Mengen, Abbildungen und Relationen Definition 2.1 (Mengen von Cantor, 1845 1918) Eine Menge M ist eine Zusammenfassung von wohlbestimmten und wohl
Exponentialfunktion & Logarithmus
 Mathematik I für Biologen, Geowissenschaftler und Geoökologen & 31. Oktober 2011 & Potenzen Definitionsbereiche Potenzrechenregeln Beispiel exp Beispiel: Lichtabsorption Definition Injektivität Beispiel:
Mathematik I für Biologen, Geowissenschaftler und Geoökologen & 31. Oktober 2011 & Potenzen Definitionsbereiche Potenzrechenregeln Beispiel exp Beispiel: Lichtabsorption Definition Injektivität Beispiel:
Karl Heinz Wagner
 Architektur der LFG Lexikalisch-Funktionale Funktionale-Grammatik Grammatik Erweiterte PG Grammatik Lexikon Lexikonregeln Formaler Aufbau der F Funktionale Beschreibungen Funktionale zur F-trukturF K-trukturen
Architektur der LFG Lexikalisch-Funktionale Funktionale-Grammatik Grammatik Erweiterte PG Grammatik Lexikon Lexikonregeln Formaler Aufbau der F Funktionale Beschreibungen Funktionale zur F-trukturF K-trukturen
5 Vektorräume. (V1) für alle x, y V : x + y = y + x; (V2) für alle x, y, z V : (x + y) + z = x + (y + z);
 5 Vektorräume Was wir in den vorangegangenen Kapiteln an Matrizen und Vektoren gesehen haben, wollen wir nun mathematisch abstrahieren. Das führt auf den Begriff des Vektorraumes, den zentralen Begriff
5 Vektorräume Was wir in den vorangegangenen Kapiteln an Matrizen und Vektoren gesehen haben, wollen wir nun mathematisch abstrahieren. Das führt auf den Begriff des Vektorraumes, den zentralen Begriff
Einführung in die Stochastik 6. Übungsblatt
 Einführung in die Stochastik 6. Übungsblatt Fachbereich Mathematik SS M. Kohler 3. Mai A. Fromkorth D. Furer Gruppen und Hausübung Aufgabe (a) Die Wahrscheinlichkeit, dass eine S Bahn Verspätung hat, betrage.3.
Einführung in die Stochastik 6. Übungsblatt Fachbereich Mathematik SS M. Kohler 3. Mai A. Fromkorth D. Furer Gruppen und Hausübung Aufgabe (a) Die Wahrscheinlichkeit, dass eine S Bahn Verspätung hat, betrage.3.
Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden.
 Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am 20.6.2015 um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden. Prof. Dr. Wolfgang Arendt Manuel Bernhard Sommersemester 2015 Achten
Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am 20.6.2015 um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden. Prof. Dr. Wolfgang Arendt Manuel Bernhard Sommersemester 2015 Achten
B. Lösungsskizzen zu den Übungsaufgaben
 B. Lösungsskizzen zu den Übungsaufgaben B.. Lösungen zum Kapitel B... Tutoraufgaben Lösungsskizze Wir gehen zuerst nach dem Lösungsverfahren vor. Schritt : Bestimmung der Lösung des homogenen DGL-Systems
B. Lösungsskizzen zu den Übungsaufgaben B.. Lösungen zum Kapitel B... Tutoraufgaben Lösungsskizze Wir gehen zuerst nach dem Lösungsverfahren vor. Schritt : Bestimmung der Lösung des homogenen DGL-Systems
( 1) k k 2. k=0. n n(n + 1) ( 1) k k 2 + ( 1) n+1 (n + 1) 2. k=0. + ( 1) n+1 (n + 1) 2 n(n + 1) + (n + 1) 2 )
 Musterlösung zum 9. Blatt 8. Aufgabe: Sei n eine natürliche Zahl. Vermuten Sie eine Formel für ( ) k k und beweisen Sie diese durch vollständige Induktion. Lösung: Für jede natürliche Zahl n sei a n =
Musterlösung zum 9. Blatt 8. Aufgabe: Sei n eine natürliche Zahl. Vermuten Sie eine Formel für ( ) k k und beweisen Sie diese durch vollständige Induktion. Lösung: Für jede natürliche Zahl n sei a n =
d(x, z) = z x = y x + z y y x + z y = d(x, y) + d(y, z). d(x, y) = 0, falls x = y.
 Metrische Räume K bezeichnet entweder den Körper R oder den Körper C. Genauer bedeutet dies: K wird in denjenigen Situationen verwendet, in denen die Ersetzung von K sowohl durch R als auch durch C einen
Metrische Räume K bezeichnet entweder den Körper R oder den Körper C. Genauer bedeutet dies: K wird in denjenigen Situationen verwendet, in denen die Ersetzung von K sowohl durch R als auch durch C einen
Mathematik für Betriebswirte I (Lineare Algebra) 2. Klausur Wintersemester 2016/
 Mathematik für Betriebswirte I (Lineare Algebra) 2. Klausur Wintersemester 206/207 20.03.207 BITTE LESERLICH IN DRUCKBUCHSTABEN AUSFÜLLEN Nachname:...................................................................
Mathematik für Betriebswirte I (Lineare Algebra) 2. Klausur Wintersemester 206/207 20.03.207 BITTE LESERLICH IN DRUCKBUCHSTABEN AUSFÜLLEN Nachname:...................................................................
