Hans-Günter Heumann PIANO KIDS. Die Klavierschule für Kinder. Band 1 ED 8301
|
|
|
- Greta Dittmar
- vor 7 Jahren
- Abrufe
Transkript
1 Hns-Günter Heumnn PIANO KIDS Die Klviershule für Kinder mit SPASS UND AKTION Bnd ED 80
2 GROSSE KLAVIERSPIELER hen uh klein ngefngen Seite 5 Ih he mein erstes Klvier stük, ein Menuett, mit fünf Jhren kompo - niert und wurde ls Wunderkind ezeihnet. Mit vier Jhren he ih shon Klvier geüt, uf einem Stuhl stehend, d ih noh niht n die Tsten hernreihen konnte. Mit neun Jhren g ih mein erstes Konzert, in dem ih ls Klviervirtuose gefeiert wurde. Bevor ih Klvier unterriht ekm, spielte ih mit meiner Shwester Ludwik shon vierhändig.
3 SPIEL NACH NOTEN Musik ist eine Sprhe. Diese Sprhe wird von llen Menshen der Welt verstnden. Ds wihtigste Mittel zur Aufzeihnung dieser Sprhe ist die Note. Tonwiederholungen zähle: RHYTHMUS Seite 5-7 Die Musik esteht us der Anordnung von kurzen und lngen Tönen. Die Komintion dieser Töne nennt mn Rhythmus. Auh die Sprhe ht einen Rhythmus: mnhe Wörter sind kurz, mnhe lng. VIERTELNOTE HALBE NOTE GANZE NOTE Seite 4 oder Einshlgnote Eine Viertelnote erhält einen Grundshlg. oder Zweishlgnote Eine hle Note erhält zwei Grundshläge. oder Viershlgnote Eine gnze Note erhält vier Grundshläge. 7 zähle: zähle: - 2 zähle:
4 QUINTE = Astnd von 5 Tönen Seite 8/9 Seite 40 FREUDE, SCHÖNER GÖTTERFUNKEN 5 Text: Friedrih Shiller ( ) Musik: Ludwig vn Beethoven ( ) Arr.: Hns-Günter Heumnn Freu de, shöner Göt ter fun ken, Toh ter us E ly si um, wir e tre ten feu er trun ken, Himm li she, dein Hei lig tum! 5 2 Brü der, wo dein snf ter Flü gel weilt. 50
5 . Welhe Note ht ein Fähnhen? Viertelnote Hle Note Ahtelnote 2. Wie nennt mn den Astnd von Tönen? Quinte Terz Sekunde Teste Dein Wissen mit dem... KLAVIER QUIZ. Wie sieht ds Wiederholungszeihen us? 4. Mit welhem Tkt zusmmen ergit der Auftkt einen vollständigen Tkt?. Tkt Shlußtkt vorletzten Tkt 5. Welhes Zeihen edeutet llmählih luter werden? 6. Auf welher Aildung ist ds Intervll Quinte? 7. Welhes ist die ndere Shreiweise für den 4 4-Tkt? 5 Antworten:, 2,, 4, 5, 6, 7
6 Diese neue Klviershule will solides musiklishes Wissen und Können vermitteln Freude n der Musik weken ttrktive, moderne Spielstüke us den Bereihen Volksund Kinderlied, Folklore, Klssik und Pop nieten lngweilige und trokene Üungen vermeiden Musiktheorie verständlih und spielerish vermitteln zum eigenen Improvisieren nregen Zu jedem Bnd der Klviershule git es ein Aktionsuh, in dem lle Themen us der Shule in spielerisher, fntsievoller Form ufgereitet und vertieft werden. Klviershule: Aktionsüher: Pino Kids ED 80 Aktionsuh ED 80-0 Pino Kids 2 ED 802 Aktionsuh 2 ED Pino Kids ED 80 Aktionsuh ED 80-0 Begleitende Spielhefte: Pino Kids im Duett Vierhändige Stüke, die Spß mhen (mit CD) ED 8886 (einsetzr Mitte des 2. Bndes) Pino Kids Finger Fun Etüden, die Spß mhen ED 800 (einsetzr Mitte des. Bndes) Pino Kids in Conert Vorspielstüke, die Spß mhen (mit CD) ED 8440 (einsetzr im Anshluß n die dreiändige Klviershule) Zu Pino Kids gehört: AKTIONSBUCH Spiel Spß Info ED 80-0 Die kretive Ergänzung zur Klviershule mit vielen Spielen und Super-Ideen! Die Themen: Wissenswertes üer ds Klvier Notenshreien Die Kltsheke Musiklishe Knoeleien Suhild Kreuzworträtsel Musikwitze Trnsponieren Notenwerte/Pusen Improvisieren Komponieren... und vieles mehr! Ds 48 Seiten strke Heft enthält ußerdem: Bstelogen für Fensterilder Spielkrten zum Notenlernen Musiklishe Wissenskärthen Noten-Shreiheft Pino Kids Clssi Fun Klssishe Stüke, die Spß mhen (mit CD) ED 8946 (einsetzr Bnd ) Pino Kids Pop Fun Jzz-, Pop-, Rok- und Folkstüke, die Spß mhen ED 929 (einsetzr Mitte des 2. Bndes) ISMN ED 80 ISBN ED 80
Hans-Günter Heumann PIANO KIDS. Die Klavierschule für Kinder. Band 3 ED 8303
 Hans-Günter Heumann PIANO KIDS Die Klavierschule für Kinder mit SPASS UND AKTION Band 3 ED 8303 DOPPELGRIFFE IN TERZEN M. M. = 26 2 3 3 ALLEGRETTO op. 823 Nr. 22 4 Carl Czerny (79-87) 3 2 2 4 3 2 996 Schott
Hans-Günter Heumann PIANO KIDS Die Klavierschule für Kinder mit SPASS UND AKTION Band 3 ED 8303 DOPPELGRIFFE IN TERZEN M. M. = 26 2 3 3 ALLEGRETTO op. 823 Nr. 22 4 Carl Czerny (79-87) 3 2 2 4 3 2 996 Schott
Ode an die Freude Text: Friedrich Schiller ( ) Melodie: aus 9. Sinfonie, 4. Satz Ludwig van Beethoven ( ) œ J. fi & œ n. J œ œ. œ œ.
 Kl B / K Sopra Alt Teor Bass 1 2 Kleie Besetzug oder Kiderhor Ode a die Freude Text: Friedrih Shiller (1759-1805) Melodie: aus 9 Sifoie, 4 Satz Ludwig va Beethove (1770-1827) Freu - Freu - Freu - Freu
Kl B / K Sopra Alt Teor Bass 1 2 Kleie Besetzug oder Kiderhor Ode a die Freude Text: Friedrih Shiller (1759-1805) Melodie: aus 9 Sifoie, 4 Satz Ludwig va Beethove (1770-1827) Freu - Freu - Freu - Freu
Lesen. Fit in Deutsch.2. circa 30 Minuten. Dieser Test hat drei Teile. In diesem Prüfungsteil findest du Anzeigen, Briefe und Artikel aus der Zeitung.
 Fit in Deutsh.2 Üungsstz 01 Kndidtenlätter ir 30 Minuten Dieser Test ht drei Teile. In diesem Prüfungsteil findest du Anzeigen, Briefe und Artikel us der Zeitung. Zu jedem Text git es Aufgen. Shreie m
Fit in Deutsh.2 Üungsstz 01 Kndidtenlätter ir 30 Minuten Dieser Test ht drei Teile. In diesem Prüfungsteil findest du Anzeigen, Briefe und Artikel us der Zeitung. Zu jedem Text git es Aufgen. Shreie m
Prüfungsteil Schriftliche Kommunikation (SK)
 SK Üerlik und Anforderungen Üerlik und Anforderungen Prüfungsteil Shriftlihe Kommuniktion (SK) Üerlik und Anforderungen Worum geht es? In diesem Prüfungsteil sollst du einen Beitrg zu einem estimmten Them
SK Üerlik und Anforderungen Üerlik und Anforderungen Prüfungsteil Shriftlihe Kommuniktion (SK) Üerlik und Anforderungen Worum geht es? In diesem Prüfungsteil sollst du einen Beitrg zu einem estimmten Them
Kandidatenblätter. Hören 40 Minuten
 Kndidtenlätter Hören 40 Minuten Ds Modul Hören esteht us vier Teilen. Sie hören mehrere Texte und lösen Aufgen dzu. Lesen Sie jeweils zuerst die Aufgen und hören Sie dnn den Text dzu. Für jede Aufge git
Kndidtenlätter Hören 40 Minuten Ds Modul Hören esteht us vier Teilen. Sie hören mehrere Texte und lösen Aufgen dzu. Lesen Sie jeweils zuerst die Aufgen und hören Sie dnn den Text dzu. Für jede Aufge git
Übungen zur Vorlesung Modellierung WS 2003/2004 Blatt 11 Musterlösungen
 Dr. Theo Lettmnn Pderorn, den 9. Jnur 24 Age 9. Jnur 24 A x, A 2 x, Üungen zur Vorlesung Modellierung WS 23/24 Bltt Musterlösungen AUFGABE 7 : Es sei der folgende prtielle deterministishe endlihe Automt
Dr. Theo Lettmnn Pderorn, den 9. Jnur 24 Age 9. Jnur 24 A x, A 2 x, Üungen zur Vorlesung Modellierung WS 23/24 Bltt Musterlösungen AUFGABE 7 : Es sei der folgende prtielle deterministishe endlihe Automt
Wurzel b bedeutet: Suche die Zahl, die mit sich selbst multipliziert gerade die Zahl ergibt, die unter der Wurzel steht.
 /0 Areitsltt Wurzel edeutet: Suhe die Zhl, die mit sih selst multipliziert gerde die Zhl ergit, die unter der Wurzel steht. Also: - suhe eine Zhl, die mit sih selst multipliziert, genu ergit. Die Lösung
/0 Areitsltt Wurzel edeutet: Suhe die Zhl, die mit sih selst multipliziert gerde die Zhl ergit, die unter der Wurzel steht. Also: - suhe eine Zhl, die mit sih selst multipliziert, genu ergit. Die Lösung
1 Aktivität 1 Sehen ohne Ton (Track 1 bis Und eine Schokolade. )
 Shritte 1/2 interntionl Hinweise für die Kursleiter Film 3:»Die Josuhe«Mteril zu Film 3 Die Josuhe : Film 3,. 05:00 Min. Zustzmteril: Mein Beruf,. 01:30 Min., 5 kurze Sttements zum Them 5 Areitslätter
Shritte 1/2 interntionl Hinweise für die Kursleiter Film 3:»Die Josuhe«Mteril zu Film 3 Die Josuhe : Film 3,. 05:00 Min. Zustzmteril: Mein Beruf,. 01:30 Min., 5 kurze Sttements zum Them 5 Areitslätter
10 1 Grundlagen der Schulgeometrie. 1.3 Das Dreieck
 10 1 Grundlgen der Shulgeometrie 13 Ds Dreiek In diesem shnitt findet lles in der ffinen Stndrdeene 2 = R 2 sttt Drei Punkte, und, die niht uf einer Gerden liegen, ilden ein Dreiek Die Punkte,, nennt mn
10 1 Grundlgen der Shulgeometrie 13 Ds Dreiek In diesem shnitt findet lles in der ffinen Stndrdeene 2 = R 2 sttt Drei Punkte, und, die niht uf einer Gerden liegen, ilden ein Dreiek Die Punkte,, nennt mn
Übungsblatt Nr. 2. Lösungsvorschlag
 Institut für Kryptogrphie und Siherheit Prof. Dr. Jörn Müller-Qude Dirk Ahenh Tois Nilges Vorlesung Theoretishe Grundlgen der Informtik Üungsltt Nr. 2 svorshlg Aufge 1: Doktor Met in Gefhr (K) (4 Punkte)
Institut für Kryptogrphie und Siherheit Prof. Dr. Jörn Müller-Qude Dirk Ahenh Tois Nilges Vorlesung Theoretishe Grundlgen der Informtik Üungsltt Nr. 2 svorshlg Aufge 1: Doktor Met in Gefhr (K) (4 Punkte)
Übungssatz 01 FIT IN DEUTSCH 1. Kandidatenblätter/Prüferblätter ISBN: FIT1_ÜS01_Kandidaten-/Prueferblaetter_Oktober_2005
 FIT IN DEUTSCH 1 Üungsstz 01 Kndidtenlätter/Prüferlätter KASTNER AG ds medienhus FIT1_ÜS01_Kndidten-/Prueferletter_Oktoer_2005 ISBN: 3-938744-76-6 Fit in Deutsh.1 Üungsstz 01 Teil 1 Du hörst drei Nhrihten
FIT IN DEUTSCH 1 Üungsstz 01 Kndidtenlätter/Prüferlätter KASTNER AG ds medienhus FIT1_ÜS01_Kndidten-/Prueferletter_Oktoer_2005 ISBN: 3-938744-76-6 Fit in Deutsh.1 Üungsstz 01 Teil 1 Du hörst drei Nhrihten
Seminarstunden S-Std. (45 min) Nr. Modul Theorie Übungen. 13 Bruchrechnung 1 5
 Mthemtik Grundlgen Mthemtik Grundlgen für Industriemeister Seminrstunden S-Std. ( min) Nr. Modul Theorie Üungen Inhlt.... Allgemeines..... Ehte Brühe..... Unehte Brühe.... Erweitern und Kürzen von Brühen....
Mthemtik Grundlgen Mthemtik Grundlgen für Industriemeister Seminrstunden S-Std. ( min) Nr. Modul Theorie Üungen Inhlt.... Allgemeines..... Ehte Brühe..... Unehte Brühe.... Erweitern und Kürzen von Brühen....
Neu gesetzt für neue Leser Hinweise für Lehrkräfte und Eltern
 Neu gesetzt für neue Leser Hinweise für Lehrkräfte und Eltern Die spnnende Geshihte von Pul Mr ist für fortgeshrittene Lesenfänger mit vielen Illustrtionen, Lesehilfen und großer Fielshrift esonders motivierend
Neu gesetzt für neue Leser Hinweise für Lehrkräfte und Eltern Die spnnende Geshihte von Pul Mr ist für fortgeshrittene Lesenfänger mit vielen Illustrtionen, Lesehilfen und großer Fielshrift esonders motivierend
Lektion 1...4 Lektion 2...9 Lektion 3...14 Lektion 4...19 Lektion 5...24 Lektion 6...29 Lektion 7...34
 Inhlt Shritte plus 5 Lektion 1...4 Lektion 2...9 Lektion 3...14 Lektion 4...19 Lektion 5...24 Lektion 6...29 Lektion 7...34 Shritte plus 6 Lektion 8...39 Lektion 9...44 Lektion 10...49 Lektion 11...54
Inhlt Shritte plus 5 Lektion 1...4 Lektion 2...9 Lektion 3...14 Lektion 4...19 Lektion 5...24 Lektion 6...29 Lektion 7...34 Shritte plus 6 Lektion 8...39 Lektion 9...44 Lektion 10...49 Lektion 11...54
Der Tigerschwanz kann als Stimmungsbarometer gesehen werden. a) Richtig b) Falsch. Tiger sind wasserscheu. a) Richtig b) Falsch
 ?37??38? Der Tigershwnz knn ls Stimmungsrometer gesehen werden. Tiger sind wssersheu.?39??40? Ds Gerüll der Tigermännhen soll die Weihen nloken. Die Anzhl der Südhinesishen Tiger eträgt nur mehr ) 2 )
?37??38? Der Tigershwnz knn ls Stimmungsrometer gesehen werden. Tiger sind wssersheu.?39??40? Ds Gerüll der Tigermännhen soll die Weihen nloken. Die Anzhl der Südhinesishen Tiger eträgt nur mehr ) 2 )
Gleichung: 11 + x = 35 Welcher Zahlenwert steckt hinter der Variablen x?
 Rettungsring Vrilen & Gleihungen gnz klr: Mthemtik - Ds Ferienheft mit Erfolgsnzeiger Vrilen & Gleihungen Vrilen (,, ) werden uh Uneknnte oder Pltzhlter gennnt. Sie smolisieren einen estimmten Zhlenwert
Rettungsring Vrilen & Gleihungen gnz klr: Mthemtik - Ds Ferienheft mit Erfolgsnzeiger Vrilen & Gleihungen Vrilen (,, ) werden uh Uneknnte oder Pltzhlter gennnt. Sie smolisieren einen estimmten Zhlenwert
SPRACHFERIEN KÜNZELSAU 2008
 SPRACHFERIEN KÜNZELSAU 2008 (Mittelstufe) CODENUMMER: I. Lesen Sie den Text. Entsheiden Sie, welhe der Antworten ( ) psst. Es git jeweils nur eine rihtige Lösung. GEMEINSAM FÚR SPRACHE UND KULTUR Ashenputtel,
SPRACHFERIEN KÜNZELSAU 2008 (Mittelstufe) CODENUMMER: I. Lesen Sie den Text. Entsheiden Sie, welhe der Antworten ( ) psst. Es git jeweils nur eine rihtige Lösung. GEMEINSAM FÚR SPRACHE UND KULTUR Ashenputtel,
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Kohls Mathe-Tandem Geometrie - Partnerrechnen im
 Unterrihtsmterilien in digitler und in gedrukter Form uszug us: Kohls Mthe-Tndem Geometrie - Prtnerrehnen im 9.-10. Shuljhr Ds komplette Mteril finden Sie hier: Shool-Sout.de Mthe-Tndem Geometrie für ds
Unterrihtsmterilien in digitler und in gedrukter Form uszug us: Kohls Mthe-Tndem Geometrie - Prtnerrehnen im 9.-10. Shuljhr Ds komplette Mteril finden Sie hier: Shool-Sout.de Mthe-Tndem Geometrie für ds
2 Kinobesuch GRAMMATIK. perfekt. Im September LEICHT. wann die Vorstellung beginnt. Schreiben Sie Sätze! Beginnen Sie mit den grün markierten Wörtern!
 DEUTSCH GRAMMATIK VERBPOSITION S. 0 Im Septemer LEICHT Shreien Sie Sätze! Beginnen Sie mit den grün mrkierten Wörtern! der Herst / m. Septemer / eginnt ds Oktoerfest / in Münhen / findet sttt die Österreiher
DEUTSCH GRAMMATIK VERBPOSITION S. 0 Im Septemer LEICHT Shreien Sie Sätze! Beginnen Sie mit den grün mrkierten Wörtern! der Herst / m. Septemer / eginnt ds Oktoerfest / in Münhen / findet sttt die Österreiher
Datenmodell = Datenobjekte + Operatoren
 Einleitung 4. eltionenlger Selektion und Projektion Mengenopertoren Vereinigung, Durhshnitt, Differenz krtesishes Produkt Verundopertionen (Join) Thet-Join ntürliher Verund Semi-Join äußerer Verund Division
Einleitung 4. eltionenlger Selektion und Projektion Mengenopertoren Vereinigung, Durhshnitt, Differenz krtesishes Produkt Verundopertionen (Join) Thet-Join ntürliher Verund Semi-Join äußerer Verund Division
Ein Winkel zwischen 0 und 90 heißt spitzer Winkel, ein Winkel zwischen 90 und 180 heißt stumpfer Winkel.
 Geometrie 1 3 Winkelsummen Der von zwei Nhrseiten eines Vieleks geildete Winkel heißt Innenwinkel. Die Summe der Innenwinkel eines Dreieks eträgt 180. + + = 180 Die Summe der Innenwinkel eines Viereks
Geometrie 1 3 Winkelsummen Der von zwei Nhrseiten eines Vieleks geildete Winkel heißt Innenwinkel. Die Summe der Innenwinkel eines Dreieks eträgt 180. + + = 180 Die Summe der Innenwinkel eines Viereks
Fragebogen E. Lothar Natter. Effizienzcoaching. Unternehmer und Führungskräfte. Firma: Straße: PLZ: Ort: Telefax: Telefon: www:
 Frgeogen E Lothr Ntter Effizienznlyse für Selstständige, Unternehmer und Führungskräfte Effizienzohing Firm: Strße: PLZ: Ort: Telefon: Telefx: E-Mil: www: Dtum: Shereiter: Untershrift: Pseudonym für die
Frgeogen E Lothr Ntter Effizienznlyse für Selstständige, Unternehmer und Führungskräfte Effizienzohing Firm: Strße: PLZ: Ort: Telefon: Telefx: E-Mil: www: Dtum: Shereiter: Untershrift: Pseudonym für die
der Zug das Taxi der Bus die U-Bahn das Flugzeug die Straßenbahn das Auto das Fahrrad das Taxi das Fahrrad das Auto Ich nehme... U-Bahn.
 Lektion 11: In er Stt unterwegs 11 A Sie müssen mit er U-Bhn fhren. A2 1 Ergänzen Sie. er Zug s Txi er Bus ie U-Bhn s Flugzeug ie Strßenhn s Auto s Fhrr er Bus........................ A2 2 Ergänzen Sie.
Lektion 11: In er Stt unterwegs 11 A Sie müssen mit er U-Bhn fhren. A2 1 Ergänzen Sie. er Zug s Txi er Bus ie U-Bhn s Flugzeug ie Strßenhn s Auto s Fhrr er Bus........................ A2 2 Ergänzen Sie.
Der Begriff der Stammfunktion
 Lernunterlgen Integrlrehnung Der Begriff der Stmmfunktion Wir gehen von folgender Frgestellung us: welhe Funktion F x liefert ls Aleitung eine gegeene Funktion f x. Wir suhen lso eine Umkehrung der Aleitung
Lernunterlgen Integrlrehnung Der Begriff der Stmmfunktion Wir gehen von folgender Frgestellung us: welhe Funktion F x liefert ls Aleitung eine gegeene Funktion f x. Wir suhen lso eine Umkehrung der Aleitung
VORKURS: MATHEMATIK RECHENFERTIGKEITEN, LÖSUNGEN. Dienstag
 Lösungen Dienstg -- VORKURS: MATHEMATIK RECHENFERTIGKEITEN, LÖSUNGEN Dienstg Blok.. - 4 3y 6 3-6y 3-3 y -. - 3y 4 - y 9 - y -93. y 0,,y Sämtlihe Lösungsmethoden liefern hier whre Aussgen. Z. Bsp. «0 0».
Lösungen Dienstg -- VORKURS: MATHEMATIK RECHENFERTIGKEITEN, LÖSUNGEN Dienstg Blok.. - 4 3y 6 3-6y 3-3 y -. - 3y 4 - y 9 - y -93. y 0,,y Sämtlihe Lösungsmethoden liefern hier whre Aussgen. Z. Bsp. «0 0».
Grundwissenkatalog / g8 Geometrie / 7. Jahrgangsstufe
 Grundwissenktlog / g8 Geometrie /. Jhrgngsstufe Die folgende ufstellung enthält mthemtishe Grundfertigkeiten, die ein Shüler nh der. Jhrgngsstufe eherrshen sollte. Dieses Wissen wird in den folgenden Jhren
Grundwissenktlog / g8 Geometrie /. Jhrgngsstufe Die folgende ufstellung enthält mthemtishe Grundfertigkeiten, die ein Shüler nh der. Jhrgngsstufe eherrshen sollte. Dieses Wissen wird in den folgenden Jhren
1 GeschäftsdiaGramme. Abbildung 1.1: Übersicht zu unterschiedlichen Grafi ktypen. 2.1.4 Unify objects: graphs e.g. org graphs, networks, and maps
 1 GeshäftsdiGrmme Wenn mn eine deutshe Üersetzung des Begriffes usiness hrts suht, so ist mn mit dem Wort Geshäftsdigrmme gnz gut edient. Wir verstehen unter einem Geshäftsdigrmm die Visulisierung von
1 GeshäftsdiGrmme Wenn mn eine deutshe Üersetzung des Begriffes usiness hrts suht, so ist mn mit dem Wort Geshäftsdigrmme gnz gut edient. Wir verstehen unter einem Geshäftsdigrmm die Visulisierung von
Kleines Deutschlandquiz
 Kleines Deutshlndquiz 0 Stimmen diese Aussgen üer Deutshlnd? Kreuzen Sie n. d e f g h i j k l Die Bundesrepulik Deutshlnd esteht us 6 Bundesländern. Jedes Bundeslnd ht einen eigenen Bundesknzler / eine
Kleines Deutshlndquiz 0 Stimmen diese Aussgen üer Deutshlnd? Kreuzen Sie n. d e f g h i j k l Die Bundesrepulik Deutshlnd esteht us 6 Bundesländern. Jedes Bundeslnd ht einen eigenen Bundesknzler / eine
SS 2018 Torsten Schreiber
 SS 08 orsten Shreier 8 Beim inneren Produkt ) wird komponentenweise multipliziert und die entstehenden Produkte nshließend. Somit hndelt es sih um keine d nur eine Zhl Sklr) ls Lösung heruskommt. Ds Sklrprodukt
SS 08 orsten Shreier 8 Beim inneren Produkt ) wird komponentenweise multipliziert und die entstehenden Produkte nshließend. Somit hndelt es sih um keine d nur eine Zhl Sklr) ls Lösung heruskommt. Ds Sklrprodukt
Fragebogen 1 zur Arbeitsmappe Durch Zusatzempfehlung zu mehr Kundenzufriedenheit
 Teilnehmer/Apotheke/Ort (Zus/1) Frgeogen 1 zur Areitsmppe Durh Zustzempfehlung zu mehr Kunenzufrieenheit Bitte kreuzen Sie jeweils ie rihtige(n) Antwort(en) in en Felern is n! 1. Worin esteht ie Beeutung
Teilnehmer/Apotheke/Ort (Zus/1) Frgeogen 1 zur Areitsmppe Durh Zustzempfehlung zu mehr Kunenzufrieenheit Bitte kreuzen Sie jeweils ie rihtige(n) Antwort(en) in en Felern is n! 1. Worin esteht ie Beeutung
ZDfB_Ü01_LV_06 120206. Felix Brandl München ZERTIFIKAT DEUTSCH FÜR DEN BERUF ÜBUNGSSATZ 01. Kandidatenblätter LESEVERSTEHEN ZEIT: 40 MINUTEN
 Felix Brndl Münhen ZDfB_Ü01_LV_06 120206 ZERTIFIKAT DEUTSCH FÜR DEN BERUF ÜBUNGSSATZ 01 Kndidtenlätter ZEIT: 40 MINUTEN Zertifikt Deutsh für den Beruf Üungsstz 01 Aufge 1 Bitte lesen Sie den folgenden
Felix Brndl Münhen ZDfB_Ü01_LV_06 120206 ZERTIFIKAT DEUTSCH FÜR DEN BERUF ÜBUNGSSATZ 01 Kndidtenlätter ZEIT: 40 MINUTEN Zertifikt Deutsh für den Beruf Üungsstz 01 Aufge 1 Bitte lesen Sie den folgenden
Facharbeit über den Beweis der Existenz der Euler schen Gerade in ebenen Dreiecken.
 Fhreit üer den Beweis der Eistenz der Euler shen Gerde in eenen Dreieken. Verfßt von Ing. Wlter Höhlhumer im Mi und ergänzt im Juli Eistenz der Euler shen Gerde Eistenz der Euler shen Gerde Eistenz der
Fhreit üer den Beweis der Eistenz der Euler shen Gerde in eenen Dreieken. Verfßt von Ing. Wlter Höhlhumer im Mi und ergänzt im Juli Eistenz der Euler shen Gerde Eistenz der Euler shen Gerde Eistenz der
Relationen: Verkettungen, Wege, Hüllen
 FH Gießen-Frieerg, Sommersemester 00 Lösungen zu Üungsltt 9 Diskrete Mthemtik (Informtik) 9./. Juni 00 Prof. Dr. Hns-Ruolf Metz Reltionen: Verkettungen, Wege, Hüllen Aufge. Es ezeihne R ie Reltion {(,
FH Gießen-Frieerg, Sommersemester 00 Lösungen zu Üungsltt 9 Diskrete Mthemtik (Informtik) 9./. Juni 00 Prof. Dr. Hns-Ruolf Metz Reltionen: Verkettungen, Wege, Hüllen Aufge. Es ezeihne R ie Reltion {(,
Kandidatenblätter. Hören 40 Minuten
 Kndidtenlätter Hören 40 Minuten Ds Modul Hören esteht us vier Teilen. Du hörst mehrere Texte und löst Aufgen dzu. Lies jeweils zuerst die Aufgen und höre dnn den Text dzu. Für jede Aufge git es nur eine
Kndidtenlätter Hören 40 Minuten Ds Modul Hören esteht us vier Teilen. Du hörst mehrere Texte und löst Aufgen dzu. Lies jeweils zuerst die Aufgen und höre dnn den Text dzu. Für jede Aufge git es nur eine
6-1 Elementare Zahlentheorie. mit 1 b n und 0 a b (zusammen mit der Ordnung ) nennt man die n-te Farey-Folge, zum Beispiel ist
 6- Elementre Zhlentheorie 6 Frey-Folgen Die Menge F n der rtionlen Zhlen mit n und (zusmmen mit der Ordnung ) nennt mn die n-te Frey-Folge, zum Beispiel ist F = { < < < < < < < < < < } Offensichtlich gilt:
6- Elementre Zhlentheorie 6 Frey-Folgen Die Menge F n der rtionlen Zhlen mit n und (zusmmen mit der Ordnung ) nennt mn die n-te Frey-Folge, zum Beispiel ist F = { < < < < < < < < < < } Offensichtlich gilt:
ÜBUNGSSATZ 01 ZERTIFIKAT DEUTSCH FÜR DEN BERUF. Kandidatenblätter STRUKTUREN UND WORTSCHATZ ZEIT: 30 MINUTEN. ZDfB_Ü01_SW_06 120206
 Felix Brndl Münhen ZDfB_Ü01_SW_06 120206 ZERTIFIKAT DEUTSCH FÜR DEN BERUF ÜBUNGSSATZ 01 Kndidtenlätter ZEIT: 30 MINUTEN Zertifikt Deutsh für den Beruf Üungsstz 01 Aufge 1 Lesen Sie den folgenden Text zuerst
Felix Brndl Münhen ZDfB_Ü01_SW_06 120206 ZERTIFIKAT DEUTSCH FÜR DEN BERUF ÜBUNGSSATZ 01 Kndidtenlätter ZEIT: 30 MINUTEN Zertifikt Deutsh für den Beruf Üungsstz 01 Aufge 1 Lesen Sie den folgenden Text zuerst
Automaten und formale Sprachen Notizen zu den Folien
 5 Ds Pumping Lemm Shufhprinzip (Folie 137) Automten und formle Sprhen Notizen zu den Folien Im Blok Ds Shufhprinzip für endlihe Automten steht m n (sttt m > n), weil die Länge eines Pfdes die Anzhl von
5 Ds Pumping Lemm Shufhprinzip (Folie 137) Automten und formle Sprhen Notizen zu den Folien Im Blok Ds Shufhprinzip für endlihe Automten steht m n (sttt m > n), weil die Länge eines Pfdes die Anzhl von
Tagesablauf Arbeit Freizeit
 Tgesluf Areit Freizeit Am Morgen Ü 1 Lesen Sie A 1. Ordnen Sie Frgen und Antworten zu. 1. Steht Sr B. gern uf? A 5 oder 6 Minuten. 2. Wnn fährt die U-Bhn? B Nein, sie leit gerne noh einen Moment liegen.
Tgesluf Areit Freizeit Am Morgen Ü 1 Lesen Sie A 1. Ordnen Sie Frgen und Antworten zu. 1. Steht Sr B. gern uf? A 5 oder 6 Minuten. 2. Wnn fährt die U-Bhn? B Nein, sie leit gerne noh einen Moment liegen.
Ober- und Untersummen, Riemann Integrale
 Oer- und Untersummen, Riemnn Integrle 1. Ds Prolem des Fläheninhlts Ausgngspunkt für die Entwiklung des Integrlegriffs wren vershiedene Frgestellungen, u.. ds Prolem der Messung des Fläheninhltes eines
Oer- und Untersummen, Riemnn Integrle 1. Ds Prolem des Fläheninhlts Ausgngspunkt für die Entwiklung des Integrlegriffs wren vershiedene Frgestellungen, u.. ds Prolem der Messung des Fläheninhltes eines
Das kleine 9er-Einmaleins mit den 10 Fingern lernen.
 Ws? Multiplizieren 9er-Finger-Einmleins Wozu? Ds kleine 9er-Einmleins mit den 10 Fingern lernen. 1. Beide Hände mit usgestrekten Fingern zeigen nh oen. 2. Die Dumen zeigen nh ußen (Hndflähen zum Gesiht).
Ws? Multiplizieren 9er-Finger-Einmleins Wozu? Ds kleine 9er-Einmleins mit den 10 Fingern lernen. 1. Beide Hände mit usgestrekten Fingern zeigen nh oen. 2. Die Dumen zeigen nh ußen (Hndflähen zum Gesiht).
a) Behauptung: Es gibt die folgenden drei stabilen Matchings:
 Musterlösung - ufgenltt 1 ufge 1 ) ehuptung: Es git ie folgenen rei stilen Mthings: ies knn mn ntürlih für ein so kleines eispiel urh etrhten ller möglihen 3! = 6 Mthings eweisen. Mn knn er uh strukturierter
Musterlösung - ufgenltt 1 ufge 1 ) ehuptung: Es git ie folgenen rei stilen Mthings: ies knn mn ntürlih für ein so kleines eispiel urh etrhten ller möglihen 3! = 6 Mthings eweisen. Mn knn er uh strukturierter
Übungssatz 01 FIT IN DEUTSCH 2. Kandidatenblätter/Prüferblätter ISBN: 3-938744-79-0. FIT2_ÜS01_Kandidaten-/Prueferblaetter_Juli_2005
 KASTNER AG ds medienhus FIT2_ÜS01_Kndidten-/Prueferletter_Juli_2005 FIT IN DEUTSCH 2 Kndidtenlätter/Prüferlätter ISBN: 3-938744-79-0 Inhlt Vorwort 3 Kndidtenlätter Hören 5 Lesen 13 Shreien 21 Sprehen 25
KASTNER AG ds medienhus FIT2_ÜS01_Kndidten-/Prueferletter_Juli_2005 FIT IN DEUTSCH 2 Kndidtenlätter/Prüferlätter ISBN: 3-938744-79-0 Inhlt Vorwort 3 Kndidtenlätter Hören 5 Lesen 13 Shreien 21 Sprehen 25
Funktionen und Mächtigkeiten
 Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
DEMO. Dreiecke: Geometrie INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK. Konstruktionen. Kongruente Dreiecke. Datei Nr
 Geometrie Dreieke: Konstruktionen Kongruente Dreieke Dtei Nr. 11111 DEM Friedrih ukel Stnd: 19. Juni 2017 INTERNETILITHEK FÜR SHULMTHEMTIK www.mthe-d.shule 11111 Dreieke 1 Kongruenz 2 Inhlt 1. Konstruktion
Geometrie Dreieke: Konstruktionen Kongruente Dreieke Dtei Nr. 11111 DEM Friedrih ukel Stnd: 19. Juni 2017 INTERNETILITHEK FÜR SHULMTHEMTIK www.mthe-d.shule 11111 Dreieke 1 Kongruenz 2 Inhlt 1. Konstruktion
Mathematische Probleme, SS 2018 Dienstag 5.6. $Id: dreieck.tex,v /06/05 15:41:51 hk Exp $ 2.1 Dreiecksberechnung mit Seiten und Winkeln
 Mthemtishe Proleme, SS 2018 Dienstg 5.6 $Id: dreiek.tex,v 1.43 2018/06/05 15:41:51 hk Exp $ 2 Dreieke 2.1 Dreiekserehnung mit Seiten und Winkeln Am Ende der letzten Sitzung htten wir den sogennnten Kongruenzstz
Mthemtishe Proleme, SS 2018 Dienstg 5.6 $Id: dreiek.tex,v 1.43 2018/06/05 15:41:51 hk Exp $ 2 Dreieke 2.1 Dreiekserehnung mit Seiten und Winkeln Am Ende der letzten Sitzung htten wir den sogennnten Kongruenzstz
Brüche gleichnamig machen
 Brüche gleichnmig mchen L Ds Erweitern von Brüchen (siehe L ) ist lediglich ein Instrument, ds vorwiegend eingesetzt wird, um Brüche mit unterschiedlichem Divisor gleichnmig zu mchen. Brüche gleichnmig
Brüche gleichnmig mchen L Ds Erweitern von Brüchen (siehe L ) ist lediglich ein Instrument, ds vorwiegend eingesetzt wird, um Brüche mit unterschiedlichem Divisor gleichnmig zu mchen. Brüche gleichnmig
Übungssatz 02 FIT IN DEUTSCH 2. Kandidatenblätter/Prüferblätter ISBN: 3-938744-85-5. FIT2_ÜS02_Kandidaten-/Prueferblaetter_April_2006
 KASTNER AG ds medienhus FIT2_ÜS02_Kndidten-/Prueferletter_April_2006 FIT IN DEUTSCH 2 Üungsstz 02 Kndidtenlätter/Prüferlätter ISBN: 3-938744-85-5 Üungsstz 02 Inhlt Vorwort 3 Kndidtenlätter Hören 5 Lesen
KASTNER AG ds medienhus FIT2_ÜS02_Kndidten-/Prueferletter_April_2006 FIT IN DEUTSCH 2 Üungsstz 02 Kndidtenlätter/Prüferlätter ISBN: 3-938744-85-5 Üungsstz 02 Inhlt Vorwort 3 Kndidtenlätter Hören 5 Lesen
Schritte plus im Beruf
 Shritte plus im Beruf A/ Lesetext: Mehr Krippenplätze, mehr erufstätige Fruen?! Lesen Sie die Üershriften und dnn den Text. Ergänzen Sie zu jedem Textshnitt die pssende Üershrift. Pläne für mehr Kinderetreuung
Shritte plus im Beruf A/ Lesetext: Mehr Krippenplätze, mehr erufstätige Fruen?! Lesen Sie die Üershriften und dnn den Text. Ergänzen Sie zu jedem Textshnitt die pssende Üershrift. Pläne für mehr Kinderetreuung
Beispiellösungen zu Blatt 24
 µthemtischer κorrespondenz- zirkel Mthemtisches Institut Georg-August-Universität Göttingen Aufge Beispiellösungen zu Bltt Mn eweise, dss mn ein Qudrt für jede Zhl n 6 in genu n kleinere Qudrte zerlegen
µthemtischer κorrespondenz- zirkel Mthemtisches Institut Georg-August-Universität Göttingen Aufge Beispiellösungen zu Bltt Mn eweise, dss mn ein Qudrt für jede Zhl n 6 in genu n kleinere Qudrte zerlegen
R. Brinkmann http://brinkmann-du.de Seite 1 17.11.2010
 R. rinkmnn http://rinkmnn-du.de Seite 7..2 Grundegriffe der Vektorrehnung Vektor und Sklr Ein Teil der in Nturwissenshft und Tehnik uftretenden Größen ist ei festgelegter Mßeinheit durh die nge einer Mßzhl
R. rinkmnn http://rinkmnn-du.de Seite 7..2 Grundegriffe der Vektorrehnung Vektor und Sklr Ein Teil der in Nturwissenshft und Tehnik uftretenden Größen ist ei festgelegter Mßeinheit durh die nge einer Mßzhl
01 Proportion Verhältnis Maßstab
 5 Ähnlihkeit und Strhlensätze LS 01.M1 01 Proportion Verhältnis Mßst 1 Lies die folgende Informtion sorgfältig. Mrkiere wihtige egriffe und Formeln. ) Proportionle Zuordnung ei einer proportionlen Zuordnung
5 Ähnlihkeit und Strhlensätze LS 01.M1 01 Proportion Verhältnis Mßst 1 Lies die folgende Informtion sorgfältig. Mrkiere wihtige egriffe und Formeln. ) Proportionle Zuordnung ei einer proportionlen Zuordnung
Mathematische Probleme, SS 2013 Montag $Id: dreieck.tex,v /04/15 09:12:15 hk Exp hk $ 1.4 Dreiecksberechnung mit Seiten und Winkeln
 Mthemtishe Proleme, SS 2013 Montg 15.4 $Id: dreiek.tex,v 1.5 2013/04/15 09:12:15 hk Exp hk $ 1 Dreieke 1.4 Dreiekserehnung mit Seiten und Winkeln In der letzten Sitzung htten wir egonnen die vershiedenen
Mthemtishe Proleme, SS 2013 Montg 15.4 $Id: dreiek.tex,v 1.5 2013/04/15 09:12:15 hk Exp hk $ 1 Dreieke 1.4 Dreiekserehnung mit Seiten und Winkeln In der letzten Sitzung htten wir egonnen die vershiedenen
5.2 Quadratische Gleichungen
 Mthemtik mit Mthd MK..0 0_0_Qud_Gleih.xmd Einfhe qudrtishe Gleihungen. Qudrtishe Gleihungen ef.: Eine Gleihung, in der x höhstens qudrtish (in der zweiten Potenz) vorkommt, heißt qudrtishe Gleihung. Gewöhnlihe
Mthemtik mit Mthd MK..0 0_0_Qud_Gleih.xmd Einfhe qudrtishe Gleihungen. Qudrtishe Gleihungen ef.: Eine Gleihung, in der x höhstens qudrtish (in der zweiten Potenz) vorkommt, heißt qudrtishe Gleihung. Gewöhnlihe
Mathematik für Studierende der Biologie und des Lehramtes Chemie
 Verfhren Mthemtik für Studierende der Biologie und des Lehrmtes Chemie Dominik Shillo Universität des Srlndes 6. Vorlesung, 4..7 (Stnd: 4..7, 4:5 Uhr) Shreibe,,n.......... n, n,n Führe den Guÿlgorithmus
Verfhren Mthemtik für Studierende der Biologie und des Lehrmtes Chemie Dominik Shillo Universität des Srlndes 6. Vorlesung, 4..7 (Stnd: 4..7, 4:5 Uhr) Shreibe,,n.......... n, n,n Führe den Guÿlgorithmus
Der Vektor lebt unabhängig vom Koordinatensystem: Bei einer Drehung des Koordinatensystems ändern zwar die Komponenten, der Vektor v aber bleibt.
 Vektorlger Vektorlger Vektoren sind Grössen, die einen Betrg sowie eine Rihtung im Rum hen. Im Gegenstz zu den Vektoren estehen Sklre nur us einer Grösse ls Zhl. In Bühern wird nsttt v oft v geshrieen.
Vektorlger Vektorlger Vektoren sind Grössen, die einen Betrg sowie eine Rihtung im Rum hen. Im Gegenstz zu den Vektoren estehen Sklre nur us einer Grösse ls Zhl. In Bühern wird nsttt v oft v geshrieen.
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Lernzirkel / Stationenlernen: Höhensätze (Pythagoras und Euklid)
 Unterrihtsmterilien in digitler und in gedrukter Form uszug us: Lernzirkel / Sttionenlernen: Höhensätze (Pythgors und Euklid) Ds komplette Mteril finden Sie hier: Downlod ei Shool-Soutde SHOOL-SOUT Lernzirkel
Unterrihtsmterilien in digitler und in gedrukter Form uszug us: Lernzirkel / Sttionenlernen: Höhensätze (Pythgors und Euklid) Ds komplette Mteril finden Sie hier: Downlod ei Shool-Soutde SHOOL-SOUT Lernzirkel
Die Näherung ist umso genauer, je kleiner die Zellen sind. Der Grenzwert ist
 Höhere Mthemtik Mehrfhintegrle sind Integrle üer eiete R n Zweifhintegrle treten B ei der Berehnung des Fläheninhltes und von Flähenträgheitsmomenten uf Dreifhintegrle kommen ei der Berehnung des Volumeninhltes
Höhere Mthemtik Mehrfhintegrle sind Integrle üer eiete R n Zweifhintegrle treten B ei der Berehnung des Fläheninhltes und von Flähenträgheitsmomenten uf Dreifhintegrle kommen ei der Berehnung des Volumeninhltes
2 Die Bildsprache Der relevante Winkel im grünen Dreieck ist stumpf; die gleichschenkligen Dreiecke haben den Basiswinkel 180 :
 Hns Wlser, [20080409] Eine Visulisierung des Kosinusstzes 1 Worum es geht Es wird eine zum Pythgors-Piktogrmm nloge Figur für niht rehtwinklige Dreieke esprohen. Dei werden ähnlihe gleihshenklige Dreieke
Hns Wlser, [20080409] Eine Visulisierung des Kosinusstzes 1 Worum es geht Es wird eine zum Pythgors-Piktogrmm nloge Figur für niht rehtwinklige Dreieke esprohen. Dei werden ähnlihe gleihshenklige Dreieke
Relationen: Äquivalenzrelationen, Ordnungsrelationen
 TH Mittelhessen, Sommersemester 202 Lösungen zu Üungsltt 9 Fchereich MNI, Diskrete Mthemtik 2. Juni 202 Prof. Dr. Hns-Rudolf Metz Reltionen: Äquivlenzreltionen, Ordnungsreltionen Aufge. Welche der folgenden
TH Mittelhessen, Sommersemester 202 Lösungen zu Üungsltt 9 Fchereich MNI, Diskrete Mthemtik 2. Juni 202 Prof. Dr. Hns-Rudolf Metz Reltionen: Äquivlenzreltionen, Ordnungsreltionen Aufge. Welche der folgenden
Ja, klar! Das weiß ich.
 J, klr! Ds weiß ih. Einstieg ins Modul 1: Wir und die nderen Areit mit den Aildungen S. XXX Lösung: 1G; 2K; 3C; 4E; 5F; 6H; 7B; 8D; 9I; 10J; 11L; 12A Einführung der Begriffe Sprehen, Shreien, Lesen und
J, klr! Ds weiß ih. Einstieg ins Modul 1: Wir und die nderen Areit mit den Aildungen S. XXX Lösung: 1G; 2K; 3C; 4E; 5F; 6H; 7B; 8D; 9I; 10J; 11L; 12A Einführung der Begriffe Sprehen, Shreien, Lesen und
Grundwissen 6. Klasse
 Grundwissen Mthemtik Klsse / Grundwissen Klsse Positive Brühe ) Grundegriffe z Brühe hen die Form n mit z I N0, n I N z heißt der Zähler, n der Nenner des Bruhes Bezeihnung Bedingung Beispiele Ehter Bruh
Grundwissen Mthemtik Klsse / Grundwissen Klsse Positive Brühe ) Grundegriffe z Brühe hen die Form n mit z I N0, n I N z heißt der Zähler, n der Nenner des Bruhes Bezeihnung Bedingung Beispiele Ehter Bruh
Die Satzgruppe des Pythagoras
 7 Die Stzgruppe des Pythgors In Klssenstufe 7 hen wir uns ei den Inhlten zur Geometrie insesondere mit Dreieken und ihren Eigenshften eshäftigt. In diesem Kpitel wirst du erkennen, dss es ei rehtwinkligen
7 Die Stzgruppe des Pythgors In Klssenstufe 7 hen wir uns ei den Inhlten zur Geometrie insesondere mit Dreieken und ihren Eigenshften eshäftigt. In diesem Kpitel wirst du erkennen, dss es ei rehtwinkligen
Verordnung über die Regionale Musikschule Wolhusen. vom 28. März 2013
 Verordnung üer die Regionle Musikshule Wolhusen Gemeinde Wolhusen Seite 2 / 10 Inhltsverzeihnis I Allgemeine Bestimmungen... 4 Art. 1 Trägershft... 4 Art. 2 Aufge und Ziel... 4 II Orgnistion... 4 Art.
Verordnung üer die Regionle Musikshule Wolhusen Gemeinde Wolhusen Seite 2 / 10 Inhltsverzeihnis I Allgemeine Bestimmungen... 4 Art. 1 Trägershft... 4 Art. 2 Aufge und Ziel... 4 II Orgnistion... 4 Art.
Download. Hausaufgaben: Trigonometrie. Üben in drei Differenzierungsstufen. Otto Mayr. Downloadauszug aus dem Originaltitel:
 Downlod Otto Myr Husufgen: Üen in drei Differenzierungsstufen Downloduszug us dem Originltitel: Husufgen: Üen in drei Differenzierungsstufen Dieser Downlod ist ein uszug us dem Originltitel Husufgen Mthemtik
Downlod Otto Myr Husufgen: Üen in drei Differenzierungsstufen Downloduszug us dem Originltitel: Husufgen: Üen in drei Differenzierungsstufen Dieser Downlod ist ein uszug us dem Originltitel Husufgen Mthemtik
Mathematik Trigonometrie Einführung
 Mthemtik Trigonometrie Einführung Ws edeutet ds Wort Trigonometrie und mit ws eshäftigt sih die Trigonometrie? Eine kleine Wortkunde: tri edeutet 'drei' Beispiel: Trithlon,... gon edeutet 'Winkel'/'Ek'
Mthemtik Trigonometrie Einführung Ws edeutet ds Wort Trigonometrie und mit ws eshäftigt sih die Trigonometrie? Eine kleine Wortkunde: tri edeutet 'drei' Beispiel: Trithlon,... gon edeutet 'Winkel'/'Ek'
Wir haben ein Koordinatensystem mit der x-achse und der y-achse. Nun wird ein Kreis gebildet mit dem Radius r=1.
 Trigonometrie In diesem Themenereih wenden wir uns den Winkeln im rehtekigen Dreiek zu. Du hst uf deinem Tshenrehner siher shon die Tsten sin, os und tn gesehen. Doh ws edeuten sie? Ds wollen wir herusfinden.
Trigonometrie In diesem Themenereih wenden wir uns den Winkeln im rehtekigen Dreiek zu. Du hst uf deinem Tshenrehner siher shon die Tsten sin, os und tn gesehen. Doh ws edeuten sie? Ds wollen wir herusfinden.
Rock? Passt der. Personen beschreiben
 10 Psst der Rok? Personen eshreien Denken Sie n drei Personen. Ws ist für die Personen typish? Mhen Sie Notizen. Ws gefällt Ihnen ( )? Ws finden Sie niht so gut ( )? Wie sieht die Person us? jung / lt
10 Psst der Rok? Personen eshreien Denken Sie n drei Personen. Ws ist für die Personen typish? Mhen Sie Notizen. Ws gefällt Ihnen ( )? Ws finden Sie niht so gut ( )? Wie sieht die Person us? jung / lt
Rund um den Satz des Pythagoras
 Wolfgng Shlottke Rund um den Stz des Pythgors Lernen n Sttionen und weiterführende ufgben für den Mthemtikunterriht uerverlg GmbH 3 Sroghty Pythgors rükwärts Die Umkehrung des Stzes des Pythgors (1) Du
Wolfgng Shlottke Rund um den Stz des Pythgors Lernen n Sttionen und weiterführende ufgben für den Mthemtikunterriht uerverlg GmbH 3 Sroghty Pythgors rükwärts Die Umkehrung des Stzes des Pythgors (1) Du
Quadratische Gleichungen. Aufgabe 1: Lösen von Gleichungen ohne Lösungsformel
 Qudrtische Gleichungen Aufge : Lösen von Gleichungen ohne Lösungsformel ) 0,8 ) 7 c) - 867 0 d) e) 9 f) - 0 g) 0 h) i) 6 0 j) Aufge : Lösen von Gleichungen durch Zerlegung in Fktoren ) 4 0 ) 4 0 c) - 4
Qudrtische Gleichungen Aufge : Lösen von Gleichungen ohne Lösungsformel ) 0,8 ) 7 c) - 867 0 d) e) 9 f) - 0 g) 0 h) i) 6 0 j) Aufge : Lösen von Gleichungen durch Zerlegung in Fktoren ) 4 0 ) 4 0 c) - 4
Transkriptionen. Lektion 1: Hallo! Ich bin Nicole... Lektion 2: Ich bin Journalistin.
 Lektion 1: Hllo! Ih in Niole... 4 Mein Nme ist Lothr Müller. Wie itte? ih uhstiere: L O T H A R M Ü L L E R Mein Nme ist Len Egger Wie itte? Wrten Sie, ih uhstiere: L E N A E G G E R Mein Nme ist Yvonne
Lektion 1: Hllo! Ih in Niole... 4 Mein Nme ist Lothr Müller. Wie itte? ih uhstiere: L O T H A R M Ü L L E R Mein Nme ist Len Egger Wie itte? Wrten Sie, ih uhstiere: L E N A E G G E R Mein Nme ist Yvonne
Kleiner Führer durch die alte Hauptstadt des römischen Helvetiens
 Ein Tg in Kleiner Führer durh die lte Huptstdt des römishen Helvetiens 3. 4. Shuljhr (Shüler/innen. 8 Jhren) Ih in Cmillus, und wer ist Du? 2011 1 Ein Tg in Geruhsnweisung Ih in ein Römer us Aventium.
Ein Tg in Kleiner Führer durh die lte Huptstdt des römishen Helvetiens 3. 4. Shuljhr (Shüler/innen. 8 Jhren) Ih in Cmillus, und wer ist Du? 2011 1 Ein Tg in Geruhsnweisung Ih in ein Römer us Aventium.
Anschlußbeispiel 2-, 3- & 4-begriffige Signale an den Funktionsdecoder LDMiba 3D oder WDMiba von Modellbahn Digital Peter Stärz
 Anshlußeispiel 2-, 3- & 4-egriffige Signle n den Funktionsdeoder LDMi 3D oder WDMi von Modellhn Digitl Peter Stärz Die folgenden Beispiele sollen zeigen, wie mn Signle n die Deoder LDMi 3D (Betriesrt )
Anshlußeispiel 2-, 3- & 4-egriffige Signle n den Funktionsdeoder LDMi 3D oder WDMi von Modellhn Digitl Peter Stärz Die folgenden Beispiele sollen zeigen, wie mn Signle n die Deoder LDMi 3D (Betriesrt )
Probeunterricht 2006 für die Realschulen in Bayern Mathematik 4. Jahrgangsstufe 1. Tag
 Probeunterricht 2006 für die Relschulen in Byern Mthemtik 4. Jhrgngsstufe 1. Tg Nme: Gruppe: Punkte: 1. In Deutschlnd (D), der Türkei (T), Frnkreich (F) und Itlien ( I ) hben die Kinder verschieden lnge
Probeunterricht 2006 für die Relschulen in Byern Mthemtik 4. Jhrgngsstufe 1. Tg Nme: Gruppe: Punkte: 1. In Deutschlnd (D), der Türkei (T), Frnkreich (F) und Itlien ( I ) hben die Kinder verschieden lnge
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt Semester ARBEITSBLATT 15 ORTHOGONALITÄT
 Mthemtik: Mg. Schmid Wolfgng Areitsltt 5. Semester ARBEITSBLATT 5 ORTHOGONALITÄT Ws versteht mn zunächst einml unter orthogonl? Dies ist nur ein nderes Wort für norml oder im rechten Winkel. Ws uns hier
Mthemtik: Mg. Schmid Wolfgng Areitsltt 5. Semester ARBEITSBLATT 5 ORTHOGONALITÄT Ws versteht mn zunächst einml unter orthogonl? Dies ist nur ein nderes Wort für norml oder im rechten Winkel. Ws uns hier
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt Semester ARBEITSBLATT 14 MULTIPLIKATION EINES VEKTORS MIT EINEM SKALAR
 Mthemtik: Mg. Schmid Wolfgng Areitsltt. Semester ARBEITSBLATT MULTIPLIKATION EINES VEKTORS MIT EINEM SKALAR Zunächst einml müssen wir den Begriff Sklr klären. Definition: Unter einem Sklr ersteht mn eine
Mthemtik: Mg. Schmid Wolfgng Areitsltt. Semester ARBEITSBLATT MULTIPLIKATION EINES VEKTORS MIT EINEM SKALAR Zunächst einml müssen wir den Begriff Sklr klären. Definition: Unter einem Sklr ersteht mn eine
Lineare Gleichungssysteme mit 3 und mehr Variablen
 Linere Gleihungssysteme mit un mehr rilen Beispiel 1 mit rilen: 11 Zunähst estimmt mn ie rile, ie mn ls Erste eliminieren will. In iesem Fll soll von hinten nh vorn vorgegngen weren,.h. zuerst soll rile
Linere Gleihungssysteme mit un mehr rilen Beispiel 1 mit rilen: 11 Zunähst estimmt mn ie rile, ie mn ls Erste eliminieren will. In iesem Fll soll von hinten nh vorn vorgegngen weren,.h. zuerst soll rile
3 Punkte, Ortsvektoren und Verbindungsvektoren. Zunächst im 2-dimensionalen: A 4 1 , C 2 4. und D 3 1 Koordinatensystem. in einem kartesischen
 Punkte Ortsvektoren und Verindungsvektoren Punkte Ortsvektoren und Verindungsvektoren Zunähst im -dimensionlen: A 4 Gegeen sind die Punkte B 5 C 4 und D Koordintensystem. in einem krtesishen AB CD d Zu
Punkte Ortsvektoren und Verindungsvektoren Punkte Ortsvektoren und Verindungsvektoren Zunähst im -dimensionlen: A 4 Gegeen sind die Punkte B 5 C 4 und D Koordintensystem. in einem krtesishen AB CD d Zu
Aussichten A1. Einstufungstest. Autorin: Sanja Mazuranic Redaktion: Renate Weber Layout: Claudia Stumpfe Satz: Regina Krawatzki, Stuttgart
 Aussihten A1 Autorin: Snj Mzurni Rektion: Rente Weer Lyout: Clui Stumpfe Stz: Regin Krwtzki, Stuttgrt Ernst Klett Sprhen GmH, Stuttgrt 2010 www.klett.e Alle Rehte vorehlten. Aussihten A1 Aussihten A1 Aufgenltt
Aussihten A1 Autorin: Snj Mzurni Rektion: Rente Weer Lyout: Clui Stumpfe Stz: Regin Krwtzki, Stuttgrt Ernst Klett Sprhen GmH, Stuttgrt 2010 www.klett.e Alle Rehte vorehlten. Aussihten A1 Aussihten A1 Aufgenltt
Mäxchen ein Würfelspiel
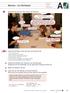 Mäxhen ein Würfelspiel A A1 Betrhten Sie ds Foto. Ws mhen die Personen? 2 + 5 Fünfundzwnzig..., hlt, nein: zweiundfünfzig. 3 + 2 Dreier Psh Ds glue ih niht. Ds will ih sehen. Ertppt! Du hst j nur eine
Mäxhen ein Würfelspiel A A1 Betrhten Sie ds Foto. Ws mhen die Personen? 2 + 5 Fünfundzwnzig..., hlt, nein: zweiundfünfzig. 3 + 2 Dreier Psh Ds glue ih niht. Ds will ih sehen. Ertppt! Du hst j nur eine
Aufgaben Mikroökonomie (mit Lösungen) 3 Wahl des Konsumenten
 Aufgen Mikroökonomie (mit Lösungen) 3 Whl des Konsumenten Budgetgerde Ein Konsument verfügt üer ein Einkommen von 300, ds er gnz für den Kuf des Gutes A und/oder B usgit. Eine Einheit A kostet 3 und eine
Aufgen Mikroökonomie (mit Lösungen) 3 Whl des Konsumenten Budgetgerde Ein Konsument verfügt üer ein Einkommen von 300, ds er gnz für den Kuf des Gutes A und/oder B usgit. Eine Einheit A kostet 3 und eine
Erkundungen. Terme vergleichen. Rechteck Fläche als Produkt der Seitenlängen Fläche als Summe der Teilflächen A B
 Erkundungen Terme vergleihen Forshungsuftrg : Fläheninhlte von Rehteken uf vershiedene Arten erehnen Die Terme () is (6) eshreien jeweils den Fläheninhlt von einem der drei Rehteke. Ordnet die Terme den
Erkundungen Terme vergleihen Forshungsuftrg : Fläheninhlte von Rehteken uf vershiedene Arten erehnen Die Terme () is (6) eshreien jeweils den Fläheninhlt von einem der drei Rehteke. Ordnet die Terme den
4 Die rationalen Zahlen
 4 Die rtionlen Zhlen Der Ring der gnzen Zhlen ht den Mngel, dß nicht jede Gleichung = X, 0 innerhl Z lösr ist. (Z.B. ist 1 = 2 X unlösr in Z). Zu seiner Beseitigung erweitert mn den Zhlereich zum Körper
4 Die rtionlen Zhlen Der Ring der gnzen Zhlen ht den Mngel, dß nicht jede Gleichung = X, 0 innerhl Z lösr ist. (Z.B. ist 1 = 2 X unlösr in Z). Zu seiner Beseitigung erweitert mn den Zhlereich zum Körper
Größter gemeinsamer Teiler und kleinstes gemeinsames Vielfaches
 Größter gemeinsmer Teiler un kleinstes gemeinsmes Vielfhes 1 Der größte gemeinsme Teiler (ggt) Zu jeer Zhl knn mn ihre Teilermenge ngeen. Τ0 {1; 2; ; 5; 6; 10; 15; 0} Τ {1; 2; ; ; 6; } Die gemeinsmen Teiler
Größter gemeinsmer Teiler un kleinstes gemeinsmes Vielfhes 1 Der größte gemeinsme Teiler (ggt) Zu jeer Zhl knn mn ihre Teilermenge ngeen. Τ0 {1; 2; ; 5; 6; 10; 15; 0} Τ {1; 2; ; ; 6; } Die gemeinsmen Teiler
Umwandlung von endlichen Automaten in reguläre Ausdrücke
 Umwndlung von endlichen Automten in reguläre Ausdrücke Wir werden sehen, wie mn us einem endlichen Automten M einen regulären Ausdruck γ konstruieren knn, der genu die von M kzeptierte Sprche erzeugt.
Umwndlung von endlichen Automten in reguläre Ausdrücke Wir werden sehen, wie mn us einem endlichen Automten M einen regulären Ausdruck γ konstruieren knn, der genu die von M kzeptierte Sprche erzeugt.
Vorkurs Mathematik. Vorlesung 3. Die rationalen Zahlen
 Prof. Dr. H. Brenner Osnrück WS 2014/2015 Vorkurs Mthemtik Vorlesung 3 Die rtionlen Zhlen Definition 3.1. Unter einer rtionlen Zhl versteht mn einen Ausdruck der Form, woei, Z und 0 sind, und woei zwei
Prof. Dr. H. Brenner Osnrück WS 2014/2015 Vorkurs Mthemtik Vorlesung 3 Die rtionlen Zhlen Definition 3.1. Unter einer rtionlen Zhl versteht mn einen Ausdruck der Form, woei, Z und 0 sind, und woei zwei
Aufgabe 1. Die Zahl 6 wird aus 3 gleichen Ziffern mit Hilfe der folgenden mathematischen
 Deprtment Mthemtik Tg der Mthemtik 5. Juli 008 Klssenstufen 9, 10 Aufge 1. Die Zhl 6 wird us 3 gleihen Ziffern mit Hilfe der folgenden mthemtishen Symole drgestellt: + Addition Sutrktion Multipliktion
Deprtment Mthemtik Tg der Mthemtik 5. Juli 008 Klssenstufen 9, 10 Aufge 1. Die Zhl 6 wird us 3 gleihen Ziffern mit Hilfe der folgenden mthemtishen Symole drgestellt: + Addition Sutrktion Multipliktion
Automaten und formale Sprachen Notizen zu den Folien
 Automten un formle Sprhen Notizen zu en Folien 1 Grunlgen un formle Beweise Venn-Digrmme (Folie 6) Im oeren Digrmm er Folie 6 sin zwei Mengen ngegeen: A un B. Es ist explizit ein Element von A ngegeen,
Automten un formle Sprhen Notizen zu en Folien 1 Grunlgen un formle Beweise Venn-Digrmme (Folie 6) Im oeren Digrmm er Folie 6 sin zwei Mengen ngegeen: A un B. Es ist explizit ein Element von A ngegeen,
Geometrische Figuren und Körper
 STNRUFGEN Geometrishe Figuren und Körper Geometrishe Figuren und Körper Welhe Shreiweisen geen den Winkel β des neenstehenden reieks PQR rihtig wieder? β = Qrp β = rp β = PQR R β = QRP β = pq q p P r Q
STNRUFGEN Geometrishe Figuren und Körper Geometrishe Figuren und Körper Welhe Shreiweisen geen den Winkel β des neenstehenden reieks PQR rihtig wieder? β = Qrp β = rp β = PQR R β = QRP β = pq q p P r Q
Mathematik Regelheft Klasse 6
 Mthemtik Regelheft Klsse 6 Inhltsverzeihnis I Them: Teilrkeit 6.) Teiler un Vielfhe 6.) Teilrkeitsregeln 6.) Primzhlen un Primfktorzerlegung 6.) ggt 6.) kgv II Them: Winkel 6.6) Kreissklen un ihre Einteilung
Mthemtik Regelheft Klsse 6 Inhltsverzeihnis I Them: Teilrkeit 6.) Teiler un Vielfhe 6.) Teilrkeitsregeln 6.) Primzhlen un Primfktorzerlegung 6.) ggt 6.) kgv II Them: Winkel 6.6) Kreissklen un ihre Einteilung
Allgemeines. Mail an muenster.de. Motivation für die Veranstaltung Übung zur Markt und Preistheorie
 Allgemeines Nme: Emil: Stefn Shrmm stefn.shrmm@wiwi.uni muenster.de Motivtion für die Vernstltung Üung zur Mrkt und Preistheorie Inhlt der Klusur Vorlesung Skrit und Üung Sehr gut vorzuereiten! Tis zur
Allgemeines Nme: Emil: Stefn Shrmm stefn.shrmm@wiwi.uni muenster.de Motivtion für die Vernstltung Üung zur Mrkt und Preistheorie Inhlt der Klusur Vorlesung Skrit und Üung Sehr gut vorzuereiten! Tis zur
Die Philosophisch-historische Fakultät der Universität Bern. erlässt
 Stuienpln für s Bhelor- un Mster-Stuienprogrmm Estern Europen Stuies / Osteurop-Stuien / Étues e l Europe orientle er Universität Bern in Zusmmenreit mit er Universität Friourg vom 1. August 2009 Die Philosophish-historishe
Stuienpln für s Bhelor- un Mster-Stuienprogrmm Estern Europen Stuies / Osteurop-Stuien / Étues e l Europe orientle er Universität Bern in Zusmmenreit mit er Universität Friourg vom 1. August 2009 Die Philosophish-historishe
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus:
 Unterrichtsmterilien in digitler und in gedruckter Form Auszug us: Die Fmilie der Rosengewächse - Sttionenlernen mit Selstkontrollkrten mit 4 Frseiten Ds komplette Mteril finden Sie hier: School-Scout.de
Unterrichtsmterilien in digitler und in gedruckter Form Auszug us: Die Fmilie der Rosengewächse - Sttionenlernen mit Selstkontrollkrten mit 4 Frseiten Ds komplette Mteril finden Sie hier: School-Scout.de
Muss der Umfang (u) oder der Flächeninhalt (A) berechnet werden? Kreuze an! Der Umfang (u) ist die Länge des Weges um eine Fläche herum.
 9 Rettungsring Umfng und Fläheninhlt von Figuren Begriffe: Umfng und Fläheninhlt 1 Muss der Umfng (u) oder der Fläheninhlt () erehnet werden? Kreuze n! u B C D E F G H Zun eines Grundstüks Rsenflähe eines
9 Rettungsring Umfng und Fläheninhlt von Figuren Begriffe: Umfng und Fläheninhlt 1 Muss der Umfng (u) oder der Fläheninhlt () erehnet werden? Kreuze n! u B C D E F G H Zun eines Grundstüks Rsenflähe eines
Die Winkelsumme im Dreieck beträgt 180. Herleitung bzw. experimentelle Begründung in der Schule: Durch Punktspiegelung. Bedeutung+Winkelsumme 1
 edeutung+winkelsumme 1 Winkelsumme Kpitel 5: Dreiekslehre 5.1 edeutung der Dreieke Durh Tringultion lssen sih Vieleke in Dreieke zerlegen ( n Ek in n- Dreieke) eweis von Sätzen mittels Sätzen üer Dreieke
edeutung+winkelsumme 1 Winkelsumme Kpitel 5: Dreiekslehre 5.1 edeutung der Dreieke Durh Tringultion lssen sih Vieleke in Dreieke zerlegen ( n Ek in n- Dreieke) eweis von Sätzen mittels Sätzen üer Dreieke
BALANCE PSYCHOLOGIE O FITNESS O GESUNDHEIT UNSERE EXPERTIN
 BALANCE PSYCHOLOGIE O FITNESS O GESUNDHEIT UNSERE EXPERTIN Die Personl Trinerin Cludi Ludeley, 37, triniert in Frnkfurt Kleingruppen und Einzelpersonen. Für BRIGITTE ht sie ds Big-Five -Workout entwikelt.
BALANCE PSYCHOLOGIE O FITNESS O GESUNDHEIT UNSERE EXPERTIN Die Personl Trinerin Cludi Ludeley, 37, triniert in Frnkfurt Kleingruppen und Einzelpersonen. Für BRIGITTE ht sie ds Big-Five -Workout entwikelt.
Denn im Unterschied zu "müssen" und "dürfen erfordert "brauchen" nach wie vor den Infinitiv mit "zu".
 Deutsh-Quiz 01 Wenn etws ds Gleihe ist, ist es noh lnge niht dssele. Welher der folgenden Sätze ist niht korrekt? ) Mrth ht keinen eigenen Lippenstift. Sie enutzt denselen wie ihre Mutter ) Florin und
Deutsh-Quiz 01 Wenn etws ds Gleihe ist, ist es noh lnge niht dssele. Welher der folgenden Sätze ist niht korrekt? ) Mrth ht keinen eigenen Lippenstift. Sie enutzt denselen wie ihre Mutter ) Florin und
McAfee Data Loss Prevention Prevent
 Shnellstrthnduh Revision B MAfee Dt Loss Prevention Prevent Version 10.x In diesem Shnellstrthnduh erhlten Sie eine llgemeine Üersiht üer die Einrihtung einer MAfee Dt Loss Prevention Prevent (MAfee DLP
Shnellstrthnduh Revision B MAfee Dt Loss Prevention Prevent Version 10.x In diesem Shnellstrthnduh erhlten Sie eine llgemeine Üersiht üer die Einrihtung einer MAfee Dt Loss Prevention Prevent (MAfee DLP
Mathematik 17 Bruchrechnen 00 Name: Vorname: Datum: Lernziele:
 Mthemtik 7 Bruhrehnen 00 Nme: Vornme: Dtum: Lernziele: Nr. Lernziel A Ih knn ie vier Grunopertionen (Aition, Subtrktion, Multipliktion un Division) uf Aufgben mit Brühen nwenen. B Ih knn ie vier Grunopertionen
Mthemtik 7 Bruhrehnen 00 Nme: Vornme: Dtum: Lernziele: Nr. Lernziel A Ih knn ie vier Grunopertionen (Aition, Subtrktion, Multipliktion un Division) uf Aufgben mit Brühen nwenen. B Ih knn ie vier Grunopertionen
Wirkung verschiedener Insektizide bei Ober- und Unterblattapplikation gegen die Kohlmottenschildlaus Aleurodes proletella in biologischem Rosenkohl
 FiBL Mittelprüfung 3/7e Seite 1 von 7 Archiviert unter: http://orgprints.org/2592/ Forschungsinstitut für iologischen Lndu Frick Nr. 3/7e Mittelprüfung 3 Projektleiter: Fchgruppe: Auftrggeer: Dr. Eric
FiBL Mittelprüfung 3/7e Seite 1 von 7 Archiviert unter: http://orgprints.org/2592/ Forschungsinstitut für iologischen Lndu Frick Nr. 3/7e Mittelprüfung 3 Projektleiter: Fchgruppe: Auftrggeer: Dr. Eric
