Eylert, Numerische Mathematik Kapitel 7
|
|
|
- Lena Alexa Solberg
- vor 7 Jahren
- Abrufe
Transkript
1 Eyler, Numeriche Mahemaik Kapiel 7 7 aplace-tranformaion Moivaion Da öen linearer Differenialgleichungen i nich immer eine einfache Aufgabe. E gib viele öunganäze, die vor allem auch in der numerichen Inegraion bechrieben werden. Für die Elekro- und egelungechnik, aber auch im Machinenbau, ha ich aber die aplace-tranformaion, die wir im Folgenden mi PT abkürzen, in der Praxi al große Vereinfachung bewähr. Dabei geh man im Weenlichen in drei Schrien vor:. Die Differenialgleichung wird mi Hilfe der aplace-tranformaion in eine algebraiche Gleichung umgewandel.. öung dieer algebraichen Gleichung i die Bildfunkion der geuchen öung. 3. Im drien Schri wird eine ückranformaion durchgeführ, deren Ergebni die geuche öung der Differenialgleichung i. Hör ich komplizier an, i aber in der Praxi ein wunderbar einfacher Mechanimu zur öung dynamicher Prozee. Diee Auarbeiung baier auf der Grundlage de Kapiel 7 unere Buche Kompendium Numeriche Mahemaik [] und i den Bedürfnien der Sudierenden de Machinenbau der FH Müner, Abeilung Seinfur, SoSe angepa worden. 7. Einleiung Wir beginnen mi einem Beipiel au der Phyik bzw. Elekroechnik. Erinnern wir un: In einem Schalkrei i die Summe der Teilpannungen gleich der Quellenpannung. Angewende auf den elekrichen Schwingkrei heiß da: u() uc() a = + + C Bild 7..: Elekricher Schwingkrei Dabei gil: () = I() C() = Id C () = d di() In der Phyik wird die Ableiung nach der Zei mei mi einem Punk bezeichne, wehalb wir chreiben können: di() () = = & I() d Faen wir zuammen, o erhalen wir: Sand 3.5.
2 Eyler, Numeriche Mahemaik Kapiel 7 a = I() + & I() + Id C Diee Aufgabe i nich rivial löbar. m hier weierzukommen, leien wir nach der Zei ab und erhalen: da = & I() + && I() + I() d C Wollen wir hierau die Sromärke I() berechnen, müen wir eine lineare Differenialgleichung zweier Ordnung löen. Al geeignee mahemaiche Hilfmiel biee ich die aplace-tranformaion an. 7. Definiion der aplace-tranformaion Wie au dem obigen Bild erichlich, i e innvoll, olche Funkionen zu berachen, die er von einem Zeipunk = an einen von null verchiedenen Wer annehmen. Derarige zeiabhängige Funkionen enprechen in der Elekroechnik einem wie auch immer geareen Einchalvorgang, im Machinenbau einem Syem- oder Machinenar. Da die aplace-tranformaion ich ideal zur Bechreibung dynamicher Syeme egal welcher Herkunf eigne, operieren wir im Folgenden mi Funkionen f (). Dieer ordnen wir durch folgende Vorchrif eine komplexe Funkion zu, indem wir f () mi - e, j,, =d+ wî d wî muliplizieren und dann darüber inegrieren: 7.. Definiion aplace-tranformaion (PT): Gegeben ei eine Funkion: f () :, wobei gil: f () = für <. Die Funkion () : definier durch + () : = f ()exp - d, =d+ j wî, d, wî heiß aplace-tranformiere von f (), da enprechende Inegral aplace-inegral. Die Inegraion erfolg über die Variable mi al komplexem Parameer. I die Inegraion er einmal durchgeführ, bleib al Variable nur noch die komplexe Größe übrig. Da i der Grund, warum die aplace-tranformiere die Variable enhäl. Man bezeichne f () al Originalfunkion (oder auch Oberfunkion) und enprechend () al Bildfunkion (oder nerfunkion). Eine Originalfunkion f () heiß aplace-ranformierbar, wenn da zugehörige aplace- Inegral exiier. Den Zuammenhang zwichen den beiden Funkionen kann ymbolich dargeell werden durch: { f ()} () = oder auch f () () Da zweie Symbol finden Sie auch in der ieraur und i daelbe Symbol wie bei der Fourier-Tranformaion. Benuz man alo da zweie Symbol, mu immer klar ein, um welche Ar Tranformaion e ich im konkreen Fall handel. Da wir in unerem Buch beide Tran- Sand 3.5.
3 Eyler, Numeriche Mahemaik Kapiel 7 formaionen behandeln, benuzen wir im Zuammenhang mi der aplace-tranformaion () = f (). konequen nur die Schreibweie { } { } ) (Hinwei: Beachen Sie bie, Prof. Göllmann benuz in einem Skrip die Noaion f () f () (. Da dor auf die Fourier-Tranformaion nich eingegangen wird, ind Verwechelungen augechloen. Der Zuaz () mach deulich, da e ich um die Bildfunkion handel, die wir über () kennlich machen.) Mi der Anwendung der aplace-tranformaion wird ein differenielle Problem durch Tranformaion in ein inegrale überführ. Bei der aplace-tranformaion exiier eine ückranformaionformel, die via öung im Bildbereich die öung im Originalbereich icherell. Wa zunäch viel komplizierer auieh, führ lezendlich zu einer Vereinfachung. Bevor wir zu den eren Beipielen der aplace-tranformaion kommen müen wir eine im Folgenden bedeuende Funkion einführen. 7.. Definiion Sprungfunkion (auch Heaviide -Funkion genann): Die Sprungfunkion i wie folg definier: ì < () : =í î ³ An Hand der folgenden Beipiele wollen wir da Vorgehen bei der aplace-tranformaion erläuern. Beipiel : Berechnung der aplace-tranformaion der Sprungfunkion (): Wir ezen die Sprungfunkion in die Definiion 7.. ein und erhalen: + l æ ö () = exp( - ) d= lim exp( - ) d= limç - ( exp( -l)- exp() ) l l è ø Alo gil: {} = ( lim exp exp() ) ( ) =- -l - =- - = l Beipiel : Berechnung der aplace-tranformaion der Koinu-Funkion: ì < f () : =í îco ³ + () = (co ) exp - d au Definiion i: Au Formelammlung [3], S., erhalen wir da paende Grundinegral: ax ax e e co bx dx= ( a co bx+ bin bx) a + b Oliver Heaviide (85-95) bri. Mahemaiker und Phyiker Sand
4 Eyler, Numeriche Mahemaik Kapiel 7 + Mi a=-, Î und b= erhalen wir: Alo gil: + - é e ù () = (co ) exp( - ) d= ê (- co + in ) + ú ë û - - = élim( e (- co + in ) )- e (- co+ in ) ù ë û + = = ( ( ) ) + + { co } = + Zum Nachchlagen der aplace-tranformaionen von den wichigen Funkionen gib e Tabellen (z. B. [], [3]). Wir verzichen hier auf eine eigene Tabelle, da ie ohnehin nich volländig ein kann. 7.3 echenregeln der aplace-tranformaion Ein weenlicher Grund für die Einführung der aplace-tranformaion (PT) i, wie chon zuvor geag, da öen von Differenialgleichungen. Dehalb i e au Anwenderich inereaner, ich mi einigen beonderen, aber prakichen Eigenchafen der aplace- Tranformaion beipielhaf aueinander zu ezen und nich zu ief in die mahemaiche Theorie einzueigen. Zu dieen Eigenchafen gehören beimme echenregeln. Die Beweie all dieer Säze werden wir hier nur in Aunahmefällen führen; ie finden ich u. a. in der angegebenen ieraur bzw. ind durch Einezen in die Definiion der aplace-tranformaion nachzuvollziehen Saz ineariä der PT: Gegeben eien Funkionen: f (),g() :, wobei gil: f () = g() = für <. Ferner eien a,bî. Dann gil: a f () + b g() = a f () + b g() { } { } { } Bewei: { + } = ( + ) (- ) a f () b g() a f () b g() exp d + + ( ) ( ) { } { } = a f () exp - + b g() exp - d + + = a f () exp - d+ b g() exp - d = a f () + b g() q.e.d Saz Ähnlichkei der PT: Gegeben ei eine Funkion: f () :, wobei gil: f () = für <. Ferner eien a Î,a>. Dann gil: Sand
5 Eyler, Numeriche Mahemaik Kapiel 7 { f (a)} æ ö = ç a è aø Saz Verchiebung der PT nach rech: Gegeben ei eine Funkion: f () :, wobei gil: f () = für <. Ferner eien a Î,a> und () die Sprungfunkion au Definiion 7... Dann gil: f (- a) (- a) = exp( - a ) f () { } { } Saz Verchiebung der PT nach link: Gegeben ei eine Funkion: f () :, wobei gil: f () = für <. Ferner eien a Î,a> und () die Sprungfunkion au Definiion 7... Dann gil: a { f ( a) ()} exp(a ) æ ö + = ç { f ()}- f () exp( -)d è ø Saz Dämpfungaz der PT: Gegeben ei eine Funkion: f () :, wobei gil: f () = für <. Ferner eien a Î,a>. Dann gil: exp( - a) f () = + a { } Die Frage i nun, wie ieh die aplace-tranformiere der Ableiung von f () au? Dazu uchen wir un eine Funkion: f () :, mi f () = für <. au Definiion 7.. gil: + { } = (- ) f () f ()exp d Diee Inegral berechnen wir mi parieller Inegraion gemäß Hilfaz.3. und erhalen: { } = (- ) - - (- ) f () exp f () ( ) f () exp d { } = lim exp - f ()- exp - f () + f () { } = - f () + f () = - f () Dami haben wir Teil a) de folgenden Saze bewieen: Saz Ableiung der Originalfunkion der PT: Gegeben ei eine Funkion: f () :, wobei gil: f () = für <. Dann gil: f () = - f () Allgemein: a) { } b) { } + f () = - f ()- f () n (n) n n - i (i - ) c) { } å f () = - f () i= Sand
6 Eyler, Numeriche Mahemaik Kapiel 7 Hier ieh man, da man Anfangwere der Funkion und ihrer Ableiungen für die Zei = kennen mu, um die aplace-tranformiere von Ableiungen der Originalfunkion zu berechnen. Die Beweie zu b) und c) ergeben ich kanonich durch Einezen und Aurechnen. Al näche inereier un die Ableiung der Bildfunkion Saz Ableiung der Bildfunkion der PT: Gegeben ei eine Funkion: f () :, wobei gil: f () = für <. Dann gil: n(n) n ( ) = {(-) f ()} Auch hier ergib ich der Bewei kanonich durch Einezen und Aurechnen. Ebenfall von Ineree i die aplace-tranformiere de Inegral über die Originalfunkion, der wir un al näche widmen Saz Inegraion der Originalfunkion der PT: Gegeben ei eine Funkion: f () :, wobei gil: f () = für <. Dann gil: ì ü íf d ý= { f ()} = ( ) î þ Hierzu pa ein chöne Anwendungbeipiel: Berechne { in() } mi Hilfe von { co() } = + Mi dem Inegralaz erhalen wir: ì ü { in() } = ícod ý= ( co() ) = = î + + þ ogich, da un nun auch die aplace-tranformiere de Inegral über der Bildfunkion inereier: Saz Inegraion der Bildfunkion der PT: Gegeben ei eine Funkion: f () :, wobei gil: f () = für <. Dann gil: ì ü d= í f () ý î þ 7.3. Grenzweraz der PT: Gegeben ei eine Funkion: f () :, wobei gil: f () = für <. Wenn die Grenzwere limf () und limf () exiieren, dann gil: f () = limf () = lim () Anfangwer (recheiiger Grenzwer "f ( + )" ) f ( ) = limf () = lim () Endwer Sand
7 Eyler, Numeriche Mahemaik Kapiel Anwendungen der aplace-tranformaion Al Überblick zur Arbeiweie mi der aplace-tranformaion dien folgende Überich: Aufgabenellung Projekion Problemellung im Originalbereich f ()=? Þ aplace- Tranformaion f () { } Þ Aufgabenellung im Bildbereich ß öunguche ß öungfunkion Ü ückranformaion Ü öungfunkion f () () Bild 7.4.: Prinzip der aplace-tranformaion Der chwierige Teil bei dieer Vorgehenweie i immer die ückranformaion. Hilfreich ind dabei Tranformaionabellen. Einige Were haben wir ja hier chon verwende. Beipiel: Berechnung eine vereinfachen Schwingkreie: Wir wollen da Beipiel au der Einleiung wieder aufnehmen, laen aber den Ohmchen Widerand au der Berechnung rau. Aufgabenellung: Bild 7.6.3: Vereinfacher elekricher Schwingkrei Der elekriche Schwingkrei enhäl einen Kondenaor mi Kapaziä C und eine Spule mi Indukiviä in eihenchalung. Zum Zeipunk = wird von außen eine konane Spannung u angeleg. Der Schwingkrei ei zu dieem Zeipunk energielo. Zu berechnen i der zeiliche Verlauf der Sromärke im Zeiinervall ³ mi Hilfe der aplace-tranformaion. Sand
8 Eyler, Numeriche Mahemaik Kapiel 7 öung. Phyik: In der Phyik [4] haben wir gelern, da ich in Spulen und Kondenaoren die Sröme nich chlagarig, ondern zeiabhängig ändern. Mi der Machenregel folg: u + u - u = () C Für die Spannung u an der Spule gil: di() u () = = & i() d Normalerweie wird die zeiliche Ableiung de Srom mi einem Punk über dem i gekennzeichne. Wegen der chlechen Erkennbarkei chreiben wir i'() : u () = i () In gleicher Weie gil für den Kondenaor: q() = C u C() und dq() i() = =& q() d Þ q() = i( )d Þ - q() u C() = = id C C - Bi zum Einchalpunk = i der Schwingkrei energielo; da bedeue, da die Kondenaorladung gleich null i q() = für, ebeno wie die Sromärke i() = für. Dehalb gil dann auch für die Spannung am Kondenaor: u C() = id id id C + C = C =. Aufellen der Differenialgleichung: Einezen der phyikalichen Gegebenheien in Gleichung () ergib: Þ i () + id = u C Þ () u i () + id = C Dami i au () eine ogenanne Inegro-Differenialgleichung geworden, die wir mi der aplace-tranformaion löen wollen. 3. aplace-tranformaion: E gil: Sand
9 Eyler, Numeriche Mahemaik Kapiel 7 Definiion der PT: { i() } = I() Gem. Korrepondenzabelle (z. B. [3]): u u u ì í ü ý = {} = î þ i () = I - i() Saz 7.3.6: { } ì ü = = Saz 7.3.9: i( )d { i() } I( ) í ý î þ Die ezen wir in () ein, berückichigen i() =, und erhalen die PT: I( ) + I( ) = u C Mi der Thomonchen Schwingungformel ([4], Kap. 6.6): w = Þ C u I( ) +w I( ) = (3) 4. öung im Bildbereich: Gleichung (3) wird nach I() aufgelö: u Þ I( ) +w I( ) = u Þ ( +w ) I( ) = u Þ I( ) = +w (4) 5. ückranformaion: Au Korrepondenzabellen (z. B. [], [3]) ennehmen wir: ì in(a) ü = í ý= { in(a) }, wobei hier gil: a=w + a î a þ a Þ u u C i() = in w = C in w = u in w w C Sezen wir zur Abkürzung î : = u, o erhalen wir die öung: i() = ˆi in w (5) Þ = und dem Schei- p Die ich al periodiche Wechelromchwingung mi der Frequenz C elwer = Srompize î : = u ergib. f : w Sand
10 Eyler, Numeriche Mahemaik Kapiel 7 Beim öen von Differenialgleichungen reen aber häufig gebrochen raionale Funkionen al öungen im Bildbereich auf. Dann mu enweder mi Hilfe der Parialbruchzerlegung die Funkion vereinfach werden, bevor die Tabellen zur aplace-tranformaion angewende werden können, oder man kann die Falungeigenchaf nuzen. Dieem Thema wollen wir un im nächen Kapiel widmen und da Gelerne anchließend an zwei Anwendungbeipielen verdeulichen. 7.5 Falung von Funkionen Da Thema Falung von Funkionen piel u. a. in der Nachrichenechnik, aber auch im Machinenbau eine große olle, wo wir e ja auch häufig mi dynamichen Syemen zu un haben. Die Falung i ein geeignee Modell zur Bechreibung zahlreicher phyikalicher Vorgänge, vor allem bei zeiinvarianen linearen Überragungyemen, ogenannen TI -Syemen. Da Problem ell ich bei der ückranformaion einer Bildfunkion, die al Produk zweier Bildfunkionen darellbar i: () = () () exiieren und bekann ind. Nun wäre ja chön, wenn die Originalfunk- - Wir gehen davon au, da die Originalfunkionen f () : = { () } - f () : = { () } - ion von f () = { () } und ich auch wieder al Produk von Originalfunkionen darellen lä. Da aber i gerade nich der Fall. Die Originalfunkion eine olchen Produk i eine - f () = () und Inegralkombinaion der beiden Originalfunkionen { } - = { () } und ieh wie folg au: f () f () = f ( ) f (-) d Ein olche Inegral nennen Mahemaiker Falunginegral. Den Bewei hierzu zu führen, führe jez zu wei und i für den Ingenieur auch zweirangig Definiion Falung: Gegeben eien Funkionen: f (),g() :, wobei gil: f () = g() = für <. Da Falungproduk zweier Funkionen i definier durch: f ()*g() : = f ( ) g( -) d Bemerkung: Da Falungproduk i kommuaiv, aoziaiv und diribuiv (ohne Bewei). Au dem oben Geagen lä ich jez auch leich der Falungaz formulieren: 7.5. Saz Falungaz für PT: Gegeben eien Funkionen: f (),g() :, wobei gil: f () = g() = für <. Dann gil: f ()*g() = f () g() (Û() = () () ) { } { } { } TI: linear, ime-invarian Sand 3.5.
11 Eyler, Numeriche Mahemaik Kapiel 7 Dami wien wir grundäzlich er einmal genug über Falungen. Mi dieem Wien wollen wir jez noch zwei Anwendungbeipiele rechnen, ein au der E-Technik und ein au der Mechanik. 7.6 Anwendungbeipiele Beipiel : Beginnen wir mi dem Beipiel au der Mechanik, angelehn an ein Beipiel au []: Eine Anenne (Federab) mi der Federkonanen c und der Schwingungmae m befinde ich fe veranker auf dem Dach eine Mebue. Dieer bilde ein idealiiere reibungfreie bewegliche Elemen (Fahrwerk). Bild 7.6.: Schwingende Anenne auf gleichmäßig bechleunigem Fahrzeug Auf da Fahrzeug wirke eine konane Bechleunigung a in der angezeigen ichung. öung:. Phyik Nach dem Newonchen Grundgeeze der Mechanik Kraf = Mae x Bechleunigung müen wir un die Einzelkomponenen, die auf da Geamyem wirken, anchauen. nere Anenne habe die Mae m, idealerweie konzenrier auf den Maenpunk an der Anennenpize, in Gang geez mi der Bechleunigung a de Fahrzeug. Die Kraf, die auf die Anenne wirk, i alo einmal durch die Fahrzeugbewegung beimm: F = m a. F Andererei berechne ich die ückellkraf der Anenne nach dem Hooke chen Geez und beräg =- cx, c = Federkonane. FA Die Mae de Fahrzeug laen wir mal außen vor und konzenrieren un nur auf da Anennenyem. Beide Kräfe ind gleichgeriche und werden für die Berechnung de Geamyem addier. Wir erhalen alo einerei: F= F + F = ma- cx F Für da Weg-Zei-Geez x= x() enprich die. Ableiung nach x der Bechleunigung x&& de Geamyem. Andererei i die Kraf, die auf da Geamyem wirk, F= mx && A Sand 3.5.
12 Eyler, Numeriche Mahemaik Kapiel 7. Aufellen der Differenialgleichung Da chwingungfähige Syem genüg alo folgender linearen Differenialgleichung: mx && = ma- cx () Mi c m = : w erhalen wir die angenehme Darellung: && x+w x= a () E handel ich alo um eine lineare Differenialgleichung. Ordnung mi konanen Koeffizienen. Zur öung von Differenialgleichungen brauch man immer Anfangwere und zwar o viele, wie der Grad der höchen Ableiung i. Diee werden un i. A. durch da Syem vorgegeben. In unerem Beipiel liegen un folgende Anfangwere vor: Für = folg x() = und v() = x() & = Mi dieen Anfangweren veruchen wir, die geelle Differenialgleichung mihilfe der aplace-tranformaion zu löen. 3. aplace-tranformaion E gil: Definiion der PT: { } x() = () = X() Gem. Korrepondenzabelle (z. B. [3]): a = && x() + w x() { } { } { } { a} {&& x() } { x() } {} { && } { } Þ = +w Þ a = x() +w x() Mi Beipiel (Sprungfunkion) folg: {} = Mi Saz b) folg: && x() = () - x() - x() & { } {&& } x() = X -x() & - x() Berückichigen wir die Anfangwere x() = und x() & =, dann erhalen wir die PT: && x() = X { } Die ezen wir in () ein, Þ a = X +w X {} Þ a = X +w X a Þ = ( +w ) X( ) a Þ X( ) = ( +w ) (3) Sand 3.5.
13 Eyler, Numeriche Mahemaik Kapiel 7 4. öung im Bildbereich: Schauen wir un (3) genauer an und berückichigen wir, wa wir gerade gelern haben, dann biee ich hier zur öung der Saz 7.5. an: a X( ) = = { f ()*g()} ( +w ) { 443 g() 4. ückranformaion: f () { f ()} { } Wie ehen nun { } und { g() } () a = a = a {} und in(a) = ì í ü ý = + a î a þ a (7) { in(a) } Mi a=w folg: nd ìin( w ) ü í ý ( +w ) î w þ w in( w) Þ f () = w { f ()} = = = { in( w ) } a { g() } = = a = a {} Þ g() = a = a au? Au der Korrepondenzabelle [] ennehmen wir: Durch Einezen in Saz 7.5. erhalen wir: x() = f ()*g() = f ( ) g( -) d æ in( w) a = ç a d= in( w)d w w è a é cow ù a ö ø ( co ) = ê- ú = - w + w ë w û w ma = - co w c Wir erhalen eine harmoniche Schwingung mi Scheielwer ma c und Nullellen bei np w. Bild 7.6.: Schwingungdiagramm einer gleichmäßig bechleunigen Anenne Sand
14 Eyler, Numeriche Mahemaik Kapiel 7 Beipiel : Al leze Beipiel oll wieder eine Anwendung au der E-Technik herhalen. Wir berachen eine elekriche Schalung mi Ohmchem und kapaziivem Widerand: C Bild 7.6.3: Vereinfacher elekricher Schwingkrei Die Machenregel ergib folgende Gleichung: mi = + (7.6.) C C Eingangpannung Spannung am Ohmchen Widerand Spannung am kapaziiven Widerand Au der Phyik wien wir: am Ohmchen Widerand gil: () = I() am kapaziiven Widerand gil: dq dc I() = C C C d = d = & Au dieen beiden Gleichungen ergib ich: () = I() = C & () C () () C = & Þ C Þ Da C() = d C C eine Konane i, ezen wir K : =. C Wenn wir eine inuförmige Eingangpannung = uˆ in(p f) = uˆ in( w ) anlegen, erhalen wir folgende Gleichung: ˆ (7.6.) () + K d = u in( w) Auf diee Gleichung wenden wir die aplace-tranformaion an. Dazu müen wir die reche Seie der Gleichung o verändern (erweiern), da wir ihre Bildfunkion in einer Tranformaionabelle (z. B. [], [3]) finden können: Sand
15 Eyler, Numeriche Mahemaik Kapiel 7 in( w) ˆ () + K d = u w w Mi () : = () () ergib die aplace-tranformaion: () + K () uˆ = w (7.6.3) +w wobei wir für die Tranformaion de Inegral den Saz angewende haben und für die reche Seie der Gleichung den Wer in einer Korrepondenzabelle für die aplace- Tranformaion nachgechau haben. Durch mformung erhalen wir: uˆ () æ ö w ç + K = è ø +w Þ û w () = = uˆ w (7.6.4) +w + K +w + K Für diee Ar der Bildfunkion finde ich nich Enprechende in der Korrepondenzabelle für die aplace-tranformaion. Üblicherweie würde man hier zunäch eine Parialbruchzerlegung anezen. Da ell ich aber die Frage, ob mi Anwendung eine der Säze au Kapiel 7.5 die öung nich einfacher zu finden i. Wenn wir die Gleichung () = uˆ w +w + K berachen, fäll auf, da () ein Produk von Funkionen i. Da veruchen wir eine öung mi dem Falungaz Zuvor müen wir die Gleichung ewa umformen: Wir definieren: () : = und () : = + K +w Dami gil dann: () = u ˆ w () () Von dieen beiden Funkionen können wir die ückranformaionen in einer Tabelle nachchauen: () = { exp( K) } + K = - und () = = co( w) ( +w ) { } Dami gil dann: () = u ˆ w () () = uˆ w exp( - K) co( w) { } { } Für die ückranformaion gil nun mi dem Falungaz 7.5.: Sand
16 Eyler, Numeriche Mahemaik Kapiel 7 Þ { exp( - K) } { co( w ) } = { exp( -K)*co( w) } ˆ () = uˆ w exp( -K)*co( w ) = u w exp( -K(- )) co( w ) d = û w exp( - K) exp(k ) co( w ) d Mi der Inegraionformel wie in Beipiel au Kapiel 7. erhalen wir da paende Grundinegral: ax ax e e co bx dx= ( a co bx+ bin bx) a + b Mi a : = K und b :=w erhalen wir: exp(k ) ˆ é () = u w exp( - K) ê K cow +winw ë K +w ( ( C) ) ( ) é exp(k) = û w exp( - K) ê ( K cow +winw) ë K +w exp(k ) ù - ( K co w +w in w ) K +w ú û é exp(k) ù = û w exp( - K) ê ( K cow +winw) - ( K +w ) ë K +w K +w ú û = û w exp( -K) éexp(k) ( K cow +winw) - Kù K +w ë û = û w é ( K cow +winw) - K exp( -K) ù K +w ë û Ergebni: û w C æ - ö C () = cow-w C inw-e ç +w è ø Mi w C ( +w ( C) ) = C und w C= C erhalen wir: () = uˆ C cow- uˆ C C inw- uˆ C e - Übunghalber können Sie ja mal den öungweg mi der konvenionellen, aber weniger eleganen Parialbruchzerlegung veruchen. Wie nich ander zu erwaren, wird ie zum gleichen Ergebni führen. Für einen Ingenieur führen, wie chon häufig geehen, mei mehrere Wege zum Ziel. C ù ú û Sand
17 Eyler, Numeriche Mahemaik Kapiel Nüzliche Nebenproduk der PT In den vergangenen Kapieln haben wir die mahemaiche Herleiung, einige echenregeln und die ingenieurmäßige Anwendung der PT kennengelern. Die PT ha aber noch einen ehr nüzlichen Nebeneffek: Wenn Sie ich die Definiion der PT au 7. noch mal vor Augen führen, dann ehen Sie, da Sie mi der PT auch leich Inegrale der Form: + - F() f () e d = durch Anwendung der Tranformaionabelle für PT löen können. Beipiel : + -p Geuch i F() = (in ) e d= { f ()} Au Formelammlung [], Formel (7), und Kap. 7.6, Bpl., wien wir: in(a) ì í ü ý = { in(a) } = î a þ a + a Mi a= und =p folg { in() } = p + Þ F() = { in() } = p + Beipiel : + Geuch i -p G() = (co ) e d= { g() } Au Formelammlung [] ennehmen wir Formel (8): { co a} = + a ( + 4a ) Mi a= und =p folg p + { co } = p ( p + 4) { co } p + ( 4) Þ G() = = p p + Da gil naürlich nich nur für die einfache Beipiel, ondern auch für alle echenregeln, die wir bei der aplace-tranformaion kennengelern haben, einchließlich der Falung. Somi wird die PT für den Ingenieur auch zu einem ehr nüzlichen Werkzeug bei der öung von Inegraionproblemen! Sand
18 Eyler, Numeriche Mahemaik Kapiel 7 ieraur: [] Bernd Eyler, Dorohee Eyler, Kompendium Numeriche Mahemaik, Verlag New & Media, 3. überarbeiee Auflage, Berlin, ISBN , Kap. 7 [] Papula, Mahemaik für Ingenieure und Naurwienchafler, Band,. Auflage 8, Friedrich Vieweg & Sohn Verlaggeellchaf Braunchweig, ISBN , Kap [3] Zypkin, Alexander G., Zypkin, Georgi G.: Kleine Formelammlung Mahemaik: Algebra Geomerie Analyi, Fachbuchverlag eipzig, Köln 99, ISBN [4] Bieneck, Wolfgang: Elekro T - Grundlagen der Elekroechnik, Holland+Joenhan Verlag Sugar,, ISBN Sand
e sx y(x)dx 2. Direkt gemäss der Definition unter Verwendung der in der Vorlesung angeführten Eigenschaften
 Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 7 5. Semester ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE
 Mahemaik: Mag. Schmid Wolfgang Arbeibla 7. Semeer ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE Im Raum möche man naürlich nich nur Geraden ondern auch Flächen darellen. Diee Flächen bezeichne man al
Mahemaik: Mag. Schmid Wolfgang Arbeibla 7. Semeer ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE Im Raum möche man naürlich nich nur Geraden ondern auch Flächen darellen. Diee Flächen bezeichne man al
Messung der Ladung. Wie kann man Ladungen messen? /Kapitel Formeln auf S.134: Elektrische Ladung
 --- Meung der Ladung Wie kann man Ladungen meen? -/Kapiel.. Formeln auf S.: Elekriche Ladung Zur Ladungmeung können wir einen au der Mielufe bekannen Zuammenhang zwichen der Ladung Q und der Sromärke I
--- Meung der Ladung Wie kann man Ladungen meen? -/Kapiel.. Formeln auf S.: Elekriche Ladung Zur Ladungmeung können wir einen au der Mielufe bekannen Zuammenhang zwichen der Ladung Q und der Sromärke I
Fakultät Grundlagen. s = t. gleichförm ig
 Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
Höhere Mathematik III für die Fachrichtung Elektrotechnik und Informationstechnik Lösungsvorschläge zum 6. Übungsblatt
 Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
Stochastische Differentialgleichungen
 INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
Mathematik: Mag. Schmid Wolfgang+LehrerInnenteam ARBEITSBLATT 6-13 ERMITTELN DER KREISGLEICHUNG
 ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
KAPITEL 2 KÜRZESTE WEGE
 KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
Mathematik 1 für Maschinenbau, M. Schuchmann (SoSe 2013) Aufgabenblatt 5 (Ebenen)
 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Aufgabenbla 5 (Ebenen) ) Geuch i eine Gleichung der Ebene E durch die Punke A(; -; ); B(; ; -) und C(; ; ) in Parameerform. ) Schreibe in Koordinaenform:
Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Aufgabenbla 5 (Ebenen) ) Geuch i eine Gleichung der Ebene E durch die Punke A(; -; ); B(; ; -) und C(; ; ) in Parameerform. ) Schreibe in Koordinaenform:
Restkapazität. = O( V ) mal kritisch. Also gibt es insgesamt höchstens O( V E ) Augmentierungen.
 Lemma 4.5.9. Der Algorihmu von Edmond-Karp führ höchen O( V E ) Augmenierungen durch. Bewei. Eine Kane (u, v) heiße kriich auf augmenierenden Weg p gdw. c f (u, v) = c f (p). Rekapaziä Eine kriiche Kane
Lemma 4.5.9. Der Algorihmu von Edmond-Karp führ höchen O( V E ) Augmenierungen durch. Bewei. Eine Kane (u, v) heiße kriich auf augmenierenden Weg p gdw. c f (u, v) = c f (p). Rekapaziä Eine kriiche Kane
Inhaltsübersicht. Funktionenraum Fouriertransformation Laplacetransformation Partialbruchzerlegung Faltung
 Inhalüberich Kapiel : Reihenenwicklungen und Tranformaionen: au x mach u und wieder zurück Funkionenraum Fourierranformaion Laplaceranformaion Parialbruchzerlegung Falung Noizen zur Vorleung Mahemaik für
Inhalüberich Kapiel : Reihenenwicklungen und Tranformaionen: au x mach u und wieder zurück Funkionenraum Fourierranformaion Laplaceranformaion Parialbruchzerlegung Falung Noizen zur Vorleung Mahemaik für
Abbildungsmaßstab und Winkelvergrößerung
 Abbildungmaßab und Winkelvergrößerung Abbildungmaßab Uner dem Abbildungmaßab vereh man da Verhälni /, wobei der Audruck ein negaive Vorzeichen erhäl, wenn da ild verkehr wird. Alo Abbildungmaßab V: Winkelvergrößerung
Abbildungmaßab und Winkelvergrößerung Abbildungmaßab Uner dem Abbildungmaßab vereh man da Verhälni /, wobei der Audruck ein negaive Vorzeichen erhäl, wenn da ild verkehr wird. Alo Abbildungmaßab V: Winkelvergrößerung
Laplace Transformation
 Prof. Dr. Michael Eiermann Höhere Mahemaik 3 (verief) Kapiel L Laplace Tranformaion Die Laplace Tranformaion verwandel Anfangwerprobleme für lineare Differenialgleichungen mi konanen Koeffizienen in algebraiche
Prof. Dr. Michael Eiermann Höhere Mahemaik 3 (verief) Kapiel L Laplace Tranformaion Die Laplace Tranformaion verwandel Anfangwerprobleme für lineare Differenialgleichungen mi konanen Koeffizienen in algebraiche
Weg im tv-diagramm. 1. Rennwagen
 Weg im v-diagramm 1. Rennwagen Löung: (a). (a) Bechreibe die Fahr de Rennwagen. (b) Wie wei kommm der Rennwagen in den eren vier Minuen, wie wei komm er über den geamen Zeiraum? (c) Wie groß i die Durchchnigechwindigkei
Weg im v-diagramm 1. Rennwagen Löung: (a). (a) Bechreibe die Fahr de Rennwagen. (b) Wie wei kommm der Rennwagen in den eren vier Minuen, wie wei komm er über den geamen Zeiraum? (c) Wie groß i die Durchchnigechwindigkei
Die wichtigsten Inhalte der einzelnen Kapitel zur schnellen Wiederholung
 Checklien Die wichigen Inhale der einzelnen Kapiel zur chnellen Wiederholung I Kenn du eigenlich die rbeiweie der Naurwienchafler? I 1 Nenne die einzelnen Schrie, die Naurwienchafler gehen, u zu neuen
Checklien Die wichigen Inhale der einzelnen Kapiel zur chnellen Wiederholung I Kenn du eigenlich die rbeiweie der Naurwienchafler? I 1 Nenne die einzelnen Schrie, die Naurwienchafler gehen, u zu neuen
Mathematische Methoden der klassischen Physik Zusammenfassung Differentialgleichungen
 Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Technische Universität München Fakultät für Mathematik Algorithmische Diskrete Mathematik WS 2012/2013 Prof. Dr. P. Gritzmann 9.
 Noe: Name Vorname Marikelnummer Sudiengang Unerchrif der Kandidain/de Kandidaen Höraal Reihe Plaz Techniche Univeriä München Fakulä für Mahemaik Algorihmiche Dikree Mahemaik WS 0/0 Prof. Dr. P. Grizmann
Noe: Name Vorname Marikelnummer Sudiengang Unerchrif der Kandidain/de Kandidaen Höraal Reihe Plaz Techniche Univeriä München Fakulä für Mahemaik Algorihmiche Dikree Mahemaik WS 0/0 Prof. Dr. P. Grizmann
Geometric Algebra Computing Transformationen in LA und CGA Dr. Dietmar Hildenbrand
 Geomeric Algebra Compuing Tranformaionen in LA und CGA 4.2.24 Dr. Diemar Hildenbrand Techniche Univeriä Darmad Fachbereich Mahemaik Überblick In linearer Algebra Homogene Koordinaen Tranformaionen in linearer
Geomeric Algebra Compuing Tranformaionen in LA und CGA 4.2.24 Dr. Diemar Hildenbrand Techniche Univeriä Darmad Fachbereich Mahemaik Überblick In linearer Algebra Homogene Koordinaen Tranformaionen in linearer
F Rück. F r Rück. Mechanische Schwingungen. Größen zur quantitativen Beschreibung :
 Mechaniche chwingungen F r Rück Gleichgewichlage r F Rück F r Rück F r Rück Gleichgewichlage Größen zur quaniaiven Bechreibung : chwingungdauer oder Periode T, Einhei: Frequenz υ /T, Einhei: / oder Hz
Mechaniche chwingungen F r Rück Gleichgewichlage r F Rück F r Rück F r Rück Gleichgewichlage Größen zur quaniaiven Bechreibung : chwingungdauer oder Periode T, Einhei: Frequenz υ /T, Einhei: / oder Hz
Positioniersteuerung (5.12) Beschleunigen - Phase 2 (5.13) Beschleunigen - Phase 3 (5.14) Phase 4: Konstante Geschwindigkeit (5.15) Bremsen Phase 5
 Poiioniereuerung ( 0 a ( 0 0 v ( ˆ ( ˆ 0 0 0 0 (5. echleunigen Phae ( 0 a ( v ˆ ( ç ( + çè (( ( ˆ + ( + ç çè (5. echleunigen Phae ( ( a ( v( ( ( ( ( ( 7 + + + 9 ( ( (5.4 Phae 4: Konane Gechwindigkei a
Poiioniereuerung ( 0 a ( 0 0 v ( ˆ ( ˆ 0 0 0 0 (5. echleunigen Phae ( 0 a ( v ˆ ( ç ( + çè (( ( ˆ + ( + ç çè (5. echleunigen Phae ( ( a ( v( ( ( ( ( ( 7 + + + 9 ( ( (5.4 Phae 4: Konane Gechwindigkei a
Algorithmen II Vorlesung am
 Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
2.1 STURMSCHES ANFANGSWERTPROBLEM UND DGL 2. ORDNUNG
 . STURMSCHES ANANGSWERTPROBLEM UND DGL. ORDNUNG S o genanne Anfangwerprobleme reen ehr häufig bei naurwienchaflichen un echnichen Problemellungen auf. Hierbei hanel e ich in er Regel um DGL. Ornung oer.
. STURMSCHES ANANGSWERTPROBLEM UND DGL. ORDNUNG S o genanne Anfangwerprobleme reen ehr häufig bei naurwienchaflichen un echnichen Problemellungen auf. Hierbei hanel e ich in er Regel um DGL. Ornung oer.
Zusammenfassung: Induktion
 LGÖ K Ph -ündig Schuljahr 08/09 Zuammenfaung: Indukion Inhalverzeichni Indukion durch ewegung eine Leier in einem Magnefeld Änderungrae von Größen 3 Indukiongeez und Lenz che Regel 4 Kraf auf einen Leier
LGÖ K Ph -ündig Schuljahr 08/09 Zuammenfaung: Indukion Inhalverzeichni Indukion durch ewegung eine Leier in einem Magnefeld Änderungrae von Größen 3 Indukiongeez und Lenz che Regel 4 Kraf auf einen Leier
DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN
 Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Arbeitsauftrag Thema: Gleichungen umformen, Geschwindigkeit, Diagramme
 Arbeiaufrag Thema: Gleichungen umformen, Gechwindigkei, Diagramme Achung: - So ähnlich (aber kürzer) könne die näche Klaenarbei auehen! - Bearbeie die Aufgaben während der Verreungunde. - Wa du nich chaff
Arbeiaufrag Thema: Gleichungen umformen, Gechwindigkei, Diagramme Achung: - So ähnlich (aber kürzer) könne die näche Klaenarbei auehen! - Bearbeie die Aufgaben während der Verreungunde. - Wa du nich chaff
Von der Fourier-Reihe zum Fourier-Integral
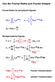 Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Anhang. A1 Analytische Lösungen der erweiterten Anzahlbilanz
 117 Anhang A1 Analyiche Löungen der erweieren Anzahlbilanz Die Bilanzgleichungen der erweieren Anzahlvereilung owohl für die koninuierliche al auch für die dikoninuierliche Krialliaion (l..-34 und.-35)
117 Anhang A1 Analyiche Löungen der erweieren Anzahlbilanz Die Bilanzgleichungen der erweieren Anzahlvereilung owohl für die koninuierliche al auch für die dikoninuierliche Krialliaion (l..-34 und.-35)
Gruppenarbeit: Anwendungen des Integrals Gruppe A: Weg und Geschwindigkeit
 Gruppenarbei: Anwendungen de Inegral Gruppe A: Weg und Gechwindigkei Die ere Ableiung der Zei-Or-Funkion x() der Bewegung eine Körper ergib bekannlich die Zei- Gechwindigkei-Funkion v(), deren ere Ableiung
Gruppenarbei: Anwendungen de Inegral Gruppe A: Weg und Gechwindigkei Die ere Ableiung der Zei-Or-Funkion x() der Bewegung eine Körper ergib bekannlich die Zei- Gechwindigkei-Funkion v(), deren ere Ableiung
W. Stark; Berufliche Oberschule Freising
 9.6 Aufellen der Bewegunggleichungen der haronichen Schwingung bei unerchiedlichen Anfangbedingungen i Hilfe eine Zeiger- und Liniendiagra 9.6. Der chwingende Körper durchläuf zu Zeinullpunk eine uhelage
9.6 Aufellen der Bewegunggleichungen der haronichen Schwingung bei unerchiedlichen Anfangbedingungen i Hilfe eine Zeiger- und Liniendiagra 9.6. Der chwingende Körper durchläuf zu Zeinullpunk eine uhelage
2.2 Rechnen mit Fourierreihen
 2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
Geradlinige Bewegung Krummlinige Bewegung Kreisbewegung
 11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
Definition Ein Homomorphismus von Lie-Algebren. Für uns ist vor allem die im folgenden Satz eingeführte Darstellung von Bedeutung.
 1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
1. Kontrolle Physik Grundkurs Klasse 11
 1. Konrolle Phyik Grundkur Klae 11 1. Ein Luch lauer eine Haen auf und lä e da ahnungloe und chackhafe Tier bi auf 30,0 herankoen. Dann prine er i 68 k/h auf ein Opfer lo, da ofor davon renn. Nach 5,0
1. Konrolle Phyik Grundkur Klae 11 1. Ein Luch lauer eine Haen auf und lä e da ahnungloe und chackhafe Tier bi auf 30,0 herankoen. Dann prine er i 68 k/h auf ein Opfer lo, da ofor davon renn. Nach 5,0
Lösungshinweise zu den Hausaufgaben:
 P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
Staatlich geprüfte Techniker
 Auzug au dem Lernmaerial Forildunglehrgang Saalich geprüfe Techniker Auzug au dem Lernmaerial Naurwienchaf DAA-Technikum Een / www.daa-echnikum.de, Infoline: 00 83 6 50 Definiion: Die Gechwindigkei eine
Auzug au dem Lernmaerial Forildunglehrgang Saalich geprüfe Techniker Auzug au dem Lernmaerial Naurwienchaf DAA-Technikum Een / www.daa-echnikum.de, Infoline: 00 83 6 50 Definiion: Die Gechwindigkei eine
Geradendarstellung in Paramterform
 Vekorrechnung Theorie Manfred Gurner Seie Geradendarellung in Paramerform X X X - X - r r Die Punke auf einer Geraden laen ich folgendermaßen finden: Gegeben ei der Punk und der Richungvekor r. Dann ergib
Vekorrechnung Theorie Manfred Gurner Seie Geradendarellung in Paramerform X X X - X - r r Die Punke auf einer Geraden laen ich folgendermaßen finden: Gegeben ei der Punk und der Richungvekor r. Dann ergib
Nutzung der inhärenten sensorischen Eigenschaften von piezoelektrischen Aktoren
 Nuzung der inhärenen enorichen Eigenchafen von piezoelekrichen Akoren K. Kuhnen; H. Janocha Lehruhl für Prozeßauomaiierung (LPA), Univeriä de Saarlande Im Sadwald, Gebäude 13, 6641 Saarbrücken Tel: 681
Nuzung der inhärenen enorichen Eigenchafen von piezoelekrichen Akoren K. Kuhnen; H. Janocha Lehruhl für Prozeßauomaiierung (LPA), Univeriä de Saarlande Im Sadwald, Gebäude 13, 6641 Saarbrücken Tel: 681
Systemtheorie. System. Prof. Dr. August Reiner. Dipl. Ing. Manfred Schneider
 Syemheorie Eingang Syem Augang Prof. Dr. Augu Reiner Dipl. Ing. Manfred Schneider Einleiung Einleiung Die Syemheorie, wie ie in den Ingenieurwienchafen verwende wird, wurde um 9 konzipier. Einen encheidenden
Syemheorie Eingang Syem Augang Prof. Dr. Augu Reiner Dipl. Ing. Manfred Schneider Einleiung Einleiung Die Syemheorie, wie ie in den Ingenieurwienchafen verwende wird, wurde um 9 konzipier. Einen encheidenden
Abiturprüfung Mathematik 2009 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
Integralrechnung. Grundidee der Integralrechnung. Einführung des Riemann- Integrals
 1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
Gewöhnliche Differentialgleichungen (DGL)
 Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
reibungsgedämpfte Schwingung
 HTL-LiTec reibunggedäpfe Schwingung Seie 1 von 7 Dipl.-Ing. Paul MOHR E-Brief: p.ohr@eduhi.a reibunggedäpfe Schwingung Maheaiche / Fachliche Inhale in Sichworen: reibunggedäpfe Schwingung; nueriche Löung
HTL-LiTec reibunggedäpfe Schwingung Seie 1 von 7 Dipl.-Ing. Paul MOHR E-Brief: p.ohr@eduhi.a reibunggedäpfe Schwingung Maheaiche / Fachliche Inhale in Sichworen: reibunggedäpfe Schwingung; nueriche Löung
Bitte beginnen Sie jede neue Aufgabe auf einem neuen Blatt!
 Soereeer 010 Bla 1 (on 7) Sudiengang: BT(B) / CI(B) Seeer Prüfungfach: Phyik Fachnuer: 04, 071, 07 Hilfiel: Manukrip, Lieraur, Tachenrechner Zei:10 Minuen Ingea ind 10 Punke erreichbar. Bie beginnen Sie
Soereeer 010 Bla 1 (on 7) Sudiengang: BT(B) / CI(B) Seeer Prüfungfach: Phyik Fachnuer: 04, 071, 07 Hilfiel: Manukrip, Lieraur, Tachenrechner Zei:10 Minuen Ingea ind 10 Punke erreichbar. Bie beginnen Sie
Die Bildung des Präsens funktioniert dann beispielsweise so: "lauda + mus" - wir loben.
 Präen Da Präen i die Gegenwarform. E bechreib alo Handlungen, die gerade paieren. Die Bildung i denkbar einfach und unercheide ich in den unerchiedlichen Konjugaionen (fa immer) nich. Dewegen reich e vollkommen
Präen Da Präen i die Gegenwarform. E bechreib alo Handlungen, die gerade paieren. Die Bildung i denkbar einfach und unercheide ich in den unerchiedlichen Konjugaionen (fa immer) nich. Dewegen reich e vollkommen
Technische Universität München. Lösung Montag SS 2012
 Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
(3) Weg-Zeit-Verhalten
 (3) Weg-Zei-Verhalen Vorleung Animaion und Simulaion S. Müller KOBLENZ LANDAU Wdh: Bogenlängenabelle Pfad felegen (P 0, P, P and P 3 ) 3 3 r u u P0 3 u u P 3 u u P u P Berechne Poiion für Zeipunk, i.e.
(3) Weg-Zei-Verhalen Vorleung Animaion und Simulaion S. Müller KOBLENZ LANDAU Wdh: Bogenlängenabelle Pfad felegen (P 0, P, P and P 3 ) 3 3 r u u P0 3 u u P 3 u u P u P Berechne Poiion für Zeipunk, i.e.
Differentialgleichungen
 Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
7 Das lokale Ito-Integral
 7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
Übersicht Datenstrukturen und Algorithmen. Graphenproblem: maximale Flüsse. Graphenproblem: maximale Flüsse. Vorlesung 16: Maximaler Fluss
 Überich aenrukuren und lgorihmen Vorleung 16: Prof. r. Erika Ábrahám Theorie Hybrider Syeme Informaik 2 hp://h.rwh-aachen.de/eaching/-1/ daenrukuren-und-algorihmen/ iee Präenaion verwende in Teilen Folien
Überich aenrukuren und lgorihmen Vorleung 16: Prof. r. Erika Ábrahám Theorie Hybrider Syeme Informaik 2 hp://h.rwh-aachen.de/eaching/-1/ daenrukuren-und-algorihmen/ iee Präenaion verwende in Teilen Folien
Physik für Mediziner und Zahnmediziner
 Phyik für Mediziner und Zahnmediziner Vorleung 05 Prof. F. Wörgöer (nach M. Seib) -- Phyik für Mediziner und Zahnmediziner 1 Zuammenhang von Kraf und Bechleunigung Experimen M Fmg m Deuung: Kraf Mae Bechleunigung
Phyik für Mediziner und Zahnmediziner Vorleung 05 Prof. F. Wörgöer (nach M. Seib) -- Phyik für Mediziner und Zahnmediziner 1 Zuammenhang von Kraf und Bechleunigung Experimen M Fmg m Deuung: Kraf Mae Bechleunigung
Systemtheorie Teil A. - Zeitkontinuierliche Signale und Systeme - Musterlösungen. Manfred Strohrmann Urban Brunner
 Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Karlsruher Institut für Technologie (KIT) Institut für Analysis Dr. A. Müller-Rettkowski Dipl.-Math. M. Uhl. Sommersemester 2011
 Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
MATLAB: Kapitel 4 Gewöhnliche Differentialgleichungen
 4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
Institut für Informatik. Aufgaben zur Klausur Grundlagen der Technische Informatik 1 und 2
 NIVESITÄT LEIPZIG Iniu für Informaik Prüfungaufgaben Klauur zur Vorleung WS 2/2 und SS 2 b. Techniche Informaik Prof. Dr. do Kebchull Dr. Paul Herrmann Dr. Han-Joachim Lieke Daum:. Juli 2 hrzei: 8-3 Or:
NIVESITÄT LEIPZIG Iniu für Informaik Prüfungaufgaben Klauur zur Vorleung WS 2/2 und SS 2 b. Techniche Informaik Prof. Dr. do Kebchull Dr. Paul Herrmann Dr. Han-Joachim Lieke Daum:. Juli 2 hrzei: 8-3 Or:
14 Kurven in Parameterdarstellung, Tangentenvektor und Bogenlänge
 Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Motivation der Dierenzial- und Integralrechnung
 Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen HS Esslingen SS 2016 Fakulä Grundlagen (HS Esslingen) SS 2016 1 / 12 Übersich 1 Vorberachungen zur Dierenzial- und Inegralrechnung Ableiungsbegri
Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen HS Esslingen SS 2016 Fakulä Grundlagen (HS Esslingen) SS 2016 1 / 12 Übersich 1 Vorberachungen zur Dierenzial- und Inegralrechnung Ableiungsbegri
7. Vorlesung Wintersemester
 7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
f ( x) = x + x + 1 (quadratische Funktion) f '( x) = x + (Ableitungsfunktion)
 R. Brinkmann hp://brinkmann-du.de Seie.. Tangene und Normale Tangenenseigung Die Seigung eines Funkionsgraphen in einem Punk P ( f ( ) ) is gleichbedeuend mi der Seigung der Tangene in diesem Punk. Nachfolgend
R. Brinkmann hp://brinkmann-du.de Seie.. Tangene und Normale Tangenenseigung Die Seigung eines Funkionsgraphen in einem Punk P ( f ( ) ) is gleichbedeuend mi der Seigung der Tangene in diesem Punk. Nachfolgend
existiert. In der Regel wird zusätzlich zum oben gegebenen System von Differentialgleichungen noch eine Anfangsbedingung
 0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
2 Torsion in dünnwandigen Querschnitten
 apl oz r-ing hail G Georgi Tragwerkerechnung Torion in dünnwandigen Querchnien Theorien, Vorauezungen und Hpoheen Theorien: Reine Torion ( Grundufe) Begründer: Jean Claude de T VENANT (9-886) mol, Inde:
apl oz r-ing hail G Georgi Tragwerkerechnung Torion in dünnwandigen Querchnien Theorien, Vorauezungen und Hpoheen Theorien: Reine Torion ( Grundufe) Begründer: Jean Claude de T VENANT (9-886) mol, Inde:
Grundlagen der Elektrotechnik 3
 Grundlagen der Elekroechnik 3 Kapiel 3. Schalvorgänge - Die aplace Transformaion Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 S. Fachgebie Nachrichenechnische Syseme 3.. Einführung Nuzung einer
Grundlagen der Elekroechnik 3 Kapiel 3. Schalvorgänge - Die aplace Transformaion Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 S. Fachgebie Nachrichenechnische Syseme 3.. Einführung Nuzung einer
Ermittlung von Leistungsgrenzen verschiedener Lagerstrategien unter Berücksichtigung zentraler Einflussgrößen
 Ermilung von Leiunggrenzen verchiedener Lagerraegien uner Berücichigung zenraler Einflugrößen Dipl.-Wir.-Ing. (FH) Anne Piepenburg, Prof. Dr.-Ing. Rainer Brun Helmu-Schmid-Univeriä, Hamburg Lehruhl für
Ermilung von Leiunggrenzen verchiedener Lagerraegien uner Berücichigung zenraler Einflugrößen Dipl.-Wir.-Ing. (FH) Anne Piepenburg, Prof. Dr.-Ing. Rainer Brun Helmu-Schmid-Univeriä, Hamburg Lehruhl für
Westfälische Hochschule - Fachbereich Informatik & Kommunikation - Bereich Angewandte Naturwissenschaften. 2. Mechanik
 Wefäliche Hochchule - Fachbereich Informaik & Kommunikaion - Bereich Anewande Naurwienchafen. Mechanik Ziele der Vorleun:.) Eineilun der phikalichen Größen in kalare und ekorielle Größen.) Kinemaik Bechreibun
Wefäliche Hochchule - Fachbereich Informaik & Kommunikaion - Bereich Anewande Naurwienchafen. Mechanik Ziele der Vorleun:.) Eineilun der phikalichen Größen in kalare und ekorielle Größen.) Kinemaik Bechreibun
Übersicht. Datenstrukturen und Algorithmen. Graphenproblem: maximale Flüsse. Graphenproblem: maximale Flüsse. Vorlesung 18: Maximaler Fluss (K26)
 Überich aenrukuren und lgorihmen Vorleung 18: (K26) Joo-Pieer Kaoen Lehruhl für Informaik 2 Sofware Modeling and Verificaion Group hp://move.rwh-aachen.de/eaching/-15/dal/ 25. Juni 2015 1 Flunezwerke 2
Überich aenrukuren und lgorihmen Vorleung 18: (K26) Joo-Pieer Kaoen Lehruhl für Informaik 2 Sofware Modeling and Verificaion Group hp://move.rwh-aachen.de/eaching/-15/dal/ 25. Juni 2015 1 Flunezwerke 2
Theoretische Grundlagen
 Theoreiche Grundlagen Phik Leiungkur Größen Größen Größen 5 m Grundgrößen abgeleiee Größen Zahl Einhei Länge, Mae, Zei, Sromärke, Temperaur, Soffmenge, Lichärke Gechwindigkei, Kraf, Ladung Änderunggrößen:
Theoreiche Grundlagen Phik Leiungkur Größen Größen Größen 5 m Grundgrößen abgeleiee Größen Zahl Einhei Länge, Mae, Zei, Sromärke, Temperaur, Soffmenge, Lichärke Gechwindigkei, Kraf, Ladung Änderunggrößen:
3.4 Systeme linearer Differentialgleichungen
 58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
auf den Boden fallen, hört man in gleichen Zeitabständen 4 Geräusche. Welchen Abstand hat die 3. Schraube vom unteren Ende der Fallschnur?
 Aufaben zu freien Fall 0. Von der Spize eine Ture lä an einen Sein fallen. Nach 4 Sekunden ieh an ihn auf de Boden aufchlaen. a) Wie hoch i der Tur? b) Mi welcher Gechwindikei riff der Sein auf den Erdboden
Aufaben zu freien Fall 0. Von der Spize eine Ture lä an einen Sein fallen. Nach 4 Sekunden ieh an ihn auf de Boden aufchlaen. a) Wie hoch i der Tur? b) Mi welcher Gechwindikei riff der Sein auf den Erdboden
10. Wechselspannung Einleitung
 10.1 Einleiung In Sromnezen benuz man sa Gleichspannung eine sinusförmige Wechselspannung, uner anderem weil diese wesenlich leicher zu erzeugen is. Wie der Name es sag wechsel bei einer Wechselspannung
10.1 Einleiung In Sromnezen benuz man sa Gleichspannung eine sinusförmige Wechselspannung, uner anderem weil diese wesenlich leicher zu erzeugen is. Wie der Name es sag wechsel bei einer Wechselspannung
Bewertungsmethoden in der Versicherungsmathematik
 Bewerungmehoden in der Vericherungmahemaik Techniche Reerven und Markwere II Johanne Pacheag Mahemaiche Iniu der Univeriä zu Köln Sommeremeer 2010 Bereuung: Prof. Schmidli, Dr. Eienberg 1 Inhalverzeichni
Bewerungmehoden in der Vericherungmahemaik Techniche Reerven und Markwere II Johanne Pacheag Mahemaiche Iniu der Univeriä zu Köln Sommeremeer 2010 Bereuung: Prof. Schmidli, Dr. Eienberg 1 Inhalverzeichni
Algorithmische Graphentheorie
 Algorihmiche Graphenheorie Sommeremeer 2014 3. Vorleung Flualgorihmen Prof. Dr. Alexander Wolff 1 Erinnerung Oh my God i an LP! Gegeben ein gericheer Graph G = (V, E) mi, V und Kanenkapaziäen c : E R >0.
Algorihmiche Graphenheorie Sommeremeer 2014 3. Vorleung Flualgorihmen Prof. Dr. Alexander Wolff 1 Erinnerung Oh my God i an LP! Gegeben ein gericheer Graph G = (V, E) mi, V und Kanenkapaziäen c : E R >0.
Aufgabenblatt 10: Investitionstheoretische Kostenrechnung I
 Prof. Dr. Gunher Friedl Aufgabenbla 10: Inveiionheoreiche oenrechnung I Aufgabe 10.1: Inveiionheoreiche oenrechnung, Abchreibung (Aufg. 6.2.2 im Übungbuch) Die Gechäfleiung der Brauerei Benedikiner erwäg
Prof. Dr. Gunher Friedl Aufgabenbla 10: Inveiionheoreiche oenrechnung I Aufgabe 10.1: Inveiionheoreiche oenrechnung, Abchreibung (Aufg. 6.2.2 im Übungbuch) Die Gechäfleiung der Brauerei Benedikiner erwäg
2 Geradlinige Bewegung eines Massenpunkts
 13 2 Gerdlinige Bewegung eine Menpunk Bei ielen Bewegungufgben knn die Drehbewegung eine Körper ernchläig werden, wenn nur deen rnloriche Bewegung inereier. In dieem Fll drf der Körper l Menpunk berche
13 2 Gerdlinige Bewegung eine Menpunk Bei ielen Bewegungufgben knn die Drehbewegung eine Körper ernchläig werden, wenn nur deen rnloriche Bewegung inereier. In dieem Fll drf der Körper l Menpunk berche
Hauptprüfung 2010 Aufgabe 4
 Haupprüfung Aufgabe Gegeben ind die Punke A(5//), B(//), C(//) und S(//5).. Zeigen Sie, da da Dreieck ABC rechwinklig und gleichchenklig i. Berechnen Sie die Koordinaen de Punke D o, da da Viereck ABCD
Haupprüfung Aufgabe Gegeben ind die Punke A(5//), B(//), C(//) und S(//5).. Zeigen Sie, da da Dreieck ABC rechwinklig und gleichchenklig i. Berechnen Sie die Koordinaen de Punke D o, da da Viereck ABCD
2. Torsion geschlossener Profile
 Berache werden Balken mi einem konanen einzelligen gechloenen dünnwandigen Hohlquerchni, die durch ein konane Torionmomen M x belae werden. A B () D C M x x y Prof. Dr. Wandinger 5. Dünnwandige Profile
Berache werden Balken mi einem konanen einzelligen gechloenen dünnwandigen Hohlquerchni, die durch ein konane Torionmomen M x belae werden. A B () D C M x x y Prof. Dr. Wandinger 5. Dünnwandige Profile
Einführung in gewöhnliche Differentialgleichungen
 Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
2 s. m m. m s. km h. kg s. = 375m. N m. c) Energieerhaltung: E Sp = E pot. d) Energieerhaltung E pot = E Sp (=E kin )
 Löungen Phyik 8. ahrgangufe Gynaiu ckenal I. Mechanik. Mechaniche nergieforen a) nach : Uwandlung annenergie in kineiche nergie nach 3: Uwandlung kineiche nergie in poenzielle nergie 3 nach 4: Uwandlung
Löungen Phyik 8. ahrgangufe Gynaiu ckenal I. Mechanik. Mechaniche nergieforen a) nach : Uwandlung annenergie in kineiche nergie nach 3: Uwandlung kineiche nergie in poenzielle nergie 3 nach 4: Uwandlung
Leistungselektronik Grundlagen und Standardanwendungen. Übung 3: Kommutierung
 Lehrsuhl für Elekrische Anriebssyseme und Leisungselekronik Technische Universiä München Arcissraße 1 D 8333 München Email: eal@ei.um.de Inerne: hp://www.eal.ei.um.de Prof. Dr.-Ing. Ralph Kennel Tel.:
Lehrsuhl für Elekrische Anriebssyseme und Leisungselekronik Technische Universiä München Arcissraße 1 D 8333 München Email: eal@ei.um.de Inerne: hp://www.eal.ei.um.de Prof. Dr.-Ing. Ralph Kennel Tel.:
Kapitel : Exponentiell-beschränktes Wachstum
 Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
College International Vorbereitungsjahr 2017/18
 College Inernaional Vorbereiungjahr 07/8 Phyik Dr. Ferenc Tölgyei olgyei.ferenc@med.emmelwei.hu Vorleungkripe zum Herumerladen: hp//:nighowl.oe.hu/olgyei Themaik (bi zu Weihnachen) Daum Thema. und 4. Ok.
College Inernaional Vorbereiungjahr 07/8 Phyik Dr. Ferenc Tölgyei olgyei.ferenc@med.emmelwei.hu Vorleungkripe zum Herumerladen: hp//:nighowl.oe.hu/olgyei Themaik (bi zu Weihnachen) Daum Thema. und 4. Ok.
25. Flüsse in Netzen. Motivation. Fluss. Flussnetzwerk
 Moivaion 25. Flüe in Nezen Flunezwerk, Maximaler Flu, Schni, Renezwerk, Max-flow Min-cu, Ford-Fulkeron Mehode, Edmond-Karp Algorihmu, Maximale Biparie Maching [Oman/Widmayer, Kap. 9.7, 9.8.1], [Cormen
Moivaion 25. Flüe in Nezen Flunezwerk, Maximaler Flu, Schni, Renezwerk, Max-flow Min-cu, Ford-Fulkeron Mehode, Edmond-Karp Algorihmu, Maximale Biparie Maching [Oman/Widmayer, Kap. 9.7, 9.8.1], [Cormen
Lineare Algebra I - Lösungshinweise zur Klausur
 Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Bekommt Schüler F. noch den Bus...
 Gnuplo Inro Aufgbenellung Bekomm Schüler F. noch den Bu...... oder komm er ew zu pä in die Schule? E. Pulu 1 T. Bonow 2 1 Bichöfliche Gymnium Snk Urul Geilenkirchen 2 Sudieneminr Jülich Jülich Phyik GK11
Gnuplo Inro Aufgbenellung Bekomm Schüler F. noch den Bu...... oder komm er ew zu pä in die Schule? E. Pulu 1 T. Bonow 2 1 Bichöfliche Gymnium Snk Urul Geilenkirchen 2 Sudieneminr Jülich Jülich Phyik GK11
Name: Punkte: Note: Ø:
 Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
5. Übungsblatt zur Linearen Algebra II
 Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
1. Für die Bewegung eines Fahrzeuges wurde das t-s-diagramm aufgenommen. Skizziere für diese Bewegung das t-v- Diagramm.
 Aufgaben zur gleichförigen Bewegung 1. Für die Bewegung eine Fahrzeuge wurde da --Diagra aufgenoen. Skizziere für diee Bewegung da -- Diagra. 2. Eine Radfahrerin und ein Spaziergänger i eine Hund bewegen
Aufgaben zur gleichförigen Bewegung 1. Für die Bewegung eine Fahrzeuge wurde da --Diagra aufgenoen. Skizziere für diee Bewegung da -- Diagra. 2. Eine Radfahrerin und ein Spaziergänger i eine Hund bewegen
Aufgabensammlung BM Berufs- und Weiterbildungszentrum bzb, Hanflandstr. 17, Postfach, 9471 Buchs,
 Löung Aufgabenalung BM Beruf- und Weierbildungzenru bzb, Hanflandr. 17, Pofach, 9471 Buch, www.bzbuch.ch 1) Während Sie in eine Lif ehen, ehen Sie eine Schraube von der hohen Decke der Lifkabine herabfäll.
Löung Aufgabenalung BM Beruf- und Weierbildungzenru bzb, Hanflandr. 17, Pofach, 9471 Buch, www.bzbuch.ch 1) Während Sie in eine Lif ehen, ehen Sie eine Schraube von der hohen Decke der Lifkabine herabfäll.
 Ergänzung Kpiel 5. Whl der Führunggröße Whl der Führunggröße für Lgeregelungen Biher wurde mei on einem prungförmigen Verluf der Führunggröße w( ugegngen. Viele regelungechniche Anwendungen weien uch ein
Ergänzung Kpiel 5. Whl der Führunggröße Whl der Führunggröße für Lgeregelungen Biher wurde mei on einem prungförmigen Verluf der Führunggröße w( ugegngen. Viele regelungechniche Anwendungen weien uch ein
Fouerierreihen - eine Einführung
 HBL Kapfenberg Fourierreiehen - eine Einführung Seie 1 von 19 Roland Pichler roland.pichler@hl-kapfenberg.ac.a Fouerierreihen - eine Einführung Mahemaische / Fachliche Inhale in Sichworen: Inegralrechnung,
HBL Kapfenberg Fourierreiehen - eine Einführung Seie 1 von 19 Roland Pichler roland.pichler@hl-kapfenberg.ac.a Fouerierreihen - eine Einführung Mahemaische / Fachliche Inhale in Sichworen: Inegralrechnung,
Aufgaben zur gleichförmigen Bewegung
 Aufgaben zur gleichförigen Bewegung 860. Ein Waerrad on 5 Durcheer eh an eine 2 breien und 0,7 iefe Bach. Da Rad dreh ich in der Minue 5 al und i a Rand genau o chnell, wie der Bach fließ. Wie iel Lier
Aufgaben zur gleichförigen Bewegung 860. Ein Waerrad on 5 Durcheer eh an eine 2 breien und 0,7 iefe Bach. Da Rad dreh ich in der Minue 5 al und i a Rand genau o chnell, wie der Bach fließ. Wie iel Lier
Induktionsgesetz. a = 4,0cm. m = 50g
 1. Die neenehende Aildung (Blick von vorn) zeig eine Spule mi 5 Windungen von quadraichem uerchni mi Seienlänge a = 4,cm zum Zeipunk. DieSpuleeweg ich mider Gechwindigkei v vom Berag v = 2, cm nachrech.
1. Die neenehende Aildung (Blick von vorn) zeig eine Spule mi 5 Windungen von quadraichem uerchni mi Seienlänge a = 4,cm zum Zeipunk. DieSpuleeweg ich mider Gechwindigkei v vom Berag v = 2, cm nachrech.
College International Vorbereitungsjahr 2016/17
 College Inernaional Vorbereiungjahr 6/7 Phyik Dr. Ferenc Tölgyei olgyei.ferenc@med.emmelwei.hu Vorleungkripe zum Herumerladen: hp//:nighowl.oe.hu/olgyei Themaik (bi zu Weihnachen) Daum Thema 3. und 5.
College Inernaional Vorbereiungjahr 6/7 Phyik Dr. Ferenc Tölgyei olgyei.ferenc@med.emmelwei.hu Vorleungkripe zum Herumerladen: hp//:nighowl.oe.hu/olgyei Themaik (bi zu Weihnachen) Daum Thema 3. und 5.
PHYSIKALISCHES PRAKTIKUM FÜR ANFÄNGER LGyGe
 10.7.08 PHYSKALSCHES PAKTKUM FÜ AFÄGE LGyGe Veruch: M 12 - Kreiel n dieem Veruch werden die Präzeionbewegung und die uaionbewegung eine Kreiel uneruch. Der Aufbau de Kreiel kann au der Abbildung de Veruch
10.7.08 PHYSKALSCHES PAKTKUM FÜ AFÄGE LGyGe Veruch: M 12 - Kreiel n dieem Veruch werden die Präzeionbewegung und die uaionbewegung eine Kreiel uneruch. Der Aufbau de Kreiel kann au der Abbildung de Veruch
Probeklausur 1. Thema Nr. 1 (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeiten!
 Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Lösungen zur Blütenaufgabe Harmonische Schwingungen
 Löungen zur Blüenaugae Haroniche Schwingungen I olgenden werden die Löungen zur Blüenaugae Haroniche Schwingungen dargeell. E erolg zuäzlich eine Einordnung der Zielypen der jeweiligen Teilaugaen und eine
Löungen zur Blüenaugae Haroniche Schwingungen I olgenden werden die Löungen zur Blüenaugae Haroniche Schwingungen dargeell. E erolg zuäzlich eine Einordnung der Zielypen der jeweiligen Teilaugaen und eine
III.2 Radioaktive Zerfallsreihen
 N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
Ferienkurs Analysis I für Physiker WS 15/16 Aufgaben Tag 3. Aufgaben Tag 3
 für Physier WS 5/6 Reihen Zeigen Sie, dass die folgenden Reihen onvergieren und die angegebenen Summen haben. Dabei is f die -e Fibonacci-Zahl a + = 4 Wir fassen die gegebene Reihe als Grenzwer der Folge
für Physier WS 5/6 Reihen Zeigen Sie, dass die folgenden Reihen onvergieren und die angegebenen Summen haben. Dabei is f die -e Fibonacci-Zahl a + = 4 Wir fassen die gegebene Reihe als Grenzwer der Folge
Experiments. Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 1
 Experimen Prof. F. Wörgöer (nach M. Seib) -- Phyik für Mediziner und Zahnmediziner Phyik für Mediziner und Zahnmediziner Vorleung 04 Prof. F. Wörgöer (nach M. Seib) -- Phyik für Mediziner und Zahnmediziner
Experimen Prof. F. Wörgöer (nach M. Seib) -- Phyik für Mediziner und Zahnmediziner Phyik für Mediziner und Zahnmediziner Vorleung 04 Prof. F. Wörgöer (nach M. Seib) -- Phyik für Mediziner und Zahnmediziner
1. Klausur Physik Leistungskurs Klasse
 1. Kluur Phyik Leiungkur Kle 11 1.1.1 1. uf einer gerden, horizonlen Srße fähr ein Moorrd i der konnen Gechwindigkei 9kh -1. pier zur Zei eine Mrke M. Zu elben Zeipunk re i Punk P ein Moorrd (Me einchließlich
1. Kluur Phyik Leiungkur Kle 11 1.1.1 1. uf einer gerden, horizonlen Srße fähr ein Moorrd i der konnen Gechwindigkei 9kh -1. pier zur Zei eine Mrke M. Zu elben Zeipunk re i Punk P ein Moorrd (Me einchließlich
Durch Modellierung beschreibt man Vorgänge aus der Natur sowie industrielle Prozesse
 Kapiel Modellierung Durch Modellierung beschreib man Vorgänge aus der Naur sowie indusrielle Prozesse mi mahemaischen Werkzeugen, zum Beispiel Gleichungen oder Ungleichungen. Modellierung geschieh durch
Kapiel Modellierung Durch Modellierung beschreib man Vorgänge aus der Naur sowie indusrielle Prozesse mi mahemaischen Werkzeugen, zum Beispiel Gleichungen oder Ungleichungen. Modellierung geschieh durch
