Figur in der Bildfläche bzw. Bildebene
|
|
|
- Alexa Wetzel
- vor 7 Jahren
- Abrufe
Transkript
1 2 ABBILDUNGSMETHODEN 2.1 Projektionsarten Um dreidimensionale Objekte wie Gebäude, Stadträume oder Bauteile darzustellen, werden diese auf eine Bildfläche bzw. eine Bildebene abgebildet. Der hierbei verwendete mathematische Abbildungsbegriff bedeutet, daß die Elemente einer Menge A eindeutig den Elementen einer Menge B zugeordnet werden, d.h. die Punkte im Raum werden eindeutig den Punkten der Bildfläche bzw. Bildebene zugeordnet. Dabei können die Objekte auch auf eine gekrümmte Bildfläche abgebildet werden. Bild 2.1 zeigt die Abbildung der räumlichen Umgebung auf eine Kugeloberfläche, also auf eine gekrümmte Bildfläche durch Spiegelung am Beispiel der Géode im Parc de la Villette in Paris. Bild 2.1: Kugel als Bildfläche - Géode, Parc de La Villette, Paris, , A. Fainsilber Bild 2.2: Methode des Projizierens: Schattentheater, Samuel van Hoogstraten, 1678 Punktmenge A Figur im Raum Original Punktmenge B Figur in der Bildfläche bzw. Bildebene Bild Bei der Abbildung der dreidimensionalen Objekte auf eine zweidimensionale Bildfläche bzw. Bildebene geht eine Dimension verloren. Es entstehen zweidimensionale Bilder dreidimensionaler Gegenstände. In den häufigsten Fällen beschränken wir uns auf die Abbildung der räumlichen Objekte auf eine Bildebene. Dabei benutzen wir die Methode des Projizierens, die der Projektion eines Gegenstandes auf eine Leinwand mit Hilfe einer Lichtquelle nachempfunden ist. Die Methode des Projizierens wird am Beispiel eines Schattentheaters deutlich, bei dem kleine Figuren mit Hilfe von Rampenlichtern an die Wand projiziert werden (Bild 2.2). Die projizierten Figuren stellen die Theaterszenen dar. Solche Schattenspiele waren in Frankreich besonders im 19. Jahrhundert beliebt. Die Projektion wird in zwei Varianten verwendet. C. Leopold, Geometrische Grundlagen der Architekturdarstellung, DOI / _2, Vieweg+Teubner Verlag Springer Fachmedien Wiesbaden GmbH
2 2.1.1 Zentralprojektion Bei der ersten Variante der Methode des Projizierens wird von einem Projektionszentrum O ( O π ) aus durch jeden Punkt P des räumlichen Objekts ein Projektionsstrahl OP gezogen und sein Durchstoßpunkt P' mit der Bildebene π ermittelt. Bild 2.3: Methode der Zentralprojektion Der Punkt P' ist das Bild von P, auch Riß genannt. Jedem Punkt P, außer dem Projektionszentrum O, wird genau ein Punkt P' in der Bildebene π zugeordnet. Die Abbildung ist also für alle Punkte P O eine eindeutige Abbildung. Diese Abbildung heißt Zentralprojektion, das entstandene Bild heißt Zentralriß oder Perspektive. Abbildungsmethode Objekt Bild des Objektes = Zentralriß / Perspektive Zentralprojektion Dieses Abbildungsverfahren ist dem natürlichen Sehvorgang so weit wie möglich nachgebildet. Dürer hat dieses Verfahren in Form einer Versuchsanordnung in einem Holzschnitt (Bild 2.4) dargestellt. Eine Zeichnung von 1583 (Bild 2.5) erläutert diese Versuchsanordnung. Die Öse in der Wand (G) stellt das Projektionszentrum dar. Der gespannte Faden zwischen der Öse in der Wand und einem Punkt des abzubildenden Objekts (L) steht für den Projektionsstrahl. Der Durchstoßpunkt (N) des Fadens mit der Bildebene wird mit Hilfe eines Fadenkreuzes festgehalten. Die Bildebene ist festgelegt durch den Rahmen und eine klappbare Zeichenebene. Nach dem Entfernen des gespannten Fadens kann die Zeichenebene in den Rahmen geklappt und der erhaltene Durchstoßpunkt mit Hilfe des Fadenkreuzes auf die Zeichenebene übertragen werden. Das Objekt wird dann punktweise in der Bildebene ermittelt. 30
3 Bis zur Erfindung der Fotografie war dieser Perspektiv-Zeichentisch weit verbreitet. Er kann das Abbildungsverfahren der Zentralprojektion anschaulich vor Augen führen. Bei der Abbildung werden Geraden im Raum auf Geraden in der Bildebene abgebildet. Die Abbildungsmethode der Zentralprojektion auf eine Bildebene ist geradentreu. Dadurch wird eine gewisse "Ähnlichkeit" zwischen Original und Bild erreicht. Dies ist bei der Abbildung auf eine Kugeloberfläche wie in Bild 2.1 nicht der Fall. Geraden erscheinen dort in der Bildfläche als gekrümmte Linien. Daher kommt nur in Sonderfällen eine Abbildung auf eine gekrümmte Bildfläche zur Anwendung. Bei einer Panorama-Perspektive wird zum Beispiel der Raum auf eine zylindrische Bildfläche abgebildet. Als Zentralriß bzw. Perspektive kann der Schatten eines Gegenstandes bei künstlicher Beleuchtung mit einer nahezu punktförmigen Lichtquelle interpretiert werden. Bild 2.4: Veranschaulichung der Methode durch A. Dürer (1525) Bild 2.5: Erläuterungszeichnung zum Visiervorgang (1583) Die Lichtquelle ist dabei das Projektionszentrum. Der Lichtstrahl kann als Projektionsstrahl gedeutet werden (Bild 2.6). Bild 2.6: Schatten bei Zentralbeleuchtung 31
4 Eine Fotografie eines Objektes (Bild 2.7) kann ebenfalls als Zentralriß gedeutet werden. Die Bildebene ist die lichtempfindliche Oberfläche des Films, das Projektionszentrum ein Punkt im Objektiv. Bild 2.7: Fotografie Die Zentralprojektion ist ein vereinfachtes Modell des Sehvorgangs und des Fotografierens. Daher kann die Zentralprojektion anschauliche, aber wenig maßgerechte Bilder liefern Parallelprojektion Die Methode des Projizierens wird in der zweiten Variante so verändert, daß das Projektionszentrum "ins Unendliche" rückt. Die Projektionsstrahlen gehen dann nicht durch ein Projektionszentrum, sondern sind alle untereinander parallel. Die Richtung der Projektionsstrahlen bestimmt das entstehende Bild (Bild 2.8). Diese Abbildung heißt Parallelprojektion, das entstandene Bild Parallelriß. Die Parallelprojektion ist wie die Zentralprojektion eine eindeutige, geradentreue Abbildung. Die Abbildungsmethode entspricht nicht dem Sehvorgang. Die Parallelprojektion liefert daher Bilder, die nicht immer sehr anschaulich sind. Dafür können die Maßverhältnisse der räumlichen Objekte aus den Bildern leichter abgelesen werden. Bild 2.8: Parallelriß eines Hauses 32
5 Ein Modell für dieses Abbildungsverfahren kann darin gesehen werden, daß die Sonne als Projektionszentrum gedeutet wird. Da die Sonne sehr weit entfernt ist, werden die Lichtstrahlen als parallel angenommen. Daher kann der Schatten eines Gegenstandes auf die Standebene bei natürlicher Beleuchtung (Sonne) als Parallelriß gedeutet werden (Bild 2.9). Bild 2.9: Schatten bei Parallelbeleuchtung Zu unterscheiden sind: 1. Schiefe (allgemeine) Parallelprojektion (0 < α < 90 ) Die Projektionsstrahlen treffen schief auf die Bildebene auf (Bild 2.10). Und der Sonderfall: 2. Normalprojektion (senkrechte Parallelprojektion) Die Projektionsstrahlen treffen senkrecht auf die Bildebene auf (Bild 2.11). Das entstandene Bild heißt Normalriß. Bild 2.10: Schiefe Parallelprojektion Bild 2.11: Senkrechte Parallelprojektion Bei der Normalprojektion kann eine Aussage darüber getroffen werden, wie eine Strecke bei der Abbildung verzerrt wird. Eine Strecke kann im Normalriß nicht länger sein als im Original. Das Bild jeder Strecke wird verkürzt. Wenn die Strecke jedoch parallel zur Bildebene ist, dann bleibt sie unverzerrt. Es ist bei Normalprojektion sogar eine einfache Aussage über den Verkürzungsfaktor möglich (vgl. Bild 2.12): AB = cosα 0 AB AB AB Das Verzerrungsverhältnis der Länge der Bildstrecke A'B' zur Originalstrecke AB ist gleich dem Kosinus ihres Neigungswinkels gegen die Bildebene (Bild 2.12). Bei schiefer Parallelprojektion ist eine solche Aussage nicht möglich. 33
6 Aus einem Normalriß lassen sich am leichtesten die wahren Größen von Strekken und Winkeln des Originals ermitteln. Die Normalprojektion ist daher zur Herstellung technischer Zeichnungen, die Grundlage für die Umsetzung eines geplanten Projektes in die Realität sind, am besten geeignet. Die Handwerker können aus den Normalrissen die wahren Abmessungen des Objektes rekonstruieren. Die Normalrisse besitzen aber im allgemeinen eine geringe Anschaulichkeit. Bild 2.12: Verzerrungsverhältnis einer Strecke bei Normalprojektion 2.2 Invarianten der Abbildungen Für das Verstehen der Bilder von räumlichen Objekten ist es wichtig zu wissen, wie sich die Bilder im Vergleich zum Original durch die Abbildung verändert haben bzw. was unverändert geblieben ist. Diese Informationen können dann zum Konstruieren der Bilder der räumlichen Objekte eingesetzt werden. Geometrische Größen, Eigenschaften oder Begriffe, die bei einer Abbildung unverändert bleiben, heißen die Invarianten der Abbildung. Diese Invarianten kennzeichnen die jeweilige Abbildungsmethode. Daher werden im folgenden die Invarianten der Parallel- und Zentralprojektion untersucht Invarianten der Parallelprojektion Bei der Parallelprojektion bleiben einige Eigenschaften und geometrische Größen der abzubildenden Objekte erhalten. Sind zwei Geraden im Raum zueinander parallel, so sind diese im Bild auch wieder parallel zueinander. Die Parallelität von Geraden bleibt somit bei Parallelprojektion erhalten, d.h. die Parallelprojektion ist eine parallelentreue Abbildung (Bild 2.13). Diese Eigenschaft ist beim Konstruieren von Parallelrissen besonders hilfreich. Bild 2.13: Parallelentreue 34
7 Bild 2.14 zeigt drei gleich lange Strecken AB, BC und CD, die auf einer Geraden liegen. Die Länge der Strecken verändert sich zwar im Bild, aber die drei Bildstrekken A p B p, B p C p und C p D p sind wieder gleich lang. Allgemein bedeutet dies, daß das Teilverhältnis bei Parallelprojektion unverändert bleibt. Das heißt z.b., daß der Mittelpunkt einer Strecke auch wieder auf den Mittelpunkt der Bildstrecke abgebildet wird. Die Parallelprojektion ist teilverhältnistreu. AB CD = A p B p C p D p Bild 2.14: Teilverhältnistreue Die wahre Größe bzw. Gestalt von Strekken, Winkeln und ebenen Figuren, welche in Ebenen parallel zur Bildebene liegen, bleibt bei Parallelprojektion erhalten. Bild 2.15 zeigt die Wand eines Hauses, die parallel zur Bildebene π liegt. Bild 2.15: Erhalt der wahren Größe Liegt eine senkrechte Parallelprojektion (Normalprojektion) vor, so kommt noch eine weitere Invariante hinzu. Es ist bei Normalprojektion eine Aussage möglich, wann ein rechter Winkel erhalten bleibt. Liegt ein Schenkel eines rechten Winkels parallel zur Bildebene π (der zweite Schenkel darf nicht in Projektionsrichtung verlaufen), so bildet sich dieser wieder als rechter Winkel ab. In Bild 2.16 wird aus dem räumlichen Rechteck des Hausdaches im Normalriß wieder ein Rechteck, da die Traufe parallel zur Bildebene liegt. Bild 2.16: Erhalt eines rechten Winkels 35
8 2.2.2 Invarianten der Zentralprojektion Eine ebene Figur ist mit ihrer Bildfigur ähnlich, wenn die Figur in einer Ebene parallel zur Bildebene liegt. Ein Winkel wird daher in wahrer Größe abgebildet, wenn beide Schenkel parallel zur Bildebene verlaufen (Bild 2.17). Bild 2.17: Ähnlichkeit ebener Figuren Das Doppelverhältnis von vier auf einer Geraden liegenden Punkten bleibt bei der Abbildung erhalten (Bild 2.18). Die Teilverhältnisse bleiben nicht erhalten. Bild 2.18: Doppelverhältnistreue Das Doppelverhältnis ist der Quotient der beiden Teilverhältnisse. Die Zentralprojektion ist doppelverhältnistreu. AC AD A c C c A c D = c BC BD B c C c B c D c 36
9 Zusammenfassung der Invarianten: Parallelprojektion Zentralprojektion Parallelität von Geraden Parallelität von Geraden nur, wenn die Geraden parallel zur Bildebene sind Teilverhältnistreue Doppelverhältnistreue Wahre Größe und Gestalt von Strekken, Winkeln und ebenen Figuren in Ebenen parallel zur Bildebene bleiben erhalten. Winkel in Ebenen parallel zur Bildebene bleiben erhalten (Ähnlichkeit ebener Figuren, die parallel zur Bildebene liegen). Senkrechte Parallelprojektion: Rechter Winkel bleibt erhalten, falls ein Schenkel parallel zur Bildebene ist. 2.3 Projektive Erweiterung des Anschauungsraumes Indem die Geometrie verwendet wird, um räumliche Objekte der Wirklichkeit zu erfassen und abzubilden, hat sie Bezüge zur empirisch erfaßbaren Welt. Daher liegt der Geometrie hier ein Raumbegriff zugrunde, der durch Idealisierung bzw. Modellbildung aus der Erfahrungswelt abgeleitet wurde. Dieser Raum ist der sogenannte Anschauungsraum. "Anschauung" kennzeichnet den Zugang zu Dingen der Wirklichkeit über die Sinne, insbesondere durch visuelles Erleben. Der Anschauungsraum enthält Punkte, Geraden und Ebenen. Diese werden mit anschaulichen Vorstellungen verknüpft, die aus der Erfahrungswelt abgeleitet und idealisiert wurden. Im Gegensatz dazu werden in der axiomatischen Geometrie, wie sie von David Hilbert begründet wurde und heute in der geometrischen Forschung zugrundegelegt wird, Punkte, Geraden, Ebenen und Beziehungen zwischen diesen Elementen ohne inhaltliche Bedeutungen eingeführt. In der anwendungsorientierten Geometrie, wie sie hier gebraucht wird, sind den geometrischen Elementen aus der Anschauung abgeleitete inhaltliche Bedeutungen zugeordnet. Räumliche Objekte des Anschauungsraumes werden mit Hilfe der Zentral- oder Parallelprojektion auf eine Bildebene abgebildet. 37
10 Diese beiden Abbildungsmethoden unterscheiden sich nur dadurch, daß sich einmal die Projektionsstrahlen in einem Punkt schneiden, sie im anderen Fall parallel zueinander sind. Durch das Einführen von Fernelementen lassen sich viele Probleme, die sich auf den Sonderfall paralleler Geraden beziehen, leichter lösen. Der Anschauungsraum wird durch das Hinzufügen von Fernelementen, Fernpunkten und Ferngeraden, projektiv erweitert. Parallele Geraden (verschiedene) haben genau einen Fernpunkt gemeinsam. Sie schneiden sich in einem Fernpunkt. Parallele Ebenen (verschiedene) haben genau eine Ferngerade gemeinsam. Sie schneiden sich in der Ferngeraden. Jede Gerade besitzt genau einen Fernpunkt, der auch als Richtung der Geraden gedeutet werden kann. Die Ferngerade einer Ebene ist die Menge der Fernpunkte der Geraden dieser Ebene. Nach dieser projektiven Erweiterung können wir die Parallelprojektion als Zentralprojektion deuten, bei der das Projektionszentrum ein Fernpunkt ist. Im projektiv erweiterten Anschauungsraum haben zwei verschiedene Ebenen genau eine Gerade gemeinsam und zwei verschiedene Geraden in einer Ebene genau einen Punkt gemeinsam. Die projektive Erweiterung des Anschauungsraumes führt zu einer sinnvollen Raumkonstruktion, da dann z.b. allen Bildpunkten jeweils auch ein Urbildpunkt zugeordnet werden kann. Werden zwei parallele Geraden g 1 und g 2 (in Bild 2.19 Beispiel einer Straße) mittels Zentralprojektion abgebildet, so sind diese im Bild (g 1 c und g 2 c ) im allgemeinen nicht parallel, sondern schneiden einander im Punkt F c. Es stellt sich die Frage, was der Urbildpunkt von diesem Punkt F c ist. Mit Hilfe der eingeführten Fernelemente kann der Punkt F c (Fluchtpunkt) als Bildpunkt des Fernpunktes der Geraden g 1 und g 2 verstanden werden. Bild 2.19: Fluchtpunkt F c als Bildpunkt des Fernpunktes zweier paralleler Geraden 38
11 2.4 Abbildungsmethoden zur Rekonstruktion des räumlichen Objektes aus der Zeichnung Die Zentral- und Parallelprojektion sind zwar eindeutige Abbildungen, da jedem Raumpunkt genau ein Punkt auf der Bildebene zugeordnet wird, aber keine umkehrbar eindeutigen, da alle Punkte auf dem Projektionsstrahl denselben Bildpunkt besitzen. Jeder Punkt der Bildebene ist das Bild von unendlich vielen Raumpunkten. Wenn jedoch das Raumobjekt aufgrund der Zeichnung rekonstruiert werden soll, ist eine umkehrbar eindeutige Abbildung nötig. Das Objekt soll durch die Zeichnung eindeutig festgelegt werden, und die Zeichnung soll nicht unendlich viele Interpretationen zulassen. Daher müssen Methoden gefunden werden, um eine umkehrbar eindeutige Abbildung zu erreichen. Die drei wichtigsten Methoden hierzu sind bei der Parallelprojektion: die kotierte Projektion, die Zweitafelprojektion und die Axonometrie. Bild 2.20 zeigt ein Wohnhaus von R. Cavadini im Foto und in Zweitafelprojektion. Bild 2.20: Räumliches Objekt und Zeichnung (Zweitafelprojektion) am Beispiel des Wohnhauses Calzascia- Vairora, Gerra Piano, Tessin, , Raffaele Cavadini Kotierte Projektion Die Kotierte Projektion wird in der Praxis nur bei der senkrechten Parallelprojektion (Normalprojektion) angewandt. Das Objekt wird auf eine horizontale Bildebene projiziert. Sie heißt deshalb auch senkrechte Eintafelprojektion. Es wird dabei an jeden Bildpunkt die auf dem Projektionsstrahl in der vorgegebenen Maßeinheit (L.E.=Längeneinheit) gemessene Entfernung des Originalpunktes von der Bildebene als Kote (von frz. 'à coté de' = 'neben') geschrieben. Bild 2.21: Kotierte Projektion 39
12 Die kotierte Projektion wird vorwiegend für Geländedarstellungen (Bild 2.23) verwendet. Eine topografische Karte stellt das Ergebnis einer kotierten Projektion dar. In Form eines Lageplans ist das vorhandene Gelände Ausgangspunkt für alle Planungen und Entwürfe. Ein zweiter Anwendungsbereich der kotierten Projektion sind Dachausmittlungen. Hier werden die Schnittgeraden von verschiedenen Dachebenen wie in Bild 2.22 ermittelt. Bild 2.22: Dachausmittlung Bild 2.23: Geländedarstellung durch Höhenlinien Zugeordnete Normalrisse (Zweitafel- bzw. Dreitafelprojektion) Das räumliche Objekt wird bei der Zweibzw. Dreitafelprojektion auf zwei bzw. drei zueinander senkrecht stehende Bildebenen senkrecht projiziert (Bild 2.24). Zur leichteren Handhabung und Orientierung kann ein räumliches Koordinatensystem eingeführt werden. Hierfür wird i.a. ein räumliches kartesisches Rechtskoordinatensystem gewählt. Bild 2.24: Dreitafelprojektion 40
13 Dieses kartesische Rechtskoordinatensystem ist durch folgende Eigenschaften gekennzeichnet: - Die drei Koordinatenachsen x, y und z stehen paarweise senkrecht aufeinander. - Auf allen drei Koordinatenachsen wird die gleiche Längeneinheit gewählt. Dadurch entsteht der sogenannte Einheitswürfel. - Die Reihenfolge und Orientierung der drei Koordinatenachsen wird in einem Rechtskoordinatensystem so gewählt, daß die positive x-achse mit der positiven y-achse und die positive y-achse mit der positiven z-achse durch eine Drehung um 90 im Uhrzeigersinn zur Deckung gebracht werden kann, wenn das Koordinatensystem in Richtung der positiven z-achse bzw. positiven x-achse betrachtet wird. Das Rechtssystem kann auch mit Hilfe der "Drei-Finger-Regel" gekennzeichnet werden (Bild 2.26). Bild 2.25: Kartesisches Rechtskoordinatensystem Bild 2.26: "Drei-Finger-Regel" des Rechtssystems Es gelingt stets mit der rechten Hand mit dem Daumen in Richtung der positiven x- Achse, dem Zeigefinger in Richtung der positiven y-achse und dem Mittelfinger in Richtung der positiven z-achse zu zeigen. Nach der Einführung eines räumlichen kartesischen Rechtskoordinatensystems ergibt sich: die xy-ebene ist die Grundrißebene π 1, die yz-ebene ist die Aufrißebene π 2, die xz-ebene ist die Kreuzrißebene π 3. Der Koordinatenursprung O und die Punkte P, P', P", P''' bestimmen einen Quader, den Koordinatenquader. Bild 2.27: Koordinatenquader 41
14 Ist ein Punkt P (x o, y o, z o ) im Raum gegeben, so gilt: Grundriß P' von P hat die Koordinaten (x o, y o, 0) Aufriß P" von P hat die Koordinaten (0, y o, z o ) Kreuzriß P"' von P hat die Koordinaten (x o, 0, z o ) Damit ist ersichtlich, daß jeder Raumpunkt durch zwei seiner Normalrisse (Grund-, Auf- oder Kreuzriß) eindeutig bestimmt ist. Um zeichnen zu können, werden die Rißebenen um eine Rißachse in eine Ebene, die Zeichenebene, geklappt (Bild 2.28). Man spricht dann von Normalrissen in zugeordneter Lage oder kurz von zugeordneten Normalrissen. Bild 2.28: Klappen der Rißebenen in die Zeichenebene Bild 2.29: Zugeordnete Normalrisse Die Koordinatenachse, um die geklappt wird (die Schnittgerade je zweier Rißebenen), heißt Rißachse und wird mit (12) bei π 1 π 2, (13) bei π 1 π 3 und (23) bei π 2 π 3 bezeichnet. Aus dieser Vorgehensweise folgt, daß zwei zugeordnete Normalrisse eines Punktes P auf einer Geraden senkrecht zur Rißachse, auf einem Ordner, liegen. Der Grundriß P' und der Aufriß P" des Raumpunktes P in Bild 2.29 liegen z.b. auf einem Ordner senkrecht zur Rißachse (12). Zwei zugeordnete Normalrisse (Grund- und Aufriß, Auf- und Kreuzriß oder Grundund Kreuzriß) können ein räumliches Objekt umkehrbar eindeutig festlegen. Daher verwendet man in der Zweitafelprojektion zwei zugeordnete Normalrisse des räumlichen Objektes, meistens Grund- und Aufriß. 42
15 Zum schnelleren Erfassen des räumlichen Objektes können auch Drei- und Mehrtafelprojektionen sinnvoll sein. Dazu werden die in Bild 2.28 gezeigten Bildebenen zu einem Quader ergänzt und das Objekt durch Normalprojektionen auf die Innenflächen des Quaders abgebildet. Zur Herstellung der zugeordneten Normalrisse kann dann der Quader abgewickelt werden. In Europa ist diese Methode nach DIN ISO : , Projektionsmethode 1 wie in Bild 2.30 üblich. In Amerika wird nach DIN ISO : , Projektionsmethode 3 vorgegangen. Nach der Projektionsmethode 3 stellt man sich den Quader durchsichtig vor ("glass box") und zeichnet die Ansichten auf den Außenflächen der "glass box" nach. Eine Abwicklung der "glass box" führt dann zur Anordnung wie in Bild Bild 2.30: Europäische Anordnung - Projektionsmethode 1 Bild 2.31: Amerikanische Anordnung - Projektionsmethode 3 43
16 Der Begriff 'Grundriß' wird in Darstellender Geometrie und in Architekturzeichnungen unterschiedlich verwendet. In der Darstellenden Geometrie versteht man unter Grundriß stets die 'Sicht von oben', während in Bauzeichnungen nach DIN : unter Grundriß folgendes verstanden wird: Grundriß Typ A: Der Grundriß ist die Draufsicht auf den unteren Teil eines horizontal geschnittenen Bauobjekts. Grundriß Typ B: Der Grundriß kann auch die gespiegelte Untersicht unter den oberen Teil eines horizontal geschnittenen Bauobjektes sein (Verwendung in der Tragwerksplanung). Bild 2.32: Grundrißtyp A nach DIN Bild 2.33: Grundrißtyp B nach DIN Die Sicht von oben, die in Bauzeichnungen als 'Draufsicht' oder 'Dachaufsicht' bezeichnet wird, heißt in der Darstellenden Geometrie Grundriß. Die Methode der Zweitafelprojektion findet Verwendung, um Werkpläne herzustellen, da die Maße leicht aus den Bildern rekonstruiert werden können. Auch zum Ausführen geometrischer Konstruktionen des Raumes in der Zeichenebene, z.b. Ermitteln der Schnittgeraden zweier Dachebenen, ist diese Methode am besten geeignet (vgl. Kapitel 5.4.4). Bild 2.34: Grundriß in Darstellender Geometrie 44
17 2.4.3 Axonometrie Die Axonometrie wird in Verbindung mit allgemeiner oder senkrechter Parallelprojektion angewandt. Dabei wird zusammen mit dem abzubildenden Objekt ein räumliches kartesisches Rechtskoordinatensystem, auf welches die Originalpunkte bezogen sind, auf die Bildebene projiziert. Es entstehen eher anschauliche Bilder, die aber im Unterschied zur Perspektive stärker die Eigenschaften des räumlichen Objektes erhalten, da die Parallelprojektion mehr Invarianten aufweist als die Zentralprojektion (vgl. Kapitel 13). Das Bild des räumlichen Koordinatensystems wird bei einer Axonometrie mit Einheiten vorgegeben (Bild 2.36). Ist ein Objekt auf das räumliche Koordinatensystem bezogen (Bild 2.35), so kann das axonometrische Bild des Objektes gezeichnet werden (s. Kapitel 4). Bild 2.35: Grund- und Aufriß eines Hauses Bild 2.36: Axonometrisches Bild des Hauses Rekonstruktion bei der Zentralprojektion Meistens wird die Zentralprojektion verwendet, um die Objekte anschaulich darzustellen. Zur Rekonstruktion des Objektes dienen dann der vorhandene Grund- und Aufriß des Objektes. Doch für einige Zwecke ist es auch nützlich, das Objekt aus einer Perspektive rekonstruieren zu können: z.b.: - Herstellung von Landkarten aus Luftaufnahmen - Rekonstruktion eines Bauwerkes aus Fotos (Bauaufnahme) - Fotomontage aus Bestand und Entwurf Die Zentralprojektion ist wie die Parallelprojektion keine umkehrbar eindeutige Abbildung. Die umkehrbare Eindeutigkeit kann nur durch Zusatzinformationen erreicht werden (vgl. Kapitel 13.8). 45
18 2.5 Navigation im dreidimensionalen Computermodell Auch wenn man mit einem dreidimensionalen CAD-Programm (Computer Aided Design) arbeitet, in das räumliche Objekte dreidimensional eingegeben werden, sind Verfahren erforderlich, die eine Navigation im dreidimensionalen Computermodell ermöglichen, da die üblichen Ein- und Ausgabemedien wie Maus, Bildschirm und Drucker nur zweidimensional sind. Dazu werden die hier vorgestellten Abbildungsmethoden verwendet. Der Bildschirm kann in den meisten CAD-Programmen in mehrere Fenster unterteilt werden, die unterschiedliche Bilder des räumlichen Objekts zeigen. Die umkehrbare Eindeutigkeit der Zweitafelprojektion ermöglicht eine Navigation im Raum mit Hilfe von zwei Fenstern, in denen Grund- und Aufriß des Objektes dargestellt werden. Im dritten Fenster wird dann häufig eine Axonometrie oder eine Perspektive gewählt, die es erleichtert, sich im räumlichen Objekt zurechtzufinden. Bild 2.37: "Drei-Fenster-Verfahren" in einem CAD-Programm (Beispiel AutoCAD ). Dadurch wird eine permanente Kontrolle mit Hilfe einer anschaulichen Visualisierung des entworfenen bzw. bearbeiteten räumlichen Objektes ermöglicht. In allen drei Fenstern kann gearbeitet werden. Es kann also immer auf das Fenster zurückgegriffen werden, das für den jeweiligen Arbeitsschritt am geeignetsten ist. Obwohl in einem dreidimensionalen CAD-Programm die Objekte dreidimensional eingegeben werden und dann Bilder mit Hilfe der Abbildungsmethoden Parallel- und Zentralprojektion automatisch erzeugt werden können, ist es sinnvoll, bei der Navigation im Raum mit Hilfe der zweidimensionalen Ein- und Ausgabemedien mit der Zweitafelprojektion zu arbeiten. 46
19
Geometrische Grundlagen der Architekturdarstellung
 Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
Projektion. FG Borrego - TU Berlin Architekturdarstellung und Gestaltung Collaborative Design Laboratory
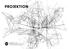 Projektion Unterscheidung nach Lage des Projektionszentrums im Unendlichen im Endlichen Parallelprojektion Zentralprojektion Projektionszentrum Z R R Q Q R P R Z' P Q Q Bildebene P Bildebene P Parallelität
Projektion Unterscheidung nach Lage des Projektionszentrums im Unendlichen im Endlichen Parallelprojektion Zentralprojektion Projektionszentrum Z R R Q Q R P R Z' P Q Q Bildebene P Bildebene P Parallelität
Darstellende Geometrie
 Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
Der Hauptsatz der Axonometrie, Aufbauverfahren
 Axonometrie Der Hauptsatz der Axonometrie, Aufbauverfahren Gegeben seien ein kartesisches Rechtssystem (U, E x, E y, E z ) und eine Bildebene π derart, daÿ bezüglich einer Parallelprojektion p keine Koordinatenebene
Axonometrie Der Hauptsatz der Axonometrie, Aufbauverfahren Gegeben seien ein kartesisches Rechtssystem (U, E x, E y, E z ) und eine Bildebene π derart, daÿ bezüglich einer Parallelprojektion p keine Koordinatenebene
Geometrische Grundlagen der Architekturdarstellung
 Geometrische Grundlagen der Architekturdarstellung von Cornelie Leopold 1. Auflage Springer Vieweg Wiesbaden 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 8348 1838 6 schnell und portofrei
Geometrische Grundlagen der Architekturdarstellung von Cornelie Leopold 1. Auflage Springer Vieweg Wiesbaden 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 8348 1838 6 schnell und portofrei
Geometrische Grundlagen der. Architekturdarstellung
 Cornelie Leopold Geometrische Grundlagen der. Architekturdarstellung 4. Auflage Mit 469 Abbildungen unter Mitwirkung von Andreas Matievits STUDIUM 11 VIEWEG+ TEUBNER INHALTSVERZEICHNIS Vorwort 1 EINFÜHRUNG
Cornelie Leopold Geometrische Grundlagen der. Architekturdarstellung 4. Auflage Mit 469 Abbildungen unter Mitwirkung von Andreas Matievits STUDIUM 11 VIEWEG+ TEUBNER INHALTSVERZEICHNIS Vorwort 1 EINFÜHRUNG
Projektionen:
 Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Parallelprojektion. Das Projektionszentrum liegt im Unendlichen. Projektionsebene. Projektionsrichtung. Quader. Bild des Quaders
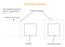 Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Geometrische Grundlagen der Architekturdarstellung
 Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
4^ Springer Vieweg. Geometrische Grundlagen der Architekturdarstellung. Cornelie Leopold. 5V überarbeitete und erweiterte Auflage.
 Cornelie Leopold Geometrische Grundlagen der Architekturdarstellung 5V überarbeitete und erweiterte Auflage Unter Mitwirkung von Andreas Matievits 4^ Springer Vieweg Affinität INHALTSVERZEICHNIS Vorwort
Cornelie Leopold Geometrische Grundlagen der Architekturdarstellung 5V überarbeitete und erweiterte Auflage Unter Mitwirkung von Andreas Matievits 4^ Springer Vieweg Affinität INHALTSVERZEICHNIS Vorwort
Projektionen:
 Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Normalprojektion. Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion.
 4. Der dreidimensionale Raum 4.5 Hauptrisse Normalprojektion Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion. Zum Beispiel:
4. Der dreidimensionale Raum 4.5 Hauptrisse Normalprojektion Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion. Zum Beispiel:
Kapitel 4: Zeichnerische Darstellung von Körpern. Darstellung von Körpern in der Ebene. Ziel bei der Darstellung von räumlichen Figuren (Körpern):
 Kapitel 4: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung von räumlichen Figuren (Körpern):
Kapitel 4: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung von räumlichen Figuren (Körpern):
Modul: Ausgewählte Kapitel der Didaktik der Mathematik
 Modul: Ausgewählte Kapitel der Didaktik der Mathematik Raumgeometrie: Körperdarstellungen, Projektionen Pascal Becker, Alexander Simon 11. Dezember 2014 1 / 16 Inhaltsverzeichnis 1 Rahmenlehrpläne 2 Projektionen
Modul: Ausgewählte Kapitel der Didaktik der Mathematik Raumgeometrie: Körperdarstellungen, Projektionen Pascal Becker, Alexander Simon 11. Dezember 2014 1 / 16 Inhaltsverzeichnis 1 Rahmenlehrpläne 2 Projektionen
Projektionen und Perspektive
 Projektionen und Perspektive 2 Beim räumlichen Zeichnen geht es um das Problem, dreidimensionale Objekte auf einer meist ebenen Zeichenfläche darzustellen. Allgemein wird diese Tätigkeit (bzw. deren Ergebnis)
Projektionen und Perspektive 2 Beim räumlichen Zeichnen geht es um das Problem, dreidimensionale Objekte auf einer meist ebenen Zeichenfläche darzustellen. Allgemein wird diese Tätigkeit (bzw. deren Ergebnis)
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 29. Februar 2016 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Prüfungsfach: Darstellende Geometrie Termin: 29. Februar 2016 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Darstellende Geometrie
 Darstellende Geometrie für Architekten und Bauingenieure Skript und Präsenzübungen WS 2010/11 Institut Computational Mathematics Technische Universität Braunschweig Inhaltsverzeichnis 1 Projektionsarten
Darstellende Geometrie für Architekten und Bauingenieure Skript und Präsenzübungen WS 2010/11 Institut Computational Mathematics Technische Universität Braunschweig Inhaltsverzeichnis 1 Projektionsarten
Ziel bei der Darstellung von räumlichen Figuren (Körpern): Startseite
 Startseite Zentralprojektion 1 Kapitel 3: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung
Startseite Zentralprojektion 1 Kapitel 3: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung
Anschauliche Parallelrisse und Hauptrisse
 Anschauliche Parallelrisse und Hauptrisse Seit frühester Kindheit wirst du im täglichen Leben immer wieder mit Bildern konfrontiert, sei es in Form von Bauanleitungen oder Produktinformationen. Du solltest
Anschauliche Parallelrisse und Hauptrisse Seit frühester Kindheit wirst du im täglichen Leben immer wieder mit Bildern konfrontiert, sei es in Form von Bauanleitungen oder Produktinformationen. Du solltest
KOP1_1_8. Die Schülerinnen und Schüler können normgerechte Zeichnungen lesen.
 Titel Risszeichnen Die Schülerinnen und Schüler können normgerechte Zeichnungen lesen. Relevante(r) Deskriptor(en) Die Schülerinnen und Schüler können Konstruktionsaufgaben mittels geeigneter Abbildungsverfahren
Titel Risszeichnen Die Schülerinnen und Schüler können normgerechte Zeichnungen lesen. Relevante(r) Deskriptor(en) Die Schülerinnen und Schüler können Konstruktionsaufgaben mittels geeigneter Abbildungsverfahren
Einerseits: Zentralperspektive
 VOM RAUM IN DIE EBENE UND ZURÜCK Ebene Figuren wie Dreiecke, Vierecke, andere Vielecke, Kreise lassen sich auf einem Zeichenblatt entweder in wahrer Größe oder unter Beibehaltung ihrer Form! maßstäblich
VOM RAUM IN DIE EBENE UND ZURÜCK Ebene Figuren wie Dreiecke, Vierecke, andere Vielecke, Kreise lassen sich auf einem Zeichenblatt entweder in wahrer Größe oder unter Beibehaltung ihrer Form! maßstäblich
iek Institut für Entwerfen und Konstruieren
 Darstellende Geometrie Institut für Entwerfen und Konstruieren Prof. José Luis Moro Matthias Rottner Heiko Stachel 1 Modul Grundlagen der Darstellung und Konstruktion Termine Grundlagen der Darstellung
Darstellende Geometrie Institut für Entwerfen und Konstruieren Prof. José Luis Moro Matthias Rottner Heiko Stachel 1 Modul Grundlagen der Darstellung und Konstruktion Termine Grundlagen der Darstellung
Geometrische Grundlagen der Architekturdarstellung
 Geometrische Grundlagen der Architekturdarstellung Cornelie Leopold Geometrische Grundlagen der Architekturdarstellung 5., überarbeitete und erweiterte Auflage Unter Mitwirkung von Andreas Matievits Cornelie
Geometrische Grundlagen der Architekturdarstellung Cornelie Leopold Geometrische Grundlagen der Architekturdarstellung 5., überarbeitete und erweiterte Auflage Unter Mitwirkung von Andreas Matievits Cornelie
Wo viel Licht ist, ist starker Schatten.
 Wo viel Licht ist, ist starker Schatten. (Goethe; Götz von Berlichingen) Perspektive & Schatten Die senkrechte Parallelprojektion (Normalperspektive) Aufriss (Vorderansicht Blick von vorne) Seitenriss
Wo viel Licht ist, ist starker Schatten. (Goethe; Götz von Berlichingen) Perspektive & Schatten Die senkrechte Parallelprojektion (Normalperspektive) Aufriss (Vorderansicht Blick von vorne) Seitenriss
KOP1_1_28. Lüftungsschacht
 Titel Relevante(r) Deskriptor(en) Lehrstoff Ausbildungsinhalte Methodisch/Didaktische Hinweise Hilfsmittel Quelle weitere Beispiele Lüftungsschacht Die Schülerinnen und Schüler können normgerechte Zeichnungen
Titel Relevante(r) Deskriptor(en) Lehrstoff Ausbildungsinhalte Methodisch/Didaktische Hinweise Hilfsmittel Quelle weitere Beispiele Lüftungsschacht Die Schülerinnen und Schüler können normgerechte Zeichnungen
Cornelie Leopold. Geometrische Grundlagen der Architekturdarstellung
 Cornelie Leopold Geometrische Grundlagen der Architekturdarstellung Cornelie Leopold Geometrische Grundlagen der Architekturdarstellung 4. Auflage Mit 469 Abbildungen unter Mitwirkung von Andreas Matievits
Cornelie Leopold Geometrische Grundlagen der Architekturdarstellung Cornelie Leopold Geometrische Grundlagen der Architekturdarstellung 4. Auflage Mit 469 Abbildungen unter Mitwirkung von Andreas Matievits
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 2. September 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 9.00 Uhr 10.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Prüfungsfach: Darstellende Geometrie Termin: 2. September 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 9.00 Uhr 10.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Thomae. Perspektive und Axonometrie
 Thomae. Perspektive und Axonometrie Reiner Thomae Perspektive und Axonometrie 7. Auflage Verlag W Kohlhammer Die Deutsche Bibliothek - CIP-Einheitsaufnahme Thomae, Reiner: Perspektive und Axonometrie/Reiner
Thomae. Perspektive und Axonometrie Reiner Thomae Perspektive und Axonometrie 7. Auflage Verlag W Kohlhammer Die Deutsche Bibliothek - CIP-Einheitsaufnahme Thomae, Reiner: Perspektive und Axonometrie/Reiner
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 5. März 2018 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 5. März 2018 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Die Zentralprojektion
 Perspektive Perspektivmodell (S. 1 von 6) / www.kunstbrowser.de Die Zentralprojektion Die Zentralprojektion eines Gegenstandes auf eine ebene Bildfläche ist das Grundprinzip, aus dem sich alle zentralperspektivischen
Perspektive Perspektivmodell (S. 1 von 6) / www.kunstbrowser.de Die Zentralprojektion Die Zentralprojektion eines Gegenstandes auf eine ebene Bildfläche ist das Grundprinzip, aus dem sich alle zentralperspektivischen
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 25. Februar 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.00 Uhr 11.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Prüfungsfach: Darstellende Geometrie Termin: 25. Februar 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.00 Uhr 11.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Geometrie 1. 1.)Geometrische Grundkonstruktionen. Halbierung einer Strecke, Mittelsenkrechte. Teilung einer Strecke. Winkelhalbierung.
 Geometrie 1 1.)Geometrische Grundkonstruktionen Halbierung einer Strecke, Mittelsenkrechte Teilung einer Strecke Winkelhalbierung Thaleskreis Konstruktion von Dreiecken Kongruenzsätze: SSS-Satz, SWS-Satz,
Geometrie 1 1.)Geometrische Grundkonstruktionen Halbierung einer Strecke, Mittelsenkrechte Teilung einer Strecke Winkelhalbierung Thaleskreis Konstruktion von Dreiecken Kongruenzsätze: SSS-Satz, SWS-Satz,
G1.02 In jedes der drei Muster hat sich ein Fehler eingeschlichen. Kennzeichne diesen, indem du den Bereich mit roter Farbe einringelst!
 1 Muster (Teil 1) G1.01 Vervollständige das Muster, sodass der gesamte Raster ausgefüllt ist! Verwende dazu ein Geodreieck und einen gespitzten Bleistift oder einen Druckbleistift mit einer 0,5 mm HB-Mine
1 Muster (Teil 1) G1.01 Vervollständige das Muster, sodass der gesamte Raster ausgefüllt ist! Verwende dazu ein Geodreieck und einen gespitzten Bleistift oder einen Druckbleistift mit einer 0,5 mm HB-Mine
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Termin: 14. September 2012 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten vor Beginn der
Prüfungsfach: Termin: 14. September 2012 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten vor Beginn der
Grundrissebene und Aufrissebene
 Grundrissebene und Aufrissebene x 3 (bzw. z) - Höhe Aufrissebene 2 (bzw. yz-ebene) Rissachse x 12 O x 2 (bzw. y) - Breite Grundrissebene 1 (bzw. xy-ebene) x 1 (bzw. x) - Tiefe Grund- / Aufrissverfahren
Grundrissebene und Aufrissebene x 3 (bzw. z) - Höhe Aufrissebene 2 (bzw. yz-ebene) Rissachse x 12 O x 2 (bzw. y) - Breite Grundrissebene 1 (bzw. xy-ebene) x 1 (bzw. x) - Tiefe Grund- / Aufrissverfahren
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 20. März 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 20. März 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Normalprojektion. Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion.
 4. Der dreidimensionale Raum 4.5 Hauptrisse Normalprojektion Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion. Zum Beispiel:
4. Der dreidimensionale Raum 4.5 Hauptrisse Normalprojektion Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion. Zum Beispiel:
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 31. August 2016 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 31. August 2016 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Termin: 9. September zugel. Hilfsmittel:
 Technische Universität München Lehrstuhl für Holzbau und Baukonstruktion Univ.-Prof. Dr.-Ing. Mike Sieder Univ.-Prof. Dr.-Ing. Stefan Winter Methoden der Darstellung Prüfung Herbst 2011 Name: Matrikelnummer:
Technische Universität München Lehrstuhl für Holzbau und Baukonstruktion Univ.-Prof. Dr.-Ing. Mike Sieder Univ.-Prof. Dr.-Ing. Stefan Winter Methoden der Darstellung Prüfung Herbst 2011 Name: Matrikelnummer:
Zeichnung: Malte Kittelmann AXONOMETRIE
 Zeichnung: Malte Kittelmann 3 AXONOMETRIE Die leichte Überlappung der axonometrischen Grundrisse in der nebenstehenden Abbildung des Reichstagsgebäudes erleichtert das Erkennen, was oben und was unten
Zeichnung: Malte Kittelmann 3 AXONOMETRIE Die leichte Überlappung der axonometrischen Grundrisse in der nebenstehenden Abbildung des Reichstagsgebäudes erleichtert das Erkennen, was oben und was unten
9"+#5(00(),(& 7(8.(5+%(
 !"#$%"&'%()*"+, 9"+#5(00(),(& 7(8.(5+%( -%)&'(*+.%/(0&12+&,"#&34(%5"1(06(+1"*+() Inhaltsverzeichnis Vorwort...5 1. Darstellung im Zweitafelverfahren...7 2. Darstellung des Punktes...9 3. Darstellung der
!"#$%"&'%()*"+, 9"+#5(00(),(& 7(8.(5+%( -%)&'(*+.%/(0&12+&,"#&34(%5"1(06(+1"*+() Inhaltsverzeichnis Vorwort...5 1. Darstellung im Zweitafelverfahren...7 2. Darstellung des Punktes...9 3. Darstellung der
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 30. August 2017 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 30. August 2017 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 25. August 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 16.00 Uhr 17.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 25. August 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 16.00 Uhr 17.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
2.3.1 Rechtshändiges und linkshändiges Koordinatensystem
 2.3. Rechtshändiges und linkshändiges Koordinatensstem Die Koordinatenachsen im dreidimensionalen Raum lassen sich auf wei verschieden Arten anordnen: Linkshändig und Rechtshändig (s. Abbildung 2.9). Um
2.3. Rechtshändiges und linkshändiges Koordinatensstem Die Koordinatenachsen im dreidimensionalen Raum lassen sich auf wei verschieden Arten anordnen: Linkshändig und Rechtshändig (s. Abbildung 2.9). Um
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Methoden der Darstellung Termin: 13. September 2013 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.30 Uhr 11.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
Prüfungsfach: Methoden der Darstellung Termin: 13. September 2013 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.30 Uhr 11.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
Perspektive Vertiefung
 Perspektive Vertiefung Hans-Peter Schröcker Arbeitsbereich Geometrie und CAD, Universität Innsbruck Wintersemester 2007/08 Teil I Einleitung Organisatorisches Perspektive Vertiefung Seminar, 2 Std. Donnerstag,
Perspektive Vertiefung Hans-Peter Schröcker Arbeitsbereich Geometrie und CAD, Universität Innsbruck Wintersemester 2007/08 Teil I Einleitung Organisatorisches Perspektive Vertiefung Seminar, 2 Std. Donnerstag,
Elemente der Zweitafelprojektion
 Teil I Elemente der Zweitafelprojektion 1 Einleitung Darstellende Geometrie: Eindeutige Darstellung der Geometrie des Raumes auf einer Zeichenebene ohne primäre Anschaulichkeit. Eine DG-Zeichnung muss
Teil I Elemente der Zweitafelprojektion 1 Einleitung Darstellende Geometrie: Eindeutige Darstellung der Geometrie des Raumes auf einer Zeichenebene ohne primäre Anschaulichkeit. Eine DG-Zeichnung muss
Kapitel 1. Koordinaten im Raum. 1.1 Schrägbilder - Kavalier-Perspektive Koordinaten
 Kapitel Koordinaten im Raum Schrägbilder - Kavalier-Perspektive Koordinaten Im Raum benötigt man drei Angaben, um die Lage eines Punktes zu beschreiben So beschreiben Geographen durch N5 0"E07 38 7"H5m
Kapitel Koordinaten im Raum Schrägbilder - Kavalier-Perspektive Koordinaten Im Raum benötigt man drei Angaben, um die Lage eines Punktes zu beschreiben So beschreiben Geographen durch N5 0"E07 38 7"H5m
Legt man die vom Betrachter aus gesehen vor den, wird die spätere Konstruktion kleiner als die Risse. Legt man die hinter das Objekt, wird die perspek
 Gegeben ist ein und ein. Der wird auf eine gezeichnet, der unterhalb von dieser in einiger Entfernung und mittig. Parallel zur wird der eingezeichnet. Dieser befindet sich in Augenhöhe. Üblicherweise wird
Gegeben ist ein und ein. Der wird auf eine gezeichnet, der unterhalb von dieser in einiger Entfernung und mittig. Parallel zur wird der eingezeichnet. Dieser befindet sich in Augenhöhe. Üblicherweise wird
Parallelprojektive Schattenbilder von Körpern mit Cabri 3D
 Heinz Schumann Parallelprojektive Schattenbilder von Körpern mit Cabri 3D Vorbereitung: die Parallelprojektion Mit Cabri 3D kann man nicht nur räumliche Abbildungen und ihre Eigenschaften im virtuellen
Heinz Schumann Parallelprojektive Schattenbilder von Körpern mit Cabri 3D Vorbereitung: die Parallelprojektion Mit Cabri 3D kann man nicht nur räumliche Abbildungen und ihre Eigenschaften im virtuellen
Axonometrie. FG Borrego - TU Berlin Architekturdarstellung und Gestaltung Collaborative Design Laboratory
 Axonometrie Rem Koolhaas mit Zoe Zenghelis: Die Stadt des gefangenen Globus, Projekt, New York City, Axonometrische Ansicht von oben, 1972 2 / 35 Parallelprojektion >> Isometrie >> Grundrissaxonometrie
Axonometrie Rem Koolhaas mit Zoe Zenghelis: Die Stadt des gefangenen Globus, Projekt, New York City, Axonometrische Ansicht von oben, 1972 2 / 35 Parallelprojektion >> Isometrie >> Grundrissaxonometrie
AXONOMETRIE. TU Berlin FG Borrego Architekturdarstellung und Gestaltung Collaborative Design Laboratory
 AXONOMETRIE Rem Koolhaas mit Zoe Zenghelis: Die Stadt des gefangenen Globus, Projekt, New York City, Axonometrische Ansicht von oben, 1972 2 / 65 Parallelprojektion >> Isometrie >> Grundrissaxonometrie
AXONOMETRIE Rem Koolhaas mit Zoe Zenghelis: Die Stadt des gefangenen Globus, Projekt, New York City, Axonometrische Ansicht von oben, 1972 2 / 65 Parallelprojektion >> Isometrie >> Grundrissaxonometrie
Termin: 8. September zugel. Hilfsmittel:
 Technische Universität München Lehrstuhl für Holzbau und Baukonstruktion Prof. Dr.-Ing. Stefan Winter Methoden der Darstellung Prüfung Herbst 2010 Name: Matrikelnummer: Prüfungsfach: Methoden der Darstellung
Technische Universität München Lehrstuhl für Holzbau und Baukonstruktion Prof. Dr.-Ing. Stefan Winter Methoden der Darstellung Prüfung Herbst 2010 Name: Matrikelnummer: Prüfungsfach: Methoden der Darstellung
Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen
 Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen Sebastian Kitz, Wuppertal I Zentralprojektion Eine brennende Kerze kann in guter Näherung als punktförmige Lichtquelle
Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen Sebastian Kitz, Wuppertal I Zentralprojektion Eine brennende Kerze kann in guter Näherung als punktförmige Lichtquelle
8.Perspektive (oder Zentralprojektion)
 8.Perspektive (oder Zentralprojektion) In unseren bisherigen Vorlesungen haben wir uns einfachheitshalber mit Parallelprojektionen beschäftigt. Das menschliche Sehen (damit meinen wir immer das Sehen mit
8.Perspektive (oder Zentralprojektion) In unseren bisherigen Vorlesungen haben wir uns einfachheitshalber mit Parallelprojektionen beschäftigt. Das menschliche Sehen (damit meinen wir immer das Sehen mit
Anwendungen der Vektorrechnung in R 3 mit GeoGebra
 Anwendungen der Vektorrechnung in R 3 mit GeoGebra 1. Parallelogramm Die Punkte A = ( 2, 1,0), B = (3, 2,2), C = (5,4,3) sind Eckpunkte eines Parallelogramms. Gesucht ist der fehlende Eckpunkt D sowie
Anwendungen der Vektorrechnung in R 3 mit GeoGebra 1. Parallelogramm Die Punkte A = ( 2, 1,0), B = (3, 2,2), C = (5,4,3) sind Eckpunkte eines Parallelogramms. Gesucht ist der fehlende Eckpunkt D sowie
Technische Darstellung
 Fakultät Maschinenwesen Institut für Festkörpermechanik Professur für Getriebelehre Prof. Dr. rer. nat. habil. Dr. h. c. Karl-Heinz Modler Bearbeiter: Dr.-Ing. Kerstin Becker Telefon: +49 351 463-32732
Fakultät Maschinenwesen Institut für Festkörpermechanik Professur für Getriebelehre Prof. Dr. rer. nat. habil. Dr. h. c. Karl-Heinz Modler Bearbeiter: Dr.-Ing. Kerstin Becker Telefon: +49 351 463-32732
14 MATHEMATISCHE GRUNDLAGEN DER COMPUTERGEOMETRIE. x y
 4 MATHEMATISCHE GRUNDLAGEN DER COMPUTERGEOMETRIE 4 Projektionen 4. Parallelprojektion (a) Senkrechte Projektion auf eine Koordinatenebene Wir wählen als Projektionsebene die Ebene, d. h. in den Beeichnungen
4 MATHEMATISCHE GRUNDLAGEN DER COMPUTERGEOMETRIE 4 Projektionen 4. Parallelprojektion (a) Senkrechte Projektion auf eine Koordinatenebene Wir wählen als Projektionsebene die Ebene, d. h. in den Beeichnungen
Wir gehen aus vom euklidischen Anschauungsraum bzw. von der euklidischen Zeichenebene. Parallele Geraden schneiden einander nicht.
 2 Ein wenig projektive Geometrie 2.1 Fernpunkte 2.1.1 Projektive Einführung von Fernpunkten Wir gehen aus vom euklidischen Anschauungsraum bzw. von der euklidischen Zeichenebene. Parallele Geraden schneiden
2 Ein wenig projektive Geometrie 2.1 Fernpunkte 2.1.1 Projektive Einführung von Fernpunkten Wir gehen aus vom euklidischen Anschauungsraum bzw. von der euklidischen Zeichenebene. Parallele Geraden schneiden
3.1.1 Anes Koordinatensystem im Raum
 3 Einführung von Koordinaten 3. Ane Koordinaten 3.. Anes Koordinatensystem im Raum Tafelskizze Im dreidimensionalen euklidischen Anschauungsraum E 3 wählen wir einen Punkt O, den Koordinatenursprung und
3 Einführung von Koordinaten 3. Ane Koordinaten 3.. Anes Koordinatensystem im Raum Tafelskizze Im dreidimensionalen euklidischen Anschauungsraum E 3 wählen wir einen Punkt O, den Koordinatenursprung und
7) Normale Axonometrie
 7) In der 7.Klasse haben wir (allgemeine) axonometrische Risse technischer Objekte hergestellt; dabei haben wir die Eigenschaften von Parallelrissen ausgenützt. Nun wollen wir axonometrische Angaben so
7) In der 7.Klasse haben wir (allgemeine) axonometrische Risse technischer Objekte hergestellt; dabei haben wir die Eigenschaften von Parallelrissen ausgenützt. Nun wollen wir axonometrische Angaben so
Numerische Punktselektion und Koordinaten
 Einführung Bei der Erstellung einer Zeichnung oder dem Generieren eines Modelles sind die Geometrieobjekte i. Allg. durch ihre Proportionen und gegenseitige Lage numerisch definiert. PICTURES by PC untersützt
Einführung Bei der Erstellung einer Zeichnung oder dem Generieren eines Modelles sind die Geometrieobjekte i. Allg. durch ihre Proportionen und gegenseitige Lage numerisch definiert. PICTURES by PC untersützt
Götter in Heißluftballonen Foto und Kameraposition
 Götter in Heißluftballonen Foto und Kameraposition Franz Gruber, Wien Kurzfassung: Bildausschnitte ebenflächiger, maßbekannter Objekte lassen im Gegensatz zu ihren Originalfotos keinen eindeutigen Rückschluss
Götter in Heißluftballonen Foto und Kameraposition Franz Gruber, Wien Kurzfassung: Bildausschnitte ebenflächiger, maßbekannter Objekte lassen im Gegensatz zu ihren Originalfotos keinen eindeutigen Rückschluss
Lehrbuch der Konstruktiven Geometrie
 H. Brauner Lehrbuch der Konstruktiven Geometrie Springer-Verlag Wien New York Inhaltsverzeichnis Abbildungsverfahren der Darstellenden Geometrie 1. Elementargeometrische Grundlagen 1.1. Grundbegriffe 12
H. Brauner Lehrbuch der Konstruktiven Geometrie Springer-Verlag Wien New York Inhaltsverzeichnis Abbildungsverfahren der Darstellenden Geometrie 1. Elementargeometrische Grundlagen 1.1. Grundbegriffe 12
Geometrische Objekte im 3-dimensionalen affinen Raum oder,... wie nützlich ist ein zugehöriger Vektorraum der Verschiebungen
 Geometrische Objekte im -dimensionalen affinen Raum Bekanntlich versteht man unter geometrischen Objekten Punktmengen, auf die man die üblichen Mengenoperationen wie z.b.: Schnittmenge bilden: - aussagenlogisch:
Geometrische Objekte im -dimensionalen affinen Raum Bekanntlich versteht man unter geometrischen Objekten Punktmengen, auf die man die üblichen Mengenoperationen wie z.b.: Schnittmenge bilden: - aussagenlogisch:
Darstellung dreidimensionaler Figuren in der Ebene. Schrägbild
 Mathematik Bl Darstellung dreidimensionaler Figuren in der Ebene Schrägbild Das Bild bei einer schrägen Parallelprojektion heisst Schrägbild und wird durch folgende Merkmale bestimmt: - Zur Zeichenebene
Mathematik Bl Darstellung dreidimensionaler Figuren in der Ebene Schrägbild Das Bild bei einer schrägen Parallelprojektion heisst Schrägbild und wird durch folgende Merkmale bestimmt: - Zur Zeichenebene
1) ie Linien der abgebildeten Bauteile entsprechen den Linienarten nach DIN EN ISO
 1) ie Linien der abgebildeten Bauteile entsprechen den Linienarten nach DIN EN ISO 128-24. Ordnen Sie den gekennzeichneten Linien die korrekten Linienarten zu! A B C D F G J K Verwenden Sie dazu die in
1) ie Linien der abgebildeten Bauteile entsprechen den Linienarten nach DIN EN ISO 128-24. Ordnen Sie den gekennzeichneten Linien die korrekten Linienarten zu! A B C D F G J K Verwenden Sie dazu die in
Mathematische Grundlagen
 Mathematische Grundlagen Oliver Deussen Mathematische Grundlagen 1 Affine Räume um Zeichenebene bzw. Raum zu beschreiben, muß vorher ein Koordinatensystem festgelegt werden durch geometrische Fragestellungen
Mathematische Grundlagen Oliver Deussen Mathematische Grundlagen 1 Affine Räume um Zeichenebene bzw. Raum zu beschreiben, muß vorher ein Koordinatensystem festgelegt werden durch geometrische Fragestellungen
DARSTELLENDE GEOMETRIE I
 DARSTELLENDE GEOMETRIE I VON DR. RUDOLF BEREIS Professor und Direktor des Instituts für Geometrie an der Technischen Universität Dresden Mit 361 Abbildungen AKADEMIE-VERLAG BERLIN 1964 h. INHALT Hinweise
DARSTELLENDE GEOMETRIE I VON DR. RUDOLF BEREIS Professor und Direktor des Instituts für Geometrie an der Technischen Universität Dresden Mit 361 Abbildungen AKADEMIE-VERLAG BERLIN 1964 h. INHALT Hinweise
Darstellende Geometrie Themenbereiche für die mündliche Reifeprüfung
 Darstellende Geometrie, Themenbereiche RP, Seite 1 von 5 Darstellende Geometrie Themenbereiche für die mündliche Reifeprüfung 1. Flächen und Körper, die durch Bewegung erzeugt werden Extrusionskörper und
Darstellende Geometrie, Themenbereiche RP, Seite 1 von 5 Darstellende Geometrie Themenbereiche für die mündliche Reifeprüfung 1. Flächen und Körper, die durch Bewegung erzeugt werden Extrusionskörper und
37 II.1. Abbildungen
 37 II.1. Abbildungen "Abbildung" und "Funktion" sind verschiedene Namen für denselben Begriff, der charakterisiert ist durch die Angabe der Definitionsmenge ("Was wird abgebildet?"), der Wertemenge ("Wohin
37 II.1. Abbildungen "Abbildung" und "Funktion" sind verschiedene Namen für denselben Begriff, der charakterisiert ist durch die Angabe der Definitionsmenge ("Was wird abgebildet?"), der Wertemenge ("Wohin
7.6. Prüfungsaufgaben zu Normalenformen
 7.6. Prüfungsaufgaben zu Normalenformen Aufgabe () Gegeben sind die Gerade g: x a + r u mit r R und die Ebene E: ( x p ) n. a) Welche geometrische Bedeutung haben die Vektoren a und u bzw. p und n? Veranschaulichen
7.6. Prüfungsaufgaben zu Normalenformen Aufgabe () Gegeben sind die Gerade g: x a + r u mit r R und die Ebene E: ( x p ) n. a) Welche geometrische Bedeutung haben die Vektoren a und u bzw. p und n? Veranschaulichen
Konstruktion einiger kartenverwandter Darstellungen mit Standard-DTP-Programmen
 Konstruktion einiger kartenverwandter Darstellungen mit Standard-DTP-Programmen HANS KERN, GUIDO LOHAUS UND EVELYN SCHMID Ziele Im Vergleich zu Karten betonen kartenverwandte Darstellungen die Anschaulichkeit
Konstruktion einiger kartenverwandter Darstellungen mit Standard-DTP-Programmen HANS KERN, GUIDO LOHAUS UND EVELYN SCHMID Ziele Im Vergleich zu Karten betonen kartenverwandte Darstellungen die Anschaulichkeit
Zentral- und parallelprojektive Darstellungen in Cabri 3D
 Heinz Schumann Zentral- und parallelprojektive Darstellungen in Cabri 3D 1. Einleitung Cabri 3D repräsentiert nicht nur geometrisches Wissen über raumgeometrische Objekte und ihre Generierung, sondern
Heinz Schumann Zentral- und parallelprojektive Darstellungen in Cabri 3D 1. Einleitung Cabri 3D repräsentiert nicht nur geometrisches Wissen über raumgeometrische Objekte und ihre Generierung, sondern
Hintergrund Geschichte - Grundbegriffe Vom Wesen der Geometrie
 Einführung in die Geometrie SS 2007 Prof.Dr.R.Deissler Einführung Literatur Titelblatt Hintergrund Geschichte - Grundbegriffe Vom Wesen der Geometrie Empirische Wissenschaft Erfahrungswissenschaft wie
Einführung in die Geometrie SS 2007 Prof.Dr.R.Deissler Einführung Literatur Titelblatt Hintergrund Geschichte - Grundbegriffe Vom Wesen der Geometrie Empirische Wissenschaft Erfahrungswissenschaft wie
Darstellende Geometrie Übungen. Tutorial. Übungsblatt: Perspektive Rekonstruktion - FSI
 Darstellende Geometrie Übungen Institut für 0Irchitektur und IIIedien Tutorial Übungsblatt: Perspektive Rekonstruktion - FSI Gegeben sind ein Foto ( mit lotrechter Bildebene ) von einem quaderförmigen
Darstellende Geometrie Übungen Institut für 0Irchitektur und IIIedien Tutorial Übungsblatt: Perspektive Rekonstruktion - FSI Gegeben sind ein Foto ( mit lotrechter Bildebene ) von einem quaderförmigen
SRP DG am BG und BRG Wieselburg 2015/16, Seite 1 von 14, Name: Schriftliche Reifeprüfung Darstellende Geometrie
 SRP DG am BG und BRG Wieselburg 2015/16, Seite 1 von 14, Name: Allgemeines Schriftliche Reifeprüfung Darstellende Geometrie BG und BRG Wieselburg, Haupttermin 2015/16 Klasse 8BD Realgymnasium mit Darstellender
SRP DG am BG und BRG Wieselburg 2015/16, Seite 1 von 14, Name: Allgemeines Schriftliche Reifeprüfung Darstellende Geometrie BG und BRG Wieselburg, Haupttermin 2015/16 Klasse 8BD Realgymnasium mit Darstellender
5A. Von der Perspektive zu den projektiven Ebenen.
 5A. Von der Perspektive zu den projektiven Ebenen. Neben der Euklidischen Geometrie, wie sie im Buch von Euklid niedergelegt und wie wir sie im vorigen Abschnitt behandelt haben, gibt es noch weitere Geometrien.
5A. Von der Perspektive zu den projektiven Ebenen. Neben der Euklidischen Geometrie, wie sie im Buch von Euklid niedergelegt und wie wir sie im vorigen Abschnitt behandelt haben, gibt es noch weitere Geometrien.
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Methoden der Darstellung Termin: 7. März 2013 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 11.30 Uhr 12.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Methoden der Darstellung Termin: 7. März 2013 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 11.30 Uhr 12.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Geometrische Anmerkungen zu den Gedankenstrichen in documenta_landschaft_kunst Hannover
 Geometrische Anmerkungen zu den Gedankenstrichen in documenta_landschaft_kunst Hannover Albert Schmid-Kirsch Die vor kurzem vorgelegte Konzeptstudie zu einer dokumenta-landschaft-kunst in Hannover durch
Geometrische Anmerkungen zu den Gedankenstrichen in documenta_landschaft_kunst Hannover Albert Schmid-Kirsch Die vor kurzem vorgelegte Konzeptstudie zu einer dokumenta-landschaft-kunst in Hannover durch
8.Kreisdarstellung in Perspektive
 8.Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel oder Hyperbel.
8.Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel oder Hyperbel.
3 Darstellungsmethoden
 3 Darstellungsmethoden 3.1 Allgemeines Zur Erstellung technischer Zeichnungen bedient man sich unterschiedlicher Darstellungsmethoden, die nach DIN ISO 5456-2 mit Projektionsmethode 1, Projektionsmethode
3 Darstellungsmethoden 3.1 Allgemeines Zur Erstellung technischer Zeichnungen bedient man sich unterschiedlicher Darstellungsmethoden, die nach DIN ISO 5456-2 mit Projektionsmethode 1, Projektionsmethode
Wir gehen aus von euklidischen Anschauungsraum bzw. von der euklidischen Zeichenebene. Parallele Geraden schneiden einander nicht.
 2 Ein wenig projektive Geometrie 2.1 Fernpunkte 2.1.1 Projektive Einführung von Fernpunkten Wir gehen aus von euklidischen Anschauungsraum bzw. von der euklidischen Zeichenebene. Parallele Geraden schneiden
2 Ein wenig projektive Geometrie 2.1 Fernpunkte 2.1.1 Projektive Einführung von Fernpunkten Wir gehen aus von euklidischen Anschauungsraum bzw. von der euklidischen Zeichenebene. Parallele Geraden schneiden
Axonometrie. 11 Axonometrien. Grundrissaxonometrie x : y : z = 1 : 1 : 1
 11 n Grundrissaonometrie : : = 1 : 1 : 1 Übersicht "... sstematisch abgewandelt, wird eine Einelfrage in Form möglichst vieler Variationen vorgetragen. Der Betrachter sieht sich in die Position eines Voeurs
11 n Grundrissaonometrie : : = 1 : 1 : 1 Übersicht "... sstematisch abgewandelt, wird eine Einelfrage in Form möglichst vieler Variationen vorgetragen. Der Betrachter sieht sich in die Position eines Voeurs
Nach Lage der Winkel im Achsenkreuz wird unterschieden zwischen:
 Darstellung In der Zeichnung gibt es verschiedene Möglichkeiten einen Körper darzustellen. Die echte perspektivische Darstellung ist gekennzeichnet, durch einen Fluchtpunkt in dem alle Linien, die in der
Darstellung In der Zeichnung gibt es verschiedene Möglichkeiten einen Körper darzustellen. Die echte perspektivische Darstellung ist gekennzeichnet, durch einen Fluchtpunkt in dem alle Linien, die in der
Grundlagen der optischen Geometrievermessung und deren Anwendungen
 Grundlagen der optischen Geometrievermessung und deren Anwendungen Christian Gerlach Innovationstag 2010 1 Gliederung: Grundlagen der Photogrammetrie Stand der Technik Industrielle Anwendungen der Photogrammetrie
Grundlagen der optischen Geometrievermessung und deren Anwendungen Christian Gerlach Innovationstag 2010 1 Gliederung: Grundlagen der Photogrammetrie Stand der Technik Industrielle Anwendungen der Photogrammetrie
Haupttermin 2012/13 Prüfer: Mag. Helgrid Müller
 Schriftliche Reifeprüfung aus Darstellender Geometrie Haupttermin 2012/13 Prüfer: Erzeuge am Laufwerk H einen Ordner mit dem Namen: Mein Nachname _DG_Matura Speichere alle folgenden Beispiele dorthin ab.
Schriftliche Reifeprüfung aus Darstellender Geometrie Haupttermin 2012/13 Prüfer: Erzeuge am Laufwerk H einen Ordner mit dem Namen: Mein Nachname _DG_Matura Speichere alle folgenden Beispiele dorthin ab.
Einleitung 2. 1 Koordinatensysteme 2. 2 Lineare Abbildungen 4. 3 Literaturverzeichnis 7
 Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
DG für Kunstpädagogik
 DG für Kunstpädagogik Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel
DG für Kunstpädagogik Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel
Angewandte Geometrie Semestralprüfung am 5. Juli 2005, Uhr
 Technische Universität München SS 2005 Zentrum Mathematik Blatt 7 apl. Prof. Dr. J. Hartl Angewandte Geometrie Semestralprüfung am 5. Juli 2005, 12.00-1.0 Uhr 1. In einem dreidimensionalen euklidischen
Technische Universität München SS 2005 Zentrum Mathematik Blatt 7 apl. Prof. Dr. J. Hartl Angewandte Geometrie Semestralprüfung am 5. Juli 2005, 12.00-1.0 Uhr 1. In einem dreidimensionalen euklidischen
Hans Walser. Raumgeometrie. Modul 1 Der Würfel
 Hans Walser Raumgeometrie Modul Der Würfel Hans Walser: Modul, Der Würfel ii Inhalt Zeichnen von Würfeln.... Würfel im Karonetz..... Der 2---Würfel.....2 Der 5-3-2-Würfel.....3 Autostereogramm... 2.2 Kavalierperspektive
Hans Walser Raumgeometrie Modul Der Würfel Hans Walser: Modul, Der Würfel ii Inhalt Zeichnen von Würfeln.... Würfel im Karonetz..... Der 2---Würfel.....2 Der 5-3-2-Würfel.....3 Autostereogramm... 2.2 Kavalierperspektive
18.7 Übungen Übungen 341
 18.7 Übungen 341 18.7 Übungen 18.1 Skizzieren Sie die dargestellten Körper (freihand) in Vorder-, Seiten- und Draufsicht. Wenn Sie Schwierigkeiten mit der räumlichen Vorstellung haben, bauen Sie die Körper
18.7 Übungen 341 18.7 Übungen 18.1 Skizzieren Sie die dargestellten Körper (freihand) in Vorder-, Seiten- und Draufsicht. Wenn Sie Schwierigkeiten mit der räumlichen Vorstellung haben, bauen Sie die Körper
3 Die Theorie des Spiegelbuches
 3 Die Theorie des Spiegelbuches 41 3 Die Theorie des Spiegelbuches Fügt man zwei Spiegel unter einem Winkel zusammen, so spricht man von einem Spiegelbuch. Blickt man in diese Spiegelanordnung, so kann
3 Die Theorie des Spiegelbuches 41 3 Die Theorie des Spiegelbuches Fügt man zwei Spiegel unter einem Winkel zusammen, so spricht man von einem Spiegelbuch. Blickt man in diese Spiegelanordnung, so kann
Externistenprüfungen aus Darstellender Geometrie
 Externistenprüfungen aus Darstellender Geometrie Zulassungsprüfung 7.Klasse Zulassungsprüfung 8. Klasse Wahlpflichtfach Reifeprüfung Juni 2008 Seite 1 von 5 Zulassungsprüfung 7. Klasse Die Prüfung teilt
Externistenprüfungen aus Darstellender Geometrie Zulassungsprüfung 7.Klasse Zulassungsprüfung 8. Klasse Wahlpflichtfach Reifeprüfung Juni 2008 Seite 1 von 5 Zulassungsprüfung 7. Klasse Die Prüfung teilt
6.4.3 Frontalperspektive
 102 KAPITEL 6. ZENTRALPRJEKTIN 6.4.3 Frontalperspektive Wir wollen den Grundriss des in Abb. 6.26 in Frontalperspektive dargestellten U-förmigen Gebäudes bestimmen. Dabei nehmen wir wieder an, dass das
102 KAPITEL 6. ZENTRALPRJEKTIN 6.4.3 Frontalperspektive Wir wollen den Grundriss des in Abb. 6.26 in Frontalperspektive dargestellten U-förmigen Gebäudes bestimmen. Dabei nehmen wir wieder an, dass das
Schrägbilder zeichnen
 Was sind Schrägbilder und welchen Zweck haben sie? Durch ein Schrägbild wird auf einer ebenen Fläche (z.b. Blatt Papier) ein Körper räumlich dargestellt (räumliche Perspektive des Körpers). Es gibt sehr
Was sind Schrägbilder und welchen Zweck haben sie? Durch ein Schrägbild wird auf einer ebenen Fläche (z.b. Blatt Papier) ein Körper räumlich dargestellt (räumliche Perspektive des Körpers). Es gibt sehr
