Vorlesung 13. Die Frequenzkennlinien / Frequenzgang
|
|
|
- Elmar Simen
- vor 7 Jahren
- Abrufe
Transkript
1 Vorlesung 3 Die Frequenzkennlinien / Frequenzgang Frequenzkennlinien geben das Antwortverhalten eines linearen Systems auf eine harmonische (sinusförmige) Anregung in Verstärkung (Amplitude) und Phasenverschiebung (Phase) an. Beispiel in Winfact: PT-System Sprungantwort
2 Vorlesung 3 Eingangssignal und Ausgangssignal unterscheiden sich voneinander abhängig von der Schwingungsfrequenz. /sec 5 /sec 20 /sec 2
3 Eingangssignal und Ausgangssignal e Vorlesung 3 ( t) = sin( ωt) e a ( t) = ( ω ) sin( ωt + α( ω)) unterscheiden sich voneinander durch Amplitude und Phasenverschiebung. a π/2 π 3π/2 2π Einschwingphase Messphase 3
4 Messung von Amplitudenverhältnis und Phasenverschiebung. Vorlesung 3 A (ω ) α(ω) = a e e a α 4
5 Amplitudenverhältnis Vorlesung 3 Phasenverschiebung A = a e ω= /sec α = =-3 5
6 Amplitudenverhältnis Vorlesung 3 Phasenverschiebung A = a e ω= 5 /sec α =0.9 =-25 6
7 Amplitudenverhältnis Vorlesung 3 Phasenverschiebung A = a e ω= 20 /sec α =0.4 =-66 7
8 Ergebnis aus der Frequenzgangmessung: Vorlesung 3 e ( t) = sin( ωt) e System a ( t) = ( ω ) sin( ωt + α( ω)) a Tabelle Kreisfrequenz Amplitudenverhältnis A Phasenverschiebung α /s -3 5 /s /s
9 Vorlesung 3 Die grafische Darstellung der Frequenzgangmessung erfolgt im Bode-Diagramm über der Kreisfrequenz ω: der Amplitudenwert A = a e die Phasenverschiebung α wird logarithmisch in Dezibel aufgetragen, wird in Grad aufgetragen. d.h. G / db = 20log0 A G / o = α 9
10 Vorlesung 3 Messwerte werden über der Kreisfrequenz aufgetragen Messwerte des Amplitudenverlauf Messwerte des Phasenverlauf 0
11 Und zu einer Linie interpoliert Vorlesung 3 Messwerte des Amplitudenverlauf Messwerte des Phasenverlauf
12 Zusammenhang zwischen Übertragungsfunktion und Frequenzgang Wird in der Übertragungsfunktion G(s) die komplexe Variable S durch die Harmonische Variable iω ersetzt, so ergibt sich der Frequenzgang F(iω) rein rechnerisch, d.h. das Bode-Diagramm des Systems kann auch rechnerisch aus der Übertragungsfunktion bestimmt werden! Der Frequenzgang F(iω) läßt sich zerlegen in Realteil und Imaginärteil F(iω)= Re (F(iω) + i * Im (F(iω)) und mit den Beziehungen für Amplitude und Phase für das Bodediagramm errechnen. Vorlesung 3 2 A = F( iω) = Re ( F( iω)) + Im Im( F( iω)) α( ω) = F ( iω) = arctan Re( F( iω)) 2 ( F( iω)) 2
13 3 Beispiel für PT-Übertragungsfunktion Vorlesung )) ( ( Im )) ( ( Re ) ( T i F i F i F A ω ω ω ω + = + = = ) arctan( )) ( Re( )) ( Im( arctan ) ( ) ( T i F i F i F ω ω ω ω ω α = = = () S T s G * + = ( ) ( ) ( ) ( ) ω ω ω ω ω i T i T i T i T i F * * * * * + = + = ( ) * * * * ω ω ω ω T T i T i F + + = ( ) ( ) 2 2 * Re ω ω T i F + = ( ) ( ) 2 2 * * Im ω ω ω T T i F + =
14 Vorlesung 3 Der Amplitudengang der Frequenzkennlinien kann dann asymptotisch konstruiert werden, indem die Verstärkung in Dezibel und die Eckfrequenz mit ω E =/T eingetragen wird und die Steigungen ein Vielfaches von +-20dB/ ω-dekade konstruiert wird. Beispiel: 0.5 PT G s = () + 0.sec* S Steigung - 20dB/Dek ω E =/T=0 /s 4
15 Vorlesung 3 Der Phasengang der Frequenzkennlinien kann asymptotisch konstruiert werden, indem eine Dekade vor/hinter der Eckfrequenz mit ω E =/T ein Knick mit der Steigungen ein Vielfaches von +-45 / ω-dekade konstruiert wird. Beispiel: PT G () s 0.5 = + 0.sec* S Steigung /Dek ω E =/T=0 /s 5
16 Vorlesung 3 Vergleich angenähert, berechnet und gemessen PT-Frequenzgang Messwerte des Amplitudenverlauf Messwerte des Phasenverlauf ω E =/T=0 /s 6
17 Übersicht Regelkreisglieder Vorlesung 3 PT Kp G( S) = Kp( ) + TS ω E =/T Steigung - 20dB/Dek ω E =/T Steigung /Dek 7
18 Übersicht Regelkreisglieder Vorlesung 3 PT2 Kp Steigung - 40dB/Dek G ( S) = + 2 Kp DT S + T 2 S 2 ω E =/T ω E =/T Steigung /Dek 8
19 Übersicht Regelkreisglieder Vorlesung 3 I Steigung - 20dB/Dek G ( S) = K S I ω E =K i Steigung 0 /Dek Constant
20 Übersicht Regelkreisglieder Vorlesung 3 D GStrecke ( S) = T D S Steigung + 20dB/Dek ω E =/T D Steigung 0 /Dek Constant
21 Übersicht Regelkreisglieder Vorlesung 3 PD Kp G Strecke ( S) = Kp( + TS) ω E =/T Steigung + 20dB/Dek Steigung 45 /Dek 2
22 Anmerkungen: Vorlesung 3 Amplituden- und Phasenverläufe können wegen des logarithmischen Massstab im Bodediagramm addiert werden, so dass eine Konstruktion von Hand möglich ist. Für Glieder. Ordnung zeigt der tatsächliche Amplitudengang an der Stelle /T (Eckfrequenz) eine Abweichung von 3 db. Für Glieder 2. Ordnung zeigt der tatsächliche Amplitudengang an der Stelle /T (Eckfrequenz) eine von der Dämpfung D abhängige Abweichung (s. Literatur). Bei kleiner Dämpfung (D<) kommt es beim PT2-Glied dort zur sog. Resonanzüberhöhung, d.h. bei Anregung mít der Eckfrequenz tritt Resonanz auf. 22
23 Vorlesung 3 Stabilität nach dem Nyquist-Kriterium im Bode-Diagramm Wenn ein nicht rückgekoppeltes Regelsystem bei einer bestimmten Anregungsfrequenz die Verstärkung.0, aber eine Phasenverschiebung von -80 Grad aufweist, so könnte sich im Falle der Rückkopplung eine ebensolche Sinusfrequenz selbständig aufrechterhalten, es wäre instabil. Der Punkt mit der Amplitude und Phasenverschiebung -80 lässt sich im Bodediagramm gut ermitteln. Er stellt den Grenzwert des stabilen Betriebs eines Regelkreises dar. Im Fall kleinerer Amplitudenwerte bei einer Phasenverschiebung von -80 ist Stabilität gegeben. Bei größeren Amplitudenwerten herrscht Instabilität. Der Frequenzwert gibt lediglich die Frequenz der instabilen Schwingung ω kritisch an. 23
24 Vorlesung 3 Zustand der stabilen Dauerschwingung im Regelkreis d U Startauslenkung WINFACT 24
25 Vorlesung 3 Wieso schwingt das? Blick auf A(ω) und α (ω) der Strecke: bei ω krit ist A=0.2 =-2.7dB und α= -80 Dummerweise hat der Regler eine Verstärkung von 5.0, so dass die Gesamtverstärkung.0 ist. Und die -80 verschobene Sinuswelle wird in der Rückführung wieder umgedreht! =>selbstaufrechterhaltene Dauerschwingung WINFACT 25
26 Vorlesung 3 Frequenzgang der Strecke: -2,6dB -80-2,6dB => K ps =0-0,63 =
27 Vorlesung 3 Man definiert die Durchtrittskreisfrequenz ω D als die Frequenz, bei der der offene Kreis genau die Verstärkung.0 hat; nach Nyquist muss hier die Phasennacheilung kleiner als 80 Grad sein für Stabilität. A(ω) Durchtrittskreisfrequenz ϖ D 0 Verstärkung.0 α (ω) stabil, wenn α< -80Grad
28 Vorlesung 3 Den Abstand der Phasennacheilung bei ω D von -80 nennt man Phasenreserve A(ω) Verstärkung.0 Phasenreserve α R α R Phasenreserve α (ω) 28
29 Vorlesung 3 Reglerentwurfskriterien im Frequenzgang: Meist wird eine Phasenreserve von α R =60 gefordert, was einem geringen Überschwingen in der Zeitantwort entspricht. Die Dämpfung zwischen D= entspricht einem Überschwingen von 5% - 25% und zeigt im Frequenzgang eine Phasenreserve von Im Bereich um die Durchtrittskreisfrequenz sollte der Amplitudengang wie ein Integralglied um -20db/Dek fallen. Die Durchtrittskreisfrequenz ϖ D kann durch Anheben und Absenken des Amplitudengang beeinflußt werden und bestimmt die Eigenschwingungsfrequenz des späteren Regelkreises. Die Übergangszeit Tg der Regelkreissprungantwort hängt näherungsweise reziprok mit der Durchtrittskreisfrequenz zusammen: Tg ~.4/ϖ D 29
30 Vorlesung 3 Reglerentwurf im Frequenzgang, Beispiel: Aufgabenstellung: Gegeben ist eine Regelstrecke aus drei PT-Gliedern mit der Zeitkonstante 0.2 sec und der Verstärkung.3. 30
31 Vorlesung 3 Reglerentwurf im Frequenzgang, Beispiel: Aufgabenstellung: Gegeben ist eine Regelstrecke aus drei PT-Gliedern mit der Zeitkonstante 0.2 sec und der Verstärkung.3. Sie soll mit einem PID-Regler geregelt werden, wobei eine Phasenreserve von α R =60 bei einer Durchtrittskreisfrequenz von ϖ D =5 /s gefordert wird. α R ω D 3
32 Reglerentwurf im Frequenzgang, Beispiel: Aufgabenstellung: Vorlesung 3 Suchen Sie die passende Einstellung für die Reglerparameter Kpr, Tn und Tv, wobei die Verzögerung des D-Anteil bei 0. Tv liegen soll! Einstellung? 32
33 Vorlesung 3 Beispiel: Vorgehensweise Struktur zur Messung des Frequenzgang aufbauen Rückkopplung rauslassen Regler auf P-Stellen mit K PR =, im FRQ-Messblock die Streckenordnung einstellen, Frequenzgang plotten 2 bei ϖ D =5 /s die Phasenreserve α R messen 3 im PID-Regler I-Anteil einschalten, T N so einstellen, dass Beule aus dem Amplitudenverlauf und im Bereich ω D der Verlauf -20dB fällt (FRQ) 4 im PID Regler T V einstellen, Faustregel: T V ~/ω D und T verz ~0.*T V Werte variieren, bis α R annähernd passt (immer wieder FRQ messen) 5 Abschliessend K p so einstellen, dass bei ω D der Amplitudenwert = 0dB 33
34 Vorlesung 3 Beispiel: Struktur zur Messung des Frequenzgang aufbauen, Rückkopplung rauslassen, Regler auf P-Stellen mit K PR =, im FRQ-Messblock die Streckenordnung einstellen, Frequenzgang plotten WINFACT 34
35 Vorlesung 3 Beispiel: 2 bei ϖ D =5 /s die Phasenreserve α R messen 35
36 Vorlesung 3 Beispiel: 3 im PID-Regler I-Anteil einschalten, T N so einstellen, dass Beule aus dem Amplitudenverlauf und im Bereich ω D der Verlauf -20dB fällt (FRQ) 36
37 Vorlesung 3 Beispiel: 4 im PID Regler T V einstellen, Faustregel: T V ~/ω D und T verz ~0.*T V Werte variieren, bis α R annähernd passt (immer wieder FRQ messen) 37
38 Vorlesung 3 Beispiel: 5 Abschliessend K p so einstellen, dass bei ω D der Amplitudenwert = 0dB 38
39 Vorlesung 3 Beispiel: Ergebnis Regelkreis schliessen 39
40 Vorlesung 3 Beispiel: Ergebnis FRQ-Block auf STEP RESPONSE und simulieren 40
41 Vorlesung 3 Konstruktion von Frequenzkennlinien im Bode-Diagramm Ausgangspunkt ist die Übertragungsfunktion Es gibt nur wenige Konstruktionsmodule (P,PT, PT2, PD, PD2, I, D) Die Übertragungsfunktion wird in die Konstruktionsmodule zerlegt; die Gesamtverstärkung wird in das P-Glied gelegt, die anderen Elemente haben die Verstärkung Im logarithmischen Massstab können die Amplitudenverläufe ebenso wie die Phasenverläufe addiert werden 4
42 Vorlesung 3 Kombination von Übertragungsfunktionselementen zum Frequenzgang. P-System PT P G( S) = 0.5 ( + 2S)( + S + S = S = P PT + 2*0.5*S + S PT 2 2 ) 2 ω E =/2 ω E =/ PT2 PT PT2 P bis
43 Vorlesung 3 Kombination von Übertragungsfunktionselementen zum Frequenzgang 2. I-System G( S) = 0.2 ( + 5S) S = S S = P PT I ω E =/5 PT I P PT P -40 I
44 Vorlesung 3 Kombination von Übertragungsfunktionselementen zum Frequenzgang 3. PI-Regler 40 G( S) = 2 = 4 = P 2 ( + 4S) PD + 4S 4S S I ω E =/4 I PD P 80 PD 40 P 0-40 I
45 Vorlesung 3 D Übung: Reglerentwurf im Frequenzgang Der gegebene Frequenzgang des offenen Regelkreises soll die Phasenreserve α R =50 haben.. Ermitteln Sie die Durchtrittsfrequenz ϖ D und die dafür notwendige Amplitudenanhebung A? 2. Rechnen Sie die Anhebung A in die Reglerverstärkung Kpr umr! 3. Wie groß ist dann die Anregelzeit des Regelkreis? 45
46 Vorlesung 3 Übung: Frequenzgang PI/PT-System 40 D + 2S G( S) = 2S = ( PI Re gler) 0.5 * + 0.3S ( PT Strecke)
47 47 Ergebnis: Vorlesung 3 S S S S S S Strecke PT gler PI S S S S G 0.3 ) 2 ( ) 2 ( ) ( ) Re ( * 2 2 ) ( + + = + + = = + + =
G S. p = = 1 T. =5 K R,db K R
 TFH Berlin Regelungstechnik Seite von 0 Aufgabe 2: Gegeben: G R p =5 p 32ms p 32 ms G S p = p 250 ms p 8 ms. Gesucht ist das Bodediagramm von G S, G R und des offenen Regelkreises. 2. Bestimmen Sie Durchtrittsfrequenz
TFH Berlin Regelungstechnik Seite von 0 Aufgabe 2: Gegeben: G R p =5 p 32ms p 32 ms G S p = p 250 ms p 8 ms. Gesucht ist das Bodediagramm von G S, G R und des offenen Regelkreises. 2. Bestimmen Sie Durchtrittsfrequenz
MAS Automation Management
 MAS Automation Management Modul: A-NLE Winterthur, 27.1./ 3.2.217 Ruprecht Altenburger, altb@zhaw.ch Lineare Regelung an einem einfachen Beispiel erstellt für das Frühlingssemester 215; Version vom 12.
MAS Automation Management Modul: A-NLE Winterthur, 27.1./ 3.2.217 Ruprecht Altenburger, altb@zhaw.ch Lineare Regelung an einem einfachen Beispiel erstellt für das Frühlingssemester 215; Version vom 12.
1 Gegenkopplung und Stabilität S107
 Regelungstechnik - Formelsammlung (Revision : 044 - powered by LATEX) Seite von 6 Gegenkopplung und Stabilität S07. LTI-Grundglieder Typ Symbol Gleichung, Dgl Sprungantwort Frequenzgang, Betrag und Argument
Regelungstechnik - Formelsammlung (Revision : 044 - powered by LATEX) Seite von 6 Gegenkopplung und Stabilität S07. LTI-Grundglieder Typ Symbol Gleichung, Dgl Sprungantwort Frequenzgang, Betrag und Argument
Labor RT Versuch RT1-1. Versuchsvorbereitung. Prof. Dr.-Ing. Gernot Freitag. FB: EuI, FH Darmstadt. Darmstadt, den
 Labor RT Versuch RT- Versuchsvorbereitung FB: EuI, Darmstadt, den 4.4.5 Elektrotechnik und Informationstechnik Rev., 4.4.5 Zu 4.Versuchvorbereitung 4. a.) Zeichnen des Bode-Diagramms und der Ortskurve
Labor RT Versuch RT- Versuchsvorbereitung FB: EuI, Darmstadt, den 4.4.5 Elektrotechnik und Informationstechnik Rev., 4.4.5 Zu 4.Versuchvorbereitung 4. a.) Zeichnen des Bode-Diagramms und der Ortskurve
3. Beschreibung dynamischer Systeme im Frequenzbereich
 3. Laplace-Transformation 3. Frequenzgang 3.3 Übertragungsfunktion Quelle: K.-D. Tieste, O.Romberg: Keine Panik vor Regelungstechnik!.Auflage, Vieweg&Teubner, Campus Friedrichshafen --- Regelungstechnik
3. Laplace-Transformation 3. Frequenzgang 3.3 Übertragungsfunktion Quelle: K.-D. Tieste, O.Romberg: Keine Panik vor Regelungstechnik!.Auflage, Vieweg&Teubner, Campus Friedrichshafen --- Regelungstechnik
Optimierung von Regelkreisen. mit P-, PI und PID Reglern
 mit P-, PI und PID Reglern Sollwert + - Regler System Istwert Infos: Skript Regelungstechnisches Praktikum (Versuch 2) + Literatur Seite 1 Ziegler und Nichols Strecke: Annäherung durch Totzeit- und PT1-Glied
mit P-, PI und PID Reglern Sollwert + - Regler System Istwert Infos: Skript Regelungstechnisches Praktikum (Versuch 2) + Literatur Seite 1 Ziegler und Nichols Strecke: Annäherung durch Totzeit- und PT1-Glied
Nr Prof. Dr. S. Zacher. Stabilitätsprüfung und Regler-Einstellung nach dem Zwei-Bode-Plots-Verfahren
 Automation-Letter Nr. 38 04.03.2018 Prof. Dr. S. Zacher Stabilitätsprüfung und Regler-Einstellung nach dem Zwei-Bode-Plots-Verfahren Die Konstruktion der negativ inversen Ortskurve ist recht unhandlich.
Automation-Letter Nr. 38 04.03.2018 Prof. Dr. S. Zacher Stabilitätsprüfung und Regler-Einstellung nach dem Zwei-Bode-Plots-Verfahren Die Konstruktion der negativ inversen Ortskurve ist recht unhandlich.
Seite 1 NAME VORNAME MATRIKEL-NR. Achtung: Schreiben Sie Ihre Antworten für die Aufgaben 1 bis 2 direkt unter den Fragen in den Fragebogen.
 144 Minuten Seite 1 NAME VORNAME MATRIKEL-NR. Achtung: Schreiben Sie Ihre Antworten für die Aufgaben 1 bis 2 direkt unter den Fragen in den Fragebogen. Aufgabe 1 (je 2 Punkte) a) Definieren Sie die Begriffe
144 Minuten Seite 1 NAME VORNAME MATRIKEL-NR. Achtung: Schreiben Sie Ihre Antworten für die Aufgaben 1 bis 2 direkt unter den Fragen in den Fragebogen. Aufgabe 1 (je 2 Punkte) a) Definieren Sie die Begriffe
G R G S. Vorlesung 11. Xd(s) W(s) Y(s) Reglerentwurfsverfahren. Zur Auswahl von Reglertyp und Reglerparameter. Typ? Parameter?
 Zur Auswahl von Reglertyp und Reglerparameter W(s) - Xd(s) Regler G R trecke G Y(s) Typ? Parameter? 1 1. Typauswahl (P, PI, PD, PID???? ) A) nach Tabellen (Faustformel mit welcher Reglertyp zu welcher
Zur Auswahl von Reglertyp und Reglerparameter W(s) - Xd(s) Regler G R trecke G Y(s) Typ? Parameter? 1 1. Typauswahl (P, PI, PD, PID???? ) A) nach Tabellen (Faustformel mit welcher Reglertyp zu welcher
Bearbeitungszeit: 120 Min
 4 6 Fachgebiet Regelungstechnik Leiter: Prof. Dr.-Ing. Johann Reger Regelungs- und Systemtechnik 1 - Übungsklausur 6 Bearbeitungszeit: 120 Min Modalitäten Es sind keine Hilfsmittel zugelassen. Bitte schreiben
4 6 Fachgebiet Regelungstechnik Leiter: Prof. Dr.-Ing. Johann Reger Regelungs- und Systemtechnik 1 - Übungsklausur 6 Bearbeitungszeit: 120 Min Modalitäten Es sind keine Hilfsmittel zugelassen. Bitte schreiben
Stellen Sie für das im folgenden Signalflussbild dargestellte dynamische System ein Zustandsraummodell K
 Aufgaben Aufgabe : Stellen Sie für das im folgenden Signalflussbild dargestellte dnamische Sstem ein Zustandsraummodell auf. u 2 7 5 Aufgabe 2: Wir betrachten das folgende Regelsstem vierter Ordnung: r
Aufgaben Aufgabe : Stellen Sie für das im folgenden Signalflussbild dargestellte dnamische Sstem ein Zustandsraummodell auf. u 2 7 5 Aufgabe 2: Wir betrachten das folgende Regelsstem vierter Ordnung: r
Bestimmung der Reglerparameter aus den Frequenzkennlinien
 1 Kapitel Bestimmung der Reglerparameter aus den Frequenzkennlinien Mit PSPICE lassen sich die Frequenzgänge der Amplitude und der Phase von Regelkreisen simulieren, graphisch darstellen und mit zwei Cursors
1 Kapitel Bestimmung der Reglerparameter aus den Frequenzkennlinien Mit PSPICE lassen sich die Frequenzgänge der Amplitude und der Phase von Regelkreisen simulieren, graphisch darstellen und mit zwei Cursors
Lösungen zur 7. Übung
 Prof. Dr.-Ing. Jörg Raisch Dipl.-Ing. Vladislav Nenchev M.Sc. Arne Passon Dipl.-Ing. Thomas Seel Fachgebiet Regelungssysteme Fakultät IV Elektrotechnik und Informatik Technische Universität Berlin Integrierte
Prof. Dr.-Ing. Jörg Raisch Dipl.-Ing. Vladislav Nenchev M.Sc. Arne Passon Dipl.-Ing. Thomas Seel Fachgebiet Regelungssysteme Fakultät IV Elektrotechnik und Informatik Technische Universität Berlin Integrierte
Grundlagen der Regelungstechnik
 Grundlagen der Regelungstechnik Dr.-Ing. Georg von Wichert Siemens AG, Corporate Technology, München Termine Dies ist der letzte Termin in diesem Jahr 17.12.2004 fällt aus Nächste Termine: 14.1., 28.1.,
Grundlagen der Regelungstechnik Dr.-Ing. Georg von Wichert Siemens AG, Corporate Technology, München Termine Dies ist der letzte Termin in diesem Jahr 17.12.2004 fällt aus Nächste Termine: 14.1., 28.1.,
Seminarübungen: Dozent: PD Dr. Gunther Reißig Ort: 33/1201 Zeit: Mo Uhr (Beginn )
 Vorlesung : Dozent: Professor Ferdinand Svaricek Ort: 33/040 Zeit: Do 5.00 6.30Uhr Seminarübungen: Dozent: PD Dr. Gunther Reißig Ort: 33/20 Zeit: Mo 5.00 6.30 Uhr (Beginn 8.0.206 Vorlesungsskript: https://www.unibw.de/lrt5/institut/lehre/vorlesung/rt_skript.pdf
Vorlesung : Dozent: Professor Ferdinand Svaricek Ort: 33/040 Zeit: Do 5.00 6.30Uhr Seminarübungen: Dozent: PD Dr. Gunther Reißig Ort: 33/20 Zeit: Mo 5.00 6.30 Uhr (Beginn 8.0.206 Vorlesungsskript: https://www.unibw.de/lrt5/institut/lehre/vorlesung/rt_skript.pdf
Regelsysteme Übung: Reglerentwurf nach Spezifikation im Zeitbereich. Damian Frick. Herbstsemester Institut für Automatik ETH Zürich
 Regelsysteme 6. Übung: Reglerentwurf nach Spezifikation im Zeitbereich Damian Frick Institut für Automatik ETH Zürich Herbstsemester 205 Damian Frick Regelsysteme Herbstsemester 205 6. Übung: Reglerentwurf
Regelsysteme 6. Übung: Reglerentwurf nach Spezifikation im Zeitbereich Damian Frick Institut für Automatik ETH Zürich Herbstsemester 205 Damian Frick Regelsysteme Herbstsemester 205 6. Übung: Reglerentwurf
() 2. K I Aufgabe 5: x(t) W(s) - X(s) G 1 (s) Z 1 (s) Z 2 (s) G 3 (s) G 2 (s) G 4 (s) X(s)
 Seite 1 von 2 Name: Matr. Nr.: Note: Punkte: Aufgabe 1: Ermitteln Sie durch grafische Umwandlung des dargestellten Systems die Übertragungsfunktion X () G s =. Z s 2 () W(s) G 1 (s) G 2 (s) Z 1 (s) G 3
Seite 1 von 2 Name: Matr. Nr.: Note: Punkte: Aufgabe 1: Ermitteln Sie durch grafische Umwandlung des dargestellten Systems die Übertragungsfunktion X () G s =. Z s 2 () W(s) G 1 (s) G 2 (s) Z 1 (s) G 3
BSc PRÜFUNGSBLOCK 2 / D-MAVT VORDIPLOMPRÜFUNG / D-MAVT. Musterlösung
 Institut für Mess- und Regeltechnik BSc PRÜFUNGSBLOCK / D-MAVT.. 005. VORDIPLOMPRÜFUNG / D-MAVT REGELUNGSTECHNIK I Musterlösung Dauer der Prüfung: Anzahl der Aufgaben: Bewertung: Zur Beachtung: Erlaubte
Institut für Mess- und Regeltechnik BSc PRÜFUNGSBLOCK / D-MAVT.. 005. VORDIPLOMPRÜFUNG / D-MAVT REGELUNGSTECHNIK I Musterlösung Dauer der Prüfung: Anzahl der Aufgaben: Bewertung: Zur Beachtung: Erlaubte
Reglerentwurf mit dem Frequenzkennlinienverfahren
 Kapitel 5 Reglerentwurf mit dem Frequenzkennlinienverfahren 5. Synthese von Regelkreisen Für viele Anwendungen genügt es, Standard Regler einzusetzen und deren Parameter nach Einstellregeln zu bestimmen.
Kapitel 5 Reglerentwurf mit dem Frequenzkennlinienverfahren 5. Synthese von Regelkreisen Für viele Anwendungen genügt es, Standard Regler einzusetzen und deren Parameter nach Einstellregeln zu bestimmen.
Prüfung im Modul Grundlagen der Regelungstechnik Studiengänge Medizintechnik / Elektrotechnik
 Brandenburgische Technische Universität Cottbus-Senftenberg Fakultät 1 Professur Systemtheorie Prof. Dr.-Ing. D. Döring Prüfung im Modul Grundlagen der Regelungstechnik Studiengänge Medizintechnik / Elektrotechnik
Brandenburgische Technische Universität Cottbus-Senftenberg Fakultät 1 Professur Systemtheorie Prof. Dr.-Ing. D. Döring Prüfung im Modul Grundlagen der Regelungstechnik Studiengänge Medizintechnik / Elektrotechnik
NANO III - MSR. Steuern Regeln Regelkreis PID-Regler Dimensionierung eines PID Reglers. Themen: Nano III MSR Physics Basel, Michael Steinacher 1
 NANO III - MSR Themen: Steuern Regeln Regelkreis PID-Regler Dimensionierung eines PID Reglers Nano III MSR Physics Basel, Michael Steinacher 1 Ziele 1. Unterschied Steuern Regeln 2. Was ist ein Regelkreis
NANO III - MSR Themen: Steuern Regeln Regelkreis PID-Regler Dimensionierung eines PID Reglers Nano III MSR Physics Basel, Michael Steinacher 1 Ziele 1. Unterschied Steuern Regeln 2. Was ist ein Regelkreis
Skriptum zur 2. Laborübung. Transiente Vorgänge und Frequenzverhalten
 Elektrotechnische Grundlagen (LU 182.692) Skriptum zur 2. Laborübung Transiente Vorgänge und Frequenzverhalten Martin Delvai Wolfgang Huber Andreas Steininger Thomas Handl Bernhard Huber Christof Pitter
Elektrotechnische Grundlagen (LU 182.692) Skriptum zur 2. Laborübung Transiente Vorgänge und Frequenzverhalten Martin Delvai Wolfgang Huber Andreas Steininger Thomas Handl Bernhard Huber Christof Pitter
Regelungs- und Systemtechnik 1 - Übungsklausur 2
 4 6 Fachgebiet Regelungstechnik Leiter: Prof. Dr.-Ing. Johann Reger Bearbeitungszeit: 12 Min Modalitäten Es sind keine Hilfsmittel zugelassen. Bitte schreiben Sie mit dokumentenechtem Schreibgerät (Tinte
4 6 Fachgebiet Regelungstechnik Leiter: Prof. Dr.-Ing. Johann Reger Bearbeitungszeit: 12 Min Modalitäten Es sind keine Hilfsmittel zugelassen. Bitte schreiben Sie mit dokumentenechtem Schreibgerät (Tinte
Gegeben sei folgender Regelkreis mit der Führungsgröße r, der Stellgröße u und der Ausgangsgröße. q r u y. R(s)
 2. Teilklausur WS 17/18 Gruppe A Name: Matr.-Nr.: Aufgabe 1 (6 Punkte) Gegeben sei folgender Regelkreis mit der Führungsgröße r, der Stellgröße u und der Ausgangsgröße y: q r u y V (s) P (s) R(s) Auf den
2. Teilklausur WS 17/18 Gruppe A Name: Matr.-Nr.: Aufgabe 1 (6 Punkte) Gegeben sei folgender Regelkreis mit der Führungsgröße r, der Stellgröße u und der Ausgangsgröße y: q r u y V (s) P (s) R(s) Auf den
Gegeben sei folgender Regelkreis mit der Führungsgröße r, dem Regelfehler e und der Ausgangsgröße y: r e R(s) P (s)
 1. Teilklausur SS 16 Gruppe A Name: Matr.-Nr.: Für beide Aufgaben gilt: Gegeben sei folgender Regelkreis mit der Führungsgröße r, dem Regelfehler e und der Ausgangsgröße y: r e R(s) P (s) y Aufgabe 1 (6
1. Teilklausur SS 16 Gruppe A Name: Matr.-Nr.: Für beide Aufgaben gilt: Gegeben sei folgender Regelkreis mit der Führungsgröße r, dem Regelfehler e und der Ausgangsgröße y: r e R(s) P (s) y Aufgabe 1 (6
Regelungstechnik für Ingenieure
 Manfred Reuter Regelungstechnik für Ingenieure 7., überarbeitete und erweiterte Auflage Mit 322 Bildern Friedr. Vieweg & Sohn Braunschweig/Wiesbaden Inhaltsverzeichnis Formelzeichen 1 Einführung 1 1.1
Manfred Reuter Regelungstechnik für Ingenieure 7., überarbeitete und erweiterte Auflage Mit 322 Bildern Friedr. Vieweg & Sohn Braunschweig/Wiesbaden Inhaltsverzeichnis Formelzeichen 1 Einführung 1 1.1
Ergänzung zur Regelungstechnik
 Ergänzung zur Regelungstechnik mathematische Erfassung Weil die einzelnen Regelkreisglieder beim Signaldurchlauf ein Zeitverhalten haben, muss der Regler den Wert der Regelabweichung verstärken und gleichzeitig
Ergänzung zur Regelungstechnik mathematische Erfassung Weil die einzelnen Regelkreisglieder beim Signaldurchlauf ein Zeitverhalten haben, muss der Regler den Wert der Regelabweichung verstärken und gleichzeitig
Regelungs- und Systemtechnik 1 - Übung 6 Sommer 2016
 4 6 Fachgebiet Regelungstechnik Leiter: Prof. Dr.-Ing. Johann Reger Regelungs- und Systemtechnik - Übung 6 Sommer 26 Vorbereitung Wiederholen Sie Vorlesungs- und Übungsinhalte zu folgenden Themen: Standardregelkreis
4 6 Fachgebiet Regelungstechnik Leiter: Prof. Dr.-Ing. Johann Reger Regelungs- und Systemtechnik - Übung 6 Sommer 26 Vorbereitung Wiederholen Sie Vorlesungs- und Übungsinhalte zu folgenden Themen: Standardregelkreis
INSTITUT FÜR REGELUNGSTECHNIK
 Aufgabe 9: Regler mit schaltendem Stellglied führen auf besonders einfache technische Lösungen. Durch pulsbreitenmoduliertes Schalten mit genügend hoher Frequenz ist auch hier eine angenähert lineare Betriebsweise
Aufgabe 9: Regler mit schaltendem Stellglied führen auf besonders einfache technische Lösungen. Durch pulsbreitenmoduliertes Schalten mit genügend hoher Frequenz ist auch hier eine angenähert lineare Betriebsweise
von der Straßenkoordinate r zur Fahrzeugkoordinate x. Straßenoberfläche Initiale Referenz
 Regelungstechnik Klausur vom 9.2.23 Zoltán Zomotor Versionsstand: 3. Januar 24, 2:59 This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike 3. Germany License. To view a
Regelungstechnik Klausur vom 9.2.23 Zoltán Zomotor Versionsstand: 3. Januar 24, 2:59 This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike 3. Germany License. To view a
Praktikum EE2 Grundlagen der Elektrotechnik. Name: Testat : Einführung
 Fachbereich Elektrotechnik Ortskurven Seite 1 Name: Testat : Einführung 1. Definitionen und Begriffe 1.1 Ortskurven für den Strom I und für den Scheinleistung S Aus den Ortskurven für die Impedanz Z(f)
Fachbereich Elektrotechnik Ortskurven Seite 1 Name: Testat : Einführung 1. Definitionen und Begriffe 1.1 Ortskurven für den Strom I und für den Scheinleistung S Aus den Ortskurven für die Impedanz Z(f)
4. Standardübertragungsglieder
 4. PT-Glied : Verzögerungsglied. Ordnung 4. P-Glied : Proportionalglied 4.3 I-Glied: Integrator 4.4 D-Glied: Differenzierer (ideal/real) 4.5 PT-Glied: Verzögerungsglied. Ordnung 4.6 Totzeitglied Campus
4. PT-Glied : Verzögerungsglied. Ordnung 4. P-Glied : Proportionalglied 4.3 I-Glied: Integrator 4.4 D-Glied: Differenzierer (ideal/real) 4.5 PT-Glied: Verzögerungsglied. Ordnung 4.6 Totzeitglied Campus
Lösungen zur 5. Übung
 Prof. Dr.-Ing. Jörg Raisch Dipl.-Ing. Anne-Kathrin Hess Dipl.-Ing. Thomas Seel Fachgebiet Regelungssysteme Fakultät IV Elektrotechnik und Informatik Technische Universität Berlin Integrierte Lehrveranstaltung
Prof. Dr.-Ing. Jörg Raisch Dipl.-Ing. Anne-Kathrin Hess Dipl.-Ing. Thomas Seel Fachgebiet Regelungssysteme Fakultät IV Elektrotechnik und Informatik Technische Universität Berlin Integrierte Lehrveranstaltung
Regelungstechnik. Zustandsgleichungcen / Übertragungsfunktionen normaler Übertragungsglieder. i c =C du dt. Zustands.- und Ausgangsgleichungen:
 Regelungstechnik Zustandsgleichungcen / Übertragungsfunktionen normaler Übertragungsglieder Energiespeicher: Zustandsgröße: Kondensator Spannung i c C du Zustands.- und Ausgangsgleichungen: Aus den Knoten:
Regelungstechnik Zustandsgleichungcen / Übertragungsfunktionen normaler Übertragungsglieder Energiespeicher: Zustandsgröße: Kondensator Spannung i c C du Zustands.- und Ausgangsgleichungen: Aus den Knoten:
Grundlagen der Regelungstechnik I (Prof. Dr.-Ing. habil. Jörg Grabow Fachgebiet Mechatronik FH Jena
 Grundlagen der Regelungstechnik I (Prof. Dr.-Ing. habil. Jörg Grabow Fachgebiet Mechatronik 1. Einführung in die Regelungstechnik 1.1 Zielsetzung der Regelungstechnik und Begriffsdefinitionen 1.2 Beispiele
Grundlagen der Regelungstechnik I (Prof. Dr.-Ing. habil. Jörg Grabow Fachgebiet Mechatronik 1. Einführung in die Regelungstechnik 1.1 Zielsetzung der Regelungstechnik und Begriffsdefinitionen 1.2 Beispiele
Frequenzganganalyse, Teil 2: P-, I- und D - Glieder
 FELJC Frequenzganganalyse_neu_2.odt 1 Frequenzganganalyse, Teil 2: P-, I- und D - Glieder 2.1 P0-Glieder P0: P-Glied ohne Verzögerung P-Glied nullter Ordnung Aufgabe 2.1: Bestimme den Proportionalbeiwert
FELJC Frequenzganganalyse_neu_2.odt 1 Frequenzganganalyse, Teil 2: P-, I- und D - Glieder 2.1 P0-Glieder P0: P-Glied ohne Verzögerung P-Glied nullter Ordnung Aufgabe 2.1: Bestimme den Proportionalbeiwert
Regelungs- und Systemtechnik 1 - Übung 6 Sommer 2016
 4 6 Fachgebiet Regelungstechnik Leiter: Prof. Dr.-Ing. Johann Reger Regelungs- und Systemtechnik - Übung 6 Sommer 26 Vorbereitung Wiederholen Sie Vorlesungs- und Übungsinhalte zu folgenden Themen: Zeitkonstantenform
4 6 Fachgebiet Regelungstechnik Leiter: Prof. Dr.-Ing. Johann Reger Regelungs- und Systemtechnik - Übung 6 Sommer 26 Vorbereitung Wiederholen Sie Vorlesungs- und Übungsinhalte zu folgenden Themen: Zeitkonstantenform
Regelungstechnik für Ingenieure
 Manfred Reuter Regelungstechnik für Ingenieure 9., überarbeitete und erweiterte Auflage Mit 291 Bildern, 43 Beispiele und 27 Aufgaben vieweg VII Inhaltsverzeichnis Formelzeichen XI 1 Einleitung 1 1.1 Das
Manfred Reuter Regelungstechnik für Ingenieure 9., überarbeitete und erweiterte Auflage Mit 291 Bildern, 43 Beispiele und 27 Aufgaben vieweg VII Inhaltsverzeichnis Formelzeichen XI 1 Einleitung 1 1.1 Das
Elementare Regelungstechnik
 Peter Busch Elementare Regelungstechnik Allgemeingültige Darstellung ohne höhere Mathematik *v Vogel Buchverlag Inhaltsverzeichnis 1 Einführung 13 1.1 Steuern - Regeln 13 1.1.1 Steuern 13 1.1.2 Regeln
Peter Busch Elementare Regelungstechnik Allgemeingültige Darstellung ohne höhere Mathematik *v Vogel Buchverlag Inhaltsverzeichnis 1 Einführung 13 1.1 Steuern - Regeln 13 1.1.1 Steuern 13 1.1.2 Regeln
Elementare Regelungstechnik
 Peter Busch Elementare Regelungstechnik Allgemeingültige Darstellung ohne höhere Mathematik 2., korrigierte Auflage Vogel Buchverlag Inhaltsverzeichnis 1 Einführung 13 1.1 Steuern - Regeln 13 1.1.1 Steuern
Peter Busch Elementare Regelungstechnik Allgemeingültige Darstellung ohne höhere Mathematik 2., korrigierte Auflage Vogel Buchverlag Inhaltsverzeichnis 1 Einführung 13 1.1 Steuern - Regeln 13 1.1.1 Steuern
Regelungstechnik I (WS 13/14) Klausur ( )
 Regelungstechnik I (WS 13/14) Klausur (13.03.2014) Prof. Dr. Ing. habil. Thomas Meurer Lehrstuhl für Regelungstechnik Name: Matrikelnummer: Bitte beachten Sie: a) Diese Klausur enthält 4 Aufgaben auf den
Regelungstechnik I (WS 13/14) Klausur (13.03.2014) Prof. Dr. Ing. habil. Thomas Meurer Lehrstuhl für Regelungstechnik Name: Matrikelnummer: Bitte beachten Sie: a) Diese Klausur enthält 4 Aufgaben auf den
Berechnung, Simulation und Messung des Übertragungsverhaltens einer PT 1 -Strecke und eines Regelkreises aus PT 1 -Strecke und P-Regler.
 Ziel des ersten Versuchs: Berechnung, Simulation und Messung des Übertragungsverhaltens einer PT 1 -Strecke und eines Regelkreises aus PT 1 -Strecke und P-Regler. 1.1 Berechnung, Simulation und Messung
Ziel des ersten Versuchs: Berechnung, Simulation und Messung des Übertragungsverhaltens einer PT 1 -Strecke und eines Regelkreises aus PT 1 -Strecke und P-Regler. 1.1 Berechnung, Simulation und Messung
2. VORDIPLOMPRÜFUNG / D-MAVT Musterlösung. Um die Note 6 zu erlangen, genügen 6 vollständig und richtig gelöste Aufgaben.
 Institut für Mess- und Regeltechnik. VORDIPLOMPRÜFUNG / D-MAVT 8.. 3 REGELUNGSTECHNIK I Musterlösung Dauer der Prüfung: Anzahl der Aufgaben: Bewertung: Zur Beachtung: Erlaubte Hilfsmittel: Minuten 8 (gleich
Institut für Mess- und Regeltechnik. VORDIPLOMPRÜFUNG / D-MAVT 8.. 3 REGELUNGSTECHNIK I Musterlösung Dauer der Prüfung: Anzahl der Aufgaben: Bewertung: Zur Beachtung: Erlaubte Hilfsmittel: Minuten 8 (gleich
b) Stellen Sie die Funktion u(t) = 1(t 1) + 2(t 2) 3(t 3) grafisch dar.
 120 Minuten Seite 1 NAME VORNAME MATRIKEL-NR. Aufgabe 1 (je 2 Punkte) a) Definieren Sie die Begriffe Stellgröße und Führungsgröße. b) Stellen Sie die Funktion u(t) = 1(t 1) + 2(t 2) 3(t 3) grafisch dar.
120 Minuten Seite 1 NAME VORNAME MATRIKEL-NR. Aufgabe 1 (je 2 Punkte) a) Definieren Sie die Begriffe Stellgröße und Führungsgröße. b) Stellen Sie die Funktion u(t) = 1(t 1) + 2(t 2) 3(t 3) grafisch dar.
Praktikum Grundlagen Regelungstechnik
 Praktikum Grundlagen Regelungstechnik Versuch P-GRT 05 Versuchsziel Versuch 5 - Reglerentwurf im Frequenzbereich COM3LAB Veränderung des Streckenfrequenzganges durch einen vorgeschalteten Regler Datum
Praktikum Grundlagen Regelungstechnik Versuch P-GRT 05 Versuchsziel Versuch 5 - Reglerentwurf im Frequenzbereich COM3LAB Veränderung des Streckenfrequenzganges durch einen vorgeschalteten Regler Datum
1 Reglerentwurf nach dem Betragsoptimum
 Reglerentwurf nach dem Betragsoptimum Für einfache d.h. einschleifige, lineare Regelungen mit ausgesprägtem Tiefpassverhalten ist der Entwurf nach dem Betragsoptimum relativ leicht anwendbar. w G K (s)
Reglerentwurf nach dem Betragsoptimum Für einfache d.h. einschleifige, lineare Regelungen mit ausgesprägtem Tiefpassverhalten ist der Entwurf nach dem Betragsoptimum relativ leicht anwendbar. w G K (s)
Frequenzgang und Übergangsfunktion
 Labor Regelungstechnik Frequenzgang und Übergangsfunktion. Einführung In diesem Versuch geht es um: Theoretische und experimentelle Ermittlung der Frequenzgänge verschiedener Übertragungsglieder (Regelstrecke,
Labor Regelungstechnik Frequenzgang und Übergangsfunktion. Einführung In diesem Versuch geht es um: Theoretische und experimentelle Ermittlung der Frequenzgänge verschiedener Übertragungsglieder (Regelstrecke,
Vorlesung 6. Übertragungsfunktion der linearen Regelkreisglieder Textuell: FederPendel. DGL: als Sprungantwort
 Textuell: FederPendel yste FederPendel Dreh- Magnet Feder c Masse l Däpfer d lf ld ollwertgeber Regler Winkelsensor Regelungstechnische Begriffe: PT-Glied it Verstärkung Kp, Däpfung D, Zeitkonstante T
Textuell: FederPendel yste FederPendel Dreh- Magnet Feder c Masse l Däpfer d lf ld ollwertgeber Regler Winkelsensor Regelungstechnische Begriffe: PT-Glied it Verstärkung Kp, Däpfung D, Zeitkonstante T
Systemtheorie. Vorlesung 25: Butterworth-Filter. Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann
 Systemtheorie Vorlesung 5: Butterworth-Filter Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann Übersicht Für den Filterentwurf stehen unterschiedliche Verfahren zur Verfügung Filter mit
Systemtheorie Vorlesung 5: Butterworth-Filter Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann Übersicht Für den Filterentwurf stehen unterschiedliche Verfahren zur Verfügung Filter mit
Die Sprungantwort ist die Reaktion auf den Einheitssprung: G 2 (s) = 2 (s +1)(s +6) 3 (s +7)(s +2)
 Aufgabe 1: Die Laplace-Transformierte der Sprungantwort ist: Y (s) = 1 s + (s +3) 3 (s +4) Die Sprungantwort ist die Reaktion auf den Einheitssprung: w(t) =σ(t) W (s) = 1 s Die Übertragungsfunktion des
Aufgabe 1: Die Laplace-Transformierte der Sprungantwort ist: Y (s) = 1 s + (s +3) 3 (s +4) Die Sprungantwort ist die Reaktion auf den Einheitssprung: w(t) =σ(t) W (s) = 1 s Die Übertragungsfunktion des
Institut für Elektrotechnik und Informationstechnik. Aufgabensammlung zur. Regelungstechnik B. Prof. Dr. techn. F. Gausch Dipl.-Ing. C.
 Institut für Elektrotechnik und Informationstechnik Aufgabensammlung zur Regelungstechnik B Prof. Dr. techn. F. Gausch Dipl.-Ing. C. Balewski 10.03.2011 Übungsaufgaben zur Regelungstechnik B Aufgabe 0
Institut für Elektrotechnik und Informationstechnik Aufgabensammlung zur Regelungstechnik B Prof. Dr. techn. F. Gausch Dipl.-Ing. C. Balewski 10.03.2011 Übungsaufgaben zur Regelungstechnik B Aufgabe 0
Frequenzganganalyse, Teil 3: PT1- und DT1- Glieder
 FELJC Frequenzganganalyse_neu_3.odt 1 Frequenzganganalyse, Teil 3: PT1- und DT1- Glieder 3.1 PT1-Glieder a) Wiederholung: Sprungantwort Beispiel: Ein Regelkreisglied hat bei einem Eingangssprung von 5V
FELJC Frequenzganganalyse_neu_3.odt 1 Frequenzganganalyse, Teil 3: PT1- und DT1- Glieder 3.1 PT1-Glieder a) Wiederholung: Sprungantwort Beispiel: Ein Regelkreisglied hat bei einem Eingangssprung von 5V
Theorie digitaler Systeme
 Theorie digitaler Systeme Vorlesung 2: Fakultät für Elektro- und Informationstechnik, anfred Strohrmann Einführung Frequenzgang zeitkontinuierlicher Systeme beschreibt die Änderung eines Spektrums bei
Theorie digitaler Systeme Vorlesung 2: Fakultät für Elektro- und Informationstechnik, anfred Strohrmann Einführung Frequenzgang zeitkontinuierlicher Systeme beschreibt die Änderung eines Spektrums bei
Elementare Regelungstechnik
 Peter Busch Elementare Regelungstechnik Allgemeingültige Darstellung ohne höhere Mathematik 7., überarbeitete Auflage Vogel Buchverlag Inhaltsverzeichnis Vorwort 5 1 Einführung 13 1.1 Steuern - Regeln
Peter Busch Elementare Regelungstechnik Allgemeingültige Darstellung ohne höhere Mathematik 7., überarbeitete Auflage Vogel Buchverlag Inhaltsverzeichnis Vorwort 5 1 Einführung 13 1.1 Steuern - Regeln
Elementare Regelungstechnik
 2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. Peter Busch Elementare Regelungstechnik Allgemeingültige Darstellung
2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. Peter Busch Elementare Regelungstechnik Allgemeingültige Darstellung
ET-Praktikumsbericht 3. Semester I (Versuch 4, Zeit-/Frequenzverhalten von Vierpolen) Inhaltsverzeichnis 1 Der RC-Tiefpass Messung bei konstante
 Praktikumsbericht Elektrotechnik 3.Semester Versuch 4, Vierpole 7. November Niels-Peter de Witt Matrikelnr. 8391 Helge Janicke Matrikelnr. 83973 1 ET-Praktikumsbericht 3. Semester I (Versuch 4, Zeit-/Frequenzverhalten
Praktikumsbericht Elektrotechnik 3.Semester Versuch 4, Vierpole 7. November Niels-Peter de Witt Matrikelnr. 8391 Helge Janicke Matrikelnr. 83973 1 ET-Praktikumsbericht 3. Semester I (Versuch 4, Zeit-/Frequenzverhalten
Aufgabe 1: Laplace-Transformation
 Aufgabe 1: Laplace-Transformation (25 Punkte) a) Teilaufgabe: 15 Punkte Gegeben sei die folgende Differenzialgleichung dritter Ordnung: mit den Anfangswerten: y (3) (t) + 4 ÿ(t) + ẏ(t) 6 y(t) = 12 u(t)
Aufgabe 1: Laplace-Transformation (25 Punkte) a) Teilaufgabe: 15 Punkte Gegeben sei die folgende Differenzialgleichung dritter Ordnung: mit den Anfangswerten: y (3) (t) + 4 ÿ(t) + ẏ(t) 6 y(t) = 12 u(t)
x 1 + u y 2 = 2 0 x 2 + 4u 2.
 3. Übung: gelkreis Aufgabe 3.. Gegeben sind die beiden linearen zeitkontinuierlichen Systeme 3 ẋ = 6 x + u 6 3 [ ] y = x (3.a) (3.b) und [ ] [ ] 8 ẋ = x + 6 4 [ ] y = x + 4u. u (3.a) (3.b) Berechnen Sie
3. Übung: gelkreis Aufgabe 3.. Gegeben sind die beiden linearen zeitkontinuierlichen Systeme 3 ẋ = 6 x + u 6 3 [ ] y = x (3.a) (3.b) und [ ] [ ] 8 ẋ = x + 6 4 [ ] y = x + 4u. u (3.a) (3.b) Berechnen Sie
x 1 + u y 2 = 2 0 x 2 + 4u 2.
 3. Übung: Regelkreis Aufgabe 3.1. Gegeben sind die beiden linearen zeitkontinuierlichen Systeme 3 2 2 ẋ 1 = 6 5 x 1 + 1 u 1 6 2 3 [ ] y 1 = 2 x 1 (3.1a) (3.1b) und [ ] [ ] 8 15 1 ẋ 2 = x 2 + 6 1 4 [ ]
3. Übung: Regelkreis Aufgabe 3.1. Gegeben sind die beiden linearen zeitkontinuierlichen Systeme 3 2 2 ẋ 1 = 6 5 x 1 + 1 u 1 6 2 3 [ ] y 1 = 2 x 1 (3.1a) (3.1b) und [ ] [ ] 8 15 1 ẋ 2 = x 2 + 6 1 4 [ ]
Grundlagen der Regelungstechnik
 Grundlagen der Regelungstechnik Dr.-Ing. Georg von Wichert Siemens AG, Corporate Technology, München Termine Nächste Termine: 28.., 4.2. Wiederholung vom letzten Mal Regelkreis Geschlossener Regelkreis
Grundlagen der Regelungstechnik Dr.-Ing. Georg von Wichert Siemens AG, Corporate Technology, München Termine Nächste Termine: 28.., 4.2. Wiederholung vom letzten Mal Regelkreis Geschlossener Regelkreis
Praktikum 2.1 Frequenzverhalten
 Elektrizitätslehre 3 Martin Schlup, Martin Weisenhorn. November 208 Praktikum 2. Frequenzverhalten Lernziele Bei diesem Versuch werden die Frequenzabhängigkeiten von elektrischen Grössenverhältnissen aus
Elektrizitätslehre 3 Martin Schlup, Martin Weisenhorn. November 208 Praktikum 2. Frequenzverhalten Lernziele Bei diesem Versuch werden die Frequenzabhängigkeiten von elektrischen Grössenverhältnissen aus
4. Der geschlossene Regelkreis mit P-Strecke und P-Regler
 FELJC 4a_Geschlossener_ Regelkreis_Störverhalten.odt 1 4. Der geschlossene Regelkreis mit P-Strecke und P-Regler 4.1. Störverhalten (disturbance behaviour, comportement au perturbations) 4.1.1 Angriffspunkt
FELJC 4a_Geschlossener_ Regelkreis_Störverhalten.odt 1 4. Der geschlossene Regelkreis mit P-Strecke und P-Regler 4.1. Störverhalten (disturbance behaviour, comportement au perturbations) 4.1.1 Angriffspunkt
Aufgabe 1 (Unsicherheitsschranke für gemessene Übertragungsfunktion)
 Prof. L. Guzzella Prof. R. D Andrea 5-59- Regelungstechnik II (FS 28) Musterlösung Übung 5 Unsicherheitsschranken, Spezifikationen im Frequenzbereich, Matlab M.B. (michael.benz@imrt.mavt.ethz.ch), 4. April
Prof. L. Guzzella Prof. R. D Andrea 5-59- Regelungstechnik II (FS 28) Musterlösung Übung 5 Unsicherheitsschranken, Spezifikationen im Frequenzbereich, Matlab M.B. (michael.benz@imrt.mavt.ethz.ch), 4. April
Aufgabe 1: Laplace-Transformation
 Aufgabe 1: Laplace-Transformation (15 Punkte) Ein technisches System sei gegeben durch folgende Differentialgleichung 3.Ordnung: y (t)+6ÿ(t)+12ẏ(t)+8y(t) =2ü(t)+1 u(t)+8u(t). Dieses System wird eingangsseitig
Aufgabe 1: Laplace-Transformation (15 Punkte) Ein technisches System sei gegeben durch folgende Differentialgleichung 3.Ordnung: y (t)+6ÿ(t)+12ẏ(t)+8y(t) =2ü(t)+1 u(t)+8u(t). Dieses System wird eingangsseitig
Technische Universität Wien Institut für Automatisierungs- und Regelungstechnik. SCHRIFTLICHE PRÜFUNG zur VU Automatisierung am
 Technische Universität Wien Institut für Automatisierungs- und Regelungstechnik SCHRIFTLICHE PRÜFUNG zur VU Automatisierung am 8.5.5 Arbeitszeit: min Name: Vorname(n): Matrikelnummer: Note: Aufgabe 3 4
Technische Universität Wien Institut für Automatisierungs- und Regelungstechnik SCHRIFTLICHE PRÜFUNG zur VU Automatisierung am 8.5.5 Arbeitszeit: min Name: Vorname(n): Matrikelnummer: Note: Aufgabe 3 4
Schriftliche Prüfung aus Control Systems 2 am
 TU Graz, Institut für Regelungs- und Automatisierungstechnik 1 Schriftliche Prüfung aus Control Sstems 2 am 23.01.2014 Name / Vorname(n): Kennzahl / Matrikel-Nummer: Bonuspunkte aus den MATLAB-Übungen:
TU Graz, Institut für Regelungs- und Automatisierungstechnik 1 Schriftliche Prüfung aus Control Sstems 2 am 23.01.2014 Name / Vorname(n): Kennzahl / Matrikel-Nummer: Bonuspunkte aus den MATLAB-Übungen:
Bode-Diagramme in der Elektrotechnik. ohne Ballast. von
 Bode-Diagramme in der Elektrotechnik ohne Ballast von Wolfgang Bengfort ET-Akademie.de / ET-Tutorials.de Elektrotechnik verstehen durch VIDEO-Tutorials Rechtlicher Hinweis: Alle Rechte vorbehalten. Dieses
Bode-Diagramme in der Elektrotechnik ohne Ballast von Wolfgang Bengfort ET-Akademie.de / ET-Tutorials.de Elektrotechnik verstehen durch VIDEO-Tutorials Rechtlicher Hinweis: Alle Rechte vorbehalten. Dieses
G R. Vorlesung 9. Identifiziert durch Sprungantwort. Sinnvoll selbst gestalten. Regler. Einschleifiger Regelkreis: Xd(s) W(s) Y(s) U(s) GFeder S
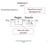 Einschleifiger Regelkreis: Identifiziert durch prungantwort W(s) - Xd(s) G R? U(s) trecke GFeder Dreh- Magnet c Masse m lm Dämpfer d lf ld ollwertgeber Winkelsensor Y(s) innvoll selbst gestalten 1 typen:
Einschleifiger Regelkreis: Identifiziert durch prungantwort W(s) - Xd(s) G R? U(s) trecke GFeder Dreh- Magnet c Masse m lm Dämpfer d lf ld ollwertgeber Winkelsensor Y(s) innvoll selbst gestalten 1 typen:
Lösungen zur 8. Übung
 Prof. Dr.-Ing. Jörg Raisch Dipl.-Ing. Vladislav Nenchev M.Sc. Arne Passon Dipl.-Ing. Thomas Seel Fachgebiet Regelungssysteme Fakultät IV Elektrotechnik und Informatik Technische Universität Berlin Integrierte
Prof. Dr.-Ing. Jörg Raisch Dipl.-Ing. Vladislav Nenchev M.Sc. Arne Passon Dipl.-Ing. Thomas Seel Fachgebiet Regelungssysteme Fakultät IV Elektrotechnik und Informatik Technische Universität Berlin Integrierte
Zusammenfassung der 3. Vorlesung
 Zusammenfassung der 3. Vorlesung Nyquist-Verfahren Motivation Ein mathematisches Modell der Strecke ist nicht notwendig Aussagen über die Stabilität des geschlossenen Regelkreises anhand des Frequenzgangs
Zusammenfassung der 3. Vorlesung Nyquist-Verfahren Motivation Ein mathematisches Modell der Strecke ist nicht notwendig Aussagen über die Stabilität des geschlossenen Regelkreises anhand des Frequenzgangs
1. Differentialgleichung der Filter zweiter Ordnung
 Prof. Dr.-Ing. F. Keller abor Elektronik 3 Filter zweiter Ordnung Info v.doc Hochschule Karlsruhe Info-Blatt: Filter zweiter Ordnung Seite /6. Differentialgleichung der Filter zweiter Ordnung Ein- und
Prof. Dr.-Ing. F. Keller abor Elektronik 3 Filter zweiter Ordnung Info v.doc Hochschule Karlsruhe Info-Blatt: Filter zweiter Ordnung Seite /6. Differentialgleichung der Filter zweiter Ordnung Ein- und
Musterlösung. 120 Minuten + 15 Minuten Lesezeit am Anfang! 36 (unterschiedlich gewichtet, total 47 Punkte)
 BSc - Sessionsprüfung 08.08.2016 Regelungstechnik I (151-0591-00 Ochsner Musterlösung Dauer der Prüfung: Anzahl der Fragen: Bewertung: 120 Minuten + 15 Minuten Lesezeit am Anfang! 36 (unterschiedlich gewichtet,
BSc - Sessionsprüfung 08.08.2016 Regelungstechnik I (151-0591-00 Ochsner Musterlösung Dauer der Prüfung: Anzahl der Fragen: Bewertung: 120 Minuten + 15 Minuten Lesezeit am Anfang! 36 (unterschiedlich gewichtet,
Schriftliche Prüfung aus Regelungssysteme am
 TU Graz, Institut für Regelungs- und Automatisierungstechnik 1 Schriftliche Prüfung aus Regelungssysteme am 12.10.2018 Name / Vorname(n): Matrikel-Nummer: Aufgabe A1 A2 A3 A4 A5 A6 A7 A8 Summe erreichbare
TU Graz, Institut für Regelungs- und Automatisierungstechnik 1 Schriftliche Prüfung aus Regelungssysteme am 12.10.2018 Name / Vorname(n): Matrikel-Nummer: Aufgabe A1 A2 A3 A4 A5 A6 A7 A8 Summe erreichbare
90 Minuten Seite 1. Einlesezeit
 90 Minuten Seite 1 Einlesezeit Für die Durchsicht der Klausur wird eine Einlesezeit von 10 Minuten gewährt. Während dieser Zeitdauer ist es Ihnen nicht gestattet, mit der Bearbeitung der Aufgaben zu beginnen.
90 Minuten Seite 1 Einlesezeit Für die Durchsicht der Klausur wird eine Einlesezeit von 10 Minuten gewährt. Während dieser Zeitdauer ist es Ihnen nicht gestattet, mit der Bearbeitung der Aufgaben zu beginnen.
Die nummerierten Felder bitte mithilfe der Videos ausfüllen:
 7 Bode-Diagramm Zoltán Zomotor Versionsstand: 22. Oktober 2015, 13:40 Die nummerierten Felder bitte mithilfe der Videos ausfüllen: http://www.z5z6.de This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike
7 Bode-Diagramm Zoltán Zomotor Versionsstand: 22. Oktober 2015, 13:40 Die nummerierten Felder bitte mithilfe der Videos ausfüllen: http://www.z5z6.de This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike
Technische Universität Wien Institut für Automatisierungs- und Regelungstechnik. SCHRIFTLICHE PRÜFUNG zur VU Automatisierung am
 Technische Universität Wien Institut für Automatisierungs- und Regelungstechnik SCHRIFTLICHE PRÜFUNG zur VU Automatisierung am 4.3.11 Arbeitszeit: 1 min Name: Vorname(n): Matrikelnummer: Note: Aufgabe
Technische Universität Wien Institut für Automatisierungs- und Regelungstechnik SCHRIFTLICHE PRÜFUNG zur VU Automatisierung am 4.3.11 Arbeitszeit: 1 min Name: Vorname(n): Matrikelnummer: Note: Aufgabe
Bearbeitungszeit: 120 Min
 4 6 Fachgebiet gelungstechnik Leiter: Prof. Dr.-Ing. Johann ger gelungs- und Systemtechnik - Übungsklausur 9 Bearbeitungszeit: Min Modalitäten Es sind keine Hilfsmittel zugelassen. Bitte schreiben Sie
4 6 Fachgebiet gelungstechnik Leiter: Prof. Dr.-Ing. Johann ger gelungs- und Systemtechnik - Übungsklausur 9 Bearbeitungszeit: Min Modalitäten Es sind keine Hilfsmittel zugelassen. Bitte schreiben Sie
Dr. Ing. Wilfried Dankmeier Eppstein im Taunus, RT2
 Fragen zur Klausurvorbereitung mit Lösungen (aber erst selbst bearbeiten, dann nachsehen, umgekehrt ist es nutzlos...) Die Seitenangaben beziehen sich auf die Stichworte zu. Die beiden folgenden Diagramme
Fragen zur Klausurvorbereitung mit Lösungen (aber erst selbst bearbeiten, dann nachsehen, umgekehrt ist es nutzlos...) Die Seitenangaben beziehen sich auf die Stichworte zu. Die beiden folgenden Diagramme
(s + 3) 1.5. w(t) = σ(t) W (s) = 1 s. G 1 (s)g 2 (s) 1 + G 1 (s)g 2 (s)g 3 (s)g 4 (s) = Y (s) Y (s) W (s)g 1 (s) Y (s)g 1 (s)g 3 (s)g 4 (s)
 Aufgabe : LAPLACE-Transformation Die Laplace-Transformierte der Sprungantwort ist: Y (s) = 0.5 s + (s + 3).5 (s + 4) Die Sprungantwort ist die Reaktion auf den Einheitssprung: w(t) = σ(t) W (s) = s Die
Aufgabe : LAPLACE-Transformation Die Laplace-Transformierte der Sprungantwort ist: Y (s) = 0.5 s + (s + 3).5 (s + 4) Die Sprungantwort ist die Reaktion auf den Einheitssprung: w(t) = σ(t) W (s) = s Die
Regelungs- und Systemtechnik 1 - Übungsklausur 7
 4 6 Fachgebiet Regelungstechnik Leiter: Prof. Dr.-Ing. Johann Reger Bearbeitungszeit: 12 Minuten Modalitäten Es sind keine Hilfsmittel zugelassen. Bitte schreiben Sie mit dokumentenechtem Schreibgerät
4 6 Fachgebiet Regelungstechnik Leiter: Prof. Dr.-Ing. Johann Reger Bearbeitungszeit: 12 Minuten Modalitäten Es sind keine Hilfsmittel zugelassen. Bitte schreiben Sie mit dokumentenechtem Schreibgerät
SSYLB2 SS06 Daniel Schrenk, Andreas Unterweger Übung 5. Laborprotokoll SSY. Reglerentwurf nach dem Frequenz- Kennlinien-Verfahren
 Laborprotokoll SSY Reglerentwurf nah dem Frequenz- Kennlinien-Verfahren Daniel Shrenk, Andreas Unterweger, ITS 24 SSYLB2 SS6 Daniel Shrenk, Andreas Unterweger Seite 1 von 13 1. Einleitung Ziel der Übung
Laborprotokoll SSY Reglerentwurf nah dem Frequenz- Kennlinien-Verfahren Daniel Shrenk, Andreas Unterweger, ITS 24 SSYLB2 SS6 Daniel Shrenk, Andreas Unterweger Seite 1 von 13 1. Einleitung Ziel der Übung
Übungsaufgaben zur Vorlesung Regelungssysteme (Grundlagen)
 Übungsaufgaben zur Vorlesung Regelungssysteme (Grundlagen) TU Bergakademie Freiberg Institut für Automatisierungstechnik Prof. Dr.-Ing. Andreas Rehkopf 27. Januar 2014 Übung 1 - Vorbereitung zum Praktikum
Übungsaufgaben zur Vorlesung Regelungssysteme (Grundlagen) TU Bergakademie Freiberg Institut für Automatisierungstechnik Prof. Dr.-Ing. Andreas Rehkopf 27. Januar 2014 Übung 1 - Vorbereitung zum Praktikum
Protokoll Elektronikpraktikum Versuch 2 am
 Protokoll Elektronikpraktikum Versuch 2 am 30.04.2013 Intsar Bangwi & Sven Köppel Passive Bauelemente Elektronische Bauelemente stellen Einzeleinheiten von elektrischen Schaltungen da. Sie werden mit versch.
Protokoll Elektronikpraktikum Versuch 2 am 30.04.2013 Intsar Bangwi & Sven Köppel Passive Bauelemente Elektronische Bauelemente stellen Einzeleinheiten von elektrischen Schaltungen da. Sie werden mit versch.
Regelungs- und Systemtechnik 1 - Übungsklausur 16
 4 6 Fachgebiet Regelungstechnik Leiter: Prof. Dr.-Ing. Johann Reger Bearbeitungszeit: Min Modalitäten Es sind keine Hilfsmittel zugelassen. Bitte schreiben Sie mit dokumentenechtem Schreibgerät (Tinte
4 6 Fachgebiet Regelungstechnik Leiter: Prof. Dr.-Ing. Johann Reger Bearbeitungszeit: Min Modalitäten Es sind keine Hilfsmittel zugelassen. Bitte schreiben Sie mit dokumentenechtem Schreibgerät (Tinte
Schriftliche Prüfung aus Regelungstechnik am
 U Graz, Institut für Regelungs- und Automatisierungstechnik 1 Schriftliche Prüfung aus Regelungstechnik am 18. 10. 01 Name / Vorname(n): Matrikel-Nummer: Bonuspunkte aus den MALAB-Übungen: O ja O nein
U Graz, Institut für Regelungs- und Automatisierungstechnik 1 Schriftliche Prüfung aus Regelungstechnik am 18. 10. 01 Name / Vorname(n): Matrikel-Nummer: Bonuspunkte aus den MALAB-Übungen: O ja O nein
Lösungen zur 8. Übung
 Prof. Dr.-Ing. Jörg Raisch Dipl.-Ing. Vladislav Nenchev M.Sc. Arne Passon Dipl.-Ing. Thomas Seel Fachgebiet Regelungssysteme Fakultät IV Elektrotechnik und Informatik Technische Universität Berlin Integrierte
Prof. Dr.-Ing. Jörg Raisch Dipl.-Ing. Vladislav Nenchev M.Sc. Arne Passon Dipl.-Ing. Thomas Seel Fachgebiet Regelungssysteme Fakultät IV Elektrotechnik und Informatik Technische Universität Berlin Integrierte
Regelungstechnik Aufgaben
 Serge Zacher Regelungstechnik Aufgaben Lineare, Zweipunkt- und digitale Regelung 2., überarbeitete und erweiterte Auflage Mit 126 Aufgaben und MATLAB-Simulationen ZACHE VII Inhalt 1. Formelsammlung 1 1.1
Serge Zacher Regelungstechnik Aufgaben Lineare, Zweipunkt- und digitale Regelung 2., überarbeitete und erweiterte Auflage Mit 126 Aufgaben und MATLAB-Simulationen ZACHE VII Inhalt 1. Formelsammlung 1 1.1
Formelsammlung. Regelungstechnik I. Basierend auf Arbeit von Florian Beermann Letzte Änderung am : Frank Bättermann
 Formelsammlung Regelungstechnik I Basierend auf Arbeit von Florian Beermann Letzte Änderung am 29.04.2008: Frank Bättermann 1 Inhaltsverzeichnis 1. Steuerung und Regelung...3 1.3 Vorteile der Regelung...3
Formelsammlung Regelungstechnik I Basierend auf Arbeit von Florian Beermann Letzte Änderung am 29.04.2008: Frank Bättermann 1 Inhaltsverzeichnis 1. Steuerung und Regelung...3 1.3 Vorteile der Regelung...3
Klausur im Fach: Regelungs- und Systemtechnik 1
 (in Druckschrift ausfüllen!) Univ.-Prof. Dr.-Ing. habil. Ch. Ament Name: Vorname: Matr.-Nr.: Sem.-Gr.: Anzahl der abgegebenen Blätter: 3 Klausur im Fach: Prüfungstermin: 26.03.2013 Prüfungszeit: 11:30
(in Druckschrift ausfüllen!) Univ.-Prof. Dr.-Ing. habil. Ch. Ament Name: Vorname: Matr.-Nr.: Sem.-Gr.: Anzahl der abgegebenen Blätter: 3 Klausur im Fach: Prüfungstermin: 26.03.2013 Prüfungszeit: 11:30
Lösungen zur 3. Übung
 Prof. Dr.-Ing. Jörg Raisch Dipl.-Ing. Anne-Kathrin Hess Dipl.-Ing. Thomas Seel Fachgebiet Regelungssysteme Fakultät IV Elektrotechnik und Informatik Technische Universität Berlin Integrierte Lehrveranstaltung
Prof. Dr.-Ing. Jörg Raisch Dipl.-Ing. Anne-Kathrin Hess Dipl.-Ing. Thomas Seel Fachgebiet Regelungssysteme Fakultät IV Elektrotechnik und Informatik Technische Universität Berlin Integrierte Lehrveranstaltung
Übung 5: Routh-Hurwitz und Nyquist Stabilitätskriterien
 Übungsaufgaben zur Vorlesung Regelsysteme Herbstsemester 25 Übung 5: Routh-Hurwitz und Nyquist Stabilitätskriterien Prof. Dr. Manfred Morari, Prof. Dr. Florian Dörfler Institut für Automatik, ETH Zürich
Übungsaufgaben zur Vorlesung Regelsysteme Herbstsemester 25 Übung 5: Routh-Hurwitz und Nyquist Stabilitätskriterien Prof. Dr. Manfred Morari, Prof. Dr. Florian Dörfler Institut für Automatik, ETH Zürich
Hauptseminar SOI Regelalgorithmen für Totzeitsysteme
 Hauptseminar SOI 6. Juli 2006 Gliederung des Vortrags Motivation Grundlagen Totzeitsysteme und deren Schwierigkeiten Lösungsansätze für Totzeitsysteme Zusammenfassung Gliederung des Vortrags Motivation
Hauptseminar SOI 6. Juli 2006 Gliederung des Vortrags Motivation Grundlagen Totzeitsysteme und deren Schwierigkeiten Lösungsansätze für Totzeitsysteme Zusammenfassung Gliederung des Vortrags Motivation
Zusammenfassung der 9. Vorlesung
 Zusammenfassung der 9. Vorlesung Analyse des Regelkreises Stationäres Verhalten des Regelkreises Bleibende Regelabweichung für Führungs- und Störverhalten Bleibende Regelabweichung für verschiedene Eingangssignale
Zusammenfassung der 9. Vorlesung Analyse des Regelkreises Stationäres Verhalten des Regelkreises Bleibende Regelabweichung für Führungs- und Störverhalten Bleibende Regelabweichung für verschiedene Eingangssignale
Regelung. Max Meiswinkel. 8. Dezember Max Meiswinkel () Regelung 8. Dezember / 12
 Regelung Max Meiswinkel 8. Dezember 2008 Max Meiswinkel () Regelung 8. Dezember 2008 1 / 12 Übersicht 1 Einführung Der Regelkreis Regelschleife 2 stetige Regelung P-Regler I-Regler PI-Regler PD-Regler
Regelung Max Meiswinkel 8. Dezember 2008 Max Meiswinkel () Regelung 8. Dezember 2008 1 / 12 Übersicht 1 Einführung Der Regelkreis Regelschleife 2 stetige Regelung P-Regler I-Regler PI-Regler PD-Regler
Regelungstechnik I. Heinz Unbehauen. Klassische Verfahren zur Analyse und Synthese linearer kontinuierlicher Regelsysteme
 Heinz Unbehauen Regelungstechnik I Klassische Verfahren zur Analyse und Synthese linearer kontinuierlicher Regelsysteme 7., überarbeitete und erweiterte Auflage Mit 192 Bildern und 28 TabeUen vieweg INHALT
Heinz Unbehauen Regelungstechnik I Klassische Verfahren zur Analyse und Synthese linearer kontinuierlicher Regelsysteme 7., überarbeitete und erweiterte Auflage Mit 192 Bildern und 28 TabeUen vieweg INHALT
Regelungstechnik I. Heinz JUnbehauen. Klassische Verfahren zur Analyse und Synthese linearer kontinuierlicher Regelsysteme. 3., durchgesehene Auflage
 Heinz JUnbehauen Regelungstechnik I Klassische Verfahren zur Analyse und Synthese linearer kontinuierlicher Regelsysteme 3., durchgesehene Auflage Mit 192 Bildern V] Friedr. Vieweg & Sohn Braunschweig/Wiesbaden
Heinz JUnbehauen Regelungstechnik I Klassische Verfahren zur Analyse und Synthese linearer kontinuierlicher Regelsysteme 3., durchgesehene Auflage Mit 192 Bildern V] Friedr. Vieweg & Sohn Braunschweig/Wiesbaden
Lösungen zur 3. Übung
 Prof. Dr.-Ing. Jörg Raisch Dipl.-Ing. Vladislav Nenchev M.Sc. Arne Passon Dipl.-Ing. Thomas Seel Fachgebiet Regelungssysteme Fakultät IV Elektrotechnik und Informatik Technische Universität Berlin Integrierte
Prof. Dr.-Ing. Jörg Raisch Dipl.-Ing. Vladislav Nenchev M.Sc. Arne Passon Dipl.-Ing. Thomas Seel Fachgebiet Regelungssysteme Fakultät IV Elektrotechnik und Informatik Technische Universität Berlin Integrierte
MR - Mechanische Resonanz Blockpraktikum Herbst 2005
 MR - Mechanische Resonanz, Blockpraktikum Herbst 5 7. September 5 MR - Mechanische Resonanz Blockpraktikum Herbst 5 Assistent Florian Jessen Tübingen, den 7. September 5 Vorwort In diesem Versuch ging
MR - Mechanische Resonanz, Blockpraktikum Herbst 5 7. September 5 MR - Mechanische Resonanz Blockpraktikum Herbst 5 Assistent Florian Jessen Tübingen, den 7. September 5 Vorwort In diesem Versuch ging
