Eingebettete Runge Kutta Verfahren DOPRI5(4) Verfahren: FSAL Verfahren
|
|
|
- Johanna Kerner
- vor 7 Jahren
- Abrufe
Transkript
1 Eingebettete Runge Kutta Verfahren DOPRI5(4) Verfahren: FSAL Verfahren p = ˆp = Kapitel IV.4 - Lineare Mehrschritt-Verfahren (rk17) 1
2 Eingebettete Runge Kutta Verfahren DOPRI8(7) Verfahren: Butcherschema entnommen aus Deuflhard/Bornemann Kapitel IV.4 - Lineare Mehrschritt-Verfahren (rk18) 2
3 Lineare Mehrschrittverfahren (MSV) Idee: Verwende zur Bestimmung von y i+1 nicht nur den zuletzt zurückliegenden Werte y i und f i, sondern zusätzlich noch weiter zurückliegende Werte. y i+1 = k 1 j=0 a j y i j + k 1 j= 1 b j f i j Es existieren zwei große Klassen: Adams Varianten basieren auf Quadraturformeln und Integration BDF Varianten basieren auf Interpolation und Differenziation Im Gegensatz zu konsistenten Einschrittverfahren sind MSV nicht automatisch Null-stabil. steigt bei MSV der Aufwand mit der Ordnung nicht an. Kapitel IV.4 - Lineare Mehrschritt-Verfahren (msv01) 3
4 Mehrschrittverfahren: Adams Bashforth Verfahren (1) Idee: y = f(t,y) y(t i+1 ) = y(t i )+ ti+1 t i f(t,y)dt Approximieref unterverwendungderbekanntenstützpunkte(t i,y i ),...,(t i+1 k,y i+1 k ) mit einem Interpolationspolynom vom Grad k 1 und integriere. f(t,y) P³(t) f(t,y) P³(t) Fehler t(i 3) t(i 2) t(i 1) t(i) t(i+1) t(i) t(i+1) Kapitel IV.4 - Lineare Mehrschritt-Verfahren (msv03) 4
5 Adams Bashforth Verfahren (ABV, explizit) (2) l : Polynomgrad, k : Schrittzahl, p : Ordnung l = 0, k = 1, p = 1 : y i+1 = y i +hf i, l = 1, k = 2, p = 2 : y i+1 = y i h(3f i f i 1 ), l = 2, k = 3, p = 3 : y i+1 = y i h(23f i 16f i 1 +5f i 2 ), l = 3, k = 4, p = 4 : y i+1 = y i h(55f i 59f i 1 +37f i 2 9f i 3 ). Bei expliziten ABV gilt: Polynomgrad+1 = Ordnung = Schrittzahl. Es existieren Verfahren beliebiger Ordnung. Kapitel IV.4 - Lineare Mehrschritt-Verfahren (msv04) 5
6 Adams Bashforth Verfahren: Verschiedene Ordnungen y = 10ty, y(0) = 1, Fehler bei t = AB2 AB AB2: Adams Bashforth Verfahren 2ter Ordnung AB3: Adams Bashforth Verfahren 3ter Ordnung : Adams Bashforth Verfahren 4ter Ordnung Kapitel IV.4 - Lineare Mehrschritt-Verfahren (msv05) 6
7 Adams Bashforth Verfahren: Verschiedene Ordnungen y = 5(y t 2 ) + 2t, y(0) = 0, Lösung y = t 2, Fehler bei t = AB2 AB AB2: Adams Bashforth Verfahren 2ter Ordnung AB3: Adams Bashforth Verfahren 3ter Ordnung : Adams Bashforth Verfahren 4ter Ordnung Kapitel IV.4 - Lineare Mehrschritt-Verfahren (msv06) 7
8 Adams Moulton Verfahren (AMV, implizit) l : Polynomgrad, k : Schrittzahl, p : Ordnung l = 0, k = 1, p = 1 : y i+1 = y i +hf i+1, l = 1, k = 1, p = 2 : y i+1 = y i h(f i+1+f i ), l = 2, k = 2, p = 3 : y i+1 = y i h(5f i+1+8f i f i 1 ), l = 3, k = 3, p = 4 : y i+1 = y i h(9f i+1+19f i 5f i 1 +1f i 2 ). Bei impliziten AMV gilt: Polynomgrad+1 = Ordnung Schrittzahl+1. Adams Bashforth Moulton / Prädiktor Korrektor Verfahren explizit l = 2, k = 2, p = 3 y (P) i+1 = y i h(3f i f i 1 ), y i+1 = y i h ( 5f ( ) ) t i+1, y (P) i+1 + 8f i f i 1. Kapitel IV.4 - Lineare Mehrschritt-Verfahren (msv09) 8
9 Vergleich: AB / AM / ABM Verfahren y = 10ty, y(0) = 1, Fehler bei t = 1 Fehler gegen Funktionsauswertungen 10 5 AM4 ABM AM4 ABM : Adams Bashforth Verfahren 4ter Ordnung AM4: Adams Moulton Verfahren 4ter Ordnung ABM4: Adams Bashforth Moulton Verfahren 4ter Ordnung Kapitel IV.4 - Lineare Mehrschritt-Verfahren (msv10) 9
10 Vergleich: AB / AM / ABM Verfahren y = 5(y t 2 ) + 2t, y(0) = 0, Lösung y = t 2, Fehler bei t = 5 Fehler gegen Funktionsauswertungen 10 5 AM4 ABM AM4 ABM : Adams Bashforth Verfahren 4ter Ordnung AM4: Adams Moulton Verfahren 4ter Ordnung ABM4: Adams Bashforth Moulton Verfahren 4ter Ordnung Kapitel IV.4 - Lineare Mehrschritt-Verfahren (msv11) 10
11 Mehrschrittverfahren: BDF Verfahren (1) Idee: Ersetze y(t) durch ein Interpolationspolynom P k (t) der Ordnung k mit den Stützstellen (t i+1, y i+1 ), (t i, y i ),..., (t i k+1, y i k+1 ), und löse Dies liefert ein Verfahren der Gestalt P k(t) = f(t,y(t)). a 1 y i+1 +a 0 y i +a 1 y i 1 + +a k 1 y i k+1 = hf (t i+1, y i+1 ), oder k 1 j= 1 a j y i j = hf (t i+1, y i+1 ). Kapitel IV.4 - Lineare Mehrschritt-Verfahren (msv25) 11
12 Mehrschrittverfahren: BDF Verfahren (2) l : Polynomgrad, k : Schrittzahl, p : Ordnung 1, 1, 1 : hf i+1 = y i+1 y i, 2, 2, 2 : hf i+1 = 3 2 y i+1 2y i y i 1, 3, 3, 3 : hf i+1 = 11 6 y i+1 3y i y i y i 2, 4, 4, 4 : hf i+1 = y i+1 4y i +3y i y i y i 3, 5, 5, 5 : hf i+1 = y i+1 5y i + 5y i y i y i y i 4 6, 6, 6 : hf i+1 = y i+1 6y i y i y i y i y i y i 5. Für k > 6 sind die Verfahren instabil. Kapitel IV.4 - Lineare Mehrschritt-Verfahren (msv26) 12
13 BDF Verfahren: Verschiedene Ordnungen y = 10ty, y(0) = 1, Fehler bei t = BDF2 BDF3 BDF BDF2: BDF Verfahren 2ter Ordnung BDF3: BDF Verfahren 3ter Ordnung BDF4: BDF Verfahren 4ter Ordnung Kapitel IV.4 - Lineare Mehrschritt-Verfahren (msv27) 13
14 BDF Verfahren: Verschiedene Ordnungen y = 5(y t 2 ) + 2t, y(0) = 0, Lösung y = t 2, Fehler bei t = BDF2 BDF3 BDF BDF2: BDF Verfahren 2ter Ordnung BDF3: BDF Verfahren 3ter Ordnung BDF4: BDF Verfahren 4ter Ordnung Kapitel IV.4 - Lineare Mehrschritt-Verfahren (msv28) 14
15 Vergleich: AB / ABM / BDF Verfahren y = 10ty, y(0) = 1, Fehler bei t = 1 Fehler gegen Funktionsauswertungen 10 5 ABM4 BDF ABM4 BDF : Adams Bashforth Verfahren 4ter Ordnung ABM4: Adams Bashforth Moulton Verfahren 4ter Ordnung BDF4: BDF Verfahren 4ter Ordnung Kapitel IV.4 - Lineare Mehrschritt-Verfahren (msv31) 15
16 Vergleich: AB / ABM / BDF Verfahren y = 5(y t 2 ) + 2t, y(0) = 0, Lösung y = t 2, Fehler bei t = 5 ABM4 BDF4 Fehler gegen Funktionsauswertungen ABM4 BDF4 : Adams Bashforth Verfahren 4ter Ordnung ABM4: Adams Bashforth Moulton Verfahren 4ter Ordnung BDF4: BDF Verfahren 4ter Ordnung Kapitel IV.4 - Lineare Mehrschritt-Verfahren (msv32) 16
17 Einfluss der Anlaufrechnung y = 5t(2+3t)y, y(0) = 1, Fehler bei t = BDF2 BDF3 BDF BDF2 BDF3 BDF BDF2 BDF3 BDF RK3 Verfahren Heun expliziter Euler BDF2: BDF Verfahren 2ter Ordnung BDF3: BDF Verfahren 3ter Ordnung BDF4: BDF Verfahren 4ter Ordnung Für MSV der Ordnung p Anlaufrechnung mit Ordnung p 1 nötig Kapitel IV.4 - Lineare Mehrschritt-Verfahren (msv36) 17
18 Konsistenz + Stabilität = Konvergenz y = y, y 0 = 1, y 1 = e h konsistent und stabil y i+1 = y i 1 +2hf i 1 y i t i h = 0.2 h = 0.1 exakt konsistent, NICHT stabil y i+1 = 3y i 1 +4y i 2hf i 1 y i t i h = 0.2 h = 0.1 exakt Kapitel IV.4 - Lineare Mehrschritt-Verfahren (msv02) 18
Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen
 Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial
Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe
 Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung
 Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel
 - Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
Lokaler Fehler y = y 2, y(0.2) = 5/9, Lösung: y = 1 Fehler nach dem 1. Schritt
 Lokaler Fehler y = y, y(.) = /9, Lösung: y = Fehler nach dem. Schritt ( t) 4 Fehler 6 8 4 (I) Euler explizit (II) Euler implizit (IIIa) Crank Nicolson (IIIb) Heun (IVa) Euler modifiziert (IVb) Euler mod.
Lokaler Fehler y = y, y(.) = /9, Lösung: y = Fehler nach dem. Schritt ( t) 4 Fehler 6 8 4 (I) Euler explizit (II) Euler implizit (IIIa) Crank Nicolson (IIIb) Heun (IVa) Euler modifiziert (IVb) Euler mod.
Gewöhnliche Differentialgleichungen
 Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Adaptive Mehrschrittverfahren
 Adaptive Mehrschrittverfahren Moritz Neumann 21. März 2011 1 Inhaltsverzeichnis 1 Vorwort 3 2 Einführung 3 3 Adaptive Seuerung der Schrittweite und Ordnung 5 3.1 Adams-Verfahren................................
Adaptive Mehrschrittverfahren Moritz Neumann 21. März 2011 1 Inhaltsverzeichnis 1 Vorwort 3 2 Einführung 3 3 Adaptive Seuerung der Schrittweite und Ordnung 5 3.1 Adams-Verfahren................................
Einführung und Beispiele
 Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB)
 Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Abschnitt 1.7: Schrittweitensteuerung 27
 Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen
 TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
ODE-Solver. Inhalt. Einleitung. grundlegende Algorithmen. weiterführende Algorithmen
 Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
3. Lineare Mehrschrittverfahren 3.1 Begriffe
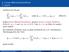 3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
Zehnte Vorlesung, 4. Juni 2009, Inhalt. Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen
 Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
Explizite, eingebettete und implizite RK-Verfahren
 Kutta-Teorie: Explizite, eingebettete und implizite RK-Verfaren Lukas Klic Kutta-Teorie: : Explizite, eingebettete und implizite RK- Verfaren Lukas Klic Seite: Gliederung -Verfaren - Explizite Verfaren
Kutta-Teorie: Explizite, eingebettete und implizite RK-Verfaren Lukas Klic Kutta-Teorie: : Explizite, eingebettete und implizite RK- Verfaren Lukas Klic Seite: Gliederung -Verfaren - Explizite Verfaren
Numerische Verfahren für gewöhnliche Differentialgleichungen
 Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Übungsblatt 10 Musterlösung
 Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
Musterlösung Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn
 D-ITET, D-MATL Musterlösung Prüfung umerische Methoden, Sommer 01 Dr. Lars Kielhorn 1. a) z = exp(iϕ) = dz = i exp(iϕ) dϕ = c n [f] = 1 π f(exp(iϕ)) exp( iϕn) dϕ π 0 b) Allgemeine zusammengesetzte Trapezregel
D-ITET, D-MATL Musterlösung Prüfung umerische Methoden, Sommer 01 Dr. Lars Kielhorn 1. a) z = exp(iϕ) = dz = i exp(iϕ) dϕ = c n [f] = 1 π f(exp(iϕ)) exp( iϕn) dϕ π 0 b) Allgemeine zusammengesetzte Trapezregel
Grundlagen der Numerischen Mathematik II
 J Manfred Reimer Grundlagen der Numerischen Mathematik II Studienbuch für Studenten der Mathematik, Informatik, Statistik und aller Naturwissenschaften Mit 29 Abbildungen Akademische Verlagsgesellschaft
J Manfred Reimer Grundlagen der Numerischen Mathematik II Studienbuch für Studenten der Mathematik, Informatik, Statistik und aller Naturwissenschaften Mit 29 Abbildungen Akademische Verlagsgesellschaft
Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik'
 Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik' 1. Diskretisierung in der Zeit: Die Evolutionsgleichung Kurzzusammenfassung Zur Erprobung der Verfahren zur zeitlichen Diskretisierung
Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik' 1. Diskretisierung in der Zeit: Die Evolutionsgleichung Kurzzusammenfassung Zur Erprobung der Verfahren zur zeitlichen Diskretisierung
9 Numerische Verfahren für Anfangswertaufgaben
 Numerik II 63 9 Numerische Verfahren für Anfangswertaufgaben Inhalt 9.1 Einige einfache Verfahren 9.2 Einschrittverfahren Definition und Eigenschaften 9.3 Runge-Kutta-Verfahren 9.4 Lineare Mehrschrittverfahren
Numerik II 63 9 Numerische Verfahren für Anfangswertaufgaben Inhalt 9.1 Einige einfache Verfahren 9.2 Einschrittverfahren Definition und Eigenschaften 9.3 Runge-Kutta-Verfahren 9.4 Lineare Mehrschrittverfahren
Kapitel 1 Gewöhnliche Differentialgleichungen
 Kapitel 1 Gewöhnliche Differentialgleichungen Eines der wichtigsten Einsatzgebiete numerischer Verfahren sind Differentialgleichungen, also Gleichungen, die Funktionen sowie deren Ableitungen in Bezug
Kapitel 1 Gewöhnliche Differentialgleichungen Eines der wichtigsten Einsatzgebiete numerischer Verfahren sind Differentialgleichungen, also Gleichungen, die Funktionen sowie deren Ableitungen in Bezug
Numerik gewöhnlicher Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2016/17 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2016/17 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Numerische Verfahren für gewöhnliche Differentialgleichungen. Literaturliste. P.Deuflhard, F.Bornemann: Numerische Mathematik II, De Gruyter, 1994.
 Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
2. Numerische Verfahren für AWPe 2.1 Das Euler-Verfahren
 2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 1. Prof. Dr. Hans Babovsky. Technische Universität Ilmenau
 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 1 Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau 1 Version vom Herbst 2006 Inhaltsverzeichnis 1 Gewöhnl. Differentialgleichungen:
NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 1 Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau 1 Version vom Herbst 2006 Inhaltsverzeichnis 1 Gewöhnl. Differentialgleichungen:
NUMERISCHE MATHEMATIK FÜR MATHEMATIKER III 1 (Numerik gewöhnlicher Differentialgleichungen) Prof. Dr. Hans Babovsky. Institut für Mathematik
 NUMERISCHE MATHEMATIK FÜR MATHEMATIKER III 1 (Numerik gewöhnlicher Differentialgleichungen) Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau WS 2003/04 1 Korrekturen, Kommentare
NUMERISCHE MATHEMATIK FÜR MATHEMATIKER III 1 (Numerik gewöhnlicher Differentialgleichungen) Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau WS 2003/04 1 Korrekturen, Kommentare
Formelsammlung zur Numerischen Mathematik mitturbo-pascal- Programmen
 Formelsammlung zur Numerischen Mathematik mitturbo-pascal- Programmen von PROF. DR. GISELA ENGELN-MÜLLGES Fachhochschule Aachen und 0. PROF. EM. DR. FRITZ REUTTER Rheinisch-Westfälische Technische Hochschule
Formelsammlung zur Numerischen Mathematik mitturbo-pascal- Programmen von PROF. DR. GISELA ENGELN-MÜLLGES Fachhochschule Aachen und 0. PROF. EM. DR. FRITZ REUTTER Rheinisch-Westfälische Technische Hochschule
Inhaltsverzeichnis. 1 Einleitung... 1
 Inhaltsverzeichnis 1 Einleitung................................................. 1 2 Fehleranalyse: Kondition, Rundungsfehler, Stabilität...... 11 2.1 Kondition eines Problems................................
Inhaltsverzeichnis 1 Einleitung................................................. 1 2 Fehleranalyse: Kondition, Rundungsfehler, Stabilität...... 11 2.1 Kondition eines Problems................................
10 Stabilität und steife Systeme
 Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Numerik gewöhnlicher Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2014/15 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2014/15 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Numerik gewöhnlicher Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen Band 2 Mehrschrittverfahren Von Dr. phil. nat. Rolf Dieter Grigorieff o. Professor an der Technischen Universität Berlin unter Mitwirkung von Dr. phil. nat.
Numerik gewöhnlicher Differentialgleichungen Band 2 Mehrschrittverfahren Von Dr. phil. nat. Rolf Dieter Grigorieff o. Professor an der Technischen Universität Berlin unter Mitwirkung von Dr. phil. nat.
Differenzialgleichungen
 Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Dr. R. Käppeli D-ITET, D-MATL Winter Numerische Methoden Punkte
 Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
Kapitel 11 Gewöhnliche Differentialgleichungen
 Kapitel 11 Gewöhnliche Differentialgleichungen 11.1 Einführung Gesucht wird eine Funktion y = y(t) einer (Zeit-)Variablen t, die der Gleichung und der Anfangsbedingung genügen soll. y (t) = f(t, y(t)),
Kapitel 11 Gewöhnliche Differentialgleichungen 11.1 Einführung Gesucht wird eine Funktion y = y(t) einer (Zeit-)Variablen t, die der Gleichung und der Anfangsbedingung genügen soll. y (t) = f(t, y(t)),
Numerische Mathematik
 ».- Numerische Mathematik Von Dr. sc. math. Hans Rudolf Schwarz o. Professor an der Universität Zürich Mit einem Beitrag von Dr. sc. math. Jörg Waldvogel Titularprofessor an der Eidg. Technischen Hochschule
».- Numerische Mathematik Von Dr. sc. math. Hans Rudolf Schwarz o. Professor an der Universität Zürich Mit einem Beitrag von Dr. sc. math. Jörg Waldvogel Titularprofessor an der Eidg. Technischen Hochschule
Inhaltsverzeichnis. 1 Einleitung 1
 Inhaltsverzeichnis 1 Einleitung 1 2 Fehleranalyse: Kondition, Rundungsfehler, Stabilitat 11 2.1 Kondition eines Problems 11 2.1.1 Elementare Beispiele 12 2.1.2 Bemessen, Normen 15 2.1.3 Relative und Absolute
Inhaltsverzeichnis 1 Einleitung 1 2 Fehleranalyse: Kondition, Rundungsfehler, Stabilitat 11 2.1 Kondition eines Problems 11 2.1.1 Elementare Beispiele 12 2.1.2 Bemessen, Normen 15 2.1.3 Relative und Absolute
Numerik gewöhnlicher Differentialgleichungen. Prof. Dr. Guido Kanschat
 Numerik gewöhnlicher Differentialgleichungen Prof. Dr. Guido Kanschat 7. Juni 03 Vorbemerkungen Bei diesen Blattern handelt es sich zur Zeit nur um eine begleitende Erganzung des Vorlesungsskriptes von
Numerik gewöhnlicher Differentialgleichungen Prof. Dr. Guido Kanschat 7. Juni 03 Vorbemerkungen Bei diesen Blattern handelt es sich zur Zeit nur um eine begleitende Erganzung des Vorlesungsskriptes von
Hohere Mathematik. fur Ingenieure, Physiker und Mathematiker von Dr. Dr. h.c. Norbert Herrmann Leibniz Universitat Hannover 2., uberarbeitete Auflage
 Hohere Mathematik fur Ingenieure, Physiker und Mathematiker von Dr. Dr. h.c. Norbert Herrmann Leibniz Universitat Hannover 2., uberarbeitete Auflage Oldenbourg Verlag MunchenWien Inhaltsverzeichnis Einleitung
Hohere Mathematik fur Ingenieure, Physiker und Mathematiker von Dr. Dr. h.c. Norbert Herrmann Leibniz Universitat Hannover 2., uberarbeitete Auflage Oldenbourg Verlag MunchenWien Inhaltsverzeichnis Einleitung
D-ITET, D-MATL. Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn
 Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
Inhaltsverzeichnis. 1 Einleitung... 1
 Inhaltsverzeichnis 1 Einleitung... 1 2 Fehleranalyse: Kondition, Rundungsfehler, Stabilität... 11 2.1 KonditioneinesProblems... 11 2.1.1 ElementareBeispiele... 12 2.1.2 Bemessen,Normen... 15 2.1.3 RelativeundAbsoluteKondition...
Inhaltsverzeichnis 1 Einleitung... 1 2 Fehleranalyse: Kondition, Rundungsfehler, Stabilität... 11 2.1 KonditioneinesProblems... 11 2.1.1 ElementareBeispiele... 12 2.1.2 Bemessen,Normen... 15 2.1.3 RelativeundAbsoluteKondition...
NUMERISCHE VERFAHREN für Naturwissenschaftler und Ingenieure
 NUMERISCHE VERFAHREN für Naturwissenschaftler und Ingenieure Eine computerorientierte Einführung Von Prof. Dr. sc. nat. HUBERT SCHWETLICK Prof. Dr. sc. nat. HORST KRETZSCHMAR Mit 74 Bildern und 34 Tabellen
NUMERISCHE VERFAHREN für Naturwissenschaftler und Ingenieure Eine computerorientierte Einführung Von Prof. Dr. sc. nat. HUBERT SCHWETLICK Prof. Dr. sc. nat. HORST KRETZSCHMAR Mit 74 Bildern und 34 Tabellen
Kapitel 6 Gewöhnliche Differenzialgleichungen (DGL)
 Kapitel 6 Gewöhnliche Differenzialgleichungen (DGL) Problemstellung Beispiele Klassifizierung von DGLs, Existenz und Eindeutigkeit des AWPs Einschrittverfahren Stabilität & Schrittweitenkontrolle Mehrschrittverfahren
Kapitel 6 Gewöhnliche Differenzialgleichungen (DGL) Problemstellung Beispiele Klassifizierung von DGLs, Existenz und Eindeutigkeit des AWPs Einschrittverfahren Stabilität & Schrittweitenkontrolle Mehrschrittverfahren
Klausur zur Vordiplom-Prüfung
 Technische Universität Hamburg-Harburg SS Arbeitsbereich Mathematik Dr. Jens-Peter M. Zemke Klausur zur Vordiplom-Prüfung Numerische Verfahren. Juli Sie haben Minuten Zeit zum Bearbeiten der Klausur. Bitte
Technische Universität Hamburg-Harburg SS Arbeitsbereich Mathematik Dr. Jens-Peter M. Zemke Klausur zur Vordiplom-Prüfung Numerische Verfahren. Juli Sie haben Minuten Zeit zum Bearbeiten der Klausur. Bitte
KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.
![KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2. KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.](/thumbs/71/65292107.jpg) MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
Inhaltsverzeichnis. Vorwort zur 10. Auflage Informationen zur Programmbibliothek Bezeichnungen VII IX
 Inhaltsverzeichnis Vorwort zur 10. Auflage Informationen zur Programmbibliothek Bezeichnungen VII IX XI I I 1 Darstellung von Zahlen und Fehleranalyse 1 1.1 Definition von Fehlergrößen..........................
Inhaltsverzeichnis Vorwort zur 10. Auflage Informationen zur Programmbibliothek Bezeichnungen VII IX XI I I 1 Darstellung von Zahlen und Fehleranalyse 1 1.1 Definition von Fehlergrößen..........................
Numerik für Ingenieure I Wintersemester 2008
 1 / 32 Numerik für Ingenieure I Wintersemester 2008 J. Michael Fried Lehrstuhl Angewandte Mathematik III 23.1.2009 2 / 32 Wiederholung Stückweise Polynominterpolation Stückweise lineare Interpolierende
1 / 32 Numerik für Ingenieure I Wintersemester 2008 J. Michael Fried Lehrstuhl Angewandte Mathematik III 23.1.2009 2 / 32 Wiederholung Stückweise Polynominterpolation Stückweise lineare Interpolierende
Zuname: Vorname: KennNr: Matr.Nr: PRÜFUNG AUS MATHEMATIK 3. 1)(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation.
 (8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
8 Gewöhnliche Differentialgleichungen
 8 Gewöhnliche Differentialgleichungen Beispiel: Radioaktiver Zerfall Sei m(t) die Menge radioaktiven Materials zur Zeit t. Der Zerfall des Materials geschieht proportional zur vorhandenen Menge mit dem
8 Gewöhnliche Differentialgleichungen Beispiel: Radioaktiver Zerfall Sei m(t) die Menge radioaktiven Materials zur Zeit t. Der Zerfall des Materials geschieht proportional zur vorhandenen Menge mit dem
Numerische Verfahren
 Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Numerik gewöhnlicher Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2014/15 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2014/15 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Numerik-Algorithmen. fyj Springer. Verfahren, Beispiele, Anwendungen. Gisela Engeln-Müllges Klaus Niederdrenk Reinhard Wodicka
 Gisela Engeln-Müllges Klaus Niederdrenk Reinhard Wodicka Numerik-Algorithmen Verfahren, Beispiele, Anwendungen Zehnte, überarbeitete und erweiterte Auflage fyj Springer Inhaltsverzeichnis Vorwort zur 10.
Gisela Engeln-Müllges Klaus Niederdrenk Reinhard Wodicka Numerik-Algorithmen Verfahren, Beispiele, Anwendungen Zehnte, überarbeitete und erweiterte Auflage fyj Springer Inhaltsverzeichnis Vorwort zur 10.
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
Dr. R. Käppeli D-ITET, D-MATL Sommer Numerische Methoden Punkte
 Dr. R. Käppeli D-ITET, D-MATL Sommer 217 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 9 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=1 Seiten) eigenhändig und handschriftlich
Dr. R. Käppeli D-ITET, D-MATL Sommer 217 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 9 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=1 Seiten) eigenhändig und handschriftlich
Differentialgleichungen
 Differentialgleichungen Viele physikalische Probleme können mathematisch als gewöhnliche Differentialgleichungen formuliert werden nur eine unabhängige Variable (meist t), z.b. Bewegungsgleichungen: gleichmäßig
Differentialgleichungen Viele physikalische Probleme können mathematisch als gewöhnliche Differentialgleichungen formuliert werden nur eine unabhängige Variable (meist t), z.b. Bewegungsgleichungen: gleichmäßig
Extrapolationsverfahren
 Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Numerik I. Gewöhnliche Differentialgleichungen. Prof.Dr.G.Wittum. Teil I:
 Numerik I Prof.Dr.G.Wittum Teil I: Gewönlice Differentialgleicungen Sommersemester 2005 INHALTSVERZEICHNIS 1 Inaltsverzeicnis 1 Numerik gewönlicer Differentialgleicungen 2 1.1 Einleitung....................................
Numerik I Prof.Dr.G.Wittum Teil I: Gewönlice Differentialgleicungen Sommersemester 2005 INHALTSVERZEICHNIS 1 Inaltsverzeicnis 1 Numerik gewönlicer Differentialgleicungen 2 1.1 Einleitung....................................
Angewandte Mathematik und Programmierung
 Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens WS 2012/13 DGL Grundlage Klassifikation Anwendung von lin. Ggln. M. konst.
Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens WS 2012/13 DGL Grundlage Klassifikation Anwendung von lin. Ggln. M. konst.
Numerische Mathematik
 Numerische Mathematik Von Prof. Dr. sc. math. Hans Rudolf Schwarz Universität Zürich Mit einem Beitrag von Prof. Dr. sc. math. Jörg Waldvogel Eidg. Technische Hochschule Zürich 4., überarbeitete und erweiterte
Numerische Mathematik Von Prof. Dr. sc. math. Hans Rudolf Schwarz Universität Zürich Mit einem Beitrag von Prof. Dr. sc. math. Jörg Waldvogel Eidg. Technische Hochschule Zürich 4., überarbeitete und erweiterte
Kapitel 3: Differentialgleichungen
 Kapitel 3: Differentialgleichungen Einführung: Vergleich zur Integration Zwischen der Integration und der Lösung von Differentialgleichungen besteht ein enger Zusammenhang: Das Aufsuchen der Lösung y(b)
Kapitel 3: Differentialgleichungen Einführung: Vergleich zur Integration Zwischen der Integration und der Lösung von Differentialgleichungen besteht ein enger Zusammenhang: Das Aufsuchen der Lösung y(b)
KAPITEL 10. Numerische Integration
 KAPITEL 10. Numerische Integration 10.1 Einleitung Sei Es gilt I Ĩ = b I = b a a f(x) f(x) dx f(x) dx, Ĩ = b b a f(x) dx. a f(x) f(x) dx (b a) f f. I Ĩ I (b a) f f b a f(x) dx = ba f dx b a f(x) dx f f
KAPITEL 10. Numerische Integration 10.1 Einleitung Sei Es gilt I Ĩ = b I = b a a f(x) f(x) dx f(x) dx, Ĩ = b b a f(x) dx. a f(x) f(x) dx (b a) f f. I Ĩ I (b a) f f b a f(x) dx = ba f dx b a f(x) dx f f
VF-3: Es seien A R n n beliebig aber regulär, b R n und gesucht sei die Lösung x R n von A x = b.
 NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
Ferienkurs Numerik Lösungsskizze. 1 Iterative Verfahren für lineare Gleichungssysteme
 Technische Universität München SoSe 1 Zentrum Mathematik Ferienkurse Dipl.-Math. Konrad Waldherr Ferienkurs Numerik Lösungsskizze 1 Iterative Verfahren für lineare Gleichungssysteme 1. Wir erhalten folgende
Technische Universität München SoSe 1 Zentrum Mathematik Ferienkurse Dipl.-Math. Konrad Waldherr Ferienkurs Numerik Lösungsskizze 1 Iterative Verfahren für lineare Gleichungssysteme 1. Wir erhalten folgende
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
 I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
2 Anfangswertprobleme gewöhnlicher Differenzialgleichungen
 2 Anfangswertprobleme gewöhnlicher Differenzialgleichungen Bei der mathematischen Modellierung von ingenieur- oder naturwissenschaftlichen Problemen treten oft Differenzialgleichungen auf. Überall dort,
2 Anfangswertprobleme gewöhnlicher Differenzialgleichungen Bei der mathematischen Modellierung von ingenieur- oder naturwissenschaftlichen Problemen treten oft Differenzialgleichungen auf. Überall dort,
2 Anfangswertprobleme gewöhnlicher Differenzialgleichungen
 2 Anfangswertprobleme gewöhnlicher Differenzialgleichungen Bei der mathematischen Modellierung von ingenieur- oder naturwissenschaftlichen Problemen treten oft Differenzialgleichungen auf. Überall dort,
2 Anfangswertprobleme gewöhnlicher Differenzialgleichungen Bei der mathematischen Modellierung von ingenieur- oder naturwissenschaftlichen Problemen treten oft Differenzialgleichungen auf. Überall dort,
Explizite Runge-Kutta-Verfahren
 Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
2.3.1 Explizite Runge-Kutta-Verfahren
 Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Numerik gewöhnlicher Differentialgleichungen
 Kapitel 3 Numerik gewöhnlicher Differentialgleichungen 3 Inhalt dieses Kapitels ist die numerische Lösung eines Systems gewöhnlicher Differentialgleichungen y (x) = f(x, y(x)) (3.) bzw. ausgeschrieben
Kapitel 3 Numerik gewöhnlicher Differentialgleichungen 3 Inhalt dieses Kapitels ist die numerische Lösung eines Systems gewöhnlicher Differentialgleichungen y (x) = f(x, y(x)) (3.) bzw. ausgeschrieben
Interpolation, numerische Integration
 Interpolation, numerische Integration 8. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 8. Mai 2014 Gliederung 1 Interpolation polynomial Spline 2 Numerische
Interpolation, numerische Integration 8. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 8. Mai 2014 Gliederung 1 Interpolation polynomial Spline 2 Numerische
Mehrschrittverfahren und Strukturerhaltung. Valentin Göbel 03. Februar 2011
 Mehrschrittverfahren und Strukturerhaltung Valentin Göbel 03. Februar 2011 1 Inhaltsverzeichnis 1 Einleitung 3 2 Arten von Mehrschrittverfahren 4 2.1 Wiederholung: Lineare Mehrschrittverfahren............
Mehrschrittverfahren und Strukturerhaltung Valentin Göbel 03. Februar 2011 1 Inhaltsverzeichnis 1 Einleitung 3 2 Arten von Mehrschrittverfahren 4 2.1 Wiederholung: Lineare Mehrschrittverfahren............
Inhaltsverzeichnis. 2 Grenzzyklen und Stabilitätskriterien VerfahrenderharmonischenBalance IdeedesVerfahrens...
 Inhaltsverzeichnis Blau nummerierte Abschnitte enthalten Grundlagen, die einen Basiskurs über nichtlineare Systeme und Regelungen bilden. Schwarz nummerierte enthalten weitergehende Informationen, die
Inhaltsverzeichnis Blau nummerierte Abschnitte enthalten Grundlagen, die einen Basiskurs über nichtlineare Systeme und Regelungen bilden. Schwarz nummerierte enthalten weitergehende Informationen, die
Klausur im Fach Numerische Methoden II Universität Siegen; Fachbereich Maschinenbau,
 Aufgabe 1 (Polynominterpolation) Abb. 1: Roboter für Positionierungsaufgaben Industrieroboter erledigen oft Positionierungsaufgaben, indem sie einen vorgegebenen Pfad abfahren. Diese Trajektorie entspricht
Aufgabe 1 (Polynominterpolation) Abb. 1: Roboter für Positionierungsaufgaben Industrieroboter erledigen oft Positionierungsaufgaben, indem sie einen vorgegebenen Pfad abfahren. Diese Trajektorie entspricht
Numerik gewöhnlicher Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2016/17 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2016/17 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
h n = (t t 0 )/n Bevor wir diesen Satz beweisen, geben wir noch einen Hilfssatz an, der eine wichtige Abschätzung liefert.
 Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
4. Runge-Kutta-Verfahren 4.1 Konstruktion und Beispiele
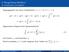 4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
4 Numerik von Anfangswertaufgaben
 4 Numerik von Anfangswertaufgaben Diese Einführung behandelt numerische Lösungsverfahren für gewöhnliche, explizite Differentialgleichungen. Ordnung. Im Folgenden wird die Variable t R die Zeit und x R
4 Numerik von Anfangswertaufgaben Diese Einführung behandelt numerische Lösungsverfahren für gewöhnliche, explizite Differentialgleichungen. Ordnung. Im Folgenden wird die Variable t R die Zeit und x R
Kap. 11: Anfangswertaufgaben: Mehrschrittverfahren
 Kap 11: Anfangswertaufgaben: Mehrschrittverfahren 111 Grundlagen und Beispiele 112 Konsistenz von Mehrschrittverfahren 113 Null-Stabilität und Konvergenz von Mehrschrittverfahren 114 Absolute und A-Stabilität
Kap 11: Anfangswertaufgaben: Mehrschrittverfahren 111 Grundlagen und Beispiele 112 Konsistenz von Mehrschrittverfahren 113 Null-Stabilität und Konvergenz von Mehrschrittverfahren 114 Absolute und A-Stabilität
(x x j ) R m [x] (3) x x j x k x j. R m [x]. (4)
![(x x j ) R m [x] (3) x x j x k x j. R m [x]. (4) (x x j ) R m [x] (3) x x j x k x j. R m [x]. (4)](/thumbs/67/57224748.jpg) 33 Interpolation 147 33 Interpolation In vielen praktischen Anwendungen der Mathematik treten Funktionen f auf, deren Werte nur näherungsweise berechnet werden können oder sogar nur auf gewissen endlichen
33 Interpolation 147 33 Interpolation In vielen praktischen Anwendungen der Mathematik treten Funktionen f auf, deren Werte nur näherungsweise berechnet werden können oder sogar nur auf gewissen endlichen
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
 I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
Numerisches Programmieren (IN0019)
 Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 11. Gewöhnliche Differenzialgleichungen................................................................................. 2
Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 11. Gewöhnliche Differenzialgleichungen................................................................................. 2
2. Gauß-Integration. Prof. Dr. Wandinger 4. Scheibenelemente FEM 4.2-1
 Die analytische Integration der Steifigkeitsmatrix für das Rechteckelement ist recht mühsam. Für Polynome gibt es eine einfachere Methode zur Berechnung von Integralen, ohne dass die Stammfunktion benötigt
Die analytische Integration der Steifigkeitsmatrix für das Rechteckelement ist recht mühsam. Für Polynome gibt es eine einfachere Methode zur Berechnung von Integralen, ohne dass die Stammfunktion benötigt
NUMERIK DER DIFFERENTIALGLEICHUNGEN. Inhaltsverzeichnis
 NUMERIK DER DIFFERENTIALGLEICHUNGEN FABIAN LUKAS MÜLLER Inhaltsverzeichnis Einschrittverfahren für Anfangsprobleme Beispiele und Problemstellung 2 Ein Existenz- und Eindeutigkeitssatz 2 3 Einschrittverfahren
NUMERIK DER DIFFERENTIALGLEICHUNGEN FABIAN LUKAS MÜLLER Inhaltsverzeichnis Einschrittverfahren für Anfangsprobleme Beispiele und Problemstellung 2 Ein Existenz- und Eindeutigkeitssatz 2 3 Einschrittverfahren
Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan :00-14:00 (120 min)
 Lehrstuhl für Angewandte Mathematik Montanuniversität Leoben 70 004 Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan. 207 2:00-4:00 (20 min) Name Matrikelnummer Mündliche Prüfung: Bitte markieren
Lehrstuhl für Angewandte Mathematik Montanuniversität Leoben 70 004 Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan. 207 2:00-4:00 (20 min) Name Matrikelnummer Mündliche Prüfung: Bitte markieren
Formelsammlung zur Numerischen Mathematik mit Turbo Pascal-Programmen
 Formelsammlung zur Numerischen Mathematik mit Turbo Pascal-Programmen von Prof. Dr. Gisela Engeln-Müllges Fachhochschule Aachen und O. Prof. em. Dr. Fritz Reutter f Rheinisch-Westfälische Technische Hochschule
Formelsammlung zur Numerischen Mathematik mit Turbo Pascal-Programmen von Prof. Dr. Gisela Engeln-Müllges Fachhochschule Aachen und O. Prof. em. Dr. Fritz Reutter f Rheinisch-Westfälische Technische Hochschule
Inhaltsverzeichnis. Kapitel 1: Rechnen mit Zahlen. Kapitel 2: Umformen von Ausdrücken. Kapitel 3: Gleichungen, Ungleichungen, Gleichungssysteme
 Kapitel 1: Rechnen mit Zahlen 1.1 Rechnen mit reellen Zahlen 1.2 Berechnen von Summen und Produkten 1.3 Primfaktorzerlegung 1.4 Größter gemeinsamer Teiler 1.5 Kleinstes gemeinsames Vielfaches 1.6 n-te
Kapitel 1: Rechnen mit Zahlen 1.1 Rechnen mit reellen Zahlen 1.2 Berechnen von Summen und Produkten 1.3 Primfaktorzerlegung 1.4 Größter gemeinsamer Teiler 1.5 Kleinstes gemeinsames Vielfaches 1.6 n-te
Numerisches Programmieren (IN0019) 11. Gewöhnliche Differenzialgleichungen. Differenzialgleichungen. Differenzialgleichungen (Physik)
 umerisches Programmieren (I19) Frank R. Schmidt 11. Gewöhnliche Differenzialgleichungen Winter Semester 16/17 Differenzialgleichungen (Phsik) Differenzialgleichungen Phsikalische Prozesse lassen sich mit
umerisches Programmieren (I19) Frank R. Schmidt 11. Gewöhnliche Differenzialgleichungen Winter Semester 16/17 Differenzialgleichungen (Phsik) Differenzialgleichungen Phsikalische Prozesse lassen sich mit
Numerik-Algorithmen VERLA3. Entscheidungshilfe zur Auswahl und Nutzung. Prof. Dr.rer.nat. Gisela Engeln-Müllges Prof. Dr.rer.techn.
 Numerik-Algorithmen Entscheidungshilfe zur Auswahl und Nutzung Prof. Dr.rer.nat. Gisela Engeln-Müllges Prof. Dr.rer.techn. Fritz Reutter t 8., neubearbeitete und erweiterte Auflage VERLA3 Inhaltsverzeichnis
Numerik-Algorithmen Entscheidungshilfe zur Auswahl und Nutzung Prof. Dr.rer.nat. Gisela Engeln-Müllges Prof. Dr.rer.techn. Fritz Reutter t 8., neubearbeitete und erweiterte Auflage VERLA3 Inhaltsverzeichnis
Unstetige Galerkin-Verfahren und die lineare Transportgleichung. Tobias G. Pfeiffer Freie Universität Berlin
 Unstetige Galerkin-Verfahren und die lineare Transportgleichung Tobias G. Pfeiffer Freie Universität Berlin Seminar DG-Verfahren, 26. Mai 2009 , Voraussetzungen & Ziele Voraussetzungen Kenntnisse in Numerik
Unstetige Galerkin-Verfahren und die lineare Transportgleichung Tobias G. Pfeiffer Freie Universität Berlin Seminar DG-Verfahren, 26. Mai 2009 , Voraussetzungen & Ziele Voraussetzungen Kenntnisse in Numerik
Numerik für Ingenieure und Naturwissenschaftler
 Springer-Lehrbuch Numerik für Ingenieure und Naturwissenschaftler Bearbeitet von Wolfgang Dahmen, Arnold Reusken überarbeitet 2008. Taschenbuch. XVIII, 633 S. Paperback ISBN 978 3 540 76492 2 Format (B
Springer-Lehrbuch Numerik für Ingenieure und Naturwissenschaftler Bearbeitet von Wolfgang Dahmen, Arnold Reusken überarbeitet 2008. Taschenbuch. XVIII, 633 S. Paperback ISBN 978 3 540 76492 2 Format (B
11. Einschrittverfahren
 H.J. Oberle Differentialgleichungen I WiSe 2012/13 A. Allgemeines. 11. Einschrittverfahren Es geht in diesem Abschnitt um die numerische Lösung einer AWA y (t) = f(t, y(t)), y(t 0 ) = y 0. (11.1) Aufgabe
H.J. Oberle Differentialgleichungen I WiSe 2012/13 A. Allgemeines. 11. Einschrittverfahren Es geht in diesem Abschnitt um die numerische Lösung einer AWA y (t) = f(t, y(t)), y(t 0 ) = y 0. (11.1) Aufgabe
Numerische Mathematik
 Hans Rudolf Schwarz I Norbert Köckler Numerische Mathematik 8., aktualisierte Auflage STUDIUM VIEWEG+, TEUBNER / Iahalt Einleitung 13 1 Fehlertheorie 15 1.1 Fehlerarten 15 1.2 Zahldarstellung 16 1.3 Rundungsfehler
Hans Rudolf Schwarz I Norbert Köckler Numerische Mathematik 8., aktualisierte Auflage STUDIUM VIEWEG+, TEUBNER / Iahalt Einleitung 13 1 Fehlertheorie 15 1.1 Fehlerarten 15 1.2 Zahldarstellung 16 1.3 Rundungsfehler
Inhaltsverzeichnis Kapitel 1: Rechnen mit Zahlen... 1 Kapitel 2: Umformen von Ausdrücken... 10
 Kapitel 1: Rechnen mit Zahlen...1 1.1 Rechnen mit reellen Zahlen...2 1.2 Berechnen von Summen und Produkten...3 1.3 Primfaktorzerlegung...4 1.4 Größter gemeinsamer Teiler...4 1.5 Kleinstes gemeinsames
Kapitel 1: Rechnen mit Zahlen...1 1.1 Rechnen mit reellen Zahlen...2 1.2 Berechnen von Summen und Produkten...3 1.3 Primfaktorzerlegung...4 1.4 Größter gemeinsamer Teiler...4 1.5 Kleinstes gemeinsames
ZWEITE KLAUSUR zur Numerik I mit Lösungen. Bitte folgende Angaben ergänzen und DEUTLICH LESBAR in Druckbuchstaben schreiben:
 MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE FELIX LIEDER DR. GEORG JANSING.9.7 ZWEITE KLAUSUR zur Numerik I mit Lösungen Bitte folgende Angaben ergänzen und DEUTLICH LESBAR in Druckbuchstaben schreiben:
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE FELIX LIEDER DR. GEORG JANSING.9.7 ZWEITE KLAUSUR zur Numerik I mit Lösungen Bitte folgende Angaben ergänzen und DEUTLICH LESBAR in Druckbuchstaben schreiben:
Numerische Mathematik I
 Numerische Mathematik I Vorlesungsmitschrift Prof. Dr. Dr. h.c. H.G. Bock Interdisziplinäres Zentrum für Wissenschaftliches Rechnen Universität Heidelberg Sommersemester 2002 Stand: 3. November 2004 Korrekturen
Numerische Mathematik I Vorlesungsmitschrift Prof. Dr. Dr. h.c. H.G. Bock Interdisziplinäres Zentrum für Wissenschaftliches Rechnen Universität Heidelberg Sommersemester 2002 Stand: 3. November 2004 Korrekturen
Stefan A. Funken Numerische Mathematik IV
 Stefan A. Funken Numerische Mathematik IV SKRIPT, UNIVERSITÄT ULM, SOMMERSEMESTER 200 i Vorbemerkung. Copyright. Alle Rechte, insbesondere das Recht auf Vervielfältigung und Verbreitung sowie der Übersetzung,
Stefan A. Funken Numerische Mathematik IV SKRIPT, UNIVERSITÄT ULM, SOMMERSEMESTER 200 i Vorbemerkung. Copyright. Alle Rechte, insbesondere das Recht auf Vervielfältigung und Verbreitung sowie der Übersetzung,
Numerische Mathematik
 Hans Rudolf Schwarz I Norbert Köckler Numerische Mathematik 8., aktualisierte Auflage STUDIUM 11 VIEWEG+ TEUBNER Inhalt Einleitung 13 1 1.1 1.2 1.3 1.4 1..5 1.6 1.7 2 2.1 2.1.1 2.1.2 2.1.3 2.2 2.2.1 2.2.2
Hans Rudolf Schwarz I Norbert Köckler Numerische Mathematik 8., aktualisierte Auflage STUDIUM 11 VIEWEG+ TEUBNER Inhalt Einleitung 13 1 1.1 1.2 1.3 1.4 1..5 1.6 1.7 2 2.1 2.1.1 2.1.2 2.1.3 2.2 2.2.1 2.2.2
