Dieses Vielfach hängt ab von der Form der Nutzenfunktion. Man bezeichnet dies auch als Arrow-Pratt Koeffizient.
|
|
|
- Martin Baum
- vor 7 Jahren
- Abrufe
Transkript
1 Die Riskoprämie ergibt sich also als ein Vielfaches der Varianz der zugrundeliegenden Unsicherheit Dieses Vielfach hängt ab von der Form der Nutzenfunktion. Man bezeichnet dies auch als Arrow-Pratt Koeffizient. Der Arrow-Pratt Koeffizient ist ein nützliches Mass für die absolute Risikoaversion des Haushaltes. Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
2 Bisher haben wir uns nur angeschaut wie Individuen Risiko bewerten. Wir haben dabei ein Maß für die Risikoeinstellung ermittelt. Ein zweiter wichtiger Punkt bleibt dabei offen: Wie messen wir überhaupt Riskiko? Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
3 Ein Maß für Risiko soll uns also zeigen wie risikoreich eine bestimmte Situation/Lotterie für ein Individuum ist. Die Idee ist dabei, dass ein risikoaverses Individuum eine Situation mit weniger Risiko einer Situation mit mehr Risiko vorzieht. Das Risikomaß soll also eine entsprechende Reihung der Lotterien generieren. Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
4 Das erste mögliche und intuitive Risikomaß ist natürlich die Varianz einer Lotterie. Eine Situation in der das Einkommen einer größeren Variation unterliegt hat auch eine höheres Risiko. Der Vorteil der Varianz ist, dass diese leicht zu ermitteln und intuitiv ist. Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
5 Der große Nachteil ist aber, dass die zu kurz greift, weil der erwartete Nutzen (bzw. payoff) nicht nur eine Funktion der Varianz ist. Eine Lotterie mit einer höheren Varianz muss nicht unbedingt mit einem höheren Risiko verbunden sein. Auch die weitere Momente der Verteilung spielen eine wichtige Rolle. Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
6 Stellen wir uns vor, dass der Haushalt sich einer (stochastischen) Auszahlung in Höhe von y s = ȳ + z s (siehe oben) gegenübersieht. Der Nutzen kann dann geschrieben werden als u(y s ) = u(ȳ + z s ) bzw. als Taylor Reihe u(y s ) = u(ȳ) + u (ȳ)z s + 1 2! u (ȳ)zs ! u (ȳ)zs 3... Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
7 Damit ergibt sich der Erwartungswert des Nutzens als E(u(y s )) = E(u(ȳ)) + 1 2! u (ȳ)e(z 2 s ) + n=3 1 n! un (ȳ)e(z n s ) Da der Erwartungswert von z s Null ist, ist die Varianz E(z 2 s ) bzw. die höheren Momente E(z n s ) Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
8 Es kann also Situationen geben in denen eine Lotterie eine höhere Varianz als eine andere hat, der erwartete Nutzen aber dennoch größer ist. Dann ist die Varianz natürlich kein vernünftiges Maß für Risiko. Dies ist nur der Fall bei speziellen Nutzenfunktionen und/oder Einkommensverteilungen. Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
9 Um diesem Problem zu begegnen wurden weitere Maße für Risiko vorgeschlagen. 1. stochastische Dominanz 2. mean-preserving spread Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
10 Nehmen wir an, das Einkommen Y sei eine Zufallsvariable. Nehmen wir weiterhin an, dass wir diese so normieren können dass y [0, 1]. Betrachten wir nun eine Verteilungsfunktion F i (y) (mit zugehöriger Dichte f i (y)), wobei i irgendeine Verteilung angibt. Von stochastischer Dominanz erster Ordnung spricht man immer dann, wenn F 1 (y) F 2 (y) y und F 1 (y) > F 2 (y) für min. ein y. Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
11 In diesem Fall hat Verteilung 2 stochastische Dominanz über Verteilung 1. Salopp kann man sagen, dass die Wahrscheinlichkeit für ein Einkommen von y oder kleiner, bei Verteilung 1 größer ist als bei Verteilung 2. damit gilt aber auch folgender Satz. Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
12 Satz Wenn Verteilung 2 die Verteilung 1 stochastisch dominiert, dann ist der erwartete Nutzen unter Verteilung 2 größer als unter Verteilung 1. Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
13 Beweis Der erwartete Nutzen (abhängig von der Verteilung i) ist E i (u(y)) = 1 0 f i (y)u(y)dy. Partielles integrieren (uv = u v + v u, hier v = f ) gibt E i (u(y)) = (u(1)f i (1) u(0)f i (0)) 1 0 F i (y)u (y)dy Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
14 Damit kann man aber zeigen, dass für E 2 (u(y)) E 1 (u(y)) folgendes gilt E 2 (u(y)) E 1 (u(y)) = 1 0 (F 1 (y) F 2 (y))u (y) > 0 Die Definition der stochastischen Dominanz beweist den Satz. Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
15 Das Konzept der stochastischen Dominanz legt strenge Restriktionen auf die zu vergleichenden Verteilungen. Faktisch sind nur Verteilungen vergleichbar, deren Verteilungsfunktionen sich nicht schneiden. Diese harte Restriktion ist aber in vielen Fällen nicht praktikabel. Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
16 Ein zweites Konzept zur Messung des Risikos zielt deshalb weniger auf die absoluten Werte der Verteilungsfunktion sondern vielmehr auf die Fläche unter der Funktion ab. Definiere die Fläche unter der Verteilungsfunktion als T (ȳ) = ȳ 0 F (y)dy. Für den Erwartungswert gilt E(y) = 1 0 yf (y)dy = [yf (y)] F (y)dy E(y) = 1 T (1) Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
17 Mit Hilfe dieser Größen kann man nun zwei Verteilungen 1 und 2 bzgl. des Risikos miteinander vergleichen. Eine Verteilung 2 hat stochastische Dominanz zweiter Ordnung über Verteilung 1, wenn T 1 (y) T 2 (y) gilt, wobei für manche y dies als Ungleichheit halten muss. Eine Verteilung hat also stochastische Dominanz zweiter Ordnung, wenn die Fläche unter der Verteilungsfunktion immer kleiner oder gleich der einer anderen Verteilung ist. Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
18 Satz Hat Verteilung 2 stochastische Dominanz zweiter Ordnung über Verteilung 1, dann ist der erwartete Nutzen unter Verteilung 2 größer als unter Verteilung 1. Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
19 Beweis Wir haben gezeigt, dass folgendes gilt: E 2 (u(y)) E 1 (u(y)) = 1 0 (F 1 (y) F 2 (y))u (y) Löst man nun die rechte Seite der Gleichung (partielles Integrieren!) so erhält man Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
20 (T 1 (1) T 2 (1))u (1) (T 1 (0) T 2 (0))u (0) 1 0 (T 1 (y) T 2 (y))u (y) > 0. Dieser Ausdruck ist aber eben wegen der Annahme der stochastischen Dominanz zweiter Ordnung positiv. Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
21 Der wichtige Punkt bei dem Konzept der stochastischen Dominanz zweiter Ordnung ist, dass es sehr eng mit dem Konzept des mean-preserving spread verbunden ist. Eine Verteilung 1 ist ein mean-preserving spread der Verteilung 2, wenn diese einen identischen Erwartungswert habe, aber Verteilung 1 mehr Wahrscheinlichkeitsmasse an den Rändern hat ( fettere Enden ). Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
22 Formal bedeutet dies, dass innerhalb eines beliebigen Intervalls f 2 (y) > f 1 (y) bzw. f 2 (y) < f 1 (y) außerhalb dieses Intervalls. Beginnen wir also am linken Rand die Werte für die Dichte zu addieren (und damit die Verteilungsfunktion zu ermitteln), so ist F 1 (y) > F 2 (y) und zwar bis zu einem Schwellenwert ȳ und danach F 1 (y) < F 2 (y). Dies ist die single crossing property des mean preserving spread. Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
23 Wegen dieser Eigenschaft muss aber für die Fläche unter der Verteilungsfunktion gelten, dass T 1 (y) T 2 (y) 0 bzw. > für einige y. Weiterhin gilt natürlich per Definition T 1 (1) = T 2 (1). Damit impliziert der mean preserving spread aber die stochastische Dominanz zweiter Ordnung. Risikoaverse Individuen verlieren also durch einen mean-preserving spread Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
24 Wir haben uns bisher angeschaut, wie die Haushalte gemäß ihrer Risikoeinstellung klassifiziert werden können und wie das Risiko verschiedener Lotterien (Verteilungen) verglichen werden kann. In einem nächsten Schritt wollen wir uns anschauen, wie ein Haushalt mit Risiko umgeht, wenn es Versicherungen gibt. Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
25 Problem: Das Einkommen des Haushaltes hängt vom Zustand der Welt s ab. Nehmen wir an, dass es 2 dieser Zustände gibt. Das Einkommen ist dann y 1 = y und y 2 = y L. L mögen dabei die Kosten eines Unfalls darstellen. Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
26 Dem Haushalt bietet sich nun die Möglichkeit über einen Versicherungskontrakt Ressourcen von einem Zustand in den anderen Zustand zu verschieben. Der Preis um einen Euro zu verschieben sei nun p. Bezahlt der Haushalt also pq, so erhält dieser q falls der Zustand 2 eintritt. Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
27 Weiterhin nehmen wir an, dass π i die Wahrscheinlichkeit für den Zustand i ist. Sowohl das Individuum als auch der Versicherer kennen diese Wahrscheinlichkeit keine Adverse Selektion. Der Versicherungsnehmer hat weder Einfluss auf die Schadenshöhe noch auf die Schadenswahrscheinlickeit kein Moral Hazard Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
28 Gegeben diese Information, kann das Einkommen des Haushaltes in den beiden Situationen dargestellt werden: y 1 = y pq y 2 = y pq L + q Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
29 Damit konstituieren diese beiden Gleichungen so etwas wie eine Budgetrestriktion. Das verbindende Element zwischen diesen beiden Zuständen der Welt ist die Höhe der Versicherung q. Der Haushalt wählt endogen die Versicherungssumme q, die den erwarteten Nutzen maximiert. Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
30 Bevor wir uns dem Maximierungsproblem des Haushaltes widmen wollen wir uns noch die Bedingung für eine faire Versicherungsprämie anschauen. Eine faire Versicherungsprämie liegt immer dann vor, wenn sich das erwartete Einkommen nicht ändert. Erwartetes Einkommen ohne Versicherung π 1 (y) + π 2 (y L) = y π 2 L, wobei natürlich π 1 + π 2 = 1. Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
31 Erwartetes Einkommen mit Versicherung π 1 (y pq) + π 2 (y L pq + q) = y pq π 2 L + π 2 q Wenn also die Prämie p der Schadenseintrittswahrscheinlichkeit π 2 entspricht, so handelt es sich um eine faire Versicherung. Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
32 Wie sieht nun das optimal Verhalten eines Haushaltes aus? Zielfunktion E(u) = π 1 u(y pq) + π 2 u(y L pq + q) Die Bedingung erster Ordnung für die optimale Wahl des Versicherungsschutzes (alle anderen Größen sind exogen!) ist dann: π 1 u (y pq)( 1)p + π 2 u (y L pq + q)(1 p) = 0 Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
33 Dies Bedingung kann umgeschrieben werden zu: p(π 1 u (y pq) + π 2 u (y L pq + q)) = π 2 u (y L pq + q) Die Grenzkosten der Versicherung (linke Seite), d.h. der Einkommenverlust in Höhe von p muss im Optimum genau so groß sein wie der Grenzertrag. Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
34 Wie hoch wir nun der optimale Versicherungsschutz sein, wenn die Prämie der Versicherung fair ist, d.h. p = π 2? In diesem Fall gilt im Optimum π 1 u (y pq) + (1 π 1 )u (y L pq + q) = u (y L pq + q) Dies impliziert aber, dass u (y pq) = u (y L pq + q). Dies kann nur wahr sein, wenn q = L Der Haushalt wird sich also bei fairer Prämie komplett absichern. Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL February 2, / 311
1. Adverse Selektion: Unsicherheit über die Schadenswahrscheinlichkeit 2. Moral Hazard: endogene Schadenshöhe.
 In der bisherigen Analyse haben wir angenommen, dass die Schadenshöhe exogen ist und die Eintrittswahrscheinlichkeit allgemein bekannt ist. Damit schließen wir aber zwei extrem wichtige Charakteristika
In der bisherigen Analyse haben wir angenommen, dass die Schadenshöhe exogen ist und die Eintrittswahrscheinlichkeit allgemein bekannt ist. Damit schließen wir aber zwei extrem wichtige Charakteristika
L mögen dabei die Kosten eines Unfalls darstellen.
 Problem: Das Einkommen des Haushaltes hängt vom Zustand der Welt s ab. Nehmen wir an, dass es 2 dieser Zustände gibt. Das Einkommen ist dann y 1 = y und y 2 = y L. L mögen dabei die Kosten eines Unfalls
Problem: Das Einkommen des Haushaltes hängt vom Zustand der Welt s ab. Nehmen wir an, dass es 2 dieser Zustände gibt. Das Einkommen ist dann y 1 = y und y 2 = y L. L mögen dabei die Kosten eines Unfalls
Vergleich von Entscheidungsträgern bzgl. ihrer Risikoaversion:
 Ist das Arrow-Pratt-Maß der absoluten Risikoaversion bekannt, so lässt sich daraus die Nutzenfunktion bestimmen: Mithilfe der Substitution y := U (w) dy = U (w)dw gilt: und daher U (w) U (w) dw = A a (w)dw
Ist das Arrow-Pratt-Maß der absoluten Risikoaversion bekannt, so lässt sich daraus die Nutzenfunktion bestimmen: Mithilfe der Substitution y := U (w) dy = U (w)dw gilt: und daher U (w) U (w) dw = A a (w)dw
wf = w 0 +E( x) Die Definition des Angebotspreises p a = wf w 0 ergibt daher: p a = E( x)
 Satz: Im Fall dass die Nutzenfunktion des Entscheidungsträgers linear bezüglich des End-Vermögens ist, stimmt der Angebotspreis einer Lotterie mit deren Erwartungswert E( x) überein Da U linear ist, gilt:
Satz: Im Fall dass die Nutzenfunktion des Entscheidungsträgers linear bezüglich des End-Vermögens ist, stimmt der Angebotspreis einer Lotterie mit deren Erwartungswert E( x) überein Da U linear ist, gilt:
Lösungshinweise zu Übungsblatt 2
 Lösungshinweise zu Übungsblatt 2 Aufgabe 1: Unsicherheit Gegeben sei ein Individuum mit streng monoton steigender und konkaver von Neumann- Morgenstern Nutzenfunktion. a) Erklären Sie anhand einer geeigneten
Lösungshinweise zu Übungsblatt 2 Aufgabe 1: Unsicherheit Gegeben sei ein Individuum mit streng monoton steigender und konkaver von Neumann- Morgenstern Nutzenfunktion. a) Erklären Sie anhand einer geeigneten
Roy s Identity. Bisher haben wir uns die Effekte von Einkommensänderungen angesehen. Nun widmen wir uns den Preisänderungen.
 Roy s Identity Bisher haben wir uns die Effekte von Einkommensänderungen angesehen. Nun widmen wir uns den Preisänderungen. Es gilt: U(f (p, W ))/ p j = λx j Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang
Roy s Identity Bisher haben wir uns die Effekte von Einkommensänderungen angesehen. Nun widmen wir uns den Preisänderungen. Es gilt: U(f (p, W ))/ p j = λx j Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang
Vorlesung 3: Versicherungsnachfrage
 Vorlesung 3: Versicherungsnachfrage Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie, FS 12 Versicherungsnachfrage 1/20 2 / 20 3. 1 Das Versicherungsnachfrageproblem
Vorlesung 3: Versicherungsnachfrage Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie, FS 12 Versicherungsnachfrage 1/20 2 / 20 3. 1 Das Versicherungsnachfrageproblem
Vorlesung 3: Risikoaversion
 Vorlesung 3: Risikoaversion Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 3 (FS 11) Risikoaversion 1 / 21 1. Modellrahmen In diesem Kapitel betrachten wir nur monetäre
Vorlesung 3: Risikoaversion Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 3 (FS 11) Risikoaversion 1 / 21 1. Modellrahmen In diesem Kapitel betrachten wir nur monetäre
Kapitel 3. Probleme der Krankenversicherung. 3.1 Überblick 3.2 Ex-ante Moral Hazard 3.3 Ex-post Moral Hazard 3.4 Lösungen bei Moral Hazard
 Kapitel 3 Probleme der Krankenversicherung 3.1 Überblick 3.2 Ex-ante Moral Hazard 3.3 Ex-post Moral Hazard 3.4 Lösungen bei Moral Hazard Literatur: BZK 6 (Auszüge), Breyer und Buchholz 6.2.1 Hendrik Schmitz
Kapitel 3 Probleme der Krankenversicherung 3.1 Überblick 3.2 Ex-ante Moral Hazard 3.3 Ex-post Moral Hazard 3.4 Lösungen bei Moral Hazard Literatur: BZK 6 (Auszüge), Breyer und Buchholz 6.2.1 Hendrik Schmitz
Ein Kerninteresse bei der Modellierung ökonomischer Fragestellungen ist die komparative Statik.
 Ein Kerninteresse bei der Modellierung ökonomischer Fragestellungen ist die komparative Statik. Es wird also gefragt was mit dem Gleichgewicht passiert, wenn sich der Vektor der exogenen Größen (der Paramter)
Ein Kerninteresse bei der Modellierung ökonomischer Fragestellungen ist die komparative Statik. Es wird also gefragt was mit dem Gleichgewicht passiert, wenn sich der Vektor der exogenen Größen (der Paramter)
Wann ist diese Vorgehensweise berechtigt? Hierzu:
 IV. Risiko und Unsicherheit Risiko: Eine Entscheidung treffen, ohne den wahren Zustand der Welt zu kennen. Aber man kennt die Wahrscheinlichkeitsverteilung für die relevanten Zustände der Welt. z. B. {
IV. Risiko und Unsicherheit Risiko: Eine Entscheidung treffen, ohne den wahren Zustand der Welt zu kennen. Aber man kennt die Wahrscheinlichkeitsverteilung für die relevanten Zustände der Welt. z. B. {
Neue Institutionenökonomik, Aufgabe 18 Seite 1
 Neue Institutionenökonomik, Aufgabe 18 Seite 1 Allgemeine Informationen zum Principal-Agent-Modell Es geht hier nun um die Vertragsausgestaltung zwischen dem Eigentümer (Prinzipal) einer Firma und dem
Neue Institutionenökonomik, Aufgabe 18 Seite 1 Allgemeine Informationen zum Principal-Agent-Modell Es geht hier nun um die Vertragsausgestaltung zwischen dem Eigentümer (Prinzipal) einer Firma und dem
Übung zu Risiko und Versicherung Entscheidungstheoretische Grundlagen
 Übung zu Risiko Entscheidungstheoretische Grundlagen Stefan Neuß Sebastian Soika http://www.inriver.bwl.lmu.de Newsletter Auf der Homepage unter http://www.inriver.bwl.uni-muenchen.de/studium/sommer_203/bachelorveranstaltungen/risiko_und_versicherungen/index.html
Übung zu Risiko Entscheidungstheoretische Grundlagen Stefan Neuß Sebastian Soika http://www.inriver.bwl.lmu.de Newsletter Auf der Homepage unter http://www.inriver.bwl.uni-muenchen.de/studium/sommer_203/bachelorveranstaltungen/risiko_und_versicherungen/index.html
Vorlesung 2: Risikopräferenzen im Zustandsraum
 Vorlesung 2: Risikopräferenzen im Zustandsraum Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie VL 2, FS 12 Risikopräferenzen im Zustandsraum 1/29 2.1 Motivation
Vorlesung 2: Risikopräferenzen im Zustandsraum Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie VL 2, FS 12 Risikopräferenzen im Zustandsraum 1/29 2.1 Motivation
Grundzüge der. Kapitel 5 Mikroökonomie (Mikro I) Entscheidungen unter Unsicherheit
 Grundzüge der Kapitel 5 Mikroökonomie (Mikro I) Entscheidungen unter Unsicherheit 1 BESCHREIBUNG VON RISIKO 2 Entscheidung unter Risiko Annahme: Wir kennen alle möglichen (sich gegenseitig ausschliessenden)
Grundzüge der Kapitel 5 Mikroökonomie (Mikro I) Entscheidungen unter Unsicherheit 1 BESCHREIBUNG VON RISIKO 2 Entscheidung unter Risiko Annahme: Wir kennen alle möglichen (sich gegenseitig ausschliessenden)
2.4 Entscheidung bei Risiko
 2.4 Entscheidung bei Risiko Entscheidung bei Risiko nimmt an, dass für jeden Zustand S j seine Eintrittswahrscheinlichkeit P(S j ) bekannt ist Eintrittswahrscheinlichkeiten bestimmbar als statistische
2.4 Entscheidung bei Risiko Entscheidung bei Risiko nimmt an, dass für jeden Zustand S j seine Eintrittswahrscheinlichkeit P(S j ) bekannt ist Eintrittswahrscheinlichkeiten bestimmbar als statistische
Vorlesung. Informationsökonomik und die Theorie der Firma
 Vorlesung Informationsökonomik und die Theorie der Firma Ulrich Schwalbe Universität Hohenheim 2. Vorlesung 24.10.2007 Ulrich Schwalbe (Universität Hohenheim) Informationsökonomik 2. Vorlesung 24.10.2007
Vorlesung Informationsökonomik und die Theorie der Firma Ulrich Schwalbe Universität Hohenheim 2. Vorlesung 24.10.2007 Ulrich Schwalbe (Universität Hohenheim) Informationsökonomik 2. Vorlesung 24.10.2007
Übung zu Risiko und Versicherung Entscheidungstheoretische Grundlagen
 Übung zu Risiko Entscheidungstheoretische Grundlagen Christoph Lex Dominik Lohmaier http://www.inriver.bwl.lmu.de Newsletter Auf der Homepage unter http://www.inriver.bwl.uni-muenchen.de/studium/sommer_04/bachelorveranstaltungen/risiko_und_versicherungen/index.html
Übung zu Risiko Entscheidungstheoretische Grundlagen Christoph Lex Dominik Lohmaier http://www.inriver.bwl.lmu.de Newsletter Auf der Homepage unter http://www.inriver.bwl.uni-muenchen.de/studium/sommer_04/bachelorveranstaltungen/risiko_und_versicherungen/index.html
I. Grundlagen. I. Grundlagen 1. Entscheidungen unter Unsicherheit. 1. Entscheidungen unter Unsicherheit
 . Entscheidungen unter Unsicherheit I. Grundlagen. Entscheidungen unter Unsicherheit Elemente des Entscheidungsproblems eines Wirtschaftssubekts: Der Entscheidungsträger kann zwischen verschiedenen Aktionen
. Entscheidungen unter Unsicherheit I. Grundlagen. Entscheidungen unter Unsicherheit Elemente des Entscheidungsproblems eines Wirtschaftssubekts: Der Entscheidungsträger kann zwischen verschiedenen Aktionen
geplante Produktion a tatsächliche Produktion ã. Abweichung von geplanter Produktion etwa durch Streiks, Klima, Ausfall von Maschinen, etc.
 Produktionsentscheidungen unter Risiko Man kann folgende Ursachen des Risikos unterscheiden: 1. Risiko durch den Markt. Unsichere Verkaufspreise: Zu Beginn der Produktion weiss der Unternehmer die Produktionskosten.
Produktionsentscheidungen unter Risiko Man kann folgende Ursachen des Risikos unterscheiden: 1. Risiko durch den Markt. Unsichere Verkaufspreise: Zu Beginn der Produktion weiss der Unternehmer die Produktionskosten.
Bachelorprüfung für Volkswirte
 Bachelorprüfung für Volkswirte Mikroökonomie II Dr. Peter Schwardmann 12. Februar 2015 Bitte beantworten Sie die folgenden drei Aufgaben. Zur Bearbeitung der Klausur stehen Ihnen 90 Minuten zur Verfügung.
Bachelorprüfung für Volkswirte Mikroökonomie II Dr. Peter Schwardmann 12. Februar 2015 Bitte beantworten Sie die folgenden drei Aufgaben. Zur Bearbeitung der Klausur stehen Ihnen 90 Minuten zur Verfügung.
Fortgeschrittene VWL Theorie
 Fortgeschrittene VWL Theorie Jörg Lingens WWU Münster October 27, 2009 Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL October 27, 2009 1 / 306 Einführung/Motivation Komplexität der Volkswirtschaftslehre
Fortgeschrittene VWL Theorie Jörg Lingens WWU Münster October 27, 2009 Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL October 27, 2009 1 / 306 Einführung/Motivation Komplexität der Volkswirtschaftslehre
Kapitel 13: Unvollständige Informationen
 Kapitel 13: Unvollständige Informationen Hauptidee: Für das Erreichen einer effizienten Allokation auf Wettbewerbsmärkten ist es notwendig, dass jeder Marktteilnehmer dieselben Informationen hat. Informationsasymmetrie
Kapitel 13: Unvollständige Informationen Hauptidee: Für das Erreichen einer effizienten Allokation auf Wettbewerbsmärkten ist es notwendig, dass jeder Marktteilnehmer dieselben Informationen hat. Informationsasymmetrie
c 2 c 1 AVWL I (WS 1996/97) 2-24 Prof. Dr. K. Schmidt 50 r r r v 30 Figur 2.7: Indierenzkurven bei Unischerheit Punkt im (c 1 ; c 2 )-Diagramm ist ein
 AVWL I (WS 1996/97) 2-23 Prof. Dr. K. Schmidt 2.7 Unsicherheit haben wir eine deterministische Welt betrachtet: Alle Bisher trafen mit Sicherheit ein. Ereignisse passiert, wenn sich der Konsument nicht
AVWL I (WS 1996/97) 2-23 Prof. Dr. K. Schmidt 2.7 Unsicherheit haben wir eine deterministische Welt betrachtet: Alle Bisher trafen mit Sicherheit ein. Ereignisse passiert, wenn sich der Konsument nicht
Aufgabe 1.3. Teil a) Teil b)
 Informationsökonomik: Anreize, Verträge, Institutionen L ösung Blatt 1 FT 2012 Aufgabe 1.3 Faire Prämie Versicherungen können nicht beobachten, welchen Typen sie vor sich haben, daher werden sie den Erwartungswert
Informationsökonomik: Anreize, Verträge, Institutionen L ösung Blatt 1 FT 2012 Aufgabe 1.3 Faire Prämie Versicherungen können nicht beobachten, welchen Typen sie vor sich haben, daher werden sie den Erwartungswert
Versicherungsökonomie Lösungshinweise zu dem Aufgabenblatt zu Vorlesung 4
 Georg Nöldeke Frühjahr 2012 Versicherungsökonomie Lösungshinweise zu dem Aufgabenblatt zu Vorlesung 4 1. Ist Individuum 1 risikoneutral, so ist u konstant. Insbesondere gilt also für beliebieg Allokationen
Georg Nöldeke Frühjahr 2012 Versicherungsökonomie Lösungshinweise zu dem Aufgabenblatt zu Vorlesung 4 1. Ist Individuum 1 risikoneutral, so ist u konstant. Insbesondere gilt also für beliebieg Allokationen
Vorlesung. Informationsökonomik und die Theorie der Firma
 Vorlesung Informationsökonomik und die Theorie der Firma Ulrich Schwalbe Universität Hohenheim 3. Vorlesung 14.11.2007 Ulrich Schwalbe (Universität Hohenheim) Informationsökonomik 3. Vorlesung 14.11.2007
Vorlesung Informationsökonomik und die Theorie der Firma Ulrich Schwalbe Universität Hohenheim 3. Vorlesung 14.11.2007 Ulrich Schwalbe (Universität Hohenheim) Informationsökonomik 3. Vorlesung 14.11.2007
Bearbeiten Sie vier der fünf Aufgaben A1-A5 und zwei der drei Aufgaben B1-B3!
 Master-Kursprüfung Kapitalmarkttheorie 2 Schwerpunktmodul Finanzmärkte 6 Kreditpunkte Bearbeitungsdauer: 90 Minuten SS 2017 21.08.2017 Prof. Dr. Lutz Arnold Bitte gut leserlich ausfüllen: Name: Vorname:
Master-Kursprüfung Kapitalmarkttheorie 2 Schwerpunktmodul Finanzmärkte 6 Kreditpunkte Bearbeitungsdauer: 90 Minuten SS 2017 21.08.2017 Prof. Dr. Lutz Arnold Bitte gut leserlich ausfüllen: Name: Vorname:
Vorlesung 4: Risikoallokation
 Vorlesung 4: Risikoallokation Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie, FS 12 Risikoallokation 1/23 2 / 23 4.1 Einleitung Bisher haben wir uns ausschliesslich
Vorlesung 4: Risikoallokation Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie, FS 12 Risikoallokation 1/23 2 / 23 4.1 Einleitung Bisher haben wir uns ausschliesslich
3. Betriebswirtschaftliche Entscheidungslehre 3.6 Entscheidung unter Risiko
 Dominanzprinzipien : Absolute Dominanz: Eine Alternative A i dominiert eine Alternative A j absolut, wenn das geringstmögliche Ergebnis von A i nicht kleiner ist als das grösstmögliche Ergebnis von A j,
Dominanzprinzipien : Absolute Dominanz: Eine Alternative A i dominiert eine Alternative A j absolut, wenn das geringstmögliche Ergebnis von A i nicht kleiner ist als das grösstmögliche Ergebnis von A j,
Beweis: Mit Hilfe des Satzes von der totalen Wahrscheinlichkeit folgt, dass
 Beweis: Mit Hilfe des Satzes von der totalen Wahrscheinlichkeit folgt, dass f Z (z) = Pr[Z = z] = x W X Pr[X + Y = z X = x] Pr[X = x] = x W X Pr[Y = z x] Pr[X = x] = x W X f X (x) f Y (z x). Den Ausdruck
Beweis: Mit Hilfe des Satzes von der totalen Wahrscheinlichkeit folgt, dass f Z (z) = Pr[Z = z] = x W X Pr[X + Y = z X = x] Pr[X = x] = x W X Pr[Y = z x] Pr[X = x] = x W X f X (x) f Y (z x). Den Ausdruck
Bachelorprüfung für Volkswirte
 Bachelorprüfung für Volkswirte Mikroökonomie II Prof. Dr. Florian Englmaier 14. Juli 2014 Bitte beantworten Sie die folgenden drei Aufgaben. Zur Bearbeitung der Klausur stehen Ihnen 90 Minuten zur Verfügung.
Bachelorprüfung für Volkswirte Mikroökonomie II Prof. Dr. Florian Englmaier 14. Juli 2014 Bitte beantworten Sie die folgenden drei Aufgaben. Zur Bearbeitung der Klausur stehen Ihnen 90 Minuten zur Verfügung.
Versicherungsmarktgleichgewicht nach Rothschild und Stiglitz
 Versicherungsmarktgleichgewicht nach Rothschild und Stiglitz Daniel Kamhöfer Universität Duisburg-Essen Gesundheitsökonomik I 1 Januar 21 Aufgabe 4 (d) Bestimmen Sie das Trenngleichgewicht nach Rothschild
Versicherungsmarktgleichgewicht nach Rothschild und Stiglitz Daniel Kamhöfer Universität Duisburg-Essen Gesundheitsökonomik I 1 Januar 21 Aufgabe 4 (d) Bestimmen Sie das Trenngleichgewicht nach Rothschild
3. Versicherungen bei symmetrischen Informationen
 1 3. Versicherungen bei symmetrischen Informationen 3.1 Mathematische Lösung: Gegeben sei eine v.nm Nutzenfunktion u(y). Das Anfangseinkommen sei z 1 = y. Die Wahrscheinlichkeit für einen Schaden (L) sei.
1 3. Versicherungen bei symmetrischen Informationen 3.1 Mathematische Lösung: Gegeben sei eine v.nm Nutzenfunktion u(y). Das Anfangseinkommen sei z 1 = y. Die Wahrscheinlichkeit für einen Schaden (L) sei.
Die Firmen maximieren den Gewinn durch Wahl von y unter der Nebenbedingung der Produktionsmöglichkeiten f (y) 0
 Firmen Die Situation der Firmen wird sehr allgemein (und gewöhnungsbedürftig) beschrieben. Von den n Gütern die in der Ökonomie existieren benutzen die Firmen einen Teil zur Produktion (also als Input)
Firmen Die Situation der Firmen wird sehr allgemein (und gewöhnungsbedürftig) beschrieben. Von den n Gütern die in der Ökonomie existieren benutzen die Firmen einen Teil zur Produktion (also als Input)
5 Erwartungswerte, Varianzen und Kovarianzen
 47 5 Erwartungswerte, Varianzen und Kovarianzen Zur Charakterisierung von Verteilungen unterscheidet man Lageparameter, wie z. B. Erwartungswert ( mittlerer Wert ) Modus (Maximum der Wahrscheinlichkeitsfunktion,
47 5 Erwartungswerte, Varianzen und Kovarianzen Zur Charakterisierung von Verteilungen unterscheidet man Lageparameter, wie z. B. Erwartungswert ( mittlerer Wert ) Modus (Maximum der Wahrscheinlichkeitsfunktion,
Bearbeiten Sie vier der fünf Aufgaben A1-A5 und zwei der drei Aufgaben B1-B3!
 Master-Kursprüfung Kapitalmarkttheorie 2 Schwerpunktmodul Finanzmärkte 6 Kreditpunkte Bearbeitungsdauer: 90 Minuten WS 2015/16 29.2.2016 Prof. Dr. Lutz Arnold Bitte gut leserlich ausfüllen: Name: Vorname:
Master-Kursprüfung Kapitalmarkttheorie 2 Schwerpunktmodul Finanzmärkte 6 Kreditpunkte Bearbeitungsdauer: 90 Minuten WS 2015/16 29.2.2016 Prof. Dr. Lutz Arnold Bitte gut leserlich ausfüllen: Name: Vorname:
In einem mathematischen Modell wird dies beschrieben durch einen funktionalen Zusammenhang: x = f (t).
 Aktueller Überblick 0 Einführende Worte ( ) 1 Geschichtlicher Überblick ( ) 2 Zufall 3 Perfekte Sicherheit und ihre Grenzen 4 Angriffsszenarien 5 Der komplexitätstheoretische Ansatz 6 Pseudozufallsgeneratoren
Aktueller Überblick 0 Einführende Worte ( ) 1 Geschichtlicher Überblick ( ) 2 Zufall 3 Perfekte Sicherheit und ihre Grenzen 4 Angriffsszenarien 5 Der komplexitätstheoretische Ansatz 6 Pseudozufallsgeneratoren
9 Entscheidungen unter Unsicherheit
 AVWL I Mikro (Sommer 2008) 9-1 Prof. Dr. M. Kocher 9 Entscheidungen unter Unsicherheit Bisher haben wir immer Situationen betrachtet, in denen Unsicherheit (Zufall, Risiko) keine Rolle spielte. Für die
AVWL I Mikro (Sommer 2008) 9-1 Prof. Dr. M. Kocher 9 Entscheidungen unter Unsicherheit Bisher haben wir immer Situationen betrachtet, in denen Unsicherheit (Zufall, Risiko) keine Rolle spielte. Für die
Kapitel 8. Erwarteter Nutzen. Intertemporaler Nutzen für Mehrperioden-Entscheidungen
 Kapitel 8 Erwarteter Nutzen Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen / 27 Lernziele Nutzenfunktion zur Risikobewertung Erwarteter Nutzen Maße für Risikoaversion Indifferenzkurven
Kapitel 8 Erwarteter Nutzen Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen / 27 Lernziele Nutzenfunktion zur Risikobewertung Erwarteter Nutzen Maße für Risikoaversion Indifferenzkurven
Folie zur Vorlesung Finanz- und Versicherungsmathematik Beispiel zu Nutzenfunktionen von risikoaversen Personen:
 Folie zur Vorlesung Finanz- und Versicherungsmathematik 16.01.2013 Beispiel zu Nutzenfunktionen von risikoaversen Personen: Im folgenden sei X ein zufälliger Schaden und P die Prämie zur Übernahme des
Folie zur Vorlesung Finanz- und Versicherungsmathematik 16.01.2013 Beispiel zu Nutzenfunktionen von risikoaversen Personen: Im folgenden sei X ein zufälliger Schaden und P die Prämie zur Übernahme des
13 Mehrdimensionale Zufallsvariablen Zufallsvektoren
 3 Mehrdimensionale Zufallsvariablen Zufallsvektoren Bisher haben wir uns ausschließlich mit Zufallsexperimenten beschäftigt, bei denen die Beobachtung eines einzigen Merkmals im Vordergrund stand. In diesem
3 Mehrdimensionale Zufallsvariablen Zufallsvektoren Bisher haben wir uns ausschließlich mit Zufallsexperimenten beschäftigt, bei denen die Beobachtung eines einzigen Merkmals im Vordergrund stand. In diesem
Fortgeschrittene VWL Theorie
 Fortgeschrittene VWL Theorie Jörg Lingens WWU Münster April 27, 2009 Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL April 27, 2009 1 / 131 Einführung/Motivation Komplexität der Volkswirtschaftslehre
Fortgeschrittene VWL Theorie Jörg Lingens WWU Münster April 27, 2009 Jörg Lingens (WWU Münster) VWL-Theorie im Masterstudiengang VWL April 27, 2009 1 / 131 Einführung/Motivation Komplexität der Volkswirtschaftslehre
Mathematik für Naturwissenschaften, Teil 2
 Lösungsvorschläge für die Aufgaben zur Vorlesung Mathematik für Naturwissenschaften, Teil Zusatzblatt SS 09 Dr. J. Schürmann keine Abgabe Aufgabe : Eine Familie habe fünf Kinder. Wir nehmen an, dass die
Lösungsvorschläge für die Aufgaben zur Vorlesung Mathematik für Naturwissenschaften, Teil Zusatzblatt SS 09 Dr. J. Schürmann keine Abgabe Aufgabe : Eine Familie habe fünf Kinder. Wir nehmen an, dass die
Bachelorprüfung für Volkswirte. Mikroökonomie II
 Seminar für Wirtschaftstheorie Prof. Thorsten Chmura Bachelorprüfung für Volkswirte Mikroökonomie II Die Klausur besteht aus drei Aufgaben auf insgesamt 16 Seiten. Alle drei Aufgaben müssen bearbeitet
Seminar für Wirtschaftstheorie Prof. Thorsten Chmura Bachelorprüfung für Volkswirte Mikroökonomie II Die Klausur besteht aus drei Aufgaben auf insgesamt 16 Seiten. Alle drei Aufgaben müssen bearbeitet
1.5.4 Quantile und Modi. Bem [Quantil, Modus]
![1.5.4 Quantile und Modi. Bem [Quantil, Modus] 1.5.4 Quantile und Modi. Bem [Quantil, Modus]](/thumbs/77/75975909.jpg) 1.5.4 Quantile und Modi 1.5 Erwartungswert und Varianz Bem. 1.73. [Quantil, Modus] und Vertei- Analog zu Statistik I kann man auch Quantile und Modi definieren. Gegeben sei eine Zufallsvariable X mit Wahrscheinlichkeitsverteilung
1.5.4 Quantile und Modi 1.5 Erwartungswert und Varianz Bem. 1.73. [Quantil, Modus] und Vertei- Analog zu Statistik I kann man auch Quantile und Modi definieren. Gegeben sei eine Zufallsvariable X mit Wahrscheinlichkeitsverteilung
0 für t < für 1 t < für 2 t < für 3 t < für 4 t < 5 1 für t 5
 4 Verteilungen und ihre Kennzahlen 1 Kapitel 4: Verteilungen und ihre Kennzahlen A: Beispiele Beispiel 1: Eine diskrete Zufallsvariable X, die nur die Werte 1,, 3, 4, 5 mit positiver Wahrscheinlichkeit
4 Verteilungen und ihre Kennzahlen 1 Kapitel 4: Verteilungen und ihre Kennzahlen A: Beispiele Beispiel 1: Eine diskrete Zufallsvariable X, die nur die Werte 1,, 3, 4, 5 mit positiver Wahrscheinlichkeit
Varianz und Kovarianz
 KAPITEL 9 Varianz und Kovarianz 9.1. Varianz Definition 9.1.1. Sei (Ω, F, P) ein Wahrscheinlichkeitsraum und X : Ω eine Zufallsvariable. Wir benutzen die Notation (1) X L 1, falls E[ X ]
KAPITEL 9 Varianz und Kovarianz 9.1. Varianz Definition 9.1.1. Sei (Ω, F, P) ein Wahrscheinlichkeitsraum und X : Ω eine Zufallsvariable. Wir benutzen die Notation (1) X L 1, falls E[ X ]
Statistische Analyseverfahren Abschnitt 2: Zufallsvektoren und mehrdimensionale Verteilungen
 Statistische Analyseverfahren Abschnitt 2: Zufallsvektoren und mehrdimensionale Verteilungen Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut für Stochastik Oktober 2018 Prof. Dr. Hans-Jörg
Statistische Analyseverfahren Abschnitt 2: Zufallsvektoren und mehrdimensionale Verteilungen Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut für Stochastik Oktober 2018 Prof. Dr. Hans-Jörg
Bestimmte Zufallsvariablen sind von Natur aus normalverteilt. - naturwissenschaftliche Variablen: originär z.b. Intelligenz, Körpergröße, Messfehler
 6.6 Normalverteilung Die Normalverteilung kann als das wichtigste Verteilungsmodell der Statistik angesehen werden. Sie wird nach ihrem Entdecker auch Gaußsche Glockenkurve genannt. Die herausragende Stellung
6.6 Normalverteilung Die Normalverteilung kann als das wichtigste Verteilungsmodell der Statistik angesehen werden. Sie wird nach ihrem Entdecker auch Gaußsche Glockenkurve genannt. Die herausragende Stellung
Der Entscheidungsträger wählt aus einer Menge von Alternativen, dem Aktionenraum A = {a 1, a 2, a m }.
 1 Grundlagen Entscheidungstheorie: Der Entscheidungsträger wählt aus einer Menge von Alternativen, dem Aktionenraum A = {a 1, a 2, a m }. Annahmen: Der Entscheidungsträger ist gezwungen, eine der betrachteten
1 Grundlagen Entscheidungstheorie: Der Entscheidungsträger wählt aus einer Menge von Alternativen, dem Aktionenraum A = {a 1, a 2, a m }. Annahmen: Der Entscheidungsträger ist gezwungen, eine der betrachteten
Kapitel 6. Verteilungsparameter. 6.1 Der Erwartungswert Diskrete Zufallsvariablen
 Kapitel 6 Verteilungsparameter Wie bei einem Merkmal wollen wir nun die Lage und die Streuung der Verteilung einer diskreten Zufallsvariablen durch geeignete Maßzahlen beschreiben. Beginnen wir mit Maßzahlen
Kapitel 6 Verteilungsparameter Wie bei einem Merkmal wollen wir nun die Lage und die Streuung der Verteilung einer diskreten Zufallsvariablen durch geeignete Maßzahlen beschreiben. Beginnen wir mit Maßzahlen
1.4 Stichproben aus einer Normalverteilung
 1.4 Stichproben aus einer Normalverteilung Die Normalverteilung ist wohl das am stärksten verbreitete Modell. Stichproben daraus führen zu nützlichen Eigenschaften der Statistiken und ergeben bekannte
1.4 Stichproben aus einer Normalverteilung Die Normalverteilung ist wohl das am stärksten verbreitete Modell. Stichproben daraus führen zu nützlichen Eigenschaften der Statistiken und ergeben bekannte
70 Wichtige kontinuierliche Verteilungen
 70 Wichtige kontinuierliche Verteilungen 70. Motivation Zufallsvariablen sind nicht immer diskret, sie können oft auch jede beliebige reelle Zahl in einem Intervall [c, d] einnehmen. Beispiele für solche
70 Wichtige kontinuierliche Verteilungen 70. Motivation Zufallsvariablen sind nicht immer diskret, sie können oft auch jede beliebige reelle Zahl in einem Intervall [c, d] einnehmen. Beispiele für solche
Einführung in die Stochastik für Informatiker Übungsaufgaben mit Lösungen
 Einführung in die Stochastik für Informatiker Übungsaufgaben mit Lösungen David Geier und Sven Middelberg RWTH Aachen, Sommersemester 27 Inhaltsverzeichnis Information 2 Aufgabe 4 Aufgabe 2 6 4 Aufgabe
Einführung in die Stochastik für Informatiker Übungsaufgaben mit Lösungen David Geier und Sven Middelberg RWTH Aachen, Sommersemester 27 Inhaltsverzeichnis Information 2 Aufgabe 4 Aufgabe 2 6 4 Aufgabe
Kapitel 5: Entscheidung unter Unsicherheit
 Kapitel 5: Entscheidung unter Unsicherheit Hauptidee: Die Konsequenzen einer Entscheidung sind oft unsicher. Wenn jeder möglichen Konsequenz eine Wahrscheinlichkeit zugeordnet wird, dann kann eine rationale
Kapitel 5: Entscheidung unter Unsicherheit Hauptidee: Die Konsequenzen einer Entscheidung sind oft unsicher. Wenn jeder möglichen Konsequenz eine Wahrscheinlichkeit zugeordnet wird, dann kann eine rationale
Nochmal: Indifferenzwahrscheinlichkeiten und Nutzenfunktion Reihung: Selbständigkeit Erfolg Geschäftsführer Vorstandsassistent Insolvenz
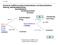 Nochmal: Indifferenzwahrscheinlichkeiten und Nutzenfunktion Reihung: Selbständigkeit Erfolg Geschäftsführer Vorstandsassistent Insolvenz Ref.-L.1: Selbst. Erfolg Sicher (300000) π = 1 1-π = 0 Selbständigkeit
Nochmal: Indifferenzwahrscheinlichkeiten und Nutzenfunktion Reihung: Selbständigkeit Erfolg Geschäftsführer Vorstandsassistent Insolvenz Ref.-L.1: Selbst. Erfolg Sicher (300000) π = 1 1-π = 0 Selbständigkeit
5.4 Verteilungsfunktion Verteilungsfunktion diskreten Zufallsvariablen stetigen Zufallsvariablen Verteilungsfunktion
 5. Verteilungsfunktion Die Verteilungsfunktion gibt an welche Wahrscheinlichkeit sich bis zu einem bestimmten Wert der Zufallsvarialben X kumuliert Die Verteilungsfunktion F() gibt an, wie groß die die
5. Verteilungsfunktion Die Verteilungsfunktion gibt an welche Wahrscheinlichkeit sich bis zu einem bestimmten Wert der Zufallsvarialben X kumuliert Die Verteilungsfunktion F() gibt an, wie groß die die
Lösungen zur Klausur WAHRSCHEINLICHKEITSTHEORIE UND STATISTIK (STOCHASTIK)
 Institut für Stochastik Dr. Steffen Winter Lösungen zur Klausur WAHRSCHEINLICHKEITSTHEORIE UND STATISTIK (STOCHASTIK) für Studierende des Maschinenbaus vom 7. Juli (Dauer: 8 Minuten) Übersicht über die
Institut für Stochastik Dr. Steffen Winter Lösungen zur Klausur WAHRSCHEINLICHKEITSTHEORIE UND STATISTIK (STOCHASTIK) für Studierende des Maschinenbaus vom 7. Juli (Dauer: 8 Minuten) Übersicht über die
2 Zufallsvariable und Verteilungsfunktionen
 8 2 Zufallsvariable und Verteilungsfunktionen Häufig ist es so, dass den Ausgängen eines Zufallexperiments, d.h. den Elementen der Ereignisalgebra, eine Zahl zugeordnet wird. Das wollen wir etwas mathematischer
8 2 Zufallsvariable und Verteilungsfunktionen Häufig ist es so, dass den Ausgängen eines Zufallexperiments, d.h. den Elementen der Ereignisalgebra, eine Zahl zugeordnet wird. Das wollen wir etwas mathematischer
Vorlesung 8b. Kovarianz, Korrelation und Regressionsgerade
 Vorlesung 8b Kovarianz, Korrelation und Regressionsgerade 1 1. Die Kovarianz und ihre Eigenschaften 2 Wir erinnern an die Definition der Kovarianz Für reellwertige Zufallsvariable X, Y mit E[X 2 ] < und
Vorlesung 8b Kovarianz, Korrelation und Regressionsgerade 1 1. Die Kovarianz und ihre Eigenschaften 2 Wir erinnern an die Definition der Kovarianz Für reellwertige Zufallsvariable X, Y mit E[X 2 ] < und
Vorlesung 5b. Zufallsvariable mit Dichten
 Vorlesung 5b 1 Vorlesung 5b Zufallsvariable mit Dichten Vorlesung 5b Zufallsvariable mit Dichten Wiederholung aus Vorlesung 2b+: Kontinuierlich uniform verteilte Zufallsvariable: Sei S eine Teilmenge des
Vorlesung 5b 1 Vorlesung 5b Zufallsvariable mit Dichten Vorlesung 5b Zufallsvariable mit Dichten Wiederholung aus Vorlesung 2b+: Kontinuierlich uniform verteilte Zufallsvariable: Sei S eine Teilmenge des
Mikroökonomik. Unsicherheit. Harald Wiese. Universität Leipzig. Harald Wiese (Universität Leipzig) Unsicherheit 1 / 46
 Mikroökonomik Unsicherheit Harald Wiese Universität Leipzig Harald Wiese (Universität Leipzig) Unsicherheit 1 / 46 Gliederung Einführung Haushaltstheorie Das Budget Präferenzen, Indi erenzkurven und Nutzenfunktionen
Mikroökonomik Unsicherheit Harald Wiese Universität Leipzig Harald Wiese (Universität Leipzig) Unsicherheit 1 / 46 Gliederung Einführung Haushaltstheorie Das Budget Präferenzen, Indi erenzkurven und Nutzenfunktionen
Einige Konzepte aus der Wahrscheinlichkeitstheorie (Wiederh.)
 Einige Konzepte aus der Wahrscheinlichkeitstheorie (Wiederh.) 1 Zusammenfassung Bedingte Verteilung: P (y x) = P (x, y) P (x) mit P (x) > 0 Produktsatz P (x, y) = P (x y)p (y) = P (y x)p (x) Kettenregel
Einige Konzepte aus der Wahrscheinlichkeitstheorie (Wiederh.) 1 Zusammenfassung Bedingte Verteilung: P (y x) = P (x, y) P (x) mit P (x) > 0 Produktsatz P (x, y) = P (x y)p (y) = P (y x)p (x) Kettenregel
Wichtige Definitionen und Aussagen
 Wichtige Definitionen und Aussagen Zufallsexperiment, Ergebnis, Ereignis: Unter einem Zufallsexperiment verstehen wir einen Vorgang, dessen Ausgänge sich nicht vorhersagen lassen Die möglichen Ausgänge
Wichtige Definitionen und Aussagen Zufallsexperiment, Ergebnis, Ereignis: Unter einem Zufallsexperiment verstehen wir einen Vorgang, dessen Ausgänge sich nicht vorhersagen lassen Die möglichen Ausgänge
Statistik I. 2. Klausur Wintersemester 2011/2012 Hamburg, BITTE LESERLICH IN DRUCKBUCHSTABEN AUSFÜLLEN!
 Statistik I A 2. Klausur Wintersemester 2011/2012 Hamburg, 20.03.2012 BITTE LESERLICH IN DRUCKBUCHSTABEN AUSFÜLLEN! Nachname:............................................................................
Statistik I A 2. Klausur Wintersemester 2011/2012 Hamburg, 20.03.2012 BITTE LESERLICH IN DRUCKBUCHSTABEN AUSFÜLLEN! Nachname:............................................................................
In der VWL-Bibliothek befindet sich ein Mikro III-Ordner:
 SS 2003 In der WL-Bibliothek befindet sich ein Mikro III-Ordner: Dort finden sie jeweils 3 Kopiervorlagen von - Literatur Eaton/Eaton, Shy und Bester - Artikel von Coase, Akerlof, Spence - Artikel von
SS 2003 In der WL-Bibliothek befindet sich ein Mikro III-Ordner: Dort finden sie jeweils 3 Kopiervorlagen von - Literatur Eaton/Eaton, Shy und Bester - Artikel von Coase, Akerlof, Spence - Artikel von
Klausur zu,,einführung in die Wahrscheinlichkeitstheorie
 Institut für angewandte Mathematik Wintersemester 2009/10 Andreas Eberle, Matthias Erbar, Bernhard Hader Klausur zu,,einführung in die Wahrscheinlichkeitstheorie Bitte diese Felder in Druckschrift ausfüllen
Institut für angewandte Mathematik Wintersemester 2009/10 Andreas Eberle, Matthias Erbar, Bernhard Hader Klausur zu,,einführung in die Wahrscheinlichkeitstheorie Bitte diese Felder in Druckschrift ausfüllen
Kapitel II Kontinuierliche Wahrscheinlichkeitsräume
 Kapitel II Kontinuierliche Wahrscheinlichkeitsräume 1. Einführung 1.1 Motivation Interpretation der Poisson-Verteilung als Grenzwert der Binomialverteilung. DWT 1.1 Motivation 211/476 Beispiel 85 Wir betrachten
Kapitel II Kontinuierliche Wahrscheinlichkeitsräume 1. Einführung 1.1 Motivation Interpretation der Poisson-Verteilung als Grenzwert der Binomialverteilung. DWT 1.1 Motivation 211/476 Beispiel 85 Wir betrachten
Entscheidungstheorie (SBWL) SS08
 Fach: Prüfer: Veranstaltung: CP anrechnen lassen für: ggfls. streichen und dann bitte Veranstaltung und Prüfungsnummer angeben Banken und Finanzierung Prof. Dr. Dr. A. Löffler Entscheidungstheorie (SBWL)
Fach: Prüfer: Veranstaltung: CP anrechnen lassen für: ggfls. streichen und dann bitte Veranstaltung und Prüfungsnummer angeben Banken und Finanzierung Prof. Dr. Dr. A. Löffler Entscheidungstheorie (SBWL)
1 1 e x2 =2 d x 1. e (x2 +y 2 )=2 d x d y : Wir gehen nun zu Polarkoordinaten uber und setzen x := r cos und y := r sin.
 Lemma 92 Beweis: Wir berechnen zunachst I 2 : I 2 = Z 1 I := e x2 =2 d x p = 2: 1 Z 1 1 Z 1 Z 1 = 1 1 Z 1 e x2 =2 d x 1 e (x2 +y 2 )=2 d x d y : e y2 =2 d y Wir gehen nun zu Polarkoordinaten uber und setzen
Lemma 92 Beweis: Wir berechnen zunachst I 2 : I 2 = Z 1 I := e x2 =2 d x p = 2: 1 Z 1 1 Z 1 Z 1 = 1 1 Z 1 e x2 =2 d x 1 e (x2 +y 2 )=2 d x d y : e y2 =2 d y Wir gehen nun zu Polarkoordinaten uber und setzen
4 Diskrete Wahrscheinlichkeitsverteilungen
 4 Diskrete Wahrscheinlichkeitsverteilungen 4.1 Wahrscheinlichkeitsräume, Ereignisse und Unabhängigkeit Definition: Ein diskreter Wahrscheinlichkeitsraum ist ein Paar (Ω, Pr), wobei Ω eine endliche oder
4 Diskrete Wahrscheinlichkeitsverteilungen 4.1 Wahrscheinlichkeitsräume, Ereignisse und Unabhängigkeit Definition: Ein diskreter Wahrscheinlichkeitsraum ist ein Paar (Ω, Pr), wobei Ω eine endliche oder
GESUNDHEITSÖKONOMIK I
 GESUNDHEITSÖKONOMIK I Christoph Strupat Universität Duisburg-Essen Wintersemester 2013/2014 Literatur: BZK, Kapitel 5; Gravelle und Rees (Kapitel 17 B, 17 E, 19 B, 19 F) und weitere Aufsätze Christoph
GESUNDHEITSÖKONOMIK I Christoph Strupat Universität Duisburg-Essen Wintersemester 2013/2014 Literatur: BZK, Kapitel 5; Gravelle und Rees (Kapitel 17 B, 17 E, 19 B, 19 F) und weitere Aufsätze Christoph
Statistik I. 2. Klausur Wintersemester 2011/2012 Hamburg, BITTE LESERLICH IN DRUCKBUCHSTABEN AUSFÜLLEN!
 Statistik I A 2. Klausur Wintersemester 2011/2012 Hamburg, 20.03.2012 BITTE LESERLICH IN DRUCKBUCHSTABEN AUSFÜLLEN! Nachname:............................................................................
Statistik I A 2. Klausur Wintersemester 2011/2012 Hamburg, 20.03.2012 BITTE LESERLICH IN DRUCKBUCHSTABEN AUSFÜLLEN! Nachname:............................................................................
1 Zielfunktionen und Restriktionen. Beispiel 1 Beispiel 2 Anna Berta Cäsar Dirk Zielfunktion U A Y A U B =X B Y B X B
 Seite 1 Ausführliche formal-analytische Herleitungen anhand von zwei Beispielen zum Kapitel 3.2 zum Kurs 42110 Preisbildung auf unvollkommenen Märkten und allgemeines Gleichgewicht Inhaltsverzeichnis 1
Seite 1 Ausführliche formal-analytische Herleitungen anhand von zwei Beispielen zum Kapitel 3.2 zum Kurs 42110 Preisbildung auf unvollkommenen Märkten und allgemeines Gleichgewicht Inhaltsverzeichnis 1
Kapitel 5: Entscheidung unter Unsicherheit
 Kapitel 5: Entscheidung unter Unsicherheit Hauptidee: Die Konsequenzen einer Entscheidung sind oft unsicher. Wenn jeder möglichen Konsequenz eine Wahrscheinlichkeit zugeordnet wird, dann kann eine rationale
Kapitel 5: Entscheidung unter Unsicherheit Hauptidee: Die Konsequenzen einer Entscheidung sind oft unsicher. Wenn jeder möglichen Konsequenz eine Wahrscheinlichkeit zugeordnet wird, dann kann eine rationale
Einführung in die Volkswirtschaftslehre
 Einführung in die Volkswirtschaftslehre Übung 1: Mathematische Analyseinstrumente Dipl.-Volksw. J.-E.Wesselhöft/ Dipl.-Volksw. J.Freese Bachelor Modul Volkswirtschaftliche Analyse (WS-14-V-03) HT 2009
Einführung in die Volkswirtschaftslehre Übung 1: Mathematische Analyseinstrumente Dipl.-Volksw. J.-E.Wesselhöft/ Dipl.-Volksw. J.Freese Bachelor Modul Volkswirtschaftliche Analyse (WS-14-V-03) HT 2009
Wichtige Informationen vorab
 Wichtige Informationen vorab Wir haben eine Mailing Liste "Vorles- UebSS09Kapitalmarkt" eingerichtet. Über diese Mailingliste erhalten Sie in Zukunft die Vorlesungsunterlagen und die Übungsunterlagen.
Wichtige Informationen vorab Wir haben eine Mailing Liste "Vorles- UebSS09Kapitalmarkt" eingerichtet. Über diese Mailingliste erhalten Sie in Zukunft die Vorlesungsunterlagen und die Übungsunterlagen.
4. Gemeinsame Verteilung und Grenzwertsätze
 4. Gemeinsame Verteilung und Grenzwertsätze Häufig in der Praxis: Man muss mehrere (n) ZV en gleichzeitig betrachten (vgl. Statistik I, Kapitel 6) Zunächst Vereinfachung: Betrachte n = 2 Zufallsvariablen
4. Gemeinsame Verteilung und Grenzwertsätze Häufig in der Praxis: Man muss mehrere (n) ZV en gleichzeitig betrachten (vgl. Statistik I, Kapitel 6) Zunächst Vereinfachung: Betrachte n = 2 Zufallsvariablen
4. Gemeinsame Verteilung und Grenzwertsätze
 4. Gemeinsame Verteilung und Grenzwertsätze Häufig in der Praxis: Man muss mehrere (n) ZV en gleichzeitig betrachten (vgl. Statistik I, Kapitel 6) Zunächst Vereinfachung: Betrachte n = 2 Zufallsvariablen
4. Gemeinsame Verteilung und Grenzwertsätze Häufig in der Praxis: Man muss mehrere (n) ZV en gleichzeitig betrachten (vgl. Statistik I, Kapitel 6) Zunächst Vereinfachung: Betrachte n = 2 Zufallsvariablen
5. Spezielle stetige Verteilungen
 5. Spezielle stetige Verteilungen 5.1 Stetige Gleichverteilung Eine Zufallsvariable X folgt einer stetigen Gleichverteilung mit den Parametern a und b, wenn für die Dichtefunktion von X gilt: f x = 1 für
5. Spezielle stetige Verteilungen 5.1 Stetige Gleichverteilung Eine Zufallsvariable X folgt einer stetigen Gleichverteilung mit den Parametern a und b, wenn für die Dichtefunktion von X gilt: f x = 1 für
Mathematik für Informatiker III im WS 05/06 Musterlösung zur 4. Übung
 Mathematik für Informatiker III im WS 5/6 Musterlösung zur. Übung erstellt von K. Kriegel Aufgabe : Wir betrachten den Wahrscheinlichkeitsraum der Punkte P =(a, b) aus dem Einheitsquadrat [, ] [, ] mit
Mathematik für Informatiker III im WS 5/6 Musterlösung zur. Übung erstellt von K. Kriegel Aufgabe : Wir betrachten den Wahrscheinlichkeitsraum der Punkte P =(a, b) aus dem Einheitsquadrat [, ] [, ] mit
Vorlesung 7a. Unabhängigkeit
 Vorlesung 7a Unabhängigkeit 1 Wir erinnern an die Definition der Unabhängigkeit von zwei Zufallsvariablen (Buch S. 61): Zufallsvariable X 1,X 2 heißen (stochastisch) unabhängig, falls für alle Ereignisse
Vorlesung 7a Unabhängigkeit 1 Wir erinnern an die Definition der Unabhängigkeit von zwei Zufallsvariablen (Buch S. 61): Zufallsvariable X 1,X 2 heißen (stochastisch) unabhängig, falls für alle Ereignisse
Statistik II. Lineare Regressionsrechnung. Wiederholung Skript 2.8 und Ergänzungen (Schira: Kapitel 4) Statistik II
 Statistik II Lineare Regressionsrechnung Wiederholung Skript 2.8 und Ergänzungen (Schira: Kapitel 4) Statistik II - 09.06.2006 1 Mit der Kovarianz und dem Korrelationskoeffizienten können wir den statistischen
Statistik II Lineare Regressionsrechnung Wiederholung Skript 2.8 und Ergänzungen (Schira: Kapitel 4) Statistik II - 09.06.2006 1 Mit der Kovarianz und dem Korrelationskoeffizienten können wir den statistischen
Einführung in die Maximum Likelihood Methodik
 in die Maximum Likelihood Methodik Thushyanthan Baskaran thushyanthan.baskaran@awi.uni-heidelberg.de Alfred Weber Institut Ruprecht Karls Universität Heidelberg Gliederung 1 2 3 4 2 / 31 Maximum Likelihood
in die Maximum Likelihood Methodik Thushyanthan Baskaran thushyanthan.baskaran@awi.uni-heidelberg.de Alfred Weber Institut Ruprecht Karls Universität Heidelberg Gliederung 1 2 3 4 2 / 31 Maximum Likelihood
Diplomprüfung Wirtschaftswissenschaften. Prüfungsfach: Volkswirtschaftslehre (60 min.) Prüfer: Professor Dr. Johann Graf Lambsdorff Matrikel-Nr.
 Diplomprüfung Wirtschaftswissenschaften Prüfungsfach: Volkswirtschaftslehre (60 min.) Prüfer: Professor Dr. Johann Graf Lambsdorff Matrikel-Nr.: Prüfungstag: Platz-Nr.: Blatt 1 Hinweise: Bitte bearbeiten
Diplomprüfung Wirtschaftswissenschaften Prüfungsfach: Volkswirtschaftslehre (60 min.) Prüfer: Professor Dr. Johann Graf Lambsdorff Matrikel-Nr.: Prüfungstag: Platz-Nr.: Blatt 1 Hinweise: Bitte bearbeiten
Dieses Quiz soll Ihnen helfen, Kapitel besser zu verstehen.
 Dieses Quiz soll Ihnen helfen, Kapitel 2.5-2. besser zu verstehen. Frage Wir betrachten ein Würfelspiel. Man wirft einen fairen, sechsseitigen Würfel. Wenn eine oder eine 2 oben liegt, muss man 2 SFr zahlen.
Dieses Quiz soll Ihnen helfen, Kapitel 2.5-2. besser zu verstehen. Frage Wir betrachten ein Würfelspiel. Man wirft einen fairen, sechsseitigen Würfel. Wenn eine oder eine 2 oben liegt, muss man 2 SFr zahlen.
Berechnung MCR unter Solvency II
 Berechnung MCR unter Solvency II Berechnung MCR unter Solvency II Die Wahl des richtigen Risikomaßes Sina Wiesinger 29. März 2018 Überblick 1 Einleitung 2 Grundlagen 3 Eigenschaften von Risikomaßen 4 Risikomaße
Berechnung MCR unter Solvency II Berechnung MCR unter Solvency II Die Wahl des richtigen Risikomaßes Sina Wiesinger 29. März 2018 Überblick 1 Einleitung 2 Grundlagen 3 Eigenschaften von Risikomaßen 4 Risikomaße
1. EINFÜHRUNG INS STATE-PRICING 1
 1. EINFÜHRUNG INS STATE-PRICING 1 1. Einführung ins State-Pricing In diesem Kapitel betrachten wir eine Periode. Das heisst, wir können nur zu den Zeitpunkten 0 und 1 handeln. Im weiteren arbeiten wir
1. EINFÜHRUNG INS STATE-PRICING 1 1. Einführung ins State-Pricing In diesem Kapitel betrachten wir eine Periode. Das heisst, wir können nur zu den Zeitpunkten 0 und 1 handeln. Im weiteren arbeiten wir
Studienschwerpunkt Finanzmarkttheorie 10 Kreditpunkte, Bearbeitungsdauer: 150 Minuten WS 2004/05, Prof. Dr. Lutz Arnold A B1 B2 B3
 Modulprüfung Kapitalmarkttheorie Studienschwerpunkt Finanzmarkttheorie 10 Kreditpunkte, Bearbeitungsdauer: 150 Minuten WS 2004/05, 7.3.2005 Prof. Dr. Lutz Arnold A B1 B2 B3 Bearbeiten Sie alle acht Aufgaben
Modulprüfung Kapitalmarkttheorie Studienschwerpunkt Finanzmarkttheorie 10 Kreditpunkte, Bearbeitungsdauer: 150 Minuten WS 2004/05, 7.3.2005 Prof. Dr. Lutz Arnold A B1 B2 B3 Bearbeiten Sie alle acht Aufgaben
1. Stationarität Definition: Ein stochastischer Prozess. heißt streng oder stark stationär, falls für
 " " " Beschreibung stochastischer Prozesse Wir betrachten diskrete Zeitpunkte und die zugehörigen Zufallsvariablen!. ann sind die Zufallsvariablen durch ihre gemeinsame ichte " #%$&#'$)(*#'$,+- charakterisiert.
" " " Beschreibung stochastischer Prozesse Wir betrachten diskrete Zeitpunkte und die zugehörigen Zufallsvariablen!. ann sind die Zufallsvariablen durch ihre gemeinsame ichte " #%$&#'$)(*#'$,+- charakterisiert.
DWT 3.3 Warteprobleme mit der Exponentialverteilung 275/467 Ernst W. Mayr
 Poisson-Prozess Wir hatten bei der Diskussion der geometrischen und der Poisson-Verteilung festgestellt: Wenn der zeitliche Abstand der Treffer geometrisch verteilt ist, so ist ihre Anzahl in einer festen
Poisson-Prozess Wir hatten bei der Diskussion der geometrischen und der Poisson-Verteilung festgestellt: Wenn der zeitliche Abstand der Treffer geometrisch verteilt ist, so ist ihre Anzahl in einer festen
Bootstrap-Methoden zur Ermittlung kritischer Werte für asymptotische FWER-Kontrolle
 Bootstrap-Methoden zur Ermittlung kritischer Werte für asymptotische FWER-Kontrolle [Dudoit, van der Laan, Pollard: Multiple Testing. Part I Single-Step Procedures for Control of General Type-I-Error Rates]
Bootstrap-Methoden zur Ermittlung kritischer Werte für asymptotische FWER-Kontrolle [Dudoit, van der Laan, Pollard: Multiple Testing. Part I Single-Step Procedures for Control of General Type-I-Error Rates]
Bearbeiten Sie vier der fünf Aufgaben A1-A5 und zwei der drei Aufgaben B1-B3!
 Master-Prüfung Kapitalmarkttheorie 2 Schwerpunktmodul Finanzmärkte 6 Kreditpunkte Bearbeitungsdauer: 90 Minuten WS 2016/17 6.3.2017 Prof. Dr. Lutz Arnold Bitte gut leserlich ausfüllen: Name: Vorname: Matr.-nr.:
Master-Prüfung Kapitalmarkttheorie 2 Schwerpunktmodul Finanzmärkte 6 Kreditpunkte Bearbeitungsdauer: 90 Minuten WS 2016/17 6.3.2017 Prof. Dr. Lutz Arnold Bitte gut leserlich ausfüllen: Name: Vorname: Matr.-nr.:
Finanzmathematische Modelle und Simulation
 Finanzmathematische Modelle und Simulation WS 9/1 Rebecca Henkelmann In meiner Ausarbeitung Grundbegriffe der Stochastik I, geht es darum die folgenden Begriffe für die nächsten Kapitel einzuführen. Auf
Finanzmathematische Modelle und Simulation WS 9/1 Rebecca Henkelmann In meiner Ausarbeitung Grundbegriffe der Stochastik I, geht es darum die folgenden Begriffe für die nächsten Kapitel einzuführen. Auf
Credibility Theory. Christoph Chlubna. 10. Januar / 18
 10. Januar 2012 1 / 18 Gliederung 1 Was ist 2 Das Problem der Risikobewertung 3 Das individuelle Risiko 4 Die verschiedenen Prämienarten 5 Die Risikofunktion 6 Die Prämie im einfachen Modell 2 / 18 Gliederung
10. Januar 2012 1 / 18 Gliederung 1 Was ist 2 Das Problem der Risikobewertung 3 Das individuelle Risiko 4 Die verschiedenen Prämienarten 5 Die Risikofunktion 6 Die Prämie im einfachen Modell 2 / 18 Gliederung
Vorlesung 8a. Kovarianz und Korrelation
 Vorlesung 8a Kovarianz und Korrelation 1 Wir erinnern an die Definition der Kovarianz Für reellwertige Zufallsvariable X, Y mit E[X 2 ] < und E[Y 2 ] < ist Cov[X, Y ] := E [ (X EX)(Y EY ) ] Insbesondere
Vorlesung 8a Kovarianz und Korrelation 1 Wir erinnern an die Definition der Kovarianz Für reellwertige Zufallsvariable X, Y mit E[X 2 ] < und E[Y 2 ] < ist Cov[X, Y ] := E [ (X EX)(Y EY ) ] Insbesondere
Grundlagen der Versicherungs- und Sozialversicherungsökonomik. Risiko: objektive oder subjektive Wahrscheinlichkeiten
 Grundlagen der Versicherungs- und Sozialversicherungsökonomik Entscheidungstheorie bei Sicherheit (z. B. trad. Mikroökonomik, lineare Programmierung etc. bei Risiko (Unsicherheit und Ungewissheit Risiko:
Grundlagen der Versicherungs- und Sozialversicherungsökonomik Entscheidungstheorie bei Sicherheit (z. B. trad. Mikroökonomik, lineare Programmierung etc. bei Risiko (Unsicherheit und Ungewissheit Risiko:
3. Gemeinsame und bedingte Verteilung, stochastische Unabhängigkeit
 3. Gemeinsame und bedingte Verteilung, stochastische Unabhängigkeit Lernziele dieses Kapitels: Mehrdimensionale Zufallsvariablen (Zufallsvektoren) (Verteilung, Kenngrößen) Abhängigkeitsstrukturen Multivariate
3. Gemeinsame und bedingte Verteilung, stochastische Unabhängigkeit Lernziele dieses Kapitels: Mehrdimensionale Zufallsvariablen (Zufallsvektoren) (Verteilung, Kenngrößen) Abhängigkeitsstrukturen Multivariate
