Lambda-Kalkül. Philipp Meyer. 28. April 2009
|
|
|
- Horst Dieter
- vor 7 Jahren
- Abrufe
Transkript
1 Lambda-Kalkül Philipp Meyer 28. April 2009
2 1 Einleitung Der λ-kalkül ist eine von Alonzo Church und Stephen Kleene in den 1930er Jahren eingeführtes Modell zur Beschreibung berechenbarer Funktionen. Es ververwendet nur fundamentale Reduktions- und Konversionsregeln zur Veränderung von textuellen Ausdrücken. Wie Turing 1937 zeigte, ist der λ-kalkül gleichmächtig im Sinne der Berechenbarkeit zu der Turing-Maschine. Hierraus folgt entsprechend, dass es im λ-kalkül unentscheidbar ist, ob zwei Terme äquivalent sind oder ein Term eine Normalform besitzt. Die typisierten Varianten des λ-kalküls bilden die Grundlage von funktionalen Programmiersprachen wie ML oder Haskell und können auch als eine Meta-Logik verwendet werden, was zu Theorembeweisern für Logiken höherer Stufe und mächtigen Typsystemen führte. 2 Syntax 2.1 Terme Definition 1 Die Menge Λ der λ-terme ist induktiv definiert durch: x Λ M Λ (λx.m) Λ M, N Λ (MN) Λ (1) (2) (3) Hierbei ist x eine Variable. Ein durch (2) konstruierter Term wird Abstraktion genannt und entspricht einer Funktionsdeklaration. Ein durch (3) konstruierter Term wird Applikation genannt und entspricht einer Funktionsanwendung. Notation Äußere Klammern werden weggelassen: M (M) Applikation ist linksassoziativ: MN 1... N n M N (... (MN 1 )... N n ) Der Körper der Abstraktion bindet so weit nach rechts wie möglich: λx.m 1... M n λx. M λx.(m 1... M n ) Bei aufeinanderfolgenden Abstraktionen werden die inneren λ. weggelassen: λx 1... x n.m λ x.m (λx 1.(... (λx n.m)... )) 2
3 Definition 2 Die Menge der Subterme eines Terms sei durch die Funktion S ub : Λ P(Λ) definiert: S ub(x) = {x} S ub(λx.m) = S ub(m) {(λx.m)} S ub(mn) = S ub(m) S ub(n) {(MN)} 2.2 Bindung und Substitution Definition 3 Die Menge der gebundenen Variablen eines Terms sei durch die Funktion BV : Λ P(Var) : definiert: BV(x) = BV(λx.M) = BV(M) {x} BV(MN) = BV(M) BV(N) Definition 4 Die Menge der freien Variablen eines Terms sei durch die Funktion FV : Λ P(Var) : definiert: FV(x) = x FV(λx.M) = FV(M)\{x} FV(MN) = FV(M) FV(N) Definition 5 Ein Term T ist geschlossen, falls FV(T) =. Definition 6 Die Substitution von x durch N in M, M[x := N], ist nach dem klassischen Ansatz von Church definiert durch: x[x := N] N y[x := N] y (λx.m)[x := N] λx.m (λy.m)[x := N] λy.m[x := N] (λy.m)[x := N] λz.(m[y := z])[x := N] (M 1 M 2 )[x := N] (M 1 [x := N])(M 2 [x := N]) falls x y falls x y y FV(N) falls x y y FV(N), z neue Variable Definition 7 Die Menge C der λ-kontexte ist definiert durch: x C [] C C[] C (λx.c[]) C C 1 [], C 2 [] C (C 1 []C 2 []) C 3
4 Ein Kontext ist ein λ-term, der [] als Löcher enthalten kann. Ist C[] ein Kontext, so bezeichnet C[T] den Term, der die Löcher durch T ersetzt. Als Beispiel für den Kontext C[] = ((λx.[]x)m) ist C[λy.y] = (λx.(λy.y)x)m. 3 Kongruenzregeln 3.1 α-konversion Definition 8 Die α-konversion α und die α-äquivalenz α sind definiert als M α M : M C[λx.N] M C[λy.(N[x := y])] y FV(N) M α N : M α N M α N falls M und N gleich sind modulo Umbenennung gebundener Variablen. Beispiel λx.x y α λz.z y α λy.y y Konventionen 1. Wir arbeiten mit α-äquivalenzklassen von Termen. Beispiel λx.x λy.y. 2. Gebundene Variablen werden automatisch umbenannt, so dass sie von allen freien Variablen verschieden sind. Damit wird die Substitution vereinfacht: Beispiel: (λy.m)[x := N] λy.m[x := N] (λy.x y)[x := F y] (λy.f y y ) (y ist frei in Fy, das gebundene y wird umbenannt) 3.2 β-reduktion Definition 9 Ein β-redex ist ein Term der Form (λx.m)n. Wir definieren β-reduktion durch C[(λx.M)N] β C[M[x := N]] Ein Term ist in β-normalform wenn er in Normalform bezüglich β ist. Beispiel λx. (λx.x x)(λx.x) } {{ } β λx. (λx.x)(λx.x) } {{ } β λx.λx.x Definition 10 Alternative induktive Definition von β : 1. (λx.m)n β M[x := N] 2. M β M (MN) β (M N) 2. M β M (NM) β (NM ) 2. M β M (λx.m) β (λx.m ) 4
5 β-reduktion ist nicht-terminierend. Beispiel: Ω := (λx.x x)(λx.x x) β Ω nicht-deterministisch aber determiniert. Beispiel: (λx.x x)((λy.y)z) kann zu (λx.x x)z oder (((λy.y)z)((λy.y)z) reduziert werden, hat als Normalform aber immer z z Konfluenz Definition 11 Ein Transitionssystem (D, ) heiß genau dann konfluent, wenn t, t 1, t 2 D. t t 1 t t 2 t D. t 1 t t 2 t In einem konfluenten Transitionssystems besitzt jedes Element höchstens eine Normalform. Ein Term, der auf verschiedenen Wegen ersetzt werden kann, wird nach weiteren Ersetzungen immer zum gleichen Term überführt. Wir versuchen Konfluenz von β über die Konfluenz von > zu beweisen: Definition 12 Parallele und geschachtelte Reduktion > 1. M > M 2. λx.m > λx.m falls M > M 3. (M N) > (M N ) falls M > M und N > N (parallel) 4. (λx.m)n > M [x := N ] falls M > M und N > N (parallel und geschachtelt) Lemma 1 M β M M > M Lemma 2 M > M M β M Korollar 1 > = β Lemma 3 λx.m > N N x.m M > M Lemma 4 > ist konfluent Beweis Durch Induktion über Definition von > wird gezeigt: M, M 1, M 2.M > M 1 M > M 2 M 3.M 1 > M 3 M 2 > M 3 M 1 M: Wähle M 3 = M 2 M λx. M 2 λx.p P > P (Nach Lemma 3) P.P > P P > P (Induktionshypothese) M 3 = λx.p 5
6 M P Q M 1 P Q P > P Q > Q : Hier gibt es zwei Fälle zu unterscheiden: 1. M 2 P Q P > P Q > Q P.P > P P > P (Induktionshypothese) Q.Q > Q Q > Q (Induktionshypothese) M 3 = P Q 2. M 2 P 1 [x := Q ] P λx.p 1 P 1 > P 1 Q > Q P λx.p 1 P 1 > P 1 (Nach Lemma 3) P 1.P 1 > P 1 P 1 > P 1 (Induktionshypothese) Q.Q > Q Q > Q (Induktionshypothese) M 3 = P 1 [x := Q ] M (λx.p)q M 1 P [x := Q ] P > P Q > Q : Analog zu oben mit Fällen für M 2 = P [x := Q ] und M 2 = (λx.p )Q. Korollar 2 β ist konfluent. 4 Berechnung im λ-kalkül 4.1 Boolsche Werte true, false und if können im λ-kalkül wie folgt definiert werden: true = λxy.x false = λxy.y if = λzxy.z x y Beispiel if true M N β M und if false M N β N. 4.2 Paare Paare werden realisiert durch fst = λp.p true snd = λp.p false pair = λxy.λz.z x y Beispiel fst(pair x y) β fst(λz.z x y) β (λz.z x y)(λxy.x) β (λxy.x) x y β x 6
7 4.3 Arithmetik Eine Möglichkeit, natürliche Zahlen darzustellen sind die Church-Numerale: 0 = λ f.λx.x 1 = λ f.λx. f x 2 = λ f.λx. f ( f x). n = λ f.λx. f n (x) = λ f.λx. f ( f (... ( f (x)) } {{ } n mal Damit können arithmetische Funktionen definiert werden: Beispiel succ = λn.λ f x. f (n f x) add = λmn.λ f x.m f (n f x) mult = λmn.λ f.m (n f ) iszero = λn.n(λx.false)true pred = λn.λ f x.n(λgh.h(g f ))(λu.x)(λu.u) add m n λ f x.m f (n f x) λ f x.m f ( f n (x)) λ f x. f m ( f n (x)) = λ f x. f m+n (x) = m + n 4.4 Rekursion Rekursion ist im λ-kalkül nicht ohne weiteres möglich, da bei einer Funktionsdefinition der Funktionsname nicht verwendet werden kann. Möchte man eine rekursive Funktion f (x) = e darstellen, so benötigt man eine nicht-rekursive Darstellung F = λ f.λx.e. Die Funktion, die an F übergeben wird, muss bestimmte Eigenschaften haben, und zwar muss f zu F( f ) expandieren. Damit ist f ein Fixpunkt von F. So eine Funktion kann mit einem Fixpunktoperator implementiert werden. Eine bekannte Lösung ist der Church sche Fixpunktoperator: Damit lässt sich f als Y F darstellen, denn Y = λ f.v f V f mit V f = λx. f (x x) Y F β (λx.f(x x))(λx.f(x x)) β F((λx.F(x x))(λx.f(x x)))) = F(YF) 7
8 Beispiel Die Fakultätsfunktion lässt sich im λ-kalkül folgendermaßen schreiben: fac = Y (λ f ac.λn.if(iszero n) 1 (mult n ( f ac(pred n)))) } {{ } F fac 2 = Y F 2 β F (Y F) 2 β if(iszero 2) 1 (mult 2 (Y F (pred 2))) β mult 2 (Y F 1) β mult 2 (mult 1(Y F 0)) β mult 2 (mult 1(F(Y F)0)) β mult 2 (mult 1(if(iszero 0) 1... ) β mult 2 (mult 1 1) β 2 Literatur [1] Barendregt, Hendrik P.: The Lambda Calculus. Its Syntax and Semantics. Amsterdam u.a. : Elsevier, 1984 [2] Hankin, Chris: An introduction to Lambda calculi for computer scientists. London : King s College Publ., 2004 [3] Nipkow, Tobias: Lambda-Kalkül. logik/ws0607/lambda.pdf. Version: 15. November
1 Geschichte. 2 Syntax und Konzepte. Lamdba-Kalkül
 1 Geschichte 1673 Gottfried Wilhelm Leibniz entwickelt eine mechanische Rechenmaschine, beginnt zu träumen: Gibt es eine universelle Sprache, in der alle Probleme dargestellt werden können? Gibt es eine
1 Geschichte 1673 Gottfried Wilhelm Leibniz entwickelt eine mechanische Rechenmaschine, beginnt zu träumen: Gibt es eine universelle Sprache, in der alle Probleme dargestellt werden können? Gibt es eine
Der untypisierte Lambda-Kalkül als Programmiersprache
 Der untypisierte Lambda-Kalkül als Programmiersprache November 29, 2006 betreut von Prof. Tobias Nipkow Einführung In den 1930er Jahren von Alonzo Church und Stephen Kleene eingeführt Der Lambda-Kalkül
Der untypisierte Lambda-Kalkül als Programmiersprache November 29, 2006 betreut von Prof. Tobias Nipkow Einführung In den 1930er Jahren von Alonzo Church und Stephen Kleene eingeführt Der Lambda-Kalkül
Der untypisierte Lambda-Kalkül
 Der untypisierte Lambda-Kalkül Fabian Immler 08.05.2008 1 Motivation und Einführung Der Lambda-Kalkül ist ein formales System zur Beschreibung von Funktionen, welches Funktionsdefinition sowie das Auswerten
Der untypisierte Lambda-Kalkül Fabian Immler 08.05.2008 1 Motivation und Einführung Der Lambda-Kalkül ist ein formales System zur Beschreibung von Funktionen, welches Funktionsdefinition sowie das Auswerten
Funktionale Programmierung - Grundlagen -
 Funktionale Programmierung - Grundlagen - λ Logische und funktionale Programmierung - Universität Potsdam - M. Thomas - Funkt. Programmierung Gundlagen - IX.1 λ-ausdrücke 1) Variablen: x, y, z,...v,v 1,...
Funktionale Programmierung - Grundlagen - λ Logische und funktionale Programmierung - Universität Potsdam - M. Thomas - Funkt. Programmierung Gundlagen - IX.1 λ-ausdrücke 1) Variablen: x, y, z,...v,v 1,...
Theoretische Informatik II
 Theoretische Informatik II Dr. Eva Richter / Holger Arnold Universität Potsdam, Theoretische Informatik, Sommersemester 2008 Übungsblatt 3 (Version 4) Abgabetermin: 13.5.2008, 12.00 Uhr Der λ-kalkül Da
Theoretische Informatik II Dr. Eva Richter / Holger Arnold Universität Potsdam, Theoretische Informatik, Sommersemester 2008 Übungsblatt 3 (Version 4) Abgabetermin: 13.5.2008, 12.00 Uhr Der λ-kalkül Da
Der untypisierte Lambda-Kalkül
 Der untypisierte Lambda-Kalkül Kern einer minimalen Programmiersprache Sabine Rieder Inhaltsverzeichnis 1 Einleitung 2 2 Grundlagen des Lambda-Kalküls 2 2.1 Syntax.....................................
Der untypisierte Lambda-Kalkül Kern einer minimalen Programmiersprache Sabine Rieder Inhaltsverzeichnis 1 Einleitung 2 2 Grundlagen des Lambda-Kalküls 2 2.1 Syntax.....................................
Theoretische Informatik II
 Vorlesung Theoretische Informatik II Bernhard Beckert Institut für Informatik Wintersemester 2007/2008 B. Beckert Theoretischen Informatik II: WS 2007/08 1 / 179 Dank Diese Vorlesungsmaterialien basieren
Vorlesung Theoretische Informatik II Bernhard Beckert Institut für Informatik Wintersemester 2007/2008 B. Beckert Theoretischen Informatik II: WS 2007/08 1 / 179 Dank Diese Vorlesungsmaterialien basieren
Funktionale Programmierung ALP I. λ Kalkül WS 2012/2013. Prof. Dr. Margarita Esponda. Prof. Dr. Margarita Esponda
 ALP I λ Kalkül WS 2012/2013 Berechenbarkeit - inspiriert durch Hilbert's Frage - im Jahr 1900, Paris - Internationaler Mathematikerkongress Gibt es ein System von Axiomen, aus denen alle Gesetze der Mathematik
ALP I λ Kalkül WS 2012/2013 Berechenbarkeit - inspiriert durch Hilbert's Frage - im Jahr 1900, Paris - Internationaler Mathematikerkongress Gibt es ein System von Axiomen, aus denen alle Gesetze der Mathematik
Programmierparadigmen
 Programmierparadigmen Teil 1: Funktionale Programmierung Kapitel 3 Lambda Kalkül (Dieses Kapitel orientiert sich an Material von Prof. Dr.-Ing. Snelting, KIT) http://www.tu-ilmenau.de/fakia/functional.html
Programmierparadigmen Teil 1: Funktionale Programmierung Kapitel 3 Lambda Kalkül (Dieses Kapitel orientiert sich an Material von Prof. Dr.-Ing. Snelting, KIT) http://www.tu-ilmenau.de/fakia/functional.html
Übersicht. Nebenläufige Programmierung: Praxis und Semantik. Semantische Modelle nebenläufiger Programmiersprachen. Einleitung
 Stand der Folien: 24. Januar 2012 Übersicht Aktuelle Themen zu Informatik der Systeme: Nebenläufige Programmierung: Praxis und Semantik Semantische Modelle nebenläufiger Programmiersprachen 1 2 Call-by-Name
Stand der Folien: 24. Januar 2012 Übersicht Aktuelle Themen zu Informatik der Systeme: Nebenläufige Programmierung: Praxis und Semantik Semantische Modelle nebenläufiger Programmiersprachen 1 2 Call-by-Name
Der untypisierte Lambda-Kalkül als Programmiersprache
 Proseminar: Programmiersprachen bei Prof. Tobias Nipkow Der untypisierte Lambda-Kalkül als Programmiersprache von Benjamin Peherstorfer betreut von Prof. Tobias Nipkow 23. November 2006 Inhaltsverzeichnis
Proseminar: Programmiersprachen bei Prof. Tobias Nipkow Der untypisierte Lambda-Kalkül als Programmiersprache von Benjamin Peherstorfer betreut von Prof. Tobias Nipkow 23. November 2006 Inhaltsverzeichnis
3 Exkurs: Der λ-kalkül
 3 Exkurs: Der λ-kalkül Alonso Churchs λ-kalkül (ca. 1940) ist der formale Kern jeder funktionalen Programmiersprache. Der λ-kalkül ist eine einfache Sprache, mit nur wenigen syntaktischen Konstrukten und
3 Exkurs: Der λ-kalkül Alonso Churchs λ-kalkül (ca. 1940) ist der formale Kern jeder funktionalen Programmiersprache. Der λ-kalkül ist eine einfache Sprache, mit nur wenigen syntaktischen Konstrukten und
Lambda-Kalkül. Dr. Eva Richter. 27.April 2012
 Lambda-Kalkül Dr. Eva Richter 27.April 2012 1 / 32 Historisches um 1200 Einführung des Zahlensystems in Europa u.a. durch Fibonacci; ist charakterisiert durch ein kleine Menge von Ziffern, deren Wert von
Lambda-Kalkül Dr. Eva Richter 27.April 2012 1 / 32 Historisches um 1200 Einführung des Zahlensystems in Europa u.a. durch Fibonacci; ist charakterisiert durch ein kleine Menge von Ziffern, deren Wert von
Einführung in das λ-kalkül
 Einführung in das λ-kalkül Max Wagner IPD Snelting 1 3.11.2017 Max Wagner - Einführung in das λ-kalkül IPD KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Syntax Abstrakte Syntax:
Einführung in das λ-kalkül Max Wagner IPD Snelting 1 3.11.2017 Max Wagner - Einführung in das λ-kalkül IPD KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Syntax Abstrakte Syntax:
Funktionale Programmierung ALP I. λ Kalkül. Teil 2 WS 2012/2013. Prof. Dr. Margarita Esponda. Prof. Dr. Margarita Esponda
 ALP I λ Kalkül Teil 2 WS 2012/2013 Lokale Variablennamen Haskell: let x = exp1 in exp2 Lambda: λ exp1. exp2 Einfache Regel: Der Geltungsbereich eines Lambda-Ausdrucks erstreckt sich soweit wie möglich
ALP I λ Kalkül Teil 2 WS 2012/2013 Lokale Variablennamen Haskell: let x = exp1 in exp2 Lambda: λ exp1. exp2 Einfache Regel: Der Geltungsbereich eines Lambda-Ausdrucks erstreckt sich soweit wie möglich
Einführung in die funktionale Programmierung
 Einführung in die funktionale Programmierung Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 17. Oktober 2006 Einführung in Haskell: Syntax, Reduktionen, Kernsprachen Haskell,
Einführung in die funktionale Programmierung Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 17. Oktober 2006 Einführung in Haskell: Syntax, Reduktionen, Kernsprachen Haskell,
Inferenzmethoden. Einheit 18. Logik höherer Stufe
 Inferenzmethoden Einheit 18 Logik höherer Stufe 1. Syntax und Semantik 2. Simulation mathematischer Konstrukte 3. Beweisführung in Logik höherer Stufe Logik höherer Stufe Logik erster Stufe hat nur einfache
Inferenzmethoden Einheit 18 Logik höherer Stufe 1. Syntax und Semantik 2. Simulation mathematischer Konstrukte 3. Beweisführung in Logik höherer Stufe Logik höherer Stufe Logik erster Stufe hat nur einfache
Funktionale Programmierung ALP I. Kombinatorische Logik (CL) SS Prof. Dr. Margarita Esponda. Prof. Dr. Margarita Esponda
 ALP I Kombinatorische Logik (CL) SS 2011 Äquivalenz vieler Berechnungsmodelle Alonzo Church λ-kalkül Kombinatorische Logik Alan Turing Turing-Maschine Mathematische Präzisierung µ-rekursive Funktionen
ALP I Kombinatorische Logik (CL) SS 2011 Äquivalenz vieler Berechnungsmodelle Alonzo Church λ-kalkül Kombinatorische Logik Alan Turing Turing-Maschine Mathematische Präzisierung µ-rekursive Funktionen
Universität Hannover Fakultät für Elektrotechnik und Informatik Institut für Theoretische Informatik. Thema: von. Paul Krüger
 1 Universität Hannover Fakultät für Elektrotechnik und Informatik Institut für Theoretische Informatik Thema: - Kalkül von Paul Krüger Betreuer: Prof. Dr. Heribert Vollmer Das Rahmenthema ist " Berechenbarkeit
1 Universität Hannover Fakultät für Elektrotechnik und Informatik Institut für Theoretische Informatik Thema: - Kalkül von Paul Krüger Betreuer: Prof. Dr. Heribert Vollmer Das Rahmenthema ist " Berechenbarkeit
Höhere Programmiersprachen
 Höhere Programmiersprachen Prof. Dr. Dr. h.c. Gerhard Goos Dipl.-Inform. Sebastian Hack (ggoos hack)@ipd.info.uni-karlsruhe.de Institut für Programmstrukturen und Datenorganisation Universität Karlsruhe
Höhere Programmiersprachen Prof. Dr. Dr. h.c. Gerhard Goos Dipl.-Inform. Sebastian Hack (ggoos hack)@ipd.info.uni-karlsruhe.de Institut für Programmstrukturen und Datenorganisation Universität Karlsruhe
Kapitel 5: λ-kalkül und Laziness
 Funktionale Programmierung (WS2005/2006) 5/1 Kapitel 5: λ-kalkül und Laziness Lernziele dieses Kapitels 1. Syntax des einfachen, ungetypten λ-kalküls Symbolische Manipulation von λ-ausdrücken in Haskell,
Funktionale Programmierung (WS2005/2006) 5/1 Kapitel 5: λ-kalkül und Laziness Lernziele dieses Kapitels 1. Syntax des einfachen, ungetypten λ-kalküls Symbolische Manipulation von λ-ausdrücken in Haskell,
Der einfach getypter Lambda-Kalkül
 Der einfach getypter Lambda-Kalkül Typprüfung und Typinferenz Tobias Nipkow und Steffen Smolka Technische Universität München 1 Einleitung 2 Explizit getypter λ-kalkül 3 Implizit getypter λ-kalkül Statische
Der einfach getypter Lambda-Kalkül Typprüfung und Typinferenz Tobias Nipkow und Steffen Smolka Technische Universität München 1 Einleitung 2 Explizit getypter λ-kalkül 3 Implizit getypter λ-kalkül Statische
Funktionale Programmierung Einführung
 Einführung Prof. Dr. Oliver Braun Fakultät für Informatik und Mathematik Hochschule München Letzte Änderung: 13.09.2017 15:29 Inhaltsverzeichnis Was ist imperative Programmierung.......................
Einführung Prof. Dr. Oliver Braun Fakultät für Informatik und Mathematik Hochschule München Letzte Änderung: 13.09.2017 15:29 Inhaltsverzeichnis Was ist imperative Programmierung.......................
Formale Methoden der Softwaretechnik 1 Vorlesung vom : Grundlage von Isabelle
 1 Formale Methoden der Softwaretechnik 1 Vorlesung vom 16.11.09: Grundlage von Isabelle Christoph Lüth, Lutz Schröder Universität Bremen Wintersemester 2009/10 2 Fahrplan Teil I: Grundlagen der Formalen
1 Formale Methoden der Softwaretechnik 1 Vorlesung vom 16.11.09: Grundlage von Isabelle Christoph Lüth, Lutz Schröder Universität Bremen Wintersemester 2009/10 2 Fahrplan Teil I: Grundlagen der Formalen
Der untypisierte Lambda-Kalkül
 Der untypisierte Lambda-Kalkül Der Lambda-Kalkül wurde zur Beschreibung des mathematischen Begriffs Funktion entwickelt. Die Menge aller Lambda-Ausdrücke Exp ist folgendermaßen definiert: x Exp wenn x
Der untypisierte Lambda-Kalkül Der Lambda-Kalkül wurde zur Beschreibung des mathematischen Begriffs Funktion entwickelt. Die Menge aller Lambda-Ausdrücke Exp ist folgendermaßen definiert: x Exp wenn x
Die Definition eines Typen kann rekursiv sein, d.h. Typ-Konstruktoren dürfen Elemente des zu definierenden Typ erhalten.
 4.5.5 Rekursive Typen Die Definition eines Typen kann rekursiv sein, d.h. Typ-Konstruktoren dürfen Elemente des zu definierenden Typ erhalten. datatype IntList = Nil Cons o f ( i n t IntList ) ; Damit
4.5.5 Rekursive Typen Die Definition eines Typen kann rekursiv sein, d.h. Typ-Konstruktoren dürfen Elemente des zu definierenden Typ erhalten. datatype IntList = Nil Cons o f ( i n t IntList ) ; Damit
Andreas Abel Ludwig-Maximilians-Universität München. Rohfassung vom 2. Juli 2010
 Lambda-Kalkül Andreas Abel Ludwig-Maximilians-Universität München Skript zur Vorlesung Lambda-Kalkül. Weiteres Material ist bereitgestellt unter http://www.tcs.ifi.lmu.de/lehre/ws06-07/lambda/ und http://www.tcs.ifi.lmu.de/lehre/ws08-09/lambda/
Lambda-Kalkül Andreas Abel Ludwig-Maximilians-Universität München Skript zur Vorlesung Lambda-Kalkül. Weiteres Material ist bereitgestellt unter http://www.tcs.ifi.lmu.de/lehre/ws06-07/lambda/ und http://www.tcs.ifi.lmu.de/lehre/ws08-09/lambda/
Einführung in die funktionale Programmierung
 Einführung in die funktionale Programmierung Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 28. Oktober 2008 Einführung in Haskell: Syntax, Reduktionen, Kernsprachen Haskell,
Einführung in die funktionale Programmierung Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 28. Oktober 2008 Einführung in Haskell: Syntax, Reduktionen, Kernsprachen Haskell,
Software Entwicklung 1
 Software Entwicklung 1 Annette Bieniusa AG Softech FB Informatik TU Kaiserslautern Überblick für heute Programmierparadigmen Imperative vs. deklarative Programmierung Beispiele Funktionale Programmierung
Software Entwicklung 1 Annette Bieniusa AG Softech FB Informatik TU Kaiserslautern Überblick für heute Programmierparadigmen Imperative vs. deklarative Programmierung Beispiele Funktionale Programmierung
Programmierparadigmen
 Programmierparadigmen Teil 1: Funktionale Programmierung Kapitel 3 Lambda Kalkül (Dieses Kapitel orientiert sich an Material von Prof. Dr.-Ing. Snelting, KIT) http://www.tu-ilmenau.de/fakia/functional.html
Programmierparadigmen Teil 1: Funktionale Programmierung Kapitel 3 Lambda Kalkül (Dieses Kapitel orientiert sich an Material von Prof. Dr.-Ing. Snelting, KIT) http://www.tu-ilmenau.de/fakia/functional.html
Interpreter (Hilfsfunktionen)
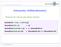 Interpreter (Hilfsfunktionen) -- Berechnet die Liste der gebundenen Variablen boundlist :: Expr -> [String] boundlist (Var x) = [] boundlist (Lambda x e) = x : (boundlist e) boundlist (App e1 e2) = (boundlist
Interpreter (Hilfsfunktionen) -- Berechnet die Liste der gebundenen Variablen boundlist :: Expr -> [String] boundlist (Var x) = [] boundlist (Lambda x e) = x : (boundlist e) boundlist (App e1 e2) = (boundlist
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2010 Lösungsblatt 11 15. Juli 2010 Einführung in die Theoretische
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2010 Lösungsblatt 11 15. Juli 2010 Einführung in die Theoretische
Gliederung. Programmierparadigmen. Mathematische Funktionen: Mathematische Funktionen: Lambda-Kalkül
 Gliederung Programmierparadigmen D. Rösner Institut für Wissens- und Sprachverarbeitung Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Sommer 2013, 9. Juli 2013, c 2009 13 D.Rösner 1 Einführung
Gliederung Programmierparadigmen D. Rösner Institut für Wissens- und Sprachverarbeitung Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Sommer 2013, 9. Juli 2013, c 2009 13 D.Rösner 1 Einführung
Einführung in die Funktionale Programmierung:
 Einführung in die Funktionale Programmierung: Funktionale Kernsprachen: Einleitung & Der Lambda-Kalkül Prof. Dr. M. Schmidt-Schauß WS 2014/15 Stand der Folien: 16. Oktober 2014 Übersicht 1 Einleitung 2
Einführung in die Funktionale Programmierung: Funktionale Kernsprachen: Einleitung & Der Lambda-Kalkül Prof. Dr. M. Schmidt-Schauß WS 2014/15 Stand der Folien: 16. Oktober 2014 Übersicht 1 Einleitung 2
1 Einleitung. 2 Normalordnungsreduktion. 3 Anwendungsordnung. 4 Verzögerte Auswertung. 5 Programmieren mit let in Haskell.
 Stand der Folien: 25. Oktober 2010 Übersicht Einführung in die Funktionale Programmierung: Funktionale Kernsprachen: Einleitung & Der Lambda-Kalkül Dr. David Sabel 1 Einleitung 2 Normalordnungsreduktion
Stand der Folien: 25. Oktober 2010 Übersicht Einführung in die Funktionale Programmierung: Funktionale Kernsprachen: Einleitung & Der Lambda-Kalkül Dr. David Sabel 1 Einleitung 2 Normalordnungsreduktion
GTI. Hannes Diener. 18. Juni. ENC B-0123,
 GTI Hannes Diener ENC B-0123, diener@math.uni-siegen.de 18. Juni 1 / 32 Als Literatur zu diesem Thema empfiehlt sich das Buch Theoretische Informatik kurzgefasst von Uwe Schöning (mittlerweile in der 5.
GTI Hannes Diener ENC B-0123, diener@math.uni-siegen.de 18. Juni 1 / 32 Als Literatur zu diesem Thema empfiehlt sich das Buch Theoretische Informatik kurzgefasst von Uwe Schöning (mittlerweile in der 5.
1 Vollständige partielle Ordnungen, stetige Funktionen
 TIDS 2, SS13, Kapitel 1, vom 11.4.2013 1 1 Vollständige partielle Ordnungen, stetige Funktionen Die Betrachtung vollständiger partieller Ordnungen soll eine einfache und verständliche Einführung in einen
TIDS 2, SS13, Kapitel 1, vom 11.4.2013 1 1 Vollständige partielle Ordnungen, stetige Funktionen Die Betrachtung vollständiger partieller Ordnungen soll eine einfache und verständliche Einführung in einen
Unentscheidbarkeitssätze der Logik
 Unentscheidbarkeitssätze der Logik Elmar Eder () Unentscheidbarkeitssätze der Logik 1 / 30 Die Zahlentheorie ist nicht formalisierbar Satz (Kurt Gödel) Zu jedem korrekten formalen System der Zahlentheorie
Unentscheidbarkeitssätze der Logik Elmar Eder () Unentscheidbarkeitssätze der Logik 1 / 30 Die Zahlentheorie ist nicht formalisierbar Satz (Kurt Gödel) Zu jedem korrekten formalen System der Zahlentheorie
Logik für Informatiker Logic for computer scientists
 Logik für Informatiker Logic for computer scientists Till Mossakowski Wintersemester 2014/15 Till Mossakowski Logik 1/ 24 Die Booleschen Junktoren Till Mossakowski Logik 2/ 24 Die Negation Wahrheitstafel
Logik für Informatiker Logic for computer scientists Till Mossakowski Wintersemester 2014/15 Till Mossakowski Logik 1/ 24 Die Booleschen Junktoren Till Mossakowski Logik 2/ 24 Die Negation Wahrheitstafel
Programmierparadigmen Software Entwicklung 1
 Programmierparadigmen Software Entwicklung 1 Annette Bieniusa, Mathias Weber, Peter Zeller 1 Imperative vs. Deklarative Programmierung Wir haben in SE1 bisher zwei Programmiersprachen näher betrachtet:
Programmierparadigmen Software Entwicklung 1 Annette Bieniusa, Mathias Weber, Peter Zeller 1 Imperative vs. Deklarative Programmierung Wir haben in SE1 bisher zwei Programmiersprachen näher betrachtet:
5. Lambda-Kalkül und Logik höherer Stufe
 5. Lambda-Kalkül und Logik höherer Stufe 5.1 Lambda-Kalkül (ungetypt) Lambda-Notation, Lambda-Terme Konversionsregeln 5.2 Einfach getypter Lambda-Kalkül 5.3 (Prädikaten-)Logik höherer Stufe Motivation
5. Lambda-Kalkül und Logik höherer Stufe 5.1 Lambda-Kalkül (ungetypt) Lambda-Notation, Lambda-Terme Konversionsregeln 5.2 Einfach getypter Lambda-Kalkül 5.3 (Prädikaten-)Logik höherer Stufe Motivation
Berechenbarkeit, Beweisbarkeit. Geschichte
 Berechenbarkeit, Beweisbarkeit Geschichte Inhalt 1. Wahrheit ausrechnen der Traum 1. Aristoteles 2. Lullus 3. Leibniz 2. Entwicklung der Grundlagen 1. Boole 2. Frege 3. Cantor 4. Russel 3. Grenzen des
Berechenbarkeit, Beweisbarkeit Geschichte Inhalt 1. Wahrheit ausrechnen der Traum 1. Aristoteles 2. Lullus 3. Leibniz 2. Entwicklung der Grundlagen 1. Boole 2. Frege 3. Cantor 4. Russel 3. Grenzen des
Übung zur Vorlesung Automatisierte Logik und Programmierung I
 Übung zur Vorlesung Automatisierte Logik und Programmierung I Prof. Chr. Kreitz Universität Potsdam, Theoretische Informatik Wintersemester 2008/09 Blatt 3 Abgabetermin: 26.11.08 nach der Übung Das dritte
Übung zur Vorlesung Automatisierte Logik und Programmierung I Prof. Chr. Kreitz Universität Potsdam, Theoretische Informatik Wintersemester 2008/09 Blatt 3 Abgabetermin: 26.11.08 nach der Übung Das dritte
1. Typen 1.1 Typsicherheit 1.2 Typprüfung
 1. Typen 1.1 Typsicherheit 1.2 Typprüfung Ein Typsystem ist ein praktikables, syntaktisches Verfahren, mit dem man die Abwesenheit gewisser Laufzeit-Eigenschaften eines Programms beweisen kann, indem man
1. Typen 1.1 Typsicherheit 1.2 Typprüfung Ein Typsystem ist ein praktikables, syntaktisches Verfahren, mit dem man die Abwesenheit gewisser Laufzeit-Eigenschaften eines Programms beweisen kann, indem man
Berühmte Informatiker
 Berühmte Informatiker Teil 12: Alonzo Church 1903-1995 John McCarthy 1927 - * 14.06.1903 in Washington 11.08.1995 in Hudson Alonzo Church 1924 Bachelor an der Princeton University 1927 Doktorarbeit an
Berühmte Informatiker Teil 12: Alonzo Church 1903-1995 John McCarthy 1927 - * 14.06.1903 in Washington 11.08.1995 in Hudson Alonzo Church 1924 Bachelor an der Princeton University 1927 Doktorarbeit an
Theoretische Informatik II
 Theoretische Informatik II Einheit 5.3 Funktionale & Logische Programme 1. Der λ-kalkül 2. Arithmetische Repräsentierbarkeit 3. Die Churchsche These Der λ-kalkül Grundlage funktionaler Programmiersprachen
Theoretische Informatik II Einheit 5.3 Funktionale & Logische Programme 1. Der λ-kalkül 2. Arithmetische Repräsentierbarkeit 3. Die Churchsche These Der λ-kalkül Grundlage funktionaler Programmiersprachen
Einführung IMP-Syntax Reduktionssemantik Maschinen-Semantik. Teil IV. Semantik imperativer Sprachen
 Teil IV Semantik imperativer Sprachen 201 1. Einführung Alternativen zur Beschreibung der Semantik: natürliche Sprache (bisher, unpräzise) operational Reduktionssemantik (vgl. Haskell-Semantik in Kap.
Teil IV Semantik imperativer Sprachen 201 1. Einführung Alternativen zur Beschreibung der Semantik: natürliche Sprache (bisher, unpräzise) operational Reduktionssemantik (vgl. Haskell-Semantik in Kap.
Imperative und funktionale Sprachen
 Imperative und funktionale Sprachen Merkmale imperativer Sprachen: Konzepte: Variablen, Zuweisungen, Sequentialität Programm-Semantik spiegelt Rechnerarchitektur wider Schleifen spielen eine große Rolle
Imperative und funktionale Sprachen Merkmale imperativer Sprachen: Konzepte: Variablen, Zuweisungen, Sequentialität Programm-Semantik spiegelt Rechnerarchitektur wider Schleifen spielen eine große Rolle
Operationale Semantik 1
 Operationae Semantik 1 Side 1 Zie: Geschossene Terme t ι ι sind Programme, die auf Eingabe n die Ausgabe [t] n erzeugen. Ein-/Ausgabekonvention: Eingaben und Ausgaben sind Numerae! Def. Ein Numera ist
Operationae Semantik 1 Side 1 Zie: Geschossene Terme t ι ι sind Programme, die auf Eingabe n die Ausgabe [t] n erzeugen. Ein-/Ausgabekonvention: Eingaben und Ausgaben sind Numerae! Def. Ein Numera ist
Reduktion. 2.1 Abstrakte Reduktion
 2 Reduktion In diesem Kapitel studieren wir abstrakte Eigenschaften von Regeln. In den ersten beiden Abschnitten betrachten wir nicht einmal die Regeln selbst, sondern nur abstrakte Reduktionssysteme,
2 Reduktion In diesem Kapitel studieren wir abstrakte Eigenschaften von Regeln. In den ersten beiden Abschnitten betrachten wir nicht einmal die Regeln selbst, sondern nur abstrakte Reduktionssysteme,
Mächtigkeit von LOOP-Programmen. Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen
 Mächtigkeit von LOOP-Programmen Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 23 Die Programmiersprache LOOP Syntax Elemente eines LOOP-Programms Variablen
Mächtigkeit von LOOP-Programmen Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 23 Die Programmiersprache LOOP Syntax Elemente eines LOOP-Programms Variablen
PCF und denotationale Semantik
 Kapitel 3 PCF und denotationale Semantik In diesem Kapitel soll ein Beispiel für eine denotationale Semantik vorgestellt und eingehend untersucht werden, die auf eine funktionale Programmiersprache mit
Kapitel 3 PCF und denotationale Semantik In diesem Kapitel soll ein Beispiel für eine denotationale Semantik vorgestellt und eingehend untersucht werden, die auf eine funktionale Programmiersprache mit
Der λ-kalkül. Frank Huch. Sommersemester 2015
 Der λ-kalkül Frank Huch Sommersemester 2015 In diesem Skript werden die Grundlagen der Funktionalen Programmierung, insbesondere der λ-kalkül eingeführt. Der hier präsentierte Stoff stellt einen teil der
Der λ-kalkül Frank Huch Sommersemester 2015 In diesem Skript werden die Grundlagen der Funktionalen Programmierung, insbesondere der λ-kalkül eingeführt. Der hier präsentierte Stoff stellt einen teil der
Berechenbarkeit und Komplexität: Mächtigkeit von Programmiersprachen: WHILE- und LOOP-Programme
 Berechenbarkeit und Komplexität: Mächtigkeit von Programmiersprachen: WHILE- und LOOP-Programme Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität 29. November 2007 Turing-mächtige
Berechenbarkeit und Komplexität: Mächtigkeit von Programmiersprachen: WHILE- und LOOP-Programme Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität 29. November 2007 Turing-mächtige
ALP I Primitiv-Rekursive Funktionen
 ALP I Primitiv-Rekursive Funktionen WS 2012/2013 Äquivalenz vieler Berechnungsmodelle Effektiv Berechenbare Funktionen Mathematische Modelle Maschinelle Modelle λ-kalkül Kombinatorische Logik Allgemein
ALP I Primitiv-Rekursive Funktionen WS 2012/2013 Äquivalenz vieler Berechnungsmodelle Effektiv Berechenbare Funktionen Mathematische Modelle Maschinelle Modelle λ-kalkül Kombinatorische Logik Allgemein
Funktionen und sprachliche Bedeutungen
 Einführung in die Semantik,4. Sitzung Mehr zu Funktionen / Mengen, Relationen, Göttingen 1. November 2006 Mengen und sprachliche Bedeutungen Abstraktion und Konversion Rekursion Charakteristische Funktionen
Einführung in die Semantik,4. Sitzung Mehr zu Funktionen / Mengen, Relationen, Göttingen 1. November 2006 Mengen und sprachliche Bedeutungen Abstraktion und Konversion Rekursion Charakteristische Funktionen
Einführung in die mathematische Logik
 Prof. Dr. H. Brenner Osnabrück SS 2014 Einführung in die mathematische Logik Vorlesung 14 Die Korrektheit des Ableitungskalküls Im Laufe der Einführung des syntaktischen Prädikatenkalküls haben wir gesehen,
Prof. Dr. H. Brenner Osnabrück SS 2014 Einführung in die mathematische Logik Vorlesung 14 Die Korrektheit des Ableitungskalküls Im Laufe der Einführung des syntaktischen Prädikatenkalküls haben wir gesehen,
Reduktionssysteme Termersetzungssysteme. Keine kritischen Paare. Betrachte Variablenüberlappung:
 Beispiele Beispiel 9.4 Betrachte f (f (x, y), z) f (x, f (y, z)) f (f (x, y ), z ) f (x, f (y, z )) Unifizierbar mit x f (x, y ), y z f (f (f (x, y ), z ), z) t 1 = f (f (x, y ), f (z, z)) f (f (x, f (y,
Beispiele Beispiel 9.4 Betrachte f (f (x, y), z) f (x, f (y, z)) f (f (x, y ), z ) f (x, f (y, z )) Unifizierbar mit x f (x, y ), y z f (f (f (x, y ), z ), z) t 1 = f (f (x, y ), f (z, z)) f (f (x, f (y,
Warum wir noch Mathematiker brauchen
 Church und das Entscheidungsproblem Warum wir noch Mathematiker brauchen Joachim Breitner * 24. Juni 2011 Gulaschprogrammiernacht 11, Karlsruhe Zusammenfassung Hilbert hatte einen Traum: Er wünschte sich
Church und das Entscheidungsproblem Warum wir noch Mathematiker brauchen Joachim Breitner * 24. Juni 2011 Gulaschprogrammiernacht 11, Karlsruhe Zusammenfassung Hilbert hatte einen Traum: Er wünschte sich
Theoretische Informatik II
 Theoretische Informatik II Einheit 5.3 Funktionale & Logische Programme 1. Der λ-kalkül 2. Arithmetische Repräsentierbarkeit 3. Die Churchsche These Der λ-kalkül Grundlage funktionaler Programmiersprachen
Theoretische Informatik II Einheit 5.3 Funktionale & Logische Programme 1. Der λ-kalkül 2. Arithmetische Repräsentierbarkeit 3. Die Churchsche These Der λ-kalkül Grundlage funktionaler Programmiersprachen
4. Spezifikation in PVS (II): Funktionen und Prädikate
 4. Spezifikation in PVS (II): Funktionen und Prädikate Definition von Funktionen: - uninterpretiert: f : [int -> int] - interpretiert, d.h. mit einer Definition: f(x: int): int = x * x f wird hierdurch
4. Spezifikation in PVS (II): Funktionen und Prädikate Definition von Funktionen: - uninterpretiert: f : [int -> int] - interpretiert, d.h. mit einer Definition: f(x: int): int = x * x f wird hierdurch
Was bisher geschah. deklarative Programmierung. funktionale Programmierung (Haskell):
 Was bisher geschah deklarative Programmierung funktional: Programm: Menge von Termgleichungen, Term Auswertung: Pattern matsching, Termumformungen logisch: Programm: Menge von Regeln (Horn-Formeln), Formel
Was bisher geschah deklarative Programmierung funktional: Programm: Menge von Termgleichungen, Term Auswertung: Pattern matsching, Termumformungen logisch: Programm: Menge von Regeln (Horn-Formeln), Formel
Kapitel 6. Programme mit Schleifen. Wir betrachten jetzt eine einfache imperative Programmiersprache IMP. IMP verfügt
 Kapitel 6 Programme mit Schleifen Wir betrachten jetzt eine einfache imperative Programmiersprache IMP. IMP verfügt über zuweisbare Variablen, Konditionale und Schleifen, hat aber keine Prozeduren. IMP
Kapitel 6 Programme mit Schleifen Wir betrachten jetzt eine einfache imperative Programmiersprache IMP. IMP verfügt über zuweisbare Variablen, Konditionale und Schleifen, hat aber keine Prozeduren. IMP
Wir betrachten jetzt eine idealisierte imperative Programmiersprache IMP mit zuweisbaren
 Kapitel 6 Programme mit Schleifen Wir betrachten jetzt eine idealisierte imperative Programmiersprache IMP mit zuweisbaren Variablen und Schleifen. Unser Ziel ist es, die Syntax und Semantik von IMP mit
Kapitel 6 Programme mit Schleifen Wir betrachten jetzt eine idealisierte imperative Programmiersprache IMP mit zuweisbaren Variablen und Schleifen. Unser Ziel ist es, die Syntax und Semantik von IMP mit
4 Terme und Σ-Algebren
 Grundlagen der Mathematik für Informatiker 1 Grundlagen der Mathematik für Informatiker 2 4 Terme und Σ-Algebren 4.1 Grundterme und Terme Menge S von unktionssymbolen funktionale Signatur: Σ S N Menge
Grundlagen der Mathematik für Informatiker 1 Grundlagen der Mathematik für Informatiker 2 4 Terme und Σ-Algebren 4.1 Grundterme und Terme Menge S von unktionssymbolen funktionale Signatur: Σ S N Menge
Einführung in Berechenbarkeit, Komplexität und Formale Sprachen
 Einführung in Berechenbarkeit, Komplexität und Formale Sprachen V8, 5.11.09 Willkommen zur Vorlesung Einführung in Berechenbarkeit, Komplexität und Formale Sprachen Friedhelm Meyer auf der Heide 1 Rückblick
Einführung in Berechenbarkeit, Komplexität und Formale Sprachen V8, 5.11.09 Willkommen zur Vorlesung Einführung in Berechenbarkeit, Komplexität und Formale Sprachen Friedhelm Meyer auf der Heide 1 Rückblick
Formale Sprachen. Grammatiken. Grammatiken und die Chomsky-Hierarchie. Rudolf FREUND, Marion OSWALD. Grammatiken: Ableitung
 Formale Sprachen rammatiken und die Chomsky-Hierarchie Rudolf FREUND, Marion OSWALD rammatiken Das fundamentale Modell zur Beschreibung von formalen Sprachen durch Erzeugungsmechanismen sind rammatiken.
Formale Sprachen rammatiken und die Chomsky-Hierarchie Rudolf FREUND, Marion OSWALD rammatiken Das fundamentale Modell zur Beschreibung von formalen Sprachen durch Erzeugungsmechanismen sind rammatiken.
Fortgeschrittene Funktionale Programmierung
 Fortgeschrittene Funktionale Programmierung 13. Vorlesung Janis Voigtländer Universität Bonn Wintersemester 2015/16 Erweiterung um Datentypen Typen: τ := Bool [τ] Terme: t := False True [ ] τ t : t case
Fortgeschrittene Funktionale Programmierung 13. Vorlesung Janis Voigtländer Universität Bonn Wintersemester 2015/16 Erweiterung um Datentypen Typen: τ := Bool [τ] Terme: t := False True [ ] τ t : t case
Kapitel 3. Syntax und Semantik von arithmetischen Ausdrücken. 3.1 Syntax
 Kapitel 3 Syntax und Semantik von arithmetischen Ausdrücken In diesem Kapitel führen wir einige grundlegende Konzepte für logische Sprachen ein. Wir tun dies am Beispiel einer einfachen Sprache AA, deren
Kapitel 3 Syntax und Semantik von arithmetischen Ausdrücken In diesem Kapitel führen wir einige grundlegende Konzepte für logische Sprachen ein. Wir tun dies am Beispiel einer einfachen Sprache AA, deren
Entwicklung korrekter Programme in Coq. Thomas Strathmann
 Entwicklung korrekter Programme in Coq Thomas Strathmann Überblick Teil 1 Was ist Coq? Theoretische Grundlagen Programmierung, Spezifikation, Beweise in
Entwicklung korrekter Programme in Coq Thomas Strathmann Überblick Teil 1 Was ist Coq? Theoretische Grundlagen Programmierung, Spezifikation, Beweise in
Berechenbarkeit und Komplexität: Mächtigkeit von Programmiersprachen: WHILE- und LOOP Programme
 Berechenbarkeit und Komplexität: Mächtigkeit von Programmiersprachen: WHILE- und LOOP Programme Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität 13. November 2006 Turing-mächtige
Berechenbarkeit und Komplexität: Mächtigkeit von Programmiersprachen: WHILE- und LOOP Programme Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität 13. November 2006 Turing-mächtige
Grundbegriffe für dreiwertige Logik
 Grundbegriffe für dreiwertige Logik Hans Kleine Büning Universität Paderborn 1.11.2011 1 Syntax und Semantik Die klassische Aussagenlogik mit den Wahrheitswerten falsch und wahr bezeichnen wir im weiteren
Grundbegriffe für dreiwertige Logik Hans Kleine Büning Universität Paderborn 1.11.2011 1 Syntax und Semantik Die klassische Aussagenlogik mit den Wahrheitswerten falsch und wahr bezeichnen wir im weiteren
Reduktionssysteme und Termersetzungssysteme
 Reduktionssysteme und Termersetzungssysteme Untersuchung von Berechnungen mittels Reduktionsregeln Simplifikation von: Datenstrukturen / Termen usw. Erkennen von gleichen Objekten durch Normalisierung
Reduktionssysteme und Termersetzungssysteme Untersuchung von Berechnungen mittels Reduktionsregeln Simplifikation von: Datenstrukturen / Termen usw. Erkennen von gleichen Objekten durch Normalisierung
Überblick. Ausdrücke. 3. Mathematische Grundlagen 3.1 Mengen und Abbildungen 3.2 Induktion und Rekursion 3.3 Ausdrücke
 Überblick 3. Mathematische Grundlagen 3.1 Mengen und Abbildungen 3.2 Induktion und Rekursion 3.3 Ausdrücke 3 Mathematische Grundlagen 3 Ausdrücke Einf. Progr. (WS 08/09) 148 Ausdrücke Betrachten wir folgende
Überblick 3. Mathematische Grundlagen 3.1 Mengen und Abbildungen 3.2 Induktion und Rekursion 3.3 Ausdrücke 3 Mathematische Grundlagen 3 Ausdrücke Einf. Progr. (WS 08/09) 148 Ausdrücke Betrachten wir folgende
Formale Sprachen. Grammatiken und die Chomsky-Hierarchie. Rudolf FREUND, Marian KOGLER
 Formale Sprachen Grammatiken und die Chomsky-Hierarchie Rudolf FREUND, Marian KOGLER Grammatiken Das fundamentale Modell zur Beschreibung von formalen Sprachen durch Erzeugungsmechanismen sind Grammatiken.
Formale Sprachen Grammatiken und die Chomsky-Hierarchie Rudolf FREUND, Marian KOGLER Grammatiken Das fundamentale Modell zur Beschreibung von formalen Sprachen durch Erzeugungsmechanismen sind Grammatiken.
Funktionsobjekte 306 operator
 Funktionsobjekte 306 Funktionsobjekte sind Objekte, bei denen der operator() definiert ist. (Siehe ISO 14882-2012, Abschnitt 20.8.) Viele Algorithmen der STL akzeptieren solche Funktionsobjekte, um aus
Funktionsobjekte 306 Funktionsobjekte sind Objekte, bei denen der operator() definiert ist. (Siehe ISO 14882-2012, Abschnitt 20.8.) Viele Algorithmen der STL akzeptieren solche Funktionsobjekte, um aus
Grammatiken. Eine Grammatik G mit Alphabet Σ besteht aus: Variablen V. Startsymbol S V. Kurzschreibweise G = (V, Σ, P, S)
 Grammatiken Eine Grammatik G mit Alphabet Σ besteht aus: Variablen V Startsymbol S V Produktionen P ( (V Σ) \ Σ ) (V Σ) Kurzschreibweise G = (V, Σ, P, S) Schreibweise für Produktion (α, β) P: α β 67 /
Grammatiken Eine Grammatik G mit Alphabet Σ besteht aus: Variablen V Startsymbol S V Produktionen P ( (V Σ) \ Σ ) (V Σ) Kurzschreibweise G = (V, Σ, P, S) Schreibweise für Produktion (α, β) P: α β 67 /
Funktionale Programmiersprachen
 Funktionale Programmiersprachen An den Beispielen Haskell und Erlang Übersicht Programmiersprachen λ-kalkül Syntax, Definitionen Besonderheiten von funktionalen Programmiersprache, bzw. Haskell Objektorientierte
Funktionale Programmiersprachen An den Beispielen Haskell und Erlang Übersicht Programmiersprachen λ-kalkül Syntax, Definitionen Besonderheiten von funktionalen Programmiersprache, bzw. Haskell Objektorientierte
Einführung in die Theoretische Informatik
 Einführung in die Theoretische Informatik Woche 4 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 Zusammenfassung Zusammenfassung der letzten LV Modus Ponens A B B A MP Axiome für
Einführung in die Theoretische Informatik Woche 4 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 Zusammenfassung Zusammenfassung der letzten LV Modus Ponens A B B A MP Axiome für
Der erste Gödelsche Unvollständigkeitssatz
 Der erste Gödelsche Unvollständigkeitssatz Referent: Tobias Gleißner 29. Januar 2013 (syntaktischer Aufbau eines arithmetischen Terms) - Jede Zahl ist ein Term - Jede Variable ist ein Term - Sind und Terme,
Der erste Gödelsche Unvollständigkeitssatz Referent: Tobias Gleißner 29. Januar 2013 (syntaktischer Aufbau eines arithmetischen Terms) - Jede Zahl ist ein Term - Jede Variable ist ein Term - Sind und Terme,
Aussagenlogik zu wenig ausdrucksstark für die meisten Anwendungen. notwendig: Existenz- und Allaussagen
 Prädikatenlogik 1. Stufe (kurz: PL1) Aussagenlogik zu wenig ausdrucksstark für die meisten Anwendungen notwendig: Existenz- und Allaussagen Beispiel: 54 Syntax der Prädikatenlogik erster Stufe (in der
Prädikatenlogik 1. Stufe (kurz: PL1) Aussagenlogik zu wenig ausdrucksstark für die meisten Anwendungen notwendig: Existenz- und Allaussagen Beispiel: 54 Syntax der Prädikatenlogik erster Stufe (in der
Seminar Mathematische Logik L-Strukturen und Syntax der Prädikatenlogik
 Seminar Mathematische Logik L-Strukturen und Syntax der Prädikatenlogik Linda Raabe 7. März 2012 1 L-Strukturen Definition 1.1 (Struktur) Eine Struktur A ist eine nichtleere Trägermenge A zusammen mit
Seminar Mathematische Logik L-Strukturen und Syntax der Prädikatenlogik Linda Raabe 7. März 2012 1 L-Strukturen Definition 1.1 (Struktur) Eine Struktur A ist eine nichtleere Trägermenge A zusammen mit
Einführung in Berechenbarkeit, Komplexität und Formale Sprachen
 Einführung in Berechenbarkeit, Komplexität und Formale Sprachen V7, 3.11.09 Willkommen zur Vorlesung Einführung in Berechenbarkeit, Komplexität und Formale Sprachen Friedhelm Meyer auf der Heide 1 Rückblick
Einführung in Berechenbarkeit, Komplexität und Formale Sprachen V7, 3.11.09 Willkommen zur Vorlesung Einführung in Berechenbarkeit, Komplexität und Formale Sprachen Friedhelm Meyer auf der Heide 1 Rückblick
Vortrag. Vortrag im Rahmen der Master-Vorlesung Semantik von Programmiersprachen an der FH München, Fachbereich Informatik
 Vortrag β- and η-conversion Vortrag im Rahmen der Master-Vorlesung Semantik von Programmiersprachen an der FH München, Fachbereich Informatik von Stefan Hertel (sh_ccbiker@gmx.de Thomas Wöllert (thomas@woellert.net
Vortrag β- and η-conversion Vortrag im Rahmen der Master-Vorlesung Semantik von Programmiersprachen an der FH München, Fachbereich Informatik von Stefan Hertel (sh_ccbiker@gmx.de Thomas Wöllert (thomas@woellert.net
Satzsemantik. Semantik und Pragmatik. Satzsemantik. Satzsemantik
 Satzsemantik 8. Mai 2007 Gerhard Jäger Erklärungsanspruch der Satzsemantik Wahrheitsbedingungen von Aussagensätzen Bedeutungsbeziehungen zwischen (Aussage-)Sätzen Kompositionale Berechnung von Satzbedeutungen
Satzsemantik 8. Mai 2007 Gerhard Jäger Erklärungsanspruch der Satzsemantik Wahrheitsbedingungen von Aussagensätzen Bedeutungsbeziehungen zwischen (Aussage-)Sätzen Kompositionale Berechnung von Satzbedeutungen
Kapitel 5. Mathematische Semantik. 1 Motivation
 Kapitel 5 Mathematische Semantik In diesem Kapitel werden wir nun eine weitere Technik zur Definition der Semantik einer Programmiersprache vorstellen: die mathematische bzw. denotationale Semantik. Außerdem
Kapitel 5 Mathematische Semantik In diesem Kapitel werden wir nun eine weitere Technik zur Definition der Semantik einer Programmiersprache vorstellen: die mathematische bzw. denotationale Semantik. Außerdem
Wir haben eine Beziehung zwischen entscheidbar und rekursiv aufzählbar hergeleitet.
 Rückschau 12.11.04 Wir haben eine Beziehung zwischen entscheidbar und rekursiv aufzählbar hergeleitet. Wir haben das Prinzip der Diagonalisierung eingeführt und mit DIAG eine erste nicht rek. aufz. Sprache
Rückschau 12.11.04 Wir haben eine Beziehung zwischen entscheidbar und rekursiv aufzählbar hergeleitet. Wir haben das Prinzip der Diagonalisierung eingeführt und mit DIAG eine erste nicht rek. aufz. Sprache
2 Hennessy-Milner-Logik
 2.1 Syntax und Semantik Hennessy-Milner-Logik (HML), auch als multi-modale Logik K bekannt, erweitert die Aussagenlogik um zwei Konstrukte ( diamond und box ), mit denen man über Nachfolger eines Zustandes
2.1 Syntax und Semantik Hennessy-Milner-Logik (HML), auch als multi-modale Logik K bekannt, erweitert die Aussagenlogik um zwei Konstrukte ( diamond und box ), mit denen man über Nachfolger eines Zustandes
HASKELL KAPITEL 2.1. Notationen: Currying und das Lambda-Kalkül
 HASKELL KAPITEL 2.1 Notationen: Currying und das Lambda-Kalkül Bisheriges (Ende VL-Teil 1) weite :: (Float,Float) ->Float weite (v0, phi) = (square(v0)/9.81) * sin(2 * phi) (10, 30 ) smaller ::(Integer,
HASKELL KAPITEL 2.1 Notationen: Currying und das Lambda-Kalkül Bisheriges (Ende VL-Teil 1) weite :: (Float,Float) ->Float weite (v0, phi) = (square(v0)/9.81) * sin(2 * phi) (10, 30 ) smaller ::(Integer,
Gröbnerbasen in Monoid- und Gruppenringen
 Gröbnerbasen in Monoid- und Gruppenringen Karsten Hiddemann 5. November 2003 Zusammenfassung Gröbnerbasen, entwickelt von Bruno Buchberger für kommutative Polynomringe, finden immer häufiger Anwendung
Gröbnerbasen in Monoid- und Gruppenringen Karsten Hiddemann 5. November 2003 Zusammenfassung Gröbnerbasen, entwickelt von Bruno Buchberger für kommutative Polynomringe, finden immer häufiger Anwendung
8 Der Kompaktheitssatz und der Satz von Löwenheim und Skolem
 8 Der Kompaktheitssatz und der Satz von Löwenheim und Skolem 8.1 Der Kompaktheitssatz Kompaktheitssatz Endlichkeitssatz Der Kompaktheitssatz ist auch unter dem Namen Endlichkeitssatz bekannt. Unter Verwendung
8 Der Kompaktheitssatz und der Satz von Löwenheim und Skolem 8.1 Der Kompaktheitssatz Kompaktheitssatz Endlichkeitssatz Der Kompaktheitssatz ist auch unter dem Namen Endlichkeitssatz bekannt. Unter Verwendung
Funktionale Programmierung ALP I. µ-rekursive Funktionen WS 2012/2013. Prof. Dr. Margarita Esponda. Prof. Dr. Margarita Esponda
 ALP I µ-rekursive Funktionen WS 2012/2013 Primitiv-rekursive Funktionen Jede primitiv-rekursive Funktion ist Loop-berechenbar. Das bedeutet, dass jede PR-Funktion in der Loop-Programmiersprache formuliert
ALP I µ-rekursive Funktionen WS 2012/2013 Primitiv-rekursive Funktionen Jede primitiv-rekursive Funktion ist Loop-berechenbar. Das bedeutet, dass jede PR-Funktion in der Loop-Programmiersprache formuliert
Fortgeschrittenenpraktikum Implementierung eines Type Checkers für das System F ω
 Fortgeschrittenenpraktikum Implementierung eines Type Checkers für das System F ω Jan Peter Gutzmann 19.12.03 Inhaltsverzeichnis 1 Einleitung 3 1.1 Der Lambda-Kalkül......................... 3 1.1.1 Der
Fortgeschrittenenpraktikum Implementierung eines Type Checkers für das System F ω Jan Peter Gutzmann 19.12.03 Inhaltsverzeichnis 1 Einleitung 3 1.1 Der Lambda-Kalkül......................... 3 1.1.1 Der
Fortgeschrittene Funktionale Programmierung
 Fortgeschrittene Funktionale Programmierung 12. Vorlesung Janis Voigtländer Universität Bonn Wintersemester 2015/16 Motivation Auf http://www-ps.iai.uni-bonn.de/ft: 1 Motivation 1 Betrachtungen zu Polymorphie
Fortgeschrittene Funktionale Programmierung 12. Vorlesung Janis Voigtländer Universität Bonn Wintersemester 2015/16 Motivation Auf http://www-ps.iai.uni-bonn.de/ft: 1 Motivation 1 Betrachtungen zu Polymorphie
Grundlagen der Programmierung 2. Operationale Semantik
 Grundlagen der Programmierung 2 Operationale Semantik Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 29. April 2009 Semantik von Programmiersprachen Semantik = Bedeutung
Grundlagen der Programmierung 2 Operationale Semantik Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 29. April 2009 Semantik von Programmiersprachen Semantik = Bedeutung
